Hierboven staan de vakken zoals ze op de middelbare school gegeven worden. Dit wil natuurlijk niet zeggen dat er hier geen ruimte is voor vragen van MBO, HBO of WO-niveau. Alle vragen die binnen het gebied van 'Bèta' vallen, kun je hier posten.
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
ln(x+7) + ln(x+3) = 0
Dat 'ln'-ding heet geloof ik een natural logarithm, voor de n00bs die dat niet weten.
Nou... los maar op.
en als spuit elf:
quote:als je iets door een deelt blijft het hetzelfde dus (z/1)=zOp dinsdag 10 januari 2006 16:17 schreef BrauN het volgende:
En hoezo kun je van:
(x/y) / (z/1)
dit maken
(x) / (yz)
dan krijg je
(x/y)/(z)=(x)/(yz)
voor x heeft het hetzelfde effect om eerst te delen door y en daarna door z als om te delen door y vermenigvuldigd met z (9/3)/(3)=1 (9)/(3x3)=1
quote:Ik zal allereerst eens beginnen met het leren van de rekenregels wat betreft de logaritmen.Op dinsdag 10 januari 2006 16:37 schreef BrauN het volgende:
Dames en heren, we gaan nu een stapje verder. Schrik niet.
ln(x+7) + ln(x+3) = 0
Dat 'ln'-ding heet geloof ik een natural logarithm, voor de n00bs die dat niet weten.
Nou... los maar op.
quote:ln(x+7) + ln(x+3) = 0Op dinsdag 10 januari 2006 16:37 schreef BrauN het volgende:
Dames en heren, we gaan nu een stapje verder. Schrik niet.
ln(x+7) + ln(x+3) = 0
Dat 'ln'-ding heet geloof ik een natural logarithm, voor de n00bs die dat niet weten.
Nou... los maar op.
ln((x+7)*(x+3)) = 0
ln(x²+10x+21) = 0
e^0 = x²+10x+21
1 = x²+10x+21
-x²-10x-20=0
x = - 2 ,76
verder kom ik niet, maar tis volgens mij wel goed
quote:Simpel zat:Dames en heren, we gaan nu een stapje verder. Schrik niet.
ln(x+7) + ln(x+3) = 0
Dat 'ln'-ding heet geloof ik een natural logarithm, voor de n00bs die dat niet weten.
Nou... los maar op.
ln(x+7) + ln(x+3) = 0
(x+7)+(x+3) = e^0 = 1
x+7+x+3 = 1
2x = -9
x = -9/2 = -4.5
[edit]
oeps foutje!!!
^^ I'm with him!
[/edit]
quote:Dit is fout.Op dinsdag 10 januari 2006 16:47 schreef SciFi het volgende:
[..]
Simpel zat:
ln(x+7) + ln(x+3) = 0
(x+7)+(x+3) = e^0 = 1
x+7+x+3 = 1
2x = -9
x = -9/2 = -4.5
quote:Dat lijkt me een zeer goed advies. Vandaar dat ik 't nog even citeer.Op dinsdag 10 januari 2006 16:43 schreef Zwansen het volgende:
[..]
Ik zal allereerst eens beginnen met het leren van de rekenregels wat betreft de logaritmen.
Kijk hier: http://en.wikipedia.org/wiki/Logarithmic_identities. of heeft men stiekem een formuleblad bij z'n tentamens tegenwoordig
quote:Ja, hoi, en doei
Il est pas slowchattopic
Zolang die brakke boommark niet gekoppeld is aan MyAT is het zinloos.
quote:Had dan TVP gezegtOp dinsdag 10 januari 2006 18:30 schreef -J-D- het volgende:
Nee, maar ik ga niet wachten tot ik inhoudelijk kan reageren en dan steeds het topic terugzoeken.
Zolang die brakke boommark niet gekoppeld is aan MyAT is het zinloos.
dan had ik niet arrogant hoeven te reageren en zwaaien met een tje 
Is goed hoor
quote:Bijna -e.Op dinsdag 10 januari 2006 16:46 schreef Repeat het volgende:
[..]
ln(x+7) + ln(x+3) = 0
ln((x+7)*(x+3)) = 0
ln(x²+10x+21) = 0
e^0 = x²+10x+21
1 = x²+10x+21
-x²-10x-20=0
x = - 2 ,76
verder kom ik niet, maar tis volgens mij wel goed
quote:Cirkelkwadratuur is onmogelijk. Komt omdat pi transcendent is. Gegeven twee punten in het vlak welke de coordinaten (0,0) en (0,1) worden gegeven kun je alleen punten met algebraische coordinaten construeren met passer en liniaal. Dat pi transcendent is, is bewezen door Lindemann. Hier is een bewijs. Ik heb geen idee of het een goed bewijs is, niet doorgelezen.Op dinsdag 10 januari 2006 18:55 schreef teletubbies het volgende:
..cirkelkwadratuur.. is het opgelost? zo ja... waar kan ik het bewijs vinden?..thanx!
quote:Het probleem is in zoverre opgelost dat bewezen is dat het niet kan. In het Engels heet het Squaring the circle. Het zit 'm erin dat Pi transcendentaal is, d.w.z. niet als nulpunt van een polynoom met alleen rationale coëfficiënten uitgedrukt kan worden. (Uiteraard wel als nulpunt van de polynoom x^2 - Pi*x, dus vandaar die rationale coëfficiënten).Op dinsdag 10 januari 2006 18:55 schreef teletubbies het volgende:
..cirkelkwadratuur.. is het opgelost? zo ja... waar kan ik het bewijs vinden?..thanx!
Helaas dus. Dat bewijs voor de transcendentie van Pi schud ik hier niet even uit m'n mouw. Als troost dan maar een liedje van Drs. P dat er ook over gaat.
ze gaan naar een boer toe.
die boer verkoopt hen een konijn voor 30 euro.
dus die jongens gooien ieder 10 euro in de pot en kopen dat konijn.
als de boer dat konijn heeft gekocht krijgt hij er spijt van.
de boer vind dat hij teveel heeft gevraagd voor het konijn.
de boer geeft aan zijn medewerker 5 euro om aan de jongens terug te geven.
de medewerker vind het niks om de kutklusjes van zijn baas op te knappen en haalt er 2 euro uit.
hij geeft de jongetjes elk 1 euro terug.
de jongens hebben nu elk 9 euro betaalt voor het konijn.
9 x 3 = 27 euro. de medewerker had ook nog 2 euro. Waar is die ene euro?
quote:Uh, nergens. Want 27 - 2 = 25. Het is overigens futue te ipsum.Op dinsdag 10 januari 2006 19:22 schreef --Christiaan-- het volgende:
er zijn 3 jongens die een konijn willen kopen.
ze gaan naar een boer toe.
die boer verkoopt hen een konijn voor 30 euro.
dus die jongens gooien ieder 10 euro in de pot en kopen dat konijn.
als de boer dat konijn heeft gekocht krijgt hij er spijt van.
de boer vind dat hij teveel heeft gevraagd voor het konijn.
de boer geeft aan zijn medewerker 5 euro om aan de jongens terug te geven.
de medewerker vind het niks om de kutklusjes van zijn baas op te knappen en haalt er 2 euro uit.
hij geeft de jongetjes elk 1 euro terug.
de jongens hebben nu elk 9 euro betaalt voor het konijn.
9 x 3 = 27 euro. de medewerker had ook nog 2 euro. Waar is die ene euro?
quote:Hmm jammer, ik had van Drs. P. toch een wat sterkere tekst verwacht.Op dinsdag 10 januari 2006 19:19 schreef AtraBilis het volgende:
[..]
Als troost dan maar een liedje van Drs. P dat er ook over gaat.
quote:Kut, typoOp dinsdag 10 januari 2006 19:25 schreef AtraBilis het volgende:
[..]
Uh, nergens. Want 27 - 2 = 25. Het is overigens futue te ipsum.
. Weet je ook wat het betekent? 
quote:Neuk jezelf. (Of: Go Fuck yourself), De -e duidt een imperativus aan.Op dinsdag 10 januari 2006 19:27 schreef --Christiaan-- het volgende:
[..]
Kut, typo
De opgave is: Geef de RV van Fe2O3 in overmaat verdund zwavelzuur
dan zou je de volgende RV moeten krijgen:
Fe2O3 + 6 H30+ -----> 2 Fe3+ + 9 H2O
zou iemand dat voor mij kunnen uitleggen aub?
De helling van die lijn is 5.
b-a = 3
Nou... hoe reken ik die a en b uit?
quote:b-a=3, dus het gaat om de punten (a,y(a) en (a+3,y(a+3)). De helling tussen die punten is (y(a+3)-y(a))/3. Ik denk dat je hiermee verder kunt komen.Een lijn snijdt de grafiek van de functie y(x) = x^2 + 7 in de punten (a,y(a)) en (b,y(b)).
De helling van die lijn is 5.
b-a = 3
[ Bericht 0% gewijzigd door GlowMouse op 10-01-2006 22:00:37 (typo [2x]) ]
quote:hehehheheheheOp dinsdag 10 januari 2006 20:21 schreef AtraBilis het volgende:
Ja. Maar voor elke epsilon geldt dat het minder grappig is.
Ik moest even gniffelen
quote:Ik denk het niet. Het gaat om de punten (a, y(a)) en (b, y(b)). Gegeven is dat a = b + 3, en dat de helling gelijk is aan 5. Ergo, we kunnen ook zeggen dat het gaat om de punten (a, y(a)) en (a - 3, y(a) - 15). Voorts weet je dat die punten aan de vergelijking moeten doen. Dat moet genoeg zijn.Op dinsdag 10 januari 2006 20:29 schreef GlowMouse het volgende:
[..]
b-a=3, dus het gaat om de punten (a,y(a) en (a+5,y(a+3)). De helling tussen die punten is (y(a+3)-y(a))/3. Ik denk dat je hiermee verder kunt komen.
quote:b = 3 + aOp dinsdag 10 januari 2006 20:24 schreef BrauN het volgende:
Een lijn snijdt de grafiek van de functie y(x) = x^2 + 7 in de punten (a,y(a)) en (b,y(b)).
De helling van die lijn is 5.
b-a = 3
Nou... hoe reken ik die a en b uit?
y(b) = y(a) + 15 {de helling is vijf en je gaat drie 'naar rechts', dus drie maal de helling 'hoger'}
b2+7 = a2+7+15
(3+a)2 +7 = a2+15+7 {b = 3 + a invullen}
a2 + 9 + 6a = a2 + 15 {haken uitwerken en de 7 aan beide kanten wegstrepen}
6a = 6
a = 1
b = 4
quote:Okee, laten we beginnen bij de Fe2O3. Dit is een zout dat gevormd wordt door positief geladen ijzerionen en negatief geladen zuurstofionen. Zuurstofionen zijn altijd 2-. Aangezien je 3 zuurstofatomen hebt in Fe2O3, is dat dus samen 6-. Fe2O3 is in zijn geheel neutraal, dus moeten de ijzerionen samen 6+ zijn. Aangezien je twee ijzerionen hebt, is elk apart ijzerion dus 3+. Oftewel: je hebt een zout dat bestaat uit O2- en Fe3+.Op dinsdag 10 januari 2006 19:44 schreef WyBo het volgende:
Ik snap de volgende zuur-base reactie niet,
De opgave is: Geef de RV van Fe2O3 in overmaat verdund zwavelzuur
dan zou je de volgende RV moeten krijgen:
Fe2O3 + 6 H30+ -----> 2 Fe3+ + 9 H2O
zou iemand dat voor mij kunnen uitleggen aub?
Als je H3O+ hebt en O2-, reageren die met elkaar in een zuur-basereactie. Even voor alle duidelijkheid: het is dus niet zo dat je Fe2O3 uit elkaar valt in Fe3+-ionen en O2--ionen. Fe2O3 blijft Fe2O3, maar de zuurstofionen reageren alsof ze losse O2-'s zijn. Om van O2- H2O te maken, moet elk zuurstofatoom dus met twee moleculen H3O+ reageren. Je had 3 zuurstofionen, dus moeten die met 6 moleculen H3O+ reageren.
Hoeveel water komt daar nou uit? Tel het aantal O'tjes en H'tjes maar. Je hebt 9 O's (3 uit de Fe2O3en 6 uit de H3O+) en 18 H'tjes (allemaal uit de H3O+), dus daar kun je precies 9 watermoleculen mee maken. Verder had je 2 ijzers in je Fe2O3 zitten. Deze waren 3+ en er gebeurt verder helemaal niks mee, dus dat blijven twee ionen Fe3+, alleen nu los.
Was dit te volgen?
quote:ok, je post was wel de moeite om te lezenOp dinsdag 10 januari 2006 21:07 schreef Lathund het volgende:
verhaal
als ze mij nou mod ses gemaakt hadden
quote:Eigenlijk heet het logaritmus naturalis, vandaar ook ln en niet nlOp dinsdag 10 januari 2006 16:37 schreef BrauN het volgende:
Dames en heren, we gaan nu een stapje verder. Schrik niet.
ln(x+7) + ln(x+3) = 0
Dat 'ln'-ding heet geloof ik een natural logarithm, voor de n00bs die dat niet weten.
Nou... los maar op.
Mijn tvp
Van logos en artihmos (Ook terug te vinden in logica, -logie en arithmetica, resp.) quote:Dat had best een goeie oplossing geweest inderdaad... jammer dat ik het nu pas leesOp dinsdag 10 januari 2006 14:55 schreef AtraBilis het volgende:
[..]
Ik snap het. Daar ik geen verstand van Excel heb weet ik niet of het haalbaar is, maar, is het dan niet logischer om de open vragen een eigen rij te geven?
(Respondent 1)
[lijst meerkeuze]
[eerste open vraag]
[tweede open vraag]
(Respondent 2)
[lijst meerkeuze]
[eerste open vraag
[tweede open vraag]
Als ze er over gaan klagen dan ga ik dit cker gebruiken... thx voor het meedenken
oh ja, link: http://home.hetnet.nl/~vanadovv/Log.html
wij hebben het hier op school het ook over logaritmen gehad en was best leuk
quote:Vraag 1 proberen gedeeltelijk te beantwoorden:1:
Machine draait 16 uur per dag. 46 werkweken in een jaar – 5 dagen per week.
Economische levensduur = 5 jaar
Gelijktijdige capaciteit= 12.800 prestaties per week
A: Omschrijf het begrip gelijktijdige capaciteit.
B: Bereken de gelijktijdige capaciteit per uur.
C: Bereken de volgtijdige capaciteit.
2:
Jaarproductie= 400.000 kg.
Kwartaal 1: 20 %
Kwartaal 2: 25 %
Kwartaal 3: 30 %
Kwartaal 4: 25 %
De reservecapaciteit is 10.000 kg per kwartaal. Er zijn 4 machines aanwezig met een capaciteit van 155.000 kg per jaar.
A: Bereken de rationele capaciteit.
B: Bepaal de rationele overcapaciteit.
C: Splits de rationele overcapaciteit naar oorzaken.
D: Is er irrationele overcapaciteit? Motiveer.
3:
1 januari is de voorraad cd-rom’s 18.000 stuks.
Er werden er 82.000 verkocht á ¤ 45 per stuk.
Kosten:
Variabele: ¤ 1.200.000
Constante: ¤ 1.700.000
Normale productie/afzet is ¤ 85.000 per jaar.
A: Wat kun je zeggen over de voorraadverandering in de afgelopen jaren?
B: Bereken de integrale kostprijs van één cd.
C: Bereken het bedrijfsresultaat volgens de integrale kostencalculatie.
D: Bereken de dekkingsbijdrage per cd.
E: Bereken het bedrijfsresultaat volgens de variabele kostencalculatie.
F: Verklaar het verschil tussen antwoord c en d. (+ berekening)
G: Wanneer is het bedrijfsresultaat bij beide methoden gelijk?
4:
Voorcalculatie berekent 1,25 kg á ¤ 8 nodig. Nacalculatie bleek 120.000 kg, waarvoor ¤ 8,5 per kg. betaald werd. Er werden 100.000 flessenrekken geproduceerd.
A: bereken het calculatieverschil op basis van grondstofverbruik.
B: berken het efficiencyverschil op grondstof
C: bereken het prijsverschil op grondstof
A: Gelijktijdige capaciteit= het aantal prestaties dat een machine per tijdseenheid kan voortbrengen. (per uur, maand of jaar)
B:
Volgtijdige capaciteit= het aantal prestaties over de gehele levensduur.
12.800 per week : 5 dagen= 2560 per dag: 16 u= 160.
C: Aantal prestaties gehele levensduur.
12.800 per week x 46= 588.000 = 1 jaar. x 5= 2.944.000.
2A en B ook:
A: Rationele capaciteit= noodzakelijke capaciteit om normale productie te kunnen voortbrengen.
De productie in het 3e kwartaal is het hoogst.
400.000 x 0.30= 120.000. De capaciteit moet daarom minstens 120.000 per kwartaal zijn. Daar komen nog 10.000 stuks reservecapaciteit bij; 130.000 stuks per kwartaal dus. De benodigde capaciteit is dan:
4 x 130.000 stuks = 520.000 stuks.
B: Rationele overcapaciteit= gedeelte van de aanwezige capaciteit dat niet voor productie wordt gebruikt, maar om andere redenen onvermijdelijk is.
De aanwezige capaciteit bedraagt 12 x 4 x 10.000 stuks= 480.000 stuks.
Normale jaarproductie: 400.000 stuks.
Overcapaciteit: 80.000 stuks.
Iemand die hier een sterk in is en dit zou kunnen?
quote:Ik schrijf gewoon log in plaats van ln als ik de natuurlijke logaritme bedoel. Een logaritme met grondtal 10 schrijf ik als log(x)/log(10).Op dinsdag 10 januari 2006 23:05 schreef Nuna het volgende:
[..]
Eigenlijk heet het logaritmus naturalis, vandaar ook ln en niet nl
Mijn tvp
quote:Waarom zou je zo moeilijk doen als het rekenmachine al automatisch 10 als grondgetal neemt?Op woensdag 11 januari 2006 17:14 schreef thabit het volgende:
[..]
Ik schrijf gewoon log in plaats van ln als ik de natuurlijke logaritme bedoel. Een logaritme met grondtal 10 schrijf ik als log(x)/log(10).
quote:eens is.Op woensdag 11 januari 2006 18:34 schreef bierglas het volgende:
[..]
Waarom zou je zo moeilijk doen als het rekenmachine al automatisch 10 als grondgetal neemt?
wij schrijven het trouwens zo op: 2log7 etc
quote:Dat alleen al is een reden om die rekenmachine bij het grofvuil te zetten.Op woensdag 11 januari 2006 18:34 schreef bierglas het volgende:
[..]
Waarom zou je zo moeilijk doen als het rekenmachine al automatisch 10 als grondgetal neemt?
quote:Grofvuil? Heb jij nog een ENIAC?Op woensdag 11 januari 2006 18:45 schreef thabit het volgende:
[..]
Dat alleen al is een reden om die rekenmachine bij het grofvuil te zetten.
quote:Dit is de ENIAC: plaatje.. beetje een hele grote computerOp woensdag 11 januari 2006 19:18 schreef thabit het volgende:
Man, ik weet niet wat een ENIAC is. Maar als de log niet met grondtal e is, dan is het waardeloos.
Het gaat om de oplossing van het Exogenuos Growth model: http://en.wikipedia.org/wiki/Exogenous_growth_model
Mijn probleem is dat de Wiki onvolledig en fouten bevat.
Heeft iemand zin/tijd om samen met mij de berekening na te lopen en mij te helpen? Alvast ter informatie, ik loop vast bij het punt waarop ze de differentiaalvergelijking gaan gebruiken. Vanaf dit punt heeft ook een andere auteur aan het stuk gewerkt volgens mij.
Er is een verschil tussen de lengte en de capaciteit. Initieel is de capaciteit = lengte+16. Maar als men via de methode StringBuffer.append("...") zaken gaat toevoegen zal die formule uit het voorbeeld dat ik hier gebruikte niet meer geldig zijn (maw capaciteit is niet langer lengte + 16).
Zit daar (bepaling van de capaciteit) enige logica in?
quote:Ik weet het ook niet maar na wat ge-Google kom ik hierop: link, de Java code van de StringBuffer class. Je kunt hier zien met welke waarden append de methode aanroept voor het uitbreiden van de capacity. De capacity wordt uiteindelijk veranderd in expandCapacity() waarbij de nieuwe capacity (value.length + 1)*2 is of de waarde die aan de methode is meegegeven vanuit append, mits deze groter is dan de al berekende waarde met die formule van daarnet.Op donderdag 12 januari 2006 08:41 schreef Masanga het volgende:
Vraag ivm StringBuffers bij Java:
Er is een verschil tussen de lengte en de capaciteit. Initieel is de capaciteit = lengte+16. Maar als men via de methode StringBuffer.append("...") zaken gaat toevoegen zal die formule uit het voorbeeld dat ik hier gebruikte niet meer geldig zijn (maw capaciteit is niet langer lengte + 16).
Zit daar (bepaling van de capaciteit) enige logica in?
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen
zal mij deugd doen
quote:Dat komt doordat het binomiaal is. Je hebt prijs óf geen prijs. In dit geval vragen ze drie keer geen prijs. De kans dat je 1x geen prijs hebt is 49500/50000. Dus de kans dat je 3x geen prijs hebt is dan (49500/50000)3.Op donderdag 12 januari 2006 17:09 schreef Ewaldus het volgende:
ok, ben bezig met kansberekeningen voor wiskundeA12, alleen door het harde leren zie ik door de bomen het bos niet meer.
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen
[afbeelding]
quote:maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?Op donderdag 12 januari 2006 18:12 schreef Nuna het volgende:
[..]
Dat komt doordat het binomiaal is. Je hebt prijs óf geen prijs. In dit geval vragen ze drie keer geen prijs. De kans dat je 1x geen prijs hebt is 49500/50000. Dus de kans dat je 3x geen prijs hebt is dan (49500/50000)3.
(3 se's op één dag zijn veel)
quote:Volgens mij welOp donderdag 12 januari 2006 18:23 schreef Ewaldus het volgende:
[..]
maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?
(3 se's op één dag zijn veel)
Niet zulke moeilijke vragen stellen he 
Ik ben het ook weer net aan het herhalen, toevallig had ik net iets gezien over de binomiale verdeling.quote:Ik denk dat er een afweging wordt gemaakt tussen ruimte en snelheid. Telkens de capaciteit een beetje verhogen (telkens met 10 of zo), geeft bij veel toevoegen natuurlijk nodeloze inspanningen om de capaciteit te verhogen. Een capaciteit in het begin die heel groot is, is ook nodeloos, want dan verkwist je ruimte.Op donderdag 12 januari 2006 08:41 schreef Masanga het volgende:
Vraag ivm StringBuffers bij Java:
Er is een verschil tussen de lengte en de capaciteit. Initieel is de capaciteit = lengte+16. Maar als men via de methode StringBuffer.append("...") zaken gaat toevoegen zal die formule uit het voorbeeld dat ik hier gebruikte niet meer geldig zijn (maw capaciteit is niet langer lengte + 16).
Zit daar (bepaling van de capaciteit) enige logica in?
Het verdubbelen is echter niet zonder goede theoretische reden. Het verdubbelen leidt ertoe dat er gemiddeld een constante tijd nog steeds gegarandeerd kan worden per toevoegen van een element aan de lijst. De kosten voor het verdubbelen worden daarbij dus verdeeld over alle elementen die je toevoegt. Resize je vaker, dan moet je vaker met data schuiven en toewijzen, en dan kost je dit gemiddeld meer tijd. (Niet O(1) in complexiteitstermen. Door verdubbeling blijft de complexiteit O(n) om n elementen toe te voegen aan de lijst. Anders wordt deze beroerder.)
Dat is volgens mij de reden.
quote:Volgens mij heb je gelijk. Als je het netjes zou doen, dan zou je gebruik maken van combinaties ('nCr'). De eerste keer geen prijs is namelijk een kanas van 49500/50000, de tweede keer van 49499/49999 en de derde keer van 49498/49998, of, hetzelfde: (49500 nCr 3)/(50000 nCr 3), beide geven als uitkomst 40426674783/41664166700. (Mits je ervan uitgaat dat men zonder terugleggen te prijzen uitdeelt, wat vaak zo is, daar op een lot meestal maar één prijs valt) Wat, in decimalen .9702984119 is. Terwijl (49500/50000)^3 = .9702990000.Op donderdag 12 januari 2006 17:09 schreef Ewaldus het volgende:
ok, ben bezig met kansberekeningen voor wiskundeA12, alleen door het harde leren zie ik door de bomen het bos niet meer.
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen
[afbeelding]
In dit geval is de populatie (het aantal loten) echter zo groot, dat het verschil verwaarloosbaar is. Je ziet het aan de decimalen, de eerste 5 zijn identiek. En volgens mij is dát de reden dat ze geen nCr gebruiken. Niet het wel of geen prijs.
quote:Als ze zouden differentieren naar hoofdprijs, tweede prijs en derde prijs en geen prijs. En ze vragen bijvoorbeeld, wat is de kans dat je met 5 loten een keer de hoofdprijs wint, en twee derde prijzen? (En de rest geen prijs), dan zou je krijgen: ((1 nCr 1)*(9 nCr 0)*(490 nCr 2)*(49500 nCr 2))/(50000 nCr 5). Zoals te verwachten is deze kans heel klein. (5.6 * 10^-8). ik hoop dat dit niet boven je wiskunde A pet gaat, anders gewoon negeren dusOp donderdag 12 januari 2006 18:23 schreef Ewaldus het volgende:
[..]
maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?
(3 se's op één dag zijn veel)
quote:Het staat gewoon in de Java hoor: linkOp donderdag 12 januari 2006 18:33 schreef AtraBilis het volgende:
[..]
Ik denk dat er een afweging wordt gemaakt tussen ruimte en snelheid. Telkens de capaciteit een beetje verhogen (telkens met 10 of zo), geeft bij veel toevoegen natuurlijk nodeloze inspanningen om de capaciteit te verhogen. Een capaciteit in het begin die heel groot is, is ook nodeloos, want dan verkwist je ruimte.
Het verdubbelen is echter niet zonder goede theoretische reden. Het verdubbelen leidt ertoe dat er gemiddeld een constante tijd nog steeds gegarandeerd kan worden per toevoegen van een element aan de lijst. De kosten voor het verdubbelen worden daarbij dus verdeeld over alle elementen die je toevoegt. Resize je vaker, dan moet je vaker met data schuiven en toewijzen, en dan kost je dit gemiddeld meer tijd. (Niet O(1) in complexiteitstermen. Door verdubbeling blijft de complexiteit O(n) om n elementen toe te voegen aan de lijst. Anders wordt deze beroerder.)
Dat is volgens mij de reden.
Bij voorbaat dank
Met begeleidende tekst:
quote:En wel hier vandaan. Dus wellicht dat inonosine monophosphate meer oplevert als je ermee zoekt in Google.Synthesis of the first fully formed purine nucleotide, inosine monophosphate, IMP begins with 5-phospho-a-ribosyl-1-pyrophosphate, PRPP. Through a series of reactions utilizing ATP, tetrahydrofolate (THF) derivatives, glutamine, glycine and aspartate this pathway yields IMP. The two indicated enzymes (A and B) are those catalyzing the rate limiting step and the reaction necessary for the purine nucleotide cycle, respectively. The structure of the nucleobase of IMP (hypoxanthine) is shown.
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
2b begrijp ik al helemaal niet
quote:Bij 2a wordt naar a gevraagd, niet naar x. Maar als het goed is, zijn er 2 mogelijkheden voor a en x (bij x ligt a vast en vice versa).Op vrijdag 13 januari 2006 19:23 schreef Frankvbr het volgende:
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
2b begrijp ik al helemaal niet
Wat je zoekt is een punt waarvoor de raaklijn door (0,0) gaat. Ken je de formule voor de lineaire benadering?
g(x)=f(c)+f'(c)(x-c)
c is het punt waarin je benadert, x is het punt waarin je de functiewaarde wilt schatten. Nu zoek je een x-waarde waarvoor de lineaire benadering door 0 gaat: precies andersom. De 'x' in de formule wordt dus 0, en de c vind je door te kijken wanneer de lineaire benadering door (0,0) gaat. Als je die c gevonden hebt, heb je a ook zo. Het antwoord kun je vrij eenvoudig exact bepalen, en de rekenmachine hiervoor gebruiken lijkt me onzin.
Bij b wil je de afstand weten tussen 2 punten op de grafiek. Dat kan met behulp van de stelling van pythagoras: afstand=wortel(deltax²+deltay²)
Nu geldt dat je deltay uit kunt drukken in deltax en a (ga na dat moet gelden 25 = deltax²+(a*deltax)²). Nu heb je een verband tussen a en deltax. Nu wil je de de functie f nog gebruiken voor een extra vergelijking, dat kan ook met de stelling van pythagoras. Noem die 2 punten a en b, bepaal deltax en deltay, bepaal de afstand tussen die twee punten, en substitueer dat in de eerder gevonden formule.
quote:dat is niet verstandig om te zeggen in dit topicOp vrijdag 13 januari 2006 19:23 schreef Frankvbr het volgende:
[[url=http://img337.imageshack.us/img337/7586/wiskundepo6qq.th.png]afbeelding][/URL]
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
en je plaatje doet t niet
quote:ex-chemicus to the rescueOp donderdag 12 januari 2006 19:23 schreef Bullet-tooth het volgende:
Scheikundigen: Hoe ziet de structuurformule van inosinemonofosfaat (ook wel IMP genaamd) eruit? Het gaat hier dus om een afbeelding van deze stof want ik kan het nergens vinden, ook niet in binas maar misschien mis ik iets.
Bij voorbaat dank
it's your lucky day!
lang leve acros
plus info
http://www.acros.be/DesktopModules/Acros_Search_Results/Acros_Search_Results.aspx?tabID=21&alias=Rainbow&lang=en&search_type=2&search=inosinemonophosphate
en als je er op klikt werkt ie wel
quote:Er zijn meerdere manieren om dit exact op te lossen, het makkelijkst is om op te schrijven waar de vergelijkingen aan moeten voldoen en daarop voort te werken. Dit is dus:Op vrijdag 13 januari 2006 20:55 schreef GlowMouse het volgende:
[..]
Bij 2a wordt naar a gevraagd, niet naar x. Maar als het goed is, zijn er 2 mogelijkheden voor a en x (bij x ligt a vast en vice versa).
Wat je zoekt is een punt waarvoor de raaklijn door (0,0) gaat. Ken je de formule voor de lineaire benadering?
g(x)=f(c)+f'(c)(x-c)
c is het punt waarin je benadert, x is het punt waarin je de functiewaarde wilt schatten. Nu zoek je een x-waarde waarvoor de lineaire benadering door 0 gaat: precies andersom. De 'x' in de formule wordt dus 0, en de c vind je door te kijken wanneer de lineaire benadering door (0,0) gaat. Als je die c gevonden hebt, heb je a ook zo. Het antwoord kun je vrij eenvoudig exact bepalen, en de rekenmachine hiervoor gebruiken lijkt me onzin.
g(x)=f(x)
g'(x)=f'(x)
g(x)=f(x) -> g(x)-f(x)=0
g'(x)=f'(x) ->2x-6=a
2x-6=a, hier heb je dus al de verbinding tussen x en a, nu kun je deze gaan invullen in de eerste vergelijking:
g(x)-f(x)=0 ->x^2-6x+13-ax=0 ->x^2-6x+13-(2x-6)x=0 -> x^2-6x-2x^2+6x+13=0
-> -x^2+13=0 -> x=+/- wortel(13)
2x-6=a, dus a= 2(+/- wortel13)-6.
Antwoord:
a=2(-3+wortel(13)) V a=2(-3-wortel(13))
Een andere methode is om gebruik te maken van de eigenschappen van de discriminant. Ziehier:
g(x)-f(x)=0, dus x^2-6x+13-ax=0. De discriminant is dus:
D=(6+a)^2-4*13=a^2+12a-16. Als de discriminant gelijk is aan 0 raakt de grafiek de x-as. Dit is wat we willen weten. Op deze discriminant gooi je dus een ABC formule:
x=(-12 +/- wortel(208))/2= -6 +- 2 wortel(13)
Antwoord:
a=2(-3+wortel(13)) V a=2(-3-wortel(13))
Is het niet wonderbaarlijk
quote:De tweede is helemaal leukOp vrijdag 13 januari 2006 19:23 schreef Frankvbr het volgende:
[[url=http://img337.imageshack.us/img337/7586/wiskundepo6qq.th.png]afbeelding][/URL]
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
2b begrijp ik al helemaal niet
Ik denk dat hij wel makkelijker kan, maar ik kreeg hem alleen zo exact opgelost, tis al laat.
Het antwoord moet aan de volgende vergelijkingen voldoen:
B=A+5
f(B)-f(A)=5a
f(A)-a*A=0
f(B)-f(A)=5a -> f(B)-f(B-5)=5a ->x^2-6x+13-((x-5)^2-6(x-5)+13)=5a.
Uitwerken geeft: a=2x-11
f(A)-a*A=0 geeft:
x^2-6x+13-ax=0 -> x^2-6x+13-(2x-11)x=0
uitwerken:
-x^2+5x+13=0
ABC-tje ertegenaan:
x=( -5 +/- wortel(25+52))/2
x= (-5+wortel(77)/2 V x=(-5 - wortel(77))/2
a=2x-11
Antwoord:
a= -6 + wortel(77) V a= -6 - wortel(77)
(excuus voor de eventuele wiskundige slordigheden qua notatie)
quote:Probeer het te begrijpen. Stel dat een gebeurtenis A op 10 verschillende manieren kan gebeuren, dan is de totale kans op gebeurtenis A 10 keer de kans dat het op een van die manieren gebeurt. nCr berekent die '10', oftewel, nCr berekent hoeveel mogelijkheden er zijn op een gebeurtenis.Op donderdag 12 januari 2006 18:23 schreef Ewaldus het volgende:
[..]
maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?
(3 se's op één dag zijn veel)
nCr is trouwens precies: n! / ((n-k)! * k!)
quote:Het grondgetal 10 is natuurlijk compleet random en nergens op gebaseerd, wiskundig gezien.Op woensdag 11 januari 2006 18:34 schreef bierglas het volgende:
[..]
Waarom zou je zo moeilijk doen als het rekenmachine al automatisch 10 als grondgetal neemt?
Het grondtal e daarentegen, hmmmm
quote:je kunt geen rechteliijnstuk met lengte pi construeren.. dus de zijde van die vierkant is het probleem?Op dinsdag 10 januari 2006 19:16 schreef thabit het volgende:
[..]
Cirkelkwadratuur is onmogelijk. Komt omdat pi transcendent is. Gegeven twee punten in het vlak welke de coordinaten (0,0) en (0,1) worden gegeven kun je alleen punten met algebraische coordinaten construeren met passer en liniaal. Dat pi transcendent is, is bewezen door Lindemann. Hier is een bewijs. Ik heb geen idee of het een goed bewijs is, niet doorgelezen.
als je een cirkel tekent met r=1/2 dan hebj e wel een omtrek van lengte pi. Dus wel 'tekenbaar'met een passer....
gaat het dus om die zijde?
quote:De oppervlakte van het vierkant moet, zeg, pi zijn (Gegeven een cirkel met straal 1). Dus dan moet een zijde wortel(pi) zijn. Het nummer wortel Pi is niet algebraïsch te construeren. Dat construeren moest met een liniaal en een passer gebeuren. Dat was dan verder aan enkele regels gebonden, welke dat zijn vind je op Wikipedia.Op zaterdag 14 januari 2006 21:35 schreef teletubbies het volgende:
[..]
je kunt geen rechteliijnstuk met lengte pi construeren.. dus de zijde van die vierkant is het probleem?
als je een cirkel tekent met r=1/2 dan hebj e wel een omtrek van lengte pi. Dus wel 'tekenbaar'met een passer....
gaat het dus om die zijde?
Het bewijs zelf is niet eenvoudig. Maar uiteindelijk komt het er dus inderdaad op neer dat als je je volgens die regels bezig houdt, je niet het goede vierkant krijgt omdat je die zijde niet kunt construeren. (Je kunt wel zo dicht bij komen als je wilt). Hippocrates heeft echter wel wat maantjes geconstrueerd (Soort sikkelvormpjes) met driehoeken die dezelfde oppervlakte hadden.
quote:Ja. Het kost wel even tijd.Op zaterdag 14 januari 2006 21:11 schreef Pauluzz_U5 het volgende:
Hallo mensen, ik was weer is druk aan het studeren en ik ben toen de formule v^2/r tegengekomen die als uitkomst de middelpuntzoekende versnelling geeft. Alleen ik zou graag willen weten hoe je dat kunt bewijzen. Iemand een id?
Je gaat uit van een versnelling a, opgebouwd uit twee vectoren:
-een versnelling loodrecht van de cirkel, de aN
-een versnelling evenwijdig aan de raaklijn van de cirkel, de aT
-(dus eT is de vector waar aT langs werkt, enz).
a = dv/dt (bekend toch?) = d(veT)/dt = dv/dt eT + v*d(eT)/dt.
Bij een rechte lijn is eT constant en vervalt de tweede term. Dan blijft er over: a = dv/dt * eT (die eT is puur de lijn waarlangs hij werkt). eT moet je herschrijven naar een functie van een sinus en een cosinus. Na herschrijven en eN invullen (ook als functie van een sinus en cosinus van de hoek phi) volgt:
deT/dt = -eN d(phi)/dt (phi is hoek tussen horizontale as en de eT). Nu moet je dus p(phi)/dt hebben. Zonder bewijs:
d(phi)/dt = v d(phi/ds), s = lengte van de boog. En d(phi)/ds is 1/r.
Ik heb eigenlijk een upload-iets nodig om het e.e.a. inzichtelijker te maken met een plaatje. Nou ja, dit linkje legt het in heel eenvoudige taal uit. Anders kun je ook wikipedia proberen natuurlijk (centripel acceleration). Hier ook een link.
[ Bericht 6% gewijzigd door Flumina op 14-01-2006 23:44:43 ]
quote:Tnx Flumina, ik snap er nog niet veel van, maar dat komt nog welOp zaterdag 14 januari 2006 23:24 schreef Flumina het volgende:
[..]
Ja. Het kost wel even tijd.
Je gaat uit van een versnelling a, opgebouwd uit twee vectoren:
-een versnelling loodrecht van de cirkel, de aN
-een versnelling evenwijdig aan de raaklijn van de cirkel, de aT
-(dus eT is de vector waar aT langs werkt, enz).
a = dv/dt (bekend toch?) = d(veT)/dt = dv/dt eT + v*d(eT)/dt.
Bij een rechte lijn is eT constant en vervalt de tweede term. Dan blijft er over: a = dv/dt * eT (die eT is puur de lijn waarlangs hij werkt). eT moet je herschrijven naar een functie van een sinus en een cosinus. Na herschrijven en eN invullen (ook als functie van een sinus en cosinus van de hoek phi) volgt:
deT/dt = -eN d(phi)/dt (phi is hoek tussen horizontale as en de eT). Nu moet je dus p(phi)/dt hebben. Zonder bewijs:
d(phi)/dt = v d(phi/ds), s = lengte van de boog. En d(phi)/ds is 1/r.
Ik heb eigenlijk een upload-iets nodig om het e.e.a. inzichtelijker te maken met een plaatje. Nou ja, dit linkje legt het in heel eenvoudige taal uit. Anders kun je ook wikipedia proberen natuurlijk (centripel acceleration). Hier ook een link.
quote:Vergeet mij uitleg en lees dit. Je ziet hieronder (zoals ook op de twee link te zien was) twee situaties van het voorwerp (namelijk een P en een Q). Bij P en Q heeft het voorwerp dezelfde snelheid, maar de snelheidsvector wijst wel naar een andere richting. Dit verschil in richting moet veroorzaakt worden door een verschil in snelheid, die dv genoemd wordt.Op zondag 15 januari 2006 00:40 schreef Pauluzz_U5 het volgende:
[..]
Tnx Flumina, ik snap er nog niet veel van, maar dat komt nog wel
Die dv, die loodrecht op de beweging staat en naar het middelpunt wijst, is nodig om die cirkelbeweging te maken. Die dv kan geschrijven worden als functie van de hoek, zoals op onderstaande te zien is.
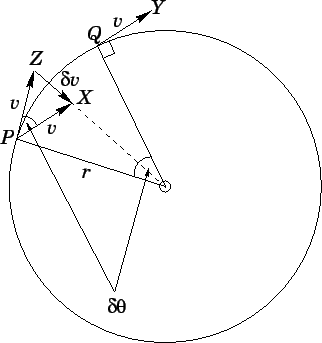
dv = v * d(theta). Met andere woorden: dat snelheidverschil is te schrijven als functie van de snelheid zelf vermedigvuldigd met een klein verschil in de hoek theta. Dit geldt alleen trouwens voor kleine hoeken, anders moet je met sinussen gaan kloten.
Nu is versnelling gedefinieerd als dv/dt (snelheid delen door tijd), dus
dv/dt = a = v * d(theta)/dt, het laatste is omega (hoeksnelheid). Dus:
a = v * omega
Omega = v/r. Deze invullen en je hebt:
a = v^2/r
[ Bericht 4% gewijzigd door Flumina op 15-01-2006 09:28:57 ]
.quote:Een baanomloop van Mercurius duurt 88 dagen. De planeet draait in 58.7 dagen om zijn as, dwz de snelheid is 2/3 keer zo groot. Laat zien dat een zonnedag op Mercurius 176 dagen duurt, precies 2 maal zolang als de baanomloop. (Dit verschijnsel wordt resonantie genoemd)
quote:Bedankt Flumina, het is me al een stuk duidelijker, alleen dat laatste wat je zegt... je zegt dat dv = v * d(theta). Is dat nou de snelheidsverandering maal de hoek, of zie ik dat nou helemaal verkeerd.Op zondag 15 januari 2006 02:01 schreef Flumina het volgende:
[..]
Vergeet mij uitleg en lees dit. Je ziet hieronder (zoals ook op de twee link te zien was) twee situaties van het voorwerp (namelijk een P en een Q). Bij P en Q heeft het voorwerp dezelfde snelheid, maar de snelheidsvector wijst wel naar een andere richting. Dit verschil in richting moet veroorzaakt worden door een verschil in snelheid, die dv genoemd wordt.
Die dv, die loodrecht op de beweging staat en naar het middelpunt wijst, is nodig om die cirkelbeweging te maken. Die dv kan geschrijven worden als functie van de hoek, zoals op onderstaande te zien is.
[afbeelding]
dv = v * d(theta). Met andere woorden: dat snelheidverschil is te schrijven als functie van de snelheid zelf vermedigvuldigd met een klein verschil in de hoek theta. Dit geldt alleen trouwens voor kleine hoeken, anders moet je met sinussen gaan kloten.
Nu is versnelling gedefinieerd als dv/dt (snelheid delen door tijd), dus
dv/dt = a = v * d(theta)/dt, het laatste is omega (hoeksnelheid). Dus:
a = v * omega
Omega = v/r. Deze invullen en je hebt:
a = v^2/r
quote:Het is een snelheid * hoekverandering. Een d ervoor betekent een (zeer) klein verschil.Op zondag 15 januari 2006 23:24 schreef Pauluzz_U5 het volgende:
[..]
Bedankt Flumina, het is me al een stuk duidelijker, alleen dat laatste wat je zegt... je zegt dat dv = v * d(theta). Is dat nou de snelheidsverandering maal de hoek, of zie ik dat nou helemaal verkeerd.
quote:tnxOp zondag 15 januari 2006 23:45 schreef Flumina het volgende:
[..]
Het is een snelheid * hoekverandering. Een d ervoor betekent een (zeer) klein verschil.
Stel a > 0 en c is de grafiek in het (x,y)-vlak van de kromme y = cosh x tussen x = 0 en x = a
a) Bereken de lengte van c
b) Stel F(x,y) = (-y,x), Bereken de integraal van F*ds over c
c) Is er een fucntie f:R^2 -> R met F = gradient f?
a en b zijn heel simpel, mits je het pad (parametrisatie van y = cosh x) weet.... en die weet ik dus niet... wie helpt me daar even uit?
Het antwoord van c is dat er geen gradient f is, omdat je nooit 2 partiele afgeleiden kan hebben met (-y,x).
d (yx)/dx = y en de(yx)/dy = x, maar die - krijg je er dus nooit voor.... correct me if I'm wrong.. maar het grootste probleem is dus het pad
quote:x(t) = tOp maandag 16 januari 2006 12:05 schreef maniack28 het volgende:
a en b zijn heel simpel, mits je het pad (parametrisatie van y = cosh x) weet.... en die weet ik dus niet... wie helpt me daar even uit?
y(t) = (et+e-t)/2
H2 Exponenten en logaritmen
89. Een bioloog heeft gedurende een groot aantal jaren onderozke gedaan naar het aantal kikkers in een waterrijk gebied. In de tabel zie je een schatting van het aantal kikkers N, telkens op 1 september van het genoemde jaar.
Jaar | 1975 | 1978 | 1980 | 1984 | 1989 | 1990 | 1992 | 1993 | 1996 | 1997 | 1998
N |15000|11700| 9900 | 7100 | 4700 | 4300 | 3600 | 3500| 3000 | 2800 | 2500
a) -
b) tot welk jaar is er sprake van exponentiële afnamen? geef voor deze periode de formule van N als functie van t. neem t in jaren en t = 0 in 1975. Rond de groeifactor af op 2 decimalen.
C) hoeveel kikkers zijn er in 1998 meer geteld dan dat er gweest zouden zijn als de exponentiële afnamen zich had doorgezet.
H5. De binomiale verdeling
53. De drie grootste automerken in nederland zijn opel, volkswagen en Ford. van de auto;s in Nederland is 13% van het merk opel , 12 % van het merk wolkswagen en 9% van het merk Ford.
Nummers vier is Renault met 8% en nummer vijf is peugeot met 7 %. Bereken in vier decimlane nauwkeurig de kans dat van 60 willekeurige aangewezen auto's er
a) precies 20 tot de drie grootste merken behoren
b) 14, 15 of 16 van het merk opel of volkswagen zijn
c) tussen de 5 en 10 van de merken renault en peugeot bij zijn.
54. Bereken in vier decimalen nauwkeurig de kans dat je bij
a) toen worpen met een dobbelsteen meer dan twee keer 6 ogen gooit
b) twaalf worpen met een dobbelsteen meer dan tien keer minstens 5 ogen gooit.
c) 30 worpen met een dobbelsteen tussen de 18 en 22 keer geen 1 of 2 ogen gooit.
56. in een labaratorium test men flesjes met het medicijn a op het voorkomen van een virus. Bekend is namelijk dat 1 op de 20 flesjes zo'n virus bevat. Bij deze controle neemt men uit elk flesje een monster. met de beschikbare apparatuur is het mogelijk maximaal tien monster tegelijk te tsten. Het nemen van een monster uit een flesje kost 2,- en elke test kost 8,-. Zo kost het gecombineerd testen van drie monster 14,- Valt deze test positief uit (dat wil zeggen het virus is aanwezig), dan moeten de drie monster afzonderlijk getest worden, hetgeen nog eens 3 x 8,- = 24,- kost
a) we bekijken de situatie waarbij de vier flesjes op het virus worden onderzicht.
- met combineert de vier monsters en de test valt negatief uit .
Wat zijn de kosten?
Bereken in vier decimalen nauwkeurig de kans dat een gecombineerde test van vier monsters negatief uitvalt.
- men combineert de vier monsters en de test valt positief uit, dus de vier monsters moeten elk afzonderlijk getest worden.
geef de kans op deze situatie en bereken de totale kosten.
- Bereken de verwachtingswaarde van de kosten en vervolgens de verwachtingswaarde van de kosten per monster.
B) wij bekijken de situatie waarbij vijf flesjes op het virus worden onderzocht. bereken in centen nauwkerugi de verwachtingswaarde. van de kosten per monster als men besluit de vijf monsters te combineren.
c) ga uit van de situatie waarbij n flesjes op het virus worden onderzocht hierbij is n > 1
toon aan dat de verwachtingswaarde E van de kosten per monster in het geval men besluit de n monsters te combineren, gelijk is aan E = 10 -8 x 0,95^n + - 8/n
H6 Veranderingen en snelheden
62. De dagelijkse kosten bij de productie van een wekkerradio zijn gegeven door de formule K = 1,2q³ - 8q² + 25q + 22. Hierin is K in duizenden gulden en is q het aantal per dag geproduceerde wekkerradio's in honderdtallen. De formule geldt voor
0 <(met = teken eronder) q < (met = teken eronder ) 8
a) schets de grafiek ( hoeft niet )
B) hoeveel zijn de gemiddelde kosten per wekkerradio bij een productie van 150 wekkerradio's
c) maak een tabel met differentiequotiënten op [0,a] met a = 1, 2, 4, 5, 6, 7, en 8. WElke betekenis hebben deze differentiequotiënten?
Met de formule GK = 10k/q ( onder elkaar) bereken je de gemiddelste kosten GK per wekkerradio
d) licht deze formule toe
e) .
f) bij welke productie zijn de gemiddelde kosten per wekkerradio minimaal?
Hoeveel zijn deze gemiddelde kosten dan?
En hoeveel de totale kosten?
quote:Per serie achtereenvolgende meetresultaten moet je kijken wat de exponentiële afname is. Exponentieel wil zeggen: steeds met een constante factor. Bij de eerste 2 zal ik het voordoen, de rest kun je dan waarschijnlijk zelf.Jaar | 1975 | 1978 | 1980 | 1984 | 1989 | 1990 | 1992 | 1993 | 1996 | 1997 | 1998
N |15000|11700| 9900 | 7100 | 4700 | 4300 | 3600 | 3500| 3000 | 2800 | 2500
a) -
b) tot welk jaar is er sprake van exponentiële afnamen? geef voor deze periode de formule van N als functie van t. neem t in jaren en t = 0 in 1975. Rond de groeifactor af op 2 decimalen.
15000 -> 11700 in 3 jaar.
15000 in jaar 1975, 15000*factor in jaar 1976, (15000*factor)*factor in jaar 1977, (15000*factor²)*factor in jaar 1978. Ofwel:
15000 * factor³ = 117000
factor = (117000/15000)^1/3
quote:a. De drie grootste merken hebben samen een marktaandeel van 34%. 20 moeten daartoe behoren, dus 40 niet. De kans wordt gegeven door 20-boven-60 * (0.34)^20 * (1-0.34)^40. De factor 20-boven-60 zorgt ervoor dat de 20 niet alleen de eerste 20 hoeven te zijn, maar bijvoorbeeld ook de laatste 20, of ergens 10 en later nog eens 10, etc.H5. De binomiale verdeling
53. De drie grootste automerken in nederland zijn opel, volkswagen en Ford. van de auto;s in Nederland is 13% van het merk opel , 12 % van het merk wolkswagen en 9% van het merk Ford.
Nummers vier is Renault met 8% en nummer vijf is peugeot met 7 %. Bereken in vier decimlane nauwkeurig de kans dat van 60 willekeurige aangewezen auto's er
a) precies 20 tot de drie grootste merken behoren
b) 14, 15 of 16 van het merk opel of volkswagen zijn
b. Zelfde als bij a; de kans voor 14, 15 en 16 optellen
54 gaat bijna hetzelfde als 53, maar dan met een dobbelsteen. De kans op 'meer dan twee keer 6 ogen' is 1-[kans minder dan 3 keer 6 ogen].
quote:Gemiddelde kosten zijn totale kosten gedeeld door het aantal stuks. Pas op dat je bij de formule in honderdtallen in moet vullen.62. De dagelijkse kosten bij de productie van een wekkerradio zijn gegeven door de formule K = 1,2q³ - 8q² + 25q + 22. Hierin is K in duizenden gulden en is q het aantal per dag geproduceerde wekkerradio's in honderdtallen. De formule geldt voor
0 <(met = teken eronder) q < (met = teken eronder ) 8
B) hoeveel zijn de gemiddelde kosten per wekkerradio bij een productie van 150 wekkerradio's
c) maak een tabel met differentiequotiënten op [0,a] met a = 1, 2, 4, 5, 6, 7, en 8. WElke betekenis hebben deze differentiequotiënten?
Het differentiequotient op [0,a] wordt gegeven door (f(a)-f(0))/(a-0). Wat dat betekent kun je, met het oog op a, zelf bedenken.
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t =
sSx(t)= 30 x t.
Hoe vind je t?
(-sin(x)+2cos(x)) en (sin(x)+2cos(x))
beiden positief zijn ?
quote:offtopic: Ik was lekker eerstOp dinsdag 17 januari 2006 15:45 schreef doepta het volgende:
Hoi mensen,
Ik heb hier een hele rare opgave voor me:
Elk getal van drie cijfers kun je achterstevoren opschrijven. 176 kun je omdraaien tot 671.
Bepaal alle getallen van drie cijfers die gelijk zijn aan 3 maal hun omgedraaide plus de som van hun cijfers.
Ik snap vooral de laatste zin niet, hoe schrijf je die om tot een formule? En wat moet je dan verder doen?
(Als dit het verkeerde forum/topic ik, hoor ik het graag).
Groeten,
Doepta
Even met de computer bepaald:
000
441
882
quote:Je rekent eerst met y(t) = 1/2 g t^2 eerst de tijd uit hoelang die bal 'onderweg' is. y(t0 = natuurlijk 1 m. Het maakt namelijk niet uit (zonder wrijving iig) of je de bal horizontaal wegschiet of gewoon laat vallen: beide ballen zullen tegelijk aankomen.Op dinsdag 17 januari 2006 13:12 schreef Koewam het volgende:
Een bal wordt met 33 m/s op 1m hoogte weggeslagen. Bereken de horizontaal afgelegde afstand als de bal de grond raakt.
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t =
Sx(t)= 30 x t.
Hoe vind je t?
Dan vul je in x(t) = v*t de horizontale afstand uit (v = 33 m/s).
Als het goed is moet x iets lager liggen dan 15 m.
20 - 1,282 * (wortel uit 20 * 80/200) - 50/200 = ...
Hoe de f*ck tik je dat goed op je rekenmachien in?!
Het antwoord moet zijn 16,12, maar ik krijg er van alles uit, behalve dat
quote:je bent er bijnaOp dinsdag 17 januari 2006 13:12 schreef Koewam het volgende:
Een bal wordt met 33 m/s op 1m hoogte weggeslagen. Bereken de horizontaal afgelegde afstand als de bal de grond raakt.
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t =
Sx(t)= 30 x t.
Hoe vind je t?
t kan je toch gewoon oplossen uit de vergelijking?Sy(t)= 1/2 * g * t 2 = 1
Dus t = Sqrt(2/g)
En dan invullen in die andere vergelijking:
Sx(t)= v * t = 33 * Sqrt(2/g) = 14.9 (afgerond)
quote:Kan je mij ook niet even helpen
Waarom komt er geen 16,12 uit? Zie boven
quote:Wat voor rekenmachine gebruik je? Als je een grafische rekenmachine gebruikt, is het heel simpel 20 - 1,282 * <<wortelteken>>(20*80/200) - 50/200. Datgene waar je dan de wortel van trekt, moet tussen haakjes staan, want anders trekt hij alleen de wortel van 20.Op woensdag 18 januari 2006 02:18 schreef sweetgirly het volgende:
Ok, even een (stom en wrs) makkelijk vraagje.
20 - 1,282 * (wortel uit 20 * 80/200) - 50/200 = ...
Hoe de f*ck tik je dat goed op je rekenmachien in?!
Het antwoord moet zijn 16,12, maar ik krijg er van alles uit, behalve dat
Als je een wat simpeler rekenmachine hebt, reken je eerst uit waar je wortel van trekt (20 * 80 /200 dus), daar trek je vervolgens de wortel van, daarna doe je dat keer -1,282 (vergeet dat minteken niet!) en vervolgens tel je daar 20 bij op en trek je er weer 50/200 van af.
quote:Thanx!Op woensdag 18 januari 2006 02:55 schreef Lathund het volgende:
Wat voor rekenmachine gebruik je? Als je een grafische rekenmachine gebruikt, is het heel simpel 20 - 1,282 * <<wortelteken>>(20*80/200) - 50/200. Datgene waar je dan de wortel van trekt, moet tussen haakjes staan, want anders trekt hij alleen de wortel van 20.
Als je een wat simpeler rekenmachine hebt, reken je eerst uit waar je wortel van trekt (20 * 80 /200 dus), daar trek je vervolgens de wortel van, daarna doe je dat keer -1,282 (vergeet dat minteken niet!) en vervolgens tel je daar 20 bij op en trek je er weer 50/200 van af.
Het is (eindelijk) gelukt, werd er helemaal tureluurs van. Kreeg er elke keer wat anders uit.
Heb je 1e vb geprobeerd (2e lukte ook niet) en die deed het! Na de 1e * een wortel, dan haakje openen, die hele vermenigvuldiging, haakje sluiten, (weer?!) wortel (gedaan, anders lukte het niet) en toen nog dat 50/200. En eindelijk kwam er 16,12 uit.
Wel vreemd dat er bij mij (eerst) van alles uitkwam, ook 16,34, terwijl ik me toch combi's heb gebruikt. Heb een casio fx-82SX fraction btw. En had hem al gemoded 0 enzo.
Nogmaals thanx
Ik moet van de volgende matrix de eigenwaardes berekenen:
[ -2 ,0 ,24 ]
[ 0 ,30 ,0 ]
[ 24 ,0 ,12]
Het probleem is niet dat ik niet weet hoe je eigenwaardes berekent ( elementen op diagonaal - lambda en vervolgens determinant berekenen). Het lukt me echter niet om de derdegraad polynoom op te lossen:
-18000 + 300 L + 40 L^2 - L^3 = 0 ( L is hierbij Lambda)
Ik weet dat eigenwaardes -20, 30 en 30 moeten zijn...kan iemand mij helpen???
Alvast bedankt!
quote:Ik volg je even niet. Je beweert eerst niet te weten wat de oplossingen van je derdegraads polynoom zijn en op de volgende regel zet je de oplossingen, waarvan je beweert dat je ze niet kent, neer.Op woensdag 18 januari 2006 14:00 schreef _Nick_ het volgende:
Hey,
Ik moet van de volgende matrix de eigenwaardes berekenen:
[ -2 ,0 ,24 ]
[ 0 ,30 ,0 ]
[ 24 ,0 ,12]
Het probleem is niet dat ik niet weet hoe je eigenwaardes berekent ( elementen op diagonaal - lambda en vervolgens determinant berekenen). Het lukt me echter niet om de derdegraad polynoom op te lossen:
-18000 + 300 L + 40 L^2 - L^3 = 0 ( L is hierbij Lambda)
Ik weet dat eigenwaardes -20, 30 en 30 moeten zijn...kan iemand mij helpen???
Alvast bedankt!
quote:Oops ja...beetje onduidelijk inderdaad...Op woensdag 18 januari 2006 14:17 schreef thabit het volgende:
[..]
Ik volg je even niet. Je beweert eerst niet te weten wat de oplossingen van je derdegraads polynoom zijn en op de volgende regel zet je de oplossingen, waarvan je beweert dat je ze niet kent, neer.
Ik heb de eigenwaardes gevonden met MatLab, maar ik weet niet hoe ik ze handmatig moet berekenen en dat ik juist wat ik wil...
quote:Ik zou beginnen met L=10x substitueren, en dan te delen door 10^3. Coefficienten blijven dan geheel en de kopcoefficient is 1. Voordeel is dat ze nu een stuk kleiner zijn. Vanwege Gauss' lemma zijn alle rationale oplossingen geheel. Gehele nulpunten moeten bovendien delers zijn van de constante term, die kun je dus vinden door uit te proberen. Zijn er geen gehele nulpunten, dan moet je meestal Cardano gebruiken, maar in dat geval kun je beter de vergelijking laten staan dan de oplossingen opschrijven.Op woensdag 18 januari 2006 14:27 schreef _Nick_ het volgende:
[..]
Oops ja...beetje onduidelijk inderdaad...
Ik heb de eigenwaardes gevonden met MatLab, maar ik weet niet hoe ik ze handmatig moet berekenen en dat ik juist wat ik wil...
.quote:Was gewoon 1/4,9 en dan de rest invullen.Op woensdag 18 januari 2006 02:22 schreef Bioman_1 het volgende:
[..]
je bent er bijna
Sy(t)= 1/2 * g * t 2 = 1
Dus t = Sqrt(2/g)
En dan invullen in die andere vergelijking:
Sx(t)= v * t = 33 * Sqrt(2/g) = 14.9 (afgerond)
quote:Ehm, makkelijkste lijkt me om de matrix gewoon de volgende te maken:Op woensdag 18 januari 2006 14:00 schreef _Nick_ het volgende:
Hey,
Ik moet van de volgende matrix de eigenwaardes berekenen:
[ -2 ,0 ,24 ]
[ 0 ,30 ,0 ]
[ 24 ,0 ,12]
Het probleem is niet dat ik niet weet hoe je eigenwaardes berekent ( elementen op diagonaal - lambda en vervolgens determinant berekenen). Het lukt me echter niet om de derdegraad polynoom op te lossen:
-18000 + 300 L + 40 L^2 - L^3 = 0 ( L is hierbij Lambda)
Ik weet dat eigenwaardes -20, 30 en 30 moeten zijn...kan iemand mij helpen???
Alvast bedankt!
[ 30 ,0 ,0 ]
[ 0 ,-2 ,24 ]
[ 0 ,24 ,12]
Dan valt meteen te zien dat 30 een eigenwaarde is (van [1,0,0] :p), en je houdt een matrix van 2x2 over die goed op te lossen is..
Wat is x en hoe reken je dat uit
log x(x+2) = log 35
x(x+2) = 35
x^2 + 2x - 35 = 0
(x-5)(x+7)=0
x=5 of x=-7
Waarbij die laatste oplossing niet kan.
(ff voor de duidelijkheid, S = het integraalteken
)-2
S (7-x)dx
-4
Het boek vult daar gewoon de boven en ondergens in voor de X, wat uiteindelijk de uitkomst 0,5 * 2 * (9+11) = 20 geeft
Maar nu heb ik een andere opgave, ook een bepaalde integraal:
4
S 3x^2dx
1
En daarin doen ze dus eerst de 3x^2 integreren tot x^3 en DAN pas de limieten invullen.
Waarom doen ze dat bij de 2e wel en bij de 1e niet
Het zijn toch allebei bepaalde integralen..xlog 10 = log 10 / log x = 2
log 10 = 2 * log x
log x = 5
quote:Op woensdag 18 januari 2006 21:12 schreef speknek het volgende:
xlog 10 = 2
xlog 10 = log 10 / log x = 2
log 10 = 2 * log xlog x = 5
x=wortel(10).
quote:en wat is X? want als X=5 dan log(10)/ log (5) = 1.4306... maar het moet 2 zijnOp woensdag 18 januari 2006 21:12 schreef speknek het volgende:
xlog 10 = 2
xlog 10 = log 10 / log x = 2
log 10 = 2 * log x
log x = 5
quote:thnx klopt
quote:Kan volgens mij het makkelijkst met behulp van de definitie van de logaritme:Op woensdag 18 januari 2006 21:12 schreef speknek het volgende:
xlog 10 = 2
alog b = c <=> ac=b
x2=10
x = 101/2 = wortel(10)
quote:De eerste functie is lineair. Je kunt de oppervlakte onder de grafiek dan makkelijk bepalen met deltax*gemiddelde functiewaardeEn daarin doen ze dus eerst de 3x^2integrerenprimitiveren tot x^3 en DAN pas de limieten invullen.
Waarom doen ze dat bij de 2e wel en bij de 1e niet Het zijn toch allebei bepaalde integralen..
[ Bericht 32% gewijzigd door GlowMouse op 18-01-2006 22:29:39 (kleine toevoeging) ]
quote:Yikes!
what a mistakeathemakea
.quote:Ow ok thxOp woensdag 18 januari 2006 22:20 schreef GlowMouse het volgende:
De eerste functie is lineair. Je kunt de oppervlakte onder de grafiek dan makkelijk bepalen met deltax*gemiddelde functiewaarde
Verdubbelingstijd = 70 / groeitpercentage
voor groeipercentage tot 10%
Maar waarom moet het 70 zijn? en waarom maar tot 10%?
(1+g/100)^v=2,
dus
v = ln(2)/ln(1+g/100).
Voor kleine g is ln(1+g/100) ongeveer gelijk aan g/100 en ln(2) is ongeveer 0.69. Zo komen ze op
v ~ 0.69/(g/100) ~ 70/g.
Mijn vraag is: Hoe werkt de redeneerregel 'contra'.
Volgens het zeer korte dictaat, dat er verder geen tijd aan besteedt, gaat de redenering zo...
A
.
.
.
!A
.
.
.
B
Okee, dat maakt niet direct sense.
Iemand inzicht over de 'contra' regel?
(En wat heeft dit te maken met de A->B implicatie wat je in de tweede zin zegt? A->B is inderdaad equivalent aan !A v B maar hoe is dat belangrijk voor 'contra'?)
Bedankt voor je hulp!
Als er een contradictie voorkomt in de hypothesen, dan zal het niet uitmaken wat er verder nog wordt afgeleid onder die hypothesen, aangezien die tak van beredenering een soort 'bizarro world' is die nooit 'afgevuurd' zal worden. Die tak zal dus nooit bijdragen aan het bewijzen/afwijzen van je verdere afleiding, dus je mag als conclusie neerzetten wat jou verder goed uitkomt?
Trippy shit...
quote:Je hebt A afgeleid maar je hebt blijkbaar ook ¬A kunnen afleiden. Dit geeft een tegenspraak en uit een tegenspraak mag je alles concluderen. Je kunt inderdaad geen nuttige conclusie trekken uit twee afleidingen die met elkaar in tegenspraak zijn dus je kunt net zo goed een conclusie B concluderen. Maar het verkrijgen van een falsum kan soms best handig zijn in je bewijsvoering hoorOp donderdag 19 januari 2006 19:30 schreef soylent het volgende:
Hmmm, ik denk dat ik een beetje op die contra begin te spacen.
Als er een contradictie voorkomt in de hypothesen, dan zal het niet uitmaken wat er verder nog wordt afgeleid onder die hypothesen, aangezien die tak van beredenering een soort 'bizarro world' is die nooit 'afgevuurd' zal worden. Die tak zal dus nooit bijdragen aan het bewijzen/afwijzen van je verdere afleiding, dus je mag als conclusie neerzetten wat jou verder goed uitkomt?
Trippy shit... [afbeelding]
quote:Ja.Op donderdag 19 januari 2006 19:14 schreef soylent het volgende:
Ik vrees dat dit een iets te korte uitleg is... Bedoel je dat als ik eenmaal een contradictie kan afleiden onder een bepaalde hypothese, dat ik dan alles hieruit kan afleiden?
quote:Vul maar voor A falsum in.En wat heeft dit te maken met de A->B implicatie wat je in de tweede zin zegt? A->B is inderdaad equivalent aan !A v B maar hoe is dat belangrijk voor 'contra'?
.
.De disjunctie introductie.
Dus als je eerst zegt
1. A (ass.)
2. !A (ass.)
3. A \/ B (disjunctie introductie op 1)
4. B (volgt uit 2 en 3)
En dit kun je natuurlijk voor alles doen.
[ Bericht 2% gewijzigd door speknek op 19-01-2006 22:56:13 ]
quote:Maar het ging nu toch gewoon om het concluderen van elke conclusie B uit A en ¬A, de implicatie werd er gewoon bijgehaald om dat uit te leggenOp donderdag 19 januari 2006 20:21 schreef speknek het volgende:
Misschien is dit wat makkelijker (en correcter, want ik weet niet of je zomaar aan A->B komt):
[afbeelding].
De disjunctie introductie.
Dus als je eerst zegt
1. A (ass.)
2. !A (ass.)
3. A \/ B (disjunctie introductie op 1)
4. B (volgt uit 3 en 4)
En dit kun je natuurlijk voor alles doen.
Ook is stap 2 in je bewijs hierboven niet nodig want je kunt gelijk stap 3 doen na 1 (en je gebruikt ass. 2 niet, die je kan gebruiken voor het concluderen van 4 uit 1 en 2). Het is wel correct wat je doet maar toch quote:Hmm nee. Je kunt een disjunctie wel introduceren, maar niet zomaar elimineren (in tegenstelling tot een conjunctie, die je wel kunt elimineren maar niet zomaar introduceren). Uit A \/ B volgt gegeven A niet B. Uit A \/ B gegeven niet A volgt wel B.Op donderdag 19 januari 2006 22:46 schreef fallrite het volgende:
Maar het ging nu toch gewoon om het concluderen van elke conclusie B uit A en ¬A, de implicatie werd er gewoon bijgehaald om dat uit te leggen
quote:OwhOp donderdag 19 januari 2006 22:52 schreef speknek het volgende:
[..]
Hmm nee. Je kunt een disjunctie wel introduceren, maar niet zomaar elimineren (in tegenstelling tot een conjunctie, die je wel kunt elimineren maar niet zomaar introduceren). Uit A \/ B volgt gegeven A niet B. Uit A \/ B gegeven niet A volgt wel B.
Ik ken de regels nog niet helemaal maja, ik mag nu nog fouten maken 
.(ik zag trouwens wel dat ik per ongeluk bij 4 (volgt uit 3 en 4) in plaats van (volgt uit 2 en 3) had geschreven, dat kan ook voor onduidelijkheid hebben gezorgd)
[ Bericht 9% gewijzigd door speknek op 19-01-2006 23:35:03 ]
quote:Als je een functie primitiveert, hoor je altijd eerst de primitieve uit te rekenen en daarna pas de grenzen in te vullen, anders gaat het fout. Lineaire functies zijn wat dat betreft een beetje een uitzondering, daar kun je ook met logisch nadenken een heel eind komen.Op woensdag 18 januari 2006 21:07 schreef bierglas het volgende:
tekst
Reken die lineaire integraal maar eens 'netjes' uit, dan zul je zien dat je ook op -20 uitkomt.
Om de respons op een enquete te vergroten, zijn 10 bonnen uitgeloofd en verloot onder 286 jongeren die de vragenlijst ingevuld hebben ingeleverd. Ieder van die jongeren kan hoogtens 1 bon winnen.
Hoe groot is de kans dat zich 4 vrouwen bevinden onder de 10 winnaars?
Antwoord is : ??
----------------------------------
ik kom er niet uit..
quote:Met de onder tafel geveegde aanname dat man/vrouw 50/50 is zeker?Op vrijdag 20 januari 2006 20:17 schreef Triple_T het volgende:
k kom niet uit deze opgave...Please somebody help.
Om de respons op een enquete te vergroten, zijn 10 bonnen uitgeloofd en verloot onder 286 jongeren die de vragenlijst ingevuld hebben ingeleverd. Ieder van die jongeren kan hoogtens 1 bon winnen.
Hoe groot is de kans dat zich 4 vrouwen bevinden onder de 10 winnaars?
Antwoord is : ??
----------------------------------
ik kom er niet uit..
Ik zou het niet (meer) weten, wel ooit gehad die kansrekening
quote:Ik bedoel gewoon dat de verdeling van man/vrouw onder de 286 jongeren gewoon 50% man, 50% vrouw isOp vrijdag 20 januari 2006 20:37 schreef Triple_T het volgende:
ik denk dat ik 1 cijfer mis.. en dat hij daarom niet uitkomt. 50/50 werkt niet:S
Volgens mij zijn er wel genoeg getallen alleen weet ik gewoon niet welke manier van kansrekenen je zou moeten gebruiken hier quote:Is alweer tijdje geleden, maar volgens mij moet je gebruik maken van de binomiale verdeling. Met rekenmachine binompdf() of binomium van newton gebruiken. Het feit dat er 286 deelnemers zijn is niet van belang, er van uitgaande dat het geslacht geen invloed heeft op de winkans.Op vrijdag 20 januari 2006 20:17 schreef Triple_T het volgende:
k kom niet uit deze opgave...Please somebody help.
Om de respons op een enquete te vergroten, zijn 10 bonnen uitgeloofd en verloot onder 286 jongeren die de vragenlijst ingevuld hebben ingeleverd. Ieder van die jongeren kan hoogtens 1 bon winnen.
Hoe groot is de kans dat zich 4 vrouwen bevinden onder de 10 winnaars?
Antwoord is : ??
----------------------------------
ik kom er niet uit..
Gegevens:
kans op vrouw: .5
aantal herhalingen: 10
aantal vrouwen: 4
Daar moet het wel mee lukken
.quote:Nou... dat weet ik niet zo zeker. Je doet nl. 10 pakkingen zónder teruglegging, oftewel: elke keer verandert de verhouding man/vrouw een klein beetje. Hoe groter de groep, hoe minder dit uitmaakt, maar bij 286 zou het nog best eens significant kunnen zijn.Op zaterdag 21 januari 2006 12:54 schreef Oscar_de_Grouch het volgende:
[..]
Het feit dat er 286 deelnemers zijn is niet van belang, er van uitgaande dat het geslacht geen invloed heeft op de winkans.
Ervan uitgaande dat er even veel mannen als vrouwen zijn.
Het antwoord moet zijn 0,1505
Maar hoe komen we daaraan?
(284C6) * (284C4) / (284C10)
Nooit echt goed geweest in die wiskunde A.
quote:Ehm, maar van die groep weet je al niet hoe hij samengesteld is. Lijkt me dat je het op moet vatten als een deel van de grotere groep jongeren (onbekende grootte, dus gokken we op oneindigOp zaterdag 21 januari 2006 21:35 schreef Lathund het volgende:
[..]
Nou... dat weet ik niet zo zeker. Je doet nl. 10 pakkingen zónder teruglegging, oftewel: elke keer verandert de verhouding man/vrouw een klein beetje. Hoe groter de groep, hoe minder dit uitmaakt, maar bij 286 zou het nog best eens significant kunnen zijn.
), en dat je dus gewoon met de gegevens moet werken die Oscar in zijn eerste post noemde.Edit: Nope, komt 0.202/0.207 uit met beide methodes, ik neem aan dat je een gegeven hebt gemist (en waarschijnlijk het aantal vrouwen of zo).
[ Bericht 3% gewijzigd door Sherkaner op 22-01-2006 13:55:16 ]
Dit dan?
Bah wat heb ik een hekel aan combinatoriek.
quote:Volgens mij moet het antwoord toch echt 0.207252 zijn.Op zondag 22 januari 2006 11:46 schreef Triple_T het volgende:
Deze opgave is zoiezo hypergeometrisch.. met de reden wat lathund zegt.
Het antwoord moet zijn 0,1505
Maar hoe komen we daaraan?
Zie ook
quote:En daar komt 0.205078 uit...Op zondag 22 januari 2006 15:15 schreef Oscar_de_Grouch het volgende:
(10 C 4) * (.5)4 * (.5)6
Dit dan?
Bah wat heb ik een hekel aan combinatoriek.
"Een wortel als sqrt(ax2+bx+c) kan door verschuiving (substitueer u=x-b/2a) altijd worden teruggebracht tot één van de types sqrt(x2-1), sqrt(x2+1), sqrt(1-x2)."
Ik zie dit eigenlijk zo niet werken... c wordt niet eens genoemd in die substitutie. Wat is hier nu precies de truc?
Ik zit bijles te geven in wiskunde, maar helaas staat statistiek op het programma en laat ik daar nu zo weinig aanleg voor hebben, dat ik alles helemaal vergeten ben (zit niet meer op de middelbare school he...
)Mijn bijleskindje heeft morgen proefwerk en ze zou het wel heel fijn vinden als ze de antwoorden wist op de volgende twee vragen (ik kom er niet uit
)1. Er wordt gegooid met dobbelstenen. Bij elke worp wordt gekeken naar de dobbelsteen met de meeste ogen en dat getal wordt genoteerd. Bij de worp (3,1) wordt de uitkomst 3 genoteerd.
> Beredeneer dat het aantal verschillende worpen met drie dobbelstenen waarbij 5 het grootste aantal ogen is, gelijk is aan 61.
2. Een vlag is samengesteld uit vijf banen. Stel dat er gekozen mag worden uit rood, wit, blauw en groen. Een kleur mag meer dan 1 keer voorkomen, maar twee aangrenzende banen mogen niet van dezelfde kleur zijn. Hoeveel verschillende vlaggen zijn er mogelijk?
Thanks alvast, namens ons allebei!
quote:Stel, de eerste dobbelsteen valt op 5, dan maakt het niet meer uit waar de andere 2 op vallen, dus die hebben 5 * 5 mogelijkheden (beiden de getallen 1 t/m 5). Dus 25 mogelijkheden.Op zondag 22 januari 2006 20:06 schreef Mr.Trelawney het volgende:
1. Er wordt gegooid met dobbelstenen. Bij elke worp wordt gekeken naar de dobbelsteen met de meeste ogen en dat getal wordt genoteerd. Bij de worp (3,1) wordt de uitkomst 3 genoteerd.
> Beredeneer dat het aantal verschillende worpen met drie dobbelstenen waarbij 5 het grootste aantal ogen is, gelijk is aan 61.
Stel, de eerste dobbelsteen valt op 4, als dan de tweede op 5 valt, maakt het niet meer uit wat de volgende is (in dat geval dus 5 mogelijkheden). stel, de tweede dobbelsteen valt NIET op 5 (dus op een van de getallen 1 t/m 4) dan moet de volgende een 5 zijn (4 mogelijkheden dus). Dat wordt dus een totaal van 5+4=9 mogelijkheden.
Ditzelfde geldt in de gevallen dat de eerste dobbelsteen op 3, 2 of 1 valt, dus het totaal is:
25+9+9+9+9=61 mogelijkheden.
Ik hoop dat m'n uitleg een beetje duidelijk is.
quote:Laten we de kleuren nummeren:Op zondag 22 januari 2006 20:06 schreef Mr.Trelawney het volgende:
2. Een vlag is samengesteld uit vijf banen. Stel dat er gekozen mag worden uit rood, wit, blauw en groen. Een kleur mag meer dan 1 keer voorkomen, maar twee aangrenzende banen mogen niet van dezelfde kleur zijn. Hoeveel verschillende vlaggen zijn er mogelijk?
rood =1
wit = 2
blauw = 3
groen = 4
Stel dat je de eerste baan begint met 1.
Dan mag de tweede baan geen 1 meer zijn, dus hier 3 keuzes.
De derde baan mag dan niet de keuze van de tweede baan zijn, dus hier ook 3 keuzes.
Idem voor vierde en vijfde baan.
Dus een totaal als de eerste baan begint met kleur 1: van 3^4 = 81 mogelijkheden.
Maar zelfs hier komen al dubbelen in voor. (Teken om het te zien een soort "boom" met de mogelijkheden (een aparte "boom" voor elke beginkleur), dat maakt het veel duidelijker. Begin bovenin met 1, dan splitsen in 2,3,4 en dan die weer splitsen enz.)
De kolom die begint met 1 en dan gaat naar 2 en verder is uniek. Maar de kolom die begint met 1 en gaat naar 3 bevat al dubbelen uit de 'vorige', namelijk degene die eindigt met 2,1 (het omgekeerde van de vorige kolom 1,2).
Dit komt hier 2x in voor.
Dan de laatste kolom in deze boom die begint met 1, de kolom 1,4 enz. Ook hier komen dubbelen in, namelijk degenen die eindigen op 2,1 en 3,1. Dit zijn er in totaal 4 (teken het voor jezelf even uit).
Dus het totaal aantal dubbelen uit de boom die begint met 1, is dan gelijk aan 2+4=6.
Het aantal mogelijkheden dat begint met kleur 1 is dan gelijk aan: 81-6=75.
Stel dat de eerste baan begint met 2.
Dan gelden daarna weer dezelfde voorwaarden voor de volgende banen.
MAAR als de laatste baan eindigt op kleur 1, dan komt hij ook voor in de mogelijkheden die beginnen met kleur 1 (dus behoort hij al tot de vorige 81 mogelijkheden). Daardoor zijn er hier nog maar:75 mogelijkheden - 18 keer dat hij op 1 eindigt. (3*3*2). 75-18 = 57.
Stel dat de eerste baan begint met 3.
Dan gelden daana weer dezelfde voorwaarden als al eerder genoemd.
Nu geldt echter dat als de laatste baan eindigt op kleur 1 OF kleur 2, dat hij al eerder is voorgekomen.
Dus: 75 - 18 - 18 = 39 mogelijkheden.
Stel dat de eerste baan begint met 4.
Dan krijg je dus:
75-18-18-18 = 21.
Totaal: 75+57+39+21 = 192 mogelijkheden.
EDIT: Ik had eerst niet overal rekening mee gehouden...
[ Bericht 36% gewijzigd door Lookbehind op 23-01-2006 10:00:08 ]
Antwoord lijkt me gewoon 4*3*3*3*3=324 mogelijkheden (eerste keuze 4 mogelijkheden, 2e keuze 3 mogelijkheden(kleur van de vorige baan mag niet), voor de 3e, 4e en 5e geldt hetzelfde... Ook al komt dit antwoord iets te laat denk ik :p)
quote:Sowieso is dit afhankelijk van de vraagstelling en hoe je die opvat. Ik ging ervan uit dat de vlag in z'n geheel een object was en dat dat dus ook 'om te draaien is', in dat geval is het dus 192.Op maandag 23 januari 2006 14:00 schreef Sherkaner het volgende:
ehm, sinds wanneer is een rood-wit-blauwe vlag gelijk aan een blauw-wit-rode vlag?
Antwoord lijkt me gewoon 4*3*3*3*3=324 mogelijkheden (eerste keuze 4 mogelijkheden, 2e keuze 3 mogelijkheden(kleur van de vorige baan mag niet), voor de 3e, 4e en 5e geldt hetzelfde... Ook al komt dit antwoord iets te laat denk ik :p)
Maar idd, 324 zou dus ook het antwoord kunnen zijn, ligt er, zoals ik al zei, aan hoe je het opvat.
ik heb behoefte aan een beetje hersenstimulatie nu ik (tijdelijk) gestopt ben met school
quote:Voer eerst die substitutie uit, en haal daarna de factor wortel c naar voren. Dan eventueel nog een substitutie doen om tot een van die drie vormen te komen.Op zondag 22 januari 2006 19:13 schreef spinor het volgende:
Het lukt me niet om willekeurige functies waar een wortel van iets kwadratisch in zit te integreren. In mijn dictaat staat het volgende:
"Een wortel als sqrt(ax2+bx+c) kan door verschuiving (substitueer u=x-b/2a) altijd worden teruggebracht tot één van de types sqrt(x2-1), sqrt(x2+1), sqrt(1-x2)."
Ik zie dit eigenlijk zo niet werken... c wordt niet eens genoemd in die substitutie. Wat is hier nu precies de truc?
quote:Ik zie het nu ja. Bedankt!Op maandag 23 januari 2006 17:14 schreef ijsklont het volgende:
[..]
Voer eerst die substitutie uit, en haal daarna de factor wortel c naar voren. Dan eventueel nog een substitutie doen om tot een van die drie vormen te komen.
hienaast zie je een voorbeeld van het zogenaamde eu teken e op een kartonnen verpakking van 1 liter melk
de eu voorschriften over de vulgewichten zijn te vinden in het hoeveelheidsaanduidingen besluit. waaruit je hieronder enkele gedeelten ziet. in artikel 3 van het besluit wordt verwezen naar een toelage die we hier niet printen. in deze bijlage staat te lezen dat de toegelate fout bij 1 liter verpakkingen 15 ml is dit betekent dat hoogstens 2% van de 1 liter verpakkingen minder dan 985 mil magbevatten
:
A in een melkfabriek wordt een vulmachine ingesteld op 1002ml. welke standaard afwijking mag de machine hebben opdat juist aan de bovenstaande eis is voldaan ga er van uit dat de inhoud van de pakken melk normaal verdeeld is
art 1-1 in dit besluit en de daarop bersutende bepaling wordt verstaan onder EU teken
de kleine letter e zoals weergeven in bijlage 1 van het besluit
e-voorverpakkingen een serie voorverpakking waarop het eu-teken in samenhang met aanduiding van de hoeveelheid van een product dat een siervoorverakking deel uitmaakt, wordt gebezigd
art 3 de e-voorverpakking moeten zodanig zijn dag:
a de werkelijke inhoud van de e voorverpakkingen gemiddeld neit kleiner is dan de nominale hoeveelheid daarvan
b het aantal e voorverpakkingen met een fout in minus groter is dan de toegelaten fouten, bepaald in bijlage 2 van het belsuit, zodanig dat, dat bij statistische controle het toelatbare aantal ondeugelijke e voorve3rpakking niet wordt overstreden en
c geen enkele van die e-voorverpakkingen een fout in de minus heeft, die groter is dan tweemaal de toegelaten fout onder b bedoeld
OPgave B
Onderzoek of met de in vraag a vermelde instelling ook aan de eis van artikel 3c is voldaan. Vat de eis 'geen enkele' op als 'minder dan een promile'
ik snap er dus niks van als jullie zo aardig wouden zijn om uitleg te geven zou ik jullie dankbaar zijn. ik heb namelijk morgen school examen er over
.antwoorden zijn
A= SD = 8.3ml
B= aan de eis wordt kenelijk voldaan
ik snap alleen niet hoe ze er bij komen
Dat lukt je voor zover ik weet alleen met een GR (zie uitleg voor de TI type D).
Bij B wordt de kans gevraagd dat er nooit minder dan het gemiddelde minus tweemaal 15mL in een verpakking terechtkomt. De kans daarop is:
P(X<=(1002-2*15) | NV; μ=1002 σ=8,3) = normalcdf(0,972,1002,8.3) = 1.5*10-4
Omdat het om een normale verdeling gaat, kun je in het wiskundig model niet uitsluiten dat er pakken met een negatieve hoeveelheid worden gevuld (de kans daarop is alleen erg klein). Bij opgave B snap ik dan ook niet hoe aan de eis voldaan kan worden.
quote:ik heb dit nu ook...Op dinsdag 24 januari 2006 21:21 schreef CrookedEye het volgende:
-knip-
ze zeggen
" hoogstens 2% van de 1 liter verpakkingen minder dan 985 mil magbevatten "
standaart is 1002 lijkt me
vegelijking
normalcdf(985,1002,1002,x) = 0,48 (dus de oppervlakte vanaf 985 (2%) tot 1002 (50%) met u=1002 en standaard afwijking x moet gelijk zijn aan 48%)
plot op je GR
y1 = normalcdf(985,1002,1002,x)
y2 = 0,48
CALC>INTERSECT--> x=8,277 dus ong 8,3
Ik hoop dat het je helpt
quote:ik snap alleen niet hoe je het in je rekenmachine stopt dat is me probleem ik heb een casio als je daar iets mee opschietOp dinsdag 24 januari 2006 21:57 schreef Agiath het volgende:
[..]
ik heb dit nu ook...
ze zeggen
" hoogstens 2% van de 1 liter verpakkingen minder dan 985 mil magbevatten "
standaart is 1002 lijkt me
vegelijking
normalcdf(985,1002,1002,x) = 0,48 (dus de oppervlakte vanaf 985 (2%) tot 1002 (50%) met u=1002 en standaard afwijking x moet gelijk zijn aan 48%)
plot op je GR
y1 = normalcdf(985,1002,1002,x)
y2 = 0,48
CALC>INTERSECT--> x=8,277 dus ong 8,3
Ik hoop dat het je helpt
http://www.student.ru.nl/wouterbekkers/rest/cirkel.jpg
Men neme een willekeurig punt op een bol, en vanuit dat punt trek je een omtrek.
In het plaatje dat ik even gemaakt heb voor het gemak een bol met diameter 10. Het punt wat je op de cirkel pakt, ligt op een hoogte 'x' van de top. (bv 1,25)
Als je deze rode lijn, nu denkbeeldig om de bol heen trek, hoe kun je de precieze omtrek van deze rode lijn dan berekenen?
bedankt in iedergeval quote:Die omtrek is een cirkel en met wat meetkunde kan je daar de straal van bepalen.Op woensdag 25 januari 2006 17:12 schreef WooZ het volgende:
Even een wiskundig vraagje waar we hier niet helemaal uitkwamen
http://www.student.ru.nl/wouterbekkers/rest/cirkel.jpg
Men neme een willekeurig punt op een bol, en vanuit dat punt trek je een omtrek.
In het plaatje dat ik even gemaakt heb voor het gemak een bol met diameter 10. Het punt wat je op de cirkel pakt, ligt op een hoogte 'x' van de top. (bv 1,25)
Als je deze rode lijn, nu denkbeeldig om de bol heen trek, hoe kun je de precieze omtrek van deze rode lijn dan berekenen?
quote:Ja je kunt het idd gewoon uittekenen, dan kan je de straal van de cirkel meten en zodoende makkelijk de omtrek van die cirkel berekenen, maar is er niet een manier om het te berekenen zonder het uit te tekenen?Op woensdag 25 januari 2006 17:29 schreef Wackyduck het volgende:
[..]
Die omtrek is een cirkel en met wat meetkunde kan je daar de straal van bepalen.
binomcdf is de binomiale kans op bijvoorbeeld 6 of minder keer kop na 10x gooien
binompdf is de binomiale kans op bijvoorbeeld precies 6 keer kop na 10x gooien.
[ Bericht 4% gewijzigd door fallrite op 25-01-2006 19:02:42 ]
quote:Met mijn simpele 6V-logica denk ik dat je alleen pythagoras en 2 pi r nodig hebt hoor.Op woensdag 25 januari 2006 17:12 schreef WooZ het volgende:
Even een wiskundig vraagje waar we hier niet helemaal uitkwamen
http://www.student.ru.nl/wouterbekkers/rest/cirkel.jpg
Men neme een willekeurig punt op een bol, en vanuit dat punt trek je een omtrek.
In het plaatje dat ik even gemaakt heb voor het gemak een bol met diameter 10. Het punt wat je op de cirkel pakt, ligt op een hoogte 'x' van de top. (bv 1,25)
Als je deze rode lijn, nu denkbeeldig om de bol heen trek, hoe kun je de precieze omtrek van deze rode lijn dan berekenen?
En wel over zijn reeksen in een willekeurig punt.
In mijn boek staat hetvolgende:
De Taylorreeks van de functie f(x) in het punt x=a is gelijk aan:
f(x)=veeltermblabla= f(k)(a)/k! * (x-a)k
Maar als je het mij vraagt komt daar gewoon 0 uit, want x-a = 0 en iets *0 is 0
Wat zie ik over het hoofd?
In het boek lijken ze gewoon *(x-a)k te verwaarlozen... om het er aan het eind weer achter te plakken
Bijv: f(x)=1/x. in het punt x = 1
f(x) = x^-1 dus a0= f(1)/0! = 1/1 = 1
f'(x) = (-1)x^-2 dus a1= f'(1)/1! = -1/1 = -1
etc etc etc
en dan komen ze op het eind met: de reeks f(x)=1/x="sigma k=0 ->inf."(-1)^k * (x-1)^k
maar die hele (x-1)^k zie je in die hele berekening nergens terug... en ik dacht toch echt dat x=1
en dus zou er weer 0 uit komen... Maar in principe heeft die hele berekening geen nut, want die reeks geldt dus voor x=a=1
en nu maken ze x weer vriabel ik nie begrijp nie
[ Bericht 11% gewijzigd door MewBie op 25-01-2006 19:21:22 ]
De blauw gekleurde hoeken zijn gelijk. Als je even rekent met tangens dingen kom je er op uit dat de rode cirkel een straal van 3,75 heeft.
Aan de hand van de straal kan je dan de omtrek berekenen.
Ik geloof het nog niet
quote:Mooi, dat voldoetOp woensdag 25 januari 2006 18:51 schreef -J-D- het volgende:
Muntje opgooien.
binomcdf is de binomiale kans op bijvoorbeeld 6 of minder keer kop na 10x gooien
binompdf is de binomiale kans op bijvoorbeeld precies 6 keer kop na 10x gooien.
Ik heb nog een andere vraag.
Ik heb twee populatievoorspellings- of Lesliematrixen die ik wil vermenigvuldigen dit om een oude situatie te berekenen. De matrixen zijn in orde maar ik weet niet hoe ik de som op de GR in moet tikken. Het ging als het goed is ongeveer zo
[A]^-1x[B]
Iemand die dit snapt en uit kan leggen?
quote:Hmm... ja. Daar zeg je wat.Op woensdag 25 januari 2006 19:07 schreef -J-D- het volgende:
HuHu ben reuze benieuwd hoe je dat dan wil berekenen
Ik geloof het nog niet
Het antwoord 3,75 klopt in ieder geval wel. Als je namelijk op de kruising van rode, groene en zwarte lijnen een cirkel tekent met dat punt als middelpunt en het centrum van de grote cirkel als straal, dan zul je zien dat deze cirkel de uiteinden van de rode lijnen snijd.
Het berekenen met tangens dingen zal waarschijnlijk niet gaan lukken nee. Wellicht kan het bewezen worden met stellingen uit de geometrie (of zoiets ? ) ?
quote:Dit is geen bewijs, hooguit iets om een gevoel te ontkrachten of te bevestigen...Op woensdag 25 januari 2006 19:15 schreef HuHu het volgende:
[..]
Hmm... ja. Daar zeg je wat.
Het antwoord 3,75 klopt in ieder geval wel. Als je namelijk op de kruising van rode, groene en zwarte lijnen een cirkel tekent met dat punt als middelpunt en het centrum van de grote cirkel als straal, dan zul je zien dat deze cirkel de uiteinden van de rode lijnen snijd.
Wiskundigen hebben daar vrij weinig aan
quote:Zonder bewijs is dat dus nog niet zekerOp woensdag 25 januari 2006 19:15 schreef HuHu het volgende:
[..]
Het antwoord 3,75 klopt in ieder geval wel.
Het zou kunnen kloppen quote:We wachten in spanning op QEDOp woensdag 25 januari 2006 19:18 schreef -J-D- het volgende:
[..]
Zonder bewijs is dat dus nog niet zeker
quote:Je kan het wel bewijzen. Door een cirkel te tekenen zie je dat de zwarte lijn van 3,75 even lang is als een rode lijn. Dat is wel degelijk een wiskundig bewijs.Op woensdag 25 januari 2006 19:18 schreef -J-D- het volgende:
[..]
Zonder bewijs is dat dus nog niet zeker
Het middelpunt van de extra cirkel valt precies op de kruising die ik eerder noemde.
quote:Het is onzin. Verklein die 1.25 maar eens. Zodat het rode lijnstuk bijna bovenin ligt. Dan is het horizontale rode lijnstukje heel klein en het lijntje (5-x) (die 3.75 bij jou) heel groot. Dan zijn ze dus niet gelijk.Op woensdag 25 januari 2006 19:24 schreef HuHu het volgende:
[..]
Je kan het wel bewijzen. Door een cirkel te tekenen zie je dat de zwarte lijn van 3,75 even lang is als een rode lijn. Dat is wel degelijk een wiskundig bewijs.
[afbeelding]
Het middelpunt van de extra cirkel valt precies op de kruising die ik eerder noemde.
Een tegenvoorbeeld is voldoende dus
quote:maar stel nu dat x groter isOp woensdag 25 januari 2006 19:24 schreef HuHu het volgende:
[..]
Je kan het wel bewijzen. Door een cirkel te tekenen zie je dat de zwarte lijn van 3,75 even lang is als een rode lijn. Dat is wel degelijk een wiskundig bewijs.
[afbeelding]
Het middelpunt van de extra cirkel valt precies op de kruising die ik eerder noemde.
dan kan het niet meer want 5-x wordt dan kleiner en de staal groter quote:Je hebt gelijk, dan gaat het niet meer op.
Fuck... weer iets wat toevallig goed uitpakt omdat de goede getallen zijn gekozen.
Zelfs dingen overnemen van degene die onder je gepost heeft.
quote:Er stond eerst iets heel anders in die post van jou, terwijl daaronder MewBie al aangaf dat het niet opgaat als x groter wordt.Op woensdag 25 januari 2006 19:31 schreef -J-D- het volgende:
Nee, ik geef mijn uitleg om aan te geven dat je verhaal niet klopt. Daar heb ik geen ander voor nodig
Dan wil ik niet zeggen dat jij daar ook niet zelf op gekomen bent, maar je hebt wel toevallig precies datgene verwoord wat MewBie ook zegt.
quote:Ik hem mijn post in de tussentijd ook nog 2x geedit ofzo hoorOp woensdag 25 januari 2006 19:33 schreef HuHu het volgende:
[..]
Er stond eerst iets heel anders in die post van jou, terwijl daaronder MewBie al aangaf dat het niet opgaat als x groter wordt.
Dan wil ik niet zeggen dat jij daar ook niet zelf op gekomen bent, maar je hebt wel toevallig precies datgene verwoord wat MewBie ook zegt.
zodat de uitleg iets completer was Maar ik heb nog steeds geen antwoord op mijn taylorkwestie
quote:Dat interesseert me geen zak. Mijn verhaal was gebaseerd op mijn eigen plaatje met x en 5-x.Op woensdag 25 januari 2006 19:33 schreef HuHu het volgende:
[..]
Er stond eerst iets heel anders in die post van jou, terwijl daaronder MewBie al aangaf dat het niet opgaat als x groter wordt.
Dan wil ik niet zeggen dat jij daar ook niet zelf op gekomen bent, maar je hebt wel toevallig precies datgene verwoord wat MewBie ook zegt.
Ik pas mn verhaal aan zodat het bij jou plaatje past. Ik ben dus alleen maar jou aan het helpen.
Geloof me, na 7 jaar wiskunde studeren heb ik, met alle respect, voor deze vraag, mn collega-meedenker in dit topic niet nodig.
Het lijkt er een beetje op dat je baalt dat je er naast zat. Waarom houden we het niet gewoon inhoudelijk?
quote:Dat is gewoon iets wat je blijft houden in redelijk snel gaande topics, dat je even iets edit en dat ineens in een paar onderelkaar staande posts ineens hetzelfde staatOp woensdag 25 januari 2006 19:35 schreef -J-D- het volgende:
[..]
Dat interesseert me geen zak. Mijn verhaal was gebaseerd op mijn eigen plaatje met x en 5-x.
Ik pas mn verhaal aan zodat het bij jou plaatje past. Ik ben dus alleen maar jou aan het helpen.
Geloof me, na 7 jaar wiskunde studeren heb ik, met alle respect, voor deze vraag, mn collega-meedenker in dit topic niet nodig.
Het lijkt er een beetje op dat je baalt dat je er naast zat. Waarom houden we het niet gewoon inhoudelijk?
moet je je niet teveel van aantrekken quote:Daar trek ik me ook niets van aan. Ik weet dat dat zo gaat. Alleen HuHu snapt het niet.Op woensdag 25 januari 2006 19:37 schreef MewBie het volgende:
[..]
Dat is gewoon iets wat je blijft houden in redelijk snel gaande topics, dat je even iets edit en dat ineens in een paar onderelkaar staande posts ineens hetzelfde staat
Ik neem dan ook aan dat je dit richting hem bedoelt
quote:Heey gast,Op woensdag 25 januari 2006 19:35 schreef -J-D- het volgende:
[..]
Dat interesseert me geen zak. Mijn verhaal was gebaseerd op mijn eigen plaatje met x en 5-x.
Ik pas mn verhaal aan zodat het bij jou plaatje past. Ik ben dus alleen maar jou aan het helpen.
Geloof me, na 7 jaar wiskunde studeren heb ik, met alle respect, voor deze vraag, mn collega-meedenker in dit topic niet nodig.
Het lijkt er een beetje op dat je baalt dat je er naast zat. Waarom houden we het niet gewoon inhoudelijk?
Ik probeer gewoon tot een antwoord te komen. Het is niet gelukt, dat is jammer voor degene die de vraag stelt. Maar ik denk tenminste wel actief mee, in plaats van met 7 jaar wiskunde studie slechts
smilies te posten en berichten te editten.Post dingen gewoon in 1 keer goed, maar ga niet de gehele strekking van je post wijzigen nadat je op Invoeren hebt geklikt.
quote:OokOp woensdag 25 januari 2006 19:38 schreef -J-D- het volgende:
[..]
Daar trek ik me ook niets van aan. Ik weet dat dat zo gaat. Alleen HuHu snapt het niet.
Ik neem dan ook aan dat je dit richting hem bedoelt
Aangezien jij 7 jaar wiskunde gestudeerd heb, zie jij misschien wat ik bij ome Taylor over het hoofd zie?
Ik heb zo'n beetje de hoop al opgegeven dat ik er ooit zelf achter kom
En dat betekend dat ik in het aankomende tentamen flink mn best moet doen bij het integreren quote:Jij snapt het niet. De strekking van mn post is niet veranderd. Vertel maar wat er geheel anders aan is. Dat zal je niet lukken want dat weet je zelf ook.Op woensdag 25 januari 2006 19:42 schreef HuHu het volgende:
[..]
Heey gast,
Ik probeer gewoon tot een antwoord te komen. Het is niet gelukt, dat is jammer voor degene die de vraag stelt. Maar ik denk tenminste wel actief mee, in plaats van met 7 jaar wiskunde studie slechts
Post dingen gewoon in 1 keer goed, maar ga niet de gehele strekking van je post wijzigen nadat je op Invoeren hebt geklikt.
Ik had het in een keer goed gepost in tegenstelling tot jouw fouten. Ik was alleen zo vriendelijk om het verhaal dusdanig te herschrijven dat jij het zou snappen. Blijkbaar raak ik daarmee een gevoelige snaar.
Het is heel goed van je dat je op zoek bent naar een antwoord, dat doen we allemaal. Maar een beetje klagen en zeiken over het feit dat iemand zn post aanpast ZONDER dat de strekking verandert, is een beetje flauw. Vind je ook niet?
quote:Ehm... Ik denk dat ik je vraag bijna begrijp. Je gebruikt als beginpunt f(1)=f(a) (omdat f(0) niet bestaat ws.), en je wilt de omringende punten f(x) berekenen met een taylorserie..Op woensdag 25 januari 2006 19:04 schreef MewBie het volgende:
Ik heb ff een vraagje over onze wiskundige vriend Taylor
En wel over zijn reeksen in een willekeurig punt.
In mijn boek staat hetvolgende:
De Taylorreeks van de functie f(x) in het punt x=a is gelijk aan:
f(x)=veeltermblabla= f(k)(a)/k! * (x-a)k
Maar als je het mij vraagt komt daar gewoon 0 uit, want x-a = 0 en iets *0 is 0
Wat zie ik over het hoofd?
In het boek lijken ze gewoon *(x-a)k te verwaarlozen... om het er aan het eind weer achter te plakken
Bijv: f(x)=1/x. in het punt x = 1
f(x) = x^-1 dus a0= f(1)/0! = 1/1 = 1
f'(x) = (-1)x^-2 dus a1= f'(1)/1! = -1/1 = -1
etc etc etc
en dan komen ze op het eind met: de reeks f(x)=1/x="sigma k=0 ->inf."(-1)^k * (x-1)^k
maar die hele (x-1)^k zie je in die hele berekening nergens terug... en ik dacht toch echt dat x=1
Maar in principe heeft die hele berekening geen nut, want die reeks geldt dus voor x=a=1
ik nie begrijp nie
Dus x is gewoon een variabele.
met z=x en z_0=a=1.
Boek rekent een paar afgeleides uit, ziet dat dit overeenkomt met n!*(-1)^n/x^n bij x=1, dus de formule wordt: som van n=0 tot oneindig (-1)^n (x-a)^n.
[ Bericht 5% gewijzigd door Sherkaner op 25-01-2006 20:11:03 ]
Met verduidelijking van onderstaand plaatje, zie je dat de omtrek wordt gegeven door 2*pi*wortel(r²-(r-x)²)
Maar om daar een discussie om te hebben, wil je hem voeren? Het liefst via de mail dan. Al lijkt het mij niet echt een iets om een discussie over te voeren.
Al sta ik niet open voor een discussie per mail, want ik vind het een kinderachtig onderwerp (het editten van een post... pfff)
Ik heb het liever inhoudelijk over dat mooie vak wiskunde
) daarom ben ik blij met de mensen die hier anderen helpen quote:Ieder z'n hobby/werk he?Op woensdag 25 januari 2006 20:13 schreef Renesite het volgende:
Vind het vak wat minder (en vooral andere bèta vakken
quote:Bij een Taylorreeks gaat het niet om de waarde f(a), want die heb je al nodig om de Taylorreeks te kunnen maken. Je maakt dan rond het punt x=a een polynoom met variabele x. Als T(x) de Talyorbenadering is, dan is T(a) = f(a) omdat alle termen (x-a)^k met k=/=0 inderdaad 0 worden.Op woensdag 25 januari 2006 19:04 schreef MewBie het volgende:
In mijn boek staat hetvolgende:
De Taylorreeks van de functie f(x) in het punt x=a is gelijk aan:
f(x)=veeltermblabla= f(k)(a)/k! * (x-a)k
Maar als je het mij vraagt komt daar gewoon 0 uit, want x-a = 0 en iets *0 is 0
Wat zie ik over het hoofd?
In het boek lijken ze gewoon *(x-a)k te verwaarlozen... om het er aan het eind weer achter te plakken
Bijv: f(x)=1/x. in het punt x = 1
Een eerste-orde Taylor polynoom is gewoon de linearisering van f(x) in a: L(x) = f(a) + f'(a)*(x-a).Als je dat begrijpt dan moeten de (x-a)^k termen in de Taylor-benadering ook begrijpbaar zijn.
quote:Misschien was ik niet geheel duidelijk...Op woensdag 25 januari 2006 19:58 schreef Sherkaner het volgende:
[..]
Ehm... Ik denk dat ik je vraag bijna begrijp. Je gebruikt als beginpunt f(1)=f(a) (omdat f(0) niet bestaat ws.), en je wilt de omringende punten f(x) berekenen met een taylorserie..
Dus x is gewoon een variabele.
[afbeelding]
met z=x en z_0=a=1.
Boek rekent een paar afgeleides uit, ziet dat dit overeenkomt met n!*(-1)^n/x^n bij x=1, dus de formule wordt: som van n=0 tot oneindig (-1)^n (x-a)^n.
In het boek zeggen ze dat x=a, vervolgens zeggen ze:
f(x) = f(k)(a)/k! * (x-a)k met k van 0 tot oneindig.
In dit stuk spreken ze zichzelf mijn inziens gigantisch tegen en krijg je van mij te horen dat het antwoord 0 is als je het mij vraagt.
Doordat x gelijk is aan a vermenigvuldig je altijd met 0.
Dat snap ik dus al niet, misschien zijn het ongelukkig gekozen letter combinaties in het boek, of het ligt aan mij, ik weet het niet
Vervolgens geven ze een voorbeeld:
We bepalen de Taylorreeks rond x=1 van de functie f(x)=1/x
Om het differentieren wat eenvoudiger te maken schrijven we f(x)=x-1
f(x)=x-1 ==> a0 = f(1<==dat is dus x of a)/0! = 1/1 = 1
f'(x) = (-1)x-2 ==> a1 = f'(1)/1! = -1/1 = -1
etc etc, nog de 2de en 3de afgeleide...
Voor de algemene term geldt:
f(k)(x) = 1/x = 1 - (x-1) + (x-1)2 - (x-1)3 + ... + (-1)k(x-1)k
En hier zit dus mijn probleem, al die afgeleides die je net hebt zitten berekenen gelden voor het punt x=1 en nu gebruiken ze diezelfde afgeleides voor elk punt van de grafiek en dus is x != a. Dus geldt je taylorreeks niet meer want die was voor x = a
quote:Je krijgt dan inderdaad steeds antwoord 0 dat je erbij op moet tellen, op het geval k=0 na. Bij k=0 krijg je de functiewaarde in x, zodat bij x=a de benadering gegeven wordt door g(x) = f(a) + 0 + 0 + 0, iets wat me vrij logisch lijkt. Let dus op dat het niet om één groot product gaat (zodat er inderdaad 0 uit komt), maar om een som van allemaal producten.Op woensdag 25 januari 2006 20:50 schreef MewBie het volgende:
In het boek zeggen ze dat x=a, vervolgens zeggen ze:
f(x) = f(k)(a)/k! * (x-a)k met k van 0 tot oneindig.
In dit stuk spreken ze zichzelf mijn inziens gigantisch tegen en krijg je van mij te horen dat het antwoord 0 is als je het mij vraagt.
quote:Weet je wel hoe de constante en lineaire benadering werken? Ze geven goed weer wat de functie 'doet' rond een bepaald punt, zodat je in de buurt van een punt kunt schatten. Wanneer je de constante benadering van f(x)=x² in 3 bekijkt, die wordt gegeven door h(x)=9, zie je dat hij in de buurt van 3 vrij nauwkeurig is, maar niet zo heel erg. Hoe groter het taylorpolynoom wordt, hoe nauwkeuriger de schatting.Vervolgens geven ze een voorbeeld:
We bepalen de Taylorreeks rond x=1 van de functie f(x)=1/x
Om het differentieren wat eenvoudiger te maken schrijven we f(x)=x-1
f(x)=x-1 ==> a0 = f(1<==dat is dus x of a)/0! = 1/1 = 1
f'(x) = (-1)x-2 ==> a1 = f'(1)/1! = -1/1 = -1
etc etc, nog de 2de en 3de afgeleide...
Voor de algemene term geldt:
f(k)(x) = 1/x = 1 - (x-1) + (x-1)2 - (x-1)3 + ... + (-1)k(x-1)k
En hier zit dus mijn probleem, al die afgeleides die je net hebt zitten berekenen gelden voor het punt x=1 en nu gebruiken ze diezelfde afgeleides voor elk punt van de grafiek en dus is x != a. Dus geldt je taylorreeks niet meer want die was voor x = a
En verdient
) moeten staan? Ik zou er erg blij van worden :$quote:Google, tweede resultaatOp zondag 29 januari 2006 16:37 schreef BierKoning het volgende:
ARGH, zou iemand mij alsjeblieft kunnen vertellen welke variabelen dr achter BinomCDF (en pdf
wat is dan het grootste verschil tussen twee opeenvolgende priemgetallen?
ik hoorde iets over het vermoedne van Peulen.. is die dan al bewezen?
stel het is bewezen..wat kan je er mee nog bewijzen? ...
Er moet toch een grootst verschil bestaan? hoe is dat te bewijzen?
quote:Dat verschil kan willekeurig groot worden. Neem een natuurlijk getal n>=2. Dan zijn alle getallen in de verzameling {n!+2,...,n!+n} samengesteld.Op zondag 29 januari 2006 21:27 schreef teletubbies het volgende:
hoi ik heb een vraagje..
wat is dan het grootste verschil tussen twee opeenvolgende priemgetallen?
ik hoorde iets over het vermoedne van Peulen.. is die dan al bewezen?
stel het is bewezen..wat kan je er mee nog bewijzen? ...
Er moet toch een grootst verschil bestaan? hoe is dat te bewijzen?
quote:Bij pdf gaat het om een precieze kans (ezelsbruggetje: p van precies). Bijvoorbeeld P(X=3).Op zondag 29 januari 2006 16:37 schreef BierKoning het volgende:
ARGH, zou iemand mij alsjeblieft kunnen vertellen welke variabelen dr achter BinomCDF (en pdf
Bij cdf gaat het juist om kleiner of gelijk aan de kans. Bijvoorbeeld P(X<=3)
(<= betekent kleiner of gelijk aan)
Als je P(X<8) hebt, dan moet je die dus ombouwen naar 'kleiner of gelijk aan'. Dan wordt het dus
P(X<=7).
Ik heb hier een tabel met percentages. De percentages in kolommen aangeduid met I t/m IV geven een relatieve waarde over een bepaald optimum aan. Vervolgens wil ik II t/m IV gaan relativeren aan I. Eerst de tabel:
In kolommen "II / I" t/m "IV / I" relativeer ik de waarde van twee items uit dezelfde rij, bijvoorbeeld: (13.30-7.99)/7.99=66.48 uit kolom "II / I" (zitten wat afrondingsverschillen in). Anyway, vervolgens doe ik netjes de som over alle elementen uit kolom "II / I", deel het door 12 en er komt 108.70% uit. Dus, claim ik, algoritme II presteert 108.70% slechter dan algoritme I.
Maar, relativeer ik alleen het gemiddelde, dan komt er wat anders uit: (63.15-45.13)/45.13 = 39.93%. Da's geen 108.70%
Ja, ik weet dat ik 5e jaars Econometrie-student ben en ik over een maand afstudeer. Dit-niet-begrijpen is dus echt een doodzonde en ik me moet doodschamen (vertel het mn afstudeerbegeleider niet!
). Edoch enig licht op de zaak zou ik waarderen quote:Neem bijvoorbeeld een erg kort lijstje, met getallen a, b, c en d:Maar, relativeer ik alleen het gemiddelde, dan komt er wat anders uit: (63.15-45.13)/45.13 = 39.93%. Da's geen 108.70%
a | b | (b-a)/a
c | d | (d-c)/c
Er zou voor gelijkheid moeten gelden dat:
(gemkolom2-gemkolom1)/gemkolom1=gemkolom3.
Dus: (((b+d)-(a+c))/2)/((a+c)/2) = ((b-a)/a + (d-c)/c)/2
Dus: (b+d-(a+c))/(a+c) = (b/a-1 + d/c-1)/2
Dus: (b+d)/(a+c)-1 = (b/a+d/c)/2-2/2
Dus: (b+d)/(a+c) = (b/a+d/c)/2
Dus: (b+d)/(a+c) = (bc+ad)/(2ac)
Dus: 2abc+2acd = abc+a²d+bc²+acd
Dus: abc+acd = a²d+bc²
Het is vrij snel in te zien dat hier niet altijd aan wordt voldaan. Je kunt het ook numeriek bekijken (ik heb expres wat uit elkaar liggende getallen gekozen):
10% | 11% | 10%
100000% | 150000% | 50%
-------------------------------
50005% | 75005,5% | 30%
Aan de hand van de onderste kolom zou je een verschil van bijna 50% verwachten. Relatief grote getallen tellen relatief zwaar mee.
Maar wat is nu de goede interpratie? Ik zou zeggen dat alleen de cijfers in het rood kloppen, maar dat is dus niet zo. Welke conclusie zou jij trekken wanneer je II met III vergelijkt? Ga er even vanuit dat I de 'benchmark' is waartegen ik ze allebei wil afzetten.
We kunnen de temperatuur van het lampje als het op vol vermogen (bij 6,0 (V)) brandt berekenen.
Dit gaat met deze formule
R(T)=R(0)*(1+a*T)
R(0) = De weerstand van het lampje bij 0 graden
a = weerstandstempratuurcoefficient van wolfraam (daarvan is het draadje van het lampje), en dat is 4,9
f) Bereken met de formule de waarde van R(0)
???
Hoe doe je dit? Je zou dan R(T) moeten weten, maar deze is toch ook gewoon R(0)?
De weerstand die we gemeten hebben bij 6,0 (V) op het lampje was trouwens 11,53846154...
Hoe bereken ik nou R(0) ???
quote:De rode waarden lijken me in de meeste gevallen meer zeggen, hoewel dat misschien van de situatie afhangt. Wanneer grote getallen zwaarder meetellen, moet je naar de zwarte waarden kijken.Op maandag 30 januari 2006 21:43 schreef Knakker het volgende:
Welke conclusie zou jij trekken wanneer je II met III vergelijkt? Ga er even vanuit dat I de 'benchmark' is waartegen ik ze allebei wil afzetten.
quote:De weerstand verandert met de temperatuur T. R(T) = R(0) valt daarom af. R(T) heb je gemeten, R(0) wil je weten, a weet je, maar T weet je nog niet. Je hebt dus 1 vergelijking met twee onbekenden, zodat je de oplossing niet exact kunt bepalen. Weet je de temperatuur van het lampje niet?R(T)=R(0)*(1+a*T)
f) Bereken met de formule de waarde van R(0)
Hoe doe je dit? Je zou dan R(T) moeten weten, maar deze is toch ook gewoon R(0)?
De weerstand die we gemeten hebben bij 6,0 (V) op het lampje was trouwens 11,53846154...
Vergeet je trouwens niet overal eenheden erachter te zetten?
[ Bericht 38% gewijzigd door GlowMouse op 30-01-2006 21:58:24 ]
Toon aan met behulp van de wetten van Newton aan dat voor de versnelling van het karretje het volgende verband geldt:
a= g sin (alpha)
a= versnelling
g= valversnelling
alpha is hellingshoek
Het is uit een practicum om een karretje van een helling te laten rijden, wrijvingskracht is verwaarloosbaar.
quote:Fz = m*gToon aan met behulp van de wetten van Newton aan dat voor de versnelling van het karretje het volgende verband geldt:
a= g sin (alpha)
a= versnelling
g= valversnelling
alpha is hellingshoek
De component van de zwaartekracht langs de helling is Fz*sin(alpha)
F=m*a dus a=F/m=m*g*sin(alpha)/m = g*sin(alpha)
quote:mmm... Ja ergens klopt het ook niet echt... We komen op een gegeven moment uit op 1,95...Op maandag 30 januari 2006 21:53 schreef GlowMouse het volgende:
[..]
De rode waarden lijken me in de meeste gevallen meer zeggen, hoewel dat misschien van de situatie afhangt. Wanneer grote getallen zwaarder meetellen, moet je naar de zwarte waarden kijken.
[..]
De weerstand verandert met de temperatuur T. R(T) = R(0) valt daarom af. R(T) heb je gemeten, R(0) wil je weten, a weet je, maar T weet je nog niet. Je hebt dus 1 vergelijking met twee onbekenden, zodat je de oplossing niet exact kunt bepalen. Weet je de temperatuur van het lampje niet?
Vergeet je trouwens niet overal eenheden erachter te zetten?
Alleen dat zou weer betekenen dat de tempratuur bij vol vermogen brandt (6,0 (V) 1,002 is...dat klopt natuurlijk ook niet
quote:schopje, ik moet dezelfde opdracht makenOp maandag 30 januari 2006 21:53 schreef Agiath het volgende:
Vraagje over Natuurkunde
We kunnen de temperatuur van het lampje als het op vol vermogen (bij 6,0 (V)) brandt berekenen.
Dit gaat met deze formule
R(T)=R(0)*(1+a*T)
R(0) = De weerstand van het lampje bij 0 graden
a = weerstandstempratuurcoefficient van wolfraam (daarvan is het draadje van het lampje), en dat is 4,9
f) Bereken met de formule de waarde van R(0)
???
Hoe doe je dit? Je zou dan R(T) moeten weten, maar deze is toch ook gewoon R(0)?
De weerstand die we gemeten hebben bij 6,0 (V) op het lampje was trouwens 11,53846154...
Hoe bereken ik nou R(0) ???
quote:Op deze manier...oke, dank je.Op zondag 29 januari 2006 21:45 schreef thabit het volgende:
[..]
Dat verschil kan willekeurig groot worden. Neem een natuurlijk getal n>=2. Dan zijn alle getallen in de verzameling {n!+2,...,n!+n} samengesteld.
wat is een proper fractional en een improper fractional exponent?
quote:Iets wat niet bestaat. Een improper fraction bestaat wel: dat is bijvoorbeeld dat je 5/2 gaat scrijven als 2 1/2. Heel fout.Op dinsdag 31 januari 2006 10:53 schreef teletubbies het volgende:
[..]
Op deze manier...oke, dank je.
wat is een proper fractional en een improper fractional exponent?
Geef de RV bij het samenvoegen van de volgende stoffen:
- loodnitraatoplossing en zoutzuur
[ Bericht 20% gewijzigd door WyBo op 31-01-2006 18:38:54 ]
quote:Dit had ik een maand geleden gevraagd, toen had Atrabilis een antwoord gegeven. Maar ik vond dat toch wel een moeilijke uitleg.weet iemand hoe differentiaalvergelijkingen precies werken. Dus dmv een kort verhaaltje erover hoe je het kan gebruiken en waarvoor etc, want het is nogal moeilijk om er wat over te vinden. Want ik heb al wat zitten zoeken, we kennen het allemaal van wiskunde maar om zoiets echt tot een verhaal te maken valt niet mee
Kan iemand differentiaalvergelijkingen uitleggen? Ik moet een verslag maken voor een 6vwo-leerling die het zeg maar nog moet leren.
Ik heb vooral moeite met het zoeken naar de geschiedenis ervan. Wie, wat waar etc.
Ik hoop dat iemand me zsm kan helpen.
quote:Differentiaalvergelijkingen zijn vergelijkingen waar afgeleides in voorkomen. DV's komen voort uit problemen uit andere vakgebieden, oorspronkelijk vooral uit de natuurwetenschappen. Dit begon met Newton en is vervolgens steeds meer uitgebreid door verschillende andere wetenschappers.Op dinsdag 31 januari 2006 19:19 schreef obl het volgende:
[..]
Dit had ik een maand geleden gevraagd, toen had Atrabilis een antwoord gegeven. Maar ik vond dat toch wel een moeilijke uitleg.
Kan iemand differentiaalvergelijkingen uitleggen? Ik moet een verslag maken voor een 6vwo-leerling die het zeg maar nog moet leren.
Ik heb vooral moeite met het zoeken naar de geschiedenis ervan. Wie, wat waar etc.
Ik hoop dat iemand me zsm kan helpen.
Een hele basale DV met beginwaarde is:
dy/dx = y
y(0) = 1
Met als oplossing y(x) = ex
int sin(Ax) sin(Bx) dx
Zit hier een beetje vast...
quote:Of via e-machten, of schijf de uitdrukking via goniometrische formules om in een makkelijk te integreren uitdrukking. Misschien werkt herhaald partieel integreren ook, maar dat zou niet mijn keuze zijn.Op dinsdag 31 januari 2006 20:34 schreef Bioman_1 het volgende:
Even een snel vraagje over een integraal die ik niet kan oplossen: Hoe bereken je:
int sin(Ax) sin(Bx) dx
Zit hier een beetje vast...
Wat thabit zegt dus.
Dat krijg je ervan als je Mathematica steeds alles laat uitrekenen Maar erg bedankt !
quote:Ik moet wel 5 pagina's vullen, dus heb wel meer nodig dan datOp dinsdag 31 januari 2006 20:19 schreef Wackyduck het volgende:
[..]
Differentiaalvergelijkingen zijn vergelijkingen waar afgeleides in voorkomen. DV's komen voort uit problemen uit andere vakgebieden, oorspronkelijk vooral uit de natuurwetenschappen. Dit begon met Newton en is vervolgens steeds meer uitgebreid door verschillende andere wetenschappers.
Een hele basale DV met beginwaarde is:
dy/dx = y
y(0) = 1
Met als oplossing y(x) = ex
De docent had een voorbeeld gegeven van een theekopje dat afkoelt, hoelang het duurt voordat het een bepaalde temperatuur had bereikt...maar ik zoek nog een voorbeeld in praktijk met uitleg hoe je dat moet oplossen...
quote:Enkele voorbeelden zijn de mathematische slinger en radioactief verval. Het voorbeeld van de slinger is gebaseerd op een tweede afgeleide, zodat de oplossing anders wordt dan bij het kopje en radioactief verval.Op woensdag 1 februari 2006 01:15 schreef obl het volgende:
De docent had een voorbeeld gegeven van een theekopje dat afkoelt, hoelang het duurt voordat het een bepaalde temperatuur had bereikt...maar ik zoek nog een voorbeeld in praktijk met uitleg hoe je dat moet oplossen...
quote:dan zoek je het opOp dinsdag 31 januari 2006 21:25 schreef Bioman_1 het volgende:
wist dat t met een van die gonio-formules kon, maar die zitten er toch nie zo goed in
Maar erg bedankt !
Wat is hier het wiskundig bewijs van?
!quote:ik neem aan dat je bedoelde ( a/b)(a/b) = a²/b² ??Op donderdag 2 februari 2006 15:14 schreef obl het volgende:
( a/b)(a/b) = (a*b)(a*b)
Wat is hier het wiskundig bewijs van?
. Dat is wat hij vroeg..maar stel dat het ( a/b)(a/b) = a²/b² is wat is dan het wiskundig bewijs ervan?
quote:Een bewijs is iets dat uit axioma\'s volgt. Één van de algebraïsche eigenschappen van reële getallen is de commutativiteit (a*b=b*a). Een andere algebraïsche eigenschap is de associativiteit ( (a*b)*c = a*(b*c) ). Verder ken je het eenheidselement (a=a*1) Met die drie eigenschappen kun je aantonen:Op zaterdag 4 februari 2006 12:42 schreef obl het volgende:
maar stel dat het ( a/b)(a/b) = a²/b² is wat is dan het wiskundig bewijs ervan?
(a/b)*(a/b) = ((a*1)/b)*((a*1)/b) = (a*(1/b))*(a*(1/b)) = a*((1/b)*a)*(1/b) = a*(a*(1/b))*(1/b) = (a*a)*((1/b)*(1/b)) = (a*a)*(1/(b*b)) = (a*a*1)/(b*b) = (a*a)/(b*b)
Vervolgens pas je toe dat je x*x noteert als x², en je krijgt a²/b².
ik hoorde dat iemand vandaag 'zondag' uit Zimbabwe een methode gaat uitproberen die hij heeft uitgevonden om de beveiliging via dit systeem te kraken..
ik heb daarna gezocht overal op google News enzo maar ik heb er nix over gevonden..
elliptische krommen worden o.a gebruikt bij gsm's en binnenkort bij stemmen (in verkiezingen)...
het lijkt me wel iets spectaculairs..als het gebeurt..
Ik hoorde hierover van iemand die onderzoek doet over het maken van dit soort 'veilige' krommen voor bijv. kpn. vandaar dat het serieus nam..
Maar hij vermeldde zelf niet waar hij dat heeft gehoord..
Ik herkende lenstra niet... ik dacht al: hij leek veel op zo'n acteur.. hij zat zelfs naast me bij een plenaire lezing, als ik wist dat hij Lenstra was.... had ik me volwassener gedragen . maar goed..
is dit een geschikt boek om Calculus een beetje te beheersen?
http://ocw.mit.edu/ans7870/textbooks/Strang/strangtext.htm
(pre-universiteit niveau)
quote:Je bedoelt of er betere boeken zijn? Want het boek staat helemaal online in PDF formaat dus je zou kunnen kijken of je vindt dat het begrijpelijk uitgelegd wordt.Op zondag 5 februari 2006 19:12 schreef teletubbies het volgende:
een vraagje!
is dit een geschikt boek om Calculus een beetje te beheersen?
http://ocw.mit.edu/ans7870/textbooks/Strang/strangtext.htm
(pre-universiteit niveau)
ik bedoel of het boek een voldoende wiskundeniveau heeft, dus diepgang, moeilijkheidsgraad etc..
het is wel te begrijpen en de toon is persoonlijk..ik vind het prettig om het zo te lezen.
quote:Zo heel toevallig is het ook weer niet. Het ritme om elliptische-krommengeesten op te trommelen verschilt nauwelijks van het trommelritme voor aardbevingsgoden. Onze Zimbabwiaan heeft daarom besloten wat extra trommellessen te nemen alvorens een tweede poging te doen. Het kan dus nog even duren voordat we weer wat van hem horen!Op maandag 6 februari 2006 16:57 schreef teletubbies het volgende:
oh bedankt, wat een toeval.. die aardbeving..!
quote:Nou is het heel lang geleden dat ik kansrekening heb gehad, maar dit kun je naar mijn idee gewoon als een vergelijking schrijven:Op dinsdag 7 februari 2006 11:18 schreef Invictus_ het volgende:
Eigenlijk zoek ik omgekeerd kans berekenen; hoe vaak moet ik met een 20-zijdige dobbelsteen gooien om een reeks te krijgen met een waarschijnlijkheid van 1 op 1*10150? Met een rijtje in excel kan je het wel benaderen (met 116 worpen kom je op 1:8*10150) maar er moet vast wel een makkelijkere oplossing zijn.
P= ( 1/ aantal mogelijkheden )n.
Dus 1/(20n ) = 1/(10150 ), dus 20n=10150.
En zo wordt n dus gelijk aan log20 ( 10150 ).
Ik heb even een snel vraagje, ik heb Wiskunde A
en ik moet een verslag uittypen. Alles goed en wel, maar hoe maak ik een normaalkromme op mijn computer? kan dit met excel? of moet ik hem er bij tekenen met de hand? thnx
quote:De standaardnormaalkromme is 1/wortel(2pi) * e^(-0.5*x²). Met andere mu en sigma ziet de formule er anders uit, maar dat kun je wel nazoekenOp dinsdag 7 februari 2006 16:14 schreef stephanie_xx het volgende:
Ik heb even een snel vraagje, ik heb Wiskunde A
quote:wat bedoel jeOp dinsdag 7 februari 2006 17:21 schreef GlowMouse het volgende:
[..]
De standaardnormaalkromme is 1/wortel(2pi) * e^(-0.5*x²). Met andere mu en sigma ziet de formule er anders uit, maar dat kun je wel nazoeken
ik wil een normaalkromme maken in excel oid, ik hoef geen formules of begrijp ik je verkeerd? ik doe wiskunde A1 hoor
quote:Er zijn genoeg formules die een formule kunnen tekenen in een grafiek. Excel niet geloof ik, maar daar gaat het ook niet in lukken...Op dinsdag 7 februari 2006 19:24 schreef stephanie_xx het volgende:
[..]
wat bedoel je
of begrijp ik je verkeerd? ik doe wiskunde A1 hoor
Tenzij je wat punten kan plotten in excel en daar een best fit lijn doorheen trekt.
Ik heb een TI-83
Het gaat om het gebruik van 1-Var stats (stat-calc-menu)
Zou het moeten gebruiken als hulpmiddel om boxplotten te tekenen en standaardafwijkingen te berekenen.
Maar als ik bij lijst 1 en 2 kloppende getallen invoer, dan komt er niet het goede antwoord uit.
voorbeeld:
Waarnemingsgetal: 12, 13, 14, 15, 16, 17, 18 (dit wordt lijst 1)
Frequentie daarbij: 15, 38, 45, 53, 46, 58, 12 (dit wordt lijst 2)
Dan 1-Vars-Stats
Zou er uit moeten komen:
Min X = 12
Q1 = 14
Med = 15
Q3 = 17
Max X = 18
Op mijn GR is Q1 = 13
(bij andere sommen kloppen er soms meer getallen niet)
Boven dat lijstje van Min X, Q1 etc. staan nog andere dingen die met de standaardafwijking te maken hebben, maar als ik die wil gebruiken klopt dat ook niet.
Iemand een idee waar het aan kan liggen?
quote:Ik denk aan je antwoorden, want als ik het gewoon bereken dan kom ik ook op 14Op woensdag 8 februari 2006 15:14 schreef appelsap het volgende:
Ik heb een probleem met mijn grafische rekenmachine.
Ik heb een TI-83
Het gaat om het gebruik van 1-Var stats (stat-calc-menu)
Zou het moeten gebruiken als hulpmiddel om boxplotten te tekenen en standaardafwijkingen te berekenen.
Maar als ik bij lijst 1 en 2 kloppende getallen invoer, dan komt er niet het goede antwoord uit.
voorbeeld:
Waarnemingsgetal: 12, 13, 14, 15, 16, 17, 18 (dit wordt lijst 1)
Frequentie daarbij: 15, 38, 45, 53, 46, 58, 12 (dit wordt lijst 2)
Dan 1-Vars-Stats
Zou er uit moeten komen:
Min X = 12
Q1 = 14
Med = 15
Q3 = 17
Max X = 18
Op mijn GR is Q1 = 13
(bij andere sommen kloppen er soms meer getallen niet)
Boven dat lijstje van Min X, Q1 etc. staan nog andere dingen die met de standaardafwijking te maken hebben, maar als ik die wil gebruiken klopt dat ook niet.
Iemand een idee waar het aan kan liggen?
quote:Ja als ik het bereken kom ik wel gewoon op 14, maar mijn grafische rekenmachine niet.Op donderdag 9 februari 2006 17:29 schreef _superboer_ het volgende:
[..]
Ik denk aan je antwoorden, want als ik het gewoon bereken dan kom ik ook op 14
Die zegt 13.
Maar het gaat erom dat ik die getallen moet gebruiken bij sommen die op papier uitrekenen veel tijd kosten. Dus het zou fijn zijn als mijn grafische rekenmachine gewoon normaal doet.
maar dat doet die dus niet
normaal gesproken wordt in excel andere methoden gebruikt om medianen of standaarddeviatie uit te rekenen..dat heb ik gelezen:
quote:misscien doet je rekenmachine hetzelfde.Excel berekent kwartielen op afwijkende manier. De methode die zij is geïntroduceerd door door J.Freund en B. Perles . Zij hanteren de volgende definitie:
Q1: kijk naar waarneming (n+3)/4
Q2: kijk naar waarneming (n+1)/2
Q3: kijk naar waarneming (3n+1)/4
quote:Ik heb het voor de lolOp dinsdag 31 januari 2006 20:58 schreef Wackyduck het volgende:
Misschien werkt herhaald partieel integreren ook, maar dat zou niet mijn keuze zijn.
even gedaan en het komt keurig uit.
Differentieer maar, hij klopt volgens mij als een bus
Productregel
quote:Zozo ijverig hoor.Op vrijdag 10 februari 2006 17:51 schreef star_gazer het volgende:
[..]
Ik heb het voor de lol
[afbeelding]
Differentieer maar, hij klopt volgens mij als een bus
u(x,y) = 2 Max(x,y) + Min(x,3y)
Nu moet ik een bepaalde grootheid berekenen die gedefinieerd is als:
M = (du/dx)/(du/dy)
Oftewel, de twee partiele afgeleiden moeten op elkaar gedeeld worden.
MAAR: hoe differentieer je een Max (of Min) functie? Kan me niet herinneren dat ik dat ooit ergens tegengekomen ben.
Heb het met Mathematica geprobeerd, en die geeft een oplossing, naar in een notatie-vorm die ik niet begrijp, dus daar kan ik ook niet zoveel mee
[ Bericht 0% gewijzigd door Bioman_1 op 10-02-2006 21:53:03 (functie aangepast, verkeerd ingetypt) ]
Maar verder dan dat kan'k je niet helpen
ik laat de algebra wel over aan de algebra-freaks
[ Bericht 90% gewijzigd door star_gazer op 10-02-2006 22:01:14 ]
quote:Marginale substitutieverhoudingen?Op vrijdag 10 februari 2006 21:29 schreef Bioman_1 het volgende:
Ik heb een probleem met differentieren. Het gaat om de functie:
u(x,y) = 2 Max(x,y) + Min(x,3y)
Nu moet ik een bepaalde grootheid berekenen die gedefinieerd is als:
M = (du/dx)/(du/dy)
Oftewel, de twee partiele afgeleiden moeten op elkaar gedeeld worden.
MAAR: hoe differentieer je een Max (of Min) functie? Kan me niet herinneren dat ik dat ooit ergens tegengekomen ben.
u(x,y) = 2 Max(x,y) + Min(x,3y) = Max(2x,2y) + Min(x,3y)
Je kunt hier met slim naar kijken niet verder vereenvoudigen. Je moet nu een heleboel situaties onderscheiden, en kijken wat de functie in zo'n situatie zou worden zonder max/min erin. Een situatie die je bijvoorbeeld kan bekijken is x<y, de functie wordt dan u(x,y)=y+x. Merk overigens op dat de partiele afgeleiden niet overal hoeven te bestaan (bijvoorbeeld bij x=y omdat het differentiequotient dan geen limiet heeft; vergelijkbaar met dat abs(x) niet diffbaar is in x=0).
quote:rationaal of irrationaal? nooit van die termen gehoord.Op zaterdag 11 februari 2006 21:32 schreef teletubbies het volgende:
klopt het dat het nog steeds onopgelost is of pi +e rationaal of irrationaal is? Ik wou dat opzoeken op google maar ik vond niet de juiste termen ... ! heeft iemand een link?
quote:Volgens mij is dat inderdaad nog steeds open.Op zaterdag 11 februari 2006 21:32 schreef teletubbies het volgende:
klopt het dat het nog steeds onopgelost is of pi +e rationaal of irrationaal is? Ik wou dat opzoeken op google maar ik vond niet de juiste termen ... ! heeft iemand een link?
http://mathworld.wolfram.com/Pi.html
Hmm, ik realiseer me nu dat ik nog nooit naar het bewijs dat pi transcendent is heb gekeken.
quote:Wie het missende integraaltekentje vindt krijgt van mij een pluimOp vrijdag 10 februari 2006 17:51 schreef star_gazer het volgende:
[..]
Ik heb het voor de lol
[afbeelding]
Differentieer maar, hij klopt volgens mij als een bus
Het antwoord klopt wel, er zit alleen ergens een notatiefoutje.quote:Bij de 2e partiele integratie.Op zondag 12 februari 2006 06:29 schreef star_gazer het volgende:
[..]
Wie het missende integraaltekentje vindt krijgt van mij een pluim
quote:Op zondag 12 februari 2006 14:42 schreef Market_Garden het volgende:
Haai,
Ik ben met een PO voor wiskunde bezig, en nu wil ik een aantal grafieken maken op de computer, die ik dan uit kan printen.
Ik heb geprobeerd om het met Excel voor mekaar te krijgen, maar ik weet niet hoe daar de notatie is voor de formule die ik erin wil hebben. Ik heb niet de versie van de Grafische rekenmachine die op de computer aangesloten kan worden, dus dat viel ook al af. Of heeft iemand misschien een wiskundig tekenprogrammaatje waarmee je dit soort dingen kan?
Het gaat om de volgende formule,
Sin(180/N) *N + Tan(180/N) *N
---------------------------------------------
2
Edit: hij haalt automatisch de spaties weg, maar dus die hele zooi boven de streep moet door 2 gedeeld worden..
Voor de geïnteresseerden, het is een formule om Pi te benaderen.
Alvast bedankt
quote:
Alstu
quote:=(SIN(PI()/B1)*B1+TAN(PI()/B1)*B1)/2Op zondag 12 februari 2006 14:42 schreef Market_Garden het volgende:
Haai,
Ik ben met een PO voor wiskunde bezig, en nu wil ik een aantal grafieken maken op de computer, die ik dan uit kan printen.
Ik heb geprobeerd om het met Excel voor mekaar te krijgen, maar ik weet niet hoe daar de notatie is voor de formule die ik erin wil hebben. Ik heb niet de versie van de Grafische rekenmachine die op de computer aangesloten kan worden, dus dat viel ook al af. Of heeft iemand misschien een wiskundig tekenprogrammaatje waarmee je dit soort dingen kan?
Het gaat om de volgende formule,
Sin(180/N) *N + Tan(180/N) *N
---------------------------------------------
2
Edit: hij haalt automatisch de spaties weg, maar dus die hele zooi boven de streep moet door 2 gedeeld worden..
Voor de geïnteresseerden, het is een formule om Pi te benaderen.
Alvast bedankt
Met in B1 de waarde voor N
quote:Hmm, die formule helpt al een stuk, alleen ik krijg t nu nog niet voor mekaar om er een grafiekje van te bouwen...Op zondag 12 februari 2006 16:59 schreef mrbombastic het volgende:
[..]
=(SIN(PI()/B1)*B1+TAN(PI()/B1)*B1)/2
Met in B1 de waarde voor N
Het is nu gelukt, beetje omslachtig, maar het staat er, bedankt!
[ Bericht 8% gewijzigd door Market_Garden op 12-02-2006 17:37:40 ]
Een machine vult pakken groente met een gemiddeld gewicht van 150 gram. De fabrikant wil dat 90% van de pakken een gewicht heeft dat maximaal 5 gram afwijkt van deze 150 gram. Welke standaardafwijking zal hij accepteen als het vulgewicht normaal verdeeld is? Rond af op 2 decimalen.
quote:Gevraagd wordt s waarvoor geldt: P(145<X<155 | NV; σ=s μ=150) = 0,90.Op maandag 13 februari 2006 19:46 schreef appelsap het volgende:
Ik kom er even niet meer uit.
Een machine vult pakken groente met een gemiddeld gewicht van 150 gram. De fabrikant wil dat 90% van de pakken een gewicht heeft dat maximaal 5 gram afwijkt van deze 150 gram. Welke standaardafwijking zal hij accepteen als het vulgewicht normaal verdeeld is? Rond af op 2 decimalen.
Ofwel 10% ligt buiten [145,155]. Vanwege symmetrie zal 5% minder dan 145 zijn. Helaas zijn de getallen slecht gekozen, zodat je een rekenmachine of tabel moet gebruiken. Bij een Ti83/84 kun je bijvoorbeeld kijken waar de volgende twee grafieken elkaar snijden: normalcdf(-10^99,145,150,X) en 0,05.
Wat wij dachten is we doen de reactie in een bekerglas met water en dan meten hoeveel graden het water verandert is en dan kunnen we de vrijgekomen/ontrokken energie meten. Maar dit lijkt ons niet echt een nauwkeurige manier, weet iemand een betere?
quote:Bedankt! Ik deed 0,10 ipv 0,05.Op maandag 13 februari 2006 20:05 schreef GlowMouse het volgende:
[..]
Gevraagd wordt s waarvoor geldt: P(145<X<155 | NV; σ=s μ=150) = 0,90.
Ofwel 10% ligt buiten [145,155]. Vanwege symmetrie zal 5% minder dan 145 zijn. Helaas zijn de getallen slecht gekozen, zodat je een rekenmachine of tabel moet gebruiken. Bij een Ti83/84 kun je bijvoorbeeld kijken waar de volgende twee grafieken elkaar snijden: normalcdf(-10^99,145,150,X) en 0,05.
Om te bepalen of een functie monotoon stijgend is kijk je naar zijn afgeleide. Is de afgeleide >= 0 dan is de functie monotoon stijgend (en zelfs strikt monotoon stijgend als afgeleide >0).
Nu is mijn vraag: hoe gaat dat met functies van meer variabelen? Is de functie f(x, y) bijvoorbeeld monotoon stijgend als geldt df/dx >=0 EN df/dy >= 0 ? Oftewel: moeten bij meer variabelen dan alle partiele afgeleiden groter-gelijk 0 zijn?
quote:Ja.Op maandag 13 februari 2006 22:41 schreef Bioman_1 het volgende:
Snel vraagje:
Om te bepalen of een functie monotoon stijgend is kijk je naar zijn afgeleide. Is de afgeleide >= 0 dan is de functie monotoon stijgend (en zelfs strikt monotoon stijgend als afgeleide >0).
Nu is mijn vraag: hoe gaat dat met functies van meer variabelen? Is de functie f(x, y) bijvoorbeeld monotoon stijgend als geldt df/dx >=0 EN df/dy >= 0 ? Oftewel: moeten bij meer variabelen dan alle partiele afgeleiden groter-gelijk 0 zijn?
Maar de wiskundige onderbouwing mis ik.
Iemand??
De kans dat je het elke keer fout hebt is (0,5)20 = 0,00000095
Heb er wel een goed gevoel over, ben wel benieuwd naar de opgaven die ik krijg
quote:Dit hoeft trouwens niet zo te zijn, want ze zegt dat ze "op het einde een keuze had uit 2 mogelijkheden".Op dinsdag 14 februari 2006 12:52 schreef Litso het volgende:
De kans is redelijk klein maar bestaat echt wel hoor
De kans dat je het elke keer fout hebt is (0,5)20 = 0,00000095
Ik weet niet of je bekend bent met het Monty Hall "probleem"? (Afkomstig uit een spelshow)
Even ter uitleg voor iedereen die het niet kent:
Stel je hebt drie deuren (A, B en C), achter 1 van die deuren staat een auto, achter de twee andere deuren staat niets. In dit geval moet je een van de deuren A, B of C kiezen.
Stel: Je kiest voor deur A.
Daarna zal de presentator van die show een van de andere twee deuren openen (B of C), hij kiest dan van een van deze twee deuren de deur waar GEEN auto achter staat (het kan natuurlijk ook dat achter allebei de deuren geen auto staat, dan kiest hij gewoon willekeurig B of C).
Nadat hij dat heeft gedaan, wordt aan jou de vraag gesteld of je nog van deur wilt wisselen. Nu blijkt dat je in dit geval WEL van deur moet wisselen, wil je de meeste kans maken om te winnen. De kansverdeling is in dit geval namelijk 1/3 dat de gekozen deur A van het begin de auto bevat, en 2/3 dat de deur andere deur die niet door de presentator is geopend de auto bevat.
Veel mensen gaan er hier ten onrechte van uit dat de kans gelijkmatig is verdeeld als 1/2 en 1/2.
Dus stel dat zij zo'n zelfde vraagstuk 20 keer heeft beantwoord en telkens bij haar eerste keuze is gebleven is de kans dat ze het 20 keer fout had zelfs: (2/3)20 = 0,0003007.
Toch een "redelijk" verschil in kans.
quote:Ik heb hem wel eens eerder gehoord maar ik snap de truc nog steeds niet helemaalOp dinsdag 14 februari 2006 19:10 schreef Lookbehind het volgende:
[..]
Dit hoeft trouwens niet zo te zijn, want ze zegt dat ze "op het einde een keuze had uit 2 mogelijkheden".
Ik weet niet of je bekend bent met het Monty Hall "probleem"? (Afkomstig uit een spelshow)
Even ter uitleg voor iedereen die het niet kent:
Stel je hebt drie deuren (A, B en C), achter 1 van die deuren staat een auto, achter de twee andere deuren staat niets. In dit geval moet je een van de deuren A, B of C kiezen.
Stel: Je kiest voor deur A.
Daarna zal de presentator van die show een van de andere twee deuren openen (B of C), hij kiest dan van een van deze twee deuren de deur waar GEEN auto achter staat (het kan natuurlijk ook dat achter allebei de deuren geen auto staat, dan kiest hij gewoon willekeurig B of C).
Nadat hij dat heeft gedaan, wordt aan jou de vraag gesteld of je nog van deur wilt wisselen. Nu blijkt dat je in dit geval WEL van deur moet wisselen, wil je de meeste kans maken om te winnen. De kansverdeling is in dit geval namelijk 1/3 dat de gekozen deur A van het begin de auto bevat, en 2/3 dat de deur andere deur die niet door de presentator is geopend de auto bevat.
Veel mensen gaan er hier ten onrechte van uit dat de kans gelijkmatig is verdeeld als 1/2 en 1/2.
Dus stel dat zij zo'n zelfde vraagstuk 20 keer heeft beantwoord en telkens bij haar eerste keuze is gebleven is de kans dat ze het 20 keer fout had zelfs: (2/3)20 = 0,0003007.
Toch een "redelijk" verschil in kans.
Daar ga ik wel even over nadenken, maar in de tussentijd denk ik dat het niet echt van toepassing is op de hierboven gestelde vraag
-edit-
o wacht, ik heb hem door ja
quote:als iemand hem niet snapt kan je het beter begrijpen door je voor te stellen dat er 100 deuren zijn, je kiest er 1, en dan doet de presentator 98 foute deuren open. Als je het op die manier bekijkt wordt het al wat logischerOp dinsdag 14 februari 2006 19:17 schreef Litso het volgende:
[..]
Ik heb hem wel eens eerder gehoord maar ik snap de truc nog steeds niet helemaal
Daar ga ik wel even over nadenken, maar in de tussentijd denk ik dat het niet echt van toepassing is op de hierboven gestelde vraag
-edit-
o wacht, ik heb hem door ja
maargoed, jij snapte em al
Ik moet in dit plaatje gelijkvormigheid bepalen voor driehoek CMD en MPD.
CD heeft als lengte 2s, DM en CM zijn beide 2s' lang.
DP en DM zijn beide raaklijnen aan de cirkel en zijn dus even lang, en DP is t', dus is PM ook t'.
Ik zie wel dat ze gelijkvormig zijn, alleen het bewijs daarvoor zie ik niet. Het moet te doen zijn, maar hoe?
quote:Hint:Op woensdag 15 februari 2006 15:01 schreef Market_Garden het volgende:
[img=http://img103.imageshack.us/img103/8086/driehoek0rl.th.gif]
Ik moet in dit plaatje gelijkvormigheid bepalen voor driehoek CMD en MPD.
CD heeft als lengte 2s, DM en CM zijn beide 2s' lang.
DP en DM zijn beide raaklijnen aan de cirkel en zijn dus even lang, en DP is t', dus is PM ook t'.
Ik zie wel dat ze gelijkvormig zijn, alleen het bewijs daarvoor zie ik niet. Het moet te doen zijn, maar hoe?
quote:
quote:Grappig, maar het helpt me niet veel
quote:Hoeken MDN en DMP zijn Z-hoeken. Vervolgens kun je het bewijs met behulp van gelijkbenigheid van beide driehoeken voltooien.Op woensdag 15 februari 2006 15:01 schreef Market_Garden het volgende:
[img=http://img103.imageshack.us/img103/8086/driehoek0rl.th.gif]
Ik moet in dit plaatje gelijkvormigheid bepalen voor driehoek CMD en MPD.
CD heeft als lengte 2s, DM en CM zijn beide 2s' lang.
DP enDPM zijn beide raaklijnen aan de cirkel en zijn dus even lang, en DP is t', dus is PM ook t'.
Ik zie wel dat ze gelijkvormig zijn, alleen het bewijs daarvoor zie ik niet. Het moet te doen zijn, maar hoe?
Gegeven:
Er rijden twee auto's. Auto A rijdt 20 m/s en heeft een gewicht van 800 kilo. Auto B rijdt 15 m/s en heeft een gewicht van 1200 kilo.
a. Bereken de snelheid die overblijft na een frontale botsing. Neem aan dat de auto's als één geheel verdergaan. (Deze was een eitje, met stoot en impuls)
b. Bereken hoeveel energie er verloren is gegaan in warmte en het kreukelen.
En hoe in hemelsnaam is dat te berekenen, als alleen maar de snelheden en massa's van de auto's zijn gegeven? Als er nou was gezegd dat de auto's na de botsing met 0,5 m/s verder gingen had ik het nog gesnapt.
Oh het kan trouwens zijn de de gegevens iets anders waren, maar dat doet er voorderest niet echt toe...
quote:ptotaal = pauto1 + pauto2 = 800*20 + 1200*(-15) = -2,0*103kg*m/sOp woensdag 15 februari 2006 17:57 schreef Me_Wesley het volgende:
Vraag met betrekking tot mijn natuurkunde toets van daarnet. Hij was best te doen, maar van een vraag snapte ik geen ene zak.
Gegeven:
Er rijden twee auto's. Auto A rijdt 20 m/s en heeft een gewicht van 800 kilo. Auto B rijdt 15 m/s en heeft een gewicht van 1200 kilo.
a. Bereken de snelheid die overblijft na een frontale botsing. Neem aan dat de auto's als één geheel verdergaan. (Deze was een eitje, met stoot en impuls)
b. Bereken hoeveel energie er verloren is gegaan in warmte en het kreukelen.
Als ze als één geheel verdergaan, wordt de eindsnelheid v = p/m = -2,0*103 / (800+1200) = -1m/s (naar links, de richting waarin auto2 reed voor de botsing).
Ek totaal = Ek auto1 + Ek auto2 = 0,5*800*20² + 0,5*1200*15² = 2,95*105J.
Ek na botsing = 0,5*(800+1200)*(-1)² = 1,0*103J
Het verschil is er verloren gegaan.
Zelf heb ik ook nog een vraag: de faculteit is eenvoudig gedefinieerd voor natuurlijke getallen door 1*2*...*n. Een rekenmachine kan ook 3,50845! uitrekenen, kan dat ook met pen en papier?
quote:Je hebt toch zelf de snelheid bij a berekend? De kinetische energie voor impact was per wagen 0,5*m*v^2... Totale kinetische energie is dus de optelsom van die twee. Na impact heb je een hoop rotzooi over die met slechts 1 m/s (even snel uit het hoofd, da's toch het antwoord bij a?) nog vooruit beweegt. Reken uit je verlies...Op woensdag 15 februari 2006 17:57 schreef Me_Wesley het volgende:
Vraag met betrekking tot mijn natuurkunde toets van daarnet. Hij was best te doen, maar van een vraag snapte ik geen ene zak.
Gegeven:
Er rijden twee auto's. Auto A rijdt 20 m/s en heeft een gewicht van 800 kilo. Auto B rijdt 15 m/s en heeft een gewicht van 1200 kilo.
a. Bereken de snelheid die overblijft na een frontale botsing. Neem aan dat de auto's als één geheel verdergaan. (Deze was een eitje, met stoot en impuls)
b. Bereken hoeveel energie er verloren is gegaan in warmte en het kreukelen.
En hoe in hemelsnaam is dat te berekenen, als alleen maar de snelheden en massa's van de auto's zijn gegeven? Als er nou was gezegd dat de auto's na de botsing met 0,5 m/s verder gingen had ik het nog gesnapt.
Oh het kan trouwens zijn de de gegevens iets anders waren, maar dat doet er voorderest niet echt toe...
quote:Maar je weet toch de snelheid waarmee ze verder gaan, die heb je net bij a) uitgerekend...Op woensdag 15 februari 2006 17:57 schreef Me_Wesley het volgende:
er verloren is gegaan in warmte en het kreukelen.
En hoe in hemelsnaam is dat te berekenen, als alleen maar de snelheden en massa's van de auto's zijn gegeven? Als er nou was gezegd dat de auto's na de botsing met 0,5 m/s verder gingen had ik het nog gesnapt.