SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik weet het ook niet maar na wat ge-Google kom ik hierop: link, de Java code van de StringBuffer class. Je kunt hier zien met welke waarden append de methode aanroept voor het uitbreiden van de capacity. De capacity wordt uiteindelijk veranderd in expandCapacity() waarbij de nieuwe capacity (value.length + 1)*2 is of de waarde die aan de methode is meegegeven vanuit append, mits deze groter is dan de al berekende waarde met die formule van daarnet.quote:Op donderdag 12 januari 2006 08:41 schreef Masanga het volgende:
Vraag ivm StringBuffers bij Java:
Er is een verschil tussen de lengte en de capaciteit. Initieel is de capaciteit = lengte+16. Maar als men via de methode StringBuffer.append("...") zaken gaat toevoegen zal die formule uit het voorbeeld dat ik hier gebruikte niet meer geldig zijn (maw capaciteit is niet langer lengte + 16).
Zit daar (bepaling van de capaciteit) enige logica in?


ok, ben bezig met kansberekeningen voor wiskundeA12, alleen door het harde leren zie ik door de bomen het bos niet meer.
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen zal mij deugd doen
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen zal mij deugd doen
niets


Dat komt doordat het binomiaal is. Je hebt prijs óf geen prijs. In dit geval vragen ze drie keer geen prijs. De kans dat je 1x geen prijs hebt is 49500/50000. Dus de kans dat je 3x geen prijs hebt is dan (49500/50000)3.quote:Op donderdag 12 januari 2006 17:09 schreef Ewaldus het volgende:
ok, ben bezig met kansberekeningen voor wiskundeA12, alleen door het harde leren zie ik door de bomen het bos niet meer.
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen zal mij deugd doen
[afbeelding]


maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?quote:Op donderdag 12 januari 2006 18:12 schreef Nuna het volgende:
[..]
Dat komt doordat het binomiaal is. Je hebt prijs óf geen prijs. In dit geval vragen ze drie keer geen prijs. De kans dat je 1x geen prijs hebt is 49500/50000. Dus de kans dat je 3x geen prijs hebt is dan (49500/50000)3.
(3 se's op één dag zijn veel)
niets


Volgens mij wel Niet zulke moeilijke vragen stellen he Ik ben het ook weer net aan het herhalen, toevallig had ik net iets gezien over de binomiale verdeling.quote:Op donderdag 12 januari 2006 18:23 schreef Ewaldus het volgende:
[..]
maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?
(3 se's op één dag zijn veel)


Ik denk dat er een afweging wordt gemaakt tussen ruimte en snelheid. Telkens de capaciteit een beetje verhogen (telkens met 10 of zo), geeft bij veel toevoegen natuurlijk nodeloze inspanningen om de capaciteit te verhogen. Een capaciteit in het begin die heel groot is, is ook nodeloos, want dan verkwist je ruimte.quote:Op donderdag 12 januari 2006 08:41 schreef Masanga het volgende:
Vraag ivm StringBuffers bij Java:
Er is een verschil tussen de lengte en de capaciteit. Initieel is de capaciteit = lengte+16. Maar als men via de methode StringBuffer.append("...") zaken gaat toevoegen zal die formule uit het voorbeeld dat ik hier gebruikte niet meer geldig zijn (maw capaciteit is niet langer lengte + 16).
Zit daar (bepaling van de capaciteit) enige logica in?
Het verdubbelen is echter niet zonder goede theoretische reden. Het verdubbelen leidt ertoe dat er gemiddeld een constante tijd nog steeds gegarandeerd kan worden per toevoegen van een element aan de lijst. De kosten voor het verdubbelen worden daarbij dus verdeeld over alle elementen die je toevoegt. Resize je vaker, dan moet je vaker met data schuiven en toewijzen, en dan kost je dit gemiddeld meer tijd. (Niet O(1) in complexiteitstermen. Door verdubbeling blijft de complexiteit O(n) om n elementen toe te voegen aan de lijst. Anders wordt deze beroerder.)
Dat is volgens mij de reden.
Het is tijd voor wat anders.


Volgens mij heb je gelijk. Als je het netjes zou doen, dan zou je gebruik maken van combinaties ('nCr'). De eerste keer geen prijs is namelijk een kanas van 49500/50000, de tweede keer van 49499/49999 en de derde keer van 49498/49998, of, hetzelfde: (49500 nCr 3)/(50000 nCr 3), beide geven als uitkomst 40426674783/41664166700. (Mits je ervan uitgaat dat men zonder terugleggen te prijzen uitdeelt, wat vaak zo is, daar op een lot meestal maar één prijs valt) Wat, in decimalen .9702984119 is. Terwijl (49500/50000)^3 = .9702990000.quote:Op donderdag 12 januari 2006 17:09 schreef Ewaldus het volgende:
ok, ben bezig met kansberekeningen voor wiskundeA12, alleen door het harde leren zie ik door de bomen het bos niet meer.
Ik vraag mij af waarom bij opdracht 8 je niet 49000 ncr 50000 hebt maar wel 49000/50000.
vaak doe ik het op gevoel of gewenning of voel ik het gewoon , maar heb geen concrete reden..
Wie kan het vertellen zal mij deugd doen
[afbeelding]
In dit geval is de populatie (het aantal loten) echter zo groot, dat het verschil verwaarloosbaar is. Je ziet het aan de decimalen, de eerste 5 zijn identiek. En volgens mij is dát de reden dat ze geen nCr gebruiken. Niet het wel of geen prijs.
Het is tijd voor wat anders.


Als ze zouden differentieren naar hoofdprijs, tweede prijs en derde prijs en geen prijs. En ze vragen bijvoorbeeld, wat is de kans dat je met 5 loten een keer de hoofdprijs wint, en twee derde prijzen? (En de rest geen prijs), dan zou je krijgen: ((1 nCr 1)*(9 nCr 0)*(490 nCr 2)*(49500 nCr 2))/(50000 nCr 5). Zoals te verwachten is deze kans heel klein. (5.6 * 10^-8). ik hoop dat dit niet boven je wiskunde A pet gaat, anders gewoon negeren dusquote:Op donderdag 12 januari 2006 18:23 schreef Ewaldus het volgende:
[..]
maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?
(3 se's op één dag zijn veel)
Het is tijd voor wat anders.


Het staat gewoon in de Java hoor: linkquote:Op donderdag 12 januari 2006 18:33 schreef AtraBilis het volgende:
[..]
Ik denk dat er een afweging wordt gemaakt tussen ruimte en snelheid. Telkens de capaciteit een beetje verhogen (telkens met 10 of zo), geeft bij veel toevoegen natuurlijk nodeloze inspanningen om de capaciteit te verhogen. Een capaciteit in het begin die heel groot is, is ook nodeloos, want dan verkwist je ruimte.
Het verdubbelen is echter niet zonder goede theoretische reden. Het verdubbelen leidt ertoe dat er gemiddeld een constante tijd nog steeds gegarandeerd kan worden per toevoegen van een element aan de lijst. De kosten voor het verdubbelen worden daarbij dus verdeeld over alle elementen die je toevoegt. Resize je vaker, dan moet je vaker met data schuiven en toewijzen, en dan kost je dit gemiddeld meer tijd. (Niet O(1) in complexiteitstermen. Door verdubbeling blijft de complexiteit O(n) om n elementen toe te voegen aan de lijst. Anders wordt deze beroerder.)
Dat is volgens mij de reden.


Scheikundigen: Hoe ziet de structuurformule van inosinemonofosfaat (ook wel IMP genaamd) eruit? Het gaat hier dus om een afbeelding van deze stof want ik kan het nergens vinden, ook niet in binas maar misschien mis ik iets.
Bij voorbaat dank
Bij voorbaat dank
Henk Knaagt Aan Schenen
Hij Kijkt Aapjes Soms
Hij Kijkt Aapjes Soms


Ik ben geen scheikundige. Doch, mijn Googlezoektocht leverde op:
Met begeleidende tekst:
Met begeleidende tekst:
En wel hier vandaan. Dus wellicht dat inonosine monophosphate meer oplevert als je ermee zoekt in Google.quote:Synthesis of the first fully formed purine nucleotide, inosine monophosphate, IMP begins with 5-phospho-a-ribosyl-1-pyrophosphate, PRPP. Through a series of reactions utilizing ATP, tetrahydrofolate (THF) derivatives, glutamine, glycine and aspartate this pathway yields IMP. The two indicated enzymes (A and B) are those catalyzing the rate limiting step and the reaction necessary for the purine nucleotide cycle, respectively. The structure of the nucleobase of IMP (hypoxanthine) is shown.
Het is tijd voor wat anders.


Bij 2a wordt naar a gevraagd, niet naar x. Maar als het goed is, zijn er 2 mogelijkheden voor a en x (bij x ligt a vast en vice versa).quote:Op vrijdag 13 januari 2006 19:23 schreef Frankvbr het volgende:
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
2b begrijp ik al helemaal niet
Wat je zoekt is een punt waarvoor de raaklijn door (0,0) gaat. Ken je de formule voor de lineaire benadering?
g(x)=f(c)+f'(c)(x-c)
c is het punt waarin je benadert, x is het punt waarin je de functiewaarde wilt schatten. Nu zoek je een x-waarde waarvoor de lineaire benadering door 0 gaat: precies andersom. De 'x' in de formule wordt dus 0, en de c vind je door te kijken wanneer de lineaire benadering door (0,0) gaat. Als je die c gevonden hebt, heb je a ook zo. Het antwoord kun je vrij eenvoudig exact bepalen, en de rekenmachine hiervoor gebruiken lijkt me onzin.
Bij b wil je de afstand weten tussen 2 punten op de grafiek. Dat kan met behulp van de stelling van pythagoras: afstand=wortel(deltax²+deltay²)
Nu geldt dat je deltay uit kunt drukken in deltax en a (ga na dat moet gelden 25 = deltax²+(a*deltax)²). Nu heb je een verband tussen a en deltax. Nu wil je de de functie f nog gebruiken voor een extra vergelijking, dat kan ook met de stelling van pythagoras. Noem die 2 punten a en b, bepaal deltax en deltay, bepaal de afstand tussen die twee punten, en substitueer dat in de eerder gevonden formule.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


dat is niet verstandig om te zeggen in dit topicquote:Op vrijdag 13 januari 2006 19:23 schreef Frankvbr het volgende:
[[url=http://img337.imageshack.us/img337/7586/wiskundepo6qq.th.png]afbeelding][/URL]
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
en je plaatje doet t niet


ex-chemicus to the rescuequote:Op donderdag 12 januari 2006 19:23 schreef Bullet-tooth het volgende:
Scheikundigen: Hoe ziet de structuurformule van inosinemonofosfaat (ook wel IMP genaamd) eruit? Het gaat hier dus om een afbeelding van deze stof want ik kan het nergens vinden, ook niet in binas maar misschien mis ik iets.
Bij voorbaat dank
it's your lucky day!
lang leve acros
plus info
http://www.acros.be/DesktopModules/Acros_Search_Results/Acros_Search_Results.aspx?tabID=21&alias=Rainbow&lang=en&search_type=2&search=inosinemonophosphate


Er zijn meerdere manieren om dit exact op te lossen, het makkelijkst is om op te schrijven waar de vergelijkingen aan moeten voldoen en daarop voort te werken. Dit is dus:quote:Op vrijdag 13 januari 2006 20:55 schreef GlowMouse het volgende:
[..]
Bij 2a wordt naar a gevraagd, niet naar x. Maar als het goed is, zijn er 2 mogelijkheden voor a en x (bij x ligt a vast en vice versa).
Wat je zoekt is een punt waarvoor de raaklijn door (0,0) gaat. Ken je de formule voor de lineaire benadering?
g(x)=f(c)+f'(c)(x-c)
c is het punt waarin je benadert, x is het punt waarin je de functiewaarde wilt schatten. Nu zoek je een x-waarde waarvoor de lineaire benadering door 0 gaat: precies andersom. De 'x' in de formule wordt dus 0, en de c vind je door te kijken wanneer de lineaire benadering door (0,0) gaat. Als je die c gevonden hebt, heb je a ook zo. Het antwoord kun je vrij eenvoudig exact bepalen, en de rekenmachine hiervoor gebruiken lijkt me onzin.
g(x)=f(x)
g'(x)=f'(x)
g(x)=f(x) -> g(x)-f(x)=0
g'(x)=f'(x) ->2x-6=a
2x-6=a, hier heb je dus al de verbinding tussen x en a, nu kun je deze gaan invullen in de eerste vergelijking:
g(x)-f(x)=0 ->x^2-6x+13-ax=0 ->x^2-6x+13-(2x-6)x=0 -> x^2-6x-2x^2+6x+13=0
-> -x^2+13=0 -> x=+/- wortel(13)
2x-6=a, dus a= 2(+/- wortel13)-6.
Antwoord:
a=2(-3+wortel(13)) V a=2(-3-wortel(13))
Een andere methode is om gebruik te maken van de eigenschappen van de discriminant. Ziehier:
g(x)-f(x)=0, dus x^2-6x+13-ax=0. De discriminant is dus:
D=(6+a)^2-4*13=a^2+12a-16. Als de discriminant gelijk is aan 0 raakt de grafiek de x-as. Dit is wat we willen weten. Op deze discriminant gooi je dus een ABC formule:
x=(-12 +/- wortel(208))/2= -6 +- 2 wortel(13)
Antwoord:
a=2(-3+wortel(13)) V a=2(-3-wortel(13))
Is het niet wonderbaarlijk


De tweede is helemaal leukquote:Op vrijdag 13 januari 2006 19:23 schreef Frankvbr het volgende:
[[url=http://img337.imageshack.us/img337/7586/wiskundepo6qq.th.png]afbeelding][/URL]
de bedoeling is dat je alles met de rekenmachine doet. ik kan solver wel gebruiken, maar ik heb geen vaste x-waarde, en er kunnen dan verschillende antwoorden zijn.
2b begrijp ik al helemaal niet
Ik denk dat hij wel makkelijker kan, maar ik kreeg hem alleen zo exact opgelost, tis al laat.
Het antwoord moet aan de volgende vergelijkingen voldoen:
B=A+5
f(B)-f(A)=5a
f(A)-a*A=0
f(B)-f(A)=5a -> f(B)-f(B-5)=5a ->x^2-6x+13-((x-5)^2-6(x-5)+13)=5a.
Uitwerken geeft: a=2x-11
f(A)-a*A=0 geeft:
x^2-6x+13-ax=0 -> x^2-6x+13-(2x-11)x=0
uitwerken:
-x^2+5x+13=0
ABC-tje ertegenaan:
x=( -5 +/- wortel(25+52))/2
x= (-5+wortel(77)/2 V x=(-5 - wortel(77))/2
a=2x-11
Antwoord:
a= -6 + wortel(77) V a= -6 - wortel(77)
(excuus voor de eventuele wiskundige slordigheden qua notatie)


Probeer het te begrijpen. Stel dat een gebeurtenis A op 10 verschillende manieren kan gebeuren, dan is de totale kans op gebeurtenis A 10 keer de kans dat het op een van die manieren gebeurt. nCr berekent die '10', oftewel, nCr berekent hoeveel mogelijkheden er zijn op een gebeurtenis.quote:Op donderdag 12 januari 2006 18:23 schreef Ewaldus het volgende:
[..]
maar als er meer mogelijkheden waren was het wel zo'n 'nCr' geval?
(3 se's op één dag zijn veel)
nCr is trouwens precies: n! / ((n-k)! * k!)


Het grondgetal 10 is natuurlijk compleet random en nergens op gebaseerd, wiskundig gezien.quote:Op woensdag 11 januari 2006 18:34 schreef bierglas het volgende:
[..]
Waarom zou je zo moeilijk doen als het rekenmachine al automatisch 10 als grondgetal neemt?
Het grondtal e daarentegen, hmmmm


Hallo mensen, ik was weer is druk aan het studeren en ik ben toen de formule v^2/r tegengekomen die als uitkomst de middelpuntzoekende versnelling geeft. Alleen ik zou graag willen weten hoe je dat kunt bewijzen. Iemand een id?


je kunt geen rechteliijnstuk met lengte pi construeren.. dus de zijde van die vierkant is het probleem?quote:Op dinsdag 10 januari 2006 19:16 schreef thabit het volgende:
[..]
Cirkelkwadratuur is onmogelijk. Komt omdat pi transcendent is. Gegeven twee punten in het vlak welke de coordinaten (0,0) en (0,1) worden gegeven kun je alleen punten met algebraische coordinaten construeren met passer en liniaal. Dat pi transcendent is, is bewezen door Lindemann. Hier is een bewijs. Ik heb geen idee of het een goed bewijs is, niet doorgelezen.
als je een cirkel tekent met r=1/2 dan hebj e wel een omtrek van lengte pi. Dus wel 'tekenbaar'met een passer....
gaat het dus om die zijde?
verlegen :)


De oppervlakte van het vierkant moet, zeg, pi zijn (Gegeven een cirkel met straal 1). Dus dan moet een zijde wortel(pi) zijn. Het nummer wortel Pi is niet algebraïsch te construeren. Dat construeren moest met een liniaal en een passer gebeuren. Dat was dan verder aan enkele regels gebonden, welke dat zijn vind je op Wikipedia.quote:Op zaterdag 14 januari 2006 21:35 schreef teletubbies het volgende:
[..]
je kunt geen rechteliijnstuk met lengte pi construeren.. dus de zijde van die vierkant is het probleem?
als je een cirkel tekent met r=1/2 dan hebj e wel een omtrek van lengte pi. Dus wel 'tekenbaar'met een passer....
gaat het dus om die zijde?
Het bewijs zelf is niet eenvoudig. Maar uiteindelijk komt het er dus inderdaad op neer dat als je je volgens die regels bezig houdt, je niet het goede vierkant krijgt omdat je die zijde niet kunt construeren. (Je kunt wel zo dicht bij komen als je wilt). Hippocrates heeft echter wel wat maantjes geconstrueerd (Soort sikkelvormpjes) met driehoeken die dezelfde oppervlakte hadden.
Het is tijd voor wat anders.


Ja. Het kost wel even tijd.quote:Op zaterdag 14 januari 2006 21:11 schreef Pauluzz_U5 het volgende:
Hallo mensen, ik was weer is druk aan het studeren en ik ben toen de formule v^2/r tegengekomen die als uitkomst de middelpuntzoekende versnelling geeft. Alleen ik zou graag willen weten hoe je dat kunt bewijzen. Iemand een id?
Je gaat uit van een versnelling a, opgebouwd uit twee vectoren:
-een versnelling loodrecht van de cirkel, de aN
-een versnelling evenwijdig aan de raaklijn van de cirkel, de aT
-(dus eT is de vector waar aT langs werkt, enz).
a = dv/dt (bekend toch?) = d(veT)/dt = dv/dt eT + v*d(eT)/dt.
Bij een rechte lijn is eT constant en vervalt de tweede term. Dan blijft er over: a = dv/dt * eT (die eT is puur de lijn waarlangs hij werkt). eT moet je herschrijven naar een functie van een sinus en een cosinus. Na herschrijven en eN invullen (ook als functie van een sinus en cosinus van de hoek phi) volgt:
deT/dt = -eN d(phi)/dt (phi is hoek tussen horizontale as en de eT). Nu moet je dus p(phi)/dt hebben. Zonder bewijs:
d(phi)/dt = v d(phi/ds), s = lengte van de boog. En d(phi)/ds is 1/r.
Ik heb eigenlijk een upload-iets nodig om het e.e.a. inzichtelijker te maken met een plaatje. Nou ja, dit linkje legt het in heel eenvoudige taal uit. Anders kun je ook wikipedia proberen natuurlijk (centripel acceleration). Hier ook een link.
[ Bericht 6% gewijzigd door Flumina op 14-01-2006 23:44:43 ]
we hebben een reëel probleem, dus we zoeken naar reële oplossingen
in dit specifieke geval maken twee helften één
in dit specifieke geval maken twee helften één


Tnx Flumina, ik snap er nog niet veel van, maar dat komt nog welquote:Op zaterdag 14 januari 2006 23:24 schreef Flumina het volgende:
[..]
Ja. Het kost wel even tijd.
Je gaat uit van een versnelling a, opgebouwd uit twee vectoren:
-een versnelling loodrecht van de cirkel, de aN
-een versnelling evenwijdig aan de raaklijn van de cirkel, de aT
-(dus eT is de vector waar aT langs werkt, enz).
a = dv/dt (bekend toch?) = d(veT)/dt = dv/dt eT + v*d(eT)/dt.
Bij een rechte lijn is eT constant en vervalt de tweede term. Dan blijft er over: a = dv/dt * eT (die eT is puur de lijn waarlangs hij werkt). eT moet je herschrijven naar een functie van een sinus en een cosinus. Na herschrijven en eN invullen (ook als functie van een sinus en cosinus van de hoek phi) volgt:
deT/dt = -eN d(phi)/dt (phi is hoek tussen horizontale as en de eT). Nu moet je dus p(phi)/dt hebben. Zonder bewijs:
d(phi)/dt = v d(phi/ds), s = lengte van de boog. En d(phi)/ds is 1/r.
Ik heb eigenlijk een upload-iets nodig om het e.e.a. inzichtelijker te maken met een plaatje. Nou ja, dit linkje legt het in heel eenvoudige taal uit. Anders kun je ook wikipedia proberen natuurlijk (centripel acceleration). Hier ook een link.


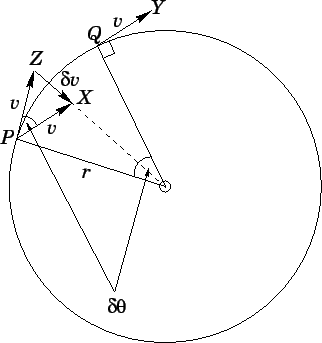
Vergeet mij uitleg en lees dit. Je ziet hieronder (zoals ook op de twee link te zien was) twee situaties van het voorwerp (namelijk een P en een Q). Bij P en Q heeft het voorwerp dezelfde snelheid, maar de snelheidsvector wijst wel naar een andere richting. Dit verschil in richting moet veroorzaakt worden door een verschil in snelheid, die dv genoemd wordt.quote:Op zondag 15 januari 2006 00:40 schreef Pauluzz_U5 het volgende:
[..]
Tnx Flumina, ik snap er nog niet veel van, maar dat komt nog wel
Die dv, die loodrecht op de beweging staat en naar het middelpunt wijst, is nodig om die cirkelbeweging te maken. Die dv kan geschrijven worden als functie van de hoek, zoals op onderstaande te zien is.
dv = v * d(theta). Met andere woorden: dat snelheidverschil is te schrijven als functie van de snelheid zelf vermedigvuldigd met een klein verschil in de hoek theta. Dit geldt alleen trouwens voor kleine hoeken, anders moet je met sinussen gaan kloten.
Nu is versnelling gedefinieerd als dv/dt (snelheid delen door tijd), dus
dv/dt = a = v * d(theta)/dt, het laatste is omega (hoeksnelheid). Dus:
a = v * omega
Omega = v/r. Deze invullen en je hebt:
a = v^2/r
[ Bericht 4% gewijzigd door Flumina op 15-01-2006 09:28:57 ]
we hebben een reëel probleem, dus we zoeken naar reële oplossingen
in dit specifieke geval maken twee helften één
in dit specifieke geval maken twee helften één


Ik heb een hele simpele vraag. Ja ik ben een loser, ja na zes jaar informatica kan ik nog steeds geen wiskunde, ja wrijf het maar in. Maar ik kom er maar niet uit .
quote:Een baanomloop van Mercurius duurt 88 dagen. De planeet draait in 58.7 dagen om zijn as, dwz de snelheid is 2/3 keer zo groot. Laat zien dat een zonnedag op Mercurius 176 dagen duurt, precies 2 maal zolang als de baanomloop. (Dit verschijnsel wordt resonantie genoemd)
They told me all of my cages were mental, so I got wasted like all my potential.


Ja, het is me zomaar ineens volkomen duidelijk.
They told me all of my cages were mental, so I got wasted like all my potential.


Nouja nu even wat minder sarcastisch, ik zie ook wel dat je bij een hele draai om de zon, de planeet anderhalf keer gedraaid was, maar wel zo met dezelfde plek naar de zon toe, dus dat het dan nacht is. Dat zie je ook wel duidelijk met een tekening. Maar ik vroeg me af of er een elegante formule was die dat liet zien.
They told me all of my cages were mental, so I got wasted like all my potential.


Bedankt Flumina, het is me al een stuk duidelijker, alleen dat laatste wat je zegt... je zegt dat dv = v * d(theta). Is dat nou de snelheidsverandering maal de hoek, of zie ik dat nou helemaal verkeerd.quote:Op zondag 15 januari 2006 02:01 schreef Flumina het volgende:
[..]
Vergeet mij uitleg en lees dit. Je ziet hieronder (zoals ook op de twee link te zien was) twee situaties van het voorwerp (namelijk een P en een Q). Bij P en Q heeft het voorwerp dezelfde snelheid, maar de snelheidsvector wijst wel naar een andere richting. Dit verschil in richting moet veroorzaakt worden door een verschil in snelheid, die dv genoemd wordt.
Die dv, die loodrecht op de beweging staat en naar het middelpunt wijst, is nodig om die cirkelbeweging te maken. Die dv kan geschrijven worden als functie van de hoek, zoals op onderstaande te zien is.
[afbeelding]
dv = v * d(theta). Met andere woorden: dat snelheidverschil is te schrijven als functie van de snelheid zelf vermedigvuldigd met een klein verschil in de hoek theta. Dit geldt alleen trouwens voor kleine hoeken, anders moet je met sinussen gaan kloten.
Nu is versnelling gedefinieerd als dv/dt (snelheid delen door tijd), dus
dv/dt = a = v * d(theta)/dt, het laatste is omega (hoeksnelheid). Dus:
a = v * omega
Omega = v/r. Deze invullen en je hebt:
a = v^2/r


Het is een snelheid * hoekverandering. Een d ervoor betekent een (zeer) klein verschil.quote:Op zondag 15 januari 2006 23:24 schreef Pauluzz_U5 het volgende:
[..]
Bedankt Flumina, het is me al een stuk duidelijker, alleen dat laatste wat je zegt... je zegt dat dv = v * d(theta). Is dat nou de snelheidsverandering maal de hoek, of zie ik dat nou helemaal verkeerd.
we hebben een reëel probleem, dus we zoeken naar reële oplossingen
in dit specifieke geval maken twee helften één
in dit specifieke geval maken twee helften één


tnxquote:Op zondag 15 januari 2006 23:45 schreef Flumina het volgende:
[..]
Het is een snelheid * hoekverandering. Een d ervoor betekent een (zeer) klein verschil.


Vraagje:
Stel a > 0 en c is de grafiek in het (x,y)-vlak van de kromme y = cosh x tussen x = 0 en x = a
a) Bereken de lengte van c
b) Stel F(x,y) = (-y,x), Bereken de integraal van F*ds over c
c) Is er een fucntie f:R^2 -> R met F = gradient f?
a en b zijn heel simpel, mits je het pad (parametrisatie van y = cosh x) weet.... en die weet ik dus niet... wie helpt me daar even uit?
Het antwoord van c is dat er geen gradient f is, omdat je nooit 2 partiele afgeleiden kan hebben met (-y,x).
d (yx)/dx = y en de(yx)/dy = x, maar die - krijg je er dus nooit voor.... correct me if I'm wrong.. maar het grootste probleem is dus het pad
Stel a > 0 en c is de grafiek in het (x,y)-vlak van de kromme y = cosh x tussen x = 0 en x = a
a) Bereken de lengte van c
b) Stel F(x,y) = (-y,x), Bereken de integraal van F*ds over c
c) Is er een fucntie f:R^2 -> R met F = gradient f?
a en b zijn heel simpel, mits je het pad (parametrisatie van y = cosh x) weet.... en die weet ik dus niet... wie helpt me daar even uit?
Het antwoord van c is dat er geen gradient f is, omdat je nooit 2 partiele afgeleiden kan hebben met (-y,x).
d (yx)/dx = y en de(yx)/dy = x, maar die - krijg je er dus nooit voor.... correct me if I'm wrong.. maar het grootste probleem is dus het pad
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


x(t) = tquote:Op maandag 16 januari 2006 12:05 schreef maniack28 het volgende:
a en b zijn heel simpel, mits je het pad (parametrisatie van y = cosh x) weet.... en die weet ik dus niet... wie helpt me daar even uit?
y(t) = (et+e-t)/2
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


ik heb een SE over 4 hoofdstukken waarvan voor elk hoofdstuk de belangrijkste sommen zijn genoteerd.. maar ik heb hiervoor niet de uitwerkingen dus misschien kunnen een aantal mensen de uitwerkingen van de sommen geven.
H2 Exponenten en logaritmen
89. Een bioloog heeft gedurende een groot aantal jaren onderozke gedaan naar het aantal kikkers in een waterrijk gebied. In de tabel zie je een schatting van het aantal kikkers N, telkens op 1 september van het genoemde jaar.
Jaar | 1975 | 1978 | 1980 | 1984 | 1989 | 1990 | 1992 | 1993 | 1996 | 1997 | 1998
N |15000|11700| 9900 | 7100 | 4700 | 4300 | 3600 | 3500| 3000 | 2800 | 2500
a) -
b) tot welk jaar is er sprake van exponentiële afnamen? geef voor deze periode de formule van N als functie van t. neem t in jaren en t = 0 in 1975. Rond de groeifactor af op 2 decimalen.
C) hoeveel kikkers zijn er in 1998 meer geteld dan dat er gweest zouden zijn als de exponentiële afnamen zich had doorgezet.
H5. De binomiale verdeling
53. De drie grootste automerken in nederland zijn opel, volkswagen en Ford. van de auto;s in Nederland is 13% van het merk opel , 12 % van het merk wolkswagen en 9% van het merk Ford.
Nummers vier is Renault met 8% en nummer vijf is peugeot met 7 %. Bereken in vier decimlane nauwkeurig de kans dat van 60 willekeurige aangewezen auto's er
a) precies 20 tot de drie grootste merken behoren
b) 14, 15 of 16 van het merk opel of volkswagen zijn
c) tussen de 5 en 10 van de merken renault en peugeot bij zijn.
54. Bereken in vier decimalen nauwkeurig de kans dat je bij
a) toen worpen met een dobbelsteen meer dan twee keer 6 ogen gooit
b) twaalf worpen met een dobbelsteen meer dan tien keer minstens 5 ogen gooit.
c) 30 worpen met een dobbelsteen tussen de 18 en 22 keer geen 1 of 2 ogen gooit.
56. in een labaratorium test men flesjes met het medicijn a op het voorkomen van een virus. Bekend is namelijk dat 1 op de 20 flesjes zo'n virus bevat. Bij deze controle neemt men uit elk flesje een monster. met de beschikbare apparatuur is het mogelijk maximaal tien monster tegelijk te tsten. Het nemen van een monster uit een flesje kost 2,- en elke test kost 8,-. Zo kost het gecombineerd testen van drie monster 14,- Valt deze test positief uit (dat wil zeggen het virus is aanwezig), dan moeten de drie monster afzonderlijk getest worden, hetgeen nog eens 3 x 8,- = 24,- kost
a) we bekijken de situatie waarbij de vier flesjes op het virus worden onderzicht.
- met combineert de vier monsters en de test valt negatief uit .
Wat zijn de kosten?
Bereken in vier decimalen nauwkeurig de kans dat een gecombineerde test van vier monsters negatief uitvalt.
- men combineert de vier monsters en de test valt positief uit, dus de vier monsters moeten elk afzonderlijk getest worden.
geef de kans op deze situatie en bereken de totale kosten.
- Bereken de verwachtingswaarde van de kosten en vervolgens de verwachtingswaarde van de kosten per monster.
B) wij bekijken de situatie waarbij vijf flesjes op het virus worden onderzocht. bereken in centen nauwkerugi de verwachtingswaarde. van de kosten per monster als men besluit de vijf monsters te combineren.
c) ga uit van de situatie waarbij n flesjes op het virus worden onderzocht hierbij is n > 1
toon aan dat de verwachtingswaarde E van de kosten per monster in het geval men besluit de n monsters te combineren, gelijk is aan E = 10 -8 x 0,95^n + - 8/n
H6 Veranderingen en snelheden
62. De dagelijkse kosten bij de productie van een wekkerradio zijn gegeven door de formule K = 1,2q³ - 8q² + 25q + 22. Hierin is K in duizenden gulden en is q het aantal per dag geproduceerde wekkerradio's in honderdtallen. De formule geldt voor
0 <(met = teken eronder) q < (met = teken eronder ) 8
a) schets de grafiek ( hoeft niet )
B) hoeveel zijn de gemiddelde kosten per wekkerradio bij een productie van 150 wekkerradio's
c) maak een tabel met differentiequotiënten op [0,a] met a = 1, 2, 4, 5, 6, 7, en 8. WElke betekenis hebben deze differentiequotiënten?
Met de formule GK = 10k/q ( onder elkaar) bereken je de gemiddelste kosten GK per wekkerradio
d) licht deze formule toe
e) .
f) bij welke productie zijn de gemiddelde kosten per wekkerradio minimaal?
Hoeveel zijn deze gemiddelde kosten dan?
En hoeveel de totale kosten?
H2 Exponenten en logaritmen
89. Een bioloog heeft gedurende een groot aantal jaren onderozke gedaan naar het aantal kikkers in een waterrijk gebied. In de tabel zie je een schatting van het aantal kikkers N, telkens op 1 september van het genoemde jaar.
Jaar | 1975 | 1978 | 1980 | 1984 | 1989 | 1990 | 1992 | 1993 | 1996 | 1997 | 1998
N |15000|11700| 9900 | 7100 | 4700 | 4300 | 3600 | 3500| 3000 | 2800 | 2500
a) -
b) tot welk jaar is er sprake van exponentiële afnamen? geef voor deze periode de formule van N als functie van t. neem t in jaren en t = 0 in 1975. Rond de groeifactor af op 2 decimalen.
C) hoeveel kikkers zijn er in 1998 meer geteld dan dat er gweest zouden zijn als de exponentiële afnamen zich had doorgezet.
H5. De binomiale verdeling
53. De drie grootste automerken in nederland zijn opel, volkswagen en Ford. van de auto;s in Nederland is 13% van het merk opel , 12 % van het merk wolkswagen en 9% van het merk Ford.
Nummers vier is Renault met 8% en nummer vijf is peugeot met 7 %. Bereken in vier decimlane nauwkeurig de kans dat van 60 willekeurige aangewezen auto's er
a) precies 20 tot de drie grootste merken behoren
b) 14, 15 of 16 van het merk opel of volkswagen zijn
c) tussen de 5 en 10 van de merken renault en peugeot bij zijn.
54. Bereken in vier decimalen nauwkeurig de kans dat je bij
a) toen worpen met een dobbelsteen meer dan twee keer 6 ogen gooit
b) twaalf worpen met een dobbelsteen meer dan tien keer minstens 5 ogen gooit.
c) 30 worpen met een dobbelsteen tussen de 18 en 22 keer geen 1 of 2 ogen gooit.
56. in een labaratorium test men flesjes met het medicijn a op het voorkomen van een virus. Bekend is namelijk dat 1 op de 20 flesjes zo'n virus bevat. Bij deze controle neemt men uit elk flesje een monster. met de beschikbare apparatuur is het mogelijk maximaal tien monster tegelijk te tsten. Het nemen van een monster uit een flesje kost 2,- en elke test kost 8,-. Zo kost het gecombineerd testen van drie monster 14,- Valt deze test positief uit (dat wil zeggen het virus is aanwezig), dan moeten de drie monster afzonderlijk getest worden, hetgeen nog eens 3 x 8,- = 24,- kost
a) we bekijken de situatie waarbij de vier flesjes op het virus worden onderzicht.
- met combineert de vier monsters en de test valt negatief uit .
Wat zijn de kosten?
Bereken in vier decimalen nauwkeurig de kans dat een gecombineerde test van vier monsters negatief uitvalt.
- men combineert de vier monsters en de test valt positief uit, dus de vier monsters moeten elk afzonderlijk getest worden.
geef de kans op deze situatie en bereken de totale kosten.
- Bereken de verwachtingswaarde van de kosten en vervolgens de verwachtingswaarde van de kosten per monster.
B) wij bekijken de situatie waarbij vijf flesjes op het virus worden onderzocht. bereken in centen nauwkerugi de verwachtingswaarde. van de kosten per monster als men besluit de vijf monsters te combineren.
c) ga uit van de situatie waarbij n flesjes op het virus worden onderzocht hierbij is n > 1
toon aan dat de verwachtingswaarde E van de kosten per monster in het geval men besluit de n monsters te combineren, gelijk is aan E = 10 -8 x 0,95^n + - 8/n
H6 Veranderingen en snelheden
62. De dagelijkse kosten bij de productie van een wekkerradio zijn gegeven door de formule K = 1,2q³ - 8q² + 25q + 22. Hierin is K in duizenden gulden en is q het aantal per dag geproduceerde wekkerradio's in honderdtallen. De formule geldt voor
0 <(met = teken eronder) q < (met = teken eronder ) 8
a) schets de grafiek ( hoeft niet )
B) hoeveel zijn de gemiddelde kosten per wekkerradio bij een productie van 150 wekkerradio's
c) maak een tabel met differentiequotiënten op [0,a] met a = 1, 2, 4, 5, 6, 7, en 8. WElke betekenis hebben deze differentiequotiënten?
Met de formule GK = 10k/q ( onder elkaar) bereken je de gemiddelste kosten GK per wekkerradio
d) licht deze formule toe
e) .
f) bij welke productie zijn de gemiddelde kosten per wekkerradio minimaal?
Hoeveel zijn deze gemiddelde kosten dan?
En hoeveel de totale kosten?


Per serie achtereenvolgende meetresultaten moet je kijken wat de exponentiële afname is. Exponentieel wil zeggen: steeds met een constante factor. Bij de eerste 2 zal ik het voordoen, de rest kun je dan waarschijnlijk zelf.quote:Jaar | 1975 | 1978 | 1980 | 1984 | 1989 | 1990 | 1992 | 1993 | 1996 | 1997 | 1998
N |15000|11700| 9900 | 7100 | 4700 | 4300 | 3600 | 3500| 3000 | 2800 | 2500
a) -
b) tot welk jaar is er sprake van exponentiële afnamen? geef voor deze periode de formule van N als functie van t. neem t in jaren en t = 0 in 1975. Rond de groeifactor af op 2 decimalen.
15000 -> 11700 in 3 jaar.
15000 in jaar 1975, 15000*factor in jaar 1976, (15000*factor)*factor in jaar 1977, (15000*factor²)*factor in jaar 1978. Ofwel:
15000 * factor³ = 117000
factor = (117000/15000)^1/3
a. De drie grootste merken hebben samen een marktaandeel van 34%. 20 moeten daartoe behoren, dus 40 niet. De kans wordt gegeven door 20-boven-60 * (0.34)^20 * (1-0.34)^40. De factor 20-boven-60 zorgt ervoor dat de 20 niet alleen de eerste 20 hoeven te zijn, maar bijvoorbeeld ook de laatste 20, of ergens 10 en later nog eens 10, etc.quote:H5. De binomiale verdeling
53. De drie grootste automerken in nederland zijn opel, volkswagen en Ford. van de auto;s in Nederland is 13% van het merk opel , 12 % van het merk wolkswagen en 9% van het merk Ford.
Nummers vier is Renault met 8% en nummer vijf is peugeot met 7 %. Bereken in vier decimlane nauwkeurig de kans dat van 60 willekeurige aangewezen auto's er
a) precies 20 tot de drie grootste merken behoren
b) 14, 15 of 16 van het merk opel of volkswagen zijn
b. Zelfde als bij a; de kans voor 14, 15 en 16 optellen
54 gaat bijna hetzelfde als 53, maar dan met een dobbelsteen. De kans op 'meer dan twee keer 6 ogen' is 1-[kans minder dan 3 keer 6 ogen].
Gemiddelde kosten zijn totale kosten gedeeld door het aantal stuks. Pas op dat je bij de formule in honderdtallen in moet vullen.quote:62. De dagelijkse kosten bij de productie van een wekkerradio zijn gegeven door de formule K = 1,2q³ - 8q² + 25q + 22. Hierin is K in duizenden gulden en is q het aantal per dag geproduceerde wekkerradio's in honderdtallen. De formule geldt voor
0 <(met = teken eronder) q < (met = teken eronder ) 8
B) hoeveel zijn de gemiddelde kosten per wekkerradio bij een productie van 150 wekkerradio's
c) maak een tabel met differentiequotiënten op [0,a] met a = 1, 2, 4, 5, 6, 7, en 8. WElke betekenis hebben deze differentiequotiënten?
Het differentiequotient op [0,a] wordt gegeven door (f(a)-f(0))/(a-0). Wat dat betekent kun je, met het oog op a, zelf bedenken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Een bal wordt met 33 m/s op 1m hoogte weggeslagen. Bereken de horizontaal afgelegde afstand als de bal de grond raakt.
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t = s
Sx(t)= 30 x t.
Hoe vind je t?
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t = s
Sx(t)= 30 x t.
Hoe vind je t?


Hoe kun je erachter komen (zonder GR) wanneer
(-sin(x)+2cos(x)) en (sin(x)+2cos(x))
beiden positief zijn ?
(-sin(x)+2cos(x)) en (sin(x)+2cos(x))
beiden positief zijn ?


Er is misschien een ingenieuzere manier te bedenken, maar ik weet nog van de middelbare school dat je dan de nulpunten moest herleiden (en eventueel limieten, maar dat zal hier wel meevallen), en dan kon je in de gedeeltes daartussen gewoon een waarde invullen en zien of ie positief of negatief was.
They told me all of my cages were mental, so I got wasted like all my potential.


offtopic: Ik was lekker eerstquote:Op dinsdag 17 januari 2006 15:45 schreef doepta het volgende:
Hoi mensen,
Ik heb hier een hele rare opgave voor me:
Elk getal van drie cijfers kun je achterstevoren opschrijven. 176 kun je omdraaien tot 671.
Bepaal alle getallen van drie cijfers die gelijk zijn aan 3 maal hun omgedraaide plus de som van hun cijfers.
Ik snap vooral de laatste zin niet, hoe schrijf je die om tot een formule? En wat moet je dan verder doen?
(Als dit het verkeerde forum/topic ik, hoor ik het graag).
Groeten,
Doepta
Even met de computer bepaald:
000
441
882


Je rekent eerst met y(t) = 1/2 g t^2 eerst de tijd uit hoelang die bal 'onderweg' is. y(t0 = natuurlijk 1 m. Het maakt namelijk niet uit (zonder wrijving iig) of je de bal horizontaal wegschiet of gewoon laat vallen: beide ballen zullen tegelijk aankomen.quote:Op dinsdag 17 januari 2006 13:12 schreef Koewam het volgende:
Een bal wordt met 33 m/s op 1m hoogte weggeslagen. Bereken de horizontaal afgelegde afstand als de bal de grond raakt.
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t = s
Sx(t)= 30 x t.
Hoe vind je t?
Dan vul je in x(t) = v*t de horizontale afstand uit (v = 33 m/s).
Als het goed is moet x iets lager liggen dan 15 m.
we hebben een reëel probleem, dus we zoeken naar reële oplossingen
in dit specifieke geval maken twee helften één
in dit specifieke geval maken twee helften één


Ok, even een (stom en wrs) makkelijk vraagje.
20 - 1,282 * (wortel uit 20 * 80/200) - 50/200 = ...
Hoe de f*ck tik je dat goed op je rekenmachien in?!
Het antwoord moet zijn 16,12, maar ik krijg er van alles uit, behalve dat
20 - 1,282 * (wortel uit 20 * 80/200) - 50/200 = ...
Hoe de f*ck tik je dat goed op je rekenmachien in?!
Het antwoord moet zijn 16,12, maar ik krijg er van alles uit, behalve dat


je bent er bijna t kan je toch gewoon oplossen uit de vergelijking?quote:Op dinsdag 17 januari 2006 13:12 schreef Koewam het volgende:
Een bal wordt met 33 m/s op 1m hoogte weggeslagen. Bereken de horizontaal afgelegde afstand als de bal de grond raakt.
Dit is meer wiskunde, ik kom er friggin' niet uit, hoe vaak ik dit gtedaan heb
Sy(t)= 1/2 x 9,81 x t 2.
1= 1/2 x 9,81 x t 2.
t = s
Sx(t)= 30 x t.
Hoe vind je t?
Sy(t)= 1/2 * g * t 2 = 1
Dus t = Sqrt(2/g)
En dan invullen in die andere vergelijking:
Sx(t)= v * t = 33 * Sqrt(2/g) = 14.9 (afgerond)
Theories come and theories go. The frog remains