W&T Wetenschap & Technologie
Een plek om te discussiëren over wetenschappelijke onderwerpen, wetenschappelijke problemen, technologische projecten en grootse uitvindingen.



Velen hebben bij Wiskunde vooral de associatie ‘saai!’, niet in het minst gevoed door ellenlange rijtjes vergelijkingen die opgelost moesten worden. En het woord ‘bewijs’ roept natuurlijk al helemaal de ergste herinneringen op.
Desondanks denk ik dat er wiskundige bewijzen zijn die toch een zekere schoonheid hebben. Het is moeilijk uit te leggen wat het precies is, dus daarom wordt het – hopelijk – duidelijk in deze topic.
Als je het niet snapt, vraag gerust. Dan zal ik het iets duidelijker proberen te maken, en anders gaan we gewoon verder naar het volgende bewijs.
Desondanks denk ik dat er wiskundige bewijzen zijn die toch een zekere schoonheid hebben. Het is moeilijk uit te leggen wat het precies is, dus daarom wordt het – hopelijk – duidelijk in deze topic.
Als je het niet snapt, vraag gerust. Dan zal ik het iets duidelijker proberen te maken, en anders gaan we gewoon verder naar het volgende bewijs.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn. De bedenker, Euklides, leefde zo ongeveer 2300 jaar geleden.
Het bewijs is zo belangrijk omdat het zo ongelooflijk elegant is, en omdat priemgetallen tot op de dag van vandaag fascinerend blijven. Er zijn veel vragen nog niet beantwoord, maar eentje in ieder geval wel: er zijn er namelijk oneindig veel. Er kan dus altijd gezocht worden naar nóg een groter priemgetal.
Als eerste: Een priemgetal is een getal dat precies twee delers heeft: 1 en zichzelf. Bijvoorbeeld 13, of 17, of 1009. Het getal 1 wordt meestal niet als priemgetal beschouwd. Maar nu het bewijs.
Neem aan dat er eindig veel priemgetallen zijn. Zeg, n priemgetallen, waarbij n misschien wel heel groot is, maar toch eindig. We kunnen al die getallen nu op een rijtje zetten: p1, p2, p3, ..., pn. Bereken nu E = p1·p2···pn + 1. Dus vermenigvuldig al die getallen met elkaar, en tel er 1 bij op.
Het is duidelijk dat dit getal E niet deelbaar is door p1, want je houdt nog rest 1 over. Ook niet door p2, daar geldt hetzelfde voor, zo geldt dat voor al die priemgetallen tot en met pn.
Dit betekent óf dat E zelf een priemgetal is, of als het geen priemgetal is (en dus deelbaar is door een ander priemgetal), dat het dan deelbaar is door een priemgetal dat niet in ons rijtje zat.
Maar we hadden aangenomen dat ons rijtje alle priemgetallen bevat. Die aanname moet wel fout zijn, want we komen nu op een tegenspraak uit. Kortom, er moeten wel oneindig veel priemgetallen zijn. □
Dat was het al. Andere, relatief eenvoudige vragen, zoals: zijn er ook oneindig veel paartjes van getallen zoals 17 en 19, of 107 en 109, die maar 2 van elkaar verschillen en allebei priem zijn, of kun je elk getal groter dan 3 als de som van precies twee priemgetallen schrijven, zijn tot op de dag van vandaag niet beantwoord.
Andere, relatief eenvoudige vragen, zoals: zijn er ook oneindig veel paartjes van getallen zoals 17 en 19, of 107 en 109, die maar 2 van elkaar verschillen en allebei priem zijn, of kun je elk getal groter dan 3 als de som van precies twee priemgetallen schrijven, zijn tot op de dag van vandaag niet beantwoord.
Het bewijs is zo belangrijk omdat het zo ongelooflijk elegant is, en omdat priemgetallen tot op de dag van vandaag fascinerend blijven. Er zijn veel vragen nog niet beantwoord, maar eentje in ieder geval wel: er zijn er namelijk oneindig veel. Er kan dus altijd gezocht worden naar nóg een groter priemgetal.
Als eerste: Een priemgetal is een getal dat precies twee delers heeft: 1 en zichzelf. Bijvoorbeeld 13, of 17, of 1009. Het getal 1 wordt meestal niet als priemgetal beschouwd. Maar nu het bewijs.
Neem aan dat er eindig veel priemgetallen zijn. Zeg, n priemgetallen, waarbij n misschien wel heel groot is, maar toch eindig. We kunnen al die getallen nu op een rijtje zetten: p1, p2, p3, ..., pn. Bereken nu E = p1·p2···pn + 1. Dus vermenigvuldig al die getallen met elkaar, en tel er 1 bij op.
Het is duidelijk dat dit getal E niet deelbaar is door p1, want je houdt nog rest 1 over. Ook niet door p2, daar geldt hetzelfde voor, zo geldt dat voor al die priemgetallen tot en met pn.
Dit betekent óf dat E zelf een priemgetal is, of als het geen priemgetal is (en dus deelbaar is door een ander priemgetal), dat het dan deelbaar is door een priemgetal dat niet in ons rijtje zat.
Maar we hadden aangenomen dat ons rijtje alle priemgetallen bevat. Die aanname moet wel fout zijn, want we komen nu op een tegenspraak uit. Kortom, er moeten wel oneindig veel priemgetallen zijn. □
Dat was het al.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


hier verlies je mequote:Neem aan dat er eindig veel priemgetallen zijn. Zeg, n priemgetallen, waarbij n misschien wel heel groot is, maar toch eindig. We kunnen al die getallen nu op een rijtje zetten: p1, p2, p3, ..., pn. Bereken nu E = p1·p2···pn + 1. Dus vermenigvuldig al die getallen met elkaar, en tel er 1 bij op.
Waarom wil je dit doen? Niet alleen alle priemgetallen met elkaar vermedigvuldigen, maar ook nog eens '1' bij optellen?
Overigens wat ik zelf een mooie wetmatigheid vind in de wiskunde:
als je alle cijfers in een getal optelt, en je kan dat door 3 delen (en de uitkomst is een heel getal), is het originele getal ook te delen door drie.
Dus: 81 = 8+1=9
9 kan je delen door 3 dus 81 kan je delen door 3
3528921= 3+5+2+8+9+2+1 = 30
30 kan je delen door 3 dus 3528921 kan je delen door 3
8592847932= 8+5+9+2+8+4+7+9+3+2 = 57
57= 5+7=12
12= 1+2 =3
enz.
lolwut


Maar heb je daar ook een bewijs voor?quote:Op maandag 28 september 2009 22:29 schreef BrandX het volgende:
Overigens wat ik zelf een mooie wetmatigheid vind in de wiskunde:
als je alle cijfers in een getal optelt, en je kan dat door 3 delen (en de uitkomst is een heel getal), is het originele getal ook te delen door drie.
Dus: 81 = 8+1=9
9 kan je delen door 3 dus 81 kan je delen door 3
3528921= 3+5+2+8+9+2+1 = 30
30 kan je delen door 3 dus 3528921 kan je delen door 3
8592847932= 8+5+9+2+8+4+7+9+3+2 = 57
57= 5+7=12
12= 1+2 =3
enz.
Ook geen sig dus


ik geef je drie rekenvoorbeelden als bewijs?quote:Op maandag 28 september 2009 22:32 schreef Dennis_enzo het volgende:
[..]
Maar heb je daar ook een bewijs voor?
edit:: ff voor je gegoogled
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.niet dat ik het verhaal snap, maar dit is de wetenschappelijke verklaring lolwut
lolwut


Een voorbeeld is nooit een bewijs in de wiskunde. Al geef je 1000 voorbeelden, je hebt het niet bewezenquote:Op maandag 28 september 2009 22:33 schreef BrandX het volgende:
[..]
ik geef je drie rekenvoorbeelden als bewijs?
Ook geen sig dus


Zie mijn editquote:Op maandag 28 september 2009 22:34 schreef Dennis_enzo het volgende:
[..]
Een voorbeeld is nooit een bewijs in de wiskunde. Al geef je 1000 voorbeelden, je hebt het niet bewezen
lolwut


quote:Op maandag 28 september 2009 22:33 schreef BrandX het volgende:
[..]
ik geef je drie rekenvoorbeelden als bewijs?
edit:: ff voor je gegoogledH0 = Het is toeval, dat hij 3 toevallig rekenvoorbeelden geeft.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.niet dat ik het verhaal snap, maar dit is de wetenschappelijke verklaring
H1 = H0 is niet waar.


Als je alle getallen met elkaar vermenigvuldigt is het getal dat je dan krijgt deelbaar door al die getallen, als je er dan 1 bij optelt is ie weer slechts deelbaar door zichzelf en door 1, dat betekent dat je een nieuw priemgetal hebt en dat er dus geen eindigheid bestaat in de reeks priemgetallen.quote:Op maandag 28 september 2009 22:29 schreef BrandX het volgende:
[..]
hier verlies je me
Waarom wil je dit doen? Niet alleen alle priemgetallen met elkaar vermedigvuldigen, maar ook nog eens '1' bij optellen?
Fietstas.


ok, ok, als dit topic uitsluitend voor wiskundebollendozen is kan ik beter wegblijven.
Iblis, kan jij mijn vraag in de fipo beantwoorden?
lolwut


ah zo! Helder, thanks.quote:Op maandag 28 september 2009 22:38 schreef Kassaa het volgende:
[..]
Als je alle getallen met elkaar vermenigvuldigt is het getal dat je dan krijgt deelbaar door al die getallen, als je er dan 1 bij optelt is ie weer slechts deelbaar door zichzelf en door 1, dat betekent dat je een nieuw priemgetal hebt en dat er dus geen eindigheid bestaat in de reeks priemgetallen.
lolwut


Nee, het produkt + 1 hoeft geen priemgetal te zijn.quote:Op maandag 28 september 2009 22:38 schreef Kassaa het volgende:
[..]
Als je alle getallen met elkaar vermenigvuldigt is het getal dat je dan krijgt deelbaar door al die getallen, als je er dan 1 bij optelt is ie weer slechts deelbaar door zichzelf en door 1, dat betekent dat je een nieuw priemgetal hebt en dat er dus geen eindigheid bestaat in de reeks priemgetallen.
Het idee is als volgt:
Stel dat Pn het n-de priemgetal is en het grootste priemgetal dat je kent. Dan is het produkt van alle priemgetallen tot en met Pn :
P1*P2*P3* ... *Pn-1*Pn
Deelbaar door elk van zijn factoren Px, oftewel door alle priemgetallen tot en met Pn
Als je er 1 bij optelt, dan hou je bij deling door een willekeurig priemgetal Px een rest 1 over. Pn is dus niet meer deelbaar door alle priemgetallen tot en met Pn en is dan of zelf een priemgetal of deelbaar door een priemgetal groter dan Pn. Je kan overigens het produkt van alle priemgetallen in dit bewijs ook prima vervangen door faculteit, als je dat makkelijker vindt
[ Bericht 9% gewijzigd door #ANONIEM op 28-09-2009 22:49:18 ]


Dat is in feite de truc. Het is slim om dat te doen. Want daarmee bereik je precies wat je wilt. Het is misschien te vergelijken met vragen waarom zet Rembrandt daar net dat lichtaccent neer? Het had ook ergens anders gekund, maar juist door het dáár te doen bereikt hij zo’n magisch effect.quote:Op maandag 28 september 2009 22:29 schreef BrandX het volgende:
[..]
hier verlies je me
Waarom wil je dit doen? Niet alleen alle priemgetallen met elkaar vermedigvuldigen, maar ook nog eens '1' bij optellen?
Het doel bij dit bewijs is dat we willen aantonen dat er oneindig veel priemgetallen zijn. We beginnen nu met aannemen dat er maar eindig veel zijn. De truc is nu om op een of andere manier te bewijzen dat je, als je dat doet, ‘enige priemgetallen overslaat’. Als je ze allemaal op een rijtje zet, dat je rijtje tóch niet compleet is.
Het rijtje is dus p1 t/m pn. De slimmigheid zit ’m nu in die vermenigvuldiging. Dat is waar het wiskundig inzicht en de genialiteit van Euklides naar voren komt. Als je dat leest denk je: dát is een slimme zet. Juist die + 1 na het vermenigvuldigen is in feit het slimme.
Doordat hij dat doet, kan hij daarna zeggen: en het nieuwe getal (E dus) is niet deelbaar door p1, niet door p2, enzovoort. Als hij die + 1 niet had gedaan, dan was het bewijs niet van de grond gekomen. Dus juist daar zit de slimmigheid van het bewijs.
Ik hoop dat het duidelijk is.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Na twee keer lezen wel ja! Het mooie zit 'em inderdaad in de simpelheid van de +1quote:Op maandag 28 september 2009 22:47 schreef Iblis het volgende:
[..]
Dat is in feite de truc. Het is slim om dat te doen. Want daarmee bereik je precies wat je wilt. Het is misschien te vergelijken met vragen waarom zet Rembrandt daar net dat lichtaccent neer? Het had ook ergens anders gekund, maar juist door het dáár te doen bereikt hij zo’n magisch effect.
Het doel bij dit bewijs is dat we willen aantonen dat er oneindig veel priemgetallen zijn. We beginnen nu met aannemen dat er maar eindig veel zijn. De truc is nu om op een of andere manier te bewijzen dat je, als je dat doet, ‘enige priemgetallen overslaat’. Als je ze allemaal op een rijtje zet, dat je rijtje tóch niet compleet is.
Het rijtje is dus p1 t/m pn. De slimmigheid zit ’m nu in die vermenigvuldiging. Dat is waar het wiskundig inzicht en de genialiteit van Euklides naar voren komt. Als je dat leest denk je: dát is een slimme zet. Juist die + 1 na het vermenigvuldigen is in feit het slimme.
Doordat hij dat doet, kan hij daarna zeggen: en het nieuwe getal (E dus) is niet deelbaar door p1, niet door p2, enzovoort. Als hij die + 1 niet had gedaan, dan was het bewijs niet van de grond gekomen. Dus juist daar zit de slimmigheid van het bewijs.
Ik hoop dat het duidelijk is.
BIjna zo simpel dat het daardoor briljant is.
lolwut


Daarmee kom je trouwens wel weer bij een nieuwe interessante vraag uit:
Had je op de een of andere manier kunnen weten dat je met +1 een bewijs kunt maken, of is dat alleen maar intuïtie en geluk?
Anders gezegd: als je een willekeurige wiskundige stelling hebt, kan een computer deze stelling dan bewijzen of weerleggen?
Nee. Om dat te laten zien moeten we de vraagstelling iets anders formuleren:
Zijn er wiskundige stellingen, waarvan een turing-machine niet zou kunnen zeggen of ze waar zijn of niet?
Ja.
Bewijzen door middel van tegenspraak zijn leuk. Dus:
Aanname: het kan wel. Dan kunnen we dus een computerprogramma maken dat de volgende taak uitvoert:
Om van enig praktisch nut te zijn, moet dit programma uiteraard ooit een antwoord geven, want als het programma voor sommige stellingen in een oneindige lus geraakt en dus nooit antwoord geeft, heb je er ook niks aan.
Stel nou dus, dat er een programma test_stelling bestaat, dat altijd eindigt. Dan kunnen we dat programma ook weer gebruiken om te kijken of andere programma's eindigen. In het bijzonder kunnen we Programma ( Programma ) eindigt als stelling nemen en deze stelling laten testen:
Wat doet deze functie?
Als de stelling Programma ( Programma ) eindigt waar is, komt het programma 'test' in een oneindige lus en eindigt dus niet.
Als Programma ( Programma ) eindigt niet waar is, is het programma 'test' meteen klaar.
En nu komt de truc:
Nou zijn er twee opties:
1. test_stelling ( test ( test ) eindigt ) == 'ja', maar dat betekent dat test ( test ) in een oneindige lus raakt en dus niet eindigt, tegenspraak!
2. test_stelling ( test ( test ) eindigt ) == 'nee', maar dat betekent dat test ( test ) meteen klaar is en dus wel eindigt, tegenspraak!
M.a.w. de aanname was fout. Het kan dus niet.
Edit: Toen ik wiskunde studeerde deden we nooit aan bronvermeldingen. Maar ik geloof dat het wel zo netjes is, dus ik zal er maar even bij vermelden dat dit bewijs werd geleverd door Turing en ook wel het 'stopprobleem' wordt genoemd.
En nou hoop ik maar dat ik zo laat op de avond met m'n slaperige hoofd geen fout heb gemaakt...
[ Bericht 3% gewijzigd door #ANONIEM op 29-09-2009 00:01:48 ]
Had je op de een of andere manier kunnen weten dat je met +1 een bewijs kunt maken, of is dat alleen maar intuïtie en geluk?
Anders gezegd: als je een willekeurige wiskundige stelling hebt, kan een computer deze stelling dan bewijzen of weerleggen?
Nee. Om dat te laten zien moeten we de vraagstelling iets anders formuleren:
Zijn er wiskundige stellingen, waarvan een turing-machine niet zou kunnen zeggen of ze waar zijn of niet?
Ja.
Bewijzen door middel van tegenspraak zijn leuk. Dus:
Aanname: het kan wel. Dan kunnen we dus een computerprogramma maken dat de volgende taak uitvoert:
| 1 2 3 | als Stelling waar: antwoord 'ja' anders: antwoord 'nee' |
Om van enig praktisch nut te zijn, moet dit programma uiteraard ooit een antwoord geven, want als het programma voor sommige stellingen in een oneindige lus geraakt en dus nooit antwoord geeft, heb je er ook niks aan.
Stel nou dus, dat er een programma test_stelling bestaat, dat altijd eindigt. Dan kunnen we dat programma ook weer gebruiken om te kijken of andere programma's eindigen. In het bijzonder kunnen we Programma ( Programma ) eindigt als stelling nemen en deze stelling laten testen:
| 1 2 | doe niks zolang test_stelling ( Programma ( Programma ) eindigt ) == 'ja' |
Wat doet deze functie?
Als de stelling Programma ( Programma ) eindigt waar is, komt het programma 'test' in een oneindige lus en eindigt dus niet.
Als Programma ( Programma ) eindigt niet waar is, is het programma 'test' meteen klaar.
En nu komt de truc:
| 1 |
Nou zijn er twee opties:
1. test_stelling ( test ( test ) eindigt ) == 'ja', maar dat betekent dat test ( test ) in een oneindige lus raakt en dus niet eindigt, tegenspraak!
2. test_stelling ( test ( test ) eindigt ) == 'nee', maar dat betekent dat test ( test ) meteen klaar is en dus wel eindigt, tegenspraak!
M.a.w. de aanname was fout. Het kan dus niet.
Edit: Toen ik wiskunde studeerde deden we nooit aan bronvermeldingen. Maar ik geloof dat het wel zo netjes is, dus ik zal er maar even bij vermelden dat dit bewijs werd geleverd door Turing en ook wel het 'stopprobleem' wordt genoemd.
En nou hoop ik maar dat ik zo laat op de avond met m'n slaperige hoofd geen fout heb gemaakt...
[ Bericht 3% gewijzigd door #ANONIEM op 29-09-2009 00:01:48 ]


Vierkantswortel van 2 is geen rationaal getal (maw kan niet als breuk van twee gehele getallen geschreven worden.)
(in het volgende stelt a een geheel getal voor)
Wat is een even getal? Een getal dat geschreven kan worden als 2*a
a=0 geeft 0 a=1 geeft 2 etc..
Een oneven getal kan geschreven worden als (2*a + 1) (dus een even getal +1)
a=0 geeft 1 a=1 geeft 3 etc...
Eerst bewijzen we dat het kwadraat van een even getal even is, en het kwadraat van een oneven getal oneven:
(2*a)2=4 * a2 = 2 * (2*a2); dus even
(2*a+1)2 = 4*a2 + 4*a + 1 = 2*(2*a2 + 2*a) + 1 (eerste term is even want factor twee; plus één wordt dus oneven)
Een rationaal getal is een getal dat geschreven kan worden als een breuk van gehele getallen. Elke breuk kan vereenvoudigd worden tot z'n eenvoudigste schrijfwijze (=met de kleinst mogelijke teller en noemer), door teller en noemer te delen door hun gemeenschappelijke delers. Daaruit volgt dat elke breuk kan geschreven worden als T/N waarbij minstens één van beide ( T of N) oneven zijn; immers: als ze beide even zijn kan je ze delen door twee, en herhalen tot T of N oneven wordt.
Stel nu dat T/N = wortel van 2. waarbij minstens één van beide oneven is.
Dus: (T/N)2 = 2
of T2 = 2*N2 ---> hieruit volgt dat T2 even is. T zelf kan dan niet oneven zijn, want dan zou het kwadraat ook oneven zijn (zie boven)
Als T even is bestaat er een geheel getal K = T/2
--> T = 2*K ---> T2 = 4*K2
vervangen we T door 2*K in bovenstaande vergelijking
4*K2=2*N2
of (linker en rechterhelft delen door twee)
2*K2=N2
dus N kwadraat is even, N zelf dus ook. En we hadden reeds gevonden dat T even was. Wat in tegenspraak is met onze veronderstelling, dat T en N niet beide even kunnen zijn.
Onze veronderstelling leidt tot een tegenspraak, maw, T en N bestaan niet (als eindige getallen)
(btw: let erop dat de conclusie T2 = even, dus T is even volgt uit de stelling dat het kwadraat van een oneven getal oneven is, niet uit de stelling dat het kwadraat van een even getal even is. Nederlanders zijn mensen betekent niet dat mensen Nederlanders zijn)
(in het volgende stelt a een geheel getal voor)
Wat is een even getal? Een getal dat geschreven kan worden als 2*a
a=0 geeft 0 a=1 geeft 2 etc..
Een oneven getal kan geschreven worden als (2*a + 1) (dus een even getal +1)
a=0 geeft 1 a=1 geeft 3 etc...
Eerst bewijzen we dat het kwadraat van een even getal even is, en het kwadraat van een oneven getal oneven:
(2*a)2=4 * a2 = 2 * (2*a2); dus even
(2*a+1)2 = 4*a2 + 4*a + 1 = 2*(2*a2 + 2*a) + 1 (eerste term is even want factor twee; plus één wordt dus oneven)
Een rationaal getal is een getal dat geschreven kan worden als een breuk van gehele getallen. Elke breuk kan vereenvoudigd worden tot z'n eenvoudigste schrijfwijze (=met de kleinst mogelijke teller en noemer), door teller en noemer te delen door hun gemeenschappelijke delers. Daaruit volgt dat elke breuk kan geschreven worden als T/N waarbij minstens één van beide ( T of N) oneven zijn; immers: als ze beide even zijn kan je ze delen door twee, en herhalen tot T of N oneven wordt.
Stel nu dat T/N = wortel van 2. waarbij minstens één van beide oneven is.
Dus: (T/N)2 = 2
of T2 = 2*N2 ---> hieruit volgt dat T2 even is. T zelf kan dan niet oneven zijn, want dan zou het kwadraat ook oneven zijn (zie boven)
Als T even is bestaat er een geheel getal K = T/2
--> T = 2*K ---> T2 = 4*K2
vervangen we T door 2*K in bovenstaande vergelijking
4*K2=2*N2
of (linker en rechterhelft delen door twee)
2*K2=N2
dus N kwadraat is even, N zelf dus ook. En we hadden reeds gevonden dat T even was. Wat in tegenspraak is met onze veronderstelling, dat T en N niet beide even kunnen zijn.
Onze veronderstelling leidt tot een tegenspraak, maw, T en N bestaan niet (als eindige getallen)
(btw: let erop dat de conclusie T2 = even, dus T is even volgt uit de stelling dat het kwadraat van een oneven getal oneven is, niet uit de stelling dat het kwadraat van een even getal even is. Nederlanders zijn mensen betekent niet dat mensen Nederlanders zijn)
I'll be back


quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn. De bedenker, Euklides, leefde zo ongeveer 2300 jaar geleden.
Het bewijs is zo belangrijk omdat het zo ongelooflijk elegant is, en omdat priemgetallen tot op de dag van vandaag fascinerend blijven. Er zijn veel vragen nog niet beantwoord, maar eentje in ieder geval wel: er zijn er namelijk oneindig veel. Er kan dus altijd gezocht worden naar nóg een groter priemgetal.
Als eerste: Een priemgetal is een getal dat precies twee delers heeft: 1 en zichzelf. Bijvoorbeeld 13, of 17, of 1009. Het getal 1 wordt meestal niet als priemgetal beschouwd. Maar nu het bewijs.
Neem aan dat er eindig veel priemgetallen zijn. Zeg, n priemgetallen, waarbij n misschien wel heel groot is, maar toch eindig. We kunnen al die getallen nu op een rijtje zetten: p1, p2, p3, ..., pn. Bereken nu E = p1·p2···pn + 1. Dus vermenigvuldig al die getallen met elkaar, en tel er 1 bij op.
Het is duidelijk dat dit getal E niet deelbaar is door p1, want je houdt nog rest 1 over. Ook niet door p2, daar geldt hetzelfde voor, zo geldt dat voor al die priemgetallen tot en met pn.
Dit betekent óf dat E zelf een priemgetal is, of als het geen priemgetal is (en dus deelbaar is door een ander priemgetal), dat het dan deelbaar is door een priemgetal dat niet in ons rijtje zat.
Maar we hadden aangenomen dat ons rijtje alle priemgetallen bevat. Die aanname moet wel fout zijn, want we komen nu op een tegenspraak uit. Kortom, er moeten wel oneindig veel priemgetallen zijn. □
Dat was het al.Andere, relatief eenvoudige vragen, zoals: zijn er ook oneindig veel paartjes van getallen zoals 17 en 19, of 107 en 109, die maar 2 van elkaar verschillen en allebei priem zijn, of kun je elk getal groter dan 3 als de som van precies twee priemgetallen schrijven, zijn tot op de dag van vandaag niet beantwoord.
Ik vind wiskunde nog steeds saai geloof ikSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Eindelijk iemand die denkt wat iedereen zegt


Tijd voor een nieuwe stelling, wederom een over priemgetallen. Ik zal eerst de stelling uitleggen, later een bewijs.
We kunnen ons afvragen welke priemgetallen p te schrijven zijn als som van twee kwadraten. De welbekende identiteit 1 + 1 = 2 laat zien dat 2 hier in elk geval aan voldoet, waarna we ons kunnen concentreren op de oneven priemgetallen.
Wil een som van twee kwadraten oneven zijn, dan zal precies 1 van deze kwadraten even moeten zijn en de andere oneven. Een even kwadraat is altijd deelbaar door 4 en een oneven kwadraat is altijd 1 modulo 4. We zien dus dat p sowieso 1 modulo 4 zal moeten zijn en priemgetallen die 3 modulo 4 zijn, zoals 3, 7, 11, etc kunnen dan ook niet als som van twee kwadraten geschreven worden. De stelling zegt nu dat ook het omgekeerde geldt:
Stelling. Elk priemgetal dat 1 modulo 4 is kan geschreven worden als de som van twee kwadraten.
Er zijn meerdere bewijzen van deze stelling bekend, eigenlijk allemaal wel behoorlijk fraai. Om de spanning op te voeren en om de stelling even te laten bezinken bij de lezer zal ik nog even wachten met het posten van het fraaiste bewijs.
We kunnen ons afvragen welke priemgetallen p te schrijven zijn als som van twee kwadraten. De welbekende identiteit 1 + 1 = 2 laat zien dat 2 hier in elk geval aan voldoet, waarna we ons kunnen concentreren op de oneven priemgetallen.
Wil een som van twee kwadraten oneven zijn, dan zal precies 1 van deze kwadraten even moeten zijn en de andere oneven. Een even kwadraat is altijd deelbaar door 4 en een oneven kwadraat is altijd 1 modulo 4. We zien dus dat p sowieso 1 modulo 4 zal moeten zijn en priemgetallen die 3 modulo 4 zijn, zoals 3, 7, 11, etc kunnen dan ook niet als som van twee kwadraten geschreven worden. De stelling zegt nu dat ook het omgekeerde geldt:
Stelling. Elk priemgetal dat 1 modulo 4 is kan geschreven worden als de som van twee kwadraten.
Er zijn meerdere bewijzen van deze stelling bekend, eigenlijk allemaal wel behoorlijk fraai. Om de spanning op te voeren en om de stelling even te laten bezinken bij de lezer zal ik nog even wachten met het posten van het fraaiste bewijs.


tvp als wiskundestudent 
-----------------------------------------------------
So happy to show us, I ate the lotus
... and I feel fine.
So happy to show us, I ate the lotus
... and I feel fine.


Geinig 
I have the cape. I make the fucking Whoosh noise.
Op donderdag 12 juli 2012 19:56 schreef Lithia het volgende:
Ik durf hier niets over te zeggen. Bart is koning hier.
Op donderdag 12 juli 2012 19:56 schreef Lithia het volgende:
Ik durf hier niets over te zeggen. Bart is koning hier.


tvp, ik ben benieuwd naar het bewijs van thabit
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten


Tijd voor een bewijs, inderdaad. Het bewijs dat ik hier geef is afkomstig van Don Zagier, onthoud die naam.quote:Op dinsdag 29 september 2009 10:41 schreef thabit het volgende:
Stelling. Elk priemgetal dat 1 modulo 4 is kan geschreven worden als de som van twee kwadraten.
Zij p = 4k + 1 een priemgetal. We gaan kijken naar alle oplossingen van de vergelijking
(*) x2 + 4yz = p
in positieve gehele getallen x, y en z. Het doel is om aan te tonen dat er een oplossing bestaat met y=z. Zo'n oplossing geeft dan namelijk x2 + (2y)2.
De grap is nu, dat we oplossingen in paren kunnen opdelen: als (x,y,z) een oplossing van (*) is, dan is (x,z,y) dat ook. De oplossingen met y=z zijn precies diegenen die onder deze paring aan zichzelf zijn gekoppeld. Het doel is nu, om aan te tonen dat (*) een oneven aantal oplossingen heeft: als dat zo is, moet er onder de paring een oplossing zijn die bij zichzelf hoort, en dus y=z heeft.
Om aan te tonen dat (*) een oneven aantal oplossingen heeft definieren we een andere paring op de verzameling oplossingen. Hiervoor jat ik gewoon een plaatje van Wikipedia:
Zagier claimt nu 2 dingen:
(a) Dit is inderdaad een paring op de oplossingen van (*).
(b) Het enige punt dat aan zichzelf gekoppeld wordt is (1, 1, k).
Laten we eerst eens aannemen dat dit klopt, dan bewijzen we de claims morgen wel.


De mooiste bewijzen zijn de bewijzen waar je een half uur naar kijkt om dan "ow zo doen ze dat" te zeggen
"Those unforgettable days, for them I live"


tvp, thabit kan het dat ik les van je hebt gehad voor Algebra 1 in Leiden? 
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.


Ik heb nog een wat simpeler bewijs, voor een andere stelling. Namelijk, de som van de eerste n oneven getallen is altijd een kwadraat. B.v. 1 + 3 = 4 = 22, 1 + 3 + 5 = 9 = 32. En 1 + 3 + 5 + 7 = 16 = 42, en 1 + 3 + 5 + 7 + 9 = 25 = 52. Dat doet zelfs vermoeden dat we kunnen zeggen: de som van de eerste n oneven getallen is n2.
Nu, zie hier:
Bron: Wikimedia Commons. Maker: Anynobody. Licentie: CC-BY-SA.
Tevens laat dit mooi zien waarom kwadraat eigenlijk ‘vierkant’ betekent.
Nu, zie hier:
Bron: Wikimedia Commons. Maker: Anynobody. Licentie: CC-BY-SA.
Tevens laat dit mooi zien waarom kwadraat eigenlijk ‘vierkant’ betekent.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


De illustratie maakt het mooi inzichtelijk maar is natuurlijk geen bewijs. Ik vind dit eigenlijk vrij triviaal en je kunt het eenvoudig ook inductief bewijzen:quote:Op dinsdag 29 september 2009 22:54 schreef Iblis het volgende:
Ik heb nog een wat simpeler bewijs, voor een andere stelling. Namelijk, de som van de eerste n oneven getallen is altijd een kwadraat. B.v. 1 + 3 = 4 = 22, 1 + 3 + 5 = 9 = 32. En 1 + 3 + 5 + 7 = 16 = 42, en 1 + 3 + 5 + 7 + 9 = 25 = 52. Dat doet zelfs vermoeden dat we kunnen zeggen: de som van de eerste n oneven getallen is n2.
Nu, zie hier:
[ link | afbeelding ]
Bron: Wikimedia Commons. Maker: Anynobody. Licentie: CC-BY-SA.
Tevens laat dit mooi zien waarom kwadraat eigenlijk ‘vierkant’ betekent.
Stel:
Sn is de som van de eerste n oneven getallen, en stel dat x = n -1
Dan is het n-de oneven getal uit te drukken als 2*n-1
Als Sn = x2 dan geldt:
Sn+1 = Sn + 2*n -1 = x2 + 2*( x+1) -1 = x2 +2*x +1 = (x+1)2
Dus als de stelling waar is voor n, dan is ie ook waar voor n+1. Voor n=1 is eenvoudig te verifieren dat de stelling klopt.
[ Bericht 0% gewijzigd door #ANONIEM op 29-09-2009 23:40:59 ]


Ik vind dat inductiebewijs veel minder inzichtelijk. Die afbeelding maakt op dezelfde manier duidelijk dat je er telkens weer een hoekje aan kunt plakken, natuurlijk, hier is ze afgekapt op het 8e oneven getal, maar de manier om naar de som van 9 oneven getallen te komen is evident. En daarmee bij 10, 11, 12, 13, enz.quote:Op dinsdag 29 september 2009 23:40 schreef ..-._---_-.- het volgende:
[..]
De illustratie maakt het mooi inzichtelijk maar is natuurlijk geen bewijs. Ik vind dit eigenlijk vrij triviaal en je kunt het eenvoudig ook inductief bewijzen:
Stel:
Sn is de som van de eerste n oneven getallen, en stel dat x = n -1
Dan is het n-de oneven getal uit te drukken als 2*n-1
Als Sn = x2 dan geldt:
Sn+1 = Sn + 2*n -1 = x2 + 2*( x+1) -1 = x2 +2*x +1 = (x+1)2
Dus als de stelling waar is voor n, dan is ie ook waar voor n+1. Voor n=1 is eenvoudig te verifieren dat de stelling klopt.
Eenzelfde soort bewijs kan overigens voor de som van 1 t/m N gegeven worden. Die som heet nota bene driehoeksgetal. Formaliseren is intens belangrijk, maar als het gaat om een idee, een beeld erachter is zo’n afbeelding m.i. van heel veel waarde.
Natuurlijk, inductie werkt ook, maar je moet inductie of als axioma aannemen of bewijzen vanuit een wel-ordenings axioma, hoe dan ook, die techniek is minder inzichtvol – maar dat is natuurlijk te betwisten als je ze al heel vaak gehanteerd hebt – dan zo’n plaatje. Wat ook echt mooi illustreert hoe een kwadraat aan z’n naam komt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Het plaatje is ook wel verhelderend, dat geef ik onmiddelijk toe. Als je trouwens de rechterbovenhoek van ieder vierkant een kleurtje zou geven dan zie je ook onmiddelijk en zonder het te hoeven uitschrijven dat (x+1)2 = x2 + 2*x +1. Het randje dat er bij komt is namelijk onder te verdelen in twee stukjes van lengte x en een los blokje, het rechterbovenhoekje.
Als je alleen maar voor inzichtelijkheid gaat kun je trouwens ook goed zonder afbeelding. Uit x2 + 2*x +1 blijkt immers al dat er 2*x+1 bijkomt en dat is altijd het volgende oneven getal.
[ Bericht 10% gewijzigd door #ANONIEM op 30-09-2009 00:02:33 ]
Als je alleen maar voor inzichtelijkheid gaat kun je trouwens ook goed zonder afbeelding. Uit x2 + 2*x +1 blijkt immers al dat er 2*x+1 bijkomt en dat is altijd het volgende oneven getal.
[ Bericht 10% gewijzigd door #ANONIEM op 30-09-2009 00:02:33 ]


Haal trouwens de fout maar even uit mijn "bewijs"  Het principe klopt, maar er zit een onnauwkeurigheid is. Dat krijg je er van als je laat op de avond met je gare hoofd nog bewijzen gaat zitten bedenken.
Het principe klopt, maar er zit een onnauwkeurigheid is. Dat krijg je er van als je laat op de avond met je gare hoofd nog bewijzen gaat zitten bedenken.
[ Bericht 0% gewijzigd door #ANONIEM op 30-09-2009 00:20:44 ]
[ Bericht 0% gewijzigd door #ANONIEM op 30-09-2009 00:20:44 ]


Stelling: Elk positief natuurlijk getal is voor wiskundigen interessant.
Bewijs: Neem aan dat er minimaal 1 positief natuurlijk getal N bestaat die voor wiskundigen niet interessant is. Dat betekent dat er ook een kleinste positief natuurlijk getal N bestaat. Het feit dat dat getal het kleinste positieve natuurlijke getal N maakt het voor wiskundigen een interessant getal. Contradictie!
QED.
[ Bericht 0% gewijzigd door Dennis_enzo op 30-09-2009 05:32:24 ]
Bewijs: Neem aan dat er minimaal 1 positief natuurlijk getal N bestaat die voor wiskundigen niet interessant is. Dat betekent dat er ook een kleinste positief natuurlijk getal N bestaat. Het feit dat dat getal het kleinste positieve natuurlijke getal N maakt het voor wiskundigen een interessant getal. Contradictie!
QED.
[ Bericht 0% gewijzigd door Dennis_enzo op 30-09-2009 05:32:24 ]
Ook geen sig dus


Tvp voor leuke bewijzen 
Ik in een aantal worden omschreven: Ondernemend | Moedig | Stout | Lief | Positief | Intuïtief | Communicatief | Humor | Creatief | Spontaan | Open | Sociaal | Vrolijk | Organisator | Pro-actief | Meedenkend | Levensgenieter | Spiritueel


quote:Op woensdag 30 september 2009 05:13 schreef Dennis_enzo het volgende:
Stelling: Elk positief natuurlijk getal is voor wiskundigen interessant.
Bewijs: Neem aan dat er minimaal 1 positief natuurlijk getal N bestaat die voor wiskundigen niet interessant is. Dat betekent dat er ook een kleinste positief natuurlijk getal N bestaat. Het feit dat dat getal het kleinste positieve natuurlijke getal N maakt het voor wiskundigen een interessant getal. Contradictie!
QED.
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.


Pythagoras is op heel veel manieren bewezen, maar het bewijs van James Garfield (de 20e president van de V.S.), alhoewel niet heel erg spectaculair, vind ik wel erg leuk:
Neem deze trapezoide (plaatje even gejat)
De oppervlakte van het ding is
O = (a+b)(a+b)/2
Dat kun je eenvoudig inzien door de trapezoide 180 gedraaid bovenop zichzelf te plaatsen, wat een vierkant met zijde (a+b) oplevert. De oppervlakte van de trapezoide is dan de helft van de oppervlakte van het vierkant.
Maar de oppervlakte is natuurlijk ook gelijk aan de som van de oppervlakten van de samenstellende rechthoekige driehoeken:
O = ab/2 + ab/2 + c2/2
Uitschrijven levert op:
(a+b)2/2 = ab + c2/2
a2 + b2 + 2ab = 2ab +c2
a2 + b2 = c2
[ Bericht 1% gewijzigd door #ANONIEM op 30-09-2009 23:26:29 ]
Neem deze trapezoide (plaatje even gejat)
De oppervlakte van het ding is
O = (a+b)(a+b)/2
Dat kun je eenvoudig inzien door de trapezoide 180 gedraaid bovenop zichzelf te plaatsen, wat een vierkant met zijde (a+b) oplevert. De oppervlakte van de trapezoide is dan de helft van de oppervlakte van het vierkant.
Maar de oppervlakte is natuurlijk ook gelijk aan de som van de oppervlakten van de samenstellende rechthoekige driehoeken:
O = ab/2 + ab/2 + c2/2
Uitschrijven levert op:
(a+b)2/2 = ab + c2/2
a2 + b2 + 2ab = 2ab +c2
a2 + b2 = c2
[ Bericht 1% gewijzigd door #ANONIEM op 30-09-2009 23:26:29 ]


Die kende ik niet, nicequote:
[quote]Op zondag 16 augustus 2009 01:12 schreef remlof het volgende:
Ik ben nog uit de tijd van de barre winters en de tolerantie [/quote]
Ik ben nog uit de tijd van de barre winters en de tolerantie [/quote]


Dit moest ik nog even afmaken. Zagier schrijft hier zelf geen bewijs van op, omdat het door een geoefende wiskundige makkelijk te verifieren is. Het is in de wiskunde dan ook zeer gebruikelijk om bewijzen die de lezer direct na kan gaan, niet op te schrijven, of daar in elk geval heel kort in te zijn. Er gebeuren hier dus ook geen bijzonder interessante dingen meer.quote:Op dinsdag 29 september 2009 22:21 schreef thabit het volgende:
[..]
Zij p = 4k + 1 een priemgetal. We gaan kijken naar alle oplossingen van de vergelijking
(*) x2 + 4yz = p
in positieve gehele getallen x, y en z. Het doel is om aan te tonen dat er een oplossing bestaat met y=z. Zo'n oplossing geeft dan namelijk x2 + (2y)2.
Zagier claimt nu 2 dingen:
(a) Dit is inderdaad een paring op de oplossingen van (*).
(b) Het enige punt dat aan zichzelf gekoppeld wordt is (1, 1, k).
Laten we eerst eens aannemen dat dit klopt, dan bewijzen we de claims morgen wel..
De fraaiheid van het bewijs zit hem er dan ook in dat het volkomen gestoord is en niet te bevatten hoe iemand erop komt; dat het volkomen elementair en direct is, maar dat het je totaal geen inzicht in wat dan ook geeft. Hieraan herken je Don Zagier: zijn voordrachten zijn ook eigenlijk altijd een soort wiskundige goochelacts, uiterst vermakelijk om naar te kijken, maar je leert er geen ene kloot van.
Laat ik vooral opmerken dat het hier cruciaal is dat p een priemgetal is: een getal als 21 is ook 1 modulo 4, maar niet te schrijven als som van twee kwadraten.
Hieruit volgt dan ook meteen dat de gevallen x = y-z en x = 2y niet kunnen voorkomen: in het eerste geval is (*) gelijk aan (y+z)2 en in het tweede geval deelbaar door 4, in geen van beide gevallen dus een priemgetal. Het is ook direct duidelijk dat door de gestelde ongelijkheden in elk van de gevallen, positieve getallen naar positieve getallen worden gestuurd. Door haakjes uit te werken kun je ook zien dat in elk van de drie gevallen de waarde van de uitdrukking x2+4yz gelijk blijft,.
We beginnen met (b): in een oplossing (x,y,z) kan x alleen naar zichzelf gestuurd worden in het tweede geval. Dan geldt ook automatisch x=y en dus p = x2 + 4xz = x(x + 4z). Omdat p een priemgetal is, moet x nu wel 1 zijn en dan hebben we automatisch y=1 en z=k.
Okee, nu (a). Hierbij moeten we eigenlijk alleen bekijken dat als je begint met een oplossing van (*) die aan een van de 3 gestelde ongelijkheden voldoet, aan welke ongelijkheid de oplossing voldoet waar je haar heenstuurt, dan weet je namelijk ook waar dat weer heen wordt gestuurd en dan kun je in alle geval direct zien dat het (x,y,z) is.
Het eerste geval wordt naar het derde geval gestuurd: er geldt altijd x+2z > 2z. Zo ook wordt het derde geval naar het eerste geval gestuurd: altijd geldt x-2y < x-2y+z = (x-y+z) + y. Een oplossing uit geval 2 wordt naar een oplossing uit geval 2 gestuurd: altijd geldt y - (x-y+z) = 2y-x-z < 2y-x en 2y-x < 2y.


Oh, mochten users ook requests kunnen plaatsen: het bewijs van 1 plus 1 gelijkstaat aan 2. Graag met zo duidelijk mogelijke uitleg!
Bedankt.
Bedankt.


Is daar wel bewijs voor? 1+1=2 is toch een axioma?quote:Op donderdag 1 oktober 2009 13:32 schreef Friek_ het volgende:
Oh, mochten users ook requests kunnen plaatsen: het bewijs van 1 plus 1 gelijkstaat aan 2. Graag met zo duidelijk mogelijke uitleg!
Bedankt.
I have the cape. I make the fucking Whoosh noise.
Op donderdag 12 juli 2012 19:56 schreef Lithia het volgende:
Ik durf hier niets over te zeggen. Bart is koning hier.
Op donderdag 12 juli 2012 19:56 schreef Lithia het volgende:
Ik durf hier niets over te zeggen. Bart is koning hier.


Hmm, toch wel:
quote:The proof starts from the Peano Postulates, which define the natural
numbers N. N is the smallest set satisfying these postulates:
P1. 1 is in N.
P2. If x is in N, then its "successor" x' is in N.
P3. There is no x such that x' = 1.
P4. If x isn't 1, then there is a y in N such that y' = x.
P5. If S is a subset of N, 1 is in S, and the implication
(x in S => x' in S) holds, then S = N.
Then you have to define addition recursively:
Def: Let a and b be in N. If b = 1, then define a + b = a'
(using P1 and P2). If b isn't 1, then let c' = b, with c in N
(using P4), and define a + b = (a + c)'.
Then you have to define 2:
Def: 2 = 1'
2 is in N by P1, P2, and the definition of 2.
Theorem: 1 + 1 = 2
Proof: Use the first part of the definition of + with a = b = 1.
Then 1 + 1 = 1' = 2 Q.E.D.
I have the cape. I make the fucking Whoosh noise.
Op donderdag 12 juli 2012 19:56 schreef Lithia het volgende:
Ik durf hier niets over te zeggen. Bart is koning hier.
Op donderdag 12 juli 2012 19:56 schreef Lithia het volgende:
Ik durf hier niets over te zeggen. Bart is koning hier.


Dat is ook al een langsgekomen in de Bèta-wiskunde huiswerktopic: [Bèta wiskunde] huiswerk- en vragentopic.quote:Op donderdag 1 oktober 2009 13:32 schreef Friek_ het volgende:
Oh, mochten users ook requests kunnen plaatsen: het bewijs van 1 plus 1 gelijkstaat aan 2. Graag met zo duidelijk mogelijke uitleg!
Bedankt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Geen idee of het een 'fraaie' afleiding is, maar ik vond deze wel fascinerend:
0,99999...=1
Uitleg: http://en.wikipedia.org/wiki/0.999...
tevens tvp
0,99999...=1
Uitleg: http://en.wikipedia.org/wiki/0.999...
tevens tvp


Bron: Wikimedia Commons. Maker: Hamilton Richards.
Licentie: CC-BY-SA. Edsger Dijkstra in 2002
Nóg een bewijs van de stelling van Pythagoras, door de Nederlandse Wiskundige en Informaticus Edsger Dijkstra. Hij is vooral bekend, nu ja, bekend – menigeen zal nooit van hem gehoord hebben, vanwege zijn werk in de informatica en zijn kortste pad algoritme: een algoritme dat je b.v. kunt gebruiken om in een applicatie als Google Maps de korste weg te vinden van A naar B. Op zich ook een elegant algoritme.
Hij was verder bekend omdat hij alles met zijn vulpen schreef. De stukjes die hij schreef worden EWD’s genoemd, en deze zijn allemaal gescand en te lezen op de universiteit waar hij lange tijd heeft gezeten: De universiteit van Austin, in Texas. In 2002 is hij in Nuenen overleden.
Dit bewijs betreft EWD 975, daarin is zijn handschrift te zien. Een HTML-versie vind je hier. Het origineel is in het Engels, maar hieronder volgt de uitwerking in het Nederlands.
Het vereist op zich alleen middelbare school kennis van wiskunde, maar is denk ik wel iets lastiger dan het vorige Pythagorasbewijs.
Stelling van Pythagoras: In een rechthoekige driehoek is het kwadraat van de lengte van de schuine zijde gelijk aan de som van de kwadraten van de twee andere zijden.
We beginnen met een willekeurige driehoek:
We weten dat de som van de hoeken α, β, γ 180°C is. Of, in radialen, π. We zouden de stelling van Pythagoras dus kunnen uitdrukken als:
γ = π/2 ⇒ a2 + b2 = c2
In woorden: Als γ een rechte hoek is, dan geldt de stelling van Pythagoras. Echter, we weten ook dat α + β + γ = π, dus als we dat invullen krijgen we:
γ = (α + β + γ) / 2 ⇔ 2γ = α + β + γ ⇔ γ = α + β
Dat is niet zo’n vreemde uitdrukking, want inderdaad als γ een rechte hoek is moet α + β ook wel 90° of π/2 zijn. We kunnen dus zeggen:
γ = α + β ⇒ a2 + b2 = c2
Dijkstra vraagt zich nu af ook geldt:
γ = α + β ≡ a2 + b2 = c2
Wat dan equivalent is aan:
γ ≠ α + β ≡ a2 + b2 ≠ c2
Hij merkt nu op dat als als x ≠ y dat dan geldt: x < y óf x > y. (Maar niet beide natuurlijk.) Zijn hypothese is nu dat je zelfs kunt zeggen dat:
α + β < γ ≡ a2 + b2 < c2
α + β > γ ≡ a2 + b2 > c2
Beschouw nu de variant van bovenstaande driehoek, we hebben twee punten H en K toegevoegd:
Dit is dus duidelijk een driehoek waarin geldt dat α + β < γ. Maar het bewijs is dus algemener, dit is alleen ter visualisatie. Maar in dit geval zien we dus dat de oppervlakte van ΔCKB en ΔAHC, die niet overlappen, kleiner is dan de oppervlakte van ΔABC. We duiden de oppervlakte van ΔCKB simpelweg aan met ‘CKB’ en van ΔAHC met ‘AHC’, enz., dan geldt voor de driehoek hierboven:
CKB + AHC < ABC
Het moge duidelijk zijn dat als α + β = γ dat H en K dan precies samenvallen (immers α + β = π/2 in dat geval) en dus geldt dan ook:
CKB + AHC = ABC.
En dat als α + β > γ, dat dan (merk trouwens op dat dit heel veel mogelijke plaatjes geeft in de relatieve positie van A, B, H, en K, dus daarom tekenen we die plaatjes ook niet ) geldt:
) geldt:
CKB + AHC > ABC.
Door nu gebruik te maken van de signum functie kunnen we heel eenvoudig schrijven:
signum(α + β - γ) = signum(CKB + AHC - ABC).
Verder valt op dat ΔABC, ΔAHC en ΔCKB gelijkvormig zijn, immers, ze hebben alle drie de hoeken α, β en γ. Omdat ze gelijkvormig zijn geldt:
CKB/a2 = AHC/b2 = ABC/c2.
Dus de oppervlakte gedeeld door het kwadraat van de langste zijde is gelijk (*), en in het bijzonder geldt dat dit positief is. We merken daarom op:
signum(CKB + AHC - ABC) = signum(a2 + b2 - c2).
Dus:
signum(α + β - γ) = signum(a2 + b2 - c2)
Deze stelling zegt, in Dijkstra’s woorden eigenlijk ‘vier keer zoveel als de stelling van Pythagoras’.
* Over die gelijkvormigheid: Neem een driehoek met basis a en hoogte h, en neem een geschaalde driehoek met basis ca en dus hoogte ch. De oppervlakte van de eerste is 1/2·a·h, en van de tweede is 1/2·a·h·c2. Hun oppervlaktes verhouden zich dus als c2, wat inderdaad ook voor de kwadraten van die zijdes geldt
Plaatjes van de driehoeken zijn eigen werk.
Licentie: CC-BY-SA. Edsger Dijkstra in 2002
Nóg een bewijs van de stelling van Pythagoras, door de Nederlandse Wiskundige en Informaticus Edsger Dijkstra. Hij is vooral bekend, nu ja, bekend – menigeen zal nooit van hem gehoord hebben, vanwege zijn werk in de informatica en zijn kortste pad algoritme: een algoritme dat je b.v. kunt gebruiken om in een applicatie als Google Maps de korste weg te vinden van A naar B. Op zich ook een elegant algoritme.
Hij was verder bekend omdat hij alles met zijn vulpen schreef. De stukjes die hij schreef worden EWD’s genoemd, en deze zijn allemaal gescand en te lezen op de universiteit waar hij lange tijd heeft gezeten: De universiteit van Austin, in Texas. In 2002 is hij in Nuenen overleden.
Dit bewijs betreft EWD 975, daarin is zijn handschrift te zien. Een HTML-versie vind je hier. Het origineel is in het Engels, maar hieronder volgt de uitwerking in het Nederlands.
Het vereist op zich alleen middelbare school kennis van wiskunde, maar is denk ik wel iets lastiger dan het vorige Pythagorasbewijs.
Stelling van Pythagoras: In een rechthoekige driehoek is het kwadraat van de lengte van de schuine zijde gelijk aan de som van de kwadraten van de twee andere zijden.
We beginnen met een willekeurige driehoek:
We weten dat de som van de hoeken α, β, γ 180°C is. Of, in radialen, π. We zouden de stelling van Pythagoras dus kunnen uitdrukken als:
γ = π/2 ⇒ a2 + b2 = c2
In woorden: Als γ een rechte hoek is, dan geldt de stelling van Pythagoras. Echter, we weten ook dat α + β + γ = π, dus als we dat invullen krijgen we:
γ = (α + β + γ) / 2 ⇔ 2γ = α + β + γ ⇔ γ = α + β
Dat is niet zo’n vreemde uitdrukking, want inderdaad als γ een rechte hoek is moet α + β ook wel 90° of π/2 zijn. We kunnen dus zeggen:
γ = α + β ⇒ a2 + b2 = c2
Dijkstra vraagt zich nu af ook geldt:
γ = α + β ≡ a2 + b2 = c2
Wat dan equivalent is aan:
γ ≠ α + β ≡ a2 + b2 ≠ c2
Hij merkt nu op dat als als x ≠ y dat dan geldt: x < y óf x > y. (Maar niet beide natuurlijk.) Zijn hypothese is nu dat je zelfs kunt zeggen dat:
α + β < γ ≡ a2 + b2 < c2
α + β > γ ≡ a2 + b2 > c2
Beschouw nu de variant van bovenstaande driehoek, we hebben twee punten H en K toegevoegd:
Dit is dus duidelijk een driehoek waarin geldt dat α + β < γ. Maar het bewijs is dus algemener, dit is alleen ter visualisatie. Maar in dit geval zien we dus dat de oppervlakte van ΔCKB en ΔAHC, die niet overlappen, kleiner is dan de oppervlakte van ΔABC. We duiden de oppervlakte van ΔCKB simpelweg aan met ‘CKB’ en van ΔAHC met ‘AHC’, enz., dan geldt voor de driehoek hierboven:
CKB + AHC < ABC
Het moge duidelijk zijn dat als α + β = γ dat H en K dan precies samenvallen (immers α + β = π/2 in dat geval) en dus geldt dan ook:
CKB + AHC = ABC.
En dat als α + β > γ, dat dan (merk trouwens op dat dit heel veel mogelijke plaatjes geeft in de relatieve positie van A, B, H, en K, dus daarom tekenen we die plaatjes ook niet
CKB + AHC > ABC.
Door nu gebruik te maken van de signum functie kunnen we heel eenvoudig schrijven:
signum(α + β - γ) = signum(CKB + AHC - ABC).
Verder valt op dat ΔABC, ΔAHC en ΔCKB gelijkvormig zijn, immers, ze hebben alle drie de hoeken α, β en γ. Omdat ze gelijkvormig zijn geldt:
CKB/a2 = AHC/b2 = ABC/c2.
Dus de oppervlakte gedeeld door het kwadraat van de langste zijde is gelijk (*), en in het bijzonder geldt dat dit positief is. We merken daarom op:
signum(CKB + AHC - ABC) = signum(a2 + b2 - c2).
Dus:
signum(α + β - γ) = signum(a2 + b2 - c2)
Deze stelling zegt, in Dijkstra’s woorden eigenlijk ‘vier keer zoveel als de stelling van Pythagoras’.
* Over die gelijkvormigheid: Neem een driehoek met basis a en hoogte h, en neem een geschaalde driehoek met basis ca en dus hoogte ch. De oppervlakte van de eerste is 1/2·a·h, en van de tweede is 1/2·a·h·c2. Hun oppervlaktes verhouden zich dus als c2, wat inderdaad ook voor de kwadraten van die zijdes geldt
Plaatjes van de driehoeken zijn eigen werk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Merk trouwens op dat Dijkstra’s bewijs nog wel wat nuttige opmerkingen op het laatst heeft, die ik niet heb overgenomen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dijkstra is een held, maar ik denk niet dat navigatie systemen het Dijkstra algoritme gebruiken  Eerder een algoritme dat heuristische schattingen doet.
Eerder een algoritme dat heuristische schattingen doet.
Ook geen sig dus


Klopt. Een variant van A* kunnen ze wel mogelijk eens gebruiken, bovendien kun je heel goed gebruik maken van het gegeven dat er snelwegen zijn en bepaalde ‘markers’ op een landkaart en het feit dat afstanden euclidisch zijn, en nog wat informatie, maar voor het idee.quote:Op dinsdag 6 oktober 2009 01:30 schreef Dennis_enzo het volgende:
Dijkstra is een held, maar ik denk niet dat navigatie systemen het Dijkstra algoritme gebruikenEerder een algoritme dat heuristische schattingen doet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dat kortste pad algortime is erg leuk. Ik heb ooit eens geprobeerd zelf een kortste pad algoritme af te leiden. Dat ging zo: Stel je voor dat de verbindingen tussen alle plaatsen/locaties worden gevormd door ideale touwtjes (dat wil zeggen dat ze niet kunnen rekken). De lengte van een touwtje tussen A en B representeert de afstand tussen A en B. Als je nu knooppunt A met je ene hand oppakt en knooppunt B met je andere hand en je trekt de touwtjes strak, dan wordt het kortste pad aangegeven door de strakgetrokken touwtjes. Dit kun je bewijzen door een willekeurig strakgetrokken touwtje door te knippen. Het pad zal dan nooit korter worden, alleen langer of eventueel gelijk als er meer dan 1 kortste pad is. Als je dat formaliseert ... komt je op Dijkstra's algoritme uit.


Recentelijk is er een nog veel sneller algoritme gepubliceerd. Maar ik weet vrij zeker dat dat (nog) niet veel in navigatiesystemen gebruikt wordt. De gangbare algoritmen zijn voor de meeste toepassingen snel genoeg voor gebruik en eenvoudig genoeg voor implementatie.quote:Op dinsdag 6 oktober 2009 08:37 schreef Iblis het volgende:
[..]
Klopt. Een variant van A* kunnen ze wel mogelijk eens gebruiken, bovendien kun je heel goed gebruik maken van het gegeven dat er snelwegen zijn en bepaalde ‘markers’ op een landkaart en het feit dat afstanden euclidisch zijn, en nog wat informatie, maar voor het idee.
Dit nieuwe algoritme maakt (grofweg) gebruik van het feit dat je deelgrafen hebt waar je in een kortste pad nooit meer dan 1 naar binnen gaat. Zo kun je een Dijkstra vanaf het beginpunt starten en vanaf het eindpunt en bij de knopen die binnen zo'n deelgraaf zitten weet je dat je daar niet meer buiten hoeft te zoeken. Het bepalen van goede deelgrafen vergt hierbij wel behoorlijk wat voorberekeningen, dus dat is dan informatie die je extra bij je kaart moet stoppen.
Als ik me niet vergis is dit de link: http://digbib.ubka.uni-karlsruhe.de/volltexte/documents/433201


quote:Op maandag 28 september 2009 22:29 schreef BrandX het volgende:
[..]
hier verlies je me
Waarom wil je dit doen? Niet alleen alle priemgetallen met elkaar vermedigvuldigen, maar ook nog eens '1' bij optellen?
Overigens wat ik zelf een mooie wetmatigheid vind in de wiskunde:
als je alle cijfers in een getal optelt, en je kan dat door 3 delen (en de uitkomst is een heel getal), is het originele getal ook te delen door drie.
Dus: 81 = 8+1=9
9 kan je delen door 3 dus 81 kan je delen door 3
3528921= 3+5+2+8+9+2+1 = 30
30 kan je delen door 3 dus 3528921 kan je delen door 3
8592847932= 8+5+9+2+8+4+7+9+3+2 = 57
57= 5+7=12
12= 1+2 =3
enz.
Het is misschien lastiger te bewijzen voor alle getallen, maar om het in ieder geval inzichtelijk te maken kun je het voor een getal ABCDE vrij makkelijk bewijzen.quote:Op maandag 28 september 2009 22:32 schreef Dennis_enzo het volgende:
[..]
Maar heb je daar ook een bewijs voor?
ABCDE is in feite 10.000A + 1000B + 100C + 10D + E
Dat is dan (9999A + A) + (999B +B) + (99C + C) + (9D + D) + E
Dit is dan weer 9999A + 999B + 99C + 9D + A + B + C + D + E
Als je dit door 3 deelt (dit geldt trouwens ook voor 9), dan zie je meteen dat de eerste vier termen deelbaar zijn door 3, en het dus afhangt van (A + B + C + D + E) of het getal in zijn geheel deelbaar is door 3. De uitkomst is namelijk (3333A + 333B + 33C + 3D) + (A + B + C + D + E)/3
"Patriotism is the last refuge of a scoundrel"


Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.


Vanaf waar volg je het niet helemaal meer?quote:Op dinsdag 6 oktober 2009 17:55 schreef Pietverdriet het volgende:
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik kan dit kort beantwoorden: Nee. Het bewijs bevat hele zware wiskunde waarvoor je jaren moet studeren om ze je eigen te maken. Er is wel een Horizon-documentaire van de BBC over het bewijs. Als je een hele kleine indruk wilt krijgen van wat erbij komt kijken, dan raad ik je aan om die te kijken, is vast wel te vinden op YouTube. Wil je meer dan alleen een kleine indruk krijgen, dan vrees ik dat je een aantal jaar flink moet studeren.quote:Op dinsdag 6 oktober 2009 17:55 schreef Pietverdriet het volgende:
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?


Deze:quote:Op dinsdag 6 oktober 2009 18:06 schreef thabit het volgende:
[..]
Ik kan dit kort beantwoorden: Nee. Het bewijs bevat hele zware wiskunde waarvoor je jaren moet studeren om ze je eigen te maken. Er is wel een Horizon-documentaire van de BBC over het bewijs. Als je een hele kleine indruk wilt krijgen van wat erbij komt kijken, dan raad ik je aan om die te kijken, is vast wel te vinden op YouTube. Wil je meer dan alleen een kleine indruk krijgen, dan vrees ik dat je een aantal jaar flink moet studeren.
Het begin is het aangrijpendst, als hij zo geëmotioneerd raakt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Het boek fermats last theorem van simon singh, daar staat het heel duidelijk in uitgelegd.quote:Op dinsdag 6 oktober 2009 17:55 schreef Pietverdriet het volgende:
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?


Ja, die bedoelde ik inderdaad.quote:Op dinsdag 6 oktober 2009 18:14 schreef Iblis het volgende:
[..]
Deze:
Het begin is het aangrijpendst, als hij zo geëmotioneerd raakt.


Ook dat boek geeft niet meer dan een kleine indruk. Als je een volledig bewijs wilt hebben, waarin elk tussenresultaat voorkomt, is dat zeker enkele duizenden pagina's. Er is een boek van Cornell, Silverman en Stevens waar wat meer wiskundige details in zitten en waarin de essentiele stappen van Wiles goed worden uitgelegd. Maar je moet wel wiskunde gestudeerd hebben om dat boek te kunnen begrijpen.quote:Op dinsdag 6 oktober 2009 18:19 schreef Basp1 het volgende:
[..]
Het boek fermats last theorem van simon singh, daar staat het heel duidelijk in uitgelegd.


Wat enorm tofquote:Op dinsdag 6 oktober 2009 18:14 schreef Iblis het volgende:
[..]
Deze:
Het begin is het aangrijpendst, als hij zo geëmotioneerd raakt.
Op donderdag 22 november 2012 00:14 schreef ondeugend het volgende:
liefdevolle gevoelens voor de duisternis
liefdevolle gevoelens voor de duisternis


Is zonder meer een van de beste afleveringen ooit van Horizon.quote:Op dinsdag 6 oktober 2009 19:42 schreef Bravebart het volgende:
[..]
Wat enorm tofIk heb de hele rits filmpjes gekeken
Respect.
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.


Niet, was ook niet nodig, hij werd niet in twijfel getrokken, alleen was er geen sluitend wiskundig bewijsquote:Op dinsdag 6 oktober 2009 19:54 schreef ReWout het volgende:
Even een vraagje over fermat... het dan destijds bewezen. Maar wat zijn we ermee verder gekomen?
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.


Nee dat bedoel ik niet. Het bewijs was dus een paar jaar geleden bewezen. Maar wat ze we als mensheid ermee opgeschotenquote:Op dinsdag 6 oktober 2009 19:57 schreef Pietverdriet het volgende:
[..]
Niet, was ook niet nodig, hij werd niet in twijfel getrokken, alleen was er geen sluitend wiskundig bewijs


volgens mij begrijp je niet helemaal waar het om gaat bij een wiskundig bewijs.quote:Op dinsdag 6 oktober 2009 19:59 schreef ReWout het volgende:
[..]
Nee dat bedoel ik niet. Het bewijs was dus een paar jaar geleden bewezen. Maar wat ze we als mensheid ermee opgeschotenwe kunnen iig nog niet met lichtsnelheid reizen daardoor helaas.
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.


Nou, tja, er zijn veel wiskundige vakgebieden ontgonnen en met elkaar verbonden. Dat is eigenlijk het grootste gedeelte. Wiskunde is veel verbanden leggen. Numerieke berekeningen en voorgaande deelbewijzen hadden eigenlijk al wel de meesten doen vermoeden dat de stelling waar was. Dus in die zin is de uitkomst niet schokkend.quote:Op dinsdag 6 oktober 2009 19:54 schreef ReWout het volgende:
Even een vraagje over fermat... het is destijds bewezen. Maar wat zijn we ermee verder gekomen?
Maar de weg ernaartoe wél. Het is een beetje te vergelijken misschien met ‘oké nu zijn de Amerikanen naar de maan geweest en staat daar een vlag’, wat hebben we aan die vlag? Nu ja, die vlag is nog het minst interessante, maar alle technieken en kennis die zijn ontwikkeld om dat haalbaar te maken, díé zijn natuurlijk superbelangrijk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Als je wilt weten hoe we dat wel moeten doen; laatst kwam er een pareltje hier bij ons op de onderzoeksgroep binnen waarin een zogenaamde "quark hyperdrive" werd beschreven waarmee dat wel kan.quote:Op dinsdag 6 oktober 2009 19:59 schreef ReWout het volgende:
Maar wat ze we als mensheid ermee opgeschotenwe kunnen iig nog niet met lichtsnelheid reizen daardoor helaas.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik geloof dat ik een paint topic in onz zie aankomenquote:Op dinsdag 6 oktober 2009 23:01 schreef Haushofer het volgende:
[..]
Als je wilt weten hoe we dat wel moeten doen; laatst kwam er een pareltje hier bij ons op de onderzoeksgroep binnen waarin een zogenaamde "quark hyperdrive" werd beschreven waarmee dat wel kan.
Tovve tekeningen ook nog erbij


Een oude bekende van de middelbare school. De kwadratische vergelijking. Je weet wel, je hebt , en om één of andere reden geldt:
Waarom? Hoe komen ze daarop… We bekijken eerst eens een wat simpeler geval: x2 + bx = c. Dit kan heel aardig gevisualiseerd worden. Bedenk dat ‘kwadraat’ van het Latijnse ‘quadratus’ komt, dat vierkant betekent.
We kunnen daarom de formule:
Ook visualiseren als een vierkant met oppervlakte x2, een rechthoek met oppervlakte bx en nog een constante term c.
De rechthoek met oppervlakte bx splitsen we nu in twee gelijke rechthoeken:
Dit komt overeen met:
Nu ‘herordenen’ we de vergelijking:
Dit is alleen als visueel hulpmiddel, aan de niet-visuele vergelijking verandert niets. We kunnen nu echter de linkerkant van de vierkant volledig maken, er een vierkant van maken. Dat is waarom deze methode ‘completing the square’ heet in het Engels. Daartoe tellen we (b/2)2 op aan beide zijden:
Of, als vergelijking:
We zien nu al, visueel, dat we nu links een vierkant hebben:
Of als vergelijking:
Dit is eigenlijk het idee achter het bewijs. Door nu wortel te trekken is zo op te lossen wat x is. De rest is af te maken door relatief eenvoudig formule manipuleren. Eigenlijk is dat saai, en niet eens heel fraai. Daarom staat het in een spoiler.
Waarom? Hoe komen ze daarop… We bekijken eerst eens een wat simpeler geval: x2 + bx = c. Dit kan heel aardig gevisualiseerd worden. Bedenk dat ‘kwadraat’ van het Latijnse ‘quadratus’ komt, dat vierkant betekent.
We kunnen daarom de formule:
Ook visualiseren als een vierkant met oppervlakte x2, een rechthoek met oppervlakte bx en nog een constante term c.
De rechthoek met oppervlakte bx splitsen we nu in twee gelijke rechthoeken:
Dit komt overeen met:
Nu ‘herordenen’ we de vergelijking:
Dit is alleen als visueel hulpmiddel, aan de niet-visuele vergelijking verandert niets. We kunnen nu echter de linkerkant van de vierkant volledig maken, er een vierkant van maken. Dat is waarom deze methode ‘completing the square’ heet in het Engels. Daartoe tellen we (b/2)2 op aan beide zijden:
Of, als vergelijking:
We zien nu al, visueel, dat we nu links een vierkant hebben:
Of als vergelijking:
Dit is eigenlijk het idee achter het bewijs. Door nu wortel te trekken is zo op te lossen wat x is. De rest is af te maken door relatief eenvoudig formule manipuleren. Eigenlijk is dat saai, en niet eens heel fraai. Daarom staat het in een spoiler.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


deze is pas echt fraai:
en dan krijg je dit soort ongein:
met oneindig veel vormen die allemaal oneindig verschillend zijn.. ik heb er even over moeten nadenken, maar na een dag lang onzoomen op de mandelbrot fractal kon ik geen 2 de zelfde vinden
en dan krijg je dit soort ongein:
met oneindig veel vormen die allemaal oneindig verschillend zijn.. ik heb er even over moeten nadenken, maar na een dag lang onzoomen op de mandelbrot fractal kon ik geen 2 de zelfde vinden


Ja, maar, ja, maar, ik wil niet vervelend doen, maar kun je ook vertellen hoe die verzameling tot stand komt? Want die kleuren zitten natuurlijk niet per se in die vergelijking.quote:Op dinsdag 6 oktober 2009 23:48 schreef alsem het volgende:
deze is pas echt fraai:
[ afbeelding ]
en dan krijg je dit soort ongein:
[ afbeelding ]
met oneindig veel vormen die allemaal oneindig verschillend zijn.. ik heb er even over moeten nadenken, maar na een dag lang onzoomen op de mandelbrot fractal kon ik geen 2 de zelfde vinden
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Eff simpel uitgelegd, de formule gaat uit van het getal i, dat getal bestaat eigenlijk niet, dus je kan het alleen benaderen.quote:Op dinsdag 6 oktober 2009 23:53 schreef Iblis het volgende:
[..]
Ja, maar, ja, maar, ik wil niet vervelend doen, maar kun je ook vertellen hoe die verzameling tot stand komt? Want die kleuren zitten natuurlijk niet per se in die vergelijking.
In de fractal heb je gewoon een x en een y as, met bijbehorende waarden.
Als je een getal door de formule heen haalt, komt er een ander getal uit dat of 0 is of groter als dat het was.
Als het antwoord 0 is dan wordt de pixel in dit plaatje zwart gemaakt.
Als je het getal dat groter is geworden nogeens door de formule haalt, wordt het nog groter.
Hoevaak je het getal door de formule haalt wordt in het engels "Itteration" genoemd.
Uiteindelijk zal het getal oneindig worden, en de waarde van de pixel is het aantal itterations.
De kleuren voor de itterations kan je zelf verzinnen, maar het aantal itterations zijn niet betekenisloos.
Het leuke eraan is dat de formule al heel lang bestaat, maar doordat de computers pas de laatste 20 jaar snel genoeg zijn om bij het inzoomen binnen een dag een plaatje te kunnen opbouwen, kunnen we nu pas de wonderlijke vormen zien.
Er bestaan ook nog julia factals, dat is een fractal die uitgaat van 1 punt op de mandelbrot fractal en die voor elk punt (dus on eindig veel)een aparte factal kan maken met oneindig veel vormen die ook allemaal verschillend zijn.
hier een zoom filmpje voor als je wilt spacen:


En het is ook nog een wetenschappelijke doorbraak die nog niet echt is doorgebroken, als we onderzoeksresultaten willen analyseren zoeken we altijd naar een patroon, parabool, lijn of andere simpele logica.
vanaf nu kunnen we naar fractals zoeken en dingen meten die onmeetbaar zijn met de huidige wetenschap.
vanaf nu kunnen we naar fractals zoeken en dingen meten die onmeetbaar zijn met de huidige wetenschap.


Alsem, volgens mij snap je toch niet heel veel van fractals. Ik zal het t.z.t. – nu is het te laat – eens proberen uit te leggen. Merk ook op dat je formule niet juist was, jij gaf de formule voor de Tricorn-fractal waarbij je de complex toegevoegde neemt. De gewone Mandelbrotiteratie wordt gegeven door .
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Overigens is het wel razend interessant, dus goed dat je het noemt. 
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Oké, fractaluitleg. Een fractal is wiskundig gezien eigenlijk alleen een verzameling punten. in een vlak (het complexe vlak om precies te zijn). Een punt hoort of wél bij die verzameling, of niet.
Bron: Wikimedia Commons. Maker: Connelly. Publiek Domein.
Hier boven zie je dus de Mandelbrotverzameling in het complexe vlak. Zwart hoort er wel bij, wit niet. Waar komen dan die kleurtjes vandaan? Dat heeft te maken met het rekenproces dat bepaalt of zo’n punt in het vlak zit of niet.
Een complex getal bestaat uit een reële en een imaginaire component, doorgaans geschreven als a + bi, a is de reële component, b de imaginaire. Dit zie je ook hierboven. Het punt (1 + 0i) ligt bijvoorbeeld ‘op de x-as’, d.w.z. de horizontale, of eigenlijk reële as, het punt (0 + i) ligt op de verticale as, of imaginaire as. En het punt (1 + i) ligt in het kwadrant rechtsboven.
Complexe getallen kun je vrij eenvoudig optellen en aftrekken, dat is ongeveer zoals je zou verwachten: (2 + 3i) + (5 + 4i) = 7 + 7i. Vermenigvuldigen is ook niet zo raar, dat geeft: (2 + 3i)(5 + 4i) = (10 + 8i + 15i + 12i2) = (10 + 23i + 12i2). Alleen nu is er wel een ding speciaal, er geldt namelijk i2 = -1. Dus we kunnen het vorige getal schrijven als (-2 + 23i).
Dat is dus de bekende i2 = -1, of soms ook als i = √(-1) geschreven. Als je dit weet, weet je eigenlijk al genoeg om die Mandelbrot fractal te kunnen teken.
Je pakt namelijk een punt uit dit complexe vlak, zeg c, en dan zeg je: z1 = c, z2 = z1*z1 + c, z3 = z2*z2 + c, en zo voort. Of in z’n algemeenheid: zn+1 = zn*zn + c. Voor sommige waarden van c levert dit een heel groot getal op, dat steeds maar groter wordt. Die zitten niet in je verzameling. Voor sommige waarden geldt dat het getal niet steeds groter wordt. Neem bijvoorbeeld i:
z1 = i
z2 = i*i + i = -1 + i
z3 = (-1 + i)2 + i = (i2 - 2i + 1) + i = -i
z4 = (-i)2 + i = -1 + i
z5 = z3
En zo voort. We komen dus in een rondje terecht. Probeer het eens voor c = 1:
z1 = 1
z2 = 1*1 + 1 = 2
z3 = 2*2 + 1 = 5
z4 = 5*5 + 1 = 26.
Dit gaat dus hopeloos mis, dit punt verdwijnt. De truc is nu: wanneer weet je zeker dat zo’n punt verdwijnt? Zoals je ziet kan een punt namelijk ‘op en neer klappen’ zoals in het geval van c = i. Als je rond de oorsprong een cirkel trekt met straal 2 in bovenstaand figuur, dan is het zeker dat als je iteratie een keertje buiten die cirkel komt, dat het dan misgaat.
Op deze manier kunnen we ook tot de kleuren komen: We tellen hoe vaak we bovenstaand proces moeten uitvoeren om buiten die cirkel te geraken. Dan krijg je zoiets:
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
De zwarte punten zitten dus in de verzameling, de gekleurde niet. En je ziet heel duidelijke banden met dezelfde kleur. De meer roodachtige aan de buitenkant zijn direct al weg in feite; de rood-paarse kleur daarbinnen doet er 1 iteratie over, die daarbinnen 2, de blauw tinten nog langer, en de groen tinten nog weer langer, en de paarse tinten binnenin, grenzend aan het zwarte vlak, doen er nóg weer langer over.
Die kleuren geven dus eigenlijk vooral het berekeningsproces weer, en hoe lang je erover doet om te berekenen dat zo’n punt niet in de verzameling zit, maar zijn niet ‘de fractal zelf’ ook al wordt misschien vaak wel zo geassocieerd. De fractal zelf, de Mandelbrotverzameling in dit geval is dus het zwarte.
Maar hoe komt men dan aan zo’n afbeelding?
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
Waarom zie je daar niet van die duidelijke strepen met dezelfde kleur? Dat is in feite gewoon een bewerkingstruc. Die strepen worden als het ware uitgevlakt en in een continue overgang geplaatst. Stel dat je een punt c hebt dat na n iteraties ‘buiten de cirkel is gekomen’ dan hoort daar dan de volgende waarde bij: v = n - log2log2 |zn|, hier is zn dus het punt dat voor het eerst buiten de cirkel valt, |zn| geeft de afstand van dat punt tot de oorsprong (dus als rechte lijn gezien). Op deze manier krijg je een continu waardenverloop: immers punten die net ietsje verder weg komen krijgen een iets andere kleur. De truc is nu om die waarden ook nog op geschikte kleuren af te beelden.. Maar als je dat doet, dan krijg je dus zulke mooie, vloeiende, afbeeldingen.
De moeilijkheid, en het fascinerende aan fractals is, dat je op een gegeven moment je iteratie moet afkappen. Je kunt wel zeker weten dat een punt niet in de verzameling zit, en van sommige punten is ook duidelijk dat ze er wél inzitten, maar op het grensvlak is het vaak niet duidelijk. Het enige dat je dan kunt doen is gewoon rekenen. 100 iteraties proberen en kijken of het punt al ontsnapt. Of 1000. Of 10000. En zo voort. In die zin is een fractal dus altijd een benadering. Die grenspunten ontsnappen misschien niet na 1000 iteraties, en zijn daarom zwart gekleurd, maar mogelijk wel na 10000!
Dat is ook de reden dat men (alleen) kan zeggen: de oppervlakte van de verzameling is 1,506 591 77 ± 0,000 000 08. Om dat precies uit te rekenen zou je oneindig lang moeten doorrekenen. Er is geen formule met een exacte uitkomst te geven.
Zo’n tekening is dus altijd een benadering. Het grappige is ook dat de uitvinder van deze verzameling, Benoît Mandelbrot, in het begin, op basis van zulke computerafbeeldingen dacht dat de verzameling niet verbonden was, m.a.w. dat je niet via een zwart punt over alleen maar zwarte punten naar elk ander zwart punt kunt komen. Er zouden dus eilandjes zijn. Dat vermoeden was gebaseerd op tekeningen gerenderd door de computer waarbij heel dunne haarlijntjes niet zichtbaar waren. Je moet immers kiezen hoe nauwkeurig je zoiets doet. Als je c = -1.1 en c = 1.2 uitrekent, moet je dan c = 1.15 ook nog doen? En c = 1.155? En c = 1.1555? Je moet ergens stoppen. Het kan best dat dus in je tekening twee pixels naast elkaar beiden een kleurtje hebben, maar dat er tussen eigenlijk nog een – in die tekening onzichtbaar – zwart lijntje loopt.
Inmiddels is bewezen dat de gehele verzameling wel verbonden is, maar die inzoomfilmpjes die je ziet tonen aan dat je in principe steekds maar kunt vergroten en vergroten op de grens en telkens nieuw detail ziet. En wát je dan precies ziet, dat is pas te zeggen nadat het is uitgerekend. Je kunt dus niet een patroon ontdekken voorspellen. Ter vergelijking, een breuk als 1/7 ≈ 1,142857142857, maar die herhaalt zichzelf telkens. Je kunt zo voorspellen dat cijfer 1, 7, 13, 19, enz. een 1 zijn. Als iemand dus wil weten wat cijfer 283043 achter de komma is kun je dat direct zeggen zonder tot 283043 cijfers achter de komma door te rekenen omdat er een patroon in zit. Dat kan bij zo’n fractal niet. Je moet het helemaal uitrekenen.
Bron: Wikimedia Commons. Maker: Connelly. Publiek Domein.
Hier boven zie je dus de Mandelbrotverzameling in het complexe vlak. Zwart hoort er wel bij, wit niet. Waar komen dan die kleurtjes vandaan? Dat heeft te maken met het rekenproces dat bepaalt of zo’n punt in het vlak zit of niet.
Een complex getal bestaat uit een reële en een imaginaire component, doorgaans geschreven als a + bi, a is de reële component, b de imaginaire. Dit zie je ook hierboven. Het punt (1 + 0i) ligt bijvoorbeeld ‘op de x-as’, d.w.z. de horizontale, of eigenlijk reële as, het punt (0 + i) ligt op de verticale as, of imaginaire as. En het punt (1 + i) ligt in het kwadrant rechtsboven.
Complexe getallen kun je vrij eenvoudig optellen en aftrekken, dat is ongeveer zoals je zou verwachten: (2 + 3i) + (5 + 4i) = 7 + 7i. Vermenigvuldigen is ook niet zo raar, dat geeft: (2 + 3i)(5 + 4i) = (10 + 8i + 15i + 12i2) = (10 + 23i + 12i2). Alleen nu is er wel een ding speciaal, er geldt namelijk i2 = -1. Dus we kunnen het vorige getal schrijven als (-2 + 23i).
Dat is dus de bekende i2 = -1, of soms ook als i = √(-1) geschreven. Als je dit weet, weet je eigenlijk al genoeg om die Mandelbrot fractal te kunnen teken.
Je pakt namelijk een punt uit dit complexe vlak, zeg c, en dan zeg je: z1 = c, z2 = z1*z1 + c, z3 = z2*z2 + c, en zo voort. Of in z’n algemeenheid: zn+1 = zn*zn + c. Voor sommige waarden van c levert dit een heel groot getal op, dat steeds maar groter wordt. Die zitten niet in je verzameling. Voor sommige waarden geldt dat het getal niet steeds groter wordt. Neem bijvoorbeeld i:
z1 = i
z2 = i*i + i = -1 + i
z3 = (-1 + i)2 + i = (i2 - 2i + 1) + i = -i
z4 = (-i)2 + i = -1 + i
z5 = z3
En zo voort. We komen dus in een rondje terecht. Probeer het eens voor c = 1:
z1 = 1
z2 = 1*1 + 1 = 2
z3 = 2*2 + 1 = 5
z4 = 5*5 + 1 = 26.
Dit gaat dus hopeloos mis, dit punt verdwijnt. De truc is nu: wanneer weet je zeker dat zo’n punt verdwijnt? Zoals je ziet kan een punt namelijk ‘op en neer klappen’ zoals in het geval van c = i. Als je rond de oorsprong een cirkel trekt met straal 2 in bovenstaand figuur, dan is het zeker dat als je iteratie een keertje buiten die cirkel komt, dat het dan misgaat.
Op deze manier kunnen we ook tot de kleuren komen: We tellen hoe vaak we bovenstaand proces moeten uitvoeren om buiten die cirkel te geraken. Dan krijg je zoiets:
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
De zwarte punten zitten dus in de verzameling, de gekleurde niet. En je ziet heel duidelijke banden met dezelfde kleur. De meer roodachtige aan de buitenkant zijn direct al weg in feite; de rood-paarse kleur daarbinnen doet er 1 iteratie over, die daarbinnen 2, de blauw tinten nog langer, en de groen tinten nog weer langer, en de paarse tinten binnenin, grenzend aan het zwarte vlak, doen er nóg weer langer over.
Die kleuren geven dus eigenlijk vooral het berekeningsproces weer, en hoe lang je erover doet om te berekenen dat zo’n punt niet in de verzameling zit, maar zijn niet ‘de fractal zelf’ ook al wordt misschien vaak wel zo geassocieerd. De fractal zelf, de Mandelbrotverzameling in dit geval is dus het zwarte.
Maar hoe komt men dan aan zo’n afbeelding?
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
Waarom zie je daar niet van die duidelijke strepen met dezelfde kleur? Dat is in feite gewoon een bewerkingstruc. Die strepen worden als het ware uitgevlakt en in een continue overgang geplaatst. Stel dat je een punt c hebt dat na n iteraties ‘buiten de cirkel is gekomen’ dan hoort daar dan de volgende waarde bij: v = n - log2log2 |zn|, hier is zn dus het punt dat voor het eerst buiten de cirkel valt, |zn| geeft de afstand van dat punt tot de oorsprong (dus als rechte lijn gezien). Op deze manier krijg je een continu waardenverloop: immers punten die net ietsje verder weg komen krijgen een iets andere kleur. De truc is nu om die waarden ook nog op geschikte kleuren af te beelden.. Maar als je dat doet, dan krijg je dus zulke mooie, vloeiende, afbeeldingen.
De moeilijkheid, en het fascinerende aan fractals is, dat je op een gegeven moment je iteratie moet afkappen. Je kunt wel zeker weten dat een punt niet in de verzameling zit, en van sommige punten is ook duidelijk dat ze er wél inzitten, maar op het grensvlak is het vaak niet duidelijk. Het enige dat je dan kunt doen is gewoon rekenen. 100 iteraties proberen en kijken of het punt al ontsnapt. Of 1000. Of 10000. En zo voort. In die zin is een fractal dus altijd een benadering. Die grenspunten ontsnappen misschien niet na 1000 iteraties, en zijn daarom zwart gekleurd, maar mogelijk wel na 10000!
Dat is ook de reden dat men (alleen) kan zeggen: de oppervlakte van de verzameling is 1,506 591 77 ± 0,000 000 08. Om dat precies uit te rekenen zou je oneindig lang moeten doorrekenen. Er is geen formule met een exacte uitkomst te geven.
Zo’n tekening is dus altijd een benadering. Het grappige is ook dat de uitvinder van deze verzameling, Benoît Mandelbrot, in het begin, op basis van zulke computerafbeeldingen dacht dat de verzameling niet verbonden was, m.a.w. dat je niet via een zwart punt over alleen maar zwarte punten naar elk ander zwart punt kunt komen. Er zouden dus eilandjes zijn. Dat vermoeden was gebaseerd op tekeningen gerenderd door de computer waarbij heel dunne haarlijntjes niet zichtbaar waren. Je moet immers kiezen hoe nauwkeurig je zoiets doet. Als je c = -1.1 en c = 1.2 uitrekent, moet je dan c = 1.15 ook nog doen? En c = 1.155? En c = 1.1555? Je moet ergens stoppen. Het kan best dat dus in je tekening twee pixels naast elkaar beiden een kleurtje hebben, maar dat er tussen eigenlijk nog een – in die tekening onzichtbaar – zwart lijntje loopt.
Inmiddels is bewezen dat de gehele verzameling wel verbonden is, maar die inzoomfilmpjes die je ziet tonen aan dat je in principe steekds maar kunt vergroten en vergroten op de grens en telkens nieuw detail ziet. En wát je dan precies ziet, dat is pas te zeggen nadat het is uitgerekend. Je kunt dus niet een patroon ontdekken voorspellen. Ter vergelijking, een breuk als 1/7 ≈ 1,142857142857, maar die herhaalt zichzelf telkens. Je kunt zo voorspellen dat cijfer 1, 7, 13, 19, enz. een 1 zijn. Als iemand dus wil weten wat cijfer 283043 achter de komma is kun je dat direct zeggen zonder tot 283043 cijfers achter de komma door te rekenen omdat er een patroon in zit. Dat kan bij zo’n fractal niet. Je moet het helemaal uitrekenen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik ben altijd bijzonder zwak in formele bewijzen geweest, toch teveel een chaoot, dus even een domme vraag:
Moet je dan niet eerst bewijzen dat combinaties van priemgetallen alleen weer deelbaar zijn door priemgetallen? Of zit dat besloten in de vermenigvuldiging?quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Dit betekent óf dat E zelf een priemgetal is, of als het geen priemgetal is (en dus deelbaar is door een ander priemgetal), dat het dan deelbaar is door een priemgetal dat niet in ons rijtje zat.
They told me all of my cages were mental, so I got wasted like all my potential.


vette uitleg, zo had ik het nog nooit bekeken! 
vanavond nog maar eens nalezen, mijn uitleg is idd erg vaag, dont blame me, ik heb 5 jaar geleden voor het laatst wiskunde gehad
Ik heb een keer een programma gedownload, fractalX.exe daarmee kan je zelf inzoomen, het is echt ongelofelijk hoe mooi die figuren zijn, ze lijken ook bekend voor te komen en te kloppen, alsof je hersens dergelijke berekeningen ook maken.
daarmee kan je ook je eigen julia fractal zoeken, itterations instellen en kleur geven, deze heb ik laatst gemaakt:
vanavond nog maar eens nalezen, mijn uitleg is idd erg vaag, dont blame me, ik heb 5 jaar geleden voor het laatst wiskunde gehad
Ik heb een keer een programma gedownload, fractalX.exe daarmee kan je zelf inzoomen, het is echt ongelofelijk hoe mooi die figuren zijn, ze lijken ook bekend voor te komen en te kloppen, alsof je hersens dergelijke berekeningen ook maken.
daarmee kan je ook je eigen julia fractal zoeken, itterations instellen en kleur geven, deze heb ik laatst gemaakt:


Ik heb inderdaad nagelaten te vermelden dat elk getal een unieke priemfactorisatie heeft. Dat was op zich opzettelijk. Elk getal heeft een unieke factorisatie in priemgetallen. En we weten dus dat die factorisatie niet de getallen kan bevatten uit ons rijtje. Ergo, ons rijtje is niet compleet.quote:Op woensdag 7 oktober 2009 12:42 schreef speknek het volgende:
Ik ben altijd bijzonder zwak in formele bewijzen geweest, toch teveel een chaoot, dus even een domme vraag:
[..]
Moet je dan niet eerst bewijzen dat combinaties van priemgetallen alleen weer deelbaar zijn door priemgetallen? Of zit dat besloten in de vermenigvuldiging?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Overigens laat ik formeel gezien wel meer steekjes vallen, maar het is niet mijn bedoeling om strikt formeel te zijn. In die fractaluitleg praat ik b.v. over ‘complexe getallen die steeds maar groter worden’, alhoewel dat natuurlijk formeel gezien niet zo zinnig is.
Ik denk dat ook zonder die formaliteiten echter het idee, de slimmigheid van de redenering, wel over komt. (Of het fascinerende erachter.)
Ik denk dat ook zonder die formaliteiten echter het idee, de slimmigheid van de redenering, wel over komt. (Of het fascinerende erachter.)
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dat hoef je niet te gebruiken. Het gaat erom dat elk getal ten minste 1 priemfactorisatie heeft. En dat is wat makkelijker te bewijzen: stel dat er een getal zonder priemfactorisatie is, dan is er ook een kleinste getal waarvoor dat geldt, zeg n. Omdat n geen priemfactorisatie heeft, is n geen priemgetal dus n = m*k met m en k kleiner dan n. Maar omdat n het kleinste getal zonder priemfactorisatie is hebben m en k dus wel een priemfactorisatie en uit n = m*k krijg je dan ook een priemfactorisatie voor n.quote:Op woensdag 7 oktober 2009 12:51 schreef Iblis het volgende:
[..]
Ik heb inderdaad nagelaten te vermelden dat elk getal een unieke priemfactorisatie heeft. Dat was op zich opzettelijk. Elk getal heeft een unieke factorisatie in priemgetallen. En we weten dus dat die factorisatie niet de getallen kan bevatten uit ons rijtje. Ergo, ons rijtje is niet compleet.


Deze vind ik eigenlijk nog eleganter dan de OP, alhoewel ik de hele tijd het gevoel heb dat ik ergens bedot wordt. Het glijdt erin als de zalvende woorden van een sekteleider, hallelujah!quote:Op woensdag 7 oktober 2009 12:55 schreef thabit het volgende:
Dat hoef je niet te gebruiken. Het gaat erom dat elk getal ten minste 1 priemfactorisatie heeft. En dat is wat makkelijker te bewijzen: stel dat er een getal zonder priemfactorisatie is, dan is er ook een kleinste getal waarvoor dat geldt, zeg n. Omdat n geen priemfactorisatie heeft, is n geen priemgetal dus n = m*k met m en k kleiner dan n. Maar omdat n het kleinste getal zonder priemfactorisatie is hebben m en k dus wel een priemfactorisatie en uit n = m*k krijg je dan ook een priemfactorisatie voor n.
They told me all of my cages were mental, so I got wasted like all my potential.


Dit bewijst natuurlijk niet dat er oneindig veel priemgetallen zijn, alleen dat elk getal een priemfactorontbinding heeft.quote:Op woensdag 7 oktober 2009 13:12 schreef speknek het volgende:
[..]
Deze vind ik eigenlijk nog eleganter dan de OP, alhoewel ik de hele tijd het gevoel heb dat ik ergens bedot wordt. Het glijdt erin als de zalvende woorden van een sekteleider, hallelujah!


het mooiste vind ik dat je met galoistheorie kan aantonen dat je geen formules kunt vinden voor meerderegraadsvergelijkingen. Da's echt prachtig opgebouwd allemaal.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.


Ja, ik heb ooit nog es de ambitie gehad om dat eens door te nemen, na een berichtje lang geleden over eendude waarvan de media beweerde dat hij polynomen van willekeurige graden exact kon oplossen.quote:Op woensdag 7 oktober 2009 16:44 schreef Beregd het volgende:
het mooiste vind ik dat je met galoistheorie kan aantonen dat je geen formules kunt vinden voor meerderegraadsvergelijkingen. Da's echt prachtig opgebouwd allemaal.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ow ja, dat was weer zo'n typische media nemen alle onzin over van andere media fail.quote:Op woensdag 7 oktober 2009 17:41 schreef Haushofer het volgende:
[..]
Ja, ik heb ooit nog es de ambitie gehad om dat eens door te nemen, na een berichtje lang geleden over eendude waarvan de media beweerde dat hij polynomen van willekeurige graden exact kon oplossen.
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten


Nog een keer de stelling van Pythagoras:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Eh ja, ik weet hoe je over Informatica denkt, maar zo'n wiskundeleek ben ik ook weer nietquote:Op woensdag 7 oktober 2009 14:30 schreef thabit het volgende:
[..]
Dit bewijst natuurlijk niet dat er oneindig veel priemgetallen zijn, alleen dat elk getal een priemfactorontbinding heeft.
They told me all of my cages were mental, so I got wasted like all my potential.


Ik heb er nu een zonder woorden voor je.quote:Op vrijdag 9 oktober 2009 00:10 schreef speknek het volgende:
[..]
Eh ja, ik weet hoe je over Informatica denkt, maar zo'n wiskundeleek ben ik ook weer niet. Ik bedoelde als een fraai bewijs tegenover het andere.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


serieus, plaatjes snap ik om een of andere reden wel. Ik tekende ook altijd venn diagrammen van alles.
They told me all of my cages were mental, so I got wasted like all my potential.


Galoistheorie, een prachtig onderwerp.quote:Op woensdag 7 oktober 2009 16:44 schreef Beregd het volgende:
het mooiste vind ik dat je met galoistheorie kan aantonen dat je geen formules kunt vinden voor meerderegraadsvergelijkingen. Da's echt prachtig opgebouwd allemaal.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
Een ander mooi onderwerp uit die fase van de wiskundestudie vind ik complexe functietheorie. Complexe functies zijn oneindig veel mooier dan reele functies. Als een complexe functie 1 keer differentieerbaar is, dan is ze gelijk oneindig vaak differentieerbaar en dat toon je aan met een paar superstrakke integraalformules.


ja, heb ik mijn thesis ovcer gemaakt (maar dan over ondeindige velduitbreidingen)quote:Op vrijdag 9 oktober 2009 14:55 schreef thabit het volgende:
[..]
Galoistheorie, een prachtig onderwerp.. Je kunt op die manier ook aantonen dat sommige dingen wel kunnen, wat anders niet zo makkelijk in te zien is, zoals het construeren van een regelmatige 65537-hoek met passer en liniaal zonder dat ook expliciet te doen.
In codetheorie heb je ook heel leuke bewijzen. Erg verschillend van de andere wiskunde vaak.
Dan zijn er ook zo van die andere wiskundige strekkingen met afschuwelijke bewijzen. Maattheorie bijvoorbeeld. Al die bewijzen zijn zodanig veel constructie en geknutsel, niks elegants aan vaak.


Even een intermezzo met een mooi gedichtje !
quote:Minus one
A carpenter named Charlie Bratticks
Who had a taste for mathematics
One summer Tuesday, just for fun
Made a wooden cube side minus one
Though this to you may seem wrong
He made it minus one foot long
Which meant (I hope your brains aren't frothing)
Its length was one foot less than nothing
Its width the same (you're not asleep?)
And likewise minus one foot deep
Giving, when multiplied (be solemn)
Minus one cubic foot of volume
With sweating brow this cube he sawed
Through areas of solid board
For though each cut had minus length
Minus times minus sapped his strength
A second cube he made, but thus
This time each one foot length was plus
Meaning of course that here one put
For volume, plus one cubic foot
So now he had, just for his sins
Two cubes as like as deviant twins
And feeling one should know the worst
He placed the second in the first
One plus, one minus - there's no doubt
The edges simply cancelled out
So did the volume, nothing gained
Only the surfaces remained
Well may you open wide your eyes
For those were now of double size
On something now, thanks to his skill
Took up no room and measured nil
From solid ebony he'd cut
These bulky objects, but
All that remained was now a thin
Black sharply angled sort of skin
Of twelve square feet - which though not small
Weighed nothing, filled no space at all
It stands there yet on Charlies floor
He can't think what to use it for
zzz


Een harmonieuze reeks leidt altijd tot oneindig.
Dus 1/1 +1/2 +1/3 +1/4 + 1/5 + ….. +1/n leidt tot oneindig.
Dit geldt ook voor 1/1000000 + 1/2000000 + 1/3000000 + etc.
Want oneindig gedeeld door miljoen is ook oneindig.
Nu komt het bewijs.
Bij de oorspronkelijke harmonieze reeks tot een willekeurig getal x is de tweede helft van de reeks altijd groter dan 0,5.
Want: de kleinste in het gezelschap is 1/x en het aantal = 0,5*x
En 0,5*x * 1/x = 0,5
En je kunt een harmonieuze reeks oneindig keer verdubbelen.
Van een lengte 1 naar een lengte 2 naar een lengte 4 en telkens komt er minimaal 0,5 bij.
Dus 1/1 +1/2 +1/3 +1/4 + 1/5 + ….. +1/n leidt tot oneindig.
Dit geldt ook voor 1/1000000 + 1/2000000 + 1/3000000 + etc.
Want oneindig gedeeld door miljoen is ook oneindig.
Nu komt het bewijs.
Bij de oorspronkelijke harmonieze reeks tot een willekeurig getal x is de tweede helft van de reeks altijd groter dan 0,5.
Want: de kleinste in het gezelschap is 1/x en het aantal = 0,5*x
En 0,5*x * 1/x = 0,5
En je kunt een harmonieuze reeks oneindig keer verdubbelen.
Van een lengte 1 naar een lengte 2 naar een lengte 4 en telkens komt er minimaal 0,5 bij.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.


Ik denk niet dat iemand chocola kan maken van je 'bewijs' voor de divergentie van de harmonische reeks. Verwijs dan gewoon even naar Wikipedia als je het niet begrijpelijk onder woorden kunt brengen.quote:Op vrijdag 9 oktober 2009 16:07 schreef Twentsche_Ros het volgende:
Een harmonieuze reeks leidt altijd tot oneindig.
Dus 1/1 +1/2 +1/3 +1/4 + 1/5 + ….. +1/n leidt tot oneindig.
[snip gibberish]


De som hiervan kan toch nooit oneindig zijn, maar zal nooit een zekere waarde (edidt: die waarde valt niet vast te stellen volgens mij, dus 'een zekere waarde' kan men met een korreltje zout nemen) ontstijgen?quote:Op vrijdag 9 oktober 2009 16:07 schreef Twentsche_Ros het volgende:
Een harmonieuze reeks leidt altijd tot oneindig.
Dus 1/1 +1/2 +1/3 +1/4 + 1/5 + .... +1/n leidt tot oneindig.
Denk ik bijvoorbeeld aan de somformule 1/1 + 1/10 + 1/100 + 1/1000 + ... + 1/n ; die zal nooit de 1,12 bereiken, of 1,112, of 1,1112, etc.
Oh really?


Lees het Wikipedia artikel eens goed door. Je begrijpt kennelijk niet dat de harmonische reeks hierboven echt divergent is. Dat is iets heel anders dan de (wel convergente) meetkundige reeks die jij geeft.quote:Op vrijdag 9 oktober 2009 21:34 schreef Matthijs- het volgende:
[..]
De som hiervan kan toch nooit oneindig zijn, maar zal nooit een zekere waarde (edidt: die waarde valt niet vast te stellen volgens mij, dus 'een zekere waarde' kan men met een korreltje zout nemen) ontstijgen?
Denk ik bijvoorbeeld aan de somformule 1/1 + 1/10 + 1/100 + 1/1000 + ... + 1/n ; die zal nooit de 1,12 bereiken, of 1,112, of 1,1112, etc.


Net die youtuub docu gezien, erg mooi! 
I am a Chinese college students, I have a loving father, but I can not help him, he needs to do heart bypass surgery, I can not help him, because the cost of 100,000 or so needed, please help me, lifelong You pray Thank you!


Kan iemand mij vertellen waarom de Fourier transformatie van een constante K gelijk is aan 2*pi*K*delta(omega)? Ik heb het op verschillende plekken op proberen te zoeken maar ik krijg alleen de - onbevredigende - verklaring dat de inverse Fourier transformatie van 2*pi*K*delta(omega) gelijk is aan K.
Ik zou dit graag willen kunnen bewijzen door de Fourier integraal op te lossen maar ik kom er niet uit?
Ik zou dit graag willen kunnen bewijzen door de Fourier integraal op te lossen maar ik kom er niet uit?


Daar is [Bèta wiskunde] Huiswerk- en vragentopic een betere plaats voor denk ik. Alhoewel de overlap in posters wel aardig hoog is.quote:Op zaterdag 10 oktober 2009 00:46 schreef Maverick_tfd het volgende:
Kan iemand mij vertellen waarom de Fourier transformatie van een constante K gelijk is aan 2*pi*K*delta(omega)? Ik heb het op verschillende plekken op proberen te zoeken maar ik krijg alleen de - onbevredigende - verklaring dat de inverse Fourier transformatie van 2*pi*K*delta(omega) gelijk is aan K.
Ik zou dit graag willen kunnen bewijzen door de Fourier integraal op te lossen maar ik kom er niet uit?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Je hebt gelijk, post ik het daar ook evenquote:Op zaterdag 10 oktober 2009 00:48 schreef Iblis het volgende:
[..]
Daar is [Bèta wiskunde] Huiswerk- en vragentopic een betere plaats voor denk ik. Alhoewel de overlap in posters wel aardig hoog is.
Dacht misschien dat (omdat het bewijs kennelijk niet geheel voor de hand liggend is) het misschien wel een elegant bewijs zou zijn.


De soldaten van Conway
De mensen die “The Curious Incident of the Dog in the Night-Time” hebben gelezen kennen dit misschien al, of ze hebben het overgeslagen omdat ze het niets zei. In het Engels heet dit probleem ‘Conway’s Soldiers’, en zo is het misschien ook beter bekend bij sommigen.
In het Engels heet dit probleem ‘Conway’s Soldiers’, en zo is het misschien ook beter bekend bij sommigen.
Het idee is in feite een eenvoudig soort solitair spelletje. Dus je hebt een aantal poppetjes op het bord staan, en je kunt ermee over naburige poppetjes springen, mits er aan de andere kant een leeg vakje is waar je kunt landen. Je mag verder alleen horizontaal en verticaal bewegen.
Bijvoorbeeld met twee stenen kun je met de onderste over de bovenste springen (of andersom natuurlijk):
Het probleem is nu als volgt: Hoeveel stenen heb je minstens nodig, als je ze allemaal onder de dikke blauwe lijn neerzet, om minstens één steen op n plaatsen boven de dikke blauwe lijn neer te zetten. Hierboven zie je al dat je 2 stenen nodig hebt om op de 1 plaats boven de blauwe lijn te komen.
De notatie gebruiken we verder ook: een pijltje geeft aan welke steen verzet gaat worden, linksboven staat het aantal gedane zetten (0 is dus de begin situatie) en een grijs rondje is een steen die is verdwenen omdat er overheen gesprongen is.
Laten we nu bekijken hoe we op de tweede regel boven de dikke blauwe lijn uitkomen:
Daar hebben we dus minstens vier stenen voor nodig. Merk overigens op dat we na twee zetten eigenlijk de situatie hebben van ons eerste voorbeeld, alleen dan 1 regel omhoog verschoven. We zouden dus daar al kunnen concluderen dat het kan. Wat wiskundig gezien genoeg is. Maar omdat ik gul ben is het helemaal uitgewerkt.
Ook de derde regel behalen is mogelijk: merk op dat de vier stenen die hier in groen zijn weergegeven precies zo staan als in het tweede voorbeeld, en de eerste drie zetten zijn dan ook gelijk aan dit tweede voorbeeld, en die gebruiken we dus om die ene groene steen op 2 regels boven de dikke blauwe streep te krijgen.
Daarna gaat het verder om met de overige stenen er eentje op drie regels boven de streep te krijgen:
Inmiddels denkt de oplettende lezer: ik heb het patroon al door, 2 stenen voor 1 regel, 4 voor voor 2 regels, 8 voor 3 regels, dus vast 16 voor vier regels: fout. Dat zijn er minstens 20, één voorbeeld zie je hier:
We gaan nu verder om in feite de begin situatie van voorbeeld drie te creëren, alleen dan alvast één regel verschoven:
Hierboven zie je een situatie die nog 8 stenen overheeft, en verder gelijk is aan de startsituatie om 3 regels omhoog te komen, behalve dat één rijtje nu al boven de streep staat.
Oké, boeiend denk je misschien, maar wat is nu het punt? Solitair spelen is niet zo spannend. Het geval is namelijk dat de volgende uitdaging, namelijk een steen op 5 regels boven de blauwe streep krijgen als je met al je stenen eronder begint überhaupt niet mogelijk is. Hoeveel stenen je ook pakt, hoe je ook beweegt, wat je ook doet, je zult nooit een steen op de vijfde regel krijgen.
En dat zullen we gaan bewijzen. Het probleem is bedacht en bewezen door John Conway in 1961. Het bewijs dat het niet kan is werkelijk heel vernuftig, en maakt slim gebruik van de gulden snede: ϕ.
Het idee is als volgt: Het is duidelijk dat elke keer dat je een zet doet dat je dan een mannetje verliest. Maar tegelijkertijd (als je tenminste niet te stom speelt) kun je een mannetje dichter bij je doel brengen. We proberen nu een soort gewicht aan de verzameling soldaatjes te hangen, en uit te drukken hoeveel gewicht er gewonnen of verloren wordt door een zet, en dan uiteindelijk zullen we zien dat hoe je ook begint, je nooit genoeg gewicht hebt om die vijfde regel te bereiken: je verliest het altijd te vroeg.
Allereerst merken we voor de volledigheid op dat het niet uitmaakt wélk punt op de vijfde regel we willen bereiken. Als we een zeker punt kunnen bereiken kunnen we ook het punt links ervan bereiken door alle stenen één plaatsje op te schuiven naar links en dan dezelfde bewegingen te doen. Kortom, die punten zijn in feite inwisselbaar en daarom maakt het niet uit welk punt we pakken. Als het niet kan met dat punt, kan het met geen enkel punt, en omgekeerd. We gaan er hierbij vanuit natuurlijk dat ons bord willekeurig groot kan worden, alhoewel we niet met oneindig veel soldaatjes gaan schuiven, maar wel met willekeurig (doch eindig) veel.
Eerst kiezen we maar eens een punt op de 5e regel (dat is blauw gekleurd hieronder) en dat punt kennen we een bepaald gewicht toe, namelijk: 1. De buurtpunten, die met één stap zijn te bereiken, kennen we gewicht x1 toe (wat x is zullen we later nog specificeren), de velden die met twee stappen bereikbaar zijn kennen we x2 toe, met drie x3, en zo voort, je krijgt dus deze situatie:
De laagste macht die we onder de streep vinden is dus x5. Een soldaatje dat op een veld staat krijgt het gewicht van het veld. Het gewicht van ons hele leger is simpelweg de som van alle veldjes waar een soldaat op staat. Merk op dat een soldaat op ons eindpunt dus per definitie gewicht 1 heeft, en een leger met een soldaat op het eindpunt dus ook minstens gewicht 1.
Voordat we specificeren wat x is, kijken we eerst nog even wat voor soort stappen we zouden kunnen doen, dat zijn er 3:
We kunnen naar het eindpunt toegaan: Dus we springen b.v. van x3 over x2 naar x1 (dan verdwijnt de soldaat op een x2-veld). In z’n algemeenheid gaan we van een veld met waarde xn+2 naar xn en verdwijnt de soldaat op xn+1.
We kunnen ook juist verder van het eindpunt afgaan: Dus we springen b.v. van x1 over x2 naar x3 (de soldaat op een x2-veld verdwijnt weer). In z’n algemeenheid gaan we van een veld met waarde xn naar xn+2 en verdwijnt de soldaat op xn+1.
We kunnen precies even ver van het eindpunt blijven: dit kan alleen als we dus over een van de twee assen door het eindpunt heenspringen, b.v. precies onder de blauwe streep kunnen we van x6 over x5 naar een ander x6 veld springen. In dit geval gaan we dus van een veld met waarde xn+1 naar een veld met waarde xn+1 en verdwijnt een soldaat met waarde xn.
Het is hopelijk niet lastig om jezelf ervan te overtuigen dat als je alleen horizontaal en verticaal mag springen dit de enige drie opties zijn.
Nu komt de truc, namelijk een geschikt waarde voor x kiezen. Dit, samen met de waardering is het briljante van het bewijs, we kiezen x = 1/ϕ, ofwel:
Het getal ϕ is de guldensnede, die heeft een paar interessante eigenschappen die ook nu van pas komen, te weten: ϕ2 = ϕ + 1, en 1/ϕ = ϕ - 1.
Laten we nu eens naar de drie soorten bewegingen kijken die we kunnen maken, eerst de eerste bewegingen waarbij we naar het eindpunt toespringen:
Het gewicht van het hele leger verandert als volgt: er komt xn bij (daar eindigen we), maar er verdwijnt xn+1 (daar springen we overheen) en er verdwijnt xn+2 (de startpositie), dus de verandering is: xn - xn+1 - xn+2. Als we xn buiten haakjes krijgen hebben we dat de verandering is:
De oplettende lezer voelt ’m nu al aankomen: de eigenschappen van de gulden snede komen nu beregoed van pas. Bedenk, x = 1/ϕ = ϕ - 1, dus x2 = 1/(ϕ2) = 1/ϕ·1/ϕ = (ϕ - 1)/ϕ = 1 - 1/ϕ = 1 - x.
Kortom:
Als we dus naar het eindpunt toe bewegen verandert het ‘gewicht’ van het leger niet. Nu bekijken we het tweede geval, dat betekent dat we van het eindpunt af bewegen, dat geeft:
Omdat x positief is geldt dat -2xn+1 < 0. Dat is voldoende: het gewicht van het leger neemt in dat geval dus af.
Nu het laatste geval waarbij we over een as door het eindpunt springen:
Ook in dát geval neemt het gewicht af. Het maakt dus niet uit wat voor sprong we maken, onder de waardering die we kiezen kan de waarde van het gehele leger niet toenemen.
Omdat het eindpunt gewicht 1 heeft, zoals we al opgemerkt hebben, zal een leger dat ooit dat eindpunt wil kunnen bereiken ook minstens gewicht 1 hebben, want het gewicht kan nooit toenemen, wat voor zetten je ook doet. Om nu aan te tonen dat ons startleger altijd te weinig gewicht zal hebben berekenen we het gewicht van het leger dat alle (oneindig veel!) vakjes onder de blauwe streep zou innemen, heeft. We doen dit per kolom. We beginnen met de kolom onder het eindpunt, deze heeft gewicht: .
Bedenk dat 0 ≤ x ≤ 1, dus dit is een geometrische reeks met als som: x5/(1 - x).
De twee kolommen aan weerszijden van deze kolom hebben elk waarde x6/(1 - x), die daarnaast x7/(1 - x), en zo voort. Dat hele halfvlak heeft dus als gewicht G:
Bedenk, we hadden x zo gekozen dat 1 - x = x2, dus bovenstaande is gelijk aan:
Kortom, als het gehele oneindige halfvlak bezet zou zijn met poppetjes, dan zouden deze samen precies gewicht 1 hebben. Elke lege plek betekent dat het gewicht minder dan 1 is, en dus de vijfde regel nooit bereikt kan worden. Geen enkel eindig leger kan die vijfde regel daarom bereiken. □
De mensen die “The Curious Incident of the Dog in the Night-Time” hebben gelezen kennen dit misschien al, of ze hebben het overgeslagen omdat ze het niets zei.
Het idee is in feite een eenvoudig soort solitair spelletje. Dus je hebt een aantal poppetjes op het bord staan, en je kunt ermee over naburige poppetjes springen, mits er aan de andere kant een leeg vakje is waar je kunt landen. Je mag verder alleen horizontaal en verticaal bewegen.
Bijvoorbeeld met twee stenen kun je met de onderste over de bovenste springen (of andersom natuurlijk):
Het probleem is nu als volgt: Hoeveel stenen heb je minstens nodig, als je ze allemaal onder de dikke blauwe lijn neerzet, om minstens één steen op n plaatsen boven de dikke blauwe lijn neer te zetten. Hierboven zie je al dat je 2 stenen nodig hebt om op de 1 plaats boven de blauwe lijn te komen.
De notatie gebruiken we verder ook: een pijltje geeft aan welke steen verzet gaat worden, linksboven staat het aantal gedane zetten (0 is dus de begin situatie) en een grijs rondje is een steen die is verdwenen omdat er overheen gesprongen is.
Laten we nu bekijken hoe we op de tweede regel boven de dikke blauwe lijn uitkomen:
Daar hebben we dus minstens vier stenen voor nodig. Merk overigens op dat we na twee zetten eigenlijk de situatie hebben van ons eerste voorbeeld, alleen dan 1 regel omhoog verschoven. We zouden dus daar al kunnen concluderen dat het kan. Wat wiskundig gezien genoeg is. Maar omdat ik gul ben is het helemaal uitgewerkt.
Ook de derde regel behalen is mogelijk: merk op dat de vier stenen die hier in groen zijn weergegeven precies zo staan als in het tweede voorbeeld, en de eerste drie zetten zijn dan ook gelijk aan dit tweede voorbeeld, en die gebruiken we dus om die ene groene steen op 2 regels boven de dikke blauwe streep te krijgen.
Daarna gaat het verder om met de overige stenen er eentje op drie regels boven de streep te krijgen:
Inmiddels denkt de oplettende lezer: ik heb het patroon al door, 2 stenen voor 1 regel, 4 voor voor 2 regels, 8 voor 3 regels, dus vast 16 voor vier regels: fout. Dat zijn er minstens 20, één voorbeeld zie je hier:
We gaan nu verder om in feite de begin situatie van voorbeeld drie te creëren, alleen dan alvast één regel verschoven:
Hierboven zie je een situatie die nog 8 stenen overheeft, en verder gelijk is aan de startsituatie om 3 regels omhoog te komen, behalve dat één rijtje nu al boven de streep staat.
Oké, boeiend denk je misschien, maar wat is nu het punt? Solitair spelen is niet zo spannend. Het geval is namelijk dat de volgende uitdaging, namelijk een steen op 5 regels boven de blauwe streep krijgen als je met al je stenen eronder begint überhaupt niet mogelijk is. Hoeveel stenen je ook pakt, hoe je ook beweegt, wat je ook doet, je zult nooit een steen op de vijfde regel krijgen.
En dat zullen we gaan bewijzen. Het probleem is bedacht en bewezen door John Conway in 1961. Het bewijs dat het niet kan is werkelijk heel vernuftig, en maakt slim gebruik van de gulden snede: ϕ.
Het idee is als volgt: Het is duidelijk dat elke keer dat je een zet doet dat je dan een mannetje verliest. Maar tegelijkertijd (als je tenminste niet te stom speelt) kun je een mannetje dichter bij je doel brengen. We proberen nu een soort gewicht aan de verzameling soldaatjes te hangen, en uit te drukken hoeveel gewicht er gewonnen of verloren wordt door een zet, en dan uiteindelijk zullen we zien dat hoe je ook begint, je nooit genoeg gewicht hebt om die vijfde regel te bereiken: je verliest het altijd te vroeg.
Allereerst merken we voor de volledigheid op dat het niet uitmaakt wélk punt op de vijfde regel we willen bereiken. Als we een zeker punt kunnen bereiken kunnen we ook het punt links ervan bereiken door alle stenen één plaatsje op te schuiven naar links en dan dezelfde bewegingen te doen. Kortom, die punten zijn in feite inwisselbaar en daarom maakt het niet uit welk punt we pakken. Als het niet kan met dat punt, kan het met geen enkel punt, en omgekeerd. We gaan er hierbij vanuit natuurlijk dat ons bord willekeurig groot kan worden, alhoewel we niet met oneindig veel soldaatjes gaan schuiven, maar wel met willekeurig (doch eindig) veel.
Eerst kiezen we maar eens een punt op de 5e regel (dat is blauw gekleurd hieronder) en dat punt kennen we een bepaald gewicht toe, namelijk: 1. De buurtpunten, die met één stap zijn te bereiken, kennen we gewicht x1 toe (wat x is zullen we later nog specificeren), de velden die met twee stappen bereikbaar zijn kennen we x2 toe, met drie x3, en zo voort, je krijgt dus deze situatie:
De laagste macht die we onder de streep vinden is dus x5. Een soldaatje dat op een veld staat krijgt het gewicht van het veld. Het gewicht van ons hele leger is simpelweg de som van alle veldjes waar een soldaat op staat. Merk op dat een soldaat op ons eindpunt dus per definitie gewicht 1 heeft, en een leger met een soldaat op het eindpunt dus ook minstens gewicht 1.
Voordat we specificeren wat x is, kijken we eerst nog even wat voor soort stappen we zouden kunnen doen, dat zijn er 3:
Het is hopelijk niet lastig om jezelf ervan te overtuigen dat als je alleen horizontaal en verticaal mag springen dit de enige drie opties zijn.
Nu komt de truc, namelijk een geschikt waarde voor x kiezen. Dit, samen met de waardering is het briljante van het bewijs, we kiezen x = 1/ϕ, ofwel:
Het getal ϕ is de guldensnede, die heeft een paar interessante eigenschappen die ook nu van pas komen, te weten: ϕ2 = ϕ + 1, en 1/ϕ = ϕ - 1.
Laten we nu eens naar de drie soorten bewegingen kijken die we kunnen maken, eerst de eerste bewegingen waarbij we naar het eindpunt toespringen:
De oplettende lezer voelt ’m nu al aankomen: de eigenschappen van de gulden snede komen nu beregoed van pas. Bedenk, x = 1/ϕ = ϕ - 1, dus x2 = 1/(ϕ2) = 1/ϕ·1/ϕ = (ϕ - 1)/ϕ = 1 - 1/ϕ = 1 - x.
Kortom:
Als we dus naar het eindpunt toe bewegen verandert het ‘gewicht’ van het leger niet. Nu bekijken we het tweede geval, dat betekent dat we van het eindpunt af bewegen, dat geeft:
Omdat x positief is geldt dat -2xn+1 < 0. Dat is voldoende: het gewicht van het leger neemt in dat geval dus af.
Nu het laatste geval waarbij we over een as door het eindpunt springen:
Ook in dát geval neemt het gewicht af. Het maakt dus niet uit wat voor sprong we maken, onder de waardering die we kiezen kan de waarde van het gehele leger niet toenemen.
Omdat het eindpunt gewicht 1 heeft, zoals we al opgemerkt hebben, zal een leger dat ooit dat eindpunt wil kunnen bereiken ook minstens gewicht 1 hebben, want het gewicht kan nooit toenemen, wat voor zetten je ook doet. Om nu aan te tonen dat ons startleger altijd te weinig gewicht zal hebben berekenen we het gewicht van het leger dat alle (oneindig veel!) vakjes onder de blauwe streep zou innemen, heeft. We doen dit per kolom. We beginnen met de kolom onder het eindpunt, deze heeft gewicht: .
Bedenk dat 0 ≤ x ≤ 1, dus dit is een geometrische reeks met als som: x5/(1 - x).
De twee kolommen aan weerszijden van deze kolom hebben elk waarde x6/(1 - x), die daarnaast x7/(1 - x), en zo voort. Dat hele halfvlak heeft dus als gewicht G:
Bedenk, we hadden x zo gekozen dat 1 - x = x2, dus bovenstaande is gelijk aan:
Kortom, als het gehele oneindige halfvlak bezet zou zijn met poppetjes, dan zouden deze samen precies gewicht 1 hebben. Elke lege plek betekent dat het gewicht minder dan 1 is, en dus de vijfde regel nooit bereikt kan worden. Geen enkel eindig leger kan die vijfde regel daarom bereiken. □
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Mooi is de formule:
x^2 + x + 41 is priem voor x = 0 t/m x = 39
2*x^2 + 29 is priem voor x = 0 t/m x = 28
Met name de eerste is een spectaculaire rij.
Verder zijn er bijna geen formules voor het berekenen van priemgetallen.
x^2 + x + 41 is priem voor x = 0 t/m x = 39
2*x^2 + 29 is priem voor x = 0 t/m x = 28
Met name de eerste is een spectaculaire rij.
Verder zijn er bijna geen formules voor het berekenen van priemgetallen.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.


Dat zijn prime-generating polynomials. Het is trouwens niet waar dat er verder 'bijna' geen van dergelijke polynomen zouden zijn, kijk maar.quote:Op zaterdag 10 oktober 2009 18:01 schreef Twentsche_Ros het volgende:
Mooi is de formule:
x^2 + x + 41 is priem voor x = 0 t/m x = 39
2*x^2 + 29 is priem voor x = 0 t/m x = 28
Met name de eerste is een spectaculaire rij.
Verder zijn er bijna geen formules voor het berekenen van priemgetallen.


Interessant, je bent een echte expert.quote:Op zaterdag 10 oktober 2009 18:20 schreef Riparius het volgende:
[..]
Dat zijn prime-generating polynomials. Het is trouwens niet waar dat er verder 'bijna' geen van dergelijke polynomen zouden zijn, kijk maar.
Ik ben wiskunde-hobby'ist.
Het is niet mijn beroep. Vandaar mijn amateuristische uitleg.
Ik ben gefascineerd door een aantal wiskundige zaken. Een ervan zijn priemgetallen. De ander zijn fractals. En bv de kubus van Rubik.
Vwb dat laatste:
Het schijnt dat je elke “in de warre” kubus binnen 20 draaien weer goed krijgt. Zijn er al algoritmen/programma’s die een dergelijk draaitraject kunnen berekenen, wanneer je de “in de war”-stand invoert?
Dat zou ik een hele fraaie formule vinden.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.


Het record staat nu op 22. Zie b.v.: Optimal solutions for Rubik's Cube
Er zijn algoritmes die je inderdaad kunnen helpen met zo’n kubus. Je hebt ook software. Die doet ’t gemiddeld in 19 moves. Het perfecte algoritme is er nog niet, maar men zit er naar verwachting niet ver af.
Voor mensen is dit echter niet heel praktisch, het zou te veel randgevallen vereisen om te leren. Mensen zijn veel meer gebaat naar het kunnen reduceren naar een toestand die ze herkennen. De standaard layer by layer methods zijn daar ook op gericht. Weinig uit je hoofd leren, toch veel kunnen doen.
Mensen die meedoen aan wedstrijden om snel kubussen op te lossen maken volgens mij gebruik van algoritmes die soms ook meer dan 100 gevallen onderscheiden. Maar dan nog ben je vaak meer dan 50 keer aan het draaien. Voor mensen maakt het echter ook uit welke kanten je na elkaar moet draaien, en of je de kubus moet verpakken. Dat kost tijd, en het gaat vaak om snelheid bij die wedstrijden. (Niet altijd overigens.)
Er zijn algoritmes die je inderdaad kunnen helpen met zo’n kubus. Je hebt ook software. Die doet ’t gemiddeld in 19 moves. Het perfecte algoritme is er nog niet, maar men zit er naar verwachting niet ver af.
Voor mensen is dit echter niet heel praktisch, het zou te veel randgevallen vereisen om te leren. Mensen zijn veel meer gebaat naar het kunnen reduceren naar een toestand die ze herkennen. De standaard layer by layer methods zijn daar ook op gericht. Weinig uit je hoofd leren, toch veel kunnen doen.
Mensen die meedoen aan wedstrijden om snel kubussen op te lossen maken volgens mij gebruik van algoritmes die soms ook meer dan 100 gevallen onderscheiden. Maar dan nog ben je vaak meer dan 50 keer aan het draaien. Voor mensen maakt het echter ook uit welke kanten je na elkaar moet draaien, en of je de kubus moet verpakken. Dat kost tijd, en het gaat vaak om snelheid bij die wedstrijden. (Niet altijd overigens.)
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Gaaf bewijs!quote:
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten


tvp ,
wellicht dat ik hier ooit een mooi bewijsje post als het hier rustig is
Het bewijs dat er oneindig veel priemgetallen zijn in de OP is zo geniaal.
Iedereen begrijpt het, maar verzin het maar eens..
[ Bericht 22% gewijzigd door qonmann op 10-10-2009 22:12:44 ]
wellicht dat ik hier ooit een mooi bewijsje post als het hier rustig is
Het bewijs dat er oneindig veel priemgetallen zijn in de OP is zo geniaal.
Iedereen begrijpt het, maar verzin het maar eens..
[ Bericht 22% gewijzigd door qonmann op 10-10-2009 22:12:44 ]
Niet geschoten is altijd mis..
Ach Margrietje, de Rozen zullen bloeien..
Ach Margrietje, de Rozen zullen bloeien..


Het bewijs dat bijvoorbeeld wortel 2 geen rationeel getal is.
Dus niet het quotient vormt van 2 gehele getallen.
Ieder rationeel getal heeft een eindig aantal kettingbreuken.
Bijvoorbeeld: 355/113:
Heeft als kettingbreuken: 3,7,16
en daarna oneindig.
Wortel 2 heeft als kettingbreuken: 1,2,2,2,2,2,2,2 etc.
Dus komt er nooit een eind aan.
Dus niet het quotient vormt van 2 gehele getallen.
Ieder rationeel getal heeft een eindig aantal kettingbreuken.
Bijvoorbeeld: 355/113:
Heeft als kettingbreuken: 3,7,16
en daarna oneindig.
Wortel 2 heeft als kettingbreuken: 1,2,2,2,2,2,2,2 etc.
Dus komt er nooit een eind aan.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.


Leuk om eens te lezen.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Ik ken eigenlijk alleen volledige inductie; wat houdt in de wiskunde "onvolledige" inductie precies in dan?quote:Op maandag 12 oktober 2009 14:15 schreef Bankfurt het volgende:
Bewijs met onvolledige (beperkte) inductie is een leuk bewijs.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


onvolledige inductie is toch geen wiskundig bewijs.
Is dat niet zo dat als iets bvb 1000 keer klopt, dat je ervan uitgaat dat het wel altijd juist zal zijn?
(zoals fysica dus )
)
Is dat niet zo dat als iets bvb 1000 keer klopt, dat je ervan uitgaat dat het wel altijd juist zal zijn?
(zoals fysica dus


Er zijn stellingen die gelden voor n = 5 of 6 en hoger, maar niet voor kleiner dan 5 of 6, met n als natuurlijk getal.quote:Op maandag 12 oktober 2009 14:26 schreef Beregd het volgende:
onvolledige inductie is toch geen wiskundig bewijs.
Is dat niet zo dat als iets bvb 1000 keer klopt, dat je ervan uitgaat dat het wel altijd juist zal zijn?
(zoals fysica dus)


dat is op zich niets anders dan stellingen die voor alle n>=0 gelden. Je kan makkelijk stellingen zoals jij ze omschrijft herschrijven naar een stelling die voor alle n>= 0 geldt.quote:Op maandag 12 oktober 2009 14:40 schreef Bankfurt het volgende:
[..]
Er zijn stellingen die gelden voor n = 5 of 6 en hoger, maar niet voor kleiner dan 5 of 6, met n als natuurlijk getal.
het komt er op neer dat N| en {x in N| | x>5} even 'groot' zijn.
Dus ook gewoon volledige inductie.


Ik gooi eerbiedig een vraag in dit gezelschap van giganten der wiskundige wetenswaardigheden: wat is het wiskundige bewijs van 1 + 1 = 2?


Is al gedaan deze topic en er is al naar gelinkt. Als je terugleest heb je het zo.quote:Op maandag 12 oktober 2009 15:50 schreef servus_universitas het volgende:
Ik gooi eerbiedig een vraag in dit gezelschap van giganten der wiskundige wetenswaardigheden: wat is het wiskundige bewijs van 1 + 1 = 2?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


quote:Op maandag 12 oktober 2009 15:50 schreef servus_universitas het volgende:
Ik gooi eerbiedig een vraag in dit gezelschap van giganten der wiskundige wetenswaardigheden: wat is het wiskundige bewijs van 1 + 1 = 2?
quote:Op dinsdag 28 oktober 2008 22:20 schreef Iblis het volgende:
[..]
Neem de lege verzameling: {}. Definieer nu een recursieve relatie van een lijst waarbij we de opvolger van element k, zeg S(k), definiëren als S(k) = k ∪ {k}. Dan hebben we de volgende lijst: {}, {{}}, {{}, {{}} }, etc. Nu noemen we het eerste element 0. Het tweede 1, en het derde 2. Aldus construeren wij de natuurlijke getallen vanuit de lege verzameling. De symbolen gaan verder als 3, 4, 5, 6, 7, 8, 9, 10, maar dit is in feite arbitrair. Doch voor nu nemen we de gebruikelijke notatie aan.
Dan zijn er nog wat definities. Zij x een natuurlijk getal, en zijn y en z dit ook. Dan, x = x, x = y dan en slechts dan y = x, verder x = y en y = z, dan x = z en als laatste, als x een natuurlijk getal is en x = x', dan is x' ook een natuurlijk getal.
Voorts stipuleren we dat {} (noemen wij ook 0) een natuurlijk getal is, en dat S(k), waarbij k een natuurlijk getal is, ook een natuurlijk getal is. Verder nemen wij aan dat er geen k is zodanig dat S(k) = {}, en ook dat als S(x) = z, en S(y) = z, dat dan x = y. (Omgekeerd volgt natuurlijk direct uit de voorgaande axiomata).
Voor het gemak duiden we de verzameling van natuurlijke getallen aan met N, dan definiëren we + : N x N -> N, met als basisstap:
+(x, {}) = x (1)
En als recursie:
+(x, S(y)) = S(+(x, y)) (2)
Soms gebruiken we ook de infix-notatie en schrijven we derhalve x + y voor +(x, y).
Let op dat deze uiteenzetting niet helemaal formeel is, maar afdoende om het idee over te brengen.
Beschouw nu: 1 + 1, ofwel +({{}}, {{}}), dit voldoet niet aan (1), dus we moeten (2) toepassen, en dit zegt dat het gelijk is aan S(+({{}}, {})). De binnenste + kan nu weer nader beken worden, en deze voldoet wel aan (1). Dit geeft dat +({{}}, {}) gelijk is aan {{}}. Dat maakt dat de vergelijking vereenvoudigt tot S({{}}), wat per definitie van S gelijk is aan {{},{{}}}, of wel 2. QED.
Dit vanuit de set-theoretische constructie van de natuurlijke getallen, en de axiomata van Peano-Arithmetica. Een minstens zo elegant bewijs kan gegeven worden middels Church-numerals in de Lambda-calculus. Uiteindelijk komt het natuurlijk meer neer op een afspraak die wij maken hoe wij bepaalde verzamelingen (of lambda-functie-expressies) kort aanduiden met een cijfer, en de opvolgingsrelatie die wij daarin veronderstellen, dat volgt dat de som van 1 + 1 inderdaad gelijk is aan de opvolger van 1. Dit correspondeert redelijk met een discreet model van dingen in de werkelijkheid. Alhoewel je zou kunnen beargumenteren dat 1 druppel samen met 1 druppel weer één druppel is, en dat bovenstaande dit niet accuraat modelleert. Voor zulke vragen, in tegen stelling tot axiomatische afleidingen moet je denk ik in een WFL topic zijn, en je zou de Principia Mathematica er eens op na kunnen slaan.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Waarbij WFL nu vervangen dient te worden door F&L.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Persoonlijk vind ik dit een prachtige fractal,
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.


quote:Op maandag 12 oktober 2009 15:52 schreef Iblis het volgende:
[..]
Is al gedaan deze topic en er is al naar gelinkt. Als je terugleest heb je het zo.
Bedankt en vergeef me mijn laksheid.quote:


Brassica oleracea convar. botrytis var. botrytisquote:Op maandag 12 oktober 2009 15:55 schreef Pietverdriet het volgende:
Persoonlijk vind ik dit een prachtige fractal,
[ afbeelding ]
Overigens zijn er heel veel van zulke repeterende systemen in de natuur te vinden, varens zijn een ander bekend voorbeeld. Een manier om dat te formaliseren zijn Lindenmayersystemen.
Die systemen bestaan uit een voudige regels (stapje naar voren, draai een slag, stapje naar voren, trek een lijntje), en door die iteratief te doen krijg je fractals. Zie die Wikipedia pagina. Een voorbeeld zie hieronder:
Bron: Wikimedia Commons. Maker: Sakurambo. Licentie: CC-BY-SA.
Het leuke is in feite dat dit heel simpele instructies zijn die zich genetisch ook gemakkelijk zouden laten coderen. Zo’n plant is dus heel compact weer te coderen. Maar toch oogt het resultaat vrij complex. Hierboven zie je ook dat de plant in feite kleinere kopieën van zichzelf bevat aan de stam.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Als je ervan uitgaat dat ze zich ook genetisch moeten kunnen laten coderen op een vrij eenvoudige manier, dan is het toch al niet zo heel vreemd? Natuurlijk is er in ‘het echt’ altijd verstoring. Dus de ‘instructie’ (zo je wilt) is weliswaar simpelweg ‘groei’ maar zonlicht/wind/beesten/iets verstoort de boel.quote:Op maandag 12 oktober 2009 16:06 schreef servus_universitas het volgende:
Echt fascinerend dat die in de natuur voorkomende patronen zich wiskundig laten beschrijven.
Maar goed:
Bron: Wikimedia Commons. Maker: L. Shyamal. Licentie: CC-BY-SA.
Van Wikipedia Fibonacci spiral (Fibonacci numbers in nature)
Het onderstreepte is de kern: evolutionair is het voordelig om zo dicht mogelijk opeen te pakken. En het resultaat is dus dat er zo’n wiskundig patroon uitkomt.quote:A model for the pattern of florets in the head of a sunflower was proposed by H. Vogel in 1979. This has the form
where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F(j):F(j + 1), the nearest neighbors of floret number n are those at n ± F(j) for some index j which depends on r, the distance from the center. It is often said that sunflowers and similar arrangements have 55 spirals in one direction and 89 in the other (or some other pair of adjacent Fibonacci numbers), but this is true only of one range of radii, typically the outermost and thus most conspicuous.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Een ander prachtig voorbeeldje van een wiskundige structuur die mooie plaatjes opgeeft is de zogenaamde wortelstructuur van de 248-dimensionale Lie group E8. Deze Lie groep wordt bijvoorbeeld in een heterotische supersnaartheorie of een 10-dimensionale N=1 supergravitatie theorie toegepast als ijkgroep.
Alhoewel het hier nog maar de vraag is of deze structuur in de natuur terug te vinden is
Alhoewel het hier nog maar de vraag is of deze structuur in de natuur terug te vinden is
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Wat ook fraai is, is om bij een rekenmethode of een raadsel de ongeldigheid aannemelijk te maken, door een extreem voorbeeld te nemen.
Stel: iemand beweert ten onrechte het volgende:
Als ik van A naar B rijd met een snelheid van 100 km/u en van B naar A met een snelheid van 150 km/u heb ik gemiddeld 125 km/u gereden. Op verjaardagen en in veel bedrijfskantines zal men dit beweren. Hoe kun je deze stelling weerleggen, zonder in allerlei rekenkundige ingewikkeldheden te verzanden.
Welnu: Stel dat ik van A naar B heb gereden met een snelheid van 100 km/u en van B naar A met een snelheid van 2 miljard km/u, heb ik dan ook gemiddeld 1 miljard km/u gereden. Niet dus.
Ander voorbeeld:
Je doet mee aan een quiz. Er zijn drie dichte deuren. Achter 1 zit een prijs, achter 2 andere niet. Je bent kandidaat en je kiest een deur. De kwismaster weet waar de prijs zit en opent een andere deur waarachter geen prijs blijkt te zitten. De door jou gekozen deur blijft dicht.
Je mag nog wisselen. Wat is wijsheid? In menige bedrijfskantine zegt men: Maakt niks uit. ’t Is fifty fifty, want er zijn immers twee deuren. Zucht.
Niet dus:
Want de kans is 2/3e dat de prijs achter de overgebleven deur zit.
Hoe maak je aannemelijk dat de fifty-fifty stelling niet klopt.
Stel er zijn honderd deuren.
Je kiest een deur.
En de kwismaster is zo vriendelijk om 98 deuren te openen waarachter geen prijs blijkt te zijn. Ook nu zijn er twee deuren over. Is het nu ook nog 50:50?
Hmmm erg onwaarschijnlijk.

Stel: iemand beweert ten onrechte het volgende:
Als ik van A naar B rijd met een snelheid van 100 km/u en van B naar A met een snelheid van 150 km/u heb ik gemiddeld 125 km/u gereden. Op verjaardagen en in veel bedrijfskantines zal men dit beweren. Hoe kun je deze stelling weerleggen, zonder in allerlei rekenkundige ingewikkeldheden te verzanden.
Welnu: Stel dat ik van A naar B heb gereden met een snelheid van 100 km/u en van B naar A met een snelheid van 2 miljard km/u, heb ik dan ook gemiddeld 1 miljard km/u gereden. Niet dus.
Ander voorbeeld:
Je doet mee aan een quiz. Er zijn drie dichte deuren. Achter 1 zit een prijs, achter 2 andere niet. Je bent kandidaat en je kiest een deur. De kwismaster weet waar de prijs zit en opent een andere deur waarachter geen prijs blijkt te zitten. De door jou gekozen deur blijft dicht.
Je mag nog wisselen. Wat is wijsheid? In menige bedrijfskantine zegt men: Maakt niks uit. ’t Is fifty fifty, want er zijn immers twee deuren. Zucht.
Niet dus:
Want de kans is 2/3e dat de prijs achter de overgebleven deur zit.
Hoe maak je aannemelijk dat de fifty-fifty stelling niet klopt.
Stel er zijn honderd deuren.
Je kiest een deur.
En de kwismaster is zo vriendelijk om 98 deuren te openen waarachter geen prijs blijkt te zijn. Ook nu zijn er twee deuren over. Is het nu ook nog 50:50?
Hmmm erg onwaarschijnlijk.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.


Het is natuurlijk wel aardig om dat patroon op je kleren te borduren als fysicus.quote:Op maandag 12 oktober 2009 16:17 schreef Haushofer het volgende:
Een ander prachtig voorbeeldje van een wiskundige structuur die mooie plaatjes opgeeft is de zogenaamde wortelstructuur van de 248-dimensionale Lie group E8. Deze Lie groep wordt bijvoorbeeld in een heterotische supersnaartheorie of een 10-dimensionale N=1 supergravitatie theorie toegepast als ijkgroep.
[ afbeelding ]
Alhoewel het hier nog maar de vraag is of deze structuur in de natuur terug te vinden is
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik vind het ook niet vreemd, maar wel fascinerend. Voor mij is deze materie dan ook geen gesneden koek, waardoor het waarschijnlijk gepaard gaat met meer verwondering dan feitelijk 'gerechtvaardigd'.quote:Op maandag 12 oktober 2009 16:17 schreef Iblis het volgende:
Als je ervan uitgaat dat ze zich ook genetisch moeten kunnen laten coderen op een vrij eenvoudige manier, dan is het toch al niet zo heel vreemd? Natuurlijk is er in ‘het echt’ altijd verstoring. Dus de ‘instructie’ (zo je wilt) is weliswaar simpelweg ‘groei’ maar zonlicht/wind/beesten/iets verstoort de boel.


Daar zou ik niet zo zeker van zijn.quote:Op maandag 12 oktober 2009 16:20 schreef Twentsche_Ros het volgende:
Wat ook fraai is, is om bij een rekenmethode of een raadsel de ongeldigheid aannemelijk te maken, door een extreem voorbeeld te nemen.
Stel er zijn honderd deuren.
Je kiest een deur.
En de kwismaster is zo vriendelijk om 98 deuren te openen waarachter geen prijs blijkt te zijn. Ook nu zijn er twee deuren over. Is het nu ook nog 50:50?
Hmmm erg onwaarschijnlijk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Fractals zijn niet alleen te beschrijven als plaatjes, maar ook als Muziek
http://www.ocf.berkeley.edu/~wwu/sounds/au/structure1.au
http://www.ocf.berkeley.edu/~wwu/sounds/au/structure1.au
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.


Dat is niet echt bewijs. Je hebt wel gelijk, maar in feite zeg je gewoon 2 keer hetzelfde alleen met andere snelheden.quote:Op maandag 12 oktober 2009 16:20 schreef Twentsche_Ros het volgende:
Wat ook fraai is, is om bij een rekenmethode of een raadsel de ongeldigheid aannemelijk te maken, door een extreem voorbeeld te nemen.
Stel: iemand beweert ten onrechte het volgende:
Als ik van A naar B rijd met een snelheid van 100 km/u en van B naar A met een snelheid van 150 km/u heb ik gemiddeld 125 km/u gereden. Op verjaardagen en in veel bedrijfskantines zal men dit beweren. Hoe kun je deze stelling weerleggen, zonder in allerlei rekenkundige ingewikkeldheden te verzanden.
Welnu: Stel dat ik van A naar B heb gereden met een snelheid van 100 km/u en van B naar A met een snelheid van 2 miljard km/u, heb ik dan ook gemiddeld 1 miljard km/u gereden. Niet dus.
Iemand die het met 100 en 150 niet begrijpt zal het ook niet met 100 en 2e9 begrijpen.


Zijn er evenveel breuken als gehele positieve getallen?
Een drieluik! Vandaag het eerste deel. Het idee voor vandaag is om te bewijzen dat er evenveel rationale getallen, ook wel bekend als breuken, zijn als natuurlijke getallen, d.w.z. de positieve gehele getallen.
Wat ‘evenveel’ is zullen we vandaag eveneens verduidelijken. Het volgende stuk is de Calkin-Wilf-reeks, en als laatste zullen we Cantors diagonaal-argument doen.
Deze aflevering is (hopelijk) goed te volgen ook al heb je nooit veel wiskunde gehad.
De natuurlijke getallen
We beginnen met de natuurlijke getallen, dit zijn de getallen 1, 2, 3, 4, 5 en zo voort. Deze verzameling wordt meestal aangeduid met een hoofdletter N (eigenlijk: ℕ):
Soms stopt men 0 er ook bij, maar ik vandaag niet.
Deze verzameling bevat uiteraard oneindig veel getallen. Er is niet zoiets als ‘een grootste natuurlijk getal’. Alhoewel het er oneindig veel zijn, kunnen we ze toch systematisch opsommen. Je begint gewoon bij 1, en dan telkens eentje meer. Je komt nooit bij het eind, maar je kunt weet zeker dat je ook geen getal overslaat als je zo opsomt. En dat is belangrijk, daarom wordt deze verzameling aftelbaar oneindig genoemd.
De gehele getallen
Nu bekijken we de verzameling van alle gehele getallen, meestal aangeduid met een Z (ℤ) van het Duitse Zahlen. Je kunt je ℤ voorstellen als:
Nu beweer ik ‘er zijn evenveel gehele getallen als natuurlijke getallen’. Wat ‘evenveel’ inhoudt zal ik nog iets preciseren. Normaliter, bij eindige verzamelingen, zeg je b.v. {a, b, c} en {1, 2, 3} bevatten evenveel elementen omdat ze allebei 3 elementen bevatten. Maar ja, het is niet in een getal uit te drukken hoeveel elementen ℕ bevat, oneindig is geen getal immers.
‘Evenveel’ precies gemaakt
Daarom is er een iets algemenere definitie voor evenveel. Namelijk, twee verzamelingen bevatten evenveel elementen als er een 1:1 koppeling te vinden tussen de elementen van beide verzamelingen. Kortom, je kunt paartjes maken met één element uit de ene verzameling, en eentje uit de andere verzameling, waarbij alle elementen gebruikt, maar waarbij je geen enkel element dubbel gebruikt, bijvoorbeeld:
Hierboven zie je twee manieren om de verzamelingen {1,2,3} en {a,b,c} aan elkaar te koppelen. Ook zie je dat voor {1,2} en {a,b,c} niet zo’n koppeling te vinden is. Je komt er immers altijd eentje te kort. In dit voorbeeld kun je c niet koppelen.
In het geval van oneindige verzamelingen kan dit een soms een wat onverwacht resultaat geven, maar hopelijk is het toch redelijk logisch als je erover nadenkt. Neem b.v. de even natuurlijke getallen ({2,4,6,…}) en alle natuurlijke getallen:
Het is duidelijk dat die koppeling helemaal door te trekken. Elk even getal n wordt gekoppeld aan n/2 en elk natuurlijk getal m aan het even getal 2m. In deze zin zijn er dus evenveel gehele getallen als even getallen. Nu is duidelijk (hopelijk) wat ik met evenveel bedoel.
Een koppeling tussen ℕ en ℤ
Er zijn op die manier ook evenveel gehele getallen als natuurlijke getallen:
Het is ook duidelijk dat deze koppeling gewoon door te trekken is, bovenaan som je de natuurlijke getallen op, onderaan gaat het verder met -4, 4, -5, 5, -6, 6 enz.
Dus er zijn ook evenveel gehele getallen als natuurlijke getallen.
Er zijn evenveel breuken als natuurlijke getallen!
Nu komen we bij de volgende stap. De eerstvolgende grotere verzameling van getallen die wiskundigen gebruiken is Q (of ℚ), die bestaat uit alle breuken. Dus b.v. 3/5, 7/3, 1/8, 9/2, enz. Hieronder zie je alle positieve breuken systematisch opgesomd als een vierkant dat oneindig is naar twee kanten:
Het misschien nog wel duidelijk hoe je één rij of één kolom kunt koppelen aan de natuurlijke getallen, maar allemaal? Toch kan dit. Het volgende werkt duidelijk niet:
Want aan welk getal wordt 2/3 bijvoorbeeld gekoppeld? Dat is niet te zeggen. Want er zijn duidelijk oneindig veel breuken in de vorm 1/n. En 2/3 komt pas ‘daarna’. Maar ‘na oneindig’ is er niet veel, en al helemaal geen getal. Dus er moet iets slimmers bedacht worden.
En dat gaat zo (volg de blauwe lijn):
Je gaat dus systematisch de diagonalen af, dit levert de volgende koppeling:
En dit systeem is wél door te trekken. Op het plaatje staat al grofweg hoe het werkt.
Tot slot
Een nadeel van deze koppeling is dat je er dubbele vormen in hebt, zoals 4/4, 3/1 en 6/2. In een volgende post zullen we een heel slimme manier van opsommen zien, die zulke ‘dubbelen’ overslaat.
Een drieluik! Vandaag het eerste deel. Het idee voor vandaag is om te bewijzen dat er evenveel rationale getallen, ook wel bekend als breuken, zijn als natuurlijke getallen, d.w.z. de positieve gehele getallen.
Wat ‘evenveel’ is zullen we vandaag eveneens verduidelijken. Het volgende stuk is de Calkin-Wilf-reeks, en als laatste zullen we Cantors diagonaal-argument doen.
Deze aflevering is (hopelijk) goed te volgen ook al heb je nooit veel wiskunde gehad.
De natuurlijke getallen
We beginnen met de natuurlijke getallen, dit zijn de getallen 1, 2, 3, 4, 5 en zo voort. Deze verzameling wordt meestal aangeduid met een hoofdletter N (eigenlijk: ℕ):
Soms stopt men 0 er ook bij, maar ik vandaag niet.
Deze verzameling bevat uiteraard oneindig veel getallen. Er is niet zoiets als ‘een grootste natuurlijk getal’. Alhoewel het er oneindig veel zijn, kunnen we ze toch systematisch opsommen. Je begint gewoon bij 1, en dan telkens eentje meer. Je komt nooit bij het eind, maar je kunt weet zeker dat je ook geen getal overslaat als je zo opsomt. En dat is belangrijk, daarom wordt deze verzameling aftelbaar oneindig genoemd.
De gehele getallen
Nu bekijken we de verzameling van alle gehele getallen, meestal aangeduid met een Z (ℤ) van het Duitse Zahlen. Je kunt je ℤ voorstellen als:
Nu beweer ik ‘er zijn evenveel gehele getallen als natuurlijke getallen’. Wat ‘evenveel’ inhoudt zal ik nog iets preciseren. Normaliter, bij eindige verzamelingen, zeg je b.v. {a, b, c} en {1, 2, 3} bevatten evenveel elementen omdat ze allebei 3 elementen bevatten. Maar ja, het is niet in een getal uit te drukken hoeveel elementen ℕ bevat, oneindig is geen getal immers.
‘Evenveel’ precies gemaakt
Daarom is er een iets algemenere definitie voor evenveel. Namelijk, twee verzamelingen bevatten evenveel elementen als er een 1:1 koppeling te vinden tussen de elementen van beide verzamelingen. Kortom, je kunt paartjes maken met één element uit de ene verzameling, en eentje uit de andere verzameling, waarbij alle elementen gebruikt, maar waarbij je geen enkel element dubbel gebruikt, bijvoorbeeld:
Hierboven zie je twee manieren om de verzamelingen {1,2,3} en {a,b,c} aan elkaar te koppelen. Ook zie je dat voor {1,2} en {a,b,c} niet zo’n koppeling te vinden is. Je komt er immers altijd eentje te kort. In dit voorbeeld kun je c niet koppelen.
In het geval van oneindige verzamelingen kan dit een soms een wat onverwacht resultaat geven, maar hopelijk is het toch redelijk logisch als je erover nadenkt. Neem b.v. de even natuurlijke getallen ({2,4,6,…}) en alle natuurlijke getallen:
Het is duidelijk dat die koppeling helemaal door te trekken. Elk even getal n wordt gekoppeld aan n/2 en elk natuurlijk getal m aan het even getal 2m. In deze zin zijn er dus evenveel gehele getallen als even getallen. Nu is duidelijk (hopelijk) wat ik met evenveel bedoel.
Een koppeling tussen ℕ en ℤ
Er zijn op die manier ook evenveel gehele getallen als natuurlijke getallen:
Het is ook duidelijk dat deze koppeling gewoon door te trekken is, bovenaan som je de natuurlijke getallen op, onderaan gaat het verder met -4, 4, -5, 5, -6, 6 enz.
Dus er zijn ook evenveel gehele getallen als natuurlijke getallen.
Er zijn evenveel breuken als natuurlijke getallen!
Nu komen we bij de volgende stap. De eerstvolgende grotere verzameling van getallen die wiskundigen gebruiken is Q (of ℚ), die bestaat uit alle breuken. Dus b.v. 3/5, 7/3, 1/8, 9/2, enz. Hieronder zie je alle positieve breuken systematisch opgesomd als een vierkant dat oneindig is naar twee kanten:
Het misschien nog wel duidelijk hoe je één rij of één kolom kunt koppelen aan de natuurlijke getallen, maar allemaal? Toch kan dit. Het volgende werkt duidelijk niet:
Want aan welk getal wordt 2/3 bijvoorbeeld gekoppeld? Dat is niet te zeggen. Want er zijn duidelijk oneindig veel breuken in de vorm 1/n. En 2/3 komt pas ‘daarna’. Maar ‘na oneindig’ is er niet veel, en al helemaal geen getal. Dus er moet iets slimmers bedacht worden.
En dat gaat zo (volg de blauwe lijn):
Je gaat dus systematisch de diagonalen af, dit levert de volgende koppeling:
En dit systeem is wél door te trekken. Op het plaatje staat al grofweg hoe het werkt.
Tot slot
Een nadeel van deze koppeling is dat je er dubbele vormen in hebt, zoals 4/4, 3/1 en 6/2. In een volgende post zullen we een heel slimme manier van opsommen zien, die zulke ‘dubbelen’ overslaat.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nog overtuigender vind ik het om het voorbeeld te stellen dat de heenreis met 100 km/h ging en de terugreis met 0 km/h.quote:Op maandag 12 oktober 2009 16:20 schreef Twentsche_Ros het volgende:
Stel: iemand beweert ten onrechte het volgende:
Als ik van A naar B rijd met een snelheid van 100 km/u en van B naar A met een snelheid van 150 km/u heb ik gemiddeld 125 km/u gereden. Op verjaardagen en in veel bedrijfskantines zal men dit beweren. Hoe kun je deze stelling weerleggen, zonder in allerlei rekenkundige ingewikkeldheden te verzanden.
Welnu: Stel dat ik van A naar B heb gereden met een snelheid van 100 km/u en van B naar A met een snelheid van 2 miljard km/u, heb ik dan ook gemiddeld 1 miljard km/u gereden. Niet dus.
[ Bericht 0% gewijzigd door #ANONIEM op 12-10-2009 22:02:32 ]


Het bewijs van de Fremant theorie natuurlijk! Helaas is dat niet ff te kopieëren en plakken 
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Met Fremant bedoel je Fermat?quote:Op dinsdag 13 oktober 2009 20:09 schreef Burakius het volgende:
Het bewijs van de Fremant theorie natuurlijk! Helaas is dat niet ff te kopieëren en plakken
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Fermantquote:
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Fermat is al langsgekomen. D.w.z. dat an + bn = cn geen oplossingen heeft voor n > 2.quote:Op dinsdag 13 oktober 2009 20:17 schreef Burakius het volgende:
[..]
FermantMaar Fermat zou ook eens kunnen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Het vermoeden is mooi (een ieder begrijpt de probleemstelling) , het bewijs minder m.i. (bijna niemand kent het)quote:Op dinsdag 13 oktober 2009 20:28 schreef Iblis het volgende:
[..]
Fermat is al langsgekomen. D.w.z. dat an + bn = cn geen oplossingen heeft voor n > 2.
Niet geschoten is altijd mis..
Ach Margrietje, de Rozen zullen bloeien..
Ach Margrietje, de Rozen zullen bloeien..


Ja het bewijs heeft toch wel een aantal jaren geduurd heb ik gehoord. Er is ook een boek over als ik het goed heb.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Misschien moet je toch even de topic doorlezen.quote:Op dinsdag 13 oktober 2009 21:43 schreef Burakius het volgende:
Ja het bewijs heeft toch wel een aantal jaren geduurd heb ik gehoord. Er is ook een boek over als ik het goed heb.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Paas me die url swa.quote:Op dinsdag 13 oktober 2009 21:57 schreef Iblis het volgende:
[..]
Misschien moet je toch even de topic doorlezen.Dan zul je ook ontdekken dat er een documentaire over is die op YouTube staat.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Jij bent liever lui dan moe hè? Ik vertik dit hoor. Je opent de topic maar op één pagina en zoekt op ‘Fermat’, kan niet missen.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik pareer door het op youtube te zoeken door Fermat uit jouw tekst te kopieërenquote:Op dinsdag 13 oktober 2009 22:00 schreef Iblis het volgende:
[..]
Jij bent liever lui dan moe hè? Ik vertik dit hoor. Je opent de topic maar op één pagina en zoekt op ‘Fermat’, kan niet missen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


De Calkin-Wilf-reeks
In het vorige deel van dit drieluik had ik laten zien hoe je de rationele getallen, d.w.z. de breuken, in een 1:1 koppeling met de natuurlijke getallen kunt zetten. Je kunt de breuken in een vierkant zetten, en dan loop je de diagonalen af. Dit is redelijk slim, maar het nadeel is dat je dubbelen tegenkomt.
Er is ook een manier – verrassend eenvoudig zelfs – om ze op te sommen zonder dat je dubbelen tegenkomt. Deze manier is in 2000 ontdekt door Neil Calkin en Herbert Wilf. Het is van een verbazingwekkende eenvoud en schoonheid.
Hun opsomming begint als volgt:
De logica is misschien nog niet direct duidelijk, maar wat wel opvalt is dat de teller van elke breuk gelijk is aan den oemer van de voorafgaande breuk. Dit is inderdaad iets dat voor de gehele reeks geldt, dus in feite kunnen we zeggen het n-e getal (we beginnen overigens bij 0 te tellen) in de reeks is gelijk aan bn/bn+1, waarbij bn gegeven wordt door:
Dit lijkt misschien een beetje een rare rij getallen, maar op zich tellen ze iets. Wat precies is verder niet zo heel relevant voor wat ik wil aantonen, maar het is wel aardig om te melden: het is namelijk het aantal manieren waarop je een getal als som van machten van twee kunt schrijven, waarbij een macht hooguit twee keer gebruikt wordt.
Dat is misschien wat duidelijker met een voorbeeld. Neem 5, dat is te schrijven als 4 + 1 = 5 (1 = 20), maar ook als 2 + 2 + 1. 1 + 1 + 1 + 1 + 1 gaat niet door, want dan gebruiken we 1 te vaak. 6 kunnen we schrijven als 4 + 1 + 1, of als 4 + 2, of als 2 + 2 + 1 + 1. 2 + 2 + 2 kan dus niet.
Deze reeks staat bekend als ‘Sterns diatomische reeks’, naar de Dutisers Stern – een reeks die overigens al in 1858 voor het eerst werd beschreven! Ook de al eerder in deze topic langsgekomen Dijkstra heeft er in EWD570 en EWD578 over geschreven.
Maar goed, we hebben die reeks dus, en we merken nog een aantal interessante eigenschappen op: Opeenvolgende getallen in bn zijn altijd relatief priem. En aangezien je breuken bouwt van opeenvolgende getallen, zijn die breuken altijd vereenvoudigd. En de lijst van breuken bevat alle positieve breuken precies 1 keer (in gereduceerde vorm dus).
Nou, oké, oké, tof, maar hoe kom ik nu op een makkelijke manier aan die reeks? Moet je echt het aantal manieren om een getal als som van machten van twee te schrijven gaan zitten uitvogelen? Nee, het kan veel gemakkelijker met behulp van een boom. Denk eraan: Het is een Wiskundige boom, dus die groeit naar beneden.
Dus 1/1 zit in de wortel van de boom, en verder heeft elke knoop r/s twee kinderen. De linker is r/(r + s) en de rechter is (r + s)/s. We bekommeren ons niet direct meer om de reeks, maar wel om de boom.
Er zijn nu vijf claims te maken:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Geen enkele breuk komt vaker dan één keer voor.
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
De lijst die je krijgt valt precies samen met bn
Claim 1:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Voor 1/1 geldt dit uiteraard. Neem nu aan dat het niet zo is, en dat er ergens, misschien zelfs wel op meerdere plekken in de boom een breuk is die nog vereenvoudigd kan worden. Van alle mogelijkheden neem je die breuk r/s, als je de boom zoals hierboven tekent, het hoogst in de boom zit.
Het is dus niet de wortel, en daarom weten we zeker dat het dan het kind van een knoop moet zijn. Als het een linker kind is, dan heeft z’n ouder de waarde r/(s - r). Maar als r/s vereenvoudigbaar is, dan is r/(s - r) dat ook[1] – tegenspraak met het feit dat we een breuk uit het hoogste niveau hadden gepakt.
Als r/s een rechter kind is, dan is z’n ouder (r-s)/s, en dat leidt tot dezelfde tegenspraak.
Claim 2:
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Dat 1/1 erin zit is duidelijk. Neem echter aan dat één of meerdere andere breuken er niet in zitten. Neem van die breuken die er niet in zitten eentje met de kleinste noemer, en als er meerdere zijn met een kleinste noemer, van die groep de breuk met de kleinste teller, zeg dat dit r/s is.
Als r > s, dan weten we dat bijgevolg ook (r-s)/s niet in de boom zou kunnen zitten, want die heeft als rechter kind r/s. Maar r - s heeft dezelfde noemer als r/s maar een kleinere teller! En dat is in tegenspraak met onze aanname dat r/s de kleinste teller had!
Omgekeerd, als r < s, dan kan r/(s - r) niet in de boom zitten, want anders zou het een linker kind hebben van de vorm r/s. Maar s - r heeft een kleinere noemer dan r/s, en dat is ook weer een tegenspraak!
Claim 3:
Geen enkele breuk komt vaker dan één keer voor.
Dit geldt sowieso voor de wortel, want stel dat 1/1 nog een keer in de boom zat, dan is het kind van een knoop r/s, maar r/s heeft kinderen in de vorm r/(r + s) en (r + s)/s, en beide kunnen uiteraard geen 1/1 zijn aangezien r en s beide > 0 moeten zijn.
Nu doen we weer het zelfde als bij de vorige claim: van alle breuken die vaker dan één keer zouden voorkomen, kies die met de kleinste noemer, en als dat er meer zijn, daarbinnen die met de kleinste teller. Als r < s, dan is r/s een linker kind, en bovendien geldt dan voor de ouder dat deze r/(s - r) is. Maar dat betekent dat er ook meer dan één van zulk soort ouders is! En r/(s-r) is in strijd met onze aanname dat we een breuk met de kleinste noemer hadden gepakt. En voor r > s hebben we hetzelfde, maar dan als rechter kind.
Claim 4:
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
Deze is iets lastiger te bewijzen. Het is natuurlijk duidelijk als het om twee breuken gaat die kind zijn van dezelfde ouder. Omdat het linker kind de vorm r/(r+s) heeft en de rechter (r+s)/s.
Ook als we van een rij naar de volgende rij gaan is het niet zo moeilijk te zien, de meest rechter breuk op een rij heeft namelijk altijd noemer 1, en de meest linker breuk op een rij altijd teller 1. Dus dat gaat ook goed.
Nu blijft over twee buren in dezelfde rij, maar die niet het kind zijn van dezelfde ouder. Dit moet even met een inductiebewijs. We praten altijd over een rechter kind, gevolgd door een linker kind in zo’n geval. Het rechter kind heeft dezelfde noemer als z’n ouder. En dat linker kind heeft dezelfde teller als z’n ouder. Die twee ouders zijn óók buren van elkaar. Dus als het voor die ouders geldt, dan geldt het ook voor die kinderen.
We hebben vastgesteld dat het voor de kinderen van de wortel sowieso klopt (noem dat de eerste rij), omdat die kinderen van dezelfde ouder zijn. Dus dan klopt het ook voor de tweede rij, en dus ook voor de derde, enz.
Kortom, dit klopt voor álle rijen in de boom.
Claim 5
Niet echt nodig voor vandaag. We hebben immers al bewezen dat alle rationale getallen 1 keer voorkomen. Dat het samenvalt met bn bewijs ik niet, maar het is wel heel aardig. Het is te vinden in het oorspronkelijke artikel, en niet lastig. Hieronder staat nog een link.
Toegift
Ook is expliciet te bepalen waar je een bepaald getal in de reeks vindt, is er expliciete successor functie te bepalen, en is er met behulp van de binaire expansie en de regels om te boom te bouwen heel gemakkelijk te vinden wat de n-breuk is (omgekeerd is aan de breuk te zien of het een linker of rechter kind is en is zo de positie te construeren). Oók is nog een mooie link te leggen met Euklides’ algoritme.
Dit verbindt dus zowel verzamelingentheorie, als getaltheorie, als combinatoriek. Lees er meer over op:
Calkin–Wilf tree (Wikipedia)
Calkin, Neil; Wilf, Herbert (2000),Recounting the rationals, American Mathematical Monthly 107 (4): 360–363
Of koop er een T-shirt van:
The Nerdiest Shirts.com.
De volgende aflevering is dat we bewijzen dat voor niet zo’n opsomming te geven is. In zekere zin is deze verzameling dus wel écht groter dan de natuurlijke getallen en is er niet meer sprake van ‘evenveel’.
Post-toegift
De reeks kan ook als H-boom-fractal weergegeven worden:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
Of als spiraal die de opsomming nog duidelijker maakt:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
[1] Dat r/s vereenvoudigbaar is wil zeggen dat er een getal d > 1 is dat zowel een deler van r als van s is. Aangezien (s - r)/d = s/d - r/d, is d dus ook een deler van s - r.
[ Bericht 0% gewijzigd door Iblis op 14-10-2009 17:41:47 ]
In het vorige deel van dit drieluik had ik laten zien hoe je de rationele getallen, d.w.z. de breuken, in een 1:1 koppeling met de natuurlijke getallen kunt zetten. Je kunt de breuken in een vierkant zetten, en dan loop je de diagonalen af. Dit is redelijk slim, maar het nadeel is dat je dubbelen tegenkomt.
Er is ook een manier – verrassend eenvoudig zelfs – om ze op te sommen zonder dat je dubbelen tegenkomt. Deze manier is in 2000 ontdekt door Neil Calkin en Herbert Wilf. Het is van een verbazingwekkende eenvoud en schoonheid.
Hun opsomming begint als volgt:
De logica is misschien nog niet direct duidelijk, maar wat wel opvalt is dat de teller van elke breuk gelijk is aan den oemer van de voorafgaande breuk. Dit is inderdaad iets dat voor de gehele reeks geldt, dus in feite kunnen we zeggen het n-e getal (we beginnen overigens bij 0 te tellen) in de reeks is gelijk aan bn/bn+1, waarbij bn gegeven wordt door:
Dit lijkt misschien een beetje een rare rij getallen, maar op zich tellen ze iets. Wat precies is verder niet zo heel relevant voor wat ik wil aantonen, maar het is wel aardig om te melden: het is namelijk het aantal manieren waarop je een getal als som van machten van twee kunt schrijven, waarbij een macht hooguit twee keer gebruikt wordt.
Dat is misschien wat duidelijker met een voorbeeld. Neem 5, dat is te schrijven als 4 + 1 = 5 (1 = 20), maar ook als 2 + 2 + 1. 1 + 1 + 1 + 1 + 1 gaat niet door, want dan gebruiken we 1 te vaak. 6 kunnen we schrijven als 4 + 1 + 1, of als 4 + 2, of als 2 + 2 + 1 + 1. 2 + 2 + 2 kan dus niet.
Deze reeks staat bekend als ‘Sterns diatomische reeks’, naar de Dutisers Stern – een reeks die overigens al in 1858 voor het eerst werd beschreven! Ook de al eerder in deze topic langsgekomen Dijkstra heeft er in EWD570 en EWD578 over geschreven.
Maar goed, we hebben die reeks dus, en we merken nog een aantal interessante eigenschappen op: Opeenvolgende getallen in bn zijn altijd relatief priem. En aangezien je breuken bouwt van opeenvolgende getallen, zijn die breuken altijd vereenvoudigd. En de lijst van breuken bevat alle positieve breuken precies 1 keer (in gereduceerde vorm dus).
Nou, oké, oké, tof, maar hoe kom ik nu op een makkelijke manier aan die reeks? Moet je echt het aantal manieren om een getal als som van machten van twee te schrijven gaan zitten uitvogelen? Nee, het kan veel gemakkelijker met behulp van een boom. Denk eraan: Het is een Wiskundige boom, dus die groeit naar beneden.
Dus 1/1 zit in de wortel van de boom, en verder heeft elke knoop r/s twee kinderen. De linker is r/(r + s) en de rechter is (r + s)/s. We bekommeren ons niet direct meer om de reeks, maar wel om de boom.
Er zijn nu vijf claims te maken:
Claim 1:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Voor 1/1 geldt dit uiteraard. Neem nu aan dat het niet zo is, en dat er ergens, misschien zelfs wel op meerdere plekken in de boom een breuk is die nog vereenvoudigd kan worden. Van alle mogelijkheden neem je die breuk r/s, als je de boom zoals hierboven tekent, het hoogst in de boom zit.
Het is dus niet de wortel, en daarom weten we zeker dat het dan het kind van een knoop moet zijn. Als het een linker kind is, dan heeft z’n ouder de waarde r/(s - r). Maar als r/s vereenvoudigbaar is, dan is r/(s - r) dat ook[1] – tegenspraak met het feit dat we een breuk uit het hoogste niveau hadden gepakt.
Als r/s een rechter kind is, dan is z’n ouder (r-s)/s, en dat leidt tot dezelfde tegenspraak.
Claim 2:
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Dat 1/1 erin zit is duidelijk. Neem echter aan dat één of meerdere andere breuken er niet in zitten. Neem van die breuken die er niet in zitten eentje met de kleinste noemer, en als er meerdere zijn met een kleinste noemer, van die groep de breuk met de kleinste teller, zeg dat dit r/s is.
Als r > s, dan weten we dat bijgevolg ook (r-s)/s niet in de boom zou kunnen zitten, want die heeft als rechter kind r/s. Maar r - s heeft dezelfde noemer als r/s maar een kleinere teller! En dat is in tegenspraak met onze aanname dat r/s de kleinste teller had!
Omgekeerd, als r < s, dan kan r/(s - r) niet in de boom zitten, want anders zou het een linker kind hebben van de vorm r/s. Maar s - r heeft een kleinere noemer dan r/s, en dat is ook weer een tegenspraak!
Claim 3:
Geen enkele breuk komt vaker dan één keer voor.
Dit geldt sowieso voor de wortel, want stel dat 1/1 nog een keer in de boom zat, dan is het kind van een knoop r/s, maar r/s heeft kinderen in de vorm r/(r + s) en (r + s)/s, en beide kunnen uiteraard geen 1/1 zijn aangezien r en s beide > 0 moeten zijn.
Nu doen we weer het zelfde als bij de vorige claim: van alle breuken die vaker dan één keer zouden voorkomen, kies die met de kleinste noemer, en als dat er meer zijn, daarbinnen die met de kleinste teller. Als r < s, dan is r/s een linker kind, en bovendien geldt dan voor de ouder dat deze r/(s - r) is. Maar dat betekent dat er ook meer dan één van zulk soort ouders is! En r/(s-r) is in strijd met onze aanname dat we een breuk met de kleinste noemer hadden gepakt. En voor r > s hebben we hetzelfde, maar dan als rechter kind.
Claim 4:
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
Deze is iets lastiger te bewijzen. Het is natuurlijk duidelijk als het om twee breuken gaat die kind zijn van dezelfde ouder. Omdat het linker kind de vorm r/(r+s) heeft en de rechter (r+s)/s.
Ook als we van een rij naar de volgende rij gaan is het niet zo moeilijk te zien, de meest rechter breuk op een rij heeft namelijk altijd noemer 1, en de meest linker breuk op een rij altijd teller 1. Dus dat gaat ook goed.
Nu blijft over twee buren in dezelfde rij, maar die niet het kind zijn van dezelfde ouder. Dit moet even met een inductiebewijs. We praten altijd over een rechter kind, gevolgd door een linker kind in zo’n geval. Het rechter kind heeft dezelfde noemer als z’n ouder. En dat linker kind heeft dezelfde teller als z’n ouder. Die twee ouders zijn óók buren van elkaar. Dus als het voor die ouders geldt, dan geldt het ook voor die kinderen.
We hebben vastgesteld dat het voor de kinderen van de wortel sowieso klopt (noem dat de eerste rij), omdat die kinderen van dezelfde ouder zijn. Dus dan klopt het ook voor de tweede rij, en dus ook voor de derde, enz.
Kortom, dit klopt voor álle rijen in de boom.
Claim 5
Niet echt nodig voor vandaag. We hebben immers al bewezen dat alle rationale getallen 1 keer voorkomen. Dat het samenvalt met bn bewijs ik niet, maar het is wel heel aardig. Het is te vinden in het oorspronkelijke artikel, en niet lastig. Hieronder staat nog een link.
Toegift
Ook is expliciet te bepalen waar je een bepaald getal in de reeks vindt, is er expliciete successor functie te bepalen, en is er met behulp van de binaire expansie en de regels om te boom te bouwen heel gemakkelijk te vinden wat de n-breuk is (omgekeerd is aan de breuk te zien of het een linker of rechter kind is en is zo de positie te construeren). Oók is nog een mooie link te leggen met Euklides’ algoritme.
Dit verbindt dus zowel verzamelingentheorie, als getaltheorie, als combinatoriek. Lees er meer over op:
Of koop er een T-shirt van:
The Nerdiest Shirts.com.
De volgende aflevering is dat we bewijzen dat voor niet zo’n opsomming te geven is. In zekere zin is deze verzameling dus wel écht groter dan de natuurlijke getallen en is er niet meer sprake van ‘evenveel’.
Post-toegift
De reeks kan ook als H-boom-fractal weergegeven worden:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
Of als spiraal die de opsomming nog duidelijker maakt:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
[1] Dat r/s vereenvoudigbaar is wil zeggen dat er een getal d > 1 is dat zowel een deler van r als van s is. Aangezien (s - r)/d = s/d - r/d, is d dus ook een deler van s - r.
[ Bericht 0% gewijzigd door Iblis op 14-10-2009 17:41:47 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Via die T-shirt-site kwam ik nu ook nog op: Math less travaled die in feite hetzelfde beschrijft. Ik had die site niet gezien echter. Hoe dan ook, wel het lezen waard!
Ook is er nog een boek aan te duiden (dat heb ik wel gebruikt), en dat is Proofs from The Book door Martin Aigner en Günter M. Ziegler. Het is hoofdstuk 16 van hun boek, op pagina 93 in deze Google Books editie. Maar Google laat mij er niet inkijken.
Ook is er nog een boek aan te duiden (dat heb ik wel gebruikt), en dat is Proofs from The Book door Martin Aigner en Günter M. Ziegler. Het is hoofdstuk 16 van hun boek, op pagina 93 in deze Google Books editie. Maar Google laat mij er niet inkijken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Toen ik de TT zag dacht ik ook direct aan dat bewijs. Zeer elegant door z'n eenvoud.quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn.
Never in the entire history of calming down did anyone ever calm down after being told to calm down.


Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.quote:Op maandag 12 oktober 2009 20:17 schreef Iblis het volgende:
Een koppeling tussen ℕ en ℤ
Er zijn op die manier ook evenveel gehele getallen als natuurlijke getallen:
[ afbeelding ]
Het is ook duidelijk dat deze koppeling gewoon door te trekken is, bovenaan som je de natuurlijke getallen op, onderaan gaat het verder met -4, 4, -5, 5, -6, 6 enz.
Dus er zijn ook evenveel gehele getallen als natuurlijke getallen.
Verder wel mijn complimenten voor de bewijzen die je hier post.


Dat kun je stellen, maar dat betekent niet dat de een "meer" elementen heeft dan de ander.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren.
Dat staat toch nergens? Er is alleen laten zien dat er een 1-op-1 'map' is tussen de elementen uit beide sets, die ook alle elementen beslaat.quote:Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
...
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here


Ja, maar daarom probeer ik duidelijk te maken wat in de Wiskunde met 'evenveel' wordt bedoeld een 1:1-koppeling (formeler: er is een bijectie te vinden tussen de verzamelingen). Ik moet deel 3 nog doen trouwens, dan zul je zien dat er voor de reële getallen ℝ zo’n bijectie niet mogelijk is.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
Verder wel mijn complimenten voor de bewijzen die je hier post.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nee, het is niet contra-intuïtief.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
Stel, ik heb twee verzamelingen, verzameling A en verzameling B. Hoe weet ik nou of beide verzamelingen even veel elementen hebben?
Wel, we kunnen een functie f : A -> B maken. Deze wijst elke waarde x in A een waarde y in B toe.
Stel, ons lukt het om een injectieve functie f te maken, dat betekent dat we aan elke waarde van x in A een unieke waarde y in B kunnen toewijzen. Dan weten we dat verzameling B minstens net zo groot is als verzameling A:
En als het omgekeerde ook lukt, als we dus ook een injectieve functie g : B -> A kunnen vinden, dan zijn beide verzamelingen even groot. In ons voorbeeld gaat dat fout:
Omdat een functie nooit voor sommige waardes ongedefinieerd mag zijn, moeten we dus naar sommige waardes in A twee pijltjes trekken, dus aan aan sommige waarden y uit B kunnen we in dit geval geen unieke waarde x uit A toewijzen. Dat geeft aan dat B groter is dan A.
Tot zo ver is het hopelijk allemaal duidelijk en intuïtief.
Neem nou het plaatje van Iblis er weer bij:
Hier zien we dat aan elke waarde uit N een unieke waarde in Z wordt toegewezen, én dat elke waarde in Z een unieke waarde in N wordt toegewezen.
Dat betekent dat Z minstens zo groot is als N, en dat N minstens zo groot is als Z. Beide zijn dus even groot.
[ Bericht 2% gewijzigd door #ANONIEM op 21-10-2009 23:24:40 ]


De ‘paradox’ is dus het (subtiele) onderscheid tussen ‘evenveel’ en ‘elementen bevatten die de andere verzameling niet bevat’.
Voor eindige verzamelingen gaat het prima op dat als verzameling A alles bevat wat B bevat, en nog een beetje meer, dat A groter is dan B. Maar voor oneindig gaat dat niet op. Immers, neem een verzameling met oneindig veel elementen, en haal er eentje uit. Hoeveel (dus niet wélke, maar het aantal) heb je er dan nog over? Dat zijn er nog steeds oneindig veel. Dus het heeft dan niet zoveel zin om te zeggen dat die laatste verzameling ‘kleiner’ is, als die óók nog oneindig is.
Dit is trouwens een andere manier om oneindig te karakteriseren: een oneindige verzameling is een verzameling waarvan een écht deelverzameling ‘even groot’ is als de verzameling zelf. M.a.w. ℕ is oneindig, want een echte deelverzameling (b.v. alle even getallen, waar 1, 3 en 5 b.v. niet in zitten) is ‘even groot’ (heeft dezelfde cardinaliteit) als ℕ zelf.
Dus ‘deelverzameling zijn van’ impliceert voor oneindige verzamelingen niet per se dat het aantal elementen ook minder is. Immers, dat aantal is in zekere zin onuitputtelijk. Zou het minder worden, dan zou je ℕ een keer ‘leeg kunnen maken’ door er maar telkens eindig veel elementen uit te halen.
Hier zit natuurlijk een lastigheid. Maar daarom wordt het straks nog raarder als ℝ eigenlijk ‘nog weer oneindiger’ blijkt te zijn dan ℕ of ℤ.
Voor eindige verzamelingen gaat het prima op dat als verzameling A alles bevat wat B bevat, en nog een beetje meer, dat A groter is dan B. Maar voor oneindig gaat dat niet op. Immers, neem een verzameling met oneindig veel elementen, en haal er eentje uit. Hoeveel (dus niet wélke, maar het aantal) heb je er dan nog over? Dat zijn er nog steeds oneindig veel. Dus het heeft dan niet zoveel zin om te zeggen dat die laatste verzameling ‘kleiner’ is, als die óók nog oneindig is.
Dit is trouwens een andere manier om oneindig te karakteriseren: een oneindige verzameling is een verzameling waarvan een écht deelverzameling ‘even groot’ is als de verzameling zelf. M.a.w. ℕ is oneindig, want een echte deelverzameling (b.v. alle even getallen, waar 1, 3 en 5 b.v. niet in zitten) is ‘even groot’ (heeft dezelfde cardinaliteit) als ℕ zelf.
Dus ‘deelverzameling zijn van’ impliceert voor oneindige verzamelingen niet per se dat het aantal elementen ook minder is. Immers, dat aantal is in zekere zin onuitputtelijk. Zou het minder worden, dan zou je ℕ een keer ‘leeg kunnen maken’ door er maar telkens eindig veel elementen uit te halen.
Hier zit natuurlijk een lastigheid. Maar daarom wordt het straks nog raarder als ℝ eigenlijk ‘nog weer oneindiger’ blijkt te zijn dan ℕ of ℤ.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 5% gewijzigd door #ANONIEM op 21-10-2009 23:42:54 ]


quote:Op woensdag 21 oktober 2009 23:42 schreef Igen het volgende:
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?Hilberts hotel moet dat zijn, logeer ik ook altijdSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt. Niet geschoten is altijd mis..
Niet geschoten is altijd mis..
Ach Margrietje, de Rozen zullen bloeien..


Ik ben dan wel benieuwd naar dat bewijs dat er voor ℝ geen bijectie mogelijk is, je kunt het tenslotte toch bewijzen op een soortgelijke manier als met ℤ en ℕ?quote:Op woensdag 21 oktober 2009 23:19 schreef Iblis het volgende:
[..]
Ja, maar daarom probeer ik duidelijk te maken wat in de Wiskunde met 'evenveel' wordt bedoeld een 1:1-koppeling (formeler: er is een bijectie te vinden tussen de verzamelingen). Ik moet deel 3 nog doen trouwens, dan zul je zien dat er voor de reële getallen ℝ zo’n bijectie niet mogelijk is.
quote:Op woensdag 21 oktober 2009 23:42 schreef Igen het volgende:
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?I.p.v. al die mensen van kamer te verhuizen kan je de nieuwe gast toch in de n+1'de kamer stoppen?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 19% gewijzigd door Diabox op 22-10-2009 01:22:46 ]


Nee, je loopt stuk met irrationale getallen. ℝ is niet aftelbaar.quote:Op donderdag 22 oktober 2009 01:14 schreef Diabox het volgende:
[..]
Ik ben dan wel benieuwd naar dat bewijs dat er voor ℝ geen bijectie mogelijk is, je kunt het tenslotte toch bewijzen op een soortgelijke manier als met ℤ en ℕ?
[..]
Nee, want n+1 is een eindig getal en alle kamers (met een welbepaald nummer) waren immers bezet.quote:I.p.v. al die mensen van kamer te verhuizen kan je de nieuwe gast toch in de n+1'de kamer stoppen?


Hm ja, niet bij stilgestaan.quote:Op donderdag 22 oktober 2009 01:36 schreef Riparius het volgende:
[..]
Nee, je loopt stuk met irrationale getallen. ℝ is niet aftelbaar.
[..]
Nee, want n+1 is een eindig getal en alle kamers (met een welbepaald nummer) waren immers bezet.


Diagonaalbewijs van Cantor
Het diagonaalbewijs
Hebben misschien alle oneindige verzamelingen hetzelfde formaat? Dit blijkt niet zo te zijn. En daar komt het diagonaalbewijs om de hoek: Er zijn meer reële getallen tussen 0 en 1 dan er natuurlijke getallen zijn. Dit bewijs gebruikt reductio ad absurdum. We nemen daarom aan dat er een bijectie, dit wil zeggen een 1-op-1 afbeelding van de natuurlijke getallen naar de reële getallen bestaat.
Zo'n afbeelding ziet er bijvoorbeeld zo uit:
enzovoort.
De lijst is in twee richtingen oneindig lang. Nu nemen we van het eerste getal het eerste cijfer achter de komma. Van het tweede getal nemen we het tweede cijfer achter de komma, enzovoort. Deze cijfers zetten we achter elkaar, zodat we een nieuwe getal krijgen, in het voorbeeld: 0,220098.... Elk cijfer in dit getal veranderen we in een willekeurig ander cijfer, bijvoorbeeld door er 1 bij op te tellen (9 wordt dan 0). Het nieuwe getal 0,331109.... dat we nu hebben gemaakt, kan nooit in de lijst staan; immers als je uit de lijst het getal n haalt dan komt het n-de cijfer van dat getal niet meer overeen met het n-de cijfer uit m. Omdat er altijd een nieuwe m gemaakt kan worden, zit er tussen 0 en 1 een overaftelbaar aantal reële getallen.
Er is een functie te beschrijven voor diagonalisatie die in zeer veel gevallen werkt:
d(i) = min{B\ {d(0),...,d(i-1),fi(i)}}, waar B het bereik is en fi(i) de waarde op de diagonaal.
Ik kwam toevallig het bewijs tegen dat het dus niet kan met ℝ.
Het diagonaalbewijs
Hebben misschien alle oneindige verzamelingen hetzelfde formaat? Dit blijkt niet zo te zijn. En daar komt het diagonaalbewijs om de hoek: Er zijn meer reële getallen tussen 0 en 1 dan er natuurlijke getallen zijn. Dit bewijs gebruikt reductio ad absurdum. We nemen daarom aan dat er een bijectie, dit wil zeggen een 1-op-1 afbeelding van de natuurlijke getallen naar de reële getallen bestaat.
Zo'n afbeelding ziet er bijvoorbeeld zo uit:
| 1 2 3 4 5 6 | 2 - 0,12345678901234... 3 - 0,00000000000120... 4 - 0,50000000000000... 5 - 0,14159265358979... 6 - 0,23562877077729... |
enzovoort.
De lijst is in twee richtingen oneindig lang. Nu nemen we van het eerste getal het eerste cijfer achter de komma. Van het tweede getal nemen we het tweede cijfer achter de komma, enzovoort. Deze cijfers zetten we achter elkaar, zodat we een nieuwe getal krijgen, in het voorbeeld: 0,220098.... Elk cijfer in dit getal veranderen we in een willekeurig ander cijfer, bijvoorbeeld door er 1 bij op te tellen (9 wordt dan 0). Het nieuwe getal 0,331109.... dat we nu hebben gemaakt, kan nooit in de lijst staan; immers als je uit de lijst het getal n haalt dan komt het n-de cijfer van dat getal niet meer overeen met het n-de cijfer uit m. Omdat er altijd een nieuwe m gemaakt kan worden, zit er tussen 0 en 1 een overaftelbaar aantal reële getallen.
Er is een functie te beschrijven voor diagonalisatie die in zeer veel gevallen werkt:
d(i) = min{B\ {d(0),...,d(i-1),fi(i)}}, waar B het bereik is en fi(i) de waarde op de diagonaal.
Ik kwam toevallig het bewijs tegen dat het dus niet kan met ℝ.


Ik plaats hier een tvp omdat dit een prachtig topic is 
I just had to get that stress off my chest like breast reduction.


Beide nog niet nee..quote:Op donderdag 22 oktober 2009 19:56 schreef Bankfurt het volgende:
Is dat bewijs van algoritme van Euclides al hier genoemd ?
en die stelling van GGD * KGV = ?


Niemand houdt je tegen.
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten


Beetje humor op de 'vroege' ochtend.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Maar zoals ik zei, dit soort analyse is nogal roestig bij me op dit moment dus als iemand anders het wel weet ben ik erg benieuwd
[ Bericht 4% gewijzigd door Haushofer op 23-10-2009 10:00:08 (Ff een spoiler toegevoegd) ]Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


quote:Op vrijdag 23 oktober 2009 09:54 schreef Haushofer het volgende:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Maar zoals ik zei, dit soort analyse is nogal roestig bij me op dit moment dus als iemand anders het wel weet ben ik erg benieuwdSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.


Ik weet het:quote:
a,b, natuurlijke getallen;
dan is GGD(a,b) * KGV (a,b) = a * b
Een vervolg is het bewijs van de priemontbinding van natuurlijke getallen.


Lijkt me toch niet zo moeilijk, want:quote:Op vrijdag 23 oktober 2009 18:38 schreef Bankfurt het volgende:
[..]
Ik weet het:
a,b, natuurlijke getallen;
dan is GGD(a,b) * KGV (a,b) = a * b
...
- Voor iedere deler D van zowel a als b geldt dat (a*b)/D een veelvoud is van a en van b, want (a*b)/D = a*(b/D) = b*(a/D)
- Als bovendien D de grootst mogelijke deler van zowel a als b is dan noemen we die per definitie GGD(a*b). Maar als D zo groot mogelijk is, dan is de corresponderende (a*b)/D zo klein mogelijk. De noemer kan dan immers niet groter worden onder voorwaarde dat D een deler van zowel a als b is.
- Conclusie als D de grootst mogelijke deler van zowel a als b is, dan is het veelvoud (a*b)/D van zowel a als b het kleinst mogelijke getal dat een veelvoud is van zowel a als b. Oftewel: (a*b)/GGD(a,b) = KGV(a,b)
en daar volgt uit:
(a*b) = GGD(a,b) * KGV(a,b)
Wellicht niet helemaal formeel, maar dit moet het wel zijn.
[ Bericht 1% gewijzigd door #ANONIEM op 23-10-2009 21:34:02 ]


Ja, toegegeven, mooi bewijs.quote:Op vrijdag 23 oktober 2009 21:01 schreef ..-._---_-.- het volgende:
[..]
Lijkt me toch niet zo moeilijk, want:
- Voor iedere deler D van zowel a als b geldt dat (a*b)/D een veelvoud is van a en van b, want (a*b)/D = a*(b/D) = b*(a/D)
- Als bovendien D de grootst mogelijke deler van zowel a als b is dan noemen we die per definitie GGD(a*b). Maar als D zo groot mogelijk is, dan is de corresponderende (a*b)/D zo klein mogelijk. De noemer kan dan immers niet groter worden onder voorwaarde dat D een deler van zowel a als b is.
- Conclusie als D de grootst mogelijke deler van zowel a als b is, dan is het veelvoud (a*b)/D van zowel a als b het kleinst mogelijke getal dat een veelvoud is van zowel a als b. Oftewel: (a*b)/GGD(a,b) = KGV(a,b)
en daar volgt uit:
(a*b) = GGD(a,b) * KGV(a,b)
Wellicht niet helemaal formeel, maar dit moet het wel zijn.


b>aquote:Op vrijdag 23 oktober 2009 08:14 schreef -J-D- het volgende:
[ afbeelding ]
Beetje humor op de 'vroege' ochtend.
Niet grappig.
Hetgeen bewezen en beklonken moest worden.


tvp
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)


Wiskunde. Leuk! Ben er niet goed in, maar wel gek op.quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn. De bedenker, Euklides, leefde zo ongeveer 2300 jaar geleden.
(...)
Maar we hadden aangenomen dat ons rijtje alle priemgetallen bevat. Die aanname moet wel fout zijn, want we komen nu op een tegenspraak uit. Kortom, er moeten wel oneindig veel priemgetallen zijn. □
Dat was het al.Andere, relatief eenvoudige vragen, zoals: zijn er ook oneindig veel paartjes van getallen zoals 17 en 19, of 107 en 109, die maar 2 van elkaar verschillen en allebei priem zijn, of kun je elk getal groter dan 3 als de som van precies twee priemgetallen schrijven, zijn tot op de dag van vandaag niet beantwoord.
Helaas werkt Latex niet op Fok dus dan maar even slordig:
Nog een bewijs dat er een oneindig aantal priemgetallen bestaat. Dit keer van Euler.
De oneindige som 1/1 + 1/2 + 1/3 +... 1/n is gelijk aan het oneindige product (1/(1-1/p) (p = priemgetal). Het bewijs hiervoor is een goed te volgen.
Aangezien de oneindige som 1/1 + 1/2 + 1/3 +... 1/n divergeert, moeten er dus ook oneindig veel priemgetallen bestaan.
Nog even over die zin in bold. Moet dat niet zijn "of kun je elk even getal groter dan 3 als de som van precies twee priemgetallen schrijven"? De Goldbach conjecture dus?
Kwam er overigens pas deze maand achter (na het maken van een programma in VBA Excel) dat als de Goldbach conjecture klopt, daarmee ook meteen de volgende stelling waar is:
"Elk getal groter dan 3 kun je op minstens één manier schrijven als het gemiddelde van twee priemgetallen."
Dus ook alle priemgetallen zelf zijn dan uit te drukken in priemgetallen. Bovendien geldt ook dat voor een priemgetal p > 7 uitgedrukt als (Px+Py)/2, de afstand tusen Px en Py altijd 12k is (of n +/- 6k). Verder ben ik helaas nog niet gekomen...
[ Bericht 0% gewijzigd door Agno op 31-10-2009 00:43:13 ]


Je bedoelt met P de verzameling der primegetallen.quote:Op vrijdag 30 oktober 2009 20:37 schreef Agno het volgende:
De oneindige som 1/1 + 1/2 + 1/3 +... 1/n is gelijk aan het oneindige product (1/(1-1/p) (p = priemgetal). Het bewijs hiervoor is een goed te volgen.
Uiteraard, dat is mijn fout. Afgezien van twee zijn er natuurlijk geen even priemgetallen en verder geldt dat een oneven + oneven getal een even getal is.quote:Nog even over die zin in bold. Moet dat niet zijn "of kun je elk even getal groter dan 3 als de som van precies twee priemgetallen schrijven"? De Goldbach conjecture dus?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik probeer me even die middelste term voor te stellen.
Je neemt voor elk priemgetal p dus de som van de reciproce van de opeenvolgende gehele machten (dus bijv. voor p=5 1/5^0 + 1/5^1 + 1/5^2 + 1/5^3 + 1/5^4 + ......... 1/5^k) en al die sommen ga je met elkaar vermenigvuldigen.
Interpreteer ik het zo goed?
Je neemt voor elk priemgetal p dus de som van de reciproce van de opeenvolgende gehele machten (dus bijv. voor p=5 1/5^0 + 1/5^1 + 1/5^2 + 1/5^3 + 1/5^4 + ......... 1/5^k) en al die sommen ga je met elkaar vermenigvuldigen.
Interpreteer ik het zo goed?
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)


Ja. En de grap is dus dat je elk getal n (uniek) kunt ontbinden en priemfactoren, dus die middelste term bevat een product van oneindige sommen met termen als 1 + 1/2 + 1/22 + 1/23 + ···, en als andere factor 1 + 1/3 + 1/32 + 1/33 ···, en als je dit vermenigvuldigt dan krijg je dus 1/(1·1·1·1···) = 1/1, en 1/(2·1·1·1···) = 1/2 en 1/(1·3·1·1···) = 1/3 maar ook 1/(2·3·1·1···) = 1/6, enz. Kortom, uiteindelijk 1/n voor alle n.quote:Op zaterdag 31 oktober 2009 00:09 schreef Kees22 het volgende:
Ik probeer me even die middelste term voor te stellen.
Je neemt voor elk priemgetal p dus de som van de reciproce van de opeenvolgende gehele machten (dus bijv. voor p=5 1/5^0 + 1/5^1 + 1/5^2 + 1/5^3 + 1/5^4 + ......... 1/5^k) en al die sommen ga je met elkaar vermenigvuldigen.
Interpreteer ik het zo goed?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Die laatste zin gaat me te snel.quote:Op zaterdag 31 oktober 2009 00:36 schreef Iblis het volgende:
[..]
Ja. En de grap is dus dat je elk getal n (uniek) kunt ontbinden en priemfactoren, dus die middelste term bevat een product van oneindige sommen met termen als 1 + 1/2 + 1/22 + 1/23 + ···, en als andere factor 1 + 1/3 + 1/32 + 1/33 ···, en als je dit vermenigvuldigt dan krijg je dus 1/(1·1·1·1···) = 1/1, en 1/(2·1·1·1···) = 1/2 en 1/(1·3·1·1···) = 1/3 maar ook 1/(2·3·1·1···) = 1/6, enz. Kortom, uiteindelijk 1/n voor alle n.
Ik zie ten eerste niet meteen de noodzaak dat in die producten alle n's een keer en niet meer dan een keer aan bod komen en ten tweede komen er aan het eind naar mijn eerste gevoel wat soorten oneindigheid in de knoop.
Het uitpuzzelen daarvan kietelt mijn wiskundige intellect, maar ik vrees dat mijn luiheid gaat winnen.
Maar dank voor je antwoord.
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)


Had er eerst ook moeite mee om dit te doorzien, maar om de invallende luiheid toch nog een laatste prikkel te geven ff het volgende.quote:Op zaterdag 31 oktober 2009 00:52 schreef Kees22 het volgende:
[..]
Die laatste zin gaat me te snel.
Ik zie ten eerste niet meteen de noodzaak dat in die producten alle n's een keer en niet meer dan een keer aan bod komen en ten tweede komen er aan het eind naar mijn eerste gevoel wat soorten oneindigheid in de knoop.
Het uitpuzzelen daarvan kietelt mijn wiskundige intellect, maar ik vrees dat mijn luiheid gaat winnen.
Maar dank voor je antwoord.
De truc is makkelijker te doorzien door te kijken hoe de priemproductformule afgeleid wordt uit de Zeta-functie. Zie bijgaande link. Dan gewoon s=1 invullen en je bent er.
http://en.wikipedia.org/w(...)iemann_zeta_function


Gnigni, je had succes!quote:Op zaterdag 31 oktober 2009 01:01 schreef Agno het volgende:
[..]
Had er eerst ook moeite mee om dit te doorzien, maar om de invallende luiheid toch nog een laatste prikkel te geven ff het volgende.
De truc is makkelijker te doorzien door te kijken hoe de priemproductformule afgeleid wordt uit de Zeta-functie. Zie bijgaande link. Dan gewoon s=1 invullen en je bent er.
http://en.wikipedia.org/w(...)iemann_zeta_function
Dat van dat een en niet meer dan een keer voorkomen van n, dat geloof ik nu wel.
Nu nog even nadenken over de staart, die diverse soorten of maten oneindigheid. Met een beetje geluk is dat probleem het voortgezette deel van het eerste.
Die zeta-functie heb ik al eens eerder gezien in een topic op FOK!
Hier hou ik verder maar eens op: morgen lekker wat spitten in mijn voortuin.
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)


Het bewijs dat de lengte van A4'tje of A3'tje wortel2 keer de breedte is.
Twee keer de breedte van A4 = de lengte van A3.
En de verhouding lengte breedte blijft het zelfde.
Dus:
l/b = 2b/l
2 b2 = l2
l/b = wortel 2.
Vandaar de vergroting 141% op het copieerapparaat.
En als je een vliegtuigje vouwt van een A4-tje blijkt de hypothenusa precies overeen te komen met de lengte van het A4-tje.

Twee keer de breedte van A4 = de lengte van A3.
En de verhouding lengte breedte blijft het zelfde.
Dus:
l/b = 2b/l
2 b2 = l2
l/b = wortel 2.
Vandaar de vergroting 141% op het copieerapparaat.
En als je een vliegtuigje vouwt van een A4-tje blijkt de hypothenusa precies overeen te komen met de lengte van het A4-tje.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.


Toch nog even door op het hierboven omgeschreven vermoeden van Goldbach:
"Elk getal groter dan 3 kun je op minstens één manier schrijven als het gemiddelde van twee priemgetallen."
Als het vermoeden van Goldbach waar blijkt te zijn dan geldt dus ook dat alle priemgetallen (behalve 2 en 3) zijn uit te drukken in een equi-distant setje andere priemgetallen. Er geldt immers dat elk priemgetal P afgeleid kan worden door (Px+Py)/2 (Px < P < Py).
Voor priemgetallen > 7 geldt bovendien dat de equidistante afstand P-Px en Py-P deelbaar is door 6 en dat de totale afstand Py-Px dus deelbaar is door 12. (We weten ook dat 2 en 3 nooit de Px kunnen zijn; 2 is immers het enige even priemgetal en 3 + 6k kan nooit een priemgetal opleveren want het is altijd deelbaar door 3. Let wel: er geldt natuurlijk ook dat bijv. (3 + 19) = 11, maar ik ben nu alleen ff geïnteresseerd in P-Px = 6k).
Waarom is die afstand altijd deelbaar door 6? We weten dat alle priemgetallende de vorm 6n+1 of 6n-1 hebben (behalve 2 en 3), omdat alle andere mogelijkheden deelbaar zijn door 2 of 3. Px en Py kunnen priemgetallen van beide vormen zijn: 6n-1 en 6n+1. Om het gemiddelde te berekenen zijn er in principe 4 combinaties te maken, maar slechts twee blijken er te werken. Er geldt namelijk altijd dat als P=6n+1 dan ook alle Px, Py = 6n+1. En vice versa voor 6n-1.
Voorbeeld:
P = 29, (Px,Py) = (17,59), (11,41), (5,53) => type 6n-1, afstand 6k, k = 2,3,4
P = 73, (Px,Py) = (67,79), (43,103), (37,109), (19,127), (7,139) => type 6n+1, afstand 6k, k = 1,5,6,9,11
Priemgetallen zijn echter niet te voorspellen, en de priemgetalstelling zegt dat als je een willekeurig getal kiest in de buurt van een groot getal N, dat dan de kans dat dit getal een priemgetal is, ongeveer gelijk is aan 1 / ln(N). Dat is dus nooit 100%.
Als de bovenstaande stelling over equi-distante priemgetallen waar is, dan zou je als volgt kunnen redeneren:
Vanaf P springen we telkens in stapjes van 6 naar beneden totdat P - 6k = 5 (voor P=6n-1) of P - 6k = 7 (voor P=6n+1). Bij elk stapje test je of het getal een priemgetal is. Indien dit niet het geval is dan wordt de kans dat het volgende stapje een paartje priemgetallen (P-6k,P+6k) is groter met 1/((P-5)/6) of 1/(P-7)/6)). Das raar. Want elke keer dat je geen setje priemgetallen vindt, dan wordt de kans groter dat P+/- 6k wel een priemgetal is. Sterker nog: stel dat je vindt dat het voorlaatste stapje nog steeds geen setje priemgetallen oplevert, dan wordt de kans dus 100% dat P+/-6k beiden priem zijn. Een 100% zekere voorspelling van een priemgetal P+6k is strijdig met de priemgetalstelling. Om deze paradox te doorbreken moeten de lagere priemgetallen elkaar dus helpen om deze zekere voorspelling te versluieren (het lijkt bijna op de EPR paradox, waarbij je door links van de bron te meten, rechts meer zekere uitspraken aan de rechter kant te kunnen doen).
Daarom mijn stelling:
De hoogste en de laagste priemcombinatie (Px, Py) met P = (Px+Py)/2 (ergo: de combinaties (P-6, P+6) en (P-6k, P+6k) met de grootst mogelijke k), kan nooit de enige priemcombinatie (Px, Py) zijn, want anders zou je voor een bepaald getal exact kunnen voorspellen waar een toekomstig priemgetal P + 6k ligt (uitgezonderd P= 11 want je hebt dan immers slechts twee mogelijke waarden voor Px: 5 en 7. In dat geval is er nog geen ‘buitenste’).
EDIT:
Er zit natuurlijk een denkfout in de aanname dat je alle stapjes van 6 altijd sequentieel doorloopt. Je zou er ook volkomen random doorheen kunnen lopen en er dan uiteindelijk twee overhouden. Als dan de voorlaatste geen priempaartje oplevert, dan moet de laatste mogelijkheid een priem op P+6k opleveren.

[ Bericht 3% gewijzigd door Agno op 31-10-2009 20:22:56 ]
"Elk getal groter dan 3 kun je op minstens één manier schrijven als het gemiddelde van twee priemgetallen."
Als het vermoeden van Goldbach waar blijkt te zijn dan geldt dus ook dat alle priemgetallen (behalve 2 en 3) zijn uit te drukken in een equi-distant setje andere priemgetallen. Er geldt immers dat elk priemgetal P afgeleid kan worden door (Px+Py)/2 (Px < P < Py).
Voor priemgetallen > 7 geldt bovendien dat de equidistante afstand P-Px en Py-P deelbaar is door 6 en dat de totale afstand Py-Px dus deelbaar is door 12. (We weten ook dat 2 en 3 nooit de Px kunnen zijn; 2 is immers het enige even priemgetal en 3 + 6k kan nooit een priemgetal opleveren want het is altijd deelbaar door 3. Let wel: er geldt natuurlijk ook dat bijv. (3 + 19) = 11, maar ik ben nu alleen ff geïnteresseerd in P-Px = 6k).
Waarom is die afstand altijd deelbaar door 6? We weten dat alle priemgetallende de vorm 6n+1 of 6n-1 hebben (behalve 2 en 3), omdat alle andere mogelijkheden deelbaar zijn door 2 of 3. Px en Py kunnen priemgetallen van beide vormen zijn: 6n-1 en 6n+1. Om het gemiddelde te berekenen zijn er in principe 4 combinaties te maken, maar slechts twee blijken er te werken. Er geldt namelijk altijd dat als P=6n+1 dan ook alle Px, Py = 6n+1. En vice versa voor 6n-1.
Voorbeeld:
P = 29, (Px,Py) = (17,59), (11,41), (5,53) => type 6n-1, afstand 6k, k = 2,3,4
P = 73, (Px,Py) = (67,79), (43,103), (37,109), (19,127), (7,139) => type 6n+1, afstand 6k, k = 1,5,6,9,11
Priemgetallen zijn echter niet te voorspellen, en de priemgetalstelling zegt dat als je een willekeurig getal kiest in de buurt van een groot getal N, dat dan de kans dat dit getal een priemgetal is, ongeveer gelijk is aan 1 / ln(N). Dat is dus nooit 100%.
Als de bovenstaande stelling over equi-distante priemgetallen waar is, dan zou je als volgt kunnen redeneren:
Vanaf P springen we telkens in stapjes van 6 naar beneden totdat P - 6k = 5 (voor P=6n-1) of P - 6k = 7 (voor P=6n+1). Bij elk stapje test je of het getal een priemgetal is. Indien dit niet het geval is dan wordt de kans dat het volgende stapje een paartje priemgetallen (P-6k,P+6k) is groter met 1/((P-5)/6) of 1/(P-7)/6)). Das raar. Want elke keer dat je geen setje priemgetallen vindt, dan wordt de kans groter dat P+/- 6k wel een priemgetal is. Sterker nog: stel dat je vindt dat het voorlaatste stapje nog steeds geen setje priemgetallen oplevert, dan wordt de kans dus 100% dat P+/-6k beiden priem zijn. Een 100% zekere voorspelling van een priemgetal P+6k is strijdig met de priemgetalstelling. Om deze paradox te doorbreken moeten de lagere priemgetallen elkaar dus helpen om deze zekere voorspelling te versluieren (het lijkt bijna op de EPR paradox, waarbij je door links van de bron te meten, rechts meer zekere uitspraken aan de rechter kant te kunnen doen).
Daarom mijn stelling:
De hoogste en de laagste priemcombinatie (Px, Py) met P = (Px+Py)/2 (ergo: de combinaties (P-6, P+6) en (P-6k, P+6k) met de grootst mogelijke k), kan nooit de enige priemcombinatie (Px, Py) zijn, want anders zou je voor een bepaald getal exact kunnen voorspellen waar een toekomstig priemgetal P + 6k ligt (uitgezonderd P= 11 want je hebt dan immers slechts twee mogelijke waarden voor Px: 5 en 7. In dat geval is er nog geen ‘buitenste’).
EDIT:
Er zit natuurlijk een denkfout in de aanname dat je alle stapjes van 6 altijd sequentieel doorloopt. Je zou er ook volkomen random doorheen kunnen lopen en er dan uiteindelijk twee overhouden. Als dan de voorlaatste geen priempaartje oplevert, dan moet de laatste mogelijkheid een priem op P+6k opleveren.
[ Bericht 3% gewijzigd door Agno op 31-10-2009 20:22:56 ]


even tvp'en, ik weet zelf even niets bij te dragen maar kan wel genieten van dit soort topics.
C'est magnifique, mais ce n'est pas la guerre.
-
-


De naald van Buffon
De naald van Buffon is een bekend probleem dat kansrekening en geometrie combineert. Het probleem stamt uit de achttiende eeuw en luidt in zijn oorspronkelijke formulering ongeveer zo:
Hiervoor zijn twee afleidingen te geven, een geometrische, en eentje die wat gebruik maakt van elementaire kansrekening en calculus. Die laatste zullen we aan het eind geven, maar eerst zullen we de geometrische behandelen. Deze geeft ook een experimentele methode om π te berekenen.
Een voorbeeld van een aantal willekeurig geworpen naalden van lengte l op een vloer met planken van breedte b.
Geometrische methode
Het idee voor deze oplossing is voor het eerst door E. Barbier in 1860 aangedragen. We zijn op zoek naar de kans dat een naald op twee planken ligt, maar de truc is dat dit samenvalt met de verwachting van het aantal naden waarop de naald ligt. Dit lijkt een subtiel onderscheid, maar is het zeker niet. Als we toch even kijken naar de verwachting van het aantal naden dat een naald van willekeurige lengte kruist, dan is dit:
waarbij p1 de kans is dat de naald één naad kruist, p2 dat ze er twee kruist, enzovoort. De kans dat deze op (minstens) twee planken ligt wordt gegeven door:
Maar, wij bekijken een korte naald met lengte l ≤ b, dus p2 = p3 = ··· = 0. En daarom geldt in het geval van een korte naald E(N1) = p. Dus als we de verwachting kunnen berekenen, dan hebben we ook de kans.1
Aan elkaar bevestigde naalden.
We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.
Nu doen we echter wat anders. we maken de punten van de naalden aan elkaar, m.a.w. twee punten van de naald vallen samen, maar op zich kunnen ze verder los bewegen, dus de naald kan in een rechte lijn vallen, of meer in een V-vorm. Als dat gebeurt zijn N1 en N2 natuurlijk niet onderling onafhankelijk, maar voor de verwachtingswaarde maakt dat niet uit, immers, er geldt:
ook als N1 en N2 niet onderling onafhankelijk zijn. Dezelfde logica gaat ook op als we aan een van de uiteinden nog een naald vastmaken, en nog één, enzovoort. Merk op dat de naalden niet eens allemaal dezelfde lengte hoeven te hebben (zo’n constructie wordt ook wel Buffon’s noodle genoemd).
Verder merken we op dat korte naalden natuurlijk naar verwachting minder naden zullen kruisen dan lange naalden. We kunnen daarom veilig stellen dat het aantal naden dat een naald kruist afhangt van de lengte. Met andere woorden E(N) = f(l), waarbij f een functie is die we nog zullen bepalen. We kunnen echter sowieso al het nodige zeggen over f. Stel je voor dat we twee naalden N1 en N2 (met lengtes l1 en l2 nemen en zo aan elkaar maken dat ze altijd in elkaars verlengde vallen. Dan geldt natuurlijk:
Maar omdat de verwachtingswaarde lineair is, geldt ook nog:
M.a.w., f(l1 + l2) = f(l1) + f(l2). Dat is alvast één eigenschap die we binnen hebben. Verder kunnen we b.v. N1 ook weer zien als m kleine naaldjes van allemaal gelijke lengte die aan elkaar gemaakt zijn, en dan krijgen we b.v.:
En zo vinden we dat f lineair is voor l ∈ ℚ. Als laatste merken we nu op dat f(l) monotoon stijgend moet zijn, en daarom ook dat f(l) = c·l voor l ∈ ℝ. Het aantal naden waar een naald N van lengte l naar verwachting op ligt wordt dus gegeven door:
Waarbij we c moeten bepalen. Merk op dat we het hier dus over een naald hebben met mogelijk veel hoeken erin, en niet per se een rechte naald.
Cirkels met straal b hebben altijd twee punten waar ze op een naad liggen.
Voordat ik duidelijk maak waarom dit precies handig is, laten we eerst eens naar een cirkel2 lijken met diameter b. Hoe je een cirkel ook gooit op de vloer, de cirkel ligt altijd precies op twee naden. Verder weten we dat de omtrek van de cirkel bπ is. Een cirkel kunnen we echter benaderen met een ingeschreven veelhoek, of met een omgeschreven veelhoek.
Een omgeschreven veelhoek (links) en ingeschreven veelhoek (rechts)
Noem de omgeschreven veelhoek met n zijden On en noem de ingeschreven In, dan kunnen we elk van die veelhoeken zien als een aan elkaar gemaakte naald bestaande uit n stukken, waarvan we weten dat E(On) = c·l(On) en E(In) = c·l(In).
Er moet dus gelden:
En, omdat:
voor n → ∞:
Kortom:
en dus geldt voor een korte naald van lengte l dat deze naar verwachting:
naden raakt, en dit is dus ook juist de kans dat deze één naad raakt.
Cirkels met omgeschreven en ingeschreven veelhoeken willekeurig geworpen, merk op dat er op een bovenste grijze baan b.v. een cirkel ligt waarvan de omgeschreven veel hoek drie snijpunten heeft met de naden. Voor n → ∞ verdwijnt dit verschil.
Nawoord
Dit geeft in feite een experimentele mogelijkheid om π te bepalen, teken een aantal lijnen op een stuk papier dat de naden tussen de planken voorstelt, gooi er een naald op die even groot is als de ruimte tussen de lijnen, en tel het aantal keren dat de naald een lijn kruist, omdat l = b, geldt dat π = (2n)/a, waarbij n het aantal keer is dat je gooit en a het aantal dat raak is. Dit is tevens vrij gemakkelijk te programmeren – echter, bedenk wel dat je heel snel al gebruik maakt van het getal π in je programma, wat eigenlijk de hele exercitie wat nutteloos maakt. Je moet vrij omzichtig programmeren om dat niet te doen.
Verder is deze methode verbonden aan een berucht experiment waarbij ene Lazzarini, een Italiaans wiskundige, 3408 keer een naald gooide, die 1808 keer een lijn raakte. Als benadering vond hij toen een getal dat tot op zes plaatsen nauwkeurig is – het heeft er echter alle schijn van dat hij zijn experiment zo inrichtte om een zo goed mogelijk resultaat te krijgen door op precies het juiste moment te stoppen.
Methode met integraal
Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt:
Met een integraal kunnen we nu de totale kans krijgen door te middelen over alle hoeken α die de naald kan aannemen ([0...π]):
1) Er is een kleine kanttekening te maken m.b.t. de mogelijkheid dat een naald met lengte gelijk aan de breedte van de planken precies zo valt dat ze alleen met de twee uiterste punten op een naad ligt, of het geval waarin de naald precies, over de gehele lengte, op een naad ligt. Aangezien dit wiskundige naalden en planken zijn, hebben beide gebeurtenissen kans 0 en kunnen ze verder genegeerd worden. Dit kan wiskundig gezien hard gemaakt worden.
2) Op zich hoef je geen cirkel te gebruiken, elke figuur met een vaste breedte zou ook werken, zoals een Reuleaux-driehoek. Hieruit volgt indirect ook dat voor deze figuren geldt dat o = π·d.
Bronnen en meer lezen:
Introduction to geometric probability, Daniel A. Klain, Gian-Carlo Rota.
Buffon’s needle (Wikipedia)
Buffon’s noodle (Wikipedia)
Buffon’s needle op cut-the-knot
Buffon's Noodle Problem, J. F. Ramaley.
De naald van Buffon is een bekend probleem dat kansrekening en geometrie combineert. Het probleem stamt uit de achttiende eeuw en luidt in zijn oorspronkelijke formulering ongeveer zo:
Het is duidelijk dat één en ander in ieder geval afhangt van de lengte van de naald, hoe langer de naald hoe groter de kans. We zullen de breedte van de planken b noemen. Tussen de planken zitten oneindig dunne naden, en als de naald dus op twee planken ligt, kruist deze één naad. De lengte van de naald zullen we met l aanduiden. Als nu geldt l ≤ d (wat we een korte naald zullen noemen), dan blijkt dat de kans p dat de naald op twee planken ligt gegeven wordt door:quote:Stel dat we een vloer hebben die bestaat uit parallelle houten planken, elk van dezelfde breedte. Als we een naald laten vallen op die vloer, wat is dan de kans dat deze naald op twee planken ligt?
Hiervoor zijn twee afleidingen te geven, een geometrische, en eentje die wat gebruik maakt van elementaire kansrekening en calculus. Die laatste zullen we aan het eind geven, maar eerst zullen we de geometrische behandelen. Deze geeft ook een experimentele methode om π te berekenen.
Een voorbeeld van een aantal willekeurig geworpen naalden van lengte l op een vloer met planken van breedte b.
Geometrische methode
Het idee voor deze oplossing is voor het eerst door E. Barbier in 1860 aangedragen. We zijn op zoek naar de kans dat een naald op twee planken ligt, maar de truc is dat dit samenvalt met de verwachting van het aantal naden waarop de naald ligt. Dit lijkt een subtiel onderscheid, maar is het zeker niet. Als we toch even kijken naar de verwachting van het aantal naden dat een naald van willekeurige lengte kruist, dan is dit:
waarbij p1 de kans is dat de naald één naad kruist, p2 dat ze er twee kruist, enzovoort. De kans dat deze op (minstens) twee planken ligt wordt gegeven door:
Maar, wij bekijken een korte naald met lengte l ≤ b, dus p2 = p3 = ··· = 0. En daarom geldt in het geval van een korte naald E(N1) = p. Dus als we de verwachting kunnen berekenen, dan hebben we ook de kans.1
Aan elkaar bevestigde naalden.
We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.
Nu doen we echter wat anders. we maken de punten van de naalden aan elkaar, m.a.w. twee punten van de naald vallen samen, maar op zich kunnen ze verder los bewegen, dus de naald kan in een rechte lijn vallen, of meer in een V-vorm. Als dat gebeurt zijn N1 en N2 natuurlijk niet onderling onafhankelijk, maar voor de verwachtingswaarde maakt dat niet uit, immers, er geldt:
ook als N1 en N2 niet onderling onafhankelijk zijn. Dezelfde logica gaat ook op als we aan een van de uiteinden nog een naald vastmaken, en nog één, enzovoort. Merk op dat de naalden niet eens allemaal dezelfde lengte hoeven te hebben (zo’n constructie wordt ook wel Buffon’s noodle genoemd).
Verder merken we op dat korte naalden natuurlijk naar verwachting minder naden zullen kruisen dan lange naalden. We kunnen daarom veilig stellen dat het aantal naden dat een naald kruist afhangt van de lengte. Met andere woorden E(N) = f(l), waarbij f een functie is die we nog zullen bepalen. We kunnen echter sowieso al het nodige zeggen over f. Stel je voor dat we twee naalden N1 en N2 (met lengtes l1 en l2 nemen en zo aan elkaar maken dat ze altijd in elkaars verlengde vallen. Dan geldt natuurlijk:
Maar omdat de verwachtingswaarde lineair is, geldt ook nog:
M.a.w., f(l1 + l2) = f(l1) + f(l2). Dat is alvast één eigenschap die we binnen hebben. Verder kunnen we b.v. N1 ook weer zien als m kleine naaldjes van allemaal gelijke lengte die aan elkaar gemaakt zijn, en dan krijgen we b.v.:
En zo vinden we dat f lineair is voor l ∈ ℚ. Als laatste merken we nu op dat f(l) monotoon stijgend moet zijn, en daarom ook dat f(l) = c·l voor l ∈ ℝ. Het aantal naden waar een naald N van lengte l naar verwachting op ligt wordt dus gegeven door:
Waarbij we c moeten bepalen. Merk op dat we het hier dus over een naald hebben met mogelijk veel hoeken erin, en niet per se een rechte naald.
Cirkels met straal b hebben altijd twee punten waar ze op een naad liggen.
Voordat ik duidelijk maak waarom dit precies handig is, laten we eerst eens naar een cirkel2 lijken met diameter b. Hoe je een cirkel ook gooit op de vloer, de cirkel ligt altijd precies op twee naden. Verder weten we dat de omtrek van de cirkel bπ is. Een cirkel kunnen we echter benaderen met een ingeschreven veelhoek, of met een omgeschreven veelhoek.
Een omgeschreven veelhoek (links) en ingeschreven veelhoek (rechts)
Noem de omgeschreven veelhoek met n zijden On en noem de ingeschreven In, dan kunnen we elk van die veelhoeken zien als een aan elkaar gemaakte naald bestaande uit n stukken, waarvan we weten dat E(On) = c·l(On) en E(In) = c·l(In).
Er moet dus gelden:
En, omdat:
voor n → ∞:
Kortom:
en dus geldt voor een korte naald van lengte l dat deze naar verwachting:
naden raakt, en dit is dus ook juist de kans dat deze één naad raakt.
Cirkels met omgeschreven en ingeschreven veelhoeken willekeurig geworpen, merk op dat er op een bovenste grijze baan b.v. een cirkel ligt waarvan de omgeschreven veel hoek drie snijpunten heeft met de naden. Voor n → ∞ verdwijnt dit verschil.
Nawoord
Dit geeft in feite een experimentele mogelijkheid om π te bepalen, teken een aantal lijnen op een stuk papier dat de naden tussen de planken voorstelt, gooi er een naald op die even groot is als de ruimte tussen de lijnen, en tel het aantal keren dat de naald een lijn kruist, omdat l = b, geldt dat π = (2n)/a, waarbij n het aantal keer is dat je gooit en a het aantal dat raak is. Dit is tevens vrij gemakkelijk te programmeren – echter, bedenk wel dat je heel snel al gebruik maakt van het getal π in je programma, wat eigenlijk de hele exercitie wat nutteloos maakt. Je moet vrij omzichtig programmeren om dat niet te doen.
Verder is deze methode verbonden aan een berucht experiment waarbij ene Lazzarini, een Italiaans wiskundige, 3408 keer een naald gooide, die 1808 keer een lijn raakte. Als benadering vond hij toen een getal dat tot op zes plaatsen nauwkeurig is – het heeft er echter alle schijn van dat hij zijn experiment zo inrichtte om een zo goed mogelijk resultaat te krijgen door op precies het juiste moment te stoppen.
Methode met integraal
Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt:
Met een integraal kunnen we nu de totale kans krijgen door te middelen over alle hoeken α die de naald kan aannemen ([0...π]):
1) Er is een kleine kanttekening te maken m.b.t. de mogelijkheid dat een naald met lengte gelijk aan de breedte van de planken precies zo valt dat ze alleen met de twee uiterste punten op een naad ligt, of het geval waarin de naald precies, over de gehele lengte, op een naad ligt. Aangezien dit wiskundige naalden en planken zijn, hebben beide gebeurtenissen kans 0 en kunnen ze verder genegeerd worden. Dit kan wiskundig gezien hard gemaakt worden.
2) Op zich hoef je geen cirkel te gebruiken, elke figuur met een vaste breedte zou ook werken, zoals een Reuleaux-driehoek. Hieruit volgt indirect ook dat voor deze figuren geldt dat o = π·d.
Bronnen en meer lezen:
Introduction to geometric probability, Daniel A. Klain, Gian-Carlo Rota.
Buffon’s needle (Wikipedia)
Buffon’s noodle (Wikipedia)
Buffon’s needle op cut-the-knot
Buffon's Noodle Problem, J. F. Ramaley.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Leuk. Had ik nog nooit van gehoord, maar de beide bewijzen zijn goed te volgen.
Roept wel de vraag op hoe de formule er uit ziet voor drie dimensionale objecten. Stel dat ik een knikker met doorsnede d laat vallen en de kans wil berekenen dat die knikker een naad kruist. Komt daar niet gewoon precies dezelfde formule uit (met l=d) ? En wat als ik kubusjes laat vallen?
Roept wel de vraag op hoe de formule er uit ziet voor drie dimensionale objecten. Stel dat ik een knikker met doorsnede d laat vallen en de kans wil berekenen dat die knikker een naad kruist. Komt daar niet gewoon precies dezelfde formule uit (met l=d) ? En wat als ik kubusjes laat vallen?


Als je een goede uitdrukking kunt vinden voor de ‘hoogte’ van zo’n voorwerp, dan is het vrij goed te doen. Want dan valt in feite die integraaltruc toe te passen.quote:Op dinsdag 3 november 2009 23:59 schreef Agno het volgende:
Leuk. Had ik nog nooit van gehoord, maar de beide bewijzen zijn goed te volgen.
Roept wel de vraag op hoe de formule er uit ziet voor drie dimensionale objecten. Stel dat ik een knikker met doorsnede d laat vallen en de kans wil berekenen dat die knikker een naad kruist. Komt daar niet gewoon precies dezelfde formule uit (met l=d) ? En wat als ik kubusjes laat vallen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Inderdaad. Maar wat als ik nu spelden laat vallen en aanneem dat ze met hun punt in het hout blijven steken (dus een halve bol kunnen beschrijven tov van het 'inslagpunt'). Waarschijnlijk lukt dat ook met de integraaltruc want de richtingshoek van de speld tov van de vloer en zijn lengte bepalen de hoogte aan de andere zijde van de speld. Of maak ik een denkfout?quote:Op woensdag 4 november 2009 00:13 schreef Iblis het volgende:
[..]
Als je een goede uitdrukking kunt vinden voor de ‘hoogte’ van zo’n voorwerp, dan is het vrij goed te doen. Want dan valt in feite die integraaltruc toe te passen.


Klopt volgens mij. Maar als het om experimenteren gaat om π uit te rekenen, heb je niet zoveel aan die integratiemethode.quote:Op woensdag 4 november 2009 00:19 schreef Agno het volgende:
[..]
Inderdaad. Maar wat als ik nu spelden laat vallen en aanneem dat ze met hun punt in het hout blijven steken (dus een halve bol kunnen beschrijven tov van het 'inslagpunt'). Waarschijnlijk lukt dat ook met de integraaltruc want de richtingshoek van de speld tov van de vloer en zijn lengte bepalen de hoogte aan de andere zijde van de speld. Of maak ik een denkfout?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik zie niet waar hhet nu niet kloptquote:Op vrijdag 23 oktober 2009 08:14 schreef -J-D- het volgende:
[ afbeelding ]
Beetje humor op de 'vroege' ochtend.


JD geeft het antwoord in een spoiler, maar het is vrij technisch.quote:Op woensdag 4 november 2009 18:36 schreef Zwavel-Zuur het volgende:
[..]
Ik zie niet waar hhet nu niet klopt
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Even terugkomend op Euclides voorzetje:
met a,b natuurlijke getallen:
Stel P(a,b) = GGD (a,b) * KGV (a,b) ; dan
impliceert:
GGD (a+1,b) * KGV (a+1,b) = (a+1) *b = a*b + b
dus:
GGD (a+1,b) * KGV (a+1,b) = GGD (a,b) * KGV (a,b) +b
dus:
P(a+1,b) = P(a,b) + b
Een belangrijke eigenschap bij priemontbindingen.
met a,b natuurlijke getallen:
Stel P(a,b) = GGD (a,b) * KGV (a,b) ; dan
impliceert:
GGD (a+1,b) * KGV (a+1,b) = (a+1) *b = a*b + b
dus:
GGD (a+1,b) * KGV (a+1,b) = GGD (a,b) * KGV (a,b) +b
dus:
P(a+1,b) = P(a,b) + b
Een belangrijke eigenschap bij priemontbindingen.


Ook een interessante is wanneer l = 3 en b = π.quote:Op woensdag 4 november 2009 00:27 schreef Iblis het volgende:
[..]
Klopt volgens mij. Maar als het om experimenteren gaat om π uit te rekenen, heb je niet zoveel aan die integratiemethode.
Dan krijg je 6/π2 en dat is 1/Zeta(2) (dus 1/(1/1 + 1/4 + 1/9 + 1/16 + .... 1/n).
Waarom zou dat zijn?


Hoewel ik wiskunde goed snap wat me voorgeschoteld wordt, snap ik hier eigenlijk de ballen van 
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Do you think you will walk away untested?


quote:Op woensdag 4 november 2009 20:42 schreef Natrium het volgende:
Hoewel ik wiskunde goed snap wat me voorgeschoteld wordt, snap ik hier eigenlijk de ballen vanNou, sommige bewijzen zullen iets verder gaan dan dat, maar:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
priemgetalbewijs is in principe wel te behappen,
ook dat je √2 niet als breuk kunt schrijven, dat de som van de eerste n oneven getallen altijd een kwadraat is ook, dit bewijs voor de stelling van Pythagoras ook evenals dit bewijs van die stelling, het bewijs van de abc-formule misschien ook.
Als laatste zijn de bewijzen over oneindigheid ook nog wel te volgen, maar misschien dat het eerst helpt om op ‘Hilberts Hotel’ te zoeken op Google. Dat behandelt hetzelfde idee.
Het laatste bewijs dat ik postte, van Buffons naald is denk ik grotendeels te volgen, behalve misschien het wat technische stukje over de verwachtingswaarde.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Mja, oke, ik heb ze niet allemaal bekeken, maar bijv. het bewijs van de abc formule vond ik wel even grappig om te zien 
Maar als ik dan zo even kijk naar wat Bankfurt boven mij aan 't bewijzen is, loop ik al vrij snel vast
Voorlopig zal ik dit topic nog wel even volgen ter vermaak, voordat ik me er mee ga bemoeien.
Ontopic weer
[ Bericht 9% gewijzigd door Natrium op 04-11-2009 21:41:37 ]
Maar als ik dan zo even kijk naar wat Bankfurt boven mij aan 't bewijzen is, loop ik al vrij snel vast
Voorlopig zal ik dit topic nog wel even volgen ter vermaak, voordat ik me er mee ga bemoeien.
Ontopic weer
[ Bericht 9% gewijzigd door Natrium op 04-11-2009 21:41:37 ]
Do you think you will walk away untested?


Er ontgaat me vast iets, maar als P(a,b) = a*b dan heb je de KGV en de GGD toch niet nodig om aan te tonen dat P(a+1,b) = P(a,b) + b ? Dat is dan toch triviaal ?quote:Op woensdag 4 november 2009 19:42 schreef Bankfurt het volgende:
Even terugkomend op Euclides voorzetje:
met a,b natuurlijke getallen:
Stel P(a,b) = GGD (a,b) * KGV (a,b) ; dan
impliceert:
GGD (a+1,b) * KGV (a+1,b) = (a+1) *b = a*b + b
dus:
GGD (a+1,b) * KGV (a+1,b) = GGD (a,b) * KGV (a,b) +b
dus:
P(a+1,b) = P(a,b) + b
Een belangrijke eigenschap bij priemontbindingen.


Triviaal wellicht, maar wel belangrijk om van een groot getal te kunnen bepalen of het priem is of niet;quote:Op woensdag 4 november 2009 22:24 schreef ..-._---_-.- het volgende:
[..]
Er ontgaat me vast iets, maar als P(a,b) = a*b dan heb je de KGV en de GGD toch niet nodig om aan te tonen dat P(a+1,b) = P(a,b) + b ? Dat is dan toch triviaal ?
Eigenlijk wordt dan een algoritme gebruikt met bijvoorbeeld een deelinvariant (er zijn veel andere mogelijkheden):
als a >b
P(a,b) = P(a-1,b) + b
en a:=a-1


Via wiskundemeisjes:
http://www.ted.com/talks/view/id/670
http://www.ted.com/talks/view/id/670
quote:About this talk
The world turns on symmetry – from the spin of subatomic particles to the dizzying beauty of an arabesque. But there's more to it than meets the eye. Here, Oxford mathematician Marcus du Sautoy offers a glimpse of the invisible numbers that marry all symmetrical objects.
About Marcus du Sautoy
Oxford's newest science ambassador Marcus du Sautoy is also author of The Times' Sexy Maths column. He'll take you footballing with prime numbers, whopping symmetry groups, higher dimensions…
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Een mooi bewijs is het bewijs van de sterke stelling van de grote aantallen (statistiek en kansberekening).


Kom maar op dan.quote:Op zondag 8 november 2009 12:20 schreef Bankfurt het volgende:
Een mooi bewijs is het bewijs van de sterke stelling van de grote aantallen (statistiek en kansberekening).
Hetgeen bewezen en beklonken moest worden.


Ik heb de details niet bij de hand, maar het mooie was dat het bewijs gebruik (en vooral de manier waarop) maakt van complexe functies en complexe getallen, om een stelling in de reele getallenwereld te bewijzen.quote:


Tof, hier hier heb ik mijn eerstejaars project over gedaan. Er zijn nog wel leuke verbanden tussen elkaars opvolgers in deze boom. Ook kun je de n-de breuk in deze boom, gemakkelijk vinden door n, binair te schrijven en steeds naar links of recht te gaan bij een 0 respectievelijk 1 in de binaire schrijfwijze. Dit alles is gemakkelijk met inductie te bewijzen, dus wellicht niet heel fraai. Hierdoor hoef je dus niet alle voorgangers te berekenen.quote:Op woensdag 14 oktober 2009 17:36 schreef Iblis het volgende:
De Calkin-Wilf-reeks


quote:Op vrijdag 6 november 2009 16:44 schreef Iblis het volgende:
Via wiskundemeisjes:
http://www.ted.com/talks/view/id/670
[..]
Heb ik.
Hetgeen bewezen en beklonken moest worden.
|
|
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |









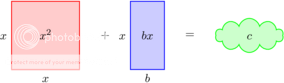
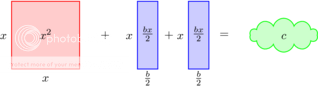
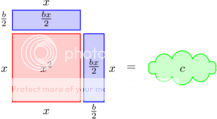
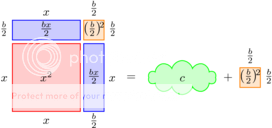
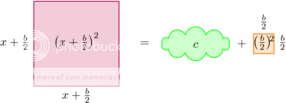














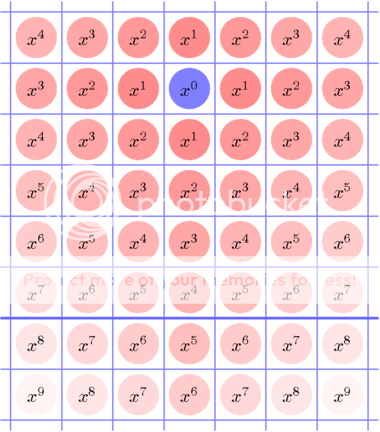












 We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.
We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.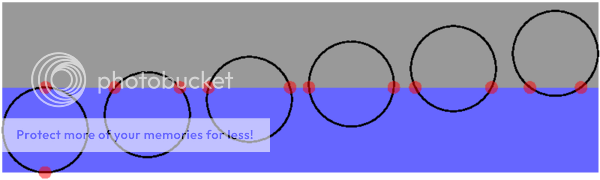


 Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt:
Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt: