De fraaiste wiskundige bewijzen #1

quote:

Op zaterdag 10 oktober 2009 00:46 schreef Maverick_tfd het volgende:
Kan iemand mij vertellen waarom de Fourier transformatie van een constante K gelijk is aan 2*pi*K*delta(omega)? Ik heb het op verschillende plekken op proberen te zoeken maar ik krijg alleen de - onbevredigende - verklaring dat de inverse Fourier transformatie van 2*pi*K*delta(omega) gelijk is aan K.

Ik zou dit graag willen kunnen bewijzen door de Fourier integraal op te lossen maar ik kom er niet uit?

Daar is [Bèta wiskunde] Huiswerk- en vragentopic een betere plaats voor denk ik. Alhoewel de overlap in posters wel aardig hoog is.

De soldaten van Conway

De mensen die “The Curious Incident of the Dog in the Night-Time” hebben gelezen kennen dit misschien al, of ze hebben het overgeslagen omdat ze het niets zei. In het Engels heet dit probleem ‘Conway’s Soldiers’, en zo is het misschien ook beter bekend bij sommigen.

Het idee is in feite een eenvoudig soort solitair spelletje. Dus je hebt een aantal poppetjes op het bord staan, en je kunt ermee over naburige poppetjes springen, mits er aan de andere kant een leeg vakje is waar je kunt landen. Je mag verder alleen horizontaal en verticaal bewegen.

Bijvoorbeeld met twee stenen kun je met de onderste over de bovenste springen (of andersom natuurlijk):


Het probleem is nu als volgt: Hoeveel stenen heb je minstens nodig, als je ze allemaal onder de dikke blauwe lijn neerzet, om minstens één steen op n plaatsen boven de dikke blauwe lijn neer te zetten. Hierboven zie je al dat je 2 stenen nodig hebt om op de 1 plaats boven de blauwe lijn te komen.

De notatie gebruiken we verder ook: een pijltje geeft aan welke steen verzet gaat worden, linksboven staat het aantal gedane zetten (0 is dus de begin situatie) en een grijs rondje is een steen die is verdwenen omdat er overheen gesprongen is.

Laten we nu bekijken hoe we op de tweede regel boven de dikke blauwe lijn uitkomen:



Daar hebben we dus minstens vier stenen voor nodig. Merk overigens op dat we na twee zetten eigenlijk de situatie hebben van ons eerste voorbeeld, alleen dan 1 regel omhoog verschoven. We zouden dus daar al kunnen concluderen dat het kan. Wat wiskundig gezien genoeg is. Maar omdat ik gul ben is het helemaal uitgewerkt.

Ook de derde regel behalen is mogelijk: merk op dat de vier stenen die hier in groen zijn weergegeven precies zo staan als in het tweede voorbeeld, en de eerste drie zetten zijn dan ook gelijk aan dit tweede voorbeeld, en die gebruiken we dus om die ene groene steen op 2 regels boven de dikke blauwe streep te krijgen.

Daarna gaat het verder om met de overige stenen er eentje op drie regels boven de streep te krijgen:



Inmiddels denkt de oplettende lezer: ik heb het patroon al door, 2 stenen voor 1 regel, 4 voor voor 2 regels, 8 voor 3 regels, dus vast 16 voor vier regels: fout. Dat zijn er minstens 20, één voorbeeld zie je hier:



We gaan nu verder om in feite de begin situatie van voorbeeld drie te creëren, alleen dan alvast één regel verschoven:



Hierboven zie je een situatie die nog 8 stenen overheeft, en verder gelijk is aan de startsituatie om 3 regels omhoog te komen, behalve dat één rijtje nu al boven de streep staat.

Oké, boeiend denk je misschien, maar wat is nu het punt? Solitair spelen is niet zo spannend. Het geval is namelijk dat de volgende uitdaging, namelijk een steen op 5 regels boven de blauwe streep krijgen als je met al je stenen eronder begint überhaupt niet mogelijk is. Hoeveel stenen je ook pakt, hoe je ook beweegt, wat je ook doet, je zult nooit een steen op de vijfde regel krijgen.

En dat zullen we gaan bewijzen. Het probleem is bedacht en bewezen door John Conway in 1961. Het bewijs dat het niet kan is werkelijk heel vernuftig, en maakt slim gebruik van de gulden snede: ϕ.

Het idee is als volgt: Het is duidelijk dat elke keer dat je een zet doet dat je dan een mannetje verliest. Maar tegelijkertijd (als je tenminste niet te stom speelt) kun je een mannetje dichter bij je doel brengen. We proberen nu een soort gewicht aan de verzameling soldaatjes te hangen, en uit te drukken hoeveel gewicht er gewonnen of verloren wordt door een zet, en dan uiteindelijk zullen we zien dat hoe je ook begint, je nooit genoeg gewicht hebt om die vijfde regel te bereiken: je verliest het altijd te vroeg.

Allereerst merken we voor de volledigheid op dat het niet uitmaakt wélk punt op de vijfde regel we willen bereiken. Als we een zeker punt kunnen bereiken kunnen we ook het punt links ervan bereiken door alle stenen één plaatsje op te schuiven naar links en dan dezelfde bewegingen te doen. Kortom, die punten zijn in feite inwisselbaar en daarom maakt het niet uit welk punt we pakken. Als het niet kan met dat punt, kan het met geen enkel punt, en omgekeerd. We gaan er hierbij vanuit natuurlijk dat ons bord willekeurig groot kan worden, alhoewel we niet met oneindig veel soldaatjes gaan schuiven, maar wel met willekeurig (doch eindig) veel.

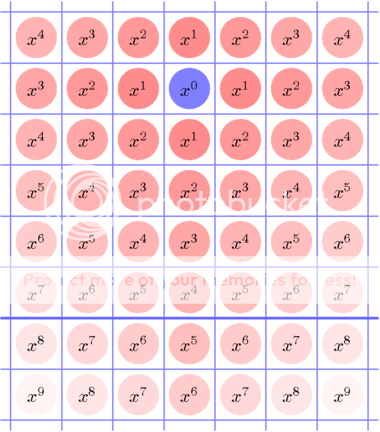
Eerst kiezen we maar eens een punt op de 5e regel (dat is blauw gekleurd hieronder) en dat punt kennen we een bepaald gewicht toe, namelijk: 1. De buurtpunten, die met één stap zijn te bereiken, kennen we gewicht x¹ toe (wat x is zullen we later nog specificeren), de velden die met twee stappen bereikbaar zijn kennen we x² toe, met drie x³, en zo voort, je krijgt dus deze situatie:



De laagste macht die we onder de streep vinden is dus x⁵. Een soldaatje dat op een veld staat krijgt het gewicht van het veld. Het gewicht van ons hele leger is simpelweg de som van alle veldjes waar een soldaat op staat. Merk op dat een soldaat op ons eindpunt dus per definitie gewicht 1 heeft, en een leger met een soldaat op het eindpunt dus ook minstens gewicht 1.

Voordat we specificeren wat x is, kijken we eerst nog even wat voor soort stappen we zouden kunnen doen, dat zijn er 3:

We kunnen naar het eindpunt toegaan: Dus we springen b.v. van x³ over x² naar x¹ (dan verdwijnt de soldaat op een x²-veld). In z’n algemeenheid gaan we van een veld met waarde xⁿ⁺² naar xⁿ en verdwijnt de soldaat op xⁿ⁺¹.

We kunnen ook juist verder van het eindpunt afgaan: Dus we springen b.v. van x¹ over x² naar x³ (de soldaat op een x²-veld verdwijnt weer). In z’n algemeenheid gaan we van een veld met waarde xⁿ naar xⁿ⁺² en verdwijnt de soldaat op xⁿ⁺¹.

We kunnen precies even ver van het eindpunt blijven: dit kan alleen als we dus over een van de twee assen door het eindpunt heenspringen, b.v. precies onder de blauwe streep kunnen we van x⁶ over x⁵ naar een ander x⁶ veld springen. In dit geval gaan we dus van een veld met waarde xⁿ⁺¹ naar een veld met waarde xⁿ⁺¹ en verdwijnt een soldaat met waarde xⁿ.

Het is hopelijk niet lastig om jezelf ervan te overtuigen dat als je alleen horizontaal en verticaal mag springen dit de enige drie opties zijn.

Nu komt de truc, namelijk een geschikt waarde voor x kiezen. Dit, samen met de waardering is het briljante van het bewijs, we kiezen x = 1/ϕ, ofwel:



Het getal ϕ is de guldensnede, die heeft een paar interessante eigenschappen die ook nu van pas komen, te weten: ϕ² = ϕ + 1, en 1/ϕ = ϕ - 1.

Laten we nu eens naar de drie soorten bewegingen kijken die we kunnen maken, eerst de eerste bewegingen waarbij we naar het eindpunt toespringen:

Het gewicht van het hele leger verandert als volgt: er komt xⁿ bij (daar eindigen we), maar er verdwijnt xⁿ⁺¹ (daar springen we overheen) en er verdwijnt xⁿ⁺² (de startpositie), dus de verandering is: xⁿ - xⁿ⁺¹ - xⁿ⁺². Als we xⁿ buiten haakjes krijgen hebben we dat de verandering is:



De oplettende lezer voelt ’m nu al aankomen: de eigenschappen van de gulden snede komen nu beregoed van pas. Bedenk, x = 1/ϕ = ϕ - 1, dus x² = 1/(ϕ²) = 1/ϕ·1/ϕ = (ϕ - 1)/ϕ = 1 - 1/ϕ = 1 - x.

Kortom:



Als we dus naar het eindpunt toe bewegen verandert het ‘gewicht’ van het leger niet. Nu bekijken we het tweede geval, dat betekent dat we van het eindpunt af bewegen, dat geeft:



Omdat x positief is geldt dat -2xⁿ⁺¹ < 0. Dat is voldoende: het gewicht van het leger neemt in dat geval dus af.

Nu het laatste geval waarbij we over een as door het eindpunt springen:



Ook in dát geval neemt het gewicht af. Het maakt dus niet uit wat voor sprong we maken, onder de waardering die we kiezen kan de waarde van het gehele leger niet toenemen.

Omdat het eindpunt gewicht 1 heeft, zoals we al opgemerkt hebben, zal een leger dat ooit dat eindpunt wil kunnen bereiken ook minstens gewicht 1 hebben, want het gewicht kan nooit toenemen, wat voor zetten je ook doet. Om nu aan te tonen dat ons startleger altijd te weinig gewicht zal hebben berekenen we het gewicht van het leger dat alle (oneindig veel!) vakjes onder de blauwe streep zou innemen, heeft. We doen dit per kolom. We beginnen met de kolom onder het eindpunt, deze heeft gewicht: .

Bedenk dat 0 ≤ x ≤ 1, dus dit is een geometrische reeks met als som: x⁵/(1 - x).

De twee kolommen aan weerszijden van deze kolom hebben elk waarde x⁶/(1 - x), die daarnaast x⁷/(1 - x), en zo voort. Dat hele halfvlak heeft dus als gewicht G:



Bedenk, we hadden x zo gekozen dat 1 - x = x², dus bovenstaande is gelijk aan:



Kortom, als het gehele oneindige halfvlak bezet zou zijn met poppetjes, dan zouden deze samen precies gewicht 1 hebben. Elke lege plek betekent dat het gewicht minder dan 1 is, en dus de vijfde regel nooit bereikt kan worden. Geen enkel eindig leger kan die vijfde regel daarom bereiken. □

Het record staat nu op 22. Zie b.v.: Optimal solutions for Rubik's Cube

Er zijn algoritmes die je inderdaad kunnen helpen met zo’n kubus. Je hebt ook software. Die doet ’t gemiddeld in 19 moves. Het perfecte algoritme is er nog niet, maar men zit er naar verwachting niet ver af.

Voor mensen is dit echter niet heel praktisch, het zou te veel randgevallen vereisen om te leren. Mensen zijn veel meer gebaat naar het kunnen reduceren naar een toestand die ze herkennen. De standaard layer by layer methods zijn daar ook op gericht. Weinig uit je hoofd leren, toch veel kunnen doen.

Mensen die meedoen aan wedstrijden om snel kubussen op te lossen maken volgens mij gebruik van algoritmes die soms ook meer dan 100 gevallen onderscheiden. Maar dan nog ben je vaak meer dan 50 keer aan het draaien. Voor mensen maakt het echter ook uit welke kanten je na elkaar moet draaien, en of je de kubus moet verpakken. Dat kost tijd, en het gaat vaak om snelheid bij die wedstrijden. (Niet altijd overigens.)

quote:

Op maandag 12 oktober 2009 15:50 schreef servus_universitas het volgende:
Ik gooi eerbiedig een vraag in dit gezelschap van giganten der wiskundige wetenswaardigheden: wat is het wiskundige bewijs van 1 + 1 = 2?

Is al gedaan deze topic en er is al naar gelinkt. Als je terugleest heb je het zo.