W&T Wetenschap & Technologie
Een plek om te discussiëren over wetenschappelijke onderwerpen, wetenschappelijke problemen, technologische projecten en grootse uitvindingen.
quote:Op maandag 28 september 2009 22:29 schreef BrandX het volgende:
[..]
hier verlies je me
Waarom wil je dit doen? Niet alleen alle priemgetallen met elkaar vermedigvuldigen, maar ook nog eens '1' bij optellen?
Overigens wat ik zelf een mooie wetmatigheid vind in de wiskunde:
als je alle cijfers in een getal optelt, en je kan dat door 3 delen (en de uitkomst is een heel getal), is het originele getal ook te delen door drie.
Dus: 81 = 8+1=9
9 kan je delen door 3 dus 81 kan je delen door 3
3528921= 3+5+2+8+9+2+1 = 30
30 kan je delen door 3 dus 3528921 kan je delen door 3
8592847932= 8+5+9+2+8+4+7+9+3+2 = 57
57= 5+7=12
12= 1+2 =3
enz.
Het is misschien lastiger te bewijzen voor alle getallen, maar om het in ieder geval inzichtelijk te maken kun je het voor een getal ABCDE vrij makkelijk bewijzen.quote:Op maandag 28 september 2009 22:32 schreef Dennis_enzo het volgende:
[..]
Maar heb je daar ook een bewijs voor?
ABCDE is in feite 10.000A + 1000B + 100C + 10D + E
Dat is dan (9999A + A) + (999B +B) + (99C + C) + (9D + D) + E
Dit is dan weer 9999A + 999B + 99C + 9D + A + B + C + D + E
Als je dit door 3 deelt (dit geldt trouwens ook voor 9), dan zie je meteen dat de eerste vier termen deelbaar zijn door 3, en het dus afhangt van (A + B + C + D + E) of het getal in zijn geheel deelbaar is door 3. De uitkomst is namelijk (3333A + 333B + 33C + 3D) + (A + B + C + D + E)/3
"Patriotism is the last refuge of a scoundrel"
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.
Vanaf waar volg je het niet helemaal meer?quote:
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik kan dit kort beantwoorden: Nee. Het bewijs bevat hele zware wiskunde waarvoor je jaren moet studeren om ze je eigen te maken. Er is wel een Horizon-documentaire van de BBC over het bewijs. Als je een hele kleine indruk wilt krijgen van wat erbij komt kijken, dan raad ik je aan om die te kijken, is vast wel te vinden op YouTube. Wil je meer dan alleen een kleine indruk krijgen, dan vrees ik dat je een aantal jaar flink moet studeren.quote:Op dinsdag 6 oktober 2009 17:55 schreef Pietverdriet het volgende:
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?
Deze:quote:
[..]
Ik kan dit kort beantwoorden: Nee. Het bewijs bevat hele zware wiskunde waarvoor je jaren moet studeren om ze je eigen te maken. Er is wel een Horizon-documentaire van de BBC over het bewijs. Als je een hele kleine indruk wilt krijgen van wat erbij komt kijken, dan raad ik je aan om die te kijken, is vast wel te vinden op YouTube. Wil je meer dan alleen een kleine indruk krijgen, dan vrees ik dat je een aantal jaar flink moet studeren.
Het begin is het aangrijpendst, als hij zo geëmotioneerd raakt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het boek fermats last theorem van simon singh, daar staat het heel duidelijk in uitgelegd.quote:Op dinsdag 6 oktober 2009 17:55 schreef Pietverdriet het volgende:
Kan iemand me het bewijs voor de laatste stelling van Fermat uitleggen?
Ja, die bedoelde ik inderdaad.quote:Op dinsdag 6 oktober 2009 18:14 schreef Iblis het volgende:
[..]
Deze:
Het begin is het aangrijpendst, als hij zo geëmotioneerd raakt.
Ook dat boek geeft niet meer dan een kleine indruk. Als je een volledig bewijs wilt hebben, waarin elk tussenresultaat voorkomt, is dat zeker enkele duizenden pagina's. Er is een boek van Cornell, Silverman en Stevens waar wat meer wiskundige details in zitten en waarin de essentiele stappen van Wiles goed worden uitgelegd. Maar je moet wel wiskunde gestudeerd hebben om dat boek te kunnen begrijpen.quote:Op dinsdag 6 oktober 2009 18:19 schreef Basp1 het volgende:
[..]
Het boek fermats last theorem van simon singh, daar staat het heel duidelijk in uitgelegd.
Wat enorm tofquote:Op dinsdag 6 oktober 2009 18:14 schreef Iblis het volgende:
[..]
Deze:
Het begin is het aangrijpendst, als hij zo geëmotioneerd raakt.
Ik heb de hele rits filmpjes gekeken 
Respect.
Op donderdag 22 november 2012 00:14 schreef ondeugend het volgende:
liefdevolle gevoelens voor de duisternis
liefdevolle gevoelens voor de duisternis
Is zonder meer een van de beste afleveringen ooit van Horizon.quote:Op dinsdag 6 oktober 2009 19:42 schreef Bravebart het volgende:
[..]
Wat enorm tof
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.
Niet, was ook niet nodig, hij werd niet in twijfel getrokken, alleen was er geen sluitend wiskundig bewijsquote:Op dinsdag 6 oktober 2009 19:54 schreef ReWout het volgende:
Even een vraagje over fermat... het dan destijds bewezen. Maar wat zijn we ermee verder gekomen?
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.
Nee dat bedoel ik niet. Het bewijs was dus een paar jaar geleden bewezen. Maar wat ze we als mensheid ermee opgeschotenquote:
[..]
Niet, was ook niet nodig, hij werd niet in twijfel getrokken, alleen was er geen sluitend wiskundig bewijs
we kunnen iig nog niet met lichtsnelheid reizen daardoor helaas.
volgens mij begrijp je niet helemaal waar het om gaat bij een wiskundig bewijs.quote:Op dinsdag 6 oktober 2009 19:59 schreef ReWout het volgende:
[..]
Nee dat bedoel ik niet. Het bewijs was dus een paar jaar geleden bewezen. Maar wat ze we als mensheid ermee opgeschoten
In Baden-Badener Badeseen kann man Baden-Badener baden sehen.
Nou, tja, er zijn veel wiskundige vakgebieden ontgonnen en met elkaar verbonden. Dat is eigenlijk het grootste gedeelte. Wiskunde is veel verbanden leggen. Numerieke berekeningen en voorgaande deelbewijzen hadden eigenlijk al wel de meesten doen vermoeden dat de stelling waar was. Dus in die zin is de uitkomst niet schokkend.quote:
Even een vraagje over fermat... het is destijds bewezen. Maar wat zijn we ermee verder gekomen
Maar de weg ernaartoe wél. Het is een beetje te vergelijken misschien met ‘oké nu zijn de Amerikanen naar de maan geweest en staat daar een vlag’, wat hebben we aan die vlag? Nu ja, die vlag is nog het minst interessante, maar alle technieken en kennis die zijn ontwikkeld om dat haalbaar te maken, díé zijn natuurlijk superbelangrijk.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Als je wilt weten hoe we dat wel moeten doen; laatst kwam er een pareltje hier bij ons op de onderzoeksgroep binnen waarin een zogenaamde "quark hyperdrive" werd beschreven waarmee dat wel kan.quote:Op dinsdag 6 oktober 2009 19:59 schreef ReWout het volgende:
Maar wat ze we als mensheid ermee opgeschoten
Tovve tekeningen ook nog erbij 
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik geloof dat ik een paint topic in onz zie aankomenquote:
[..]
Als je wilt weten hoe we dat wel moeten doen; laatst kwam er een pareltje hier bij ons op de onderzoeksgroep binnen waarin een zogenaamde "quark hyperdrive" werd beschreven waarmee dat wel kan.
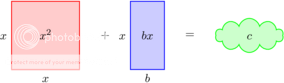
Een oude bekende van de middelbare school. De kwadratische vergelijking. Je weet wel, je hebt , en om één of andere reden geldt:
Waarom? Hoe komen ze daarop… We bekijken eerst eens een wat simpeler geval: x2 + bx = c. Dit kan heel aardig gevisualiseerd worden. Bedenk dat ‘kwadraat’ van het Latijnse ‘quadratus’ komt, dat vierkant betekent.
We kunnen daarom de formule:
Ook visualiseren als een vierkant met oppervlakte x2, een rechthoek met oppervlakte bx en nog een constante term c.
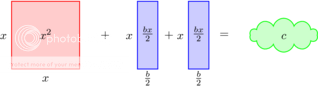
De rechthoek met oppervlakte bx splitsen we nu in twee gelijke rechthoeken:
Dit komt overeen met:
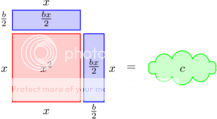
Nu ‘herordenen’ we de vergelijking:
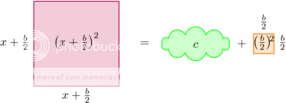
Dit is alleen als visueel hulpmiddel, aan de niet-visuele vergelijking verandert niets. We kunnen nu echter de linkerkant van de vierkant volledig maken, er een vierkant van maken. Dat is waarom deze methode ‘completing the square’ heet in het Engels. Daartoe tellen we (b/2)2 op aan beide zijden:
Of, als vergelijking:
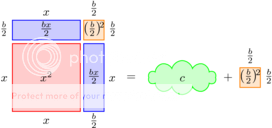
We zien nu al, visueel, dat we nu links een vierkant hebben:
Of als vergelijking:
Dit is eigenlijk het idee achter het bewijs. Door nu wortel te trekken is zo op te lossen wat x is. De rest is af te maken door relatief eenvoudig formule manipuleren. Eigenlijk is dat saai, en niet eens heel fraai. Daarom staat het in een spoiler.
Waarom? Hoe komen ze daarop… We bekijken eerst eens een wat simpeler geval: x2 + bx = c. Dit kan heel aardig gevisualiseerd worden. Bedenk dat ‘kwadraat’ van het Latijnse ‘quadratus’ komt, dat vierkant betekent.
We kunnen daarom de formule:
Ook visualiseren als een vierkant met oppervlakte x2, een rechthoek met oppervlakte bx en nog een constante term c.
De rechthoek met oppervlakte bx splitsen we nu in twee gelijke rechthoeken:
Dit komt overeen met:
Nu ‘herordenen’ we de vergelijking:
Dit is alleen als visueel hulpmiddel, aan de niet-visuele vergelijking verandert niets. We kunnen nu echter de linkerkant van de vierkant volledig maken, er een vierkant van maken. Dat is waarom deze methode ‘completing the square’ heet in het Engels. Daartoe tellen we (b/2)2 op aan beide zijden:
Of, als vergelijking:
We zien nu al, visueel, dat we nu links een vierkant hebben:
Of als vergelijking:
Dit is eigenlijk het idee achter het bewijs. Door nu wortel te trekken is zo op te lossen wat x is. De rest is af te maken door relatief eenvoudig formule manipuleren. Eigenlijk is dat saai, en niet eens heel fraai. Daarom staat het in een spoiler.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
deze is pas echt fraai:
en dan krijg je dit soort ongein:
met oneindig veel vormen die allemaal oneindig verschillend zijn.. ik heb er even over moeten nadenken, maar na een dag lang onzoomen op de mandelbrot fractal kon ik geen 2 de zelfde vinden
en dan krijg je dit soort ongein:
met oneindig veel vormen die allemaal oneindig verschillend zijn.. ik heb er even over moeten nadenken, maar na een dag lang onzoomen op de mandelbrot fractal kon ik geen 2 de zelfde vinden
Ja, maar, ja, maar, ik wil niet vervelend doen, maar kun je ook vertellen hoe die verzameling tot stand komt? Want die kleuren zitten natuurlijk niet per se in die vergelijking.quote:
deze is pas echt fraai:
[ afbeelding ]
en dan krijg je dit soort ongein:
[ afbeelding ]
met oneindig veel vormen die allemaal oneindig verschillend zijn.. ik heb er even over moeten nadenken, maar na een dag lang onzoomen op de mandelbrot fractal kon ik geen 2 de zelfde vinden
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Eff simpel uitgelegd, de formule gaat uit van het getal i, dat getal bestaat eigenlijk niet, dus je kan het alleen benaderen.quote:Op dinsdag 6 oktober 2009 23:53 schreef Iblis het volgende:
[..]
Ja, maar, ja, maar, ik wil niet vervelend doen, maar kun je ook vertellen hoe die verzameling tot stand komt? Want die kleuren zitten natuurlijk niet per se in die vergelijking.
In de fractal heb je gewoon een x en een y as, met bijbehorende waarden.
Als je een getal door de formule heen haalt, komt er een ander getal uit dat of 0 is of groter als dat het was.
Als het antwoord 0 is dan wordt de pixel in dit plaatje zwart gemaakt.
Als je het getal dat groter is geworden nogeens door de formule haalt, wordt het nog groter.
Hoevaak je het getal door de formule haalt wordt in het engels "Itteration" genoemd.
Uiteindelijk zal het getal oneindig worden, en de waarde van de pixel is het aantal itterations.
De kleuren voor de itterations kan je zelf verzinnen, maar het aantal itterations zijn niet betekenisloos.
Het leuke eraan is dat de formule al heel lang bestaat, maar doordat de computers pas de laatste 20 jaar snel genoeg zijn om bij het inzoomen binnen een dag een plaatje te kunnen opbouwen, kunnen we nu pas de wonderlijke vormen zien.
Er bestaan ook nog julia factals, dat is een fractal die uitgaat van 1 punt op de mandelbrot fractal en die voor elk punt (dus on eindig veel)een aparte factal kan maken met oneindig veel vormen die ook allemaal verschillend zijn.
hier een zoom filmpje voor als je wilt spacen:
En het is ook nog een wetenschappelijke doorbraak die nog niet echt is doorgebroken, als we onderzoeksresultaten willen analyseren zoeken we altijd naar een patroon, parabool, lijn of andere simpele logica.
vanaf nu kunnen we naar fractals zoeken en dingen meten die onmeetbaar zijn met de huidige wetenschap.
vanaf nu kunnen we naar fractals zoeken en dingen meten die onmeetbaar zijn met de huidige wetenschap.
Alsem, volgens mij snap je toch niet heel veel van fractals. Ik zal het t.z.t. – nu is het te laat – eens proberen uit te leggen. Merk ook op dat je formule niet juist was, jij gaf de formule voor de Tricorn-fractal waarbij je de complex toegevoegde neemt. De gewone Mandelbrotiteratie wordt gegeven door .
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Overigens is het wel razend interessant, dus goed dat je het noemt. 
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Oké, fractaluitleg. Een fractal is wiskundig gezien eigenlijk alleen een verzameling punten. in een vlak (het complexe vlak om precies te zijn). Een punt hoort of wél bij die verzameling, of niet.
Bron: Wikimedia Commons. Maker: Connelly. Publiek Domein.
Hier boven zie je dus de Mandelbrotverzameling in het complexe vlak. Zwart hoort er wel bij, wit niet. Waar komen dan die kleurtjes vandaan? Dat heeft te maken met het rekenproces dat bepaalt of zo’n punt in het vlak zit of niet.
Een complex getal bestaat uit een reële en een imaginaire component, doorgaans geschreven als a + bi, a is de reële component, b de imaginaire. Dit zie je ook hierboven. Het punt (1 + 0i) ligt bijvoorbeeld ‘op de x-as’, d.w.z. de horizontale, of eigenlijk reële as, het punt (0 + i) ligt op de verticale as, of imaginaire as. En het punt (1 + i) ligt in het kwadrant rechtsboven.
Complexe getallen kun je vrij eenvoudig optellen en aftrekken, dat is ongeveer zoals je zou verwachten: (2 + 3i) + (5 + 4i) = 7 + 7i. Vermenigvuldigen is ook niet zo raar, dat geeft: (2 + 3i)(5 + 4i) = (10 + 8i + 15i + 12i2) = (10 + 23i + 12i2). Alleen nu is er wel een ding speciaal, er geldt namelijk i2 = -1. Dus we kunnen het vorige getal schrijven als (-2 + 23i).
Dat is dus de bekende i2 = -1, of soms ook als i = √(-1) geschreven. Als je dit weet, weet je eigenlijk al genoeg om die Mandelbrot fractal te kunnen teken.
Je pakt namelijk een punt uit dit complexe vlak, zeg c, en dan zeg je: z1 = c, z2 = z1*z1 + c, z3 = z2*z2 + c, en zo voort. Of in z’n algemeenheid: zn+1 = zn*zn + c. Voor sommige waarden van c levert dit een heel groot getal op, dat steeds maar groter wordt. Die zitten niet in je verzameling. Voor sommige waarden geldt dat het getal niet steeds groter wordt. Neem bijvoorbeeld i:
z1 = i
z2 = i*i + i = -1 + i
z3 = (-1 + i)2 + i = (i2 - 2i + 1) + i = -i
z4 = (-i)2 + i = -1 + i
z5 = z3
En zo voort. We komen dus in een rondje terecht. Probeer het eens voor c = 1:
z1 = 1
z2 = 1*1 + 1 = 2
z3 = 2*2 + 1 = 5
z4 = 5*5 + 1 = 26.
Dit gaat dus hopeloos mis, dit punt verdwijnt. De truc is nu: wanneer weet je zeker dat zo’n punt verdwijnt? Zoals je ziet kan een punt namelijk ‘op en neer klappen’ zoals in het geval van c = i. Als je rond de oorsprong een cirkel trekt met straal 2 in bovenstaand figuur, dan is het zeker dat als je iteratie een keertje buiten die cirkel komt, dat het dan misgaat.
Op deze manier kunnen we ook tot de kleuren komen: We tellen hoe vaak we bovenstaand proces moeten uitvoeren om buiten die cirkel te geraken. Dan krijg je zoiets:
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
De zwarte punten zitten dus in de verzameling, de gekleurde niet. En je ziet heel duidelijke banden met dezelfde kleur. De meer roodachtige aan de buitenkant zijn direct al weg in feite; de rood-paarse kleur daarbinnen doet er 1 iteratie over, die daarbinnen 2, de blauw tinten nog langer, en de groen tinten nog weer langer, en de paarse tinten binnenin, grenzend aan het zwarte vlak, doen er nóg weer langer over.
Die kleuren geven dus eigenlijk vooral het berekeningsproces weer, en hoe lang je erover doet om te berekenen dat zo’n punt niet in de verzameling zit, maar zijn niet ‘de fractal zelf’ ook al wordt misschien vaak wel zo geassocieerd. De fractal zelf, de Mandelbrotverzameling in dit geval is dus het zwarte.
Maar hoe komt men dan aan zo’n afbeelding?
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
Waarom zie je daar niet van die duidelijke strepen met dezelfde kleur? Dat is in feite gewoon een bewerkingstruc. Die strepen worden als het ware uitgevlakt en in een continue overgang geplaatst. Stel dat je een punt c hebt dat na n iteraties ‘buiten de cirkel is gekomen’ dan hoort daar dan de volgende waarde bij: v = n - log2log2 |zn|, hier is zn dus het punt dat voor het eerst buiten de cirkel valt, |zn| geeft de afstand van dat punt tot de oorsprong (dus als rechte lijn gezien). Op deze manier krijg je een continu waardenverloop: immers punten die net ietsje verder weg komen krijgen een iets andere kleur. De truc is nu om die waarden ook nog op geschikte kleuren af te beelden.. Maar als je dat doet, dan krijg je dus zulke mooie, vloeiende, afbeeldingen.
De moeilijkheid, en het fascinerende aan fractals is, dat je op een gegeven moment je iteratie moet afkappen. Je kunt wel zeker weten dat een punt niet in de verzameling zit, en van sommige punten is ook duidelijk dat ze er wél inzitten, maar op het grensvlak is het vaak niet duidelijk. Het enige dat je dan kunt doen is gewoon rekenen. 100 iteraties proberen en kijken of het punt al ontsnapt. Of 1000. Of 10000. En zo voort. In die zin is een fractal dus altijd een benadering. Die grenspunten ontsnappen misschien niet na 1000 iteraties, en zijn daarom zwart gekleurd, maar mogelijk wel na 10000!
Dat is ook de reden dat men (alleen) kan zeggen: de oppervlakte van de verzameling is 1,506 591 77 ± 0,000 000 08. Om dat precies uit te rekenen zou je oneindig lang moeten doorrekenen. Er is geen formule met een exacte uitkomst te geven.
Zo’n tekening is dus altijd een benadering. Het grappige is ook dat de uitvinder van deze verzameling, Benoît Mandelbrot, in het begin, op basis van zulke computerafbeeldingen dacht dat de verzameling niet verbonden was, m.a.w. dat je niet via een zwart punt over alleen maar zwarte punten naar elk ander zwart punt kunt komen. Er zouden dus eilandjes zijn. Dat vermoeden was gebaseerd op tekeningen gerenderd door de computer waarbij heel dunne haarlijntjes niet zichtbaar waren. Je moet immers kiezen hoe nauwkeurig je zoiets doet. Als je c = -1.1 en c = 1.2 uitrekent, moet je dan c = 1.15 ook nog doen? En c = 1.155? En c = 1.1555? Je moet ergens stoppen. Het kan best dat dus in je tekening twee pixels naast elkaar beiden een kleurtje hebben, maar dat er tussen eigenlijk nog een – in die tekening onzichtbaar – zwart lijntje loopt.
Inmiddels is bewezen dat de gehele verzameling wel verbonden is, maar die inzoomfilmpjes die je ziet tonen aan dat je in principe steekds maar kunt vergroten en vergroten op de grens en telkens nieuw detail ziet. En wát je dan precies ziet, dat is pas te zeggen nadat het is uitgerekend. Je kunt dus niet een patroon ontdekken voorspellen. Ter vergelijking, een breuk als 1/7 ≈ 1,142857142857, maar die herhaalt zichzelf telkens. Je kunt zo voorspellen dat cijfer 1, 7, 13, 19, enz. een 1 zijn. Als iemand dus wil weten wat cijfer 283043 achter de komma is kun je dat direct zeggen zonder tot 283043 cijfers achter de komma door te rekenen omdat er een patroon in zit. Dat kan bij zo’n fractal niet. Je moet het helemaal uitrekenen.
Bron: Wikimedia Commons. Maker: Connelly. Publiek Domein.
Hier boven zie je dus de Mandelbrotverzameling in het complexe vlak. Zwart hoort er wel bij, wit niet. Waar komen dan die kleurtjes vandaan? Dat heeft te maken met het rekenproces dat bepaalt of zo’n punt in het vlak zit of niet.
Een complex getal bestaat uit een reële en een imaginaire component, doorgaans geschreven als a + bi, a is de reële component, b de imaginaire. Dit zie je ook hierboven. Het punt (1 + 0i) ligt bijvoorbeeld ‘op de x-as’, d.w.z. de horizontale, of eigenlijk reële as, het punt (0 + i) ligt op de verticale as, of imaginaire as. En het punt (1 + i) ligt in het kwadrant rechtsboven.
Complexe getallen kun je vrij eenvoudig optellen en aftrekken, dat is ongeveer zoals je zou verwachten: (2 + 3i) + (5 + 4i) = 7 + 7i. Vermenigvuldigen is ook niet zo raar, dat geeft: (2 + 3i)(5 + 4i) = (10 + 8i + 15i + 12i2) = (10 + 23i + 12i2). Alleen nu is er wel een ding speciaal, er geldt namelijk i2 = -1. Dus we kunnen het vorige getal schrijven als (-2 + 23i).
Dat is dus de bekende i2 = -1, of soms ook als i = √(-1) geschreven. Als je dit weet, weet je eigenlijk al genoeg om die Mandelbrot fractal te kunnen teken.
Je pakt namelijk een punt uit dit complexe vlak, zeg c, en dan zeg je: z1 = c, z2 = z1*z1 + c, z3 = z2*z2 + c, en zo voort. Of in z’n algemeenheid: zn+1 = zn*zn + c. Voor sommige waarden van c levert dit een heel groot getal op, dat steeds maar groter wordt. Die zitten niet in je verzameling. Voor sommige waarden geldt dat het getal niet steeds groter wordt. Neem bijvoorbeeld i:
z1 = i
z2 = i*i + i = -1 + i
z3 = (-1 + i)2 + i = (i2 - 2i + 1) + i = -i
z4 = (-i)2 + i = -1 + i
z5 = z3
En zo voort. We komen dus in een rondje terecht. Probeer het eens voor c = 1:
z1 = 1
z2 = 1*1 + 1 = 2
z3 = 2*2 + 1 = 5
z4 = 5*5 + 1 = 26.
Dit gaat dus hopeloos mis, dit punt verdwijnt. De truc is nu: wanneer weet je zeker dat zo’n punt verdwijnt? Zoals je ziet kan een punt namelijk ‘op en neer klappen’ zoals in het geval van c = i. Als je rond de oorsprong een cirkel trekt met straal 2 in bovenstaand figuur, dan is het zeker dat als je iteratie een keertje buiten die cirkel komt, dat het dan misgaat.
Op deze manier kunnen we ook tot de kleuren komen: We tellen hoe vaak we bovenstaand proces moeten uitvoeren om buiten die cirkel te geraken. Dan krijg je zoiets:
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
De zwarte punten zitten dus in de verzameling, de gekleurde niet. En je ziet heel duidelijke banden met dezelfde kleur. De meer roodachtige aan de buitenkant zijn direct al weg in feite; de rood-paarse kleur daarbinnen doet er 1 iteratie over, die daarbinnen 2, de blauw tinten nog langer, en de groen tinten nog weer langer, en de paarse tinten binnenin, grenzend aan het zwarte vlak, doen er nóg weer langer over.
Die kleuren geven dus eigenlijk vooral het berekeningsproces weer, en hoe lang je erover doet om te berekenen dat zo’n punt niet in de verzameling zit, maar zijn niet ‘de fractal zelf’ ook al wordt misschien vaak wel zo geassocieerd. De fractal zelf, de Mandelbrotverzameling in dit geval is dus het zwarte.
Maar hoe komt men dan aan zo’n afbeelding?
Bron: Wikimedia Commons. Maker: Wolfgang Beyer. Licentie: CC-BY-SA.
Waarom zie je daar niet van die duidelijke strepen met dezelfde kleur? Dat is in feite gewoon een bewerkingstruc. Die strepen worden als het ware uitgevlakt en in een continue overgang geplaatst. Stel dat je een punt c hebt dat na n iteraties ‘buiten de cirkel is gekomen’ dan hoort daar dan de volgende waarde bij: v = n - log2log2 |zn|, hier is zn dus het punt dat voor het eerst buiten de cirkel valt, |zn| geeft de afstand van dat punt tot de oorsprong (dus als rechte lijn gezien). Op deze manier krijg je een continu waardenverloop: immers punten die net ietsje verder weg komen krijgen een iets andere kleur. De truc is nu om die waarden ook nog op geschikte kleuren af te beelden.. Maar als je dat doet, dan krijg je dus zulke mooie, vloeiende, afbeeldingen.
De moeilijkheid, en het fascinerende aan fractals is, dat je op een gegeven moment je iteratie moet afkappen. Je kunt wel zeker weten dat een punt niet in de verzameling zit, en van sommige punten is ook duidelijk dat ze er wél inzitten, maar op het grensvlak is het vaak niet duidelijk. Het enige dat je dan kunt doen is gewoon rekenen. 100 iteraties proberen en kijken of het punt al ontsnapt. Of 1000. Of 10000. En zo voort. In die zin is een fractal dus altijd een benadering. Die grenspunten ontsnappen misschien niet na 1000 iteraties, en zijn daarom zwart gekleurd, maar mogelijk wel na 10000!
Dat is ook de reden dat men (alleen) kan zeggen: de oppervlakte van de verzameling is 1,506 591 77 ± 0,000 000 08. Om dat precies uit te rekenen zou je oneindig lang moeten doorrekenen. Er is geen formule met een exacte uitkomst te geven.
Zo’n tekening is dus altijd een benadering. Het grappige is ook dat de uitvinder van deze verzameling, Benoît Mandelbrot, in het begin, op basis van zulke computerafbeeldingen dacht dat de verzameling niet verbonden was, m.a.w. dat je niet via een zwart punt over alleen maar zwarte punten naar elk ander zwart punt kunt komen. Er zouden dus eilandjes zijn. Dat vermoeden was gebaseerd op tekeningen gerenderd door de computer waarbij heel dunne haarlijntjes niet zichtbaar waren. Je moet immers kiezen hoe nauwkeurig je zoiets doet. Als je c = -1.1 en c = 1.2 uitrekent, moet je dan c = 1.15 ook nog doen? En c = 1.155? En c = 1.1555? Je moet ergens stoppen. Het kan best dat dus in je tekening twee pixels naast elkaar beiden een kleurtje hebben, maar dat er tussen eigenlijk nog een – in die tekening onzichtbaar – zwart lijntje loopt.
Inmiddels is bewezen dat de gehele verzameling wel verbonden is, maar die inzoomfilmpjes die je ziet tonen aan dat je in principe steekds maar kunt vergroten en vergroten op de grens en telkens nieuw detail ziet. En wát je dan precies ziet, dat is pas te zeggen nadat het is uitgerekend. Je kunt dus niet een patroon ontdekken voorspellen. Ter vergelijking, een breuk als 1/7 ≈ 1,142857142857, maar die herhaalt zichzelf telkens. Je kunt zo voorspellen dat cijfer 1, 7, 13, 19, enz. een 1 zijn. Als iemand dus wil weten wat cijfer 283043 achter de komma is kun je dat direct zeggen zonder tot 283043 cijfers achter de komma door te rekenen omdat er een patroon in zit. Dat kan bij zo’n fractal niet. Je moet het helemaal uitrekenen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik ben altijd bijzonder zwak in formele bewijzen geweest, toch teveel een chaoot, dus even een domme vraag:
Moet je dan niet eerst bewijzen dat combinaties van priemgetallen alleen weer deelbaar zijn door priemgetallen? Of zit dat besloten in de vermenigvuldiging?quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Dit betekent óf dat E zelf een priemgetal is, of als het geen priemgetal is (en dus deelbaar is door een ander priemgetal), dat het dan deelbaar is door een priemgetal dat niet in ons rijtje zat.
They told me all of my cages were mental, so I got wasted like all my potential.
vette uitleg, zo had ik het nog nooit bekeken!
vanavond nog maar eens nalezen, mijn uitleg is idd erg vaag, dont blame me, ik heb 5 jaar geleden voor het laatst wiskunde gehad
Ik heb een keer een programma gedownload, fractalX.exe daarmee kan je zelf inzoomen, het is echt ongelofelijk hoe mooi die figuren zijn, ze lijken ook bekend voor te komen en te kloppen, alsof je hersens dergelijke berekeningen ook maken.
daarmee kan je ook je eigen julia fractal zoeken, itterations instellen en kleur geven, deze heb ik laatst gemaakt:
vanavond nog maar eens nalezen, mijn uitleg is idd erg vaag, dont blame me, ik heb 5 jaar geleden voor het laatst wiskunde gehad
Ik heb een keer een programma gedownload, fractalX.exe daarmee kan je zelf inzoomen, het is echt ongelofelijk hoe mooi die figuren zijn, ze lijken ook bekend voor te komen en te kloppen, alsof je hersens dergelijke berekeningen ook maken.
daarmee kan je ook je eigen julia fractal zoeken, itterations instellen en kleur geven, deze heb ik laatst gemaakt:
Ik heb inderdaad nagelaten te vermelden dat elk getal een unieke priemfactorisatie heeft. Dat was op zich opzettelijk. Elk getal heeft een unieke factorisatie in priemgetallen. En we weten dus dat die factorisatie niet de getallen kan bevatten uit ons rijtje. Ergo, ons rijtje is niet compleet.quote:Op woensdag 7 oktober 2009 12:42 schreef speknek het volgende:
Ik ben altijd bijzonder zwak in formele bewijzen geweest, toch teveel een chaoot, dus even een domme vraag:
[..]
Moet je dan niet eerst bewijzen dat combinaties van priemgetallen alleen weer deelbaar zijn door priemgetallen? Of zit dat besloten in de vermenigvuldiging?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Overigens laat ik formeel gezien wel meer steekjes vallen, maar het is niet mijn bedoeling om strikt formeel te zijn. In die fractaluitleg praat ik b.v. over ‘complexe getallen die steeds maar groter worden’, alhoewel dat natuurlijk formeel gezien niet zo zinnig is.
Ik denk dat ook zonder die formaliteiten echter het idee, de slimmigheid van de redenering, wel over komt. (Of het fascinerende erachter.)
Ik denk dat ook zonder die formaliteiten echter het idee, de slimmigheid van de redenering, wel over komt. (Of het fascinerende erachter.)
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dat hoef je niet te gebruiken. Het gaat erom dat elk getal ten minste 1 priemfactorisatie heeft. En dat is wat makkelijker te bewijzen: stel dat er een getal zonder priemfactorisatie is, dan is er ook een kleinste getal waarvoor dat geldt, zeg n. Omdat n geen priemfactorisatie heeft, is n geen priemgetal dus n = m*k met m en k kleiner dan n. Maar omdat n het kleinste getal zonder priemfactorisatie is hebben m en k dus wel een priemfactorisatie en uit n = m*k krijg je dan ook een priemfactorisatie voor n.quote:Op woensdag 7 oktober 2009 12:51 schreef Iblis het volgende:
[..]
Ik heb inderdaad nagelaten te vermelden dat elk getal een unieke priemfactorisatie heeft. Dat was op zich opzettelijk. Elk getal heeft een unieke factorisatie in priemgetallen. En we weten dus dat die factorisatie niet de getallen kan bevatten uit ons rijtje. Ergo, ons rijtje is niet compleet.
Deze vind ik eigenlijk nog eleganter dan de OP, alhoewel ik de hele tijd het gevoel heb dat ik ergens bedot wordt. Het glijdt erin als de zalvende woorden van een sekteleider, hallelujah!quote:Op woensdag 7 oktober 2009 12:55 schreef thabit het volgende:
Dat hoef je niet te gebruiken. Het gaat erom dat elk getal ten minste 1 priemfactorisatie heeft. En dat is wat makkelijker te bewijzen: stel dat er een getal zonder priemfactorisatie is, dan is er ook een kleinste getal waarvoor dat geldt, zeg n. Omdat n geen priemfactorisatie heeft, is n geen priemgetal dus n = m*k met m en k kleiner dan n. Maar omdat n het kleinste getal zonder priemfactorisatie is hebben m en k dus wel een priemfactorisatie en uit n = m*k krijg je dan ook een priemfactorisatie voor n.
They told me all of my cages were mental, so I got wasted like all my potential.
Dit bewijst natuurlijk niet dat er oneindig veel priemgetallen zijn, alleen dat elk getal een priemfactorontbinding heeft.quote:Op woensdag 7 oktober 2009 13:12 schreef speknek het volgende:
[..]
Deze vind ik eigenlijk nog eleganter dan de OP, alhoewel ik de hele tijd het gevoel heb dat ik ergens bedot wordt. Het glijdt erin als de zalvende woorden van een sekteleider, hallelujah!
het mooiste vind ik dat je met galoistheorie kan aantonen dat je geen formules kunt vinden voor meerderegraadsvergelijkingen. Da's echt prachtig opgebouwd allemaal.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
Ja, ik heb ooit nog es de ambitie gehad om dat eens door te nemen, na een berichtje lang geleden over eendude waarvan de media beweerde dat hij polynomen van willekeurige graden exact kon oplossen.quote:Op woensdag 7 oktober 2009 16:44 schreef Beregd het volgende:
het mooiste vind ik dat je met galoistheorie kan aantonen dat je geen formules kunt vinden voor meerderegraadsvergelijkingen. Da's echt prachtig opgebouwd allemaal.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ow ja, dat was weer zo'n typische media nemen alle onzin over van andere media fail.quote:Op woensdag 7 oktober 2009 17:41 schreef Haushofer het volgende:
[..]
Ja, ik heb ooit nog es de ambitie gehad om dat eens door te nemen, na een berichtje lang geleden over eendude waarvan de media beweerde dat hij polynomen van willekeurige graden exact kon oplossen.
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Nog een keer de stelling van Pythagoras:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Eh ja, ik weet hoe je over Informatica denkt, maar zo'n wiskundeleek ben ik ook weer nietquote:Op woensdag 7 oktober 2009 14:30 schreef thabit het volgende:
[..]
Dit bewijst natuurlijk niet dat er oneindig veel priemgetallen zijn, alleen dat elk getal een priemfactorontbinding heeft.
. Ik bedoelde als een fraai bewijs tegenover het andere.
They told me all of my cages were mental, so I got wasted like all my potential.
Ik heb er nu een zonder woorden voor je.quote:
[..]
Eh ja, ik weet hoe je over Informatica denkt, maar zo'n wiskundeleek ben ik ook weer niet
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
.serieus, plaatjes snap ik om een of andere reden wel. Ik tekende ook altijd venn diagrammen van alles.
They told me all of my cages were mental, so I got wasted like all my potential.
Galoistheorie, een prachtig onderwerp.quote:Op woensdag 7 oktober 2009 16:44 schreef Beregd het volgende:
het mooiste vind ik dat je met galoistheorie kan aantonen dat je geen formules kunt vinden voor meerderegraadsvergelijkingen. Da's echt prachtig opgebouwd allemaal.
En ook straf, want bewijzen dat iets niet kan is veel moeilijker dan het omgekeerde.
. Je kunt op die manier ook aantonen dat sommige dingen wel kunnen, wat anders niet zo makkelijk in te zien is, zoals het construeren van een regelmatige 65537-hoek met passer en liniaal zonder dat ook expliciet te doen.Een ander mooi onderwerp uit die fase van de wiskundestudie vind ik complexe functietheorie. Complexe functies zijn oneindig veel mooier dan reele functies. Als een complexe functie 1 keer differentieerbaar is, dan is ze gelijk oneindig vaak differentieerbaar en dat toon je aan met een paar superstrakke integraalformules.
ja, heb ik mijn thesis ovcer gemaakt (maar dan over ondeindige velduitbreidingen)quote:Op vrijdag 9 oktober 2009 14:55 schreef thabit het volgende:
[..]
Galoistheorie, een prachtig onderwerp.
In codetheorie heb je ook heel leuke bewijzen. Erg verschillend van de andere wiskunde vaak.
Dan zijn er ook zo van die andere wiskundige strekkingen met afschuwelijke bewijzen. Maattheorie bijvoorbeeld. Al die bewijzen zijn zodanig veel constructie en geknutsel, niks elegants aan vaak.
Even een intermezzo met een mooi gedichtje !
quote:Minus one
A carpenter named Charlie Bratticks
Who had a taste for mathematics
One summer Tuesday, just for fun
Made a wooden cube side minus one
Though this to you may seem wrong
He made it minus one foot long
Which meant (I hope your brains aren't frothing)
Its length was one foot less than nothing
Its width the same (you're not asleep?)
And likewise minus one foot deep
Giving, when multiplied (be solemn)
Minus one cubic foot of volume
With sweating brow this cube he sawed
Through areas of solid board
For though each cut had minus length
Minus times minus sapped his strength
A second cube he made, but thus
This time each one foot length was plus
Meaning of course that here one put
For volume, plus one cubic foot
So now he had, just for his sins
Two cubes as like as deviant twins
And feeling one should know the worst
He placed the second in the first
One plus, one minus - there's no doubt
The edges simply cancelled out
So did the volume, nothing gained
Only the surfaces remained
Well may you open wide your eyes
For those were now of double size
On something now, thanks to his skill
Took up no room and measured nil
From solid ebony he'd cut
These bulky objects, but
All that remained was now a thin
Black sharply angled sort of skin
Of twelve square feet - which though not small
Weighed nothing, filled no space at all
It stands there yet on Charlies floor
He can't think what to use it for
zzz
Een harmonieuze reeks leidt altijd tot oneindig.
Dus 1/1 +1/2 +1/3 +1/4 + 1/5 + ….. +1/n leidt tot oneindig.
Dit geldt ook voor 1/1000000 + 1/2000000 + 1/3000000 + etc.
Want oneindig gedeeld door miljoen is ook oneindig.
Nu komt het bewijs.
Bij de oorspronkelijke harmonieze reeks tot een willekeurig getal x is de tweede helft van de reeks altijd groter dan 0,5.
Want: de kleinste in het gezelschap is 1/x en het aantal = 0,5*x
En 0,5*x * 1/x = 0,5
En je kunt een harmonieuze reeks oneindig keer verdubbelen.
Van een lengte 1 naar een lengte 2 naar een lengte 4 en telkens komt er minimaal 0,5 bij.
Dus 1/1 +1/2 +1/3 +1/4 + 1/5 + ….. +1/n leidt tot oneindig.
Dit geldt ook voor 1/1000000 + 1/2000000 + 1/3000000 + etc.
Want oneindig gedeeld door miljoen is ook oneindig.
Nu komt het bewijs.
Bij de oorspronkelijke harmonieze reeks tot een willekeurig getal x is de tweede helft van de reeks altijd groter dan 0,5.
Want: de kleinste in het gezelschap is 1/x en het aantal = 0,5*x
En 0,5*x * 1/x = 0,5
En je kunt een harmonieuze reeks oneindig keer verdubbelen.
Van een lengte 1 naar een lengte 2 naar een lengte 4 en telkens komt er minimaal 0,5 bij.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.
|
|
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |