W&T Wetenschap & Technologie
Een plek om te discussiëren over wetenschappelijke onderwerpen, wetenschappelijke problemen, technologische projecten en grootse uitvindingen.
Jij bent liever lui dan moe hè? Ik vertik dit hoor. Je opent de topic maar op één pagina en zoekt op ‘Fermat’, kan niet missen.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik pareer door het op youtube te zoeken door Fermat uit jouw tekst te kopieërenquote:Op dinsdag 13 oktober 2009 22:00 schreef Iblis het volgende:
[..]
Jij bent liever lui dan moe hè? Ik vertik dit hoor. Je opent de topic maar op één pagina en zoekt op ‘Fermat’, kan niet missen.
. Daarmee heb ik én niet gezocht én heb JIJ mij alsnog geholpen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
De Calkin-Wilf-reeks
In het vorige deel van dit drieluik had ik laten zien hoe je de rationele getallen, d.w.z. de breuken, in een 1:1 koppeling met de natuurlijke getallen kunt zetten. Je kunt de breuken in een vierkant zetten, en dan loop je de diagonalen af. Dit is redelijk slim, maar het nadeel is dat je dubbelen tegenkomt.
Er is ook een manier – verrassend eenvoudig zelfs – om ze op te sommen zonder dat je dubbelen tegenkomt. Deze manier is in 2000 ontdekt door Neil Calkin en Herbert Wilf. Het is van een verbazingwekkende eenvoud en schoonheid.
Hun opsomming begint als volgt:
De logica is misschien nog niet direct duidelijk, maar wat wel opvalt is dat de teller van elke breuk gelijk is aan den oemer van de voorafgaande breuk. Dit is inderdaad iets dat voor de gehele reeks geldt, dus in feite kunnen we zeggen het n-e getal (we beginnen overigens bij 0 te tellen) in de reeks is gelijk aan bn/bn+1, waarbij bn gegeven wordt door:
Dit lijkt misschien een beetje een rare rij getallen, maar op zich tellen ze iets. Wat precies is verder niet zo heel relevant voor wat ik wil aantonen, maar het is wel aardig om te melden: het is namelijk het aantal manieren waarop je een getal als som van machten van twee kunt schrijven, waarbij een macht hooguit twee keer gebruikt wordt.
Dat is misschien wat duidelijker met een voorbeeld. Neem 5, dat is te schrijven als 4 + 1 = 5 (1 = 20), maar ook als 2 + 2 + 1. 1 + 1 + 1 + 1 + 1 gaat niet door, want dan gebruiken we 1 te vaak. 6 kunnen we schrijven als 4 + 1 + 1, of als 4 + 2, of als 2 + 2 + 1 + 1. 2 + 2 + 2 kan dus niet.
Deze reeks staat bekend als ‘Sterns diatomische reeks’, naar de Dutisers Stern – een reeks die overigens al in 1858 voor het eerst werd beschreven! Ook de al eerder in deze topic langsgekomen Dijkstra heeft er in EWD570 en EWD578 over geschreven.
Maar goed, we hebben die reeks dus, en we merken nog een aantal interessante eigenschappen op: Opeenvolgende getallen in bn zijn altijd relatief priem. En aangezien je breuken bouwt van opeenvolgende getallen, zijn die breuken altijd vereenvoudigd. En de lijst van breuken bevat alle positieve breuken precies 1 keer (in gereduceerde vorm dus).
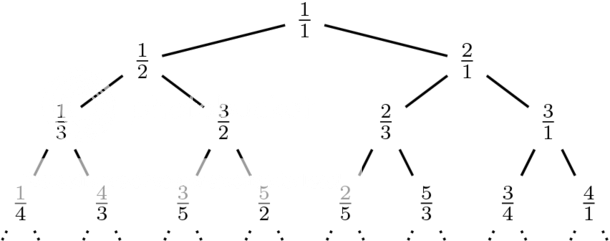
Nou, oké, oké, tof, maar hoe kom ik nu op een makkelijke manier aan die reeks? Moet je echt het aantal manieren om een getal als som van machten van twee te schrijven gaan zitten uitvogelen? Nee, het kan veel gemakkelijker met behulp van een boom. Denk eraan: Het is een Wiskundige boom, dus die groeit naar beneden.
Dus 1/1 zit in de wortel van de boom, en verder heeft elke knoop r/s twee kinderen. De linker is r/(r + s) en de rechter is (r + s)/s. We bekommeren ons niet direct meer om de reeks, maar wel om de boom.
Er zijn nu vijf claims te maken:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Geen enkele breuk komt vaker dan één keer voor.
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
De lijst die je krijgt valt precies samen met bn
Claim 1:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Voor 1/1 geldt dit uiteraard. Neem nu aan dat het niet zo is, en dat er ergens, misschien zelfs wel op meerdere plekken in de boom een breuk is die nog vereenvoudigd kan worden. Van alle mogelijkheden neem je die breuk r/s, als je de boom zoals hierboven tekent, het hoogst in de boom zit.
Het is dus niet de wortel, en daarom weten we zeker dat het dan het kind van een knoop moet zijn. Als het een linker kind is, dan heeft z’n ouder de waarde r/(s - r). Maar als r/s vereenvoudigbaar is, dan is r/(s - r) dat ook[1] – tegenspraak met het feit dat we een breuk uit het hoogste niveau hadden gepakt.
Als r/s een rechter kind is, dan is z’n ouder (r-s)/s, en dat leidt tot dezelfde tegenspraak.
Claim 2:
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Dat 1/1 erin zit is duidelijk. Neem echter aan dat één of meerdere andere breuken er niet in zitten. Neem van die breuken die er niet in zitten eentje met de kleinste noemer, en als er meerdere zijn met een kleinste noemer, van die groep de breuk met de kleinste teller, zeg dat dit r/s is.
Als r > s, dan weten we dat bijgevolg ook (r-s)/s niet in de boom zou kunnen zitten, want die heeft als rechter kind r/s. Maar r - s heeft dezelfde noemer als r/s maar een kleinere teller! En dat is in tegenspraak met onze aanname dat r/s de kleinste teller had!
Omgekeerd, als r < s, dan kan r/(s - r) niet in de boom zitten, want anders zou het een linker kind hebben van de vorm r/s. Maar s - r heeft een kleinere noemer dan r/s, en dat is ook weer een tegenspraak!
Claim 3:
Geen enkele breuk komt vaker dan één keer voor.
Dit geldt sowieso voor de wortel, want stel dat 1/1 nog een keer in de boom zat, dan is het kind van een knoop r/s, maar r/s heeft kinderen in de vorm r/(r + s) en (r + s)/s, en beide kunnen uiteraard geen 1/1 zijn aangezien r en s beide > 0 moeten zijn.
Nu doen we weer het zelfde als bij de vorige claim: van alle breuken die vaker dan één keer zouden voorkomen, kies die met de kleinste noemer, en als dat er meer zijn, daarbinnen die met de kleinste teller. Als r < s, dan is r/s een linker kind, en bovendien geldt dan voor de ouder dat deze r/(s - r) is. Maar dat betekent dat er ook meer dan één van zulk soort ouders is! En r/(s-r) is in strijd met onze aanname dat we een breuk met de kleinste noemer hadden gepakt. En voor r > s hebben we hetzelfde, maar dan als rechter kind.
Claim 4:
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
Deze is iets lastiger te bewijzen. Het is natuurlijk duidelijk als het om twee breuken gaat die kind zijn van dezelfde ouder. Omdat het linker kind de vorm r/(r+s) heeft en de rechter (r+s)/s.
Ook als we van een rij naar de volgende rij gaan is het niet zo moeilijk te zien, de meest rechter breuk op een rij heeft namelijk altijd noemer 1, en de meest linker breuk op een rij altijd teller 1. Dus dat gaat ook goed.
Nu blijft over twee buren in dezelfde rij, maar die niet het kind zijn van dezelfde ouder. Dit moet even met een inductiebewijs. We praten altijd over een rechter kind, gevolgd door een linker kind in zo’n geval. Het rechter kind heeft dezelfde noemer als z’n ouder. En dat linker kind heeft dezelfde teller als z’n ouder. Die twee ouders zijn óók buren van elkaar. Dus als het voor die ouders geldt, dan geldt het ook voor die kinderen.
We hebben vastgesteld dat het voor de kinderen van de wortel sowieso klopt (noem dat de eerste rij), omdat die kinderen van dezelfde ouder zijn. Dus dan klopt het ook voor de tweede rij, en dus ook voor de derde, enz.
Kortom, dit klopt voor álle rijen in de boom.
Claim 5
Niet echt nodig voor vandaag. We hebben immers al bewezen dat alle rationale getallen 1 keer voorkomen. Dat het samenvalt met bn bewijs ik niet, maar het is wel heel aardig. Het is te vinden in het oorspronkelijke artikel, en niet lastig. Hieronder staat nog een link.
Toegift
Ook is expliciet te bepalen waar je een bepaald getal in de reeks vindt, is er expliciete successor functie te bepalen, en is er met behulp van de binaire expansie en de regels om te boom te bouwen heel gemakkelijk te vinden wat de n-breuk is (omgekeerd is aan de breuk te zien of het een linker of rechter kind is en is zo de positie te construeren). Oók is nog een mooie link te leggen met Euklides’ algoritme.
Dit verbindt dus zowel verzamelingentheorie, als getaltheorie, als combinatoriek. Lees er meer over op:
Calkin–Wilf tree (Wikipedia)
Calkin, Neil; Wilf, Herbert (2000),Recounting the rationals, American Mathematical Monthly 107 (4): 360–363
Of koop er een T-shirt van:
The Nerdiest Shirts.com.
De volgende aflevering is dat we bewijzen dat voor niet zo’n opsomming te geven is. In zekere zin is deze verzameling dus wel écht groter dan de natuurlijke getallen en is er niet meer sprake van ‘evenveel’.
Post-toegift
De reeks kan ook als H-boom-fractal weergegeven worden:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
Of als spiraal die de opsomming nog duidelijker maakt:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
[1] Dat r/s vereenvoudigbaar is wil zeggen dat er een getal d > 1 is dat zowel een deler van r als van s is. Aangezien (s - r)/d = s/d - r/d, is d dus ook een deler van s - r.
[ Bericht 0% gewijzigd door Iblis op 14-10-2009 17:41:47 ]
In het vorige deel van dit drieluik had ik laten zien hoe je de rationele getallen, d.w.z. de breuken, in een 1:1 koppeling met de natuurlijke getallen kunt zetten. Je kunt de breuken in een vierkant zetten, en dan loop je de diagonalen af. Dit is redelijk slim, maar het nadeel is dat je dubbelen tegenkomt.
Er is ook een manier – verrassend eenvoudig zelfs – om ze op te sommen zonder dat je dubbelen tegenkomt. Deze manier is in 2000 ontdekt door Neil Calkin en Herbert Wilf. Het is van een verbazingwekkende eenvoud en schoonheid.
Hun opsomming begint als volgt:
De logica is misschien nog niet direct duidelijk, maar wat wel opvalt is dat de teller van elke breuk gelijk is aan den oemer van de voorafgaande breuk. Dit is inderdaad iets dat voor de gehele reeks geldt, dus in feite kunnen we zeggen het n-e getal (we beginnen overigens bij 0 te tellen) in de reeks is gelijk aan bn/bn+1, waarbij bn gegeven wordt door:
Dit lijkt misschien een beetje een rare rij getallen, maar op zich tellen ze iets. Wat precies is verder niet zo heel relevant voor wat ik wil aantonen, maar het is wel aardig om te melden: het is namelijk het aantal manieren waarop je een getal als som van machten van twee kunt schrijven, waarbij een macht hooguit twee keer gebruikt wordt.
Dat is misschien wat duidelijker met een voorbeeld. Neem 5, dat is te schrijven als 4 + 1 = 5 (1 = 20), maar ook als 2 + 2 + 1. 1 + 1 + 1 + 1 + 1 gaat niet door, want dan gebruiken we 1 te vaak. 6 kunnen we schrijven als 4 + 1 + 1, of als 4 + 2, of als 2 + 2 + 1 + 1. 2 + 2 + 2 kan dus niet.
Deze reeks staat bekend als ‘Sterns diatomische reeks’, naar de Dutisers Stern – een reeks die overigens al in 1858 voor het eerst werd beschreven! Ook de al eerder in deze topic langsgekomen Dijkstra heeft er in EWD570 en EWD578 over geschreven.
Maar goed, we hebben die reeks dus, en we merken nog een aantal interessante eigenschappen op: Opeenvolgende getallen in bn zijn altijd relatief priem. En aangezien je breuken bouwt van opeenvolgende getallen, zijn die breuken altijd vereenvoudigd. En de lijst van breuken bevat alle positieve breuken precies 1 keer (in gereduceerde vorm dus).
Nou, oké, oké, tof, maar hoe kom ik nu op een makkelijke manier aan die reeks? Moet je echt het aantal manieren om een getal als som van machten van twee te schrijven gaan zitten uitvogelen? Nee, het kan veel gemakkelijker met behulp van een boom. Denk eraan: Het is een Wiskundige boom, dus die groeit naar beneden.
Dus 1/1 zit in de wortel van de boom, en verder heeft elke knoop r/s twee kinderen. De linker is r/(r + s) en de rechter is (r + s)/s. We bekommeren ons niet direct meer om de reeks, maar wel om de boom.
Er zijn nu vijf claims te maken:
Claim 1:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Voor 1/1 geldt dit uiteraard. Neem nu aan dat het niet zo is, en dat er ergens, misschien zelfs wel op meerdere plekken in de boom een breuk is die nog vereenvoudigd kan worden. Van alle mogelijkheden neem je die breuk r/s, als je de boom zoals hierboven tekent, het hoogst in de boom zit.
Het is dus niet de wortel, en daarom weten we zeker dat het dan het kind van een knoop moet zijn. Als het een linker kind is, dan heeft z’n ouder de waarde r/(s - r). Maar als r/s vereenvoudigbaar is, dan is r/(s - r) dat ook[1] – tegenspraak met het feit dat we een breuk uit het hoogste niveau hadden gepakt.
Als r/s een rechter kind is, dan is z’n ouder (r-s)/s, en dat leidt tot dezelfde tegenspraak.
Claim 2:
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Dat 1/1 erin zit is duidelijk. Neem echter aan dat één of meerdere andere breuken er niet in zitten. Neem van die breuken die er niet in zitten eentje met de kleinste noemer, en als er meerdere zijn met een kleinste noemer, van die groep de breuk met de kleinste teller, zeg dat dit r/s is.
Als r > s, dan weten we dat bijgevolg ook (r-s)/s niet in de boom zou kunnen zitten, want die heeft als rechter kind r/s. Maar r - s heeft dezelfde noemer als r/s maar een kleinere teller! En dat is in tegenspraak met onze aanname dat r/s de kleinste teller had!
Omgekeerd, als r < s, dan kan r/(s - r) niet in de boom zitten, want anders zou het een linker kind hebben van de vorm r/s. Maar s - r heeft een kleinere noemer dan r/s, en dat is ook weer een tegenspraak!
Claim 3:
Geen enkele breuk komt vaker dan één keer voor.
Dit geldt sowieso voor de wortel, want stel dat 1/1 nog een keer in de boom zat, dan is het kind van een knoop r/s, maar r/s heeft kinderen in de vorm r/(r + s) en (r + s)/s, en beide kunnen uiteraard geen 1/1 zijn aangezien r en s beide > 0 moeten zijn.
Nu doen we weer het zelfde als bij de vorige claim: van alle breuken die vaker dan één keer zouden voorkomen, kies die met de kleinste noemer, en als dat er meer zijn, daarbinnen die met de kleinste teller. Als r < s, dan is r/s een linker kind, en bovendien geldt dan voor de ouder dat deze r/(s - r) is. Maar dat betekent dat er ook meer dan één van zulk soort ouders is! En r/(s-r) is in strijd met onze aanname dat we een breuk met de kleinste noemer hadden gepakt. En voor r > s hebben we hetzelfde, maar dan als rechter kind.
Claim 4:
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
Deze is iets lastiger te bewijzen. Het is natuurlijk duidelijk als het om twee breuken gaat die kind zijn van dezelfde ouder. Omdat het linker kind de vorm r/(r+s) heeft en de rechter (r+s)/s.
Ook als we van een rij naar de volgende rij gaan is het niet zo moeilijk te zien, de meest rechter breuk op een rij heeft namelijk altijd noemer 1, en de meest linker breuk op een rij altijd teller 1. Dus dat gaat ook goed.
Nu blijft over twee buren in dezelfde rij, maar die niet het kind zijn van dezelfde ouder. Dit moet even met een inductiebewijs. We praten altijd over een rechter kind, gevolgd door een linker kind in zo’n geval. Het rechter kind heeft dezelfde noemer als z’n ouder. En dat linker kind heeft dezelfde teller als z’n ouder. Die twee ouders zijn óók buren van elkaar. Dus als het voor die ouders geldt, dan geldt het ook voor die kinderen.
We hebben vastgesteld dat het voor de kinderen van de wortel sowieso klopt (noem dat de eerste rij), omdat die kinderen van dezelfde ouder zijn. Dus dan klopt het ook voor de tweede rij, en dus ook voor de derde, enz.
Kortom, dit klopt voor álle rijen in de boom.
Claim 5
Niet echt nodig voor vandaag. We hebben immers al bewezen dat alle rationale getallen 1 keer voorkomen. Dat het samenvalt met bn bewijs ik niet, maar het is wel heel aardig. Het is te vinden in het oorspronkelijke artikel, en niet lastig. Hieronder staat nog een link.
Toegift
Ook is expliciet te bepalen waar je een bepaald getal in de reeks vindt, is er expliciete successor functie te bepalen, en is er met behulp van de binaire expansie en de regels om te boom te bouwen heel gemakkelijk te vinden wat de n-breuk is (omgekeerd is aan de breuk te zien of het een linker of rechter kind is en is zo de positie te construeren). Oók is nog een mooie link te leggen met Euklides’ algoritme.
Dit verbindt dus zowel verzamelingentheorie, als getaltheorie, als combinatoriek. Lees er meer over op:
Of koop er een T-shirt van:
The Nerdiest Shirts.com.
De volgende aflevering is dat we bewijzen dat voor niet zo’n opsomming te geven is. In zekere zin is deze verzameling dus wel écht groter dan de natuurlijke getallen en is er niet meer sprake van ‘evenveel’.
Post-toegift
De reeks kan ook als H-boom-fractal weergegeven worden:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
Of als spiraal die de opsomming nog duidelijker maakt:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
[1] Dat r/s vereenvoudigbaar is wil zeggen dat er een getal d > 1 is dat zowel een deler van r als van s is. Aangezien (s - r)/d = s/d - r/d, is d dus ook een deler van s - r.
[ Bericht 0% gewijzigd door Iblis op 14-10-2009 17:41:47 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Via die T-shirt-site kwam ik nu ook nog op: Math less travaled die in feite hetzelfde beschrijft. Ik had die site niet gezien echter. Hoe dan ook, wel het lezen waard!
Ook is er nog een boek aan te duiden (dat heb ik wel gebruikt), en dat is Proofs from The Book door Martin Aigner en Günter M. Ziegler. Het is hoofdstuk 16 van hun boek, op pagina 93 in deze Google Books editie. Maar Google laat mij er niet inkijken.
Ook is er nog een boek aan te duiden (dat heb ik wel gebruikt), en dat is Proofs from The Book door Martin Aigner en Günter M. Ziegler. Het is hoofdstuk 16 van hun boek, op pagina 93 in deze Google Books editie. Maar Google laat mij er niet inkijken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Toen ik de TT zag dacht ik ook direct aan dat bewijs. Zeer elegant door z'n eenvoud.quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn.
Never in the entire history of calming down did anyone ever calm down after being told to calm down.
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.quote:Op maandag 12 oktober 2009 20:17 schreef Iblis het volgende:
Een koppeling tussen ℕ en ℤ
Er zijn op die manier ook evenveel gehele getallen als natuurlijke getallen:
[ afbeelding ]
Het is ook duidelijk dat deze koppeling gewoon door te trekken is, bovenaan som je de natuurlijke getallen op, onderaan gaat het verder met -4, 4, -5, 5, -6, 6 enz.
Dus er zijn ook evenveel gehele getallen als natuurlijke getallen.
Verder wel mijn complimenten voor de bewijzen die je hier post.
Dat kun je stellen, maar dat betekent niet dat de een "meer" elementen heeft dan de ander.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren.
Dat staat toch nergens? Er is alleen laten zien dat er een 1-op-1 'map' is tussen de elementen uit beide sets, die ook alle elementen beslaat.quote:Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
...
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Ja, maar daarom probeer ik duidelijk te maken wat in de Wiskunde met 'evenveel' wordt bedoeld een 1:1-koppeling (formeler: er is een bijectie te vinden tussen de verzamelingen). Ik moet deel 3 nog doen trouwens, dan zul je zien dat er voor de reële getallen ℝ zo’n bijectie niet mogelijk is.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
Verder wel mijn complimenten voor de bewijzen die je hier post.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nee, het is niet contra-intuïtief.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contraïntuïtief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
Stel, ik heb twee verzamelingen, verzameling A en verzameling B. Hoe weet ik nou of beide verzamelingen even veel elementen hebben?
Wel, we kunnen een functie f : A -> B maken. Deze wijst elke waarde x in A een waarde y in B toe.
Stel, ons lukt het om een injectieve functie f te maken, dat betekent dat we aan elke waarde van x in A een unieke waarde y in B kunnen toewijzen. Dan weten we dat verzameling B minstens net zo groot is als verzameling A:
En als het omgekeerde ook lukt, als we dus ook een injectieve functie g : B -> A kunnen vinden, dan zijn beide verzamelingen even groot. In ons voorbeeld gaat dat fout:
Omdat een functie nooit voor sommige waardes ongedefinieerd mag zijn, moeten we dus naar sommige waardes in A twee pijltjes trekken, dus aan aan sommige waarden y uit B kunnen we in dit geval geen unieke waarde x uit A toewijzen. Dat geeft aan dat B groter is dan A.
Tot zo ver is het hopelijk allemaal duidelijk en intuïtief.
Neem nou het plaatje van Iblis er weer bij:
Hier zien we dat aan elke waarde uit N een unieke waarde in Z wordt toegewezen, én dat elke waarde in Z een unieke waarde in N wordt toegewezen.
Dat betekent dat Z minstens zo groot is als N, en dat N minstens zo groot is als Z. Beide zijn dus even groot.
[ Bericht 2% gewijzigd door #ANONIEM op 21-10-2009 23:24:40 ]
De ‘paradox’ is dus het (subtiele) onderscheid tussen ‘evenveel’ en ‘elementen bevatten die de andere verzameling niet bevat’.
Voor eindige verzamelingen gaat het prima op dat als verzameling A alles bevat wat B bevat, en nog een beetje meer, dat A groter is dan B. Maar voor oneindig gaat dat niet op. Immers, neem een verzameling met oneindig veel elementen, en haal er eentje uit. Hoeveel (dus niet wélke, maar het aantal) heb je er dan nog over? Dat zijn er nog steeds oneindig veel. Dus het heeft dan niet zoveel zin om te zeggen dat die laatste verzameling ‘kleiner’ is, als die óók nog oneindig is.
Dit is trouwens een andere manier om oneindig te karakteriseren: een oneindige verzameling is een verzameling waarvan een écht deelverzameling ‘even groot’ is als de verzameling zelf. M.a.w. ℕ is oneindig, want een echte deelverzameling (b.v. alle even getallen, waar 1, 3 en 5 b.v. niet in zitten) is ‘even groot’ (heeft dezelfde cardinaliteit) als ℕ zelf.
Dus ‘deelverzameling zijn van’ impliceert voor oneindige verzamelingen niet per se dat het aantal elementen ook minder is. Immers, dat aantal is in zekere zin onuitputtelijk. Zou het minder worden, dan zou je ℕ een keer ‘leeg kunnen maken’ door er maar telkens eindig veel elementen uit te halen.
Hier zit natuurlijk een lastigheid. Maar daarom wordt het straks nog raarder als ℝ eigenlijk ‘nog weer oneindiger’ blijkt te zijn dan ℕ of ℤ.
Voor eindige verzamelingen gaat het prima op dat als verzameling A alles bevat wat B bevat, en nog een beetje meer, dat A groter is dan B. Maar voor oneindig gaat dat niet op. Immers, neem een verzameling met oneindig veel elementen, en haal er eentje uit. Hoeveel (dus niet wélke, maar het aantal) heb je er dan nog over? Dat zijn er nog steeds oneindig veel. Dus het heeft dan niet zoveel zin om te zeggen dat die laatste verzameling ‘kleiner’ is, als die óók nog oneindig is.
Dit is trouwens een andere manier om oneindig te karakteriseren: een oneindige verzameling is een verzameling waarvan een écht deelverzameling ‘even groot’ is als de verzameling zelf. M.a.w. ℕ is oneindig, want een echte deelverzameling (b.v. alle even getallen, waar 1, 3 en 5 b.v. niet in zitten) is ‘even groot’ (heeft dezelfde cardinaliteit) als ℕ zelf.
Dus ‘deelverzameling zijn van’ impliceert voor oneindige verzamelingen niet per se dat het aantal elementen ook minder is. Immers, dat aantal is in zekere zin onuitputtelijk. Zou het minder worden, dan zou je ℕ een keer ‘leeg kunnen maken’ door er maar telkens eindig veel elementen uit te halen.
Hier zit natuurlijk een lastigheid. Maar daarom wordt het straks nog raarder als ℝ eigenlijk ‘nog weer oneindiger’ blijkt te zijn dan ℕ of ℤ.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 5% gewijzigd door #ANONIEM op 21-10-2009 23:42:54 ]
quote:Op woensdag 21 oktober 2009 23:42 schreef Igen het volgende:
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?Hilberts hotel moet dat zijn, logeer ik ook altijdSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Niet geschoten is altijd mis..
Ach Margrietje, de Rozen zullen bloeien..
Ik ben dan wel benieuwd naar dat bewijs dat er voor ℝ geen bijectie mogelijk is, je kunt het tenslotte toch bewijzen op een soortgelijke manier als met ℤ en ℕ?quote:Op woensdag 21 oktober 2009 23:19 schreef Iblis het volgende:
[..]
Ja, maar daarom probeer ik duidelijk te maken wat in de Wiskunde met 'evenveel' wordt bedoeld een 1:1-koppeling (formeler: er is een bijectie te vinden tussen de verzamelingen). Ik moet deel 3 nog doen trouwens, dan zul je zien dat er voor de reële getallen ℝ zo’n bijectie niet mogelijk is.
quote:Op woensdag 21 oktober 2009 23:42 schreef Igen het volgende:
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?I.p.v. al die mensen van kamer te verhuizen kan je de nieuwe gast toch in de n+1'de kamer stoppen?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 19% gewijzigd door Diabox op 22-10-2009 01:22:46 ]
Nee, je loopt stuk met irrationale getallen. ℝ is niet aftelbaar.quote:Op donderdag 22 oktober 2009 01:14 schreef Diabox het volgende:
[..]
Ik ben dan wel benieuwd naar dat bewijs dat er voor ℝ geen bijectie mogelijk is, je kunt het tenslotte toch bewijzen op een soortgelijke manier als met ℤ en ℕ?
[..]
Nee, want n+1 is een eindig getal en alle kamers (met een welbepaald nummer) waren immers bezet.quote:I.p.v. al die mensen van kamer te verhuizen kan je de nieuwe gast toch in de n+1'de kamer stoppen?
Hm ja, niet bij stilgestaan.quote:Op donderdag 22 oktober 2009 01:36 schreef Riparius het volgende:
[..]
Nee, je loopt stuk met irrationale getallen. ℝ is niet aftelbaar.
[..]
Nee, want n+1 is een eindig getal en alle kamers (met een welbepaald nummer) waren immers bezet.
Diagonaalbewijs van Cantor
Het diagonaalbewijs
Hebben misschien alle oneindige verzamelingen hetzelfde formaat? Dit blijkt niet zo te zijn. En daar komt het diagonaalbewijs om de hoek: Er zijn meer reële getallen tussen 0 en 1 dan er natuurlijke getallen zijn. Dit bewijs gebruikt reductio ad absurdum. We nemen daarom aan dat er een bijectie, dit wil zeggen een 1-op-1 afbeelding van de natuurlijke getallen naar de reële getallen bestaat.
Zo'n afbeelding ziet er bijvoorbeeld zo uit:
enzovoort.
De lijst is in twee richtingen oneindig lang. Nu nemen we van het eerste getal het eerste cijfer achter de komma. Van het tweede getal nemen we het tweede cijfer achter de komma, enzovoort. Deze cijfers zetten we achter elkaar, zodat we een nieuwe getal krijgen, in het voorbeeld: 0,220098.... Elk cijfer in dit getal veranderen we in een willekeurig ander cijfer, bijvoorbeeld door er 1 bij op te tellen (9 wordt dan 0). Het nieuwe getal 0,331109.... dat we nu hebben gemaakt, kan nooit in de lijst staan; immers als je uit de lijst het getal n haalt dan komt het n-de cijfer van dat getal niet meer overeen met het n-de cijfer uit m. Omdat er altijd een nieuwe m gemaakt kan worden, zit er tussen 0 en 1 een overaftelbaar aantal reële getallen.
Er is een functie te beschrijven voor diagonalisatie die in zeer veel gevallen werkt:
d(i) = min{B\ {d(0),...,d(i-1),fi(i)}}, waar B het bereik is en fi(i) de waarde op de diagonaal.
Ik kwam toevallig het bewijs tegen dat het dus niet kan met ℝ.
Het diagonaalbewijs
Hebben misschien alle oneindige verzamelingen hetzelfde formaat? Dit blijkt niet zo te zijn. En daar komt het diagonaalbewijs om de hoek: Er zijn meer reële getallen tussen 0 en 1 dan er natuurlijke getallen zijn. Dit bewijs gebruikt reductio ad absurdum. We nemen daarom aan dat er een bijectie, dit wil zeggen een 1-op-1 afbeelding van de natuurlijke getallen naar de reële getallen bestaat.
Zo'n afbeelding ziet er bijvoorbeeld zo uit:
| 1 2 3 4 5 6 | 2 - 0,12345678901234... 3 - 0,00000000000120... 4 - 0,50000000000000... 5 - 0,14159265358979... 6 - 0,23562877077729... |
enzovoort.
De lijst is in twee richtingen oneindig lang. Nu nemen we van het eerste getal het eerste cijfer achter de komma. Van het tweede getal nemen we het tweede cijfer achter de komma, enzovoort. Deze cijfers zetten we achter elkaar, zodat we een nieuwe getal krijgen, in het voorbeeld: 0,220098.... Elk cijfer in dit getal veranderen we in een willekeurig ander cijfer, bijvoorbeeld door er 1 bij op te tellen (9 wordt dan 0). Het nieuwe getal 0,331109.... dat we nu hebben gemaakt, kan nooit in de lijst staan; immers als je uit de lijst het getal n haalt dan komt het n-de cijfer van dat getal niet meer overeen met het n-de cijfer uit m. Omdat er altijd een nieuwe m gemaakt kan worden, zit er tussen 0 en 1 een overaftelbaar aantal reële getallen.
Er is een functie te beschrijven voor diagonalisatie die in zeer veel gevallen werkt:
d(i) = min{B\ {d(0),...,d(i-1),fi(i)}}, waar B het bereik is en fi(i) de waarde op de diagonaal.
Ik kwam toevallig het bewijs tegen dat het dus niet kan met ℝ.
Ik plaats hier een tvp omdat dit een prachtig topic is 
I just had to get that stress off my chest like breast reduction.
Beide nog niet nee..quote:Op donderdag 22 oktober 2009 19:56 schreef Bankfurt het volgende:
Is dat bewijs van algoritme van Euclides al hier genoemd ?
en die stelling van GGD * KGV = ?
Niemand houdt je tegen.
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Beetje humor op de 'vroege' ochtend.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Maar zoals ik zei, dit soort analyse is nogal roestig bij me op dit moment dus als iemand anders het wel weet ben ik erg benieuwd
[ Bericht 4% gewijzigd door Haushofer op 23-10-2009 10:00:08 (Ff een spoiler toegevoegd) ]Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
quote:Op vrijdag 23 oktober 2009 09:54 schreef Haushofer het volgende:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Maar zoals ik zei, dit soort analyse is nogal roestig bij me op dit moment dus als iemand anders het wel weet ben ik erg benieuwdSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
Ik weet het:quote:
a,b, natuurlijke getallen;
dan is GGD(a,b) * KGV (a,b) = a * b
Een vervolg is het bewijs van de priemontbinding van natuurlijke getallen.
Lijkt me toch niet zo moeilijk, want:quote:
[..]
Ik weet het:
a,b, natuurlijke getallen;
dan is GGD(a,b) * KGV (a,b) = a * b
...
- Voor iedere deler D van zowel a als b geldt dat (a*b)/D een veelvoud is van a en van b, want (a*b)/D = a*(b/D) = b*(a/D)
- Als bovendien D de grootst mogelijke deler van zowel a als b is dan noemen we die per definitie GGD(a*b). Maar als D zo groot mogelijk is, dan is de corresponderende (a*b)/D zo klein mogelijk. De noemer kan dan immers niet groter worden onder voorwaarde dat D een deler van zowel a als b is.
- Conclusie als D de grootst mogelijke deler van zowel a als b is, dan is het veelvoud (a*b)/D van zowel a als b het kleinst mogelijke getal dat een veelvoud is van zowel a als b. Oftewel: (a*b)/GGD(a,b) = KGV(a,b)
en daar volgt uit:
(a*b) = GGD(a,b) * KGV(a,b)
Wellicht niet helemaal formeel, maar dit moet het wel zijn.
[ Bericht 1% gewijzigd door #ANONIEM op 23-10-2009 21:34:02 ]
Ja, toegegeven, mooi bewijs.quote:Op vrijdag 23 oktober 2009 21:01 schreef ..-._---_-.- het volgende:
[..]
Lijkt me toch niet zo moeilijk, want:
- Voor iedere deler D van zowel a als b geldt dat (a*b)/D een veelvoud is van a en van b, want (a*b)/D = a*(b/D) = b*(a/D)
- Als bovendien D de grootst mogelijke deler van zowel a als b is dan noemen we die per definitie GGD(a*b). Maar als D zo groot mogelijk is, dan is de corresponderende (a*b)/D zo klein mogelijk. De noemer kan dan immers niet groter worden onder voorwaarde dat D een deler van zowel a als b is.
- Conclusie als D de grootst mogelijke deler van zowel a als b is, dan is het veelvoud (a*b)/D van zowel a als b het kleinst mogelijke getal dat een veelvoud is van zowel a als b. Oftewel: (a*b)/GGD(a,b) = KGV(a,b)
en daar volgt uit:
(a*b) = GGD(a,b) * KGV(a,b)
Wellicht niet helemaal formeel, maar dit moet het wel zijn.
b>aquote:
[ afbeelding ]
Beetje humor op de 'vroege' ochtend.
Niet grappig.
Hetgeen bewezen en beklonken moest worden.
tvp
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Wiskunde. Leuk! Ben er niet goed in, maar wel gek op.quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn. De bedenker, Euklides, leefde zo ongeveer 2300 jaar geleden.
(...)
Maar we hadden aangenomen dat ons rijtje alle priemgetallen bevat. Die aanname moet wel fout zijn, want we komen nu op een tegenspraak uit. Kortom, er moeten wel oneindig veel priemgetallen zijn. □
Dat was het al.
Helaas werkt Latex niet op Fok dus dan maar even slordig:
Nog een bewijs dat er een oneindig aantal priemgetallen bestaat. Dit keer van Euler.
De oneindige som 1/1 + 1/2 + 1/3 +... 1/n is gelijk aan het oneindige product (1/(1-1/p) (p = priemgetal). Het bewijs hiervoor is een goed te volgen.
Aangezien de oneindige som 1/1 + 1/2 + 1/3 +... 1/n divergeert, moeten er dus ook oneindig veel priemgetallen bestaan.
Nog even over die zin in bold. Moet dat niet zijn "of kun je elk even getal groter dan 3 als de som van precies twee priemgetallen schrijven"? De Goldbach conjecture dus?
Kwam er overigens pas deze maand achter (na het maken van een programma in VBA Excel) dat als de Goldbach conjecture klopt, daarmee ook meteen de volgende stelling waar is:
"Elk getal groter dan 3 kun je op minstens één manier schrijven als het gemiddelde van twee priemgetallen."
Dus ook alle priemgetallen zelf zijn dan uit te drukken in priemgetallen. Bovendien geldt ook dat voor een priemgetal p > 7 uitgedrukt als (Px+Py)/2, de afstand tusen Px en Py altijd 12k is (of n +/- 6k). Verder ben ik helaas nog niet gekomen...
[ Bericht 0% gewijzigd door Agno op 31-10-2009 00:43:13 ]
Je bedoelt met P de verzameling der primegetallen.quote:
De oneindige som 1/1 + 1/2 + 1/3 +... 1/n is gelijk aan het oneindige product (1/(1-1/p) (p = priemgetal). Het bewijs hiervoor is een goed te volgen.
Uiteraard, dat is mijn fout. Afgezien van twee zijn er natuurlijk geen even priemgetallen en verder geldt dat een oneven + oneven getal een even getal is.quote:Nog even over die zin in bold. Moet dat niet zijn "of kun je elk even getal groter dan 3 als de som van precies twee priemgetallen schrijven"? De Goldbach conjecture dus?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik probeer me even die middelste term voor te stellen.
Je neemt voor elk priemgetal p dus de som van de reciproce van de opeenvolgende gehele machten (dus bijv. voor p=5 1/5^0 + 1/5^1 + 1/5^2 + 1/5^3 + 1/5^4 + ......... 1/5^k) en al die sommen ga je met elkaar vermenigvuldigen.
Interpreteer ik het zo goed?
Je neemt voor elk priemgetal p dus de som van de reciproce van de opeenvolgende gehele machten (dus bijv. voor p=5 1/5^0 + 1/5^1 + 1/5^2 + 1/5^3 + 1/5^4 + ......... 1/5^k) en al die sommen ga je met elkaar vermenigvuldigen.
Interpreteer ik het zo goed?
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Ja. En de grap is dus dat je elk getal n (uniek) kunt ontbinden en priemfactoren, dus die middelste term bevat een product van oneindige sommen met termen als 1 + 1/2 + 1/22 + 1/23 + ···, en als andere factor 1 + 1/3 + 1/32 + 1/33 ···, en als je dit vermenigvuldigt dan krijg je dus 1/(1·1·1·1···) = 1/1, en 1/(2·1·1·1···) = 1/2 en 1/(1·3·1·1···) = 1/3 maar ook 1/(2·3·1·1···) = 1/6, enz. Kortom, uiteindelijk 1/n voor alle n.quote:
Ik probeer me even die middelste term voor te stellen.
Je neemt voor elk priemgetal p dus de som van de reciproce van de opeenvolgende gehele machten (dus bijv. voor p=5 1/5^0 + 1/5^1 + 1/5^2 + 1/5^3 + 1/5^4 + ......... 1/5^k) en al die sommen ga je met elkaar vermenigvuldigen.
Interpreteer ik het zo goed?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Die laatste zin gaat me te snel.quote:Op zaterdag 31 oktober 2009 00:36 schreef Iblis het volgende:
[..]
Ja. En de grap is dus dat je elk getal n (uniek) kunt ontbinden en priemfactoren, dus die middelste term bevat een product van oneindige sommen met termen als 1 + 1/2 + 1/22 + 1/23 + ···, en als andere factor 1 + 1/3 + 1/32 + 1/33 ···, en als je dit vermenigvuldigt dan krijg je dus 1/(1·1·1·1···) = 1/1, en 1/(2·1·1·1···) = 1/2 en 1/(1·3·1·1···) = 1/3 maar ook 1/(2·3·1·1···) = 1/6, enz. Kortom, uiteindelijk 1/n voor alle n.
Ik zie ten eerste niet meteen de noodzaak dat in die producten alle n's een keer en niet meer dan een keer aan bod komen en ten tweede komen er aan het eind naar mijn eerste gevoel wat soorten oneindigheid in de knoop.
Het uitpuzzelen daarvan kietelt mijn wiskundige intellect, maar ik vrees dat mijn luiheid gaat winnen.
Maar dank voor je antwoord.
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Had er eerst ook moeite mee om dit te doorzien, maar om de invallende luiheid toch nog een laatste prikkel te geven ff het volgende.quote:Op zaterdag 31 oktober 2009 00:52 schreef Kees22 het volgende:
[..]
Die laatste zin gaat me te snel.
Ik zie ten eerste niet meteen de noodzaak dat in die producten alle n's een keer en niet meer dan een keer aan bod komen en ten tweede komen er aan het eind naar mijn eerste gevoel wat soorten oneindigheid in de knoop.
Het uitpuzzelen daarvan kietelt mijn wiskundige intellect, maar ik vrees dat mijn luiheid gaat winnen.
Maar dank voor je antwoord.
De truc is makkelijker te doorzien door te kijken hoe de priemproductformule afgeleid wordt uit de Zeta-functie. Zie bijgaande link. Dan gewoon s=1 invullen en je bent er.
http://en.wikipedia.org/w(...)iemann_zeta_function
Gnigni, je had succes!quote:Op zaterdag 31 oktober 2009 01:01 schreef Agno het volgende:
[..]
Had er eerst ook moeite mee om dit te doorzien, maar om de invallende luiheid toch nog een laatste prikkel te geven ff het volgende.
De truc is makkelijker te doorzien door te kijken hoe de priemproductformule afgeleid wordt uit de Zeta-functie. Zie bijgaande link. Dan gewoon s=1 invullen en je bent er.
http://en.wikipedia.org/w(...)iemann_zeta_function
Dat van dat een en niet meer dan een keer voorkomen van n, dat geloof ik nu wel.
Nu nog even nadenken over de staart, die diverse soorten of maten oneindigheid. Met een beetje geluk is dat probleem het voortgezette deel van het eerste.
Die zeta-functie heb ik al eens eerder gezien in een topic op FOK!
Hier hou ik verder maar eens op: morgen lekker wat spitten in mijn voortuin.
Onderschat nooit de kracht van domme mensen in grote groepen!
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Der Irrsinn ist bei Einzelnen etwas Seltenes - aber bei Gruppen, Parteien, Völkern, Zeiten die Regel. (Friedrich Nietzsche)
Het bewijs dat de lengte van A4'tje of A3'tje wortel2 keer de breedte is.
Twee keer de breedte van A4 = de lengte van A3.
En de verhouding lengte breedte blijft het zelfde.
Dus:
l/b = 2b/l
2 b2 = l2
l/b = wortel 2.
Vandaar de vergroting 141% op het copieerapparaat.
En als je een vliegtuigje vouwt van een A4-tje blijkt de hypothenusa precies overeen te komen met de lengte van het A4-tje.
Twee keer de breedte van A4 = de lengte van A3.
En de verhouding lengte breedte blijft het zelfde.
Dus:
l/b = 2b/l
2 b2 = l2
l/b = wortel 2.
Vandaar de vergroting 141% op het copieerapparaat.
En als je een vliegtuigje vouwt van een A4-tje blijkt de hypothenusa precies overeen te komen met de lengte van het A4-tje.
Je kunt beter één kaars opsteken dan duizend maal de duisternis vervloeken.
Toch nog even door op het hierboven omgeschreven vermoeden van Goldbach:
"Elk getal groter dan 3 kun je op minstens één manier schrijven als het gemiddelde van twee priemgetallen."
Als het vermoeden van Goldbach waar blijkt te zijn dan geldt dus ook dat alle priemgetallen (behalve 2 en 3) zijn uit te drukken in een equi-distant setje andere priemgetallen. Er geldt immers dat elk priemgetal P afgeleid kan worden door (Px+Py)/2 (Px < P < Py).
Voor priemgetallen > 7 geldt bovendien dat de equidistante afstand P-Px en Py-P deelbaar is door 6 en dat de totale afstand Py-Px dus deelbaar is door 12. (We weten ook dat 2 en 3 nooit de Px kunnen zijn; 2 is immers het enige even priemgetal en 3 + 6k kan nooit een priemgetal opleveren want het is altijd deelbaar door 3. Let wel: er geldt natuurlijk ook dat bijv. (3 + 19) = 11, maar ik ben nu alleen ff geïnteresseerd in P-Px = 6k).
Waarom is die afstand altijd deelbaar door 6? We weten dat alle priemgetallende de vorm 6n+1 of 6n-1 hebben (behalve 2 en 3), omdat alle andere mogelijkheden deelbaar zijn door 2 of 3. Px en Py kunnen priemgetallen van beide vormen zijn: 6n-1 en 6n+1. Om het gemiddelde te berekenen zijn er in principe 4 combinaties te maken, maar slechts twee blijken er te werken. Er geldt namelijk altijd dat als P=6n+1 dan ook alle Px, Py = 6n+1. En vice versa voor 6n-1.
Voorbeeld:
P = 29, (Px,Py) = (17,59), (11,41), (5,53) => type 6n-1, afstand 6k, k = 2,3,4
P = 73, (Px,Py) = (67,79), (43,103), (37,109), (19,127), (7,139) => type 6n+1, afstand 6k, k = 1,5,6,9,11
Priemgetallen zijn echter niet te voorspellen, en de priemgetalstelling zegt dat als je een willekeurig getal kiest in de buurt van een groot getal N, dat dan de kans dat dit getal een priemgetal is, ongeveer gelijk is aan 1 / ln(N). Dat is dus nooit 100%.
Als de bovenstaande stelling over equi-distante priemgetallen waar is, dan zou je als volgt kunnen redeneren:
Vanaf P springen we telkens in stapjes van 6 naar beneden totdat P - 6k = 5 (voor P=6n-1) of P - 6k = 7 (voor P=6n+1). Bij elk stapje test je of het getal een priemgetal is. Indien dit niet het geval is dan wordt de kans dat het volgende stapje een paartje priemgetallen (P-6k,P+6k) is groter met 1/((P-5)/6) of 1/(P-7)/6)). Das raar. Want elke keer dat je geen setje priemgetallen vindt, dan wordt de kans groter dat P+/- 6k wel een priemgetal is. Sterker nog: stel dat je vindt dat het voorlaatste stapje nog steeds geen setje priemgetallen oplevert, dan wordt de kans dus 100% dat P+/-6k beiden priem zijn. Een 100% zekere voorspelling van een priemgetal P+6k is strijdig met de priemgetalstelling. Om deze paradox te doorbreken moeten de lagere priemgetallen elkaar dus helpen om deze zekere voorspelling te versluieren (het lijkt bijna op de EPR paradox, waarbij je door links van de bron te meten, rechts meer zekere uitspraken aan de rechter kant te kunnen doen).
Daarom mijn stelling:
De hoogste en de laagste priemcombinatie (Px, Py) met P = (Px+Py)/2 (ergo: de combinaties (P-6, P+6) en (P-6k, P+6k) met de grootst mogelijke k), kan nooit de enige priemcombinatie (Px, Py) zijn, want anders zou je voor een bepaald getal exact kunnen voorspellen waar een toekomstig priemgetal P + 6k ligt (uitgezonderd P= 11 want je hebt dan immers slechts twee mogelijke waarden voor Px: 5 en 7. In dat geval is er nog geen ‘buitenste’).
EDIT:
Er zit natuurlijk een denkfout in de aanname dat je alle stapjes van 6 altijd sequentieel doorloopt. Je zou er ook volkomen random doorheen kunnen lopen en er dan uiteindelijk twee overhouden. Als dan de voorlaatste geen priempaartje oplevert, dan moet de laatste mogelijkheid een priem op P+6k opleveren.
[ Bericht 3% gewijzigd door Agno op 31-10-2009 20:22:56 ]
"Elk getal groter dan 3 kun je op minstens één manier schrijven als het gemiddelde van twee priemgetallen."
Als het vermoeden van Goldbach waar blijkt te zijn dan geldt dus ook dat alle priemgetallen (behalve 2 en 3) zijn uit te drukken in een equi-distant setje andere priemgetallen. Er geldt immers dat elk priemgetal P afgeleid kan worden door (Px+Py)/2 (Px < P < Py).
Voor priemgetallen > 7 geldt bovendien dat de equidistante afstand P-Px en Py-P deelbaar is door 6 en dat de totale afstand Py-Px dus deelbaar is door 12. (We weten ook dat 2 en 3 nooit de Px kunnen zijn; 2 is immers het enige even priemgetal en 3 + 6k kan nooit een priemgetal opleveren want het is altijd deelbaar door 3. Let wel: er geldt natuurlijk ook dat bijv. (3 + 19) = 11, maar ik ben nu alleen ff geïnteresseerd in P-Px = 6k).
Waarom is die afstand altijd deelbaar door 6? We weten dat alle priemgetallende de vorm 6n+1 of 6n-1 hebben (behalve 2 en 3), omdat alle andere mogelijkheden deelbaar zijn door 2 of 3. Px en Py kunnen priemgetallen van beide vormen zijn: 6n-1 en 6n+1. Om het gemiddelde te berekenen zijn er in principe 4 combinaties te maken, maar slechts twee blijken er te werken. Er geldt namelijk altijd dat als P=6n+1 dan ook alle Px, Py = 6n+1. En vice versa voor 6n-1.
Voorbeeld:
P = 29, (Px,Py) = (17,59), (11,41), (5,53) => type 6n-1, afstand 6k, k = 2,3,4
P = 73, (Px,Py) = (67,79), (43,103), (37,109), (19,127), (7,139) => type 6n+1, afstand 6k, k = 1,5,6,9,11
Priemgetallen zijn echter niet te voorspellen, en de priemgetalstelling zegt dat als je een willekeurig getal kiest in de buurt van een groot getal N, dat dan de kans dat dit getal een priemgetal is, ongeveer gelijk is aan 1 / ln(N). Dat is dus nooit 100%.
Als de bovenstaande stelling over equi-distante priemgetallen waar is, dan zou je als volgt kunnen redeneren:
Vanaf P springen we telkens in stapjes van 6 naar beneden totdat P - 6k = 5 (voor P=6n-1) of P - 6k = 7 (voor P=6n+1). Bij elk stapje test je of het getal een priemgetal is. Indien dit niet het geval is dan wordt de kans dat het volgende stapje een paartje priemgetallen (P-6k,P+6k) is groter met 1/((P-5)/6) of 1/(P-7)/6)). Das raar. Want elke keer dat je geen setje priemgetallen vindt, dan wordt de kans groter dat P+/- 6k wel een priemgetal is. Sterker nog: stel dat je vindt dat het voorlaatste stapje nog steeds geen setje priemgetallen oplevert, dan wordt de kans dus 100% dat P+/-6k beiden priem zijn. Een 100% zekere voorspelling van een priemgetal P+6k is strijdig met de priemgetalstelling. Om deze paradox te doorbreken moeten de lagere priemgetallen elkaar dus helpen om deze zekere voorspelling te versluieren (het lijkt bijna op de EPR paradox, waarbij je door links van de bron te meten, rechts meer zekere uitspraken aan de rechter kant te kunnen doen).
Daarom mijn stelling:
De hoogste en de laagste priemcombinatie (Px, Py) met P = (Px+Py)/2 (ergo: de combinaties (P-6, P+6) en (P-6k, P+6k) met de grootst mogelijke k), kan nooit de enige priemcombinatie (Px, Py) zijn, want anders zou je voor een bepaald getal exact kunnen voorspellen waar een toekomstig priemgetal P + 6k ligt (uitgezonderd P= 11 want je hebt dan immers slechts twee mogelijke waarden voor Px: 5 en 7. In dat geval is er nog geen ‘buitenste’).
EDIT:
Er zit natuurlijk een denkfout in de aanname dat je alle stapjes van 6 altijd sequentieel doorloopt. Je zou er ook volkomen random doorheen kunnen lopen en er dan uiteindelijk twee overhouden. Als dan de voorlaatste geen priempaartje oplevert, dan moet de laatste mogelijkheid een priem op P+6k opleveren.
[ Bericht 3% gewijzigd door Agno op 31-10-2009 20:22:56 ]
even tvp'en, ik weet zelf even niets bij te dragen maar kan wel genieten van dit soort topics.
C'est magnifique, mais ce n'est pas la guerre.
-
-
De naald van Buffon
De naald van Buffon is een bekend probleem dat kansrekening en geometrie combineert. Het probleem stamt uit de achttiende eeuw en luidt in zijn oorspronkelijke formulering ongeveer zo:
Hiervoor zijn twee afleidingen te geven, een geometrische, en eentje die wat gebruik maakt van elementaire kansrekening en calculus. Die laatste zullen we aan het eind geven, maar eerst zullen we de geometrische behandelen. Deze geeft ook een experimentele methode om π te berekenen.
Een voorbeeld van een aantal willekeurig geworpen naalden van lengte l op een vloer met planken van breedte b.
Geometrische methode
Het idee voor deze oplossing is voor het eerst door E. Barbier in 1860 aangedragen. We zijn op zoek naar de kans dat een naald op twee planken ligt, maar de truc is dat dit samenvalt met de verwachting van het aantal naden waarop de naald ligt. Dit lijkt een subtiel onderscheid, maar is het zeker niet. Als we toch even kijken naar de verwachting van het aantal naden dat een naald van willekeurige lengte kruist, dan is dit:
waarbij p1 de kans is dat de naald één naad kruist, p2 dat ze er twee kruist, enzovoort. De kans dat deze op (minstens) twee planken ligt wordt gegeven door:
Maar, wij bekijken een korte naald met lengte l ≤ b, dus p2 = p3 = ··· = 0. En daarom geldt in het geval van een korte naald E(N1) = p. Dus als we de verwachting kunnen berekenen, dan hebben we ook de kans.1
Aan elkaar bevestigde naalden.
We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.
Nu doen we echter wat anders. we maken de punten van de naalden aan elkaar, m.a.w. twee punten van de naald vallen samen, maar op zich kunnen ze verder los bewegen, dus de naald kan in een rechte lijn vallen, of meer in een V-vorm. Als dat gebeurt zijn N1 en N2 natuurlijk niet onderling onafhankelijk, maar voor de verwachtingswaarde maakt dat niet uit, immers, er geldt:
ook als N1 en N2 niet onderling onafhankelijk zijn. Dezelfde logica gaat ook op als we aan een van de uiteinden nog een naald vastmaken, en nog één, enzovoort. Merk op dat de naalden niet eens allemaal dezelfde lengte hoeven te hebben (zo’n constructie wordt ook wel Buffon’s noodle genoemd).
Verder merken we op dat korte naalden natuurlijk naar verwachting minder naden zullen kruisen dan lange naalden. We kunnen daarom veilig stellen dat het aantal naden dat een naald kruist afhangt van de lengte. Met andere woorden E(N) = f(l), waarbij f een functie is die we nog zullen bepalen. We kunnen echter sowieso al het nodige zeggen over f. Stel je voor dat we twee naalden N1 en N2 (met lengtes l1 en l2 nemen en zo aan elkaar maken dat ze altijd in elkaars verlengde vallen. Dan geldt natuurlijk:
Maar omdat de verwachtingswaarde lineair is, geldt ook nog:
M.a.w., f(l1 + l2) = f(l1) + f(l2). Dat is alvast één eigenschap die we binnen hebben. Verder kunnen we b.v. N1 ook weer zien als m kleine naaldjes van allemaal gelijke lengte die aan elkaar gemaakt zijn, en dan krijgen we b.v.:
En zo vinden we dat f lineair is voor l ∈ ℚ. Als laatste merken we nu op dat f(l) monotoon stijgend moet zijn, en daarom ook dat f(l) = c·l voor l ∈ ℝ. Het aantal naden waar een naald N van lengte l naar verwachting op ligt wordt dus gegeven door:
Waarbij we c moeten bepalen. Merk op dat we het hier dus over een naald hebben met mogelijk veel hoeken erin, en niet per se een rechte naald.
Cirkels met straal b hebben altijd twee punten waar ze op een naad liggen.
Voordat ik duidelijk maak waarom dit precies handig is, laten we eerst eens naar een cirkel2 lijken met diameter b. Hoe je een cirkel ook gooit op de vloer, de cirkel ligt altijd precies op twee naden. Verder weten we dat de omtrek van de cirkel bπ is. Een cirkel kunnen we echter benaderen met een ingeschreven veelhoek, of met een omgeschreven veelhoek.
Een omgeschreven veelhoek (links) en ingeschreven veelhoek (rechts)
Noem de omgeschreven veelhoek met n zijden On en noem de ingeschreven In, dan kunnen we elk van die veelhoeken zien als een aan elkaar gemaakte naald bestaande uit n stukken, waarvan we weten dat E(On) = c·l(On) en E(In) = c·l(In).
Er moet dus gelden:
En, omdat:
voor n → ∞:
Kortom:
en dus geldt voor een korte naald van lengte l dat deze naar verwachting:
naden raakt, en dit is dus ook juist de kans dat deze één naad raakt.
Cirkels met omgeschreven en ingeschreven veelhoeken willekeurig geworpen, merk op dat er op een bovenste grijze baan b.v. een cirkel ligt waarvan de omgeschreven veel hoek drie snijpunten heeft met de naden. Voor n → ∞ verdwijnt dit verschil.
Nawoord
Dit geeft in feite een experimentele mogelijkheid om π te bepalen, teken een aantal lijnen op een stuk papier dat de naden tussen de planken voorstelt, gooi er een naald op die even groot is als de ruimte tussen de lijnen, en tel het aantal keren dat de naald een lijn kruist, omdat l = b, geldt dat π = (2n)/a, waarbij n het aantal keer is dat je gooit en a het aantal dat raak is. Dit is tevens vrij gemakkelijk te programmeren – echter, bedenk wel dat je heel snel al gebruik maakt van het getal π in je programma, wat eigenlijk de hele exercitie wat nutteloos maakt. Je moet vrij omzichtig programmeren om dat niet te doen.
Verder is deze methode verbonden aan een berucht experiment waarbij ene Lazzarini, een Italiaans wiskundige, 3408 keer een naald gooide, die 1808 keer een lijn raakte. Als benadering vond hij toen een getal dat tot op zes plaatsen nauwkeurig is – het heeft er echter alle schijn van dat hij zijn experiment zo inrichtte om een zo goed mogelijk resultaat te krijgen door op precies het juiste moment te stoppen.
Methode met integraal
Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt:
Met een integraal kunnen we nu de totale kans krijgen door te middelen over alle hoeken α die de naald kan aannemen ([0...π]):
1) Er is een kleine kanttekening te maken m.b.t. de mogelijkheid dat een naald met lengte gelijk aan de breedte van de planken precies zo valt dat ze alleen met de twee uiterste punten op een naad ligt, of het geval waarin de naald precies, over de gehele lengte, op een naad ligt. Aangezien dit wiskundige naalden en planken zijn, hebben beide gebeurtenissen kans 0 en kunnen ze verder genegeerd worden. Dit kan wiskundig gezien hard gemaakt worden.
2) Op zich hoef je geen cirkel te gebruiken, elke figuur met een vaste breedte zou ook werken, zoals een Reuleaux-driehoek. Hieruit volgt indirect ook dat voor deze figuren geldt dat o = π·d.
Bronnen en meer lezen:
Introduction to geometric probability, Daniel A. Klain, Gian-Carlo Rota.
Buffon’s needle (Wikipedia)
Buffon’s noodle (Wikipedia)
Buffon’s needle op cut-the-knot
Buffon's Noodle Problem, J. F. Ramaley.
De naald van Buffon is een bekend probleem dat kansrekening en geometrie combineert. Het probleem stamt uit de achttiende eeuw en luidt in zijn oorspronkelijke formulering ongeveer zo:
Het is duidelijk dat één en ander in ieder geval afhangt van de lengte van de naald, hoe langer de naald hoe groter de kans. We zullen de breedte van de planken b noemen. Tussen de planken zitten oneindig dunne naden, en als de naald dus op twee planken ligt, kruist deze één naad. De lengte van de naald zullen we met l aanduiden. Als nu geldt l ≤ d (wat we een korte naald zullen noemen), dan blijkt dat de kans p dat de naald op twee planken ligt gegeven wordt door:quote:Stel dat we een vloer hebben die bestaat uit parallelle houten planken, elk van dezelfde breedte. Als we een naald laten vallen op die vloer, wat is dan de kans dat deze naald op twee planken ligt?
Hiervoor zijn twee afleidingen te geven, een geometrische, en eentje die wat gebruik maakt van elementaire kansrekening en calculus. Die laatste zullen we aan het eind geven, maar eerst zullen we de geometrische behandelen. Deze geeft ook een experimentele methode om π te berekenen.
Een voorbeeld van een aantal willekeurig geworpen naalden van lengte l op een vloer met planken van breedte b.
Geometrische methode
Het idee voor deze oplossing is voor het eerst door E. Barbier in 1860 aangedragen. We zijn op zoek naar de kans dat een naald op twee planken ligt, maar de truc is dat dit samenvalt met de verwachting van het aantal naden waarop de naald ligt. Dit lijkt een subtiel onderscheid, maar is het zeker niet. Als we toch even kijken naar de verwachting van het aantal naden dat een naald van willekeurige lengte kruist, dan is dit:
waarbij p1 de kans is dat de naald één naad kruist, p2 dat ze er twee kruist, enzovoort. De kans dat deze op (minstens) twee planken ligt wordt gegeven door:
Maar, wij bekijken een korte naald met lengte l ≤ b, dus p2 = p3 = ··· = 0. En daarom geldt in het geval van een korte naald E(N1) = p. Dus als we de verwachting kunnen berekenen, dan hebben we ook de kans.1
Aan elkaar bevestigde naalden.
We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.
We zullen verder gaan met de verwachting, de verwachtingswaarde heeft namelijk een aantal interessante eigenschappen, die goed van pas komen. Stel namelijk, we gooien nog een naald, en laat het aantal naden deze naald kruist aangeduid worden door N2. Natuurlijk geldt E(N1) = E(N2), en ook de kans dat deze naald op een naad ligt blijft is hetzelfde als voor de eerste naald.Nu doen we echter wat anders. we maken de punten van de naalden aan elkaar, m.a.w. twee punten van de naald vallen samen, maar op zich kunnen ze verder los bewegen, dus de naald kan in een rechte lijn vallen, of meer in een V-vorm. Als dat gebeurt zijn N1 en N2 natuurlijk niet onderling onafhankelijk, maar voor de verwachtingswaarde maakt dat niet uit, immers, er geldt:
ook als N1 en N2 niet onderling onafhankelijk zijn. Dezelfde logica gaat ook op als we aan een van de uiteinden nog een naald vastmaken, en nog één, enzovoort. Merk op dat de naalden niet eens allemaal dezelfde lengte hoeven te hebben (zo’n constructie wordt ook wel Buffon’s noodle genoemd).
Verder merken we op dat korte naalden natuurlijk naar verwachting minder naden zullen kruisen dan lange naalden. We kunnen daarom veilig stellen dat het aantal naden dat een naald kruist afhangt van de lengte. Met andere woorden E(N) = f(l), waarbij f een functie is die we nog zullen bepalen. We kunnen echter sowieso al het nodige zeggen over f. Stel je voor dat we twee naalden N1 en N2 (met lengtes l1 en l2 nemen en zo aan elkaar maken dat ze altijd in elkaars verlengde vallen. Dan geldt natuurlijk:
Maar omdat de verwachtingswaarde lineair is, geldt ook nog:
M.a.w., f(l1 + l2) = f(l1) + f(l2). Dat is alvast één eigenschap die we binnen hebben. Verder kunnen we b.v. N1 ook weer zien als m kleine naaldjes van allemaal gelijke lengte die aan elkaar gemaakt zijn, en dan krijgen we b.v.:
En zo vinden we dat f lineair is voor l ∈ ℚ. Als laatste merken we nu op dat f(l) monotoon stijgend moet zijn, en daarom ook dat f(l) = c·l voor l ∈ ℝ. Het aantal naden waar een naald N van lengte l naar verwachting op ligt wordt dus gegeven door:
Waarbij we c moeten bepalen. Merk op dat we het hier dus over een naald hebben met mogelijk veel hoeken erin, en niet per se een rechte naald.
Cirkels met straal b hebben altijd twee punten waar ze op een naad liggen.
Voordat ik duidelijk maak waarom dit precies handig is, laten we eerst eens naar een cirkel2 lijken met diameter b. Hoe je een cirkel ook gooit op de vloer, de cirkel ligt altijd precies op twee naden. Verder weten we dat de omtrek van de cirkel bπ is. Een cirkel kunnen we echter benaderen met een ingeschreven veelhoek, of met een omgeschreven veelhoek.
Een omgeschreven veelhoek (links) en ingeschreven veelhoek (rechts)
Noem de omgeschreven veelhoek met n zijden On en noem de ingeschreven In, dan kunnen we elk van die veelhoeken zien als een aan elkaar gemaakte naald bestaande uit n stukken, waarvan we weten dat E(On) = c·l(On) en E(In) = c·l(In).
Er moet dus gelden:
En, omdat:
voor n → ∞:
Kortom:
en dus geldt voor een korte naald van lengte l dat deze naar verwachting:
naden raakt, en dit is dus ook juist de kans dat deze één naad raakt.
Cirkels met omgeschreven en ingeschreven veelhoeken willekeurig geworpen, merk op dat er op een bovenste grijze baan b.v. een cirkel ligt waarvan de omgeschreven veel hoek drie snijpunten heeft met de naden. Voor n → ∞ verdwijnt dit verschil.
Nawoord
Dit geeft in feite een experimentele mogelijkheid om π te bepalen, teken een aantal lijnen op een stuk papier dat de naden tussen de planken voorstelt, gooi er een naald op die even groot is als de ruimte tussen de lijnen, en tel het aantal keren dat de naald een lijn kruist, omdat l = b, geldt dat π = (2n)/a, waarbij n het aantal keer is dat je gooit en a het aantal dat raak is. Dit is tevens vrij gemakkelijk te programmeren – echter, bedenk wel dat je heel snel al gebruik maakt van het getal π in je programma, wat eigenlijk de hele exercitie wat nutteloos maakt. Je moet vrij omzichtig programmeren om dat niet te doen.
Verder is deze methode verbonden aan een berucht experiment waarbij ene Lazzarini, een Italiaans wiskundige, 3408 keer een naald gooide, die 1808 keer een lijn raakte. Als benadering vond hij toen een getal dat tot op zes plaatsen nauwkeurig is – het heeft er echter alle schijn van dat hij zijn experiment zo inrichtte om een zo goed mogelijk resultaat te krijgen door op precies het juiste moment te stoppen.
Methode met integraal
Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt:
Zij l de lengte van de naald, b de afstand tussen de planken, en p de kans dat de naald op twee planken ligt. Gegeven de hoek α die de naald met de horizontaal maakt, is de hoogte h van de naald l sin α, en daarmee de kans dat een naald die onder een hoek α ligt op twee planken ligt:Met een integraal kunnen we nu de totale kans krijgen door te middelen over alle hoeken α die de naald kan aannemen ([0...π]):
1) Er is een kleine kanttekening te maken m.b.t. de mogelijkheid dat een naald met lengte gelijk aan de breedte van de planken precies zo valt dat ze alleen met de twee uiterste punten op een naad ligt, of het geval waarin de naald precies, over de gehele lengte, op een naad ligt. Aangezien dit wiskundige naalden en planken zijn, hebben beide gebeurtenissen kans 0 en kunnen ze verder genegeerd worden. Dit kan wiskundig gezien hard gemaakt worden.
2) Op zich hoef je geen cirkel te gebruiken, elke figuur met een vaste breedte zou ook werken, zoals een Reuleaux-driehoek. Hieruit volgt indirect ook dat voor deze figuren geldt dat o = π·d.
Bronnen en meer lezen:
Introduction to geometric probability, Daniel A. Klain, Gian-Carlo Rota.
Buffon’s needle (Wikipedia)
Buffon’s noodle (Wikipedia)
Buffon’s needle op cut-the-knot
Buffon's Noodle Problem, J. F. Ramaley.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Leuk. Had ik nog nooit van gehoord, maar de beide bewijzen zijn goed te volgen.
Roept wel de vraag op hoe de formule er uit ziet voor drie dimensionale objecten. Stel dat ik een knikker met doorsnede d laat vallen en de kans wil berekenen dat die knikker een naad kruist. Komt daar niet gewoon precies dezelfde formule uit (met l=d) ? En wat als ik kubusjes laat vallen?
Roept wel de vraag op hoe de formule er uit ziet voor drie dimensionale objecten. Stel dat ik een knikker met doorsnede d laat vallen en de kans wil berekenen dat die knikker een naad kruist. Komt daar niet gewoon precies dezelfde formule uit (met l=d) ? En wat als ik kubusjes laat vallen?
Als je een goede uitdrukking kunt vinden voor de ‘hoogte’ van zo’n voorwerp, dan is het vrij goed te doen. Want dan valt in feite die integraaltruc toe te passen.quote:
Leuk. Had ik nog nooit van gehoord, maar de beide bewijzen zijn goed te volgen.
Roept wel de vraag op hoe de formule er uit ziet voor drie dimensionale objecten. Stel dat ik een knikker met doorsnede d laat vallen en de kans wil berekenen dat die knikker een naad kruist. Komt daar niet gewoon precies dezelfde formule uit (met l=d) ? En wat als ik kubusjes laat vallen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Inderdaad. Maar wat als ik nu spelden laat vallen en aanneem dat ze met hun punt in het hout blijven steken (dus een halve bol kunnen beschrijven tov van het 'inslagpunt'). Waarschijnlijk lukt dat ook met de integraaltruc want de richtingshoek van de speld tov van de vloer en zijn lengte bepalen de hoogte aan de andere zijde van de speld. Of maak ik een denkfout?quote:Op woensdag 4 november 2009 00:13 schreef Iblis het volgende:
[..]
Als je een goede uitdrukking kunt vinden voor de ‘hoogte’ van zo’n voorwerp, dan is het vrij goed te doen. Want dan valt in feite die integraaltruc toe te passen.
Klopt volgens mij. Maar als het om experimenteren gaat om π uit te rekenen, heb je niet zoveel aan die integratiemethode.quote:
[..]
Inderdaad. Maar wat als ik nu spelden laat vallen en aanneem dat ze met hun punt in het hout blijven steken (dus een halve bol kunnen beschrijven tov van het 'inslagpunt'). Waarschijnlijk lukt dat ook met de integraaltruc want de richtingshoek van de speld tov van de vloer en zijn lengte bepalen de hoogte aan de andere zijde van de speld. Of maak ik een denkfout?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik zie niet waar hhet nu niet kloptquote:Op vrijdag 23 oktober 2009 08:14 schreef -J-D- het volgende:
[ afbeelding ]
Beetje humor op de 'vroege' ochtend.
|
|
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |