W&T Wetenschap & Technologie
Een plek om te discussiŰren over wetenschappelijke onderwerpen, wetenschappelijke problemen, technologische projecten en grootse uitvindingen.



Jij bent liever lui dan moe hŔ? Ik vertik dit hoor. Je opent de topic maar op ÚÚn pagina en zoekt op ‘Fermat’, kan niet missen.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik pareer door het op youtube te zoeken door Fermat uit jouw tekst te kopieŰrenquote:Op dinsdag 13 oktober 2009 22:00 schreef Iblis het volgende:
[..]
Jij bent liever lui dan moe hŔ? Ik vertik dit hoor. Je opent de topic maar op ÚÚn pagina en zoekt op ‘Fermat’, kan niet missen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


De Calkin-Wilf-reeks
In het vorige deel van dit drieluik had ik laten zien hoe je de rationele getallen, d.w.z. de breuken, in een 1:1 koppeling met de natuurlijke getallen kunt zetten. Je kunt de breuken in een vierkant zetten, en dan loop je de diagonalen af. Dit is redelijk slim, maar het nadeel is dat je dubbelen tegenkomt.
Er is ook een manier – verrassend eenvoudig zelfs – om ze op te sommen zonder dat je dubbelen tegenkomt. Deze manier is in 2000 ontdekt door Neil Calkin en Herbert Wilf. Het is van een verbazingwekkende eenvoud en schoonheid.
Hun opsomming begint als volgt:
De logica is misschien nog niet direct duidelijk, maar wat wel opvalt is dat de teller van elke breuk gelijk is aan den oemer van de voorafgaande breuk. Dit is inderdaad iets dat voor de gehele reeks geldt, dus in feite kunnen we zeggen het n-e getal (we beginnen overigens bij 0 te tellen) in de reeks is gelijk aan bn/bn+1, waarbij bn gegeven wordt door:
Dit lijkt misschien een beetje een rare rij getallen, maar op zich tellen ze iets. Wat precies is verder niet zo heel relevant voor wat ik wil aantonen, maar het is wel aardig om te melden: het is namelijk het aantal manieren waarop je een getal als som van machten van twee kunt schrijven, waarbij een macht hooguit twee keer gebruikt wordt.
Dat is misschien wat duidelijker met een voorbeeld. Neem 5, dat is te schrijven als 4 + 1 = 5 (1 = 20), maar ook als 2 + 2 + 1. 1 + 1 + 1 + 1 + 1 gaat niet door, want dan gebruiken we 1 te vaak. 6 kunnen we schrijven als 4 + 1 + 1, of als 4 + 2, of als 2 + 2 + 1 + 1. 2 + 2 + 2 kan dus niet.
Deze reeks staat bekend als ‘Sterns diatomische reeks’, naar de Dutisers Stern – een reeks die overigens al in 1858 voor het eerst werd beschreven! Ook de al eerder in deze topic langsgekomen Dijkstra heeft er in EWD570 en EWD578 over geschreven.
Maar goed, we hebben die reeks dus, en we merken nog een aantal interessante eigenschappen op: Opeenvolgende getallen in bn zijn altijd relatief priem. En aangezien je breuken bouwt van opeenvolgende getallen, zijn die breuken altijd vereenvoudigd. En de lijst van breuken bevat alle positieve breuken precies 1 keer (in gereduceerde vorm dus).
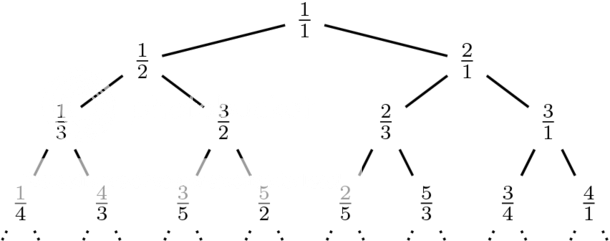
Nou, okÚ, okÚ, tof, maar hoe kom ik nu op een makkelijke manier aan die reeks? Moet je echt het aantal manieren om een getal als som van machten van twee te schrijven gaan zitten uitvogelen? Nee, het kan veel gemakkelijker met behulp van een boom. Denk eraan: Het is een Wiskundige boom, dus die groeit naar beneden.
Dus 1/1 zit in de wortel van de boom, en verder heeft elke knoop r/s twee kinderen. De linker is r/(r + s) en de rechter is (r + s)/s. We bekommeren ons niet direct meer om de reeks, maar wel om de boom.
Er zijn nu vijf claims te maken:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Geen enkele breuk komt vaker dan ÚÚn keer voor.
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
De lijst die je krijgt valt precies samen met bn
Claim 1:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Voor 1/1 geldt dit uiteraard. Neem nu aan dat het niet zo is, en dat er ergens, misschien zelfs wel op meerdere plekken in de boom een breuk is die nog vereenvoudigd kan worden. Van alle mogelijkheden neem je die breuk r/s, als je de boom zoals hierboven tekent, het hoogst in de boom zit.
Het is dus niet de wortel, en daarom weten we zeker dat het dan het kind van een knoop moet zijn. Als het een linker kind is, dan heeft z’n ouder de waarde r/(s - r). Maar als r/s vereenvoudigbaar is, dan is r/(s - r) dat ook[1] – tegenspraak met het feit dat we een breuk uit het hoogste niveau hadden gepakt.
Als r/s een rechter kind is, dan is z’n ouder (r-s)/s, en dat leidt tot dezelfde tegenspraak.
Claim 2:
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Dat 1/1 erin zit is duidelijk. Neem echter aan dat ÚÚn of meerdere andere breuken er niet in zitten. Neem van die breuken die er niet in zitten eentje met de kleinste noemer, en als er meerdere zijn met een kleinste noemer, van die groep de breuk met de kleinste teller, zeg dat dit r/s is.
Als r > s, dan weten we dat bijgevolg ook (r-s)/s niet in de boom zou kunnen zitten, want die heeft als rechter kind r/s. Maar r - s heeft dezelfde noemer als r/s maar een kleinere teller! En dat is in tegenspraak met onze aanname dat r/s de kleinste teller had!
Omgekeerd, als r < s, dan kan r/(s - r) niet in de boom zitten, want anders zou het een linker kind hebben van de vorm r/s. Maar s - r heeft een kleinere noemer dan r/s, en dat is ook weer een tegenspraak!
Claim 3:
Geen enkele breuk komt vaker dan ÚÚn keer voor.
Dit geldt sowieso voor de wortel, want stel dat 1/1 nog een keer in de boom zat, dan is het kind van een knoop r/s, maar r/s heeft kinderen in de vorm r/(r + s) en (r + s)/s, en beide kunnen uiteraard geen 1/1 zijn aangezien r en s beide > 0 moeten zijn.
Nu doen we weer het zelfde als bij de vorige claim: van alle breuken die vaker dan ÚÚn keer zouden voorkomen, kies die met de kleinste noemer, en als dat er meer zijn, daarbinnen die met de kleinste teller. Als r < s, dan is r/s een linker kind, en bovendien geldt dan voor de ouder dat deze r/(s - r) is. Maar dat betekent dat er ook meer dan ÚÚn van zulk soort ouders is! En r/(s-r) is in strijd met onze aanname dat we een breuk met de kleinste noemer hadden gepakt. En voor r > s hebben we hetzelfde, maar dan als rechter kind.
Claim 4:
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
Deze is iets lastiger te bewijzen. Het is natuurlijk duidelijk als het om twee breuken gaat die kind zijn van dezelfde ouder. Omdat het linker kind de vorm r/(r+s) heeft en de rechter (r+s)/s.
Ook als we van een rij naar de volgende rij gaan is het niet zo moeilijk te zien, de meest rechter breuk op een rij heeft namelijk altijd noemer 1, en de meest linker breuk op een rij altijd teller 1. Dus dat gaat ook goed.
Nu blijft over twee buren in dezelfde rij, maar die niet het kind zijn van dezelfde ouder. Dit moet even met een inductiebewijs. We praten altijd over een rechter kind, gevolgd door een linker kind in zo’n geval. Het rechter kind heeft dezelfde noemer als z’n ouder. En dat linker kind heeft dezelfde teller als z’n ouder. Die twee ouders zijn ˇˇk buren van elkaar. Dus als het voor die ouders geldt, dan geldt het ook voor die kinderen.
We hebben vastgesteld dat het voor de kinderen van de wortel sowieso klopt (noem dat de eerste rij), omdat die kinderen van dezelfde ouder zijn. Dus dan klopt het ook voor de tweede rij, en dus ook voor de derde, enz.
Kortom, dit klopt voor ßlle rijen in de boom.
Claim 5
Niet echt nodig voor vandaag. We hebben immers al bewezen dat alle rationale getallen 1 keer voorkomen. Dat het samenvalt met bn bewijs ik niet, maar het is wel heel aardig. Het is te vinden in het oorspronkelijke artikel, en niet lastig. Hieronder staat nog een link.
Toegift
Ook is expliciet te bepalen waar je een bepaald getal in de reeks vindt, is er expliciete successor functie te bepalen, en is er met behulp van de binaire expansie en de regels om te boom te bouwen heel gemakkelijk te vinden wat de n-breuk is (omgekeerd is aan de breuk te zien of het een linker of rechter kind is en is zo de positie te construeren). Oˇk is nog een mooie link te leggen met Euklides’ algoritme.
Dit verbindt dus zowel verzamelingentheorie, als getaltheorie, als combinatoriek. Lees er meer over op:
Calkin–Wilf tree (Wikipedia)
Calkin, Neil; Wilf, Herbert (2000),Recounting the rationals, American Mathematical Monthly 107 (4): 360–363
Of koop er een T-shirt van:
The Nerdiest Shirts.com.
De volgende aflevering is dat we bewijzen dat voor niet zo’n opsomming te geven is. In zekere zin is deze verzameling dus wel Úcht groter dan de natuurlijke getallen en is er niet meer sprake van ‘evenveel’.
Post-toegift
De reeks kan ook als H-boom-fractal weergegeven worden:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
Of als spiraal die de opsomming nog duidelijker maakt:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
[1] Dat r/s vereenvoudigbaar is wil zeggen dat er een getal d > 1 is dat zowel een deler van r als van s is. Aangezien (s - r)/d = s/d - r/d, is d dus ook een deler van s - r.
[ Bericht 0% gewijzigd door Iblis op 14-10-2009 17:41:47 ]
In het vorige deel van dit drieluik had ik laten zien hoe je de rationele getallen, d.w.z. de breuken, in een 1:1 koppeling met de natuurlijke getallen kunt zetten. Je kunt de breuken in een vierkant zetten, en dan loop je de diagonalen af. Dit is redelijk slim, maar het nadeel is dat je dubbelen tegenkomt.
Er is ook een manier – verrassend eenvoudig zelfs – om ze op te sommen zonder dat je dubbelen tegenkomt. Deze manier is in 2000 ontdekt door Neil Calkin en Herbert Wilf. Het is van een verbazingwekkende eenvoud en schoonheid.
Hun opsomming begint als volgt:
De logica is misschien nog niet direct duidelijk, maar wat wel opvalt is dat de teller van elke breuk gelijk is aan den oemer van de voorafgaande breuk. Dit is inderdaad iets dat voor de gehele reeks geldt, dus in feite kunnen we zeggen het n-e getal (we beginnen overigens bij 0 te tellen) in de reeks is gelijk aan bn/bn+1, waarbij bn gegeven wordt door:
Dit lijkt misschien een beetje een rare rij getallen, maar op zich tellen ze iets. Wat precies is verder niet zo heel relevant voor wat ik wil aantonen, maar het is wel aardig om te melden: het is namelijk het aantal manieren waarop je een getal als som van machten van twee kunt schrijven, waarbij een macht hooguit twee keer gebruikt wordt.
Dat is misschien wat duidelijker met een voorbeeld. Neem 5, dat is te schrijven als 4 + 1 = 5 (1 = 20), maar ook als 2 + 2 + 1. 1 + 1 + 1 + 1 + 1 gaat niet door, want dan gebruiken we 1 te vaak. 6 kunnen we schrijven als 4 + 1 + 1, of als 4 + 2, of als 2 + 2 + 1 + 1. 2 + 2 + 2 kan dus niet.
Deze reeks staat bekend als ‘Sterns diatomische reeks’, naar de Dutisers Stern – een reeks die overigens al in 1858 voor het eerst werd beschreven! Ook de al eerder in deze topic langsgekomen Dijkstra heeft er in EWD570 en EWD578 over geschreven.
Maar goed, we hebben die reeks dus, en we merken nog een aantal interessante eigenschappen op: Opeenvolgende getallen in bn zijn altijd relatief priem. En aangezien je breuken bouwt van opeenvolgende getallen, zijn die breuken altijd vereenvoudigd. En de lijst van breuken bevat alle positieve breuken precies 1 keer (in gereduceerde vorm dus).
Nou, okÚ, okÚ, tof, maar hoe kom ik nu op een makkelijke manier aan die reeks? Moet je echt het aantal manieren om een getal als som van machten van twee te schrijven gaan zitten uitvogelen? Nee, het kan veel gemakkelijker met behulp van een boom. Denk eraan: Het is een Wiskundige boom, dus die groeit naar beneden.
Dus 1/1 zit in de wortel van de boom, en verder heeft elke knoop r/s twee kinderen. De linker is r/(r + s) en de rechter is (r + s)/s. We bekommeren ons niet direct meer om de reeks, maar wel om de boom.
Er zijn nu vijf claims te maken:
Claim 1:
Teller en noemer van de breuken die aan deze boom groeien zijn relatief priem.
Voor 1/1 geldt dit uiteraard. Neem nu aan dat het niet zo is, en dat er ergens, misschien zelfs wel op meerdere plekken in de boom een breuk is die nog vereenvoudigd kan worden. Van alle mogelijkheden neem je die breuk r/s, als je de boom zoals hierboven tekent, het hoogst in de boom zit.
Het is dus niet de wortel, en daarom weten we zeker dat het dan het kind van een knoop moet zijn. Als het een linker kind is, dan heeft z’n ouder de waarde r/(s - r). Maar als r/s vereenvoudigbaar is, dan is r/(s - r) dat ook[1] – tegenspraak met het feit dat we een breuk uit het hoogste niveau hadden gepakt.
Als r/s een rechter kind is, dan is z’n ouder (r-s)/s, en dat leidt tot dezelfde tegenspraak.
Claim 2:
Elke positieve vereenvoudigde breuk zit ergens in deze boom.
Dat 1/1 erin zit is duidelijk. Neem echter aan dat ÚÚn of meerdere andere breuken er niet in zitten. Neem van die breuken die er niet in zitten eentje met de kleinste noemer, en als er meerdere zijn met een kleinste noemer, van die groep de breuk met de kleinste teller, zeg dat dit r/s is.
Als r > s, dan weten we dat bijgevolg ook (r-s)/s niet in de boom zou kunnen zitten, want die heeft als rechter kind r/s. Maar r - s heeft dezelfde noemer als r/s maar een kleinere teller! En dat is in tegenspraak met onze aanname dat r/s de kleinste teller had!
Omgekeerd, als r < s, dan kan r/(s - r) niet in de boom zitten, want anders zou het een linker kind hebben van de vorm r/s. Maar s - r heeft een kleinere noemer dan r/s, en dat is ook weer een tegenspraak!
Claim 3:
Geen enkele breuk komt vaker dan ÚÚn keer voor.
Dit geldt sowieso voor de wortel, want stel dat 1/1 nog een keer in de boom zat, dan is het kind van een knoop r/s, maar r/s heeft kinderen in de vorm r/(r + s) en (r + s)/s, en beide kunnen uiteraard geen 1/1 zijn aangezien r en s beide > 0 moeten zijn.
Nu doen we weer het zelfde als bij de vorige claim: van alle breuken die vaker dan ÚÚn keer zouden voorkomen, kies die met de kleinste noemer, en als dat er meer zijn, daarbinnen die met de kleinste teller. Als r < s, dan is r/s een linker kind, en bovendien geldt dan voor de ouder dat deze r/(s - r) is. Maar dat betekent dat er ook meer dan ÚÚn van zulk soort ouders is! En r/(s-r) is in strijd met onze aanname dat we een breuk met de kleinste noemer hadden gepakt. En voor r > s hebben we hetzelfde, maar dan als rechter kind.
Claim 4:
Als je de breuken achter elkaar schrijft, van boven naar beneden, en van links naar rechts (dus laag voor laag als het ware), dan is de noemer van elke breuk gelijk aan de teller van z’n opvolger.
Deze is iets lastiger te bewijzen. Het is natuurlijk duidelijk als het om twee breuken gaat die kind zijn van dezelfde ouder. Omdat het linker kind de vorm r/(r+s) heeft en de rechter (r+s)/s.
Ook als we van een rij naar de volgende rij gaan is het niet zo moeilijk te zien, de meest rechter breuk op een rij heeft namelijk altijd noemer 1, en de meest linker breuk op een rij altijd teller 1. Dus dat gaat ook goed.
Nu blijft over twee buren in dezelfde rij, maar die niet het kind zijn van dezelfde ouder. Dit moet even met een inductiebewijs. We praten altijd over een rechter kind, gevolgd door een linker kind in zo’n geval. Het rechter kind heeft dezelfde noemer als z’n ouder. En dat linker kind heeft dezelfde teller als z’n ouder. Die twee ouders zijn ˇˇk buren van elkaar. Dus als het voor die ouders geldt, dan geldt het ook voor die kinderen.
We hebben vastgesteld dat het voor de kinderen van de wortel sowieso klopt (noem dat de eerste rij), omdat die kinderen van dezelfde ouder zijn. Dus dan klopt het ook voor de tweede rij, en dus ook voor de derde, enz.
Kortom, dit klopt voor ßlle rijen in de boom.
Claim 5
Niet echt nodig voor vandaag. We hebben immers al bewezen dat alle rationale getallen 1 keer voorkomen. Dat het samenvalt met bn bewijs ik niet, maar het is wel heel aardig. Het is te vinden in het oorspronkelijke artikel, en niet lastig. Hieronder staat nog een link.
Toegift
Ook is expliciet te bepalen waar je een bepaald getal in de reeks vindt, is er expliciete successor functie te bepalen, en is er met behulp van de binaire expansie en de regels om te boom te bouwen heel gemakkelijk te vinden wat de n-breuk is (omgekeerd is aan de breuk te zien of het een linker of rechter kind is en is zo de positie te construeren). Oˇk is nog een mooie link te leggen met Euklides’ algoritme.
Dit verbindt dus zowel verzamelingentheorie, als getaltheorie, als combinatoriek. Lees er meer over op:
Of koop er een T-shirt van:
The Nerdiest Shirts.com.
De volgende aflevering is dat we bewijzen dat voor niet zo’n opsomming te geven is. In zekere zin is deze verzameling dus wel Úcht groter dan de natuurlijke getallen en is er niet meer sprake van ‘evenveel’.
Post-toegift
De reeks kan ook als H-boom-fractal weergegeven worden:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
Of als spiraal die de opsomming nog duidelijker maakt:
Bron: Wikimedia Commons. Maker: David Eppstein. Publiek Domein.
[1] Dat r/s vereenvoudigbaar is wil zeggen dat er een getal d > 1 is dat zowel een deler van r als van s is. Aangezien (s - r)/d = s/d - r/d, is d dus ook een deler van s - r.
[ Bericht 0% gewijzigd door Iblis op 14-10-2009 17:41:47 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Via die T-shirt-site kwam ik nu ook nog op: Math less travaled die in feite hetzelfde beschrijft. Ik had die site niet gezien echter. Hoe dan ook, wel het lezen waard!
Ook is er nog een boek aan te duiden (dat heb ik wel gebruikt), en dat is Proofs from The Book door Martin Aigner en GŘnter M. Ziegler. Het is hoofdstuk 16 van hun boek, op pagina 93 in deze Google Books editie. Maar Google laat mij er niet inkijken.
Ook is er nog een boek aan te duiden (dat heb ik wel gebruikt), en dat is Proofs from The Book door Martin Aigner en GŘnter M. Ziegler. Het is hoofdstuk 16 van hun boek, op pagina 93 in deze Google Books editie. Maar Google laat mij er niet inkijken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Toen ik de TT zag dacht ik ook direct aan dat bewijs. Zeer elegant door z'n eenvoud.quote:Op maandag 28 september 2009 22:18 schreef Iblis het volgende:
Als eerste bewijs, een klassieker, namelijk, dat er oneindig veel priemgetallen zijn.
Never in the entire history of calming down did anyone ever calm down after being told to calm down.


Dit vind ik toch een beetje contra´ntu´tief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.quote:Op maandag 12 oktober 2009 20:17 schreef Iblis het volgende:
Een koppeling tussen ℕ en ℤ
Er zijn op die manier ook evenveel gehele getallen als natuurlijke getallen:
[ afbeelding ]
Het is ook duidelijk dat deze koppeling gewoon door te trekken is, bovenaan som je de natuurlijke getallen op, onderaan gaat het verder met -4, 4, -5, 5, -6, 6 enz.
Dus er zijn ook evenveel gehele getallen als natuurlijke getallen.
Verder wel mijn complimenten voor de bewijzen die je hier post.


Dat kun je stellen, maar dat betekent niet dat de een "meer" elementen heeft dan de ander.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contra´ntu´tief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren.
Dat staat toch nergens? Er is alleen laten zien dat er een 1-op-1 'map' is tussen de elementen uit beide sets, die ook alle elementen beslaat.quote:Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
...
More oneness, less categories
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here
Open hearts, no strategies
Decisions based upon faith and not fear
People who live right now and right here


Ja, maar daarom probeer ik duidelijk te maken wat in de Wiskunde met 'evenveel' wordt bedoeld een 1:1-koppeling (formeler: er is een bijectie te vinden tussen de verzamelingen). Ik moet deel 3 nog doen trouwens, dan zul je zien dat er voor de reŰle getallen ℝ zo’n bijectie niet mogelijk is.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contra´ntu´tief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
Verder wel mijn complimenten voor de bewijzen die je hier post.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Nee, het is niet contra-intu´tief.quote:Op woensdag 21 oktober 2009 22:54 schreef lyolyrc het volgende:
[..]
Dit vind ik toch een beetje contra´ntu´tief. Je kunt immers ook stellen dat alle elementen in ℕ ook voorkomen in ℤ, terwijl er in ℤ elementen voorkomen die niet tot ℕ behoren. Op deze manier lijkt het dat je ze gelijkstelt wat betreft het aantal elementen, omdat het aantal elementen in ℕ en ℤ veel te groot is om te overzien.
Stel, ik heb twee verzamelingen, verzameling A en verzameling B. Hoe weet ik nou of beide verzamelingen even veel elementen hebben?
Wel, we kunnen een functie f : A -> B maken. Deze wijst elke waarde x in A een waarde y in B toe.
Stel, ons lukt het om een injectieve functie f te maken, dat betekent dat we aan elke waarde van x in A een unieke waarde y in B kunnen toewijzen. Dan weten we dat verzameling B minstens net zo groot is als verzameling A:
En als het omgekeerde ook lukt, als we dus ook een injectieve functie g : B -> A kunnen vinden, dan zijn beide verzamelingen even groot. In ons voorbeeld gaat dat fout:
Omdat een functie nooit voor sommige waardes ongedefinieerd mag zijn, moeten we dus naar sommige waardes in A twee pijltjes trekken, dus aan aan sommige waarden y uit B kunnen we in dit geval geen unieke waarde x uit A toewijzen. Dat geeft aan dat B groter is dan A.
Tot zo ver is het hopelijk allemaal duidelijk en intu´tief.
Neem nou het plaatje van Iblis er weer bij:
Hier zien we dat aan elke waarde uit N een unieke waarde in Z wordt toegewezen, Ún dat elke waarde in Z een unieke waarde in N wordt toegewezen.
Dat betekent dat Z minstens zo groot is als N, en dat N minstens zo groot is als Z. Beide zijn dus even groot.
[ Bericht 2% gewijzigd door #ANONIEM op 21-10-2009 23:24:40 ]


De ‘paradox’ is dus het (subtiele) onderscheid tussen ‘evenveel’ en ‘elementen bevatten die de andere verzameling niet bevat’.
Voor eindige verzamelingen gaat het prima op dat als verzameling A alles bevat wat B bevat, en nog een beetje meer, dat A groter is dan B. Maar voor oneindig gaat dat niet op. Immers, neem een verzameling met oneindig veel elementen, en haal er eentje uit. Hoeveel (dus niet wÚlke, maar het aantal) heb je er dan nog over? Dat zijn er nog steeds oneindig veel. Dus het heeft dan niet zoveel zin om te zeggen dat die laatste verzameling ‘kleiner’ is, als die ˇˇk nog oneindig is.
Dit is trouwens een andere manier om oneindig te karakteriseren: een oneindige verzameling is een verzameling waarvan een Úcht deelverzameling ‘even groot’ is als de verzameling zelf. M.a.w. ℕ is oneindig, want een echte deelverzameling (b.v. alle even getallen, waar 1, 3 en 5 b.v. niet in zitten) is ‘even groot’ (heeft dezelfde cardinaliteit) als ℕ zelf.
Dus ‘deelverzameling zijn van’ impliceert voor oneindige verzamelingen niet per se dat het aantal elementen ook minder is. Immers, dat aantal is in zekere zin onuitputtelijk. Zou het minder worden, dan zou je ℕ een keer ‘leeg kunnen maken’ door er maar telkens eindig veel elementen uit te halen.
Hier zit natuurlijk een lastigheid. Maar daarom wordt het straks nog raarder als ℝ eigenlijk ‘nog weer oneindiger’ blijkt te zijn dan ℕ of ℤ.
Voor eindige verzamelingen gaat het prima op dat als verzameling A alles bevat wat B bevat, en nog een beetje meer, dat A groter is dan B. Maar voor oneindig gaat dat niet op. Immers, neem een verzameling met oneindig veel elementen, en haal er eentje uit. Hoeveel (dus niet wÚlke, maar het aantal) heb je er dan nog over? Dat zijn er nog steeds oneindig veel. Dus het heeft dan niet zoveel zin om te zeggen dat die laatste verzameling ‘kleiner’ is, als die ˇˇk nog oneindig is.
Dit is trouwens een andere manier om oneindig te karakteriseren: een oneindige verzameling is een verzameling waarvan een Úcht deelverzameling ‘even groot’ is als de verzameling zelf. M.a.w. ℕ is oneindig, want een echte deelverzameling (b.v. alle even getallen, waar 1, 3 en 5 b.v. niet in zitten) is ‘even groot’ (heeft dezelfde cardinaliteit) als ℕ zelf.
Dus ‘deelverzameling zijn van’ impliceert voor oneindige verzamelingen niet per se dat het aantal elementen ook minder is. Immers, dat aantal is in zekere zin onuitputtelijk. Zou het minder worden, dan zou je ℕ een keer ‘leeg kunnen maken’ door er maar telkens eindig veel elementen uit te halen.
Hier zit natuurlijk een lastigheid. Maar daarom wordt het straks nog raarder als ℝ eigenlijk ‘nog weer oneindiger’ blijkt te zijn dan ℕ of ℤ.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 5% gewijzigd door #ANONIEM op 21-10-2009 23:42:54 ]


quote:Op woensdag 21 oktober 2009 23:42 schreef Igen het volgende:
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?Hilberts hotel moet dat zijn, logeer ik ook altijdSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt. Niet geschoten is altijd mis..
Niet geschoten is altijd mis..
Ach Margrietje, de Rozen zullen bloeien..


Ik ben dan wel benieuwd naar dat bewijs dat er voor ℝ geen bijectie mogelijk is, je kunt het tenslotte toch bewijzen op een soortgelijke manier als met ℤ en ℕ?quote:Op woensdag 21 oktober 2009 23:19 schreef Iblis het volgende:
[..]
Ja, maar daarom probeer ik duidelijk te maken wat in de Wiskunde met 'evenveel' wordt bedoeld een 1:1-koppeling (formeler: er is een bijectie te vinden tussen de verzamelingen). Ik moet deel 3 nog doen trouwens, dan zul je zien dat er voor de reŰle getallen ℝ zo’n bijectie niet mogelijk is.
quote:Op woensdag 21 oktober 2009 23:42 schreef Igen het volgende:
Bij dit thema past ook een leuk klein wiskundig raadseltje:
Stel, je hebt een hotel met oneindig veel kamers en al die kamers zijn bezet. Dan komt er een nieuwe reiziger binnen, op zoek naar onderdak. Kan die een kamer krijgen?I.p.v. al die mensen van kamer te verhuizen kan je de nieuwe gast toch in de n+1'de kamer stoppen?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 19% gewijzigd door Diabox op 22-10-2009 01:22:46 ]


Nee, je loopt stuk met irrationale getallen. ℝ is niet aftelbaar.quote:Op donderdag 22 oktober 2009 01:14 schreef Diabox het volgende:
[..]
Ik ben dan wel benieuwd naar dat bewijs dat er voor ℝ geen bijectie mogelijk is, je kunt het tenslotte toch bewijzen op een soortgelijke manier als met ℤ en ℕ?
[..]
Nee, want n+1 is een eindig getal en alle kamers (met een welbepaald nummer) waren immers bezet.quote:I.p.v. al die mensen van kamer te verhuizen kan je de nieuwe gast toch in de n+1'de kamer stoppen?


Hm ja, niet bij stilgestaan.quote:Op donderdag 22 oktober 2009 01:36 schreef Riparius het volgende:
[..]
Nee, je loopt stuk met irrationale getallen. ℝ is niet aftelbaar.
[..]
Nee, want n+1 is een eindig getal en alle kamers (met een welbepaald nummer) waren immers bezet.


Diagonaalbewijs van Cantor
Het diagonaalbewijs
Hebben misschien alle oneindige verzamelingen hetzelfde formaat? Dit blijkt niet zo te zijn. En daar komt het diagonaalbewijs om de hoek: Er zijn meer reŰle getallen tussen 0 en 1 dan er natuurlijke getallen zijn. Dit bewijs gebruikt reductio ad absurdum. We nemen daarom aan dat er een bijectie, dit wil zeggen een 1-op-1 afbeelding van de natuurlijke getallen naar de reŰle getallen bestaat.
Zo'n afbeelding ziet er bijvoorbeeld zo uit:
enzovoort.
De lijst is in twee richtingen oneindig lang. Nu nemen we van het eerste getal het eerste cijfer achter de komma. Van het tweede getal nemen we het tweede cijfer achter de komma, enzovoort. Deze cijfers zetten we achter elkaar, zodat we een nieuwe getal krijgen, in het voorbeeld: 0,220098.... Elk cijfer in dit getal veranderen we in een willekeurig ander cijfer, bijvoorbeeld door er 1 bij op te tellen (9 wordt dan 0). Het nieuwe getal 0,331109.... dat we nu hebben gemaakt, kan nooit in de lijst staan; immers als je uit de lijst het getal n haalt dan komt het n-de cijfer van dat getal niet meer overeen met het n-de cijfer uit m. Omdat er altijd een nieuwe m gemaakt kan worden, zit er tussen 0 en 1 een overaftelbaar aantal reŰle getallen.
Er is een functie te beschrijven voor diagonalisatie die in zeer veel gevallen werkt:
d(i) = min{B\ {d(0),...,d(i-1),fi(i)}}, waar B het bereik is en fi(i) de waarde op de diagonaal.
Ik kwam toevallig het bewijs tegen dat het dus niet kan met ℝ.
Het diagonaalbewijs
Hebben misschien alle oneindige verzamelingen hetzelfde formaat? Dit blijkt niet zo te zijn. En daar komt het diagonaalbewijs om de hoek: Er zijn meer reŰle getallen tussen 0 en 1 dan er natuurlijke getallen zijn. Dit bewijs gebruikt reductio ad absurdum. We nemen daarom aan dat er een bijectie, dit wil zeggen een 1-op-1 afbeelding van de natuurlijke getallen naar de reŰle getallen bestaat.
Zo'n afbeelding ziet er bijvoorbeeld zo uit:
| 1 2 3 4 5 6 | 2 - 0,12345678901234... 3 - 0,00000000000120... 4 - 0,50000000000000... 5 - 0,14159265358979... 6 - 0,23562877077729... |
enzovoort.
De lijst is in twee richtingen oneindig lang. Nu nemen we van het eerste getal het eerste cijfer achter de komma. Van het tweede getal nemen we het tweede cijfer achter de komma, enzovoort. Deze cijfers zetten we achter elkaar, zodat we een nieuwe getal krijgen, in het voorbeeld: 0,220098.... Elk cijfer in dit getal veranderen we in een willekeurig ander cijfer, bijvoorbeeld door er 1 bij op te tellen (9 wordt dan 0). Het nieuwe getal 0,331109.... dat we nu hebben gemaakt, kan nooit in de lijst staan; immers als je uit de lijst het getal n haalt dan komt het n-de cijfer van dat getal niet meer overeen met het n-de cijfer uit m. Omdat er altijd een nieuwe m gemaakt kan worden, zit er tussen 0 en 1 een overaftelbaar aantal reŰle getallen.
Er is een functie te beschrijven voor diagonalisatie die in zeer veel gevallen werkt:
d(i) = min{B\ {d(0),...,d(i-1),fi(i)}}, waar B het bereik is en fi(i) de waarde op de diagonaal.
Ik kwam toevallig het bewijs tegen dat het dus niet kan met ℝ.


Ik plaats hier een tvp omdat dit een prachtig topic is 
I just had to get that stress off my chest like breast reduction.


Beide nog niet nee..quote:Op donderdag 22 oktober 2009 19:56 schreef Bankfurt het volgende:
Is dat bewijs van algoritme van Euclides al hier genoemd ?
en die stelling van GGD * KGV = ?


Niemand houdt je tegen.
Want ik heb destijds besloten, dat ik de harde weg ontwijk.
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten
Dus blijf ik lopen door de sloten, het liefst in zeven tegelijk.
BZB - Zeven Sloten


Beetje humor op de 'vroege' ochtend.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
|
|
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |