Hierboven staan de vakken zoals ze op de middelbare school gegeven worden. Dit wil natuurlijk niet zeggen dat er hier geen ruimte is voor vragen van MBO, HBO of WO-niveau. Alle vragen die binnen het gebied van 'Bèta' vallen, kun je hier posten.
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
[ Bericht 0% gewijzigd door Rene op 24-02-2006 20:04:52 ]
mara ik heb het over de Polya oplossingstrategien of probleemoplossen-heuristiken (ik weet niet hoe je dat nog spelt) In ieder geval.
mijn vraag is of ze wel nuttig zijn als je die toepast? Ik ben ze pas dit jaar (dit blok) tegengekomen..:
de methode is als volgt
1) probleem begrijpen
2)plan ontwerpen
3)plan uitvoeren
4)evalueren..
waarom ga je dat dan bewust aanleren? ..zal dat dan wel helpen? heeft dat wel ooit geholpen?
quote:Lang niet iedereen leert dit zo vanzelfsprekend. Nog steeds kom ik er op school vaak achter dat mensen helemaal geen idee hebben hoe ze een probleemstelling aan moeten pakken en wat ze allemaal zouden kunnen en/of moeten doen om een oplossing te vinden. Het ligt er maar net aan op wat voor manier jij denkt, leert, opgevoed bent en hoe ze op school met zulke dingen om zijn gegaan.Op vrijdag 17 februari 2006 20:05 schreef teletubbies het volgende:
zoiets leer je toch onbewust tijdens het oplossen van opgaven..
waarom ga je dat dan bewust aanleren? ..zal dat dan wel helpen? heeft dat wel ooit geholpen?
quote:De meeste opgaven die je maakt volgen direct op een klein stukje theorie en de oplossing van die opgave is na de theorie, met eventuele voorbeelden, bijna triviaal. Je wordt dan meestal met problemen geconfronteerd waarvan de oplossingmethode duidelijk is. Voor een aantal problemen zijn er standaardtrucjes waarmee je redelijk eenvoudig tot een oplossing komt.Op vrijdag 17 februari 2006 20:05 schreef teletubbies het volgende:
zoiets leer je toch onbewust tijdens het oplossen van opgaven..
waarom ga je dat dan bewust aanleren? ..zal dat dan wel helpen? heeft dat wel ooit geholpen?
Als je echter een echt probleem tegenkomt is de oplossing niet altijd voor de hand liggend. En dan moet je echt dieper over het plan van aanpak nadenken, zeker als de uitvoering maanden zou duren is het van te voren handig om te kijken of die aanpak nut heeft.
quote:Er is maar 1 manier waarop je problemen leert oplossen en dat is HEEL VEEL, maar dan ook echt HEEL VEEL oefenen en zorgen dat je alles wat je tijdens dat oefenen ziet ook NIET MEER VERGEET.Op vrijdag 17 februari 2006 20:05 schreef teletubbies het volgende:
zoiets leer je toch onbewust tijdens het oplossen van opgaven..
waarom ga je dat dan bewust aanleren? ..zal dat dan wel helpen? heeft dat wel ooit geholpen?
het lijkt mere op reproduceren
[ Bericht 2% gewijzigd door McCarthy op 18-02-2006 01:09:47 ]
Wat wij dachten is we doen de reactie in een bekerglas met water en dan meten hoeveel graden het water verandert is en dan kunnen we de vrijgekomen/ontrokken energie meten. Maar dit lijkt ons niet echt een nauwkeurige manier, weet iemand een betere?
Ik heb 2 gonioformules, die heb ik nodig om een aantal berekeningen te kunnen maken, en wil ook weten waarom deze 2 vergelijkingen zo zijn.
Ik ben echter al een hele tijd bezig, en ik kom er niet uit.
Het gaat om de volgende 2:
Sin(x) = 2 * Sin(x/2) * Cos (x/2)
en
Cos (x) = 2 Cos²(x/2) -1
Kunnen jullie me helpen?
quote:Die zijn makkelijk af te leiden met de bekende formules:Op zaterdag 18 februari 2006 13:48 schreef Market_Garden het volgende:
Hallooo!
Ik heb 2 gonioformules, die heb ik nodig om een aantal berekeningen te kunnen maken, en wil ook weten waarom deze 2 vergelijkingen zo zijn.
Ik ben echter al een hele tijd bezig, en ik kom er niet uit.
Het gaat om de volgende 2:
Sin(x) = 2 * Sin(x/2) * Cos (x/2)
en
Cos (x) = 2 Cos²(x/2) -1
Kunnen jullie me helpen?
sin(x+y) = sin(x)·cos(y) + cos(x)·sin(y)
cos(x+y) = cos(x)·cos(y) - sin(x)·sin(y)
sin2(x) + cos2(x) = 1
Probeer het maar eens.
Of als je daar geen zin hebt:
SPOILERsin(x+y) = sin(x)·cos(y) + cos(x)·sin(y)
sin(2x) = 2·sin(x)·cos(x)
sin(x) = 2·sin(x/2)·cos(x/2)
cos(x+y) = cos(x)·cos(y) - sin(x)·sin(y)
cos(2x) = cos2(x) - sin2(x)
cos(2x) = cos2(x) - (1 - cos2(x))
cos(2x) = 2·cos2(x) - 1
*heb toch stiekem in de spoiler gekeken*
Het gaat om de DV:
dy/dx = -2 y/x + xy2, waarbij y(1) =0 als voorwaarde
We moeten dit oplossen mbv "de methode van variatie van constanten van Lagrange".
Nu staat in het boek uitgelegd hoe dit in zijn werking gaat voor een een inhomogene lineaire DV, dus
dy/dx = a(x) y + b(x)
en de opgaven in die vorm lukken ook wel, maar ik krijg de bovenstaande DV niet in deze vorm (wat waarschijnlijk te maken heeft met het feit dat deze DV volgens mij niet lineair is).
Dus nu is mn vraag: hoe los ik dit dan wel op (mbv "de methode van variatie van constanten van Lagrange") ???
Toevoeging: mocht het helpen, ik weet dat de oplossing is: y(x) = -1/(x2 * (Log(x) - 1))
quote:als je nou nog eens een keer de afgeleide naar y neemt of anders substitueert of zo. y ^2 = u bijvoorbeeld. deze richting moet je uit. Zal er zelf ook nog eens wat beter naar kijken.Op zondag 19 februari 2006 15:19 schreef Bioman_1 het volgende:
Ben bezig met een vak differentiaalvergelijkingen en moet wat opgaven maken, maar het wel echt niet lukkenMisschien dat jullie me kunnen helpen.
Het gaat om de DV:
dy/dx = -2 y/x + xy2, waarbij y(1) =0 als voorwaarde
We moeten dit oplossen mbv "de methode van variatie van constanten van Lagrange".
Nu staat in het boek uitgelegd hoe dit in zijn werking gaat voor een een inhomogene lineaire DV, dus
dy/dx = a(x) y + b(x)
en de opgaven in die vorm lukken ook wel, maar ik krijg de bovenstaande DV niet in deze vorm (wat waarschijnlijk te maken heeft met het feit dat deze DV volgens mij niet lineair is).
Dus nu is mn vraag: hoe los ik dit dan wel op (mbv "de methode van variatie van constanten van Lagrange") ???
Toevoeging: mocht het helpen, ik weet dat de oplossing is: y(x) = -1/(x2 * (Log(x) - 1))
of een nieuwe functie introduceren: f(x) = y(x) * x
[ Bericht 2% gewijzigd door McCarthy op 19-02-2006 19:17:25 ]
quote:Op vrijdag 17 februari 2006 18:21 schreef FritsFluitketel het volgende:
tvp
quote:Deze vergelijking is inderdaad niet lineair, het is echter een DV van Bernouilli. Een substitutie z = 1/y zorgt ervoor dat de vergelijking wél lineair wordt (met z(x) en y(x), uiteraard. Vergeet ook y'(x) niet te substitueren in functie van z(x) en x).Op zondag 19 februari 2006 15:19 schreef Bioman_1 het volgende:
Het gaat om de DV:
dy/dx = -2 y/x + xy2, waarbij y(1) =0 als voorwaarde
We moeten dit oplossen mbv "de methode van variatie van constanten van Lagrange".
Nu staat in het boek uitgelegd hoe dit in zijn werking gaat voor een een inhomogene lineaire DV, dus
dy/dx = a(x) y + b(x)
en de opgaven in die vorm lukken ook wel, maar ik krijg de bovenstaande DV niet in deze vorm (wat waarschijnlijk te maken heeft met het feit dat deze DV volgens mij niet lineair is).
Daarna bekom je zoals ik al zei een lineaire DV die je dan kan oplossen, achteraf terug substitueren (hetgeen zal neerkomen op omkeren van de oplossing).
mvg,
TD
http://www.miniscience.com/kits/DNAmodel/DNA_model5.jpg
http://www.open.ac.uk/science/biosci/images/research/DNA.jpg
Zijn 2 voorbeelden, maar ik heb geen idee hoe ik dit in elkaar ga krijgen
quote:Als tekening of als "kunstwerk"?Op maandag 20 februari 2006 20:53 schreef GotenSSJ het volgende:
Heeft iemand hier een goed idee om een DNA structuur te maken voor Biologie ?
http://www.miniscience.com/kits/DNAmodel/DNA_model5.jpg
http://www.open.ac.uk/science/biosci/images/research/DNA.jpg
Zijn 2 voorbeelden, maar ik heb geen idee hoe ik dit in elkaar ga krijgen
quote:KunstwerkOp maandag 20 februari 2006 22:32 schreef FritsFluitketel het volgende:
[..]
Als tekening of als "kunstwerk"?
____________ ____________
|____________| |____________|
____________ ____________
|____________| |____________|
Onderschrift
Oftewel. Ik heb 4 (.eps) figuren, die ik in LaTeX wil zetten als één figuur. Kan dit ??? Of moet ik echt met Paint (of iets dergelijks) gaan knippen en plakken en er zelf één figuur van maken???
quote:IJzerdraad en piepschuim? Of bedoel je niet zoiets?
quote:Als je een beetje een fatsoenlijk grafisch programma (photoshop, fireworks) hebt, dan lijkt me dat het handigst. Het zal ook wel rechtstreeks in LaTeX kunnen, maar precieze lay-out bepalen is daar gewoonlijk nogal wat geknutsel. Voor dit probleem ken ik de syntax niet uit men hoofd (kan je het niet in een array doen?), maar zoek eens op google: er zijn veel gratis LaTeX manuals te vinden.Op dinsdag 21 februari 2006 00:28 schreef Bioman_1 het volgende:
Oftewel. Ik heb 4 (.eps) figuren, die ik in LaTeX wil zetten als één figuur. Kan dit ??? Of moet ik echt met Paint (of iets dergelijks) gaan knippen en plakken en er zelf één figuur van maken???
ik heb een vraag over de vergelijking van Pell. ALs je een oplossing vindt, dan zijn de andere oplossingen niet moeilijk te generen. Dat kan bijv. met lineaire algebra(het kan oko met kettingbreuken):
matrices, diagonalisering etc.
Heeft iemand hier een site over?Zou iemand een voorbeeld willen geven? alvast bedankt
Laten we beginnen met kettingbreuken. Zij a0, a1,... een rij gehele getallen met ai>0 voor i>0. De n'de kettingbreuk die bij deze rij hoort is de uitdrukking
a0+1/(a1+1/(a2+1/(...)..)) (beetje lastig om het mooi op te schrijven).
Dit convergeert naar een bepaalde waarde in R. Het mooie is dat je ook andersom voor elk reeel getal een kettingbreuk kunt opschrijven. Er is zelfs een methode voor.
Begin met i := 0 en voer vervolgens
ai := [x], x := 1/(x-[x]), i := i+1 ([x] is hier de entier van x).
herhaaldelijk achterelkaar uit. Mocht x per ongeluk rationaal zijn dan stopt dit na een bepaald aantal stappen omdat x dan op een gegeven moment gelijk is aan [x].
Als je de kettingbreuk nu uitrekent behorende bij a0 t/m an voor een bepaalde n, dan komt daar een rationaal getal p/q uit dat een hele goede benadering is voor x (altijd is het zo dat |x-p/q|<1/q2 maar vaak nog wat beter).
Lees dit eerst maar even door, dan ga ik er straks wat meer over vertellen in connectie met Pellvergelijkingen.
Ondertussen een vraagje: heeft iedere pellvergelijking een oplossing?(hoe kan je zien of er geen oplo. bestaat)?
tot laters
quote:Laten we een eenvoudig voorbeeld geven met n=2. Voor een oplossing van x2-2y2=1 geldt dat x/y een goede benadering van w=wortel(2) is.Op donderdag 23 februari 2006 10:45 schreef thabit het volgende:
Als n kwadraatvrij is heeft x2-ny2=1 altijd een oplossing.
Laten we de kettingbreuk voor 2 eens opschrijven:
x=w, a0=[x]=1,
x:=1/(w-1)=w+1. a1=[x']=2.
x:=1/(w-1)=w+1, s2=2.
En dit blijft zo herhalen: 1,2,2,2,... zijn de kettingbreuk coefficienten.
In het algemeen heeft de kettingbreuk voor wortel(n) een herhalend deel. Laten we eens kijken wat voor convergenten we hebben.
1, 1+1/2=3/2, 1+1/(2+1/2)=7/5, etc.
Om een oplossing voor de Pell te pakken moet je geloof ik ofwel tot de helft van het herhalende stuk gaan ofwel het hele ding pakken.
In dit geval je zie dat (3,2) wel een oplossing is maar (7,5) niet.
Als we nu de kleinste oplossing gevonden hebben kunnen we ze ook allemaal vinden: werk (in ons geval) (3+2w)n uit tot a+bw, dan is (a,b) een oplossing en zo krijgen we ook alle oplossingen. Voorbeeld (3+2w)2=9+12w+8=17+12w en (17,12) is een oplossing.
[ Bericht 1% gewijzigd door thabit op 23-02-2006 11:22:06 ]
Twee even lange studenten gooien een bal naar elkaar in een hal van een groot gebouw. De initiele snelheid van de bal is V0. De hoogte van het plafond is H en elke bal wordt geworpen en gevangen (onder een zekere hoek theta) op schouderhoogte h van beide studenten.
Vraag 1: stel de bewegingsvergelijking op (=>- g = d2z/dt2)
Vraag 2: los op (=> z(t) = -1/2 g t 2+ v0t sin (theta) + h
Vraag 3: Laat d de maximale afstand zijn tussen de studenten zodat de bal het plafond niet raakt.. Toon aan dat :
d= 4 Sqrt [ (H-h) (v02/2g - (H-h)) ]
Die laatste vraag zorgt voor een probleem... wie helpt? (en controleerd of het antwoord bij 1 en 2 goed is
quote:Dit lijkt me flauwekul. Als H heel groot is staat er namelijk iets negatiefs binnen de wortel.Op donderdag 23 februari 2006 14:38 schreef maniack28 het volgende:
d= 4 Sqrt [ (H-h) (v02/2g - (H-h)) ]
x = v0*t*cos(a)
y=-1/2*g*t2 + v0*t*sin(a)+h
Het handigste is om gewoon bij x'' en y'' te beginnen, en dan 2 maal naar t te integreren. Dus x''=0, x'=v0cos(a), en y''=-g, y'=-g*t+v0sin(a).
Dan weet je r via r2=x2+y2 en
v2=(x')2+(y')2.
Bedenk eerst even dat allebei studenten even lang zijn, dus je kunt die h wel weglaten naar mijn idee; je trekt het hele systeem gewoon h naar beneden. Hiervoor compenseer je door in plaats van H, H-h te nemen. Het probleem is ook nog es symmetrisch rond R=1/2, ( met R de totale afgelegde weg in de x-richting )dus je weet dat op de helft van de x-waarde geldt dat y=maximaal. De afgelegde weg in de x-richting krijg je door y=0 op te lossen voor t ongelijk aan 0.
y=0--> t[v0*sin(a)-1/2*g*t]=0, en je hebt je t. Noem deze even T. Dan geldt dus dat de afgelegde weg in de x-richting gelijk is aan x(T), noem die ff R. Dus R=x(T). Nou weet je ook dat y maximaal is op R/2. Dan kom je een heel end, lijkt me
-edit:
ben ff in de war, die gonioregel kun je gebruiken om het bereik leuk uit te drukken. Wat jij natuurlijk nodig hebt is dat y(T/2)=H-h en x(T)=d. Dit kun je doen door de symmetrie en omdat x lineair is in t.
[ Bericht 2% gewijzigd door Haushofer op 23-02-2006 15:48:40 ]
Ik zit met een vraag (demand) naar een product die normaal verdeeld is met een gemiddelde van 100 en een standaardafwijking (sigma) van 50 per maand. Het is alleen praktischer als ik kan rekenen met weken, omdat ik dat daarna ook moet doen.
Het gemiddelde per week is eenvoudig: 100 / 4.33 (we gaan in deze casus uit van 4.33 weken per maand).
Nu zegt mijn vermoeden me dat de standaardafwijking, geen 50 blijft, maar ook geen (50 / 4.33). Mijn vermoeden zegt dat het (50 / (wortel(4.33))) moet worden, maar ik kan geen bewijs vinden en weet het ook niet 100% zeker.
Kan iemand me uit de brand helpen. Dan zoek ik ondertussen mijn statistiekboek nog maar eens door.
Ik begin toch weer te twijfelen
omdat de var een kwadraat is van je eenheid (bijvoorbeeld meters) is de sigma de wortel van de variantie, je wil de sigma in meters, niet in meters kwadraat.
dus Var(X) = 502 = sigma2
dus Var(X/4.33) = Var(X) / 4.332 = 502/4.332
dus je nieuwe sigma = 50/4.33
nu kan ik ff een stapje verder
Is een 'subgroup' hetgene dat men in het nederlands een 'ondergroep' noemt? Zo ja, waarom heet het niet gewoon een 'deelgroep' dan?
Ik ben wat opgaven aan 't maken en er zijn er een paar waar ik een beetje van in de war raak. Zo is er een opgave: "In Z6, the group of integers modulo 6, find the order of each element". Er staat echter niet bij of ze nu de additieve groep of de multiplicatieve groep bedoelen. Is er iets dat ik verkeerd of niet begrijp en zou ik moeten weten wat er precies bedoelt wordt of zou die vraag inderdaad duidelijker gesteld kunnen worden?
edit: oh wacht, nu realiseer ik me ineens dat Z6 onder de vermenigvuldiging helemaal geen groep is (maar een monoïde?).
En een willekeurige opgave waar ik niet uit kwam: "If G is a finite abelian group, show that G has an element g such that |g| is the least common multiple of { |a| : a is an element of G }.
[ Bericht 6% gewijzigd door spinor op 24-02-2006 20:44:05 ]
Z6 is een kutnotatie, beter is Z/6Z. (de indexnotatie wordt gebruikt voor p-adische getallen).
Ze bedoelen de additive groep. Z/6Z is immers geen groep onder vermenigvuldiging: 0 heeft bijvoorbeeld geen inverse.
Ken je de structuurstelling voor eindige abelse groepen?
En daarom geef ik hem vast de volgende informatie:
http://nl.wikipedia.org/wiki/Explosie
http://nl.wikipedia.org/wiki/gas
quote:Kijk eens naar de reactie boven je, misschien heb je daar wat aan?Op maandag 27 februari 2006 14:43 schreef Dr. het volgende:
mijn topic word overal geblokt maar ja iemand die wt hoe je gas tot ontploffing kan brengen en niet gelijk gaan doordenke en domme reacties plaatsen
Voor de rest kan ik je weinig helpen, misschien dat anderen er wat meer over kunnen zeggen
Is het huiswerk of gewoon interesse, enzovoorts
quote:Op dinsdag 21 februari 2006 00:28 schreef Bioman_1 het volgende:
Oftewel. Ik heb 4 (.eps) figuren, die ik in LaTeX wil zetten als één figuur. Kan dit ??? Of moet ik echt met Paint (of iets dergelijks) gaan knippen en plakken en er zelf één figuur van maken???
Aan de late kant: Gebruik subfigure of maak een figure omgeving met daarin minipages waar je de figuren in plaatst.
quote:Iig bedankt. Ik heb inmiddels ook al een andere manier gevonden. Ik gebruike het epsfig-package om figuren te includen, maar dat schijnt nogal ouderwets te zijn. Tegenwoordig gebruikt iedereen includegraphics ipv epsfig. En in deze omgeving kan je gewoon een array maken van je figuren. En daarbij hoeven je figuren ook niet meer .eps te zijn maar werken .pdf figuren ook gewoon.Op maandag 27 februari 2006 15:40 schreef Nekto het volgende:
[..]
Aan de late kant: Gebruik subfigure of maak een figure omgeving met daarin minipages waar je de figuren in plaatst.
* Et-Cetera denkt aan elektrocutie
In brandblussers zit ook vast vast CO2
quote:Dit antwoord komt een beetje laat vrees ik. Na 2 dagen zal de tv toch wel helemaal uitgefikt zijn.Op woensdag 1 maart 2006 11:31 schreef teigan het volgende:
Ik zou zeggen met een poederblusser, zand zou je ook kunnen doen, maar iig geen water dus..
In brandblussers zit ook vast vast CO2
quote:Op woensdag 1 maart 2006 11:54 schreef thabit het volgende:
[..]
Dit antwoord komt een beetje laat vrees ik. Na 2 dagen zal de tv toch wel helemaal uitgefikt zijn.
Hoeveel pentomino’s kan je vormen? (Afspraak: pentomino’s die je spiegelt of roteert leveren geen nieuwe pentomino’s op).
het antwoord is : 12
de oplossing: gewoon tekenen. En de geroteerde of gespiegelde pentomino's doorstrepen.
Ik vroeg me af hoe het anders kan: met algebra ofzo?!
Enig idee hoe het moet?
alvast bedankt
http://www.research.att.com/~njas/sequences/A000105

Kan iemand mij kort uitleggen wat deze 3 dingen inhouden en wat ik nu uit de grafiek kan afleiden?
Transmissie is doorlating dus het percentage dat doorgelaten wordt.
Emissie is wat het uitzendt, maar dat kan ik niet echt plaatsen, mischien licht dat op een andere golflengte wordt uitgezonden dan dat het ontvangen wordt.
De volgende uitspraken zijn equivalent:
Waarom is dat ? Wie kan er een lichtje over laten schijnen?
Zij S een deelverzameling van de complexe getallen. Bewijs dat de volgende uitspraken equivalent zijn.
Morgen tik ik het antwoord wel in, want ik ben nu te moe. Welke implicaties heb je trouwens al?
ik was bezig iets uit te zoeken over public key encrypton
ik laat mijn eigen voorbeeld zien van RSA
n = p * q 7 * 13 = 91
φ(n) = (p – 1) * (q – 1) 6 * 12 = 72
Dit is Eulers totient functie.
φ(n) = φ(p) * φ(q) omdat 7 en 13 beide priemgetallen zijn.
Dus het aantal relatieve priemgetallen voor 7 is 6 want dat zijn namelijk 1,2,3,4,5,6
Nu moet ik e kiezen.
e moet relatief priem zijn met 72 en kleiner zijn dan 72. Is 15 dan een goed antwoord of doe ik iets fout? de factoren van 72 zijn 6 en 12 en die van 15 5 en 3?
bij 15 werkt de berekening niet goed
van 5 weet ik dat die wel goed is maar waarom?
[ Bericht 12% gewijzigd door the_jasper op 05-03-2006 15:29:18 ]
(1)=>(3). Stel we hebben een oneindige deelverzameling Z van S die geen verdichtingspunt in S heeft. In het bijzonder is S dan zelf oneindig. Ook geldt voor elk punt van S dat we een open omgeving hebben die geen enkel element van Z bevat, behalve misschien dat punt zelf. Zo verkrijgen we een open overdekking van S. Deze open overdekking heeft geen eindige deel overdekking: de open delen om de punten in Z kunnen we niet weghalen omdat elk punt in Z slechts in 1 open deel ligt.
(2)=>(1). Zij S gegeven, tezamen met een oneindige open overdekking. We gaan nu de stelling gebruiken dat deze overdekking een aftelbare deeloverdekking heeft. Dit volgt uit het feit dat C een aftelbare basis heeft: we kunnen de open overdekking zien als verzameling open delen van C. Bij elk basiselement U kijken we of er een open deel in onze overdekking zit waarin U bevat is. Zo ja, dan nemen dit deel mee in de deeloverdekking. Zo nee, dan niet.
Onze aftelbare overdekking gaan we schrijven als een rij U1,U2,... . Als S niet compact is dan is er voor elke n een sn in S die niet in de vereniging van U1 t/m Un zit. De elementen s1,s2,... vormen nu ook weer een rij. Deze rij heeft per veronderstelling een verdichtingspunt s in S. Omdat de rij open delen nog altijd een overdekking is, zit s in een Un. Per constructie van onze rij geldt echter dat de open omgeving Un van s slechts eindig veel punten, geteld met multipliciteit, van de rij kan bevatten. Dit is in tegenspraak met het feit dat s een verdichtingspunt is.
quote:72=3*24.Op zondag 5 maart 2006 15:12 schreef the_jasper het volgende:
Hoi mijn post opniew, ik dacht dat dit alleen middelbare school wiskunde was.
ik was bezig iets uit te zoeken over public key encrypton
ik laat mijn eigen voorbeeld zien van RSA
n = p * q 7 * 13 = 91
φ(n) = (p – 1) * (q – 1) 6 * 12 = 72
Dit is Eulers totient functie.
φ(n) = φ(p) * φ(q) omdat 7 en 13 beide priemgetallen zijn.
Dus het aantal relatieve priemgetallen voor 7 is 6 want dat zijn namelijk 1,2,3,4,5,6
Nu moet ik e kiezen.
e moet relatief priem zijn met 72 en kleiner zijn dan 72. Is 15 dan een goed antwoord of doe ik iets fout? de factoren van 72 zijn 6 en 12 en die van 15 5 en 3?
bij 15 werkt de berekening niet goed
van 5 weet ik dat die wel goed is maar waarom?
quote:sorry die snap ik niet helemaal
ik probeer dit voor een werkstuk te doen ( 6 vwo)
en het werkt al wel helemaal en ik snap het verder ook wel (denk ik
kan je het plz een beetje meer uitleggen?
quote:Zowel 15 als 72 zijn deelbaar door 3, dus ze niet relatief priemOp zondag 5 maart 2006 17:02 schreef the_jasper het volgende:
[..]
sorry die snap ik niet helemaal
ik probeer dit voor een werkstuk te doen ( 6 vwo)
en het werkt al wel helemaal en ik snap het verder ook wel (denk ik)maar alleen deze stap snap ik gewoon nog niet en ik wil niet zomaar iets opschrijven
kan je het plz een beetje meer uitleggen?
ik begrijp het
Voor Biologie moet ik een praktische opdracht doen. Die bestaat uit een theoretisch gedeelte, en uit, jawel, een praktisch gedeelte. Ik moet kiezen uit 4 onderwerpen: suikerziekte, longcollaps, caissonziekte of uit insuline. Van 1 van die 4 onderwerpen moet ik informatie zoeken en dan een hypothese verzinnen en die dan vervolgens bewijzen met een proefje.
Hebben jullie misschien een idee over een proefje dat ik zou kunnen doen? Ik vraag dit niet op deze manier uit gemakzucht, want ik heb echt geen flauw idee.
misschien kan je cassionziekte simuleren door bepaalde beesten onder een drukpomp te leggen?
kijken welke beesten er wel en niet tegen kunnen (en nee ik bedeol geen formaat kat beesten ofzo)
Kan iemand mij meer vertellen over dit type vergelijking? Stel dat ik als resultaat 3 wil hebben, is dan te voorspellen wat x*y moet zijn?
quote:Zij a = x*y. Substitueer x=a/y in je vergelijking, dan krijg je:Op maandag 6 maart 2006 01:27 schreef bankrupcy het volgende:
(1+x/100)y is ongeveer 2 voor x*y =72
Kan iemand mij meer vertellen over dit type vergelijking? Stel dat ik als resultaat 3 wil hebben, is dan te voorspellen wat x*y moet zijn?
(1+a/(100*y))y=((1+a/(100*y))100*y/a)a/100
Schrijf nu z=y*100/a, dan staat er
((1+1/z)z)a/100
Dat ding in z heeft als limiet e als z naar oneindig gaat. Dus als je a zodanig kiest dat a/100 > ln( 3 ) dan weet je zeker dat er x en y zijn die aan jouw vergelijking voldoen.
@ WyBo : al iets bedacht?
quote:mja, vaag.Op maandag 6 maart 2006 12:36 schreef the_jasper het volgende:
ja ik zag al zo'n rondje staan
@ WyBo : al iets bedacht?
Insuline wordt aangetast door maagsap, vandaar dat het wordt ingespoten en niet door de mond. Misschien dat ik insuline en een zuur met dezelfde pH als maagsap bij elkaar zou kunnen doen, alleen hoe kan ik dan bewijzen dat het insuline is aangetast? Door pH te meten ofzo? Of door papierchromotografie? (dat zei mijn sk leraar maar zelf snap ik dat niet)
quote:als zuur kan je iig zoutzuur nemen dat zit ook in je maag.Op maandag 6 maart 2006 15:02 schreef WyBo het volgende:
[..]
mja, vaag.
Insuline wordt aangetast door maagsap, vandaar dat het wordt ingespoten en niet door de mond. Misschien dat ik insuline en een zuur met dezelfde pH als maagsap bij elkaar zou kunnen doen, alleen hoe kan ik dan bewijzen dat het insuline is aangetast? Door pH te meten ofzo? Of door papierchromotografie? (dat zei mijn sk leraar maar zelf snap ik dat niet)
dat over insuline weet ik niet precies
is er wel een indicator voor insuline?
mss moet je kijken of er een is voor de reactie producten die ontstaan
quote:is dat zo? Maar toon je dan ook werkelijk aan dat het is aangetast?Op maandag 6 maart 2006 15:22 schreef teigan het volgende:
Met papierchromatografie laat je denk ik de insuline lopen naast de insuline die dus in een pH"bad" is geweest.... Iedere stof heeft zijn eigen looptijd....
Mijn vraag gaat over kernfysica, ik ben bezig met een profielwerkstuk over onder andere kernsplijting en kernfusie. Ik ben echter nog niet helemaal zeker over het onderwerp bindingsenergie. Het is me bekend dat de som van de massa's van de nucleonen die een kern opbouwen groter is dan de massa van de kern zelf. In een kern is dus een deel van die massa van die nucleonen omgezet in energie. Nu wat ik niet snap: waar komt die massa vandaan? Leveren de nucleonen allemaal massa in, en zo ja, hoe is die verdeling, en hoe zit dat op quark niveau?
Ten tweede, wat gebeurd er met die energie die vrijkomt? Hier zijn bronnen niet allemaal even duidelijk over, de één zegt dat deze energie gebruikt wordt om de nucleonen te binden, dat ze de sterke kernkracht vormen die de kern bij elkaar houdt, die de onderlinge afstoting van de protonen tegen gaat. Of wordt deze energie afgestaan door de kern aan zijn omgeving, zo ja, hoe, doormiddel van fotonen met bepaalde kinetische energie?
Dan het kernsplijting/fusie verhaal. Ik ben bekend met de grafiek waar de bindingsenergie per nucleon uit wordt gezet tegen het massagetal. Wanneer de typische U-235 kern gespleten wordt ontstaan er twee dochterkernen die meer bindingsenergie per nucleon bevatten. Volgens mij is het zo dat het aantal nucleonen (grofweg) gelijk blijft en dat dus de opgetelde bindingsenergie toeneemt. Maar aan de andere kant, er komen ook drie neutronen in de reactie vrij, waardoor het totaal aantal nucleonen in de dochterkernen kleiner is dan in de moederkern, ik weet dat dit netto maar een verschil van twee neutronen is, maar is dit een verwaarloosbaar verschil? En daarbij weer de vraag over de bindingsenergie, waar komt die energie precies vandaan, en wat gebeurd er met die energie?
Dezelfde vraag is van toepassing op het kernfusie verhaal, idee dat twee lichtere kernen een zwaardere kern vormen die dus een hogere bindingsenergie per nucleon heeft, enz.
Ik begrijp het geloof ik allemaal wel in grote lijnen, maar er zijn nog genoeg punten waar ik nog erg onzeker over ben, en hoewel ik wel een aantal schoolboeken en (oude) universiteitsboeken heb, staat het er nergens duidelijk in. Zou iemand hier met enige zekerheid antwoord op kunnen geven?
Erhm, mijn broertje vertelde vanmiddag dus precies hetzelfde vraagstuk aan mij, had ie vandaag gehoord op school, jij ook misschien?
quote:Ik kan er geen touw aan vastknopen.Op maandag 6 maart 2006 22:04 schreef -jos- het volgende:
Even mijn reactie op het gesloten topic van die kansberekening:
Erhm, mijn broertje vertelde vanmiddag dus precies hetzelfde vraagstuk aan mij, had ie vandaag gehoord op school, jij ook misschien?
Wanneer hij op het begin 4 kiest, is er 10% kans dat hij in 4 zit, en 90% kan dat hij in de rest zit.. Wanneer er op het laatste dus alles 4 en 9 over zijn, is het dus een veel grotere kans dat hij in 9 zit dan in 4
Dat was vroeger ook met zo quizmaster met een auto op 1 van de drie plaatsen, je mocht dan altijd op het laatste nog kiezen of je wilde ruilen, nadat er 1 geopend was waar geen auto in zat... ik weet niet waarbij het was, maar ik ben dan ook pas 17
[ Bericht 16% gewijzigd door elby1988 op 06-03-2006 22:15:23 ]
quote:vraagje kansbereking
Ik vind het wel frappant want ik zeg dus dan mijn broertje vandaag precies hetzelfde vraagstuk op school heeft gehoord
Start:
Kans op goed geraden (#4 is prijs (#4P)) = 10%
Kans op #9P (maar dus niet geraden) = 10%
Kans op een van de acht andere kluizen = 80%
Na het openen van de acht lege kluizen is de kans op #4P nog steeds gelijk aan #9p alleen nu 50%.
Het openen van de lege kluizen heeft de kans dat de oorspronkelijke keus goed was groter gemaakt maar helemaal niets veranderd aan de verhouding tussen de nog niet geopende kluizen, er is van de inhoud van die kluizen geen informatie gegeven.
quote:Wat is dan het verschil met het Monty Hall Probleem a.k.a. 3 deuren probleem?Op maandag 6 maart 2006 22:29 schreef Barbaaf het volgende:
In het kort komt het hierop uit geloof ik:
Start:
Kans op goed geraden (#4 is prijs (#4P)) = 10%
Kans op #9P (maar dus niet geraden) = 10%
Kans op een van de acht andere kluizen = 80%
Na het openen van de acht lege kluizen is de kans op #4P nog steeds gelijk aan #9p alleen nu 50%.
Het openen van de lege kluizen heeft de kans dat de oorspronkelijke keus goed was groter gemaakt maar helemaal niets veranderd aan de verhouding tussen de nog niet geopende kluizen, er is van de inhoud van die kluizen geen informatie gegeven.
quote:In ieder geval dat in het geval van de TS de 8 deuren geopend zijn door de kandidaat, die niet weet of die kluis ook leeg zou zijn (wat gebeurt als de kandidaat een volle kiest vermeldt het verhaal niet).Op maandag 6 maart 2006 22:53 schreef _superboer_ het volgende:
[..]
Wat is dan het verschil met het Monty Hall Probleem a.k.a. 3 deuren probleem?
Bij het 3-deuren probleem is het anders: je hebt initieel 2/3 kans dat je het fout hebt. Als je het fout hebt is, na het openen van de bekende lege deur, de alternatieve zeker gevuld. Als je het goed had, met een kans van 1/3, moet je niet switchen maar die kans is dus kleiner.
... nu ik er meer over nadenk denk ik dat je met die 10 deuren ook moet switchen, aan de andere kant, bekijk het zo: Je moet 10 kluizen openen, ééntje heeft inhoud en die mag je pas op het laatst openen, open je hem eerder ben je af. Als je er dan 8 gehad hebt, maakt het dan uit welke kluis je in eerste instantie in gedachten had?
quote:Iemand?Op maandag 6 maart 2006 15:24 schreef WyBo het volgende:
[..]
is dat zo? Maar toon je dan ook werkelijk aan dat het is aangetast?
quote:Nou, ik heb niet echt een idee hoe dit aan te moeten tonen. Het stond in het Complexe Analyse boek van Serge Lang, en ik was er dit weekend weer even mee bezig. Nou is het niet heel belangrijk ofzo, maar ik vroeg het me gewoon af.Op zaterdag 4 maart 2006 23:33 schreef thabit het volgende:
Die vraag is verkeerd gesteld. De eerste uitspraak is namelijk waar en de tweede en de derde zijn onzin want je veronderstelt daar niets over S. De vraag moet waarschijnlijk luiden:
Zij S een deelverzameling van de complexe getallen. Bewijs dat de volgende uitspraken equivalent zijn.S is compact. Elke rij van elementen van S heeft een verdichtingspunt in S. Elke ondeindige deelverzameling van elementen van S heeft een verdichtingspunt in S. Elke rij elementen in S heeft een convergente deelrij met limiet in S.
Morgen tik ik het antwoord wel in, want ik ben nu te moe. Welke implicaties heb je trouwens al?
quote:Als je drie afzonderlijke massa's hebt, en die bind je tot een deeltje, dan is de totale gebonden massa iets minder dan de som van de massa's. De rest wordt in bindingsenergie omgezet, via E=mc2. Hoe dat zit op quarkniveau is iets subtieler; je kunt niet een losse quark nemen en daar de massa van meten. Ze zitten namelijk opgesloten in een systeem, het zogeheten "confinement problem". De sterke kernkracht tussen 2 deeltjes heeft een erg kort bereik, maar ze neemt wel toe als de afstand tussen de quarks toeneemt ! Dat is dus het tegenovergestelde van de andere krachten.Op maandag 6 maart 2006 18:47 schreef -Mzraki- het volgende:
Mijn vraag gaat over kernfysica, ik ben bezig met een profielwerkstuk over onder andere kernsplijting en kernfusie. Ik ben echter nog niet helemaal zeker over het onderwerp bindingsenergie. Het is me bekend dat de som van de massa's van de nucleonen die een kern opbouwen groter is dan de massa van de kern zelf. In een kern is dus een deel van die massa van die nucleonen omgezet in energie. Nu wat ik niet snap: waar komt die massa vandaan? Leveren de nucleonen allemaal massa in, en zo ja, hoe is die verdeling, en hoe zit dat op quark niveau?
quote:Wat bedoel je precies met "de energie die vrijkomt"? Die bindingsenergie? Die wordt veroorzaakt door de sterke kernkracht. Die wordt voortgezet door zogenaamde pionen, tenminste, dat nam men aan. Nou blijken die pionen ook weer uit 2 quarks te bestaan, dus dat is niet helemaal juist. Die quarks worden echter weer bijmekaar gehouden door gluonen, en deze worden dan gezien als de ware overbrengers van de sterke kernkracht.Ten tweede, wat gebeurd er met die energie die vrijkomt? Hier zijn bronnen niet allemaal even duidelijk over, de één zegt dat deze energie gebruikt wordt om de nucleonen te binden, dat ze de sterke kernkracht vormen die de kern bij elkaar houdt, die de onderlinge afstoting van de protonen tegen gaat. Of wordt deze energie afgestaan door de kern aan zijn omgeving, zo ja, hoe, doormiddel van fotonen met bepaalde kinetische energie?
quote:Ik weet niet of je de term al kent, maar google eens even op Liquid Drop model Een heel simpel model waarbij de kern wordt gezien als een heel stevig druppeltje vloeistof. Dit model wordt in heel veel takken van de kernfysica gebruikt. De bindingsenergie per nucleon blijkt eerst toe te nemen, daarna heel langzaam te stijgen totdat Z=60, en daarna weer af te nemen. Het is dus energetisch economischer om elementen met Z<60 te fuseren, en om elementen met Z>60 te splitsen ( fisseren ).Dan het kernsplijting/fusie verhaal. Ik ben bekend met de grafiek waar de bindingsenergie per nucleon uit wordt gezet tegen het massagetal. Wanneer de typische U-235 kern gespleten wordt ontstaan er twee dochterkernen die meer bindingsenergie per nucleon bevatten. Volgens mij is het zo dat het aantal nucleonen (grofweg) gelijk blijft en dat dus de opgetelde bindingsenergie toeneemt. Maar aan de andere kant, er komen ook drie neutronen in de reactie vrij, waardoor het totaal aantal nucleonen in de dochterkernen kleiner is dan in de moederkern, ik weet dat dit netto maar een verschil van twee neutronen is, maar is dit een verwaarloosbaar verschil? En daarbij weer de vraag over de bindingsenergie, waar komt die energie precies vandaan, en wat gebeurd er met die energie?
Je moet bij zo'n splitsing dus kijken wat de totale energie voor en na is, en daarbij kun je zeker geen 3 neutronen gaan verwaarlozen.
quote:Er wordt tijdens de reactie dus massa omgezet, dat begrijp ik, maar hoe moet ik dat dan precies zien? Wat voor massa verdwijnt er? Ik neem aan dat het niet zo is dat alle nucleonen een bepaald deel van hun massa inleveren en dat die dan om wordt gezet in energie, puur alleen al omdat nucleonen blijkbaar weer uit quarks bestaan, en je daar niet zomaar een deel van af kan schaven. Maar hoe valt dan het verschil in massa te verklaren? Heeft het te maken met het verschil tussen de rustmassa (waar ik bij mijn berekeningen van uitga) en een bewegingsmassa?Op dinsdag 7 maart 2006 09:51 schreef Haushofer het volgende:
[..]
Als je drie afzonderlijke massa's hebt, en die bind je tot een deeltje, dan is de totale gebonden massa iets minder dan de som van de massa's. De rest wordt in bindingsenergie omgezet, via E=mc2. Hoe dat zit op quarkniveau is iets subtieler; je kunt niet een losse quark nemen en daar de massa van meten. Ze zitten namelijk opgesloten in een systeem, het zogeheten "confinement problem". De sterke kernkracht tussen 2 deeltjes heeft een erg kort bereik, maar ze neemt wel toe als de afstand tussen de quarks toeneemt ! Dat is dus het tegenovergestelde van de andere krachten.
quote:Inderdaad, die bindingsenergie die gevormd wordt uit de omzetting van massa. Wordt die opgeslagen in de vorm van potentiële energie? Aangezien in een kern de afstotende coulombkracht is overwonnen kan ik me voorstellen dat de nucleonen een aanzienlijke potentiële energie bezitten. Maar aan de andere kant, ze zitten wat sterke kernkracht betreft al in een energie gunstige positie, want, hoe verder de nucleonen van elkaar afzitten, hoe sterker de sterke kernkracht wordt (Of gaat dit alleen voor quarks op?). Is dat het geval dan zou het dus energie kosten om de nucleonen van elkaar te trekken, en is er dus geen potentiële energie. Waar is die bindingsenergie dan heen?Wat bedoel je precies met "de energie die vrijkomt"? Die bindingsenergie? Die wordt veroorzaakt door de sterke kernkracht. Die wordt voortgezet door zogenaamde pionen, tenminste, dat nam men aan. Nou blijken die pionen ook weer uit 2 quarks te bestaan, dus dat is niet helemaal juist. Die quarks worden echter weer bijmekaar gehouden door gluonen, en deze worden dan gezien als de ware overbrengers van de sterke kernkracht.
quote:Liquid Drop ken ik nog niet, ik zal daar ook nog even naar zoeken. Gisteravond heb ik ook nog wat berekeningen gedaan aan de splijting van een uranium-235 kern, nadat ik een site had gevonden waar ze het volgende deden:Ik weet niet of je de term al kent, maar google eens even op Liquid Drop model Een heel simpel model waarbij de kern wordt gezien als een heel stevig druppeltje vloeistof. Dit model wordt in heel veel takken van de kernfysica gebruikt. De bindingsenergie per nucleon blijkt eerst toe te nemen, daarna heel langzaam te stijgen totdat Z=60, en daarna weer af te nemen. Het is dus energetisch economischer om elementen met Z<60 te fuseren, en om elementen met Z>60 te splitsen ( fisseren ).
Je moet bij zo'n splitsing dus kijken wat de totale energie voor en na is, en daarbij kun je zeker geen 3 neutronen gaan verwaarlozen.
quote:http://www.einstein-online.info/en/spotlights/binding_energy/Uranium-235 (consisting of 92 protons and 143 neutrons) has a binding energy of roundabout 7.6 MeV per nucleon. For barium-141 (56 protons, 85 neutrons) the binding energy is 8.3 MeV, for krypton-92 (36 protons, 56 neutrons) 8.5 MeV per nucleon. Nuclear fission occurs when uranium-235 is bombarded by an additional neutron, and for every nucleus of uranium-235 results in one nucleus of barium-141, one of krypton-92, and three single neutrons. Before the fission, the total binding energy is 235 times 7.6 MeV = 1786 MeV. For the fission products barium and krypton however, the binding energies of 141 times 8.3 MeV (barium) and 92 times 8.5 MeV (krypton) sum up to 1952 MeV. The difference, 166 MeV, is the energy released in the fission process.
Hier nemen ze de drie neutronen dus niet mee in de vergelijking, laat een beetje zien wat ik bedoelde met dat verwaarlozen van die drie neutronen. Daarna heb ik naar de exacte massa's voor en na de reactie gekeken, om zo het massadefect te bepalen, daarin heb ik natuurlijk wel die drie neutronen meegenomen. Ik heb voor het gemak dezelfde splijtingsreactie gebruikt:
quote:Opvallend verschil, zij zeggen 166 MeV, ik zeg 266 MeV, ik denk dat dat vooral te wijten is aan de onnauwkeurige bepaling van de bindingsenergie per nucleon die zij gebruikt hebben, of niet?Voor de reactie was er een totale massa van:
massa uranium-235 atoom – massa 92 elektronen + massa neutron =
235,04393 u – 92 x 0,00054858 u + 1,008665 u = 236,0021256 u
Na de reactie was er een krypton-92 kern, een barium-141 kern en drie neutronen, dit heeft een totale massa van:
massa krypton-92 atoom – massa 36 elektronen + massa barium-141 atoom – 56 elektronen + massa drie neutronen =
91,826111 u – 36 x 0,00054858 u + 140,91441 u – 56 x 0,00054858 u + 3 x 1,008665 u = 235,7160466 u.
Het verschil in massa is dus massa voor reactie – massa na reactie = 236,0021256 u – 235,7160466 u = 0,28607896 u. De atomaire massaeenheid u is gelijk aan 1,66054 x 10^-27 kg, dus 0,28607896 u = 4,7505556 x 10^-28 kg. Dit is de massa die verdwenen is tijdens de splijtingsreactie. De massa moet dus omgezet zijn in energie. Als we de massa invullen in de formule E=mc^2 krijgen we: (4,7595556 x 10^-28 kg) x (2,99792458 x 10^8 m/s)^2 = 4,26949654 x 10^-11 Joule. Dit is gelijk aan 266,48 x 10^6 elektron volt= 266,48 MeV. Bij de splijting van één uranium-235 kern komt er dus ongeveer 266,48 MeV vrij als het volgens deze splijtingsreactie verloopt.
Afgelopen vrijdag een toets van mn wiskunde bijles (om zonder achterstand naar het hbo te kunnen na het mbo) redelijk verkloot, ik dacht dat ik het snapte, niet dus, extra opdrachten gevraagd maar nu zit ik dus vast.
De vraag:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
Dat betekent: x - 6 = 0 of x + 1 = 0 En dus zijn de oplossingen x=6 en x=-1
'controleer ze maar'
Ik snap er werkelijk NIETS van.. waar haalt ze die 6 en 1 vandaan en waar is mn x^2 gebleven
Mare, werk dat eens uit dan, vanaf het begin?? hier heb ik natuurlijk geen reed aan he
quote:Je vergelijking is daardoor echter (x + 6)(x - 1) = 0. Wat zij zegt is onzin, maar als je het had gesnapt was dat het probleem niet geweest. Echter, een (lange) uitleg, maar wel met de goede vergelijking. De uitleg komt eerst, die is ook voor het snappen, dan komt het stukje Truuk, die vooral de truuk uitlegt.Op dinsdag 7 maart 2006 16:24 schreef Robin__ het volgende:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
We bekijken x^2 + 5x = 6. Merk op dat x^2 natuurlijk gewoon hetzelfde is als x * x. En 5x is 5 * x. (Dat als allereerste).
Ik neem aan dat je bekend bent met haakjes wegwerken. Dat wil zeggen, als er x*(3 + 5x) staat, dan is dit hetzelfde als x*3 + x*5x. Je vermenigvuldigt die x met alle termen die binnen de haakjes staan. Merk dan op dat je na dat vermenigvuldigen in elke term termen zijn overigens de naam voor de losse 'dingen' in een optelling, dus 3 + 5 + 9 heeft termen 3, 5 en 9, en 3x + 5 heeft termen 3x en 5 dezelfde factorfactor is een onderdeel van een vermenigvuldiging, dus 3x heeft factoren 3 en x aantreft, namelijk 'x'.
Die factor kun je zogezegd weer buiten haakjes halen. Dat is ook wel logisch, want als x(3 + 5x) gelijk is aan 3x + 5x^2, dan moet natuurlijk 3x + 5x^2 ook gelijk zijn aan x(3 + 5x). En inderdaad, door driftig uitschrijven kun je dat oefenen.
Ik hoop dat je bijvoorbeeld inziet dat x(5 + 8x) = 5x + 8x^2, en ook omgekeerd, of dat x^2(6 + 9x) = 6x^2 + 9x^3. En dat je net zogoed in plaats van 4x + 8x^2 ook 4x(1 + 2x) kunt schrijven (die is al wat gemener, want we halen de factor 4x eruit).
In jouw voorbeeld halen ze ook buiten haakjes. De eerste stap begint met:
x^2 + 5x = 6 om te zetten in x^2 +5x - 6 = 0 (dat levert geen problemen). Nu moeten er echter die haakjes gevonden worden. Ik denk dat je wel ziet dat als je (x + 6)(x - 1) uitschrijft, je weer op x^2 + 5x - 6 uitkomt, immers:
(x + 6)(x - 1) = (x + 6)*x + (x + 6)*1 = x*x + 6*x - 1*x - 6 = x^2 +(6 - 1)*x - 6 = x^2 +5x - 6.
Merk op dat we bij die laatste stap in feite weer factoren binnen haakjes brengen, want er zijn twee termen die een 'x' gemeen hebben, dus die kunnen we samenvoegen.
Truuk
De truuk is nu (en dat is het belangrijkste) hoe te herkennen wat je moet doen als je een kwadratische vergelijking hebt, en je die als product van twee sommen (x + a)(x + b) wilt schrijven.
Welnu, laten we eerst de som (x + a)(x + b) uitschrijven, dat geeft:
(x + a)(x + b) = (x + a)x + (x + a)b = x^2 + a*x + x*b + a*b = x^2 + (a + b)*x + a*b
Merk weer hoe we haakjes inbrengen om de twee termen die elk een factor x hebben samen te nemen. Nu komt de truuk, als je een willekeurige vergelijking x^2 + c*x + d hebt, vindt dan twee getallen a en b zodat c = a + b en d = a * b. Daar moet je wellicht even op broeden, maar dat is eigenlijk wat hierboven in die formule staat.
En als we dat dan nu gaan toepassen op jouw formule:
x^2 + 5x -6 = 0.
We zien dat c = 5, en d = -6. Nu wordt het gewoon wat proberen om a en b te vinden meestal, Zeg a = 2, b = 3. Dan a + b = 5, dat klopt, maar a * b = 6, dus dat kan niet kloppen. Sterker nog, we zien aan de -6 dat of a of b wel negatief moet zijn. (Goede truuk om te onthouden, is d negatief, dan is een van a of b ook negatief). Dus, zeg a = -2, dan moet b wel 3 zijn, maar -2 + 3 = 1, dus dat kan ook niet. Enfin, om een al lang verhaal toch iets korter te maken: a = 6 en b = -1. Dit klopt precies, immers 6 *- 1 = -6 en 6 + (-1) = 5.
Dus, je vult nu de linkerkant van die hele vergelijking in, en je krijgt dat in dit geval:
(x + a)(x + b) moet zijn: (x + 6)(x - 1).
Nou, hopelijk is dat na een tijdje oefenen duidelijk genoeg.
[ Bericht 0% gewijzigd door Nekto op 07-03-2006 16:57:14 ]
quote:Sorry maar hier gaat het al mis.. 6 punt x^2????
snap je dat?
quote:Die punt is een zins-einde teken daar.Op dinsdag 7 maart 2006 16:52 schreef Robin__ het volgende:
[..]
Sorry maar hier gaat het al mis.. 6 punt x^2????
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
quote:Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1Op dinsdag 7 maart 2006 16:34 schreef McCarthy het volgende:
x = -6 en x = +1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
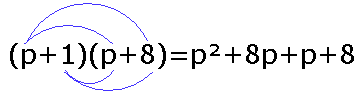
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
quote:Op dinsdag 7 maart 2006 16:24 schreef Robin__ het volgende:
Sorry dat ik zo kom binnenvallen.. maar ik heb ook een vraag
Afgelopen vrijdag een toets van mn wiskunde bijles (om zonder achterstand naar het hbo te kunnen na het mbo) redelijk verkloot, ik dacht dat ik het snapte, niet dus, extra opdrachten gevraagd maar nu zit ik dus vast.
De vraag:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
Dat betekent: x - 6 = 0 of x + 1 = 0 En dus zijn de oplossingen x=6 en x=-1
'controleer ze maar'
Ik snap er werkelijk NIETS van.. waar haalt ze die 6 en 1 vandaan en waar is mn x^2 gebleven
quote:Ja, maar, in zijn voorbeeld wordt niet juist ontbonden. Als de vergelijking x^2 + 5x - 6 is, dan is de ontbinding niet (x - 6)(x + 1), maar (x + 6)(x - 1). Als de ontbinding (x - 6)(x + 1) is, dan is de vergelijking echter x^2 -5x -6.Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
quote:Ah, overheen gezienOp dinsdag 7 maart 2006 17:07 schreef Nekto het volgende:
[..]
Ja, maar, in zijn voorbeeld wordt niet juist ontbonden. Als de vergelijking x^2 + 5x - 6 is, dan is de ontbinding niet (x - 6)(x + 1), maar (x + 6)(x - 1). Als de ontbinding (x - 6)(x + 1) is, dan is de vergelijking echter x^2 -5x -6.
quote:zal ik het maar overnemen want dit gaat didactisch gezien helemaal foutOp dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
[afbeelding]
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
quote:Jaja, ik heb het al gezien, maar de rest van wat ik vertel klopt toch aardig of niet?Op dinsdag 7 maart 2006 17:10 schreef McCarthy het volgende:
[..]
zal ik het maar overnemen want dit gaat didactisch gezien helemaal fout
quote:ik zei alleen dat het didactisch gezien niet echt handig isOp dinsdag 7 maart 2006 17:11 schreef Litso het volgende:
[..]
Jaja, ik heb het al gezien, maar de rest van wat ik vertel klopt toch aardig of niet?
quote:Ach, als je maar weet hoe het werktOp dinsdag 7 maart 2006 17:14 schreef Nekto het volgende:
Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.
Als je er in geïnteresseerd bent of van plan er verder mee te werken is het wel zo handig als je dat weet inderdaad, maar ik kan me voorstellen dat er mensen zijn die liefst na hun examen niks meer met wiskunde te maken willen hebben
quote:Want?Op dinsdag 7 maart 2006 17:15 schreef McCarthy het volgende:
[..]
ik zei alleen dat het didactisch gezien niet echt handig is
quote:omfgOp dinsdag 7 maart 2006 17:14 schreef Nekto het volgende:
Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.
anders onthouden ze het niet of zo?
dat het eigenlijk de regel x(y + z) = xy + xz is wordt ze ook al niet verteld
onderwijs in NEderland
allemaal de schuld van de PvdA
quote:Tussen droom en daad staan wetten in de weg, en praktische bezwaren.Op dinsdag 7 maart 2006 17:16 schreef Litso het volgende:
maar ik kan me voorstellen dat er mensen zijn die liefst na hun examen niks meer met wiskunde te maken willen hebben
quote:papagaaienregels en zo
da's niks
quote:versus die van jouOp dinsdag 7 maart 2006 16:58 schreef McCarthy het volgende:
in brief
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
quote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
[afbeelding]
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
quote:Voor iemand die van deze som al geen hout snapt en zich afvraagt waar zijn kwadraat heen is kan ik me voorstellen dat diegene ook niet al teveel aan jouw post heeft.
quote:Begrijp me niet verkeerd, ik heb niks tegen wiskunde, ik ben zelf meer een bètamens dan wat anders. Ik zie ook wel degelijk het nut in van wiskunde, ook voor later. Maar als iemand het ontbinden in factoren nou eenmaal makkelijker begrijpt door de naam papegaaienbek te gebruiken denk ik dat je beter gelukkig kan zijn dat hij weet hoe hij het toe moet passen dan zeuren dat hij de goede naam niet gebruiktOp dinsdag 7 maart 2006 17:16 schreef Nekto het volgende:
[..]
Tussen droom en daad staan wetten in de weg, en praktische bezwaren.
quote:ik stel voor dat we dan thabit op hem af sturenOp dinsdag 7 maart 2006 17:18 schreef Litso het volgende:
[..]
Voor iemand die van deze som al geen hout snapt en zich afvraagt waar zijn kwadraat heen is kan ik me voorstellen dat diegene ook niet al teveel aan jouw post heeft.
enes kijken hoe dat uitpakt.
quote:toch lijkt me dit makkelijkerOp dinsdag 7 maart 2006 17:20 schreef Litso het volgende:
[..]
Begrijp me niet verkeerd, ik heb niks tegen wiskunde, ik ben zelf meer een bètamens dan wat anders. Ik zie ook wel degelijk het nut in van wiskunde, ook voor later. Maar als iemand het ontbinden in factoren nou eenmaal makkelijker begrijpt door de naam papegaaienbek te gebruiken denk ik dat je beter gelukkig kan zijn dat hij weet hoe hij het toe moet passen dan zeuren dat hij de goede naam niet gebruikt
x(y + z) = xy + xz
quote:Makkelijker, wiskundig sowieso veel verantwoorder, maar ik pretendeer dan ook niet dat ik beter wiskunde kan dan jij (integendeel, ik ben bang dat mijn kennis het snel af laat weten). Maar misschien is wat extra uitleg eromheen wel handig. Misschien ook niet. We merken het wel als hij nog reageertOp dinsdag 7 maart 2006 17:22 schreef McCarthy het volgende:
[..]
toch lijkt me dit makkelijker
x(y + z) = xy + xz
quote:
En wow wat een reacties verder
Even een check, ik ben al aan de volgende som begonnen en wil even weten of ik goed onderweg ben
Los op: x^2 + x = 4x + 28
x^2 + x = 4x + 28 (-4x)
x^2 -3x = 28 (-28)
x^2 -3x - 28 = 0
Dan uit nekto's verhaal het a+b=c en a*b=d
a+b = c (-3)
axb = d (-28)
wat dan word
(x a)(x b) = 0 En dan vervolgens het antwoord maar dat is een eitje
Klopt dit tot zo ver? En er is dus geen andere manier, behalve een beetje puzzelen, om A en B te vinden?
Maar mooi dat het nu wil lukken
quote:Beetje puzzelen kom je er wel. Als het beide een negatief getal weet je wel dat van a en b eentje negatief is, en eentje positief. In dit geval is het -7 en 4.Op dinsdag 7 maart 2006 17:32 schreef Robin__ het volgende:
[..]


En wow wat een reacties verderNekto heel erg bedankt voor je uitleg, al werd ik er wat draaiering van
Even een check, ik ben al aan de volgende som begonnen en wil even weten of ik goed onderweg ben
Los op: x^2 + x = 4x + 28
x^2 + x = 4x + 28 (-4x)
x^2 -3x = 28 (-28)
x^2 -3x - 28 = 0
Dan uit nekto's verhaal het a+b=c en a*b=d
a+b = c (-3)
axb = d (-28)
wat dan word
(x a)(x b) = 0 En dan vervolgens het antwoord maar dat is een eitje
Klopt dit tot zo ver? En er is dus geen andere manier, behalve een beetje puzzelen, om A en B te vinden?
Dus in dit geval wil je 2 getallen hebben die: opgeteld 5 en vermenigvuldigt -6 zijn...
dus -1 en 6 zijn geschikt...
Werk (x-6)(x+1) maar eens uit, haal de haakjes maar weer weg, en je hebt (als het goed is) je eerste vergelijking weer
quote:Ik ben goed voor een aardige discussie zie ikOp dinsdag 7 maart 2006 17:25 schreef Litso het volgende:
[..]
Makkelijker, wiskundig sowieso veel verantwoorder, maar ik pretendeer dan ook niet dat ik beter wiskunde kan dan jij (integendeel, ik ben bang dat mijn kennis het snel af laat weten). Maar misschien is wat extra uitleg eromheen wel handig. Misschien ook niet. We merken het wel als hij nog reageert
Ik ben wel bekend met het papagaaienbek verhaal (vorig jaar ergens) en mn natuurkunde leraar heeft ooit tussen neus en lippen door gemeld dat dat hetzelfde is als 'x(y + z) = xy + xz'
quote:wat studeer je dan?Op dinsdag 7 maart 2006 17:25 schreef Litso het volgende:
[..]
Makkelijker, wiskundig sowieso veel verantwoorder, maar ik pretendeer dan ook niet dat ik beter wiskunde kan dan jij (integendeel, ik ben bang dat mijn kennis het snel af laat weten).
quote:Dat woord uitgesproken door mijn wiskunde lerares lijkt me zwaar humorOp dinsdag 7 maart 2006 17:56 schreef Nekto het volgende:
distributiviteitsaxioma
Ik blijf dit topic zeker volgen, misschien steek ik er nog wat van op, of kan ik zelf eens iemand helpen, al gaan de meeste vragen hier mij voorlopig zwaar de pet te boven. Ik volg trouwens een opleiding werktuigbouwkunde, mbo, niv 4, 3e jaar. Dit jaar alleen maar een of ander competentie gestuurd bullshit project en sporadisch een les pneumatiek of autocad. Op vrijdag middag dus 2 uur natuurkunde en 2 uur wiskunde voor hbo doorstroom.. en schijnbaar is de tijd dat ik lekker achterover kan leunen en toch goede cijvers halen nu toch voorbij (ben er zowaar een beetje blij om
Thanks voor de uitleg
quote:Digitale Communicatie. Ik vind wiskunde wel interessant maar ik ben er niet super goed in.
quote:Omdat de vermenigvuldiging ' x ' teveel lijkt op de variabele x, vriendelijk doch dringend het verzoek het de vermenigvuldigings ' x ' niet te gebruiken. axb betekent a vermenigvuldigd met x vermenigvuldigd met b. Jij bedoelt ab.
quote:Wat bedoel je met ' (x a)(x b) = 0 '. Het lijkt allemaal onbelangrijk, maar netjes werken in de wiskunde is erg belangrijk. Alles heeft een betekenis, dus wees precies.wat dan word
(x a)(x b) = 0 En dan vervolgens het antwoord maar dat is een eitje
quote:abc-formule: x1,2=(-b±SQR(b2-4ac))/2aKlopt dit tot zo ver? En er is dus geen andere manier, behalve een beetje puzzelen, om A en B te vinden?
Uitgaande van x2 -3x - 28 = 0 geeft dit
a=1
b=-3
c=-28
Invullen levert dan
x1,2=(3±SQR(9-(-112)))/2
x1,2=(3±11)/2
x1=(3-11)/2=-4 en x2=(3+11)/2=7
Je gebruikt hier de volgende regel, die alleen bij tweedegraads vergelijkingen werkt.
Je hebt de vorm x^2 + Qx - P
Nu moet je 2 getallen vinden, die opgeteld Q zijn, en vermenigvuldigd P. Als het goed is, is dit de regel. Waarom het zo is, vraag het me niet, dat is gewoon zo :p
Dus bij jou moet je 2 getallen vinden, die opgeteld 5 zijn, en vermenigvuldigd -6.
Beetje puzzelen, en dan kom je op -1 en 6
-1 * 6 = -6
-1 + 6 = 5
Je vergelijking is daardoor (x-6)(x+1)=0
Hier vermenigvuldig je 2 getallen met elkaar, die dan 0 zijn.
Dat kan alleen maar als 1 van die 2 getallen nul is.
Dus
x - 6 = 0
of
x + 1 = 0
x is dus 6 of -1.
En dat klopt, dat zie je ook als je 'm plot in je rekenmachine...
Ik hoop dat je een beetje geholpen bent
__
Zoo, dan had ik zelf ook nog een vraag
Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig
quote:Op woensdag 8 maart 2006 15:16 schreef Market_Garden het volgende:
Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig

Erg goed boek. Goed leesbaar voor leken, tevens zeer interessant voor vakmensen.
quote:Op woensdag 8 maart 2006 15:16 schreef Market_Garden het volgende:
En dat klopt, dat zie je ook als je 'm plot in je rekenmachine...
quote:Ik neem aan dat je dit bewijs van Ivan Niven hebt gevonden.Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig
Dat is een elegant bewijs, ik heb het ooit gesnapt (was volgens mij ook niet zo moeilijk), maar het helemaal uittypen, dat wordt me te veel werk, dus zeg waar je vastloopt. Let op de notatie f<sup>(2)</sup> betekent de tweede afgeleide van f, etc. (De rest lijkt me wel duidelijk).
Onderstaand boek bevat ook een goed volgbaar bewijs van de irrationaliteit van Pi (en nog andere elegante bewijzen):

[ Bericht 11% gewijzigd door Nekto op 08-03-2006 15:43:15 ]
Omdat ik de oppervlakte moet uitrekenen van een bepaald gedeelte onder een grafiek, heb ik een integraal opgesteld. Om die integraal op te lossen moet ik de volgende functie primitiveren:
f(x) = 100 * 0,998x
Iemand enig idee hoe ik dit moet oplossen en wat de uitkomst is? Ik heb zelf wel wat zitten klungelen, maar op het goede antwoord kwam ik niet.
Bedankt alvast
quote:Als je een exponent differentieert met als grondgetal ongelijk aan e krijg je: f(x) = g^x -> f'(x) = ln(g).g^xOp woensdag 8 maart 2006 18:55 schreef Floriz87 het volgende:
Wiskunde - primitiveren:
Omdat ik de oppervlakte moet uitrekenen van een bepaald gedeelte onder een grafiek, heb ik een integraal opgesteld. Om die integraal op te lossen moet ik de volgende functie primitiveren:
f(x) = 100 * 0,998x
Iemand enig idee hoe ik dit moet oplossen en wat de uitkomst is? Ik heb zelf wel wat zitten klungelen, maar op het goede antwoord kwam ik niet.
Bedankt alvast!
Vang die ln(g) op en je hebt je primitieve.
De primitieve is btw: F(x) = ( 100 / ln0,998 ) * 0,998^x
Bedankt iig!
Ik heb dus insuline, 3 ml geregeld. Die gaan we onder andere samenvoegen met pepsine en dan gaan we bij de drie stoffen die we dan hebben kijken hoe ze uitlopen bij papierchromotografie.
Ik wil dus gaan aantonen dan insuline wordt aangetast door het maagsap.
Dus 1x bij insuline, 1x bij pepsine en HCL en 1x bij insuline met pepsine en HCL.
Ik zit alleen met 2 vraagjes. Ik heb 3 ml, dat is voor insuline best veel, maar kan ik daar wel papierchromotografie mee doen? Of moet ik het dan eerst verdunnen?
En welke loopvloeistof moet ik nemen? Alvast erg bedankt
[ Bericht 7% gewijzigd door WyBo op 08-03-2006 20:37:50 ]
quote:In de praktijk zijn de oplossingen zeer zelden gehele getallen. Formules gebruik je juist om dom toe te passen. Je moet nadenken over welke formule je moet toepassen.Op woensdag 8 maart 2006 14:20 schreef Nekto het volgende:
De abc- of wortelformule leidt vaak tot dom toepassen. (En is zeker niet altijd sneller.) Ik heb vaak wel esthetische voorkeuren voor ontbinden, en daar zie je ook sneller dat het goed is.
quote:Niemand die mij kan of wil helpen?Op woensdag 8 maart 2006 19:57 schreef WyBo het volgende:
Nog even over mijn experiment met insuline.
Ik heb dus insuline, 3 ml geregeld. Die gaan we onder andere samenvoegen met pepsine en dan gaan we bij de drie stoffen die we dan hebben kijken hoe ze uitlopen bij papierchromotografie.
Ik wil dus gaan aantonen dan insuline wordt aangetast door het maagsap.
Dus 1x bij insuline, 1x bij pepsine en HCL en 1x bij insuline met pepsine en HCL.
Alleen welke loopvloeistof moet ik nemen? Met ammonia of is loopvloeistof met ethanol of alcohol beter? Alvast erg bedankt
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
quote:Een noob-bui? Jij komt hier met de huiswerkvraag, dus is het logisch dat je er zelf ook even wat energie in steekt. Ik snap de vraag nu iig niet, dus misschien is het verstandig dat je zelf even uitzoekt hoe je dit wat beter kan formuleren?Op donderdag 9 maart 2006 15:54 schreef Floriz87 het volgende:
Iemand enig idee hoe ik dit vereenvoudig?
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
quote:Op donderdag 9 maart 2006 15:54 schreef Floriz87 het volgende:
Iemand enig idee hoe ik dit vereenvoudig?
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
Dus, zorg eerst dat je in de noemer van de grote breuk eens één breuk in plaats van een som krijgt, en deel dan.
quote:Ik bedoel te zeggen dat ik het inzicht vandaag ff mis. Zit er nu al tijd mee, maar krijg hem niet opgelost. Duidelijker geformuleerd krijg ik hem denk ik niet. Misschien als ik hem uitteken en vervolgens inscanOp donderdag 9 maart 2006 16:39 schreef Litso het volgende:
[..]
Een noob-bui? Jij komt hier met de huiswerkvraag, dus is het logisch dat je er zelf ook even wat energie in steekt. Ik snap de vraag nu iig niet, dus misschien is het verstandig dat je zelf even uitzoekt hoe je dit wat beter kan formuleren?
Maar reactie op de post hiervoor: Inderdaad zag ik dat nu net dus ook. Maar ik krijg er niet eens een normale breuk van. Je kan die 1 toch niet zomaar bij die teller optellen? Want wil je breuken op kunnen tellen, dan moet wel de noemer gelijk zijn. En kheb geen idee hoe ik die gelijk moet krijgen.
quote:Snap niet hoe je met die hints wat kunt doen hier.Op donderdag 9 maart 2006 16:41 schreef Nekto het volgende:Onder een noemer brengen Delen door een breuk is vermenigvuldigen met het omgekeerde.
Het makkelijkste is denk ik het eenheidselement gebruiken: x*1 = x. Als je met 1 vermenigvuldigt, verandert de breuk niet. Vermenigvuldig met (1+x)/(1+x). Dat doe je door zowel teller als noemer ermee te vermenigvuldigen. Pas distributiviteit goed toe in de noemer, en je bent klaar.
quote:Werd toch net ook gezegd?Op donderdag 9 maart 2006 19:03 schreef GlowMouse het volgende:
[..]
Snap niet hoe je met die hints wat kunt doen hier.
Het makkelijkste is denk ik het eenheidselement gebruiken: x*1 = x. Als je met 1 vermenigvuldigt, verandert de breuk niet. Vermenigvuldig met (1+x)/(1+x). Dat doe je door zowel teller als noemer ermee te vermenigvuldigen. Pas distributiviteit goed toe in de noemer, en je bent klaar.
quote:Waar precies? "En 1 = 1/1 = a/a = (b+q)/(b+q) = patat/patat." komt erg uit de lucht vallen.Werd toch net ook gezegd?
Bedankt iig, kheb weer wat inzichten opgedaan
| 1 2 3 4 5 6 7 | --- 1+x ------- 1 1 + --- 1+x |
De ‘noemer’ onder een noemer brengen:
| 1 2 3 4 5 6 7 | --- 1+x -------- 1+x 1 --- + --- 1+x 1+x |
Wat gelijk is aan:
| 1 2 3 4 5 6 7 | --- 1+x -------- 2+x --- 1+x |
Delen door een breuk, vermenigvuldigen met het omgekeerde:
| 1 2 3 | ---------- (1+x)(2+x) |
Dus: 1/(2+x)
Anders:
| 1 2 3 4 5 6 7 | --- 1+x ------- 1 1 + --- 1+x |
Breng van de noemer van de teller (i.e. 1/1+x bovenin) direct in de noemer:
| 1 2 3 4 | 1 ------- 1+x + 1 |
Is ook 1/(2+x)
quote:Is de inhoud een beetje goed van dit stukje tekst, of staat er echt grote fouten in. Jullie hoeven niet te kijken naar spelfouten e.d.Endotherme reacties
Hoe komt het dat als je barium….. en ammonium……. met elkaar mengt dat het kouder wordt!!!?????!!??!?!?!?!?!
De antwoord op die vraag is eigenlijk niet zo heel erg moeilijk. Nee? Nee, nauw misschien toch wel.
In oplossing gaan is niet echt een chemische reactie, dus als je echt een reactie wilt blijven alleen processen waarbij een gas vrijkomt over.....
Het “ontstaan” of “verdwijnen” van warmte kan je uitleggen met de begrippen enthalpie en entropie.
Wat houd dit in? Enthalpie staat voor de hoeveelheid energie die door de molecuul is opgenomen.
Entropie is een maat voor de wanorde in een systeem
Dat betekend dus dat entropie staat voor hoe ordelijk je moleculen gerangschikt zijn, dus of ze in een mooi rooster zitten of lekker door elkaar aan ’t zweven zijn. Zeg maar hoe groter de ruimte tussen de moleculen hoe groter de entropie.
Men heeft ook ooit de deze mooie formule bedacht: ΔG= ΔH – TΔS
Bij een spontaan endotherm proces zal de G altijd afnemen, in een endotherme reactie neemt de enthalpie(ΔH) toe, vind je ’t gek, de energie moet toch ergens naartoe. Dus ΔG is negatief, ΔH is positief, dus moet TΔS wel heel positief zijn, namelijk (│ΔG+ΔH│)
Dat is allemaal wel mooi en aardig maar wat is die TΔS dan? De T staat voor temperatuur in kelvin en ΔS staat voor de entropie. Aangezien er zoiets bestaat als ’t absolute nulpunt moet T wel positief zijn en dus is ΔS ook positief.
Dat verklaart ook waarom de stoffen kouder worden als er een gas vrij komt. “Echt waar?? Vertel eens waarom dan?”
Kijk de beginstoffen waren allemaal zouten, die zitten allemaal netjes in kristalroosters, de Entropie is dus laag. Maar als ze met elkaar reageren dan veranderen ze in gassen, vloeistoffen en zouten. Dus van 2 geordende stoffen ga je naar meerdere ongeordende stoffen ΔH neemt toe, denk aan de vanderwaals bindingen die verbroken moeten worden, dat kost ook energie.ΔS neemt toe, je gaat namelijk van een geordende zaak naar een warboel. Omdat de T min of meer constant is en ΔS heel groot is zal er dus veel energie worden opgenomen uit de omgeving en wordt ’t dus kouder.
Ik weet trouwens niet waar het stukje voor bedoelt is, maar je schrijfstijl laat nogal te wensen over, voor het geval je het hebt geschreven om anderen het uit te leggen
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
Klopt dit?
quote:tvp, antwoord volgtOp zaterdag 11 maart 2006 23:55 schreef Crazykill het volgende:
Ik moet voor Scheikude P.O. een practicum doen. We moeten dus een Ester maken..
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
Klopt dit?
quote:Bij propanol weet je niet waar de alcoholgroep zit, de naam is dus niet volledig. Verder ziet het er goed uit.Ik moet voor Scheikude P.O. een practicum doen. We moeten dus een Ester maken..
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
quote:Hoe bedoel jeOp zondag 12 maart 2006 13:04 schreef GlowMouse het volgende:
[..]
Bij propanol weet je niet waar de alcoholgroep zit, de naam is dus niet volledig. Verder ziet het er goed uit.
Oja, hoe kan ik berekenen hoeveel propanol en methaanzuur ik nodig heb om 2mL ester (2-propylmethanoaat) te krijgen?
quote:De alcoholgroep kan zowel aan een de middelste C (2-propanol) als aan een C aan de zijkant (1-propanol) zitten. In dit geval wil je methanoaat aan de middelste C hebben, dus kies je voor 2-propanol.Hoe bedoel je ?
quote:Weet je zeker dat de ester vloeibaar is, dat je hem in mL meet? Zoja, dan heb je de dichtheid nodig om naar massa te gaan. Via massa kun je via molaire massa naar aantal mol.Oja, hoe kan ik berekenen hoeveel propanol en methaanzuur ik nodig heb om 2mL ester (2-propylmethanoaat) te krijgen?
Als het om een ester in oplossing gaat, heb je de gewenste molariteit nodig om bij mol te komen.
Als je het aantal mol 2-propylmethanoaat weet, neem ik aan dat je de rest zelf weer kunt
quote:Uhmm ja, dat zei de leraar welOp zondag 12 maart 2006 15:02 schreef GlowMouse het volgende:
Weet je zeker dat de ester vloeibaar is, dat je hem in mL meet? Zoja, dan heb je de dichtheid nodig om naar massa te gaan. Via massa kun je via molaire massa naar aantal mol.
Als het om een ester in oplossing gaat, heb je de gewenste molariteit nodig om bij mol te komen.
Als je het aantal mol 2-propylmethanoaat weet, neem ik aan dat je de rest zelf weer kunt
C4H8O2
dichtheid = 0.904
Volume = 2 ML
M = 2*0,904 = 1,808 gram
Mol. massa = 88.106
aantal mol = 1,808 / 88.106 =0.020 mol
C3H8O+HCOOH >>> C4H8O2+H2O
mol massa:
C3H8O = 60.09
HCOOH = 46.02
Uhmm hier zit ik dus vast, ik snap niet zo goed hoe je dan die 2mL kunt krijgen.. (ik begrijp deze onderwerp niet zo goed
(Je hoeft die berekening niet te doen voor me hoor
Je zei al dat het om een evenwichtsreactie ging. De volgende stap is daarom het opstellen van de evenwichtsvoorwaarde. Je hebt daarbij de evenwichtsconstante nodig. Daarna is het een kwestie van oplossen.
Edit: De Kz van HCOOH staat wel in Binas, maar kan ik die ook gebruiken?
[ Bericht 17% gewijzigd door Crazykill op 12-03-2006 16:20:32 ]
quote:In enkele gevallen wel, maar hier lijkt me het lastig. Je kunt alleen aan evenwichten rekenen als je de evenwichtsconstante hebt. Zonder die constante kun je er wel aan rekenen, maar dan moet je het evenwicht verstoren door een beginstof weg te nemen. Omdat je C4H8O2 over wilt houden, zou dat water zijn.Is er geen andere manier om het te berekenen, want ik heb de evenwichtsconstante niet.
Een andere manier is om dmv de temperatuur de evenwichtsreactie toch zoveel mogelijk naar rechts te laten verlopen, maar je weet dan niet of de reactie voor 5 of voor 99% verloopt.
quote:Nee.Edit: De Kz van HCOOH staat wel in Binas, maar kan ik die ook gebruiken?
quote:Ja inderdaad, we moeten zoutzuur toevoegen waardoor water word ontrokken. Dus de evenwicht gaat naar rechts waardoor we de ester overhouden.Op zondag 12 maart 2006 16:23 schreef GlowMouse het volgende:
[..]
In enkele gevallen wel, maar hier lijkt me het lastig. Je kunt alleen aan evenwichten rekenen als je de evenwichtsconstante hebt. Zonder die constante kun je er wel aan rekenen, maar dan moet je het evenwicht verstoren door een beginstof weg te nemen. Omdat je C4H8O2 over wilt houden, zou dat water zijn.
Een andere manier is om dmv de temperatuur de evenwichtsreactie toch zoveel mogelijk naar rechts te laten verlopen, maar je weet dan niet of de reactie voor 5 of voor 99% verloopt.
Maar ik dacht dus...
De verhouding is 1:1
C3H8O + HCOOH >>>> C4H8O2 + H2O
0,020 mol C4H8O2 had ik nodig
Dus C3H8O en HCOOH moeten ook 0,020 mol zijn.
Als ik dan uitreken hoeveel gram 0,020 mol C3H8O en HCOOH zijn, dan weet ik toch hoeveel ik nodig heb? Of klopt dit niet?
quote:Thnx voor je hulp/moeite !Op zondag 12 maart 2006 17:10 schreef GlowMouse het volgende:
Dat klopt.
Ik heb ff een klein vraagje waar ik niet helemaal uitkom.
We laten een bal op de tafel vallen, waarvandaan deze wordt teruggekaatst. De tijd tot de volgende impact is dan:
t = (2 v) / g,
met v de snelheid en g de gravitatieversnelling. Stellen we nu g=1/2, dan kunnen we de stuiterende bal modelleren dmv de volgende afbeelding:
t -> t + v
v -> a v,
waarbij a een parameter is met 0 < a < 1.
Dit is de beginsituatie en dit is mij volkomen duidelijk. Heb hier al wat aan gerekend (dekpunten enzo) en dat lukt allemaal wel. Maar nu verandert er het volgende aan de situatie.
Nu laten we de bal vallen op een oppervlak dat periodiek aangedreven wordt. Het tafelblad blijft loodrecht op de verticale as, maar beweegt nu op en neer volgens -B*sin(t). Stel nu c = (1+a)*B.
Laat nu zien dat deze nieuwe situatie gemodelleerd kan worden door de afbeelding:
t -> t + v
v -> av - c*cos(t+v)
Volgens mij is dit niet zo moelijk, maar ik zie gewoonweg niet waarom dit zo is.
Wie helpt me uit de brand?
{a1,a2,a3,...,an} en {b1,2,b3,..bn}
two sets of real numbers. Find a necessary and (a) sufficient condition for {a1,a2,a3,...,an} and {b1,2,b3,..bn}
such that there are real numbers A and B with
(a1x+b1)²+(a2x+b2)²+...+(anx+bn)²
=(Ax+B)²
voor all values of x.
Het lijkt me sterk dat deze vraag veel te maken heeft met de vraag:
toon aan dat:
a²+b²+c²+d²=ab+bc+cd+ad
slechts en slechts als a=b=c=d
deze vraag is niet moeilijk te beantwoorden:
a²+b²+c²+d²=ab+bc+cd+ad ==> 2(a²+b²+c²+d²)=2(ab+bc+cd+ad)
dan krijg je iets van (a-b)²+(b-c)²...=0 dan is a=b, b=c,c=d,d=a dus a=b=c=d.
De 2e vraag is een geval van de algemene vraag1.
[ Bericht 79% gewijzigd door thabit op 13-03-2006 19:17:38 ]
ik moet een breuksplitsen namenlijk
x − 5
------------
x^3 − x^2 − 2x
nu ben ik tot hier gekomen
| 1 2 3 | - + ------ + --------- x x+1 x-2 |
maar ik kan nu niet verder want ik zit met drie variabelen?
hoe los ik dit op
quote:Je moet die breuken met A, B en C onder een noemer brengen. Dan krijg je in de tellerOp maandag 13 maart 2006 20:53 schreef icecreamfarmer_NL het volgende:
Ik heb een breuk probleem
ik moet een breuksplitsen namenlijk
x − 5
------------
x^3 − x^2 − 2x
nu ben ik tot hier gekomen
[ code verwijderd ]
maar ik kan nu niet verder want ik zit met drie variabelen?
hoe los ik dit op
A (x + 1)(x - 2) + B x(x - 2) + C x(x + 1).
De haakjes moet je zelf even uitwerken. Het moet dan gelijk zijn aan x-5 voor zekere waarden van A, B en C. Je moet ze dus zodanig kiezen dat de coefficient van (A+B+C)x^2 gelijk is aan 0, ofwel A+B+C=0. Ditzelfde moet je doen voor de coefficient van x en de constante term. Dan krijg je drie lineaire vergelijkingen in 3 onbekenden die je wel kunt oplossen.
A + Bx/(x+1) + Cx/(x-2) = x(x-5)/(x^3-x^2-2x) = (x-5)/(x+1)(x-2).
Daarna vul je simpelweg x=0 in en voila:
A + 0 + 0 = 5/2.
Dezelfde truuk kun je gebruiken om B en C te bepalen. Bij B moet je dan dus met x+1 vermenigvuldigen en x=-1 invullen.
quote:ik heb dezelfde methode gebruikt.Op maandag 13 maart 2006 21:51 schreef Wolfje het volgende:
[..]
Je moet die breuken met A, B en C onder een noemer brengen. Dan krijg je in de teller
A (x + 1)(x - 2) + B x(x - 2) + C x(x + 1).
De haakjes moet je zelf even uitwerken. Het moet dan gelijk zijn aan x-5 voor zekere waarden van A, B en C. Je moet ze dus zodanig kiezen dat de coefficient van (A+B+C)x^2 gelijk is aan 0, ofwel A+B+C=0. Ditzelfde moet je doen voor de coefficient van x en de constante term. Dan krijg je drie lineaire vergelijkingen in 3 onbekenden die je wel kunt oplossen.
maar ik zie nu wat ik fout deed ik ben de x bij C vergeten
en dan krijg je dat A=B wat dus niet met het antwoordt overeenkomt
en ik kom er dan nog niet uit
dat A= 5/2 heb je zo daarna doe ik
0=A+B+C
-5/2=B+C B=-C-5/2
-5/2=-C-5/2+C
0=-C+C
0=0
maar daar kan ik zo weinig mee
[ Bericht 7% gewijzigd door icecreamfarmer_NL op 14-03-2006 11:04:11 ]
quote:Daarom moet je ook de methode gebruiken die ik gepost heb, minder kans op rekenfouten.Op dinsdag 14 maart 2006 10:32 schreef icecreamfarmer_NL het volgende:
[..]
ik heb dezelfde methode gebruikt.
maar ik zie nu wat ik fout deed ik ben de x bij C vergeten
en dan krijg je dat A=B wat dus niet met het antwoordt overeenkomt
en ik kom er dan nog niet uit
dat A= 5/2 heb je zo daarna doe ik
0=A+B+C
-5/2=B+C B=-C-5/2
-5/2=-C-5/2+C
0=-C+C
0=0
maar daar kan ik zo weinig mee
quote:Je wil het maximum van Q weten, dus met andere woorden, de waarde waarbij de afgeleide van Q nul is(dan heb je nl. een (plaatselijk) minimum of maximum...Op dinsdag 14 maart 2006 12:54 schreef el-Fenomeno het volgende:
Ik moet het maximum weten van de formule: Q= -20A + 12A^2 - A^3. Ik wil graag gebruik maken van de ABC formule, maar ik heb geen idee hoe ik dat doe. Kan iemand me helpen?
De afgeleide van Q is wel een functie waarop je de ABC formule kan toepassen..
Nu moet het vast wel lukken..
quote:Een maximum (of minimum) vind je door de afgeleide te berekenen en de nulpunten ervan te bepalen.Op dinsdag 14 maart 2006 12:54 schreef el-Fenomeno het volgende:
Ik moet het maximum weten van de formule: Q= -20A + 12A^2 - A^3. Ik wil graag gebruik maken van de ABC formule, maar ik heb geen idee hoe ik dat doe. Kan iemand me helpen?
-20+24A-3A2=0
Bepalen van die nulpunten doe je met de ABC formule. Je bepaalt de nulpunten, vult deze in in de oorspronkelijke formule en berekent de waarde Q
Dan krijg je het lokaal maximum en minimum. Als A naar -oneindig gaat wordt het maximum natuurlijk +oneindig en omgekeerd voor a gaande naar +oneindig wordt het minimum -oneindig
quote:Dat snap ik, maar hoe moet je dat precies invullen in de ABC formule. Je moet toch wat doen met de formules: ax^2+bx+c=0, x=(-b+wortel D)/2a, x=(-b-wortel D)/2a en D=b^2-4ac? Hoe moet ik dat precies invullen?Op dinsdag 14 maart 2006 13:53 schreef Doderok het volgende:
[..]
Een maximum (of minimum) vind je door de afgeleide te berekenen en de nulpunten ervan te bepalen.
-20+24A-3A2=0
Bepalen van die nulpunten doe je met de ABC formule. Je bepaalt de nulpunten, vult deze in in de oorspronkelijke formule en berekent de waarde Q
Dan krijg je het lokaal maximum en minimum. Als A naar -oneindig gaat wordt het maximum natuurlijk +oneindig en omgekeerd voor a gaande naar +oneindig wordt het minimum -oneindig
quote:-20+24A-3A2=0 ofOp dinsdag 14 maart 2006 14:08 schreef el-Fenomeno het volgende:
[..]
Dat snap ik, maar hoe moet je dat precies invullen in de ABC formule. Je moet toch wat doen met de formules: ax^2+bx+c=0, x=(-b+wortel D)/2a, x=(-b-wortel D)/2a en D=b^2-4ac? Hoe moet ik dat precies invullen?
-3A2+24A-20=0
dan is a=-3
b=24
c=-20
D=242-4*60=336
x1=(-24+wortel 336)/(-6)=0.94495..
x2=(-24-wortel 336)/(-6)=7.05505..
Invullen geeft voor Q1=-9.0276..
Q2=105.0276..
quote:Thnx, ik snap het. Wat gebeurt er als je de formule f(x) = x^3-3x-4 hebt? De afgeleide is dan 3x^2-3, maar de b van de ABC formule ontbreekt en daardoor kun je de D niet uitrekenen.Op dinsdag 14 maart 2006 14:39 schreef Doderok het volgende:
[..]
-20+24A-3A2=0 of
-3A2+24A-20=0
dan is a=-3
b=24
c=-20
D=242-4*60=336
x1=(-24+wortel 336)/(-6)=0.94495..
x2=(-24-wortel 336)/(-6)=7.05505..
Invullen geeft voor Q1=-9.0276..
Q2=105.0276..
quote:b ontbreekt niet, b=0Op dinsdag 14 maart 2006 15:00 schreef el-Fenomeno het volgende:
[..]
Thnx, ik snap het. Wat gebeurt er als je de formule f(x) = x^3-3x-4 hebt? De afgeleide is dan 3x^2-3, maar de b van de ABC formule ontbreekt en daardoor kun je de D niet uitrekenen.
dus D=36 etc.
maar dat los je eenvoudiger op:
3x2-3=0
3x2=3
x2=1 dus x=1 of x=-1
quote:Een complexe wortelOp woensdag 15 maart 2006 12:45 schreef mrbombastic het volgende:
http://www.hhofstede.nl/bewijzen/cardano.htm
Op dit moment ben ik bezig met het programma SPSS. Hierbij snap ik de volgende opdracht niet:
In een stad zijn 660 mensen gevraagd met welk vervoermiddel zij dagelijks van hun huis naar hun werk reizen. Het resultaat van dit onderzoek staat vermeld in onderstaande tabel:
Vervoermiddel Aantal Mensen
Openbaar vervoer 160
Auto 350
(brom)fiets/te voet 150
Voer deze gegevens in in SPSS en presenteer ze in een staafdiagram (vermeld de aantalllen in de staven)
quote:Hoe komt het dat dat je zo'n opdracht moet doen je geen idee hebt hoe je het aan moet pakken? Hadden jullie dit moeten weten? Kan de leraar of het lesboek geen uitleg bieden?Op donderdag 16 maart 2006 09:34 schreef mariekesmulders het volgende:
Zijn er scheikundigen in de zaal? Want:
Wij moeten voor scheikunde een opdracht doen met wasmiddelen als Vanish, Tricel,Sil,...Allemaal producten die bij oplossen zorgen voor zuurstofproductie. We hebben allemaal proefjes gedaan, waardoor blijkt dat niet alle vlekken waarvan wordt beweerd dat ze eruit gaan met deze " wondermiddelen" er ook werkelijk uitgaan. Motor-olievlekken en markkerstif blijken bijvoorbeeld niet uit kleding te gaan door de stukken stof, net als in de reclame, in een warm sopje te hangen. Slaolie, rode wijn en grasvlekken gaan w'el redelijk tot goed uit de kleding. Wij moeten nu verklaren wat de invloed van het vrijkomen van zuustof op het verwijderen van vlekken is. We hoeven dus niet de hele werking van de zeep te verklaren, omdat dat te moeilijk was voor ons (redoxreacties )
Iemand die kan helpen? Dit wordt een ramp zonder hulp van iemand die ons kan duidelijk maken hoe het precies zit!!
dus:::::
HELP!!!!!
Groetjes,
Kim en Marieke
Ik kan me niet voorstellen dat je zomaar zo'n opdracht in je schoot krijgt geworpen zonder uitleg eromheen.
elke info is welkom, bedankt, groeten Gian.
http://en.wikipedia.org/wiki/Chaos_theory
100sinωt dt is de functie die ik moet integreren.
In het boek maken ze er dan:
-100/ω cos ωt van als die functie geprimitiveerd is. Die -cos snap ik wel, maar waarom -100 delen door ω ?? Ik zou zeggen ω * 100 omdat constanten naar voren worden gehaald volgens mij wiskunde leraar. Of is het eigenlijk 1/ω wat dan naar voor gaat, en waarom?
Hoe het vroeger was.
Toen je nog op de basischool zat in welk jaar ongeveer kwam er bij jou een of meerdere computer(s) in de klas?
Wat kon je ermee? wat vond je er leuk of juist niet leuk aan, wat miste je in die tijd?
Wat zijn de dingen die je zijn bij gebleven van die computers,
wat vind je een grote uitvinding op ict gebied wat handig is binnen het basisonderwijs.?
Wat zijn de voordelen en nadelen van informatica (ict) in het basisonderwijs)
Heb je een praktijk voorbeeld vertel die hier ook graag
Alle info is welkom, nog verwijzingen naar websites met handige info zijn ook zeer welkom.
THX
quote:Ok, maar waarom?Op donderdag 16 maart 2006 19:15 schreef thabit het volgende:
Omdat bij differentieren w naar voren gaat, moet bij primitiveren 1/w naar voren.
Bij differentieren moet het omdat de kettingregel dat zegt
Ik krijg van iemand die ik zo nu en dan help met wiskunde een vraag voorgelegd waar ik zo 123 het antwoord niet op weet. Het is 5e jaars VWO, maar vrees dat ik al wat te lang uit de running ben om al die trucjes te onthouden.
a * b = 11a + 4b + 97
Als het goed is moeten er 4 positieve oplossingen in hele getallen.
quote:Dat is omdat differentieren het tegenovergestelde is van integreren. Dus als je bij differentieren een factor w krijgt, krijg je bij integreren een factor 1/w, zodat als je het geintegreerde weer differentieert je dezelfde functie terugkrijgt.Op donderdag 16 maart 2006 20:23 schreef bierglas het volgende:
[..]
Ok, maar waarom?
Bij differentieren moet het omdat de kettingregel dat zegtmaar bij integreren vind ik er niet 123 een regel voor.. ?
quote:Het is weer zo'n vrijdagmorgenOp vrijdag 17 maart 2006 11:02 schreef thabit het volgende:
Ontbinden als (a-4)(b-11)=nog iets.
(a-4)(b-11)=141
Ik kan in ieder geval zeggen dat a géén 4 moet zijn en b geen 11... still stuck dus
quote:Ah, zo ging dat inderdaad! Daar moet ik verder mee kunnen, bedankt Thabit.Op vrijdag 17 maart 2006 11:33 schreef thabit het volgende:
141 ontbinden in priemfactoren en zo alle delers vinden.
dat nulpunt is x=-B/A
Dan moet links ook gelijk zijn aan 0.
subsitueren links levert :
(-a1B/A+b1)²+(-a2B/A+b2)²+...+(anB/A+bn)²=0
ieder kwadraat moet gelijk zijn aan 0.
dus:
-a1B/A+b1=0 dus b1/a1=B/A
en en in het algemeen: b1/a1=b2/a2=...=bn/an met (a1,a2,..an) ongelijk aan nul
ben ik op de goede weg? of al klaar?
Trouwens, als een bepaalde functie continu is op een bepaald interval, is de inverse d'r van ook continu?
waarom is lnx continu op (0,-->)?
Ik denk dat ik iets moet substitueren, maar ik zie niet wat.
quote:De logische oplossing: (n^4+100) < n^4 als n gaat naar oneindigOp zaterdag 18 maart 2006 11:07 schreef Oscar_de_Grouch het volgende:
Toon aan dat de limiet van sqrt(n^4 + 100)/4n bij n -> oneindig, gelijk is aan oneindig.
Ik denk dat ik iets moet substitueren, maar ik zie niet wat.
De limiet van sqrt(n^4)/4n = n^2/4n = n/4 is dus kleiner dan de limiet die jij zoekt. Deze limiet n/4 gaat natuurlijk naar oneindig als n naar oneindig gaat. Jouw limiet is groter dan deze limiet en groter dan oneindig is.... oneindig....
quote:Ik snap. Ook al denk ik dat dikgedrukte een typo is..?Op zaterdag 18 maart 2006 11:17 schreef Drive-r het volgende:
[..]
De logische oplossing: (n^4+100) < n^4 als n gaat naar oneindig
De limiet van sqrt(n^4)/4n = n^2/4n = n/4 is dus kleiner dan de limiet die jij zoekt. Deze limiet n/4 gaat natuurlijk naar oneindig als n naar oneindig gaat. Jouw limiet is groter dan deze limiet en groter dan oneindig is.... oneindig....
[ Bericht 90% gewijzigd door thabit op 18-03-2006 11:54:01 ]
Antwoord 0.
Reden: (pi^2) < 10 dus noemer gaat sneller naar oneindig dan de teller.
Voldoet dit..?
quote:Help me 'es dan?Op zaterdag 18 maart 2006 12:09 schreef thabit het volgende:
Voor zo'n oplossing zou ik zelf niet het volle puntenaantal geven.
quote:Ik zou het iets uitgebreider doen:Op zaterdag 18 maart 2006 12:00 schreef Oscar_de_Grouch het volgende:
Limiet van (pi^(2n) + 3)/(10^n + 3), als n --> oneindig.
Antwoord 0.
Reden: (pi^2) < 10 dus noemer gaat sneller naar oneindig dan de teller.
Voldoet dit..?
(pi^(2n) + 3)/(10^n + 3)=(pi^(2n)/(10^n + 3) + ( 3)/(10^n + 3)
Die laatste breuk gaat naar nul voor n gaat naar oneindig.
Vervolgens wederom (pi^(2n)/(10^n + 3) < (pi^(2n))/(10^n)
(pi^(2n))/(10^n) = pi^n/10, en dit gaat naar nul voor oneindig. De gezocht limiet is nog kleiner en gaat dus ook naar nul.
quote:Eens, maar hoe bewijst dat het?Op zaterdag 18 maart 2006 12:15 schreef thabit het volgende:
pi^(2n)+3 < 2pi^(2n). 10^n+3 > 10^n.
Waarom haal je er 2pi^(2n) bij?
quote:Hm? Dat zie ik niet...Op zaterdag 18 maart 2006 12:17 schreef Drive-r het volgende:
[..]
(pi^(2n))/(10^n) = pi^n/10, en dit gaat naar nul voor oneindig.
En dat die tweede uitdrukking naar nul gaat al helemaal niet.
Limiet van [sqrt(n^2 + n) - n] bij n -> oneindig.
quote:Het belangrijkste is dat je de wortel herkent. Ook weet je dat (a-b)(a+b) = a²-b². Vermenigvuldig teller en noemer (de noemer is 1) met wortel(n²+n)+n. Dat geeft n/(wortel(n²+n)+n). Deel daarna teller en noemer door n en je krijgt: 1/(wortel(1+1/n)+1). Hiervan is het eenvoudig in te zien dat dit naar 1/2 gaat.Op zaterdag 18 maart 2006 13:20 schreef Oscar_de_Grouch het volgende:
Ook hier weet ik niet hoe ik het aan moet pakken:
Limiet van [sqrt(n^2 + n) - n] bij n -> oneindig.
quote:SuperOp zaterdag 18 maart 2006 14:18 schreef GlowMouse het volgende:
[..]
Het belangrijkste is dat je de wortel herkent. Ook weet je dat (a-b)(a+b) = a²-b². Vermenigvuldig teller en noemer (de noemer is 1) met wortel(n²+n)+n. Dat geeft n/(wortel(n²+n)+n). Deel daarna teller en noemer door n en je krijgt: 1/(wortel(1+1/n)+1). Hiervan is het eenvoudig in te zien dat dit naar 1/2 gaat.
Overige limieten ook gelukt.
Bereken het differentiequotiënt van f(x) op het interval L,.
Δf(x) / Δx = f(x+Δx) - f(x) / Δx }
f(x)= -2x^2+5x L= [x,x+Δx]
Ik heb het nu zo gedaan!

Maar het antwoord moet zijn -4x + 5 + Δx
quote:Dat is voor zover ik zie de enige regel die fout gaat omdat haakjes ontbreken, maar verder doe je het wel goed. Het verschil zit hem in de Δx. Aangezien een term bΔx in het antwoord alleen kan ontstaan door in de teller van het differentiequotient een term bΔx² te hebben, en die alleen kan onstaan door -2(x+Δx)², lijkt mij zijn antwoord fout.Δf(x) / Δx = f(x+Δx) - f(x) / Δx }
In een vaas zitten 16 rode en 9 witte knikkers. Wouter pakt in één greep twee knikkers uit de vaas. Wouter voert dit experiment 15 keer uit. Uiteraard doet hij elke keer de twee getrokken knikkers terug in de vaas.
Bereken de kans dat Wouter;
a)minstens dertien keer minstens één witte knikker pakt
b)precies twee keer twee witte knikkers pakt
Wat is de kans dat hij bij één trekking een of twee knikkers pakt? Zijn de trekkingen onderling onafhankelijk? Wat is dan de kans dat hij 13/14/15 keer succes heeft (d.w.z. een of twee knikkers)?
b) Wat is de kans op twee knikkers? Definieer dat als je succes, en iets anders als niet succes. Doe 15 pogingen, bereken wat de kans is op precies twee keer succes.
quote:Kans op twee rode is: (16/25) * (15/24) [kans dat eerste bal rood is maal de kans dat volgende bal rood is, met 1 rode bal minder in de vaas]= 6/15Op zondag 19 maart 2006 16:54 schreef alyel het volgende:
ik vraag me af of iemand weet hoe ik dit moet berekenen..:
In een vaas zitten 16 rode en 9 witte knikkers. Wouter pakt in één greep twee knikkers uit de vaas. Wouter voert dit experiment 15 keer uit. Uiteraard doet hij elke keer de twee getrokken knikkers terug in de vaas.
Bereken de kans dat Wouter;
a)minstens dertien keer minstens één witte knikker pakt
b)precies twee keer twee witte knikkers pakt
Daaruit volgt: kans dat er minstens 1 wit is: 1-(6/15)= 9/15=3/5
Kans dat op 15 beurten minstens dertien keer een witte verschijnt:
We hebben drie mogelijke gevallen: 15 maal wit, 14 maal wit en 13 maal wit.
De totale kans is de som van de kansen in deze drie gevallen.
kans op 15 maal wit: (3/5)15
kans op 14 maal wit: (3/5)14 * (2/5) * 15 [eerst 14 keer wit , dan één keer niet: geeft (3/5)14 * (2/5); Maar de éne keer geen wit kan ook gebeuren bij de eerste beurt, bij de tweede, etc.. dus in totaal op 15 verschillende wijzen]
kans op 13 maal wit: (3/5)13 * (2/5)2 * (15 * 14 / 2)
Als je deze waarden berekent en optelt krijg je: 0.027114001
(of je brengt alles op gelijke noemer zodat je de kans krijgt uitgedrukt als breuk)
Geval b): precies twee keer twee witte ballen. De kans om twee witte ballen te nemen is: (9/25) * (8/24)=3/25
Dus kans dat het niet gebeurt is 22/25
Precies twee keer in 15 beurten: (22/25)13 * (3/25)2 * (15 * 14 / 2)
Uitwerken, klaar
Ben niet helemaal nuchter, dus je kan het beter nakijken op domme fouten
[ Bericht 9% gewijzigd door Doderok op 19-03-2006 17:49:59 ]
en ehm hier nog een probleem waar ik niet uitkom;
Van de Nederlandse vakantiegangers naar Spanje gaat 45% met het vliegtuig, 30% met de auto, 20% met de bus en 5% met de trein.
Bij een onderzoek worden 13 vakantiegangers naar Spanje ondervraagd. Bereken de kans dat tussen de 10% en 30% met de bus gaat.
Je stelt u = x², dan is du = (du/dx) dx = 2 x dx, dus: 1/2 du = x dx.
Dan heb je dus de integraal 1/2 sin (u) du, dat levert -1/2cos(u)+C op, terugsubstitueren geeft -1/2cos(x²)+C en klaar is kees
Je kan het controleren door wat uit de integraal komt weer te primitiveren.
quote:Zo ver kwam ik ook, maar wat doe je met de X die je bij x * sin (x²) gebruikt?Op maandag 20 maart 2006 17:00 schreef SNArky het volgende:
Je moet de substitutieregel gebruiken.
Je stelt u = x², dan is du = (du/dx) dx = 2 x dx, dus: 1/2 du = x dx.
Dan heb je dus de integraal 1/2 sin (u) du, dat levert -1/2cos(u)+C op, terugsubstitueren geeft -1/2cos(x²)+C en klaar is kees.
Je kan het controleren door wat uit de integraal komt weer te primitiveren.
quote:Je bent daar toch met de substitutie van de x² bezig die in sin(x²) staat? Heeft dacht ik weinig met de x te maken uit x*sin(x²)Op maandag 20 maart 2006 17:07 schreef SNArky het volgende:
Die "verdwijnt" als je die differentiaal neemt. Je krijgt 1/2 du = x dx, en daar verdwijnt die x toch mee?
If u = g(x) is a differentiable function whose range is an interval I and f is continous on I, then:
int( f(g(x)) g'(x)) dx = int( f(u)) du
Hierin is dus g(x) = x² , dus g'(x) = 2x en f(u) = 1/2 sin u.
(Moeilijk om integralen op te schrijven
x * sin(x²)
neem u = x², du/dx = 2x, dus dx = 1/(2x) du
invullen (zowel x² als dx vervangen): x * sin(u) 1/(2x) du = 1/2 sin(u) du.
Een docent gebruikte een iets andere manier van noteren, die ik nog wel graag wil snappen. Hij veranderde dx op het eind door wat hij ging substitueren, dan lijkt het hierop: x*sin(x²)dx = x*sin(x²) dx². Heeft iemand meer informatie over deze manier van noteren?
quote:Gebruik dan dx2 =2 x dxOp maandag 20 maart 2006 19:02 schreef GlowMouse het volgende:
De substitutieregel heeft me, voordat ik hem snapte, wel wat hoofdbrekens gekost. Uiteindelijk snapte ik hem zo:
x * sin(x²)
neem u = x², du/dx = 2x, dus dx = 1/(2x) du
invullen (zowel x² als dx vervangen): x * sin(u) 1/(2x) du = 1/2 sin(u) du.
Een docent gebruikte een iets andere manier van noteren, die ik nog wel graag wil snappen. Hij veranderde dx op het eind door wat hij ging substitueren, dan lijkt het hierop: x*sin(x²)dx = x*sin(x²) dx². Heeft iemand meer informatie over deze manier van noteren?
Dan: x sin(x2) dx = 1/2 sin(x2) dx2
En dan naar x2 integreren, als dit te abstract is kun je nog altijd u = x2 gebruiken.
Hoe reken ik 'x' uit?
quote:Even omzetten naar de wat duidelijkere (standaard) notatie
-6x2 - 6x + 12 = 0
delen door -6
x2 + x - 2 = 0
ontbinden in factoren:
(x - 1) (x + 2) = 0
x = 1 of x = -2
quote:Bedankt! Nét toen ik het postte bedacht ik dat ik het effe moest herschrijven. Ik heb het trouwens met de ABC-formule opgelost, want na al die jaren kan ik nog steeds niet ontbinden in factoren.Op dinsdag 21 maart 2006 12:01 schreef Litso het volgende:
[..]
Even omzetten naar de wat duidelijkere (standaard) notatie
-6x2 - 6x + 12 = 0
delen door -6
x2 + x - 2 = 0
ontbinden in factoren:
(x - 1) (x + 2) = 0
x = 1 of x = -2
Kijk... ik snap niet hoe je van:
delen door -6
x2 + x - 2 = 0
Dít maakt...
ontbinden in factoren:
(x - 1) (x + 2) = 0
Hoe je dat 'ziet' of 'verzint' zeg maar... Die -1 en die +2 dan met name.
quote:ABC formule werkt ook, maar ontbinden is makkelijker voor uit je hoofd.Op dinsdag 21 maart 2006 12:29 schreef BrauN het volgende:
[..]
Bedankt! Nét toen ik het postte bedacht ik dat ik het effe moest herschrijven. Ik heb het trouwens met de ABC-formule opgelost, want na al die jaren kan ik nog steeds niet ontbinden in factoren.
Kijk... ik snap niet hoe je van:
delen door -6
x2 + x - 2 = 0
Dít maakt...
ontbinden in factoren:
(x - 1) (x + 2) = 0
Hoe je dat 'ziet' of 'verzint' zeg maar... Die -1 en die +2 dan met name.
En dat -1 en +2... Je moet twee getallen krijgen die bij elkaar +1 zijn (van de +x) en met elkaar vermenigvuldigd -2.
Bij mij meestal een kwestie van snel hoofdrekenen, geen idee of daar ook ezelsbruggetjes voor zijn
Het Grote PokerTopique 40: Bad Beat Central
dit is de vraag:
Je zit aan een full-ring 10 handed table. Je ziet KK verschijnen, hoe groot is dan de kans dat 1 vd overige 9 spelers AA heeft?
dus 10 personen, eentje heeft KK wat is de kans dat iemand anders AA heeft?
mijn berekening was als volgt:
Jij ziet KK dan blijft er over, 9 spelers en 50 kaarten.
Kans dat iemand AA dan krijgt is (4 boven 2)/(50 boven 2) = 12/(50*49) = 12/2450 = 1/204
dus je wilt weten de kans dat van die 9 man eentje of meer AA krijgt = 1 - P(niemand van de overige 9 AA)
dit is weer gelijk aan 1 - (1-1/204)^9 = 1 - (203/204)^9 = 4.3%
dus 1 op 23 zelfs ongeveer
Wie kan ons uit de brand helpen en het juiste antwoord geven???
quote:Dit is fout, want de kaarten die de tweede speler heeft hebben weer invloed op de kansverdeling van de derde, etc.Op dinsdag 21 maart 2006 14:49 schreef superbient het volgende:
Naar aanleiding van deze discussie wil ik wat experts te hulp roepen....
Het Grote PokerTopique 40: Bad Beat Central
dit is de vraag:
Je zit aan een full-ring 10 handed table. Je ziet KK verschijnen, hoe groot is dan de kans dat 1 vd overige 9 spelers AA heeft?
dus 10 personen, eentje heeft KK wat is de kans dat iemand anders AA heeft?
mijn berekening was als volgt:
Jij ziet KK dan blijft er over, 9 spelers en 50 kaarten.
Kans dat iemand AA dan krijgt is (4 boven 2)/(50 boven 2) = 12/(50*49) = 12/2450 = 1/204
dus je wilt weten de kans dat van die 9 man eentje of meer AA krijgt = 1 - P(niemand van de overige 9 AA)
dit is weer gelijk aan 1 - (1-1/204)^9 = 1 - (203/204)^9 = 4.3%
dus 1 op 23 zelfs ongeveer
Wie kan ons uit de brand helpen en het juiste antwoord geven???
quote:maar je ziet alleen je eigen kaarten, kan jij een betere berekening geven?Op dinsdag 21 maart 2006 15:07 schreef thabit het volgende:
[..]
Dit is fout, want de kaarten die de tweede speler heeft hebben weer invloed op de kansverdeling van de derde, etc.
quote:Jazeker. Ik vind dit probleem alleen niet interessant genoeg om dat ook echt te gaan doen.Op dinsdag 21 maart 2006 15:27 schreef superbient het volgende:
[..]
maar je ziet alleen je eigen kaarten, kan jij een betere berekening geven?
Het gaat om het Patching Problem; gegeven twee cycles, het verwijderen van twee arcs en het toevoegen van twee nieuwe arcs zodanig dat de twee cycles tot één 'gepatched' worden.
Ik vind dit erg lastig te formaliseren... ik heb al iets in elkaar gedraaid wat wel redelijk is, alleen zie ik volgens mij iets cruciaals over het hoofd.
Als een wiskundige onder jullie hier een korte blik op zou willen schijnen, graag
Tis een pdf-je van 1 A4: klik hier voor de PDF.
Ik heb je pdf-je bekeken en heb een aantal opmerkingen.
Ik hoop dat je er wat aan hebt!
Wij moeten voor scheikunde een opdracht doen met wasmiddelen als Vanish, Tricel,Sil,...Allemaal producten die bij oplossen zorgen voor zuurstofproductie. We hebben allemaal proefjes gedaan, waardoor blijkt dat niet alle vlekken waarvan wordt beweerd dat ze eruit gaan met deze " wondermiddelen" er ook werkelijk uitgaan. Motor-olievlekken en markkerstif blijken bijvoorbeeld niet uit kleding te gaan door de stukken stof, net als in de reclame, in een warm sopje te hangen. Slaolie, rode wijn en grasvlekken gaan w'el redelijk tot goed uit de kleding. Wij moeten nu verklaren wat de invloed van het vrijkomen van zuustof op het verwijderen van vlekken is. We hoeven dus niet de hele werking van de zeep te verklaren, omdat dat te moeilijk was voor ons (redoxreacties )
Iemand die kan helpen? Dit wordt een ramp zonder hulp van iemand die ons kan duidelijk maken hoe het precies zit!!
dus:::::
HELP!!!!!
Groetjes,
Kim en Marieke
quote:Super, erg helpvol!Op dinsdag 21 maart 2006 23:15 schreef Wolfje het volgende:
Ik weet dat dit nauwelijks een 'probleem' te noemen is, het is eigenlijk heel triviaal. Ik heb een experimentele studie gedaan, waarin ik upper & lower tolerances met betrekking tot de oplossing van dit probleem heb gebruikt. Bij het doorlezen kwam ik er alleen achter dat ik het probleem en zn optimale oplossing nooit geformaliseerd heb, dus vandaar.
En zoals je op heb kunnen maken uit mijn PDFje is theoretische wiskunde nooit mijn favoriet geweest
Daar een cycle een begrip is wat iedereen (die dit leest) wel kent, kan ik beter gewoon refereren naar een goed standaard werk over graph theory voor formele definities.
De rest (mbt tot het PP) zal ik zéker verwerken. Bedankt
quote:Dat lijkt me niet zo verstandig. Er zijn verschillende definities van het begrip cykel in omloop, dus het is wel handig om de lezer mede te delen welke jij hanteert.Op woensdag 22 maart 2006 16:26 schreef Knakker het volgende:
[..]
Daar een cycle een begrip is wat iedereen (die dit leest) wel kent, kan ik beter gewoon refereren naar een goed standaard werk over graph theory voor formele definities.
quote:Goed punt, zal hem dan maar toevoegen.Op woensdag 22 maart 2006 16:43 schreef thabit het volgende:
[..]
Dat lijkt me niet zo verstandig. Er zijn verschillende definities van het begrip cykel in omloop, dus het is wel handig om de lezer mede te delen welke jij hanteert.
Wat het geval is: Iemand stort elke 2 jaar, te beginnen op 1/1/2003, 25.000 op een spaarrekening. Hij stort 11 keer. Interestpercentage is 9% per jaar.
Gevraagd: De eindwaarde op 1/1/2024.
Met behulp van een meetkundige reeks zou dit opgelost moeten kunnen worden. Dit lukt me wel bij een jaarlijkse storting en jaarlijks rentepercentage, maar in dit geval wordt er dus maar eens in de 2 jaar gestort.
De formule die ik gebruik bij jaarlijkse rente en storting is E = K * (1+i) * ((1+i)^n) / i.
Hierbij is E het eindkapitaal. K het startkapitaal (de eerste storting). i de rente op jaarbasis en n de looptijd in jaren.
Iemand enig idee hoe ik de formule moet aanpassen om bovenstaande vraag te beantwoorden?
quote:Dat is het nadeel van formules leren zonder te weten wat erachter zit.Iemand enig idee hoe ik de formule moet aanpassen om bovenstaande vraag te beantwoorden?
De elfde storting blijft 1 jaar staan
De tiende storting blijft 3 jaar staan
De negende storting blijft 5 jaar staan
...
De eerste storting blijft 21 jaar staan
E = K*1,09^1 + K*1,09^3 + K*1,09^5+...+K*1,09^21
Daar heb je weer een meetkundige rij met reden 1,09^2. De som daarvan ([opvolger laatste term]-[eerste term]) / (r-1).
S = a * (r^n-1) / r-1
Dat wordt dan dus: S = 1,08^1 * ((1,08^2)^21-1) / (1,08^2)-1.
Correct? Want als ik de uitkomst daarvan vermenigvuldig met 25000 kom ik enkele tonnen lager uit dan wat als antwoord in de syllabus staat.
quote:Die tonnen zijn verdwenen door een te lage rente. Ik kom uit op ongeveerCorrect? Want als ik de uitkomst daarvan vermenigvuldig met 25000 kom ik enkele tonnen lager uit dan wat als antwoord in de syllabus staat.
quote:De formule klopt wel, je vult hem alleen verkeerd in: S = a * (r^n-1) / r-1 = 1,09 * ((1,09²)^11 - 1) / (1,09²-1)Hm, de formule klopt dus niet.
[ Bericht 33% gewijzigd door GlowMouse op 23-03-2006 20:03:01 ]
Maar waarom neem je n=11? Is n altijd het aantal investeringen? In andere opgaven was de looptijd in jaren gelijk aan het aantal investeringen en in de opgaven ervoor is n altijd de looptijd in jaren geweest. Vandaar dat ik 21 invulde.
quote:In de onderste lagen van het OSI-model liggen al veel afspraken vast. Naarmate we hoger in het model komen, zijn de afspraken vager en verlopen de onderhandelingen moeizamer. Waarom is dit zo?
quote:Euh, de onderste lagen zijn ouder? (min of meer geïnspireerd door telefonie...)Op maandag 27 maart 2006 18:13 schreef Thrilled het volgende:
Hallo, ik heb problemen met de volgende vraag die gaat over het OSI-model (datacommunicatie):
[..]
Edit: toen het OSI model gedefinieerd werd, bestond TCP/IP al. Verder steunt elke laag op de voorgaande, als de fysieke lagen niet met elkaar kunnen communiceren, dan heeft het weinig zin om protocollen voor de datalink laag op te stellen...
Hoe hoger men gaat, hoe meer verscheideinheid van toepassingen men tegenkomt.
(als je toekomst ervan afhangt zou ik wel betere bronnen raadplegen)
[ Bericht 40% gewijzigd door Doderok op 27-03-2006 18:39:00 ]
quote:Nee dit is gewoon een huiswerkopgave, hij heeft 20 vragen gegeven en dit was de enige die ik nog niet had, dank je welOp maandag 27 maart 2006 18:23 schreef Doderok het volgende:
[..]
Euh, de onderste lagen zijn ouder? (min of meer geïnspireerd door telefonie...)
Edit: toen het OSI model gedefinieerd werd, bestond TCP/IP al. Verder steunt elke laag op de voorgaande, als de fysieke lagen niet met elkaar kunnen communiceren, dan heeft het weinig zin om protocollen voor de datalink laag op te stellen...
Hoe hoger men gaat, hoe meer verscheideinheid van toepassingen men tegenkomt.
(als je toekomst ervan afhangt zou ik wel betere bronnen raadplegen)
In mijn boek staat dat het altijd positief is. Logisch ook wel, want bijv. de absolute waarde van |-5| is 5.
Maar eronder staat als defenitie:
|g| = g als g >- 0 en -g als g < 0
En daar snap ik het dus ff niet, eerst zeggen ze dat de absolut waarde altijd positief is, en dan komt bij de defenitie -g te staan, wat voor mij toch echt een negatief getal oplevert.
Hoe zit het nu? Kan iemand mij misschien wat meer info daarover vertellen
quote:als g negatief is, dan is -g positief ...Op maandag 27 maart 2006 19:42 schreef bierglas het volgende:
Hoe zit het nu met absolute waardes?
In mijn boek staat dat het altijd positief is. Logisch ook wel, want bijv. de absolute waarde van |-5| is 5.
Maar eronder staat als defenitie:
|g| = g als g >- 0 en -g als g < 0
En daar snap ik het dus ff niet, eerst zeggen ze dat de absolut waarde altijd positief is, en dan komt bij de defenitie -g te staan, wat voor mij toch echt een negatief getal oplevert.
Hoe zit het nu? Kan iemand mij misschien wat meer info daarover vertellen
quote:ow dat moet ik dan zien als -(-g) ?Op maandag 27 maart 2006 19:49 schreef Doderok het volgende:
[..]
als g negatief is, dan is -g positief ...
dan is het wel duidelijk ja..
quote:Neem g = -a, met a positief.Op maandag 27 maart 2006 19:53 schreef bierglas het volgende:
[..]
ow dat moet ik dan zien als -(-g) ?
dan is het wel duidelijk ja..
Dan |g| = a = - (-a) = -g.
Teken anders de grafieken van y = |x|, y = x en y = -x, dan wordt het wel duidelijk.
quote:Dat is dan fout, een absolute waarde is altijd niet-negatief.Hoe zit het nu met absolute waardes?
In mijn boek staat dat het altijd positief is
quote:Jij wilt g hier zo graag zien als een positief getal, zodat -(-g) ook positief is. Maar |g| = -g als g<0. Neem bijvoorbeeld g = -3, dan zie je al direct dat |g| = 3. Maar |g| != -(-g) want -(-g) is -(-(-3)) = -3.ow dat moet ik dan zien als -(-g) ?
dan is het wel duidelijk ja..
Alle atomen die geen edelgas zijn streven naar een edelgasconfiguratie. Waarom kan kalium zijn schillen dan niet op de volgende manier indelen: 2+8+1+8 ? (ipv 2+8+8+1)
Want ik zie dat Xenon ook binnen zijn eigen schillen ermee schuift: 2+8+18+18+8. De derde schil kan namelijk 32 elektronen bevatten dus als alle schillen zo vol mogelijk zouden moeten zitten had Xenon er als volgt uit gezien: 2+8+18+25+1.
Wat zie ik over het hoofd?
Alvast bedankt voor de moeite!
Kalium heeft de volgende elektronenconfiguratie: 1s22s22p63s23p64s1.
Dat heeft ermee te maken dat een physisch systeem er naar streeft in een zo laag mogelijke energie te zitten. De hierboven beschreven configuratie is de meest energetisch gunstige en daarom heeft kalium ook die configuratie (als het atoom in de grondtoestand is uiteraard).
quote:ziehierHoi, wat is een alkylgroep?
quote:De edelgasconfiguratie gaat voor veel elementen op, maar voor andere kun je beter een ander model gebruiken. In dit wikipedia artikel staat een iets uitgebreider model.Alle atomen die geen edelgas zijn streven naar een edelgasconfiguratie. Waarom kan kalium zijn schillen dan niet op de volgende manier indelen: 2+8+1+8 ? (ipv 2+8+8+1)
Want ik zie dat Xenon ook binnen zijn eigen schillen ermee schuift: 2+8+18+18+8. De derde schil kan namelijk 32 elektronen bevatten dus als alle schillen zo vol mogelijk zouden moeten zitten had Xenon er als volgt uit gezien: 2+8+18+25+1.
Van wat ik me ervan kan herinneren is de standaard configuratie energetisch het best haalbare is.
Hoi SNArky
quote:Een alkaan waar één H+ atoom ontbreekt.Op maandag 27 maart 2006 22:19 schreef -Mzraki- het volgende:
Hoi, wat is een alkylgroep?
quote:Hier staat een applet waarmee je kan zien in welke volgorde de schillen opgevuld worden.Op maandag 27 maart 2006 22:21 schreef Odin83 het volgende:
Het volgende kom ik met mijn boek niet uit:
Alle atomen die geen edelgas zijn streven naar een edelgasconfiguratie. Waarom kan kalium zijn schillen dan niet op de volgende manier indelen: 2+8+1+8 ? (ipv 2+8+8+1)
Want ik zie dat Xenon ook binnen zijn eigen schillen ermee schuift: 2+8+18+18+8. De derde schil kan namelijk 32 elektronen bevatten dus als alle schillen zo vol mogelijk zouden moeten zitten had Xenon er als volgt uit gezien: 2+8+18+25+1.
Wat zie ik over het hoofd?
Alvast bedankt voor de moeite!
http://www.webelements.com/webelements/elements/text/K/econ.html
Als men zegt "streeft naar een edelgasconfiguratie" dan heeft men het over de meest stabiele verbindingen die het atoom vormt, niet over hoe het z'n eigen elektronen over de schillen verdeelt.
quote:Ja, maar in het scheikundeboek hebben ze nooit gezegd dat bijvoorbeeld een methyl een methaanradicaal is, ze smijten heel eenvoudig met jaa een alkylgroepOp maandag 27 maart 2006 22:48 schreef Doderok het volgende:
[..]
Een alkaan waar één H+ atoom ontbreekt.
Beetje vreemd, maar ok, ik snap het, bedankt.
Nog een; primitieve van log(500/x)?
quote:hmm, log(500/x) = log500 - log xOp maandag 27 maart 2006 22:57 schreef -Mzraki- het volgende:
[..]
Ja, maar in het scheikundeboek hebben ze nooit gezegd dat bijvoorbeeld een methyl een methaanradicaal is, ze smijten heel eenvoudig met jaa een alkylgroep.
Beetje vreemd, maar ok, ik snap het, bedankt.
Nog een; primitieve van log(500/x)?.
wordt: (log500)x - (x logx - x) ?
quote:sorry, 10logx schrijf ik gewoon als logxOp maandag 27 maart 2006 23:06 schreef SNArky het volgende:
Wat is het grondtal van jouw logaritme?
Maar volgens mij heb ik hem met (log500)x - (x*logx - x), is het niet?
1/ln(10)*ln(500/x)*x+1/ln(10)*x
en ik heb nu geen zin om dat terug te rekenen
quote:Ik ook niet, volgens mij heb je als begingrafiek f = log(500/x) ingevuld of niet?Op maandag 27 maart 2006 23:19 schreef SNArky het volgende:
Volgens maple is het:
1/ln(10)*ln(500/x)*x+1/ln(10)*x
en ik heb nu geen zin om dat terug te rekenen.
probeer dan liever f = log(500) - log(x), volgens mij krijg je dan hetzelfde als ik
Of nee, afgeleide log(x) is niet 1/x ?
dan moet het zijn: F = log(500)x - (x*ln(x) - x)
Opdracht is: toon aan of de somrij van de rij un = log(500/n) convergeert ja of nee, volgens mij niet dus.
[ Bericht 8% gewijzigd door -Mzraki- op 27-03-2006 23:28:39 ]
quote:Als een rij sommeerbaar is, dan convergeert de rij naar 0.Moet aantonen of de somrij van de rij un = log(500/n) convergeert ja of nee, volgens mij niet dus.
Het wordt volgens mij tijd om te gaan slapen...:P
quote:Somrij? bedoel je de rij van Si=u1 + u2 + ... ui ?Op maandag 27 maart 2006 23:23 schreef -Mzraki- het volgende:
[..]
Ik ook niet, volgens mij heb je als begingrafiek f = log(500/x) ingevuld of niet?
probeer dan liever f = log(500) - log(x), volgens mij krijg je dan hetzelfde als ik.
Of nee, afgeleide log(x) is niet 1/x ?
dan moet het zijn: F = log(500)x - (x*ln(x) - x)
Opdracht is: toon aan of de somrij van de rij un = log(500/n) convergeert ja of nee, volgens mij niet dus.
Die kan toch niet convergeren aangezien un niet naar nul gaat voor n gaande naar oneindig... ?
Edit: wat hij zegt