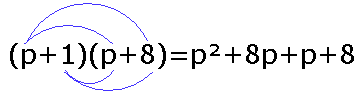SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Je vergelijking is daardoor echter (x + 6)(x - 1) = 0. Wat zij zegt is onzin, maar als je het had gesnapt was dat het probleem niet geweest. Echter, een (lange) uitleg, maar wel met de goede vergelijking. De uitleg komt eerst, die is ook voor het snappen, dan komt het stukje Truuk, die vooral de truuk uitlegt.quote:Op dinsdag 7 maart 2006 16:24 schreef Robin__ het volgende:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
We bekijken x^2 + 5x = 6. Merk op dat x^2 natuurlijk gewoon hetzelfde is als x * x. En 5x is 5 * x. (Dat als allereerste).
Ik neem aan dat je bekend bent met haakjes wegwerken. Dat wil zeggen, als er x*(3 + 5x) staat, dan is dit hetzelfde als x*3 + x*5x. Je vermenigvuldigt die x met alle termen die binnen de haakjes staan. Merk dan op dat je na dat vermenigvuldigen in elke term termen zijn overigens de naam voor de losse 'dingen' in een optelling, dus 3 + 5 + 9 heeft termen 3, 5 en 9, en 3x + 5 heeft termen 3x en 5 dezelfde factorfactor is een onderdeel van een vermenigvuldiging, dus 3x heeft factoren 3 en x aantreft, namelijk 'x'.
Die factor kun je zogezegd weer buiten haakjes halen. Dat is ook wel logisch, want als x(3 + 5x) gelijk is aan 3x + 5x^2, dan moet natuurlijk 3x + 5x^2 ook gelijk zijn aan x(3 + 5x). En inderdaad, door driftig uitschrijven kun je dat oefenen.
Ik hoop dat je bijvoorbeeld inziet dat x(5 + 8x) = 5x + 8x^2, en ook omgekeerd, of dat x^2(6 + 9x) = 6x^2 + 9x^3. En dat je net zogoed in plaats van 4x + 8x^2 ook 4x(1 + 2x) kunt schrijven (die is al wat gemener, want we halen de factor 4x eruit).
In jouw voorbeeld halen ze ook buiten haakjes. De eerste stap begint met:
x^2 + 5x = 6 om te zetten in x^2 +5x - 6 = 0 (dat levert geen problemen). Nu moeten er echter die haakjes gevonden worden. Ik denk dat je wel ziet dat als je (x + 6)(x - 1) uitschrijft, je weer op x^2 + 5x - 6 uitkomt, immers:
(x + 6)(x - 1) = (x + 6)*x + (x + 6)*1 = x*x + 6*x - 1*x - 6 = x^2 +(6 - 1)*x - 6 = x^2 +5x - 6.
Merk op dat we bij die laatste stap in feite weer factoren binnen haakjes brengen, want er zijn twee termen die een 'x' gemeen hebben, dus die kunnen we samenvoegen.
Truuk
De truuk is nu (en dat is het belangrijkste) hoe te herkennen wat je moet doen als je een kwadratische vergelijking hebt, en je die als product van twee sommen (x + a)(x + b) wilt schrijven.
Welnu, laten we eerst de som (x + a)(x + b) uitschrijven, dat geeft:
(x + a)(x + b) = (x + a)x + (x + a)b = x^2 + a*x + x*b + a*b = x^2 + (a + b)*x + a*b
Merk weer hoe we haakjes inbrengen om de twee termen die elk een factor x hebben samen te nemen. Nu komt de truuk, als je een willekeurige vergelijking x^2 + c*x + d hebt, vindt dan twee getallen a en b zodat c = a + b en d = a * b. Daar moet je wellicht even op broeden, maar dat is eigenlijk wat hierboven in die formule staat.
En als we dat dan nu gaan toepassen op jouw formule:
x^2 + 5x -6 = 0.
We zien dat c = 5, en d = -6. Nu wordt het gewoon wat proberen om a en b te vinden meestal, Zeg a = 2, b = 3. Dan a + b = 5, dat klopt, maar a * b = 6, dus dat kan niet kloppen. Sterker nog, we zien aan de -6 dat of a of b wel negatief moet zijn. (Goede truuk om te onthouden, is d negatief, dan is een van a of b ook negatief). Dus, zeg a = -2, dan moet b wel 3 zijn, maar -2 + 3 = 1, dus dat kan ook niet. Enfin, om een al lang verhaal toch iets korter te maken: a = 6 en b = -1. Dit klopt precies, immers 6 *- 1 = -6 en 6 + (-1) = 5.
Dus, je vult nu de linkerkant van die hele vergelijking in, en je krijgt dat in dit geval:
(x + a)(x + b) moet zijn: (x + 6)(x - 1).
Nou, hopelijk is dat na een tijdje oefenen duidelijk genoeg.
[ Bericht 0% gewijzigd door Nekto op 07-03-2006 16:57:14 ]


stap 1: x2 + 5x - 6 = 0
snap je dat?
snap je dat?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Die punt is een zins-einde teken daar.quote:Op dinsdag 7 maart 2006 16:52 schreef Robin__ het volgende:
[..]
Sorry maar hier gaat het al mis.. 6 punt x^2????


in brief
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1quote:Op dinsdag 7 maart 2006 16:34 schreef McCarthy het volgende:
x = -6 en x = +1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
"Dat is echt ontzettend zielig" ©


welles
quote:Op dinsdag 7 maart 2006 16:24 schreef Robin__ het volgende:
Sorry dat ik zo kom binnenvallen.. maar ik heb ook een vraag
Afgelopen vrijdag een toets van mn wiskunde bijles (om zonder achterstand naar het hbo te kunnen na het mbo) redelijk verkloot, ik dacht dat ik het snapte, niet dus, extra opdrachten gevraagd maar nu zit ik dus vast.
De vraag:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
Dat betekent: x - 6 = 0 of x + 1 = 0 En dus zijn de oplossingen x=6 en x=-1
'controleer ze maar'
Ik snap er werkelijk NIETS van.. waar haalt ze die 6 en 1 vandaan en waar is mn x^2 gebleven
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Ja, maar, in zijn voorbeeld wordt niet juist ontbonden. Als de vergelijking x^2 + 5x - 6 is, dan is de ontbinding niet (x - 6)(x + 1), maar (x + 6)(x - 1). Als de ontbinding (x - 6)(x + 1) is, dan is de vergelijking echter x^2 -5x -6.quote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1


Ah, overheen gezienquote:Op dinsdag 7 maart 2006 17:07 schreef Nekto het volgende:
[..]
Ja, maar, in zijn voorbeeld wordt niet juist ontbonden. Als de vergelijking x^2 + 5x - 6 is, dan is de ontbinding niet (x - 6)(x + 1), maar (x + 6)(x - 1). Als de ontbinding (x - 6)(x + 1) is, dan is de vergelijking echter x^2 -5x -6.
"Dat is echt ontzettend zielig" ©


Kijk nou eens goed naar de bold gemaakte vergl modje van me
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


zal ik het maar overnemen want dit gaat didactisch gezien helemaal foutquote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
[afbeelding]
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Jaja, ik heb het al gezien, maar de rest van wat ik vertel klopt toch aardig of niet?quote:Op dinsdag 7 maart 2006 17:10 schreef McCarthy het volgende:
[..]
zal ik het maar overnemen want dit gaat didactisch gezien helemaal fout
"Dat is echt ontzettend zielig" ©


Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.


ik zei alleen dat het didactisch gezien niet echt handig isquote:Op dinsdag 7 maart 2006 17:11 schreef Litso het volgende:
[..]
Jaja, ik heb het al gezien, maar de rest van wat ik vertel klopt toch aardig of niet?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Ach, als je maar weet hoe het werktquote:Op dinsdag 7 maart 2006 17:14 schreef Nekto het volgende:
Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.
Als je er in geïnteresseerd bent of van plan er verder mee te werken is het wel zo handig als je dat weet inderdaad, maar ik kan me voorstellen dat er mensen zijn die liefst na hun examen niks meer met wiskunde te maken willen hebben
"Dat is echt ontzettend zielig" ©


Want?quote:Op dinsdag 7 maart 2006 17:15 schreef McCarthy het volgende:
[..]
ik zei alleen dat het didactisch gezien niet echt handig is
"Dat is echt ontzettend zielig" ©


omfgquote:Op dinsdag 7 maart 2006 17:14 schreef Nekto het volgende:
Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.
anders onthouden ze het niet of zo?
dat het eigenlijk de regel x(y + z) = xy + xz is wordt ze ook al niet verteld
onderwijs in NEderland
allemaal de schuld van de PvdA
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Tussen droom en daad staan wetten in de weg, en praktische bezwaren.quote:Op dinsdag 7 maart 2006 17:16 schreef Litso het volgende:
maar ik kan me voorstellen dat er mensen zijn die liefst na hun examen niks meer met wiskunde te maken willen hebben


papagaaienregels en zoquote:
da's niks
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


die van mij
versus die van jouquote:Op dinsdag 7 maart 2006 16:58 schreef McCarthy het volgende:
in brief
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
quote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
[afbeelding]
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Voor iemand die van deze som al geen hout snapt en zich afvraagt waar zijn kwadraat heen is kan ik me voorstellen dat diegene ook niet al teveel aan jouw post heeft.quote:
"Dat is echt ontzettend zielig" ©


Begrijp me niet verkeerd, ik heb niks tegen wiskunde, ik ben zelf meer een bètamens dan wat anders. Ik zie ook wel degelijk het nut in van wiskunde, ook voor later. Maar als iemand het ontbinden in factoren nou eenmaal makkelijker begrijpt door de naam papegaaienbek te gebruiken denk ik dat je beter gelukkig kan zijn dat hij weet hoe hij het toe moet passen dan zeuren dat hij de goede naam niet gebruiktquote:Op dinsdag 7 maart 2006 17:16 schreef Nekto het volgende:
[..]
Tussen droom en daad staan wetten in de weg, en praktische bezwaren.
"Dat is echt ontzettend zielig" ©


ik stel voor dat we dan thabit op hem af sturenquote:Op dinsdag 7 maart 2006 17:18 schreef Litso het volgende:
[..]
Voor iemand die van deze som al geen hout snapt en zich afvraagt waar zijn kwadraat heen is kan ik me voorstellen dat diegene ook niet al teveel aan jouw post heeft.
enes kijken hoe dat uitpakt.
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


toch lijkt me dit makkelijkerquote:Op dinsdag 7 maart 2006 17:20 schreef Litso het volgende:
[..]
Begrijp me niet verkeerd, ik heb niks tegen wiskunde, ik ben zelf meer een bètamens dan wat anders. Ik zie ook wel degelijk het nut in van wiskunde, ook voor later. Maar als iemand het ontbinden in factoren nou eenmaal makkelijker begrijpt door de naam papegaaienbek te gebruiken denk ik dat je beter gelukkig kan zijn dat hij weet hoe hij het toe moet passen dan zeuren dat hij de goede naam niet gebruikt
x(y + z) = xy + xz
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Makkelijker, wiskundig sowieso veel verantwoorder, maar ik pretendeer dan ook niet dat ik beter wiskunde kan dan jij (integendeel, ik ben bang dat mijn kennis het snel af laat weten). Maar misschien is wat extra uitleg eromheen wel handig. Misschien ook niet. We merken het wel als hij nog reageertquote:Op dinsdag 7 maart 2006 17:22 schreef McCarthy het volgende:
[..]
toch lijkt me dit makkelijker
x(y + z) = xy + xz
"Dat is echt ontzettend zielig" ©


quote:
En wow wat een reacties verder Nekto heel erg bedankt voor je uitleg, al werd ik er wat draaiering van
Even een check, ik ben al aan de volgende som begonnen en wil even weten of ik goed onderweg ben
Los op: x^2 + x = 4x + 28
x^2 + x = 4x + 28 (-4x)
x^2 -3x = 28 (-28)
x^2 -3x - 28 = 0
Dan uit nekto's verhaal het a+b=c en a*b=d
a+b = c (-3)
axb = d (-28)
wat dan word
(x a)(x b) = 0 En dan vervolgens het antwoord maar dat is een eitje
Klopt dit tot zo ver? En er is dus geen andere manier, behalve een beetje puzzelen, om A en B te vinden?


Ik had die lange reply van Nekto helemaal gemist
Maar mooi dat het nu wil lukken
Maar mooi dat het nu wil lukken
"Dat is echt ontzettend zielig" ©


Beetje puzzelen kom je er wel. Als het beide een negatief getal weet je wel dat van a en b eentje negatief is, en eentje positief. In dit geval is het -7 en 4.quote:Op dinsdag 7 maart 2006 17:32 schreef Robin__ het volgende:
[..]
En wow wat een reacties verder Nekto heel erg bedankt voor je uitleg, al werd ik er wat draaiering van
Even een check, ik ben al aan de volgende som begonnen en wil even weten of ik goed onderweg ben
Los op: x^2 + x = 4x + 28
x^2 + x = 4x + 28 (-4x)
x^2 -3x = 28 (-28)
x^2 -3x - 28 = 0
Dan uit nekto's verhaal het a+b=c en a*b=d
a+b = c (-3)
axb = d (-28)
wat dan word
(x a)(x b) = 0 En dan vervolgens het antwoord maar dat is een eitje
Klopt dit tot zo ver? En er is dus geen andere manier, behalve een beetje puzzelen, om A en B te vinden?
"Dat is echt ontzettend zielig" ©


Als je het linkerdeel tussen haakjes gaat zetten, wil je 2 getallen hebben op zo'n manier, dat als je ze optelt, je het getal wat voor de x staat hebt, en vermenigvuldigt, het enkele getal...
Dus in dit geval wil je 2 getallen hebben die: opgeteld 5 en vermenigvuldigt -6 zijn...
dus -1 en 6 zijn geschikt...
Werk (x-6)(x+1) maar eens uit, haal de haakjes maar weer weg, en je hebt (als het goed is) je eerste vergelijking weer
Dus in dit geval wil je 2 getallen hebben die: opgeteld 5 en vermenigvuldigt -6 zijn...
dus -1 en 6 zijn geschikt...
Werk (x-6)(x+1) maar eens uit, haal de haakjes maar weer weg, en je hebt (als het goed is) je eerste vergelijking weer
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"


Ik ben goed voor een aardige discussie zie ikquote:Op dinsdag 7 maart 2006 17:25 schreef Litso het volgende:
[..]
Makkelijker, wiskundig sowieso veel verantwoorder, maar ik pretendeer dan ook niet dat ik beter wiskunde kan dan jij (integendeel, ik ben bang dat mijn kennis het snel af laat weten). Maar misschien is wat extra uitleg eromheen wel handig. Misschien ook niet. We merken het wel als hij nog reageert
Ik ben wel bekend met het papagaaienbek verhaal (vorig jaar ergens) en mn natuurkunde leraar heeft ooit tussen neus en lippen door gemeld dat dat hetzelfde is als 'x(y + z) = xy + xz' Maar de toepassing op deze manier, 2 sets haakjes achter elkaar = 0 is in de les iniedergeval nooit behandeld.. er is eigenlijk gewoon helemaal niets uitgelegd (das nieuw ofzo? en in een lokaal met geluidsniveau kinderboerderij op vrijdag middag 3 uur lukt het mij ook echt niet zelf een nutige vraag te formuleren.. de helft van de aanwezigen (vrijwillig) komt alleen zodat ze niet op stage hoeven te zijn maar kunnen lullen met klasgenoten)


De meesten denken dat het ze niet duidelijker wordt als ze de toepassing van het distributiviteitsaxioma x(y + z) = x*y + x*z wordt uitgelegd. Maar dat komt eigenlijk vooral door de naam en de onwil. Want feitelijk is het dat gewoon. En distributiviteit komt op allerhande plekken terug in de wiskunde.


wat studeer je dan?quote:Op dinsdag 7 maart 2006 17:25 schreef Litso het volgende:
[..]
Makkelijker, wiskundig sowieso veel verantwoorder, maar ik pretendeer dan ook niet dat ik beter wiskunde kan dan jij (integendeel, ik ben bang dat mijn kennis het snel af laat weten).
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Dat woord uitgesproken door mijn wiskunde lerares lijkt me zwaar humorquote:Op dinsdag 7 maart 2006 17:56 schreef Nekto het volgende:
distributiviteitsaxioma
Ik blijf dit topic zeker volgen, misschien steek ik er nog wat van op, of kan ik zelf eens iemand helpen, al gaan de meeste vragen hier mij voorlopig zwaar de pet te boven. Ik volg trouwens een opleiding werktuigbouwkunde, mbo, niv 4, 3e jaar. Dit jaar alleen maar een of ander competentie gestuurd bullshit project en sporadisch een les pneumatiek of autocad. Op vrijdag middag dus 2 uur natuurkunde en 2 uur wiskunde voor hbo doorstroom.. en schijnbaar is de tijd dat ik lekker achterover kan leunen en toch goede cijvers halen nu toch voorbij (ben er zowaar een beetje blij om )
Thanks voor de uitleg


Digitale Communicatie. Ik vind wiskunde wel interessant maar ik ben er niet super goed in.quote:
"Dat is echt ontzettend zielig" ©


Omdat de vermenigvuldiging ' x ' teveel lijkt op de variabele x, vriendelijk doch dringend het verzoek het de vermenigvuldigings ' x ' niet te gebruiken. axb betekent a vermenigvuldigd met x vermenigvuldigd met b. Jij bedoelt ab.quote:
Wat bedoel je met ' (x a)(x b) = 0 '. Het lijkt allemaal onbelangrijk, maar netjes werken in de wiskunde is erg belangrijk. Alles heeft een betekenis, dus wees precies.quote:wat dan word
(x a)(x b) = 0 En dan vervolgens het antwoord maar dat is een eitje
abc-formule: x1,2=(-b±SQR(b2-4ac))/2aquote:Klopt dit tot zo ver? En er is dus geen andere manier, behalve een beetje puzzelen, om A en B te vinden?
Uitgaande van x2 -3x - 28 = 0 geeft dit
a=1
b=-3
c=-28
Invullen levert dan
x1,2=(3±SQR(9-(-112)))/2
x1,2=(3±11)/2
x1=(3-11)/2=-4 en x2=(3+11)/2=7


De abc- of wortelformule leidt vaak tot dom toepassen. (En is zeker niet altijd sneller.) Ik heb vaak wel esthetische voorkeuren voor ontbinden, en daar zie je ook sneller dat het goed is.


x^2 + 5x - 6 = (x-6)(x+1)
Je gebruikt hier de volgende regel, die alleen bij tweedegraads vergelijkingen werkt.
Je hebt de vorm x^2 + Qx - P
Nu moet je 2 getallen vinden, die opgeteld Q zijn, en vermenigvuldigd P. Als het goed is, is dit de regel. Waarom het zo is, vraag het me niet, dat is gewoon zo :p
Dus bij jou moet je 2 getallen vinden, die opgeteld 5 zijn, en vermenigvuldigd -6.
Beetje puzzelen, en dan kom je op -1 en 6
-1 * 6 = -6
-1 + 6 = 5
Je vergelijking is daardoor (x-6)(x+1)=0
Hier vermenigvuldig je 2 getallen met elkaar, die dan 0 zijn.
Dat kan alleen maar als 1 van die 2 getallen nul is.
Dus
x - 6 = 0
of
x + 1 = 0
x is dus 6 of -1.
En dat klopt, dat zie je ook als je 'm plot in je rekenmachine...
Ik hoop dat je een beetje geholpen bent
__
Zoo, dan had ik zelf ook nog een vraag
Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig
Je gebruikt hier de volgende regel, die alleen bij tweedegraads vergelijkingen werkt.
Je hebt de vorm x^2 + Qx - P
Nu moet je 2 getallen vinden, die opgeteld Q zijn, en vermenigvuldigd P. Als het goed is, is dit de regel. Waarom het zo is, vraag het me niet, dat is gewoon zo :p
Dus bij jou moet je 2 getallen vinden, die opgeteld 5 zijn, en vermenigvuldigd -6.
Beetje puzzelen, en dan kom je op -1 en 6
-1 * 6 = -6
-1 + 6 = 5
Je vergelijking is daardoor (x-6)(x+1)=0
Hier vermenigvuldig je 2 getallen met elkaar, die dan 0 zijn.
Dat kan alleen maar als 1 van die 2 getallen nul is.
Dus
x - 6 = 0
of
x + 1 = 0
x is dus 6 of -1.
En dat klopt, dat zie je ook als je 'm plot in je rekenmachine...
Ik hoop dat je een beetje geholpen bent
__
Zoo, dan had ik zelf ook nog een vraag
Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig
De sint verzon op z'n gemak,
dit voor het oude wrak.
dit voor het oude wrak.


quote:Op woensdag 8 maart 2006 15:16 schreef Market_Garden het volgende:
Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig
Erg goed boek. Goed leesbaar voor leken, tevens zeer interessant voor vakmensen.


quote:Op woensdag 8 maart 2006 15:16 schreef Market_Garden het volgende:
En dat klopt, dat zie je ook als je 'm plot in je rekenmachine...
Ik neem aan dat je dit bewijs van Ivan Niven hebt gevonden.quote:Ik ben aan het bewijs bezig dat Pi irrationaal is. Ik ben al een aardig eind gekomen, maar er zijn nog veel stappen waar ik geen kaas van kan maken
Heeft iemand hier een goede bron voor, waar het bewijs goed staat beschreven? Google geeft weinig
Dat is een elegant bewijs, ik heb het ooit gesnapt (was volgens mij ook niet zo moeilijk), maar het helemaal uittypen, dat wordt me te veel werk, dus zeg waar je vastloopt. Let op de notatie f<sup>(2)</sup> betekent de tweede afgeleide van f, etc. (De rest lijkt me wel duidelijk).
Onderstaand boek bevat ook een goed volgbaar bewijs van de irrationaliteit van Pi (en nog andere elegante bewijzen):
[ Bericht 11% gewijzigd door Nekto op 08-03-2006 15:43:15 ]


Wiskunde - primitiveren:
Omdat ik de oppervlakte moet uitrekenen van een bepaald gedeelte onder een grafiek, heb ik een integraal opgesteld. Om die integraal op te lossen moet ik de volgende functie primitiveren:
f(x) = 100 * 0,998x
Iemand enig idee hoe ik dit moet oplossen en wat de uitkomst is? Ik heb zelf wel wat zitten klungelen, maar op het goede antwoord kwam ik niet.
Bedankt alvast !
Omdat ik de oppervlakte moet uitrekenen van een bepaald gedeelte onder een grafiek, heb ik een integraal opgesteld. Om die integraal op te lossen moet ik de volgende functie primitiveren:
f(x) = 100 * 0,998x
Iemand enig idee hoe ik dit moet oplossen en wat de uitkomst is? Ik heb zelf wel wat zitten klungelen, maar op het goede antwoord kwam ik niet.
Bedankt alvast !
Woei!


Als je een exponent differentieert met als grondgetal ongelijk aan e krijg je: f(x) = g^x -> f'(x) = ln(g).g^xquote:Op woensdag 8 maart 2006 18:55 schreef Floriz87 het volgende:
Wiskunde - primitiveren:
Omdat ik de oppervlakte moet uitrekenen van een bepaald gedeelte onder een grafiek, heb ik een integraal opgesteld. Om die integraal op te lossen moet ik de volgende functie primitiveren:
f(x) = 100 * 0,998x
Iemand enig idee hoe ik dit moet oplossen en wat de uitkomst is? Ik heb zelf wel wat zitten klungelen, maar op het goede antwoord kwam ik niet.
Bedankt alvast !
Vang die ln(g) op en je hebt je primitieve.
Sea Shepherd
Virtus omnia vincit
Virtus omnia vincit


Haha, sorry, maar khad echt een hele domme fout gemaakt. Ik had de primitieve wel goed, de fout zat ergens anders. Mijn excuses .
De primitieve is btw: F(x) = ( 100 / ln0,998 ) * 0,998^x
Bedankt iig!
De primitieve is btw: F(x) = ( 100 / ln0,998 ) * 0,998^x
Bedankt iig!
Woei!


Nog even over mijn experiment met insuline.
Ik heb dus insuline, 3 ml geregeld. Die gaan we onder andere samenvoegen met pepsine en dan gaan we bij de drie stoffen die we dan hebben kijken hoe ze uitlopen bij papierchromotografie.
Ik wil dus gaan aantonen dan insuline wordt aangetast door het maagsap.
Dus 1x bij insuline, 1x bij pepsine en HCL en 1x bij insuline met pepsine en HCL.
Ik zit alleen met 2 vraagjes. Ik heb 3 ml, dat is voor insuline best veel, maar kan ik daar wel papierchromotografie mee doen? Of moet ik het dan eerst verdunnen?
En welke loopvloeistof moet ik nemen? Alvast erg bedankt
[ Bericht 7% gewijzigd door WyBo op 08-03-2006 20:37:50 ]
Ik heb dus insuline, 3 ml geregeld. Die gaan we onder andere samenvoegen met pepsine en dan gaan we bij de drie stoffen die we dan hebben kijken hoe ze uitlopen bij papierchromotografie.
Ik wil dus gaan aantonen dan insuline wordt aangetast door het maagsap.
Dus 1x bij insuline, 1x bij pepsine en HCL en 1x bij insuline met pepsine en HCL.
Ik zit alleen met 2 vraagjes. Ik heb 3 ml, dat is voor insuline best veel, maar kan ik daar wel papierchromotografie mee doen? Of moet ik het dan eerst verdunnen?
En welke loopvloeistof moet ik nemen? Alvast erg bedankt
[ Bericht 7% gewijzigd door WyBo op 08-03-2006 20:37:50 ]


In de praktijk zijn de oplossingen zeer zelden gehele getallen. Formules gebruik je juist om dom toe te passen. Je moet nadenken over welke formule je moet toepassen.quote:Op woensdag 8 maart 2006 14:20 schreef Nekto het volgende:
De abc- of wortelformule leidt vaak tot dom toepassen. (En is zeker niet altijd sneller.) Ik heb vaak wel esthetische voorkeuren voor ontbinden, en daar zie je ook sneller dat het goed is.


Niemand die mij kan of wil helpen?quote:Op woensdag 8 maart 2006 19:57 schreef WyBo het volgende:
Nog even over mijn experiment met insuline.
Ik heb dus insuline, 3 ml geregeld. Die gaan we onder andere samenvoegen met pepsine en dan gaan we bij de drie stoffen die we dan hebben kijken hoe ze uitlopen bij papierchromotografie.
Ik wil dus gaan aantonen dan insuline wordt aangetast door het maagsap.
Dus 1x bij insuline, 1x bij pepsine en HCL en 1x bij insuline met pepsine en HCL.
Alleen welke loopvloeistof moet ik nemen? Met ammonia of is loopvloeistof met ethanol of alcohol beter? Alvast erg bedankt


Pfff, ik zit even te denken, misschien dat je op chemieforum.nl meer respons krijgt, ik weet hier verder ook niet zoveel vanaf..
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"


Iemand enig idee hoe ik dit vereenvoudig?
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
Woei!


Een noob-bui? Jij komt hier met de huiswerkvraag, dus is het logisch dat je er zelf ook even wat energie in steekt. Ik snap de vraag nu iig niet, dus misschien is het verstandig dat je zelf even uitzoekt hoe je dit wat beter kan formuleren?quote:Op donderdag 9 maart 2006 15:54 schreef Floriz87 het volgende:
Iemand enig idee hoe ik dit vereenvoudig?
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
"Dat is echt ontzettend zielig" ©


quote:Op donderdag 9 maart 2006 15:54 schreef Floriz87 het volgende:
Iemand enig idee hoe ik dit vereenvoudig?
http://img417.imageshack.us/my.php?image=sommetje4uu.jpg
Ben echt in n00b-bui vandaag. Weet niet hoe ik met computers en wiskunde om moet gaan.
Dus, zorg eerst dat je in de noemer van de grote breuk eens één breuk in plaats van een som krijgt, en deel dan.


Ik bedoel te zeggen dat ik het inzicht vandaag ff mis. Zit er nu al tijd mee, maar krijg hem niet opgelost. Duidelijker geformuleerd krijg ik hem denk ik niet. Misschien als ik hem uitteken en vervolgens inscan . Geen idee hoe ik dat met de computer moet doen...quote:Op donderdag 9 maart 2006 16:39 schreef Litso het volgende:
[..]
Een noob-bui? Jij komt hier met de huiswerkvraag, dus is het logisch dat je er zelf ook even wat energie in steekt. Ik snap de vraag nu iig niet, dus misschien is het verstandig dat je zelf even uitzoekt hoe je dit wat beter kan formuleren?
Maar reactie op de post hiervoor: Inderdaad zag ik dat nu net dus ook. Maar ik krijg er niet eens een normale breuk van. Je kan die 1 toch niet zomaar bij die teller optellen? Want wil je breuken op kunnen tellen, dan moet wel de noemer gelijk zijn. En kheb geen idee hoe ik die gelijk moet krijgen.
Woei!


Snap niet hoe je met die hints wat kunt doen hier.quote:Op donderdag 9 maart 2006 16:41 schreef Nekto het volgende:Onder een noemer brengen Delen door een breuk is vermenigvuldigen met het omgekeerde.
Het makkelijkste is denk ik het eenheidselement gebruiken: x*1 = x. Als je met 1 vermenigvuldigt, verandert de breuk niet. Vermenigvuldig met (1+x)/(1+x). Dat doe je door zowel teller als noemer ermee te vermenigvuldigen. Pas distributiviteit goed toe in de noemer, en je bent klaar.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Werd toch net ook gezegd?quote:Op donderdag 9 maart 2006 19:03 schreef GlowMouse het volgende:
[..]
Snap niet hoe je met die hints wat kunt doen hier.
Het makkelijkste is denk ik het eenheidselement gebruiken: x*1 = x. Als je met 1 vermenigvuldigt, verandert de breuk niet. Vermenigvuldig met (1+x)/(1+x). Dat doe je door zowel teller als noemer ermee te vermenigvuldigen. Pas distributiviteit goed toe in de noemer, en je bent klaar.


Waar precies? "En 1 = 1/1 = a/a = (b+q)/(b+q) = patat/patat." komt erg uit de lucht vallen.quote:Werd toch net ook gezegd?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Eendere methode komt (vrijwel) op hetzelfde neer. Doch, als hij de ene uitleg wel snapt, maar de andere niet, dan kan dat alleen maar baatzaam zijn.


Nee, de hints zijn iets te ingewikkeld. Ik zal het morgen wel even aan mijn wiskundeleraar vragen, het is wat moeilijk alles uit te schrijven zoals ik het gedaan heb. Anders hadden jullie even aan kunnen wijzen waar het fout ging.
Bedankt iig, kheb weer wat inzichten opgedaan .
Bedankt iig, kheb weer wat inzichten opgedaan .
Woei!


Goed, er zijn verschillende mogelijkheden… ik zal eens een ASCII-art oplossing aanreiken.
De ‘noemer’ onder een noemer brengen:
Wat gelijk is aan:
Delen door een breuk, vermenigvuldigen met het omgekeerde:
Dus: 1/(2+x)
Anders:
Breng van de noemer van de teller (i.e. 1/1+x bovenin) direct in de noemer:
Is ook 1/(2+x)
| 1 2 3 4 5 6 7 | --- 1+x ------- 1 1 + --- 1+x |
De ‘noemer’ onder een noemer brengen:
| 1 2 3 4 5 6 7 | --- 1+x -------- 1+x 1 --- + --- 1+x 1+x |
Wat gelijk is aan:
| 1 2 3 4 5 6 7 | --- 1+x -------- 2+x --- 1+x |
Delen door een breuk, vermenigvuldigen met het omgekeerde:
| 1 2 3 | ---------- (1+x)(2+x) |
Dus: 1/(2+x)
Anders:
| 1 2 3 4 5 6 7 | --- 1+x ------- 1 1 + --- 1+x |
Breng van de noemer van de teller (i.e. 1/1+x bovenin) direct in de noemer:
| 1 2 3 4 | 1 ------- 1+x + 1 |
Is ook 1/(2+x)


Je wordt bedankt! Erg overzichtelijk! Nu weet ik gelijk hoe voortaan formules kan 'digitaliseren'. Bovendien snap ik de vereenvoudiging ook nog eens !
Woei!


Is de inhoud een beetje goed van dit stukje tekst, of staat er echt grote fouten in. Jullie hoeven niet te kijken naar spelfouten e.d.quote:Endotherme reacties
Hoe komt het dat als je barium….. en ammonium……. met elkaar mengt dat het kouder wordt!!!?????!!??!?!?!?!?!
De antwoord op die vraag is eigenlijk niet zo heel erg moeilijk. Nee? Nee, nauw misschien toch wel.
In oplossing gaan is niet echt een chemische reactie, dus als je echt een reactie wilt blijven alleen processen waarbij een gas vrijkomt over.....
Het “ontstaan” of “verdwijnen” van warmte kan je uitleggen met de begrippen enthalpie en entropie.
Wat houd dit in? Enthalpie staat voor de hoeveelheid energie die door de molecuul is opgenomen.
Entropie is een maat voor de wanorde in een systeem
Dat betekend dus dat entropie staat voor hoe ordelijk je moleculen gerangschikt zijn, dus of ze in een mooi rooster zitten of lekker door elkaar aan ’t zweven zijn. Zeg maar hoe groter de ruimte tussen de moleculen hoe groter de entropie.
Men heeft ook ooit de deze mooie formule bedacht: ΔG= ΔH – TΔS
Bij een spontaan endotherm proces zal de G altijd afnemen, in een endotherme reactie neemt de enthalpie(ΔH) toe, vind je ’t gek, de energie moet toch ergens naartoe. Dus ΔG is negatief, ΔH is positief, dus moet TΔS wel heel positief zijn, namelijk (│ΔG+ΔH│)
Dat is allemaal wel mooi en aardig maar wat is die TΔS dan? De T staat voor temperatuur in kelvin en ΔS staat voor de entropie. Aangezien er zoiets bestaat als ’t absolute nulpunt moet T wel positief zijn en dus is ΔS ook positief.
Dat verklaart ook waarom de stoffen kouder worden als er een gas vrij komt. “Echt waar?? Vertel eens waarom dan?”
Kijk de beginstoffen waren allemaal zouten, die zitten allemaal netjes in kristalroosters, de Entropie is dus laag. Maar als ze met elkaar reageren dan veranderen ze in gassen, vloeistoffen en zouten. Dus van 2 geordende stoffen ga je naar meerdere ongeordende stoffen ΔH neemt toe, denk aan de vanderwaals bindingen die verbroken moeten worden, dat kost ook energie.ΔS neemt toe, je gaat namelijk van een geordende zaak naar een warboel. Omdat de T min of meer constant is en ΔS heel groot is zal er dus veel energie worden opgenomen uit de omgeving en wordt ’t dus kouder.
"Those unforgettable days, for them I live"


" Zeg maar hoe groter de ruimte tussen de moleculen hoe groter de entropie." ? Da's toch echt niet waar. De entropie is gedefinieerd als S=k*log(O), waarbij O je vertelt op hoeveel manieren je de verzameling kunt rangschikken. Een evenwicht komt dan overeen met een maximale entropie.
Ik weet trouwens niet waar het stukje voor bedoelt is, maar je schrijfstijl laat nogal te wensen over, voor het geval je het hebt geschreven om anderen het uit te leggen
Ik weet trouwens niet waar het stukje voor bedoelt is, maar je schrijfstijl laat nogal te wensen over, voor het geval je het hebt geschreven om anderen het uit te leggen
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik moet voor Scheikude P.O. een practicum doen. We moeten dus een Ester maken..
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
Klopt dit?
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
Klopt dit?


tvp, antwoord volgtquote:Op zaterdag 11 maart 2006 23:55 schreef Crazykill het volgende:
Ik moet voor Scheikude P.O. een practicum doen. We moeten dus een Ester maken..
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
Klopt dit?


Bij propanol weet je niet waar de alcoholgroep zit, de naam is dus niet volledig. Verder ziet het er goed uit.quote:Ik moet voor Scheikude P.O. een practicum doen. We moeten dus een Ester maken..
De stof die ik moet maken is 2-propylmethanoaat. Dit geeft toch deze reactie...
propanol + methaanzuur >>> 2-propylmethanoaat + water
(evenwichtsreactie)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hoe bedoel je ?quote:Op zondag 12 maart 2006 13:04 schreef GlowMouse het volgende:
[..]
Bij propanol weet je niet waar de alcoholgroep zit, de naam is dus niet volledig. Verder ziet het er goed uit.
Oja, hoe kan ik berekenen hoeveel propanol en methaanzuur ik nodig heb om 2mL ester (2-propylmethanoaat) te krijgen?


De alcoholgroep kan zowel aan een de middelste C (2-propanol) als aan een C aan de zijkant (1-propanol) zitten. In dit geval wil je methanoaat aan de middelste C hebben, dus kies je voor 2-propanol.quote:Hoe bedoel je ?
Weet je zeker dat de ester vloeibaar is, dat je hem in mL meet? Zoja, dan heb je de dichtheid nodig om naar massa te gaan. Via massa kun je via molaire massa naar aantal mol.quote:Oja, hoe kan ik berekenen hoeveel propanol en methaanzuur ik nodig heb om 2mL ester (2-propylmethanoaat) te krijgen?
Als het om een ester in oplossing gaat, heb je de gewenste molariteit nodig om bij mol te komen.
Als je het aantal mol 2-propylmethanoaat weet, neem ik aan dat je de rest zelf weer kunt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Uhmm ja, dat zei de leraar welquote:Op zondag 12 maart 2006 15:02 schreef GlowMouse het volgende:
Weet je zeker dat de ester vloeibaar is, dat je hem in mL meet? Zoja, dan heb je de dichtheid nodig om naar massa te gaan. Via massa kun je via molaire massa naar aantal mol.
Als het om een ester in oplossing gaat, heb je de gewenste molariteit nodig om bij mol te komen.
Als je het aantal mol 2-propylmethanoaat weet, neem ik aan dat je de rest zelf weer kunt
C4H8O2
dichtheid = 0.904
Volume = 2 ML
M = 2*0,904 = 1,808 gram
Mol. massa = 88.106
aantal mol = 1,808 / 88.106 =0.020 mol
C3H8O+HCOOH >>> C4H8O2+H2O
mol massa:
C3H8O = 60.09
HCOOH = 46.02
Uhmm hier zit ik dus vast, ik snap niet zo goed hoe je dan die 2mL kunt krijgen.. (ik begrijp deze onderwerp niet zo goed )
(Je hoeft die berekening niet te doen voor me hoor alleen ff uitleggen hoe ik het moet doen )


Hier en daar missen wat eenheden, maar ik ga er even vanuit dat al je berekeningen tot nu toe kloppen.
Je zei al dat het om een evenwichtsreactie ging. De volgende stap is daarom het opstellen van de evenwichtsvoorwaarde. Je hebt daarbij de evenwichtsconstante nodig. Daarna is het een kwestie van oplossen.
Je zei al dat het om een evenwichtsreactie ging. De volgende stap is daarom het opstellen van de evenwichtsvoorwaarde. Je hebt daarbij de evenwichtsconstante nodig. Daarna is het een kwestie van oplossen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Is er geen andere manier om het te berekenen, want ik heb de evenwichtsconstante niet. :
Edit: De Kz van HCOOH staat wel in Binas, maar kan ik die ook gebruiken?
[ Bericht 17% gewijzigd door Crazykill op 12-03-2006 16:20:32 ]
Edit: De Kz van HCOOH staat wel in Binas, maar kan ik die ook gebruiken?
[ Bericht 17% gewijzigd door Crazykill op 12-03-2006 16:20:32 ]


In enkele gevallen wel, maar hier lijkt me het lastig. Je kunt alleen aan evenwichten rekenen als je de evenwichtsconstante hebt. Zonder die constante kun je er wel aan rekenen, maar dan moet je het evenwicht verstoren door een beginstof weg te nemen. Omdat je C4H8O2 over wilt houden, zou dat water zijn.quote:Is er geen andere manier om het te berekenen, want ik heb de evenwichtsconstante niet.
Een andere manier is om dmv de temperatuur de evenwichtsreactie toch zoveel mogelijk naar rechts te laten verlopen, maar je weet dan niet of de reactie voor 5 of voor 99% verloopt.
Nee.quote:Edit: De Kz van HCOOH staat wel in Binas, maar kan ik die ook gebruiken?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja inderdaad, we moeten zoutzuur toevoegen waardoor water word ontrokken. Dus de evenwicht gaat naar rechts waardoor we de ester overhouden.quote:Op zondag 12 maart 2006 16:23 schreef GlowMouse het volgende:
[..]
In enkele gevallen wel, maar hier lijkt me het lastig. Je kunt alleen aan evenwichten rekenen als je de evenwichtsconstante hebt. Zonder die constante kun je er wel aan rekenen, maar dan moet je het evenwicht verstoren door een beginstof weg te nemen. Omdat je C4H8O2 over wilt houden, zou dat water zijn.
Een andere manier is om dmv de temperatuur de evenwichtsreactie toch zoveel mogelijk naar rechts te laten verlopen, maar je weet dan niet of de reactie voor 5 of voor 99% verloopt.
Maar ik dacht dus...
De verhouding is 1:1
C3H8O + HCOOH >>>> C4H8O2 + H2O
0,020 mol C4H8O2 had ik nodig
Dus C3H8O en HCOOH moeten ook 0,020 mol zijn.
Als ik dan uitreken hoeveel gram 0,020 mol C3H8O en HCOOH zijn, dan weet ik toch hoeveel ik nodig heb? Of klopt dit niet?


Thnx voor je hulp/moeite !quote:Op zondag 12 maart 2006 17:10 schreef GlowMouse het volgende:
Dat klopt.


Ik heb ff een klein vraagje waar ik niet helemaal uitkom.
We laten een bal op de tafel vallen, waarvandaan deze wordt teruggekaatst. De tijd tot de volgende impact is dan:
t = (2 v) / g,
met v de snelheid en g de gravitatieversnelling. Stellen we nu g=1/2, dan kunnen we de stuiterende bal modelleren dmv de volgende afbeelding:
t -> t + v
v -> a v,
waarbij a een parameter is met 0 < a < 1.
Dit is de beginsituatie en dit is mij volkomen duidelijk. Heb hier al wat aan gerekend (dekpunten enzo) en dat lukt allemaal wel. Maar nu verandert er het volgende aan de situatie.
Nu laten we de bal vallen op een oppervlak dat periodiek aangedreven wordt. Het tafelblad blijft loodrecht op de verticale as, maar beweegt nu op en neer volgens -B*sin(t). Stel nu c = (1+a)*B.
Laat nu zien dat deze nieuwe situatie gemodelleerd kan worden door de afbeelding:
t -> t + v
v -> av - c*cos(t+v)
Volgens mij is dit niet zo moelijk, maar ik zie gewoonweg niet waarom dit zo is.
Wie helpt me uit de brand?
Theories come and theories go. The frog remains


hier een vraagje:
{a1,a2,a3,...,an} en {b1,2,b3,..bn}
two sets of real numbers. Find a necessary and (a) sufficient condition for {a1,a2,a3,...,an} and {b1,2,b3,..bn}
such that there are real numbers A and B with
(a1x+b1)²+(a2x+b2)²+...+(anx+bn)²
=(Ax+B)²
voor all values of x.
Het lijkt me sterk dat deze vraag veel te maken heeft met de vraag:
toon aan dat:
a²+b²+c²+d²=ab+bc+cd+ad
slechts en slechts als a=b=c=d
deze vraag is niet moeilijk te beantwoorden:
a²+b²+c²+d²=ab+bc+cd+ad ==> 2(a²+b²+c²+d²)=2(ab+bc+cd+ad)
dan krijg je iets van (a-b)²+(b-c)²...=0 dan is a=b, b=c,c=d,d=a dus a=b=c=d.
De 2e vraag is een geval van de algemene vraag1.
{a1,a2,a3,...,an} en {b1,2,b3,..bn}
two sets of real numbers. Find a necessary and (a) sufficient condition for {a1,a2,a3,...,an} and {b1,2,b3,..bn}
such that there are real numbers A and B with
(a1x+b1)²+(a2x+b2)²+...+(anx+bn)²
=(Ax+B)²
voor all values of x.
Het lijkt me sterk dat deze vraag veel te maken heeft met de vraag:
toon aan dat:
a²+b²+c²+d²=ab+bc+cd+ad
slechts en slechts als a=b=c=d
deze vraag is niet moeilijk te beantwoorden:
a²+b²+c²+d²=ab+bc+cd+ad ==> 2(a²+b²+c²+d²)=2(ab+bc+cd+ad)
dan krijg je iets van (a-b)²+(b-c)²...=0 dan is a=b, b=c,c=d,d=a dus a=b=c=d.
De 2e vraag is een geval van de algemene vraag1.
verlegen :)


Haakjes uitwerken is een vrij directe manier die hier wel werkt. Een andere manier is opmerken dat (Ax+B)2 een nulpunt in R heeft mits A niet nul is.
[ Bericht 79% gewijzigd door thabit op 13-03-2006 19:17:38 ]
[ Bericht 79% gewijzigd door thabit op 13-03-2006 19:17:38 ]


De vraag is wel slecht geformuleerd trouwens. In een verzameling staan de elementen namelijk niet op een bepaalde volgorde terwijl dat hier wel wordt gebruikt.


Ik heb een breuk probleem
ik moet een breuksplitsen namenlijk
x − 5
------------
x^3 − x^2 − 2x
nu ben ik tot hier gekomen
maar ik kan nu niet verder want ik zit met drie variabelen?
hoe los ik dit op
ik moet een breuksplitsen namenlijk
x − 5
------------
x^3 − x^2 − 2x
nu ben ik tot hier gekomen
| 1 2 3 | - + ------ + --------- x x+1 x-2 |
maar ik kan nu niet verder want ik zit met drie variabelen?
hoe los ik dit op
1/10 Van de rappers dankt zijn bestaan in Amerika aan de Nederlanders die zijn voorouders met een cruiseschip uit hun hongerige landen ophaalde om te werken op prachtige plantages.
"Oorlog is de overtreffende trap van concurrentie."
"Oorlog is de overtreffende trap van concurrentie."


Je moet die breuken met A, B en C onder een noemer brengen. Dan krijg je in de tellerquote:Op maandag 13 maart 2006 20:53 schreef icecreamfarmer_NL het volgende:
Ik heb een breuk probleem
ik moet een breuksplitsen namenlijk
x − 5
------------
x^3 − x^2 − 2x
nu ben ik tot hier gekomen
[ code verwijderd ]
maar ik kan nu niet verder want ik zit met drie variabelen?
hoe los ik dit op
A (x + 1)(x - 2) + B x(x - 2) + C x(x + 1).
De haakjes moet je zelf even uitwerken. Het moet dan gelijk zijn aan x-5 voor zekere waarden van A, B en C. Je moet ze dus zodanig kiezen dat de coefficient van (A+B+C)x^2 gelijk is aan 0, ofwel A+B+C=0. Ditzelfde moet je doen voor de coefficient van x en de constante term. Dan krijg je drie lineaire vergelijkingen in 3 onbekenden die je wel kunt oplossen.


Je kunt hier A bepalen door links en rechts met x te vermenigvuldigen:
A + Bx/(x+1) + Cx/(x-2) = x(x-5)/(x^3-x^2-2x) = (x-5)/(x+1)(x-2).
Daarna vul je simpelweg x=0 in en voila:
A + 0 + 0 = 5/2.
Dezelfde truuk kun je gebruiken om B en C te bepalen. Bij B moet je dan dus met x+1 vermenigvuldigen en x=-1 invullen.
A + Bx/(x+1) + Cx/(x-2) = x(x-5)/(x^3-x^2-2x) = (x-5)/(x+1)(x-2).
Daarna vul je simpelweg x=0 in en voila:
A + 0 + 0 = 5/2.
Dezelfde truuk kun je gebruiken om B en C te bepalen. Bij B moet je dan dus met x+1 vermenigvuldigen en x=-1 invullen.


ik heb dezelfde methode gebruikt.quote:Op maandag 13 maart 2006 21:51 schreef Wolfje het volgende:
[..]
Je moet die breuken met A, B en C onder een noemer brengen. Dan krijg je in de teller
A (x + 1)(x - 2) + B x(x - 2) + C x(x + 1).
De haakjes moet je zelf even uitwerken. Het moet dan gelijk zijn aan x-5 voor zekere waarden van A, B en C. Je moet ze dus zodanig kiezen dat de coefficient van (A+B+C)x^2 gelijk is aan 0, ofwel A+B+C=0. Ditzelfde moet je doen voor de coefficient van x en de constante term. Dan krijg je drie lineaire vergelijkingen in 3 onbekenden die je wel kunt oplossen.
maar ik zie nu wat ik fout deed ik ben de x bij C vergeten
en dan krijg je dat A=B wat dus niet met het antwoordt overeenkomt
en ik kom er dan nog niet uit
dat A= 5/2 heb je zo daarna doe ik
0=A+B+C
-5/2=B+C B=-C-5/2
-5/2=-C-5/2+C
0=-C+C
0=0
maar daar kan ik zo weinig mee
[ Bericht 7% gewijzigd door icecreamfarmer_NL op 14-03-2006 11:04:11 ]
1/10 Van de rappers dankt zijn bestaan in Amerika aan de Nederlanders die zijn voorouders met een cruiseschip uit hun hongerige landen ophaalde om te werken op prachtige plantages.
"Oorlog is de overtreffende trap van concurrentie."
"Oorlog is de overtreffende trap van concurrentie."


Ik moet het maximum weten van de formule: Q= -20A + 12A^2 - A^3. Ik wil graag gebruik maken van de ABC formule, maar ik heb geen idee hoe ik dat doe. Kan iemand me helpen?


Daarom moet je ook de methode gebruiken die ik gepost heb, minder kans op rekenfouten.quote:Op dinsdag 14 maart 2006 10:32 schreef icecreamfarmer_NL het volgende:
[..]
ik heb dezelfde methode gebruikt.
maar ik zie nu wat ik fout deed ik ben de x bij C vergeten
en dan krijg je dat A=B wat dus niet met het antwoordt overeenkomt
en ik kom er dan nog niet uit
dat A= 5/2 heb je zo daarna doe ik
0=A+B+C
-5/2=B+C B=-C-5/2
-5/2=-C-5/2+C
0=-C+C
0=0
maar daar kan ik zo weinig mee


Je wil het maximum van Q weten, dus met andere woorden, de waarde waarbij de afgeleide van Q nul is(dan heb je nl. een (plaatselijk) minimum of maximum...quote:Op dinsdag 14 maart 2006 12:54 schreef el-Fenomeno het volgende:
Ik moet het maximum weten van de formule: Q= -20A + 12A^2 - A^3. Ik wil graag gebruik maken van de ABC formule, maar ik heb geen idee hoe ik dat doe. Kan iemand me helpen?
De afgeleide van Q is wel een functie waarop je de ABC formule kan toepassen..
Nu moet het vast wel lukken..
You don't have to know why you do something to stop doing it. All you have to do is to take a close look at what you are actually doing and decide to stop doing it for that moment!"


Een maximum (of minimum) vind je door de afgeleide te berekenen en de nulpunten ervan te bepalen.quote:Op dinsdag 14 maart 2006 12:54 schreef el-Fenomeno het volgende:
Ik moet het maximum weten van de formule: Q= -20A + 12A^2 - A^3. Ik wil graag gebruik maken van de ABC formule, maar ik heb geen idee hoe ik dat doe. Kan iemand me helpen?
-20+24A-3A2=0
Bepalen van die nulpunten doe je met de ABC formule. Je bepaalt de nulpunten, vult deze in in de oorspronkelijke formule en berekent de waarde Q
Dan krijg je het lokaal maximum en minimum. Als A naar -oneindig gaat wordt het maximum natuurlijk +oneindig en omgekeerd voor a gaande naar +oneindig wordt het minimum -oneindig


Dat snap ik, maar hoe moet je dat precies invullen in de ABC formule. Je moet toch wat doen met de formules: ax^2+bx+c=0, x=(-b+wortel D)/2a, x=(-b-wortel D)/2a en D=b^2-4ac? Hoe moet ik dat precies invullen?quote:Op dinsdag 14 maart 2006 13:53 schreef Doderok het volgende:
[..]
Een maximum (of minimum) vind je door de afgeleide te berekenen en de nulpunten ervan te bepalen.
-20+24A-3A2=0
Bepalen van die nulpunten doe je met de ABC formule. Je bepaalt de nulpunten, vult deze in in de oorspronkelijke formule en berekent de waarde Q
Dan krijg je het lokaal maximum en minimum. Als A naar -oneindig gaat wordt het maximum natuurlijk +oneindig en omgekeerd voor a gaande naar +oneindig wordt het minimum -oneindig


-20+24A-3A2=0 ofquote:Op dinsdag 14 maart 2006 14:08 schreef el-Fenomeno het volgende:
[..]
Dat snap ik, maar hoe moet je dat precies invullen in de ABC formule. Je moet toch wat doen met de formules: ax^2+bx+c=0, x=(-b+wortel D)/2a, x=(-b-wortel D)/2a en D=b^2-4ac? Hoe moet ik dat precies invullen?
-3A2+24A-20=0
dan is a=-3
b=24
c=-20
D=242-4*60=336
x1=(-24+wortel 336)/(-6)=0.94495..
x2=(-24-wortel 336)/(-6)=7.05505..
Invullen geeft voor Q1=-9.0276..
Q2=105.0276..


Thnx, ik snap het. Wat gebeurt er als je de formule f(x) = x^3-3x-4 hebt? De afgeleide is dan 3x^2-3, maar de b van de ABC formule ontbreekt en daardoor kun je de D niet uitrekenen.quote:Op dinsdag 14 maart 2006 14:39 schreef Doderok het volgende:
[..]
-20+24A-3A2=0 of
-3A2+24A-20=0
dan is a=-3
b=24
c=-20
D=242-4*60=336
x1=(-24+wortel 336)/(-6)=0.94495..
x2=(-24-wortel 336)/(-6)=7.05505..
Invullen geeft voor Q1=-9.0276..
Q2=105.0276..


b ontbreekt niet, b=0quote:Op dinsdag 14 maart 2006 15:00 schreef el-Fenomeno het volgende:
[..]
Thnx, ik snap het. Wat gebeurt er als je de formule f(x) = x^3-3x-4 hebt? De afgeleide is dan 3x^2-3, maar de b van de ABC formule ontbreekt en daardoor kun je de D niet uitrekenen.
dus D=36 etc.
maar dat los je eenvoudiger op:
3x2-3=0
3x2=3
x2=1 dus x=1 of x=-1


Ik heb hier een probleem. Ik moet de formule van Cardano afleiden, maar ik zou echt niet weten waar of hoe ik moet beginnen. Heeft iemand tips?


Een complexe wortelquote:Op woensdag 15 maart 2006 12:45 schreef mrbombastic het volgende:
http://www.hhofstede.nl/bewijzen/cardano.htm


Hooi ik heb een klein vraagje. Ben bezig met een opdracht voor informatica...
Op dit moment ben ik bezig met het programma SPSS. Hierbij snap ik de volgende opdracht niet:
In een stad zijn 660 mensen gevraagd met welk vervoermiddel zij dagelijks van hun huis naar hun werk reizen. Het resultaat van dit onderzoek staat vermeld in onderstaande tabel:
Vervoermiddel Aantal Mensen
Openbaar vervoer 160
Auto 350
(brom)fiets/te voet 150
Voer deze gegevens in in SPSS en presenteer ze in een staafdiagram (vermeld de aantalllen in de staven)
Op dit moment ben ik bezig met het programma SPSS. Hierbij snap ik de volgende opdracht niet:
In een stad zijn 660 mensen gevraagd met welk vervoermiddel zij dagelijks van hun huis naar hun werk reizen. Het resultaat van dit onderzoek staat vermeld in onderstaande tabel:
Vervoermiddel Aantal Mensen
Openbaar vervoer 160
Auto 350
(brom)fiets/te voet 150
Voer deze gegevens in in SPSS en presenteer ze in een staafdiagram (vermeld de aantalllen in de staven)


Uit scheikunde wasmiddelen :S
Ik kan me niet voorstellen dat je zomaar zo'n opdracht in je schoot krijgt geworpen zonder uitleg eromheen.
Hoe komt het dat dat je zo'n opdracht moet doen je geen idee hebt hoe je het aan moet pakken? Hadden jullie dit moeten weten? Kan de leraar of het lesboek geen uitleg bieden?quote:Op donderdag 16 maart 2006 09:34 schreef mariekesmulders het volgende:
Zijn er scheikundigen in de zaal? Want:
Wij moeten voor scheikunde een opdracht doen met wasmiddelen als Vanish, Tricel,Sil,...Allemaal producten die bij oplossen zorgen voor zuurstofproductie. We hebben allemaal proefjes gedaan, waardoor blijkt dat niet alle vlekken waarvan wordt beweerd dat ze eruit gaan met deze " wondermiddelen" er ook werkelijk uitgaan. Motor-olievlekken en markkerstif blijken bijvoorbeeld niet uit kleding te gaan door de stukken stof, net als in de reclame, in een warm sopje te hangen. Slaolie, rode wijn en grasvlekken gaan w'el redelijk tot goed uit de kleding. Wij moeten nu verklaren wat de invloed van het vrijkomen van zuustof op het verwijderen van vlekken is. We hoeven dus niet de hele werking van de zeep te verklaren, omdat dat te moeilijk was voor ons (redoxreacties )
Iemand die kan helpen? Dit wordt een ramp zonder hulp van iemand die ons kan duidelijk maken hoe het precies zit!!
dus:::::
HELP!!!!!
Groetjes,
Kim en Marieke
Ik kan me niet voorstellen dat je zomaar zo'n opdracht in je schoot krijgt geworpen zonder uitleg eromheen.
"Dat is echt ontzettend zielig" ©


Hoi, ik moet een presentatie doen voor wiskunde over chaos en orde, met sommen als voorbeeld, maar ik weet nog niet echt wat chaos is. bijvoorbeeld op deze site: http://www.vuiksvertier.nl/wetenschap/chaos-maken.htm staan 5 grafieken, vanaf welke is het nou chaos? want bij de eerste 4 zit een patroon, kan chaos een patroon hebben?
elke info is welkom, bedankt, groeten Gian.
elke info is welkom, bedankt, groeten Gian.


Ik denk dat dit wel een goede intro is (mits je niet al te veel moeite hebt met Engels):
http://en.wikipedia.org/wiki/Chaos_theory
http://en.wikipedia.org/wiki/Chaos_theory


Snap ff iets niet van een sinus te integreren. Het gaat om de gemiddelde waarde bepalen ervan.
100sinωt dt is de functie die ik moet integreren.
In het boek maken ze er dan:
-100/ω cos ωt van als die functie geprimitiveerd is. Die -cos snap ik wel, maar waarom -100 delen door ω ?? Ik zou zeggen ω * 100 omdat constanten naar voren worden gehaald volgens mij wiskunde leraar. Of is het eigenlijk 1/ω wat dan naar voor gaat, en waarom?
100sinωt dt is de functie die ik moet integreren.
In het boek maken ze er dan:
-100/ω cos ωt van als die functie geprimitiveerd is. Die -cos snap ik wel, maar waarom -100 delen door ω ?? Ik zou zeggen ω * 100 omdat constanten naar voren worden gehaald volgens mij wiskunde leraar. Of is het eigenlijk 1/ω wat dan naar voor gaat, en waarom?
♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫ ♪♫


Voor school moet ik een presentatie geven over de komst van computers (ICT) binnen het basis onderwijs.
Hoe het vroeger was.
Toen je nog op de basischool zat in welk jaar ongeveer kwam er bij jou een of meerdere computer(s) in de klas?
Wat kon je ermee? wat vond je er leuk of juist niet leuk aan, wat miste je in die tijd?
Wat zijn de dingen die je zijn bij gebleven van die computers,
wat vind je een grote uitvinding op ict gebied wat handig is binnen het basisonderwijs.?
Wat zijn de voordelen en nadelen van informatica (ict) in het basisonderwijs)
Heb je een praktijk voorbeeld vertel die hier ook graag
Alle info is welkom, nog verwijzingen naar websites met handige info zijn ook zeer welkom.
THX
Hoe het vroeger was.
Toen je nog op de basischool zat in welk jaar ongeveer kwam er bij jou een of meerdere computer(s) in de klas?
Wat kon je ermee? wat vond je er leuk of juist niet leuk aan, wat miste je in die tijd?
Wat zijn de dingen die je zijn bij gebleven van die computers,
wat vind je een grote uitvinding op ict gebied wat handig is binnen het basisonderwijs.?
Wat zijn de voordelen en nadelen van informatica (ict) in het basisonderwijs)
Heb je een praktijk voorbeeld vertel die hier ook graag
Alle info is welkom, nog verwijzingen naar websites met handige info zijn ook zeer welkom.
THX
Ado is the pride of Holland!