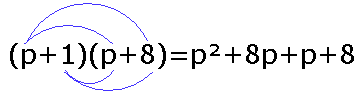SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Als dat zo is dan klopt er dus geen hout van (ook fijn)
Mare, werk dat eens uit dan, vanaf het begin?? hier heb ik natuurlijk geen reed aan he
Mare, werk dat eens uit dan, vanaf het begin?? hier heb ik natuurlijk geen reed aan he


Je vergelijking is daardoor echter (x + 6)(x - 1) = 0. Wat zij zegt is onzin, maar als je het had gesnapt was dat het probleem niet geweest. Echter, een (lange) uitleg, maar wel met de goede vergelijking. De uitleg komt eerst, die is ook voor het snappen, dan komt het stukje Truuk, die vooral de truuk uitlegt.quote:Op dinsdag 7 maart 2006 16:24 schreef Robin__ het volgende:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
We bekijken x^2 + 5x = 6. Merk op dat x^2 natuurlijk gewoon hetzelfde is als x * x. En 5x is 5 * x. (Dat als allereerste).
Ik neem aan dat je bekend bent met haakjes wegwerken. Dat wil zeggen, als er x*(3 + 5x) staat, dan is dit hetzelfde als x*3 + x*5x. Je vermenigvuldigt die x met alle termen die binnen de haakjes staan. Merk dan op dat je na dat vermenigvuldigen in elke term termen zijn overigens de naam voor de losse 'dingen' in een optelling, dus 3 + 5 + 9 heeft termen 3, 5 en 9, en 3x + 5 heeft termen 3x en 5 dezelfde factorfactor is een onderdeel van een vermenigvuldiging, dus 3x heeft factoren 3 en x aantreft, namelijk 'x'.
Die factor kun je zogezegd weer buiten haakjes halen. Dat is ook wel logisch, want als x(3 + 5x) gelijk is aan 3x + 5x^2, dan moet natuurlijk 3x + 5x^2 ook gelijk zijn aan x(3 + 5x). En inderdaad, door driftig uitschrijven kun je dat oefenen.
Ik hoop dat je bijvoorbeeld inziet dat x(5 + 8x) = 5x + 8x^2, en ook omgekeerd, of dat x^2(6 + 9x) = 6x^2 + 9x^3. En dat je net zogoed in plaats van 4x + 8x^2 ook 4x(1 + 2x) kunt schrijven (die is al wat gemener, want we halen de factor 4x eruit).
In jouw voorbeeld halen ze ook buiten haakjes. De eerste stap begint met:
x^2 + 5x = 6 om te zetten in x^2 +5x - 6 = 0 (dat levert geen problemen). Nu moeten er echter die haakjes gevonden worden. Ik denk dat je wel ziet dat als je (x + 6)(x - 1) uitschrijft, je weer op x^2 + 5x - 6 uitkomt, immers:
(x + 6)(x - 1) = (x + 6)*x + (x + 6)*1 = x*x + 6*x - 1*x - 6 = x^2 +(6 - 1)*x - 6 = x^2 +5x - 6.
Merk op dat we bij die laatste stap in feite weer factoren binnen haakjes brengen, want er zijn twee termen die een 'x' gemeen hebben, dus die kunnen we samenvoegen.
Truuk
De truuk is nu (en dat is het belangrijkste) hoe te herkennen wat je moet doen als je een kwadratische vergelijking hebt, en je die als product van twee sommen (x + a)(x + b) wilt schrijven.
Welnu, laten we eerst de som (x + a)(x + b) uitschrijven, dat geeft:
(x + a)(x + b) = (x + a)x + (x + a)b = x^2 + a*x + x*b + a*b = x^2 + (a + b)*x + a*b
Merk weer hoe we haakjes inbrengen om de twee termen die elk een factor x hebben samen te nemen. Nu komt de truuk, als je een willekeurige vergelijking x^2 + c*x + d hebt, vindt dan twee getallen a en b zodat c = a + b en d = a * b. Daar moet je wellicht even op broeden, maar dat is eigenlijk wat hierboven in die formule staat.
En als we dat dan nu gaan toepassen op jouw formule:
x^2 + 5x -6 = 0.
We zien dat c = 5, en d = -6. Nu wordt het gewoon wat proberen om a en b te vinden meestal, Zeg a = 2, b = 3. Dan a + b = 5, dat klopt, maar a * b = 6, dus dat kan niet kloppen. Sterker nog, we zien aan de -6 dat of a of b wel negatief moet zijn. (Goede truuk om te onthouden, is d negatief, dan is een van a of b ook negatief). Dus, zeg a = -2, dan moet b wel 3 zijn, maar -2 + 3 = 1, dus dat kan ook niet. Enfin, om een al lang verhaal toch iets korter te maken: a = 6 en b = -1. Dit klopt precies, immers 6 *- 1 = -6 en 6 + (-1) = 5.
Dus, je vult nu de linkerkant van die hele vergelijking in, en je krijgt dat in dit geval:
(x + a)(x + b) moet zijn: (x + 6)(x - 1).
Nou, hopelijk is dat na een tijdje oefenen duidelijk genoeg.
[ Bericht 0% gewijzigd door Nekto op 07-03-2006 16:57:14 ]


stap 1: x2 + 5x - 6 = 0
snap je dat?
snap je dat?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Die punt is een zins-einde teken daar.quote:Op dinsdag 7 maart 2006 16:52 schreef Robin__ het volgende:
[..]
Sorry maar hier gaat het al mis.. 6 punt x^2????


in brief
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1quote:Op dinsdag 7 maart 2006 16:34 schreef McCarthy het volgende:
x = -6 en x = +1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
"Dat is echt ontzettend zielig" ©


welles
quote:Op dinsdag 7 maart 2006 16:24 schreef Robin__ het volgende:
Sorry dat ik zo kom binnenvallen.. maar ik heb ook een vraag
Afgelopen vrijdag een toets van mn wiskunde bijles (om zonder achterstand naar het hbo te kunnen na het mbo) redelijk verkloot, ik dacht dat ik het snapte, niet dus, extra opdrachten gevraagd maar nu zit ik dus vast.
De vraag:
bekijk de vergelijking x^2 + 5x = 6 allereerst merk je op dat terugrekenen niet gaat (de eerdere sommen was simpel weg alle x-en naar 1 kant schuiven) dus moet je wel wat andres verzinnen je gaat de vergelijking eerst de vorm ... =0 geven door aan beide kanten 6 af te trekken: x^2 + 5x -6 = 0 vervolgens ga je in het linkerdeel haakjes inbrengen. met behulp van ontbinden in factoren: x^2 + 5x - 6 = (x-6)(x+1)
Je vergelijking is daardoor (x-6)(x+1)=0
Dat betekent: x - 6 = 0 of x + 1 = 0 En dus zijn de oplossingen x=6 en x=-1
'controleer ze maar'
Ik snap er werkelijk NIETS van.. waar haalt ze die 6 en 1 vandaan en waar is mn x^2 gebleven
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Ja, maar, in zijn voorbeeld wordt niet juist ontbonden. Als de vergelijking x^2 + 5x - 6 is, dan is de ontbinding niet (x - 6)(x + 1), maar (x + 6)(x - 1). Als de ontbinding (x - 6)(x + 1) is, dan is de vergelijking echter x^2 -5x -6.quote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1


Ah, overheen gezienquote:Op dinsdag 7 maart 2006 17:07 schreef Nekto het volgende:
[..]
Ja, maar, in zijn voorbeeld wordt niet juist ontbonden. Als de vergelijking x^2 + 5x - 6 is, dan is de ontbinding niet (x - 6)(x + 1), maar (x + 6)(x - 1). Als de ontbinding (x - 6)(x + 1) is, dan is de vergelijking echter x^2 -5x -6.
"Dat is echt ontzettend zielig" ©


Kijk nou eens goed naar de bold gemaakte vergl modje van me
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


zal ik het maar overnemen want dit gaat didactisch gezien helemaal foutquote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
[afbeelding]
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Jaja, ik heb het al gezien, maar de rest van wat ik vertel klopt toch aardig of niet?quote:Op dinsdag 7 maart 2006 17:10 schreef McCarthy het volgende:
[..]
zal ik het maar overnemen want dit gaat didactisch gezien helemaal fout
"Dat is echt ontzettend zielig" ©


Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.


ik zei alleen dat het didactisch gezien niet echt handig isquote:Op dinsdag 7 maart 2006 17:11 schreef Litso het volgende:
[..]
Jaja, ik heb het al gezien, maar de rest van wat ik vertel klopt toch aardig of niet?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Ach, als je maar weet hoe het werktquote:Op dinsdag 7 maart 2006 17:14 schreef Nekto het volgende:
Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.
Als je er in geïnteresseerd bent of van plan er verder mee te werken is het wel zo handig als je dat weet inderdaad, maar ik kan me voorstellen dat er mensen zijn die liefst na hun examen niks meer met wiskunde te maken willen hebben
"Dat is echt ontzettend zielig" ©


Want?quote:Op dinsdag 7 maart 2006 17:15 schreef McCarthy het volgende:
[..]
ik zei alleen dat het didactisch gezien niet echt handig is
"Dat is echt ontzettend zielig" ©


omfgquote:Op dinsdag 7 maart 2006 17:14 schreef Nekto het volgende:
Als ze maar ook weten dat de 'papegaaiebek' normaliter 'ontbinden in factoren' wordt genoemd, dan vind ik het best. Ik heb mensen gezien die je glazig aankeken als je ze vroeg naar de afgeleide van f(x), en alleen f-accent snapten.
anders onthouden ze het niet of zo?
dat het eigenlijk de regel x(y + z) = xy + xz is wordt ze ook al niet verteld
onderwijs in NEderland
allemaal de schuld van de PvdA
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Tussen droom en daad staan wetten in de weg, en praktische bezwaren.quote:Op dinsdag 7 maart 2006 17:16 schreef Litso het volgende:
maar ik kan me voorstellen dat er mensen zijn die liefst na hun examen niks meer met wiskunde te maken willen hebben


papagaaienregels en zoquote:
da's niks
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


die van mij
versus die van jouquote:Op dinsdag 7 maart 2006 16:58 schreef McCarthy het volgende:
in brief
0 = x2 + 5x - 6 = (x + a)(x + b) = x2 + (a + b)x + ab
dus
ab = -6 en
a + b = 5
Rara wat zijn a en b
quote:Op dinsdag 7 maart 2006 17:02 schreef Litso het volgende:
[..]
Nee hoor, als (x-6)(x+1) = 0 dan geldt voor x=6 of x=-1
en Robin__, ik ben waarschijnlijk niet de geschiktste om het uit te leggen maar ik zal het proberen.
Ik neem aan dat je bekent bent met het buiten haakjes stellen als je deze sommen voor je krijgt. Dus bij een formule 3 (x-2) kan je ook zeggen 3x - 6 (eerst de x maal de 3 die er voor staat, dan de -2 maal de 3 die er voor staat.
Bij een som als (x+3)(x-2) geldt eerst de eerste x maal de tweede x: x2
Dan de eerste x maal de -2: -2x
Dan de +3 maal de eerste x: +3x
Dan de +3 maal de -2: -6.
Bij elkaar is dit x2 - 2x + 3x - 6
oftewel x2 +x -6
Deze methode noemen ze ook wel de papegaaienbek.
De lijntjes tussen de elementen die je moet vermenigvuldigen maken een vorm van een soort pagegaaienbek
[afbeelding]
Andersom kan het ook. De formule die jij hebt gekregen, x2 +5x -6 is ook te schrijven als (x-6)(x+1). Reken maar na op dezelfde manier als hierboven. Beide formules komen op het zelfde neer.
En nu kan je dus zeggen (x-6)(x+1) = 0. Als a maal b 0 is, betekent dat dat óf a, óf b 0 is.
In dit geval is dus óf (x-6) = 0, óf (x+1) = 0.
En als (x-6) = 0 dan is x dus 6.
Als (x+1) = 0 dan is x -1.
Duidelijk?
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy


Voor iemand die van deze som al geen hout snapt en zich afvraagt waar zijn kwadraat heen is kan ik me voorstellen dat diegene ook niet al teveel aan jouw post heeft.quote:
"Dat is echt ontzettend zielig" ©


Begrijp me niet verkeerd, ik heb niks tegen wiskunde, ik ben zelf meer een bètamens dan wat anders. Ik zie ook wel degelijk het nut in van wiskunde, ook voor later. Maar als iemand het ontbinden in factoren nou eenmaal makkelijker begrijpt door de naam papegaaienbek te gebruiken denk ik dat je beter gelukkig kan zijn dat hij weet hoe hij het toe moet passen dan zeuren dat hij de goede naam niet gebruiktquote:Op dinsdag 7 maart 2006 17:16 schreef Nekto het volgende:
[..]
Tussen droom en daad staan wetten in de weg, en praktische bezwaren.
"Dat is echt ontzettend zielig" ©


ik stel voor dat we dan thabit op hem af sturenquote:Op dinsdag 7 maart 2006 17:18 schreef Litso het volgende:
[..]
Voor iemand die van deze som al geen hout snapt en zich afvraagt waar zijn kwadraat heen is kan ik me voorstellen dat diegene ook niet al teveel aan jouw post heeft.
enes kijken hoe dat uitpakt.
Het nationaal product is hetzelfde als een taart waar uiteraard iedereen recht op heeft, als overheden met geld smijten heet het investeren en als bedrijven investeren heet het een sprinkhanenplaag. McCarthy