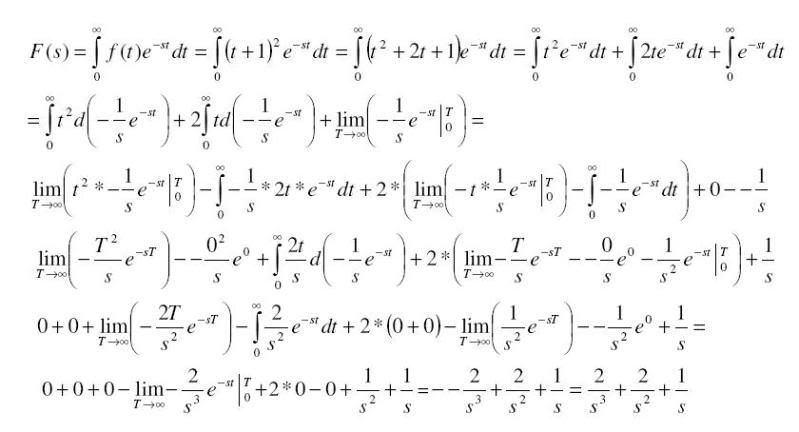SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
miss. beetje ontopic , maar dankzij jouw wiskundetopics heb ik een 6,5 gehaald voor mn vwo wiskunde examen 
, Thanks dus! 
, Thanks dus!
.
Hé, dat is mijn avatar!
IAh, ja, ik zie al wat ik fout doe. Ik had nog sqrt(24)-24/sqrt(24) moeten doen en dan komt er wel nul uit.
IAh, ja, ik zie al wat ik fout doe. Ik had nog sqrt(24)-24/sqrt(24) moeten doen en dan komt er wel nul uit.
Door het examenforum zo te zienquote:Op zondag 1 november 2009 16:07 schreef Rainb0ws het volgende:
miss. beetje ontopic , maar dankzij jouw wiskundetopics heb ik een 6,5 gehaald voor mn vwo wiskunde examen
Graag gedaan hoor 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe komen ze aan 123 ft?
Dat is zeker weer zo'n rare omzetting met feet enzo?
Dat is zeker weer zo'n rare omzetting met feet enzo?
Blues ain't nothing but a good man feeling bad...
60(3+e^(-3)) - 60(0+e^(-0)) uitrekenen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Er is toch niets om te zetten als je alles in feet uitdrukt? Begrijp je de berekening van de integraal wel?quote:Op zondag 1 november 2009 17:01 schreef GoodGawd het volgende:
Hoe komen ze aan 123 ft?
[ afbeelding ]
Dat is zeker weer zo'n rare omzetting met feet enzo?
je bedoeltquote:
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:31:00 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
@Iblis & GlowMouse: is geen van beide goed.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
Die Wolfram-sites in de OP 
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Wat snap je er niet aan?quote:Op zondag 1 november 2009 17:01 schreef GoodGawd het volgende:
Hoe komen ze aan 123 ft?
[ afbeelding ]
Dat is zeker weer zo'n rare omzetting met feet enzo?
Ten percent faster with a sturdier frame
nooit van een tvp gehoord?quote:
@Iblis & GlowMouse: is geen van beide goed.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik had eigenlijk geen fysische interpretatie in gedachten. Ik wilde gewoon een onbeschaamde tvp plaatsen.quote:
@Iblis & GlowMouse: is geen van beide goed.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Plaats van een puntmassa wordt zo gedefineerd:
r = 5 cos 2t i + 4 sin 2t j
differentiëren naar snelheid
-5 sin 2 i + 4 cos 2 j
differentiëren naar versnelling
-5 cos 2 i - 4 sin 2 j
Klopt dit?
r = 5 cos 2t i + 4 sin 2t j
differentiëren naar snelheid
-5 sin 2 i + 4 cos 2 j
differentiëren naar versnelling
-5 cos 2 i - 4 sin 2 j
Klopt dit?
Blues ain't nothing but a good man feeling bad...
dit is het wiskundetopic, zonder beschrijving van i, t en j snap ik het niet en ik denk ook dat het fout gaat omdat er een t verdwijnt en de kettingregel niet wordt gebruikt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zonder de i en j:
r = 5 cos 2t + 4 sin 2t
differentiëren naar snelheid
-10 sin 2t + 8 cos 2
differentiëren naar versnelling
-10 cos 2 - 8 sin 2
Zo?
r = 5 cos 2t + 4 sin 2t
differentiëren naar snelheid
-10 sin 2t + 8 cos 2
differentiëren naar versnelling
-10 cos 2 - 8 sin 2
Zo?
Blues ain't nothing but a good man feeling bad...
bij de tweede keer differentiëren mis je nog de kettingregel
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh ja typo >_> Nou dan iig diff ook weer opgefrist
Blues ain't nothing but a good man feeling bad...
Heeft iemand hier ervaring met het programma Eviews? Wij moeten dat namelijk gebruiken tijdens ons vak econometrie en vind het zelf een vrij onhandig programma.
Het betreft een string aan data waar we een econometrisch model aan moeten toeschrijven op een specifieke manier zodat het "can be estimated by least squares regression".
Het betreft een string aan data waar we een econometrisch model aan moeten toeschrijven op een specifieke manier zodat het "can be estimated by least squares regression".
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
GlowMouse, ligt het aan mij of moet ik op http://betahw.mine.nu/index.php alle backslashes dubbel invoeren om resultaat te hebben? Dus \\int en niet \int?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
vanaf nu ligt het aan jouquote:Op zondag 1 november 2009 23:17 schreef Iblis het volgende:
GlowMouse, ligt het aan mij of moet ik op http://betahw.mine.nu/index.php alle backslashes dubbel invoeren om resultaat te hebben? Dus \int en niet \int?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik snap hoe A eruit ziet uitgedrukt in v1 en v2, maar heb echt nog geen idee hoe ik kern en bereik moet vinden. Ik kan niet rijvegen in die matrix, geloof ik.quote:Op zondag 1 november 2009 02:05 schreef Hanneke12345 het volgende:
4. Laat v ∈ R^2 een vector zijn van lengte één, dus ||v|| = 1. Definieer de matrix A door A=vvT
a. Bepaal kern en beeld (=bereik?) van A
- wat is A? ik heb echt geen idee eigenlijk.
+ vraag b; geef zonder berekening de eigenwaarden en eigenvectoren van A, eigenwaarde 0 is triviaal, maar ook één is v1^2+v2^2, waar komt die vandaan?
Kijk nou eens naar twee voorbeeldjesquote:
[..]
Ik snap hoe A eruit ziet uitgedrukt in v1 en v2, maar heb echt nog geen idee hoe ik kern en bereik moet vinden. Ik kan niet rijvegen in die matrix, geloof ik.
Van het spoor. Of van je kolomruimte.quote:+ vraag b; geef zonder berekening de eigenwaarden en eigenvectoren van A, eigenwaarde 0 is triviaal, maar ook één is v1^2+v2^2, waar komt die vandaan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dan kom ik een dezer dagen nog wel met de vraag op de proppen, heb woensdag weer les in 'Eviews' en ben op dit moment niet eens in staat een fatsoenlijk antwoord te geven op de vragen die ik hebquote:
Wij moeten namelijk naar alle waarschijnlijkheid tijdens ons examen econometrie ook een klein gedeelte in Eviews doen.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ik heb een vraag over de odds ratio. Stel je hebt een kruistabel met 4 cellen. Is de odds ratio dan altijd a x d / b x c ?
...and that's the way the cookie crumbles.
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Ik ben een pure Turk.
Reset proces gebruiken in het systeem van je GR? Dan gaat alles terug naar normaal en werkt het allemaal weer!quote:Op maandag 2 november 2009 18:31 schreef Bilmiyorem het volgende:
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Zorg wel dat je je programmas ff beschermt anders flikkert hij die ook weg.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Heb je een Ti-84 (plus)?quote:Op maandag 2 november 2009 18:31 schreef Bilmiyorem het volgende:
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Ga dan eens naar Window en verander de waardes van xmin, xmax etc.
Cool story, Hansel.
vast dom, maar heb de gr nooit eerder gebruikt, hoe doe ik dat?quote:Op maandag 2 november 2009 18:49 schreef sitting_elfling het volgende:
[..]
Reset proces gebruiken in het systeem van je GR? Dan gaat alles terug naar normaal en werkt het allemaal weer!
Ik ben een pure Turk.
ja, die staan al goed volgens mij:quote:Op maandag 2 november 2009 18:50 schreef wikwakka2 het volgende:
[..]
Heb je een Ti-84 (plus)?
Ga dan eens naar Window en verander de waardes van xmin, xmax etc.
-10
10
1
-10
10
1
1
Ik ben een pure Turk.
Dat ligt aan de grafiek die je aan wilt plotten.quote:Op maandag 2 november 2009 19:03 schreef Bilmiyorem het volgende:
[..]
ja, die staan al goed volgens mij:
-10
10
1
-10
10
1
1
Maar een reset kan je doen door 2nd/ + knop / Reset / All / All memory te gaan. Je verliest dan wel programma's die je er zelf op hebt gezet.
Cool story, Hansel.
Ja, maar eerst waren deze waardes goed, dat bedoel ik. Heb er nog niets op gezet, gr is nog niet nodig geweest.quote:Op maandag 2 november 2009 19:05 schreef wikwakka2 het volgende:
[..]
Dat ligt aan de grafiek die je aan wilt plotten.
Maar een reset kan je doen door 2nd/ + knop / Reset / All / All memory te gaan. Je verliest dan wel programma's die je er zelf op hebt gezet.
Ik ben een pure Turk.
Dan zou ik hem dus gewoon even resetten. Of anders even alle zooms afgaan.quote:Op maandag 2 november 2009 19:08 schreef Bilmiyorem het volgende:
[..]
Ja, maar eerst waren deze waardes goed, dat bedoel ik. Heb er nog niets op gezet, gr is nog niet nodig geweest.
Cool story, Hansel.
Gedaan, dankjewel.quote:Op maandag 2 november 2009 19:08 schreef wikwakka2 het volgende:
[..]
Dan zou ik hem dus gewoon even resetten.
Het leven zonder rekenmachine is leuker.
Ik ben een pure Turk.
GR's maken het leven zoveel makkelijkerquote:Op maandag 2 november 2009 19:11 schreef Bilmiyorem het volgende:
[..]
Gedaan, dankjewel.
Het leven zonder rekenmachine is leuker.
als je het logisch denken/rekenen maar niet afleert.
Cool story, Hansel.
ik snap niet wat ik met de gr moet, vond "gewone" wiskunde beter (wat ik eerst had zonder gr)quote:Op maandag 2 november 2009 19:18 schreef wikwakka2 het volgende:
[..]
GR's maken het leven zoveel makkelijker
Ik ben een pure Turk.
Ik heb een vraagje. Ik verschil een beetje in antwoorden en wil weten of dit correct is:
e^2zi = e^1/2 pi * i
Daar maak ik van:
2zi = (1/2 pi + 2pi k )i
zi = (1/4 pi + pi k ) i
z = (1/4 pi + pi k)
Zo moet deze correct zijn?
e^2zi = e^1/2 pi * i
Daar maak ik van:
2zi = (1/2 pi + 2pi k )i
zi = (1/4 pi + pi k ) i
z = (1/4 pi + pi k)
Zo moet deze correct zijn?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
e2zi = e1/2πi.quote:
Ik heb een vraagje. Ik verschil een beetje in antwoorden en wil weten of dit correct is:
e^2zi = e^1/2 pi * i
Daar maak ik van:
2zi = (1/2 pi + 2pi k )i
zi = (1/4 pi + pi k ) i
z = (1/4 pi + pi k)
Zo moet deze correct zijn?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik heb het gewoon correct dus... , vriend had i.p.v. z = (pi/4 + pi k ) ---> z = (pi/4 + 2pi k) . Die 2pi k kan natuurlijk niet, omdat je nog door 2 deelt. Wat hij voor die pi/2 wel doet , maar voor die 2pi niet.quote:
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Klopt.quote:
[..]
Ik heb het gewoon correct dus... , vriend had i.p.v. z = (pi/4 + pi k ) ---> z = (pi/4 + 2pi k) . Die 2pi k kan natuurlijk niet, omdat je nog door 2 deelt. Wat hij voor die pi/2 wel doet , maar voor die 2pi niet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Denk je alles te snappen, loop ik tegen een oefenvraag aan die me toch nog hoofdbrekens bezorgt:
Op een van de inkoopfacturen van de Wadtrappers staat een totaal factuurbedrag van ¤ 158,32 vermeld. Een deel hiervan is belast met 6% omzetbelasting (BTW) en een ander deel met 19%. De omzetbelasting van 6% is ¤ 1,35.
Welk bedrag vermeldt de factuur voor de betaalde omzetbelasting van 19%?
Wat zie ik over het hoofd?
Op een van de inkoopfacturen van de Wadtrappers staat een totaal factuurbedrag van ¤ 158,32 vermeld. Een deel hiervan is belast met 6% omzetbelasting (BTW) en een ander deel met 19%. De omzetbelasting van 6% is ¤ 1,35.
Welk bedrag vermeldt de factuur voor de betaalde omzetbelasting van 19%?
Wat zie ik over het hoofd?
Zeg dat het deel dat met 6% is belast x is, en het deel dat met 19% is belast y is, dan is het totaalbedrag dus: 1,06x + 1,19y.
Je weet dat 0,06x = 1,35, dus x moet je kunnen uitrekenen. Dan moet het verder lukken hoop ik?
Je weet dat 0,06x = 1,35, dus x moet je kunnen uitrekenen. Dan moet het verder lukken hoop ik?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik kom er niet uit, heb weer hetzelfdequote:Op maandag 2 november 2009 18:31 schreef Bilmiyorem het volgende:
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Weet iemand hoe ik dit kan oplossen?
Ik ben een pure Turk.
Heb je met de zoom zitten klooien? Je hebt toch wel íéts veranderd?quote:Op maandag 2 november 2009 22:39 schreef Bilmiyorem het volgende:
[..]
Ik kom er niet uit, heb weer hetzelfde
Cool story, Hansel.
Ja, maar die herstel je toch altijd met ZStandard en dat werkt nu nietquote:Op maandag 2 november 2009 22:49 schreef wikwakka2 het volgende:
[..]
Heb je met de zoom zitten klooien? Je hebt toch wel íéts veranderd?
Ik ben een pure Turk.
Scroll eens naar beneden en druk op ZoomFitquote:Op maandag 2 november 2009 22:51 schreef Bilmiyorem het volgende:
[..]
Ja, maar die herstel je toch altijd met ZStandard en dat werkt nu niet
Cool story, Hansel.
Wat doet dat? Stomme rekenmachinequote:Op maandag 2 november 2009 22:52 schreef wikwakka2 het volgende:
[..]
Scroll eens naar beneden en druk op ZoomFit
Ik dacht lekker een hoog cijfer halen, zodat ik eindelijk afgerond een 10 sta
Ik ben een pure Turk.
Dan stelt hij het scherm zo af dat je grafiek er precies op past. Probeer het nou gewoonquote:Op maandag 2 november 2009 22:54 schreef Bilmiyorem het volgende:
[..]
Wat doet dat? Stomme rekenmachine
.
Cool story, Hansel.
Ik wil niets verkeerds doen, rekenmachine was al bijna niet meer af te lezen, daarom wilde ik weten wat het betekende. Ik wil wel die 10 op m'n rapport hequote:Op maandag 2 november 2009 22:56 schreef wikwakka2 het volgende:
[..]
Dan stelt hij het scherm zo af dat je grafiek er precies op past. Probeer het nou gewoon
Ik ben een pure Turk.
En wat was het resultaat toen je mijn instructies opvolgde?quote:Op maandag 2 november 2009 22:57 schreef Bilmiyorem het volgende:
[..]
Ik wil niets verkeerds doen, rekenmachine was al bijna niet meer af te lezen, daarom wilde ik weten wat het betekende. Ik wil wel die 10 op m'n rapport he
Cool story, Hansel.
Het werkt! Beste kan ik het dus altijd gebruiken?quote:Op maandag 2 november 2009 22:58 schreef wikwakka2 het volgende:
[..]
En wat was het resultaat toen je mijn instructies opvolgde?
Ik ben een pure Turk.
Ja, lijkt me wel het handigste want dan staat je functie er tenminste altijd helemaal op. Je moet wel uitkijken dat je limieten gebruikt indien nodig, (door de xmin en xmax etc. te veranderen) want soms hoef je maar naar een deel van je functie te kijken.quote:Op maandag 2 november 2009 22:59 schreef Bilmiyorem het volgende:
[..]
Het werkt! Beste kan ik het dus altijd gebruiken?
Cool story, Hansel.
Ik weet helemaal niets van de gr, weet ook niet wat ik ervan moet weten, dat is het hele probleem. Ik bekijk daarom een beetje wat ik met die grafieken kan, maar bedankt voor de tip.quote:Op maandag 2 november 2009 23:01 schreef wikwakka2 het volgende:
[..]
Ja, lijkt me wel het handigste want dan staat je functie er tenminste altijd helemaal op. Je moet wel uitkijken dat je limieten gebruikt indien nodig, (door de xmin en xmax etc. te veranderen) want soms hoef je maar naar een deel van je functie te kijken.
(ik hoop op een 10, valse hoop)
Ik ben een pure Turk.
x=22,5 dan? Maar wat kan ik met die info?quote:Op maandag 2 november 2009 22:12 schreef Iblis het volgende:
Zeg dat het deel dat met 6% is belast x is, en het deel dat met 19% is belast y is, dan is het totaalbedrag dus: 1,06x + 1,19y.
Je weet dat 0,06x = 1,35, dus x moet je kunnen uitrekenen. Dan moet het verder lukken hoop ik?
Welke denkwijze moet ik hanteren? Ik heb een black-out!
Aparte toets dan als je niet weet wat je ervoor moet lerenquote:Op maandag 2 november 2009 23:02 schreef Bilmiyorem het volgende:
[..]
Ik weet helemaal niets van de gr, weet ook niet wat ik ervan moet weten, dat is het hele probleem. Ik bekijk daarom een beetje wat ik met die grafieken kan, maar bedankt voor de tip.
.
Cool story, Hansel.
Invullen, dan weet je dus dat 158,32 = 1,06·22,5 + 1,19y.quote:
[..]
x=22,5 dan? Maar wat kan ik met die info?
Welke denkwijze moet ik hanteren? Ik heb een black-out!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Boek ligt op schoolquote:Op maandag 2 november 2009 23:05 schreef wikwakka2 het volgende:
[..]
Aparte toets dan als je niet weet wat je ervoor moet leren
Ik ben een pure Turk.
Doh! Tnx!quote:Op maandag 2 november 2009 23:06 schreef Iblis het volgende:
[..]
Invullen, dan weet je dus dat 158,32 = 1,06·22,5 + 1,19y.
Vandaag mn toets. Jullie krijgen mn tentamencijfer nog te horen
'Een ijscoman weet uit ervaring dat hij op een zonnige dag bij een prijs van 1.30 per ijsje 700 stuks verkoopt. Bij elke 10 cent prijsverhoging verkoopt hij er 50 minder. Er bestaat een lineair verband tussen de prijs p in euro's en het aantal verkochte ijsjes q'
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
mundus vult decipi
Je a is goed. Je hebt alleen nog niet gebruikt dat bij een prijs van 1.30 per ijsje 700 stuks verkoopt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
welke methode heb je?quote:Op dinsdag 3 november 2009 19:52 schreef Gratau het volgende:
'Een ijscoman weet uit ervaring dat hij op een zonnige dag bij een prijs van 1.30 per ijsje 700 stuks verkoopt. Bij elke 10 cent prijsverhoging verkoopt hij er 50 minder. Er bestaat een lineair verband tussen de prijs p in euro's en het aantal verkochte ijsjes q'
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
Ik ben een pure Turk.
Er staat geen vraag/opdrachtquote:
'Een ijscoman weet uit ervaring dat hij op een zonnige dag bij een prijs van 1.30 per ijsje 700 stuks verkoopt. Bij elke 10 cent prijsverhoging verkoopt hij er 50 minder. Er bestaat een lineair verband tussen de prijs p in euro's en het aantal verkochte ijsjes q'
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
Neem aan dat je dat lineair verband moet geven?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
huh ik snap het even niet. bereken je b zo?quote:Op dinsdag 3 november 2009 19:53 schreef GlowMouse het volgende:
Je a is goed. Je hebt alleen nog niet gebruikt dat bij een prijs van 1.30 per ijsje 700 stuks verkoopt.
mundus vult decipi
Dat je een modelletje moet uitrekenen mischienquote:
[..]
Er staat geen vraag/opdracht
Neem aan dat je dat lineair verband moet geven?
?
Cool story, Hansel.
jaquote:Op dinsdag 3 november 2009 19:54 schreef -J-D- het volgende:
[..]
Er staat geen vraag/opdracht
Neem aan dat je dat lineair verband moet geven?
stel de formule van p als functie van q
mundus vult decipi
als je 1.30 invult als prijs moet er 700 uitkomen.quote:
[..]
huh ik snap het even niet. bereken je b zo?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je kan toch de variablen invullen die je weet en zo de variabel die je niet weet uitrekenen.quote:Op dinsdag 3 november 2009 19:55 schreef Gratau het volgende:
[..]
huh ik snap het even niet. bereken je b zo?
Cool story, Hansel.
Ik zou q als functie van p nemen. Je wil toch het effect van de prijs op de verkochte aantallen beschrijven in een formule?quote:Op dinsdag 3 november 2009 19:55 schreef Gratau het volgende:
[..]
ja
stel de formule van p als functie van q
Het is hem al gelukt, me dunkt.quote:
[..]
Ik zou q als functie van p nemen. Je wil toch het effect van de prijs op de verkochte aantallen beschrijven in een formule?
Cool story, Hansel.
Misschien, maar dat heeft hij/zij hier dan niet laten zien. En als je met een kromme redenatie of een verkeerde aanpak bij het 'goede' antwoord uitkomt wil dat niet zeggen dat je het goed hebt gedaan.quote:
Heej Einsteins ik heb weer een vraag:. Dit keer is de vraag over linker-en rechterafgeleide f 'l(0) en fr ' 0) van:
f (x) = { x^2 +2x als x >(of gelijk) 0
en { -x^2 + x + 1 als x<0
Nu weten we dat we f(a) = f(a+h) - f(a) / h moeten gebruiken.
De rechterafgeleide geeft dan:
h^2 + 2h - 0 /h = h + 2
lim x-> 0 = 2
Maar de linkerafgeleide komen we niet uit met het antwoord. Someone can solve this nut?
f (x) = { x^2 +2x als x >(of gelijk) 0
en { -x^2 + x + 1 als x<0
Nu weten we dat we f(a) = f(a+h) - f(a) / h moeten gebruiken.
De rechterafgeleide geeft dan:
h^2 + 2h - 0 /h = h + 2
lim x-> 0 = 2
Maar de linkerafgeleide komen we niet uit met het antwoord. Someone can solve this nut?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Het differentiequotiënt voor f als h < 0 is (f(h)-f(0))/(x-0) = (-h² + h + 1 - 0)/h = -h+1 + 1/h.
Als h van onderen naar 0 gaat, gaat dit naar -oneindig.
[ Bericht 11% gewijzigd door GlowMouse op 04-11-2009 13:52:07 ]
Als h van onderen naar 0 gaat, gaat dit naar -oneindig.
[ Bericht 11% gewijzigd door GlowMouse op 04-11-2009 13:52:07 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wij hadden hier dus ook -h + 1 uit!!!! En naar 0 is dat natuurlijk 1.quote:Op woensdag 4 november 2009 13:43 schreef GlowMouse het volgende:
Het differentiequotiënt voor f als h < 0 is (f(h)-f(0))/(x-0) = (-h² + h - 0)/h = -h+1.
Als h van onderen naar 0 gaat, komt hier 1 uit.
Maar de juffrouw heeft iets anders gegoogeld namelijk:
lim h --> 0 -h^2 + h +1 - 0 /h (die 0 kan niet eens maar ja) = lim h->0 -h+1 + 1/h
= - oneindig dus f ' l (0) bestaat niet. Is haar antwoord.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Verdammt, nee ik, moet leren lezen, was de 1 in f(h) vergeten. Zie edit.quote:
De functie is discontinu in 0 dus het is ook logisch dat een van beide afgeleiden niet bestaat.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
maar die linkerafgeleide wordt toch:
(-h^2 + h +1 + 0 - 1)/(h) = -h+1
Want f(0) is toch -0^2 + 0 + 1 = 1 ?
(-h^2 + h +1 + 0 - 1)/(h) = -h+1
Want f(0) is toch -0^2 + 0 + 1 = 1 ?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
f (x) = { x^2 +2x als x >(of gelijk) 0
dus f(0) = 0²+2*0 = 0.
dus f(0) = 0²+2*0 = 0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Thx we snappen em!!! brontosaurus dat ge bent!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik merk wel dat het zwaar vervelend is om wiskundige vragen in het Nederlands uit te leggen als je Engels gewend bent .
.
Cool story, Hansel.
Dat is gewoon integreren m.b.v. substitutie, je gaat van een integraal over dy over naar een integraal over dp, misschien dat deze voorbeelden bij Wikipedia je wat helpen, maar kort gezegd (ik heb even geen tijd om het helemaal uit te werken), het doel is om een makkelijker integraal te krijgen, m.a.w. men wil van integratie over y naar integratie over p, waarbij dat een ‘handige’ vorm heeft, daarvoor kiest men de substitutie p = y3 + 2, en dan geldt dp/dy = 3y2 (lijkt me logisch) en dan maakt men weer gebruik van de voordelen die Leibniz’ notatie biedt, en dan kun je stellen dat dp=3y2dy geldt, ofwel dy=dp/3y2, en dat proppen ze dan in die formule, dus waar dy staat, kun je dan dp/3y2 neerzetten.quote:
[ afbeelding ]
Waarom gaan ze in dat rode blok differentiëren?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Even een makkelijke vraag die ik nergens in mijn boek kan vinden
Wat bereken je met een eigenvector. Ik kan het uitrekenen, maar weet niet wat het betekend.
De eigenwaarde is de verlenging/ verkorting van een vector, dat is dan wel weer meteen duidelijk.
Wat bereken je met een eigenvector. Ik kan het uitrekenen, maar weet niet wat het betekend.
De eigenwaarde is de verlenging/ verkorting van een vector, dat is dan wel weer meteen duidelijk.
C'est magnifique, mais ce n'est pas la guerre.
-
-
Een eigenvector is een vector die na de transformatie niet verandert van richting, althans, kan wel omklappen, maar verschuift verder niet.quote:
Even een makkelijke vraag die ik nergens in mijn boek kan vinden
Wat bereken je met een eigenvector. Ik kan het uitrekenen, maar weet niet wat het betekend.
De eigenwaarde is de verlenging/ verkorting van een vector, dat is dan wel weer meteen duidelijk.
Wikipedia illustreert het mooit met de Mona Lisa.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik zit hier met de vaag wanneer de golffunctie (in de quantum) een oscillerend karakter heeft (en wanneer deze een monotoom karakter heeft)
Mijn ene bron zegt: Etot > Epot -> oscillerend karakter, terwijl de andere bron zegt Ekin>Epot, wat niet op hetzelfde neerkomt. Immers kan Etot > Epot als Ekin < Epot.
Mijn ene bron zegt: Etot > Epot -> oscillerend karakter, terwijl de andere bron zegt Ekin>Epot, wat niet op hetzelfde neerkomt. Immers kan Etot > Epot als Ekin < Epot.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
er is ook een niet-wiskundetopic.quote:
Ik zit hier met de vaag wanneer de golffunctie (in de quantum) een oscillerend karakter heeft (en wanneer deze een monotoom karakter heeft)
Mijn ene bron zegt: Etot > Epot -> oscillerend karakter, terwijl de andere bron zegt Ekin>Epot, wat niet op hetzelfde neerkomt. Immers kan Etot > Epot als Ekin < Epot.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik moet 2 natuurlijke getallen p,q vinden met 35p=55q.
Lastig. Ik kwam tot nu toe niet verder dan priemontbinding maken;
(5*7)p=(5*11)q
5p*7p =5q*11q
Wie ziet hoe het verder moet en wil een tip geven?
Lastig. Ik kwam tot nu toe niet verder dan priemontbinding maken;
(5*7)p=(5*11)q
5p*7p =5q*11q
Wie ziet hoe het verder moet en wil een tip geven?
kloep kloep
Als q>0 is het rechterlid deelbaar door 11, maar het linkerlid niet. Als p>0 zelfde met 7. Dus p=q=0.quote:Op woensdag 4 november 2009 21:50 schreef Borizzz het volgende:
Ik moet 2 natuurlijke getallen p,q vinden met 35p=55q.
Lastig. Ik kwam tot nu toe niet verder dan priemontbinding maken;
(5*7)p=(5*11)q
5p*7p =5q*11q
Wie ziet hoe het verder moet en wil een tip geven?
thabit vindt 0 een natuurlijk getal
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus geen oplossingen.quote:Op woensdag 4 november 2009 22:09 schreef thabit het volgende:
[..]
Als q>0 is het rechterlid deelbaar door 11, maar het linkerlid niet. Als p>0 zelfde met 7. Dus p=q=0.
Kan je dit ook concluderen met hoofdstelling?
kloep kloep
Ik gebruik de term 'natuurlijk getal' zelf zelden. Ik spreek liever van positieve danwel niet-negatieve gehele getallen.quote:Op woensdag 4 november 2009 22:11 schreef GlowMouse het volgende:
thabit vindt 0 een natuurlijk getal
Zeker, al kan je ook zonder de hoofdstelling wel bewijzen dat een 5-macht maal een 7-macht niet deelbaar is door 11, maar met de hoofdstelling is het wel zo makkelijk.quote:Op woensdag 4 november 2009 22:13 schreef Borizzz het volgende:
[..]
Dus geen oplossingen.
Kan je dit ook concluderen met hoofdstelling?
Iets wat ik een paar maanden geleden perfect kon maar nu ben "vergeten". Opzich een hele simpele vergelijking.
N(t) = N(0) x (1/2)(t/t0,5)
Kan iemand vertellen hoe ik dit oplos als t OF t0,5 de onbekende is? Bedankt!
bijvoorbeeld:
1 = 100 x (1/2)20/t0,50)
N(t) = N(0) x (1/2)(t/t0,5)
Kan iemand vertellen hoe ik dit oplos als t OF t0,5 de onbekende is? Bedankt!
bijvoorbeeld:
1 = 100 x (1/2)20/t0,50)
Op vrijdag 11 september 2009 18:32 schreef jogy het volgende:
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Het toverwoord is logartime, maar voordat ik het voor je uitwerk moet ik eerst even weten hoe die exponent in elkaar zit, bij de eerste heb je (t/t0,5) wat denk ik is: (t/(0,5t)), maar ja, dat is weer gewoon gelijk aan 2. En bij die tweede komt er opeens 20 te staan? Dat snap ik ook niet helemaal.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nee het is geen 0,5t, het is officieel t1/2, het is een waarde, het is de halveringstijd van een bepaald isotoop.quote:
Het toverwoord is logartime, maar voordat ik het voor je uitwerk moet ik eerst even weten hoe die exponent in elkaar zit, bij de eerste heb je (t/t0,5) wat denk ik is: (t/(0,5t)), maar ja, dat is weer gewoon gelijk aan 2. En bij die tweede komt er opeens 20 te staan? Dat snap ik ook niet helemaal.
Dit is kernfysica, en de formule die ik je gegeven heb is een formule voor radioactief verval. Ik was er al wel achter dat ik log zou moeten gebruiken, maar ik dacht dat ik zelf een paar maanden terug een slim truukje had om log te voorkomen en het makkelijk uit te rekenen.
1 = 100 x (1/2)(20/t0,50)
1/100 = (1/2)(20/t0,50)
En nu?
Op vrijdag 11 september 2009 18:32 schreef jogy het volgende:
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Ik snap ’m, nou, in dit dit laatste geval wil je dus uitrekenen wat t1/2 is. Ik zal het eerst gewoon uitrekenen:
Dit is gelijk aan:
Neem links en rechts een logaritme:
Die log2 en de 2-macht heffen elkaar op in feite:
Wat links staat kun je numeriek uitrekenen, het is hetzelfde als log(1/100)/log(2) (immers: loga x = logb x / logb a), en dat is ≈ -6,643, dus dat vullen we in:
En daar komt uit:
t1/2 = -20/-6,643 ≈ 3,01.
Kun je het ook ‘handiger’ doen, ja en nee. Je kunt een inschatting maken, namelijk (1/2)2 = 1/4, (1/2)3 = 1/8, (1/2)6 = 1/64, (1/2)7 = 1/128, dus die exponent zal wel ergens tussen 6 en 7 moeten liggen, maar dat is weinig precies.
Ik hoop dat je het een beetje volgt.
Dit is gelijk aan:
Neem links en rechts een logaritme:
Die log2 en de 2-macht heffen elkaar op in feite:
Wat links staat kun je numeriek uitrekenen, het is hetzelfde als log(1/100)/log(2) (immers: loga x = logb x / logb a), en dat is ≈ -6,643, dus dat vullen we in:
En daar komt uit:
t1/2 = -20/-6,643 ≈ 3,01.
Kun je het ook ‘handiger’ doen, ja en nee. Je kunt een inschatting maken, namelijk (1/2)2 = 1/4, (1/2)3 = 1/8, (1/2)6 = 1/64, (1/2)7 = 1/128, dus die exponent zal wel ergens tussen 6 en 7 moeten liggen, maar dat is weinig precies.
Ik hoop dat je het een beetje volgt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik volg het wel, heel duidelijk, maar dit is niet precies wat ik zoek. De vraag is namelijk niet namens mij zelf maar namens iemand die weinig van logaritme snapt. Voor mij is het weer opgeheldert maar als ik log helemaal moet gaan uitleggen ben ik weer 2 maanden verder ofzo. Ik meen me te herinneren dat de formule zo om te zetten was dat logaritme niet nodig was, kan dat? Anders ga ik wel even in mn archieven kijken.quote:Op donderdag 5 november 2009 12:54 schreef Iblis het volgende:
Ik snap ’m, nou, in dit dit laatste geval wil je dus uitrekenen wat t1/2 is. Ik zal het eerst gewoon uitrekenen:
[ afbeelding ]
Dit is gelijk aan:
[ afbeelding ]
Neem links en rechts een logaritme:
[ afbeelding ]
Die log2 en de 2-macht heffen elkaar op in feite:
[ afbeelding ]
Wat links staat kun je numeriek uitrekenen, het is hetzelfde als log(1/100)/log(2) (immers: loga x = logb x / logb a), en dat is ≈ -6,643, dus dat vullen we in:
[ afbeelding ]
En daar komt uit:
t1/2 = -20/-6,643 ≈ 3,01.
Kun je het ook ‘handiger’ doen, ja en nee. Je kunt een inschatting maken, namelijk (1/2)2 = 1/4, (1/2)3 = 1/8, (1/2)6 = 1/64, (1/2)7 = 1/128, dus die exponent zal wel ergens tussen 6 en 7 moeten liggen, maar dat is weinig precies.
Ik hoop dat je het een beetje volgt.
Op vrijdag 11 september 2009 18:32 schreef jogy het volgende:
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Volgens mij kan het niet in z’n algemeenheid zonder log. In sommige gevallen wel, als de waarden mooi uitkomen, dan kun je het in feite beredeneren (b.v. omdat er nog maar 1/8 over is, dan moet dit wel 3 halfwaardetijden zijn).
Je kunt de vergelijking namelijk ook in z’n algemeenheid oplossen, dan krijg je:
Dus tenzij N(t)/N(0) een mooie breuk met een twee-macht is in de noemer (of N(0)/N(t) een 2-macht is) valt hier niet veel aan te vereenvoudigen.
[ Bericht 8% gewijzigd door Iblis op 05-11-2009 13:58:32 ]
Je kunt de vergelijking namelijk ook in z’n algemeenheid oplossen, dan krijg je:
Dus tenzij N(t)/N(0) een mooie breuk met een twee-macht is in de noemer (of N(0)/N(t) een 2-macht is) valt hier niet veel aan te vereenvoudigen.
[ Bericht 8% gewijzigd door Iblis op 05-11-2009 13:58:32 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het laatste.
Edit: nvm, ik zie het al in mijn wiskundeboek. Het gedeelte over Lagrange hadden we overgeslagen destijds. Tyfus, wat logisch.
Edit: nvm, ik zie het al in mijn wiskundeboek. Het gedeelte over Lagrange hadden we overgeslagen destijds. Tyfus, wat logisch.
Oh really?
Als je twee maanden nodig hebt om iemand het principe van logaritmen uit te leggen dan word je nooit een goede docent ... Niet dat ik wil suggereren dat dat daar je ambities zouden liggen, maar mijn ervaring is dat je dingen beter uit kunt leggen naarmate je er zelf meer inzicht in hebt, dus dat voorspelt niet veel goeds voor wat betreft je eigen inzicht. Ik denk - net als Iblis - dat je je vergist wat dat 'trucje' betreft. Alleen in eenvoudige gevallen kun je je vergelijking omwerken zodanig dat je links en rechts exponenten krijgt van eenzelfde grondtal, waarna je de exponenten aan elkaar gelijk kunt stellen. Maar als je dat vermeende trucje nog boven water kunt krijgen, laat het hier dan maar eens zien. Ik ben benieuwd ...quote:Op donderdag 5 november 2009 13:04 schreef appelsjap het volgende:
[..]
Ik volg het wel, heel duidelijk, maar dit is niet precies wat ik zoek. De vraag is namelijk niet namens mij zelf maar namens iemand die weinig van logaritmen snapt. Voor mij is het weer opgehelderd maar als ik log helemaal moet gaan uitleggen ben ik weer 2 maanden verder ofzo. Ik meen me te herinneren dat de formule zo om te zetten was dat logaritme niet nodig was, kan dat? Anders ga ik wel even in m'n archieven kijken.
We zoeken 30 + 31 + 32 + ... + 49. Dit is 20*(30+49)/2 = 790.quote:Op vrijdag 6 november 2009 16:18 schreef EmileVanDoorne het volgende:
Ik heb een vraagje in verband met wiskunde :
In een bioscoopzaal zijn er 20 rijen stoelen. Op de eerste rij zijn er 30 zitjes en elke rij heeft één zijde
meer dan de rij ervoor. Hoeveel stoelen zijn er in deze zaal?
A. 790 B. 800 C. 810 D. 820 E. 830
ik heb dit ook al berekend en ik kom altijd 790 uit ...
toch blijkt dit volgens mijn leerkracht niet de juiste oplossing te zijn ...
!!! HELP !!!
wie kan beter ????????????
thanks
Emile
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Horen hier ook Logica vragen? We zijn net begonnen met Verzamelingenleer en Logica maar ik vind het best wel lastig. Dingen als verzamelingenalgebra lukken wel maar het bewijzen van dingen vind ik erg lastig. Bijvoorbeeld de volgende opgave:
Laat zien dat A in B zit. A heeft alle 21-vouden, B alle 3-vouden. Omdat natuurlijk alle 21-vouden ook 3-vouden zijn klopt dit wel maar hoe ik dit echt moet bewijzen snap ik niet goed, hoe moet je zoiets aanpakken? Uit ons dictaat wordt ik ook niet echt wijzer.
Kan het niet goed opschrijven aangezien ik nog geen LaTeX kan, sorry!
Laat zien dat A in B zit. A heeft alle 21-vouden, B alle 3-vouden. Omdat natuurlijk alle 21-vouden ook 3-vouden zijn klopt dit wel maar hoe ik dit echt moet bewijzen snap ik niet goed, hoe moet je zoiets aanpakken? Uit ons dictaat wordt ik ook niet echt wijzer.
Kan het niet goed opschrijven aangezien ik nog geen LaTeX kan, sorry!
"Reality is an illusion created by a lack of alcohol."
Je redenering is juist inderdaad. Je kunt ze formeel maken, en dan moet je bewijzen: A ⊆ B, dit betekent a ∈ A ⇒ a ∈ B. Dan kijk je ‘wat betekent a ∈ A’, en ‘wat betekent b ∈ B’. Je zegt het zelf al, voor het eerste geldt dat als een getal een 21-voud is, dat het dan in A zit, voor het tweede geldt dat een het een 3-voud moet zijn. Omdat elk 21-voud ook een 3-voud is, zal gelden dat a ∈ A ⇒ a ∈ B.quote:
Horen hier ook Logica vragen? We zijn net begonnen met Verzamelingenleer en Logica maar ik vind het best wel lastig. Dingen als verzamelingenalgebra lukken wel maar het bewijzen van dingen vind ik erg lastig. Bijvoorbeeld de volgende opgave:
Laat zien dat A in B zit. A heeft alle 21-vouden, B alle 3-vouden. Omdat natuurlijk alle 21-vouden ook 3-vouden zijn klopt dit wel maar hoe ik dit echt moet bewijzen snap ik niet goed, hoe moet je zoiets aanpakken? Uit ons dictaat wordt ik ook niet echt wijzer.
Kan het niet goed opschrijven aangezien ik nog geen LaTeX kan, sorry!
Je kunt het helemaal formaliseren:
A ⊆ B ⇔ a ∈ A ⇒ a ∈ B, a ∈ A ⇔ ∃n ∈ ℤ: 21n = a, zeg m = 7n, dan m ∈ ℤ en 21n = 3m = a en dus per definitie van B (∃n ∈ ℤ: 3n = b ⇔ b ∈ B) ook a ∈ B.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik moet het dus inderdaad formaliseren, maar ik vind dit al behoorlijk lastig te volgen, laat staan hier zelf op te komen. Ik ga nog even met deze som stoeien. De volgende som heb ik zelf opgelost maar ik denk dat het wel mooier kan:
A:= {1,2,3}
B := ( x ∈ |R : x3 - 6x2 + 11x - 6 = 0}
Bewijs of weerleg de inclusie A ⊆ B.
Ik ben nu gewoon de drie mogelijkheden langsgegaan, op de volgende manier:
1 ∈ B want (1-6+1-6=0)
2 ∈ B want (8-24+22-6=0)
3 ∈ B want (27-54+33-6=0)
Dus ∀x : x ∈ A ⇒ x∈ B
Maar dit moet ook mooier kunnen, nu zijn het toevallig maar drie elementen in A met meer of oneindig kan dit niet zo natuurlijk..
A:= {1,2,3}
B := ( x ∈ |R : x3 - 6x2 + 11x - 6 = 0}
Bewijs of weerleg de inclusie A ⊆ B.
Ik ben nu gewoon de drie mogelijkheden langsgegaan, op de volgende manier:
1 ∈ B want (1-6+1-6=0)
2 ∈ B want (8-24+22-6=0)
3 ∈ B want (27-54+33-6=0)
Dus ∀x : x ∈ A ⇒ x∈ B
Maar dit moet ook mooier kunnen, nu zijn het toevallig maar drie elementen in A met meer of oneindig kan dit niet zo natuurlijk..
"Reality is an illusion created by a lack of alcohol."
De matrix moet ik van bewijzen dat 'ie alleen reële eigenwaardes heeft.
c is een complex getal 'c' (de c met streepje erop wat me teveel werk is ;p) de complex geconjugeerde van c.
Voor eigenwaarde l moet (a-l)(b-l) gelijk zijn aan c'c'
Als c = c1+c2i dan c'c'=c12+c22
(a-l)(b-l)=c'c'
2ab-(a+b)l+l2=c12+c22
Vanaf hier kom ik niet echt meer verder. c12+c22 is natuurlijk reëel, maar kan ik dan gelijk concluderen dat l ook reëel moet zijn?
[ Bericht 1% gewijzigd door GlowMouse op 08-11-2009 15:56:30 ([sub]-fix) ]
c is een complex getal 'c' (de c met streepje erop wat me teveel werk is ;p) de complex geconjugeerde van c.
Voor eigenwaarde l moet (a-l)(b-l) gelijk zijn aan c'c'
Als c = c1+c2i dan c'c'=c12+c22
(a-l)(b-l)=c'c'
2ab-(a+b)l+l2=c12+c22
Vanaf hier kom ik niet echt meer verder. c12+c22 is natuurlijk reëel, maar kan ik dan gelijk concluderen dat l ook reëel moet zijn?
[ Bericht 1% gewijzigd door GlowMouse op 08-11-2009 15:56:30 ([sub]-fix) ]
Bij 3 elementen is dit de mooiste methode. Bij meer is het probleem ook anders en kun je een andere methode gebruiken.quote:
Maar dit moet ook mooier kunnen, nu zijn het toevallig maar drie elementen in A met meer of oneindig kan dit niet zo natuurlijk..
Van a en b weet je dat ze reëel zijn (toch?).quote:
Vanaf hier kom ik niet echt meer verder. c12+c22 is natuurlijk reëel, maar kan ik dan gelijk concluderen dat l ook reëel moet zijn?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
a en b zijn reëel, ja. Maar door die l^2 weet ik niet zeker of ik gelijk kan zeggen of 't reëel is
Uitschrijven van l als l1+l2i geeft:
2ab-al1+bl1+l12-l22 + al2i+bl2i+2l1l2i = (reëel deel) + (a+b+2l1)l2i
en dat moet gelijk zijn aan een reëel getal, dus dan moet l2 nul zijn, toch? (ja, of (a+b+2l1)...)
[ Bericht 1% gewijzigd door Hanneke12345 op 08-11-2009 18:05:34 ]
Uitschrijven van l als l1+l2i geeft:
2ab-al1+bl1+l12-l22 + al2i+bl2i+2l1l2i = (reëel deel) + (a+b+2l1)l2i
en dat moet gelijk zijn aan een reëel getal, dus dan moet l2 nul zijn, toch? (ja, of (a+b+2l1)...)
[ Bericht 1% gewijzigd door Hanneke12345 op 08-11-2009 18:05:34 ]
Wat GlowMouse zegt klopt in feite, maar om nog iets meer te zeggen: bedenk dat je hier een derdegraads polynoom te pakken hebt, die heeft simpelweg hooguit drie (reële) oplossingen.quote:
Ik moet het dus inderdaad formaliseren, maar ik vind dit al behoorlijk lastig te volgen, laat staan hier zelf op te komen. Ik ga nog even met deze som stoeien. De volgende som heb ik zelf opgelost maar ik denk dat het wel mooier kan:
A:= {1,2,3}
B := ( x ∈ |R : x3 - 6x2 + 11x - 6 = 0}
Bewijs of weerleg de inclusie A ⊆ B.
Ik ben nu gewoon de drie mogelijkheden langsgegaan, op de volgende manier:
1 ∈ B want (1-6+1-6=0)
2 ∈ B want (8-24+22-6=0)
3 ∈ B want (27-54+33-6=0)
Dus ∀x : x ∈ A ⇒ x∈ B
Maar dit moet ook mooier kunnen, nu zijn het toevallig maar drie elementen in A met meer of oneindig kan dit niet zo natuurlijk..
Bij een verzameling met vier of meer elementen weet je dus sowieso dat deze geen deelverzameling kan zijn. Dus dat probleem ‘met oneindig veel elementen’ bestaat niet voor zo’n polynoom.
En nu is wat jij doet het simpelst.
[ Bericht 0% gewijzigd door Iblis op 08-11-2009 17:54:52 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
A direction field for the differential equation y ' = y(1-1/4 y^2)
a) Sketch the graphs of the solutions that satisfy the given initial conditions
i) y(o) = 1
Oke hoe kom ik aan die x waardes dan? Een vriend zei dat het kont makkelijk was en dat lijkt me eigenlijk ook best wel. Heb even die start-up nodig van jullie brontosaurussen. In die voorbeeldjes geven ze net ook weer iets waar ik niets aan heb.
-brachiosaurus
a) Sketch the graphs of the solutions that satisfy the given initial conditions
i) y(o) = 1
Oke hoe kom ik aan die x waardes dan? Een vriend zei dat het kont makkelijk was en dat lijkt me eigenlijk ook best wel. Heb even die start-up nodig van jullie brontosaurussen. In die voorbeeldjes geven ze net ook weer iets waar ik niets aan heb.
-brachiosaurus
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
edit: En ik snap natuurlijk dat ik een coordinaat moet hebben van (0,1)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Laat maar heb het al, wat een kontsom.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Schrijf om: l² - (a+b)l +ab - c'c' = 0 (jij had 2ab)quote:
De matrix [ afbeelding ] moet ik van bewijzen dat 'ie alleen reële eigenwaardes heeft.
c is een complex getal 'c' (de c met streepje erop wat me teveel werk is ;p) de complex geconjugeerde van c.
Voor eigenwaarde l moet (a-l)(b-l) gelijk zijn aan c'c'
Als c = c1+c2i dan c'c'=c12+c22
(a-l)(b-l)=c'c'
En dan de discriminant gebruiken; je krijgt de som van drie kwadraten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh, ik weet niet waar ik die 2ab van vandaan heb gehaald. ;x
Wat bedoel je met discriminant gebruiken? Want ik gebruik de discriminant toch al om die vergelijking (l² - (a+b)l +ab - c'c' = 0) te krijgen?
Wat bedoel je met discriminant gebruiken? Want ik gebruik de discriminant toch al om die vergelijking (l² - (a+b)l +ab - c'c' = 0) te krijgen?
Ok ja dat was een beetje een domme opmerking in dit geval. Ik vind het in ieder geval erg lastig die bewijzen te formaliseren. Ik zal hier binnenkort nog wel vaker komen met vragen. Hartstikke bedankt in ieder geval!quote:Op zondag 8 november 2009 17:14 schreef Iblis het volgende:
[..]
Wat GlowMouse zegt klopt in feite, maar om nog iets meer te zeggen: bedenk dat je hier een derdegraads polynoom te pakken hebt, die heeft simpelweg hooguit drie (reële) oplossingen.
Bij een verzameling met vier of meer elementen weet je dus sowieso dat deze geen deelverzameling kan zijn. Dus dat probleem ‘met oneindig veel elementen’ bestaat niet voor zo’n polynoom.
En nu is wat jij doet het simpelst.
"Reality is an illusion created by a lack of alcohol."
b) geef een matrix V en een diagonaalmaatrix D waarvoor geldt dat
A=VDV-1 (A is
Heb hier door V eigenvectoren te nemen een D gevonden
Definieer nu:
Laat zien dat u en v voldoen aan het volgende stelsel differentiaalvergelijkingen,
Dit doe ik door gebruik te maken van m'n eerder gevonden V (daar heb ik de inverse van berekend)
Maar nu is vraag e. Bereken V-1
Begrijp ik de som nou helemaal verkeerd, of doe ik dingen te omslachtig?
Je begrijpt het principe van conjugatie niet. Het idee is dat een matrix een lineaire afbeelding voorstelt, die ten aanzien van een gegeven basis is opgeschreven. Door de conjugeren schrijf je dezelfde lineaire afbeelding ten aanzien van een andere basis.
Ik ken het woord geconjugeerd alleen uit de scheikundelessen. Ik heb wel sommen gehad waarbij ik coördinaten ten opzcihte van een basis moest berekenen ([x]B enzo), maar dat zie ik hier niet in terug?
a+bi is de geconjugeerde van a-bi en vice versa
voor een vector of matrix is de geconjugeerde elementsgewijs gedefinieerd
voor een vector of matrix is de geconjugeerde elementsgewijs gedefinieerd
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, daar doelde ik niet op. Conjugatie is het uitvoeren van een operatie A -> SAS-1.quote:Op zondag 8 november 2009 23:00 schreef GlowMouse het volgende:
a+bi is de geconjugeerde van a-bi en vice versa
voor een vector of matrix is de geconjugeerde elementsgewijs gedefinieerd
Een matrix is diagonaliseerbaar als er een diagonaalmatrix D bestaat met A = SDS-1. In dat geval beschrijft D dezelfde lineaire afbeelding als A, maar dan ten aanzien van de basis die wordt gegeven door de kolommen van S.
Stel je hebt basis S, dan is [A]S = D ?
Maargoed, dan nog, is de V die later in de som terugkomt (bij e) dezelfde V als die ik vind bij b?
Maargoed, dan nog, is de V die later in de som terugkomt (bij e) dezelfde V als die ik vind bij b?
Geen idee, omdat later gevraagd wordt V-1 uit te rekenen.
Maar then again; Ik kan de som dus ook oplossen door V-1 te bepalen (dmv rijvegen tov standaardmatrix) en daarmee u(t) en v(t) te berekenen? Is dat ook de bedoeling of willen ze waarschijnlijk dat ik iets heel anders doe?
Maar then again; Ik kan de som dus ook oplossen door V-1 te bepalen (dmv rijvegen tov standaardmatrix) en daarmee u(t) en v(t) te berekenen? Is dat ook de bedoeling of willen ze waarschijnlijk dat ik iets heel anders doe?
Ah, ja, dat had ik bij een eerdere som ook vergeten. Herinner me opeens weer dat die tip in de les ook was gegeven. Ik geloof dat ik nu snap wat ik moet doen!
Klopt het dat ik dan krijg dat V-1 = l (want karakteristieke polynoom van A = l^2+1)? En betekent dat dan dat u(t) = f(t) en v(t) = g(t)?
Nee, wat V is heeft niets met het karakteristieke polynoom van A te maken. V bestaat uit de eigenvectoren van A.
Ah, shit, ja. Maar meot ik wel werken met het karakteristieke polynoom van V (= -(5+i)l+l^2, dus V-1=l-(5+i))? Dus dan is v(t)=g(t)-5-i?
(ik twijfel overigens over m'n - bij 5+i, maar dat is bijzaak)
(ik twijfel overigens over m'n - bij 5+i, maar dat is bijzaak)
Kan iemand me hier helpen met een opstapje? Heb een vaag idee waar ik ong. moet uitkomen in de stappen die ik moet doen, maar weet absoluut niet hoe ik moet beginnen. Hoe turn ik het zo om dat het berekend kan worden door de LSR?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
kijk naar log(Y)quote:
Kan iemand me hier helpen met een opstapje? Heb een vaag idee waar ik ong. moet uitkomen in de stappen die ik moet doen, maar weet absoluut niet hoe ik moet beginnen. Hoe turn ik het zo om dat het berekend kan worden door de LSR?
[ afbeelding ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, zo werkt dat niet. Het idee is dat je u(x) en v(x) kan schrijven als lineaire combinatie van f(x) en g(x).quote:Op maandag 9 november 2009 00:17 schreef Hanneke12345 het volgende:
Ah, shit, ja. Maar meot ik wel werken met het karakteristieke polynoom van V (= -(5+i)l+l^2, dus V-1=l-(5+i))? Dus dan is v(t)=g(t)-5-i?
(ik twijfel overigens over m'n - bij 5+i, maar dat is bijzaak)
Even een vraag mbt absolute waarde.
Bepaal de kritieke punten van f(x)= ln(x2 - |x| +1)
Klopt nu dat:
f(x) = ln(x2-x+1) als ln(x2-x+1) => 0
f(x) = ln(x2+x+1) als ln(x2-x+1) < 0
Of moet je alleen de term binnen de absolute waarde nemen (dus krijg je ... als x =>0; ... als x<0)
Of moet ik dit anders aanpakken
Bepaal de kritieke punten van f(x)= ln(x2 - |x| +1)
Klopt nu dat:
f(x) = ln(x2-x+1) als ln(x2-x+1) => 0
f(x) = ln(x2+x+1) als ln(x2-x+1) < 0
Of moet je alleen de term binnen de absolute waarde nemen (dus krijg je ... als x =>0; ... als x<0)
Of moet ik dit anders aanpakken
Kritieke punten bepaal je aan de hand van de afgeleide. En jouw functie definitie is gelijk aan:
Kortom, het gaat alleen om die term tussen absoluutstrepen. Maar dan moet je volgens mij nog de afgeleide bepalen…
Kortom, het gaat alleen om die term tussen absoluutstrepen. Maar dan moet je volgens mij nog de afgeleide bepalen…
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ah bedankt. Ik wilde alleen die eerste stap hier weten, voor de rest lukt het me wel.quote:Op maandag 9 november 2009 14:42 schreef Iblis het volgende:
Kritieke punten bepaal je aan de hand van de afgeleide. En jouw functie definitie is gelijk aan:
[ afbeelding ]
Kortom, het gaat alleen om die term tussen absoluutstrepen. Maar dan moet je volgens mij nog de afgeleide bepalen…
Ik zoek een formule om de trend te bereken van de omzet van een artikel.
Ik heb 12 maanden historische data. Hij moet nu de 13e maand omzet berekenen en voor de 14e maand moet hij weer 12 maanden pakken (werkelijk verkocht maand 2 tm 13 zou maar zeggen).
Lineair Trend model werkt niet, daar het niet altijd lineair is.
Quadratic Trend model werkt ook niet, daar de aantallen soms onder 0 komen!
Ik heb 12 maanden historische data. Hij moet nu de 13e maand omzet berekenen en voor de 14e maand moet hij weer 12 maanden pakken (werkelijk verkocht maand 2 tm 13 zou maar zeggen).
Lineair Trend model werkt niet, daar het niet altijd lineair is.
Quadratic Trend model werkt ook niet, daar de aantallen soms onder 0 komen!
Hoe komt de omzet onder 0?
Beste is een plaatje pakken en kijken wat er gebeurt. Maar simple moving average of exponential smoothing zijn wel voor de hand liggende technieken.
Beste is een plaatje pakken en kijken wat er gebeurt. Maar simple moving average of exponential smoothing zijn wel voor de hand liggende technieken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik bedoel dat als ik het quadratic trend model gebruik de aantallen soms onder 0 komen.
Exponential smoothing is volgens mij ook niet de juiste omdat de aantallen niet altijd hoeven te stijgen.
Exponential smoothing is volgens mij ook niet de juiste omdat de aantallen niet altijd hoeven te stijgen.
Owh exponential smoothing hoeven de aantallen ook niet altijd te stijgen nog niet zo scherp 's morgens .
.
Wat is centripetale versnelling precies? En hoe zit het met dat voorbeeld van die twee schaatser in een bocht (Welke heeft grotere centripetale versnelling etc.?)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Begin even hiermee.quote:Op donderdag 12 november 2009 18:32 schreef Burakius het volgende:
Wat is centripetale versnelling precies? En hoe zit het met dat voorbeeld van die twee schaatser in een bocht (Welke heeft grotere centripetale versnelling etc.?)
Is dit wiskunde? http://nl.wikipedia.org/wiki/Middelpuntzoekende_krachtquote:
Wat is centripetale versnelling precies? En hoe zit het met dat voorbeeld van die twee schaatser in een bocht (Welke heeft grotere centripetale versnelling etc.?)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
even voor de zekerheid: de somregel bij differentieren gaat ook op in geval van min? dus f(x) - g(x) en dan afgeleide is f'(x) - g'(x)?
Ja. Als je bv x - x² hebt dan kun je dat ook zien als x + (-x²) en dan zie je gelijk dat het goed gaat.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ojaquote:Op vrijdag 13 november 2009 21:11 schreef GlowMouse het volgende:
Ja. Als je bv x - x² hebt dan kun je dat ook zien als x + (-x²) en dan zie je gelijk dat het goed gaat.
merci
je kunt een breuk uitdelen, dan splits je de teller en de noemer blijft gelijk. werkt dit andersom ook zo? dus de noemer splitsen en de teller gelijk houden?
zoals dit?:
1/(3x^2) = (1/3) . (1/x^2) = (1/3) . x^(-2)
zoals dit?:
1/(3x^2) = (1/3) . (1/x^2) = (1/3) . x^(-2)
Dat werkt en is in feite een factor buiten haakjes halen. Maar waar je volgens mij op doelt is:quote:
je kunt een breuk uitdelen, dan splits je de teller en de noemer blijft gelijk. werkt dit andersom ook zo? dus de noemer splitsen en de teller gelijk houden?
zoals dit?:
1/(3x^2) = (1/3) . (1/x^2) = (1/3) . x^(-2)
Wat geldt.
Maar er geldt niet:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik kom er niet helemaal uit.
Ik heb
(slechte kwaliteit, verkeerd gesaved)
1. is de Cauchy-schwarz ongelijkheid dus bekend en bewezen
2. is de functie, V een reële inproductruimte
3. moet ik bewijzen.
Het probleem is vooral dat als ik 3 uitwerk er overal + staat, terwijl 1 allemaal vermenigvuldigingen heeft.
Ik heb
(slechte kwaliteit, verkeerd gesaved)
1. is de Cauchy-schwarz ongelijkheid dus bekend en bewezen
2. is de functie, V een reële inproductruimte
3. moet ik bewijzen.
Het probleem is vooral dat als ik 3 uitwerk er overal + staat, terwijl 1 allemaal vermenigvuldigingen heeft.
Als je met de linkerkant begint dan heb je <x+y,x+y> = <x,x> + <y,y> + 2<x,y>
doe hetzelfde voor de rechterkant en dan zie je het toch direct?
doe hetzelfde voor de rechterkant en dan zie je het toch direct?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Aan de rechterkant heb je <x,x>+<y,y>
Dan krijg je <x,x>+<y,y>+2<x,y> < <x,x>+<y,y>
Dan heb ik dus 2<x,y> < 0?
Dan krijg je <x,x>+<y,y>+2<x,y> < <x,x>+<y,y>
Dan heb ik dus 2<x,y> < 0?
neequote:
Aan de rechterkant heb je <x,x>+<y,y>
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Determine the values of r for wich the given differential equiation has solutions of the form y=e^rt
y '' + y ' - 6y = 0
Ik kom hier niet op het goede antwoord. Ik heb zelf wel een beetje gefrutseld:
---> y '' + y ' - 6y = 0
---> y '' + y '= 6y
---> 1/6 (y '' + y ') = y
---> y '' + y ' = y / (1/6)
---> y '' + y '/ y = 6
En nu komt het stuk waar ik niet echt zeker van ben:
--> y ' * ln | y | = 6t + c En hier ging ik er vanuit dat na kloten r = 6 zou zijn. Maar ik doe duidelijk iets niet goed of denk verkeerd. Can someone help?
y '' + y ' - 6y = 0
Ik kom hier niet op het goede antwoord. Ik heb zelf wel een beetje gefrutseld:
---> y '' + y ' - 6y = 0
---> y '' + y '= 6y
---> 1/6 (y '' + y ') = y
---> y '' + y ' = y / (1/6)
---> y '' + y '/ y = 6
En nu komt het stuk waar ik niet echt zeker van ben:
--> y ' * ln | y | = 6t + c En hier ging ik er vanuit dat na kloten r = 6 zou zijn. Maar ik doe duidelijk iets niet goed of denk verkeerd. Can someone help?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
---> y '' + y '/ y = 6
die klopt niet.
En vul y' en y'' gewoon eens in
die klopt niet.
En vul y' en y'' gewoon eens in
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oja natuurlijk dat moet 1/6 zijn. Ik krijg:
y ' = e^rt * r
y '' = e^rt * r^2
Invullen geeft van de originele formule:
e^rt * r^2 + e^rt * r - 6y = 0
Schiet ik niet echt iets mee op??
1.Of moet ik het invullen in --> y '' + y' / y = 1/6
2. Klopte het trouwens van die y ' * ln | y | = 6t + c ???
y ' = e^rt * r
y '' = e^rt * r^2
Invullen geeft van de originele formule:
e^rt * r^2 + e^rt * r - 6y = 0
Schiet ik niet echt iets mee op??
1.Of moet ik het invullen in --> y '' + y' / y = 1/6
2. Klopte het trouwens van die y ' * ln | y | = 6t + c ???
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
functievoorschrift van een parabool opstellen gegeven is:
symetrie-as x=3
punten op de grafiek
P(5,17) en Q(2,8)
Wie helpt me?
PS: Ik woon in Nederland en zit in Belgie op school.
symetrie-as x=3
punten op de grafiek
P(5,17) en Q(2,8)
Wie helpt me?
PS: Ik woon in Nederland en zit in Belgie op school.
waarom vul je y niet in? Dan kun je hem gewoon oplossen.quote:
Oja natuurlijk dat moet 1/6 zijn. Ik krijg:
y ' = e^rt * r
y '' = e^rt * r^2
Invullen geeft van de originele formule:
e^rt * r^2 + e^rt * r - 6y = 0
Het punt (3,a) ligt op de parabool. Als je 1 opzij gaat, ga je 8-a omhoog en als je 2 opzij gaat, ga je 17-a omhoog.quote:
functievoorschrift van een parabool opstellen gegeven is:
symetrie-as x=3
punten op de grafiek
P(5,17) en Q(2,8)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
f: V--> R: x-> sqrt(<x,x>) (functie als in regel 2 in het eerdere plaatje)
Ik heb bewezen dat voor alle x,y uit V geldt dat ||x+y||2+||x-y||2=2||x||2+2||y||2
Schets x, y, x+y en x-y in een plaatje en begrijp de naam paralellogramwet
Ik kan hier toch willekeurige coördinaten voor x en y kiezen? Ik had x = (1,2) en y=(2,-3). Dan kan ik x+y en x-y toch gewoon uitrekenen door x+y=(1+2, 2-3)? Als ik dat doe snap ik de naam parallelogramwet nog altijd niet. ;x
Ik heb bewezen dat voor alle x,y uit V geldt dat ||x+y||2+||x-y||2=2||x||2+2||y||2
Schets x, y, x+y en x-y in een plaatje en begrijp de naam paralellogramwet
Ik kan hier toch willekeurige coördinaten voor x en y kiezen? Ik had x = (1,2) en y=(2,-3). Dan kan ik x+y en x-y toch gewoon uitrekenen door x+y=(1+2, 2-3)? Als ik dat doe snap ik de naam parallelogramwet nog altijd niet. ;x
e^rt * r^2 + e^rt * r - 6 * e^rt = 0
En nu kan ik het gewoon oplossen? Het ontgaat me even welke stappen ik zou moeten ondernemen.... black-out time...
En nu kan ik het gewoon oplossen? Het ontgaat me even welke stappen ik zou moeten ondernemen.... black-out time...
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
verbind x met x+y en y ook met x+y, en transleer x-y zodat hij x en y verbindt.quote:
f: V--> R: x-> sqrt(<x,x>) (functie als in regel 2 in het eerdere plaatje)
Ik heb bewezen dat voor alle x,y uit V geldt dat ||x+y||2+||x-y||2=2||x||2+2||y||2
Schets x, y, x+y en x-y in een plaatje en begrijp de naam paralellogramwet
Ik kan hier toch willekeurige coördinaten voor x en y kiezen? Ik had x = (1,2) en y=(2,-3). Dan kan ik x+y en x-y toch gewoon uitrekenen door x+y=(1+2, 2-3)? Als ik dat doe snap ik de naam parallelogramwet nog altijd niet. ;x
ontbinden in factoren, heb je dat In Delft niet?quote:
e^rt * r^2 + e^rt * r - 6 * e^rt = 0
En nu kan ik het gewoon oplossen? Het ontgaat me even welke stappen ik zou moeten ondernemen.... black-out time...
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nu snap ik er nog minder van?quote:Op zondag 15 november 2009 17:29 schreef GlowMouse het volgende:
[..]
[..]
Het punt (3,a) ligt op de parabool. Als je 1 opzij gaat, ga je 8-a omhoog en als je 2 opzij gaat, ga je 17-a omhoog.
Ah, dat laatste was ik nog niet opgekomen dat dat kon. Maarr dan heb ik toch een driehoek (x, x+y, y) en geen parallelogram?quote:Op zondag 15 november 2009 17:36 schreef GlowMouse het volgende:
[..]
verbind x met x+y en y ook met x+y, en transleer x-y zodat hij x en y verbindt.
[..]
ontbinden in factoren, heb je dat In Delft niet?
Als je een afbeelding hebt van R2 naar R, en je hebt de normaxioma f(av)=|a|f(v) voor alle a bla Dan geldt dat av = (a*v1, av2), toch?
plaatje makenquote:
hoekpunten zijn O, x, y en x+y. De vector x teken je niet als een punt maar als een lijn van O naar x, idem voor y.quote:
[..]
Ah, dat laatste was ik nog niet opgekomen dat dat kon. Maarr dan heb ik toch een driehoek (x, x+y, y) en geen parallelogram?
Als je een afbeelding hebt van R2 naar R, en je hebt de normaxioma f(av)=|a|f(v) voor alle a bla Dan geldt dat av = (a*v1, av2), toch?
En je vergeet absoluuttekens.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:Op zondag 15 november 2009 17:36 schreef GlowMouse het volgende:
[..]
verbind x met x+y en y ook met x+y, en transleer x-y zodat hij x en y verbindt.
[..]
ontbinden in factoren, heb je dat In Delft niet?
I regret the day I posted there
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ah, opnieuw een plaatje gemaakt, en nu zijn a+x en a-x zijn niet de zijkanten van de parallelogram maar de diagonalenquote:Op zondag 15 november 2009 17:46 schreef GlowMouse het volgende:
[..]
plaatje maken
[..]
hoekpunten zijn O, x, y en x+y. De vector x teken je niet als een punt maar als een lijn van O naar x, idem voor y.
En je vergeet absoluuttekens.
Waar moeten de absoluuttekens precies |a|v1, |a|v2?
waarom daar?quote:
[..]
Waar moeten de absoluuttekens precies |a|v1, |a|v2?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je kunt nu ert in het linkerlid van je vergelijking (niet: formule) buiten haakjes halen. Tussen haakjes houd je dan een kwadratisch polynoom in r over. Een product van twee grootheden kan alleen gelijk zijn aan 0 als (tenminste) één der beide grootheden gelijk is aan 0. Maar nu weet je ook dat ert nooit 0 kan zijn. Dus kan y = ert alleen een oplossing zijn van je DV als r voldoet aan de vierkantsvergelijking r2 + r - 6 = 0. Nu mag je zelf weer even verder.quote:Op zondag 15 november 2009 17:32 schreef Burakius het volgende:
e^rt * r^2 + e^rt * r - 6 * e^rt = 0
En nu kan ik het gewoon oplossen? Het ontgaat me even welke stappen ik zou moeten ondernemen.... black-out time...
Kijk gewoon naar je functies en bedenk wat er gebeurt als er iets negatief is en of jouw functie hetzelfde doet.quote:
[..]
Omdat het niet in av moet, want dat staat zo in de opdracht / in m'n aantekeningen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
In de functie staan absoluuttekens om x,f(av)=max(|ax1|,|ax2|), dus volgens mij maken absoluutteken om de a niks uit, die staan er al. Toch?
Volgens mij klopt je vraag niet; av = (a*v1, av2) geldt altijd.
Maar f(av) = (a*f(v1), af(v2)) klopt niet omdat het rechterlid negatief kan zijn.
Maar f(av) = (a*f(v1), af(v2)) klopt niet omdat het rechterlid negatief kan zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:
Medemensen!
ik heb 2, misschien ietwat uitgebreide vragen.
ik moet voor mijn volgende les weten hoe ik een beta kan schatten met het gebruik van the single index model. Ik weet dat ik alle outcomes van de S&P500 en van het andere aandeel in Excel kan zetten deze in een mooie grafiek zetten en daarna gewoon via de tools een trendline erdoorheen laten zetten en zo dus, via de bijbehorende formule de beta af kan lezen, maar is er ook nog een andere manier? Een numerieke bv. dat ik met spss outcomes de beta vinden kan?
mijn 2e vraag is. Hoe kan ik aan de hand van spss-gegevens(regression statistics, ANOVA en nog een tabel met gegevens van Intercept en X variable 1) van 2 aandelen berekenen wat hun expected return is..wanneer ook nog de expected return van de S&P500 gegeven is. Moet ik dan de beruchte formule:
E(Ri)= Rf + beta(E(Rm)-Rf) gebruiken en zoja...Hoe dan, want daar kwam ik niet uit
Ik hoop dat dit niet teveel voor jullie is!
Ja doei.
Max(|x1+y1|, |x2+y2|) =< max(|x1|, x2|)+max(|y1|, |y2|)
Logisch. Omdat y negatief kan zijn maar x+y nog steeds positief, of y1 het maximum van y maar x2 het maximum van x. Maar hoe kan ik dit bewijzen?
Logisch. Omdat y negatief kan zijn maar x+y nog steeds positief, of y1 het maximum van y maar x2 het maximum van x. Maar hoe kan ik dit bewijzen?
|x1+y1| =< max(|x1|, x2|)+max(|y1|, |y2|)
lukt dat wel?
lukt dat wel?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
1. numeriek gaat met lineaire regressie.quote:
2. je weet Rf, beta, E(Rm) dus je kunt E(Ri) uitrekenen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:Op zondag 15 november 2009 19:39 schreef GlowMouse het volgende:
[..]
1. numeriek gaat met lineaire regressie.
2. je weet Rf, beta, E(Rm) dus je kunt E(Ri) uitrekenen
maar er is voor 1. geen bepaalde formule met standaard deviaties van de s&p500 in relatie met wat anders?
en ik weet voor het 2e gedeelte wel al de dingen, maar de beta is niet te vinden, omdat ik wel de spss resultaten heb, maar blijkbaar dus beperkt en ik heb zelf niet de data inspss om alle analyses zelf uit te voeren
1. geen idee, maar je zult toch excess returns moeten berekenen op een of andere manier
2. toch een beta vinden, anders lukt het niet
2. toch een beta vinden, anders lukt het niet
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
thanks, ik ga mijn best doenquote:Op zondag 15 november 2009 19:45 schreef GlowMouse het volgende:
1. geen idee, maar je zult toch excess returns moeten berekenen op een of andere manier
2. toch een beta vinden, anders lukt het niet
Hmm, het enige wat ik kan bedenken is iets als:quote:Op zondag 15 november 2009 19:37 schreef GlowMouse het volgende:
|x1+y1| =< max(|x1|, x2|)+max(|y1|, |y2|)
lukt dat wel?
Max(|x1|, |x2|)+max(|y1|, |y2| =
max(|x1|+|y1|, |x1|+|y2|, |x2|+|y1|, |x2|+|y2|) >=|x1+y1|
Moet het zo?
waarom?quote:
[..]
Hmm, het enige wat ik kan bedenken is iets als:
Max(|x1|, |x2|)+max(|y1|, |y2| =
max(|x1|+|y1|, |x1|+|y2|, |x2|+|y1|, |x2|+|y2|) >=|x1+y1|
Moet het zo?
Begin met |x1+y1| en doe dan gelijk de driehoeksongelijkheid, veel korter.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Maar ik ben nog aan het aantonen dat het een norm is. Dan weet ik toch niet zeker of de driehoeksongelijkheid geldt? Ikb en die volgens mij nu juist aan het bewijzen bij deze functie. ;o
Oh, | is geen absolutie waarde hier?quote:
Maar ik ben nog aan het aantonen dat het een norm is. Dan weet ik toch niet zeker of de driehoeksongelijkheid geldt? Ikb en die volgens mij nu juist aan het bewijzen bij deze functie. ;o
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat wel. Maar de vraag is "laat zien dat f een norm op R2 definieert", ik heb laten zien dat f(x)>o voor alle x, dat f(av)=|a|f(v) en nu dus nog dat f(x+y)<= f(x)+f(y). Dat laatste is volgens mij precies wat de driehoeksongelijkheid zegt, toch?
ja, maar je kunt de driehoeksongelijkheid voor de absolute waarde gebruikenquote:
Dat wel. Maar de vraag is "laat zien dat f een norm op R2 definieert", ik heb laten zien dat f(x)>o voor alle x, dat f(av)=|a|f(v) en nu dus nog dat f(x+y)<= f(x)+f(y). Dat laatste is volgens mij precies wat de driehoeksongelijkheid zegt, toch?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Voor absolute waarde geldt ook dat |x+y| <= |x|+|y|?
|x1+y1| <= |x1|+|y1|<=max(|x1|, |x2|)+max(|y1|, |y2|)?
En die manier die ik net deed, is die fout, onvolledig of gewoon omslachtig? Hij overtuide mij meer dan zo eigenlijk ;o
|x1+y1| <= |x1|+|y1|<=max(|x1|, |x2|)+max(|y1|, |y2|)?
En die manier die ik net deed, is die fout, onvolledig of gewoon omslachtig? Hij overtuide mij meer dan zo eigenlijk ;o
omslachtig, dit is veel duidelijker.quote:
Voor absolute waarde geldt ook dat |x+y| <= |x|+|y|?
|x1+y1| <= |x1|+|y1|<=max(|x1|, |x2|)+max(|y1|, |y2|)?
En die manier die ik net deed, is die fout, onvolledig of gewoon omslachtig? Hij overtuide mij meer dan zo eigenlijk ;o
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oke ik doe duidelijk iets verkeerds?
Find the solution of the given initial value problem:
y ' + 3y = t e^ -3t met y(1) = 0
Daar maak ik van:
--> y ' * u(t) + 3y * u(t) = te^-3t * u(t)
--> u '(t) = 3y * u(t) --> u '(t)/u(t) = 3y
--> ln |u(t)| = 3/2 y^2 + c
Ik neem c = 0 en vind:
- u(t) = +/- e^3/2 y^2
Voordat ik verder kan met invullen van de gevonden u(t) zie ik al aan het antwoord dat mijn u(t) = (t^2-1) moet zijn.
De voorbeelden van het college kan ik wel perfect uitvoeren, maar in het werkboek faal ik hopeloos. Help me someone !
Find the solution of the given initial value problem:
y ' + 3y = t e^ -3t met y(1) = 0
Daar maak ik van:
--> y ' * u(t) + 3y * u(t) = te^-3t * u(t)
--> u '(t) = 3y * u(t) --> u '(t)/u(t) = 3y
--> ln |u(t)| = 3/2 y^2 + c
Ik neem c = 0 en vind:
- u(t) = +/- e^3/2 y^2
Voordat ik verder kan met invullen van de gevonden u(t) zie ik al aan het antwoord dat mijn u(t) = (t^2-1) moet zijn.
De voorbeelden van het college kan ik wel perfect uitvoeren, maar in het werkboek faal ik hopeloos. Help me someone !
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Is het mijn fout dat ik die y meeneem?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
waar komt die tweede regel vandaan?quote:
--> y ' * u(t) + 3y * u(t) = te^-3t * u(t)
--> u '(t) = 3y * u(t) --> u '(t)/u(t) = 3y
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vermenigvuldigd met een integratie factor...en daarna u'(t) vinden Die moet gelijk zijn met P(x)y ( van: dy/dx + P(x)y = Q(x) )quote:Op zondag 15 november 2009 21:09 schreef GlowMouse het volgende:
[..]
waar komt die tweede regel vandaan?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
De DV die je moet oplossen is y ' + 3y = te-3t met als randvoorwaarde y(1) = 0. Dit is een lineaire inhomogene DV van de eerste orde. De algemene aanpak is dat je eerst de corresponderende homogene DV y' + 3y = 0 oplost en dan een particuliere oplossing vindt van de inhomogene DV. Voor dat laatste kun je gebruik maken van de methode van de onbepaalde constanten die ik hier al eens kort heb uiteengezet. De algemene oplossing van je inhomogene DV wordt dan gegeven door de som van de algemene oplossing van de homogene DV en de reeds gevonden particuliere oplossing. Tenslotte kun je dan bepalen welke oplossing(en) voldoet c.q. voldoen aan de gegeven randvoorwaarde(n).quote:Op zondag 15 november 2009 20:59 schreef Burakius het volgende:
Oke ik doe duidelijk iets verkeerds?
Find the solution of the given initial value problem:
y ' + 3y = t e^ -3t met y(1) = 0
[snip]
Ik zie nu dat ik die y elke keer heb meegenomen. Als ik die niet meeneem, kom ik voor de rest van de rit helemaal uit. Nu nog even uitvogelen wat er nou precies bedoelt wordt met y(1) = 0 en wat ik er mee moet, maar dat zal ik even moeten lezen in je link. Thx!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik.quote:Op zondag 15 november 2009 17:24 schreef cojonesm het volgende:
Functievoorschrift van een parabool opstellen. Gegeven is:
Symmetrie-as x=3
Punten op de grafiek
P(5,17) en Q(2,8)
Wie helpt me?
Wat wil je daarmee zeggen? Dat het wiskunde-onderwijs in België op een hoger plan staat en dat je er daarom (extra) moeite mee hebt?quote:PS: Ik woon in Nederland en zit in België op school.
De grafiek is een parabool met als (verticale) symmetrie-as de lijn met als vergelijking x = 3. Nu weet je dat een parabool met een verticale symmetrie-as in zijn algemeenheid de grafiek voorstelt van een kwadratische functie. We zoeken dus een vergelijking (c.q. functie) van de gedaante:
(1) y = ax2 + bx + c,
waarbij we a ongelijk aan nul mogen veronderstellen, anders is het immers geen kwadratische functie meer.
De kunst is nu natuurlijk om de waarden van a, b en c te bepalen. Daarvoor gaan we gebruik maken van de gegevens die we hebben. Het eerste gegeven is dat de symmetrie-as van de parabool de lijn met vergelijking x = 3 is. Maar nu weet je - hopelijk - dat de symmetrie-as van een parabool met vergelijking (1) wordt gegeven door:
(2) x = -b/2a
Zodoende weten we dus al dat moet gelden:
(3) -b/2a = 3
Vermenigvuldigen we in (3) beide leden met -2a, dan kunnen we voor (3) dus ook schrijven:
(4) b = -6a
Verder weten we dat de punten P(5;17) en Q(2;8) op de grafiek liggen, zodat de coördinaten van deze punten ook moeten voldoen aan (1). Invullen in (1) van x = 5 en y = 17 (voor punt P) geeft:
(5) 17 = 25a + 5b + c
En invullen in (1) van x = 2 en y = 8 (voor punt Q) geeft:
(6) 8 = 4a + 2b + c
Nu vormen (4), (5) en (6) samen een stelsel van drie vergelijkingen in de drie onbekenden a, b en c, en daarmee hebben we voldoende informatie om de waarden van a,b en c te bepalen.
Het eenvoudigst is hier om de leden van vergelijking (6) af te trekken van de leden van vergelijking (5), zodat we c kwijtraken. We krijgen dan:
(7) 9 = 21a + 3b
En aangezien we uit (4) weten dat b = -6a, kunnen we dit substitueren in (7), zodat we krijgen
9 = 21a - 18a
9 = 3a
a = 3
Op grond van (4) weten we dan ook meteen dat b = -18, en invullen van a=3 en b=-18 in (5) of (6) levert dan c = 32. Daarmee is de gevraagde vergelijking gevonden:
(8) y = 3x2 -18x + 32
Toch nog maar even reageren, omdat ik nu pas zie dat je voor het oplossen van een lineaire inhomogene dv van de eerste orde gebruik probeert te maken van de methode van de integrerende factor. De methode van de onbepaalde coëfficienten die ik je in de hierboven genoemde link aan de hand heb gedaan is hier uiteraard ook te gebruiken, aangezien het gaat om een lineaire dv met constante coëfficiënten, maar is voor een eerste orde dv wat omslachtiger.quote:Op zondag 15 november 2009 21:25 schreef Burakius het volgende:
Ik zie nu dat ik die y elke keer heb meegenomen. Als ik die niet meeneem, kom ik voor de rest van de rit helemaal uit. Nu nog even uitvogelen wat er nou precies bedoelt wordt met y(1) = 0 en wat ik er mee moet, maar dat zal ik even moeten lezen in je link. Thx!
De algemene gedaante van een lineaire dv van de eerste orde in standaardvorm is:
(1) y'(t) + p(t)∙y(t) = q(t)
De gedachte achter de methode van de integrerende factor is dat we het linkerlid van (1) gaan proberen om te vormen tot de afgeleide van een product van y(t) en een nader te bepalen functie µ(t). Het linkerlid van (1) bestaat immers uit twee termen, waarvan één met een factor y'(t) en één met een factor y(t), en dat herinnert aan de productregel. Immers, de afgeleide van een product y(t)∙µ(t) is gelijk aan:
(2) y'(t)∙µ(t) + y(t)∙µ'(t)
Vermenigvuldigen we nu beide leden van (1) met µ(t), dan kunnen we voor (1) schrijven:
(3) y'(t)∙µ(t) + y(t)∙p(t)∙µ(t) = q(t)∙µ(t)
Vergelijken we nu het linkerlid van (3) met de gewenste vorm (2), dan zien we dat de eerste van de twee termen van het linkerlid (3) al overeenstemt met (2) maar de tweede term niet. Toch kunnen we ervoor zorgen dat de tweede term van het linkerlid van (3) ook overeenstemt met het tweede lid van (2) als we µ(t) zodanig zouden kunnen kiezen dat geldt:
(4) y(t)∙µ'(t) = y(t)∙p(t)∙µ(t),
en dus:
(5) µ'(t) = p(t)∙µ(t)
Het is nu niet zo moeilijk om te zien hoe we µ(t) zodanig kunnen kiezen dat deze functie voldoet aan (5). We zoeken een functie µ(t) waarvan de afgeleide µ'(t) gelijk is aan de oorspronkelijke functie µ(t) vermenigvuldigd met p(t). Denken we aan de exponentiële functie, die zichzelf als afgeleide heeft, en aan de kettingregel, dan is eenvoudig in te zien dat de gezochte functie µ(t) wordt gegeven door:
(6) µ(t) = eP(t),
waarbij P(t) een primitieve is van p(t). Immers, volgens de kettingregel is de afgeleide van µ(t) = eP(t) dan gelijk aan µ'(t) = P'(t)∙eP(t) = p(t)∙eP(t) = p(t)∙µ(t), zoals gewenst.
De oplossingsmethode met de integrerende factor voor een dv van de gedaante (1) bestaat er dus in dat we eerst een primitieve P(t) van p(t) bepalen en dan beide leden vermenigvuldigen met eP(t), waarna we het linkerlid van de dv kunnen opvatten als de afgeleide van het product y(t)∙eP(t). Vervolgens kunnen we dan beide leden van de DV integreren en daarna door deling van beide leden door eP(t) de gezochte functies y(t) vinden die aan de dv (1) voldoen.
De DV die je moest oplossen is:
(7) y'(t) + 3∙y(t) = t∙e-3t
Hier is p(t) = 3, en een primitieve daarvan is P(t) =3t. We kiezen er dus voor beide leden van (7) te vermenigvuldigen met µ(t) = eP(t) = e3t en krijgen dan:
(8) y'(t)∙e3t + y(t)∙3∙e3t = t
Het linkerlid is nu de afgeleide van y(t)∙e3t, zodat integreren van beide leden geeft:
(9) y(t)∙e3t = ½t2 + c
Delen van beide leden door e3t oftewel vermenigvuldiging van beide leden met e-3t geeft dan:
(10) y(t) = (½t2 + c)∙e-3t
Nu rest alleen nog de bepaling van c aan de hand van de gegeven randvoorwaarde y(1) = 0. Substitutie van t = 1 en dus ook y(t) = y(1) = 0 in (10) geeft dan 0 = (½ + c)∙e-3, en dus c = -½. Substitutie hiervan in (10) levert dan als gezochte oplossing van de dv onder de gegeven randvoorwaarde:
(11) y(t) = ½∙(t2 - 1)∙e-3t
Nog even één detail. Moet het niet zijn c = - 1/2 ??
edit: Laat maar had je ook
edit: Laat maar had je ook
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Hey Riparius kan het ook op deze manier?:
(1) y '(t) + 3y(t) = te^-3t
Alles met integratiefactor vermenigvuldigen geeft:
(2) y '(t)*u(t) + 3y(t)*u(t) = te^-3t * u(t)
Daarna moet ik zoals jij aangaf (P(x)= 3):
(3) u '(t) = 3 * u(t)
Dan wordt u(t) --> ln |u(t)| = 3t
(4)u(t) = +/- e^3t+c
Dan vullen we die weer in als:
{u(t) y} ' = u(t)y' + u ' (t) y
(5) e^3t *y = te^-3t * e^3t+c
(6) y = (te^-3t * e^3t+c)/ e^3t
Nu weet ik niet meer goed wat ik moet doen (gewoon die y =1 invullen, maar ik kan (6) eerst vereenvoudigen lijkt me?
Maar heb ik het tot stap (6) goed op deze manier?
edit MIS IK TUSSEN STAP 5 en STAP 6 een INTEGRATIE? ? (als ik zo even in mijn boek kijk)
(1) y '(t) + 3y(t) = te^-3t
Alles met integratiefactor vermenigvuldigen geeft:
(2) y '(t)*u(t) + 3y(t)*u(t) = te^-3t * u(t)
Daarna moet ik zoals jij aangaf (P(x)= 3):
(3) u '(t) = 3 * u(t)
Dan wordt u(t) --> ln |u(t)| = 3t
(4)u(t) = +/- e^3t+c
Dan vullen we die weer in als:
{u(t) y} ' = u(t)y' + u ' (t) y
(5) e^3t *y = te^-3t * e^3t+c
(6) y = (te^-3t * e^3t+c)/ e^3t
Nu weet ik niet meer goed wat ik moet doen (gewoon die y =1 invullen, maar ik kan (6) eerst vereenvoudigen lijkt me?
Maar heb ik het tot stap (6) goed op deze manier?
edit MIS IK TUSSEN STAP 5 en STAP 6 een INTEGRATIE? ? (als ik zo even in mijn boek kijk)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Hallo,
Voor het vak Operations Research I moet er een aantal grafieken gemaakt worden van lineaire vergelijkingen.
Zoals:
Nu moeten daar in Excel of Calc dit soort grafiekjes bij worden gemaakt:
Helaas, omdat ik nog nooit met Excel heb gewerkt weet ik niet hoe dit moet.
Hopelijk kan iemand het me uitleggen
Voor het vak Operations Research I moet er een aantal grafieken gemaakt worden van lineaire vergelijkingen.
Zoals:
Z=18=3x1 + 2x2quote:Maximize: Z=3x1 + 2x2
subject to:
x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≤18
en x1 ≥ 0 en x2 ≥ 0
Nu moeten daar in Excel of Calc dit soort grafiekjes bij worden gemaakt:
Helaas, omdat ik nog nooit met Excel heb gewerkt weet ik niet hoe dit moet.
Hopelijk kan iemand het me uitleggen
cracka frakka ass
In DIG loopt een Exceltopic, misschien word je daar net zo goed of zelfs beter geholpen. Ik raak Excel namelijk zelfs met handschoenen ook nog niet aan.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Okee, bedankt.quote:Op maandag 16 november 2009 14:31 schreef Iblis het volgende:
In DIG loopt een Exceltopic, misschien word je daar net zo goed of zelfs beter geholpen. Ik raak Excel namelijk zelfs met handschoenen ook nog niet aan.
cracka frakka ass
Je bedoelt p(t) = 3 (met kleine letter p). De coëfficiënt van y(t) in de standaardvorm y'(t) + p(t)∙y(t) = q(t) van je lineaire inhomogene dv y'(t) + 3∙y(t) = t∙e-3t is hier immers p(t) = 3.quote:Op maandag 16 november 2009 12:21 schreef Burakius het volgende:
Hey Riparius kan het ook op deze manier?:
(1) y '(t) + 3y(t) = te^-3t
Alles met integratiefactor vermenigvuldigen geeft:
(2) y '(t)*u(t) + 3y(t)*u(t) = te^-3t * u(t)
Daarna moet ik zoals jij aangaf (P(x)= 3):
Er zijn natuurlijk oneindig veel functies µ(t) die aan betrekking (3) voldoen, maar je hebt er maar één nodig. Je probleem ontstaat doordat je - onnodig - wil werken met een algemene vorm van µ(t) maar daar dan vervolgens weer niet consequent mee omgaat.quote:(3) u '(t) = 3 * u(t)
Dan wordt u(t) --> ln |u(t)| = 3t
(4)u(t) = +/- e^3t+c
Je moet wel consequent zijn in je notatie. Als je de haakjesnotatie gebruikt bij µ(t) (traditioneel met de Griekse letter µ, maar je mag van mij ook de Latijnse letter u gebruiken), dan moet je dat bij y(t) in dezelfde vergelijking ook doen. y is immers net zo goed een functie van t.quote:Dan vullen we die weer in als:
{u(t) y} ' = u(t)y' + u ' (t) y
Nee, hier gaat het fout. Je hebt gekozen voor µ(t) = e3t+c. Dat is overigens nog steeds niet de meest algemene vorm, omdat, zoals je bij (4) hebt gevonden, ook µ(t) = -e3t+c bruikbaar is, maar dat is het probleem niet. Wat je hier fout doet is dat je weliswaar het rechterlid van je vergelijking hebt vermenigvuldigd met µ(t) = e3t+c, maar dan moet je het linkerlid ook vermenigvuldigen met µ(t) = e3t+c, en dat heb je (impliciet) niet gedaan, want in (5) ga je er plotseling van uit dat je het linkerlid had vermenigvuldigd met µ(t) = e3t, en dan klopt je vergelijking niet meer. Wat je had moeten opschrijven voor (5) is dus:quote:(5) e^3t *y = te^-3t * e^3t+c
e3t+c∙y(t) = t∙e-3t∙e3t+c
Nu is het zo dat e3t+c gelijk is aan het product van e3t en ec, dus zie je ook meteen waarom het geen nut heeft te werken met een algemene vorm van µ(t): zowel in het linkerlid als in het rechterlid van je vergelijking heb je nu een constante factor ec, en door beide leden van je vergelijking te delen door ec - hetgeen is toegestaan omdat ec niet gelijk aan nul kan zijn en hetgeen ook noodzakelijk is om y(t) te isoleren - valt de constante c weg uit je vergelijking. Deze constante is dus irrelevant voor de oplossing van de dv.
Nee, zoals uitgelegd ging het bij stap (5) al mis omdat je het jezelf onnodig moeilijk had gemaakt. Verder moet je natuurlijk niet y = 1 invullen, want de gegeven randvoorwaarde was immers y(1) = 0. Hier zie je ook hoe nuttig het is om consequent met de haakjesnotatie te werken, dan kunnen dit soort begripsverwarringen niet optreden. Je moest invullen t = 1 en dus ook y(t) = y(1) = 0.quote:(6) y = (te^-3t * e^3t+c)/ e^3t
Nu weet ik niet meer goed wat ik moet doen (gewoon die y =1 invullen, maar ik kan (6) eerst vereenvoudigen lijkt me?
Maar heb ik het tot stap (6) goed op deze manier?
Nee. Maar je hebt wel eerst een onnodige constante c geïntroduceerd, daar niet consequent mee gewerkt, en tenslotte bij je integratie in stap (5) de wel benodigde constante in het rechterlid weer helemaal vergeten toe te voegen. Je hebt nog een hoop werk te doen, denk ik zo.quote:edit MIS IK TUSSEN STAP 5 en STAP 6 een INTEGRATIE? ? (als ik zo even in mijn boek kijk)
[ Bericht 0% gewijzigd door Riparius op 16-11-2009 21:33:08 ]
xgem=4.715
m=4.100
SD= 2.2421
Ik zou ik deze gegevens kunnen logtransformeren?
[ Bericht 45% gewijzigd door Brons_Juweel op 16-11-2009 19:04:18 ]
m=4.100
SD= 2.2421
Ik zou ik deze gegevens kunnen logtransformeren?
[ Bericht 45% gewijzigd door Brons_Juweel op 16-11-2009 19:04:18 ]
Gangstarr
niet zonder meerquote:
xgem=4.715
m=4.100
SD= 2.2421
Ik zou ik deze gegevens kunnen logtransformeren?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Morgen tussententamen micro en liep net bij de oefentoets tegen het volgende aan:
nutsfunctie U(x,Y) = X1/2Y1/2, inkomen M=100, en de prijzen zijn Px=0,5 en Py=1
Lagrange:
L = X1/2Y1/2 - l (0,5X+Y-100)
Mijn antwoordblad geeft vervolgens:
1) dL/dX = 0.5X -0.5Y0.5 - 0.5 l
2) dL/dY = 0.5X -0.5Y0.5 - l
Ik had bij de 2e differentiatie echter dL/dY = 0.5X0.5Y -0.5 - l
Staat er een fout in het antwoordblad of heb ik zelf een fout gemaakt? Thanks.
nutsfunctie U(x,Y) = X1/2Y1/2, inkomen M=100, en de prijzen zijn Px=0,5 en Py=1
Lagrange:
L = X1/2Y1/2 - l (0,5X+Y-100)
Mijn antwoordblad geeft vervolgens:
1) dL/dX = 0.5X -0.5Y0.5 - 0.5 l
2) dL/dY = 0.5X -0.5Y0.5 - l
Ik had bij de 2e differentiatie echter dL/dY = 0.5X0.5Y -0.5 - l
Staat er een fout in het antwoordblad of heb ik zelf een fout gemaakt? Thanks.
Oh really?
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
Dikgedrukte is gelijk aan: 2 sin t cos t?
Blues ain't nothing but a good man feeling bad...
Ja. a + a = 2a. (En uiteraard is vermenigvuldiging op de reële getallen commutatief, dus a·b = b·a).quote:
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
[ Bericht 3% gewijzigd door Iblis op 17-11-2009 10:31:00 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
standaarddeviatiequote:
Hoe deed je dat ook al weer op een rekenmachine (CASIO)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
[ Bericht 7% gewijzigd door motorbloempje op 17-11-2009 11:36:40 ]
Ja doei.
Wat is dat?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
EDIT: Standaarddeviatie, variantie en gemiddelde?
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
[ Bericht 4% gewijzigd door mezzy op 17-11-2009 11:50:10 ]
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
[ Bericht 4% gewijzigd door mezzy op 17-11-2009 11:50:10 ]
Wat voor Casio heb je?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
handig om te vermelden dat je de standaarddeviatie wilde wetenquote:
Hoe deed je dat ook al weer op een rekenmachine (CASIO)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Ja doei.
quote:Op dinsdag 17 november 2009 11:38 schreef motorbloempje het volgende:
[..]
handig om te vermelden dat je de standaarddeviatie wilde weten
idd
te snel gecopy/paste 
Bepaal met behulp van de definitie Laplace getransformeerde unctie F(s) van f(t) = (1+t)2
Is er niet iets snellers en makkelijkers om deze shit op te lossen, wat een geschrijf allemaal zeg of met GR?
Is er niet iets snellers en makkelijkers om deze shit op te lossen, wat een geschrijf allemaal zeg of met GR?
Blues ain't nothing but a good man feeling bad...
Als het m.b.v. de definitie moet heb je al snel zulke grappen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja wat een ramp hè, ik sla die som op de toets wel overquote:Op dinsdag 17 november 2009 17:25 schreef Iblis het volgende:
Als het m.b.v. de definitie moet heb je al snel zulke grappen.
Als hij met die ongein gaat komen. Ik verwacht het eigenlijk niet.
Blues ain't nothing but a good man feeling bad...
Ach, het is wel wat werk, maar het vereist weinig inzicht. Dus op zich is het makkelijk punten scoren.quote:
[..]
Ja wat een ramp hè, ik sla die som op de toets wel over
Als hij met die ongein gaat komen. Ik verwacht het eigenlijk niet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik denk dat je een plusteken bent vergeten. Voor 2∙sin t∙cos t kun je trouwens sin 2t schrijven. Dus krijg je:quote:Op dinsdag 17 november 2009 10:22 schreef GoodGawd het volgende:
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
(cos t + sin t)2 = 1 + sin 2t
Ye, ik moest gewoon even op dat formule blad kijken >_>;quote:Op dinsdag 17 november 2009 17:42 schreef Riparius het volgende:
[..]
Ik denk dat je een plusteken bent vergeten. Voor 2∙sin t∙cos t kun je trouwens sin 2t schrijven. Dus krijg je:
(cos t + sin t)2 = 1 + sin 2t
Blues ain't nothing but a good man feeling bad...
Waarom? Zulke dingen moet je gewoon uit het blote hoofd weten (gangbare goniometrische identiteiten).quote:Op dinsdag 17 november 2009 17:48 schreef GoodGawd het volgende:
[..]
Ye, ik moest gewoon even op dat formule blad kijken >_>;
http://www.math4all.nl/MathAdore/hb-b34-ex2b.html
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
nevermind, 1 / wortel x = x^-0,5 uiteraard...
[ Bericht 33% gewijzigd door petrelli op 17-11-2009 18:21:41 ]
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
nevermind, 1 / wortel x = x^-0,5 uiteraard...
[ Bericht 33% gewijzigd door petrelli op 17-11-2009 18:21:41 ]
Begrijp je wel dat a-p (voor a ongelijk aan 0) hetzelfde is als 1/ap ?quote:Op dinsdag 17 november 2009 18:05 schreef petrelli het volgende:
http://www.math4all.nl/MathAdore/hb-b34-ex2b.html
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
Zit te kutten nu met partiele afgeleide en dan maximum punten:
f(x,y) = -2x² - 2xy - 2y² +36x + 42y - 158
f1 (x,y) = -4x-2y+36 = 0 (eerste order conditie)
f2 (x,y) = -2x-4y+42= 0
En hier krijgen ze het punt (5,8) uit, ik snap niet hoe mijn boek hier ineens aan komt.
Het klopt wel maar ik probeer het zelf na te rekenen maar dat is nogal irritant met een x en een y en ik heb het gevoel dat ik iets niet weet.
f(x,y) = -2x² - 2xy - 2y² +36x + 42y - 158
f1 (x,y) = -4x-2y+36 = 0 (eerste order conditie)
f2 (x,y) = -2x-4y+42= 0
En hier krijgen ze het punt (5,8) uit, ik snap niet hoe mijn boek hier ineens aan komt.
Het klopt wel maar ik probeer het zelf na te rekenen maar dat is nogal irritant met een x en een y en ik heb het gevoel dat ik iets niet weet.
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?quote:Op dinsdag 17 november 2009 19:22 schreef thabit het volgende:
Waarschijnlijk weet je niet hoe je een lineair stelsel vergelijkingen moet oplossen.
Wiskunde is het niet waard zulke dingen te onthouden. Steek me tijd liever in interessantere vakkenquote:Op dinsdag 17 november 2009 17:50 schreef Riparius het volgende:
[..]
Waarom? Zulke dingen moet je gewoon uit het blote hoofd weten (gangbare goniometrische identiteiten).
Blues ain't nothing but a good man feeling bad...
Dan begin ik me toch af te vragen waarom je voor een studie hebt gekozen waarbij kennelijk toch aardig wat wiskunde komt kijken. Je krijgt die wiskunde niet voor niets, die zul je later voor dat vak gewoon nodig hebben.quote:Op dinsdag 17 november 2009 19:38 schreef GoodGawd het volgende:
[..]
Wiskunde is het niet waard zulke dingen te onthouden. Steek me tijd liever in interessantere vakken
Nee, gewoon 2xfunctie1 - functie twee zodat je X krijgt. Dan x in de eerste formule proppen en y uitrekenen. Dan krijg je x=5 en y =8.quote:Op dinsdag 17 november 2009 19:26 schreef petrelli het volgende:
[..]
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?
Cool story, Hansel.
Een stelsel vergelijkingen kan toch ook lineair zijn? En het stelsel dat je moet oplossen is inderdaad lineair. Vermenigvuldig bijvoorbeeld beide leden van de tweede vergelijking met 2 en trek daarna de leden van de tweede vergelijking af van de leden van de eerste vergelijking. Moet je eens kijken wat je dan overhoudt ...quote:Op dinsdag 17 november 2009 19:26 schreef petrelli het volgende:
[..]
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?
Wiskunde kan heel handig zijn ja, met m'n vakken zoals mechanica en meet en regeltechniek, electrotechniek etc. Maar dat Laplace geneuzel en zoveelste orde differentiaal vergelijkingen heb ik nog nul keer hoeven toepassen. Dat maakt het vak wiskunde er nou niet bepaald leuker van. En ik acht de kans klein dat ik het ooit nog zal gebruiken. Zo ja dan ben ik het toch al weer vergetenquote:Op dinsdag 17 november 2009 20:05 schreef Riparius het volgende:
[..]
Dan begin ik me toch af te vragen waarom je voor een studie hebt gekozen waarbij kennelijk toch aardig wat wiskunde komt kijken. Je krijgt die wiskunde niet voor niets, die zul je later voor dat vak gewoon nodig hebben.
Die standaard dingen zijn handig om te weten integreren zus differentieren zo, maar al die theorien, van laplace en de zoveelste professor die weer eens wat heeft uitgevonden, ik vind het allemaal wel gezegend.
Blues ain't nothing but a good man feeling bad...
Argh ik krijg nu Laplace . En ja soms vraag ik me ook af waarom ik het moet doen voor mijn latere carriere
. En ja soms vraag ik me ook af waarom ik het moet doen voor mijn latere carriere
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Vorig jaar had ik na 2 hoor colleges zoiets iets van ja right dit gaat nergens meer overquote:Op dinsdag 17 november 2009 21:53 schreef Burakius het volgende:
Argh ik krijg nu Laplace
Ben er niet meer heen geweest en had ook geen poging @ tentamen gedaan. Maar wat meer tijd aan andere vakken besteed. Maargoed ik moet het toch nog even halen, gelukkig heb ik dit jaar vrij weinig te doen Dat noem ik nog eens efficient verdelen. SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
quote:Op dinsdag 17 november 2009 23:14 schreef GoodGawd het volgende:
[..]
Vorig jaar had ik na 2 hoor colleges zoiets iets van ja right dit gaat nergens meer overJa maar ik heb een HARDE KNIPSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Heb even een vraag die waarschijnlijk voor jullie wel makkelijk zijn maar ik kom er even niet uit.
3
-
7
Die moet ik opschrijven als decimaal getal. Maar hoe krijg ik die noemer tot een rationeel getal? Om zodoende de drie te vermenigvuldigen?
3
-
7
Die moet ik opschrijven als decimaal getal. Maar hoe krijg ik die noemer tot een rationeel getal? Om zodoende de drie te vermenigvuldigen?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
Vladimir Putin
Ik heb een vraagje. Als ik hypothesis test, hoe weet ik dan welke kant het pijltje (> en <) opstaat bij de Rejection Region?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
zwakken overleven moeilijk, sterken zitten in de wolken
Dit is (in decimale vorm) een repeterende breuk. Daar heb je toch hopelijk wel eens van gehoord?quote:Op woensdag 18 november 2009 14:36 schreef phpmystyle het volgende:
Heb even een vraag die waarschijnlijk voor jullie wel makkelijk zijn maar ik kom er even niet uit.
3
-
7
Die moet ik opschrijven als decimaal getal. Maar hoe krijg ik die noemer tot een rationeel getal? Om zodoende de drie te vermenigvuldigen?
Dat kreeg ik ook op het vmbo-basisquote:Op woensdag 18 november 2009 15:28 schreef Skylark. het volgende:
Ik heb een vraagje. Als ik hypothesis test, hoe weet ik dan welke kant het pijltje (> en <) opstaat bij de Rejection Region?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
Vladimir Putin
Leg het me dan eens uit.quote:
[..]
Dat kreeg ik ook op het vmbo-basis
zwakken overleven moeilijk, sterken zitten in de wolken
Of bedoelde hoe je nu kunt weten dat 3/7 = 0.42857.... ?quote:Op woensdag 18 november 2009 15:39 schreef Riparius het volgende:
[..]
Dit is (in decimale vorm) een repeterende breuk. Daar heb je toch hopelijk wel eens van gehoord?
Keer dat keer dat, uitkomsten valideren, breuk van maken, wortel eruit halen, keer pie. Simpel toch.quote:
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
Vladimir Putin
Je bedoelt het groene gebied?quote:Op woensdag 18 november 2009 15:28 schreef Skylark. het volgende:
Ik heb een vraagje. Als ik hypothesis test, hoe weet ik dan welke kant het pijltje (> en <) opstaat bij de Rejection Region?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
Dus rejection gebied x is Z(a/2) < x < -Z(a/2)
Dan is het logisch dat als H1 >0, je rejection gebied x > Z(a/2)
En H1<0, x< -Z(a/2)
Of was dat je vraag niet?
Ja ik snap wel hoe ik de t/F/z-waarde moet berekenen, maar ik twijfel dan altijd welke kant de pijltjes op moeten staan. Vooral bij 1-sided hypotheses.quote:
[..]
Je bedoelt het groene gebied?
[ afbeelding ]
Dus rejection gebied x is Z(a/2) < x < -Z(a/2)
Dan is het logisch dat als H1 >0, je rejection gebied x > Z(a/2)
En H1<0, x< -Z(a/2)
Of was dat je vraag niet?
zwakken overleven moeilijk, sterken zitten in de wolken
Bij het bepalen van H1 ? Daar kan ik me namelijk van herrineren dat mensen er moeite mee hadden.quote:Op woensdag 18 november 2009 16:03 schreef Skylark. het volgende:
[..]
Ja ik snap wel hoe ik de t/F/z-waarde moet berekenen, maar ik twijfel dan altijd welke kant de pijltjes op moeten staan. Vooral bij 1-sided hypotheses.
Oftewel, over welke pijltjes heb je het nou precies?
Nee, bij het bepalen van de Rejection Region. Ik heb dan in de tabel gekeken en dan heb ik bijvoorbeeld waarde 1.949.quote:
[..]
Bij het bepalen van H1 ? Daar kan ik me namelijk van herrineren dat mensen er moeite mee hadden.
Oftewel, over welke pijltjes heb je het nou precies?
Dan weet ik niet of ik H0 reject als het > 1.949 is of < 1.949 of misschien wel >= 1.949
zwakken overleven moeilijk, sterken zitten in de wolken
Ah, nu weet ik waar je het over hebt.quote:Op woensdag 18 november 2009 16:08 schreef Skylark. het volgende:
[..]
Nee, bij het bepalen van de Rejection Region. Ik heb dan in de tabel gekeken en dan heb ik bijvoorbeeld waarde 1.949.
Dan weet ik niet of ik H0 reject als het > 1.949 is of < 1.949 of misschien wel >= 1.949
Wat je moet doen is je de grafiek voorstellen. H0 is het middelpunt.
Dan heb je H1 gegeven*, dus groter of kleiner dan H0.
Dan heb je nog het waarnemingsgetal.
Je wilt dus weten of het wel mogelijk is dat je zo'n waarnemingsgetal krijgt ( hoe groot de kans daarop is).
Die kans zoek je op, en kijkt wat de waarde is.
Bij H1>0 moet die waarde groter zijn dan de alpha waarde.
Bij H1<0 moet die waarde kleiner zijn dan de alpha waarde.
En als 1 van die dingen geldt, dan verwerp je H0.
Oftewel, valt het waarnemingsgetal binnen het groene gebied: Dan heb je een 'onmogelijke' waarneming gezien en verwerp je dus H0.
* stel je hebt H1 niet gegeven, dan kun je die in een som meestal heel handig zelf bepalen: Is het waarnemingsgetal kleiner dan H0, dan is het dus logisch H1<0, en andersom. Dit geldt bij een eenzijdige-toets. Bij two-sided niet, maar daar heb je dan ook geen probleem.
En als het dan zeg maar eentje is waarbij H0: B1+B2+B3=0 en H1: B1,B2,B3 =/ 0?quote:
[..]
Ah, nu weet ik waar je het over hebt.
Wat je moet doen is je de grafiek voorstellen. H0 is het middelpunt.
Dan heb je H1 gegeven*, dus groter of kleiner dan H0.
Dan heb je nog het waarnemingsgetal.
Je wilt dus weten of het wel mogelijk is dat je zo'n waarnemingsgetal krijgt ( hoe groot de kans daarop is).
Die kans zoek je op, en kijkt wat de waarde is.
Bij H1>0 moet die waarde groter zijn dan de alpha waarde.
Bij H1<0 moet die waarde kleiner zijn dan de alpha waarde.
En als 1 van die dingen geldt, dan verwerp je H0.
Oftewel, valt het waarnemingsgetal binnen het groene gebied: Dan heb je een 'onmogelijke' waarneming gezien en verwerp je dus H0.
* stel je hebt H1 niet gegeven, dan kun je die in een som meestal heel handig zelf bepalen: Is het waarnemingsgetal kleiner dan H0, dan is het dus logisch H1<0, en andersom. Dit geldt bij een eenzijdige-toets. Bij two-sided niet, maar daar heb je dan ook geen probleem.
zwakken overleven moeilijk, sterken zitten in de wolken
Ik weet niet precies wat je bedoelt daarmee, maar het zal niks uitmaken qua gebied.quote:Op woensdag 18 november 2009 16:19 schreef Skylark. het volgende:
[..]
En als het dan zeg maar eentje is waarbij H0: B1+B2+B3=0 en H1: B1,B2,B3 =/ 0?
Ik heb zelf ook een vraag:
Hoe kan ik de volgende breuk vereenvoudigen:
Ik kwam zelf uit op 2x-5/ x-2
Maar dat kan niet.
[ Bericht 12% gewijzigd door motorbloempje op 01-09-2013 21:31:42 ]
Is dat niet gewoon 2x² - x + 4? Of zeg ik nou iets doms?
zwakken overleven moeilijk, sterken zitten in de wolken
Dat kan niet, vul maar een willekeurige x in.quote:Op woensdag 18 november 2009 17:31 schreef Skylark. het volgende:
Is dat niet gewoon 2x² - x + 4? Of zeg ik nou iets doms?
Er staat toch geen '= 0' achter of wel?quote:
[..]
Dat kan niet, vul maar een willekeurige x in.
zwakken overleven moeilijk, sterken zitten in de wolken
Als je de noemer en teller ontbindt in factoren, zie je dat ze beiden een gemeenschappelijke factor hebben. Deze kan je er dan dus uitdelen.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Je bepaalt eerst de nulpunten van de polynomen in teller en noemer. Dan zie je dat beiden een wortel x = 3/2 hebben, en aangezien de coëfficiënten van x2 van beide polynomen een tweevoud zijn, betekent dit dat teller en noemer een factor (2x - 3) gemeenschappelijk hebben. De breuk laat zich dus inderdaad vereenvoudigen. Je kunt de teller schrijven als (2x - 3)(2x + 4) en de noemer als (2x - 3)(x + 1).quote:Op woensdag 18 november 2009 17:25 schreef Siddartha het volgende:
[..]
Ik weet niet precies wat je bedoelt daarmee, maar het zal niks uitmaken qua gebied.
Ik heb zelf ook een vraag:
Hoe kan ik de volgende breuk vereenvoudigen:
[ afbeelding ]
Ik kwam zelf uit op 2x-5/ x-2
Maar dat kan niet.
Standaarddeviatie, variantie en gemiddelde?
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Moet determineren of deze reeks convergeert of divergeert:
(3^n+2 )/ 5^n
En als deze convergeert vind het limiet. Ik kom er bij deze niet uit, waar ik bij de andere sommen mooi uit de voeten kan komen met delen door de hoogste macht of andere truucjes. Als ik deze meteen invul zie ik eigenlijk al:
3^oneindig / 5^oneindig = een getal , maar goed ik moet zeker iets doen kom er niet uit.
Verder heb ik wel een andere som die er op lijkt, maar waar ik niet begrijp welke stappen zijn ondernomen:
an = 2^n / 3^(n+1) = 1/3 (2/3) ^n. Die 1/3 halen ze eruit waardoor je krijgt
--> 1/3 lim n-> oneindig (2/3)^n = 1/3 * 0 = 0 convergeert. Maar die eerste stap kan ik maar niet begrijpen. Help me brontosaurussen
(3^n+2 )/ 5^n
En als deze convergeert vind het limiet. Ik kom er bij deze niet uit, waar ik bij de andere sommen mooi uit de voeten kan komen met delen door de hoogste macht of andere truucjes. Als ik deze meteen invul zie ik eigenlijk al:
3^oneindig / 5^oneindig = een getal , maar goed ik moet zeker iets doen kom er niet uit.
Verder heb ik wel een andere som die er op lijkt, maar waar ik niet begrijp welke stappen zijn ondernomen:
an = 2^n / 3^(n+1) = 1/3 (2/3) ^n. Die 1/3 halen ze eruit waardoor je krijgt
--> 1/3 lim n-> oneindig (2/3)^n = 1/3 * 0 = 0 convergeert. Maar die eerste stap kan ik maar niet begrijpen. Help me brontosaurussen
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Tip: (3^n+2 )/ 5^n = 3^n / 5^n + 2/5^n.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zou je het misschien met haakjes willen schrijven??? Zie even niet wat bij wat hoort...
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je notatie is wat onduidelijk, maar ik neem aan dat je (3n + 2)/5n bedoelt? Gebruik superscript voor exponenten. Je kunt dit ook schrijven als:quote:Op woensdag 18 november 2009 19:24 schreef Burakius het volgende:
Moet determineren of deze reeks convergeert of divergeert:
(3^n+2 )/ 5^n
En als deze convergeert vind de limiet. Ik kom er bij deze niet uit, waar ik bij de andere sommen mooi uit de voeten kan komen met delen door de hoogste macht of andere truucjes. Als ik deze meteen invul zie ik eigenlijk al:
3^oneindig / 5^oneindig = een getal , maar goed ik moet zeker iets doen kom er niet uit.
(3/5)n + 2/5n
Nu is het niet moeilijk meer om de limiet voor n → ∞ te bepalen.
Elementaire rekenregels voor machten gebruiken. Die 3n+1 in de noemer is gelijk aan het product van 31 = 3 en 3n.quote:
Verder heb ik wel een andere som die er op lijkt, maar waar ik niet begrijp welke stappen zijn ondernomen:
an = 2^n / 3^(n+1) = 1/3 (2/3) ^n. Die 1/3 halen ze eruit waardoor je krijgt
--> 1/3 lim n-> oneindig (2/3)^n = 1/3 * 0 = 0 convergeert. Maar die eerste stap kan ik maar niet begrijpen. Help me brontosaurussen
Ik bedoel 3n+2/5nquote:Op woensdag 18 november 2009 19:39 schreef Riparius het volgende:
[..]
Je notatie is wat onduidelijk, maar ik neem aan dat je (3n + 2)/5n bedoelt? Gebruik superscript voor exponenten. Je kunt dit ook schrijven als:
(3/5)n + 2/5n
Nu is het niet moeilijk meer om de limiet voor n → ∞ te bepalen.
[..]
Elementaire rekenregels voor machten gebruiken. Die 3n+1 in de noemer is gelijk aan het product van 31 = 3 en 3n.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
OK. In dat geval bedenk je dat 3n+2 in de teller gelijk is aan het product van 3n en 32 = 9. Dus geldt:quote:
3n+2/5n = 9∙(3/5)n
Hoe kun je met behulp van inductie bewijzen dat voor
x> -1, voor elke natuurlijke n geld:
Ik heb een 'uitwerking' hier liggen, maar word er niet echt wijs uit.
Voor P(k+1) aan de linkerkant snap ik het nog wel, maar rechts krijgen ze dit:
Ps: dit is Bernouilli's inequality.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:31:48 ]
x> -1, voor elke natuurlijke n geld:
Ik heb een 'uitwerking' hier liggen, maar word er niet echt wijs uit.
Voor P(k+1) aan de linkerkant snap ik het nog wel, maar rechts krijgen ze dit:
Ps: dit is Bernouilli's inequality.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:31:48 ]
NICE! Je bent een echte brontosaurus! Vaak willen ze ook de squeeze theorem gebruiken( bijvoorbeeld bijquote:Op woensdag 18 november 2009 19:45 schreef Riparius het volgende:
[..]
OK. In dat geval bedenk je dat 3n+2 in de teller gelijk is aan het product van 3n en 32 = 9. Dus geldt:
3n+2/5n = 9∙(3/5)n
an = (cos n)2 / 2n
Hoe kan ik nou makkelijk zien wanneer wat toe te passen?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je bewijs via (volledige) inductie bestaat uit twee stappen. Eerst bewijs je dat de bewering juist is voor n = 1 (dit is triviaal, waarom eigenlijk?), en vervolgens bewijs je dat de bewering juist is voor n=k+1 áls de bewering juist is voor n=k. Je verkrijgt (1+x)k+1 door (1+x)k met (1+x) te vermenigvuldigen, maar als je het linkerlid van je ongelijkheid met (1+x) vermenigvuldigt, dan moet je dat rechts ook doen. En begrijp je ook waarom x groter dan -1 moet zijn?quote:Op woensdag 18 november 2009 19:49 schreef Siddartha het volgende:
Hoe kun je met behulp van inductie bewijzen dat voor
x> -1, voor elke natuurlijke n geldt:
[ afbeelding ]
Ik heb een 'uitwerking' hier liggen, maar word er niet echt wijs uit.
Voor P(k+1) aan de linkerkant snap ik het nog wel, maar rechts krijgen ze dit:
[ afbeelding ]
Ps: dit is Bernouilli's inequality.
Daar zijn geen algemene regels voor te geven, en er bestaan nog veel meer convergentiecriteria voor rijen (en voor reeksen). Maar aangezien (cos n)2 niet convergeert vanwege de periodiciteit van de cosinusfunctie, terwijl je wel kunt zeggen dat geldt 0 ≤ (cos n)2 ≤ 1 ligt het gebruik van de insluitstelling (c.q. een majorante rij die naar 0 convergeert) hier wel voor de hand.quote:Op woensdag 18 november 2009 19:55 schreef Burakius het volgende:
[..]
NICE! Je bent een echte brontosaurus! Vaak willen ze ook de squeeze theorem gebruiken( bijvoorbeeld bij
an = (cos n)2 / 2n
Hoe kan ik nou makkelijk zien wanneer wat toe te passen?
an = (1 + (2/n) 2
Bij deze heb ik twee manieren...
(1) :
Gewoon droog invullen lim n-> oneindig ---> (1+0)^oneindig = 1 = convergent (dit is niet goed zoals ik het doe vermoed ik)
(2):
an = (1 + (2/n) 2 --> omschrijven --> n ln(1+ (2/n)) --> ln(1) * oneindig = 0 (dit is de goede methode?)
En toch vind ik het moeilijk te zien welke methode toe te passen.
Bij deze heb ik twee manieren...
(1) :
Gewoon droog invullen lim n-> oneindig ---> (1+0)^oneindig = 1 = convergent (dit is niet goed zoals ik het doe vermoed ik)
(2):
an = (1 + (2/n) 2 --> omschrijven --> n ln(1+ (2/n)) --> ln(1) * oneindig = 0 (dit is de goede methode?)
En toch vind ik het moeilijk te zien welke methode toe te passen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik snap de redenering niet dat je het ook rechts met (x+1) moet vermenigvuldigen. Het enige dat je doet is in beide vergelijkingen K+1 invullen, niet 'willekeurig' vermenigvuldigen. Anders heb je stap 2 immers niet nodig:quote:Op woensdag 18 november 2009 20:01 schreef Riparius het volgende:
[..]
Je bewijs via (volledige) inductie bestaat uit twee stappen. Eerst bewijs je dat de bewering juist is voor n = 1 (dit is triviaal, waarom eigenlijk?), en vervolgens bewijs je dat de bewering juist is voor n=k+1 áls de bewering juist is voor n=k. Je verkrijgt (1+x)k+1 door (1+x)k met (1+x) te vermenigvuldigen, maar als je het linkerlid van je ongelijkheid met (1+x) vermenigvuldigt, dan moet je dat rechts ook doen. En begrijp je ook waarom x groter dan -1 moet zijn?
als
5> 2
dan is
5x3> 2x3
(beide vermenigvuldigt met hetzelfde)
En dat slaat natuurlijk nergens op.
Nee, zo werkt het bewijs niet. Je gaat ervan uit dat de bewering juist is voor een gegeven n=k, dus ga je ervan uit dat geldt:quote:Op woensdag 18 november 2009 20:11 schreef Siddartha het volgende:
[..]
Ik snap de redenering niet dat je het ook rechts met (x+1) moet vermenigvuldigen. Het enige dat je doet is in beide vergelijkingen K+1 invullen, niet 'willekeurig' vermenigvuldigen. Anders heb je stap 2 immers niet nodig:
als
5> 2
dan is
5x3> 2x3
(beide vermenigvuldigt met hetzelfde)
En dat slaat natuurlijk nergens op.
(1) (1 + x)k ≥ 1 + kx
Nu moeten we, uitgaande van deze bewering dus, aantonen dat de ongelijkheid ook geldig is voor n=k+1. De ongelijkheid blijft geldig als we beide leden met eenzelfde positieve (!) factor vermenigvuldigen. We vermenigvuldigen nu beide leden met (1 + x) en krijgen dan:
(2) (1 + x)k+1 ≥ (1 + kx)(1 + x)
Werk nu het rechterlid van deze ongelijkheid eens uit en bedenk hoe je dan verder kunt gaan.
Maar waar blijft dan de k+1 ?quote:Op woensdag 18 november 2009 20:21 schreef Riparius het volgende:
[..]
Nee, zo werkt het bewijs niet. Je gaat ervan uit dat de bewering juist is voor een gegeven n=k, dus ga je ervan uit dat geldt:
(1) (1 + x)k ≥ 1 + kx
Nu moeten we, uitgaande van deze bewering dus, aantonen dat de ongelijkheid ook geldig is voor n=k+1. De ongelijkheid blijft geldig als we beide leden met eenzelfde positieve (!) factor vermenigvuldigen. We vermenigvuldigen nu beide leden met (1 + x) en krijgen dan:
(2) (1 + x)k+1 ≥ (1 + kx)(1 + x)
Werk nu het rechterlid van deze ongelijkheid eens uit en bedenk hoe je dan verder kunt gaan.
Ja in het linkerlid, maar die moet je ook in het rechterlid invoeren.
Ze komen aan die (x+1) omdat:
(1+x)^(K+1) gelijk is aan (1+x)^k x (1+x)
Niet omdat ze willekeurig daarmee vermenigvuldigen....
Ik weet dat
(1 + x)k+1 ≥ (1 + kx)(1 + x)
Er uiteindelijk moet komen te staan, en waarom dat het bewijs is. Dat is het punt niet. Alleen hoe ze tot daar komen.
Nee, je mist het punt. Mijn ongelijkheid (2) is niet het eindpunt van het bewijs maar een tussenstap.quote:Op woensdag 18 november 2009 20:24 schreef Siddartha het volgende:
[..]
Maar waar blijft dan de k+1 ?
Ja in het linkerlid, maar die moet je ook in het rechterlid invoeren.
Ze komen aan die (x+1) omdat:
(1+x)^(K+1) gelijk is aan (1+x)^k x (1+x)
Niet omdat ze willekeurig daarmee vermenigvuldigen....
Ik weet dat
(1 + x)k+1 ≥ (1 + kx)(1 + x)
Er uiteindelijk moet komen te staan, en waarom dat het bewijs is. Dat is het punt niet. Alleen hoe ze tot daar komen.
Je gaat ervan uit dat de bewering juist is voor een gegeven n = k, dus
(1) (1 + x)k ≥ 1 + kx
Vermenigvuldiging van beide leden van deze ongelijkheid met (1 + x) levert, mits x > -1, dan op dat ook moet gelden:
(2) (1 + x)k+1 ≥ (1 + kx)(1 +x)
Hiervoor is ook te schrijven:
(3) (1 + x)k+1 ≥ 1 + (k+1)x + kx2
Maar nu is k een natuurlijk getal, en x2 is zeker niet negatief, dus geldt ook:
(4) kx2 ≥ 0
En dus kunnen we zeggen dat voor het rechterlid van (3) geldt:
(5) 1 + (k+1)x + kx2 ≥ 1 + (k+1)x
Maar uit de ongelijkheden (3) en (5) volgt nu:
(6) (1 + x)k+1 ≥ 1 + (k+1)x
En dit laatste betekent niets anders dan dat de uitspraak geldt voor n = k +1. Aangezien (6) een consequentie is van (1), hebben we zo dus bewezen dat de ongelijkheid geldt voor n = k + 1 áls deze geldt voor n = k. Samen met de juistheid van de uitspraak voor n = 1 is het bewijs met volledige inductie daarmee compleet.
quote:Op woensdag 18 november 2009 21:00 schreef Riparius het volgende:
[..]
Nee, je mist het punt. Mijn ongelijkheid (2) is niet het eindpunt van het bewijs maar een tussenstap.
Je gaat ervan uit dat de bewering juist is voor een gegeven n = k, dus
(1) (1 + x)k ≥ 1 + kx
Vermenigvuldiging van beide leden van deze ongelijkheid met (1 + x) levert, mits x > -1, dan op dat ook moet gelden:
(2) (1 + x)k+1 ≥ (1 + kx)(1 +x)
Hiervoor is ook te schrijven:
(3) (1 + x)k+1 ≥ 1 + (k+1)x + kx2
Maar nu is k een natuurlijk getal, en x2 is zeker niet negatief, dus geldt ook:
(4) kx2 ≥ 0
En dus kunnen we zeggen dat voor het rechterlid van (3) geldt:
(5) 1 + (k+1)x + kx2 ≥ 1 + (k+1)x
Maar uit de ongelijkheden (3) en (5) volgt nu:
(6) (1 + x)k+1 ≥ 1 + (k+1)x
En dit laatste betekent niets anders dan dat de uitspraak geldt voor n = k +1. Aangezien (6) een consequentie is van (1), hebben we zo dus bewezen dat de ongelijkheid geldt voor n = k + 1 áls deze geldt voor n = k. Samen met de juistheid van de uitspraak voor n = 1 is het bewijs met volledige inductie daarmee compleet.
Voor de moeite Mijn probleem ligt denk ik bij de manier van bewijzen: Inductie.
Als k waar is, dan moet ook k+1 waar zijn. Dat snap ik.
Maar ik verwacht dan dat ze voor n/de variable dan bij P(k+1) die
k+1 voor de formule invoeren ( en niet zoals in dit bewijs gewoon vermenigvuldingen?)
Misschien moet ik dus eerst vragen hoe inductie nou precies werkt?
Hoe je het kan bewijzen.
Ik wilde som 5 maken, maar maakte per ongeluk som 6, waar geen antwoord van in het boek staat. Wil toch graag even checken of ik 't goed doe.
x= sin t
y = sin t- t cos t
Waar is de raaklijn horizontaal en waar verticaal
Horizontaal op t = 0, dus (0,0)
Verticaal op t = 1/2 pi dus (1,1)
Klotp dit?
x= sin t
y = sin t- t cos t
Waar is de raaklijn horizontaal en waar verticaal
Horizontaal op t = 0, dus (0,0)
Verticaal op t = 1/2 pi dus (1,1)
Klotp dit?
x'(t) = cost
y'(t) = tsin(t)
je kijkt op [0, pi/2] ? Dan gaat het goed.
y'(t) = tsin(t)
je kijkt op [0, pi/2] ? Dan gaat het goed.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Er staat geen interval bij, maar als het interval groter zou zijn zouden de coördinaten niet veranderen geloof ik?
x'(t)=0 ook voor bv. t=3pi/2 (en y'(t) ongelijk aan 0 dan). Je hebt dan (x,y) = (-1, -1).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Met een beetje invullen bewijs je niets. Je kunt niet zomaar ervan uitgaan dat een uitspraak waar is voor n=k, dan overal k vervangen door k+1 en vervolgens roepen, hé moet je kijken, hij doet het ook met k+1, want dan ben je nog steeds niet verder dan je oorspronkelijke aanname, maar nu met k+1 in plaats van k, meer niet. Je moet echt laten zien dat de juistheid van de uitspraak voor n=k+1 volgt uit de juistheid van de uitspraak voor n=k.quote:Op woensdag 18 november 2009 21:08 schreef Siddartha het volgende:
[..]
Mijn probleem ligt denk ik bij de manier van bewijzen: Inductie.
Als k waar is, dan moet ook k+1 waar zijn. Dat snap ik.
Maar ik verwacht dan dat ze voor n/de variable dan bij P(k+1) die
k+1 voor de formule invoeren ( en niet zoals in dit bewijs gewoon vermenigvuldingen?)
Misschien moet ik dus eerst vragen hoe inductie nou precies werkt?
Hoe je het kan bewijzen.
Het is pie niet pi.quote:Op woensdag 18 november 2009 15:56 schreef phpmystyle het volgende:
[..]
Keer dat keer dat, uitkomsten valideren, breuk van maken, wortel eruit halen, keer pie. Simpel toch.
Tevens, hou eens op met Skylark bashen. Je komt hier om een vraag te stellen, die wordt beantwoord door 2 mensen en vervolgens reageer jij niet meer op ze, lekker fatsoenlijk.
quote:Op woensdag 18 november 2009 15:39 schreef Riparius het volgende:
[..]
Dit is (in decimale vorm) een repeterende breuk. Daar heb je toch hopelijk wel eens van gehoord?
quote:Op woensdag 18 november 2009 15:49 schreef Siddartha het volgende:
[..]
Of bedoelde hoe je nu kunt weten dat 3/7 = 0.42857.... ?
Op woensdag 23 juni 2010 22:44 schreef Chuck_Norris het volgende:
Haha Jap jonge trollgod
Op woensdag 23 juni 2010 22:48 schreef Skylark. het volgende:
Chuck is mastertrolled _O_.
Haha Jap jonge trollgod
Op woensdag 23 juni 2010 22:48 schreef Skylark. het volgende:
Chuck is mastertrolled _O_.
Even kijken of ik het nu wel begrijp:quote:Op woensdag 18 november 2009 22:19 schreef Riparius het volgende:
[..]
Met een beetje invullen bewijs je niets. Je kunt niet zomaar ervan uitgaan dat een uitspraak waar is voor n=k, dan overal k vervangen door k+1 en vervolgens roepen, hé moet je kijken, hij doet het ook met k+1, want dan ben je nog steeds niet verder dan je oorspronkelijke aanname, maar nu met k+1 in plaats van k, meer niet. Je moet echt laten zien dat de juistheid van de uitspraak voor n=k+1 volgt uit de juistheid van de uitspraak voor n=k.
Stel ik moet bewijzen dat
Dus stap 1: Bewijs dat P(1) waar is. Klopt
Stap 2: Aanname dat P(k) klopt,
dus nu uitzoeken of het dan ook voor (elke) volgende stap geld, dus P(k+1).
Dan krijg ik:
Wat ik weer kan opschrijven als:
Waarna ik alleen nog hoef te bewijzen dat 2 kleiner gelijk is aan (k+2), wat logisch is.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:32:24 ]
en dat is wat je nu wel doet.quote:Je kunt niet zomaar ervan uitgaan dat een uitspraak waar is voor n=k, dan overal k vervangen door k+1
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus ik had beide kanten gewoon met 2 moeten vermenigvuldigen, rechterkant uitwerken?quote:Op donderdag 19 november 2009 11:37 schreef GlowMouse het volgende:
[..]
en dat is wat je nu wel doet.
Sorry, maar ik snap het principe denk ik gewoon niet?
Je wilt laten zien dat 
Je weet
en hier kun je je inductieaanname gebruiken, namelijk dat
het truukje is om met één kant te beginnen, en dan net zolang om te schrijven tot je op de rechterkant uitkomt, daarbij ergens de inductieaanname gebruikend.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:32:29 ]
Je weet
en hier kun je je inductieaanname gebruiken, namelijk dat
het truukje is om met één kant te beginnen, en dan net zolang om te schrijven tot je op de rechterkant uitkomt, daarbij ergens de inductieaanname gebruikend.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:32:29 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Maar dat doe ik toch?quote:Op donderdag 19 november 2009 11:46 schreef GlowMouse het volgende:
Je wilt laten zien dat [ afbeelding ]
Je weet
[ afbeelding ]
en hier kun je je inductieaanname gebruiken, namelijk dat
[ afbeelding ]
het truukje is om met één kant te beginnen, en dan net zolang om te schrijven tot je op de rechterkant uitkomt, daarbij ergens de inductieaanname gebruikend.
2^k x 2 = (k+2)!
Rechterkant wordt dan: (k+2)((k+1)!
En dan hoef ik alleen te bewijzen dat 2 kleiner gelijk (k+2)
Ik word helemaal gek .. hoe kan ik deze vergelijking oplossen, weet iemand dat??
x0.5 - 0.75(x + 720)0.5 = 9
heb de wortels voor het gemak even vervangen door een 0.5de macht. Ik heb echt al van alles geprobeerd, maar ik weet niet hoe ik dit moet aanpakken
.. hoe kan ik deze vergelijking oplossen, weet iemand dat??x0.5 - 0.75(x + 720)0.5 = 9
heb de wortels voor het gemak even vervangen door een 0.5de macht. Ik heb echt al van alles geprobeerd, maar ik weet niet hoe ik dit moet aanpakken
ik ben het mannetje in de chinese kamer
Vraag:
De 4e regel zie je dat -y'' (0)
Waarom is dat?
Blues ain't nothing but a good man feeling bad...
Beide kanten kwadrateren en dan is het een eitjequote:Op donderdag 19 november 2009 15:34 schreef sefer het volgende:
Ik word helemaal gek
x0.5 - 0.75(x + 720)0.5 = 9
heb de wortels voor het gemak even vervangen door een 0.5de macht. Ik heb echt al van alles geprobeerd, maar ik weet niet hoe ik dit moet aanpakken
Blues ain't nothing but a good man feeling bad...
dan is het geen eitje hoor, volgens mij..quote:Op donderdag 19 november 2009 16:38 schreef GoodGawd het volgende:
[..]
Beide kanten kwadrateren en dan is het een eitje
ik ben het mannetje in de chinese kamer
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |