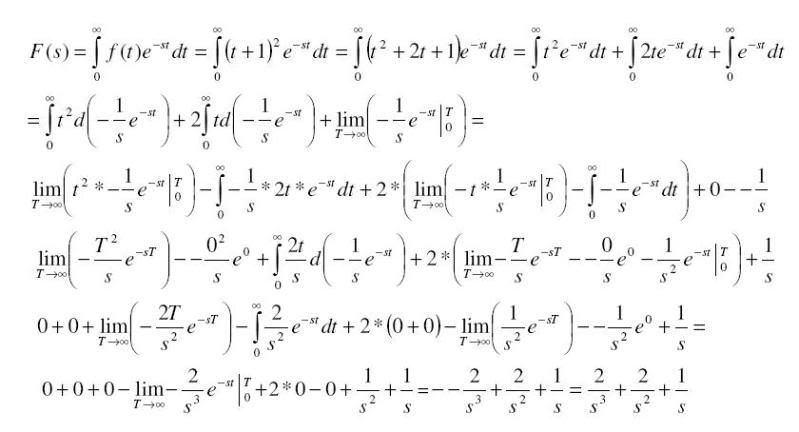SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Wat voor Casio heb je?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
handig om te vermelden dat je de standaarddeviatie wilde wetenquote:Op dinsdag 17 november 2009 11:37 schreef mezzy het volgende:
Hoe deed je dat ook al weer op een rekenmachine (CASIO)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Ja doei.
quote:Op dinsdag 17 november 2009 11:38 schreef motorbloempje het volgende:
[..]
handig om te vermelden dat je de standaarddeviatie wilde weten
idd
te snel gecopy/paste 
Bepaal met behulp van de definitie Laplace getransformeerde unctie F(s) van f(t) = (1+t)2
Is er niet iets snellers en makkelijkers om deze shit op te lossen, wat een geschrijf allemaal zeg of met GR?
Is er niet iets snellers en makkelijkers om deze shit op te lossen, wat een geschrijf allemaal zeg of met GR?
Blues ain't nothing but a good man feeling bad...
Als het m.b.v. de definitie moet heb je al snel zulke grappen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja wat een ramp hè, ik sla die som op de toets wel overquote:Op dinsdag 17 november 2009 17:25 schreef Iblis het volgende:
Als het m.b.v. de definitie moet heb je al snel zulke grappen.
Als hij met die ongein gaat komen. Ik verwacht het eigenlijk niet.
Blues ain't nothing but a good man feeling bad...
Ach, het is wel wat werk, maar het vereist weinig inzicht. Dus op zich is het makkelijk punten scoren.quote:
[..]
Ja wat een ramp hè, ik sla die som op de toets wel over
Als hij met die ongein gaat komen. Ik verwacht het eigenlijk niet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik denk dat je een plusteken bent vergeten. Voor 2∙sin t∙cos t kun je trouwens sin 2t schrijven. Dus krijg je:quote:Op dinsdag 17 november 2009 10:22 schreef GoodGawd het volgende:
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
(cos t + sin t)2 = 1 + sin 2t
Ye, ik moest gewoon even op dat formule blad kijken >_>;quote:Op dinsdag 17 november 2009 17:42 schreef Riparius het volgende:
[..]
Ik denk dat je een plusteken bent vergeten. Voor 2∙sin t∙cos t kun je trouwens sin 2t schrijven. Dus krijg je:
(cos t + sin t)2 = 1 + sin 2t
Blues ain't nothing but a good man feeling bad...
Waarom? Zulke dingen moet je gewoon uit het blote hoofd weten (gangbare goniometrische identiteiten).quote:Op dinsdag 17 november 2009 17:48 schreef GoodGawd het volgende:
[..]
Ye, ik moest gewoon even op dat formule blad kijken >_>;
http://www.math4all.nl/MathAdore/hb-b34-ex2b.html
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
nevermind, 1 / wortel x = x^-0,5 uiteraard...
[ Bericht 33% gewijzigd door petrelli op 17-11-2009 18:21:41 ]
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
nevermind, 1 / wortel x = x^-0,5 uiteraard...
[ Bericht 33% gewijzigd door petrelli op 17-11-2009 18:21:41 ]
Begrijp je wel dat a-p (voor a ongelijk aan 0) hetzelfde is als 1/ap ?quote:Op dinsdag 17 november 2009 18:05 schreef petrelli het volgende:
http://www.math4all.nl/MathAdore/hb-b34-ex2b.html
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
Zit te kutten nu met partiele afgeleide en dan maximum punten:
f(x,y) = -2x² - 2xy - 2y² +36x + 42y - 158
f1 (x,y) = -4x-2y+36 = 0 (eerste order conditie)
f2 (x,y) = -2x-4y+42= 0
En hier krijgen ze het punt (5,8) uit, ik snap niet hoe mijn boek hier ineens aan komt.
Het klopt wel maar ik probeer het zelf na te rekenen maar dat is nogal irritant met een x en een y en ik heb het gevoel dat ik iets niet weet.
f(x,y) = -2x² - 2xy - 2y² +36x + 42y - 158
f1 (x,y) = -4x-2y+36 = 0 (eerste order conditie)
f2 (x,y) = -2x-4y+42= 0
En hier krijgen ze het punt (5,8) uit, ik snap niet hoe mijn boek hier ineens aan komt.
Het klopt wel maar ik probeer het zelf na te rekenen maar dat is nogal irritant met een x en een y en ik heb het gevoel dat ik iets niet weet.
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?quote:Op dinsdag 17 november 2009 19:22 schreef thabit het volgende:
Waarschijnlijk weet je niet hoe je een lineair stelsel vergelijkingen moet oplossen.
Wiskunde is het niet waard zulke dingen te onthouden. Steek me tijd liever in interessantere vakkenquote:Op dinsdag 17 november 2009 17:50 schreef Riparius het volgende:
[..]
Waarom? Zulke dingen moet je gewoon uit het blote hoofd weten (gangbare goniometrische identiteiten).
Blues ain't nothing but a good man feeling bad...
Dan begin ik me toch af te vragen waarom je voor een studie hebt gekozen waarbij kennelijk toch aardig wat wiskunde komt kijken. Je krijgt die wiskunde niet voor niets, die zul je later voor dat vak gewoon nodig hebben.quote:Op dinsdag 17 november 2009 19:38 schreef GoodGawd het volgende:
[..]
Wiskunde is het niet waard zulke dingen te onthouden. Steek me tijd liever in interessantere vakken
Nee, gewoon 2xfunctie1 - functie twee zodat je X krijgt. Dan x in de eerste formule proppen en y uitrekenen. Dan krijg je x=5 en y =8.quote:Op dinsdag 17 november 2009 19:26 schreef petrelli het volgende:
[..]
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?
Cool story, Hansel.
Een stelsel vergelijkingen kan toch ook lineair zijn? En het stelsel dat je moet oplossen is inderdaad lineair. Vermenigvuldig bijvoorbeeld beide leden van de tweede vergelijking met 2 en trek daarna de leden van de tweede vergelijking af van de leden van de eerste vergelijking. Moet je eens kijken wat je dan overhoudt ...quote:Op dinsdag 17 november 2009 19:26 schreef petrelli het volgende:
[..]
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?
Wiskunde kan heel handig zijn ja, met m'n vakken zoals mechanica en meet en regeltechniek, electrotechniek etc. Maar dat Laplace geneuzel en zoveelste orde differentiaal vergelijkingen heb ik nog nul keer hoeven toepassen. Dat maakt het vak wiskunde er nou niet bepaald leuker van. En ik acht de kans klein dat ik het ooit nog zal gebruiken. Zo ja dan ben ik het toch al weer vergetenquote:Op dinsdag 17 november 2009 20:05 schreef Riparius het volgende:
[..]
Dan begin ik me toch af te vragen waarom je voor een studie hebt gekozen waarbij kennelijk toch aardig wat wiskunde komt kijken. Je krijgt die wiskunde niet voor niets, die zul je later voor dat vak gewoon nodig hebben.
Die standaard dingen zijn handig om te weten integreren zus differentieren zo, maar al die theorien, van laplace en de zoveelste professor die weer eens wat heeft uitgevonden, ik vind het allemaal wel gezegend.
Blues ain't nothing but a good man feeling bad...
Argh ik krijg nu Laplace . En ja soms vraag ik me ook af waarom ik het moet doen voor mijn latere carriere
. En ja soms vraag ik me ook af waarom ik het moet doen voor mijn latere carriere
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Vorig jaar had ik na 2 hoor colleges zoiets iets van ja right dit gaat nergens meer overquote:Op dinsdag 17 november 2009 21:53 schreef Burakius het volgende:
Argh ik krijg nu Laplace
Ben er niet meer heen geweest en had ook geen poging @ tentamen gedaan. Maar wat meer tijd aan andere vakken besteed. Maargoed ik moet het toch nog even halen, gelukkig heb ik dit jaar vrij weinig te doen Dat noem ik nog eens efficient verdelen. SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
quote:Op dinsdag 17 november 2009 23:14 schreef GoodGawd het volgende:
[..]
Vorig jaar had ik na 2 hoor colleges zoiets iets van ja right dit gaat nergens meer overJa maar ik heb een HARDE KNIPSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |