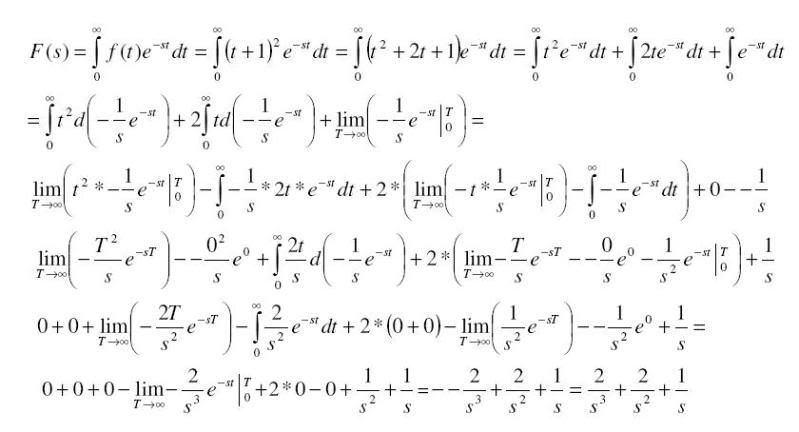SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Is het mijn fout dat ik die y meeneem?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
waar komt die tweede regel vandaan?quote:Op zondag 15 november 2009 20:59 schreef Burakius het volgende:
--> y ' * u(t) + 3y * u(t) = te^-3t * u(t)
--> u '(t) = 3y * u(t) --> u '(t)/u(t) = 3y
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vermenigvuldigd met een integratie factor...en daarna u'(t) vinden Die moet gelijk zijn met P(x)y ( van: dy/dx + P(x)y = Q(x) )quote:Op zondag 15 november 2009 21:09 schreef GlowMouse het volgende:
[..]
waar komt die tweede regel vandaan?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
De DV die je moet oplossen is y ' + 3y = te-3t met als randvoorwaarde y(1) = 0. Dit is een lineaire inhomogene DV van de eerste orde. De algemene aanpak is dat je eerst de corresponderende homogene DV y' + 3y = 0 oplost en dan een particuliere oplossing vindt van de inhomogene DV. Voor dat laatste kun je gebruik maken van de methode van de onbepaalde constanten die ik hier al eens kort heb uiteengezet. De algemene oplossing van je inhomogene DV wordt dan gegeven door de som van de algemene oplossing van de homogene DV en de reeds gevonden particuliere oplossing. Tenslotte kun je dan bepalen welke oplossing(en) voldoet c.q. voldoen aan de gegeven randvoorwaarde(n).quote:Op zondag 15 november 2009 20:59 schreef Burakius het volgende:
Oke ik doe duidelijk iets verkeerds?
Find the solution of the given initial value problem:
y ' + 3y = t e^ -3t met y(1) = 0
[snip]
Ik zie nu dat ik die y elke keer heb meegenomen. Als ik die niet meeneem, kom ik voor de rest van de rit helemaal uit. Nu nog even uitvogelen wat er nou precies bedoelt wordt met y(1) = 0 en wat ik er mee moet, maar dat zal ik even moeten lezen in je link. Thx!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik.quote:Op zondag 15 november 2009 17:24 schreef cojonesm het volgende:
Functievoorschrift van een parabool opstellen. Gegeven is:
Symmetrie-as x=3
Punten op de grafiek
P(5,17) en Q(2,8)
Wie helpt me?
Wat wil je daarmee zeggen? Dat het wiskunde-onderwijs in België op een hoger plan staat en dat je er daarom (extra) moeite mee hebt?quote:PS: Ik woon in Nederland en zit in België op school.
De grafiek is een parabool met als (verticale) symmetrie-as de lijn met als vergelijking x = 3. Nu weet je dat een parabool met een verticale symmetrie-as in zijn algemeenheid de grafiek voorstelt van een kwadratische functie. We zoeken dus een vergelijking (c.q. functie) van de gedaante:
(1) y = ax2 + bx + c,
waarbij we a ongelijk aan nul mogen veronderstellen, anders is het immers geen kwadratische functie meer.
De kunst is nu natuurlijk om de waarden van a, b en c te bepalen. Daarvoor gaan we gebruik maken van de gegevens die we hebben. Het eerste gegeven is dat de symmetrie-as van de parabool de lijn met vergelijking x = 3 is. Maar nu weet je - hopelijk - dat de symmetrie-as van een parabool met vergelijking (1) wordt gegeven door:
(2) x = -b/2a
Zodoende weten we dus al dat moet gelden:
(3) -b/2a = 3
Vermenigvuldigen we in (3) beide leden met -2a, dan kunnen we voor (3) dus ook schrijven:
(4) b = -6a
Verder weten we dat de punten P(5;17) en Q(2;8) op de grafiek liggen, zodat de coördinaten van deze punten ook moeten voldoen aan (1). Invullen in (1) van x = 5 en y = 17 (voor punt P) geeft:
(5) 17 = 25a + 5b + c
En invullen in (1) van x = 2 en y = 8 (voor punt Q) geeft:
(6) 8 = 4a + 2b + c
Nu vormen (4), (5) en (6) samen een stelsel van drie vergelijkingen in de drie onbekenden a, b en c, en daarmee hebben we voldoende informatie om de waarden van a,b en c te bepalen.
Het eenvoudigst is hier om de leden van vergelijking (6) af te trekken van de leden van vergelijking (5), zodat we c kwijtraken. We krijgen dan:
(7) 9 = 21a + 3b
En aangezien we uit (4) weten dat b = -6a, kunnen we dit substitueren in (7), zodat we krijgen
9 = 21a - 18a
9 = 3a
a = 3
Op grond van (4) weten we dan ook meteen dat b = -18, en invullen van a=3 en b=-18 in (5) of (6) levert dan c = 32. Daarmee is de gevraagde vergelijking gevonden:
(8) y = 3x2 -18x + 32
Toch nog maar even reageren, omdat ik nu pas zie dat je voor het oplossen van een lineaire inhomogene dv van de eerste orde gebruik probeert te maken van de methode van de integrerende factor. De methode van de onbepaalde coëfficienten die ik je in de hierboven genoemde link aan de hand heb gedaan is hier uiteraard ook te gebruiken, aangezien het gaat om een lineaire dv met constante coëfficiënten, maar is voor een eerste orde dv wat omslachtiger.quote:Op zondag 15 november 2009 21:25 schreef Burakius het volgende:
Ik zie nu dat ik die y elke keer heb meegenomen. Als ik die niet meeneem, kom ik voor de rest van de rit helemaal uit. Nu nog even uitvogelen wat er nou precies bedoelt wordt met y(1) = 0 en wat ik er mee moet, maar dat zal ik even moeten lezen in je link. Thx!
De algemene gedaante van een lineaire dv van de eerste orde in standaardvorm is:
(1) y'(t) + p(t)∙y(t) = q(t)
De gedachte achter de methode van de integrerende factor is dat we het linkerlid van (1) gaan proberen om te vormen tot de afgeleide van een product van y(t) en een nader te bepalen functie µ(t). Het linkerlid van (1) bestaat immers uit twee termen, waarvan één met een factor y'(t) en één met een factor y(t), en dat herinnert aan de productregel. Immers, de afgeleide van een product y(t)∙µ(t) is gelijk aan:
(2) y'(t)∙µ(t) + y(t)∙µ'(t)
Vermenigvuldigen we nu beide leden van (1) met µ(t), dan kunnen we voor (1) schrijven:
(3) y'(t)∙µ(t) + y(t)∙p(t)∙µ(t) = q(t)∙µ(t)
Vergelijken we nu het linkerlid van (3) met de gewenste vorm (2), dan zien we dat de eerste van de twee termen van het linkerlid (3) al overeenstemt met (2) maar de tweede term niet. Toch kunnen we ervoor zorgen dat de tweede term van het linkerlid van (3) ook overeenstemt met het tweede lid van (2) als we µ(t) zodanig zouden kunnen kiezen dat geldt:
(4) y(t)∙µ'(t) = y(t)∙p(t)∙µ(t),
en dus:
(5) µ'(t) = p(t)∙µ(t)
Het is nu niet zo moeilijk om te zien hoe we µ(t) zodanig kunnen kiezen dat deze functie voldoet aan (5). We zoeken een functie µ(t) waarvan de afgeleide µ'(t) gelijk is aan de oorspronkelijke functie µ(t) vermenigvuldigd met p(t). Denken we aan de exponentiële functie, die zichzelf als afgeleide heeft, en aan de kettingregel, dan is eenvoudig in te zien dat de gezochte functie µ(t) wordt gegeven door:
(6) µ(t) = eP(t),
waarbij P(t) een primitieve is van p(t). Immers, volgens de kettingregel is de afgeleide van µ(t) = eP(t) dan gelijk aan µ'(t) = P'(t)∙eP(t) = p(t)∙eP(t) = p(t)∙µ(t), zoals gewenst.
De oplossingsmethode met de integrerende factor voor een dv van de gedaante (1) bestaat er dus in dat we eerst een primitieve P(t) van p(t) bepalen en dan beide leden vermenigvuldigen met eP(t), waarna we het linkerlid van de dv kunnen opvatten als de afgeleide van het product y(t)∙eP(t). Vervolgens kunnen we dan beide leden van de DV integreren en daarna door deling van beide leden door eP(t) de gezochte functies y(t) vinden die aan de dv (1) voldoen.
De DV die je moest oplossen is:
(7) y'(t) + 3∙y(t) = t∙e-3t
Hier is p(t) = 3, en een primitieve daarvan is P(t) =3t. We kiezen er dus voor beide leden van (7) te vermenigvuldigen met µ(t) = eP(t) = e3t en krijgen dan:
(8) y'(t)∙e3t + y(t)∙3∙e3t = t
Het linkerlid is nu de afgeleide van y(t)∙e3t, zodat integreren van beide leden geeft:
(9) y(t)∙e3t = ½t2 + c
Delen van beide leden door e3t oftewel vermenigvuldiging van beide leden met e-3t geeft dan:
(10) y(t) = (½t2 + c)∙e-3t
Nu rest alleen nog de bepaling van c aan de hand van de gegeven randvoorwaarde y(1) = 0. Substitutie van t = 1 en dus ook y(t) = y(1) = 0 in (10) geeft dan 0 = (½ + c)∙e-3, en dus c = -½. Substitutie hiervan in (10) levert dan als gezochte oplossing van de dv onder de gegeven randvoorwaarde:
(11) y(t) = ½∙(t2 - 1)∙e-3t
Nog even één detail. Moet het niet zijn c = - 1/2 ??
edit: Laat maar had je ook
edit: Laat maar had je ook
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Hey Riparius kan het ook op deze manier?:
(1) y '(t) + 3y(t) = te^-3t
Alles met integratiefactor vermenigvuldigen geeft:
(2) y '(t)*u(t) + 3y(t)*u(t) = te^-3t * u(t)
Daarna moet ik zoals jij aangaf (P(x)= 3):
(3) u '(t) = 3 * u(t)
Dan wordt u(t) --> ln |u(t)| = 3t
(4)u(t) = +/- e^3t+c
Dan vullen we die weer in als:
{u(t) y} ' = u(t)y' + u ' (t) y
(5) e^3t *y = te^-3t * e^3t+c
(6) y = (te^-3t * e^3t+c)/ e^3t
Nu weet ik niet meer goed wat ik moet doen (gewoon die y =1 invullen, maar ik kan (6) eerst vereenvoudigen lijkt me?
Maar heb ik het tot stap (6) goed op deze manier?
edit MIS IK TUSSEN STAP 5 en STAP 6 een INTEGRATIE? ? (als ik zo even in mijn boek kijk)
(1) y '(t) + 3y(t) = te^-3t
Alles met integratiefactor vermenigvuldigen geeft:
(2) y '(t)*u(t) + 3y(t)*u(t) = te^-3t * u(t)
Daarna moet ik zoals jij aangaf (P(x)= 3):
(3) u '(t) = 3 * u(t)
Dan wordt u(t) --> ln |u(t)| = 3t
(4)u(t) = +/- e^3t+c
Dan vullen we die weer in als:
{u(t) y} ' = u(t)y' + u ' (t) y
(5) e^3t *y = te^-3t * e^3t+c
(6) y = (te^-3t * e^3t+c)/ e^3t
Nu weet ik niet meer goed wat ik moet doen (gewoon die y =1 invullen, maar ik kan (6) eerst vereenvoudigen lijkt me?
Maar heb ik het tot stap (6) goed op deze manier?
edit MIS IK TUSSEN STAP 5 en STAP 6 een INTEGRATIE? ? (als ik zo even in mijn boek kijk)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Hallo,
Voor het vak Operations Research I moet er een aantal grafieken gemaakt worden van lineaire vergelijkingen.
Zoals:
Nu moeten daar in Excel of Calc dit soort grafiekjes bij worden gemaakt:
Helaas, omdat ik nog nooit met Excel heb gewerkt weet ik niet hoe dit moet.
Hopelijk kan iemand het me uitleggen
Voor het vak Operations Research I moet er een aantal grafieken gemaakt worden van lineaire vergelijkingen.
Zoals:
Z=18=3x1 + 2x2quote:Maximize: Z=3x1 + 2x2
subject to:
x1 ≤ 4
2x2 ≤ 12
3x1 + 2x2 ≤18
en x1 ≥ 0 en x2 ≥ 0
Nu moeten daar in Excel of Calc dit soort grafiekjes bij worden gemaakt:
Helaas, omdat ik nog nooit met Excel heb gewerkt weet ik niet hoe dit moet.
Hopelijk kan iemand het me uitleggen
cracka frakka ass
In DIG loopt een Exceltopic, misschien word je daar net zo goed of zelfs beter geholpen. Ik raak Excel namelijk zelfs met handschoenen ook nog niet aan.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Okee, bedankt.quote:Op maandag 16 november 2009 14:31 schreef Iblis het volgende:
In DIG loopt een Exceltopic, misschien word je daar net zo goed of zelfs beter geholpen. Ik raak Excel namelijk zelfs met handschoenen ook nog niet aan.
cracka frakka ass
Je bedoelt p(t) = 3 (met kleine letter p). De coëfficiënt van y(t) in de standaardvorm y'(t) + p(t)∙y(t) = q(t) van je lineaire inhomogene dv y'(t) + 3∙y(t) = t∙e-3t is hier immers p(t) = 3.quote:Op maandag 16 november 2009 12:21 schreef Burakius het volgende:
Hey Riparius kan het ook op deze manier?:
(1) y '(t) + 3y(t) = te^-3t
Alles met integratiefactor vermenigvuldigen geeft:
(2) y '(t)*u(t) + 3y(t)*u(t) = te^-3t * u(t)
Daarna moet ik zoals jij aangaf (P(x)= 3):
Er zijn natuurlijk oneindig veel functies µ(t) die aan betrekking (3) voldoen, maar je hebt er maar één nodig. Je probleem ontstaat doordat je - onnodig - wil werken met een algemene vorm van µ(t) maar daar dan vervolgens weer niet consequent mee omgaat.quote:(3) u '(t) = 3 * u(t)
Dan wordt u(t) --> ln |u(t)| = 3t
(4)u(t) = +/- e^3t+c
Je moet wel consequent zijn in je notatie. Als je de haakjesnotatie gebruikt bij µ(t) (traditioneel met de Griekse letter µ, maar je mag van mij ook de Latijnse letter u gebruiken), dan moet je dat bij y(t) in dezelfde vergelijking ook doen. y is immers net zo goed een functie van t.quote:Dan vullen we die weer in als:
{u(t) y} ' = u(t)y' + u ' (t) y
Nee, hier gaat het fout. Je hebt gekozen voor µ(t) = e3t+c. Dat is overigens nog steeds niet de meest algemene vorm, omdat, zoals je bij (4) hebt gevonden, ook µ(t) = -e3t+c bruikbaar is, maar dat is het probleem niet. Wat je hier fout doet is dat je weliswaar het rechterlid van je vergelijking hebt vermenigvuldigd met µ(t) = e3t+c, maar dan moet je het linkerlid ook vermenigvuldigen met µ(t) = e3t+c, en dat heb je (impliciet) niet gedaan, want in (5) ga je er plotseling van uit dat je het linkerlid had vermenigvuldigd met µ(t) = e3t, en dan klopt je vergelijking niet meer. Wat je had moeten opschrijven voor (5) is dus:quote:(5) e^3t *y = te^-3t * e^3t+c
e3t+c∙y(t) = t∙e-3t∙e3t+c
Nu is het zo dat e3t+c gelijk is aan het product van e3t en ec, dus zie je ook meteen waarom het geen nut heeft te werken met een algemene vorm van µ(t): zowel in het linkerlid als in het rechterlid van je vergelijking heb je nu een constante factor ec, en door beide leden van je vergelijking te delen door ec - hetgeen is toegestaan omdat ec niet gelijk aan nul kan zijn en hetgeen ook noodzakelijk is om y(t) te isoleren - valt de constante c weg uit je vergelijking. Deze constante is dus irrelevant voor de oplossing van de dv.
Nee, zoals uitgelegd ging het bij stap (5) al mis omdat je het jezelf onnodig moeilijk had gemaakt. Verder moet je natuurlijk niet y = 1 invullen, want de gegeven randvoorwaarde was immers y(1) = 0. Hier zie je ook hoe nuttig het is om consequent met de haakjesnotatie te werken, dan kunnen dit soort begripsverwarringen niet optreden. Je moest invullen t = 1 en dus ook y(t) = y(1) = 0.quote:(6) y = (te^-3t * e^3t+c)/ e^3t
Nu weet ik niet meer goed wat ik moet doen (gewoon die y =1 invullen, maar ik kan (6) eerst vereenvoudigen lijkt me?
Maar heb ik het tot stap (6) goed op deze manier?
Nee. Maar je hebt wel eerst een onnodige constante c geïntroduceerd, daar niet consequent mee gewerkt, en tenslotte bij je integratie in stap (5) de wel benodigde constante in het rechterlid weer helemaal vergeten toe te voegen. Je hebt nog een hoop werk te doen, denk ik zo.quote:edit MIS IK TUSSEN STAP 5 en STAP 6 een INTEGRATIE? ? (als ik zo even in mijn boek kijk)
[ Bericht 0% gewijzigd door Riparius op 16-11-2009 21:33:08 ]
xgem=4.715
m=4.100
SD= 2.2421
Ik zou ik deze gegevens kunnen logtransformeren?
[ Bericht 45% gewijzigd door Brons_Juweel op 16-11-2009 19:04:18 ]
m=4.100
SD= 2.2421
Ik zou ik deze gegevens kunnen logtransformeren?
[ Bericht 45% gewijzigd door Brons_Juweel op 16-11-2009 19:04:18 ]
Gangstarr
niet zonder meerquote:
xgem=4.715
m=4.100
SD= 2.2421
Ik zou ik deze gegevens kunnen logtransformeren?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Morgen tussententamen micro en liep net bij de oefentoets tegen het volgende aan:
nutsfunctie U(x,Y) = X1/2Y1/2, inkomen M=100, en de prijzen zijn Px=0,5 en Py=1
Lagrange:
L = X1/2Y1/2 - l (0,5X+Y-100)
Mijn antwoordblad geeft vervolgens:
1) dL/dX = 0.5X -0.5Y0.5 - 0.5 l
2) dL/dY = 0.5X -0.5Y0.5 - l
Ik had bij de 2e differentiatie echter dL/dY = 0.5X0.5Y -0.5 - l
Staat er een fout in het antwoordblad of heb ik zelf een fout gemaakt? Thanks.
nutsfunctie U(x,Y) = X1/2Y1/2, inkomen M=100, en de prijzen zijn Px=0,5 en Py=1
Lagrange:
L = X1/2Y1/2 - l (0,5X+Y-100)
Mijn antwoordblad geeft vervolgens:
1) dL/dX = 0.5X -0.5Y0.5 - 0.5 l
2) dL/dY = 0.5X -0.5Y0.5 - l
Ik had bij de 2e differentiatie echter dL/dY = 0.5X0.5Y -0.5 - l
Staat er een fout in het antwoordblad of heb ik zelf een fout gemaakt? Thanks.
Oh really?
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
Dikgedrukte is gelijk aan: 2 sin t cos t?
Blues ain't nothing but a good man feeling bad...
Ja. a + a = 2a. (En uiteraard is vermenigvuldiging op de reële getallen commutatief, dus a·b = b·a).quote:
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
[ Bericht 3% gewijzigd door Iblis op 17-11-2009 10:31:00 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
standaarddeviatiequote:Op dinsdag 17 november 2009 11:18 schreef mezzy het volgende:
Hoe deed je dat ook al weer op een rekenmachine (CASIO)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
[ Bericht 7% gewijzigd door motorbloempje op 17-11-2009 11:36:40 ]
Ja doei.
Wat is dat?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
EDIT: Standaarddeviatie, variantie en gemiddelde?
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
[ Bericht 4% gewijzigd door mezzy op 17-11-2009 11:50:10 ]
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
[ Bericht 4% gewijzigd door mezzy op 17-11-2009 11:50:10 ]
Wat voor Casio heb je?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
handig om te vermelden dat je de standaarddeviatie wilde wetenquote:
Hoe deed je dat ook al weer op een rekenmachine (CASIO)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Ja doei.
quote:Op dinsdag 17 november 2009 11:38 schreef motorbloempje het volgende:
[..]
handig om te vermelden dat je de standaarddeviatie wilde weten
idd
te snel gecopy/paste 
Bepaal met behulp van de definitie Laplace getransformeerde unctie F(s) van f(t) = (1+t)2
Is er niet iets snellers en makkelijkers om deze shit op te lossen, wat een geschrijf allemaal zeg of met GR?
Is er niet iets snellers en makkelijkers om deze shit op te lossen, wat een geschrijf allemaal zeg of met GR?
Blues ain't nothing but a good man feeling bad...
Als het m.b.v. de definitie moet heb je al snel zulke grappen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja wat een ramp hè, ik sla die som op de toets wel overquote:Op dinsdag 17 november 2009 17:25 schreef Iblis het volgende:
Als het m.b.v. de definitie moet heb je al snel zulke grappen.
Als hij met die ongein gaat komen. Ik verwacht het eigenlijk niet.
Blues ain't nothing but a good man feeling bad...
Ach, het is wel wat werk, maar het vereist weinig inzicht. Dus op zich is het makkelijk punten scoren.quote:
[..]
Ja wat een ramp hè, ik sla die som op de toets wel over
Als hij met die ongein gaat komen. Ik verwacht het eigenlijk niet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik denk dat je een plusteken bent vergeten. Voor 2∙sin t∙cos t kun je trouwens sin 2t schrijven. Dus krijg je:quote:Op dinsdag 17 november 2009 10:22 schreef GoodGawd het volgende:
(sin t cos t)2 = sin2 t+sin t cos t + cos t sin t + cos2t
Dikgedrukte is gelijk aan: 2 sin t cos t?
(cos t + sin t)2 = 1 + sin 2t
Ye, ik moest gewoon even op dat formule blad kijken >_>;quote:Op dinsdag 17 november 2009 17:42 schreef Riparius het volgende:
[..]
Ik denk dat je een plusteken bent vergeten. Voor 2∙sin t∙cos t kun je trouwens sin 2t schrijven. Dus krijg je:
(cos t + sin t)2 = 1 + sin 2t
Blues ain't nothing but a good man feeling bad...
Waarom? Zulke dingen moet je gewoon uit het blote hoofd weten (gangbare goniometrische identiteiten).quote:Op dinsdag 17 november 2009 17:48 schreef GoodGawd het volgende:
[..]
Ye, ik moest gewoon even op dat formule blad kijken >_>;
http://www.math4all.nl/MathAdore/hb-b34-ex2b.html
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
nevermind, 1 / wortel x = x^-0,5 uiteraard...
[ Bericht 33% gewijzigd door petrelli op 17-11-2009 18:21:41 ]
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
nevermind, 1 / wortel x = x^-0,5 uiteraard...
[ Bericht 33% gewijzigd door petrelli op 17-11-2009 18:21:41 ]
Begrijp je wel dat a-p (voor a ongelijk aan 0) hetzelfde is als 1/ap ?quote:Op dinsdag 17 november 2009 18:05 schreef petrelli het volgende:
http://www.math4all.nl/MathAdore/hb-b34-ex2b.html
Dan bij de n'= blabla gaatie opeens over naar een breuk, ik snap die stap niet.
Zit te kutten nu met partiele afgeleide en dan maximum punten:
f(x,y) = -2x² - 2xy - 2y² +36x + 42y - 158
f1 (x,y) = -4x-2y+36 = 0 (eerste order conditie)
f2 (x,y) = -2x-4y+42= 0
En hier krijgen ze het punt (5,8) uit, ik snap niet hoe mijn boek hier ineens aan komt.
Het klopt wel maar ik probeer het zelf na te rekenen maar dat is nogal irritant met een x en een y en ik heb het gevoel dat ik iets niet weet.
f(x,y) = -2x² - 2xy - 2y² +36x + 42y - 158
f1 (x,y) = -4x-2y+36 = 0 (eerste order conditie)
f2 (x,y) = -2x-4y+42= 0
En hier krijgen ze het punt (5,8) uit, ik snap niet hoe mijn boek hier ineens aan komt.
Het klopt wel maar ik probeer het zelf na te rekenen maar dat is nogal irritant met een x en een y en ik heb het gevoel dat ik iets niet weet.
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?quote:Op dinsdag 17 november 2009 19:22 schreef thabit het volgende:
Waarschijnlijk weet je niet hoe je een lineair stelsel vergelijkingen moet oplossen.
Wiskunde is het niet waard zulke dingen te onthouden. Steek me tijd liever in interessantere vakkenquote:Op dinsdag 17 november 2009 17:50 schreef Riparius het volgende:
[..]
Waarom? Zulke dingen moet je gewoon uit het blote hoofd weten (gangbare goniometrische identiteiten).
Blues ain't nothing but a good man feeling bad...
Dan begin ik me toch af te vragen waarom je voor een studie hebt gekozen waarbij kennelijk toch aardig wat wiskunde komt kijken. Je krijgt die wiskunde niet voor niets, die zul je later voor dat vak gewoon nodig hebben.quote:Op dinsdag 17 november 2009 19:38 schreef GoodGawd het volgende:
[..]
Wiskunde is het niet waard zulke dingen te onthouden. Steek me tijd liever in interessantere vakken
Nee, gewoon 2xfunctie1 - functie twee zodat je X krijgt. Dan x in de eerste formule proppen en y uitrekenen. Dan krijg je x=5 en y =8.quote:Op dinsdag 17 november 2009 19:26 schreef petrelli het volgende:
[..]
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?
Cool story, Hansel.
Een stelsel vergelijkingen kan toch ook lineair zijn? En het stelsel dat je moet oplossen is inderdaad lineair. Vermenigvuldig bijvoorbeeld beide leden van de tweede vergelijking met 2 en trek daarna de leden van de tweede vergelijking af van de leden van de eerste vergelijking. Moet je eens kijken wat je dan overhoudt ...quote:Op dinsdag 17 november 2009 19:26 schreef petrelli het volgende:
[..]
Lineair wel, maar nu met die 2 variabelen is het toch iets anders of zie ik iets over het hoofd?
Wiskunde kan heel handig zijn ja, met m'n vakken zoals mechanica en meet en regeltechniek, electrotechniek etc. Maar dat Laplace geneuzel en zoveelste orde differentiaal vergelijkingen heb ik nog nul keer hoeven toepassen. Dat maakt het vak wiskunde er nou niet bepaald leuker van. En ik acht de kans klein dat ik het ooit nog zal gebruiken. Zo ja dan ben ik het toch al weer vergetenquote:Op dinsdag 17 november 2009 20:05 schreef Riparius het volgende:
[..]
Dan begin ik me toch af te vragen waarom je voor een studie hebt gekozen waarbij kennelijk toch aardig wat wiskunde komt kijken. Je krijgt die wiskunde niet voor niets, die zul je later voor dat vak gewoon nodig hebben.
Die standaard dingen zijn handig om te weten integreren zus differentieren zo, maar al die theorien, van laplace en de zoveelste professor die weer eens wat heeft uitgevonden, ik vind het allemaal wel gezegend.
Blues ain't nothing but a good man feeling bad...
Argh ik krijg nu Laplace . En ja soms vraag ik me ook af waarom ik het moet doen voor mijn latere carriere
. En ja soms vraag ik me ook af waarom ik het moet doen voor mijn latere carriere
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Vorig jaar had ik na 2 hoor colleges zoiets iets van ja right dit gaat nergens meer overquote:Op dinsdag 17 november 2009 21:53 schreef Burakius het volgende:
Argh ik krijg nu Laplace
Ben er niet meer heen geweest en had ook geen poging @ tentamen gedaan. Maar wat meer tijd aan andere vakken besteed. Maargoed ik moet het toch nog even halen, gelukkig heb ik dit jaar vrij weinig te doen Dat noem ik nog eens efficient verdelen. SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
quote:Op dinsdag 17 november 2009 23:14 schreef GoodGawd het volgende:
[..]
Vorig jaar had ik na 2 hoor colleges zoiets iets van ja right dit gaat nergens meer overJa maar ik heb een HARDE KNIPSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Heb even een vraag die waarschijnlijk voor jullie wel makkelijk zijn maar ik kom er even niet uit.
3
-
7
Die moet ik opschrijven als decimaal getal. Maar hoe krijg ik die noemer tot een rationeel getal? Om zodoende de drie te vermenigvuldigen?
3
-
7
Die moet ik opschrijven als decimaal getal. Maar hoe krijg ik die noemer tot een rationeel getal? Om zodoende de drie te vermenigvuldigen?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Ik heb een vraagje. Als ik hypothesis test, hoe weet ik dan welke kant het pijltje (> en <) opstaat bij de Rejection Region?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
zwakken overleven moeilijk, sterken zitten in de wolken
Dit is (in decimale vorm) een repeterende breuk. Daar heb je toch hopelijk wel eens van gehoord?quote:Op woensdag 18 november 2009 14:36 schreef phpmystyle het volgende:
Heb even een vraag die waarschijnlijk voor jullie wel makkelijk zijn maar ik kom er even niet uit.
3
-
7
Die moet ik opschrijven als decimaal getal. Maar hoe krijg ik die noemer tot een rationeel getal? Om zodoende de drie te vermenigvuldigen?
Dat kreeg ik ook op het vmbo-basisquote:Op woensdag 18 november 2009 15:28 schreef Skylark. het volgende:
Ik heb een vraagje. Als ik hypothesis test, hoe weet ik dan welke kant het pijltje (> en <) opstaat bij de Rejection Region?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Leg het me dan eens uit.quote:
[..]
Dat kreeg ik ook op het vmbo-basis
zwakken overleven moeilijk, sterken zitten in de wolken
Of bedoelde hoe je nu kunt weten dat 3/7 = 0.42857.... ?quote:Op woensdag 18 november 2009 15:39 schreef Riparius het volgende:
[..]
Dit is (in decimale vorm) een repeterende breuk. Daar heb je toch hopelijk wel eens van gehoord?
Keer dat keer dat, uitkomsten valideren, breuk van maken, wortel eruit halen, keer pie. Simpel toch.quote:
"Fifty years ago the Leningrad street taught me a rule - if a fight is inevitable, you have to throw the first punch."
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Vladimir Putin
“To forgive the terrorists is up to God, but to send them there is up to me.”
Vladimir Putin
Je bedoelt het groene gebied?quote:Op woensdag 18 november 2009 15:28 schreef Skylark. het volgende:
Ik heb een vraagje. Als ik hypothesis test, hoe weet ik dan welke kant het pijltje (> en <) opstaat bij de Rejection Region?
Bijvoorbeeld, is er een regel dat als ik H0: B1 >= 0 en H1: B1<0 is dat bij de Rejection Region het pijltje altijd zo staat als de H1?
Dus rejection gebied x is Z(a/2) < x < -Z(a/2)
Dan is het logisch dat als H1 >0, je rejection gebied x > Z(a/2)
En H1<0, x< -Z(a/2)
Of was dat je vraag niet?
Ja ik snap wel hoe ik de t/F/z-waarde moet berekenen, maar ik twijfel dan altijd welke kant de pijltjes op moeten staan. Vooral bij 1-sided hypotheses.quote:
[..]
Je bedoelt het groene gebied?
[ afbeelding ]
Dus rejection gebied x is Z(a/2) < x < -Z(a/2)
Dan is het logisch dat als H1 >0, je rejection gebied x > Z(a/2)
En H1<0, x< -Z(a/2)
Of was dat je vraag niet?
zwakken overleven moeilijk, sterken zitten in de wolken
Bij het bepalen van H1 ? Daar kan ik me namelijk van herrineren dat mensen er moeite mee hadden.quote:Op woensdag 18 november 2009 16:03 schreef Skylark. het volgende:
[..]
Ja ik snap wel hoe ik de t/F/z-waarde moet berekenen, maar ik twijfel dan altijd welke kant de pijltjes op moeten staan. Vooral bij 1-sided hypotheses.
Oftewel, over welke pijltjes heb je het nou precies?
Nee, bij het bepalen van de Rejection Region. Ik heb dan in de tabel gekeken en dan heb ik bijvoorbeeld waarde 1.949.quote:
[..]
Bij het bepalen van H1 ? Daar kan ik me namelijk van herrineren dat mensen er moeite mee hadden.
Oftewel, over welke pijltjes heb je het nou precies?
Dan weet ik niet of ik H0 reject als het > 1.949 is of < 1.949 of misschien wel >= 1.949
zwakken overleven moeilijk, sterken zitten in de wolken
Ah, nu weet ik waar je het over hebt.quote:Op woensdag 18 november 2009 16:08 schreef Skylark. het volgende:
[..]
Nee, bij het bepalen van de Rejection Region. Ik heb dan in de tabel gekeken en dan heb ik bijvoorbeeld waarde 1.949.
Dan weet ik niet of ik H0 reject als het > 1.949 is of < 1.949 of misschien wel >= 1.949
Wat je moet doen is je de grafiek voorstellen. H0 is het middelpunt.
Dan heb je H1 gegeven*, dus groter of kleiner dan H0.
Dan heb je nog het waarnemingsgetal.
Je wilt dus weten of het wel mogelijk is dat je zo'n waarnemingsgetal krijgt ( hoe groot de kans daarop is).
Die kans zoek je op, en kijkt wat de waarde is.
Bij H1>0 moet die waarde groter zijn dan de alpha waarde.
Bij H1<0 moet die waarde kleiner zijn dan de alpha waarde.
En als 1 van die dingen geldt, dan verwerp je H0.
Oftewel, valt het waarnemingsgetal binnen het groene gebied: Dan heb je een 'onmogelijke' waarneming gezien en verwerp je dus H0.
* stel je hebt H1 niet gegeven, dan kun je die in een som meestal heel handig zelf bepalen: Is het waarnemingsgetal kleiner dan H0, dan is het dus logisch H1<0, en andersom. Dit geldt bij een eenzijdige-toets. Bij two-sided niet, maar daar heb je dan ook geen probleem.
En als het dan zeg maar eentje is waarbij H0: B1+B2+B3=0 en H1: B1,B2,B3 =/ 0?quote:
[..]
Ah, nu weet ik waar je het over hebt.
Wat je moet doen is je de grafiek voorstellen. H0 is het middelpunt.
Dan heb je H1 gegeven*, dus groter of kleiner dan H0.
Dan heb je nog het waarnemingsgetal.
Je wilt dus weten of het wel mogelijk is dat je zo'n waarnemingsgetal krijgt ( hoe groot de kans daarop is).
Die kans zoek je op, en kijkt wat de waarde is.
Bij H1>0 moet die waarde groter zijn dan de alpha waarde.
Bij H1<0 moet die waarde kleiner zijn dan de alpha waarde.
En als 1 van die dingen geldt, dan verwerp je H0.
Oftewel, valt het waarnemingsgetal binnen het groene gebied: Dan heb je een 'onmogelijke' waarneming gezien en verwerp je dus H0.
* stel je hebt H1 niet gegeven, dan kun je die in een som meestal heel handig zelf bepalen: Is het waarnemingsgetal kleiner dan H0, dan is het dus logisch H1<0, en andersom. Dit geldt bij een eenzijdige-toets. Bij two-sided niet, maar daar heb je dan ook geen probleem.
zwakken overleven moeilijk, sterken zitten in de wolken
Ik weet niet precies wat je bedoelt daarmee, maar het zal niks uitmaken qua gebied.quote:Op woensdag 18 november 2009 16:19 schreef Skylark. het volgende:
[..]
En als het dan zeg maar eentje is waarbij H0: B1+B2+B3=0 en H1: B1,B2,B3 =/ 0?
Ik heb zelf ook een vraag:
Hoe kan ik de volgende breuk vereenvoudigen:
Ik kwam zelf uit op 2x-5/ x-2
Maar dat kan niet.
[ Bericht 12% gewijzigd door motorbloempje op 01-09-2013 21:31:42 ]
Is dat niet gewoon 2x² - x + 4? Of zeg ik nou iets doms?
zwakken overleven moeilijk, sterken zitten in de wolken
Dat kan niet, vul maar een willekeurige x in.quote:Op woensdag 18 november 2009 17:31 schreef Skylark. het volgende:
Is dat niet gewoon 2x² - x + 4? Of zeg ik nou iets doms?
Er staat toch geen '= 0' achter of wel?quote:
[..]
Dat kan niet, vul maar een willekeurige x in.
zwakken overleven moeilijk, sterken zitten in de wolken
Als je de noemer en teller ontbindt in factoren, zie je dat ze beiden een gemeenschappelijke factor hebben. Deze kan je er dan dus uitdelen.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Je bepaalt eerst de nulpunten van de polynomen in teller en noemer. Dan zie je dat beiden een wortel x = 3/2 hebben, en aangezien de coëfficiënten van x2 van beide polynomen een tweevoud zijn, betekent dit dat teller en noemer een factor (2x - 3) gemeenschappelijk hebben. De breuk laat zich dus inderdaad vereenvoudigen. Je kunt de teller schrijven als (2x - 3)(2x + 4) en de noemer als (2x - 3)(x + 1).quote:Op woensdag 18 november 2009 17:25 schreef Siddartha het volgende:
[..]
Ik weet niet precies wat je bedoelt daarmee, maar het zal niks uitmaken qua gebied.
Ik heb zelf ook een vraag:
Hoe kan ik de volgende breuk vereenvoudigen:
[ afbeelding ]
Ik kwam zelf uit op 2x-5/ x-2
Maar dat kan niet.
Standaarddeviatie, variantie en gemiddelde?
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Hoe deed je dat ook al weer op een rekenmachine (CASIO fx82MS)? Ik kan zo even niet snel een rekenopgave vinden, ik zou het zeer op prijs stellen als iemand het me kan uitleggen aan de hand van een voorbeeld..
Moet determineren of deze reeks convergeert of divergeert:
(3^n+2 )/ 5^n
En als deze convergeert vind het limiet. Ik kom er bij deze niet uit, waar ik bij de andere sommen mooi uit de voeten kan komen met delen door de hoogste macht of andere truucjes. Als ik deze meteen invul zie ik eigenlijk al:
3^oneindig / 5^oneindig = een getal , maar goed ik moet zeker iets doen kom er niet uit.
Verder heb ik wel een andere som die er op lijkt, maar waar ik niet begrijp welke stappen zijn ondernomen:
an = 2^n / 3^(n+1) = 1/3 (2/3) ^n. Die 1/3 halen ze eruit waardoor je krijgt
--> 1/3 lim n-> oneindig (2/3)^n = 1/3 * 0 = 0 convergeert. Maar die eerste stap kan ik maar niet begrijpen. Help me brontosaurussen
(3^n+2 )/ 5^n
En als deze convergeert vind het limiet. Ik kom er bij deze niet uit, waar ik bij de andere sommen mooi uit de voeten kan komen met delen door de hoogste macht of andere truucjes. Als ik deze meteen invul zie ik eigenlijk al:
3^oneindig / 5^oneindig = een getal , maar goed ik moet zeker iets doen kom er niet uit.
Verder heb ik wel een andere som die er op lijkt, maar waar ik niet begrijp welke stappen zijn ondernomen:
an = 2^n / 3^(n+1) = 1/3 (2/3) ^n. Die 1/3 halen ze eruit waardoor je krijgt
--> 1/3 lim n-> oneindig (2/3)^n = 1/3 * 0 = 0 convergeert. Maar die eerste stap kan ik maar niet begrijpen. Help me brontosaurussen
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Tip: (3^n+2 )/ 5^n = 3^n / 5^n + 2/5^n.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zou je het misschien met haakjes willen schrijven??? Zie even niet wat bij wat hoort...
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je notatie is wat onduidelijk, maar ik neem aan dat je (3n + 2)/5n bedoelt? Gebruik superscript voor exponenten. Je kunt dit ook schrijven als:quote:Op woensdag 18 november 2009 19:24 schreef Burakius het volgende:
Moet determineren of deze reeks convergeert of divergeert:
(3^n+2 )/ 5^n
En als deze convergeert vind de limiet. Ik kom er bij deze niet uit, waar ik bij de andere sommen mooi uit de voeten kan komen met delen door de hoogste macht of andere truucjes. Als ik deze meteen invul zie ik eigenlijk al:
3^oneindig / 5^oneindig = een getal , maar goed ik moet zeker iets doen kom er niet uit.
(3/5)n + 2/5n
Nu is het niet moeilijk meer om de limiet voor n → ∞ te bepalen.
Elementaire rekenregels voor machten gebruiken. Die 3n+1 in de noemer is gelijk aan het product van 31 = 3 en 3n.quote:
Verder heb ik wel een andere som die er op lijkt, maar waar ik niet begrijp welke stappen zijn ondernomen:
an = 2^n / 3^(n+1) = 1/3 (2/3) ^n. Die 1/3 halen ze eruit waardoor je krijgt
--> 1/3 lim n-> oneindig (2/3)^n = 1/3 * 0 = 0 convergeert. Maar die eerste stap kan ik maar niet begrijpen. Help me brontosaurussen
Ik bedoel 3n+2/5nquote:Op woensdag 18 november 2009 19:39 schreef Riparius het volgende:
[..]
Je notatie is wat onduidelijk, maar ik neem aan dat je (3n + 2)/5n bedoelt? Gebruik superscript voor exponenten. Je kunt dit ook schrijven als:
(3/5)n + 2/5n
Nu is het niet moeilijk meer om de limiet voor n → ∞ te bepalen.
[..]
Elementaire rekenregels voor machten gebruiken. Die 3n+1 in de noemer is gelijk aan het product van 31 = 3 en 3n.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
OK. In dat geval bedenk je dat 3n+2 in de teller gelijk is aan het product van 3n en 32 = 9. Dus geldt:quote:
3n+2/5n = 9∙(3/5)n
Hoe kun je met behulp van inductie bewijzen dat voor
x> -1, voor elke natuurlijke n geld:
Ik heb een 'uitwerking' hier liggen, maar word er niet echt wijs uit.
Voor P(k+1) aan de linkerkant snap ik het nog wel, maar rechts krijgen ze dit:
Ps: dit is Bernouilli's inequality.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:31:48 ]
x> -1, voor elke natuurlijke n geld:
Ik heb een 'uitwerking' hier liggen, maar word er niet echt wijs uit.
Voor P(k+1) aan de linkerkant snap ik het nog wel, maar rechts krijgen ze dit:
Ps: dit is Bernouilli's inequality.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:31:48 ]
NICE! Je bent een echte brontosaurus! Vaak willen ze ook de squeeze theorem gebruiken( bijvoorbeeld bijquote:Op woensdag 18 november 2009 19:45 schreef Riparius het volgende:
[..]
OK. In dat geval bedenk je dat 3n+2 in de teller gelijk is aan het product van 3n en 32 = 9. Dus geldt:
3n+2/5n = 9∙(3/5)n
an = (cos n)2 / 2n
Hoe kan ik nou makkelijk zien wanneer wat toe te passen?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je bewijs via (volledige) inductie bestaat uit twee stappen. Eerst bewijs je dat de bewering juist is voor n = 1 (dit is triviaal, waarom eigenlijk?), en vervolgens bewijs je dat de bewering juist is voor n=k+1 áls de bewering juist is voor n=k. Je verkrijgt (1+x)k+1 door (1+x)k met (1+x) te vermenigvuldigen, maar als je het linkerlid van je ongelijkheid met (1+x) vermenigvuldigt, dan moet je dat rechts ook doen. En begrijp je ook waarom x groter dan -1 moet zijn?quote:Op woensdag 18 november 2009 19:49 schreef Siddartha het volgende:
Hoe kun je met behulp van inductie bewijzen dat voor
x> -1, voor elke natuurlijke n geldt:
[ afbeelding ]
Ik heb een 'uitwerking' hier liggen, maar word er niet echt wijs uit.
Voor P(k+1) aan de linkerkant snap ik het nog wel, maar rechts krijgen ze dit:
[ afbeelding ]
Ps: dit is Bernouilli's inequality.
Daar zijn geen algemene regels voor te geven, en er bestaan nog veel meer convergentiecriteria voor rijen (en voor reeksen). Maar aangezien (cos n)2 niet convergeert vanwege de periodiciteit van de cosinusfunctie, terwijl je wel kunt zeggen dat geldt 0 ≤ (cos n)2 ≤ 1 ligt het gebruik van de insluitstelling (c.q. een majorante rij die naar 0 convergeert) hier wel voor de hand.quote:Op woensdag 18 november 2009 19:55 schreef Burakius het volgende:
[..]
NICE! Je bent een echte brontosaurus! Vaak willen ze ook de squeeze theorem gebruiken( bijvoorbeeld bij
an = (cos n)2 / 2n
Hoe kan ik nou makkelijk zien wanneer wat toe te passen?
an = (1 + (2/n) 2
Bij deze heb ik twee manieren...
(1) :
Gewoon droog invullen lim n-> oneindig ---> (1+0)^oneindig = 1 = convergent (dit is niet goed zoals ik het doe vermoed ik)
(2):
an = (1 + (2/n) 2 --> omschrijven --> n ln(1+ (2/n)) --> ln(1) * oneindig = 0 (dit is de goede methode?)
En toch vind ik het moeilijk te zien welke methode toe te passen.
Bij deze heb ik twee manieren...
(1) :
Gewoon droog invullen lim n-> oneindig ---> (1+0)^oneindig = 1 = convergent (dit is niet goed zoals ik het doe vermoed ik)
(2):
an = (1 + (2/n) 2 --> omschrijven --> n ln(1+ (2/n)) --> ln(1) * oneindig = 0 (dit is de goede methode?)
En toch vind ik het moeilijk te zien welke methode toe te passen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik snap de redenering niet dat je het ook rechts met (x+1) moet vermenigvuldigen. Het enige dat je doet is in beide vergelijkingen K+1 invullen, niet 'willekeurig' vermenigvuldigen. Anders heb je stap 2 immers niet nodig:quote:Op woensdag 18 november 2009 20:01 schreef Riparius het volgende:
[..]
Je bewijs via (volledige) inductie bestaat uit twee stappen. Eerst bewijs je dat de bewering juist is voor n = 1 (dit is triviaal, waarom eigenlijk?), en vervolgens bewijs je dat de bewering juist is voor n=k+1 áls de bewering juist is voor n=k. Je verkrijgt (1+x)k+1 door (1+x)k met (1+x) te vermenigvuldigen, maar als je het linkerlid van je ongelijkheid met (1+x) vermenigvuldigt, dan moet je dat rechts ook doen. En begrijp je ook waarom x groter dan -1 moet zijn?
als
5> 2
dan is
5x3> 2x3
(beide vermenigvuldigt met hetzelfde)
En dat slaat natuurlijk nergens op.
Nee, zo werkt het bewijs niet. Je gaat ervan uit dat de bewering juist is voor een gegeven n=k, dus ga je ervan uit dat geldt:quote:Op woensdag 18 november 2009 20:11 schreef Siddartha het volgende:
[..]
Ik snap de redenering niet dat je het ook rechts met (x+1) moet vermenigvuldigen. Het enige dat je doet is in beide vergelijkingen K+1 invullen, niet 'willekeurig' vermenigvuldigen. Anders heb je stap 2 immers niet nodig:
als
5> 2
dan is
5x3> 2x3
(beide vermenigvuldigt met hetzelfde)
En dat slaat natuurlijk nergens op.
(1) (1 + x)k ≥ 1 + kx
Nu moeten we, uitgaande van deze bewering dus, aantonen dat de ongelijkheid ook geldig is voor n=k+1. De ongelijkheid blijft geldig als we beide leden met eenzelfde positieve (!) factor vermenigvuldigen. We vermenigvuldigen nu beide leden met (1 + x) en krijgen dan:
(2) (1 + x)k+1 ≥ (1 + kx)(1 + x)
Werk nu het rechterlid van deze ongelijkheid eens uit en bedenk hoe je dan verder kunt gaan.
Maar waar blijft dan de k+1 ?quote:Op woensdag 18 november 2009 20:21 schreef Riparius het volgende:
[..]
Nee, zo werkt het bewijs niet. Je gaat ervan uit dat de bewering juist is voor een gegeven n=k, dus ga je ervan uit dat geldt:
(1) (1 + x)k ≥ 1 + kx
Nu moeten we, uitgaande van deze bewering dus, aantonen dat de ongelijkheid ook geldig is voor n=k+1. De ongelijkheid blijft geldig als we beide leden met eenzelfde positieve (!) factor vermenigvuldigen. We vermenigvuldigen nu beide leden met (1 + x) en krijgen dan:
(2) (1 + x)k+1 ≥ (1 + kx)(1 + x)
Werk nu het rechterlid van deze ongelijkheid eens uit en bedenk hoe je dan verder kunt gaan.
Ja in het linkerlid, maar die moet je ook in het rechterlid invoeren.
Ze komen aan die (x+1) omdat:
(1+x)^(K+1) gelijk is aan (1+x)^k x (1+x)
Niet omdat ze willekeurig daarmee vermenigvuldigen....
Ik weet dat
(1 + x)k+1 ≥ (1 + kx)(1 + x)
Er uiteindelijk moet komen te staan, en waarom dat het bewijs is. Dat is het punt niet. Alleen hoe ze tot daar komen.
Nee, je mist het punt. Mijn ongelijkheid (2) is niet het eindpunt van het bewijs maar een tussenstap.quote:Op woensdag 18 november 2009 20:24 schreef Siddartha het volgende:
[..]
Maar waar blijft dan de k+1 ?
Ja in het linkerlid, maar die moet je ook in het rechterlid invoeren.
Ze komen aan die (x+1) omdat:
(1+x)^(K+1) gelijk is aan (1+x)^k x (1+x)
Niet omdat ze willekeurig daarmee vermenigvuldigen....
Ik weet dat
(1 + x)k+1 ≥ (1 + kx)(1 + x)
Er uiteindelijk moet komen te staan, en waarom dat het bewijs is. Dat is het punt niet. Alleen hoe ze tot daar komen.
Je gaat ervan uit dat de bewering juist is voor een gegeven n = k, dus
(1) (1 + x)k ≥ 1 + kx
Vermenigvuldiging van beide leden van deze ongelijkheid met (1 + x) levert, mits x > -1, dan op dat ook moet gelden:
(2) (1 + x)k+1 ≥ (1 + kx)(1 +x)
Hiervoor is ook te schrijven:
(3) (1 + x)k+1 ≥ 1 + (k+1)x + kx2
Maar nu is k een natuurlijk getal, en x2 is zeker niet negatief, dus geldt ook:
(4) kx2 ≥ 0
En dus kunnen we zeggen dat voor het rechterlid van (3) geldt:
(5) 1 + (k+1)x + kx2 ≥ 1 + (k+1)x
Maar uit de ongelijkheden (3) en (5) volgt nu:
(6) (1 + x)k+1 ≥ 1 + (k+1)x
En dit laatste betekent niets anders dan dat de uitspraak geldt voor n = k +1. Aangezien (6) een consequentie is van (1), hebben we zo dus bewezen dat de ongelijkheid geldt voor n = k + 1 áls deze geldt voor n = k. Samen met de juistheid van de uitspraak voor n = 1 is het bewijs met volledige inductie daarmee compleet.
quote:Op woensdag 18 november 2009 21:00 schreef Riparius het volgende:
[..]
Nee, je mist het punt. Mijn ongelijkheid (2) is niet het eindpunt van het bewijs maar een tussenstap.
Je gaat ervan uit dat de bewering juist is voor een gegeven n = k, dus
(1) (1 + x)k ≥ 1 + kx
Vermenigvuldiging van beide leden van deze ongelijkheid met (1 + x) levert, mits x > -1, dan op dat ook moet gelden:
(2) (1 + x)k+1 ≥ (1 + kx)(1 +x)
Hiervoor is ook te schrijven:
(3) (1 + x)k+1 ≥ 1 + (k+1)x + kx2
Maar nu is k een natuurlijk getal, en x2 is zeker niet negatief, dus geldt ook:
(4) kx2 ≥ 0
En dus kunnen we zeggen dat voor het rechterlid van (3) geldt:
(5) 1 + (k+1)x + kx2 ≥ 1 + (k+1)x
Maar uit de ongelijkheden (3) en (5) volgt nu:
(6) (1 + x)k+1 ≥ 1 + (k+1)x
En dit laatste betekent niets anders dan dat de uitspraak geldt voor n = k +1. Aangezien (6) een consequentie is van (1), hebben we zo dus bewezen dat de ongelijkheid geldt voor n = k + 1 áls deze geldt voor n = k. Samen met de juistheid van de uitspraak voor n = 1 is het bewijs met volledige inductie daarmee compleet.
Voor de moeite Mijn probleem ligt denk ik bij de manier van bewijzen: Inductie.
Als k waar is, dan moet ook k+1 waar zijn. Dat snap ik.
Maar ik verwacht dan dat ze voor n/de variable dan bij P(k+1) die
k+1 voor de formule invoeren ( en niet zoals in dit bewijs gewoon vermenigvuldingen?)
Misschien moet ik dus eerst vragen hoe inductie nou precies werkt?
Hoe je het kan bewijzen.
Ik wilde som 5 maken, maar maakte per ongeluk som 6, waar geen antwoord van in het boek staat. Wil toch graag even checken of ik 't goed doe.
x= sin t
y = sin t- t cos t
Waar is de raaklijn horizontaal en waar verticaal
Horizontaal op t = 0, dus (0,0)
Verticaal op t = 1/2 pi dus (1,1)
Klotp dit?
x= sin t
y = sin t- t cos t
Waar is de raaklijn horizontaal en waar verticaal
Horizontaal op t = 0, dus (0,0)
Verticaal op t = 1/2 pi dus (1,1)
Klotp dit?
x'(t) = cost
y'(t) = tsin(t)
je kijkt op [0, pi/2] ? Dan gaat het goed.
y'(t) = tsin(t)
je kijkt op [0, pi/2] ? Dan gaat het goed.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Er staat geen interval bij, maar als het interval groter zou zijn zouden de coördinaten niet veranderen geloof ik?
x'(t)=0 ook voor bv. t=3pi/2 (en y'(t) ongelijk aan 0 dan). Je hebt dan (x,y) = (-1, -1).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Met een beetje invullen bewijs je niets. Je kunt niet zomaar ervan uitgaan dat een uitspraak waar is voor n=k, dan overal k vervangen door k+1 en vervolgens roepen, hé moet je kijken, hij doet het ook met k+1, want dan ben je nog steeds niet verder dan je oorspronkelijke aanname, maar nu met k+1 in plaats van k, meer niet. Je moet echt laten zien dat de juistheid van de uitspraak voor n=k+1 volgt uit de juistheid van de uitspraak voor n=k.quote:Op woensdag 18 november 2009 21:08 schreef Siddartha het volgende:
[..]
Mijn probleem ligt denk ik bij de manier van bewijzen: Inductie.
Als k waar is, dan moet ook k+1 waar zijn. Dat snap ik.
Maar ik verwacht dan dat ze voor n/de variable dan bij P(k+1) die
k+1 voor de formule invoeren ( en niet zoals in dit bewijs gewoon vermenigvuldingen?)
Misschien moet ik dus eerst vragen hoe inductie nou precies werkt?
Hoe je het kan bewijzen.
Het is pie niet pi.quote:Op woensdag 18 november 2009 15:56 schreef phpmystyle het volgende:
[..]
Keer dat keer dat, uitkomsten valideren, breuk van maken, wortel eruit halen, keer pie. Simpel toch.
Tevens, hou eens op met Skylark bashen. Je komt hier om een vraag te stellen, die wordt beantwoord door 2 mensen en vervolgens reageer jij niet meer op ze, lekker fatsoenlijk.
quote:Op woensdag 18 november 2009 15:39 schreef Riparius het volgende:
[..]
Dit is (in decimale vorm) een repeterende breuk. Daar heb je toch hopelijk wel eens van gehoord?
quote:Op woensdag 18 november 2009 15:49 schreef Siddartha het volgende:
[..]
Of bedoelde hoe je nu kunt weten dat 3/7 = 0.42857.... ?
Op woensdag 23 juni 2010 22:44 schreef Chuck_Norris het volgende:
Haha Jap jonge trollgod
Op woensdag 23 juni 2010 22:48 schreef Skylark. het volgende:
Chuck is mastertrolled _O_.
Haha Jap jonge trollgod
Op woensdag 23 juni 2010 22:48 schreef Skylark. het volgende:
Chuck is mastertrolled _O_.
Even kijken of ik het nu wel begrijp:quote:Op woensdag 18 november 2009 22:19 schreef Riparius het volgende:
[..]
Met een beetje invullen bewijs je niets. Je kunt niet zomaar ervan uitgaan dat een uitspraak waar is voor n=k, dan overal k vervangen door k+1 en vervolgens roepen, hé moet je kijken, hij doet het ook met k+1, want dan ben je nog steeds niet verder dan je oorspronkelijke aanname, maar nu met k+1 in plaats van k, meer niet. Je moet echt laten zien dat de juistheid van de uitspraak voor n=k+1 volgt uit de juistheid van de uitspraak voor n=k.
Stel ik moet bewijzen dat
Dus stap 1: Bewijs dat P(1) waar is. Klopt
Stap 2: Aanname dat P(k) klopt,
dus nu uitzoeken of het dan ook voor (elke) volgende stap geld, dus P(k+1).
Dan krijg ik:
Wat ik weer kan opschrijven als:
Waarna ik alleen nog hoef te bewijzen dat 2 kleiner gelijk is aan (k+2), wat logisch is.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:32:24 ]
en dat is wat je nu wel doet.quote:Je kunt niet zomaar ervan uitgaan dat een uitspraak waar is voor n=k, dan overal k vervangen door k+1
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus ik had beide kanten gewoon met 2 moeten vermenigvuldigen, rechterkant uitwerken?quote:Op donderdag 19 november 2009 11:37 schreef GlowMouse het volgende:
[..]
en dat is wat je nu wel doet.
Sorry, maar ik snap het principe denk ik gewoon niet?
Je wilt laten zien dat 
Je weet
en hier kun je je inductieaanname gebruiken, namelijk dat
het truukje is om met één kant te beginnen, en dan net zolang om te schrijven tot je op de rechterkant uitkomt, daarbij ergens de inductieaanname gebruikend.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:32:29 ]
Je weet
en hier kun je je inductieaanname gebruiken, namelijk dat
het truukje is om met één kant te beginnen, en dan net zolang om te schrijven tot je op de rechterkant uitkomt, daarbij ergens de inductieaanname gebruikend.
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:32:29 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Maar dat doe ik toch?quote:Op donderdag 19 november 2009 11:46 schreef GlowMouse het volgende:
Je wilt laten zien dat [ afbeelding ]
Je weet
[ afbeelding ]
en hier kun je je inductieaanname gebruiken, namelijk dat
[ afbeelding ]
het truukje is om met één kant te beginnen, en dan net zolang om te schrijven tot je op de rechterkant uitkomt, daarbij ergens de inductieaanname gebruikend.
2^k x 2 = (k+2)!
Rechterkant wordt dan: (k+2)((k+1)!
En dan hoef ik alleen te bewijzen dat 2 kleiner gelijk (k+2)
Ik word helemaal gek .. hoe kan ik deze vergelijking oplossen, weet iemand dat??
x0.5 - 0.75(x + 720)0.5 = 9
heb de wortels voor het gemak even vervangen door een 0.5de macht. Ik heb echt al van alles geprobeerd, maar ik weet niet hoe ik dit moet aanpakken
.. hoe kan ik deze vergelijking oplossen, weet iemand dat??x0.5 - 0.75(x + 720)0.5 = 9
heb de wortels voor het gemak even vervangen door een 0.5de macht. Ik heb echt al van alles geprobeerd, maar ik weet niet hoe ik dit moet aanpakken
ik ben het mannetje in de chinese kamer
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |