SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
miss. beetje ontopic , maar dankzij jouw wiskundetopics heb ik een 6,5 gehaald voor mn vwo wiskunde examen 
, Thanks dus! 
, Thanks dus!
.
Hé, dat is mijn avatar!
IAh, ja, ik zie al wat ik fout doe. Ik had nog sqrt(24)-24/sqrt(24) moeten doen en dan komt er wel nul uit.
IAh, ja, ik zie al wat ik fout doe. Ik had nog sqrt(24)-24/sqrt(24) moeten doen en dan komt er wel nul uit.
Door het examenforum zo te zienquote:Op zondag 1 november 2009 16:07 schreef Rainb0ws het volgende:
miss. beetje ontopic , maar dankzij jouw wiskundetopics heb ik een 6,5 gehaald voor mn vwo wiskunde examen
Graag gedaan hoor 
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
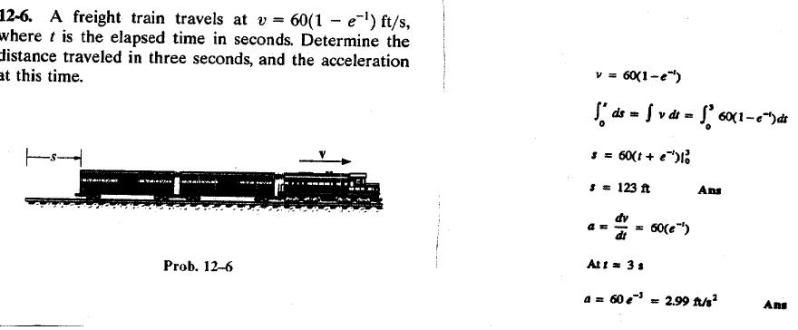
Hoe komen ze aan 123 ft?
Dat is zeker weer zo'n rare omzetting met feet enzo?
Dat is zeker weer zo'n rare omzetting met feet enzo?
Blues ain't nothing but a good man feeling bad...
60(3+e^(-3)) - 60(0+e^(-0)) uitrekenen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Er is toch niets om te zetten als je alles in feet uitdrukt? Begrijp je de berekening van de integraal wel?quote:Op zondag 1 november 2009 17:01 schreef GoodGawd het volgende:
Hoe komen ze aan 123 ft?
[ afbeelding ]
Dat is zeker weer zo'n rare omzetting met feet enzo?
je bedoeltquote:
[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:31:00 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
@Iblis & GlowMouse: is geen van beide goed.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
Die Wolfram-sites in de OP 
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Wat snap je er niet aan?quote:Op zondag 1 november 2009 17:01 schreef GoodGawd het volgende:
Hoe komen ze aan 123 ft?
[ afbeelding ]
Dat is zeker weer zo'n rare omzetting met feet enzo?
Ten percent faster with a sturdier frame
nooit van een tvp gehoord?quote:
@Iblis & GlowMouse: is geen van beide goed.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik had eigenlijk geen fysische interpretatie in gedachten. Ik wilde gewoon een onbeschaamde tvp plaatsen.quote:
@Iblis & GlowMouse: is geen van beide goed.
We hebben immers v(t) = s'(t) en s(0) = 0, zodat:
s(T) = ∫0T v(t)dt
Maar doe geen moeite, de vragensteller vond ONZ en KLB kennelijk toch een stuk belangrijker.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Plaats van een puntmassa wordt zo gedefineerd:
r = 5 cos 2t i + 4 sin 2t j
differentiëren naar snelheid
-5 sin 2 i + 4 cos 2 j
differentiëren naar versnelling
-5 cos 2 i - 4 sin 2 j
Klopt dit?
r = 5 cos 2t i + 4 sin 2t j
differentiëren naar snelheid
-5 sin 2 i + 4 cos 2 j
differentiëren naar versnelling
-5 cos 2 i - 4 sin 2 j
Klopt dit?
Blues ain't nothing but a good man feeling bad...
dit is het wiskundetopic, zonder beschrijving van i, t en j snap ik het niet en ik denk ook dat het fout gaat omdat er een t verdwijnt en de kettingregel niet wordt gebruikt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Zonder de i en j:
r = 5 cos 2t + 4 sin 2t
differentiëren naar snelheid
-10 sin 2t + 8 cos 2
differentiëren naar versnelling
-10 cos 2 - 8 sin 2
Zo?
r = 5 cos 2t + 4 sin 2t
differentiëren naar snelheid
-10 sin 2t + 8 cos 2
differentiëren naar versnelling
-10 cos 2 - 8 sin 2
Zo?
Blues ain't nothing but a good man feeling bad...
bij de tweede keer differentiëren mis je nog de kettingregel
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh ja typo >_> Nou dan iig diff ook weer opgefrist
Blues ain't nothing but a good man feeling bad...
Heeft iemand hier ervaring met het programma Eviews? Wij moeten dat namelijk gebruiken tijdens ons vak econometrie en vind het zelf een vrij onhandig programma.
Het betreft een string aan data waar we een econometrisch model aan moeten toeschrijven op een specifieke manier zodat het "can be estimated by least squares regression".
Het betreft een string aan data waar we een econometrisch model aan moeten toeschrijven op een specifieke manier zodat het "can be estimated by least squares regression".
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
GlowMouse, ligt het aan mij of moet ik op http://betahw.mine.nu/index.php alle backslashes dubbel invoeren om resultaat te hebben? Dus \\int en niet \int?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
vanaf nu ligt het aan jouquote:Op zondag 1 november 2009 23:17 schreef Iblis het volgende:
GlowMouse, ligt het aan mij of moet ik op http://betahw.mine.nu/index.php alle backslashes dubbel invoeren om resultaat te hebben? Dus \int en niet \int?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik snap hoe A eruit ziet uitgedrukt in v1 en v2, maar heb echt nog geen idee hoe ik kern en bereik moet vinden. Ik kan niet rijvegen in die matrix, geloof ik.quote:Op zondag 1 november 2009 02:05 schreef Hanneke12345 het volgende:
4. Laat v ∈ R^2 een vector zijn van lengte één, dus ||v|| = 1. Definieer de matrix A door A=vvT
a. Bepaal kern en beeld (=bereik?) van A
- wat is A? ik heb echt geen idee eigenlijk.
+ vraag b; geef zonder berekening de eigenwaarden en eigenvectoren van A, eigenwaarde 0 is triviaal, maar ook één is v1^2+v2^2, waar komt die vandaan?
Kijk nou eens naar twee voorbeeldjesquote:
[..]
Ik snap hoe A eruit ziet uitgedrukt in v1 en v2, maar heb echt nog geen idee hoe ik kern en bereik moet vinden. Ik kan niet rijvegen in die matrix, geloof ik.
Van het spoor. Of van je kolomruimte.quote:+ vraag b; geef zonder berekening de eigenwaarden en eigenvectoren van A, eigenwaarde 0 is triviaal, maar ook één is v1^2+v2^2, waar komt die vandaan?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dan kom ik een dezer dagen nog wel met de vraag op de proppen, heb woensdag weer les in 'Eviews' en ben op dit moment niet eens in staat een fatsoenlijk antwoord te geven op de vragen die ik hebquote:
Wij moeten namelijk naar alle waarschijnlijkheid tijdens ons examen econometrie ook een klein gedeelte in Eviews doen.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ik heb een vraag over de odds ratio. Stel je hebt een kruistabel met 4 cellen. Is de odds ratio dan altijd a x d / b x c ?
...and that's the way the cookie crumbles.
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Ik ben een pure Turk.
Reset proces gebruiken in het systeem van je GR? Dan gaat alles terug naar normaal en werkt het allemaal weer!quote:Op maandag 2 november 2009 18:31 schreef Bilmiyorem het volgende:
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Zorg wel dat je je programmas ff beschermt anders flikkert hij die ook weg.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Heb je een Ti-84 (plus)?quote:Op maandag 2 november 2009 18:31 schreef Bilmiyorem het volgende:
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Ga dan eens naar Window en verander de waardes van xmin, xmax etc.
Cool story, Hansel.
vast dom, maar heb de gr nooit eerder gebruikt, hoe doe ik dat?quote:Op maandag 2 november 2009 18:49 schreef sitting_elfling het volgende:
[..]
Reset proces gebruiken in het systeem van je GR? Dan gaat alles terug naar normaal en werkt het allemaal weer!
Ik ben een pure Turk.
ja, die staan al goed volgens mij:quote:Op maandag 2 november 2009 18:50 schreef wikwakka2 het volgende:
[..]
Heb je een Ti-84 (plus)?
Ga dan eens naar Window en verander de waardes van xmin, xmax etc.
-10
10
1
-10
10
1
1
Ik ben een pure Turk.
Dat ligt aan de grafiek die je aan wilt plotten.quote:Op maandag 2 november 2009 19:03 schreef Bilmiyorem het volgende:
[..]
ja, die staan al goed volgens mij:
-10
10
1
-10
10
1
1
Maar een reset kan je doen door 2nd/ + knop / Reset / All / All memory te gaan. Je verliest dan wel programma's die je er zelf op hebt gezet.
Cool story, Hansel.
Ja, maar eerst waren deze waardes goed, dat bedoel ik. Heb er nog niets op gezet, gr is nog niet nodig geweest.quote:Op maandag 2 november 2009 19:05 schreef wikwakka2 het volgende:
[..]
Dat ligt aan de grafiek die je aan wilt plotten.
Maar een reset kan je doen door 2nd/ + knop / Reset / All / All memory te gaan. Je verliest dan wel programma's die je er zelf op hebt gezet.
Ik ben een pure Turk.
Dan zou ik hem dus gewoon even resetten. Of anders even alle zooms afgaan.quote:Op maandag 2 november 2009 19:08 schreef Bilmiyorem het volgende:
[..]
Ja, maar eerst waren deze waardes goed, dat bedoel ik. Heb er nog niets op gezet, gr is nog niet nodig geweest.
Cool story, Hansel.
Gedaan, dankjewel.quote:Op maandag 2 november 2009 19:08 schreef wikwakka2 het volgende:
[..]
Dan zou ik hem dus gewoon even resetten.
Het leven zonder rekenmachine is leuker.
Ik ben een pure Turk.
GR's maken het leven zoveel makkelijkerquote:Op maandag 2 november 2009 19:11 schreef Bilmiyorem het volgende:
[..]
Gedaan, dankjewel.
Het leven zonder rekenmachine is leuker.
als je het logisch denken/rekenen maar niet afleert.
Cool story, Hansel.
ik snap niet wat ik met de gr moet, vond "gewone" wiskunde beter (wat ik eerst had zonder gr)quote:Op maandag 2 november 2009 19:18 schreef wikwakka2 het volgende:
[..]
GR's maken het leven zoveel makkelijker
Ik ben een pure Turk.
Ik heb een vraagje. Ik verschil een beetje in antwoorden en wil weten of dit correct is:
e^2zi = e^1/2 pi * i
Daar maak ik van:
2zi = (1/2 pi + 2pi k )i
zi = (1/4 pi + pi k ) i
z = (1/4 pi + pi k)
Zo moet deze correct zijn?
e^2zi = e^1/2 pi * i
Daar maak ik van:
2zi = (1/2 pi + 2pi k )i
zi = (1/4 pi + pi k ) i
z = (1/4 pi + pi k)
Zo moet deze correct zijn?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
e2zi = e1/2πi.quote:
Ik heb een vraagje. Ik verschil een beetje in antwoorden en wil weten of dit correct is:
e^2zi = e^1/2 pi * i
Daar maak ik van:
2zi = (1/2 pi + 2pi k )i
zi = (1/4 pi + pi k ) i
z = (1/4 pi + pi k)
Zo moet deze correct zijn?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik heb het gewoon correct dus... , vriend had i.p.v. z = (pi/4 + pi k ) ---> z = (pi/4 + 2pi k) . Die 2pi k kan natuurlijk niet, omdat je nog door 2 deelt. Wat hij voor die pi/2 wel doet , maar voor die 2pi niet.quote:
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Klopt.quote:
[..]
Ik heb het gewoon correct dus... , vriend had i.p.v. z = (pi/4 + pi k ) ---> z = (pi/4 + 2pi k) . Die 2pi k kan natuurlijk niet, omdat je nog door 2 deelt. Wat hij voor die pi/2 wel doet , maar voor die 2pi niet.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Denk je alles te snappen, loop ik tegen een oefenvraag aan die me toch nog hoofdbrekens bezorgt:
Op een van de inkoopfacturen van de Wadtrappers staat een totaal factuurbedrag van ¤ 158,32 vermeld. Een deel hiervan is belast met 6% omzetbelasting (BTW) en een ander deel met 19%. De omzetbelasting van 6% is ¤ 1,35.
Welk bedrag vermeldt de factuur voor de betaalde omzetbelasting van 19%?
Wat zie ik over het hoofd?
Op een van de inkoopfacturen van de Wadtrappers staat een totaal factuurbedrag van ¤ 158,32 vermeld. Een deel hiervan is belast met 6% omzetbelasting (BTW) en een ander deel met 19%. De omzetbelasting van 6% is ¤ 1,35.
Welk bedrag vermeldt de factuur voor de betaalde omzetbelasting van 19%?
Wat zie ik over het hoofd?
Zeg dat het deel dat met 6% is belast x is, en het deel dat met 19% is belast y is, dan is het totaalbedrag dus: 1,06x + 1,19y.
Je weet dat 0,06x = 1,35, dus x moet je kunnen uitrekenen. Dan moet het verder lukken hoop ik?
Je weet dat 0,06x = 1,35, dus x moet je kunnen uitrekenen. Dan moet het verder lukken hoop ik?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik kom er niet uit, heb weer hetzelfdequote:Op maandag 2 november 2009 18:31 schreef Bilmiyorem het volgende:
ik heb een probleem met m'n gr, kan ik m'n vraag hier stellen?
probleem:
ik kan geen grafieken meer zien als ik ze heb geplot, ik heb iets met de zoom gedaan, als ik ZStandard gebruik, zie ik nog steeds niet de grafiek die ik heb geplot
Weet iemand hoe ik dit kan oplossen?
Ik ben een pure Turk.
Heb je met de zoom zitten klooien? Je hebt toch wel íéts veranderd?quote:Op maandag 2 november 2009 22:39 schreef Bilmiyorem het volgende:
[..]
Ik kom er niet uit, heb weer hetzelfde
Cool story, Hansel.
Ja, maar die herstel je toch altijd met ZStandard en dat werkt nu nietquote:Op maandag 2 november 2009 22:49 schreef wikwakka2 het volgende:
[..]
Heb je met de zoom zitten klooien? Je hebt toch wel íéts veranderd?
Ik ben een pure Turk.
Scroll eens naar beneden en druk op ZoomFitquote:Op maandag 2 november 2009 22:51 schreef Bilmiyorem het volgende:
[..]
Ja, maar die herstel je toch altijd met ZStandard en dat werkt nu niet
Cool story, Hansel.
Wat doet dat? Stomme rekenmachinequote:Op maandag 2 november 2009 22:52 schreef wikwakka2 het volgende:
[..]
Scroll eens naar beneden en druk op ZoomFit
Ik dacht lekker een hoog cijfer halen, zodat ik eindelijk afgerond een 10 sta
Ik ben een pure Turk.
Dan stelt hij het scherm zo af dat je grafiek er precies op past. Probeer het nou gewoonquote:Op maandag 2 november 2009 22:54 schreef Bilmiyorem het volgende:
[..]
Wat doet dat? Stomme rekenmachine
.
Cool story, Hansel.
Ik wil niets verkeerds doen, rekenmachine was al bijna niet meer af te lezen, daarom wilde ik weten wat het betekende. Ik wil wel die 10 op m'n rapport hequote:Op maandag 2 november 2009 22:56 schreef wikwakka2 het volgende:
[..]
Dan stelt hij het scherm zo af dat je grafiek er precies op past. Probeer het nou gewoon
Ik ben een pure Turk.
En wat was het resultaat toen je mijn instructies opvolgde?quote:Op maandag 2 november 2009 22:57 schreef Bilmiyorem het volgende:
[..]
Ik wil niets verkeerds doen, rekenmachine was al bijna niet meer af te lezen, daarom wilde ik weten wat het betekende. Ik wil wel die 10 op m'n rapport he
Cool story, Hansel.
Het werkt! Beste kan ik het dus altijd gebruiken?quote:Op maandag 2 november 2009 22:58 schreef wikwakka2 het volgende:
[..]
En wat was het resultaat toen je mijn instructies opvolgde?
Ik ben een pure Turk.
Ja, lijkt me wel het handigste want dan staat je functie er tenminste altijd helemaal op. Je moet wel uitkijken dat je limieten gebruikt indien nodig, (door de xmin en xmax etc. te veranderen) want soms hoef je maar naar een deel van je functie te kijken.quote:Op maandag 2 november 2009 22:59 schreef Bilmiyorem het volgende:
[..]
Het werkt! Beste kan ik het dus altijd gebruiken?
Cool story, Hansel.
Ik weet helemaal niets van de gr, weet ook niet wat ik ervan moet weten, dat is het hele probleem. Ik bekijk daarom een beetje wat ik met die grafieken kan, maar bedankt voor de tip.quote:Op maandag 2 november 2009 23:01 schreef wikwakka2 het volgende:
[..]
Ja, lijkt me wel het handigste want dan staat je functie er tenminste altijd helemaal op. Je moet wel uitkijken dat je limieten gebruikt indien nodig, (door de xmin en xmax etc. te veranderen) want soms hoef je maar naar een deel van je functie te kijken.
(ik hoop op een 10, valse hoop)
Ik ben een pure Turk.
x=22,5 dan? Maar wat kan ik met die info?quote:Op maandag 2 november 2009 22:12 schreef Iblis het volgende:
Zeg dat het deel dat met 6% is belast x is, en het deel dat met 19% is belast y is, dan is het totaalbedrag dus: 1,06x + 1,19y.
Je weet dat 0,06x = 1,35, dus x moet je kunnen uitrekenen. Dan moet het verder lukken hoop ik?
Welke denkwijze moet ik hanteren? Ik heb een black-out!
Aparte toets dan als je niet weet wat je ervoor moet lerenquote:Op maandag 2 november 2009 23:02 schreef Bilmiyorem het volgende:
[..]
Ik weet helemaal niets van de gr, weet ook niet wat ik ervan moet weten, dat is het hele probleem. Ik bekijk daarom een beetje wat ik met die grafieken kan, maar bedankt voor de tip.
.
Cool story, Hansel.
Invullen, dan weet je dus dat 158,32 = 1,06·22,5 + 1,19y.quote:
[..]
x=22,5 dan? Maar wat kan ik met die info?
Welke denkwijze moet ik hanteren? Ik heb een black-out!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Boek ligt op schoolquote:Op maandag 2 november 2009 23:05 schreef wikwakka2 het volgende:
[..]
Aparte toets dan als je niet weet wat je ervoor moet leren
Ik ben een pure Turk.
Doh! Tnx!quote:Op maandag 2 november 2009 23:06 schreef Iblis het volgende:
[..]
Invullen, dan weet je dus dat 158,32 = 1,06·22,5 + 1,19y.
Vandaag mn toets. Jullie krijgen mn tentamencijfer nog te horen
'Een ijscoman weet uit ervaring dat hij op een zonnige dag bij een prijs van 1.30 per ijsje 700 stuks verkoopt. Bij elke 10 cent prijsverhoging verkoopt hij er 50 minder. Er bestaat een lineair verband tussen de prijs p in euro's en het aantal verkochte ijsjes q'
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
mundus vult decipi
Je a is goed. Je hebt alleen nog niet gebruikt dat bij een prijs van 1.30 per ijsje 700 stuks verkoopt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
welke methode heb je?quote:Op dinsdag 3 november 2009 19:52 schreef Gratau het volgende:
'Een ijscoman weet uit ervaring dat hij op een zonnige dag bij een prijs van 1.30 per ijsje 700 stuks verkoopt. Bij elke 10 cent prijsverhoging verkoopt hij er 50 minder. Er bestaat een lineair verband tussen de prijs p in euro's en het aantal verkochte ijsjes q'
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
Ik ben een pure Turk.
Er staat geen vraag/opdrachtquote:
'Een ijscoman weet uit ervaring dat hij op een zonnige dag bij een prijs van 1.30 per ijsje 700 stuks verkoopt. Bij elke 10 cent prijsverhoging verkoopt hij er 50 minder. Er bestaat een lineair verband tussen de prijs p in euro's en het aantal verkochte ijsjes q'
ik heb eerst a berekend ( uitgaande van p = aq + b ) ik kwam uit op -0.002.
maar hoe verder?
ik weet trouwens niet of het bij beta hoort
Neem aan dat je dat lineair verband moet geven?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
huh ik snap het even niet. bereken je b zo?quote:Op dinsdag 3 november 2009 19:53 schreef GlowMouse het volgende:
Je a is goed. Je hebt alleen nog niet gebruikt dat bij een prijs van 1.30 per ijsje 700 stuks verkoopt.
mundus vult decipi
Dat je een modelletje moet uitrekenen mischienquote:
[..]
Er staat geen vraag/opdracht
Neem aan dat je dat lineair verband moet geven?
?
Cool story, Hansel.
jaquote:Op dinsdag 3 november 2009 19:54 schreef -J-D- het volgende:
[..]
Er staat geen vraag/opdracht
Neem aan dat je dat lineair verband moet geven?
stel de formule van p als functie van q
mundus vult decipi
als je 1.30 invult als prijs moet er 700 uitkomen.quote:
[..]
huh ik snap het even niet. bereken je b zo?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je kan toch de variablen invullen die je weet en zo de variabel die je niet weet uitrekenen.quote:Op dinsdag 3 november 2009 19:55 schreef Gratau het volgende:
[..]
huh ik snap het even niet. bereken je b zo?
Cool story, Hansel.
Ik zou q als functie van p nemen. Je wil toch het effect van de prijs op de verkochte aantallen beschrijven in een formule?quote:Op dinsdag 3 november 2009 19:55 schreef Gratau het volgende:
[..]
ja
stel de formule van p als functie van q
Het is hem al gelukt, me dunkt.quote:
[..]
Ik zou q als functie van p nemen. Je wil toch het effect van de prijs op de verkochte aantallen beschrijven in een formule?
Cool story, Hansel.
Misschien, maar dat heeft hij/zij hier dan niet laten zien. En als je met een kromme redenatie of een verkeerde aanpak bij het 'goede' antwoord uitkomt wil dat niet zeggen dat je het goed hebt gedaan.quote:
Heej Einsteins ik heb weer een vraag:. Dit keer is de vraag over linker-en rechterafgeleide f 'l(0) en fr ' 0) van:
f (x) = { x^2 +2x als x >(of gelijk) 0
en { -x^2 + x + 1 als x<0
Nu weten we dat we f(a) = f(a+h) - f(a) / h moeten gebruiken.
De rechterafgeleide geeft dan:
h^2 + 2h - 0 /h = h + 2
lim x-> 0 = 2
Maar de linkerafgeleide komen we niet uit met het antwoord. Someone can solve this nut?
f (x) = { x^2 +2x als x >(of gelijk) 0
en { -x^2 + x + 1 als x<0
Nu weten we dat we f(a) = f(a+h) - f(a) / h moeten gebruiken.
De rechterafgeleide geeft dan:
h^2 + 2h - 0 /h = h + 2
lim x-> 0 = 2
Maar de linkerafgeleide komen we niet uit met het antwoord. Someone can solve this nut?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Het differentiequotiënt voor f als h < 0 is (f(h)-f(0))/(x-0) = (-h² + h + 1 - 0)/h = -h+1 + 1/h.
Als h van onderen naar 0 gaat, gaat dit naar -oneindig.
[ Bericht 11% gewijzigd door GlowMouse op 04-11-2009 13:52:07 ]
Als h van onderen naar 0 gaat, gaat dit naar -oneindig.
[ Bericht 11% gewijzigd door GlowMouse op 04-11-2009 13:52:07 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Wij hadden hier dus ook -h + 1 uit!!!! En naar 0 is dat natuurlijk 1.quote:Op woensdag 4 november 2009 13:43 schreef GlowMouse het volgende:
Het differentiequotiënt voor f als h < 0 is (f(h)-f(0))/(x-0) = (-h² + h - 0)/h = -h+1.
Als h van onderen naar 0 gaat, komt hier 1 uit.
Maar de juffrouw heeft iets anders gegoogeld namelijk:
lim h --> 0 -h^2 + h +1 - 0 /h (die 0 kan niet eens maar ja) = lim h->0 -h+1 + 1/h
= - oneindig dus f ' l (0) bestaat niet. Is haar antwoord.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Verdammt, nee ik, moet leren lezen, was de 1 in f(h) vergeten. Zie edit.quote:
De functie is discontinu in 0 dus het is ook logisch dat een van beide afgeleiden niet bestaat.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
maar die linkerafgeleide wordt toch:
(-h^2 + h +1 + 0 - 1)/(h) = -h+1
Want f(0) is toch -0^2 + 0 + 1 = 1 ?
(-h^2 + h +1 + 0 - 1)/(h) = -h+1
Want f(0) is toch -0^2 + 0 + 1 = 1 ?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
f (x) = { x^2 +2x als x >(of gelijk) 0
dus f(0) = 0²+2*0 = 0.
dus f(0) = 0²+2*0 = 0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Thx we snappen em!!! brontosaurus dat ge bent!
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik merk wel dat het zwaar vervelend is om wiskundige vragen in het Nederlands uit te leggen als je Engels gewend bent .
.
Cool story, Hansel.
Dat is gewoon integreren m.b.v. substitutie, je gaat van een integraal over dy over naar een integraal over dp, misschien dat deze voorbeelden bij Wikipedia je wat helpen, maar kort gezegd (ik heb even geen tijd om het helemaal uit te werken), het doel is om een makkelijker integraal te krijgen, m.a.w. men wil van integratie over y naar integratie over p, waarbij dat een ‘handige’ vorm heeft, daarvoor kiest men de substitutie p = y3 + 2, en dan geldt dp/dy = 3y2 (lijkt me logisch) en dan maakt men weer gebruik van de voordelen die Leibniz’ notatie biedt, en dan kun je stellen dat dp=3y2dy geldt, ofwel dy=dp/3y2, en dat proppen ze dan in die formule, dus waar dy staat, kun je dan dp/3y2 neerzetten.quote:
[ afbeelding ]
Waarom gaan ze in dat rode blok differentiëren?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Even een makkelijke vraag die ik nergens in mijn boek kan vinden
Wat bereken je met een eigenvector. Ik kan het uitrekenen, maar weet niet wat het betekend.
De eigenwaarde is de verlenging/ verkorting van een vector, dat is dan wel weer meteen duidelijk.
Wat bereken je met een eigenvector. Ik kan het uitrekenen, maar weet niet wat het betekend.
De eigenwaarde is de verlenging/ verkorting van een vector, dat is dan wel weer meteen duidelijk.
C'est magnifique, mais ce n'est pas la guerre.
-
-
Een eigenvector is een vector die na de transformatie niet verandert van richting, althans, kan wel omklappen, maar verschuift verder niet.quote:
Even een makkelijke vraag die ik nergens in mijn boek kan vinden
Wat bereken je met een eigenvector. Ik kan het uitrekenen, maar weet niet wat het betekend.
De eigenwaarde is de verlenging/ verkorting van een vector, dat is dan wel weer meteen duidelijk.
Wikipedia illustreert het mooit met de Mona Lisa.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik zit hier met de vaag wanneer de golffunctie (in de quantum) een oscillerend karakter heeft (en wanneer deze een monotoom karakter heeft)
Mijn ene bron zegt: Etot > Epot -> oscillerend karakter, terwijl de andere bron zegt Ekin>Epot, wat niet op hetzelfde neerkomt. Immers kan Etot > Epot als Ekin < Epot.
Mijn ene bron zegt: Etot > Epot -> oscillerend karakter, terwijl de andere bron zegt Ekin>Epot, wat niet op hetzelfde neerkomt. Immers kan Etot > Epot als Ekin < Epot.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.
er is ook een niet-wiskundetopic.quote:
Ik zit hier met de vaag wanneer de golffunctie (in de quantum) een oscillerend karakter heeft (en wanneer deze een monotoom karakter heeft)
Mijn ene bron zegt: Etot > Epot -> oscillerend karakter, terwijl de andere bron zegt Ekin>Epot, wat niet op hetzelfde neerkomt. Immers kan Etot > Epot als Ekin < Epot.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik moet 2 natuurlijke getallen p,q vinden met 35p=55q.
Lastig. Ik kwam tot nu toe niet verder dan priemontbinding maken;
(5*7)p=(5*11)q
5p*7p =5q*11q
Wie ziet hoe het verder moet en wil een tip geven?
Lastig. Ik kwam tot nu toe niet verder dan priemontbinding maken;
(5*7)p=(5*11)q
5p*7p =5q*11q
Wie ziet hoe het verder moet en wil een tip geven?
kloep kloep
Als q>0 is het rechterlid deelbaar door 11, maar het linkerlid niet. Als p>0 zelfde met 7. Dus p=q=0.quote:Op woensdag 4 november 2009 21:50 schreef Borizzz het volgende:
Ik moet 2 natuurlijke getallen p,q vinden met 35p=55q.
Lastig. Ik kwam tot nu toe niet verder dan priemontbinding maken;
(5*7)p=(5*11)q
5p*7p =5q*11q
Wie ziet hoe het verder moet en wil een tip geven?
thabit vindt 0 een natuurlijk getal
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dus geen oplossingen.quote:Op woensdag 4 november 2009 22:09 schreef thabit het volgende:
[..]
Als q>0 is het rechterlid deelbaar door 11, maar het linkerlid niet. Als p>0 zelfde met 7. Dus p=q=0.
Kan je dit ook concluderen met hoofdstelling?
kloep kloep
Ik gebruik de term 'natuurlijk getal' zelf zelden. Ik spreek liever van positieve danwel niet-negatieve gehele getallen.quote:Op woensdag 4 november 2009 22:11 schreef GlowMouse het volgende:
thabit vindt 0 een natuurlijk getal
Zeker, al kan je ook zonder de hoofdstelling wel bewijzen dat een 5-macht maal een 7-macht niet deelbaar is door 11, maar met de hoofdstelling is het wel zo makkelijk.quote:Op woensdag 4 november 2009 22:13 schreef Borizzz het volgende:
[..]
Dus geen oplossingen.
Kan je dit ook concluderen met hoofdstelling?
Iets wat ik een paar maanden geleden perfect kon maar nu ben "vergeten". Opzich een hele simpele vergelijking.
N(t) = N(0) x (1/2)(t/t0,5)
Kan iemand vertellen hoe ik dit oplos als t OF t0,5 de onbekende is? Bedankt!
bijvoorbeeld:
1 = 100 x (1/2)20/t0,50)
N(t) = N(0) x (1/2)(t/t0,5)
Kan iemand vertellen hoe ik dit oplos als t OF t0,5 de onbekende is? Bedankt!
bijvoorbeeld:
1 = 100 x (1/2)20/t0,50)
Op vrijdag 11 september 2009 18:32 schreef jogy het volgende:
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Ik ben zo trots op je dat ik je in brons wil gieten, in de achtertuin wil zetten met een tuinslang door je mond als appelsjapfontein.
Het toverwoord is logartime, maar voordat ik het voor je uitwerk moet ik eerst even weten hoe die exponent in elkaar zit, bij de eerste heb je (t/t0,5) wat denk ik is: (t/(0,5t)), maar ja, dat is weer gewoon gelijk aan 2. En bij die tweede komt er opeens 20 te staan? Dat snap ik ook niet helemaal.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
