SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Uitleg staat hier.quote:Op maandag 14 juli 2014 23:16 schreef netchip het volgende:
[..]
Dit zegt mij niet erg veel.Ik zal er een nachtje overslapen.
Ik zal binnenkort nog iets posten over de meetkundige interpretatie van een vermenigvuldiging met een willekeurig complex getal ongelijk nul, die in het algemeen beantwoordt aan een draaistrekking in het complexe vlak. Dat wordt eigenlijk nooit goed uitgelegd in inleidende cursussen complexe getallen die ik heb gezien, dus dit is een goede gelegenheid om daar eens iets over te vertellen.quote:Leuk dat je er tijd insteekt om mij iets te leren over complexe getallen, Riparius.Ik merk dat ik nu nieuwe inzichten heb, jij vertelde dat een vermenigvuldiging met i een rotatie van 90 graden tegen de klok in betekent. Erg leuk (voor mij) om die kennis dan ook te gebruiken, omdat ik nu weet wat een vermenigvuldiging met i inhoudt.
Als t je parameter is, dan zijn x en y elk een functie van t. Oefeningetje nog gelukt?quote:Het kwartje met de parametervoorstellingen is nu ook gevallen. Het principe is mij duidelijk.
Die laatste helaas niet ... Ik kwam er echt niet uit.quote:
[..]
Uitleg staat hier.
[..]
Ik zal binnenkort nog iets posten over de meetkundige interpretatie van een vermenigvuldiging met een willekeurig complex getal ongelijk nul, die in het algemeen beantwoordt aan een draaistrekking in het complexe vlak. Dat wordt eigenlijk nooit goed uitgelegd in inleidende cursussen complexe getallen die ik heb gezien, dus dit is een goede gelegenheid om daar eens iets over te vertellen.
[..]
Als t je parameter is, dan zijn x en y elk een functie van t. Oefeningetje nog gelukt?
Is echt heel eenvoudig hoor (als je je goniometrische identiteiten kent ...). We hadden een kromme met als parametervoorstellingquote:
[..]
Die laatste helaas niet ... Ik kwam er echt niet uit.
(1) x = 2·sin t
(2) y = sin 2t
en gevraagd werd een cartesische vergelijking van deze kromme op te stellen. Dit is een zogeheten Lissajous figuur (zie hier voor een grafiek). Als we vergelijking (2) kwadrateren, dan hebben we
(3) y2 = (sin 2t)2 = (2·sin t·cos t)2 = 4·sin2t·cos2t = 4·sin2t(1 − sin2t) = 4·sin2t − 4·sin4t
En substitutie van (1) in (3) levert dan
y2 = 4·(½x)2 − 4·(½x)4
y2 = x2 − ¼x4
4y2 = 4x2 − x4
en dus
x4 − 4x2 + 4y2 = 0
De grafiek van deze vierdegraads kromme is uiteraard precies dezelfde Lissajous figuur.
Geen echte wiskunde, maar een stukje natuurkunde.
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Die druk voel je wel degelijk. Stel dat deze druk ineens wegvalt, ben je op zijn minst bewusteloos, als je al niet 'explodeert'.quote:
Geen echte wiskunde, maar een stukje natuurkunde.
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Die druk voel je zowel onder aan je arm als erboven. Daarom dat ie niet één kant op gelanceerd wordtquote:
Geen echte wiskunde, maar een stukje natuurkunde.
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Waarom stel je deze vraag dan niet in het andere bèta topic?quote:
Geen echte wiskunde, maar een stukje natuurkunde.
De druk binnen in je lichaam is min of meer gelijk aan de buitendruk. Maar als je bijvoorbeeld ademhaalt creëer je een onderdruk, waardoor lucht naar binnen stroomt.quote:De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Je kunt een eenvoudig proefje doen om de luchtdruk te demonstreren. Vul een beker geheel met water, zet er een onderzetter bovenop die de opening geheel afsluit, en keer de gevulde beker dan om terwijl je de onderzetter tegenhoudt zodat deze niet weg kan glijden. Als je dan bij de omgekeerde beker de onderzetter los laat maar de beker wel vast blijft houden, dan blijft de onderzetter tegen de beker zitten. Dat bewijst dus dat er van onderaf een kracht omhoog op de onderzetter wordt uitgeoefend die groter is dan de kracht omlaag die door het gravitatieveld van de aarde op het water en de onderzetter wordt uitgeoefend. En die kracht omhoog wordt uiteraard veroorzaakt door de luchtdruk.
Zoals Riparius aangeeft, jij maakt de redeneerfout om naar 1 absolute druk te kijken in plaats van naar het drukverschil tussen binnen en buiten het lichaam, boven en onder je hand etc.quote:
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Als jij je hand uitsteekt dan is de druk boven je hand even groot als onder de hand, er is dus geen drukverschil (nu ja, een verwaarloosbaar kleine waarschijnlijk maar dat is nu niet relevant) en dus geen netto kracht van die lucht. Het gaat om het drukverschil. Aanvullende opmerking: op het moment dat wij inademen wordt een onderdruk gecreëerd doordat de spieren de longen oprekken en zodoende het volume vergroten.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Op die manier. Ik dacht er inderdaad fundamenteel verkeerd over na; bedankt voor de antwoorden! Hier heb ik heel veel aan.
Ik snap niet helemaal wat je hier mee bedoelt: "En substitutie van (1) in (3) levert dan" ... Wat valt er te substitueren?quote:
[..]
Is echt heel eenvoudig hoor (als je je goniometrische identiteiten kent ...). We hadden een kromme met als parametervoorstelling
(1) x = 2·sin t
(2) y = sin 2t
en gevraagd werd een cartesische vergelijking van deze kromme op te stellen. Dit is een zogeheten Lissajous figuur (zie hier voor een grafiek). Als we vergelijking (2) kwadrateren, dan hebben we
(3) y2 = (sin 2t)2 = (2·sin t·cos t)2 = 4·sin2t·cos2t = 4·sin2t(1 − sin2t) = 4·sin2t − 4·sin4t
En substitutie van (1) in (3) levert dan
y2 = 4·(½x)2 − 4·(½x)4
y2 = x2 − ¼x4
4y2 = 4x2 − x4
en dus
x4 − 4x2 + 4y2 = 0
De grafiek van deze vierdegraads kromme is uiteraard precies dezelfde Lissajous figuur.
Ah, ik zie het nu.
sin t = x / 2quote:
[..]
Ik snap niet helemaal wat je hier mee bedoelt: "En substitutie van (1) in (3) levert dan" ... Wat valt er te substitueren?
Ah, ik zie het nu.
Hmm. Ik probeer de inverse functie van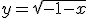 
te bepalen... Ik dacht, kwadrateer beide kanten, dan krijg je y2 = -1-x. Dan breng je de x naar links, en de y2 naar rechts, daaruit volgt dan: x = -y2-1. Maar dat blijkt dus fout te zijn...
Waarom blijkt dat fout te zijn?quote:
Hmm. Ik probeer de inverse functie van
Je moet natuurlijk wel kijken naar de domeinen waarop de functies geldig zijn.
Ik controleerde mijn antwoord aan de hand van Wolfram Alpha: http://www.wolframalpha.c(...)f+y%3Dsqrt%28-1-x%29 Ik werd in verwarring gebracht doordat WA de x in hun inverse functie laat terugkomen, maar dat is natuurlijk omdat de functie y(x) een parameter x nodig heeft. x(y) was logischer geweest, maar goed.quote:
[..]
Waarom blijkt dat fout te zijn?
Je moet natuurlijk wel kijken naar de domeinen waarop de functies geldig zijn.
[ Bericht 3% gewijzigd door netchip op 06-08-2014 14:50:07 ]
Gebruikelijke notatie is y(x) voor een functie, en y-1(x) voor de inverse. De notatie x(y) vind ik ook wel leuk, maar is ongebruikelijk en kan verwarrend zijn. Zeker als x als vrije variabele gebruikt wordt, en dan ook nog een functie moet voorstellen.quote:
[..]
Ik controleerde mijn antwoord aan de hand van Wolfram Alpha: http://www.wolframalpha.c(...)f+y%3Dsqrt%28-1-x%29 Ik werd in verwarring gebracht doordat WA de x in hun inverse functie laat terugkomen, maar dat is natuurlijk omdat de functie y(x) een parameter x nodig heeft. x(y) was logischer geweest, maar goed.
Het is beter om aanduidingen van variabelen en namen van functies niet door elkaar te gebruiken, want dan krijg je inderdaad al gauw allerlei conceptuele verwarringen. Ik heb Netchip daar overigens al eens op gewezen.quote:
[..]
Gebruikelijke notatie is y(x) voor een functie, en y-1(x) voor de inverse. De notatie x(y) vind ik ook wel leuk, maar is ongebruikelijk en kan verwarrend zijn. Zeker als x als vrije variabele gebruikt wordt, en dan ook nog een functie moet voorstellen.
Het probleem zit vooral in de notatie die je zelf hebt gekozen. Als je nu gewoon dit had gedaan dan was je vast niet in verwarring gebracht. Overigens is de notatie f−1 voor de inverse van een functie f en daarmee bijvoorbeeld sin−1x voor arcsin x nu ook niet bepaald gelukkig gekozen, zie hier mijn kanttekeningen over deze notatie.quote:
[..]
Ik controleerde mijn antwoord aan de hand van Wolfram Alpha: http://www.wolframalpha.c(...)f+y%3Dsqrt%28-1-x%29 Ik werd in verwarring gebracht doordat WA de x in hun inverse functie laat terugkomen, maar dat is natuurlijk omdat de functie y(x) een parameter x nodig heeft. x(y) was logischer geweest, maar goed.
y(x) is een functie geëvalueerd op het punt x, y is een functie en y-1 is de bijbehorende inverse functie.quote:
[..]
Gebruikelijke notatie is y(x) voor een functie, en y-1(x) voor de inverse. De notatie x(y) vind ik ook wel leuk, maar is ongebruikelijk en kan verwarrend zijn. Zeker als x als vrije variabele gebruikt wordt, en dan ook nog een functie moet voorstellen.
En het is altijd makkelijk om te controleren of je de inverse te pakken hebt, immers moet gelden dat y(y-1(x)) = y-1(y(x)) = x voor alle x.
En zo moet je dit dus niet opschrijven, zoals ik hierboven beargumenteer. Hier gebruik je y als aanduiding van een functienaam maar tevens als variabele, en dat is conceptueel onjuist. De notatie y−1 is nu ambigu, want dit stelt ook de multiplicatieve inverse van de variabele y voor. Als je daarentegen f en f−1 exclusief als namen van functies gebruikt, dan kan f−1 niet worden aangezien voor een multiplicatieve inverse, wat natuurlijk niet wegneemt dat de notatie f−1 voor de inverse functie van een functie f ongelukkig blijft.quote:
[..]
y(x) is een functie geëvalueerd op het punt x, y is een functie en y-1 is de bijbehorende inverse functie.
En het is altijd makkelijk om te controleren of je de inverse te pakken hebt, immers moet gelden dat y(y-1(x)) = y-1(y(x)) = x voor alle x.
Waar gebruik ik y als variabele? En f en f-1 zijn inderdaad beter, maar omdat de rest toch al bezig waren met het gebruiken van y en y-1, ben ik daar for the sake of consistency mee doorgegaan.quote:
[..]
En zo moet je dit dus niet opschrijven, zoals ik hierboven beargumenteer. Hier gebruik je y als aanduiding van een functienaam maar tevens als variabele, en dat is conceptueel onjuist. De notatie y−1 is nu ambigu, want dit stelt ook de multiplicatieve inverse van de variabele y voor. Als je daarentegen f en f−1 exclusief als namen van functies gebruikt, dan kan f−1 niet worden aangezien voor een multiplicatieve inverse, wat natuurlijk niet wegneemt dat de notatie f−1 voor de inverse functie van een functie f ongelukkig blijft.
Inderdaad niet expliciet, maar wel impliciet. Als je een reële functie hebt van een reële variabele x, hoe zou je dan de afhankelijke variabele willen noemen? Om iets als f(x) = √(−1 − x) te inverteren moet je de afhankelijke variabele toch ook (even) een naam geven. En als je een grafiek gaat tekenen en de horizontale as noem je de x-as, hoe zou je dan de verticale as willen noemen?quote:
[..]
Waar gebruik ik y als variabele?
Jaja. Als je namen van variabelen als namen van functies gaat gebruiken of omgekeerd, en je gaat dit dan ook nog mixen met de notatie van de multiplicatieve inverse van een variabele als inverse van een functie, dan is de chaos compleet, en dat verdient geen navolging.quote:En f en f-1 zijn inderdaad beter, maar omdat de rest toch al bezig waren was met het gebruiken van y en y-1, ben ik daar for the sake of consistency mee doorgegaan.
@netchip: de grafiek van een inverse functie verkrijg je door de grafiek van de gegeven (inverteerbare) functie te spiegelen in de lijn met vergelijking y = x. Bij een spiegeling in de lijn met vergelijking y = x gaat een punt met coördinaten (x, y) over in het punt met coördinaten (y, x). Dat impliceert dat je een vergelijking van de grafiek van het spiegelbeeld van de grafiek van een gegeven functie bij spiegeling in de lijn met vergelijking y = x kunt verkrijgen door de variabelen x en y met elkaar te verwisselen in de vergelijking y = f(x) van de grafiek van de oorspronkelijke functie.
Hebben we dus een functie f: (−∞, −1] → R met als functievoorschrift f(x) = √(−1 − x), dan heeft de grafiek van deze functie de vergelijking y = √(−1 − x). Verwisselen van x en y geeft x = √(−1 − y) en oplossen van y uit deze betrekking geeft y = −x² − 1 als vergelijking van het spiegelbeeld van de grafiek van f bij spiegeling in de lijn met vergelijking y = x. De functie f is dus inverteerbaar en de inverse van f is de functie g: [0, ∞) → R met als functievoorschrift g(x) = −x² − 1.
De notatie f−1 voor de inverse van een functie f is gebruikelijk, maar verdient geen aanbeveling, net zo min als het aanbeveling verdient om bijvoorbeeld de notatie sin−1x te gebruiken voor arcsin x. Merk ook op dat f−1(x) iets anders betekent dan f(x−1) en dat dit weer iets anders is dan f(x)−1 = (f(x))−1. Men heeft ook voorgesteld om de notatie f[−1] te gebruiken voor de inverse functie van een functie f, maar we gebruiken ook al f(n) voor de n-de afgeleide van f, en je zou dus zeggen dat f(−1) dan weer een primitieve voorstelt van f. Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi.
Een alternatief is de notatie finv voor de inverse functie van een functie f.
[ Bericht 0% gewijzigd door Riparius op 07-08-2014 05:52:49 ]
Interessant.quote:
[..]
Inderdaad niet expliciet, maar wel impliciet. Als je een reële functie hebt van een reële variabele x, hoe zou je dan de afhankelijke variabele willen noemen? Om iets als f(x) = √(−1 − x) te inverteren moet je de afhankelijke variabele toch ook (even) een naam geven. En als je een grafiek gaat tekenen en de horizontale as noem je de x-as, hoe zou je dan de verticale as willen noemen?
[..]
Jaja. Als je namen van variabelen als namen van functies gaat gebruiken of omgekeerd, en je gaat dit dan ook nog mixen met de notatie van de multiplicatieve inverse van een variabele als inverse van een functie, dan is de chaos compleet, en dat verdient geen navolging.
@netchip: de grafiek van een inverse functie verkrijg je door de grafiek van de gegeven (inverteerbare) functie te spiegelen in de lijn met vergelijking y = x. Bij een spiegeling in de lijn met vergelijking y = x gaat een punt met coördinaten (x, y) over in het punt met coördinaten (y, x). Dat impliceert dat je een vergelijking van de grafiek van het spiegelbeeld van de grafiek van een gegeven functie bij spiegeling in de lijn met vergelijking y = x kunt verkrijgen door de variabelen x en y met elkaar te verwisselen in de vergelijking y = f(x) van de grafiek van de oorspronkelijke functie.
Hebben we dus een functie f: (−∞, −1] → R met als functievoorschrift f(x) = √(−1 − x), dan heeft de grafiek van deze functie de vergelijking y = √(−1 − x). Verwisselen van x en y geeft x = √(−1 − y) en oplossen van y uit deze betrekking geeft y = −x² − 1 als vergelijking van het spiegelbeeld van de grafiek van f bij spiegeling in de lijn met vergelijking y = x. De functie f is dus inverteerbaar en de inverse van f is de functie g: [0, ∞) → R met als functievoorschrift g(x) = −x² − 1.
De notatie f−1 voor de inverse van een functie f is gebruikelijk, maar verdient geen aanbeveling, net zo min als het aanbeveling verdient om bijvoorbeeld de notatie sin−1x te gebruiken voor arcsin x. Merk ook op dat f−1(x) iets anders betekent dan f(x−1) en dat dit weer iets anders is dan f(x)−1 = (f(x))−1. Men heeft ook voorgesteld om de notatie f[−1] te gebruiken voor de inverse functie van een functie f, maar we gebruiken ook al f(n) voor de n-de afgeleide van f, en je zou dus zeggen dat f(−1) dan weer een primitieve voorstelt van f. Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi.
Een alternatief is de notatie finv voor de inverse functie van een functie f.
"Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi."
Bedoel je met de -1 bij dy/dx, de inverse functie, of 1/(dy/dx)? Volgens mij is dit geen functie (geen 'haakjesnotatie'), dus moet het wel het laatste zijn...
Dus differentiëren met de kettingregel geeft
Met y=f(x) en x=f^{-1}(y) krijg je dus
De ^-1 die Riparius aanhaalde was daar dus multiplicatief.
De waarde van de afgeleide functie is (bij een reële functie van een reële variabele) niets anders dan de richtingscoëfficiënt van de raaklijn in een punt op de grafiek van de functie. Welnu, bij twee rechte lijnen die elkaars spiegelbeeld zijn bij spiegeling in de lijn met vergelijking y = x is het product van de richtingscoëfficiënten van die lijnen gelijk aan 1, mits de lijnen niet parallel zijn aan de coördinaatassen (bewijs dit).quote:
[..]
Interessant.
"Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi."
Bedoel je met de -1 bij dy/dx, de inverse functie, of 1/(dy/dx)? Volgens mij is dit geen functie (geen 'haakjesnotatie'), dus moet het wel het laatste zijn...
Een raaklijn in een punt (x, y) op de grafiek van f gaat bij spiegeling in de lijn y = x over in de raaklijn in het punt (y, x) op de grafiek van f−1 zodat je dus direct ziet dat moet gelden
f'(x)·(f−1)'(y) = 1
oftewel, in de veel transparantere notatie van Leibniz
(dy/dx)·(dx/dy) = 1.
Easy. f(x) = 6x. f(x)-1 = x/6. m = 6, minv = 1/6. 6 * (1/6) = 1.quote:
[..]
De waarde van de afgeleide functie is (bij een reële functie van een reële variabele) niets anders dan de richtingscoëfficiënt van de raaklijn in een punt op de grafiek van de functie. Welnu, bij twee rechte lijnen die elkaars spiegelbeeld zijn bij spiegeling in de lijn met vergelijking y = x is het product van de richtingscoëfficiënten van die lijnen gelijk aan 1, mits de lijnen niet parallel zijn aan de coördinaatassen (bewijs dit).
Een raaklijn in een punt (x, y) op de grafiek van f gaat bij spiegeling in de lijn y = x over in de raaklijn in het punt (y, x) op de grafiek van f−1 zodat je dus direct ziet dat moet gelden
f'(x)·(f−1)'(y) = 1
oftewel, in de veel transparantere notatie van Leibniz
(dy/dx)·(dx/dy) = 1.
Dat is natuurlijk nog geen algemeen bewijs, een rechte lijn hoeft geen richtingscoëfficiënt 6 te hebben en hoeft ook niet door de oorsprong te gaan.quote:
[..]
Easy. f(x) = 6x. f(x)-1 = x/6. m = 6, minv = 1/6. 6 * (1/6) = 1.
f(x) = mx. f(x)-1 = x/m. m * (1/m) = 1. Ik weet dat ik de constante b mis, maar op het moment heb ik geen papier bij de hand. Ik kijk er morgen wel naar.quote:
[..]
Dat is natuurlijk nog geen algemeen bewijs, een rechte lijn hoeft geen richtingscoëfficiënt 6 te hebben en hoeft ook niet door de oorsprong te gaan.
Het is vast een kwestie van voorkeur, maar ik vind die meetkundige argumenten veel minder prettig dan een simpele toepassing van een kettingregel.quote:
[..]
De waarde van de afgeleide functie is (bij een reële functie van een reële variabele) niets anders dan de richtingscoëfficiënt van de raaklijn in een punt op de grafiek van de functie. Welnu, bij twee rechte lijnen die elkaars spiegelbeeld zijn bij spiegeling in de lijn met vergelijking y = x is het product van de richtingscoëfficiënten van die lijnen gelijk aan 1, mits de lijnen niet parallel zijn aan de coördinaatassen (bewijs dit).
Een raaklijn in een punt (x, y) op de grafiek van f gaat bij spiegeling in de lijn y = x over in de raaklijn in het punt (y, x) op de grafiek van f−1 zodat je dus direct ziet dat moet gelden
f'(x)·(f−1)'(y) = 1
oftewel, in de veel transparantere notatie van Leibniz
(dy/dx)·(dx/dy) = 1.
Riparius, ik heb 'm nu volledig uitgewerkt.
f(x) = mx+b
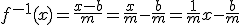
Hieruit blijkt dat de richtingscoëfficient 1/m is. m*(1/m) = 1.
f(x) = mx+b
Hieruit blijkt dat de richtingscoëfficient 1/m is. m*(1/m) = 1.
Tja, ik werk zelf graag met meetkundige argumenten om dingen te visualiseren. Uiteraard mag een bewijs in de analyse niet op meetkundige argumenten zijn gebaseerd, maar voor het begrip is het wel belangrijk om te laten zien wat een en ander meetkundig betekent. Als een leerling bijvoorbeeld niet begrijpt dat een waarde van een afgeleide functie de richtingscoëfficiënt voorstelt van de raaklijn in een punt op de grafiek van de oorspronkelijke functie, dan zal die leerling ook niet begrijpen waarom je (locale en globale) extrema van de functie op kunt sporen door de nulpunten van de afgeleide functie te bepalen, en dan verwordt differentiaalrekening tot het slaafs en mechanisch toepassen van een paar half begrepen of geheel niet begrepen regeltjes. Voorbeelden van dergelijk onbegrip hoef je niet ver te zoeken, dit forum staat er vol mee.quote:
[..]
Het is vast een kwestie van voorkeur, maar ik vind die meetkundige argumenten veel minder prettig dan een simpele toepassing van een kettingregel.
Uiteraard kun je volstaan met te zeggen dat uit (g ∘ f)' = (g' ∘ f) · f' en f ∘ f−1 = I volgt dat (f−1)' = (f' ∘ f−1)−1, waarbij f−1 de reciproke functie is van f maar (f' ∘ f−1)−1 de multiplicatieve inverse van f' ∘ f−1 voorstelt (!), maar hoe verhelderend denk je dat dit is voor een leerling die nog nauwelijks enig begrip heeft van differentiaalrekening?
Bij de differentiaalrekening blijkt met name de kettingregel vaak problemen op te leveren voor scholieren en (beginnende) studenten, en dat komt niet omdat die regel zo moeilijk zou zijn maar omdat er kennelijk het nodige schort aan de didactiek. Als je reële functies van reële variabelen opvat als afbeeldingen van een getallenlijn op een andere getallenlijn, dan kun je gemakkelijk laten zien dat de afgeleide een locale schaalfactor voorstelt en dat een samenstelling van afbeeldingen zo dus beantwoordt aan een vermenigvuldiging van locale schaalfactoren.
[ Bericht 2% gewijzigd door Riparius op 09-08-2014 00:10:09 ]
Hey,quote:
[..]
Tja, ik werk zelf graag met meetkundige argumenten om dingen te visualiseren. Uiteraard mag een bewijs in de analyse niet op meetkundige argumenten zijn gebaseerd, maar voor het begrip is het wel belangrijk om te laten zien wat een en ander meetkundig betekent. Als een leerling bijvoorbeeld niet begrijpt dat een waarde van een afgeleide functie de richtingscoëfficiënt voorstelt van de raaklijn in een punt op de grafiek van de oorspronkelijke functie, dan zal die leerling ook niet begrijpen waarom je (locale en globale) extrema van de functie op kunt sporen door de nulpunten van de afgeleide functie te bepalen, en dan verwordt differentiaalrekening tot het slaafs en mechanisch toepassen van een paar half begrepen of geheel niet begrepen regeltjes. Voorbeelden van dergelijk onbegrip hoef je niet ver te zoeken, dit forum staat er vol mee.
Uiteraard kun je volstaan met te zeggen dat uit (g ∘ f)' = (g' ∘ f) · f' en f ∘ f−1 = I volgt dat (f−1)' = (f' ∘ f−1)−1, waarbij f−1 de reciproke functie is van f maar (f' ∘ f−1)−1 de multiplicatieve inverse van f' ∘ f−1 voorstelt (!), maar hoe verhelderend denk je dat dit is voor een leerling die nog nauwelijks enig begrip heeft van differentiaalrekening?
Bij de differentiaalrekening blijkt met name de kettingregel vaak problemen op te leveren voor scholieren en (beginnende) studenten, en dat komt niet omdat die regel zo moeilijk zou zijn maar omdat er kennelijk het nodige schort aan de didactiek. Als je reële functies van reële variabelen opvat als afbeeldingen van een getallenlijn op een andere getallenlijn, dan kun je gemakkelijk laten zien dat de afgeleide een locale schaalfactor voorstelt en dat een samenstelling van afbeeldingen zo dus beantwoordt aan een vermenigvuldiging van locale schaalfactoren.
Zou jij shadowseer de beginselen van wiskunde willen uitleggen? Ik heb hem net een PM gestuurd met uitleg over het cartesisch coordinatenstelsel, en een beginnetje over variabelen en formules, en een opdracht waarbij het de bedoeling is dat hij de waardes van y voor x = 1 tot en met x = 6 uitrekent, met de formule y = 3x + 1. En dat hij de punten die volgen uit de formule aanstipt op het cartesisch assenstelsel, en dan een lijn trekt.
Jouw didactisch vermogen is een stuk beter dan de mijne.
Ik vraag dit namens shadowsheer, omdat hij dat fijner vindt.Lokquote voor shadowseer:
quote:
Ik heb zijn OP gelezen en ik voel er naar aanleiding van de lectuur daarvan niets voor om op dit verzoek in te gaan. Ik denk dat hij een psychiater nodig heeft, geen instructie in elementaire schoolwiskunde.quote:
[..]
Hey,
Zou jij shadowseer de beginselen van wiskunde willen uitleggen? Ik heb hem net een PM gestuurd met uitleg over het cartesisch coordinatenstelsel, en een beginnetje over variabelen en formules, en een opdracht waarbij het de bedoeling is dat hij de waardes van y voor x = 1 tot en met x = 6 uitrekent, met de formule y = 3x + 1. En dat hij de punten die volgen uit de formule aanstipt op het cartesisch assenstelsel, en dan een lijn trekt.
Jouw didactisch vermogen is een stuk beter dan de mijne.
Verder moeten mensen die vragen hebben die vragen hier zelf stellen, en niet via derden. Een hele tijd geleden was er hier ook een joker die - overigens hopeloos geformuleerde en nauwelijks begrijpelijke - vragen stelde namens zijn vriendin, en beweerde dat hij de antwoorden weer over zou brengen aan zijn vriendin. Op mijn vraag of zijn vriendin die vragen hier zelf niet kon stellen kwam geen bevredigend antwoord. Ik kan me voorstellen dat iemand bijvoorbeeld de Nederlandse taal niet machtig is of een lichamelijke handicap heeft waardoor hij of zij niet gebruik kan maken van een computer, maar dat was niet het geval. Volgens de vragensteller was zijn vriendin alleen niet in staat FOK te gebruiken, maar waarom dat zo was kwam niet uit de verf en wenste hij kennelijk ook niet duidelijk te maken. En dan houdt het voor mij op.
Eens. Het ligt alleen niet zo simpel voor hem, daar zit een reden achter. Het beste wat je dan kan doen, is iemand iets leren over iets wat hij vroeger interessant vond, neem ik aan.quote:
[..]
Ik heb zijn OP gelezen en ik voel er naar aanleiding van de lectuur daarvan niets voor om op dit verzoek in te gaan. Ik denk dat hij een psychiater nodig heeft, geen instructie in elementaire schoolwiskunde.
Verder moeten mensen die vragen hebben die vragen hier zelf stellen, en niet via derden. Een hele tijd geleden was er hier ook een joker die - overigens hopeloos geformuleerde en nauwelijks begrijpelijke - vragen stelde namens zijn vriendin, en beweerde dat hij de antwoorden weer over zou brengen aan zijn vriendin. Op mijn vraag of zijn vriendin die vragen hier zelf niet kon stellen kwam geen bevredigend antwoord. Ik kan me voorstellen dat iemand bijvoorbeeld de Nederlandse taal niet machtig is of een lichamelijke handicap heeft waardoor hij of zij niet gebruik kan maken van een computer, maar dat was niet het geval. Volgens de vragensteller was zijn vriendin alleen niet in staat FOK te gebruiken, maar waarom dat zo was kwam niet uit de verf en wenste hij kennelijk ook niet duidelijk te maken. En dan houdt het voor mij op.
Wie heeft een goede site met inhoud en opgaven in de analytische meetkunde? In het nieuwe schoolprogramma is daar het eea over opgenomen en ik wil me hier even in verdiepen.
kloep kloep
Wordt lastig. Ik kan je in ieder geval het oude Prisma Compendium Analytische meetkunde van C. van der Linden aanraden, waarin de vroegere stof van het middelbaar wordt behandeld. Verder bijvoorbeeld dit Amerikaanse schoolboek van bijna een eeuw geleden. Sites met specifiek opgaven over analytische meetkunde ken ik niet maar ik kwam een hele tijd geleden wel dit tegen, een vraagstuk over het bepalen van de vergelijkingen van de twee raaklijnen aan een gegeven cirkel waarbij de gebruikelijke methoden met de richtingscoëfficiënt m van de raaklijn als variabele falen voor één van beide raaklijnen om de eenvoudige reden dat één van de beide raaklijnen verticaal loopt. Kun je je leerlingen eens voorleggen en kijken of ze het probleem correct kunnen identificeren, en, belangrijker nog, of ze een algebraïsche aanpak kunnen bedenken die wél de vergelijkingen van beide raaklijnen oplevert.quote:
Wie heeft een goede site met inhoud en opgaven in de analytische meetkunde? In het nieuwe schoolprogramma is daar het eea over opgenomen en ik wil me hier even in verdiepen.
[ Bericht 0% gewijzigd door Riparius op 12-08-2014 20:00:20 ]
http://www.fi.uu.nl/wiskrant/artikelen/264/264juni_broek.pdf
Niet echt een partij waar ik veel vertrouwen in heb (realistisch rekenen en contextwiskunde) maar het is interessant om te lezen.
http://www.ru.nl/publish/(...)13_ruud_stolwijk.ppt
Wat uitleg over het nieuwe programma (PP), blijkbaar mocht ook BON aan de tafel zitten wat ik toejuich.
Niet echt een partij waar ik veel vertrouwen in heb (realistisch rekenen en contextwiskunde) maar het is interessant om te lezen.
http://www.ru.nl/publish/(...)13_ruud_stolwijk.ppt
Wat uitleg over het nieuwe programma (PP), blijkbaar mocht ook BON aan de tafel zitten wat ik toejuich.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Dit artikel is inmiddels al zeven jaar oud. Het laatste stuk is vooral een pleidooi om weer wat aan vectoren te gaan doen op school, al dan niet in combinatie met klassieke analytische meetkunde, maar het lijkt er niet op dat daar gevolg aan is gegeven. Met vectoren gaan bewijzen van sommige stellingen uit de vlakke meetkunde, de stereometrie, de analytische meetkunde en ook uit de goniometrie (additietheorema's) heel elegant en eenvoudig, maar goed dat weet je zelf allang als je mij een beetje volgt (zie bijvoorbeeld het bewijs dat het hoogtepunt H, het zwaartepunt Z en het middelpunt van de omgeschreven cirkel O in een driehoek op één rechte liggen, de zogeheten rechte van Euler, en wel zo dat HZ : ZO = 2 : 1, en zie ook je eigen vraag over de transformatieformules bij rotatie van een cartesisch assenstelsel om de oorsprong).quote:
http://www.fi.uu.nl/wiskrant/artikelen/264/264juni_broek.pdf
Niet echt een partij waar ik veel vertrouwen in heb (realistisch rekenen en contextwiskunde) maar het is interessant om te lezen.
Je kunt hier het materiaal vinden dat in de pilots is en wordt gebruikt.quote:
Wie heeft een goede site met inhoud en opgaven in de analytische meetkunde? In het nieuwe schoolprogramma is daar het eea over opgenomen en ik wil me hier even in verdiepen.
Stel, je gooit met 3 dobbelstenen. Hoeveel combinaties heb je dan in totaal om 16 te krijgen? 5 + 5 + 6 is een voorbeeld.
Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?
Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?
Er moet tenminste één 6 bij zitten, anders kan het totaal van de aantallen ogen van de drie dobbelstenen niet groter zijn dan 15. En als je een 6 hebt voor één dobbelsteen, dan zal de som van de ogen van de beide andere dobbelstenen dus 10 moeten zijn, en dat kan alleen met één 6 en één 4 of met twee maal 5. Er zijn dus slechts twee combinaties mogelijk, namelijk één maal 6 met twee maal 5 en twee maal 6 met één maal 4.quote:
Stel, je gooit met 3 dobbelstenen. Hoeveel combinaties heb je dan in totaal om 16 te krijgen? 5 + 5 + 6 is een voorbeeld.
Nee, niet echt. Kijk eens naar partities.quote:Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?
Werk (x + x2 + x3 + x4 + x5 + x6)3 uit. Dan is de coëfficiënt van x16 het antwoord.quote:
Stel, je gooit met 3 dobbelstenen. Hoeveel combinaties heb je dan in totaal om 16 te krijgen? 5 + 5 + 6 is een voorbeeld.
Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?
quote:
[..]
Werk (x + x2 + x3 + x4 + x5 + x6)3 uit. Dan is de coëfficiënt van x16 het antwoord.
Fervent tegenstander van het korps lasergamers.
Daar heb je WolframAlpha voor en dan vind je 6 als coëfficiënt van x16. Maar dat is wel het aantal combinaties dat een totaal van 16 oplevert bij het werpen met drie dobbelstenen die zich van elkaar laten onderscheiden (bijvoorbeeld één rode, één groene en één blauwe). Als de drie dobbelstenen niet van elkaar zijn te onderscheiden heb je maar 2 combinaties die 16 opleveren omdat steeds twee van de drie dobbelstenen een gelijk aantal ogen hebben bij een worp die een totaal van 16 oplevert.quote:
Op
Ja dat begrijp ik. Ik snap alleen even niet de redenatie achter dit trucje.quote:
[..]
Daar heb je WolframAlpha voor en dan vind je 6 als coëfficiënt van x16. Maar dat is wel het aantal combinaties dat een totaal van 16 oplevert bij het werpen met drie dobbelstenen die zich van elkaar laten onderscheiden (bijvoorbeeld één rode, één groene en één blauwe). Als de drie dobbelstenen niet van elkaar zijn te onderscheiden heb je maar 2 combinaties die 16 opleveren omdat steeds twee van de drie dobbelstenen een gelijk aantal ogen hebben bij een worp die een totaal van 16 oplevert.
Fervent tegenstander van het korps lasergamers.
Deze techniek staat bekend als voortbrengende functies. Als f(n) het aantal mogelijkheden is om n ogen te gooien, dan is de voortbrengende machtreeks (of polynoom in dit geval) van f(n):quote:Op woensdag 20 augustus 2014 14:14 schreef Amoeba het volgende:
[..]
Ja dat begrijp ik. Ik snap alleen even niet de redenatie achter dit trucje. [ afbeelding ]
Andere typen voortbrengende functies bestaan ook, maar laten we het simpel houden.
De voortbrengende functie voor 1 dobbelsteen is dan x + x2 + x3 + x4 + x5 + x6.
Voor m dobbelstenen krijg je als voortbrengende functie (x + x2 + x3 + x4 + x5 + x6)m. Dit kun je inzien door de haakjes uit te werken in dit product van m factoren: de factoren komen overeen met de dobbelstenen, en bij elke factor kies je een term xn die overeenkomt met de mogelijkheid dat er n ogen zijn bij die dobbelsteen. Het product van die termen is xn1+n2+...+nm, zo dat de exponent overeenkomt met de som van de ogen.
[ Bericht 0% gewijzigd door thabit op 20-08-2014 16:08:18 ]
Mooi, dan heb ik nog een sommetje voor je.quote:
Op Als je twee "gewone" dobbelstenen gooit ("gewoon" wil zeggen dat vlakken 1, 2, 3, 4, 5, en 6 ogen hebben), dan weet je hoe de verdeling van de som van de ogen is: je kunt op 1 manier 2 gooien, op 2 manieren 3, op 3 manieren 4, etc t/m op 1 manier 12.
Geef nu twee "ongewone" dobbelstenen (dwz wel met 6 vlakken, maar met andere ogenverdelingen) zo dat de som van de ogen van de twee dezelfde verdeling heeft als bij 2 gewone dobbelstenen.
OK, snap echt niet waar hier de fout inzit...
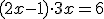dan,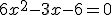 
. abc-formule (gebruikt mijn boek): D = 9 - 4 * 6 * -6 = 153. En mijn boek komt aan met 17?
Door 3 delen, dan ABC.quote:
OK, snap echt niet waar hier de fout inzit...
Is hetzelfde want 153 / 32 = 17
Ik zie het nu. Dank je!quote:
[..]
Door 3 delen, dan ABC.
Is hetzelfde want 153 / 32 = 17
Maar waarom delen door 32?
Gewoon datquote:
[..]
Ik zie het nu. Dank je!
D = b2 - 4ac
Jouw a,b en c zijn 3 keer zo groot, dus je D is 9 keer zo groot.
Omdat je daarna nog de wortel neemt en deelt door 2a (ook 3 keer zo groot) enz. komt er hetzelfde uit.
Ik heb een aantal vraagstukken en hopelijk kan iemand mij hiermee helpen:
Simplificeren van..
(4² * 6²) / (3³ * 2³)
(34(2³)6) / ((-3)1537)
(py(pq)o ) / (p 2y + o q o - 2 ) ---> de o is een standaardafwijking teken..
Het bovenstaande (delen met machten) vind ik best lastig omdat de grondgetallen niet gelijk aan elkaar zijn
- Een bedrijf heeft van 1990 tot 1991 haar winst verhoogd met 20%, maar heeft het verlaagd met 17% vanaf 1991 tot 1992. Wat voor percentage in de daling van de winst van 1991 tot 1992 laat zien dat de winsten gelijk waren in 1990 en 1992? -
Simplificeren van..
(4² * 6²) / (3³ * 2³)
(34(2³)6) / ((-3)1537)
(py(pq)o ) / (p 2y + o q o - 2 ) ---> de o is een standaardafwijking teken..
Het bovenstaande (delen met machten) vind ik best lastig omdat de grondgetallen niet gelijk aan elkaar zijn
- Een bedrijf heeft van 1990 tot 1991 haar winst verhoogd met 20%, maar heeft het verlaagd met 17% vanaf 1991 tot 1992. Wat voor percentage in de daling van de winst van 1991 tot 1992 laat zien dat de winsten gelijk waren in 1990 en 1992? -
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 1% gewijzigd door Andijvie_ op 22-08-2014 11:48:31 ]
Hint;quote:
Ik heb een aantal vraagstukken en hopelijk kan iemand mij hiermee helpen:
(4² * 6²) / (3³ * 2³)
4 = 22
6 = 3 * 2
quote:
Ik heb een aantal vraagstukken en hopelijk kan iemand mij hiermee helpen:
(4² * 6²) / (3³ * 2³)
(34(2³)6) / ((-3)1537)
(py(pq)o ) / (p 2y + o q o - 2 ) ---> de o is een standaardafwijking teken..
Het bovenstaande (delen met machten) vind ik best lastig omdat de grondgetallen niet gelijk aan elkaar zijn
- Een bedrijf heeft van 1990 tot 1991 haar winst verhoogd met 20%, maar heeft het verlaagd met 17% vanaf 1991 tot 1992. Wat voor percentage in de daling van de winst van 1991 tot 1992 laat zien dat de winsten gelijk waren in 1990 en 1992? -De winst is in 1991 met 20% gestegen ten opzichte van 1990. Hoeveel moet de winst dalen in 1992 ten opzichte van 1991 zodat de winst in 1992 gelijk is aan die van 1990?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Ohh zo, dan heb ik het wellicht verkeerd vertaald..quote:Op vrijdag 22 augustus 2014 00:02 schreef OllieWilliams het volgende:
[..]
De winst is in 1991 met 20% gestegen ten opzichte van 1990. Hoeveel moet de winst dalen in 1992 ten opzichte van 1991 zodat de winst in 1992 gelijk is aan die van 1990?
"What percentage decrease in profits from 1991 to 1992 would imply that the profits were equal in 1990 and 1992"
Ik snap hem niet? Ik heb gezien dat het niet in mijn post stond, nu wel, dat het gesimplificeerd opgeachreven moest worden.quote:
Ik kom dan uit opquote:
( 24 * 32 * 24 ) / (33 * 23)
En dat maakt
( 28 * 32 ) / ( 33 * 23 )
Dan zou ik er het volgende van maken
25 / 3 -1
Ten eerste
32 / 33 = 3-1 = 1/3
Niet 1/3-1
Dus het antwoord is
23 / 3 = 8 / 3
Ten tweedequote:
[..]
Ik kom dan uit op
( 24 * 32 * 22 ) / (33 * 23)
32 / 33 = 3-1 = 1/3
Niet 1/3-1
Dus het antwoord is
23 / 3 = 8 / 3
Zou je me ook kunnen helpen met die derde? Die tweede ga ik zelf even goed uitpuzzelen.. Die derde lukt mij niet i.v.m. die standaardafwijking teken en omdat het letters zijn..quote:
Ten eerste
[..]
Ten tweede
32 / 33 = 3-1 = 1/3
Niet 1/3-1
Dus het antwoord is
23 / 3 = 8 / 3
[ Bericht 0% gewijzigd door Andijvie_ op 22-08-2014 15:49:23 ]
De standaardafwijking wordt gewoonlijk aangegeven met de kleine Griekse letter sigma: σquote:
[..]
Zou je me ook kunnen helpen met die derde? Die tweede ga ik zelf even goed uitpuzzelen.. Die derde lukt mij niet i.v.m. die standaardafwijking teken en omdat het letters zijn..
Deze letter kun je krijgen door & sigma; te typen, maar dan zonder spatie na de ampersand.
Verder is het gewoon een kwestie van het toepassen van de standaard rekenregels voor het werken met machten.
Thnx. Ik heb nog een onduidelijkheidje:quote:
[..]
De standaardafwijking wordt gewoonlijk aangegeven met de kleine Griekse letter sigma: σ
Deze letter kun je krijgen door & sigma; te typen, maar dan zonder spatie na de ampersand.
Verder is het gewoon een kwestie van het toepassen van de standaard rekenregels voor het werken met machten.
Ontbinden in factoren van:
21x²y³
en
8x²y² - 16xy :
Ik had:
7xy² (3xy), maar het antwoordenboek geeft aan: 3 * 7 * xxyyy
en
8xy (xy - 2), maar het antwoordenboek geeft aan: 2 * 2 * 2xy ( xy - 2)
Dit ben ik niet gewend, aangezien ik het op de wijze als het antwoordenboek nooit geleerd heb..
quote:Op woensdag 20 augustus 2014 17:19 schreef thabit het volgende:
[..]
Mooi, dan heb ik nog een sommetje voor je.
Als je twee "gewone" dobbelstenen gooit ("gewoon" wil zeggen dat vlakken 1, 2, 3, 4, 5, en 6 ogen hebben), dan weet je hoe de verdeling van de som van de ogen is: je kunt op 1 manier 2 gooien, op 2 manieren 3, op 3 manieren 4, etc t/m op 1 manier 12.
Geef nu twee "ongewone" dobbelstenen (dwz wel met 6 vlakken, maar met andere ogenverdelingen) zo dat de som van de ogen van de twee dezelfde verdeling heeft als bij 2 gewone dobbelstenen.
Ik heb oneindig veel paren voor je: (1,2,3,4,5,6) + ke6 & (1,2,3,4,5,6) - ke6 voor k in N, waar e6 = (1,1,1,1,1,1). (OK, alleen k=1 en k=0 tellen dan nietquote:
O ja, (0, 1, 2, 3, 4, 5) en (2, 3, 4, 5, 6, 7) telt niet.
)
Het aantal ogen op elk van de vlakjes van elk van de beide dobbelstenen moet positief en geheel zijn aangezien je geen negatief aantal ogen kunt hebben, en dan is er precies één oplossing (afgezien van de triviale mogelijkheid om de beide dobbelstenen met elkaar te verwisselen).quote:Op vrijdag 22 augustus 2014 16:24 schreef thenxero het volgende:
[..]
[..]
Ik heb oneindig veel paren voor je: (1,2,3,4,5,6) + ke6 & (1,2,3,4,5,6) - ke6 voor k in N, waar e6 = (1,1,1,1,1,1). (OK, alleen k=1 en k=0 tellen dan niet
Kennelijk wordt bedoeld dat je de gegeven uitdrukkingen zo ver mogelijk moet ontbinden in factoren, waarmee dan wordt bedoeld dat je voor deze opgave machten moet uitschrijven als een product van gelijke factoren en tevens dat je (gehele) getallen moet ontbinden in priemfactoren.quote:
[..]
Dit ben ik niet gewend, aangezien ik het op de wijze als het antwoordenboek nooit geleerd heb..
Een wiskundige neemt nooit stilzwijgend aan dat een aantal ogen positief moet zijnquote:
[..]
Het aantal ogen op elk van de vlakjes van elk van de beide dobbelstenen moet positief en geheel zijn aangezien je geen negatief aantal ogen kunt hebben, en dan is er precies één oplossing (afgezien van de triviale mogelijkheid om de beide dobbelstenen met elkaar te verwisselen).
. Als je zeker weet dat er dan precies één oplossing is, dan is de oplossingsverzameling leeg na Thabit's opmerking.
Nee, dat laatste is niet zo. Zoals gezegd is er precies één oplossing waarbij het aantal ogen op elk van de vlakjes van elk van beide dobbelstenen geheel en positief is, de dobbelstenen niet 'normaal' zijn en de verdeling van de mogelijke uitkomsten bij het werpen met deze twee 'speciale' dobbelstenen niettemin identiek is aan de verdeling van de mogelijke uitkomsten bij het werpen met twee 'normale' dobbelstenen. Thabit heeft het vraagstuk helaas niet exact genoeg geformuleerd.quote:
[..]
Een wiskundige neemt nooit stilzwijgend aan dat een aantal ogen positief moet zijn
Hoi Riparius ik had nog een vraag.. waar ik helemaal niet uitkom. Althans ik vind het lastig, ondanks het toepassen van de rekenregels:quote:
[..]
Nee, dat laatste is niet zo. Zoals gezegd is er precies één oplossing waarbij het aantal ogen op elk van de vlakjes van elk van beide dobbelstenen geheel en positief is, de dobbelstenen niet 'normaal' zijn en de verdeling van de mogelijke uitkomsten bij het werpen met deze twee 'speciale' dobbelstenen niettemin identiek is aan de verdeling van de mogelijke uitkomsten bij het werpen met twee 'normale' dobbelstenen. Thabit heeft het vraagstuk helaas niet exact genoeg geformuleerd.
K -3 - K -6
(ontbinden in factoren)
Bedenk dat je kunt schrijven K−6 = K−3·K−3 waarna je een factor K−3 buiten haakjes kunt halen. Dan krijg je dusquote:
[..]
Hoi Riparius ik had nog een vraag.. waar ik helemaal niet uitkom. Althans ik vind het lastig, ondanks het toepassen van de rekenregels:
K -3 - K -6
(ontbinden in factoren)
K−3 − K−6 = K−3(1 − K−3)
Maar je zou ook kunnen bedenken dat K−3 = K−6·K3 waarna je een factor K−6 buiten haakjes kunt halen en je dus krijgt
K−3 − K−6 = K−6(K3 − 1)
Hierna zou je verder kunnen gaan omdat K3 − 1 = (K − 1)(K2 + K + 1), maar je zult eerst duidelijk moeten maken wat precies de bedoeling is van de opgave, aangezien je K−3 − K−6 op meerdere manieren kunt herschrijven als een product van twee of meer factoren.
Jou kan ik wel volgen, maar het antwoordenboek niet:quote:
[..]
Bedenk dat je kunt schrijven K−6 = K−3·K−3 waarna je een factor K−3 buiten haakjes kunt halen. Dan krijg je dus
K−3 − K−6 = K−3(1 − K−3)
Maar je zou ook kunnen bedenken dat K−3 = K−6·K3 waarna je een factor K−6 buiten haakjes kunt halen en je dus krijgt
K−3 − K−6 = K−6(K3 − 1)
Hierna zou je verder kunnen gaan omdat K3 − 1 = (K − 1)(K2 + K + 1), maar je zult eerst duidelijk moeten maken wat precies de bedoeling is van de opgave, aangezien je K−3 − K−6 op meerdere manieren kunt herschrijven als een product van twee of meer factoren.
K -6 (K - 1)(K2+ K + 1)
Dat is exact wat Riparius doet?quote:
[..]
Jou kan ik wel volgen, maar het antwoordenboek niet:
K -6 (K - 1)(K2+ K + 1)
Ja maar bij zijn eindantwoord stond er geen K -6 ervoor.quote:
[..]
Dat is exact wat Riparius doet?
Dat was geen 'eindantwoord', want ik verwachtte dat je de laatste stap nu zelf wel zou kunnen zetten. Ik heb gezegd datquote:
[..]
Ja maar bij zijn eindantwoord stond er geen K -6 ervoor.
K−3 − K−6 = K−6(K3 − 1)
en ook dat
K3 − 1 = (K − 1)(K2 + K + 1)
En wat krijg je dan als je de tweede betrekking in de eerste substitueert, oftewel, als je in de eerste betrekking (K3 − 1) door (K − 1)(K2 + K + 1) vervangt?
Weleens een dobbelsteen met een negatief aantal ogen gezien? Dobbelstenen met halve ogen, halve of negatief tellende zijden, of nog meer van dat soort flauwekul, daar doen we niet aan. Gewoon 6 vlakken met een positief geheel aantal ogen op elk van de vlakken, zoals Riparius opmerkte.quote:
[..]
[..]
Ik heb oneindig veel paren voor je: (1,2,3,4,5,6) + ke6 & (1,2,3,4,5,6) - ke6 voor k in N, waar e6 = (1,1,1,1,1,1). (OK, alleen k=1 en k=0 tellen dan niet
Maar goed, ik neem aan dat je de oplossing inmiddels al hebt gevonden?
Ow, dan was het een misinterpretatie geweest van mij. Ik dacht dat je het vergeten was.quote:
[..]
Dat was geen 'eindantwoord', want ik verwachtte dat je de laatste stap nu zelf wel zou kunnen zetten. Ik heb gezegd dat
K−3 − K−6 = K−6(K3 − 1)
en ook dat
K3 − 1 = (K − 1)(K2 + K + 1)
En wat krijg je dan als je de tweede betrekking in de eerste substitueert, oftewel, als je in de eerste betrekking (K3 − 1) door (K − 1)(K2 + K + 1) vervangt?
Ik heb nog een onduidelijkheid over het onderwerp ongelijkheden:
Bij de volgende ongelijkheid vraag ik me af hoe de getallenlijn eruit ziet en wat het antwoord is:
( (x-2) + 3(x+1) ) / (x+3) -< [gelijk of kleiner als] 0
Ik maakte er het volgende van:
(4x + 1) / (x+3) -< 0
Ik vraag me alleen af hoe ik zonder calculator een getallenlijn kan maken en achter het antwoord kan komen? Is het trial and error ofzo?
Bij de volgende ongelijkheid vraag ik me af hoe de getallenlijn eruit ziet en wat het antwoord is:
( (x-2) + 3(x+1) ) / (x+3) -< [gelijk of kleiner als] 0
Ik maakte er het volgende van:
(4x + 1) / (x+3) -< 0
Ik vraag me alleen af hoe ik zonder calculator een getallenlijn kan maken en achter het antwoord kan komen? Is het trial and error ofzo?
Het teken ≤ maak je door & le; te typen zonder spatie na de &. De ongelijkheid isquote:
Ik heb nog een onduidelijkheid over het onderwerp ongelijkheden:
Bij de volgende ongelijkheid vraag ik me af hoe de getallenlijn eruit ziet en wat het antwoord is:
( (x-2) + 3(x+1) ) / (x+3) -< [gelijk of kleiner als] 0
Ik maakte er het volgende van:
(4x + 1) / (x+3) -< 0
Ik vraag me alleen af hoe ik zonder calculator een getallenlijn kan maken en achter het antwoord kan komen? Is het trial and error ofzo?
(4x + 1) / (x + 3) ≤ 0
Het oplossen van een dergelijke ongelijkheid doe je niet via trial and error. In het linkerlid van de ongelijkheid heb je een breuk, en we moeten nu bepalen voor welke waarden van x de waarde van deze breuk ofwel negatief is ofwel nul.
In het algemeen is de waarde van een breuk negatief of nul als (a) de teller kleiner dan of gelijk is aan nul terwijl de noemer groter is dan nul of als (b) de teller groter dan of gelijk is aan nul terwijl de noemer kleiner is dan nul. Dus krijgen we als voorwaarden
(4x + 1 ≤ 0 ∧ x + 3 > 0) ∨ (4x + 1 ≥ 0 ∧ x + 3 < 0)
en dit geeft
(x ≤ −¼ ∧ x > −3) ∨ (x ≥ −¼ ∧ x < −3)
De tweede voorwaarde is strijdig, want een getal x kan niet gelijktijdig groter zijn dan −¼ en kleiner dan −3, zodat we alleen de eerste voorwaarde overhouden. En hiervoor kunnen we schrijven
−3 < x ≤ −¼
Anders gezegd, x moet liggen op het interval (−3, −¼].
Is dit de enige manier of zijn er nog meer makkelijke methoden?quote:
[..]
Het teken ≤ maak je door & le; te typen zonder spatie na de &. De ongelijkheid is
(4x + 1) / (x + 3) ≤ 0
Het oplossen van een dergelijke ongelijkheid doe je niet via trial and error. In het linkerlid van de ongelijkheid heb je een breuk, en we moeten nu bepalen voor welke waarden van x de waarde van deze breuk ofwel negatief is ofwel nul.
In het algemeen is de waarde van een breuk negatief of nul als (a) de teller kleiner dan of gelijk is aan nul terwijl de noemer groter is dan nul of als (b) de teller groter dan of gelijk is aan nul terwijl de noemer kleiner is dan nul. Dus krijgen we als voorwaarden
(4x + 1 ≤ 0 ∧ x + 3 > 0) ∨ (4x + 1 ≥ 0 ∧ x + 3 < 0)
en dit geeft
(x ≤ −¼ ∧ x > −3) ∨ (x ≥ −¼ ∧ x < −3)
De tweede voorwaarde is strijdig, want een getal x kan niet gelijktijdig groter zijn dan −¼ en kleiner dan −3, zodat we alleen de eerste voorwaarde overhouden. En hiervoor kunnen we schrijven
−3 < x ≤ −¼
Anders gezegd, x moet liggen op het interval (−3, −¼].
Enorm duidelijke uitleg en daar dank ik je dan ook zeer voor Riparius!
Je zou in dit geval de breuk ook kunnen herleiden door eerst de teller 4x + 1 te herschrijven als 4(x + 3) − 11, zodat je de breuk als geheel daarna kunt herschrijven als 4 − (11/(x + 3)), maar de oplossing van de ongelijkheid wordt hiermee niet eenvoudiger.quote:
[..]
Is dit de enige manier of zijn er nog meer makkelijke methoden?
In het algemeen herleid je bij ongelijkheden waarbij de onbekende in de noemer van een breuk voorkomt eerst het rechterlid op nul, en herschrijf je het linkerlid als één breuk, waarna je in het algemeen twee mogelijkheden hebt, zoals in het uitgewerkte voorbeeld hierboven. Dan houd je twee sets ongelijkheden over waarbij de onbekende niet meer in de noemer van een breuk voorkomt.
Graag gedaan.quote:Enorm duidelijke uitleg en daar dank ik je dan ook zeer voor Riparius!
Aangezien Amoeba, aan wie het vraagstuk was opgegeven, het volledig af heeft laten weten en jij kennelijk ook niet meer genegen bent om je erin te verdiepen geef ik hier voor eventuele andere geïnteresseerden maar even mijn uitwerking.quote:
De voortbrengende functie voor de uitkomsten van een worp met één reguliere dobbelsteen is
x + x2 + x3 + x4 + x5 + x6
Dit polynoom heeft 6 termen waarbij de coëfficiënt van elke term 1 is en de exponent van x van elke term het aantal ogen voorstelt op een zijde van de dobbelsteen. Door dit polynoom met zichzelf te vermenigvuldigen krijgen we de voortbrengende functie voor de uitkomsten van een worp met twee reguliere dobbelstenen. Het is eenvoudig in te zien waarom dit zo is. Als we namelijk dit polynoom met zichzelf vermenigvuldigen, dan vermenigvuldigen we elke term uit de eerste factor met elke term uit de tweede factor. Elk product stelt daarbij één mogelijke uitkomst voor bij een worp met de twee dobbelstenen. Aangezien exponenten optellen bij vermenigvuldiging krijgen we zo een polynoom waarvan de exponenten van x van de termen lopen van 2 tot en met 12 en waarbij de coëfficiënt van elke term het aantal manieren geeft waarop met twee dobbelstenen het totaal aantal ogen gelijk aan de exponent van die term kan worden verkregen. En dus hebben we zo inderdaad de voortbrengende functie voor de uitkomsten van een worp met twee reguliere dobbelstenen.
Willen we nu twee dobbelstenen vinden waarbij het aantal ogen op elk van de zes vlakjes van elk van beide dobbelstenen geheel en positief is, de dobbelstenen niet 'normaal' zijn en de verdeling van de mogelijke uitkomsten bij het werpen met deze twee 'speciale' dobbelstenen niettemin identiek is aan de verdeling van de mogelijke uitkomsten bij het werpen met twee 'normale' dobbelstenen, dan moet dus het product van de voortbrengende functies P(x) en Q(x) voor de uitkomsten van een worp met elk van deze 'speciale' dobbelstenen identiek zijn aan het kwadraat van de voortbrengende functie van de uitkomsten van een worp met één reguliere dobbelsteen, zodat moet gelden
(1) P(x)Q(x) = (x + x2 + x3 + x4 + x5 + x6)2
Nu moeten de polynomen P(x) en Q(x) wel aan een aantal voorwaarden voldoen. De algemene gedaante van een voortbrengende functie voor de uitkomsten van worp met een dobbelsteen met zes vlakjes is
xm + xn + xp + xq + xr + xs
waarbij m, n, p, q, r, s positieve gehele getallen zijn die de aantallen ogen voorstellen op elk van de zes vlakjes van de dobbelsteen. Aangezien een dergelijk polynoom geen constante term heeft, moet voor de te vinden polynomen P(x) en Q(x) dus gelden
(2) P(0) = 0, Q(0) = 0
Verder is de som van de coëfficiënten van de termen van een voortbrengende functie voor de uitkomsten van een worp met een dobbelsteen met zes vlakjes gelijk aan 6. Dit geldt uiteraard ook als twee of meer van de positieve gehele getallen m, n, p, q, r, s gelijk aan elkaar zijn en het aantal termen van het polynoom dus minder is dan 6. Als bijvoorbeeld n = m, dan is xm + xn = 2xm zodat aan de som van de coëfficiënten van het polynoom niets verandert. De coëfficiënten van de te vinden polynomen P(x) en Q(x) zijn dus positief en geheel en voor deze polynomen moet ook gelden
(3) P(1) = 6, Q(1) = 6
Nu volgt uit (1) dat het product P(x)Q(x) dezelfde factoren bevat als (x + x2 + x3 + x4 + x5 + x6)2 en dat betekent dat elk van de factoren van (x + x2 + x3 + x4 + x5 + x6)2 een factor is van hetzij P(x) hetzij Q(x). Ontbinden we dus x + x2 + x3 + x4 + x5 + x6 en daarmee (x + x2 + x3 + x4 + x5 + x6)2 in factoren, dan kunnen we nagaan of we deze factoren op een zodanige wijze over P(x) en Q(x) kunnen verdelen dat beide polynomen ongelijk zijn aan x + x2 + x3 + x4 + x5 + x6 terwijl nog steeds aan de voorwaarden (2) en (3) wordt voldaan. Als dit lukt, dan hebben we de voortbrengende functies en daarmee de verdeling van de ogen van de gevraagde speciale dobbelstenen gevonden.
Welnu, het ontbinden in factoren van de veelterm x + x2 + x3 + x4 + x5 + x6 is niet moeilijk. Om te beginnen kunnen we een factor x buiten haakjes halen, en dit geeft
x(1 + x + x2 + x3 + x4 + x5)
Nu is gemakkelijk te zien dat de veelterm 1 + x + x2 + x3 + x4 + x5 een nulpunt x = −1 heeft, zodat deze veelterm een factor (x + 1) bevat. Halen we per tweetal opeenvolgende termen een factor (1 + x) buiten haakjes, dan krijgen we
1 + x + x2 + x3 + x4 + x5 = (1 + x) + (1 + x)x2 + (1 + x)x4 = (1 + x)(1 + x2 + x4)
De veelterm 1 + x2 + x4 kunnen we nog ontbinden in twee kwadratische veeltermen. Met behulp van kwadraatafsplitsing krijgen we
1 + x2 + x4 = (1 + x2)2 − x2 = (1 + x + x2)(1 − x + x2)
De kwadratische veeltermen 1 + x + x2 en 1 − x + x2 zijn niet verder te ontbinden in reële lineaire factoren (en dus a fortiori niet in lineaire factoren met gehele coëfficiënten) aangezien de discriminanten van deze kwadratische veeltermen negatief zijn. We vinden dus
x + x2 + x3 + x4 + x5 + x6 = x(1 + x)(1 + x + x2)(1 − x + x2)
zodat we op grond van (1) hebben
(4) P(x)Q(x) = x2(1 + x)2(1 + x + x2)2(1 − x + x2)2
We hebben nu acht factoren die we moeten verdelen over P(x) en Q(x). Het is duidelijk dat P(x) en Q(x) elk één factor x moeten bevatten, aangezien op grond van (2) moet gelden P(0) = 0 en tevens Q(0) = 0. Verder is het zo dat de factoren (1 + x), (1 + x + x2) en (1 − x + x2) voor x = 1 gelijk zijn aan resp. 2, 3 en 1. En aangezien op grond van (3) moet gelden P(1) = 6 en tevens Q(1) = 6 volgt uit (4) dat P(x) en Q(x) elk één factor (1 + x) en één factor (1 + x + x2) moeten bevatten.
Nu blijven alleen nog de beide factoren (1 − x + x2) over om te verdelen over P(x) en Q(x). Het is echter duidelijk dat de beide factoren (1 − x + x2) samen in één van de beide polynomen P(x) en Q(x) moeten zitten als deze polynomen ongelijk moeten zijn aan x + x2 + x3 + x4 + x5 + x6. Er is dus, afgezien van de verwisseling van P(x) en Q(x), precies één paar voortbrengende functies P(x) en Q(x) dat aan het gevraagde voldoet. Stoppen we de beide factoren (1 − x + x2) in Q(x) dan hebben we
(5) P(x) = x(1 + x)(1 + x + x2) = x + 2x2 + 2x3 + x4
en
(6) Q(x) = x(1 + x)(1 + x + x2)(1 − x + x2)2 = x + x3 + x4 + x5 + x6 + x8
De gevraagde verdeling van de aantallen ogen op de speciale dobbelstenen is dus (1, 2, 2, 3, 3, 4) en (1, 3, 4, 5, 6, 8).
[ Bericht 0% gewijzigd door Riparius op 24-08-2014 23:46:06 ]
Mooi uitgewerkt!quote:
Ik vind het leuke puzzels maar ik heb er nu weinig tijd voor. Ben bezig met mijn masterscriptie en het regelen van een Phd plek, dus er zijn al voldoende puzzels die ik moet oplossen
.
Ik wil 2(x+2)^2 ontbinden in factoren. Na een (mislukte) poging kwam ik uit op:
2x^2+4^2, maar dat klopt natuurlijk niet. Kan iemand mij een opstapje geven over hoe ik deze formule moet ontbinden in factoren (m.n. hoe ik die kwadraat daarin moet verwerken).
Edit:
Laat maar: 2x^2+8x+8
[ Bericht 3% gewijzigd door Holograph op 28-08-2014 21:13:31 ]
2x^2+4^2, maar dat klopt natuurlijk niet. Kan iemand mij een opstapje geven over hoe ik deze formule moet ontbinden in factoren (m.n. hoe ik die kwadraat daarin moet verwerken).
Edit:
Laat maar: 2x^2+8x+8
[ Bericht 3% gewijzigd door Holograph op 28-08-2014 21:13:31 ]
Nu heb je de haakjes uitgewerkt. Ontbinden in factoren wordt iets van de vorm
(2x+...)(x+...)
(2x+...)(x+...)
Opinion is the medium between knowledge and ignorance (Plato)
Ik moest iig de haakjes wegwerkenquote:
Nu heb je de haakjes uitgewerkt. Ontbinden in factoren wordt iets van de vorm
(2x+...)(x+...)
Ik dacht dat dat 'ontbinden in factoren' heet, maar de laatste keer dat ik wiskunde heb gehad is ook alweer 4 jaar geleden..
Ontbinden in factoren is min of meer het tegenovergestelde. Maar eigenlijk was waarmee je begon al ontbonden in factoren.quote:
[..]
Ik moest iig de haakjes wegwerken
Opinion is the medium between knowledge and ignorance (Plato)
M = aY + B(r - y)-8
*: Y en y zijn twee verschillende tekens (variabelen). -8 is ook een teken-variabele maar ik heb geen idee hoe ik dat invoer hier...
De vraag is:
Solve the equation for r.
Ik heb geen idee.
Kunnen jullie mij helpen?
Verderop staat dat ik makkelijk moet kunnen zien dat de functie gelijk is aan
(r - y)-8 = (M - aY)/B
Ik snap het niet en kan het niet inzien. Daarnaast snap ik nog ook niet waarom het M - aY is en niet aY - M
*: Y en y zijn twee verschillende tekens (variabelen). -8 is ook een teken-variabele maar ik heb geen idee hoe ik dat invoer hier...
De vraag is:
Solve the equation for r.
Ik heb geen idee.
Kunnen jullie mij helpen?
Verderop staat dat ik makkelijk moet kunnen zien dat de functie gelijk is aan
(r - y)-8 = (M - aY)/B
Ik snap het niet en kan het niet inzien. Daarnaast snap ik nog ook niet waarom het M - aY is en niet aY - M
Je haalt de aY naar links, plus wordt min dus M - aY. Dan haal je B naar links, vermenigvuldigen wordt delen. Dan schrijven met r aan één kant van het = teken en de rest aan de andere kant.quote:
M = aY + B(r - y)-8
*: Y en y zijn twee verschillende tekens (variabelen). -8 is ook een teken-variabele maar ik heb geen idee hoe ik dat invoer hier...
De vraag is:
Solve the equation for r.
Ik heb geen idee.
Kunnen jullie mij helpen?
Verderop staat dat ik makkelijk moet kunnen zien dat de functie gelijk is aan
(r - y)-8 = (M - aY)/B
Ik snap het niet en kan het niet inzien. Daarnaast snap ik nog ook niet waarom het M - aY is en niet aY - M
Dankje.quote:
[..]
Je haalt de aY naar links, plus wordt min dus M - aY. Dan haal je B naar links, vermenigvuldigen wordt delen. Dan schrijven met r aan één kant van het = teken en de rest aan de andere kant.
Ik weet niet hoe je een verbonden functie uit elkaar moet halen (r - y)-8
Alles wat er tussen de haakjes staat kun je voor nu beschouwen als één ding. Zaak is om de macht weg te werken, weet je hoe dat werkt?quote:
[..]
Dankje.
Ik weet niet hoe je een verbonden functie uit elkaar moet halen (r - y)-8
Ja een negatieve macht is hetzelfde als delen.quote:
[..]
Alles wat er tussen de haakjes staat kun je voor nu beschouwen als één ding. Zaak is om de macht weg te werken, weet je hoe dat werkt?
Bijv. x-5 is gelijk aan
1 / x5
Klopt, maar we willen r hebben en niet r8quote:
[..]
Ja een negatieve macht is hetzelfde als delen.
Bijv. x-5 is gelijk aan
1 / x5
Dus moeten we die macht zien weg te krijgen, weet je ook hoe dat werkt?
Die 8 wegkrijgen ehmm..quote:
[..]
Klopt, maar we willen r hebben en niet r8
Dat wordt dan 1/8 (als exponent) aan de rechterzijde van de = teken.
Edit: ik heb hem door. Jij legt ook, net als Riparius, uit alsof je een docent bent.
Dankje!!
Goed bezigquote:
[..]
Die 8 wegkrijgen ehmm..
Dat wordt dan 1/8 (als exponent) aan de rechterzijde van de = teken.
Edit: ik heb hem door. Jij legt ook, net als Riparius, uit alsof je een docent bent.
Dankje!!
Heb moeite met n polynoomfunctie
Kan een van jullie mij helpen met het volgende;
x^4+2x^2=8
Zonder gebruik van een GR kom ik er niet uit, moet ik bekennen
Kan een van jullie mij helpen met het volgende;
x^4+2x^2=8
Zonder gebruik van een GR kom ik er niet uit, moet ik bekennen
Ik heb een paar bladzijdes volgeschreven (met onzin), maar het juiste antwoord heb ik niet gevonden.quote:
Jouw reactie gaf me nieuwe inzichten maar t is me niet gelukt chef
ik kan wel beredeneren dat x √2 of -√2 moet zijn : x^2(x^2+2)=8 maar of dat de juiste (geaccepteerde) methode van tot de uitkomst komen is ben ik me niet zeker vanquote:
Tsja Henk, zo moeilijk is dit toch niet?
Hoe heb je dat beredeneerd?quote:
[..]
ik kan wel beredeneren dat x √2 of -√2 moet zijn : x^2(x^2+2)=8 maar of dat de juiste (geaccepteerde) methode van tot de uitkomst komen is ben ik me niet zeker van
Ik neem trouwens aan dat je alleen reële oplossingen hoeft te geven?
Opinion is the medium between knowledge and ignorance (Plato)
x4 + 2x2 = 8quote:
Heb moeite met n polynoomfunctie
Kan een van jullie mij helpen met het volgende;
x^4+2x^2=8
Zonder gebruik van een GR kom ik er niet uit, moet ik bekennen
x4 + 2x2 − 8 = 0
Het linkerlid kun je nu gemakkelijk ontbinden in (kwadratische) factoren. Daarvoor zoek je twee (gehele) getallen waarvan de som +2 is en het product −8. Die getallen zijn +4 en −2. Dan krijgen we
(x2 + 4)(x2 − 2) = 0
x2 + 4 = 0 ∨ x2 − 2 = 0
x2 = −4 ∨ x2 = 2
De eerste vergelijking heeft in R geen oplossingen aangezien het kwadraat van een reëel getal niet negatief kan zijn. Voor de tweede vergelijking vinden we dan
x = √2 ∨ x = −√2
Dat is alles.
Bedankt voor je reactie chefquote:
[..]
x4 + 2x2 = 8
x4 + 2x2 − 8 = 0
Het linkerlid kun je nu gemakkelijk ontbinden in (kwadratische) factoren. Daarvoor zoek je twee (gehele) getallen waarvan de som +2 is en het product −8. Die getallen zijn +4 en −2. Dan krijgen we
(x2 + 4)(x2 − 2) = 0
x2 + 4 = 0 ∨ x2 − 2 = 0
x2 = −4 ∨ x2 = 2
De eerste vergelijking heeft in R geen oplossingen aangezien het kwadraat van een reëel getal niet negatief kan zijn. Voor de tweede vergelijking vinden we dan
x = √2 ∨ x = −√2
Dat is alles.
Zeer verhelderend
Bereken de afgeleide en herleid tot 1 breuk:
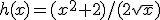
h'(x)= 3/4*sqrtx - 1/(2x*sqrtx)
Ik kom er niet echt uit hoe ik hem verder kan oplossen.
[ Bericht 7% gewijzigd door rareziekte op 31-08-2014 13:50:19 ]
h'(x)= 3/4*sqrtx - 1/(2x*sqrtx)
Ik kom er niet echt uit hoe ik hem verder kan oplossen.
[ Bericht 7% gewijzigd door rareziekte op 31-08-2014 13:50:19 ]
Dit is in principe gewoon toepassen van de regels voor differentiëren. Waar loop je vast?quote:
Bereken de afgeleide en herleid tot 1 breuk:
h'(x)= 3/4*sqrtx - 1/(2x*sqrtx)
Ik kom er niet echt uit hoe ik hem verder kan oplossen.
Het is duidelijk dat hij vastloopt op het herleiden van de twee termen van zijn afgeleide tot gelijknamige breuken. Dat heeft an sich niets met differentiëren te maken maar alles met gebrekkige algebraïsche vaardigheden die weer zijn terug te voeren op onvoldoende rekenvaardigheid.quote:
[..]
Dit is in principe gewoon toepassen van de regels voor differentiëren. Waar loop je vast?
Je hebt gelijk. Ik weet dat ik de noemer gelijk kan stellen, maar heb geen idee hoe dat te doen met (3/4)*sqrtxquote:
[..]
Het is duidelijk dat hij vastloopt op het herleiden van de twee termen van zijn afgeleide tot gelijknamige breuken. Dat heeft an sich niets met differentiëren te maken maar alles met gebrekkige algebraïsche vaardigheden die weer zijn terug te voeren op onvoldoende rekenvaardigheid.
Vermenigvuldig de eerste term met x2 / x2 en de tweede term met 2√x / 2√x, dan krijg je twee gelijknamige breuken met als noemer 4x2.quote:
[..]
Je hebt gelijk. Ik weet dat ik de noemer gelijk kan stellen, maar heb geen idee hoe dat te doen met (3/4)*sqrtx
Ik had niet gezien dat de afgeleide al in de post stond.quote:
[..]
Het is duidelijk dat hij vastloopt op het herleiden van de twee termen van zijn afgeleide tot gelijknamige breuken. Dat heeft an sich niets met differentiëren te maken maar alles met gebrekkige algebraïsche vaardigheden die weer zijn terug te voeren op onvoldoende rekenvaardigheid.
Ik snap het volgende niet wat betrekking heeft tot een uitleg over de abc formule en zou daar graag wat hulp bij willen, mits dat mogelijk is van één van jullie wiskundigen
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die laatste spoiler is totaal onbekend voor mij met name doordat alles door elkaar is (exponenten, letters, wortels etc etc.) ..
En tenslotte een simpele, waar ik alleen niet begrijp waarom er een a staat aan de rechterzijde van de vergelijking:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 17% gewijzigd door BroodjeKebab op 01-09-2014 23:12:04 ]quote:
Ik snap het volgende niet wat betrekking heeft tot een uitleg over de abc formule en zou daar graag wat hulp bij willen, mits dat mogelijk is van één van jullie wiskundigenSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die laatste spoiler is totaal onbekend voor mij met name doordat alles door elkaar is (exponenten, letters, wortels etc etc.) ..
En tenslotte een simpele, waar ik alleen niet begrijp waarom er een a staat aan de rechterzijde van de vergelijking:Ik moet zeggen dat ik de tekst (of de vertaling ervan?) onder de eerste spoiler niet begrijp. Ik denk wel dat ik weet wat er bedoeld wordt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Er wordt geprobeerd van de linkerkant een kwadraat (in Engelse literatuur noemt men dit, als ik het me goed herinner, vaak een 'perfect square') te maken. Door toepassing van
(a + b)² = a² + 2ab + b²
kunnen we zien dat
(x + p/2)² = x² + px + (p/2)²
En deze laatste term, (p/2)2, kunnen we dus aan x² + px = -q toevoegen om zo een 'perfect square' aan de linkerkant te krijgen:
(x + p/2)² = (p/2)² - q
En vervolgens kan je gebruiken dat als a² = b dan a = √b of a = -√b, om een formule voor x te krijgen.
Wat je bedoelt met 'oplossen' weet ik niet, ik neem dat je de formules moet vereenvoudigen. Dan nog is het me niet helemaal duidelijk in welke vorm de formules het meest vereenvoudigd zijn (want volgens mij bestaat er geen echt simpele uitdrukking voor de gegeven formules).
Om de formules in je tweede spoiler te vereenvoudigen moet je gebruikmaken van de rekenregels voor machten en wortels, zoals je ongetwijfeld weet. Het werkt beter als je uitlegt tot waar je komt en waar je vastloopt of niet zeker over bent. De eerste formule zullen de meeste mensen simpeler te vereenvoudigen vinden dan de tweede (hoewel beide goede testen zijn of je de rekenregels goed toepast). Heb je met allebei problemen?
Onthoud
apar = ap+r
De r-de machtswortel van a is a1/r
1/(a/b)=b/a
(ap)r = apr
En als laatste:
Als a er niet zou staan aan de rechterkant, zou er x² ipv ax² na het wegwerken van de haakjes van (x - x1)(x - x2).
[ Bericht 2% gewijzigd door defineaz op 02-09-2014 02:40:02 ]quote:
Ik snap het volgende niet wat betrekking heeft tot op een uitleg over de abc formule en zou daar graag wat hulp bij willen, mits dat mogelijk is van één van jullie wiskundigenOm te beginnen: als je citeert, gebruik dan liever geen spoilers, dat maakt het quoten van passages van je post onnodig lastig en je bericht zelf minder leesbaar.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Het lijkt erop dat je hier een Engelse tekst door een vertaalmachine hebt gehaald, het is althans niet te hopen dat dit je eigen vertaling is. Zoals ik al eerder heb opgemerkt heeft het gebruik van het Engels in een Nederlandse onderwijssituatie niet zelden een dramatische verslechtering van de kennisoverdracht tot gevolg, en dat wordt hier weer eens treffend geïllustreerd.
Het gaat hier feitelijk om een afleiding van de wortelformule voor de oplossing van de kwadratische vergelijking x2 + px + q = 0, en deze formule wordt de pq-formule genoemd, niet de abc-formule. In het Duitse taalgebied spreekt men om het onderscheid aan te geven wel van de kleine Lösungsformel terwijl de abc-formule die de oplossingen geeft van ax2 + bx + c = 0 (a ≠ 0) de große Lösungsformel wordt genoemd. Het is overigens heel goed mogelijk de abc-formule af te leiden uit de pq-formule door p = b/a en q = c/a te substitueren.
Om te begrijpen hoe de pq-formule resp. de abc-formule kan worden afgeleid is het nodig de techniek van de kwadraatafsplitsing te begrijpen. In het Engels heet deze techniek (vanuit een iets ander perspectief) completing the square oftewel het completeren van een (volkomen) kwadraat. Het komt erop neer dat we de constante term q van de kwadratische vergelijking x2 + px + q = 0 overbrengen naar het rechterlid door van beide leden q af te trekken, zodat we x2 + px = −q krijgen. Vervolgens gaan we dan het linkerlid aanvullen tot een volkomen kwadraat door bij beide leden een geschikt gekozen constante op te tellen. Daarna kunnen we gebruik maken van één van de merkwaardige producten (identiteiten)
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
om het linkerlid van de vergelijking te herschrijven als een kwadraat. Om deze techniek beter te begrijpen moet je dit eens goed doornemen. Het is ook van belang de techniek van het kwadraatafsplitsen te oefenen door een aantal kwadratische vergelijkingen met deze methode op te lossen, zie bijvoorbeeld hier en hier voor uitgewerkte voorbeelden.
Heb je de techniek van het kwadraatafsplitsen onder de knie, dan zul je ook deze afleiding van de pq-formule alsmede deze afleiding van de abc-formule goed kunnen begrijpen.quote:Dit zijn geen functies maar uitdrukkingen, waarbij het kennelijk de bedoeling is dat je deze uitdrukkingen zo ver mogelijk vereenvoudigt. Het is natuurlijk onzin om op te merken dat iets 'totaal onbekend' is omdat het er wat ingewikkelder uitziet dan je wellicht gewend bent. Het is ook niet nodig om in één oogopslag te kunnen overzien wat een dergelijke uitdrukking nu eigenlijk voorstelt. Je kunt bij het vereenvoudigen stap voor stap te werk gaan, waarbij je voor elke stap een jou bekende rekenregel gebruikt om de uitdrukking in een eenvoudiger vorm te brengen, totdat je op een punt aan bent gekomen waarbij verdere vereenvoudigingen niet meer mogelijk zijn of in ieder geval niet zinvol.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die laatste spoiler is totaal onbekend voor mij met name doordat alles door elkaar is (exponenten, letters, wortels etc etc.) ..
Voor de eerste uitdrukking kun je bedenken dat
p√a = a1/p en r√a = a1/r
zodat
p√a · r√a = a1/p·a1/r
en dit geeft ons dan weer de mogelijkheid om de rekenregel te gebruiken die zegt dat exponenten optellen bij het vermenigvuldigen van twee machten van hetzelfde grondtal. We hebben 1/p + 1/r = r/pr + p/pr = (r+p)/pr = (p+r)/pr en dus ook
a1/p·a1/r = a(p+r)/pr
Nu zien we dat de breuk die we moeten vereenvoudigen in zowel de teller als de noemer een factor a(p+r)/pr heeft. Dat betekent dat we de breuk kunnen vereenvoudigen door teller en noemer elk door deze factor a(p+r)/pr te delen en dan houden we over
apr / 1 = apr
en dit is niet verder te vereenvoudigen. Je ziet dus dat de wat ingewikkeld ogende uitdrukking niets anders is dan apr.
De tweede opgave is niet meer dan een simpele invuloefening, omdat hier immers is gegeven dat x = 2. Maar we kunnen onszelf hier wel wat rekenwerk besparen door gebruik te maken van de gekende rekenregels woor het werken met machten, en het is kennelijk ook de bedoeling geweest van de maker van de opgave dat je dit inziet. Kijken we naar de teller van de breuk onder het wortelteken dan hebben we met x = 2
2(x²)·42x = 24·42·2 = 16·(42)2 = 16·162 = 163
zodat de teller en de noemer van de breuk onder het wortelteken voor x = 2 beide gelijk zijn aan 163. Maar dat betekent dat de waarde van de breuk onder het wortelteken voor x = 2 dus gelijk is aan 163 / 163 = 1. En de wortel uit 1 is 1. De uitdrukking is dus gelijk aan 1 voor x = 2.quote:En tenslotte een simpele, waar ik alleen niet begrijp waarom er een a staat aan de rechterzijde van de vergelijking:Hebben we een veelterm oftewel een polynoom P(x) in de variabele x, dan zegt de factorstelling dat P(x) een factor (x − x0) bevat dan en slechts dan als x0 een nulpunt is van P(x), oftewel dan en slechts dan als x0 een oplossing is van de vergelijking P(x) = 0 en dus geldt P(x0) = 0.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Welnu, als x1 en x2 de oplossingen zijn van de vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
dan is dus volgens de factorstelling zowel (x − x1) als (x − x2) een factor van de veelterm ax2 + bx + c. En daarmee is het product (x − x1)(x − x2) eveneens een factor van ax2 + bx + c. Maar het is ook duidelijk dat dit product in het algemeen niet identiek is met
ax2 + bx + c
want als we (x − x1)(x − x2) uitwerken, dan krijgen we
x2 − (x1 + x2)x + x1x2
Er ontbreekt dus nog een factor a. We kunnen nu concluderen dat een vierkantsvergelijking
(1) ax2 + bx + c = 0 (a ≠ 0)
met als oplossingen x1 en x2 ook is te schrijven als
(2) ax2 − a(x1 + x2)x + ax1x2 = 0 (a ≠ 0)
Aangezien (1) en (2) dezelfde vergelijking voorstellen, moeten de coëfficiënten van (1) en (2) identiek zijn, zodat dus geldt −a(x1 + x2) = b en dus
(3) x1 + x2 = −b/a
en ook ax1x2 = c en dus
(4) x1x2 = c/a
De betrekkingen (3) en (4) die een verband geven tussen de oplossingen x1 en x2 en de coëfficiënten a, b en c van de vierkantsvergelijking (1) heten de formules van Viète voor de vierkantsvergelijking (1). Uitgaande van de betrekkingen (3) en (4) zou je uitdrukkingen voor x1 en x2 in a, b en c af kunnen leiden, en dan heb je dus een alternatieve methode om de abc-formule af te leiden, zie ook hier.Enorm bedankt voor je uitleg. De eerste twee is mij enorm duidelijk.quote:
[..]
Om te beginnen: als je citeert, gebruik dan liever geen spoilers, dat maakt het quoten van passages van je post onnodig lastig en je bericht zelf minder leesbaar.
Het lijkt erop dat je hier een Engelse tekst door een vertaalmachine hebt gehaald, het is althans niet te hopen dat dit je eigen vertaling is. Zoals ik al eerder heb opgemerkt heeft het gebruik van het Engels in een Nederlandse onderwijssituatie niet zelden een dramatische verslechtering van de kennisoverdracht tot gevolg, en dat wordt hier weer eens treffend geïllustreerd.
Het gaat hier feitelijk om een afleiding van de wortelformule voor de oplossing van de kwadratische vergelijking x2 + px + q = 0, en deze formule wordt de pq-formule genoemd, niet de abc-formule. In het Duitse taalgebied spreekt men om het onderscheid aan te geven wel van de kleine Lösungsformel terwijl de abc-formule die de oplossingen geeft van ax2 + bx + c = 0 (a ≠ 0) de große Lösungsformel wordt genoemd. Het is overigens heel goed mogelijk de abc-formule af te leiden uit de pq-formule door p = b/a en q = c/a te substitueren.
Om te begrijpen hoe de pq-formule resp. de abc-formule kan worden afgeleid is het nodig de techniek van de kwadraatafsplitsing te begrijpen. In het Engels heet deze techniek (vanuit een iets ander perspectief) completing the square oftewel het completeren van een (volkomen) kwadraat. Het komt erop neer dat we de constante term q van de kwadratische vergelijking x2 + px + q = 0 overbrengen naar het rechterlid door van beide leden q af te trekken, zodat we x2 + px = −q krijgen. Vervolgens gaan we dan het linkerlid aanvullen tot een volkomen kwadraat door bij beide leden een geschikt gekozen constante op te tellen. Daarna kunnen we gebruik maken van één van de merkwaardige producten (identiteiten)
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
om het linkerlid van de vergelijking te herschrijven als een kwadraat. Om deze techniek beter te begrijpen moet je dit eens goed doornemen. Het is ook van belang de techniek van het kwadraatafsplitsen te oefenen door een aantal kwadratische vergelijkingen met deze methode op te lossen, zie bijvoorbeeld hier en hier voor uitgewerkte voorbeelden.
Heb je de techniek van het kwadraatafsplitsen onder de knie, dan zul je ook deze afleiding van de pq-formule alsmede deze afleiding van de abc-formule goed kunnen begrijpen.
[..]
Dit zijn geen functies maar uitdrukkingen, waarbij het kennelijk de bedoeling is dat je deze uitdrukkingen zo ver mogelijk vereenvoudigt. Het is natuurlijk onzin om op te merken dat iets 'totaal onbekend' is omdat het er wat ingewikkelder uitziet dan je wellicht gewend bent. Het is ook niet nodig om in één oogopslag te kunnen overzien wat een dergelijke uitdrukking nu eigenlijk voorstelt. Je kunt bij het vereenvoudigen stap voor stap te werk gaan, waarbij je voor elke stap een jou bekende rekenregel gebruikt om de uitdrukking in een eenvoudiger vorm te brengen, totdat je op een punt aan bent gekomen waarbij verdere vereenvoudigingen niet meer mogelijk zijn of in ieder geval niet zinvol.
Voor de eerste uitdrukking kun je bedenken dat
p√a = a1/p en r√a = a1/r
zodat
p√a · r√a = a1/p·a1/r
en dit geeft ons dan weer de mogelijkheid om de rekenregel te gebruiken die zegt dat exponenten optellen bij het vermenigvuldigen van twee machten van hetzelfde grondtal. We hebben 1/p + 1/r = r/pr + p/pr = (r+p)/pr = (p+r)/pr en dus ook
a1/p·a1/r = a(p+r)/pr
Nu zien we dat de breuk die we moeten vereenvoudigen in zowel de teller als de noemer een factor a(p+r)/pr heeft. Dat betekent dat we de breuk kunnen vereenvoudigen door teller en noemer elk door deze factor a(p+r)/pr te delen en dan houden we over
apr / 1 = apr
en dit is niet verder te vereenvoudigen. Je ziet dus dat de wat ingewikkeld ogende uitdrukking niets anders is dan apr.
De tweede opgave is niet meer dan een simpele invuloefening, omdat hier immers is gegeven dat x = 2. Maar we kunnen onszelf hier wel wat rekenwerk besparen door gebruik te maken van de gekende rekenregels woor het werken met machten, en het is kennelijk ook de bedoeling geweest van de maker van de opgave dat je dit inziet. Kijken we naar de teller van de breuk onder het wortelteken dan hebben we met x = 2
2(x²)·42x = 24·42·2 = 16·(42)2 = 16·162 = 163
zodat de teller en de noemer van de breuk onder het wortelteken voor x = 2 beide gelijk zijn aan 163. Maar dat betekent dat de waarde van de breuk onder het wortelteken voor x = 2 dus gelijk is aan 163 / 163 = 1. En de wortel uit 1 is 1. De uitdrukking is dus gelijk aan 1 voor x = 2.
[..]
Hebben we een veelterm oftewel een polynoom P(x) in de variabele x, dan zegt de factorstelling dat P(x) een factor (x − x0) bevat dan en slechts dan als x0 een nulpunt is van P(x), oftewel dan en slechts dan als x0 een oplossing is van de vergelijking P(x) = 0 en dus geldt P(x0) = 0.
Welnu, als x1 en x2 de oplossingen zijn van de vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
dan is dus volgens de factorstelling zowel (x − x1) als (x − x2) een factor van de veelterm ax2 + bx + c. En daarmee is het product (x − x1)(x − x2) eveneens een factor van ax2 + bx + c. Maar het is ook duidelijk dat dit product in het algemeen niet identiek is met
ax2 + bx + c
want als we (x − x1)(x − x2) uitwerken, dan krijgen we
x2 − (x1 + x2)x + x1x2
Er ontbreekt dus nog een factor a. We kunnen nu concluderen dat een vierkantsvergelijking
(1) ax2 + bx + c = 0 (a ≠ 0)
met als oplossingen x1 en x2 ook is te schrijven als
(2) ax2 − a(x1 + x2)x + ax1x2 = 0 (a ≠ 0)
Aangezien (1) en (2) dezelfde vergelijking voorstellen, moeten de coëfficiënten van (1) en (2) identiek zijn, zodat dus geldt −a(x1 + x2) = b en dus
(3) x1 + x2 = −b/a
en ook ax1x2 = c en dus
(4) x1x2 = c/a
De betrekkingen (3) en (4) die een verband geven tussen de oplossingen x1 en x2 en de coëfficiënten a, b en c van de vierkantsvergelijking (1) heten de formules van Viète voor de vierkantsvergelijking (1). Uitgaande van de betrekkingen (3) en (4) zou je uitdrukkingen voor x1 en x2 in a, b en c af kunnen leiden, en dan heb je dus een alternatieve methode om de abc-formule af te leiden, zie ook hier.
Laatste is mij niet duidelijker geworden, aangezien ik de materie al lastig vind en daarnaast gebruik je termen die het dan ook voor mij lastiger maken, omdat ik de materie niet begrijp..
Het is meer dat ik niet begrijp waarom de a er staat en de b en c niet terug te vinden is.. ik weet wel dat de formule
Ax^2 + bx + c gelijk is aan de functie met de oplossingen (waarin a ) voorkomt..: a(x - x1) ( x - x2)Hello,
Snapt iemand waarom bij het volgende geen 3 onder de 'onzichtbare noemer' van de gehele getallen komt?:
3x - 24 + 8/3x = -7
Ik zou zeggen alles vermenigvuldigen met 3, en daarnaast de gehele getallen zien als breuken (3x/1 en 24/1 )
Dus
9x/3 - 72/3 + 8x = -21/3
Dit klopt volgens mij niet, maar waarom behandel je de gehele getallen niet als breuken?quote:
Hello,
Snapt iemand waarom bij het volgende geen 3 onder de 'onzichtbare noemer' van de gehele getallen komt?:
3x - 24 + 8/3x = -7
Ik zou zeggen alles vermenigvuldigen met 3, en daarnaast de gehele getallen zien als breuken (3x/1 en 24/1 )
Dus
9x/3 - 72/3 + 8x = -21/3
Dit klopt volgens mij niet, maar waarom behandel je de gehele getallen niet als breuken?. Dan doe je alles keer 3x, dus
. Dan krijg je,
, en het antwoord:
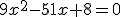
Dat b en c niet terug zouden zijn te vinden is natuurlijk niet waar. Je vergeet namelijk dat x1 en x2 zijn uit te drukken in a, b en c. Hebben we een kwadratische veelterm ax2 + bx + c met reële coëfficiënten waarvan de discriminant D = b2 − 4ac niet negatief is, dan geldt voor de reële nulpunten x1 en x2 van deze veeltermquote:
[..]
Enorm bedankt voor je uitleg. De eerste twee is mij enorm duidelijk.
Laatste is mij niet duidelijker geworden, aangezien ik de materie al lastig vind en daarnaast gebruik je termen die het dan ook voor mij lastiger maken, omdat ik de materie niet begrijp.
Het is meer dat ik niet begrijp waarom de a er staat en de b en c niet terug te vinden zijn. Ik weet wel dat de formule
ax2 + bx + c gelijk is aan de functie met de oplossingen (waarin a voorkomt): a(x - x1) (x - x2)
zodat we voor
kunnen schrijven
Bekijk eens een eenvoudig voorbeeld met concrete getallen voor de coëficiënten a, b en c van de vierkantsvergelijking ax2 + bx + c = 0. Kies a = 2, b = −10, c = 12, dan hebben we
2x2 − 10x + 12 = 0
De oplossingen van deze vergelijking zijn x1 = 2 en x2 = 3, zodat de veelterm 2x2 − 10x + 12 dus een factor (x − 2) en een factor (x − 3) bevat. Maar als we deze factoren met elkaar vermenigvuldigen, dan krijgen we
(x − 2)(x − 3) = x2 − (2+3)x + (2·3) = x2 − 5x + 6
en dat is niet identiek met 2x2 − 10x + 12. Dit komt omdat 2x2 − 10x + 12 behalve de factoren (x − 2) en (x − 3) ook nog een (constante) factor 2 bevat. De vergelijking is dan ook te schrijven als
2(x − 2)(x − 3) = 0
Voor de som van de oplossingen geldt x1 + x2 = 2 + 3 = 5 en dit is gelijk aan −b/a = 10/2 en voor het product van de oplossingen geldt x1x2 = 2·3 = 6 en dit is gelijk aan c/a = 12/2, zoals de formules van Viète ook aangeven.
[ Bericht 11% gewijzigd door Riparius op 05-09-2014 02:09:13 ]Klopt, maar waarom mag je de gehele getallen niet benaderen als breuken ( gehele getal/1 ) ?quote:
[..]Ik vermoed dat je bedoeltquote:
Hello,
Snapt iemand waarom bij het volgende geen 3 onder de 'onzichtbare noemer' van de gehele getallen komt?:
3x - 24 + 8/3x = -7
3x − 24 + (8/3)·x = −7
Beide leden vermenigvuldigen met 3 geeft dan
9x − 72 + 8x = −21
en dus
17x − 72 = −21
zodat
17x = 72 − 21
oftewel
17x = 51
en dus
x = 3Dat mag je wel? 10 delen door 5 isquote:
[..]
Klopt, maar waarom mag je de gehele getallen niet benaderen als breuken ( gehele getal/1 ) ?
( 1-W2)2
Hoe moet deze (w is wortel)?
Ik kom uit op 1-2= -1
Maar het antwoordenboek komt uit op 3 - 2W2(a + b)2 = a2 + 2ab + b2quote:
( 1-W2)2
Hoe moet deze (w is wortel)?
Ik kom uit op 1-2= -1
Maar het antwoordenboek komt uit op 3 - 2W2
Jij vergeet 2ab en je vergeet dat min keer min plus is.(a-b)2 = a2 -2ab +b2 is misschien handiger als je niet meteen ziet dat b ook een negatief getal mag zijn.Dit had je nu zonder meer moeten kunnen herleiden als je de moeite had genomen dit te bestuderen, zoals ik je ook heb aangeraden. Merkwaardige producten dien je van buiten te kennen en ook te allen tijde te herkennen.quote:
( 1-W2)2
Hoe moet deze (w is wortel)?
Ik kom uit op 1-2= -1
Maar het antwoordenboek komt uit op 3 - 2W2
(1 − √2)2 = 1 − 2·1·√2 + (√2)2 = 1 − 2√2 + 2 = 3 − 2√2.Waar komt die wortel 2 opeens vandaan?quote:
[..]
Dit had je nu zonder meer moeten kunnen herleiden als je de moeite had genomen dit te bestuderen, zoals ik je ook heb aangeraden. Merkwaardige producten dien je van buiten te kennen en ook te allen tijde te herkennen.
(1 − √2)2 = 1 − 2·1·√2 + (√2)2 = 1 − 2√2 + 2 = 3 − 2√2.quote:
[..]
Waar komt die wortel 2 opeens vandaan?Heb je dit gelezen?quote:
(a-b)2 = a2 -2ab +b2 is misschien handiger als je niet meteen ziet dat b ook een negatief getal mag zijn.Kan iemand mij deze uitleggen. Vooral de natuurlijke logaritme in combinatie met een absolute waarde functie maakt het mij enorm lastig. :
Weet je wanneer een logaritme negatief is?quote:
Kan iemand mij deze uitleggen. Vooral de natuurlijke logaritme in combinatie met een absolute waarde functie maakt het mij enorm lastig. :
[ afbeelding ]
Zoja kijk wanneer dat logaritme negatief, 0, positief is en hetzelfde doe je voor
En daarna kan je beiden combineren om je antwoord te krijgen.
Bekijk nu voor elk afzonderlijk deel wanneer alles gedefinieerd is, wanneer deze nul is of wanneer deze positief/negatief is.x^2-5x+6
A = 1
B = -5
C = 6
Ik krijg x = 2 and x = 3
dus x^2 - 5x + 6 = (x + 2)(x+3)
Maar als ik het ontbind in factoren krijg ik :
x^2 - 5x + 6 = (x - 2)(x - 3)
Als ik de abc formule gebruik, zijn de factoren positief en als ik het ontbind in factoren, zijn de factoren negatief (wat klopt), waarom is het dan positief als ik de abc formule gebruik?
@BrandX bedankt voor de link hierna toe.Als x = 2 en x = 3 de nulpunten zijn, dan is het (x - 2)(x - 3).quote:
x^2-5x+6
A = 1
B = -5
C = 6
Ik krijg x = 2 and x = 3
dus x^2 - 5x + 6 = (x + 2)(x+3)Dit zijn inderdaad de nulpunten van de kwadratische veelterm x2 − 5x + 6.quote:
x^2-5x+6
A = 1
B = -5
C = 6
Ik krijg x = 2 and x = 3Nee, dit klopt niet. Zie mijn uitleg hierboven.quote:dus x^2 - 5x + 6 = (x + 2)(x+3)Dit is weer wel juist. Een polynoom oftewel veelterm P(x) heeft een factor (x − x0) dan en slechts dan als x = x0 een nulpunt is van P(x), oftewel dan en slechts dan als x = x0 een oplossing is van de vergelijking P(x) = 0.quote:Maar als ik het ontbind in factoren krijg ik :
x^2 - 5x + 6 = (x - 2)(x - 3)Je vergist je, omdat je kennelijk de factorstelling niet begrijpt. Een nulpunt x = x0 geeft een factor (x − x0), niet een factor (x + x0).quote:Als ik de abc formule gebruik, zijn de factoren positief en als ik het ontbind in factoren, zijn de factoren negatief (wat klopt), waarom is het dan positief als ik de abc formule gebruik?Ik weet dus niet hoe dat moet.quote:
Bekijk nu voor elk afzonderlijk deel wanneer alles gedefinieerd is, wanneer deze nul is of wanneer deze positief/negatief is.
Dit is nieuw voor me, zowel de logaritme als de absolute waarde functie. Ik vind dat al helemaal lastig door die absolute waarde functie, want y kan nooit lager dan 0 zijn, want het wordt altijd positief doordat het absoluut is.quote:
[..]
Weet je wanneer een logaritme negatief is?
Zoja kijk wanneer dat logaritme negatief, 0, positief is en hetzelfde doe je voor
En daarna kan je beiden combineren om je antwoord te krijgen.Het lastige van deze opgave schuilt niet in die logaritme van een absolute waarde maar in het verkrijgen van een goed overzicht. Dit is nu typisch een opgave waarbij je heel goed met tekenschema's kunt werken. Ik heb je al vaker aangeraden gebruik te maken van tekenschema's, maar dat ben je kennelijk alweer vergeten, of je verkiest mijn adviezen te negeren.quote:
Kan iemand mij deze uitleggen. Vooral de natuurlijke logaritme in combinatie met een absolute waarde functie maakt het mij enorm lastig. :
[ afbeelding ]
We kijken nu eerst naar de teller x2 − 10x + 16 van de breuk, waarvoor we (x − 2)(x − 8) kunnen schrijven. De grafiek van f(x) = x2 − 10x + 16 is een dalparabool die de x-as snijdt bij x = 2 en x = 8, zodat we voor deze teller het volgende tekenschema krijgen:
1
2
3++++++++++++++++++++++++++++++++0-----------------------0++++++++
________________________________|_______________________|________
2 8
Voor de noemer x2 − 16 van de breuk kunnen we (x + 4)(x − 4) schrijven. De grafiek van g(x) = x2 − 16 is eveneens een dalparabool, maar deze snijdt de x-as bij x = −4 en x = 4, zodat we voor deze noemer het volgende tekenschema krijgen:
1
2
3++++++++0-------------------------------0++++++++++++++++++++++++
________|_______________________________|________________________
-4 4
Nu we tekenschema's hebben voor de teller en noemer van onze breuk, kunnen we hieruit een tekenschema afleiden voor de breuk als geheel, omdat de waarde van een breuk immers positief is als teller en noemer hetzij beide positief zijn, hetzij beide negatief. Voorts is de waarde van de breuk negatief als hetzij de teller positief is en tevens de noemer negatief hetzij de teller negatief is en tevens de noemer positief. Ook is de waarde van een breuk nul als de teller nul is terwijl de noemer niet nul is. Is daarentegen de noemer nul, dan is de waarde van de breuk ongedefinieerd. In tekenschema's kunnen we een asterisk (*) gebruiken om aan te geven dat de waarde van een uitdrukking waarvan we het tekenverloop weergeven niet is gedefinieerd. Voor het tekenschema van de breuk als geheel krijgen we aldus:
1
2
3++++++++*-----------------------0+++++++*---------------0++++++++
________|_______________________|_______|_______________|________
-4 2 4 8
Nu moeten we nog kijken naar het tekenverloop van de uitdrukking ln(| x − 2 |). Om te beginnen hebben we | x − 2 | = 0 voor x = 2, wat dus betekent dat ln(| x − 2 |) voor x = 2 niet is gedefinieerd, aangezien de logaritme van 0 niet is gedefinieerd. Voor x ≠ 2 is | x − 2 | > 0, zodat ln(| x − 2 |) dan wel is gedefinieerd. De logaritme van 1 is 0, zodat ln(| x − 2 |) = 0 als | x − 2 | = 1, en dat is het geval voor x = 1 of x = 3. De uitdrukking | x − 2 | geeft de afstand op de getallenlijn van het beeldpunt van het getal x tot het beeldpunt van het getal 2, zodat het duidelijk is dat 0 < | x − 2 | < 1 voor 1 < x < 3 ∧ x ≠ 2 terwijl | x − 2 | > 1 voor x < 1 ∨ x > 3. De logaritme van getallen tussen 0 en 1 is negatief, en de logaritme van getallen groter dan 1 is positief, zodat we voor ln(| x − 2 |) het volgende tekenschema krijgen:
1
2
3++++++++++++++++++++++++++++0---*---0++++++++++++++++++++++++++++
____________________________|___|___|____________________________
1 2 3
Tenslotte moeten we nu de tekenschema's van het quotiënt (x2 − 10x + 16)/(x2 − 16) en van ln(| x − 2 |) combineren om een tekenschema van de gegeven uitdrukking te verkrijgen. Het product van twee grootheden is positief als die grootheden hetzij beide positief zijn hetzij beide negatief, en het product van twee grootheden is negatief als één van beide grootheden positief is en de andere negatief. Voorts is een product van twee grootheden nul als (tenminste) één van beide grootheden zelf nul is. En uiteraard is een product van twee grootheden niet gedefinieerd zodra één van beide grootheden zelf niet is gedefinieerd. Aldus krijgen we voor de gegeven uitdrukking het volgende tekenschema:
1
2
3++++++++*-------------------0+++*---0+++*---------------0++++++++
________|___________________|___|___|___|_______________|________
-4 1 2 3 4 8
Uit dit tekenschema lezen we nu het volgende af:
De uitdrukking is positief voor
x ∈ (−∞, −4) ∪ (1, 2) ∪ (3,4) ∪ (8, ∞)
De uitdrukking is negatief voor
x ∈ (−4, 1) ∪ (2, 3) ∪ (4, 8)
De uitdrukking is nul voor
x ∈ { 1, 3, 8 }
De uitdrukking is niet gedefinieerd voor
x ∈ { −4, 2, 4 }
Hiermee is de opgave opgelost.
[ Bericht 1% gewijzigd door Riparius op 05-09-2014 02:28:22 ]Nou heeft Riparius het je al voor gekauwd maar je kon mijn vraag toch nog wel beantwoorden, zo moeilijk was dat niet te vinden.quote:
[..]
Dit is nieuw voor me, zowel de logaritme als de absolute waarde functie. Ik vind dat al helemaal lastig door die absolute waarde functie, want y kan nooit lager dan 0 zijn, want het wordt altijd positief doordat het absoluut is.
Wanneer is een logaritme negatief, 0, positief? Als het niet weet kan je dit vast wel vinden.
Welke y?
En je kon ook alvast uitrekenen wanneer die polynomen positief, 0 of negatief zijn.Goedennacht,
Kan iemand mij de overgang, van stap 3 naar stap 4, uitleggen in het volgende plaatje?
Waarom mag dit en kan dit? Wat is de gedachte erachter? En daarnaast; waarom moet de p vóór ln staan en kan het niet staan naast de x?
Ten tweede:
Die laatste stap?! Eigenlijk hetzelfde als het eerste plaatje, alleen andere vorm.
Tenslotte begrijp ik dit niet (zowel links als rechts):
[ Bericht 17% gewijzigd door BroodjeKebab op 06-09-2014 00:26:29 ]http://nl.wikipedia.org/w(...)kenen_met_logaritmesquote:
Goedennacht,
Kan iemand mij de overgang, van stap 3 naar stap 4, uitleggen in het volgende plaatje?
[ afbeelding ]
Waarom mag dit en kan dit? Wat is de gedachte erachter? En daarnaast; waarom moet de p vóór ln staan en kan het niet staan naast de x?
Ten tweede:
[ afbeelding ]
Die laatste stap?! Eigenlijk hetzelfde als het eerste plaatje, alleen andere vorm.
Tenslotte begrijp ik dit niet (zowel links als rechts):
[ afbeelding ]( 5 / (2x - 1) ) = (1 / (2 - x) )
( 5 / (2x - 1) ) - (1 / (2 - x) ) = 0
(5(2-x) - 2x - 1 ) / (2x - 1)(2 - x) = 0
(10 - 5x) - (2x - 1 ) / (2x - 1)(2 - x) = 0
Dan loop ik vast. HELP!Als een breuk gelijk aan 0 moet zijn, dan is dat alleen zo als de teller gelijk aan nul is en de noemer niet. Bovenkant gelijk aan 0 stellen dus.
Maar let op, je maakt een mintekenfout, en daarnaast ben je sneller af als je vanaf het begin de keuze maakt om kruislings te vermenigvuldigen:
Hint: a/b = c/d dan en slechts dan als ad = cb onder de voorwaarde dat b≠0 en d≠0.Opinion is the medium between knowledge and ignorance (Plato)Dankjewel!! Ben eruit gekomen.quote:
Als een breuk gelijk aan 0 moet zijn, dan is dat alleen zo als de teller gelijk aan nul is en de noemer niet. Bovenkant gelijk aan 0 stellen dus.
Maar let op, je maakt een mintekenfout, en daarnaast ben je sneller af als je vanaf het begin de keuze maakt om kruislings te vermenigvuldigen:
Hint: a/b = c/d dan en slechts dan als ad = cb onder de voorwaarde dat b≠0 en d≠0.
Ik heb nu iets heel anders waar ik ook mee zit, ik dacht laat ik eerst even die breukenvraag vragen en vervolgens deze vragen m.b.t. een ander onderwerp:
Px (Px + Q)-1/3 + ( Px + Q)2/3 = 0 --> functie zo omzetten dat er komt te staan x = ....
Hiervan dan r berekenen (formule zo omzetten dat er komt te staan r = ....SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 6% gewijzigd door Brainstorm245 op 06-09-2014 15:04:34 ]Tip bij de eerste: haal een van beide termen naar de andere kant en verhef links en rechts tot de derde macht.
Tip bij de tweede: vermenigvuldig in de grote breuk boven en onder met (1+r).Opinion is the medium between knowledge and ignorance (Plato)Zie edit overigens.quote:
Tip bij de eerste: haal een van beide termen naar de andere kant en verhef links en rechts tot de derde macht.
Tip bij de tweede: vermenigvuldig in de grote breuk boven en onder met (1+r).
Bij die eerste weet ik dat ik het moet verheffen tot de derde macht, maar ik weet niet hoe ik moet uitvoeren, want er zit nog een Px buiten de haakjes.
Bij die tweede snap ik er niks van, want ik zie 3 deelstrepen (waarvan twee breuken).Opmerking over de edit in je spoiler: 'Naar rechts halen' of 'naar de andere kant halen' is eigenlijk een onterechte term, die ik zelf ook met de regelmaat van de klok misbruik, maar je moet goed in de gaten houden wat je eigenlijk doet.
Het is-teken betekent dat links en rechts evenveel is. Als je links en rechts dezelfde elementaire bewerking toepast, zoals vermeningvuldigen met 37, of aan beide kanten 19 optellen, zal dat niet veranderen. Bij vermenigvuldiging met x ook niet, tenzij x per ongeluk 0 zou zijn, dus die moet je dan even uitsluiten.
Terug naar jouw uitdrukking:
3K-1/2 L1/3 = 1/5
Als je links en rechts met K1/2 vermenigvuldigt wordt dit
3L1/3 = 1/5K1/2.
Reken dat zelf maar even na.
Voor de andere 2 opgaven geldt: probeer ze stap voor stap uit te schrijven met behulp van de hints. Ik kan ze wel voor je gaan uitschrijven, maar daar leer je weinig van.Opinion is the medium between knowledge and ignorance (Plato)quote:
[..]
Dankjewel!! Ben eruit gekomen.
Ik heb nu iets heel anders waar ik ook mee zit, ik dacht laat ik eerst even die breukenvraag vragen en vervolgens deze vragen m.b.t. een ander onderwerp:
Px (Px + Q)-1/3 + ( Px + Q)2/3 = 0 --> functie zo omzetten dat er komt te staan x = ....
Hiervan dan r berekenen (formule zo omzetten dat er komt te staan r = ....
[ afbeelding ]Over die spoiler: een negatieve macht is het zelfde als delen door een positieve macht, ie x-1 = 1/x. Naar de andere kant halen dus delen wordt vermenigvuldiging.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.2e opgave is gelukt met Px is nu wel gelukt, dankje !!. Echter die breuken met deelstreep zit mij nog steeds in de weg...quote:
Opmerking over de edit in je spoiler: 'Naar rechts halen' of 'naar de andere kant halen' is eigenlijk een onterechte term, die ik zelf ook met de regelmaat van de klok misbruik, maar je moet goed in de gaten houden wat je eigenlijk doet.
Het is-teken betekent dat links en rechts evenveel is. Als je links en rechts dezelfde elementaire bewerking toepast, zoals vermeningvuldigen met 37, of aan beide kanten 19 optellen, zal dat niet veranderen. Bij vermenigvuldiging met x ook niet, tenzij x per ongeluk 0 zou zijn, dus die moet je dan even uitsluiten.
Terug naar jouw uitdrukking:
3K-1/2 L1/3 = 1/5
Als je links en rechts met K1/2 vermenigvuldigt wordt dit
3L1/3 = 1/5K1/2.
Reken dat zelf maar even na.
Voor de andere 2 opgaven geldt: probeer ze stap voor stap uit te schrijven met behulp van de hints. Ik kan ze wel voor je gaan uitschrijven, maar daar leer je weinig van.(1−λ)a−ρ +λb−ρ = c−ρ
Hier moet ik b = van zien te maken.. Ik weet wel hoe ik de exponenten wegkrijg, maar niet wat er gebeurt met de functie als ik c naar links haal en b naar rechts.Ik post nu misschien té veel achter elkaar, maar dit komt omdat ik komende week een toets heb en nu alles aan het herhalen ben heel vlug.Je haalt niets naar links en naar rechts, maar je vermenigvuldigt links en rechts met hetzelfde. Heb je het voorbeeld uit post #145 al negerekend?quote:
(1−λ)a−ρ +λb−ρ = c−ρ
Hier moet ik b = van zien te maken.. Ik weet wel hoe ik de exponenten wegkrijg, maar niet wat er gebeurt met de functie als ik c naar links haal en b naar rechts.
In dit geval zou je links en rechts met cp kunnen vermenigvuldigen.Opinion is the medium between knowledge and ignorance (Plato)Uhu, maar ik snap niet hoe het antwoord dan dit is:quote:
[..]
Je haalt niets naar links en naar rechts, maar je vermenigvuldigt links en rechts met hetzelfde. Heb je het voorbeeld uit post #145 al negerekend?
In dit geval zou je links en rechts met cp kunnen vermenigvuldigen.
λ−1(c−ρ −(1−λ)a−ρ).
Ik snap de verschijning van λ−1 buiten de haakjes niet.Ik begrijp niet waarom je deze 'tip' geeft. Als je namelijk beide leden met (Px + Q)1/3 vermenigvuldigt, dan krijg je meteenquote:
Tip bij de eerste: haal een van beide termen naar de andere kant en verhef links en rechts tot de derde macht.
Px + (Px + Q) = 0
en dus
x = −Q/2P (P ≠ 0, Q ≠ 0)
En ja, dat gaat gewoon uit het blote hoofd, zonder pen en papier.
[ Bericht 0% gewijzigd door Riparius op 06-09-2014 18:43:55 ]Ik geef die tip omdat die voor leerlingen/studenten die minder algebraïsch begaafd zijn makkelijker te zien is en bovendien algemener toepasbaar.quote:
Ik begrijp niet waarom je deze 'tip' geeft.
Neemt niet weg dat jouw oplossing in dit geval handiger is.
[ Bericht 0% gewijzigd door Janneke141 op 06-09-2014 17:21:52 ]Opinion is the medium between knowledge and ignorance (Plato)Ik denk juist dat met jouw advies veel meer leerlingen de mist ingaan. Maar laten we de proef op de som nemen:quote:
[..]
Ik geef dit tip omdat die voor leerlingen/studenten die minder algebraïsch begaafd zijn makkelijker te zien is en bovendien algemener toepasbaar.
Neemt niet weg dat jouw oplossing in dit geval handiger is.
@Brainstorm245: post je uitwerking van deze opgave volgens het advies van Janneke eens, ik ben benieuwd ...
[ Bericht 0% gewijzigd door Riparius op 06-09-2014 17:37:35 ]Om te beginnen: dit is niet het juiste antwoord als de opdracht luidde om b op te lossen uit je betrekking, want wat je hier geeft is een uitdrukking voor bρ.quote:
[..]
Uhu, maar ik snap niet hoe het antwoord dan dit is:
λ−1(c−ρ −(1−λ)a−ρ).
Ik snap de verschijning van λ−1 buiten de haakjes niet.
We hadden:
(1 − λ)a−ρ + λbρ = c−ρ
Van beide leden (1 − λ)a−ρ aftrekken geeft:
λbρ = c−ρ − (1 − λ)a−ρ
En nu beide leden vermenigvuldigen met λ−1 geeft:
bρ = λ−1(c−ρ − (1 − λ)a−ρ)
De clou is natuurlijk dat λ−1·λ = λ0 = 1 (voor λ ≠ 0), zodat de coëfficiënt van bρ in het linkerlid gelijk wordt aan 1 door beide leden met λ−1 te vermenigvuldigen.Waar is (Px + Q) -1/3 gebleven? Die vaststond aan Px ---> Px(Px + Q) -1/3 ?quote:
[..]
Ik begrijp niet waarom je deze 'tip' geeft. Als je namelijk beide leden met met (Px + Q)1/3 vermenigvuldigt, dan krijg je meteen
Px + (Px + Q) = 0
en dus
x = −Q/2P (P ≠ 0, Q ≠ 0)
En ja, dat gaat gewoon uit het blote hoofd, zonder pen en papier.Als je een macht vermenigvuldigt met zijn tegengestelde, dan is dat gelijk aan 1.quote:
[..]
Waar is (Px + Q) -1/3 gebleven? Die vaststond aan Px ---> Px(Px + Q) -1/3 ?
Dit is op twee manieren in te zien: Als je twee machten van hetzelfde grondtal vermenigvuldigt, dan tel je de exponenten op. Voorbeeld:
x3·x5 = x8
In dit geval staat er
y-1/3·y1/3 = y0 = 1 (waarbij y = Px + Q)
Tweede manier: denk even terug hoe de negatieve exponenten zijn geïntroduceerd: als "één gedeeld door", oftewel:
x-a = 1 / xa
Hieruit kun je ook afleiden dat x-a·xa = xa/xa = 1.
[ Bericht 2% gewijzigd door Janneke141 op 06-09-2014 18:43:21 ]Opinion is the medium between knowledge and ignorance (Plato)We hadden:quote:
[..]
Waar is (Px + Q) -1/3 gebleven? Die vaststond aan Px ---> Px(Px + Q) -1/3 ?
Px(Px + Q)−1/3 + (Px + Q)2/3 = 0
Nu vermenigvuldigen we beide leden met (Px + Q)1/3, en dan krijgen we:
Px(Px + Q)−1/3(Px + Q)1/3 + (Px + Q)2/3(Px + Q)1/3 = 0
Nu passen we de rekenregel toe die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal (dat is: ab·ac = ab+c). We zien nu dat (Px + Q)−1/3(Px + Q)1/3 = (Px + Q)−1/3+1/3 = (Px + Q)0 = 1 en (Px + Q)2/3(Px + Q)1/3 = (Px + Q)2/3+1/3 = (Px + Q)1 = (Px + Q). De vergelijking wordt nu dus
Px + (Px + Q) = 0
en dus
2Px + Q = 0
Van beide leden Q aftrekken geeft:
2Px = −Q
Tenslotte beide leden delen door 2P en we krijgen:
x = −Q/2P
Merk op dat zowel P als Q ongelijk aan nul moeten zijn.
Ik zie in je postgeschiedenis dat je net bent begonnen met Econometrie. Ik denk dat je het heel zwaar gaat krijgen, dit is een studie waarbij aardig wat wiskunde komt kijken, terwijl je nauwelijks op het niveau van een brugklasser zit (ja, uit de tijd dat er nog goed onderwijs was) voor wat betreft je algebraïsche vaardigheden.
Post nu nog even je eigen uitwerking van deze opgave aan de hand van het advies dat je van Janneke had gekregen, zoals ik je heb gevraagd. Ik heb zo'n donkerbruin vermoeden dat daar ook niet veel van deugt.
[ Bericht 0% gewijzigd door Riparius op 06-09-2014 18:42:56 ]Op mijn vooropleidingen stond ik gemiddeld meestal 8,5 tot 9,5 voor wiskunde. Dit behoort tot de stof van de eerste twee weken op de opleiding econometrie. De opgaven van de eerste drie hoofdstukken heb ik foutloos gemaakt, op de vragen (van verschillende opgaven) die ik hier gepost heb na.quote:
[..]
We hadden:
Px(Px + Q)−1/3 + (Px + Q)2/3 = 0
Nu vermenigvuldigen we beide leden met (Px + Q)1/3, en dan krijgen we:
Px(Px + Q)−1/3(Px + Q)1/3 + (Px + Q)2/3(Px + Q)1/3 = 0
Nu passen we de rekenregel toe die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal (dat is: ab·ac = ab+c). We zien nu dat (Px + Q)−1/3(Px + Q)1/3 = (Px + Q)−1/3+1/3 = (Px + Q)0 = 1 en (Px + Q)2/3(Px + Q)1/3 = (Px + Q)2/3+1/3 = (Px + Q)1 = (Px + Q). De vergelijking wordt nu dus
Px + (Px + Q) = 0
en dus
2Px + Q = 0
Van beide leden Q aftrekken geeft:
2Px = −Q
en tenslotte beide leden delen door 2P en we krijgen:
x = −Q/2P
Merk op dat zowel P als Q ongelijk aan nul moeten zijn.
Ik zie in je postgeschiedenis dat je net bent begonnen met Econometrie. Ik denk dat je het heel zwaar gaat krijgen, dit is een studie waarbij aardig wat wiskunde komt kijken, terwijl je nauwelijks op het niveau van een brugklasser zit (ja, uit de tijd dat er nog goed onderwijs was) voor wat betreft je algebraïsche vaardigheden.
Post nu nog even je eigen uitwerking van deze opgave aan de hand van het advies dat je van Janneke had gekregen, zoals ik je heb gevraagd. Ik heb zo'n donkerbruin vermoeden dat daar ook niet veel van deugt.Die cijfers die je bij je vooropleidingen hebt behaald (welke vooropleidingen waren dat overigens?) zijn dan kennelijk onderhevig aan een enorme inflatie, of die opleidingen sjoemelen met de cijfers om zo een hoger slagingspercentage en minder uitval te krijgen en daarmee ook meer subsidie te blijven ontvangen. Je bent kennelijk ook niet op de hoogte met de juiste termen voor allerlei begrippen uit de elementaire algebra, nog even afgezien van het gebrek aan vaardigheden.quote:
[..]
Op mijn vooropleidingen stond ik gemiddeld meestal 8,5 tot 9,5 voor wiskunde. Dit behoort tot de stof van de eerste twee weken op de opleiding econometrie. De opgaven van de eerste drie hoofdstukken heb ik foutloos gemaakt, op de vragen (van verschillende opgaven) die ik hier gepost heb na.Havo (en wisk a) en hbo. Nu wo econometrie.quote:
[..]
Die cijfers die je bij je vooropleidingen hebt behaald (welke vooropleidingen waren dat overigens?) zijn dan kennelijk onderhevig aan een enorme inflatie, of die opleidingen sjoemelen met de cijfers om zo een hoger slagingspercentage en minder uitval te krijgen en daarmee ook meer subsidie te blijven ontvangen. Je bent kennelijk ook niet op de hoogte met de juiste termen voor allerlei begrippen uit de elementaire algebra, nog even afgezien van het gebrek aan vaardigheden.Ik zou graag nog een vraag willen stellen en dat is het volgende (over implications):
Bij x² = 16 --> x = 4 heb ik dat --> false is en <-- true. --> heb ik false, aangezien het ook (-4)² kan zijn.
Ik weet niet of dit goed is? Ik ga uit van wel?
Maar hier komt het moeilijkste:
(x-3)² (y+2) > 0 --> y > -2 hier is ---> true en <--- false en ik weet niet waarom. Ik kan het ook niet 123 eruit halen zoals ik bij andere opgaven dat wel kan.. Ik zie het, soort van, trucje niet en ik begrijp het niet als het zo complex is. Ondanks dat ik de implications wel begrijp bij x² = 16 --> x = 4, maar toch begrijp ik het niet bij wat complexere vergelijkingen/inequalities.Als x = 3 dan geldt (x-3)² (y+2) = 0 ongeacht wat y is.quote:
(x-3)² (y+2) > 0 --> y > -2 hier is ---> true en <--- false en ik weet niet waarom. Ik kan het ook niet 123 eruit halen zoals ik bij andere opgaven dat wel kan.. Ik zie het, soort van, trucje niet en ik begrijp het niet als het zo complex is. Ondanks dat ik de implications wel begrijp bij x² = 16 --> x = 4, maar toch begrijp ik het niet bij wat complexere vergelijkingen/inequalities.
Dus <--- is false want als x = 3 dan gaat het mis.
Was dit het probleem (dat je niet zag dat er ook een x variabele was) of snap je niet wat implicaties precies inhouden?
[ Bericht 6% gewijzigd door Anoonumos op 06-09-2014 22:15:26 ]Dank je wel.quote:
[..]
Vermenigvuldig de eerste term met x2 / x2 en de tweede term met 2√x / 2√x, dan krijg je twee gelijknamige breuken met als noemer 4x2.
Ik zit nu met een soortgelijk probleem, namelijk:
Het tweede klopt niet. Hoe doe ik het wel goed?Ik heb het idee dat jequote:
[..]
Dank je wel.
Ik zit nu met een soortgelijk probleem, namelijk:
[ afbeelding ]
Het tweede klopt niet. Hoe doe ik het wel goed?
probeert te differentiëren met behulp van de quotiëntregel, maar dan klopt je eerste regel ook niet. En je herleiding is sowieso onjuist, want als je √(x² + x) vermenigvuldigt met 2√(x² + 2) krijg je niet 2(x² + x).Je hebt gelijk. Het eerste moet 2x+1 gedeeld door 2sqrt(x^2+x) zijn, en niet 2sqrt(x^2+2). (En het tweede moet *2sqrt(x^2+x) zijn).quote:
[..]
Ik heb het idee dat je
probeert te differentiëren met behulp van de quotiëntregel, maar dan klopt je eerste regel ook niet. En je herleiding is sowieso onjuist, want als je √(x² + x) vermenigvuldigt met 2√(x² + 2) krijg je niet 2(x² + x).
Maar nu zit ik nog steeds vast.In ieder geval zul je in je tweede regel haakjes om (2x+1) moeten zetten. Daarna kun je er ongetwijfeld een factor (x+1) uitdelen boven en beneden.
[ Bericht 71% gewijzigd door Janneke141 op 07-09-2014 12:02:25 ]Opinion is the medium between knowledge and ignorance (Plato)Gegeven zijn de functies y1 = 2x^2+5x+2 / x+3 en y2 = 2x^2+2x-7 / x+3
Bereken y1-y2
Y1-y2 = 2x^2+5x+2 / x+3 - 2x^2+2x-7 / 3
= 2x^2+5x+2-2x^2+2x-7 / x+3
= 7x-5 / x+3
Het antwoorden boek zegt y1-y2 = 3x+9 / x+3
= 3(x+9) / x+3
= 3
Wat doe ik fout?Haakjes vergeten.quote:
Gegeven zijn de functies y1 = 2x^2+5x+2 / x+3 en y2 = 2x^2+2x-7 / x+3
Bereken y1-y2
Y1-y2 = 2x^2+5x+2 / x+3 - 2x^2+2x-7 / x + 3
Y1-y2 = 2x^2+5x+2 / x+3 - ( 2x^2+2x-7 / x + 3 )Tekenfout. Als je 2x2 + 2x − 7 aftrekt van 2x2 + 5x + 2 dan krijg jequote:
Gegeven zijn de functies y1 = 2x^2+5x+2 / x+3 en y2 = 2x^2+2x-7 / x+3
Bereken y1-y2
Y1-y2 = 2x^2+5x+2 / x+3 - 2x^2+2x-7 / 3
= 2x^2+5x+2-2x^2+2x-7 / x+3
= 7x-5 / x+3
Het antwoorden boek zegt y1-y2 = 3x+9 / x+3
= 3(x+9) / x+3
= 3
Wat doe ik fout?
1
2
3
42x² + 5x + 2
2x² + 2x - 7
------------ -
0 + 3x + 9
Het antwoordenboekje heeft het overigens ook niet helemaal correct, y1 en y2 zijn immers niet gedefinieerd voor x = −3, zodat y1 − y2 = 3 uitsluitend geldt voor x ≠ −3.
Als je de slash (/) gebruikt voor een breuk, dan moet je wel haakjes gebruiken als de teller en of de noemer van een breuk uit meerdere termen bestaat om ambiguïteiten te vermijden. De manier waarop je y1 en y2 noteert is zo niet correct, en dit heeft ook bijgedragen aan je fout. Schrijf dus
y1 = (2x2 + 5x + 2) / (x + 3)
y2 = (2x2 + 2x − 7) / (x + 3)Goed, we hebbenquote:
[..]
Je hebt gelijk. Het eerste moet 2x+1 gedeeld door 2sqrt(x^2+x) zijn, en niet 2sqrt(x^2+2). (En het tweede moet *2sqrt(x^2+x) zijn).
Maar nu zit ik nog steeds vast.
Met behulp van de quotiëntregel (en de kettingregel!) krijgen we dan
Nu vermenigvuldigen we teller en noemer van de breuk met 2√(x²+x) en dan hebben we
Voor de teller van de breuk hebben we nu
zodat het quotiënt wordt
Nu kunnen we teller en noemer van deze breuk nog door (x+1) delen, en dan krijgen we
Bedankt voor je heldere uitleg!quote:
[..]
Goed, we hebben
Met behulp van de quotiëntregel (en de kettingregel!) krijgen we dan
Nu vermenigvuldigen we teller en noemer van de breuk met 2√(x²+x) en dan hebben we
Voor de teller van de breuk hebben we nu
zodat het quotiënt wordt
Nu kunnen we teller en noemer van deze breuk nog door (x+1) delen, en dan krijgen weIk heb de volgende formule:
C(x) = Ax√x + B
Ik moet hem substitueren met ( x+h)
Ik maak er dan het volgende van:
C(x) = C(10) = A(10)√(10) + B
Heb ik het goed gedaan? Zo ja, kan ik het korter opschrijven? Ik zat eraan te denken om het te kwadrateren om zo van de wortel af te komen, dus:
A²(10)²(10) + B²Je moet x+h invullen? En waarom vul je dan 10 in? Leg eens duidelijk uit wat de opgave is.quote:
Ik heb de volgende formule:
C(x) = Ax√x + B
Ik moet hem substitueren met ( x+h)
Ik maak er dan het volgende van:
C(x) = C(10) = A(10)√(10) + B
Heb ik het goed gedaan? Zo ja, kan ik het korter opschrijven? Ik zat eraan te denken om het te kwadrateren om zo van de wortel af te komen, dus:
A²(10)²(10) + B²
En dat laatste deel is pure onzin natuurlijk. Je mag toch hopelijk nu wel weten dat (A+B)2 niet gelijk is aan A2 + B2. En als je het kwadraat neemt verander je de functie. Dat lijkt mij ook niet de bedoeling.Ik heb de volgende formule:quote:
[..]
Je moet x+h invullen? En waarom vul je dan 10 in? Leg eens duidelijk uit wat de opgave is.
En dat laatste deel is pure onzin natuurlijk. Je mag toch hopelijk nu wel weten dat (A+B)2 niet gelijk is aan A2 + B2. En als je het kwadraat neemt verander je de functie. Dat lijkt mij ook niet de bedoeling.
C(x) = Ax√x + B
Ik moet hem substitueren met ( x+h)
Ik maak er dan het volgende van:
C(x) = C(10) = A(10)√(10) + B
Ik wou alleen weten of het korter kon en of ik hem goed had gesubstitueerd.Wat moet je precies substitueren? X voor x+h? Lijkt me niet moeilijk,quote:
Ik heb de volgende formule:
C(x) = Ax√x + B
Ik moet hem substitueren met ( x+h)
Ik maak er dan het volgende van:
C(x) = C(10) = A(10)√(10) + B
Heb ik het goed gedaan? Zo ja, kan ik het korter opschrijven? Ik zat eraan te denken om het te kwadrateren om zo van de wortel af te komen, dus:
A²(10)²(10) + B²
C(x+h) = A(x+h)√(x+h) + BJe moet eerst maar eens werken aan je terminologie. Substitueren met (x+h) is geen begrijpelijke formulering. En botweg dezelfde vraag nog een keer posten met dezelfde onzin nadat iemand je erop heeft gewezen dat het nergens op slaat wat je aan het doen bent is natuurlijk ook not done.quote:
[..]
Ik heb de volgende formule:
C(x) = Ax√x + B
Ik moet hem substitueren met (x+h)
Vermoedelijk gaat het om het bepalen van de afgeleide van je functie C(x) = Ax√x + B met behulp van de definitie van de afgeleide, dus
C'(x) = limh→0 (C(x+h) − C(x))/h
Om deze limiet en daarmee de afgeleide C'(x) te bepalen moeten we eerst het differentiequotiënt (C(x+h) − C(x))/h herleiden tot een geschikte vorm zodanig dat we van dit differentiequotiënt de limiet voor h → 0 kunnen bepalen.
We hebben
(C(x+h) − C(x))/h = A·((x+h)√(x+h) − x√x)/h
aangezien de constante B wegvalt bij de bepaling van het verschil van C(x+h) en C(x), terwijl we de constante factor A hier buiten haakjes kunnen halen. Bedenk nu zelf maar eens hoe je dit differentiequotiënt zodanig kunt herleiden dat je hiervan de limiet voor h → 0 kunt bepalen.Dit ja. X substitueren voor x+h. Had ik het goed gedaan? Zo ja, kan het korter geschreven worden (zoals wortels wegwerken?)quote:
[..]
Wat moet je precies substitueren? X voor x+h? Lijkt me niet moeilijk,
C(x+h) = A(x+h)√(x+h) + BNee het was niet de afgeleide dat bepaald moest worden. Dat komt later.quote:
[..]
Je moet eerst maar eens werken aan je terminologie. Substitueren met (x+h) is geen begrijpelijke formulering. En botweg dezelfde vraag nog een keer posten met dezelfde onzin nadat iemand je erop heeft gewezen dat het nergens op slaat wat je aan het doen bent is natuurlijk ook not done.
Vermoedelijk gaat het om het bepalen van de afgeleide van je functie C(x) = Ax√x + B met behulp van de definitie van de afgeleide, dus
C'(x) = limh→0 (C(x+h) − C(x))/h
Om deze limiet en daarmee de afgeleide C'(x) te bepalen moeten we eerst het differentiequotiënt (C(x+h) − C(x))/h herleiden tot een geschikte vorm zodanig dat we van dit differentiequotiënt de limiet voor h → 0 kunnen bepalen.
We hebben
(C(x+h) − C(x))/h = A·((x+h)√(x+h) − x√x)/h
aangezien de constante B wegvalt bij de bepaling van het verschil van C(x+h) en C(x), terwijl we de constante factor A hier buiten haakjes kunnen halen. Bedenk nu zelf maar eens hoe je dit differentiequotiënt zodanig kunt herleiden dat je hiervan de limiet voor h → 0 kunt bepalen.
Ik bedoelde natuurlijk ' x substitueren met x+h 'Volgens mij heb je geen idee wat je precies gedaan hebt. De vraag of je dat goed gedaan hebt, is daarom nogal misplaatst.quote:
[..]
Dit ja. X substitueren voor x+h. Had ik het goed gedaan? Zo ja, kan het korter geschreven worden (zoals wortels wegwerken?)
Als je moet substitueren met x+h, waar komt die '10' dan vandaan?Opinion is the medium between knowledge and ignorance (Plato)Ja ik had de post even ge-edit met 10 ipv x+h om het maar even simpel te houden.quote:
[..]
Volgens mij heb je geen idee wat je precies gedaan hebt. De vraag of je dat goed gedaan hebt, is daarom nogal misplaatst.
Als je moet substitueren met x+h, waar komt die '10' dan vandaan?Iets, dat onduidelijk is voor mij: ''Show that f(-x) = -f(x) for all x, and that f(1/x) = f(x) for x /= 0 by the formula: f(x) = x / (1+x²)''.
Ik snap niet echt wat ik moet doen? Moet ik nou eigenlijk verklaren dat de variabele -x ervoor zal zorgen dat er een -y output wordt geleverd? Hetzelfde dan dat een 1/x variabele bij x ervoor zal zorgen dat er een positieve y variabele als output zal weergeven?Ja, daar komt het wel op neer.quote:
Iets, dat onduidelijk is voor mij: ''Show that f(-x) = -f(x) for all x, and that f(1/x) = f(x) for x /= 0 by the formula: f(x) = x / (1+x²)''.
Ik snap niet echt wat ik moet doen? Moet ik nou eigenlijk verklaren dat de variabele -x ervoor zal zorgen dat er een -y output wordt geleverd? Hetzelfde dan dat een 1/x variabele bij x ervoor zal zorgen dat er een positieve y variabele als output zal weergeven?
Als je in je functievoorschrift f(x) x vervangt door -x, en je schrijft dat netjes uit, dan moet je laten zien dat daar -f(x) uitkomt.
Idem voor 1/x, waarbij de voorwaarde x ≠ 0 natuurlijk logisch is.Opinion is the medium between knowledge and ignorance (Plato)Ik raak alleen in de war doordat er steeds f(x) staat.. Ik weet wel dat die f in principe staat voor de functie (y) en dan de (x) staat voor de input, maar het is zo verwarrend als het dan allemaal in 1 zin staat. Dan weet ik bijvoorbeeld niet wat -f(x) dan moet voorstellen, de input of output zeg maar.quote:
[..]
Ja, daar komt het wel op neer.
Als je in je functievoorschrift f(x) x vervangt door -x, en je schrijft dat netjes uit, dan moet je laten zien dat daar -f(x) uitkomt.
Idem voor 1/x, waarbij de voorwaarde x ≠ 0 natuurlijk logisch is.
Je moet niet dezelfde vraag in twee topics tegelijk stellen en dan ook nog je vraag weer weghalen als ik die juist voor je heb beantwoord. Stel je vragen over wiskunde hier, daar is dit topic voor bedoeld.quote:
Iets, dat onduidelijk is voor mij: ''Show that f(-x) = -f(x) for all x, and that f(1/x) = f(x) for x /= 0 by the formula: f(x) = x / (1+x²)''.
Ik snap niet echt wat ik moet doen? Moet ik nou eigenlijk verklaren dat de variabele -x ervoor zal zorgen dat er een -y output wordt geleverd? Hetzelfde dan dat een 1/x variabele bij x ervoor zal zorgen dat er een positieve y variabele als output zal weergeven?Ik dacht dat ik het in dit topic had gepost, echter bleek dat ik het in mijn eigen topic had gepost. Vandaar dat ik het verwijderde. Jouw post kwam vlak na de verwijdering...quote:
[..]
Je moet niet dezelfde vraag in twee topics tegelijk stellen en dan ook nog je vraag weer weghalen als ik die juist voor je heb beantwoord. Stel je vragen over wiskunde hier, daar is dit topic voor bedoeld.
Maar bedankt voor de tip.Stel f(x) = x2, dan is -f(x) = -x2.quote:
[..]
Ik raak alleen in de war doordat er steeds f(x) staat.. Ik weet wel dat die f in principe staat voor de functie (y) en dan de (x) staat voor de input, maar het is zo verwarrend als het dan allemaal in 1 zin staat. Dan weet ik bijvoorbeeld niet wat -f(x) dan moet voorstellen, de input of output zeg maar.
Het doel van deze opgave is dus dat je moet laten zien dat als je -x als input gebruikt in de functie, dat dat resulteert in x als input gebruiken en dan een minteken voor de functie zetten.
In mijn voorbeeld geldt dit bijvoorbeeld niet. Want: f(-x) = (-x)2 = x2 = f(x)Om even wat duidelijkheid in het gebruik van de letters te scheppen:
In een gebruikelijk, 2-dimensionaal, assenstelsel geeft x de horizontale coördinaat aan en y de verticale coördinaat.
De letter f (en indien nodig g, h..) worden gebruikt om een functievoorschrift aan te geven die, bij een gegeven x-coördinaat (in jouw woorden: de input) één unieke y-coördinaat levert. Die y-coördinaat, die bij de genoemde x hoort, noteren we als f(x).
De waarde die bij 3 hoort, noteren we als f(3)
De waarde die bij -3 hoort, noteren we als f(-3)
De waarde die bij -x hoort, noteren we als f(-x).
-f(x) is niets anders dan -1 ∙ f(x).
Ik zie dat ik me de moeite kan besparen om ze verder uit te werken, omdat Riparius dat (in een ander topic) al keurig voor je gedaan heeft.Opinion is the medium between knowledge and ignorance (Plato)Hoe wil jij hier wortels wegwerken?quote:
[..]
Dit ja. X substitueren voor x+h. Had ik het goed gedaan? Zo ja, kan het korter geschreven worden (zoals wortels wegwerken?)
Het enige wat je nog kunt doen is C(x+h)=A(x+h)1,5+B ervan maken. Maar vanwege de onduidelijke vraagstellen weet ik niet of dit de bedoeling is.
Verder moet je niet zomaar 10 invullen om `het simpel te houden`. De hele essentie van de opgave doe je hiermee teniet.kloep kloepHoe is 82/3 makkelijk op te lossen uit het hoofd?
Als het 1/3 was dan was het een kwestie geweest van de derdemachtswortel nemen..Hint: als het goed is weet je dat 8ab = (8a)bquote:
Hoe is 82/3 makkelijk op te lossen uit het hoofd?
Als het 1/3 was dan was het een kwestie geweest van de derdemachtswortel nemen..Opinion is the medium between knowledge and ignorance (Plato)8^(2/3) is het kwadraat van 8^(1/3).quote:
Hoe is 82/3 makkelijk op te lossen uit het hoofd?
Als het 1/3 was dan was het een kwestie geweest van de derdemachtswortel nemen..kloep kloepRekenregel:quote:
Hoe is 82/3 makkelijk op te lossen uit het hoofd?
Als het 1/3 was dan was het een kwestie geweest van de derdemachtswortel nemen..
(ap)q = apq
(voor a ∈ R+, p, q ∈ R)
Dus:
82/3 = (81/3)2 = 22 = 4
Of:
82/3 = (23)2/3 = 22 = 4hoe zou je dat moeten doen als het grondtal 2 was geweest? Want 2 kun je niet verder verkleinen..quote:
[..]
Rekenregel:
(ap)q = apq
(voor a ∈ R+, p, q ∈ R)
Dus:
82/3 = (81/3)2 = 22 = 4
Of:
82/3 = (23)2/3 = 22 = 4Dan wordt het 3√4, maar die weet ik ook niet uit mijn hoofd.quote:
[..]
hoe zou je dat moeten doen als het grondtal 2 was geweest? Want 2 kun je niet verder verkleinen..Opinion is the medium between knowledge and ignorance (Plato)22/3 = (22)1/3 = 41/3 is geen rationaal getal, dus dit kun je niet (uit het hoofd of met pen en papier) exact berekenen, hoogstens benaderen. Je kunt wel uit het hoofd nagaan dat dit getal groter moet zijn dan 1,5 = 3/2, want (3/2)3 = 27/8 < 32/8 = 4, en dat dit getal kleiner moet zijn dan 1,6 = 8/5, want (8/5)3 = 512/125 > 500/125 = 4. Dus heb je 1,5 < 41/3 < 1,6.quote:
[..]
hoe zou je dat moeten doen als het grondtal 2 was geweest? Want 2 kun je niet verder verkleinen..Er is iets wat ik niet begrijp en ik hoop hier meer duidelijkheid over te verkrijgen. De essentie van het onderstaande verhaal (wat er in de afbeeldingen staat) begrijp ik, echter begrijp ik een paar dingen niet, welke uitgebreid worden uitgelegd. Ik kan 'het' niet volgen.
Van dit plaatje begrijp ik het laatste gedeelte niet. Dat gedeelte begint bij de formule waar aan de rechterzijde (2) staat. De tekst onder de functie begrijp ik ook niet.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Van dit plaatje begrijp ik de eerste alinea niet (tot aan de blauwe tekst toe, blauwe tekst begrijp ik wel). Vervolgens ik de functie/formule niet waarin breuken te zien is (onder andere met au² e.d.)
Tenslotte begrijp ik de twee functies onderaan het plaatje niet ('solution'). Ik weet wel wat er gevraagd wordt en wat er geantwoord moet worden, maar ik begrijp de functie niet, deze wordt waarschijnlijk afgeleid van de stof welke ik dan weer niet begrijp... Overigens begrijp ik de * bij de twee functies ook niet.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Ik hoop dat iemand mij uit de brand kan helpen en bij voorbaat dank.
Excuseer mij voor een zijliggende foto, maar dat deed tinypic uit zich zelf tijdens het uploaden, want ik had het de foto's toch echt rechtop genomen, daarnaast stonden ze op mijn pc ook wel goed.
[ Bericht 5% gewijzigd door Brainstorm245 op 09-09-2014 18:42:50 ]We gaan op zoek naar de waarde van x waarvoor de kwadratische functie f zijn minimale of maximale waarde bereikt. Hebben we een dalparabool, dus met a>0, dan hebben we een minimum; bij a<0 hebben we een bergparabool en vinden we dus een maximum.quote:
Van dit plaatje begrijp ik het laatste gedeelte niet. Dat gedeelte begint bij de formule waar aan de rechterzijde (2) staat. De tekst onder de functie begrijp ik ook niet.
De uitdrukking die bij (2) wordt gegeven is niets anders dan een andere wijze van opschrijven van de algemene kwadratische functie waarmee werd begonnen. Dit is niet al te moeilijk in te zien door de haakjes weer uit te werken, maar ik denk dat het in paragraaf 2.3 ook netjes staat uitgeschreven, vermoedelijk onderweg naar het afleiden van de abc- of wortelformule.
In de uitdrukking bij (2) is het gedeelte achter het minteken constant - het hangt niet af van x. Het eerste gedeelte is slechts 0 als x = -b/2a (Oh ja?) Bij deze waarde van x moet dus wel de extreme waarde van de parabool liggen.
(Als je graag grafisch denkt: de parabool wordt eigenlijk verticaal zó opgeschoven dat ze raakt aan de x-as; dan is er precies één nulpunt dat op de top van de parabool ligt.)
Dat de top van de parabool precies daar moet liggen is ook makkelijk te zien als je gaat differentiëren:
f(x) = ax2 + bx + c, dan
f'(x) = 2ax + b, en dan
f'(x) = 0, dus 2ax + b = 0, dus 2ax = -b, dus x = -b/2a.Deze uitdrukking vertelt je dat, als je eenmaal de x-waarde van het maximum gevonden hebt, de symmetrie-as van de parabool de verticale lijn door die x-waarde is, en (logischerwijs), de functiewaarde op een afstand u links van het midden, even groot is als de functiewaarde op een afstand u rechts van het midden. Bedenk dat, nog steeds, dat midden ligt bij x = -b / 2a.quote:Van dit plaatje begrijp ik de eerste alinea niet (tot aan de blauwe tekst toe, blauwe tekst begrijp ik wel). Vervolgens ik de functie/formule niet waarin breuken te zien is (onder andere met au² e.d.)Ik ga er dan maar van uit dat je het economische gedeelte (hoe komt de formule van π tot stand) begrijpt. Dit is een kwadratische functie, namelijk π(Q) = 100Q - 5/2Q2quote:Tenslotte begrijp ik de twee functies onderaan het plaatje niet ('solution'). Ik weet wel wat er gevraagd wordt en wat er geantwoord moet worden, maar ik begrijp de functie niet, deze wordt waarschijnlijk afgeleid van de stof welke ik dan weer niet begrijp... Overigens begrijp ik de * bij de twee functies ook niet.
Als we deze in dezelfde volgorde schrijven als voorheen, dus met de hoogste machten eerst, dan wordt dat
π(Q) = -5/2Q2 + 100Q.
In deze kwadratische formule is dus a = -5/2, b = 100 en c = 0. Met de hierboven afgeleide formule berekenen we eenvoudig de positie van het maximum (want a<0), en dat is precies wat ze doen bij 'Solution'. Daarna wordt de waarde van dat maximum π*(Q) berekend met behulp van de tweede regel van je tweede scan, waar de waarde van f(x) bij de top wordt uitgeschreven als c - b2/4a.
Succes.
[ Bericht 1% gewijzigd door Janneke141 op 09-09-2014 00:38:27 ]Opinion is the medium between knowledge and ignorance (Plato)Je zult het wel niet willen horen, maar ik denk dat het niet kunnen volgen van de argumentatie ook te maken heeft met het feit dat het een Engels leerboek is. Ik zie steeds weer hier op FOK dat het gebruik van Engels lesmateriaal bij studenten een goed begrip in de weg staat. Is ook nergens voor nodig bij zulke elementaire dingen, er zijn genoeg Nederlandse boeken of dictaten waarin dit soort zaken worden uitgelegd, en als die er niet zijn is het hoog tijd dat ze geschreven worden.quote:
Er is iets wat ik niet begrijp en ik hoop hier meer duidelijkheid over te verkrijgen. De essentie van het onderstaande verhaal (wat er in de afbeeldingen staat) begrijp ik, echter begrijp ik een paar dingen niet, welke uitgebreid worden uitgelegd. Ik kan 'het' niet volgen.Formule (2) wordt verkregen via kwadraatafsplitsing. Dat is een standaardtechniek voor het herleiden van kwadratische veeltermen die je gewoon moet leren gebruiken. Ik heb dit al heel vaak uitgelegd, als je even terugleest in dit topic vind je wel een paar linkjes naar eerdere posts van mij om je op weg te helpen.quote:Van dit plaatje begrijp ik het laatste gedeelte niet. Dat gedeelte begint bij de formule waar aan de rechterzijde (2) staat. De tekst onder de functie begrijp ik ook niet.
De tekst onder (2) zegt dat je deze formule eenvoudig kunt verifiëren door de haakjes weer uit te werken en gelijksoortige termen samen te nemen. De clou is dat alleen de eerste term in het rechterlid van (2) afhangt van x en dat deze eerste term een kwadraat is, vermenigvuldigd met de constante a. Aangezien een kwadraat niet negatief kan zijn volgt dat de uitdrukking een extreme waarde bereikt als x + b/2a = 0 oftewel x = −b/2a. Deze extreme waarde is een minimum voor a > 0 aangezien a(x + b/2a)² dan niet kleiner kan worden dan nul, en een maximum voor a < 0 aangezien a(x + b/2a)² dan niet groter kan worden dan nul.quote:Dit kan niet. De blauwe tekst is een samenvatting van de tekst erboven waarvan je zelf beweert dat je deze niet begrijpt, en dus volgt dat je de blauwe tekst ook niet echt begrijpt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Van dit plaatje begrijp ik de eerste alinea niet (tot aan de blauwe tekst toe, blauwe tekst begrijp ik wel).quote:Vervolgens ik de functie/formule niet waarin breuken te zien is (onder andere met au² e.d.)
Tenslotte begrijp ik de twee functies onderaan het plaatje niet ('solution'). Ik weet wel wat er gevraagd wordt en wat er geantwoord moet worden, maar ik begrijp de functie niet, deze wordt waarschijnlijk afgeleid van de stof welke ik dan weer niet begrijp... Overigens begrijp ik de * bij de twee functies ook niet.Hier wordt een simpele substitutie x = −b/2a + u resp. x = −b/a2 − u uitgevoerd om aan te tonen dat de functiewaarden hetzelfde zijn voor elk tweetal waarden van x die symmetrisch liggen ten opzichte van −b/2a, zodat volgt dat de verticale lijn met vergelijking x = −b/2a een symmetrie-as is van de grafiek van de functie. In de tekst daaronder gaat het gewoon om het bepalen van het maximum van de functie π(Q) = 100Q − (5/2)·Q² alsmede de waarde van Q waarbij dit maximum wordt bereikt. Andere letters, zelfde principe.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Ik zal dit toch maar even voordoen met kwadraatafsplitsing, want de manier waarop het boek het doet is didactisch niet al te handig en foutgevoelig. We halen eerst even de coëfficiënt −5/2 van de kwadratische term buiten haakjes, dan hebben we
π(Q) = (−5/2)·(Q² − 40Q)
Nu gaan we kwadraatafsplitsing toepassen op de kwadratische veelterm binnen de haakjes. Daarvoor halveren we de coëfficiënt van Q en maken we gebruik van het merkwaardig product
(a − b)² = a² − 2ab + b²
om te bedenken dat (Q −20)² = Q² − 40Q + 400, zodat we dus hebben
Q² − 40Q = (Q − 20)² − 400
Voor de functie kunnen we dus schrijven
π(Q) = (−5/2)·((Q − 20)² − 400)
Nu werken we de buitenste haakjes in het functievoorschrift weer uit, en dan hebben we
π(Q) = (−5/2)·(Q − 20)² + 1000
En zie, nu kunnen we direct uit het functievoorschrift aflezen dat π(Q) een maximum van 1000 bereikt voor Q = 20. Dat komt uiteraard doordat (Q − 20)² niet negatief kan zijn, zodat de eerste term (−5/2)·(Q − 20)² niet groter kan worden dan nul omdat deze term steeds negatief is, behalve als Q = 20. En dus kan (−5/2)·(Q − 20)² + 1000 oftewel π(Q) niet groter worden dan 1000.Kwadraatafsplitsen kan ik wel. In het voorbeeld in 2.3 wordt ook een tweedegraads polynoom gebruikt, maar dan met getallen ipv a, b en c. Echter komt het niet voor dat er een breuk e.d. ontstaat.quote:
[..]
Je zult het wel niet willen horen, maar ik denk dat het niet kunnen volgen van de argumentatie ook te maken heeft met het feit dat het een Engels leerboek is. Ik zie steeds weer hier op FOK dat het gebruik van Engels lesmateriaal bij studenten een goed begrip in de weg staat. Is ook nergens voor nodig bij zulke elementaire dingen, er zijn genoeg Nederlandse boeken of dictaten waarin dit soort zaken worden uitgelegd, en als die er niet zijn is het hoog tijd dat ze geschreven worden.
[..]
Formule (2) wordt verkregen via kwadraatafsplitsing. Dat is een standaardtechniek voor het herleiden van kwadratische veeltermen die je gewoon moet leren gebruiken. Ik heb dit al heel vaak uitgelegd, als je even terugleest in dit topic vind je wel een paar linkjes naar eerdere posts van mij om je op weg te helpen.
De tekst onder (2) zegt dat je deze formule eenvoudig kunt verifiëren door de haakjes weer uit te werken en gelijksoortige termen samen te nemen. De clou is dat alleen de eerste term in het rechterlid van (2) afhangt van x en dat deze eerste term een kwadraat is, vermenigvuldigd met de constante a. Aangezien een kwadraat niet negatief kan zijn volgt dat de uitdrukking een extreme waarde bereikt als x + b/2a = 0 oftewel x = −b/2a. Deze extreme waarde is een minimum voor a > 0 aangezien a(x + b/2a)² dan niet kleiner kan worden dan nul, en een maximum voor a < 0 aangezien a(x + b/2a)² dan niet groter kan worden dan nul.
[..]
Dit kan niet. De blauwe tekst is een samenvatting van de tekst erboven waarvan je zelf beweert dat je deze niet begrijpt, en dus volgt dat je de blauwe tekst ook niet echt begrijpt.
[..]
Hier wordt een simpele substitutie x = −b/2a + u resp. x = −b/a2 − u uitgevoerd om aan te tonen dat de functiewaarden hetzelfde zijn voor elk tweetal waarden van x die symmetrisch liggen ten opzichte van −b/2a, zodat volgt dat de verticale lijn met vergelijking x = −b/2a een symmetrie-as is van de grafiek van de functie. In de tekst daaronder gaat het gewoon om het bepalen van het maximum van de functie π(Q) = 100Q − (5/2)·Q² alsmede de waarde van Q waarbij dit maximum wordt bereikt. Andere letters, zelfde principe.
Ik zal dit toch maar even voordoen met kwadraatafsplitsing, want de manier waarop het boek het doet is didactisch niet al te handig en foutgevoelig. We halen eerst even de coëfficiënt −5/2 van de kwadratische term buiten haakjes, dan hebben we
π(Q) = (−5/2)·(Q² − 40Q)
Nu gaan we kwadraatafsplitsing toepassen op de kwadratische veelterm binnen de haakjes. Daarvoor halveren we de coëfficiënt van Q en maken we gebruik van het merkwaardig product
(a − b)² = a² − 2ab + b²
om te bedenken dat (Q −20)² = Q² − 40Q + 400, zodat we dus hebben
Q² − 40Q = (Q − 20)² − 400
Voor de functie kunnen we dus schrijven
π(Q) = (−5/2)·((Q − 20)² − 400)
Nu werken we de buitenste haakjes in het functievoorschrift weer uit, en dan hebben we
π(Q) = (−5/2)·(Q − 20)² + 1000
En zie, nu kunnen we direct uit het functievoorschrift aflezen dat π(Q) een maximum van 1000 bereikt voor Q = 20. Dat komt uiteraard doordat (Q − 20)² niet negatief kan zijn, zodat de eerste term (−5/2)·(Q − 20)² niet groter kan worden dan nul omdat deze term steeds negatief is, behalve als Q = 20. En dus kan (−5/2)·(Q − 20)² + 1000 oftewel π(Q) niet groter worden dan 1000.Wat er in 2.3 staat, begrijp ik, maar er komen dan ook geen voorbeelden voor waarin zo'n kwadraatafsplitsing tevoorschijn komt met breuken en al.quote:
[..]
We gaan op zoek naar de waarde van x waarvoor de kwadratische functie f zijn minimale of maximale waarde bereikt. Hebben we een dalparabool, dus met a>0, dan hebben we een minimum; bij a<0 hebben we een bergparabool en vinden we dus een maximum.
De uitdrukking die bij (2) wordt gegeven is niets anders dan een andere wijze van opschrijven van de algemene kwadratische functie waarmee werd begonnen. Dit is niet al te moeilijk in te zien door de haakjes weer uit te werken, maar ik denk dat het in paragraaf 2.3 ook netjes staat uitgeschreven, vermoedelijk onderweg naar het afleiden van de abc- of wortelformule.
In de uitdrukking bij (2) is het gedeelte achter het minteken constant - het hangt niet af van x. Het eerste gedeelte is slechts 0 als x = -b/2a (Oh ja?) Bij deze waarde van x moet dus wel de extreme waarde van de parabool liggen.
(Als je graag grafisch denkt: de parabool wordt eigenlijk verticaal zó opgeschoven dat ze raakt aan de x-as; dan is er precies één nulpunt dat op de top van de parabool ligt.)
Dat de top van de parabool precies daar moet liggen is ook makkelijk te zien als je gaat differentiëren:
f(x) = ax2 + bx + c, dan
f'(x) = 2ax + b, en dan
f'(x) = 0, dus 2ax + b = 0, dus 2ax = -b, dus x = -b/2a.
[..]
Deze uitdrukking vertelt je dat, als je eenmaal de x-waarde van het maximum gevonden hebt, de symmetrie-as van de parabool de verticale lijn door die x-waarde is, en (logischerwijs), de functiewaarde op een afstand u links van het midden, even groot is als de functiewaarde op een afstand u rechts van het midden. Bedenk dat, nog steeds, dat midden ligt bij x = -b / 2a.
[..]
Ik ga er dan maar van uit dat je het economische gedeelte (hoe komt de formule van π tot stand) begrijpt. Dit is een kwadratische functie, namelijk π(Q) = 100Q - 5/2Q2
Als we deze in dezelfde volgorde schrijven als voorheen, dus met de hoogste machten eerst, dan wordt dat
π(Q) = -5/2Q2 + 100Q.
In deze kwadratische formule is dus a = -5/2, b = 100 en c = 0. Met de hierboven afgeleide formule berekenen we eenvoudig de positie van het maximum (want a<0), en dat is precies wat ze doen bij 'Solution'. Daarna wordt de waarde van dat maximum π*(Q) berekend met behulp van de tweede regel van je tweede scan, waar de waarde van f(x) bij de top wordt uitgeschreven als c - b2/4a.
Succes.
Dit is 2.3:
[ Bericht 1% gewijzigd door Brainstorm245 op 09-09-2014 09:54:56 ]Ik begrijp je probleem niet zo goed. Het lijkt er eerder op dat je moeite hebt met de herleiding middels kwadraatafsplitsing van de algemene kwadratische functiequote:
[..]
Kwadraatafsplitsen kan ik wel. In het voorbeeld in 2.3 wordt ook een tweedegraads polynoom gebruikt, maar dan met getallen ipv a, b en c. Echter komt het niet voor dat er een breuk e.d. ontstaat.
Je kunt trouwens in plaats van te beginnen met het buiten haakjes halen van een factor a en te schrijven
ook beginnen om een factor 1/4a buiten haakjes te halen, dan krijg je
waarvoor je weer kunt schrijven
De buitenste haakjes uitwerken geeft dan
En door bij de teller van de eerste term een factor 4a² = (2a)² buiten de haakjes te brengen hebben we dan inderdaad
Zo kan het dus ook. Begrijp je dit wel?waar haal je opeena die 1/4 vandaan? Overigens begrijp ik de overgang van stap 3 naar 4 niet. Uitgaande dat stap 1 gewoon het opschrijven vd kwadratische functie is.quote:
[..]
Ik begrijp je probleem niet zo goed. Het lijkt er eerder op dat je moeite hebt met de herleiding middels kwadraatafsplitsing van de algemene kwadratische functie
Je kunt trouwens in plaats van te beginnen met het buiten haakjes halen van een factor a en te schrijven
ook beginnen om een factor 1/4a buiten haakjes te halen, dan krijg je
waarvoor je weer kunt schrijven
De buitenste haakjes uitwerken geeft dan
En door bij de teller van de eerste term een factor 4a² = (2a)² buiten de haakjes te brengen hebben we dan inderdaad
Zo kan het dus ook. Begrijp je dit wel?overgang van n/a laatste naar laatste stap begrijp ik ook niet.quote:
[..]
Ik begrijp je probleem niet zo goed. Het lijkt er eerder op dat je moeite hebt met de herleiding middels kwadraatafsplitsing van de algemene kwadratische functie
Je kunt trouwens in plaats van te beginnen met het buiten haakjes halen van een factor a en te schrijven
ook beginnen om een factor 1/4a buiten haakjes te halen, dan krijg je
waarvoor je weer kunt schrijven
De buitenste haakjes uitwerken geeft dan
En door bij de teller van de eerste term een factor 4a² = (2a)² buiten de haakjes te brengen hebben we dan inderdaad
Zo kan het dus ook. Begrijp je dit wel?
excuus als het dom overkomt.Ik zie dat er een eenvoudig voorbeeld wordt gegeven voor het completeren van het linkerlid van een kwadratische vergelijking tot een volkomen kwadraat, waarna de pq formule wordt afgeleid die de oplossingen geeft van de vergelijkingquote:
[..]
Wat er in 2.3 staat, begrijp ik, maar er komen dan ook geen voorbeelden voor waarin zo'n kwadraatafsplitsing tevoorschijn komt met breuken en al.
Nu kun je vervolgens om de abc formule voor de oplossingen van de algemene vierkantsvergelijking
af te leiden beginnen om beide leden van deze vergelijking door a te delen, waardoor we dus krijgen
Hiermee is de vergelijking herleid tot een vergelijking die we met de pq formule op kunnen lossen, en waarbij dus p = b/a en q = c/a. Door deze substituties uit te voeren in de pq formule wordt in het boek de abc formule verkregen.
Bestudeer dit eens goed en ook deze en deze uitwerkingen waarbij een vierkantsvergelijking wordt opgelost middels kwadraatafsplitsing. En bekijk ook mijn post over de afleiding van de pq formule en deze post over de directe afleiding van de abc formule met de methode van Sridhara.Dit begrijp ik niet. Sorry...quote:
[..]
We gaan op zoek naar de waarde van x waarvoor de kwadratische functie f zijn minimale of maximale waarde bereikt. Hebben we een dalparabool, dus met a>0, dan hebben we een minimum; bij a<0 hebben we een bergparabool en vinden we dus een maximum.
De uitdrukking die bij (2) wordt gegeven is niets anders dan een andere wijze van opschrijven van de algemene kwadratische functie waarmee werd begonnen. Dit is niet al te moeilijk in te zien door de haakjes weer uit te werken, maar ik denk dat het in paragraaf 2.3 ook netjes staat uitgeschreven, vermoedelijk onderweg naar het afleiden van de abc- of wortelformule.
In de uitdrukking bij (2) is het gedeelte achter het minteken constant - het hangt niet af van x. Het eerste gedeelte is slechts 0 als x = -b/2a (Oh ja?) Bij deze waarde van x moet dus wel de extreme waarde van de parabool liggen.
(Als je graag grafisch denkt: de parabool wordt eigenlijk verticaal zó opgeschoven dat ze raakt aan de x-as; dan is er precies één nulpunt dat op de top van de parabool ligt.)
Dat de top van de parabool precies daar moet liggen is ook makkelijk te zien als je gaat differentiëren:
f(x) = ax2 + bx + c, dan
f'(x) = 2ax + b, en dan
f'(x) = 0, dus 2ax + b = 0, dus 2ax = -b, dus x = -b/2a.
[..]
Deze uitdrukking vertelt je dat, als je eenmaal de x-waarde van het maximum gevonden hebt, de symmetrie-as van de parabool de verticale lijn door die x-waarde is, en (logischerwijs), de functiewaarde op een afstand u links van het midden, even groot is als de functiewaarde op een afstand u rechts van het midden. Bedenk dat, nog steeds, dat midden ligt bij x = -b / 2a.
[..]
Ik ga er dan maar van uit dat je het economische gedeelte (hoe komt de formule van π tot stand) begrijpt. Dit is een kwadratische functie, namelijk π(Q) = 100Q - 5/2Q2
Als we deze in dezelfde volgorde schrijven als voorheen, dus met de hoogste machten eerst, dan wordt dat
π(Q) = -5/2Q2 + 100Q.
In deze kwadratische formule is dus a = -5/2, b = 100 en c = 0. Met de hierboven afgeleide formule berekenen we eenvoudig de positie van het maximum (want a<0), en dat is precies wat ze doen bij 'Solution'. Daarna wordt de waarde van dat maximum π*(Q) berekend met behulp van de tweede regel van je tweede scan, waar de waarde van f(x) bij de top wordt uitgeschreven als c - b2/4a.
Succes.
er staat staat dat de waarde (bij het bepalen van een maxima/minima) van x= -b/2a gelijk is aan f(-b /2a) = -(b^2 - 4ac) / 4a = c - b^2 /4a
Het vetgedrukte begrijp ik dus niet.. als ik i.p.v. x -b/2a invul, hoe komt het tot het vetgedrukte formule? En waarin verschilt dat met -b/2a waardoor -b/2a gebruikt kan worden voor de maximalisatie van de profit bij Q (begrijp ik wel) en de maximalisatie profit bij aantal euro (die met die 100^2)... ??
Overigens voor alle duidelijkheid: ik snap de essentie en de bedoeling erachter en waar ik mee bezig ben.. het is meer de uitleg en de diepgang die ik niet begrijp..Ik vermenigvuldig de veelterm ax2 + bx + c met 4a, waardoor we 4a2x2 + 4abx + 4ac krijgen. Maar dit kan ik bij een functie niet zomaar doen, omdat ik dan een andere functie zou krijgen. Daarom moet ik dit compenseren door ook weer door 4a te delen oftewel met 1/4a te vermenigvuldigen. Dit komt uiteindelijk neer op het buiten haakjes halen van een factor 1/4a.quote:
[..]
waar haal je opeena die 1/4 vandaan?Dit is gewoon kwadraatafsplitsing. We kunnen binnen de haakjesquote:Overigens begrijp ik de overgang van stap 3 naar 4 niet. Uitgaande dat stap 1 gewoon het opschrijven vd kwadratische functie is.
4a2x2 + 4abx + 4ac
herschrijven als
(2ax)2 + 2·(2ax)·b + b2 − (b2 − 4ac)
en dit is weer te schrijven als
(2ax + b)2 − (b2 − 4ac)
Maar bestudeer nu eerst maar eens alle posts waarnaar ik hierboven link, dan moet het wel duidelijk worden.Ja die post had ik al eerder bestudeerd. Ze stonden ook nog eens letterlijk in mijn boek.quote:
[..]
Ik vermenigvuldig de veelterm ax2 + bx + c met 4a, waardoor we 4a2x2 + 4abx + 4ac krijgen. Maar dit kan ik bij een functie niet zomaar doen, omdat ik dan een andere functie zou krijgen. Daarom moet ik dit compenseren door ook weer door 4a te delen oftewel met 1/4a te vermenigvuldigen. Dit komt uiteindelijk neer op het buiten haakjes halen van een factor 1/4a.
[..]
Dit is gewoon kwadraatafsplitsing. We kunnen binnen de haakjes
4a2x2 + 4abx + 4ac
herschrijven als
(2ax)2 + 2·(2ax)·b + b2 − (b2 − 4ac)
en dit is weer te schrijven als
(2ax + b)2 − (b2 − 4ac)
Maar bestudeer nu eerst maar eens alle posts waarnaar ik hierboven link, dan moet het wel duidelijk worden.
Ik begrijp alleen niet waarom die -(b² - 4ac) erbij komt.. Voor de rest was het wel duidelijk ( de overgang).Jammer dat ik op google geen fatsoenlijke Nederlandse uitleg kan vinden over de kwadratische functies... en dan heb ik het over die
a( x + b/2a)² - b² - 4ac / 4a
etc. Eigenlijk gewoon mijn eerste post met die twee scans.
Als iemand dat toevallig heeft kunnen vinden, zou ik dat enorm waarderen (!!!)Aangezien mijn les zo zal beginnen, wil ik nog even alvast (!) mijn twee laatste vragen stellen:
Stel dat een winstformule het volgende is:
(a - c)Q - (b + d)Q²
Waarom is de maximalisatie van de winst op een bepaalde Q dan :
Q = (a - c) / 2(b + d) ?
Ik zou denken dat het
Q = (-a + c) / 2(b + d) is omdat er staat -b / 2a en niet b/2a
Tenslotte:
Stel er is een supply en demand functie, waarbij ze gelijk zijn en dus een quilibruim hebben bij:
P = a - bQ = c + 2dQ
dan zou:
Q = (a - c) / (b + 2d) zijn, daar ben ik nog wel uitgekomen, maar ik weet niet hoe ik de evenwichtsprijs functie kan opstellen evenals de evenwichts winstfunctie?Hierboven heb ik laten zien hoe je de algemene kwadratische functiequote:
[..]
Dit begrijp ik niet. Sorry...
er staat staat dat de waarde (bij het bepalen van een maxima/minima) van x= -b/2a gelijk is aan f(-b /2a) = -(b^2 - 4ac) / 4a = c - b^2 /4a
Het vetgedrukte begrijp ik dus niet.. als ik i.p.v. x -b/2a invul, hoe komt het tot het vetgedrukte formule?
kunt herschrijven als
Uit deze gedaante van de algemene kwadratische functie kunnen we aflezen dat f(x) een extreme waarde bereikt bij x = −b/2a en dat deze extreme waarde een minimum is indien a > 0 en een maximum indien a < 0.
Immers, als a > 0 dan is de term a(x + b/2a)2 positief of nul, zodat een minimum wordt bereikt als (x + b/2a) nul is, en dat is het geval voor x = −b/2a. Is daarentegen a < 0 dan is de term a(x + b/2a)2 negatief of nul zodat een maximum wordt bereikt als (x + b/2a) nul is, en dat is wederom het geval voor x = −b/2a.
Vullen we nu x = −b/2a in in het herleide functievoorschrift, dan is de eerste term nul en houden we dus over
De waarde van het bereikte extremum (minimum indien a > 0, maximum indien a < 0) is dus −(b² − 4ac)/4a = −b²/4a + c. Overigens vind ik het zelf prettiger om te schrijven
waarbij
de discriminant is van de kwadratische veelterm ax² + bx + c (a ≠ 0). De discriminant bepaalt bij een kwadratische veelterm met reële coëfficiënten het aantal (verschillende) reële nulpunten van de veelterm, dat 0, 1 of 2 kan bedragen.Dit is niet begrijpelijk. Beter uitleggen wat precies je probleem is. Overigens heb ik je al gezegd dat je hier beter de functie π(Q) om kunt werken met kwadraatafsplitsing in een vorm waarbij je direct kunt aflezen dat voor Q = 20 een maximum van 1000 wordt bereikt.quote:En waarin verschilt dat met -b/2a waardoor -b/2a gebruikt kan worden voor de maximalisatie van de profit bij Q (begrijp ik wel) en de maximalisatie profit bij aantal euro (die met die 100^2)... ??Dit is geen kwestie van diepgang, je hebt kennelijk nauwelijks enig benul van elementaire schoolalgebra. Dit was vroeger allemaal stof voor de tweede klas.quote:Overigens voor alle duidelijkheid: ik snap de essentie en de bedoeling erachter en waar ik mee bezig ben.. het is meer de uitleg en de diepgang die ik niet begrijp..Super bedankt.quote:
[..]
Hierboven heb ik laten zien hoe je de algemene kwadratische functie
kunt herschrijven als
Uit deze gedaante van de algemene kwadratische functie kunnen we aflezen dat f(x) een extreme waarde bereikt bij x = −b/2a en dat deze extreme waarde een minimum is indien a > 0 en een maximum indien a < 0.
Immers, als a > 0 dan is de term a(x + b/2a)2 positief of nul, zodat een minimum wordt bereikt als (x + b/2a) nul is, en dat is het geval voor x = −b/2a. Is daarentegen a < 0 dan is de term a(x + b/2a)2 negatief of nul zodat een maximum wordt bereikt als (x + b/2a) nul is, en dat is wederom het geval voor x = −b/2a.
Vullen we nu x = −b/2a in in het herleide functievoorschrift, dan is de eerste term nul en houden we dus over
De waarde van het bereikte extremum (minimum indien a > 0, maximum indien a < 0) is dus −(b² − 4ac)/4a = −b²/4a + c. Overigens vind ik het zelf prettiger om te schrijven
waarbij
de discriminant is van de kwadratische veelterm ax² + bx + c (a ≠ 0). De discriminant bepaalt bij een kwadratische veelterm met reële coëfficiënten het aantal (verschillende) reële nulpunten van de veelterm, dat 0, 1 of 2 kan bedragen.
[..]
Dit is niet begrijpelijk. Beter uitleggen wat precies je probleem is. Overigens heb ik je al gezegd dat je hier beter de functie π(Q) om kunt werken met kwadraatafsplitsing in een vorm waarbij je direct kunt aflezen dat voor Q = 20 een maximum van 1000 wordt bereikt.
[..]
Dit is geen kwestie van diepgang, je hebt kennelijk nauwelijks enig benul van elementaire schoolalgebra. Dit was vroeger allemaal stof voor de tweede klas.
Ja klopt... Maar ik had havo wiskunde A en dat stelde niks voor op mijn middelbare school i.t.t. het vwo.Dan begrijp je dus echt niet hoe het completeren van het kwadraat werkt.quote:
[..]
Ja die post had ik al eerder bestudeerd. Ze stonden ook nog eens letterlijk in mijn boek.
Ik begrijp alleen niet waarom die -(b² - 4ac) erbij komt.. Voor de rest was het wel duidelijk ( de overgang).
Om te beginnen: die 4ac komt er niet bij, want die stond er al. Waar het om gaat dat is dat we
4a2x2 + 4abx
oftewel
(2ax)2 + 2·2ax·b
willen completeren tot een volkomen kwadraat, en dat kunnen we doen door hier b2 bij op te tellen. Maar ik mag niet zomaar b2 optellen in een functievoorschrift want dan zou ik een andere functie krijgen. Dus moet ik die b2 ook weer meteen aftrekken. We herschrijven dus
4a2x2 + 4abx + 4ac
oftewel
(2ax)2 + 2·2ax·b + 4ac
als
(2ax)2 + 2·2ax·b + b2 − b2 + 4ac
en nu kunnen we dit weer schrijven als
(2ax + b)2 − b2 + 4ac
oftewel
(2ax + b)2 − (b2 − 4ac)Ik begrijp gewoon niet hoe die c/a opeens 4ac wordt..quote:
[..]
Dan begrijp je dus echt niet hoe het completeren van het kwadraat werkt.
Om te beginnen: die 4ac komt er niet bij, want die stond er al. Waar het om gaat dat is dat we
4a2x2 + 4abx
oftewel
(2ax)2 + 2·2ax·b
willen completeren tot een volkomen kwadraat, en dat kunnen we doen door hier b2 bij op te tellen. Maar ik mag niet zomaar b2 optellen in een functievoorschrift want dan zou ik een andere functie krijgen. Dus moet ik die b2 ook weer meteen aftrekken. We herschrijven dus
4a2x2 + 4abx + 4ac
oftewel
(2ax)2 + 2·2ax·b + 4ac
als
(2ax)2 + 2·2ax·b + b2 − b2 + 4ac
en nu kunnen we dit weer schrijven als
(2ax + b)2 − b2 + 4ac
oftewel
(2ax + b)2 − (b2 − 4ac)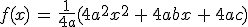
quote:Ik vermenigvuldig de veelterm ax2 + bx + c met 4a, waardoor we 4a2x2 + 4abx + 4ac krijgen. Maar dit kan ik bij een functie niet zomaar doen, omdat ik dan een andere functie zou krijgen. Daarom moet ik dit compenseren door ook weer door 4a te delen oftewel met 1/4a te vermenigvuldigen. Dit komt uiteindelijk neer op het buiten haakjes halen van een factor 1/4a.ja ik snap de nut er niet van? Je vermenigvuldigt met 4a? Sowieso al, waarom 4a en niet alleen met 4? Wat is de reden voor de keuze voor 4 en niet voor 2 oid? en dan inderdaad weer delen met 1/4a, maar dan bereik je toch niks? is gewoon hetzelfde functie alleen anders geschreven? ik begrijp de hele nut ervan niet.quote:
ik stel steeds waarom vragen en denk extreem veel door, waardoor ik in mijn eigen doordenken in de war raak. ik wil alles weten.. waarom het zo is etc.Is gewoon een herschrijving om het je gemakkelijker te maken.quote:
[..]
ja ik snap de nut er niet van? Je vermenigvuldigt met 4a? Sowieso al, waarom 4a en niet alleen met 4? Wat is de reden voor de keuze voor 4 en niet voor 2 oid? en dan inderdaad weer delen met 1/4a, maar dan bereik je toch niks? is gewoon hetzelfde functie alleen anders geschreven? ik begrijp de hele nut ervan niet.
ik stel steeds waarom vragen en denk extreem veel door, waardoor ik in mijn eigen doordenken in de war raak. ik wil alles weten.. waarom het zo is etc.
lees post op dinsdag 9 september 2014 @ 11:24 • 214
[ Bericht 3% gewijzigd door wiskundenoob op 09-09-2014 13:23:14 ]
Deze vraag gaat over lineair programmeren. De kosten dienen geminimaliseerd te worden en de tabel geeft weer welke boete men heeft ontvangen (kosten), na aanleiding van de gereden rit op een dag. Taxichauffeurs mogen maar 1 route per dag rijden. Ik moet dus een optimale situatie weer kunnen geven met behulp van excel (Solver?). Er zijn dus 64 variabelen met chauffeurs en route?
Als iemand me kan helpen, zou mooi zijn!--http://tinypic.com/r/rqxij4/8
Is de link van de tabel, hij wil hem helaas hier niet openen
Objective is dus dat ik de chauffeurs moet toewijzen aan de routes, waar een bepaalde optimale situatie voor is
Bij voorbaat dank!--quote:
Aangezien mijn les zo zal beginnen, wil ik nog even alvast (!) mijn twee laatste vragen stellen:
Stel dat een winstformule het volgende is:
(a - c)Q - (b + d)Q²
Waarom is de maximalisatie van de winst op een bepaalde Q dan :
Q = (a - c) / 2(b + d) ?
Ik zou denken dat het
Q = (-a + c) / 2(b + d) is omdat er staat -b / 2a en niet b/2a
Tenslotte:
Stel er is een supply en demand functie, waarbij ze gelijk zijn en dus een quilibruim hebben bij:
P = a - bQ = c + 2dQ
dan zou:
Q = (a - c) / (b + 2d) zijn, daar ben ik nog wel uitgekomen, maar ik weet niet hoe ik de evenwichtsprijs functie kan opstellen evenals de evenwichts winstfunctie?Bekijk het eens andersom. Stel dat we precies bovenstaand functievoorschrift hebben en dat we hier de haakjes weer uit willen werken. Dan krijgen we dusquote:
[..]
Ik begrijp gewoon niet hoe die c/a opeens 4ac wordt..
oftewel
Nu zie je dat we de drie breuken kunnen vereenvoudigen, want de teller en de noemer van elk van de drie breuken heeft een factor 4a. We kunnen dus de drie breuken vereenvoudigen door bij elke breuk teller en noemer door 4a te delen. En dan krijgen we
oftewel
Zo zie je dus dat beide uitdrukkingen voor f(x) inderdaad identiek zijn.Als je mijn post over de afleiding van de abc formule met de methode van Sridhara had bestudeerd dan zou je hebben begrepen waarom we met 4a vermenigvuldigen.quote:
[..]
ja ik snap de nut er niet van? Je vermenigvuldigt met 4a? Sowieso al, waarom 4a en niet alleen met 4? Wat is de reden voor de keuze voor 4 en niet voor 2 oid?Inderdaad, we moeten bij de herleiding van een functievoorschrift natuurlijk wel ervoor zorgen dat de functie hetzelfde blijft. Ik vermenigvuldig de veeltermquote:en dan inderdaad weer delen vermenigvuldigen met 1/4a, maar dan bereik je toch niks? is gewoon hetzelfde functie alleen anders geschreven?
ax² + bx + c
met 4a om zo
4a²x² + 4abx + 4ac
te krijgen oftewel
(2ax)² + 2·(2ax)·b + 4ac
zodat ik kwadraatafsplitsing kan toepassen zonder vervelende breuken en je dus krijgt
(2ax + b)² − b² + 4ac
Maar bij de herleiding van een functievoorschrift mag ik niet zomaar alles met een factor vermenigvuldigen, want dan zouden we een andere functie krijgen, en dat is niet de bedoeling. Dus moeten we die vermenigvuldiging van de termen van (ax² + bx + c) met 4a compenseren door meteen buiten de haakjes een factor 1/4a toe te voegen. En effectief komt dit neer op het buiten haakjes halen van een factor 1/4a.Dat blijkt. Nog één keer dan. Als we een kwadratische functiequote:ik begrijp de hele nut ervan niet.
hebben, dan kunnen we hier met het 'blote oog' niet aan zien of deze functie een extreme waarde heeft, laat staan wat het maximum of het minimum is van deze functie, en voor welke waarde van x dit maximum of minimum wordt bereikt. Maar als we dit functievoorschrift omwerken naar
dan kunnen we opeens wél in één oogopslag zien dat de functie een extreme waarde bereikt bij x = −b/2a, en dat deze extreme waarde een minimum is als a > 0 maar een maximum als a < 0. Ook kunnen we direct zien dat deze extreme waarde f(−b/2a) = −D/4a bedraagt, waarbij D = b² − 4ac. De top van de parabool die de grafiek is van deze functie heeft dus de coördinaten (−b/2a, −D/4a).
Je ziet dat we nu opeens een heleboel informatie over deze kwadratische functie boven water hebben gekregen die we nooit hadden gekregen als we alleen maar stom naar het functievoorschrift
f(x) = ax² + bx + c
waren blijven staren.
Bovendien is de techiek van het kwadraatafsplitsen uitermate nuttig voor het oplossen van vierkantsvergelijkingen (en voor tal van andere zaken waar ik nu niet op in ga).Dat 'extreem doordenken' valt nogal mee (of tegen, afhankelijk van het perspectief van de beschouwer). Ik vind dat je een en ander nog wel wat beter mag overdenken, en ook is het zaak om je vaardigheden met het uitvoeren van algebraïsche herleidingen snel op peil te brengen, anders zal dit je je hele studie blijven achtervolgen en zul je mogelijk je studie moeten staken. Laat het eens lekker doorwaaien in die grijze massa van je!quote:Ik stel steeds waarom vragen en denk extreem veel door, waardoor ik in mijn eigen doordenken in de war raak. ik wil alles weten.. waarom het zo is etc.
[ Bericht 0% gewijzigd door Riparius op 11-09-2014 15:11:20 ]Ik begrijp er geen reet meer van. In mijn boek wordt er gewerkt met b/a en c/a. Ik weet dat je dat in je andere post wel had uitgelegd waarom (iets met Sdhara oid.) maar ik ben gewoon helemaal in de war...quote:
[..]
Als je mijn post over de afleiding van de abc formule met de methode van Sridhara had bestudeerd dan zou je hebben begrepen waarom we met 4a vermenigvuldigen.
[..]
Inderdaad, we moeten bij de herleiding van een functievoorschrift natuurlijk wel ervoor zorgen dat de functie hetzelfde blijft. Ik vermenigvuldig de veelterm
ax² + bx + c
met 4a om zo
4a²x² + 4abx + 4ac
te krijgen oftewel
(2ax)² + 2·(2ax)·b + 4ac
zodat ik kwadraatafsplitsing kan toepassen zonder vervelende breuken en je dus krijgt
(2ax + b)² − b² + 4ac
Maar bij de herleiding van een functievoorschrift mag ik niet zomaar alles met een factor vermenigvuldigen, want dan zouden we een andere functie krijgen, en dat is niet de bedoeling. Dus moeten we die vermenigvuldiging van de termen van (ax² + bx + c) met 4a compenseren door meteen buiten de haakjes een factor 1/4a toe te voegen. En effectief komt dit neer op het buiten haakjes halen van een factor 1/4a.
[..]
Dat blijkt. Nog één keer dan. Als we een kwadratische functie
hebben, dan kunnen we hier met het 'blote oog' niet aan zien of deze functie een extreme waarde heeft, laat staan wat het maximum of het minimum is van deze functie, en voor welke waarde van x dit maximum of minimum wordt bereikt. Maar als we dit functievoorschrift omwerken naar
dan kunnen we opeens wél in één oogopslag zien dat de functie een extreme waarde bereikt bij x = −b/2a, en dat deze extreme waarde een minimum is als a > 0 maar een maximum als a < 0. Ook kunnen we direct zien dat deze extreme waarde f(−b/2a) = −D/4a bedraagt, waarbij D = b² − 4ac. De top van de parabool die de grafiek is van deze functie heeft dus de coördinaten (−b/2a, −D/4a).
Je ziet dat we nu opeens een heleboel informatie over deze kwadratische functie boven water hebben gekregen die we nooit hadden gekregen als we alleen maar stom naar het functievoorschrift
f(x) = ax² + bx + c
waren blijven staren.
Bovendien is de techiek van het kwadraatafsplitsen uitermate nuttig voor het oplossen van vierkantsvergelijkingen (en voor tal van andere zaken waar ik nu niet op in ga).
[..]
Dat 'extreem doordenken valt nogal mee (of tegen, afhankelijk van het perspectief van de beschouwer). Ik vind dat je een en ander nog wel wat beter mag overdenken, en ook is het zaak om je vaardigheden met het uitvoeren van algebraïsche herleidingen snel op peil te brengen, anders zal dit je je hele studie blijven achtervolgen en zul je mogelijk je studie moeten staken. Laat het eens lekker doorwaaien in die grijze massa van je!
Excuus nogmaals voor het verdoen van je tijd, maar de middelbare school heeft mij geen wiskunde gegeven maar een klote vak 'hoe ga je met een GR'' om, want wat ik had, was echt geen wiskunde.Is er overigens een video op youtube te vinden hierover? Ik weet niet specifiek een trefwoord. Ik tik quadratic functions vertex completing the square, maar ik tref niet de juiste video's.
Dit soort dingen snap ik gemakkelijk:
Maar mij gaat het dus om die a(x + b/2a)² - Discriminant/4a. Dat wat Riparius mij dus al twee dagen probeert te verduidelijken.ax² + bx + c = 0
Nu vermenigvuldigen we het linker- en rechterlid met 4a. Dit levert:
4a(ax² + bx + c) = 0, uitgeschreven levert dit:
4a²x² + 4abx + 4ac = 0, tel nu links en rechts b² erbij op. Dit levert:
4a²x² + 4abx + 4ac + b² = b², breng nu 4ac van linkerlid naar rechterlid. Dit levert:
4a²x² + 4abx + b² = b² - 4ac, je ziet nu iets bekend staan bij het rechterlid.
Let wel: Het linkerlid kunnen we nu ontbinden in de volgende factoren (2ax + b)(2ax + b). Dit levert:
(2ax + b)² = b² - 4ac
Je weet als: x² = a, dan zijn de oplossingen: x = √(a) of x = -√(a). Hieruit volgt:
(2ax + b) = ±√(b² - 4ac)
Links en rechts 'b' aftrekken, levert:
2ax = -b ±√(b² - 4ac)
Daarna links en rechts delen door 2a, levert:
x = -b ±√(b² - 4ac) / 2a
Hieruit volgen de oplossingen met de abc formule:
x1 = -b - √(b² - 4ac) / 2a
en
x2 = -b + √(b² - 4ac) / 2a
Dit begrijp ik gewoon; bewijstlast voor de abc formule. Maar het is echt die a(x+b/2a)² ... etc.. dat ik niet snap..Er zijn natuurlijk altijd meerdere wegen die naar Rome leiden. De methode van Sridhara voor kwadraatafsplitsing (eigenlijk: het oplossen van een vierkantsvergelijking) heeft het grote voordeel dat breuken worden vermeden bij de herleiding van de abc formule (behalve op het laatst, als we door 2a moeten delen). De andere, meer conventionele methode om de abc formule af te leiden houdt in dat we bij de vierkantsvergelijkingquote:
[..]
Ik begrijp er geen reet meer van. In mijn boek wordt er gewerkt met b/a en c/a. Ik weet dat je dat in je andere post wel had uitgelegd waarom (iets met Sridhara oid.) maar ik ben gewoon helemaal in de war...
eerst beide leden delen door a (hetgeen is toegestaan aangezien a ≠ 0) zodat we krijgen
Nu hebben we dus een vergelijking van de gedaante
met p = b/a en q = c/a.
Bestudeer deze pagina eens (print de pagina eventueel ook uit) om het verschil te zien tussen de beide methoden om middels kwadraatafsplitsing de abc formule af te leiden.Dat begrijp ik, maar je mist ook gewoon een hoop basiskennis die je nu hard nodig zult hebben, namelijk de stof van Wiskunde B op VWO niveau.quote:Excuus nogmaals voor het verdoen van je tijd, maar de middelbare school heeft mij geen wiskunde gegeven maar een klote vak 'hoe ga je met een GR'' om, want wat ik had, was echt geen wiskunde.Add a term to both sides for completing square --> dat stuk begrijp ik niet.quote:
[..]
Er zijn natuurlijk altijd meerdere wegen die naar Rome leiden. De methode van Sridhara voor kwadraatafsplitsing (eigenlijk: het oplossen van een vierkantsvergelijking) heeft het grote voordeel dat breuken worden vermeden bij de herleiding van de abc formule (behalve op het laatst, als we door 2a moeten delen). De andere, meer conventionele methode om de abc formule af te leiden houdt in dat we bij de vierkantsvergelijking
eerst beide leden delen door a (hetgeen is toegestaan aangezien a ≠ 0) zodat we krijgen
Nu hebben we dus een vergelijking van de gedaante
met p = b/a en q = c/a.
Bestudeer deze pagina eens (print de pagina eventueel ook uit) om het verschil te zien tussen de beide methoden om middels kwadraatafsplitsing de abc formule af te leiden.
[..]
Dat begrijp ik, maar je mist ook gewoon een hoop basiskennis die je nu hard nodig zult hebben, namelijk de stof van Wiskunde B op VWO niveau.Getallenvoorbeeldje:quote:
[..]
Add a term to both sides for completing square --> dat stuk begrijp ik niet.
x2 + 6x + 5 = 0, en we willen een kwadraat afsplitsen.
De logische kandidaat is (x + 3)2, dat wordt x2 + 6x + 9
Dat is niet helemaal hetzelfde, dus om het kwadraat compleet te maken, moeten we links en rechts een term toevoegen. In dit geval + 4:
x2 + 6x + 5 + 4 = 4
Nu staat links namelijk een kwadraat, een square.Opinion is the medium between knowledge and ignorance (Plato)aha duidelijk..quote:
[..]
Getallenvoorbeeldje:
x2 + 6x + 5 = 0, en we willen een kwadraat afsplitsen.
De logische kandidaat is (x + 3)2, dat wordt x2 + 6x + 9
Dat is niet helemaal hetzelfde, dus om het kwadraat compleet te maken, moeten we links en rechts een term toevoegen. In dit geval + 4:
x2 + 6x + 5 + 4 = 4
Nu staat links namelijk een kwadraat, een square.
Weet jij ook hoe je van
-b /2a +/- √(b² / 4a² - c/a) gaat naar: (-b +/- √b²- 4ac) / 2a
Die linkerterm begrijp ik met die -b/2a, wat ik niet begrijp is de Discriminant omzetten naar .... met een deling van 2a.quote:
[..]
aha duidelijk..
Weet jij ook hoe je van
-b /2a +/- √(b² / 4a² - c/a) gaat naar: (-b +/- √b²- 4ac) / 2a
Die linkerterm begrijp ik met die -b/2a, wat ik niet begrijp is de Discriminant omzetten naar .... met een deling van 2a.Opinion is the medium between knowledge and ignorance (Plato)Ik zal de herleiding van de algemene kwadratische functiequote:
Maar mij gaat het dus om die a(x + b/2a)² - Discriminant/4a. Dat wat Riparius mij dus al twee dagen probeert te verduidelijken.
nog een keertje voor je uitwerken, maar nu op de conventionele manier. We halen eerst een factor a buiten haakjes, dan krijgen we
Nu halveren we de coëfficiënt b/a van x, dat geeft b/2a, en hiervan nemen we het kwadraat, dat is (b/2a)² = b²/4a². Dit tellen we op bij de termen tussen haakjes, maar dan moeten we dit ook meteen weer aftrekken, anders blijft de functie niet hetzelfde. Zo hebben we dus
Nu kunnen we de eerste drie termen binnen de grote haakjes schrijven als een kwadraat, want we hebben immers
Ook kunnen we de laatste twee termen binnen de grote haakjes samennemen. Dit zijn twee breuken, die we wel eerst gelijknamig moeten maken door de teller en de noemer van de tweede breuk c/a met 4a te vermenigvuldigen, zodat we krijgen
Voor het functievoorschrift krijgen we zo
Tenslotte werken we de grote haakjes weer uit en dan hebben we inderdaad
En aangezien
de discriminant is van de kwadratische veelterm ax² + bx + c kunnen we dus ook schrijven
Nu lezen we gemakkelijk af dat deze functie voor x = −b/2a een extreme waarde
bereikt, en dat dit extremum een minimum is indien a > 0 en een maximum indien a < 0.Dit is het laatste stukje waar ik nog vastloop, want ik zit met die kwadraatsplitsing dat je:quote:
[..]
Ik zal de herleiding van de algemene kwadratische functie
nog een keertje voor je uitwerken, maar nu op de conventionele manier. We halen eerst een factor a buiten haakjes, dan krijgen we
Nu halveren we de coëfficiënt b/a van x, dat geeft b/2a, en hiervan nemen we het kwadraat, dat is (b/2a)² = b²/4a². Dit tellen we op bij de termen tussen haakjes, maar dan moeten we dit ook meteen weer aftrekken, anders blijft de functie niet hetzelfde. Zo hebben we dus
Nu kunnen we de eerste drie termen binnen de grote haakjes schrijven als een kwadraat, want we hebben immers
Ook kunnen we de laatste twee termen binnen de grote haakjes samennemen. Dit zijn twee breuken, die we wel eerst gelijknamig moeten maken door de teller en de noemer van de tweede breuk c/a met 4a te vermenigvuldigen, zodat we krijgen
Voor het functievoorschrift krijgen we zo
Tenslotte werken we de grote haakjes weer uit en dan hebben we inderdaad
En aangezien
de discriminant is van de kwadratische veelterm ax² + bx + c kunnen we dus ook schrijven
Nu lezen we gemakkelijk af dat deze functie voor x = −b/2a een extreme waarde
bereikt, en dat dit extremum een minimum is indien a > 0 en een maximum indien a < 0.
(p/2)² doet en vervolgens deze toevoegt aan het linkerlid en c naar het rechterlid (rechts van het = teken brengt) en daarna vervolgens (p/2)² ook toevoegt aan het rechterlid zoals:
x² + 2x - 4 = 0
x² + 2x = 4
x² + 2x + (2/2)² = 4 + (2/2)²
x² + 2x + 1 = 4 + 1
(x+1)² = 5
Dat zie ik niet terug zeg maar in het vetgedrukte stap.hoe kom je opeens aan die 2 * x * b/2a ?quote:
[..]
Ik zal de herleiding van de algemene kwadratische functie
nog een keertje voor je uitwerken, maar nu op de conventionele manier. We halen eerst een factor a buiten haakjes, dan krijgen we
Nu halveren we de coëfficiënt b/a van x, dat geeft b/2a, en hiervan nemen we het kwadraat, dat is (b/2a)² = b²/4a². Dit tellen we op bij de termen tussen haakjes, maar dan moeten we dit ook meteen weer aftrekken, anders blijft de functie niet hetzelfde. Zo hebben we dus
Nu kunnen we de eerste drie termen binnen de grote haakjes schrijven als een kwadraat, want we hebben immers
Ook kunnen we de laatste twee termen binnen de grote haakjes samennemen. Dit zijn twee breuken, die we wel eerst gelijknamig moeten maken door de teller en de noemer van de tweede breuk c/a met 4a te vermenigvuldigen, zodat we krijgen
Voor het functievoorschrift krijgen we zo
Tenslotte werken we de grote haakjes weer uit en dan hebben we inderdaad
En aangezien
de discriminant is van de kwadratische veelterm ax² + bx + c kunnen we dus ook schrijven
Nu lezen we gemakkelijk af dat deze functie voor x = −b/2a een extreme waarde
bereikt, en dat dit extremum een minimum is indien a > 0 en een maximum indien a < 0.Overigens snap ik ook niet waaromquote:
[..]
Ik zal de herleiding van de algemene kwadratische functie
nog een keertje voor je uitwerken, maar nu op de conventionele manier. We halen eerst een factor a buiten haakjes, dan krijgen we
Nu halveren we de coëfficiënt b/a van x, dat geeft b/2a, en hiervan nemen we het kwadraat, dat is (b/2a)² = b²/4a². Dit tellen we op bij de termen tussen haakjes, maar dan moeten we dit ook meteen weer aftrekken, anders blijft de functie niet hetzelfde. Zo hebben we dus
Nu kunnen we de eerste drie termen binnen de grote haakjes schrijven als een kwadraat, want we hebben immers
Ook kunnen we de laatste twee termen binnen de grote haakjes samennemen. Dit zijn twee breuken, die we wel eerst gelijknamig moeten maken door de teller en de noemer van de tweede breuk c/a met 4a te vermenigvuldigen, zodat we krijgen
Voor het functievoorschrift krijgen we zo
Tenslotte werken we de grote haakjes weer uit en dan hebben we inderdaad
En aangezien
de discriminant is van de kwadratische veelterm ax² + bx + c kunnen we dus ook schrijven
Nu lezen we gemakkelijk af dat deze functie voor x = −b/2a een extreme waarde
bereikt, en dat dit extremum een minimum is indien a > 0 en een maximum indien a < 0.
ze zeggen dat a(x + b/2a)² 0 is wanneer x= -b/2a ?
Tenslotte:
-(b² - 4ac)/4a hoe kan dit gelijk zijn aan : c - b² / 4a ?
Ik denk dat met de antwoorden op deze vragen (evenals mijn eerdere posts hierboven) ik wel voor de rest zelfstandig dingen kan uitpuzzelen.Bij je eerste vraag: een kwadraat is slechts nul als wat eronder staat 0 is, dus x + iets = 0, dus x = -iets.quote:
[..]
Overigens snap ik ook niet waarom
ze zeggen dat a(x + b/2a)² 0 is wanneer x= -b/2a ?
Tenslotte:
-(b² - 4ac)/4a hoe kan dit gelijk zijn aan : c - b² / 4a ?
Ik denk dat met de antwoorden op deze vragen (evenals mijn eerdere posts hierboven) ik wel voor de rest zelfstandig dingen kan uitpuzzelen.
Bij je tweede vraag: splits de breuk. eerste stuk: -b2/4a, tweede deel: 4ac/4a = c. Samen: c - b2/4a
Moet ik ook nog voor je narekenen hoeveel drie keer drie is?Opinion is the medium between knowledge and ignorance (Plato)4ac/4a = c. Dat wist ik, maar dan heb jequote:
[..]
Bij je eerste vraag: een kwadraat is slechts nul als wat eronder staat 0 is, dus x + iets = 0, dus x = -iets.
Bij je tweede vraag: splits de breuk. eerste stuk: -b2/4a, tweede deel: 4ac/4a = c. Samen: c - b2/4a
Moet ik ook nog voor je narekenen hoeveel drie keer drie is?
c - ( b² / 4a) en dan moet je het weer gelijknamig maken en dan krijg je :
(4ac - b²) / 4a.., weer vanaf begin af aan...Komt door de onduidelijkheid in de schrijfwijze. Met het stukje dat ik dikgedrukt heb gemaakt ben je er namelijk al.quote:
[..]
4ac/4a = c. Dat wist ik, maar dan heb je
c - ( b² / 4a) en dan moet je het weer gelijknamig maken en dan krijg je :
(4ac - b²) / 4a.., weer vanaf begin af aan...
-(b² - 4ac)/4a = c - ( b² / 4a)
dus NIET
-(b² - 4ac)/4a = (c - b²)/4aOpinion is the medium between knowledge and ignorance (Plato)Oh dan las ik het verkeerd hahaha. Bedankt!!quote:
[..]
Komt door de onduidelijkheid in de schrijfwijze. Met het stukje dat ik dikgedrukt heb gemaakt ben je er namelijk al.
-(b² - 4ac)/4a = c - ( b² / 4a)
dus NIET
-(b² - 4ac)/4a = (c - b²)/4aEvenwichtshoeveelheid functie opstellen van twee functies:quote:
[..]
Komt door de onduidelijkheid in de schrijfwijze. Met het stukje dat ik dikgedrukt heb gemaakt ben je er namelijk al.
-(b² - 4ac)/4a = c - ( b² / 4a)
dus NIET
-(b² - 4ac)/4a = (c - b²)/4a
P = prijs
Q = hoeveelheid
P = a - bQ
P = c + 2dQ
Dus ik maakte er van:
a - bQ = c + 2dQ en dan
a - bQ - c - 2dQ
en dan
(a-c) - (b + 2d)Q
Maar moet ik het dan naar rechts halen?
(a-c) = (b + 2d)Q
en dan:
Q = (a-c)/(b + 2d)
Is dit goed? Zo ja, hoe doe ik dit voor de prijs?
[ Bericht 8% gewijzigd door Brainstorm245 op 09-09-2014 21:12:14 ]Ja, maar je vergeet wel wat isnullen te noteren in de eerste paar regels.quote:
[..]
Is dit goed? Zo ja, hoe doe ik dit voor de prijs?
Je hebt nu de waarde van Q gevonden waarbij je evenwichtssituatie optreedt. Hoe reken je de prijs P uit bij een gegeven waarde Q ?Opinion is the medium between knowledge and ignorance (Plato)Bij het oplossen van een vergelijking kun je bij het linkerlid termen optellen of het linkerlid met een factor vermenigvuldigen, zolang je dit ook in het rechterlid doet. Maar bij het herleiden van een functievoorschrift heb je niet twee leden, maar één uitdrukking die je moet herleiden, en dan moet je dus zorgen dat die uitdrukking equivalent blijft.quote:
[..]
Dit is het laatste stukje waar ik nog vastloop, want ik zit met die kwadraatsplitsing dat je:
(p/2)² doet en vervolgens deze toevoegt aan het linkerlid en c naar het rechterlid (rechts van het = teken brengt) en daarna vervolgens (p/2)² ook toevoegt aan het rechterlid zoals:
x² + 2x - 4 = 0
x² + 2x = 4
x² + 2x + (2/2)² = 4 + (2/2)²
x² + 2x + 1 = 4 + 1
(x+1)² = 5
Dat zie ik niet terug zeg maar in het vetgedrukte stap.
Het verschil in aanpak is goed te illustreren met de vergelijking die je geeft, omdat je bij een vergelijking ook de vrijheid hebt om alleen iets aan het linkerlid te veranderen, zolang de uitdrukking in het linkerlid maar equivalent blijft.
Eerste aanpak (balansmethode):
x² + 2x − 4 = 0
Bij beide leden 4 optellen
x² + 2x − 4 + 4 = 0 + 4
oftewel
x² + 2x = 4
Nu de coëfficiënt 2 van x halveren, dat geeft 1, en hier weer het kwadraat van nemen, dat geeft 1² = 1. Deze 1 nu optellen bij beide leden geeft
x² + 2x + 1 = 4 + 1
oftewel
x² + 2x + 1 = 5
Nu gebruik maken van het merkwaardig product (identiteit) a² + 2ab + b² = (a + b)² om het linkerlid te herschrijven als een volkomen kwadraat, dit geeft
(x + 1)² = 5
Als nu het kwadraat van (x + 1) gelijk moet zijn aan 5, dan moet (x + 1) zelf dus gelijk zijn aan hetzij √5 hetzij −√5, zodat we dus krijgen
x + 1 = √5 ∨ x + 1 = −√5
Tenslotte nog bij deze beide vergelijkingen van beide leden 1 aftrekken oftewel bij beide leden −1 optellen(!) en we hebben
x = −1 + √5 ∨ x = −1 − √5
Tweede aanpak (herleiding van het linkerlid):
x² + 2x − 4 = 0
We halveren weer de coëfficiënt 2 van x, dit geeft 1, en hiervan het kwadraat nemen geeft 1² = 1. Deze 1 tellen we nu alleen op bij het linkerlid, maar dan moeten we deze 1 ook meteen weer aftrekken, anders is de uitdrukking in het linkerlid en daarmee de vergelijking niet meer equivalent. Zo krijgen we
x² + 2x + 1 − 1 − 4 = 0
Nu kunnen we x² + 2x + 1 weer herschrijven als (x + 1)² en zo krijgen we dus
(x + 1)² − 1 − 4 = 0
oftewel
(x + 1)² − 5 = 0
Zie je het verschil in aanpak? Het vervolg kan nu uiteraard op dezelfde manier als bij de eerste aanpak, want door bij beide leden 5 op te tellen krijgen we nu
(x + 1)² − 5 + 5 = 0 + 5
oftewel
(x + 1)² = 5
We kunnen echter ook doorgaan met het herleiden van het linkerlid van
(x + 1)² − 5 = 0
We kunnen 5 namelijk schrijven als het kwadraat van √5 zodat we krijgen
(x + 1)² − (√5)² = 0
Nu hebben we in het linkerlid een verschil van twee kwadraten, en dat betekent dat we nu het merkwaardig product a² − b² = (a − b)(a + b) kunnen gebruiken om het linkerlid te herschrijven als een product van twee factoren, zodat we krijgen
(x + 1 − √5)(x + 1 + √5) = 0
Nu kan een product van twee factoren alleen gelijk zijn aan nul als (tenminste) één van de beide factoren zelf nul is, zodat dus moet gelden
x + 1 − √5 = 0 ∨ x + 1 + √5 = 0
Tellen we tenslotte − 1 + √5 op bij beide leden van de eerste vergelijking en −1 − √5 bij beide leden van de tweede vergelijking, dan krijgen we
x = −1 + √5 ∨ x = −1 − √5
De gevonden oplossingen stemmen uiteraard overeen met de oplossingen die we met de eerste methode vonden.
Het leuke is dat het verschil in aanpak tussen de eerste en de tweede methode ook tot uitdrukking komt in de verschillende termen die het Engels en het Nederlands gebruiken. Bij de eerste aanpak hebben we x² + 2x aangevuld tot een volkomen kwadraat x² + 2x + 1 = (x + 1)² en dat is wat eigenlijk met completing the square wordt bedoeld. Maar bij de tweede aanpak hebben we x² + 2x − 4 herleid tot (x + 1)² − 5 en dat is wat eigenlijk met kwadraatafsplitsing wordt bedoeld. In de praktijk worden beide termen echter meestal voor beide methodes gebruikt.
[ Bericht 1% gewijzigd door Riparius op 10-09-2014 05:47:03 ]Door een getal bij Q in te vullen. Maar die is er dus nietquote:
[..]
Ja, maar je vergeet wel wat isnullen te noteren in de eerste paar regels.
Je hebt nu de waarde van Q gevonden waarbij je evenwichtssituatie optreedt. Hoe reken je de prijs P uit bij een gegeven waarde Q ?Jawel, die heb je net uitgerekend. Alleen is het geen getal, maar een uitdrukking in wat letters.quote:
[..]
Door een getal bij Q in te vullen. Maar die is er dus niet
En... waar moet je die invullen? Niet waar je het in de post hieronder hebt gedaan, want die leidt slechts tot de conclusie 1 = 1.
Een waarheid als een koe, dat wel.
[ Bericht 12% gewijzigd door Janneke141 op 09-09-2014 21:15:09 ]Opinion is the medium between knowledge and ignorance (Plato)Dus... (a-c)/(b + 2d) invullen als Q?quote:
[..]
Jawel, die heb je net uitgerekend. Alleen is het geen getal, maar een uitdrukking in wat letters.
(a-c) = (b + 2d)* (a-c)/(b + 2d)Geen idee?quote:
[..]
Jawel, die heb je net uitgerekend. Alleen is het geen getal, maar een uitdrukking in wat letters.
En... waar moet je die invullen? Niet waar je het in de post hieronder hebt gedaan, want die leidt slechts tot de conclusie 1 = 1.
Een waarheid als een koe, dat wel.Ga slapen en probeer het morgen nog eens. Je maakt jezelf nu alleen maar gek terwijl je vragen moet stellen over dingen die je echt wel weet - en die je wel weer ziet als je er morgen of overmorgen met frisse ogen naar kijkt.quote:Opinion is the medium between knowledge and ignorance (Plato)evalueer de volgende functies:
f(ab) voor f(x) = (ax b√x) / a(ln(x)/ln a) waarbij a =/ 0
en
f(e-3) voor f(x) = √((-x) ln(x(12e) ) --> hele functie zit onder de wortel.
Kan iemand mij hierbij helpen?Inderdaad. Dat zal zeker helpen. Bovendien heb je zelf al een antwoord gegeven.quote:
[..]
Ga slapen en probeer het morgen nog eens. Je maakt jezelf nu alleen maar gek terwijl je vragen moet stellen over dingen die je echt wel weet - en die je wel weer ziet als je er morgen of overmorgen met frisse ogen naar kijkt.Wat heb je al geprobeerd?quote:
evalueer de volgende functies:
f(ab) voor f(x) = (ax b√x) / a(ln(x)/ln a) waarbij a =/ 0
en
f(e-3) voor f(x) = √((-x) ln(x(12e) ) --> hele functie zit onder de wortel.
Kan iemand mij hierbij helpen?kloep kloepniks. de reden hiervan is dat ik niet begrijp wat de vraagstelling nou eigenlijk is en daarnaast is ln nieuw voor me, evenala het getal e.quote:
[..]
Inderdaad. Dat zal zeker helpen. Bovendien heb je zelf al een antwoord gegeven.
[..]
Wat heb je al geprobeerd?De vraagstelling houdt in dat je de waarde van de functie uit moet rekenen voor een bepaalde x. f(3) evalueren betekent de waarde van f uitrekenen bij x=3, f(ab) evalueren betekent dat je de waarde van f moet uitrekenen voor x=ab.quote:
[..]
niks. de reden hiervan is dat ik niet begrijp wat de vraagstelling nou eigenlijk is en daarnaast is ln nieuw voor me, evenala het getal e.
Dat betekent invullen, en daarna heel goed laten zien dat je alle rekenregeltjes met machten en logaritmes kent. En nauwkeurig werken.
e Is het grondtal van de natuurlijke logaritme. Rings a bell?Opinion is the medium between knowledge and ignorance (Plato)Janneke, hij moet f(e-3) uitrekenen. Maar goed, inderdaad:
f(e-3) betekent voor x de waarde e-3 invullen in het functievoorschrift.
Evenzo betekent f(ab) betekent voor x de waarde ab invullen in het functievoorschrift.
Wat uitleg over het getal e vind je hier.kloep kloepIk denk dat dit hem allemaal niets zegt, omdat hij kennelijk nog nooit wat aan calculus heeft gedaan. Het blijft voor mij onbegrijpelijk waarom opleidingen waarbij dit soort zaken nodig zijn niet gewoon harde eisen stellen aan de vooropleiding of toelatingsexamens instellen, bij voorkeur voor iedereen die met de betreffende studie wil beginnen, dus niet alleen voor studenten met een deficiëntie.quote:
Wat uitleg over het getal e vind je hier.
Vroeger werd de behandeling van het getal e trouwens vaak uitgesteld totdat de beginselen van de integraalrekening waren behandeld, omdat je dan ln x kunt introduceren als de unieke primitieve F(x) van f(x) = x−1 op R+ waarvoor F(1) = 0 oftewel ln x = ∫1x t−1dt. Een dergelijke behandeling heeft veel voordelen, onder meer een eenvoudig bewijs voor limh→0 (ah − 1)/h = ln a. Je hebt deze limiet en de natuurlijke logaritme namelijk sowieso nodig alvorens je de afgeleide van f(x) = ax (a ∈ R+) kunt behandelen.Ik ben vroeg naar bed gegaan en zojuist opgestaan en ik begrijp het nu allemaal. Ik loop alleen nog vast bjj die prijsfunctie.quote:
[..]
Ga slapen en probeer het morgen nog eens. Je maakt jezelf nu alleen maar gek terwijl je vragen moet stellen over dingen die je echt wel weet - en die je wel weer ziet als je er morgen of overmorgen met frisse ogen naar kijkt.geen idee...quote:
[..]
Jawel, die heb je net uitgerekend. Alleen is het geen getal, maar een uitdrukking in wat letters.
En... waar moet je die invullen? Niet waar je het in de post hieronder hebt gedaan, want die leidt slechts tot de conclusie 1 = 1.
Een waarheid als een koe, dat wel.ik kom uit op de volgende evenwichtsprijsfunctie:
-b * (a-c)/(b+2d) + 2d* (a-c)/(b+2d)
dus..
(-ab + bd) / (b+2d) + (2ad - 2cd)/(b+2d)Misschien moet je jouw vraag eerst evén opnieuw stellen. Ik kan zo niet inzien wat jij wil weten.quote:
ik kom uit op de volgende evenwichtsprijsfunctie:
-b * (a-c)/(b+2d) + 2d* (a-c)/(b+2d)
dus..
(-ab + bd) / (b+2d) + (2ad - 2cd)/(b+2d)kloep kloepquote:
[..]
Evenwichtshoeveelheid functie opstellen van twee functies:
P = prijs
Q = hoeveelheid
P = a - bQ
P = c + 2dQ
Dus ik maakte er van:
a - bQ = c + 2dQ en dan
a - bQ - c - 2dQ
en dan
(a-c) - (b + 2d)Q
Maar moet ik het dan naar rechts halen?
(a-c) = (b + 2d)Q
en dan:
Q = (a-c)/(b + 2d)
Is dit goed? Zo ja, hoe doe ik dit voor de prijs?zie de postquote boven deze post.quote:
[..]
Misschien moet je jouw vraag eerst evén opnieuw stellen. Ik kan zo niet inzien wat jij wil weten.Even een compleet andere vraag, misschien dat ik je daarmee weer op het goede spoor krijg:
Je hebt 2 verschillende prijsfuncties:
P = a - bQ
P = c + 2dQ
Ik maak 100 dingen. Wat wordt de prijs in de bovenste prijsfunctie, en wat wordt het in de onderste?Opinion is the medium between knowledge and ignorance (Plato)bij die eerste: a - B * 100quote:
Even een compleet andere vraag, misschien dat ik je daarmee weer op het goede spoor krijg:
Je hebt 2 verschillende prijsfuncties:
P = a - bQ
P = c + 2dQ
Ik maak 100 dingen. Wat wordt de prijs in de bovenste prijsfunctie, en wat wordt het in de onderste?
en bjj de onderste: c + 2d*100Je hebt een stelsel van twee lineaire vergelijkingen in de twee onbekenden P en Q. Een (correcte) uitdrukking voor Q heb je al gevonden, namelijkquote:
[..]
zie de postquote boven deze post.
Q = (a − c)/(b + 2d)
Substitueer nu deze uitdrukking voor Q in één van de twee gegeven vergelijkingen. Dan heb je een vergelijking waaruit je P kunt oplossen. Als je het goed doet vind je dan
P = (2ad + bc)/(b + 2d).
Je kunt ook als volgt te werk gaan. Vermenigvuldig beide leden van de eerste vergelijking met 2d en beide leden van de tweede vergelijking met b en tel de linker en de rechter leden van de vergelijkingen dan bij elkaar op. Dan krijg je
1
2
3
42dP = 2ad - 2bdQ
bP = bc + 2bdQ
-------------------- +
(b+2d)P = 2ad+bcEn nu maak je niet 100 dingen, maar (a-c)/(b + 2d).quote:
[..]
bij die eerste: a - B * 100
en bjj de onderste: c + 2d*100Opinion is the medium between knowledge and ignorance (Plato)in 1 van de twee?ohhh ik dacht in beide.. en er een vergelijking van maken.quote:
[..]
Je hebt een stelsel van twee lineaire vergelijkingen in de twee onbekenden P en Q. Een (correcte) uitdrukking voor Q heb je al gevonden, namelijk
Q = (a − c)/(b + 2d)
Substitueer nu deze uitdrukking voor Q in één van de twee gegeven vergelijkingen. Dan heb je een vergelijking waaruit je P kunt oplossen. Als je het goed doet vind je dan
P = (2ad + bc)/(b + 2d).
Je kunt ook als volgt te werk gaan. Vermenigvuldig beide leden van de eerste vergelijking met 2d en beide leden van de tweede vergelijking met b en tel de linker en de rechter leden van de vergelijkingen dan bij elkaar op. Dan krijg je
[ code verwijderd ]
functie 1 = functie 2
Bedankt!!
Op tijd slapen (21.00) en ochtend leren bijv van 06.00 tot 10.00 helpt beter dan laat slapen (01.00) en dan weer in de avond leren van 19.30 tot 01.00.Dat laatste werkt goed inderdaad. Kan ik mij ook nog herinneren van mijn eigen wiskunde opleiding. En toen werd in midden in de nacht wakker met het bewijs van de rechte van Wallace; die ik de avond ervoor niet inzag.quote:
[..]
in 1 van de twee?ohhh ik dacht in beide.. en er een vergelijking van maken.
functie 1 = functie 2
Bedankt!!
Op tijd slapen (21.00) en ochtend leren bijv van 06.00 tot 10.00 helpt beter dan laat slapen (01.00) en dan weer in de avond leren van 19.30 tot 01.00.
Als je het nu begrepen hebt, dan loont het de moeite om een vergelijkbare opdracht te maken om te checken of je het een beetje in de vingers hebt.kloep kloep2x^3 + 2x - 1 : (x-1) (staartdeling)
Ik kwam uit op: (2x^2 + 2x - 2) + ( -3 )
-3 is dus de remainder
Antwoordenboek zegt echter 2x^2 + 2x + 4 + 3Wat dacht je er van om ook je uitwerking te plaatsen? Anders kunnen we toch nooit zien wat je fout hebt gedaan?quote:
2x^3 + 2x - 1 : (x-1) (staartdeling)
Ik kwam uit op: (2x^2 + 2x - 2) + ( -3 )
-3 is dus de remainder
Antwoordenboek zegt echter 2x^2 + 2x + 4 + 3Als f(x) een polynoom is, dan is de rest bij deling door x-a gelijk aan f(a). In dit geval is dat f(1)=3.Ik heb de fout inmiddels al gevonden. Ik had ergens -2x gezet i.p.v +2xquote:Op donderdag 11 september 2014 09:11 schreef Ensemble het volgende:
[..]
Wat dacht je er van om ook je uitwerking te plaatsen? Anders kunnen we toch nooit zien wat je fout hebt gedaan?(x5 − 3x4 + 1) ÷ (x2 + x + 1) =
Waarom is het antwoord uiteindelijk gedeeld door een andere polynoom?
Ik zou toch echt denken vermenigvuldigen als je de 6/2 = 3 en 3 * 2 = 6 en 6/3 = 2 methode toepast..Goedenmorgen, ik heb een vraag over het onderwerp machten/exponenten. De vraag is het volgende:
Zoek uit wat t is wanneer 9t = (27) 1/5 /3
Ik deed het volgende":
9t = 27 1/5 /3
9t = 3 3/5 / 3
9t = 3 -2/5
en dan loop ik vast... want ik weet niet wat t moet zijn bij 9 t om hetzelfde te krijgen als 3 -2/5
Dat denk ik??
Of moet ik er PER SE hetzelfde grondtal maken door
32t = 3 -2/5Dus ik had die zgn vergelijking met 2t niet kunnen maken als het niet dezelfde grondtal was geweest?quote:
het simpelst is als je meteen *3 doet dan krijg je meteen de oplossing:
t = 1/5
En ja het grondgetal moet altijd gelijk zijn je kan er 3 of 9 van maken.sorry het eerste wat ik zei klopt niet, wat jij doet klopt.quote:
[..]
Dus ik had die zgn vergelijking met 2t niet kunnen maken als het niet dezelfde grondtal was geweest?Je houdt hier een rest −4x over bij deling omdat de deling niet verder is voort te zetten. De rest bij polynoomstaartdelingen die niet opgaan is altijd een polynoom waarvan de graad ten hoogste één lager is dan de graad van het polynoom waardoor je deelt. In dit geval deel je door een polynoom van de tweede graad en is de rest een polynoom van de eerste graad. Alleen als je door een polynoom van de eerste graad deelt kan de rest een constante zijn, oftewel een polynoom van de graad nul. Je hebt hierquote:
(x5 − 3x4 + 1) ÷ (x2 + x + 1) =
[ afbeelding ]
[ afbeelding ]
Waarom is het antwoord uiteindelijk gedeeld door een ander polynoom?
x5 − 3x4 + 1 = (x2 + x + 1)(x3 − 4x2 + 3x + 1) − 4x
Als we nog een term 4x bij het oorspronkelijke polynoom hadden gevoegd, dan hadden we dus een deling door (x2 + x + 1) gehad die wel opgaat, want je hebt immers ook
x5 − 3x4 + 4x + 1 = (x2 + x + 1)(x3 − 4x2 + 3x + 1)
[ Bericht 0% gewijzigd door Riparius op 11-09-2014 17:44:59 ]Misschien dat ik gek word hoor (zou zo maar kunnen), maar als je in het voorbeeld dat jij geeft waar de deling wél opgaatquote:
[..]
De rest bij polynoomstaartdelingen die niet opgaan is altijd een polynoom waarvan de graad één lager is dan de graad van het polynoom waardoor je deelt. In dit geval deel je door een polynoom van de tweede graad en is de rest een polynoom van de eerste graad. Alleen als je door een polynoom van de eerste graad deelt kan de rest een constante zijn, oftewel een polynoom van de graad nul.Een constante factor +1 toevoegt, en dan de deling door (x2 + x + 1) zou willen maken, dan hou je toch een constante rest over (van +1)?quote:x5 − 3x4 + 4x + 1 = (x2 + x + 1)(x3 − 4x2 + 3x + 1)Opinion is the medium between knowledge and ignorance (Plato)Mea culpa, je hebt gelijk. De coëfficiënt van x in een eerstegraadspolynoom kan ook nul zijn, en dan heb je een constante. Ik had moeten zeggen dat de rest bij deling een constante kan zijn of een polynoom waarvan de graad ten hoogste gelijk is aan de graad van de deler verminderd met één.quote:
[..]
Misschien dat ik gek word hoor (zou zo maar kunnen), maar als je in het voorbeeld dat jij geeft waar de deling wél opgaat
[..]
Een constante factor +1 toevoegt, en dan de deling door (x2 + x + 1) zou willen maken, dan hou je toch een constante rest over (van +1)?Ik heb het niet begrepen? Dus omdat er een rest is, wordt er gedeeld?quote:
[..]
Je houdt hier een rest −4x over bij deling omdat de deling niet verder is voort te zetten. De rest bij polynoomstaartdelingen die niet opgaan is altijd een polynoom waarvan de graad ten hoogste één lager is dan de graad van het polynoom waardoor je deelt. In dit geval deel je door een polynoom van de tweede graad en is de rest een polynoom van de eerste graad. Alleen als je door een polynoom van de eerste graad deelt kan de rest een constante zijn, oftewel een polynoom van de graad nul. Je hebt hier
x5 − 3x4 + 1 = (x2 + x + 1)(x3 − 4x2 + 3x + 1) − 4x
Als we nog een term 4x bij het oorspronkelijke polynoom hadden gevoegd, dan hadden we dus een deling door (x2 + x + 1) gehad die wel opgaat, want je hebt immers ook
x5 − 3x4 + 4x + 1 = (x2 + x + 1)(x3 − 4x2 + 3x + 1)Vergelijk het maar met een normale staartdeling. Als je 37 door 5 deelt, heb je 7 rest 2. Oftewel:quote:
[..]
Ik heb het niet begrepen? Dus omdat er een rest is, wordt er gedeeld?
37 / 5 = 7 + 2/5.Opinion is the medium between knowledge and ignorance (Plato)Nee, niet achterstevoren redeneren, er wordt een deling uitgevoerd, en die levert hier een rest −4x op. Kijk nog eens naar de uitgewerkte staartdeling. Dan zie je dat de graad van het polynoom waarmee je verder werkt steeds met één daalt in de staartdeling. Zolang de graad van het polynoom waarmee je verder werkt groter dan of gelijk is aan de graad van de deler x² + x + 1 kun je de staartdeling verder voortzetten. Maar zodra je die −4x hebt gekregen kun je de staartdeling niet verder voortzetten, en dit is dan je rest.quote:
[..]
Ik heb het niet begrepen? Dus omdat er een rest is, wordt er gedeeld?Doctor in de weetnietkunde?quote:
Als het goed is moeten jullie me over 4 jaar aanspreken als dr. ThenxeroIs dat een referentie naar mijn username?quote:
thenxero = den xero = δεν ξερω = Grieks voor "ik weet niet".
Maar nee, doctor in de wiskunde uiteraardUiteraard was dat het. Ben je Grieks?quote:
[..]
Is dat een referentie naar mijn username?
thenxero = den xero = δεν ξερω = Grieks voor "ik weet niet".
Maar nee, doctor in de wiskunde uiteraardΟὐδὲν οἶσθα;quote:
[..]
Is dat een referentie naar mijn username?
thenxero = den xero = δεν ξερω = Grieks voor "ik weet niet".
Maar nee, doctor in de wiskunde uiteraardWaarnaar ga je onderzoek doen?quote:
Als het goed is moeten jullie me over 4 jaar aanspreken als dr. ThenxeroNee. Toen ik vroeger niks te doen had ging ik mezelf Russisch en modern Grieks aanleren. Je moet toch watquote:
[..]
Uiteraard was dat het. Ben je Grieks?Dat is denk ik oud Grieks.quote:Het eerste jaar zal ik ermee bezig zijn om te begrijpen waar ik precies onderzoek naar ga doenquote:
[..]
Waarnaar ga je onderzoek doen?Gefeliciteerd met je promotieplek!quote:
Als het goed is moeten jullie me over 4 jaar aanspreken als dr. ThenxeroCroce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.Niet van tevoren ervan uitgaan dat het 4 jaar duurt, 5 of 6 mag ook als het resultaat de moeite waard is.quote:
Als het goed is moeten jullie me over 4 jaar aanspreken als dr. Thenxero
Proficiat! Welk vakgebied (meer generiek i.v.m. je privacy)?ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPLquote:
[..]
Gefeliciteerd met je promotieplek!Bedankt!quote:
[..]
Niet van tevoren ervan uitgaan dat het 4 jaar duurt, 5 of 6 mag ook als het resultaat de moeite waard is.
Proficiat! Welk vakgebied (meer generiek i.v.m. je privacy)?
Schijnt dat 4 jaar best wel vaak lukt, dus ik ga er ook wel vanuit dat het gaat lukken. Ze letten daar tegenwoordig sowieso meer op. Als je eenmaal afstudeert krijgen ze geld, dus het is ook in hun belang dat je het zo snel mogelijk afrondt. Ik zou ook niet 1 of 2 jaar zonder salaris willen zitten, zeker niet als je in het bedrijfsleven makkelijk ¤3000 p/m verdient.Ik hoop daarom ook stiekem dat het NWO dit jaar nog wordt doodgetrapt en dat de faculteiten zelf weer geld krijgen voor phd-posities. Anders hoef ik geen phd te doen XDquote:
[..]
[..]
Bedankt!
Schijnt dat 4 jaar best wel vaak lukt, dus ik ga er ook wel vanuit dat het gaat lukken. Ze letten daar tegenwoordig sowieso meer op. Als je eenmaal afstudeert krijgen ze geld, dus het is ook in hun belang dat je het zo snel mogelijk afrondt. Ik zou ook niet 1 of 2 jaar zonder salaris willen zitten, zeker niet als je in het bedrijfsleven makkelijk ¤3000 p/m verdient.Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.Ik heb een kwadratische vergelijking met 3 integere variabelen, deze moet geminimaliseerd worden.
Is dit nog analytisch te doen of kan dit alleen opgelost worden door te proberen?
(en misschien is dat ook wel makkelijker)
G = a^2 + b^2 + 2c^2 + ab - 2ca - 2cb
-edit-
G != 0, anders was het niet zo moeilijk
En dan moet ik dus "alle" oplossingen vinden.
[ Bericht 26% gewijzigd door t4rt4rus op 13-09-2014 12:20:30 ]Hallo,
Het is al een tijd geleden dat ik wat in dit topic had gevraagd, maar nu heb ik toch wel weer wat vragen. Komende week heb ik een tentamen en de basics begrijp ik onderhand wel, echter zijn de wat 'harder problems' een probleem voor mij. In plaats van het topic vol te spammen met posts met vragen, heb ik besloten om al mijn vragen in één post te verwerken:
Van het volgende snap ik niet waar ik moet beginnen en wat de bedoeling is.. met 'implies that..''
a-1b-1 c-1 = 1/4 implies (abc)4
Van het volgende ben ik ten einde raad vanwege de -c...
''Show that the division below leaves a remainder for all values of c''
(x4 + 3x² + 5) : (x-c)
''Solve the following equations'' --> ik weet niet wat ik moet doen als er een ln bij staat... Zelf dacht ik om gewoon te bepalen wanneer x = 0 en de ln even wegdenkend, maar dat werkte dus niet..
ln[x(x-2)] = 0
x ln(x+3) / (x² + 1) = 0
en tenslotte:
ln√(x-5) = 0Zie je dat ding ooit negatief worden?quote:
Ik heb een kwadratische vergelijking met 3 integere variabelen, deze moet geminimaliseerd worden.
Is dit nog analytisch te doen of kan dit alleen opgelost worden door te proberen?
(en misschien is dat ook wel makkelijker)
G = a^2 + b^2 + 2c^2 + ab - 2ca - 2cb
Als het je helpt: G = (a-c)2 + (b-c)2 + ab.Opinion is the medium between knowledge and ignorance (Plato)Ja sorry kom er net ook achter, moet nog bij dat G geen 0 mag zijn.quote:
[..]
Zie je dat ding ooit negatief worden?
Als het je helpt: G = (a-c)2 + (b-c)2 + ab.
Ik was het net aan het aanpassen, bedankt!Geen idee, volgens mij als ln 0 is?quote:
Wanneer is ln gelijk aan nul?
@SuperIk heb het gevoel dat de opgave zoals je die hier neerzet niet klopt. Moet het niet toevallig zijnquote:
Hallo,
Het is al een tijd geleden dat ik wat in dit topic had gevraagd, maar nu heb ik toch wel weer wat vragen. Komende week heb ik een tentamen en de basics begrijp ik onderhand wel, echter zijn de wat 'harder problems' een probleem voor mij. In plaats van het topic vol te spammen met posts met vragen, heb ik besloten om al mijn vragen in één post te verwerken:
Van het volgende snap ik niet waar ik moet beginnen en wat de bedoeling is.. met 'implies that..''
a-1b-1 c-1 = 1/4 implies (abc)4
a-1b-1 c-1 = 1/4 implies (abc) =4Ze willen dat je aantoont dat (x-c) geen deler is van het gegeven polynoom, oftewel dat er geen ontbinding te vinden is waarvan (x-c) een van de termen is, voor welke waarde van c dan ook.quote:Van het volgende ben ik ten einde raad vanwege de -c...
''Show that the division below leaves a remainder for all values of c''
(x4 + 3x² + 5) : (x-c)
Eerder in het topic zijn enkele posts besteed aan het maken van staartdelingen met polynomen, ik denk dat je daarmee deze opgave relatief eenvoudig kan oplossen.Voor welk getal q is ln q = 0?quote:''Solve the following equations'' --> ik weet niet wat ik moet doen als er een ln bij staat... Zelf dacht ik om gewoon te bepalen wanneer x = 0 en de ln even wegdenkend, maar dat werkte dus niet..Opinion is the medium between knowledge and ignorance (Plato)
Forum Opties Forumhop: Hop naar:
