SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Hoe heb je dat beredeneerd?quote:Op zaterdag 30 augustus 2014 16:08 schreef rumiii het volgende:
[..]
ik kan wel beredeneren dat x √2 of -√2 moet zijn : x^2(x^2+2)=8 maar of dat de juiste (geaccepteerde) methode van tot de uitkomst komen is ben ik me niet zeker van
Ik neem trouwens aan dat je alleen reële oplossingen hoeft te geven?
Opinion is the medium between knowledge and ignorance (Plato)
x4 + 2x2 = 8quote:
Heb moeite met n polynoomfunctie
Kan een van jullie mij helpen met het volgende;
x^4+2x^2=8
Zonder gebruik van een GR kom ik er niet uit, moet ik bekennen
x4 + 2x2 − 8 = 0
Het linkerlid kun je nu gemakkelijk ontbinden in (kwadratische) factoren. Daarvoor zoek je twee (gehele) getallen waarvan de som +2 is en het product −8. Die getallen zijn +4 en −2. Dan krijgen we
(x2 + 4)(x2 − 2) = 0
x2 + 4 = 0 ∨ x2 − 2 = 0
x2 = −4 ∨ x2 = 2
De eerste vergelijking heeft in R geen oplossingen aangezien het kwadraat van een reëel getal niet negatief kan zijn. Voor de tweede vergelijking vinden we dan
x = √2 ∨ x = −√2
Dat is alles.
Bedankt voor je reactie chefquote:
[..]
x4 + 2x2 = 8
x4 + 2x2 − 8 = 0
Het linkerlid kun je nu gemakkelijk ontbinden in (kwadratische) factoren. Daarvoor zoek je twee (gehele) getallen waarvan de som +2 is en het product −8. Die getallen zijn +4 en −2. Dan krijgen we
(x2 + 4)(x2 − 2) = 0
x2 + 4 = 0 ∨ x2 − 2 = 0
x2 = −4 ∨ x2 = 2
De eerste vergelijking heeft in R geen oplossingen aangezien het kwadraat van een reëel getal niet negatief kan zijn. Voor de tweede vergelijking vinden we dan
x = √2 ∨ x = −√2
Dat is alles.
Zeer verhelderend
Bereken de afgeleide en herleid tot 1 breuk:
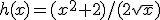
h'(x)= 3/4*sqrtx - 1/(2x*sqrtx)
Ik kom er niet echt uit hoe ik hem verder kan oplossen.
[ Bericht 7% gewijzigd door rareziekte op 31-08-2014 13:50:19 ]
h'(x)= 3/4*sqrtx - 1/(2x*sqrtx)
Ik kom er niet echt uit hoe ik hem verder kan oplossen.
[ Bericht 7% gewijzigd door rareziekte op 31-08-2014 13:50:19 ]
Dit is in principe gewoon toepassen van de regels voor differentiëren. Waar loop je vast?quote:
Bereken de afgeleide en herleid tot 1 breuk:
h'(x)= 3/4*sqrtx - 1/(2x*sqrtx)
Ik kom er niet echt uit hoe ik hem verder kan oplossen.
Het is duidelijk dat hij vastloopt op het herleiden van de twee termen van zijn afgeleide tot gelijknamige breuken. Dat heeft an sich niets met differentiëren te maken maar alles met gebrekkige algebraïsche vaardigheden die weer zijn terug te voeren op onvoldoende rekenvaardigheid.quote:
[..]
Dit is in principe gewoon toepassen van de regels voor differentiëren. Waar loop je vast?
Je hebt gelijk. Ik weet dat ik de noemer gelijk kan stellen, maar heb geen idee hoe dat te doen met (3/4)*sqrtxquote:
[..]
Het is duidelijk dat hij vastloopt op het herleiden van de twee termen van zijn afgeleide tot gelijknamige breuken. Dat heeft an sich niets met differentiëren te maken maar alles met gebrekkige algebraïsche vaardigheden die weer zijn terug te voeren op onvoldoende rekenvaardigheid.
Vermenigvuldig de eerste term met x2 / x2 en de tweede term met 2√x / 2√x, dan krijg je twee gelijknamige breuken met als noemer 4x2.quote:
[..]
Je hebt gelijk. Ik weet dat ik de noemer gelijk kan stellen, maar heb geen idee hoe dat te doen met (3/4)*sqrtx
Ik had niet gezien dat de afgeleide al in de post stond.quote:
[..]
Het is duidelijk dat hij vastloopt op het herleiden van de twee termen van zijn afgeleide tot gelijknamige breuken. Dat heeft an sich niets met differentiëren te maken maar alles met gebrekkige algebraïsche vaardigheden die weer zijn terug te voeren op onvoldoende rekenvaardigheid.
Ik snap het volgende niet wat betrekking heeft tot een uitleg over de abc formule en zou daar graag wat hulp bij willen, mits dat mogelijk is van één van jullie wiskundigen 
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die laatste spoiler is totaal onbekend voor mij met name doordat alles door elkaar is (exponenten, letters, wortels etc etc.) ..
En tenslotte een simpele, waar ik alleen niet begrijp waarom er een a staat aan de rechterzijde van de vergelijking:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 17% gewijzigd door BroodjeKebab op 01-09-2014 23:12:04 ]quote:
Ik snap het volgende niet wat betrekking heeft tot een uitleg over de abc formule en zou daar graag wat hulp bij willen, mits dat mogelijk is van één van jullie wiskundigenSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die laatste spoiler is totaal onbekend voor mij met name doordat alles door elkaar is (exponenten, letters, wortels etc etc.) ..
En tenslotte een simpele, waar ik alleen niet begrijp waarom er een a staat aan de rechterzijde van de vergelijking:Ik moet zeggen dat ik de tekst (of de vertaling ervan?) onder de eerste spoiler niet begrijp. Ik denk wel dat ik weet wat er bedoeld wordt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Er wordt geprobeerd van de linkerkant een kwadraat (in Engelse literatuur noemt men dit, als ik het me goed herinner, vaak een 'perfect square') te maken. Door toepassing van
(a + b)² = a² + 2ab + b²
kunnen we zien dat
(x + p/2)² = x² + px + (p/2)²
En deze laatste term, (p/2)2, kunnen we dus aan x² + px = -q toevoegen om zo een 'perfect square' aan de linkerkant te krijgen:
(x + p/2)² = (p/2)² - q
En vervolgens kan je gebruiken dat als a² = b dan a = √b of a = -√b, om een formule voor x te krijgen.
Wat je bedoelt met 'oplossen' weet ik niet, ik neem dat je de formules moet vereenvoudigen. Dan nog is het me niet helemaal duidelijk in welke vorm de formules het meest vereenvoudigd zijn (want volgens mij bestaat er geen echt simpele uitdrukking voor de gegeven formules).
Om de formules in je tweede spoiler te vereenvoudigen moet je gebruikmaken van de rekenregels voor machten en wortels, zoals je ongetwijfeld weet. Het werkt beter als je uitlegt tot waar je komt en waar je vastloopt of niet zeker over bent. De eerste formule zullen de meeste mensen simpeler te vereenvoudigen vinden dan de tweede (hoewel beide goede testen zijn of je de rekenregels goed toepast). Heb je met allebei problemen?
Onthoud
apar = ap+r
De r-de machtswortel van a is a1/r
1/(a/b)=b/a
(ap)r = apr
En als laatste:
Als a er niet zou staan aan de rechterkant, zou er x² ipv ax² na het wegwerken van de haakjes van (x - x1)(x - x2).
[ Bericht 2% gewijzigd door defineaz op 02-09-2014 02:40:02 ]quote:
Ik snap het volgende niet wat betrekking heeft tot op een uitleg over de abc formule en zou daar graag wat hulp bij willen, mits dat mogelijk is van één van jullie wiskundigenOm te beginnen: als je citeert, gebruik dan liever geen spoilers, dat maakt het quoten van passages van je post onnodig lastig en je bericht zelf minder leesbaar.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Het lijkt erop dat je hier een Engelse tekst door een vertaalmachine hebt gehaald, het is althans niet te hopen dat dit je eigen vertaling is. Zoals ik al eerder heb opgemerkt heeft het gebruik van het Engels in een Nederlandse onderwijssituatie niet zelden een dramatische verslechtering van de kennisoverdracht tot gevolg, en dat wordt hier weer eens treffend geïllustreerd.
Het gaat hier feitelijk om een afleiding van de wortelformule voor de oplossing van de kwadratische vergelijking x2 + px + q = 0, en deze formule wordt de pq-formule genoemd, niet de abc-formule. In het Duitse taalgebied spreekt men om het onderscheid aan te geven wel van de kleine Lösungsformel terwijl de abc-formule die de oplossingen geeft van ax2 + bx + c = 0 (a ≠ 0) de große Lösungsformel wordt genoemd. Het is overigens heel goed mogelijk de abc-formule af te leiden uit de pq-formule door p = b/a en q = c/a te substitueren.
Om te begrijpen hoe de pq-formule resp. de abc-formule kan worden afgeleid is het nodig de techniek van de kwadraatafsplitsing te begrijpen. In het Engels heet deze techniek (vanuit een iets ander perspectief) completing the square oftewel het completeren van een (volkomen) kwadraat. Het komt erop neer dat we de constante term q van de kwadratische vergelijking x2 + px + q = 0 overbrengen naar het rechterlid door van beide leden q af te trekken, zodat we x2 + px = −q krijgen. Vervolgens gaan we dan het linkerlid aanvullen tot een volkomen kwadraat door bij beide leden een geschikt gekozen constante op te tellen. Daarna kunnen we gebruik maken van één van de merkwaardige producten (identiteiten)
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
om het linkerlid van de vergelijking te herschrijven als een kwadraat. Om deze techniek beter te begrijpen moet je dit eens goed doornemen. Het is ook van belang de techniek van het kwadraatafsplitsen te oefenen door een aantal kwadratische vergelijkingen met deze methode op te lossen, zie bijvoorbeeld hier en hier voor uitgewerkte voorbeelden.
Heb je de techniek van het kwadraatafsplitsen onder de knie, dan zul je ook deze afleiding van de pq-formule alsmede deze afleiding van de abc-formule goed kunnen begrijpen.quote:Dit zijn geen functies maar uitdrukkingen, waarbij het kennelijk de bedoeling is dat je deze uitdrukkingen zo ver mogelijk vereenvoudigt. Het is natuurlijk onzin om op te merken dat iets 'totaal onbekend' is omdat het er wat ingewikkelder uitziet dan je wellicht gewend bent. Het is ook niet nodig om in één oogopslag te kunnen overzien wat een dergelijke uitdrukking nu eigenlijk voorstelt. Je kunt bij het vereenvoudigen stap voor stap te werk gaan, waarbij je voor elke stap een jou bekende rekenregel gebruikt om de uitdrukking in een eenvoudiger vorm te brengen, totdat je op een punt aan bent gekomen waarbij verdere vereenvoudigingen niet meer mogelijk zijn of in ieder geval niet zinvol.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die laatste spoiler is totaal onbekend voor mij met name doordat alles door elkaar is (exponenten, letters, wortels etc etc.) ..
Voor de eerste uitdrukking kun je bedenken dat
p√a = a1/p en r√a = a1/r
zodat
p√a · r√a = a1/p·a1/r
en dit geeft ons dan weer de mogelijkheid om de rekenregel te gebruiken die zegt dat exponenten optellen bij het vermenigvuldigen van twee machten van hetzelfde grondtal. We hebben 1/p + 1/r = r/pr + p/pr = (r+p)/pr = (p+r)/pr en dus ook
a1/p·a1/r = a(p+r)/pr
Nu zien we dat de breuk die we moeten vereenvoudigen in zowel de teller als de noemer een factor a(p+r)/pr heeft. Dat betekent dat we de breuk kunnen vereenvoudigen door teller en noemer elk door deze factor a(p+r)/pr te delen en dan houden we over
apr / 1 = apr
en dit is niet verder te vereenvoudigen. Je ziet dus dat de wat ingewikkeld ogende uitdrukking niets anders is dan apr.
De tweede opgave is niet meer dan een simpele invuloefening, omdat hier immers is gegeven dat x = 2. Maar we kunnen onszelf hier wel wat rekenwerk besparen door gebruik te maken van de gekende rekenregels woor het werken met machten, en het is kennelijk ook de bedoeling geweest van de maker van de opgave dat je dit inziet. Kijken we naar de teller van de breuk onder het wortelteken dan hebben we met x = 2
2(x²)·42x = 24·42·2 = 16·(42)2 = 16·162 = 163
zodat de teller en de noemer van de breuk onder het wortelteken voor x = 2 beide gelijk zijn aan 163. Maar dat betekent dat de waarde van de breuk onder het wortelteken voor x = 2 dus gelijk is aan 163 / 163 = 1. En de wortel uit 1 is 1. De uitdrukking is dus gelijk aan 1 voor x = 2.quote:En tenslotte een simpele, waar ik alleen niet begrijp waarom er een a staat aan de rechterzijde van de vergelijking:Hebben we een veelterm oftewel een polynoom P(x) in de variabele x, dan zegt de factorstelling dat P(x) een factor (x − x0) bevat dan en slechts dan als x0 een nulpunt is van P(x), oftewel dan en slechts dan als x0 een oplossing is van de vergelijking P(x) = 0 en dus geldt P(x0) = 0.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Welnu, als x1 en x2 de oplossingen zijn van de vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
dan is dus volgens de factorstelling zowel (x − x1) als (x − x2) een factor van de veelterm ax2 + bx + c. En daarmee is het product (x − x1)(x − x2) eveneens een factor van ax2 + bx + c. Maar het is ook duidelijk dat dit product in het algemeen niet identiek is met
ax2 + bx + c
want als we (x − x1)(x − x2) uitwerken, dan krijgen we
x2 − (x1 + x2)x + x1x2
Er ontbreekt dus nog een factor a. We kunnen nu concluderen dat een vierkantsvergelijking
(1) ax2 + bx + c = 0 (a ≠ 0)
met als oplossingen x1 en x2 ook is te schrijven als
(2) ax2 − a(x1 + x2)x + ax1x2 = 0 (a ≠ 0)
Aangezien (1) en (2) dezelfde vergelijking voorstellen, moeten de coëfficiënten van (1) en (2) identiek zijn, zodat dus geldt −a(x1 + x2) = b en dus
(3) x1 + x2 = −b/a
en ook ax1x2 = c en dus
(4) x1x2 = c/a
De betrekkingen (3) en (4) die een verband geven tussen de oplossingen x1 en x2 en de coëfficiënten a, b en c van de vierkantsvergelijking (1) heten de formules van Viète voor de vierkantsvergelijking (1). Uitgaande van de betrekkingen (3) en (4) zou je uitdrukkingen voor x1 en x2 in a, b en c af kunnen leiden, en dan heb je dus een alternatieve methode om de abc-formule af te leiden, zie ook hier.Enorm bedankt voor je uitleg. De eerste twee is mij enorm duidelijk.quote:
[..]
Om te beginnen: als je citeert, gebruik dan liever geen spoilers, dat maakt het quoten van passages van je post onnodig lastig en je bericht zelf minder leesbaar.
Het lijkt erop dat je hier een Engelse tekst door een vertaalmachine hebt gehaald, het is althans niet te hopen dat dit je eigen vertaling is. Zoals ik al eerder heb opgemerkt heeft het gebruik van het Engels in een Nederlandse onderwijssituatie niet zelden een dramatische verslechtering van de kennisoverdracht tot gevolg, en dat wordt hier weer eens treffend geïllustreerd.
Het gaat hier feitelijk om een afleiding van de wortelformule voor de oplossing van de kwadratische vergelijking x2 + px + q = 0, en deze formule wordt de pq-formule genoemd, niet de abc-formule. In het Duitse taalgebied spreekt men om het onderscheid aan te geven wel van de kleine Lösungsformel terwijl de abc-formule die de oplossingen geeft van ax2 + bx + c = 0 (a ≠ 0) de große Lösungsformel wordt genoemd. Het is overigens heel goed mogelijk de abc-formule af te leiden uit de pq-formule door p = b/a en q = c/a te substitueren.
Om te begrijpen hoe de pq-formule resp. de abc-formule kan worden afgeleid is het nodig de techniek van de kwadraatafsplitsing te begrijpen. In het Engels heet deze techniek (vanuit een iets ander perspectief) completing the square oftewel het completeren van een (volkomen) kwadraat. Het komt erop neer dat we de constante term q van de kwadratische vergelijking x2 + px + q = 0 overbrengen naar het rechterlid door van beide leden q af te trekken, zodat we x2 + px = −q krijgen. Vervolgens gaan we dan het linkerlid aanvullen tot een volkomen kwadraat door bij beide leden een geschikt gekozen constante op te tellen. Daarna kunnen we gebruik maken van één van de merkwaardige producten (identiteiten)
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
om het linkerlid van de vergelijking te herschrijven als een kwadraat. Om deze techniek beter te begrijpen moet je dit eens goed doornemen. Het is ook van belang de techniek van het kwadraatafsplitsen te oefenen door een aantal kwadratische vergelijkingen met deze methode op te lossen, zie bijvoorbeeld hier en hier voor uitgewerkte voorbeelden.
Heb je de techniek van het kwadraatafsplitsen onder de knie, dan zul je ook deze afleiding van de pq-formule alsmede deze afleiding van de abc-formule goed kunnen begrijpen.
[..]
Dit zijn geen functies maar uitdrukkingen, waarbij het kennelijk de bedoeling is dat je deze uitdrukkingen zo ver mogelijk vereenvoudigt. Het is natuurlijk onzin om op te merken dat iets 'totaal onbekend' is omdat het er wat ingewikkelder uitziet dan je wellicht gewend bent. Het is ook niet nodig om in één oogopslag te kunnen overzien wat een dergelijke uitdrukking nu eigenlijk voorstelt. Je kunt bij het vereenvoudigen stap voor stap te werk gaan, waarbij je voor elke stap een jou bekende rekenregel gebruikt om de uitdrukking in een eenvoudiger vorm te brengen, totdat je op een punt aan bent gekomen waarbij verdere vereenvoudigingen niet meer mogelijk zijn of in ieder geval niet zinvol.
Voor de eerste uitdrukking kun je bedenken dat
p√a = a1/p en r√a = a1/r
zodat
p√a · r√a = a1/p·a1/r
en dit geeft ons dan weer de mogelijkheid om de rekenregel te gebruiken die zegt dat exponenten optellen bij het vermenigvuldigen van twee machten van hetzelfde grondtal. We hebben 1/p + 1/r = r/pr + p/pr = (r+p)/pr = (p+r)/pr en dus ook
a1/p·a1/r = a(p+r)/pr
Nu zien we dat de breuk die we moeten vereenvoudigen in zowel de teller als de noemer een factor a(p+r)/pr heeft. Dat betekent dat we de breuk kunnen vereenvoudigen door teller en noemer elk door deze factor a(p+r)/pr te delen en dan houden we over
apr / 1 = apr
en dit is niet verder te vereenvoudigen. Je ziet dus dat de wat ingewikkeld ogende uitdrukking niets anders is dan apr.
De tweede opgave is niet meer dan een simpele invuloefening, omdat hier immers is gegeven dat x = 2. Maar we kunnen onszelf hier wel wat rekenwerk besparen door gebruik te maken van de gekende rekenregels woor het werken met machten, en het is kennelijk ook de bedoeling geweest van de maker van de opgave dat je dit inziet. Kijken we naar de teller van de breuk onder het wortelteken dan hebben we met x = 2
2(x²)·42x = 24·42·2 = 16·(42)2 = 16·162 = 163
zodat de teller en de noemer van de breuk onder het wortelteken voor x = 2 beide gelijk zijn aan 163. Maar dat betekent dat de waarde van de breuk onder het wortelteken voor x = 2 dus gelijk is aan 163 / 163 = 1. En de wortel uit 1 is 1. De uitdrukking is dus gelijk aan 1 voor x = 2.
[..]
Hebben we een veelterm oftewel een polynoom P(x) in de variabele x, dan zegt de factorstelling dat P(x) een factor (x − x0) bevat dan en slechts dan als x0 een nulpunt is van P(x), oftewel dan en slechts dan als x0 een oplossing is van de vergelijking P(x) = 0 en dus geldt P(x0) = 0.
Welnu, als x1 en x2 de oplossingen zijn van de vierkantsvergelijking
ax2 + bx + c = 0 (a ≠ 0)
dan is dus volgens de factorstelling zowel (x − x1) als (x − x2) een factor van de veelterm ax2 + bx + c. En daarmee is het product (x − x1)(x − x2) eveneens een factor van ax2 + bx + c. Maar het is ook duidelijk dat dit product in het algemeen niet identiek is met
ax2 + bx + c
want als we (x − x1)(x − x2) uitwerken, dan krijgen we
x2 − (x1 + x2)x + x1x2
Er ontbreekt dus nog een factor a. We kunnen nu concluderen dat een vierkantsvergelijking
(1) ax2 + bx + c = 0 (a ≠ 0)
met als oplossingen x1 en x2 ook is te schrijven als
(2) ax2 − a(x1 + x2)x + ax1x2 = 0 (a ≠ 0)
Aangezien (1) en (2) dezelfde vergelijking voorstellen, moeten de coëfficiënten van (1) en (2) identiek zijn, zodat dus geldt −a(x1 + x2) = b en dus
(3) x1 + x2 = −b/a
en ook ax1x2 = c en dus
(4) x1x2 = c/a
De betrekkingen (3) en (4) die een verband geven tussen de oplossingen x1 en x2 en de coëfficiënten a, b en c van de vierkantsvergelijking (1) heten de formules van Viète voor de vierkantsvergelijking (1). Uitgaande van de betrekkingen (3) en (4) zou je uitdrukkingen voor x1 en x2 in a, b en c af kunnen leiden, en dan heb je dus een alternatieve methode om de abc-formule af te leiden, zie ook hier.
Laatste is mij niet duidelijker geworden, aangezien ik de materie al lastig vind en daarnaast gebruik je termen die het dan ook voor mij lastiger maken, omdat ik de materie niet begrijp..
Het is meer dat ik niet begrijp waarom de a er staat en de b en c niet terug te vinden is.. ik weet wel dat de formule
Ax^2 + bx + c gelijk is aan de functie met de oplossingen (waarin a ) voorkomt..: a(x - x1) ( x - x2)Hello,
Snapt iemand waarom bij het volgende geen 3 onder de 'onzichtbare noemer' van de gehele getallen komt?:
3x - 24 + 8/3x = -7
Ik zou zeggen alles vermenigvuldigen met 3, en daarnaast de gehele getallen zien als breuken (3x/1 en 24/1 )
Dus
9x/3 - 72/3 + 8x = -21/3
Dit klopt volgens mij niet, maar waarom behandel je de gehele getallen niet als breuken?quote:Op dinsdag 2 september 2014 18:56 schreef RustCohle het volgende:
Hello,
Snapt iemand waarom bij het volgende geen 3 onder de 'onzichtbare noemer' van de gehele getallen komt?:
3x - 24 + 8/3x = -7
Ik zou zeggen alles vermenigvuldigen met 3, en daarnaast de gehele getallen zien als breuken (3x/1 en 24/1 )
Dus
9x/3 - 72/3 + 8x = -21/3
Dit klopt volgens mij niet, maar waarom behandel je de gehele getallen niet als breuken?. Dan doe je alles keer 3x, dus
. Dan krijg je,
, en het antwoord:
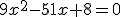
Dat b en c niet terug zouden zijn te vinden is natuurlijk niet waar. Je vergeet namelijk dat x1 en x2 zijn uit te drukken in a, b en c. Hebben we een kwadratische veelterm ax2 + bx + c met reële coëfficiënten waarvan de discriminant D = b2 − 4ac niet negatief is, dan geldt voor de reële nulpunten x1 en x2 van deze veeltermquote:
[..]
Enorm bedankt voor je uitleg. De eerste twee is mij enorm duidelijk.
Laatste is mij niet duidelijker geworden, aangezien ik de materie al lastig vind en daarnaast gebruik je termen die het dan ook voor mij lastiger maken, omdat ik de materie niet begrijp.
Het is meer dat ik niet begrijp waarom de a er staat en de b en c niet terug te vinden zijn. Ik weet wel dat de formule
ax2 + bx + c gelijk is aan de functie met de oplossingen (waarin a voorkomt): a(x - x1) (x - x2)
zodat we voor
kunnen schrijven
Bekijk eens een eenvoudig voorbeeld met concrete getallen voor de coëficiënten a, b en c van de vierkantsvergelijking ax2 + bx + c = 0. Kies a = 2, b = −10, c = 12, dan hebben we
2x2 − 10x + 12 = 0
De oplossingen van deze vergelijking zijn x1 = 2 en x2 = 3, zodat de veelterm 2x2 − 10x + 12 dus een factor (x − 2) en een factor (x − 3) bevat. Maar als we deze factoren met elkaar vermenigvuldigen, dan krijgen we
(x − 2)(x − 3) = x2 − (2+3)x + (2·3) = x2 − 5x + 6
en dat is niet identiek met 2x2 − 10x + 12. Dit komt omdat 2x2 − 10x + 12 behalve de factoren (x − 2) en (x − 3) ook nog een (constante) factor 2 bevat. De vergelijking is dan ook te schrijven als
2(x − 2)(x − 3) = 0
Voor de som van de oplossingen geldt x1 + x2 = 2 + 3 = 5 en dit is gelijk aan −b/a = 10/2 en voor het product van de oplossingen geldt x1x2 = 2·3 = 6 en dit is gelijk aan c/a = 12/2, zoals de formules van Viète ook aangeven.
[ Bericht 11% gewijzigd door Riparius op 05-09-2014 02:09:13 ]Klopt, maar waarom mag je de gehele getallen niet benaderen als breuken ( gehele getal/1 ) ?quote:
[..]Ik vermoed dat je bedoeltquote:
Hello,
Snapt iemand waarom bij het volgende geen 3 onder de 'onzichtbare noemer' van de gehele getallen komt?:
3x - 24 + 8/3x = -7
3x − 24 + (8/3)·x = −7
Beide leden vermenigvuldigen met 3 geeft dan
9x − 72 + 8x = −21
en dus
17x − 72 = −21
zodat
17x = 72 − 21
oftewel
17x = 51
en dus
x = 3Dat mag je wel? 10 delen door 5 isquote:
[..]
Klopt, maar waarom mag je de gehele getallen niet benaderen als breuken ( gehele getal/1 ) ?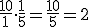
( 1-W2)2
Hoe moet deze (w is wortel)?
Ik kom uit op 1-2= -1
Maar het antwoordenboek komt uit op 3 - 2W2(a + b)2 = a2 + 2ab + b2quote:
( 1-W2)2
Hoe moet deze (w is wortel)?
Ik kom uit op 1-2= -1
Maar het antwoordenboek komt uit op 3 - 2W2
Jij vergeet 2ab en je vergeet dat min keer min plus is.(a-b)2 = a2 -2ab +b2 is misschien handiger als je niet meteen ziet dat b ook een negatief getal mag zijn.Dit had je nu zonder meer moeten kunnen herleiden als je de moeite had genomen dit te bestuderen, zoals ik je ook heb aangeraden. Merkwaardige producten dien je van buiten te kennen en ook te allen tijde te herkennen.quote:
( 1-W2)2
Hoe moet deze (w is wortel)?
Ik kom uit op 1-2= -1
Maar het antwoordenboek komt uit op 3 - 2W2
(1 − √2)2 = 1 − 2·1·√2 + (√2)2 = 1 − 2√2 + 2 = 3 − 2√2.Waar komt die wortel 2 opeens vandaan?quote:
[..]
Dit had je nu zonder meer moeten kunnen herleiden als je de moeite had genomen dit te bestuderen, zoals ik je ook heb aangeraden. Merkwaardige producten dien je van buiten te kennen en ook te allen tijde te herkennen.
(1 − √2)2 = 1 − 2·1·√2 + (√2)2 = 1 − 2√2 + 2 = 3 − 2√2.
Forum Opties Forumhop: Hop naar:
