SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
OK, snap echt niet waar hier de fout inzit...
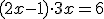dan, 
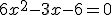. abc-formule (gebruikt mijn boek): D = 9 - 4 * 6 * -6 = 153. En mijn boek komt aan met 17?
Door 3 delen, dan ABC.quote:Op donderdag 21 augustus 2014 17:28 schreef netchip het volgende:
OK, snap echt niet waar hier de fout inzit...
Is hetzelfde want 153 / 32 = 17
Ik zie het nu. Dank je!quote:
[..]
Door 3 delen, dan ABC.
Is hetzelfde want 153 / 32 = 17
Maar waarom delen door 32?
Gewoon datquote:
[..]
Ik zie het nu. Dank je!
D = b2 - 4ac
Jouw a,b en c zijn 3 keer zo groot, dus je D is 9 keer zo groot.
Omdat je daarna nog de wortel neemt en deelt door 2a (ook 3 keer zo groot) enz. komt er hetzelfde uit.
Ik heb een aantal vraagstukken en hopelijk kan iemand mij hiermee helpen:
Simplificeren van..
(4² * 6²) / (3³ * 2³)
(34(2³)6) / ((-3)1537)
(py(pq)o ) / (p 2y + o q o - 2 ) ---> de o is een standaardafwijking teken..
Het bovenstaande (delen met machten) vind ik best lastig omdat de grondgetallen niet gelijk aan elkaar zijn
- Een bedrijf heeft van 1990 tot 1991 haar winst verhoogd met 20%, maar heeft het verlaagd met 17% vanaf 1991 tot 1992. Wat voor percentage in de daling van de winst van 1991 tot 1992 laat zien dat de winsten gelijk waren in 1990 en 1992? -
Simplificeren van..
(4² * 6²) / (3³ * 2³)
(34(2³)6) / ((-3)1537)
(py(pq)o ) / (p 2y + o q o - 2 ) ---> de o is een standaardafwijking teken..
Het bovenstaande (delen met machten) vind ik best lastig omdat de grondgetallen niet gelijk aan elkaar zijn
- Een bedrijf heeft van 1990 tot 1991 haar winst verhoogd met 20%, maar heeft het verlaagd met 17% vanaf 1991 tot 1992. Wat voor percentage in de daling van de winst van 1991 tot 1992 laat zien dat de winsten gelijk waren in 1990 en 1992? -
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 1% gewijzigd door Andijvie_ op 22-08-2014 11:48:31 ]
Hint;quote:
Ik heb een aantal vraagstukken en hopelijk kan iemand mij hiermee helpen:
(4² * 6²) / (3³ * 2³)
4 = 22
6 = 3 * 2
quote:
Ik heb een aantal vraagstukken en hopelijk kan iemand mij hiermee helpen:
(4² * 6²) / (3³ * 2³)
(34(2³)6) / ((-3)1537)
(py(pq)o ) / (p 2y + o q o - 2 ) ---> de o is een standaardafwijking teken..
Het bovenstaande (delen met machten) vind ik best lastig omdat de grondgetallen niet gelijk aan elkaar zijn
- Een bedrijf heeft van 1990 tot 1991 haar winst verhoogd met 20%, maar heeft het verlaagd met 17% vanaf 1991 tot 1992. Wat voor percentage in de daling van de winst van 1991 tot 1992 laat zien dat de winsten gelijk waren in 1990 en 1992? -De winst is in 1991 met 20% gestegen ten opzichte van 1990. Hoeveel moet de winst dalen in 1992 ten opzichte van 1991 zodat de winst in 1992 gelijk is aan die van 1990?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Ohh zo, dan heb ik het wellicht verkeerd vertaald..quote:Op vrijdag 22 augustus 2014 00:02 schreef OllieWilliams het volgende:
[..]
De winst is in 1991 met 20% gestegen ten opzichte van 1990. Hoeveel moet de winst dalen in 1992 ten opzichte van 1991 zodat de winst in 1992 gelijk is aan die van 1990?
"What percentage decrease in profits from 1991 to 1992 would imply that the profits were equal in 1990 and 1992"
Ik snap hem niet? Ik heb gezien dat het niet in mijn post stond, nu wel, dat het gesimplificeerd opgeachreven moest worden.quote:
Ik kom dan uit opquote:
( 24 * 32 * 24 ) / (33 * 23)
En dat maakt
( 28 * 32 ) / ( 33 * 23 )
Dan zou ik er het volgende van maken
25 / 3 -1
Ten eerste
32 / 33 = 3-1 = 1/3
Niet 1/3-1
Dus het antwoord is
23 / 3 = 8 / 3
Ten tweedequote:
[..]
Ik kom dan uit op
( 24 * 32 * 22 ) / (33 * 23)
32 / 33 = 3-1 = 1/3
Niet 1/3-1
Dus het antwoord is
23 / 3 = 8 / 3
Zou je me ook kunnen helpen met die derde? Die tweede ga ik zelf even goed uitpuzzelen.. Die derde lukt mij niet i.v.m. die standaardafwijking teken en omdat het letters zijn..quote:
Ten eerste
[..]
Ten tweede
32 / 33 = 3-1 = 1/3
Niet 1/3-1
Dus het antwoord is
23 / 3 = 8 / 3
[ Bericht 0% gewijzigd door Andijvie_ op 22-08-2014 15:49:23 ]
De standaardafwijking wordt gewoonlijk aangegeven met de kleine Griekse letter sigma: σquote:
[..]
Zou je me ook kunnen helpen met die derde? Die tweede ga ik zelf even goed uitpuzzelen.. Die derde lukt mij niet i.v.m. die standaardafwijking teken en omdat het letters zijn..
Deze letter kun je krijgen door & sigma; te typen, maar dan zonder spatie na de ampersand.
Verder is het gewoon een kwestie van het toepassen van de standaard rekenregels voor het werken met machten.
Thnx. Ik heb nog een onduidelijkheidje:quote:
[..]
De standaardafwijking wordt gewoonlijk aangegeven met de kleine Griekse letter sigma: σ
Deze letter kun je krijgen door & sigma; te typen, maar dan zonder spatie na de ampersand.
Verder is het gewoon een kwestie van het toepassen van de standaard rekenregels voor het werken met machten.
Ontbinden in factoren van:
21x²y³
en
8x²y² - 16xy :
Ik had:
7xy² (3xy), maar het antwoordenboek geeft aan: 3 * 7 * xxyyy
en
8xy (xy - 2), maar het antwoordenboek geeft aan: 2 * 2 * 2xy ( xy - 2)
Dit ben ik niet gewend, aangezien ik het op de wijze als het antwoordenboek nooit geleerd heb..
quote:Op woensdag 20 augustus 2014 17:19 schreef thabit het volgende:
[..]
Mooi, dan heb ik nog een sommetje voor je.
Als je twee "gewone" dobbelstenen gooit ("gewoon" wil zeggen dat vlakken 1, 2, 3, 4, 5, en 6 ogen hebben), dan weet je hoe de verdeling van de som van de ogen is: je kunt op 1 manier 2 gooien, op 2 manieren 3, op 3 manieren 4, etc t/m op 1 manier 12.
Geef nu twee "ongewone" dobbelstenen (dwz wel met 6 vlakken, maar met andere ogenverdelingen) zo dat de som van de ogen van de twee dezelfde verdeling heeft als bij 2 gewone dobbelstenen.
Ik heb oneindig veel paren voor je: (1,2,3,4,5,6) + ke6 & (1,2,3,4,5,6) - ke6 voor k in N, waar e6 = (1,1,1,1,1,1). (OK, alleen k=1 en k=0 tellen dan nietquote:Op woensdag 20 augustus 2014 17:32 schreef thabit het volgende:
O ja, (0, 1, 2, 3, 4, 5) en (2, 3, 4, 5, 6, 7) telt niet.
)
Het aantal ogen op elk van de vlakjes van elk van de beide dobbelstenen moet positief en geheel zijn aangezien je geen negatief aantal ogen kunt hebben, en dan is er precies één oplossing (afgezien van de triviale mogelijkheid om de beide dobbelstenen met elkaar te verwisselen).quote:Op vrijdag 22 augustus 2014 16:24 schreef thenxero het volgende:
[..]
[..]
Ik heb oneindig veel paren voor je: (1,2,3,4,5,6) + ke6 & (1,2,3,4,5,6) - ke6 voor k in N, waar e6 = (1,1,1,1,1,1). (OK, alleen k=1 en k=0 tellen dan niet
Kennelijk wordt bedoeld dat je de gegeven uitdrukkingen zo ver mogelijk moet ontbinden in factoren, waarmee dan wordt bedoeld dat je voor deze opgave machten moet uitschrijven als een product van gelijke factoren en tevens dat je (gehele) getallen moet ontbinden in priemfactoren.quote:
[..]
Dit ben ik niet gewend, aangezien ik het op de wijze als het antwoordenboek nooit geleerd heb..
Een wiskundige neemt nooit stilzwijgend aan dat een aantal ogen positief moet zijnquote:
[..]
Het aantal ogen op elk van de vlakjes van elk van de beide dobbelstenen moet positief en geheel zijn aangezien je geen negatief aantal ogen kunt hebben, en dan is er precies één oplossing (afgezien van de triviale mogelijkheid om de beide dobbelstenen met elkaar te verwisselen).
. Als je zeker weet dat er dan precies één oplossing is, dan is de oplossingsverzameling leeg na Thabit's opmerking.
Nee, dat laatste is niet zo. Zoals gezegd is er precies één oplossing waarbij het aantal ogen op elk van de vlakjes van elk van beide dobbelstenen geheel en positief is, de dobbelstenen niet 'normaal' zijn en de verdeling van de mogelijke uitkomsten bij het werpen met deze twee 'speciale' dobbelstenen niettemin identiek is aan de verdeling van de mogelijke uitkomsten bij het werpen met twee 'normale' dobbelstenen. Thabit heeft het vraagstuk helaas niet exact genoeg geformuleerd.quote:
[..]
Een wiskundige neemt nooit stilzwijgend aan dat een aantal ogen positief moet zijn
Hoi Riparius ik had nog een vraag.. waar ik helemaal niet uitkom. Althans ik vind het lastig, ondanks het toepassen van de rekenregels:quote:
[..]
Nee, dat laatste is niet zo. Zoals gezegd is er precies één oplossing waarbij het aantal ogen op elk van de vlakjes van elk van beide dobbelstenen geheel en positief is, de dobbelstenen niet 'normaal' zijn en de verdeling van de mogelijke uitkomsten bij het werpen met deze twee 'speciale' dobbelstenen niettemin identiek is aan de verdeling van de mogelijke uitkomsten bij het werpen met twee 'normale' dobbelstenen. Thabit heeft het vraagstuk helaas niet exact genoeg geformuleerd.
K -3 - K -6
(ontbinden in factoren)
Bedenk dat je kunt schrijven K−6 = K−3·K−3 waarna je een factor K−3 buiten haakjes kunt halen. Dan krijg je dusquote:
[..]
Hoi Riparius ik had nog een vraag.. waar ik helemaal niet uitkom. Althans ik vind het lastig, ondanks het toepassen van de rekenregels:
K -3 - K -6
(ontbinden in factoren)
K−3 − K−6 = K−3(1 − K−3)
Maar je zou ook kunnen bedenken dat K−3 = K−6·K3 waarna je een factor K−6 buiten haakjes kunt halen en je dus krijgt
K−3 − K−6 = K−6(K3 − 1)
Hierna zou je verder kunnen gaan omdat K3 − 1 = (K − 1)(K2 + K + 1), maar je zult eerst duidelijk moeten maken wat precies de bedoeling is van de opgave, aangezien je K−3 − K−6 op meerdere manieren kunt herschrijven als een product van twee of meer factoren.
Jou kan ik wel volgen, maar het antwoordenboek niet:quote:
[..]
Bedenk dat je kunt schrijven K−6 = K−3·K−3 waarna je een factor K−3 buiten haakjes kunt halen. Dan krijg je dus
K−3 − K−6 = K−3(1 − K−3)
Maar je zou ook kunnen bedenken dat K−3 = K−6·K3 waarna je een factor K−6 buiten haakjes kunt halen en je dus krijgt
K−3 − K−6 = K−6(K3 − 1)
Hierna zou je verder kunnen gaan omdat K3 − 1 = (K − 1)(K2 + K + 1), maar je zult eerst duidelijk moeten maken wat precies de bedoeling is van de opgave, aangezien je K−3 − K−6 op meerdere manieren kunt herschrijven als een product van twee of meer factoren.
K -6 (K - 1)(K2+ K + 1)
Dat is exact wat Riparius doet?quote:
[..]
Jou kan ik wel volgen, maar het antwoordenboek niet:
K -6 (K - 1)(K2+ K + 1)
Ja maar bij zijn eindantwoord stond er geen K -6 ervoor.quote:
[..]
Dat is exact wat Riparius doet?
Dat was geen 'eindantwoord', want ik verwachtte dat je de laatste stap nu zelf wel zou kunnen zetten. Ik heb gezegd datquote:
[..]
Ja maar bij zijn eindantwoord stond er geen K -6 ervoor.
K−3 − K−6 = K−6(K3 − 1)
en ook dat
K3 − 1 = (K − 1)(K2 + K + 1)
En wat krijg je dan als je de tweede betrekking in de eerste substitueert, oftewel, als je in de eerste betrekking (K3 − 1) door (K − 1)(K2 + K + 1) vervangt?
Weleens een dobbelsteen met een negatief aantal ogen gezien? Dobbelstenen met halve ogen, halve of negatief tellende zijden, of nog meer van dat soort flauwekul, daar doen we niet aan. Gewoon 6 vlakken met een positief geheel aantal ogen op elk van de vlakken, zoals Riparius opmerkte.quote:
[..]
[..]
Ik heb oneindig veel paren voor je: (1,2,3,4,5,6) + ke6 & (1,2,3,4,5,6) - ke6 voor k in N, waar e6 = (1,1,1,1,1,1). (OK, alleen k=1 en k=0 tellen dan niet
Maar goed, ik neem aan dat je de oplossing inmiddels al hebt gevonden?
Ow, dan was het een misinterpretatie geweest van mij. Ik dacht dat je het vergeten was.quote:
[..]
Dat was geen 'eindantwoord', want ik verwachtte dat je de laatste stap nu zelf wel zou kunnen zetten. Ik heb gezegd dat
K−3 − K−6 = K−6(K3 − 1)
en ook dat
K3 − 1 = (K − 1)(K2 + K + 1)
En wat krijg je dan als je de tweede betrekking in de eerste substitueert, oftewel, als je in de eerste betrekking (K3 − 1) door (K − 1)(K2 + K + 1) vervangt?
Ik heb nog een onduidelijkheid over het onderwerp ongelijkheden:
Bij de volgende ongelijkheid vraag ik me af hoe de getallenlijn eruit ziet en wat het antwoord is:
( (x-2) + 3(x+1) ) / (x+3) -< [gelijk of kleiner als] 0
Ik maakte er het volgende van:
(4x + 1) / (x+3) -< 0
Ik vraag me alleen af hoe ik zonder calculator een getallenlijn kan maken en achter het antwoord kan komen? Is het trial and error ofzo?
Bij de volgende ongelijkheid vraag ik me af hoe de getallenlijn eruit ziet en wat het antwoord is:
( (x-2) + 3(x+1) ) / (x+3) -< [gelijk of kleiner als] 0
Ik maakte er het volgende van:
(4x + 1) / (x+3) -< 0
Ik vraag me alleen af hoe ik zonder calculator een getallenlijn kan maken en achter het antwoord kan komen? Is het trial and error ofzo?
Het teken ≤ maak je door & le; te typen zonder spatie na de &. De ongelijkheid isquote:
Ik heb nog een onduidelijkheid over het onderwerp ongelijkheden:
Bij de volgende ongelijkheid vraag ik me af hoe de getallenlijn eruit ziet en wat het antwoord is:
( (x-2) + 3(x+1) ) / (x+3) -< [gelijk of kleiner als] 0
Ik maakte er het volgende van:
(4x + 1) / (x+3) -< 0
Ik vraag me alleen af hoe ik zonder calculator een getallenlijn kan maken en achter het antwoord kan komen? Is het trial and error ofzo?
(4x + 1) / (x + 3) ≤ 0
Het oplossen van een dergelijke ongelijkheid doe je niet via trial and error. In het linkerlid van de ongelijkheid heb je een breuk, en we moeten nu bepalen voor welke waarden van x de waarde van deze breuk ofwel negatief is ofwel nul.
In het algemeen is de waarde van een breuk negatief of nul als (a) de teller kleiner dan of gelijk is aan nul terwijl de noemer groter is dan nul of als (b) de teller groter dan of gelijk is aan nul terwijl de noemer kleiner is dan nul. Dus krijgen we als voorwaarden
(4x + 1 ≤ 0 ∧ x + 3 > 0) ∨ (4x + 1 ≥ 0 ∧ x + 3 < 0)
en dit geeft
(x ≤ −¼ ∧ x > −3) ∨ (x ≥ −¼ ∧ x < −3)
De tweede voorwaarde is strijdig, want een getal x kan niet gelijktijdig groter zijn dan −¼ en kleiner dan −3, zodat we alleen de eerste voorwaarde overhouden. En hiervoor kunnen we schrijven
−3 < x ≤ −¼
Anders gezegd, x moet liggen op het interval (−3, −¼].
Is dit de enige manier of zijn er nog meer makkelijke methoden?quote:
[..]
Het teken ≤ maak je door & le; te typen zonder spatie na de &. De ongelijkheid is
(4x + 1) / (x + 3) ≤ 0
Het oplossen van een dergelijke ongelijkheid doe je niet via trial and error. In het linkerlid van de ongelijkheid heb je een breuk, en we moeten nu bepalen voor welke waarden van x de waarde van deze breuk ofwel negatief is ofwel nul.
In het algemeen is de waarde van een breuk negatief of nul als (a) de teller kleiner dan of gelijk is aan nul terwijl de noemer groter is dan nul of als (b) de teller groter dan of gelijk is aan nul terwijl de noemer kleiner is dan nul. Dus krijgen we als voorwaarden
(4x + 1 ≤ 0 ∧ x + 3 > 0) ∨ (4x + 1 ≥ 0 ∧ x + 3 < 0)
en dit geeft
(x ≤ −¼ ∧ x > −3) ∨ (x ≥ −¼ ∧ x < −3)
De tweede voorwaarde is strijdig, want een getal x kan niet gelijktijdig groter zijn dan −¼ en kleiner dan −3, zodat we alleen de eerste voorwaarde overhouden. En hiervoor kunnen we schrijven
−3 < x ≤ −¼
Anders gezegd, x moet liggen op het interval (−3, −¼].
Enorm duidelijke uitleg en daar dank ik je dan ook zeer voor Riparius!
Je zou in dit geval de breuk ook kunnen herleiden door eerst de teller 4x + 1 te herschrijven als 4(x + 3) − 11, zodat je de breuk als geheel daarna kunt herschrijven als 4 − (11/(x + 3)), maar de oplossing van de ongelijkheid wordt hiermee niet eenvoudiger.quote:
[..]
Is dit de enige manier of zijn er nog meer makkelijke methoden?
In het algemeen herleid je bij ongelijkheden waarbij de onbekende in de noemer van een breuk voorkomt eerst het rechterlid op nul, en herschrijf je het linkerlid als één breuk, waarna je in het algemeen twee mogelijkheden hebt, zoals in het uitgewerkte voorbeeld hierboven. Dan houd je twee sets ongelijkheden over waarbij de onbekende niet meer in de noemer van een breuk voorkomt.
Graag gedaan.quote:Enorm duidelijke uitleg en daar dank ik je dan ook zeer voor Riparius!
Aangezien Amoeba, aan wie het vraagstuk was opgegeven, het volledig af heeft laten weten en jij kennelijk ook niet meer genegen bent om je erin te verdiepen geef ik hier voor eventuele andere geïnteresseerden maar even mijn uitwerking.quote:
De voortbrengende functie voor de uitkomsten van een worp met één reguliere dobbelsteen is
x + x2 + x3 + x4 + x5 + x6
Dit polynoom heeft 6 termen waarbij de coëfficiënt van elke term 1 is en de exponent van x van elke term het aantal ogen voorstelt op een zijde van de dobbelsteen. Door dit polynoom met zichzelf te vermenigvuldigen krijgen we de voortbrengende functie voor de uitkomsten van een worp met twee reguliere dobbelstenen. Het is eenvoudig in te zien waarom dit zo is. Als we namelijk dit polynoom met zichzelf vermenigvuldigen, dan vermenigvuldigen we elke term uit de eerste factor met elke term uit de tweede factor. Elk product stelt daarbij één mogelijke uitkomst voor bij een worp met de twee dobbelstenen. Aangezien exponenten optellen bij vermenigvuldiging krijgen we zo een polynoom waarvan de exponenten van x van de termen lopen van 2 tot en met 12 en waarbij de coëfficiënt van elke term het aantal manieren geeft waarop met twee dobbelstenen het totaal aantal ogen gelijk aan de exponent van die term kan worden verkregen. En dus hebben we zo inderdaad de voortbrengende functie voor de uitkomsten van een worp met twee reguliere dobbelstenen.
Willen we nu twee dobbelstenen vinden waarbij het aantal ogen op elk van de zes vlakjes van elk van beide dobbelstenen geheel en positief is, de dobbelstenen niet 'normaal' zijn en de verdeling van de mogelijke uitkomsten bij het werpen met deze twee 'speciale' dobbelstenen niettemin identiek is aan de verdeling van de mogelijke uitkomsten bij het werpen met twee 'normale' dobbelstenen, dan moet dus het product van de voortbrengende functies P(x) en Q(x) voor de uitkomsten van een worp met elk van deze 'speciale' dobbelstenen identiek zijn aan het kwadraat van de voortbrengende functie van de uitkomsten van een worp met één reguliere dobbelsteen, zodat moet gelden
(1) P(x)Q(x) = (x + x2 + x3 + x4 + x5 + x6)2
Nu moeten de polynomen P(x) en Q(x) wel aan een aantal voorwaarden voldoen. De algemene gedaante van een voortbrengende functie voor de uitkomsten van worp met een dobbelsteen met zes vlakjes is
xm + xn + xp + xq + xr + xs
waarbij m, n, p, q, r, s positieve gehele getallen zijn die de aantallen ogen voorstellen op elk van de zes vlakjes van de dobbelsteen. Aangezien een dergelijk polynoom geen constante term heeft, moet voor de te vinden polynomen P(x) en Q(x) dus gelden
(2) P(0) = 0, Q(0) = 0
Verder is de som van de coëfficiënten van de termen van een voortbrengende functie voor de uitkomsten van een worp met een dobbelsteen met zes vlakjes gelijk aan 6. Dit geldt uiteraard ook als twee of meer van de positieve gehele getallen m, n, p, q, r, s gelijk aan elkaar zijn en het aantal termen van het polynoom dus minder is dan 6. Als bijvoorbeeld n = m, dan is xm + xn = 2xm zodat aan de som van de coëfficiënten van het polynoom niets verandert. De coëfficiënten van de te vinden polynomen P(x) en Q(x) zijn dus positief en geheel en voor deze polynomen moet ook gelden
(3) P(1) = 6, Q(1) = 6
Nu volgt uit (1) dat het product P(x)Q(x) dezelfde factoren bevat als (x + x2 + x3 + x4 + x5 + x6)2 en dat betekent dat elk van de factoren van (x + x2 + x3 + x4 + x5 + x6)2 een factor is van hetzij P(x) hetzij Q(x). Ontbinden we dus x + x2 + x3 + x4 + x5 + x6 en daarmee (x + x2 + x3 + x4 + x5 + x6)2 in factoren, dan kunnen we nagaan of we deze factoren op een zodanige wijze over P(x) en Q(x) kunnen verdelen dat beide polynomen ongelijk zijn aan x + x2 + x3 + x4 + x5 + x6 terwijl nog steeds aan de voorwaarden (2) en (3) wordt voldaan. Als dit lukt, dan hebben we de voortbrengende functies en daarmee de verdeling van de ogen van de gevraagde speciale dobbelstenen gevonden.
Welnu, het ontbinden in factoren van de veelterm x + x2 + x3 + x4 + x5 + x6 is niet moeilijk. Om te beginnen kunnen we een factor x buiten haakjes halen, en dit geeft
x(1 + x + x2 + x3 + x4 + x5)
Nu is gemakkelijk te zien dat de veelterm 1 + x + x2 + x3 + x4 + x5 een nulpunt x = −1 heeft, zodat deze veelterm een factor (x + 1) bevat. Halen we per tweetal opeenvolgende termen een factor (1 + x) buiten haakjes, dan krijgen we
1 + x + x2 + x3 + x4 + x5 = (1 + x) + (1 + x)x2 + (1 + x)x4 = (1 + x)(1 + x2 + x4)
De veelterm 1 + x2 + x4 kunnen we nog ontbinden in twee kwadratische veeltermen. Met behulp van kwadraatafsplitsing krijgen we
1 + x2 + x4 = (1 + x2)2 − x2 = (1 + x + x2)(1 − x + x2)
De kwadratische veeltermen 1 + x + x2 en 1 − x + x2 zijn niet verder te ontbinden in reële lineaire factoren (en dus a fortiori niet in lineaire factoren met gehele coëfficiënten) aangezien de discriminanten van deze kwadratische veeltermen negatief zijn. We vinden dus
x + x2 + x3 + x4 + x5 + x6 = x(1 + x)(1 + x + x2)(1 − x + x2)
zodat we op grond van (1) hebben
(4) P(x)Q(x) = x2(1 + x)2(1 + x + x2)2(1 − x + x2)2
We hebben nu acht factoren die we moeten verdelen over P(x) en Q(x). Het is duidelijk dat P(x) en Q(x) elk één factor x moeten bevatten, aangezien op grond van (2) moet gelden P(0) = 0 en tevens Q(0) = 0. Verder is het zo dat de factoren (1 + x), (1 + x + x2) en (1 − x + x2) voor x = 1 gelijk zijn aan resp. 2, 3 en 1. En aangezien op grond van (3) moet gelden P(1) = 6 en tevens Q(1) = 6 volgt uit (4) dat P(x) en Q(x) elk één factor (1 + x) en één factor (1 + x + x2) moeten bevatten.
Nu blijven alleen nog de beide factoren (1 − x + x2) over om te verdelen over P(x) en Q(x). Het is echter duidelijk dat de beide factoren (1 − x + x2) samen in één van de beide polynomen P(x) en Q(x) moeten zitten als deze polynomen ongelijk moeten zijn aan x + x2 + x3 + x4 + x5 + x6. Er is dus, afgezien van de verwisseling van P(x) en Q(x), precies één paar voortbrengende functies P(x) en Q(x) dat aan het gevraagde voldoet. Stoppen we de beide factoren (1 − x + x2) in Q(x) dan hebben we
(5) P(x) = x(1 + x)(1 + x + x2) = x + 2x2 + 2x3 + x4
en
(6) Q(x) = x(1 + x)(1 + x + x2)(1 − x + x2)2 = x + x3 + x4 + x5 + x6 + x8
De gevraagde verdeling van de aantallen ogen op de speciale dobbelstenen is dus (1, 2, 2, 3, 3, 4) en (1, 3, 4, 5, 6, 8).
[ Bericht 0% gewijzigd door Riparius op 24-08-2014 23:46:06 ]
Mooi uitgewerkt!quote:
Ik vind het leuke puzzels maar ik heb er nu weinig tijd voor. Ben bezig met mijn masterscriptie en het regelen van een Phd plek, dus er zijn al voldoende puzzels die ik moet oplossen
.
Ik wil 2(x+2)^2 ontbinden in factoren. Na een (mislukte) poging kwam ik uit op:
2x^2+4^2, maar dat klopt natuurlijk niet. Kan iemand mij een opstapje geven over hoe ik deze formule moet ontbinden in factoren (m.n. hoe ik die kwadraat daarin moet verwerken).
Edit:
Laat maar: 2x^2+8x+8
[ Bericht 3% gewijzigd door Holograph op 28-08-2014 21:13:31 ]
2x^2+4^2, maar dat klopt natuurlijk niet. Kan iemand mij een opstapje geven over hoe ik deze formule moet ontbinden in factoren (m.n. hoe ik die kwadraat daarin moet verwerken).
Edit:
Laat maar: 2x^2+8x+8
[ Bericht 3% gewijzigd door Holograph op 28-08-2014 21:13:31 ]
Nu heb je de haakjes uitgewerkt. Ontbinden in factoren wordt iets van de vorm
(2x+...)(x+...)
(2x+...)(x+...)
Opinion is the medium between knowledge and ignorance (Plato)
Ik moest iig de haakjes wegwerkenquote:
Nu heb je de haakjes uitgewerkt. Ontbinden in factoren wordt iets van de vorm
(2x+...)(x+...)
Ik dacht dat dat 'ontbinden in factoren' heet, maar de laatste keer dat ik wiskunde heb gehad is ook alweer 4 jaar geleden..
Ontbinden in factoren is min of meer het tegenovergestelde. Maar eigenlijk was waarmee je begon al ontbonden in factoren.quote:
[..]
Ik moest iig de haakjes wegwerken
Opinion is the medium between knowledge and ignorance (Plato)
M = aY + B(r - y)-8
*: Y en y zijn twee verschillende tekens (variabelen). -8 is ook een teken-variabele maar ik heb geen idee hoe ik dat invoer hier...
De vraag is:
Solve the equation for r.
Ik heb geen idee.
Kunnen jullie mij helpen?
Verderop staat dat ik makkelijk moet kunnen zien dat de functie gelijk is aan
(r - y)-8 = (M - aY)/B
Ik snap het niet en kan het niet inzien. Daarnaast snap ik nog ook niet waarom het M - aY is en niet aY - M
*: Y en y zijn twee verschillende tekens (variabelen). -8 is ook een teken-variabele maar ik heb geen idee hoe ik dat invoer hier...
De vraag is:
Solve the equation for r.
Ik heb geen idee.
Kunnen jullie mij helpen?
Verderop staat dat ik makkelijk moet kunnen zien dat de functie gelijk is aan
(r - y)-8 = (M - aY)/B
Ik snap het niet en kan het niet inzien. Daarnaast snap ik nog ook niet waarom het M - aY is en niet aY - M
Je haalt de aY naar links, plus wordt min dus M - aY. Dan haal je B naar links, vermenigvuldigen wordt delen. Dan schrijven met r aan één kant van het = teken en de rest aan de andere kant.quote:
M = aY + B(r - y)-8
*: Y en y zijn twee verschillende tekens (variabelen). -8 is ook een teken-variabele maar ik heb geen idee hoe ik dat invoer hier...
De vraag is:
Solve the equation for r.
Ik heb geen idee.
Kunnen jullie mij helpen?
Verderop staat dat ik makkelijk moet kunnen zien dat de functie gelijk is aan
(r - y)-8 = (M - aY)/B
Ik snap het niet en kan het niet inzien. Daarnaast snap ik nog ook niet waarom het M - aY is en niet aY - M
Dankje.quote:
[..]
Je haalt de aY naar links, plus wordt min dus M - aY. Dan haal je B naar links, vermenigvuldigen wordt delen. Dan schrijven met r aan één kant van het = teken en de rest aan de andere kant.
Ik weet niet hoe je een verbonden functie uit elkaar moet halen (r - y)-8
Alles wat er tussen de haakjes staat kun je voor nu beschouwen als één ding. Zaak is om de macht weg te werken, weet je hoe dat werkt?quote:
[..]
Dankje.
Ik weet niet hoe je een verbonden functie uit elkaar moet halen (r - y)-8
Ja een negatieve macht is hetzelfde als delen.quote:
[..]
Alles wat er tussen de haakjes staat kun je voor nu beschouwen als één ding. Zaak is om de macht weg te werken, weet je hoe dat werkt?
Bijv. x-5 is gelijk aan
1 / x5
Klopt, maar we willen r hebben en niet r8quote:
[..]
Ja een negatieve macht is hetzelfde als delen.
Bijv. x-5 is gelijk aan
1 / x5
Dus moeten we die macht zien weg te krijgen, weet je ook hoe dat werkt?
Die 8 wegkrijgen ehmm..quote:
[..]
Klopt, maar we willen r hebben en niet r8
Dat wordt dan 1/8 (als exponent) aan de rechterzijde van de = teken.
Edit: ik heb hem door. Jij legt ook, net als Riparius, uit alsof je een docent bent.
Dankje!!
Goed bezigquote:
[..]
Die 8 wegkrijgen ehmm..
Dat wordt dan 1/8 (als exponent) aan de rechterzijde van de = teken.
Edit: ik heb hem door. Jij legt ook, net als Riparius, uit alsof je een docent bent.
Dankje!!
Heb moeite met n polynoomfunctie
Kan een van jullie mij helpen met het volgende;
x^4+2x^2=8
Zonder gebruik van een GR kom ik er niet uit, moet ik bekennen
Kan een van jullie mij helpen met het volgende;
x^4+2x^2=8
Zonder gebruik van een GR kom ik er niet uit, moet ik bekennen
Ik heb een paar bladzijdes volgeschreven (met onzin), maar het juiste antwoord heb ik niet gevonden.quote:
Jouw reactie gaf me nieuwe inzichten maar t is me niet gelukt chef
ik kan wel beredeneren dat x √2 of -√2 moet zijn : x^2(x^2+2)=8 maar of dat de juiste (geaccepteerde) methode van tot de uitkomst komen is ben ik me niet zeker vanquote:
Tsja Henk, zo moeilijk is dit toch niet?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |