SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


Uitleg staat hier.quote:Op maandag 14 juli 2014 23:16 schreef netchip het volgende:
[..]
Dit zegt mij niet erg veel.Ik zal er een nachtje overslapen.
Ik zal binnenkort nog iets posten over de meetkundige interpretatie van een vermenigvuldiging met een willekeurig complex getal ongelijk nul, die in het algemeen beantwoordt aan een draaistrekking in het complexe vlak. Dat wordt eigenlijk nooit goed uitgelegd in inleidende cursussen complexe getallen die ik heb gezien, dus dit is een goede gelegenheid om daar eens iets over te vertellen.quote:Leuk dat je er tijd insteekt om mij iets te leren over complexe getallen, Riparius.Ik merk dat ik nu nieuwe inzichten heb, jij vertelde dat een vermenigvuldiging met i een rotatie van 90 graden tegen de klok in betekent. Erg leuk (voor mij) om die kennis dan ook te gebruiken, omdat ik nu weet wat een vermenigvuldiging met i inhoudt.
Als t je parameter is, dan zijn x en y elk een functie van t. Oefeningetje nog gelukt?quote:Het kwartje met de parametervoorstellingen is nu ook gevallen. Het principe is mij duidelijk.Het is eigenlijk een redelijk abstract principe als je gewend bent dat y een functie van x is.


Die laatste helaas niet ... Ik kwam er echt niet uit.quote:Op maandag 14 juli 2014 23:45 schreef Riparius het volgende:
[..]
Uitleg staat hier.
[..]
Ik zal binnenkort nog iets posten over de meetkundige interpretatie van een vermenigvuldiging met een willekeurig complex getal ongelijk nul, die in het algemeen beantwoordt aan een draaistrekking in het complexe vlak. Dat wordt eigenlijk nooit goed uitgelegd in inleidende cursussen complexe getallen die ik heb gezien, dus dit is een goede gelegenheid om daar eens iets over te vertellen.
[..]
Als t je parameter is, dan zijn x en y elk een functie van t. Oefeningetje nog gelukt?


Is echt heel eenvoudig hoor (als je je goniometrische identiteiten kent ...). We hadden een kromme met als parametervoorstellingquote:Op maandag 14 juli 2014 23:47 schreef netchip het volgende:
[..]
Die laatste helaas niet ... Ik kwam er echt niet uit.
(1) x = 2·sin t
(2) y = sin 2t
en gevraagd werd een cartesische vergelijking van deze kromme op te stellen. Dit is een zogeheten Lissajous figuur (zie hier voor een grafiek). Als we vergelijking (2) kwadrateren, dan hebben we
(3) y2 = (sin 2t)2 = (2·sin t·cos t)2 = 4·sin2t·cos2t = 4·sin2t(1 − sin2t) = 4·sin2t − 4·sin4t
En substitutie van (1) in (3) levert dan
y2 = 4·(½x)2 − 4·(½x)4
y2 = x2 − ¼x4
4y2 = 4x2 − x4
en dus
x4 − 4x2 + 4y2 = 0
De grafiek van deze vierdegraads kromme is uiteraard precies dezelfde Lissajous figuur.


Geen echte wiskunde, maar een stukje natuurkunde.
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?


Die druk voel je wel degelijk. Stel dat deze druk ineens wegvalt, ben je op zijn minst bewusteloos, als je al niet 'explodeert'.quote:Op woensdag 23 juli 2014 12:57 schreef m.w. het volgende:
Geen echte wiskunde, maar een stukje natuurkunde.
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?


Die druk voel je zowel onder aan je arm als erboven. Daarom dat ie niet één kant op gelanceerd wordtquote:Op woensdag 23 juli 2014 12:57 schreef m.w. het volgende:
Geen echte wiskunde, maar een stukje natuurkunde.
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?


Waarom stel je deze vraag dan niet in het andere bèta topic?quote:Op woensdag 23 juli 2014 12:57 schreef m.w. het volgende:
Geen echte wiskunde, maar een stukje natuurkunde.
De druk binnen in je lichaam is min of meer gelijk aan de buitendruk. Maar als je bijvoorbeeld ademhaalt creëer je een onderdruk, waardoor lucht naar binnen stroomt.quote:De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Je kunt een eenvoudig proefje doen om de luchtdruk te demonstreren. Vul een beker geheel met water, zet er een onderzetter bovenop die de opening geheel afsluit, en keer de gevulde beker dan om terwijl je de onderzetter tegenhoudt zodat deze niet weg kan glijden. Als je dan bij de omgekeerde beker de onderzetter los laat maar de beker wel vast blijft houden, dan blijft de onderzetter tegen de beker zitten. Dat bewijst dus dat er van onderaf een kracht omhoog op de onderzetter wordt uitgeoefend die groter is dan de kracht omlaag die door het gravitatieveld van de aarde op het water en de onderzetter wordt uitgeoefend. En die kracht omhoog wordt uiteraard veroorzaakt door de luchtdruk.


Zoals Riparius aangeeft, jij maakt de redeneerfout om naar 1 absolute druk te kijken in plaats van naar het drukverschil tussen binnen en buiten het lichaam, boven en onder je hand etc.quote:Op woensdag 23 juli 2014 12:57 schreef m.w. het volgende:
De SI eenheid voor druk is Pascal. 1 Pascal is 1 newton gedeeld door 1 vierkante meter. Op de oppervlakte van de aarde is de atmosferische druk ongeveer 100 kilonewton per vierkante meter.
Waarom ervaren wij die druk dan niet? Als ik mijn hand uitsteek, waarom is het dan alleen de zwaartekracht die een neerwaartse kracht uitoefent op mijn hand?
Als jij je hand uitsteekt dan is de druk boven je hand even groot als onder de hand, er is dus geen drukverschil (nu ja, een verwaarloosbaar kleine waarschijnlijk maar dat is nu niet relevant) en dus geen netto kracht van die lucht. Het gaat om het drukverschil. Aanvullende opmerking: op het moment dat wij inademen wordt een onderdruk gecreëerd doordat de spieren de longen oprekken en zodoende het volume vergroten.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Op die manier. Ik dacht er inderdaad fundamenteel verkeerd over na; bedankt voor de antwoorden! Hier heb ik heel veel aan.


Ik snap niet helemaal wat je hier mee bedoelt: "En substitutie van (1) in (3) levert dan" ... Wat valt er te substitueren?quote:Op dinsdag 15 juli 2014 00:11 schreef Riparius het volgende:
[..]
Is echt heel eenvoudig hoor (als je je goniometrische identiteiten kent ...). We hadden een kromme met als parametervoorstelling
(1) x = 2·sin t
(2) y = sin 2t
en gevraagd werd een cartesische vergelijking van deze kromme op te stellen. Dit is een zogeheten Lissajous figuur (zie hier voor een grafiek). Als we vergelijking (2) kwadrateren, dan hebben we
(3) y2 = (sin 2t)2 = (2·sin t·cos t)2 = 4·sin2t·cos2t = 4·sin2t(1 − sin2t) = 4·sin2t − 4·sin4t
En substitutie van (1) in (3) levert dan
y2 = 4·(½x)2 − 4·(½x)4
y2 = x2 − ¼x4
4y2 = 4x2 − x4
en dus
x4 − 4x2 + 4y2 = 0
De grafiek van deze vierdegraads kromme is uiteraard precies dezelfde Lissajous figuur.
Ah, ik zie het nu.


sin t = x / 2quote:Op zondag 3 augustus 2014 14:56 schreef netchip het volgende:
[..]
Ik snap niet helemaal wat je hier mee bedoelt: "En substitutie van (1) in (3) levert dan" ... Wat valt er te substitueren?
Ah, ik zie het nu.


Hmm. Ik probeer de inverse functie van 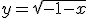 te bepalen... Ik dacht, kwadrateer beide kanten, dan krijg je y2 = -1-x. Dan breng je de x naar links, en de y2 naar rechts, daaruit volgt dan: x = -y2-1. Maar dat blijkt dus fout te zijn...
te bepalen... Ik dacht, kwadrateer beide kanten, dan krijg je y2 = -1-x. Dan breng je de x naar links, en de y2 naar rechts, daaruit volgt dan: x = -y2-1. Maar dat blijkt dus fout te zijn...


Waarom blijkt dat fout te zijn?quote:Op woensdag 6 augustus 2014 12:15 schreef netchip het volgende:
Hmm. Ik probeer de inverse functie vante bepalen... Ik dacht, kwadrateer beide kanten, dan krijg je y2 = -1-x. Dan breng je de x naar links, en de y2 naar rechts, daaruit volgt dan: x = -y2-1. Maar dat blijkt dus fout te zijn...
Je moet natuurlijk wel kijken naar de domeinen waarop de functies geldig zijn.


Ik controleerde mijn antwoord aan de hand van Wolfram Alpha: http://www.wolframalpha.c(...)f+y%3Dsqrt%28-1-x%29 Ik werd in verwarring gebracht doordat WA de x in hun inverse functie laat terugkomen, maar dat is natuurlijk omdat de functie y(x) een parameter x nodig heeft. x(y) was logischer geweest, maar goed.quote:Op woensdag 6 augustus 2014 13:58 schreef thenxero het volgende:
[..]
Waarom blijkt dat fout te zijn?
Je moet natuurlijk wel kijken naar de domeinen waarop de functies geldig zijn.
[ Bericht 3% gewijzigd door netchip op 06-08-2014 14:50:07 ]


Gebruikelijke notatie is y(x) voor een functie, en y-1(x) voor de inverse. De notatie x(y) vind ik ook wel leuk, maar is ongebruikelijk en kan verwarrend zijn. Zeker als x als vrije variabele gebruikt wordt, en dan ook nog een functie moet voorstellen.quote:Op woensdag 6 augustus 2014 14:10 schreef netchip het volgende:
[..]
Ik controleerde mijn antwoord aan de hand van Wolfram Alpha: http://www.wolframalpha.c(...)f+y%3Dsqrt%28-1-x%29 Ik werd in verwarring gebracht doordat WA de x in hun inverse functie laat terugkomen, maar dat is natuurlijk omdat de functie y(x) een parameter x nodig heeft. x(y) was logischer geweest, maar goed.


Het is beter om aanduidingen van variabelen en namen van functies niet door elkaar te gebruiken, want dan krijg je inderdaad al gauw allerlei conceptuele verwarringen. Ik heb Netchip daar overigens al eens op gewezen.quote:Op woensdag 6 augustus 2014 16:23 schreef thenxero het volgende:
[..]
Gebruikelijke notatie is y(x) voor een functie, en y-1(x) voor de inverse. De notatie x(y) vind ik ook wel leuk, maar is ongebruikelijk en kan verwarrend zijn. Zeker als x als vrije variabele gebruikt wordt, en dan ook nog een functie moet voorstellen.


Het probleem zit vooral in de notatie die je zelf hebt gekozen. Als je nu gewoon dit had gedaan dan was je vast niet in verwarring gebracht. Overigens is de notatie f−1 voor de inverse van een functie f en daarmee bijvoorbeeld sin−1x voor arcsin x nu ook niet bepaald gelukkig gekozen, zie hier mijn kanttekeningen over deze notatie.quote:Op woensdag 6 augustus 2014 14:10 schreef netchip het volgende:
[..]
Ik controleerde mijn antwoord aan de hand van Wolfram Alpha: http://www.wolframalpha.c(...)f+y%3Dsqrt%28-1-x%29 Ik werd in verwarring gebracht doordat WA de x in hun inverse functie laat terugkomen, maar dat is natuurlijk omdat de functie y(x) een parameter x nodig heeft. x(y) was logischer geweest, maar goed.


y(x) is een functie geëvalueerd op het punt x, y is een functie en y-1 is de bijbehorende inverse functie.quote:Op woensdag 6 augustus 2014 16:23 schreef thenxero het volgende:
[..]
Gebruikelijke notatie is y(x) voor een functie, en y-1(x) voor de inverse. De notatie x(y) vind ik ook wel leuk, maar is ongebruikelijk en kan verwarrend zijn. Zeker als x als vrije variabele gebruikt wordt, en dan ook nog een functie moet voorstellen.
En het is altijd makkelijk om te controleren of je de inverse te pakken hebt, immers moet gelden dat y(y-1(x)) = y-1(y(x)) = x voor alle x.


En zo moet je dit dus niet opschrijven, zoals ik hierboven beargumenteer. Hier gebruik je y als aanduiding van een functienaam maar tevens als variabele, en dat is conceptueel onjuist. De notatie y−1 is nu ambigu, want dit stelt ook de multiplicatieve inverse van de variabele y voor. Als je daarentegen f en f−1 exclusief als namen van functies gebruikt, dan kan f−1 niet worden aangezien voor een multiplicatieve inverse, wat natuurlijk niet wegneemt dat de notatie f−1 voor de inverse functie van een functie f ongelukkig blijft.quote:Op woensdag 6 augustus 2014 22:15 schreef Novermars het volgende:
[..]
y(x) is een functie geëvalueerd op het punt x, y is een functie en y-1 is de bijbehorende inverse functie.
En het is altijd makkelijk om te controleren of je de inverse te pakken hebt, immers moet gelden dat y(y-1(x)) = y-1(y(x)) = x voor alle x.


Waar gebruik ik y als variabele? En f en f-1 zijn inderdaad beter, maar omdat de rest toch al bezig waren met het gebruiken van y en y-1, ben ik daar for the sake of consistency mee doorgegaan.quote:Op woensdag 6 augustus 2014 22:37 schreef Riparius het volgende:
[..]
En zo moet je dit dus niet opschrijven, zoals ik hierboven beargumenteer. Hier gebruik je y als aanduiding van een functienaam maar tevens als variabele, en dat is conceptueel onjuist. De notatie y−1 is nu ambigu, want dit stelt ook de multiplicatieve inverse van de variabele y voor. Als je daarentegen f en f−1 exclusief als namen van functies gebruikt, dan kan f−1 niet worden aangezien voor een multiplicatieve inverse, wat natuurlijk niet wegneemt dat de notatie f−1 voor de inverse functie van een functie f ongelukkig blijft.


Inderdaad niet expliciet, maar wel impliciet. Als je een reële functie hebt van een reële variabele x, hoe zou je dan de afhankelijke variabele willen noemen? Om iets als f(x) = √(−1 − x) te inverteren moet je de afhankelijke variabele toch ook (even) een naam geven. En als je een grafiek gaat tekenen en de horizontale as noem je de x-as, hoe zou je dan de verticale as willen noemen?quote:Op donderdag 7 augustus 2014 00:24 schreef Novermars het volgende:
[..]
Waar gebruik ik y als variabele?
Jaja. Als je namen van variabelen als namen van functies gaat gebruiken of omgekeerd, en je gaat dit dan ook nog mixen met de notatie van de multiplicatieve inverse van een variabele als inverse van een functie, dan is de chaos compleet, en dat verdient geen navolging.quote:En f en f-1 zijn inderdaad beter, maar omdat de rest toch al bezig waren was met het gebruiken van y en y-1, ben ik daar for the sake of consistency mee doorgegaan.
@netchip: de grafiek van een inverse functie verkrijg je door de grafiek van de gegeven (inverteerbare) functie te spiegelen in de lijn met vergelijking y = x. Bij een spiegeling in de lijn met vergelijking y = x gaat een punt met coördinaten (x, y) over in het punt met coördinaten (y, x). Dat impliceert dat je een vergelijking van de grafiek van het spiegelbeeld van de grafiek van een gegeven functie bij spiegeling in de lijn met vergelijking y = x kunt verkrijgen door de variabelen x en y met elkaar te verwisselen in de vergelijking y = f(x) van de grafiek van de oorspronkelijke functie.
Hebben we dus een functie f: (−∞, −1] → R met als functievoorschrift f(x) = √(−1 − x), dan heeft de grafiek van deze functie de vergelijking y = √(−1 − x). Verwisselen van x en y geeft x = √(−1 − y) en oplossen van y uit deze betrekking geeft y = −x² − 1 als vergelijking van het spiegelbeeld van de grafiek van f bij spiegeling in de lijn met vergelijking y = x. De functie f is dus inverteerbaar en de inverse van f is de functie g: [0, ∞) → R met als functievoorschrift g(x) = −x² − 1.
De notatie f−1 voor de inverse van een functie f is gebruikelijk, maar verdient geen aanbeveling, net zo min als het aanbeveling verdient om bijvoorbeeld de notatie sin−1x te gebruiken voor arcsin x. Merk ook op dat f−1(x) iets anders betekent dan f(x−1) en dat dit weer iets anders is dan f(x)−1 = (f(x))−1. Men heeft ook voorgesteld om de notatie f[−1] te gebruiken voor de inverse functie van een functie f, maar we gebruiken ook al f(n) voor de n-de afgeleide van f, en je zou dus zeggen dat f(−1) dan weer een primitieve voorstelt van f. Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi.
Een alternatief is de notatie finv voor de inverse functie van een functie f.
[ Bericht 0% gewijzigd door Riparius op 07-08-2014 05:52:49 ]


Interessant.quote:Op donderdag 7 augustus 2014 03:38 schreef Riparius het volgende:
[..]
Inderdaad niet expliciet, maar wel impliciet. Als je een reële functie hebt van een reële variabele x, hoe zou je dan de afhankelijke variabele willen noemen? Om iets als f(x) = √(−1 − x) te inverteren moet je de afhankelijke variabele toch ook (even) een naam geven. En als je een grafiek gaat tekenen en de horizontale as noem je de x-as, hoe zou je dan de verticale as willen noemen?
[..]
Jaja. Als je namen van variabelen als namen van functies gaat gebruiken of omgekeerd, en je gaat dit dan ook nog mixen met de notatie van de multiplicatieve inverse van een variabele als inverse van een functie, dan is de chaos compleet, en dat verdient geen navolging.
@netchip: de grafiek van een inverse functie verkrijg je door de grafiek van de gegeven (inverteerbare) functie te spiegelen in de lijn met vergelijking y = x. Bij een spiegeling in de lijn met vergelijking y = x gaat een punt met coördinaten (x, y) over in het punt met coördinaten (y, x). Dat impliceert dat je een vergelijking van de grafiek van het spiegelbeeld van de grafiek van een gegeven functie bij spiegeling in de lijn met vergelijking y = x kunt verkrijgen door de variabelen x en y met elkaar te verwisselen in de vergelijking y = f(x) van de grafiek van de oorspronkelijke functie.
Hebben we dus een functie f: (−∞, −1] → R met als functievoorschrift f(x) = √(−1 − x), dan heeft de grafiek van deze functie de vergelijking y = √(−1 − x). Verwisselen van x en y geeft x = √(−1 − y) en oplossen van y uit deze betrekking geeft y = −x² − 1 als vergelijking van het spiegelbeeld van de grafiek van f bij spiegeling in de lijn met vergelijking y = x. De functie f is dus inverteerbaar en de inverse van f is de functie g: [0, ∞) → R met als functievoorschrift g(x) = −x² − 1.
De notatie f−1 voor de inverse van een functie f is gebruikelijk, maar verdient geen aanbeveling, net zo min als het aanbeveling verdient om bijvoorbeeld de notatie sin−1x te gebruiken voor arcsin x. Merk ook op dat f−1(x) iets anders betekent dan f(x−1) en dat dit weer iets anders is dan f(x)−1 = (f(x))−1. Men heeft ook voorgesteld om de notatie f[−1] te gebruiken voor de inverse functie van een functie f, maar we gebruiken ook al f(n) voor de n-de afgeleide van f, en je zou dus zeggen dat f(−1) dan weer een primitieve voorstelt van f. Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi.
Een alternatief is de notatie finv voor de inverse functie van een functie f.
"Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi."
Bedoel je met de -1 bij dy/dx, de inverse functie, of 1/(dy/dx)? Volgens mij is dit geen functie (geen 'haakjesnotatie'), dus moet het wel het laatste zijn...


Dus differentiëren met de kettingregel geeft
Met y=f(x) en x=f^{-1}(y) krijg je dus
De ^-1 die Riparius aanhaalde was daar dus multiplicatief.


De waarde van de afgeleide functie is (bij een reële functie van een reële variabele) niets anders dan de richtingscoëfficiënt van de raaklijn in een punt op de grafiek van de functie. Welnu, bij twee rechte lijnen die elkaars spiegelbeeld zijn bij spiegeling in de lijn met vergelijking y = x is het product van de richtingscoëfficiënten van die lijnen gelijk aan 1, mits de lijnen niet parallel zijn aan de coördinaatassen (bewijs dit).quote:Op donderdag 7 augustus 2014 11:09 schreef netchip het volgende:
[..]
Interessant.
"Overigens heb je met y = f(x), x = f−1(y) wel dx/dy = (dy/dx)−1 en dat is dan weer mooi."
Bedoel je met de -1 bij dy/dx, de inverse functie, of 1/(dy/dx)? Volgens mij is dit geen functie (geen 'haakjesnotatie'), dus moet het wel het laatste zijn...
Een raaklijn in een punt (x, y) op de grafiek van f gaat bij spiegeling in de lijn y = x over in de raaklijn in het punt (y, x) op de grafiek van f−1 zodat je dus direct ziet dat moet gelden
f'(x)·(f−1)'(y) = 1
oftewel, in de veel transparantere notatie van Leibniz
(dy/dx)·(dx/dy) = 1.


Easy. f(x) = 6x. f(x)-1 = x/6. m = 6, minv = 1/6. 6 * (1/6) = 1.quote:Op donderdag 7 augustus 2014 17:59 schreef Riparius het volgende:
[..]
De waarde van de afgeleide functie is (bij een reële functie van een reële variabele) niets anders dan de richtingscoëfficiënt van de raaklijn in een punt op de grafiek van de functie. Welnu, bij twee rechte lijnen die elkaars spiegelbeeld zijn bij spiegeling in de lijn met vergelijking y = x is het product van de richtingscoëfficiënten van die lijnen gelijk aan 1, mits de lijnen niet parallel zijn aan de coördinaatassen (bewijs dit).
Een raaklijn in een punt (x, y) op de grafiek van f gaat bij spiegeling in de lijn y = x over in de raaklijn in het punt (y, x) op de grafiek van f−1 zodat je dus direct ziet dat moet gelden
f'(x)·(f−1)'(y) = 1
oftewel, in de veel transparantere notatie van Leibniz
(dy/dx)·(dx/dy) = 1.


Dat is natuurlijk nog geen algemeen bewijs, een rechte lijn hoeft geen richtingscoëfficiënt 6 te hebben en hoeft ook niet door de oorsprong te gaan.quote:Op donderdag 7 augustus 2014 18:41 schreef netchip het volgende:
[..]
Easy. f(x) = 6x. f(x)-1 = x/6. m = 6, minv = 1/6. 6 * (1/6) = 1.


f(x) = mx. f(x)-1 = x/m. m * (1/m) = 1. Ik weet dat ik de constante b mis, maar op het moment heb ik geen papier bij de hand. Ik kijk er morgen wel naar.quote:Op donderdag 7 augustus 2014 20:17 schreef Riparius het volgende:
[..]
Dat is natuurlijk nog geen algemeen bewijs, een rechte lijn hoeft geen richtingscoëfficiënt 6 te hebben en hoeft ook niet door de oorsprong te gaan.


Het is vast een kwestie van voorkeur, maar ik vind die meetkundige argumenten veel minder prettig dan een simpele toepassing van een kettingregel.quote:Op donderdag 7 augustus 2014 17:59 schreef Riparius het volgende:
[..]
De waarde van de afgeleide functie is (bij een reële functie van een reële variabele) niets anders dan de richtingscoëfficiënt van de raaklijn in een punt op de grafiek van de functie. Welnu, bij twee rechte lijnen die elkaars spiegelbeeld zijn bij spiegeling in de lijn met vergelijking y = x is het product van de richtingscoëfficiënten van die lijnen gelijk aan 1, mits de lijnen niet parallel zijn aan de coördinaatassen (bewijs dit).
Een raaklijn in een punt (x, y) op de grafiek van f gaat bij spiegeling in de lijn y = x over in de raaklijn in het punt (y, x) op de grafiek van f−1 zodat je dus direct ziet dat moet gelden
f'(x)·(f−1)'(y) = 1
oftewel, in de veel transparantere notatie van Leibniz
(dy/dx)·(dx/dy) = 1.


Riparius, ik heb 'm nu volledig uitgewerkt.
f(x) = mx+b
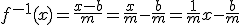
Hieruit blijkt dat de richtingscoëfficient 1/m is. m*(1/m) = 1.
f(x) = mx+b
Hieruit blijkt dat de richtingscoëfficient 1/m is. m*(1/m) = 1.


Tja, ik werk zelf graag met meetkundige argumenten om dingen te visualiseren. Uiteraard mag een bewijs in de analyse niet op meetkundige argumenten zijn gebaseerd, maar voor het begrip is het wel belangrijk om te laten zien wat een en ander meetkundig betekent. Als een leerling bijvoorbeeld niet begrijpt dat een waarde van een afgeleide functie de richtingscoëfficiënt voorstelt van de raaklijn in een punt op de grafiek van de oorspronkelijke functie, dan zal die leerling ook niet begrijpen waarom je (locale en globale) extrema van de functie op kunt sporen door de nulpunten van de afgeleide functie te bepalen, en dan verwordt differentiaalrekening tot het slaafs en mechanisch toepassen van een paar half begrepen of geheel niet begrepen regeltjes. Voorbeelden van dergelijk onbegrip hoef je niet ver te zoeken, dit forum staat er vol mee.quote:Op vrijdag 8 augustus 2014 10:42 schreef thenxero het volgende:
[..]
Het is vast een kwestie van voorkeur, maar ik vind die meetkundige argumenten veel minder prettig dan een simpele toepassing van een kettingregel.
Uiteraard kun je volstaan met te zeggen dat uit (g ∘ f)' = (g' ∘ f) · f' en f ∘ f−1 = I volgt dat (f−1)' = (f' ∘ f−1)−1, waarbij f−1 de reciproke functie is van f maar (f' ∘ f−1)−1 de multiplicatieve inverse van f' ∘ f−1 voorstelt (!), maar hoe verhelderend denk je dat dit is voor een leerling die nog nauwelijks enig begrip heeft van differentiaalrekening?
Bij de differentiaalrekening blijkt met name de kettingregel vaak problemen op te leveren voor scholieren en (beginnende) studenten, en dat komt niet omdat die regel zo moeilijk zou zijn maar omdat er kennelijk het nodige schort aan de didactiek. Als je reële functies van reële variabelen opvat als afbeeldingen van een getallenlijn op een andere getallenlijn, dan kun je gemakkelijk laten zien dat de afgeleide een locale schaalfactor voorstelt en dat een samenstelling van afbeeldingen zo dus beantwoordt aan een vermenigvuldiging van locale schaalfactoren.
[ Bericht 2% gewijzigd door Riparius op 09-08-2014 00:10:09 ]


Hey,quote:Op vrijdag 8 augustus 2014 21:23 schreef Riparius het volgende:
[..]
Tja, ik werk zelf graag met meetkundige argumenten om dingen te visualiseren. Uiteraard mag een bewijs in de analyse niet op meetkundige argumenten zijn gebaseerd, maar voor het begrip is het wel belangrijk om te laten zien wat een en ander meetkundig betekent. Als een leerling bijvoorbeeld niet begrijpt dat een waarde van een afgeleide functie de richtingscoëfficiënt voorstelt van de raaklijn in een punt op de grafiek van de oorspronkelijke functie, dan zal die leerling ook niet begrijpen waarom je (locale en globale) extrema van de functie op kunt sporen door de nulpunten van de afgeleide functie te bepalen, en dan verwordt differentiaalrekening tot het slaafs en mechanisch toepassen van een paar half begrepen of geheel niet begrepen regeltjes. Voorbeelden van dergelijk onbegrip hoef je niet ver te zoeken, dit forum staat er vol mee.
Uiteraard kun je volstaan met te zeggen dat uit (g ∘ f)' = (g' ∘ f) · f' en f ∘ f−1 = I volgt dat (f−1)' = (f' ∘ f−1)−1, waarbij f−1 de reciproke functie is van f maar (f' ∘ f−1)−1 de multiplicatieve inverse van f' ∘ f−1 voorstelt (!), maar hoe verhelderend denk je dat dit is voor een leerling die nog nauwelijks enig begrip heeft van differentiaalrekening?
Bij de differentiaalrekening blijkt met name de kettingregel vaak problemen op te leveren voor scholieren en (beginnende) studenten, en dat komt niet omdat die regel zo moeilijk zou zijn maar omdat er kennelijk het nodige schort aan de didactiek. Als je reële functies van reële variabelen opvat als afbeeldingen van een getallenlijn op een andere getallenlijn, dan kun je gemakkelijk laten zien dat de afgeleide een locale schaalfactor voorstelt en dat een samenstelling van afbeeldingen zo dus beantwoordt aan een vermenigvuldiging van locale schaalfactoren.
Zou jij shadowseer de beginselen van wiskunde willen uitleggen? Ik heb hem net een PM gestuurd met uitleg over het cartesisch coordinatenstelsel, en een beginnetje over variabelen en formules, en een opdracht waarbij het de bedoeling is dat hij de waardes van y voor x = 1 tot en met x = 6 uitrekent, met de formule y = 3x + 1. En dat hij de punten die volgen uit de formule aanstipt op het cartesisch assenstelsel, en dan een lijn trekt.
Jouw didactisch vermogen is een stuk beter dan de mijne.
Lokquote voor shadowseer:
quote:


Ik heb zijn OP gelezen en ik voel er naar aanleiding van de lectuur daarvan niets voor om op dit verzoek in te gaan. Ik denk dat hij een psychiater nodig heeft, geen instructie in elementaire schoolwiskunde.quote:Op zaterdag 9 augustus 2014 19:14 schreef netchip het volgende:
[..]
Hey,
Zou jij shadowseer de beginselen van wiskunde willen uitleggen? Ik heb hem net een PM gestuurd met uitleg over het cartesisch coordinatenstelsel, en een beginnetje over variabelen en formules, en een opdracht waarbij het de bedoeling is dat hij de waardes van y voor x = 1 tot en met x = 6 uitrekent, met de formule y = 3x + 1. En dat hij de punten die volgen uit de formule aanstipt op het cartesisch assenstelsel, en dan een lijn trekt.
Jouw didactisch vermogen is een stuk beter dan de mijne.Ik vraag dit namens shadowsheer, omdat hij dat fijner vindt.
Verder moeten mensen die vragen hebben die vragen hier zelf stellen, en niet via derden. Een hele tijd geleden was er hier ook een joker die - overigens hopeloos geformuleerde en nauwelijks begrijpelijke - vragen stelde namens zijn vriendin, en beweerde dat hij de antwoorden weer over zou brengen aan zijn vriendin. Op mijn vraag of zijn vriendin die vragen hier zelf niet kon stellen kwam geen bevredigend antwoord. Ik kan me voorstellen dat iemand bijvoorbeeld de Nederlandse taal niet machtig is of een lichamelijke handicap heeft waardoor hij of zij niet gebruik kan maken van een computer, maar dat was niet het geval. Volgens de vragensteller was zijn vriendin alleen niet in staat FOK te gebruiken, maar waarom dat zo was kwam niet uit de verf en wenste hij kennelijk ook niet duidelijk te maken. En dan houdt het voor mij op.


Eens. Het ligt alleen niet zo simpel voor hem, daar zit een reden achter. Het beste wat je dan kan doen, is iemand iets leren over iets wat hij vroeger interessant vond, neem ik aan.quote:Op zaterdag 9 augustus 2014 19:32 schreef Riparius het volgende:
[..]
Ik heb zijn OP gelezen en ik voel er naar aanleiding van de lectuur daarvan niets voor om op dit verzoek in te gaan. Ik denk dat hij een psychiater nodig heeft, geen instructie in elementaire schoolwiskunde.
Verder moeten mensen die vragen hebben die vragen hier zelf stellen, en niet via derden. Een hele tijd geleden was er hier ook een joker die - overigens hopeloos geformuleerde en nauwelijks begrijpelijke - vragen stelde namens zijn vriendin, en beweerde dat hij de antwoorden weer over zou brengen aan zijn vriendin. Op mijn vraag of zijn vriendin die vragen hier zelf niet kon stellen kwam geen bevredigend antwoord. Ik kan me voorstellen dat iemand bijvoorbeeld de Nederlandse taal niet machtig is of een lichamelijke handicap heeft waardoor hij of zij niet gebruik kan maken van een computer, maar dat was niet het geval. Volgens de vragensteller was zijn vriendin alleen niet in staat FOK te gebruiken, maar waarom dat zo was kwam niet uit de verf en wenste hij kennelijk ook niet duidelijk te maken. En dan houdt het voor mij op.


Wie heeft een goede site met inhoud en opgaven in de analytische meetkunde? In het nieuwe schoolprogramma is daar het eea over opgenomen en ik wil me hier even in verdiepen.
kloep kloep


Wordt lastig. Ik kan je in ieder geval het oude Prisma Compendium Analytische meetkunde van C. van der Linden aanraden, waarin de vroegere stof van het middelbaar wordt behandeld. Verder bijvoorbeeld dit Amerikaanse schoolboek van bijna een eeuw geleden. Sites met specifiek opgaven over analytische meetkunde ken ik niet maar ik kwam een hele tijd geleden wel dit tegen, een vraagstuk over het bepalen van de vergelijkingen van de twee raaklijnen aan een gegeven cirkel waarbij de gebruikelijke methoden met de richtingscoëfficiënt m van de raaklijn als variabele falen voor één van beide raaklijnen om de eenvoudige reden dat één van de beide raaklijnen verticaal loopt. Kun je je leerlingen eens voorleggen en kijken of ze het probleem correct kunnen identificeren, en, belangrijker nog, of ze een algebraïsche aanpak kunnen bedenken die wél de vergelijkingen van beide raaklijnen oplevert.quote:Op zondag 10 augustus 2014 17:36 schreef Borizzz het volgende:
Wie heeft een goede site met inhoud en opgaven in de analytische meetkunde? In het nieuwe schoolprogramma is daar het eea over opgenomen en ik wil me hier even in verdiepen.
[ Bericht 0% gewijzigd door Riparius op 12-08-2014 20:00:20 ]


http://www.fi.uu.nl/wiskrant/artikelen/264/264juni_broek.pdf
Niet echt een partij waar ik veel vertrouwen in heb (realistisch rekenen en contextwiskunde) maar het is interessant om te lezen.
http://www.ru.nl/publish/(...)13_ruud_stolwijk.ppt
Wat uitleg over het nieuwe programma (PP), blijkbaar mocht ook BON aan de tafel zitten wat ik toejuich.
Niet echt een partij waar ik veel vertrouwen in heb (realistisch rekenen en contextwiskunde) maar het is interessant om te lezen.
http://www.ru.nl/publish/(...)13_ruud_stolwijk.ppt
Wat uitleg over het nieuwe programma (PP), blijkbaar mocht ook BON aan de tafel zitten wat ik toejuich.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Dit artikel is inmiddels al zeven jaar oud. Het laatste stuk is vooral een pleidooi om weer wat aan vectoren te gaan doen op school, al dan niet in combinatie met klassieke analytische meetkunde, maar het lijkt er niet op dat daar gevolg aan is gegeven. Met vectoren gaan bewijzen van sommige stellingen uit de vlakke meetkunde, de stereometrie, de analytische meetkunde en ook uit de goniometrie (additietheorema's) heel elegant en eenvoudig, maar goed dat weet je zelf allang als je mij een beetje volgt (zie bijvoorbeeld het bewijs dat het hoogtepunt H, het zwaartepunt Z en het middelpunt van de omgeschreven cirkel O in een driehoek op één rechte liggen, de zogeheten rechte van Euler, en wel zo dat HZ : ZO = 2 : 1, en zie ook je eigen vraag over de transformatieformules bij rotatie van een cartesisch assenstelsel om de oorsprong).quote:Op maandag 11 augustus 2014 00:42 schreef Bram_van_Loon het volgende:
http://www.fi.uu.nl/wiskrant/artikelen/264/264juni_broek.pdf
Niet echt een partij waar ik veel vertrouwen in heb (realistisch rekenen en contextwiskunde) maar het is interessant om te lezen.


Je kunt hier het materiaal vinden dat in de pilots is en wordt gebruikt.quote:Op zondag 10 augustus 2014 17:36 schreef Borizzz het volgende:
Wie heeft een goede site met inhoud en opgaven in de analytische meetkunde? In het nieuwe schoolprogramma is daar het eea over opgenomen en ik wil me hier even in verdiepen.


Stel, je gooit met 3 dobbelstenen. Hoeveel combinaties heb je dan in totaal om 16 te krijgen? 5 + 5 + 6 is een voorbeeld.
Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?
Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?


Er moet tenminste één 6 bij zitten, anders kan het totaal van de aantallen ogen van de drie dobbelstenen niet groter zijn dan 15. En als je een 6 hebt voor één dobbelsteen, dan zal de som van de ogen van de beide andere dobbelstenen dus 10 moeten zijn, en dat kan alleen met één 6 en één 4 of met twee maal 5. Er zijn dus slechts twee combinaties mogelijk, namelijk één maal 6 met twee maal 5 en twee maal 6 met één maal 4.quote:Op dinsdag 19 augustus 2014 16:59 schreef netchip het volgende:
Stel, je gooit met 3 dobbelstenen. Hoeveel combinaties heb je dan in totaal om 16 te krijgen? 5 + 5 + 6 is een voorbeeld.
Nee, niet echt. Kijk eens naar partities.quote:Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?


Werk (x + x2 + x3 + x4 + x5 + x6)3 uit. Dan is de coëfficiënt van x16 het antwoord.quote:Op dinsdag 19 augustus 2014 16:59 schreef netchip het volgende:
Stel, je gooit met 3 dobbelstenen. Hoeveel combinaties heb je dan in totaal om 16 te krijgen? 5 + 5 + 6 is een voorbeeld.
Ik zou ze systematisch kunnen noteren, maar ik dacht dat er misschien een formule voor is?


quote:Op dinsdag 19 augustus 2014 21:32 schreef thabit het volgende:
[..]
Werk (x + x2 + x3 + x4 + x5 + x6)3 uit. Dan is de coëfficiënt van x16 het antwoord.


Daar heb je WolframAlpha voor en dan vind je 6 als coëfficiënt van x16. Maar dat is wel het aantal combinaties dat een totaal van 16 oplevert bij het werpen met drie dobbelstenen die zich van elkaar laten onderscheiden (bijvoorbeeld één rode, één groene en één blauwe). Als de drie dobbelstenen niet van elkaar zijn te onderscheiden heb je maar 2 combinaties die 16 opleveren omdat steeds twee van de drie dobbelstenen een gelijk aantal ogen hebben bij een worp die een totaal van 16 oplevert.quote:


Ja dat begrijp ik. Ik snap alleen even niet de redenatie achter dit trucje.quote:Op woensdag 20 augustus 2014 13:38 schreef Riparius het volgende:
[..]
Daar heb je WolframAlpha voor en dan vind je 6 als coëfficiënt van x16. Maar dat is wel het aantal combinaties dat een totaal van 16 oplevert bij het werpen met drie dobbelstenen die zich van elkaar laten onderscheiden (bijvoorbeeld één rode, één groene en één blauwe). Als de drie dobbelstenen niet van elkaar zijn te onderscheiden heb je maar 2 combinaties die 16 opleveren omdat steeds twee van de drie dobbelstenen een gelijk aantal ogen hebben bij een worp die een totaal van 16 oplevert.


Deze techniek staat bekend als voortbrengende functies. Als f(n) het aantal mogelijkheden is om n ogen te gooien, dan is de voortbrengende machtreeks (of polynoom in dit geval) van f(n):quote:Op woensdag 20 augustus 2014 14:14 schreef Amoeba het volgende:
[..]
Ja dat begrijp ik. Ik snap alleen even niet de redenatie achter dit trucje. [ afbeelding ]
Andere typen voortbrengende functies bestaan ook, maar laten we het simpel houden.
De voortbrengende functie voor 1 dobbelsteen is dan x + x2 + x3 + x4 + x5 + x6.
Voor m dobbelstenen krijg je als voortbrengende functie (x + x2 + x3 + x4 + x5 + x6)m. Dit kun je inzien door de haakjes uit te werken in dit product van m factoren: de factoren komen overeen met de dobbelstenen, en bij elke factor kies je een term xn die overeenkomt met de mogelijkheid dat er n ogen zijn bij die dobbelsteen. Het product van die termen is xn1+n2+...+nm, zo dat de exponent overeenkomt met de som van de ogen.
[ Bericht 0% gewijzigd door thabit op 20-08-2014 16:08:18 ]


Mooi, dan heb ik nog een sommetje voor je.quote:
Als je twee "gewone" dobbelstenen gooit ("gewoon" wil zeggen dat vlakken 1, 2, 3, 4, 5, en 6 ogen hebben), dan weet je hoe de verdeling van de som van de ogen is: je kunt op 1 manier 2 gooien, op 2 manieren 3, op 3 manieren 4, etc t/m op 1 manier 12.
Geef nu twee "ongewone" dobbelstenen (dwz wel met 6 vlakken, maar met andere ogenverdelingen) zo dat de som van de ogen van de twee dezelfde verdeling heeft als bij 2 gewone dobbelstenen.

 Op
Op 
 Op
Op