Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Hoe voer je hier wiskundige formules in want dit typt niet zo fijn
R'(t) = < 3, 4 cos t , -4 sin t>
R''(t) = <0, - 4 sin t, -4 cos t>
|R"(t)| = wortel (16 sin^2 (t) + 16 cos^2 (t) = 4
Is hiermee bewezen dat de kromming overal constant is ?
| 1 | [tex]||R''(t)|| = \sqrt{ 16\sin^2 (t) + 16\cos^2 (t) }[/tex] |
de oorsprong (0; 0) over de hoek a.
(1) Wat zijn de beelden p((1; 0)) en p((0; 1))?
(2) Laat zien dat er geldt
p((x; y)) = (x cos a - y sin a; x sin a + y cos a):
Heeft iemand een tip voor de 2e vraag?
gebruik je antwoord bij a en gebruik dat (x,y) = x[1;0] + y[0;1].quote:Op dinsdag 4 oktober 2011 20:26 schreef Anoonumos het volgende:
Zij p: R² -> R² de lineaire afbeelding gegeven door rotatie om
de oorsprong (0; 0) over de hoek a.
(1) Wat zijn de beelden p((1; 0)) en p((0; 1))?
(2) Laat zien dat er geldt
p((x; y)) = (x cos a - y sin a; x sin a + y cos a):
Heeft iemand een tip voor de 2e vraag?
Raakvlak in (0,0,0)
z = f(0,0) + fx(0,0)(x) + fy(0,0)(y)
fx = 6xy/(x^2+y^2+1) (quotientregel) -> fx (0,0) = 0
fy = -3x^2 - 3y^2 - 3 + 6y/(x^2+y^2+1) (quotientregel) -> fy(0,0 = -3/1 = -3
z = 0 + 0 + (-3*y) = -3y
Is dit correct ?
P((1,0)), is dat nou (cos a, sin a) of (cos a, -sin a).quote:
twaalf: nosml ipv code
[..]
gebruik je antwoord bij a en gebruik dat (x,y) = x[1;0] + y[0;1].
Bij de eerste beweegt het punt over de cirkel naar links als je het punt draait over hoek a, en bij de tweede naar rechts. Naar rechts leek mij het meest logisch, maar het is dus de eerste?
Je draait natuurlijk naar links. Bedankt.
[ Bericht 4% gewijzigd door Anoonumos op 04-10-2011 21:05:48 ]
Het eindantwoord is goed, maar je partiële afgeleides zijn verkeerd. Afgeleide naarquote:
f(x,y) = =3y/x^2 + y^2 + 1
Raakvlak in (0,0,0)
z = f(0,0) + fx(0,0)(x) + fy(0,0)(y)
fx = 6xy/(x^2+y^2+1) (quotientregel) -> fx (0,0) = 0
fy = -3x^2 - 3y^2 - 3 + 6y/(x^2+y^2+1) (quotientregel) -> fy(0,0 = -3/1 = -3
z = 0 + 0 + (-3*y) = -3y
Is dit correct ?
Nee. Lees dit maar eens.quote:
R(t) = <3t, 4 sin (t), 4 cos (t)>
R'(t) = < 3, 4 cos t , -4 sin t>
R''(t) = <0, - 4 sin t, -4 cos t>
|R"(t)| = wortel (16 sin^2 (t) + 16 cos^2 (t) = 4
Is hiermee bewezen dat de kromming overal constant is ?
For a parametrically defined space curve in three-dimensions given in Cartesian coordinates by γ(t) = (x(t),y(t),z(t)), the curvature is:
Deze formule heb ik nog nooit eerder gezien.Ga er wel even mee aan de slag
quote:
Wat moet ik me voorstellen bij ℝ^2, het kwadraat van alle reëele getallen, wat houdt dat ooit in?
x' = 3
x'' = 0
y' = 4 cos (t)
y'' = - 4 sin (t)
z' = -4 sin (t)
z'' = -4 cos (t)
Invullen van de formule K = wortel (z'' y' - y'' z')^2 + (x'' z' - z'' x')^2 + (y''x' - x''y')^2/((x'^2)+(y'^2) + (z'^2)^3/2)
Als ik dit invul valt de eerste term weg ( -16 cos ^2 t + 16 cos^2)^2 = 0
De tweede term blijft staan (-12 cos^2 (t))^2
De derde term blijft staan (-12 sin^2 (t))^2
Delen door ( 9 + 16 cos^2 (t) + 16 sin^2 (t))^3/2 = (9+16)^3/2 = 125
Wat kan ik met de tweede en derde term doen om te bewijzing dat de kromming overal gelijk is voor deze functie?
Bij die link staat toch precies wat ik al eerder zei, namelijk dat de krommingquote:
Als je twee verzamelingen cartesisch vermenigvuldigt, krijg je de verzameling van alle mogelijke paren van die verzamelingen. Dus {2,3} x {4,5} = { {2,4},{2,5},{3,4},{3,5} }. Bij R^2 krijg je dan inderdaad een vlak waarbij de coördinaten reële getallen zijn.quote:
Wat moet ik me voorstellen bij ℝ^2, het kwadraat van alle reëele getallen, wat houdt dat ooit in?
In mijn boek staat wel een dergelijke formule die volgens mij hetzelfde is:
k(t) = | R'(t) x R''(t)|/ | R'(t)|^3
Dit uitwerken geeft:
R'(t) = <3, 4cos t, -4 sin t>
R''(t) = <0, -4 sin t, - 3 cos 2>
UItproduct geeft: - 16 cos^2 t + 16 sin^2 t - 12 cos t - 12 sin 2
Lengte van het uiproduct is de wortel van het uitproduct^2 , dus:
256 * cos ^2 (t)^2 + 256 * sin ^2 (t)^2 + 144 cos ^2 (t) + 144 sin^2 = 256 + 144 = 400
K = 400/125 = 3,2 en is dus niet afhankelijk van t en voor ieder punt hetzelfde
Met "deelbaar" bedoel je dat er een natuurlijk getal uitkomt?quote:
Bewijs dat n^3-n deelbaar door 6 is voor n>=0. Is toch echt deelbaar door 6 vanaf 2?
Is niet gespecificeerd maar bij de andere opgaven betekent deelbaar idd dat er een natuurlijk getal uitkomt.quote:
[..]
Met "deelbaar" bedoel je dat er een natuurlijk getal uitkomt?
De formule van de wikilink is dus in feite de lengte van het uitproduct van de eerste en tweede afgeleide gedeelt door de lengte van de eerste afgeleide tot de macht 3.
0 is ook deelbaar door 6.quote:
Bewijs dat n^3-n deelbaar door 6 is voor n>=0. Is toch echt deelbaar door 6 vanaf 2?
Meh je hebt gelijk, 0 is ook een natuurlijk getal.quote:
Maar 0 is volgens mij per afspraak deelbaar door alles.
Ook door 0?quote:
Niet in alle vakgebieden...
Maar 0 is volgens mij per afspraak deelbaar door alles.
Trouwens bij B(n+1) kom ik tot: 1. bewezen bij basis b(0) (n^3-n) + (3n^2+3n) waarbij laatste deel ook voor alle n deelbaar door 6 is, alleen is dat genoeg bewijs?
Het laatste deel kun je schrijven als 3n(n+1), waarbij ofwel n ofwel n+1 een deler twee heeft.quote:
[..]
Ook door 0?
Trouwens bij B(n+1) kom ik tot: 1. bewezen bij basis b(0) (n^3-n) + (3n^2+3n) waarbij laatste deel ook voor alle n deelbaar door 6 is, alleen is dat genoeg bewijs?
En je hoeft het niet met inductie te doen, bedenk ik nu. Je kunt n^3-n ook schrijven als (n-1)n(n+1), waarvan één een deler drie heeft en tenminste één een deler twee.
Hoezo per afspraak?quote:
Niet in alle vakgebieden...
Maar 0 is volgens mij per afspraak deelbaar door alles.
0/6=0 en 0 is een geheel getal
Delen door 0 is geen goed idee, ook 0/0 niet.
Maar Physics zei dat het een natuurlijk getal moest zijn, en 0 is dat niet altijd.quote:
[..]
Hoezo per afspraak?
0/6=0 en 0 is een geheel getal
Als je inductie over de natuurlijke getallen wilt doen voor n=0 dan neem je dus ook aan dat 0 een element is van de natuurlijke getallen.quote:
[..]
Maar Physics zei dat het een natuurlijk getal moest zijn, en 0 is dat niet altijd.
De modulus moet 0 zijn, anders zou -4 niet deelbaar zijn door 2.quote:
[..]
Met "deelbaar" bedoel je dat er een natuurlijk getal uitkomt?
'Alles' is wat veel, deelbaarheid door een fiets is bijvoorbeeld niet gedefinieerd.quote:
Niet in alle vakgebieden...
Maar 0 is volgens mij per afspraak deelbaar door alles.
Hmm, in mijn boek (Mathematics for Economists, Simon & Blume) niet, maar misschien bij jou wel.quote:
[..]
Meh je hebt gelijk, 0 is ook een natuurlijk getal.
De meningen verschillen daarover inderdaadquote:
[..]
Hmm, in mijn boek (Mathematics for Economists, Simon & Blume) niet, maar misschien bij jou wel.
Wie kan mij stap voor stap uitleggen wat #1, #2 en #3 is.
Nee, want 0 geeft geen rest bij deling door 6. Verder lijkt mij dit triviaal. Je hebt:quote:
Bewijs dat n^3-n deelbaar door 6 is voor n >= 0. Is toch echt deelbaar door 6 vanaf n = 2?
n3 - n = n(n2 - 1) = n(n-1)(n+1)
Welnu, voor n > 1 zijn (n-1), n en (n+1) drie opeenvolgende natuurlijke getallen, en daarvan is er altijd één een drievoud en tenminste één even, zodat het product inderdaad deelbaar is door 6, QED.
Waarschijnlijk een domme vraag van mij, maar hebben die hekjes nog een speciale betekenis, of zou je net zo goed A, B en C neer kunnen zetten?quote:
Ik heb het volgende stelsel:
[ afbeelding ]
Wie kan mij stap voor stap uitleggen wat #1, #2 en #3 is.
Volgens mijn geen speciale tekens in de dit geval. Het zijn namelijk aantal stappen keer kans, zeg maar.quote:
[..]
Waarschijnlijk een domme vraag van mij, maar hebben die hekjes nog een speciale betekenis, of zou je net zo goed A, B en C neer kunnen zetten?
Nee, dat staat er niet. Je hebt wel κ(s) = |γ''(s)| als je een booglengteparametrisatie hebt van je curve.quote:
[..]
Bij die link staat toch precies wat ik al eerder zei, namelijk dat de krommingis?
De 2e vergelijking luidt #2=2/5#1+3/7#2quote:
[..]
Volgens mijn geen speciale tekens in de dit geval. Het zijn namelijk aantal stappen keer kans, zeg maar.
Dat is hetzelfde als 4/7#2=2/5#1
Oftewel, #2=7/10#1 en #1=10/7#2
En dan kan je hem zo invullen. Lukt het dan? Je krijgt in de bovenste vergelijking uiteindelijk 1 = ...#1 (of #2, of #3) en daarmee bereken je het antwoord.
Er staat trouwens toch wel "1" en geen "I"? Onduidelijk lettertype zeg, onhandig, nauwelijks verschil tussen hoofdletter i en 1.
Dank, maar zo ver was ik ookquote:
[..]
De 2e vergelijking luidt #2=2/5#1+3/7#2
Dat is hetzelfde als 4/7#2=2/5#1
Oftewel, #2=7/10#1 en #1=10/7#2
En dan kan je hem zo invullen. Lukt het dan? Je krijgt in de bovenste vergelijking uiteindelijk 1 = ...#1 (of #2, of #3) en daarmee bereken je het antwoord.
Als dat niet de bedoeling is heb ik trouwens geen idee
Wetende dat de antwoorden: #1 = 80/39 #2 = 56/39 #3 = 24/39, kom ik er nog niet uit
Als in, je snapt niet hoe ze bij die antwoorden zijn gekomen?quote:
[..]
Dank, maar zo ver was ik ook
Wetende dat de antwoorden: #1 = 80/39 #2 = 56/39 #3 = 24/39, kom ik er nog niet uit
Nou, eigenlijk niet nee. Want ik twijfel nu aan de stappen die ik maak. Oftwel, doe ik het goed?quote:
[..]
Als in, je snapt niet hoe ze bij die antwoorden zijn gekomen?
Het gaat dus zo:quote:
[..]
Nou, eigenlijk niet nee. Want ik twijfel nu aan de stappen die ik maak. Oftwel, doe ik het goed?
Je was zover dat je had #2=7/10#1 en #1=10/7#2. De derde vergelijking is #3=3/7#2.
Dan krijg je dus #3=3/7*(7/10*#1)=3/10#1.
Dat vul je in in vergelijking 1, dan krijg je:
#1=1+2/5#1+3/8*(3/10#1)
#1-2/5#1-3/8*3/10#1=1
39/80#1=1
#1=80/39
En dan vul je dat getal in en krijg je de antwoorden op #2 en #3.
Aight.quote:
[..]
Het gaat dus zo:
Je was zover dat je had #2=7/10#1 en #1=10/7#2. De derde vergelijking is #3=3/7#2.
Dan krijg je dus #3=3/7*(7/10*#1)=3/10#1.
Dat vul je in in vergelijking 1, dan krijg je:
#1=1+2/5#1+3/8*(3/10#1)
#1-2/5#1-3/8*3/10#1=1
39/80#1=1
#1=80/39
En dan vul je dat getal in en krijg je de antwoorden op #2 en #3.
[ Bericht 4% gewijzigd door Self-Catering op 05-10-2011 15:20:05 ]
1. Stel je hebt een continue kansdichtingsheidfunctie.
X = continue stochastische variabel
Y = continue stochastische variabel
Wat betekent:
E(E(X|Y is y))
In woorden betekent dit, volgens mij: De verwachtingswaarde van de verwachtingswaarde van (X met als voorwaarde dat Y gelijk is aan y). Maar ik begrijp niet meer wat ik dan precies aan het uitrekenen ben.
En waarom is dit gewoon gelijk aan de E(X).
2. Ook is dit misschien een domme vraag, maar stel ik heb een continue kansdichtheidsfunctie 8xy.
Wat betekent het dan precies als ik daar gewoon x = 0.4 en y = 0.4 invul? Wat zegt mijn antwoord dan?
3. Stel:
Kansdichtheidsfunctie:
8xy , 0 < x < y , 0 < y < 1
Ik wil de marginale kansdichtheidsfunctie van x.
Dit krijg ik door de integraal van 8xy (naar y, dus dy) te nemen, op het interval [1,x]. (volgens het boek).
In andere woorden, ik moet het domein van y (wat eerst 0 < y < 1 was) omschrijven naar een domein afhankelijk van x. Dit is (als ik een schets maak) [1, x].
Ik begrijp niet zo goed waarom ik het eerst moet omschrijven. Waarom mag ik y niet gewoon [0,1] laten en dan integreren. Ik begrijp dus blijkbaar niet echt goed wat ik hier doe omdat ik het antwoord hier niet op weet.
Alvast bedankt
2. dat betekent niets, een kansdichtheid moet je integreren om er betekenis aan toe te kennen.
3. het interval is [x,1]. Je moet eigenlijk doen:
maar f(x,y) = 0 voor y die niet voldoen aan "0 < x < y , 0 < y < 1".
Op vraag 3. Ohja, ik bedoelde inderdaad [x,1] , maar waarom zou ik het interval niet gewoon [0,1] kunnen laten? Waarom moet ik dit omschrijven in een interval afhankelijk van x (ik weet niet of ik dit goed zeg, maar je begrijpt hopelijk wat ik bedoel)quote:
1. De buitenste E is over Y, de binnenste over X.
2. dat betekent niets, een kansdichtheid moet je integreren om er betekenis aan toe te kennen.
3. het interval is [x,1]. Je moet eigenlijk doen:
maar f(x,y) = 0 voor y die niet voldoen aan "0 < x < y , 0 < y < 1".
Op vraag 2. Oke!
Op vraag 1. Ik begrijp nog niet helemaal wat je bedoelt.
Zie hier voor een bewijs dat het gelijk is aan E(X).
http://en.wikipedia.org/wiki/Expected_value#Iterated_expectation
Stel dat je het op [0,1] laat. Voor x=0.5 integreer je dan ook over het stuk y=[0,0.5], terwijl de kansdichtheid daar helemaal niet gegeven is door 8xy. Daar is de kansdichtheid gewoon 0. Maar omdat de integraal van 0 toch 0 is, laat je dat deel gewoon helemaal weg. Dan houd je [x,1] over.quote:
[..]
Op vraag 3. Ohja, ik bedoelde inderdaad [x,1] , maar waarom zou ik het interval niet gewoon [0,1] kunnen laten? Waarom moet ik dit omschrijven in een interval afhankelijk van x (ik weet niet of ik dit goed zeg, maar je begrijpt hopelijk wat ik bedoel)
Het is dus zoiets van:quote:
Volgens mij bedoel je E(E(X|Y)). Omdat Y een stochast is, is de verwachtingswaarde van X gegeven Y nog afhankelijk van Y. Dus E(X|Y) kan je zien als een nieuwe stochast die door Y bepaald wordt. Van deze "nieuwe stochast" kan je dus weer de verwachtingswaarde bepalen.
Zie hier voor een bewijs dat het gelijk is aan E(X).
http://en.wikipedia.org/wiki/Expected_value#Iterated_expectation
Je krijgt E(X|Y) door eerst de conditionele kansdichtheidsfunctie te bepalen, wat de joint kansdichtheidsfunctie is(8xy), geschaald naar de marginale kansdichtheidsfunctie van y.
Dat is dan 8xy/(4y^3) = 2x/y
Dat geeft mij dus een kansdichtheidsfunctie van x, als ik de variabel y zou invulle
Als ik dus de verwachtingswaarde van (2x/y) pak over alle mogelijke y waarden dan zou ik logischerwijs de verwachtingswaarde krijgen van x omdat ik voor elke y kijk wat mijn x waarden dan zou zijn.
Klopt deze gedachtegang een beetje?
Maar het hoeft niet weg gelaten te worden? Als de integraal toch 0 is dan maakt het voor het antwoord niet zoveel uit of je over [0,1] of [x,1] integreert?quote:
[..]
Stel dat je het op [0,1] laat. Voor x=0.5 integreer je dan ook over het stuk y=[0,0.5], terwijl de kansdichtheid daar helemaal niet gegeven is door 8xy. Daar is de kansdichtheid gewoon 0. Maar omdat de integraal van 0 toch 0 is, laat je dat deel gewoon helemaal weg. Dan houd je [x,1] over.
Maar de uitkomst is wel degelijk een andere functie. Als ik zou integeren over [0,1] dan zou het 4xy^2 = 4x zijn, terwijl het over [x,1] 4x - 4x^3 is.
[ Bericht 26% gewijzigd door JohnSpek op 05-10-2011 21:22:25 ]
Je berekent (in het discrete geval)
Dan vul je in plaats van y weer Y in, en dan neem je daar weer de verwachtingswaarde van.
Klopt, maar dan moet je dus een andere integrand nemen. De functie is op [0,x] gedefinieerd als 0, en op [x,1] gedefinieerd als 8xy.quote:
[..]
Maar het hoeft niet weg gelaten te worden? Als de integraal toch 0 is dan maakt het voor het antwoord niet zoveel uit of je over [0,1] of [x,1] integreert?
Wat je eigenlijk doet is, zoals GlowMouse zegt,
waarbij je dus de functie opdeelt in een deel waarin f=0, en een deel waarin f=8xy.
Als ik 8xy integreer naar y over [1,x] dan komt daar 4x - 4x^3 uit. Dat integreren op 0 < X < 0.5
Dat zou dan zijn 2 * 0.5^2 - 0.5^4
Hoe zou ik dat doen als je gewoon het 0 stuk erbij laat als het waren?
(Dus als ik 8xy eerst integreer naar y over interval [0,1] om de marginale kansdichtheidsfunctie van x te bepalen)
Wat is X? En wat is de berekening.
Klas: Atheneum 4
Haakjes wegwerkenquote:Op woensdag 5 oktober 2011 21:45 schreef verwarmingsbank het volgende:
x(2x-3)=2(3x+1)
Wat is X? En wat is de berekening.
Klas: Atheneum 4
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
Dat begrijp ik, maar de uitkomst is steeds fout. Hoe moet ik deze doen volgens jullie?quote:
Iedereen aan wie ik het gevraagd heb begrijpt het niet bij mij op school.
Schrijf maar de stappen op die je al hebt gemaakt.quote:
[..]
Dat begrijp ik, maar de uitkomst is steeds fout. Hoe moet ik deze doen volgens jullie?
Iedereen aan wie ik het gevraagd heb begrijpt het niet bij mij op school.
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23
Aha, ik had de tekening al wel gemaakt voor mezelf, maar nog niet zo naar gekekenquote:
Ik heb het even voor je gepaint:
[ afbeelding ]
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
Bedankt voor de moeite en uitleg! en xero/glowmouse ook bedankt ;
Je hebt gezegd C=1 terwijl het moet zijn C=-1.quote:
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel
Je methode is goed. Als je je antwoord invult in x(2x-3)=2(3x+1) dan weet je of het antwoord ook klopt.quote:
Bedankt voor de opmerking.
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
Is zo'n klein verschil niet erg of wat doe ik nu weer fout
Je weet pas echt zeker of het klopt als je het antwoord in "wortelvorm" laat staan, in plaats van numerieke benaderingen te gebruiken. Nu weet je alleen maar dat het waarschijnlijk goed is omdat een afwijking van 0,02 wel te verklaren is als je afrondt op 2 decimalen, maar zeker weten doe je niet.quote:
Als ik X = 4,71 invul dan krijg ik 30,2382 = 30,26
Is zo'n klein verschil niet erg of wat doe ik nu weer fout
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
één minnetje moet een plusje zijn. Dan krijg je -0,2122... en voor de andere 4.71221...quote:
Wow: in het antwoorden boekje staat dit:
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
Volgende keer dus gewoon die wortel laten staan. Dan heb je een precies antwoord, en daar zijn wiskundigen altijd blij mee.
--------------
Even mijn laatste post naar beneden brengen:
quote:Weet iemand een goede buitenlandse universiteit waar ze vakken als Statistics, Stochastic Integration, Lévy Processes, Financial Stochastics, Financial Time Series, Measure Theory, etc geven? Een master in Financial mathematics / stochastics dus.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
[ Bericht 16% gewijzigd door thenxero op 05-10-2011 22:31:12 ]
Al die opgaven is aantonen voor 1 en dan voor k+1 aantonen met inductie, als je eenmaal 1 gehad hebt zijn ze allemaal hetzelfde.quote:
[..]
Is niet gespecificeerd maar bij de andere opgaven betekent deelbaar idd dat er een natuurlijk getal uitkomt.
Hoeveel tijd ben je trouwens tot nu toe voor alles kwijt?
En waarom was meneer Heij trouwens eigenlijk een week afwezig?
Ja ik heb ze nu allemaal gemaakt. Hoeveel tijd ik kwijt ben vind ik moeilijk te zeggen, ik doe nu zeg maar wat opgegeven staat en dat kost me ongeveer 20 uur per week, dus contact + zelfstudie. Alleen wil ik eigenlijk wel wat harder studeren voor de betere cijfers.quote:
[..]
Al die opgaven is aantonen voor 1 en dan voor k+1 aantonen met inductie, als je eenmaal 1 gehad hebt zijn ze allemaal hetzelfde.
Hoeveel tijd ben je trouwens tot nu toe voor alles kwijt?
En waarom was meneer Heij trouwens eigenlijk een week afwezig?
)Dan doe ik eerst de partiele elasticiteit van x.quote:F(x,y) = √(ln(x2) - ln(y2)) (de hele formule staat dus onder de wortel
Bepaal de partiële elasticiteit van F naar x en de partiële elasticiteit van F naar y en tel beide bij elkaar op.
ELx = X / √(ln(x2) - ln(y2)) * De afgeleide F(x,y) naar X. Maar ik kom niet uit die afgeleide volgens mij
Ik dacht dat de afgeleide 1/2(ln(x2) - ln(y2))-1/2 * (2x/x2) was maar dat weet ik niet zeker. Kan iemand mij helpen/vertellen of ik op de goede weg ben?
Alvast heel erg bedankt
Oke dankjewelquote:
De part. afgeleide is goed, twee keer de kettingregel gebruiken inderdaad.
Het uitwerken hiervan lukt me alleen niet zo goed, zou je misschien kunnen helpen?dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus
Super bedanktquote:
Als ik die formule volg die je hebt geplaatst:
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus
NevermindOh dus beide elasticiteiten optellen zal op 0 uitkomen?quote:
Nee, want je hebt daar nog een factor -1 staan bij de tweede keer dat je de kettingregel toepast.
Heel erg bedankt!!quote:
⇒ ln(x + 1/2) = 0
Waarom kan ik ex hier weglaten?
In vervolg op wat GlowMouse zegt:quote:
ex ln(x + 1/2) = 0
⇒ ln(x + 1/2) = 0
Waarom kan ik ex hier weglaten?
en e^x kan nooit 0 zijn, dus moet het andere stuk wel gelijk aan 0 zijn en kan je e^x gewoon weg laten.
Ik snap er niks van
(hints worden ook erg op prijs gesteld
)[ Bericht 16% gewijzigd door minibeer op 07-10-2011 23:00:41 ]
Er staat een binomiaalcoëfficient in de formule, dus we hebben
Nu prop ik daar vrolijk een x-macht bij:
Dit moeten we dan evalueren in x=1.
Nog meer hints?
.Als je hints wil hebben is het wel handig als iedereen je plaatje kan zien. Ik zie het hier niet omdat de links naar plaatjes van Wolfram maar een beperkte tijd geldig zijn.quote:Op vrijdag 7 oktober 2011 17:31 schreef minibeer het volgende:
Waarom geldt:
[ afbeelding ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld
Excuses, ik kan geen latex, anders zou ik het wel even ingetypt hebben. Gefixt nu.quote:
[..]
Als je hints wil hebben is het wel handig als iedereen je plaatje kan zien. Ik zie het hier niet omdat de links naar plaatjes van Wolfram maar een beperkte tijd geldig zijn.
[ Bericht 0% gewijzigd door minibeer op 07-10-2011 23:01:48 ]
Kan ook makkelijk zonder inductie.quote:
Waarom geldt:
[ afbeelding ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld
Hint:
Volgens het Binomium van Newton.
Ik zie het nu wel inderdaad, ik zie het helaas alleen de andere kant op, als ik met jou hint begin en die vervolgens vermenigvuldig met n zie ik vrij makkelijk dat het gelijk is aanquote:
[..]
Kan ook makkelijk zonder inductie.
Hint:
Volgens het Binomium van Newton.
Andersom echter nog niet, maar dat zal wel aan mijn inzicht liggen (sowieso heb ik nog nooit met die binomiaalcoëfficiënten gerekend op deze manier, dus ik moet gewoon die rekenregels nog wat beter leren kennen)
. Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.True. Het grappige is dat ik deze vraag op een tentamen trouwens goed hadquote:
Als je het de ene kant opziet dan is dat genoeg, want je werkt met = tekens
. Ik was er alleen op gekomen door de eerste 5 of 6 gevallen uit te schrijven en daar de formule uit te concluderen (het was geen wiskunde, dus er werd gelukkig geen bewijs gevraagd), maar ik had geen idee waarom deze formule nou eigenlijk gold.Dat is eigenlijk hetzelfde idee als inductie, alleen doe je het met inductie algemener. Dat het in de eerste 5 a 6 gevallen klopt garandeert niets over het 7e geval of daarna. Inductie is denk ik ook nog sneller dan die gevallen uitschrijven.quote:
[..]
True. Het grappige is dat ik deze vraag op een tentamen trouwens goed had
Ik vind het prettiger om een paar vergelijkingen op te schrijven dan om een beredenering te houden wat je aan het tellen bent.quote:
Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met,
en
,
Hmm, zo heb ik er nooit tegenaan gekeken, maar ik weet niet of ik dat zo gelijk kan zienquote:
Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met
.Na 10 min is het leeg.
Welke formule geeft het verband tussen de waterhoogte h in cm en de tijd t in minuten?
Je startwaarde is 40 en het waterhoogte daalt met 40/10 = 4 cm per minuut,
In dit geval wel.quote:
Het wordt leeggeheveld, dat lijkt me niet lineair te verlopen.
Sorry, mijn fout.
Zo zie je maar weer dat ik niet bepaald de briljanste ben in wiskunde.
Edit : Geen dank !
Ik snap het, dank u!quote:
H = 40 - (4t)
Je startwaarde is 40 en het waterhoogte daalt met 40/10 = 4 cm per minuut,
leg even uit waarom de haakjes er staanquote:
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
(x²-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
oj, zie http://www.khanacademy.or(...)t=Developmental+Mathquote:
De haakjes staan er om ervoor te zorgen dat de vermenigvuldiging eerst plaatsvindt.
Indien je "40 - 4t" zou opschrijven, krijg je :
40 - 4 = 36 en dan
36 * t
quote:
Ik kom niet uit de volgende limiet
(x²-1) = (x-1)(x+1), maar verder kom ik niet. Sin (a -b) = sin a cos a - cos a sin b leverde me niets op. L'hospital's rule ken ik niet. Kan iemand helpen?
Oh ja.quote:
[..]
oj, zie http://www.khanacademy.or(...)t=Developmental+Math
Tja, dit bevestigt mijn eerdere stelling.
Heb 'em.quote:
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
[ Bericht 14% gewijzigd door Anoonumos op 08-10-2011 15:57:47 ]
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Impliciet differentiëren van de vergelijking van de curve naar x en subsitutie van y' = 3 levert als voorwaarde voor de coördinaten van de gevraagde punten op de curve:quote:
De kromme K bestaat uit alle puntendie voldoen aan
Deze kromme heeft een raaklijn L in het punt (0, 0).
(a) Geef de vergelijking van L in de vorm y = rx + b.
(b) Er zijn twee punten op K waar de raaklijnen zo zijn dat ze de lijn L
ergens loodrecht snijden. Bereken de co¨ordinaten van deze punten.
Met impliciet differentieren krijg ik bij a) L = -1/3 x.
Dus voor de andere raaklijn geldt helling = 3. Ik weet niet hoe ik nu x en y kan vinden.
(x + y)2 = (3/4)∙81
Nu jij weer.
[ Bericht 0% gewijzigd door Riparius op 08-10-2011 18:21:13 ]
Dank
dus:
(-∞,3) (5,+∞)?
http://en.wikipedia.org/wiki/SI_prefix#List_of_SI_prefixesquote:
Heeft iemand hier dat trapje waar staat hoeveel x je moet gaan van centiliter naar ml naar liter enz en meters naar centimeters naar decimeters enz.. ?
Dank
Ja. Je bedoelt vast:quote:Op zaterdag 8 oktober 2011 16:58 schreef Sokz het volgende:
Domein van sq.(x-3)(x-5) is toch (x-3)(x-5) > 0?
dus:
(-∞,3) (5,+∞)?
3 en 5 ook.quote:
Domein van sq.(x-3)(x-5) is toch (x-3)(x-5) > 0?
dus:
(-∞,3) (5,+∞)?
Misschien heb je iets aan het blaadje dat voor me ligt, en dan vooral de zin na het woordje 'de'?quote:
Calculus van James Stewart
Section 7.1
Example 6
Ik probeer al een half uur lang te begijpen hoe men aan het antwoor na de zin: cos^2x = 1-sin^2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Lekker duidelijk zo. Jij denkt zeker dat iedereen hier die je mogelijk kan helpen een exemplaar van dat boek (en dan ook nog de juiste druk, die je niet vermeldt) bij de hand heeft?quote:
Calculus van James Stewart
Section 7.1
Example 6
Ik probeer al een half uur lang te begrijpen hoe men aan het antwoord komt na de zin: cos2x = 1-sin2x
Waarom staan er plots 2 integralen met daarvoor (n-1)
Ik heb hier een PDF, dus je boft. Het gaat om het afleiden van een recursieve formule voor de onbepaalde integraal van sinnx. De stap waar je over struikelt is gewoon elementaire algebra:
(n-1)∙sinn-2x∙cos2x = (n-1)∙sinn-2x∙(1 - sin2x) = (n-1)∙sinn-2x - (n-1)∙sinnx
Kijk anders even hier.
[ Bericht 4% gewijzigd door Riparius op 08-10-2011 18:18:38 ]
quote:
Yes bedankt beiden had ik 't toch wel correct. Kloteboek brengt me elke keer weer in de war met foute antwoorden. :Squote:
We must have (x - 3)(x - 5) > 0 i.e. 3 < x < 5 (using a sign diagram)
say what?quote:
[..]
We must have (x - 3)(x - 5) > 0 i.e. 3 < x < 5 (using a sign diagram)
ja snapte het dus ook al niet.quote:
Op Geplot en alles [tex]9x+27y - \frac{10}{81} * (x + y)^{3} = 0[/tex] implicitiet diffquote:
[..]
Impliciet differentiëren van de vergelijking van de curve naar x en subsitutie van y' = 3 levert als voorwaarde voor de coördinaten van de gevraagde punten op de curve:
(x + y)2 = 81
Nu jij weer.
[tex]9 + 27y' - \frac{30}{81} * (x+y)^{2} * (y + x*y')[/tex] y' = 3 substitueren
[tex]90 - \frac{30}{81} * (x+y)^{2} * (y + 3x)[/tex]
[tex](x+y)^{2} * (y + 3x) = 243[/tex]
Toch? Hoezo moet (x + y)2 dan 81 zijn?
Oeps!
[ Bericht 26% gewijzigd door Anoonumos op 08-10-2011 17:31:23 ]
Kijk pi is ook maar een raar tekentje maar dat is wel de verhouding tussen omtrek en diameter. Waar haalt men die e vandaan?
Is dat gewoon een kwestie van de eerste en tweede orde afgeleide aan elkaar gelijkstellen en dan de discriminant berekenen? Ik heb hier geen antwoorden bij de hand.
Heb ik ook. Ben er wel mee bezig, maar heb eigenlijk geen idee waar het voor dient.quote:
Wat is trouwens e? Ik snap dat het een waarde heeft (2.7 ofzo) maar hoe komen ze aan dat getal?
Kijk pi is ook maar een raar tekentje maar dat is wel de verhouding tussen omtrek en diameter. Waar haalt men die e vandaan?
Oeps, stomme fout. Maar is het dan niet (x+y)² * 4 = 243, dus (x+y)² = 60.75?quote:
Alhoewel 81 mooier uitkomt.. maar afgeleide van (x+y)³ is hier toch 3(x+y)²(1 + y')
[ Bericht 8% gewijzigd door Anoonumos op 08-10-2011 17:56:58 ]
Ja.quote:
y(x)=ex^2, toon aan dat y'(x) =/ y''(x) voor alle x.
Is dat gewoon een kwestie van de eerste en tweede orde afgeleide aan elkaar gelijkstellen en dan de discriminant berekenen? Ik heb hier geen antwoorden bij de hand.
quote:
De waarde van a waarvoor de afgeleide van a^x gelijk is aan a^x.
kijk PI werd me na het zien van http://upload.wikimedia.o(...)-Pi-unrolled-720.gif gelijk duidelijk. Is zoiets ook voor e?| 1 2 3 4 5 6 7 8 9 10 11 | n: (1+1/n)^n: 1 2.00000000000000 21 2.65626321392610 41 2.68585634753775 61 2.69633049628226 81 2.70168999138345 101 2.70494597748516 121 2.70713368818803 141 2.70870477667918 161 2.70988774063937 181 2.71081059248709 |
Modelijke interpretatie: rentebetalingen. Als je op een kapitaal 1 aan het einde van het jaar een rente van 100% krijgt, dan heb je 1+1=2. Stel nu dat je ipv eenmaal per jaar, tweemaal per jaar (halverwege en aan het eind) een rente van 50% krijgt. Dan heb je halverwege het jaar 1+1/2, en aan het einde van het jaar heb je (1+1/2)*(1+1/2)=(1+1/2)^2. In het algemeen, als je het jaar in n stukjes verdeelt en aan het einde van elke periode een rente van 100/n % krijgt, dan heb je aan het einde van het jaar (1+1/n)^n. Als je nu n groter en groter maakt, komt het bedrag dat je aan het einde van het jaar hebt steeds dichter bij het getal e.
[ Bericht 23% gewijzigd door keesjeislief op 08-10-2011 18:04:44 ]
Het oppervlak onder de functie y=1/x tussen x=1 en x=e is gelijk aan 1.
Inderdaad, je hebt gelijk. Maar los de opgave nu eens verder op.quote:
[..]
IOeps, stomme fout. Maar is het dan niet (x+y)² * 4 = 243, dus (x+y)² = 60.75?
Alhoewel 81 mooier uitkomt.. maar afgeleide van (x+y)³ is hier toch 3(x+y)²(1 + y')
quote:
[..]
Inderdaad, je hebt gelijk. Maar los de opgave nu eens verder op.
Dus
Delen door 9, x + 3y = ...
Dus je hebt 2 vergelijking en 2 onbekenden en dat kan ik op zich wel uitwerken, maar volgens mij komt hier geen mooi getal uit en dat vind ik toch vreemd.
Edit: ik zie nu pas je stelsel
z(3, 2) = 2 (volgens de uitwerkingen)
Is het niet z(3, 2) = 3?
Ja, z(3,2)=3.quote:
z(x, y) = min{x, 2y}
z(3, 2) = 2 (volgens de uitwerkingen)
Is het niet z(3, 2) = 3?
Niet met decimale breuken werken. En vergeet niet dat er twee punten zijn op de curve die aan het gevraagde voldoen.quote:
[..]
Dus
Delen door 9, x + 3y = ...
Dus je hebt 2 vergelijking en 2 onbekenden en dat kan ik op zich wel uitwerken, maar volgens mij komt hier geen mooi getal uit en dat vind ik toch vreemd.
Thanks. Fijn, die foute antwoorden in een dictaat.quote:
Was ik niet vergeten(wel in mijn post). Ik krijg nuquote:
[..]
Niet met decimale breuken werken. En vergeet niet dat er twee punten zijn op de curve die aan het gevraagde voldoen.
quote:Op zaterdag 8 oktober 2011 17:58 schreef keesjeislief het volgende:
maakt, komt het bedrag dat je aan het einde van het jaar hebt steeds dichter bij het getal e.
Dank beiden!quote:
[ afbeelding ]
Het oppervlak onder de functie y=1/x tussen x=1 en x=e is gelijk aan 1.
Dat klopt.quote:
[..]
Was ik niet vergeten(wel in mijn post). Ik krijg nuen dan nog de negatieve waarden hiervan voor de andere oplossing.
Haha sorry, maar ik dacht dat de meesten hier wel met een bètastudie Calculus hebben gekregen en dus al het boek in hun la hadden liggen, het betreft trouwens het vijfde drukquote:
[..]
Lekker duidelijk zo. Jij denkt zeker dat iedereen hier die je mogelijk kan helpen een exemplaar van dat boek (en dan ook nog de juiste druk, die je niet vermeldt) bij de hand heeft?
Ik heb hier een PDF, dus je boft. Het gaat om het afleiden van een recursieve formule voor de onbepaalde integraal van sinnx. De stap waar je over struikelt is gewoon elementaire algebra:
(n-1)∙sinn-2x∙cos2x = (n-1)∙sinn-2x∙(1 - sin2x) = (n-1)∙sinn-2x - (n-1)∙sinnx
Kijk anders even hier.
Trouwens de uitleg in je link begrijp ik nog minder dan het antwoord zelf, waar ik ook al een
voor heb...Wat ik niet begrijp is hoe je aan de laatste antwoord komt, (n-1)∙sinn-2x∙(1 - sin2x)
oke tot hier begrijp ik, maar:
= (n-1)∙sinn-2x - (n-1)∙sinnx
Ik weet dat het eerste deel vermenigvuldigd wordt met de 1 in het haakje, die wordt dus (n-1)∙sinn-2x, maar hoe ontstaat het tweede deel, daar kom ik maar niet uit
(n-1)∙sinn-2x∙1 - (n-1)∙sinn-2x ∙ sin2x =
(n-1)∙sinn-2x∙1 - (n-1)∙sinn-2+2x =
(n-1)∙sinn-2x∙1 - (n-1)∙sinnx
remember: ea * eb = ea+b
Ah, door dat laatste heb ik nu eindelijk het Eureka moment gekregen na al die uren aan 1 somquote:
(n-1)∙sinn-2x ∙ (1 - sin2x) =
(n-1)∙sinn-2x∙1 - (n-1)∙sinn-2x ∙ sin2x =
(n-1)∙sinn-2x∙1 - (n-1)∙sinn-2+2x =
(n-1)∙sinn-2x∙1 - (n-1)∙sinnx
remember: ea * eb = ea+b
Super bedankt!
Man wat is wiskunde moeilijk, en dan MOET ik dit blok de vakken Regeltechniek 2, Analyse en Linreaire Algebra halen, anders word ik eruitgekickt van de opleiding
Werk soms wel van 9 - 22 in de bibliotheek van TU Delft, hou ENORM van de opleiding, maar het is freaking taai! 
Dit jaar is het zelfs moeilijker geworden en mogen geen rekenmachines meer worden gebruikt, dus alle regels als tan 1 = pi/4 uit je kop rammen
Maar genoeg zelfmedelijden, thanx voor het antwoord
[ Bericht 26% gewijzigd door MoetPoepen op 08-10-2011 21:57:53 ]
Als je wat van vectoren weet:quote:
waarom staan twee lijnen loodrecht op elkaar als het product van de twee hellingen gelijk is aan -1?
De lijnen y=ax+b en y'=a'x'+b' staan loodrecht op elkaar staan, desda als y=ax en y' = a'x' dat ook doen. Vul in die laatste vergelijking x=x'=1 in. Dan krijg je de vectors (1,a) en (1,a'). De lijnen zijn loodrecht desda de vectoren loodrecht op elkaar staan. De vectoren staan loodrecht op elkaar als het inproduct nul is, d.w.z. 1 + a*a' = 0. Oftewel a*a'=-1.
Het kan vast ook anders, zonder vectoren, maar dit is het eerste wat in me opkwam.
Ik ken die getalletjes ook niet allemaal uit mijn hoofd maar ik weet wel dat tan[1] geen pi/4 isquote:
[..]
Ah, door dat laatste heb ik nu eindelijk het Eureka moment gekregen na al die uren aan 1 som
Super bedankt!
Man wat is wiskunde moeilijk, en dan MOET ik dit blok de vakken Regeltechniek 2, Analyse en Linreaire Algebra halen, anders word ik eruitgekickt van de opleiding
Dit jaar is het zelfs moeilijker geworden en mogen geen rekenmachines meer worden gebruikt, dus alle regels als tan 1 = pi/4 uit je kop rammen
Maar genoeg zelfmedelijden, thanx voor het antwoord
. Welke opleiding doe je ?Ja, hij moet nog even doorstuderenquote:
Hij bedoelt waarschijnlijk tan(1/4*pi) = 1 => arctan 1 = 1/4*pi
Yupsquote:
Die dingen moet je bovendien op het vwo al kennen.
, wij kregen de trigonometrische functies al in Ath4 voor de kiezen, en de cyclometrische functies kwamen halverwege Ath5 aan bod. Overigens hoef je niet eens de complete reeks in je kop te stampen. Dr is een makkelijk te onthouden reeks voor bijv sinx: x = 0 => sinx = 1/2*SQRT(0)
x = 1/6*pi => sinx = 1/2*SQRT(1)
x = 1/4*pi => sinx = 1/2*SQRT(2)
x = 1/3*pi => sinx = 1/2*SQRT(3)
x = 1/2*pi => sinx = 1/2*SQRT(4)
x = 2/3*pi => sinx = 1/2*SQRT(3)
x = 3/4*pi => sinx = 1/2*SQRT(2)
x = 5/6*pi => sinx = 1/2*SQRT(1)
x = pi => sinx = 1/2*SQRT(0)
De integerwaarden [-4,-3..,0..,3,4] volgen heel mooi het verloop van de grafieken van sinx en cosx, dus je hoeft eigenlijk alleen die 1/2*SQRT(x) te onthouden.
quote:
[..]
Ik ken die getalletjes ook niet allemaal uit mijn hoofd maar ik weet wel dat tan[1] geen pi/4 is
Voila, het antwoordquote:
Hij bedoelt waarschijnlijk tan(1/4*pi) = 1 => arctan 1 = 1/4*pi
Helaas kom ik niet van het vwo af, de tering ik had na de havo het vwo moeten doen, maar neeeee hoor 'het wordt te moeilijk' zeiden ze op schoolquote:
Die dingen moet je bovendien op het vwo al kennen.
Ik moet dus belachelijk veel kennis bijspijkeren. Het lijkt erop dat Analyse niet eens de basis is maar een vergevorderd stadium
Kom zelf van het hbo, nauwelijks wiskunde gekregen daar. Beetje imaginaire getallen maar verder niets.
oh mijn god zeg me niet dat je ook een TippieTop kloon bent.quote:
[..]
[..]
Voila, het antwoord
[..]
Helaas kom ik niet van het vwo af, de tering ik had na de havo het vwo moeten doen, maar neeeee hoor 'het wordt te moeilijk' zeiden ze op school
Ik moet dus belachelijk veel kennis bijspijkeren. Het lijkt erop dat Analyse niet eens de basis is maar een vergevorderd stadium
Kom zelf van het hbo, nauwelijks wiskunde gekregen daar. Beetje imaginaire getallen maar verder niets.
Geen kloon hierquote:
[..]
oh mijn god zeg me niet dat je ook een TippieTop kloon bent.
Ik hou van je.quote:
[..]
Yups
x = 0 => sinx = 1/2*SQRT(0)
x = 1/6*pi => sinx = 1/2*SQRT(1)
x = 1/4*pi => sinx = 1/2*SQRT(2)
x = 1/3*pi => sinx = 1/2*SQRT(3)
x = 1/2*pi => sinx = 1/2*SQRT(4)
x = 2/3*pi => sinx = 1/2*SQRT(3)
x = 3/4*pi => sinx = 1/2*SQRT(2)
x = 5/6*pi => sinx = 1/2*SQRT(1)
x = pi => sinx = 1/2*SQRT(0)
De integerwaarden [-4,-3..,0..,3,4] volgen heel mooi het verloop van de grafieken van sinx en cosx, dus je hoeft eigenlijk alleen die 1/2*SQRT(x) te onthouden.
Wanneer ik de tekst kopieer en plak in een tekstveld, krijg ik een reguliere A te zien.
Lambda (of \Lambda in LaTeX).quote:
Misschien niet echt een pure wiskunde-vraag, maar jullie weten dit soort dingen over het algemeen erg goed.. Kan iemand me vertellen hoe het gemarkeerde symbool hieronder heet (of hoe ik 'm kan typen in LaTeX)?
[ afbeelding ]
Wanneer ik de tekst kopieer en plak in een tekstveld, krijg ik een A te zien.
Ah, oke! Cursief en als hoofdletter had ik 'm niet herkend. Thankyou!quote:
4 ln L + 2 ln K = 10
2 ln K = 10 − 4 ln L
ln K = 5 − 2 ln
Hier zit ik vast. Hoe krijg ik ln aan de linkerkant weg?
Metquote:
We have an equation of the form 4 ln L + 2 ln K = 10. Solving this for K gives:
4 ln L + 2 ln K = 10
2 ln K = 10 − 4 ln L
ln K = 5 − 2 ln
Hier zit ik vast. Hoe krijg ik ln aan de linkerkant weg?
Thanks!quote:
Neem een lijn met helling a_1 en eentje met helling a_2:quote:
waarom staan twee lijnen loodrecht op elkaar als het product van de twee hellingen gelijk is aan -1?
Dan geldt dat
(waarbij je gebruikt dat
Er is dus een rechte hoek tussen de lijnen desda
Je kunt ook Pythagorad gebruiken. Als de lijn met positieve helling de grafiek van f is en de andere lijn de grafiek van g, dan geldt dat de lengte van het lijnstuk tussen (0,2) en (1,f(1)) gelijk is aan
[ Bericht 10% gewijzigd door keesjeislief op 09-10-2011 16:15:55 ]
Zo kan het dus ookquote:
[..]
Neem een lijn met helling a_1 en eentje met helling a_2:
[ afbeelding ]
Dan geldt daten
. Dus
(waarbij je gebruikt dat) en dus
Er is dus een rechte hoek tussen de lijnen desda.
Je kunt ook Pythagorad gebruiken. Als de lijn met positieve helling de grafiek van f is en de andere lijn de grafiek van g, dan geldt dat de lengte van het lijnstuk tussen (0,2) en (1,f(1)) gelijk is aanen de lengte van het lijnstuk tussen (0,2) en (1,g(1)) gelijk aan
. Er is een rechte hoek tussen beide lijnen als Pythagoras geldt voor de grote driehoek bestaande uit hoekpunten (0,2), (1,f(1)) en (1,g(1)). Dit geeft:
. Met vectoren is wel het korst en eenvoudigst.hee, die moet ik onthouden!!!quote:
[..]
Neem een lijn met helling a_1 en eentje met helling a_2:
[ afbeelding ]
Dan geldt dat
(waarbij je gebruikt dat
Er is dus een rechte hoek tussen de lijnen desda
Je kunt ook Pythagorad gebruiken. Als de lijn met positieve helling de grafiek van f is en de andere lijn de grafiek van g, dan geldt dat de lengte van het lijnstuk tussen (0,2) en (1,f(1)) gelijk is aan
Daar herformuleer je de vraag alleen in termen van het inproduct en gebruik je een equivalente uitspraak, nl. dat vectoren loodrecht op elkaar staan als het inproduct 0 is. Als je dat wilt laten zien moet je ook iets met goniometrie of Pythagoras doen, komt op hetzelfde neer.quote:
[..]
Zo kan het dus ook
Klopt ja, maar als je dat eenmaal een keer gezien hebt...quote:
[..]
Daar herformuleer je de vraag alleen in termen van het inproduct en gebruik je een equivalente uitspraak, nl. dat vectoren loodrecht op elkaar staan als het inproduct 0 is. Als je dat wilt laten zien moet je ook iets met goniometrie of Pythagoras doen, komt op hetzelfde neer.
Bedankt!quote:
[..]
Neem een lijn met helling a_1 en eentje met helling a_2:
[ afbeelding ]
Dan geldt dat
(waarbij je gebruikt dat
Er is dus een rechte hoek tussen de lijnen desda
Je kunt ook Pythagorad gebruiken. Als de lijn met positieve helling de grafiek van f is en de andere lijn de grafiek van g, dan geldt dat de lengte van het lijnstuk tussen (0,2) en (1,f(1)) gelijk is aan
dat zocht ikLaat zien dat voor elke a in
Zij T de afbeelding van
Wat betekent het precies dat a wordt gestuurd naar de afbeelding
A. Voor welke a snijdt de lijn de x-as in(3.0)?
B. Voor welke a is de lijn evenwijdig met de lijn y= 3x -1?
Wat willen ze nu bij vraag B. ?
Met een klein beetje basiskennis van formules van rechte lijnen moet dat lukken. Welk getal geeft het hellingsgetal weer in y=ax+b?
a wordt niet gestuurd, maar de x uit F^n wordt gestuurd. a is maar een parameter. Voor de rest lijkt dit me gewoon definities gebruiken?quote:
Wat betekent het precies dat a wordt gestuurd naar de afbeelding? Ik moet dus aantonen dat T lineair, injectief en subjectief is maar ik snap niet helemaal wat er met a gebeurt.
[ Bericht 3% gewijzigd door twaalf op 09-10-2011 20:47:35 ]
Het kan ook zonder vectoren een stuk korter dan wat keesjeislief doet als je gebruik maakt van de identiteitquote:
[..]
Zo kan het dus ook
tan(α-β) = (tan α - tan β)/(1+ tan α∙tan β)
Hebben we twee lijnen met een richtingscoëfficiënt a resp. b, dan maken deze lijnen hoeken α resp. β met de (positieve) x-as zodanig dat a = tan α en b = tan β. Als nu het product ab, en daarmee het product tan α∙tan β, gelijk is aan -1, dan is tan(α-β) ongedefinieerd, en dat kan alleen als α - β = ½π + κ∙π (k ∈Z), QED.
[ Bericht 0% gewijzigd door Riparius op 10-10-2011 12:14:58 ]
(In de vorm van y(t+2) - y(t+1) - 6y(t) = 0 , dus de y 2 periodes in de toekomst is te verklaren in termen van het heden en de eerst volgende periode.) Ik zet het dik gedrukt neer wanneer ik het niet snap.
Stel y(t+2) - y(t+1) - 6y(t) = 0 en we willen de algemene oplossing vinden. Dan zegt de docent dat we gewoon is moeten proberen om y(t) = m^t
Dan:
y(t) = m^(t)
y(t+1) = m^(t+1)
y(t+2) = m^(t+2)
Invullen in de difference equation
m^(t+2) - m^(t+1) - 6*m^t = 0
m^t * ( m^2 - m - 6 ) = 0
Dan zegt hij m^t is 0 of m^2 - m -6 is 0 , maar m^t is 0 is geen interessante oplossing. (Waarom niet?) Ook al is het m = 0 , waarom is dat niet interessant?
Dus we gaan verder met m^2 - m - 6 = 0
m = 3 v m = -2
Dus y(t) = 3^t of y(t) = (-2)^t
Nu zegt de docent
Dus y(t) = 3^t * A + B * (-2)^t
Waarom? Ik begrijp niet waarom hij beide oplossingen bij elkaar optelt? En waarom kan dat?
Waarom zou je de A en B er ook voor zetten?
Ik begrijp niet waarom je niet gewoon de 2 losse oplossingen houdt, het doel van het bij elkaar optellen ontgaat mij dus een beetje.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
En met die A en B kan je aan beginvoorwaarden voldoen. Als je bijvoorbeeld de waarden van y op t=0 en t=1 weet, weet je ook de waarden voor A en Bquote:
- Je weet al dat y=0 een oplossing is.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
Aha, net even ingevuld en er komt inderdaad gewoon 0 uit. Bedankt!quote:
- Je weet al dat y=0 een oplossing is.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
Stel y0 = 0 en y1 = 1quote:
[..]
En met die A en B kan je aan beginvoorwaarden voldoen. Als je bijvoorbeeld de waarden van y op t=0 en t=1 weet, weet je ook de waarden voor A en B
Dan zou je toch ook dit systeem van vergelijkingen kunnen oplossen:
0 = 3^t
1 = 3^t
0 = (-2)^t
1 = (-2)^t
Of werkt dat zo niet? (3^t = 0 wordt al onmogelijk?)
In plaats van A*3^0 + B*(-2)^0 = 0 en A*3^1 + B*(-2)^1 = 1 oplossen.
Het doel is om alle oplossingen te vinden. Het idee is dat het een lineaire vergelijking is, d.w.z. als y0(t) en y1(t) twee oplossingen zijn, dan is de functie y2(t)=A*y0(t)+B*y1(t) voor willekeurige constanten A en B ook een oplossing. In feite is de ruimte van alle oplossingen een 2-dimensionale deelruimte. De algemene oplossingsmethode is als volgt: ten eerste vind je zoveel mogelijk lineair onafhankelijke oplossingen y1,...,yn. Die oplossingen spannen dan de oplossingsruimte op, in de zin dat elk element in de oplossingsruimte dan van de vorm a1*y1(t)+a2*y2(t)+...+an*yn(t) is. Om de lineair onafhankelijke oplossingen te vinden gebruik je die 'gok' y(t)=m^t. (Dat is natuurlijk niet echt een gok, die werkt altijd voor dit soort vergelijkingen, net zoals je voor gewone lineaire dv's exponentiele functies gebruikt als 'gok').quote:
Ik snap iets niet bij het oplossen van homogeneous 2de order lineaire difference equations
(In de vorm van y(t+2) - y(t+1) - 6y(t) = 0 , dus de y 2 periodes in de toekomst is te verklaren in termen van het heden en de eerst volgende periode.) Ik zet het dik gedrukt neer wanneer ik het niet snap.
Stel y(t+2) - y(t+1) - 6y(t) = 0 en we willen de algemene oplossing vinden. Dan zegt de docent dat we gewoon is moeten proberen om y(t) = m^t
Dan:
y(t) = m^(t)
y(t+1) = m^(t+1)
y(t+2) = m^(t+2)
Invullen in de difference equation
m^(t+2) - m^(t+1) - 6*m^t = 0
m^t * ( m^2 - m - 6 ) = 0
Dan zegt hij m^t is 0 of m^2 - m -6 is 0 , maar m^t is 0 is geen interessante oplossing. (Waarom niet?) Ook al is het m = 0 , waarom is dat niet interessant?
Dus we gaan verder met m^2 - m - 6 = 0
m = 3 v m = -2
Dus y(t) = 3^t of y(t) = (-2)^t
Nu zegt de docent
Dus y(t) = 3^t * A + B * (-2)^t
Waarom? Ik begrijp niet waarom hij beide oplossingen bij elkaar optelt? En waarom kan dat?
Waarom zou je de A en B er ook voor zetten?
Ik begrijp niet waarom je niet gewoon de 2 losse oplossingen houdt, het doel van het bij elkaar optellen ontgaat mij dus een beetje.
[ Bericht 2% gewijzigd door keesjeislief op 10-10-2011 18:26:27 ]
Wat een gemiereneuk, je spaart misschien twee regels uit en moet in ruil daarvoor een veel onbekendere goneometrische identiteit gebruiken. Pythagoras is natuurlijk verreweg de meest elegante en simpele oplossing.quote:
[..]
Het kan ook zonder vectoren een stuk korter dan wat keesjeislief doet als je gebruik maakt van de identiteit
tan(α-β) = (tan α - tan β)/(1+ tan α∙tan β)
Hebben we twee lijnen met een richtingscoëfficiënt a resp. b, dan maken deze lijnen hoeken α resp. β met de (positieve) x-as zodanig dat a = tan α en b = tan β. Als nu het product ab, en daarmee het product tan α∙tan β, gelijk is aan -1, dan is tan(α-β) ongedefinieerd, en dat kan alleen als α - β = ½π + κ∙π (k ∈Z), QED.
Nee, zo werkt dat niet. Je kunt niet uitgaan van twee - willekeurige - randvoorwaarden en dan verwachten dat je de algemene oplossing zult vinden. Er is precies één oplossing die aan jouw randvoorwaarden voldoet, namelijk y(t) = (1/5)∙3t - (1/5)∙(-2)t, maar die vind je nu juist door uit te gaan van de algemene oplossing y(t) = A∙3t + B∙(-2)t, niet omgekeerd.quote:
[..]
Stel y(0) = 0 en y(1) = 1
Dan zou je toch ook dit systeem van vergelijkingen kunnen oplossen:
[snip]
5x^2+28x-63 = 1259x-7
Alvast bedankt
gebruik logarithmsquote:Op dinsdag 11 oktober 2011 10:51 schreef Snuf. het volgende:
Zou iemand mij kunnen uitleggen hoe ik een vergelijking als dit op moet lossen?
5x^2+28x-63 = 1259x-7
Alvast bedankt
Bedenk dat 125 = 53. Dan hebben we:quote:
Zou iemand mij kunnen uitleggen hoe ik een vergelijking als dit op moet lossen?
5x^2+28x-63 = 1259x-7
Alvast bedankt
5x²+28x-63 = 53(9x-7)
En dus:
x2 + 28x - 63 = 3(9x - 7)
Nu jij weer.
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
ln(N) = ln(25-3L)quote:
Hoe bereken ik de inverse van N=2^(5-3L)
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
ln(N) = (5-3L)*ln(2)
Je kunt i.p.v. ln ook log gebruiken. Ik neem aan dat je de rest zelf kunt.
Ik reageerde op de opvatting van thenxzero dat het gebruik van vectoren het eenvoudigst zou zijn. Maar los daarvan begrijp ik de kritiek niet. Je leidt namelijk zelf eerst een andere goniometrische identiteit af, tan α1∙tan α2 = 1 - cos(α1 + α2)/cos α1∙cos α2, die zo mogelijk nog veel onbekender is dan de formules voor tan(α-β) (resp. tan(α+β)) die gewoon tot het standaardrepertoire van goniometrische identiteiten behoren.quote:Op maandag 10 oktober 2011 18:24 schreef keesjeislief het volgende:
[..]
Wat een gemiereneuk, je spaart misschien twee regels uit en moet in ruil daarvoor een veel onbekendere goniometrische identiteit gebruiken.
Zo 'natuurlijk' is dat niet. Als geldt a1a2 = -1 dan is 1 : a1 = -a2 : 1, zodat in je figuur de rechthoekige driehoek met hoekpunten (0,2), (1,2), (1, f(1)) gelijkvormig is met de rechthoekige driehoek met hoekpunten (1, g(1)), (1,2), (0,2), waaruit volgt dat α1 + α2 = π/2. Is omgekeerd α1 + α2 = π/2, dan zijn de genoemde driehoeken gelijkvormig, waaruit volgt dat 1 : a1 = -a2 : 1 en dus a1a2 = -1. Daar heb ik 'Pythagoras' niet voor nodig.quote:Pythagoras is natuurlijk verreweg de meest elegante en simpele oplossing.
oke bedankt, ik kom nu op:quote:Op dinsdag 11 oktober 2011 15:07 schreef lyolyrc het volgende:
[..]
ln(N) = ln(25-3L)
ln(N) = (5-3L)*ln(2)
Je kunt i.p.v. ln ook log gebruiken. Ik neem aan dat je de rest zelf kunt.
ln(N)=5-3L * ln(2)
ln(N)/ln(2)=5-3L
ln(N)/ln(2)-5=-3L
3L=5- ln(N)/ln(2)
L= 1/3 (5- ((ln)N/(ln)2) )
[ Bericht 1% gewijzigd door bezemsteeltaart op 11-10-2011 15:52:12 ]
Nee, hoe kom je daarbij?quote:
[..]
die LN kan ik weglaten bij ln(N)/ln(2) toch
//oja ik controleer net en dit klopt inderdaad niet, je hebt gelijk
Je lijdt aan een wegstreepsyndroom.quote:
dacht dat dezelfde termen die vermenigvulden in de noemer en teller, je die mag wegstrepen. Of geldt dit alleen bij XY^2/XY = Y bijvoorbeeld en niet bij ln/log/e??
Bekijk het eens aan de hand van een voorbeeld. We nemen 'gewone' logaritmen met grondtal 10. Nu weet je dat:
log(100) = 2 en log(10) = 1.
Jij beweert nu dat log(100)/log(10) = 2/1 = 2 hetzelfde zou zijn als 100/10 = 10, en dat is duidelijk onzin.
Wat wel kan is ln[ N^(ln(2))^-1 ], niet dat dit duidelijker is maar okquote:
Je vergeet dat je niet met ln vermenigvuldigt, maar dat ln een functie is.quote:
dacht dat dezelfde termen die vermenigvulden in de noemer en teller, je die mag wegstrepen. Of geldt dit alleen bij XY^2/XY = Y bijvoorbeeld en niet bij ln/log/e??
//oja ik controleer net en dit klopt inderdaad niet, je hebt gelijk
Ik begrijp het eigenlijk, bedanktquote:
[..]
Nee, zo werkt dat niet. Je kunt niet uitgaan van twee - willekeurige - randvoorwaarden en dan verwachten dat je de algemene oplossing zult vinden. Er is precies één oplossing die aan jouw randvoorwaarden voldoet, namelijk y(t) = (1/5)∙3t - (1/5)∙(-2)t, maar die vind je nu juist door uit te gaan van de algemene oplossing y(t) = A∙3t + B∙(-2)t, niet omgekeerd.
Op één of andere manier dacht ik dat 3^t of (-2)^t de echte oplossingen waren terwijl A*3^t ook een oplossing kan zijn, maar het is natuurlijk zo dat 3^t slechtst één oplossing is van A*3^t. en A*3^t slechtst een deel van de oplossingen van A*3^t + B*(-2)^t.
Best raar dat je soms zo scheef kan denken en het niet doorhebt.
Hee, dat is precies dezelfde opdracht als een die ik moest doenquote:
Hoe bereken ik de inverse van N=2^(5-3L)
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
Doe je ook het oefententamen bij Wiskunde 1 op de Eur? Nog bedankt voor het helpen, op het moment dat ik mijn vraag enkele posts hier boven stelde schoot het me te binnen, het is best wel simpel eigenlijk..
Ik ga hier verder maar niet op in, daar is het het topic niet voor. Laten we het er maar op houden dat we duidelijk van mening verschillen over toedracht en inhoud.quote:
[..]
Ik reageerde op de opvatting van thenxzero dat het gebruik van vectoren het eenvoudigst zou zijn. Maar los daarvan begrijp ik de kritiek niet. Je leidt namelijk zelf eerst een andere goniometrische identiteit af, tan α1∙tan α2 = 1 - cos(α1 + α2)/cos α1∙cos α2, die zo mogelijk nog veel onbekender is dan de formules voor tan(α-β) (resp. tan(α+β)) die gewoon tot het standaardrepertoire van goniometrische identiteiten behoren.
[..]
Zo 'natuurlijk' is dat niet. Als geldt a1a2 = -1 dan is 1 : a1 = -a2 : 1, zodat in je figuur de rechthoekige driehoek met hoekpunten (0,2), (1,2), (1, f(1)) gelijkvormig is met de rechthoekige driehoek met hoekpunten (1, g(1)), (1,2), (0,2), waaruit volgt dat α1 + α2 = π/2. Is omgekeerd α1 + α2 = π/2, dan zijn de genoemde driehoeken gelijkvormig, waaruit volgt dat 1 : a1 = -a2 : 1 en dus a1a2 = -1. Daar heb ik 'Pythagoras' niet voor nodig.
u'y(8, 20) = 0 (volgens de uitwerkingen)
Moet dit niet u'y(8, 20) = 1 zijn?
Jij leest die posts ook echt?!?!quote:
[..]
Ik ga hier verder maar niet op in, daar is het het topic niet voor. Laten we het er maar op houden dat we duidelijk van mening verschillen over toedracht en inhoud.
quote:
Volgens dictaat: y′(x) = (2x−1)e2x−1(2) = (4x-2)e2x−1
Ik dacht: y'(x) = 2(e2x-1), want de afgeleide van ex = ex
Wie zit er fout?
Waarom kan een universiteit geen fatsoenlijke uitwerkingen online zetten? Het stikt echt van de fouten.
Klunzige fout zelfs. Dit is geen tikfoutje of zo maar echt een technische fout.quote:
Thanks.
Waarom kan een universiteit geen fatsoenlijke uitwerkingen online zetten? Het stikt echt van de fouten.
f '(x) = (e2x-1) ' = (2x-1) ' * de2x-1/d(2x-1) = 2e2x-1quote:
Bepaal de afgeleide van y(x) = e2x−1
Volgens dictaat: y′(x) = (2x−1)e2x−1(2) = (4x-2)e2x−1
Ik dacht: y'(x) = 2(e2x-1), want de afgeleide van ex = ex
Wie zit er fout?
Het dictaat heeft het fout. Beste blunder van die Uni
.8000 births, 3000 single mom, 5000 /w partner
Out of 3000 single moms, 1450 gave birth to son
Out of 5000 /w partner, 2250 gave birth to son.
Test at 5% significance
(a) Test whether the probability for a mom /w partner getting a son exceeds 50%
(b) Test whether the probability for a single mom getting a son is smaller than 50%.
(c) Test whether the probability of getting a son differs between the two groups of mothers.
(a) Nee
(b) Nee
(c) Nee
Dacht ik, maar nu twijfel of ik de juiste methode gebruikt heb..
Ik heb een 95% betrouwbaarheidsinterval van de fractie p (zoon) geconstrueerd. Bij (a) krijg ik 0.496-0.523, bij (b) .465-.5012quote:
Normale benadering van dit geval.
Thanks man, dit was idd wat ik zocht.quote:
Je hebt hier een leuke test voor, p. 498 van het grijze deel van je boek als ik het goed heb.
Normale benadering van dit geval.
Bij (b) krijg ik uit dat z=-1.83 en het significantieniveau komt uit op -1.645. Dus -1.83<-1.645. De verwachting bij verwerpen van H0 dan zou z<-1.645 moeten zijn toch? Dus verwerpen in dit geval en accepteren Ha.
Het moet toch ook pooled variance test zijn?quote:
c is leuk, gepoolde variantie nemen anders trekt Heij puntjes af
Het is tenslotte niet dezelfde groep die je twee keer test.
Correct.quote:
[..]
Het moet toch ook pooled variance test zijn?
Het is tenslotte niet dezelfde groep die je twee keer test.
Maar over die filosofie moet je je na een tijdje maar heen zetten. Ik zeg na een toets gewoon altijd H0 is waar of H1 is waar, iedereen snapt toch wat je daarmee bedoelt.
Ja je toetst of H0 verworpen kan worden dus de uitkomst is wel of niet verwerpen. Toch snap ik het niet helemaal waarom je niet het woord accepteren mag gebruiken, zeker als je dat resultaat wel in je verdere berekeningen voor waar aanneemt.quote:
Daar zit nog een bepaald filosofisch verschil tussen. Aangezien de inferentiële methode bestaat uit het verwerpen van H0, kan het resultaat van die methode nooit zijn dat je H0 accepteert. De methode heeft maar twee uitkomsten, of je verwerpt wel of je verwerpt niet.
Maar over die filosofie moet je je na een tijdje maar heen zetten. Ik zeg na een toets gewoon altijd H0 is waar of H1 is waar, iedereen snapt toch wat je daarmee bedoelt.
Even een voorbeeld:
H0: P is waar
H1: P is niet waar
Je gaat een toets doen en je kan H0 niet verwerpen. Vervolgens neem je aan dat P waar is in je verdere berekeningen. Dan heb je de uitspraak "P is waar" toch niet alleen niet verworpen, maar ook geaccepteerd? Dat je het niet zeker weet dat P echt waar is, dat klopt. Maar ook als je H0 verwerpt weet je niet zeker of dat terecht is en dat P niet waar is.
Dat jij H0 is waar of H1 is waar zegt is eigenlijk hetzelfde als zeggen dat je H0 of H1 accepteert, dus dat mag dan ook niet. En wat is de filosofie precies?
Blijven oefenen en doorzetten. Hoe meer je oefent hoe sneller je het op gaat pikken... je moet die manier van denken trainenquote:
Jongens, ik heb ENORM veel problemen met mijn schakeljaar, de wiskundige vakken steek ik ENORM veel tijd in, de theorie, vooral achter Lineaire Algebra, is onbegrijpelijk. Weet niet hoe ik dit moet oppakken, werk soms tot 10 uur 's avonds op de TU door met het huiswerk, en voornamelijk de theoretsiche vragen zijn moeilijk en onbegrijpelijk... dit is trowuens mijn tweede keer... hoe pak ik dit nou op?
.Veel vragen lukt het mij om te maken... de manier om het op te schrijven en te verklaren, DAAR heb ik problemen mee, en daar verneuk ik tentamens mee, terwijl ik de sommen gewoon kan maken...quote:
[..]
Blijven oefenen en doorzetten. Hoe meer je oefent hoe sneller je het op gaat pikken... je moet die manier van denken trainen
http://liesandstats.wordp(...)r-fail-to-reject-it/quote:
[..]
Ja je toetst of H0 verworpen kan worden dus de uitkomst is wel of niet verwerpen. Toch snap ik het niet helemaal waarom je niet het woord accepteren mag gebruiken, zeker als je dat resultaat wel in je verdere berekeningen voor waar aanneemt.
Even een voorbeeld:
H0: P is waar
H1: P is niet waar
Je gaat een toets doen en je kan H0 niet verwerpen. Vervolgens neem je aan dat P waar is in je verdere berekeningen. Dan heb je de uitspraak "P is waar" toch niet alleen niet verworpen, maar ook geaccepteerd? Dat je het niet zeker weet dat P echt waar is, dat klopt. Maar ook als je H0 verwerpt weet je niet zeker of dat terecht is en dat P niet waar is.
Dat jij H0 is waar of H1 is waar zegt is eigenlijk hetzelfde als zeggen dat je H0 of H1 accepteert, dus dat mag dan ook niet. En wat is de filosofie precies?
Het is wat stelliger om te zeggen dat iets waar is, dan dat er niet genoeg bewijs is om de veronderstelde situatie te verwerpen. Je weet niet of iets waar is of niet, je weet enkel dat er geen reden is om de veronderstelde situatie te verwerpen indien er geen significante afwijkingen zijn gevonden.
Ik heb m'n post al veranderdquote:
Waarom zou je er niet mee doorrekenen als je niet kunt aantonen dat het niet waar is?
Ik vroeg mij dat zelf ook af.Schakeljaar waarvan precies?quote:
Jongens, ik heb ENORM veel problemen met mijn schakeljaar, de wiskundige vakken steek ik ENORM veel tijd in, de theorie, vooral achter Lineaire Algebra, is onbegrijpelijk. Weet niet hoe ik dit moet oppakken, werk soms tot 10 uur 's avonds op de TU door met het huiswerk, en voornamelijk de theoretsiche vragen zijn moeilijk en onbegrijpelijk... dit is trowuens mijn tweede keer... hoe pak ik dit nou op?
dratische factoren met een negatieve discriminant
Bij z^4+2z^2+1 = (z^2+1)^2
Bij z^4-2z^2+1 = ((z-1)^2)*((z+1)^2)
Waarom bij de 2e niet gewoon (z^2-1)^2?
Heel eenvoudig, omdat je bij de tweede conform de opdracht kunt factoriseren in lineaire factoren met reële coëfficiënten, en bij de eerste niet. z2 - 1 heeft dan ook geen negatieve discriminant.quote:
3.11 Splits de volgende reële polynomen in reële lineaire factoren en reële kwadratische factoren met een negatieve discriminant
Bij z^4+2z^2+1 = (z^2+1)^2
Bij z^4-2z^2+1 = ((z-1)^2)*((z+1)^2)
Waarom bij de 2e niet gewoon (z^2-1)^2?
Oh, misschien had ik de opdracht moeten lezenquote:
[..]
Heel eenvoudig, omdat je bij de tweede conform de opdracht kunt factoriseren in lineaire factoren met reële coëfficiënten, en bij de eerste niet. z2 - 1 heeft dan ook geen negatieve discriminant.
Mag ik dan gebruiken dat de som van k=1 t/m N met k gelijk is aan 1/2n(n+1)?
Ik snap het punt, maar je zou ook kunnen zeggen dat je met accepteren niet bedoelt dat het waar is, maar dat er niet voldoende reden is om iets anders aan te nemen.quote:
[..]
http://liesandstats.wordp(...)r-fail-to-reject-it/
Het is wat stelliger om te zeggen dat iets waar is, dan dat er niet genoeg bewijs is om de veronderstelde situatie te verwerpen. Je weet niet of iets waar is of niet, je weet enkel dat er geen reden is om de veronderstelde situatie te verwerpen indien er geen significante afwijkingen zijn gevonden.
Zo werkt het ook in de natuurkunde. Een theorie als quantummechanica wordt geaccepteerd door onderzoekers, mede omdat de theorie overeenkomt met experimenten (oftewel: er is niet voldoende bewijs om H0: quantummechanica klopt te verwerpen), maar dat betekent nog niet dat de theorie echt klopt.
Dus: je kan best iets accepteren zonder dat je zeker weet of het zo is. Het zit 'm denk ik in je definitie van accepteren.
[ Bericht 4% gewijzigd door thenxero op 15-10-2011 12:47:00 ]
Het nadeel van een bewijs met inductie is dat het niet heuristisch is, dus je moet al weten wat de formule is voor e.g. de som van de kwadraten of kubieken (derde machten) van de eerste n natuurlijke getallen alvorens je een bewijs met inductie kunt geven. Een afleiding van een dergelijke formule is toch wat anders. In dit geval weet Physics al wat hij moet bewijzen, en is gebruik van inductie dus inderdaad de aangewezen weg, maar eerder vroeg Physics ook al naar een uitdrukking voor de som van de kwadraten van de eerste n natuurlijke getallen en hoe je aan die formule komt, en dan is het geven van de kant en klare formule met de opmerking dat je deze kunt bewijzen met inductie geen antwoord op de eigenlijke vraag.quote:
Het mag wel (want het is makkelijk aan te tonen), maar ik vraag me af of inductie niet simpeler is.
[ Bericht 0% gewijzigd door Riparius op 15-10-2011 20:01:30 ]
Ja, en dat is inderdaad zelfs handig als je het gevraagde middels inductie wil bewijzen. Als je wil zien waarom en hoe het bewijs dan gaat moet je maar even hier kijken. Wil je daarentegen een afleiding van de somformule zonder gebruik van inductie, dan kan ik je aanraden eens naar het verschil van de vierde machten van opeenvolgende natuurlijke getallen te kijken en deze verschillen te sommeren. Je krijgt dan een zogeheten telescoopreeks waarin alle termen uitgezonderd de eerste en de laatste tegen elkaar weg vallen.quote:
Bewijs dat de som van k=1 t/m N met k^3 gelijk is aan (de som van k=1 t/m N met k)^2
Mag ik dan gebruiken dat de som van k=1 t/m N met k gelijk is aan 1/2n(n+1)?
Ik heb eerst die somformule bewezen en daarmee de oorspronkelijke vraag bewezen dmv volledige inductie.quote:
Ik zie dat je met inductie ook de somformule nodig hebt van. Met die formule is het bewijs vijf regeltjes.
Ja bedankt, het is me zelf ook al gelukt!quote:
[..]
Ja, en dat is inderdaad zelfs handig als je het gevraagde middels inductie wil bewijzen. Als je wil zien waarom en hoe het bewijs dan gaat moet je maar even hier kijken. Wil je daarentegen een afleiding van de somformule zonder gebruik van inductie, dan kan ik je aanraden eens naar het verschil van de vierde machten van opeenvolgende natuurlijke getallen te kijken en deze verschillen te sommeren. Je krijgt dan een zogeheten telescoopreeks waarin alle termen uitgezonderd de eerste en de laatste tegen elkaar weg vallen.
[ Bericht 42% gewijzigd door Physics op 15-10-2011 19:19:04 ]
Waarom is het u′y(1, 1) = 0 en niet 1?
Soortgelijke vraag van pagina 9:
quote:
u(x, y) = min{2x, y}, bepaal u'y(8, 20).
u'y(8, 20) = 0 (volgens de uitwerkingen)
Moet dit niet u'y(8, 20) = 1 zijn?
Dit is het antwoord van een tentamen van vorig jaar, dus ik kan me niet voorstellen dat het fout is.quote:
min{2x,y} geeft de kleinste van 2x en y, voor (x,y) = (8,20) geeft hij dus 16; de 2x is actief daar, dus de afgeleide naar y is 0.
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
5.3 = 15
6.2 + 2 = 14
15 > 14
u′y(3, 2) = 6
Redeneer ik zo goed?
Dat je hier 5x = 6y+2 mist.quote:
5x > 6y+2, dan u′y(3, 2) = 6
5x < 6y+2, dan u′y(3, 2) = 0
Hello waar komt die 32,5 vandaan?
In de opgave staat:
....reduce sales prices by only 2.5% instead of 4%
"The cost of goods sold as a percentage of revenue would change proportionally with the price change."
Toen de price change nog 4% was, was de COGS 57.5% van Sales.
Hoeveel % is de COGS nu van Sales?
*Ik dacht zelf 0,975/0,96 * 0,575*
Ik doe echt mijn best maar bijvoorbeeld onderstaande opgave: ik weet gewoon niet goed waar ik moet beginnen...Ik begrijp steeds wel het idee van wat er moet gebeuren, maar de notatie is zo ingewikkeld. Ik zou graag iets hebben wat ik goed begreep waar ik kon beginnen. Kan iemand me helpen met het beter begrijpen van bijvoorbeeld het onderwerp "limieten van rijen" zoals bij de opgave hierboven?quote:Veronderstel daten
convergente rijen zijn in
.
Noteeren
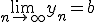
opgave
Doe een voorstel voor de limiet van de rijen bewijs je voorstel m.b.v. de definitie van de limiet van een rij.
definitie limiet van een rij
We zeggen dat een rijin
convergeert naar een
als:
We noemende limiet van de rij
Als je de notatie ingewikkeld vindt: probeer het eens (deels) in woorden op te schrijven. Als je het snapt dan stap je waarschijnlijk snel weer over op de wiskundige notatie want dat scheelt een hoop schrijfwerk en maakt het een stuk overzichtelijker.quote:
Dag allemaal. Ik heb nu het vak hogere wiskunde (wo) en ik vind het echt zooooo moeilijk.
[..]
Ik begrijp steeds wel het idee van wat er moet gebeuren, maar de notatie is zo ingewikkeld. Ik zou graag iets hebben wat ik goed begreep waar ik kon beginnen. Kan iemand me helpen met het beter begrijpen van bijvoorbeeld het onderwerp "limieten van rijen" zoals bij de opgave hierboven?
Snap je waar die definitie van de limiet vandaan komt? Zie je een beetje voor je wat er gebeurt, of vind je het maar vaag?
Ik moet zeggen dat ik haar zijn notatie van een rij ook niet helemaal vat, wat betekent (3xn - 2)n?quote:
[..]
Als je de notatie ingewikkeld vindt: probeer het eens (deels) in woorden op te schrijven. Als je het snapt dan stap je waarschijnlijk snel weer over op de wiskundige notatie want dat scheelt een hoop schrijfwerk en maakt het een stuk overzichtelijker.
Snap je waar die definitie van de limiet vandaan komt? Zie je een beetje voor je wat er gebeurt, of vind je het maar vaag?
Dat is best normale notatie. Het betekent:quote:
[..]
Ik moet zeggen dat ik haar notatie van een rij ook niet helemaal vat, wat betekent (3xn - 2)n?
3x1-2, 3x2-2 , ...
Het is dus gewoon de rij met n=1, n=2, ...
[ Bericht 2% gewijzigd door thenxero op 17-10-2011 19:54:11 ]
COGS = kosten / omzet * 100%quote:
Niet echt een wiskunde vraag, maar ik denk dat ik hier de beste antwoorden krijg :p
In de opgave staat:
....reduce sales prices by only 2.5% instead of 4%
"The cost of goods sold as a percentage of revenue would change proportionally with the price change."
Toen de price change nog 4% was, was de COGS 57.5% van Sales.
Hoeveel % is de COGS nu van Sales?
*Ik dacht zelf 0,975/0,96 * 0,575*
De kosten blijven gelijk, de prijs en dus de omzet stijgt met een factor 0.975/0.96 dus de COGS stijgen met een factor 0.96/0.975.
Dus ik zou zeggen 0,96/0,975 * 0,575.
Aha, dat klopt volgens het antwoordmodel inderdaad. thxquote:
[..]
COGS = kosten / omzet * 100%
De kosten blijven gelijk, de prijs en dus de omzet stijgt met een factor 0.975/0.96 dus de COGS stijgen met een factor 0.96/0.975.
Dus ik zou zeggen 0,96/0,975 * 0,575.
Je bent de notatie van een rij met accolades gewend? Of ken je die ook niet?quote:
[..]
Ik moet zeggen dat ik haar zijn notatie van een rij ook niet helemaal vat, wat betekent (3xn - 2)n?
Die inderdaad, of gewoon als an = 3n - 2quote:
[..]
Je bent de notatie van een rij met accolades gewend? Of ken je die ook niet?
Subtiel verschil: an = 3n - 2 is een element van de rij, en niet de rij zelfquote:
[..]
Die inderdaad, of gewoon als an = 3n - 2
.De definitie voor een limiet van een rij is nauw verwant met de bekende ε,δ definitie van een limiet van een functie. Begin even met dit door te nemen. Het gebruik van kwantoren maakt de notatie van de definitie compacter en overzichtelijker. De definitie voor een limiet L van een rij (an) of {an} is niets meer dan een formalisering van wat je je hier intuïtief bij voorstelt, namelijk dat je an zo dicht tegen L kunt laten aankruipen als je zelf wil als je n maar groot genoeg kiest.quote:
Dag allemaal. Ik heb nu het vak hogere wiskunde (wo) en ik vind het echt zooooo moeilijk.
[..]
Ik begrijp steeds wel het idee van wat er moet gebeuren, maar de notatie is zo ingewikkeld. Ik zou graag iets hebben wat ik goed begreep waar ik kon beginnen. Kan iemand me helpen met het beter begrijpen van bijvoorbeeld het onderwerp "limieten van rijen" zoals bij de opgave hierboven?
Vind je het correct als ik erachter had gehad n element uit {natuurlijke getallen} ?quote:
[..]
Subtiel verschil: an = 3n - 2 is een element van de rij, en niet de rij zelf
In het boek werd het altijd zo of met accolades gegeven dacht ik.
Ik moet zeggen dat ik wel altijd rijen en reeksen door elkaar haalde, omdat mensen ze vaak door elkaar gebruiken.
(ik moet toegeven dat het wel een beetje mierenneuken is)
Ah, bedankt. Ik ben nu de wiki pagina's aan het doornemen en zal morgen hier nog even terugkomen met wat ik ervan begrijpquote:
[..]
De definitie voor een limiet van een rij is nauw verwant met de bekende ε,δ definitie van een limiet van een functie. Begin even met dit door te nemen. Het gebruik van kwantoren maakt de notatie van de definitie compacter en overzichtelijker. De definitie voor een limiet L van een rij (an) of {an} is niets meer dan een formalisering van wat je je hier intuïtief bij voorstelt, namelijk dat je an zo dicht tegen L kunt laten aankruipen als je zelf wil als je n maar groot genoeg kiest.
Maar wat ik ook niet zo goed begrijp aan de hele notatie is het kommagebruik.Ik snap wel dat je bijvoorbeeld zegt:
(voor elk kind (k) bestaat er precies 1 moeder (v).
Maar in de omschrijving:
is me dit al een stuk minder duidelijk. Ik vind het moeilijk om dit "onder woorden te brengen" zegmaar...
Je kan het lezen als:quote:
[..]
Ah, bedankt. Ik ben nu de wiki pagina's aan het doornemen en zal morgen hier nog even terugkomen met wat ik ervan begrijp
Ik snap wel dat je bijvoorbeeld zegt:
(voor elk kind (k) bestaat er precies 1 moeder (v).
Maar in de omschrijving:
is me dit al een stuk minder duidelijk. Ik vind het moeilijk om dit "onder woorden te brengen" zegmaar...
Voor iedere epsilon groter dan 0 bestaat er een natuurlijk getal k0 zodat als k groter of gelijk is aan k0, dan is de afstand tussen xk en a kleiner dan epsilon.
Okequote:
[..]
Je kan het lezen als:
Voor iedere epsilon groter dan 0 bestaat er een natuurlijk getal k0 zodat als k groter of gelijk is aan k0, dan is de afstand tussen xk en a kleiner dan epsilon.
en waar is dan het stukje na de laatste komma? dus:want ik begrijp inderdaad: Voor "eerste stuk" bestaat "tweede stuk" zodat "achter dubbele punt"
Maar het "derde stuk" lijk ik dan te missen...
Ik vind het zelf mooier om het zo neer te zetten, al is het equivalent met jouw uitspraak:
Laat k0 en k natuurlijke getallen zijn en epsilon reëel. Dan is per definitie de limiet van xk gelijk aan a dan en slechts dan als
of eventueel
Snap je waarom dat allemaal hetzelfde is?
Dat is weliswaar wat beter te verteren dan drie kwantoren achter elkaar, maar formeel (syntactisch) is de eerste regel niet juist omdat je na ∀k≥k₀ een uitspraak verwacht.quote:
Daarmee geef je eigenlijk alleen nog aan dat k een natuurlijk getal is. Wat er gebeurt is het volgende: eerst neem je k als een willekeurig natuurlijk getal. Dan zeg je als hij groot genoeg is, dan geldt een bepaalde ongelijkheid. (een beetje omslachtig maar wel correct).
Ik vind het zelf mooier om het zo neer te zetten, al is het equivalent met jouw uitspraak:
Laat k0 en k natuurlijke getallen zijn en epsilon reëel. Dan is per definitie de limiet van xk gelijk aan a dan en slechts dan als
of eventueel
Snap je waarom dat allemaal hetzelfde is?
Je hebt gelijk, het is wel inzichtelijker alleen formeel misschien niet zo netjes. Die tweede is wat netter.quote:
[..]
Dat is weliswaar wat beter te verteren dan drie kwantoren achter elkaar, maar formeel (syntactisch) is het niet juist omdat je na ∀k≥k₀ een uitspraak verwacht.
Kan de afgeleide f' van een functie f een groter domein hebben dan de functie f zelf?
Een concreet voorbeeld:
Zeg je dat f'(x) = 1/x een groter domein heeft dan f(x)=log(x)?
De afgeleide van f:R naar R gedefinieerd door f(x) = log( |x| ) is f'(x)=1/x op heel R. Maar de afgeleide van g:R+ naar R, g(x) = log(x) is g' : R+ naar R, g'(x)=1/x.
Ik zou zeggen van niet omdat f'(x) is gedefinieerd als de limiet voor h → 0 van het differentiequotiënt (f(x+h)-f(x))/h en die limiet kan niet zijn gedefinieerd als f(x) niet is gedefinieerd. Je kunt hier wel zeggen dat f'(x) = 1/x de afgeleide is van f(x) = log |x| en dan kun je het domein van beide oprekken tot R\{0}.quote:
Een kleine vraag over een definitie:
Kan de afgeleide f' van een functie f een groter domein hebben dan de functie f zelf?
Een concreet voorbeeld:
Zeg je dat f'(x) = 1/x een groter domein heeft dan f(x)=log(x)?
quote:
Nee, kijk maar naar de definitie van de afgeleide: daar heb je toch echt de functiewaardes nodig en daar moet de functie dus wel gedefinieerd zijn.
De afgeleide van f:R naar R gedefinieerd door f(x) = log( |x| ) is f'(x)=1/x op heel R. Maar de afgeleide van g:R+ naar R, g(x) = log(x) is g' : R+ naar R, g'(x)=1/x.
quote:
[..]
Ik zou zeggen van niet omdat f'(x) is gedefinieerd als de limiet voor h → 0 van het differentiequotiënt (f(x+h)-f(x))/h en die limiet kan niet zijn gedefinieerd als f(x) niet is gedefinieerd. Je kunt hier wel zeggen dat f'(x) = 1/x de afgeleide is van f(x) = log |x| en dan kun je het domein van beide oprekken tot R\{0}.
Ok, dat is ook wel zo logisch jaquote:
Minibeer, bij jouw voorbeeldt geldt f'(x) = 1/x alleen voor x>0.
Danks!
Van wat?quote:
Vrij irritant die oefententamens die makkelijker zijn dan echte tentamens.. Voor deze had ik een 10 kunnen halen maar de echte is sowieso een stuk moeilijker, als ik de trial exams met de echte vergelijk was het vorige jaren ook zo..
Geef de differentiaalvergelijking die bij dit model hoort.
O'(t) =
Iemand die me op weg kan helpen?
Huh ben ik nu gek aan het worden, of klopt die 70cos60 gewoon niet. Ze rekenen de tangentiële versnelling uit. Dat is in de richting van de pijl.
Je doet toch 70 / cos60
Want.
Aanliggende delen door schuine zijde. Dus 70 ft/s2 / tangentiële zijde. = Cos 60
Dus omschrijven geeft 70 / cos 60. om at te krijgen
Het klopt wel, de tangentiële versnelling is de aanliggende zijde, de radiale versnelling is de overstaande zijde. De gegeven versnelling van 70 ft/s2 is dus de schuine zijde.quote:
[ afbeelding ]
Huh ben ik nu gek aan het worden, of klopt die 70cos60 gewoon niet. Ze rekenen de tangentiële versnelling uit. Dat is in de richting van de pijl.
Je doet toch 70 / cos60
Want.
Aanliggende delen door schuine zijde. Dus 70 ft/s2 / tangentiële zijde. = Cos 60
Dus omschrijven geeft 70 / cos 60. om at te krijgen
Dat geeft cos(60°) = at/a en dus at = a*cos(60°)
Jij denkt dat je alsnog het antwoord krijgt voorgekauwd als je gewoon de vraag herhaalt?quote:
Leid uit de formule van opdracht a (O(t) = 0,5*2t) de differentiaalvergelijking af die bij dit model hoort, d.w.z. geef de vergelijking die het verband legt tussen de afgeleide O'(t) en de functie O(t): O'(t) =
Een hint: schrijf 2t eerst even als een e-macht, dat maakt het opschrijven van de afgeleide eenvoudiger.
de afgeleide van de formule zou toch ln2*2t moeten zijn?
Is dat al een begin?
(Even voor de duidelijkheid, voor vandaag had ik alleen nog maar de afgeleide van makkelijke formules gemaakt en thats it. Dus ik heb geen idee waar dit allemaal over gaat..)
Oh ja..., maar de normaal versnelling die wijst wel naar het middelpunt right. Of hoeft dat niet per sé?quote:
[..]
Het klopt wel, de tangentiële versnelling is de aanliggende zijde, de radiale versnelling is de overstaande zijde. De gegeven versnelling van 70 ft/s2 is dus de schuine zijde.
Dat geeft cos(60°) = at/a en dus at = a*cos(60°)
De afgeleide van O(t) = ½∙2t = ½∙et∙ln 2 is O'(t) = ½∙ln2∙2tquote:
Nee ik dacht ik verduidelijk eventjes.
de afgeleide van de formule zou toch ln2*2t moeten zijn?
Is dat al een begin?
(Even voor de duidelijkheid, voor vandaag had ik alleen nog maar de afgeleide van makkelijke formules gemaakt en thats it. Dus ik heb geen idee waar dit allemaal over gaat..)
Dus heb je: O'(t) = ln 2 ∙ O(t)
Je kunt dit ook met differentialen opschrijven, dan wordt het:
dO = ln 2 ∙ O ∙ dt
Ja, anders zou het deeltje (of in dit geval de straaljager) niet een cirkelvormige baan kunnen beschrijven. Anders gezegd, zonder radiale versnelling vliegt het deeltje rechtdoor.quote:
[..]
Oh ja..., maar de normaal versnelling die wijst wel naar het middelpunt right. Of hoeft dat niet per sé?
Ik vraag me serieus af of je wel vorderingen maakt in je studie. Twee jaar geleden was je namelijk ook al bezig met dezelfde soort sommetjes over versnellingen en kromtestralen, en zo te zien ook uit precies hetzelfde boek.quote:
[..]
Oh ja..., maar de normaal versnelling die wijst wel naar het middelpunt right. Of hoeft dat niet per sé?
Er staat "x>-1" Lim (Sin(2*pi*x))/2x; substitueer y=2*pi*x
En vervolgens staat er "y->-2*pi" Lim Sin(y)/y;
edit: oh wacht, ze nemen de grenzen mee.
wat doet die -, en waar blijft pi in de noemer?quote:
Ik ben hier naar een uitwerking aan het staren en iets bevalt me niet.
Er staat "x>-1" Lim (Sin(2*pi*x))/2x; substitueer y=2*pi*x
En vervolgens staat er "y->-2*pi" Lim Sin(y)/y;
edit: oh wacht, ze nemen de grenzen mee.
Gastquote:
[..]
Ik vraag me serieus af of je wel vorderingen maakt in je studie. Twee jaar geleden was je namelijk ook al bezig met dezelfde soort sommetjes over versnellingen en kromtestralen, en zo te zien ook uit precies hetzelfde boek.
[ Bericht 87% gewijzigd door lipper op 18-10-2011 19:42:24 ]
Damn wat een geheugenquote:
Op Maar inderdaad wel interessante vraag.Ik weet dat ik de middelwaarde stelling moet gebruiken, maar ik kan geen ln 0 nemen. Hoe vermijd ik dit?
[ Bericht 49% gewijzigd door GlowMouse op 18-10-2011 20:56:04 ]
x-1 voor x>0 is minimaal -1. Je hoeft de stelling daarom voor heel kleine x niet te controleren.quote:
Bewijs de volgende ongelijkheid:voor alle x>0
Ik weet dat ik de middelwaarde stelling moet gebruiken, maar ik kan geen ln 0 nemen. Hoe vermijd ik dit?
Nu stuit ik op het volgende:
Algemene oplossing voor N uitgedrukt in t en k: N(t) = 53660*e-k*t(deze formule is juist)
En de volgende vraag luidt: De halfwaardetijd van C14 is 5750 jaar. Bereken hieruit de waarde van k in 5 decimalen.
k =
- De halfwaardetijd is 5750 jaar, is het juist als ik dan dit zeg: N(5750) = 53660/2?
- Dan weet je dus de N en de t=5750
- Dan: 26830 = 53660*e-k*5750
- En dan weet ik niet hoe ik verder moet...
Hint:quote:
Thanks! Ik ben inmiddels een stukje verder gekomen.
Nu stuit ik op het volgende:
Algemene oplossing voor N uitgedrukt in t en k: N(t) = 53660*e-k*t(deze formule is juist)
En de volgende vraag luidt: De halfwaardetijd van C14 is 5750 jaar. Bereken hieruit de waarde van k in 5 decimalen.
k =
- De halfwaardetijd is 5750 jaar, is het juist als ik dan dit zeg: N(5750) = 533660/2?
- Dan weet je dus de N en de t=5750
- Dan: 266830 = 53660*e-k*5750
- En dan weet ik niet hoe ik verder moet...
ln(ek) = k
Alleen heb ik geen idee of je op de goede weg zit, wat is de output van N(t)?
Dan krijg ik als totale output: 1,20547