SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Stel dat je het op [0,1] laat. Voor x=0.5 integreer je dan ook over het stuk y=[0,0.5], terwijl de kansdichtheid daar helemaal niet gegeven is door 8xy. Daar is de kansdichtheid gewoon 0. Maar omdat de integraal van 0 toch 0 is, laat je dat deel gewoon helemaal weg. Dan houd je [x,1] over.quote:Op woensdag 5 oktober 2011 20:54 schreef JohnSpek het volgende:
[..]
Op vraag 3. Ohja, ik bedoelde inderdaad [x,1] , maar waarom zou ik het interval niet gewoon [0,1] kunnen laten? Waarom moet ik dit omschrijven in een interval afhankelijk van x (ik weet niet of ik dit goed zeg, maar je begrijpt hopelijk wat ik bedoel)


Het is dus zoiets van:quote:Op woensdag 5 oktober 2011 20:59 schreef thenxero het volgende:
Volgens mij bedoel je E(E(X|Y)). Omdat Y een stochast is, is de verwachtingswaarde van X gegeven Y nog afhankelijk van Y. Dus E(X|Y) kan je zien als een nieuwe stochast die door Y bepaald wordt. Van deze "nieuwe stochast" kan je dus weer de verwachtingswaarde bepalen.
Zie hier voor een bewijs dat het gelijk is aan E(X).
http://en.wikipedia.org/wiki/Expected_value#Iterated_expectation
Je krijgt E(X|Y) door eerst de conditionele kansdichtheidsfunctie te bepalen, wat de joint kansdichtheidsfunctie is(8xy), geschaald naar de marginale kansdichtheidsfunctie van y.
Dat is dan 8xy/(4y^3) = 2x/y
Dat geeft mij dus een kansdichtheidsfunctie van x, als ik de variabel y zou invulle
Als ik dus de verwachtingswaarde van (2x/y) pak over alle mogelijke y waarden dan zou ik logischerwijs de verwachtingswaarde krijgen van x omdat ik voor elke y kijk wat mijn x waarden dan zou zijn.
Klopt deze gedachtegang een beetje?
Maar het hoeft niet weg gelaten te worden? Als de integraal toch 0 is dan maakt het voor het antwoord niet zoveel uit of je over [0,1] of [x,1] integreert?quote:Op woensdag 5 oktober 2011 21:13 schreef twaalf het volgende:
[..]
Stel dat je het op [0,1] laat. Voor x=0.5 integreer je dan ook over het stuk y=[0,0.5], terwijl de kansdichtheid daar helemaal niet gegeven is door 8xy. Daar is de kansdichtheid gewoon 0. Maar omdat de integraal van 0 toch 0 is, laat je dat deel gewoon helemaal weg. Dan houd je [x,1] over.
Maar de uitkomst is wel degelijk een andere functie. Als ik zou integeren over [0,1] dan zou het 4xy^2 = 4x zijn, terwijl het over [x,1] 4x - 4x^3 is.
[ Bericht 26% gewijzigd door JohnSpek op 05-10-2011 21:22:25 ]


Ja dat klopt wel.
Je berekent (in het discrete geval)
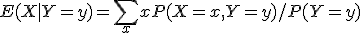
Dan vul je in plaats van y weer Y in, en dan neem je daar weer de verwachtingswaarde van.
Je berekent (in het discrete geval)
Dan vul je in plaats van y weer Y in, en dan neem je daar weer de verwachtingswaarde van.


Klopt, maar dan moet je dus een andere integrand nemen. De functie is op [0,x] gedefinieerd als 0, en op [x,1] gedefinieerd als 8xy.quote:Op woensdag 5 oktober 2011 21:16 schreef JohnSpek het volgende:
[..]
Maar het hoeft niet weg gelaten te worden? Als de integraal toch 0 is dan maakt het voor het antwoord niet zoveel uit of je over [0,1] of [x,1] integreert?
Wat je eigenlijk doet is, zoals GlowMouse zegt,
waarbij je dus de functie opdeelt in een deel waarin f=0, en een deel waarin f=8xy.


Oke, maar stel ik wil dus de kans weten dat 0 < X < 0.5. (en dit wil doen vanuit de marginale kansdichtheidsfunctie, gewoon als oefening).
Als ik 8xy integreer naar y over [1,x] dan komt daar 4x - 4x^3 uit. Dat integreren op 0 < X < 0.5
Dat zou dan zijn 2 * 0.5^2 - 0.5^4
Hoe zou ik dat doen als je gewoon het 0 stuk erbij laat als het waren?
(Dus als ik 8xy eerst integreer naar y over interval [0,1] om de marginale kansdichtheidsfunctie van x te bepalen)
Als ik 8xy integreer naar y over [1,x] dan komt daar 4x - 4x^3 uit. Dat integreren op 0 < X < 0.5
Dat zou dan zijn 2 * 0.5^2 - 0.5^4
Hoe zou ik dat doen als je gewoon het 0 stuk erbij laat als het waren?
(Dus als ik 8xy eerst integreer naar y over interval [0,1] om de marginale kansdichtheidsfunctie van x te bepalen)


Haakjes wegwerkenquote:Op woensdag 5 oktober 2011 21:45 schreef verwarmingsbank het volgende:
x(2x-3)=2(3x+1)
Wat is X? En wat is de berekening.
Klas: Atheneum 4


Ik heb het even voor je gepaint:
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.


Dat begrijp ik, maar de uitkomst is steeds fout. Hoe moet ik deze doen volgens jullie?quote:
Iedereen aan wie ik het gevraagd heb begrijpt het niet bij mij op school.


Schrijf maar de stappen op die je al hebt gemaakt.quote:Op woensdag 5 oktober 2011 21:48 schreef verwarmingsbank het volgende:
[..]
Dat begrijp ik, maar de uitkomst is steeds fout. Hoe moet ik deze doen volgens jullie?
Iedereen aan wie ik het gevraagd heb begrijpt het niet bij mij op school.


x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23


Aha, ik had de tekening al wel gemaakt voor mezelf, maar nog niet zo naar gekekenquote:Op woensdag 5 oktober 2011 21:47 schreef twaalf het volgende:
Ik heb het even voor je gepaint:
[ afbeelding ]
• Jij houdt nogal vast aan f(x,y)=8xy. Het punt is, dat dat alleen maar in het gearceerde gebied hierboven geldt. Daarbuiten is f(x,y) gelijk aan 0 - als het goed is staat dat ook zo gedefinieerd in je opgave.
• Wat doe je precies als je van 0 tot 1 integreert? Dan integreer je 8xy over de gehele blauwe lijn. Maar dat heeft geen zin, want op het b-gedeelte van de lijn is f(x,y) niet gelijk aan 8xy. Daarom heeft het alleen maar zin om over het a-gedeelte te integreren.
Bedankt voor de moeite en uitleg! en xero/glowmouse ook bedankt ;


Je hebt gezegd C=1 terwijl het moet zijn C=-1.quote:Op woensdag 5 oktober 2011 21:52 schreef verwarmingsbank het volgende:
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*1 = 16,25
X1 = (-b + Wortel van 16,25) / 2*1 = 4,27
X2 = (-b - Wortel van 16,25) / 2*1 = 0,23


Bedankt voor de opmerking.
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel


Je methode is goed. Als je je antwoord invult in x(2x-3)=2(3x+1) dan weet je of het antwoord ook klopt.quote:Op woensdag 5 oktober 2011 21:58 schreef verwarmingsbank het volgende:
Bedankt voor de opmerking.
x(2x-3)=2(3x+1)
2x² - 3x = 6x + 2
2x² -9x -2 = 0
x² - 4,5x -1 = 0
D=B²-4AC
D= (-4,5)² -4*1*-1 = 24,25
X1 = (-b + Wortel van 24,25) / 2*1 = 4,71
X2 = (-b - Wortel van 24,25) / 2*1 = 0,21
Klopt dit dan wel


En als tip voor de volgende keer om niet 2x² -9x -2 = 0 door twee te delen als je daarmee breuken krijgt. Want de abc-formule werkt ook prima met a=2.


Weet iemand een goede buitenlandse universiteit waar ze vakken als Statistics, Stochastic Integration, Lévy Processes, Financial Stochastics, Financial Time Series, Measure Theory, etc geven? Een master in Financial mathematics / stochastics dus.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.


Als ik X = 4,71 invul dan krijg ik 30,2382 = 30,26
Is zo'n klein verschil niet erg of wat doe ik nu weer fout
Is zo'n klein verschil niet erg of wat doe ik nu weer fout


Je weet pas echt zeker of het klopt als je het antwoord in "wortelvorm" laat staan, in plaats van numerieke benaderingen te gebruiken. Nu weet je alleen maar dat het waarschijnlijk goed is omdat een afwijking van 0,02 wel te verklaren is als je afrondt op 2 decimalen, maar zeker weten doe je niet.quote:Op woensdag 5 oktober 2011 22:03 schreef verwarmingsbank het volgende:
Als ik X = 4,71 invul dan krijg ik 30,2382 = 30,26
Is zo'n klein verschil niet erg of wat doe ik nu weer fout


Wow: in het antwoorden boekje staat dit:
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122


één minnetje moet een plusje zijn. Dan krijg je -0,2122... en voor de andere 4.71221...quote:Op woensdag 5 oktober 2011 22:10 schreef verwarmingsbank het volgende:
Wow: in het antwoorden boekje staat dit:
9/4 - 1/4 Wortel 97 OF 9/4 - 1/4 Wortel 97
Oftewel er staat 2 keer hetzelfde getal
Wanneer ik dit trouwens in de rekenmachine gooi dan krijg ik uit:-0,2122
Volgende keer dus gewoon die wortel laten staan. Dan heb je een precies antwoord, en daar zijn wiskundigen altijd blij mee.
--------------
Even mijn laatste post naar beneden brengen:
quote:Weet iemand een goede buitenlandse universiteit waar ze vakken als Statistics, Stochastic Integration, Lévy Processes, Financial Stochastics, Financial Time Series, Measure Theory, etc geven? Een master in Financial mathematics / stochastics dus.
Ik zit een beetje rond te kijken maar de UK is onbetaalbaar, en Duitse websites geven vaak vage of weinig informatie.
[ Bericht 16% gewijzigd door thenxero op 05-10-2011 22:31:12 ]


Al die opgaven is aantonen voor 1 en dan voor k+1 aantonen met inductie, als je eenmaal 1 gehad hebt zijn ze allemaal hetzelfde.quote:Op woensdag 5 oktober 2011 10:48 schreef Physics het volgende:
[..]
Is niet gespecificeerd maar bij de andere opgaven betekent deelbaar idd dat er een natuurlijk getal uitkomt.
Hoeveel tijd ben je trouwens tot nu toe voor alles kwijt?
En waarom was meneer Heij trouwens eigenlijk een week afwezig?
Beneath the gold, bitter steel


Ja ik heb ze nu allemaal gemaakt. Hoeveel tijd ik kwijt ben vind ik moeilijk te zeggen, ik doe nu zeg maar wat opgegeven staat en dat kost me ongeveer 20 uur per week, dus contact + zelfstudie. Alleen wil ik eigenlijk wel wat harder studeren voor de betere cijfers.quote:Op woensdag 5 oktober 2011 22:41 schreef Fingon het volgende:
[..]
Al die opgaven is aantonen voor 1 en dan voor k+1 aantonen met inductie, als je eenmaal 1 gehad hebt zijn ze allemaal hetzelfde.
Hoeveel tijd ben je trouwens tot nu toe voor alles kwijt?
En waarom was meneer Heij trouwens eigenlijk een week afwezig?


Hee jongens ik heb een vraag (joh, echt?  )
)
ELx = X / √(ln(x2) - ln(y2)) * De afgeleide F(x,y) naar X. Maar ik kom niet uit die afgeleide volgens mij
Ik dacht dat de afgeleide 1/2(ln(x2) - ln(y2))-1/2 * (2x/x2) was maar dat weet ik niet zeker. Kan iemand mij helpen/vertellen of ik op de goede weg ben?
Alvast heel erg bedankt
Dan doe ik eerst de partiele elasticiteit van x.quote:F(x,y) = √(ln(x2) - ln(y2)) (de hele formule staat dus onder de wortel)
Bepaal de partiële elasticiteit van F naar x en de partiële elasticiteit van F naar y en tel beide bij elkaar op.
ELx = X / √(ln(x2) - ln(y2)) * De afgeleide F(x,y) naar X. Maar ik kom niet uit die afgeleide volgens mij
Ik dacht dat de afgeleide 1/2(ln(x2) - ln(y2))-1/2 * (2x/x2) was maar dat weet ik niet zeker. Kan iemand mij helpen/vertellen of ik op de goede weg ben?
Alvast heel erg bedankt


Oke dankjewelquote:Op donderdag 6 oktober 2011 17:15 schreef twaalf het volgende:
De part. afgeleide is goed, twee keer de kettingregel gebruiken inderdaad.


Als ik die formule volg die je hebt geplaatst:
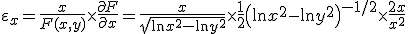
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus
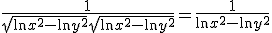
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus


Super bedanktquote:Op donderdag 6 oktober 2011 17:28 schreef twaalf het volgende:
Als ik die formule volg die je hebt geplaatst:
dan valt de 1/2 weg tegen de 2, valt de x^2 in de noemer weg tegen de twee factoren x in de teller. In de noemer houd je dan het kwadraat van een wortel over, dus


Oh dus beide elasticiteiten optellen zal op 0 uitkomen?quote:Op donderdag 6 oktober 2011 17:38 schreef twaalf het volgende:
Nee, want je hebt daar nog een factor -1 staan bij de tweede keer dat je de kettingregel toepast.


In vervolg op wat GlowMouse zegt:quote:Op vrijdag 7 oktober 2011 15:22 schreef Tauchmeister het volgende:
ex ln(x + 1/2) = 0
⇒ ln(x + 1/2) = 0
Waarom kan ik ex hier weglaten?
en e^x kan nooit 0 zijn, dus moet het andere stuk wel gelijk aan 0 zijn en kan je e^x gewoon weg laten.


Waarom geldt:
Ik snap er niks van
(hints worden ook erg op prijs gesteld )
)
[ Bericht 16% gewijzigd door minibeer op 07-10-2011 23:00:41 ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld
[ Bericht 16% gewijzigd door minibeer op 07-10-2011 23:00:41 ]
Finally, someone let me out of my cage


Ik zal alvast een aanzet geven:
Er staat een binomiaalcoëfficient in de formule, dus we hebben
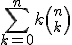
Nu prop ik daar vrolijk een x-macht bij:
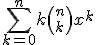
Dit moeten we dan evalueren in x=1.
Nog meer hints? .
.
Er staat een binomiaalcoëfficient in de formule, dus we hebben
Nu prop ik daar vrolijk een x-macht bij:
Dit moeten we dan evalueren in x=1.
Nog meer hints?


Het kan zelfs nog simpeler bedenk ik me opeens, je kan factoren k in de teller en noemer tegen elkaar wegstrepen, dan staat het er zowat.


Als je hints wil hebben is het wel handig als iedereen je plaatje kan zien. Ik zie het hier niet omdat de links naar plaatjes van Wolfram maar een beperkte tijd geldig zijn.quote:Op vrijdag 7 oktober 2011 17:31 schreef minibeer het volgende:
Waarom geldt:
[ afbeelding ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld)


Excuses, ik kan geen latex, anders zou ik het wel even ingetypt hebben. Gefixt nu.quote:Op vrijdag 7 oktober 2011 19:24 schreef Riparius het volgende:
[..]
Als je hints wil hebben is het wel handig als iedereen je plaatje kan zien. Ik zie het hier niet omdat de links naar plaatjes van Wolfram maar een beperkte tijd geldig zijn.
[ Bericht 0% gewijzigd door minibeer op 07-10-2011 23:01:48 ]
Finally, someone let me out of my cage


Kan ook makkelijk zonder inductie.quote:Op vrijdag 7 oktober 2011 17:31 schreef minibeer het volgende:
Waarom geldt:
[ afbeelding ]
Ik snap er niks van
(hints worden ook erg op prijs gesteld)
Hint:
Volgens het Binomium van Newton.


Ik zie het nu wel inderdaad, ik zie het helaas alleen de andere kant op, als ik met jou hint begin en die vervolgens vermenigvuldig met n zie ik vrij makkelijk dat het gelijk is aanquote:Op vrijdag 7 oktober 2011 23:41 schreef thenxero het volgende:
[..]
Kan ook makkelijk zonder inductie.
Hint:
Volgens het Binomium van Newton.
Andersom echter nog niet, maar dat zal wel aan mijn inzicht liggen (sowieso heb ik nog nooit met die binomiaalcoëfficiënten gerekend op deze manier, dus ik moet gewoon die rekenregels nog wat beter leren kennen)
Finally, someone let me out of my cage


Als je het de ene kant opziet dan is dat genoeg, want je werkt met = tekens  . Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.
. Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.


True. Het grappige is dat ik deze vraag op een tentamen trouwens goed hadquote:Op vrijdag 7 oktober 2011 23:55 schreef thenxero het volgende:
Als je het de ene kant opziet dan is dat genoeg, want je werkt met = tekens. Vaak werkt één bepaalde kant op heel intuïtief, maar de andere kant op heel erg getruct... dat is normaal.
Finally, someone let me out of my cage


Dat is eigenlijk hetzelfde idee als inductie, alleen doe je het met inductie algemener. Dat het in de eerste 5 a 6 gevallen klopt garandeert niets over het 7e geval of daarna. Inductie is denk ik ook nog sneller dan die gevallen uitschrijven.quote:Op zaterdag 8 oktober 2011 00:39 schreef minibeer het volgende:
[..]
True. Het grappige is dat ik deze vraag op een tentamen trouwens goed had. Ik was er alleen op gekomen door de eerste 5 of 6 gevallen uit te schrijven en daar de formule uit te concluderen (het was geen wiskunde, dus er werd gelukkig geen bewijs gevraagd), maar ik had geen idee waarom deze formule nou eigenlijk gold.


Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met 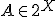 ,
, 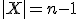 en
en 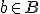 ,
, 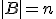


Ik vind het prettiger om een paar vergelijkingen op te schrijven dan om een beredenering te houden wat je aan het tellen bent.quote:Op zaterdag 8 oktober 2011 00:48 schreef twaalf het volgende:
Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met,
en
,


Wat heb je aan de formule die je bewijst als je niet weet voor welk probleem je precies een andere uitdrukking hebt gevonden? Natuurlijk maakt het uiteindelijk niet uit of je het met formulemanipulatie of tellen doet, maar dit is nou samen met gonio juist een vakgebied waar je eens iets anders kunt doen dan manipuleren.


Hmm, zo heb ik er nooit tegenaan gekeken, maar ik weet niet of ik dat zo gelijk kan zienquote:Op zaterdag 8 oktober 2011 00:48 schreef twaalf het volgende:
Het is m.i. beter en plezieriger om zulke sommen met combinatoriek te bewijzen, door daadwerkelijk te kijken naar wat je telt. Je kunt in dit geval wel beredeneren dat je zowel links als rechts het aantal paren telt (A,b) met,
en
,
Finally, someone let me out of my cage


 Op
Op 