SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Ze willen weten welk getal je op de plaats van de a moet invullen om een lijn te krijgen die evenwijdig loopt aan y=3x-1
Met een klein beetje basiskennis van formules van rechte lijnen moet dat lukken. Welk getal geeft het hellingsgetal weer in y=ax+b?
Met een klein beetje basiskennis van formules van rechte lijnen moet dat lukken. Welk getal geeft het hellingsgetal weer in y=ax+b?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Twee lijnen zijn evenwijdig als ze elkaar nooit snijden, dus beide lijnen moeten even stijl lopen, anders snijden ze elkaar ooit. En er is een a waarvoor dat geldt.
a wordt niet gestuurd, maar de x uit F^n wordt gestuurd. a is maar een parameter. Voor de rest lijkt dit me gewoon definities gebruiken?quote:Op zondag 9 oktober 2011 20:19 schreef Anoonumos het volgende:
Wat betekent het precies dat a wordt gestuurd naar de afbeelding? Ik moet dus aantonen dat T lineair, injectief en subjectief is maar ik snap niet helemaal wat er met a gebeurt.
[ Bericht 3% gewijzigd door twaalf op 09-10-2011 20:47:35 ]
Het kan ook zonder vectoren een stuk korter dan wat keesjeislief doet als je gebruik maakt van de identiteitquote:
[..]
Zo kan het dus ook. Met vectoren is wel het kortst en eenvoudigst.
tan(α-β) = (tan α - tan β)/(1+ tan α∙tan β)
Hebben we twee lijnen met een richtingscoëfficiënt a resp. b, dan maken deze lijnen hoeken α resp. β met de (positieve) x-as zodanig dat a = tan α en b = tan β. Als nu het product ab, en daarmee het product tan α∙tan β, gelijk is aan -1, dan is tan(α-β) ongedefinieerd, en dat kan alleen als α - β = ½π + κ∙π (k ∈Z), QED.
[ Bericht 0% gewijzigd door Riparius op 10-10-2011 12:14:58 ]
Ik snap iets niet bij het oplossen van homogeneous 2de order lineaire difference equations
(In de vorm van y(t+2) - y(t+1) - 6y(t) = 0 , dus de y 2 periodes in de toekomst is te verklaren in termen van het heden en de eerst volgende periode.) Ik zet het dik gedrukt neer wanneer ik het niet snap.
Stel y(t+2) - y(t+1) - 6y(t) = 0 en we willen de algemene oplossing vinden. Dan zegt de docent dat we gewoon is moeten proberen om y(t) = m^t
Dan:
y(t) = m^(t)
y(t+1) = m^(t+1)
y(t+2) = m^(t+2)
Invullen in de difference equation
m^(t+2) - m^(t+1) - 6*m^t = 0
m^t * ( m^2 - m - 6 ) = 0
Dan zegt hij m^t is 0 of m^2 - m -6 is 0 , maar m^t is 0 is geen interessante oplossing. (Waarom niet?) Ook al is het m = 0 , waarom is dat niet interessant?
Dus we gaan verder met m^2 - m - 6 = 0
m = 3 v m = -2
Dus y(t) = 3^t of y(t) = (-2)^t
Nu zegt de docent
Dus y(t) = 3^t * A + B * (-2)^t
Waarom? Ik begrijp niet waarom hij beide oplossingen bij elkaar optelt? En waarom kan dat?
Waarom zou je de A en B er ook voor zetten?
Ik begrijp niet waarom je niet gewoon de 2 losse oplossingen houdt, het doel van het bij elkaar optellen ontgaat mij dus een beetje.
(In de vorm van y(t+2) - y(t+1) - 6y(t) = 0 , dus de y 2 periodes in de toekomst is te verklaren in termen van het heden en de eerst volgende periode.) Ik zet het dik gedrukt neer wanneer ik het niet snap.
Stel y(t+2) - y(t+1) - 6y(t) = 0 en we willen de algemene oplossing vinden. Dan zegt de docent dat we gewoon is moeten proberen om y(t) = m^t
Dan:
y(t) = m^(t)
y(t+1) = m^(t+1)
y(t+2) = m^(t+2)
Invullen in de difference equation
m^(t+2) - m^(t+1) - 6*m^t = 0
m^t * ( m^2 - m - 6 ) = 0
Dan zegt hij m^t is 0 of m^2 - m -6 is 0 , maar m^t is 0 is geen interessante oplossing. (Waarom niet?) Ook al is het m = 0 , waarom is dat niet interessant?
Dus we gaan verder met m^2 - m - 6 = 0
m = 3 v m = -2
Dus y(t) = 3^t of y(t) = (-2)^t
Nu zegt de docent
Dus y(t) = 3^t * A + B * (-2)^t
Waarom? Ik begrijp niet waarom hij beide oplossingen bij elkaar optelt? En waarom kan dat?
Waarom zou je de A en B er ook voor zetten?
Ik begrijp niet waarom je niet gewoon de 2 losse oplossingen houdt, het doel van het bij elkaar optellen ontgaat mij dus een beetje.
- Je weet al dat y=0 een oplossing is.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
En met die A en B kan je aan beginvoorwaarden voldoen. Als je bijvoorbeeld de waarden van y op t=0 en t=1 weet, weet je ook de waarden voor A en Bquote:
- Je weet al dat y=0 een oplossing is.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!
Aha, net even ingevuld en er komt inderdaad gewoon 0 uit. Bedankt!quote:
- Je weet al dat y=0 een oplossing is.
- De vraag waarom optellen (en vermenigvuldigen met A of B) kan, kan je zelf beantwoorden: vul hem maar in in de oorspronkelijke vergelijking en gebruik dat elk van te termen voldoet.
- Het doel is om alle oplossingen in 1x weer te geven. Het geval y=0 vermeld je zo ook.
Stel y0 = 0 en y1 = 1quote:Op maandag 10 oktober 2011 18:10 schreef freiss het volgende:
[..]
En met die A en B kan je aan beginvoorwaarden voldoen. Als je bijvoorbeeld de waarden van y op t=0 en t=1 weet, weet je ook de waarden voor A en B
Dan zou je toch ook dit systeem van vergelijkingen kunnen oplossen:
0 = 3^t
1 = 3^t
0 = (-2)^t
1 = (-2)^t
Of werkt dat zo niet? (3^t = 0 wordt al onmogelijk?)
In plaats van A*3^0 + B*(-2)^0 = 0 en A*3^1 + B*(-2)^1 = 1 oplossen.
Het doel is om alle oplossingen te vinden. Het idee is dat het een lineaire vergelijking is, d.w.z. als y0(t) en y1(t) twee oplossingen zijn, dan is de functie y2(t)=A*y0(t)+B*y1(t) voor willekeurige constanten A en B ook een oplossing. In feite is de ruimte van alle oplossingen een 2-dimensionale deelruimte. De algemene oplossingsmethode is als volgt: ten eerste vind je zoveel mogelijk lineair onafhankelijke oplossingen y1,...,yn. Die oplossingen spannen dan de oplossingsruimte op, in de zin dat elk element in de oplossingsruimte dan van de vorm a1*y1(t)+a2*y2(t)+...+an*yn(t) is. Om de lineair onafhankelijke oplossingen te vinden gebruik je die 'gok' y(t)=m^t. (Dat is natuurlijk niet echt een gok, die werkt altijd voor dit soort vergelijkingen, net zoals je voor gewone lineaire dv's exponentiele functies gebruikt als 'gok').quote:
Ik snap iets niet bij het oplossen van homogeneous 2de order lineaire difference equations
(In de vorm van y(t+2) - y(t+1) - 6y(t) = 0 , dus de y 2 periodes in de toekomst is te verklaren in termen van het heden en de eerst volgende periode.) Ik zet het dik gedrukt neer wanneer ik het niet snap.
Stel y(t+2) - y(t+1) - 6y(t) = 0 en we willen de algemene oplossing vinden. Dan zegt de docent dat we gewoon is moeten proberen om y(t) = m^t
Dan:
y(t) = m^(t)
y(t+1) = m^(t+1)
y(t+2) = m^(t+2)
Invullen in de difference equation
m^(t+2) - m^(t+1) - 6*m^t = 0
m^t * ( m^2 - m - 6 ) = 0
Dan zegt hij m^t is 0 of m^2 - m -6 is 0 , maar m^t is 0 is geen interessante oplossing. (Waarom niet?) Ook al is het m = 0 , waarom is dat niet interessant?
Dus we gaan verder met m^2 - m - 6 = 0
m = 3 v m = -2
Dus y(t) = 3^t of y(t) = (-2)^t
Nu zegt de docent
Dus y(t) = 3^t * A + B * (-2)^t
Waarom? Ik begrijp niet waarom hij beide oplossingen bij elkaar optelt? En waarom kan dat?
Waarom zou je de A en B er ook voor zetten?
Ik begrijp niet waarom je niet gewoon de 2 losse oplossingen houdt, het doel van het bij elkaar optellen ontgaat mij dus een beetje.
[ Bericht 2% gewijzigd door keesjeislief op 10-10-2011 18:26:27 ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Wat een gemiereneuk, je spaart misschien twee regels uit en moet in ruil daarvoor een veel onbekendere goneometrische identiteit gebruiken. Pythagoras is natuurlijk verreweg de meest elegante en simpele oplossing.quote:
[..]
Het kan ook zonder vectoren een stuk korter dan wat keesjeislief doet als je gebruik maakt van de identiteit
tan(α-β) = (tan α - tan β)/(1+ tan α∙tan β)
Hebben we twee lijnen met een richtingscoëfficiënt a resp. b, dan maken deze lijnen hoeken α resp. β met de (positieve) x-as zodanig dat a = tan α en b = tan β. Als nu het product ab, en daarmee het product tan α∙tan β, gelijk is aan -1, dan is tan(α-β) ongedefinieerd, en dat kan alleen als α - β = ½π + κ∙π (k ∈Z), QED.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Nee, zo werkt dat niet. Je kunt niet uitgaan van twee - willekeurige - randvoorwaarden en dan verwachten dat je de algemene oplossing zult vinden. Er is precies één oplossing die aan jouw randvoorwaarden voldoet, namelijk y(t) = (1/5)∙3t - (1/5)∙(-2)t, maar die vind je nu juist door uit te gaan van de algemene oplossing y(t) = A∙3t + B∙(-2)t, niet omgekeerd.quote:
[..]
Stel y(0) = 0 en y(1) = 1
Dan zou je toch ook dit systeem van vergelijkingen kunnen oplossen:
[snip]
Zou iemand mij kunnen uitleggen hoe ik een vergelijking als dit op moet lossen?
5x^2+28x-63 = 1259x-7
Alvast bedankt
5x^2+28x-63 = 1259x-7
Alvast bedankt
gebruik logarithmsquote:Op dinsdag 11 oktober 2011 10:51 schreef Snuf. het volgende:
Zou iemand mij kunnen uitleggen hoe ik een vergelijking als dit op moet lossen?
5x^2+28x-63 = 1259x-7
Alvast bedankt
En de regel dat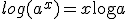 
.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Bedenk dat 125 = 53. Dan hebben we:quote:
Zou iemand mij kunnen uitleggen hoe ik een vergelijking als dit op moet lossen?
5x^2+28x-63 = 1259x-7
Alvast bedankt
5x²+28x-63 = 53(9x-7)
En dus:
x2 + 28x - 63 = 3(9x - 7)
Nu jij weer.
Hoe bereken ik de inverse van N=2^(5-3L)
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
ln(N) = ln(25-3L)quote:
Hoe bereken ik de inverse van N=2^(5-3L)
Dus L=...N
ik weet dat ik ln/e moet gebruiken maar ik kom er niet echt uit, een voorzet is ook goed. BVD
ln(N) = (5-3L)*ln(2)
Je kunt i.p.v. ln ook log gebruiken. Ik neem aan dat je de rest zelf kunt.
Ik reageerde op de opvatting van thenxzero dat het gebruik van vectoren het eenvoudigst zou zijn. Maar los daarvan begrijp ik de kritiek niet. Je leidt namelijk zelf eerst een andere goniometrische identiteit af, tan α1∙tan α2 = 1 - cos(α1 + α2)/cos α1∙cos α2, die zo mogelijk nog veel onbekender is dan de formules voor tan(α-β) (resp. tan(α+β)) die gewoon tot het standaardrepertoire van goniometrische identiteiten behoren.quote:Op maandag 10 oktober 2011 18:24 schreef keesjeislief het volgende:
[..]
Wat een gemiereneuk, je spaart misschien twee regels uit en moet in ruil daarvoor een veel onbekendere goniometrische identiteit gebruiken.
Zo 'natuurlijk' is dat niet. Als geldt a1a2 = -1 dan is 1 : a1 = -a2 : 1, zodat in je figuur de rechthoekige driehoek met hoekpunten (0,2), (1,2), (1, f(1)) gelijkvormig is met de rechthoekige driehoek met hoekpunten (1, g(1)), (1,2), (0,2), waaruit volgt dat α1 + α2 = π/2. Is omgekeerd α1 + α2 = π/2, dan zijn de genoemde driehoeken gelijkvormig, waaruit volgt dat 1 : a1 = -a2 : 1 en dus a1a2 = -1. Daar heb ik 'Pythagoras' niet voor nodig.quote:Pythagoras is natuurlijk verreweg de meest elegante en simpele oplossing.
oke bedankt, ik kom nu op:quote:Op dinsdag 11 oktober 2011 15:07 schreef lyolyrc het volgende:
[..]
ln(N) = ln(25-3L)
ln(N) = (5-3L)*ln(2)
Je kunt i.p.v. ln ook log gebruiken. Ik neem aan dat je de rest zelf kunt.
ln(N)=5-3L * ln(2)
ln(N)/ln(2)=5-3L
ln(N)/ln(2)-5=-3L
3L=5- ln(N)/ln(2)
L= 1/3 (5- ((ln)N/(ln)2) )
[ Bericht 1% gewijzigd door bezemsteeltaart op 11-10-2011 15:52:12 ]
Nee, hoe kom je daarbij?quote:
[..]
die LN kan ik weglaten bij ln(N)/ln(2) toch
dacht dat dezelfde termen die vermenigvulden in de noemer en teller, je die mag wegstrepen. Of geldt dit alleen bij XY^2/XY = Y bijvoorbeeld en niet bij ln/log/e??
//oja ik controleer net en dit klopt inderdaad niet, je hebt gelijk
//oja ik controleer net en dit klopt inderdaad niet, je hebt gelijk
Je lijdt aan een wegstreepsyndroom.quote:
dacht dat dezelfde termen die vermenigvulden in de noemer en teller, je die mag wegstrepen. Of geldt dit alleen bij XY^2/XY = Y bijvoorbeeld en niet bij ln/log/e??
Bekijk het eens aan de hand van een voorbeeld. We nemen 'gewone' logaritmen met grondtal 10. Nu weet je dat:
log(100) = 2 en log(10) = 1.
Jij beweert nu dat log(100)/log(10) = 2/1 = 2 hetzelfde zou zijn als 100/10 = 10, en dat is duidelijk onzin.
Wat wel kan is ln[ N^(ln(2))^-1 ], niet dat dit duidelijker is maar okquote:
Beneath the gold, bitter steel
Je vergeet dat je niet met ln vermenigvuldigt, maar dat ln een functie is.quote:
dacht dat dezelfde termen die vermenigvulden in de noemer en teller, je die mag wegstrepen. Of geldt dit alleen bij XY^2/XY = Y bijvoorbeeld en niet bij ln/log/e??
//oja ik controleer net en dit klopt inderdaad niet, je hebt gelijk
Ik begrijp het eigenlijk, bedanktquote:
[..]
Nee, zo werkt dat niet. Je kunt niet uitgaan van twee - willekeurige - randvoorwaarden en dan verwachten dat je de algemene oplossing zult vinden. Er is precies één oplossing die aan jouw randvoorwaarden voldoet, namelijk y(t) = (1/5)∙3t - (1/5)∙(-2)t, maar die vind je nu juist door uit te gaan van de algemene oplossing y(t) = A∙3t + B∙(-2)t, niet omgekeerd.
Op één of andere manier dacht ik dat 3^t of (-2)^t de echte oplossingen waren terwijl A*3^t ook een oplossing kan zijn, maar het is natuurlijk zo dat 3^t slechtst één oplossing is van A*3^t. en A*3^t slechtst een deel van de oplossingen van A*3^t + B*(-2)^t.
Best raar dat je soms zo scheef kan denken en het niet doorhebt.
