SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP


Laatste post kopie:
Ik heb zelf geprobeerd met weka iets te vinden, maar nog niet veel succes daarmee geboekt (vanwege dat afronden en linear regression altijd een E toevoegt ).
).
Ik heb wel succes geboekt met evolutionary algorithm (simpele GA met real values, gaussian perturbation mutation, scattered crossover, etcetera met een eigen fitness functie die voor alle instanties kijkt wat de uitkomst is met de waardens en vervolgens afrondt naar halve getallen (kun je simpel doen door je uitkomst *2 te doen en vervolgens afronden op een geheel getal om weer te delen door 2 om afrondingen te krijgen op halve (dus 5, 5.5, 6, 6.5, etc)). Ik heb zelf Matlab gebruikt hiervoor, maar je kunt ook Mobat gebruiken (moet je even eigen functie uitschrijven) of je kunt het helemaal zelf programmeren. Ik wou zelf nog een andere methode proberen omdat ik issues heb met missing values (heb nog niet achterhaald wat zijn methode daarvoor is, ik heb wel al een oplossing met 0 fouten gevonden als ik enkel de data gebruik die geen missing values bevatten).
Toevallig data mining techniques bij de VU?quote:Op woensdag 10 maart 2010 22:10 schreef Dzy het volgende:
Hey hey,
ik ben bezig met een probleempje voor een vriend. Het gaat erom om de gewichten van een formule te vinden waarmee een eindcijfer berekend is. Er is gegeven dat de formule uit 5 onderdelen met 5 gewichten bestaat, de cijfers waarmee de gewichten worden vermenigvuldigd en dan bij elkaar worden opgeteld zijn bekend. Er is een dataset van 60 mensen, dus in principe meer dan genoeg om gewoon een stelsel van 5 vergelijkingen met 5 onbekenden op te lossen, alleen is het probleem dat de cijfers afgerond zijn in de dataset. De bedoeling is om de gewichten zo dicht mogelijk te benaderen, hoe dat staat vrij maar het lijkt me waarschijnlijk dat dit met een wiskundig programma moet, of zijn er suggesties om dit mooi met de hand zelf te doen? De cijfers worden op halven afgerond. Iemand een idee hoe dit aan te pakken? Thanks!
Dit is de formule trouwens:
f(x) = g1 * D + g2 * S1 + g3 * S2 + g4 * e^(-3(D-S1)2 + g5 * e^(-3(D-S2)2
Waarbij D het cijfer is dat gegeven is door de docent, S1 is het cijfer gegeven door de eerste student en S2 is het cijfer gegeven door de tweede student. g1 tot en met g5 zijn de gewichten. D, S1 en S2 zijn dus gewoon bekend, net als de e-machten die erin voorkomen.
Ik heb zelf geprobeerd met weka iets te vinden, maar nog niet veel succes daarmee geboekt (vanwege dat afronden en linear regression altijd een E toevoegt
Ik heb wel succes geboekt met evolutionary algorithm (simpele GA met real values, gaussian perturbation mutation, scattered crossover, etcetera met een eigen fitness functie die voor alle instanties kijkt wat de uitkomst is met de waardens en vervolgens afrondt naar halve getallen (kun je simpel doen door je uitkomst *2 te doen en vervolgens afronden op een geheel getal om weer te delen door 2 om afrondingen te krijgen op halve (dus 5, 5.5, 6, 6.5, etc)). Ik heb zelf Matlab gebruikt hiervoor, maar je kunt ook Mobat gebruiken (moet je even eigen functie uitschrijven) of je kunt het helemaal zelf programmeren. Ik wou zelf nog een andere methode proberen omdat ik issues heb met missing values (heb nog niet achterhaald wat zijn methode daarvoor is, ik heb wel al een oplossing met 0 fouten gevonden als ik enkel de data gebruik die geen missing values bevatten).


Wat is 32/16 ?quote:Op woensdag 10 maart 2010 20:46 schreef Bilmiyorem het volgende:
[..]
Geen tijd meer voor. Wat ik ook niet snap.. wat moet ik met dit? Het ging eerst namelijk de hele tijd over MK=TK', dacht daarom dat ik die 16000 ook moest weglaten.
En wij kunnen ook niet weten wat je ermee moet als je niet zegt wat de vraag is


Ja, volgens mij gaat het om dat vak (zoals gezegd, het gaat om een vriend van me). Ik heb hem de link gestuurd, weet er zelf niet zoveel van. Heb wel een manier bedacht om met excel Solver het op te lossen, gewoon als beslissingsvariabelen de gewichten gebruiken en dan over alle volledige data de verschillen tussen het echte cijfer en het berekende cijfer met de gevonden gewichten bij elkaar op te tellen en dat getal te minimaliseren. Daarbij zou je ook de verschillen tussen de echte cijfers en de afronding van het berekende cijfer op nul kunnen stellen om ervoor te zorgen dat alle afrondingen met de gevonden gewichten ook daadwerkelijk op hetzelfde cijfer komen.quote:Op woensdag 10 maart 2010 23:38 schreef koffiegast het volgende:
Laatste post kopie:
[..]
Toevallig data mining techniques bij de VU?
Ik heb zelf geprobeerd met weka iets te vinden, maar nog niet veel succes daarmee geboekt (vanwege dat afronden en linear regression altijd een E toevoegt).
Ik heb wel succes geboekt met evolutionary algorithm (simpele GA met real values, gaussian perturbation mutation, scattered crossover, etcetera met een eigen fitness functie die voor alle instanties kijkt wat de uitkomst is met de waardens en vervolgens afrondt naar halve getallen (kun je simpel doen door je uitkomst *2 te doen en vervolgens afronden op een geheel getal om weer te delen door 2 om afrondingen te krijgen op halve (dus 5, 5.5, 6, 6.5, etc)). Ik heb zelf Matlab gebruikt hiervoor, maar je kunt ook Mobat gebruiken (moet je even eigen functie uitschrijven) of je kunt het helemaal zelf programmeren. Ik wou zelf nog een andere methode proberen omdat ik issues heb met missing values (heb nog niet achterhaald wat zijn methode daarvoor is, ik heb wel al een oplossing met 0 fouten gevonden als ik enkel de data gebruik die geen missing values bevatten).
"Reality is an illusion created by a lack of alcohol."


sin(0)=0quote:Op donderdag 11 maart 2010 17:17 schreef beertenderrr het volgende:
Kan iemand mij het volgende uitleggen?
[ afbeelding ]
Waarom volgt uit deze vergelijking [ afbeelding ] en niet [ afbeelding ]
In mijn boek wordt het nergens uitgelegd en ik heb maandag pas weer wiskunde, dus duurt het nog wel even tot de volgende les. Daarom hoop ik dat jullie mij kunnen uitleggen waarom dit nou zo is. Ik kan het niet plaatsen en het frustreert me
Ow en tussen de k en de pi moet een vermenigvuldigingsteken, maar die zit niet in het pakket van Latex ofzo
sin(pi)=0
sin(2pi)=0
sin(3pi)=0
Zie je een patroon?
sin(x)=0 als x=k pi, met k een geheel getal.
\cdot is denk ik wat je zoekt.


ja dat patroon zie ik, en snap ook dat dat altijd 0 zal zijn. Echter snap ik dan nog niet waarom ze als eerste stap x = k pi pakken en niet x = k 2pi. Ik dacht dat deze laatste altijd de regel was binnen de gonio.quote:Op donderdag 11 maart 2010 17:21 schreef RQPS het volgende:
[..]
sin(0)=0
sin(pi)=0
sin(2pi)=0
sin(3pi)=0
Zie je een patroon?
sin(x)=0 als x=k pi, met k een geheel getal.
\cdot is denk ik wat je zoekt.
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me


tvp
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Ja, er is een periode van 2*pi. Dat wil zeggen dat als sin(A)=y, dan is ook sin(A+k*2*pi)=y, waarbij k een element uit Z is. Dus in die zin kunnen we ons beperken tot de sinus op het interval [0,2*pi]. Als je nu een grafiekje daarvan maakt, dan zie je dat er in dat interval 3 nulpunten zijn, nl. 0, pi en 2*pi. Als je hier nu die periodiciteit op toepast, krijg je 3 setjes punten: 0+k*2*pi, pi+k*2*pi en 2*pi+k*2*pi. Natuurlijk zijn de eerste en de laatste identiek (omdat 0 en 2*pi al precies een periode uit elkaar liggen), en de twee die je overhoudt vormen samen precies de set punten k*pi.quote:Op donderdag 11 maart 2010 17:44 schreef beertenderrr het volgende:
[..]
ja dat patroon zie ik, en snap ook dat dat altijd 0 zal zijn. Echter snap ik dan nog niet waarom ze als eerste stap x = k pi pakken en niet x = k 2pi. Ik dacht dat deze laatste altijd de regel was binnen de gonio.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


ahh op die manier! Thnx voor de uitlegquote:Op donderdag 11 maart 2010 18:07 schreef keesjeislief het volgende:
[..]
Ja, er is een periode van 2*pi. Dat wil zeggen dat als sin(A)=y, dan is ook sin(A+k*2*pi)=y, waarbij k een element uit Z is. Dus in die zin kunnen we ons beperken tot de sinus op het interval [0,2*pi]. Als je nu een grafiekje daarvan maakt, dan zie je dat er in dat interval 3 nulpunten zijn, nl. 0, pi en 2*pi. Als je hier nu die periodiciteit op toepast, krijg je 3 setjes punten: 0+k*2*pi, pi+k*2*pi en 2*pi+k*2*pi. Natuurlijk zijn de eerste en de laatste identiek (omdat 0 en 2*pi al precies een periode uit elkaar liggen), en de twee die je overhoudt vormen samen precies de set punten k*pi.
A "Nederlands restaurant" is a 'contradictio in terminus'.
If it don't matter to you, it don't matter to me
If it don't matter to you, it don't matter to me


Let A and B be nonempty bounded subsets of R, and let S be the set of all sums a + b where a in A and b in B
-Prove that sup S = sup A + sup B
Voor alle a in A: Sup A ≥ a
Voor alle b in B: sup B ≥ b
Dus voor alle (a+b) in S: sup A + sup B ≥ a+b
Dus is sup A + sup B in ieder geval een bovengrens van S, maar nog niet ook het supremum. Ik denk dat ik op de een of andere manier ook moet komen tot sup S ≥ sup A + sup B, maar ik weet niet zo goed hoe.
-Prove that sup S = sup A + sup B
Voor alle a in A: Sup A ≥ a
Voor alle b in B: sup B ≥ b
Dus voor alle (a+b) in S: sup A + sup B ≥ a+b
Dus is sup A + sup B in ieder geval een bovengrens van S, maar nog niet ook het supremum. Ik denk dat ik op de een of andere manier ook moet komen tot sup S ≥ sup A + sup B, maar ik weet niet zo goed hoe.


Per definitie van het supremum zijn er rijtjes (a_n) in A en (b_n) in B wiens respectievelijke limieten de suprema in die sets zijn. Kijk dan eens naar het rijtje (a_n+b_n)?quote:Op vrijdag 12 maart 2010 16:35 schreef Hanneke12345 het volgende:
Let A and B be nonempty bounded subsets of R, and let S be the set of all sums a + b where a in A and b in B
-Prove that sup S = sup A + sup B
Voor alle a in A: Sup A ≥ a
Voor alle b in B: sup B ≥ b
Dus voor alle (a+b) in S: sup A + sup B ≥ a+b
Dus is sup A + sup B in ieder geval een bovengrens van S, maar nog niet ook het supremum. Ik denk dat ik op de een of andere manier ook moet komen tot sup S ≥ sup A + sup B, maar ik weet niet zo goed hoe.
Of, als je niet met rijtjes wilt werken (wat misschien 'netter' is), zou je het als volgt kunnen doen:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 18% gewijzigd door keesjeislief op 12-03-2010 17:25:34 ]heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek


Limieten heb ik nog niet gehad (althans bij analyse nog niet. En eigenlijk bij analyse ook wel, maar ik ben een achterstand aan 't inhalen.  ). De tweede methode lijkt me prima
). De tweede methode lijkt me prima 


Als ik een tabel in moet voeren uitgaande van de klasenbreedten
moet ik dan als er bijvoorbeeld deze tabel staat
0-5
6-10
10-15
16-20
21-25
26-30
de xscl op 5 instellen en bij L1 de klassen beginwaarden?
dus:
0
6
10
16
21
26
moet ik dan als er bijvoorbeeld deze tabel staat
0-5
6-10
10-15
16-20
21-25
26-30
de xscl op 5 instellen en bij L1 de klassen beginwaarden?
dus:
0
6
10
16
21
26


Ik moet een rij verzinnen die bestaat uit rationale getallen, maar met een irrationale limiet. En ik kan er geen één bedenken!


Of doe een Newton-Rhapson-benadering van een wortel. Bijv. een rijtje (x_n) gegeven door x_{n+1} = x_n - f(x_n)/f'(x_n), met f(x)=x2-a geeft je een rijtje rationale getallen dat naar a1/2 convergeert.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Is het mogelijk om een bepaalde imputation als stabiel (voor pre-bargaining set) te bewijzen door middel van excessen? Dus zonder dat ik beetje voor elke mogelijke objection die er ook maar is een counter objection moet verzinnen?
Ik lees op een of andere slide bv het volgende:
A coalition T is a counterobjection to the objection S
of i against j if T includes j but not i, and
e(T, x) >= e(S, x).
Dat is in mijn assignment volgensmij het volgende (weighted voting game met 6 players en q=3):
0 >= 0
(want v(T) en v(S) = 1 en x(T) en x(S) = 1, dus excess is 1-1).
Ik snap alleen niet hoe dit eigenlijk als counterobjection kan worden gezien (Counterobjection!! But then look at this coalition T without you!! With the current imputation x, coalition T sacrifices not less than your S!! staat erbij)
[ Bericht 23% gewijzigd door koffiegast op 13-03-2010 16:49:35 ]
Ik lees op een of andere slide bv het volgende:
A coalition T is a counterobjection to the objection S
of i against j if T includes j but not i, and
e(T, x) >= e(S, x).
Dat is in mijn assignment volgensmij het volgende (weighted voting game met 6 players en q=3):
0 >= 0
(want v(T) en v(S) = 1 en x(T) en x(S) = 1, dus excess is 1-1).
Ik snap alleen niet hoe dit eigenlijk als counterobjection kan worden gezien (Counterobjection!! But then look at this coalition T without you!! With the current imputation x, coalition T sacrifices not less than your S!! staat erbij)
[ Bericht 23% gewijzigd door koffiegast op 13-03-2010 16:49:35 ]


Dat is geen directe formule. Ik bedoel zonder recursie dusquote:Op zaterdag 13 maart 2010 16:50 schreef BasementDweller het volgende:
[..]
Werkt dit ook niet gewoon?
[ afbeelding ]


Ah, op die manier. Nee dan weet ik het nietquote:Op zaterdag 13 maart 2010 17:00 schreef Hanneke12345 het volgende:
[..]
Dat is geen directe formule. Ik bedoel zonder recursie dus


Je krijgt natuurlijk xn = fn+1/fn, waarbij fn de rij van Fibonacci voorstelt. Die kun je weer in een directe formule uitdrukken (gemakshalve van Wikipedia geplukt):


De tweede ronde van de Vlaamse Wiskunde Olympiade is uit. ( http://www.vwo.be/vwo/2ronde2010.PDF )
29 vragen kon ik prima oplossen maar 1 vraag vind ik echt niet.
22. De kleuren van een club zijn rood, wit, blauw. Bij wedstrijden dragen de fans van die
club twee kousen van dezelfde kleur, een short, een shirt, een sjaal en een pet. Elk van
die kledingstukken is in één van die drie kleuren en zo dat in de kledingcombinatie van
iedere fan precies drie kleuren voorkomen. Hoeveel verschillende uitrustingen zijn zo
mogelijk?
A 146
B 147
C 150
D 231
E 243
Iemand?
29 vragen kon ik prima oplossen maar 1 vraag vind ik echt niet.
22. De kleuren van een club zijn rood, wit, blauw. Bij wedstrijden dragen de fans van die
club twee kousen van dezelfde kleur, een short, een shirt, een sjaal en een pet. Elk van
die kledingstukken is in één van die drie kleuren en zo dat in de kledingcombinatie van
iedere fan precies drie kleuren voorkomen. Hoeveel verschillende uitrustingen zijn zo
mogelijk?
A 146
B 147
C 150
D 231
E 243
Iemand?
When all things seem to end, the future still remains..


Er zijn vijf dingen te kleuren, dus inclusief dubbele zijn er 3^5 = 243 mogelijkheden.
Teveel geteld is alles dat je ook met twee kleuren kunt kleuren. Dit kan op 2^5 mogelijkheden, en je kunt 3 paren van twee kleuren pakken, dus totaal 3*2^5 = 96 mogelijkheden
Maar nu heb je de situatie waarin alles dezelfde kleur krijgt teveel eraf getrokken, dus moet er nog drie bij.
kom je op 150
verder kom ik op
cceab
baedd
aee.d
ddd.d
dc.b.
c....
[ Bericht 14% gewijzigd door GlowMouse op 13-03-2010 23:45:31 ]
Teveel geteld is alles dat je ook met twee kleuren kunt kleuren. Dit kan op 2^5 mogelijkheden, en je kunt 3 paren van twee kleuren pakken, dus totaal 3*2^5 = 96 mogelijkheden
Maar nu heb je de situatie waarin alles dezelfde kleur krijgt teveel eraf getrokken, dus moet er nog drie bij.
kom je op 150
verder kom ik op
cceab
baedd
aee.d
ddd.d
dc.b.
c....
[ Bericht 14% gewijzigd door GlowMouse op 13-03-2010 23:45:31 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ken de definities niet van veel van je woorden, maar als het een andere karakterisatie van de nucleolus is, kun je naar het Kohlberg criterium kijken.quote:Op zaterdag 13 maart 2010 16:35 schreef koffiegast het volgende:
Is het mogelijk om een bepaalde imputation als stabiel (voor pre-bargaining set) te bewijzen door middel van excessen? Dus zonder dat ik beetje voor elke mogelijke objection die er ook maar is een counter objection moet verzinnen?
Ik lees op een of andere slide bv het volgende:
A coalition T is a counterobjection to the objection S
of i against j if T includes j but not i, and
e(T, x) >= e(S, x).
Dat is in mijn assignment volgensmij het volgende (weighted voting game met 6 players en q=3):
0 >= 0
(want v(T) en v(S) = 1 en x(T) en x(S) = 1, dus excess is 1-1).
Ik snap alleen niet hoe dit eigenlijk als counterobjection kan worden gezien (Counterobjection!! But then look at this coalition T without you!! With the current imputation x, coalition T sacrifices not less than your S!! staat erbij)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb het net 2 minuten geleden opgelost (door gewoonweg voor alle mogelijke objections counterobjections te vindenquote:Op zaterdag 13 maart 2010 22:12 schreef GlowMouse het volgende:
[..]
Ik ken de definities niet van veel van je woorden, maar als het een andere karakterisatie van de nucleolus is, kun je naar het Kohlberg criterium kijken.
Ik heb wel nu een andere vraag.
Ik weet dat de Nucleolus een subset is van de core. Maar kan ik ook b.v. zeggen dat als de core een unieke imputatie bevat (dus er is maar 1 oplossing dat in de core zit) dat dit ook automatisch de Nucleolus is? Bespaart me een hoopje typwerk, want volgensmij kan ik het aantonen door een random imputatie maken waarbij ik gewoon kan zeggen dat in de exces van deze imputatie er een waarde is dat hoger dan 0 is en daarmee al gelijk lexicographisch groter is dan de exces van de imputatie in de core (wat (0,0,0,0,-30,-40,-50) is, unieke imputatie in de core is (50,40,30) fyi).


Dat is niet zo mooi, want de core kan leeg zijn terwijl de nucleolus altijd bestaat.quote:Op zaterdag 13 maart 2010 22:56 schreef koffiegast het volgende:
[..]
Ik heb het net 2 minuten geleden opgelost (door gewoonweg voor alle mogelijke objections counterobjections te vinden)
Ik heb wel nu een andere vraag.
Ik weet dat de Nucleolus een subset is van de core.
Ja, dat wel.quote:Maar kan ik ook b.v. zeggen dat als de core een unieke imputatie bevat (dus er is maar 1 oplossing dat in de core zit) dat dit ook automatisch de Nucleolus is?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


was erbij vergeten te zeggen dat het in het geval van een game met een non empty core gaatquote:Op zaterdag 13 maart 2010 23:16 schreef GlowMouse het volgende:
[..]
Dat is niet zo mooi, want de core kan leeg zijn terwijl de nucleolus altijd bestaat.
[..]
Ja, dat wel.
Ik ben helaas nog geen methode tegengekomen in de slides die me gelijk de nucleolus laat uitrekenen aan de hand van imputaties (dus niet dat ik letterlijk elke mogelijke imputatie moet uitschrijven, zelfs niet met variabelen enzo), is daar een specifieke methode voor (moet haast wel he!)?
Bedankt voor het snelle antwoord


Nee, de nucleolus is heel vervelend. Voor compromise stable spelletjes lukt het wel door het spel om te zetten naar een bankroetspel en daar de Aumann Maschler-regel toe te passen.quote:Op zaterdag 13 maart 2010 23:24 schreef koffiegast het volgende:
[..]
was erbij vergeten te zeggen dat het in het geval van een game met een non empty core gaat
Ik ben helaas nog geen methode tegengekomen in de slides die me gelijk de nucleolus laat uitrekenen aan de hand van imputaties (dus niet dat ik letterlijk elke mogelijke imputatie moet uitschrijven, zelfs niet met variabelen enzo), is daar een specifieke methode voor (moet haast wel he!)?
Bedankt voor het snelle antwoord
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt! Je kan de oplossing controleren op http://www.vwo.be/vwo/tweederonde2010/Berekenscore .quote:Op zaterdag 13 maart 2010 21:53 schreef GlowMouse het volgende:
Er zijn vijf dingen te kleuren, dus inclusief dubbele zijn er 3^5 = 243 mogelijkheden.
Teveel geteld is alles dat je ook met twee kleuren kunt kleuren. Dit kan op 2^5 mogelijkheden, en je kunt 3 paren van twee kleuren pakken, dus totaal 3*2^5 = 96 mogelijkheden
Maar nu heb je de situatie waarin alles dezelfde kleur krijgt teveel eraf getrokken, dus moet er nog drie bij.
kom je op 150
verder kom ik op
cceab
baedd
aee.d
ddd.d
dc.b.
c....
De test is bedoeld voor leerlingen van 16 tot 18 jaar en ze krijgen 2u de tijd om alles op te lossen.
When all things seem to end, the future still remains..


Ah, ik zag de antwoorden nog niet staan op de site.quote:Op zondag 14 maart 2010 00:29 schreef Masanga het volgende:
[..]
Bedankt! Je kan de oplossing controleren op http://www.vwo.be/vwo/tweederonde2010/Berekenscore .
De test is bedoeld voor leerlingen van 16 tot 18 jaar en ze krijgen 2u de tijd om alles op te lossen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wat is een goede score?quote:Op zondag 14 maart 2010 00:29 schreef Masanga het volgende:
[..]
Bedankt! Je kan de oplossing controleren op http://www.vwo.be/vwo/tweederonde2010/Berekenscore .
De test is bedoeld voor leerlingen van 16 tot 18 jaar en ze krijgen 2u de tijd om alles op te lossen.


Zoals eerder vermeld betreft het hier de tweede ronde, je kan het vergelijken met provinciale finales.quote:
Om door te gaan naar de nationale finale moet je normaal minstens ergens tussen 95 en 110 scoren. De 6 besten van die nationale finales vertegenwoordigen België komende zomer in Astana op de 51ste International Mathematical Olympiad van 6 tot 12 juli 2010.
In de Nationale finales krijg je trouwens 3 open vragen ipv 30 meerkeuzevragen.
When all things seem to end, the future still remains..


Okequote:Op zondag 14 maart 2010 15:52 schreef Masanga het volgende:
[..]
Zoals eerder vermeld betreft het hier de tweede ronde, je kan het vergelijken met provinciale finales.
Om door te gaan naar de nationale finale moet je normaal minstens ergens tussen 95 en 110 scoren. De 6 besten van die nationale finales vertegenwoordigen België komende zomer in Astana op de 51ste International Mathematical Olympiad van 6 tot 12 juli 2010.
In de Nationale finales krijg je trouwens 3 open vragen ipv 30 meerkeuzevragen.


Ik heb hier een makkelijke vraag, ik weet het antwoord wel al, maar snap de logica niet...
Een gemeenteraad bestaat uit 9 leden. Er zijn 3 CDA leden, 3 PVDA, 2 VVD en 1 GL
Er moet een commissie van drie leden worden samengesteld.
Hoeveel commissies zijn in totaal mogelijk?
Het antwoorden boeken geeft (9 nCr 2) Combinatie van 9 boven 2 mogelijkheden. Maar het bestaat toch uit drie leden, waarom is het dan niet 9 nCr 3?
Een gemeenteraad bestaat uit 9 leden. Er zijn 3 CDA leden, 3 PVDA, 2 VVD en 1 GL
Er moet een commissie van drie leden worden samengesteld.
Hoeveel commissies zijn in totaal mogelijk?
Het antwoorden boeken geeft (9 nCr 2) Combinatie van 9 boven 2 mogelijkheden. Maar het bestaat toch uit drie leden, waarom is het dan niet 9 nCr 3?


Hebben die partijen nog wat met het antwoord te maken? Anders zou ik ook 9 nCr 3 zeggen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De vorige vraag was: Hoeveel commissies zijn er mogelijk met twee CDA leden?
Maar het lijkt mij dat die vraag er niks te maken mee heeft...
Maar het lijkt mij dat die vraag er niks te maken mee heeft...


Nee, daar krijg je een 3 nCr 2 en een 6 nCr 1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Klopt. Nouja, iedergeval bedankt voor je antwoorden. Zal wel gewoon verder gaan met de opdrachten, moet er nog een hoop...


Heb twee korte vraagjes:
Vraag 1:
Hoeveel data heb ik nodig om een pearson correlatie coefficient (r) te berekenen? Is twee lijsten van twee waarden genoeg? Dat werkt wel, maar zegt dat nog iets, of heb je eigenlijk minimaal 3 waarden nodig per lijst?
Vraag 2:
Mag je r berekenen met log2 ratio's? Hier is 1 waarde van 1 lijst dus een verschil tussen twee condities. Ik wilde dit gaan doen om te kijken of de lijsten overeenkomsten vertonen in verschillende omgevingen. Maar ik vraag me af of dit dé manier is.
Alvast bedankt
[ Bericht 0% gewijzigd door tactician op 15-03-2010 13:04:26 ]
Vraag 1:
Hoeveel data heb ik nodig om een pearson correlatie coefficient (r) te berekenen? Is twee lijsten van twee waarden genoeg? Dat werkt wel, maar zegt dat nog iets, of heb je eigenlijk minimaal 3 waarden nodig per lijst?
Vraag 2:
Mag je r berekenen met log2 ratio's? Hier is 1 waarde van 1 lijst dus een verschil tussen twee condities. Ik wilde dit gaan doen om te kijken of de lijsten overeenkomsten vertonen in verschillende omgevingen. Maar ik vraag me af of dit dé manier is.
Alvast bedankt
[ Bericht 0% gewijzigd door tactician op 15-03-2010 13:04:26 ]


1. 2 is genoeg, maar hoe meer hoe beter.
2. waarom niet?
2. waarom niet?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Gegroet mijn mede Gaussiaanse bewonderaars,
Graag zou ik ter controle de berekeningen van jullie willen hebben op de volgende vraag:
Gebruik de Modified Euler methode om de oplossing te benaderen van het volgende beginwaardeprobleem...: y ' = 1+(t-y)2 , 2 <= t <= 3, y(2)= 1, h= 0.5 .
De exacte oplossing wordt gegeven door y(t) = t + 1/(1-t). Bepaal de fout in de nummerieke benadering. De tweede subvraag hoeven jullie niet te doen, dat is een eitje .
De modified Euler formule (even handig om het te zien wanneer je het maakt):
Predictor: W*n+1 = Wn + h f(tn, Wn)
Corrector: Wn+1= Wn + h/2 [ f(tn, Wn) + f(tn+1, W*n+1)
Mijn berekeningen:
W1* = 1 + 0.5 * ( 1 + (0.5 * 0 - 1)2 ) = 1+1 = 2
W1 = 1 + 0.25 ((1+(0.5*0 - 1)2 ) + (1 + (2.5 - 2)2))
= 1,8125
Het vetgedrukte heb ik problemen mee. Men zegt dus dat:
w0 = 2
w1 = 2.5 <---- hier komt die 2.5 natuurlijk vandaan
w2 = 3
Echter was ik gewend om op de plek van het vetgedrukte gewoon 0.5 * n te zetten (Tn = 0.5 * n). Graag opheldering hierover.
Voor de rest kwam ik met w2 op een andere waarde uit dan de antwoorden. Ik wil graag weten wat jullie als antwoord hebben voor w2.
Dank jullie wel.
Graag zou ik ter controle de berekeningen van jullie willen hebben op de volgende vraag:
Gebruik de Modified Euler methode om de oplossing te benaderen van het volgende beginwaardeprobleem...: y ' = 1+(t-y)2 , 2 <= t <= 3, y(2)= 1, h= 0.5 .
De exacte oplossing wordt gegeven door y(t) = t + 1/(1-t). Bepaal de fout in de nummerieke benadering. De tweede subvraag hoeven jullie niet te doen, dat is een eitje .
De modified Euler formule (even handig om het te zien wanneer je het maakt):
Predictor: W*n+1 = Wn + h f(tn, Wn)
Corrector: Wn+1= Wn + h/2 [ f(tn, Wn) + f(tn+1, W*n+1)
Mijn berekeningen:
W1* = 1 + 0.5 * ( 1 + (0.5 * 0 - 1)2 ) = 1+1 = 2
W1 = 1 + 0.25 ((1+(0.5*0 - 1)2 ) + (1 + (2.5 - 2)2))
= 1,8125
Het vetgedrukte heb ik problemen mee. Men zegt dus dat:
w0 = 2
w1 = 2.5 <---- hier komt die 2.5 natuurlijk vandaan
w2 = 3
Echter was ik gewend om op de plek van het vetgedrukte gewoon 0.5 * n te zetten (Tn = 0.5 * n). Graag opheldering hierover.
Voor de rest kwam ik met w2 op een andere waarde uit dan de antwoorden. Ik wil graag weten wat jullie als antwoord hebben voor w2.
Dank jullie wel.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


De afgeleide van -1/2 sin(x) is -1/2cos(x).
Zie het maar zo:
f(x)= -Sin (x) * c
De afgeleide wordt dan :
f '(x) = -Cos(x) * c * "de afgeleide van die x "
Dus in jouw geval:
-1/2 sin (2x) + c afleiden wordt:
-1/2 cos (2x) * 2 = - cos (2x)
Zie het maar zo:
f(x)= -Sin (x) * c
De afgeleide wordt dan :
f '(x) = -Cos(x) * c * "de afgeleide van die x "
Dus in jouw geval:
-1/2 sin (2x) + c afleiden wordt:
-1/2 cos (2x) * 2 = - cos (2x)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Je moet de kettingregel toepassen. Als je dan de afgeleide neemt van - 1/2 sin(2x) krijg je dus - 1/2 cos(2x)*2=-cos(2x)quote:Op woensdag 17 maart 2010 21:04 schreef afcabrk het volgende:
vraagje:
in mijn antwoordblad staat dat
[ afbeelding ]
is de afgeleide van -1/2 sin dus gewoon -cos of...?


Ook nog een leuke (hier had ik vroeger veel moeite mee) :quote:Op woensdag 17 maart 2010 21:20 schreef afcabrk het volgende:
ohja ik snap het :d thnx
Het cyclus van sinus en cosinus als je die moet differentieren:
Sin (x) --> differentieren --> Cos(x)
Cos(x) --> differentieren --> -Sin(x)
-Sin(x) --> differentieren --> -Cos(x)
-Cos(x) --> differentieren --> Sin(x)
En daarna begint het weer opnieuw.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Die vond ik ook wel lastig, maar het is eigenlijk slechts een kwestie van weten wanneer er een minteken voor komtquote:Op woensdag 17 maart 2010 21:31 schreef Burakius het volgende:
[..]
Ook nog een leuke (hier had ik vroeger veel moeite mee) :
Het cyclus van sinus en cosinus als je die moet differentieren:
Sin (x) --> differentieren --> Cos(x)
Cos(x) --> differentieren --> -Sin(x)
-Sin(x) --> differentieren --> -Cos(x)
-Cos(x) --> differentieren --> Sin(x)
En daarna begint het weer opnieuw.


Je moet je eenheidscirkeltje gewoon kennen. En snappen waarom een eenheidscirkel bovenin Sinus heeft, en waarom rechts horizontaal Cosinus. Het beste is dit uit te tekenen. Mijn lerares heeft een hele goede animatie hiervan (lange link):quote:Op woensdag 17 maart 2010 22:07 schreef BasementDweller het volgende:
[..]
Die vond ik ook wel lastig, maar het is eigenlijk slechts een kwestie van weten wanneer er een minteken voor komt. Verder geldt altijd cos->sin en sin->cos
http://www.ies.co.jp/math/java/samples/graphSinX.html
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik onthou het doormiddel van de grafieken van sinus en cosinusquote:Op woensdag 17 maart 2010 22:17 schreef Burakius het volgende:
[..]
Je moet je eenheidscirkeltje gewoon kennen. En snappen waarom een eenheidscirkel bovenin Sinus heeft, en waarom rechts horizontaal Cosinus. Het beste is dit uit te tekenen. Mijn lerares heeft een hele goede animatie hiervan (lange link):
http://www.ies.co.jp/math/java/samples/graphSinX.html


Vraagje... waarvoor staat lambda in deze functie?
http://en.wikipedia.org/wiki/Lagrange_multipliers
ps. de hoofdletter, niet de kleine letter
http://en.wikipedia.org/wiki/Lagrange_multipliers
ps. de hoofdletter, niet de kleine letter


Voor de Lagrange functie. Is gewoon een naampje dus, ze hadden het net zo goed g(x,y,lambda) kunnen noemen.quote:Op donderdag 18 maart 2010 10:38 schreef ReWout het volgende:
Vraagje... waarvoor staat lambda in deze functie?
[ afbeelding ]
http://en.wikipedia.org/wiki/Lagrange_multipliers
ps. de hoofdletter, niet de kleine letter


Als je weet hoe de cosinus en sinus gedefinieerd worden aan de hand van de eenheidscirkel en je weet dat een raaklijn aan een cirkel loodrecht op de straal naar het raakpunt staat, dan zou je kunnen inzien dat geldt:quote:Op woensdag 17 maart 2010 21:31 schreef Burakius het volgende:
[..]
Ook nog een leuke (hier had ik vroeger veel moeite mee) :
Het cyclus van sinus en cosinus als je die moet differentieren:
Sin (x) --> differentieren --> Cos(x)
Cos(x) --> differentieren --> -Sin(x)
-Sin(x) --> differentieren --> -Cos(x)
-Cos(x) --> differentieren --> Sin(x)
En daarna begint het weer opnieuw.
d(cos φ)/dφ = cos (φ + ½π)
d(sin φ)/dφ = sin (φ + ½π)
En aangezien de cosinus en sinus periodieke functies zijn met een periode 2π kom je na viermaal differentiëren dus weer op de oorspronkelijke functie uit.


ik ben nu even bezig met wiskunde, en moet nu de volgende som oplossen
Rekenudige rij, beginterm is 7, en de zesde term is 37.
Berekend de 80ste term van de rij
bereken de som van de eerste 80 termen.
Op wikipedia staat opzich wel de formule die we gebruikt hebben, maar dan veel uitgebreider. Is er iemand die me hier mee kan helpen?
Rekenudige rij, beginterm is 7, en de zesde term is 37.
Berekend de 80ste term van de rij
bereken de som van de eerste 80 termen.
Op wikipedia staat opzich wel de formule die we gebruikt hebben, maar dan veel uitgebreider. Is er iemand die me hier mee kan helpen?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Een rekenkundige rij wil zeggen dat er telkens een bepaald getal bijgeteld wordt. Dus je begint met 7 (term 1), en dan tel je er 5 maal een bepaald getal bij op om de zesde term te krijgen. Wat is dat getal?quote:Op vrijdag 19 maart 2010 13:08 schreef kanovinnie het volgende:
ik ben nu even bezig met wiskunde, en moet nu de volgende som oplossen
Rekenudige rij, beginterm is 7, en de zesde term is 37.
Berekend de 80ste term van de rij
bereken de som van de eerste 80 termen.
Op wikipedia staat opzich wel de formule die we gebruikt hebben, maar dan veel uitgebreider. Is er iemand die me hier mee kan helpen?


In dit geval is datquote:Op vrijdag 19 maart 2010 13:15 schreef BasementDweller het volgende:
[..]
Een rekenkundige rij wil zeggen dat er telkens een bepaald getal bijgeteld wordt. Dus je begint met 7 (term 1), en dan tel je er 5 maal een bepaald getal bij op om de zesde term te krijgen. Wat is dat getal?
(37-7)/5=6
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


duuuus.... de 80ste term is 7+80*6=487?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Nee, want hoeveel keer moet je er 6 bij optellen om van de 1ste bij de 80ste term van de rij uit te komen?quote:Op vrijdag 19 maart 2010 13:22 schreef kanovinnie het volgende:
duuuus.... de 80ste term is 7+80*6=487?


Om van term 1 naar term 2 te gaan moet je er één keer 6 bij optellen
Om van term 1 naar term 3 te gaan, moet je er twee keer 6 bij optellen
...
...
Om van term 1 naar term 80 te gaan, moet je er .... keer 6 bij optellen
Ga dit altijd even na, want hier maak je snel fouten mee!
Om van term 1 naar term 3 te gaan, moet je er twee keer 6 bij optellen
...
...
Om van term 1 naar term 80 te gaan, moet je er .... keer 6 bij optellen
Ga dit altijd even na, want hier maak je snel fouten mee!


79 keer? dus N-1?quote:Op vrijdag 19 maart 2010 13:30 schreef BasementDweller het volgende:
Om van term 1 naar term 2 te gaan moet je er één keer 6 bij optellen
Om van term 1 naar term 3 te gaan, moet je er twee keer 6 bij optellen
...
...
Om van term 1 naar term 80 te gaan, moet je er .... keer 6 bij optellen
Ga dit altijd even na, want hier maak je snel fouten mee!
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Inderdaad. Dus de 80 term is? Kun je nu de som berekenen?quote:
(Het is beter om het elke keer even na te gaan dan te onthouden dat het (n-1) keer is, want soms begint men bij de nulde of een andere willekeurige term )


7+79*6=481?quote:Op vrijdag 19 maart 2010 13:35 schreef BasementDweller het volgende:
[..]
Inderdaad. Dus de 80 term is? Kun je nu de som berekenen?
En de som is dan....
0.5*6*(6+481)=8658?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


481 is goed.quote:Op vrijdag 19 maart 2010 13:37 schreef kanovinnie het volgende:
[..]
7+79*6=481?
En de som is dan....
0.5*6*(6+481)=8658?
De som klopt niet.


Je hebt deze formule toch?quote:Op vrijdag 19 maart 2010 13:38 schreef BasementDweller het volgende:
[..]
481 is goed.
De som klopt niet.
½ n(u1+un).
dus
0.5*6*(6+481)?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


o wacht, er stond op mijn rekenmachine een * ipv +
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Je moet je niet zo vastbijten in formules (die je kennelijk ook niet begrijpt). Wat is de truc die men gebruikt om de som van de termen van een rekenkundige rij te bepalen?quote:Op vrijdag 19 maart 2010 13:42 schreef kanovinnie het volgende:
[..]
Je hebt deze formule toch?
½ n(u1+un).
dus
0.5*6*(6+481)?


En dat niet alleen, n = het aantal termen.quote:Op vrijdag 19 maart 2010 13:43 schreef kanovinnie het volgende:
o wacht, er stond op mijn rekenmachine een * ipv +


Doel je er nu op dat de eerste, plus de laatste term hetzelfde zijn als de tweede plus de 1 na laatste term?quote:Op vrijdag 19 maart 2010 13:44 schreef Riparius het volgende:
[..]
Je moet je niet zo vastbijten in formules (die je kennelijk ook niet begrijpt). Wat is de truc die men gebruikt om de som van de termen van een rekenkundige rij te bepalen?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Inderdaad. Ik kan je sterk adviseren om de afleiding opquote:Op vrijdag 19 maart 2010 13:44 schreef Riparius het volgende:
[..]
Je moet je niet zo vastbijten in formules (die je kennelijk ook niet begrijpt). Wat is de truc die men gebruikt om de som van de termen van een rekenkundige rij te bepalen?
http://nl.wikipedia.org/wiki/Rekenkundige_rij
door te nemen.
Het is niet zo moeilijk als het misschien op het eerste gezicht lijkt, maar dan snap je de formule zometeen wel echt goed.


Inderdaad. En als je in totaal 80 termen hebt, hoeveel van die paren met dezelfde som kun je dan vormen? En wat is (dus) de totale som van alle termen?quote:Op vrijdag 19 maart 2010 13:46 schreef kanovinnie het volgende:
[..]
Doel je er nu op dat de eerste, plus de laatste term hetzelfde zijn als de tweede plus de 1 na laatste term?


Juist. En hoeveel keer wil je de (eerste + laatste term)/2 hebben? Je hebt nu 6.quote:Op vrijdag 19 maart 2010 13:46 schreef kanovinnie het volgende:
[..]
Doel je er nu op dat de eerste, plus de laatste term hetzelfde zijn als de tweede plus de 1 na laatste term?
Riparius beats me to it


40*(7+481)?quote:Op vrijdag 19 maart 2010 13:48 schreef Riparius het volgende:
[..]
Inderdaad. En als je in totaal 80 termen hebt, hoeveel van die paren met dezelfde som kun je dan vormen? En wat is (dus) de totale som van alle termen?
Dus 19.520?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Ja, en de formule nu ook. Ik zal nog even die wiki doornemen.quote:Op vrijdag 19 maart 2010 13:53 schreef Riparius het volgende:
[..]
Dat is correct. Laat de vraagtekens maar weg. Snap je het principe nu ook?
Bedankt beiden
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


You're welcomequote:Op vrijdag 19 maart 2010 13:55 schreef kanovinnie het volgende:
[..]
Ja, en de formule nu ook. Ik zal nog even die wiki doornemen.
Bedankt beiden


Dus, even terugkomend op waar we het gister over hadden.
Om het de een bepaalde term uit een reeks te berekenen gebruik je de formule:
Sn=S1+(Sn-1)*V
Sn=de gevraagde term
S1= de eerste term
V=Verschil tussen 2 opeenvolgende reeksen.
Om de totale som uit te rekenen doe je eigenlijk je eerste +je laatste term, tweede+ 1 nalaatste term, derde + twee nalaatste term etc
De formule hiervan is
Tr=0,5*V*(T1+Tn)
Tr=totaal van de reeksen
V=verschil tussen twee termen
T1= de eerste term
Tn=de laatste term
Om het de een bepaalde term uit een reeks te berekenen gebruik je de formule:
Sn=S1+(Sn-1)*V
Sn=de gevraagde term
S1= de eerste term
V=Verschil tussen 2 opeenvolgende reeksen.
Om de totale som uit te rekenen doe je eigenlijk je eerste +je laatste term, tweede+ 1 nalaatste term, derde + twee nalaatste term etc
De formule hiervan is
Tr=0,5*V*(T1+Tn)
Tr=totaal van de reeksen
V=verschil tussen twee termen
T1= de eerste term
Tn=de laatste term
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Ik zie echt niet wat hier gebeurt. Tot zo ver snap ik 't (althans, denk ik 't te snappen):
Nou zeggen ze: "If n-m is odd, the last term of A is -an, so
and also
"
Ik snap niet hoe ze nou aan die tweede vergelijking komen.
Nou zeggen ze: "If n-m is odd, the last term of A is -an, so
and also
"
Ik snap niet hoe ze nou aan die tweede vergelijking komen.


Wat is je vraag?quote:Op zaterdag 20 maart 2010 13:16 schreef kanovinnie het volgende:
Dus, even terugkomend op waar we het gister over hadden.
Om het de een bepaalde term uit een reeks te berekenen gebruik je de formule:
Sn=S1+(Sn-1)*V
Sn=de gevraagde term
S1= de eerste term
V=Verschil tussen 2 opeenvolgende reeksen.
Om de totale som uit te rekenen doe je eigenlijk je eerste +je laatste term, tweede+ 1 nalaatste term, derde + twee nalaatste term etc
De formule hiervan is
Tr=0,5*V*(T1+Tn)
Tr=totaal van de reeksen
V=verschil tussen twee termen
T1= de eerste term
Tn=de laatste term


Of dat kloptquote:
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Het is gewoon een kwestie van de haakjes anders zetten, en gebruik maken van het feit dat a1 >= a2 >=a3 >=... 0 (want daarom is het verschil tussen haakjes steeds niet-negatief. Dus als je dat van a_m afhaalt krijg je iets wat kleiner of gelijk is aan a_m).quote:Op zaterdag 20 maart 2010 13:42 schreef Hanneke12345 het volgende:
Ik zie echt niet wat hier gebeurt. Tot zo ver snap ik 't (althans, denk ik 't te snappen):
[ afbeelding ]
Nou zeggen ze: "If n-m is odd, the last term of A is -an, so
[ [url=http://latex.codecogs.com/gif.latex?A%20=%20[a_m%20-%20a_{m+1}]+[a_{m+2}-a_{m+3}]+...+%20[a_{n-1}-a_n]%20\geq%200]afbeelding[/url] ]
and also
[ [url=http://latex.codecogs.com/gif.latex?A%20=%20a_m%20-%20[a_{m+1}-a_{m+2}]-[a_{m+3}-a_{m+4}]-...-%20[a_{n-2}-a_{n-1}]-a_n%20\leq%20a_m]afbeelding[/url] ]"
Ik snap niet hoe ze nou aan die tweede vergelijking komen.


Ik zie dat je het woord reeks verkeerd gebruikt. Een reeks is bestaat uit termen (a1,a2,...). Dus V is het verschil tussen twee termen (en niet reeksen). Voor de rest zie ik geen fouten.quote:


Slordig bewijs; de alterende reeks zelf wordt met zijn somrij verward, s_n wordt niet gedefinieerd, en het is ook onduidelijk waarom ze van m+1 naar m-1 springen. Het stukje na 'omdat' (derde regel bewijs) slaat ook nergens op, want je mag best een andere epsilon pakken. De stukjes na (2) en (3) zijn ook alleen maar ruis.quote:Op zaterdag 20 maart 2010 13:42 schreef Hanneke12345 het volgende:
Ik zie echt niet wat hier gebeurt. Tot zo ver snap ik 't (althans, denk ik 't te snappen):
[ afbeelding ]
Nou zeggen ze: "If n-m is odd, the last term of A is -an, so
[ [url=http://latex.codecogs.com/gif.latex?A%20=%20[a_m%20-%20a_{m+1}]+[a_{m+2}-a_{m+3}]+...+%20[a_{n-1}-a_n]%20\geq%200]afbeelding[/url] ]
and also
[ [url=http://latex.codecogs.com/gif.latex?A%20=%20a_m%20-%20[a_{m+1}-a_{m+2}]-[a_{m+3}-a_{m+4}]-...-%20[a_{n-2}-a_{n-1}]-a_n%20\leq%20a_m]afbeelding[/url] ]"
Ik snap niet hoe ze nou aan die tweede vergelijking komen.
Die tweede vergelijking is juist omdat je begint met a_m en daar alleen maar niet-negatieve termen vanaf trekt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


daar heb je inderdaad gelijk in. Ik heb de twee woorden met elkaar door elkaar gehaald.quote:Op zaterdag 20 maart 2010 13:54 schreef BasementDweller het volgende:
[..]
Ik zie dat je het woord reeks verkeerd gebruikt. Een reeks is bestaat uit termen (a1,a2,...). Dus V is het verschil tussen twee termen (en niet reeksen). Voor de rest zie ik geen fouten.
Dank je
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Oeps! Ik zie trouwens een fout in de tweede formule, die fout heb je al eerder gemaakt!quote:Op zaterdag 20 maart 2010 13:57 schreef kanovinnie het volgende:
[..]
daar heb je inderdaad gelijk in. Ik heb de twee woorden met elkaar door elkaar gehaald.
Dank je
En ik wil je erop wijzen dat het in de eerste formule eigenlijk moet zijn:
Sn=S1+(Sn-1)*V
(dus met die "n-1" beneden). Voor als je het misschien niet door had


Hehe, goed dat je ziet. Nu nog even de meetkundige rij doornemen, en dan kan ik de rest van de dingen met mijn vader doornemen morgen.quote:Op zaterdag 20 maart 2010 14:03 schreef BasementDweller het volgende:
[..]
Oeps! Ik zie trouwens een fout in de tweede formule, die fout heb je al eerder gemaakt!
En ik wil je erop wijzen dat het in de eerste formule eigenlijk moet zijn:
Sn=S1+(Sn-1)*V
(dus met die "n-1" beneden). Voor als je het misschien niet door had
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Zie je het zelf ook (daar gaat het om natuurlijk)? Verbeter de formule eens. (de 2e dus)quote:Op zaterdag 20 maart 2010 14:09 schreef kanovinnie het volgende:
[..]
Hehe, goed dat je ziet. Nu nog even de meetkundige rij doornemen, en dan kan ik de rest van de dingen met mijn vader doornemen morgen.


Tr=0,5*V*(T1+Tn)quote:Op zaterdag 20 maart 2010 14:10 schreef BasementDweller het volgende:
[..]
Zie je het zelf ook (daar gaat het om natuurlijk)? Verbeter de formule eens. (de 2e dus)
die? die is zo toch goed, of niet?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Nee, die is niet goed.quote:Op zaterdag 20 maart 2010 14:14 schreef kanovinnie het volgende:
[..]
Tr=0,5*V*(T1+Tn)
die? die is zo toch goed, of niet?


Tr=0,5*V*(T1+Tn)quote:
Moet zijn
Tr=0,5*Tn*(T1+Tn)
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


not quite. Vul hem gewoon eens in:quote:Op zaterdag 20 maart 2010 14:18 schreef kanovinnie het volgende:
[..]
Tr=0,5*V*(T1+Tn)
Moet zijn
Tr=0,5*Tn*(T1+Tn)
n=3
T1=0
T2=1
T3=2
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


de fout: ik vermenigvulde met het verschil, terwijl je met het aantal termen moet vermenigvuldigen.
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Juistquote:Op zaterdag 20 maart 2010 14:18 schreef kanovinnie het volgende:
de fout: ik vermenigvulde met het verschil, terwijl je met het aantal termen moet vermenigvuldigen.


0.5*3*(0+2)=3quote:Op zaterdag 20 maart 2010 14:18 schreef GlowMouse het volgende:
[..]
not quite. Vul hem gewoon eens in:
n=3
T1=0
T2=1
T3=2
T1+T2+T3=3
gelijk, dus goed? of doe ik nu nog steeds iets fout?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Je zei "Tr=0,5*Tn*(T1+Tn)". Waarom vul je voor Tn op de ene plek 3 in, en op de andere plek 2?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


goed punt. Maar ik ben nu in de war, want jij zegt dat het niet klopt, en BasementDweller zegt dat het wel klopt.quote:Op zaterdag 20 maart 2010 14:23 schreef GlowMouse het volgende:
Je zei "Tr=0,5*Tn*(T1+Tn)". Waarom vul je voor Tn op de ene plek 3 in, en op de andere plek 2?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Nja, het is vooral bedoelt dat ik zelf min of meer snap wat er gebeurt. Maar dan alsnog.quote:Op zaterdag 20 maart 2010 13:55 schreef GlowMouse het volgende:
[..]
Slordig bewijs; de alterende reeks zelf wordt met zijn somrij verward, s_n wordt niet gedefinieerd, en het is ook onduidelijk waarom ze van m+1 naar m-1 springen. Het stukje na 'omdat' (derde regel bewijs) slaat ook nergens op, want je mag best een andere epsilon pakken. De stukjes na (2) en (3) zijn ook alleen maar ruis.
Die tweede vergelijking is juist omdat je begint met a_m en daar alleen maar niet-negatieve termen vanaf trekt.
De alternerende reeks is de somrij, maar dan zonder de sigma ervoor, toch? Of zeg ik dan iets heel stoms ;x Waar wordt dat met elkaar verward?
Wat bedoel je met "de stukjes na (2) en (3)", dat wat daarvoor staat? Was vooral omdat ik niet gelijk zag dat die sommen aan elkaar gelijk zijn.
Weet ik dan ook zeker dat a_n niet negatief is?


Omdat je daar het aantal termen invult en niet Tn of V, zoals je ook al aangaf dat dat de fout was. Je doet het nu dus gewoon goedquote:Op zaterdag 20 maart 2010 14:29 schreef kanovinnie het volgende:
[..]
goed punt. Maar ik ben nu in de war, want jij zegt dat het niet klopt, en BasementDweller zegt dat het wel klopt.
[ Bericht 0% gewijzigd door BasementDweller op 20-03-2010 14:57:41 ]


Dit is de alternerende rij:quote:Op zaterdag 20 maart 2010 14:43 schreef Hanneke12345 het volgende:
[..]
Nja, het is vooral bedoelt dat ik zelf min of meer snap wat er gebeurt. Maar dan alsnog.
De alternerende reeks is de somrij, maar dan zonder de sigma ervoor, toch? Of zeg ik dan iets heel stoms ;x Waar wordt dat met elkaar verward?
[ afbeelding ]
Wat bedoel je met "de stukjes na (2) en (3)", dat wat daarvoor staat? Was vooral omdat ik niet gelijk zag dat die sommen aan elkaar gelijk zijn.
Weet ik dan ook zeker dat a_n niet negatief is?
a_n is niet negatief bij aanname (eerste regel van je stelling).
De stap van (1) naar (4) is triviaal.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Het lukt me niet om de afgeleide te berekenen als er een kwadraat in de noemer staat.
Voorbeeld:
(-4x^2+4)/(x^2+1)^2
Het moet dan zijn (8x(x^2-3))/(x^2+1)^3 , maar ik weet niet hoe ze dat vereenvoudigen vanuit deze som:
( (x^2+1)^2(-8x)-4(1-x^2)*2(x^2+1)(2x) ) / (x^2+1)^4
[ Bericht 45% gewijzigd door pietpiraat88 op 20-03-2010 15:44:13 ]
Voorbeeld:
(-4x^2+4)/(x^2+1)^2
Het moet dan zijn (8x(x^2-3))/(x^2+1)^3 , maar ik weet niet hoe ze dat vereenvoudigen vanuit deze som:
( (x^2+1)^2(-8x)-4(1-x^2)*2(x^2+1)(2x) ) / (x^2+1)^4
[ Bericht 45% gewijzigd door pietpiraat88 op 20-03-2010 15:44:13 ]


Vereenvoudigen is het sleutelwoord. Die lelijke uitdrukking waar je op uitkomt, of de uitdrukking waar je mee begint, dat maakt niet uit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wat ik gisteren al zei: bijt je niet zo vast in die formules. Het gaat om het verkrijgen van inzicht, niet om het hersenloos invullen van formuletjes. Bovendien is de formule die je geeft voor de som van de termen van een rekenkundige rij ook nog eens fout. Als het aantal temen van de rekenkundige rij n is, en de eerste term is t1 en de laatste term tn, dan geldt voor de som s van die termen:quote:Op zaterdag 20 maart 2010 14:29 schreef kanovinnie het volgende:
[..]
goed punt. Maar ik ben nu in de war, want jij zegt dat het niet klopt, en BasementDweller zegt dat het wel klopt.
s = ½n(t1 + tn)
O ja, maak gebruik van de mogelijkheden voor subscript en superscript als die in je formules te pas komen, dat voorkomt een hoop onduidelijkheden en nutteloze welles-nietes discussies.
[ Bericht 0% gewijzigd door Riparius op 20-03-2010 16:48:10 ]


Ja ik heb m'n bericht even aangepast, bleek dat ik toch de goede formule had. Maar ik zie alleen niet hoe ze het vereenvoudigen tot het korte antwoord.quote:Op zaterdag 20 maart 2010 15:38 schreef GlowMouse het volgende:
Vereenvoudigen is het sleutelwoord. Die lelijke uitdrukking waar je op uitkomt, of de uitdrukking waar je mee begint, dat maakt niet uit.


Ik zie overal wel x²+1 terugkomen, die kun je wegdelen dus.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Teller en noemer van je breuk hebben een factor (x2 + 1) gemeenschappelijk. En gebruik alsjeblieft superscript, die carets zijn nergens voor nodig op FOK.quote:Op zaterdag 20 maart 2010 15:45 schreef pietpiraat88 het volgende:
[..]
Ja ik heb m'n bericht even aangepast, bleek dat ik toch de goede formule had. Maar ik zie alleen niet hoe ze het vereenvoudigen tot het korte antwoord.


Hallo allemaal,
Ik ben opzoek naar een wiskundig programma dat laat zien hoe je aan uitkomsten komt. Ik zou dit graag als ondersteuning willen gebruiken om te differentiëren.
Wie kan mij verder helpen:?
Ik ben opzoek naar een wiskundig programma dat laat zien hoe je aan uitkomsten komt. Ik zou dit graag als ondersteuning willen gebruiken om te differentiëren.
Wie kan mij verder helpen:?


Dit klinkt nog iets te vaag. Kan je iets concreter zijn?quote:Op zondag 21 maart 2010 11:41 schreef snakeman123 het volgende:
Hallo allemaal,
Ik ben opzoek naar een wiskundig programma dat laat zien hoe je aan uitkomsten komt. Ik zou dit graag als ondersteuning willen gebruiken om te differentiëren.
Wie kan mij verder helpen:?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Ik zou graag een som willen invullen en dan dat het programma mij stap voor stap laat zien hoe je tot het antwoord komt.quote:Op zondag 21 maart 2010 11:52 schreef -J-D- het volgende:
[..]
Dit klinkt nog iets te vaag. Kan je iets concreter zijn?


www.wolframpalpha.com, probeer daar eens wat? Met differentieren en integreren kan hij wat stappen laten zien.
"Reality is an illusion created by a lack of alcohol."


en waar moet ik dan kijken:? ik vind wel van alles over computers en filmsquote:Op zondag 21 maart 2010 12:08 schreef Dzy het volgende:
www.wolframpalpha.com, probeer daar eens wat? Met differentieren en integreren kan hij wat stappen laten zien.
ik heb derive op mijn pc staan maar deze laat alleen het antwoord zien en niet in stappen


Met wolframalpha mathematica krijg je ook alleen de eindantwoorden voor zover ik weet. Ik betwijfel of er zo'n programma bestaat waar je naar op zoek bent.quote:Op zondag 21 maart 2010 12:12 schreef snakeman123 het volgende:
[..]
en waar moet ik dan kijken:? ik vind wel van alles over computers en films
ik heb derive op mijn pc staan maar deze laat alleen het antwoord zien en niet in stappen


Als je een URL geeft, geef dan wel de juiste URL. In die URL van jou zit een typo, en er zijn altijd misselijke commerciële figuren die daar misbruik van maken en het nietsvermoedende slachtoffer naar een site toe laten gaan die geen moer met de officiële site heeft te maken.quote:Op zondag 21 maart 2010 12:08 schreef Dzy het volgende:
www.wolframpalpha.com, probeer daar eens wat? Met differentieren en integreren kan hij wat stappen laten zien.
Dit is de juiste URL.


Ik ken wel een site die voor integratie stapsgewijs uitwerkingen kan laten zien, maar niet voor differentiatie. Dat laatste is ook niet zo nuttig, want leren differentiëren is toch vooral een kwestie van oefenen en het krijgen van routine in het juist toepassen van de bekende regels zoals de regels voor het bepalen van de afgeleide van een product of quotiënt of de kettingregel. Daarnaast moet je natuurlijk de afgeleiden van een aantal standaardfuncties gewoon uit het blote hoofd kunnen opschrijven.quote:Op zondag 21 maart 2010 13:20 schreef BasementDweller het volgende:
[..]
Met wolframalpha mathematica krijg je ook alleen de eindantwoorden voor zover ik weet. Ik betwijfel of er zo'n programma bestaat waar je naar op zoek bent.


Excuseer, ik maakte een typo, het is dus www.wolframalpha.com, als je daar iets in typt in de trant van:quote:Op zondag 21 maart 2010 12:12 schreef snakeman123 het volgende:
[..]
en waar moet ik dan kijken:? ik vind wel van alles over computers en films
ik heb derive op mijn pc staan maar deze laat alleen het antwoord zien en niet in stappen
derivative ln(x^2 + 3x)
dan geeft hij de afgeleide. Hiernaast kun je op Show Steps drukken waarin hij uitlegt hoe je er zelf zou kunnen komen.
[ Bericht 0% gewijzigd door Dzy op 21-03-2010 14:25:29 (goede url deze keer.) ]
"Reality is an illusion created by a lack of alcohol."


Ben je dyslectisch? Je geeft weer de verkeerde URL.quote:Op zondag 21 maart 2010 14:13 schreef Dzy het volgende:
[..]
Excuseer, ik maakte een typo, het is dus www.wolframpalpha.com, als je daar iets in typt in de trant van:
derivative ln(x^2 + 3x)
dan geeft hij de afgeleide. Hiernaast kun je op Show Steps drukken waarin hij uitlegt hoe je er zelf zou kunnen komen.


Ik ben nu bezig met meetkundige rijen, en er staat hier de volgende formule:
Waarom klopt dit? 1- x is toch niet hetzelfde als x-1?
Waarom klopt dit? 1- x is toch niet hetzelfde als x-1?
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


zelfde als 8/4 hetzelfde is als 1/2: je vermenigvuldigt teller/noemer met hetzelfde getal (hier -1).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oh, ik had niet door dat de noemer ook verandert wasquote:Op zondag 21 maart 2010 15:25 schreef GlowMouse het volgende:
zelfde als 8/4 hetzelfde is als 1/2: je vermenigvuldigt teller/noemer met hetzelfde getal (hier -1).
Op dinsdag 25 augustus 2015 15:48 schreef Toekito het volgende:
de grootste schande van heel FOK! naast Fylax is Kano als mod.
de grootste schande van heel FOK! naast Fylax is Kano als mod.


Je bedoelt dat je niet doorhad dat de teller ook veranderd was.quote:Op zondag 21 maart 2010 15:27 schreef kanovinnie het volgende:
[..]
Oh, ik had niet door dat de noemer ook veranderd was


x=r?quote:Op zondag 21 maart 2010 15:39 schreef Riparius het volgende:
[..]
Je bedoelt dat je niet doorhad dat de teller ook veranderd was.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Te bewijzen:
Een normal operator waarvan alle eigenwaardes voldoen aan |L|=1, is unitair. Hint: diagonalisatie.
Hoe pak ik dit aan? Ik weet ook niet wat ik met die hint moet.
Een normal operator waarvan alle eigenwaardes voldoen aan |L|=1, is unitair. Hint: diagonalisatie.
Hoe pak ik dit aan? Ik weet ook niet wat ik met die hint moet.


welke site ken je voor integratie?quote:Op zondag 21 maart 2010 14:06 schreef Riparius het volgende:
[..]
Ik ken wel een site die voor integratie stapsgewijs uitwerkingen kan laten zien, maar niet voor differentiatie. Dat laatste is ook niet zo nuttig, want leren differentiëren is toch vooral een kwestie van oefenen en het krijgen van routine in het juist toepassen van de bekende regels zoals de regels voor het bepalen van de afgeleide van een product of quotiënt of de kettingregel. Daarnaast moet je natuurlijk de afgeleiden van een aantal standaardfuncties gewoon uit het blote hoofd kunnen opschrijven.


Ik zie dat je dit ook op www.wolframalpha.com kan doen. Zeg bijvoorbeeld:quote:Op zondag 21 maart 2010 16:30 schreef snakeman123 het volgende:
[..]
welke site ken je voor integratie?
Integrate[Log[x]/x] en druk op show steps.


Ik heb een beetje moeite met partieel differentieren bij wiskundige economie, het gaat om het bewijs van de stelling van Slutsky. De stelling is:
δdj(p,m) δhj(p,u) δdj(p,m)
-------------- = ------- - -----------
δpi δpi δm
Nu gaat het bewijs als volgt, er geldt dat hj(p,u) = dj(p,e(p,u)) en die gaan ze beiden naar pi differentieren. Er geldt dat m = e(p,u).
Even kijken of het er goed uit ziet, ik kan niet meer previewen?
δdj(p,m) δhj(p,u) δdj(p,m)
-------------- = ------- - -----------
δpi δpi δm
Nu gaat het bewijs als volgt, er geldt dat hj(p,u) = dj(p,e(p,u)) en die gaan ze beiden naar pi differentieren. Er geldt dat m = e(p,u).
Even kijken of het er goed uit ziet, ik kan niet meer previewen?
"Reality is an illusion created by a lack of alcohol."


Meh, dat ziet er niet zo goed uit  Nouja, mijn concrete vraag is, hoe differentieer je dj(p,e(p,u)) naar pi? De di functie is de marshilliaanse vraagfunctie waar een vector uit komt met de vraag naar goed i, de e functie is de minimale uitgavenfunctie welke bestaat uit de som van de kosten-minimaliserende vraag naar elk goed vermenigvuldigd met de prijs van dat goed.
Nouja, mijn concrete vraag is, hoe differentieer je dj(p,e(p,u)) naar pi? De di functie is de marshilliaanse vraagfunctie waar een vector uit komt met de vraag naar goed i, de e functie is de minimale uitgavenfunctie welke bestaat uit de som van de kosten-minimaliserende vraag naar elk goed vermenigvuldigd met de prijs van dat goed.
"Reality is an illusion created by a lack of alcohol."


Beter gebruik je http://betahw.mine.nu/ . Voor breuken doe je dan \frac{a}{b} en de kromme d's krijg je met \partial . Ziet er overzichtelijker uitquote:Op zondag 21 maart 2010 17:00 schreef Dzy het volgende:
Ik heb een beetje moeite met partieel differentieren bij wiskundige economie, het gaat om het bewijs van de stelling van Slutsky. De stelling is:
δdj(p,m) δhj(p,u) δdj(p,m)
-------------- = ------- - -----------
δpi δpi δm
Nu gaat het bewijs als volgt, er geldt dat hj(p,u) = dj(p,e(p,u)) en die gaan ze beiden naar pi differentieren. Er geldt dat m = e(p,u).
Even kijken of het er goed uit ziet, ik kan niet meer previewen?


Even op terugkeren: iedereen die 96 of meer scoorde mag naar de finale in Brussel.quote:
De finalevragen van vorig jaar:
Hoeveel massieve regelmatige viervlakken kan men maximaal tegen mekaar plaatsen zodat één van hun ribben samenvalt met een gegeven lijnstuk in de ruimte?
Een natuurlijk getal heeft vier natuurlijke delers: 1, het getal zelf en twee echte delers. Dat getal vermeerderd met 9 is gelijk aan het zevenvoud van de som van de echte delers. Bepaal dat getal en bewijs dat het uniek is.
In een poging het Belgisch record handjes schudden te verbeteren komen op 20/09/2009 precies 2009 Belgen samen in een grote sporthal. Onder hen bevinden zich Nathalie en Thomas. Tijdens dit evenement schudt iedereen precies één keer de hand van alle andere aanwezigen. Na afloop zegt Nathalie: "Ik heb precies 5 keer zoveel Vlamingen als Brusselaars de hand geschud." Thomas antwoordt met "Ik heb precies 3 keer zoveel Walen als Brusselaars de hand geschud". Uit welk gewest komt Nathalie en uit welk gewest komt Thomas?
Beschouw een lijnstuk [AB] met midden M en middelloodlijn m. Voor elk punt X (verschillend van M) op m beschouwen we het snijpunt Y van de rechte BX met de bissectrice van de hoek BAX. Als X tot M nadert, dan nadert Y tot een punt van [AB]. Welk?
When all things seem to end, the future still remains..


Voor subscript: _quote:
Voor superscript: ^
Als je meerdere tekens in je sub/super-script hebt gebruik dan accolades, bijv.: a_{k+1} of x^{-1}


Zat ik toch wel aardig in de buurt met een score in de 90quote:Op zondag 21 maart 2010 17:20 schreef Masanga het volgende:
[..]
Even op terugkeren: iedereen die 96 of meer scoorde mag naar de finale in Brussel.


Ok, blijkbaar geldt dit:

Met m = e(p,u)
Het heeft met de kettingregel e.d. te maken maar ik kom hier niet zo goed uit.
De di functie is de marshilliaanse vraagfunctie waar een vector uit komt met de vraag naar goed i, de e functie is de minimale uitgavenfunctie welke bestaat uit de som van de kosten-minimaliserende vraag naar elk goed vermenigvuldigd met de prijs van dat goed.
Met m = e(p,u)
Het heeft met de kettingregel e.d. te maken maar ik kom hier niet zo goed uit.
De di functie is de marshilliaanse vraagfunctie waar een vector uit komt met de vraag naar goed i, de e functie is de minimale uitgavenfunctie welke bestaat uit de som van de kosten-minimaliserende vraag naar elk goed vermenigvuldigd met de prijs van dat goed.
"Reality is an illusion created by a lack of alcohol."


quote:Op zondag 21 maart 2010 16:02 schreef BasementDweller het volgende:
Te bewijzen:
Een normal operator waarvan alle eigenwaardes voldoen aan |L|=1, is unitair. Hint: diagonalisatie.
Hoe pak ik dit aan? Ik weet ook niet wat ik met die hint moet.


Vraagje:
Gegeven het stelsel: y1'= 1195 y1 - 1995 y2, y1(0)=2 , y2'=1197y1-1197y2 , y2(0)=-2
Het inverse gedeelte snap ik niet. Ik wou zelf gewoon de rechter w1 (1) en w2 (1) naar links halen. Daarna links herschrijven zodat ik daar één w1 (1) en één w2(2) heb en dan 2/ waarde
Zo zou het toch ook moeten lukken op mijn manier?
Gegeven het stelsel: y1'= 1195 y1 - 1995 y2, y1(0)=2 , y2'=1197y1-1197y2 , y2(0)=-2
Het inverse gedeelte snap ik niet. Ik wou zelf gewoon de rechter w1 (1) en w2 (1) naar links halen. Daarna links herschrijven zodat ik daar één w1 (1) en één w2(2) heb en dan 2/ waarde
Zo zou het toch ook moeten lukken op mijn manier?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik heb een vraag bij mij huiswerk staat die als volgt is:
Bewijs dat als c|a en c|b, dan c|(a-b)
Maar ik snap eigenlijk al niet wat '|' nu eigenlijk doet
In de stof staan ook wel andere voorbeelden met '|', maar het lijkt me handig om te weten wat het nu eigenlijk doet.
Bewijs dat als c|a en c|b, dan c|(a-b)
Maar ik snap eigenlijk al niet wat '|' nu eigenlijk doet
In de stof staan ook wel andere voorbeelden met '|', maar het lijkt me handig om te weten wat het nu eigenlijk doet.


Ik ken die notatie niet maar aan het probleem te zien betekent het deelbaar door?
"Reality is an illusion created by a lack of alcohol."


Die notatie betekent volgens mij " niet "
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


c|a en c|b (lees: c deelt a en c deelt b) betekent dat a/c=k en b/c=l met k,l gehele getallen.quote:Op zondag 21 maart 2010 20:57 schreef Keiichi het volgende:
Ik heb een vraag bij mij huiswerk staat die als volgt is:
Bewijs dat als c|a en c|b, dan c|(a-b)
Maar ik snap eigenlijk al niet wat '|' nu eigenlijk doet
In de stof staan ook wel andere voorbeelden met '|', maar het lijkt me handig om te weten wat het nu eigenlijk doet.


Oke dus wel gedeelt. Grappig. Soms gebruiken ze het als "niet", naar mijn weten.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Dat zou best wel kunnen, maar dat is in deze context een beetje raar vind je niet? Het betekent ook "gegeven dat" maar dat zou hier ook niet echt ergens op slaan 
"Reality is an illusion created by a lack of alcohol."


Beetje vreemd, dan maar aanmenen dat het gewoon gedeeld door is.
Weten jullie trouwens een goede tool voor het maken van simpele grafen? Het hoeft niets flashies te zijn (liever niet zelfs )
)
Weten jullie trouwens een goede tool voor het maken van simpele grafen? Het hoeft niets flashies te zijn (liever niet zelfs


Volgensmij is dit heel makkelijk voor jullie maar ik snap er niks van  kan iemand dit met berekening oplossen:
kan iemand dit met berekening oplossen:
De kwadratische vergelijking is : (y+1)² = 25
het antwoord is: y = 4 of y = -6, maar ik snap niet waarom??
(ik heb vanmiddag een toets)
[ Bericht 2% gewijzigd door stievun1234 op 22-03-2010 00:17:29 ]
De kwadratische vergelijking is : (y+1)² = 25
het antwoord is: y = 4 of y = -6, maar ik snap niet waarom??
(ik heb vanmiddag een toets)
[ Bericht 2% gewijzigd door stievun1234 op 22-03-2010 00:17:29 ]


Omdat 5 in het kwadraat en alleen 5 , 25 kan maken.
5*5=25 . Dus 52 = 25
De enige manier om daar een 5 te krijgen is (links), is door een cijfer(s) te vinden die 5 maken.
Dus wat +1 maakt 5? . Juist dat is 4!
Maar omdat een kwadraat het negatieve weghaalt (kijk maar, negatief *negatief = positief): -5*-5 = 25 , kun je ook iets vinden wat -5 maakt! Dus wat + 1 maakt -5? Juist! -6 natuurlijk.
Je kon ook dit doen:
(y+1)(y+1) = 25
Vermenigvuldigen van linkerkant geeft:
y2 + 2y + 1 = 25 En vervolgens op je rekenmachine (gr ) als je die mag gebruiken:
Y1 = x^2 + 2x + 1
Y2 = 25
En daar dan de intersecties van. (2nd , calc , intersect) (wel even y max op 26 zetten, via window)
5*5=25 . Dus 52 = 25
De enige manier om daar een 5 te krijgen is (links), is door een cijfer(s) te vinden die 5 maken.
Dus wat +1 maakt 5? . Juist dat is 4!
Maar omdat een kwadraat het negatieve weghaalt (kijk maar, negatief *negatief = positief): -5*-5 = 25 , kun je ook iets vinden wat -5 maakt! Dus wat + 1 maakt -5? Juist! -6 natuurlijk.
Je kon ook dit doen:
(y+1)(y+1) = 25
Vermenigvuldigen van linkerkant geeft:
y2 + 2y + 1 = 25 En vervolgens op je rekenmachine (gr ) als je die mag gebruiken:
Y1 = x^2 + 2x + 1
Y2 = 25
En daar dan de intersecties van. (2nd , calc , intersect) (wel even y max op 26 zetten, via window)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Zie de update, als je een GR mag gebruiken is het nog makkelijker (GR=grafische rekenmachine)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ja maar ik zit pas in de 2e klas daar gebruiken we die niet 
die kwadratische vergelijkingen zijn wel rot
die kwadratische vergelijkingen zijn wel rot


Komt wel goed. Op een dag ga je het snappen. Gewoon veel oefenen vooral. Dat is waar wiskunde om draait.
En nog belangrijker: vind iemand die het goed uitlegt.
En nog belangrijker: vind iemand die het goed uitlegt.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Ik snap nu iets niet met een afgeleide van een functie met 2 variabelen.
f (x,y) = x2exy
Ik kom uit op dit:
fx (x,y) = 2x exy + x2 exy
fy (x,y) = x2exy
Maar het moet zijn:
fx (x,y) = 2x exy + x2 y exy
fy (x,y) = x3exy
Ziet iemand wat ik fout doe?
Ik dacht dat ik die fx wel goed had, en bij fy twijfelde ik zelf al.
f (x,y) = x2exy
Ik kom uit op dit:
fx (x,y) = 2x exy + x2 exy
fy (x,y) = x2exy
Maar het moet zijn:
fx (x,y) = 2x exy + x2 y exy
fy (x,y) = x3exy
Ziet iemand wat ik fout doe?
Ik dacht dat ik die fx wel goed had, en bij fy twijfelde ik zelf al.


Bij die exy is in het eerste geval (differentiëren naar x) de y een constante, en in het tweede geval (differentiëren naar y) de x een constante. Je past hier de kettingregel niet correct toe, immers d(ect)/dt = c∙ect.quote:Op maandag 22 maart 2010 15:30 schreef pietpiraat88 het volgende:
Ik snap nu iets niet met een afgeleide van een functie met 2 variabelen.
f (x,y) = x2exy
Ik kom uit op dit:
fx (x,y) = 2x exy + x2 exy
fy (x,y) = x2exy
Maar het moet zijn:
fx (x,y) = 2x exy + x2 y exy
fy (x,y) = x3exy
Ziet iemand wat ik fout doe?
Ik dacht dat ik die fx wel goed had, en bij fy twijfelde ik zelf al.


Kreeg de volgende tentamenvraag:
Is de volgende bewering waar of niet? Licht antwoorden bondig toe.
Als A en B gelijksoortige matrices zijn en A is inverteerbaar, dan is B ook inverteerbaar.
Toen heb ik de AS=SB gebruikt, om proberen te schrijven zodat je aantoont dat B^-1 bestaat, maar hier kwam ik niet uit.
Heb dus uiteindelijk opgeschreven dat deze bewering onjuist is, omdat uit de AS=SB niet blijkt dat B^-1 bestaat.
Weet iemand hier het goede antwoord + uitleg op?
Is de volgende bewering waar of niet? Licht antwoorden bondig toe.
Als A en B gelijksoortige matrices zijn en A is inverteerbaar, dan is B ook inverteerbaar.
Toen heb ik de AS=SB gebruikt, om proberen te schrijven zodat je aantoont dat B^-1 bestaat, maar hier kwam ik niet uit.
Heb dus uiteindelijk opgeschreven dat deze bewering onjuist is, omdat uit de AS=SB niet blijkt dat B^-1 bestaat.
Weet iemand hier het goede antwoord + uitleg op?


Als A inverteerbaar is, dan is de determinant van A ongelijk aan nul. Gelijksoortige matrices hebben dezelfde determinant (waarom?), dus is de determinant van B ongelijk aan nul, waaruit volgt dat B inverteerbaar is. Helpt dat?


Ik ken gelijksoortige matrices niet maar ik heb het even opgezocht en er staat dat ze dezelfde determinant hebben. Als A inverteerbaar is betekent dat dat det(A) ongelijk aan 0 is. Det(A) = det(B) waaruit volgt dat B dus ook inverteerbaar moet zijn.
Nog bedankt voor je boek trouwens, heb vandaag wiskundige economie gehaald met een goed cijfer verwacht ik
Nog bedankt voor je boek trouwens, heb vandaag wiskundige economie gehaald met een goed cijfer verwacht ik
"Reality is an illusion created by a lack of alcohol."


Ik ben bezig met mijn wiskunde huiswerk en kom er nu even niet meer uit..
De opdracht is:
Wouter laat de schijf (2x appel, 2x peer, 1x banaan) zes keer draaien.
Bereken de kans op drie keer appel en drie keer peer
Nu ben ik al uitgekomen op:
en dit klopt ook volgens het antwoordenmodel maar hoe moet ik dit op mijn GR invoeren?
De opdracht is:
Wouter laat de schijf (2x appel, 2x peer, 1x banaan) zes keer draaien.
Bereken de kans op drie keer appel en drie keer peer
Nu ben ik al uitgekomen op:
en dit klopt ook volgens het antwoordenmodel maar hoe moet ik dit op mijn GR invoeren?


GR? Grrr ...quote:Op maandag 22 maart 2010 20:09 schreef AE86_Trueno het volgende:
Ik ben bezig met mijn wiskunde huiswerk en kom er nu even niet meer uit..
De opdracht is:
Wouter laat de schijf (2x appel, 2x peer, 1x banaan) zes keer draaien.
Bereken de kans op drie keer appel en drie keer peer
Nu ben ik al uitgekomen op:
[ afbeelding ] en dit klopt ook volgens het antwoordenmodel maar hoe moet ik dit op mijn GR invoeren?
Maar je weet toch hopelijk wel dat:
(nk) = n!/k!(n-k)!
Klik
[ Bericht 4% gewijzigd door Riparius op 22-03-2010 20:20:21 ]


Ja, ben er ook al uit.. maakte een domme fout.
Zo voer ik het in: 6nCr3 x (2/5)^3 x (2/5)^3
Ik deed eerst met mijn domme hoofd 2nCr5 ipv 2/5.

[ Bericht 37% gewijzigd door AE86_Trueno op 22-03-2010 20:42:07 ]
Zo voer ik het in: 6nCr3 x (2/5)^3 x (2/5)^3
Ik deed eerst met mijn domme hoofd 2nCr5 ipv 2/5.
[ Bericht 37% gewijzigd door AE86_Trueno op 22-03-2010 20:42:07 ]


Ik ben er trouwens uitgekomen met de Lagrange interpolatie. Wikipedia was super handig. Nu nog even hermite interpolatie uitvoeren hahaha.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Stel dat de limiet als x->a van f(x) gelijk is aan p, en de limiet als x->a van g(x) gelijk is aan q, met p>q. Volgt hier dan uit dat f(x)>g(x) voor een bepaald delta interval? Zoja, hoe kan ik dit interval omschrijven?
Dank!
Dank!


Tip: S is inverteerbaar (per definitie van gelijksoortig, anders zou je altijd S=0 kunnen nemen). Gebruik dat.quote:Op maandag 22 maart 2010 18:01 schreef martijnnum1 het volgende:
Kreeg de volgende tentamenvraag:
Is de volgende bewering waar of niet? Licht antwoorden bondig toe.
Als A en B gelijksoortige matrices zijn en A is inverteerbaar, dan is B ook inverteerbaar.
Toen heb ik de AS=SB gebruikt, om proberen te schrijven zodat je aantoont dat B^-1 bestaat, maar hier kwam ik niet uit.
Heb dus uiteindelijk opgeschreven dat deze bewering onjuist is, omdat uit de AS=SB niet blijkt dat B^-1 bestaat.
Weet iemand hier het goede antwoord + uitleg op?


Pak de definitie van de limiet en doe wat met epsilon en (p+q)/2.quote:Op maandag 22 maart 2010 22:55 schreef BasementDweller het volgende:
Stel dat de limiet als x->a van f(x) gelijk is aan p, en de limiet als x->a van g(x) gelijk is aan q, met p>q. Volgt hier dan uit dat f(x)>g(x) voor een bepaald delta interval? Zoja, hoe kan ik dit interval omschrijven?
Dank!
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je bedoelt: kies ε < (p-q)/2.quote:Op maandag 22 maart 2010 22:56 schreef GlowMouse het volgende:
[..]
Pak de definitie van de limiet en doe wat met epsilon en (p+q)/2.


Nee, anders zei ik dat welquote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik geloof toch niet dat het zo werkt. Je moet een omgeving van p en een omgeving van q kiezen die elkaar niet overlappen. Bij p > q en eenzelfde ε voor beide functies kom je dan tot ε < (p-q)/2.quote:Op maandag 22 maart 2010 23:01 schreef GlowMouse het volgende:
[..]
Nee, anders zei ik dat welHet idee is gewoon dat je met epsilon zorgt dat je altijd aan de goede kant van (p+q)/2 zit en de uitwerking laat ik aan hemzelf over.


daar kom je op uit ja, dat is dan ook precies de afstand van p tot (p+q)/2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat lijkt me ook, en dit had ik ook al zelf bedacht. Alleen hiermee kwam ik niet tot de conclusie dat f(x)>g(x).quote:Op maandag 22 maart 2010 23:06 schreef Riparius het volgende:
[..]
Ik geloof toch niet dat het zo werkt. Je moet een omgeving van p en een omgeving van q kiezen die elkaar niet overlappen. Bij p > q en eenzelfde ε voor beide functies kom je dan tot ε < (p-q)/2.


Uit de definitie van de limiet:
Voor alle e>0 bestaat er een d>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d, dan d(f(x),p)<e.
Kies nu 0 < e < (p-q)/2. Dan bestaat er een d'>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d', dan d(f(x),p) < (p-q)/2.
Voor alle e>0 bestaat er een d>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d, dan d(f(x),p)<e.
Kies nu 0 < e < (p-q)/2. Dan bestaat er een d'>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d', dan d(f(x),p) < (p-q)/2.


Waarom niet? Kies een ε < (p-q)/2. Volgens de definitie van de limiet is er dan een δf zodanig dat:quote:Op maandag 22 maart 2010 23:12 schreef BasementDweller het volgende:
[..]
Dat lijkt me ook, en dit had ik ook al zelf bedacht. Alleen hiermee kwam ik niet tot de conclusie dat f(x)>g(x).
| f(x) - p | < ε voor 0 < | x - a | < δf
En tevens een δg zodanig dat
| g(x) - q | < ε voor 0 < | x - a | < δg
Kies nu δ = min(δf,δg), dan is
f(x) > g(x) voor 0 < | x - a | < δ


Dat ik dat zelf niet op papier krijgquote:Op maandag 22 maart 2010 23:19 schreef Riparius het volgende:
[..]
Waarom niet? Kies een ε < (p-q)/2. Volgens de definitie van de limiet is er dan een δf zodanig dat:
| f(x) - p | < ε voor 0 < | x - a | < δf
En tevens een δg zodanig dat
| g(x) - q | < ε voor 0 < | x - a | < δg
Kies nu δ = min(δf,δg), dan is
f(x) > g(x) voor 0 < | x - a | < δ


vraagje(s):

van stap 2 naar 3 snap ik wel, maar stap 1 naar 2 is voor mij een raadsel.... er staat wel iets met dat je cos(2x) = 2(cos(x))² - 1 moet gebruiken maar zou niet weten hoe

hier snap ik helemaal niks van

hier kom ik zelf uit op
alvast bedankt
van stap 2 naar 3 snap ik wel, maar stap 1 naar 2 is voor mij een raadsel.... er staat wel iets met dat je cos(2x) = 2(cos(x))² - 1 moet gebruiken maar zou niet weten hoe
hier snap ik helemaal niks van
hier kom ik zelf uit op
alvast bedankt


De eerste integraal: elementaire goniometrie. Je kunt het kwadraat van een cosinus of een sinus omzetten in de cosinus van de dubbele hoek. Kijk even hier.quote:Op dinsdag 23 maart 2010 01:47 schreef afcabrk het volgende:
vraagje(s):
[ afbeelding ]
van stap 2 naar 3 snap ik wel, maar stap 1 naar 2 is voor mij een raadsel.... er staat wel iets met dat je cos(2x) = 2(cos(x))² - 1 moet gebruiken maar zou niet weten hoe
[ afbeelding ]
hier snap ik helemaal niks van
[ afbeelding ]
hier kom ik zelf uit op [ afbeelding ]
alvast bedankt
De tweede en derde integraal: probeer de primitieve eens te differentiëren. Ik heb het idee dat je de kettingregel niet goed begrijpt. Uiteraard kun je deze integralen oplossen met de substitutieregel (de tegenhanger van de kettingregel bij het differentiëren), maar als je de kettingregel begrijpt zou je de primitieve ook zo moeten kunnen 'zien'.


oke dat eerste snap ik nu toch wel.
maar die tweede en derde.. moet je bij die (x+1)e^(4x²+8x)
4x²+8x als schakel nemen? zo ja, wat doe je dan met x+1, want die zie ik nergens terug in de primitieve..
of moet je ze allebei als schakels nemen?
edit: ikzie dat het in dit geval niet uitmaakt of x+1 als schakel wordt genomen, want delen door 1 geeft hetzelfde. ikkom zelf uit op e^(4x²+8x) / (8x+8)
zonder die 8x komik wel uit op wat ik hoor te krijgen...
en die met wortel in de integraal : die x die vooraan staat wordt gewoon weggelaten ? of waarschijnlijk zie ik iets over het hoofd
[ Bericht 22% gewijzigd door afcabrk op 23-03-2010 02:12:10 ]
maar die tweede en derde.. moet je bij die (x+1)e^(4x²+8x)
4x²+8x als schakel nemen? zo ja, wat doe je dan met x+1, want die zie ik nergens terug in de primitieve..
of moet je ze allebei als schakels nemen?
edit: ikzie dat het in dit geval niet uitmaakt of x+1 als schakel wordt genomen, want delen door 1 geeft hetzelfde. ikkom zelf uit op e^(4x²+8x) / (8x+8)
zonder die 8x komik wel uit op wat ik hoor te krijgen...
en die met wortel in de integraal : die x die vooraan staat wordt gewoon weggelaten ? of waarschijnlijk zie ik iets over het hoofd
[ Bericht 22% gewijzigd door afcabrk op 23-03-2010 02:12:10 ]


Probeer nu eerst eens de (juiste) primitieven te differentiëren met behulp van de kettingregel, dat kun je toch wel?quote:Op dinsdag 23 maart 2010 02:06 schreef afcabrk het volgende:
oke dat eerste snap ik nu toch wel.
maar die tweede en derde.. moet je bij die (x+1)e^(4x²+8x)
4x²+8x als schakel nemen? zo ja, wat doe je dan met x+1, want die zie ik nergens terug in de primitieve..
of moet je ze allebei als schakels nemen?
en die met wortel in de integraal : die x die vooraan staat wordt gewoon weggelaten ? of waarschijnlijk zie ik iets over het hoofd


ja dan kom ik uit op
1/8e^u ---> 1/8e^u
4x²+8x ---> 8x + 8
f'(x) = (8x+8) 1/8e^u
= (x+1) e^u
en dit klopt, maar het probleem ligt ook niet bij het differentieren bij mij.
ik doe gewoon iets fout bij het berekenen van het primitieve, en ikdacht dat één van jullie
wist waar :p heb binnekort een toelatingstentamen voor econometrie, en ikheb maar paar weekjes ervaring
met integraalrekening dus vandaar datik zuig
1/8e^u ---> 1/8e^u
4x²+8x ---> 8x + 8
f'(x) = (8x+8) 1/8e^u
= (x+1) e^u
en dit klopt, maar het probleem ligt ook niet bij het differentieren bij mij.
ik doe gewoon iets fout bij het berekenen van het primitieve, en ikdacht dat één van jullie
wist waar :p heb binnekort een toelatingstentamen voor econometrie, en ikheb maar paar weekjes ervaring
met integraalrekening dus vandaar datik zuig


Inderdaad, differentiëren van e4x²+8x geeft e4x²+8x(8x+8) = 8(x+1)e4x²+8x, en dat is een factor 8 teveel. De gezochte primitieve van (x+1)e4x²+8x is dus 1/8∙e4x²+8x.quote:Op dinsdag 23 maart 2010 02:06 schreef afcabrk het volgende:
edit: ikzie dat het in dit geval niet uitmaakt of x+1 als schakel wordt genomen, want delen door 1 geeft hetzelfde. ikkom zelf uit op e^(4x²+8x) / (8x+8)
zonder die 8x komik wel uit op wat ik hoor te krijgen...


Je kunt ook formeel de substitutiemethode gebruiken. De op te lossen (onbepaalde) integraal is:quote:Op dinsdag 23 maart 2010 02:17 schreef afcabrk het volgende:
ja dan kom ik uit op
1/8e^u ---> 1/8e^u
4x²+8x ---> 8x + 8
f'(x) = (8x+8) 1/8e^u
= (x+1) e^u
en dit klopt, maar het probleem ligt ook niet bij het differentieren bij mij.
ik doe gewoon iets fout bij het berekenen van het primitieve, en ikdacht dat één van jullie
wist waar :p heb binnekort een toelatingstentamen voor econometrie, en ikheb maar paar weekjes ervaring
met integraalrekening dus vandaar datik zuig
∫ (x+1)∙e4x²+8x∙dx
Ik kies nu de substitutie:
u = 4x2 + 8x
Dan is:
du/dx = 8x + 8
En dus:
du = 8(x+1)∙dx
En dus:
1/8∙du = (x+1)∙dx
De integraal wordt dan:
∫ 1/8∙eudu = 1/8∙eu + C
Terugsubstitueren van u = 4x2 + 8x geeft dan als resultaat
∫ (x+1)∙e4x²+8x∙dx = 1/8∙e4x²+8x + C


zo'n uitleg hadik nodig om het te laten doordringen dankjewel! 
en dat andere wordt dan..

u = 9x²-1
du/dx = 18x
du = 18x * dx
1/18du = x * dx (<-- is die x in het rechterlid de x in het begin van het integraal?)
f = wortel(u)
primitiveren = 2/3(9x²-1)^3/2
F = 1/18 * 2/3(9x²-1)^3/2
klopt dit?
en dat andere wordt dan..
u = 9x²-1
du/dx = 18x
du = 18x * dx
1/18du = x * dx (<-- is die x in het rechterlid de x in het begin van het integraal?)
f = wortel(u)
primitiveren = 2/3(9x²-1)^3/2
F = 1/18 * 2/3(9x²-1)^3/2
klopt dit?


Ja, zo klopt het, maar je moet het iets netter proberen op te schrijven (zoals in mijn uitwerking van je tweede integraal) en in je oorspronkelijke integraal niet de dx vergeten natuurlijk.quote:Op dinsdag 23 maart 2010 02:42 schreef afcabrk het volgende:
zo'n uitleg hadik nodig om het te laten doordringen dankjewel!
en dat andere wordt dan..
[ afbeelding ]
u = 9x²-1
du/dx = 18x
du = 18x * dx
1/18du = x * dx (<-- is die x in het rechterlid de x in het begin van het integraal?)
f = wortel(u)
primitiveren = 2/3(9x²-1)^3/2
F = 1/18 * 2/3(9x²-1)^3/2


Ik zit met een probleempje: ik moet iets integreren, maar ik weet niet hoe. We hebben verschillende methoden hiervoor gehad: partieel integreren, substitutiemethode en nog wat.
De formule gaat
(x+2) / (x^2+4x-12)
Welke methode voor integreren moet ik hiervoor gebruiken?
De formule gaat
(x+2) / (x^2+4x-12)
Welke methode voor integreren moet ik hiervoor gebruiken?
New in town


Voor de noemer van je breuk hebben we:quote:Op dinsdag 23 maart 2010 14:25 schreef AliKebap het volgende:
Ik zit met een probleempje: ik moet iets integreren, maar ik weet niet hoe. We hebben verschillende methoden hiervoor gehad: partieel integreren, substitutiemethode en nog wat.
De formule gaat
(x+2) / (x^2+4x-12)
Welke methode voor integreren moet ik hiervoor gebruiken?
x2 + 4x - 12 = (x + 6)(x - 2)
Je kunt nu splitsen in deelbreuken (partiële breuken), door je oorspronkelijke breuk te herschrijven als een lineaire combinatie van 1/(x + 6) en 1/(x - 2), als volgt:
(x+2)/(x2+4x-12) = A/(x + 6) + B/(x - 2)
Werk dit eerst eens uit en bepaal hieruit A en B.


Ik moet de oppervlakte van het vlakdeel dat word ingesloten door de formule
f(x) = (x^2 + x + 1) / x
en de lijn
y = -1,5
uitrekenen.
Nu is dat het gebied tussen -2 en -0.5. Hoe kan ik dat uitrekenen? Door x en y om te wisselen?
f(x) = (x^2 + x + 1) / x
en de lijn
y = -1,5
uitrekenen.
Nu is dat het gebied tussen -2 en -0.5. Hoe kan ik dat uitrekenen? Door x en y om te wisselen?


Je hebt de x-coordinaten van de snijpunten al bepaald. Met integreren reken je het vlakdeel dat wordt ingesloten tussen een formule en de x-as uit. Als je nu f(x) aanpast door er 1.5 bij op te tellen verschuif je de functie 1.5 omhoog en gaat het nu om het vlakdeel tussen de nieuwe functie en de x-as, welke je dus kunt oplossen met integreren.
"Reality is an illusion created by a lack of alcohol."


Nee, niet gaan goochelen. Maak even een tekening met daarin de grafiek van y = (x2 + x + 1)/x en de grafiek van y = -3/2 op het interval [-2,-½]. Dan zie je dat het gaat om de verticale afstand tussen de curve en de rechte lijn, en dus het verschil van deze twee. Je moet dus:quote:Op dinsdag 23 maart 2010 16:04 schreef Siddartha het volgende:
Ik moet de oppervlakte van het vlakdeel dat wordt ingesloten door de grafiek van
f(x) = (x^2 + x + 1) / x
en de lijn
y = -1,5
uitrekenen.
Nu is dat het gebied tussen x=-2 en x=-½. Hoe kan ik dat uitrekenen? Door x en y om te wisselen?
(x2 + x + 1)/x - (-3/2)
integreren over het interval [-2,-½] om de oppervlakte van het vlakdeel ingesloten door de curve en de lijn te berekenen.


Maar dan krijg ik uit als primitive:quote:Op dinsdag 23 maart 2010 16:20 schreef Riparius het volgende:
[..]
Nee, niet gaan goochelen. Maak even een tekening met daarin de grafiek van y = (x2 + x + 1)/x en de grafiek van y = -3/2 op het interval [-2,-½]. Dan zie je dat het gaat om de verticale afstand tussen de curve en de rechte lijn, en dus het verschil van deze twee. Je moet dus:
(x2 + x + 1)/x - (-3/2)
integreren over het interval [-2,-½] om de oppervlakte van het vlakdeel ingesloten door de curve en de lijn te berekenen.
0.5x^2 + x + ln x - 1.5x
Hoe vul ik dan een negatief getal in (aangezien er ln instaat)?


Om te beginnen: je maakt een tekenfout. Kijk nog eens goed naar mijn functie.quote:Op dinsdag 23 maart 2010 16:34 schreef Siddartha het volgende:
[..]
Maar dan krijg ik uit als primitive:
0.5x^2 + x + ln x - 1.5x
Hoe vul ik dan een negatief getal in (aangezien er ln instaat)?
Verder: voor x < 0 kun je ln(-x) als primitieve van 1/x nemen. Controleer dit door ln(-x) te differentiëren.


Ah, een min vergeten:quote:Op dinsdag 23 maart 2010 16:38 schreef Riparius het volgende:
[..]
Om te beginnen: je maakt een tekenfout. Kijk nog eens goed naar mijn functie.
Verder: voor x < 0 kun je ln(-x) als primitieve van 1/x nemen. Controleer dit door ln(-x) te differentiëren.
0.5x^2 + x + ln (-x) + 1.5x
En dan kan ik dus wel de negatieve getallen invullen.
En dan klopt het!
Bedankt!


Ja. Wat krijg je als (exact) eindantwoord?quote:Op dinsdag 23 maart 2010 16:45 schreef Siddartha het volgende:
[..]
Ah, een min vergeten:
0.5x^2 + x + ln (-x) + 1.5x
En dan kan ik dus wel de negatieve getallen invullen.
En dan klopt het!
Bedankt!


Gegeven: CD staat loodrecht op AB, DE loodrecht op AC en DF loodrecht op BC.
Bewijs dat ABFE een koordenvierhoek is.
Van m'n toets van vandaag


CEDF is een kv want hoek E en hoek F zijn beide recht. Hieruit volgt dat hoek DFE gelijk is aan hoek DCE. Nu gaan we in ABFE overstaande hoeken optellen: hoek A + hoek BFE = hoek A + hoek BFD + hoek DFE = hoek A + 90 + hoek DCE = hoek A + hoek ADC + hoek DCA = som van 3 hoeken van driehoek ADC = 180 graden.


Waarom?quote:Op dinsdag 23 maart 2010 22:39 schreef thabit het volgende:
CEDF is een kv want hoek E en hoek F zijn beide recht. Hieruit volgt dat hoek DFE gelijk is aan hoek DCE.


Grmbl, even over het hoofd gezien DEFC is natuurlijk ook een koordenvierhoek. Dan kan ik gewoon constante hoek gebruiken inderdaad. Dankjewel!quote:Op dinsdag 23 maart 2010 22:50 schreef thabit het volgende:
Dat is altijd zo in koordenvierhoeken. Teken er een cirkel omheen: de omtrekshoek is constant.


Ik probeer de Wetten van Mrogan te bewijzen, maar kom niet erg ver 
Ik kom niet verder dan het complement weghalen door 1 - (vereniging van a_i). Hoe kan ik van ene vereniging een doorsnede maken?
Ik kom niet verder dan het complement weghalen door 1 - (vereniging van a_i). Hoe kan ik van ene vereniging een doorsnede maken?


Ik zou gewoon een element uit het linkerdeel nemen en bewijzen dat dat in het rechterdeel zit, en vice versa.


Hm, ik dacht het vorige keer op deze manier gedaan te hebben, maar oké! Ik weet alleen niet goed hoe ik dit moet noteren, hoe ik het nu heb staan:
Maar ik k anme voorstellen dat het op een iets meer wiskundige manier kan ipv die puntjes ;x
Maar ik k anme voorstellen dat het op een iets meer wiskundige manier kan ipv die puntjes ;x


Beide notaties kom ik wel eens tegen, zijn ze eigenlijk allebei 'goed'?


eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ah, oké. Maar die notatie is dan wel gewoon oké, en het gevolg ("voor alle i: e niet in Ai" -> "voor alle i: e zit in Aic") is wel triviaal toch?


Die tweede zou ik niet doen. Eerst allerlei symbolen gebruiken en ze achteraf pas introduceren is heel vervelend om te moeten lezen.quote:Op woensdag 24 maart 2010 21:08 schreef GlowMouse het volgende:
Beide notaties kom ik wel eens tegen, zijn ze eigenlijk allebei 'goed'?
[ afbeelding ]
[ afbeelding ]


Ze worden allebei wel gebruikt, maar eigenlijk kom ik in artikelen in mijn vakgebied veel vaker een beschrijving in woorden tegen dan zulke constructies met logische symbolen, a la "for all $i \in \mathbb{N}$ we have $e_i \not\in A_i$".quote:Op woensdag 24 maart 2010 21:08 schreef GlowMouse het volgende:
Beide notaties kom ik wel eens tegen, zijn ze eigenlijk allebei 'goed'?
[ afbeelding ]
[ afbeelding ]
Voor de volledigheid, wat je op regel 3 en 4 schrijft klopt semantisch niet, de $e$ weglaten voor de $\in$/$\not\in$ is voor zover ik weet geen geaccepteerd gebruik.quote:Op woensdag 24 maart 2010 21:15 schreef Hanneke12345 het volgende:
Ah, oké. Maar die notatie is dan wel gewoon oké, en het gevolg ("voor alle i: e niet in Ai" -> "voor alle i: e zit in Aic") is wel triviaal toch?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Bewijs dat de inhoud van een bol gelijk is aan:

Doormiddel van Integreren.
Wat doe ik fout?

Dus:

Maar dan kom ik uit op:

Wat dus niet klopt, ik mis een factor 2?
Doormiddel van Integreren.
Wat doe ik fout?
Dus:
Maar dan kom ik uit op:
Wat dus niet klopt, ik mis een factor 2?


Je hebt de functiequote:Op donderdag 25 maart 2010 12:22 schreef Siddartha het volgende:
Bewijs dat de inhoud van een bol gelijk is aan:
[ afbeelding ]
Doormiddel van Integreren.
Wat doe ik fout?
[ afbeelding ]
Dus:
[ afbeelding ]
Maar dan kom ik uit op:
[ afbeelding ]
Wat dus niet klopt, ik mis een factor 2?
f(x) = √(r2 - x2)
De grafiek hiervan is een halve cirkel in de kwadranten I en II, die bij wenteling om de x-as een bol met als middelpunt de oorsprong en straal r oplevert. Om nu het volume van deze bol te berekenen, moet je {f(x)}2 integreren over het interval [-r,r] en het resultaat met π vermenigvuldigen. Jij integreert echter over het interval [0,r], zodat je het volume vindt van een halve bol met straal r.
Heb je trouwens de opgave over het berekenen van de oppervlakte van een bol met straal r nog uitgewerkt? Ik heb zo het idee van niet, anders had je geweten dat je over het interval [-r,r] moet integreren.


In het antwoordboekje staat het volgende:quote:Op donderdag 25 maart 2010 14:14 schreef Riparius het volgende:
[..]
Je hebt de functie
f(x) = √(r2 - x2)
De grafiek hiervan is een halve cirkel in de kwadranten I en II, die bij wenteling om de x-as een bol met als middelpunt de oorsprong en straal r oplevert. Om nu het volume van deze bol te berekenen, moet je {f(x)}2 integreren over het interval [-r,r] en het resultaat met π vermenigvuldigen. Jij integreert echter over het interval [0,r], zodat je het volume vindt van een halve bol met straal r.
Heb je trouwens de opgave over het berekenen van de oppervlakte van een bol met straal r nog uitgewerkt? Ik heb zo het idee van niet, anders had je geweten dat je over het interval [-r,r] moet integreren.
En dat is gelijk aan 4/3Pir^3 (Volgens het antwoordboekje dan). Waarom klopt dat dan niet?


Het antwoordenboekje klopt, hoewel ik het zelf niet zo zou opschrijven. Je hebt kennelijk de integraal niet correct uitgerekend.quote:Op donderdag 25 maart 2010 14:47 schreef Siddartha het volgende:
[..]
In het antwoordboekje staat het volgende:
[ afbeelding ]
En dat is gelijk aan 4/3Pir^3 (Volgens het antwoordboekje dan). Waarom klopt dat dan niet?


Integraal van Pi(r^2 - x^2) is toch gewoon Pi r^2 - 1/3x^3 + c ?quote:Op donderdag 25 maart 2010 14:50 schreef Riparius het volgende:
[..]
Het antwoordenboekje klopt, hoewel ik het zelf niet zo zou opschrijven. Je hebt kennelijk de integraal niet correct uitgerekend.
Invullen voor x=r en vermenigvuldigen met 2 geeft dan 2/3 ipv 4/3.


Nee, dit klopt niet. Bovendien vind ik het jammer dat je kennelijk eerst in het antwoordenboekje kijkt en dan probeert na te doen wat daar wordt gedaan, anders was je nooit op het idee gekomen om de integraal over het interval [-r,r] te vervangen door tweemaal de integraal over het interval [0,r].quote:Op donderdag 25 maart 2010 14:53 schreef Siddartha het volgende:
[..]
Integraal van Pi(r^2 - x^2) is toch gewoon Pi r^2 - 1/3x^3 + c ?
Invullen voor x=r en vermenigvuldigen met 2 geeft dan 2/3 ipv 4/3.


Verdomme, ik ben gewoon r^2 vergeten te integreren!quote:Op donderdag 25 maart 2010 14:56 schreef Riparius het volgende:
[..]
Nee, dit klopt niet. Bovendien vind ik het jammer dat je kennelijk eerst in het antwoordenboekje kijkt en dan probeert na te doen wat daar wordt gedaan, anders was je nooit op het idee gekomen om de integraal over het interval [-r,r] te vervangen door tweemaal de integraal over het interval [0,r].
Stomme fout die ik vaak maak, helaas.
Ik kan je geruststellen dat ik eerst een hele tijd zelf over het antwoord heb nagedacht. Pas daarna zocht ik het antwoord op.


Inderdaad, een primitieve van {f(x)}2 = r2 - x2 is r2x - 1/3∙x3. Integreren over [-r,r] en vermenigvuldigen met π geeft dan 4/3∙π∙r3 voor het volume van een bol met straal r. Heb je nu de oppervlakte van een bol met straal r ook kunnen berekenen via integratie?quote:Op donderdag 25 maart 2010 15:07 schreef Siddartha het volgende:
[..]
Verdomme, ik ben gewoon r^2 vergeten te integreren!
Stomme fout die ik vaak maak, helaas.
Ik kan je geruststellen dat ik eerst een hele tijd zelf over het antwoord heb nagedacht. Pas daarna zocht ik het antwoord op.


Ik kom tot dit:quote:Op donderdag 25 maart 2010 15:12 schreef Riparius het volgende:
[..]
Inderdaad, een primitieve van {f(x)}2 = r2 - x2 is r2x - 1/3∙x3. Integreren over [-r,r] en vermenigvuldigen met π geeft dan 4/3∙π∙r3 voor het volume van een bol met straal r. Heb je nu de oppervlakte van een bol met straal r ook kunnen berekenen via integratie?
f(x): y = Wortel(r^2 - x^2)
f'(x)= x / wortel(r^2-x^2)
Dat kwadrateren levert op(?):
x^2 (r^2 - x^2)^1,5
Invullen in de formule voor lengte geeft:
Primitiveer Wortel(1+(f'(x)^2 )
Maar hoe moet ik zoiets primitiveren?


Nee, dit gaat niet goed. Ik had het meeste werk trouwens al voor je gedaan. Kijk nog even hier. We hebben:quote:Op donderdag 25 maart 2010 15:40 schreef Siddartha het volgende:
[..]
Ik kom tot dit:
f(x): y = Wortel(r^2 - x^2)
f'(x)= x / wortel(r^2-x^2)
Dat kwadrateren levert op(?):
x^2 (r^2 - x^2)^1,5
1 + (f'(x))2 = r2/(r2 - x2)
En dus:
√(1 + (f'(x))2) = r/√(r2 - x2)
En dus:
f(x)∙√(1 + (f'(x))2) = r
Je krijgt dus een heel eenvoudige (constante) functie om te integreren! Kun je ook een meetkundige interpretatie geven van dit resultaat? En wat wordt nu de oppervlakte van een bol met straal r?


Weet iemand hoe je met http://www.wolframalpha.com/ de hoekfrequentie, periode en frequentie kan uitrekenen? Ik snap die sommen maar niet...


Hoe komen ze bij die vergelijking, ik zie de logica niet? Dus die onder de zin, via breuksplitsen krijgen we.
Blues ain't nothing but a good man feeling bad...


Oppervlakte van een bol is dusquote:Op donderdag 25 maart 2010 16:00 schreef Riparius het volgende:
[..]
Nee, dit gaat niet goed. Ik had het meeste werk trouwens al voor je gedaan. Kijk nog even hier. We hebben:
1 + (f'(x))2 = r2/(r2 - x2)
En dus:
√(1 + (f'(x))2) = r/√(r2 - x2)
En dus:
f(x)∙√(1 + (f'(x))2) = r
Je krijgt dus een heel eenvoudige (constante) functie om te integreren! Kun je ook een meetkundige interpretatie geven van dit resultaat? En wat wordt nu de oppervlakte van een bol met straal r?
4pi r^2
Ik bedacht me trouwens, is de omtrek niet gewoon de afgeleide van de inhoud?
Inhoud = 4/3Pi r^3
Inhoud '= 4Pi r^2 = Omtrek


Breuksplitsing is een standaardtechniek bij o.a. integreren. Het idee is dat je een breuk gaat schrijven als een som van een aantal breuken waarbij de noemer steeds één van de factoren is van de noemer van de oorspronkelijke breuk. Vervolgens moet je die deelbreuken weer gelijknamig maken om ze op te kunnen tellen. Dat is wat hier gebeurt. Tenslotte vermenigvuldig je beide leden van de vergelijking met de noemer van de oorspronkelijke breuk en stel je de coëfficiënten van de veeltermen in linker en rechter lid aan elkaar gelijk. Dit levert dan een stelsel lineaire vergelijkingen op in A, B, C ... dat je op kunt lossen om uiteindelijk te weten te komen hoe je de oorspronkelijke breuk kunt schrijven als een som van deelbreuken.quote:Op donderdag 25 maart 2010 16:22 schreef GoodGawd het volgende:
[ afbeelding ]
Hoe komen ze bij die vergelijking, ik zie de logica niet? Dus die onder de zin, via breuksplitsen krijgen we.


Inderdaad, dit klopt. De meetkundige interpretatie van die constante functie die je krijgt is dat de oppervlakte van een bol gelijk is aan de manteloppervlakte van een omgeschreven cilinder. En aangezien dit resultaat ook geldt als je integreert over een willekeurig deelinterval van [-r,r] zien we dus dat de oppervlakte van een willekeurig bolsegment ook gelijk is aan het corresponderende deel van de oppervlakte van de omgeschreven cilinder.quote:Op donderdag 25 maart 2010 16:24 schreef Siddartha het volgende:
[..]
Oppervlakte van een bol is dus
4pi r^2
Dat is een hele goede observatie. Als je een bol neemt met een straal r en een iets grotere concentrische bol met een straal r + Δr, dan kun je het verschil in volume benaderen door de oppervlakte O(r) van de bol te vermenigvuldigen met de dikte Δr van de 'schil'. En dus geldt:quote:Ik bedacht me trouwens, is de oppervlakte niet gewoon de afgeleide van de inhoud?
Inhoud = 4/3Pi r^3
Inhoud '= 4Pi r^2 = Oppervlakte
V(r+Δr) - V(r) ≈ O(r)∙Δr
En dus ook:
(V(r+Δr) - V(r))/Δr ≈ O(r)
De benadering wordt beter naarmate we de dikte Δr van de 'schil' tot nul laten naderen, en dus geldt inderdaad:
V'(r) = O(r)
Voor een cirkel geldt iets dergelijks: als je de formule πr2 voor de oppervlakte van een cirkel met straal r differentieert naar r krijg je 2πr, en dat is inderdaad de formule voor de omtrek van een cirkel met straal r.
[ Bericht 1% gewijzigd door Riparius op 25-03-2010 18:05:40 ]


Breuksplitsen is echt iets wat je even moet leren door op het internet naar voorbeeldjes te kijken. Verder kun je in je rekenmachine handig de matrix oplossen die je bij breuksplitsen krijgt.quote:Op donderdag 25 maart 2010 16:22 schreef GoodGawd het volgende:
[ afbeelding ]
Hoe komen ze bij die vergelijking, ik zie de logica niet? Dus die onder de zin, via breuksplitsen krijgen we.
Bij de Tu Delft, kregen we een pdf'je om het te leren. Maar het meest heb ik gehad aan mijn leraar van het HBO en een vriend die het door had.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Geef eens een voorbeeld van een opgave. Met deze vraag kan niemand iets omdat we jouw gedachten niet kunnen lezen.quote:Op donderdag 25 maart 2010 16:17 schreef snakeman123 het volgende:
Weet iemand hoe je met http://www.wolframalpha.com/ de hoekfrequentie, periode en frequentie kan uitrekenen? Ik snap die sommen maar niet...


Okay, met als er twee letters om de hoek komen kijken volg ik het wel maar met meer wordt het een beetje een doolhofquote:Op donderdag 25 maart 2010 16:52 schreef Burakius het volgende:
[..]
Breuksplitsen is echt iets wat je even moet leren door op het internet naar voorbeeldjes te kijken. Verder kun je in je rekenmachine handig de matrix oplossen die je bij breuksplitsen krijgt.
Bij de Tu Delft, kregen we een pdf'je om het te leren. Maar het meest heb ik gehad aan mijn leraar van het HBO en een vriend die het door had.
Blues ain't nothing but a good man feeling bad...


Maakt verder niet uit, je krijgt uiteindelijk een vergelijking met een vierdegraads polynoom in s en gelijkstelling van de vijf coëfficiënten in beide leden van je vergelijking levert je dan een stelsel van vijf lineaire vergelijkingen in A,B,C,D en E op.quote:Op donderdag 25 maart 2010 17:52 schreef GoodGawd het volgende:
[..]
Okay, met als er twee letters om de hoek komen kijken volg ik het wel maar met meer wordt het een beetje een doolhof


Het principe blijft hetzelfde steeds. Er zijn meerdere manieren om het te doen. Ik heb mijn eigen illegale manierquote:Op donderdag 25 maart 2010 17:52 schreef GoodGawd het volgende:
[..]
Okay, met als er twee letters om de hoek komen kijken volg ik het wel maar met meer wordt het een beetje een doolhof
y '' + y = u3pi(t) , met y(0)=1 en y'(0) = 0
Met Laplace wordt dit:
(s2+1)*Y(s) -s = 1/s * e-3pi*s
Y(s) = e-3pi*s * 1/s(s2 +1 ) + s/(s2+1) (de laatste term is getransformeerd cos t, dus die hebben we mooi al).
Nu komt het BREUKSPLITSEN, let goed op
Wat er aan de rechterkant staat (behalve s/(s2+1), want dat is vervangen met cos t) , gaan we breuksplitsen
We hebben daar nu de term 1/s(s2 + 1 ) staan. Dit kunnen we splitsen in:
1/s en 1/s2 +1 , we vervangen de letters erboven met A en B en C. De tweede term heeft namelijk een kwadraat erin. Daarom komt daar B*s + C . Zie maar:
A/s + B*s + C / s2 +1 = 1/s(s2 +1 ) ( zoals je merkt zet je aan de rechterkant van de vergelijking hetgeen wat je hebt "gebreuksplitst" )
Nu gaan we er een matrix van maken. Dit noem ik de Johan methode. Omdat een vriend die Johan heet het heeft voorgedaan. We moeten eerst kruislingsvermenigvuldigen. Of eigenlijk zorg je ervoor dat er aan de rechterkant van de vergelijking alleen de 1 overblijft. Daarom moeten we vermenigvuldigen met s(s2+1)
Waardoor we krijgen:
A(s2 +1) +B*s*s + C*s = 1
Dit zetten we in een matrix met :
s=0
s=1
s=2
, omdat er drie letters zijn, namelijk A, B en C. We vermenigvuldigen het aangegeven S met de letters om te komen tot:
A:
s=0 A=1 , (immers A(02 +1 ) , je houdt 1 over tussen de haakjes waardoor A =1 )
s=1 A=2
s= 2 A= 5
B:
s=0 B=0
s=1 B=1
s=2 B=4
C:
s=0 C=0
s=1 C=1
s=2 C=2
Matrix:
A , B , C
s=0 [1 , 0, 0] = [1]
s=1 [2, 1 , 1] = [1]
s=2 [5 , 4 , 2] = [1]
Dit vul je in in je GR en laat je oplossen, waardoor je krijgt
A=1
B=-1
C=0
Deze voeren we weer terug naar onze formule die we hadden (de splitsing): A/s + B*s + C / s2 +1
Waardoor je krijgt:
1/s - s/s2+1 ==> (1-cost)e3pi*s + cos t
===> oplossing: (1-cost)u3pi(t) + cos t
Hoop dat ik geen tikfoutjes heb gemaakt.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Okay duidelijk! Moet alleen nog uitvogelen hoe je die matrix in je GR invult, hehe. 
Blues ain't nothing but a good man feeling bad...


De 'methode Johan' hierboven berust nog steeds op het opstellen van een lineair stelsel, en dat gaat in dit geval toch handiger en sneller met de traditionele manier. Als je hebt:
A∙(s2 +1) +B∙s2 + C∙s = 1
Dan kunnen we dit schrijven als:
(A+B)∙s2 + C∙s + A = 1,
en dan zie ik meteen dat A = 1, B = -1 (want A+B=0) en C = 0.
Maar als het aantal coëfficiënten groot is dan kan het oplossen van het lineaire stelsel wat meer werk opleveren, en dan kun je met voordeel gebruik maken van de methode van Heaviside. Bij die methode moet je echter weer goed opletten als er meervoudige factoren zijn in de noemer van de breuk die je wil splitsen. Zie deze uitleg.
A∙(s2 +1) +B∙s2 + C∙s = 1
Dan kunnen we dit schrijven als:
(A+B)∙s2 + C∙s + A = 1,
en dan zie ik meteen dat A = 1, B = -1 (want A+B=0) en C = 0.
Maar als het aantal coëfficiënten groot is dan kan het oplossen van het lineaire stelsel wat meer werk opleveren, en dan kun je met voordeel gebruik maken van de methode van Heaviside. Bij die methode moet je echter weer goed opletten als er meervoudige factoren zijn in de noemer van de breuk die je wil splitsen. Zie deze uitleg.


2nd x^-1quote:Op donderdag 25 maart 2010 19:09 schreef GoodGawd het volgende:
Okay duidelijk! Moet alleen nog uitvogelen hoe je die matrix in je GR invult, hehe.
Daarna in dit geval een 3 * 4 matrix. Die invullen met de cijfers die je hebt. En vervolgens oplossen door.
1. 2nd x^-1 (daar staat matrix)
2. Math
3. rref()
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Als je die rref hebt gekozen dan de letters invullen op deze manier?:
rref(A,B,C,D)
rref(A,B,C,D)
Blues ain't nothing but a good man feeling bad...


Overigens zou ik de methode die Riparius voorstelt gebruiken. Bespaart je veel tijd.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


Je hebt bij het maken van de Matrix als het goed is bij [A] deze matrix gemaakt.quote:Op donderdag 25 maart 2010 20:02 schreef GoodGawd het volgende:
Als je die rref hebt gekozen dan de letters invullen op deze manier?:
rref(A,B,C,D)
Dus je moet nu rref (A) doen. Dan gaat de GR het oplossen voor je (de cijfers aan de rechterkant).
(zie 2nd , matrix , edit 1:[A]--> 3x4 matrix doen en invullen, daarna rref (A))
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


NP bro. Nerds support each other enzo 
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.


"Gegeven zijn een punt P uit P3(R), een projectieve lijn L subset van P3(R) met P niet uit L, en een projectief vlak V subset van P3. Gegeven is verder dat er bij elk punt R uit V een punt Q uit L bestaat zo dat P, Q en R op één lijn liggen. Bewijs dat L een subset is van V."
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.


Hallo iedereen
Ik heb een vraag over een dubbellogaritmisch assenstelsel,
al heb je zo een grafiek voor je, dus een grafiek van een machtsfunctie,
hoe kun je daar een formule van maken??
aub de stappen die je moet maken uitleggen en sorry dat ik er geen voorbeeld grafiek bij heb
Ik snap het echt niet
hiervoor zei iemand dat ik het hier moest poste dus
alvast bedankt!

Ik heb een vraag over een dubbellogaritmisch assenstelsel,
al heb je zo een grafiek voor je, dus een grafiek van een machtsfunctie,
hoe kun je daar een formule van maken??
aub de stappen die je moet maken uitleggen en sorry dat ik er geen voorbeeld grafiek bij heb
Ik snap het echt niet
hiervoor zei iemand dat ik het hier moest poste dus
alvast bedankt!
babababa


is je optelling goed gedefinieerd? (-3:-2:1)=(3:2:-1) en toch krijg je:quote:Op donderdag 25 maart 2010 20:24 schreef Hanneke12345 het volgende:
"Gegeven zijn een punt P uit P3(R), een projectieve lijn L subset van P3(R) met P niet uit L, en een projectief vlak V subset van P3. Gegeven is verder dat er bij elk punt R uit V een punt Q uit L bestaat zo dat P, Q en R op één lijn liggen. Bewijs dat L een subset is van V."
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.
(-3:-2:1)+(1:2:0)=(-2:0:1)
(3:2:-1)+(1:2:0)=(4:4:-1)
dus totaal verschillende uitkomsten....
Voor punten op bijv elliptische krommen bestaat er een optelling en dan geldt P+Q+R=O als de punten op 1 lijn liggen, waarbij O een punt die je als eenheidselement hebt gekozen voor optelling.
Opmerking: een punt in P4 geef je aan met vier coordinaten.


Mja, op deze manier hoor je wel coördinaten op te tellen voor zover ik weet.quote:Op donderdag 25 maart 2010 20:52 schreef Optimistic1 het volgende:
[..]
is je optelling goed gedefinieerd? (-3:-2:1)=(3:2:-1) en toch krijg je:
(-3:-2:1)+(1:2:0)=(-2:0:1)
(3:2:-1)+(1:2:0)=(4:4:-1)
dus totaal verschillende uitkomsten....
Voor punten op bijv elliptische krommen bestaat er een optelling en dan geldt P+Q+R=O als de punten op 1 lijn liggen, waarbij O een punt die je als eenheidselement hebt gekozen voor optelling.
Opmerking: een punt in P4 geef je aan met vier coordinaten.
Het gaat nergens om P4, toch?
pff, kutvak. ;x


Oh, en om een functie B(f,g) bilineair te laten zijn, moet het dan lineair zijn met g vast én met f vast (dus B(f_1+f_2, g) = B(f_1, g) + B(f_2, g) en B(f, g_1+g_2) = ... ), of is het genoeg met één van beiden?


Je kunt punten in een projectieve ruimte niet optellen. Drie punten liggen op een lijn als hun coordinaatvectoren lineair afhankelijk zijn, gebruik dat.quote:Op donderdag 25 maart 2010 20:24 schreef Hanneke12345 het volgende:
"Gegeven zijn een punt P uit P3(R), een projectieve lijn L subset van P3(R) met P niet uit L, en een projectief vlak V subset van P3. Gegeven is verder dat er bij elk punt R uit V een punt Q uit L bestaat zo dat P, Q en R op één lijn liggen. Bewijs dat L een subset is van V."
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.


Moet met allebei, anders zou je, bijvoorbeeld, voor A een lineaire functie kunnen nemen en B(f, g) = A(f), dat is iha niet lineair in g.quote:Op donderdag 25 maart 2010 21:22 schreef Hanneke12345 het volgende:
Oh, en om een functie B(f,g) bilineair te laten zijn, moet het dan lineair zijn met g vast én met f vast (dus B(f_1+f_2, g) = B(f_1, g) + B(f_2, g) en B(f, g_1+g_2) = ... ), of is het genoeg met één van beiden?


Ik heb hier in een som staan:
Laplace(f(5t)) = 1/5 F (s/5)
Waarom is dat zo? Kan je dat herleiden aan de hand van een rekenregel?
Laplace(f(5t)) = 1/5 F (s/5)
Waarom is dat zo? Kan je dat herleiden aan de hand van een rekenregel?
Blues ain't nothing but a good man feeling bad...


Je kunt dit rechtstreeks herleiden uit de definitie van de Laplacetransformatie:quote:Op vrijdag 26 maart 2010 13:06 schreef GoodGawd het volgende:
Ik heb hier in een som staan:
Laplace(f(5t)) = 1/5 F (s/5)
Waarom is dat zo? Kan je dat herleiden aan de hand van een rekenregel?
Zij ℒ[f(t)](s) = F(s). Om nu aan de hand van de definitie ℒ[f(5t)](s) te bepalen voer je een integraalsubstitutie t = τ/5 (en dus dt = dτ/5) uit, en dan zie je direct dat ℒ[f(5t)](s) = 1/5∙F(s/5).


Is dat convolutie product gebeuren moeilijk of ligt dat aan mij?
Blues ain't nothing but a good man feeling bad...


Hallo, weet iemand hier op je op een casio fx-9850gb de standaardafwijking kunt bepalen als je de gemiddelde en de opp hebt (bij een normale verdeling)?


De oppervlakte is altijd 1, dus dat zegt niet zoveel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja maar niet als er een oppervlakje uitgesneden is met 1 (en dan verder tot zo ver mogelijk links, of rechts) of 2 verticale strepen, waar een getal bij staatquote:Op vrijdag 26 maart 2010 19:55 schreef GlowMouse het volgende:
De oppervlakte is altijd 1, dus dat zegt niet zoveel.


sorry,Ik bedoelde P3quote:Op donderdag 25 maart 2010 21:19 schreef Hanneke12345 het volgende:
[..]
Mja, op deze manier hoor je wel coördinaten op te tellen voor zover ik weet.
Het gaat nergens om P4, toch?
pff, kutvak. ;x


Een vraagje:
Zij X < Am en Y < An twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < Am+n de geinduceerde Zariski topologie krijgt.
Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!
Heeft iemand een idee?
Zij X < Am en Y < An twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < Am+n de geinduceerde Zariski topologie krijgt.
Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!
Heeft iemand een idee?


Ik probeer de volgende stelling te bewijzen:
Stelling: Als A=A* (A* is de getransponeerde complex geconjugeerde van A), dan A>0 (A is "positive definite") desda alle eigenwaarden van A positief zijn.
Bewijs:
Stel alle eigenwaarden zijn positief. Omdat A=A* is A orthogonaal te diagonaliseren. Er bestaat dus een unitaire matrix U zo dat A=UDU* met D=diag(L1,...,Ln) met Lk positieve eigenwaarden voor alle k.
en nu?
Stelling: Als A=A* (A* is de getransponeerde complex geconjugeerde van A), dan A>0 (A is "positive definite") desda alle eigenwaarden van A positief zijn.
Bewijs:
Stel alle eigenwaarden zijn positief. Omdat A=A* is A orthogonaal te diagonaliseren. Er bestaat dus een unitaire matrix U zo dat A=UDU* met D=diag(L1,...,Ln) met Lk positieve eigenwaarden voor alle k.
en nu?


Moet je dat niet juist bewijzen?quote:Op zondag 28 maart 2010 12:07 schreef BasementDweller het volgende:
Bewijs:
Stel alle eigenwaarden zijn positief. Omdat A=A* is A orthogonaal te diagonaliseren. Er bestaat dus een unitaire matrix U zo dat A=UDU* met D=diag(L1,...,Ln) met Lk positieve eigenwaarden voor alle k.
A>0 => alle ew. positief kun je uit het ongerijmde bewijzen
alle ew. positief => A>0 kun je bewijzen door gebruik te maken dat de eigenvectoren R^n opspannen.
[ Bericht 0% gewijzigd door GlowMouse op 28-03-2010 17:12:33 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel A = A* > 0 en niet alle e.w. zijn positief. Dan bestaat er een Lk=<0. Voor de bijbehorende eigenvector vk geldt: Mvk= Lk vk. Aan beide kanten het inproduct nemen met vk* geeft: (M vk,vk)=Lk(vk,vk). Omdat het inproduct van een vector ongelijk aan nul met zichzelf groter of gelijk is aan nul en Lk niet-positief is, volgt: (M vk,vk)=<0), tegenspraak.
Nu de andere kant nog.
Nu de andere kant nog.


De andere kant op:
Stel A>0. Omdat A=A*, bestaat er een orthonormaal stelsel van eigenvectoren en dus een unitaire matrix U zdd D=U*AU=diag(L1,..,Ln). Dus A=UDU*. Uit A>0 volgt UDU*>0.
Kan ik hier iets mee?
(en was mijn eerste bewijs goed?)
Stel A>0. Omdat A=A*, bestaat er een orthonormaal stelsel van eigenvectoren en dus een unitaire matrix U zdd D=U*AU=diag(L1,..,Ln). Dus A=UDU*. Uit A>0 volgt UDU*>0.
Kan ik hier iets mee?
(en was mijn eerste bewijs goed?)


"de bijbehorende eigenvector" bestaat niet.
En nee, probeer de hint tegebruiken
En nee, probeer de hint tegebruiken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met de bijbehorende eigenvector bedoel ik de eigenvector die bij die eigenwaarde hoort. Bestaat deze niet volgens jou?quote:Op zondag 28 maart 2010 15:41 schreef GlowMouse het volgende:
"de bijbehorende eigenvector" bestaat niet.
En nee, probeer de hint tegebruiken
En die hint, dat de eigenvectoren R^n opspannen heb ik gebruikt (want omdat ze R^n opspannen bestaat er een unitaire matrix U). Ik zou niet weten hoe ik het anders kan gebruiken... (we werken trouwens niet alleen in R^n maar ook in C^n)


Ik zou gebruiken dat de dimensie gelijk is aan de transcendentiegraad van het functielichaam.quote:Op zaterdag 27 maart 2010 18:25 schreef Optimistic1 het volgende:
Een vraagje:
Zij X < Am en Y < An twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < Am+n de geinduceerde Zariski topologie krijgt.
Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!
Heeft iemand een idee?


Het idee is dat je bij <Ax,x> x schrijft als lineaire combinatie van eigenvectoren. Maar ik vraag me even af of je niet nodig hebt dat A reëel is (anders weet ik niet of de eigenwaarden en -vectoren reëel zijn).quote:Op zondag 28 maart 2010 15:44 schreef BasementDweller het volgende:
[..]
Met de bijbehorende eigenvector bedoel ik de eigenvector die bij die eigenwaarde hoort. Bestaat deze niet volgens jou?
En die hint, dat de eigenvectoren R^n opspannen heb ik gebruikt (want omdat ze R^n opspannen bestaat er een unitaire matrix U). Ik zou niet weten hoe ik het anders kan gebruiken... (we werken trouwens niet alleen in R^n maar ook in C^n)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Als je wil aantonen dat een verzameling gesloten is, kan je laten zien dat de verzameling gelijk is aan zijn afsluiting. Als je echter wil aantonen dat een verzameling gesloten is in een andere verzameling, wat moet je dan precies laten zien?


Mijn vragen: Stel je hebt een empirical cumulative distribution function en hier moet je een histogram van maken.
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de bucket sizes en bucket boundaries krijgt?
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de optimale bucket sizes en bucket boundaries krijgt?
Ik ben erachter dat je een ecdf kan benaderen met een cdf en dan ook een bijbehorende pdf hebt. Er wordt gehint naar lineaire functies omdat het differentieren van lineaire functies getallen opleveren die volgens mij het antwoord op de vraag zijn. De ecdf benaderen met een lineaire functie lijkt me onverantwoord. De enige andere lineaire functies die ik hier tevoorschijn kan toveren zijn de raaklijnen van de cdf en pdf.
Ik heb een manier gevonden om op een arbitrair punt de hoogte en breedte van een bucket te vinden. Er is ook gehint naar de mate van optimaliteit gelijk stellen aan de goodness of fit van de cdf op de ecdf alleen zie ik totaal niet hoe ik hier optimale bucket boundaries af kan leiden. Ik hoop zeer dat ik duidelijk ben en dat iemand me op weg kan helpen.
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de bucket sizes en bucket boundaries krijgt?
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de optimale bucket sizes en bucket boundaries krijgt?
Ik ben erachter dat je een ecdf kan benaderen met een cdf en dan ook een bijbehorende pdf hebt. Er wordt gehint naar lineaire functies omdat het differentieren van lineaire functies getallen opleveren die volgens mij het antwoord op de vraag zijn. De ecdf benaderen met een lineaire functie lijkt me onverantwoord. De enige andere lineaire functies die ik hier tevoorschijn kan toveren zijn de raaklijnen van de cdf en pdf.
Ik heb een manier gevonden om op een arbitrair punt de hoogte en breedte van een bucket te vinden. Er is ook gehint naar de mate van optimaliteit gelijk stellen aan de goodness of fit van de cdf op de ecdf alleen zie ik totaal niet hoe ik hier optimale bucket boundaries af kan leiden. Ik hoop zeer dat ik duidelijk ben en dat iemand me op weg kan helpen.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


A is gesloten in S als A gelijk is aan de afsluiting van A doorsneden met S.quote:Op maandag 29 maart 2010 23:46 schreef BasementDweller het volgende:
Als je wil aantonen dat een verzameling gesloten is, kan je laten zien dat de verzameling gelijk is aan zijn afsluiting. Als je echter wil aantonen dat een verzameling gesloten is in een andere verzameling, wat moet je dan precies laten zien?


Bedankt!quote:Op dinsdag 30 maart 2010 17:19 schreef thabit het volgende:
[..]
A is gesloten in S als A gelijk is aan de afsluiting van A doorsneden met S.


Hey ik heb ook een vraagje
Ik heb zeg maar een data set met 6 attributes die allemaal numeriek zijn.
Het idee is dat je 5 coefficienten vindt die de dataset zeg maar goed fitten. Die heb ik dus gevonden, nou heb ik alleen een ander probleem waarmee ik zit. Het gaat over de sufficient/necessary number of instances die je nodig moet hebben om aan je beste score te komen (dus b.v. 0 fouten). Ik probeerde dit op te lossen met sum squared error, nou heb ik alleen eerlijk gezegd geen flauw benul hoe ik kan bepalen welke instances ik nodig zou moeten hebben om er voor te zorgen dat de error laag blijft.
Ik heb dit al op een experimentele wijze opgelost (simpelweg random setje instances nemen en kijken of de methode erop coefficienten vindt die 0 error oplevert), maar er zou ook een theoretische methode moeten zijn om dit uit te zoeken. Daarbij werd me verteld dat ik partieel differentieren moest gebruiken. En dat als alle partieel differenties gelijk aan 0 zijn je de coefficients hebt gevonden want dan heb je 0 error. Het probleem nu alleen is, hoe haal ik hiermee eruit welke instances ik moet hebben? Mijn differentieren knobbel is daarbij wat verroest, maar ik kwam ermee dat (x-y)^2 differentieert naar df/dx: 2x-2y en df/dy: 2y-2x en d^2f/dxdy: -2 (?).
Ik heb al overal en nergens gezocht, boek doorgelezen, meerdere sites over linear regression gelezen en ik kan het gewoon niet vinden :/
Elk klein beetje help (als je weet hoe je met behulp uit een differentie kunt bepalen welke instances je moet hebben bijvoorbeeld) is van harte welkom.
Ik heb zeg maar een data set met 6 attributes die allemaal numeriek zijn.
Het idee is dat je 5 coefficienten vindt die de dataset zeg maar goed fitten. Die heb ik dus gevonden, nou heb ik alleen een ander probleem waarmee ik zit. Het gaat over de sufficient/necessary number of instances die je nodig moet hebben om aan je beste score te komen (dus b.v. 0 fouten). Ik probeerde dit op te lossen met sum squared error, nou heb ik alleen eerlijk gezegd geen flauw benul hoe ik kan bepalen welke instances ik nodig zou moeten hebben om er voor te zorgen dat de error laag blijft.
Ik heb dit al op een experimentele wijze opgelost (simpelweg random setje instances nemen en kijken of de methode erop coefficienten vindt die 0 error oplevert), maar er zou ook een theoretische methode moeten zijn om dit uit te zoeken. Daarbij werd me verteld dat ik partieel differentieren moest gebruiken. En dat als alle partieel differenties gelijk aan 0 zijn je de coefficients hebt gevonden want dan heb je 0 error. Het probleem nu alleen is, hoe haal ik hiermee eruit welke instances ik moet hebben? Mijn differentieren knobbel is daarbij wat verroest, maar ik kwam ermee dat (x-y)^2 differentieert naar df/dx: 2x-2y en df/dy: 2y-2x en d^2f/dxdy: -2 (?).
Ik heb al overal en nergens gezocht, boek doorgelezen, meerdere sites over linear regression gelezen en ik kan het gewoon niet vinden :/
Elk klein beetje help (als je weet hoe je met behulp uit een differentie kunt bepalen welke instances je moet hebben bijvoorbeeld) is van harte welkom.


Wat een rare manier, om partiële afgeleiden te pakken. ik zou eerder naar lineaire algebra kijken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zij X een open verzameling. Is de afsluiting van het inwendige van een verzameling X dan een deelverzameling van X?


Ja om coefficienten te vinden enzo is lineaire algebra prima, het is alleen hoe haal ik hieruit welke instances ik moet hebben? De vraag lijkt wel incompleet, want er staat niet bij of ik een aantal moet noteren of specifieke instances moet nemen. Daarbij weet ik niet of ik de coefficienten bij voorbaat al mag invullen, aangezien als ik al de coefficienten mag gebruiken die voor perfecte score kan gebruiken, kan ik net zo goed 1 instance zeggen, het is alleen dat als je 1 instance pakt en je moet de coefficienten juist vinden, dan heb je goeie kans dat je niet dezelfde coefficienten vindt. En daar ben ik dus naar op zoek, ik snap wel dat partial derivatives daarbij zouden moeten helpen om aan te geven dat je nulpunten vindt, maar om dan te zeggen welke instances?quote:Op woensdag 31 maart 2010 08:22 schreef GlowMouse het volgende:
Wat een rare manier, om partiële afgeleiden te pakken. ik zou eerder naar lineaire algebra kijken.
Klopt mijn partieel differentieren overigens?
Ja, ik heb al al het andere af en ik wil dit ook oplossen op een andere manierquote:


Ik zit vast met een formule die ik moet differentiëren, en ik hoop dat iemand mij hieruit kan redden.
Ik moet de volgende formule differentiëren:
2x^2√(1-x^2)
Nu heb ik de uitwerkingen voor me, maar er staat één ding in waar ik niet uitkom.
Waar komt die *-2x aan het einde van 'stap 1' vandaan? Ik zit al een kwartier naar de opgave te staren maar het wil niet dagen..
Alvast bedankt!
Ik moet de volgende formule differentiëren:
2x^2√(1-x^2)
Nu heb ik de uitwerkingen voor me, maar er staat één ding in waar ik niet uitkom.
Waar komt die *-2x aan het einde van 'stap 1' vandaan? Ik zit al een kwartier naar de opgave te staren maar het wil niet dagen..
Alvast bedankt!


Kettingregel. Schrijf de functie even als 2x2∙(1-x2)1/2, dan zie je het wellicht wel direct.quote:Op woensdag 31 maart 2010 17:52 schreef BlackSaint het volgende:
Ik zit vast met een formule die ik moet differentiëren, en ik hoop dat iemand mij hieruit kan redden.
Ik moet de volgende formule differentiëren:
2x^2√(1-x^2)
Nu heb ik de uitwerkingen voor me, maar er staat één ding in waar ik niet uitkom.
[ afbeelding ]
Waar komt die *-2x aan het einde van 'stap 1' vandaan? Ik zit al een kwartier naar de opgave te staren maar het wil niet dagen..
Alvast bedankt!


Yes, dat is 'm.quote:Op woensdag 31 maart 2010 18:02 schreef Riparius het volgende:
[..]
Kettingregel. Schrijf de functie even als 2x2∙(1-x2)1/2, dan zie je het wellicht wel direct.


Je afgeleides kloppen ja. Je hebt sowieso een perfect fit als de vector met de verklaarde variabele in het kolomruimte zit van de matrix met regressoren, daar komt weinig calculus bij kijken.quote:Op woensdag 31 maart 2010 13:57 schreef koffiegast het volgende:
[..]
Ja om coefficienten te vinden enzo is lineaire algebra prima, het is alleen hoe haal ik hieruit welke instances ik moet hebben? De vraag lijkt wel incompleet, want er staat niet bij of ik een aantal moet noteren of specifieke instances moet nemen. Daarbij weet ik niet of ik de coefficienten bij voorbaat al mag invullen, aangezien als ik al de coefficienten mag gebruiken die voor perfecte score kan gebruiken, kan ik net zo goed 1 instance zeggen, het is alleen dat als je 1 instance pakt en je moet de coefficienten juist vinden, dan heb je goeie kans dat je niet dezelfde coefficienten vindt. En daar ben ik dus naar op zoek, ik snap wel dat partial derivatives daarbij zouden moeten helpen om aan te geven dat je nulpunten vindt, maar om dan te zeggen welke instances?
Klopt mijn partieel differentieren overigens?
[..]
Ja, ik heb al al het andere af en ik wil dit ook oplossen op een andere manier
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ok, mmh heb je enig idee welke richting ik überhaupt moet nemen om zeg maar op een bepaald nummer instances moet komen? Ik heb vandaag ook al uren lopen lezen en ik vind maar niet iets concreets dat gewoon zegt "zo kun je zeggen dat deze weg moeten". Sterker nog, de meeste gaan alleen over attribute weglaten en information gain/loss. Of gaan juist over hoe je kunt clusteren.quote:Op woensdag 31 maart 2010 19:18 schreef GlowMouse het volgende:
[..]
Je afgeleides kloppen ja. Je hebt sowieso een perfect fit als de vector met de verklaarde variabele in het kolomruimte zit van de matrix met regressoren, daar komt weinig calculus bij kijken.
Ik zie verder nog niet hoe partieel differentieren mij precies gaat helpen. Het ersgte is dat naarmate ik meer en meer lees begin ik de vraag minder goed te begrijpen hehe
Kortom, hoe kan ik met een set instanties data (numeriek) bepalen hoe veel ik ervan nodig heb?
[ Bericht 4% gewijzigd door koffiegast op 31-03-2010 22:08:51 ]


hoe kun je met http://www.wolframalpha.com deze som oplossen : 5log(1/25)sqrt5 Zou het mogelijk zijn om dit ook in stappen te laten weergeven.


Ik denk dat dit een huiswerkopgave is en dat je daarom stappen moet kunnen laten zien. Maar systemen zoals WolframAlpha kunnen alleen overweg met logaritmen met grondtal 10 of grondtal e, en dat is hier niet handig, als je met je notatie een log met grondtal 5 bedoelt (zoals ik vermoed). Waarom vermoed ik dat? Wel, omdat de opgave dan eenvoudig uit het blote hoofd is te doen:quote:Op donderdag 1 april 2010 10:50 schreef snakeman123 het volgende:
hoe kun je met http://www.wolframalpha.com deze som oplossen : 5log(1/25)sqrt5 Zou het mogelijk zijn om dit ook in stappen te laten weergeven.
5log(1/25∙√5) = 5log(5-2) + 5log(5½) = -2 + ½ = -1½.
Begrijp je dit nu ook?


Nog even even een aanvulling: WolframAlpha blijkt toch wel overweg te kunnen met logaritmen met een ander grondtal dan 10 of e. Alleen heb je niet zoveel aan die uitwerking voor je huiswerkopgave zoals je zult zien. Je voert dan in:quote:
log[5,((1/25)*sqrt(5))]


Is er iemand die me uit kan leggen waarom dit klopt?
Ik kan van links met geen mogelijkheid maken wat er rechts staat.
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


Voer een polynoomstaartdeling uit (waarbij je dus een rest van 915/2 zult vinden), óf vermenigvuldig eerst teller en noemer van de breuk met 2 en pas vervolgens breuksplitsing toe (splitsing in partiële breuken).quote:Op donderdag 1 april 2010 13:32 schreef Jesse_ het volgende:
[ afbeelding ]
Is er iemand die me uit kan leggen waarom dit klopt?
Ik kan van links met geen mogelijkheid maken wat er rechts staat.


Zou je misschien een tussen stap van het breuksplitsen kunnen opschrijven? Ik zie het namelijk niet 
En mijn boek biedt helaas geen soelaas voor dit geval.
En mijn boek biedt helaas geen soelaas voor dit geval.
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


Teller en noemer van de breuk met 2 vermenigvuldigen levert:quote:Op donderdag 1 april 2010 15:25 schreef Jesse_ het volgende:
Zou je misschien een tussen stap van het breuksplitsen kunnen opschrijven? Ik zie het namelijk niet
En mijn boek biedt helaas geen soelaas voor dit geval.
(-3y3 + 48y2 -288y + 576)/2∙(y+1)
Nu opsplitsen in een breuk met noemer 2 en een breuk met noemer (y+1), als volgt:
(-3y3 + 48y2 -288y + 576)/2∙(y+1) = (Ay2 + By + C)/2 + D/(y+1)
De ratio hierachter is dat je bij deling van een derdegraads polynoom door een lineair polynoom een kwadratisch polynoom krijgt, plus een rest (tenzij het nulpunt van het lineaire polynoom in de noemer ook een nulpunt is van het derdegraads polynoom in de teller). Door in bovenstaande vergelijking beide leden te vermenigvuldigen met 2(y + 1) en (na herleiding) de coëfficiënten van het derdegraadspolynoom in linker en rechter lid aan elkaar gelijk te stellen krijg je vier lineaire vergelijkingen in A,B,C en D, waaruit je deze kunt bepalen.
Zelf zou ik hier overigens veel liever een polynoomstaartdeling uitvoeren, dat is eenvoudiger en sneller.


Bedankt voor je hulp, volgens mij kom ik er nu uit 
Edit: ik kom er uit en een staartdeling is inderdaad een stuk eenvoudiger, bedankt!
[ Bericht 23% gewijzigd door Jesse_ op 01-04-2010 18:26:17 ]
Edit: ik kom er uit en een staartdeling is inderdaad een stuk eenvoudiger, bedankt!
[ Bericht 23% gewijzigd door Jesse_ op 01-04-2010 18:26:17 ]
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


Een open verzameling is gelijk aan haar inwendige. De afsluiting kan dan best strikt groter zijn.quote:Op woensdag 31 maart 2010 11:39 schreef BasementDweller het volgende:
Zij X een open verzameling. Is de afsluiting van het inwendige van een verzameling X dan een deelverzameling van X?


Een conic heeft de vergelijking:
Met de matrix
Hoe kom ik ook alweer vanaf die vergelijking van de conic op de matrix, moet ik achter de matrix dan ook nog =0 zetten? En is de conic automatisch bilineair en symetrisch (ja toch?)
Ik ben het even kwijt hoe dit ook alweer werkte. En ik ken wel die matrix en vergelijking nu, maar toch. ;x
Met de matrix
Hoe kom ik ook alweer vanaf die vergelijking van de conic op de matrix, moet ik achter de matrix dan ook nog =0 zetten? En is de conic automatisch bilineair en symetrisch (ja toch?)
Ik ben het even kwijt hoe dit ook alweer werkte. En ik ken wel die matrix en vergelijking nu, maar toch. ;x


Als v de vector (x0, x1, x2) is, en A is je matrix, dan kan de vergelijking geschreven worden als vAvt = 0. A is per definitie symmetrisch.


Ik snap dat het zo is, omdat even+even=even, maar hoe moet je dat bewijzen?quote:Gegeven is de taal
L1 := { w ∈ {a,b}* | w bevat een even aantal a's }
Bewijs dat L1 = L1*


a/2=pquote:Op zondag 4 april 2010 13:00 schreef .aeon het volgende:
[..]
Ik snap dat het zo is, omdat even+even=even, maar hoe moet je dat bewijzen?
b/2=q
a+b=2(p+q) => a+b deelbaar door 2


Voor een kleine opdracht moet ik een zo kort mogelijk prefixcode boom maken voor een bepaalde tekst.
Ik ben niet veel verder gekomen dan het tellen van hoe vaak elke letter voor komt, maar ik heb geen idee hoe ik het aanpak om een zo kort mogelijke prefixcode boom hiervoor te maken.
Ik kan opzich wel zo'n boom uit m'n mouw schudden, maar hoe ik weet dat ie zo kort mogelijk is en hoe ik dat aan kan tonen, ik zou geen idee van de aanpak hebben
Ik ben niet veel verder gekomen dan het tellen van hoe vaak elke letter voor komt, maar ik heb geen idee hoe ik het aanpak om een zo kort mogelijke prefixcode boom hiervoor te maken.
Ik kan opzich wel zo'n boom uit m'n mouw schudden, maar hoe ik weet dat ie zo kort mogelijk is en hoe ik dat aan kan tonen, ik zou geen idee van de aanpak hebben
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |

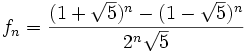




 en dit klopt ook volgens het antwoordenmodel maar hoe moet ik dit op mijn GR invoeren?
en dit klopt ook volgens het antwoordenmodel maar hoe moet ik dit op mijn GR invoeren?