SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



daar kom je op uit ja, dat is dan ook precies de afstand van p tot (p+q)/2.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat lijkt me ook, en dit had ik ook al zelf bedacht. Alleen hiermee kwam ik niet tot de conclusie dat f(x)>g(x).quote:Op maandag 22 maart 2010 23:06 schreef Riparius het volgende:
[..]
Ik geloof toch niet dat het zo werkt. Je moet een omgeving van p en een omgeving van q kiezen die elkaar niet overlappen. Bij p > q en eenzelfde ε voor beide functies kom je dan tot ε < (p-q)/2.


Uit de definitie van de limiet:
Voor alle e>0 bestaat er een d>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d, dan d(f(x),p)<e.
Kies nu 0 < e < (p-q)/2. Dan bestaat er een d'>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d', dan d(f(x),p) < (p-q)/2.
Voor alle e>0 bestaat er een d>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d, dan d(f(x),p)<e.
Kies nu 0 < e < (p-q)/2. Dan bestaat er een d'>0 met als eigenschap dat als x in Dom(f) en d(x,a)<d', dan d(f(x),p) < (p-q)/2.


Waarom niet? Kies een ε < (p-q)/2. Volgens de definitie van de limiet is er dan een δf zodanig dat:quote:Op maandag 22 maart 2010 23:12 schreef BasementDweller het volgende:
[..]
Dat lijkt me ook, en dit had ik ook al zelf bedacht. Alleen hiermee kwam ik niet tot de conclusie dat f(x)>g(x).
| f(x) - p | < ε voor 0 < | x - a | < δf
En tevens een δg zodanig dat
| g(x) - q | < ε voor 0 < | x - a | < δg
Kies nu δ = min(δf,δg), dan is
f(x) > g(x) voor 0 < | x - a | < δ


Dat ik dat zelf niet op papier krijgquote:Op maandag 22 maart 2010 23:19 schreef Riparius het volgende:
[..]
Waarom niet? Kies een ε < (p-q)/2. Volgens de definitie van de limiet is er dan een δf zodanig dat:
| f(x) - p | < ε voor 0 < | x - a | < δf
En tevens een δg zodanig dat
| g(x) - q | < ε voor 0 < | x - a | < δg
Kies nu δ = min(δf,δg), dan is
f(x) > g(x) voor 0 < | x - a | < δ


vraagje(s):

van stap 2 naar 3 snap ik wel, maar stap 1 naar 2 is voor mij een raadsel.... er staat wel iets met dat je cos(2x) = 2(cos(x))² - 1 moet gebruiken maar zou niet weten hoe

hier snap ik helemaal niks van

hier kom ik zelf uit op
alvast bedankt
van stap 2 naar 3 snap ik wel, maar stap 1 naar 2 is voor mij een raadsel.... er staat wel iets met dat je cos(2x) = 2(cos(x))² - 1 moet gebruiken maar zou niet weten hoe
hier snap ik helemaal niks van
hier kom ik zelf uit op
alvast bedankt


De eerste integraal: elementaire goniometrie. Je kunt het kwadraat van een cosinus of een sinus omzetten in de cosinus van de dubbele hoek. Kijk even hier.quote:Op dinsdag 23 maart 2010 01:47 schreef afcabrk het volgende:
vraagje(s):
[ afbeelding ]
van stap 2 naar 3 snap ik wel, maar stap 1 naar 2 is voor mij een raadsel.... er staat wel iets met dat je cos(2x) = 2(cos(x))² - 1 moet gebruiken maar zou niet weten hoe
[ afbeelding ]
hier snap ik helemaal niks van
[ afbeelding ]
hier kom ik zelf uit op [ afbeelding ]
alvast bedankt
De tweede en derde integraal: probeer de primitieve eens te differentiëren. Ik heb het idee dat je de kettingregel niet goed begrijpt. Uiteraard kun je deze integralen oplossen met de substitutieregel (de tegenhanger van de kettingregel bij het differentiëren), maar als je de kettingregel begrijpt zou je de primitieve ook zo moeten kunnen 'zien'.


oke dat eerste snap ik nu toch wel.
maar die tweede en derde.. moet je bij die (x+1)e^(4x²+8x)
4x²+8x als schakel nemen? zo ja, wat doe je dan met x+1, want die zie ik nergens terug in de primitieve..
of moet je ze allebei als schakels nemen?
edit: ikzie dat het in dit geval niet uitmaakt of x+1 als schakel wordt genomen, want delen door 1 geeft hetzelfde. ikkom zelf uit op e^(4x²+8x) / (8x+8)
zonder die 8x komik wel uit op wat ik hoor te krijgen...
en die met wortel in de integraal : die x die vooraan staat wordt gewoon weggelaten ? of waarschijnlijk zie ik iets over het hoofd
[ Bericht 22% gewijzigd door afcabrk op 23-03-2010 02:12:10 ]
maar die tweede en derde.. moet je bij die (x+1)e^(4x²+8x)
4x²+8x als schakel nemen? zo ja, wat doe je dan met x+1, want die zie ik nergens terug in de primitieve..
of moet je ze allebei als schakels nemen?
edit: ikzie dat het in dit geval niet uitmaakt of x+1 als schakel wordt genomen, want delen door 1 geeft hetzelfde. ikkom zelf uit op e^(4x²+8x) / (8x+8)
zonder die 8x komik wel uit op wat ik hoor te krijgen...
en die met wortel in de integraal : die x die vooraan staat wordt gewoon weggelaten ? of waarschijnlijk zie ik iets over het hoofd
[ Bericht 22% gewijzigd door afcabrk op 23-03-2010 02:12:10 ]


Probeer nu eerst eens de (juiste) primitieven te differentiëren met behulp van de kettingregel, dat kun je toch wel?quote:Op dinsdag 23 maart 2010 02:06 schreef afcabrk het volgende:
oke dat eerste snap ik nu toch wel.
maar die tweede en derde.. moet je bij die (x+1)e^(4x²+8x)
4x²+8x als schakel nemen? zo ja, wat doe je dan met x+1, want die zie ik nergens terug in de primitieve..
of moet je ze allebei als schakels nemen?
en die met wortel in de integraal : die x die vooraan staat wordt gewoon weggelaten ? of waarschijnlijk zie ik iets over het hoofd


ja dan kom ik uit op
1/8e^u ---> 1/8e^u
4x²+8x ---> 8x + 8
f'(x) = (8x+8) 1/8e^u
= (x+1) e^u
en dit klopt, maar het probleem ligt ook niet bij het differentieren bij mij.
ik doe gewoon iets fout bij het berekenen van het primitieve, en ikdacht dat één van jullie
wist waar :p heb binnekort een toelatingstentamen voor econometrie, en ikheb maar paar weekjes ervaring
met integraalrekening dus vandaar datik zuig
1/8e^u ---> 1/8e^u
4x²+8x ---> 8x + 8
f'(x) = (8x+8) 1/8e^u
= (x+1) e^u
en dit klopt, maar het probleem ligt ook niet bij het differentieren bij mij.
ik doe gewoon iets fout bij het berekenen van het primitieve, en ikdacht dat één van jullie
wist waar :p heb binnekort een toelatingstentamen voor econometrie, en ikheb maar paar weekjes ervaring
met integraalrekening dus vandaar datik zuig


Inderdaad, differentiëren van e4x²+8x geeft e4x²+8x(8x+8) = 8(x+1)e4x²+8x, en dat is een factor 8 teveel. De gezochte primitieve van (x+1)e4x²+8x is dus 1/8∙e4x²+8x.quote:Op dinsdag 23 maart 2010 02:06 schreef afcabrk het volgende:
edit: ikzie dat het in dit geval niet uitmaakt of x+1 als schakel wordt genomen, want delen door 1 geeft hetzelfde. ikkom zelf uit op e^(4x²+8x) / (8x+8)
zonder die 8x komik wel uit op wat ik hoor te krijgen...


Je kunt ook formeel de substitutiemethode gebruiken. De op te lossen (onbepaalde) integraal is:quote:Op dinsdag 23 maart 2010 02:17 schreef afcabrk het volgende:
ja dan kom ik uit op
1/8e^u ---> 1/8e^u
4x²+8x ---> 8x + 8
f'(x) = (8x+8) 1/8e^u
= (x+1) e^u
en dit klopt, maar het probleem ligt ook niet bij het differentieren bij mij.
ik doe gewoon iets fout bij het berekenen van het primitieve, en ikdacht dat één van jullie
wist waar :p heb binnekort een toelatingstentamen voor econometrie, en ikheb maar paar weekjes ervaring
met integraalrekening dus vandaar datik zuig
∫ (x+1)∙e4x²+8x∙dx
Ik kies nu de substitutie:
u = 4x2 + 8x
Dan is:
du/dx = 8x + 8
En dus:
du = 8(x+1)∙dx
En dus:
1/8∙du = (x+1)∙dx
De integraal wordt dan:
∫ 1/8∙eudu = 1/8∙eu + C
Terugsubstitueren van u = 4x2 + 8x geeft dan als resultaat
∫ (x+1)∙e4x²+8x∙dx = 1/8∙e4x²+8x + C


zo'n uitleg hadik nodig om het te laten doordringen dankjewel! 
en dat andere wordt dan..

u = 9x²-1
du/dx = 18x
du = 18x * dx
1/18du = x * dx (<-- is die x in het rechterlid de x in het begin van het integraal?)
f = wortel(u)
primitiveren = 2/3(9x²-1)^3/2
F = 1/18 * 2/3(9x²-1)^3/2
klopt dit?
en dat andere wordt dan..
u = 9x²-1
du/dx = 18x
du = 18x * dx
1/18du = x * dx (<-- is die x in het rechterlid de x in het begin van het integraal?)
f = wortel(u)
primitiveren = 2/3(9x²-1)^3/2
F = 1/18 * 2/3(9x²-1)^3/2
klopt dit?


Ja, zo klopt het, maar je moet het iets netter proberen op te schrijven (zoals in mijn uitwerking van je tweede integraal) en in je oorspronkelijke integraal niet de dx vergeten natuurlijk.quote:Op dinsdag 23 maart 2010 02:42 schreef afcabrk het volgende:
zo'n uitleg hadik nodig om het te laten doordringen dankjewel!
en dat andere wordt dan..
[ afbeelding ]
u = 9x²-1
du/dx = 18x
du = 18x * dx
1/18du = x * dx (<-- is die x in het rechterlid de x in het begin van het integraal?)
f = wortel(u)
primitiveren = 2/3(9x²-1)^3/2
F = 1/18 * 2/3(9x²-1)^3/2


Ik zit met een probleempje: ik moet iets integreren, maar ik weet niet hoe. We hebben verschillende methoden hiervoor gehad: partieel integreren, substitutiemethode en nog wat.
De formule gaat
(x+2) / (x^2+4x-12)
Welke methode voor integreren moet ik hiervoor gebruiken?
De formule gaat
(x+2) / (x^2+4x-12)
Welke methode voor integreren moet ik hiervoor gebruiken?
New in town


Voor de noemer van je breuk hebben we:quote:Op dinsdag 23 maart 2010 14:25 schreef AliKebap het volgende:
Ik zit met een probleempje: ik moet iets integreren, maar ik weet niet hoe. We hebben verschillende methoden hiervoor gehad: partieel integreren, substitutiemethode en nog wat.
De formule gaat
(x+2) / (x^2+4x-12)
Welke methode voor integreren moet ik hiervoor gebruiken?
x2 + 4x - 12 = (x + 6)(x - 2)
Je kunt nu splitsen in deelbreuken (partiële breuken), door je oorspronkelijke breuk te herschrijven als een lineaire combinatie van 1/(x + 6) en 1/(x - 2), als volgt:
(x+2)/(x2+4x-12) = A/(x + 6) + B/(x - 2)
Werk dit eerst eens uit en bepaal hieruit A en B.


Ik moet de oppervlakte van het vlakdeel dat word ingesloten door de formule
f(x) = (x^2 + x + 1) / x
en de lijn
y = -1,5
uitrekenen.
Nu is dat het gebied tussen -2 en -0.5. Hoe kan ik dat uitrekenen? Door x en y om te wisselen?
f(x) = (x^2 + x + 1) / x
en de lijn
y = -1,5
uitrekenen.
Nu is dat het gebied tussen -2 en -0.5. Hoe kan ik dat uitrekenen? Door x en y om te wisselen?


Je hebt de x-coordinaten van de snijpunten al bepaald. Met integreren reken je het vlakdeel dat wordt ingesloten tussen een formule en de x-as uit. Als je nu f(x) aanpast door er 1.5 bij op te tellen verschuif je de functie 1.5 omhoog en gaat het nu om het vlakdeel tussen de nieuwe functie en de x-as, welke je dus kunt oplossen met integreren.
"Reality is an illusion created by a lack of alcohol."


Nee, niet gaan goochelen. Maak even een tekening met daarin de grafiek van y = (x2 + x + 1)/x en de grafiek van y = -3/2 op het interval [-2,-½]. Dan zie je dat het gaat om de verticale afstand tussen de curve en de rechte lijn, en dus het verschil van deze twee. Je moet dus:quote:Op dinsdag 23 maart 2010 16:04 schreef Siddartha het volgende:
Ik moet de oppervlakte van het vlakdeel dat wordt ingesloten door de grafiek van
f(x) = (x^2 + x + 1) / x
en de lijn
y = -1,5
uitrekenen.
Nu is dat het gebied tussen x=-2 en x=-½. Hoe kan ik dat uitrekenen? Door x en y om te wisselen?
(x2 + x + 1)/x - (-3/2)
integreren over het interval [-2,-½] om de oppervlakte van het vlakdeel ingesloten door de curve en de lijn te berekenen.


Maar dan krijg ik uit als primitive:quote:Op dinsdag 23 maart 2010 16:20 schreef Riparius het volgende:
[..]
Nee, niet gaan goochelen. Maak even een tekening met daarin de grafiek van y = (x2 + x + 1)/x en de grafiek van y = -3/2 op het interval [-2,-½]. Dan zie je dat het gaat om de verticale afstand tussen de curve en de rechte lijn, en dus het verschil van deze twee. Je moet dus:
(x2 + x + 1)/x - (-3/2)
integreren over het interval [-2,-½] om de oppervlakte van het vlakdeel ingesloten door de curve en de lijn te berekenen.
0.5x^2 + x + ln x - 1.5x
Hoe vul ik dan een negatief getal in (aangezien er ln instaat)?


Om te beginnen: je maakt een tekenfout. Kijk nog eens goed naar mijn functie.quote:Op dinsdag 23 maart 2010 16:34 schreef Siddartha het volgende:
[..]
Maar dan krijg ik uit als primitive:
0.5x^2 + x + ln x - 1.5x
Hoe vul ik dan een negatief getal in (aangezien er ln instaat)?
Verder: voor x < 0 kun je ln(-x) als primitieve van 1/x nemen. Controleer dit door ln(-x) te differentiëren.


Ah, een min vergeten:quote:Op dinsdag 23 maart 2010 16:38 schreef Riparius het volgende:
[..]
Om te beginnen: je maakt een tekenfout. Kijk nog eens goed naar mijn functie.
Verder: voor x < 0 kun je ln(-x) als primitieve van 1/x nemen. Controleer dit door ln(-x) te differentiëren.
0.5x^2 + x + ln (-x) + 1.5x
En dan kan ik dus wel de negatieve getallen invullen.
En dan klopt het!
Bedankt!


Ja. Wat krijg je als (exact) eindantwoord?quote:Op dinsdag 23 maart 2010 16:45 schreef Siddartha het volgende:
[..]
Ah, een min vergeten:
0.5x^2 + x + ln (-x) + 1.5x
En dan kan ik dus wel de negatieve getallen invullen.
En dan klopt het!
Bedankt!


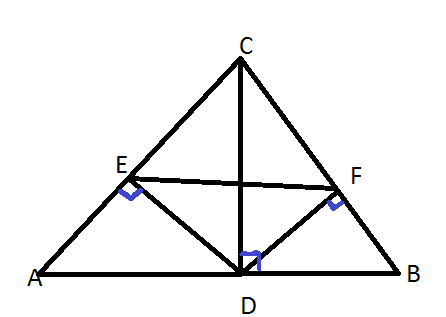
Gegeven: CD staat loodrecht op AB, DE loodrecht op AC en DF loodrecht op BC.
Bewijs dat ABFE een koordenvierhoek is.
Van m'n toets van vandaag


CEDF is een kv want hoek E en hoek F zijn beide recht. Hieruit volgt dat hoek DFE gelijk is aan hoek DCE. Nu gaan we in ABFE overstaande hoeken optellen: hoek A + hoek BFE = hoek A + hoek BFD + hoek DFE = hoek A + 90 + hoek DCE = hoek A + hoek ADC + hoek DCA = som van 3 hoeken van driehoek ADC = 180 graden.


Waarom?quote:Op dinsdag 23 maart 2010 22:39 schreef thabit het volgende:
CEDF is een kv want hoek E en hoek F zijn beide recht. Hieruit volgt dat hoek DFE gelijk is aan hoek DCE.


Grmbl, even over het hoofd gezien DEFC is natuurlijk ook een koordenvierhoek. Dan kan ik gewoon constante hoek gebruiken inderdaad. Dankjewel!quote:Op dinsdag 23 maart 2010 22:50 schreef thabit het volgende:
Dat is altijd zo in koordenvierhoeken. Teken er een cirkel omheen: de omtrekshoek is constant.


Ik probeer de Wetten van Mrogan te bewijzen, maar kom niet erg ver 
Ik kom niet verder dan het complement weghalen door 1 - (vereniging van a_i). Hoe kan ik van ene vereniging een doorsnede maken?
Ik kom niet verder dan het complement weghalen door 1 - (vereniging van a_i). Hoe kan ik van ene vereniging een doorsnede maken?


Ik zou gewoon een element uit het linkerdeel nemen en bewijzen dat dat in het rechterdeel zit, en vice versa.


Hm, ik dacht het vorige keer op deze manier gedaan te hebben, maar oké! Ik weet alleen niet goed hoe ik dit moet noteren, hoe ik het nu heb staan:
Maar ik k anme voorstellen dat het op een iets meer wiskundige manier kan ipv die puntjes ;x
Maar ik k anme voorstellen dat het op een iets meer wiskundige manier kan ipv die puntjes ;x


Beide notaties kom ik wel eens tegen, zijn ze eigenlijk allebei 'goed'?


eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ah, oké. Maar die notatie is dan wel gewoon oké, en het gevolg ("voor alle i: e niet in Ai" -> "voor alle i: e zit in Aic") is wel triviaal toch?


Die tweede zou ik niet doen. Eerst allerlei symbolen gebruiken en ze achteraf pas introduceren is heel vervelend om te moeten lezen.quote:Op woensdag 24 maart 2010 21:08 schreef GlowMouse het volgende:
Beide notaties kom ik wel eens tegen, zijn ze eigenlijk allebei 'goed'?
[ afbeelding ]
[ afbeelding ]


Ze worden allebei wel gebruikt, maar eigenlijk kom ik in artikelen in mijn vakgebied veel vaker een beschrijving in woorden tegen dan zulke constructies met logische symbolen, a la "for all $i \in \mathbb{N}$ we have $e_i \not\in A_i$".quote:Op woensdag 24 maart 2010 21:08 schreef GlowMouse het volgende:
Beide notaties kom ik wel eens tegen, zijn ze eigenlijk allebei 'goed'?
[ afbeelding ]
[ afbeelding ]
Voor de volledigheid, wat je op regel 3 en 4 schrijft klopt semantisch niet, de $e$ weglaten voor de $\in$/$\not\in$ is voor zover ik weet geen geaccepteerd gebruik.quote:Op woensdag 24 maart 2010 21:15 schreef Hanneke12345 het volgende:
Ah, oké. Maar die notatie is dan wel gewoon oké, en het gevolg ("voor alle i: e niet in Ai" -> "voor alle i: e zit in Aic") is wel triviaal toch?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Bewijs dat de inhoud van een bol gelijk is aan:

Doormiddel van Integreren.
Wat doe ik fout?

Dus:

Maar dan kom ik uit op:

Wat dus niet klopt, ik mis een factor 2?
Doormiddel van Integreren.
Wat doe ik fout?
Dus:
Maar dan kom ik uit op:
Wat dus niet klopt, ik mis een factor 2?


Je hebt de functiequote:Op donderdag 25 maart 2010 12:22 schreef Siddartha het volgende:
Bewijs dat de inhoud van een bol gelijk is aan:
[ afbeelding ]
Doormiddel van Integreren.
Wat doe ik fout?
[ afbeelding ]
Dus:
[ afbeelding ]
Maar dan kom ik uit op:
[ afbeelding ]
Wat dus niet klopt, ik mis een factor 2?
f(x) = √(r2 - x2)
De grafiek hiervan is een halve cirkel in de kwadranten I en II, die bij wenteling om de x-as een bol met als middelpunt de oorsprong en straal r oplevert. Om nu het volume van deze bol te berekenen, moet je {f(x)}2 integreren over het interval [-r,r] en het resultaat met π vermenigvuldigen. Jij integreert echter over het interval [0,r], zodat je het volume vindt van een halve bol met straal r.
Heb je trouwens de opgave over het berekenen van de oppervlakte van een bol met straal r nog uitgewerkt? Ik heb zo het idee van niet, anders had je geweten dat je over het interval [-r,r] moet integreren.


In het antwoordboekje staat het volgende:quote:Op donderdag 25 maart 2010 14:14 schreef Riparius het volgende:
[..]
Je hebt de functie
f(x) = √(r2 - x2)
De grafiek hiervan is een halve cirkel in de kwadranten I en II, die bij wenteling om de x-as een bol met als middelpunt de oorsprong en straal r oplevert. Om nu het volume van deze bol te berekenen, moet je {f(x)}2 integreren over het interval [-r,r] en het resultaat met π vermenigvuldigen. Jij integreert echter over het interval [0,r], zodat je het volume vindt van een halve bol met straal r.
Heb je trouwens de opgave over het berekenen van de oppervlakte van een bol met straal r nog uitgewerkt? Ik heb zo het idee van niet, anders had je geweten dat je over het interval [-r,r] moet integreren.
En dat is gelijk aan 4/3Pir^3 (Volgens het antwoordboekje dan). Waarom klopt dat dan niet?


Het antwoordenboekje klopt, hoewel ik het zelf niet zo zou opschrijven. Je hebt kennelijk de integraal niet correct uitgerekend.quote:Op donderdag 25 maart 2010 14:47 schreef Siddartha het volgende:
[..]
In het antwoordboekje staat het volgende:
[ afbeelding ]
En dat is gelijk aan 4/3Pir^3 (Volgens het antwoordboekje dan). Waarom klopt dat dan niet?


Integraal van Pi(r^2 - x^2) is toch gewoon Pi r^2 - 1/3x^3 + c ?quote:Op donderdag 25 maart 2010 14:50 schreef Riparius het volgende:
[..]
Het antwoordenboekje klopt, hoewel ik het zelf niet zo zou opschrijven. Je hebt kennelijk de integraal niet correct uitgerekend.
Invullen voor x=r en vermenigvuldigen met 2 geeft dan 2/3 ipv 4/3.