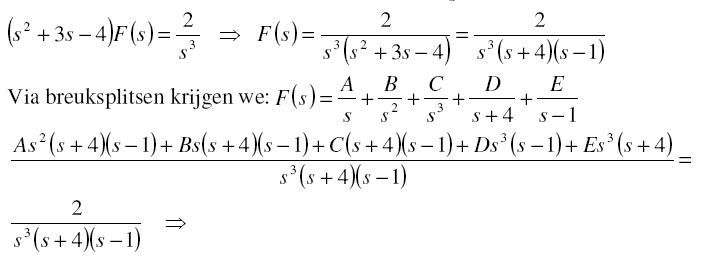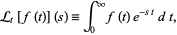[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op donderdag 25 maart 2010 14:53 schreef Siddartha het volgende:

[..]

Integraal van Pi(r^2 - x^2) is toch gewoon Pi r^2 - 1/3x^3 + c ?
Invullen voor x=r en vermenigvuldigen met 2 geeft dan 2/3 ipv 4/3.

Nee, dit klopt niet. Bovendien vind ik het jammer dat je kennelijk eerst in het antwoordenboekje kijkt en dan probeert na te doen wat daar wordt gedaan, anders was je nooit op het idee gekomen om de integraal over het interval [-r,r] te vervangen door tweemaal de integraal over het interval [0,r].

quote:

Op donderdag 25 maart 2010 14:56 schreef Riparius het volgende:

[..]

Nee, dit klopt niet. Bovendien vind ik het jammer dat je kennelijk eerst in het antwoordenboekje kijkt en dan probeert na te doen wat daar wordt gedaan, anders was je nooit op het idee gekomen om de integraal over het interval [-r,r] te vervangen door tweemaal de integraal over het interval [0,r].

Verdomme, ik ben gewoon r^2 vergeten te integreren!
Stomme fout die ik vaak maak, helaas.

Ik kan je geruststellen dat ik eerst een hele tijd zelf over het antwoord heb nagedacht. Pas daarna zocht ik het antwoord op.

quote:

Op donderdag 25 maart 2010 15:07 schreef Siddartha het volgende:

[..]

Verdomme, ik ben gewoon r^2 vergeten te integreren!
Stomme fout die ik vaak maak, helaas.

Ik kan je geruststellen dat ik eerst een hele tijd zelf over het antwoord heb nagedacht. Pas daarna zocht ik het antwoord op.

Inderdaad, een primitieve van {f(x)}² = r² - x² is r²x - 1/3∙x³. Integreren over [-r,r] en vermenigvuldigen met π geeft dan 4/3∙π∙r³ voor het volume van een bol met straal r. Heb je nu de oppervlakte van een bol met straal r ook kunnen berekenen via integratie?

quote:

Op donderdag 25 maart 2010 15:12 schreef Riparius het volgende:

[..]

Inderdaad, een primitieve van {f(x)}² = r² - x² is r²x - 1/3∙x³. Integreren over [-r,r] en vermenigvuldigen met π geeft dan 4/3∙π∙r³ voor het volume van een bol met straal r. Heb je nu de oppervlakte van een bol met straal r ook kunnen berekenen via integratie?

Ik kom tot dit:
f(x): y = Wortel(r^2 - x^2)
f'(x)= x / wortel(r^2-x^2)
Dat kwadrateren levert op(?):
x^2 (r^2 - x^2)^1,5

Invullen in de formule voor lengte geeft:
Primitiveer Wortel(1+(f'(x)^2 )
Maar hoe moet ik zoiets primitiveren?

quote:

Op donderdag 25 maart 2010 15:40 schreef Siddartha het volgende:

[..]

Ik kom tot dit:
f(x): y = Wortel(r^2 - x^2)
f'(x)= x / wortel(r^2-x^2)
Dat kwadrateren levert op(?):
x^2 (r^2 - x^2)^1,5

Nee, dit gaat niet goed. Ik had het meeste werk trouwens al voor je gedaan. Kijk nog even hier. We hebben:


1 + (f'(x))² = r²/(r² - x²)

En dus:

√(1 + (f'(x))²) = r/√(r² - x²)

En dus:

f(x)∙√(1 + (f'(x))²) = r

Je krijgt dus een heel eenvoudige (constante) functie om te integreren! Kun je ook een meetkundige interpretatie geven van dit resultaat? En wat wordt nu de oppervlakte van een bol met straal r?

Weet iemand hoe je met http://www.wolframalpha.com/ de hoekfrequentie, periode en frequentie kan uitrekenen? Ik snap die sommen maar niet...

Hoe komen ze bij die vergelijking, ik zie de logica niet? Dus die onder de zin, via breuksplitsen krijgen we.

quote:

Op donderdag 25 maart 2010 16:00 schreef Riparius het volgende:

[..]

Nee, dit gaat niet goed. Ik had het meeste werk trouwens al voor je gedaan. Kijk nog even hier. We hebben:


1 + (f'(x))² = r²/(r² - x²)

En dus:

√(1 + (f'(x))²) = r/√(r² - x²)

En dus:

f(x)∙√(1 + (f'(x))²) = r

Je krijgt dus een heel eenvoudige (constante) functie om te integreren! Kun je ook een meetkundige interpretatie geven van dit resultaat? En wat wordt nu de oppervlakte van een bol met straal r?

Oppervlakte van een bol is dus
4pi r^2

Ik bedacht me trouwens, is de omtrek niet gewoon de afgeleide van de inhoud?
Inhoud = 4/3Pi r^3
Inhoud '= 4Pi r^2 = Omtrek

quote:

Op donderdag 25 maart 2010 16:22 schreef GoodGawd het volgende:
[ afbeelding ]

Hoe komen ze bij die vergelijking, ik zie de logica niet? Dus die onder de zin, via breuksplitsen krijgen we.

Breuksplitsing is een standaardtechniek bij o.a. integreren. Het idee is dat je een breuk gaat schrijven als een som van een aantal breuken waarbij de noemer steeds één van de factoren is van de noemer van de oorspronkelijke breuk. Vervolgens moet je die deelbreuken weer gelijknamig maken om ze op te kunnen tellen. Dat is wat hier gebeurt. Tenslotte vermenigvuldig je beide leden van de vergelijking met de noemer van de oorspronkelijke breuk en stel je de coëfficiënten van de veeltermen in linker en rechter lid aan elkaar gelijk. Dit levert dan een stelsel lineaire vergelijkingen op in A, B, C ... dat je op kunt lossen om uiteindelijk te weten te komen hoe je de oorspronkelijke breuk kunt schrijven als een som van deelbreuken.

quote:

Op donderdag 25 maart 2010 16:24 schreef Siddartha het volgende:

[..]

Oppervlakte van een bol is dus
4pi r^2

Inderdaad, dit klopt. De meetkundige interpretatie van die constante functie die je krijgt is dat de oppervlakte van een bol gelijk is aan de manteloppervlakte van een omgeschreven cilinder. En aangezien dit resultaat ook geldt als je integreert over een willekeurig deelinterval van [-r,r] zien we dus dat de oppervlakte van een willekeurig bolsegment ook gelijk is aan het corresponderende deel van de oppervlakte van de omgeschreven cilinder.

quote:

Ik bedacht me trouwens, is de oppervlakte niet gewoon de afgeleide van de inhoud?
Inhoud = 4/3Pi r^3
Inhoud '= 4Pi r^2 = Oppervlakte

Dat is een hele goede observatie. Als je een bol neemt met een straal r en een iets grotere concentrische bol met een straal r + Δr, dan kun je het verschil in volume benaderen door de oppervlakte O(r) van de bol te vermenigvuldigen met de dikte Δr van de 'schil'. En dus geldt:

V(r+Δr) - V(r) ≈ O(r)∙Δr

En dus ook:

(V(r+Δr) - V(r))/Δr ≈ O(r)

De benadering wordt beter naarmate we de dikte Δr van de 'schil' tot nul laten naderen, en dus geldt inderdaad:

V'(r) = O(r)

Voor een cirkel geldt iets dergelijks: als je de formule πr² voor de oppervlakte van een cirkel met straal r differentieert naar r krijg je 2πr, en dat is inderdaad de formule voor de omtrek van een cirkel met straal r.

[ Bericht 1% gewijzigd door Riparius op 25-03-2010 18:05:40 ]

quote:

Op donderdag 25 maart 2010 16:46 schreef Riparius het volgende:

[..]

Ah, nu is het een stuk duidelijker geworden.
Heel erg bedankt voor de uitleg (en je geduld!).

quote:

Op donderdag 25 maart 2010 16:22 schreef GoodGawd het volgende:
[ afbeelding ]

Hoe komen ze bij die vergelijking, ik zie de logica niet? Dus die onder de zin, via breuksplitsen krijgen we.

Breuksplitsen is echt iets wat je even moet leren door op het internet naar voorbeeldjes te kijken. Verder kun je in je rekenmachine handig de matrix oplossen die je bij breuksplitsen krijgt.

Bij de Tu Delft, kregen we een pdf'je om het te leren. Maar het meest heb ik gehad aan mijn leraar van het HBO en een vriend die het door had.

quote:

Op donderdag 25 maart 2010 16:17 schreef snakeman123 het volgende:
Weet iemand hoe je met http://www.wolframalpha.com/ de hoekfrequentie, periode en frequentie kan uitrekenen? Ik snap die sommen maar niet...

Geef eens een voorbeeld van een opgave. Met deze vraag kan niemand iets omdat we jouw gedachten niet kunnen lezen.

quote:

Op donderdag 25 maart 2010 16:52 schreef Burakius het volgende:

[..]

Breuksplitsen is echt iets wat je even moet leren door op het internet naar voorbeeldjes te kijken. Verder kun je in je rekenmachine handig de matrix oplossen die je bij breuksplitsen krijgt.

Bij de Tu Delft, kregen we een pdf'je om het te leren. Maar het meest heb ik gehad aan mijn leraar van het HBO en een vriend die het door had.

Okay, met als er twee letters om de hoek komen kijken volg ik het wel maar met meer wordt het een beetje een doolhof

quote:

Op donderdag 25 maart 2010 17:52 schreef GoodGawd het volgende:

[..]

Okay, met als er twee letters om de hoek komen kijken volg ik het wel maar met meer wordt het een beetje een doolhof

Maakt verder niet uit, je krijgt uiteindelijk een vergelijking met een vierdegraads polynoom in s en gelijkstelling van de vijf coëfficiënten in beide leden van je vergelijking levert je dan een stelsel van vijf lineaire vergelijkingen in A,B,C,D en E op.

quote:

Op donderdag 25 maart 2010 17:52 schreef GoodGawd het volgende:

[..]

Okay, met als er twee letters om de hoek komen kijken volg ik het wel maar met meer wordt het een beetje een doolhof

Het principe blijft hetzelfde steeds. Er zijn meerdere manieren om het te doen. Ik heb mijn eigen illegale manier . Ik zal nu een voorbeeldje posten om je te verhelderen. Was wel even graven naar mijn oude aantekeningen:

y '' + y = u_3pi(t) , met y(0)=1 en y'(0) = 0

Met Laplace wordt dit:

(s²+1)*Y(s) -s = 1/s * e^-3pi*s

Y(s) = e^-3pi*s * 1/s(s² +1 ) + s/(s²+1) (de laatste term is getransformeerd cos t, dus die hebben we mooi al).

Nu komt het BREUKSPLITSEN, let goed op

Wat er aan de rechterkant staat (behalve s/(s²+1), want dat is vervangen met cos t) , gaan we breuksplitsen

We hebben daar nu de term 1/s(s² + 1 ) staan. Dit kunnen we splitsen in:

1/s en 1/s² +1 , we vervangen de letters erboven met A en B en C. De tweede term heeft namelijk een kwadraat erin. Daarom komt daar B*s + C . Zie maar:

A/s + B*s + C / s² +1 = 1/s(s² +1 ) ( zoals je merkt zet je aan de rechterkant van de vergelijking hetgeen wat je hebt "gebreuksplitst" )

Nu gaan we er een matrix van maken. Dit noem ik de Johan methode. Omdat een vriend die Johan heet het heeft voorgedaan. We moeten eerst kruislingsvermenigvuldigen. Of eigenlijk zorg je ervoor dat er aan de rechterkant van de vergelijking alleen de 1 overblijft. Daarom moeten we vermenigvuldigen met s(s²+1)

Waardoor we krijgen:

A(s² +1) +B*s*s + C*s = 1

Dit zetten we in een matrix met :

s=0
s=1
s=2

, omdat er drie letters zijn, namelijk A, B en C. We vermenigvuldigen het aangegeven S met de letters om te komen tot:

A:

s=0 A=1 , (immers A(0² +1 ) , je houdt 1 over tussen de haakjes waardoor A =1 )
s=1 A=2
s= 2 A= 5

B:

s=0 B=0
s=1 B=1
s=2 B=4

C:

s=0 C=0
s=1 C=1
s=2 C=2


Matrix:
A , B , C
s=0 [1 , 0, 0] = [1]
s=1 [2, 1 , 1] = [1]
s=2 [5 , 4 , 2] = [1]


Dit vul je in in je GR en laat je oplossen, waardoor je krijgt


A=1
B=-1
C=0

Deze voeren we weer terug naar onze formule die we hadden (de splitsing): A/s + B*s + C / s² +1

Waardoor je krijgt:

1/s - s/s²+1 ==> (1-cost)e^3pi*s + cos t

===> oplossing: (1-cost)u_3pi(t) + cos t

Hoop dat ik geen tikfoutjes heb gemaakt.

Okay duidelijk! Moet alleen nog uitvogelen hoe je die matrix in je GR invult, hehe.

De 'methode Johan' hierboven berust nog steeds op het opstellen van een lineair stelsel, en dat gaat in dit geval toch handiger en sneller met de traditionele manier. Als je hebt:

A∙(s² +1) +B∙s² + C∙s = 1

Dan kunnen we dit schrijven als:

(A+B)∙s² + C∙s + A = 1,

en dan zie ik meteen dat A = 1, B = -1 (want A+B=0) en C = 0.

Maar als het aantal coëfficiënten groot is dan kan het oplossen van het lineaire stelsel wat meer werk opleveren, en dan kun je met voordeel gebruik maken van de methode van Heaviside. Bij die methode moet je echter weer goed opletten als er meervoudige factoren zijn in de noemer van de breuk die je wil splitsen. Zie deze uitleg.

quote:

Op donderdag 25 maart 2010 19:09 schreef GoodGawd het volgende:
Okay duidelijk! Moet alleen nog uitvogelen hoe je die matrix in je GR invult, hehe.

2nd x^-1

Daarna in dit geval een 3 * 4 matrix. Die invullen met de cijfers die je hebt. En vervolgens oplossen door.
1. 2nd x^-1 (daar staat matrix)
2. Math
3. rref()

Als je die rref hebt gekozen dan de letters invullen op deze manier?:

rref(A,B,C,D)

Overigens zou ik de methode die Riparius voorstelt gebruiken. Bespaart je veel tijd.

quote:

Op donderdag 25 maart 2010 20:02 schreef GoodGawd het volgende:
Als je die rref hebt gekozen dan de letters invullen op deze manier?:

rref(A,B,C,D)

Je hebt bij het maken van de Matrix als het goed is bij [A] deze matrix gemaakt.

Dus je moet nu rref (A) doen. Dan gaat de GR het oplossen voor je (de cijfers aan de rechterkant).

(zie 2nd , matrix , edit 1:[A]--> 3x4 matrix doen en invullen, daarna rref (A))

Oh wacht ja op die fiets !

Ik snap hem thanks!

NP bro. Nerds support each other enzo

"Gegeven zijn een punt P uit P³(R), een projectieve lijn L subset van P³(R) met P niet uit L, en een projectief vlak V subset van P³. Gegeven is verder dat er bij elk punt R uit V een punt Q uit L bestaat zo dat P, Q en R op één lijn liggen. Bewijs dat L een subset is van V."
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.

Hallo iedereen
Ik heb een vraag over een dubbellogaritmisch assenstelsel,
al heb je zo een grafiek voor je, dus een grafiek van een machtsfunctie,
hoe kun je daar een formule van maken??
aub de stappen die je moet maken uitleggen en sorry dat ik er geen voorbeeld grafiek bij heb
Ik snap het echt niet
hiervoor zei iemand dat ik het hier moest poste dus
alvast bedankt!

quote:

Op donderdag 25 maart 2010 20:24 schreef Hanneke12345 het volgende:
"Gegeven zijn een punt P uit P³(R), een projectieve lijn L subset van P³(R) met P niet uit L, en een projectief vlak V subset van P³. Gegeven is verder dat er bij elk punt R uit V een punt Q uit L bestaat zo dat P, Q en R op één lijn liggen. Bewijs dat L een subset is van V."
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.

is je optelling goed gedefinieerd? (-3:-2:1)=(3:2:-1) en toch krijg je:
(-3:-2:1)+(1:2:0)=(-2:0:1)
(3:2:-1)+(1:2:0)=(4:4:-1)
dus totaal verschillende uitkomsten....
Voor punten op bijv elliptische krommen bestaat er een optelling en dan geldt P+Q+R=O als de punten op 1 lijn liggen, waarbij O een punt die je als eenheidselement hebt gekozen voor optelling.

Opmerking: een punt in P4 geef je aan met vier coordinaten.

quote:

Op donderdag 25 maart 2010 20:52 schreef Optimistic1 het volgende:

[..]

is je optelling goed gedefinieerd? (-3:-2:1)=(3:2:-1) en toch krijg je:
(-3:-2:1)+(1:2:0)=(-2:0:1)
(3:2:-1)+(1:2:0)=(4:4:-1)
dus totaal verschillende uitkomsten....
Voor punten op bijv elliptische krommen bestaat er een optelling en dan geldt P+Q+R=O als de punten op 1 lijn liggen, waarbij O een punt die je als eenheidselement hebt gekozen voor optelling.

Opmerking: een punt in P4 geef je aan met vier coordinaten.

Mja, op deze manier hoor je wel coördinaten op te tellen voor zover ik weet.

Het gaat nergens om P⁴, toch?

pff, kutvak. ;x

Oh, en om een functie B(f,g) bilineair te laten zijn, moet het dan lineair zijn met g vast én met f vast (dus B(f_1+f_2, g) = B(f_1, g) + B(f_2, g) en B(f, g_1+g_2) = ... ), of is het genoeg met één van beiden?

quote:

Op donderdag 25 maart 2010 21:19 schreef Hanneke12345 het volgende:
pff, kutvak. ;x

Wat voor vak is dat?

Projectieve meetkunde.

quote:

Op donderdag 25 maart 2010 20:24 schreef Hanneke12345 het volgende:
"Gegeven zijn een punt P uit P³(R), een projectieve lijn L subset van P³(R) met P niet uit L, en een projectief vlak V subset van P³. Gegeven is verder dat er bij elk punt R uit V een punt Q uit L bestaat zo dat P, Q en R op één lijn liggen. Bewijs dat L een subset is van V."
Ik heb bij deze som gezet "Q+P=R", is het zo dat dat geldt als ze op één lijn liggen? Dan geldt toch ook dat P+R=Q en Q+R=P. (Is dit wel zo? Ik probeer het na te rekenen maar (-3:-2:1)+(1:2:0)=(-2:0:1), maar (1:2:0)+(-2:0:1)=(-1:2:1)=/=(-3:-2:1)). Ik zie echt niet hoe ik dit moet aanpakken.

Je kunt punten in een projectieve ruimte niet optellen. Drie punten liggen op een lijn als hun coordinaatvectoren lineair afhankelijk zijn, gebruik dat.

quote:

Op donderdag 25 maart 2010 21:22 schreef Hanneke12345 het volgende:
Oh, en om een functie B(f,g) bilineair te laten zijn, moet het dan lineair zijn met g vast én met f vast (dus B(f_1+f_2, g) = B(f_1, g) + B(f_2, g) en B(f, g_1+g_2) = ... ), of is het genoeg met één van beiden?

Moet met allebei, anders zou je, bijvoorbeeld, voor A een lineaire functie kunnen nemen en B(f, g) = A(f), dat is iha niet lineair in g.

B is constant in g

Ik heb hier in een som staan:

Laplace(f(5t)) = 1/5 F (s/5)

Waarom is dat zo? Kan je dat herleiden aan de hand van een rekenregel?

Volgt direct uit de definitie. Zie ook http://en.wikipedia.org/wiki/Laplace_transform

quote:

Op vrijdag 26 maart 2010 13:06 schreef GoodGawd het volgende:
Ik heb hier in een som staan:

Laplace(f(5t)) = 1/5 F (s/5)

Waarom is dat zo? Kan je dat herleiden aan de hand van een rekenregel?

Je kunt dit rechtstreeks herleiden uit de definitie van de Laplacetransformatie:



Zij ℒ[f(t)](s) = F(s). Om nu aan de hand van de definitie ℒ[f(5t)](s) te bepalen voer je een integraalsubstitutie t = τ/5 (en dus dt = dτ/5) uit, en dan zie je direct dat ℒ[f(5t)](s) = 1/5∙F(s/5).

Is dat convolutie product gebeuren moeilijk of ligt dat aan mij?

Hallo, weet iemand hier op je op een casio fx-9850gb de standaardafwijking kunt bepalen als je de gemiddelde en de opp hebt (bij een normale verdeling)?

De oppervlakte is altijd 1, dus dat zegt niet zoveel.

quote:

Op vrijdag 26 maart 2010 19:55 schreef GlowMouse het volgende:
De oppervlakte is altijd 1, dus dat zegt niet zoveel.

Ja maar niet als er een oppervlakje uitgesneden is met 1 (en dan verder tot zo ver mogelijk links, of rechts) of 2 verticale strepen, waar een getal bij staat

quote:

Op donderdag 25 maart 2010 21:19 schreef Hanneke12345 het volgende:

[..]

Mja, op deze manier hoor je wel coördinaten op te tellen voor zover ik weet.

Het gaat nergens om P⁴, toch?

pff, kutvak. ;x

sorry,Ik bedoelde P³

Een vraagje:
Zij X < A^m en Y < Aⁿ twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < A^m+n de geinduceerde Zariski topologie krijgt.

Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!

Heeft iemand een idee?