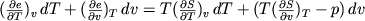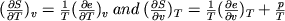Post hier weer al je vragen, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
Vorige deeltje Beta-huiswerkvragen
verkeerd gepostIQ aankomende studenten is normaal verdeeld met u=105 en o=15. Vanaf welk IQ behoort een student tot de 15% hoogste IQ-groep?
Mijn oplossing ->
y1 = normalcdf(X,10000,105,15). Bij X =120 y1 = 0.15 = 15%. IQ dus 120 of hoger. Vervolgens kijk ik wat het goede antwoord is, dat is 125.0. In mijn table is x=125 y1=0.09..
De vraag is dus of ik fout zit of het antwoordenvel.
Gevraagd is c zodat P(Y<c) = 0,85. Eenvoudig omschrijfwerk levert dat P((Y-105)/15 < (c-105)/15) = P(Z < (c-105)/15) = 0,85. Een tabellenboek levert dat (c-105)/15 gelijk is aan 1,04. Hieruit volgt dat c=120,6. Gebruikmakend van de tabel wordt er wat afgerond, maar 120 lijkt mij een juist antwoord.
[ Bericht 47% gewijzigd door spinor op 01-09-2006 11:33:18 ]
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
quote:Ik weet niet wat je wil vinden, maar als links de rode lijn parallel is aan RT, dan is, onder de juiste voorwaarden, die driehoek gelijkbenig. De hoeken volgen daaruit en ook de lengtes zijn uit te rekenen. Maar ik weet niet wat je wilt weten.Op vrijdag 1 september 2006 12:59 schreef lj_lightning het volgende:
Vraagje, als ik van een driehoek 2 onbekende heb, hoe kan ik die dan vinden? situatie:
[afbeelding]
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
quote:Ja ik was op school en heb er een kwartier over gedaan om mijn bericht proberen te editenOp vrijdag 1 september 2006 15:23 schreef Wackyduck het volgende:
[..]
Ik weet niet wat je wil vinden, maar als links de rode lijn parallel is aan RT, dan is, onder de juiste voorwaarden, die driehoek gelijkbenig. De hoeken volgen daaruit en ook de lengtes zijn uit te rekenen. Maar ik weet niet wat je wilt weten.
Ik wil weten op welke hoogte die rode lijn 4cm is (dus ik wil de lengte weten van die zwarte verticale streep) en om die hoogte te weten moet ik de lengte van de aanliggende zijde en overstaande zijde weten...maar hoe?
We onderscheiden twee situaties:
l<0 of l>4: geen oplossing
0<=l<=4:
Voor de eerste mogelijkheid geldt (l / (2h)) = tan(45) = 1 (waarom?). Omschrijven naar de hoogte is denk ik geen probleem.
Zolang h!=2 is de tweede oplossing gelijk aan 4-h.
Hierbij heb ik gebruik gemaakt dat het zij-aanzicht een vierkant is, en symmetrisch is in een verticale lijn.
[ Bericht 1% gewijzigd door GlowMouse op 02-09-2006 14:17:04 (grote fout :() ]
We komen van de 1e wet v d TD uit op:
quote:Nu zie ik wel hoe de auteur er bij komt, maar wat hij nou wiskundig doet snap ik niet. dus wat dat uitdelen nu precies inhoudt...(..)
equating the dT and dv terms gives:
mvg en bvd.
quote:Je hebtOp woensdag 6 september 2006 12:36 schreef pfaf het volgende:
Hey allen, even een kort vraagje. Bij Thermo kom ik in de tekst het volgende tegen waar ik niet helemaal begrijp wat ze doen.
We komen van de 1e wet v d TD uit op:
[..]
Nu zie ik wel hoe de auteur er bij komt, maar wat hij nou wiskundig doet snap ik niet. dus wat dat uitdelen nu precies inhoudt...
mvg en bvd.
a dT + b dv = c dT + d dv,
met a b c d variabel.
Ofwel
(a - c) dT = (d - b) dv.
Dit moet altijd waar zijn onafhankelijk van dT en dv, dat kan alleen maar als a-c en d-b 0 zijn, ofwel
a = c,
b = d.
Ik heb ff wat vraagjes over het vier-kleurenprobleem. Heb er vandaag college over gehad, maar kon de docent niet echt volgen... Hij bleef maar lachen om zn eigen anekdotes en opmerkingen enzo
Maar goed, we hebben het volgende:
Gegeven is een kaart op de bol met de volgende eigenschappen:
1) Elk land is een evenhoek. Dus de grens van een land vormt een rondweg met een even aantal ribben.
2) Elk meerlandenpunt is een drielandenpunt. Dus een ribbe verbindt twee drielandenpunten.
3) Er zijn eindig veel landen, en ze vullen het boloppervlak.
Nu de vragen:
1)
2) Leg uit waarom er een land is met hoogstens vier ribben in zn grens
3) Laat zien dat we de drielandenpunten van een + of - kunnen voorzien, zo dat elke ribbe een + met een - verbindt (beschouw een minimaal tegenvoorbeeld)
Tijdens het verhaal van de docent kwam ook een stelling van Euler naar voren. Die was iets van:
V - E + F = 2,
met V=vertices (hoekpunten), E=edges(ribben) en F=faces(landen),
maar ik zie ook niet hoe dat hier iets mee te maken heeft.
Wie kan mij helpen???
Elk punt heeft graad 3, dus je weet dat 2.E = 3.V. Dit invullen in de formule geeft 3.F = 6 + E. Als alle vlakken nu meer dan 4 kanten zou hebben, dus tenminste 6, dan heb je E >= 3.F en dit levert dan een tegenspraak.
Voor je derde vraag heb ik momenteel geen tijd
..Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
@ Wolfje: dank je. Nu snap ik t. Tijdens college had de docent dat 2E = 3V ook wel laten zien, maar ik had geen idee wat 'ie nou bedoelde... maar nu dus wel
quote:Als je dan begint ergens een + te zetten, dan zet je op elk punt met oneven afstand van die + een - en elk punt met even afstand van die + een +. Als elke cykel even lengte heeft, dan is de pariteit van het aantal stappen om van het ene punt naar het andere punt te komen onafhankelijk van het gekozen pad.Op dinsdag 12 september 2006 15:28 schreef Bioman_1 het volgende:
@ thabit: mijn bewijskunst is nogal waardeloos, dus ik zie niet hoe ik wat jij zegt aan moet tonen. Dit neemt niet weg dat ik wel snap waarom het zo is, ik kan t alleen niet echt verwoorden :S
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
Het makkelijkst is hier om de drielandenpunt-voorwaarde op je graaf te laten vallen en te veronderstellen dat je een planaire graaf hebt waarvan elk land even grenslengte heeft. Dan kun je namelijk wat makkelijker gebruik maken van inductie.
we moeten dat 5| Fn <==> 5|n
Fn staat voor de nste term van de fibonacci rij.
ik heb nu moeite met het bewijzen van 5|n ==> 5| Fn of wel NIET( 5| Fn) ==> NIET (5|n)
ik dacht, schrijf n=5k+1 of 5k+2 of 5k+3 of 5k+4 maar verder dan dat kwam ik niet verder...
enige tips.. die kunnen helpen?
alvast bedankt
als m|n dan Fm|Fn
en voor alle m,n dat Fggd(m,n)=ggd(Fm,Fn) geldt.
quote:Ik koos dus antwoord c omdat niet alle levenden mannen zijn, waardoor je nooit kunt concluderen dat alle mannen lui zijn. Maak ik nu een denkfout»alle mannen zijn levenden - sommige mannen zijn lui
A. geen levenden zijn lui
B. niet alle levenden zijn lui
C. tenminste sommige levenden zijn lui
D. geen conclusie mogelijk
Je koos antwoord c. Het juiste antwoord is b.
quote:Bedankt voor de bevestiging, ik zat echt aan mijzelf te twijfelen.Op woensdag 13 september 2006 14:21 schreef thabit het volgende:
C is correct. B is fout.
Ik wil RQ-waardes experimenteel bepalen. De vorige poging was echter een regelrechte mislukking. Ik vermoed dat dit gedeeltelijk veroorzaakt wordt door het verschil in temperatuur van de ingeademde en de uitgeademde lucht.
De RQ-waarde is de verhouding tussen de geproduceerde CO2 (in l) en de gebruikte O2 (in l).
Om het volume geproduceerde CO2 te berekenen moet ik de ingeademde CO2 van de uitgeademde CO2 aftrekken.
Om het volume gebruikte O2 te berekenen moet ik de uitgeademde O2 aftrekken van de ingeademde O2.
De uitgeademde gassen zijn echter warmer, en hebben dus een groter volume dan de ingeademde gassen.
Is er een formule waarmee ik de volumes uitgeademde gassen terug kan brengen naar hun volume bij kamertemperatuur?
De ideale gasformule is een eerste benadering in dit geval. Maar de temperatuursstijging lijkt me niet echt hoog 25 en 35 C, scheelt 10 K op 300 K. De rest van je metingen zal waarschijnlijk meer dan een 3% foutmarge hebben.
Deze opstelling geeft het gasvolume en de temperatuur van de aangezogen lucht aan. Vervolgens wordt er door het apparaat een staaltje van de aangezogen lucht geanalyseerd mbv een CO2-meter en een O2-meter die percentages aangeven. Mbv deze percentages en het gasvolume heb ik de volumes per gas berekend, voor zowel de ingeademde als de uitgeademde lucht. We hebben er dus geen rekening mee gehouden dat het volume aan uitgeademde gassen gewoon groter is.
Onze precieze werkwijze:
We bekijken de constante waardes van de ingeademde lucht.
Vervolgens laten we een proefpersoon uitademen in het apparaat. Per 0,01 m^3 uitgeademde lucht noteren we het percentage aan O2 en CO2.
We berekenen het verschil in uitgeademde CO2 en ingeademde CO2 en het verschil van de ingeademde O2 en de uitgeademde CO2. We delen dan de volumes van de verschillende gassen door elkaar
[ Bericht 26% gewijzigd door vliegtuigje op 15-09-2006 21:04:35 ]
Wat is het temperatuurverschil, wat zijn je meetwaarden en in hoeverre wijken die af van je verwachtingen.
Bedoel je hier met volume het volumedebiet (volume/tijd [m3/s]) en meet je dat continu?
Misschien is het een idee om niet in absolute volumens, maar om in volumepercentages te werken. Als je ervan uit gaat dat bij dit kleine temperatuurverschil alle gassen evenveel uitzetten is dat ook een mogelijkheid.
Het temperatuurverschil is redelijk klein, meer dan 4 graden is het zeker niet.
De meetwaarden leken eerst te kloppen. Zoals we verwachtten neemt het percentage CO2 toe nadat men gegeten heeft. De hoeveelheid CO2 in de ingeademde lucht leek echter groter dan de theorie deed verwachten.
De verhouding klopt echter niet. We verkrijgen RQ-waardes die hoger zijn dan 1, wat onmogelijk is.
Het volume is echt puur het volume wat door het apparaat stroomt.
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?
Maar kun je ook stellen dat er zulke G1 en G2 bestaan die disjunct zijn? Dat is namelijk precies wat ik nog nodig heb om een bepaald bewijs af te maken, maar ik zie eigenlijk zelf niet zo in dat er ook altijd disjuncte G1 en G2 zouden moeten bestaan.
Neem maar een oneindige verzameling X met de co-eindige topologie (dwz de lege verzameling en alle complementen van eindige deelverzamelingen zijn open). Dit is een topologische ruimte waarin 2 niet-lege open delen altijd een niet-lege doorsnede hebben. Neem voor E een deelverzameling bestaande uit 2 punten en voor V een deelverzameling van E die uit 1 punt bestaat.
Klopt het dat je wel altijd zo'n disjunct open paar of gesloten paar kan vinden als V onsamenhangend is?
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".
quote:Ik heb weinig biologische kenins, maar ik betwijfel het. Omdat een deel van de stoffen (vooral zuurstof) wordt opgenomen door het lichaam.Op vrijdag 15 september 2006 21:16 schreef vliegtuigje het volgende:
V = (m * K * T) / p
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.
quote:Reken eerst dV/dT (partiële afgeleide uit, of zoek de waarde op in een tabel) en kijk of er daadwerkelijk sprake is van een beetje toename in volume.Op vrijdag 15 september 2006 21:20 schreef vliegtuigje het volgende:
Iemand hier merkte net op dat het logisch zou zijn als de apparaten steeds het volumepercentage berekenen van stalen met hetzelfde volume.
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?
Wat ik me wel afvraag is of je gemeten inademwaardes overeen komen met die waardes bij het uitademen, of dat het überhaupt goed mogelijk om dit soort dingen niet-continu te meten. Als er iemand overdreven uitademt in een apparaat krijg je waarschijnlijk gekke dingen.
De telling van een mechanische tapecounter om te zetten in minuten en seconden.
Bijvoorbeeld dat je weet dat als de teller 0500 aanwijst dat je op 5:30 minuten van je tape zit.
De formule die hiervoor gebruikt kan worden is :
t = K1 * theta - K2*theta2
waarbij t = de tijd, theta de tellerstand en K1 en K2 constanten. Nu moet je dus eerst die constanten berekenen.
Nu is dit 1 vergelijking met 2 onbekenden, maar je kunt gewoon 2 waarden pakken.
Bijvoorbeeld
Bij 23 minuten staat de tapecounter op 1450
Bij 45 minuten (1 kant van een 90min bandje) staat de tapecounter op 2356
Maar ik kom er toch niet uit.
t1 = K1 * theta - K2*theta2
t2 = K1 * theta - K2*theta2
Dus:
23 = K1 * 1450 - K2 * 14502
45 = K1 * 2356 - K2 * 23562
K1 * 1450 - K2 * 14502 - 23 = 0
K1 * 2356 - K2 * 23562 - 45 = 0
1450K1 - 2102500K2 - 23 = 0
2356K1 - 5550736K2 - 45 = 0
1450K1 - 2345K1 - 2102500K2 + 5550736K2 - 23 + 45 = 0
Gaat dit wel goed? Hoe nu verder? 'k ben verdorie de hele avond al aan het rekenen maar ik kom er niet uit.
Het zijn 2 vergelijkingen met 2 onbekenden dus dat zou op te lossen moeten zijn.
Je loopt met een groep van 10 man in een rotswoestijn bij 45 graden. Jullie hebben te weinig water en er komt diarree. De tocht duurt 3-4 dagen en je hebt voor 1.5 dag water.
Langs de weg kom je poeltjes en artesisch water tegen. Je mag een rugzak van met 10 kg meenemen. Wat neem je mee en waarom? (ook werden we verwezen naar Norit, Immodium en ORS). Wie heeft een idee?
quote:Ik zou een vouwfiets mee nemen, dan kun je vast wel 3 keer zo snel gaan en heb je dus voldoende water voor de hele tochtOp zondag 17 september 2006 14:10 schreef alyel het volgende:
een opdracht van ANW waar ik niet uitkom;
Je loopt met een groep van 10 man in een rotswoestijn bij 45 graden. Jullie hebben te weinig water en er komt diarree. De tocht duurt 3-4 dagen en je hebt voor 1.5 dag water.
Langs de weg kom je poeltjes en artesisch water tegen. Je mag een rugzak van met 10 kg meenemen. Wat neem je mee en waarom? (ook werden we verwezen naar Norit, Immodium en ORS). Wie heeft een idee?
.quote:Of een radio-installatie om hulp in te roepen.Op zondag 17 september 2006 14:26 schreef Wolfje het volgende:
[..]
Ik zou een vouwfiets mee nemen, dan kun je vast wel 3 keer zo snel gaan en heb je dus voldoende water voor de hele tocht
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking
quote:Maak gebruik van wortel(x) = x^0.5 en van de kettingregelOp zondag 17 september 2006 15:04 schreef -tK- het volgende:
Ik zoek de afgeleide van de volgende functie:
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking
quote:Het is al opgelost. De stelling die ik moest bewijzen blijkt helemaal niet te kloppen.Op zaterdag 16 september 2006 16:30 schreef thabit het volgende:
Nog maar een voorbeeld dan. Neem voor X het projectieve vlak over een oneindig lichaam waarbij de gesloten delen alle eindige verenigingen van punten en lijnen zijn (en natuurlijk de hele X). Kies hierin twee lijnen L1 en L2 en noem het snijpunt P. Neem E = L1 U L2 - {P}, V = {L1} - P. Als ik me niet heb vergist is dit een voorbeeld waar je je disjuncte G1 en G2 noch allebei open, noch allebei gesloten kunt kiezen.
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".
quote:f[x] = sqrt(x^2 + 4)Op zondag 17 september 2006 15:04 schreef -tK- het volgende:
Ik zoek de afgeleide van de volgende functie:
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking
f[x] = (x^2 + 4)^0.5
f'[x] = 0.5(x^2 + 4)^-0,5 * 2x = (x^2 + 4)^-0.5 * x = (1 / sqrt(x^2 + 4)) * x
[ Bericht 2% gewijzigd door thomzor op 20-09-2006 00:26:58 ]
quote:En om het helemaal af te maken kan je er ook nog x/sqrt(4+x^2) van makenOp woensdag 20 september 2006 00:21 schreef thomzor het volgende:
[..]
f[x] = sqrt(x^2 + 4)
f[x] = (x^2 + 4)^0.5
f'[x] = 0.5(x^2 + 4)^-0,5 * 2x = (x^2 + 4)^-0.5 * x = (1 / sqrt(x^2 + 4)) * x
quote:dat staat er al...Op woensdag 20 september 2006 19:15 schreef Thundertje het volgende:
[..]
En om het helemaal af te maken kan je er ook nog x/sqrt(4+x^2) van maken
ik heb gehoord over een functie die overal continu is en toch nergens differentieerbaar is..
ik bedoel niet de functie
f(x)=1 als x uit Q is
f(x)=0 als x uit RQ is
want deze is toch niet continu...
ik weet niet meer van wie die functie was... dus wie die had geconstrueerd...
groetjes
. (Plaatje kan er ik niet bijdoen ivm ontbreken scanner).Iemand staat voorovergebukt. Beschouw romp, hoofd en armen als een hefboom. In de heupen ligt het scharnierpunt S. Het zwaartepunt van de hefboom ligt op 20cm van S. Spieren oefenen bij de schouders (die 60 cm van het scharnierpunt liggen) een kracht uit van 900N om de hefboom in evenwicht te houden. Deze spierkracht maakt een hoek van 9,3 graden met de horizontaal.
a) Bereken de massa van de hefboom (hoofd, romp en armen).
b) Bereken hoe groot de kracht is die in het scharnierpunt S op de onderrug werkt.
Bij a dacht ik aan het volgende antwoord: 0,2 x m x 9,8 = 0,6 x 900
m = 32 kg (afgerond). IK weet niet of het klopt, maar persoonlijk vind het erg weinig voor de romp, hoofd en armen van een volwassen man.
Bij b dacht ik aan: sin 9,3 graden = overstaande / 900
Overstaande = sin 9,3 graden x 900 = 145 newton (naar beneden afgerond).
Alvast bedankt voor het helpen
while statement....
int count = 3;
while ( count-- > 0)
cout << count << " ";
de uitput is 2 1 0 (waarom ook 0 ?)
en wat betekent het als er --count stond..? dus wat is eigenlijk --count?
kan iemand mij helpen? thanx.
lastige taal is dit, visual basic was een stukje makkelijker
Wie kan mij een tip geven?
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet.
[ Bericht 6% gewijzigd door de_priester op 25-09-2006 11:18:42 ]
quote:Een werkende link zou handig zijn...Op zondag 24 september 2006 21:46 schreef de_priester het volgende:
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Wie kan mij een tip geven?
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet.
quote:Je kunt natuurlijk ook de 2 commando's/expressies apart opschrijven in plaats van in 1 expressie te willen stoppen, wordt je code heel wat leesbaarder door.Op zondag 24 september 2006 20:50 schreef teletubbies het volgende:
okee! thanx
lastige taal is dit, visual basic was een stukje makkelijker
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet, want bij substitutie van de vgls gaat het steeds mis. (en dat doe ik in maple)
De gangbare aanpak is volgens mij met massabehoud, impulsbehoud, en bernouillie
massabehoud en impulsbehoud staan hieronder, maar hoe moet ik bernouillie toepassen?
kan iemand ff checken of dit de goede kant op werkt
Ik zit nog in de basis met differentieren maar ik snap echt niet hoe je in godsnaam dit doet.
Interval is dus [X, X+DeltaX]
En dan voor de Functie, f(x) = X^3
Dan doe je Delta Y/Detla X.
Delta Y wordt dan:
Maar hoe ga je in godsnaam daarheen? Dit vond ik in het antwoordenboekje, maar ik snap niet hoe je dit doet
Kan iemand dit met stap voor stap uitleggen?
b=delta x^3
(a+b)^3 -a^3=
(a+b)(a+b)(a+b) - a^3= (a+b)(a^2+2ab+b^2) -a^3
= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 - a^3
= 3a^2b + 3ab^2 + b^3
Ik kom dus hier op uit.
Ik mis dus de factor x^3 want die vervalt bij mij en bij jou niet.
f'(x) = 3x^2
x^g = g*x^(g-1)
^ basisregel afgeleiden
edit: laatmaar ik begrijp geloof ik de vraag niet echt
quote:Tjah dat is meer 4 Havo stofOp maandag 25 september 2006 20:16 schreef thomzor het volgende:
f(x) = x^3
f'(x) = 3x^2
x^g = g*x^(g-1)
^ basisregel afgeleiden
edit: laatmaar ik begrijp geloof ik de vraag niet echt
Het gaat erom dat je het op een andere manier laat zien hoe je van X^3 naar 3X^2 gaat. En dat moet met heel veel machten en delta's
quote:Heel erg bedankt, hier begin ik al iets meer van te snappen.Op maandag 25 september 2006 20:16 schreef -J-D- het volgende:
a=x^3
b=delta x^3
(a+b)^3 -a^3=
(a+b)(a+b)(a+b) - a^3= (a+b)(a^2+2ab+b^2) -a^3
= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 - a^3
= 3a^2b + 3ab^2 + b^3
Ik kom dus hier op uit.
Ik mis dus de factor x^3 want die vervalt bij mij en bij jou niet.
quote:Das dan 5 euro.Op maandag 25 september 2006 21:13 schreef HomerJ het volgende:
[..]
Heel erg bedankt, hier begin ik al iets meer van te snappen.
quote:nog iemand ? (heb tot morgen 11.00 u)Op maandag 25 september 2006 11:22 schreef de_priester het volgende:
nogmaals, met werkende link:
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet, want bij substitutie van de vgls gaat het steeds mis. (en dat doe ik in maple)
De gangbare aanpak is volgens mij met massabehoud, impulsbehoud, en bernouillie
massabehoud en impulsbehoud staan hieronder, maar hoe moet ik bernouillie toepassen?
kan iemand ff checken of dit de goede kant op werkt
[afbeelding]
quote:lolOp maandag 25 september 2006 21:09 schreef HomerJ het volgende:
[..]
Tjah dat is meer 4 Havo stof
Het gaat erom dat je het op een andere manier laat zien hoe je van X^3 naar 3X^2 gaat. En dat moet met heel veel machten en delta's
, ik heb wiskunde B2 gedaan op t vwo en ik heb nog nooit gezien wat jij daar deed XDzal wel aan mijn school (of de jouwe) liggen dan
Anyway, weet iemand anders nog hoe je kan laten zien dat:
f(x)= X^3 = f'(x) 3X^2
Zonder dus differentieregels maar meer met Delta Y
hoe moet ik bewijzen dat er oneindig veel priemgetallen zijn die bij deling door 4, rest 3 geven.
thanx
quote:De aanpak is hetzelfde als hoe je bewijst dat er oneindig veel priemgetallen zijn. Stel dat er maar N (eindig uiteraard) priemgetallen -1 mod 4 zijn. Definieer x = 2 + p_1^2....p_N^2. Er geldt dat x = -1 mod 4. Als x geen priemgetal is, dan moet het wel een deler -1 mod 4 hebben. Maar dit kan niet omdat het wel p_1^2...p_N^2 deelt maar niet 2. Dus er zijn oneindig veel priemgetallen van de vorm 3 mod 4.Op dinsdag 26 september 2006 21:40 schreef teletubbies het volgende:
he hee!
hoe moet ik bewijzen dat er oneindig veel priemgetallen zijn die bij deling door 4, rest 3 geven.
thanx
Leuk sommetje! Ik had hem zelf nog niet eerder gezien
. quote:Wat een gelijkheden, klopt geen zak van. Je zegt nu dat f(x) gelijk is aan f'(x).f(x)= X^3 = f'(x) 3X^2
Met behulp van de definitie: lim(k->0) (f(c+k)-f(c)) / k = lim(k->0) ((c+k)³-c³)/k = lim(k->0) (3c²k+3ck²+k³)/k = lim(k->0) 3c²+3ck+k² = 3c².
quote:ik dacht aan die aanpak ook.Op dinsdag 26 september 2006 22:12 schreef Wolfje het volgende:
[..]
De aanpak is hetzelfde als hoe je bewijst dat er oneindig veel priemgetallen zijn. Stel dat er maar N (eindig uiteraard) priemgetallen -1 mod 4 zijn. Definieer x = 2 + p_1^2....p_N^2. Er geldt dat x = -1 mod 4. Als x geen priemgetal is, dan moet het wel een deler -1 mod 4 hebben. Maar dit kan niet omdat het wel p_1^2...p_N^2 deelt maar niet 2. Dus er zijn oneindig veel priemgetallen van de vorm 3 mod 4.
Leuk sommetje! Ik had hem zelf nog niet eerder gezien
alleen ik gebruikte p1...pn*4+3= N (n het nieuwe priemgetal ). maar goed k kwam moeilijkheden tegen..
k ga het zo doorlezen
thanx
quote:Jouw getalletje werkt inderdaad ook wel als je eist dat p_i <> 3. Het gaat erom dat een getal dat 3 mod 4 is, altijd een factor 3 mod 4 heeft. Maak hierbij gebruik van (a mod c)*(b mod c) = (a*b) mod c.Op dinsdag 26 september 2006 22:53 schreef teletubbies het volgende:
[..]
ik dacht aan die aanpak ook.
alleen ik gebruikte p1...pn*4+3= N (n het nieuwe priemgetal ). maar goed k kwam moeilijkheden tegen..
k ga het zo doorlezen
thanx
quote:Laat antwoord, maar ik ben het er niet mee eens. Stel dat er wel levenden zijn maar geen van dezen zijn mannelijk, en aangezien alleen mannen lui kunnen zijn zijn er dan niet per se luie levenden.Op woensdag 13 september 2006 14:21 schreef thabit het volgende:
C is correct. B is fout.
quote:"Sommige mannen zijn lui". Hieruit kun je afleiden dat er mannen zijn.Op woensdag 27 september 2006 19:38 schreef Aibmi het volgende:
[..]
Laat antwoord, maar ik ben het er niet mee eens. Stel dat er wel levenden zijn maar geen van dezen zijn mannelijk, en aangezien alleen mannen lui kunnen zijn zijn er dan niet per se luie levenden.
quote:Er staat nergens dat alleen mannen lui kunnen zijn. Voor de rest verwijs ik naar thabit's commentaarOp woensdag 27 september 2006 19:38 schreef Aibmi het volgende:
[..]
Laat antwoord, maar ik ben het er niet mee eens. Stel dat er wel levenden zijn maar geen van dezen zijn mannelijk, en aangezien alleen mannen lui kunnen zijn zijn er dan niet per se luie levenden.
.quote:Oei, ik had meerdere keren moeten lezen/nadenken voordat ik tegen thabit in zou gaan op zijn terrein. Maar wat jij zegt klopt niet. Als er niet staat dat niet-mannen lui kunnen zijn, weet je het niet zeker, en kun je er dus van uit gaan dat ze niet lui zijn(bij dit soort logische redeneringen moet je alleen van zekerheden uitgaan).Op woensdag 27 september 2006 19:54 schreef Wolfje het volgende:
[..]
Er staat nergens dat alleen mannen lui kunnen zijn. Voor de rest verwijs ik naar thabit's commentaar
quote:Het enige wat je zeker weet is dat je er niks over kunt zeggen. En toch doe jij dat door te stellen dat je er vanuit kunt gaan dat ze niet lui zijn.weet je het niet zeker, en kun je er dus van uit gaan dat ze niet lui zijn(bij dit soort logische redeneringen moet je alleen van zekerheden uitgaan).
quote:Ok, knullig geformuleerd. Daar ben ik het mee eens. Maar ik bedoelde in ieder geval dat je nooit er van uit kan gaan dat het wel zo is als het niet zeker is. In dit geval had ik dus wel gelijk, want het niet conclusies kunnen trekken uit niet bestaande informatie komt op het zelfde neer als negatief aannemen.Op woensdag 27 september 2006 20:05 schreef GlowMouse het volgende:
[..]
Het enige wat je zeker weet is dat je er niks over kunt zeggen. En toch doe jij dat door te stellen dat je er vanuit kunt gaan dat ze niet lui zijn.
Impliciet Differentiëren
de opgave:
xy=6e^(2x-3y)
Mijn gedachte was:
xy'+y=(2-3y')6e^(2x-3y)
xy'+y=(12-18y')e^(2x-3y)
Kan iemand mij helpen?
Dat was idd mijn volgende gedachte, maar ik kwam er niet verder uit.
Ik wist maar niet hoe ik y'= zou moeten krijgen.
Ik weet het nog steeds niet:'(
[ Bericht 10% gewijzigd door Rejected op 28-09-2006 13:40:10 ]
Dan y' buiten haakjes halen: y'(x+18*exp(2x-3y) = 12*exp(2x-3y)-y
Dan links en rechts delen door 18*exp(2x-3y): y' = (12*exp(2x-3y)-y) / 18*exp(2x-3y) = 2/3 - y/ 18*exp(2x-3y).
quote:Ik snap niet precies wat er in de 1e regel gebeurt, om y' aan uitsluitend aan de linkerkant te krijgen moet je toch delen door (12-18y')??Op donderdag 28 september 2006 17:53 schreef GlowMouse het volgende:
Zorg eerst dat je y' aan een kant krijgt: xy' + 18y'*exp(2x-3y) = 12*exp(2x-3y)-y
Dan y' buiten haakjes halen: y'(x+18*exp(2x-3y) = 12*exp(2x-3y)-y
Dan links en rechts delen door 18*exp(2x-3y): y' = (12*exp(2x-3y)-y) / 18*exp(2x-3y) = 2/3 - y/ 18*exp(2x-3y).
Wat ik doe, is rechts de haakjes wegwerken en dan 18y'*exp(2x-3y) links en rechts optellen.
Hulde GlowMouse
Held Heel erg bedankt
het gaat om het volgende: 
Ik moet 'Punt X' berekenen, ik moet namelijk weten op welke hoogte het vierkantje (dat blauwe vlakje) 4x4 cm is... hoe is dit te doen? Cos Tas Toa is even geleden maar ik weet alleen dat hoek Q 45graden is... kan je dan Cos/Tas/Toa toepassen?
Kan je hier iets mee?
Verhoudingen
btw. het is SOS CAS TOA en niet TAS of zo
Maar dat heb je dus nu ff niet nodig.
quote:Van 'cos/tas/toa' heb ik niet gehoord, maar als je dit op kunt lossen, kan het met goniometrie. Als de bissectrice van Q tekent, kún je twee rechthoekige driehoeken zien ontstaan. Voorwaarde is dan wel dat het blauwe vlakje recht ligt.Op vrijdag 29 september 2006 14:02 schreef lj_lightning het volgende:
Ik heb het al een keer eerder gevraagt maar ik kom er niet uit
[afbeelding]
Ik moet 'Punt X' berekenen, ik moet namelijk weten op welke hoogte het vierkantje (dat blauwe vlakje) 4x4 cm is... hoe is dit te doen? Cos Tas Toa is even geleden maar ik weet alleen dat hoek Q 45graden is... kan je dan Cos/Tas/Toa toepassen?
Waarom zou het blauwe vlakje trouwens niet bovenin de balk zitten?
Op je tekening lijkt hoek Q trouwens eerder 90 graden, maar dat maakt verder niet uit.
quote:Ehh ja goniometrie en bissectrice komen niet in mijn woordeboekje voorOp vrijdag 29 september 2006 14:10 schreef GlowMouse het volgende:
[..]
Van 'cos/tas/toa' heb ik niet gehoord, maar als je dit op kunt lossen, kan het met goniometrie. Als de bissectrice van Q tekent, kún je twee rechthoekige driehoeken zien ontstaan. Voorwaarde is dan wel dat het blauwe vlakje recht ligt.
Waarom zou het blauwe vlakje trouwens niet bovenin de balk zitten?
Op je tekening lijkt hoek Q trouwens eerder 90 graden, maar dat maakt verder niet uit.
Het is 5Havo btw en hoek Q is 90 graden, foutje van mij
quote:Kun je nagaan hoelang het geleden isOp vrijdag 29 september 2006 14:09 schreef -J-D- het volgende:
[afbeelding]
Kan je hier iets mee?
Verhoudingen
btw. het is SOS CAS TOA en niet TAS of zo
Maar dat heb je dus nu ff niet nodig.
komt gelukkig niet opt examen dacht ik 
Maar met verhoudings tabellen heb ik eik nog nooit gezien bij meetkunde
het klopt wel (ik gebruik sketchup en die laat de afmetingen zien en het is 2,0cm en 4x2,85/5,65 is 2,0 beide Ging er wel vanuit dat het nu zou lukken.
Succes
a. Druk AB uit in x
b. Druk de oppervlakte O van het af te zetten stuk land uit in x.
c. Onderzoek de grootst mogelijke oppervlakte van het land dat Boer op deze manier af kan zetten.
De antwoorden
SPOILERDie antwoorden zijn natuurlijk wel leuk, en c snap ik ook wel, max intoetsen op je GR, maar ik snap A en B niet, want buiten de antwoorden heb ik geen uitwerkingen. Wie kan me helpen?Antwoord op A is AB = 44 - 2x
Antwoord op B is O = 44x - 2x²
Antwoord op C is 242m²
Rechterlengte X-4
Totale lengte AB + X + X-4 = AB + 2X - 4 = 40
AB = 44 - 2x
O = AB * X = 44X - 2X2
Maximum bij dO/dX = 0
dO/dX = 44 - 4X = 0
X = 11
En dat in O invullen
quote:Het is me geluktOp vrijdag 29 september 2006 18:24 schreef -J-D- het volgende:
Het ging me dan ook te ver om het helemaal voor je uit te rekenen.
Ging er wel vanuit dat het nu zou lukken.
Succes
ben net klaar, pff wat een werk (mocht je ge-intresseerd zijn: hier is de opgave oa te vinden ) Morgen de foutjes eruit halen, nu eerst pitten
quote:En het dan wel snappen
Goed, afgeleide bepalen, p schrijven als x, invullen, en dan krijg ik er uiteindelijk dit uit:
y = (x2+4)/(2x3+8x)
dan moet ik dat dus herleiden tot 1/(2x)
Je ziet dat het antwoord goed is, als je (x2+4)/(2x3+8x) = 1/(2x) kruislings vermenigvuldigt zie je dat het klopt. Maar het lukt me maar niet om via de officiële stappen die functie te herleiden. Ik denk waarschijnlijk heel raar na (bovendien ben ik slecht in deelstrepen etc.)
Kan iemand me laten zien hoe je dat herleidt?
| 1 2 3 4 5 6 7 8 9 10 11 12 | ih: 3^(n-1) >= 1 + 2(n-1)^2 3^n = 3 * 3^(n-1) >= { ih } 3 * (1 + 2(n-1)^2) = 3 * (1 + 2n^2) - 12x + 6 >= 1 + 2n^2 |
volgens mij klopt het opzich wel (typefouten daargelaten), alleen vind ik mijn laatste stap vrij onduidelijk
is er iemand hier (ongetwijfeld) die het beter/duidelijker kan en eventueel feedback kan geven
bvd
>=
1 + 2n^2
Is dit de stap die je niet volgt?
Dit is waar als 8 + 4 n^2 >= 12n , als je dat bewijst ben je er.
quote:ja ik volg het wel, ik heb het namelijk zelf gedaan - maar ik kan me voorstellen dat het nogal een grote stap is / onduidelijk isOp zondag 1 oktober 2006 17:43 schreef Wackyduck het volgende:
3 * (1 + 2n^2) - 12n + 6
>=
1 + 2n^2
Is dit de stap die je niet volgt?
Dit is waar als 8 + 4 n^2 >= 12n , als je dat bewijst ben je er.
ik vroeg me af of het niet makkelijker kon :p
A_t zijn binaire variabelen
s is een integer variabele
Y_t zijn (binaire) parameters
Nu wil ik het volgende lineariseren:
A_{t+s} >= Y_t voor alle t
Iemand enig idee hoe ik dit aanpak? Het probleem zit hem er dus in dat in de index van variabele A een variabele zit... Als iemand een oplossing weet in het geval dat A_t geen variabele, maar een parameter is hoor ik dat ook graag.
hoe reken je dat uit op de rekenmachine
4x5 = 12 ?
Dan x = (12/4)^(1/5) = 31/5
Zit er niet zo'n xy knop op je rekenapparaat?
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
Vandaag dus geleerd dat als je twee getallen a en b hebt (die allebei een onnauwkeurigheid bevatten - denk bijv. aan meetwaarden) dat de berekening erg uit kan maken voor de propagatie van je afrondfouten.
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.
Zo is het bijvoorbeeld ook beter (nauwkeuriger) om NIET sin(a) - sin(b) te berekenen, maar juist
2 * sin((a-b)/2) * cos((a+b)/2)
(wat uiteraard gelijk is aan sin(a) - sin(b) als je over EXACTE waarde zou beschikken, maar dat is dus niet zo).
Nu vraag ik mij bijvoorbeeld af wat de beste (meest nauwkeurige) manier is om bijv:
log(x) - log(x-1) , x>>1
uit te rekenen. Of bijv:
(ex - 1)/x, |x|<<1
Tot aan vandaag had ik gedacht dat je gewoon de log van x zou berekenen, dan de log van x-1 en dan die van elkaar aftrekken. Maar na vandaag twijfel ik of dat nog wel de meest nauwkeurige manier is.
Iemand suggesties?
ik weet hoe ik t moet uitrekenen alleen niet op de calculator
quote:Als je weet hoe je het uit moet rekenen, gebruik je daar toch al de calculator voor? Waarom zou je dat anders willen? Verder is het natuurlijk van belang of er sprake is van discreet/continu samengestelde of van enkelvoudige interest.b) Een bedrag van ¤6000 is op 1 januari 2005 op een bankrekening gestort. Na 10 jaar staat er ¤8881,47 op deze rekening. Wat is het gehanteerde rentepercentage op jaarbasis?
ik weet hoe ik t moet uitrekenen alleen niet op de calculator
quote:log(x) - log(x-1) = log(x/(x-1)) = log(1 + 1/(x-1)).Op woensdag 4 oktober 2006 21:25 schreef Bioman_1 het volgende:
Zelf ook een vraag:
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
Vandaag dus geleerd dat als je twee getallen a en b hebt (die allebei een onnauwkeurigheid bevatten - denk bijv. aan meetwaarden) dat de berekening erg uit kan maken voor de propagatie van je afrondfouten.
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.
Zo is het bijvoorbeeld ook beter (nauwkeuriger) om NIET sin(a) - sin(b) te berekenen, maar juist
2 * sin((a-b)/2) * cos((a+b)/2)
(wat uiteraard gelijk is aan sin(a) - sin(b) als je over EXACTE waarde zou beschikken, maar dat is dus niet zo).
Nu vraag ik mij bijvoorbeeld af wat de beste (meest nauwkeurige) manier is om bijv:
log(x) - log(x-1) , x>>1
uit te rekenen. Of bijv:
(ex - 1)/x, |x|<<1
Tot aan vandaag had ik gedacht dat je gewoon de log van x zou berekenen, dan de log van x-1 en dan die van elkaar aftrekken. Maar na vandaag twijfel ik of dat nog wel de meest nauwkeurige manier is.
Iemand suggesties?
Als x >> 1, dan is y = 1/(x-1) heel dicht bij 0.
Nu is log(1+y) = y - y2/2 + y3/3 - ...
Dit convergeert natuurlijk heel snel als y heel klein is.
Evenzo kun je gebruiken dat ex = 1 + x + x2/2! + x3/3! + ... .
dus
(ex - 1)/x = 1 + x/2! + x2/3! + ... .
quote:jaa via het uitwerking boekje heb ik gezien hoe het moet,alleen op me rekenmachine krijg ik het niet voor elkaarOp woensdag 4 oktober 2006 22:52 schreef GlowMouse het volgende:
Steeds zie je dat het nauwkeuriger kan door een uitdrukking om te schrijven. log(x) - log(x-1) kun je denk ik niet omschrijven. (exp(x)-1)/x wel: exp(x)/x - 1/x = x-log(x)-1/x. Of het nauwkeuriger is, kun je zelf zo proberen.
[..]
Als je weet hoe je het uit moet rekenen, gebruik je daar toch al de calculator voor? Waarom zou je dat anders willen? Verder is het natuurlijk van belang of er sprake is van discreet/continu samengestelde of van enkelvoudige interest.
Ik geef je als tip de algemene regel voor logaritmen.
a log b = c <=> a^c=b
Als je er niet uit komt, vertel dan waar je nu vast komt te zitten.
quote:Je hebt op je rekenmachine een "e" toets, deze heeft het variabele "× 10n" Dan moet je dus intypen 6000Xe10.Op donderdag 5 oktober 2006 07:15 schreef italiaan1987 het volgende:
6000 X x tot de 10 = 8881,47
quote:De meeste rekenmachines kunnen niet 6000*x10 uitrekenen. En zelfs als je een luxe rekenmachine hebt die dat wel kan, zal het je vertellen dat dat gelijk is aan 6000*x10.Op donderdag 5 oktober 2006 07:26 schreef --Christiaan-- het volgende:
[..]
Je hebt op je rekenmachine een "e" toets, deze heeft het variabele "× 10n" Dan moet je dus intypen 6000Xe10.
De tip voor logaritmen is trouwens ook nutteloos. Het is nu eenvoudige algebra. De enige regel die je misschien niet kent luidt dat als ab = c, dan a = c1/b.
x^10 = 1,4802 berekend door 8881,47 door 6000 te delen
x = ^10wortel van 1,4802
en dit ken ik dus nie berekenen op de calculator
quote:Tuurlijk wel. Er zit toch wel een toets voor xy o.i.d. op je calculator, en een toets voor inverse functies? Met de calculator in Windows XP gaat het trouwens ook gemakkelijk. Vinkje bij Inv aanzetten en dan intoetsen: 1.4802 x^y 10 = en je krijgt als antwoord 1.0399968885584896330874361342892. De rente is dus 4%.Op donderdag 5 oktober 2006 15:33 schreef italiaan1987 het volgende:
x = ^10wortel van 1,4802
en dit kan ik dus niet berekenen op de calculator
Je kunt natuurlijk ook bedenken dat het trekken van de 10-de machtswortel gelijk staat aan verheffen tot de macht 1/10, dan heb je de inverse functietoets van je calculator niet eens nodig.
het is 10 Shift ^1,4802 en dan kom je indd op 4% rente uit
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
Ik zou degene die me 't antwoord verschaf bijzonder dankbaar zijn
quote:Heb je het al geprobeerd met zwavelzuur?Op zaterdag 7 oktober 2006 20:03 schreef Greus het volgende:
Ik ben met Elektrostatica de volgende integraal tegengekomen en het lukt me niet 't onding op te lossen. Weet iemand raad?
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
[afbeelding]
Ik zou degene die me 't antwoord verschaf bijzonder dankbaar zijn
quote:Je vraagt in feite naar het primitiveren van de functie x∙(x2 - √2∙a∙x + a2)-½. In eerste instantie zou je dus (x2 - √2∙a∙x + a2)½ kunnen uitproberen. Differentiëren van de laatste geeft:Op zaterdag 7 oktober 2006 20:03 schreef Greus het volgende:
Ik ben met Elektrostatica de volgende integraal tegengekomen en het lukt me niet 't onding op te lossen. Weet iemand raad?
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
[afbeelding]
Ik zou degene die me 't antwoord verschaft bijzonder dankbaar zijn
½∙(x2 - √2∙a∙x + a2)-½∙ (2x - √2∙a) =
x∙(x2 - √2∙a∙x + a2)-½ - ½∙√2∙a∙(x2 - √2∙a∙x + a2)-½
De eerste term is precies de functie waarvan we een primitieve willen vinden, maar de tweede term willen we er niet bij hebben. Dat betekent dat we nu nog een functie moeten vinden waarvan de afgeleide gelijk is aan het tegendeel van de tweede term, anders gezegd, we zoeken nu nog een primitieve van:
½∙√2∙a∙(x2 - √2∙a∙x + a2)-½
De som van een primitieve van deze functie en (x2 - √2∙a∙x + a2)½ zal dan bij differentiatie het gewenste resultaat x∙(x2 - √2∙a∙x + a2)-½ opleveren.
Om nu een primitieve te vinden van ½∙√2∙a∙(x2 - √2∙a∙x + a2)-½ moet je de kwadratische veelterm onder het wortelteken eerst schrijven als een som van twee kwadraten. Je hebt:
(x - ½∙√2∙a)2 = x2 - √2∙a∙x + (½∙√2∙a)2 = x2 - √2∙a∙x + ½∙a2, zodat we vinden dat:
x2 - √2∙a∙x + a2 = (x - ½∙√2∙a)2 + (½∙√2∙a)2
Nu kun je de factor ½∙√2∙a buiten het wortelteken halen (we nemen aan dat a > 0) en een substitutie z = (x - ½∙√2∙a)/(½∙√2∙a) uitvoeren. We hebben dan:
½∙√2∙a∙(x2 - √2∙a∙x + a2)-½ = (z2 + 1)-½
Uit z = (x - ½∙√2∙a)/(½∙√2∙a) volgt dz/dx = 1/(½∙√2∙a) dus dx/dz = ½∙√2∙a. Het probleem is nu herleid tot het vinden van een primitieve van
½∙√2∙a∙ (z2 + 1)-½
Deze laatste functie is, op de factor ½∙√2∙a na, een standaardfunctie. Een primitieve hiervan is de inverse functie van de hyperbolische functie sinh(z), oftewel arcsinh(z). Deze laatste kun je ook schrijven als
ln(z + (z2 + 1)½)
Substitutie van z = (x - ½∙√2∙a)/(½∙√2∙a) levert dan, op een constante na, hetzelfde resultaat als Mathematica. Bedenk hierbij dat je een constante ½∙√2∙a∙ln(√2∙a) bij de gevonden primitieve op kunt tellen om op precies hetzelfde resultaat uit te komen als Mathematica. Maak hiervoor gebruik van ln(p) + ln(q) = ln(p∙q) en breng dan de factor ½∙√2∙a weer onder het wortelteken.
Nog een opmerking over het primitiveren van de functie
(z2 + 1)-½
Om hiervan een primitieve te vinden maakt men gebruik van de substitutie z = sinh(u) zodat dz/du = cosh(u). Aangezien cosh2(u) - sinh2(u) = 1 volgt dan direct dat u = arcsinh(z) een primitieve is.
[ Bericht 1% gewijzigd door Riparius op 08-10-2006 03:54:21 ]
quote:Fantastisch, bedanktOp zondag 8 oktober 2006 03:41 schreef Riparius het volgende:
[..]
Je vraagt in feite naar het primitiveren van de functie x∙(x2 - √2∙a∙x + a2)-½. In eerste instantie
...
z = sinh(u) zodat dz/du = cosh(u). Aangezien cosh2(u) - sinh2(u) = 1 volgt dan direct dat u = arcsinh(z) een primitieve is.
Hoe los ik bijvoorbeeld 3 vergelijkingen met evenveel onbekenden op?
Ik heb geen problemen om alles te definieren, maar kom er maar niet achter hoe ik er uitkomsten voor alle onbekenden uitkrijg.
quote:solve( { je vergelijkingen gescheiden door komma's} );Op maandag 9 oktober 2006 11:19 schreef Innocence het volgende:
Maple-vraagje:
Hoe los ik bijvoorbeeld 3 vergelijkingen met evenveel onbekenden op?
Ik heb geen problemen om alles te definieren, maar kom er maar niet achter hoe ik er uitkomsten voor alle onbekenden uitkrijg.
quote:Graag gedaan. Ik zag dat je een poos geleden, hier, ook al zat te worstelen met het bepalen van de integraal van (2∙e2t + 1)½ over het interval van 0 tot 2π. Er waren wel wat suggesties maar de gouden tip zat er duidelijk niet bij, laat staan dat iemand de moeite nam om het echt uit te werken. Ik heb dat inmiddels wel gedaan en de oplossing die je gaf uit het boekje blijkt te kloppen. Ik vond die integraal trouwens nog wat pittiger dan deze.
quote:Kan ik deze oplossing misschien van je overnemen?Op maandag 9 oktober 2006 14:29 schreef Riparius het volgende:
[..]
Graag gedaan. Ik zag dat je een poos geleden, hier, ook al zat te worstelen met het bepalen van de integraal van (2∙e2t + 1)½ over het interval van 0 tot 2π. Er waren wel wat suggesties maar de gouden tip zat er duidelijk niet bij, laat staan dat iemand de moeite nam om het echt uit te werken. Ik heb dat inmiddels wel gedaan en de oplossing die je gaf uit het boekje blijkt te kloppen. Ik vond die integraal trouwens nog wat pittiger dan deze.
de vraag is:
bepaal alle cykeltypes in S<sub>5</sub> van alle even permutaties en die orde 4 hebben.
..
hoe pak ik dit het beste aan?
trouwens, hoeveel permutaties zijn er van ieder cykeltype?
alvast bedankt
quote:Volgens mij zijn er geen permutaties die daar aan voldoen, maar wellicht heb ik er niet genoeg over na gedacht.Op maandag 9 oktober 2006 18:50 schreef teletubbies het volgende:
hee!
de vraag is:
bepaal alle cykeltypes in S<sub>5</sub> van alle even permutaties en die orde 4 hebben.
..
hoe pak ik dit het beste aan?
trouwens, hoeveel permutaties zijn er van ieder cykeltype?
alvast bedankt
De orde van een permutatie is gelijk aan het kleinste gemene veelvoud van de ordes van zijn cykels. Aangezien de orde 4 moet zijn, bevat de permutatie dus een 4-cykel en een 1-cykel. Maar een 4-cykel is een oneven permutatie, dus dergelijke permutaties bestaan niet in S_5.
nu een vraag die daarop lijkt:bepaal alle cykeltypes in S6 van alle even permutaties en die orde 5 hebben.
het gaat om een 5-cykel:
5=5.1
de permutatie bevat een 5-cykel en een 1-cykel. Een 5-cykel is even, dit is de enige oplossing.
bepaal alle cykeltypes in S8 van alle Oneven permutaties en die orde 4 hebben.
het gaat om een 4-cykel:
4=4*1, (2*2 gaat niet..kgv(2,2)=2)
de permutatie bevat een 4-cykel en een 1-cykel. Een 4-cykel is oneven, dit is de enige oplossing.
hoeveel permutaties voldoen hieraan?
je hebt bijv (1234), (1243), (1324), (1342) ....(5678),(5687)...
maar (1234)=(2341)=(3412)=(4123)
het aantal permutaties is volgens mij 4*8/4=16
of is dit fout?
[ Bericht 0% gewijzigd door teletubbies op 09-10-2006 20:56:59 (foutje) ]
quote:Ja, dit klopt naar mijn weten.Op maandag 9 oktober 2006 20:29 schreef teletubbies het volgende:
okee..
bepaal alle cykeltypes in S6 van alle even permutaties en die orde 5 hebben.
het gaat om een 5-cykel:
5=5.1
de permutatie bevat een 5-cykel en een 1-cykel. Een 5-cykel is even, dit is de enige oplossing.
quote:Nee, een permutatie met cykels ter lengte 4, 2 en 2 voldoet ook.bepaal alle cykeltypes in S8 van alle Oneven permutaties en die orde 4 hebben.
het gaat om een 4-cykel:
4=4*1, (2*2 gaat niet..kgv(2,2)=2)
de permutatie bevat een 4-cykel en een 1-cykel. Een 4-cykel is oneven, dit is de enige oplossing.
quote:Ja, dit is fout omdat 4*8/4=8. Bovendien heb je niet goed geteld. Je kunt op 8 kies 4 manieren de 4 elementen in je cykel kiezen. Deze kun je op 4! manieren ordenen. Zoals je al opmerkte zijn telkens 4 van deze ordeningen hetzelfde. Het gevraagde aantal is dus (8 kies 4)*4!/4 = (8 kies 4)*3!.hoeveel permutaties voldoen hieraan?
je hebt bijv (1234), (1243), (1324), (1342) ....(5678),(5687)...
maar (1234)=(2341)=(3412)=(4123)
het aantal permutaties is volgens mij 4*8/4=16
of is dit fout?
8 kies 4= 8 boven 4 ..betekende 8!/(4!4!) als het goed is.
merci:)
quote:Gevraagd werd de integraal te bepalen van de functie √(2∙e2t + 1) over het interval [0, 2π].Op maandag 9 oktober 2006 17:17 schreef Greus het volgende:
[..]
Kan ik deze oplossing misschien van je overnemen?
Bij integralen met een vierkantswortel uit een kwadratische veelterm bestaat de oplossingsmethode erin dat je de veelterm door kwadraatafsplitsing en een geschikt gekozen lineaire substitutie herleidt tot een vorm van de gedaante z2 + 1, z2 -1 of 1 - z2. De reden hiervoor is dat je dan met een substitutie van een goniometrische of hyperbolische functie de integraal in een vorm kunt brengen waarin geen wortelteken meer voorkomt. Hierbij wordt gebruik gemaakt van de bekende identiteiten
cos2(x) + sin2(x) =1
cosh2(x) - sinh2(x) = 1
In dit geval hebben we onder het wortelteken echter geen kwadratische veelterm, maar we kunnen 2∙e2t + 1 wel herleiden tot z2 + 1 als we substitueren z2 = 2∙e2t oftewel
z = √2∙et
Merk op dat geldt z > 0 voor alle (reële) waarden van t. We hebben nu dz/dt = √2∙et = z, dus dt/dz = z-1. Hiermee is de integraal omgevormd tot
∫ z-1∙√(z2 + 1)∙dz
Nu kunnen we een substitutie met een hyperbolische functie uitvoeren om de wortel kwijt te raken. Kiezen we z = sinh(u) (waarbij geldt dat u > 0 daar z > 0), dan is √(z2 + 1) = cosh(u) en dz/du = cosh(u) zodat we krijgen
∫ (1/sinh(u))∙cosh(u)∙cosh(u)∙du
Aangezien cosh2(u) = 1 + sinh2(u) kunnen we dit schrijven als:
∫ ((1/sinh(u)) + sinh(u))∙du
De tweede term is eenvoudig te primitiveren, want sinh(u) en cosh(u) zijn elkaars afgeleiden, zodat cosh(u) een primitieve is van sinh(u). Maar een primitieve van 1/sinh(u) is niet zo eenvoudig te bepalen. Aangezien 1/x de afgeleide is van ln(x) zou je kunnen denken aan ln(sinh(u)), maar de afgeleide daarvan is, vanwege de kettingregel, (1/sinh(u))∙cosh(u) = coth(u). Evenzo geeft ln(cosh(u)) als afgeleide tanh(u).
Nu valt op dat het differentiëren van de natuurlijke logaritme van een hyperbolische functie een andere hyperbolische functie oplevert, en je zou je daarom kunnen afvragen of ln(tanh(u)) misschien het gewenste resultaat geeft. De afgeleide van tanh(u) is 1/cosh2(u) en dus vinden we voor de afgeleide van ln(tanh(u)) :
(1/tanh(u)) ∙ (1/cosh2(u)) = (cosh(u)/sinh(u)) ∙ (1/cosh2(u)) = (1/ sinh(u))∙(1/cosh(u)) = 1/(sinh(u)∙cosh(u))
Dit is nog niet het gewenste resultaat 1/sinh(u) maar toch kunnen we hier verder mee omdat het mogelijk is sinh(u) te herschrijven als een produkt van een sinh en een cosh. We hebben de volgende identiteit:
sinh(2x) = 2∙sinh(x)∙cosh(x)
Substitutie van 2x = u en dus x = ½∙u levert
sinh(u) = 2∙sinh(½∙u)∙cosh(½∙u)
Nu is eenvoudig te zien dat 1/sinh(u) = 1/(2∙sinh(½∙u)∙cosh(½∙u)) de afgeleide is van ln(tan(½∙u)) en dus vinden we
∫ ((1/sinh(u)) + sinh(u))∙du = cosh(u) + ln(tan(½∙u))
De hyperbolische substitutie was alleen bedoeld om de wortel kwijt te raken, zodat we de primitieve nu weer om gaan zetten naar een uitdrukking in z (die dan op zijn beurt weer is om te zetten naar een uitdrukking in t). We weten al dat cosh(u) = √(z2 + 1) maar om de term ln(tan(½∙u)) uit te drukken in z moeten we deze term eerst omzetten naar een uitdruking in sinh(u) of cosh(u). We hebben de volgende identiteit:
cosh(2x) = cosh2(x) + sinh2(x) = 2∙cosh2(x) - 1 = 2∙sinh2(x) + 1
Na substitutie van 2x = u ofwel x = ½∙u kunnen we hieruit afleiden dat geldt
sinh2(½∙u) = (cosh(u) - 1)/2
cosh2(½∙u) = (cosh(u) + 1)/2
Delen we de eerste betrekking door de tweede en nemen we de vierkantswortel dan vinden we dus (voor u ≥ 0):
tanh(½∙u) = √((cosh(u) - 1)/(cosh(u) + 1))
Aangezien ln(√a) = ½∙ln(a) hebben we dan:
∫ ((1/sinh(u)) + sinh(u))∙du = cosh(u) + ½∙ln((cosh(u) - 1)/(cosh(u) + 1))
Hierin is cosh(u) = √(z2 + 1) zodat we voor de primitieve uitgedrukt in z vinden:
√(z2 + 1) + ½∙ln((√(z2 + 1) - 1)/(√(z2 + 1) + 1))
Nu kunnen we de breuk (√(z2 + 1) - 1)/(√(z2 + 1) + 1) nog wat vereenvoudigen door teller en noemer te vermenigvuldigen met (√(z2 + 1) - 1) en gebruik te maken van (a+b)(a-b) = a2 - b2. Merk op dat (√(z2 + 1) - 1) positief is aangezien z > 0. De noemer van de breuk wordt dan (z2 + 1) - 12 = z2 en voor de teller krijgen we:
(√(z2 + 1) - 1)2 = (z2 + 1) - 2∙√(z2 + 1)∙1 + 12 = z2 + 2 - 2∙√(z2 + 1)
Voor de primitieve uitgedrukt in z hebben we nu:
∫ z-1∙√(z2 + 1)∙dz = √(z2 + 1) + ½∙ln((z2 + 2 - 2∙√(z2 + 1))/z2)
Substitutie van z2 = 2∙e2t geeft tenslotte als resultaat:
∫√(2∙e2t + 1)∙dt = √(2∙e2t + 1) + ½∙ln((e2t + 1 - √(2∙e2t + 1))/e2t)
Vullen we nu eerst t=2π in en dan t=0 en trekken we het tweede resultaat af van het eerste dan vinden we voor de bepaalde integraal over het interval [0,2π] inderdaad:
Hiermee is de opgave voltooid. Nog enkele aanvullingen. Aangezien ln(a) = - ln(1/a) kunnen we voor de primitieve uitgedrukt in z ook schrijven:
√(z2 + 1) - ½∙ln((√(z2 + 1) + 1)/(√(z2 + 1) - 1))
Vereenvoudigen we weer de breuk door teller en noemer nu met (√(z2 + 1) + 1) te vermenigvuldigen dan wordt de noemer weer gereduceerd tot z2 terwijl we voor de teller (√(z2 + 1) + 1)2 krijgen. Beide zijn een kwadraat zodat de gehele breuk ook als een kwadraat ((√(z2 + 1) + 1)/z)2 is te schrijven, en aangezien ln(a2) = 2∙ln(a) kunnen we de primitieve schrijven als:
√(z2 + 1) - ln((√(z2 + 1) + 1)/z)
Dit is eenvoudig te herleiden tot
√(z2 + 1) - ln(z-1 + √(z-2 + 1))
Aangezien arcsinh(z) = ln(z + √(z2 + 1)) en dus arcsinh(1/z) = ln(z-1 + √(z-2 + 1)) vinden we dat:
∫ z-1∙√(z2 + 1)∙dz = √(z2 + 1) - arcsinh(1/z)
Substitutie van z = √2∙et, z2 = 2∙e2t geeft dan:
∫√(2∙e2t + 1)∙dt = √(2∙e2t + 1) - arcsinh(e-t/√2)
Hiermee is de bepaalde integraal eenvoudiger numeriek te berekenen met een gewone calculator. Voor de waarde van de bepaalde integraal over het interval [0, 2π] vinden we dan 756,225...
Tot slot nog een opmerking over de wijze waarop Mathematica deze integraal behandelt. Aangezien de waarde van tanh(x) tussen -1 en +1 ligt, is de waarde van de inverse functie arctanh(x) strict genomen alleen gedefinieerd voor -1 < x < 1. Voor deze waarden van x geldt:
arctanh(x) = ½∙ln((1+x)/(1-x))
De afgeleide van arctanh(x) is 1/(1-x2) maar deze laatste functie is ook gedefinieerd voor x < -1 en x > 1. Om deze reden is het voor toepassing in de integraalrekening nuttig om het domein van arctanh(x) uit te breiden naar waarden van x < -1 of x > 1. Te vergelijken is de functie x-1 die ook gedefinieerd is voor x < 0, terwijl de bijbehorende primitieve functie ln(x) binnen de reële getallen alleen is gedefinieerd voor x > 0. We kunnen de primitieve functie van x-1 echter ongeacht het teken van x weergeven als ln(|x|). Op vergelijkbare wijze is het domein van arctanh(x) uit te breiden door deze functie voor x < -1 of x > 1 te definiëren als:
arctanh(x) = ½∙ln(|(1+x)/(1-x)|)
Grafisch zien de uitgebreide functie arctanh(x) en de bijbehorende afgeleide er als volgt uit:
Voor x > 1 geldt |(1+x)/(1-x)| = (x+1)/(x-1) zodat we voor ½∙ln((√(z2 + 1) + 1)/(√(z2 + 1) - 1)) bij gebruik van de uitgebreide definitie van arctanh mogen schrijven:
arctanh(√(z2 + 1))
Zo krijgen we dan:
∫ z-1∙√(z2 + 1)∙dz = √(z2 + 1) - arctanh(√(z2 + 1))
En substitutie van z2 = 2∙e2t geeft:
∫√(2∙e2t + 1)∙dt = √(2∙e2t + 1) - arctanh(√(2∙e2t + 1))
Deze laatste variant is alleen geschikt voor de berekening van de bepaalde integraal als de gebruikte calculator of het gebruikte programma de uitgebreide definitie van arctanh hanteert.
Het snijpunt van twee bissectrices in een driehoek is het middelpunt van de ingeschreven cirkel. Kijk nu naar het snijpunt van de buiten bissectrices bij twee hoekpunten. Dat snijpunt is ook het middelpunt van een bijzondere cirkel. Verklaar dat ?
Geen idee ?????
Wat voor cirkel moet dat wezen ? Appolonius cirkel? Hoe valt dat te verklaren.
[ Bericht 1% gewijzigd door sitting_elfling op 10-10-2006 22:11:24 ]
wat is het verschil tussen wiskunde A en B??
wat krijgt B wat A niet krijgt
quote:sin(2x) > 0,4, en hier kun je zonder intersect vrij weinig mee. Het zou wat anders zijn als we het bijvoorbeeld over sin(2x) > wortel(2)/2 hadden.Hoe los je 2sin 2x > 0,8 op, zonder intersect en hoe schrijf je dat precies op
quote:Logisch nadenken: wat gebeurt er nu eigenlijk? 5*sin(x) -> de sinus wordt 5x uitgerekt. Sin(0,5x) -> pas bij x=2pi gaat hij weer door 0, dus de sinus wordt uit elkaar getrokken in horizontale richting. Sin(x+5) -> Ipv x wordt er nu steeds x+5 ingevuld, ofwel een verschuiving van 5 naar links.# Hoe bepaal je de horizontale verschuiving van Y = sin x met verschillende formule( bv. 5 * Sin (0,5x) + 6) of wat is de algemene regel hoe kan je dat zien in de grafiek
quote:B is iets algebraïscher. Dingen die A niet krijgt zijn integralen, wat goniometrie, en misschien nog wel meer.gewoon een vraagje
wat is het verschil tussen wiskunde A en B??
wat krijgt B wat A niet krijgt
quote:B krijgt het bewijzen en redeneren. En gaat volgens mij dieper op de 'abstracte' stof in.Op dinsdag 10 oktober 2006 21:51 schreef italiaan1987 het volgende:
gewoon een vraagje
wat is het verschil tussen wiskunde A en B??
wat krijgt B wat A niet krijgt
Maar meer weet ik er ook niet vanaf. Alleen dat bewijzen en meetkunde verschil is wel aanwezig. Groot verschil ook
Als een driehoek een zijde heeft van 5 en een zijde
van 8. Kan de 3e zijde dan 13 zijn ?
Hoe zit dat met de cosinus/sinus regel in dit vlak ?
quote:Nee, want de som van de lengtes van twee zijden van een driehoek is altijd groter dan de lengte van de derde zijde.Op dinsdag 10 oktober 2006 23:48 schreef sitting_elfling het volgende:
Een vraagje
Als een driehoek een zijde heeft van 5 en een zijde
van 8. Kan de 3e zijde dan 13 zijn ?
quote:Onduidelijke vraagstelling. De cosinusregel luidt:
Hoe zit dat met de cosinus/sinus regel in dit vlak ?
a2 = b2 + c2 - 2bc∙cos α
Als nu a = b + c dan is a2 = (b+c)2 = b2 + 2bc + c2. Bij een driehoek met a = b + c zou dus moeten gelden cos α = -1 dus α = 180°, maar dat kan niet aangezien de beide andere hoeken dan 0 graden zouden moeten zijn.
quote:Oke bedankt nu weet ik ook weer wanneer ik dat moet gebruikenOp woensdag 11 oktober 2006 00:01 schreef Riparius het volgende:
[..]
Nee, want de som van de lengtes van twee zijden van een driehoek is altijd groter dan de lengte van de derde zijde.
[..]
Onduidelijke vraagstelling. De cosinusregel luidt:
a2 = b2 + c2 - 2bc?cos ?
Als nu a = b + c dan is a2 = (b+c)2 = b2 + 2bc + c2. Bij een driehoek met a = b + c zou dus moeten gelden cos ? = -1 dus ? = 180°, maar dat kan niet aangezien de beide andere hoeken dan 0 graden zouden moeten zijn.
.Nog een bewijs vraag waar ik niet uitkom
Gegeven is een vierkant EFGH
Je verlengt EF met FA
Je verlengt FG met GB
Je verlengt GH met HC
Je verlengt HE met ED
verder is FA = GB = HC = ED
bewijs dat ABCD een vierkant is.
Als ik het teken zie ik ook wel dat het een vierkant is. Maar hoe bewijs ik dat
Er komen gewoon bij vierkant EFGH 4 rechthoekige driehoeken bij.
4 rechthoekige driehoeken passen mooi inelkaar
Maar das geen goed bewijs
quote:Je moet eerst aantonen dat de vier rechthoekige driehoeken congruent zijn (congruentiekenmerken gebruiken). Dan weet je al dat de vier schuine zijden die samen de grote vierhoek vormen gelijk zijn. Verder moet je laten zien dat de vier hoeken van de grote figuur elk 90 graden zijn. Dat is ook eenvoudig omdat de vier toegevoegde driehoeken rechthoekig zijn zodat de som van de twee andere hoeken van elke driehoek ook 90 graden is.Op woensdag 11 oktober 2006 00:09 schreef sitting_elfling het volgende:
[..]
Oke bedankt nu weet ik ook weer wanneer ik dat moet gebruiken
Nog een bewijs vraag waar ik niet uitkom
Gegeven is een vierkant EFGH
Je verlengt EF met FA
Je verlengt FG met GB
Je verlengt GH met HC
Je verlengt HE met ED
verder is FA = GB = HC = ED
bewijs dat ABCD een vierkant is.
Als ik het teken zie ik ook wel dat het een vierkant is. Maar hoe bewijs ik dat
[ Bericht 2% gewijzigd door Riparius op 11-10-2006 00:25:41 ]
quote:Ik heb m opgelost met mn Grafische Rekenmachine:Op 1-1-2006 zet iemand ¤ 6000,- op een spaarrekening. De rente is 3% per jaar en wordt aan het eind van elk jaar bijgeschreven op de spaarrekening. Verder wordt er niets op de spaarrekening gestort en er wordt ook niets afgehaald.
Hoeveel jaar duurt het voor het saldo verdubbeld is?
y1 = 6000*1,03^x
y2 = 12000
En dan het snijpunt opzoeken, en dat geeft x = 23,45 jaar, dus na 24 jaar.
Maar ik moet m natuurlijk berekenen
Zover was ik: 6000*(1,03x) = 12000
Hoe los je zoiets op
1.03log2=x
En daar zul je toch je rekenmachine moeten pakken vrees ik.
http://scp.thrijswijk.nl/vakken/prog3t1/index.html en dan Practicum Handleiding staan de opdrachten in.
Ik maak het in JBuilder. Heb al begin gemaakt, maar lukt mij verder niet..
Bedankt alvast!
quote:Zover was ik al gekomen, maar dan kom ik op 0.31006Op woensdag 11 oktober 2006 17:48 schreef Aibmi het volgende:
2=1.03x
1.03log2=x
En daar zul je toch je rekenmachine moeten pakken vrees ik.
quote:[Java] voor dummies - Deel 1Op woensdag 11 oktober 2006 17:49 schreef Elle4 het volgende:
Hier een vraag over Java Programmeren? Wie kan mij helpen en/of tips geven?
quote:Simpel:Op woensdag 11 oktober 2006 17:51 schreef Piles het volgende:
[..]
Zover was ik al gekomen, maar dan kom ik op 0.31006
[..]
[Java] voor dummies - Deel 1
(1,03)x = 2
log((1,03)x) = log(2)
x∙log(1,03) = log(2)
x = log(2) / log (1,03)
Dit laatste even uitrekenen met de calculator
Je hoeft dus niet met logaritmen met grondtal 2 te werken, gewone logaritmen voldoen prima.
[ Bericht 1% gewijzigd door Riparius op 11-10-2006 18:12:57 ]
quote:Op woensdag 11 oktober 2006 18:00 schreef Riparius het volgende:
log((1,03)x) = log 2
x∙log(1,03) = log(2)
Ik kende de logica van deze stap nog niet, maar die ga ik zeker ff opschrijven
Bedankt voor de hulp
quote:Dit is toch echt een basisregel voor het rekenen met logaritmen hoor. Kijk maar eens op je formulekaart:Op woensdag 11 oktober 2006 18:06 schreef Piles het volgende:
[..]
Ik kende de logica van deze stap nog niet, maar die ga ik zeker ff opschrijven
Bedankt voor de hulp
log(ap) = p∙log(a)
quote:Die heb ik nietOp woensdag 11 oktober 2006 18:08 schreef Riparius het volgende:
[..]
Dit is toch echt een basisregel voor het rekenen met logaritmen hoor. Kijk maar eens op je formulekaart:
log(ap) = p∙log(a)
Het staat vast ergens in mn boek, maar dat heb ik denk ik gemist
Ik ben nogal een idioot op het vlak van bètavakken (Ik doe dan ook de meest alpha opleiding die er is) en heb dus problemen met een vraag die normaal simpel zou moeten zijn: Eerst moet ik de vergelijking bepalen van een cirkel met M(-4, 1) als middelpunt en r=3
Dat is c <-> (x+4)2 + ( y-1)2 = 9 (toch?)
Als ik ervanuitga dat dat juist is, dan moet ik nu zien wat de snijpunten met de X-as zijn, dat was toch Y=0 en dan uitrekenen ?
Dan krijg je
(x+4)2 + (0-1)2 = 9
Hier overal de wortel uit nemen om die kwadraathaakjesdingetjes weg te werken:
x + 4 + 1 = 3
x + 5 = 3
x = -2
En dan denk ik, zo idioot als ik ben, dat de snijpunten met de X-as... oh wacht ik heb er twee nodig
Dat heb ik ergens lang geleden gehad, maar ik weet het al lang niet meer.
Wat doe ik fout ?
quote:Mag ik zeggen dat de 4 toegevoegde driehoeken congruent zijn omdat ze voldoen aan ZHZOp woensdag 11 oktober 2006 00:20 schreef Riparius het volgende:
[..]
Je moet eerst aantonen dat de vier rechthoekige driehoeken congruent zijn (congruentiekenmerken gebruiken). Dan weet je al dat de vier schuine zijden die samen de grote vierhoek vormen gelijk zijn. Verder moet je laten zien dat de vier hoeken van de grote figuur elk 90 graden zijn. Dat is ook eenvoudig omdat de vier toegevoegde driehoeken rechthoekig zijn zodat de som van de twee andere hoeken van elke driehoek ook 90 graden is.
ZHZ = 2 zijden en een ingesloten hoek. De 4 schuine zijden zijn dus even lang. En omdat de 4 toegevoegde driehoeken rechthoekig zijn, zijn de 2 overige hoeken 90 graden. Wat het dus een vierkant maakt.
quote:Ja, dat is het, heel compact opgeschreven.Op woensdag 11 oktober 2006 20:06 schreef sitting_elfling het volgende:
[..]
Mag ik zeggen dat de 4 toegevoegde driehoeken congruent zijn omdat ze voldoen aan ZHZ
ZHZ = 2 zijden en een ingesloten hoek. De 4 schuine zijden zijn dus even lang. En omdat de 4 toegevoegde driehoeken rechthoekig zijn, zijn de 2 overige hoeken 90 graden. Wat het dus een vierkant maakt.
quote:Maar ik snap eigenlijk niet wat ik met jouw raad moet (als je eerste post voor mij bedoelt is)Op woensdag 11 oktober 2006 20:15 schreef GlowMouse het volgende:
Het kan, maar is niet aan te raden omdat het veel makkelijker kan.
Je deed zelf trouwens dat wortel((x+4)² + (0-1)²) = (x+4) + (0-1), maar dit gaat fout (voorbeeld: wortel(2+2) = 2, terwijl wortel(2) geen 1 is).
quote:De grote fout die je maakt is dat je denkt dat de wortel uit de som van twee termen gelijk is aan de som van de wortels van die termen. Je denkt dus dat √(a+b) hetzelfde is als √a + √b, maar dat is niet zo.Op woensdag 11 oktober 2006 19:58 schreef Secretus het volgende:
Ok, hallo
Eerst moet ik de vergelijking bepalen van een cirkel met M(-4, 1) als middelpunt en r=3
Dat is c <-> (x+4)2 + ( y-1)2 = 9 (toch?)
Als ik ervanuitga dat dat juist is, dan moet ik nu zien wat de snijpunten met de X-as zijn, dat was toch Y=0 en dan uitrekenen ?
Dan krijg je
(x+4)2 + (0-1)2 = 9
Hier overal de wortel uit nemen om die kwadraathaakjesdingetjes weg te werken:
x + 4 + 1 = 3
x + 5 = 3
x = -2
En dan denk ik, zo idioot als ik ben, dat de snijpunten met de X-as... oh wacht ik heb er twee nodig
Dat heb ik ergens lang geleden gehad, maar ik weet het al lang niet meer.
Wat doe ik fout ?
Je hebt:
(x+4)2 + (0-1)2 = 9
(x+4)2 + 1 = 9
(x+4)2 = 8
Nu is:
x+4 = √8 of x+4 = -√8
De rest kun je nu denk ik zelf wel oplossen. Merk nog op dat √8 = 2√2.
quote:Ja, die fout heb ik bijna juist na het typen van mijn post ook ontdektOp woensdag 11 oktober 2006 20:20 schreef GlowMouse het volgende:
Als (x+4)² + (0-1)² = 9 dan (x+4)² = 8. Ofwel x+4 = wortel(8) of x+4 = -wortel(8)
Je deed zelf trouwens dat wortel((x+4)² + (0-1)²) = (x+4) + (0-1), maar dit gaat fout (voorbeeld: wortel(2+2) = 2, terwijl wortel(2) geen 1 is).
Bedankt voor het helpen, nu ik terugkijk is het wel makkelijk, maarja, ik kom niet zo snel op die dingen.
Ik moet een driehoek construeren met die 3 zijdes. Als 'hint' staat er een passer. :S Snap er geen knurft van. Als ik een driehoek teken kom ik niet verder dan 9.5 cm als 3e schuine zijde.
In I zitten 0 en 2. Bovendien geldt f(0)=f(1)=0 en f(2)=1.
Toon aan dat er getallen a,b in I zitten zodat:
f'(a)=1/2
f''(b) > 1/2
de eerste vraag doet me denken aan: als f(0)=f(1) dan f(m)=f(m+1/2) voor een of ander m uit [0,1/2]
dus ook f'(m)=f'(m+1/2)
maar goed, k weet niet of dit helpt..
weet iemand het? thanx
quote:In zijn algemeenheid klopt je bewering niet. Als ik in de calculator van WinXP deze berekening uitvoer dan komt er op beide manieren toch echt precies hetzelfde uit, namelijk 0.02002001.Op woensdag 4 oktober 2006 21:25 schreef Bioman_1 het volgende:
Zelf ook een vraag:
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
[...]
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.
quote:Teken een lijnstuk van 10 cm. Zet de punt van de passer in het ene eindpunt en trek een cirkel met straal 5 cm. Zet dan de punt van de passer in het andere eindpunt en trek een cirkel met straal 8 cm. Het snijpunt van de cirkels (nu ja, één van beide snijpunten) is nu het derde punt van je driehoek, samen met de twee eindpunten van je lijnstuk van 10 cm waar je mee begon.Op woensdag 11 oktober 2006 21:00 schreef sitting_elfling het volgende:
Ik heb een vraagje. Je hebt een driehoek met een zijde 5 cm 8 cm en 10 cm.
Ik moet een driehoek construeren met die 3 zijdes. Als 'hint' staat er een passer. :S Snap er geen knurft van. Als ik een driehoek teken kom ik niet verder dan 9.5 cm als 3e schuine zijde.
quote:Gebruik de middelwaardestelling, eerst toegepast op f(x) en dan toegepast op f'(x).Op woensdag 11 oktober 2006 21:00 schreef teletubbies het volgende:
stel f is twee keer differentieerbaar op een interval I.
In I zitten 0 en 2. Bovendien geldt f(0)=f(1)=0 en f(2)=1.
Toon aan dat er getallen a,b in I zitten zodat:
f'(a)=1/2
f''(b) > 1/2
quote:Voor f'(a)=1/2 in ieder geval gecombineerd met de tussenwaardestelling.Op woensdag 11 oktober 2006 21:21 schreef Riparius het volgende:
[..]
Gebruik de middelwaardestelling, eerst toegepast op f(x) en dan toegepast op f'(x).
Persoon A gaat iedere ochtend hardlopen. Het is even waarschijnlijk dat A het huis via de voordeur of via de achterdeur verlaat. Bij het verlaten van het huis, trekt A een paar schoenen aan (indien aanwezig, anders gaat A blootvoets naar buiten).
Bij terugkeer laat A de schoenen achter bij de voordeur of achterdeur, al naar gelang waar A binnenkomt (waarbij voor- of achterdeur weer willekeurig wordt gekozen).
Neem aan dat A 3 paar schoenen heeft, en laat Xn het aantal paar schoenen zijn dat aan het begin van de n-de dag bij de deur van vertrek staan.
(a) Bepaal de overgangsmatrix van de Markovketen {Xn : n >= 0}.
(b) Met welke frequentie zal A blootvoets rondhollen?
quote:Onduidelijke vraag. Ik denk trouwens dat je een beetje in de war bent. Kijk maar eens hier.Op woensdag 11 oktober 2006 23:29 schreef sitting_elfling het volgende:
waarom is de congruentie zhz en zhh gelijk ?
quote:Oh ik heb hier namelijk een opgave waarin staat.Op woensdag 11 oktober 2006 23:52 schreef Riparius het volgende:
[..]
Onduidelijke vraag. Ik denk trouwens dat je een beetje in de war bent. Kijk maar eens hier.
Als 2 driehoeken congruent zijn volgens ZHZ zijn dat ook volgens ZHH. Waarom is dat zo ?
Dat is de Letterlijke vraag in mn boekje staat. Ik zie niet in waarom, de site die je me gaf geeft aan dat beide opzich wat anders betekenen.
En dan nog een laatste vraag, de afsluiting van mijn boekje met vragen.
Gegeven is driehoek ABC die congruent is met XYZ en gegeven is AB = 3 XY
CD is de loodlijn vanuit C op AB
ZW is de loodlijn vanuit Z op XY
Laat zien dat CD = 3 ZW
men dit bewijzen zeg pfft
bedankt btw voor het helpen
bewijzen en redeneren vind ik altijd pittig.quote:Het enige wat ik zo gauw kan bedenken is dat ZHZ in je boek een drukfout is voor HZH. Gelijkheid van twee hoeken impliceert namelijk altijd gelijkheid van de derde hoek, omdat de som van de hoeken van een driehoek 180 graden is.Op donderdag 12 oktober 2006 00:26 schreef sitting_elfling het volgende:
[..]
Oh ik heb hier namelijk een opgave waarin staat.
Als 2 driehoeken congruent zijn volgens ZHZ zijn dat ook volgens ZHH. Waarom is dat zo ?
Dat is de Letterlijke vraag in mn boekje staat. Ik zie niet in waarom, de site die je me gaf geeft aan dat beide opzich wat anders betekenen.
quote:Zoals het hier staat kan het strict genomen niet kloppen, want als je stelt dat driehoek ABC congruent is met driehoek XYZ dan impliceer je daarmee dat AB=XY, BC=YZ en CA=ZX, terwijl is gegeven dat AB = 3*XY: een tegenstrijdigheid dus.En dan nog een laatste vraag, de afsluiting van mijn boekje met vragen.
Gegeven is driehoek ABC die congruent is met XYZ en gegeven is AB = 3 XY
CD is de loodlijn vanuit C op AB
ZW is de loodlijn vanuit Z op XY
Laat zien dat CD = 3 ZW
Geef eerst eens een tekening die volgens jou alle gegevens die je hebt laat zien.
quote:Logisch leren denken en redeneren is altijd goed.men dit bewijzen zeg pfft
quote:bedankt btw voor het helpen
Som 1
Integraal Wortel X * exp(2xwortel x) dx
De bedoeling bij deze is substitueren.
Mij lijkt dan:
u=2xwortelx
du/dx = (2x)/(2wortelx) +2 wortelx
du= (2x*dx)/(2wortelx) +2 wortelx
En dan moet du de originele vergelijking met het integraal teken in, maar hoe gaat dit nu precies?
Som 2
De bedoeling is hier partitieel integreren
Integraal ln(1+x²)
ik dacht dus:
x*ln(1+x²) - [integraal] (2x*dx)/1+x²
Hoe los ik dat integraal op?
quote:Probeer eens u = wortel(x)Integraal Wortel X * exp(2xwortel x) dx
De bedoeling bij deze is substitueren.
Mij lijkt dan:
u=2xwortelx
du/dx = (2x)/(2wortelx) +2 wortelx
Bovendien zou ik niet du maar dx los schrijven.
We krijgen: du/dx = 1/(2wortel(x)), dus dx = 2 wortel(x) du = 2 u du. Dit kun je in de integraal gewoon invullen voor dx.
Mocht je toch 2xwortel(x) doen, differentieer dan 2x3/2 in plaats van de kettingregel te gebruiken.
Partieel integreren is handig wanneer je een product van twee functies hebt. Bij je tweede opgave zie ik die niet terug. Door u=1+x² te substitueren krijg je wel een product.
[Integraal] 2*u*du* exp (2xu) ?
Dat snap ik niet helemaal, daarom dacht ik dat ik 2xwortelx moest substitueren.
quote:De x in de integrand moet je dan uiteraard wel door u² vervangen. En waar is wortel(x) gebleven?Op donderdag 12 oktober 2006 22:07 schreef Rejected het volgende:
Dus dan krijg ik bij som 1:
[Integraal] 2*u*du* exp (2xu) ?
Dat snap ik niet helemaal, daarom dacht ik dat ik 2xwortelx moest substitueren.
[Integraal] 2*u*du* exp (2u³)
antwoord= 1/3 exp 2xwortelx
Ik snap wel hoe je aan dat 1/3 komt, ik snap niet hoe die u voor de exp verdwijnt.
Heb Som 1 opgelost.
quote:Nou het product is een beetje "verborgen"Op donderdag 12 oktober 2006 21:59 schreef GlowMouse het volgende:
Partieel integreren is handig wanneer je een product van twee functies hebt. Bij je tweede opgave zie ik die niet terug. Door u=1+x² te substitueren krijg je wel een product.
[Integraal] 1* ln(1+x²), verder kom ik dus niet.
[integraal] (2x*dx)/1+x²
u= x²
du/dx=2x dus du=2xdx
Dit geeft:
[integraal] du/(1+u) = 0.5ln (1+u)+C = 0.5ln (1+x²) +C Klopt dit?
Nu ga ik met een fijn hoofd naar bed.
Kan iemand mij uitleggen hoe je hiervan de uitkomst berekend??Gegeven: f(x) = 2x4 + 2x3 - 2x2 - 2
Bereken f '(3). (Vul als antwoord een geheel getal in.)
Maak de afgeleide van f(x). Vul daarna x=3 in. Als je geen afgeleides kunt maken zou ik goed in je boek kijken, want ik kan me niet voorstellen dat een methode dit níet goed uit legt (of in ieder geval het "trucje" waarmee je het kunt berekenen).
Zo nee:f'(x)=10, dus f'(3) is dan ook 10.
quote:Nu ik er nog eens naar kijk, zie ik dat je te kort door de bocht bent gegaan bij de tweede vraag. x*ln(1+x²) - [integraal] (2x*dx)/1+x² is namelijk fout. Wat je krijgt, is x*ln(1+x²) - [integraal] (2x2*dx)/(1+x²). Het uitwerken van deze integraal vergt iets meer inzicht: 2x²/(1+x²) = 2*(x²+1-1) / (x²+1) = 2(1 - 1/(x²+1)). Je ziet dan de afgeleide van de arctangens terugkomen, en de uitwerking is niet zo moeilijk meer.Op donderdag 12 oktober 2006 23:06 schreef Rejected het volgende:
Bedankt!! Je zou een fotoboek moeten openen, het zou vollopen door bedankjes!
Nu ga ik met een fijn hoofd naar bed.
8x^3 6x^2 4x
216 54 12 258
quote:Klopt idd!Op vrijdag 13 oktober 2006 12:37 schreef GlowMouse het volgende:
[..]
Nu ik er nog eens naar kijk, zie ik dat je te kort door de bocht bent gegaan bij de tweede vraag. x*ln(1+x²) - [integraal] (2x*dx)/1+x² is namelijk fout. Wat je krijgt, is x*ln(1+x²) - [integraal] (2x2*dx)/(1+x²). Het uitwerken van deze integraal vergt iets meer inzicht: 2x²/(1+x²) = 2*(x²+1-1) / (x²+1) = 2(1 - 1/(x²+1)). Je ziet dan de afgeleide van de arctangens terugkomen, en de uitwerking is niet zo moeilijk meer.
Ik heb hem vandaag alsnog opgelost
Wat is de afegeleide van ln(x^2+1)?
Het antwoord moet zijn 2x/(x^2+1) .... Hoe kom je daaraan?
We hebben hier f(g(x)) met g(x) = x²+1 en f(x) = ln(x). Let goed op deze notatie: f(g(x)) betekent dat je eerst g uitrekent in x, en de uitkomst daarvan in f stopt.
De afgeleide van f(g(x)) is f'(g(x)) * g'(x) (zegt de kettingregel). Let weer op de notatie: je berekent voor de eerste factor eerst g uit in x, en dat vul je in bij f'.
f'(x) = 1/x, g'(x) = 2x.
Dit vullen we in: f'(g(x)) * g'(x) = 1/(x²+1) * 2x = 2x/(x²+1).
f(x)=ln(u) met u=x2+1
dy/du=1/u du/dx = 2x
dy/dx = 1/x2+2 * 2x = 2x/x2+2
Thx
Laat X een banach ruimte zijn S een deelverzameling van X met de eigenschap dat sup |x'(x) | < oneindig, waarbij het supremum genomen wordt over alle x in S, en dat deze eigenschap geldt voor alle x' in de duale van X. Bewijs nu dat sup_{x in S} ||x|| < oneindig
We moeten een Praktische opdracht maken over het Amylase enzym.
Je krijgt een Amylase oplossing, deze hoef je niet zelf meer te maken. Je moet het overgebleven zetmeel aantonen met Jood-oplossing.
Het probleem is echter dat we zelf het onderzoek moeten bedenken. Wij komen niet verder dan wat met de pH of de temperatuur, maar onze docente vind dat dat onder ons niveau is. (we zijn 6V, en wel de betere van de klas, anderen mogen wel pH of temperatuur doen)
We hadden bijvoorbeeld al bedacht:
Wat is het temperatuur-optimum van amylase?
Wat is het pH-optimum van amylase?
Bij welke pH werkt amylase helemaal niet meer?
Bij welke temperatuur denatureert amylase?
Deze zijn allen niet goed genoeg. Er moeten blijkbaar nog meer dingen zijn die van invloed zijn op de werking van amylase. Kan iemand ons een voorzetje geven?
Alvast hartstikke bedankt!
quote:Dat kan ook zonder elasticiteit: Q(X) ≈ Q(P) + Q'(P)(X-P) (Taylor). Als X dicht bij P ligt, geeft dit heel aardige benaderingen. Wat de elasticiteit juist benadrukt, is de procentuele verandering. Een verandering van 1000 klinkt misschien heel veel, maar als dat maar 0,01% is, komt dat uit de elasticiteit naar voren. Maar waarom nou juist die formule, en niet iets dat erop lijkt?Met de procentuele verandering van de prijselasticiteit kan je berekenen wat Q gaat doen als P verandert.
De elasticiteit wil je zo definieren dat Q(P(1+h)) ≈ Q(P)*(1+e(P)h) (in formulevorm dat als je P met een paar procent verhoogt, dat Q(P) met e(P)*paar procent verhoogt).
Omschrijven levert e(P) ≈ [Q(P+Ph) - Q(P)] / [h*Q(P)].
Dit kun je weer omschrijven tot e(P) ≈ [Q(P+Ph) - Q(P)] / [Ph] * P/Q(P). Als je nu de verandering erg klein maakt, ofwel h naar 0 stuurt (en daarmee ook Ph), krijg je e(P) ≈ dQ/dP * P/Q (volgt uit de definitie van de afgeleide).
quote:Je hebt een onbekende amylase oplossing, misschien kun je onderzoek doen of je α- of β- amylaseoplossing hebt door te kijken naar het afbraakproduct? (bij β-amylase ontstaat maltose, en bij α-amylase verschillende suikers)Op zondag 15 oktober 2006 19:04 schreef K-mail het volgende:
Ik heb een vraagje over Biologie...
We moeten een Praktische opdracht maken over het Amylase enzym.
Je krijgt een Amylase oplossing, deze hoef je niet zelf meer te maken. Je moet het overgebleven zetmeel aantonen met Jood-oplossing.
Het probleem is echter dat we zelf het onderzoek moeten bedenken. Wij komen niet verder dan wat met de pH of de temperatuur, maar onze docente vind dat dat onder ons niveau is. (we zijn 6V, en wel de betere van de klas, anderen mogen wel pH of temperatuur doen)
We hadden bijvoorbeeld al bedacht:
Wat is het temperatuur-optimum van amylase?
Wat is het pH-optimum van amylase?
Bij welke pH werkt amylase helemaal niet meer?
Bij welke temperatuur denatureert amylase?
Deze zijn allen niet goed genoeg. Er moeten blijkbaar nog meer dingen zijn die van invloed zijn op de werking van amylase. Kan iemand ons een voorzetje geven?
Alvast hartstikke bedankt!
Je zou voor veel info over amylase eens kunnen kijken in boeken waarin in wordt gegaan op het bierbrouwproces, amylase is heel belangrijk bij bier brouwen. Misschien kun je daar nog wat ideetjes uit opdoen
Een producent produceert per jaar xk stuks van een bepaald goed. Hiervan slaat hij (1 - uk) * xk op (met 0 <= uk <= 1) en inversteert het restant (xk*uk), zodat volgend jaar voor de productie geldt:
xk+1 = xk + wk*uk*xk, met k = 0,1,...,N-1
The getallen wk zijn random variabelen (onafhankelijk en identiek verdeeld, met een verdeling die NIET afhangt van xk danwel uk).
Verder geldt E{wk} = W > 0.
We zoeken nu het optimale investeringsbeleid, zodat we het totale aantal opgeslagen stukken goed over N jaren maximaliseren. Oftewel:
max Ew k { xN + SOM(van k=0 t/m N-1)[ (1 - uk) * xk ] },
waarbij het maximum genomen wordt over alle mogelijke uk.
Het hoofdstuk waar deze opgave uitkomt gaat over het Dynamisch Programerings Algorithme (DPA), dus daar zal t wel iets mee te maken hebben
Nu snap ik (denk ik) wel een beetje hoe DPA werkt, maar om één of andere reden krijg ik dit niet echt opgelost.Wie kan helpen???
Alvast bedankt!
We gaan er in deze proef vanuit dat Fv ~ u. Leg uit dat voor de veerenergie bij een bepaalde uitrekking van het elastiek geldt: Ev = 1/2 x Fv x u
Maar we hebben wat weinig informatie om dit uit te leggen.
Staat er niet nog meer info bij?
Ik denk niet dat ik je echt verder kan helpen, aangezien ik te weinig weet over veerkracht en veerenergie.
quote:Zo moet het ookOp dinsdag 17 oktober 2006 19:07 schreef midje het volgende:
nee dat is het.. ik dacht zelf iets met de grafiek die je van Fv en u kan tekenen. die gaat als het goed is rechtsschuin omhoog zegmaar. en dat je dan met die 0.5 de oppervlakte onder de grafiek kan berekenen en dat je daar ev uit haalt
De arbeid is F*s, oftewel Fv * u. Je berekent dus eigenlijk de oppervlakte van die grafiek.midje: Als Fv ~ u dan is Fv recht evenredig met u (door de oorsprong dus), en kun je schrijven dat c = Fv/u.
We kunnen afleiden dat Eveer = 1/2 c u² (eenvoudig in te zien als oppervlak van een driehoek), substitueren levert Eveer = 1/2 Fv u.
[ Bericht 19% gewijzigd door GlowMouse op 17-10-2006 19:21:17 ]
quote:Ik weet dat ik de substitutieregel moet gebruiken maar heb geen flauw idee hoeOp dinsdag 17 oktober 2006 19:15 schreef GlowMouse het volgende:
Jopie: bij 1 t/m 3 de substitutieregel gebruiken (bij 3 evt eerst teller en noemer met e^x vermenigvuldigen), bij 4 een integraal maken waarbij je naar de tijd integreert en de hoeveelheid die binnenkomt in de integrand zetten.
Ik moet aantonen dat voor de warmte, die door de wrijvingskracht ontstaat geldt dat Q = f x m x g x X
daarin is f de wrijvingscoëfficiënt, m de massa van een schijf en X de afstand die de schijf aflegt wanneer hij met een bepaalde kracht weggeschoten wordt.
midje: kijk eens naar de definitie cq eenheid van de wrijvingscoëfficient.
quote:Je kunt alle drie de integralen simpel oplossen, zonder substitutie als je maar even de kettingregel in gedachten houdt.Op dinsdag 17 oktober 2006 17:59 schreef Jopie_Pringle het volgende:
Mijn wiskundige inzicht laat me weer eens in de steek :
[afbeelding]
Alvast bedankt!
1. x∙sin(x2) : Je weet dat de afgeleide van cos(x) gelijk is aan -sin(x). Dus proberen we eerst cos(x2). De afgeleide hiervan (kettingregel) is -2x∙sin(x2). Dat is bijna goed op een factor -½ na. De gezochte primitieve is dus -½∙cos(x2).
2. sin(2x)/(1 + cos2x): Je weet dat 1/x de afgeleide is van ln(x). Daarom proberen we hier eerst ln(1 + cos2x). De afgeleide hiervan (kettingregel) is 1/(1 + cos2x) ∙ 2cos(x) ∙ -sin(x). Nu is volgens een bekende goniometrische identiteit sin(2x) = 2∙sin(x)∙cos(x), dus zien we dat we weer bijna goed zitten, op een factor -½ na. De gezochte primitieve is dus -½∙ln(1 + cos2x).
3. 1/(ex + e-x). Hier vermenigvuldigen we eerst even teller en noemer van de breuk met ex om zodoende e-x = 1/ex in de noemer kwijt te raken. We krijgen dan ex / (e2x + 1). Als je een beetje goed bent in het herkennen van patronen en ziet dat e2x het kwadraat is van ex dan kun je denken aan arctan(x), waarvan de afgeleide immers is: 1/(x2 + 1). We proberen dus arctan(ex) en dit levert via de kettingregel inderdaad de gewenste afgeleide op.
Voor de vierde opgave moet je eerst een vergelijking opstellen die aangeeft wat de nog openstaande oppervlakte is op een tijdstip t tijdens het dichtschuiven van de deksel. Vervolgens kun je dan berekenen hoeveel water er in de bak valt gedurende een heel klein tijdsinterval [t, t+Δt] waarbij je aanneemt dat de deksel in dit heel kleine tijdsinterval niet noemenswaardig verschuift. De hoeveelheid water in al deze deelintervalletjes moet je sommeren om de totale hoeveelheid water die in de bak valt te bepalen. Door Δt naar 0 te laten gaan verkrijg je dan een integraal en oplossing hiervan levert de totale hoeveelheid water die tijdens het dichtschuiven van de deksel in de bak valt. Nu mag je het verder weer even zelf proberen.
[ Bericht 0% gewijzigd door Riparius op 17-10-2006 23:21:25 ]
quote:Met die redenatie hoef je nooit te substitueren. Dit terwijl substitueren een integraal vaak zoveel eenvoudiger maakt.Op dinsdag 17 oktober 2006 23:15 schreef Riparius het volgende:
[..]
Je kunt alle drie de integralen simpel oplossen, zonder substitutie als je maar even de kettingregel in gedachten houdt.
quote:Nee dat beweer ik niet. Kijk maar eens hier voor de uitwerking van een integraal waarbij je er echt niet komt zonder (meervoudige) substitutie.Op dinsdag 17 oktober 2006 23:26 schreef GlowMouse het volgende:
[..]
Met die redenatie hoef je nooit te substitueren. Dit terwijl substitueren een integraal vaak zoveel eenvoudiger maakt.
Ik heb een stelsel vergelijkingen, waar ik de volgende oplossing uit moet destileren.
{{U}*v+{V}} = 0 en v =| 0
Ik weet dat het kan door het determinant te nemen, en dan oplossen voor v. Dit gaat prima voor een 12x12 matrix (in mijn geval) maar bij een 14x14 matrix gaat het al mis. Resultaten komen dan niet overheen met de verwachting. En ik wil hem nog gebruiken voor een 50x50
Iemand die kan helpen?
quote:Substitutie is het integrale equivalent van de kettingregel bij differentieren. En bovendien is het gebruik van de substitutie regel in de bovenstaande integralen veel gemakkelijker en sneller dan het "proberen" van de juiste functies. Wat jij hierboven in jouw antwoorden doet is in feite gewoon de substitutie regel toepassen in een wat minder rigoreuze vorm.Op dinsdag 17 oktober 2006 23:15 schreef Riparius het volgende:
Je kunt alle drie de integralen simpel oplossen, zonder substitutie als je maar even de kettingregel in gedachten houdt.
quote:Ik heb een beetje ervaring met Mathematica. Als ik je goed begrijp dan wordt er voor de grotere matrix wel een oplossing gevonden maar niet de juiste? Dan lijkt me, uitgaande van de weinige info die gegeven hebt, dat er problemen optreden met de numerieke nauwkeurigheid (wat een bekend fenomeen is voor grote stelsels en puur numerieke input). Ik meen eens gezien te hebben dat er een speciale methode, iets van "SparseArray" oid, is voor dit soort dingen die daarmee rekening houdt als je een ijle matrix hebt (dwz dat er relatief veel nulelementen in voorkomen), is dat idd het geval?Op woensdag 18 oktober 2006 16:55 schreef FoRAiN het volgende:
Zijn er hier ook mensen die ervaring hebben met mathematica.
Ik heb een stelsel vergelijkingen, waar ik de volgende oplossing uit moet destileren.
{{U}*v+{V}} = 0 en v =| 0
Ik weet dat het kan door het determinant te nemen, en dan oplossen voor v. Dit gaat prima voor een 12x12 matrix (in mijn geval) maar bij een 14x14 matrix gaat het al mis. Resultaten komen dan niet overheen met de verwachting. En ik wil hem nog gebruiken voor een 50x50
Iemand die kan helpen?
quote:Dat is ie zeker zie hieronder.En mijn vermoeden was ook numerieke nauwkeurigheid.Op donderdag 19 oktober 2006 01:19 schreef keesjeislief het volgende:
[..]
Ik heb een beetje ervaring met Mathematica. Als ik je goed begrijp dan wordt er voor de grotere matrix wel een oplossing gevonden maar niet de juiste? Dan lijkt me, uitgaande van de weinige info die gegeven hebt, dat er problemen optreden met de numerieke nauwkeurigheid (wat een bekend fenomeen is voor grote stelsels en puur numerieke input). Ik meen eens gezien te hebben dat er een speciale methode, iets van "SparseArray" oid, is voor dit soort dingen die daarmee rekening houdt als je een ijle matrix hebt (dwz dat er relatief veel nulelementen in voorkomen), is dat idd het geval?
quote:Hierin is mg de zwaartekracht en ook de normaal kracht (bij een horizontale baan), de wrijvingskracht is (onder voorwaarden bij benadering) recht evenredig met de normaalkracht. En de arbeid verricht door de wrijvingskracht is warmte, deze arbeid is de integraal over het pad.Op dinsdag 17 oktober 2006 19:30 schreef midje het volgende:
ok volgende vraag. beetje lastig practicum dit.
Ik moet aantonen dat voor de warmte, die door de wrijvingskracht ontstaat geldt dat Q = f x m x g x X
daarin is f de wrijvingscoëfficiënt, m de massa van een schijf en X de afstand die de schijf aflegt wanneer hij met een bepaalde kracht weggeschoten wordt.
FN = FG = m g
Fwr = f FN = f m g
Q = W = IntegraalX0 (Fwr . dx) = f m g X
"bereken de absolute entropy S van de volgende systemen"
2,5 mol argon bij p = 0,25 bar
[ Bericht 43% gewijzigd door vliegtuigje op 19-10-2006 21:24:39 ]
quote:Wat moet ik met dat grote kruiswoordraadsel?Op donderdag 19 oktober 2006 10:46 schreef FoRAiN het volgende:
[..]
Dat is ie zeker zie hieronder.En mijn vermoeden was ook numerieke nauwkeurigheid.
[afbeelding]
Heb je gekeken in de documentatie bij LinearSolve? Daar staat dat er speciaal voor ijle systemen twee methoden zijn, nl. "Multifrontal" en "Krylov" (versie 5.1), misschien dat je daarmee verder komt?quote:De kruiswoord puzzel, is de listdensityplot van mijn matrix.. een 0 is wit. Maar de oplossing is al gevonden.Op donderdag 19 oktober 2006 21:27 schreef keesjeislief het volgende:
[..]
Wat moet ik met dat grote kruiswoordraadsel?
quote:En die was?Op vrijdag 20 oktober 2006 19:11 schreef FoRAiN het volgende:
[..]
De kruiswoord puzzel, is de listdensityplot van mijn matrix.. een 0 is wit. Maar de oplossing is al gevonden.
quote:De oplossing is
LinearSolve[U,-V] ==> krijg je een n x n matrix waar U*x=-V
Eigenvalues[%] ==> hiermee krijg je de eigenwaarden van x
Min[Select[Cases[%,_Real],Positive]] ==> hiermee krijg je de laagste positive reeele antwoord
Eigenlijk best makkelijk, maar je moet er maar op komen
quote:Ok, maar ik bedoelde eigenlijk of je hebt uitgevonden waarom het in eerste instantie fout ging voor grotere matrices?Op vrijdag 20 oktober 2006 22:07 schreef FoRAiN het volgende:
[..]
De oplossing is
LinearSolve[U,-V] ==> krijg je een n x n matrix waar U*x=-V
Eigenvalues[%] ==> hiermee krijg je de eigenwaarden van x
Min[Select[Cases[%,_Real],Positive]] ==> hiermee krijg je de laagste positive reeele antwoord
Eigenlijk best makkelijk, maar je moet er maar op komen
Leid af:
voor k >= 2.
Ik heb al geprobeerd (sinx)^k te schrijven als sinx * (sinx)^(k-1) en dan partieel integreren toe te passen, maar dat bood helaas geen soelaas.
Wie helpt me?
Als we het rechterlid differentieren, krijgen we 1/2-1/2 cos(2x). Dit lijkt me niet kloppen.
[ Bericht 0% gewijzigd door GlowMouse op 21-10-2006 20:01:43 ]
quote:Het klopt WEL voor k=2. Je differentieert niet goed. De afgeleide van het rechterlid is:Op zaterdag 21 oktober 2006 19:50 schreef GlowMouse het volgende:
Voor k=2 staat er primitieve sin²x dx = -1/2 cos(x)sin(x) + 1/2x + c.
Als we het rechterlid differentieren, krijgen we 1/2-1/2 cos(2x). Dit lijkt me niet kloppen.
-½∙-sin(x)∙sin(x) - ½∙cos(x)∙cos(x) + ½ = ½∙sin2(x) - ½∙cos2(x) + ½
Voor die ½ kun je schrijven ½∙cos2(x) + ½∙sin2(x). Zie je het nu?
quote:Hint: maak gebruik van sink(x) = sin2(x)∙sink-2(x) = sink-2(x) - cos2(x)∙sink-2(x).Op zaterdag 21 oktober 2006 19:21 schreef Oscar_de_Grouch het volgende:
Bij het hoofdstuk hogere afgeleiden van infinitesimaalrekening (1e jaars natuurkunde/wiskunde) kom ik niet uit de volgende vraag:
Leid af:
[afbeelding]
voor k >= 2.
Ik heb al geprobeerd (sinx)^k te schrijven als sinx * (sinx)^(k-1) en dan partieel integreren toe te passen, maar dat bood helaas geen soelaas.
Wie helpt me?
quote:Ik begon te vroeg met omschrijven zodat je niet sin² niet direct terugzag. Het klopt wel, maar 1/2-1/2 cos(2x) is gelijk aan sin²x (op zich ook logisch uit de identiteit cos(2x) = 1-2sin²x).Op zaterdag 21 oktober 2006 20:16 schreef Riparius het volgende:
[..]
Het klopt WEL voor k=2. Je differentieert niet goed.
quote:Populaire vraag blijkbaar, zie hier.Op zaterdag 21 oktober 2006 19:21 schreef Oscar_de_Grouch het volgende:
Bij het hoofdstuk hogere afgeleiden van infinitesimaalrekening (1e jaars natuurkunde/wiskunde) kom ik niet uit de volgende vraag:
Leid af:
[afbeelding]
voor k >= 2.
Ik heb al geprobeerd (sinx)^k te schrijven als sinx * (sinx)^(k-1) en dan partieel integreren toe te passen, maar dat bood helaas geen soelaas.
Wie helpt me?
quote:Ach, het is gewoon een heel bekende (recursieve) formule uit de integraalrekening en altijd een goede oefening in het partieel integreren en het omgaan met goniometrische functies. Ik had trouwens een iets andere afleiding dan in de link die je geeft, als volgt:Op woensdag 25 oktober 2006 23:03 schreef TomD het volgende:
[..]
Populaire vraag blijkbaar, zie hier.
Aangezien cos2(x) + sin2(x) = 1 hebben we sink(x) = sink-2(x)∙sin2(x) = sink-2(x) - sink-2(x)∙cos2(x) en dus:
(1) ∫ sink(x)∙dx = ∫ sink-2(x)∙dx - ∫ sink-2(x)∙cos2(x)∙dx
De eerste integraal in het rechterlid laten we staan, en de tweede gaan we nu herleiden met partiële integratie. De afgeleide van f(x)∙g(x) is f'(x)∙g(x) + f(x)∙g'(x), zodat:
∫ f'(x)∙g(x)∙dx = f(x)∙g(x) - ∫ f(x)∙g'(x)∙dx
De afgeleide van sink-1(x) (met k>1) is (k-1)∙sink-2(x)∙cos(x) (kettingregel), zodat omgekeerd (1/(k-1))∙sink-1(x) een primitieve is van sink-2(x)∙cos(x). We kiezen dus f'(x) = sink-2(x)∙cos(x) zodat f(x) = (1/(k-1))∙sink-1(x) en g(x) = cos(x) zodat g'(x) = -sin(x). We hebben dan:
∫ sink-2(x)∙cos2(x)∙dx = (1/(k-1))∙sink-1(x)∙cos(x) - ∫ (1/(k-1))∙sink-1(x)∙-sin(x)∙dx
Door de constante (1/(k-1)) en het minteken voor het integraalteken te brengen is dit te schrijven als:
(2) ∫ sink-2(x)∙cos2(x)∙dx = (1/(k-1))∙sink-1(x)∙cos(x) + (1/(k-1))∙∫ sink(x)∙dx
Substitutie van (2) in (1) levert nu:
∫ sink(x)∙dx = ∫ sink-2(x)∙dx - (1/(k-1))∙sink-1(x)∙cos(x) - (1/(k-1))∙∫ sink(x)∙dx
Brengen we nu de term met ∫ sink(x)∙dx uit het rechterlid over naar het linkerlid en bedenken we dat 1 + (1/(k-1)) = ((k-1)/(k-1)) + (1/(k-1)) = k/(k-1) dan hebben we:
k/(k-1)∙∫ sink(x)∙dx = -(1/(k-1))∙sink-1(x)∙cos(x) + ∫ sink-2(x)∙dx
Vermenigvuldiging van beide leden met (k-1)/k levert dan:
∫ sink(x)∙dx = -(1/k)∙sink-1(x)∙cos(x) + ((k-1)/k)∙∫ sink-2(x)∙dx
QED
=>
f'( a) niet gedefinieerd is en limx->a f'( x) = +/- oneindig.
Nu, best voor mijn vraag is als je zo een functie grafisch voorstelt.
Mijn vraag, is zo iets wel een functie. Om een vertikale raaklijn te hebben heb je toch 2 (infenitesimaal dichte) punten nodig met dezelfde x-coördinaat?
Mijn redenering is vrij intuïtief, kan iemand mij een rationeel onderbouwd antwoord geven ? Dank!
quote:Nee, dat is niet zo, want je kunt bijv. een functie hebben waarvan de grafiek een buigpunt heeft met een verticale raaklijn in het buigpunt.Op zaterdag 28 oktober 2006 12:21 schreef Masanga het volgende:
beschouw een "functie" met een perfect vertikale raaklijn in punt a.
=>
f'( a) niet gedefinieerd is en limx->a f'( x) = +/- oneindig.
Nu, best voor mijn vraag is als je zo een functie grafisch voorstelt.
Mijn vraag, is zo iets wel een functie. Om een vertikale raaklijn te hebben heb je toch 2 (infinitesimaal dichte) punten nodig met dezelfde x-coördinaat?
Een bekend voorbeeld is de functie f(x) = x1/3. Deze functie is continu in x=0 maar niet differentieerbaar in x=0. Zie hier.
quote:Je past eerst een substitutie toe, en wel z = x1/3. Dan is x = z3 dus dx/dz = 3∙z2. De integraal is daarmee herleid tot:Op zondag 29 oktober 2006 21:38 schreef Asmodean het volgende:
iemand enig idee hoe ik de integraal van cos(x^(1/3)) uitreken? Ik moet het morgen inleveren, maar heb echt geen idee hoe ik dit oplos....
∫ 3∙z2∙cos(z)∙dz
Nu kun je (herhaald) gebruik maken van partiële integratie om deze integraal verder op te lossen. Hierbij kun je gebruik maken van:
en:
quote:ah, na een hele tijd van alles proberen is het nu eindelijk duidelijk. Hartelijk bedanktOp zondag 29 oktober 2006 21:56 schreef Riparius het volgende:
[..]
Je past eerst een substitutie toe, en wel z = x1/3. Dan is x = z3 dus dx/dz = 3∙z2. De integraal is daarmee herleid tot:
∫ 3∙z2∙cos(z)∙dz
Nu kun je (herhaald) gebruik maken van partiële integratie om deze integraal verder op te lossen. Hierbij kun je gebruik maken van:
[afbeelding]
en:
[afbeelding]
We hebben het systeem:
x'1(t) = -x1(t) + u(t)
x'2(t) = x1(t)
met 0 <= u(t) <= 1 voor alle t. Verder x1(0) = x2(0) = 0.
Nu is de vraag: Maximaliseer: 2 x2(1) + x1(1).
Dit moet gebeuren aan de hand van Pontryagin's minimum principe. Ik hb al wat zitten rekenen, maar dat heeft tot niets geleid.
Wie kan mij hiermee op weg helpen???
3X^2 + 6x -16 = 0
Ik moet het algebraisch uitrekenen maar ik krijg het maar niet voor elkaar.
fp(x) = X^3 + 2px^2 + px
a. Bewijs dat elke functie fp ten hoogste 1 nulpunt heeft met een positieve waarde van x
b Voor welke waarden van p het fp precies 1 extreme waarde
c voor welke waarden van p heeft de grafiek van fp een buigpunt met daarin een horizontale raaklijn?
Heb nog nooit zoiets gehad met 2 variabelen, dus als iemand mij een beetje op weg kan helpen lukt het wel
quote:Je formulering algebraïsch uitrekenen is onduidelijk, maar ik neem aan dat je bedoelt dat je niet van de abc formule gebruik mag maken.Op maandag 30 oktober 2006 17:11 schreef HomerJ het volgende:
Even wat vraagjes:Ik heb deze vergelijking:
3X^2 + 6x -16 = 0
Ik moet het algebraisch uitrekenen maar ik krijg het maar niet voor elkaar.
Welnu, je kunt dan de methode van kwadraatafsplitsing gebruiken (in het engels heet dat overigens completing the square, voor het geval je dat na wil zoeken op internet).We delen eerst beide leden door 3 om de factor van x2 kwijt te raken en krijgen dan:
x2 + 2x - 16/3 = 0
Nu de constante term naar het rechterlid overbrengen:
x2 + 2x = 16/3
Nu halveer je de coefficiënt van x, kwadrateer je die en tel je die bij beide leden op. Waarom? Wel we hebben (x+1)2 = x2 + 2x + 1, dus als we nu bij beide leden 1 optellen dan kunnen we het linkerlid herschrijven als een kwadraat, dus:
x2 + 2x = 16/3
x2 + 2x +1 = 16/3 + 1
(x+1)2 = 19/3
Nu kun je deze vergelijking verder wel zelf oplossen: (x+1) is gelijk aan plus of min de vierkantswortel uit 19/3.
quote:Je kunt een x buiten haakjes halen en de functie herschrijven als:
fp(x) = X^3 + 2px^2 + px
a. Bewijs dat elke functie fp ten hoogste 1 nulpunt heeft met een positieve waarde van x
b Voor welke waarden van p het fp precies 1 extreme waarde
c voor welke waarden van p heeft de grafiek van fp een buigpunt met daarin een horizontale raaklijn?
Heb nog nooit zoiets gehad met 2 variabelen, dus als iemand mij een beetje op weg kan helpen lukt het wel
fp(x) = x(x2 + 2px + p)
Je ziet dat elke functie fp een nulpunt heeft voor x=0. Om de (eventuele) overige nulpunten te bepalen moeten we het deel tussen haakjes gelijk aan nul nemen, dus:
x2 + 2px + p = 0
Dit is gewoon een vierkantvergelijking, die je eenvoudig met kwadraatafsplitsing kunt behandelen. We hebben:
x2 + 2px = -p
Kwadraat completeren door links en rechts p2 op te tellen:
x2 + 2px + p2 = p2 - p
Linkerlid herschrijven als kwadraat:
(x+p)2 = p2 - p
Nu kan een kwadraat (van een reëel getal) niet negatief zijn, en dus moet p2 - p groter of gelijk aan 0 zijn. Deze uitdrukking is gelijk aan 0 als p=0 of als p=1 en positief als p<0 of als p>1. In dat geval hebben we als oplossingen van de vergelijking:
x1 = -p + √(p2 - p) en x2 = -p - √(p2 - p)
Nu kun je (hoop ik) inzien dat voor p > 1 beide wortels negatief zijn, en dat voor p<0 één wortel positief is en één wortel negatief. Daarmee is (a) beantwoord.
Voor (b) bepalen we eerst de afgeleide van fp, die is:
fp'(x) = 3x2 + 4px + p
Als er precies 1 extreme waarde moet zijn, dan moet er dus ook precies één waarde van x zijn waarvoor geldt fp'(x) = 0. Er wordt dus gevraagd voor welke waarde(n) van p de vergelijking
3x2 + 4px + p = 0
precies één oplossing heeft. Dat is het geval als de discriminant D = b2 - 4ac van deze vierkantsvergelijking gelijk is aan 0, dus:
(4p)2 - 4∙3∙p = 0
16p2 - 12p = 0
p(16p - 12) = 0
p = 0 of p = 3/4
Daarmee zijn we er nog niet, want voor een (locaal) minimum of maximum moet ook nog voldaan worden aan de voorwaarde dat de tweede afgeleide voor de betreffende waarde van x niet gelijk is aan nul, en daarover gaat dan ook het derde deel van je opgave.
Voor opgave (c) moet je ook de tweede afgeleide van fp(x) bepalen, deze is:
fp''(x) = 6x + 4p
In een buigpunt is de tweede afgeleide gelijk aan 0, dat is het geval als 6x + 4p = 0, dus x = -(2/3)∙p.
Maar nu wordt gevraagd naar buigpunten met een horizontale raaklijn, en dat betekent dat voor deze waarde van x ook de eerste afgeleide gelijk moet zijn aan 0. We substitueren dus x = -(2/3)∙p in fp'(x) = 0 en krijgen dan:
3∙((-2/3)∙p)2 + 4∙p∙((-2/3)∙p) + p = 0
(12/9)∙p2 - (8/3)∙p2 + p = 0
- (4/3)∙p2 + p = 0
p(1 - (4/3)∙p) = 0
p = 0 of p = 3/4
Je ziet dat dit precies de waarden van p zijn waarvoor er één extreme waarde zou kunnen zijn. Maar aangezien we voor deze waarden van p een buigpunt hebben met een horizontale raaklijn is de conclusie dat er geen waarden van p zijn waarvoor de functie fp(x) precies één extreme waarde bezit.
[ Bericht 0% gewijzigd door Riparius op 30-10-2006 23:17:44 ]
Heel erg bedankt
ik heb een vraagje over deze functie:
f(x)=xx
vraag 1: toon aan f is strict stijgend op [e-1, oo) dit is niet moeilijk, gewoon afgeleide uitrekenen en kijken wanneer di e groter is dan nul .
vraag 2: als g de inverse is van f. laat zien dat
lim ( y --> oo) (g(y)ln(lny))/lny= 1
de hint is: begin met y=xx dan
lny=xlnx.
alvast bedankt
dus stel je moet bijv uitrekenen wat
lim ( y --> oo) (g(y)ln(lny))/lny
met g de inverse van lnx.
dan mag je gewoon subsitueren: y =xx
thanks
quote:Als functie g de inverse is van functie f en je hebt y = f(x), dan is x = g(y).Op dinsdag 31 oktober 2006 20:47 schreef teletubbies het volgende:
mmm, ik dacht te moeilijk!
dus stel je moet bijv uitrekenen wat
lim ( y --> oo) (g(y)ln(lny))/lny
met g de inverse van lnx.
dan mag je gewoon subsitueren: y =xx
thanks
Probleem is alleen dat je nu weer iets anders beweert dan vanmiddag, want toen zei je dat g de inverse was van de functie f(x) = xx en nu zeg je dat g de inverse is van ln(x), maar dat is toch echt iets anders. Ik vraag me dus wel een beetje af of je weet waar je mee bezig bent.
[ Bericht 0% gewijzigd door Riparius op 01-11-2006 00:48:15 ]
De vergelijking: x² + y² = 25
Dit wordt:
2x + 2yy' = 0
y' = -2x/2y = -x/y
dy/dx = -(x/y)
Nu moet ik de raaklijn weten in het punt (3,4). Dus invullen:
dy/dx = -3/4.
Ik snap echter totaal niet hoe het boek nu aan het volgende komt:
quote:Hoe komen ze nou aan de vergelijking voor die raaklijn?An equation of the tangent to the circle at (3,4) is therefore: y - 4 = -3/4(x-3) or 3x+4y = 25
[ Bericht 50% gewijzigd door GlowMouse op 01-11-2006 21:26:03 ]
).y = -0,75x + b
b = 4 + 0,75x
y = -0,75x + 4 + 0,75x
y-4 = -0,75x + 0,75x
Kom er nog steeds niet op uit. En hoe komen ze aan die tweede vorm van 3x+4y = 25 dan?
Overigens slaat 'therefore' op dy/dx = -3/4.
daar staat dat y-4 = 0. Leuk voor dat ene punt, maar je hebt nog steeds geen raaklijnvergelijking. Na y = -0,75x+b vul je wel y in, maar niet x. Je vindt b juist door zowel x als y in te vullen. b is namelijk een constante term, die niet meer van x of y afhangt. In jouw geval hangt hij nog van x af.
Ik heb het volgende elektronisch circuit:
De blokjes stellen weerstanden van 300 Ohm voor. Ik moet het gedissipeerde vermogen in weerstand R2 bepalen, daartoe moet ik dus de stroom of het voltage over deze weerstand weten. Overigens heb ik de vervangingsweerstand van hele circuit al uitgerekend, dit is 1000 Ohm.
Het antwoord is 0.033mW, maar hoe kom ik hierop?
Edit: Dit circuit wordt op een DC voltage bron aangesloten van 1 Volt.
[ Bericht 5% gewijzigd door Schuifpui op 01-11-2006 22:12:45 ]
quote:Bedoel je deze: (ben nooit zo van die namenOp woensdag 1 november 2006 22:15 schreef GlowMouse het volgende:
Heb je de kirchhoff vergelijkingen al?
)P=UI
P=V^2/R
U=IR
serie:
Rv = R1 + R2 + ..
parallel:
Rv=1/R1 + 1/R2 + ..
quote:Snap eigenlijk niet zo goed wat je bedoeltOp woensdag 1 november 2006 22:22 schreef GlowMouse het volgende:
Nee, meer van de som der spanningsvallen in elke kring (5 stuks hier) 0 is, het dat de som der stromen op elk punt (4 relevante hier) 0 is. Zonder lastige transformaties zie ik trouwens niet hoe je hier met U=IR uit zou komen.
Zou je misschien eens voor kunnen doen wat ik moet doen om op een antwoord te komen, of iig een begin kunnen maken, ben niet zo heel erg thuis in de electriciteit eigenlijk.quote:Dank jeOp woensdag 1 november 2006 22:27 schreef GlowMouse het volgende:
Hier staat een voorbeeldje. Staat Kirchhoff ook helemaal niet in je studieboeken?
Ik ga er even naar kijken, nu je het zegt heb ik idd wel eens van deze wet gehoord.
Kirchhoff wordt wel genoemd in het boek, maar de wetten staan er niet echt duidelijk in, ze gaan er vanuit dat je wat basis kennis hebt, die bij mij weleens wil ontbreken of iig weggezakt is.
quote:Jeey, ik heb hemOp woensdag 1 november 2006 22:34 schreef GlowMouse het volgende:
Het kan ook met een ster-driehoektransformatie. Dat is hier denk ik sneller, maar minder universeel toepasbaar.
Dank je wel
Dat laatste deed het hem. Zo even een aantekening maken, tis een openboek tentamen
Nogmaals dank.
quote:Stel je hebt een lijn door het punt P(x,0,y0) met richtingscoëfficiënt m. Kies nu een willekeurig ander punt (x,y) op die lijn, dan is:Op woensdag 1 november 2006 20:55 schreef TC03 het volgende:
Ik snap echter totaal niet hoe het boek nu aan het volgende komt:
[..]
Hoe komen ze nou aan de vergelijking voor die raaklijn?
Δx = x - x0 en Δy = y - y0
Verder is
Δy/Δx = m, dus Δy = m∙Δx.
De vergelijking van een lijn door het punt P(x0,y0) met richtingscoëfficiënt m is dus:
y - y0 = m∙(x - x0)
quote:g is inverse van x^x, al opgelost.thank u!Op dinsdag 31 oktober 2006 21:13 schreef Riparius het volgende:
[..]
Als functie g de inverse is van functie f en je hebt y = f(x), dan is x = g(y).
Probleem is alleen dat je nu weer iets anders beweert dan vanmiddag, want toen zei je dat g de inverse was van de functie f(x) = xx en nu zeg je dat g de inverse is van ln(x), maar dat is toch echt iets anders. Ik vraag me dus wel een beetje af of je weet waar je mee bezig bent.
:
Hoe moet ik dit oplossen? Ik heb substitutie met u = cos x gebruikt, maar dat kwam ook nergens op uit. Antwoord is 2/3 overigens. Help
.quote:Stapsgewijze herleiden met partiële integratie, zie hier in dit topic (had je dus zelf kunnen vinden).Op donderdag 2 november 2006 21:55 schreef Merkie het volgende:
Help. Ik heb de volgende integraal.
[afbeelding]
Hoe moet ik dit oplossen? Ik heb substitutie met u = cos x gebruikt, maar dat kwam ook nergens op uit. Antwoord is 2/3 overigens. Help
Je kunt ook bedenken dat cos3(x) = cos(x)∙cos2(x) = cos(x) - cos(x)∙sin2(x), dan zou het je moeten lukken om rechtstreeks een primitieve te bepalen.
[ Bericht 1% gewijzigd door Riparius op 02-11-2006 22:15:15 ]
deze cauchy rijtjes convergeren niet 'altijd' in Q. maar wel altijd in R.
Bestaan er Cauchy rijtjes in R?
ik vraag me af waarom ze in R convergeren ..dit heeft te maken met metrische afsluiting ofzo..
kan iemand me dit eventjes uitleggen?
groetjes..
quote:Daar waar xn staat dient xn gelezen te worden.Op zaterdag 4 november 2006 20:29 schreef teletubbies het volgende:
R= {Cauchy-rijtjes} \ ~
deze cauchy rijtjes convergeren niet 'altijd' in Q. maar wel altijd in R.
Bestaan er Cauchy rijtjes in R?
ik vraag me af waarom ze in R convergeren ..dit heeft te maken met metrische afsluiting ofzo..
kan iemand me dit eventjes uitleggen?
groetjes..
In R hanteer je als afstandsmaat tussen Cauchyrijtjes d((xn),(yn)) = (|xn-yn|), dit is een Cauchyrijtje dus een element van R. Je hebt ook een ordening op R, (xn)>(yn) als
er een epsilon>0 en een N bestaan met xn-yn>epsilon voor alle n>N.
Het is eenvoudig te bewijzen dat deze afstandsmaat ook echt een afstandsmaat is (i.e. d(x,y)=0 desda x=y, d(x,y)=d(y,x) en d(x,y)+d(y,z)>=d(x,z)).
Nu je een afstandsmaat hebt op R kun je dus ook Cauchyrijtjes (yn) in R bekijken. Dit zijn dus eigenlijk Cauchyrijtjes van Cauchyrijtjes in Q. Laten we zeggen dat (yn)=(xnm). Om te laten zien dat die convergeren moet je dus een Cauchyrijtje in Q zien te produceren die de limiet van die rijtjes is.
Dat kan op meerdere manieren. Ik stel de volgende manier voor: voor elke n is er een N(n) zdd voor alle m,k>=N(n) geldt dat |xnm-xnk|<2-n. Dan is het rijtje zn=xn,N(n) de limiet. Probeer dat maar eens te bewijzen. Je moet dus bewijzen dat voor alle epsilon>0 er een M bestaat zodanig dat voor alle m>M de ongelijkheid d(ym,(zn))<epsilon geldt. Je moet bijvoorbeeld ergens gebruiken dat (yn) zelf ook een Cauchyrijtje is. Als je er niet uitkomt geef ik je nog wel een hint.
De stoffen jood en chloor reageren met elkaar tot joodmonochloride of joodtrichloride. Bij een experiment wordt 0,50 mmol chloorgas over 0,10 mmol jood geleid. Er ontstaat 0,20 mmol joodmonochloride volgens de reactie I2 + Cl2 -> 2ICl. Leid af of de reactie tot joodmonochloride een aflopende of evenwichtsreactie is.
Geen idee hoe 'k het aan moet pakken, iemand hier
[ Bericht 5% gewijzigd door MeScott op 05-11-2006 11:41:54 ]
quote:Het is erg lang geleden dat ik scheikunde gehad hebOp zondag 5 november 2006 11:26 schreef MeScott het volgende:
Morgen scheikundetentamen en natuurlijk weer veel te laat begonnen, k hoop dat m'n laatste vraag (vragen probably) hier beantwoord kunnen worden (gaat over evenwichtsreacties e.d.)
De stoffen jood en chloor reageren met elkaar tot joodmonochloride of joodtrichloride. Bij een experiment wordt 0,50 mmol chloorgas over 0,10 mmol jood geleid. Er ontstaat 0,20 mmol joodmonochloride volgens de reactie I2 + Cl2 -> 2ICl. Leid af of de reactie tot joodmonochloride een aflopende of evenwichtsreactie is.
Geen idee hoe 'k het aan moet pakken, iemand hier
, maar is het niet gewoon zo dat het verschil tussen een evenwichts- en aflopende reactie is dat er in het eerste geval een evenwicht tussen alle stoffen ontstaat en in het tweede uiteindelijk alleen joodmonochloride overblijft? Als dat zo is, moet je gewoon kijken hoe het zit met de hoeveelheden, uit 1 deeltje I2 en 1 deeltje Cl2 ontstaan twee deeltjes ICl. Heb je alle ingangshoeveelheden I2 en Cl2 nodig om tot 0,20 mmol lCl te komen? Zo ja, dan aflopende reactie, zo niet, dan evenwichtsreactie. Helpt dat? Edit: meer concreet zou ik denken dat het als volgt is. Een (m)mol is een eenheid voor een absoluut aantal deeltjes niet. Dus, gezien de verhoudingen in de reactievergelijking, als je 1 mmol jood hebt en 1 mmol chloorgas, ontstaat er 2 mmol joodmonochloride. Nu heb je 0,10 mmol jood. Als je daar 0,50 mmol chloorgas bijdoet, reageert 0,10 mmol daarvan met de 0,10 mmol jood tot 0,20 mmol joodmonochloride en blijft er 0,40 mmol chloorgas over. Het is dus een aflopende reactie, omdat een van de "inputstoffen" (ik weet niet hoe je dat schiekundig noemt) op raakt, als het een evenwichtsreactie zou zijn zouden van elk van de drie stoffen hoeveelheden aanwezig blijven.
[ Bericht 17% gewijzigd door keesjeislief op 05-11-2006 13:34:33 ]
De stoffen jood en chloor reageren met elkaar tot joodmonochloride of joodtrichloride. Bij een experiment wordt 0,50 mmol chloorgas over 0,10 mmol jood geleid. Er ontstaat 0,20 mmol joodmonochloride volgens de volgende reactie:
I2 + Cl2 -> 2ICl
Per mol jood ontstaat er twee mol joodchloride. In totaal is er 0,20 mmol joodmonochloride ontstaan. Dit ontstaat uit 0,10 mol jood. De reactie is dus aflopend. Er is nog 0,40 mol chloor over.
Wat ik niet snap: hoe komen ze tot de conclusie dat de reactie aflopend is, als er uit 0,10 mol jood 0,20 mmol joodmonochloride ontstaat
quote:Zie edit, is dat duidelijk?Op zondag 5 november 2006 13:29 schreef MeScott het volgende:
Hmm, begrijp het nog niet helemaal.. Heb de uitwerkingen en daar staat dit als antwoord:
De stoffen jood en chloor reageren met elkaar tot joodmonochloride of joodtrichloride. Bij een experiment wordt 0,50 mmol chloorgas over 0,10 mmol jood geleid. Er ontstaat 0,20 mmol joodmonochloride volgens de volgende reactie:
I2 + Cl2 -> 2ICl
Per mol jood ontstaat er twee mol joodchloride. In totaal is er 0,20 mmol joodmonochloride ontstaan. Dit ontstaat uit 0,10 mol jood. De reactie is dus aflopend. Er is nog 0,40 mol chloor over.
Wat ik niet snap: hoe komen ze tot de conclusie dat de reactie aflopend is, als er uit 0,10 mol jood 0,20 mmol joodmonochloride ontstaat
quote:Ja, ik snap wel hoe je aan die 0,10 mmol komt en dat dat reageert tot 0,20 mmol joodmonochloride, maar niet hoezo je daaruit kunt concluderen dat het een aflopende reactie is. Althans, snapte, wantOp zondag 5 november 2006 13:32 schreef GlowMouse het volgende:
Als de reactievergelijking I2 + Cl2 -> 2ICl luidt, en er ontstaat 0,20 mmol joodmonochloride, dan is er 0,10 mmol jood gereageerd. De coëfficienten in de reactievergelijking geven namelijk de reactieverhouding in mol weer.
quote:Dat klaar het op
De jood in het begin raakt op en omdat de reactie dan niet meer verder kan, kan hij ook niet omgedraaid worden en dus is hij aflopend. Toch ?quote:Wat bedoel je met omgedraaid worden? Ik stel me het als volgt voor (niet gehinderd door een overdaad aan relevante kennis thoughOp zondag 5 november 2006 13:49 schreef MeScott het volgende:
[..]
Ja, ik snap wel hoe je aan die 0,10 mmol komt en dat dat reageert tot 0,20 mmol joodmonochloride, maar niet hoezo je daaruit kunt concluderen dat het een aflopende reactie is. Althans, snapte, want
[..]
Dat klaar het op
). Bij een evenwichtsreactie raakt nooit één van de stoffen op maar convergeren de hoeveelheden (een beetje fluctuerend misschien) naar een stabiele situatie waarin de drie stoffen in een bepaalde verhouding aanwezig zijn, geen van allen raakt helemaal op. Bij een aflopende reactie nemen de hoeveelheden van de "inputstoffen" vanaf het begin alleen maar steeds verder af en neemt de hoeveelheid van de "outputstof" alleen maar toe, net zolang tot een van de inputstoffen op is en de reactie dus niet verder meer kan plaatsvinden. Als je de beginhoeveelheden in de juiste verhouding kiest (in jouw voorbeeld zou dat betekenen evenveel van beide inputstoffen) raken allebei de inputstoffen op en blijft er alleen maar outputstof over, maar dat hoeft dus niet per sé.quote:Lijkt me eerst dat je het herschrijft tot iets zonder wortels. Heb je niet zo een standaard blauw velletje met regels hoe je wortels moet differentiëren. Ik heb het niet terug kunnen vindenOp zondag 17 september 2006 15:04 schreef -tK- het volgende:
Ik zoek de afgeleide van de volgende functie:
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking
. Je kan ook proberen. Eerst alles buiten de haakjes te differentiëren. en daarna alles binnen de haakjes. Sorry weet dat het niet veel is
. Ik ben beetje roestig geworden.quote:Je kunt gewoon de kettingregel toepassen, als je de wortel als een macht schrijft krijg je (x2+4)1/2, differentiëren geeft dan (1/2)*(x2+4)-1/2*2x = x/sqrt(x2+4).Op zondag 5 november 2006 14:18 schreef Burakius het volgende:
[..]
Lijkt me eerst dat je het herschrijft tot iets zonder wortels. Heb je niet zo een standaard blauw velletje met regels hoe je wortels moet differentiëren. Ik heb het niet terug kunnen vinden
Je kan ook proberen. Eerst alles buiten de haakjes te differentiëren. en daarna alles binnen de haakjes. Sorry weet dat het niet veel is
Weet iemand hoe je C doet?
Ik hoop dat iemand me ermee op weg kan helpen
Ik weet dat lineariseren in principe inhoudt dat je de functie benadert met een lijn:
y = f(a) + (x-a)f'(a) als x=a
Maar in de functie van de opgave komt ook nog een vertraging voor waarvan ik niet weet wat ik ermee moet...
bvd.
Op welke wijze wordt op het kadastrale uittreksel het aantal vierkante meters correct
weergegeven? In hectare....? Are.....? Ca......?
quote:Correct volgens wie???Op woensdag 8 november 2006 11:28 schreef BadKeukenTegel het volgende:
De grondoppervlakte van een perceel bedraagt 7.426 m².
Op welke wijze wordt op het kadastrale uittreksel het aantal vierkante meters correct
weergegeven? In hectare....? Are.....? Ca......?
Natuurkundig gezien mag je het in vierkante lichtjaren uitdrukken, of in A4-tjes, zolang je de eenheid maar netjes vermeldt.
SI-eenheden zijn wel aan te raden, dus dan zou ik vierkante meters doen.
Of het via de een of andere juridische norm een andere voorgeschreven eenheid moet zijn weet ik niet, bedoel je dat?
quote:Je moet het of in hectare, are en ca neerzetten, dus bijv. 7ha 4a 26ca, ik vraag me alleen af of die wel klopt.Op woensdag 8 november 2006 11:34 schreef Pie.er het volgende:
[..]
Correct volgens wie???
Natuurkundig gezien mag je het in vierkante lichtjaren uitdrukken, of in A4-tjes, zolang je de eenheid maar netjes vermeldt.
SI-eenheden zijn wel aan te raden, dus dan zou ik vierkante meters doen.
Of het via de een of andere juridische norm een andere voorgeschreven eenheid moet zijn weet ik niet, bedoel je dat?
quote:Je probleem is dat je kennelijk niet weet wat een hectare, are of centiare is. Kijk eens hier.Op woensdag 8 november 2006 11:36 schreef BadKeukenTegel het volgende:
[..]
Je moet het of in hectare, are en ca neerzetten, dus bijv. 7ha 4a 26ca, ik vraag me alleen af of die wel klopt.
quote:In Mathematica is er zoiets als ImplicitPlot, bestaat zoiets niet in Maple?Op dinsdag 7 november 2006 13:49 schreef pfaf het volgende:
Misschien niet helemaal een beta-huiswerkvraag, maar er zijn hier vast wel mensen die me kunnen helpen. M'n vraag is hoe ik in Maple een vergelijking als: 10y+2Pi*arctan(y/x)=2 kan plotten.
bvd.
Edit: dit: http://hornacek.coa.edu/d(...)ts/implicit.plot.pdf ?
quote:Held!Op woensdag 8 november 2006 13:00 schreef keesjeislief het volgende:
[..]
In Mathematica is er zoiets als ImplicitPlot, bestaat zoiets niet in Maple?
Edit: dit: http://hornacek.coa.edu/d(...)ts/implicit.plot.pdf ?
Dank u!Ik ben me aan het orienteren voor een onderwerp. Vorig jaar heb ik voor een gewone PO de transcendentie van Pi bewezen, met hulp van een globale uitwerking in 5 stappen. Daarbij kwam flink wat algebra kijken, en een stuk meetkunde...
Nu wil ik voor m'n pws weer zoiets doen, alleen dan wel iets dat verder gaat... Alleen heb ik geen idee wat, zijn er hier mensen met leuke ideeen?
quote:Je zou kunnen bewijzen dat een vijfdegraadsvergelijking niet op te lossen is met een soort abc-formule.Op woensdag 8 november 2006 17:20 schreef Market_Garden het volgende:
Ik ben me aan het orienteren voor m'n PWS wiskunde... (6 vwo)
Ik ben me aan het orienteren voor een onderwerp. Vorig jaar heb ik voor een gewone PO de transcendentie van Pi bewezen, met hulp van een globale uitwerking in 5 stappen. Daarbij kwam flink wat algebra kijken, en een stuk meetkunde...
Nu wil ik voor m'n pws weer zoiets doen, alleen dan wel iets dat verder gaat... Alleen heb ik geen idee wat, zijn er hier mensen met leuke ideeen?
Of bewijzen dat een regelmatige n-hoek te construeren is met passer en liniaal dan en slechts dan als n een tweemacht maal een product van verschillende Fermatpriemgetallen is.
Hier heb je wel een pittige hoeveelheid algebra bij nodig, dus als je zoiets wilt doen moet je wel op tijd beginnen.
tip 1+x mag je substitueren voor t^3
Nu weet ik al dat het antwoord 1/3 moet zijn, wat ik nog niet weet is hoe ik hier in vredesnaam op moet komen. Kan iemand dit in stapjes eens opschrijven?