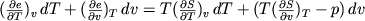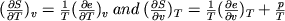SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Nieuw deeltje, vorige was vol.
Post hier weer al je vragen, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Wiskunde
Natuurkunde
Informatica
Scheikunde
Biologie
Algemene Natuurwetenschappen
Alles wat in de richting komt
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
Vorige deeltje Beta-huiswerkvragen
Post hier weer al je vragen, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
Vorige deeltje Beta-huiswerkvragen
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Sticky
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Die link linkt naar 2 betatopics terug. Dat moet deze zijn
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Vraag :
IQ aankomende studenten is normaal verdeeld met u=105 en o=15. Vanaf welk IQ behoort een student tot de 15% hoogste IQ-groep?
Mijn oplossing ->
y1 = normalcdf(X,10000,105,15). Bij X =120 y1 = 0.15 = 15%. IQ dus 120 of hoger. Vervolgens kijk ik wat het goede antwoord is, dat is 125.0. In mijn table is x=125 y1=0.09..
De vraag is dus of ik fout zit of het antwoordenvel.
IQ aankomende studenten is normaal verdeeld met u=105 en o=15. Vanaf welk IQ behoort een student tot de 15% hoogste IQ-groep?
Mijn oplossing ->
y1 = normalcdf(X,10000,105,15). Bij X =120 y1 = 0.15 = 15%. IQ dus 120 of hoger. Vervolgens kijk ik wat het goede antwoord is, dat is 125.0. In mijn table is x=125 y1=0.09..
De vraag is dus of ik fout zit of het antwoordenvel.


Y~N(105,225), Z~N(0,1).
Gevraagd is c zodat P(Y<c) = 0,85. Eenvoudig omschrijfwerk levert dat P((Y-105)/15 < (c-105)/15) = P(Z < (c-105)/15) = 0,85. Een tabellenboek levert dat (c-105)/15 gelijk is aan 1,04. Hieruit volgt dat c=120,6. Gebruikmakend van de tabel wordt er wat afgerond, maar 120 lijkt mij een juist antwoord.
Gevraagd is c zodat P(Y<c) = 0,85. Eenvoudig omschrijfwerk levert dat P((Y-105)/15 < (c-105)/15) = P(Z < (c-105)/15) = 0,85. Een tabellenboek levert dat (c-105)/15 gelijk is aan 1,04. Hieruit volgt dat c=120,6. Gebruikmakend van de tabel wordt er wat afgerond, maar 120 lijkt mij een juist antwoord.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


120 dacht ik dus ook... Ik heb nog een paar soortgelijke vragen gemaakt met andere gegevens en daarbij kwam mijn antwoord wel overeen met het antwoordenvel, dus ik denk dat bij bovenstaande vraag het antwoordenvel gewoon fout zit. Iig bedankt voor jouw berekening, al vind ik die van mij wat eenvoudiger


edit: Ok, laat maar... dit was een hele stomme vraag.
[ Bericht 47% gewijzigd door spinor op 01-09-2006 11:33:18 ]
[ Bericht 47% gewijzigd door spinor op 01-09-2006 11:33:18 ]


Vraagje, als ik van een driehoek 2 onbekende heb, hoe kan ik die dan vinden? situatie:
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
Bram! Boterham!


Ik weet niet wat je wil vinden, maar als links de rode lijn parallel is aan RT, dan is, onder de juiste voorwaarden, die driehoek gelijkbenig. De hoeken volgen daaruit en ook de lengtes zijn uit te rekenen. Maar ik weet niet wat je wilt weten.quote:Op vrijdag 1 september 2006 12:59 schreef lj_lightning het volgende:
Vraagje, als ik van een driehoek 2 onbekende heb, hoe kan ik die dan vinden? situatie:
[afbeelding]
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Ja ik was op school en heb er een kwartier over gedaan om mijn bericht proberen te editen Ik wil weten op welke hoogte die rode lijn 4cm is (dus ik wil de lengte weten van die zwarte verticale streep)quote:Op vrijdag 1 september 2006 15:23 schreef Wackyduck het volgende:
[..]
Ik weet niet wat je wil vinden, maar als links de rode lijn parallel is aan RT, dan is, onder de juiste voorwaarden, die driehoek gelijkbenig. De hoeken volgen daaruit en ook de lengtes zijn uit te rekenen. Maar ik weet niet wat je wilt weten.
en om die hoogte te weten moet ik de lengte van de aanliggende zijde en overstaande zijde weten...maar hoe?
Bram! Boterham!


Voor de hoogte zijn bij een gegeven lengte vaak 2 mogelijkheden (zowel in de driehoek onder- als bovenin). Noem die lengte van de rode lijn l en de lengte van de zwarte lijn h.
We onderscheiden twee situaties:
l<0 of l>4: geen oplossing
0<=l<=4:
Voor de eerste mogelijkheid geldt (l / (2h)) = tan(45) = 1 (waarom?). Omschrijven naar de hoogte is denk ik geen probleem.
Zolang h!=2 is de tweede oplossing gelijk aan 4-h.
Hierbij heb ik gebruik gemaakt dat het zij-aanzicht een vierkant is, en symmetrisch is in een verticale lijn.
[ Bericht 1% gewijzigd door GlowMouse op 02-09-2006 14:17:04 (grote fout :() ]
We onderscheiden twee situaties:
l<0 of l>4: geen oplossing
0<=l<=4:
Voor de eerste mogelijkheid geldt (l / (2h)) = tan(45) = 1 (waarom?). Omschrijven naar de hoogte is denk ik geen probleem.
Zolang h!=2 is de tweede oplossing gelijk aan 4-h.
Hierbij heb ik gebruik gemaakt dat het zij-aanzicht een vierkant is, en symmetrisch is in een verticale lijn.
[ Bericht 1% gewijzigd door GlowMouse op 02-09-2006 14:17:04 (grote fout :() ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hey allen, even een kort vraagje. Bij Thermo kom ik in de tekst het volgende tegen waar ik niet helemaal begrijp wat ze doen.
We komen van de 1e wet v d TD uit op:
mvg en bvd.
We komen van de 1e wet v d TD uit op:
Nu zie ik wel hoe de auteur er bij komt, maar wat hij nou wiskundig doet snap ik niet. dus wat dat uitdelen nu precies inhoudt...quote:(..)
equating the dT and dv terms gives:
mvg en bvd.


Je hebtquote:Op woensdag 6 september 2006 12:36 schreef pfaf het volgende:
Hey allen, even een kort vraagje. Bij Thermo kom ik in de tekst het volgende tegen waar ik niet helemaal begrijp wat ze doen.
We komen van de 1e wet v d TD uit op:
[..]
Nu zie ik wel hoe de auteur er bij komt, maar wat hij nou wiskundig doet snap ik niet. dus wat dat uitdelen nu precies inhoudt...
mvg en bvd.
a dT + b dv = c dT + d dv,
met a b c d variabel.
Ofwel
(a - c) dT = (d - b) dv.
Dit moet altijd waar zijn onafhankelijk van dT en dv, dat kan alleen maar als a-c en d-b 0 zijn, ofwel
a = c,
b = d.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Hoi allemaal.
Ik heb ff wat vraagjes over het vier-kleurenprobleem. Heb er vandaag college over gehad, maar kon de docent niet echt volgen... Hij bleef maar lachen om zn eigen anekdotes en opmerkingen enzo
Maar goed, we hebben het volgende:
Gegeven is een kaart op de bol met de volgende eigenschappen:
1) Elk land is een evenhoek. Dus de grens van een land vormt een rondweg met een even aantal ribben.
2) Elk meerlandenpunt is een drielandenpunt. Dus een ribbe verbindt twee drielandenpunten.
3) Er zijn eindig veel landen, en ze vullen het boloppervlak.
Nu de vragen:
1) Laat aan een voorbeeld zien dat een land minder buren kan hebben dan er ribben in zn grens zitten Die heb ik al
2) Leg uit waarom er een land is met hoogstens vier ribben in zn grens
3) Laat zien dat we de drielandenpunten van een + of - kunnen voorzien, zo dat elke ribbe een + met een - verbindt (beschouw een minimaal tegenvoorbeeld)
Tijdens het verhaal van de docent kwam ook een stelling van Euler naar voren. Die was iets van:
V - E + F = 2,
met V=vertices (hoekpunten), E=edges(ribben) en F=faces(landen),
maar ik zie ook niet hoe dat hier iets mee te maken heeft.
Wie kan mij helpen???
Ik heb ff wat vraagjes over het vier-kleurenprobleem. Heb er vandaag college over gehad, maar kon de docent niet echt volgen... Hij bleef maar lachen om zn eigen anekdotes en opmerkingen enzo
Maar goed, we hebben het volgende:
Gegeven is een kaart op de bol met de volgende eigenschappen:
1) Elk land is een evenhoek. Dus de grens van een land vormt een rondweg met een even aantal ribben.
2) Elk meerlandenpunt is een drielandenpunt. Dus een ribbe verbindt twee drielandenpunten.
3) Er zijn eindig veel landen, en ze vullen het boloppervlak.
Nu de vragen:
1) Laat aan een voorbeeld zien dat een land minder buren kan hebben dan er ribben in zn grens zitten Die heb ik al
2) Leg uit waarom er een land is met hoogstens vier ribben in zn grens
3) Laat zien dat we de drielandenpunten van een + of - kunnen voorzien, zo dat elke ribbe een + met een - verbindt (beschouw een minimaal tegenvoorbeeld)
Tijdens het verhaal van de docent kwam ook een stelling van Euler naar voren. Die was iets van:
V - E + F = 2,
met V=vertices (hoekpunten), E=edges(ribben) en F=faces(landen),
maar ik zie ook niet hoe dat hier iets mee te maken heeft.
Wie kan mij helpen???
Theories come and theories go. The frog remains


V - E + F = 2 is Eulers formule voor planaire grafen. De juistheid hiervan kun je inzien door uit te gaan van een boom. Hiervoor geldt V - E = 1. Bij planaire (ook wel vlakke genoemd) grafen heb je altijd een buitenvlak. Dus voor een boom geldt dat V - E + F = 2. Door nu kanten toe te voegen creeer je ook telkens een extra vlak, waardoor de formule blijft gelden.
Elk punt heeft graad 3, dus je weet dat 2.E = 3.V. Dit invullen in de formule geeft 3.F = 6 + E. Als alle vlakken nu meer dan 4 kanten zou hebben, dus tenminste 6, dan heb je E >= 3.F en dit levert dan een tegenspraak.
Voor je derde vraag heb ik momenteel geen tijd .
Elk punt heeft graad 3, dus je weet dat 2.E = 3.V. Dit invullen in de formule geeft 3.F = 6 + E. Als alle vlakken nu meer dan 4 kanten zou hebben, dus tenminste 6, dan heb je E >= 3.F en dit levert dan een tegenspraak.
Voor je derde vraag heb ik momenteel geen tijd .


Bij die derde vraag moet je eerst proberen aan te tonen dat uit de voorwaarde dat elk land een evenhoek is volgt dat elke cykel in de puntengraaf even lengte heeft.


@ thabit: mijn bewijskunst is nogal waardeloos, dus ik zie niet hoe ik wat jij zegt aan moet tonen. Dit neemt niet weg dat ik wel snap waarom het zo is, ik kan t alleen niet echt verwoorden :S
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
@ Wolfje: dank je. Nu snap ik t. Tijdens college had de docent dat 2E = 3V ook wel laten zien, maar ik had geen idee wat 'ie nou bedoelde... maar nu dus wel
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
@ Wolfje: dank je. Nu snap ik t. Tijdens college had de docent dat 2E = 3V ook wel laten zien, maar ik had geen idee wat 'ie nou bedoelde... maar nu dus wel
Theories come and theories go. The frog remains


Als je dan begint ergens een + te zetten, dan zet je op elk punt met oneven afstand van die + een - en elk punt met even afstand van die + een +. Als elke cykel even lengte heeft, dan is de pariteit van het aantal stappen om van het ene punt naar het andere punt te komen onafhankelijk van het gekozen pad.quote:Op dinsdag 12 september 2006 15:28 schreef Bioman_1 het volgende:
@ thabit: mijn bewijskunst is nogal waardeloos, dus ik zie niet hoe ik wat jij zegt aan moet tonen. Dit neemt niet weg dat ik wel snap waarom het zo is, ik kan t alleen niet echt verwoorden :S
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
Het makkelijkst is hier om de drielandenpunt-voorwaarde op je graaf te laten vallen en te veronderstellen dat je een planaire graaf hebt waarvan elk land even grenslengte heeft. Dan kun je namelijk wat makkelijker gebruik maken van inductie.


heeloo!
we moeten dat 5| Fn <==> 5|n
Fn staat voor de nste term van de fibonacci rij.
ik heb nu moeite met het bewijzen van 5|n ==> 5| Fn of wel NIET( 5| Fn) ==> NIET (5|n)
ik dacht, schrijf n=5k+1 of 5k+2 of 5k+3 of 5k+4 maar verder dan dat kwam ik niet verder...
enige tips.. die kunnen helpen?
alvast bedankt
we moeten dat 5| Fn <==> 5|n
Fn staat voor de nste term van de fibonacci rij.
ik heb nu moeite met het bewijzen van 5|n ==> 5| Fn of wel NIET( 5| Fn) ==> NIET (5|n)
ik dacht, schrijf n=5k+1 of 5k+2 of 5k+3 of 5k+4 maar verder dan dat kwam ik niet verder...
enige tips.. die kunnen helpen?
alvast bedankt
verlegen :)


In dit speciale geval kun je de Fibonacci-rij modulo 5 opschrijven en constateren dat dat repeteert. In het algemeen kun je bewijzen dat
als m|n dan Fm|Fn
en voor alle m,n dat Fggd(m,n)=ggd(Fm,Fn) geldt.
als m|n dan Fm|Fn
en voor alle m,n dat Fggd(m,n)=ggd(Fm,Fn) geldt.


Een logica vraagje van de IQ-test van intermediar.nl:
Ik koos dus antwoord c omdat niet alle levenden mannen zijn, waardoor je nooit kunt concluderen dat alle mannen lui zijn. Maak ik nu een denkfoutquote:»alle mannen zijn levenden - sommige mannen zijn lui
A. geen levenden zijn lui
B. niet alle levenden zijn lui
C. tenminste sommige levenden zijn lui
D. geen conclusie mogelijk
Je koos antwoord c. Het juiste antwoord is b.


Bedankt voor de bevestiging, ik zat echt aan mijzelf te twijfelen.quote:Op woensdag 13 september 2006 14:21 schreef thabit het volgende:
C is correct. B is fout.


Help
Ik wil RQ-waardes experimenteel bepalen. De vorige poging was echter een regelrechte mislukking. Ik vermoed dat dit gedeeltelijk veroorzaakt wordt door het verschil in temperatuur van de ingeademde en de uitgeademde lucht.
De RQ-waarde is de verhouding tussen de geproduceerde CO2 (in l) en de gebruikte O2 (in l).
Om het volume geproduceerde CO2 te berekenen moet ik de ingeademde CO2 van de uitgeademde CO2 aftrekken.
Om het volume gebruikte O2 te berekenen moet ik de uitgeademde O2 aftrekken van de ingeademde O2.
De uitgeademde gassen zijn echter warmer, en hebben dus een groter volume dan de ingeademde gassen.
Is er een formule waarmee ik de volumes uitgeademde gassen terug kan brengen naar hun volume bij kamertemperatuur?
Ik wil RQ-waardes experimenteel bepalen. De vorige poging was echter een regelrechte mislukking. Ik vermoed dat dit gedeeltelijk veroorzaakt wordt door het verschil in temperatuur van de ingeademde en de uitgeademde lucht.
De RQ-waarde is de verhouding tussen de geproduceerde CO2 (in l) en de gebruikte O2 (in l).
Om het volume geproduceerde CO2 te berekenen moet ik de ingeademde CO2 van de uitgeademde CO2 aftrekken.
Om het volume gebruikte O2 te berekenen moet ik de uitgeademde O2 aftrekken van de ingeademde O2.
De uitgeademde gassen zijn echter warmer, en hebben dus een groter volume dan de ingeademde gassen.
Is er een formule waarmee ik de volumes uitgeademde gassen terug kan brengen naar hun volume bij kamertemperatuur?


Vertel eens wat meer. Wat meet je precies en hoe meet je het?
De ideale gasformule is een eerste benadering in dit geval. Maar de temperatuursstijging lijkt me niet echt hoog 25 en 35 C, scheelt 10 K op 300 K. De rest van je metingen zal waarschijnlijk meer dan een 3% foutmarge hebben.
De ideale gasformule is een eerste benadering in dit geval. Maar de temperatuursstijging lijkt me niet echt hoog 25 en 35 C, scheelt 10 K op 300 K. De rest van je metingen zal waarschijnlijk meer dan een 3% foutmarge hebben.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Ik heb een bepaalde opstelling. De ingeademde lucht en de uitgeademde lucht kunnen hiermee niet tegelijk geanalyseerd worden.
Deze opstelling geeft het gasvolume en de temperatuur van de aangezogen lucht aan. Vervolgens wordt er door het apparaat een staaltje van de aangezogen lucht geanalyseerd mbv een CO2-meter en een O2-meter die percentages aangeven. Mbv deze percentages en het gasvolume heb ik de volumes per gas berekend, voor zowel de ingeademde als de uitgeademde lucht. We hebben er dus geen rekening mee gehouden dat het volume aan uitgeademde gassen gewoon groter is.
Onze precieze werkwijze:
We bekijken de constante waardes van de ingeademde lucht.
Vervolgens laten we een proefpersoon uitademen in het apparaat. Per 0,01 m^3 uitgeademde lucht noteren we het percentage aan O2 en CO2.
We berekenen het verschil in uitgeademde CO2 en ingeademde CO2 en het verschil van de ingeademde O2 en de uitgeademde CO2. We delen dan de volumes van de verschillende gassen door elkaar
[ Bericht 26% gewijzigd door vliegtuigje op 15-09-2006 21:04:35 ]
Deze opstelling geeft het gasvolume en de temperatuur van de aangezogen lucht aan. Vervolgens wordt er door het apparaat een staaltje van de aangezogen lucht geanalyseerd mbv een CO2-meter en een O2-meter die percentages aangeven. Mbv deze percentages en het gasvolume heb ik de volumes per gas berekend, voor zowel de ingeademde als de uitgeademde lucht. We hebben er dus geen rekening mee gehouden dat het volume aan uitgeademde gassen gewoon groter is.
Onze precieze werkwijze:
We bekijken de constante waardes van de ingeademde lucht.
Vervolgens laten we een proefpersoon uitademen in het apparaat. Per 0,01 m^3 uitgeademde lucht noteren we het percentage aan O2 en CO2.
We berekenen het verschil in uitgeademde CO2 en ingeademde CO2 en het verschil van de ingeademde O2 en de uitgeademde CO2. We delen dan de volumes van de verschillende gassen door elkaar
[ Bericht 26% gewijzigd door vliegtuigje op 15-09-2006 21:04:35 ]


Meet je volume percentages of massa percentages.
Wat is het temperatuurverschil, wat zijn je meetwaarden en in hoeverre wijken die af van je verwachtingen.
Bedoel je hier met volume het volumedebiet (volume/tijd [m3/s]) en meet je dat continu?
Misschien is het een idee om niet in absolute volumens, maar om in volumepercentages te werken. Als je ervan uit gaat dat bij dit kleine temperatuurverschil alle gassen evenveel uitzetten is dat ook een mogelijkheid.
Wat is het temperatuurverschil, wat zijn je meetwaarden en in hoeverre wijken die af van je verwachtingen.
Bedoel je hier met volume het volumedebiet (volume/tijd [m3/s]) en meet je dat continu?
Misschien is het een idee om niet in absolute volumens, maar om in volumepercentages te werken. Als je ervan uit gaat dat bij dit kleine temperatuurverschil alle gassen evenveel uitzetten is dat ook een mogelijkheid.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Dat eerste is nog niet geheel duidelijk. Ze komen echter wel ongeveer overheen met de percentages die normale 'lucht' zou moeten hebben. Ik ga er dus vanuit dat het volumepercentages zijn.
Het temperatuurverschil is redelijk klein, meer dan 4 graden is het zeker niet.
De meetwaarden leken eerst te kloppen. Zoals we verwachtten neemt het percentage CO2 toe nadat men gegeten heeft. De hoeveelheid CO2 in de ingeademde lucht leek echter groter dan de theorie deed verwachten.
De verhouding klopt echter niet. We verkrijgen RQ-waardes die hoger zijn dan 1, wat onmogelijk is.
Het volume is echt puur het volume wat door het apparaat stroomt.
Het temperatuurverschil is redelijk klein, meer dan 4 graden is het zeker niet.
De meetwaarden leken eerst te kloppen. Zoals we verwachtten neemt het percentage CO2 toe nadat men gegeten heeft. De hoeveelheid CO2 in de ingeademde lucht leek echter groter dan de theorie deed verwachten.
De verhouding klopt echter niet. We verkrijgen RQ-waardes die hoger zijn dan 1, wat onmogelijk is.
Het volume is echt puur het volume wat door het apparaat stroomt.


V = (m * K * T) / p
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.


Iemand hier merkte net op dat het logisch zou zijn als de apparaten steeds het volumepercentage berekenen van stalen met hetzelfde volume.
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?


Zij (X,T) een topologische ruimte, E een topologische deelruimte van X en V een open-gesloten verzameling in E. Omdat V open is in E kun je stellen dat er een deelverzameling G1 van X is zodat de doorsnede van E en G1 gelijk is aan V. Omdat V ook gesloten is in E, is E \ V open en kun je dus ook stellen dat er een deelverzameling G2 van X is zodat de doorsnede van E en G2 gelijk is aan E \ V.
Maar kun je ook stellen dat er zulke G1 en G2 bestaan die disjunct zijn? Dat is namelijk precies wat ik nog nodig heb om een bepaald bewijs af te maken, maar ik zie eigenlijk zelf niet zo in dat er ook altijd disjuncte G1 en G2 zouden moeten bestaan.
Maar kun je ook stellen dat er zulke G1 en G2 bestaan die disjunct zijn? Dat is namelijk precies wat ik nog nodig heb om een bepaald bewijs af te maken, maar ik zie eigenlijk zelf niet zo in dat er ook altijd disjuncte G1 en G2 zouden moeten bestaan.


Ik neem aan dat G1 en G2 open moeten zijn? In dat geval kan het niet.
Neem maar een oneindige verzameling X met de co-eindige topologie (dwz de lege verzameling en alle complementen van eindige deelverzamelingen zijn open). Dit is een topologische ruimte waarin 2 niet-lege open delen altijd een niet-lege doorsnede hebben. Neem voor E een deelverzameling bestaande uit 2 punten en voor V een deelverzameling van E die uit 1 punt bestaat.
Neem maar een oneindige verzameling X met de co-eindige topologie (dwz de lege verzameling en alle complementen van eindige deelverzamelingen zijn open). Dit is een topologische ruimte waarin 2 niet-lege open delen altijd een niet-lege doorsnede hebben. Neem voor E een deelverzameling bestaande uit 2 punten en voor V een deelverzameling van E die uit 1 punt bestaat.


G1 en G2 mogen ook allebei gesloten zijn, maar jouw voorbeeld brengt me wel in verwarring dus ik ga alle definities nog even heel goed nalezen.


Als G1 en G2 allebei gesloten zijn kan het ook niet. Neem bijvoorbeeld X = R (i.e. de verzameling reele getallen met standaardtopologie), E = R-{0}, V = (0,oneindig).


Huh? Maar in dat geval kun je toch wel open G1 en G2 vinden? Namelijk (-oneindig,0) en (0,+oneindig).
Klopt het dat je wel altijd zo'n disjunct open paar of gesloten paar kan vinden als V onsamenhangend is?
Klopt het dat je wel altijd zo'n disjunct open paar of gesloten paar kan vinden als V onsamenhangend is?


Nog maar een voorbeeld dan. Neem voor X het projectieve vlak over een oneindig lichaam waarbij de gesloten delen alle eindige verenigingen van punten en lijnen zijn (en natuurlijk de hele X). Kies hierin twee lijnen L1 en L2 en noem het snijpunt P. Neem E = L1 U L2 - {P}, V = {L1} - P. Als ik me niet heb vergist is dit een voorbeeld waar je je disjuncte G1 en G2 noch allebei open, noch allebei gesloten kunt kiezen.
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".


Ik heb weinig biologische kenins, maar ik betwijfel het. Omdat een deel van de stoffen (vooral zuurstof) wordt opgenomen door het lichaam.quote:Op vrijdag 15 september 2006 21:16 schreef vliegtuigje het volgende:
V = (m * K * T) / p
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.
Reken eerst dV/dT (partiële afgeleide uit, of zoek de waarde op in een tabel) en kijk of er daadwerkelijk sprake is van een beetje toename in volume.quote:Op vrijdag 15 september 2006 21:20 schreef vliegtuigje het volgende:
Iemand hier merkte net op dat het logisch zou zijn als de apparaten steeds het volumepercentage berekenen van stalen met hetzelfde volume.
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?
Wat ik me wel afvraag is of je gemeten inademwaardes overeen komen met die waardes bij het uitademen, of dat het überhaupt goed mogelijk om dit soort dingen niet-continu te meten. Als er iemand overdreven uitademt in een apparaat krijg je waarschijnlijk gekke dingen.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...