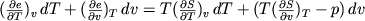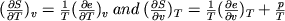SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Nieuw deeltje, vorige was vol.
Post hier weer al je vragen, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Wiskunde
Natuurkunde
Informatica
Scheikunde
Biologie
Algemene Natuurwetenschappen
Alles wat in de richting komt
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
Vorige deeltje Beta-huiswerkvragen
Post hier weer al je vragen, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen
Heb je een vraag die niet binnen het gebied 'Bèta' valt? Neem eens een kijkje in één van de volgende topics:
[Centraal] Gamma 'huiswerk en vragen topic'
[Centraal] Alfa 'huiswerk en vragen topic'
Vorige deeltje Beta-huiswerkvragen
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Sticky
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Die link linkt naar 2 betatopics terug. Dat moet deze zijn
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Vraag :
IQ aankomende studenten is normaal verdeeld met u=105 en o=15. Vanaf welk IQ behoort een student tot de 15% hoogste IQ-groep?
Mijn oplossing ->
y1 = normalcdf(X,10000,105,15). Bij X =120 y1 = 0.15 = 15%. IQ dus 120 of hoger. Vervolgens kijk ik wat het goede antwoord is, dat is 125.0. In mijn table is x=125 y1=0.09..
De vraag is dus of ik fout zit of het antwoordenvel.
IQ aankomende studenten is normaal verdeeld met u=105 en o=15. Vanaf welk IQ behoort een student tot de 15% hoogste IQ-groep?
Mijn oplossing ->
y1 = normalcdf(X,10000,105,15). Bij X =120 y1 = 0.15 = 15%. IQ dus 120 of hoger. Vervolgens kijk ik wat het goede antwoord is, dat is 125.0. In mijn table is x=125 y1=0.09..
De vraag is dus of ik fout zit of het antwoordenvel.


Y~N(105,225), Z~N(0,1).
Gevraagd is c zodat P(Y<c) = 0,85. Eenvoudig omschrijfwerk levert dat P((Y-105)/15 < (c-105)/15) = P(Z < (c-105)/15) = 0,85. Een tabellenboek levert dat (c-105)/15 gelijk is aan 1,04. Hieruit volgt dat c=120,6. Gebruikmakend van de tabel wordt er wat afgerond, maar 120 lijkt mij een juist antwoord.
Gevraagd is c zodat P(Y<c) = 0,85. Eenvoudig omschrijfwerk levert dat P((Y-105)/15 < (c-105)/15) = P(Z < (c-105)/15) = 0,85. Een tabellenboek levert dat (c-105)/15 gelijk is aan 1,04. Hieruit volgt dat c=120,6. Gebruikmakend van de tabel wordt er wat afgerond, maar 120 lijkt mij een juist antwoord.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


120 dacht ik dus ook... Ik heb nog een paar soortgelijke vragen gemaakt met andere gegevens en daarbij kwam mijn antwoord wel overeen met het antwoordenvel, dus ik denk dat bij bovenstaande vraag het antwoordenvel gewoon fout zit. Iig bedankt voor jouw berekening, al vind ik die van mij wat eenvoudiger


edit: Ok, laat maar... dit was een hele stomme vraag.
[ Bericht 47% gewijzigd door spinor op 01-09-2006 11:33:18 ]
[ Bericht 47% gewijzigd door spinor op 01-09-2006 11:33:18 ]


Vraagje, als ik van een driehoek 2 onbekende heb, hoe kan ik die dan vinden? situatie:
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
Bram! Boterham!


Ik weet niet wat je wil vinden, maar als links de rode lijn parallel is aan RT, dan is, onder de juiste voorwaarden, die driehoek gelijkbenig. De hoeken volgen daaruit en ook de lengtes zijn uit te rekenen. Maar ik weet niet wat je wilt weten.quote:Op vrijdag 1 september 2006 12:59 schreef lj_lightning het volgende:
Vraagje, als ik van een driehoek 2 onbekende heb, hoe kan ik die dan vinden? situatie:
[afbeelding]
Het gaat dan nu om de linkse situatie...volgens mij is het heel simpel maar ik weet niet (meer) hoe
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Ja ik was op school en heb er een kwartier over gedaan om mijn bericht proberen te editen Ik wil weten op welke hoogte die rode lijn 4cm is (dus ik wil de lengte weten van die zwarte verticale streep)quote:Op vrijdag 1 september 2006 15:23 schreef Wackyduck het volgende:
[..]
Ik weet niet wat je wil vinden, maar als links de rode lijn parallel is aan RT, dan is, onder de juiste voorwaarden, die driehoek gelijkbenig. De hoeken volgen daaruit en ook de lengtes zijn uit te rekenen. Maar ik weet niet wat je wilt weten.
en om die hoogte te weten moet ik de lengte van de aanliggende zijde en overstaande zijde weten...maar hoe?
Bram! Boterham!


Voor de hoogte zijn bij een gegeven lengte vaak 2 mogelijkheden (zowel in de driehoek onder- als bovenin). Noem die lengte van de rode lijn l en de lengte van de zwarte lijn h.
We onderscheiden twee situaties:
l<0 of l>4: geen oplossing
0<=l<=4:
Voor de eerste mogelijkheid geldt (l / (2h)) = tan(45) = 1 (waarom?). Omschrijven naar de hoogte is denk ik geen probleem.
Zolang h!=2 is de tweede oplossing gelijk aan 4-h.
Hierbij heb ik gebruik gemaakt dat het zij-aanzicht een vierkant is, en symmetrisch is in een verticale lijn.
[ Bericht 1% gewijzigd door GlowMouse op 02-09-2006 14:17:04 (grote fout :() ]
We onderscheiden twee situaties:
l<0 of l>4: geen oplossing
0<=l<=4:
Voor de eerste mogelijkheid geldt (l / (2h)) = tan(45) = 1 (waarom?). Omschrijven naar de hoogte is denk ik geen probleem.
Zolang h!=2 is de tweede oplossing gelijk aan 4-h.
Hierbij heb ik gebruik gemaakt dat het zij-aanzicht een vierkant is, en symmetrisch is in een verticale lijn.
[ Bericht 1% gewijzigd door GlowMouse op 02-09-2006 14:17:04 (grote fout :() ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hey allen, even een kort vraagje. Bij Thermo kom ik in de tekst het volgende tegen waar ik niet helemaal begrijp wat ze doen.
We komen van de 1e wet v d TD uit op:
mvg en bvd.
We komen van de 1e wet v d TD uit op:
Nu zie ik wel hoe de auteur er bij komt, maar wat hij nou wiskundig doet snap ik niet. dus wat dat uitdelen nu precies inhoudt...quote:(..)
equating the dT and dv terms gives:
mvg en bvd.


Je hebtquote:Op woensdag 6 september 2006 12:36 schreef pfaf het volgende:
Hey allen, even een kort vraagje. Bij Thermo kom ik in de tekst het volgende tegen waar ik niet helemaal begrijp wat ze doen.
We komen van de 1e wet v d TD uit op:
[..]
Nu zie ik wel hoe de auteur er bij komt, maar wat hij nou wiskundig doet snap ik niet. dus wat dat uitdelen nu precies inhoudt...
mvg en bvd.
a dT + b dv = c dT + d dv,
met a b c d variabel.
Ofwel
(a - c) dT = (d - b) dv.
Dit moet altijd waar zijn onafhankelijk van dT en dv, dat kan alleen maar als a-c en d-b 0 zijn, ofwel
a = c,
b = d.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Hoi allemaal.
Ik heb ff wat vraagjes over het vier-kleurenprobleem. Heb er vandaag college over gehad, maar kon de docent niet echt volgen... Hij bleef maar lachen om zn eigen anekdotes en opmerkingen enzo
Maar goed, we hebben het volgende:
Gegeven is een kaart op de bol met de volgende eigenschappen:
1) Elk land is een evenhoek. Dus de grens van een land vormt een rondweg met een even aantal ribben.
2) Elk meerlandenpunt is een drielandenpunt. Dus een ribbe verbindt twee drielandenpunten.
3) Er zijn eindig veel landen, en ze vullen het boloppervlak.
Nu de vragen:
1) Laat aan een voorbeeld zien dat een land minder buren kan hebben dan er ribben in zn grens zitten Die heb ik al
2) Leg uit waarom er een land is met hoogstens vier ribben in zn grens
3) Laat zien dat we de drielandenpunten van een + of - kunnen voorzien, zo dat elke ribbe een + met een - verbindt (beschouw een minimaal tegenvoorbeeld)
Tijdens het verhaal van de docent kwam ook een stelling van Euler naar voren. Die was iets van:
V - E + F = 2,
met V=vertices (hoekpunten), E=edges(ribben) en F=faces(landen),
maar ik zie ook niet hoe dat hier iets mee te maken heeft.
Wie kan mij helpen???
Ik heb ff wat vraagjes over het vier-kleurenprobleem. Heb er vandaag college over gehad, maar kon de docent niet echt volgen... Hij bleef maar lachen om zn eigen anekdotes en opmerkingen enzo
Maar goed, we hebben het volgende:
Gegeven is een kaart op de bol met de volgende eigenschappen:
1) Elk land is een evenhoek. Dus de grens van een land vormt een rondweg met een even aantal ribben.
2) Elk meerlandenpunt is een drielandenpunt. Dus een ribbe verbindt twee drielandenpunten.
3) Er zijn eindig veel landen, en ze vullen het boloppervlak.
Nu de vragen:
1) Laat aan een voorbeeld zien dat een land minder buren kan hebben dan er ribben in zn grens zitten Die heb ik al
2) Leg uit waarom er een land is met hoogstens vier ribben in zn grens
3) Laat zien dat we de drielandenpunten van een + of - kunnen voorzien, zo dat elke ribbe een + met een - verbindt (beschouw een minimaal tegenvoorbeeld)
Tijdens het verhaal van de docent kwam ook een stelling van Euler naar voren. Die was iets van:
V - E + F = 2,
met V=vertices (hoekpunten), E=edges(ribben) en F=faces(landen),
maar ik zie ook niet hoe dat hier iets mee te maken heeft.
Wie kan mij helpen???
Theories come and theories go. The frog remains


V - E + F = 2 is Eulers formule voor planaire grafen. De juistheid hiervan kun je inzien door uit te gaan van een boom. Hiervoor geldt V - E = 1. Bij planaire (ook wel vlakke genoemd) grafen heb je altijd een buitenvlak. Dus voor een boom geldt dat V - E + F = 2. Door nu kanten toe te voegen creeer je ook telkens een extra vlak, waardoor de formule blijft gelden.
Elk punt heeft graad 3, dus je weet dat 2.E = 3.V. Dit invullen in de formule geeft 3.F = 6 + E. Als alle vlakken nu meer dan 4 kanten zou hebben, dus tenminste 6, dan heb je E >= 3.F en dit levert dan een tegenspraak.
Voor je derde vraag heb ik momenteel geen tijd .
Elk punt heeft graad 3, dus je weet dat 2.E = 3.V. Dit invullen in de formule geeft 3.F = 6 + E. Als alle vlakken nu meer dan 4 kanten zou hebben, dus tenminste 6, dan heb je E >= 3.F en dit levert dan een tegenspraak.
Voor je derde vraag heb ik momenteel geen tijd .


Bij die derde vraag moet je eerst proberen aan te tonen dat uit de voorwaarde dat elk land een evenhoek is volgt dat elke cykel in de puntengraaf even lengte heeft.


@ thabit: mijn bewijskunst is nogal waardeloos, dus ik zie niet hoe ik wat jij zegt aan moet tonen. Dit neemt niet weg dat ik wel snap waarom het zo is, ik kan t alleen niet echt verwoorden :S
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
@ Wolfje: dank je. Nu snap ik t. Tijdens college had de docent dat 2E = 3V ook wel laten zien, maar ik had geen idee wat 'ie nou bedoelde... maar nu dus wel
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
@ Wolfje: dank je. Nu snap ik t. Tijdens college had de docent dat 2E = 3V ook wel laten zien, maar ik had geen idee wat 'ie nou bedoelde... maar nu dus wel
Theories come and theories go. The frog remains


Als je dan begint ergens een + te zetten, dan zet je op elk punt met oneven afstand van die + een - en elk punt met even afstand van die + een +. Als elke cykel even lengte heeft, dan is de pariteit van het aantal stappen om van het ene punt naar het andere punt te komen onafhankelijk van het gekozen pad.quote:Op dinsdag 12 september 2006 15:28 schreef Bioman_1 het volgende:
@ thabit: mijn bewijskunst is nogal waardeloos, dus ik zie niet hoe ik wat jij zegt aan moet tonen. Dit neemt niet weg dat ik wel snap waarom het zo is, ik kan t alleen niet echt verwoorden :S
Maar wat ik eigenlijk niet zie is: waarom heeft dat wat je zegt iets te maken met de vraag?
Het makkelijkst is hier om de drielandenpunt-voorwaarde op je graaf te laten vallen en te veronderstellen dat je een planaire graaf hebt waarvan elk land even grenslengte heeft. Dan kun je namelijk wat makkelijker gebruik maken van inductie.


heeloo!
we moeten dat 5| Fn <==> 5|n
Fn staat voor de nste term van de fibonacci rij.
ik heb nu moeite met het bewijzen van 5|n ==> 5| Fn of wel NIET( 5| Fn) ==> NIET (5|n)
ik dacht, schrijf n=5k+1 of 5k+2 of 5k+3 of 5k+4 maar verder dan dat kwam ik niet verder...
enige tips.. die kunnen helpen?
alvast bedankt
we moeten dat 5| Fn <==> 5|n
Fn staat voor de nste term van de fibonacci rij.
ik heb nu moeite met het bewijzen van 5|n ==> 5| Fn of wel NIET( 5| Fn) ==> NIET (5|n)
ik dacht, schrijf n=5k+1 of 5k+2 of 5k+3 of 5k+4 maar verder dan dat kwam ik niet verder...
enige tips.. die kunnen helpen?
alvast bedankt
verlegen :)


In dit speciale geval kun je de Fibonacci-rij modulo 5 opschrijven en constateren dat dat repeteert. In het algemeen kun je bewijzen dat
als m|n dan Fm|Fn
en voor alle m,n dat Fggd(m,n)=ggd(Fm,Fn) geldt.
als m|n dan Fm|Fn
en voor alle m,n dat Fggd(m,n)=ggd(Fm,Fn) geldt.


Een logica vraagje van de IQ-test van intermediar.nl:
Ik koos dus antwoord c omdat niet alle levenden mannen zijn, waardoor je nooit kunt concluderen dat alle mannen lui zijn. Maak ik nu een denkfoutquote:»alle mannen zijn levenden - sommige mannen zijn lui
A. geen levenden zijn lui
B. niet alle levenden zijn lui
C. tenminste sommige levenden zijn lui
D. geen conclusie mogelijk
Je koos antwoord c. Het juiste antwoord is b.


Bedankt voor de bevestiging, ik zat echt aan mijzelf te twijfelen.quote:Op woensdag 13 september 2006 14:21 schreef thabit het volgende:
C is correct. B is fout.


Help
Ik wil RQ-waardes experimenteel bepalen. De vorige poging was echter een regelrechte mislukking. Ik vermoed dat dit gedeeltelijk veroorzaakt wordt door het verschil in temperatuur van de ingeademde en de uitgeademde lucht.
De RQ-waarde is de verhouding tussen de geproduceerde CO2 (in l) en de gebruikte O2 (in l).
Om het volume geproduceerde CO2 te berekenen moet ik de ingeademde CO2 van de uitgeademde CO2 aftrekken.
Om het volume gebruikte O2 te berekenen moet ik de uitgeademde O2 aftrekken van de ingeademde O2.
De uitgeademde gassen zijn echter warmer, en hebben dus een groter volume dan de ingeademde gassen.
Is er een formule waarmee ik de volumes uitgeademde gassen terug kan brengen naar hun volume bij kamertemperatuur?
Ik wil RQ-waardes experimenteel bepalen. De vorige poging was echter een regelrechte mislukking. Ik vermoed dat dit gedeeltelijk veroorzaakt wordt door het verschil in temperatuur van de ingeademde en de uitgeademde lucht.
De RQ-waarde is de verhouding tussen de geproduceerde CO2 (in l) en de gebruikte O2 (in l).
Om het volume geproduceerde CO2 te berekenen moet ik de ingeademde CO2 van de uitgeademde CO2 aftrekken.
Om het volume gebruikte O2 te berekenen moet ik de uitgeademde O2 aftrekken van de ingeademde O2.
De uitgeademde gassen zijn echter warmer, en hebben dus een groter volume dan de ingeademde gassen.
Is er een formule waarmee ik de volumes uitgeademde gassen terug kan brengen naar hun volume bij kamertemperatuur?


Vertel eens wat meer. Wat meet je precies en hoe meet je het?
De ideale gasformule is een eerste benadering in dit geval. Maar de temperatuursstijging lijkt me niet echt hoog 25 en 35 C, scheelt 10 K op 300 K. De rest van je metingen zal waarschijnlijk meer dan een 3% foutmarge hebben.
De ideale gasformule is een eerste benadering in dit geval. Maar de temperatuursstijging lijkt me niet echt hoog 25 en 35 C, scheelt 10 K op 300 K. De rest van je metingen zal waarschijnlijk meer dan een 3% foutmarge hebben.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Ik heb een bepaalde opstelling. De ingeademde lucht en de uitgeademde lucht kunnen hiermee niet tegelijk geanalyseerd worden.
Deze opstelling geeft het gasvolume en de temperatuur van de aangezogen lucht aan. Vervolgens wordt er door het apparaat een staaltje van de aangezogen lucht geanalyseerd mbv een CO2-meter en een O2-meter die percentages aangeven. Mbv deze percentages en het gasvolume heb ik de volumes per gas berekend, voor zowel de ingeademde als de uitgeademde lucht. We hebben er dus geen rekening mee gehouden dat het volume aan uitgeademde gassen gewoon groter is.
Onze precieze werkwijze:
We bekijken de constante waardes van de ingeademde lucht.
Vervolgens laten we een proefpersoon uitademen in het apparaat. Per 0,01 m^3 uitgeademde lucht noteren we het percentage aan O2 en CO2.
We berekenen het verschil in uitgeademde CO2 en ingeademde CO2 en het verschil van de ingeademde O2 en de uitgeademde CO2. We delen dan de volumes van de verschillende gassen door elkaar
[ Bericht 26% gewijzigd door vliegtuigje op 15-09-2006 21:04:35 ]
Deze opstelling geeft het gasvolume en de temperatuur van de aangezogen lucht aan. Vervolgens wordt er door het apparaat een staaltje van de aangezogen lucht geanalyseerd mbv een CO2-meter en een O2-meter die percentages aangeven. Mbv deze percentages en het gasvolume heb ik de volumes per gas berekend, voor zowel de ingeademde als de uitgeademde lucht. We hebben er dus geen rekening mee gehouden dat het volume aan uitgeademde gassen gewoon groter is.
Onze precieze werkwijze:
We bekijken de constante waardes van de ingeademde lucht.
Vervolgens laten we een proefpersoon uitademen in het apparaat. Per 0,01 m^3 uitgeademde lucht noteren we het percentage aan O2 en CO2.
We berekenen het verschil in uitgeademde CO2 en ingeademde CO2 en het verschil van de ingeademde O2 en de uitgeademde CO2. We delen dan de volumes van de verschillende gassen door elkaar
[ Bericht 26% gewijzigd door vliegtuigje op 15-09-2006 21:04:35 ]


Meet je volume percentages of massa percentages.
Wat is het temperatuurverschil, wat zijn je meetwaarden en in hoeverre wijken die af van je verwachtingen.
Bedoel je hier met volume het volumedebiet (volume/tijd [m3/s]) en meet je dat continu?
Misschien is het een idee om niet in absolute volumens, maar om in volumepercentages te werken. Als je ervan uit gaat dat bij dit kleine temperatuurverschil alle gassen evenveel uitzetten is dat ook een mogelijkheid.
Wat is het temperatuurverschil, wat zijn je meetwaarden en in hoeverre wijken die af van je verwachtingen.
Bedoel je hier met volume het volumedebiet (volume/tijd [m3/s]) en meet je dat continu?
Misschien is het een idee om niet in absolute volumens, maar om in volumepercentages te werken. Als je ervan uit gaat dat bij dit kleine temperatuurverschil alle gassen evenveel uitzetten is dat ook een mogelijkheid.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Dat eerste is nog niet geheel duidelijk. Ze komen echter wel ongeveer overheen met de percentages die normale 'lucht' zou moeten hebben. Ik ga er dus vanuit dat het volumepercentages zijn.
Het temperatuurverschil is redelijk klein, meer dan 4 graden is het zeker niet.
De meetwaarden leken eerst te kloppen. Zoals we verwachtten neemt het percentage CO2 toe nadat men gegeten heeft. De hoeveelheid CO2 in de ingeademde lucht leek echter groter dan de theorie deed verwachten.
De verhouding klopt echter niet. We verkrijgen RQ-waardes die hoger zijn dan 1, wat onmogelijk is.
Het volume is echt puur het volume wat door het apparaat stroomt.
Het temperatuurverschil is redelijk klein, meer dan 4 graden is het zeker niet.
De meetwaarden leken eerst te kloppen. Zoals we verwachtten neemt het percentage CO2 toe nadat men gegeten heeft. De hoeveelheid CO2 in de ingeademde lucht leek echter groter dan de theorie deed verwachten.
De verhouding klopt echter niet. We verkrijgen RQ-waardes die hoger zijn dan 1, wat onmogelijk is.
Het volume is echt puur het volume wat door het apparaat stroomt.


V = (m * K * T) / p
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.


Iemand hier merkte net op dat het logisch zou zijn als de apparaten steeds het volumepercentage berekenen van stalen met hetzelfde volume.
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?


Zij (X,T) een topologische ruimte, E een topologische deelruimte van X en V een open-gesloten verzameling in E. Omdat V open is in E kun je stellen dat er een deelverzameling G1 van X is zodat de doorsnede van E en G1 gelijk is aan V. Omdat V ook gesloten is in E, is E \ V open en kun je dus ook stellen dat er een deelverzameling G2 van X is zodat de doorsnede van E en G2 gelijk is aan E \ V.
Maar kun je ook stellen dat er zulke G1 en G2 bestaan die disjunct zijn? Dat is namelijk precies wat ik nog nodig heb om een bepaald bewijs af te maken, maar ik zie eigenlijk zelf niet zo in dat er ook altijd disjuncte G1 en G2 zouden moeten bestaan.
Maar kun je ook stellen dat er zulke G1 en G2 bestaan die disjunct zijn? Dat is namelijk precies wat ik nog nodig heb om een bepaald bewijs af te maken, maar ik zie eigenlijk zelf niet zo in dat er ook altijd disjuncte G1 en G2 zouden moeten bestaan.


Ik neem aan dat G1 en G2 open moeten zijn? In dat geval kan het niet.
Neem maar een oneindige verzameling X met de co-eindige topologie (dwz de lege verzameling en alle complementen van eindige deelverzamelingen zijn open). Dit is een topologische ruimte waarin 2 niet-lege open delen altijd een niet-lege doorsnede hebben. Neem voor E een deelverzameling bestaande uit 2 punten en voor V een deelverzameling van E die uit 1 punt bestaat.
Neem maar een oneindige verzameling X met de co-eindige topologie (dwz de lege verzameling en alle complementen van eindige deelverzamelingen zijn open). Dit is een topologische ruimte waarin 2 niet-lege open delen altijd een niet-lege doorsnede hebben. Neem voor E een deelverzameling bestaande uit 2 punten en voor V een deelverzameling van E die uit 1 punt bestaat.


G1 en G2 mogen ook allebei gesloten zijn, maar jouw voorbeeld brengt me wel in verwarring dus ik ga alle definities nog even heel goed nalezen.


Als G1 en G2 allebei gesloten zijn kan het ook niet. Neem bijvoorbeeld X = R (i.e. de verzameling reele getallen met standaardtopologie), E = R-{0}, V = (0,oneindig).


Huh? Maar in dat geval kun je toch wel open G1 en G2 vinden? Namelijk (-oneindig,0) en (0,+oneindig).
Klopt het dat je wel altijd zo'n disjunct open paar of gesloten paar kan vinden als V onsamenhangend is?
Klopt het dat je wel altijd zo'n disjunct open paar of gesloten paar kan vinden als V onsamenhangend is?


Nog maar een voorbeeld dan. Neem voor X het projectieve vlak over een oneindig lichaam waarbij de gesloten delen alle eindige verenigingen van punten en lijnen zijn (en natuurlijk de hele X). Kies hierin twee lijnen L1 en L2 en noem het snijpunt P. Neem E = L1 U L2 - {P}, V = {L1} - P. Als ik me niet heb vergist is dit een voorbeeld waar je je disjuncte G1 en G2 noch allebei open, noch allebei gesloten kunt kiezen.
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".


Ik heb weinig biologische kenins, maar ik betwijfel het. Omdat een deel van de stoffen (vooral zuurstof) wordt opgenomen door het lichaam.quote:Op vrijdag 15 september 2006 21:16 schreef vliegtuigje het volgende:
V = (m * K * T) / p
Kan ik er vanuit gaan dat het aantal mol ingeademde lucht gelijk is aan het aantal mol ingeademde lucht? dan zou ik nl met de algemene gaswet kunnen berekenen wat de toename in volume is.
Deze is dan vrij verwaarloosbaar.
Reken eerst dV/dT (partiële afgeleide uit, of zoek de waarde op in een tabel) en kijk of er daadwerkelijk sprake is van een beetje toename in volume.quote:Op vrijdag 15 september 2006 21:20 schreef vliegtuigje het volgende:
Iemand hier merkte net op dat het logisch zou zijn als de apparaten steeds het volumepercentage berekenen van stalen met hetzelfde volume.
Het enige wat er dan zou verandere bij een temperatuurstijging is het aantal mol van zo'n staal.
Dan zou ik met de volgende formule kunnen berekenen hoeveel mol er per liter is bij een temperatuurstijging van enkele graden:
(p * V) / (K * T) = n
Klopt dat?
Wat ik me wel afvraag is of je gemeten inademwaardes overeen komen met die waardes bij het uitademen, of dat het überhaupt goed mogelijk om dit soort dingen niet-continu te meten. Als er iemand overdreven uitademt in een apparaat krijg je waarschijnlijk gekke dingen.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Waar het om gaat is dit:
De telling van een mechanische tapecounter om te zetten in minuten en seconden.
Bijvoorbeeld dat je weet dat als de teller 0500 aanwijst dat je op 5:30 minuten van je tape zit.
De formule die hiervoor gebruikt kan worden is :
t = K1 * theta - K2*theta2
waarbij t = de tijd, theta de tellerstand en K1 en K2 constanten. Nu moet je dus eerst die constanten berekenen.
Nu is dit 1 vergelijking met 2 onbekenden, maar je kunt gewoon 2 waarden pakken.
Bijvoorbeeld
Bij 23 minuten staat de tapecounter op 1450
Bij 45 minuten (1 kant van een 90min bandje) staat de tapecounter op 2356
Maar ik kom er toch niet uit.
t1 = K1 * theta - K2*theta2
t2 = K1 * theta - K2*theta2
Dus:
23 = K1 * 1450 - K2 * 14502
45 = K1 * 2356 - K2 * 23562
K1 * 1450 - K2 * 14502 - 23 = 0
K1 * 2356 - K2 * 23562 - 45 = 0
1450K1 - 2102500K2 - 23 = 0
2356K1 - 5550736K2 - 45 = 0
1450K1 - 2345K1 - 2102500K2 + 5550736K2 - 23 + 45 = 0
Gaat dit wel goed? Hoe nu verder? 'k ben verdorie de hele avond al aan het rekenen maar ik kom er niet uit.
Het zijn 2 vergelijkingen met 2 onbekenden dus dat zou op te lossen moeten zijn.
De telling van een mechanische tapecounter om te zetten in minuten en seconden.
Bijvoorbeeld dat je weet dat als de teller 0500 aanwijst dat je op 5:30 minuten van je tape zit.
De formule die hiervoor gebruikt kan worden is :
t = K1 * theta - K2*theta2
waarbij t = de tijd, theta de tellerstand en K1 en K2 constanten. Nu moet je dus eerst die constanten berekenen.
Nu is dit 1 vergelijking met 2 onbekenden, maar je kunt gewoon 2 waarden pakken.
Bijvoorbeeld
Bij 23 minuten staat de tapecounter op 1450
Bij 45 minuten (1 kant van een 90min bandje) staat de tapecounter op 2356
Maar ik kom er toch niet uit.
t1 = K1 * theta - K2*theta2
t2 = K1 * theta - K2*theta2
Dus:
23 = K1 * 1450 - K2 * 14502
45 = K1 * 2356 - K2 * 23562
K1 * 1450 - K2 * 14502 - 23 = 0
K1 * 2356 - K2 * 23562 - 45 = 0
1450K1 - 2102500K2 - 23 = 0
2356K1 - 5550736K2 - 45 = 0
1450K1 - 2345K1 - 2102500K2 + 5550736K2 - 23 + 45 = 0
Gaat dit wel goed? Hoe nu verder? 'k ben verdorie de hele avond al aan het rekenen maar ik kom er niet uit.
Het zijn 2 vergelijkingen met 2 onbekenden dus dat zou op te lossen moeten zijn.
Geduld
(zelfst. naamw.)
Iets dat op is tegen de middag.
(zelfst. naamw.)
Iets dat op is tegen de middag.


Je moet die eerste vergelijking vermenigvuldigen met 2356/1450. Als je dan de vergelijkingen van elkaar aftrekt is de konstante K_1 verdwenen, dus kan je K_2 gewoon berekenen. K_1 volgt hier dan weer uit.


een opdracht van ANW waar ik niet uitkom;
Je loopt met een groep van 10 man in een rotswoestijn bij 45 graden. Jullie hebben te weinig water en er komt diarree. De tocht duurt 3-4 dagen en je hebt voor 1.5 dag water.
Langs de weg kom je poeltjes en artesisch water tegen. Je mag een rugzak van met 10 kg meenemen. Wat neem je mee en waarom? (ook werden we verwezen naar Norit, Immodium en ORS). Wie heeft een idee?
Je loopt met een groep van 10 man in een rotswoestijn bij 45 graden. Jullie hebben te weinig water en er komt diarree. De tocht duurt 3-4 dagen en je hebt voor 1.5 dag water.
Langs de weg kom je poeltjes en artesisch water tegen. Je mag een rugzak van met 10 kg meenemen. Wat neem je mee en waarom? (ook werden we verwezen naar Norit, Immodium en ORS). Wie heeft een idee?
my future seems like one big past...


Ik zou een vouwfiets mee nemen, dan kun je vast wel 3 keer zo snel gaan en heb je dus voldoende water voor de hele tocht .quote:Op zondag 17 september 2006 14:10 schreef alyel het volgende:
een opdracht van ANW waar ik niet uitkom;
Je loopt met een groep van 10 man in een rotswoestijn bij 45 graden. Jullie hebben te weinig water en er komt diarree. De tocht duurt 3-4 dagen en je hebt voor 1.5 dag water.
Langs de weg kom je poeltjes en artesisch water tegen. Je mag een rugzak van met 10 kg meenemen. Wat neem je mee en waarom? (ook werden we verwezen naar Norit, Immodium en ORS). Wie heeft een idee?


Of een radio-installatie om hulp in te roepen.quote:Op zondag 17 september 2006 14:26 schreef Wolfje het volgende:
[..]
Ik zou een vouwfiets mee nemen, dan kun je vast wel 3 keer zo snel gaan en heb je dus voldoende water voor de hele tocht .
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Ik zoek de afgeleide van de volgende functie:
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking


Maak gebruik van wortel(x) = x^0.5 en van de kettingregelquote:Op zondag 17 september 2006 15:04 schreef -tK- het volgende:
Ik zoek de afgeleide van de volgende functie:
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking


Het is al opgelost. De stelling die ik moest bewijzen blijkt helemaal niet te kloppen.quote:Op zaterdag 16 september 2006 16:30 schreef thabit het volgende:
Nog maar een voorbeeld dan. Neem voor X het projectieve vlak over een oneindig lichaam waarbij de gesloten delen alle eindige verenigingen van punten en lijnen zijn (en natuurlijk de hele X). Kies hierin twee lijnen L1 en L2 en noem het snijpunt P. Neem E = L1 U L2 - {P}, V = {L1} - P. Als ik me niet heb vergist is dit een voorbeeld waar je je disjuncte G1 en G2 noch allebei open, noch allebei gesloten kunt kiezen.
Ik vrees dat je toch een andere aanpak moet verzinnen voor je "bepaald bewijs".


f[x] = sqrt(x^2 + 4)quote:Op zondag 17 september 2006 15:04 schreef -tK- het volgende:
Ik zoek de afgeleide van de volgende functie:
f1(x) = Wortel(x2+4)
Het antwoord weet ik want die staat achterin het boek, maar de berekening mist en ik zou het zelf niet meer weten
Ook kon ik geen vergelijkbare functies terugvinden in het boek met een uitwerking
f[x] = (x^2 + 4)^0.5
f'[x] = 0.5(x^2 + 4)^-0,5 * 2x = (x^2 + 4)^-0.5 * x = (1 / sqrt(x^2 + 4)) * x
[ Bericht 2% gewijzigd door thomzor op 20-09-2006 00:26:58 ]


Stel A is een aftelbare deelverzameling van [0,1] en g een toenemende functie van [0,1] naar R+. Kan de (stieltjes)integraal [0 tot 1] 1Adg gedefinieerd zijn als A oneindig veel elementen bevat?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


En om het helemaal af te maken kan je er ook nog x/sqrt(4+x^2) van makenquote:Op woensdag 20 september 2006 00:21 schreef thomzor het volgende:
[..]
f[x] = sqrt(x^2 + 4)
f[x] = (x^2 + 4)^0.5
f'[x] = 0.5(x^2 + 4)^-0,5 * 2x = (x^2 + 4)^-0.5 * x = (1 / sqrt(x^2 + 4)) * x
"I'm trained not to see beautiful women, because they might distract me from my mission."


dat staat er al...quote:Op woensdag 20 september 2006 19:15 schreef Thundertje het volgende:
[..]
En om het helemaal af te maken kan je er ook nog x/sqrt(4+x^2) van maken


he hee!
ik heb gehoord over een functie die overal continu is en toch nergens differentieerbaar is..
ik bedoel niet de functie
f(x)=1 als x uit Q is
f(x)=0 als x uit RQ is
want deze is toch niet continu...
ik weet niet meer van wie die functie was... dus wie die had geconstrueerd...
groetjes
ik heb gehoord over een functie die overal continu is en toch nergens differentieerbaar is..
ik bedoel niet de functie
f(x)=1 als x uit Q is
f(x)=0 als x uit RQ is
want deze is toch niet continu...
ik weet niet meer van wie die functie was... dus wie die had geconstrueerd...
groetjes
verlegen :)


Een mechanicavraagje . (Plaatje kan er ik niet bijdoen ivm ontbreken scanner).
Iemand staat voorovergebukt. Beschouw romp, hoofd en armen als een hefboom. In de heupen ligt het scharnierpunt S. Het zwaartepunt van de hefboom ligt op 20cm van S. Spieren oefenen bij de schouders (die 60 cm van het scharnierpunt liggen) een kracht uit van 900N om de hefboom in evenwicht te houden. Deze spierkracht maakt een hoek van 9,3 graden met de horizontaal.
a) Bereken de massa van de hefboom (hoofd, romp en armen).
b) Bereken hoe groot de kracht is die in het scharnierpunt S op de onderrug werkt.
Bij a dacht ik aan het volgende antwoord: 0,2 x m x 9,8 = 0,6 x 900
m = 32 kg (afgerond). IK weet niet of het klopt, maar persoonlijk vind het erg weinig voor de romp, hoofd en armen van een volwassen man.
Bij b dacht ik aan: sin 9,3 graden = overstaande / 900
Overstaande = sin 9,3 graden x 900 = 145 newton (naar beneden afgerond).
Alvast bedankt voor het helpen
Iemand staat voorovergebukt. Beschouw romp, hoofd en armen als een hefboom. In de heupen ligt het scharnierpunt S. Het zwaartepunt van de hefboom ligt op 20cm van S. Spieren oefenen bij de schouders (die 60 cm van het scharnierpunt liggen) een kracht uit van 900N om de hefboom in evenwicht te houden. Deze spierkracht maakt een hoek van 9,3 graden met de horizontaal.
a) Bereken de massa van de hefboom (hoofd, romp en armen).
b) Bereken hoe groot de kracht is die in het scharnierpunt S op de onderrug werkt.
Bij a dacht ik aan het volgende antwoord: 0,2 x m x 9,8 = 0,6 x 900
m = 32 kg (afgerond). IK weet niet of het klopt, maar persoonlijk vind het erg weinig voor de romp, hoofd en armen van een volwassen man.
Bij b dacht ik aan: sin 9,3 graden = overstaande / 900
Overstaande = sin 9,3 graden x 900 = 145 newton (naar beneden afgerond).
Alvast bedankt voor het helpen


hehee.. twee vraagjes over c++
while statement....
int count = 3;
while ( count-- > 0)
cout << count << " ";
de uitput is 2 1 0 (waarom ook 0 ?)
en wat betekent het als er --count stond..? dus wat is eigenlijk --count?
kan iemand mij helpen? thanx.
while statement....
int count = 3;
while ( count-- > 0)
cout << count << " ";
de uitput is 2 1 0 (waarom ook 0 ?)
en wat betekent het als er --count stond..? dus wat is eigenlijk --count?
kan iemand mij helpen? thanx.
verlegen :)


Bij count-- > 0 bekijkt hij eerst count > 0 en dan pas wordt count-- uitgevoerd. Bij --count > 0 wordt eerst --count gedaan en dan pas count > 0 bekeken.


Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Wie kan mij een tip geven?
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet.
[ Bericht 6% gewijzigd door de_priester op 25-09-2006 11:18:42 ]
Wie kan mij een tip geven?
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet.
[ Bericht 6% gewijzigd door de_priester op 25-09-2006 11:18:42 ]
Imperare sibi maximum imperium est


Een werkende link zou handig zijn...quote:Op zondag 24 september 2006 21:46 schreef de_priester het volgende:
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Wie kan mij een tip geven?
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je kunt natuurlijk ook de 2 commando's/expressies apart opschrijven in plaats van in 1 expressie te willen stoppen, wordt je code heel wat leesbaarder door.quote:Op zondag 24 september 2006 20:50 schreef teletubbies het volgende:
okee! thanx
lastige taal is dit, visual basic was een stukje makkelijker


nogmaals, met werkende link:
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet, want bij substitutie van de vgls gaat het steeds mis. (en dat doe ik in maple)
De gangbare aanpak is volgens mij met massabehoud, impulsbehoud, en bernouillie
massabehoud en impulsbehoud staan hieronder, maar hoe moet ik bernouillie toepassen?
kan iemand ff checken of dit de goede kant op werkt
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet, want bij substitutie van de vgls gaat het steeds mis. (en dat doe ik in maple)
De gangbare aanpak is volgens mij met massabehoud, impulsbehoud, en bernouillie
massabehoud en impulsbehoud staan hieronder, maar hoe moet ik bernouillie toepassen?
kan iemand ff checken of dit de goede kant op werkt
Imperare sibi maximum imperium est


Kan iemand mij helpen? Ik doe nu VWO en alles gaat me prima af behalve Wiskunde B1.
Ik zit nog in de basis met differentieren maar ik snap echt niet hoe je in godsnaam dit doet.
Interval is dus [X, X+DeltaX]
En dan voor de Functie, f(x) = X^3
Dan doe je Delta Y/Detla X.
Delta Y wordt dan:
Maar hoe ga je in godsnaam daarheen? Dit vond ik in het antwoordenboekje, maar ik snap niet hoe je dit doet
Kan iemand dit met stap voor stap uitleggen?
Ik zit nog in de basis met differentieren maar ik snap echt niet hoe je in godsnaam dit doet.
Interval is dus [X, X+DeltaX]
En dan voor de Functie, f(x) = X^3
Dan doe je Delta Y/Detla X.
Delta Y wordt dan:
Maar hoe ga je in godsnaam daarheen? Dit vond ik in het antwoordenboekje, maar ik snap niet hoe je dit doet
Kan iemand dit met stap voor stap uitleggen?
"the female orgasme is a mythe, I hae had sex with 26 women in my life and not one of them had a orgasme."


a=x^3
b=delta x^3
(a+b)^3 -a^3=
(a+b)(a+b)(a+b) - a^3= (a+b)(a^2+2ab+b^2) -a^3
= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 - a^3
= 3a^2b + 3ab^2 + b^3
Ik kom dus hier op uit.
Ik mis dus de factor x^3 want die vervalt bij mij en bij jou niet.
b=delta x^3
(a+b)^3 -a^3=
(a+b)(a+b)(a+b) - a^3= (a+b)(a^2+2ab+b^2) -a^3
= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 - a^3
= 3a^2b + 3ab^2 + b^3
Ik kom dus hier op uit.
Ik mis dus de factor x^3 want die vervalt bij mij en bij jou niet.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


f(x) = x^3
f'(x) = 3x^2
x^g = g*x^(g-1)
^ basisregel afgeleiden
edit: laatmaar ik begrijp geloof ik de vraag niet echt
f'(x) = 3x^2
x^g = g*x^(g-1)
^ basisregel afgeleiden
edit: laatmaar ik begrijp geloof ik de vraag niet echt


Tjah dat is meer 4 Havo stofquote:Op maandag 25 september 2006 20:16 schreef thomzor het volgende:
f(x) = x^3
f'(x) = 3x^2
x^g = g*x^(g-1)
^ basisregel afgeleiden
edit: laatmaar ik begrijp geloof ik de vraag niet echt
Het gaat erom dat je het op een andere manier laat zien hoe je van X^3 naar 3X^2 gaat. En dat moet met heel veel machten en delta's
"the female orgasme is a mythe, I hae had sex with 26 women in my life and not one of them had a orgasme."


Heel erg bedankt, hier begin ik al iets meer van te snappen.quote:Op maandag 25 september 2006 20:16 schreef -J-D- het volgende:
a=x^3
b=delta x^3
(a+b)^3 -a^3=
(a+b)(a+b)(a+b) - a^3= (a+b)(a^2+2ab+b^2) -a^3
= a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 - a^3
= 3a^2b + 3ab^2 + b^3
Ik kom dus hier op uit.
Ik mis dus de factor x^3 want die vervalt bij mij en bij jou niet.
"the female orgasme is a mythe, I hae had sex with 26 women in my life and not one of them had a orgasme."


Das dan 5 euro.quote:Op maandag 25 september 2006 21:13 schreef HomerJ het volgende:
[..]
Heel erg bedankt, hier begin ik al iets meer van te snappen.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


nog iemand ? (heb tot morgen 11.00 u)quote:Op maandag 25 september 2006 11:22 schreef de_priester het volgende:
nogmaals, met werkende link:
Ik heb een vraagje, over een vraagstuk waar ik in zijn geheel niet uitkom.
Het gaat om het volgende:
http://www.ahd.tudelft.nl(...)/vraagst/Vrgst-5.pdf
en dan B
Ik weet niet welke vgl's ik het beste kan gebruiken om tot een kloppend antwoord te komen!
Het lukt me steeds niet, want bij substitutie van de vgls gaat het steeds mis. (en dat doe ik in maple)
De gangbare aanpak is volgens mij met massabehoud, impulsbehoud, en bernouillie
massabehoud en impulsbehoud staan hieronder, maar hoe moet ik bernouillie toepassen?
kan iemand ff checken of dit de goede kant op werkt
[afbeelding]
Imperare sibi maximum imperium est


lol , ik heb wiskunde B2 gedaan op t vwo en ik heb nog nooit gezien wat jij daar deed XDquote:Op maandag 25 september 2006 21:09 schreef HomerJ het volgende:
[..]
Tjah dat is meer 4 Havo stof
Het gaat erom dat je het op een andere manier laat zien hoe je van X^3 naar 3X^2 gaat. En dat moet met heel veel machten en delta's
zal wel aan mijn school (of de jouwe) liggen dan


Ik heb Wiskunde B1, misschien ligt het daar aan?
Anyway, weet iemand anders nog hoe je kan laten zien dat:
f(x)= X^3 = f'(x) 3X^2
Zonder dus differentieregels maar meer met Delta Y
Anyway, weet iemand anders nog hoe je kan laten zien dat:
f(x)= X^3 = f'(x) 3X^2
Zonder dus differentieregels maar meer met Delta Y
"the female orgasme is a mythe, I hae had sex with 26 women in my life and not one of them had a orgasme."


he hee!
hoe moet ik bewijzen dat er oneindig veel priemgetallen zijn die bij deling door 4, rest 3 geven.
thanx
hoe moet ik bewijzen dat er oneindig veel priemgetallen zijn die bij deling door 4, rest 3 geven.
thanx
verlegen :)


De aanpak is hetzelfde als hoe je bewijst dat er oneindig veel priemgetallen zijn. Stel dat er maar N (eindig uiteraard) priemgetallen -1 mod 4 zijn. Definieer x = 2 + p_1^2....p_N^2. Er geldt dat x = -1 mod 4. Als x geen priemgetal is, dan moet het wel een deler -1 mod 4 hebben. Maar dit kan niet omdat het wel p_1^2...p_N^2 deelt maar niet 2. Dus er zijn oneindig veel priemgetallen van de vorm 3 mod 4.quote:Op dinsdag 26 september 2006 21:40 schreef teletubbies het volgende:
he hee!
hoe moet ik bewijzen dat er oneindig veel priemgetallen zijn die bij deling door 4, rest 3 geven.
thanx
Leuk sommetje! Ik had hem zelf nog niet eerder gezien .


Wat een gelijkheden, klopt geen zak van. Je zegt nu dat f(x) gelijk is aan f'(x).quote:f(x)= X^3 = f'(x) 3X^2
Met behulp van de definitie: lim(k->0) (f(c+k)-f(c)) / k = lim(k->0) ((c+k)³-c³)/k = lim(k->0) (3c²k+3ck²+k³)/k = lim(k->0) 3c²+3ck+k² = 3c².
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ik dacht aan die aanpak ook.quote:Op dinsdag 26 september 2006 22:12 schreef Wolfje het volgende:
[..]
De aanpak is hetzelfde als hoe je bewijst dat er oneindig veel priemgetallen zijn. Stel dat er maar N (eindig uiteraard) priemgetallen -1 mod 4 zijn. Definieer x = 2 + p_1^2....p_N^2. Er geldt dat x = -1 mod 4. Als x geen priemgetal is, dan moet het wel een deler -1 mod 4 hebben. Maar dit kan niet omdat het wel p_1^2...p_N^2 deelt maar niet 2. Dus er zijn oneindig veel priemgetallen van de vorm 3 mod 4.
Leuk sommetje! Ik had hem zelf nog niet eerder gezien .
alleen ik gebruikte p1...pn*4+3= N (n het nieuwe priemgetal ). maar goed k kwam moeilijkheden tegen..
k ga het zo doorlezen
thanx
verlegen :)


Jouw getalletje werkt inderdaad ook wel als je eist dat p_i <> 3. Het gaat erom dat een getal dat 3 mod 4 is, altijd een factor 3 mod 4 heeft. Maak hierbij gebruik van (a mod c)*(b mod c) = (a*b) mod c.quote:Op dinsdag 26 september 2006 22:53 schreef teletubbies het volgende:
[..]
ik dacht aan die aanpak ook.
alleen ik gebruikte p1...pn*4+3= N (n het nieuwe priemgetal ). maar goed k kwam moeilijkheden tegen..
k ga het zo doorlezen
thanx


Laat antwoord, maar ik ben het er niet mee eens. Stel dat er wel levenden zijn maar geen van dezen zijn mannelijk, en aangezien alleen mannen lui kunnen zijn zijn er dan niet per se luie levenden.quote:Op woensdag 13 september 2006 14:21 schreef thabit het volgende:
C is correct. B is fout.


"Sommige mannen zijn lui". Hieruit kun je afleiden dat er mannen zijn.quote:Op woensdag 27 september 2006 19:38 schreef Aibmi het volgende:
[..]
Laat antwoord, maar ik ben het er niet mee eens. Stel dat er wel levenden zijn maar geen van dezen zijn mannelijk, en aangezien alleen mannen lui kunnen zijn zijn er dan niet per se luie levenden.


Er staat nergens dat alleen mannen lui kunnen zijn. Voor de rest verwijs ik naar thabit's commentaar .quote:Op woensdag 27 september 2006 19:38 schreef Aibmi het volgende:
[..]
Laat antwoord, maar ik ben het er niet mee eens. Stel dat er wel levenden zijn maar geen van dezen zijn mannelijk, en aangezien alleen mannen lui kunnen zijn zijn er dan niet per se luie levenden.


Oei, ik had meerdere keren moeten lezen/nadenken voordat ik tegen thabit in zou gaan op zijn terrein. Maar wat jij zegt klopt niet. Als er niet staat dat niet-mannen lui kunnen zijn, weet je het niet zeker, en kun je er dus van uit gaan dat ze niet lui zijn(bij dit soort logische redeneringen moet je alleen van zekerheden uitgaan).quote:Op woensdag 27 september 2006 19:54 schreef Wolfje het volgende:
[..]
Er staat nergens dat alleen mannen lui kunnen zijn. Voor de rest verwijs ik naar thabit's commentaar .


Het enige wat je zeker weet is dat je er niks over kunt zeggen. En toch doe jij dat door te stellen dat je er vanuit kunt gaan dat ze niet lui zijn.quote:weet je het niet zeker, en kun je er dus van uit gaan dat ze niet lui zijn(bij dit soort logische redeneringen moet je alleen van zekerheden uitgaan).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ok, knullig geformuleerd. Daar ben ik het mee eens. Maar ik bedoelde in ieder geval dat je nooit er van uit kan gaan dat het wel zo is als het niet zeker is. In dit geval had ik dus wel gelijk, want het niet conclusies kunnen trekken uit niet bestaande informatie komt op het zelfde neer als negatief aannemen.quote:Op woensdag 27 september 2006 20:05 schreef GlowMouse het volgende:
[..]
Het enige wat je zeker weet is dat je er niks over kunt zeggen. En toch doe jij dat door te stellen dat je er vanuit kunt gaan dat ze niet lui zijn.


Ik heb een vraagje over:
Impliciet Differentiëren
de opgave:
xy=6e^(2x-3y)
Mijn gedachte was:
xy'+y=(2-3y')6e^(2x-3y)
xy'+y=(12-18y')e^(2x-3y)
Kan iemand mij helpen?
Impliciet Differentiëren
de opgave:
xy=6e^(2x-3y)
Mijn gedachte was:
xy'+y=(2-3y')6e^(2x-3y)
xy'+y=(12-18y')e^(2x-3y)
Kan iemand mij helpen?


Je gedachten kloppen. Mocht je nog willen herschrijven naar y'= ..., zorg dan eerst dat je y' aan een kant krijgt en haal y' buiten haakjes.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt voor je reactie!
Dat was idd mijn volgende gedachte, maar ik kwam er niet verder uit.
Ik wist maar niet hoe ik y'= zou moeten krijgen.
Ik weet het nog steeds niet:'(
[ Bericht 10% gewijzigd door Rejected op 28-09-2006 13:40:10 ]
Dat was idd mijn volgende gedachte, maar ik kwam er niet verder uit.
Ik wist maar niet hoe ik y'= zou moeten krijgen.
Ik weet het nog steeds niet:'(
[ Bericht 10% gewijzigd door Rejected op 28-09-2006 13:40:10 ]


Zorg eerst dat je y' aan een kant krijgt: xy' + 18y'*exp(2x-3y) = 12*exp(2x-3y)-y
Dan y' buiten haakjes halen: y'(x+18*exp(2x-3y) = 12*exp(2x-3y)-y
Dan links en rechts delen door 18*exp(2x-3y): y' = (12*exp(2x-3y)-y) / 18*exp(2x-3y) = 2/3 - y/ 18*exp(2x-3y).
Dan y' buiten haakjes halen: y'(x+18*exp(2x-3y) = 12*exp(2x-3y)-y
Dan links en rechts delen door 18*exp(2x-3y): y' = (12*exp(2x-3y)-y) / 18*exp(2x-3y) = 2/3 - y/ 18*exp(2x-3y).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik snap niet precies wat er in de 1e regel gebeurt, om y' aan uitsluitend aan de linkerkant te krijgen moet je toch delen door (12-18y')??quote:Op donderdag 28 september 2006 17:53 schreef GlowMouse het volgende:
Zorg eerst dat je y' aan een kant krijgt: xy' + 18y'*exp(2x-3y) = 12*exp(2x-3y)-y
Dan y' buiten haakjes halen: y'(x+18*exp(2x-3y) = 12*exp(2x-3y)-y
Dan links en rechts delen door 18*exp(2x-3y): y' = (12*exp(2x-3y)-y) / 18*exp(2x-3y) = 2/3 - y/ 18*exp(2x-3y).


Als je daardoor deelt, is hij rechts weg maar houd je links een term y/(12-18y') over. Je krijgt dan y' niet meer los zonder weer met 12-18y' te vermenigvuldigen.
Wat ik doe, is rechts de haakjes wegwerken en dan 18y'*exp(2x-3y) links en rechts optellen.
Wat ik doe, is rechts de haakjes wegwerken en dan 18y'*exp(2x-3y) links en rechts optellen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik heb het al een keer eerder gevraagt maar ik kom er niet uit het gaat om het volgende:
Ik moet 'Punt X' berekenen, ik moet namelijk weten op welke hoogte het vierkantje (dat blauwe vlakje) 4x4 cm is... hoe is dit te doen? Cos Tas Toa is even geleden maar ik weet alleen dat hoek Q 45graden is... kan je dan Cos/Tas/Toa toepassen?
Ik moet 'Punt X' berekenen, ik moet namelijk weten op welke hoogte het vierkantje (dat blauwe vlakje) 4x4 cm is... hoe is dit te doen? Cos Tas Toa is even geleden maar ik weet alleen dat hoek Q 45graden is... kan je dan Cos/Tas/Toa toepassen?
Bram! Boterham!


Kan je hier iets mee?
Verhoudingen
btw. het is SOS CAS TOA en niet TAS of zo
Maar dat heb je dus nu ff niet nodig.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Van 'cos/tas/toa' heb ik niet gehoord, maar als je dit op kunt lossen, kan het met goniometrie. Als de bissectrice van Q tekent, kún je twee rechthoekige driehoeken zien ontstaan. Voorwaarde is dan wel dat het blauwe vlakje recht ligt.quote:Op vrijdag 29 september 2006 14:02 schreef lj_lightning het volgende:
Ik heb het al een keer eerder gevraagt maar ik kom er niet uit het gaat om het volgende:
[afbeelding]
Ik moet 'Punt X' berekenen, ik moet namelijk weten op welke hoogte het vierkantje (dat blauwe vlakje) 4x4 cm is... hoe is dit te doen? Cos Tas Toa is even geleden maar ik weet alleen dat hoek Q 45graden is... kan je dan Cos/Tas/Toa toepassen?
Waarom zou het blauwe vlakje trouwens niet bovenin de balk zitten?
Op je tekening lijkt hoek Q trouwens eerder 90 graden, maar dat maakt verder niet uit.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ehh ja goniometrie en bissectrice komen niet in mijn woordeboekje voor Het is 5Havo btwquote:Op vrijdag 29 september 2006 14:10 schreef GlowMouse het volgende:
[..]
Van 'cos/tas/toa' heb ik niet gehoord, maar als je dit op kunt lossen, kan het met goniometrie. Als de bissectrice van Q tekent, kún je twee rechthoekige driehoeken zien ontstaan. Voorwaarde is dan wel dat het blauwe vlakje recht ligt.
Waarom zou het blauwe vlakje trouwens niet bovenin de balk zitten?
Op je tekening lijkt hoek Q trouwens eerder 90 graden, maar dat maakt verder niet uit.
en hoek Q is 90 graden, foutje van mij
Bram! Boterham!


Kun je nagaan hoelang het geleden is komt gelukkig niet opt examen dacht ikquote:Op vrijdag 29 september 2006 14:09 schreef -J-D- het volgende:
[afbeelding]
Kan je hier iets mee?
Verhoudingen
btw. het is SOS CAS TOA en niet TAS of zo
Maar dat heb je dus nu ff niet nodig.
Maar met verhoudings tabellen heb ik eik nog nooit gezien bij meetkunde het klopt wel (ik gebruik sketchup en die laat de afmetingen zien en het is 2,0cm en 4x2,85/5,65 is 2,0
Bram! Boterham!


Het ging me dan ook te ver om het helemaal voor je uit te rekenen.
Ging er wel vanuit dat het nu zou lukken.
Succes
Ging er wel vanuit dat het nu zou lukken.
Succes
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Boer wil land afzetten, maar alleen het gedeelte dat niet aan de sloot grenst, zie Figuur. Er is 40m schrikdraad
a. Druk AB uit in x
b. Druk de oppervlakte O van het af te zetten stuk land uit in x.
c. Onderzoek de grootst mogelijke oppervlakte van het land dat Boer op deze manier af kan zetten.
De antwoorden
a. Druk AB uit in x
b. Druk de oppervlakte O van het af te zetten stuk land uit in x.
c. Onderzoek de grootst mogelijke oppervlakte van het land dat Boer op deze manier af kan zetten.
De antwoorden
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Die antwoorden zijn natuurlijk wel leuk, en c snap ik ook wel, max intoetsen op je GR, maar ik snap A en B niet, want buiten de antwoorden heb ik geen uitwerkingen. Wie kan me helpen?Op maandag 9 november 2009 12:25 schreef Whiskey_Tango het volgende:
Dat interesseert GroenLinks voor geen meter, ze zien je als een wandelende zak euro's waar ze handig een tap in kunnen drukken voor hun socialistische hobbies.


Linkerlengte X
Rechterlengte X-4
Totale lengte AB + X + X-4 = AB + 2X - 4 = 40
AB = 44 - 2x
O = AB * X = 44X - 2X2
Maximum bij dO/dX = 0
dO/dX = 44 - 4X = 0
X = 11
En dat in O invullen
Rechterlengte X-4
Totale lengte AB + X + X-4 = AB + 2X - 4 = 40
AB = 44 - 2x
O = AB * X = 44X - 2X2
Maximum bij dO/dX = 0
dO/dX = 44 - 4X = 0
X = 11
En dat in O invullen
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Het is me gelukt ben net klaar, pff wat een werk (mocht je ge-intresseerd zijn: hier is de opgave oa te vinden )quote:Op vrijdag 29 september 2006 18:24 schreef -J-D- het volgende:
Het ging me dan ook te ver om het helemaal voor je uit te rekenen.
Ging er wel vanuit dat het nu zou lukken.
Succes
Morgen de foutjes eruit halen, nu eerst pitten
Bram! Boterham!


"Max intoetsen op je GR"
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


En het dan wel snappenquote:Op zaterdag 30 september 2006 17:51 schreef Haushofer het volgende:
"Max intoetsen op je GR"
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


In een huiswerk opdracht moest ik bewijzen dat van een bepaalde parameterfunctie de functie door alle toppen van die parameterfunctie gelijk was aan 1/(2x).
Goed, afgeleide bepalen, p schrijven als x, invullen, en dan krijg ik er uiteindelijk dit uit:
y = (x2+4)/(2x3+8x)
dan moet ik dat dus herleiden tot 1/(2x)
Je ziet dat het antwoord goed is, als je (x2+4)/(2x3+8x) = 1/(2x) kruislings vermenigvuldigt zie je dat het klopt. Maar het lukt me maar niet om via de officiële stappen die functie te herleiden. Ik denk waarschijnlijk heel raar na (bovendien ben ik slecht in deelstrepen etc.)
Kan iemand me laten zien hoe je dat herleidt?
Goed, afgeleide bepalen, p schrijven als x, invullen, en dan krijg ik er uiteindelijk dit uit:
y = (x2+4)/(2x3+8x)
dan moet ik dat dus herleiden tot 1/(2x)
Je ziet dat het antwoord goed is, als je (x2+4)/(2x3+8x) = 1/(2x) kruislings vermenigvuldigt zie je dat het klopt. Maar het lukt me maar niet om via de officiële stappen die functie te herleiden. Ik denk waarschijnlijk heel raar na (bovendien ben ik slecht in deelstrepen etc.)
Kan iemand me laten zien hoe je dat herleidt?
- Als een wijs man een goede reden heeft het woord te voeren houdt hij moeiteloos een goed betoog.
- You can say that again
- You can say that again


Haal bij 2x³+8x eens 2x buiten haakjes.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


| 1 2 3 4 5 6 7 8 9 10 11 12 | ih: 3^(n-1) >= 1 + 2(n-1)^2 3^n = 3 * 3^(n-1) >= { ih } 3 * (1 + 2(n-1)^2) = 3 * (1 + 2n^2) - 12x + 6 >= 1 + 2n^2 |
volgens mij klopt het opzich wel (typefouten daargelaten), alleen vind ik mijn laatste stap vrij onduidelijk
is er iemand hier (ongetwijfeld) die het beter/duidelijker kan en eventueel feedback kan geven
bvd


3 * (1 + 2n^2) - 12n + 6
>=
1 + 2n^2
Is dit de stap die je niet volgt?
Dit is waar als 8 + 4 n^2 >= 12n , als je dat bewijst ben je er.
>=
1 + 2n^2
Is dit de stap die je niet volgt?
Dit is waar als 8 + 4 n^2 >= 12n , als je dat bewijst ben je er.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


ja ik volg het wel, ik heb het namelijk zelf gedaan - maar ik kan me voorstellen dat het nogal een grote stap is / onduidelijk isquote:Op zondag 1 oktober 2006 17:43 schreef Wackyduck het volgende:
3 * (1 + 2n^2) - 12n + 6
>=
1 + 2n^2
Is dit de stap die je niet volgt?
Dit is waar als 8 + 4 n^2 >= 12n , als je dat bewijst ben je er.
ik vroeg me af of het niet makkelijker kon :p


Een tijdje terug postte ik al een aantal vragen mbt linear programmeren. Het meeste heb ik inmiddels wel op kunnen lossen alleen zit ik nog met één probleem.
A_t zijn binaire variabelen
s is een integer variabele
Y_t zijn (binaire) parameters
Nu wil ik het volgende lineariseren:
A_{t+s} >= Y_t voor alle t
Iemand enig idee hoe ik dit aanpak? Het probleem zit hem er dus in dat in de index van variabele A een variabele zit... Als iemand een oplossing weet in het geval dat A_t geen variabele, maar een parameter is hoor ik dat ook graag.
A_t zijn binaire variabelen
s is een integer variabele
Y_t zijn (binaire) parameters
Nu wil ik het volgende lineariseren:
A_{t+s} >= Y_t voor alle t
Iemand enig idee hoe ik dit aanpak? Het probleem zit hem er dus in dat in de index van variabele A een variabele zit... Als iemand een oplossing weet in het geval dat A_t geen variabele, maar een parameter is hoor ik dat ook graag.


Bedoel je:
4x5 = 12 ?
Dan x = (12/4)^(1/5) = 31/5
Zit er niet zo'n xy knop op je rekenapparaat?
4x5 = 12 ?
Dan x = (12/4)^(1/5) = 31/5
Zit er niet zo'n xy knop op je rekenapparaat?
Theories come and theories go. The frog remains


Zelf ook een vraag:
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
Vandaag dus geleerd dat als je twee getallen a en b hebt (die allebei een onnauwkeurigheid bevatten - denk bijv. aan meetwaarden) dat de berekening erg uit kan maken voor de propagatie van je afrondfouten.
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.
Zo is het bijvoorbeeld ook beter (nauwkeuriger) om NIET sin(a) - sin(b) te berekenen, maar juist
2 * sin((a-b)/2) * cos((a+b)/2)
(wat uiteraard gelijk is aan sin(a) - sin(b) als je over EXACTE waarde zou beschikken, maar dat is dus niet zo).
Nu vraag ik mij bijvoorbeeld af wat de beste (meest nauwkeurige) manier is om bijv:
log(x) - log(x-1) , x>>1
uit te rekenen. Of bijv:
(ex - 1)/x, |x|<<1
Tot aan vandaag had ik gedacht dat je gewoon de log van x zou berekenen, dan de log van x-1 en dan die van elkaar aftrekken. Maar na vandaag twijfel ik of dat nog wel de meest nauwkeurige manier is.
Iemand suggesties?
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
Vandaag dus geleerd dat als je twee getallen a en b hebt (die allebei een onnauwkeurigheid bevatten - denk bijv. aan meetwaarden) dat de berekening erg uit kan maken voor de propagatie van je afrondfouten.
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.
Zo is het bijvoorbeeld ook beter (nauwkeuriger) om NIET sin(a) - sin(b) te berekenen, maar juist
2 * sin((a-b)/2) * cos((a+b)/2)
(wat uiteraard gelijk is aan sin(a) - sin(b) als je over EXACTE waarde zou beschikken, maar dat is dus niet zo).
Nu vraag ik mij bijvoorbeeld af wat de beste (meest nauwkeurige) manier is om bijv:
log(x) - log(x-1) , x>>1
uit te rekenen. Of bijv:
(ex - 1)/x, |x|<<1
Tot aan vandaag had ik gedacht dat je gewoon de log van x zou berekenen, dan de log van x-1 en dan die van elkaar aftrekken. Maar na vandaag twijfel ik of dat nog wel de meest nauwkeurige manier is.
Iemand suggesties?
Theories come and theories go. The frog remains


b) Een bedrag van ¤6000 is op 1 januari 2005 op een bankrekening gestort. Na 10 jaar staat er ¤8881,47 op deze rekening. Wat is het gehanteerde rentepercentage op jaarbasis?
ik weet hoe ik t moet uitrekenen alleen niet op de calculator
ik weet hoe ik t moet uitrekenen alleen niet op de calculator
bier


Steeds zie je dat het nauwkeuriger kan door een uitdrukking om te schrijven. log(x) - log(x-1) kun je denk ik niet omschrijven. (exp(x)-1)/x wel: exp(x)/x - 1/x = x-log(x)-1/x. Of het nauwkeuriger is, kun je zelf zo proberen.
Als je weet hoe je het uit moet rekenen, gebruik je daar toch al de calculator voor? Waarom zou je dat anders willen? Verder is het natuurlijk van belang of er sprake is van discreet/continu samengestelde of van enkelvoudige interest.quote:b) Een bedrag van ¤6000 is op 1 januari 2005 op een bankrekening gestort. Na 10 jaar staat er ¤8881,47 op deze rekening. Wat is het gehanteerde rentepercentage op jaarbasis?
ik weet hoe ik t moet uitrekenen alleen niet op de calculator
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


log(x) - log(x-1) = log(x/(x-1)) = log(1 + 1/(x-1)).quote:Op woensdag 4 oktober 2006 21:25 schreef Bioman_1 het volgende:
Zelf ook een vraag:
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
Vandaag dus geleerd dat als je twee getallen a en b hebt (die allebei een onnauwkeurigheid bevatten - denk bijv. aan meetwaarden) dat de berekening erg uit kan maken voor de propagatie van je afrondfouten.
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.
Zo is het bijvoorbeeld ook beter (nauwkeuriger) om NIET sin(a) - sin(b) te berekenen, maar juist
2 * sin((a-b)/2) * cos((a+b)/2)
(wat uiteraard gelijk is aan sin(a) - sin(b) als je over EXACTE waarde zou beschikken, maar dat is dus niet zo).
Nu vraag ik mij bijvoorbeeld af wat de beste (meest nauwkeurige) manier is om bijv:
log(x) - log(x-1) , x>>1
uit te rekenen. Of bijv:
(ex - 1)/x, |x|<<1
Tot aan vandaag had ik gedacht dat je gewoon de log van x zou berekenen, dan de log van x-1 en dan die van elkaar aftrekken. Maar na vandaag twijfel ik of dat nog wel de meest nauwkeurige manier is.
Iemand suggesties?
Als x >> 1, dan is y = 1/(x-1) heel dicht bij 0.
Nu is log(1+y) = y - y2/2 + y3/3 - ...
Dit convergeert natuurlijk heel snel als y heel klein is.
Evenzo kun je gebruiken dat ex = 1 + x + x2/2! + x3/3! + ... .
dus
(ex - 1)/x = 1 + x/2! + x2/3! + ... .


jaa via het uitwerking boekje heb ik gezien hoe het moet,alleen op me rekenmachine krijg ik het niet voor elkaarquote:Op woensdag 4 oktober 2006 22:52 schreef GlowMouse het volgende:
Steeds zie je dat het nauwkeuriger kan door een uitdrukking om te schrijven. log(x) - log(x-1) kun je denk ik niet omschrijven. (exp(x)-1)/x wel: exp(x)/x - 1/x = x-log(x)-1/x. Of het nauwkeuriger is, kun je zelf zo proberen.
[..]
Als je weet hoe je het uit moet rekenen, gebruik je daar toch al de calculator voor? Waarom zou je dat anders willen? Verder is het natuurlijk van belang of er sprake is van discreet/continu samengestelde of van enkelvoudige interest.
bier


Weet je al wel welke vergelijking je op moet lossen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


6000*x^10=8881,47 dus.
Ik geef je als tip de algemene regel voor logaritmen.
a log b = c <=> a^c=b
Als je er niet uit komt, vertel dan waar je nu vast komt te zitten.
Ik geef je als tip de algemene regel voor logaritmen.
a log b = c <=> a^c=b
Als je er niet uit komt, vertel dan waar je nu vast komt te zitten.


Je hebt op je rekenmachine een "e" toets, deze heeft het variabele "× 10n" Dan moet je dus intypen 6000Xe10.quote:Op donderdag 5 oktober 2006 07:15 schreef italiaan1987 het volgende:
6000 X x tot de 10 = 8881,47
Op maandag 9 november 2009 12:25 schreef Whiskey_Tango het volgende:
Dat interesseert GroenLinks voor geen meter, ze zien je als een wandelende zak euro's waar ze handig een tap in kunnen drukken voor hun socialistische hobbies.
Dat interesseert GroenLinks voor geen meter, ze zien je als een wandelende zak euro's waar ze handig een tap in kunnen drukken voor hun socialistische hobbies.


De meeste rekenmachines kunnen niet 6000*x10 uitrekenen. En zelfs als je een luxe rekenmachine hebt die dat wel kan, zal het je vertellen dat dat gelijk is aan 6000*x10.quote:Op donderdag 5 oktober 2006 07:26 schreef --Christiaan-- het volgende:
[..]
Je hebt op je rekenmachine een "e" toets, deze heeft het variabele "× 10n" Dan moet je dus intypen 6000Xe10.
De tip voor logaritmen is trouwens ook nutteloos. Het is nu eenvoudige algebra. De enige regel die je misschien niet kent luidt dat als ab = c, dan a = c1/b.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


6000*x^10=8881,47
x^10 = 1,4802 berekend door 8881,47 door 6000 te delen
x = ^10wortel van 1,4802
en dit ken ik dus nie berekenen op de calculator
x^10 = 1,4802 berekend door 8881,47 door 6000 te delen
x = ^10wortel van 1,4802
en dit ken ik dus nie berekenen op de calculator
bier


Kun je wel x^y berekenen voor willekeurige x en y? Zoja, zie mijn tip, zonee, dan gaat jou dit niet lukken met deze rekenmachine (of je moet met inklemmen willen werken).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Tuurlijk wel. Er zit toch wel een toets voor xy o.i.d. op je calculator, en een toets voor inverse functies? Met de calculator in Windows XP gaat het trouwens ook gemakkelijk. Vinkje bij Inv aanzetten en dan intoetsen: 1.4802 x^y 10 = en je krijgt als antwoord 1.0399968885584896330874361342892. De rente is dus 4%.quote:Op donderdag 5 oktober 2006 15:33 schreef italiaan1987 het volgende:
x = ^10wortel van 1,4802
en dit kan ik dus niet berekenen op de calculator
Je kunt natuurlijk ook bedenken dat het trekken van de 10-de machtswortel gelijk staat aan verheffen tot de macht 1/10, dan heb je de inverse functietoets van je calculator niet eens nodig.


ik heb het knopje gevonden om het te berekenen op de calculator
het is 10 Shift ^1,4802 en dan kom je indd op 4% rente uit
het is 10 Shift ^1,4802 en dan kom je indd op 4% rente uit
bier


Ik ben met Elektrostatica de volgende integraal tegengekomen en het lukt me niet 't onding op te lossen. Weet iemand raad?
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
Ik zou degene die me 't antwoord verschaf bijzonder dankbaar zijn
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
Ik zou degene die me 't antwoord verschaf bijzonder dankbaar zijn


Heb je het al geprobeerd met zwavelzuur?quote:Op zaterdag 7 oktober 2006 20:03 schreef Greus het volgende:
Ik ben met Elektrostatica de volgende integraal tegengekomen en het lukt me niet 't onding op te lossen. Weet iemand raad?
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
[afbeelding]
Ik zou degene die me 't antwoord verschaf bijzonder dankbaar zijn
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


Je vraagt in feite naar het primitiveren van de functie x∙(x2 - √2∙a∙x + a2)-½. In eerste instantie zou je dus (x2 - √2∙a∙x + a2)½ kunnen uitproberen. Differentiëren van de laatste geeft:quote:Op zaterdag 7 oktober 2006 20:03 schreef Greus het volgende:
Ik ben met Elektrostatica de volgende integraal tegengekomen en het lukt me niet 't onding op te lossen. Weet iemand raad?
Het gaat om de volgende integraal (oplossing komt van Wolfram, maar het gaat me uiteraard om de uitwerking):
[afbeelding]
Ik zou degene die me 't antwoord verschaft bijzonder dankbaar zijn
½∙(x2 - √2∙a∙x + a2)-½∙ (2x - √2∙a) =
x∙(x2 - √2∙a∙x + a2)-½ - ½∙√2∙a∙(x2 - √2∙a∙x + a2)-½
De eerste term is precies de functie waarvan we een primitieve willen vinden, maar de tweede term willen we er niet bij hebben. Dat betekent dat we nu nog een functie moeten vinden waarvan de afgeleide gelijk is aan het tegendeel van de tweede term, anders gezegd, we zoeken nu nog een primitieve van:
½∙√2∙a∙(x2 - √2∙a∙x + a2)-½
De som van een primitieve van deze functie en (x2 - √2∙a∙x + a2)½ zal dan bij differentiatie het gewenste resultaat x∙(x2 - √2∙a∙x + a2)-½ opleveren.
Om nu een primitieve te vinden van ½∙√2∙a∙(x2 - √2∙a∙x + a2)-½ moet je de kwadratische veelterm onder het wortelteken eerst schrijven als een som van twee kwadraten. Je hebt:
(x - ½∙√2∙a)2 = x2 - √2∙a∙x + (½∙√2∙a)2 = x2 - √2∙a∙x + ½∙a2, zodat we vinden dat:
x2 - √2∙a∙x + a2 = (x - ½∙√2∙a)2 + (½∙√2∙a)2
Nu kun je de factor ½∙√2∙a buiten het wortelteken halen (we nemen aan dat a > 0) en een substitutie z = (x - ½∙√2∙a)/(½∙√2∙a) uitvoeren. We hebben dan:
½∙√2∙a∙(x2 - √2∙a∙x + a2)-½ = (z2 + 1)-½
Uit z = (x - ½∙√2∙a)/(½∙√2∙a) volgt dz/dx = 1/(½∙√2∙a) dus dx/dz = ½∙√2∙a. Het probleem is nu herleid tot het vinden van een primitieve van
½∙√2∙a∙ (z2 + 1)-½
Deze laatste functie is, op de factor ½∙√2∙a na, een standaardfunctie. Een primitieve hiervan is de inverse functie van de hyperbolische functie sinh(z), oftewel arcsinh(z). Deze laatste kun je ook schrijven als
ln(z + (z2 + 1)½)
Substitutie van z = (x - ½∙√2∙a)/(½∙√2∙a) levert dan, op een constante na, hetzelfde resultaat als Mathematica. Bedenk hierbij dat je een constante ½∙√2∙a∙ln(√2∙a) bij de gevonden primitieve op kunt tellen om op precies hetzelfde resultaat uit te komen als Mathematica. Maak hiervoor gebruik van ln(p) + ln(q) = ln(p∙q) en breng dan de factor ½∙√2∙a weer onder het wortelteken.
Nog een opmerking over het primitiveren van de functie
(z2 + 1)-½
Om hiervan een primitieve te vinden maakt men gebruik van de substitutie z = sinh(u) zodat dz/du = cosh(u). Aangezien cosh2(u) - sinh2(u) = 1 volgt dan direct dat u = arcsinh(z) een primitieve is.
[ Bericht 1% gewijzigd door Riparius op 08-10-2006 03:54:21 ]


Fantastisch, bedanktquote:Op zondag 8 oktober 2006 03:41 schreef Riparius het volgende:
[..]
Je vraagt in feite naar het primitiveren van de functie x∙(x2 - √2∙a∙x + a2)-½. In eerste instantie
...
z = sinh(u) zodat dz/du = cosh(u). Aangezien cosh2(u) - sinh2(u) = 1 volgt dan direct dat u = arcsinh(z) een primitieve is.


Maple-vraagje:
Hoe los ik bijvoorbeeld 3 vergelijkingen met evenveel onbekenden op?
Ik heb geen problemen om alles te definieren, maar kom er maar niet achter hoe ik er uitkomsten voor alle onbekenden uitkrijg.
Hoe los ik bijvoorbeeld 3 vergelijkingen met evenveel onbekenden op?
Ik heb geen problemen om alles te definieren, maar kom er maar niet achter hoe ik er uitkomsten voor alle onbekenden uitkrijg.
Sweet and innocent...


solve( { je vergelijkingen gescheiden door komma's} );quote:Op maandag 9 oktober 2006 11:19 schreef Innocence het volgende:
Maple-vraagje:
Hoe los ik bijvoorbeeld 3 vergelijkingen met evenveel onbekenden op?
Ik heb geen problemen om alles te definieren, maar kom er maar niet achter hoe ik er uitkomsten voor alle onbekenden uitkrijg.


Graag gedaan. Ik zag dat je een poos geleden, hier, ook al zat te worstelen met het bepalen van de integraal van (2∙e2t + 1)½ over het interval van 0 tot 2π. Er waren wel wat suggesties maar de gouden tip zat er duidelijk niet bij, laat staan dat iemand de moeite nam om het echt uit te werken. Ik heb dat inmiddels wel gedaan en de oplossing die je gaf uit het boekje blijkt te kloppen. Ik vond die integraal trouwens nog wat pittiger dan deze.quote:


Kan ik deze oplossing misschien van je overnemen?quote:Op maandag 9 oktober 2006 14:29 schreef Riparius het volgende:
[..]
Graag gedaan. Ik zag dat je een poos geleden, hier, ook al zat te worstelen met het bepalen van de integraal van (2∙e2t + 1)½ over het interval van 0 tot 2π. Er waren wel wat suggesties maar de gouden tip zat er duidelijk niet bij, laat staan dat iemand de moeite nam om het echt uit te werken. Ik heb dat inmiddels wel gedaan en de oplossing die je gaf uit het boekje blijkt te kloppen. Ik vond die integraal trouwens nog wat pittiger dan deze.


hee!
de vraag is:
bepaal alle cykeltypes in S<sub>5</sub> van alle even permutaties en die orde 4 hebben.
..
hoe pak ik dit het beste aan?
trouwens, hoeveel permutaties zijn er van ieder cykeltype?
alvast bedankt
de vraag is:
bepaal alle cykeltypes in S<sub>5</sub> van alle even permutaties en die orde 4 hebben.
..
hoe pak ik dit het beste aan?
trouwens, hoeveel permutaties zijn er van ieder cykeltype?
alvast bedankt
verlegen :)


Volgens mij zijn er geen permutaties die daar aan voldoen, maar wellicht heb ik er niet genoeg over na gedacht.quote:Op maandag 9 oktober 2006 18:50 schreef teletubbies het volgende:
hee!
de vraag is:
bepaal alle cykeltypes in S<sub>5</sub> van alle even permutaties en die orde 4 hebben.
..
hoe pak ik dit het beste aan?
trouwens, hoeveel permutaties zijn er van ieder cykeltype?
alvast bedankt
De orde van een permutatie is gelijk aan het kleinste gemene veelvoud van de ordes van zijn cykels. Aangezien de orde 4 moet zijn, bevat de permutatie dus een 4-cykel en een 1-cykel. Maar een 4-cykel is een oneven permutatie, dus dergelijke permutaties bestaan niet in S_5.


okee..
nu een vraag die daarop lijkt:
bepaal alle cykeltypes in S6 van alle even permutaties en die orde 5 hebben.
het gaat om een 5-cykel:
5=5.1
de permutatie bevat een 5-cykel en een 1-cykel. Een 5-cykel is even, dit is de enige oplossing.
bepaal alle cykeltypes in S8 van alle Oneven permutaties en die orde 4 hebben.
het gaat om een 4-cykel:
4=4*1, (2*2 gaat niet..kgv(2,2)=2)
de permutatie bevat een 4-cykel en een 1-cykel. Een 4-cykel is oneven, dit is de enige oplossing.
hoeveel permutaties voldoen hieraan?
je hebt bijv (1234), (1243), (1324), (1342) ....(5678),(5687)...
maar (1234)=(2341)=(3412)=(4123)
het aantal permutaties is volgens mij 4*8/4=16
of is dit fout?
[ Bericht 0% gewijzigd door teletubbies op 09-10-2006 20:56:59 (foutje) ]
nu een vraag die daarop lijkt:
bepaal alle cykeltypes in S6 van alle even permutaties en die orde 5 hebben.
het gaat om een 5-cykel:
5=5.1
de permutatie bevat een 5-cykel en een 1-cykel. Een 5-cykel is even, dit is de enige oplossing.
bepaal alle cykeltypes in S8 van alle Oneven permutaties en die orde 4 hebben.
het gaat om een 4-cykel:
4=4*1, (2*2 gaat niet..kgv(2,2)=2)
de permutatie bevat een 4-cykel en een 1-cykel. Een 4-cykel is oneven, dit is de enige oplossing.
hoeveel permutaties voldoen hieraan?
je hebt bijv (1234), (1243), (1324), (1342) ....(5678),(5687)...
maar (1234)=(2341)=(3412)=(4123)
het aantal permutaties is volgens mij 4*8/4=16
of is dit fout?
[ Bericht 0% gewijzigd door teletubbies op 09-10-2006 20:56:59 (foutje) ]
verlegen :)


Ja, dit klopt naar mijn weten.quote:Op maandag 9 oktober 2006 20:29 schreef teletubbies het volgende:
okee..
nu een vraag die daarop lijkt:
bepaal alle cykeltypes in S6 van alle even permutaties en die orde 5 hebben.
het gaat om een 5-cykel:
5=5.1
de permutatie bevat een 5-cykel en een 1-cykel. Een 5-cykel is even, dit is de enige oplossing.
Nee, een permutatie met cykels ter lengte 4, 2 en 2 voldoet ook.quote:bepaal alle cykeltypes in S8 van alle Oneven permutaties en die orde 4 hebben.
het gaat om een 4-cykel:
4=4*1, (2*2 gaat niet..kgv(2,2)=2)
de permutatie bevat een 4-cykel en een 1-cykel. Een 4-cykel is oneven, dit is de enige oplossing.
Ja, dit is fout omdat 4*8/4=8. Bovendien heb je niet goed geteld. Je kunt op 8 kies 4 manieren de 4 elementen in je cykel kiezen. Deze kun je op 4! manieren ordenen. Zoals je al opmerkte zijn telkens 4 van deze ordeningen hetzelfde. Het gevraagde aantal is dus (8 kies 4)*4!/4 = (8 kies 4)*3!.quote:hoeveel permutaties voldoen hieraan?
je hebt bijv (1234), (1243), (1324), (1342) ....(5678),(5687)...
maar (1234)=(2341)=(3412)=(4123)
het aantal permutaties is volgens mij 4*8/4=16
of is dit fout?


okee . ik snap het nu... kgv(4,2,2) is ook twee. en zo'n cykel is oneven.
8 kies 4= 8 boven 4 ..betekende 8!/(4!4!) als het goed is.
merci:)
8 kies 4= 8 boven 4 ..betekende 8!/(4!4!) als het goed is.
merci:)
verlegen :)


Gevraagd werd de integraal te bepalen van de functie √(2∙e2t + 1) over het interval [0, 2π].quote:Op maandag 9 oktober 2006 17:17 schreef Greus het volgende:
[..]
Kan ik deze oplossing misschien van je overnemen?
Bij integralen met een vierkantswortel uit een kwadratische veelterm bestaat de oplossingsmethode erin dat je de veelterm door kwadraatafsplitsing en een geschikt gekozen lineaire substitutie herleidt tot een vorm van de gedaante z2 + 1, z2 -1 of 1 - z2. De reden hiervoor is dat je dan met een substitutie van een goniometrische of hyperbolische functie de integraal in een vorm kunt brengen waarin geen wortelteken meer voorkomt. Hierbij wordt gebruik gemaakt van de bekende identiteiten
cos2(x) + sin2(x) =1
cosh2(x) - sinh2(x) = 1
In dit geval hebben we onder het wortelteken echter geen kwadratische veelterm, maar we kunnen 2∙e2t + 1 wel herleiden tot z2 + 1 als we substitueren z2 = 2∙e2t oftewel
z = √2∙et
Merk op dat geldt z > 0 voor alle (reële) waarden van t. We hebben nu dz/dt = √2∙et = z, dus dt/dz = z-1. Hiermee is de integraal omgevormd tot
∫ z-1∙√(z2 + 1)∙dz
Nu kunnen we een substitutie met een hyperbolische functie uitvoeren om de wortel kwijt te raken. Kiezen we z = sinh(u) (waarbij geldt dat u > 0 daar z > 0), dan is √(z2 + 1) = cosh(u) en dz/du = cosh(u) zodat we krijgen
∫ (1/sinh(u))∙cosh(u)∙cosh(u)∙du
Aangezien cosh2(u) = 1 + sinh2(u) kunnen we dit schrijven als:
∫ ((1/sinh(u)) + sinh(u))∙du
De tweede term is eenvoudig te primitiveren, want sinh(u) en cosh(u) zijn elkaars afgeleiden, zodat cosh(u) een primitieve is van sinh(u). Maar een primitieve van 1/sinh(u) is niet zo eenvoudig te bepalen. Aangezien 1/x de afgeleide is van ln(x) zou je kunnen denken aan ln(sinh(u)), maar de afgeleide daarvan is, vanwege de kettingregel, (1/sinh(u))∙cosh(u) = coth(u). Evenzo geeft ln(cosh(u)) als afgeleide tanh(u).
Nu valt op dat het differentiëren van de natuurlijke logaritme van een hyperbolische functie een andere hyperbolische functie oplevert, en je zou je daarom kunnen afvragen of ln(tanh(u)) misschien het gewenste resultaat geeft. De afgeleide van tanh(u) is 1/cosh2(u) en dus vinden we voor de afgeleide van ln(tanh(u)) :
(1/tanh(u)) ∙ (1/cosh2(u)) = (cosh(u)/sinh(u)) ∙ (1/cosh2(u)) = (1/ sinh(u))∙(1/cosh(u)) = 1/(sinh(u)∙cosh(u))
Dit is nog niet het gewenste resultaat 1/sinh(u) maar toch kunnen we hier verder mee omdat het mogelijk is sinh(u) te herschrijven als een produkt van een sinh en een cosh. We hebben de volgende identiteit:
sinh(2x) = 2∙sinh(x)∙cosh(x)
Substitutie van 2x = u en dus x = ½∙u levert
sinh(u) = 2∙sinh(½∙u)∙cosh(½∙u)
Nu is eenvoudig te zien dat 1/sinh(u) = 1/(2∙sinh(½∙u)∙cosh(½∙u)) de afgeleide is van ln(tan(½∙u)) en dus vinden we
∫ ((1/sinh(u)) + sinh(u))∙du = cosh(u) + ln(tan(½∙u))
De hyperbolische substitutie was alleen bedoeld om de wortel kwijt te raken, zodat we de primitieve nu weer om gaan zetten naar een uitdrukking in z (die dan op zijn beurt weer is om te zetten naar een uitdrukking in t). We weten al dat cosh(u) = √(z2 + 1) maar om de term ln(tan(½∙u)) uit te drukken in z moeten we deze term eerst omzetten naar een uitdruking in sinh(u) of cosh(u). We hebben de volgende identiteit:
cosh(2x) = cosh2(x) + sinh2(x) = 2∙cosh2(x) - 1 = 2∙sinh2(x) + 1
Na substitutie van 2x = u ofwel x = ½∙u kunnen we hieruit afleiden dat geldt
sinh2(½∙u) = (cosh(u) - 1)/2
cosh2(½∙u) = (cosh(u) + 1)/2
Delen we de eerste betrekking door de tweede en nemen we de vierkantswortel dan vinden we dus (voor u ≥ 0):
tanh(½∙u) = √((cosh(u) - 1)/(cosh(u) + 1))
Aangezien ln(√a) = ½∙ln(a) hebben we dan:
∫ ((1/sinh(u)) + sinh(u))∙du = cosh(u) + ½∙ln((cosh(u) - 1)/(cosh(u) + 1))
Hierin is cosh(u) = √(z2 + 1) zodat we voor de primitieve uitgedrukt in z vinden:
√(z2 + 1) + ½∙ln((√(z2 + 1) - 1)/(√(z2 + 1) + 1))
Nu kunnen we de breuk (√(z2 + 1) - 1)/(√(z2 + 1) + 1) nog wat vereenvoudigen door teller en noemer te vermenigvuldigen met (√(z2 + 1) - 1) en gebruik te maken van (a+b)(a-b) = a2 - b2. Merk op dat (√(z2 + 1) - 1) positief is aangezien z > 0. De noemer van de breuk wordt dan (z2 + 1) - 12 = z2 en voor de teller krijgen we:
(√(z2 + 1) - 1)2 = (z2 + 1) - 2∙√(z2 + 1)∙1 + 12 = z2 + 2 - 2∙√(z2 + 1)
Voor de primitieve uitgedrukt in z hebben we nu:
∫ z-1∙√(z2 + 1)∙dz = √(z2 + 1) + ½∙ln((z2 + 2 - 2∙√(z2 + 1))/z2)
Substitutie van z2 = 2∙e2t geeft tenslotte als resultaat:
∫√(2∙e2t + 1)∙dt = √(2∙e2t + 1) + ½∙ln((e2t + 1 - √(2∙e2t + 1))/e2t)
Vullen we nu eerst t=2π in en dan t=0 en trekken we het tweede resultaat af van het eerste dan vinden we voor de bepaalde integraal over het interval [0,2π] inderdaad:
Hiermee is de opgave voltooid. Nog enkele aanvullingen. Aangezien ln(a) = - ln(1/a) kunnen we voor de primitieve uitgedrukt in z ook schrijven:
√(z2 + 1) - ½∙ln((√(z2 + 1) + 1)/(√(z2 + 1) - 1))
Vereenvoudigen we weer de breuk door teller en noemer nu met (√(z2 + 1) + 1) te vermenigvuldigen dan wordt de noemer weer gereduceerd tot z2 terwijl we voor de teller (√(z2 + 1) + 1)2 krijgen. Beide zijn een kwadraat zodat de gehele breuk ook als een kwadraat ((√(z2 + 1) + 1)/z)2 is te schrijven, en aangezien ln(a2) = 2∙ln(a) kunnen we de primitieve schrijven als:
√(z2 + 1) - ln((√(z2 + 1) + 1)/z)
Dit is eenvoudig te herleiden tot
√(z2 + 1) - ln(z-1 + √(z-2 + 1))
Aangezien arcsinh(z) = ln(z + √(z2 + 1)) en dus arcsinh(1/z) = ln(z-1 + √(z-2 + 1)) vinden we dat:
∫ z-1∙√(z2 + 1)∙dz = √(z2 + 1) - arcsinh(1/z)
Substitutie van z = √2∙et, z2 = 2∙e2t geeft dan:
∫√(2∙e2t + 1)∙dt = √(2∙e2t + 1) - arcsinh(e-t/√2)
Hiermee is de bepaalde integraal eenvoudiger numeriek te berekenen met een gewone calculator. Voor de waarde van de bepaalde integraal over het interval [0, 2π] vinden we dan 756,225...
Tot slot nog een opmerking over de wijze waarop Mathematica deze integraal behandelt. Aangezien de waarde van tanh(x) tussen -1 en +1 ligt, is de waarde van de inverse functie arctanh(x) strict genomen alleen gedefinieerd voor -1 < x < 1. Voor deze waarden van x geldt:
arctanh(x) = ½∙ln((1+x)/(1-x))
De afgeleide van arctanh(x) is 1/(1-x2) maar deze laatste functie is ook gedefinieerd voor x < -1 en x > 1. Om deze reden is het voor toepassing in de integraalrekening nuttig om het domein van arctanh(x) uit te breiden naar waarden van x < -1 of x > 1. Te vergelijken is de functie x-1 die ook gedefinieerd is voor x < 0, terwijl de bijbehorende primitieve functie ln(x) binnen de reële getallen alleen is gedefinieerd voor x > 0. We kunnen de primitieve functie van x-1 echter ongeacht het teken van x weergeven als ln(|x|). Op vergelijkbare wijze is het domein van arctanh(x) uit te breiden door deze functie voor x < -1 of x > 1 te definiëren als:
arctanh(x) = ½∙ln(|(1+x)/(1-x)|)
Grafisch zien de uitgebreide functie arctanh(x) en de bijbehorende afgeleide er als volgt uit:
Voor x > 1 geldt |(1+x)/(1-x)| = (x+1)/(x-1) zodat we voor ½∙ln((√(z2 + 1) + 1)/(√(z2 + 1) - 1)) bij gebruik van de uitgebreide definitie van arctanh mogen schrijven:
arctanh(√(z2 + 1))
Zo krijgen we dan:
∫ z-1∙√(z2 + 1)∙dz = √(z2 + 1) - arctanh(√(z2 + 1))
En substitutie van z2 = 2∙e2t geeft:
∫√(2∙e2t + 1)∙dt = √(2∙e2t + 1) - arctanh(√(2∙e2t + 1))
Deze laatste variant is alleen geschikt voor de berekening van de bepaalde integraal als de gebruikte calculator of het gebruikte programma de uitgebreide definitie van arctanh hanteert.


Morgen toets over periodieke functies, maar heb nog een paar vraagjes:
Hoe los je 2sin 2x > 0,8 op, zonder intersect en hoe schrijf je dat precies op
Hoe bepaal je de horizontale verschuiving van Y = sin x met verschillende formule( bv. 5 * Sin (0,5x) + 6) of wat is de algemene regel hoe kan je dat zien in de grafiek
"the female orgasme is a mythe, I hae had sex with 26 women in my life and not one of them had a orgasme."


Ik had zo een vraagje
Het snijpunt van twee bissectrices in een driehoek is het middelpunt van de ingeschreven cirkel. Kijk nu naar het snijpunt van de buiten bissectrices bij twee hoekpunten. Dat snijpunt is ook het middelpunt van een bijzondere cirkel. Verklaar dat ?
Geen idee ????? Wat voor cirkel moet dat wezen ?
Appolonius cirkel? Hoe valt dat te verklaren.
[ Bericht 1% gewijzigd door sitting_elfling op 10-10-2006 22:11:24 ]
Het snijpunt van twee bissectrices in een driehoek is het middelpunt van de ingeschreven cirkel. Kijk nu naar het snijpunt van de buiten bissectrices bij twee hoekpunten. Dat snijpunt is ook het middelpunt van een bijzondere cirkel. Verklaar dat ?
Geen idee ????? Wat voor cirkel moet dat wezen ?
Appolonius cirkel? Hoe valt dat te verklaren.
[ Bericht 1% gewijzigd door sitting_elfling op 10-10-2006 22:11:24 ]
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


sin(2x) > 0,4, en hier kun je zonder intersect vrij weinig mee. Het zou wat anders zijn als we het bijvoorbeeld over sin(2x) > wortel(2)/2 hadden.quote:Hoe los je 2sin 2x > 0,8 op, zonder intersect en hoe schrijf je dat precies op
Logisch nadenken: wat gebeurt er nu eigenlijk? 5*sin(x) -> de sinus wordt 5x uitgerekt. Sin(0,5x) -> pas bij x=2pi gaat hij weer door 0, dus de sinus wordt uit elkaar getrokken in horizontale richting. Sin(x+5) -> Ipv x wordt er nu steeds x+5 ingevuld, ofwel een verschuiving van 5 naar links.quote:# Hoe bepaal je de horizontale verschuiving van Y = sin x met verschillende formule( bv. 5 * Sin (0,5x) + 6) of wat is de algemene regel hoe kan je dat zien in de grafiek
B is iets algebraïscher. Dingen die A niet krijgt zijn integralen, wat goniometrie, en misschien nog wel meer.quote:gewoon een vraagje
wat is het verschil tussen wiskunde A en B??
wat krijgt B wat A niet krijgt
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


B krijgt het bewijzen en redeneren. En gaat volgens mij dieper op de 'abstracte' stof in.quote:Op dinsdag 10 oktober 2006 21:51 schreef italiaan1987 het volgende:
gewoon een vraagje
wat is het verschil tussen wiskunde A en B??
wat krijgt B wat A niet krijgt
Maar meer weet ik er ook niet vanaf. Alleen dat bewijzen en meetkunde verschil is wel aanwezig. Groot verschil ook
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Het is inderdaad alleen meetkunde en bewijzen(op VWO niveau in ieder geval). Verder is het volgens mij exact hetzelfde(heb zelf wb1,2 gehad).


Een vraagje
Als een driehoek een zijde heeft van 5 en een zijde
van 8. Kan de 3e zijde dan 13 zijn ?
Hoe zit dat met de cosinus/sinus regel in dit vlak ?
Als een driehoek een zijde heeft van 5 en een zijde
van 8. Kan de 3e zijde dan 13 zijn ?
Hoe zit dat met de cosinus/sinus regel in dit vlak ?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Nee, want de som van de lengtes van twee zijden van een driehoek is altijd groter dan de lengte van de derde zijde.quote:Op dinsdag 10 oktober 2006 23:48 schreef sitting_elfling het volgende:
Een vraagje
Als een driehoek een zijde heeft van 5 en een zijde
van 8. Kan de 3e zijde dan 13 zijn ?
Onduidelijke vraagstelling. De cosinusregel luidt:quote:
Hoe zit dat met de cosinus/sinus regel in dit vlak ?
a2 = b2 + c2 - 2bc∙cos α
Als nu a = b + c dan is a2 = (b+c)2 = b2 + 2bc + c2. Bij een driehoek met a = b + c zou dus moeten gelden cos α = -1 dus α = 180°, maar dat kan niet aangezien de beide andere hoeken dan 0 graden zouden moeten zijn.


Oke bedankt nu weet ik ook weer wanneer ik dat moet gebruiken .quote:Op woensdag 11 oktober 2006 00:01 schreef Riparius het volgende:
[..]
Nee, want de som van de lengtes van twee zijden van een driehoek is altijd groter dan de lengte van de derde zijde.
[..]
Onduidelijke vraagstelling. De cosinusregel luidt:
a2 = b2 + c2 - 2bc?cos ?
Als nu a = b + c dan is a2 = (b+c)2 = b2 + 2bc + c2. Bij een driehoek met a = b + c zou dus moeten gelden cos ? = -1 dus ? = 180°, maar dat kan niet aangezien de beide andere hoeken dan 0 graden zouden moeten zijn.
Nog een bewijs vraag waar ik niet uitkom
Gegeven is een vierkant EFGH
Je verlengt EF met FA
Je verlengt FG met GB
Je verlengt GH met HC
Je verlengt HE met ED
verder is FA = GB = HC = ED
bewijs dat ABCD een vierkant is.
Als ik het teken zie ik ook wel dat het een vierkant is. Maar hoe bewijs ik dat
Er komen gewoon bij vierkant EFGH 4 rechthoekige driehoeken bij.
4 rechthoekige driehoeken passen mooi inelkaar
Maar das geen goed bewijs
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Je moet eerst aantonen dat de vier rechthoekige driehoeken congruent zijn (congruentiekenmerken gebruiken). Dan weet je al dat de vier schuine zijden die samen de grote vierhoek vormen gelijk zijn. Verder moet je laten zien dat de vier hoeken van de grote figuur elk 90 graden zijn. Dat is ook eenvoudig omdat de vier toegevoegde driehoeken rechthoekig zijn zodat de som van de twee andere hoeken van elke driehoek ook 90 graden is.quote:Op woensdag 11 oktober 2006 00:09 schreef sitting_elfling het volgende:
[..]
Oke bedankt nu weet ik ook weer wanneer ik dat moet gebruiken .
Nog een bewijs vraag waar ik niet uitkom
Gegeven is een vierkant EFGH
Je verlengt EF met FA
Je verlengt FG met GB
Je verlengt GH met HC
Je verlengt HE met ED
verder is FA = GB = HC = ED
bewijs dat ABCD een vierkant is.
Als ik het teken zie ik ook wel dat het een vierkant is. Maar hoe bewijs ik dat
[ Bericht 2% gewijzigd door Riparius op 11-10-2006 00:25:41 ]


Nog even een hele simpele opdracht, maar hij lukt mij niet
y1 = 6000*1,03^x
y2 = 12000
En dan het snijpunt opzoeken, en dat geeft x = 23,45 jaar, dus na 24 jaar.
Maar ik moet m natuurlijk berekenen
Zover was ik: 6000*(1,03x) = 12000
Hoe los je zoiets op
Ik heb m opgelost met mn Grafische Rekenmachine:quote:Op 1-1-2006 zet iemand ¤ 6000,- op een spaarrekening. De rente is 3% per jaar en wordt aan het eind van elk jaar bijgeschreven op de spaarrekening. Verder wordt er niets op de spaarrekening gestort en er wordt ook niets afgehaald.
Hoeveel jaar duurt het voor het saldo verdubbeld is?
y1 = 6000*1,03^x
y2 = 12000
En dan het snijpunt opzoeken, en dat geeft x = 23,45 jaar, dus na 24 jaar.
Maar ik moet m natuurlijk berekenen
Zover was ik: 6000*(1,03x) = 12000
Hoe los je zoiets op


Hier een vraag over Java Programmeren? Wie kan mij helpen en/of tips geven?
http://scp.thrijswijk.nl/vakken/prog3t1/index.html en dan Practicum Handleiding staan de opdrachten in.
Ik maak het in JBuilder. Heb al begin gemaakt, maar lukt mij verder niet..
Bedankt alvast!
http://scp.thrijswijk.nl/vakken/prog3t1/index.html en dan Practicum Handleiding staan de opdrachten in.
Ik maak het in JBuilder. Heb al begin gemaakt, maar lukt mij verder niet..
Bedankt alvast!


Zover was ik al gekomen, maar dan kom ik op 0.31006quote:Op woensdag 11 oktober 2006 17:48 schreef Aibmi het volgende:
2=1.03x
1.03log2=x
En daar zul je toch je rekenmachine moeten pakken vrees ik.
[Java] voor dummies - Deel 1quote:Op woensdag 11 oktober 2006 17:49 schreef Elle4 het volgende:
Hier een vraag over Java Programmeren? Wie kan mij helpen en/of tips geven?


Simpel:quote:Op woensdag 11 oktober 2006 17:51 schreef Piles het volgende:
[..]
Zover was ik al gekomen, maar dan kom ik op 0.31006
[..]
[Java] voor dummies - Deel 1
(1,03)x = 2
log((1,03)x) = log(2)
x∙log(1,03) = log(2)
x = log(2) / log (1,03)
Dit laatste even uitrekenen met de calculator
Je hoeft dus niet met logaritmen met grondtal 2 te werken, gewone logaritmen voldoen prima.
[ Bericht 1% gewijzigd door Riparius op 11-10-2006 18:12:57 ]


De GR ziet 1.03log2 als 1.03 maal de 10log van 2. Je zult het dus inderdaad op de manier van Riparius in de GR moeten doen.


quote:Op woensdag 11 oktober 2006 18:00 schreef Riparius het volgende:
log((1,03)x) = log 2
x∙log(1,03) = log(2)
Ik kende de logica van deze stap nog niet, maar die ga ik zeker ff opschrijven
Bedankt voor de hulp


Dit is toch echt een basisregel voor het rekenen met logaritmen hoor. Kijk maar eens op je formulekaart:quote:Op woensdag 11 oktober 2006 18:06 schreef Piles het volgende:
[..]
Ik kende de logica van deze stap nog niet, maar die ga ik zeker ff opschrijven
Bedankt voor de hulp
log(ap) = p∙log(a)


Die heb ik nietquote:Op woensdag 11 oktober 2006 18:08 schreef Riparius het volgende:
[..]
Dit is toch echt een basisregel voor het rekenen met logaritmen hoor. Kijk maar eens op je formulekaart:
log(ap) = p∙log(a)
Het staat vast ergens in mn boek, maar dat heb ik denk ik gemist


Ok, hallo Ik ben nogal een idioot op het vlak van bètavakken (Ik doe dan ook de meest alpha opleiding die er is) en heb dus problemen met een vraag die normaal simpel zou moeten zijn:
Eerst moet ik de vergelijking bepalen van een cirkel met M(-4, 1) als middelpunt en r=3
Dat is c <-> (x+4)2 + ( y-1)2 = 9 (toch?)
Als ik ervanuitga dat dat juist is, dan moet ik nu zien wat de snijpunten met de X-as zijn, dat was toch Y=0 en dan uitrekenen ?
Dan krijg je
(x+4)2 + (0-1)2 = 9
Hier overal de wortel uit nemen om die kwadraathaakjesdingetjes weg te werken:
x + 4 + 1 = 3
x + 5 = 3
x = -2
En dan denk ik, zo idioot als ik ben, dat de snijpunten met de X-as... oh wacht ik heb er twee nodig
Dat heb ik ergens lang geleden gehad, maar ik weet het al lang niet meer.
Wat doe ik fout ?
Eerst moet ik de vergelijking bepalen van een cirkel met M(-4, 1) als middelpunt en r=3
Dat is c <-> (x+4)2 + ( y-1)2 = 9 (toch?)
Als ik ervanuitga dat dat juist is, dan moet ik nu zien wat de snijpunten met de X-as zijn, dat was toch Y=0 en dan uitrekenen ?
Dan krijg je
(x+4)2 + (0-1)2 = 9
Hier overal de wortel uit nemen om die kwadraathaakjesdingetjes weg te werken:
x + 4 + 1 = 3
x + 5 = 3
x = -2
En dan denk ik, zo idioot als ik ben, dat de snijpunten met de X-as... oh wacht ik heb er twee nodig
Dat heb ik ergens lang geleden gehad, maar ik weet het al lang niet meer.
Wat doe ik fout ?


Mag ik zeggen dat de 4 toegevoegde driehoeken congruent zijn omdat ze voldoen aan ZHZquote:Op woensdag 11 oktober 2006 00:20 schreef Riparius het volgende:
[..]
Je moet eerst aantonen dat de vier rechthoekige driehoeken congruent zijn (congruentiekenmerken gebruiken). Dan weet je al dat de vier schuine zijden die samen de grote vierhoek vormen gelijk zijn. Verder moet je laten zien dat de vier hoeken van de grote figuur elk 90 graden zijn. Dat is ook eenvoudig omdat de vier toegevoegde driehoeken rechthoekig zijn zodat de som van de twee andere hoeken van elke driehoek ook 90 graden is.
ZHZ = 2 zijden en een ingesloten hoek. De 4 schuine zijden zijn dus even lang. En omdat de 4 toegevoegde driehoeken rechthoekig zijn, zijn de 2 overige hoeken 90 graden. Wat het dus een vierkant maakt.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Het kan, maar is niet aan te raden omdat het veel makkelijker kan.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, dat is het, heel compact opgeschreven.quote:Op woensdag 11 oktober 2006 20:06 schreef sitting_elfling het volgende:
[..]
Mag ik zeggen dat de 4 toegevoegde driehoeken congruent zijn omdat ze voldoen aan ZHZ
ZHZ = 2 zijden en een ingesloten hoek. De 4 schuine zijden zijn dus even lang. En omdat de 4 toegevoegde driehoeken rechthoekig zijn, zijn de 2 overige hoeken 90 graden. Wat het dus een vierkant maakt.


Maar ik snap eigenlijk niet wat ik met jouw raad moet (als je eerste post voor mij bedoelt is)quote:Op woensdag 11 oktober 2006 20:15 schreef GlowMouse het volgende:
Het kan, maar is niet aan te raden omdat het veel makkelijker kan.


Als (x+4)² + (0-1)² = 9 dan (x+4)² = 8. Ofwel x+4 = wortel(8) of x+4 = -wortel(8)
Je deed zelf trouwens dat wortel((x+4)² + (0-1)²) = (x+4) + (0-1), maar dit gaat fout (voorbeeld: wortel(2+2) = 2, terwijl wortel(2) geen 1 is).
Je deed zelf trouwens dat wortel((x+4)² + (0-1)²) = (x+4) + (0-1), maar dit gaat fout (voorbeeld: wortel(2+2) = 2, terwijl wortel(2) geen 1 is).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De grote fout die je maakt is dat je denkt dat de wortel uit de som van twee termen gelijk is aan de som van de wortels van die termen. Je denkt dus dat √(a+b) hetzelfde is als √a + √b, maar dat is niet zo.quote:Op woensdag 11 oktober 2006 19:58 schreef Secretus het volgende:
Ok, hallo Ik ben nogal een idioot op het vlak van bètavakken (Ik doe dan ook de meest alpha opleiding die er is) en heb dus problemen met een vraag die normaal simpel zou moeten zijn:
Eerst moet ik de vergelijking bepalen van een cirkel met M(-4, 1) als middelpunt en r=3
Dat is c <-> (x+4)2 + ( y-1)2 = 9 (toch?)
Als ik ervanuitga dat dat juist is, dan moet ik nu zien wat de snijpunten met de X-as zijn, dat was toch Y=0 en dan uitrekenen ?
Dan krijg je
(x+4)2 + (0-1)2 = 9
Hier overal de wortel uit nemen om die kwadraathaakjesdingetjes weg te werken:
x + 4 + 1 = 3
x + 5 = 3
x = -2
En dan denk ik, zo idioot als ik ben, dat de snijpunten met de X-as... oh wacht ik heb er twee nodig
Dat heb ik ergens lang geleden gehad, maar ik weet het al lang niet meer.
Wat doe ik fout ?
Je hebt:
(x+4)2 + (0-1)2 = 9
(x+4)2 + 1 = 9
(x+4)2 = 8
Nu is:
x+4 = √8 of x+4 = -√8
De rest kun je nu denk ik zelf wel oplossen. Merk nog op dat √8 = 2√2.


Ja, die fout heb ik bijna juist na het typen van mijn post ook ontdektquote:Op woensdag 11 oktober 2006 20:20 schreef GlowMouse het volgende:
Als (x+4)² + (0-1)² = 9 dan (x+4)² = 8. Ofwel x+4 = wortel(8) of x+4 = -wortel(8)
Je deed zelf trouwens dat wortel((x+4)² + (0-1)²) = (x+4) + (0-1), maar dit gaat fout (voorbeeld: wortel(2+2) = 2, terwijl wortel(2) geen 1 is).
Bedankt voor het helpen, nu ik terugkijk is het wel makkelijk, maarja, ik kom niet zo snel op die dingen.


Ik heb een vraagje. Je hebt een driehoek met een zijde 5 cm 8 cm en 10 cm.
Ik moet een driehoek construeren met die 3 zijdes. Als 'hint' staat er een passer. :S Snap er geen knurft van. Als ik een driehoek teken kom ik niet verder dan 9.5 cm als 3e schuine zijde.
Ik moet een driehoek construeren met die 3 zijdes. Als 'hint' staat er een passer. :S Snap er geen knurft van. Als ik een driehoek teken kom ik niet verder dan 9.5 cm als 3e schuine zijde.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


stel f is twee keer differentieerbaar op een interval I.
In I zitten 0 en 2. Bovendien geldt f(0)=f(1)=0 en f(2)=1.
Toon aan dat er getallen a,b in I zitten zodat:
f'(a)=1/2
f''(b) > 1/2
de eerste vraag doet me denken aan: als f(0)=f(1) dan f(m)=f(m+1/2) voor een of ander m uit [0,1/2]
dus ook f'(m)=f'(m+1/2)
maar goed, k weet niet of dit helpt..
weet iemand het? thanx
In I zitten 0 en 2. Bovendien geldt f(0)=f(1)=0 en f(2)=1.
Toon aan dat er getallen a,b in I zitten zodat:
f'(a)=1/2
f''(b) > 1/2
de eerste vraag doet me denken aan: als f(0)=f(1) dan f(m)=f(m+1/2) voor een of ander m uit [0,1/2]
dus ook f'(m)=f'(m+1/2)
maar goed, k weet niet of dit helpt..
weet iemand het? thanx
verlegen :)


In zijn algemeenheid klopt je bewering niet. Als ik in de calculator van WinXP deze berekening uitvoer dan komt er op beide manieren toch echt precies hetzelfde uit, namelijk 0.02002001.quote:Op woensdag 4 oktober 2006 21:25 schreef Bioman_1 het volgende:
Zelf ook een vraag:
Vandaag bezig geweest met het onderwerp: Hoe rekent een computer? (over machine-getallen enzo en de afrondfouten die daarbij gemaakt worden).
[...]
Zo is het beter om a2 - b2 te bereken als (a+b)*(a-b) en niet als (zoals ik had verwacht) a*a - b*b. In het eerste geval is namelijk de relatieve rekenfout die je maakt kleiner dan bij de tweede.
Reken bovenstaande bijvoorbeeld maar eens uit met a = 100.1001 en b = 100.1000 Dan komt uit beide berekeningen NIET hetzelfde antwoord.


Teken een lijnstuk van 10 cm. Zet de punt van de passer in het ene eindpunt en trek een cirkel met straal 5 cm. Zet dan de punt van de passer in het andere eindpunt en trek een cirkel met straal 8 cm. Het snijpunt van de cirkels (nu ja, één van beide snijpunten) is nu het derde punt van je driehoek, samen met de twee eindpunten van je lijnstuk van 10 cm waar je mee begon.quote:Op woensdag 11 oktober 2006 21:00 schreef sitting_elfling het volgende:
Ik heb een vraagje. Je hebt een driehoek met een zijde 5 cm 8 cm en 10 cm.
Ik moet een driehoek construeren met die 3 zijdes. Als 'hint' staat er een passer. :S Snap er geen knurft van. Als ik een driehoek teken kom ik niet verder dan 9.5 cm als 3e schuine zijde.


Gebruik de middelwaardestelling, eerst toegepast op f(x) en dan toegepast op f'(x).quote:Op woensdag 11 oktober 2006 21:00 schreef teletubbies het volgende:
stel f is twee keer differentieerbaar op een interval I.
In I zitten 0 en 2. Bovendien geldt f(0)=f(1)=0 en f(2)=1.
Toon aan dat er getallen a,b in I zitten zodat:
f'(a)=1/2
f''(b) > 1/2


Voor f'(a)=1/2 in ieder geval gecombineerd met de tussenwaardestelling.quote:Op woensdag 11 oktober 2006 21:21 schreef Riparius het volgende:
[..]
Gebruik de middelwaardestelling, eerst toegepast op f(x) en dan toegepast op f'(x).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik blijf erg moeite houden met mn kansrekening. Hier weer een vraag mbt Markov-ketens. Heb dit nu al zo vaak gezien, maar weet nog steeds niet hoe ik dit soort problemen op moet lossen. Op één of andere manier wil het er gewoon niet in :S
Persoon A gaat iedere ochtend hardlopen. Het is even waarschijnlijk dat A het huis via de voordeur of via de achterdeur verlaat. Bij het verlaten van het huis, trekt A een paar schoenen aan (indien aanwezig, anders gaat A blootvoets naar buiten).
Bij terugkeer laat A de schoenen achter bij de voordeur of achterdeur, al naar gelang waar A binnenkomt (waarbij voor- of achterdeur weer willekeurig wordt gekozen).
Neem aan dat A 3 paar schoenen heeft, en laat Xn het aantal paar schoenen zijn dat aan het begin van de n-de dag bij de deur van vertrek staan.
(a) Bepaal de overgangsmatrix van de Markovketen {Xn : n >= 0}.
(b) Met welke frequentie zal A blootvoets rondhollen?
Persoon A gaat iedere ochtend hardlopen. Het is even waarschijnlijk dat A het huis via de voordeur of via de achterdeur verlaat. Bij het verlaten van het huis, trekt A een paar schoenen aan (indien aanwezig, anders gaat A blootvoets naar buiten).
Bij terugkeer laat A de schoenen achter bij de voordeur of achterdeur, al naar gelang waar A binnenkomt (waarbij voor- of achterdeur weer willekeurig wordt gekozen).
Neem aan dat A 3 paar schoenen heeft, en laat Xn het aantal paar schoenen zijn dat aan het begin van de n-de dag bij de deur van vertrek staan.
(a) Bepaal de overgangsmatrix van de Markovketen {Xn : n >= 0}.
(b) Met welke frequentie zal A blootvoets rondhollen?
Theories come and theories go. The frog remains


waarom is de congruentie zhz en zhh gelijk ?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Onduidelijke vraag. Ik denk trouwens dat je een beetje in de war bent. Kijk maar eens hier.quote:Op woensdag 11 oktober 2006 23:29 schreef sitting_elfling het volgende:
waarom is de congruentie zhz en zhh gelijk ?


Oh ik heb hier namelijk een opgave waarin staat.quote:Op woensdag 11 oktober 2006 23:52 schreef Riparius het volgende:
[..]
Onduidelijke vraag. Ik denk trouwens dat je een beetje in de war bent. Kijk maar eens hier.
Als 2 driehoeken congruent zijn volgens ZHZ zijn dat ook volgens ZHH. Waarom is dat zo ?
Dat is de Letterlijke vraag in mn boekje staat. Ik zie niet in waarom, de site die je me gaf geeft aan dat beide opzich wat anders betekenen.
En dan nog een laatste vraag, de afsluiting van mijn boekje met vragen.
Gegeven is driehoek ABC die congruent is met XYZ en gegeven is AB = 3 XY
CD is de loodlijn vanuit C op AB
ZW is de loodlijn vanuit Z op XY
Laat zien dat CD = 3 ZW
men dit bewijzen zeg pfft
bedankt btw voor het helpen bewijzen en redeneren vind ik altijd pittig.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.


Het enige wat ik zo gauw kan bedenken is dat ZHZ in je boek een drukfout is voor HZH. Gelijkheid van twee hoeken impliceert namelijk altijd gelijkheid van de derde hoek, omdat de som van de hoeken van een driehoek 180 graden is.quote:Op donderdag 12 oktober 2006 00:26 schreef sitting_elfling het volgende:
[..]
Oh ik heb hier namelijk een opgave waarin staat.
Als 2 driehoeken congruent zijn volgens ZHZ zijn dat ook volgens ZHH. Waarom is dat zo ?
Dat is de Letterlijke vraag in mn boekje staat. Ik zie niet in waarom, de site die je me gaf geeft aan dat beide opzich wat anders betekenen.
Zoals het hier staat kan het strict genomen niet kloppen, want als je stelt dat driehoek ABC congruent is met driehoek XYZ dan impliceer je daarmee dat AB=XY, BC=YZ en CA=ZX, terwijl is gegeven dat AB = 3*XY: een tegenstrijdigheid dus.quote:En dan nog een laatste vraag, de afsluiting van mijn boekje met vragen.
Gegeven is driehoek ABC die congruent is met XYZ en gegeven is AB = 3 XY
CD is de loodlijn vanuit C op AB
ZW is de loodlijn vanuit Z op XY
Laat zien dat CD = 3 ZW
Geef eerst eens een tekening die volgens jou alle gegevens die je hebt laat zien.
Logisch leren denken en redeneren is altijd goed.quote:men dit bewijzen zeg pfft
quote:bedankt btw voor het helpen bewijzen en redeneren vind ik altijd pittig.


Volgens mij maken ZHZ en HZH beiden unieke driehoeken. Als je twee zijdes hebt, en de hoek er tussen, dan kun je de 3e zijde maar op 1 manier tekenen, namelijk tussen de uiteindes van de twee zijden. HZH is logisch, je weet immers 2 van de 3 hoeken, en daarmee is het al gelijkvormig, je voegt een zijde toe en het is congruent. Zelfde voor ZHH.


Ik heb 2 sommen over integralen
Som 1
Integraal Wortel X * exp(2xwortel x) dx
De bedoeling bij deze is substitueren.
Mij lijkt dan:
u=2xwortelx
du/dx = (2x)/(2wortelx) +2 wortelx
du= (2x*dx)/(2wortelx) +2 wortelx
En dan moet du de originele vergelijking met het integraal teken in, maar hoe gaat dit nu precies?
Som 2
De bedoeling is hier partitieel integreren
Integraal ln(1+x²)
ik dacht dus:
x*ln(1+x²) - [integraal] (2x*dx)/1+x²
Hoe los ik dat integraal op?
Som 1
Integraal Wortel X * exp(2xwortel x) dx
De bedoeling bij deze is substitueren.
Mij lijkt dan:
u=2xwortelx
du/dx = (2x)/(2wortelx) +2 wortelx
du= (2x*dx)/(2wortelx) +2 wortelx
En dan moet du de originele vergelijking met het integraal teken in, maar hoe gaat dit nu precies?
Som 2
De bedoeling is hier partitieel integreren
Integraal ln(1+x²)
ik dacht dus:
x*ln(1+x²) - [integraal] (2x*dx)/1+x²
Hoe los ik dat integraal op?


Probeer eens u = wortel(x)quote:Integraal Wortel X * exp(2xwortel x) dx
De bedoeling bij deze is substitueren.
Mij lijkt dan:
u=2xwortelx
du/dx = (2x)/(2wortelx) +2 wortelx
Bovendien zou ik niet du maar dx los schrijven.
We krijgen: du/dx = 1/(2wortel(x)), dus dx = 2 wortel(x) du = 2 u du. Dit kun je in de integraal gewoon invullen voor dx.
Mocht je toch 2xwortel(x) doen, differentieer dan 2x3/2 in plaats van de kettingregel te gebruiken.
Partieel integreren is handig wanneer je een product van twee functies hebt. Bij je tweede opgave zie ik die niet terug. Door u=1+x² te substitueren krijg je wel een product.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dus dan krijg ik bij som 1:
[Integraal] 2*u*du* exp (2xu) ?
Dat snap ik niet helemaal, daarom dacht ik dat ik 2xwortelx moest substitueren.
[Integraal] 2*u*du* exp (2xu) ?
Dat snap ik niet helemaal, daarom dacht ik dat ik 2xwortelx moest substitueren.


De x in de integrand moet je dan uiteraard wel door u² vervangen. En waar is wortel(x) gebleven?quote:Op donderdag 12 oktober 2006 22:07 schreef Rejected het volgende:
Dus dan krijg ik bij som 1:
[Integraal] 2*u*du* exp (2xu) ?
Dat snap ik niet helemaal, daarom dacht ik dat ik 2xwortelx moest substitueren.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oja natuurlijk!
[Integraal] 2*u*du* exp (2u³)
antwoord= 1/3 exp 2xwortelx
Ik snap wel hoe je aan dat 1/3 komt, ik snap niet hoe die u voor de exp verdwijnt.
[Integraal] 2*u*du* exp (2u³)
antwoord= 1/3 exp 2xwortelx
Ik snap wel hoe je aan dat 1/3 komt, ik snap niet hoe die u voor de exp verdwijnt.


Je hebt exp(2xwortel(x)) door exp(2u³) vervangen, dx door 2udu, maar de wortel(x) die ervoor staat heb je helemaal laten verdwijnen. Hoe je toch op het juiste antwoord uitkomt, is me een raadsel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Thank you very much!
Heb Som 1 opgelost.
[Integraal] 1* ln(1+x²), verder kom ik dus niet.
Heb Som 1 opgelost.
Nou het product is een beetje "verborgen"quote:Op donderdag 12 oktober 2006 21:59 schreef GlowMouse het volgende:
Partieel integreren is handig wanneer je een product van twee functies hebt. Bij je tweede opgave zie ik die niet terug. Door u=1+x² te substitueren krijg je wel een product.
[Integraal] 1* ln(1+x²), verder kom ik dus niet.


Substitueren van u=x² was al makkelijker zie ik, maar wat je nu hebt kun je dezelfde substitutie alsnog uitvoeren. Je ziet dan dat de 2x in de teller wegvalt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


ff kijken ik heb
[integraal] (2x*dx)/1+x²
u= x²
du/dx=2x dus du=2xdx
Dit geeft:
[integraal] du/(1+u) = 0.5ln (1+u)+C = 0.5ln (1+x²) +C Klopt dit?
[integraal] (2x*dx)/1+x²
u= x²
du/dx=2x dus du=2xdx
Dit geeft:
[integraal] du/(1+u) = 0.5ln (1+u)+C = 0.5ln (1+x²) +C Klopt dit?


d/dx 0.5ln(1+x²)+C = x/(1+x²). De factor 0,5 moet er dus niet voor.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt!! Je zou een fotoboek moeten openen, het zou vollopen door bedankjes!
Nu ga ik met een fijn hoofd naar bed.
Nu ga ik met een fijn hoofd naar bed.


Ik kom hier helaas niet uit. Kan iemand mij uitleggen hoe je hiervan de uitkomst berekend??
Gegeven: f(x) = 2x4 + 2x3 - 2x2 - 2
Bereken f '(3). (Vul als antwoord een geheel getal in.)
Gegeven: f(x) = 2x4 + 2x3 - 2x2 - 2
Bereken f '(3). (Vul als antwoord een geheel getal in.)


Zijn die getallen machten? Zo ja:
Maak de afgeleide van f(x). Vul daarna x=3 in. Als je geen afgeleides kunt maken zou ik goed in je boek kijken, want ik kan me niet voorstellen dat een methode dit níet goed uit legt (of in ieder geval het "trucje" waarmee je het kunt berekenen).
Zo nee:f'(x)=10, dus f'(3) is dan ook 10.
Maak de afgeleide van f(x). Vul daarna x=3 in. Als je geen afgeleides kunt maken zou ik goed in je boek kijken, want ik kan me niet voorstellen dat een methode dit níet goed uit legt (of in ieder geval het "trucje" waarmee je het kunt berekenen).
Zo nee:f'(x)=10, dus f'(3) is dan ook 10.


Nu ik er nog eens naar kijk, zie ik dat je te kort door de bocht bent gegaan bij de tweede vraag. x*ln(1+x²) - [integraal] (2x*dx)/1+x² is namelijk fout. Wat je krijgt, is x*ln(1+x²) - [integraal] (2x2*dx)/(1+x²). Het uitwerken van deze integraal vergt iets meer inzicht: 2x²/(1+x²) = 2*(x²+1-1) / (x²+1) = 2(1 - 1/(x²+1)). Je ziet dan de afgeleide van de arctangens terugkomen, en de uitwerking is niet zo moeilijk meer.quote:Op donderdag 12 oktober 2006 23:06 schreef Rejected het volgende:
Bedankt!! Je zou een fotoboek moeten openen, het zou vollopen door bedankjes!
Nu ga ik met een fijn hoofd naar bed.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |