SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


Bedankt voor de snelle reactie!quote:Op woensdag 8 oktober 2014 22:14 schreef Anoonumos het volgende:
[..]
Laat zien dat de verdelingsfuncties hetzelfde zijn.
voor alle u in [0,1]
Maar ik begrijp dat er gevraagd wordt om de verdelingsfuncties gelijk te stellen. Echter snap ik niet hoe ik dat moet doen, want ik zie gewoon niet anders dan dat 1 - U negatieve getallen geeft en dat kan toch niet?
Kom maar konijntje, doe maar wiebelen wiebelen...


Aangezien U ∈ [0,1], is 1-U nooit kleiner dan 0. Sterker nog, 1-U∈ [0,1]quote:Op woensdag 8 oktober 2014 22:25 schreef Hoplahopla het volgende:
[..]
Bedankt voor de snelle reactie!
Maar ik begrijp dat er gevraagd wordt om de verdelingsfuncties gelijk te stellen. Echter snap ik niet hoe ik dat moet doen, want ik zie gewoon niet anders dan dat 1 - U negatieve getallen geeft en dat kan toch niet?
Opinion is the medium between knowledge and ignorance (Plato)


Misschien bekijk ik het te algebraïsch. Ik zie niet in hoe de functies identiek kunnen zijn. Ik snap dat de lijn hetzelfde patroon volgt, maar dan gespiegeld. Maar ik denk niet dat het hetzelfde is... U is niet gelijk aan U want f(U) = 1 en f(1-U) = -1.quote:Op woensdag 8 oktober 2014 22:27 schreef Janneke141 het volgende:
[..]
Aangezien U ∈ [0,1], is 1-U nooit kleiner dan 0. Sterker nog, 1-U∈ [0,1]
Kom maar konijntje, doe maar wiebelen wiebelen...


Dat U een kansdichtheid f heeft impliceert niet dat 1 - U een kansdichtheid 1 - f heeft. (Dat zou ook niet kunnen want dat is geen kansdichtheid)
Je moet laten zien dat U ook kansdichtheid f heeft.
Dat kan door te laten zien dat de verdelingsfuncties van U en 1-U hetzelfde zijn.
Je moet laten zien dat U ook kansdichtheid f heeft.
Dat kan door te laten zien dat de verdelingsfuncties van U en 1-U hetzelfde zijn.


lim x --> 0quote:Op woensdag 8 oktober 2014 21:53 schreef Riparius het volgende:
[..]
Weer hetzelfde advies: lees hier niet alleen de antwoorden op je eigen vragen, maar ook de antwoorden op vragen van je studiegenoten die vaak over precies dezelfde opgaven gaan.
Ik vermoed (c.q. weet bijna wel zeker) dat je probeert deze limiet te bepalen met behulp van de regel van L'Hôpital, maar dan heb je fouten gemaakt bij het differentiëren.
(-1/2(1+x) -3/2 ) / [ 2(1 + x + x²) -1/2 + ( 1 + 2x)² ( -1/2) ( (1 + x + x²) -3/2 ]
Er moest een 2 weg, welke ik nu weggehaald heb. De afgeleide klopt exact met wat er in het antwoordenboek staat.


Goedenavond,
Ziet iemand de overgang van wat er links voor het = teken staat naar wat er rechts van het = teken staat?:
Wat mij onduidelijk is (de vraag heeft betrekking op de extreme punten) is x1 en x2... Ik vind het erg lastig om te weten wat voor getal x1 en x2 nou voorstellen en hoe ik dit moet invullen, want de functie maakt het er niet gemakkelijker op met wortels en al..
Ziet iemand de overgang van wat er links voor het = teken staat naar wat er rechts van het = teken staat?:
Wat mij onduidelijk is (de vraag heeft betrekking op de extreme punten) is x1 en x2... Ik vind het erg lastig om te weten wat voor getal x1 en x2 nou voorstellen en hoe ik dit moet invullen, want de functie maakt het er niet gemakkelijker op met wortels en al..


Ik neem aan dat jij geen moeite hebt met van rechts naar links te gaan. Doe dat dan eens en je zal er vanzelf achter komen hoe ze van links naar rechts gaan.quote:Op woensdag 8 oktober 2014 22:49 schreef GeschiktX het volgende:
Goedenavond,
Ziet iemand de overgang van wat er links voor het = teken staat naar wat er rechts van het = teken staat?:
[ afbeelding ]
Wat mij onduidelijk is (de vraag heeft betrekking op de extreme punten) is x1 en x2... Ik vind het erg lastig om te weten wat voor getal x1 en x2 nou voorstellen en hoe ik dit moet invullen, want de functie maakt het er niet gemakkelijker op met wortels en al..
Die wortel maakt het in dit geval trouwens niet moeilijker.
[ Bericht 2% gewijzigd door Bram_van_Loon op 08-10-2014 22:59:22 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Om te beginnen zie ik een fout (en een typo). De afgeleide van arctan x naar x is 1/(1 + x²). Om √(x² + a²) te primitiveren met behulp van partiële integratie vat je de integrand op als het product van 1 en √(x² + a²) en dan krijg jequote:Op woensdag 8 oktober 2014 21:00 schreef Aardappeltaart het volgende:
Eerste keer dat ik dit topic nodig heb tijdens mijn studie wiskunde. Bevalt erg goed.
Uit g(x)=ln(x+sqrt(x2+a2)) zijn afgeleide g'(x)= 1 / (sqrt(a2+x2) en die van d/dx artcan(x) = 1/sqrt(a2-x2) moet ik de primitieve van h(x)=sqrt(x2+a2) kunnen halen door middel van partiële integratie (ik vermoed op h(x). Ik zie alleen niet hoe, met welke keuzes dus. De delen van de vraag over het differentiëren van g(x) en de primitieve vinden van 1/h(x) zijn me gelukkig al gelukt. Op dit stuk loop ik echter vast. Iemand een tip of idee? Goniometrische substituties zijn dus niet de bedoeling. Alvast bedankt!
Nu hebben we ook
zodat we dus krijgen
en dit geeft
en dus
aangezien we al wisten dat
Er is overigens een interessante manier om deze laatste integraal met behulp van een substitutie te behandelen. Je mag zonder verlies van algemeenheid a > 0 veronderstellen, en als je nu
substitueert, waarin je dan u > 0 mag veronderstellen zodat
dan vind je dat de integraal reduceert tot
aangezien
en dus
terwijl
Het is eenvoudig om het verband te zien tussen deze algebraïsche substitutie en de meer gebruikelijke hyperbolische substitutie om deze integraal te behandelen. Substitueren we namelijk
in
dan hebben we
en daarmee
en dan is ook
en
zodat de integraal reduceert tot
en we dus hebben
als tegenhanger van
[ Bericht 8% gewijzigd door Riparius op 09-10-2014 20:30:17 ]


De verdelingsfunctie van U is de volgende:quote:Op woensdag 8 oktober 2014 22:45 schreef Anoonumos het volgende:
Dat U een kansdichtheid f heeft impliceert niet dat 1 - U een kansdichtheid 1 - f heeft. (Dat zou ook niet kunnen want dat is geen kansdichtheid)
Je moet laten zien dat U ook kansdichtheid f heeft.
Dat kan door te laten zien dat de verdelingsfuncties van U en 1-U hetzelfde zijn.
Maar moet ik de 1 buiten de functie laten of niet? Dus 1 - f(u) is 1 - U ?
Kom maar konijntje, doe maar wiebelen wiebelen...


Als je links in de teller haakjes uitwerkt en de 8 buiten haakjes laat staat er 8(3x2+4-6x2)= 8(4-3x2). Via het merkwaardig product a2-b2=(a+b)(a-b) kom je aan de rechterkant uit.quote:Op woensdag 8 oktober 2014 22:49 schreef GeschiktX het volgende:
Goedenavond,
Ziet iemand de overgang van wat er links voor het = teken staat naar wat er rechts van het = teken staat?:
[ afbeelding ]
Wat mij onduidelijk is (de vraag heeft betrekking op de extreme punten) is x1 en x2... Ik vind het erg lastig om te weten wat voor getal x1 en x2 nou voorstellen en hoe ik dit moet invullen, want de functie maakt het er niet gemakkelijker op met wortels en al..
En over die extreme waarden:
Je hebt de functie (8x)/(3x2+4) gedifferentieerd, en om de extreme waarden van die functie te vinden stel je de afgeleide gelijk aan 0. Immers, waar de afgeleide functie gelijk aan nul is, is de raaklijn horizontaal en dan heb je óf een extremum óf een buigpunt te pakken.
Om de nulpunten van je afgeleide te vinden is de ontbinding van de teller uit je post handig. Want voor welke twee waarden van x is de teller, en dus de breuk, gelijk aan 0?
Opinion is the medium between knowledge and ignorance (Plato)


Tot zover was het mij wel gelukt, maar de merkwaardigheid ervan zie ik niet. Daar stoot ik mijzelf tegen de 'douchekop'.quote:Op woensdag 8 oktober 2014 22:59 schreef Janneke141 het volgende:
[..]
Als je links in de teller haakjes uitwerkt en de 8 buiten haakjes laat staat er 8(3x2+4-6x2)= 8(4-3x2). Via het merkwaardig product a2-b2=(a+b)(a-b) kom je aan de rechterkant uit.


http://nl.wikipedia.org/wiki/Merkwaardig_productquote:Op woensdag 8 oktober 2014 23:04 schreef GeschiktX het volgende:
[..]
Tot zover was het mij wel gelukt, maar de merkwaardigheid ervan zie ik niet. Daar stoot ik mijzelf tegen de 'douchekop'.
Opinion is the medium between knowledge and ignorance (Plato)


Ja die ken ik allemaal... Dit was nog zelfs nog middelbare school wiskunde. Toch zie ik hem niet.. Het ziet er veel anders uit die 8(4-3x²).. dan ik gewend ben voor een merkwaardig product zoals bijv. (a-b)²quote:Op woensdag 8 oktober 2014 23:05 schreef Janneke141 het volgende:
[..]
http://nl.wikipedia.org/wiki/Merkwaardig_product


Vergeet even de 8, en kijk alleen naar 4-3x². Dat is van de vorm a²-b², waarbij a=2 en b=x√3.quote:Op woensdag 8 oktober 2014 23:07 schreef GeschiktX het volgende:
[..]
Ja die ken ik allemaal... Dit was nog zelfs nog middelbare school wiskunde. Toch zie ik hem niet.. Het ziet er veel anders uit die 8(4-3x²).. dan ik gewend ben voor een merkwaardig product zoals bijv. (a-b)²
Je weet dat a²-b²=(a+b)(a-b), dus dan is ook, in dit geval:
4-3x² = (2+x√3)(2-x√3)
Opinion is the medium between knowledge and ignorance (Plato)


Noem dat FU. De verdelingsfunctie van 1-U is dan (voor alle u in [0,1])quote:Op woensdag 8 oktober 2014 22:59 schreef Hoplahopla het volgende:
[..]
De verdelingsfunctie van U is de volgende:
Maar moet ik de 1 buiten de functie laten of niet? Dus 1 - f(u) is 1 - U ?
Waar jij nog de laatste één a twee tussenstappen kan invullen.
Snap je het zo? Ik weet niet wat je bedoelt met je laatste vraag.


Ohh wat oliedom van me.quote:Op woensdag 8 oktober 2014 23:10 schreef Janneke141 het volgende:
[..]
Vergeet even de 8, en kijk alleen naar 4-3x². Dat is van de vorm a²-b², waarbij a=2 en b=x√3.
Je weet dat a²-b²=(a+b)(a-b), dus dan is ook, in dit geval:
4-3x² = (2+x√3)(2-x√3)
Dit is dan zeker ook een merkwaardig product?
4x5 - 8x5 ?


Om te beginnen: de term merkwaardig product is ergens in de 19e eeuw in het onderwijs geïntroduceerd. Niet omdat er iets 'merkwaardigs' mee aan de hand zou zijn, maar omdat ze het (be)merken waard zijn, oftewel omdat ze het waard zijn onthouden te worden. Dit klinkt nu een beetje ouderwets, en de term wordt door hedendaagse generaties vaak verkeerd begrepen, maar de term is blijven hangen en deze identiteiten heten nu eenmaal zo. En inderdaad moet je ze gewoon van buiten kennen, en dan niet alleen van links naar rechts maar ook van rechts naar links. En daarnaast moet je ze ook altijd kunnen herkennen en toepassen, anders heb je er tenslotte nog niets aan. En aan dat laatste schort het bij jou. Als je zietquote:Op woensdag 8 oktober 2014 23:07 schreef GeschiktX het volgende:
[..]
Ja die ken ik allemaal... Dit was nog zelfs nog middelbare school wiskunde. Toch zie ik hem niet.. Het ziet er veel anders uit die 8(4-3x²).. dan ik gewend ben voor een merkwaardig product zoals bijv. (a-b)²
4 − 3x²
en je wil dit ontbinden in lineaire factoren (en ja, dat wil je, waarom eigenlijk?) dan moet je direct zien dat je dit op kunt vatten als een verschil van twee kwadraten, namelijk als
2² − (√3·x)²
en dus als
(2 − √3·x)(2 + √3·x)


Dat is gewoon -4x5.quote:Op woensdag 8 oktober 2014 23:17 schreef GeschiktX het volgende:
[..]
Ohh wat oliedom van me.Dankje.
Dit is dan zeker ook een merkwaardig product?
4x5 - 8x5 ?


Dit stuk schort bij mij, waardoor ik het laatste dus niet kan zien.quote:Op woensdag 8 oktober 2014 23:18 schreef Riparius het volgende:
[..]
Om te beginnen: de term merkwaardig product is ergens in de 19e eeuw in het onderwijs geïntroduceerd. Niet omdat er iets 'merkwaardigs' mee aan de hand zou zijn, maar omdat ze het (be)merken waard zijn, oftewel omdat ze het waard zijn onthouden te worden. Dit klinkt nu een beetje ouderwets, en de term wordt door hedendaagse generaties vaak verkeerd begrepen, maar de term is blijven hangen en deze identiteiten heten nu eenmaal zo. En inderdaad moet je ze gewoon van buiten kennen, en dan niet alleen van links naar rechts maar ook van rechts naar links. En daarnaast moet je ze ook altijd kunnen herkennen en toepassen, anders heb je er tenslotte nog niets aan. En aan dat laatste schort het bij jou. Als je ziet
4 − 3x²
en je wil dit ontbinden in lineaire factoren (en ja, dat wil je, waarom eigenlijk?) dan moet je direct zien dat je dit op kunt vatten als een verschil van twee kwadraten, namelijk als
2² − (√3·x)²
en dus als
(2 − √3·x)(2 + √3·x)


Nee. Bedenk zelf maar waarom niet.quote:Op woensdag 8 oktober 2014 23:17 schreef GeschiktX het volgende:
Dit is dan zeker ook een merkwaardig product?
4x5 - 8x5 ?


Oeps verkeerde functie gekopieerd..quote:Op woensdag 8 oktober 2014 23:19 schreef Riparius het volgende:
[..]
Nee. Bedenk zelf maar waarom niet.


quote:Op woensdag 8 oktober 2014 23:19 schreef Riparius het volgende:
[..]
Nee. Bedenk zelf maar waarom niet.
quote:Op woensdag 8 oktober 2014 23:19 schreef GeschiktX het volgende:
[..]
Klopt, maar als je dit wilt factoriseren, hoe doe je dit?
[ 4x ( x4 + 1 ) - 2x² 4x³ ]quote:Op woensdag 8 oktober 2014 23:21 schreef GeschiktX het volgende:
[..]
Oeps verkeerde functie gekopieerd..
ofwel
4x5 + 4x - 8x5
Het zou moeten resulteren tot:
4x( 1 + x² ) ( 1 + x) ( 1-x)


Ik denk dat het een goede oefening voor jou is als je zelf eens (a+b)(a+b) , (a+b)(a-b) en (a-b)(a-b) uitrekent en er op let wat het patroon is. Je zou binnen een seconde moeten kunnen opdreunen wat er uit komt als a en b een ander ander getal zijn.quote:Op woensdag 8 oktober 2014 23:19 schreef GeschiktX het volgende:
[..]
Dit stuk schort bij mij, waardoor ik het laatste dus niet kan zien.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Die factoren staan al voor je neus, het is namelijk −4·x·x·x·x·x maar zo moet je dit natuurlijk niet opschrijven, Descartes heeft niet voor niets de notatie van een exponent met superscript bedacht.quote:Op woensdag 8 oktober 2014 23:19 schreef GeschiktX het volgende:
[..]
Klopt, maar als je dit wilt factoriseren, hoe doe je dit?


Omslachtig, maar klopt welquote:Op woensdag 8 oktober 2014 23:22 schreef GeschiktX het volgende:
[..]
[..]
[..]
[ 4x ( x4 + 1 ) - 2x² 4x³ ]
ofwel
4x5 + 4x - 8x5
Het zou moeten resulteren tot:
4x( 1 + x² ) ( 1 + x) ( 1-x)
4x5 + 4x - 8x5
=-4x5 + 4x
=4x(1-x4)
= 4x(1+x2)(1-x2)
= 4x(1+x2)(1-x)(1+x)
Hetzelfde merkwaardig product als boven wordt twee keer gebruikt.
Opinion is the medium between knowledge and ignorance (Plato)


De fout is inderdaad een typo, helaas. Omdat ik een nieuwe laptop heb is een werkende Mathtype niet meer beschikbaar en zo typen is enorm onoverzichtelijk. Tijd om misschien een LaTeX te gaan leren...quote:
Fijn deze uitwerking, ik snap hem! Heel erg bedankt! Het blijkt dat ik dit spoor niet heb afgemaakt omdat ik bij het afleiden van de wortel vergat te compenseren met 2x, waardoor er geen kwadraat in de teller kwam, enz. Wat haat ik slordigheidsfouten zeg.


@Geschiktquote:Op woensdag 8 oktober 2014 23:23 schreef Janneke141 het volgende:
[..]
Omslachtig, maar klopt wel
4x5 + 4x - 8x5
=-4x5 + 4x
=4x(1-x4)
= 4x(1+x2)(1-x2)
= 4x(1+x2)(1-x)(1+x)
Hetzelfde merkwaardig product als boven wordt twee keer gebruikt.
Hier zie je nu een goede demonstratie waarom het belangrijk is dat je het merkwaardige product direct herkent. Je ziet dan direct bij de derde regel van Janneke haar uitleg hoe je dat verder opschrijft waardoor je niet zelf hoeft te zoeken door willekeurig wat uit te proberen.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Ik zie het écht niet. Ben me er nu al een paar uur op aan het blindstaren...quote:Op woensdag 8 oktober 2014 23:13 schreef Anoonumos het volgende:
[..]
Noem dat FU. De verdelingsfunctie van 1-U is dan (voor alle u in [0,1])
Waar jij nog de laatste één a twee tussenstappen kan invullen.
Snap je het zo? Ik weet niet wat je bedoelt met je laatste vraag.
Kom maar konijntje, doe maar wiebelen wiebelen...


Werkt je registratiecode niet meer? Of heb je nu een ander besturingssysteem waarmee MathType niet meer werkt?quote:Op woensdag 8 oktober 2014 23:27 schreef Aardappeltaart het volgende:
[..]
De fout is inderdaad een typo, helaas. Omdat ik een nieuwe laptop heb is een werkende Mathtype niet meer beschikbaar en zo typen is enorm onoverzichtelijk. Tijd om misschien een LaTeX te gaan leren...
quote:Fijn deze uitwerking, ik snap hem! Heel erg bedankt! Het blijkt dat ik dit spoor niet heb afgemaakt omdat ik bij het afleiden van de wortel vergat te compenseren met 2x, waardoor er geen kwadraat in de teller kwam, enz. Wat haat ik slordigheidsfouten zeg.


De ontbrekende stappen zie je niet, of begrijp je niet wat ik tot nu toe doe?quote:Op woensdag 8 oktober 2014 23:29 schreef Hoplahopla het volgende:
[..]
Ik zie het écht niet. Ben me er nu al een paar uur op aan het blindstaren...


Ja inderdaad Bram_Van_Loon, het is zoals je in een post hiervoor al zei een kwestie voor mij om het goed in mijn hoofd te stampen. Ik zal er goed naar kijken!~quote:Op woensdag 8 oktober 2014 23:28 schreef Bram_van_Loon het volgende:
[..]
@Geschikt
Hier zie je nu een goede demonstratie waarom het belangrijk is dat je het merkwaardige product direct herkent. Je ziet dan direct bij de derde regel van Janneke haar uitleg hoe je dat verder opschrijft waardoor je niet zelf hoeft te zoeken door willekeurig wat uit te proberen.
Vanaf de derde regel is het inderdaad al gelijk te zien... en dan is het een kwestie van het 'verkleinen' van de vierde macht naar tweede machten en dat dan weer verkleinen naar een 1e graad (1e exponent).
Ik wou bijna vragen waarom (1+x²) zo blijft staan, maar dat komt omdat beide plus is (neem ik aan?). Als het bijv x² - 1 was geweest, had (x+1) (x-1) gemogen toch?


Het is belangrijk om een beetje systematisch na te denken bij zoiets. Als je een vergelijking hebt van de vorm ax²+ bx + c, waar komen die a, b en c vandaan? Wat is het gevolg voor de a, b en c als je bij (d+e)(f+g) twee keer een - of 1 keer een - hebt in plaats van een plus? Kan a, b of c 0 zijn en wanneer gebeurt dat? Probeer voor jezelf eens alle variaties uit en je zal vanzelf inzien hoe het werkt zodat je niets van buiten hoeft te leren, in ieder geval niet voor de tweede graad. Bij de een duurt het langer dan bij de ander maar dat inzicht komt wel als je dat doet.quote:Op woensdag 8 oktober 2014 23:34 schreef GeschiktX het volgende:
[..]
Ja inderdaad Bram_Van_Loon, het is zoals je in een post hiervoor al zei een kwestie voor mij om het goed in mijn hoofd te stampen. Ik zal er goed naar kijken!~
Vanaf de derde regel is het inderdaad al gelijk te zien... en dan is het een kwestie van het 'verkleinen' van de vierde macht naar tweede machten en dat dan weer verkleinen naar een 1e graad (1e exponent).
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Ik heb geen Word meer. Ik moet nog kijken of ik de code terug kan vinden en het kan installeren enzovoorts op Openoffice.quote:Op woensdag 8 oktober 2014 23:30 schreef Riparius het volgende:
[..]
Werkt je registratiecode niet meer? Of heb je nu een ander besturingssysteem waarmee MathType niet meer werkt?
[..]


Een som van twee kwadraten kun je niet schrijven als een product van reële lineaire factoren en daarom heeft bijvoorbeeld de vergelijkingquote:Op woensdag 8 oktober 2014 23:34 schreef GeschiktX het volgende:
[..]
Ik wou bijna vragen waarom (1+x²) zo blijft staan, maar dat komt omdat beide plus is (neem ik aan?). Als het bijv x² - 1 was geweest, had (x+1) (x-1) gemogen toch?
ook geen oplossingen binnen R, de verzameling van alle reële getallen. Begrijp je het verband tussen het niet kunnen ontbinden van x² + 1 in reële factoren en het ontbreken van reële oplossingen van deze vergelijking?
Een som van twee oneven machten kun je overigens wel ontbinden, want als n oneven is dan heeft de som an + bn een factor (a + b). Zo heb je bijvoorbeeld
Als je ook irrationale coëfficiënten toestaat, dan is een tweeterm als
wel te ontbinden in twee reële kwadratische veeltermen in a en b. Probeer nu zelf te bedenken hoe je dit zou ontbinden.


Als je in dit quotiënt x = 0 invult, dan komt erquote:Op woensdag 8 oktober 2014 22:48 schreef Super-B het volgende:
[..]
lim x --> 0
(-1/2(1+x) -3/2 ) / [ 2(1 + x + x²) -1/2 + ( 1 + 2x)² ( -1/2) ( (1 + x + x²) -3/2 ]
Er moest een 2 weg, welke ik nu weggehaald heb. De afgeleide klopt exact met wat er in het antwoordenboek staat.


Voor mij verdwijnt die 1 op magische wijze. Ik kan me niet bedenken waarom dat gebeurt namelijk.quote:Op woensdag 8 oktober 2014 23:13 schreef Anoonumos het volgende:
[..]
Noem dat FU. De verdelingsfunctie van 1-U is dan (voor alle u in [0,1])
Waar jij nog de laatste één a twee tussenstappen kan invullen.
Snap je het zo? Ik weet niet wat je bedoelt met je laatste vraag.
Ik vermoed dat de uitwerking op de puntjes iets in de trant van
Kom maar konijntje, doe maar wiebelen wiebelen...


Hartstikke bedankt!quote:Op donderdag 9 oktober 2014 00:46 schreef Riparius het volgende:
[..]
Als je in dit quotiënt x = 0 invult, dan komt er


quote:Op donderdag 9 oktober 2014 06:00 schreef Hoplahopla het volgende:
[..]
Voor mij verdwijnt die 1 op magische wijze. Ik kan me niet bedenken waarom dat gebeurt namelijk.
Ik vermoed dat de uitwerking op de puntjes iets in de trant vanis, maar echt lekker voelt het niet aan.
(alleen als u=1/2 is het wel een gelijkheid)
Dus dat klopt inderdaad niet.


Even een kleine vraagje:
Stel ik heb:
ax + by = c
en
dx + ey = f
Waar x dan vervolgens: (ce - bf) / (ae - bd) is..
Hoe bereken ik y?
Ik vulde gewoon x in één van de twee vergelijkingen ( ik deed het in de eerste) en ik kwam uit op het volgende:
y = (ace - abf) / (ae - bd) + by - c
Klopt dit?
Stel ik heb:
ax + by = c
en
dx + ey = f
Waar x dan vervolgens: (ce - bf) / (ae - bd) is..
Hoe bereken ik y?
Ik vulde gewoon x in één van de twee vergelijkingen ( ik deed het in de eerste) en ik kwam uit op het volgende:
y = (ace - abf) / (ae - bd) + by - c
Klopt dit?


Nee, dit klopt niet, en dat is ook onmiddellijk te zien. Subsitutie geeft namelijkquote:Op donderdag 9 oktober 2014 18:36 schreef Super-B het volgende:
Even een kleine vraagje:
Stel ik heb:
ax + by = c
en
dx + ey = f
Waar x dan vervolgens: (ce - bf) / (ae - bd) is..
Hoe bereken ik y?
Ik vulde gewoon x in één van de twee vergelijkingen ( ik deed het in de eerste) en ik kwam uit op het volgende:
y = (ace - abf) / (ae - bd) + by - c
Klopt dit?
(ace - abf) / (ae - bd) + by - c = 0
en het is niet zo dat y hier steeds gelijk is aan nul, zodat het linkerlid van deze gelijkheid niet gelijk kan zijn aan y zoals jij hier beweert.


Je hebt 2 lineaire verbanden. Waar x dan vervolgens *iets* is. Hoezo is x dat? Hoe kom je aan die x?quote:Op donderdag 9 oktober 2014 18:36 schreef Super-B het volgende:
Even een kleine vraagje:
Stel ik heb:
ax + by = c
en
dx + ey = f
Waar x dan vervolgens: (ce - bf) / (ae - bd) is..
Hoe bereken ik y?
Ik vulde gewoon x in één van de twee vergelijkingen ( ik deed het in de eerste) en ik kwam uit op het volgende:
y = (ace - abf) / (ae - bd) + by - c
Klopt dit?
Ik heb het niet nagerekend, maar het zal wel het evenwichtspunt zijn, oftewel de x-waarde van het snijpunt van die twee rechte lijnen. Dit soort dingen moet je vermelden in je post!. Áls dat zo is, dan kun je y uitrekenen door x in te vullen in één van beide vergelijkingen. Hebben we het niet over een evenwichtspunt, dan werkt het natuurlijk niet omdat er bij allebei wat anders uitkomt.
OK, we gaan invullen in de bovenste:
ax+by=c
a((ce - bf) / (ae - bd)) + by = c
(ace-abf)/(ae-bd) + by = c
even een onnodige tussenstap, behalve om je denkfout te laten zien
(ace-abf)/(ae-bd) + by - c = 0
Jij concludeert dat gedeelte links van het =-teken gelijk moet zijn aan y. Klopt niet, het is gelijk aan 0. Je eigen uitdrukking voor y hangt trouwens af van y, wat al niet handig is)
einde intermezzo
(ace-abf)/(ae-bd) + by = c
by = c - (ace-abf)/(ae-bd)
y = (c - (ace-abf)/(ae-bd))/b
Dat laatste verder netjes uitschrijven mag je zelf doen. Mag je daarna uittesten of er hetzelfde uitkomt als je de x-waarde invult in de onderste.
Opinion is the medium between knowledge and ignorance (Plato)


Ik moet er uiteindelijk (af - cd) / (ae - bd) van maken.... Ik zie het niet. Dat laatste stap maakt het mij dus lastig. Wat jij had, had ik dus ook, alleen had ik per ongeluk uit automatisme y = opgeschreven..quote:Op donderdag 9 oktober 2014 18:48 schreef Janneke141 het volgende:
[..]
Je hebt 2 lineaire verbanden. Waar x dan vervolgens *iets* is. Hoezo is x dat? Hoe kom je aan die x?
Ik heb het niet nagerekend, maar het zal wel het evenwichtspunt zijn, oftewel de x-waarde van het snijpunt van die twee rechte lijnen. Dit soort dingen moet je vermelden in je post!. Áls dat zo is, dan kun je y uitrekenen door x in te vullen in één van beide vergelijkingen. Hebben we het niet over een evenwichtspunt, dan werkt het natuurlijk niet omdat er bij allebei wat anders uitkomt.
OK, we gaan invullen in de bovenste:
ax+by=c
a((ce - bf) / (ae - bd)) + by = c
(ace-abf)/(ae-bd) + by = c
even een onnodige tussenstap, behalve om je denkfout te laten zien
(ace-abf)/(ae-bd) + by - c = 0
Jij concludeert dat gedeelte links van het =-teken gelijk moet zijn aan y. Klopt niet, het is gelijk aan 0. Je eigen uitdrukking voor y hangt trouwens af van y, wat al niet handig is)
einde intermezzo
(ace-abf)/(ae-bd) + by = c
by = c - (ace-abf)/(ae-bd)
y = (c - (ace-abf)/(ae-bd))/b
Dat laatste verder netjes uitschrijven mag je zelf doen. Mag je daarna uittesten of er hetzelfde uitkomt als je de x-waarde invult in de onderste.


Tja, dit is algebra die ze in 2-vmbo-t zonder al te veel problemen uitvoeren.quote:Op donderdag 9 oktober 2014 19:12 schreef Super-B het volgende:
[..]
Ik moet er uiteindelijk (af - cd) / (ae - bd) van maken.... Ik zie het niet. Dat laatste stap maakt het mij dus lastig. Wat jij had, had ik dus ook, alleen had ik per ongeluk uit automatisme y = opgeschreven..
Overigens, nog steeds onder het vermoeden dat het om een evenwichtspunt gaat, kan het natuurlijk ook anders:
Schrijven in de vorm x=..., zodat we ze gelijk kunnen stellen met y als variabele, levertquote:ax + by = c
en
dx + ey = f
x = (c-by)/a
en
x = (f-ey)/d
Gelijkstellen:
(c-by)/a = (f-ey)/d
dc-dby = af - aey
aey - dby = af - dc
(ae - db)y = af - dc
y = (af - cd)/(ae - bd)
Klaar.
Opinion is the medium between knowledge and ignorance (Plato)


De vraag is hoe je x hebt bepaald uit je lineaire stelsel. Als je dat zelfstandig kunt, dan kun je op dezelfde manier ook y bepalen.quote:Op donderdag 9 oktober 2014 19:12 schreef Super-B het volgende:
[..]
Ik moet er uiteindelijk (af - cd) / (ae - bd) van maken.... Ik zie het niet. Dat laatste stap maakt het mij dus lastig. Wat jij had, had ik dus ook, alleen had ik per ongeluk uit automatisme y = opgeschreven..
Bedenk trouwens wel dat je lineaire stelsel uitsluitend een eenduidige oplossing heeft als
ae − bd ≠ 0
want delen door nul heeft geen betekenis. De waarde ae − bd heet de determinant van je lineaire stelsel. Is deze determinant gelijk aan nul, dan is je stelsel ofwel strijdig (dan zijn er geen oplossingen) ofwel onbepaald (dan zijn er oneindig veel oplossingen). Het is gemakkelijk in te zien waarom je deze drie mogelijkheden hebt: de twee lineaire vergelijkingen in x en y stellen elk een rechte lijn voor in een cartesisch coördinatenstelsel, en twee rechte lijnen kunnen elkaar snijden (één oplossing), evenwijdig lopen (geen oplossing) of geheel en al samenvallen (oneindig veel oplossingen).


Waarom mogen de noemers weg?quote:Op donderdag 9 oktober 2014 19:18 schreef Janneke141 het volgende:
[..]
Tja, dit is algebra die ze in 2-vmbo-t zonder al te veel problemen uitvoeren.
Overigens, nog steeds onder het vermoeden dat het om een evenwichtspunt gaat, kan het natuurlijk ook anders:
[..]
Schrijven in de vorm x=..., zodat we ze gelijk kunnen stellen met y als variabele, levert
x = (c-by)/a
en
x = (f-ey)/d
Gelijkstellen:
(c-by)/a = (f-ey)/d
dc-dby = af - aey
aey - dby = af - dc
(ae - db)y = af - dc
y = (af - cd)/(ae - bd)
Klaar.
Ik kwam namelijk uit op
(( dc - dby) / ad ) - ((a - aey) / ad)


Hoe vaak is je in dit topic al verteld dat je zorgvuldig moet zijn met het opschrijven van vergelijkingen en dus niet het =-teken en alles wat erachter staat moet vergeten?quote:Op donderdag 9 oktober 2014 19:45 schreef Super-B het volgende:
[..]
Waarom mogen de noemers weg?
Ik kwam namelijk uit op
(( dc - dby) / ad ) - ((a - aey) / ad)
Maar goed,
Vermenigvuldig links en rechts alles met a en d.quote:(c-by)/a = (f-ey)/d
dc-dby = af - aey
Opinion is the medium between knowledge and ignorance (Plato)


Dus dan moet ik weer met ad vermenigvuldigen om zo de noemer weg te krijgen?quote:Op donderdag 9 oktober 2014 19:48 schreef Janneke141 het volgende:
[..]
Hoe vaak is je in dit topic al verteld dat je zorgvuldig moet zijn met het opschrijven van vergelijkingen en dus niet het =-teken en alles wat erachter staat moet vergeten?
Maar goed,
[..]
Vermenigvuldig links en rechts alles met a en d.


Hallo.. Ik heb een drietal vragen:
Voor de volgende twee functies moet ik de logaritmes differentiëren toepassen om y'/y te vinden:
f(x) = ((x+1) / (x-1) ) 1/3
en
g(x) = √(x-2) (x²+1) (x4 + 6)
Ik kwam bij de afgeleide van g'(x) niet uit, laat staan g'(x) vinden met log. differentiëren. Bij die eerste deed ik het volgende:
y = ((x+1) / (x-1) ) 1/3
ln y = ln (x+1)1/3 - ln(x-1) 1/3
y' / y = 1/3 * 1/(x+1) - 1/3 * 1/(x-1)
Mijn derde vraag is het volgende:
Hoe kan ik van de volgende functie het 'solven' voor P en vervolgens dP/dQ vinden:
Q = ea P -b
Voor de volgende twee functies moet ik de logaritmes differentiëren toepassen om y'/y te vinden:
f(x) = ((x+1) / (x-1) ) 1/3
en
g(x) = √(x-2) (x²+1) (x4 + 6)
Ik kwam bij de afgeleide van g'(x) niet uit, laat staan g'(x) vinden met log. differentiëren. Bij die eerste deed ik het volgende:
y = ((x+1) / (x-1) ) 1/3
ln y = ln (x+1)1/3 - ln(x-1) 1/3
y' / y = 1/3 * 1/(x+1) - 1/3 * 1/(x-1)
Mijn derde vraag is het volgende:
Hoe kan ik van de volgende functie het 'solven' voor P en vervolgens dP/dQ vinden:
Q = ea P -b


Wat heb je voor g(x) geprobeerd dan?quote:Op donderdag 9 oktober 2014 20:50 schreef RustCohle het volgende:
Ik kwam bij de afgeleide van g'(x) niet uit, laat staan g'(x) vinden met log. differentiëren. Bij die eerste deed ik het volgende:
[...]
"solven" is oplossen, dus los een vergelijking voor P op en neem de afgeleide.quote:Mijn derde vraag is het volgende:
Hoe kan ik van de volgende functie het 'solven' voor P en vervolgens dP/dQ vinden:
Q = ea P -b
Wat lukt hier niet?


Voor P oplossen wordt het :quote:Op donderdag 9 oktober 2014 21:24 schreef t4rt4rus het volgende:
[..]
Wat heb je voor g(x) geprobeerd dan?
[..]
"solven" is oplossen, dus los een vergelijking voor P op en neem de afgeleide.
Wat lukt hier niet?
Q / ea = P-b
Maar dat is dus niet goed..


Nee P-b is ook geen P...quote:Op donderdag 9 oktober 2014 21:36 schreef RustCohle het volgende:
[..]
Voor P oplossen wordt het :
Q / ea = P-b
Maar dat is dus niet goed..
Dus hoe krijg je dat weg?
En wat heb je voor die andere gedaan?


De clou van logaritmisch differentiëren is dat je eerst van beide leden de (natuurlijke) logaritme neemt en dan beide leden differentieert. Welnu, je hebtquote:Op donderdag 9 oktober 2014 20:50 schreef RustCohle het volgende:
Hallo.. Ik heb een drietal vragen:
Voor de volgende twee functies moet ik de logaritmes differentiëren toepassen om y'/y te vinden:
f(x) = ((x+1) / (x-1) ) 1/3
en
g(x) = √(x-2) (x²+1) (x4 + 6)
Ik kwam bij de afgeleide van g'(x) niet uit, laat staan g'(x) vinden met log. differentiëren. Bij die eerste deed ik het volgende:
y = ((x+1) / (x-1) ) 1/3
ln y = ln (x+1)1/3 - ln(x-1) 1/3
y' / y = 1/3 * 1/(x+1) - 1/3 * 1/(x-1)
en dus
zodat
Vermenigvuldig eerst beide leden met PbQ−1 en je hebtquote:Mijn derde vraag is het volgende:
Hoe kan ik van de volgende functie het 'solven' voor P en vervolgens dP/dQ vinden:
Q = ea P -b
en dus
en dit geeft
en dus
zodat


Goed opgemerkt. Er had moeten staan dat de functie f niet differentieerbaar is in het punt x = 2. Voor elke andere waarde van x uit het domein is deze functie f wel differentieerbaar. Maar je moet even nakijken welke definitie ze precies hanteren voor een differentieerbare functie tout court.quote:Op donderdag 9 oktober 2014 22:01 schreef Super-B het volgende:
[ afbeelding ]
Waarom staat er op het einde dat f(x) niet differentieerbaar is? Het is tóch juist wel differentieerbaar, alleen het is niet differentieerbaar op het punt x = 2.. (?)


De definitie is dat het overal differentieerbaar moet zijn...quote:Op donderdag 9 oktober 2014 22:01 schreef Super-B het volgende:
[ afbeelding ]
Waarom staat er op het einde dat f(x) niet differentieerbaar is? Het is tóch juist wel differentieerbaar, alleen het is niet differentieerbaar op het punt x = 2.. (?)
Dit kon je niet zelf bedenken?


quote:Op donderdag 9 oktober 2014 22:09 schreef t4rt4rus het volgende:
[..]
De definitie is dat het overal differentieerbaar moet zijn...
Dit kon je niet zelf bedenken?


Je moet hier gewoon goed naar het gegeven functievoorschrift kijken voor f(x) en de definitie voor continuïteit hanteren. Een reële functie f van een reële variabele gedefinieerd op een domein Df is continu indien f continu is voor elke a ∈ Df en een functie f is continu in een punt a ∈ Df dan en slechts dan als limx→a f(x) = f(a). En dat is hier het geval voor elke a ∈ R terwijl R het domein is van deze functie.quote:Op donderdag 9 oktober 2014 22:06 schreef Super-B het volgende:
Ten tweede:
[ afbeelding ]
Waarom is de functie continu voor alle x, terwijl (2x - 2)/ ln (x) alleen continu is als x > 0, Dus dan zou de hele functie toch continu moeten zijn als x > 0? Daarnaast waarom x > 0 en niet x > 1? Want als x = 1 dan is de noemer 0...


Dat trucje van logaritmisch differentiëren kende ik nog niet trouwens.quote:Op donderdag 9 oktober 2014 21:54 schreef Riparius het volgende:
[..]
De clou van logaritmisch differentiëren is dat je eerst van beide leden de (natuurlijke) logaritme neemt en dan beide leden differentieert. Welnu, je hebt
en dus
zodat
[..]
Vermenigvuldig eerst beide leden met PbQ−1 en je hebt
en dus
en dit geeft
en dus
zodat


Het is niet echt iets waarvoor deze draad is bedoeld, helaas misschien, maar het lijkt me aardig om het toch maar eens te doen.
Ik kwam een interessant vraagstuk tegen wat gemakkelijk te begrijpen is maar desalniettemin erg leerzaam is.
Heron's probleem. De vraag. Plaatsen A en B liggen langs een rivier, je moet via die rivier van A naar B. Wat is de kortste weg? Probeer het geometrisch op te lossen als je het zelf probeert, niet met rekenen.
[ Bericht 5% gewijzigd door Bram_van_Loon op 09-10-2014 23:57:42 ]
Ik kwam een interessant vraagstuk tegen wat gemakkelijk te begrijpen is maar desalniettemin erg leerzaam is.
Heron's probleem. De vraag. Plaatsen A en B liggen langs een rivier, je moet via die rivier van A naar B. Wat is de kortste weg? Probeer het geometrisch op te lossen als je het zelf probeert, niet met rekenen.
[ Bericht 5% gewijzigd door Bram_van_Loon op 09-10-2014 23:57:42 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Ik ben even in de war met iets.. als h richting 0 gaat vanaf de linkerkant.. dan wordt het toch geen 3, maar 0/0?quote:Op donderdag 9 oktober 2014 22:01 schreef Super-B het volgende:
[ afbeelding ]
Waarom staat er op het einde dat f(x) niet differentieerbaar is? Het is tóch juist wel differentieerbaar, alleen het is niet differentieerbaar op het punt x = 2.. (?)


Waarom vermenigvuldig je ook met Q-1?quote:Op donderdag 9 oktober 2014 21:54 schreef Riparius het volgende:
[..]
De clou van logaritmisch differentiëren is dat je eerst van beide leden de (natuurlijke) logaritme neemt en dan beide leden differentieert. Welnu, je hebt
en dus
zodat
[..]
Vermenigvuldig eerst beide leden met PbQ−1 en je hebt
en dus
en dit geeft
en dus
zodat


Als ik dat niet zou doen, dan zou in het linkerlid een factor Q blijven staan, en dat wil ik niet, want ik wil een gelijkheid krijgen waarbij in het linkerlid alleen P voorkomt. Uiteraard is vermenigvuldigen met Q−1 hetzelfde als delen door Q.quote:Op vrijdag 10 oktober 2014 00:43 schreef RustCohle het volgende:
[..]
Waarom vermenigvuldig je ook met Q-1?


Niemand kan die vraag met zekerheid beantwoorden als je niet de oorspronkelijke opgave laat zien, maar alleen een fragment van een uitwerking.quote:
Welke afgeleide van welke functie? En hoezo 'dus' ? Ik zie helemaal geen gevolgtrekking.quote:Ik had dat de afgeleide dus (-2y)-2 is
Nee, wat je hier beweert is met zekerheid fout. Leer nu eindelijk eens rekenregels voor machten (en ook voor breuken, wortels, logaritmen ...) alsmede haakjes consequent toe te passen. We hebbenquote:en de afgeleide daar weer van is dan:
(4y-3 )
voor a, b ∈ R+, p ∈ R, waarbij a en of b evenwel ook negatief mogen zijn als p geheel is, en dus hebben we
en de afgeleide hiervan naar y is
Maar wat je bedoelde maar niet opschreef was wellicht
en de afgeleide naar y hiervan is inderdaad
Hola! Nog meer onzin. Om te beginnen, wat bedoel je hier precies mee,quote:en dus: 1/4y³,
of
?
En dan nog: hoe kom je erbij dat 4y−3 opeens verandert in hetzij (1/4)·y3 hetzij 1/(4y3) louter en alleen door haakjes om 4y−3 te zetten? Het is natuurlijk conform bovenstaande rekenregel alsmede de rekenregel (ap)q = apq wel zo dat
maar het is niet in te zien waarom je hier meent het omgekeerde te moeten nemen van een afgeleide die je zojuist hebt berekend.
Ja, dat is voor jouw een vraag, en zeker gezien het scala aan goocheltrucs dat je hier ten beste geeft. Zoals gezegd is je vraag feitelijk niet te beantwoorden omdat je de oorspronkelijke opgave achterhoudt, maar ik doe een poging tot reconstructie. Als we hebbenquote:dus hoe komen ze op 1/y³ ?
dan is de inverse van deze functie
Goed, nu gaan we eens lekker differentiëren. De eerste afgeleide wordt
en hiervoor kunnen we uiteraard ook schrijven
Nu is het verder een kwestie van braaf de regel
toepassen. Voor de tweede afgeleide krijgen we zo
en de derde afgeleide wordt nu
Nog even een opmerking over de Leibniz notatie voor hogere afgeleiden. Zoals eerder uiteengezet kunnen we schrijven
waarbij we
dus als operator voor differentiatie naar x kunnen opvatten, zodat we voor de tweede afgeleide naar x zouden kunnen schrijven
Nu heeft Leibniz al bedacht dat je voor iets als
louter symbolisch
en daarmee ook
kunt schrijven en zo dus in het algemeen als operator voor de n-de afgeleide naar x
zodat we dus hebben
Overigens laat men de haakjes rond dx meestal weg, dus je zult ook vaak de notatie
of
tegenkomen voor wat in de notatie van Lagrange als
wordt geschreven, en waarbij we voor n < 4 gewoonlijk primes gebruiken, dus f'(x), f''(x) en f'''(x). Zie ook hier. Verwar de superscript n in de Leibniz notatie van de n-de afgeleide vooral niet met een exponent van een uitdrukking waarvan een afgeleide wordt genomen. Je hebt voor n ∈ N bijvoorbeeld
maar
waarvoor je ook
kunt schrijven, terwijl
en dus voor elke n > 1 ook
oftewel
[ Bericht 0% gewijzigd door Riparius op 12-10-2014 04:37:45 ]


Ik heb vandaag een tentamen en ik heb een klein vraagje:
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
[ Bericht 43% gewijzigd door GeschiktX op 10-10-2014 09:52:49 ]
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
[ Bericht 43% gewijzigd door GeschiktX op 10-10-2014 09:52:49 ]


quote:Op vrijdag 10 oktober 2014 09:46 schreef GeschiktX het volgende:
Ik heb vandaag een tentamen en ik heb een klein vraagje:
[ afbeelding ]
[ afbeelding ]
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
f(x) is gedefinieerd als
Dan dus we weten dat f(x) in iedergeval continue voor alle
Dan hoef je dus alleen nog maar te kijken naar het punt x = 1, beiden hebben een limiet van 2 voor x = 1.
En dus geldt dat f(x) is continu.


Zelfde probleem staat hier ook al:quote:Op vrijdag 10 oktober 2014 09:46 schreef GeschiktX het volgende:
Ik heb vandaag een tentamen en ik heb een klein vraagje:
[ afbeelding ]
[ afbeelding ]
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
SES / [Bèta wiskunde] Huiswerk- en vragentopic.
Het functievoorschrift is
f(x) = x6 - 2x3 + 3x, voor alle x≤1.
Dat polynoom is continu op heet R, dus zeker ook voor alle x≤1. Dus hoe je er precies bij komt dat de functie niet continu zou zijn voor x≤0 ontgaat me.
Opinion is the medium between knowledge and ignorance (Plato)


f is niet gedefinieerd in x=2 en kan dus per definitie niet continu zijn. Probeer de grafiek op het interval [1,2] maar eens te tekenen zonder je pen van het papier te halen. Dat lukt je niet.
En verder kan f(x) niet continu zijn, aangezien dat slechts een getal is. De functie f kan daarentegen wel continu zijn.
En als laatste, er zijn functies die wel continu zijn (op een deelverzameling van het domein) maar je niet kunt tekenen zonder je pen van het papier te halen. Thomae's functie bijvoorbeeld.
En verder kan f(x) niet continu zijn, aangezien dat slechts een getal is. De functie f kan daarentegen wel continu zijn.
En als laatste, er zijn functies die wel continu zijn (op een deelverzameling van het domein) maar je niet kunt tekenen zonder je pen van het papier te halen. Thomae's functie bijvoorbeeld.


Ter verduidelijking, we zeggen dat 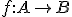 continu is als geldt dat voor elke
continu is als geldt dat voor elke 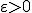 , voor elke
, voor elke 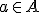 bestaat er een
bestaat er een 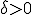 zodat voor elke
zodat voor elke 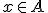 met
met 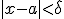 impliceert dat
impliceert dat 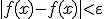
Verder, we zeggen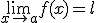 als geldt dat voor elke
als geldt dat voor elke 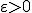 bestaat er een
bestaat er een 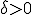 zodat voor elke
zodat voor elke 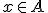 met
met 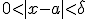 impliceert dat
impliceert dat 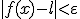
Zie je het cruciale verschil?
Verder, we zeggen
Zie je het cruciale verschil?


En, hoe ging het?quote:Op vrijdag 10 oktober 2014 11:59 schreef GeschiktX het volgende:
Hallo, ik heb nog één vraag voor mijn tentamen zal starten:
Opinion is the medium between knowledge and ignorance (Plato)


Mocht het je nog interesseren, voor x=2 krijg je in de noemer een 0. Delen door nul kan niet, wel kan je delen door een getal wat een heel klein beetje (laten we zeggen 0,0001) kleiner of groter is dan 0. In beide gevallen krijg je een zeer grote waarde maar doordat het teken verandert is de ene waarde erg groot en positief en de andere even groot en negatief. Hoe ziet zo'n grafiek er uit?quote:Op vrijdag 10 oktober 2014 11:59 schreef GeschiktX het volgende:
Hallo, ik heb nog één vraag voor mijn tentamen zal starten:
[ afbeelding ]
[ afbeelding ]
De limiet van 2 bestaat en dus waarom staat er op het einde ''f(x) is continu voor alle x =/ 2 en x =/ 3'' ? Er moet toch staan: ''f(x) is continu voor alle x =/ 3''
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Nee? Voor a = 2 bestaat de limiet. Voor a = 3 niet.quote:Op vrijdag 10 oktober 2014 17:18 schreef Bram_van_Loon het volgende:
[..]
Mocht het je nog interesseren, voor x=2 krijg je in de noemer een 0. Delen door nul kan niet, wel kan je delen door een getal wat een heel klein beetje (laten we zeggen 0,0001) kleiner of groter is dan 0. In beide gevallen krijg je een zeer grote waarde maar doordat het teken verandert is de ene waarde erg groot en positief en de andere even groot en negatief. Hoe ziet zo'n grafiek er uit?
quote:Op vrijdag 10 oktober 2014 12:04 schreef Novermars het volgende:
f is niet gedefinieerd in x=2 en kan dus per definitie niet continu zijn.


Weet iemand het antwoord op deze vragen?
Opgave
Een krant ontving een klacht van een lezer die beweerde dat hij 500 keer aan de wekelijkse
kruiswoord- puzzel had meegedaan, altijd met de correcte oplossing, maar dat hij nog nooit
een prijs had gewonnen. De krant antwoordde dat ze gemiddeld 4000 oplossingen ontvangen
voor elke kruiswoordpuzzel, waarvan 25% correct zijn. Elke week worden willekeurige
oplossingen getrokken tot de eerste correcte wordt getrokken, die dan de prijs wint.
(a) Bereken de exacte kans dat de lezer nooit een prijs wint als hij 500 keer een correcte
oplossing had.
(d) Neem aan dat de lezer oplossingen instuurt van een groot aantal kruiswoordpuzzels. We
zijn geïnteresseerd in de kans dat hij meer dan 2000 correcte oplossingen moet insturen
voordat hij voor de tweede keer een prijs wint.
 Geef de exacte formule voor deze kans.
Geef de exacte formule voor deze kans.
(ii) Gebruik een geschikte benadering voor het berekenen van een (benaderende) numerieke
waarde van deze kans.
(e) Bij de laatste kruiswoord-puzzel duurde het tot de tiende trekking voordat een correcte
oplossing werd gevonden. Toets of het percentage goede inzendingen kleiner is dan 25%, met
een significantieniveau van 0.05.
Opgave
Een krant ontving een klacht van een lezer die beweerde dat hij 500 keer aan de wekelijkse
kruiswoord- puzzel had meegedaan, altijd met de correcte oplossing, maar dat hij nog nooit
een prijs had gewonnen. De krant antwoordde dat ze gemiddeld 4000 oplossingen ontvangen
voor elke kruiswoordpuzzel, waarvan 25% correct zijn. Elke week worden willekeurige
oplossingen getrokken tot de eerste correcte wordt getrokken, die dan de prijs wint.
(a) Bereken de exacte kans dat de lezer nooit een prijs wint als hij 500 keer een correcte
oplossing had.
(d) Neem aan dat de lezer oplossingen instuurt van een groot aantal kruiswoordpuzzels. We
zijn geïnteresseerd in de kans dat hij meer dan 2000 correcte oplossingen moet insturen
voordat hij voor de tweede keer een prijs wint.
 Geef de exacte formule voor deze kans.
Geef de exacte formule voor deze kans. (ii) Gebruik een geschikte benadering voor het berekenen van een (benaderende) numerieke
waarde van deze kans.
(e) Bij de laatste kruiswoord-puzzel duurde het tot de tiende trekking voordat een correcte
oplossing werd gevonden. Toets of het percentage goede inzendingen kleiner is dan 25%, met
een significantieniveau van 0.05.


Wat is de kans dat hij in week 1 wint? Wat is dus de kans dat hij in week 1 niet wint? Wat is dan de kans dat hij in 500 weken niet wint?quote:Op vrijdag 10 oktober 2014 18:34 schreef Wouterw17 het volgende:
(a) Bereken de exacte kans dat de lezer nooit een prijs wint als hij 500 keer een correcte
oplossing had.


Aan de ene kant kut en aan de andere kant tamelijk goed. Ik had 5 opgaven, waarvan 1 opgave een a en een b vraag had. Ik heb sowieso drie opgaven goed, maar er zijn er twee die ik verziekt heb.. en ik ben er zojuist nog even bezig mee geweest om te kijken hoe het moet (ik weet de vragen nog wel zo ongeveer), maar kwam er totaal niet uit:quote:
1. Er is een functie ln ( (x+5)/(x+1) ) met het domein (0, oneindig). Bepaal wanneer deze functie stijgt/daalt en bepaal wanneer die convex/concaaf is.
-Hier wist ik wat ik moest doen, maar ik vond de functie lastig. Ik vond bovendien raar dat het domein [0, oneindig) is, aangezien x = -0,50 nog best mogelijk is bijvoorbeeld.
Ik had dus.. de functie verandert in:
Ln (x+5) - ln (x+1) en vervolgens de afgeleide genomen;
1/(x+5) - 1/(x+1) en toen liep ik vast...ik snapte dus niet hoe ik de getallenlijn moest opstellen hiervoor.. ik had mijzelf, tijdens het leren, te veel geconcentreerd op afgeleiden met een vermenigvuldiging ipv een min/plusteken... de tweede afgeleide vinden snapte ik niet (om de convexiteit/concaviteit) te bepalen.. want moest ik nou de quotientregel toepassen of de breuk weghalen en er bijv (x+5)^-1 van maken...
2. Er is een aanbodfunctie: s(p) = p^p ln p, waar de s voor aanbod staay en de p voor de prijs. In dit geval is p = e
Hier had ik:
Ln s(p) = p ln p * 1 ( want ln p valt weg omdat ln e is 1)
Ln s(p) = e ln e
ln s(p) = e
afgeleide hiervan is 0, omdat e een constante is en dit resulteert dat het een prijsinelastisch is.
----
Het kunnen domme antwoorden zijn, dat kan.. ik ben er ook behoorlijk om gefrustreerd dat deze fout konden gaan..


Als in de vraag staat dat ie gedefinieerd is voor het domein (0, inf) dan hoef je dus alleen maar naar dat domein te kijken.quote:Op vrijdag 10 oktober 2014 19:45 schreef GeschiktX het volgende:
1. Er is een functie ln ( (x+5)/(x+1) ) met het domein (0, oneindig). Bepaal wanneer deze functie stijgt/daalt en bepaal wanneer die convex/concaaf is.
-Hier wist ik wat ik moest doen, maar ik vond de functie lastig. Ik vond bovendien raar dat het domein [0, oneindig) is, aangezien x = -0,50 nog best mogelijk is bijvoorbeeld.
Voor andere x is de functie dus niet gedefinieerd, ook al is ln((x+5)/(x+1)) op een groter domein gedefinieerd.
Maak er eens één breuk van.quote:Ik had dus.. de functie verandert in:
Ln (x+5) - ln (x+1) en vervolgens de afgeleide genomen;
1/(x+5) - 1/(x+1) en toen liep ik vast...ik snapte dus niet hoe ik de getallenlijn moest opstellen hiervoor.. ik had mijzelf, tijdens het leren, te veel geconcentreerd op afgeleiden met een vermenigvuldiging ipv een min/plusteken...
Ook al had je er niet één breuk van gemaakt dan kan je toch nog wel de afgeleide bepalen van 1/(x+1) en 1/(x+5)?quote:de tweede afgeleide vinden snapte ik niet (om de convexiteit/concaviteit) te bepalen.. want moest ik nou de quotientregel toepassen of de breuk weghalen en er bijv (x+5)^-1 van maken...
Heb je hier ook de volledige vraag van?quote:2. Er is een aanbodfunctie: s(p) = p^p ln p, waar de s voor aanbod staay en de p voor de prijs. In dit geval is p = e
Hier had ik:
Ln s(p) = p ln p * 1 ( want ln p valt weg omdat ln e is 1)
Ln s(p) = e ln e
ln s(p) = e
afgeleide hiervan is 0, omdat e een constante is en dit resulteert dat het een prijsinelastisch is.


Dit is de volledige vraag zo ongeveer.. ik kon er trouwens geen 1 breuk van maken.. ik ken de regels, maar wist het ff niet met die x en al..quote:Op vrijdag 10 oktober 2014 20:27 schreef t4rt4rus het volgende:
[..]
Als in de vraag staat dat ie gedefinieerd is voor het domein (0, inf) dan hoef je dus alleen maar naar dat domein te kijken.
Voor andere x is de functie dus niet gedefinieerd, ook al is ln((x+5)/(x+1)) op een groter domein gedefinieerd.
[..]
Maak er eens één breuk van.
[..]
Ook al had je er niet één breuk van gemaakt dan kan je toch nog wel de afgeleide bepalen van 1/(x+1) en 1/(x+5)?
[..]
Heb je hier ook de volledige vraag van?


Plaatst hier dan eens een vollediger vraag.quote:Op vrijdag 10 oktober 2014 20:31 schreef GeschiktX het volgende:
[..]
Dit is de volledige vraag zo ongeveer.. ik kon er trouwens geen 1 breuk van maken.. ik ken de regels, maar wist het ff niet met die x en al..
a/b + c/d = (b c + a d)/(b d) ?


Oeps.. ik had het niet volledig opgeschreven:quote:Op vrijdag 10 oktober 2014 20:33 schreef t4rt4rus het volgende:
[..]
Plaatst hier dan eens een vollediger vraag.
a/b + c/d = (b c + a d)/(b d) ?
er is een aanbodfunctie s(p) = p^p ln p, waarbij p staat voor de prijs en s voor supply (aanbod). In dit geval is p = e. Bereken/bepaal de elasticiteit.


Oh je moet de elasticiteit van s(p) uitrekenen voor p = e.quote:Op vrijdag 10 oktober 2014 20:49 schreef GeschiktX het volgende:
[..]
Oeps.. ik had het niet volledig opgeschreven:
er is een aanbodfunctie s(p) = p^p ln p, waarbij p staat voor de prijs en s voor supply (aanbod). In dit geval is p = e. Bereken/bepaal de elasticiteit.
Hoe bepaal je de elasticiteit? Kan je daar een functie voor opstellen?
Als je dat hebt hoef je alleen nog maar p=e in te vullen, dit moet je natuurlijk niet doen voordat je de elasticiteit hebt uitgerekend.


De formule voor de elasticiteit is x/y * f'(x)quote:Op vrijdag 10 oktober 2014 20:57 schreef t4rt4rus het volgende:
[..]
Oh je moet de elasticiteit van s(p) uitrekenen voor p = e.
Hoe bepaal je de elasticiteit? Kan je daar een functie voor opstellen?
Als je dat hebt hoef je alleen nog maar p=e in te vullen, dit moet je natuurlijk niet doen voordat je de elasticiteit hebt uitgerekend.
Tijdens de toets.. vulde ik hem wel in... waarom moet dat niet eigenlijk?


-edit- moet je het wel goed opschrijven hè! Ef(x)=x/f(x) f'(x)quote:Op vrijdag 10 oktober 2014 21:06 schreef GeschiktX het volgende:
[..]
De formule voor de elasticiteit is x/y * f'(x)
Of nog makkelijker
Dan kan je deze opgave vrij makkelijk oplossen.
[ Bericht 5% gewijzigd door t4rt4rus op 10-10-2014 21:20:43 ]


Ik had dit enkele dagen geleden hier al uitgebreider uitgelegd, maar kennelijk worden zulke posts niet gelezen door de personen die daar het meeste baat bij zouden hebben en voor wie ze eigenlijk ook bedoeld zijn.quote:Op vrijdag 10 oktober 2014 12:29 schreef Novermars het volgende:
Ter verduidelijking, we zeggen datcontinu is als geldt dat voor elke
, voor elke
bestaat er een
zodat voor elke
met
impliceert dat
Verder, we zeggenals geldt dat voor elke
bestaat er een
zodat voor elke
met
impliceert dat
Zie je het cruciale verschil?


y = p^p * ln pquote:Op vrijdag 10 oktober 2014 21:11 schreef t4rt4rus het volgende:
[..]
Of nog makkelijker
Dan kan je deze opgave vrij makkelijk oplossen.
-edit- iets te snelnee eigenlijk niet
Als ik deze wil vermenigvuldigen met ln om zodoende jouw formule te kunnen gebruiken krijg ik:
ln y = ln p^p * (ln p * ln)
Hoe los ik dit op? ln * ln p? Zo liep ik dus ook op de toets vast.. Anders was het me waarschijnlijk gewoon gelukt!
Die breukopgaven ga ik nu even opnieuw doen met het advies van jouw post.


Wat ben je nou aan het doen? :Squote:Op vrijdag 10 oktober 2014 21:20 schreef GeschiktX het volgende:
[..]
y = p^p * ln p
Als ik deze wil vermenigvuldigen met ln om zodoende jouw formule te kunnen gebruiken krijg ik:
ln y = ln p^p * (ln p * ln)
Hoe los ik dit op? ln * ln p? Zo liep ik dus ook op de toets vast.. Anders was het me waarschijnlijk gewoon gelukt!
Je kan ln niet vermenigvuldigen, het is een operator geen variabele.
[ Bericht 1% gewijzigd door t4rt4rus op 10-10-2014 21:33:02 ]


Ik snap het niet meer... Ik moet toch zowel links als rechts ln bij doen eerst en daarna de afgeleide nemen?quote:Op vrijdag 10 oktober 2014 21:21 schreef t4rt4rus het volgende:
[..]
Wat ben je nou aan het doen? :S
Je kan ln niet vermenigvuldigen, het is een operator geen variabele.


quote:Op vrijdag 10 oktober 2014 21:32 schreef GeschiktX het volgende:
[..]
Ik snap het niet meer... Ik moet toch zowel links als rechts ln bij doen eerst en daarna de afgeleide nemen?
Elasticiteit is dan gegeven door
De laatste term is heel makkelijk te berekenen
Kettingregel gebruiken en dan kunnen we de afgeleide in de eerste term herschrijven tot
Dus dan hebben we
Dan nog de productregel gebruiken en je krijgt
Vul je p = e in dan krijg je
[ Bericht 1% gewijzigd door t4rt4rus op 10-10-2014 22:40:49 ]


ln ( x+5) / (x+1)quote:Op vrijdag 10 oktober 2014 20:33 schreef t4rt4rus het volgende:
[..]
Plaatst hier dan eens een vollediger vraag.
a/b + c/d = (b c + a d)/(b d) ?
ln ( x+5) - ln ( x+1)
f'(x) = 1 / (x+5) - 1/(x+1)
Ik kan niet vinden waar ik de noemer gemeenschappelijk kan maken..


Zou jij je bericht kunnen editen in ln ipv log? Want ik ben ln gewend..quote:Op vrijdag 10 oktober 2014 21:37 schreef t4rt4rus het volgende:
[..]
Elasticiteit is dan gegeven door
De laatste term is heel makkelijk te berekenen
Kettingregel gebruiken en dan kunnen we de afgeleide in de eerste term herschrijven tot
Dus dan hebben we
Dan nog de productregel gebruiken en je krijgt
Vul je p = e in dan krijg je


Waar zie je iets in de vorm "a/b + c/d" staan?quote:Op vrijdag 10 oktober 2014 21:37 schreef GeschiktX het volgende:
[..]
ln ( x+5) / (x+1)
ln ( x+5) - ln ( x+1)
f'(x) = 1 / (x+5) - 1/(x+1)
Ik kan niet vinden waar ik de noemer gemeenschappelijk kan maken..


In de noemer.. Het verschil is +4quote:Op vrijdag 10 oktober 2014 21:38 schreef t4rt4rus het volgende:
[..]
Waar zie je iets in de vorm "a/b + c/d" staan?


Dat maakt toch helemaal niks uit?quote:Op vrijdag 10 oktober 2014 21:37 schreef GeschiktX het volgende:
[..]
Zou jij je bericht kunnen editen in ln ipv log? Want ik ben ln gewend..
In de Engelstalige literatuur is trouwens


Ik snap je niet.quote:Op vrijdag 10 oktober 2014 21:39 schreef GeschiktX het volgende:
[..]
In de noemer.. Het verschil is +4
Ach was heel makkelijk te "find and replacen".quote:Op vrijdag 10 oktober 2014 21:40 schreef Novermars het volgende:
[..]
Dat maakt toch helemaal niks uit?
In de Engelstalige literatuur is trouwens
En nu ook nog eens minder noise van 1 symbool per log
Het lettertype dat deze TeX gebruikt is ook niet echt super om te lezen, 1 symbool minder maakt het al leesbaarder. (vind ik)


Maar is zijn hele probleem niet dat hij het best redelijk kan, maar als er ook iets net anders is dan het standaardprobleem, dat het helemaal mis gaat?quote:Op vrijdag 10 oktober 2014 21:41 schreef t4rt4rus het volgende:
[..]
Ik snap je niet.
[..]
Ach was heel makkelijk te "find and replacen".
En nu ook nog eens minder noise van 1 symbool per log


Die laatste term is juist niet zo lastig te begrijpen, maar die eerste met name doordat er p ln p staat..quote:Op vrijdag 10 oktober 2014 21:37 schreef t4rt4rus het volgende:
[..]
Elasticiteit is dan gegeven door
De laatste term is heel makkelijk te berekenen
Kettingregel gebruiken en dan kunnen we de afgeleide in de eerste term herschrijven tot
Dus dan hebben we
Dan nog de productregel gebruiken en je krijgt
Vul je p = e in dan krijg je
ln p valt gewoon weg omdat het d ln s(p) / ln p is.. maar door die p naast de ln p raak ik in de war...


Ik mijzelf ook niet eigenlijk.quote:Op vrijdag 10 oktober 2014 21:41 schreef t4rt4rus het volgende:
[..]
Ik snap je niet.
[..]
Ach was heel makkelijk te "find and replacen".
En nu ook nog eens minder noise van 1 symbool per log
Het lettertype dat deze TeX gebruikt is ook niet echt super om te lezen, 1 symbool minder maakt het al leesbaarder. (vind ik)
Denk dat het probleem is.quote:Op vrijdag 10 oktober 2014 21:44 schreef Novermars het volgende:
[..]
Maar is zijn hele probleem niet dat hij het best redelijk kan, maar als er ook iets net anders is dan het standaardprobleem, dat het helemaal mis gaat?


Klopt alleen het 'base' getal verschilt, maar ln leest lekkerder dan log. Of ligt het nou aan mij ?quote:Op vrijdag 10 oktober 2014 21:40 schreef Novermars het volgende:
[..]
Dat maakt toch helemaal niks uit?
In de Engelstalige literatuur is trouwens


Substitueer u = log p, dan krijg jequote:Op vrijdag 10 oktober 2014 21:44 schreef GeschiktX het volgende:
[..]
Die laatste term is juist niet zo lastig te begrijpen, maar die eerste met name doordat er p ln p staat..
d/d(log p) log(log p) = d/du log(u) = 1/u
ln p valt niet "gewoon" weg...quote:ln p valt gewoon weg omdat het d ln s(p) / ln p is.. maar door die p naast de ln p raak ik in de war...
Je kent toch de productregel?


Nee het basisgetal verschilt niet Log(x) = ln(x).quote:Op vrijdag 10 oktober 2014 21:46 schreef GeschiktX het volgende:
[..]
Klopt alleen het 'base' getal verschilt, maar ln leest lekkerder dan log. Of ligt het nou aan mij ?
Als ze een logaritme met basisgetal 10 willen dan geven ze dat expliciet aan.


Ja, dat snap ik allemaal wel, maar wat moet ik met die losse p doen als ln p = u.. .Er is nog een losse pquote:Op vrijdag 10 oktober 2014 21:46 schreef t4rt4rus het volgende:
[..]
Substitueer u = log p, dan krijg je
d/d(log p) log(log p) = d/du log(u) = 1/u
[..]
ln p valt niet "gewoon" weg...
Je kent toch de productregel?
p ln p
-------> p <---------- ln p


Ja die pijltjes maken het allemaal heel duidelijk... Maar ik gebruik je niet.quote:Op vrijdag 10 oktober 2014 21:49 schreef GeschiktX het volgende:
[..]
Ja, dat snap ik allemaal wel, maar wat moet ik met die losse p doen als ln p = u.. .Er is nog een losse p
p ln p
-------> p <---------- ln p


In het eerste term heb je P * ln pquote:Op vrijdag 10 oktober 2014 21:51 schreef t4rt4rus het volgende:
[..]
Ja die pijltjes maken het allemaal heel duidelijk... Maar ik gebruik je niet.
Ik snap dus niet wat je met die LOSSE P moet doen links van ln p als je door ln p moet differentieren


Dat heb ik toch uitgelegd.quote:Op vrijdag 10 oktober 2014 21:52 schreef GeschiktX het volgende:
[..]
In het eerste term heb je P * ln p
Ik snap dus niet wat je met die LOSSE P moet doen links van ln p als je door ln p moet differentieren
Ik gebruik de kettingregel om de afgeleide te herschrijven naar p d/dp.
Heb je de uitwerking van mij wel gelezen? Of heb ik dat voor niks gedaan?
-edit-
Oké ik raakte in de war door jouw taalgebruik
Ik had in de uitwerking staan dat de tweede term makkelijk te berekenen was en jij reageert dan met "juist niet ... lastig".quote:Op vrijdag 10 oktober 2014 21:44 schreef GeschiktX het volgende:
[..]
Die laatste term is juist niet zo lastig te begrijpen, maar die eerste met name doordat er p ln p staat..
ln p valt gewoon weg omdat het d ln s(p) / ln p is.. maar door die p naast de ln p raak ik in de war...
Maar de uitleg van die andere term staat gewoon in de uitwerking.
[ Bericht 9% gewijzigd door t4rt4rus op 10-10-2014 21:59:46 ]


Ik heb hem gelezen, maar ik snap de leibniz notatie niet zo vanaf de 'kettingregel' stuk in je post.. Ik gebruik de standaard methode gewoon:quote:Op vrijdag 10 oktober 2014 21:53 schreef t4rt4rus het volgende:
[..]
Dat heb ik toch uitgelegd.
Ik gebruik de kettingregel om de afgeleide te herschrijven naar p d/dp.
Heb je de uitwerking van mij wel gelezen? Of heb ik dat voor niks gedaan?
y' en f'(x). Dat soort dingen...


f'(ln(x)) = x f'(x), ofzo...quote:Op vrijdag 10 oktober 2014 21:56 schreef GeschiktX het volgende:
[..]
Ik heb hem gelezen, maar ik snap de leibniz notatie niet zo vanaf de 'kettingregel' stuk in je post.. Ik gebruik de standaard methode gewoon:
y' en f'(x). Dat soort dingen...
d/d(ln x) = d/dx dx/d(ln x) = x d/dx
De Leibniz notatie maakt het veel makkelijker.


Ik weet niet hoe ik het moet uitleggen, maar hoe moet ik die P zien?quote:Op vrijdag 10 oktober 2014 21:37 schreef t4rt4rus het volgende:
[..]
Elasticiteit is dan gegeven door
De laatste term is heel makkelijk te berekenen
Kettingregel gebruiken en dan kunnen we de afgeleide in de eerste term herschrijven tot
Dus dan hebben we
Dan nog de productregel gebruiken en je krijgt
Vul je p = e in dan krijg je
Als ik d ln y / d ln p zie dan is het voor mij een ezelsbruggetje dat ik gewoon ln y moet differentieren door ln x net als d y / d x en dus de ln p kan 'zien' als een x..
als ik ln p differentieer wordt dat gewoon 1, maar die losse p....!!


Die Leibniz begrijp ik tot dusverre wel, evenals wat Riparius al enige tijd geleden heeft uitgelegd in meerdere posts.. Maar vanaf 'kettingregel' in je post snap ik die ene term niet met p ln p!quote:Op vrijdag 10 oktober 2014 22:03 schreef t4rt4rus het volgende:
[..]
f'(ln(x)) = x f'(x), ofzo...
d/d(ln x) = d/dx dx/d(ln x) = x d/dx
De Leibniz notatie maakt het veel makkelijker.
HOE MOET IK DIE P BENADEREN!!


Ik weet niet wat voor gemeenschappelijke noemer ik ervan kan maken..quote:Op vrijdag 10 oktober 2014 21:38 schreef t4rt4rus het volgende:
[..]
Waar zie je iets in de vorm "a/b + c/d" staan?


d/dp p ln p = p d/dp ln p + ln p d/dp p...quote:Op vrijdag 10 oktober 2014 22:04 schreef GeschiktX het volgende:
[..]
Die Leibniz begrijp ik tot dusverre wel, evenals wat Riparius al enige tijd geleden heeft uitgelegd in meerdere posts.. Maar vanaf 'kettingregel' in je post snap ik die ene term niet met p ln p!
HOE MOET IK DIE P BENADEREN!!
Dat is gewoon de kettingregel...
En als je weet wat de kettingregel is, plaats dan even duidelijk vanaf welke regel je het niet snapt.


kan je het zonder leibniz notatie opschrijven, dus gewoon beetje op basisniveau ala y' etc..quote:Op vrijdag 10 oktober 2014 22:11 schreef t4rt4rus het volgende:
[..]
d/dp p ln p = p d/dp ln p + ln p d/dp p...
Dat is gewoon de kettingregel...
En als je weet wat de kettingregel is, plaats dan even duidelijk vanaf welke regel je het niet snapt.


(p ln p)' = p (ln p)' + p' ln p = 1 + ln pquote:Op vrijdag 10 oktober 2014 22:20 schreef GeschiktX het volgende:
[..]
kan je het zonder leibniz notatie opschrijven, dus gewoon beetje op basisniveau ala y' etc..
Waar ' staat voor het afleiden naar p...


Dat klopt, maar even voor de duidelijkheid:quote:Op vrijdag 10 oktober 2014 22:25 schreef t4rt4rus het volgende:
[..]
(p ln p)' = p (ln p)' + p' ln p = 1 + ln p
Waar ' staat voor het afleiden naar p...
(ln p)' is gewoon 1 neem ik aan?
ln p is gewoon ln p..
Wat gebeurd er met die p en p' ?
Want je differentieert door ln p en niet door p --> d ln y / d ln p en dus niet d y / d p


Lees mijn laatste zin eens...quote:Op vrijdag 10 oktober 2014 22:32 schreef GeschiktX het volgende:
[..]
Dat klopt, maar even voor de duidelijkheid:
(ln p)' is gewoon 1 neem ik aan?
ln p is gewoon ln p..
Wat gebeurd er met die p en p' ?
Want je differentieert door ln p en niet door p --> d ln y / d ln p en dus niet d y / d p


Ow... Maar waarom pas je dan bij die term 'afleiden naar p' toe en niet ''afleiden naar ln p '' zoals die laatste term met ln(ln p) ?quote:
Want bij de elasticiteit van log/ln draait het erom om juist de hele functie af te leiden van ln y naar ln p..


Omdat... lees mijn uitwerking nog eens!quote:Op vrijdag 10 oktober 2014 22:39 schreef GeschiktX het volgende:
[..]
Ow... Maar waarom pas je dan bij die term 'afleiden naar p' toe en niet ''afleiden naar ln p '' zoals die laatste term met ln(ln p) ?
Want bij de elasticiteit van log/ln draait het erom om juist de hele functie af te leiden van ln y naar ln p..
quote:Kettingregel gebruiken en dan kunnen we de afgeleide in de eerste term herschrijven tot


Ja en hoe kan d / d ln p hetzelfde zijn als d / dp * dp / d ln p ?quote:Op vrijdag 10 oktober 2014 22:40 schreef t4rt4rus het volgende:
[..]
Omdat... lees mijn uitwerking nog eens!
[..]
En wat is dp / d ln p dan? p naar ln p differentieren WHAAT??!


Als je nu eens begint met te bedenken dat je voor x > 0 hebtquote:Op vrijdag 10 oktober 2014 21:37 schreef GeschiktX het volgende:
[..]
f(x) = ln (( x+5) / (x+1))
f(x) = ln (x+5) - ln (x+1)
f'(x) = 1/(x+5) - 1/(x+1)
Ik kan niet vinden waar ik de noemer gemeenschappelijk kan maken..
1/(x+5) < 1/(x+1)
dan zie je dus direct dat
f'(x) < 0
voor x > 0. Je functie f is dus strict monotoon dalend op het gegeven domein Df = (0, ∞). Wat denk je daarvan?


Kettingregelquote:Op vrijdag 10 oktober 2014 22:42 schreef GeschiktX het volgende:
[..]
Ja en hoe kan d / d ln p hetzelfde zijn als d / dp * dp / d ln p ?
Ik dacht dat je die tweede term "juist niet zo lastig" begreep?quote:En wat is dp / d ln p dan? p naar ln p differentieren WHAAT??!


Ik snap er echt geen ruk van.quote:Op vrijdag 10 oktober 2014 22:45 schreef t4rt4rus het volgende:
[..]
Kettingregel
[..]
Ik dacht dat je die tweede term "juist niet zo lastig" begreep?
Ja d ln y / d ln p van ln p dan is dat gewoon 1... (afgeleide). Maar ik heb geen flauw idee wat de afgeleide van p is als je door ln p differentieert. Het gaat mij niet om de regel of whatever, maar om die losse p.


Dit snap ik, maar ik was meer benieuwd naar de ''berekening''quote:Op vrijdag 10 oktober 2014 22:45 schreef Riparius het volgende:
[..]
Als je nu eens begint met te bedenken dat je voor x > 0 hebt
1/(x+5) < 1/(x+1)
dan zie je dus direct dat
f'(x) < 0
voor x > 0. Je functie f is dus strict monotoon dalend op het gegeven domein Df = (0, ∞). Wat denk je daarvan?


Nee, (ln p)' is niet 'gewoon' 1, maar 1/p.quote:Op vrijdag 10 oktober 2014 22:32 schreef GeschiktX het volgende:
[..]
Dat klopt, maar even voor de duidelijkheid:
(ln p)' is gewoon 1 neem ik aan?
ln p is gewoon ln p..
Wat gebeurd er met die p en p' ?
Want je differentieert door ln p en niet door p --> d ln y / d ln p en dus niet d y / d p
Je hebt dus (p ln p)' = p (ln p)' + p' ln p = 1 + ln p = p*(1/p) + 1*ln p = 1 + ln p.


Maar waarom benader je deze als d / dp en niet als d ln y / ln p zoals het hoort voor de elasticiteit en zoals de tweede term van de functie juist wel benadert is.quote:Op vrijdag 10 oktober 2014 22:54 schreef zerak het volgende:
[..]
Nee, (ln p)' is niet 'gewoon' 1, maar 1/p.
Je hebt dus (p ln p)' = p (ln p)' + p' ln p = 1 + ln p = p*(1/p) + 1*ln p = 1 + ln p.


Kan je de afgeleide naar p van ln p nemen? En neem daar eens de reciprocal van.quote:Op vrijdag 10 oktober 2014 22:48 schreef GeschiktX het volgende:
[..]
Ik snap er echt geen ruk van.
Ja d ln y / d ln p van ln p dan is dat gewoon 1... (afgeleide). Maar ik heb geen flauw idee wat de afgeleide van p is als je door ln p differentieert. Het gaat mij niet om de regel of whatever, maar om die losse p.
Je kan ook een subtitutie gebruik van u = ln p.
Doe ze beide eens!


Ik benader helemaal niks.quote:Op vrijdag 10 oktober 2014 22:56 schreef GeschiktX het volgende:
[..]
Maar waarom benader je deze als d / dp en niet als d ln y / ln p zoals het hoort voor de elasticiteit en zoals de tweede term van de functie juist wel benadert is.
Maar gebruik de kettingregel en dan hoef je alleen nog maar een afgeleide naar p te nemen.


Heb je al eens eerder logaritmisch gedifferentieerd?quote:Op vrijdag 10 oktober 2014 22:56 schreef GeschiktX het volgende:
[..]
Maar waarom benader je deze als d / dp en niet als d ln y / ln p zoals het hoort voor de elasticiteit en zoals de tweede term van de functie juist wel benadert is.


In mijn boek staat bijv:quote:Op vrijdag 10 oktober 2014 22:58 schreef t4rt4rus het volgende:
[..]
Ik benader helemaal niks.
Maar gebruik de kettingregel en dan hoef je alleen nog maar een afgeleide naar p te nemen.
y = a + xb
Als je de elasticiteit wilt nemen dan :
d ln y / d ln x
Dus:
ln y = ln a + b ln x
ln a = constante dus die valt weg:
y' = 0 + b * 1
Deze methode staat dus in mijn boek en zo probeer ik dit dus te benaderen.


Ja dat is makkelijk.quote:Op vrijdag 10 oktober 2014 23:02 schreef zerak het volgende:
[..]
Heb je al eens eerder logaritmisch gedifferentieerd?
t4r4us gebruikt alleen twee verschillende dingen: hij differentieert naar ln p ( d ln y / d ln p ) en daarna past die voor één term opeens d y / d p toe en dat snap ik dus niet.


ln y is daar linear in ln x, dus dan is de afgeleide nemen heel makkelijk.quote:Op vrijdag 10 oktober 2014 23:02 schreef GeschiktX het volgende:
[..]
In mijn boek staat bijv:
y = a + xb
Als je de elasticiteit wilt nemen dan :
d ln y / d ln x
Dus:
ln y = ln a + b ln x
ln a = constante dus die valt weg:
y' = 0 + b * 1
Deze methode staat dus in mijn boek en zo probeer ik dit dus te benaderen.
-edit-
Moet je het natuurlijk wel goed opschrijven.
Het is niet y' maar (ln y)'(ln x)...
Snap je nu waarom de Leibniz notatie makkelijker is?


Ja,..quote:Op vrijdag 10 oktober 2014 23:03 schreef t4rt4rus het volgende:
[..]
ln y is daar linear in ln x, dus dan is de afgeleide nemen heel makkelijk.


Ik ben er denk ik uit.quote:
Als ik ln p = x neem is het wat overzichtelijker.. voor mij..
En als ik dan gewoon voor alle ln p gewoon x neerzet dan is het zo op te lossen.


Je kan het inderdaad ook zo doenquote:Op vrijdag 10 oktober 2014 23:34 schreef GeschiktX het volgende:
[..]
Ik ben er denk ik uit.Dank je wel voor de uitleg..
Als ik ln p = x neem is het wat overzichtelijker.. voor mij..
En als ik dan gewoon voor alle ln p gewoon x neerzet dan is het zo op te lossen.
f(x) = x^x ln x
Ef(x) = d(ln f(x)) / d(ln x) = d/d(ln x) (x ln x + ln ln x)
Substitueer u = ln x <=> x = e^u
Ef(x) = d/du (u e^u + ln u) = e^u + u e^u + 1/u = e^u (1 + u) + 1/u
Substitutie weer toepassen en klaar
Ef(x) = x(1+ ln x) + 1/(ln x)


oh ik dacht als ik er x van maak dan wordt het ook gewoon d ln y / d xquote:Op vrijdag 10 oktober 2014 23:54 schreef t4rt4rus het volgende:
[..]
Je kan het inderdaad ook zo doen
f(x) = x^x ln x
Ef(x) = d(ln f(x)) / d(ln x) = d/d(ln x) (x ln x + ln ln x)
Substitueer u = ln x <=> x = e^u
Ef(x) = d/du (u e^u + ln u) = e^u + u e^u + 1/u = e^u (1 + u) + 1/u
Substitutie weer toepassen en klaar
Ef(x) = x(1+ ln x) + 1/(ln x)


Ik snap dat w.r.t. ln x niet.. ik ben gewoon gewend dat ik w.r.t. x doe bijv.. en dat als je x^2 hebt het 2x wordt en als je hebt x dat het dan 1 wordt. Dus als je w.r.t. ln x doet en je hebt ln x, dan wordt het gewoon 1 toch? Maar wat doe je als je bijv... hebtquote:Op vrijdag 10 oktober 2014 23:54 schreef t4rt4rus het volgende:
[..]
Je kan het inderdaad ook zo doen
f(x) = x^x ln x
Ef(x) = d(ln f(x)) / d(ln x) = d/d(ln x) (x ln x + ln ln x)
Substitueer u = ln x <=> x = e^u
Ef(x) = d/du (u e^u + ln u) = e^u + u e^u + 1/u = e^u (1 + u) + 1/u
Substitutie weer toepassen en klaar
Ef(x) = x(1+ ln x) + 1/(ln x)
ln y = ln x + x
En je wilt de afgeleide berekenen van ln y w.r.t. ln x?


Dan pas je dus of substitutie toequote:Op zaterdag 11 oktober 2014 00:16 schreef GeschiktX het volgende:
[..]
Ik snap dat w.r.t. ln x niet.. ik ben gewoon gewend dat ik w.r.t. x doe bijv.. en dat als je x^2 hebt het 2x wordt en als je hebt x dat het dan 1 wordt. Dus als je w.r.t. ln x doet en je hebt ln x, dan wordt het gewoon 1 toch? Maar wat doe je als je bijv... hebt
ln y = ln x + x
En je wilt de afgeleide berekenen van ln y w.r.t. ln x?
u=ln x
=> ln y = u + e^u
d(ln y)/du = 1 + e^u = 1 + x
of de kettingregel
d(ln y)/d(ln x) = d(ln y)/dx dx/d(ln x) = x d(ln y)/dx = 1 + x
of in dit geval nog makkelijker
d(ln y)/d(ln x) = d(ln x)/d(ln x) + dx/d(ln x) = 1 + x
( dx/d(ln x) = 1/(d(ln x)/dx) = 1/(1/x) = x )


Jouw probleem is hier dat je de Leibniz notatie kennelijk nog niet voldoende begrijpt het daarom zonder die notatie wil stellen. Maar dat is nu precies de reden dat je het overzicht kwijt raakt, in de war raakt, en gaat proberen om je er doorheen te slaan met trucjes en ezelsbruggetjes die je eigenlijk al helemaal niet begrijpt, en waarmee je gegarandeerd fouten gaat maken. Dat moet je dus allemaal niet doen.quote:Op vrijdag 10 oktober 2014 22:20 schreef GeschiktX het volgende:
[..]
Kan je het zonder Leibniz notatie opschrijven, dus gewoon beetje op basisniveau ala y' etc ...
De notatie van Leibniz is bij uitstek geschikt om te beschrijven hoe variabelen van elkaar afhangen, omdat deze notatie werkt met namen van variabelen, en niet met namen van functies zoals de notatie van Lagrange. Ook hoeven we zo niet elke afhankelijkheidsrelatie eerst een eigen naam te geven om de rate of change van een variabele ten opzichte van een andere variabele te kunnen noteren. En, de kettingregel is in de notatie van Leibniz ook nog eens heel transparant en intuïtief en daarmee gemakkelijk te onthouden en op te schrijven, dus wat wil je nog meer?
Hybride notaties zoals y' voor de rate of change van een variabele y in relatie tot een andere variabele (welke andere variabele?) resp. de afgeleide van een functie (hoe heet die functie?) waarbij y de afhankelijke variabele is (maar welke variabele is dan de onafhankelijke variabele?) zijn af te keuren omdat de prime notatie van Lagrange de afgeleide functie f' aangeeft van een functie f en niet de rate of change van een variabele ten opzichte van een andere variabele. Aan deze hybride notatie ligt dus de verwarring van namen van variabelen met namen van functies ten grondslag, en daarom is deze notatie niet goed.
In feite geeft de prime bij y' alleen maar aan dat dit een andere grootheid is dan y, net zo goed als als de prime bij een punt P' in een meetkundige figuur aangeeft dat dit een ander punt is dan punt P in dezelfde figuur. En uiteraard suggereert de overeenkomst in naamgeving dan dat er een zeker verband bestaat, maar de prime zegt an sich helemaal niets over de aard van dat verband. In een meetkundige figuur kan punt P' bijvoorbeeld het beeld zijn van punt P bij een translatie (om maar wat te noemen), en als punt P bijvoorbeeld de coördinaten (x, y) heeft, dan zouden we de coördinaten van punt P' heel goed kunnen noteren als (x', y'), maar het is duidelijk dat de primes hier niets met differentiëren van doen hebben.
De verwarring tussen namen van functies en namen van variabelen wordt nog verder in de hand gewerkt door een notatie als s(p) waarmee gewoonlijk wordt bedoeld dat s een variabele is die afhangt van een andere variabele p, versus een notatie als f(x) waarmee gewoonlijk wordt bedoeld dat f een functie is waarbij x de onafhankelijke variabele is en waarbij de notatie f(x) staat voor de bij die variabele x behorende functiewaarde. En nu weet ik ook wel dat hybride notaties als y' vaak worden gebruikt, ik gebruik ze zelf ook, maar zeker in het (elementaire) onderwijs zouden dit soort notaties vermeden moeten worden omdat ze getuigen van een conceptuele verwarring en die het studenten die de materie proberen te doorgronden daarmee nog lastiger maakt dan het voor velen kennelijk toch al is.
Heb je nu een variabele s die afhangt van een variabele p, dan hebben we voor de zogeheten elasticiteit Es(p) in de notatie van Leibniz
Zo zie je dus dat we ds/dp moeten vemenigvuldigen met p/s om een uitdrukking voor de elasticiteit van s ten opzichte van p te verkrijgen, waarbij we s in het quotiënt p/s dan uiteraard in p uitdrukken. Heb je nu s = pp·ln p dan is het enige lastige eigenlijk de bepaling van ds/dp, maar het aardige is dat we hier voor de bepaling van de elasticiteit een directe bepaling van ds/dp kunnen vermijden, als volgt.
Noteren we ds/dp als s'(p) dan hebben we blijkens bovenstaande herleiding ook
en zo zie je wellicht duidelijker dat we ook gebruik kunnen maken van logaritmisch differentiëren, want de afgeleide van ln s(p) naar p is immers s'(p)/s(p) en dit hoeven we dan alleen nog te vermenigvuldigen met p om een uitdrukking in p voor Es(p) te verkrijgen.
Dus, om je opgave nog even uit te werken in pseudo Lagrange notatie (pseudo omdat s een naam is van een variabele, en geen naam van een functie) doen we het volgende. We hebben
Van beide leden de natuurlijke logaritme nemen geeft
Nu beide leden differentiëren naar p en we krijgen
dus
Nu moeten we de uitdrukking in het rechterlid nog vermenigvuldigen met p om de elasticiteit Es(p) in p uit te drukken, dus hebben we
en dit geeft
Nu werd de elasticiteit gevraagd voor p = e, dus vullen we dit in en dan vinden we
Het kan dus allemaal best zonder Leibniz, en zonder de draad kwijt te raken, maar je hebt de Leibniz notatie toch nodig om te begrijpen wat er wordt bedoeld met een notatie als
als definitie voor de elasticiteit van een (positieve) variabele s die afhangt van een (positieve) variabele p, en ook om op een eenvoudige en overzichtelijke wijze in te zien dat dit gelijk is aan
oftewel
[ Bericht 16% gewijzigd door Riparius op 11-10-2014 05:58:55 ]


Nee! Je zou toch ondertussen wel in de gaten moeten hebben datquote:Op vrijdag 10 oktober 2014 23:02 schreef GeschiktX het volgende:
[..]
In mijn boek staat bijv:
y = a + xb
Als je de elasticiteit wilt nemen dan :
d ln y / d ln x
Dus:
ln y = ln a + b ln x
ln(p + q)
niet equivalent is met
ln p + ln q
Als dat wel zo was dan zou ln x lineair afhangen van x en dat is niet zo. Bovendien is ln p + ln q al equivalent met
ln pq
en je wil toch niet beweren dat p + q hetzelfde is als pq ?
Je mag nooit het =-teken misbruiken als vervanging van de werkwoordsvorm is in een zin.quote:ln a is een constante dus die valt weg:
Ik geloof er niets van dat dit zo in je boek staat. Waarschijnlijk staat erquote:y' = 0 + b * 1
Deze methode staat dus in mijn boek en zo probeer ik dit dus te benaderen.
y = abx
Zie ook hier.
Gebruik ook niet het woord benaderen voor het aanpakken van een vraagstuk of probleem want hiermee wek je misverstanden. Het gaat hier niet om het vinden van een numerieke benadering van de elasticiteit maar om het vinden van een (exacte) uitdrukking voor de elasticiteit.


Hartelijk dank. Alleen 1 iets mij niet duidelijk.. stel je hebt dan gedifferentieerd tot s(p)'/s(p) waarom moet je dan nog vermenigvuldigen met p?quote:Op zaterdag 11 oktober 2014 00:30 schreef Riparius het volgende:
[..]
Jouw probleem is hier dat je de Leibniz notatie kennelijk nog niet voldoende begrijpt het daarom zonder die notatie wil stellen. Maar dat is nu precies de reden dat je het overzicht kwijt raakt, in de war raakt, en gaat proberen om je er doorheen te slaan met trucjes en ezelsbruggetjes die je eigenlijk al helemaal niet begrijpt, en waarmee je gegarandeerd fouten gaat maken. Dat moet je dus allemaal niet doen.
De notatie van Leibniz is bij uitstek geschikt om te beschrijven hoe variabelen van elkaar afhangen, omdat deze notatie werkt met namen van variabelen, en niet met namen van functies zoals de notatie van Lagrange. Ook hoeven we zo niet elke afhankelijkheidsrelatie eerst een eigen naam te geven om de rate of change van een variabele ten opzichte van een andere variabele te kunnen noteren. En, de kettingregel is in de notatie van Leibniz ook nog eens heel transparant en intuïtief en daarmee gemakkelijk te onthouden en op te schrijven, dus wat wil je nog meer?
Hybride notaties zoals y' voor de rate of change van een variabele y in relatie tot een andere variabele (welke andere variabele?) resp. de afgeleide van een functie (hoe heet die functie?) waarbij y de afhankelijke variabele is (maar welke variabele is dan de onafhankelijke variabele?) zijn af te keuren omdat de prime notatie van Lagrange de afgeleide functie f' aangeeft van een functie f en niet de rate of change van een variabele ten opzichte van een andere variabele. Aan deze hybride notatie ligt dus de verwarring van namen van variabelen met namen van functies ten grondslag, en daarom is deze notatie niet goed.
In feite geeft de prime bij y' alleen maar aan dat dit een andere grootheid is dan y, net zo goed als als de prime bij een punt P' in een meetkundige figuur aangeeft dat dit een ander punt is dan punt P in dezelfde figuur. En uiteraard suggereert de overeenkomst in naamgeving dan dat er een zeker verband bestaat, maar de prime zegt an sich helemaal niets over de aard van dat verband. In een meetkundige figuur kan punt P' bijvoorbeeld het beeld zijn van punt P bij een translatie (om maar wat te noemen), en als punt P bijvoorbeeld de coördinaten (x, y) heeft, dan zouden we de coördinaten van punt P' heel goed kunnen noteren als (x', y'), maar het is duidelijk dat de primes hier niets met differentiëren van doen hebben.
De verwarring tussen namen van functies en namen van variabelen wordt nog verder in de hand gewerkt door een notatie als s(p) waarmee gewoonlijk wordt bedoeld dat s een variabele is die afhangt van een andere variabele p, versus een notatie als f(x) waarmee gewoonlijk wordt bedoeld dat f een functie is waarbij x de onafhankelijke variabele is en waarbij de notatie f(x) staat voor de bij die variabele x behorende functiewaarde. En nu weet ik ook wel dat hybride notaties als y' vaak worden gebruikt, ik gebruik ze zelf ook, maar zeker in het (elementaire) onderwijs zouden dit soort notaties vermeden moeten worden omdat ze getuigen van een conceptuele verwarring en die het studenten die de materie proberen te doorgronden daarmee nog lastiger maakt dan het voor velen kennelijk toch al is.
Heb je nu een variabele s die afhangt van een variabele p, dan hebben we voor de zogeheten elasticiteit Es(p) in de notatie van Leibniz
Zo zie je dus dat we ds/dp moeten vemenigvuldigen met p/s om een uitdrukking voor de elasticiteit van s ten opzichte van p te verkrijgen, waarbij we s in het quotiënt p/s dan uiteraard in p uitdrukken. Heb je nu s = pp·ln p dan is het enige lastige eigenlijk de bepaling van ds/dp, maar het aardige is dat we hier voor de bepaling van de elasticiteit een directe bepaling van ds/dp kunnen vermijden, als volgt.
Noteren we ds/dp als s'(p) dan hebben we blijkens bovenstaande herleiding ook
en zo zie je wellicht duidelijker dat we ook gebruik kunnen maken van logaritmisch differentiëren, want de afgeleide van ln s(p) naar p is immers s'(p)/s(p) en dit hoeven we dan alleen nog te vermenigvuldigen met p om een uitdrukking in p voor Es(p) te verkrijgen.
Dus, om je opgave nog even uit te werken in pseudo Lagrange notatie (pseudo omdat s een naam is van een variabele, en geen naam van een functie) doen we het volgende. We hebben
Van beide leden de natuurlijke logaritme nemen geeft
Nu beide leden differentiëren naar p en we krijgen
dus
Nu moeten we de uitdrukking in het rechterlid nog vermenigvuldigen met p om de elasticiteit Es(p) in p uit te drukken, dus hebben we
en dit geeft
Nu werd de elasticiteit gevraagd voor p = e, dus vullen we dit in en dan vinden we
Het kan dus allemaal best zonder Leibniz, en zonder de draad kwijt te raken, maar je hebt de Leibniz notatie toch nodig om te begrijpen wat er wordt bedoeld met een notatie als
als definitie voor de elasticiteit van een (positieve) variabele s die afhangt van een (positieve) variabele p, en ook om op een eenvoudige en overzichtelijke wijze in te zien dat dit gelijk is aan
oftewel
in mijn boek staat dat de elasticiteit te berekenen is door d ln y/ d ln p en dat is dan toch gedaanm


Misschien is een simpele handiger om het te begrijpen...
Stel: ax^b
Dan is de elasticiteit te berekenen door d ln y / d ln x te nemen
Dus: ln a + b ln x
ln x is hier de variabele die verandert en de overige zijn constante, dus
D ln y / d ln x = b
maar stel nou dat het ax^x was en dus
ln y = ln a + x ln x
dan weet ik dus niet wat ik met die x links van ln x moet doen want ik differentieer w.r.t. ln x en niet naar x. Als het w.r.t. x was dan had ik het gemakkelijk gekund..
Overigens snap ik de leibniz notatie wel, maar tijdens het differentieren begrijp ik het niet meer
Stel: ax^b
Dan is de elasticiteit te berekenen door d ln y / d ln x te nemen
Dus: ln a + b ln x
ln x is hier de variabele die verandert en de overige zijn constante, dus
D ln y / d ln x = b
maar stel nou dat het ax^x was en dus
ln y = ln a + x ln x
dan weet ik dus niet wat ik met die x links van ln x moet doen want ik differentieer w.r.t. ln x en niet naar x. Als het w.r.t. x was dan had ik het gemakkelijk gekund..
Overigens snap ik de leibniz notatie wel, maar tijdens het differentieren begrijp ik het niet meer


De helft van het werk zit in nauwkeurigheid en juist gebruik van notaties, omdat je vooral jezelf in de war brengt als je dat niet doet. Iets waar je (en anderen) met enige regelmaat op wordt gewezen in dit topic. Probeer hier, maar zeker ook in de opgaves die je op school en in je toetsen maakt, om de tips die je krijgt ter hand te nemen. Eigenlijk zijn het ook geen tips, maar dwingende adviezen.quote:Op zaterdag 11 oktober 2014 10:07 schreef GeschiktX het volgende:
Misschien is een simpele handiger om het te begrijpen...
Stel: ax^b
Net als Engels of Russisch heeft ook de wiskunde zijn grammatica, en als je ergens een lettertje vergeet of verkeerd zet is het gewoon fout.
Want wat staat er nu eigenlijk in je post? Je stelt iets. Je doet dus een bewering. En je bewering is 'koe'. Het is geen zin, en we weten dus ook niet wat er met 'koe' aan de hand is, of in dit geval met ax^b. Het wordt nog erger als er in je volgende regel ineens een y uit de lucht komt vallen.
Dus als je van jouw 'stel' en net zinnetje zou maken, staat er "Stel: Dat dier is een koe".
Oftewel: Stel:
y = axb
[ Bericht 5% gewijzigd door Janneke141 op 11-10-2014 10:27:50 ]
Opinion is the medium between knowledge and ignorance (Plato)


Stom stom stom. Volgens mij heb ik het door.. alleen ik raakte in de war door d ln y / d ln p.. met dat w.r.t. p... maar de methode die gebruikt wordt is gewoon d p volgens mij..


Ik vraag me echt af hoe goed je mijn teksten leest, want het antwoord staat gewoon clip en klaar voor je neus en wordt volledig uitgelegd. Ik laat immers zien dat je hebtquote:Op zaterdag 11 oktober 2014 09:59 schreef GeschiktX het volgende:
[..]
Hartelijk dank. Alleen één iets is mij niet duidelijk. Stel je hebt dan gedifferentieerd tot s(p)'/s(p), waarom moet je dan nog vermenigvuldigen met p?


Duidelijk: tenslotte nog één vraagje:quote:Op zaterdag 11 oktober 2014 10:58 schreef Riparius het volgende:
[..]
Ik vraag me echt af hoe goed je mijn teksten leest, want het antwoord staat gewoon clip en klaar voor je neus en wordt volledig uitgelegd. Ik laat immers zien dat je hebt
De productregel is toch:
f'(x)=g'(x)·h(x)+g(x)·h'(x)
Dus dan is g(x) = p ln p
en h(x) = ln ( ln p )
g'(x) = 1 * ln p + p * 1/p
h'(x) = 1/ln p * 1/p
Waarom zou het dan niet het volgende moeten zijn:
(1 * ln p + p * 1/p ) * ln (ln p ) + p ln p * ( 1/ln p * 1/p) ?
Dan heb ik het even puur om de afgeleide en dus nog even vóórdat het met p vermenigvuldigt moet worden.
[ Bericht 2% gewijzigd door GeschiktX op 11-10-2014 11:24:13 ]


Als ik de productregel wil toepassen doe ik het volgende:
y = p^p * ln p
ln y = p ln p ln(ln p)
x = ln p
ln y = px * ln(x)
de losse p van px is een constante:
y'/y = p * 1/ln(p)
y = p^p * ln p
ln y = p ln p ln(ln p)
x = ln p
ln y = px * ln(x)
de losse p van px is een constante:
y'/y = p * 1/ln(p)


Het gaat mij om die p ln p
Als je gaat differentiëren door ln p, dan is die p toch gewoon die p links van ln een constante?
Dus dan wordt het toch gewoon p * 1 = p ? En waarom vermenigvuldig je die p uiteindelijk met de afgeleide?
[ Bericht 24% gewijzigd door GeschiktX op 11-10-2014 11:45:09 ]


Ik snap er echt niks meer van sorry...
Het is echt met die losse p dat ik niet weet wat ik moet doen. Ik loop er steeds tegen aan, mijn methode is gewoon de ln erbij toevoegen en dan de afgeleide nemen d ln y / d ln x (of p)
y = p^p ln p
ln y = ln p^p ln (ln (p) )
ln(p) = x
f'(x) = x^p ln(x)
Nu zit ik met die p dus..
Het is echt met die losse p dat ik niet weet wat ik moet doen. Ik loop er steeds tegen aan, mijn methode is gewoon de ln erbij toevoegen en dan de afgeleide nemen d ln y / d ln x (of p)
y = p^p ln p
ln y = ln p^p ln (ln (p) )
ln(p) = x
f'(x) = x^p ln(x)
Nu zit ik met die p dus..


Je moet niet zomaar een expressie opschrijven en dan vervolgens een tweede variabele uit je hoge hoed toveren die helemaal niet in je expressie voorkomt. Je kunt niet spreken over d(ln y)/d(ln x) als je niet eerst hebt gedefinieerd wat y is en hoe die afhangt van x. Als y namelijk niet af zou hangen van x dan gebeurt er helemaal niets met y als je iets aan x verandert en dan heb je d(ln y)/d(ln x) = 0 en hoef je verder ook niets uit te rekenen.quote:Op zaterdag 11 oktober 2014 10:07 schreef GeschiktX het volgende:
Misschien is een simpele handiger om het te begrijpen...
Stel: y = ax^b
Dan is de elasticiteit te berekenen door d ln y / d ln x te nemen
Je zegt dat je d(ln y)/d(ln x) wil gaan bepalen, maar dan moet je wel een betrekking hebben waar x én y in voorkomen.quote:Dus: ln y = ln a + b ln x
Hier geen hoofdletter D gebruiken, ook al staat je formule aan het begin van een nieuwe regel.quote:ln x is hier de variabele die verandert en de overige zijn constantes, dus
d ln y / d ln x = b
Nee, niks dus. Je had y nog niet gedefinieerd.quote:Maar stel nou dat het y = ax^x was en dus
Kijk, en dit is nu precies je probleem: je hebt een kunstje geleerd dat in een heel eenvoudig geval het correcte antwoord produceert, maar nu hangt y op een iets andere manier af van x en werkt je kunstje niet meer.quote:ln y = ln a + x ln x
dan weet ik dus niet wat ik met die x links van ln x moet doen want ik differentieer w.r.t. ln x en niet naar x. Als het w.r.t. x was dan had ik het gemakkelijk gekund.
Dit is een non sequitur om je eigen onbegrip te bagatelliseren en dat weet je zelf ook wel. Dit is net zo'n onzin als beweren dat je de letters van het alfabet snapt maar dat je ze tijdens het lezen niet meer begrijpt terwijl je toch echt niet dyslectisch bent. Als je mijn uitleg hierboven over elasticiteit had begrepen dan zou je toch moeten zien en zelfstandig kunnen afleiden dat je hebtquote:Overigens snap ik de Leibniz notatie wel, maar tijdens het differentieren begrijp ik het niet meer.
Of laten we dit eens iets anders schrijven. Je kunt hier gemakkelijk uit afleiden dat we hebben
In woorden: om hier de elasticiteit d(ln y)/d(ln x) te berekenen moeten we onze uitdrukking voor ln y naar x differentiëren en het resultaat vervolgens nog met x vermenigvuldigen. Goed, dat is precies wat we nu gaan doen. We hadden
Beide leden differentiëren naar x geeft
En dus hebben we


Hoe weet je dat d x / d(ln x) gelijk is aan x?quote:Op zaterdag 11 oktober 2014 12:11 schreef Riparius het volgende:
[..]
Je moet niet zomaar een expressie opschrijven en dan vervolgens een tweede variabele uit je hoge hoed toveren die helemaal niet in je expressie voorkomt. Je kunt niet spreken over d(ln y)/d(ln x) als je niet eerst hebt gedefinieerd wat y is en hoe die afhangt van x. Als y namelijk niet af zou hangen van x dan gebeurt er helemaal niets met y als je iets aan x verandert en dan heb je d(ln y)/d(ln x) = 0 en hoef je verder ook niets uit te rekenen.
[..]
Je zegt dat je d(ln y)/d(ln x) wil gaan bepalen, maar dan moet je wel een betrekking hebben waar x én y in voorkomen.
[..]
Hier geen hoofdletter D gebruiken, ook al staat je formule aan het begin van een nieuwe regel.
[..]
Nee, niks dus. Je had y nog niet gedefinieerd.
[..]
Kijk, en dit is nu precies je probleem: je hebt een kunstje geleerd dat in een heel eenvoudig geval het correcte antwoord produceert, maar nu hangt y op een iets andere manier af van x en werkt je kunstje niet meer.
[..]
Dit is een non sequitur om je eigen onbegrip te bagatelliseren en dat weet je zelf ook wel. Dit is net zo'n onzin als beweren dat je de letters van het alfabet snapt maar dat je ze tijdens het lezen niet meer begrijpt terwijl je toch echt niet dyslectisch bent. Als je mijn uitleg hierboven over elasticiteit had begrepen dan zou je toch moeten zien en zelfstandig kunnen afleiden dat je hebt
Of laten we dit eens iets anders schrijven. Je kunt hier gemakkelijk uit afleiden dat we hebben
In woorden: om hier de elasticiteit d(ln y)/d(ln x) te berekenen moeten we onze uitdrukking voor ln y naar x differentiëren en het resultaat vervolgens nog met x vermenigvuldigen. Goed, dat is precies wat we nu gaan doen. We hadden
Beide leden differentiëren naar x geeft
En dus hebben we


d x / d ln xquote:Op zaterdag 11 oktober 2014 12:11 schreef Riparius het volgende:
[..]
Je moet niet zomaar een expressie opschrijven en dan vervolgens een tweede variabele uit je hoge hoed toveren die helemaal niet in je expressie voorkomt. Je kunt niet spreken over d(ln y)/d(ln x) als je niet eerst hebt gedefinieerd wat y is en hoe die afhangt van x. Als y namelijk niet af zou hangen van x dan gebeurt er helemaal niets met y als je iets aan x verandert en dan heb je d(ln y)/d(ln x) = 0 en hoef je verder ook niets uit te rekenen.
[..]
Je zegt dat je d(ln y)/d(ln x) wil gaan bepalen, maar dan moet je wel een betrekking hebben waar x én y in voorkomen.
[..]
Hier geen hoofdletter D gebruiken, ook al staat je formule aan het begin van een nieuwe regel.
[..]
Nee, niks dus. Je had y nog niet gedefinieerd.
[..]
Kijk, en dit is nu precies je probleem: je hebt een kunstje geleerd dat in een heel eenvoudig geval het correcte antwoord produceert, maar nu hangt y op een iets andere manier af van x en werkt je kunstje niet meer.
[..]
Dit is een non sequitur om je eigen onbegrip te bagatelliseren en dat weet je zelf ook wel. Dit is net zo'n onzin als beweren dat je de letters van het alfabet snapt maar dat je ze tijdens het lezen niet meer begrijpt terwijl je toch echt niet dyslectisch bent. Als je mijn uitleg hierboven over elasticiteit had begrepen dan zou je toch moeten zien en zelfstandig kunnen afleiden dat je hebt
Of laten we dit eens iets anders schrijven. Je kunt hier gemakkelijk uit afleiden dat we hebben
In woorden: om hier de elasticiteit d(ln y)/d(ln x) te berekenen moeten we onze uitdrukking voor ln y naar x differentiëren en het resultaat vervolgens nog met x vermenigvuldigen. Goed, dat is precies wat we nu gaan doen. We hadden
Beide leden differentiëren naar x geeft
En dus hebben we
Is eigenlijk hetzelfde wat hier staat:
Maar waarom is de afgeleide van x naar ln x gewoon x dan?
Ik begrijp wel wat er staat dat u = ln x en dat x = e^u, maar ik begrijp dan niet waarom de afgeleide van e^u dan x is ? Want de afgeleide zou gewoon e^u moeten blijven.


Het klopt inderdaad dat de afgeleide e^u is. Maar als je vervolgens weer u = ln(x) invult krijg je:quote:Op zaterdag 11 oktober 2014 12:28 schreef GeschiktX het volgende:
[..]
d x / d ln x
Is eigenlijk hetzelfde wat hier staat:
[ afbeelding ]
Maar waarom is de afgeleide van x naar ln x gewoon x dan?
Ik begrijp wel wat er staat dat u = ln x en dat x = e^u, maar ik begrijp dan niet waarom de afgeleide van e^u dan x is ? Want de afgeleide zou gewoon e^u moeten blijven.
Je zat dus goed, maar je moest nog net een stap meer maken


heb het al thnx.quote:Op zaterdag 11 oktober 2014 12:33 schreef Alrac4 het volgende:
[..]
Het klopt inderdaad dat de afgeleide e^u is. Maar als je vervolgens weer u = ln(x) invult krijg je:
Je zat dus goed, maar je moest nog net een stap meer maken


Ik heb dus nu:
y = p^p ln p
ln y = ln p^p * ln(ln(p))
De afgeleide is dus:
d ln y / d ln p = d ln y / d p * dp / d ln p
ln y = p ln p * ln(ln(p))
d p / d ln p bepalen vind ik lastig... want ik snap hier de bedoeling niet p naar ln p afleiden?!?! P is hier niet de functie maar ln y, dus ik snap niet echt wat ik moet doen.
Ik weet dus niet of dit de meest makkelijke en handige manier is, maar dit is dus wat ik tot nu toe heb. Ja ik heb jullie posts gelezen ,maar ik probeer het stap voor stap om het ook echt te begrijpen.
y = p^p ln p
ln y = ln p^p * ln(ln(p))
De afgeleide is dus:
d ln y / d ln p = d ln y / d p * dp / d ln p
ln y = p ln p * ln(ln(p))
d p / d ln p bepalen vind ik lastig... want ik snap hier de bedoeling niet p naar ln p afleiden?!?! P is hier niet de functie maar ln y, dus ik snap niet echt wat ik moet doen.
Ik weet dus niet of dit de meest makkelijke en handige manier is, maar dit is dus wat ik tot nu toe heb. Ja ik heb jullie posts gelezen ,maar ik probeer het stap voor stap om het ook echt te begrijpen.


Ik begrijp je post nu na het vier keer gelezen te hebben, alleen twee onduidelijkheden. Hoe weet je dat d p / d ln p = p ? Moet je de hele ln y functie afleiden naar p of wat? En waarom moet je het vermenigvuldigen met p en niet met de hele ln y functie?quote:Op zaterdag 11 oktober 2014 00:30 schreef Riparius het volgende:
[..]
Jouw probleem is hier dat je de Leibniz notatie kennelijk nog niet voldoende begrijpt het daarom zonder die notatie wil stellen. Maar dat is nu precies de reden dat je het overzicht kwijt raakt, in de war raakt, en gaat proberen om je er doorheen te slaan met trucjes en ezelsbruggetjes die je eigenlijk al helemaal niet begrijpt, en waarmee je gegarandeerd fouten gaat maken. Dat moet je dus allemaal niet doen.
De notatie van Leibniz is bij uitstek geschikt om te beschrijven hoe variabelen van elkaar afhangen, omdat deze notatie werkt met namen van variabelen, en niet met namen van functies zoals de notatie van Lagrange. Ook hoeven we zo niet elke afhankelijkheidsrelatie eerst een eigen naam te geven om de rate of change van een variabele ten opzichte van een andere variabele te kunnen noteren. En, de kettingregel is in de notatie van Leibniz ook nog eens heel transparant en intuïtief en daarmee gemakkelijk te onthouden en op te schrijven, dus wat wil je nog meer?
Hybride notaties zoals y' voor de rate of change van een variabele y in relatie tot een andere variabele (welke andere variabele?) resp. de afgeleide van een functie (hoe heet die functie?) waarbij y de afhankelijke variabele is (maar welke variabele is dan de onafhankelijke variabele?) zijn af te keuren omdat de prime notatie van Lagrange de afgeleide functie f' aangeeft van een functie f en niet de rate of change van een variabele ten opzichte van een andere variabele. Aan deze hybride notatie ligt dus de verwarring van namen van variabelen met namen van functies ten grondslag, en daarom is deze notatie niet goed.
In feite geeft de prime bij y' alleen maar aan dat dit een andere grootheid is dan y, net zo goed als als de prime bij een punt P' in een meetkundige figuur aangeeft dat dit een ander punt is dan punt P in dezelfde figuur. En uiteraard suggereert de overeenkomst in naamgeving dan dat er een zeker verband bestaat, maar de prime zegt an sich helemaal niets over de aard van dat verband. In een meetkundige figuur kan punt P' bijvoorbeeld het beeld zijn van punt P bij een translatie (om maar wat te noemen), en als punt P bijvoorbeeld de coördinaten (x, y) heeft, dan zouden we de coördinaten van punt P' heel goed kunnen noteren als (x', y'), maar het is duidelijk dat de primes hier niets met differentiëren van doen hebben.
De verwarring tussen namen van functies en namen van variabelen wordt nog verder in de hand gewerkt door een notatie als s(p) waarmee gewoonlijk wordt bedoeld dat s een variabele is die afhangt van een andere variabele p, versus een notatie als f(x) waarmee gewoonlijk wordt bedoeld dat f een functie is waarbij x de onafhankelijke variabele is en waarbij de notatie f(x) staat voor de bij die variabele x behorende functiewaarde. En nu weet ik ook wel dat hybride notaties als y' vaak worden gebruikt, ik gebruik ze zelf ook, maar zeker in het (elementaire) onderwijs zouden dit soort notaties vermeden moeten worden omdat ze getuigen van een conceptuele verwarring en die het studenten die de materie proberen te doorgronden daarmee nog lastiger maakt dan het voor velen kennelijk toch al is.
Heb je nu een variabele s die afhangt van een variabele p, dan hebben we voor de zogeheten elasticiteit Es(p) in de notatie van Leibniz
Zo zie je dus dat we ds/dp moeten vemenigvuldigen met p/s om een uitdrukking voor de elasticiteit van s ten opzichte van p te verkrijgen, waarbij we s in het quotiënt p/s dan uiteraard in p uitdrukken. Heb je nu s = pp·ln p dan is het enige lastige eigenlijk de bepaling van ds/dp, maar het aardige is dat we hier voor de bepaling van de elasticiteit een directe bepaling van ds/dp kunnen vermijden, als volgt.
Noteren we ds/dp als s'(p) dan hebben we blijkens bovenstaande herleiding ook
en zo zie je wellicht duidelijker dat we ook gebruik kunnen maken van logaritmisch differentiëren, want de afgeleide van ln s(p) naar p is immers s'(p)/s(p) en dit hoeven we dan alleen nog te vermenigvuldigen met p om een uitdrukking in p voor Es(p) te verkrijgen.
Dus, om je opgave nog even uit te werken in pseudo Lagrange notatie (pseudo omdat s een naam is van een variabele, en geen naam van een functie) doen we het volgende. We hebben
Van beide leden de natuurlijke logaritme nemen geeft
Nu beide leden differentiëren naar p en we krijgen
dus
Nu moeten we de uitdrukking in het rechterlid nog vermenigvuldigen met p om de elasticiteit Es(p) in p uit te drukken, dus hebben we
en dit geeft
Nu werd de elasticiteit gevraagd voor p = e, dus vullen we dit in en dan vinden we
Het kan dus allemaal best zonder Leibniz, en zonder de draad kwijt te raken, maar je hebt de Leibniz notatie toch nodig om te begrijpen wat er wordt bedoeld met een notatie als
als definitie voor de elasticiteit van een (positieve) variabele s die afhangt van een (positieve) variabele p, en ook om op een eenvoudige en overzichtelijke wijze in te zien dat dit gelijk is aan
oftewel
Want als je x^x hebt dan moet je uiteindelijk vermenigvuldigen met x^x.


Ik heb nu:
y = p^p ln p
ln y = p ln p + ln (ln (p))
y' / y = 1 * ln p + p * 1/p + 1/ln p * 1/p
y'/y = ln p + 1 + 1 / p* ln p
Ik zou dus nu y = p^p ln p moeten vermenigvuldigen om y' te krijgen.. en vervolgens kan ik de elasticiteit berekenen door:
p / y * y'
ln y / ln x lukt mij niet...
y = p^p ln p
ln y = p ln p + ln (ln (p))
y' / y = 1 * ln p + p * 1/p + 1/ln p * 1/p
y'/y = ln p + 1 + 1 / p* ln p
Ik zou dus nu y = p^p ln p moeten vermenigvuldigen om y' te krijgen.. en vervolgens kan ik de elasticiteit berekenen door:
p / y * y'
ln y / ln x lukt mij niet...


Hoeft die dx/d lnx nou maar eenmaal berekent te worden, ongeacht hoe groot de functie is?
En dat is dan gewoon x en dan vermenigvuldigen met d ln y / dx?
En dat is dan gewoon x en dan vermenigvuldigen met d ln y / dx?


Beste GeschiktX, je stelt nu al een aantal keer achter elkaar min of meer dezelfde vraag. Het antwoord is al voorbij gekomen en bijzonder duidelijk en uitgebreid uitgelegd.
Helaas zit voor jou het probleem er in, dat je voorkennis onvoldoende is om je deze materie eigen te maken. Ik ben bang dat je voor dit moment moet accepteren dat dit forum geen antwoord kan geven op je vraag, in ieder geval niet op zo'n manier dat je daarmee voldoende begrip van de stof krijgt, en dat je je hulp irl moet gaan zoeken. Iemand die naast je gaat zitten en je stap voor stap door dit soort afleidingen loodst, maar belangrijker nog: door de basisvaardigheden die hier voor nodig zijn.
Als je zo iemand kan vinden, moet je hem ook vragen of hij je kan trainen in het op een zorgvuldige manier stellen van je vragen.
[ Bericht 48% gewijzigd door Janneke141 op 11-10-2014 14:07:07 ]
Helaas zit voor jou het probleem er in, dat je voorkennis onvoldoende is om je deze materie eigen te maken. Ik ben bang dat je voor dit moment moet accepteren dat dit forum geen antwoord kan geven op je vraag, in ieder geval niet op zo'n manier dat je daarmee voldoende begrip van de stof krijgt, en dat je je hulp irl moet gaan zoeken. Iemand die naast je gaat zitten en je stap voor stap door dit soort afleidingen loodst, maar belangrijker nog: door de basisvaardigheden die hier voor nodig zijn.
Als je zo iemand kan vinden, moet je hem ook vragen of hij je kan trainen in het op een zorgvuldige manier stellen van je vragen.
[ Bericht 48% gewijzigd door Janneke141 op 11-10-2014 14:07:07 ]
Opinion is the medium between knowledge and ignorance (Plato)


Het blijft voor mij een lastige materie:quote:Op zaterdag 11 oktober 2014 13:53 schreef Janneke141 het volgende:
Beste GeschiktX, je stelt nu al een aantal keer achter elkaar min of meer dezelfde vraag. Het antwoord is al voorbij gekomen en bijzonder duidelijk en uitgebreid uitgelegd.
Helaas zit voor jou het probleem er in, dat je voorkennis onvoldoende is om je deze materie eigen te maken. Ik ben bang dat je voor dit moment moet accepteren dat dit forum geen antwoord kan geven op je vraag, in ieder geval niet op zo'n manier dat je daarmee voldoende begrip van de stof krijgt, en dat je je hulp irl moet gaan zoeken. Iemand die naast je gaat zitten en je stap voor stap door dit soort afleidingen, maar belangrijker nog: door de basisvaardigheden die hier voor nodig zijn.
Als je zo iemand kan vinden, moet je hem ook vragen of hij je kan trainen in het op een zorgvuldige manier stellen van je vragen.
Ik ben er wel uitgekomen dat:
d ln y / dp = ln p + 1 + 1 / p* ln p
d ln p / dp = e^u + e^u * u + 1/u
moet ik dit dan met elkaar vermenigvuldigen?


Alleen de laatste zin wordt gelezen.quote:Op zaterdag 11 oktober 2014 10:58 schreef Riparius het volgende:
[..]
Ik vraag me echt af hoe goed je mijn teksten leest, want het antwoord staat gewoon clip en klaar voor je neus en wordt volledig uitgelegd. Ik laat immers zien dat je hebt
Daarom is het denk ik ook niet handig om bij deze lui de hele uitwerking te geven.
Laat ze zelf maar eens zelf een goede uitwerking geven.
Hoe vaak is gezegd om niet zomaar een kant van een vergelijking weg te laten. En toch doet hij dat weer in zijn laatste bericht.
-edit- Mobiel verstuurde reactie met een flinke vertraging. Hij heeft al weer meer rotzooi geplaatst.
[ Bericht 6% gewijzigd door t4rt4rus op 11-10-2014 14:34:27 ]


quote:Op zaterdag 11 oktober 2014 13:53 schreef Janneke141 het volgende:
Beste GeschiktX, je stelt nu al een aantal keer achter elkaar min of meer dezelfde vraag. Het antwoord is al voorbij gekomen en bijzonder duidelijk en uitgebreid uitgelegd.
Helaas zit voor jou het probleem er in, dat je voorkennis onvoldoende is om je deze materie eigen te maken. Ik ben bang dat je voor dit moment moet accepteren dat dit forum geen antwoord kan geven op je vraag, in ieder geval niet op zo'n manier dat je daarmee voldoende begrip van de stof krijgt, en dat je je hulp irl moet gaan zoeken. Iemand die naast je gaat zitten en je stap voor stap door dit soort afleidingen loodst, maar belangrijker nog: door de basisvaardigheden die hier voor nodig zijn.
Als je zo iemand kan vinden, moet je hem ook vragen of hij je kan trainen in het op een zorgvuldige manier stellen van je vragen.


Ik lees alles hoor.quote:Op zaterdag 11 oktober 2014 14:20 schreef t4rt4rus het volgende:
[..]
Alleen de laatste zin wordt gelezen.
Daarom is het denk ik ook niet handig om bij deze lui de hele uitwerking te geven.
Laat ze zelf maar eens zelf een goede uitwerking geven.
Hoe vaak is gezegd om niet zomaar een kant van een vergelijking weg te laten. En toch doet hij dat weer in zijn laatste bericht.
-edit- Mobiel verstuurde reactie met een flinke vertraging. Hij heeft al weer meer rotzooi geplaatst.


Hallo , weet iemand het antwoord op deze vraag:
Laat F(K,L) = 10K1/2 L 1/3 zijn voor K > 0 en L > 0 en vind F(2K, 2L)
Ik vulde dat gewoon netjes in om zodoende het volgende te krijgen:
20K3/2 * 2L 4/3
40K3/2 * L 4/3
Ik ben er naar mijn idee heilig van overtuigd dat ik goed zit, echter ben ik in de verwarring geraakt door het antwoordenmodel, welke het volgende zegt:
25/6 K 1/2 L 1/3 = 25/6 F(K,L)
Laat F(K,L) = 10K1/2 L 1/3 zijn voor K > 0 en L > 0 en vind F(2K, 2L)
Ik vulde dat gewoon netjes in om zodoende het volgende te krijgen:
20K3/2 * 2L 4/3
40K3/2 * L 4/3
Ik ben er naar mijn idee heilig van overtuigd dat ik goed zit, echter ben ik in de verwarring geraakt door het antwoordenmodel, welke het volgende zegt:
25/6 K 1/2 L 1/3 = 25/6 F(K,L)


F(2K, 2L) = 10(2K)1/2 (2L) 1/3quote:Op zaterdag 11 oktober 2014 15:42 schreef GoldenHeart het volgende:
Hallo , weet iemand het antwoord op deze vraag:
Laat F(K,L) = 10K1/2 L 1/3 zijn voor K > 0 en L > 0 en vind F(2K, 2L)
Ik vulde dat gewoon netjes in om zodoende het volgende te krijgen:
20K3/2 * 2L 4/3
40K3/2 * L 4/3
Ik ben er naar mijn idee heilig van overtuigd dat ik goed zit, echter ben ik in de verwarring geraakt door het antwoordenmodel, welke het volgende zegt:
25/6 K 1/2 L 1/3 = 25/6 F(K,L)
= 10∙21/2K 1/2 2 1/3 L 1/3
= 21/2∙21/3∙10∙K1/2∙L 1/3
= 25/6∙10∙K1/2∙L 1/3
= 25/6∙F(K,L)
Je gaat dus al de fout in bij het invullen van 2K.
Opinion is the medium between knowledge and ignorance (Plato)


Waarom mag het eigenlijk niet 205/6 K1/2 L1/3 zijn ?quote:Op zaterdag 11 oktober 2014 15:52 schreef Janneke141 het volgende:
[..]
F(2K, 2L) = 10(2K)1/2 (2L) 1/3
= 10∙21/2K 1/2 2 1/3 L 1/3
= 21/2∙21/3∙10∙K1/2∙L 1/3
= 25/6∙10∙K1/2∙L 1/3
= 25/6∙F(K,L)
Je gaat dus al de fout in bij het invullen van 2K.


Omdat 25/6∙10 ≠ 205/6quote:Op zaterdag 11 oktober 2014 16:04 schreef GoldenHeart het volgende:
[..]
Waarom mag het eigenlijk niet 205/6 K1/2 L1/3 zijn ?
Opinion is the medium between knowledge and ignorance (Plato)


Dit slaat weer helemaal nergens op.quote:Op zaterdag 11 oktober 2014 14:00 schreef GeschiktX het volgende:
[..]
Het blijft voor mij een lastige materie:
Ik ben er wel uitgekomen dat:
d ln y / dp = ln p + 1 + 1 / p* ln p
d ln p / dp = e^u + e^u * u + 1/u
moet ik dit dan met elkaar vermenigvuldigen?
d ln p/dp = 1/p.
Wat jij er van gemaakt hebt, staat ergens in mijn uitwerking. Maar dan weer verkeerd over genomen.
Maak nou eens één keer een gehele uitwerking waar je begint met het vraagstuk en uit eindelijk op op het antwoord uitkomt.
En dan duidelijk aangeveb wat je doet en waarom iets volgt uit het andere.
En we willen dus geen dingen zijn als "dus" waar dus nergens op slaat.


Hoe kan ik dat gebruiken met machten?quote:Op zaterdag 11 oktober 2014 17:19 schreef Novermars het volgende:
Gebruik ofof de sup/sub tags, nu is het niet duidelijk wat je precies bedoelt.


Hallo , weet iemand het antwoord op nog een vraag van mij, ditmaal heeft het betrekking op het partieel differentiëren. Hopelijk is iemand hier bekend mee.
Er is een gegeven functie: (x-y)/(x+y) en ik zou f' xy moeten berekenen:
Allereerst dus f'x: Dit deed ik door de quotientregel te gebruiken:
![[(x+y ) - (x - y)] /](https://forum.fok.nl/lib/mimetex.cgi?%20%5B%28x%2By%20%29%20%20-%20%28x%20-%20y%29%5D%20%20%2F%20) (x+y)²
(x+y)²
![\frac [x+y - x + y]](https://forum.fok.nl/lib/mimetex.cgi?%20%5Cfrac%20%5Bx%2By%20-%20x%20%2B%20y%5D) / (x+y)²
/ (x+y)²
2y / (x+y)²
Nu ga ik f'xy berekenen door de d f'x / dy te nemen dmv het quotientregel alweer:
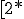 (x+y)²
(x+y)² ![- 2y * 2(x+y)] /](https://forum.fok.nl/lib/mimetex.cgi?%20-%202y%20%2A%202%28x%2By%29%5D%20%2F%20) (x+y) 4 --> Overigens ook de exponent in de noemer vermenigvuldigen met 2.
(x+y) 4 --> Overigens ook de exponent in de noemer vermenigvuldigen met 2.
Alle termen delen door (x+y)
![[2 * (x+y) - 4y ] /](https://forum.fok.nl/lib/mimetex.cgi?%5B2%20%2A%20%28x%2By%29%20-%204y%20%5D%20%2F) (x+y)³
(x+y)³
Is dit goed? Zo iemand die kunnen controleren voor mij?
[ Bericht 0% gewijzigd door GoldenHeart op 11-10-2014 17:31:26 ]
Er is een gegeven functie: (x-y)/(x+y) en ik zou f' xy moeten berekenen:
Allereerst dus f'x: Dit deed ik door de quotientregel te gebruiken:
2y / (x+y)²
Nu ga ik f'xy berekenen door de d f'x / dy te nemen dmv het quotientregel alweer:
Alle termen delen door (x+y)
Is dit goed? Zo iemand die kunnen controleren voor mij?
[ Bericht 0% gewijzigd door GoldenHeart op 11-10-2014 17:31:26 ]


quote:Op zaterdag 11 oktober 2014 17:23 schreef GoldenHeart het volgende:
Hallo , weet iemand het antwoord op nog een vraag van mij, ditmaal heeft het betrekking op het partieel differentiëren. Hopelijk is iemand hier bekend mee.
Er is een gegeven functie: (x-y)/(x+y) en ik zou f' xy moeten berekenen:
Allereerst dus f'x: Dit deed ik door de quotientregel te gebruiken:(x+y)²
/ (x+y)²
2y / (x+y)²
Nu ga ik f'xy berekenen door de d f'x / dy te nemen dmv het quotientregel alweer:(x+y)²
(x+y) 4 --> Overigens ook de exponent in de noemer vermenigvuldigen met 2.
Alle termen delen door (x+y)(x+y)³
Is dit goed? Zo iemand die kunnen controleren voor mij?
Quote mijn post even om te zien hoe je een breuk maakt in
Opinion is the medium between knowledge and ignorance (Plato)


Ten eerste is het niet te lezen.quote:Op zaterdag 11 oktober 2014 17:23 schreef GoldenHeart het volgende:
Hallo , weet iemand het antwoord op nog een vraag van mij, ditmaal heeft het betrekking op het partieel differentiëren. Hopelijk is iemand hier bekend mee.
Er is een gegeven functie: (x-y)/(x+y) en ik zou f' xy moeten berekenen:
Allereerst dus f'x: Dit deed ik door de quotientregel te gebruiken:(x+y)²
/ (x+y)²
2y / (x+y)²
Nu ga ik f'xy berekenen door de d f'x / dy te nemen dmv het quotientregel alweer:(x+y)²
(x+y) 4 --> Overigens ook de exponent in de noemer vermenigvuldigen met 2.
Alle termen delen door (x+y)(x+y)³
Is dit goed? Zo iemand die kunnen controleren voor mij?
Ten tweede is je notatie niet duidelijk.


Na wat ontcijferwerk kan ik melden dat je antwoord klopt. Als je trouwens antwoorden wilt 'checken', kan je ook altijd even kijken op Wolfram. Ik zou je overigens aanraden je eerst enigzins in te lezen over LATEXquote:Op zaterdag 11 oktober 2014 17:23 schreef GoldenHeart het volgende:
Hallo , weet iemand het antwoord op nog een vraag van mij, ditmaal heeft het betrekking op het partieel differentiëren. Hopelijk is iemand hier bekend mee.
Er is een gegeven functie: (x-y)/(x+y) en ik zou f' xy moeten berekenen:
Allereerst dus f'x: Dit deed ik door de quotientregel te gebruiken:(x+y)²
/ (x+y)²
2y / (x+y)²
Nu ga ik f'xy berekenen door de d f'x / dy te nemen dmv het quotientregel alweer:(x+y)²
(x+y) 4 --> Overigens ook de exponent in de noemer vermenigvuldigen met 2.
Alle termen delen door (x+y)(x+y)³
Is dit goed? Zo iemand die kunnen controleren voor mij?


Momenteel is het te druk voor onze databaseservers om alle verzoeken te kunnen verwerken. De gevraagde pagina kon daardoor niet getoond worden of de gevraagde actie kon niet worden uitgevoerd. Wacht even een ogenblik en probeer het daarna nog eens. <br/><br/><i><small>(:mysql_busy)</small></i>quote:Op zaterdag 11 oktober 2014 18:04 schreef Anoonumos het volgende:
Ja het is goed.
2(x+y) - 4y kan je nog schrijven als 2(x-y)
Enorm bedankt voor jullie tijd en moeite. Ik zal die Wolfram Alpha eens bekijken voortaan en alleen vragen stellen wanneer ik er echt niet uit kom.


De kans dat hij wint is toch 1/1000? Want er zijn 4000 deelnemers waarvan 25% een goede oplossing heeft. Dus de kans dat hij nooit wint is (999/1000)^500.quote:Op vrijdag 10 oktober 2014 18:58 schreef Anoonumos het volgende:
[..]
Wat is de kans dat hij in week 1 wint? Wat is dus de kans dat hij in week 1 niet wint? Wat is dan de kans dat hij in 500 weken niet wint?
Weet je toevallig ook het antwoord op de laatste vraag? Want daar kom ik echt niet uit.
En weet je misschien ook hoe je een benadering moet geven op de negatief binomiale verdeling? Kan dat gewoon met Poisson?
[ Bericht 7% gewijzigd door Wouterw17 op 11-10-2014 19:12:54 ]


Hmm.. iets als:quote:Op zaterdag 11 oktober 2014 19:07 schreef Wouterw17 het volgende:
[..]
De kans dat hij wint is toch 1/1000? Want er zijn 4000 deelnemers waarvan 25% een goede oplossing heeft. Dus de kans dat hij nooit wint is (999/1000)^500.
Weet je toevallig ook het antwoord op de laatste vraag? Want daar kom ik echt niet uit.
En weet je misschien ook hoe je een benadering moet geven op de negatief binomiale verdeling? Kan dat gewoon met Poisson?
Nulhypothese: De kans op succes is kleiner dan 25%.
Onder de nulhypothese is de kans dat je de eerste 9 keer een foutieve inzending trekt groter dan (3/4)9 = 0.075
(dus de p-waarde is groter dan 0.075, als dat je iets zegt)
(eigenlijk moet je erop corrigeren dat je steeds een foute inzending verwijdert maar dat zal niet veel verschil geven)
Dus we verwerpen de nulhypothese niet, want de kans onder de nulhypothese op de gegeven uitkomst of extremer is groter dan 0.05. (want de p-waarde is kleiner dan het significantieniveau)
Die andere vraag weet ik niet, zou kunnen.


Oh je neemt dus eigenlijk een geometrische verdeling onder aanname van de nulhypothese? Wordt de kans dan niet (3/4)^9 * (1/4)? Want dat is uiteindelijk de kans dat je pas na de tiende trekking een goede inzending hebt. En die kans is 0.019 dus een P-waarde kleiner dan het significantieniveau. Dus je verwerpt de nulhypothese wel. Of klopt dat niet?quote:Op zaterdag 11 oktober 2014 20:03 schreef Anoonumos het volgende:
[..]
Hmm.. iets als:
Nulhypothese: De kans op succes is kleiner dan 25%.
Onder de nulhypothese is de kans dat je de eerste 9 keer een foutieve inzending trekt groter dan (3/4)9 = 0.075
(dus de p-waarde is groter dan 0.075, als dat je iets zegt)
(eigenlijk moet je erop corrigeren dat je steeds een foute inzending verwijdert maar dat zal niet veel verschil geven)
Dus we verwerpen de nulhypothese niet, want de kans onder de nulhypothese op de gegeven uitkomst of extremer is groter dan 0.05. (want de p-waarde is kleiner dan het significantieniveau)
Die andere vraag weet ik niet, zou kunnen.


The p-value is the probability under the null hypothesis of a result as or more extreme than that actually observed.quote:Op zaterdag 11 oktober 2014 20:09 schreef Wouterw17 het volgende:
[..]
Oh je neemt dus eigenlijk een geometrische verdeling onder aanname van de nulhypothese? Wordt de kans dan niet (3/4)^9 * (1/4)? Want dat is uiteindelijk de kans dat je pas na de tiende trekking een goede inzending hebt. En die kans is 0.019 dus een P-waarde kleiner dan het significantieniveau. Dus je verwerpt de nulhypothese wel. Of klopt dat niet?
Volgens mij kijk je altijd naar de kans op de data of extremer, maar ik zou het niet met 100% zekerheid durven zeggen.


Die p he die vermenigvuldigt moet worden om de elasticiteit te vinden (d p / d ln p ). Kun je die uitwerking geven?quote:Op zaterdag 11 oktober 2014 00:30 schreef Riparius het volgende:
[..]
Jouw probleem is hier dat je de Leibniz notatie kennelijk nog niet voldoende begrijpt het daarom zonder die notatie wil stellen. Maar dat is nu precies de reden dat je het overzicht kwijt raakt, in de war raakt, en gaat proberen om je er doorheen te slaan met trucjes en ezelsbruggetjes die je eigenlijk al helemaal niet begrijpt, en waarmee je gegarandeerd fouten gaat maken. Dat moet je dus allemaal niet doen.
De notatie van Leibniz is bij uitstek geschikt om te beschrijven hoe variabelen van elkaar afhangen, omdat deze notatie werkt met namen van variabelen, en niet met namen van functies zoals de notatie van Lagrange. Ook hoeven we zo niet elke afhankelijkheidsrelatie eerst een eigen naam te geven om de rate of change van een variabele ten opzichte van een andere variabele te kunnen noteren. En, de kettingregel is in de notatie van Leibniz ook nog eens heel transparant en intuïtief en daarmee gemakkelijk te onthouden en op te schrijven, dus wat wil je nog meer?
Hybride notaties zoals y' voor de rate of change van een variabele y in relatie tot een andere variabele (welke andere variabele?) resp. de afgeleide van een functie (hoe heet die functie?) waarbij y de afhankelijke variabele is (maar welke variabele is dan de onafhankelijke variabele?) zijn af te keuren omdat de prime notatie van Lagrange de afgeleide functie f' aangeeft van een functie f en niet de rate of change van een variabele ten opzichte van een andere variabele. Aan deze hybride notatie ligt dus de verwarring van namen van variabelen met namen van functies ten grondslag, en daarom is deze notatie niet goed.
In feite geeft de prime bij y' alleen maar aan dat dit een andere grootheid is dan y, net zo goed als als de prime bij een punt P' in een meetkundige figuur aangeeft dat dit een ander punt is dan punt P in dezelfde figuur. En uiteraard suggereert de overeenkomst in naamgeving dan dat er een zeker verband bestaat, maar de prime zegt an sich helemaal niets over de aard van dat verband. In een meetkundige figuur kan punt P' bijvoorbeeld het beeld zijn van punt P bij een translatie (om maar wat te noemen), en als punt P bijvoorbeeld de coördinaten (x, y) heeft, dan zouden we de coördinaten van punt P' heel goed kunnen noteren als (x', y'), maar het is duidelijk dat de primes hier niets met differentiëren van doen hebben.
De verwarring tussen namen van functies en namen van variabelen wordt nog verder in de hand gewerkt door een notatie als s(p) waarmee gewoonlijk wordt bedoeld dat s een variabele is die afhangt van een andere variabele p, versus een notatie als f(x) waarmee gewoonlijk wordt bedoeld dat f een functie is waarbij x de onafhankelijke variabele is en waarbij de notatie f(x) staat voor de bij die variabele x behorende functiewaarde. En nu weet ik ook wel dat hybride notaties als y' vaak worden gebruikt, ik gebruik ze zelf ook, maar zeker in het (elementaire) onderwijs zouden dit soort notaties vermeden moeten worden omdat ze getuigen van een conceptuele verwarring en die het studenten die de materie proberen te doorgronden daarmee nog lastiger maakt dan het voor velen kennelijk toch al is.
Heb je nu een variabele s die afhangt van een variabele p, dan hebben we voor de zogeheten elasticiteit Es(p) in de notatie van Leibniz
Zo zie je dus dat we ds/dp moeten vemenigvuldigen met p/s om een uitdrukking voor de elasticiteit van s ten opzichte van p te verkrijgen, waarbij we s in het quotiënt p/s dan uiteraard in p uitdrukken. Heb je nu s = pp·ln p dan is het enige lastige eigenlijk de bepaling van ds/dp, maar het aardige is dat we hier voor de bepaling van de elasticiteit een directe bepaling van ds/dp kunnen vermijden, als volgt.
Noteren we ds/dp als s'(p) dan hebben we blijkens bovenstaande herleiding ook
en zo zie je wellicht duidelijker dat we ook gebruik kunnen maken van logaritmisch differentiëren, want de afgeleide van ln s(p) naar p is immers s'(p)/s(p) en dit hoeven we dan alleen nog te vermenigvuldigen met p om een uitdrukking in p voor Es(p) te verkrijgen.
Dus, om je opgave nog even uit te werken in pseudo Lagrange notatie (pseudo omdat s een naam is van een variabele, en geen naam van een functie) doen we het volgende. We hebben
Van beide leden de natuurlijke logaritme nemen geeft
Nu beide leden differentiëren naar p en we krijgen
dus
Nu moeten we de uitdrukking in het rechterlid nog vermenigvuldigen met p om de elasticiteit Es(p) in p uit te drukken, dus hebben we
en dit geeft
Nu werd de elasticiteit gevraagd voor p = e, dus vullen we dit in en dan vinden we
Het kan dus allemaal best zonder Leibniz, en zonder de draad kwijt te raken, maar je hebt de Leibniz notatie toch nodig om te begrijpen wat er wordt bedoeld met een notatie als
als definitie voor de elasticiteit van een (positieve) variabele s die afhangt van een (positieve) variabele p, en ook om op een eenvoudige en overzichtelijke wijze in te zien dat dit gelijk is aan
oftewel


Die staat verdomme in de tekst die je quote.quote:Op zaterdag 11 oktober 2014 23:25 schreef GeschiktX het volgende:
[..]
Die p he die vermenigvuldigt moet worden om de elasticiteit te vinden (d p / d ln p ). Kun je die uitwerking geven?
Je kan me niet zeggen dat je alles leest. Blijkt wel dat je alleen het laatste leest, zoals ik al eerder zei


Nee hoor. Ik snap het gewoon niet. Het ging ook de hele tijd om die p..quote:Op zaterdag 11 oktober 2014 23:40 schreef t4rt4rus het volgende:
[..]
Die staat verdomme in de tekst die je quote.
Je kan me niet zeggen dat je alles leest. Blijkt wel dat je alleen het laatste leest, zoals ik al eerder zei


Vertel dan vanaf waar je het niet begrijpt.quote:Op zondag 12 oktober 2014 00:03 schreef GeschiktX het volgende:
[..]
Nee hoor. Ik snap het gewoon niet. Het ging ook de hele tijd om die p..
Anders kan Riparius wel weer hetzelfde plaatsen.
Doe ook een beetje moeite!


Als je alles leest, dan heb je dit ook gelezen:quote:Op zondag 12 oktober 2014 00:03 schreef GeschiktX het volgende:
[..]
Nee hoor. Ik snap het gewoon niet. Het ging ook de hele tijd om die p..
quote:Op zaterdag 11 oktober 2014 13:53 schreef Janneke141 het volgende:
Beste GeschiktX, je stelt nu al een aantal keer achter elkaar min of meer dezelfde vraag. Het antwoord is al voorbij gekomen en bijzonder duidelijk en uitgebreid uitgelegd.
Helaas zit voor jou het probleem er in, dat je voorkennis onvoldoende is om je deze materie eigen te maken. Ik ben bang dat je voor dit moment moet accepteren dat dit forum geen antwoord kan geven op je vraag, in ieder geval niet op zo'n manier dat je daarmee voldoende begrip van de stof krijgt, en dat je je hulp irl moet gaan zoeken. Iemand die naast je gaat zitten en je stap voor stap door dit soort afleidingen loodst, maar belangrijker nog: door de basisvaardigheden die hier voor nodig zijn.
Als je zo iemand kan vinden, moet je hem ook vragen of hij je kan trainen in het op een zorgvuldige manier stellen van je vragen.
Opinion is the medium between knowledge and ignorance (Plato)


Om te beginnen: nu quote je al voor de derde keer mijn complete tekst om een detail in mijn tekst aan de orde te stellen. Dat moet je niet doen, quote alleen de specifieke passage waar het je om te doen is. Dan vervuil je het topic niet met onnodige herhalingen van complete teksten en dan is het meestal ook duidelijker waar het nu precies om gaat.quote:Op zaterdag 11 oktober 2014 23:25 schreef GeschiktX het volgende:
[..]
Die p waarmee vermenigvuldigd moet worden om de elasticiteit te vinden (d p / d ln p ). Kun je die uitwerking geven?
Je hebt kennelijk een probleem met de betekenis van
Welnu, juist de notatie van Leibniz maakt het heel eenvoudig om dit te begrijpen, je hebt namelijk
Hangt een variabele z af van een variabele y en hangt die variabele y weer af van een variabele x, dan zal de variabele z afhangen van de variabele x en dan heb je voor de rate of change van z ten opzichte van x oftewel dz/dx in de notatie van Leibniz
In woorden: de rate of change van z ten opzichte van x is gelijk aan de rate of change van z ten opzichte van y vermenigvuldigd met de rate of change van y ten opzichte van x.
Dit is uiteraard de kettingregel, maar in de notatie van Leibniz is deze bijzonder gemakkelijk te onthouden en op te schrijven, want de symboliek van Leibniz maakt dat de kettingregel er net zo uitziet als de vermenigvuldiging van twee gewone breuken, vergelijk dit maar met
Dit laat zien dat het differentiequotiënt Δz/Δx gelijk is aan het product van het differentiequotiënt Δz/Δy en het differentiequotiënt Δy/Δx, en aangezien een afgeleide oftewel een zogeheten differentiaalquotiënt zoals dy/dx niets anders is dan de limiet van het bijbehorende differentiequotiënt Δy/Δx als we Δx naar nul laten gaan, is het duidelijk waarom de kettingregel in de notatie van Leibniz als twee druppels water lijkt op de vermenigvuldiging van twee gewone breuken.
Dit kun je misschien nog wat beter zien als je in
Δx, Δy en Δz even vervangt door resp. a, b en c, want dan staat er gewoon
Laten we dit nog eens van rechts naar links bekijken. Als je de breuken c/b en b/a met elkaar vermenigvuldigt, dan heb je
Maar nu zien we dat we de breuk cb/ba kunnen vereenvoudigen, want zowel in de teller cb als in de noemer ba zit een factor b. Dat betekent dat we teller en noemer elk door deze gemeenschappelijke factor b kunnen delen zonder dat de waarde van de breuk verandert, en dan hebben we
en dus inderdaad
Nu gaan we weer terug naar onze differentiaalquotiënten en de kettingregel in de notatie van Leibniz. Zoals we hebben gezien lijkt deze regel als twee druppels water op de vermenigvuldiging van twee gewone breuken. Echter, differentiaalquotiënten zijn geen breuken want het zijn immers limieten van differentiequotiënten (die wel breuken zijn). Maar de grap is dat we bij de vermenigvuldiging van differentiaalquotiënten wel kunnen doen alsof we werken met gewone breuken, en dat maakt het werken met de kettingregel in de notatie van Leibniz nu juist zo eenvoudig en overzichtelijk. Als we in
a, b en c vervangen door resp. dx, dy en dz, dan hebben we
en dat is uiteraard weer de kettingregel, maar nu opgeschreven van rechts naar links.
Nu gaan we nog een stapje verder. Stel nu eens dat de variabele z identiek gelijk is aan de variabele x, oftewel z is gewoon een andere naam (zeg maar een alias) van x. Dan mogen we in bovenstaande regel dus z vervangen door x en dan hebben we
Maar nu weet je dat dx/dx de afgeleide is van x naar x en die is gelijk aan de constante 1, dus hebben we
Je ziet dat het ook hier weer net zo werkt als bij gewone breuken, vergelijk dit maar met
We zien dus dat dx/dy en dy/dx elkaars omgekeerde zijn, en we kunnen dus ook schrijven
Nu zal het toch echt wel duidelijk zijn dat je hebt
want dit is immers het omgekeerde van
Natuurlijk kunnen we dit ook nog op een andere manier inzien. Laten we zeggen dat
dan is
maar q = ln p is equivalent met
en dus hebben we ook
Maar nu weten we dat q = ln p en eq = p zodat we hier dus q kunnen vervangen door ln p en eq kunnen vervangen door p, en zie, dan staat er inderdaad


Thanks. Maar is d ln p / dp van de hele functie p^p * ln p gewoon 1/p? Omdat p^p dan een constante is? En dus 1/p overblijft. En hoezo mag je de inverse gebruiken? Want 1/p is anders dan p.quote:Op zondag 12 oktober 2014 01:14 schreef Riparius het volgende:
[..]
Om te beginnen: nu quote je al voor de derde keer mijn complete tekst om een detail in mijn tekst aan de orde te stellen. Dat moet je niet doen, quote alleen de specifieke passage waar het je om te doen is. Dan vervuil je het topic niet met onnodige herhalingen van complete teksten en dan is het meestal ook duidelijker waar het nu precies om gaat.
Je hebt kennelijk een probleem met de betekenis van
Welnu, juist de notatie van Leibniz maakt het heel eenvoudig om dit te begrijpen, je hebt namelijk
Hangt een variabele z af van een variabele y en hangt die variabele y weer af van een variabele x, dan zal de variabele z afhangen van de variabele x en dan heb je voor de rate of change van z ten opzichte van x oftewel dz/dx in de notatie van Leibniz
In woorden: de rate of change van z ten opzichte van x is gelijk aan de rate of change van z ten opzichte van y vermenigvuldigd met de rate of change van y ten opzichte van x.
Dit is uiteraard de kettingregel, maar in de notatie van Leibniz is deze bijzonder gemakkelijk te onthouden en op te schrijven, want de symboliek van Leibniz maakt dat de kettingregel er net zo uitziet als de vermenigvuldiging van twee gewone breuken, vergelijk dit maar met
Dit laat zien dat het differentiequotiënt Δz/Δx gelijk is aan het product van het differentiequotiënt Δz/Δy en het differentiequotiënt Δy/Δx, en aangezien een afgeleide oftewel een zogeheten differentiaalquotiënt zoals dy/dx niets anders is dan de limiet van het bijbehorende differentiequotiënt Δy/Δx als we Δx naar nul laten gaan, is het duidelijk waarom de kettingregel in de notatie van Leibniz als twee druppels water lijkt op de vermenigvuldiging van twee gewone breuken.
Dit kun je misschien nog wat beter zien als je in
Δx, Δy en Δz even vervangt door resp. a, b en c, want dan staat er gewoon
Laten we dit nog eens van rechts naar links bekijken. Als je de breuken c/b en b/a met elkaar vermenigvuldigt, dan heb je
Maar nu zien we dat we de breuk cb/ba kunnen vereenvoudigen, want zowel in de teller cb als in de noemer ba zit een factor b. Dat betekent dat we teller en noemer elk door deze gemeenschappelijke factor b kunnen delen zonder dat de waarde van de breuk verandert, en dan hebben we
en dus inderdaad
Nu gaan we weer terug naar onze differentiaalquotiënten en de kettingregel in de notatie van Leibniz. Zoals we hebben gezien lijkt deze regel als twee druppels water op de vermenigvuldiging van twee gewone breuken. Echter, differentiaalquotiënten zijn geen breuken want het zijn immers limieten van differentiequotiënten (die wel breuken zijn). Maar de grap is dat we bij de vermenigvuldiging van differentiaalquotiënten wel kunnen doen alsof we werken met gewone breuken, en dat maakt het werken met de kettingregel in de notatie van Leibniz nu juist zo eenvoudig en overzichtelijk. Als we in
a, b en c vervangen door resp. dx, dy en dz, dan hebben we
en dat is uiteraard weer de kettingregel, maar nu opgeschreven van rechts naar links.
Nu gaan we nog een stapje verder. Stel nu eens dat de variabele z identiek gelijk is aan de variabele x, oftewel z is gewoon een andere naam (zeg maar een alias) van x. Dan mogen we in bovenstaande regel dus z vervangen door x en dan hebben we
Maar nu weet je dat dx/dx de afgeleide is van x naar x en die is gelijk aan de constante 1, dus hebben we
Je ziet dat het ook hier weer net zo werkt als bij gewone breuken, vergelijk dit maar met
We zien dus dat dx/dy en dy/dx elkaars omgekeerde zijn, en we kunnen dus ook schrijven
Nu zal het toch echt wel duidelijk zijn dat je hebt
want dit is immers het omgekeerde van
Natuurlijk kunnen we dit ook nog op een andere manier inzien. Laten we zeggen dat
dan is
maar q = ln p is equivalent met
en dus hebben we ook
Maar nu weten we dat q = ln p en eq = p zodat we hier dus q kunnen vervangen door ln p en eq kunnen vervangen door p, en zie, dan staat er inderdaad


quote:Op zondag 12 oktober 2014 10:21 schreef GeschiktX het volgende:
[..]
Thanks. Maar is d ln p / dp van de hele functie p^p * ln p gewoon 1/p? Omdat p^p dan een constante is? En dus 1/p overblijft. En hoezo mag je de inverse gebruiken? Want 1/p is anders dan p.
Verder reageer ik niet...quote:Om te beginnen: nu quote je al voor de derde keer mijn complete tekst om een detail in mijn tekst aan de orde te stellen. Dat moet je niet doen, quote alleen de specifieke passage waar het je om te doen is. Dan vervuil je het topic niet met onnodige herhalingen van complete teksten en dan is het meestal ook duidelijker waar het nu precies om gaat.


Om te beginnen: ik had je toch gevraagd niet meer mijn volledige teksten te quoten als je een vraag hebt over een detail dat je niet duidelijk is?quote:
Uit deze vraag blijkt helaas dat je er nog werkelijk niets van begrijpt. Je vraag is ook betekenisloos, want wat zou d ln p / dp van de hele functie p^p * ln p moeten betekenen? We hebbenquote:Thanks. Maar is d ln p / dp van de hele functie p^p * ln p gewoon 1/p?
maar als je de uitdrukking pp·ln p naar p differentieert, dan noteer je dit als
of als
en het is toch zonneklaar, ook zonder dit te evalueren, dat dit niet hetzelfde kan zijn als d(ln p)/dp, al was het maar omdat we hier de productregel moeten gebruiken en pp niet identiek gelijk is aan 1.
Dit is echt lariekoek, en dat weet je zelf ook wel. Als pp constant zou moeten zijn, dan kan dat alleen als p zelf een constante is, en dan is ook ln p een constante en daarmee is dan je hele uitdrukking pp·ln p een constante, en dan is differentiëren van deze uitdrukking naar p of naar ln p per definitie onmogelijk.quote:Omdat p^p dan een constante is?
Nee. Ik heb het idee dat je echt nog geen steek verder bent dan het imiteren van wat onbegrepen regeltjes zoals d(ln x)/dx = 1/x.quote:En dus 1/p overblijft.
Dit is onduidelijk. Welke inverse bedoel je precies? Ja, ik heb zo'n donkerbruin vermoeden wat je bedoelt, maar ik wil dat van jou horen. Anders gezegd, je moet leren je vraagstellingen helder, exact en niet voor tweeerlei uitleg vatbaar op te schrijven.quote:En hoezo mag je de inverse gebruiken? Want 1/p is anders dan p.
Nog één keertje dan. Laten we zeggen dat we hebben
en dat wordt gevraagd de elasticiteit van q ten opzichte van p te bepalen. We hebben
In woorden: om hier de elasticiteit d(ln q)/d(ln p) van q ten opzichte van p te berekenen moeten we ln q naar p differentiëren en het resultaat vervolgens nog met p vermenigvuldigen. We nemen dus eerst de logaritme van beide leden van onze gelijkheid om een uitdrukking voor ln q in p te krijgen, en dit geeft
Beide leden differentiëren naar p geeft
dus
en voor de elasticiteit vinden we dus


Hallo wiskundigen,
Ik zat te denken over differentieerbaarheid en ik vroeg mij dus het volgende af:
-Waarom is | x | niet differentieerbaar in het punt x= 0? Ik weet dat er op dat punt een knik is, echter vraag ik mij af hoe dit te berekenen is, evenals hoe je kunt berekenen of | x | differentieerbaar is in het punt x=2.
Kort samengevat: hoe kun je de differentieerbaarheid in bepaalde punten berekenen?
Ik zat te denken over differentieerbaarheid en ik vroeg mij dus het volgende af:
-Waarom is | x | niet differentieerbaar in het punt x= 0? Ik weet dat er op dat punt een knik is, echter vraag ik mij af hoe dit te berekenen is, evenals hoe je kunt berekenen of | x | differentieerbaar is in het punt x=2.
Kort samengevat: hoe kun je de differentieerbaarheid in bepaalde punten berekenen?


Heb je ooit uitleg gehad over de achtergrond van differentiëren, met limieten en dergelijke?quote:Op zondag 12 oktober 2014 22:31 schreef GoldenHeart het volgende:
Hallo wiskundigen,
Ik zat te denken over differentieerbaarheid en ik vroeg mij dus het volgende af:
-Waarom is | x | niet differentieerbaar in het punt x= 0? Ik weet dat er op dat punt een knik is, echter vraag ik mij af hoe dit te berekenen is, evenals hoe je kunt berekenen of | x | differentieerbaar is in het punt x=2.
Kort samengevat: hoe kun je de differentieerbaarheid in bepaalde punten berekenen?
Opinion is the medium between knowledge and ignorance (Plato)


Ja tot op zekere hoogte. Ik weet van de volgende onderwerpen af:quote:Op zondag 12 oktober 2014 22:33 schreef Janneke141 het volgende:
[..]
Heb je ooit uitleg gehad over de achtergrond van differentiëren, met limieten en dergelijke?
-Differentiëren (constante, som-, product-, quotiëntregel)
-Limieten berekenen
-L'hopital
Wat betreft de achtergrond: ik heb wel bepaalde theorie waar ik dus nog niet alles van begrijp zoals de differentieerbaarheid, newton quotient en de afgeleiden berekenen met de standaard rate of change formule i.p.v. standaardregels.
Omdat de achtergrond van het differentieren er niet goed in zit bij mij, stel ik mijzelf veel waarom vragen en dan stel ik mij de vragen, zoals gesteld op de vorige pagina.


Differentieerbaarheid bereken je niet maar toon je aan. Begin maar eens met deze post van mij goed door te nemen.quote:Op zondag 12 oktober 2014 22:31 schreef GoldenHeart het volgende:
Hallo wiskundigen,
Ik zat te denken over differentieerbaarheid en ik vroeg mij dus het volgende af:
-Waarom is | x | niet differentieerbaar in het punt x= 0? Ik weet dat er op dat punt een knik is, echter vraag ik mij af hoe dit te berekenen is, evenals hoe je kunt berekenen of | x | differentieerbaar is in het punt x=2.
Kort samengevat: hoe kun je de differentieerbaarheid in bepaalde punten berekenen?


Ik had mij even beperkt tot het stuk m.b.t. differentieerbaarheid en daar impliceer je dat de differentieerbaarheid te berekenen is d.m.v. de definitie van de afgeleide. Echter vraag ik mij af of er ook dit aan te tonen is d.m.v. een tweede methode; zoals het direct te bepalen van de afgeleide (d.m.v. de regels) en verbolgens dan wat met het punt (laten we stellen) x = 2 moeten doen (zoals invullen in f(x) of f'(x) ).quote:Op zondag 12 oktober 2014 22:39 schreef Riparius het volgende:
[..]
Differentieerbaarheid bereken je niet maar toon je aan. Begin maar eens met deze post van mij goed door te nemen.


Differentieerbaarheid is een eigenschap, en eigenschappen toon je aan. Het hellingsgetal op een bepaalde plek is een getal, en die kan je berekenen.quote:Op zondag 12 oktober 2014 22:47 schreef GoldenHeart het volgende:
[..]
Ik had mij even beperkt tot het stuk m.b.t. differentieerbaarheid en daar impliceer je dat de differentieerbaarheid te berekenen is d.m.v. de definitie van de afgeleide. Echter vraag ik mij af of er ook dit aan te tonen is d.m.v. een tweede methode; zoals het direct te bepalen van de afgeleide (d.m.v. de regels) en verbolgens dan wat met het punt (laten we stellen) x = 2 moeten doen (zoals invullen in f(x) of f'(x) ).
Wat je weet van differentieerbaarheid zijn een aantal rekenregels voor het differentiëren van bepaalde functies. Afhankelijk van wat je precies moet kunnen zou je daar nog wel een heel eind mee kunnen komen, maar voor je kennis van het begrip 'differentieerbaarheid', en ook hoe die rekenregels nou precies tot stand zijn gekomen, is meer achtergrondkennis nodig. Zie de link van Riparius. Die kennis heb je eigenlijk wel nodig om op een nette manier differentieerbaarheid te kunnen aantonen.
Blijft het bij huis-, tuin- en keukenfuncties, zoals f(x) = |x|, dan kun je met wat rekenregels nog wel een eind komen.
Omdat f(x) = x voor x>0 en f(x) = -x voor x<0, kun je met de jou bekende rekenregels makkelijk zien dat f'(x) = 1 (voor x>0) en f'(x) = -1 (voor x<0).
Wil een functie f in een bepaald punt a differentieerbaar zijn, dan zal limx →af'(x) moeten bestaan. Voor x=2 is dit wel duidelijk.
Voor x=0 is vrij makkelijk te zien dat f daar niet differentieerbaar is, omdat
limx ↓0f'(x) = 1, en limx ↑0f'(x) = -1
Opinion is the medium between knowledge and ignorance (Plato)


Nee Janneke, dit is niet waar. Kijk hier maar eens.quote:Op zondag 12 oktober 2014 22:57 schreef Janneke141 het volgende:
[..]
Wil een functie f in een bepaald punt a differentieerbaar zijn, dan zal limx →af'(x) moeten bestaan.


Wel voor huis-, tuin- en keukenfunctiesquote:Op zondag 12 oktober 2014 23:08 schreef Riparius het volgende:
[..]
Nee Janneke, dit is niet waar. Kijk hier maar eens.
Maar je hebt (uiteraard) gelijk.
Opinion is the medium between knowledge and ignorance (Plato)


Nee, want dan maak je je schuldig aan een petitio principii. Dat wil zeggen dat je datgene wat je wil bewijzen al op voorhand voor waar aanneemt, en dan bewijs je niets. Die regels die jij wil toepassen gelden namelijk voor differentieerbare functies, dus als je op die regels steunt, dan neem je impliciet al differentieerbaarheid aan en is je 'bewijs' dus sowieso ongeldig.quote:Op zondag 12 oktober 2014 22:47 schreef GoldenHeart het volgende:
[..]
Ik had mij even beperkt tot het stuk m.b.t. differentieerbaarheid en daar impliceer je dat de differentieerbaarheid te berekenen is d.m.v. de definitie van de afgeleide. Echter vraag ik mij af of er ook dit aan te tonen is d.m.v. een tweede methode; zoals het direct te bepalen van de afgeleide (d.m.v. de regels) en vervolgens dan wat met het punt (laten we stellen) x = 2 moeten doen (zoals invullen in f(x) of f'(x) ).


Ik lees soms door deze reeks omdat ik het wel kan waarderen dat wiskunde een soort apart taaltje is, waardoor ik een Nederlandse tekst kan lezen en toch geen flauw idee heb waar het over gaat 
+ omdat het cool is dat hier mensen zitten die anderen écht helpen iets te begrijpen
+ omdat het cool is dat hier mensen zitten die anderen écht helpen iets te begrijpen


Hey, daar ben ik weer en ik heb weer eens wat vragen. Ditmaal over partiële afgeleiden. Ik hoop dat iemand mij uit de brand kan helpen:
Ik zou de partiële elasticiteit van z = xnexyney moeten vinden voor z with respect to x ( d z / d x).
Hierbij heb ik de volgende elasticiteitsformule gebruikt: (x / z) * (d z / d x)
( x / xnexyney ) * nxn-1exyney
Dit maakt:
x * ( nxn-1exyney ) / xnexyney
de -1 exponent eruit halen door x -1 buiten de haakjes te halen, evenals de n, zodat zowel de noemer als teller gedeeld kunnen worden door één dezelfde term:
x * x -1 * n ( xn-1exyney ) / xnexyney
Het antwoord wordt dus gewoon = n
Echter moet het x + n zijn...
Tenslotte:
''let z = x1p ...... xnp exp(a1x1 + ...... + an xn) , where a1, ..... , an, and p are constants. Find the partial elasticities of z w.r.t. x1, ...... , xn.''
Hoe moet ik dit doen? Ik ben het recht toe recht aan gewend en niet met de sommatie notatie.
[ Bericht 4% gewijzigd door Super-B op 13-10-2014 19:29:03 ]
Ik zou de partiële elasticiteit van z = xnexyney moeten vinden voor z with respect to x ( d z / d x).
Hierbij heb ik de volgende elasticiteitsformule gebruikt: (x / z) * (d z / d x)
( x / xnexyney ) * nxn-1exyney
Dit maakt:
x * ( nxn-1exyney ) / xnexyney
de -1 exponent eruit halen door x -1 buiten de haakjes te halen, evenals de n, zodat zowel de noemer als teller gedeeld kunnen worden door één dezelfde term:
x * x -1 * n ( xn-1exyney ) / xnexyney
Het antwoord wordt dus gewoon = n
Echter moet het x + n zijn...
Tenslotte:
''let z = x1p ...... xnp exp(a1x1 + ...... + an xn) , where a1, ..... , an, and p are constants. Find the partial elasticities of z w.r.t. x1, ...... , xn.''
Hoe moet ik dit doen? Ik ben het recht toe recht aan gewend en niet met de sommatie notatie.
[ Bericht 4% gewijzigd door Super-B op 13-10-2014 19:29:03 ]


Je moet de productregel gebruiken, dz/dx ≠ nxn-1exyney.quote:Op maandag 13 oktober 2014 19:18 schreef Super-B het volgende:
Hey, daar ben ik weer en ik heb weer eens wat vragen. Ditmaal over partiële afgeleiden. Ik hoop dat iemand mij uit de brand kan helpen:
Ik zou de partiële elasticiteit van z = xnexyney moeten vinden voor z with respect to x ( d z / d x).
Hierbij heb ik de volgende elasticiteitsformule gebruikt: (x / z) * (d z / d x)
( x / xnexyney ) * nxn-1exyney
Dit maakt:
x * ( nxn-1exyney ) / xnexyney
de -1 exponent eruit halen door x -1 buiten de haakjes te halen, evenals de n, zodat zowel de noemer als teller gedeeld kunnen worden door één dezelfde term:
x * x -1 * n ( xn-1exyney ) / xnexyney
Het antwoord wordt dus gewoon = n
Echter moet het x + n zijn...


Dat komt vanwege de e^x neem ik aan? Hoe moet ik bovendien de overige constante zien (y^n en e^y)? Moet ik die even wegdenken of..?quote:Op maandag 13 oktober 2014 19:33 schreef zerak het volgende:
[..]
Je moet de productregel gebruiken, dz/dx ≠ nxn-1exyney.


Inderdaad. yney behandel je gewoon als elke andere constante.quote:Op maandag 13 oktober 2014 19:39 schreef Super-B het volgende:
[..]
Dat komt vanwege de e^x neem ik aan? Hoe moet ik bovendien de overige constante zien (y^n en e^y)? Moet ik die even wegdenken of..?
Je krijgt hier dz/dx = nxn-1exyney + xnexyney.


quote:Op maandag 13 oktober 2014 19:41 schreef zerak het volgende:
[..]
Inderdaad. yney behandel je gewoon als elke andere constante.
Je krijgt hier dz/dx = nxn-1exyney + xnexyney.
Top, bedankt!quote:


Je hebt dus z(xi) = xipeai·xi voor i ∈ {1, ...., n}.quote:Op maandag 13 oktober 2014 19:18 schreef Super-B het volgende:
Tenslotte:
''let z = x1p ...... xnp exp(a1x1 + ...... + an xn) , where a1, ..... , an, and p are constants. Find the partial elasticities of z w.r.t. x1, ...... , xn.''
Hoe moet ik dit doen? Ik ben het recht toe recht aan gewend en niet met de sommatie notatie.
z'(xi) = pxip-1eai·xi + aixipeai·xi.
Elzi = x/z(xi) * z'(xi) = ((p + aixi) xipeai·xi) / (xipeai·xi) = p + aixi.
[ Bericht 0% gewijzigd door zerak op 13-10-2014 20:49:45 ]


Hoi, zou iemand mij met een kleine onduidelijkheid kunnen helpen?
Het vraagstuk dat ik moet oplossen is als volgt:
Find dz / dt for the following cases:
z =(x - y) / (x + y), x = et +s , y = ets
Ik heb het antwoord opgezocht in een antwoordenmodel op het internet en het antwoord luidt:
Ik heb exact hetzelfde antwoord op één iets na en dat is dat ik in het rechterdeel op -2x uitkom i.p.v -2sx..
Omdat ik het oplos met de quotientregel, was mijn methode voor het rechterdeel als volgt:
Het vraagstuk dat ik moet oplossen is als volgt:
Find dz / dt for the following cases:
z =(x - y) / (x + y), x = et +s , y = ets
Ik heb het antwoord opgezocht in een antwoordenmodel op het internet en het antwoord luidt:
Ik heb exact hetzelfde antwoord op één iets na en dat is dat ik in het rechterdeel op -2x uitkom i.p.v -2sx..
Omdat ik het oplos met de quotientregel, was mijn methode voor het rechterdeel als volgt:


Kettingregel. Wat is de afgeleide van exp(ts) naar t?quote:Op dinsdag 14 oktober 2014 11:26 schreef GoldenHeart het volgende:
Find dz / dt for the following cases:


s, ow.. ik heb hem al door... Dankjewel voor de wake-up call.quote:Op dinsdag 14 oktober 2014 11:28 schreef Novermars het volgende:
[..]
Kettingregel. Wat is de afgeleide van exp(ts) naar t?


Weer een vraag vanuit mijn kant:
If u = ln (x³ + y³ + z³ - 3xyz ), show that:
( i ) x * du/dx + y * du/dy + z * du/dz = 3
&
(ii) (x + y + z) (du/dx + du/dy + du/dz) = 3
( i ) Ik kom toch echt uit op: 3 + 3 + 3 = 9 i.p.v 3. Want als ik x * du/dx bereken, dan kom ik uit op 3 want ik krijg de mogelijkheid (na het berekenen van de afgeleide en het vermenigvuldigen van x) om zowel de teller als de noemer te delen door wat er in de noemer staat..zodat er alleen 3 overblijft, en dit geldt dan ook voor y * du/dy en z * du/dz
(ii) ik heb de afgeleiden berekend, maar hoe kan ik bewijzen dat het gelijk is aan 3 uiteindelijk? Want ik weet niet hoe ik dat kan laten zien met nog de vermenigvuldigen met (x + y + z) ernaast.. Ik 'zie het' niet zeg maar.
If u = ln (x³ + y³ + z³ - 3xyz ), show that:
( i ) x * du/dx + y * du/dy + z * du/dz = 3
&
(ii) (x + y + z) (du/dx + du/dy + du/dz) = 3
( i ) Ik kom toch echt uit op: 3 + 3 + 3 = 9 i.p.v 3. Want als ik x * du/dx bereken, dan kom ik uit op 3 want ik krijg de mogelijkheid (na het berekenen van de afgeleide en het vermenigvuldigen van x) om zowel de teller als de noemer te delen door wat er in de noemer staat..zodat er alleen 3 overblijft, en dit geldt dan ook voor y * du/dy en z * du/dz
(ii) ik heb de afgeleiden berekend, maar hoe kan ik bewijzen dat het gelijk is aan 3 uiteindelijk? Want ik weet niet hoe ik dat kan laten zien met nog de vermenigvuldigen met (x + y + z) ernaast.. Ik 'zie het' niet zeg maar.


Laat je werk maar zien. Wolfram|alpha geeft een verschrikkelijke afgeleide en ik heb geen zin om alles uit te werken.


quote:Op dinsdag 14 oktober 2014 13:20 schreef Novermars het volgende:
Laat je werk maar zien. Wolfram|alpha geeft een verschrikkelijke afgeleide en ik heb geen zin om alles uit te werken.


Ow top!quote:Op dinsdag 14 oktober 2014 13:38 schreef Riparius het volgende:
[..]
Prachtig toch? Als je dat nog even optelt krijg je 3v/v = 3.
Nog een vraagstuk:
Find y'' for y5 - x6 = 0
Eerst ging ik op zoek naar y'
5y4 * y' - 6x5 = 0
y' = 6x5 / 5y4 = 0
Nu y'' berekenen:
20y³ * y' * y' + 5y4 * y'' - 30x4 = 0
y' invullen voor bovenstaande levert:
(120x5y3 / 5y4) *( 6x5 / 5y4) + 5y4 * y'' - 30x4 = 0
(720x10y³ / 25y8 )+ 5y4 * y'' = 30x4
Breuk delen door 5:
(144x10 / 5y5) + 5y4 * y'' = 30x4
y'' = (6x4 / y4 ) - (144x10 / 5y5)
Doe ik het goed?
[ Bericht 0% gewijzigd door GoldenHeart op 14-10-2014 15:21:12 ]


STOP. Waar komt dat =-teken opeens vandaan?quote:Op dinsdag 14 oktober 2014 13:58 schreef GoldenHeart het volgende:
[..]
Ow top!
Nog een vraagstuk:
Find y'' for y5 - x6
Eerst ging ik op zoek naar y'
5y4 * y' - 6x5
y' = 6x5 / 5y4
Kijk nog eens goed naar de precieze formulering van het vraagstuk. Je lijdt aan dezelfde kwaal als veel anderen hier de laatste tijd, namelijk het negeren van =-tekens en hetgeen rechts daarvan staat om het =-teken dan als het je zo uitkomt plotseling weer op te laten duiken. Maar dat is geen geldige herleiding. Zoals jij de vraag weergeeft is die niet te beantwoorden.
Nee.quote:Doe ik het goed?


Zie edit.quote:Op dinsdag 14 oktober 2014 14:09 schreef Riparius het volgende:
[..]
STOP. Waar komt dat =-teken opeens vandaan?
Kijk nog eens goed naar de precieze formulering van het vraagstuk. Je lijdt aan dezelfde kwaal als veel anderen hier de laatste tijd, namelijk het negeren van =-tekens en hetgeen rechts daarvan staat om het =-teken dan als het je zo uitkomt plotseling weer op te laten duiken. Maar dat is geen geldige herleiding. Zoals jij de vraag weergeeft is die niet te beantwoorden.
[..]
Nee.


Nee, dit is weer fout opgeschreven. Hier beweer je namelijk dat y' = 0, maar dan hoef je niets meer te berekenen, want dan is ook y'' = 0.quote:Op dinsdag 14 oktober 2014 13:58 schreef GoldenHeart het volgende:
[..]
Ow top!
Nog een vraagstuk:
Find y'' for y5 - x6 = 0
Eerst ging ik op zoek naar y'
5y4 * y' - 6x5 = 0
y' = 6x5 / 5y4 = 0
Nu y'' berekenen:


Daar ben ik mij bewust van.quote:Op dinsdag 14 oktober 2014 14:21 schreef Riparius het volgende:
[..]
Nee, dit is weer fout opgeschreven. Hier beweer je namelijk dat y' = 0, maar dan hoef je niets meer te berekenen, want dan is ook y'' = 0.
Je hoeft trouwens y' helemaal niet vrij te maken voordat je opnieuw (impliciet) gaat differentiëren, had je dat al bedacht?
Ik maak y' alleen vrij om het later weer in te vullen..


Ja, ik zag het nu.quote:Op dinsdag 14 oktober 2014 14:23 schreef GoldenHeart het volgende:
[..]
Daar ben ik mij bewust van.
Ik maak y' alleen vrij om het later weer in te vullen..


Nee, het klopt nog steeds niet. Je maakt op het laatst een fout. Verder is het overzichtelijker om eerst een uitdrukking voor y'' op te schrijven en dan pas de gevonden uitdrukking voor y' te substitueren.quote:


Kun je quoten waar ik de fout bega??quote:Op dinsdag 14 oktober 2014 14:42 schreef Riparius het volgende:
[..]
Nee, het klopt nog steeds niet. Je maakt op het laatst een fout. Verder is het overzichtelijker om eerst een uitdrukking voor y'' op te schrijven en dan pas de gevonden uitdrukking voor y' te substitueren.


Overgang naar de laatste regel. Daar ga je te snel en daarmee ook de fout in.quote:Op dinsdag 14 oktober 2014 14:45 schreef GoldenHeart het volgende:
[..]
Kun je quoten waar ik de fout bega??


Ik heb het niet door hahah.quote:Op dinsdag 14 oktober 2014 14:51 schreef Riparius het volgende:
[..]
Overgang naar de laatste regel. Daar ga je te snel en daarmee ook de fout in.


quote:Op dinsdag 14 oktober 2014 14:51 schreef Riparius het volgende:
[..]
Overgang naar de laatste regel. Daar ga je te snel en daarmee ook de fout in.
Wat zou ik precies fout gedaan moeten hebben? Ik zit er al enige tijd naar te zoeken, maar ik kan de fout niet vinden (althans tot nu toe).quote:


Je vergeet in de tweede term door 5y^4 te delenquote:Op dinsdag 14 oktober 2014 15:12 schreef GoldenHeart het volgende:
[..]
[..]
Wat zou ik precies fout gedaan moeten hebben? Ik zit er al enige tijd naar te zoeken, maar ik kan de fout niet vinden (althans tot nu toe).


Ja maar het klopt wel? Ik keek even in het antwoordenmodel en het blijkt dat ik 5y9 moet hebben i.p.v. 5y4. Echter zie ik niet bij welk stuk ik op 5y^9 moest komen..quote:Op dinsdag 14 oktober 2014 15:17 schreef Alrac4 het volgende:
[..]
Je vergeet in de tweede term door 5y^4 te delen


Volgens mij klopt het tot aan de voorlaatste regel.quote:Op dinsdag 14 oktober 2014 15:20 schreef GoldenHeart het volgende:
[..]
Ja maar het klopt wel? Ik keek even in het antwoordenmodel en het blijkt dat ik 5y9 moet hebben i.p.v. 5y4. Echter zie ik niet bij welk stuk ik op 5y^9 moest komen..
Je hebt:
Om y" te elimineren moet je de eerste term naar de rechterkant halen en dan alles delen door 5y^4.
De eerste term in je uitdrukking voor y" (de laatste regel) klopt. Bij de tweede term vergeet je echter te delen door 5y^4:


Jeetje.. Een detail dat ik overzag, maar wel een cruciale fout. Dank voor je tijd.quote:Op dinsdag 14 oktober 2014 15:37 schreef Alrac4 het volgende:
[..]
Volgens mij klopt het tot aan de voorlaatste regel.
Je hebt:
Om y" te elimineren moet je de eerste term naar de rechterkant halen en dan alles delen door 5y^4.
De eerste term in je uitdrukking voor y" (de laatste regel) klopt. Bij de tweede term vergeet je echter te delen door 5y^4:


Hey,
Ik heb een vraag met betrekking tot de homogeniteit van een functie. Het gaat om deze functie:
F( K, L ) = A[aK-e + bL-e) -1/e
Dit is de vraagstelling:'' Prove the CES function F (K, L ) is homogenous of degree one. Express F(K,L) / L as a function of k = K / L''
Ik begon met de bewijslast van de homogeniteit van graad 1:
F( tK, tL) = A[a * t-e * K-e + b * t -e * L-e) -1/e
(t-e ) -1/ e F(K , L )
t * F(K , L )
Is dit een goed antwoord of niet? De antwoorden achterin mijn boek is wat kort door de bocht om het te controleren. Daarnaast vraag ik mij af hoe ik het laatste stuk van de opgave kan maken: ''Express F(K,L) / L as a function of k = K / L''
Ik snap de bedoeling van dit laatste niet eens.. laat staan het maken ervan.
Ik heb een vraag met betrekking tot de homogeniteit van een functie. Het gaat om deze functie:
F( K, L ) = A[aK-e + bL-e) -1/e
Dit is de vraagstelling:'' Prove the CES function F (K, L ) is homogenous of degree one. Express F(K,L) / L as a function of k = K / L''
Ik begon met de bewijslast van de homogeniteit van graad 1:
F( tK, tL) = A[a * t-e * K-e + b * t -e * L-e) -1/e
(t-e ) -1/ e F(K , L )
t * F(K , L )
Is dit een goed antwoord of niet? De antwoorden achterin mijn boek is wat kort door de bocht om het te controleren. Daarnaast vraag ik mij af hoe ik het laatste stuk van de opgave kan maken: ''Express F(K,L) / L as a function of k = K / L''
Ik snap de bedoeling van dit laatste niet eens.. laat staan het maken ervan.


Hoi goedenavond,
Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan? Ik vind het zelf een vrij lastig onderwerp, met name omdat ik niet echt snap waarvoor het dient, want je kunt toch al een maximum/minimum berekenen d.m.v. partieel afgeleiden, waarom zou je de Lagrange functie nodig moeten hebben..? Op internet tref ik veel literatuur wat er al vanuit gaat dat je al een redelijke kennis over het onderwerp beschikt, wat het voor mij lastig maakt.
Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan? Ik vind het zelf een vrij lastig onderwerp, met name omdat ik niet echt snap waarvoor het dient, want je kunt toch al een maximum/minimum berekenen d.m.v. partieel afgeleiden, waarom zou je de Lagrange functie nodig moeten hebben..? Op internet tref ik veel literatuur wat er al vanuit gaat dat je al een redelijke kennis over het onderwerp beschikt, wat het voor mij lastig maakt.


Heb je je boek gelezen?quote:Op dinsdag 14 oktober 2014 21:34 schreef RustCohle het volgende:
Hoi goedenavond,
Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan?
Staat daar niks in over Lagrange multipliers?


Simpel voorbeeld waarom partiële afgeleides niet nuttig zijn: Stel je hebt de functie gedefinieerd door f(x)=x^2 op het domein A=[2,4]. en je wilt 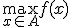 bepalen. Hoe ga je dit doen met partiële afgeleides?
bepalen. Hoe ga je dit doen met partiële afgeleides?
Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.
Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.


Jawel, maar er wordt het niet fatsoenlijk uitgelegd.quote:Op dinsdag 14 oktober 2014 22:02 schreef t4rt4rus het volgende:
[..]
Heb je je boek gelezen?
Staat daar niks in over Lagrange multipliers?


Het stationaire punt bepalen door f'(x) te bepalen en vervolgens te kijken wanneer f'(x) = 0 en dan een getallenlijn maken voor de getallen van het domein om zodoende het hoogste punt te bepalen.., het zijn overigens maar 3 getallen.. In dit geval is het maximum bij x= 4 want y= 16 dan. (?)quote:Op dinsdag 14 oktober 2014 22:09 schreef Novermars het volgende:
Simpel voorbeeld waarom partiële afgeleides niet nuttig zijn: Stel je hebt de functie gedefinieerd door f(x)=x^2 op het domein A=[2,4]. en je wiltbepalen. Hoe ga je dit doen met partiële afgeleides?
Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.
Misschien spreek ik mijzelf weer tegen, want het stationaire punt is bij x = 0... dus x =4 kan nooit een stationaire punt zijn..
Ik ben nu wel mindfucked.


Kan iemand me vertellen hoe je een multinomiaal experiment bepaalt waarbij er geen onderscheid is tussen de groepen? Dus bijvoorbeeld: er is een kaartspel tussen 4 spelers. Elke speler krijgt 13 kaarten. Hoeveel mogelijke verdelingen zijn er als er geen onderscheid is tussen de spelers?
Edit: een kaartspel bestaat uiteraard uit 52 kaarten.
Edit: een kaartspel bestaat uiteraard uit 52 kaarten.


52!/(13!13!13!13!4!)?quote:Op dinsdag 14 oktober 2014 22:24 schreef Wouterw17 het volgende:
Kan iemand me vertellen hoe je een multinomiaal experiment bepaalt waarbij er geen onderscheid is tussen de groepen? Dus bijvoorbeeld: er is een kaartspel tussen 4 spelers. Elke speler krijgt 13 kaarten. Hoeveel mogelijke verdelingen zijn er als er geen onderscheid is tussen de spelers?
Edit: een kaartspel bestaat uiteraard uit 52 kaarten.
Opinion is the medium between knowledge and ignorance (Plato)


Het lijkt me juist prima om af en toe dit soort dingen te doen. Lees de OP nog even, daar is sprake van passies toch?quote:Op donderdag 9 oktober 2014 23:52 schreef Bram_van_Loon het volgende:
Het is niet echt iets waarvoor deze draad is bedoeld, helaas misschien, maar het lijkt me aardig om het toch maar eens te doen.
Het is een beetje jammer dat je dit vraagstuk niet in de oorspronkelijke vorm geeft, want die is wel interessanter. Maar eerst iets over de man zelf en zijn werk. Heron van Alexandrië was zeker geen zuiver wiskundige, eerder iemand die je nu een werktuigbouwkundig ingenieur zou noemen, en hij construeerde dan ook diverse toestellen zoals een verkoopautomaat, pompen, en een voorloper van de stoommachine. Als men het belang van deze en soortgelijke uitvindingen had ingezien, dan had de industriële revolutie wellicht 1500 jaar eerder kunnen plaatsvinden. Daarnaast was hij uitstekend op de hoogte met de wiskunde van zijn tijd en leverde hij ook originele bijdragen, zoals een bewijs voor de parallellogramconstructie bij de samenstelling van twee verplaatsingen, oftewel de optelling van vectoren avant la lettre.quote:Ik kwam een interessant vraagstuk tegen wat gemakkelijk te begrijpen is maar desalniettemin erg leerzaam is.
Heron's probleem. De vraag. Plaatsen A en B liggen langs een rivier, je moet via die rivier van A naar B. Wat is de kortste weg? Probeer het geometrisch op te lossen als je het zelf probeert, niet met rekenen.
Zijn naam is nog verbonden aan de methode van Heron voor het berekenen van vierkantswortels, een methode die echter veel eerder ook al aan de Babyloniërs bekend was. Deze methode komt er (in moderne notatie) op neer dat als xn een benadering is van √A die iets te klein is, dat A/xn dan een iets te grote benadering is van √A en vice versa, zodat we dus een betere benadering kunnen krijgen dan de slechtste van deze twee benaderingen door ze te middelen, wat een nieuwe benadering xn+1 = ½(xn + A/xn) geeft. Het is gemakkelijk na te gaan dat deze iteratie equivalent is met de Newton-Raphson iteratie voor √A.
Daarnaast is zijn naam verbonden aan de formule van Heron voor de bepaling van de oppervlakte van een driehoek waarvan de lengtes van de drie zijden zijn gegeven, in moderne notatie
waarin a, b, c de lengtes zijn van de drie zijden, terwijl
de halve omtrek is van de driehoek. De gewoonte om de halve omtrek van een driehoek oftewel de halve som van de zijden (semisumma laterum) aan te geven met de letter s gaat terug op Euler, die ook een bewijs gaf van de formule van Heron. Er zijn veel verschillende bewijzen (meetkundig, algebraïsch, goniometrisch) voor de formule van Heron, maar het originele (en zeer ingenieuze) bewijs van Heron was lange tijd onbekend, totdat in 1896 een manuscript met de complete tekst van zijn Metrica werd ontdekt.
Voor een bespreking van dit bewijs en het overige wiskundige werk van Heron kun je voor een eerste oriëntatie uitstekend terecht in het onvolprezen werk van Sir Thomas Heath, A History of Greek Mathematics (2 dln., Oxford 1921), dat online beschikbaar is (Volume 1, Volume 2). Heath opent zijn hoofdstuk over Heron met de lang omstreden kwestie van de datering van Heron. In 1938 liet Otto Neugebauer echter zien dat een in Heron's werk Dioptra beschreven maansverduistering, waargenomen te Alexandrië, alleen de maansverduistering van 13 maart 62 (Juliaanse kalender) kan zijn geweest, wat dus een terminus post quem oplevert voor het ontstaan van de tekst en daarmee voor het einde van zijn leven. Men neemt nu algemeen aan dat hij heeft geleefd in de eerste eeuw n.C.
Van alle bewaard gebleven werken van Heron is in de periode 1899-1914 bij Teubner in Leipzig een wetenschappelijke uitgave verschenen met een kritisch apparaat, uitvoerige commentaren en inleidingen, alsmede een Duitse vertaling van alle teksten. Deze editie (herdrukt in 1976 bij de destijds West-Duitse divisie van Teubner in Stuttgart) is online beschikbaar via Gallica.
Het vraagstuk dat je aan de orde stelt is in feite een stelling afkomstig uit een werk van Heron dat bekend staat als de Catoptrica, wat al aangeeft dat het handelt over spiegelingen (Gr. κάτοπτρον 'spiegel'). De Griekse tekst is ergens in de middeleeuwen verloren gegaan, maar de Vlaamse geestelijke Willem van Moerbeke heeft er een Latijnse vertaling van gemaakt die wel bewaard is gebleven, zodat we er nu nog kennis van kunnen nemen. In de Teubner editie is de Latijnse tekst van de Catoptrica (met Duitse vertaling) opgenomen in Vol. 2, en de stelling waar het om gaat komt aan de orde in hoofdstuk IV, hier. Heron stelt dat bij een spiegel de gelijkheid van de hoek van inval en de hoek van uitval impliceert dat het licht vanaf een object naar een waarnemer die het object via de spiegel waarneemt de kortst mogelijke weg aflegt.
Uitgaande van het diagram dat je zelf postte kunnen we dit als volgt inzien.
Zij s een rechte en laten A en B twee punten zijn aan dezelfde zijde van de rechte s zodanig dat lijnstuk AB niet loodrecht staat op de rechte s. Zij verder C het spiegelbeeld van A in s. Aangezien de punten A en C en daarmee ook de punten B en C aan weerszijden van de rechte s liggen, snijdt het lijnstuk BC de rechte s in een punt P. Kies nu een willekeurig tweede punt Q ≠ P op de rechte s. Ik beweer nu dat
AP + PB < AQ + QB
Bewijs:
Zij R het snijpunt van lijnstuk AC met de rechte s. Dan is AR = CR en AC ⊥ RP en dus ∠ARP = ∠CRP en daarmee △ARP ≅ △CRP (ZHZ) en dus AP = CP. Evenzo is △ARQ ≅ △CRQ (ZHZ) en dus AQ = CQ. Merk op dat AQ = CQ ook geldt als Q = R aangezien AR = CR. Nu is
AP + PB = CP + PB = CB < CQ + QB = AQ + QB
en dus
AP + PB < AQ + QB
QED
Aangezien △ARP ≅ △CRP is ∠(AP, s) = ∠APR = ∠CPR en aangezien ook (overstaande hoeken) ∠CPR = ∠BPQ = ∠(BP, s) is dus inderdaad
∠(AP, s) = ∠(PB, s)
Het is verder gemakkelijk in te zien dat in de figuur voor △APQ geldt ∠APQ + ∠AQP = (180° − ∠(AP, s)) + ∠(AQ, s) < 180° en daarmee ∠(AQ, s) < ∠(AP, s). Evenzo kunnen we zien dat voor △BPQ geldt ∠BPQ + ∠BQP = ∠(PB, s) + (180° − ∠(QB, s)) < 180° en daarmee ∠(PB, s) < ∠(QB, s). Dus hebben we
∠(AQ, s) < ∠(AP, s) = ∠(PB, s) < ∠(QB, s)
en daarmee ∠(AQ, s) < ∠(QB, s). Uiteraard geldt dit voor een punt Q op de rechte s tussen punt P en het voetpunt van de loodlijn uit punt B op s, maar het is triviaal dat dit eveneens geldt als punt Q samenvalt met het voetpunt van de loodlijn uit B op s of rechts van dit voetpunt op s ligt, aangezien AQ dan hoek PQB deelt. Ligt punt Q daarentegen tussen punt R en punt P, dan kunnen we volkomen analoog laten zien dat ∠(AQ, s) > ∠(QB, s), en uiteraard geldt dit eveneens als punt Q samenvalt met punt R of links daarvan op de rechte s ligt, aangezien QB dan hoek AQP deelt. Daarmee is ∠(AQ, s) ≠ ∠(QB, s) voor elk punt Q op de rechte s anders dan P. De gelijkheid van de hoek van inval en de hoek van uitval impliceert dus inderdaad dat het licht van een object in punt A naar een waarnemer in punt B die het object via de spiegel s waarneemt de kortst mogelijke weg aflegt.
[ Bericht 0% gewijzigd door Riparius op 16-10-2014 14:13:10 ]


quote:Op dinsdag 14 oktober 2014 21:34 schreef RustCohle het volgende:
Hoi goedenavond,
Zou iemand mij iets kunnen vertellen over de Lagrange functie (waaronder de eerste en de voldoende voorwaarden) en de geometrische interpretatie hiervan? Ik vind het zelf een vrij lastig onderwerp, met name omdat ik niet echt snap waarvoor het dient, want je kunt toch al een maximum/minimum berekenen d.m.v. partieel afgeleiden, waarom zou je de Lagrange functie nodig moeten hebben..? Op internet tref ik veel literatuur wat er al vanuit gaat dat je al een redelijke kennis over het onderwerp beschikt, wat het voor mij lastig maakt.
quote:Op dinsdag 14 oktober 2014 22:09 schreef Novermars het volgende:
Simpel voorbeeld waarom partiële afgeleides niet nuttig zijn: Stel je hebt de functie gedefinieerd door f(x)=x^2 op het domein A=[2,4]. en je wiltbepalen. Hoe ga je dit doen met partiële afgeleides?
Voor wat extra literatuur. In Simon & Blume's Mathematics for Economists staat heel erg veel beschreven over dit soort problemen.
quote:Op dinsdag 14 oktober 2014 22:19 schreef RustCohle het volgende:
[..]
Het stationaire punt bepalen door f'(x) te bepalen en vervolgens te kijken wanneer f'(x) = 0 en dan een getallenlijn maken voor de getallen van het domein om zodoende het hoogste punt te bepalen.., het zijn overigens maar 3 getallen.. In dit geval is het maximum bij x= 4 want y= 16 dan. (?)
Misschien spreek ik mijzelf weer tegen, want het stationaire punt is bij x = 0... dus x =4 kan nooit een stationaire punt zijn..
Ik ben nu wel mindfucked.


Het probleem is dat aan de rand van het interval de afgeleide niet nul hoeft te zijn om een maximum te hebben.quote:


Hoezo? Dat is toch een noodzakelijje voorwaarde? Daarnaast kun je hier toch geen lagrange op toepassen? Want dat betreft op twee variabelenquote:Op woensdag 15 oktober 2014 11:24 schreef thenxero het volgende:
[..]
Het probleem is dat aan de rand van het interval de afgeleide niet nul hoeft te zijn om een maximum te hebben.


Die factor 4! staat daar prima. Die krijg je er namelijk bij omdat er geen onderscheid wordt gemaakt tussen de spelers.quote:Op dinsdag 14 oktober 2014 23:26 schreef Novermars het volgende:
[..]
Volgens mij is die factor 4! overbodig. En sowieso moet de noemer optellen tot aan de teller.


Nee, aan de rand is de afgeleide niet noodzakelijk 0 in een maximum (dat geldt alleen voor maxima in het interieur van het domein waarop je werkt).quote:Op woensdag 15 oktober 2014 11:44 schreef RustCohle het volgende:
[..]
Hoezo? Dat is toch een noodzakelijje voorwaarde? Daarnaast kun je hier toch geen lagrange op toepassen? Want dat betreft op twee variabelen
Simpel voorbeeld: f:[0,1]-->[0,1] gedefinieerd door f(x)=x. De afgeleide is f'(x)=1 voor alle x, maar het maximum ligt bij x=1.
Je kan met "inequality constraints" niet direct Lagrange toepassen inderdaad, maar dat het één variable is maakt niet zoveel uit. Voor inequalities heb je een iets algemenere theorie nodig: http://en.wikipedia.org/w(...)%93Tucker_conditions .


Thanks!quote:Op woensdag 15 oktober 2014 14:05 schreef thenxero het volgende:
[..]
Nee, aan de rand is de afgeleide niet noodzakelijk 0 in een maximum (dat geldt alleen voor maxima in het interieur van het domein waarop je werkt).
Simpel voorbeeld: f:[0,1]-->[0,1] gedefinieerd door f(x)=x. De afgeleide is f'(x)=1 voor alle x, maar het maximum ligt bij x=1.
Je kan met "inequality constraints" niet direct Lagrange toepassen inderdaad, maar dat het één variable is maakt niet zoveel uit. Voor inequalities heb je een iets algemenere theorie nodig: http://en.wikipedia.org/w(...)%93Tucker_conditions .
ik wacht nog op een leuke uitleg over lagrange van Riparius.


Hoezo zou het overbodig zijn? Er is geen onderscheid tussen de 4 spelers. En wat bedoel je met de noemer optellen tot aan de teller?quote:Op dinsdag 14 oktober 2014 23:26 schreef Novermars het volgende:
[..]
Volgens mij is die factor 4! overbodig. En sowieso moet de noemer optellen tot aan de teller.


Bij een multinomiaal telprobleemquote:Op woensdag 15 oktober 2014 17:09 schreef Wouterw17 het volgende:
[..]
Hoezo zou het overbodig zijn? Er is geen onderscheid tussen de 4 spelers. En wat bedoel je met de noemer optellen tot aan de teller?
Verder zuig ik in Combinatoriek, dus zal ik me verder afzijdig houden.


Wat wil je er over weten? Concreet alsjeblieft, je kan hier hele boeken over schrijven.quote:Op woensdag 15 oktober 2014 15:48 schreef RustCohle het volgende:
[..]
Thanks!
ik wacht nog op een leuke uitleg over lagrange van Riparius.


De oplossing die ik geef telt als volgt: het aantal mogelijke volgorden van een stock is 52!, en daar zou je dan 4 stapeltjes van maken voor de vier spelers. Ieder stapeltje kan je op 13! manieren steken, dus die komen in de noemer. Daarnaast zijn er ook nog eens 4! mogelijkheden identiek, omdat je de 4 spelers mag verwisselen.quote:Op woensdag 15 oktober 2014 22:10 schreef Novermars het volgende:
[..]
Bij een multinomiaal telprobleemmoet gelden dat
Verder zuig ik in Combinatoriek, dus zal ik me verder afzijdig houden.
Levert als oplossing 52!/(13!44!)
Merk op dat 52!/(13!4) hetzelfde is als het product van (52 | 13)(39 | 13)(26 | 13)(13 | 13)
Sorry, lelijke schrijfwijze van binomiaalcoëfficiënten, maar ik heb geen zin om te texen.
Opinion is the medium between knowledge and ignorance (Plato)


Ik zou graag willen weten waarom je het gebruikt en waarom i.p.v. niet de gewone maximum/minimum methode volgens de partiele afgeleiden. Daarnaast ben ik benieuwd wat ik 'visueel' gezien aan het berekenen ben.. want het is toch anders (functie met 2variabelen en een voorwaarde) dan een functie met 1 variabele..quote:Op woensdag 15 oktober 2014 22:13 schreef Novermars het volgende:
[..]
Wat wil je er over weten? Concreet alsjeblieft, je kan hier hele boeken over schrijven.
Ook ben ik benieuwd wat een level curve is.


Je hebt volledig gelijk. Zoals ik zei is combinatoriek niet mijn sterkste kant. Dit krijg je er dus van als je trucjes uit je hoofd leert!quote:Op woensdag 15 oktober 2014 22:18 schreef Janneke141 het volgende:
[..]
De oplossing die ik geef telt als volgt: het aantal mogelijke volgorden van een stock is 52!, en daar zou je dan 4 stapeltjes van maken voor de vier spelers. Ieder stapeltje kan je op 13! manieren steken, dus die komen in de noemer. Daarnaast zijn er ook nog eens 4! mogelijkheden identiek, omdat je de 4 spelers mag verwisselen.
Levert als oplossing 52!/(13!44!)
Merk op dat 52!/(13!4) hetzelfde is als het product van (52 | 13)(39 | 13)(26 | 13)(13 | 13)
Sorry, lelijke schrijfwijze van binomiaalcoëfficiënten, maar ik heb geen zin om te texen.


Alles wat je nodig hebt staat in Simon en Blume's Mathematics for Economists. PDF is relatief makkelijk te vinden online.quote:Op woensdag 15 oktober 2014 22:43 schreef RustCohle het volgende:
[..]
Ik zou graag willen weten waarom je het gebruikt en waarom i.p.v. niet de gewone maximum/minimum methode volgens de partiele afgeleiden. Daarnaast ben ik benieuwd wat ik 'visueel' gezien aan het berekenen ben.. want het is toch anders (functie met 2variabelen en een voorwaarde) dan een functie met 1 variabele..
Ook ben ik benieuwd wat een level curve is.


Even nog ter controle van de rest van de vraag: wat is de kans dat elke speler 1 aas krijgt als er opnieuw geen onderscheid is tussen de spelers? Is dat dan 4!/1!^4 * 48!/12!^4*4! delen door het antwoord van de eerdere vraag?quote:Op woensdag 15 oktober 2014 22:18 schreef Janneke141 het volgende:
[..]
De oplossing die ik geef telt als volgt: het aantal mogelijke volgorden van een stock is 52!, en daar zou je dan 4 stapeltjes van maken voor de vier spelers. Ieder stapeltje kan je op 13! manieren steken, dus die komen in de noemer. Daarnaast zijn er ook nog eens 4! mogelijkheden identiek, omdat je de 4 spelers mag verwisselen.
Levert als oplossing 52!/(13!44!)
Merk op dat 52!/(13!4) hetzelfde is als het product van (52 | 13)(39 | 13)(26 | 13)(13 | 13)
Sorry, lelijke schrijfwijze van binomiaalcoëfficiënten, maar ik heb geen zin om te texen.


Houd de vier azen even apart en volg voor de 48 kaarten die je over de 4 spelers verdeelt dezelfde telwijze als Janneke hanteert. Dan weet je op hoeveel manieren je die 48 kaarten over de vier spelers kunt verdelen waarbij elke speler 12 kaarten krijgt. Tenslotte geef je elke speler nog één aas.quote:Op woensdag 15 oktober 2014 22:58 schreef Wouterw17 het volgende:
[..]
Even nog ter controle van de rest van de vraag: wat is de kans dat elke speler 1 aas krijgt als er opnieuw geen onderscheid is tussen de spelers?
[ Bericht 6% gewijzigd door Riparius op 16-10-2014 05:07:24 ]


Ik heb een leuke opdracht voor mezelf bedacht: 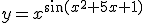 , bepaal dy/dx.
, bepaal dy/dx.
Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan: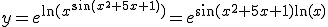
m = sin(x2+5x+1) * ln(x), dan is y = em.
u = x2+5x+1
i = sin(u)
du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x2+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = ln(x) (2x + 5) cos(x2+5x+1) + sin(x2+5x+1)/x
Maar wat dan? Ik weet dy/dm = em
[ Bericht 0% gewijzigd door netchip op 16-10-2014 17:09:22 ]
Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan:
m = sin(x2+5x+1) * ln(x), dan is y = em.
u = x2+5x+1
i = sin(u)
du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x2+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = ln(x) (2x + 5) cos(x2+5x+1) + sin(x2+5x+1)/x
Maar wat dan? Ik weet dy/dm = em
[ Bericht 0% gewijzigd door netchip op 16-10-2014 17:09:22 ]


De inverse vanquote:Op donderdag 16 oktober 2014 16:35 schreef jatochneetoch het volgende:
Hallo, simpel vraagje maar ben het even kwijt.
Hoe kom ik van:
naar:
?


dy/dx = dy/dm * dm/dxquote:Op donderdag 16 oktober 2014 16:41 schreef netchip het volgende:
Ik heb een leuke opdracht voor mezelf bedacht:, bepaal dy/dx.
Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan:
m = sin(x2+5x+1) * ln(x), dan is y = em.
u = x2+5x+1
i = sin(u)
du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x2+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = (2x + 5) cos(x2+5x+1) + sin(x2+5x+1)/x
Maar wat dan? Ik weet dy/dm = em
Kon je dit zelf niet verzinnen? Dit heb je namelijk voor di/dx en dm/dx ook al gedaan.


Ik zie 'm nu, ik was de draad een beetje kwijt.quote:Op donderdag 16 oktober 2014 16:53 schreef Alrac4 het volgende:
[..]
dy/dx = dy/dm * dm/dx
Kon je dit zelf niet verzinnen? Dit heb je namelijk voor di/dx en dm/dx ook al gedaan.


Oke, dan is dy/dx = dy/dm * dm/dx =quote:Op donderdag 16 oktober 2014 16:41 schreef netchip het volgende:
Ik heb een leuke opdracht voor mezelf bedacht:, bepaal dy/dx.
Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan:
m = sin(x2+5x+1) * ln(x), dan is y = em.
u = x2+5x+1
i = sin(u)
du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x2+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = (2x + 5) cos(x2+5x+1) + sin(x2+5x+1)/x
Maar wat dan? Ik weet dy/dm = em
Opgelost.


Je uitdrukking voor dm/dx klopt niet, je raakt hier een factor ln x kwijt. Maar met al die substituties raak je sowieso snel de draad kwijt. Gebruik de Leibniz notatie zonder expliciete substituties. Zie hier voor het idee.quote:Op donderdag 16 oktober 2014 16:41 schreef netchip het volgende:
Ik heb een leuke opdracht voor mezelf bedacht:, bepaal dy/dx.
Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan:
m = sin(x2+5x+1) * ln(x), dan is y = em.
u = x2+5x+1
i = sin(u)
du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x2+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = (2x + 5) cos(x2+5x+1) + sin(x2+5x+1)/x
Maar wat dan? Ik weet dy/dm = em


Hier 2 vragen over limieten van functies waar ik niet uitkom:
Bepaal de limiet van arccos(x)/x
x nadert 0
Bepaal de limiet van
(ln(x)-ln(a))/ (x-a)
x nadert a.
Bepaal de limiet van arccos(x)/x
x nadert 0
Bepaal de limiet van
(ln(x)-ln(a))/ (x-a)
x nadert a.


Oja zo was het bedankt!quote:Op donderdag 16 oktober 2014 16:51 schreef Alrac4 het volgende:
[..]
De inverse vanis
. Aan beide kanten vermenigvuldigen met deze inverse levert op:
. Deze matrix vermenigvuldiging uitwerken levert het antwoord
Alleen verder in de opgaven komen er grotere matrices voor, en dat is best veel werk als ik op internet zoek hoe je daar de inverse van uitrekent. Wel zit er een bepaalde structuur in, weet jij misschien of er trucjes zijn om deze snel op te lossen?:


Ik snap niet helemaal wat je daar doet, zou je dat alsjeblieft uit kunnen leggen?quote:Op donderdag 16 oktober 2014 17:07 schreef Riparius het volgende:
[..]
Je uitdrukking voor dm/dx klopt niet, je raakt hier een factor ln x kwijt. Maar met al die substituties raak je sowieso snel de draad kwijt. Gebruik de Leibniz notatie zonder expliciete substituties. Zie hier voor het idee.


Als je mijn stuk over de kettingregel en de notaties van Leibniz en Lagrange hebt gelezen, dan zou je bijvoorbeeld dit moeten begrijpen:quote:Op donderdag 16 oktober 2014 17:29 schreef netchip het volgende:
[..]
Ik snap niet helemaal wat je daar doet, zou je dat alsjeblieft uit kunnen leggen?


Het inverteren van matrices is in het algemeen een vervelend werkje. Als je dan toch zo'n 4x4 matrix moet inverteren doe ik het altijd op deze manier:quote:Op donderdag 16 oktober 2014 17:26 schreef jatochneetoch het volgende:
[..]
Oja zo was het bedankt!
Alleen verder in de opgaven komen er grotere matrices voor, en dat is best veel werk als ik op internet zoek hoe je daar de inverse van uitrekent. Wel zit er een bepaalde structuur in, weet jij misschien of er trucjes zijn om deze snel op te lossen?:
http://www.mathsisfun.com(...)s-gauss-jordan.html
Dit is waarschijnlijk niet de snelste manier, maar het werkt altijd (als de matrix inverteerbaar is uiteraard) en het is redelijk overzichtelijk. In het geval van jouw matrix kan het vrij snel volgens deze methode, omdat je maar een paar niet-diagonaal elementen hebt (al is er waarschijnlijk een slim trukje waar Riparius je meer over kan vertellen bij dit specifieke soort matrices).


Deze limiet bestaat niet, want de teller gaat niet naar nul, terwijl de noemer wel naar nul gaat.quote:Op donderdag 16 oktober 2014 17:23 schreef Wouterw17 het volgende:
Hier 2 vragen over limieten van functies waar ik niet uitkom:
Bepaal de limiet van arccos(x)/x
x nadert 0
Doet je dit niet denken aan een afgeleide? Hint: limiet van een differentiequotiënt.quote:Bepaal de limiet van
(ln(x)-ln(a))/ (x-a)
x nadert a.


Bij de eerste zegt het antwoordenboek dat de limiet 1 is. Heb jij wel eens van speciale limieten gehoord? zoals lim sin(x)/x =1? Want zo zou je het op moeten lossen.quote:Op donderdag 16 oktober 2014 17:44 schreef Riparius het volgende:
[..]
Deze limiet bestaat niet, want de teller gaat niet naar nul, terwijl de noemer wel naar nul gaat.
[..]
Doet je dit niet denken aan een afgeleide? Hint: limiet van een differentiequotiënt.


Ja, uiteraard ken ik die standaardlimieten. Maar dan vraag ik me af of je de opgave niet verkeerd hebt overgenomen. Wellicht gaat het om de limiet van arcsin(x)/x voor x → 0.quote:Op donderdag 16 oktober 2014 17:48 schreef Wouterw17 het volgende:
[..]
Bij de eerste zegt het antwoordenboek dat de limiet 1 is. Heb jij wel eens van speciale limieten gehoord? zoals lim sin(x)/x =1? Want zo zou je het op moeten lossen.


Ik had zelf gesubstitueerd door te nemen y=arccos(x). In dat geval geldt x=cos(y). Als je dan y=0 invult krijg je 0/cos(0)=0 maar de antwoorden zeggen dus 1... En ik weet zeker dat ik de vraag goed heb overgenomen.quote:Op donderdag 16 oktober 2014 17:53 schreef Riparius het volgende:
[..]
Ja, uiteraard ken ik die standaardlimieten. Maar dan vraag ik me af of je de opgave niet verkeerd hebt overgenomen. Wellicht gaat het om de limiet van arcsin(x)/x voor x → 0.


Nee, zo werkt het niet. Als je hebt y = arccos(x) dan is inderdaad x = cos(y) maar dan mag je natuurlijk niet zonder nadenken y = 0 gaan stellen want dat klopt niet. Immers, de cosinus van 0 is 1 en niet 0, dus als je y naar 0 laat gaan, dan gaat x naar 1 en dat was toch niet de bedoeling?quote:Op donderdag 16 oktober 2014 17:59 schreef Wouterw17 het volgende:
[..]
Ik had zelf gesubstitueerd door te nemen y=arccos(x). In dat geval geldt x=cos(y). Als je dan y=0 invult krijg je 0/cos(0)=0 maar de antwoorden zeggen dus 1... En ik weet zeker dat ik de vraag goed heb overgenomen.
Je zou meteen moeten zien dat de limiet van arccos(x)/x voor x → 0 niet bestaat, want de teller gaat naar arccos(0) = ½π en de noemer gaat naar 0. Verder kun je limieten ook laten bepalen door WolframAlpha, en die zegt uiteraard ook dat je limiet niet bestaat.


Ik zou wel graag zien dat je in het vervolg eerst je opgave controleert voordat je deze post, want nu hebben we allebei onze tijd verdaan.quote:Op donderdag 16 oktober 2014 18:11 schreef Wouterw17 het volgende:
Btw, heb de vraag wel fout overgenomen.Het was (½π - arccos(x))/ x
Kun je er nu wel uitkomen?
Goed, nieuwe ronde, nieuwe kansen. Je ziet nu dat de teller en de noemer van je quotiënt beide naar nul gaan voor x → 0, en dat betekent dat deze limiet inderdaad kan bestaan (maar niet hoeft te bestaan). Je kunt dit op verschillende manieren aanpakken, afhankelijk van je kennis. Je weet bijvoorbeeld dat
arccos(0) = ½π
dus zou je de limiet kunnen herschrijven als
Wat denk je hiervan?


Ik kan hier nog steeds vrij weinig mee. In de opgave staat als hint dat je gebruik moet maken van de speciale limieten sin(x)/x =1 en tan(x)/x= 1. Maar ik zie niet hoe je die kan toepassen.quote:Op donderdag 16 oktober 2014 18:24 schreef Riparius het volgende:
[..]
Ik zou wel graag zien dat je in het vervolg eerst je opgave controleert voordat je deze post, want nu hebben we allebei onze tijd verdaan.
Goed, nieuwe ronde, nieuwe kansen. Je ziet nu dat de teller en de noemer van je quotiënt beide naar nul gaan voor x → 0, en dat betekent dat deze limiet inderdaad kan bestaan (maar niet hoeft te bestaan). Je kunt dit op verschillende manieren aanpakken, afhankelijk van je kennis. Je weet bijvoorbeeld dat
arccos(0) = ½π
dus zou je de limiet kunnen herschrijven als
Wat denk je hiervan?


Wat is de definitie van de afgeleide in een punt? (uitschrijven)quote:Op donderdag 16 oktober 2014 18:31 schreef Wouterw17 het volgende:
[..]
Ik kan hier nog steeds vrij weinig mee. In de opgave staat als hint dat je gebruik moet maken van de speciale limieten sin(x)/x =1 en tan(x)/x= 1. Maar ik zie niet hoe je die kan toepassen.


Het gaat bij deze opdracht niet om de afgeleide maar om een limiet. En daarbij moet je gebruik maken van de speciale limieten.quote:Op donderdag 16 oktober 2014 18:34 schreef Novermars het volgende:
[..]
Wat is de definitie van de afgeleide in een punt?


En sinds wanneer is de afgeleide geen limiet meer?quote:Op donderdag 16 oktober 2014 18:35 schreef Wouterw17 het volgende:
[..]
Het gaat bij deze opdracht niet om de afgeleide maar om een limiet. En daarbij moet je gebruik maken van de speciale limieten.


Stel dat je een eindige on onderbroken reeks van natuurlijke getallen hebt (Dus 1,2,3... kan terwijl 1, 2, 4... ongeldig is). En je weet dat de volgende getallen in die reeks voorkomen:
kun je vanaf dit punt een zinnige schattig doen over waar de getallenreeks begint en ophoudt?quote:145, 84, 161, 85, 152, 47, 109, 16, 106, 101, 64, 73, 57, 83, 88, 135, 119, 120, 121, 122, 42, 8, 104, 112, 89, 82
“An interesting thing is a good thing.”


Ja hoor, hij begint bij een integer kleiner dan of gelijk aan acht, en eindigt bij een natuurlijk getal groter dan of gelijk aan 161.quote:Op donderdag 16 oktober 2014 18:39 schreef Repelsteeltju het volgende:
Stel dat je een eindige on onderbroken reeks van natuurlijke getallen hebt (Dus 1,2,3... kan terwijl 1, 2, 4... ongeldig is). En je weet dat de volgende getallen in die reeks voorkomen:
[..]
kun je vanaf dit punt een zinnige schattig doen over waar de getallenreeks begint en ophoudt?
Opinion is the medium between knowledge and ignorance (Plato)


Afgeleide is wel een limiet maar daarmee kan ik deze som nog steeds niet oplossen.quote:Op donderdag 16 oktober 2014 18:36 schreef Novermars het volgende:
[..]
En sinds wanneer is de afgeleide geen limiet meer?


Ik had gehoopt dat je zou herkennen dat ik het quotiënt had omgevormd naar een differentiequotiënt en dat je dus zou zien dat de limiet gelijk moet zijn aan het tegengestelde van de waarde van de afgeleide bij 0. Maar goed, andere aanpak. Stel datquote:Op donderdag 16 oktober 2014 18:31 schreef Wouterw17 het volgende:
[..]
Ik kan hier nog steeds vrij weinig mee. In de opgave staat als hint dat je gebruik moet maken van de speciale limieten sin(x)/x =1 en tan(x)/x= 1. Maar ik zie niet hoe je die kan toepassen.
arccos x = θ
dan is
0 ≤ θ ≤ π
en ook
cos θ = x
dus ook
sin(½π − θ) = x
waarbij
−½π ≤ ½π − θ ≤ ½π
en dus
arcsin x = ½π − θ
oftewel
arcsin x = ½π − arccos x
kijk, en dit is mooi, want dit betekent dat we hebben
Zie je?


Kun je niet ook op basis van de frequentie van de andere getallen een uitspraak doen over waar de reeks ongeveer begint of stopt? Met de getallen die gegeven zijn lijkt het me intuïtief onwaarschijnlijk dat de doorgaat na pakweg de driehonderd.quote:Op donderdag 16 oktober 2014 18:41 schreef Janneke141 het volgende:
[..]
Ja hoor, hij begint bij een integer kleiner dan of gelijk aan acht, en eindigt bij een natuurlijk getal groter dan of gelijk aan 161.
“An interesting thing is a good thing.”


Stel f(x) = arccos(x), dan isquote:Op donderdag 16 oktober 2014 18:42 schreef Wouterw17 het volgende:
[..]
Afgeleide is wel een limiet maar daarmee kan ik deze som nog steeds niet oplossen.


Zo lang je niet weet welk gedeelte van de reeks te pakken hebt of hoe de deelreeks tot stand is gekomen, is er geen zinnig woord over te zeggen. Intuïtief heb je natuurlijk wel gelijk, maar de reeks 1...999.999 voldoet evengoed. Er is simpelweg te weinig informatie.quote:Op donderdag 16 oktober 2014 18:46 schreef Repelsteeltju het volgende:
[..]
Kun je niet ook op basis van de frequentie van de andere getallen een uitspraak doen over waar de reeks ongeveer begint of stopt? Met de getallen die gegeven zijn lijkt het me intuïtief onwaarschijnlijk dat de doorgaat na pakweg de driehonderd.
[ Bericht 2% gewijzigd door Janneke141 op 16-10-2014 18:57:59 ]
Opinion is the medium between knowledge and ignorance (Plato)


Ervaring zullen we maar zeggen?quote:Op donderdag 16 oktober 2014 18:49 schreef Riparius het volgende:
[..]
Dat is uiteraard precies wat ik wilde dat hij zou zien.


Eerder creativiteit. Maar die is vaak ver te zoeken. Hoe dan ook, hij is alweer vertrokken zonder mijn alternatieve uitwerking af te wachten en zonder verder naar de tweede opgave te vragen.quote:Op donderdag 16 oktober 2014 18:53 schreef Novermars het volgende:
[..]
Ervaring zullen we maar zeggen?


Ik was even eten maar deze snap ik. Thanksquote:Op donderdag 16 oktober 2014 18:44 schreef Riparius het volgende:
[..]
Ik had gehoopt dat je zou herkennen dat ik het quotiënt had omgevormd naar een differentiequotiënt en dat je dus zou zien dat de limiet gelijk moet zijn aan het tegengestelde van de waarde van de afgeleide bij 0. Maar goed, andere aanpak. Stel dat
arccos x = θ
dan is
0 ≤ θ ≤ π
en ook
cos θ = x
dus ook
sin(½π − θ) = x
waarbij
−½π ≤ ½π − θ ≤ ½π
en dus
arcsin x = ½π − θ
oftewel
arcsin x = ½π − arccos x
kijk, en dit is mooi, want dit betekent dat we hebben
Zie je?


Dat heb ik nog nooit gehad en volgens mij mogen wij het ook niet zo aanpakken. Misschien komt dat volgend blok nog.quote:


Ik kan me niet voorstellen dat je wel limieten behandeld maar niet de definitie van de afgeleide hebt gezien.quote:Op donderdag 16 oktober 2014 19:17 schreef Wouterw17 het volgende:
[..]
Dat heb ik nog nooit gehad en volgens mij mogen wij het ook niet zo aanpakken. Misschien komt dat volgend blok nog.


Definitie van afgeleiden heb ik wel gezien maar ik heb het nog nooit zo toegepast zien worden zoals jullie net lieten zien. Voorlopig moeten wij nog limieten oplossen mbv speciale limieten. Misschien krijg ik in een ander vak volgend blok jullie manier ook nog uitgelegd.quote:Op donderdag 16 oktober 2014 19:19 schreef Novermars het volgende:
[..]
Ik kan me niet voorstellen dat je wel limieten behandeld maar niet de definitie van de afgeleide hebt gezien.


Daar staat:quote:Op donderdag 16 oktober 2014 17:38 schreef Riparius het volgende:
[..]
Als je mijn stuk over de kettingregel en de notaties van Leibniz en Lagrange hebt gelezen, dan zou je bijvoorbeeld dit moeten begrijpen:
Waarom doe je hier de verandering van z ten opzichte van y keer de verandering van y ten opzichte van x? Ik zie niet in hoe dit de verandering van z tegenover x geeft...

 Op
Op