[Bèta wiskunde] Huiswerk- en vragentopic.

woensdag 15 oktober 2014 @ 11:48:54 #251

thabit

quote:
Op dinsdag 14 oktober 2014 23:26 schreef Novermars het volgende:

[..]

Volgens mij is die factor 4! overbodig. En sowieso moet de noemer optellen tot aan de teller.

Die factor 4! staat daar prima. Die krijg je er namelijk bij omdat er geen onderscheid wordt gemaakt tussen de spelers.

woensdag 15 oktober 2014 @ 14:05:01 #252

thenxero

quote:
Op woensdag 15 oktober 2014 11:44 schreef RustCohle het volgende:
[..]
Hoezo? Dat is toch een noodzakelijje voorwaarde? Daarnaast kun je hier toch geen lagrange op toepassen? Want dat betreft op twee variabelen

Nee, aan de rand is de afgeleide niet noodzakelijk 0 in een maximum (dat geldt alleen voor maxima in het interieur van het domein waarop je werkt).

Simpel voorbeeld: f:[0,1]-->[0,1] gedefinieerd door f(x)=x. De afgeleide is f'(x)=1 voor alle x, maar het maximum ligt bij x=1.

Je kan met "inequality constraints" niet direct Lagrange toepassen inderdaad, maar dat het één variable is maakt niet zoveel uit. Voor inequalities heb je een iets algemenere theorie nodig: http://en.wikipedia.org/w(...)%93Tucker_conditions .

woensdag 15 oktober 2014 @ 15:48:39 #253

RustCohle

quote:
Op woensdag 15 oktober 2014 14:05 schreef thenxero het volgende:

[..]

Nee, aan de rand is de afgeleide niet noodzakelijk 0 in een maximum (dat geldt alleen voor maxima in het interieur van het domein waarop je werkt).

Simpel voorbeeld: f:[0,1]-->[0,1] gedefinieerd door f(x)=x. De afgeleide is f'(x)=1 voor alle x, maar het maximum ligt bij x=1.

Je kan met "inequality constraints" niet direct Lagrange toepassen inderdaad, maar dat het één variable is maakt niet zoveel uit. Voor inequalities heb je een iets algemenere theorie nodig: http://en.wikipedia.org/w(...)%93Tucker_conditions .

Thanks!

ik wacht nog op een leuke uitleg over lagrange van Riparius.

woensdag 15 oktober 2014 @ 17:09:02 #254

Wouterw17

quote:
Op dinsdag 14 oktober 2014 23:26 schreef Novermars het volgende:
[..]
Volgens mij is die factor 4! overbodig. En sowieso moet de noemer optellen tot aan de teller.

Hoezo zou het overbodig zijn? Er is geen onderscheid tussen de 4 spelers. En wat bedoel je met de noemer optellen tot aan de teller?

woensdag 15 oktober 2014 @ 22:10:21 #255

Novermars

quote:
Op woensdag 15 oktober 2014 17:09 schreef Wouterw17 het volgende:
[..]
Hoezo zou het overbodig zijn? Er is geen onderscheid tussen de 4 spelers. En wat bedoel je met de noemer optellen tot aan de teller?

Bij een multinomiaal telprobleem $n \choose k_1,k_2, \dots , k_j$ moet gelden dat $\sum_{i=1}^j k_i = n$

Verder zuig ik in Combinatoriek, dus zal ik me verder afzijdig houden.

woensdag 15 oktober 2014 @ 22:13:56 #256

Novermars

quote:
Op woensdag 15 oktober 2014 15:48 schreef RustCohle het volgende:
[..]
Thanks!
ik wacht nog op een leuke uitleg over lagrange van Riparius.

Wat wil je er over weten? Concreet alsjeblieft, je kan hier hele boeken over schrijven.

woensdag 15 oktober 2014 @ 22:18:39 #257

Janneke141

Green, green grass of home

quote:
Op woensdag 15 oktober 2014 22:10 schreef Novermars het volgende:
[..]
Bij een multinomiaal telprobleem $n \choose k_1,k_2, \dots , k_j$ moet gelden dat $\sum_{i=1}^j k_i = n$
Verder zuig ik in Combinatoriek, dus zal ik me verder afzijdig houden.

De oplossing die ik geef telt als volgt: het aantal mogelijke volgorden van een stock is 52!, en daar zou je dan 4 stapeltjes van maken voor de vier spelers. Ieder stapeltje kan je op 13! manieren steken, dus die komen in de noemer. Daarnaast zijn er ook nog eens 4! mogelijkheden identiek, omdat je de 4 spelers mag verwisselen.
Levert als oplossing 52!/(13!⁴4!)

Merk op dat 52!/(13!⁴) hetzelfde is als het product van (52 | 13)(39 | 13)(26 | 13)(13 | 13)

Sorry, lelijke schrijfwijze van binomiaalcoëfficiënten, maar ik heb geen zin om te texen.

Opinion is the medium between knowledge and ignorance (Plato)

woensdag 15 oktober 2014 @ 22:43:02 #258

RustCohle

quote:
Op woensdag 15 oktober 2014 22:13 schreef Novermars het volgende:

[..]

Wat wil je er over weten? Concreet alsjeblieft, je kan hier hele boeken over schrijven.

Ik zou graag willen weten waarom je het gebruikt en waarom i.p.v. niet de gewone maximum/minimum methode volgens de partiele afgeleiden. Daarnaast ben ik benieuwd wat ik 'visueel' gezien aan het berekenen ben.. want het is toch anders (functie met 2variabelen en een voorwaarde) dan een functie met 1 variabele..

Ook ben ik benieuwd wat een level curve is.

woensdag 15 oktober 2014 @ 22:51:01 #259

Novermars

quote:
Op woensdag 15 oktober 2014 22:18 schreef Janneke141 het volgende:
[..]
De oplossing die ik geef telt als volgt: het aantal mogelijke volgorden van een stock is 52!, en daar zou je dan 4 stapeltjes van maken voor de vier spelers. Ieder stapeltje kan je op 13! manieren steken, dus die komen in de noemer. Daarnaast zijn er ook nog eens 4! mogelijkheden identiek, omdat je de 4 spelers mag verwisselen.
Levert als oplossing 52!/(13!⁴4!)
Merk op dat 52!/(13!⁴) hetzelfde is als het product van (52 | 13)(39 | 13)(26 | 13)(13 | 13)
Sorry, lelijke schrijfwijze van binomiaalcoëfficiënten, maar ik heb geen zin om te texen.

Je hebt volledig gelijk. Zoals ik zei is combinatoriek niet mijn sterkste kant. Dit krijg je er dus van als je trucjes uit je hoofd leert!

woensdag 15 oktober 2014 @ 22:52:51 #260

Novermars

quote:
Op woensdag 15 oktober 2014 22:43 schreef RustCohle het volgende:
[..]
Ik zou graag willen weten waarom je het gebruikt en waarom i.p.v. niet de gewone maximum/minimum methode volgens de partiele afgeleiden. Daarnaast ben ik benieuwd wat ik 'visueel' gezien aan het berekenen ben.. want het is toch anders (functie met 2variabelen en een voorwaarde) dan een functie met 1 variabele..
Ook ben ik benieuwd wat een level curve is.

Alles wat je nodig hebt staat in Simon en Blume's Mathematics for Economists. PDF is relatief makkelijk te vinden online.

woensdag 15 oktober 2014 @ 22:58:36 #261

Wouterw17

quote:
Op woensdag 15 oktober 2014 22:18 schreef Janneke141 het volgende:
[..]
De oplossing die ik geef telt als volgt: het aantal mogelijke volgorden van een stock is 52!, en daar zou je dan 4 stapeltjes van maken voor de vier spelers. Ieder stapeltje kan je op 13! manieren steken, dus die komen in de noemer. Daarnaast zijn er ook nog eens 4! mogelijkheden identiek, omdat je de 4 spelers mag verwisselen.
Levert als oplossing 52!/(13!⁴4!)
Merk op dat 52!/(13!⁴) hetzelfde is als het product van (52 | 13)(39 | 13)(26 | 13)(13 | 13)
Sorry, lelijke schrijfwijze van binomiaalcoëfficiënten, maar ik heb geen zin om te texen.

Even nog ter controle van de rest van de vraag: wat is de kans dat elke speler 1 aas krijgt als er opnieuw geen onderscheid is tussen de spelers? Is dat dan 4!/1!^4 * 48!/12!^4*4! delen door het antwoord van de eerdere vraag?

woensdag 15 oktober 2014 @ 23:53:27 #262

Riparius

quote:
Op woensdag 15 oktober 2014 22:58 schreef Wouterw17 het volgende:
[..]
Even nog ter controle van de rest van de vraag: wat is de kans dat elke speler 1 aas krijgt als er opnieuw geen onderscheid is tussen de spelers?

Houd de vier azen even apart en volg voor de 48 kaarten die je over de 4 spelers verdeelt dezelfde telwijze als Janneke hanteert. Dan weet je op hoeveel manieren je die 48 kaarten over de vier spelers kunt verdelen waarbij elke speler 12 kaarten krijgt. Tenslotte geef je elke speler nog één aas.

[ Bericht 6% gewijzigd door Riparius op 16-10-2014 05:07:24 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 16 oktober 2014 @ 16:35:54 #263

jatochneetoch

Hallo, simpel vraagje maar ben het even kwijt.
Hoe kom ik van:
$\frac{AE}{2L}\begin{bmatrix}2 & -1\\ -1 & 3\end{bmatrix}\begin{Bmatrix}u2\\ u3\end{Bmatrix}=\begin{Bmatrix}Fa\\Fb\end{Bmatrix}$
naar:
$u2=\frac{2L}{EA}(\frac{3}{5}Fa+\frac{1}{5}Fb)\\u3=\frac{2L}{EA}(\frac{1}{5}Fa+\frac{2}{5}Fb)$

?

donderdag 16 oktober 2014 @ 16:41:26 #264

netchip

Ik heb een leuke opdracht voor mezelf bedacht: 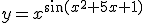$y = x^{\sin(x^2+5x+1)}$ , bepaal dy/dx.

Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan: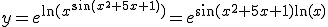 $y = e^{\ln(x^{\sin(x^2+5x+1)})} = e^{\sin(x^2+5x+1)\ln(x)}$

m = sin(x²+5x+1) * ln(x), dan is y = e^m.
u = x²+5x+1
i = sin(u)

du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x²+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = ln(x) (2x + 5) cos(x²+5x+1) + sin(x²+5x+1)/x

Maar wat dan? Ik weet dy/dm = e^m

[ Bericht 0% gewijzigd door netchip op 16-10-2014 17:09:22 ]

donderdag 16 oktober 2014 @ 16:51:33 #265

Alrac4

quote:
Op donderdag 16 oktober 2014 16:35 schreef jatochneetoch het volgende:
Hallo, simpel vraagje maar ben het even kwijt.
Hoe kom ik van:
$\frac{AE}{2L}\begin{bmatrix}2 & -1\\ -1 & 3\end{bmatrix}\begin{Bmatrix}u2\\ u3\end{Bmatrix}=\begin{Bmatrix}Fa\\Fb\end{Bmatrix}$
naar:
$u2=\frac{2L}{EA}(\frac{3}{5}Fa+\frac{1}{5}Fb)\\u3=\frac{2L}{EA}(\frac{1}{5}Fa+\frac{2}{5}Fb)$

?

De inverse van $\frac{AE}{2L}\begin{bmatrix}2 & -1\\ -1 & 3\end{bmatrix}$ is $\frac{2L}{5AE}\begin{bmatrix}3 & 1\\ 1 & 2\end{bmatrix}$ . Aan beide kanten vermenigvuldigen met deze inverse levert op: $\begin{Bmatrix}u2\\ u3\end{Bmatrix}=\frac{2L}{5AE}\begin{bmatrix}3 & 1\\ 1 & 2\end{bmatrix}\begin{Bmatrix}Fa\\Fb\end{Bmatrix}$ . Deze matrix vermenigvuldiging uitwerken levert het antwoord

donderdag 16 oktober 2014 @ 16:53:09 #266

Alrac4

quote:
Op donderdag 16 oktober 2014 16:41 schreef netchip het volgende:
Ik heb een leuke opdracht voor mezelf bedacht: $y = x^{\sin(x^2+5x+1)}$ , bepaal dy/dx.

Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan: $y = e^{\ln(x^{\sin(x^2+5x+1)})} = e^{\sin(x^2+5x+1)\ln(x)}$

m = sin(x²+5x+1) * ln(x), dan is y = e^m.
u = x²+5x+1
i = sin(u)

du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x²+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = (2x + 5) cos(x²+5x+1) + sin(x²+5x+1)/x

Maar wat dan? Ik weet dy/dm = e^m

dy/dx = dy/dm * dm/dx

Kon je dit zelf niet verzinnen? Dit heb je namelijk voor di/dx en dm/dx ook al gedaan.

donderdag 16 oktober 2014 @ 17:01:49 #267

netchip

quote:
Op donderdag 16 oktober 2014 16:53 schreef Alrac4 het volgende:

[..]

dy/dx = dy/dm * dm/dx

Kon je dit zelf niet verzinnen? Dit heb je namelijk voor di/dx en dm/dx ook al gedaan.

Ik zie 'm nu, ik was de draad een beetje kwijt.

donderdag 16 oktober 2014 @ 17:06:25 #268

netchip

quote:
Op donderdag 16 oktober 2014 16:41 schreef netchip het volgende:
Ik heb een leuke opdracht voor mezelf bedacht: $y = x^{\sin(x^2+5x+1)}$ , bepaal dy/dx.

Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan: $y = e^{\ln(x^{\sin(x^2+5x+1)})} = e^{\sin(x^2+5x+1)\ln(x)}$

m = sin(x²+5x+1) * ln(x), dan is y = e^m.
u = x²+5x+1
i = sin(u)

du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x²+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = (2x + 5) cos(x²+5x+1) + sin(x²+5x+1)/x

Maar wat dan? Ik weet dy/dm = e^m

Oke, dan is dy/dx = dy/dm * dm/dx = $(\ln(x)(2x + 5) \cos(x^2+5x+1) + \frac{\sin(x^2+5x+1)}{x}) e^{\sin(x^2+5x+1)\ln(x)}$

Opgelost.

donderdag 16 oktober 2014 @ 17:07:58 #269

Riparius

quote:
Op donderdag 16 oktober 2014 16:41 schreef netchip het volgende:
Ik heb een leuke opdracht voor mezelf bedacht: $y = x^{\sin(x^2+5x+1)}$ , bepaal dy/dx.

Ik heb dit op de volgende manier aangepakt: schrijf dit eerst als een e-macht, dus dit wordt dan: $y = e^{\ln(x^{\sin(x^2+5x+1)})} = e^{\sin(x^2+5x+1)\ln(x)}$

m = sin(x²+5x+1) * ln(x), dan is y = e^m.
u = x²+5x+1
i = sin(u)

du/dx = 2x + 5
di/dx = di/du * du/dx = (2x + 5) cos(x²+5x+1)
dm/dx = di/dx * ln(x) + i * 1/x = (2x + 5) cos(x²+5x+1) + sin(x²+5x+1)/x

Maar wat dan? Ik weet dy/dm = e^m

Je uitdrukking voor dm/dx klopt niet, je raakt hier een factor ln x kwijt. Maar met al die substituties raak je sowieso snel de draad kwijt. Gebruik de Leibniz notatie zonder expliciete substituties. Zie hier voor het idee.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 16 oktober 2014 @ 17:23:49 #270

Wouterw17

Hier 2 vragen over limieten van functies waar ik niet uitkom:
Bepaal de limiet van arccos(x)/x
x nadert 0

Bepaal de limiet van
(ln(x)-ln(a))/ (x-a)
x nadert a.

donderdag 16 oktober 2014 @ 17:26:10 #271

jatochneetoch

quote:
Op donderdag 16 oktober 2014 16:51 schreef Alrac4 het volgende:

[..]

De inverse van $\frac{AE}{2L}\begin{bmatrix}2 & -1\\ -1 & 3\end{bmatrix}$ is $\frac{2L}{5AE}\begin{bmatrix}3 & 1\\ 1 & 2\end{bmatrix}$ . Aan beide kanten vermenigvuldigen met deze inverse levert op: $\begin{Bmatrix}u2\\ u3\end{Bmatrix}=\frac{2L}{5AE}\begin{bmatrix}3 & 1\\ 1 & 2\end{bmatrix}\begin{Bmatrix}Fa\\Fb\end{Bmatrix}$ . Deze matrix vermenigvuldiging uitwerken levert het antwoord

Oja zo was het bedankt!
Alleen verder in de opgaven komen er grotere matrices voor, en dat is best veel werk als ik op internet zoek hoe je daar de inverse van uitrekent. Wel zit er een bepaalde structuur in, weet jij misschien of er trucjes zijn om deze snel op te lossen?:
$10^{5}\begin{bmatrix}4&-4&0&0\\-4&(4+3)&-3&0\\0&-3&(3+5)&-5\\0&0&-5&5\end{bmatrix}\begin{Bmatrix}0\\u_{2}\\u_{3}\\u_{4}\end{Bmatrix}=\begin{Bmatrix}R1\\0\\0\\10^{4}\end{Bmatrix}$

donderdag 16 oktober 2014 @ 17:29:36 #272

netchip

quote:
Op donderdag 16 oktober 2014 17:07 schreef Riparius het volgende:

[..]

Je uitdrukking voor dm/dx klopt niet, je raakt hier een factor ln x kwijt. Maar met al die substituties raak je sowieso snel de draad kwijt. Gebruik de Leibniz notatie zonder expliciete substituties. Zie hier voor het idee.

Ik snap niet helemaal wat je daar doet, zou je dat alsjeblieft uit kunnen leggen?

donderdag 16 oktober 2014 @ 17:38:05 #273

Riparius

quote:
Op donderdag 16 oktober 2014 17:29 schreef netchip het volgende:

[..]

Ik snap niet helemaal wat je daar doet, zou je dat alsjeblieft uit kunnen leggen?

Als je mijn stuk over de kettingregel en de notaties van Leibniz en Lagrange hebt gelezen, dan zou je bijvoorbeeld dit moeten begrijpen:

$\frac{\rm{d}(\ln(x^2\,+\,1))}{\rm{d}x}\,=\,\frac{\rm{d}(\ln(x^2\,+\,1))}{\rm{d}(x^2\,+\,1)}\,\cdot\,\frac{\rm{d}(x^2\,+\,1)}{\rm{d}x}\,=\,\frac{1}{x^2\,+\,1}\,\cdot\,2x\,=\,\frac{2x}{x^2\,+\,1}$

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

donderdag 16 oktober 2014 @ 17:43:53 #274

Alrac4

quote:
Op donderdag 16 oktober 2014 17:26 schreef jatochneetoch het volgende:

[..]

Oja zo was het bedankt!
Alleen verder in de opgaven komen er grotere matrices voor, en dat is best veel werk als ik op internet zoek hoe je daar de inverse van uitrekent. Wel zit er een bepaalde structuur in, weet jij misschien of er trucjes zijn om deze snel op te lossen?:
$10^{5}\begin{bmatrix}4&-4&0&0\\-4&(4+3)&-3&0\\0&-3&(3+5)&-5\\0&0&-5&5\end{bmatrix}\begin{Bmatrix}0\\u_{2}\\u_{3}\\u_{4}\end{Bmatrix}=\begin{Bmatrix}R1\\0\\0\\10^{4}\end{Bmatrix}$

Het inverteren van matrices is in het algemeen een vervelend werkje. Als je dan toch zo'n 4x4 matrix moet inverteren doe ik het altijd op deze manier:

http://www.mathsisfun.com(...)s-gauss-jordan.html

Dit is waarschijnlijk niet de snelste manier, maar het werkt altijd (als de matrix inverteerbaar is uiteraard) en het is redelijk overzichtelijk. In het geval van jouw matrix kan het vrij snel volgens deze methode, omdat je maar een paar niet-diagonaal elementen hebt (al is er waarschijnlijk een slim trukje waar Riparius je meer over kan vertellen bij dit specifieke soort matrices).

donderdag 16 oktober 2014 @ 17:44:34 #275

Riparius

quote:
Op donderdag 16 oktober 2014 17:23 schreef Wouterw17 het volgende:
Hier 2 vragen over limieten van functies waar ik niet uitkom:
Bepaal de limiet van arccos(x)/x
x nadert 0

Deze limiet bestaat niet, want de teller gaat niet naar nul, terwijl de noemer wel naar nul gaat.

quote:
Bepaal de limiet van
(ln(x)-ln(a))/ (x-a)
x nadert a.

Doet je dit niet denken aan een afgeleide? Hint: limiet van een differentiequotiënt.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs