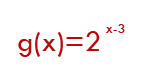SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Volledigquote:Op maandag 19 oktober 2009 17:53 schreef thabit het volgende:
Antwoord op laatste vraag in vorige topic: inductie.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Sobald du dir vertraust, sobald weißt du zu leben. – Omdat Goethe niet in het Engels schreef.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dat is zo, maar niet iedereen kan Duits.quote:Op maandag 19 oktober 2009 18:34 schreef Iblis het volgende:
[..]
Sobald du dir vertraust, sobald weißt du zu leben. – Omdat Goethe niet in het Engels schreef.
& Minister Rouvoet heeft alle melk opgedroken
Hetgeen bewezen en beklonken moest worden.
Ja de hoeveelste? 
(Tvp)
(Tvp)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Kan iemand mij een beetje op weg helpen met deze formule.
Hij moet zo ver mogelijk vereenvoudigd worden.
61/2n x 12n+1 x 27-1/2n / 321/2n
[ Bericht 0% gewijzigd door IHVK op 19-10-2009 22:26:30 ]
Hij moet zo ver mogelijk vereenvoudigd worden.
61/2n x 12n+1 x 27-1/2n / 321/2n
[ Bericht 0% gewijzigd door IHVK op 19-10-2009 22:26:30 ]
Begin eens met te bedenken dat (ab)k = akbk en apaq = ap+q. De getallen 6, 12 en 27 hebben een GGD van 3, dus ...quote:Op maandag 19 oktober 2009 21:56 schreef IHVK het volgende:
Kan iemand mij een beetje op weg helpen met deze formule.
Hij moet zo ver mogelijk vereenvoudigd worden.
61/2n x 12n+1 x 27-1/2n / 321/2n
En verder dat je die negatieve exponent naar de noemer kunt verplaatsen.quote:
[..]
Begin eens met te bedenken dat (ab)k = akbk en apaq = ap+q. De getallen 6, 12 en 27 hebben een GGD van 3, dus ...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Hm ik kom uit op 11.5n+1
...................................12n
Kan dat kloppen?
Stappen: (haakje=macht)
6(0.5n) x 12(n+1)
-----------------------
32 (0.5n) x 27 (0.5n)
72(1.5n+1)
---------
864(n)
/ 72 teller en noemer
=antwoord
...................................12n
Kan dat kloppen?
Stappen: (haakje=macht)
6(0.5n) x 12(n+1)
-----------------------
32 (0.5n) x 27 (0.5n)
72(1.5n+1)
---------
864(n)
/ 72 teller en noemer
=antwoord
Nee dat gaat mis. Sowieso mag je niet stellen dat 6(0.5n) x 12(n+1) = 72(1.5n+1). 'Delen' door 72 mag ook niet. Gebruik de rekenregels van Riparius.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een tussenjaar gehad dus de regels zijn echt weggeëbd.
Ik mag niet door 72 'delen' omdat ze een ander soort exponent hebben?
En die rekenregels heb ik al lang en breed genoteerd, alleen de uitvoering gaat dus niet zo best.
Ik mag niet door 72 'delen' omdat ze een ander soort exponent hebben?
En die rekenregels heb ik al lang en breed genoteerd, alleen de uitvoering gaat dus niet zo best.
'Delen door 72': is 72^2 / 73 gelijk aan 1^2 / 1?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe het wel moet: 12^4 * 4^9 = (3*4)^4 * 4^9 = 3^4 * 4^4 * 4^9 = 3^4 * 4^13.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je mag dus zeggen:
2a·3a = 6a, óf:
2a·2b = 2a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
[ Bericht 0% gewijzigd door Iblis op 19-10-2009 22:55:12 ]
2a·3a = 6a, óf:
2a·2b = 2a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
[ Bericht 0% gewijzigd door Iblis op 19-10-2009 22:55:12 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Deze volg ik alleen niet.quote:
Je mag dus zeggen:
2a·3a = 6a, óf:
2a·2b = 6a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
Terecht, want die was ook onzin. Nu staat het er beter.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ok thx, maar ik ga nog wel even nog een noob vraag stellen dan.
Omdat ik de negatieve exponent in de noemer tip (van Iblis) opvolg, want dat lijkt me logisch.
Krijg ik dit
6(0.5n) x 12 (n+1)
_____________
32 (0.5n) x 27 (0.5n)
In principe kan ik nu de onderste met elkaar vermenigvuldigen en zeggen dat ik klaar ben, maar iets zeg me dat ik een andere richting op moet met die (0.5n) en dat het verder vereenvoudigd kan worden.
Ja toch?
Omdat ik de negatieve exponent in de noemer tip (van Iblis) opvolg, want dat lijkt me logisch.
Krijg ik dit
6(0.5n) x 12 (n+1)
_____________
32 (0.5n) x 27 (0.5n)
In principe kan ik nu de onderste met elkaar vermenigvuldigen en zeggen dat ik klaar ben, maar iets zeg me dat ik een andere richting op moet met die (0.5n) en dat het verder vereenvoudigd kan worden.
Ja toch?
Jups. Sowieso:
En dan kun al eens proberen of je nu een 6n/2 kunt krijgen in de noemer.
En dan kun al eens proberen of je nu een 6n/2 kunt krijgen in de noemer.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
6(0.5n) x 12 (n+1)quote:
Jups. Sowieso:
[ afbeelding ]
En dan kun al eens proberen of je nu een 6n/2 kunt krijgen in de noemer.
-------------
6(0.5n) x 144 (0.5n)
12(n+1)
-------------
144 (1/2n)
Ik hoop en denk dat dit klopt.
En anders hoor ik het morgen wel.
Thx.
Die 144 = 122 en (122)1/2n = 12n. Dus het eind-antwoord is ‘12’.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
vergeet ax*bx = (ab)x nietquote:Op maandag 19 oktober 2009 22:48 schreef Iblis het volgende:
Je mag dus zeggen:
2a·3a = 6a, óf:
2a·2b = 2a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
Ik heb het vast gemist, maar de latexcode doet het nog steeds niet goed. Is de link niet meer goed ofzo?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik moet het nog een keer fixen. Als iemand anders een vhost kan opzetten op zijn webserver wil ik de dns daarnaartoe wel aanpassen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Lukt dat niet makkelijk met De Moivre?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
is dat niet iets met e^iy = cos x nog wat?quote:Op dinsdag 20 oktober 2009 20:27 schreef GlowMouse het volgende:
Lukt dat niet makkelijk met Euler?
Was voor je edit:
Even kijken naar Moivre
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Nou ik kom er echt niet uit:
Ik blijf steken bij:
Eerst schrijf ik de bovenste term naar polaire vorm:
r = ((-1)^2 + 1^2) = wortel(2)
z = wortel(2) (cos pi/4 + i sin pi/4 )
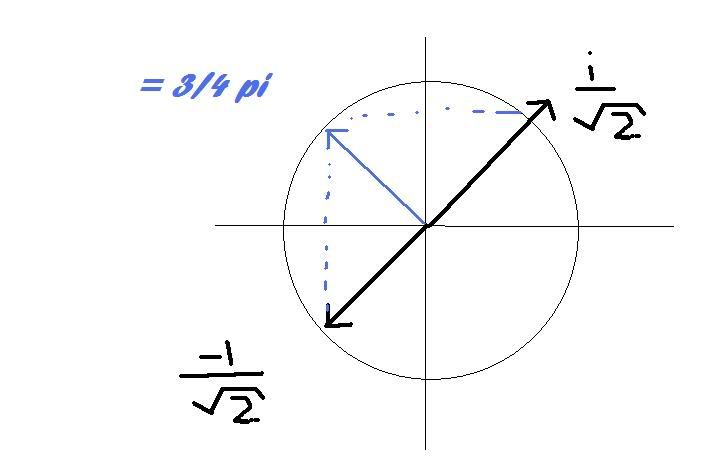
-1/wortel(2) + i/wortel(2) --> ((wortel(2)/wortel(2) (cos(pi/4) + i sin(pi/4) )^1001
--> 1 * ( cos(1001pi/4) + i sin (1001pi/4) )
---> aangezien 2pi een rondje is. 1000/2 = 500. Hou je 1 pi over?? Dus dan:
---> ( cos(5pi/4) + i sin (5 pi/4) ) en daarna raakt het een beetje in de soep.
Ik blijf steken bij:
Eerst schrijf ik de bovenste term naar polaire vorm:
r = ((-1)^2 + 1^2) = wortel(2)
z = wortel(2) (cos pi/4 + i sin pi/4 )
-1/wortel(2) + i/wortel(2) --> ((wortel(2)/wortel(2) (cos(pi/4) + i sin(pi/4) )^1001
--> 1 * ( cos(1001pi/4) + i sin (1001pi/4) )
---> aangezien 2pi een rondje is. 1000/2 = 500. Hou je 1 pi over?? Dus dan:
---> ( cos(5pi/4) + i sin (5 pi/4) ) en daarna raakt het een beetje in de soep.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Welk getal doe je nou? Want r=1 voor beide getallen.
En de hoek bij -1 + i is niet pi/4.
En de hoek bij -1 + i is niet pi/4.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
r = 1??? ehh... ik pak zeg maar -1 + 1*i voor de bovenste term.....quote:Op dinsdag 20 oktober 2009 21:09 schreef GlowMouse het volgende:
Welk getal doe je nou? Want r=1 voor beide getallen.
En de hoek bij -1 + i is niet pi/4.
Edit: en die hoek is natuurlijk 3/4 pi.
Maar als ik naar polaire vorm schrijf, dan wordt die -1+1i toch z = wortel ( 1 +1 ) ??
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
quote:Op dinsdag 20 oktober 2009 21:30 schreef GlowMouse het volgende:
waar komt -1+i vandaan dan?
van die boventerm : ( -1/wortel2 + i 1/wortel 2 )
In het boek zag ik dat ze hetzelfde doen met : 1/2 + 1/2 i gebruikten ze 1+i .. dus vandaar..
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Het is toch makkelijker om -1/wortel2 + i 1/wortel 2 te schrijven als cos(3pi/4) + i sin(3pi/4)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ff denken.... -1 wortel 2 = 5/4 pi + pi 1/4 --> ja idd dat wordt op de éénheidscirkel 3/4 pi. Ik ga even een paint maken om het te verduidelijken. kijken of ik het goed doe.quote:Op dinsdag 20 oktober 2009 21:42 schreef GlowMouse het volgende:
Het is toch makkelijker om -1/wortel2 + i 1/wortel 2 te schrijven als cos(3pi/4) + i sin(3pi/4)?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Schrijf eens de breuk als 1 e-macht, zoiets als et/en = et-n, en kijk wat de rest wordt als je de resulterende exponent modulo 2pi neemt.quote:Op dinsdag 20 oktober 2009 20:22 schreef Burakius het volgende:
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
[ afbeelding ]
btw. Even mijn totale noob plaatje:
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
i / wortel2 ligt op de 'y-as' en -1/wortel2 ligt op de x-as
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Goed, het nemen van machten staat gelijk aan het doorcirkelen van dat ding op de eenheidsschijf. De vierde macht van dat ding is daarbij duidelijk 1. De 1000ste macht is dan ook 1, aangezien 1000 een veelvoud van 4 is. De 1001ste macht is dus gelijk aan het getal zelf.quote:Op dinsdag 20 oktober 2009 21:52 schreef Burakius het volgende:
btw. Even mijn totale noob plaatje:
[ afbeelding ]
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
Ik begrijp het niet helemaal. De vierde macht van zowel cos ¾π + i∙sin ¾π als cos(-¼π) + i∙sin(-¼π) is -1, dus je kunt de machten van zowel teller als noemer mod 8 nemen. Niet dat daardoor iets verandert aan de uitwerking natuurlijk.quote:Op dinsdag 20 oktober 2009 22:08 schreef thabit het volgende:
[..]
Goed, het nemen van machten staat gelijk aan het doorcirkelen van dat ding op de eenheidsschijf. De vierde macht van dat ding is daarbij duidelijk 1. De 1000ste macht is dan ook 1, aangezien 1000 een veelvoud van 4 is. De 1001ste macht is dus gelijk aan het getal zelf.
Bij dit soort sommen schrijf ik altijd de zaak even om naar exponenten. In het meest algemene geval heb je iets alsquote:Op dinsdag 20 oktober 2009 20:22 schreef Burakius het volgende:
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
[ afbeelding ]
(a+bi)n
Nu ga je (a+bi) omschrijven in de vorm (a+bi)=reix, want dan kun je makkelijk uitrekenen dat
(a+bi)n = (reix)n = rneinx
In het algemeen geldt (teken het plaatje maar) dat
r = [a2+b2]1/2
en
tan(x) = b/a --> b/a=tan-1(x)
Hieruit kun je x en r oplossen in termen van a en b. Vervolgens schrijf je
rneinx
op. Dit doe je met de teller, en hetzelfde doe je met de noemer, en wat je overhoudt is een uitdrukking in de vorm
rneinx/[smeimx] = [rn/sm]ei(n-m)x.
Maar je kunt natuurlijk ook de plaatjes tekenen zoals werd aangegeven
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Okee, ja, vergissinkje.quote:Op woensdag 21 oktober 2009 00:22 schreef Riparius het volgende:
[..]
Ik begrijp het niet helemaal. De vierde macht van zowel cos ¾π + i∙sin ¾π als cos(-¼π) + i∙sin(-¼π) is -1, dus je kunt de machten van zowel teller als noemer mod 8 nemen. Niet dat daardoor iets verandert aan de uitwerking natuurlijk.
quote:
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Is dit toegestaan:
(1) (- 1/wortel(2) + i/wortel(2)) herschrijven tot 1/wortel(2) ( -1 + i ) ?
(2) modulus is wortel(2) en danzou het argument tan 1 zijn en dat is pi/4 , en dan klap ik het natuurlijk om door die -1 en dan wordt het 3/4 pi.
correct?
(1) (- 1/wortel(2) + i/wortel(2)) herschrijven tot 1/wortel(2) ( -1 + i ) ?
(2) modulus is wortel(2) en danzou het argument tan 1 zijn en dat is pi/4 , en dan klap ik het natuurlijk om door die -1 en dan wordt het 3/4 pi.
correct?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
1 ja
2 tan(x) = -1 dus x=3/4 pi (of x=-pi/4 maar die is het niet), niks 'klap ik het natuurlijk om', gewoon in 1x goed doen
2 tan(x) = -1 dus x=3/4 pi (of x=-pi/4 maar die is het niet), niks 'klap ik het natuurlijk om', gewoon in 1x goed doen
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat is correct, maar ik zou beginnen om wortels in de noemer weg te werken. Je hebt immers:quote:Op woensdag 21 oktober 2009 18:52 schreef Burakius het volgende:
Is dit toegestaan:
(1) (- 1/wortel(2) + i/wortel(2)) herschrijven tot 1/wortel(2) ( -1 + i ) ?
1/√2 = ½√2
Lijkt me op zijn minst onnodig verwarrend om het zo te doen. Je moet het gewoon even visualiseren in het complexe vlak. Het beeldpunt van -1 + i ligt in het tweede kwadrant, dan zie je meteen dat het argument ¾π (mod 2π) is.quote:(2) modulus is wortel(2) en danzou het argument tan 1 zijn en dat is pi/4 , en dan klap ik het natuurlijk om door die -1 en dan wordt het 3/4 pi.
correct?
Ja maar ik schrijf het eerst om naar een driehoek met a= 1 b = 1 en r = wortel(2).
Want ik heb dus een tabel tot mijn beschikking die ik uit mijn hoofd ken. Daarin komt tan-1 niet voor, mar bij tan 1 weet ik wel dat het pi/4 is. En dan "klap ik het om" .
Want ik heb dus een tabel tot mijn beschikking die ik uit mijn hoofd ken. Daarin komt tan-1 niet voor, mar bij tan 1 weet ik wel dat het pi/4 is. En dan "klap ik het om" .
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ja bij deze wel, maar bij pi/6 en pi/3 etc. vind ik het al moeilijker om te zien. Het liefst doe ik het dan op de langzame officiele wijze. Maar in een geval van pi/4 zou ik het wel zien natuurlijk. pi/2 trouwens ook.quote:Op woensdag 21 oktober 2009 19:15 schreef Riparius het volgende:
[..]
Dat is correct, maar ik zou beginnen om wortels in de noemer weg te werken. Je hebt immers:
1/√2 = ½√2
[..]
Lijkt me op zijn minst onnodig verwarrend om het zo te doen. Je moet het gewoon even visualiseren in het complexe vlak. Het beeldpunt van -1 + i ligt in het tweede kwadrant, dan zie je meteen dat het argument ¾π (mod 2π) is.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Tja, het is natuurlijk ook niet goed dat pi de verhouding tussen de omtrek en de middellijn van een cirkel aanduidt, in plaats van de verhouding tussen omtrek en straal. Het is op de een of andere manier historisch zo gegroeid natuurlijk, maar handig is anders omdat je je heel makkelijk in factoren 2 vergist. Maar goed, zo zijn er wel meer voorbeelden van slechte notatie te vinden die we toch nog dagelijks blijven gebruiken.quote:
Leg ees beter uit thabit . Ik kom nog wel eens in de war met dat rad gedoe. Ik haat het.
. Ik kom nog wel eens in de war met dat rad gedoe. Ik haat het.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
In de meeste formules en stellingen waar pi in voorkomt, komt eigenlijk 2*pi voor. Zo is de omtrek van de eenheidscirkel gelijk aan 2*pi. En als gevolg daarvan de periode van de sinus en cosinus gelijk aan 2*pi. Als je een hoek van pi hebt gemaakt dan ben je nog maar halverwege het hele rondje, etc.
Oke jongens nog eentje.Deze is wat simpeler.
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Het oudst bekende gebruik van de letter π in de 'moderne' betekenis komt voor bij William Jones, Synopsis palmariorum matheseos (London, 1706) p. 263, maar de notatie lijkt mede te zijn geïnspireerd door het gebruik van de letters π en δ voor respectievelijk de omtrek (periferie) en diameter van een cirkel bij Oughtred, Clauis mathematicae (1652) p. 66. De notatie π voor de verhouding van de omtrek tot de middellijn van een cirkel is populair geworden doordat Euler deze consequent gebruikte in zijn invloedrijke Introductio in analysin inifinitorum (1748). Opmerkelijk is echter dat Euler in een brief aan d'Alembert gedateerd 15 april 1747 schrijft: soit π la circonférence d'un cercle dont le rayon = 1, en daarmee definieert hij π dan weer op de manier die jij graag zou willen, wat wel opmerkelijk mag heten omdat Euler het manuscript voor de Introductio al medio 1745 had voltooid.quote:Op woensdag 21 oktober 2009 19:54 schreef thabit het volgende:
In de meeste formules en stellingen waar pi in voorkomt, komt eigenlijk 2*pi voor. Zo is de omtrek van de eenheidscirkel gelijk aan 2*pi. En als gevolg daarvan de periode van de sinus en cosinus gelijk aan 2*pi. Als je een hoek van pi hebt gemaakt dan ben je nog maar halverwege het hele rondje, etc.
[ Bericht 0% gewijzigd door Riparius op 21-10-2009 21:04:32 ]
Heb je sin(x) al getekend van π/2 tot 3/2π?quote:
Oke jongens nog eentje.Deze is wat simpeler.
[ afbeelding ]
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik weet niet wie die vraag heeft gemaakt, maar geen van de vier gegeven antwoorden is juist als je althans de gangbare definitie van arcsin x hanteert.quote:Op woensdag 21 oktober 2009 20:46 schreef Burakius het volgende:
Oke jongens nog eentje.Deze is wat simpeler.
[ afbeelding ]
Nou snap ik de notatie van de domein(en?) niet helemaal. Maar wat ik iig wel kan is: (als hij dus invers is) is natuurlijk:
f(x)=sin x ---> y=sinx ---> arcsiny=x -----> arcsinx= y is de inverse.
MAAarr... daarna komt het antwoord met arcsin(x + pi ) . En dat zal wel te maken hebben met die domein(en). Kan het even niet zien.
p.s.
wij hanteren het domein pi tot -pi ... als dat hiermee te maken heeft
Heb het getekend, alhoewel ik het niet vanuit de oorsprong laat gaan...quote:Op woensdag 21 oktober 2009 20:51 schreef Iblis het volgende:
[..]
Heb je sin(x) al getekend van π/2 tot 3/2π?
Dus ik heb de gewone sinus grafiek (die begint in 0,0) getekend. En daarna domeinen gesteld bij pi/2 en 3pi/2 ...
Maar uberhaupt snap ik dat [pi/2 , 3pi/2] --> [-1,1] gedoe niet. Wat wil dat zeggen.
Een grafiek is toch invers als dezelfde waarde y niet voor de tweede keer voorkomt...
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Kan iemand mij uitleggen wat de definitie\restricties van een lineair programmeringsprobleem zijn?
Ik moet morgen op mn tentamen lp's formuleren adhv een verhaal, maar ik weet niet exact waar het aan moet voldoen.
Ik heb het idee dat in je uiteindelijke probleem alle vergelijkingen aan de volgende voorwaarden moet voldoen
:
- Elke kant is steeds of een losse Beslissingsvariabele/Constante of een som waarvan de termen maximaal uit 1 Beslissingsvariabele bestaan.
- Je mag dus niet Xi/Yj = Zj doen
- Je mag ook niet Lj = A(j-1) + B(j-1) doen
Die laatste 2 zouden mijn leven namelijk zóooo veel makkelijker maken
Ik moet morgen op mn tentamen lp's formuleren adhv een verhaal, maar ik weet niet exact waar het aan moet voldoen.
Ik heb het idee dat in je uiteindelijke probleem alle vergelijkingen aan de volgende voorwaarden moet voldoen
:
- Elke kant is steeds of een losse Beslissingsvariabele/Constante of een som waarvan de termen maximaal uit 1 Beslissingsvariabele bestaan.
- Je mag dus niet Xi/Yj = Zj doen
- Je mag ook niet Lj = A(j-1) + B(j-1) doen
Die laatste 2 zouden mijn leven namelijk zóooo veel makkelijker maken
Een compacte notatie van domein en codomein van de functie.quote:Op donderdag 22 oktober 2009 00:15 schreef Burakius het volgende:
[..]
Heb het getekend, alhoewel ik het niet vanuit de oorsprong laat gaan...
Dus ik heb de gewone sinus grafiek (die begint in 0,0) getekend. En daarna domeinen gesteld bij pi/2 en 3pi/2 ...
Maar uberhaupt snap ik dat [pi/2 , 3pi/2] --> [-1,1] gedoe niet. Wat wil dat zeggen.
Je moet niet grafiek en functie met elkaar identificeren.quote:Een grafiek is toch invers als dezelfde waarde y niet voor de tweede keer voorkomt...
Lees nog even na wat men onder domein en bereik verstaat en bekijk de gehanteerde notaties, ook in de artikelen waarnaar wordt verwezen.
Zie het voorbeeld: http://nl.wikipedia.org/wiki/Lineair_programmeren
>> Elke kant is steeds of een losse Beslissingsvariabele/Constante of een som waarvan de termen maximaal uit 1 Beslissingsvariabele bestaan.
Bijna goed, maar het valt altijd om te schrijven naar wat jij zegt. 3x=2y kun je bv omschrijven naar 3x-2y=0.
>> - Je mag dus niet Xi/Yj = Zj doen
klopt, dit is een kwadratische constraint
>> - Je mag ook niet Lj = A(j-1) + B(j-1) doen
Waarom niet? Valt om te schrijven naar A+B-L = 0 dus gewoon toegestaan (ook zonder om te schrijven).
>> Elke kant is steeds of een losse Beslissingsvariabele/Constante of een som waarvan de termen maximaal uit 1 Beslissingsvariabele bestaan.
Bijna goed, maar het valt altijd om te schrijven naar wat jij zegt. 3x=2y kun je bv omschrijven naar 3x-2y=0.
>> - Je mag dus niet Xi/Yj = Zj doen
klopt, dit is een kwadratische constraint
>> - Je mag ook niet Lj = A(j-1) + B(j-1) doen
Waarom niet? Valt om te schrijven naar A+B-L = 0 dus gewoon toegestaan (ook zonder om te schrijven).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ok meer specifiek hoe ik bij dat laatste kwam, ik zit met productieproces waarbij er elke maand een overschot op voorraad kan blijven, hier betaal je dan geld voor.quote:Op donderdag 22 oktober 2009 01:18 schreef GlowMouse het volgende:
Zie het voorbeeld: http://nl.wikipedia.org/wiki/Lineair_programmeren
>> Elke kant is steeds of een losse Beslissingsvariabele/Constante of een som waarvan de termen maximaal uit 1 Beslissingsvariabele bestaan.
Bijna goed, maar het valt altijd om te schrijven naar wat jij zegt. 3x=2y kun je bv omschrijven naar 3x-2y=0.
>> - Je mag dus niet Xi/Yj = Zj doen
klopt, dit is een kwadratische constraint
>> - Je mag ook niet Lj = A(j-1) + B(j-1) doen
Waarom niet? Valt om te schrijven naar A+B-L = 0 dus gewoon toegestaan (ook zonder om te schrijven).
Mijn omslachtige idee was: definieer overschot aan begin van elke maand als een beslissingvariabele en voeg een constraint toe die stelt dat overschot gelijk moet zijn aan ' productie + overschot - verkoop ' van vorige maand:
Oj = Pj-1 + Oj-1 - Vj-1
Het lijkt me niet dat dit mag maar het ziet er wel aannemelijk uit als je het opschrijft dus ik twijfelde.
Sorry! Had injectief en invers door elkaar gehaald
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Als f(x) = eg(x), dan geldt volgens de kettingregel dat
f(x)' = g(x)'eg(x).
In jouw geval dus
f(x)' = 2e2x-4
aangezien (2x-4)'=2.
f(x)' = g(x)'eg(x).
In jouw geval dus
f(x)' = 2e2x-4
aangezien (2x-4)'=2.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Nee, kettingregel gebruiken, Leibniz’ notatie:quote:
Hoe was die regel ook weer?
Als f(x) = e2x - 4 dan is f '(x) = -4e2x - 4 ?
Dus, in dit geval y=2x - 4, dus dan krijg je:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Bedankt. Nog eentje:
De relatie tussen de prijs p en de vraaghoeveelheid q is gegeven door q = 10-0.02p+2
a) Voor welke waarden van p is de vraag q groter dan 10?
Ik begon:
10-0.02p+2 > 101
-0.02p + 2 > 1
-0.02 p > -1
p > 50
Maar het antwoord moet volgens het antwoordenblad p < 50 zijn, net andersom dus. Waarom? Als je aan beide kanten een minteken hebt hoef je het pijltje toch niet om te keren?
De relatie tussen de prijs p en de vraaghoeveelheid q is gegeven door q = 10-0.02p+2
a) Voor welke waarden van p is de vraag q groter dan 10?
Ik begon:
10-0.02p+2 > 101
-0.02p + 2 > 1
-0.02 p > -1
p > 50
Maar het antwoord moet volgens het antwoordenblad p < 50 zijn, net andersom dus. Waarom? Als je aan beide kanten een minteken hebt hoef je het pijltje toch niet om te keren?
Oh really?
Wel. Als je deelt door een negatief getal (en dat doe jij, door -0,02) dan klapt het minteken om. Het maakt niet uit of er aan beide zijden een positief of negatief getal staat, als je deelt door een negatief getal, dan klapt het om, b.v.:quote:Op donderdag 22 oktober 2009 16:20 schreef Matthijs- het volgende:
Bedankt. Nog eentje:
De relatie tussen de prijs p en de vraaghoeveelheid q is gegeven door q = 10-0.02p+2
a) Voor welke waarden van p is de vraag q groter dan 10?
Ik begon:
10-0.02p+2 > 101
-0.02p + 2 > 1
-0.02 p > -1
p > 50
Maar het antwoord moet volgens het antwoordenblad p < 50 zijn, net andersom dus. Waarom? Als je aan beide kanten een minteken hebt hoef je het pijltje toch niet om te keren?
Voorbeeld 1: -1 < 1
Deel door -1: 1 > -1.
Voorbeeld 2: -2 < -1:
Deel door -1: 2 > 1.
Voorbeeld 3: 3 < 4
Deel door -1: -3 > -4
Voorbeeld 4: 1 > -1:
Deel door -1: -1 < 1.
Dit is geen bewijs, maar je ziet: het maakt niet uit of er positieve of negatieve getallen staan, als je deelt door een negatief getal dán klapt het om.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ah oke, dank je. Scheelt toch weer 2 punten op het tentamen!
[ Bericht 43% gewijzigd door Matthijs- op 22-10-2009 16:35:57 ]
[ Bericht 43% gewijzigd door Matthijs- op 22-10-2009 16:35:57 ]
Oh really?
Edit: Ik vermenigvuldigde in mijn hoofd overigens met -50 ipv door -0,02 te delen (wat natuurlijk op hetzelfde neerkomt). Denk dat ik daardoor in de war ben geraakt.
Oh really?
Dat maakt niet uit: als je beide leden van een ongelijkheid met een negatief getal vermenigvuldigt dien je het teken ook om te klappen. En een beetje gezond verstand kan geen kwaad. Je kunt zo wel bedenken dat de vraag niet zal toenemen als de prijs almaar stijgt.quote:Op donderdag 22 oktober 2009 16:35 schreef Matthijs- het volgende:
Edit: Ik vermenigvuldigde in mijn hoofd overigens met -50 ipv door -0,02 te delen (wat natuurlijk op hetzelfde neerkomt). Denk dat ik daardoor in de war ben geraakt.
[ Bericht 0% gewijzigd door Riparius op 22-10-2009 18:12:06 ]
En we gaan vrolijk verder. 
Als f (x, y) = 4x3 + 4(x - y)3 - 60x + 12y
Dan zou f'y = 12(x - y)2 + 12 moeten zijn volgens mij. Het goede antwoord volgens het antwoordmodel is echter f'y = -12(x - y)2 + 12. Weer dat minteken dus!
Waarom zit ik er dit maal naast? Thanks.
Als f (x, y) = 4x3 + 4(x - y)3 - 60x + 12y
Dan zou f'y = 12(x - y)2 + 12 moeten zijn volgens mij. Het goede antwoord volgens het antwoordmodel is echter f'y = -12(x - y)2 + 12. Weer dat minteken dus!
Waarom zit ik er dit maal naast? Thanks.
Oh really?
Je moet wat er tussen de haakjes staat ook nog diferentieren --> -y = -
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Je paste de kettingregel niet correct toe.quote:Op donderdag 22 oktober 2009 18:26 schreef Matthijs- het volgende:
En we gaan vrolijk verder.
Als f (x, y) = 4x3 + 4(x - y)3 - 60x + 12y
Dan zou f'y = 12(x - y)2 + 12 moeten zijn volgens mij. Het goede antwoord volgens het antwoordmodel is echter f'y = -12(x - y)2 + 12. Weer dat minteken dus!
Waarom zit ik er dit maal naast? Thanks.
Oftewel
f(x) = a( g(x) )^n
f '(x)= a*n( g(x) )^n-1 * g '(x)
f(x) = a( g(x) )^n
f '(x)= a*n( g(x) )^n-1 * g '(x)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik snap niet goed wat er bedoeld wordt. Ik dacht a: L=1-labda en L=2+labda, maar ik denk dat ik hier al de fout in ga? Zo nee, hoe moet ik c dan doen?
Edit: Of moet ik het zien als twee punten (1,-1labda) en (2,1labda) en daar een y=ax+b formule voor opstellen?
>> Edit: Of moet ik het zien als twee punten (1,-1labda) en (2,1labda) en daar een y=ax+b formule voor opstellen?
Dat denk ik ja.
Ik kwam trouwens een echt gemene vraag tegen: voor welke p heeft px²+p = (x-1)² twee oplossingen?
Dat denk ik ja.
Ik kwam trouwens een echt gemene vraag tegen: voor welke p heeft px²+p = (x-1)² twee oplossingen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dan zou ik dus krijgen y=-(4/3)labda*x-(1/3)labda? Beetje kut dat hiervan de antwoorden niet online staan ;o
Met die p, ik zou denk gewoon haakjes uitwerken en dan de abc-formule, als 4(p-1)^2>4 is er iig geen antwoord, als 4(p-1)^2=4 is er één antwoord?
Met die p, ik zou denk gewoon haakjes uitwerken en dan de abc-formule, als 4(p-1)^2>4 is er iig geen antwoord, als 4(p-1)^2=4 is er één antwoord?
je moet iets in de vorm c1 x1 + c2 x2 = c3 krijgen.quote:
Dan zou ik dus krijgen y=-(4/3)labda*x-(1/3)labda? Beetje kut dat hiervan de antwoorden niet online staan ;o
juist, maar dat is de vraag niet.quote:Met die p, ik zou denk gewoon haakjes uitwerken en dan de abc-formule, als 4(p-1)^2>4 is er iig geen antwoord, als 4(p-1)^2=4 is er één antwoord?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het eerste wat je bij zo'n vraag moet bekijken zijn de gedegenereerde gevallen natuurlijk: wanneer is het een eerstegraadsvergelijking?
Ja inderdaad. Deze komt uit een tentamen voor eerstejaars economiestudenten en de docent had hem in eerste instantie zelf ook foutquote:Op donderdag 22 oktober 2009 20:21 schreef thabit het volgende:
Het eerste wat je bij zo'n vraag moet bekijken zijn de gedegenereerde gevallen natuurlijk: wanneer is het een eerstegraadsvergelijking?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dr zal vast een Huysse-se Instinker inzitten, maar toch maar eerst de standaardmethode erop loslaten.quote:Op donderdag 22 oktober 2009 19:59 schreef GlowMouse het volgende:
>> Edit: Of moet ik het zien als twee punten (1,-1labda) en (2,1labda) en daar een y=ax+b formule voor opstellen?
Dat denk ik ja.
Ik kwam trouwens een echt gemene vraag tegen: voor welke p heeft px²+p = (x-1)² twee oplossingen?
px2 + p = x2 - 2x + 1
px2 + p - x2 + 2x - 1 = 0
(p-1)x2 + 2x + p-1 = 0
ABC-formule
A = (p-1)
B = 2
C = (p-1)
D = B2 - 4AC = 4 - 4*(p-1)*(p-1) = 4 - 4p2 + 8p - 4 = 4p(2-p)
voor 2 oplossingen moet 4p(2-p) > 0 zijn; dan geldt voor het interval <0,2>, dus bij inpluggen zou deze moeten kloppen. Maar als we bijv 1 invullen in de originele vgl dat blijkt deze strijdig te zijn.
je antwoord mag natuurlijk niet van lambda afhangen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Correct, dus we zoeken (0,2)\{1}.quote:
[..]
Dr zal vast een Huyssense Instinker inzitten, maar toch maar eerst de standaardmethode erop loslaten.
px2 + p = x2 - 2x + 1
px2 + p - x2 + 2x - 1 = 0
(p-1)x2 + 2x + p-1 = 0
ABC-formule
A = (p-1)
B = 2
C = (p-1)
D = B2 - 4AC = 4 - 4*(p-1)*(p-1) = 4 - 4p2 + 8p - 4 = 4p(2-p)
voor 2 oplossingen moet 4p(2-p) > 0 zijn; dan geldt voor het interval <0,2>, dus bij inpluggen zou deze moeten kloppen. Maar als we bijv 1 invullen in de originele vgl dat blijkt deze strijdig te zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
want voor p=1 reduceert de resulterende vgl. tot 2x=0, en dâkanniequote:Op donderdag 22 oktober 2009 20:32 schreef GlowMouse het volgende:
[..]
Correct, dus we zoeken (0,2)\{1}.
idd, een Huysse-se Instinker van het zuiverste water, enne...
<mierenneukmodus>
de pipo in kwestie had bij jouw ook wel de rode pen gehanteerd vanwege de verkeerde notatie voor een open interval; daar worden nl. deze <x,y> haken gebruikt
<mierenneukmodus>
[ Bericht 29% gewijzigd door ErictheSwift op 22-10-2009 20:48:14 ]
quote:
[..]
want voor p=1 reduceert de resulterende vgl. tot 2x=0, en dâkannie
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oh, wacht, je kan er een basis van maken metquote:Op donderdag 22 oktober 2009 20:32 schreef GlowMouse het volgende:
je antwoord mag natuurlijk niet van lambda afhangen.
Dus dan heb je ?
Klopt iig met dat het geen deelruimte is, want 0-0=/=-2/3
En c zou dan inplaatsvan -2/3 achter de = 0?
Je basis en het resultaat kloppen niet. Sowieso, als je een basis hebt dan heb je een lineaire deelruimte.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:Op donderdag 22 oktober 2009 20:43 schreef GlowMouse het volgende:
want voor p=1 reduceert de resulterende vgl. tot 2x=0, en dâkannie
Damn, kloppen niet met elkaar bedoel je, dus de basis los klopt wel of wat? En is een rechte lijn in R2 niet een lineaire deelruimte? Ik dacht het te snappen, maar dat valt tegen. ;xquote:Op donderdag 22 oktober 2009 20:50 schreef GlowMouse het volgende:
Je basis en het resultaat kloppen niet. Sowieso, als je een basis hebt dan heb je een lineaire deelruimte.
Nog eens legendre symbolen
x2 +7x+13 = 0 mod 17 oplossen.
Dit wilde ik doen met kwadraat afsplitsen, dus als k2 = c (mod 17) schrijven.
maar 7 is oneven. Hoe kan ik dit doen? Vermenigvuldigen met inverse van 7 (mod 17)? Of een ander handigheidje?
x2 +7x+13 = 0 mod 17 oplossen.
Dit wilde ik doen met kwadraat afsplitsen, dus als k2 = c (mod 17) schrijven.
maar 7 is oneven. Hoe kan ik dit doen? Vermenigvuldigen met inverse van 7 (mod 17)? Of een ander handigheidje?
kloep kloep
x1 = 1-lquote:
[..]
Damn, kloppen niet met elkaar bedoel je, dus de basis los klopt wel of wat? En is een rechte lijn in R2 niet een lineaire deelruimte? Ik dacht het te snappen, maar dat valt tegen. ;x
x2 = 2+l
je kunt het omschrijven naar bv. x2 = (1-l)+1+2l = x1+1+2l maar als je l dan invult dan heb je helemaal geen garantie meer dat x1=1-l want voor x1 kun je dan nog alles kiezen.
De juiste methode is om l helemaal kwijt te raken. Dat lukt bv. door beide vergelijkingen op te tellen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
4(x2 + 7x + 13) = 4x2 + 28x + 52 = (2x + 7)2 + 3.quote:Op donderdag 22 oktober 2009 21:04 schreef Borizzz het volgende:
Nog eens legendre symbolen
x2 +7x+13 = 0 mod 17 oplossen.
Dit wilde ik doen met kwadraat afsplitsen, dus als k2 = c (mod 17) schrijven.
maar 7 is oneven. Hoe kan ik dit doen? Vermenigvuldigen met inverse van 7 (mod 17)? Of een ander handigheidje?
Volgens mijn docent moet ik b=2*k schrijven en dan b maal de inverse van 2 (mod 17) schrijven. Maar dit zie ik nog niet zo gebeuren...quote:Op donderdag 22 oktober 2009 21:23 schreef Riparius het volgende:
[..]
4(x2 + 7x + 13) = 4x2 + 28x + 52 = (2x + 7)2 + 3.
kloep kloep
Modulo 17 bestaat er geen even of oneven, 2 is immers inverteerbaar. Delen door 2 is ofwel 2n=1 mod 17 oplossen (bijvoorbeeld met Euclides als) ofwel direct zien dat 9 een inverse van 2 is en dus met 9 vermenigvuldigen.quote:Op donderdag 22 oktober 2009 21:04 schreef Borizzz het volgende:
Nog eens legendre symbolen
x2 +7x+13 = 0 mod 17 oplossen.
Dit wilde ik doen met kwadraat afsplitsen, dus als k2 = c (mod 17) schrijven.
maar 7 is oneven. Hoe kan ik dit doen? Vermenigvuldigen met inverse van 7 (mod 17)? Of een ander handigheidje?
Oh, zo oké. Dus x1+x2=3 dan.quote:Op donderdag 22 oktober 2009 21:16 schreef GlowMouse het volgende:
[..]
x1 = 1-l
x2 = 2+l
je kunt het omschrijven naar bv. x2 = (1-l)+1+2l = x1+1+2l maar als je l dan invult dan heb je helemaal geen garantie meer dat x1=1-l want voor x1 kun je dan nog alles kiezen.
De juiste methode is om l helemaal kwijt te raken. Dat lukt bv. door beide vergelijkingen op te tellen.
Laatste keer vanavond dat ik stoor:
Klopt het dat wanneer f(x) = 5 . ewortel[6x], dan is f'(x) = 5 . ewortel[6x] . 3x-1/2 ?
Heb dan de kettingregel en de productregel gebruikt.
Klopt het dat wanneer f(x) = 5 . ewortel[6x], dan is f'(x) = 5 . ewortel[6x] . 3x-1/2 ?
Heb dan de kettingregel en de productregel gebruikt.
Oh really?
De afgeleide van wortel[6x] is 3*(6x)^(-0.5)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nee, klopt niet.quote:Op donderdag 22 oktober 2009 21:58 schreef Matthijs- het volgende:
Laatste keer vanavond dat ik stoor:
Klopt het dat wanneer f(x) = 5 . ewortel[6x], dan is f'(x) = 5 . ewortel[6x] . 3x-1/2 ?
Heb dan de kettingregel en de productregel gebruikt.
Hoe herschrijf je wortel[6x] dan GM? Ik had het herschreven als 6x-1/2, wat waarschijnlijk de foute differentiatie opleverde.quote:Op donderdag 22 oktober 2009 22:00 schreef GlowMouse het volgende:
De afgeleide van wortel[6x] is 3*(6x)^(-0.5)
Ik en wiskunde
Oh really?
Doe maar (6x)1/2quote:Op donderdag 22 oktober 2009 22:12 schreef Matthijs- het volgende:
[..]
Hoe herschrijf je wortel[6x] dan GM? Ik had het herschreven als 6x-1/2, wat waarschijnlijk de foute differentiatie opleverde.
Ik en wiskunde
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
In het algemeen geldt (ab)^c = a^c * b^c.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dat is het niet.quote:
[..]
Maar waarom is de afgeleide daarvan dan 18x-1/2?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Rondje spreek je uit als 'na'. S na T Dus eerst T dan S: S(T(x)).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een vraagje over elliptische krommen.
Gegeven een rationaal punt (a,b) op de kromme gedefinieerd door de vergelijking y2=-x4+ c (met c een rationaal getal ongelijk aan 0) wil ik deze vergelijking transformeren tot de weierstrass vgl y'2 =(polynoom van graad 3).
Enig idee hoe dat werkte?
Gegeven een rationaal punt (a,b) op de kromme gedefinieerd door de vergelijking y2=-x4+ c (met c een rationaal getal ongelijk aan 0) wil ik deze vergelijking transformeren tot de weierstrass vgl y'2 =(polynoom van graad 3).
Enig idee hoe dat werkte?
Ken je Riemann-Roch?quote:Op vrijdag 23 oktober 2009 12:41 schreef Optimistic1 het volgende:
Ik heb een vraagje over elliptische krommen.
Gegeven een rationaal punt (a,b) op de kromme gedefinieerd door de vergelijking y2=-x4+ c (met c een rationaal getal ongelijk aan 0) wil ik deze vergelijking transformeren tot de weierstrass vgl y'2 =(polynoom van graad 3).
Enig idee hoe dat werkte?
Calculus 17.1 vraag 21:
y'' + 16y = 0
y(pi/4) = -3
y'(pi/4) = 4
Ik heb bij die opgave moeite met het begrijpen van een tussenstap die ik op een uitwerking vond. (Toen ik het op mezelf probeerde kwam ik niet van de dubbele paren sinus en cosinus af.
Hier is mijn poging:
Als afbeelding:
y'' + 16y = 0
y(pi/4) = -3
y'(pi/4) = 4
Ik heb bij die opgave moeite met het begrijpen van een tussenstap die ik op een uitwerking vond. (Toen ik het op mezelf probeerde kwam ik niet van de dubbele paren sinus en cosinus af.
| 1 2 | y = c_1 cos(4x) + c_2 sin(4x) |
Hier is mijn poging:
| 1 2 3 4 5 | y = c_1 * e ^ 4 (cos x - i sin x) + c_2 * e ^ 4 (cos x - i sin x) \\ y = (c_1 + c_2) * e ^ 4 (cos x - i sin x) \\ how? \\ y = c_1 cos(4x) + c_2 sin(4x) \\ |
Als afbeelding:
Jesus hates you.
Klopt geen hout van, je respecteert om te beginnen de elementaire rekenregels voor machten al niet. Je kunt niet zomaar die e-macht (met een reële exponent) buiten haakjes halen. Oftewel, apq is niet hetzelfde als het product van ap en aq.quote:Op vrijdag 23 oktober 2009 17:17 schreef Hondenbrokken het volgende:
Calculus 17.1 vraag 21:
y'' + 16y = 0
y(pi/4) = -3
y'(pi/4) = 4
Ik heb bij die opgave moeite met het begrijpen van een tussenstap die ik op een uitwerking vond. (Toen ik het op mezelf probeerde kwam ik niet van de dubbele paren sinus en cosinus af.
[ code verwijderd ]
Hier is mijn poging:
[ code verwijderd ]
Als afbeelding:
[ afbeelding ]
[ Bericht 0% gewijzigd door Riparius op 23-10-2009 17:40:51 ]
Je hebt gelijk. Die exponenten worden vermenigvuldigd in plaats van opgeteld.
Dan krijg ik:
En het maakt natuurlijk niet uit hoe je de constanten noemt.
Dan krijg ik:
| 1 2 3 4 5 6 7 | y = c_1 * (cos 4x - i sin 4x) + c_2 * (cos -4x - i sin -4x) \\ y = c_1 * (cos 4x - i sin 4x) + c_2 * (cos 4x + i sin 4x) \\ y = (c_1 + c_2) * (cos 4x) + (c_2 - c_1) * sin(4x) \\ \\ Subs: d_1 = (c_1 + c_2) en d_2 = (c_2 - c_1) \\ y = d_1 * (cos 4x) + d_2 * sin(4x) \\ |
En het maakt natuurlijk niet uit hoe je de constanten noemt.
Jesus hates you.
Dit is nog steeds niet goed. Je kent toch wel de formule van Euler:quote:Op vrijdag 23 oktober 2009 19:37 schreef Hondenbrokken het volgende:
Je hebt gelijk. Die exponenten worden vermenigvuldigd in plaats van opgeteld.
Dan krijg ik:
[ code verwijderd ]
En het maakt natuurlijk niet uit hoe je de constanten noemt.
eiφ = cos φ + i∙sin φ
En waar blijft in jouw uitwerking die i bij je sinustermen?
| 1 2 3 4 5 6 7 | y = c_1 * (\cos 4x + i \sin 4x) + c_2 * (\cos -4x + i \sin -4x) \\ y = c_1 * (\cos 4x + i \sin 4x) + c_2 * (\cos 4x - i \sin 4x) \\ y = (c_1 + c_2) * (\cos 4x) + (c_1 - c_2) * i \sin(4x) \\ \\ Subs: d_1 = (c_1 + c_2) ; d_2 = (c_1 - c_2) \\ y = d_1 * (\cos 4x) + d_2 * i \sin(4x) \\ |
Maar dan snap ik alsnog niet hoe ik van die i af moet komen.
Jesus hates you.
Nou, niet door de i te verdonkeremanen natuurlijk. Je hebt:quote:Op vrijdag 23 oktober 2009 20:27 schreef Hondenbrokken het volgende:
[ code verwijderd ]
Maar dan snap ik alsnog niet hoe ik van die i af moet komen.
d1 = c1 + c2
d2 = i∙(c1 - c2)
Dan zijn de oplossingen van de DV te schrijven als:
y = d1∙cos 4x + d2∙sin 4x
Wat is nu het probleem?
Ik ken de stelling zoals het in Silverman staat. Die stelling 'geeft' geen algortime om gegeven een rationaal punt op 'y^2= (irri. polynoom van graad 4) om dit te transformeren tot een elliptische kromme. In het boek van Cassels is er wel een algortime dat een aantal transformaties gebruikt. Ik geloof dat Riemann-Roch kan helpen uitleggen hoe men op het idee komt dit soort transformaties te doen maar bij mijn ontbreekt het inzicht.quote:
Klopt, er zijn inderdaad een aantal boeken die met formules goochelen. Dat zijn van die methoden die je nooit kunt onthouden. Zou je zoiets willen toepassen, moet je elke keer weer dat boek erbij pakken.quote:Op zaterdag 24 oktober 2009 13:01 schreef Optimistic1 het volgende:
[..]
Ik ken de stelling zoals het in Silverman staat. Die stelling 'geeft' geen algortime om gegeven een rationaal punt op 'y^2= (irri. polynoom van graad 4) om dit te transformeren tot een elliptische kromme. In het boek van Cassels is er wel een algortime dat een aantal transformaties gebruikt. Ik geloof dat Riemann-Roch kan helpen uitleggen hoe men op het idee komt dit soort transformaties te doen maar bij mijn ontbreekt het inzicht.
Met Riemann-Roch heb je een methode die in je hoofd past. Misschien dat die methode wat meer stappen vergt, maar je begrijpt in elk geval wat je aan het doen bent.
Goed, R-R dus. Zij C je kromme en P een rationaal punt op C. We gaan ervan uit dat C compleet en niet-singulier is. Voor gehele n heb je de ruimte L(nP) van rationale functies op C die in P een pool van orde hooguit n hebben en buiten P regulier zijn. De ruimte L(nP) is eindig-dimensionaal en R-R zegt iets over de dimensie ervan. In het geval van krommen van geslacht 1 kun je op die manier zelfs precies de dimensie bepalen. Er komt dan het volgende uit:
dim L(nP) = 0 als n<0 (niet-constante functies hebben evenveel nulpunten als polen, geteld met multipliciteit),
dim L(nP) = 1 als n=0 of n=1 (je hebt dan alleen constante functies),
dim L(nP) = n als n>1 (dus als je n groter maakt krijg je altijd functies die je nog niet eerder had).
Hieruit volgt dat L(2P) een niet-constante functie x bevat en L(3P) een y bevat die niet al in L(2P) ligt.
Nu zitten x3, x2, x, 1, y2, xy, y allemaal in L(6P). Dit zijn 7 elementen van een 6-dimensionale ruimte, dus er is een relatie tussen. Die relatie geeft je een Weierstrassvgl.
Nu geeft het bovenstaande nog niet een manier om de x en de y ook te vinden. Dat gaan we ook pas doen als je eerst goed begrijpt wat ik zojuist ingetikt heb.
.
Magma kan het. Maar dat is geen gratis programma dus dan moet je maar hopen dat je universiteit het heeft.quote:Op zaterdag 24 oktober 2009 13:31 schreef Optimistic1 het volgende:
Bestaat er een programma dat dat doet? ik zie dat dat algoritme veel prutswerk is.
Ik heb een coole site gevonden. Je kunt er van alles en nog wat berekenen! Ik dacht ik deel het met jullie:
http://www.martindalecenter.com/Calculators.html
http://www.martindalecenter.com/Calculators.html
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Hoi S&S:
Ik heb een vraag over de normaalkromme. Wat ik weet:
De kans om in het rode gebied te vallen is 68%. (1 Sigma buiten het gemiddelde, zo zeg je dat toch?)
De kans om in het groene gebied te vallen is 27% (2 sigma buiten het gemiddelde)
De kans om buiten de groene en rode gebieden te vallen is 5%.
Mijn vraag: Weet iemand wat de exacte kans zijn om in het gebied van 3 sigma, 4 sigma en 5 sigma te vallen. Ik weet dat die kansen zeer klein zijn, maar ik kan ze nergens vinden op internet en ben vergeten of je dat ook zelf kan berekenen.
Ik heb een vraag over de normaalkromme. Wat ik weet:
De kans om in het rode gebied te vallen is 68%. (1 Sigma buiten het gemiddelde, zo zeg je dat toch?)
De kans om in het groene gebied te vallen is 27% (2 sigma buiten het gemiddelde)
De kans om buiten de groene en rode gebieden te vallen is 5%.
Mijn vraag: Weet iemand wat de exacte kans zijn om in het gebied van 3 sigma, 4 sigma en 5 sigma te vallen. Ik weet dat die kansen zeer klein zijn, maar ik kan ze nergens vinden op internet en ben vergeten of je dat ook zelf kan berekenen.
How you play the cards you are dealt is all that matters.
hier heb je het lijstje:
| 1 2 3 4 5 6 7 8 9 10 11 | >> 2*(normcdf( i)-normcdf(i-1)) ans = 0.68268949213709 0.27181024396656 0.04280046783310 0.00263645357959 0.00006276918052 0.00000057132997 |
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Dankjewel.quote:Op zaterdag 24 oktober 2009 20:57 schreef GlowMouse het volgende:
hier heb je het lijstje:
[ code verwijderd ]
How you play the cards you are dealt is all that matters.
Kan iemand hier mij grafisch tonen hoe het nou zit met codomein. Gewoon een voorbeeld in een grafiek ofzo, wat nou precies het codomein is. Jipjanneke stijl. Want codomein is ook bereik toch? Echt een epic fail ben ik 
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Kijk even naar het plaatje bij dit artikel. Bereik en codomein zijn niet hetzelfde begrip. Het is wel zo dat het bereik altijd een deelverzameling van het codomein is, dus bereik en codomein kunnen wel samenvallen.quote:Op zaterdag 24 oktober 2009 21:26 schreef Burakius het volgende:
Kan iemand hier mij grafisch tonen hoe het nou zit met codomein. Gewoon een voorbeeld in een grafiek ofzo, wat nou precies het codomein is. Jipjanneke stijl. Want codomein is ook bereik toch? Echt een epic fail ben ik
Ja die had ik al bekeken en snapte er vrij weinig van. Is het niet mogelijk een grafiekje te tekenen ofzo waarin ze staan aangegeven?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Er is verder weinig aan te tekenen. Neem als voorbeeld de functiequote:Op zaterdag 24 oktober 2009 22:16 schreef Burakius het volgende:
Ja die had ik al bekeken en snapte er vrij weinig van. Is het niet mogelijk een grafiekje te tekenen ofzo waarin ze staan aangegeven?
f: ℝ ↦ ℝ,
gedefinieerd door f(x) = x2, of zoals het (in een soort hybride notatie) ook wel wordt geschreven:
f: x ↦ x2
Dan is de verzameling ℝ van de reële getallen het domein van de functie en tevens het codomein, maar het bereik bestaat uit de niet-negatieve reële getallen, want het kwadraat van een reëel getal is immers nooit negatief.
Bij een (formele) definitie van een functie geef je ook het domein en het codomein, b.v.:
f(x): , x ex.
De definitie zegt: het domein (in rood) is ℝ en het codomein (in blauw) is óók ℝ. Dus je kijkt gewoon naar de functiedefinitie om domein en codomein af te lezen.
Het bereik hangt echter (formeel) gezien af van de waarden die daadwerkelijk optreden, in het geval van ex zijn dit alleen positieve getallen, kortom het bereik van die functie is ℝ+. En dat is ook wat dat plaatje laat zien:
Bron: Wikipedia. Maker: Damien Karras. Publiek Domein.
Het domein is rood, het codomein is blauw, en het bereik is gelig. Dit omdat het bereik niet hoeft samen te vallen met het codomein. Soms is dit wel het geval, heb je b.v.:
f(x): ℝ → ℝ, x 2x dan is zowel codomein als bereik ℝ.
f(x): , x ex.
De definitie zegt: het domein (in rood) is ℝ en het codomein (in blauw) is óók ℝ. Dus je kijkt gewoon naar de functiedefinitie om domein en codomein af te lezen.
Het bereik hangt echter (formeel) gezien af van de waarden die daadwerkelijk optreden, in het geval van ex zijn dit alleen positieve getallen, kortom het bereik van die functie is ℝ+. En dat is ook wat dat plaatje laat zien:
Bron: Wikipedia. Maker: Damien Karras. Publiek Domein.
Het domein is rood, het codomein is blauw, en het bereik is gelig. Dit omdat het bereik niet hoeft samen te vallen met het codomein. Soms is dit wel het geval, heb je b.v.:
f(x): ℝ → ℝ, x 2x dan is zowel codomein als bereik ℝ.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Oke dus als ik het goed begrijp, is het "domein" de getallen die je kunt invullen voor een functie waarbij deze geldig is. En de codomein is het resultaat van het invullen van die reële getallen. Zoals bij het voorbeeld is dan bij het invullen van x^2 nooit een negatief getal mogelijk. Waardoor het bereik alle positieve getallen van R is.
Ik snap het begrip bereik dan. Maar het begrip codomein is mij dan nog een beetje vaag. Is er een voorbeeld te geven waarbij domein en codomein verschillend zijn?
Ik snap het begrip bereik dan. Maar het begrip codomein is mij dan nog een beetje vaag. Is er een voorbeeld te geven waarbij domein en codomein verschillend zijn?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Codomein is gewoon een definitiekwestie, als iemand zegt:
f(x): ℝ → , x x2, dan is het codomein dus alle niet-negatieve getallen.
Of neem b.v. | | voor 2-dimensionale vectoren:
|v|: ℝ2 → ℝ, v √(v1² + v2²).
Domein is ℝ², codomein ℝ (volgt gewoon uit de definitie), maar het bereik is natuurlijk alleen de positieve getallen, want een vector heeft geen negatieve lengte.
f(x): ℝ → , x x2, dan is het codomein dus alle niet-negatieve getallen.
Of neem b.v. | | voor 2-dimensionale vectoren:
|v|: ℝ2 → ℝ, v √(v1² + v2²).
Domein is ℝ², codomein ℝ (volgt gewoon uit de definitie), maar het bereik is natuurlijk alleen de positieve getallen, want een vector heeft geen negatieve lengte.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Oke nou het is me eindelijk duidelijk. Nu ga ik Fermat oplossen (of spel ik die dude zijn achternaam nog steeds verkeerd )
)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik kan je de Kleine stelling van Fermat dan aanraden om mee te beginnen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Laat ik eerst me pre-master + master halenquote:Op zaterdag 24 oktober 2009 23:07 schreef Iblis het volgende:
Ik kan je de Kleine stelling van Fermat dan aanraden om mee te beginnen.
Daarna heb ik een jaar werkvrij . Wie weet dan.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Zoals ik het begrijp is codomein het domein van de inverse.
Alleen als f(x) = x^2 dan heeft f(x): R -> R geen zin, want de inverse f{^-1}(x) = sqrt(x) geeft als x < 0 complexe resultaten en die vallen buiten R, dus hebben die dan geen oplossing, dus dan kan R helemaal geen codomein van f zijn.
Dus ik snap het eigenlijk nog steeds niet.
Alleen als f(x) = x^2 dan heeft f(x): R -> R geen zin, want de inverse f{^-1}(x) = sqrt(x) geeft als x < 0 complexe resultaten en die vallen buiten R, dus hebben die dan geen oplossing, dus dan kan R helemaal geen codomein van f zijn.
Dus ik snap het eigenlijk nog steeds niet.
Jesus hates you.
Nee, dat is het bereik (mits f inverteerbaar is). Lees de posts hierboven; Riparius legt het prima uit.quote:
Zoals ik het begrijp is codomein het domein van de inverse.
Alleen als f(x) = x^2 dan heeft f(x): R -> R geen zin, want de inverse f{^-1}(x) = sqrt(x) geeft als x < 0 complexe resultaten en die vallen buiten R, dus hebben die dan geen oplossing, dus dan kan R helemaal geen codomein van f zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een vraag over een som invoeren in excell.
De som is
Hoe doe ik die met haakjes en dakjes invoeren dat hij niet denkt dat die -3 geen deel meer is van het verband?
De som is
Hoe doe ik die met haakjes en dakjes invoeren dat hij niet denkt dat die -3 geen deel meer is van het verband?
wat bedoel je met 'geen deel van het verband'?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik weet het ook niet helemaal meerquote:Op zondag 25 oktober 2009 @ 13:44 schreef GlowMouse het volgende:
wat bedoel je met 'geen deel van het verband'?
Maar dat hij denkt dat. ^x-3 is, dat de x nog klein is maar de -3 een normaal getal.Volgens mij maak ik het alleen maar moeilijker om te begrijpen
Zoals hij daar staat wil je =2^(x-3).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Nog een vraag (Lekker bezig )
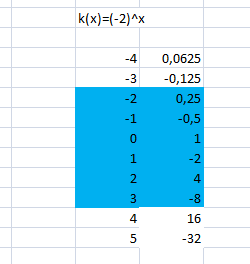
Nu moet ik een exponentiele functie doen.
Die lopen vloeiend enzo.
Hoe kán dit de uitkomst zijn? Ik heb alleen geprobeerd om (-2)^x te doen, en -2^x, maar allebei heeft dezelfde uitkomst. Ik ben niet wiskundig, maar wat er uit deze berekening komt is géén exponentiele functie.
Wat heb ik verkeerd gedaan?
) Nu moet ik een exponentiele functie doen.
Die lopen vloeiend enzo.
Hoe kán dit de uitkomst zijn? Ik heb alleen geprobeerd om (-2)^x te doen, en -2^x, maar allebei heeft dezelfde uitkomst. Ik ben niet wiskundig, maar wat er uit deze berekening komt is géén exponentiele functie.
Wat heb ik verkeerd gedaan?
Je hebt nu f(x) = a*b^t met a=1 en b=-2. En dat is geen exponentiële functie want dan moet b positief zijn.
-2^x zou wel een andere grafiek moeten geven (dan a=-1 en b=2).
-2^x zou wel een andere grafiek moeten geven (dan a=-1 en b=2).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
-2^x geeft juist die tabel, even kijken wat er gebeurt met haakjes bij allesquote:Op zondag 25 oktober 2009 @ 14:54 schreef GlowMouse het volgende:
Je hebt nu f(x) = a*b^t met a=1 en b=-2. En dat is geen exponentiële functie want dan moet b positief zijn.
-2^x zou wel een andere grafiek moeten geven (dan a=-1 en b=2).
Edit, met haakjes is het hetzelfde
Lelijk van Excel, dan moet je haakjes gebruiken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Maar hoe dan? Als ik -2 tussen haakjes zet, krijg ik dus dezelfde uitkomst als zonder haakjes Daarom ben ik zo in de war.
Daarom ben ik zo in de war.
Wat wil je eerst doen? -2 uitrekenen of eerst 2^x uitrekenen?quote:
Maar hoe dan? Als ik -2 tussen haakjes zet, krijg ik dus dezelfde uitkomst als zonder haakjes
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik weet het nietquote:Op zondag 25 oktober 2009 @ 15:13 schreef GlowMouse het volgende:
[..]
Wat wil je eerst doen? -2 uitrekenen of eerst 2^x uitrekenen?
In mijn reader staat dus.-2^x
En aangezien ik dan een of ander puntig ding krijg als grafiek, is dat zekerweten fout. En als ik de -2 tussen haakjes zet. Heb ik nogsteeds een puntig ding
http://nl.wikipedia.org/wiki/Bewerkingsvolgordequote:
[..]
Ik weet het niet
-2^x
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ja, dat weet ik allemaal, maar nog snap ik niet wat ik verkeerd doe. Omdat haakjes eerst verwerkt worden, zou ik -2 eerst tussen haakjes moeten zetten, toch? Omdat anders de min genegerd wordt en gelijk naar de ^ gekeken wordt, toch?quote:Op zondag 25 oktober 2009 @ 15:17 schreef GlowMouse het volgende:
[..]
http://nl.wikipedia.org/wiki/Bewerkingsvolgorde
Als je -2x hebt, moet je eerst 2x uitrekenen. Excel doet dat blijkbaar niet. Hoe los je dat op.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Om heel eerlijk te zijn gaat het volgende om een opdracht die ik moet maken.
Maar ik ben zelf helemaal geen wiskundige, althans ik ben bij lange na niet zo diep de wiskunde ingegaan als voor mijn idee deze vraag eist.
Ultrametric Trees
Definition 1: ultrametric tree
Let D be a symmetric n x n matrix of real numbers. An ultrametric tree T is a tree with the following properties:
* T contains n leaves and each leave is labeled by one row/column of D;
* Each internal node of T is labeled by a value of D and has at least two children;
* For each path from a leaf to the root, the values on the nodes are given in increasing order;
* For each pair (i,j) of leaves the following holds: The last common ancestor of i and j in T is labeled using the value D(i,j).
Definition 2: Ultrametric Distance
A symmetric Matrix D of real numbers defines an ultrametric Distance if and only if for each triple of indices i,j,k holds:
The maximum of the three distances D(i,j), D(i,k) and D(j,k) is not unique; or in other words, two of the distances are equal while a third is smaller (or equal as well).
Exercise
Prove the following statement:
A symmetric Matrix D corresponds to an ultrametric tree T if and only if D defines an ultrametric distance.
Ik vraag niet om een direct antwoord, maar of iemand mij kan uitleggen hoe ik nou eigenlijk een ultrametric tree maak. En als tweede hoe ik een vector k kan hebben als ik enkel i & j heb? Of moet ik soms voor een willekeurige vector k nagaan dat de definitie van ultrametric distance klopt wanneer mijn matrix symmetrisch is? Ik heb me al een ongeluk gezocht naar websites die het me uitleggen, maar ze lijken elkaar zelfs tegen te spreken? De ene geeft als 4e conditie d(x,y) =< d(x,z)+d(y,z) en de andere d(x,y) =< max(d(x,z),d(y,z))...
Het ergste nog wel is dat het vak tot nu toe helemaal niet echt gaat over dit soort wiskunde bewijzen (het is juist biologie...) en in geen van de slides wordt ook maar een stap richting 'trees' gemaakt. Het is dus hopeloos zoeken en proberen te begrijpen tot je een ons weegt.
Maar ik ben zelf helemaal geen wiskundige, althans ik ben bij lange na niet zo diep de wiskunde ingegaan als voor mijn idee deze vraag eist.
Ultrametric Trees
Definition 1: ultrametric tree
Let D be a symmetric n x n matrix of real numbers. An ultrametric tree T is a tree with the following properties:
* T contains n leaves and each leave is labeled by one row/column of D;
* Each internal node of T is labeled by a value of D and has at least two children;
* For each path from a leaf to the root, the values on the nodes are given in increasing order;
* For each pair (i,j) of leaves the following holds: The last common ancestor of i and j in T is labeled using the value D(i,j).
Definition 2: Ultrametric Distance
A symmetric Matrix D of real numbers defines an ultrametric Distance if and only if for each triple of indices i,j,k holds:
The maximum of the three distances D(i,j), D(i,k) and D(j,k) is not unique; or in other words, two of the distances are equal while a third is smaller (or equal as well).
Exercise
Prove the following statement:
A symmetric Matrix D corresponds to an ultrametric tree T if and only if D defines an ultrametric distance.
Ik vraag niet om een direct antwoord, maar of iemand mij kan uitleggen hoe ik nou eigenlijk een ultrametric tree maak. En als tweede hoe ik een vector k kan hebben als ik enkel i & j heb? Of moet ik soms voor een willekeurige vector k nagaan dat de definitie van ultrametric distance klopt wanneer mijn matrix symmetrisch is? Ik heb me al een ongeluk gezocht naar websites die het me uitleggen, maar ze lijken elkaar zelfs tegen te spreken? De ene geeft als 4e conditie d(x,y) =< d(x,z)+d(y,z) en de andere d(x,y) =< max(d(x,z),d(y,z))...
Het ergste nog wel is dat het vak tot nu toe helemaal niet echt gaat over dit soort wiskunde bewijzen (het is juist biologie...) en in geen van de slides wordt ook maar een stap richting 'trees' gemaakt. Het is dus hopeloos zoeken en proberen te begrijpen tot je een ons weegt.
is het niet zo dat bij -2^x dat je een positief getal krijgt bij een x dat even is en een negatief getal bij oneven?quote:Op zondag 25 oktober 2009 15:21 schreef RenRen- het volgende:
Ik heb geen idee, mijn hoofd blokkeert alles op het moment
-2^2 -> -2*-2 = 4, -2^3 -> -2*-2*-2 = -8. In dat geval zou je gewoon 2^x doen en zeggen dat als even -> positief, en oneven zet er een - voor.
(-2)^x is voor mijn idee doorgaans hetzelfde als -2^x.
Als je enkel negatief wilt moet je iets als -(2)^x doen... iets als -1 * 2^x.
Mogelijk is de - voor de 2^x gewoon als een aanduiding als in:
- je hebt zus
- je hebt zo
[ Bericht 23% gewijzigd door koffiegast op 25-10-2009 17:25:52 ]
Nee, normaliter heeft machtsverheffen prioriteit. Dus -2x is -(2x), en als je wilt wat jij wilt doe je (-2)x. Excel interpreteert -2x echter blijkbaar als (-2)x en niet als -(2x).quote:
[..]
is het niet zo dat bij -2^x dat je een positief getal krijgt bij een x dat even is en een negatief getal bij oneven?
-2^2 -> -2*-2 = 4, -2^3 -> -2*-2*-2 = -8
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja, al verholpen voordat ik jouw bericht las.quote:
Je zit er ook bovenop!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ja, dát werkte dus.quote:Op zondag 25 oktober 2009 @ 17:24 schreef Iblis het volgende:
[..]
Nee, normaliter heeft machtsverheffen prioriteit. Dus -2x is -(2x), en als je wilt wat jij wilt doe je (-2)x. Excel interpreteert -2x echter blijkbaar als (-2)x en niet als -(2x).
Daarom raakte ik zo in de war.
Heel erg bedankt
kan iemand mij helpen met deze formule: N = 480x2(kwadraat) - 40x3(kwadraat).
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?
mundus vult decipi
N = 480x² - 40x³ ?
Kun je toch zo invullen op een grafische rekenmachine?
Kun je toch zo invullen op een grafische rekenmachine?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
y1 = (480*X^2) - (40*X^3)quote:Op zondag 25 oktober 2009 18:08 schreef Gratau het volgende:
kan iemand mij helpen met deze formule: N = 480x2(kwadraat) - 40x3(kwadraat).
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?
doe ik dan, de ( ) is wellicht niet eens nodig, maar doe ik voor de zekerheid.
* gaat voor -, de haakjes zijn dus niet nodig.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Schijf die formule om te beginnen eens wat begrijpelijker op. Je kunt hier gebruik maken van subscript en superscript, dus doe dat dan ook.quote:Op zondag 25 oktober 2009 18:08 schreef Gratau het volgende:
kan iemand mij helpen met deze formule: N = 480x2(kwadraat) - 40x3(kwadraat).
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?
ja, maar dan zie ik hem niet of heel klein ofzo. ik kan de juiste waarden niet vinden voor de X en Y min/maxquote:Op zondag 25 oktober 2009 18:15 schreef GlowMouse het volgende:
N = 480x² - 40x³ ?
Kun je toch zo invullen op een grafische rekenmachine?
mundus vult decipi
window aanpassen, eerst je x kiezen en dan bedenken welke y daarbij horen.quote:
[..]
ja, maar dan zie ik hem niet of heel klein ofzo. ik kan de juiste waarden niet vinden voor de X en Y min/max
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je moet twee implicaties bewijzen: boom => matrix en matrix => boom. Ik zou beginnen met die eerste als ik jou was. Daarna kan het handig zijn om wat simpele voorbeeldjes uit te werken voor de ander implicatie, zodat je ziet wat er gebeurt.quote:Op zondag 25 oktober 2009 17:15 schreef koffiegast het volgende:
Om heel eerlijk te zijn gaat het volgende om een opdracht die ik moet maken.
Maar ik ben zelf helemaal geen wiskundige, althans ik ben bij lange na niet zo diep de wiskunde ingegaan als voor mijn idee deze vraag eist.
Ultrametric Trees
Definition 1: ultrametric tree
Let D be a symmetric n x n matrix of real numbers. An ultrametric tree T is a tree with the following properties:
* T contains n leaves and each leave is labeled by one row/column of D;
* Each internal node of T is labeled by a value of D and has at least two children;
* For each path from a leaf to the root, the values on the nodes are given in increasing order;
* For each pair (i,j) of leaves the following holds: The last common ancestor of i and j in T is labeled using the value D(i,j).
Definition 2: Ultrametric Distance
A symmetric Matrix D of real numbers defines an ultrametric Distance if and only if for each triple of indices i,j,k holds:
The maximum of the three distances D(i,j), D(i,k) and D(j,k) is not unique; or in other words, two of the distances are equal while a third is smaller (or equal as well).
Exercise
Prove the following statement:
A symmetric Matrix D corresponds to an ultrametric tree T if and only if D defines an ultrametric distance.
Ik vraag niet om een direct antwoord, maar of iemand mij kan uitleggen hoe ik nou eigenlijk een ultrametric tree maak. En als tweede hoe ik een vector k kan hebben als ik enkel i & j heb? Of moet ik soms voor een willekeurige vector k nagaan dat de definitie van ultrametric distance klopt wanneer mijn matrix symmetrisch is? Ik heb me al een ongeluk gezocht naar websites die het me uitleggen, maar ze lijken elkaar zelfs tegen te spreken? De ene geeft als 4e conditie d(x,y) =< d(x,z)+d(y,z) en de andere d(x,y) =< max(d(x,z),d(y,z))...
Het ergste nog wel is dat het vak tot nu toe helemaal niet echt gaat over dit soort wiskunde bewijzen (het is juist biologie...) en in geen van de slides wordt ook maar een stap richting 'trees' gemaakt. Het is dus hopeloos zoeken en proberen te begrijpen tot je een ons weegt.
En i, j en k zijn geen vectoren maar indices, D(i, j) is dan het getal dat in de matrix op plek (i, j) staat, etc. Je moet het zo zien: je hebt n punten, en daartussen staan afstanden gedefinieerd, je indices komen met die punten overeen. De afstand tussen i en j staat dus op plek (i, j). Een afstand moet normaliter voldoen aan de driehoeksongelijkheid, dat wil zeggen D(i, j) + D(j, k) <= D(i, k) voor elk drietal punten i, j, k. Zo'n afstand heet ultrametrisch als-ie aan de sterkere vorm van de driehoeksongelijkheid voldoet die jij boven beschreven hebt.
maar wat is dan k? Dat kan ik dus niet echt terugvinden in een symmetrische matrix van i en j enkel, het lijkt me verder stug k willekeurig te doen, ik bedoel dus: is er iets waarvan ik het kan afleiden? Verder zit ik nog beetje vast met hoe ik zo'n boom precies maak.
k is net als i en j gewoon een index, dus een element van {1, ..., n}.quote:Op zondag 25 oktober 2009 22:58 schreef koffiegast het volgende:
maar wat is dan k? Dat kan ik dus niet echt terugvinden in een symmetrische matrix van i en j enkel, het lijkt me verder stug k willekeurig te doen, ik bedoel dus: is er iets waarvan ik het kan afleiden? Verder zit ik nog beetje vast met hoe ik zo'n boom precies maak.
Maar dat is mijn probleem, als ik slechts 2 strings heb met elk een eigen index, van wat is dan index k? Ik bekijk het zeker compleet verkeerd ofzoquote:Op zondag 25 oktober 2009 23:12 schreef thabit het volgende:
[..]
k is net als i en j gewoon een index, dus een element van {1, ..., n}.
In de driehoeksongelijkheid heb je er 3 nodig. Je relateert dan immers de 3 onderlinge afstanden tussen 3 punten met elkaar.quote:Op zondag 25 oktober 2009 23:14 schreef koffiegast het volgende:
[..]
Maar dat is mijn probleem, als ik slechts 2 strings heb met elk een eigen index, van wat is dan index k? Ik bekijk het zeker compleet verkeerd ofzo
Hoi ik heb morgen een wiskunde B toets en ik snap niet hoe ik het volgend kan uitreken
1.5^x = .5log(x)
ik moet x weten
iemand suggesties??
1.5^x = .5log(x)
ik moet x weten
iemand suggesties??
Beware of the Raping Zebra's
In het algemeen kun je zulke vergelijkingen niet symbolisch oplossen. Probeer nu eerst maar eens na te gaan of de vergelijking überhaupt wel oplossingen heeft; het linkerdeel van de vergelijking lijkt een stuk groter dan het rechterdeel.quote:Op maandag 26 oktober 2009 18:16 schreef netolk het volgende:
Hoi ik heb morgen een wiskunde B toets en ik snap niet hoe ik het volgend kan uitreken
1.5^x = .5log(x)
ik moet x weten
iemand suggesties??
Hij is op te lossen ik heb hem geplot en toen had ik x is bij benadering 0,44 maar ik moet x dus exact wetenquote:Op maandag 26 oktober 2009 18:18 schreef thabit het volgende:
[..]
In het algemeen kun je zulke vergelijkingen niet symbolisch oplossen. Probeer nu eerst maar eens na te gaan of de vergelijking überhaupt wel oplossingen heeft; het linkerdeel van de vergelijking lijkt een stuk groter dan het rechterdeel.
Beware of the Raping Zebra's
Als x ongeveer 0,44 is, zal 1.5x groter dan 0 zijn en log(x) kleiner dan 0 (want x<1). Dus ik denk dat je iets fout hebt gedaan.
dit heb ik zo uit mijn boek overgenomen en als je hem plot en intersect komt er uit x = .43711598 en y = 1.193912
Beware of the Raping Zebra's
nee hoor
y1 = 1.5^x
y2 = .5log(x)
en dan plotten
en ik had 1.5^x = .5log(x) hier neer gezet
y1 = 1.5^x
y2 = .5log(x)
en dan plotten
en ik had 1.5^x = .5log(x) hier neer gezet
Beware of the Raping Zebra's
Als dat echt de vgl is die je moet oplossen, dan heb je het fout gedaan in je plotprogramma. Die vergelijking van jou heeft geen oplossingen met x<1 (en waarschijnlijk zelfs helemaal geen oplossingen maar dat mag je zelf uitwerken).
Hij heeft geen oplossing in R maar wel een in C
Maak maar een screenshot/foto van je plotding, want er gaat iets fout.
Maak maar een screenshot/foto van je plotding, want er gaat iets fout.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
nee, moet ongeveer 0.44 zijn maar ik kan die zooi dus niet met algebra oplossen. Had deze som van een klasgenootje gekregen en die komt er nu pas mee dat het niet exact hoefde...
Toch harstike bedankt thabit
Toch harstike bedankt thabit
Beware of the Raping Zebra's
log(x) is niet gedefinieerd op C.quote:Op maandag 26 oktober 2009 18:41 schreef GlowMouse het volgende:
Hij heeft geen oplossing in R maar wel een in C
Ik twijfelde al toen ik het postte. Waar staat een goed overzichtje van al die standaardfuncties met hun domein?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vast wel op Wikipedia.quote:Op maandag 26 oktober 2009 18:46 schreef GlowMouse het volgende:
Ik twijfelde al toen ik het postte. Waar staat een goed overzichtje van al die standaardfuncties met hun domein?
.Het handigst is natuurlijk om gewoon een keer een vak complexe functietheorie gevolgd te hebben, dan zit het gelijk goed in je hoofd.
log(z) is niet eenduidig gedefinieerd want als exp(z+2*pi*i) = exp(z). De waarde ligt dus altijd vast op een veelvoud van 2*pi*i na. Een holomorfe functie log(z) (dwz inverse van exp(z)) kun je definieren op een open deel U van C-{0} waarin geen gesloten pad bestaat dat om het punt 0 heen draait, dus bijvoorbeeld op C - (-oneindig, 0].
Het kán geen 0,44 zijn. Hier heb je een grafiekje tussen 0 en 1.quote:
nee, moet ongeveer 0.44 zijn maar ik kan die zooi dus niet met algebra oplossen. Had deze som van een klasgenootje gekregen en die komt er nu pas mee dat het niet exact hoefde...
Toch harstike bedankt thabit
Rood is 1.5x, groen is .5log(x). Zie je hoe ze nooit snijden?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Morgen tentamen "wiskundesommen correct overtikken op je GR" 
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik snap het al, het heeft geen oplossingen.quote:
dit heb ik zo uit mijn boek overgenomen en als je hem plot en intersect komt er uit x = .43711598 en y = 1.193912
Wellicht bedoel je 1.5^x = .5logx/logx
Probeer ipv intersect ook eens de gewone solver in het hoofdmenu.
Meer info: http://world.casio.com/ed(...)d/f07_01f/f07_01.pdf
[ Bericht 12% gewijzigd door Q.E.D. op 26-10-2009 20:43:01 ]
Hetgeen bewezen en beklonken moest worden.
Wat is de volgende pivot. Die 1 of die 3. En ja dit is noob.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Die 3, en daarom moet je ook de derde en vierde rij omwisselen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Die regel helemaal vergeten ja.quote:Op maandag 26 oktober 2009 22:16 schreef GlowMouse het volgende:
Die 3, en daarom moet je ook de derde en vierde rij omwisselen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Ik denk dat Netolk de vgl (1.5)x = 0.5log(x) bedoelt.quote:Op maandag 26 oktober 2009 18:59 schreef Iblis het volgende:
[..]
Het kán geen 0,44 zijn. Hier heb je een grafiekje tussen 0 en 1.
[ afbeelding ]
Rood is 1.5x, groen is .5log(x). Zie je hoe ze nooit snijden?
Inderdaad. Numeriek oplossen levert dan x = 0,4371159833 ...quote:Op dinsdag 27 oktober 2009 03:29 schreef ErictheSwift het volgende:
[..]
Ik denk dat Netolk de vgl (1.5)x = 0.5log(x) bedoelt.
Als Netolk nu even de moeite had genomen 0,5 te superscripten dan had dat een hoop nutteloze discussie gescheeld. Laat maar weer eens zien hoe belangrijk een goede notatie is.
Ja, hou potdomme es op met die noobvragen hieroquote:
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik heb een pagina ingescand van mijn "rekenboek" Mijn kennis van kansverdelingen is echt gebaseerd op dit boek. Maar ik moet zeggen dat het boek niet echt duidelijk is voor mij.
http://img9.imageshack.us/img9/2681/img342u.jpg
Zo heb ik bij vraag 1 al de eerste vraagtekens. 1a, kan ik nog gewoon beantwoorden. (gewoon uit de tekst links halen) maar 1b en 1c zijn voor mij een raadsel. Zouden jullie mij een beetje op weg kunnen helpen? Het is voor mij nog veel te vaag. (ook die zogenaamde diagram waar ik net niets vanaf kan lezen..)
p.s. de antwoorden volgens het antwoordenboek zijn: 1a. ruim 68% 1b. 95,4% en c. 2,3%
Bedankt voor jullie hulp!
p.p.s. als ik dit snap, dan ga ik naar de volgende vragen, en heb ik jullie hulp wellicht weer nodig
http://img9.imageshack.us/img9/2681/img342u.jpg
Zo heb ik bij vraag 1 al de eerste vraagtekens. 1a, kan ik nog gewoon beantwoorden. (gewoon uit de tekst links halen) maar 1b en 1c zijn voor mij een raadsel. Zouden jullie mij een beetje op weg kunnen helpen? Het is voor mij nog veel te vaag. (ook die zogenaamde diagram waar ik net niets vanaf kan lezen..)
p.s. de antwoorden volgens het antwoordenboek zijn: 1a. ruim 68% 1b. 95,4% en c. 2,3%
Bedankt voor jullie hulp!
p.p.s. als ik dit snap, dan ga ik naar de volgende vragen, en heb ik jullie hulp wellicht weer nodig
Je moet die opmerking onder op de linkerpagina gebruiken onder het kopje ‘Kenmerken Normale Verdeling’.quote:
Ik heb een pagina ingescand van mijn "rekenboek" Mijn kennis van kansverdelingen is echt gebaseerd op dit boek. Maar ik moet zeggen dat het boek niet echt duidelijk is voor mij.
http://img9.imageshack.us/img9/2681/img342u.jpg
Zo heb ik bij vraag 1 al de eerste vraagtekens. 1a, kan ik nog gewoon beantwoorden. (gewoon uit de tekst links halen) maar 1b en 1c zijn voor mij een raadsel. Zouden jullie mij een beetje op weg kunnen helpen? Het is voor mij nog veel te vaag. (ook die zogenaamde diagram waar ik net niets vanaf kan lezen..)
p.s. de antwoorden volgens het antwoordenboek zijn: 1a. ruim 68% 1b. 95,4% en c. 2,3%
Bedankt voor jullie hulp!
p.p.s. als ik dit snap, dan ga ik naar de volgende vragen, en heb ik jullie hulp wellicht weer nodig
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Los op: y'' + 2y' + y = x e ^ {-x}
Complementaire oplossing:
y'' + 2y' + y = 0
r2 + 2r + 1 = 0
(r + 1)2 = 0
r = -1
y_c = c_1 e ^ {-x} + c_2 x e ^{-x}
Particuliere oplossing:
y_p = (Ax + B) e ^ {-x}
y_p' = (-Ax - B + A) e ^ {-x}
y_p'' = (Ax + B - 2A) e ^ {-x}
Als ik dit nu substitueer dan kom ik uit op:
((Ax + B - 2A) + 2(-Ax - B + A) + (Ax + B)) e ^ {-x} = x e^{-x}
Vereenvoudigen geeft:
0 = x e^{-x}
Dus welke waarden moet ik nu voor A en B invullen of heb ik wat fout gedaan?
Complementaire oplossing:
y'' + 2y' + y = 0
r2 + 2r + 1 = 0
(r + 1)2 = 0
r = -1
y_c = c_1 e ^ {-x} + c_2 x e ^{-x}
Particuliere oplossing:
y_p = (Ax + B) e ^ {-x}
y_p' = (-Ax - B + A) e ^ {-x}
y_p'' = (Ax + B - 2A) e ^ {-x}
Als ik dit nu substitueer dan kom ik uit op:
((Ax + B - 2A) + 2(-Ax - B + A) + (Ax + B)) e ^ {-x} = x e^{-x}
Vereenvoudigen geeft:
0 = x e^{-x}
Dus welke waarden moet ik nu voor A en B invullen of heb ik wat fout gedaan?
Jesus hates you.
Blijkbaar werkt het voor geen waarden van A en B. Je zult dus een ander soort functie moeten zoeken als particuliere oplossing.quote:Op dinsdag 27 oktober 2009 14:55 schreef Hondenbrokken het volgende:
Los op: y'' + 2y' + y = x e ^ {-x}
Complementaire oplossing:
y'' + 2y' + y = 0
r2 + 2r + 1 = 0
(r + 1)2 = 0
r = -1
y_c = c_1 e ^ {-x} + c_2 x e ^{-x}
Particuliere oplossing:
y_p = (Ax + B) e ^ {-x}
y_p' = (-Ax - B + A) e ^ {-x}
y_p'' = (Ax + B - 2A) e ^ {-x}
Als ik dit nu substitueer dan kom ik uit op:
((Ax + B - 2A) + 2(-Ax - B + A) + (Ax + B)) e ^ {-x} = x e^{-x}
Vereenvoudigen geeft:
0 = x e^{-x}
Dus welke waarden moet ik nu voor A en B invullen of heb ik wat fout gedaan?
Wat voor soort moet ik dan hebben?quote:Op dinsdag 27 oktober 2009 15:09 schreef thabit het volgende:
[..]
Blijkbaar werkt het voor geen waarden van A en B. Je zult dus een ander soort functie moeten zoeken als particuliere oplossing.
Jesus hates you.
Je zou misschien iets als x2e-x kunnen proberen of zo.quote:Op dinsdag 27 oktober 2009 15:11 schreef Hondenbrokken het volgende:
[..]
Wat voor soort moet ik dan hebben?
1b. snap ik dan ook. Ik heb (u-1o) (u+1o) 14 centimer is 2x de standaarddeviattie. Dus: 95,4%. (u-2o) (u+2o)quote:Op dinsdag 27 oktober 2009 14:40 schreef Iblis het volgende:
[..]
Je moet die opmerking onder op de linkerpagina gebruiken onder het kopje ‘Kenmerken Normale Verdeling’.
1c. Na lang denken snap ik hem. Eerst dacht ik 100%-95,4= 4,6%??? Dus dat is de rest! Maar de rest zit natuurlijk ook onder 180-14. Dus!! 4,6% / 2 = 2,3% (ik heb wel het gevoel dat mijn manier de onorthodoxe manier is. Klopt dat)
(u en o gebruik ik even als die wiskundige tekentjes)
Ik vind je manier van opschrijven wat verwarrend. Bij 1b heb je dus een verdeling met μ = 180cm, en de vraag is nu naar tussen (180 - 14) en (180 + 14), omdat σ = 7, is dit dus (μ - 2σ) en (μ + 2σ) – wat jij nog met (μ - 1σ) en (μ + 1σ) doet bij 1b) is me niet duidelijk.quote:
[..]
1b. snap ik dan ook. Ik heb (u-1o) (u+1o) 14 centimer is 2x de standaarddeviattie. Dus: 95,4%. (u-2o) (u+2o)
1c. Na lang denken snap ik hem. Eerst dacht ik 100%-95,4= 4,6%??? Dus dat is de rest! Maar de rest zit natuurlijk ook onder 180-14. Dus!! 4,6% / 2 = 2,3% (ik heb wel het gevoel dat mijn manier de onorthodoxe manier is. Klopt dat)
(u en o gebruik ik even als die wiskundige tekentjes)
Maar goed, 1c. Je aanpak en antwoord is in principe goed, en ook wel orthodox, maar ik zal dan even toelichten waarom dat zo is. Er staat bovenaan de linker bladzijde opgemerkt dat de kromme symmetrisch is. Dus dat betekent dat inderdaad de helft van de rest onder 180 - 14 moet zitten, zoals jij het zegt, en de andere helft erboven, anders zou het niet symmetrisch zijn. Vandaar dat je dus 4,6%/2 = 2,3% krijgt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik probeerde y_p = (Ax^2 + BX) e ^ {-x}quote:Op dinsdag 27 oktober 2009 15:14 schreef thabit het volgende:
[..]
Je zou misschien iets als x2e-x kunnen proberen of zo.
Dat kwam uit op:
(-2Ax + 2A) e ^ {-x} = x e {-x}
-2A = 1 en 2A = 0
Een dergelijke waarde van A bestaat niet.
Ik heb nog steeds hulp nodig.
Jesus hates you.
Ok dankjewel, maar in dit geval weet ik dus (gelukkig) dat die eerste met standaarddeviatie 68% is. (dat staat gegeven) kan ik daar zonder die 68% ook zelf achter komen door bijv. de grafiek af te lezen? (formule?) Of heb ik daar in dit geval te weinig informatie voor en moet ik het maar "aannemen"?quote:Op dinsdag 27 oktober 2009 15:33 schreef Iblis het volgende:
[..]
Ik vind je manier van opschrijven wat verwarrend. Bij 1b heb je dus een verdeling met μ = 180cm, en de vraag is nu naar tussen (180 - 14) en (180 + 14), omdat σ = 7, is dit dus (μ - 2σ) en (μ + 2σ) – wat jij nog met (μ - 1σ) en (μ + 1σ) doet bij 1b) is me niet duidelijk.
Maar goed, 1c. Je aanpak en antwoord is in principe goed, en ook wel orthodox, maar ik zal dan even toelichten waarom dat zo is. Er staat bovenaan de linker bladzijde opgemerkt dat de kromme symmetrisch is. Dus dat betekent dat inderdaad de helft van de rest onder 180 - 14 moet zitten, zoals jij het zegt, en de andere helft erboven, anders zou het niet symmetrisch zijn. Vandaar dat je dus 4,6%/2 = 2,3% krijgt.
Er geldt altijd (voor een Normale Verdeling) dat tussen (μ - 1σ) en (μ + 1σ) 68,3% van de waarnemingen ligt. Als dat niet zo is, dan is het geen Normale Verdeling, idem m.b.t. 95,4% voor (μ - 2σ) t/m (μ + 2σ) en 99,7% voor (μ - 3σ) t/m (μ + 3σ). Maar dat zijn getallen die inderdaad gegeven moeten zijn.quote:
[..]
Ok dankjewel, maar in dit geval weet ik dus (gelukkig) dat die eerste met standaarddeviatie 68% is. (dat staat gegeven) kan ik daar zonder die 68% ook zelf achter komen door bijv. de grafiek af te lezen? (formule?) Of heb ik daar in dit geval te weinig informatie voor en moet ik het maar "aannemen"?
Ze zijn natuurlijk wel uit te rekenen (b.v. ook wel wat tussen (μ - 1.5σ) en (μ + 2,3σ) moet liggen), maar de formule daarvoor is niet iets wat je eenvoudig kunt uitdrukken. Grafische rekenmachines hebben die tabel wel tot hun beschikking, maar dat komt vast later in het hoofdstuk hoe je daarbij kunt komen.
Voor nu is het vooral belangrijk dat je die kenmerken van die Normale Verdeling nog even goed onthoudt.
Stel b.v. dat iemand zegt ik heb een normale verdeling over flessen cola met μ = 1 liter en σ = 1 deciliter dan kun je op grond van die gegevens al zeggen dat 68,3% van de flessen tussen de 0,9 liter en 1,1 liter bevat. Dat vanwege de kenmerken van die normale verdeling.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
ah top! Vraag 2 en 3 heb ik nu ook kunnen beantwoorden. Op naar het volgende hoofdstuk: "standaardnormale verdeling"
Kijk eens wat er onderaan je linker bladzijde staat ... De antwoorden op 1b en 1c krijg je ook (bijna) kado. Welk niveau is dit als ik vragen mag?quote:Op dinsdag 27 oktober 2009 14:35 schreef Thije het volgende:
Ik heb een pagina ingescand van mijn "rekenboek" Mijn kennis van kansverdelingen is echt gebaseerd op dit boek. Maar ik moet zeggen dat het boek niet echt duidelijk is voor mij.
http://img9.imageshack.us/img9/2681/img342u.jpg
Zo heb ik bij vraag 1 al de eerste vraagtekens. 1a, kan ik nog gewoon beantwoorden. (gewoon uit de tekst links halen) maar 1b en 1c zijn voor mij een raadsel. Zouden jullie mij een beetje op weg kunnen helpen? Het is voor mij nog veel te vaag. (ook die zogenaamde diagram waar ik net niets vanaf kan lezen..)
p.s. de antwoorden volgens het antwoordenboek zijn: 1a. ruim 68% 1b. 95,4% en c. 2,3%
Bedankt voor jullie hulp!
p.p.s. als ik dit snap, dan ga ik naar de volgende vragen, en heb ik jullie hulp wellicht weer nodig
Je aanpak is niet generiek genoeg. Als y (de gezochte functie) een product is van een kwadratisch polynoom in x en e-x, dan zullen de eerste afgeleide y' en de tweede afgeleide y'' dat ook zijn (waarom?). En het rechterlid van je DV is ook zo op te vatten, zij het dat de coëfficient van x2 hier nul is. Ik zou dus uitgaan van:quote:Op dinsdag 27 oktober 2009 15:41 schreef Hondenbrokken het volgende:
[..]
Ik probeerde y_p = (Ax^2 + BX) e ^ {-x}
Dat kwam uit op:
(-2Ax + 2A) e ^ {-x} = x e {-x}
-2A = 1 en 2A = 0
Een dergelijke waarde van A bestaat niet.
Ik heb nog steeds hulp nodig.
y = (Ax2 + Bx + C)e-x
Door differentiëren, invullen in de DV, herleiden van het linkerlid op een product van een kwadratisch polynoom en e-x en gelijkstellen van de coëfficienten van het kwadratisch polynoom in linker en rechter lid krijg je dan een stelsel van drie lineaire vergelijkingen in de drie onbekenden A,B,C. Dan zou het moeten lukken.
[ Bericht 0% gewijzigd door Riparius op 27-10-2009 17:50:33 ]
Met lineaire en constante termen in het polynoom zal het niet gaan werken, die worden toch naar 0 gestuurd door de differentiaaloperator (het lineaire stelsel waarnaar je verwijst zal gegarandeerd strijdig zijn). Maar je zou natuurlijk nog een graadje verder kunnen gaan of gewoon in het algemeen xne-x invullen en kijken wat er gebeurt. Als zoiets niet werkt, dan weet ik het ook niet zo gauw maar het lijkt me dat het wel moet werken.quote:Op dinsdag 27 oktober 2009 17:45 schreef Riparius het volgende:
[..]
Je aanpak is niet generiek genoeg. Als y (de gezochte functie) een product is van een kwadratisch polynoom in x en e-x, dan zullen de eerste afgeleide y' en de tweede afgeleide y'' dat ook zijn (waarom?). En het rechterlid van je DV is ook zo op te vatten, zij het dat de coëfficient van x2 hier nul is. Ik zou dus uitgaan van:
y = (Ax2 + Bx + C)e-x
Door differentiëren, invullen in de DV, herleiden van het linkerlid op een product van een kwadratisch polynoom en e-x en gelijkstellen van de coëfficienten van het kwadratisch polynoom in linker en rechter lid krijg je dan een stelsel van drie lineaire vergelijkingen in de drie onbekenden A,B,C. Dan zou het moeten lukken.
Werkt niet.quote:Op dinsdag 27 oktober 2009 17:45 schreef Riparius het volgende:
[..]
Je aanpak is niet generiek genoeg. Als y (de gezochte functie) een product is van een kwadratisch polynoom in x en e-x, dan zullen de eerste afgeleide y' en de tweede afgeleide y'' dat ook zijn (waarom?). En het rechterlid van je DV is ook zo op te vatten, zij het dat de coëfficient van x2 hier nul is. Ik zou dus uitgaan van:
y = (Ax2 + Bx + C)e-x
Door differentiëren, invullen in de DV, herleiden van het linkerlid op een product van een kwadratisch polynoom en e-x en gelijkstellen van de coëfficienten van het kwadratisch polynoom in linker en rechter lid krijg je dan een stelsel van drie lineaire vergelijkingen in de drie onbekenden A,B,C. Dan zou het moeten lukken.
y_p = (Ax^2 + Bx + C) e {-x}
y'_p = (-Ax^2 + (2A-B)x + (B - C)) e {-x}
y''_p = (Ax^2 + (B-4A)x + (2A - 2B + C) e {-x}
Invullen in y'' + 2y' + y = x e ^ {-x}
(A - 2A + A) x^2 + (B - 4A +4A -2B + B)x + (2A - 2B + C +2B -2C + C) e ^ {-x} = e^{-x}
Vereenvoudigen
2A e^{-x} = e^{-x}
Jesus hates you.
Ah, ik zie het. Probeer de eerste suggestie van Thabit nog even uit (een derdegraads polynoom). Anders zou ik het zo gauw ook niet weten. Heb nu geen tijd om er echt in te duiken.quote:Op dinsdag 27 oktober 2009 18:32 schreef Hondenbrokken het volgende:
[..]
Werkt niet.
y_p = (Ax^2 + Bx + C) e {-x}
y'_p = (-Ax^2 + (2A-B)x + (B - C)) e {-x}
y''_p = (Ax^2 + (B-4A)x + (2A - 2B + C) e {-x}
Invullen in y'' + 2y' + y = x e ^ {-x}
(A - 2A + A) x^2 + (B - 4A +4A -2B + B)x + (2A - 2B + C +2B -2C + C) e ^ {-x} = e^{-x}
Vereenvoudigen
2A e^{-x} = e^{-x}
Deze heb ik iets sneller en slordiger uitgerekend, maar weer geen oplossing.
y_p = (Dx^3 + Ax^2 + Bx + C) e^{-x}
y'_p = (-Dx^3 + (3D - A)x^2 + (2A-B)x + (B - C)) e^{-x}
y''_p = (Dx^3 + (A - 3D)x^2 + (B-4A + 6D)x + (2A - 2B + C) e^{-x}
Invullen in y'' + 2y' + y = x e ^ {-x}
(D -2D +D) x^3 (A - 2A + A + 6D - 3D) x^2 + (B - 4A +4A -2B + B + 6D)x + (2A - 2B + C +2B -2C + C) e ^ {-x} = e^{-x}
Vereenvoudigen
(3Dx^2 + 6Dx + 2A) e^{-x} = x e^{-x}
3D = 0
6D = 1
2A = 0
Boven de vraag staat dat je het op moet lossen middels "the method of undetermined constants".
Ik heb ook gehad dat als de oplossingen gelijk zijn aan de complementaire functie je dan alle termen met x moest vermeningvuldigen, maar dat heb ik al 2 keer geprobeerd. Hoe je dit zou moeten doen met een onbepaald aantal coefficiënten weet ik niet en vraag me af of dat dan wel een oplossing oplevert.
[ Bericht 0% gewijzigd door Hondenbrokken op 27-10-2009 21:31:42 ]
y_p = (Dx^3 + Ax^2 + Bx + C) e^{-x}
y'_p = (-Dx^3 + (3D - A)x^2 + (2A-B)x + (B - C)) e^{-x}
y''_p = (Dx^3 + (A - 3D)x^2 + (B-4A + 6D)x + (2A - 2B + C) e^{-x}
Invullen in y'' + 2y' + y = x e ^ {-x}
(D -2D +D) x^3 (A - 2A + A + 6D - 3D) x^2 + (B - 4A +4A -2B + B + 6D)x + (2A - 2B + C +2B -2C + C) e ^ {-x} = e^{-x}
Vereenvoudigen
(3Dx^2 + 6Dx + 2A) e^{-x} = x e^{-x}
3D = 0
6D = 1
2A = 0
Boven de vraag staat dat je het op moet lossen middels "the method of undetermined constants".
Ik heb ook gehad dat als de oplossingen gelijk zijn aan de complementaire functie je dan alle termen met x moest vermeningvuldigen, maar dat heb ik al 2 keer geprobeerd. Hoe je dit zou moeten doen met een onbepaald aantal coefficiënten weet ik niet en vraag me af of dat dan wel een oplossing oplevert.
[ Bericht 0% gewijzigd door Hondenbrokken op 27-10-2009 21:31:42 ]
Jesus hates you.
Misschien moet je dan proberen om het langzamer en nauwkeuriger uit te rekenen want volgens mij komt er namelijk wel wat uit.quote:Op dinsdag 27 oktober 2009 20:23 schreef Hondenbrokken het volgende:
Deze heb ik iets sneller en slordiger uitgerekend, maar weer geen oplossing.
Je hebt van doen met een tweede orde lineaire inhomogene DV met constante coëfficienten. De algemene aanpak is dat je een particuliere oplossing yp(x) vindt van deze DV en de algemene oplossing yh(x) van de corresponderende homogene DV. De algemene oplossing van de inhomogene DV wordt dan gegeven door y(x) = yp(x) + yh(x).quote:Op dinsdag 27 oktober 2009 20:23 schreef Hondenbrokken het volgende:
Boven de vraag staat dat je het op moet lossen middels "the method of undetermined constants".
Ik heb ook gehad dat als de oplossingen gelijk zijn aan de complementaire functie je dan alle termen met x moest vermeningvuldigen, maar dat heb ik al 2 keer geprobeerd. Hoe je dit zou moeten doen met een onbepaald aantal coefficiënten weet ik niet en vraag me af of dat dan wel een oplossing oplevert.
Nu lees ik hier dat als het rechterlid van je inhomogene DV van de gedaante Pnekx is, waarbij Pn een polynoom van graad n is, dat er dan een particuliere oplossing van de inhomogene DV van de gedaante yp(x) = Qnekx is, waarbij Qn eveneens een polynoom van graad n is. Maar dat lijkt hier niet te werken?
[ Bericht 0% gewijzigd door Riparius op 27-10-2009 21:49:11 ]
Ik vroeg me af of iemand me met mijn sommen kan helpen? We hebben hier geen boek bij, alleen hoorcollege materiaal (waar niet voldoende instaat om dit te antwoorden)
Wat bedoelen ze met die X ~ N(8,16)? Het doet me wat denken aan een normale verdeling (die wel voorkwam in het materiaal wat we hebben) maar ik kan hier verder niks mee.
Moet ik het zien als de mogelijkheid dat X de tussen 8 en 16 kan zitten? Zo niet zou de kans dan niet iets rondom een 0.5 liggen?
Wat bedoelen ze met die X ~ N(8,16)? Het doet me wat denken aan een normale verdeling (die wel voorkwam in het materiaal wat we hebben) maar ik kan hier verder niks mee.
Moet ik het zien als de mogelijkheid dat X de tussen 8 en 16 kan zitten? Zo niet zou de kans dan niet iets rondom een 0.5 liggen?
Ik weet het wel
X is normaal verdeeld met mu=8 en sigma² = 16.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik denk dat ik het begrijp. Normaliter zou ik zoiets op de GR doen, met in geval van vraag 2A, (12, 1099,8,16) om zo de kans van boven de 12 uit te rekenen. GR is alleen niet toegestaanquote:Op dinsdag 27 oktober 2009 22:32 schreef GlowMouse het volgende:
X is normaal verdeeld met mu=8 en sigma² = 16.
En nu ik zo naar die 12 kijk, klopt dat volgens mij ook net, greater than 12 lijkt mij dus te berekenen als je het vlak van 13 tot en met 16 neemt?
Ik weet het wel
13 t/m 16? 
a kun je nog wel schatten met vuistregels; heb je geen tabel met z-waarden die je erbij mag houden?
a kun je nog wel schatten met vuistregels; heb je geen tabel met z-waarden die je erbij mag houden?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Er zit om te beginnen een fout in je uitdrukking voor y''. De coëfficiënt van x2 moet (A-6D) zijn. Uitwerken levert dan:quote:Op dinsdag 27 oktober 2009 20:23 schreef Hondenbrokken het volgende:
Deze heb ik iets sneller en slordiger uitgerekend, maar weer geen oplossing.
y_p = (Dx^3 + Ax^2 + Bx + C) e^{-x}
y'_p = (-Dx^3 + (3D - A)x^2 + (2A-B)x + (B - C)) e^{-x}
y''_p = (Dx^3 + (A - 3D)x^2 + (B-4A + 6D)x + (2A - 2B + C) e^{-x}
Invullen in y'' + 2y' + y = x e ^ {-x}
(D -2D +D) x^3 (A - 2A + A + 6D - 3D) x^2 + (B - 4A +4A -2B + B + 6D)x + (2A - 2B + C +2B -2C + C) e ^ {-x} = e^{-x}
Vereenvoudigen
(3Dx^2 + 6Dx + 2A) e^{-x} = x e^{-x}
3D = 0
6D = 1
2A = 0
Boven de vraag staat dat je het op moet lossen middels "the method of undetermined constants".
Ik heb ook gehad dat als de oplossingen gelijk zijn aan de complementaire functie je dan alle termen met x moest vermeningvuldigen, maar dat heb ik al 2 keer geprobeerd. Hoe je dit zou moeten doen met een onbepaald aantal coefficiënten weet ik niet en vraag me af of dat dan wel een oplossing oplevert.
(1) y'' + 2y' + y = (6Dx + 2A)∙e-x,
Zodat je vindt:
(2) D = 1/6 en A = 0
(B en C vallen weg). En inderdaad is
(3) y = (1/6)∙x3∙e-x
een particuliere oplossing van je inhomogene DV.
De methode van de onbepaalde coëfficiënten voor het vinden van een particuliere oplossing van een inhomogene lineaire DV met constante coëfficienten houdt in dat je een particuliere oplossing zoekt die is te schrijven als een lineaire combinatie van het rechterlid g(x) en de eerste k afgeleiden van g(x), dus:
(4) yp(x) = c0∙g(x) + c1∙g'(x) + ... + ck∙g(k)(x)
Dit is mogelijk als elke afgeleide van g(x) hoger dan g(k)(x) is te schrijven als een lineaire combinatie van g(x), g'(x) ... g(k)(x).
In de DV die je moet oplossen is g(x) = x∙e-x en dus g'(x) = (-x+1)∙e-x, zodat het duidelijk is dat je elke hogere afgeleide kunt schrijven als een lineaire combinatie van g(x) en g'(x), i.e. we hebben hier k = 1. We zouden dus in eerste instantie denken dat we moeten zoeken naar een particuliere oplossing van de gedaante:
(5) yp(x) = c0∙x∙e-x + c1∙(-x+1)∙e-x
Nemen we
(6) A = c0 - c1 en B = c1,
dan is dit eenvoudiger te schrijven als:
(7) yp(x) = (Ax + B)∙e-x
Maar dit is nog niet voldoende om de methode van de onbepaalde coëfficiënten voor het vinden van een particuliere oplossing van de inhomogene DV te kunnen gebruiken. Het moet namelijk ook nog zo zijn dat geen van de functies g(x), g'(x) ... g(k)(x) een oplossing is van de corresponderende homogene DV. En aan die voorwaarde is hier niet voldaan, omdat (zoals je eenvoudig na kunt gaan) g(x) = x∙e-x en g'(x) = (-x+1)∙e-x beide oplossingen zijn van y'' + 2y + y = 0, zodat ook elke lineaire combinatie van g(x) en g'(x) een oplossing is van deze homogene DV. Dit verklaart meteen waarom de methode van de onbepaalde coëfficiënten voor het vinden van een particuliere oplossing van de inhomogene DV mislukt als we uitgaan van een particuliere oplossing van de gedaante (5) ofwel (7). Immers, als elke functie van de gedaante (7) voldoet aan y'' + 2y' + y = 0, dan kan geen enkele functie van deze gedaante voldoen aan y" + 2y' + y = x∙e-x.
De remedie is dan om het rechterlid van (5) resp. (7) te vermenigvuldigen met een voldoend hoge macht van x zodanig dat yp(x), yp'(x), yp''(x) lineair onafhankelijk is van g(x), g'(x). Vermenigvuldigen met x is hier niet voldoende omdat yp''(x) + 2yp'(x) + yp(x) dan reduceert tot e-x maal een constante en dus niet gelijk kan zijn aan x∙e-x. We vermenigvuldigen het rechterlid van (7) daarom met x2, zodat we krijgen:
(8) yp(x) = (Ax3 + Bx2)∙e-x
Substitutie in de inhomogene DV en gelijkstellen van de coëfficiënten levert dan A = 1/6, B = 0, en daarmee zijn we weer terug bij (3) als particuliere oplossing van de inhomogene DV.
Beginnersniveauquote:Op dinsdag 27 oktober 2009 17:27 schreef Riparius het volgende:
[..]
Kijk eens wat er onderaan je linker bladzijde staat ... De antwoorden op 1b en 1c krijg je ook (bijna) kado. Welk niveau is dit als ik vragen mag?
http://img2.imageshack.us/img2/5572/img343.jpg
Bij 1b. hebben ze het over een tabel. Ik kan die tabel niet vinden? Moet ik die zelf maken en met welke formule?
Bij 1b. hebben ze het over een tabel. Ik kan die tabel niet vinden? Moet ik die zelf maken en met welke formule?
Ah, tabel op andere pagina. (sorry voor de spam)quote:Op woensdag 28 oktober 2009 10:08 schreef Thije het volgende:
http://img2.imageshack.us/img2/5572/img343.jpg
Bij 1b. hebben ze het over een tabel. Ik kan die tabel niet vinden? Moet ik die zelf maken en met welke formule?
(ik heb dinsdag tentamen, dus ik wil het snappen)
Vraag 1c. vraagt om het percentage wat langer brandt dan 2500. Wat kan ik dan met die 0,9772 en wat betekent die 0.9772?
Vraag 1c. vraagt om het percentage wat langer brandt dan 2500. Wat kan ik dan met die 0,9772 en wat betekent die 0.9772?
Die 0.9772 is de kans dat de levensduur minder dan 2z is.quote:
(ik heb dinsdag tentamen, dus ik wil het snappen)
Vraag 1c. vraagt om het percentage wat langer brandt dan 2500. Wat kan ik dan met die 0,9772 en wat betekent die 0.9772?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik moest het woordje ' compleet' opzoeken. In hartshorne stond wat het betekent . Ik heb ook een bewijsje opgezocht voor " niet-constante functies hebben evenveel nulpunten als polen".quote:Op zaterdag 24 oktober 2009 13:49 schreef thabit het volgende:
[..]
Klopt, er zijn inderdaad een aantal boeken die met formules goochelen. Dat zijn van die methoden die je nooit kunt onthouden. Zou je zoiets willen toepassen, moet je elke keer weer dat boek erbij pakken.
Met Riemann-Roch heb je een methode die in je hoofd past. Misschien dat die methode wat meer stappen vergt, maar je begrijpt in elk geval wat je aan het doen bent.
Goed, R-R dus. Zij C je kromme en P een rationaal punt op C. We gaan ervan uit dat C compleet en niet-singulier is. Voor gehele n heb je de ruimte L(nP) van rationale functies op C die in P een pool van orde hooguit n hebben en buiten P regulier zijn. De ruimte L(nP) is eindig-dimensionaal en R-R zegt iets over de dimensie ervan. In het geval van krommen van geslacht 1 kun je op die manier zelfs precies de dimensie bepalen. Er komt dan het volgende uit:
dim L(nP) = 0 als n<0 (niet-constante functies hebben evenveel nulpunten als polen, geteld met multipliciteit),
dim L(nP) = 1 als n=0 of n=1 (je hebt dan alleen constante functies),
dim L(nP) = n als n>1 (dus als je n groter maakt krijg je altijd functies die je nog niet eerder had).
Hieruit volgt dat L(2P) een niet-constante functie x bevat en L(3P) een y bevat die niet al in L(2P) ligt.
Nu zitten x3, x2, x, 1, y2, xy, y allemaal in L(6P). Dit zijn 7 elementen van een 6-dimensionale ruimte, dus er is een relatie tussen. Die relatie geeft je een Weierstrassvgl.
Nu geeft het bovenstaande nog niet een manier om de x en de y ook te vinden. Dat gaan we ook pas doen als je eerst goed begrijpt wat ik zojuist ingetikt heb.
In Silverman wordt steeds gewerkt met Poo het punt op oneindig. Het gaat toch prima als je een ander rationaal punt op C neemt?
By the way, gegeven dat op een elliptische kromme C: y2=x3+Ax+B een rationaal punt ligt (a,b) met a,b ongelijk aan 0. Verder is gegeven dat a of b een kwadraat is. Kun je hiermee nieuwe punten genereren die op C liggen en waarvan beide coordinaten niet nul zijn en een van de coordinaten is een kwadraat? Is er iets bekend over het bestaan van zulke punten en hoeveel er zijn als ze bestaan?
Je kan elk rationaal punt op C hier nemen. Voorwaarde is natuurlijk wel dat je er een moet kennen. Zo'n vierdegraads C hoeft geen rationaal punt te hebben en zelfs als-ie er wel een heeft dan is het nog maar de vraag of je zo'n punt ook makkelijk kunt vinden. Het punt op oneindig mag je hier niet zomaar nemen want dat is singulier. In een niet-singulier model valt het punt in 2 punten uiteen, en die hoeven dan weer niet rationaal te zijn.quote:Op woensdag 28 oktober 2009 10:55 schreef Optimistic1 het volgende:
[..]
Ik moest het woordje ' compleet' opzoeken. In hartshorne stond wat het betekent . Ik heb ook een bewijsje opgezocht voor " niet-constante functies hebben evenveel nulpunten als polen".
In Silverman wordt steeds gewerkt met Poo het punt op oneindig. Het gaat toch prima als je een ander rationaal punt op C neemt?
Dat zullen er altijd eindig veel zijn. Je zoekt namelijk eigenlijk naar rationale punten op andere krommen: ofwel y4=x3+Ax+B ofwel y2 = x6+Ax2+B. Dit zijn krommen van hoger geslacht (3 in het eerste geval en 2 in het tweede geval). De stelling van Faltings zegt dat er altijd eindig veel rationale punten op een kromme van geslacht >= 2 liggen. Hoe je die punten vervolgens moet vinden, is weer een hele andere tak van sport en in de meeste gevallen gewoon onbekend, hoewel je in dit geval misschien nog wat kan doen met het gegeven dat de beide krommen een niet-constante afbeelding naar een elliptische kromme toelaten.quote:Op woensdag 28 oktober 2009 10:55 schreef Optimistic1 het volgende:
[..]
By the way, gegeven dat op een elliptische kromme C: y2=x3+Ax+B een rationaal punt ligt (a,b) met a,b ongelijk aan 0. Verder is gegeven dat a of b een kwadraat is. Kun je hiermee nieuwe punten genereren die op C liggen en waarvan beide coordinaten niet nul zijn en een van de coordinaten is een kwadraat? Is er iets bekend over het bestaan van zulke punten en hoeveel er zijn als ze bestaan?
Dat merkte ik ook toen ik het later nog eens op papier probeerde. Ik dacht alleen dat ik hem weer fout had gedaan omdat B en C weggevallen waren uit de vergelijking(hier kom ik op terug) en had het eigenlijk al opgegeven.quote:Op woensdag 28 oktober 2009 06:14 schreef Riparius het volgende:
[..]
Er zit om te beginnen een fout in je uitdrukking voor y''. De coëfficiënt van x2 moet (A-6D) zijn. Uitwerken levert dan:
(1) y'' + 2y' + y = (6Dx + 2A)∙e-x,
Zodat je vindt:
(2) D = 1/6 en A = 0
Dat je ineens meer coëfficienten nodig hebt dan er in het rechterlid voorkomen is waarschijnlijk de strik in deze vraag en is er denk ik tussengestopt om je wakker te houden.
Als B en C wegvallen uit de vergelijking, is het dan niet zo dat je voor deze variabelen elke mogelijke waarde in kan vullen en B en C moet laten staan om de meest generale oplossing te krijgen?quote:(B en C vallen weg). En inderdaad is
(3) y = (1/6)∙x3∙e-x
een particuliere oplossing van je inhomogene DV.
(Ik weet niet of ik het in dit topic erbij gezet heb, maar de opgave was oorspronkelijk een 'initial value problem')
De laatste methode die je beschreef heb ik nog niet gehad, maar heb ik doorgelezen (en snap eigenlijk niet alles), maar zal ik bewaren voor als iets dergelijks nog aan bod komt.
Jesus hates you.
Dat zijn dan dus ook precies de oplossingen van de homogene vergelijking.quote:Op woensdag 28 oktober 2009 14:08 schreef Hondenbrokken het volgende:
[..]
Als B en C wegvallen uit de vergelijking, is het dan niet zo dat je voor deze variabelen elke mogelijke waarde in kan vullen en B en C moet laten staan om de meest generale oplossing te krijgen?
http://img94.imageshack.us/img94/625/img344.jpg
1a. en 1b. heb ik makkelijk opgelost. Door de 'z' uit te rekenen.
Nu moet ik bij 1c. de formule omdraaien.
Dat heb ik gedaan door uit de standaardnormale tabel het getal te pakken dat het dichtst bij de 10% komt. 1,28 is dat in mijn optiek (1 - 0.8997 = 0,01003 =10,03%) Als ik dan de formule invul: ..... - 6000 / 500 = 1,28 Komt het ontbrekende getal uit op 6640 branduren. Dit zijn volgens het antwoordenboek echter 5 uren te kort. Wat doe ik fout?
1a. en 1b. heb ik makkelijk opgelost. Door de 'z' uit te rekenen.
Nu moet ik bij 1c. de formule omdraaien.
Dat heb ik gedaan door uit de standaardnormale tabel het getal te pakken dat het dichtst bij de 10% komt. 1,28 is dat in mijn optiek (1 - 0.8997 = 0,01003 =10,03%) Als ik dan de formule invul: ..... - 6000 / 500 = 1,28 Komt het ontbrekende getal uit op 6640 branduren. Dit zijn volgens het antwoordenboek echter 5 uren te kort. Wat doe ik fout?
Integreren:
4t
zou kunnen zijn:
2t2
maar ook
t4
Maar toch is het wat anders hoe kan dat nou.
4t
zou kunnen zijn:
2t2
maar ook
t4
Maar toch is het wat anders hoe kan dat nou.
Blues ain't nothing but a good man feeling bad...
t4 kan het nooit zijn. De afgeleide daarvan is namelijk 4t3
2t2 is het wel want de afgeleide daarvan is 4t. (+ evt. constante)
Ken je de regel:
f(x) = xn
f'(x) = n*xn-1
2t2 is het wel want de afgeleide daarvan is 4t. (+ evt. constante)
Ken je de regel:
f(x) = xn
f'(x) = n*xn-1
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
quote:Op woensdag 28 oktober 2009 16:15 schreef -J-D- het volgende:
t4 kan het nooit zijn. De afgeleide daarvan is namelijk 4t3
2t2 is het wel want de afgeleide daarvan is 4t. (+ evt. constante)
Ken je de regel:
f(x) = xn
f'(x) = n*xn-1
Okay het is tijd voor een pauze denk ik, ik zit nu al moeilijk te doen om de simpelste dingen
Blues ain't nothing but a good man feeling bad...
Nee, maar 1,29 > 0,9015 is ook geen 10.... toch?quote:
100%- 90,15 % = 9,85 %
Dus 6645 hoort bij de beste 9,85% lampen?
Als zij op 6645 uitkomen hebben ze dus (6645 - 6000)/500 = 1,29 gekozen… ik weet de precieze reden daar niet voor.quote:
http://img94.imageshack.us/img94/625/img344.jpg
1a. en 1b. heb ik makkelijk opgelost. Door de 'z' uit te rekenen.
Nu moet ik bij 1c. de formule omdraaien.
Dat heb ik gedaan door uit de standaardnormale tabel het getal te pakken dat het dichtst bij de 10% komt. 1,28 is dat in mijn optiek (1 - 0.8997 = 0,01003 =10,03%) Als ik dan de formule invul: ..... - 6000 / 500 = 1,28 Komt het ontbrekende getal uit op 6640 branduren. Dit zijn volgens het antwoordenboek echter 5 uren te kort. Wat doe ik fout?
Jouw antwoord is natuurlijk net iets te laag, maar 1,29 is duidelijk te hoog. Misschien dat zij als redenatie hebben ‘1,28 is nog te laag, want het moet minder dan 10% zijn, dus daarom pakken we 1,29’.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
quote:Op woensdag 28 oktober 2009 16:20 schreef Iblis het volgende:
[..]
Als zij op 6645 uitkomen hebben ze dus (6645 - 6000)/500 = 1,29 gekozen… ik weet de precieze reden daar niet voor.
Jouw antwoord is natuurlijk net iets te laag, maar 1,29 is duidelijk te hoog. Misschien dat zij als redenatie hebben ‘1,28 is nog te laag, want het moet minder dan 10% zijn, dus daarom pakken we 1,29’.Duidelijk jaSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Wat heb je al gedaan?quote:
Hoe los ik vraag 3a. en 3b. op?
Het draait en kraakt bij me
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Is er een leesbare bron (boek, site,..) over rationale punten op krommen van de vorm y4=x3+Ax+B of y2 = x6+Ax2+B of de meer eigenschappen/technieken die gebruik maken van die niet constante afbeelding van die krommen naar een elliptische kromme? Het lijkt me leuk om hier over te lezen.quote:Op woensdag 28 oktober 2009 12:08 schreef thabit het volgende:
[..]
Dat zullen er altijd eindig veel zijn. Je zoekt namelijk eigenlijk naar rationale punten op andere krommen: ofwel y4=x3+Ax+B ofwel y2 = x6+Ax2+B. Dit zijn krommen van hoger geslacht (3 in het eerste geval en 2 in het tweede geval). De stelling van Faltings zegt dat er altijd eindig veel rationale punten op een kromme van geslacht >= 2 liggen. Hoe je die punten vervolgens moet vinden, is weer een hele andere tak van sport en in de meeste gevallen gewoon onbekend, hoewel je in dit geval misschien nog wat kan doen met het gegeven dat de beide krommen een niet-constante afbeelding naar een elliptische kromme toelaten.
Ik weet niet of er bronnen zijn die dit van A tot Z behandelen, maar je zou kunnen zoeken op: Chabauty method.quote:Op woensdag 28 oktober 2009 20:45 schreef Optimistic1 het volgende:
[..]
Is er een leesbare bron (boek, site,..) over rationale punten op krommen van de vorm y4=x3+Ax+B of y2 = x6+Ax2+B of de meer eigenschappen/technieken die gebruik maken van die niet constante afbeelding van die krommen naar een elliptische kromme? Het lijkt me leuk om hier over te lezen.
http://img522.imageshack.us/img522/3449/img345c.jpg
1a. en 1b. zijn makkelijk. 1c en 1d. vragen mij om de formules te gebruiken. Hoe dat moet is mij onduidelijk, hebben jullie wat tips?
1a. en 1b. zijn makkelijk. 1c en 1d. vragen mij om de formules te gebruiken. Hoe dat moet is mij onduidelijk, hebben jullie wat tips?
Deze had ik over het hoofd gezien, ben je daar inmiddels al uit?quote:
[..]
52-56 / 2.2 = -1,82 = 0.0344
en
56-56 / 2,2 = 0 = 0.50
Maarja, ik weet het eigenlijk niet
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Je hebt dus deze formule gekregen:quote:
http://img522.imageshack.us/img522/3449/img345c.jpg
1a. en 1b. zijn makkelijk. 1c en 1d. vragen mij om de formules te gebruiken. Hoe dat moet is mij onduidelijk, hebben jullie wat tips?
Nu moet je P(3) uitrekenen, dat betekent dus voor k het getal 3 invullen in die formule. Ik neem aan dat je de notatie dus weet uit te rekenen (en het staat ook op de linkerbladzijde die je geeft).
[ Bericht 1% gewijzigd door Iblis op 29-10-2009 15:53:06 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Nee eigenlijk niet... Maar ik ben alvast doorgegaan naar het volgende hoofdstuk. Ik zie je uitleg graag tegemoet!quote:Op donderdag 29 oktober 2009 15:43 schreef Iblis het volgende:
[..]
Deze had ik over het hoofd gezien, ben je daar inmiddels al uit?
Oké, eerst deze, je vult inderdaad de berekening voor de z-waarde juist in, alhoewel je eigenlijk haakjes moet gebruiken: (52 - 56)/2,2 = -1,82.quote:
Wat je echter absoluut niet mag zeggen is: -1,82 = 0,0344 – dat is gewoon onzin. -1,82 is geen 0,0344. Je bedoelt: Φ(-1,82) = 0,0344, of eventueel als je de Φ niet kunt typen schrijf je van mijn part Phi(-1,82).
Als je nog eens naar de uitleg kijkt bovenaan de linkerpagina, dan zie je dat de interpretatie moet zijn dat 3,4% van de hoofden 52 cm of kleiner is.
Het gaat nu om de 80% meestvoorkomende schedelafmetingen, en daar zit het niet bij, iedereen die immers een schedelafmeting heeft die bij de kleinste 10% of grootste 10% hoort, zit niet bij die 80%, kortom, geen hoed voor die man.
Wat je hiermee wilt is me niet duidelijk, aangezien dat weinig betrekking heeft op de vraag.quote:56-56 / 2,2 = 0 = 0.50
Vraag b) kun je in feite, als je gebruik maakt van de symmetrie van die kromme direct beantwoorden. 4 cm (of meer) boven het gemiddelde komt net zo vaak voor als 4 cm eronder, dus ook in 3,8% van de gevallen, kortom, ook geen hoed. Je kunt het ook uitrekenen.
Maarja, ik weet het eigenlijk niet
[/quote]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
En lukt die nieuwe vraag met wat ik aangeef?quote:
[..]
Nee eigenlijk niet... Maar ik ben alvast doorgegaan naar het volgende hoofdstuk. Ik zie je uitleg graag tegemoet!
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Na Riemann-Roch, hoe ging het weer met complete niet-sing. krommen van geslacht 1 transformeren naar een Weierstrass vorm?quote:Op woensdag 28 oktober 2009 20:53 schreef thabit het volgende:
[..]
Ik weet niet of er bronnen zijn die dit van A tot Z behandelen, maar je zou kunnen zoeken op: Chabauty method.
Ik zou zeggen, scroll naar de post waar ik het beschreef en vertel me waar je precies vastloopt. Dan kunnen we daarover wat meer uitwijden. Heb je misschien een concreet voorbeeld van een kromme waarop je het toepassen wilt?quote:Op donderdag 29 oktober 2009 18:50 schreef Optimistic1 het volgende:
[..]
Na Riemann-Roch, hoe ging het weer met complete niet-sing. krommen van geslacht 1 transformeren naar een Weierstrass vorm?
Ok zo ver kom ik : (let niet teveel op de notatie, ik denk dat het een doorn in je oog is, maar ik heb geen idee hoe ik het anders kan neerzetten in 'plain' tekst)quote:Op donderdag 29 oktober 2009 15:46 schreef Iblis het volgende:
[..]
Je hebt dus deze formule gekregen:
[ afbeelding ]
Nu moet je P(3) uitrekenen, dat betekent dus voor k het getal 3 invullen in die formule. Ik neem aan dat je de notatie [ afbeelding ] dus weet uit te rekenen (en het staat ook op de linkerbladzijde die je geeft).
P (3) = ⎛6⎞* 0.25² * 0,75³ = en dan snap ik niet hoe ik die getallen in grote haakjes moet uitschrijven en
............... (3)
hoe ik bepaal met welke hoeveelheden ik moet toevoegen: met wat gokken kwam ik op 6*5*4 / 3*2*1 en dat bleek nog goed te zijn ook :S
Kun je aangeven hoe ik dat moet zien?
Wiskunde is geen gokspelletje (hoewel je gokken weer prima wiskundig kunt analyseren). Die notatie met de langgerekte haakjes (6 over 3) geeft aan op hoeveel manieren je 3 objecten kunt kiezen uit een verzameling van 6. Dus, er liggen zes verschillende bonbons op een schaal en je mag er drie nemen. Hoeveel verschillende combinaties van drie bonbons kun je dan kiezen?quote:Op donderdag 29 oktober 2009 21:28 schreef Thije het volgende:
[..]
hoe ik bepaal met welke hoeveelheden ik moet toevoegen: met wat gokken kwam ik op 6*5*4 / 3*2*1 en dat bleek nog goed te zijn ook :S
Kun je aangeven hoe ik dat moet zien?
Ik denk dat je 0,253·0,753 bedoelt, en dat die exponent van 0,25 een typefoutje is. Wat ‘die grote haken’ betreft: in je boek staat:
Als je dat invult voor n = 6 en k = 3 dan krijg je dus (n - k + 1 = 4):
.
Maar goed, nu heb ik het gewoon ingevuld, en dat is eigenlijk niet zo nuttig, het is nuttiger om te begrijpen wat het betekent, en dat heb ik laatst al uitgetypt, en dat zal ik eens opzoeken.
Als je dat invult voor n = 6 en k = 3 dan krijg je dus (n - k + 1 = 4):
.
Maar goed, nu heb ik het gewoon ingevuld, en dat is eigenlijk niet zo nuttig, het is nuttiger om te begrijpen wat het betekent, en dat heb ik laatst al uitgetypt, en dat zal ik eens opzoeken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dat was ook voor jou! Dus ik denk dat het niet zo nuttig was omdat ik wat moeilijk termen heb gebruikt.quote:
Maar goed, nu heb ik het gewoon ingevuld, en dat is eigenlijk niet zo nuttig, het is nuttiger om te begrijpen wat het betekent, en dat heb ik laatst al uitgetypt, en dat zal ik eens opzoeken.
Welk niveau is je opleiding? (HAVO/VWO/MBO schat ik het?). Dan weet ik iets beter wat ik wel en niet moet zeggen, het schiet ook niet op om mensen te verwarren met begrippen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Laat ik het zo zeggen. Ik heb nooit wiskunde A of B gehad op de middelbare school. (MAVO/ MBO welzijn studie en nu Communicatie waarbij ik een basis van economie moet kennen)quote:Op donderdag 29 oktober 2009 21:49 schreef Iblis het volgende:
[..]
Dat was ook voor jou! Dus ik denk dat het niet zo nuttig was omdat ik wat moeilijk termen heb gebruikt.
Welk niveau is je opleiding? (HAVO/VWO/MBO schat ik het?). Dan weet ik iets beter wat ik wel en niet moet zeggen, het schiet ook niet op om mensen te verwarren met begrippen.
Oké, maar lukt al?quote:
[..]
Laat ik het zo zeggen. Ik heb nooit wiskunde A of B gehad op de middelbare school. (MAVO/ MBO welzijn studie en nu Communicatie waarbij ik een basis van economie moet kennen)
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Als ik het voorbeeld met P(4) neem:
Is hetgeen mij in verwarring brengt die puntjes in: 6*5*... (6-k+1) en daaronder k(k-1)... 3*2
Zeggen de (6-k+1) en de (k-1) hoeveel getallen je daar moet gebruiken? En wat zegt het eigenlijk nog meer?
En waarom je nou specifiek de getallen: 6*5*4*3 moet gebruiken en daaronder 4*3*2..?
Is hetgeen mij in verwarring brengt die puntjes in: 6*5*... (6-k+1) en daaronder k(k-1)... 3*2
Zeggen de (6-k+1) en de (k-1) hoeveel getallen je daar moet gebruiken? En wat zegt het eigenlijk nog meer?
En waarom je nou specifiek de getallen: 6*5*4*3 moet gebruiken en daaronder 4*3*2..?
iets specifieker?quote:
iemand hier verstand van randomized response?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ja eh hoe moet ik dat zeggen...ik snap het hele principe niet.quote:
Dit staat er in mijn boek: Bij een even aantal ogen antwoord je 'ja', bij een oneven aantal geef je eerlijk antwoord. 70% van de respondenten heeft ja geantwoord, dan is de schatting van het percentage mensen dat hun partner slaat 40%. Van de 70% 'ja' antwoorden is immers 50% naar verwachting 'ja' omdat zij een even aantal gooide en dus wel ja moesten antwoorden. De resterende 20% gaat boven die verwachte 50% uit en kunnen we dus toeschrijven aan daadwerkelijk daderschap.
Hoe komen ze dan aan 40%???
...and that's the way the cookie crumbles.
Bij de mensen die een even aantal ogen gooiden en (dus) ja antwoordden zaten evengoed mensen die de waarheid spraken natuurlijk als bij de mensen die een oneven aantal ogen gooiden. Wat dacht je daarvan?quote:Op vrijdag 30 oktober 2009 16:04 schreef hetismijrobbert het volgende:
[..]
ja eh hoe moet ik dat zeggen...ik snap het hele principe niet.
Dit staat er in mijn boek: Bij een even aantal ogen antwoord je 'ja', bij een oneven aantal geef je eerlijk antwoord. 70% van de respondenten heeft ja geantwoord, dan is de schatting van het percentage mensen dat hun partner slaat 40%. Van de 70% 'ja' antwoorden is immers 50% naar verwachting 'ja' omdat zij een even aantal gooide en dus wel ja moesten antwoorden. De resterende 20% gaat boven die verwachte 50% uit en kunnen we dus toeschrijven aan daadwerkelijk daderschap.
Hoe komen ze dan aan 40%???
Die puntjes staan voor ‘hier is een boel weggelaten’. Dus: 1 + 2 + 3 + ··· + 10 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10. En evenzo 1·2·3···6 = 1·2·3·4·5·6.quote:
Als ik het voorbeeld met P(4) neem:
Is hetgeen mij in verwarring brengt die puntjes in: 6*5*... (6-k+1) en daaronder k(k-1)... 3*2
Zeggen de (6-k+1) en de (k-1) hoeveel getallen je daar moet gebruiken? En wat zegt het eigenlijk nog meer?
En waarom je nou specifiek de getallen: 6*5*4*3 moet gebruiken en daaronder 4*3*2..?
Als nu:
Neemt en je vult n = 6 en k = 4 in krijg je dus:
En dat is gelijk aan:
Als we nou de puntjes invullen zie je dat er bovenin niets meer in te vullen is, dat wordt gewoon 6·5·4·3 en onderin mist alleen de 2. Dus je krijgt uiteindelijk als je wegstreept (6·5)/(2·1) = 15.
Maar goed, soms kan het dus wat gekke situaties opleveren als je het al te letterlijk invult, want als je neemt k = 1 krijg je bovenin 6·5·4···(6 - 1 + 1), maar goed, dat is gewoon ‘6’. Die (n - 1)(n - 2) zijn vooral om aan te geven dat elke factor eentje kleiner wordt totdat je bij de eindfactor (n -k + 1) komt, maar soms kan de beginfactor al gelijk zijn aan de eindfactor.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Van de 70% 'ja' antwoorden is 50% naar verwachting 'ja' omdat zij een even aantal gooide en dus wel ja moesten antwoorden. De resterende 20% gaat boven die verwachte 50% uit en kunnen we dus toeschrijven aan daadwerkelijk daderschap. Maar die 20% is ten opzichte van het totaal en we kijken nu naar de 50% die de waarheid spreekt. 20/50 = 40%.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Muchos gracias !!!!quote:Op vrijdag 30 oktober 2009 16:11 schreef GlowMouse het volgende:
Van de 70% 'ja' antwoorden is 50% naar verwachting 'ja' omdat zij een even aantal gooide en dus wel ja moesten antwoorden. De resterende 20% gaat boven die verwachte 50% uit en kunnen we dus toeschrijven aan daadwerkelijk daderschap. Maar die 20% is ten opzichte van het totaal en we kijken nu naar de 50% die de waarheid spreekt. 20/50 = 40%.
...and that's the way the cookie crumbles.
Ik loop even vast
Vind de vergelijking van het raakvlak op het gegeven punt
z = y*cos(x-y) op (2,2,2) ( = (x0,y0,z0) )
De formule is volgens Stewart
z - z0 = fx(x0,y0)(x-x0) + fy(x0,y0)(y-y0)
Maar de partiële afgeleiden zijn dan toch sowieso
fx = -y*sin(x-y)*1 en fy = -y*sin(x-y)*-1
Maar vul je daar x=2 en y=2 in krijg je in beide gevallen sin(0) = 0. Dus is de vergelijking
z =2
Het antwoord is echter z = y. Dus ergens bij mijn partiële afgeleide ga ik de fout in, wat doe ik fout?
[ Bericht 31% gewijzigd door Agiath op 30-10-2009 17:47:57 ]
Vind de vergelijking van het raakvlak op het gegeven punt
z = y*cos(x-y) op (2,2,2) ( = (x0,y0,z0) )
De formule is volgens Stewart
z - z0 = fx(x0,y0)(x-x0) + fy(x0,y0)(y-y0)
Maar de partiële afgeleiden zijn dan toch sowieso
fx = -y*sin(x-y)*1 en fy = -y*sin(x-y)*-1
Maar vul je daar x=2 en y=2 in krijg je in beide gevallen sin(0) = 0. Dus is de vergelijking
z =2
Het antwoord is echter z = y. Dus ergens bij mijn partiële afgeleide ga ik de fout in, wat doe ik fout?
[ Bericht 31% gewijzigd door Agiath op 30-10-2009 17:47:57 ]
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Als je gewoon tekst typt, kun je dat beter gewoon hier doen. Tex heeft anders geen voordeel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Het is wel wat duidelijker vind ik. Maar je hebt op zich gelijkquote:
Als je gewoon tekst typt, kun je dat beter gewoon hier doen. Tex heeft anders geen voordeel.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Ik vind het hardstikke onduidelijk, ik kan namelijk je plaatjes helemaal niet zien, alleen een rood gekleurde foutmelding.quote:Op vrijdag 30 oktober 2009 17:39 schreef Agiath het volgende:
[..]
Het is wel wat duidelijker vind ik. Maar je hebt op zich gelijk
Oh ik zie het ook na een ctrl+F5, ik zal het even makenquote:
[..]
Ik vind het hardstikke onduidelijk, ik kan namelijk je plaatjes helemaal niet zien, alleen een rood gekleurde foutmelding.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
daar doelde ik niet op; doe nog maar eens ctrl-f5quote:Op vrijdag 30 oktober 2009 17:45 schreef Agiath het volgende:
[..]
Oh ik zie het ook na een ctrl+F5, ik zal het even maken
wel op
[ Bericht 14% gewijzigd door motorbloempje op 01-09-2013 21:30:39 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik kreeg trouwens net wel de notering zoals ik dat wou (dat tweede plaatje)quote:
[..]
daar doelde ik niet op; doe nog maar eens ctrl-f5
wel op [ afbeelding ] vs [ afbeelding ]
iig het is nu plain tekst
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
ik snap al niks van z - z0 = fx(x0,y0)(x-x0) + fy(x0,y0)(y-y0)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Plain text works for me.quote:Op vrijdag 30 oktober 2009 17:48 schreef Agiath het volgende:
[..]
Ik kreeg trouwens net wel de notering zoals ik dat wou (dat tweede plaatje)
iig het is nu plain tekst
Je partiële afgeleide naar y is fout, y is dan immers je variabele, dus moet je hier (ook) de productregel toepassen. Dat heb je niet gedaan.
Ah, je hebt gelijk, dan krijg je waarschijnlijk welquote:
[..]
Plain text works for me.
Je partiële afgeleide naar y is fout, y is dan immers je variabele, dus moet je hier (ook) de productregel toepassen. Dat heb je niet gedaan.
z - 2 = y -2 --> z = y
Bedankt
fx(x0,y0) is dus de waarde van de partiele afgeleide naar x voor x=2 en y=2quote:
ik snap al niks van z - z0 = fx(x0,y0)(x-x0) + fy(x0,y0)(y-y0)
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Dat is gewoon de vergelijking van het raakvlak in het punt (x0,y0,z0) van het gekromde vlak gegeven door z = f(x,y).quote:Op vrijdag 30 oktober 2009 17:50 schreef GlowMouse het volgende:
ik snap al niks van z - z0 = fx(x0,y0)(x-x0) + fy(x0,y0)(y-y0)
Vergelijk het maar met het tweedimensionale analogon: de vergelijking van de raaklijn aan de grafiek van y = f(x) in het punt (x0,y0) wordt gegeven door y - y0 = f'(x0)(x - x0).
Dan mis ik al een functie f om te beginnen. Verder is het dan wel te volgen, productregel inderdaad.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een aantal vragen over matrices waar ik niet uitkom. Hoop dat iemand ze kan uitleggen.
1. (som van matrices)
Laat zien dat A - AT is niet symmetrisch voor een 2 x 2 matrix A.
2. (matrix-matrix product)
A = [ 1 2 ]
[ 3 4 ]
B = [ 0 -2 ] [ 1 3 ]
[ 1 8 ] [- 4 -1]
Antwoord = [ -54 -8 ]
[ -100 -14]
3. De volgende matrices zijn er:
A = [ 2 0 0 ]
[1 2 0 ]
[ 1 1 2 ]
B = [ 0 0 1 ]
[ 0 1 0 ]
[ 1 0 0 ]
Bepaal ABAT ik kom er niet uit om dus 3 matrices te vermenigvuldigen..
Antwoord =
[ 0 0 4 ]
[ 0 4 4 ]
[ 4 4 5 ]
1. (som van matrices)
Laat zien dat A - AT is niet symmetrisch voor een 2 x 2 matrix A.
2. (matrix-matrix product)
A = [ 1 2 ]
[ 3 4 ]
B = [ 0 -2 ] [ 1 3 ]
[ 1 8 ] [- 4 -1]
Antwoord = [ -54 -8 ]
[ -100 -14]
3. De volgende matrices zijn er:
A = [ 2 0 0 ]
[1 2 0 ]
[ 1 1 2 ]
B = [ 0 0 1 ]
[ 0 1 0 ]
[ 1 0 0 ]
Bepaal ABAT ik kom er niet uit om dus 3 matrices te vermenigvuldigen..
Antwoord =
[ 0 0 4 ]
[ 0 4 4 ]
[ 4 4 5 ]
Leuke nick
1. probeer eens een A. Overigens is de uitspraak niet waar voor alle A, je zult toch makkelijk eentje moeten kunnen vinden.
2. reken eerst B uit
3. bereken eerst AB (of eerst BAT)
1. probeer eens een A. Overigens is de uitspraak niet waar voor alle A, je zult toch makkelijk eentje moeten kunnen vinden.
2. reken eerst B uit
3. bereken eerst AB (of eerst BAT)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heb je al iets geprobeerd?quote:
Ik heb een aantal vragen over matrices waar ik niet uitkom. Hoop dat iemand ze kan uitleggen.
1. (som van matrices)
Laat zien dat A - AT is niet symmetrisch voor een 2 x 2 matrix A.
Wat lukt hier niet?quote:2. (matrix-matrix product)
A = [ 1 2 ]
[ 3 4 ]
B = [ 0 -2 ] [ 1 3 ]
[ 1 8 ] [- 4 -1]
Antwoord = [ -54 -8 ]
[ -100 -14]
Lukt twee wel?quote:3. De volgende matrices zijn er:
A = [ 2 0 0 ]
[1 2 0 ]
[ 1 1 2 ]
B = [ 0 0 1 ]
[ 0 1 0 ]
[ 1 0 0 ]
Bepaal ABAT ik kom er niet uit om dus 3 matrices te vermenigvuldigen..
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
(Logica, hoort ook wel in dit topic, toch? ;x )
Toon aan dat voor elke formule phi het aantal subformules van phi kleiner of gelijk is aan de lengte van phi.
Met volledige inductie naar L(φ)
E(n): voor alle φ zo dat L(φ) = n geldt dat |sfor(φ) ≤ L(φ)
E(0): Er is geen φ met L(φ) = 0, dus hiervoor klopt E(n)
E(1): Als L(φ)=1, dan is φ een propositieletter, dus |sfor(φ)| = 1, hiervoor klopt E(n) ook.
Stel E(n) is bewezen voor alle n.
Dan geldt voor E(n+1):
Neem een φ met L(φ) = n+1
Twee mogelijkheden:
• φ = ¬ψ: sfor(φ) = sfor(¬ψ) = {¬ψ} ∪ sfor(ψ)
|sfor(φ)| = |sfor(ψ)|+1, dus L(φ) = n+1
Bewezen voor unaire connectief
• φ = ψ^χ: sfor(φ) = sfor(ψ^χ ) = {ψ^χ} ∪ sfor(ψ) ∪ sfor(χ)
|sfor(ψ)|+|sfor(χ)|≤ |sfor(φ)|-1
Dus |sfor(φ)|≤ L(n+1)
Bewezen voor binaire connectieven
Ik weet bij de laatste stap niet goed hoe ik het moet bewijzen. Het klopt trouwens niet eens, want sfor(\phi) kunnen ook dubbeltellingen al uitgehaald zijn. Ik weet echt niet goed hoe ik deze stap wel moet doen.
Is het verder wel een goed en vooral volledig bewijs?
Toon aan dat voor elke formule phi het aantal subformules van phi kleiner of gelijk is aan de lengte van phi.
Met volledige inductie naar L(φ)
E(n): voor alle φ zo dat L(φ) = n geldt dat |sfor(φ) ≤ L(φ)
E(0): Er is geen φ met L(φ) = 0, dus hiervoor klopt E(n)
E(1): Als L(φ)=1, dan is φ een propositieletter, dus |sfor(φ)| = 1, hiervoor klopt E(n) ook.
Stel E(n) is bewezen voor alle n.
Dan geldt voor E(n+1):
Neem een φ met L(φ) = n+1
Twee mogelijkheden:
• φ = ¬ψ: sfor(φ) = sfor(¬ψ) = {¬ψ} ∪ sfor(ψ)
|sfor(φ)| = |sfor(ψ)|+1, dus L(φ) = n+1
Bewezen voor unaire connectief
• φ = ψ^χ: sfor(φ) = sfor(ψ^χ ) = {ψ^χ} ∪ sfor(ψ) ∪ sfor(χ)
|sfor(ψ)|+|sfor(χ)|≤ |sfor(φ)|-1
Dus |sfor(φ)|≤ L(n+1)
Bewezen voor binaire connectieven
Ik weet bij de laatste stap niet goed hoe ik het moet bewijzen. Het klopt trouwens niet eens, want sfor(\phi) kunnen ook dubbeltellingen al uitgehaald zijn. Ik weet echt niet goed hoe ik deze stap wel moet doen.
Is het verder wel een goed en vooral volledig bewijs?
fx en fy zijn de partiële afgeleide van z naar x en z naar yquote:
Dan mis ik al een functie f om te beginnen. Verder is het dan wel te volgen, productregel inderdaad.
Buy it, use it, break it, fix it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Trash it, change it, mail - upgrade it,
Charge it, point it, zoom it, press it,
Snap it, work it, quick - erase it,
Logica is m.i. meer een onderdeel van de filosofie dan van de wiskunde, maar dat terzijde.quote:Op vrijdag 30 oktober 2009 23:02 schreef Hanneke12345 het volgende:
(Logica, hoort ook wel in dit topic, toch? ;x )
Toon aan dat voor elke formule phi het aantal subformules van phi kleiner of gelijk is aan de lengte van phi.
Met volledige inductie naar L(φ)
E(n): voor alle φ zo dat L(φ) = n geldt dat |sfor(φ) ≤ L(φ)
E(0): Er is geen φ met L(φ) = 0, dus hiervoor klopt E(n)
E(1): Als L(φ)=1, dan is φ een propositieletter, dus |sfor(φ)| = 1, hiervoor klopt E(n) ook.
Stel E(n) is bewezen voor alle n.
Dan geldt voor E(n+1):
Neem een φ met L(φ) = n+1
Twee mogelijkheden:
• φ = ¬ψ: sfor(φ) = sfor(¬ψ) = {¬ψ} ∪ sfor(ψ)
|sfor(φ)| = |sfor(ψ)|+1, dus L(φ) = n+1
Bewezen voor unaire connectief
• φ = ψ^χ: sfor(φ) = sfor(ψ^χ ) = {ψ^χ} ∪ sfor(ψ) ∪ sfor(χ)
|sfor(ψ)|+|sfor(χ)|≤ |sfor(φ)|-1
Dus |sfor(φ)|≤ L(n+1)
Bewezen voor binaire connectieven
Ik weet bij de laatste stap niet goed hoe ik het moet bewijzen. Het klopt trouwens niet eens, want sfor(\phi) kunnen ook dubbeltellingen al uitgehaald zijn. Ik weet echt niet goed hoe ik deze stap wel moet doen.
Is het verder wel een goed en vooral volledig bewijs?
Ik neem aan, dat L(phi * psi) = L(phi) + L(psi) + 1? Dus i.h.b. hebben phi en psi kleinere lengte dan phi * psi zodat we de inductiehypothese kunnen toepassen. Dan heb je toch dat #sfor(phi * psi) = #(sfor(phi) U sfor(psi) U {phi * psi}) <= #sfor(phi) + #sfor(psi) + 1 <= L(phi) + L(psi) + 1 = L(phi * psi), of zie ik dat verkeerd (ik ben immers geen filosoof)?
[ Bericht 1% gewijzigd door thabit op 31-10-2009 11:03:36 ]
quote:
Logica is m.i. meer een onderdeel van de filosofie dan van de wiskunde, maar dat terzijde.
Filosofen gebruiken het vaak om een zweempje formaliteit aan hun werk te geven, maar zodra er een kwantor bij komt kijken geven ze zich meestal gewonnen. Ik denk dat de meeste logica-research nu echter bij informatica zit, alhoewel het vaak wel tegen wiskunde aanhangt. Veel manieren om over computerprogramma’s en protocollen te redeneren zijn op logica gebaseerd, en maken gebruik van Markov-keten-achtige modellen, waarop je dan met probabilistische kwantoren kunt stellen dat P<0.01(systeem belandt in een deadlock) o.i.d. Maar om zulke soort logica’s rigoureus te maken moet je natuurlijk wel een maat definiëren waarmee je die P betekenis geeft. Ook in geautomatiseerde taalverwerking wordt logica veel gebruikt. En dat is ook echt geen pakkie-an van filosofen.
Ja, dat lijkt me de goede kijk op de zaken.quote:Ik neem aan, dat L(phi * psi) = L(phi) + L(psi) + 1? Dus i.h.b. hebben phi en psi kleinere lengte dan phi * psi zodat we de inductiehypothese kunnen toepassen. Dan heb je toch dat #sfor(phi * psi) = #(sfor(phi) U sfor(psi) U {phi * psi}) <= #sfor(phi) + #sfor(psi) + 1 <= L(phi) + L(psi) + 1 = L(phi * psi), of zie ik dat verkeerd (ik ben immers geen filosoof)?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Mwah, ben ik niet helemaal met je eens. Hoewel het onderdeel is van filosofie vind ik het met dit soort dingen (inductiebewijzen alles) toch meer wiskunde lijken.quote:Op zaterdag 31 oktober 2009 10:55 schreef thabit het volgende:
[..]
Logica is m.i. meer een onderdeel van de filosofie dan van de wiskunde, maar dat terzijde.
Ik neem aan, dat L(phi * psi) = L(phi) + L(psi) + 1? Dus i.h.b. hebben phi en psi kleinere lengte dan phi * psi zodat we de inductiehypothese kunnen toepassen. Dan heb je toch dat #sfor(phi * psi) = #(sfor(phi) U sfor(psi) U {phi * psi}) <= #sfor(phi) + #sfor(psi) + 1 <= L(phi) + L(psi) + 1 = L(phi * psi), of zie ik dat verkeerd (ik ben immers geen filosoof)?
Maar oké, eigenlijk heel voor de hand liggend, ja. Kwam er niet op gister.
Verder; "Gegeven j ∈{1,2,3} laat Lj: R^2-->R^2 de lineaire afbeelding zijn waarvan de matrix ten opzichte van de standaard bases gelijk is aan Aj met: [insert drie matrices]
Bepaal de eigenwaarden en eigenvectoren van de afbeelding Lj "
Dan moet ik gewoon de eigenwaarden en -vectoren van de matrices Aj bepalen, toch?
Oké, dacht ik al. Maar het is ook weer zo jammer als ik iets totaal verkeerds doe. ;x
Verder, ik ben even een avondje bezig geweest. ;o
1. Vraag b bij vorige vraag; "geef voor iedere j ∈{1,2,3} een basis Bj van R^2 ten opzichte waarvan de matrix Lj een diagonaalsmatrix is.
Dus moet ik een basis V vinden zodat V-1AV=D en D is diagonaalsmatrix. Ik heb het geprobeerd met
Maar dan kwam ik uiteindelijk op
En daar kon ik het niet mee oplossen.
2. Is het een probleem als de eigenvector 0 is, volgens mij wel toch?
3.
Klopt het dat ik hier krijg als eigenwaarde l1,2 = 5 +/- sqrt(100-4*14399)/2 en dus een negatieve wortel / complexe eigenwaarde? Ik denk eigenlijk dat die 14399 niet klopt, want zo'n hoog getal.
4. Laat v ∈ R^2 een vector zijn van lengte één, dus ||v|| = 1. Definieer de matrix A door A=vvT
a. Bepaal kern en beeld (=bereik?) van A
- wat is A? ik heb echt geen idee eigenlijk.
Veel vragen, maar volgens mij kan ik als ik deze dingen weet/snap wel alles maken.
Verder, ik ben even een avondje bezig geweest. ;o
1. Vraag b bij vorige vraag; "geef voor iedere j ∈{1,2,3} een basis Bj van R^2 ten opzichte waarvan de matrix Lj een diagonaalsmatrix is.
Dus moet ik een basis V vinden zodat V-1AV=D en D is diagonaalsmatrix. Ik heb het geprobeerd met
Maar dan kwam ik uiteindelijk op
En daar kon ik het niet mee oplossen.
2. Is het een probleem als de eigenvector 0 is, volgens mij wel toch?
3.
Klopt het dat ik hier krijg als eigenwaarde l1,2 = 5 +/- sqrt(100-4*14399)/2 en dus een negatieve wortel / complexe eigenwaarde? Ik denk eigenlijk dat die 14399 niet klopt, want zo'n hoog getal.
4. Laat v ∈ R^2 een vector zijn van lengte één, dus ||v|| = 1. Definieer de matrix A door A=vvT
a. Bepaal kern en beeld (=bereik?) van A
- wat is A? ik heb echt geen idee eigenlijk.
Veel vragen, maar volgens mij kan ik als ik deze dingen weet/snap wel alles maken.
1. denk aan diagonaliseren
2. een eigenvector is per definitie een nonzero vector
3. je krijgt drie reële eigenwaarden
4. A is een 2x2 matrix. Beeld kunnen ze niet over spreken want er is geen functie gedefinieerd, maar ze bedoelen kolomruimte. Probeer eens wat vectoren v om een idee te krijgen.
2. een eigenvector is per definitie een nonzero vector
3. je krijgt drie reële eigenwaarden
4. A is een 2x2 matrix. Beeld kunnen ze niet over spreken want er is geen functie gedefinieerd, maar ze bedoelen kolomruimte. Probeer eens wat vectoren v om een idee te krijgen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Diagonaliseren heb ik nog nooit gehad. Is er een andere manier om het te beredeneren of door het met die D die ik gevonden heb (geen idee of die klopt, best kans dat er rekenfouten inzitten) op te lossen, of kan ik beter diagonaliseren even googelen?
2 en 3, ik heb een dingetje gevonden die de eigenwaardes en -vectoren kan vinden van matrices en daar bleek inderdaad dat ik ergens rekenfouten moet hebben gemaakt, daar ga ik zo nog eens naar kijkenl
2 en 3, ik heb een dingetje gevonden die de eigenwaardes en -vectoren kan vinden van matrices en daar bleek inderdaad dat ik ergens rekenfouten moet hebben gemaakt, daar ga ik zo nog eens naar kijkenl
Eigenwaarde is 5-sqrt(24), ik probeer bijbehorende vectoren te vinden, maar ergens gaat iets fout. Ik kom op deze manier op de nulvector uit
Je zegt 5-sqrt(24) maar gebruikt 5+sqrt(24).
5+sqrt(24) is een eigenwaarde als A-(5+sqrt(24))I singulier zou zijn. A-(5+sqrt(24))I is niet singulier, dus is 5+sqrt(24) geen eigenwaarde.
5-sqrt(24) is overigens ook geen eigenwaarde. Hoe ben je daarop gekomen?
5+sqrt(24) is een eigenwaarde als A-(5+sqrt(24))I singulier zou zijn. A-(5+sqrt(24))I is niet singulier, dus is 5+sqrt(24) geen eigenwaarde.
5-sqrt(24) is overigens ook geen eigenwaarde. Hoe ben je daarop gekomen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ah sorry, zat nog met die oude matrix, die lijkt er erg op.
Dus (1-L)((5-L)^2 - 24) = 0
Dus L = 1 of L = 5+sqrt(24) of L = 5-sqrt(24)
Ik snap niet wat er gebeurt in de laatste matrix; de tweede rij is een veelvoud van de eerste rij in de derde matrix
Dus (1-L)((5-L)^2 - 24) = 0
Dus L = 1 of L = 5+sqrt(24) of L = 5-sqrt(24)
Ik snap niet wat er gebeurt in de laatste matrix; de tweede rij is een veelvoud van de eerste rij in de derde matrix
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |