SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Vorige deel: [Bèta wiskunde] Huiswerk- en vragentopic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
Een uitleg over LaTeX-code kun je hier vinden
Wiskundig inhoudelijk:
OP
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Volledigquote:Op maandag 19 oktober 2009 17:53 schreef thabit het volgende:
Antwoord op laatste vraag in vorige topic: inductie.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Sobald du dir vertraust, sobald weißt du zu leben. – Omdat Goethe niet in het Engels schreef.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Dat is zo, maar niet iedereen kan Duits.quote:Op maandag 19 oktober 2009 18:34 schreef Iblis het volgende:
[..]
Sobald du dir vertraust, sobald weißt du zu leben. – Omdat Goethe niet in het Engels schreef.
& Minister Rouvoet heeft alle melk opgedroken
Hetgeen bewezen en beklonken moest worden.
Ja de hoeveelste? 
(Tvp)
(Tvp)
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Kan iemand mij een beetje op weg helpen met deze formule.
Hij moet zo ver mogelijk vereenvoudigd worden.
61/2n x 12n+1 x 27-1/2n / 321/2n
[ Bericht 0% gewijzigd door IHVK op 19-10-2009 22:26:30 ]
Hij moet zo ver mogelijk vereenvoudigd worden.
61/2n x 12n+1 x 27-1/2n / 321/2n
[ Bericht 0% gewijzigd door IHVK op 19-10-2009 22:26:30 ]
Begin eens met te bedenken dat (ab)k = akbk en apaq = ap+q. De getallen 6, 12 en 27 hebben een GGD van 3, dus ...quote:Op maandag 19 oktober 2009 21:56 schreef IHVK het volgende:
Kan iemand mij een beetje op weg helpen met deze formule.
Hij moet zo ver mogelijk vereenvoudigd worden.
61/2n x 12n+1 x 27-1/2n / 321/2n
En verder dat je die negatieve exponent naar de noemer kunt verplaatsen.quote:
[..]
Begin eens met te bedenken dat (ab)k = akbk en apaq = ap+q. De getallen 6, 12 en 27 hebben een GGD van 3, dus ...
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Hm ik kom uit op 11.5n+1
...................................12n
Kan dat kloppen?
Stappen: (haakje=macht)
6(0.5n) x 12(n+1)
-----------------------
32 (0.5n) x 27 (0.5n)
72(1.5n+1)
---------
864(n)
/ 72 teller en noemer
=antwoord
...................................12n
Kan dat kloppen?
Stappen: (haakje=macht)
6(0.5n) x 12(n+1)
-----------------------
32 (0.5n) x 27 (0.5n)
72(1.5n+1)
---------
864(n)
/ 72 teller en noemer
=antwoord
Nee dat gaat mis. Sowieso mag je niet stellen dat 6(0.5n) x 12(n+1) = 72(1.5n+1). 'Delen' door 72 mag ook niet. Gebruik de rekenregels van Riparius.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik heb een tussenjaar gehad dus de regels zijn echt weggeëbd.
Ik mag niet door 72 'delen' omdat ze een ander soort exponent hebben?
En die rekenregels heb ik al lang en breed genoteerd, alleen de uitvoering gaat dus niet zo best.
Ik mag niet door 72 'delen' omdat ze een ander soort exponent hebben?
En die rekenregels heb ik al lang en breed genoteerd, alleen de uitvoering gaat dus niet zo best.
'Delen door 72': is 72^2 / 73 gelijk aan 1^2 / 1?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Hoe het wel moet: 12^4 * 4^9 = (3*4)^4 * 4^9 = 3^4 * 4^4 * 4^9 = 3^4 * 4^13.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Je mag dus zeggen:
2a·3a = 6a, óf:
2a·2b = 2a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
[ Bericht 0% gewijzigd door Iblis op 19-10-2009 22:55:12 ]
2a·3a = 6a, óf:
2a·2b = 2a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
[ Bericht 0% gewijzigd door Iblis op 19-10-2009 22:55:12 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Deze volg ik alleen niet.quote:
Je mag dus zeggen:
2a·3a = 6a, óf:
2a·2b = 6a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
Terecht, want die was ook onzin. Nu staat het er beter.quote:
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ok thx, maar ik ga nog wel even nog een noob vraag stellen dan.
Omdat ik de negatieve exponent in de noemer tip (van Iblis) opvolg, want dat lijkt me logisch.
Krijg ik dit
6(0.5n) x 12 (n+1)
_____________
32 (0.5n) x 27 (0.5n)
In principe kan ik nu de onderste met elkaar vermenigvuldigen en zeggen dat ik klaar ben, maar iets zeg me dat ik een andere richting op moet met die (0.5n) en dat het verder vereenvoudigd kan worden.
Ja toch?
Omdat ik de negatieve exponent in de noemer tip (van Iblis) opvolg, want dat lijkt me logisch.
Krijg ik dit
6(0.5n) x 12 (n+1)
_____________
32 (0.5n) x 27 (0.5n)
In principe kan ik nu de onderste met elkaar vermenigvuldigen en zeggen dat ik klaar ben, maar iets zeg me dat ik een andere richting op moet met die (0.5n) en dat het verder vereenvoudigd kan worden.
Ja toch?
Jups. Sowieso:
En dan kun al eens proberen of je nu een 6n/2 kunt krijgen in de noemer.
En dan kun al eens proberen of je nu een 6n/2 kunt krijgen in de noemer.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
6(0.5n) x 12 (n+1)quote:
Jups. Sowieso:
[ afbeelding ]
En dan kun al eens proberen of je nu een 6n/2 kunt krijgen in de noemer.
-------------
6(0.5n) x 144 (0.5n)
12(n+1)
-------------
144 (1/2n)
Ik hoop en denk dat dit klopt.
En anders hoor ik het morgen wel.
Thx.
Die 144 = 122 en (122)1/2n = 12n. Dus het eind-antwoord is ‘12’.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
vergeet ax*bx = (ab)x nietquote:Op maandag 19 oktober 2009 22:48 schreef Iblis het volgende:
Je mag dus zeggen:
2a·3a = 6a, óf:
2a·2b = 2a+b, maar niet 2a·3b=6a+b.
Ga maar na: 23 = 2·2·2 en 33 = 3·3·3 en natuurlijk 2·2·2·3·3·3=6·6·6. (En natuurlijk 22 · 23 = 2·2·2·2·2 = 25.) Maar 22 · 33 = 4 · 27 en dat is natuurlijk heel wat anders dan 65, wat jij doet.
Ik heb het vast gemist, maar de latexcode doet het nog steeds niet goed. Is de link niet meer goed ofzo?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Ik moet het nog een keer fixen. Als iemand anders een vhost kan opzetten op zijn webserver wil ik de dns daarnaartoe wel aanpassen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Lukt dat niet makkelijk met De Moivre?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
is dat niet iets met e^iy = cos x nog wat?quote:Op dinsdag 20 oktober 2009 20:27 schreef GlowMouse het volgende:
Lukt dat niet makkelijk met Euler?
Was voor je edit:
Even kijken naar Moivre
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Nou ik kom er echt niet uit:
Ik blijf steken bij:
Eerst schrijf ik de bovenste term naar polaire vorm:
r = ((-1)^2 + 1^2) = wortel(2)
z = wortel(2) (cos pi/4 + i sin pi/4 )
-1/wortel(2) + i/wortel(2) --> ((wortel(2)/wortel(2) (cos(pi/4) + i sin(pi/4) )^1001
--> 1 * ( cos(1001pi/4) + i sin (1001pi/4) )
---> aangezien 2pi een rondje is. 1000/2 = 500. Hou je 1 pi over?? Dus dan:
---> ( cos(5pi/4) + i sin (5 pi/4) ) en daarna raakt het een beetje in de soep.
Ik blijf steken bij:
Eerst schrijf ik de bovenste term naar polaire vorm:
r = ((-1)^2 + 1^2) = wortel(2)
z = wortel(2) (cos pi/4 + i sin pi/4 )
-1/wortel(2) + i/wortel(2) --> ((wortel(2)/wortel(2) (cos(pi/4) + i sin(pi/4) )^1001
--> 1 * ( cos(1001pi/4) + i sin (1001pi/4) )
---> aangezien 2pi een rondje is. 1000/2 = 500. Hou je 1 pi over?? Dus dan:
---> ( cos(5pi/4) + i sin (5 pi/4) ) en daarna raakt het een beetje in de soep.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Welk getal doe je nou? Want r=1 voor beide getallen.
En de hoek bij -1 + i is niet pi/4.
En de hoek bij -1 + i is niet pi/4.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
r = 1??? ehh... ik pak zeg maar -1 + 1*i voor de bovenste term.....quote:Op dinsdag 20 oktober 2009 21:09 schreef GlowMouse het volgende:
Welk getal doe je nou? Want r=1 voor beide getallen.
En de hoek bij -1 + i is niet pi/4.
Edit: en die hoek is natuurlijk 3/4 pi.
Maar als ik naar polaire vorm schrijf, dan wordt die -1+1i toch z = wortel ( 1 +1 ) ??
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
quote:Op dinsdag 20 oktober 2009 21:30 schreef GlowMouse het volgende:
waar komt -1+i vandaan dan?
van die boventerm : ( -1/wortel2 + i 1/wortel 2 )
In het boek zag ik dat ze hetzelfde doen met : 1/2 + 1/2 i gebruikten ze 1+i .. dus vandaar..
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
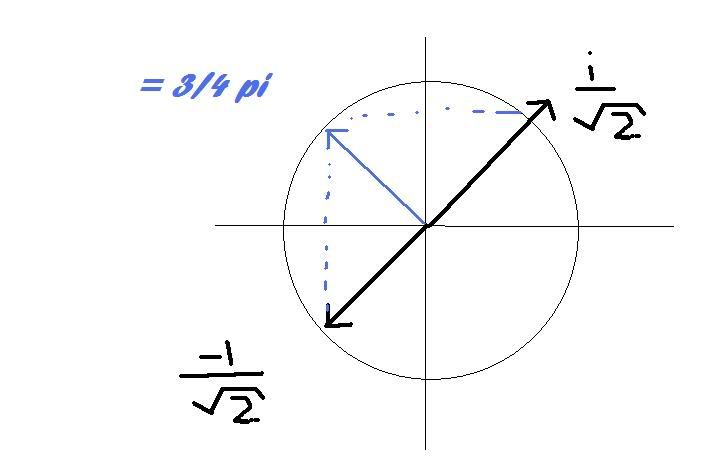
Het is toch makkelijker om -1/wortel2 + i 1/wortel 2 te schrijven als cos(3pi/4) + i sin(3pi/4)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
ff denken.... -1 wortel 2 = 5/4 pi + pi 1/4 --> ja idd dat wordt op de éénheidscirkel 3/4 pi. Ik ga even een paint maken om het te verduidelijken. kijken of ik het goed doe.quote:Op dinsdag 20 oktober 2009 21:42 schreef GlowMouse het volgende:
Het is toch makkelijker om -1/wortel2 + i 1/wortel 2 te schrijven als cos(3pi/4) + i sin(3pi/4)?
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
Schrijf eens de breuk als 1 e-macht, zoiets als et/en = et-n, en kijk wat de rest wordt als je de resulterende exponent modulo 2pi neemt.quote:Op dinsdag 20 oktober 2009 20:22 schreef Burakius het volgende:
Heey genialen,
Vrienden en ik kwamen niet uit deze som. (uitwerking is perongeluk boven i.p.v. beneden). Hoe kom je nou op die onderste term ^3( dus welk truukje wordt er nou uitgehaald bij de eerste bewerking). Help ons uit de brand.
[ afbeelding ]
btw. Even mijn totale noob plaatje:
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
Het is echt lang geleden, ik moet me maar eens totaal inlezen.
In fact, recent observations and simulations have suggested that a network of cosmic strings stretches across the entire universe.
