[Bčta wiskunde] Huiswerk- en vragentopic

Lelijk van Excel, dan moet je haakjes gebruiken.

Maar hoe dan? Als ik -2 tussen haakjes zet, krijg ik dus dezelfde uitkomst als zonder haakjes Daarom ben ik zo in de war.

quote:

Op zondag 25 oktober 2009 15:12 schreef RenRen- het volgende:
Maar hoe dan? Als ik -2 tussen haakjes zet, krijg ik dus dezelfde uitkomst als zonder haakjes Daarom ben ik zo in de war.

Wat wil je eerst doen? -2 uitrekenen of eerst 2^x uitrekenen?

quote:

Op zondag 25 oktober 2009 @ 15:13 schreef GlowMouse het volgende:

[..]

Wat wil je eerst doen? -2 uitrekenen of eerst 2^x uitrekenen?

Ik weet het niet In mijn reader staat dus.
-2^x
En aangezien ik dan een of ander puntig ding krijg als grafiek, is dat zekerweten fout. En als ik de -2 tussen haakjes zet. Heb ik nogsteeds een puntig ding

quote:

Op zondag 25 oktober 2009 15:15 schreef RenRen- het volgende:

[..]

Ik weet het niet In mijn reader staat dus.
-2^x
En aangezien ik dan een of ander puntig ding krijg als grafiek, is dat zekerweten fout. En als ik de -2 tussen haakjes zet. Heb ik nogsteeds een puntig ding

http://nl.wikipedia.org/wiki/Bewerkingsvolgorde

quote:

Op zondag 25 oktober 2009 @ 15:17 schreef GlowMouse het volgende:

[..]

http://nl.wikipedia.org/wiki/Bewerkingsvolgorde

Ja, dat weet ik allemaal, maar nog snap ik niet wat ik verkeerd doe. Omdat haakjes eerst verwerkt worden, zou ik -2 eerst tussen haakjes moeten zetten, toch? Omdat anders de min genegerd wordt en gelijk naar de ^ gekeken wordt, toch?

Als je -2^x hebt, moet je eerst 2^x uitrekenen. Excel doet dat blijkbaar niet. Hoe los je dat op.

Ik heb geen idee, mijn hoofd blokkeert alles op het moment Moet 2^x tussen haakjes dan?

Om heel eerlijk te zijn gaat het volgende om een opdracht die ik moet maken.
Maar ik ben zelf helemaal geen wiskundige, althans ik ben bij lange na niet zo diep de wiskunde ingegaan als voor mijn idee deze vraag eist.


Ultrametric Trees

Definition 1: ultrametric tree
Let D be a symmetric n x n matrix of real numbers. An ultrametric tree T is a tree with the following properties:
* T contains n leaves and each leave is labeled by one row/column of D;
* Each internal node of T is labeled by a value of D and has at least two children;
* For each path from a leaf to the root, the values on the nodes are given in increasing order;
* For each pair (i,j) of leaves the following holds: The last common ancestor of i and j in T is labeled using the value D(i,j).

Definition 2: Ultrametric Distance
A symmetric Matrix D of real numbers defines an ultrametric Distance if and only if for each triple of indices i,j,k holds:
The maximum of the three distances D(i,j), D(i,k) and D(j,k) is not unique; or in other words, two of the distances are equal while a third is smaller (or equal as well).

Exercise
Prove the following statement:
A symmetric Matrix D corresponds to an ultrametric tree T if and only if D defines an ultrametric distance.


Ik vraag niet om een direct antwoord, maar of iemand mij kan uitleggen hoe ik nou eigenlijk een ultrametric tree maak. En als tweede hoe ik een vector k kan hebben als ik enkel i & j heb? Of moet ik soms voor een willekeurige vector k nagaan dat de definitie van ultrametric distance klopt wanneer mijn matrix symmetrisch is? Ik heb me al een ongeluk gezocht naar websites die het me uitleggen, maar ze lijken elkaar zelfs tegen te spreken? De ene geeft als 4e conditie d(x,y) =< d(x,z)+d(y,z) en de andere d(x,y) =< max(d(x,z),d(y,z))...

Het ergste nog wel is dat het vak tot nu toe helemaal niet echt gaat over dit soort wiskunde bewijzen (het is juist biologie...) en in geen van de slides wordt ook maar een stap richting 'trees' gemaakt. Het is dus hopeloos zoeken en proberen te begrijpen tot je een ons weegt.

quote:

Op zondag 25 oktober 2009 15:21 schreef RenRen- het volgende:
Ik heb geen idee, mijn hoofd blokkeert alles op het moment Moet 2^x tussen haakjes dan?

is het niet zo dat bij -2^x dat je een positief getal krijgt bij een x dat even is en een negatief getal bij oneven?
-2^2 -> -2*-2 = 4, -2^3 -> -2*-2*-2 = -8. In dat geval zou je gewoon 2^x doen en zeggen dat als even -> positief, en oneven zet er een - voor.

(-2)^x is voor mijn idee doorgaans hetzelfde als -2^x.
Als je enkel negatief wilt moet je iets als -(2)^x doen... iets als -1 * 2^x.

Mogelijk is de - voor de 2^x gewoon als een aanduiding als in:
- je hebt zus
- je hebt zo

[ Bericht 23% gewijzigd door koffiegast op 25-10-2009 17:25:52 ]

typo

quote:

Op zondag 25 oktober 2009 @ 17:24 schreef Iblis het volgende:

[..]

Nee, normaliter heeft machtsverheffen prioriteit. Dus -2^x is -(2^x), en als je wilt wat jij wilt doe je (-2)^x. Excel interpreteert -2^x echter blijkbaar als (-2)^x en niet als -(2^x).

Ja, dát werkte dus.
Daarom raakte ik zo in de war.
Heel erg bedankt

kan iemand mij helpen met deze formule: N = 480x2(kwadraat) - 40x3(kwadraat).
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?

N = 480x˛ - 40xł ?
Kun je toch zo invullen op een grafische rekenmachine?

quote:

Op zondag 25 oktober 2009 18:08 schreef Gratau het volgende:
kan iemand mij helpen met deze formule: N = 480x2(kwadraat) - 40x3(kwadraat).
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?

y1 = (480*X^2) - (40*X^3)

doe ik dan, de ( ) is wellicht niet eens nodig, maar doe ik voor de zekerheid.

* gaat voor -, de haakjes zijn dus niet nodig.

quote:

Op zondag 25 oktober 2009 18:08 schreef Gratau het volgende:
kan iemand mij helpen met deze formule: N = 480x2(kwadraat) - 40x3(kwadraat).
de formule snap ik wel enzo, maar ik krijg het maar niet op m'n grafische rekenmachine. welke waarden moet ik hebben om de grafiek te plotten?

Schijf die formule om te beginnen eens wat begrijpelijker op. Je kunt hier gebruik maken van subscript en superscript, dus doe dat dan ook.

quote:

Op zondag 25 oktober 2009 18:15 schreef GlowMouse het volgende:
N = 480x˛ - 40xł ?
Kun je toch zo invullen op een grafische rekenmachine?

ja, maar dan zie ik hem niet of heel klein ofzo. ik kan de juiste waarden niet vinden voor de X en Y min/max

quote:

Op zondag 25 oktober 2009 18:17 schreef Gratau het volgende:

[..]

ja, maar dan zie ik hem niet of heel klein ofzo. ik kan de juiste waarden niet vinden voor de X en Y min/max

window aanpassen, eerst je x kiezen en dan bedenken welke y daarbij horen.

heb het al

quote:

Op zondag 25 oktober 2009 17:15 schreef koffiegast het volgende:
Om heel eerlijk te zijn gaat het volgende om een opdracht die ik moet maken.
Maar ik ben zelf helemaal geen wiskundige, althans ik ben bij lange na niet zo diep de wiskunde ingegaan als voor mijn idee deze vraag eist.


Ultrametric Trees

Definition 1: ultrametric tree
Let D be a symmetric n x n matrix of real numbers. An ultrametric tree T is a tree with the following properties:
* T contains n leaves and each leave is labeled by one row/column of D;
* Each internal node of T is labeled by a value of D and has at least two children;
* For each path from a leaf to the root, the values on the nodes are given in increasing order;
* For each pair (i,j) of leaves the following holds: The last common ancestor of i and j in T is labeled using the value D(i,j).

Definition 2: Ultrametric Distance
A symmetric Matrix D of real numbers defines an ultrametric Distance if and only if for each triple of indices i,j,k holds:
The maximum of the three distances D(i,j), D(i,k) and D(j,k) is not unique; or in other words, two of the distances are equal while a third is smaller (or equal as well).

Exercise
Prove the following statement:
A symmetric Matrix D corresponds to an ultrametric tree T if and only if D defines an ultrametric distance.


Ik vraag niet om een direct antwoord, maar of iemand mij kan uitleggen hoe ik nou eigenlijk een ultrametric tree maak. En als tweede hoe ik een vector k kan hebben als ik enkel i & j heb? Of moet ik soms voor een willekeurige vector k nagaan dat de definitie van ultrametric distance klopt wanneer mijn matrix symmetrisch is? Ik heb me al een ongeluk gezocht naar websites die het me uitleggen, maar ze lijken elkaar zelfs tegen te spreken? De ene geeft als 4e conditie d(x,y) =< d(x,z)+d(y,z) en de andere d(x,y) =< max(d(x,z),d(y,z))...

Het ergste nog wel is dat het vak tot nu toe helemaal niet echt gaat over dit soort wiskunde bewijzen (het is juist biologie...) en in geen van de slides wordt ook maar een stap richting 'trees' gemaakt. Het is dus hopeloos zoeken en proberen te begrijpen tot je een ons weegt.

Je moet twee implicaties bewijzen: boom => matrix en matrix => boom. Ik zou beginnen met die eerste als ik jou was. Daarna kan het handig zijn om wat simpele voorbeeldjes uit te werken voor de ander implicatie, zodat je ziet wat er gebeurt.

En i, j en k zijn geen vectoren maar indices, D(i, j) is dan het getal dat in de matrix op plek (i, j) staat, etc. Je moet het zo zien: je hebt n punten, en daartussen staan afstanden gedefinieerd, je indices komen met die punten overeen. De afstand tussen i en j staat dus op plek (i, j). Een afstand moet normaliter voldoen aan de driehoeksongelijkheid, dat wil zeggen D(i, j) + D(j, k) <= D(i, k) voor elk drietal punten i, j, k. Zo'n afstand heet ultrametrisch als-ie aan de sterkere vorm van de driehoeksongelijkheid voldoet die jij boven beschreven hebt.

maar wat is dan k? Dat kan ik dus niet echt terugvinden in een symmetrische matrix van i en j enkel, het lijkt me verder stug k willekeurig te doen, ik bedoel dus: is er iets waarvan ik het kan afleiden? Verder zit ik nog beetje vast met hoe ik zo'n boom precies maak.

quote:

Op zondag 25 oktober 2009 22:58 schreef koffiegast het volgende:
maar wat is dan k? Dat kan ik dus niet echt terugvinden in een symmetrische matrix van i en j enkel, het lijkt me verder stug k willekeurig te doen, ik bedoel dus: is er iets waarvan ik het kan afleiden? Verder zit ik nog beetje vast met hoe ik zo'n boom precies maak.

k is net als i en j gewoon een index, dus een element van {1, ..., n}.

quote:

Op zondag 25 oktober 2009 23:12 schreef thabit het volgende:

[..]

k is net als i en j gewoon een index, dus een element van {1, ..., n}.

Maar dat is mijn probleem, als ik slechts 2 strings heb met elk een eigen index, van wat is dan index k? Ik bekijk het zeker compleet verkeerd ofzo

quote:

Op zondag 25 oktober 2009 23:14 schreef koffiegast het volgende:

[..]

Maar dat is mijn probleem, als ik slechts 2 strings heb met elk een eigen index, van wat is dan index k? Ik bekijk het zeker compleet verkeerd ofzo

In de driehoeksongelijkheid heb je er 3 nodig. Je relateert dan immers de 3 onderlinge afstanden tussen 3 punten met elkaar.

Hoi ik heb morgen een wiskunde B toets en ik snap niet hoe ik het volgend kan uitreken
1.5^x = .5log(x)

ik moet x weten

iemand suggesties??

quote:

Op maandag 26 oktober 2009 18:16 schreef netolk het volgende:
Hoi ik heb morgen een wiskunde B toets en ik snap niet hoe ik het volgend kan uitreken
1.5^x = .5log(x)

ik moet x weten

iemand suggesties??

In het algemeen kun je zulke vergelijkingen niet symbolisch oplossen. Probeer nu eerst maar eens na te gaan of de vergelijking überhaupt wel oplossingen heeft; het linkerdeel van de vergelijking lijkt een stuk groter dan het rechterdeel.

quote:

Op maandag 26 oktober 2009 18:18 schreef thabit het volgende:

[..]

In het algemeen kun je zulke vergelijkingen niet symbolisch oplossen. Probeer nu eerst maar eens na te gaan of de vergelijking überhaupt wel oplossingen heeft; het linkerdeel van de vergelijking lijkt een stuk groter dan het rechterdeel.

Hij is op te lossen ik heb hem geplot en toen had ik x is bij benadering 0,44 maar ik moet x dus exact weten

Als x ongeveer 0,44 is, zal 1.5^x groter dan 0 zijn en log(x) kleiner dan 0 (want x<1). Dus ik denk dat je iets fout hebt gedaan.

dit heb ik zo uit mijn boek overgenomen en als je hem plot en intersect komt er uit x = .43711598 en y = 1.193912

In dat geval heb je de som hier verkeerd overgetikt.

nee hoor

y1 = 1.5^x
y2 = .5log(x)

en dan plotten
en ik had 1.5^x = .5log(x) hier neer gezet

Als dat echt de vgl is die je moet oplossen, dan heb je het fout gedaan in je plotprogramma. Die vergelijking van jou heeft geen oplossingen met x<1 (en waarschijnlijk zelfs helemaal geen oplossingen maar dat mag je zelf uitwerken).

Hij heeft geen oplossing in R maar wel een in C

Maak maar een screenshot/foto van je plotding, want er gaat iets fout.

nee, moet ongeveer 0.44 zijn maar ik kan die zooi dus niet met algebra oplossen. Had deze som van een klasgenootje gekregen en die komt er nu pas mee dat het niet exact hoefde...

Toch harstike bedankt thabit

quote:

Op maandag 26 oktober 2009 18:41 schreef GlowMouse het volgende:
Hij heeft geen oplossing in R maar wel een in C

log(x) is niet gedefinieerd op C.

Ik twijfelde al toen ik het postte. Waar staat een goed overzichtje van al die standaardfuncties met hun domein?

quote:

Op maandag 26 oktober 2009 18:46 schreef GlowMouse het volgende:
Ik twijfelde al toen ik het postte. Waar staat een goed overzichtje van al die standaardfuncties met hun domein?

Vast wel op Wikipedia. .

Het handigst is natuurlijk om gewoon een keer een vak complexe functietheorie gevolgd te hebben, dan zit het gelijk goed in je hoofd.

log(z) is niet eenduidig gedefinieerd want als exp(z+2*pi*i) = exp(z). De waarde ligt dus altijd vast op een veelvoud van 2*pi*i na. Een holomorfe functie log(z) (dwz inverse van exp(z)) kun je definieren op een open deel U van C-{0} waarin geen gesloten pad bestaat dat om het punt 0 heen draait, dus bijvoorbeeld op C - (-oneindig, 0].

Morgen tentamen "wiskundesommen correct overtikken op je GR"

quote:

Op maandag 26 oktober 2009 18:26 schreef netolk het volgende:
dit heb ik zo uit mijn boek overgenomen en als je hem plot en intersect komt er uit x = .43711598 en y = 1.193912

Ik snap het al, het heeft geen oplossingen.

Wellicht bedoel je 1.5^x = .5logx/logx

Probeer ipv intersect ook eens de gewone solver in het hoofdmenu.

Meer info: http://world.casio.com/ed(...)d/f07_01f/f07_01.pdf

[ Bericht 12% gewijzigd door Q.E.D. op 26-10-2009 20:43:01 ]

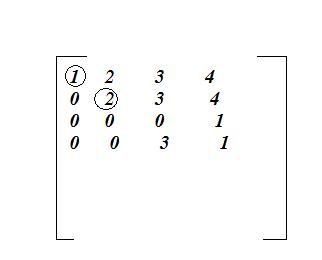
Wat is de volgende pivot. Die 1 of die 3. En ja dit is noob.

Die 3, en daarom moet je ook de derde en vierde rij omwisselen.

quote:

Op maandag 26 oktober 2009 22:16 schreef GlowMouse het volgende:
Die 3, en daarom moet je ook de derde en vierde rij omwisselen.

Die regel helemaal vergeten ja.

quote:

Op maandag 26 oktober 2009 18:59 schreef Iblis het volgende:

[..]

Het kán geen 0,44 zijn. Hier heb je een grafiekje tussen 0 en 1.

[ afbeelding ]

Rood is 1.5^x, groen is .5log(x). Zie je hoe ze nooit snijden?

Ik denk dat Netolk de vgl (1.5)^x = ^0.5log(x) bedoelt.

quote:

Op dinsdag 27 oktober 2009 03:29 schreef ErictheSwift het volgende:

[..]

Ik denk dat Netolk de vgl (1.5)^x = ^0.5log(x) bedoelt.

Inderdaad. Numeriek oplossen levert dan x = 0,4371159833 ...

Als Netolk nu even de moeite had genomen 0,5 te superscripten dan had dat een hoop nutteloze discussie gescheeld. Laat maar weer eens zien hoe belangrijk een goede notatie is.

quote:

Op maandag 26 oktober 2009 22:15 schreef Burakius het volgende:
[ afbeelding ]
En ja dit is noob.

Ja, hou potdomme es op met die noobvragen hiero

Ik heb een pagina ingescand van mijn "rekenboek" Mijn kennis van kansverdelingen is echt gebaseerd op dit boek. Maar ik moet zeggen dat het boek niet echt duidelijk is voor mij.

http://img9.imageshack.us/img9/2681/img342u.jpg

Zo heb ik bij vraag 1 al de eerste vraagtekens. 1a, kan ik nog gewoon beantwoorden. (gewoon uit de tekst links halen) maar 1b en 1c zijn voor mij een raadsel. Zouden jullie mij een beetje op weg kunnen helpen? Het is voor mij nog veel te vaag. (ook die zogenaamde diagram waar ik net niets vanaf kan lezen..)

p.s. de antwoorden volgens het antwoordenboek zijn: 1a. ruim 68% 1b. 95,4% en c. 2,3%

Bedankt voor jullie hulp!

p.p.s. als ik dit snap, dan ga ik naar de volgende vragen, en heb ik jullie hulp wellicht weer nodig