SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Vorig deel: [Centraal] Bèta huiswerk en vragen topic
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Wiskunde
Natuurkunde
Informatica
Scheikunde
Biologie
Algemene Natuurwetenschappen
Alles wat in de richting komt
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen. Vragen over coderingstheorie en het gelijknamig maken van breuken worden extra op prijs gesteld.
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de vakken:
Van MBO tot WO, hier is het topic wat antwoord kan geven op je vragen. Vragen over coderingstheorie en het gelijknamig maken van breuken worden extra op prijs gesteld.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wat is een frequentietabel?:o
Celebrities walk on red carpet because they are famous, I walk on toilet paper because I'm the shit
5 Xbox360 spellen: Halo 3 , Fable 2 ,Saints Row 2 , Pure en Virtua Tennis 3 te koop!
5 Xbox360 spellen: Halo 3 , Fable 2 ,Saints Row 2 , Pure en Virtua Tennis 3 te koop!


ik doe atheneum!!1
Celebrities walk on red carpet because they are famous, I walk on toilet paper because I'm the shit
5 Xbox360 spellen: Halo 3 , Fable 2 ,Saints Row 2 , Pure en Virtua Tennis 3 te koop!
5 Xbox360 spellen: Halo 3 , Fable 2 ,Saints Row 2 , Pure en Virtua Tennis 3 te koop!


Dan moet ik alles wat ik er nog over wil zeggen dus nog in één post proppen . Ik ben het niet met jouw berekening eens. De notatie u(x, y(x), z) = x + y(x) + z gebruiken en dan deze tweede variabele constant willen houden is fout en veroorzaakt de verwarring. Je schrijft de functie x -> x + cos(x) ook niet als f(x,cos(x)) = x + cos(x) en gaat dan cos(x) constant houden als je de afgeleide wilt bepalen. Je moet gewoon schrijven u(x,z) = x + y(x) + z, of, correcter imo als je met u(x,y,z)=x+y+z begonnen bent, (u ○ f)(x,z), waarbij f(x,z) = (x,y(x),z) voor een zekere functie y. Dan geeft de partiële afgeleide naar x je keurig het juiste antwoord.quote:Op zaterdag 25 augustus 2007 23:48 schreef GlowMouse het volgende:
[..]
Hierna nog één post, dan zit het topic vol en is de discussie ten einde. Heb jij het laatste woord als niemand je voor is
[..]
Dat 'gewoon per definitie' klopt niet. Als y een functie is van x, dan kun je schrijven u(x, y(x), z) = x + y(x) + z. Neem je bij deze functie de partiële afgeleide nemen naar x, dan blijkt uit de definitie dat andere parameters buiten beschouwing moeten worden gelaten. Zou je toch y(x+h) gebruiken, blijft de tweede parameter niet constant. ∂u/∂x is dus 1, onafhankelijk van de relatie tussen x en y. Omdat je in praktijk ook wel eens wilt weten wat y doet als alleen x een infinitesimaalkleine wijziging ondergaat, is ook de totale afgeleide maar geïntroduceerd.
Verdorie, te laat
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


had het over mezelf
frequentietable is bijv over wat voor cijfers er voorkomen bij een toets in een klas
bijv 30 leerlingen
1 | 2 keer
2 | 3 keer
3 | 5 keer
4 | 2 keer
5 | 1 keer
6 | 12 keer
7 | 1 keer
8 | 0 keer
9 | 0 keer
10| 4 keer
Maar zo moet je hem niet noteren
frequentietable is bijv over wat voor cijfers er voorkomen bij een toets in een klas
bijv 30 leerlingen
1 | 2 keer
2 | 3 keer
3 | 5 keer
4 | 2 keer
5 | 1 keer
6 | 12 keer
7 | 1 keer
8 | 0 keer
9 | 0 keer
10| 4 keer
Maar zo moet je hem niet noteren
When I get sad, I stop being sad and just be awesome instead.


Wat dacht je van een tabel waarin je de verschillende mogelijke uitkomsten samen met het aantal maal dat ze voorkomen neerzet? Uitgekauwd voorbeeld: 10 x muntje flippen geeft 7 x kop en 3 x munt. Dan tabel:quote:Op zondag 26 augustus 2007 00:14 schreef UnderTheWingsOfLove het volgende:
Wat is een frequentietabel?:o
| K | M |
-----------
| 7 | 3 |
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Oh ja, ik heb ook nog een probleempje dat ik met jullie wil delen!
Een zekere koning gaat een groot feest geven! Een paar dagen voor het feest vangen zijn bewakers een vijandelijke spion. Ze doen hem eens lekker martelen en komen zo te weten dat precies een van de 1000 flessen wijn is vergiftigd . Iedereen die daarvan drinkt gaat altijd dood na een paar dagen, zelfs van de kleinste hoeveelheid! Nu wil de koning het feest niet uitstellen, maar zijn slaven gebruiken om te testen welke fles wijn dodelijk is. Een slaaf mag best van meerdere flessen drinken, maar er is dus niet voldoende tijd voor een tweede drink ronde. Hoeveel slaven moet de koning gebruiken om met 100% zekerheid de dodelijke fles wijn te achterhalen?
Aangezien ik een 0.0000478432 op de schaal van thabit score, wist ik dit probleem vrij makkelijk op te lossen, maar kunnen jullie dat ook? .
Een zekere koning gaat een groot feest geven! Een paar dagen voor het feest vangen zijn bewakers een vijandelijke spion. Ze doen hem eens lekker martelen en komen zo te weten dat precies een van de 1000 flessen wijn is vergiftigd . Iedereen die daarvan drinkt gaat altijd dood na een paar dagen, zelfs van de kleinste hoeveelheid! Nu wil de koning het feest niet uitstellen, maar zijn slaven gebruiken om te testen welke fles wijn dodelijk is. Een slaaf mag best van meerdere flessen drinken, maar er is dus niet voldoende tijd voor een tweede drink ronde. Hoeveel slaven moet de koning gebruiken om met 100% zekerheid de dodelijke fles wijn te achterhalen?
Aangezien ik een 0.0000478432 op de schaal van thabit score, wist ik dit probleem vrij makkelijk op te lossen, maar kunnen jullie dat ook? .


Eerst ingeving is 2*sqrt(1000). Je legt de flessen in een matrix en laat elke slaaf een hele rij of kolom drinken. 2 Slaven gaan dood, en het kruispunt van hun rij en kolom is de vergiftigde fles. 64 slaven zouden hiervoor nodig zijn, maar iets zegt me dat het efficienter kan..
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.


Ah, je kan die matrix ook opdelen in kleinere matrixen, en dat nog meerdere keren ook.. Wat daar het optimale geval van is bereken ik morgen wel
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.


Ok, een ingeving gehad, nu kan ik het met 10 slaven. Ben nog niet helemaal tevreden, misschien dat ik er morgen nog eentje af kan afschaven. Maar nu echt slapen.
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.


En centraal
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


Ik denk inderdaad ook 10, maar ik wil je natuurlijk niet de verdiende eer van de eerste oplossing ontnemen dus ik zal mijn poging in een spoiler zetten.quote:Op zondag 26 augustus 2007 02:56 schreef Gebraden_Wombat het volgende:
Ok, een ingeving gehad, nu kan ik het met 10 slaven. Ben nog niet helemaal tevreden, misschien dat ik er morgen nog eentje af kan afschaven. Maar nu echt slapen.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek


tvp
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


quote:Op zondag 26 augustus 2007 03:55 schreef keesjeislief het volgende:
[..]
Ik denk inderdaad ook 10, maar ik wil je natuurlijk niet de verdiende eer van de eerste oplossing ontnemen dus ik zal mijn poging in een spoiler zetten.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Mijn oplossing was niet zo wiskundig, maar goed.
Mijn idee was dat je maar 2 slaven nodig hebt om de dodelijke uit 4 opties te kiezen. Ze gaan namelijk allebei dood, 1 van 2ën of geen van beiden.
Nu deel je de 32x32 matrix op in 162 2x2 matrixjes en laat die slaven dezelfde test uitvoeren op al die matrixjes. Maar nu weet je nog niet in welke van die 162 matrixjes nu de dodelijke zit. Maar dat is hetzelfde probleem als net, maar nu met een 16x16 matrix.
Doe dus nu hetzelfde: laat 2 slaven het hele veld afgaan, maar ipv dat een slaaf 1 fles drinkt, drinkt hij alle 4 de flessen uit een 2x2 matrix.
Als je dit 5x doet met steeds 2x zo grote hokjes heb je de hele matrix van 32x32 gehad, en je hebt er maar 5*2 = 10 slaven voor nodig.
En toch bevallen die 24 lege plekken me niet
Edit:
Waarom zou je je beperken tot het platte vlak. In drie dimensies gaat het efficiënter, je hebt dan maar 3 slaven nodig voor 2*2*2=8 keuzes. Ook wordt de kubus mooier, namelijk 10x10x10.
Helaas komt de uitbreiding hier minder mooi uit. In 3 stappen zit je op 8*8*8=512, en heb je alsnog 1 slaaf extra nodig om tussen 2 8*8*8-kubussen te kiezen, en dus totaal 10 slaven.
[ Bericht 18% gewijzigd door Gebraden_Wombat op 26-08-2007 10:55:42 ]
Mijn idee was dat je maar 2 slaven nodig hebt om de dodelijke uit 4 opties te kiezen. Ze gaan namelijk allebei dood, 1 van 2ën of geen van beiden.
Nu deel je de 32x32 matrix op in 162 2x2 matrixjes en laat die slaven dezelfde test uitvoeren op al die matrixjes. Maar nu weet je nog niet in welke van die 162 matrixjes nu de dodelijke zit. Maar dat is hetzelfde probleem als net, maar nu met een 16x16 matrix.
Doe dus nu hetzelfde: laat 2 slaven het hele veld afgaan, maar ipv dat een slaaf 1 fles drinkt, drinkt hij alle 4 de flessen uit een 2x2 matrix.
Als je dit 5x doet met steeds 2x zo grote hokjes heb je de hele matrix van 32x32 gehad, en je hebt er maar 5*2 = 10 slaven voor nodig.
En toch bevallen die 24 lege plekken me niet
Edit:
Waarom zou je je beperken tot het platte vlak. In drie dimensies gaat het efficiënter, je hebt dan maar 3 slaven nodig voor 2*2*2=8 keuzes. Ook wordt de kubus mooier, namelijk 10x10x10.
Helaas komt de uitbreiding hier minder mooi uit. In 3 stappen zit je op 8*8*8=512, en heb je alsnog 1 slaaf extra nodig om tussen 2 8*8*8-kubussen te kiezen, en dus totaal 10 slaven.
[ Bericht 18% gewijzigd door Gebraden_Wombat op 26-08-2007 10:55:42 ]
Op dinsdag 23 augustus 2011 23:18 schreef problematiQue het volgende:
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.
Mensen die zomaar claimen dat A beter is dan B moet je gewoon negeren. Internetruis.


De koning heeft inderdaad 10 slaven nodig .
Nu een vraagje over algoritmen!
Gegeven n haaien waarvan de kracht, snelheid en intelligentie (dit zijn constanten) bekend zijn. Een haai kan een andere haai opeten als hij minstens net zo sterk, snel en slim is. Voorts is gegeven dat een haai maximaal 2 andere haaien kan opeten. Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen .
Nu een vraagje over algoritmen!
Gegeven n haaien waarvan de kracht, snelheid en intelligentie (dit zijn constanten) bekend zijn. Een haai kan een andere haai opeten als hij minstens net zo sterk, snel en slim is. Voorts is gegeven dat een haai maximaal 2 andere haaien kan opeten. Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen .


Je kunt mijn idee en jouw eerste idee met elkaar verenigen door n-dimensionale matrices te bekijken, en dan te kijken welke n het beste resultaat geeft. Dat moet ook 10 opleveren.quote:Op zondag 26 augustus 2007 10:34 schreef Gebraden_Wombat het volgende:
Mijn oplossing was niet zo wiskundig, maar goed.
Mijn idee was dat je maar 2 slaven nodig hebt om de dodelijke uit 4 opties te kiezen. Ze gaan namelijk allebei dood, 1 van 2ën of geen van beiden.
Nu deel je de 32x32 matrix op in 162 2x2 matrixjes en laat die slaven dezelfde test uitvoeren op al die matrixjes. Maar nu weet je nog niet in welke van die 162 matrixjes nu de dodelijke zit. Maar dat is hetzelfde probleem als net, maar nu met een 16x16 matrix.
Doe dus nu hetzelfde: laat 2 slaven het hele veld afgaan, maar ipv dat een slaaf 1 fles drinkt, drinkt hij alle 4 de flessen uit een 2x2 matrix.
Als je dit 5x doet met steeds 2x zo grote hokjes heb je de hele matrix van 32x32 gehad, en je hebt er maar 5*2 = 10 slaven voor nodig.
En toch bevallen die 24 lege plekken me niet
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Minstens net zo sterk, snel en slim is. Kan het dus zo zijn dat twee haaien, H1 en H2 precies even sterk, snel en slim zijn en derhalve H1 opgegeten zou kunnen worden door H2, maar ook omgekeerd? Ik wilde iets met een partiële ordening en naar een gerichte acyclische graaf toe, en dan een bipartite graaf construeren waar twee matchings op worden uitgevoerd. Maar, ik zit even te denken of dat wel zo fijn gaat als het geen partiële ordening geeft.quote:Op zondag 26 augustus 2007 10:47 schreef Wolfje het volgende:
De koning heeft inderdaad 10 slaven nodig .
Nu een vraagje over algoritmen!
Gegeven n haaien waarvan de kracht, snelheid en intelligentie (dit zijn constanten) bekend zijn. Een haai kan een andere haai opeten als hij minstens net zo sterk, snel en slim is. Voorts is gegeven dat een haai maximaal 2 andere haaien kan opeten. Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen .
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Als onderstaand algoritme klopt, is O(n²) een bovengrens.quote:Op zondag 26 augustus 2007 10:47 schreef Wolfje het volgende:
De koning heeft inderdaad 10 slaven nodig .
Nu een vraagje over algoritmen!
Gegeven n haaien waarvan de kracht, snelheid en intelligentie (dit zijn constanten) bekend zijn. Een haai kan een andere haai opeten als hij minstens net zo sterk, snel en slim is. Voorts is gegeven dat een haai maximaal 2 andere haaien kan opeten. Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen .
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 2% gewijzigd door GlowMouse op 26-08-2007 11:42:44 ]eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 26 augustus 2007 11:30 schreef GlowMouse het volgende:
[..]
Als onderstaand algoritme klopt, is O(n²) een bovengrens.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Er zit niet zo'n definitieve ordening in, daar b.v. kracht groter kan zijn, maar snelheid en intelligentie niet. Verder lijkt je algoritme me greedy, qua opeten. (D.w.z. het eet de eerste 'kleinere' haai die het tegenkomt.) Ik weet niet helemaal of je daar met het sorteren rekening mee houdt ... sorteren kan nog steeds natuurlijk.
Er is dus geen strikt lineaire ordening, aangezien sommige elementen onvergelijkbaar zijn. Wel kun je ervoor zorgen dat 'kleinere' haaien altijd rechts staan van een element in de array. Ik denk dat je dat wilt. Als je dan zoals jij doet, achteraan begint, en dan greedy laat opeten, dan gaat het volgens mij mis, je hebt b.v. de volgende situatie (ik ga ervanuit dat alle eigenschappen strikt groter moeten zijn, wil een haai kunnen eten, net als jij doet):
Drie haaien: (1,1,2), (1,2,1) en (2,1,1): Deze kunnen elkaar niet opeten.
Nog drie haaien: (1,1,3), (3,3,3) en (3,1,1): Deze kunnen elkaar niet opeten.
Haai (1,1,3) kan (1,1,2) eten, en verder niet. (3,1,1) kan (2,1,1) eten. (3,3,3) eet alle drie de haaien uit het eerste rijtje.
Als je ordening in de array nu zo is (en ik zie niet in waarom dat niet zo zou zijn, daar de eerste drie elementen onderling niet vergelijkbaar zijn, evt. maak je er (1,1,10) en (10,1,1) van):
[(1,1,3),(3,1,1),(3,3,3),(1,1,2),(2,1,1),(1,2,1)] dan pakt haai (3,3,3) de eerste de twee haaien die hij pakken kan. Nu hebben (1,1,3) en (3,1,1) niets meer. De optimale oplossing is echter niet dat er twee haaien worden opgegeten en 4 overblijven, maar dat er 3 worden opgegeten. En dat kan. Maar dan moet wel (1,1,3) (1,1,2) opeten, of (3,1,1) (2,1,1) -- de overige twee kunnen dan b.v. door (3,3,3) opgegeten worden, en het is klaar.
[edit]
Bovenstaande is een wat rommelig verhaal geworden. Maar ik denk dus dat je greedy aanpak niet werkt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Dat strikt groter heb ik later gewijzigd. Haai a kan haai b eten als haai b geen eigenschap heeft die strikt groter is, dat is wat ik van Wolfjes uitleg begrijp. Het sorteeralgoritme had ik nog niet goed aangepast, dat zou zo moeten zijn:quote:Op zondag 26 augustus 2007 11:49 schreef Iblis het volgende:
[..]
Er zit niet zo'n definitieve ordening in, daar b.v. kracht groter kan zijn, maar snelheid en intelligentie niet. Verder lijkt je algoritme me greedy, qua opeten. (D.w.z. het eet de eerste 'kleinere' haai die het tegenkomt.) Ik weet niet helemaal of je daar met het sorteren rekening mee houdt ... sorteren kan nog steeds natuurlijk.
Er is dus geen strikt lineaire ordening, aangezien sommige elementen onvergelijkbaar zijn. Wel kun je ervoor zorgen dat 'kleinere' haaien altijd rechts staan van een element in de array. Ik denk dat je dat wilt. Als je dan zoals jij doet, achteraan begint, en dan greedy laat opeten, dan gaat het volgens mij mis, je hebt b.v. de volgende situatie (ik ga ervanuit dat alle eigenschappen strikt groter moeten zijn, wil een haai kunnen eten, net als jij doet):
Drie haaien: (1,1,2), (1,2,1) en (2,1,1): Deze kunnen elkaar niet opeten.
Nog drie haaien: (1,1,3), (3,3,3) en (3,1,1): Deze kunnen elkaar niet opeten.
Haai (1,1,3) kan (1,1,2) eten, en verder niet. (3,1,1) kan (2,1,1) eten. (3,3,3) eet alle drie de haaien uit het eerste rijtje.
Als je ordening in de array nu zo is (en ik zie niet in waarom dat niet zo zou zijn, daar de eerste drie elementen onderling niet vergelijkbaar zijn, evt. maak je er (1,1,10) en (10,1,1) van):
[(1,1,3),(3,1,1),(3,3,3),(1,1,2),(2,1,1),(1,2,1)] dan pakt haai (3,3,3) de eerste de twee haaien die hij pakken kan. Nu hebben (1,1,3) en (3,1,1) niets meer. De optimale oplossing is echter niet dat er twee haaien worden opgegeten en 4 overblijven, maar dat er 3 worden opgegeten. En dat kan. Maar dan moet wel (1,1,3) (1,1,2) opeten, of (3,1,1) (2,1,1) -- de overige twee kunnen dan b.v. door (3,3,3) opgegeten worden, en het is klaar.
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.De volgorde wordt dan:
[(3,3,3), (1,1,3), (3,1,1), (1,1,2), (2,1,1), (1,2,1)]
(3,1,1) eet (2,1,1) op, (1,1,3) eet (1,1,2) op, en (3,3,3) eet (1,1,3) en (3,1,1) op.eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


quote:Op zondag 26 augustus 2007 12:32 schreef GlowMouse het volgende:
Dat strikt groter heb ik later gewijzigd. Haai a kan haai b eten als haai b geen eigenschap heeft die strikt groter is, dat is wat ik van Wolfjes uitleg begrijp. Het sorteeralgoritme had ik nog niet goed aangepast, dat zou zo moeten zijn:Daarom had ik (1,1,10) en (10,1,1) nog genoemd i.p.v. (1,1,3) en (3,1,1). Als we nu vergelijken:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.De volgorde wordt dan:
[(3,3,3), (1,1,3), (3,1,1), (1,1,2), (2,1,1), (1,2,1)]
(3,1,1) eet (2,1,1) op, (1,1,3) eet (1,1,2) op, en (3,3,3) eet (1,1,3) en (3,1,1) op.
(3,3,3) is niet groter dan (10,1,1), maar ook (10,1,1) is niet groter dan (3,3,3) => Ze zijn gelijk. Ergo, de volgorde in de array zou kunnen worden:
[(10,1,1),(1,1,10),(3,3,3),(1,1,2), (2,1,1), (1,2,1)]
En dit gaat mis.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja, dat is inderdaad zo. En ze kunnen elkaar ook niet tegelijkertijd op eten .quote:Op zondag 26 augustus 2007 11:26 schreef Iblis het volgende:
[..]
Minstens net zo sterk, snel en slim is. Kan het dus zo zijn dat twee haaien, H1 en H2 precies even sterk, snel en slim zijn en derhalve H1 opgegeten zou kunnen worden door H2, maar ook omgekeerd?
De probeersels in dit topic heb ik nog niet uitvoerig bestudeerd, maar naar mijn weten is een greedy algoritme fout . Ik zal er later nog eens naar kijken, maar ik ga eerst douchen (van hardlopen word je vies).


Ja het gaat inderdaad mis, ik zie het. Efficientie dan maar even vergeten, en blij zijn als het uberhaupt werkt. Vanmiddag weer een poging wagen.
#1
#1
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.En #2SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 82% gewijzigd door GlowMouse op 26-08-2007 13:20:31 ]eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Volgende poging:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


quote:Op zondag 26 augustus 2007 13:33 schreef Iblis het volgende:
Volgende poging:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt. Ik had het gevoel dat je door de sorteren de boel zou kunnen optimaliseren, daar je een bepaald segment aangeeft waaruit gegeten kan worden. De graaf hoeft zo niet expliciet gemaakt te worden.quote:Het matching algoritme twee keer uitvoeren is volgens mij ook niet correct! Het kan mis gaan als een eter precies twee mogelijke prooien heeft en een daarvan wordt in de eerste matching door een andere haai opgegeten. Een voorbeeld hiervan is:
eters: (10,10,101) en (100,100,100)
prooien: (5,10,5), (10,9,10), (11,1,10) en (11,10,1).
Het kan zijn dat de eerste matching eter 1 - prooi 1 en eter 2 - prooi 2 geeft. In de tweede matching is er dus niks meer voor eter 1. De beste keuze zou zijn dat eter 1 de eerste twee prooien eet en de andere de rest.
Klopt. Is dat te verhelpen door de eters twee maal op te nemen? En dan één keer te machten? Dan zal eter1 b.v. aan prooi1 gematcht worden, eter1' aan prooi2, en eter2 aan prooi3 en eter2' aan prooi 4.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


quote:Op zondag 26 augustus 2007 14:40 schreef Iblis het volgende:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.


Waarom telkens die irritante spoilers?
When I get sad, I stop being sad and just be awesome instead.


Max flow problemen zou ik over twee weken krijgen . Het geeft hier een hele nette oplossing. In ieder geval netter dan de dingen die ik voorstelde.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hulp nodig met wiskunde:
De functie g(x) is gegeven door: g(x) = 3e-machtswortel uit x+1
i) bepaal de tweede orde Taylorreeksonwikkeling rond x = 0
ii) laat zien dat |R3(x)|< 5x^3 / 81
iii) Bepaal de 3e-machtswortel uit 1003
En nog een over limieten:
Bepaal de volgende limiet:
Lim x-> oneindig ln(x) / x
Dank u vriendelijk.
De functie g(x) is gegeven door: g(x) = 3e-machtswortel uit x+1
i) bepaal de tweede orde Taylorreeksonwikkeling rond x = 0
ii) laat zien dat |R3(x)|< 5x^3 / 81
iii) Bepaal de 3e-machtswortel uit 1003
En nog een over limieten:
Bepaal de volgende limiet:
Lim x-> oneindig ln(x) / x
Dank u vriendelijk.
9 levens lang bier drinken!


Weet je wel wat een Taylorreeks is? Als je de definituie bekijkt, kun je de ontwikkeling toch gewoon uitschrijven? De restterm schatten is heel eenvoudig. Kom, iets meer eigen initiatief , probeer het eerst even zelf en geef dan aan waar je vastloopt.quote:Op maandag 27 augustus 2007 10:15 schreef KaterPils het volgende:
Hulp nodig met wiskunde:
De functie g(x) is gegeven door: g(x) = 3e-machtswortel uit x+1
i) bepaal de tweede orde Taylorreeksonwikkeling rond x = 0
ii) laat zien dat |R3(x)|< 5x^3 / 81
iii) Bepaal de 3e-machtswortel uit 1003
En nog een over limieten:
Bepaal de volgende limiet:
Lim x-> oneindig ln(x) / x
Dank u vriendelijk.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Mogen er in een samenhangende ongerichte graaf twee kanten zijn tussen twee knopen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nee. Een ongerichte graaf is een paar verzamelingen (V,E) waarbij de elementen van E ongeordende paren van verschillende elementen van V zijn. Deze definitie laat niet toe dat er twee kanten tussen twee knopen lopen.quote:Op dinsdag 28 augustus 2007 22:59 schreef GlowMouse het volgende:
Mogen er in een samenhangende ongerichte graaf twee kanten zijn tussen twee knopen?
[ Bericht 2% gewijzigd door thabit op 29-08-2007 17:48:21 ]


Even een hele simpele:
Corrinne travels from home to work at an average speed of 50 miles per hour, and returns home by the same route at 60 miles per hour. It takes her 10 more minutes to get to work than it takes her to get home. How many miles is it from Corinne's home to work?
A 25
B 35
C 50
D 75
E 90
Het antwoord is C. Hoe kun je daar komen zonder alle oplossingen na te rekenen?
Corrinne travels from home to work at an average speed of 50 miles per hour, and returns home by the same route at 60 miles per hour. It takes her 10 more minutes to get to work than it takes her to get home. How many miles is it from Corinne's home to work?
A 25
B 35
C 50
D 75
E 90
Het antwoord is C. Hoe kun je daar komen zonder alle oplossingen na te rekenen?


Gewoon uitproberen en dan zie je dat het 50 miles is.
Heenweg is dan 1 uur.
Terugweg is dan 50 minuten (60 m/uur --> 10 m/10 min --> 50 m / 50 min)
En dan is ze dus 10 min sneller.
-edit-
ah, en nu wil je het zonder allemaal uit te rekenen.
Het is me wat
-edit-edit-
Stel x = afstand.
Heenweg duurt dan x / 50 in uren
Terugweg duurt dan x / 60 in uren
Dan geldt er: x / 50 - x / 60 = verschil in tijd tussen heenweg en terugweg.
Herschrijven levert op: 6x/300 - 5x/300= x/ 300
Dat antwoord moet hetzelfde zijn als 10 minuten, oftewel 1/6 uur
Dat kan alleen als x 1/6 deel is van 300, en dus 50 mile.
Want 50/300 = 1/6
[ Bericht 24% gewijzigd door -J-D- op 29-08-2007 16:34:11 ]
Heenweg is dan 1 uur.
Terugweg is dan 50 minuten (60 m/uur --> 10 m/10 min --> 50 m / 50 min)
En dan is ze dus 10 min sneller.
-edit-
ah, en nu wil je het zonder allemaal uit te rekenen.
Het is me wat
-edit-edit-
Stel x = afstand.
Heenweg duurt dan x / 50 in uren
Terugweg duurt dan x / 60 in uren
Dan geldt er: x / 50 - x / 60 = verschil in tijd tussen heenweg en terugweg.
Herschrijven levert op: 6x/300 - 5x/300= x/ 300
Dat antwoord moet hetzelfde zijn als 10 minuten, oftewel 1/6 uur
Dat kan alleen als x 1/6 deel is van 300, en dus 50 mile.
Want 50/300 = 1/6
[ Bericht 24% gewijzigd door -J-D- op 29-08-2007 16:34:11 ]
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Ik vermoed dat er een voorwaarde m.b.t. timing mist? Kan een haai die al een andere haai gegeten heeft nu wel of niet opgegeten worden door nog een andere haai? Logisch gezien kan een haai natuurlijk niet tegelijkertijd twee haaien eten, dus zou een haai zowel eter als prooi moeten kunnen zijn. Dit zie ik echter niet terug in de aangedragen oplossingen?quote:Op zondag 26 augustus 2007 10:47 schreef Wolfje het volgende:
De koning heeft inderdaad 10 slaven nodig .
Nu een vraagje over algoritmen!
Gegeven n haaien waarvan de kracht, snelheid en intelligentie (dit zijn constanten) bekend zijn. Een haai kan een andere haai opeten als hij minstens net zo sterk, snel en slim is. Voorts is gegeven dat een haai maximaal 2 andere haaien kan opeten. Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen .
Stel je hebt de haaien (1,1,2), (1,2,1), (2,1,1), (1,1,3), (1,2,3) en (3,3,3). Volgens de voorwaarden is het zelfs mogelijk dat (1,1,3) (1,1,2) opeet en dat vervolgens (1,2,3) (1,2,1) en (1,1,3) opeet en weer vervolgens dat (3,3,3) (2,1,1) en (1,2,3) opeet.


quote:Op zondag 2 september 2007 02:54 schreef cjs het volgende:
[..]
Ik vermoed dat er een voorwaarde m.b.t. timing mist? Kan een haai die al een andere haai gegeten heeft nu wel of niet opgegeten worden door nog een andere haai?
Waaruit ik zou afleiden dat een haai zeker niet postuum nog een andere haai kan eten.quote:Op zondag 26 augustus 2007 12:43 schreef Wolfje het volgende:
En ze kunnen elkaar ook niet tegelijkertijd op eten .
Jawel, mijn oplossing houdt daar impiliciet met de manier van coderen van de bipartiete graaf rekening mee.quote:Logisch gezien kan een haai natuurlijk niet tegelijkertijd twee haaien eten, dus zou een haai zowel eter als prooi moeten kunnen zijn. Dit zie ik echter niet terug in de aangedragen oplossingen?
We kunnen een partiële ordening op jouw haaien aanbrengen, van klein naar groot:quote:Stel je hebt de haaien (1,1,2), (1,2,1), (2,1,1), (1,1,3), (1,2,3) en (3,3,3). Volgens de voorwaarden is het zelfs mogelijk dat (1,1,3) (1,1,2) opeet en dat vervolgens (1,2,3) (1,2,1) en (1,1,3) opeet en weer vervolgens dat (3,3,3) (2,1,1) en (1,2,3) opeet.
[ (1, 1, 2), (1,2,1) (2, 1, 1) ] ; [ (1, 1, 3) ] ; [(1,2,3) ] ; [(3,3,3)]
De haaien in een 'blok' (tussen [ ]) kunnen elkaar niet opeten, maar ze kunnen wel opgegeten worden door alle haaien in een blok 'rechts' ervan. De lunch moet dus beginnen doordat in het eerste 'tijdsmoment' alleen haaien uit het kleinste blok gegeten worden. Het volgende moment mogen alle haaien uit het blok erna gegeten worden, et cetera. Dat levert de optimale haaiconsumptie op. De vraag is namelijk wat is het “kleinste aantal dat over is”, en daarvoor ga je van deze optimale consumptie uit.
Er is alleen één valkuil, namelijk gelijke haaien (b.v. (1,1,1) en (1,1,1) ). Want die zitten in hetzelfde blok, maar kunnen elkaar eventueel opeten. Dat is niet mogelijk, bij het coderen van de graaf wordt zo'n cykel arbitrair doorbroken door een willekeurige ordening onder deze haaien aan te brengen, zodat er geen cyklische afhankelijkheden ontstaan.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Cjs heeft gelijk dat de volgorde van eten wel belangrijk is, maar daar is in de vraagstelling rekening mee gehouden: "Geef een algoritme om het kleinst aantal haaien dat na de lunch nog in leven is, te bepalen". Je moet dus op zoek naar de manier waarbij de minste haaien overblijven.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hmm, ik moet eens beter lezen, ookal is het 's nachts.
Ik ging eerst hier vanuit:
Ik ging eerst hier vanuit:
Om vervolgens dit stukje te missen:quote:Op zondag 26 augustus 2007 11:49 schreef Iblis het volgende:
[..]
Drie haaien: (1,1,2), (1,2,1) en (2,1,1): Deze kunnen elkaar niet opeten.
Nog drie haaien: (1,1,3), (3,3,3) en (3,1,1): Deze kunnen elkaar niet opeten. (Wel dus!)
Haai (1,1,3) kan (1,1,2) eten, en verder niet. (3,1,1) kan (2,1,1) eten. (3,3,3) eet alle drie de haaien uit het eerste rijtje.
quote:Op zondag 26 augustus 2007 12:32 schreef GlowMouse het volgende:
[..]
]
De volgorde wordt dan:
[(3,3,3), (1,1,3), (3,1,1), (1,1,2), (2,1,1), (1,2,1)]
(3,1,1) eet (2,1,1) op, (1,1,3) eet (1,1,2) op, en (3,3,3) eet (1,1,3) en (3,1,1) op.


Dat haaien probleem ben ik overigens tegengekomen bij een wedstrijdje in het bedenken en programmeren van algoritmes. Dergelijke wedstrijden worden vrijwel wekelijks door topcoder georganiseerd. Je krijgt dan 75 minuten de tijd om drie problemen van verschillende moeilijkheid op te lossen (de haaien waren lastig ). Als je dat heel goed doet, stijgt je rating en anders zakt ie natuurlijk. Voor degenen die zulk soort dingen leuk vinden, is het absoluut een aanrader!


Ik heb een probleem met een wiskunde project. Het gaat over grafen. De opgave is:
Hoeveel 2-reguliere grafen G=(V,E) bestaan er met V={1,2,3,4,5,6}? En hoeveel 3-reguliere grafen?
Onze hele klas (6VWO) komt er niet uit, en de leraar werkt niet mee. Wijzelf dachten 60, maar dat was in elk geval niet goed, er moet nog iets bij volgens de projectleidster.
Iemand die mij kan helpen?
Hoeveel 2-reguliere grafen G=(V,E) bestaan er met V={1,2,3,4,5,6}? En hoeveel 3-reguliere grafen?
Onze hele klas (6VWO) komt er niet uit, en de leraar werkt niet mee. Wijzelf dachten 60, maar dat was in elk geval niet goed, er moet nog iets bij volgens de projectleidster.
Iemand die mij kan helpen?


Wat maakt een graaf verschillend? 2 reguliere grafen zijn per definitie alleen cykels (i.e. rondjes), dus op 6 punten heb je of:quote:Op donderdag 6 september 2007 16:23 schreef Leso_Varen het volgende:
Ik heb een probleem met een wiskunde project. Het gaat over grafen. De opgave is:
Hoeveel 2-reguliere grafen G=(V,E) bestaan er met V={1,2,3,4,5,6}? En hoeveel 3-reguliere grafen?
Onze hele klas (6VWO) komt er niet uit, en de leraar werkt niet mee. Wijzelf dachten 60, maar dat was in elk geval niet goed, er moet nog iets bij volgens de projectleidster.
Iemand die mij kan helpen?
| 1 2 3 | | | *--*--* |
Of:
| 1 2 3 | \ / \ / * * |
De labelling maakt het dan eventueel verschillend. Voor een 3 reguliere graaf begin je met de cykel op zes punten:
| 1 2 3 4 5 | / \ * * \ / *--* |
Immers, twee losse grafen zijn niet mogelijk, daar je als je 1 punt 3 buren geeft, al 4 van de 6 punten gebruikt. De andere twee moeten bij je graaf.
Je krijgt dus:
| 1 2 3 4 5 | / \ /| |\ / \ / \ * * --> *-+---+-* of *---X---* \ / \| |/ \ / \ / *---* *---* *---* |
Andere mogelijkheden zijn voor de basisstructuur niet. Aangezien zo'n graaf symmetrisch is maakt het in beginsel niet uit met welke knoop je begint. In de rechtse is elke knoop verbonden met de knoop 3 stapjes verder over de cykel. In de 2e is je beginknoop verbonden met twee stapjes over de cykel (duidelijk anders). Dat kun je met nog 1 knoop doen, 2 stapjes de andere kant op. Je kunt ze niet alle 3 2 stapjes over de cykel heen doen. Want dan krijg je dat er 1 knoop vier lijnen krijgt (2 stapjes de ene kant op verbonden, 2 stapjes de andere kant op met 1 knoop verbonden); ergo, je houdt deze twee over.
Dus ik zou zeggen, feitelijk zijn er slechts 2 verschillende grafen mogelijk bij 2 regulier, en 2 bij drie regulier.
Dan kun je je verder druk maken over de labelling (toewijzing welke knopen welk nummer krijgen):
Op de eerste graaf met 2 x 3 maakt de volgorde op de cykel niet uit. Je krijgt het aantal door (6 boven 3) te doen. Dat geeft 20 mogelijkheden. Als je er 3 voor 1 driehoek hebt gekozen, liggen de volgende 3 direct vast voor de andere driehoek.
Voor de cykel. In totaal zijn er 6! = 720 rijtjes mogelijk van zes getallen, maar aangezien het cyclisch is het rijtje 123456 op de graaf niet anders dan 612345, of 561234. Etc. Je telt dus 6x te veel rijtjes in feite. Dus: 720/6 = 120 die je nog overhoudt. En dan kun je nog gratis spiegelen. Dus dan houd je er nog maar 60 over. (Hier kan ik trouwens miszitten. Ik vertel me nog wel eens met zulk soort dingen).
Geeft 60 + 20 voor de 2-reguliere.
De drie reguliere is op zich ongeveer gelijk. Bij rechter van de 2 zijn alle knopen equivalent. Je hebt hier dus weer 60 rijtjes. Bij de rechter zijn de knopen niet per se equivalent. Daar moet ik even langer over nadenken, maar heb ik geen tijd voor.
[edit]
Er schoot me het volgende te binnen, je hebt feitelijk deze 3 labellingen:
| 1 2 3 4 5 6 7 | *---* *---* *---* /| |\ /| |\ /| |\ 6*-+---+-*3 5*-+---+-*2 4*-+---+-*1 \| |/ \| |/ \| |/ *---* *---* *---* 5 4 4 3 3 2 |
Je ziet dat deze, ondanks dat ze alleen maar verschoven zijn langs de graaf via de cykel wel degelijk anders zijn. In de eerste zijn de buren van 1 : {2, 5, 6}, bij de 2e zijn de buren van 1: {2,3,6}, en bij de derde: {2,4,6}. Draai je verder, dan kom je weer op een situate uit die je al hebt, nl. dat 1 buur is van {2,5,6}. Dus, van alle rijtjes is de helft maar echt anders. Het rijtje 123456 verschilt niet van 456123 (d.w.z. als je linksboven begint te nummeren en met de klok meegaat en dan bekijkt welke buren elk punt heeft). En idem voor andere rijtjes. Van de 6! = 720 houd je er dus nog 360 over. Maar, dat is ook nog niet alles. Want, je ziet dat de rechter graaf spiegelsymmetrisch is. 654321 levert dezelfde graaf op, maar dan gespiegeld. Dat is niet 'echt' een andere graaf. Verder zie je dat dit voor de andere 2 ook geldt. Enfin, volgens mij kom je dan (misschien dat er nog wat mis hoor...) op 360 / 2 = 180 over.
Maar goed, dit is wel het idee... hopelijk heb je er wat aan.
[ Bericht 20% gewijzigd door Iblis op 06-09-2007 21:18:06 ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


een lineaire vectorruimte kan je zien als een additief geschreven abelse groep waarop een lichaam K werkt. Als ik kijk naar de defintie van zo'n vectorruimte dan kan ook een commutatieve ring nemen in plaats van een lichaam, nergens staat er iets over een inverse van een element uit K. Is dat zo? Leidt de werking van een commutatieve ring op een addetief geschreven abelse groep tot een lineaire vectorruimte?..wat gaat mis?
verlegen :)


Hartstikke bedankt Hier kom ik verder mee, echt topquote:Op donderdag 6 september 2007 21:00 schreef Iblis het volgende:
[..]Uitleg.
Maar goed, dit is wel het idee... hopelijk heb je er wat aan.


Volgens mij heb je gelijk. Je hebt een scalaire vermenigvuldiging nodig, maar deze hoeft niet inverteerbaar te zijn in een lineaire ruimte.quote:Op donderdag 6 september 2007 21:23 schreef teletubbies het volgende:
een lineaire vectorruimte kan je zien als een additief geschreven abelse groep waarop een lichaam K werkt. Als ik kijk naar de defintie van zo'n vectorruimte dan kan ook een commutatieve ring nemen in plaats van een lichaam, nergens staat er iets over een inverse van een element uit K. Is dat zo? Leidt de werking van een commutatieve ring op een addetief geschreven abelse groep tot een lineaire vectorruimte?..wat gaat mis?


In dat geval heet het geen vectorruimte, maar een moduul. Hierbij hoeven we niet eens aan te nemen dat de ring commutatief is.quote:Op donderdag 6 september 2007 21:23 schreef teletubbies het volgende:
een lineaire vectorruimte kan je zien als een additief geschreven abelse groep waarop een lichaam K werkt. Als ik kijk naar de defintie van zo'n vectorruimte dan kan ook een commutatieve ring nemen in plaats van een lichaam, nergens staat er iets over een inverse van een element uit K. Is dat zo? Leidt de werking van een commutatieve ring op een addetief geschreven abelse groep tot een lineaire vectorruimte?..wat gaat mis?


Even een simpel vraagje: als G de groeifactor is per 3 dagen, is de groeifactor per uur dan gewoon G^1/72?
Eins, zwei, hoeplakai.


Correct.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Okey,quote:Op vrijdag 7 september 2007 09:42 schreef thabit het volgende:
[..]
In dat geval heet het geen vectorruimte, maar een moduul. Hierbij hoeven we niet eens aan te nemen dat de ring commutatief is.
een andere vraag, kansrekening/statistiek en algebra lijken me twee zaken die veel van elkaar verschillen, toch ben ik nieuwsgierig naar kansen in algebra, bijv bij groepen ofzo... ik zag ooit iets wat te maken met kansen bij groepen en het had te maken met een of andere soort deler/orde of iets dergelijks...
kun je me bijv nuttig links geven
verlegen :)


Veel mensen die zich met algebra bezighouden interesseren zich niet voor statistiek en veel mensen die zich met statistiek bezighouden hebben geen zin om algebra te leren. Gevolg is dat er niet veel verbanden tussen de vakgebieden bekend zijn. Ik heb er zelf in elk geval vrij weinig van gezien.quote:Op zaterdag 8 september 2007 23:54 schreef teletubbies het volgende:
[..]
Okey,
een andere vraag, kansrekening/statistiek en algebra lijken me twee zaken die veel van elkaar verschillen, toch ben ik nieuwsgierig naar kansen in algebra, bijv bij groepen ofzo... ik zag ooit iets wat te maken met kansen bij groepen en het had te maken met een of andere soort deler/orde of iets dergelijks...
kun je me bijv nuttig links geven
Er bestaat wel zoiets als ergodentheorie voor topologische groepen. Random matrix theorie heeft hier en daar wat toepassingen in de L-functies. Bepaalde stukken statistische analyse op Riemannoppervlakken hebben weer raakvlakken met arithmetische meetkunde. Verder kun je wat kansrekening loslaten op de analyse van probabilistische algoritmen in de getaltheorie. En om bepaalde voortbrengen functies in de combinatoriek te bestuderen zul je ook vast stukken algebra toepassen.


Ook weer even een vraag:
Om maar even een begin te maken:
De taylor polynoom is:
p(x) = u(0) + Du(0)/1! *x + D2u(0)/2! *x2 + .. + Dnu(0)/n! *xn
Waar Du de eerste afgeleide is D2u de tweede enz.
Df(x) = eh - 1
D2f(x) = eh
D3f(x) = eh
und so weiter.
dus:
p(h) = 0 + 0/1 * h +1/2 *h2 + 1/6 * h3 ...
= 1/2 *h2 + 1/6 * h3 ...
= Sigma n=2 tot oneindig eh/n! *hn
En nu?
[edit] ik heb nu eigenlijk de helft van de h's wel en de andere helft niet ingevuld, geen idee waarom ik dat heb gedaan, snap er toch geen bal van.
[ Bericht 5% gewijzigd door Schuifpui op 10-09-2007 19:14:12 ]
Eigenlijk snap ik de vraag al niet. Wat willen ze nu precies.quote:Use taylor expansions to establish the order (as h -> 0) of:
f(x) = eh-(1+h)
Om maar even een begin te maken:
De taylor polynoom is:
p(x) = u(0) + Du(0)/1! *x + D2u(0)/2! *x2 + .. + Dnu(0)/n! *xn
Waar Du de eerste afgeleide is D2u de tweede enz.
Df(x) = eh - 1
D2f(x) = eh
D3f(x) = eh
und so weiter.
dus:
p(h) = 0 + 0/1 * h +1/2 *h2 + 1/6 * h3 ...
= 1/2 *h2 + 1/6 * h3 ...
= Sigma n=2 tot oneindig eh/n! *hn
En nu?
[edit] ik heb nu eigenlijk de helft van de h's wel en de andere helft niet ingevuld, geen idee waarom ik dat heb gedaan, snap er toch geen bal van.
[ Bericht 5% gewijzigd door Schuifpui op 10-09-2007 19:14:12 ]


De 'orde' geeft aan met welk polynoom je functie 'vergelijkbaar' is in de omgeving van 0. Dwz zoek polynoom p zodat f(x)/p(x) convergeert voor x -> 0 naar een 'mooie' limiet, dwz geen 0 of oneindig. Jouw Taylorbenadering laat zien dat p tweedegraads moet zijn en dat f(x)/p(x) = 1/2 + <hogere orde termen> voor x -> 0, waarbij <hogere orde termen> staan voor de overige machten die naar 0 gaan als x -> 0. Dit wordt vaak genoteerd als "f(x) ~ (1/2)*x^2 voor x -> 0".quote:Op maandag 10 september 2007 19:05 schreef Schuifpui het volgende:
Ook weer even een vraag:
[..]
Eigenlijk snap ik de vraag al niet. Wat willen ze nu precies.
Om maar even een begin te maken:
De taylor polynoom is:
p(x) = u(0) + Du(0)/1! *x + D2u(0)/2! *x2 + .. + Dnu(0)/n! *xn
Waar Du de eerste afgeleide is D2u de tweede enz.
Df(x) = eh - 1
D2f(x) = eh
D3f(x) = eh
und so weiter.
dus:
p(h) = 0 + 0/1 * h +1/2 *h2 + 1/6 * h3 ...
= 1/2 *h2 + 1/6 * h3 ...
= Sigma n=2 tot oneindig eh/n! *hn
En nu?
[edit] ik heb nu eigenlijk de helft van de h's wel en de andere helft niet ingevuld, geen idee waarom ik dat heb gedaan, snap er toch geen bal van.
.
[ Bericht 7% gewijzigd door keesjeislief op 10-09-2007 19:27:35 ]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Thanks ik denk dat ik heel vaag een klein beetje begin te begrijpen. We werken ook met Landau symbolen en die f(x)/p(x) komt me dan wel bekend voor. Dus incl Landau kan ik zeggen dat f(x) = 1/2x2 +O(x3)?quote:Op maandag 10 september 2007 19:21 schreef keesjeislief het volgende:
[..]
De 'orde' geeft aan met welk polynoom je functie 'vergelijkbaar' is in de omgeving van 0. Dwz zoek polynoom p zodat f(x)/p(x) convergeert voor x -> 0 naar een 'mooie' limiet, dwz geen 0 of oneindig. Jouw Taylorbenadering laat zien dat p tweedegraads moet zijn en dat f(x)/p(x) = 1/2 + <hogere orde termen> voor x -> 0, waarbij <hogere orde termen> staan voor de overige machten die naar 0 gaan als x -> 0. Dit wordt vaak genoteerd als "f(x) ~ (1/2)*x^2 voor x -> 0".
.
Moet het trouwens niet naar 2 zijn dan? (delen door een half)
Nog even een edit, want eigenlijk snap ik het toch niet.
f(x)/p(x) = [eh-(1+h)]/[eh/2*h2 + ... ]
Voor h -> 0 wordt dit toch geen half (of twee) of zie ik het nou verkeerd?
[ Bericht 9% gewijzigd door Schuifpui op 10-09-2007 19:58:24 ]


Ja, dat klopt. Om helemaal precies te zijn zou je eigenlijk nog "x -> 0" aan de uitdrukking moeten toevoegen. Het is niet zo moeilijk hoor, het gaat er gewoon om het limietgedrag van de functie uit te drukken in makkelijkere termen. Dit wordt meestal in termen van machtsfuncties gedaan, dwz x -> xa, maar dat hoeft niet noodzakelijkerwijs, het kan ook een andere familie van functies x -> ga(x) zijn.quote:Op maandag 10 september 2007 19:41 schreef Schuifpui het volgende:
[..]
Thanks ik denk dat ik heel vaag een klein beetje begin te begrijpen. We werken ook met Landau symbolen en die f(x)/p(x) komt me dan wel bekend voor. Dus incl Landau kan ik zeggen dat f(x) = 1/2x2 +O(x3)?
Moet het trouwens niet naar 2 zijn dan? (delen door een half)
Het nut van dit soort uitdrukkingen is dat je bijv. makkelijker de limiet van verschillende uitdrukkingen met elkaar kunt vergelijken als je eerst ieder van die uitdrukkingen in zulke makkelijkere termen schrijft. Nog een tip is dat je in een aantal gevallen makkelijke trucs hebt om ingewikkelde uitdrukkingen asymptotisch te ontwikkelen, zoals partiële integratie wanneer je met integralen van doen hebt.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Sorry, mijn notatie was een beetje verwarrend. Je hebt gegeven de functie f(h) = eh-(1+h). Met behulp van Taylor had jij al f(h) = (1/2)*h2 + O(h3). Dit laat meteen zien dat f van orde 2 is dichtbij 0, nl. met p(h)=h2 vind je f(h)/p(h) = 1/2 + O(h), dus f(h)/p(h) -> 1/2, wat betekent dat f en p "van dezelfde orde" zijn voor h -> 0. Duidelijk?quote:Op maandag 10 september 2007 19:41 schreef Schuifpui het volgende:
[..]
Thanks ik denk dat ik heel vaag een klein beetje begin te begrijpen. We werken ook met Landau symbolen en die f(x)/p(x) komt me dan wel bekend voor. Dus incl Landau kan ik zeggen dat f(x) = 1/2x2 +O(x3)?
Moet het trouwens niet naar 2 zijn dan? (delen door een half)
Nog even een edit, want eigenlijk snap ik het toch niet.
f(x)/p(x) = [eh-(1+h)]/[eh/2*h2 + ... ]
Voor h -> 0 wordt dit toch geen half (of twee) of zie ik het nou verkeerd?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Ik denk dat ik het zo ga snappen, moet nu even weg, kijk er morgen even iets uitgebreider naar.
Heel veel dank iig.
Heel veel dank iig.


Ik zie me weer genoodzaakt de hulp van Glowmouse/Riparius/KeesjeisLief ijn te roepen. Kan er iemand mij de afleiding van de "Euler chain relation"/"triple product rule" (hoe je het beestje noemen wilt) van a tot z uitleggen? Onthouden en toepassen is totaal geen probleem (δy/δxz * δz/δyx * δx/δzy = -1), alleen de afleidingen die ik tot nu toe heb gevonden zijn zo counterintuitief als wat.


Kijk hier eens, echt veel duidelijker zou ik het zelf ook niet uit kunnen leggen. En anders moet je misschien eens in het Euler archief gaan zoeken om te kijken hoe Euler het zelf deed.quote:Op vrijdag 14 september 2007 14:55 schreef harrypiel het volgende:
Ik zie me weer genoodzaakt de hulp van Glowmouse/Riparius/KeesjeisLief ijn te roepen. Kan er iemand mij de afleiding van de "Euler chain relation"/"triple product rule" (hoe je het beestje noemen wilt) van a tot z uitleggen? Onthouden en toepassen is totaal geen probleem (δy/δxz * δz/δyx * δx/δzy = -1), alleen de afleidingen die ik tot nu toe heb gevonden zijn zo counterintuitief als wat.


Hoi! geldt dat R en Ropp (tegengestelde ring) isomorf zijn dan en slechts dan als R commutatief is? mag ik een hint!
Thanks!
Thanks!
verlegen :)


hoii, het antwoord is nee, ik denk momenteel aan H (dat met quaternionen). Als ik niet een isomorfie vind,post ik hier weer een bericht..quote:Op zaterdag 15 september 2007 19:53 schreef teletubbies het volgende:
Hoi! geldt dat R en Ropp (tegengestelde ring) isomorf zijn dan en slechts dan als R commutatief is? mag ik een hint!
Thanks!
Is er nog een voorbeeld ?
verlegen :)


Even nog een iets simpelere:
If f^2 - g^2 = -10 and f + g = 2, than what is the value of f - g?
Het antwoord moet zijn -5
If f^2 - g^2 = -10 and f + g = 2, than what is the value of f - g?
Het antwoord moet zijn -5


Hint: werk (a+b)(a-b) eens uit (dit is een bekend merkwaardig product).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met quaternionen gaat het niet lukken: stuur a + ib + jc + kd naar a - ib - jc - kd, dat is een isomorfisme van H naar Hopp.quote:Op zaterdag 15 september 2007 20:42 schreef teletubbies het volgende:
[..]
hoii, het antwoord is nee, ik denk momenteel aan H (dat met quaternionen). Als ik niet een isomorfie vind,post ik hier weer een bericht..
Is er nog een voorbeeld ?
Ik zit zelf meer te denken aan het volgende: neem Q[X,Y], maar dan met een vreemd soort vermenigvuldiging: YX=X2Y.
edit: O, hmm. Je bent op zoek naar een niet-commutatieve ring die isomorf is met z'n tegengestelde, niet naar een die er niet mee isomorf is. In dat geval werken de quaternionen dus wel. .


okey dank je, maar ' stuur a + ib + jc + kd naar a - ib - jc - kd' is inderdaad handiger.quote:Op maandag 17 september 2007 13:55 schreef thabit het volgende:
[..]
Met quaternionen gaat het niet lukken: stuur a + ib + jc + kd naar a - ib - jc - kd, dat is een isomorfisme van H naar Hopp.
Ik zit zelf meer te denken aan het volgende: neem Q[X,Y], maar dan met een vreemd soort vermenigvuldiging: YX=X2Y.
edit: O, hmm. Je bent op zoek naar een niet-commutatieve ring die isomorf is met z'n tegengestelde, niet naar een die er niet mee isomorf is. In dat geval werken de quaternionen dus wel. .
verlegen :)


Die andere ring die ik noemde is juist niet isomorf met z'n tegengestelde.quote:Op dinsdag 18 september 2007 18:04 schreef teletubbies het volgende:
[..]
okey dank je, maar ' stuur a + ib + jc + kd naar a - ib - jc - kd' is inderdaad handiger.


Kan iemand me deze uitleggen, ik zie niet hoe "FE, ED equal to the square of the tangent E is" in de bewijsvoering.
Given a circle ABC and two points D, E external to it, to draw straight lines DB, EB from D, E to a point B on the circle such that, if DB, EB produced meet the circle again in C, A, AC shall be parallel to DE.
Given a circle ABC and two points D, E external to it, to draw straight lines DB, EB from D, E to a point B on the circle such that, if DB, EB produced meet the circle again in C, A, AC shall be parallel to DE.


Wat is nu precies de vraag, kun je het wat duidelijker formuleren?quote:Op woensdag 19 september 2007 21:40 schreef Ogala het volgende:
Kan iemand me deze uitleggen, ik zie niet hoe "FE, ED equal to the square of the tangent E is" in de bewijsvoering.
Given a circle ABC and two points D, E external to it, to draw straight lines DB, EB from D, E to a point B on the circle such that, if DB, EB produced meet the circle again in C, A, AC shall be parallel to DE.
[afbeelding]
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


(Part I. Construction.)quote:Op woensdag 19 september 2007 22:36 schreef keesjeislief het volgende:
[..]
Wat is nu precies de vraag, kun je het wat duidelijker formuleren?
Ik snap puntje 2 dus niet bij het construeren (EF = square on the tangent to E) en zodoende in de bewijsvoering dus ook niet dat FE,ED = to the square of the tangent E.


OK.quote:Op woensdag 19 september 2007 22:54 schreef Ogala het volgende:
[..]
(Part I. Construction.)1. Suppose the circle ABC and the points D, E given.
Hiermee wordt bedoeld dat je op het verlengde van ED een punt F moet bepalen, zodanig dat ED∙EF gelijk is aan het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E. Deze raaklijn heb je niet getekend in je figuur.quote:2. Take a rectangle contained by ED and by a certain straight line EF equal to the square on the tangent to the circle from E.
De reden om punt F zo te bepalen is gelegen in een bekende stelling van Euclides (Boek III, stelling 36). Volgens deze stelling is namelijk het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E gelijk aan het product EB∙EA. En aangezien het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E ook gelijk is aan ED∙EF hebben we dus EB∙EA = ED∙EF.
quote:3. From F draw FA touching the circle in A; join ABE and then DB, producing DB to meet the circle at C. Join AC. I say then that AC is parallel to DE.
Ik snap puntje 2 dus niet bij het construeren (EF = square on the tangent to E) en zodoende in de bewijsvoering dus ook niet dat FE,ED = to the square of the tangent E.


If x is an integer and 2 < x < 7 , how many different triangles are there with sides of lengths 2, 7 and x?
Het antwoord moet zijn een. Waarom?
Het antwoord moet zijn een. Waarom?


x mag dus 3, 4, 5 of 6 zijn.
x = 3 kan niet, want dan heb je een driehoek met zijde 2, 3, 7 en dan kan niet. (De 2 kleinste zijden moeten samen meer zijn dan de langste zijde)
x = 4 idem.
x = 5 wordt ook lastig Een driehoek met zijde van 2, 5 en 7 is niet haalbaar. Probeer maar eens te tekenen. Zie het als een graaf. Een omweg kan nooit korter of evenlang zijn als rechtstreeks.
x= 6 is de enige die kan.
x = 3 kan niet, want dan heb je een driehoek met zijde 2, 3, 7 en dan kan niet. (De 2 kleinste zijden moeten samen meer zijn dan de langste zijde)
x = 4 idem.
x = 5 wordt ook lastig Een driehoek met zijde van 2, 5 en 7 is niet haalbaar. Probeer maar eens te tekenen. Zie het als een graaf. Een omweg kan nooit korter of evenlang zijn als rechtstreeks.
x= 6 is de enige die kan.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Thnx die stelling had ik nog niet gezien (achteraf gezien heel logisch)quote:Op donderdag 20 september 2007 09:31 schreef Riparius het volgende:
...Hiermee wordt bedoeld dat je op het verlengde van ED een punt F moet bepalen, zodanig dat ED∙EF gelijk is aan het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E. Deze raaklijn heb je niet getekend in je figuur.
De reden om punt F zo te bepalen is gelegen in een bekende stelling van Euclides (Boek III, stelling 36).
...


Ja. Alleen zijn we er hiermee nog niet. Zoals gezegd hebben we EB∙EA = ED∙EF, waaruit volgt dat de punten A,B,D,F op een cirkel liggen, of anders gezegd, ABDF is een koordenvierhoek (begrijp je dat ook?). Nu zijn de overstaande hoeken in een koordenvierhoek supplementair, en dus is hoek FAE gelijk aan hoek BDE. So far so good. Maar dan zegt Heath:quote:Op donderdag 20 september 2007 21:24 schreef Ogala het volgende:
[..]
Thnx die stelling had ik nog niet gezien (achteraf gezien heel logisch)
En dat zie ik dus even niet. Ik begrijp met name niet wat Heath bedoelt met the alternate segment. Die term is niet gebruikelijk, en wordt verder in het hele betoog ook niet gebruikt, zodat niet duidelijk is waar hij op doelt. Nu jij weer ...quote:But the angle FAE is equal to the angle ACB in the alternate segment
[ Bericht 1% gewijzigd door Riparius op 20-09-2007 22:47:48 ]


Yup concyclic quadrilateral, Book III Proposition 22quote:Op donderdag 20 september 2007 21:41 schreef Riparius het volgende:
... ABDF is een koordenvierhoek (begrijp je dat ook?). Nu zijn de overstaande hoeken in een koordenvierhoek supplementair, en dus is hoek FAE gelijk aan hoek BDE..
alternate segment theorem (Heath heeft het probleem uit Hankel from Pappus)quote:...wat Heath bedoelt met the alternate segment....
The angles between a tangent and a chord through the point of contact are equal respectively to the angles in the alternate segment.
(heb ik wel even aangenomen anders kan ik alles tot aan het bestaan van een punt toe bewijzen )
[ Bericht 7% gewijzigd door Ogala op 20-09-2007 23:34:35 ]


Ah, dank je wel. Dat is inderdaad stelling 32 uit boek III bij Euclides. Dan is het bewijs helemaal duidelijk. Maar waarom wilde je uitgerekend dit bewijs bij Heath nalopen? Ik ben zelf erg geïnteresseerd in de geschiedenis van de wiskunde, dus vandaar dat ik het vraag.quote:Op donderdag 20 september 2007 23:11 schreef Ogala het volgende:
[..]
Yup concyclic quadrilateral, Book III Proposition 22
[..]
alternate segment theorem (Heath heeft het probleem uit Hankel from Pappus)
The angles between a tangent and a chord through the point of contact are equal respectively to the angles in the alternate segment.
[afbeelding]


Ik ben pas begonnen met Book I en in de intro stond deze stelling als ideaal voorbeeld voor de analyse van problemen. (transformatie, resolutie, synthese) vandaar! Toch wel leuk om eens door te lezen!quote:Op donderdag 20 september 2007 23:39 schreef Riparius het volgende:
[..]
Ah, dank je wel. Dat is inderdaad stelling 32 uit boek III bij Euclides. Dan is het bewijs helemaal duidelijk. Maar waarom wilde je uitgerekend dit bewijs bij Heath nalopen? Ik ben zelf erg geïnteresseerd in de geschiedenis van de wiskunde, dus vandaar dat ik het vraag.


Als I en J idealen zijn van een commutatieve ring R dan geldt (I +J)(I^J) C IJ. het symbool ^ staat voor de 'doorsende'. Is het waar dat voor iedere een commutatieve ring de gelijkheid t (I +J)(I^J) =IJ geldt? (zonder bewijs aub!)
verlegen :)


Nee.quote:Op zondag 23 september 2007 15:41 schreef teletubbies het volgende:
Als I en J idealen zijn van een commutatieve ring R dan geldt (I +J)(I^J) C IJ. het symbool ^ staat voor de 'doorsende'. Is het waar dat voor iedere een commutatieve ring de gelijkheid t (I +J)(I^J) =IJ geldt? (zonder bewijs aub!)


nu begin ik een zochttocht naar een tegenvoorbeeld..quote:
tot nu toe is me voorbeelden set bijna op!
verlegen :)


De ringen :d zijn Z[x], euuh R, C en Z.
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..
:S welke richting moet ik eigenlijk gaan?
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
Im+Jn=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jn=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I2+Jn=R maar verder kom ik niet uit..
ALvast bedankt
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..
:S welke richting moet ik eigenlijk gaan?
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
Im+Jn=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jn=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I2+Jn=R maar verder kom ik niet uit..
ALvast bedankt
verlegen :)


In Z[x] moet het lukken een tegenvoorbeeld te vinden. Endomorfismen-, groepen- en matrixringen zijn iha niet commutatief.quote:Op maandag 24 september 2007 13:16 schreef teletubbies het volgende:
De ringen :d zijn Z[x], euuh R, C en Z.
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..


Kun je dan niet je argument van 'eerst' toepassen op het paar (Jn,I)? Die zijn immers ook onderling ondeelbaar.quote:Op maandag 24 september 2007 13:16 schreef teletubbies het volgende:
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
Im+Jn=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jn=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I2+Jn=R maar verder kom ik niet uit..
ALvast bedankt


Gewoon optellen kjalquote:Op maandag 24 september 2007 22:12 schreef MaximumRush het volgende:
OMG. Schaam me echt dood dat ik dit moet vragen, maar ben het echt eventjes helemaal kwijt. De resultant force van deze 2 forces is duidelijk. Gewoon een parallelogram van maken en dan weet je de resultant.
[afbeelding]
Maar wat als de forces er zo uitzien?
[afbeelding,link]
 .
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Het parallellogram hoef je ook niet helemaal te tekenen, ook door daar de twee pijltjes achter elkaar te tekenen krijg je de juiste resultante.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Vraagje over statistiek:
Reken percentiel P10, P45, P60 en P90 uit
Formule
Wie kan me nu helpen met het invullen van de formule?
frequentie distributie:quote:1. Stel de cumulatieve frequentieverdeling op.
2. Bepaal de cumulatieve frequentie die met het K-de percentiel correspondeert: nK/100
3. Zoek in de cumulatieve frequentieverdeling de klasse op waarin K-de percentiel moet liggen.
Dit is de klasse waarvan de cumulatieve frequentie net groter is dan (of gelijk is aan) nK/100. Van deze klasse bepalen we:
a) De frequentie f
b) De exacte benedengrens ll
c) De klassenbreedte w = verschil tussen de exacte boven- en benedengrens :
| 1 2 3 4 5 6 7 8 9 10 11 12 | 3.8-4.0 4 120 3.5-3.7 8 116 3.2-3.4 15 108 2.9-3.1 18 93 2.6-2.8 20 75 2.3-2.5 17 55 2.0-2.2 12 38 1.7-1.9 12 26 1.4-1.6 10 14 1.1-1.3 4 4 0.8-1.0 0 0 |
Reken percentiel P10, P45, P60 en P90 uit
Formule
Wie kan me nu helpen met het invullen van de formule?
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


Ehm...quote:Op dinsdag 25 september 2007 19:55 schreef crossover het volgende:
Vraagje over statistiek:
[..]
frequentie distributie:
[ code verwijderd ]
Reken percentiel P10, P45, P60 en P90 uit
Formule
[afbeelding]
Wie kan me nu helpen met het invullen van de formule?
correct me if i'm wrong.
Je moet de formule invullen voor achtereenvolgens K = {10,45,60,90}
Als K=10 zoek je de bijbehorende entry in je tabel, dit is waar cF voor het eerst >= 10 (hier cF=14)
ll is dan 1.4 (exacte benedengrens iig)
w is 0.2 (boven - benedengrens)
cf is 14
f is 10
invullen, doorrekenen en klaar is klara, zelfde trucje herhalen voor K = 45, K=60 en K=90
En dat voor iemand die nooit statistiek gehad heeft
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Ben vergeten te vermelden dat cF betrekking heeft op de net lagere klasse. lower limit is 1.35.quote:Op dinsdag 25 september 2007 20:03 schreef MPG het volgende:
[..]
Ehm...
correct me if i'm wrong.
Je moet de formule invullen voor achtereenvolgens K = {10,45,60,90}
Als K=10 zoek je de bijbehorende entry in je tabel, dit is waar cF voor het eerst >= 10 (hier cF=14)
ll is dan 1.4 (exacte benedengrens iig) 1.35
w is 0.2 (boven - benedengrens)
cf is 14 4
f is 10
invullen, doorrekenen en klaar is klara, zelfde trucje herhalen voor K = 45, K=60 en K=90
En dat voor iemand die nooit statistiek gehad heeft
N(totale scores) = 120?
Dat wordt dan 1.35+(120x10/100-4)/10 * 0.2 = 0.43
Edit: misschien klopt het niet dat cF correspondeert met de net lagere klasse, dan zou het 14 zijn en komt er 1.15 uit.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


cF correspondeert voor zover ik uit hetgeen ik heb gelezen in jouw eerste post niet met de net lagere klasse. Jouw edit lijkt mij dan ook juistquote:Op dinsdag 25 september 2007 20:13 schreef crossover het volgende:
[..]
Ben vergeten te vermelden dat cF betrekking heeft op de net lagere klasse. lower limit is 1.35.
[afbeelding]
N(totale scores) = 120?
Dat wordt dan 1.35+(120x10/100-4)/10 * 0.2 = 0.43
Edit: misschien klopt het niet dat cF correspondeert met de net lagere klasse, dan zou het 14 zijn en komt er 1.15 uit.
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Lieve mensen,
Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.
e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.
Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.
e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.


e-x + SQRT(y) = 1
e-x -1= SQRT(y)
kwadateren levert e-2x -2e-x + 1 = y (merkwaardig product)
stel e-x = p ; daaruit volgt p2 - 2p + 1 = y
nu moet het moet niet zo moeilijk zijn om nulpunten te bereken.
[ Bericht 0% gewijzigd door harrypiel op 26-09-2007 15:08:51 ]
e-x -1= SQRT(y)
kwadateren levert e-2x -2e-x + 1 = y (merkwaardig product)
stel e-x = p ; daaruit volgt p2 - 2p + 1 = y
nu moet het moet niet zo moeilijk zijn om nulpunten te bereken.
[ Bericht 0% gewijzigd door harrypiel op 26-09-2007 15:08:51 ]


e-x+wortel(y) = 1quote:Op woensdag 26 september 2007 13:07 schreef moeffiemoeffie het volgende:
Lieve mensen,
Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.
e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.
ex = a is hetzelfde als x = ln(a)
dus -x+wortel(y) = ln(1)
ln(1) = 0
dus -x+wortel(y) = 0
dus wortel(y) = x
dus y = x2
Zorg er wel voor dat je goed met haakjes werkt als je een macht aangeeft met ^, anders krijg je dus antwoorden als die van meneer piel te zien.
[ Bericht 29% gewijzigd door Jordy-B op 26-09-2007 13:24:07 ]
Bestiality sure is a fun thing to do. But I have to say this as a warning to you:
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.


anders met tekst in subscript of tekst in superscript werken om de zaak te verduidelijkenquote:Op woensdag 26 september 2007 13:17 schreef Jordy-B het volgende:
[..]
e-x+wortel(y) = 1
ex = a is hetzelfde als x = ln(a)
dus -x+wortel(y) = ln(1)
ln(1) = 0
dus -x+wortel(y) = 0
dus wortel(y) = x
dus y = x2
Zorg er wel voor dat je goed met haakjes werkt als je een macht aangeeft met ^, anders krijg je dus antwoorden als die van meneer piel te zien.
druk op de quote bericht knop voor de precieze code


Ik heb weer eens een proef gedaan bij scheikunde met heel aantal vragen erbij. De meeste snap ik natuurlijk. Echter zit er ook een vraag bij die ik niet snap. De volgende:
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.


* Mergequote:Op zondag 30 september 2007 12:34 schreef Curri het volgende:
Ik heb weer eens een proef gedaan bij scheikunde met heel aantal vragen erbij. De meeste snap ik natuurlijk. Echter zit er ook een vraag bij die ik niet snap. De volgende:
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
[afbeelding]
[afbeelding]
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


Ik heb ook weer eens een vraag.
Ik heb de volgende functie:
ABS((1+0.5f)/(1-0.5f)) <= 1
(ABS = absolute waarde dus, en <= betekent kleiner of gelijk.)
waarbij f een complex getal is. Ik moet het gebied in het complex vlak schetsen wat hier aan voldoet. Het lukt alleen niet. Ik mag ook MATLAB gebruiken, dat zou zelfs wat handiger zijn, omdat ik nog een aantal van dit soort dingen moet oplossen.
Ik heb de volgende functie:
ABS((1+0.5f)/(1-0.5f)) <= 1
(ABS = absolute waarde dus, en <= betekent kleiner of gelijk.)
waarbij f een complex getal is. Ik moet het gebied in het complex vlak schetsen wat hier aan voldoet. Het lukt alleen niet. Ik mag ook MATLAB gebruiken, dat zou zelfs wat handiger zijn, omdat ik nog een aantal van dit soort dingen moet oplossen.


quote:Op zondag 7 oktober 2007 14:08 schreef Schuifpui het volgende:
Ik heb ook weer eens een vraag.
Ik heb de volgende functie:
ABS((1+0.5f)/(1-0.5f)) <= 1
(ABS = absolute waarde dus, en <= betekent kleiner of gelijk.)
waarbij f een complex getal is. Ik moet het gebied in het complex vlak schetsen wat hier aan voldoet. Het lukt alleen niet. Ik mag ook MATLAB gebruiken, dat zou zelfs wat handiger zijn, omdat ik nog een aantal van dit soort dingen moet oplossen.
Is f complex in de zin dat f = (a + b*i), of complex in de zin dat f = b*i? Dat eerste lijkt me een rottige vergelijking opleveren… dat laatste is volgens mij wel te doen als je je realiseert dat complexe deling opgelost kan worden door met de complex geconjugeerde te vermenigvuldigen… dan kun je de complexe modulus uitrekenen en berekenen wat b moet zijn.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Toch. Dacht al dat zoiets eruit zou komen, door wat proberen.. Tijdens college met andere voorbeelden kwam er altijd iets met een rondje uit. Toch nog maar eens checken of de afleiding goed is. Thanks anyway.
[edit] dan gelijk nog maar een:
ABS(1+f+1/2f^2) <= 1
Ik zie dus gewoon echt niet goed hoe ik dit moet doen.
[ Bericht 29% gewijzigd door Schuifpui op 07-10-2007 17:12:27 ]
[edit] dan gelijk nog maar een:
ABS(1+f+1/2f^2) <= 1
Ik zie dus gewoon echt niet goed hoe ik dit moet doen.
[ Bericht 29% gewijzigd door Schuifpui op 07-10-2007 17:12:27 ]


PWS vraagje, Ik heb voor mijn profielwerkstuk een elektromotor gebouwd die tevens als generator zou moeten werken. Nou als elektromotor werkt hij prima, maar als generator geeft hij in een stroomkring alleen maar spanning en géén stroom. Hoe is dit mogelijk?
De motor loopt op gelijkspaning, heeft 2 permanente magneten van 0,4 Tesla.
Op de as zitten de spoelen, 2 om precies te zijn ieder van 60 windingen.
Omdat de motor op gelijkspanning loopt zit er dus ook een commutator op, daar zou volgens mij misschien wel het probleem kunnen liggen. Maar toch, hoe kan het dat er wel spanning loopt maar geen stroom als je de as ronddraait.
De motor loopt op gelijkspaning, heeft 2 permanente magneten van 0,4 Tesla.
Op de as zitten de spoelen, 2 om precies te zijn ieder van 60 windingen.
Omdat de motor op gelijkspanning loopt zit er dus ook een commutator op, daar zou volgens mij misschien wel het probleem kunnen liggen. Maar toch, hoe kan het dat er wel spanning loopt maar geen stroom als je de as ronddraait.


Ten eerste: Spanning loopt niet, die staat over twee punten.quote:Op donderdag 11 oktober 2007 20:21 schreef DJ90 het volgende:
PWS vraagje, Ik heb voor mijn profielwerkstuk een elektromotor gebouwd die tevens als generator zou moeten werken. Nou als elektromotor werkt hij prima, maar als generator geeft hij in een stroomkring alleen maar spanning en géén stroom. Hoe is dit mogelijk?
De motor loopt op gelijkspaning, heeft 2 permanente magneten van 0,4 Tesla.
Op de as zitten de spoelen, 2 om precies te zijn ieder van 60 windingen.
Omdat de motor op gelijkspanning loopt zit er dus ook een commutator op, daar zou volgens mij misschien wel het probleem kunnen liggen. Maar toch, hoe kan het dat er wel spanning loopt maar geen stroom als je de as ronddraait.
Ten tweede, wat heb je bij generatorwerking aan de klemmen van de motor aangesloten?Alleen een multimeter? Dan meet je inderdaad alleen spanning.
Tip: Een weerstand zet spanning over de klemmen om in een stroom, geheel volgens de wet van Ohm.
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Meet je de spanning wanneer de generator op de stroomkring is aangesloten? Wanneer je het los van elkaar meet, kan de spanning direct inzakken wanneer je de stroomkring sluit omdat het vermogen niet toereikend is maar dat merk je direct wanneer je gelijktijdig meet.
Meet je wel gelijktijdig, dan is de stroomkring waarschijnlijk niet gesloten.
Meet je wel gelijktijdig, dan is de stroomkring waarschijnlijk niet gesloten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Beetje laat antwoord...quote:Op zondag 30 september 2007 12:34 schreef Curri het volgende:
Ik heb weer eens een proef gedaan bij scheikunde met heel aantal vragen erbij. De meeste snap ik natuurlijk. Echter zit er ook een vraag bij die ik niet snap. De volgende:
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
[afbeelding]
[afbeelding]
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.
Als je de overmaat OH- toevoegt en het kookt, wordt het zuurrest-ion omgezet naar het salycilaat-ion en azijnzuur. Vervolgens ga je terugtitreren met HCl om te kijken hoeveel van de OH- niet gereageerd heeft. Het verschil tussen het aantal mol OH- dat je in het begin hebt toegevoegd (25 mL 0,05M oplossing) en het aantal mol HCl dat je getitreerd hebt, geeft de concentratie acetylsalicylzuur (a.k.a. aspirine).
Je hebt in beide metingen 25mL 0,05M NaOH toegevoegd. Dit is 25×0,05=1,25 mmol OH-
Vervolgens ga je terugtitreren met HCl. De eerste keer kom je uit op 14 mL (×0.05013 M = 0,70182 mmol) en de tweede keer kom je uit op 14,67 mL (×0.05013 M = 0,735407 mmol)
Vervolgens trek je deze van elkaar af:
1,25 mmol NaOH - 0,702 mmol HCl = 0,548 mmol aspirine
1,25 mmol NaOH - 0,735 mmol HCl = 0,515 mmol aspirine
je hebt 10 mL oplossing C gebruikt, dus de concentraties aspirine in oplossing C waren:
0,548mmol / 10mL = 0,0548 M
en dus 0,0515 M in de tweede meting.
Om oplossing C te maken zijn 25 tabletten opgelost in 1 liter, 1M is hetzelfde als 1 mol per liter, dus om het aantal mol in een tablet te vinden, moet je de boel delen door 25. Vervolgens vermenigvuldigen met de molecuulmassa om de hoeveelheid aspirine in een tablet in grammen te krijgen... De molecuulmassa schijnt 180,16 g/mol te zijn
0,0548 / 25 = 2,19 mmol × 180,16 g/mol = 394,6 mg per tablet
0,0515 / 25 = 2,06 mmol × 180,16 g/mol = 371,1 mg per tablet
Dat moet je vervolgens controleren met de waarde die op het pakje bruistabletten staat.
Bestiality sure is a fun thing to do. But I have to say this as a warning to you:
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.


vraagje. 1.08^n=100/75
wat is n en hoe bereken je dat?
wat is n en hoe bereken je dat?
Sei wachsam,
Fall nicht auf sie rein! Paß auf, daß du deine Freiheit nutzt,
Die Freiheit nutzt sich ab, wenn du sie nicht nutzt!
Fall nicht auf sie rein! Paß auf, daß du deine Freiheit nutzt,
Die Freiheit nutzt sich ab, wenn du sie nicht nutzt!


Dat is het teken voor een sommatie. In plaats van a_1+a_2+a_3+...+a_n schrijft men vaakquote:Op dinsdag 16 oktober 2007 13:30 schreef alors het volgende:
n00bvraagje, maar wat betekent deze?
[ afbeelding ]
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Okay bedankt, ik had al zo'n vermoeden.quote:Op dinsdag 16 oktober 2007 14:17 schreef keesjeislief het volgende:
[..]
Dat is het teken voor een sommatie. In plaats van a_1+a_2+a_3+...+a_n schrijft men vaak
[ afbeelding ].
know'm sayin?
×
word? word.
×
word? word.


Ik moet twee integralen oplossen, kom op twee manieren op verschillende antwoorden uit en Maple kan hem niet oplossen. Zou iemand het voor me uit kunnen rekenen?


productregel bij integreren, altijd lastig. Truc hierbij is te beseffen dat we hier alleen naar e integreren en dat elke andere term zonder e als constante beschouwd dient te worden.
INT (x-e)
------------------------------------------ de =
((x-e)2 + y2)
INT -(x-e)
----------------------------------------- d(x-e) =
((x-e)2 + y2)
(eerst de x voor de d halen en compenseren voor minteken)
1/2 * ln | ((x-e)2 + y2) |
(compenseren voor het differentieren van (x-e)2 naar e, dus een factor -1/2 meenemen. Remember: (-x2)' = -2x )
De tweede is er eentje die je op een dwaalspoor zal zetten. De truc hier is in te zien dat we met de afgeleide van een arctangens-functie te maken hebben. So let's try that way.
INT y
------------------------------------------ de =
(x-e)2 + y2
INT -y
------------------------------------------ d(x-e) =
(x-e)2 + y2
(eerst x voor de d halen en compenseren voor het minteken)
INT (1/y2 * -y)
--------------------------------------------------------------- d(x-e) =
(1/y2) * ((x-e)2 + y2)
(teller en noemer met (1/y2) vermenigvuldigen)
INT y*1/y2
--------------------------------- d(x-e) =
((x-e)/y)2 + 1
(de door de vermenigvuldiging ontstane breuken in teller en noemer apart uitdelen)
INT (-y/y2) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
INT (-1/y) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
(teller als aparte factor van de breuk afsplitsen en -y/y2 tot -1/y uitschrijven)
-1*arctan ((x-e)/y)
(integratie uitvoeren. Note to self; VERGEET VOORAL NIET DAT DE AFGELEIDE VAN ( (x-e)/y ) NAAR e, -e/y IS, MORON!!)
tering, dat was een zware bevalling zeg.
[ Bericht 6% gewijzigd door harrypiel op 18-10-2007 21:31:07 ]
INT (x-e)
------------------------------------------ de =
((x-e)2 + y2)
INT -(x-e)
----------------------------------------- d(x-e) =
((x-e)2 + y2)
(eerst de x voor de d halen en compenseren voor minteken)
1/2 * ln | ((x-e)2 + y2) |
(compenseren voor het differentieren van (x-e)2 naar e, dus een factor -1/2 meenemen. Remember: (-x2)' = -2x )
De tweede is er eentje die je op een dwaalspoor zal zetten. De truc hier is in te zien dat we met de afgeleide van een arctangens-functie te maken hebben. So let's try that way.
INT y
------------------------------------------ de =
(x-e)2 + y2
INT -y
------------------------------------------ d(x-e) =
(x-e)2 + y2
(eerst x voor de d halen en compenseren voor het minteken)
INT (1/y2 * -y)
--------------------------------------------------------------- d(x-e) =
(1/y2) * ((x-e)2 + y2)
(teller en noemer met (1/y2) vermenigvuldigen)
INT y*1/y2
--------------------------------- d(x-e) =
((x-e)/y)2 + 1
(de door de vermenigvuldiging ontstane breuken in teller en noemer apart uitdelen)
INT (-y/y2) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
INT (-1/y) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
(teller als aparte factor van de breuk afsplitsen en -y/y2 tot -1/y uitschrijven)
-1*arctan ((x-e)/y)
(integratie uitvoeren. Note to self; VERGEET VOORAL NIET DAT DE AFGELEIDE VAN ( (x-e)/y ) NAAR e, -e/y IS, MORON!!)
tering, dat was een zware bevalling zeg.
[ Bericht 6% gewijzigd door harrypiel op 18-10-2007 21:31:07 ]


Thanks
Die eerste heb ik idd ook. De tweede had ik als:
arctan((-x+e)/y), dat kwam uit maple. Ik ga er nog even naar kijken, nogmaals dank.
Die eerste heb ik idd ook. De tweede had ik als:
arctan((-x+e)/y), dat kwam uit maple. Ik ga er nog even naar kijken, nogmaals dank.


Kan wel kloppen; de arctangens functie is namelijk symmetrisch voor de bewerking (x,y) -> -(-x,y)quote:Op dinsdag 16 oktober 2007 22:29 schreef Schuifpui het volgende:
Thanks
Die eerste heb ik idd ook. De tweede had ik als:
arctan((-x+e)/y), dat kwam uit maple. Ik ga er nog even naar kijken, nogmaals dank.


P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1)
Maar hoe bereken je P(Y = 1 EN X3 = 1)?
edit
Dit dus:
en maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
[ Bericht 54% gewijzigd door R-Mon op 17-10-2007 19:55:47 ]
Maar hoe bereken je P(Y = 1 EN X3 = 1)?
edit
Dit dus:
en maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
[ Bericht 54% gewijzigd door R-Mon op 17-10-2007 19:55:47 ]
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Eindelijk weer kansrekening
Die tweede regel die je daar noemt geldt voor twee onafhankelijke gebeurtenissen A en B. En wanneer A en B onafhankelijk zijn, is het inderdaad logisch dat geldt P(A|B) = P(A). Zijn A en B niet onafhankelijk, dan zul je P(A en B) op een andere manier uit moeten rekenen.
Voorbeeld: een worp met een dobbelsteen, we kijken naar het aantal oogjes. A = 'minder dan 4', B = 'gelijk aan 1'.
Nu geldt dat P(A) = 1/2, P(B) = 1/6, P(A en B) = 1/2 (dus niet P(A en B) = P(A)P(B), A en B zijn immers niet onafhankelijk). P(A|B) = 1.
Die tweede regel die je daar noemt geldt voor twee onafhankelijke gebeurtenissen A en B. En wanneer A en B onafhankelijk zijn, is het inderdaad logisch dat geldt P(A|B) = P(A). Zijn A en B niet onafhankelijk, dan zul je P(A en B) op een andere manier uit moeten rekenen.
Voorbeeld: een worp met een dobbelsteen, we kijken naar het aantal oogjes. A = 'minder dan 4', B = 'gelijk aan 1'.
Nu geldt dat P(A) = 1/2, P(B) = 1/6, P(A en B) = 1/2 (dus niet P(A en B) = P(A)P(B), A en B zijn immers niet onafhankelijk). P(A|B) = 1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt GlowMouse, helaas is mijn som niet zo makkelijk om te schrijven naar een dobbelstenen voorbeeld... Het is van Machine Learning, ik moet (moest, deadline was gisteravond, geen colleges meer voor tentamen) gegeven een train set een conditional entropy uitrekenen... Dit is wat ik heb gedaan:
Train set
x1 x2 x3 y
WearsBlack SavesPrincess HorseColour GoodOrEvil
No Yes Black Good
Yes No Black Evil
No No White Good
Yes Yes Brown Good
Schattingen van de kansen
Y=1 Good Estimate P = 3/4
Y=2 Evil Estimate P = 1/4
P(X3 = 1 (Black)) = 1/2
P(X3 = 2 (White)) = ¼
P(X3 = 3 (Brown)) = ¼
Definitie conditional entropy
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
Versimpelen
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1) = P(Y = 1) * P(X3 = 1) / P(Y = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(Y = 2) = P(Y = 2) * P(X3 = 1) / P(Y = 2) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
Uitrekenen
p = ¾ * 1/2 / ¾ = 1/2
q = ¼ * 1/2 / ¼ = 1/2
H(Y | X3 = 1) = 1/2 * -log2 (1/2) + 1/2 * -log2 (1/2)
log(1/2) = -0,30
log2 (1/2) = log(1/2) / log 2 = -1
H(Y | X3 = 1) = 1/2 * -1 + 1/2 * -1 = -1
Het lijkt mij dus niet dat X en Y onafhankelijk zijn, of wel?
Train set
x1 x2 x3 y
WearsBlack SavesPrincess HorseColour GoodOrEvil
No Yes Black Good
Yes No Black Evil
No No White Good
Yes Yes Brown Good
Schattingen van de kansen
Y=1 Good Estimate P = 3/4
Y=2 Evil Estimate P = 1/4
P(X3 = 1 (Black)) = 1/2
P(X3 = 2 (White)) = ¼
P(X3 = 3 (Brown)) = ¼
Definitie conditional entropy
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
Versimpelen
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1) = P(Y = 1) * P(X3 = 1) / P(Y = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(Y = 2) = P(Y = 2) * P(X3 = 1) / P(Y = 2) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
Uitrekenen
p = ¾ * 1/2 / ¾ = 1/2
q = ¼ * 1/2 / ¼ = 1/2
H(Y | X3 = 1) = 1/2 * -log2 (1/2) + 1/2 * -log2 (1/2)
log(1/2) = -0,30
log2 (1/2) = log(1/2) / log 2 = -1
H(Y | X3 = 1) = 1/2 * -1 + 1/2 * -1 = -1
Het lijkt mij dus niet dat X en Y onafhankelijk zijn, of wel?
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Dit gaat fout: P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1)
Je moet hier delen door P(X3=1).
Daarnaast: ik heb nooit met entropy's gewerkt, dus ik weet niet of je hieruit al kunt afleiden dat X3 en Y onafhankelijk zijn. Dit kun je in ieder geval aantonen via P(Y=a en X3=b) = P(Y=a)P(X3=b) voor iedere a en b (heb dit zelf niet gecheckt).
Je moet hier delen door P(X3=1).
Daarnaast: ik heb nooit met entropy's gewerkt, dus ik weet niet of je hieruit al kunt afleiden dat X3 en Y onafhankelijk zijn. Dit kun je in ieder geval aantonen via P(Y=a en X3=b) = P(Y=a)P(X3=b) voor iedere a en b (heb dit zelf niet gecheckt).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Aargh ik zie het ook nu... Ook zo leuk als er in de formule X en Y wordt gebruikt maar in het voorbeeld Y en X. Dit komt er nu uit:
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(X3 = 1) = P(Y = 1) * P(X3 = 1) / P(X3 = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(X3 = 1) = P(Y = 2) * P(X3 = 1) / P(X3 = 1) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
p = ¾ * 1/2 / 1/2 = ¾
q = ¼ * 1/2 / 1/2 = ¼
H(Y | X3 = 1) = 3/4 * -log2 (3/4) + 3/4 * -log2 (3/4)
log(3/4) = -0,12
log2 (3/4) = log(3/4) / log 2 = -0,42
H(Y | X3 = 1) = ¾ * -0,42 + ¾ * -0,42 = -0,63
Verder maakt het weinig uit, bedankt in elk geval.
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(X3 = 1) = P(Y = 1) * P(X3 = 1) / P(X3 = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(X3 = 1) = P(Y = 2) * P(X3 = 1) / P(X3 = 1) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
p = ¾ * 1/2 / 1/2 = ¾
q = ¼ * 1/2 / 1/2 = ¼
H(Y | X3 = 1) = 3/4 * -log2 (3/4) + 3/4 * -log2 (3/4)
log(3/4) = -0,12
log2 (3/4) = log(3/4) / log 2 = -0,42
H(Y | X3 = 1) = ¾ * -0,42 + ¾ * -0,42 = -0,63
Verder maakt het weinig uit, bedankt in elk geval.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Help
Ik probeer iets in Mathematica te implementeren, maar het lukt me gewoon echt niet.
Ik wil eigenlijk een soort van loop maken waarin ik steeds achtereenvolgens 2 functies laat uitvoeren waarvan de 1e gebruik maakt van het resultaat van de tweede en de tweede gebruik maakt van het resultaat van de eerste (volgen jullie het nog ?):
Ik voer een functie f1 uit op een plaatje 'alle cellen' -> resultaat: plaatje 'cel 1'
Ik pas plaatje 'alle cellen' aan door pixels uit plaatje 'cel 1' te verwijderen
etc etc.
Dit doe ik totdat Apply[Plus,'alle cellen'] 0 oplevert.
Uiteindelijk wil ik een lijst met alle plaatjes 'cel 1'
De afzonderlijke stappen werken, alleen moet ik ze steeds zelf opnieuw evalueren omdat ik geen loop heb .
Ik probeer iets in Mathematica te implementeren, maar het lukt me gewoon echt niet.
Ik wil eigenlijk een soort van loop maken waarin ik steeds achtereenvolgens 2 functies laat uitvoeren waarvan de 1e gebruik maakt van het resultaat van de tweede en de tweede gebruik maakt van het resultaat van de eerste (volgen jullie het nog ?):
Ik voer een functie f1 uit op een plaatje 'alle cellen' -> resultaat: plaatje 'cel 1'
Ik pas plaatje 'alle cellen' aan door pixels uit plaatje 'cel 1' te verwijderen
etc etc.
Dit doe ik totdat Apply[Plus,'alle cellen'] 0 oplevert.
Uiteindelijk wil ik een lijst met alle plaatjes 'cel 1'
De afzonderlijke stappen werken, alleen moet ik ze steeds zelf opnieuw evalueren omdat ik geen loop heb .


Ja ik heb ook weer wat... Afleiden met natuurlijke deductie:
1. ~(p of q) |- ~(p en q)
het verste dat ik kom:
3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
En kan iemand deze controleren, dat ik niks illegaals doe:
2. (p en q) of ~p |- p -> q
1. ~(p of q) |- ~(p en q)
het verste dat ik kom:
| 1 2 3 4 5 6 7 8 9 10 11 | ... |------------------ (box) | ~~(p en q) (assumptie) | p en q (~~eliminatie) | p (en-eliminatie1) | q (en-eliminatie2) | ... | contradictie |---------------------- ~(p en q) (PBC) |
3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
En kan iemand deze controleren, dat ik niks illegaals doe:
2. (p en q) of ~p |- p -> q
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | - |------------------------box 2 | p en q (assumptie) 3 | p (en-eliminatie1 op 2) 4 | q (en-eliminatie2 op 2) - | |-----------------------------box2 5 | | p (assumptie) 6 | | q (copy 4) - | |----------------------------- 7 | p -> q (impl.-introductie 5-6) - |------------------------------- - |-------------------------------box 8 | ~p (assumptie) - | |-----------------------------box2 9 | | p (assumptie) 10 | | ~p (copy 8) 11 | | contradictie (~eliminatie 9,10) 12 | | p (contr. eliminatie 11) 13 | | q (assumptie) - | |---------------------------- 14 | p -> q (impl. introductie 9-13) - |----------------------------- 15 p -> q (of eliminatie 1-7,8-14) |
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Niet meer nodig Je kan dus opeenvolgens dingen uit laten voeren door ze in een for loopje te zetten met méérdere functies.quote:Op zaterdag 20 oktober 2007 12:02 schreef vliegtuigje het volgende:
Help
Ik probeer iets in Mathematica te implementeren, maar het lukt me gewoon echt niet.
Ik wil eigenlijk een soort van loop maken waarin ik steeds achtereenvolgens 2 functies laat uitvoeren waarvan de 1e gebruik maakt van het resultaat van de tweede en de tweede gebruik maakt van het resultaat van de eerste (volgen jullie het nog ?):
Ik voer een functie f1 uit op een plaatje 'alle cellen' -> resultaat: plaatje 'cel 1'
Ik pas plaatje 'alle cellen' aan door pixels uit plaatje 'cel 1' te verwijderen
etc etc.
Dit doe ik totdat Apply[Plus,'alle cellen'] 0 oplevert.
Uiteindelijk wil ik een lijst met alle plaatjes 'cel 1'
De afzonderlijke stappen werken, alleen moet ik ze steeds zelf opnieuw evalueren omdat ik geen loop heb .
For[i=1,i>=blabla,i++,{functie1,functie2}]
Misschien heeft iemand er nog wat aan


Dit heb ik al lang niet gedaan, ik ken de terminologie die je gebruikt ook niet helemaal, zoals 'LEM', maar ik denk dat de truc 'm erin zit dat je inderdaadquote:Op zaterdag 20 oktober 2007 16:24 schreef R-Mon het volgende:
Ja ik heb ook weer wat... Afleiden met natuurlijke deductie:
1. ~(p of q) |- ~(p en q)
het verste dat ik kom:
[ code verwijderd ]
~~(p & q) aanneemt, dan zoals jij doet (p & q) afleidt, daarvan of p of q afleidt, dan een of introduceert (voorgesteld door 'v'), dus dat je dan p v q hebt, en dat is in tegenspraak met je premisse. Dus ~~(p & q) leidt tot een contradictie.
Ik weet niet wat LEM is.quote:3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
Lijkt me correct.quote:En kan iemand deze controleren, dat ik niks illegaals doe:
2. (p en q) of ~p |- p -> q
[ code verwijderd ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Overigens kan ik hier wel een afleiding voor geven:quote:Op zaterdag 20 oktober 2007 16:24 schreef R-Mon het volgende:
3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
1) ~(p en q) (premisse)
2) ~(~p of ~q) (aanname)
3) ~p (aanname)
4) ~p of ~q (of-introductie op de vorige aanname)
5) p (contradictie met aanname 2, dus onder 2 is aanname 3 ongeldig)
6) ~q (aanname, gaat natuurlijk hetzelfde als ~p)
7) ~p of ~q (of-introductie op de vorige)
8) q (contradictie met aanname 2, dus onder 2 is aanname 6 ongeldig)
9) p en q (uit 5 en 8)
10) ~p of ~q (p en q is een contradictie met de premisse (1), en dat komt door de aanname (2), want die geldt op het moment, die aanname is dus fout, en de elimineren we).
Met jouw 'LEM' regel worden vast een paar stappen samengevat in dit proces.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ah p v q is wat ik zocht, stom dat ik die niet zag.quote:Op zaterdag 20 oktober 2007 20:50 schreef Iblis het volgende:
[..]
Dit heb ik al lang niet gedaan, ik ken de terminologie die je gebruikt ook niet helemaal, zoals 'LEM', maar ik denk dat de truc 'm erin zit dat je inderdaad
~~(p & q) aanneemt, dan zoals jij doet (p & q) afleidt, daarvan of p of q afleidt, dan een of introduceert (voorgesteld door 'v'), dus dat je dan p v q hebt, en dat is in tegenspraak met je premisse. Dus ~~(p & q) leidt tot een contradictie.
LEM is Law of Excluded Middle, p v ~p. Bedankt iigquote:[..]
Ik weet niet wat LEM is.
[..]
Lijkt me correct.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


ik moet voor een moment generating function een limit uitrekenen, maar ik snap niet hoe dit moet. Bijvoorbeeld deze functie
Als ik het in maple stop, of een waarde heel dicht bij 0 uitreken, dan weet ik dat als x naar 0 gaat, de functie 1 wordt. Maar Ik moet het eigenlijk algebraisch oplossen. Hoe doe ik dat?
Als ik het in maple stop, of een waarde heel dicht bij 0 uitreken, dan weet ik dat als x naar 0 gaat, de functie 1 wordt. Maar Ik moet het eigenlijk algebraisch oplossen. Hoe doe ik dat?


Is dit niet op te lossen met de stelling van l'Hospital? Ik dacht dat je dan de afgeleide van de teller en de noemer een nieuwe breuk moet maken en daar de lim x->0 van moet uit rekenen. Die stelling kan je dacht ik gebruiken wanneer de teller en de noemer allebei 0 zijn of oneindig.
/Edit: Spuitelf
Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link .
/Edit2: En omdat ik vandaag helemaal in een goede bui ben en dit best een makkelijke opgave is:
lim x->0 (e2x-1)/(2x) = lim x->0 (2e2x)/2 = 1
/Edit3: En omdat ik het calculus boek toch moest pakken voor m'n tentamen over anderhalve week:
(Ik gok dat je het boek Calculus: early transcendentals 5e editie ook hebt) Op p.308 staat de boel uitgelegd, enjoy
[ Bericht 27% gewijzigd door fart op 21-10-2007 17:54:58 ]
/Edit: Spuitelf
Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link .
/Edit2: En omdat ik vandaag helemaal in een goede bui ben en dit best een makkelijke opgave is:
lim x->0 (e2x-1)/(2x) = lim x->0 (2e2x)/2 = 1
/Edit3: En omdat ik het calculus boek toch moest pakken voor m'n tentamen over anderhalve week:
(Ik gok dat je het boek Calculus: early transcendentals 5e editie ook hebt) Op p.308 staat de boel uitgelegd, enjoy
[ Bericht 27% gewijzigd door fart op 21-10-2007 17:54:58 ]


Moet je voor die afgeleide de quotientregel niet toepassen?quote:Op zondag 21 oktober 2007 17:42 schreef fart het volgende:
Is dit niet op te lossen met de stelling van l'Hospital? Ik dacht dat je dan de afgeleide van de teller en de noemer een nieuwe breuk moet maken en daar de lim x->0 van moet uit rekenen. Die stelling kan je dacht ik gebruiken wanneer de teller en de noemer allebei 0 zijn of oneindig.
/Edit: Spuitelf
Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link .
/Edit2: En omdat ik vandaag helemaal in een goede bui ben en dit best een makkelijke opgave is:
lim x->0 (e2x-1)/(2x) = lim x->0 (2e2x)/2 = 1
/Edit3: En omdat ik het calculus boek toch moest pakken voor m'n tentamen over anderhalve week:
(Ik gok dat je het boek Calculus: early transcendentals 5e editie ook hebt) Op p.308 staat de boel uitgelegd, enjoy
Zou dan zijn: (4xe^(2x)-2e^(2x)+2)/(4x²)
Ik weet overigens ook niet hoe je die limiet verder moet doen, dat is meer de reden dat ik hier keek


Nope, je komt dan ook niets verder trouwens, aangezien lim x->0 van die functie nog steeds 0/0 is.quote:Op zondag 21 oktober 2007 18:15 schreef Fhm het volgende:
[..]
Moet je voor die afgeleide de quotientregel niet toepassen?
Zou dan zijn: (4xe^(2x)-2e^(2x)+2)/(4x²)
Ik weet overigens ook niet hoe je die limiet verder moet doen, dat is meer de reden dat ik hier keek
De stelling van l'Hôpital kan je gebruiken wanneer je een limiet van een breuk moet nemen en je 0/0 krijgt of oneindig/oneindig. Wanneer je dat krijgt, moet je de de teller als functie zien en de noemer ook.
Je hebt dan lim x->c f(x)/g(x) wat dan gelijk is aan lim x->c f'(x)/g'(x)


Oh ja, tuurlijk, wat dom!quote:Op zondag 21 oktober 2007 18:19 schreef fart het volgende:
[..]
Nope, je komt dan ook niets verder trouwens, aangezien lim x->0 van die functie nog steeds 0/0 is.
De stelling van l'Hôpital kan je gebruiken wanneer je een limiet van een breuk moet nemen en je 0/0 krijgt of oneindig/oneindig. Wanneer je dat krijgt, moet je de de teller als functie zien en de noemer ook.
Je hebt dan lim x->c f(x)/g(x) wat dan gelijk is aan lim x->c f'(x)/g'(x)
Dank je


Topic gemerged.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


tnx, met deze regel is het inderdaad op te lossen. Ik zie dat deze regel alleen beperkt te gebruiken is, namelijk als beide expressies tot 0 of inf evalueren bij dezelfde c. Stel dat er geen -1 maar -2 in de expressie had gestaan, dan was dit dus niet het geval geweest en had ik het niet kunnen oplossen? Of zie ik nu wat over het hoofd?quote:Op zondag 21 oktober 2007 17:42 schreef fart het volgende:Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link.


In dat geval zou je de stelling niet juist toepassen. In het algemeen is de limiet van de afgeleide van een functie ook niet gelijk aan de limiet van die functie zelf.quote:Op zondag 21 oktober 2007 18:15 schreef Fhm het volgende:
[..]
Moet je voor die afgeleide de quotientregel niet toepassen?
Zou dan zijn: (4xe^(2x)-2e^(2x)+2)/(4x²)
Ik weet overigens ook niet hoe je die limiet verder moet doen, dat is meer de reden dat ik hier keek
In dat geval was je nog sneller klaar geweest, want dan kun je direct zien wat de limiet is. Gaat de teller naar oneindig en de noemer naar 5, dan gaat bijvoorbeeld de hele breuk naar oneindig. Gaat de teller naar 1 en de noemer naar 2, dan gaat de hele breuk naar 1/2. Het wordt alleen lastig wanneer de noemer naar 0 gaat, en de teller niet.quote:Op zondag 21 oktober 2007 21:54 schreef jeroenisblij het volgende:
[..]
tnx, met deze regel is het inderdaad op te lossen. Ik zie dat deze regel alleen beperkt te gebruiken is, namelijk als beide expressies tot 0 of inf evalueren bij dezelfde c. Stel dat er geen -1 maar -2 in de expressie had gestaan, dan was dit dus niet het geval geweest en had ik het niet kunnen oplossen? Of zie ik nu wat over het hoofd?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel je hebt een vectorveld xi+yj+zk en je wilt de arbeid weten van een deetltje dat langs de parabool y=x^2, z=0 beweegt, van x=-1 tot x=2.... hoe weet ik dan hoe dat pad eruit ziet? maw, hoe parametriseer ik iets van (x,y,z) naar iets in de vorm van t. Als ik dat weet word het gewoon:
Int (Fds)= Int ( F(c(t)) . c'(t)) dt
Kortom: is er een makkelijke algemene methode om te parametriseren?
Int (Fds)= Int ( F(c(t)) . c'(t)) dt
Kortom: is er een makkelijke algemene methode om te parametriseren?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Dat zal wel goed zijn, maar mijn vraag is meer, hoe kom ik tot die/een parametrisatie.. is daar een standaard werkwijze voor of is dat "inzicht" of wat? Ik bedoel.... dx/dt kan je uitreken, Fds kan je uitrekenen, maar hoe kom je voor een willekeurig pad uitgedrukt in x,y,z-coordinaten naar een pad in t?quote:Op maandag 22 oktober 2007 10:44 schreef thabit het volgende:
Wat dacht je van (x,y,z) = (t,t^2,0), waarbij t van -1 tot 2 loopt?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


In het algemeen is dat niet zo eenvoudig, maar in dit geval staat er gewoon "y = uitdrukking in x" en ook "z = uitdrukking in x" (weliswaar een die x niet gebruikt maar dat doet er niet toe).


Ok, dus je noemt 1 van de variablen x,y,z t en dan schrijf je de rest ook om naar tquote:Op maandag 22 oktober 2007 12:03 schreef thabit het volgende:
In het algemeen is dat niet zo eenvoudig, maar in dit geval staat er gewoon "y = uitdrukking in x" en ook "z = uitdrukking in x" (weliswaar een die x niet gebruikt maar dat doet er niet toe).
y= x^2 z= 0*x, neem x = t, geeft c(t)=t,t^2,0
Beetje jammer dat het niet eenvoudig is, want ik heb het heel vaak nodig, maar ik snap het nooit
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


De voorbeelden die je voor je tentamensommen enzo moet uitwerken zijn altijd wel eenvoudig. Er bestaat alleen geen "algemene methode" voor (buiten het feit dat je ook nog eens goed moet definieren wat je met een parametrisatie bedoelt).


A path in R^n is a map c: [a,b] -> R^n; it is a path in the plane if n=2 and a path in the space if n=3. The collection C of points c(t) as t varies in [a,b] is called a curve, and c(a) and c(b) are its endpoints. The path c is said to parametrize the curve C.quote:Op maandag 22 oktober 2007 12:26 schreef thabit het volgende:
De voorbeelden die je voor je tentamensommen enzo moet uitwerken zijn altijd wel eenvoudig. Er bestaat alleen geen "algemene methode" voor (buiten het feit dat je ook nog eens goed moet definieren wat je met een parametrisatie bedoelt).
Voor de tentamensommen, tjsa... zo makkelijk vind ik het niet, maar ik zal er nog even verder op oefenen... alsi k iets tegenkom wat echt niet werkt vraag ik het hier wel aan de experts
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Boek weggooien.quote:Op maandag 22 oktober 2007 12:50 schreef maniack28 het volgende:
[..]
A path in R^n is a map c: [a,b] -> R^n; it is a path in the plane if n=2 and a path in the space if n=3. The collection C of points c(t) as t varies in [a,b] is called a curve, and c(a) and c(b) are its endpoints. The path c is said to parametrize the curve C.


Staat er niet bij, maar hij is idd wel differentieerbaar (Dat komt laterquote:Op maandag 22 oktober 2007 13:38 schreef thabit het volgende:
[..]
Boek weggooien.. Dit lijkt me niet hoe je het wilt definieren namelijk. Je zal toch enkele voorwaarden op c moeten veronderstellen. Een pad zal toch op z'n minst continu moeten zijn en in veel toepassingen stuksgewijs differentieerbaar.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Hi,
ik heb ff een vraagje over de representativiteit van mijn steekproef onder ouderen in de gemeente.
Ik wil een enquete houden onder ouderen vanaf 55 jaar. De gemeente telt ongeveer 17700 ouderen.
Nu wil de gemeente dat ik de enquete aan 1500 respondenten verstuur. Alleen al om het feit dat ik de enquete per post verstuur, zou ik eigenlijk de helft minder respondenten willen benaderen(moet namelijk alles handmatig invoeren).
Maar is de steekproef nog steeds representatief wanneer ik 750 of minder ouderen zou benaderen?
Iemand enig idee waar die grens ligt?
[ Bericht 0% gewijzigd door Fibonacci22 op 23-10-2007 11:27:52 ]
ik heb ff een vraagje over de representativiteit van mijn steekproef onder ouderen in de gemeente.
Ik wil een enquete houden onder ouderen vanaf 55 jaar. De gemeente telt ongeveer 17700 ouderen.
Nu wil de gemeente dat ik de enquete aan 1500 respondenten verstuur. Alleen al om het feit dat ik de enquete per post verstuur, zou ik eigenlijk de helft minder respondenten willen benaderen(moet namelijk alles handmatig invoeren).
Maar is de steekproef nog steeds representatief wanneer ik 750 of minder ouderen zou benaderen?
Iemand enig idee waar die grens ligt?
[ Bericht 0% gewijzigd door Fibonacci22 op 23-10-2007 11:27:52 ]


Voor zover mij bekend bestaat er geen hard criterium om te bepalen of een steekproef representatief is. Zolang de steekproef aselect is, kun je vrij eenvoudig statistisch juiste uitspraken doen maar representativiteit is daarbij niet gegarandeerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je kunt toch uitrekenen wat je betrouwbaarheid wordt onder bepaalde aannames. Ik weet niet welke betrouwbaarheid je wilt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik heb ook een domme vraag. Bij de chikwadraat test.
Als je berekende chi waarde, hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
Als je berekende chi waarde, hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
"AAAAAHH ZENNE MOAT, WOARST VLEISCH"


Hier het volgende:
lengte van een lijnstuk berekenen:
Zie het lijnstuk gegeven door de formule y=-(a/b)x+a
De lengte is simpel te berekenen door gebruik van de formule van pythagoras: L = sqrt(a^2 + b^2)
Maar kan het ook door te integreren???
Stel ik benader de lijn door een trappetje.
De lengte van één 'tree' is dx - dy = dx + dx (dy/dx) = dx - dx [ -(a/b) ] = dx + dx (a/b) = dx [ 1 + (a/b) ]
Integreren van x = 0 tot x = b geeft:
[ 1 + (a/b) ] b = b + a
WTF???????
Blijkbaar mag ik de benadering van de trap niet toepassen, maar waarom niet?
Bij het gebruik van infinitesimale traptreden (in de limiet van dx --> 0 ) valt toch de trap gelijk met de lijn?
Wie helpt mij?
lengte van een lijnstuk berekenen:
Zie het lijnstuk gegeven door de formule y=-(a/b)x+a
De lengte is simpel te berekenen door gebruik van de formule van pythagoras: L = sqrt(a^2 + b^2)
Maar kan het ook door te integreren???
Stel ik benader de lijn door een trappetje.
De lengte van één 'tree' is dx - dy = dx + dx (dy/dx) = dx - dx [ -(a/b) ] = dx + dx (a/b) = dx [ 1 + (a/b) ]
Integreren van x = 0 tot x = b geeft:
[ 1 + (a/b) ] b = b + a
WTF???????
Blijkbaar mag ik de benadering van de trap niet toepassen, maar waarom niet?
Bij het gebruik van infinitesimale traptreden (in de limiet van dx --> 0 ) valt toch de trap gelijk met de lijn?
Wie helpt mij?


Moet het niet dx + dy zijn voor de lengte van één tree?
Daarmee is je probleem niet opgelost, maar wordt het verhaal "iets" anders.
[ 1 + (a/b) ] b = b + a wordt dan [ 1 - (a/b) ] b = b - a
Of begrijp ik het nu niet?
Daarmee is je probleem niet opgelost, maar wordt het verhaal "iets" anders.
[ 1 + (a/b) ] b = b + a wordt dan [ 1 - (a/b) ] b = b - a
Of begrijp ik het nu niet?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Dat dacht ik ook maar dat zou HELEMAAL nergens op slaanquote:Op dinsdag 23 oktober 2007 20:06 schreef -J-D- het volgende:
Moet het niet dx + dy zijn voor de lengte van één tree?
Daarmee is je probleem niet opgelost, maar wordt het verhaal "iets" anders.


ik wil een formule differienteiren
dit is de formule:
f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
ik dacht kettingregel = f(g(x)) = f'(g(x)) * g'(x)
dus eerst de afgeleide van sinx (cosx)zonder wat er binnenin staat veranderen
f'(x) 4cos (1/2 PI x - 1/4 PI)
dan het gedeelte tussen haakjes doen (1/2 PI x - 1/4 PI)
is 1/2 PI want 1/4PI is gewoon een getal en mag je dus wegahalen?
dan komt mijn afgeleide op
f'(x) 4cos (1/2 PI x - 1/4 PI) * 1/2 PI
dus kan ik nog even de hele formule keer 1/2 PI doen of niet?
dit is de formule:
f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
ik dacht kettingregel = f(g(x)) = f'(g(x)) * g'(x)
dus eerst de afgeleide van sinx (cosx)zonder wat er binnenin staat veranderen
f'(x) 4cos (1/2 PI x - 1/4 PI)
dan het gedeelte tussen haakjes doen (1/2 PI x - 1/4 PI)
is 1/2 PI want 1/4PI is gewoon een getal en mag je dus wegahalen?
dan komt mijn afgeleide op
f'(x) 4cos (1/2 PI x - 1/4 PI) * 1/2 PI
dus kan ik nog even de hele formule keer 1/2 PI doen of niet?


f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
f'(g(x)) = 4/2 PI * cos (1/2 PI x - 1/4 PI) = 2 * PI * cos (1/2 PI x - 1/4 PI)
g'(x) = 1/2 PI
geeft f'(g(x))*g'(x) = PI^2 * cos (1/2 PI x - 1/4 PI)
Wat je zegt klopt dus idd, alleen je bent vergeten datgeen wat voor de afgeleide komt van de sin x (dus 1/2 PI * 4 = 2 PI) erbij te zetten, waardoor je een factor 2 PI te weinig hebt...
edit - wat je op het eind zegt is dus waar
edit2 - probeer het in nette stappen waarin je f(x),g(x) en g'(x) netjes opschrijft en definieert, dat scheelt fouten!
f'(g(x)) = 4/2 PI * cos (1/2 PI x - 1/4 PI) = 2 * PI * cos (1/2 PI x - 1/4 PI)
g'(x) = 1/2 PI
geeft f'(g(x))*g'(x) = PI^2 * cos (1/2 PI x - 1/4 PI)
Wat je zegt klopt dus idd, alleen je bent vergeten datgeen wat voor de afgeleide komt van de sin x (dus 1/2 PI * 4 = 2 PI) erbij te zetten, waardoor je een factor 2 PI te weinig hebt...
edit - wat je op het eind zegt is dus waar
edit2 - probeer het in nette stappen waarin je f(x),g(x) en g'(x) netjes opschrijft en definieert, dat scheelt fouten!
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Ja, dat kan.quote:Op dinsdag 23 oktober 2007 20:05 schreef Greus het volgende:
Hier het volgende:
lengte van een lijnstuk berekenen:
[ afbeelding ]
Zie het lijnstuk gegeven door de formule y=-(a/b)x+a
De lengte is simpel te berekenen door gebruik van de formule van pythagoras: L = sqrt(a^2 + b^2)
Maar kan het ook door te integreren???
Hoe kom je hier nu bij? De lengte van een tree is niet dx - dy, bovendien gaat het niet om de lengtes van de treden, de totale lengte hiervan is immers constant als je de treden kleiner maakt en niet gelijk aan de lengte van je lijnstuk.quote:Stel ik benader de lijn door een trappetje.
De lengte van één 'tree' is dx - dy = dx + dx (dy/dx) = dx - dx [ -(a/b) ] = dx + dx (a/b) = dx [ 1 + (a/b) ]
Bij rectificatie (de bepaling van de lengte van een curve (of in dit geval een rechte) verdeel je het interval waarover je de lengte wil bepalen in stukjes en benader je de curve door lijnsegmentjes. Volgens Pythagoras is de lengte van één zo'n segmentje:quote:Wie helpt mij?
√(Δx2 + Δy2) = Δx√(1 + (Δy/Δx)2)
Deze segmentjes sommeer je dan, waarbij de benadering beter wordt naarmate Δx kleiner wordt. Oftewel, de lengte van de curve over een interval [a,b] wordt gegeven door
∫ab √(1 + (f'(x))2)dx
[ Bericht 0% gewijzigd door Riparius op 23-10-2007 22:19:16 ]


okee gelukkig dat t kloptquote:Op dinsdag 23 oktober 2007 20:54 schreef maniack28 het volgende:
f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
f'(g(x)) = 4/2 PI * cos (1/2 PI x - 1/4 PI) = 2 * PI * cos (1/2 PI x - 1/4 PI)
g'(x) = 1/2 PI
geeft f'(g(x))*g'(x) = PI^2 * cos (1/2 PI x - 1/4 PI)
Wat je zegt klopt dus idd, alleen je bent vergeten datgeen wat voor de afgeleide komt van de sin x (dus 1/2 PI * 4 = 2 PI) erbij te zetten, waardoor je een factor 2 PI te weinig hebt...
edit - wat je op het eind zegt is dus waar
edit2 - probeer het in nette stappen waarin je f(x),g(x) en g'(x) netjes opschrijft en definieert, dat scheelt fouten!
kun je me misschien uitleggen hoe je precies ziet wanner ketting/som/die andere regel te gebruiken?


Je moet goed weten wat een functie is, en dan kun je gewoon kijken hoe je je functie kunt schrijven: is dat het product van twee functies, of zijn het twee functies die na elkaar worden uitgevoerd.quote:Op dinsdag 23 oktober 2007 22:00 schreef Principessa.Farfalla het volgende:
[..]
kun je me misschien uitleggen hoe je precies ziet wanner ketting/som/die andere regel te gebruiken?
Als de berekende waarde groter is dan de kritische waarde zit je bij de chi-kwadraattoets in het kritieke gebied (bij andere toetsen kan het kritieke gebied ook links van de kritieke waarde zitten), wat betekent dat je de nulhypothese verwerpt. Wat de nulhypothese is, ligt bij een chi-kwadraattoets niet vast omdat er verschillende chi-kwadraattoetsen bestaan. Voordat je gaat toetsen, moet je die hypothesen uiteraard goed definieren. Je conclusie zal zijn dat er waarschijnlijk geen verband bestaat.quote:Op dinsdag 23 oktober 2007 19:31 schreef znarch het volgende:
Ik heb ook een vraag. Bij de chikwadraat test.
Als je berekende chi waarde hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hmmm.. even kijken of ik dat kan. Je hebt de kettingregel en de productregel. De kettingregel gebruik je als je de afgeleide wilt weten van een "samengestelde" functie. In de meeste gevallen functies die zijn samengesteld uit cosinus/sinus/exponent/logaritme en iets waarvan je de cosinus/sinus/exponent/logarimte neemt waarvan de afgeleide ongelijk aan 0 is.quote:Op dinsdag 23 oktober 2007 22:00 schreef Principessa.Farfalla het volgende:
[..]
okee gelukkig dat t klopt
kun je me misschien uitleggen hoe je precies ziet wanner ketting/som/die andere regel te gebruiken?
Dus in gevallen als bereken de afgeleide van:
f(x) = cos (2*x+1) of f(x) = sin (x^2) of f(x) = exp (x^2+4x)
Maar eigenlijk kan je hem altijd toepassen. Neem bijv. f(x) = sin (2*x). Gebruik de kettingregel:
f'(g(x)) = cos (2*x)
g'(x) = 2
Geeft f'(x)= 2 cos (2*x), maar goed, dat kan je zonder de kettingregel ook doen
De productregel gebruik je enkel als de functie een product van 2 andere functies is, dus bijv. f(x) = x^2 * cos (x) of f(x) = 1/x * exp (x). Je leidt dan eerst naar de een af (houdt de ander constant) en daarna nara de ander af en houdt de een constant: (fg)' = f'g+fg'
Je kan ze ook combineren en beide gebruiken, probeer maar eens de afgeleide van f(x) = x^3 * cos (x^2) te berekenen.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Volgens mij is er een significant verschil als de waarde groter is dan de kritieke waarde. Dacht ik...quote:Op dinsdag 23 oktober 2007 19:31 schreef znarch het volgende:
Ik heb ook een domme vraag. Bij de chikwadraat test.
Als je berekende chi waarde, hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
Theories come and theories go. The frog remains


Zelf ook nog een vraagje:
Ben in R bezig met wat data-mining, maar heb een vraag waar ik niet uitkom. Ik moet voor een dataset de zogenaamde hyperedges berekenen. Nu is dit niet zo moelijk, want het algoritme wat ik gebruik, kan dit gewoon. Maar een andere vraag is: wat is een hyperedgeset?
Als ik google op hyperedgeset krijg ik als results alleen de papers/websites waar ik juist de vraag vandaan heb, maar daar staat alleen in uitgelegd dat het algoritme wat ik gebruik dat kan uitrekenen (en hoe), maar niet wat het is.
Is er hier toevallig iemand die weet wat een hyperedgeset is???
Ben in R bezig met wat data-mining, maar heb een vraag waar ik niet uitkom. Ik moet voor een dataset de zogenaamde hyperedges berekenen. Nu is dit niet zo moelijk, want het algoritme wat ik gebruik, kan dit gewoon. Maar een andere vraag is: wat is een hyperedgeset?
Als ik google op hyperedgeset krijg ik als results alleen de papers/websites waar ik juist de vraag vandaan heb, maar daar staat alleen in uitgelegd dat het algoritme wat ik gebruik dat kan uitrekenen (en hoe), maar niet wat het is.
Is er hier toevallig iemand die weet wat een hyperedgeset is???
Theories come and theories go. The frog remains


Een hyperedge is een gewoon een kant die meerdere punten tegelijk met elkaar verbindt. En die set is dan natuurlijk de verzameling van hyperedges.quote:Op dinsdag 23 oktober 2007 22:49 schreef Bioman_1 het volgende:
Zelf ook nog een vraagje:
Ben in R bezig met wat data-mining, maar heb een vraag waar ik niet uitkom. Ik moet voor een dataset de zogenaamde hyperedges berekenen. Nu is dit niet zo moelijk, want het algoritme wat ik gebruik, kan dit gewoon. Maar een andere vraag is: wat is een hyperedgeset?
Als ik google op hyperedgeset krijg ik als results alleen de papers/websites waar ik juist de vraag vandaan heb, maar daar staat alleen in uitgelegd dat het algoritme wat ik gebruik dat kan uitrekenen (en hoe), maar niet wat het is.
Is er hier toevallig iemand die weet wat een hyperedgeset is???


Leo  Jij ook weer hier?
Jij ook weer hier?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Halloquote:
@wolfje: ik dacht al iets in die richting, maar kon dat niet 'vertalen' in data-mining taal. Het gaat over frequent itemsets, closed frequent itemsets, maximal frequent itemsets en hyperedgesets. En ik zou dus graag in data-mining jargon uitleggen wat een hyperedgeset is.
Theories come and theories go. The frog remains


Heey:) ik heb weer wat vragen:
Nu even ringen:
soms hoort f(1)=1 bij de defnitie van ringhomomorfisme en soms wordt f(1)=1 als extra eis genomen en in dit geval wordt t ringhomomorfisme een lichaamshomomorfisme... Waarom is het niet één definitie?
Zij p een priemgetal ongelijk aan 5. Stel dat p = x^2 + 5y^2 met x en y in Z. Te bewijzen: p is 1 of 9 mod 20.
Het is wel duidelijk dat of x of y even zijn. Maar volgens mij moet ik nog aantonen dat y even moet zijn...
hoe gaat dit verder?
groetjes
Nu even ringen:
soms hoort f(1)=1 bij de defnitie van ringhomomorfisme en soms wordt f(1)=1 als extra eis genomen en in dit geval wordt t ringhomomorfisme een lichaamshomomorfisme... Waarom is het niet één definitie?
Zij p een priemgetal ongelijk aan 5. Stel dat p = x^2 + 5y^2 met x en y in Z. Te bewijzen: p is 1 of 9 mod 20.
Het is wel duidelijk dat of x of y even zijn. Maar volgens mij moet ik nog aantonen dat y even moet zijn...
hoe gaat dit verder?
groetjes
verlegen :)


Dat is categorie-theorie. Wijze heren met grijze baarden hebben ooit bedacht dat je wiskundige objecten veel beter kunt bestuderen door ze in een categorie te stoppen en er morfismen tussen te gooien dan 'los', en eigenlijk meer op de morfismen te focussen dan op de objecten. Een inzicht dat mijns inziens getuigt van een uitzonderlijke genialiteit. Dan maakt het natuurlijk wel uit welke morfismen je tussen je objecten definieert; zoiets ligt nog geenszins vast bij de definitie van de objecten. Voor verschillende en/of toepassingen van een theorie blijken soms verschillende definities van de morfismen het best te werken.quote:Op donderdag 25 oktober 2007 20:59 schreef teletubbies het volgende:
Heey:) ik heb weer wat vragen:
Nu even ringen:
soms hoort f(1)=1 bij de defnitie van ringhomomorfisme en soms wordt f(1)=1 als extra eis genomen en in dit geval wordt t ringhomomorfisme een lichaamshomomorfisme... Waarom is het niet één definitie?


Merk eerst op dat p niet gelijk is aan 2 en dat y niet congruent is met 0 mod p.quote:Op donderdag 25 oktober 2007 20:59 schreef teletubbies het volgende:
Zij p een priemgetal ongelijk aan 5. Stel dat p = x^2 + 5y^2 met x en y in Z. Te bewijzen: p is 1 of 9 mod 20.
Het is wel duidelijk dat of x of y even zijn. Maar volgens mij moet ik nog aantonen dat y even moet zijn...
hoe gaat dit verder?
groetjes
Kwadraten zijn 0 of 1 mod 4, hieruit volgt eenvoudig dat p zelf 1 mod 4 moet zijn. Verder zien we dat -5=(x/y)^2 mod p, dus -5 is een kwadraatrest (ongelijk aan 0) mod p. Dan pluggen we nu de kwadratische reciprociteitswet in: (-5/p) = (p/5) want p=1 mod 4. Nu is (p/5)=1 desda p = 1 of 4 mod 5. Tezamen met p = 1 mod 4 geeft de Chinese Reststelling nu p = 1 of 9 mod 20.


Z/(Z-5) + 1/3 = -5/(5-Z)quote:Op dinsdag 30 oktober 2007 15:21 schreef duncannn het volgende:
Z/(Z-5) + 1/3 = -5/(5-Z)
hoe moet je dit ook alweer oplossen.
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
-Z (Z-5)/(Z-5) - 1/3 (Z-5) = -5
-Z - 1/3Z +5/3 = -5 = -15/3
-4/3Z= - 20/3
Z= 5
Even invullen en je komt dat de conclusie dat ik ergens een fout maak, want delen door 0 mag niet
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


NEE!quote:Op dinsdag 30 oktober 2007 16:40 schreef maniack28 het volgende:
[..]
Z/(Z-5) + 1/3 = -5/(5-Z)
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
-Z (Z-5)/(Z-5) - 1/3 (Z-5) = -5
Als je beide leden met (Z-5) vermenigvuldigt krijg je in het rechterlid +5, niet -5.


Ah kijk, slordigheidje, maar goed..het idee is helder, kandie het verder zelf wel uitwerkenquote:Op dinsdag 30 oktober 2007 17:09 schreef Riparius het volgende:
[..]
NEE!
Als je beide leden met (Z-5) vermenigvuldigt krijg je in het rechterlid +5, niet -5.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Ja. Je vergelijking heeft overigens geen oplossing. Had je dat ook al gezien?quote:Op dinsdag 30 oktober 2007 17:31 schreef maniack28 het volgende:
[..]
Ah kijk, slordigheidje, maar goed..het idee is helder, kandie het verder zelf wel uitwerken


Nope, had hem niet uitgewerkt met de -, ben te luiquote:Op dinsdag 30 oktober 2007 17:33 schreef Riparius het volgende:
[..]
Ja. Je vergelijking heeft overigens geen oplossing. Had je dat ook al gezien?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Z/(Z-5) + 1/3 = -5/(5-Z)
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
Z/(Z-5) + 1/3 = 5/(Z-5)
Z + 1/3(Z-5) = 5
4/3Z-5/3=5
4/3Z= 6 2/3
Z = 5
.... kom ik er weer op
Ik had het trouwens wel goed gedaan, ik had gedeeld door vermenigvuldigd met -(Z-5), daarom kwam er in mijn oorspronkelijke antwoord een - voor de termen Z en 1/3(Z-5) aan de linkerkant, rechts bleef er gewoon -5 staan, nu doe ik het andersom en komt er nog steeds 5 uit. Ben ik nu blond of is de werkwijze gewoon goed en is er geen oplossing
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
Z/(Z-5) + 1/3 = 5/(Z-5)
Z + 1/3(Z-5) = 5
4/3Z-5/3=5
4/3Z= 6 2/3
Z = 5
.... kom ik er weer op
Ik had het trouwens wel goed gedaan, ik had gedeeld door vermenigvuldigd met -(Z-5), daarom kwam er in mijn oorspronkelijke antwoord een - voor de termen Z en 1/3(Z-5) aan de linkerkant, rechts bleef er gewoon -5 staan, nu doe ik het andersom en komt er nog steeds 5 uit. Ben ik nu blond of is de werkwijze gewoon goed en is er geen oplossing
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Je werkwijze is ditmaal juist, en de oplossingsverzameling van het stelsel is inderdaad leeg.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De vorige keer ook, zie toelichting post boven je... maakt niet uit of je links vervangt met - of rechts met + of omgedraaid... komt op hetzelfde neerquote:Op dinsdag 30 oktober 2007 18:46 schreef GlowMouse het volgende:
Je werkwijze is ditmaal juist, en de oplossingsverzameling van het stelsel is inderdaad leeg.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Je kunt het ook zo bekijken: vermenigvuldig teller en noemer van de breuk in het rechterlid met -1, dan heb je:quote:Op dinsdag 30 oktober 2007 18:51 schreef maniack28 het volgende:
[..]
De vorige keer ook, zie toelichting post boven je... maakt niet uit of je links vervangt met - of rechts met + of omgedraaid... komt op hetzelfde neer
Z/(Z-5) + 1/3 = 5/(Z-5)
Rechterlid herleiden op nul geeft dan:
(Z-5)/(Z-5) + 1/3 = 0
Nu is (Z-5)/(Z-5) gelijk aan 1 als Z ongelijk is aan 5, en niet gedefinieerd als Z=5, dus is het meteen duidelijk dat de vergelijking geen oplossing kan hebben.


Oeh nice  Ik geloof dat degene die de vraag vroeg nu wel genoeg antwoord heeft
Ik geloof dat degene die de vraag vroeg nu wel genoeg antwoord heeft 
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Hoii
ik zoek een leuk bewijsje van de kwadratische reciprociteit..
 zijn er bewijzen mbv ringen theorie of iets dergelijks?
zijn er bewijzen mbv ringen theorie of iets dergelijks?
Ik heb wel analytische bewijzen gevonden.. maar variatie doet geen kwaad
ik zoek een leuk bewijsje van de kwadratische reciprociteit..
Ik heb wel analytische bewijzen gevonden.. maar variatie doet geen kwaad
verlegen :)


Er is een bewijs met algebraische getaltheorie. De essentie is dat Z[wortel((-1/p)p)] een deelring van Z[zeta_p] is. De ontbinding van q in Z[wortel((-1/p)p)] hangt samen met (p/q) en de ontbinding van q in Z[zeta_p] hangt samen met (q/p). Maar om hiervan de details uit te werken moet je nog wel wat doen.
Er is ook een bewijs dat het volgende gebruikt: vermenigvuldiging met p geeft een permutatie van Z/qZ. Het teken van deze permutatie is precies (p/q). Alleen hoe dat bewijs verder ging weet ik niet meer precies, maar als je in Google iets als permutation quadratic reciprocity intikt dan vind je het wel.
En zo zijn er veel en veel meer bewijzen.
Er is ook een bewijs dat het volgende gebruikt: vermenigvuldiging met p geeft een permutatie van Z/qZ. Het teken van deze permutatie is precies (p/q). Alleen hoe dat bewijs verder ging weet ik niet meer precies, maar als je in Google iets als permutation quadratic reciprocity intikt dan vind je het wel.
En zo zijn er veel en veel meer bewijzen.


op je grafische rekenmachine kan je bijvoorbeeld het aantal keren dat een dobbelsteen gegooid word weergeven,
Math -> PRB -> RandInt (
je doet dan 1,6,50 ( 1 voor het begin 6 voor het eindgetal, het aantal ogen dus en 50x wil ik werpen)
dus randInt(1,6,50)
je krijgt dan (2,5,6,2,1,2,4,5 etc etc 50 getallen lang
nu heeft die leraar uitgelegt hoe ik hier een staafgrafiek van krijg, maar ik weet het niet meer
help me plz
Math -> PRB -> RandInt (
je doet dan 1,6,50 ( 1 voor het begin 6 voor het eindgetal, het aantal ogen dus en 50x wil ik werpen)
dus randInt(1,6,50)
je krijgt dan (2,5,6,2,1,2,4,5 etc etc 50 getallen lang
nu heeft die leraar uitgelegt hoe ik hier een staafgrafiek van krijg, maar ik weet het niet meer
help me plz


Je bedoelt waarschijnlijk een histogram. Maar volgens mij is dat een ***werk wat gewoon veel handelingen vereist:
RandInt(1,6,50) -> L1
Seq(X,1,6) -> L3
SUM(L1=1) -> L3(1)
SUM(L1=2) -> L3(2)
. .
. .
SUM(L1=6) -> L3(6)
Daarna kun je via stat plot een histogram tekenen met Freq L2 en Xlist L3.
Met L1, L2 en L3 lijsten (bv via 2nd, 1).
RandInt(1,6,50) -> L1
Seq(X,1,6) -> L3
SUM(L1=1) -> L3(1)
SUM(L1=2) -> L3(2)
. .
. .
SUM(L1=6) -> L3(6)
Daarna kun je via stat plot een histogram tekenen met Freq L2 en Xlist L3.
Met L1, L2 en L3 lijsten (bv via 2nd, 1).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Een product dat uit 25 onderdelen bestaat, moet worden gemonteerd. Voor elk onderdeel geldt dat één op de driehonderd ervan een fout heeft. Hoe groot is de kans op goede producten?
Het is wat te lang geleden voor me, ik heb al eerder zo'n vraagstuk voor mijn snufferd gehad maar ik kom er gewoon niet uit.
Hellup!!
Het is wat te lang geleden voor me, ik heb al eerder zo'n vraagstuk voor mijn snufferd gehad maar ik kom er gewoon niet uit.
Hellup!!


kans op goed product = goed EN goed EN goed EN (...) = goed^25 = (299/300)^25 = 0,9199quote:Op woensdag 31 oktober 2007 18:23 schreef Cracka-ass het volgende:
Een product dat uit 25 onderdelen bestaat, moet worden gemonteerd. Voor elk onderdeel geldt dat één op de driehonderd ervan een fout heeft. Hoe groot is de kans op goede producten?
Het is wat te lang geleden voor me, ik heb al eerder zo'n vraagstuk voor mijn snufferd gehad maar ik kom er gewoon niet uit.
Hellup!!
kans op fout product = fout OF fout OF fout OF (...) = 25 * (1/300) = 0,0833
kans op goed product + kans op fout product = 0,9199 + 0,0833 = ~ 1 door onnauwkeurige afronding
Maar pin me er niet op vast
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Even een hele simpele van de SAT Test:
If the sum of the consecutive integers from -22 tot x, inclusive, is 72, what is the value of x?
Antwoord: 25
Hoe?
If the sum of the consecutive integers from -22 tot x, inclusive, is 72, what is the value of x?
Antwoord: 25
Hoe?


Dit is fout. Je berekening voor een goed product is correct, maar voor een fout product niet.quote:Op woensdag 31 oktober 2007 19:16 schreef R-Mon het volgende:
[..]
kans op goed product = goed EN goed EN goed EN (...) = goed^25 = (299/300)^25 = 0,9199
kans op fout product = fout OF fout OF fout OF (...) = 25 * (1/300) = 0,0833
kans op goed product + kans op fout product = 0,9199 + 0,0833 = ~ 1 door onnauwkeurige afronding
Maar pin me er niet op vast
Je hebt een fout product als het eerste onderdeel fout gaat en de rest goed. Of het tweede onderdeel, en de rest goed, of het eerste én tweede onderdeel, en de rest goed. De som van al deze mogelijkheden (incl. de mogelijkheid dat alles fout gaat, welke (1/300)^25 is) wordt gewoon gegeven door 1 - (299/300)^25.
Wat jij uitrekent is niet correct. Stel, je hebt een dobbelsteen, wat is de kans dat je één keer 6 gaat, terwijl je 10x gooit? Dat is niet 1/6 + 1/6 ... en dat 10 keer, dat zou groter zijn dan 1. Want de kans dat je de eerste keer weliswaar 6 gooit is wel 1/6e, maar er zit bij die mogelijkheden ook al een mogelijkheid dat je de 2e keer 6 gooit. En die mogelijkheid tel je weer mee bij de volgende 1/6e. Je telt zaken dubbel. Dat doe jij ook.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


som van y = -22 tot y = 22 over y = 0quote:Op woensdag 31 oktober 2007 19:42 schreef nickybol het volgende:
Even een hele simpele van de SAT Test:
If the sum of the consecutive integers from -22 tot x, inclusive, is 72, what is the value of x?
Antwoord: 25
Hoe?
dus x = 22 levert nul op, kleinere x levert iets negatiefs op.
72 - 23 = 49
49 - 24 = 25
25 - 25 = 0
tada
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Ok bedankt voor de controle. En Cracka-ass heeft z'n antwoordquote:Op woensdag 31 oktober 2007 19:52 schreef Iblis het volgende:
[..]
Dit is fout. Je berekening voor een goed product is correct, maar voor een fout product niet.
Je hebt een fout product als het eerste onderdeel fout gaat en de rest goed. Of het tweede onderdeel, en de rest goed, of het eerste én tweede onderdeel, en de rest goed. De som van al deze mogelijkheden (incl. de mogelijkheid dat alles fout gaat, welke (1/300)^25 is) wordt gewoon gegeven door 1 - (299/300)^25.
Wat jij uitrekent is niet correct. Stel, je hebt een dobbelsteen, wat is de kans dat je één keer 6 gaat, terwijl je 10x gooit? Dat is niet 1/6 + 1/6 ... en dat 10 keer, dat zou groter zijn dan 1. Want de kans dat je de eerste keer weliswaar 6 gooit is wel 1/6e, maar er zit bij die mogelijkheden ook al een mogelijkheid dat je de 2e keer 6 gooit. En die mogelijkheid tel je weer mee bij de volgende 1/6e. Je telt zaken dubbel. Dat doe jij ook.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Als je een eiwit denatureerd veranderd de tertiaire structuur. Bij het koken van serumeiwit verbreken de S-S bruggen en is de tertiaire structuur permanent verneukt. Waarom is het eiwit dan wit geworden?


Ik heb
Y(X) = e^2x / x+2
Y’ = (2x+3)e^2x / (x+2)^ 2
maar hoe kom je eraan, de quotient regel toepassen. maar ik kom er niet meer uit.
Y(X) = e^2x / x+2
Y’ = (2x+3)e^2x / (x+2)^ 2
maar hoe kom je eraan, de quotient regel toepassen. maar ik kom er niet meer uit.
winnaar wielerprono 2007 :) Last.FM


quotientregel = (noemer * afgeleide teller - teller * afgeleide noemer) / noemer in het kwadraat.
n * at = (x+2) * 2e2x
t * an = e2x * 1 = e2x
n*at - t*an = (x+2) * 2e2x - e2x
= 2(x+2)e2x - e2x
= (2x+4)e2x- e2x
= (2x+3)e2x
(n*at-t*an)/n2 = (2x+3)e2x / (x+2)2
n * at = (x+2) * 2e2x
t * an = e2x * 1 = e2x
n*at - t*an = (x+2) * 2e2x - e2x
= 2(x+2)e2x - e2x
= (2x+4)e2x- e2x
= (2x+3)e2x
(n*at-t*an)/n2 = (2x+3)e2x / (x+2)2
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


dank, eerste deel ging nog goed, maar toen vanaf n*at - t*an = (x+2) * 2e2x - e2x wist ik het niet meer
winnaar wielerprono 2007 :) Last.FM


Even een (waarschijnlijk stom) scheikundevraagje m.b.t. zuur-base-reacties.
Men voegt de volgende oplossingen bij elkaar: KCN-opl. + HCl-opl.
KCN-opl: K+ + CN-
HCl-opl: H3O+ + Cl-
Nu zal het sterkste zuur reageren met de sterkste base:
CN- + H3O+ --> HCN + H2O
Nu is gegeven dat CN- in OVERMAAT aanwezig is (ten opzichte van H3O+).
Dit betekent dus dat aan het einde van bovenstaande reactie aanwezig is:
CN- (deze is in overmaat) en HCN (deze is gevormd)
Aangezien er geen H3O+ meer aanwezig is zal een van de stoffen (of misschien wel beide?) verder reageren met water (H2O).
Maar hoe kan ik nu bepalen welke reactie er plaatsvindt?
Volgens het antwoordenmodel gaat de volgende reactie verder:
HCN + H2O <--> CN- + H3O+
Maar waarom niet deze reactie?
CN- + H2O <--> HCN + OH-
Iemand enig idee?
Verder gegeven: de pKZ van NH4+ = 9,25
Ik zal wel dom zijn, maar ik kom er ff niet uit.


Men voegt de volgende oplossingen bij elkaar: KCN-opl. + HCl-opl.
KCN-opl: K+ + CN-
HCl-opl: H3O+ + Cl-
Nu zal het sterkste zuur reageren met de sterkste base:
CN- + H3O+ --> HCN + H2O
Nu is gegeven dat CN- in OVERMAAT aanwezig is (ten opzichte van H3O+).
Dit betekent dus dat aan het einde van bovenstaande reactie aanwezig is:
CN- (deze is in overmaat) en HCN (deze is gevormd)
Aangezien er geen H3O+ meer aanwezig is zal een van de stoffen (of misschien wel beide?) verder reageren met water (H2O).
Maar hoe kan ik nu bepalen welke reactie er plaatsvindt?
Volgens het antwoordenmodel gaat de volgende reactie verder:
HCN + H2O <--> CN- + H3O+
Maar waarom niet deze reactie?
CN- + H2O <--> HCN + OH-
Iemand enig idee?
Verder gegeven: de pKZ van NH4+ = 9,25
Ik zal wel dom zijn, maar ik kom er ff niet uit.


Waarschijnlijk moet je daarvoor in de redoxtabel kijken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Nope. Helaas mogen we geen tabellen(boek) gebruiken, dus geen BINAS o.i.d.quote:Op vrijdag 2 november 2007 19:15 schreef GlowMouse het volgende:
Waarschijnlijk moet je daarvoor in de redoxtabel kijken.


Je hebt een bufferoplossing van HCN (errug giftig, net als zn chemische broertjes zwavelwaterstof en koolstofmonoxide) en CN-, dus de reacties zijn met elkaar in evenwicht. Ze treden dus beiden tegelijkertijd op. Om de uiteindelijke pH te kunnen berekenen moet je dus de -log nemen van de evenwichtsvergelijking Kacid = [CN-]*[H3O+]/[HCN] en daar je pKz en de concentraties [CN-] en [HCN] in de breuk invoeren. Als de pKb in plaats van de pKz gegeven is kun je de laatste berekenen uit Kz*Kb = 10-14.
[ Bericht 26% gewijzigd door harrypiel op 02-11-2007 21:33:53 ]
[ Bericht 26% gewijzigd door harrypiel op 02-11-2007 21:33:53 ]


Jep, ben er uit nu.quote:Op vrijdag 2 november 2007 21:23 schreef harrypiel het volgende:
Je hebt een bufferoplossing van HCN (errug giftig, net als zn chemische broertjes zwavelwaterstof en koolstofmonoxide) en CN-, dus de reacties zijn met elkaar in evenwicht. Ze treden dus beiden tegelijkertijd op. Om de uiteindelijke pH te kunnen berekenen moet je dus de -log nemen van de evenwichtsvergelijking Kacid = [CN-]*[H3O+]/[HCN] en daar je pKz en de concentraties [CN-] en [HCN] in de breuk invoeren. Als de pKb in plaats van de pKz gegeven is kun je de laatste berekenen uit Kz*Kb = 10-14.


Nog een scheikundige vraag:
In een geroerde tankreactor vindt de volgende vloeistoffase reactie plaats:
A -> P
De reactie wordt isotherm uitgevoerd. Technoloog Karin wordt gevraagd de kinetiek van de reactie te bestuderen. Ze voert 4 experimenten uit bij verschillende verblijftijden en allen met een ingaande reactorstroom die 10 kmol/m3 aan A bevat en 1 kmol/m3 aan P. De experimenten worden stationair uitgevoerd. Dit geeft de volgende resultaten:
t(tau) in minuten ::::::: 1 ////////// 4 ////// 7 /////// 10
Xa (conversie van A) 0.09 / 0.28 / 0.41 / 0.5
Bepaal uit deze gegevens de orde van de reactie en de waarde van de kinetiekconstante.
[ Bericht 2% gewijzigd door KaterPils op 03-11-2007 13:52:22 ]
In een geroerde tankreactor vindt de volgende vloeistoffase reactie plaats:
A -> P
De reactie wordt isotherm uitgevoerd. Technoloog Karin wordt gevraagd de kinetiek van de reactie te bestuderen. Ze voert 4 experimenten uit bij verschillende verblijftijden en allen met een ingaande reactorstroom die 10 kmol/m3 aan A bevat en 1 kmol/m3 aan P. De experimenten worden stationair uitgevoerd. Dit geeft de volgende resultaten:
t(tau) in minuten ::::::: 1 ////////// 4 ////// 7 /////// 10
Xa (conversie van A) 0.09 / 0.28 / 0.41 / 0.5
Bepaal uit deze gegevens de orde van de reactie en de waarde van de kinetiekconstante.
[ Bericht 2% gewijzigd door KaterPils op 03-11-2007 13:52:22 ]
9 levens lang bier drinken!


Ik kan je nu al zeggen dat dat een eerste orde reactie gaat worden: Dr is nl. maar 1 reactant betrokken in de reactie.


Zover wa sik ook dus dan wordt de reactiekinetiekformule toch: R(a) = -k. C(a)^1?quote:Op zaterdag 3 november 2007 13:39 schreef harrypiel het volgende:
Ik kan je nu al zeggen dat dat een eerste orde reactie gaat worden: Dr is nl. maar 1 reactant betrokken in de reactie.
9 levens lang bier drinken!


En met de gegeven conversie X(a) en de gegeven verblijftijd tau kan ik het dus invullen in de formule:quote:Op zaterdag 3 november 2007 14:26 schreef harrypiel het volgende:
Eerder iets in de vorm van C[tx] = C[t0] * B * e-t*k
A/RT= k oftewel de Arrheniusfactor
X(a) = (k*tau) / (1+ k*tau)
Of zeg ik nu wee riets verkeerds?
9 levens lang bier drinken!


Wiskunde vraagje: als er een lijnenveld voor me is getekend en de differentiaalvergelijking dy/dt = 0,5t + y en een oplossingskromme gaat door het punt (0,3), hoe moet ik dan weten hoe ik de oplossingskromme moet tekenen ? Is dit te berekenen of moet ik gewoon m'n fantasie gebruiken door te kijken hoe de lijnelementen naar elkaar toe lopen ?
edit: Ik geloof dat ik differentiaalvergelijkingen sowieso niet echt lekker snap. In het boek staat het wel uitgelegd maar ik begrijp het toch niet echt goed. Kan iemand me dat eens uitleggen, liefst met voorbeelden want dat helpt vaak goed
[ Bericht 32% gewijzigd door MeScott op 03-11-2007 15:05:38 ]
edit: Ik geloof dat ik differentiaalvergelijkingen sowieso niet echt lekker snap. In het boek staat het wel uitgelegd maar ik begrijp het toch niet echt goed. Kan iemand me dat eens uitleggen, liefst met voorbeelden want dat helpt vaak goed
[ Bericht 32% gewijzigd door MeScott op 03-11-2007 15:05:38 ]


Hoe precies moet het? Je hebt het lijnenveld, en je hebt de vergelijking hoe een punt van richting verandert (dy/dt). In het punt (0,3) kun je dus uitrekenen wat de richting van de kromme daar is. Dan volg je dat een stukje zeg maar, en dan in een nieuw punt reken je weer de richting uit. Het is niet supernauwkeurig, maar goed.
Je kunt het bijv. met dfield controleren.
Je kunt het bijv. met dfield controleren.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja, dat snap ik wel, maar die lijnelementen zijn al gegeven, alleen ik snap niet goed hoe ik weet of ik van (0,3) naar (-1, 2) of (-1;1,5) moet bij het tekenen van de oplossingskromme. De richting uitrekenen in elk punt is het probleem niet zo (vooral omdat dat al voor me gedaan wordt  ), maar meer hoe ik moet weten welke punten ik met elkaar moet verbinden..
), maar meer hoe ik moet weten welke punten ik met elkaar moet verbinden..


Hoe kleiner je je stapjes maakt hoe nauwkeuriger het is natuurlijk. Maar je moet een beetje gevoel krijgen… Als je direct een lijn trekt van 10cm, dan heb je een wel heel grove benadering van de oplossingskromme, teken je telkens maar 0.5mm, dan blijf je bezig…quote:Op zaterdag 3 november 2007 15:10 schreef MeScott het volgende:
Ja, dat snap ik wel, maar die lijnelementen zijn al gegeven, alleen ik snap niet goed hoe ik weet of ik van (0,3) naar (-1, 2) of (-1;1,5) moet bij het tekenen van de oplossingskromme. De richting uitrekenen in elk punt is het probleem niet zo (vooral omdat dat al voor me gedaan wordt), maar meer hoe ik moet weten welke punten ik met elkaar moet verbinden..
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


klein kort vraagje
opgave is Suppose π (L) = PF(L) – wL, where F is a differentiable function a P and w are constants. Find an expression for d π/dL
ik had (q) = PF(L) – wL
d π / DL = F’(L) – L omdat P en F constanten waren vielen die weg dacht ik. Klopt dit want andere mensen hadden
dπ/dL= p * dF/dL – w * dW/dL
opgave is Suppose π (L) = PF(L) – wL, where F is a differentiable function a P and w are constants. Find an expression for d π/dL
ik had (q) = PF(L) – wL
d π / DL = F’(L) – L omdat P en F constanten waren vielen die weg dacht ik. Klopt dit want andere mensen hadden
dπ/dL= p * dF/dL – w * dW/dL
winnaar wielerprono 2007 :) Last.FM


Het juiste antwoord moet zijn dπ/dL= p * dF/dL – w. Je gedachte dat een constante wegvalt bij differentieren is juist wanneer je hem ergens bij optelt, maar niet wanneer je ermee vermenigvuldigt:
g(L) = 8L dan g'(x) = 8 (constante blijft staan)
h(L) = 8L+5 dan h'(x) = 8 (5 valt weg)
Dat wL naar L gedifferentieert w geeft, zie je in met het voorbeeld met de functie g hierboven. Hoe anderen aan dW/dL komen zie ik echt niet. W is immers constant (mits ze de kleine w bedoelen), zodat dW/dL=0.
g(L) = 8L dan g'(x) = 8 (constante blijft staan)
h(L) = 8L+5 dan h'(x) = 8 (5 valt weg)
Dat wL naar L gedifferentieert w geeft, zie je in met het voorbeeld met de functie g hierboven. Hoe anderen aan dW/dL komen zie ik echt niet. W is immers constant (mits ze de kleine w bedoelen), zodat dW/dL=0.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dus je wilt van t-coord. 0 naar t-coord. -1, weet je dat zeker? Sowieso blijft het tekenen van een oplossingskromme enkel met behulp van richtingsvectoren een erg grove aangelegenheid hoor, vergelijkbaar met hokjes ruitjespapier tellen om een oppervlakte te bepalenquote:Op zaterdag 3 november 2007 15:10 schreef MeScott het volgende:
Ja, dat snap ik wel, maar die lijnelementen zijn al gegeven, alleen ik snap niet goed hoe ik weet of ik van (0,3) naar (-1, 2) of (-1;1,5) moet bij het tekenen van de oplossingskromme. De richting uitrekenen in elk punt is het probleem niet zo (vooral omdat dat al voor me gedaan wordt), maar meer hoe ik moet weten welke punten ik met elkaar moet verbinden..
Wat begrijp je niet aan de differentiaalvergelijking? De vergelijking dy/dt = 0,5t + y geeft in het punt (0,3) de waarde dy/dt = 3. Dus als je een raaklijn aan de oplossingskromme in dat punt zou tekenen, zou deze lijn een richtingscoëffcient van 3 hebben, en dit wordt in een lijnenveld aanschouwbaar gemaakt door een klein lijntje te tekenen die door het punt (0,3) gaat en r.c. 3 heeft. Door dit in meer punten te doen, krijg je een gevoel voor het gedrag van de oplossingen.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Als je een eiwit denatureerd veranderd de tertiaire structuur. Bij het koken van serumeiwit verbreken de S-S bruggen en is de tertiaire structuur permanent verneukt. Waarom is het eiwit dan wit geworden?


Pinocytose is aspecifiek, maar is fagocytose wel specifiek dan? En receptor-mediated endocytose dan? 


Ik nog meer hulp nodig, ik kom er echt niet uit.
Gedurende een dialyse worden de volgende concentraties en volumestromen gemeten:
Volumestroom (ml/min) Inkomend bloed: 200.0 / uitgaand bloed 195.0
Concentraties ureum (mg/ml) inkomend bloed: 1.90 / uitgaand bloed 1.75
a. Bereken de snelheden waarmee water (in ml/min) en ureum (in mg/min) uit het bloed verwijderd worden.
b. Stel dat de ingaande dialysevloeistof volumestroom 1500 ml/min bedraagt, wat is dan de concentraties ureum in de uitgaande dialysevloeistofstroom?
c. Stel we willen de concentratie ureum in een patient reduceren van 2.7 mg/ml naar 1.1 mg/ml. Hoelang moet de patient aan het dialyse apparaat gekoppeld worden als we aannemen dat:
- het totale bloedvolume 5L begraagt
- de gemiddelde snelheid van ureum verwijdering gelijk is aan de in onderdeel a. berekende waarde
En een laatste vraag:
Geef voor onderstaande reactie een relatie die de verhouding van de reactiesnelheden voor de deelnemende componenten beschrijft:
2 NO2 + 0.5 O2 --> N2O5
Gedurende een dialyse worden de volgende concentraties en volumestromen gemeten:
Volumestroom (ml/min) Inkomend bloed: 200.0 / uitgaand bloed 195.0
Concentraties ureum (mg/ml) inkomend bloed: 1.90 / uitgaand bloed 1.75
a. Bereken de snelheden waarmee water (in ml/min) en ureum (in mg/min) uit het bloed verwijderd worden.
b. Stel dat de ingaande dialysevloeistof volumestroom 1500 ml/min bedraagt, wat is dan de concentraties ureum in de uitgaande dialysevloeistofstroom?
c. Stel we willen de concentratie ureum in een patient reduceren van 2.7 mg/ml naar 1.1 mg/ml. Hoelang moet de patient aan het dialyse apparaat gekoppeld worden als we aannemen dat:
- het totale bloedvolume 5L begraagt
- de gemiddelde snelheid van ureum verwijdering gelijk is aan de in onderdeel a. berekende waarde
En een laatste vraag:
Geef voor onderstaande reactie een relatie die de verhouding van de reactiesnelheden voor de deelnemende componenten beschrijft:
2 NO2 + 0.5 O2 --> N2O5
9 levens lang bier drinken!


blalala
Maak van de volgende onderdelen een verslag:
-blalala...
-uitslagen
-doorsneden
iemand enig idee wat ik kan vertellen/voorbeelden geven over uitslagen en doorsneden? alvast bedankt (gaat over meetkunde enzo)
Maak van de volgende onderdelen een verslag:
-blalala...
-uitslagen
-doorsneden
iemand enig idee wat ik kan vertellen/voorbeelden geven over uitslagen en doorsneden? alvast bedankt (gaat over meetkunde enzo)


haha domme boerquote:Op zondag 4 november 2007 17:13 schreef Index het volgende:
blalala
Maak van de volgende onderdelen een verslag:
-blalala...
-uitslagen
-doorsneden
iemand enig idee wat ik kan vertellen/voorbeelden geven over uitslagen en doorsneden? alvast bedankt (gaat over meetkunde enzo)


Zou iemand willen uitleggen hoe men Jordan vorm van een matrix vindt?
wat ik dus weet is het volgende:
Neem een matrix A. (neem aan dat niet alle eigenwaarden zijn verschillend)
ZOek de karakteristieke polynoom p(x).
Vind de bijbehorende eigenwaarden.
de dimensie van ker(A-L1*I)zegt: er zijn minstens dim(ker A-L1*I) blokjes van afmeting minstens 1.
de rang van (A-L1*I)² zegt: er zijn minstens rang(A-L1*I)-rang(A-L1*I)² blokjes van afmeting minstens 2.
de rang van (A-L1*I)^3 zegt: er zijn minstens rang(A-L1*I)^2-rang(A-L1*I)^3 blokjes van afmeting minstens 3.
enzovoort (tot dat er en nul matrix uitkomt bij (A-L1*I)^k..
dit doe je bij iedere eigenwaarde L_i.
wanneer weet je dat je een gegeneraliseerde eigenwaarde moet vinden en wanneer niet?
Is dit trouwens goed? op internet staat dit vaag uitgelegd.
alvast bedankt
wat ik dus weet is het volgende:
Neem een matrix A. (neem aan dat niet alle eigenwaarden zijn verschillend)
ZOek de karakteristieke polynoom p(x).
Vind de bijbehorende eigenwaarden.
de dimensie van ker(A-L1*I)zegt: er zijn minstens dim(ker A-L1*I) blokjes van afmeting minstens 1.
de rang van (A-L1*I)² zegt: er zijn minstens rang(A-L1*I)-rang(A-L1*I)² blokjes van afmeting minstens 2.
de rang van (A-L1*I)^3 zegt: er zijn minstens rang(A-L1*I)^2-rang(A-L1*I)^3 blokjes van afmeting minstens 3.
enzovoort (tot dat er en nul matrix uitkomt bij (A-L1*I)^k..
dit doe je bij iedere eigenwaarde L_i.
wanneer weet je dat je een gegeneraliseerde eigenwaarde moet vinden en wanneer niet?
Is dit trouwens goed? op internet staat dit vaag uitgelegd.
alvast bedankt
verlegen :)


quote:Op zondag 4 november 2007 18:08 schreef Index het volgende:
[..]
en je moeder is een hoer [afbeelding]
[ Bericht 7% gewijzigd door MPG op 04-11-2007 18:22:04 ]
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Ik doe altijd zo:quote:Op zondag 4 november 2007 17:50 schreef teletubbies het volgende:
Zou iemand willen uitleggen hoe men Jordan vorm van een matrix vindt?
- vind alle eigenwaarden met zowel hun algebraïsche (macht van die eigenwaarde in het gefactoriseerde karakteristieke polynoom) als meetkundige (dim(ker(A-Li*I)) multipliciteit (am en mm)
- maak voor iedere eigenwaarde een serie van mm jordanmatrices zodanig dat het totaal aantal kolommen van die jordanmatrices gelijk is aan am (bij een eigenwaarde met am=4 en mm=3 moet je dus 2x een 1x1 jordanmatrix maken en 1x een 2x2 jordanmatrix).
- zet alle jordanmatrices op de diagonaal van J, dat is de jordanvorm
- construeer P door bij iedere 1x1 jordanmatrix een unieke eigenvector te nemen, voor iedere 2x2 jordanmatrix een unieke eigenvector en een gegeneraliseerde eigenvector, en die allemaal naast elkaar te plaatsen in dezelfde volgorde als waarin je de jordanmatrices had geplaatst. Bij 3x3 jordanmatrices weet ik het helaas niet
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Een vraagje over iets waar ik maar niet uit lijk te komen:
f(x,y)=-e^(xy)
En dan afleiden naar zowel x als y.
Ik weet wat de uitkomst moet zijn, maar niet hoe ik daar moet komen.
Het zou fijn zijn als iemand me dit duidelijk kon maken
f(x,y)=-e^(xy)
En dan afleiden naar zowel x als y.
Ik weet wat de uitkomst moet zijn, maar niet hoe ik daar moet komen.
Het zou fijn zijn als iemand me dit duidelijk kon maken
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


Als je afleidt naar x dan "doe je net of y een constante is". Als je -e3x afleidt naar x wordt dat -3 e3x niet? Op dezelfde manier krijg je als je -exy afleidt naar x de uitdrukking -y exy.quote:Op maandag 5 november 2007 12:26 schreef Jesse_ het volgende:
Een vraagje over iets waar ik maar niet uit lijk te komen:
f(x,y)=-e^(xy)
En dan afleiden naar zowel x als y.
Ik weet wat de uitkomst moet zijn, maar niet hoe ik daar moet komen.
Het zou fijn zijn als iemand me dit duidelijk kon maken
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Dat klopt.quote:Op maandag 5 november 2007 17:19 schreef keesjeislief het volgende:
[..]
Als je afleidt naar x dan "doe je net of y een constante is". Als je -e3x afleidt naar x wordt dat -3 e3x niet? Op dezelfde manier krijg je als je -exy afleidt naar x de uitdrukking -y exy.
Maar ik bedoelde; hoe leid je hem af als je tegelijk naar x en y afleidt?
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


Je kunt maar differentieren naar een variabele tegelijk, dus óf naar x, óf naar y. Je kunt ook eerst naar x en dan naar y afleiden, maar dat is gewoon achterelkaar uitvoeren van hetzelfde trucje (eerst naar x dan krijg je -y*exy, vervolgens dat weer naar y, dan krijg je *knip*; het maakt niet uit of je eerst naar x en dan naar y differentieert, of andersom).quote:Op maandag 5 november 2007 18:53 schreef Jesse_ het volgende:
[..]
Dat klopt.
Maar ik bedoelde; hoe leid je hem af als je tegelijk naar x en y afleidt?
[ Bericht 1% gewijzigd door GlowMouse op 06-11-2007 18:18:51 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zo moet het dus niet precies, de uitkomst van de opgave is namelijk -e^(xy)-xye^(xy)quote:Op maandag 5 november 2007 21:55 schreef GlowMouse het volgende:
[..]
Je kunt maar differentieren naar een variabele tegelijk, dus óf naar x, óf naar y. Je kunt ook eerst naar x en dan naar y afleiden, maar dat is gewoon achterelkaar uitvoeren van hetzelfde trucje (eerst naar x dan krijg je -y*exy, vervolgens dat weer naar y, dan krijg je -xy*exy; het maakt niet uit of je eerst naar x en dan naar y differentieert, of andersom).
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


En tóch heeft hij gelijk, je kunt niet gelijktijdig naar x en y afleiden – wa tje hooguit kan doen is eerst naar x afleiden, en dan naar y, of omgekeerd, zoals ook al gezegd. Dat is hoe partiële afgleiden werken; in dit geval maakt het niet uit of je eerst naar y afleidt, en dan naar x of omgekeerd.quote:Op maandag 5 november 2007 22:34 schreef Jesse_ het volgende:
[..]
Zo moet het dus niet precies, de uitkomst van de opgave is namelijk -e^(xy)-xye^(xy)
Maa wat is de precieze vraag in je boek? Wnat het concept van 'tgelijk' afleiden is een beetje vreemd.
Er zal allicht iets als ∂2f/∂x∂y staan? (Alhoewel antwoord dan bovenstaande zou moeten zijn.)
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Wacht eens even, maar ik zie dat ik even te makkelijk was met de partiële afgeleide in m'n hoofd, er moet ook een product regel bij. Maar die notatie is me dus niet helemaal duidelijk, want er moet duidelijk zijn (denk ik), wat de eerste en wat de tweede variabele is.quote:
Maar goed, het lijkt me dus:
f''12 = (f'1)'2 of zo… Misschien is ’t andersom, maar dat maakt in dit geval niets uit.
Eerst differentiëren we naar x, ‘y’ beschouwen de dus als constant:
∂ -exy/∂x = -y exy.
Nu differentiëren we naar ‘y’ en beschouwen we ‘x’ als constant – let echter op dat je nu met de productregel te maken krijgt, omdat je net ‘y’ constant hield, en er daardoor eentje voor de e-xy gekomen is.
∂ -y exy/∂y = (-y)' * e-xy + -y(exy) = -exy - xy*e-xy.
Dit zal ongeveer het idee zijn … behalve met een iets andere notatie in jouw geval.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


dank je, het is nu iig duidelijk 
(notatie is trouwens wel hetzelfde, alleen die tekens zijn me te moeilijk om te maken )
)
(notatie is trouwens wel hetzelfde, alleen die tekens zijn me te moeilijk om te maken
Het is geel en staat in mijn ondertitel!
3DS friend code: 2191-7623-9035
3DS friend code: 2191-7623-9035


wilt u AUB dan voortaan de correcte notatie van δ2e-xy/δx*δy hanteren jaquote:Op dinsdag 6 november 2007 11:55 schreef Jesse_ het volgende:
dank je, het is nu iig duidelijk
(notatie is trouwens wel hetzelfde, alleen die tekens zijn me te moeilijk om te maken)


yo mensen, aangezien ik echt niet weet waar ik deze vraag moet plaatsen doe ik het hier maar.
Ik studeer Software Engineering en ga binnekort een nieuwe laptop aanschaffen. Deze zal ik ook voor school gaan gebruiken. Is er dan een mogelijkheid dat ik iets van de belasting af kan trekken?
Ik studeer Software Engineering en ga binnekort een nieuwe laptop aanschaffen. Deze zal ik ook voor school gaan gebruiken. Is er dan een mogelijkheid dat ik iets van de belasting af kan trekken?


WGR is een beter forum.quote:Op woensdag 7 november 2007 17:11 schreef Darow het volgende:
yo mensen, aangezien ik echt niet weet waar ik deze vraag moet plaatsen doe ik het hier maar.
Ik studeer Software Engineering en ga binnekort een nieuwe laptop aanschaffen. Deze zal ik ook voor school gaan gebruiken. Is er dan een mogelijkheid dat ik iets van de belasting af kan trekken?
Delta's?quote:Op dinsdag 6 november 2007 21:44 schreef harrypiel het volgende:
[..]
wilt u AUB dan voortaan de correcte notatie van δ2e-xy/δx*δy hanteren ja? Partiele afgeleiden zijn al verwarrend genoeg zonder inconsistente schrijfwijzen


eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik wil de volgende functie minimaliseren voor phi:
E = Ea*cos^2(phi)+Eb*sin^2(phi)+2*cos(phi)*sin(phi)*h^2
Ea, Eb en h zijn constantes. Uiteraard afgeleide nemen naar phi maar dan krijg ik allerlei nare dingen. Ik kom zelf tot het volgende:
dE/dphi = -2 Ea cos(phi) sin(phi) + 2 Eb sin(phi) cos(phi) - 2 sin^2(phi) *h^2 + 2 cos^2(phi)* h^2 = 0
Verdubbelingsformules toepassen: (Eb-Ea)*sin(2phi)+2*h^2*cos(2*phi) = 0
Vervolgens: tan(2phi) = -(2*h^2)/(Eb-Ea)
En dan zit ik vast Iemand die hulp kan bieden?
Iemand die hulp kan bieden?
E = Ea*cos^2(phi)+Eb*sin^2(phi)+2*cos(phi)*sin(phi)*h^2
Ea, Eb en h zijn constantes. Uiteraard afgeleide nemen naar phi maar dan krijg ik allerlei nare dingen. Ik kom zelf tot het volgende:
dE/dphi = -2 Ea cos(phi) sin(phi) + 2 Eb sin(phi) cos(phi) - 2 sin^2(phi) *h^2 + 2 cos^2(phi)* h^2 = 0
Verdubbelingsformules toepassen: (Eb-Ea)*sin(2phi)+2*h^2*cos(2*phi) = 0
Vervolgens: tan(2phi) = -(2*h^2)/(Eb-Ea)
En dan zit ik vast


Zie ik wat over hoofd, of is de rest eenvoudig 
2phi = arctan(-(2*h^2)/(Eb-Ea)) + k*π (k in Z)
phi = arctan(-(2*h^2)/(Eb-Ea))/2 + k/2*π (k in Z)
Het teken van de tweede afgeleide checken lijkt me erger
2phi = arctan(-(2*h^2)/(Eb-Ea)) + k*π (k in Z)
phi = arctan(-(2*h^2)/(Eb-Ea))/2 + k/2*π (k in Z)
Het teken van de tweede afgeleide checken lijkt me erger
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


dan heb je inderdaad de exacte oplossing maar als je die phi vervolgens weer invult in je vergelijking voor E krijg je er nog geen mooie dingen uit..
Ik heb wel een oplossing van het boek. Die gaan op de volgende manier verder:
tan 2phi = sin(2 phi) / sqrt(1-sin^2(2phi) = -c (c = 2h^2/(Eb-Ea) )
kwadrateren geeft dan: sin^2(2 phi) = c^2(1- sin^2(2phi))
oftewel sin^2(2phi)(1+c^2) = c^2
dus: sin(2phi) = +- c / sqrt(1+c^2)
cos(2phi) kun je dan op een zelfde manier eruit halen. Hetzelfde geldt voor cos^2(phi) sin^2(phi).
Tot hier volg ik het nog wel (alleen geen idee hoe ik dit ooit zelf zou moeten bedenken). Ik zie in dat het goed is maar ik zie de gedachtengang niet hoe bij het eindpunt te komen vanuit mijn eerste vergelijking...
Ik heb wel een oplossing van het boek. Die gaan op de volgende manier verder:
tan 2phi = sin(2 phi) / sqrt(1-sin^2(2phi) = -c (c = 2h^2/(Eb-Ea) )
kwadrateren geeft dan: sin^2(2 phi) = c^2(1- sin^2(2phi))
oftewel sin^2(2phi)(1+c^2) = c^2
dus: sin(2phi) = +- c / sqrt(1+c^2)
cos(2phi) kun je dan op een zelfde manier eruit halen. Hetzelfde geldt voor cos^2(phi) sin^2(phi).
Tot hier volg ik het nog wel (alleen geen idee hoe ik dit ooit zelf zou moeten bedenken). Ik zie in dat het goed is maar ik zie de gedachtengang niet hoe bij het eindpunt te komen vanuit mijn eerste vergelijking...


gvd ik moet natuurlijk weer een kutonderwerp kiezen voor m'n pws
de aarde
weet iemand een goeie hoofdvraag? dan kan ik zelf wel deelvragen verzinnen
gvd waarom denk ik daar niet eerst aan voordat ik zo'n brak onderwerp neem
de aarde
weet iemand een goeie hoofdvraag? dan kan ik zelf wel deelvragen verzinnen
gvd waarom denk ik daar niet eerst aan voordat ik zo'n brak onderwerp neem


F(qt) = 13,33 – 4/3Qt(Qt-1)
= 13,33 - 1,33Qt2 + 1,33Qt
F'(Qt) = -2,67Qt +1,33

= 13,33 - 1,33Qt2 + 1,33Qt
F'(Qt) = -2,67Qt +1,33
Bestiality sure is a fun thing to do. But I have to say this as a warning to you:
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.


Wat is pws? Profielwerkstuk? (Wilde gok.) En om welk profiel gaat het? Natuur & Techniek? En 'de aarde', dat klinkt als een nogal vaag onderwerp. Wat wil je? Het over het onstaan van de aarde hebben? Of hoe de aarde nu in elkaar zit (d.w.z. met tectonische platen, aardkorst, e.d.) of meer een soort beschouwing over het eco-systeem op aarde? Of wil je gewoon een staatkundige indeling erop loslaten? Wat is het doel?quote:Op donderdag 8 november 2007 11:11 schreef warchaser44 het volgende:
gvd ik moet natuurlijk weer een kutonderwerp kiezen voor m'n pws
de aarde
weet iemand een goeie hoofdvraag? dan kan ik zelf wel deelvragen verzinnen
gvd waarom denk ik daar niet eerst aan voordat ik zo'n brak onderwerp neem
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


laat maar zitten, gaat niet helemaal goedquote:Op donderdag 8 november 2007 11:27 schreef Jordy-B het volgende:
F(qt) = 13,33 – 4/3Qt(Qt-1)
= 13,33 - 1,33Qt2 + 1,33Qt
F'(Qt) = -2,67Qt +1,33
winnaar wielerprono 2007 :) Last.FM


profielwerkstuk, profiel van economie-maatschappij 
ik kom er dus achter dat ik echt een verkeerd onderwerp heb genomen wat veel te breed is, maar nu ik ermee door moet gaan denk ik toch dat er over het eco systeem wel het meeste te vinden is
het doel is dus dat je hoofd en deelvragen geeft, dan je plan van aanpak, en dan dat je een soort onderzoek doet naar de hoofd en deelvragen
--- eigenlijk heb ik alleen nog maar het vak gekozen: Aardrijkskunde, denk je dat het beter is dat ik een ander onderwerp pak omdat - de aarde een veel te breed onderwerp is ?
ik kom er dus achter dat ik echt een verkeerd onderwerp heb genomen wat veel te breed is, maar nu ik ermee door moet gaan denk ik toch dat er over het eco systeem wel het meeste te vinden is
het doel is dus dat je hoofd en deelvragen geeft, dan je plan van aanpak, en dan dat je een soort onderzoek doet naar de hoofd en deelvragen
--- eigenlijk heb ik alleen nog maar het vak gekozen: Aardrijkskunde, denk je dat het beter is dat ik een ander onderwerp pak omdat - de aarde een veel te breed onderwerp is ?


Wordt zo'n onderwerp niet goedgekeurd door een docent die dan zegt of het niet te specifiek of te ruim is?
Je kunt natuurlijk je vraagstuk makkelijk specificeren, d.w.z. op een nader onderwerp toespitsen binnen de aardrijkskunde.
Klimaatzones van de aarde
- Welke zijn er
- Wat zijn de kenmerken
- Hoe beinvloeden ze landbouw en veeteelt
- Hoe veranderen ze?
- Blah blah broeikaseffect
Plaattectoniek
- Platen/breuklijnen
- Aardbevingen (tsunami's, lekker actueel)
- Vulkanen, vertel iets over vruchtbare grond en gevaren
Ecosysteem
- Definitie ecosysteem
- Voorbeelden, land/water verschillende regio's
- Evenwichten, verandering, nieuw evenwicht
- Gevaren, klimaatverandering, jacht/(over)bevissing
Geschiedenis van de aarde (evt. inspelen op creationisme-debat)
- Ouderdomsbepaling; hoe doe je dat? Wat zijn de bewijzen?
- Gloeiend bolletje
- Afkoeling
- Rotsvorming
- Continentvorming
- Etc. Je kunt een beetje beschrijven welke processen nog steeds in gang zijn (Een kleine geschiedenis van bijna alles is wat dat betreft wel leuk om te lezen); hoe er heuvels zijn, waarom de aarde niet vlak is (uiteindelijk zou erosie alles vlak moeten maken); hoe rivieren landschappen vormen, et cetera.
Naar het boek van Friedman: The World is Flat: beschrijf de mondialisering van economieen, et cetera, ook actueel.
Kortom, er zijn genoeg ideeen. Verder kun je iets met de opkomst van het concect 'staat' doen in de geschiedenis, hoe de aarde de staatkundige indeling heeft gekregen die het nu heeft (vroeger was het begrip staat natuurlijk niet zo bestaand, en leefden mensen veel meer in een dorp of gemeenschap of als nomaden). En als ik nog even uit m'n duim zuig kan ik vast nog wel wat bedenken.
Je kunt natuurlijk je vraagstuk makkelijk specificeren, d.w.z. op een nader onderwerp toespitsen binnen de aardrijkskunde.
- Welke zijn er
- Wat zijn de kenmerken
- Hoe beinvloeden ze landbouw en veeteelt
- Hoe veranderen ze?
- Blah blah broeikaseffect
- Platen/breuklijnen
- Aardbevingen (tsunami's, lekker actueel)
- Vulkanen, vertel iets over vruchtbare grond en gevaren
- Definitie ecosysteem
- Voorbeelden, land/water verschillende regio's
- Evenwichten, verandering, nieuw evenwicht
- Gevaren, klimaatverandering, jacht/(over)bevissing
- Ouderdomsbepaling; hoe doe je dat? Wat zijn de bewijzen?
- Gloeiend bolletje
- Afkoeling
- Rotsvorming
- Continentvorming
- Etc. Je kunt een beetje beschrijven welke processen nog steeds in gang zijn (Een kleine geschiedenis van bijna alles is wat dat betreft wel leuk om te lezen); hoe er heuvels zijn, waarom de aarde niet vlak is (uiteindelijk zou erosie alles vlak moeten maken); hoe rivieren landschappen vormen, et cetera.
Kortom, er zijn genoeg ideeen. Verder kun je iets met de opkomst van het concect 'staat' doen in de geschiedenis, hoe de aarde de staatkundige indeling heeft gekregen die het nu heeft (vroeger was het begrip staat natuurlijk niet zo bestaand, en leefden mensen veel meer in een dorp of gemeenschap of als nomaden). En als ik nog even uit m'n duim zuig kan ik vast nog wel wat bedenken.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


nee, het is zo dat ik een vak invoer, en morgen moet ik dan hoofd en deelvragen invoeren, maar ik twijfel of ik tussen Klimaatzones van de aarde wat jij hebt uitgelegd ga, of een nieuw onderwerp wat ook onder ak valt namelijk: De allochtoon, hier zijn mooie vraagstukken over zoals bv
- Wat is een allochtoon volgens de wet en volgens de buurman?
- Zijn Marokkaanse kinderen die in Nederland zijn geboren ook allochtoon?
- Is Maxima een allochtoon?
- Wat is een autochtoon?
- Om welke redenen komen mensen uit andere landen naar Nederland?
- Hoe denkt men in Nederland over allochtonen?
- Is er een integratieprobleem en zo ja, wat doen we eraan?
dus ik twijfel nog over welk onderwerp ik zal nemen
- Wat is een allochtoon volgens de wet en volgens de buurman?
- Zijn Marokkaanse kinderen die in Nederland zijn geboren ook allochtoon?
- Is Maxima een allochtoon?
- Wat is een autochtoon?
- Om welke redenen komen mensen uit andere landen naar Nederland?
- Hoe denkt men in Nederland over allochtonen?
- Is er een integratieprobleem en zo ja, wat doen we eraan?
dus ik twijfel nog over welk onderwerp ik zal nemen


Ik heb een probleem met een aantal sommen van wiskunde wiskunde:
* Ik mag geen rekenmachine gebruiken, antwoorden moet ik geven als x = ln(3) bijvoorbeeld
Geef x:
1: e^(x*(x-2)) = e
2: e^x > e^-x
3: (1/5)^(x²) < 5^(-12-4x)
4: ln(x)-ln(x-4) = 4
5: ln(1-x) < 0
hoe ver ik zelf ben gekomen:
1: e^(x² -2x) = e
x²-2x = 1
x² -2x -1 = 0
abc formule:
2+-wortel(-2²-4*1*-1)
2
x=2,41 v x=0,41
dit kan je toch niet uit je hoofd volgens t antwoordenboekje moest t zijn 1+- wortel(2), hoe kwamen ze daar aan?
volgens t antwoordenboekje moest t zijn 1+- wortel(2), hoe kwamen ze daar aan?
2:e^x > e^-x
Ik dacht dat t antwoord simpel: x > -x zou zijn, maar t blijkt x > 0 te zijn, hoe kwamen ze daarbij en is mijn antwoord niet goed?
3: (1/5)^(x²) < 5^(-12-4x)
5^(-x²) < 5^(-12-4x)
-x² < -12-4x
0 < x²-4x-12
(x-6) (x+2)
x=6 v x=-2
oke, hier luidt mijn vraag hoe weet ik of t x<6 of x>6 is, of x<-2 of x>-2 is. dit doe ik altijd fout kan iemand uitleggen hoe t zit?
kan iemand uitleggen hoe t zit?
4: ln(x)-ln(x-4) = 4
ln(x/(x-4)) = 4
x/(x-4) = e^4
x=e^4*(x-4)
x=e^4x-4e^4
4e^4=e^4x+x
en daar loop ik vast.
5: ln(1-x) < 0
1-x < 1
0 < x
maar volgens t antwoordenboekje moest t zijn 1>x>0
kheb echt een probleem met die > <
* Ik mag geen rekenmachine gebruiken, antwoorden moet ik geven als x = ln(3) bijvoorbeeld
Geef x:
1: e^(x*(x-2)) = e
2: e^x > e^-x
3: (1/5)^(x²) < 5^(-12-4x)
4: ln(x)-ln(x-4) = 4
5: ln(1-x) < 0
hoe ver ik zelf ben gekomen:
1: e^(x² -2x) = e
x²-2x = 1
x² -2x -1 = 0
abc formule:
2+-wortel(-2²-4*1*-1)
2
x=2,41 v x=0,41
dit kan je toch niet uit je hoofd
2:e^x > e^-x
Ik dacht dat t antwoord simpel: x > -x zou zijn, maar t blijkt x > 0 te zijn, hoe kwamen ze daarbij en is mijn antwoord niet goed?
3: (1/5)^(x²) < 5^(-12-4x)
5^(-x²) < 5^(-12-4x)
-x² < -12-4x
0 < x²-4x-12
(x-6) (x+2)
x=6 v x=-2
oke, hier luidt mijn vraag hoe weet ik of t x<6 of x>6 is, of x<-2 of x>-2 is. dit doe ik altijd fout
4: ln(x)-ln(x-4) = 4
ln(x/(x-4)) = 4
x/(x-4) = e^4
x=e^4*(x-4)
x=e^4x-4e^4
4e^4=e^4x+x
en daar loop ik vast.
5: ln(1-x) < 0
1-x < 1
0 < x
maar volgens t antwoordenboekje moest t zijn 1>x>0
kheb echt een probleem met die > <


Sommetje 1.
Je weet dus al dat de argumenten gelijk moeten zijn, dus
x2 - 2x = 1 --> x2 -2x -1 =0
ABC formule toepassen:
x= ( 2 +/- sqrt ( 4+4) ) /2 = 1 +\\- 1/2 sqrt (8) = 1 +\\- sqrt(2)
Je gebruikt hierbij dat sqrt(8) = sqrt(4)*sqrt(2) = 2*sqrt(2).
Sommetje 2
x > -x betekent precies dat x>0. Immers, als x=0 gaat de ongelijkheid niet meer op, en als x bijvoorbeeld -1 is, dan al helemaal niet meer.
Sommetje 5
Die x moet groter zijn dan 0, omdat je anders rare fratsen krijgt; die logaritme is dan niet meer gedefinieerd.
Bijvoorbeeld,neem es ln(-80), en noem dit y:
y=ln(-80)
Dan dus ook ey= -80. Echter, een e-macht kan nooit negatief zijn, als je het argument naar -oo stuurt kan de functie hooguit naar 0 gaan. Maar niet verder dan dat.
Sommetje 4
Je kunt inderdaad gebruiken dat ln(x) - ln(y)= ln(x/y). Dus:
ln [ x/(x-4) ] = 4 --> x/(x-4) = e4.
Dus x = (x-4)e4
x-e4 x = 4
x ( 1- e4 ) =4
x= 4/ ( 1-e4 )
Je weet dus al dat de argumenten gelijk moeten zijn, dus
x2 - 2x = 1 --> x2 -2x -1 =0
ABC formule toepassen:
x= ( 2 +/- sqrt ( 4+4) ) /2 = 1 +\\- 1/2 sqrt (8) = 1 +\\- sqrt(2)
Je gebruikt hierbij dat sqrt(8) = sqrt(4)*sqrt(2) = 2*sqrt(2).
Sommetje 2
x > -x betekent precies dat x>0. Immers, als x=0 gaat de ongelijkheid niet meer op, en als x bijvoorbeeld -1 is, dan al helemaal niet meer.
Sommetje 5
Die x moet groter zijn dan 0, omdat je anders rare fratsen krijgt; die logaritme is dan niet meer gedefinieerd.
Bijvoorbeeld,neem es ln(-80), en noem dit y:
y=ln(-80)
Dan dus ook ey= -80. Echter, een e-macht kan nooit negatief zijn, als je het argument naar -oo stuurt kan de functie hooguit naar 0 gaan. Maar niet verder dan dat.
Sommetje 4
Je kunt inderdaad gebruiken dat ln(x) - ln(y)= ln(x/y). Dus:
ln [ x/(x-4) ] = 4 --> x/(x-4) = e4.
Dus x = (x-4)e4
x-e4 x = 4
x ( 1- e4 ) =4
x= 4/ ( 1-e4 )
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Overigens, dat x > -a*x met a een positief getal hetzelfde is als x>0,kun je triviaal bewijzen:
x > -a*x
x+ a*x > 0
x(1+a) > 0
En omdat 1+a altijd groter is dan 0, geldt dat x>0.
x > -a*x
x+ a*x > 0
x(1+a) > 0
En omdat 1+a altijd groter is dan 0, geldt dat x>0.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Sommetje 3:
Je kijkt of je een berg- of dalparabool hebt; x²-4x-12 is een dalparabool.
Je hebt 0 < x²-4x-12, dus de dalparabool moet groot zijn. Het middenstuk ligt altijd erg laag bij een dalparabool, dus je moet aan de uiteinden zijn. Met zo'n argumentatie gaat het nooit fout.
Bij 5 lijkt me de verwarring veroorzaakt doordat bij het antwoordenboek x=0 ook meedoet. Dit is echter een fout in het antwoordenboek.
Je kijkt of je een berg- of dalparabool hebt; x²-4x-12 is een dalparabool.
Je hebt 0 < x²-4x-12, dus de dalparabool moet groot zijn. Het middenstuk ligt altijd erg laag bij een dalparabool, dus je moet aan de uiteinden zijn. Met zo'n argumentatie gaat het nooit fout.
Bij 5 lijkt me de verwarring veroorzaakt doordat bij het antwoordenboek x=0 ook meedoet. Dit is echter een fout in het antwoordenboek.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Differentiere, doe ik het goed? en kan het compacter dan dit?
1: y=x-x*ln(x)
y'= -x*(1/x) + -ln(x) = -x/x + -ln(x)
2: y=xe^(2x)
y'=x*2e^(2x)+e^2(x)
3: y=3x*log(x)
y'= 3x*1/(x*ln(10))+3*log(x) = 3x/(x*ln(10))+3*log(x) = 3/ln(10)+3*log(x)
1: y=x-x*ln(x)
y'= -x*(1/x) + -ln(x) = -x/x + -ln(x)
2: y=xe^(2x)
y'=x*2e^(2x)+e^2(x)
3: y=3x*log(x)
y'= 3x*1/(x*ln(10))+3*log(x) = 3x/(x*ln(10))+3*log(x) = 3/ln(10)+3*log(x)


Die eerste doe je alvast niet goed, je moet hier niet alleen de productregel maar ook de somregel gebruiken. En gebruik liever superscript, dat maakt de zaak wat prettiger leesbaar.quote:Op maandag 12 november 2007 00:31 schreef stekemrt het volgende:
Differentiëren, doe ik het goed? en kan het compacter dan dit?


Nee, differentieren kan soms waar hufwerk of doom zijnquote:Op maandag 12 november 2007 00:31 schreef stekemrt het volgende:
En kan het compacter dan dit?
Je differentieert nou alleen de tweede term, maar je had ook nog een x. De afgeleide wordt dan -ln(x)quote:1: y=x-x*ln(x)
y'= -x*(1/x) + -ln(x) = -x/x + -ln(x)
quote:2: y=xe^(2x)
y'=x*2e^(2x)+e^2(x)
quote:3: y=3x*log(x)
y'= 3x*1/(x*ln(10))+3*log(x) = 3x/(x*ln(10))+3*log(x) = 3/ln(10)+3*log(x)
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Z = X/Y
∂z/∂x ? en ∂z/∂y ?
Het zal wel weer zo simpel zijn, maar ik kom er niet uit
∂z/∂x ? en ∂z/∂y ?
Het zal wel weer zo simpel zijn, maar ik kom er niet uit
winnaar wielerprono 2007 :) Last.FM


De eerste moet je dus differentiëren naar X (en Y als constant beschouwen) en de tweede naar Y, en X als constant beschouwen. Vervang eerst eens Y en X respectievelijk door een échte constante, zeg 3. Kijk eens of het dan wel lukt. Dan moet het niet zo moeilijk zijn.quote:Op maandag 12 november 2007 14:55 schreef borisz het volgende:
Z = X/Y
∂z/∂x ? en ∂z/∂y ?
Het zal wel weer zo simpel zijn, maar ik kom er niet uit
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ja tenzij X en Y functies van de variabelen x en y zijn (en eventueel zelfs van elkaar). Dan zit je met de productregel en impliciete afgeleides.


Daar heb je helemaal gelijk in, maar daar ging ik even niet vanuit. Het zou echter best kunnen zijn dat er een functie in x bedoeld wordt met X, daar wordt het echter niet veel moeilijker van. Als Y een functie in y is, dan heb je wel een kettingregel nodig.quote:Op maandag 12 november 2007 18:24 schreef Marinus het volgende:
Ja tenzij X en Y functies van de variabelen x en y zijn (en eventueel zelfs van elkaar). Dan zit je met de productregel en impliciete afgeleides.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


De deelstreep maakt het een beetje raar, ik wist niet meer wat ik toe moest passen.
dat was vooral het probleem Maar dank iig
Maar dank iig 
dat was vooral het probleem
winnaar wielerprono 2007 :) Last.FM


Voortaan sticky.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


Helllo:)
Als R een commutatieve ring is en M en N twee R-modulen zijn.
Dan is HomR(M,N) ook een R-moduul door te definieren (rf)(x)=rf(x) voor alle r in R en alle x in M.
Om dit na te gaan, moet men o.a nagaan dat als r en s in R zitten dan geldt:
((rs)f)(x)=(r(sf))(x)
Ik deed het als volgt:
((rs)f)(x)=((sr)f)(x)
=(sr)f(x)
=s(rf(x)) want HomR(M,N) is een R-moduul dus zo ' spelen' met haakjes is toegestaan.
=sf(rx)
=(sf)(rx)
=r(sf)(x) want HomR(M,N) is een R-moduul dusf f(rx)=rf(x).
=(r(sf))(x)
is dit goed..of maak ik fouten?
Als R een commutatieve ring is en M en N twee R-modulen zijn.
Dan is HomR(M,N) ook een R-moduul door te definieren (rf)(x)=rf(x) voor alle r in R en alle x in M.
Om dit na te gaan, moet men o.a nagaan dat als r en s in R zitten dan geldt:
((rs)f)(x)=(r(sf))(x)
Ik deed het als volgt:
((rs)f)(x)=((sr)f)(x)
=(sr)f(x)
=s(rf(x)) want HomR(M,N) is een R-moduul dus zo ' spelen' met haakjes is toegestaan.
=sf(rx)
=(sf)(rx)
=r(sf)(x) want HomR(M,N) is een R-moduul dusf f(rx)=rf(x).
=(r(sf))(x)
is dit goed..of maak ik fouten?
verlegen :)


Ik lees hierin dat je wilt aantonen dat HomR(M,N) een R-moduul is, en dat je in je argument om dit aan te tonen al gebruikt dat HomR(M,N) een R-moduul is?quote:Op dinsdag 13 november 2007 19:27 schreef teletubbies het volgende:
Helllo:)
Als R een commutatieve ring is en M en N twee R-modulen zijn.
Dan is HomR(M,N) ook een R-moduul door te definieren (rf)(x)=rf(x) voor alle r in R en alle x in M.
Om dit na te gaan, moet men o.a nagaan dat als r en s in R zitten dan geldt:
((rs)f)(x)=(r(sf))(x)
Ik deed het als volgt:
((rs)f)(x)=((sr)f)(x)
=(sr)f(x)
=s(rf(x)) want HomR(M,N) is een R-moduul dus zo ' spelen' met haakjes is toegestaan.
=sf(rx)
=(sf)(rx)
=r(sf)(x) want HomR(M,N) is een R-moduul dusf f(rx)=rf(x).
=(r(sf))(x)
is dit goed..of maak ik fouten?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Nee nEE nee.. ik wil niet gebruiken wat ik wou bewijzen..
ik gebruikte per ongeluk een fout argument, maar de uitwerking is voor de rest goed denk ik:
Ik wou zeggeN:
Hom(M,N) van R-modulen is een abelse groep. Ieder homomorfisme van M naar N voldoet aan:
f(rm)=rf(m).
Hom(M,N) R is slechts een ondergroep van Hom(M,N) en voldoet dus ook aan f(rm)=rf(m)..deze eigenschap heb ik een paar keer gebruikt...
ik gebruikte per ongeluk een fout argument, maar de uitwerking is voor de rest goed denk ik:
Ik wou zeggeN:
Hom(M,N) van R-modulen is een abelse groep. Ieder homomorfisme van M naar N voldoet aan:
f(rm)=rf(m).
Hom(M,N) R is slechts een ondergroep van Hom(M,N) en voldoet dus ook aan f(rm)=rf(m)..deze eigenschap heb ik een paar keer gebruikt...
verlegen :)


Zij M een R-moduul is en f:M->M een R-homomorfisme. Als je moet bewijzen dat M isomorf met de directe som van twee deelmodulen ker(f) en im(f) , wat moet je eigenlijk nagaan?
verlegen :)


Je hebt een exacte rij 0 -> ker(f) -> M -> im(f) -> 0. Een van de dingen die voldoende is om na te gaan is dat f:M->im(f) een sectie heeft, dus dat er een g:im(f)->M is met fg de identiteit op im(f).quote:Op donderdag 15 november 2007 22:12 schreef teletubbies het volgende:
Zij M een R-moduul is en f:M->M een R-homomorfisme. Als je moet bewijzen dat M isomorf met de directe som van twee deelmodulen ker(f) en im(f) , wat moet je eigenlijk nagaan?


even controle Matrixen (beide 2x2)
A =(2 4) B = (-2 4)
(1 2 ) (1 -2)
bereken AB
Ik weet niet zeker of het goed is
AB = (0 12)
(-3 0)
uitwerking
AB= (2*-2 +4*1 , 4*4 + 2*-2)
(1*1 + 2*-2 , -2*2 4*1)
klopt het of niet ?
[ Bericht 0% gewijzigd door borisz op 16-11-2007 11:36:35 ]
A =(2 4) B = (-2 4)
(1 2 ) (1 -2)
bereken AB
Ik weet niet zeker of het goed is
AB = (0 12)
(-3 0)
uitwerking
AB= (2*-2 +4*1 , 4*4 + 2*-2)
(1*1 + 2*-2 , -2*2 4*1)
klopt het of niet ?
[ Bericht 0% gewijzigd door borisz op 16-11-2007 11:36:35 ]
winnaar wielerprono 2007 :) Last.FM


Nee.quote:Op vrijdag 16 november 2007 10:54 schreef borisz het volgende:
even controle Matrixen
A =(2 4) B = (-2 4)
(1 2 ) (1 -2)
bereken AB
Ik weet niet zeker of het goed is
AB = (0 12)
(-3 0)
uitwerking
AB= (2*-2 +4*1 , 4*4 + 2*-2)
(1*1 + 2*-2 , -2*2 4*1)
klopt het of niet ?


moet je nu gewoon simpel doen dus (2*-2 , 4*4) en dan daaronder (1*1 , 2*-2) ?
en zo nee hoe moet het dan ? ik weet het niet... en met het boek wordt ik ook niet veel wijzer.
en zo nee hoe moet het dan ? ik weet het niet... en met het boek wordt ik ook niet veel wijzer.
winnaar wielerprono 2007 :) Last.FM


Nee, Matrices gaan niet elementsgewijs. Dat zou ook niet kunnen. Want in het algemeen kun je matrices met elkaar vermenigvuldigen als het aantal kolommen van de linker gelijk is aan het aantal rijen van de rechter. Heb je een m x k matrix die je met een k x n matrix vermenigvuldigt is het resultaat een m x n matrix. Dat gaat altijd op. Als je zo zou doen als jij zou willen zou het niet kunnen.quote:Op vrijdag 16 november 2007 11:38 schreef borisz het volgende:
moet je nu gewoon simpel doen dus (2*-2 , 4*4) en dan daaronder (1*1 , 2*-2) ?
en zo nee hoe moet het dan ? ik weet het niet... en met het boek wordt ik ook niet veel wijzer.
Wat je doet met vermenigvuldiging, is dat je de rijen van de eerste matrix stuk voor stuk ‘langs de kolommen’ van de andere matrix legt. Jij doet dat in je eerste poging in het eerste geval goed. Elke rij-kolom combinatie levert uiteindelijk één getal op in het antwoord.
Concreet:
| 1 2 | [1 2] [ 1 -2] |
We nemen de eerste rij van A, en leggen die langs de eerste kolom van B. Die rij is [2 4], die kolom is [-2 1].
En pas dán gaan we elementsgewijs vermenigvuldigen. Dus 2*-2 + 4*1 = -4 + 4 = 0. Die had jij ook goed. Dan pakken we de tweede kolom van B (we blijven nog bij de eerste rij van A). En we leggen ze weer naast elkaar: [2 4] van A, en [4 -2] van B. Levert: 2 * 4 + -4 * 2 = 8 - 8 = 0.
Nu hebben we alle kolommen van B gehad, en gaan we naar een volgende rij in A (ook in de antwoordmatrix beginnen we dan met een nieuwe rij). Nu pakken we dus de rij [1 2] en gaan we weer alle kolommen van B af. Dat kun je nu hopelijk zelf doen.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


[1 2] en [-2 1] = 1*-2 + 2*1 = -2 + 2 = 0
en
[1 2] en [4 -2] = 1*4 + 2*-2 = 4-4 = 0
bedankt Ik wist het niet meer helemaal. En na andere voorbeelden bekeken kwam ik er niet uit wat ik dacht dat eruit moest komen
Ik wist het niet meer helemaal. En na andere voorbeelden bekeken kwam ik er niet uit wat ik dacht dat eruit moest komen
ik was wel aardig opweg maar dat was dan ook alles.
en
[1 2] en [4 -2] = 1*4 + 2*-2 = 4-4 = 0
bedankt
ik was wel aardig opweg maar dat was dan ook alles.
winnaar wielerprono 2007 :) Last.FM


kort vraagje nog, de volgende opgave is C(AB) moet je dan de uitkomsten van AB 'vermeningvuldigen' met tabel C (dus op de matrix manier)?
edit: Ja antwoord stond een paar paragraven verder in het boek
edit: Ja antwoord stond een paar paragraven verder in het boek
winnaar wielerprono 2007 :) Last.FM


De extreme waarde van de functie f(x) = px² + (p + 2)x + 5 is 3.
Bereken algebraïsch de x-coördinaat van de top van de grafiek.
Zelf gedaan:
Xtop = -b / 2a = -p + 2 / 2p = -p - 2 / 2p
Ytop = f(-p - 2 / 2p) = p * (-p - 2 / 2p)² + (p + 2) * -p - 2 / 2p + 5 = - 1/4p - 1/p + 4 = 3
En dan? Hoe krijg ik hier p uit?
Bereken algebraïsch de x-coördinaat van de top van de grafiek.
Zelf gedaan:
Xtop = -b / 2a = -p + 2 / 2p = -p - 2 / 2p
Ytop = f(-p - 2 / 2p) = p * (-p - 2 / 2p)² + (p + 2) * -p - 2 / 2p + 5 = - 1/4p - 1/p + 4 = 3
En dan? Hoe krijg ik hier p uit?


Je mist wat haakjes, let daar altijd goed op.
Xtop = -b / 2a = -(p + 2) / (2p) = -1/2 - 1/p
Ytop = p*(-1/2 - 1/p)² + (p+2)*(-1/2 - 1/p) + 5
= p*(1/4 + 1/p + 1/p²) + (p+2)*(-1/2 - 1/p) + 5
= p/4 + 1 + 1/p - p/2 - 1 - 1 - 2/p + 5
= -p/4 - 1/p + 4
Op te lossen is dus -p/4 - 1/p + 4 = 3. Vermenigvuldig links en rechts met p en je hebt weer een kwadratische vergelijking.
Xtop = -b / 2a = -(p + 2) / (2p) = -1/2 - 1/p
Ytop = p*(-1/2 - 1/p)² + (p+2)*(-1/2 - 1/p) + 5
= p*(1/4 + 1/p + 1/p²) + (p+2)*(-1/2 - 1/p) + 5
= p/4 + 1 + 1/p - p/2 - 1 - 1 - 2/p + 5
= -p/4 - 1/p + 4
Op te lossen is dus -p/4 - 1/p + 4 = 3. Vermenigvuldig links en rechts met p en je hebt weer een kwadratische vergelijking.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


g=f zelf toch?Trouwens formeel moet ik in feite een linkerinverse zoeken dus eigenlijk een g met gf de identiteit op imf(f)?quote:Op donderdag 15 november 2007 22:26 schreef thabit het volgende:
[..]
Je hebt een exacte rij 0 -> ker(f) -> M -> im(f) -> 0. Een van de dingen die voldoende is om na te gaan is dat f:M->im(f) een sectie heeft, dus dat er een g:im(f)->M is met fg de identiteit op im(f).
f[f[M]]=f[im(f)]=im(f) met de identiteit op im(f) bedoel je de identieke afbeelding.. gewoon f(x)=x.
In ieder geval, ik doe nu alsof ik met groepen werk, de extra structuur die men krijgt omdat M een moduul is ..wordt niet aangetast toch?
verlegen :)


f(x,y) = X^2 + Y^2 – 6x + 8Y + 35
hoe kan je dit herschrijven naar ?
F(x,y) = (x-3)^2 + (y+4)^2 + 10
let niet op hoofdletters/kleine letters dat is hetzelfde
hoe kan je dit herschrijven naar ?
F(x,y) = (x-3)^2 + (y+4)^2 + 10
let niet op hoofdletters/kleine letters dat is hetzelfde
winnaar wielerprono 2007 :) Last.FM


Je kijkt eerst naar x²-6x + c, dat kun je herschrijven naar (x-3)² met c=9
Daarna naar y²+8y+c, dat kun je herschrijven naar (y+4)² met c=16
En daarna kijk je hoeveel van de 35 je al hebt verwerkt in de kwadraten, en dan houd je nog 10 over.
Daarna naar y²+8y+c, dat kun je herschrijven naar (y+4)² met c=16
En daarna kijk je hoeveel van de 35 je al hebt verwerkt in de kwadraten, en dan houd je nog 10 over.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


dank  dat met die constante was niet helemaal duidelijk voor mij hoe je die naar beneden kreeg
dat met die constante was niet helemaal duidelijk voor mij hoe je die naar beneden kreeg  nu wel
nu wel 
winnaar wielerprono 2007 :) Last.FM


Klopt dit nu ?
P(x,y) = -x^2 – Y^2 +22x +18y – 102
Kan je herschrijven naar
Kijken naar -x^2 + 22x + C = -(x+11)^2 met c = 144
Kijken naar –Y^2 + 18Y + C = -(Y+9)^2 met C = 181
P(x,y) = (-x+11)^2 (-Y+9)^2 + 427
?
P(x,y) = -x^2 – Y^2 +22x +18y – 102
Kan je herschrijven naar
Kijken naar -x^2 + 22x + C = -(x+11)^2 met c = 144
Kijken naar –Y^2 + 18Y + C = -(Y+9)^2 met C = 181
P(x,y) = (-x+11)^2 (-Y+9)^2 + 427
?
winnaar wielerprono 2007 :) Last.FM


-(x+11)² = -(x²+22x+121) = -x² - 22x - 121, en dus wat anders dan -x²+22x+144. De tweede is helaas ook fout.quote:Op zondag 18 november 2007 11:53 schreef borisz het volgende:
Klopt dit nu ?
P(x,y) = -x^2 – Y^2 +22x +18y – 102
Kan je herschrijven naar
Kijken naar -x^2 + 22x + C = -(x+11)^2 met c = 144
Kijken naar –Y^2 + 18Y + C = -(Y+9)^2 met C = 181
P(x,y) = (-x+11)^2 (-Y+9)^2 + 427
?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Die ene was een typo op de rekenmachine had 12 ipv 11 en die ander is 81 ipv 181.
het wordt dus P(x,y) = -(x+11)^2 + -(Y+9)^2 + 100
het wordt dus P(x,y) = -(x+11)^2 + -(Y+9)^2 + 100
winnaar wielerprono 2007 :) Last.FM


Dan blijft hij fout, zie edit. En in je uiteindelijke functie komt het minteken plotseling binnen de haakjes, dat is ook opmerkelijk.quote:Op zondag 18 november 2007 12:03 schreef borisz het volgende:
Die ene was een typo op de rekenmachine had 12 ipv 11 en die ander is 81 ipv 181.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


hoe ik die daar neer heb gezetquote:Op zondag 18 november 2007 12:04 schreef GlowMouse het volgende:
[..]
Dan blijft hij fout, zie edit. En in je uiteindelijke functie komt het minteken plotseling binnen de haakjes, dat is ook opmerkelijk.
P(x,y) = -x^2 – Y^2 +22x +18y – 102
Kan je herschrijven naar
Kijken naar -x^2 + 22x + C = -(x+11)^2 met c = -121
Kijken naar –Y^2 + 18Y + C = -(Y+9)^2 met C = -81
P(x,y) = -(x+11)^2 + -(Y+9)^2 -304
dan
winnaar wielerprono 2007 :) Last.FM


Nee, je krijgt dan nog steeds -22x ipv +22x bij de eerste, en -18y ipv +18y bij de tweede.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


P(x,y) = -(x-11)^2 -(Y-9)^2 -304
want dan is het -- = +. Nu heb ik hem eindelijk denk ik
want dan is het -- = +. Nu heb ik hem eindelijk denk ik
winnaar wielerprono 2007 :) Last.FM


Bijna goed, alleen de 304 klopt nog niet. Van het eerste kwadraat krijg je -121, van het tweede -81, dus je hebt al -202. Je moet op -102 uitkomen, dus je krijgt +100 ipv -304 als laatste term. Om het antwoord te controleren kun je de haakjes gewoon weer wegwerken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Als je g=f neemt zal dat in het algemeen niet werken. Sterker nog, voor de meeste f'en bestaat g niet.quote:Op zaterdag 17 november 2007 23:26 schreef teletubbies het volgende:
[..]
g=f zelf toch?Trouwens formeel moet ik in feite een linkerinverse zoeken dus eigenlijk een g met gf de identiteit op imf(f)?
f[f[M]]=f[im(f)]=im(f) met de identiteit op im(f) bedoel je de identieke afbeelding.. gewoon f(x)=x.
In ieder geval, ik doe nu alsof ik met groepen werk, de extra structuur die men krijgt omdat M een moduul is ..wordt niet aangetast toch?


Zij A een ring waarin er voor elk element x een n>1 is zodat dat xn=x. Ik moet laten zien dat elke priemideaal van A ook een maximaal ideaal is, maar het wil niet bepaald lukken. Ik dacht dat het misschien zinvol zou zijn om voor een priemideaal p te kijken naar de ring A/p, maar ik zie niet in hoe ik de bijzondere eigenschap (xn=x) en het feit dat A/p een domein is kan combineren om tot de conclusie te komen dat elk element van A/p een eenheid is. Enig idee?


Kies x ongelijk aan 0 in A/p. Je weet xn=x of wel xn-x=0 ofwel x(xn-1-1)=0. Omdat x ongelijk aan 0 is en A/p een domein geldt xn-1-1=0 ofwel xn-1=1. Omdat n-1 > 0 is x een factor van 1, dus een eenheid.


ff natuurkundig vraagje:
Op het SE ging het over een sleetje dat van een helling af ging.
Nu moest je een grafiek maken: Ek uitzetten tegen de afstand.
Wrijving was gemiddeld 25N.
Nu dacht ik dat het een kromme lijn was (als wortel(x)),
maar iemand anders dacht dat het een rechte lijn was.
Ik begin zelf eigenlijk ook steeds meer te twijfelen .
.
Anyone?
Op het SE ging het over een sleetje dat van een helling af ging.
Nu moest je een grafiek maken: Ek uitzetten tegen de afstand.
Wrijving was gemiddeld 25N.
Nu dacht ik dat het een kromme lijn was (als wortel(x)),
maar iemand anders dacht dat het een rechte lijn was.
Ik begin zelf eigenlijk ook steeds meer te twijfelen
Anyone?


We hebben a=F/m, dus a is constant (F is namelijk de component langs de helling van de zwaartekracht, minus de wrijvingskracht en de massa verandert ook niet). Omdat x=1/2*a*t2, geldt dat t=sqrt(2x/a). Vul in: Ek = 1/2*m*v2 = 1/2*m*(at)2 = 1/2*m*a2*2x/a = m*a*x. Dit is lineair in x.quote:Op maandag 19 november 2007 15:07 schreef luckass het volgende:
ff natuurkundig vraagje:
Op het SE ging het over een sleetje dat van een helling af ging.
Nu moest je een grafiek maken: Ek uitzetten tegen de afstand.
Wrijving was gemiddeld 25N.
Nu dacht ik dat het een kromme lijn was (als wortel(x)),
maar iemand anders dacht dat het een rechte lijn was.
Ik begin zelf eigenlijk ook steeds meer te twijfelen.
Anyone?
Met de stoot gaat het nog makkelijker: delta Ek = F*s. Omdat F niet van s afhangt, is Ek lineair in s.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt, dat dacht ik dus ook, alleen jammer dat het me pas 2 uur na het examen te binnen schietquote:Op maandag 19 november 2007 17:07 schreef GlowMouse het volgende:
[..]
We hebben a=F/m, dus a is constant (F is namelijk de component langs de helling van de zwaartekracht, minus de wrijvingskracht en de massa verandert ook niet). Omdat x=1/2*a*t2, geldt dat t=sqrt(2x/a). Vul in: Ek = 1/2*m*v2 = 1/2*m*(at)2 = 1/2*m*a2*2x/a = m*a*x. Dit is lineair in x.
Met de stoot gaat het nog makkelijker: delta Ek = F*s. Omdat F niet van s afhangt, is Ek lineair in s.


Goed, ook even van mijn kant een vraagje. Thermodynamica, deze keer
Stel, ik heb een gesloten cilinder, die ik aan beide uiteinden op verschillende temperaturen houdt. Tk en Th, laat ik ze zo noemen. In deze cilinder plaats ik een zeer los passende cilinder, zodat er als het ware 2 temperatuurzones onstaan. De lucht kan echter vrij langs deze grens bewegen. Is het nu mogelijk de druk die in het vat ontstaat te berekenen? Of ontstaan er 2 aparte drukgebieden?
overigens wel raar dat ik in 6 vwo NT nog steeds niets geen thermodynamica heb gehad...
Stel, ik heb een gesloten cilinder, die ik aan beide uiteinden op verschillende temperaturen houdt. Tk en Th, laat ik ze zo noemen. In deze cilinder plaats ik een zeer los passende cilinder, zodat er als het ware 2 temperatuurzones onstaan. De lucht kan echter vrij langs deze grens bewegen. Is het nu mogelijk de druk die in het vat ontstaat te berekenen? Of ontstaan er 2 aparte drukgebieden?
overigens wel raar dat ik in 6 vwo NT nog steeds niets geen thermodynamica heb gehad...
Moeder, waar is mijn pils?


Je vraag is me niet helemaal duidelijk. In de cilinder doe je nog een cilinder, of moet dit een zuiger zijn die geen wrijving ondervindt? Het laatste kan ik me beter voorstellen. In dat geval moet je nog aannemen dat de warmteoverdracht door die zuiger verwaarloosbaar is, anders wordt het erg lastig. De druk is in de hele cilinder nu hetzelfde, anders zou de zuiger wel bewegen. De preciese druk laat zich berekenen met pV=nrT, en hangt af van de begincondities.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De cilinder zit dus zo los in het vat dat de lucht er vrij langs kan stromen, echter, er ontstaan wel 2 aparte temperatuurzones. Nu is mijn vraag, welke druk komt er in het gehele vat, of ontstaan er 2 drukgebieden die met pV = nRT te berekenen zijn.
Moeder, waar is mijn pils?


Twee drukgebieden kan natuurlijk hier ook niet: dan zou de lucht wel gaan stromen. Wat je hier krijgt, is geen statische situatie. Lucht wordt verwarmd en kan naar een koeler gebied stromen om weer af te koelen. Dit gaat oneindig lang door. De uiteindelijke druk zal zich dan denk ik niet zomaar laten berekenen, Misschien kun je wat met de gemiddelde temperatuur proberen. Maar ook de startcondities zijn nog van belang.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |



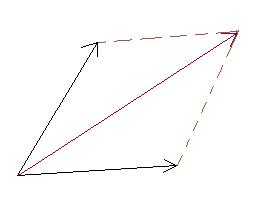







 .
.

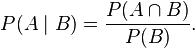 en
en  maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
