SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik heb weer eens een proef gedaan bij scheikunde met heel aantal vragen erbij. De meeste snap ik natuurlijk. Echter zit er ook een vraag bij die ik niet snap. De volgende:
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.


* Mergequote:Op zondag 30 september 2007 12:34 schreef Curri het volgende:
Ik heb weer eens een proef gedaan bij scheikunde met heel aantal vragen erbij. De meeste snap ik natuurlijk. Echter zit er ook een vraag bij die ik niet snap. De volgende:
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
[afbeelding]
[afbeelding]
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


Ik heb ook weer eens een vraag.
Ik heb de volgende functie:
ABS((1+0.5f)/(1-0.5f)) <= 1
(ABS = absolute waarde dus, en <= betekent kleiner of gelijk.)
waarbij f een complex getal is. Ik moet het gebied in het complex vlak schetsen wat hier aan voldoet. Het lukt alleen niet. Ik mag ook MATLAB gebruiken, dat zou zelfs wat handiger zijn, omdat ik nog een aantal van dit soort dingen moet oplossen.
Ik heb de volgende functie:
ABS((1+0.5f)/(1-0.5f)) <= 1
(ABS = absolute waarde dus, en <= betekent kleiner of gelijk.)
waarbij f een complex getal is. Ik moet het gebied in het complex vlak schetsen wat hier aan voldoet. Het lukt alleen niet. Ik mag ook MATLAB gebruiken, dat zou zelfs wat handiger zijn, omdat ik nog een aantal van dit soort dingen moet oplossen.


quote:Op zondag 7 oktober 2007 14:08 schreef Schuifpui het volgende:
Ik heb ook weer eens een vraag.
Ik heb de volgende functie:
ABS((1+0.5f)/(1-0.5f)) <= 1
(ABS = absolute waarde dus, en <= betekent kleiner of gelijk.)
waarbij f een complex getal is. Ik moet het gebied in het complex vlak schetsen wat hier aan voldoet. Het lukt alleen niet. Ik mag ook MATLAB gebruiken, dat zou zelfs wat handiger zijn, omdat ik nog een aantal van dit soort dingen moet oplossen.
Is f complex in de zin dat f = (a + b*i), of complex in de zin dat f = b*i? Dat eerste lijkt me een rottige vergelijking opleveren… dat laatste is volgens mij wel te doen als je je realiseert dat complexe deling opgelost kan worden door met de complex geconjugeerde te vermenigvuldigen… dan kun je de complexe modulus uitrekenen en berekenen wat b moet zijn.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Toch. Dacht al dat zoiets eruit zou komen, door wat proberen.. Tijdens college met andere voorbeelden kwam er altijd iets met een rondje uit. Toch nog maar eens checken of de afleiding goed is. Thanks anyway.
[edit] dan gelijk nog maar een:
ABS(1+f+1/2f^2) <= 1
Ik zie dus gewoon echt niet goed hoe ik dit moet doen.
[ Bericht 29% gewijzigd door Schuifpui op 07-10-2007 17:12:27 ]
[edit] dan gelijk nog maar een:
ABS(1+f+1/2f^2) <= 1
Ik zie dus gewoon echt niet goed hoe ik dit moet doen.
[ Bericht 29% gewijzigd door Schuifpui op 07-10-2007 17:12:27 ]


PWS vraagje, Ik heb voor mijn profielwerkstuk een elektromotor gebouwd die tevens als generator zou moeten werken. Nou als elektromotor werkt hij prima, maar als generator geeft hij in een stroomkring alleen maar spanning en géén stroom. Hoe is dit mogelijk?
De motor loopt op gelijkspaning, heeft 2 permanente magneten van 0,4 Tesla.
Op de as zitten de spoelen, 2 om precies te zijn ieder van 60 windingen.
Omdat de motor op gelijkspanning loopt zit er dus ook een commutator op, daar zou volgens mij misschien wel het probleem kunnen liggen. Maar toch, hoe kan het dat er wel spanning loopt maar geen stroom als je de as ronddraait.
De motor loopt op gelijkspaning, heeft 2 permanente magneten van 0,4 Tesla.
Op de as zitten de spoelen, 2 om precies te zijn ieder van 60 windingen.
Omdat de motor op gelijkspanning loopt zit er dus ook een commutator op, daar zou volgens mij misschien wel het probleem kunnen liggen. Maar toch, hoe kan het dat er wel spanning loopt maar geen stroom als je de as ronddraait.


Ten eerste: Spanning loopt niet, die staat over twee punten.quote:Op donderdag 11 oktober 2007 20:21 schreef DJ90 het volgende:
PWS vraagje, Ik heb voor mijn profielwerkstuk een elektromotor gebouwd die tevens als generator zou moeten werken. Nou als elektromotor werkt hij prima, maar als generator geeft hij in een stroomkring alleen maar spanning en géén stroom. Hoe is dit mogelijk?
De motor loopt op gelijkspaning, heeft 2 permanente magneten van 0,4 Tesla.
Op de as zitten de spoelen, 2 om precies te zijn ieder van 60 windingen.
Omdat de motor op gelijkspanning loopt zit er dus ook een commutator op, daar zou volgens mij misschien wel het probleem kunnen liggen. Maar toch, hoe kan het dat er wel spanning loopt maar geen stroom als je de as ronddraait.
Ten tweede, wat heb je bij generatorwerking aan de klemmen van de motor aangesloten?Alleen een multimeter? Dan meet je inderdaad alleen spanning.
Tip: Een weerstand zet spanning over de klemmen om in een stroom, geheel volgens de wet van Ohm.
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Meet je de spanning wanneer de generator op de stroomkring is aangesloten? Wanneer je het los van elkaar meet, kan de spanning direct inzakken wanneer je de stroomkring sluit omdat het vermogen niet toereikend is maar dat merk je direct wanneer je gelijktijdig meet.
Meet je wel gelijktijdig, dan is de stroomkring waarschijnlijk niet gesloten.
Meet je wel gelijktijdig, dan is de stroomkring waarschijnlijk niet gesloten.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Beetje laat antwoord...quote:Op zondag 30 september 2007 12:34 schreef Curri het volgende:
Ik heb weer eens een proef gedaan bij scheikunde met heel aantal vragen erbij. De meeste snap ik natuurlijk. Echter zit er ook een vraag bij die ik niet snap. De volgende:
Bereken uit de titratiegegevens het aantal mg acetylsaliclzuur in 1 bruistablet
Hier zitten volgende gegevens bij:
(afbeeldingen toegevoegd..)
[afbeelding]
[afbeelding]
Bij buretstand 2 is het verschil 14,67.
Iemand enig idee hoe ik dus dat aantal mg bereken? Eventueel met uitwerking en antwoord..
Bvd,
C.
Als je de overmaat OH- toevoegt en het kookt, wordt het zuurrest-ion omgezet naar het salycilaat-ion en azijnzuur. Vervolgens ga je terugtitreren met HCl om te kijken hoeveel van de OH- niet gereageerd heeft. Het verschil tussen het aantal mol OH- dat je in het begin hebt toegevoegd (25 mL 0,05M oplossing) en het aantal mol HCl dat je getitreerd hebt, geeft de concentratie acetylsalicylzuur (a.k.a. aspirine).
Je hebt in beide metingen 25mL 0,05M NaOH toegevoegd. Dit is 25×0,05=1,25 mmol OH-
Vervolgens ga je terugtitreren met HCl. De eerste keer kom je uit op 14 mL (×0.05013 M = 0,70182 mmol) en de tweede keer kom je uit op 14,67 mL (×0.05013 M = 0,735407 mmol)
Vervolgens trek je deze van elkaar af:
1,25 mmol NaOH - 0,702 mmol HCl = 0,548 mmol aspirine
1,25 mmol NaOH - 0,735 mmol HCl = 0,515 mmol aspirine
je hebt 10 mL oplossing C gebruikt, dus de concentraties aspirine in oplossing C waren:
0,548mmol / 10mL = 0,0548 M
en dus 0,0515 M in de tweede meting.
Om oplossing C te maken zijn 25 tabletten opgelost in 1 liter, 1M is hetzelfde als 1 mol per liter, dus om het aantal mol in een tablet te vinden, moet je de boel delen door 25. Vervolgens vermenigvuldigen met de molecuulmassa om de hoeveelheid aspirine in een tablet in grammen te krijgen... De molecuulmassa schijnt 180,16 g/mol te zijn
0,0548 / 25 = 2,19 mmol × 180,16 g/mol = 394,6 mg per tablet
0,0515 / 25 = 2,06 mmol × 180,16 g/mol = 371,1 mg per tablet
Dat moet je vervolgens controleren met de waarde die op het pakje bruistabletten staat.
Bestiality sure is a fun thing to do. But I have to say this as a warning to you:
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.


vraagje. 1.08^n=100/75
wat is n en hoe bereken je dat?
wat is n en hoe bereken je dat?
Sei wachsam,
Fall nicht auf sie rein! Paß auf, daß du deine Freiheit nutzt,
Die Freiheit nutzt sich ab, wenn du sie nicht nutzt!
Fall nicht auf sie rein! Paß auf, daß du deine Freiheit nutzt,
Die Freiheit nutzt sich ab, wenn du sie nicht nutzt!


Dat is het teken voor een sommatie. In plaats van a_1+a_2+a_3+...+a_n schrijft men vaakquote:Op dinsdag 16 oktober 2007 13:30 schreef alors het volgende:
n00bvraagje, maar wat betekent deze?
[ afbeelding ]
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Okay bedankt, ik had al zo'n vermoeden.quote:Op dinsdag 16 oktober 2007 14:17 schreef keesjeislief het volgende:
[..]
Dat is het teken voor een sommatie. In plaats van a_1+a_2+a_3+...+a_n schrijft men vaak
[ afbeelding ].
know'm sayin?
×
word? word.
×
word? word.


Ik moet twee integralen oplossen, kom op twee manieren op verschillende antwoorden uit en Maple kan hem niet oplossen. Zou iemand het voor me uit kunnen rekenen?


productregel bij integreren, altijd lastig. Truc hierbij is te beseffen dat we hier alleen naar e integreren en dat elke andere term zonder e als constante beschouwd dient te worden.
INT (x-e)
------------------------------------------ de =
((x-e)2 + y2)
INT -(x-e)
----------------------------------------- d(x-e) =
((x-e)2 + y2)
(eerst de x voor de d halen en compenseren voor minteken)
1/2 * ln | ((x-e)2 + y2) |
(compenseren voor het differentieren van (x-e)2 naar e, dus een factor -1/2 meenemen. Remember: (-x2)' = -2x )
De tweede is er eentje die je op een dwaalspoor zal zetten. De truc hier is in te zien dat we met de afgeleide van een arctangens-functie te maken hebben. So let's try that way.
INT y
------------------------------------------ de =
(x-e)2 + y2
INT -y
------------------------------------------ d(x-e) =
(x-e)2 + y2
(eerst x voor de d halen en compenseren voor het minteken)
INT (1/y2 * -y)
--------------------------------------------------------------- d(x-e) =
(1/y2) * ((x-e)2 + y2)
(teller en noemer met (1/y2) vermenigvuldigen)
INT y*1/y2
--------------------------------- d(x-e) =
((x-e)/y)2 + 1
(de door de vermenigvuldiging ontstane breuken in teller en noemer apart uitdelen)
INT (-y/y2) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
INT (-1/y) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
(teller als aparte factor van de breuk afsplitsen en -y/y2 tot -1/y uitschrijven)
-1*arctan ((x-e)/y)
(integratie uitvoeren. Note to self; VERGEET VOORAL NIET DAT DE AFGELEIDE VAN ( (x-e)/y ) NAAR e, -e/y IS, MORON!!)
tering, dat was een zware bevalling zeg.
[ Bericht 6% gewijzigd door harrypiel op 18-10-2007 21:31:07 ]
INT (x-e)
------------------------------------------ de =
((x-e)2 + y2)
INT -(x-e)
----------------------------------------- d(x-e) =
((x-e)2 + y2)
(eerst de x voor de d halen en compenseren voor minteken)
1/2 * ln | ((x-e)2 + y2) |
(compenseren voor het differentieren van (x-e)2 naar e, dus een factor -1/2 meenemen. Remember: (-x2)' = -2x )
De tweede is er eentje die je op een dwaalspoor zal zetten. De truc hier is in te zien dat we met de afgeleide van een arctangens-functie te maken hebben. So let's try that way.
INT y
------------------------------------------ de =
(x-e)2 + y2
INT -y
------------------------------------------ d(x-e) =
(x-e)2 + y2
(eerst x voor de d halen en compenseren voor het minteken)
INT (1/y2 * -y)
--------------------------------------------------------------- d(x-e) =
(1/y2) * ((x-e)2 + y2)
(teller en noemer met (1/y2) vermenigvuldigen)
INT y*1/y2
--------------------------------- d(x-e) =
((x-e)/y)2 + 1
(de door de vermenigvuldiging ontstane breuken in teller en noemer apart uitdelen)
INT (-y/y2) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
INT (-1/y) * 1
----------------------------------------------------------- d(x-e) =
((x-e)/y)2 + 1)
(teller als aparte factor van de breuk afsplitsen en -y/y2 tot -1/y uitschrijven)
-1*arctan ((x-e)/y)
(integratie uitvoeren. Note to self; VERGEET VOORAL NIET DAT DE AFGELEIDE VAN ( (x-e)/y ) NAAR e, -e/y IS, MORON!!)
tering, dat was een zware bevalling zeg.
[ Bericht 6% gewijzigd door harrypiel op 18-10-2007 21:31:07 ]


Thanks
Die eerste heb ik idd ook. De tweede had ik als:
arctan((-x+e)/y), dat kwam uit maple. Ik ga er nog even naar kijken, nogmaals dank.
Die eerste heb ik idd ook. De tweede had ik als:
arctan((-x+e)/y), dat kwam uit maple. Ik ga er nog even naar kijken, nogmaals dank.


Kan wel kloppen; de arctangens functie is namelijk symmetrisch voor de bewerking (x,y) -> -(-x,y)quote:Op dinsdag 16 oktober 2007 22:29 schreef Schuifpui het volgende:
Thanks
Die eerste heb ik idd ook. De tweede had ik als:
arctan((-x+e)/y), dat kwam uit maple. Ik ga er nog even naar kijken, nogmaals dank.


P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1)
Maar hoe bereken je P(Y = 1 EN X3 = 1)?
edit
Dit dus:
en maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
[ Bericht 54% gewijzigd door R-Mon op 17-10-2007 19:55:47 ]
Maar hoe bereken je P(Y = 1 EN X3 = 1)?
edit
Dit dus:
en maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
[ Bericht 54% gewijzigd door R-Mon op 17-10-2007 19:55:47 ]
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Eindelijk weer kansrekening
Die tweede regel die je daar noemt geldt voor twee onafhankelijke gebeurtenissen A en B. En wanneer A en B onafhankelijk zijn, is het inderdaad logisch dat geldt P(A|B) = P(A). Zijn A en B niet onafhankelijk, dan zul je P(A en B) op een andere manier uit moeten rekenen.
Voorbeeld: een worp met een dobbelsteen, we kijken naar het aantal oogjes. A = 'minder dan 4', B = 'gelijk aan 1'.
Nu geldt dat P(A) = 1/2, P(B) = 1/6, P(A en B) = 1/2 (dus niet P(A en B) = P(A)P(B), A en B zijn immers niet onafhankelijk). P(A|B) = 1.
Die tweede regel die je daar noemt geldt voor twee onafhankelijke gebeurtenissen A en B. En wanneer A en B onafhankelijk zijn, is het inderdaad logisch dat geldt P(A|B) = P(A). Zijn A en B niet onafhankelijk, dan zul je P(A en B) op een andere manier uit moeten rekenen.
Voorbeeld: een worp met een dobbelsteen, we kijken naar het aantal oogjes. A = 'minder dan 4', B = 'gelijk aan 1'.
Nu geldt dat P(A) = 1/2, P(B) = 1/6, P(A en B) = 1/2 (dus niet P(A en B) = P(A)P(B), A en B zijn immers niet onafhankelijk). P(A|B) = 1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedankt GlowMouse, helaas is mijn som niet zo makkelijk om te schrijven naar een dobbelstenen voorbeeld... Het is van Machine Learning, ik moet (moest, deadline was gisteravond, geen colleges meer voor tentamen) gegeven een train set een conditional entropy uitrekenen... Dit is wat ik heb gedaan:
Train set
x1 x2 x3 y
WearsBlack SavesPrincess HorseColour GoodOrEvil
No Yes Black Good
Yes No Black Evil
No No White Good
Yes Yes Brown Good
Schattingen van de kansen
Y=1 Good Estimate P = 3/4
Y=2 Evil Estimate P = 1/4
P(X3 = 1 (Black)) = 1/2
P(X3 = 2 (White)) = ¼
P(X3 = 3 (Brown)) = ¼
Definitie conditional entropy
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
Versimpelen
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1) = P(Y = 1) * P(X3 = 1) / P(Y = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(Y = 2) = P(Y = 2) * P(X3 = 1) / P(Y = 2) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
Uitrekenen
p = ¾ * 1/2 / ¾ = 1/2
q = ¼ * 1/2 / ¼ = 1/2
H(Y | X3 = 1) = 1/2 * -log2 (1/2) + 1/2 * -log2 (1/2)
log(1/2) = -0,30
log2 (1/2) = log(1/2) / log 2 = -1
H(Y | X3 = 1) = 1/2 * -1 + 1/2 * -1 = -1
Het lijkt mij dus niet dat X en Y onafhankelijk zijn, of wel?
Train set
x1 x2 x3 y
WearsBlack SavesPrincess HorseColour GoodOrEvil
No Yes Black Good
Yes No Black Evil
No No White Good
Yes Yes Brown Good
Schattingen van de kansen
Y=1 Good Estimate P = 3/4
Y=2 Evil Estimate P = 1/4
P(X3 = 1 (Black)) = 1/2
P(X3 = 2 (White)) = ¼
P(X3 = 3 (Brown)) = ¼
Definitie conditional entropy
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
Versimpelen
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1) = P(Y = 1) * P(X3 = 1) / P(Y = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(Y = 2) = P(Y = 2) * P(X3 = 1) / P(Y = 2) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
Uitrekenen
p = ¾ * 1/2 / ¾ = 1/2
q = ¼ * 1/2 / ¼ = 1/2
H(Y | X3 = 1) = 1/2 * -log2 (1/2) + 1/2 * -log2 (1/2)
log(1/2) = -0,30
log2 (1/2) = log(1/2) / log 2 = -1
H(Y | X3 = 1) = 1/2 * -1 + 1/2 * -1 = -1
Het lijkt mij dus niet dat X en Y onafhankelijk zijn, of wel?
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Dit gaat fout: P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(Y = 1)
Je moet hier delen door P(X3=1).
Daarnaast: ik heb nooit met entropy's gewerkt, dus ik weet niet of je hieruit al kunt afleiden dat X3 en Y onafhankelijk zijn. Dit kun je in ieder geval aantonen via P(Y=a en X3=b) = P(Y=a)P(X3=b) voor iedere a en b (heb dit zelf niet gecheckt).
Je moet hier delen door P(X3=1).
Daarnaast: ik heb nooit met entropy's gewerkt, dus ik weet niet of je hieruit al kunt afleiden dat X3 en Y onafhankelijk zijn. Dit kun je in ieder geval aantonen via P(Y=a en X3=b) = P(Y=a)P(X3=b) voor iedere a en b (heb dit zelf niet gecheckt).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Aargh ik zie het ook nu... Ook zo leuk als er in de formule X en Y wordt gebruikt maar in het voorbeeld Y en X. Dit komt er nu uit:
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(X3 = 1) = P(Y = 1) * P(X3 = 1) / P(X3 = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(X3 = 1) = P(Y = 2) * P(X3 = 1) / P(X3 = 1) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
p = ¾ * 1/2 / 1/2 = ¾
q = ¼ * 1/2 / 1/2 = ¼
H(Y | X3 = 1) = 3/4 * -log2 (3/4) + 3/4 * -log2 (3/4)
log(3/4) = -0,12
log2 (3/4) = log(3/4) / log 2 = -0,42
H(Y | X3 = 1) = ¾ * -0,42 + ¾ * -0,42 = -0,63
Verder maakt het weinig uit, bedankt in elk geval.
H(Y | X3 = 1) = P(Y = 1 | X3 = 1) *(-log2 (P(Y = 1 | X3 = 1)) + P(Y = 2 | X3 = 1) *(-log2 (P(Y = 2 | X3 = 1))
P(Y = 1 | X3 = 1) = P(Y = 1 EN X3 = 1) / P(X3 = 1) = P(Y = 1) * P(X3 = 1) / P(X3 = 1) = p
P(Y = 2 | X3 = 1) = P(Y = 2 EN X3 = 1) / P(X3 = 1) = P(Y = 2) * P(X3 = 1) / P(X3 = 1) = q
H(Y | X3 = 1) = p * -log2 (p) + q * -log2 (q)
p = ¾ * 1/2 / 1/2 = ¾
q = ¼ * 1/2 / 1/2 = ¼
H(Y | X3 = 1) = 3/4 * -log2 (3/4) + 3/4 * -log2 (3/4)
log(3/4) = -0,12
log2 (3/4) = log(3/4) / log 2 = -0,42
H(Y | X3 = 1) = ¾ * -0,42 + ¾ * -0,42 = -0,63
Verder maakt het weinig uit, bedankt in elk geval.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Help
Ik probeer iets in Mathematica te implementeren, maar het lukt me gewoon echt niet.
Ik wil eigenlijk een soort van loop maken waarin ik steeds achtereenvolgens 2 functies laat uitvoeren waarvan de 1e gebruik maakt van het resultaat van de tweede en de tweede gebruik maakt van het resultaat van de eerste (volgen jullie het nog ?):
Ik voer een functie f1 uit op een plaatje 'alle cellen' -> resultaat: plaatje 'cel 1'
Ik pas plaatje 'alle cellen' aan door pixels uit plaatje 'cel 1' te verwijderen
etc etc.
Dit doe ik totdat Apply[Plus,'alle cellen'] 0 oplevert.
Uiteindelijk wil ik een lijst met alle plaatjes 'cel 1'
De afzonderlijke stappen werken, alleen moet ik ze steeds zelf opnieuw evalueren omdat ik geen loop heb .
Ik probeer iets in Mathematica te implementeren, maar het lukt me gewoon echt niet.
Ik wil eigenlijk een soort van loop maken waarin ik steeds achtereenvolgens 2 functies laat uitvoeren waarvan de 1e gebruik maakt van het resultaat van de tweede en de tweede gebruik maakt van het resultaat van de eerste (volgen jullie het nog ?):
Ik voer een functie f1 uit op een plaatje 'alle cellen' -> resultaat: plaatje 'cel 1'
Ik pas plaatje 'alle cellen' aan door pixels uit plaatje 'cel 1' te verwijderen
etc etc.
Dit doe ik totdat Apply[Plus,'alle cellen'] 0 oplevert.
Uiteindelijk wil ik een lijst met alle plaatjes 'cel 1'
De afzonderlijke stappen werken, alleen moet ik ze steeds zelf opnieuw evalueren omdat ik geen loop heb .


Ja ik heb ook weer wat... Afleiden met natuurlijke deductie:
1. ~(p of q) |- ~(p en q)
het verste dat ik kom:
3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
En kan iemand deze controleren, dat ik niks illegaals doe:
2. (p en q) of ~p |- p -> q
1. ~(p of q) |- ~(p en q)
het verste dat ik kom:
| 1 2 3 4 5 6 7 8 9 10 11 | ... |------------------ (box) | ~~(p en q) (assumptie) | p en q (~~eliminatie) | p (en-eliminatie1) | q (en-eliminatie2) | ... | contradictie |---------------------- ~(p en q) (PBC) |
3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
En kan iemand deze controleren, dat ik niks illegaals doe:
2. (p en q) of ~p |- p -> q
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | - |------------------------box 2 | p en q (assumptie) 3 | p (en-eliminatie1 op 2) 4 | q (en-eliminatie2 op 2) - | |-----------------------------box2 5 | | p (assumptie) 6 | | q (copy 4) - | |----------------------------- 7 | p -> q (impl.-introductie 5-6) - |------------------------------- - |-------------------------------box 8 | ~p (assumptie) - | |-----------------------------box2 9 | | p (assumptie) 10 | | ~p (copy 8) 11 | | contradictie (~eliminatie 9,10) 12 | | p (contr. eliminatie 11) 13 | | q (assumptie) - | |---------------------------- 14 | p -> q (impl. introductie 9-13) - |----------------------------- 15 p -> q (of eliminatie 1-7,8-14) |
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Niet meer nodig Je kan dus opeenvolgens dingen uit laten voeren door ze in een for loopje te zetten met méérdere functies.quote:Op zaterdag 20 oktober 2007 12:02 schreef vliegtuigje het volgende:
Help
Ik probeer iets in Mathematica te implementeren, maar het lukt me gewoon echt niet.
Ik wil eigenlijk een soort van loop maken waarin ik steeds achtereenvolgens 2 functies laat uitvoeren waarvan de 1e gebruik maakt van het resultaat van de tweede en de tweede gebruik maakt van het resultaat van de eerste (volgen jullie het nog ?):
Ik voer een functie f1 uit op een plaatje 'alle cellen' -> resultaat: plaatje 'cel 1'
Ik pas plaatje 'alle cellen' aan door pixels uit plaatje 'cel 1' te verwijderen
etc etc.
Dit doe ik totdat Apply[Plus,'alle cellen'] 0 oplevert.
Uiteindelijk wil ik een lijst met alle plaatjes 'cel 1'
De afzonderlijke stappen werken, alleen moet ik ze steeds zelf opnieuw evalueren omdat ik geen loop heb .
For[i=1,i>=blabla,i++,{functie1,functie2}]
Misschien heeft iemand er nog wat aan


Dit heb ik al lang niet gedaan, ik ken de terminologie die je gebruikt ook niet helemaal, zoals 'LEM', maar ik denk dat de truc 'm erin zit dat je inderdaadquote:Op zaterdag 20 oktober 2007 16:24 schreef R-Mon het volgende:
Ja ik heb ook weer wat... Afleiden met natuurlijke deductie:
1. ~(p of q) |- ~(p en q)
het verste dat ik kom:
[ code verwijderd ]
~~(p & q) aanneemt, dan zoals jij doet (p & q) afleidt, daarvan of p of q afleidt, dan een of introduceert (voorgesteld door 'v'), dus dat je dan p v q hebt, en dat is in tegenspraak met je premisse. Dus ~~(p & q) leidt tot een contradictie.
Ik weet niet wat LEM is.quote:3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
Lijkt me correct.quote:En kan iemand deze controleren, dat ik niks illegaals doe:
2. (p en q) of ~p |- p -> q
[ code verwijderd ]
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Overigens kan ik hier wel een afleiding voor geven:quote:Op zaterdag 20 oktober 2007 16:24 schreef R-Mon het volgende:
3. ~(p en q) |- ~p of ~q "(hint: gebruik LEM)" zelfde als de vorige, hoe ga je met die negatie in de premisse om?
1) ~(p en q) (premisse)
2) ~(~p of ~q) (aanname)
3) ~p (aanname)
4) ~p of ~q (of-introductie op de vorige aanname)
5) p (contradictie met aanname 2, dus onder 2 is aanname 3 ongeldig)
6) ~q (aanname, gaat natuurlijk hetzelfde als ~p)
7) ~p of ~q (of-introductie op de vorige)
8) q (contradictie met aanname 2, dus onder 2 is aanname 6 ongeldig)
9) p en q (uit 5 en 8)
10) ~p of ~q (p en q is een contradictie met de premisse (1), en dat komt door de aanname (2), want die geldt op het moment, die aanname is dus fout, en de elimineren we).
Met jouw 'LEM' regel worden vast een paar stappen samengevat in dit proces.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ah p v q is wat ik zocht, stom dat ik die niet zag.quote:Op zaterdag 20 oktober 2007 20:50 schreef Iblis het volgende:
[..]
Dit heb ik al lang niet gedaan, ik ken de terminologie die je gebruikt ook niet helemaal, zoals 'LEM', maar ik denk dat de truc 'm erin zit dat je inderdaad
~~(p & q) aanneemt, dan zoals jij doet (p & q) afleidt, daarvan of p of q afleidt, dan een of introduceert (voorgesteld door 'v'), dus dat je dan p v q hebt, en dat is in tegenspraak met je premisse. Dus ~~(p & q) leidt tot een contradictie.
LEM is Law of Excluded Middle, p v ~p. Bedankt iigquote:[..]
Ik weet niet wat LEM is.
[..]
Lijkt me correct.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


ik moet voor een moment generating function een limit uitrekenen, maar ik snap niet hoe dit moet. Bijvoorbeeld deze functie
Als ik het in maple stop, of een waarde heel dicht bij 0 uitreken, dan weet ik dat als x naar 0 gaat, de functie 1 wordt. Maar Ik moet het eigenlijk algebraisch oplossen. Hoe doe ik dat?
Als ik het in maple stop, of een waarde heel dicht bij 0 uitreken, dan weet ik dat als x naar 0 gaat, de functie 1 wordt. Maar Ik moet het eigenlijk algebraisch oplossen. Hoe doe ik dat?


Is dit niet op te lossen met de stelling van l'Hospital? Ik dacht dat je dan de afgeleide van de teller en de noemer een nieuwe breuk moet maken en daar de lim x->0 van moet uit rekenen. Die stelling kan je dacht ik gebruiken wanneer de teller en de noemer allebei 0 zijn of oneindig.
/Edit: Spuitelf
Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link .
/Edit2: En omdat ik vandaag helemaal in een goede bui ben en dit best een makkelijke opgave is:
lim x->0 (e2x-1)/(2x) = lim x->0 (2e2x)/2 = 1
/Edit3: En omdat ik het calculus boek toch moest pakken voor m'n tentamen over anderhalve week:
(Ik gok dat je het boek Calculus: early transcendentals 5e editie ook hebt) Op p.308 staat de boel uitgelegd, enjoy
[ Bericht 27% gewijzigd door fart op 21-10-2007 17:54:58 ]
/Edit: Spuitelf
Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link .
/Edit2: En omdat ik vandaag helemaal in een goede bui ben en dit best een makkelijke opgave is:
lim x->0 (e2x-1)/(2x) = lim x->0 (2e2x)/2 = 1
/Edit3: En omdat ik het calculus boek toch moest pakken voor m'n tentamen over anderhalve week:
(Ik gok dat je het boek Calculus: early transcendentals 5e editie ook hebt) Op p.308 staat de boel uitgelegd, enjoy
[ Bericht 27% gewijzigd door fart op 21-10-2007 17:54:58 ]


Moet je voor die afgeleide de quotientregel niet toepassen?quote:Op zondag 21 oktober 2007 17:42 schreef fart het volgende:
Is dit niet op te lossen met de stelling van l'Hospital? Ik dacht dat je dan de afgeleide van de teller en de noemer een nieuwe breuk moet maken en daar de lim x->0 van moet uit rekenen. Die stelling kan je dacht ik gebruiken wanneer de teller en de noemer allebei 0 zijn of oneindig.
/Edit: Spuitelf
Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link .
/Edit2: En omdat ik vandaag helemaal in een goede bui ben en dit best een makkelijke opgave is:
lim x->0 (e2x-1)/(2x) = lim x->0 (2e2x)/2 = 1
/Edit3: En omdat ik het calculus boek toch moest pakken voor m'n tentamen over anderhalve week:
(Ik gok dat je het boek Calculus: early transcendentals 5e editie ook hebt) Op p.308 staat de boel uitgelegd, enjoy
Zou dan zijn: (4xe^(2x)-2e^(2x)+2)/(4x²)
Ik weet overigens ook niet hoe je die limiet verder moet doen, dat is meer de reden dat ik hier keek


Nope, je komt dan ook niets verder trouwens, aangezien lim x->0 van die functie nog steeds 0/0 is.quote:Op zondag 21 oktober 2007 18:15 schreef Fhm het volgende:
[..]
Moet je voor die afgeleide de quotientregel niet toepassen?
Zou dan zijn: (4xe^(2x)-2e^(2x)+2)/(4x²)
Ik weet overigens ook niet hoe je die limiet verder moet doen, dat is meer de reden dat ik hier keek
De stelling van l'Hôpital kan je gebruiken wanneer je een limiet van een breuk moet nemen en je 0/0 krijgt of oneindig/oneindig. Wanneer je dat krijgt, moet je de de teller als functie zien en de noemer ook.
Je hebt dan lim x->c f(x)/g(x) wat dan gelijk is aan lim x->c f'(x)/g'(x)


Oh ja, tuurlijk, wat dom!quote:Op zondag 21 oktober 2007 18:19 schreef fart het volgende:
[..]
Nope, je komt dan ook niets verder trouwens, aangezien lim x->0 van die functie nog steeds 0/0 is.
De stelling van l'Hôpital kan je gebruiken wanneer je een limiet van een breuk moet nemen en je 0/0 krijgt of oneindig/oneindig. Wanneer je dat krijgt, moet je de de teller als functie zien en de noemer ook.
Je hebt dan lim x->c f(x)/g(x) wat dan gelijk is aan lim x->c f'(x)/g'(x)
Dank je


Topic gemerged.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>


tnx, met deze regel is het inderdaad op te lossen. Ik zie dat deze regel alleen beperkt te gebruiken is, namelijk als beide expressies tot 0 of inf evalueren bij dezelfde c. Stel dat er geen -1 maar -2 in de expressie had gestaan, dan was dit dus niet het geval geweest en had ik het niet kunnen oplossen? Of zie ik nu wat over het hoofd?quote:Op zondag 21 oktober 2007 17:42 schreef fart het volgende:Het is dus inderdaad de stelling van l'Hôpital. Hier de wiki link.


In dat geval zou je de stelling niet juist toepassen. In het algemeen is de limiet van de afgeleide van een functie ook niet gelijk aan de limiet van die functie zelf.quote:Op zondag 21 oktober 2007 18:15 schreef Fhm het volgende:
[..]
Moet je voor die afgeleide de quotientregel niet toepassen?
Zou dan zijn: (4xe^(2x)-2e^(2x)+2)/(4x²)
Ik weet overigens ook niet hoe je die limiet verder moet doen, dat is meer de reden dat ik hier keek
In dat geval was je nog sneller klaar geweest, want dan kun je direct zien wat de limiet is. Gaat de teller naar oneindig en de noemer naar 5, dan gaat bijvoorbeeld de hele breuk naar oneindig. Gaat de teller naar 1 en de noemer naar 2, dan gaat de hele breuk naar 1/2. Het wordt alleen lastig wanneer de noemer naar 0 gaat, en de teller niet.quote:Op zondag 21 oktober 2007 21:54 schreef jeroenisblij het volgende:
[..]
tnx, met deze regel is het inderdaad op te lossen. Ik zie dat deze regel alleen beperkt te gebruiken is, namelijk als beide expressies tot 0 of inf evalueren bij dezelfde c. Stel dat er geen -1 maar -2 in de expressie had gestaan, dan was dit dus niet het geval geweest en had ik het niet kunnen oplossen? Of zie ik nu wat over het hoofd?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel je hebt een vectorveld xi+yj+zk en je wilt de arbeid weten van een deetltje dat langs de parabool y=x^2, z=0 beweegt, van x=-1 tot x=2.... hoe weet ik dan hoe dat pad eruit ziet? maw, hoe parametriseer ik iets van (x,y,z) naar iets in de vorm van t. Als ik dat weet word het gewoon:
Int (Fds)= Int ( F(c(t)) . c'(t)) dt
Kortom: is er een makkelijke algemene methode om te parametriseren?
Int (Fds)= Int ( F(c(t)) . c'(t)) dt
Kortom: is er een makkelijke algemene methode om te parametriseren?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Dat zal wel goed zijn, maar mijn vraag is meer, hoe kom ik tot die/een parametrisatie.. is daar een standaard werkwijze voor of is dat "inzicht" of wat? Ik bedoel.... dx/dt kan je uitreken, Fds kan je uitrekenen, maar hoe kom je voor een willekeurig pad uitgedrukt in x,y,z-coordinaten naar een pad in t?quote:Op maandag 22 oktober 2007 10:44 schreef thabit het volgende:
Wat dacht je van (x,y,z) = (t,t^2,0), waarbij t van -1 tot 2 loopt?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


In het algemeen is dat niet zo eenvoudig, maar in dit geval staat er gewoon "y = uitdrukking in x" en ook "z = uitdrukking in x" (weliswaar een die x niet gebruikt maar dat doet er niet toe).


Ok, dus je noemt 1 van de variablen x,y,z t en dan schrijf je de rest ook om naar tquote:Op maandag 22 oktober 2007 12:03 schreef thabit het volgende:
In het algemeen is dat niet zo eenvoudig, maar in dit geval staat er gewoon "y = uitdrukking in x" en ook "z = uitdrukking in x" (weliswaar een die x niet gebruikt maar dat doet er niet toe).
y= x^2 z= 0*x, neem x = t, geeft c(t)=t,t^2,0
Beetje jammer dat het niet eenvoudig is, want ik heb het heel vaak nodig, maar ik snap het nooit
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


De voorbeelden die je voor je tentamensommen enzo moet uitwerken zijn altijd wel eenvoudig. Er bestaat alleen geen "algemene methode" voor (buiten het feit dat je ook nog eens goed moet definieren wat je met een parametrisatie bedoelt).


A path in R^n is a map c: [a,b] -> R^n; it is a path in the plane if n=2 and a path in the space if n=3. The collection C of points c(t) as t varies in [a,b] is called a curve, and c(a) and c(b) are its endpoints. The path c is said to parametrize the curve C.quote:Op maandag 22 oktober 2007 12:26 schreef thabit het volgende:
De voorbeelden die je voor je tentamensommen enzo moet uitwerken zijn altijd wel eenvoudig. Er bestaat alleen geen "algemene methode" voor (buiten het feit dat je ook nog eens goed moet definieren wat je met een parametrisatie bedoelt).
Voor de tentamensommen, tjsa... zo makkelijk vind ik het niet, maar ik zal er nog even verder op oefenen... alsi k iets tegenkom wat echt niet werkt vraag ik het hier wel aan de experts
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Boek weggooien.quote:Op maandag 22 oktober 2007 12:50 schreef maniack28 het volgende:
[..]
A path in R^n is a map c: [a,b] -> R^n; it is a path in the plane if n=2 and a path in the space if n=3. The collection C of points c(t) as t varies in [a,b] is called a curve, and c(a) and c(b) are its endpoints. The path c is said to parametrize the curve C.


Staat er niet bij, maar hij is idd wel differentieerbaar (Dat komt laterquote:Op maandag 22 oktober 2007 13:38 schreef thabit het volgende:
[..]
Boek weggooien.. Dit lijkt me niet hoe je het wilt definieren namelijk. Je zal toch enkele voorwaarden op c moeten veronderstellen. Een pad zal toch op z'n minst continu moeten zijn en in veel toepassingen stuksgewijs differentieerbaar.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Hi,
ik heb ff een vraagje over de representativiteit van mijn steekproef onder ouderen in de gemeente.
Ik wil een enquete houden onder ouderen vanaf 55 jaar. De gemeente telt ongeveer 17700 ouderen.
Nu wil de gemeente dat ik de enquete aan 1500 respondenten verstuur. Alleen al om het feit dat ik de enquete per post verstuur, zou ik eigenlijk de helft minder respondenten willen benaderen(moet namelijk alles handmatig invoeren).
Maar is de steekproef nog steeds representatief wanneer ik 750 of minder ouderen zou benaderen?
Iemand enig idee waar die grens ligt?
[ Bericht 0% gewijzigd door Fibonacci22 op 23-10-2007 11:27:52 ]
ik heb ff een vraagje over de representativiteit van mijn steekproef onder ouderen in de gemeente.
Ik wil een enquete houden onder ouderen vanaf 55 jaar. De gemeente telt ongeveer 17700 ouderen.
Nu wil de gemeente dat ik de enquete aan 1500 respondenten verstuur. Alleen al om het feit dat ik de enquete per post verstuur, zou ik eigenlijk de helft minder respondenten willen benaderen(moet namelijk alles handmatig invoeren).
Maar is de steekproef nog steeds representatief wanneer ik 750 of minder ouderen zou benaderen?
Iemand enig idee waar die grens ligt?
[ Bericht 0% gewijzigd door Fibonacci22 op 23-10-2007 11:27:52 ]


Voor zover mij bekend bestaat er geen hard criterium om te bepalen of een steekproef representatief is. Zolang de steekproef aselect is, kun je vrij eenvoudig statistisch juiste uitspraken doen maar representativiteit is daarbij niet gegarandeerd.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Je kunt toch uitrekenen wat je betrouwbaarheid wordt onder bepaalde aannames. Ik weet niet welke betrouwbaarheid je wilt.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Ik heb ook een domme vraag. Bij de chikwadraat test.
Als je berekende chi waarde, hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
Als je berekende chi waarde, hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
"AAAAAHH ZENNE MOAT, WOARST VLEISCH"


Hier het volgende:
lengte van een lijnstuk berekenen:
Zie het lijnstuk gegeven door de formule y=-(a/b)x+a
De lengte is simpel te berekenen door gebruik van de formule van pythagoras: L = sqrt(a^2 + b^2)
Maar kan het ook door te integreren???
Stel ik benader de lijn door een trappetje.
De lengte van één 'tree' is dx - dy = dx + dx (dy/dx) = dx - dx [ -(a/b) ] = dx + dx (a/b) = dx [ 1 + (a/b) ]
Integreren van x = 0 tot x = b geeft:
[ 1 + (a/b) ] b = b + a
WTF???????
Blijkbaar mag ik de benadering van de trap niet toepassen, maar waarom niet?
Bij het gebruik van infinitesimale traptreden (in de limiet van dx --> 0 ) valt toch de trap gelijk met de lijn?
Wie helpt mij?
lengte van een lijnstuk berekenen:
Zie het lijnstuk gegeven door de formule y=-(a/b)x+a
De lengte is simpel te berekenen door gebruik van de formule van pythagoras: L = sqrt(a^2 + b^2)
Maar kan het ook door te integreren???
Stel ik benader de lijn door een trappetje.
De lengte van één 'tree' is dx - dy = dx + dx (dy/dx) = dx - dx [ -(a/b) ] = dx + dx (a/b) = dx [ 1 + (a/b) ]
Integreren van x = 0 tot x = b geeft:
[ 1 + (a/b) ] b = b + a
WTF???????
Blijkbaar mag ik de benadering van de trap niet toepassen, maar waarom niet?
Bij het gebruik van infinitesimale traptreden (in de limiet van dx --> 0 ) valt toch de trap gelijk met de lijn?
Wie helpt mij?


Moet het niet dx + dy zijn voor de lengte van één tree?
Daarmee is je probleem niet opgelost, maar wordt het verhaal "iets" anders.
[ 1 + (a/b) ] b = b + a wordt dan [ 1 - (a/b) ] b = b - a
Of begrijp ik het nu niet?
Daarmee is je probleem niet opgelost, maar wordt het verhaal "iets" anders.
[ 1 + (a/b) ] b = b + a wordt dan [ 1 - (a/b) ] b = b - a
Of begrijp ik het nu niet?
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Dat dacht ik ook maar dat zou HELEMAAL nergens op slaanquote:Op dinsdag 23 oktober 2007 20:06 schreef -J-D- het volgende:
Moet het niet dx + dy zijn voor de lengte van één tree?
Daarmee is je probleem niet opgelost, maar wordt het verhaal "iets" anders.


ik wil een formule differienteiren
dit is de formule:
f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
ik dacht kettingregel = f(g(x)) = f'(g(x)) * g'(x)
dus eerst de afgeleide van sinx (cosx)zonder wat er binnenin staat veranderen
f'(x) 4cos (1/2 PI x - 1/4 PI)
dan het gedeelte tussen haakjes doen (1/2 PI x - 1/4 PI)
is 1/2 PI want 1/4PI is gewoon een getal en mag je dus wegahalen?
dan komt mijn afgeleide op
f'(x) 4cos (1/2 PI x - 1/4 PI) * 1/2 PI
dus kan ik nog even de hele formule keer 1/2 PI doen of niet?
dit is de formule:
f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
ik dacht kettingregel = f(g(x)) = f'(g(x)) * g'(x)
dus eerst de afgeleide van sinx (cosx)zonder wat er binnenin staat veranderen
f'(x) 4cos (1/2 PI x - 1/4 PI)
dan het gedeelte tussen haakjes doen (1/2 PI x - 1/4 PI)
is 1/2 PI want 1/4PI is gewoon een getal en mag je dus wegahalen?
dan komt mijn afgeleide op
f'(x) 4cos (1/2 PI x - 1/4 PI) * 1/2 PI
dus kan ik nog even de hele formule keer 1/2 PI doen of niet?


f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
f'(g(x)) = 4/2 PI * cos (1/2 PI x - 1/4 PI) = 2 * PI * cos (1/2 PI x - 1/4 PI)
g'(x) = 1/2 PI
geeft f'(g(x))*g'(x) = PI^2 * cos (1/2 PI x - 1/4 PI)
Wat je zegt klopt dus idd, alleen je bent vergeten datgeen wat voor de afgeleide komt van de sin x (dus 1/2 PI * 4 = 2 PI) erbij te zetten, waardoor je een factor 2 PI te weinig hebt...
edit - wat je op het eind zegt is dus waar
edit2 - probeer het in nette stappen waarin je f(x),g(x) en g'(x) netjes opschrijft en definieert, dat scheelt fouten!
f'(g(x)) = 4/2 PI * cos (1/2 PI x - 1/4 PI) = 2 * PI * cos (1/2 PI x - 1/4 PI)
g'(x) = 1/2 PI
geeft f'(g(x))*g'(x) = PI^2 * cos (1/2 PI x - 1/4 PI)
Wat je zegt klopt dus idd, alleen je bent vergeten datgeen wat voor de afgeleide komt van de sin x (dus 1/2 PI * 4 = 2 PI) erbij te zetten, waardoor je een factor 2 PI te weinig hebt...
edit - wat je op het eind zegt is dus waar
edit2 - probeer het in nette stappen waarin je f(x),g(x) en g'(x) netjes opschrijft en definieert, dat scheelt fouten!
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Ja, dat kan.quote:Op dinsdag 23 oktober 2007 20:05 schreef Greus het volgende:
Hier het volgende:
lengte van een lijnstuk berekenen:
[ afbeelding ]
Zie het lijnstuk gegeven door de formule y=-(a/b)x+a
De lengte is simpel te berekenen door gebruik van de formule van pythagoras: L = sqrt(a^2 + b^2)
Maar kan het ook door te integreren???
Hoe kom je hier nu bij? De lengte van een tree is niet dx - dy, bovendien gaat het niet om de lengtes van de treden, de totale lengte hiervan is immers constant als je de treden kleiner maakt en niet gelijk aan de lengte van je lijnstuk.quote:Stel ik benader de lijn door een trappetje.
De lengte van één 'tree' is dx - dy = dx + dx (dy/dx) = dx - dx [ -(a/b) ] = dx + dx (a/b) = dx [ 1 + (a/b) ]
Bij rectificatie (de bepaling van de lengte van een curve (of in dit geval een rechte) verdeel je het interval waarover je de lengte wil bepalen in stukjes en benader je de curve door lijnsegmentjes. Volgens Pythagoras is de lengte van één zo'n segmentje:quote:Wie helpt mij?
√(Δx2 + Δy2) = Δx√(1 + (Δy/Δx)2)
Deze segmentjes sommeer je dan, waarbij de benadering beter wordt naarmate Δx kleiner wordt. Oftewel, de lengte van de curve over een interval [a,b] wordt gegeven door
∫ab √(1 + (f'(x))2)dx
[ Bericht 0% gewijzigd door Riparius op 23-10-2007 22:19:16 ]


okee gelukkig dat t kloptquote:Op dinsdag 23 oktober 2007 20:54 schreef maniack28 het volgende:
f(x)= 12 + 4 sin(1/2 PI x - 1/4 PI)
f'(g(x)) = 4/2 PI * cos (1/2 PI x - 1/4 PI) = 2 * PI * cos (1/2 PI x - 1/4 PI)
g'(x) = 1/2 PI
geeft f'(g(x))*g'(x) = PI^2 * cos (1/2 PI x - 1/4 PI)
Wat je zegt klopt dus idd, alleen je bent vergeten datgeen wat voor de afgeleide komt van de sin x (dus 1/2 PI * 4 = 2 PI) erbij te zetten, waardoor je een factor 2 PI te weinig hebt...
edit - wat je op het eind zegt is dus waar
edit2 - probeer het in nette stappen waarin je f(x),g(x) en g'(x) netjes opschrijft en definieert, dat scheelt fouten!
kun je me misschien uitleggen hoe je precies ziet wanner ketting/som/die andere regel te gebruiken?


Je moet goed weten wat een functie is, en dan kun je gewoon kijken hoe je je functie kunt schrijven: is dat het product van twee functies, of zijn het twee functies die na elkaar worden uitgevoerd.quote:Op dinsdag 23 oktober 2007 22:00 schreef Principessa.Farfalla het volgende:
[..]
kun je me misschien uitleggen hoe je precies ziet wanner ketting/som/die andere regel te gebruiken?
Als de berekende waarde groter is dan de kritische waarde zit je bij de chi-kwadraattoets in het kritieke gebied (bij andere toetsen kan het kritieke gebied ook links van de kritieke waarde zitten), wat betekent dat je de nulhypothese verwerpt. Wat de nulhypothese is, ligt bij een chi-kwadraattoets niet vast omdat er verschillende chi-kwadraattoetsen bestaan. Voordat je gaat toetsen, moet je die hypothesen uiteraard goed definieren. Je conclusie zal zijn dat er waarschijnlijk geen verband bestaat.quote:Op dinsdag 23 oktober 2007 19:31 schreef znarch het volgende:
Ik heb ook een vraag. Bij de chikwadraat test.
Als je berekende chi waarde hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hmmm.. even kijken of ik dat kan. Je hebt de kettingregel en de productregel. De kettingregel gebruik je als je de afgeleide wilt weten van een "samengestelde" functie. In de meeste gevallen functies die zijn samengesteld uit cosinus/sinus/exponent/logaritme en iets waarvan je de cosinus/sinus/exponent/logarimte neemt waarvan de afgeleide ongelijk aan 0 is.quote:Op dinsdag 23 oktober 2007 22:00 schreef Principessa.Farfalla het volgende:
[..]
okee gelukkig dat t klopt
kun je me misschien uitleggen hoe je precies ziet wanner ketting/som/die andere regel te gebruiken?
Dus in gevallen als bereken de afgeleide van:
f(x) = cos (2*x+1) of f(x) = sin (x^2) of f(x) = exp (x^2+4x)
Maar eigenlijk kan je hem altijd toepassen. Neem bijv. f(x) = sin (2*x). Gebruik de kettingregel:
f'(g(x)) = cos (2*x)
g'(x) = 2
Geeft f'(x)= 2 cos (2*x), maar goed, dat kan je zonder de kettingregel ook doen
De productregel gebruik je enkel als de functie een product van 2 andere functies is, dus bijv. f(x) = x^2 * cos (x) of f(x) = 1/x * exp (x). Je leidt dan eerst naar de een af (houdt de ander constant) en daarna nara de ander af en houdt de een constant: (fg)' = f'g+fg'
Je kan ze ook combineren en beide gebruiken, probeer maar eens de afgeleide van f(x) = x^3 * cos (x^2) te berekenen.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Volgens mij is er een significant verschil als de waarde groter is dan de kritieke waarde. Dacht ik...quote:Op dinsdag 23 oktober 2007 19:31 schreef znarch het volgende:
Ik heb ook een domme vraag. Bij de chikwadraat test.
Als je berekende chi waarde, hoger is dan de gevonde kritische waarde (dmv vrijheidsgraden) Is er dan een verband of niet ?
Anders geformuleerd: Wanner was er nu een verband ? Als de berekende (chi) waarde groter is dan de kritische waarde (dmv vrijheidsgraden) of juist andersom ?
Theories come and theories go. The frog remains


Zelf ook nog een vraagje:
Ben in R bezig met wat data-mining, maar heb een vraag waar ik niet uitkom. Ik moet voor een dataset de zogenaamde hyperedges berekenen. Nu is dit niet zo moelijk, want het algoritme wat ik gebruik, kan dit gewoon. Maar een andere vraag is: wat is een hyperedgeset?
Als ik google op hyperedgeset krijg ik als results alleen de papers/websites waar ik juist de vraag vandaan heb, maar daar staat alleen in uitgelegd dat het algoritme wat ik gebruik dat kan uitrekenen (en hoe), maar niet wat het is.
Is er hier toevallig iemand die weet wat een hyperedgeset is???
Ben in R bezig met wat data-mining, maar heb een vraag waar ik niet uitkom. Ik moet voor een dataset de zogenaamde hyperedges berekenen. Nu is dit niet zo moelijk, want het algoritme wat ik gebruik, kan dit gewoon. Maar een andere vraag is: wat is een hyperedgeset?
Als ik google op hyperedgeset krijg ik als results alleen de papers/websites waar ik juist de vraag vandaan heb, maar daar staat alleen in uitgelegd dat het algoritme wat ik gebruik dat kan uitrekenen (en hoe), maar niet wat het is.
Is er hier toevallig iemand die weet wat een hyperedgeset is???
Theories come and theories go. The frog remains


Een hyperedge is een gewoon een kant die meerdere punten tegelijk met elkaar verbindt. En die set is dan natuurlijk de verzameling van hyperedges.quote:Op dinsdag 23 oktober 2007 22:49 schreef Bioman_1 het volgende:
Zelf ook nog een vraagje:
Ben in R bezig met wat data-mining, maar heb een vraag waar ik niet uitkom. Ik moet voor een dataset de zogenaamde hyperedges berekenen. Nu is dit niet zo moelijk, want het algoritme wat ik gebruik, kan dit gewoon. Maar een andere vraag is: wat is een hyperedgeset?
Als ik google op hyperedgeset krijg ik als results alleen de papers/websites waar ik juist de vraag vandaan heb, maar daar staat alleen in uitgelegd dat het algoritme wat ik gebruik dat kan uitrekenen (en hoe), maar niet wat het is.
Is er hier toevallig iemand die weet wat een hyperedgeset is???


Leo  Jij ook weer hier?
Jij ook weer hier?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Halloquote:
@wolfje: ik dacht al iets in die richting, maar kon dat niet 'vertalen' in data-mining taal. Het gaat over frequent itemsets, closed frequent itemsets, maximal frequent itemsets en hyperedgesets. En ik zou dus graag in data-mining jargon uitleggen wat een hyperedgeset is.
Theories come and theories go. The frog remains


Heey:) ik heb weer wat vragen:
Nu even ringen:
soms hoort f(1)=1 bij de defnitie van ringhomomorfisme en soms wordt f(1)=1 als extra eis genomen en in dit geval wordt t ringhomomorfisme een lichaamshomomorfisme... Waarom is het niet één definitie?
Zij p een priemgetal ongelijk aan 5. Stel dat p = x^2 + 5y^2 met x en y in Z. Te bewijzen: p is 1 of 9 mod 20.
Het is wel duidelijk dat of x of y even zijn. Maar volgens mij moet ik nog aantonen dat y even moet zijn...
hoe gaat dit verder?
groetjes
Nu even ringen:
soms hoort f(1)=1 bij de defnitie van ringhomomorfisme en soms wordt f(1)=1 als extra eis genomen en in dit geval wordt t ringhomomorfisme een lichaamshomomorfisme... Waarom is het niet één definitie?
Zij p een priemgetal ongelijk aan 5. Stel dat p = x^2 + 5y^2 met x en y in Z. Te bewijzen: p is 1 of 9 mod 20.
Het is wel duidelijk dat of x of y even zijn. Maar volgens mij moet ik nog aantonen dat y even moet zijn...
hoe gaat dit verder?
groetjes
verlegen :)


Dat is categorie-theorie. Wijze heren met grijze baarden hebben ooit bedacht dat je wiskundige objecten veel beter kunt bestuderen door ze in een categorie te stoppen en er morfismen tussen te gooien dan 'los', en eigenlijk meer op de morfismen te focussen dan op de objecten. Een inzicht dat mijns inziens getuigt van een uitzonderlijke genialiteit. Dan maakt het natuurlijk wel uit welke morfismen je tussen je objecten definieert; zoiets ligt nog geenszins vast bij de definitie van de objecten. Voor verschillende en/of toepassingen van een theorie blijken soms verschillende definities van de morfismen het best te werken.quote:Op donderdag 25 oktober 2007 20:59 schreef teletubbies het volgende:
Heey:) ik heb weer wat vragen:
Nu even ringen:
soms hoort f(1)=1 bij de defnitie van ringhomomorfisme en soms wordt f(1)=1 als extra eis genomen en in dit geval wordt t ringhomomorfisme een lichaamshomomorfisme... Waarom is het niet één definitie?


Merk eerst op dat p niet gelijk is aan 2 en dat y niet congruent is met 0 mod p.quote:Op donderdag 25 oktober 2007 20:59 schreef teletubbies het volgende:
Zij p een priemgetal ongelijk aan 5. Stel dat p = x^2 + 5y^2 met x en y in Z. Te bewijzen: p is 1 of 9 mod 20.
Het is wel duidelijk dat of x of y even zijn. Maar volgens mij moet ik nog aantonen dat y even moet zijn...
hoe gaat dit verder?
groetjes
Kwadraten zijn 0 of 1 mod 4, hieruit volgt eenvoudig dat p zelf 1 mod 4 moet zijn. Verder zien we dat -5=(x/y)^2 mod p, dus -5 is een kwadraatrest (ongelijk aan 0) mod p. Dan pluggen we nu de kwadratische reciprociteitswet in: (-5/p) = (p/5) want p=1 mod 4. Nu is (p/5)=1 desda p = 1 of 4 mod 5. Tezamen met p = 1 mod 4 geeft de Chinese Reststelling nu p = 1 of 9 mod 20.


Z/(Z-5) + 1/3 = -5/(5-Z)quote:Op dinsdag 30 oktober 2007 15:21 schreef duncannn het volgende:
Z/(Z-5) + 1/3 = -5/(5-Z)
hoe moet je dit ook alweer oplossen.
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
-Z (Z-5)/(Z-5) - 1/3 (Z-5) = -5
-Z - 1/3Z +5/3 = -5 = -15/3
-4/3Z= - 20/3
Z= 5
Even invullen en je komt dat de conclusie dat ik ergens een fout maak, want delen door 0 mag niet
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


NEE!quote:Op dinsdag 30 oktober 2007 16:40 schreef maniack28 het volgende:
[..]
Z/(Z-5) + 1/3 = -5/(5-Z)
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
-Z (Z-5)/(Z-5) - 1/3 (Z-5) = -5
Als je beide leden met (Z-5) vermenigvuldigt krijg je in het rechterlid +5, niet -5.


Ah kijk, slordigheidje, maar goed..het idee is helder, kandie het verder zelf wel uitwerkenquote:Op dinsdag 30 oktober 2007 17:09 schreef Riparius het volgende:
[..]
NEE!
Als je beide leden met (Z-5) vermenigvuldigt krijg je in het rechterlid +5, niet -5.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Ja. Je vergelijking heeft overigens geen oplossing. Had je dat ook al gezien?quote:Op dinsdag 30 oktober 2007 17:31 schreef maniack28 het volgende:
[..]
Ah kijk, slordigheidje, maar goed..het idee is helder, kandie het verder zelf wel uitwerken


Nope, had hem niet uitgewerkt met de -, ben te luiquote:Op dinsdag 30 oktober 2007 17:33 schreef Riparius het volgende:
[..]
Ja. Je vergelijking heeft overigens geen oplossing. Had je dat ook al gezien?
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Z/(Z-5) + 1/3 = -5/(5-Z)
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
Z/(Z-5) + 1/3 = 5/(Z-5)
Z + 1/3(Z-5) = 5
4/3Z-5/3=5
4/3Z= 6 2/3
Z = 5
.... kom ik er weer op
Ik had het trouwens wel goed gedaan, ik had gedeeld door vermenigvuldigd met -(Z-5), daarom kwam er in mijn oorspronkelijke antwoord een - voor de termen Z en 1/3(Z-5) aan de linkerkant, rechts bleef er gewoon -5 staan, nu doe ik het andersom en komt er nog steeds 5 uit. Ben ik nu blond of is de werkwijze gewoon goed en is er geen oplossing
Zie in dat:
(5-Z) = -(Z-5)
Geeft:
Z/(Z-5) + 1/3 = 5/(Z-5)
Z + 1/3(Z-5) = 5
4/3Z-5/3=5
4/3Z= 6 2/3
Z = 5
.... kom ik er weer op
Ik had het trouwens wel goed gedaan, ik had gedeeld door vermenigvuldigd met -(Z-5), daarom kwam er in mijn oorspronkelijke antwoord een - voor de termen Z en 1/3(Z-5) aan de linkerkant, rechts bleef er gewoon -5 staan, nu doe ik het andersom en komt er nog steeds 5 uit. Ben ik nu blond of is de werkwijze gewoon goed en is er geen oplossing
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Je werkwijze is ditmaal juist, en de oplossingsverzameling van het stelsel is inderdaad leeg.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


De vorige keer ook, zie toelichting post boven je... maakt niet uit of je links vervangt met - of rechts met + of omgedraaid... komt op hetzelfde neerquote:Op dinsdag 30 oktober 2007 18:46 schreef GlowMouse het volgende:
Je werkwijze is ditmaal juist, en de oplossingsverzameling van het stelsel is inderdaad leeg.
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Je kunt het ook zo bekijken: vermenigvuldig teller en noemer van de breuk in het rechterlid met -1, dan heb je:quote:Op dinsdag 30 oktober 2007 18:51 schreef maniack28 het volgende:
[..]
De vorige keer ook, zie toelichting post boven je... maakt niet uit of je links vervangt met - of rechts met + of omgedraaid... komt op hetzelfde neer
Z/(Z-5) + 1/3 = 5/(Z-5)
Rechterlid herleiden op nul geeft dan:
(Z-5)/(Z-5) + 1/3 = 0
Nu is (Z-5)/(Z-5) gelijk aan 1 als Z ongelijk is aan 5, en niet gedefinieerd als Z=5, dus is het meteen duidelijk dat de vergelijking geen oplossing kan hebben.


Oeh nice  Ik geloof dat degene die de vraag vroeg nu wel genoeg antwoord heeft
Ik geloof dat degene die de vraag vroeg nu wel genoeg antwoord heeft 
Cause I'd rather continue my trip to the top of the mountain then freeze to death in the valley.


Hoii
ik zoek een leuk bewijsje van de kwadratische reciprociteit..
 zijn er bewijzen mbv ringen theorie of iets dergelijks?
zijn er bewijzen mbv ringen theorie of iets dergelijks?
Ik heb wel analytische bewijzen gevonden.. maar variatie doet geen kwaad
ik zoek een leuk bewijsje van de kwadratische reciprociteit..
Ik heb wel analytische bewijzen gevonden.. maar variatie doet geen kwaad
verlegen :)


Er is een bewijs met algebraische getaltheorie. De essentie is dat Z[wortel((-1/p)p)] een deelring van Z[zeta_p] is. De ontbinding van q in Z[wortel((-1/p)p)] hangt samen met (p/q) en de ontbinding van q in Z[zeta_p] hangt samen met (q/p). Maar om hiervan de details uit te werken moet je nog wel wat doen.
Er is ook een bewijs dat het volgende gebruikt: vermenigvuldiging met p geeft een permutatie van Z/qZ. Het teken van deze permutatie is precies (p/q). Alleen hoe dat bewijs verder ging weet ik niet meer precies, maar als je in Google iets als permutation quadratic reciprocity intikt dan vind je het wel.
En zo zijn er veel en veel meer bewijzen.
Er is ook een bewijs dat het volgende gebruikt: vermenigvuldiging met p geeft een permutatie van Z/qZ. Het teken van deze permutatie is precies (p/q). Alleen hoe dat bewijs verder ging weet ik niet meer precies, maar als je in Google iets als permutation quadratic reciprocity intikt dan vind je het wel.
En zo zijn er veel en veel meer bewijzen.


op je grafische rekenmachine kan je bijvoorbeeld het aantal keren dat een dobbelsteen gegooid word weergeven,
Math -> PRB -> RandInt (
je doet dan 1,6,50 ( 1 voor het begin 6 voor het eindgetal, het aantal ogen dus en 50x wil ik werpen)
dus randInt(1,6,50)
je krijgt dan (2,5,6,2,1,2,4,5 etc etc 50 getallen lang
nu heeft die leraar uitgelegt hoe ik hier een staafgrafiek van krijg, maar ik weet het niet meer
help me plz
Math -> PRB -> RandInt (
je doet dan 1,6,50 ( 1 voor het begin 6 voor het eindgetal, het aantal ogen dus en 50x wil ik werpen)
dus randInt(1,6,50)
je krijgt dan (2,5,6,2,1,2,4,5 etc etc 50 getallen lang
nu heeft die leraar uitgelegt hoe ik hier een staafgrafiek van krijg, maar ik weet het niet meer
help me plz


Je bedoelt waarschijnlijk een histogram. Maar volgens mij is dat een ***werk wat gewoon veel handelingen vereist:
RandInt(1,6,50) -> L1
Seq(X,1,6) -> L3
SUM(L1=1) -> L3(1)
SUM(L1=2) -> L3(2)
. .
. .
SUM(L1=6) -> L3(6)
Daarna kun je via stat plot een histogram tekenen met Freq L2 en Xlist L3.
Met L1, L2 en L3 lijsten (bv via 2nd, 1).
RandInt(1,6,50) -> L1
Seq(X,1,6) -> L3
SUM(L1=1) -> L3(1)
SUM(L1=2) -> L3(2)
. .
. .
SUM(L1=6) -> L3(6)
Daarna kun je via stat plot een histogram tekenen met Freq L2 en Xlist L3.
Met L1, L2 en L3 lijsten (bv via 2nd, 1).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Een product dat uit 25 onderdelen bestaat, moet worden gemonteerd. Voor elk onderdeel geldt dat één op de driehonderd ervan een fout heeft. Hoe groot is de kans op goede producten?
Het is wat te lang geleden voor me, ik heb al eerder zo'n vraagstuk voor mijn snufferd gehad maar ik kom er gewoon niet uit.
Hellup!!
Het is wat te lang geleden voor me, ik heb al eerder zo'n vraagstuk voor mijn snufferd gehad maar ik kom er gewoon niet uit.
Hellup!!


kans op goed product = goed EN goed EN goed EN (...) = goed^25 = (299/300)^25 = 0,9199quote:Op woensdag 31 oktober 2007 18:23 schreef Cracka-ass het volgende:
Een product dat uit 25 onderdelen bestaat, moet worden gemonteerd. Voor elk onderdeel geldt dat één op de driehonderd ervan een fout heeft. Hoe groot is de kans op goede producten?
Het is wat te lang geleden voor me, ik heb al eerder zo'n vraagstuk voor mijn snufferd gehad maar ik kom er gewoon niet uit.
Hellup!!
kans op fout product = fout OF fout OF fout OF (...) = 25 * (1/300) = 0,0833
kans op goed product + kans op fout product = 0,9199 + 0,0833 = ~ 1 door onnauwkeurige afronding
Maar pin me er niet op vast
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Even een hele simpele van de SAT Test:
If the sum of the consecutive integers from -22 tot x, inclusive, is 72, what is the value of x?
Antwoord: 25
Hoe?
If the sum of the consecutive integers from -22 tot x, inclusive, is 72, what is the value of x?
Antwoord: 25
Hoe?


Dit is fout. Je berekening voor een goed product is correct, maar voor een fout product niet.quote:Op woensdag 31 oktober 2007 19:16 schreef R-Mon het volgende:
[..]
kans op goed product = goed EN goed EN goed EN (...) = goed^25 = (299/300)^25 = 0,9199
kans op fout product = fout OF fout OF fout OF (...) = 25 * (1/300) = 0,0833
kans op goed product + kans op fout product = 0,9199 + 0,0833 = ~ 1 door onnauwkeurige afronding
Maar pin me er niet op vast
Je hebt een fout product als het eerste onderdeel fout gaat en de rest goed. Of het tweede onderdeel, en de rest goed, of het eerste én tweede onderdeel, en de rest goed. De som van al deze mogelijkheden (incl. de mogelijkheid dat alles fout gaat, welke (1/300)^25 is) wordt gewoon gegeven door 1 - (299/300)^25.
Wat jij uitrekent is niet correct. Stel, je hebt een dobbelsteen, wat is de kans dat je één keer 6 gaat, terwijl je 10x gooit? Dat is niet 1/6 + 1/6 ... en dat 10 keer, dat zou groter zijn dan 1. Want de kans dat je de eerste keer weliswaar 6 gooit is wel 1/6e, maar er zit bij die mogelijkheden ook al een mogelijkheid dat je de 2e keer 6 gooit. En die mogelijkheid tel je weer mee bij de volgende 1/6e. Je telt zaken dubbel. Dat doe jij ook.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


som van y = -22 tot y = 22 over y = 0quote:Op woensdag 31 oktober 2007 19:42 schreef nickybol het volgende:
Even een hele simpele van de SAT Test:
If the sum of the consecutive integers from -22 tot x, inclusive, is 72, what is the value of x?
Antwoord: 25
Hoe?
dus x = 22 levert nul op, kleinere x levert iets negatiefs op.
72 - 23 = 49
49 - 24 = 25
25 - 25 = 0
tada
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties


Ok bedankt voor de controle. En Cracka-ass heeft z'n antwoordquote:Op woensdag 31 oktober 2007 19:52 schreef Iblis het volgende:
[..]
Dit is fout. Je berekening voor een goed product is correct, maar voor een fout product niet.
Je hebt een fout product als het eerste onderdeel fout gaat en de rest goed. Of het tweede onderdeel, en de rest goed, of het eerste én tweede onderdeel, en de rest goed. De som van al deze mogelijkheden (incl. de mogelijkheid dat alles fout gaat, welke (1/300)^25 is) wordt gewoon gegeven door 1 - (299/300)^25.
Wat jij uitrekent is niet correct. Stel, je hebt een dobbelsteen, wat is de kans dat je één keer 6 gaat, terwijl je 10x gooit? Dat is niet 1/6 + 1/6 ... en dat 10 keer, dat zou groter zijn dan 1. Want de kans dat je de eerste keer weliswaar 6 gooit is wel 1/6e, maar er zit bij die mogelijkheden ook al een mogelijkheid dat je de 2e keer 6 gooit. En die mogelijkheid tel je weer mee bij de volgende 1/6e. Je telt zaken dubbel. Dat doe jij ook.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


Als je een eiwit denatureerd veranderd de tertiaire structuur. Bij het koken van serumeiwit verbreken de S-S bruggen en is de tertiaire structuur permanent verneukt. Waarom is het eiwit dan wit geworden?


Ik heb
Y(X) = e^2x / x+2
Y’ = (2x+3)e^2x / (x+2)^ 2
maar hoe kom je eraan, de quotient regel toepassen. maar ik kom er niet meer uit.
Y(X) = e^2x / x+2
Y’ = (2x+3)e^2x / (x+2)^ 2
maar hoe kom je eraan, de quotient regel toepassen. maar ik kom er niet meer uit.
winnaar wielerprono 2007 :) Last.FM


quotientregel = (noemer * afgeleide teller - teller * afgeleide noemer) / noemer in het kwadraat.
n * at = (x+2) * 2e2x
t * an = e2x * 1 = e2x
n*at - t*an = (x+2) * 2e2x - e2x
= 2(x+2)e2x - e2x
= (2x+4)e2x- e2x
= (2x+3)e2x
(n*at-t*an)/n2 = (2x+3)e2x / (x+2)2
n * at = (x+2) * 2e2x
t * an = e2x * 1 = e2x
n*at - t*an = (x+2) * 2e2x - e2x
= 2(x+2)e2x - e2x
= (2x+4)e2x- e2x
= (2x+3)e2x
(n*at-t*an)/n2 = (2x+3)e2x / (x+2)2
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.





 .
.

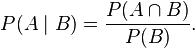 en
en  maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?
maar dan krijg je P(A) * P(B) / P(B) = P(A) dat slaat toch nergens op?