SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
If x is an integer and 2 < x < 7 , how many different triangles are there with sides of lengths 2, 7 and x?
Het antwoord moet zijn een. Waarom?
Het antwoord moet zijn een. Waarom?
x mag dus 3, 4, 5 of 6 zijn.
x = 3 kan niet, want dan heb je een driehoek met zijde 2, 3, 7 en dan kan niet. (De 2 kleinste zijden moeten samen meer zijn dan de langste zijde)
x = 4 idem.
x = 5 wordt ook lastig Een driehoek met zijde van 2, 5 en 7 is niet haalbaar. Probeer maar eens te tekenen. Zie het als een graaf. Een omweg kan nooit korter of evenlang zijn als rechtstreeks.
x= 6 is de enige die kan.
x = 3 kan niet, want dan heb je een driehoek met zijde 2, 3, 7 en dan kan niet. (De 2 kleinste zijden moeten samen meer zijn dan de langste zijde)
x = 4 idem.
x = 5 wordt ook lastig Een driehoek met zijde van 2, 5 en 7 is niet haalbaar. Probeer maar eens te tekenen. Zie het als een graaf. Een omweg kan nooit korter of evenlang zijn als rechtstreeks.
Een driehoek met zijde van 2, 5 en 7 is niet haalbaar. Probeer maar eens te tekenen. Zie het als een graaf. Een omweg kan nooit korter of evenlang zijn als rechtstreeks.x= 6 is de enige die kan.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.
Thnx die stelling had ik nog niet gezien (achteraf gezien heel logisch)quote:Op donderdag 20 september 2007 09:31 schreef Riparius het volgende:
...Hiermee wordt bedoeld dat je op het verlengde van ED een punt F moet bepalen, zodanig dat ED∙EF gelijk is aan het kwadraat van de lengte van de raaklijn aan de cirkel vanuit punt E. Deze raaklijn heb je niet getekend in je figuur.
De reden om punt F zo te bepalen is gelegen in een bekende stelling van Euclides (Boek III, stelling 36).
...
die stelling had ik nog niet gezien (achteraf gezien heel logisch)
Ja. Alleen zijn we er hiermee nog niet. Zoals gezegd hebben we EB∙EA = ED∙EF, waaruit volgt dat de punten A,B,D,F op een cirkel liggen, of anders gezegd, ABDF is een koordenvierhoek (begrijp je dat ook?). Nu zijn de overstaande hoeken in een koordenvierhoek supplementair, en dus is hoek FAE gelijk aan hoek BDE. So far so good. Maar dan zegt Heath:quote:Op donderdag 20 september 2007 21:24 schreef Ogala het volgende:
[..]
Thnx die stelling had ik nog niet gezien (achteraf gezien heel logisch)
En dat zie ik dus even niet. Ik begrijp met name niet wat Heath bedoelt met the alternate segment. Die term is niet gebruikelijk, en wordt verder in het hele betoog ook niet gebruikt, zodat niet duidelijk is waar hij op doelt. Nu jij weer ...quote:But the angle FAE is equal to the angle ACB in the alternate segment
[ Bericht 1% gewijzigd door Riparius op 20-09-2007 22:47:48 ]
Yup concyclic quadrilateral, Book III Proposition 22quote:Op donderdag 20 september 2007 21:41 schreef Riparius het volgende:
... ABDF is een koordenvierhoek (begrijp je dat ook?). Nu zijn de overstaande hoeken in een koordenvierhoek supplementair, en dus is hoek FAE gelijk aan hoek BDE..
alternate segment theorem (Heath heeft het probleem uit Hankel from Pappus)quote:...wat Heath bedoelt met the alternate segment....
The angles between a tangent and a chord through the point of contact are equal respectively to the angles in the alternate segment.
(heb ik wel even aangenomen anders kan ik alles tot aan het bestaan van een punt toe bewijzen )
)[ Bericht 7% gewijzigd door Ogala op 20-09-2007 23:34:35 ]
Ah, dank je wel. Dat is inderdaad stelling 32 uit boek III bij Euclides. Dan is het bewijs helemaal duidelijk. Maar waarom wilde je uitgerekend dit bewijs bij Heath nalopen? Ik ben zelf erg geīnteresseerd in de geschiedenis van de wiskunde, dus vandaar dat ik het vraag.quote:Op donderdag 20 september 2007 23:11 schreef Ogala het volgende:
[..]
Yup concyclic quadrilateral, Book III Proposition 22
[..]
alternate segment theorem (Heath heeft het probleem uit Hankel from Pappus)
The angles between a tangent and a chord through the point of contact are equal respectively to the angles in the alternate segment.
[afbeelding]
Ik ben pas begonnen met Book I en in de intro stond deze stelling als ideaal voorbeeld voor de analyse van problemen. (transformatie, resolutie, synthese) vandaar! Toch wel leuk om eens door te lezen!quote:Op donderdag 20 september 2007 23:39 schreef Riparius het volgende:
[..]
Ah, dank je wel. Dat is inderdaad stelling 32 uit boek III bij Euclides. Dan is het bewijs helemaal duidelijk. Maar waarom wilde je uitgerekend dit bewijs bij Heath nalopen? Ik ben zelf erg geīnteresseerd in de geschiedenis van de wiskunde, dus vandaar dat ik het vraag.
Als I en J idealen zijn van een commutatieve ring R dan geldt (I +J)(I^J) C IJ. het symbool ^ staat voor de 'doorsende'. Is het waar dat voor iedere een commutatieve ring de gelijkheid t (I +J)(I^J) =IJ geldt? (zonder bewijs aub!)
verlegen :)
Nee.quote:Op zondag 23 september 2007 15:41 schreef teletubbies het volgende:
Als I en J idealen zijn van een commutatieve ring R dan geldt (I +J)(I^J) C IJ. het symbool ^ staat voor de 'doorsende'. Is het waar dat voor iedere een commutatieve ring de gelijkheid t (I +J)(I^J) =IJ geldt? (zonder bewijs aub!)
nu begin ik een zochttocht naar een tegenvoorbeeld..quote:
tot nu toe is me voorbeelden set bijna op!
verlegen :)
De ringen :d zijn Z[x], euuh R, C en Z.
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..
:S welke richting moet ik eigenlijk gaan?
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
Im+Jn=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jn=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I2+Jn=R maar verder kom ik niet uit..
ALvast bedankt
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..
:S welke richting moet ik eigenlijk gaan?
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
Im+Jn=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jn=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I2+Jn=R maar verder kom ik niet uit..
ALvast bedankt
verlegen :)
In Z[x] moet het lukken een tegenvoorbeeld te vinden. Endomorfismen-, groepen- en matrixringen zijn iha niet commutatief.quote:Op maandag 24 september 2007 13:16 schreef teletubbies het volgende:
De ringen :d zijn Z[x], euuh R, C en Z.
Ik dacht aan endomorfismenring. Misschien ook groepenringen, matrices..
Kun je dan niet je argument van 'eerst' toepassen op het paar (Jn,I)? Die zijn immers ook onderling ondeelbaar.quote:Op maandag 24 september 2007 13:16 schreef teletubbies het volgende:
Nog een vraagje, als I+J=R met I en J idealen die onderling ondeelbaar zijn en R is een ring. Ik moet laten zien dat
Im+Jn=R. Hiervoor heb ik inductie gebruikt, eerst heb ik laten zien dat:
I+Jn=R voor n=1,2,3,...
Maar daarna wil ik n vast nemen en dan inductie gebruiken naar de macht van I. Ik heb al:
I2+Jn=R maar verder kom ik niet uit..
ALvast bedankt
OMG. Schaam me echt dood dat ik dit moet vragen, maar ben het echt eventjes helemaal kwijt. De resultant force van deze 2 forces is duidelijk. Gewoon een parallelogram van maken en dan weet je de resultant.
Maar wat als de forces er zo uitzien?
Maar wat als de forces er zo uitzien?
Gewoon optellen kjalquote:Op maandag 24 september 2007 22:12 schreef MaximumRush het volgende:
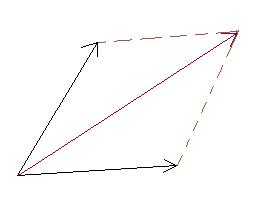
OMG. Schaam me echt dood dat ik dit moet vragen, maar ben het echt eventjes helemaal kwijt. De resultant force van deze 2 forces is duidelijk. Gewoon een parallelogram van maken en dan weet je de resultant.
[afbeelding]
Maar wat als de forces er zo uitzien?
[afbeelding,link]
.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Het parallellogram hoef je ook niet helemaal te tekenen, ook door daar de twee pijltjes achter elkaar te tekenen krijg je de juiste resultante.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Vraagje over statistiek:
Reken percentiel P10, P45, P60 en P90 uit
Formule
Wie kan me nu helpen met het invullen van de formule?
frequentie distributie:quote:1. Stel de cumulatieve frequentieverdeling op.
2. Bepaal de cumulatieve frequentie die met het K-de percentiel correspondeert: nK/100
3. Zoek in de cumulatieve frequentieverdeling de klasse op waarin K-de percentiel moet liggen.
Dit is de klasse waarvan de cumulatieve frequentie net groter is dan (of gelijk is aan) nK/100. Van deze klasse bepalen we:
a) De frequentie f
b) De exacte benedengrens ll
c) De klassenbreedte w = verschil tussen de exacte boven- en benedengrens :
| 1 2 3 4 5 6 7 8 9 10 11 12 | 3.8-4.0 4 120 3.5-3.7 8 116 3.2-3.4 15 108 2.9-3.1 18 93 2.6-2.8 20 75 2.3-2.5 17 55 2.0-2.2 12 38 1.7-1.9 12 26 1.4-1.6 10 14 1.1-1.3 4 4 0.8-1.0 0 0 |
Reken percentiel P10, P45, P60 en P90 uit
Formule
Wie kan me nu helpen met het invullen van de formule?
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
Ehm...quote:Op dinsdag 25 september 2007 19:55 schreef crossover het volgende:
Vraagje over statistiek:
[..]
frequentie distributie:
[ code verwijderd ]
Reken percentiel P10, P45, P60 en P90 uit
Formule
[afbeelding]
Wie kan me nu helpen met het invullen van de formule?
correct me if i'm wrong.
Je moet de formule invullen voor achtereenvolgens K = {10,45,60,90}
Als K=10 zoek je de bijbehorende entry in je tabel, dit is waar cF voor het eerst >= 10 (hier cF=14)
ll is dan 1.4 (exacte benedengrens iig)
w is 0.2 (boven - benedengrens)
cf is 14
f is 10
invullen, doorrekenen en klaar is klara, zelfde trucje herhalen voor K = 45, K=60 en K=90
En dat voor iemand die nooit statistiek gehad heeft
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
Ben vergeten te vermelden dat cF betrekking heeft op de net lagere klasse. lower limit is 1.35.quote:Op dinsdag 25 september 2007 20:03 schreef MPG het volgende:
[..]
Ehm...
correct me if i'm wrong.
Je moet de formule invullen voor achtereenvolgens K = {10,45,60,90}
Als K=10 zoek je de bijbehorende entry in je tabel, dit is waar cF voor het eerst >= 10 (hier cF=14)
ll is dan 1.4 (exacte benedengrens iig) 1.35
w is 0.2 (boven - benedengrens)
cf is 14 4
f is 10
invullen, doorrekenen en klaar is klara, zelfde trucje herhalen voor K = 45, K=60 en K=90
En dat voor iemand die nooit statistiek gehad heeft
N(totale scores) = 120?
Dat wordt dan 1.35+(120x10/100-4)/10 * 0.2 = 0.43
Edit: misschien klopt het niet dat cF correspondeert met de net lagere klasse, dan zou het 14 zijn en komt er 1.15 uit.
'Expand my brain, learning juice!'
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
<a href="http://www.last.fm/user/crossover1" rel="nofollow" target="_blank">Last.fm</a>
cF correspondeert voor zover ik uit hetgeen ik heb gelezen in jouw eerste post niet met de net lagere klasse. Jouw edit lijkt mij dan ook juistquote:Op dinsdag 25 september 2007 20:13 schreef crossover het volgende:
[..]
Ben vergeten te vermelden dat cF betrekking heeft op de net lagere klasse. lower limit is 1.35.
[afbeelding]
N(totale scores) = 120?
Dat wordt dan 1.35+(120x10/100-4)/10 * 0.2 = 0.43
Edit: misschien klopt het niet dat cF correspondeert met de net lagere klasse, dan zou het 14 zijn en komt er 1.15 uit.
KSC JUBILEUM topic
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
"Sleep: A completely inadequate substitute for caffeine"
#TeamHumbug
Heeft patent op Mosterd-Maaltijd situaties
Lieve mensen,
Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.
e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.
Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.
e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.
e-x + SQRT(y) = 1
e-x -1= SQRT(y)
kwadateren levert e-2x -2e-x + 1 = y (merkwaardig product)
stel e-x = p ; daaruit volgt p2 - 2p + 1 = y
nu moet het moet niet zo moeilijk zijn om nulpunten te bereken.
[ Bericht 0% gewijzigd door harrypiel op 26-09-2007 15:08:51 ]
e-x -1= SQRT(y)
kwadateren levert e-2x -2e-x + 1 = y (merkwaardig product)
stel e-x = p ; daaruit volgt p2 - 2p + 1 = y
nu moet het moet niet zo moeilijk zijn om nulpunten te bereken.
[ Bericht 0% gewijzigd door harrypiel op 26-09-2007 15:08:51 ]
e-x+wortel(y) = 1quote:Op woensdag 26 september 2007 13:07 schreef moeffiemoeffie het volgende:
Lieve mensen,
Ik was eens aan mijn achterstallig huiswerk begonnen en stuitte op dit prachtige iets.
e^-X+wortelY=1 In mijn boek zeggen ze ineens simpel dat je dit ook kunt schrijven als y = x^2, maar ik heb geen flauw idee hoe ze hierbij komen.
ex = a is hetzelfde als x = ln(a)
dus -x+wortel(y) = ln(1)
ln(1) = 0
dus -x+wortel(y) = 0
dus wortel(y) = x
dus y = x2
Zorg er wel voor dat je goed met haakjes werkt als je een macht aangeeft met ^, anders krijg je dus antwoorden als die van meneer piel te zien.
[ Bericht 29% gewijzigd door Jordy-B op 26-09-2007 13:24:07 ]
Bestiality sure is a fun thing to do. But I have to say this as a warning to you:
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.
With almost all animals you can have a ball, but the hedgehog can never be buggered at all.
anders met tekst in subscript of tekst in superscript werken om de zaak te verduidelijkenquote:Op woensdag 26 september 2007 13:17 schreef Jordy-B het volgende:
[..]
e-x+wortel(y) = 1
ex = a is hetzelfde als x = ln(a)
dus -x+wortel(y) = ln(1)
ln(1) = 0
dus -x+wortel(y) = 0
dus wortel(y) = x
dus y = x2
Zorg er wel voor dat je goed met haakjes werkt als je een macht aangeeft met ^, anders krijg je dus antwoorden als die van meneer piel te zien.
druk op de quote bericht knop voor de precieze code
