SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Hahahahha nee zeker niet. Had het liefst voor de sier gewild, maar ja.quote:Op maandag 5 mei 2014 17:16 schreef Anoonumos het volgende:
Dat heet de absolute waarde. Die streepjes staan er niet voor de sier.
Ik snap hem niet helemaal... In mijn boek is het zeer kort uitgelegd en op internet is er ook zeer weinig te vinden over de absolute-waardefunctie, althans weinig goede naar mijn mening..
In mijn boek staat er alleen dit:
f(x) = |x| die gedefinieerd is door |x| = x als x > 0 en |x| = -x als x < 0. Voor alle x geldt dat |x|² = x².
Maar ja dan zou ik ervan uit moeten gaan dat |x|³ = -x³ ?
Ja.quote:
[..]
f(x) = |x| die gedefinieerd is door |x| = x als x > 0 en |x| = -x als x < 0.
|x| = - x als x < 0
-0.5 is negatief dus
|-0.5| = - (-0.5) = 0.5
Dus |-0.5| = 0.5
Absolute waarde nemen is niets anders dan een getal positief maken. Als een getal al positief is, dan verandert er niks.
Oh die - bij -x is losstaand wat x zal zijn bij x < 0 ? Dus zoals jij zegt als x = -0,5 dan is het -(-0,5) omdat die - niks te maken heeft met x die <0 kan zijn?quote:
[..]
Ja.
|x| = - x als x < 0
-0.5 is negatief dus
|-0.5| = - (-0.5) = 0.5
Dus |-0.5| = 0.5
Absolute waarde nemen is niets anders dan een getal positief maken. Als een getal al positief is, dan verandert er niks.
In principe los je toch absolute waarde functies twee keer op?quote:
[..]
Ja.
|x| = - x als x < 0
-0.5 is negatief dus
|-0.5| = - (-0.5) = 0.5
Dus |-0.5| = 0.5
Absolute waarde nemen is niets anders dan een getal positief maken. Als een getal al positief is, dan verandert er niks.
Dus x^4 < |x^(1/3)| los je op als volgt:
x^4 - x^(1/3) < 0 en als x^4 + x^(1/3) toch?
Ja precies.quote:
[..]
In principe los je toch absolute waarde functies twee keer op?
Dus x^4 < |x^(1/3)| los je op als volgt:
x^4 - x^(1/3) < 0 en als x^4 + x^(1/3) toch?
Je moet wel opletten dat je dan voor
x^4 - x^(1/3) < 0 alleen naar x ≥ 0 kijkt
en voor
x^4 + x^(1/3) < 0 alleen naar x < 0
Hoe bedoel je? En wat is de gedachte achter dit hele gebeuren waarom je bij absolute waarden altijd dubbel moet gaan oplossen? Geldt dit ook voor even machten of alleen voor oneven machten?quote:
[..]
Ja precies.
Je moet wel opletten dat je dan voor
x^4 - x^(1/3) < 0 alleen naar x ≥ 0 kijkt
en voor
x^4 + x^(1/3) < 0 alleen naar x < 0
Daarnaast snap ik niet wat de bedoeling er dus van is, als alles toch als een positief getal benadert gaat worden...
Vooral dit bijvoorbeeld:
x^(1/n) = | x | als n even is, en x^(1/n) = x als n oneven is..
Ik zie het verschil niet echt...want of het nou | x | of x is, x kan altijd zowel negatief als positief zijn..
x^(1/n) = | x | als n even is, en x^(1/n) = x als n oneven is..
Ik zie het verschil niet echt...want of het nou | x | of x is, x kan altijd zowel negatief als positief zijn..
Dan zou ik toch even een goed boek of internetsite (Of youtube, Khan academy ... ) zoeken die het uitlegt.
Gewoon even vanaf het begin beginnen met de definitie.
Gewoon even vanaf het begin beginnen met de definitie.
Thanks. Ik heb gekeken naar een aantal video's op zowel khan academy als op Youtube, maar de basis is mij geheel duidelijk.. Moeilijkheden beginnen met vergelijkingen:quote:
| 2x + 3 | = 2
Het oplossen is geen probleem, maar het begrijpen ervan.
Ik zal een voorbeeld geven wat ik niet kan begrijpen eraan:
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
hoe kom je opeens aan 1^(1/3)?quote:
Ik zal een voorbeeld geven wat ik niet kan begrijpen eraan:
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
oh is blijkbaar gelijk aan 1
[ Bericht 5% gewijzigd door wiskundenoob op 05-05-2014 18:26:03 ]
| -1 | = 1 = 1^4quote:
[..]
(x³ - 1 ) --> ik zou denken x³= 1 waardoor x = 1^(1/3)
| 1 | = 1 = 1^4
| 0 | = 0 = 0^4
1^(1/3) = 1, klopt toch ook? Je moet alleen niet de negatieve oplossing vergeten. Net zoals x²=4 ook twee oplossingen heeft, x=2 en x=-2.quote:
[..]
(x³ - 1 ) --> ik zou denken x³= 1 waardoor x = 1^(1/3)
Wacht, maar het is een derde macht dus -1 is helemaal geen oplossing van x³ - 1 =0
.
ohjaaquote:
[..]
| -1 | = 1 = 1^4
| 1 | = 1 = 1^4
| 0 | = 0 = 0^4
Je snapt dat de derdemachtswortel van een gewoon een is?quote:
Ik zal een voorbeeld geven wat ik niet kan begrijpen eraan:
x^4 = | x |
x (x³ - 1)
x = 0 of x = 1^(1/3) zou ik zeggen, maar het is
x = 0 of x = 1 of x = -1
Vind het gewoon al helemaal raar dat (x³ - 1 ) --> x = 1 is ... ik zou denken x³= 1 waardoor x = 1^(1/3)
En een hint: x^4 = | x | geeft x^4 = x v x^4 = -x
De basis van absolute-waardefuncties is hartstikke makkelijk, maar wanneer er vergelijkingen en ongelijkheden erbij komen kijken, snap ik er niks van..quote:
[..]
1^(1/3) = 1, klopt toch ook? Je moet alleen niet de negatieve oplossing vergeten. Net zoals x²=4 ook twee oplossingen heeft, x=2 en x=-2.
Precies, gewoon deze definitie opschrijven en dat uitwerken. Je moet er wel rekening mee houden dat x^4 = x alleen geldt voor x>=0, en x^4=-x voor x <0.quote:Op maandag 5 mei 2014 18:17 schreef jordyqwerty het volgende:
[..]
Je snapt dat de derdemachtswortel van een gewoon een is?
En een hint: x^4 = | x | geeft x^4 = x v x^4 = -x
Mooie! Dankjewel!quote:
[..]
Je snapt dat de derdemachtswortel van een gewoon een is?
En een hint: x^4 = | x | geeft x^4 = x v x^4 = -x
Denk ik het net te begrijpen gaat het weer fout...quote:
[..]
Precies, gewoon deze definitie opschrijven en dat uitwerken. Je moet er wel rekening mee houden dat x^4 = x alleen geldt voor x>=0, en x^4=-x voor x <0.
x^4 < x^(1/3)
Dus ik doe
x^7 - x want (x^1/3 = x)
en
x^7 + x
dus
x ( x^6 - 1 ) en x (x^6 +1 ) -- > x = 0, x > 1 en x = 0, x < -1
Dus x =0 , x > 1 en x < -1
Hoe ik op die tekens kom?
Gewoon de getallenrij gemaakt:
-------------- -1 ++++++ 0 ----------- 1 +++++++++
Toch blijkt het fout te zijn want het is x < 1 en x > -1
[ Bericht 0% gewijzigd door Super-B op 05-05-2014 18:40:35 ]
quote:
[..]
Denk ik het net te begrijpen gaat het weer fout...
x^4 < x^(1/3)
Dus ik doe
x^7 - x want (x^1/3 = x)
en
x^7 + x
dus
x ( x^6 - 1 ) en x (x^6 +1 ) -- > x = 0, x > 1 en x = 0, x < -1
Dus x =0 , x > 1 en x < -1
Hoe ik op die tekens kom?
Gewoon de getallenrij gemaakt:
-------------- -1 ++++++ 0 ----------- 1 +++++++++
Toch blijkt het fout te zijn want het is x=0, x < 1 en x > -1
x = | x³ |quote:
Los straks even |x^3| = x op, om te zien of je het begrijpt.
x(1 - x²) en x(1 + x³ )
x = 0 of x = -1 (want beide kanten komen uit op -1)
Je tweede vergelijking moet x(1 + x^2 ) zijn.quote:
[..]
x = | x³ |
x(1 - x²) en x(1 + x³ )
x = 0 of x = -1 (want beide kanten komen uit op -1)
En -1 klopt natuurlijk niet. Vul maar in.
Zie daarvoor de opmerking van thenxero
SES / [Bèta wiskunde] Huiswerk- en vragentopic
x³ = |x| geeft x³ = x v x³ = -xquote:
Los straks even |x^3| = x op, om te zien of je het begrijpt.
x(x²-1) v x(x² + 1)
dus x = 0 , x = 1 , x = -1
x³ = x als x ≥ 0quote:
x³ = -x als x < 0
Dus -1 is geen oplossing want je vergelijking x(x²-1) = 0 geldt alleen als x ≥ 0.
Huh?quote:
[..]
x³ = x als x ≥ 0
x³ = -x als x < 0
Dus -1 is geen oplossing want je vergelijking x(x²-1) = 0 geldt alleen als x ≥ 0.
Voor welke x geldt x^3 = |x| ?
Absolute waarde, altijd twee gevallen onderscheiden.
Geval 1: x ≥ 0.
Dan |x| = x.
Voor welke x ≥ 0 geldt x^3 = x oftewel x(x^2 - 1) = 0?
x(x^2 - 1) = 0 oplossen geeft x =0 of x = 1 of x = -1.
Maar we hadden aangenomen dat x ≥ 0 ! Anders mogen we niet zeggen dat |x| = x.
Dus x = 0 en x = 1 zijn oplossingen. Van x = -1 kunnen we nog niet zeggen of het een oplossing is. Daarvoor moeten we naar geval 2 kijken.
Geval 2: x < 0.
Dan |x| = -x.
Voor welke x < 0 geldt x^3 = -x oftewel x(x^2 + 1) = 0?
Voor geen enkele x. Dus we vinden geen extra oplossingen.
Conclusie: x^3 = |x| voor x = 0 en voor x = 1.
Door invullen zien we ook dat x = -1 geen oplossing is.
(-1)^3 = -1
| -1| = 1
En dat is niet gelijk.
quote:
[..]
Wat snap je niet?
(Wow er zijn ineens veel pagina's bijgekomen zeg.)
11:16
Bedankt voor je reactie.. Ik kijk even een video, gepost hierboven.. Ik begrijp er even helemaal niks meer van.quote:
Voor welke x geldt x^3 = |x| ?
Absolute waarde, altijd twee gevallen onderscheiden.
Geval 1: x ≥ 0.
Dan |x| = x.
Voor welke x ≥ 0 geldt x^3 = x oftewel x(x^2 - 1) = 0?
x(x^2 - 1) = 0 oplossen geeft x =0 of x = 1 of x = -1.
Maar we hadden aangenomen dat x ≥ 0 ! Anders mogen we niet zeggen dat |x| = x.
Dus x = 0 en x = 1 zijn oplossingen. Van x = -1 kunnen we nog niet zeggen of het een oplossing is. Daarvoor moeten we naar geval 2 kijken.
Geval 2: x < 0.
Dan |x| = -x.
Voor welke x < 0 geldt x^3 = -x oftewel x(x^2 + 1) = 0?
Voor geen enkele x. Dus we vinden geen extra oplossingen.
Conclusie: x^3 = |x| voor x = 0 en voor x = 1.
Door invullen zien we ook dat x = -1 geen oplossing is.
(-1)^3 = -1
| -1| = 1
En dat is niet gelijk.
Dat ''opsplitsen'' begrijp ik niet, vanaf 11:16 in de video.. Ik denk dat het daar ligt, waar ik de fout in ga.
Correct. This is a bifurcation.quote:
Bifurcartion. Can you define in your own words?
Splitting it up in two statements, yeah. Or the way mathematicians break up with their girlfriends.
That's like their facebookstatus." I've bifurcated! "
Wat een popie jopie Sorry hiervoor.
Ja ik weet het..quote:
[..]
Correct. This is a bifurcation.
Bifurcartion. Can you define in your own words?
Splitting it up in two statements, yeah. Or the way mathematicians break up with their girlfriends.
That's like their facebookstatus." I've bifurcated! "
Sorry hiervoor.
Ik kon even geen uitgebreidere vinden.
Neem de rekenregels voor exponenten eens doorquote:
[..]
Denk ik het net te begrijpen gaat het weer fout...
x^4 < x^(1/3)
Dus ik doe
x^7 - x want (x^1/3 = x)
en
x^7 + x
dus
x ( x^6 - 1 ) en x (x^6 +1 ) -- > x = 0, x > 1 en x = 0, x < -1
Dus x =0 , x > 1 en x < -1
Hoe ik op die tekens kom?
Gewoon de getallenrij gemaakt:
-------------- -1 ++++++ 0 ----------- 1 +++++++++
Toch blijkt het fout te zijn want het is x < 1 en x > -1
Bereken mbv de productregel de afgeleide van:
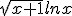
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
Filmpje bekeken en het wordt steeds duidelijker!quote:
[..]
Neem de rekenregels voor exponenten eens door
x^4 > x³
Dit wordt opgesplitst in
x^4 > x³ en x^4 < -x³
x³(x - 1 ) > 0 en x³(x + 1) < 0
x > 1 en x < -1 echter begrijp ik niet wat ik dus met die 0 moet doen? x =0 , x>0 of x<0 ?
En wat ik ik me afvraag die -x³, stel het is -2 is dat dan -(-2)³ en dus 8 en -2^4 = -16 waardoor dus -x³ groter is dan x^4 ?
Één gedachtenkronkel: waarvoor dient de absolute waardefunctie? Dus waarom zou ik berekenen wanneer x^4< -x³ als het om x^4 > x³ gaat?
Dat is hetzelfde.quote:
Bereken mbv de productregel de afgeleide van:
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
a-p = 1/apquote:
Bereken mbv de productregel de afgeleide van:
Dus ik kom op:
(1/2) (x+1) ^(-1/2) ln x
+
wortel(x+1)/x
Maar het moet zijn: wortel(x+1)/x + ln x / (2*wortel(x+1))
Wat doe ik verkeerd?
Edit: Ah, iemand was me weer voor
Pff... het antwoord is x > 1 en x < 0 .....quote:
[..]
Filmpje bekeken en het wordt steeds duidelijker!
x^4 > x³
Dit wordt opgesplitst in
x^4 > x³ en x^4 < -x³
x³(x - 1 ) > 0 en x³(x + 1) < 0
x > 1 en x < -1 echter begrijp ik niet wat ik dus met die 0 moet doen? x =0 , x>0 of x<0 ?
En wat ik ik me afvraag die -x³, stel het is -2 is dat dan -(-2)³ en dus 8 en -2^4 = -16 waardoor dus -x³ groter is dan x^4 ?
Één gedachtenkronkel: waarvoor dient de absolute waardefunctie? Dus waarom zou ik berekenen wanneer x^4< -x³ als het om x^4 > x³ gaat?
volgens wolframalpha.comHoe kan dat....
maar volgens het antwoordenmodel heb ik het wel goed met x > 1 en x < -1. Maar ik snap niet hoe x = 0? Omdat het x > 0 en x < 0 is en daarom x=0 is?
Ik doe alles om niet aan bacheloronderzoek en presentaties te hoeven werken op het moment.quote:
[..]
a-p = 1/ap
Edit: Ah, iemand was me weer voor
quote:
Akkoord! Ik heb hem doorquote:
[..]
a-p = 1/ap
Edit: Ah, iemand was me weer voor
Dank heren
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
Hahahaha. Iedereen wordt denk ik wel gek en misselijk van onze vragen.quote:
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
als je x^4 < √x hebt en je stelt √x = x
wordt x^4 dan x^8 of x^6? Want zover ik weet is bij vermenigvuldiging dat machten opgeteld worden?
wordt x^4 dan x^8 of x^6? Want zover ik weet is bij vermenigvuldiging dat machten opgeteld worden?
Zoals ik x * (1/(1^(1/3))) lees is het gewoon gelijk aan x. Typo?quote:
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
http://www.wolframalpha.com/input/?i=+x+*+%281%2F%281%5E%281%2F3%29%29%29+
Typo inderdaad!quote:
envoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
Zoals ik x * (1/(1^(1/3))) lees is het gewoon gelijk aan x. Typo?
http://www.wolframalpha.com/input/?i=+x+*+%281%2F%281%5E%281%2F3%29%29%29+
Zo klopt die als je hem in wolfram stopt:
x * (1/(x^(1/3)))
En wat was het probleem precies?quote:Op maandag 5 mei 2014 20:13 schreef nodig het volgende:
[..]
Typo inderdaad!
Zo klopt die als je hem in wolfram stopt:
x * (1/(x^(1/3)))
'' als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3? "
De opdracht is differentieer mbv productregel:quote:
[..]
En wat was het probleem precies?
'' als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3? "
Dus kom ik op:
+
Dat vereenvoudig als
x / x^(1/3)
Maar dan? Die x'en kan je tegen elkaar wegstrepen maar wat doe je met de macht?
Maar het antwoord is:
[ Bericht 6% gewijzigd door nodig op 05-05-2014 20:32:22 ]
Zoals Anoonumos al zegt, volgensmij heb je een typo gemaakt. Er staat nu eigenlijk x * 1.quote:
Oke, nog een (voor jullie makkelijke) vraag.
Ik kom nu op x * (1/(1^(1/3))) uit.
Dit wordt in het antwoordmodel vereenvoudigt tot 1/3
Maar als ik hem vereenvoudig houd ik ^(1/3) over, hoezo mag je dit herschrijven tot 1/3?
Zie post boven jouw postquote:
[..]
Zoals Anoonumos al zegt, volgensmij heb je een typo gemaakt. Er staat nu eigenlijk x * 1.
Jouw afgeleide van
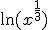
klopt niet.
Je vergeet de kettingregel.
Maar de kettingregel kan je vermijden.
Hint:
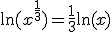
klopt niet.
Je vergeet de kettingregel.
Maar de kettingregel kan je vermijden.
Hint:
Gebruik bij substitutie niet je oorspronkelijke variabele als substitutievariabele. Stellen dat √x = x is als stellen dat 2 = 4 en dat slaat nergens op.quote:
als je x^4 < √x hebt en je stelt √x = x
wordt x^4 dan x^8 of x^6? Want zover ik weet is bij vermenigvuldiging dat machten opgeteld worden?
Als je y = √x definieert, dan is y2 = (√x)2 = x en kun je x4 = √x schrijven als (y2)4 = y, dus y8 = y.
Nog een tip voor logaritmes differentiëren (zo doe ik het tenminste altijd):
Je hebt y = ln(x), laten we de term waarvan het logaritme bepaald moet worden h(x) noemen (y = ln(h(x)). Dan volgt dat de afgeleide is: h'(x)/h(x)
Je hebt y = ln(x), laten we de term waarvan het logaritme bepaald moet worden h(x) noemen (y = ln(h(x)). Dan volgt dat de afgeleide is: h'(x)/h(x)
Ah, dus dan krijg je:quote:
Jouw afgeleide van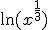
klopt niet.
Je vergeet de kettingregel.
Maar de kettingregel kan je vermijden.
Hint:
x * ((1/3)/x)
=
(1/3x / x)
=
1/3
?
Correctquote:
[..]
Ah, dus dan krijg je:
x * ((1/3)/x)
=
(1/3x / x)
=
1/3
?
Dus in deze situatie het logaritme van x^1/3quote:
Nog een tip voor logaritmes differentiëren (zo doe ik het tenminste altijd):
Je hebt y = ln(x), laten we de term waarvan het logaritme bepaald moet worden h(x) noemen (y = ln(h(x)). Dan volgt dat de afgeleide is: h'(x)/h(x)
Afgeleide hiervan (1/3)x^-(2/3)
Dit gedeeld door x^1/3?
Dat klopt, en via de regel die ik je zojuist gaf krijg je dus (1/3)/x = 1/(3x), en als je dat keer die x die ervoor stond doet krijg je inderdaad 1/3. Echter is het bij deze opgave natuurlijk veel makkelijker om gebruik te maken van de rekenregel log(ap) = plog(a).quote:
[..]
Dus in deze situatie het logaritme van x^1/3
Afgeleide hiervan (1/3)x^-(2/3)
Dit gedeeld door x^1/3?
Dat hele absolute waardefuncties gebeuren is mij duidelijker dan vanmiddag...
Deze is wel een pittige...
| 2x + 3 | > | 4x |
Deze is wel een pittige...
| 2x + 3 | > | 4x |
voor x ≥ 0quote:
Dat hele absolute waardefuncties gebeuren is mij duidelijker dan vanmiddag...
Deze is wel een pittige...
| 2x + 3 | > | 4x |
2x + 3 > 4x
-2x > -3
x < 3/2
voor x < 0
2x + 3 > -4x
6x > -3
x > -1/2
Dus -1/2 < x < 3/2
is toch een apart gebied, omdat er ook absoluut strepen om de 2x + 3 staan?
Maar ik zie aardig scheel van die absoluut strepen inmiddels dus misschien mis ik iets.
Je kan meteen wel zien dat het geen nieuwe oplossingen geeft, maar wel nodig om te vermelden.
Moet je niet iets anders doen omdat beide absoluut zijn ofzo..? En waarom klapt het teken van x < 0 naar x > op het eind opeens?quote:
[..]
voor x ≥ 0
2x + 3 > 4x
-2x > -3
x < 3/2
voor x < 0
2x + 3 > -4x
6x > -3
x > -1/2
Dus -1/2 < x < 3/2
| x^2 - 2x | < 1
Ik deed
x^2 - 2x - 1 < 0 en x^2 - 2x + 1 > 0
Bij de eerste abc formule toegepast te hebben kom ik uit op
x < 1 - W2 , x < 1 + W2 en x > 1, x >1
Nu heb ik wel de goede antwoorden, maar heb ik niet de juiste combinatie van oplossingen bij elkaar en onjuiste ongelijkheidstekens...? Wat doe ik fout..?
Ik deed
x^2 - 2x - 1 < 0 en x^2 - 2x + 1 > 0
Bij de eerste abc formule toegepast te hebben kom ik uit op
x < 1 - W2 , x < 1 + W2 en x > 1, x >1
Nu heb ik wel de goede antwoorden, maar heb ik niet de juiste combinatie van oplossingen bij elkaar en onjuiste ongelijkheidstekens...? Wat doe ik fout..?
Dit deel van je uitwerking is fout, want je gaat ervan uit dat (2x + 3) positief is voor elke x < 0, maar dat is niet zo.quote:
[..]
voor x < 0
2x + 3 > -4x
6x > -3
x > -1/2
Dus -1/2 < x < 3/2
Je bent enorm aan het goochelen terwijl je er nog niet veel van begrijpt. Ga nu eerst eens serieus studeren en kom dan pas met wat vragen. Het is niet de bedoeling dit topic als een slowchat te gebruiken.quote:
Ben er al ruim 4-5 uur mee bezig geweest.quote:
[..]
Je bent enorm aan het goochelen terwijl je er nog niet veel van begrijpt. Ga nu eerst eens serieus studeren en kom dan pas met wat vragen. Het is niet de bedoeling dit topic als een slowchat te gebruiken.
Dat zegt niet veel. Mensen die aan zelfstudie doen voor een toelatingsexamen wiskunde studeren vaak bijzonder inefficiënt en vliegen voordurend uit de bocht, zo heb ik gemerkt. Een goede leraar die ook echt les geeft is onvervangbaar. Voor welke toets bereid je je voor, en welke boeken gebruik je daarbij?quote:Op maandag 5 mei 2014 21:43 schreef Super-B het volgende:
[..]
Ben er al ruim 4-5 uur mee bezig geweest.
Basisboek Wiskunde van Jan van Craats en eventueel extra materiaal op Youtube.quote:
[..]
Dat zegt niet veel. Mensen die aan zelfstudie doen voor een toelatingsexamen wiskunde studeren vaak bijzonder inefficiënt en vliegen voordurend uit de bocht, zo heb ik gemerkt. Een goede leraar die ook echt les geeft is onvervangbaar. Voor welke toets bereid je je voor, en welke boeken gebruik je daarbij?
Nee klopt.. heb je gelijk in. Ik heb het nu wel door.. de antwoorden kloppen ook... echter hebben ze niet de juiste combinatie.. dus dat laatste is voor mij een groot struikelblok..quote:
[..]
Je bent enorm aan het goochelen terwijl je er nog niet veel van begrijpt. Ga nu eerst eens serieus studeren en kom dan pas met wat vragen. Het is niet de bedoeling dit topic als een slowchat te gebruiken.
ik kom uit op x > ... en x >... en daarnaast x < ... en x< ... maar ze zijn niet op de juiste manier gecombineerd..
Als je mijn post nog eens bekijkt, het klopt wel..alleen waar ik dan vast zit is wat ik dus moet doen met de tekens en oplossingen..? Normaal gesproken kan ik het gewoon laten zoals het hoort.
Er moet ook gezegd worden dat het boek bijzonder ongeschikt is voor zelfstudie..quote:
[..]
Dat zegt niet veel. Mensen die aan zelfstudie doen voor een toelatingsexamen wiskunde studeren vaak bijzonder inefficiënt en vliegen voordurend uit de bocht, zo heb ik gemerkt. Een goede leraar die ook echt les geeft is onvervangbaar. Voor welke toets bereid je je voor, en welke boeken gebruik je daarbij?
Snap jij opgave 16.34 e?quote:
[..]
Er moet ook gezegd worden dat het boek bijzonder ongeschikt is voor zelfstudie..
Gedaan.. zie de post hierna die ik ga quoten (zit op mijn mobiel). Ik zit vast bij het schrijven vh eindantwoord.quote:
[..]
Zowel de - als de + versie van het linkerlid berekenen?
antwoordenboek zegt:quote:
| x^2 - 2x | < 1
Ik deed
x^2 - 2x - 1 < 0 en x^2 - 2x + 1 > 0
Bij de eerste abc formule toegepast te hebben kom ik uit op
x < 1 - W2 , x < 1 + W2 en x > 1, x >1
Nu heb ik wel de goede antwoorden, maar heb ik niet de juiste combinatie van oplossingen bij elkaar en onjuiste ongelijkheidstekens...? Wat doe ik fout..?
1 - W2 < x < 1 , 1 < x < 1 + W2
Regard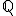 
as a metric space, with 
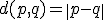. Let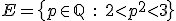 
. Show that 
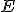is closed and bounded in 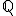, but that 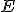is not compact. Is 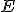open in ?
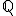Help?
Overduidelijk,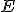 is begrensd. Dat was het makkelijke gedeelte. Volgens de definitie is een set closed iff als zij al haar limietpunten bevat. Omdat 
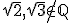, lijkt me dat deze set is gesloten is. Waarom mag ik Heine-Borel niet 'invoken'?
[ Bericht 18% gewijzigd door Novermars op 05-05-2014 22:22:26 ]
Help?
Overduidelijk,
[ Bericht 18% gewijzigd door Novermars op 05-05-2014 22:22:26 ]
Grafiek schetsen, daaruit kan je het vervolgens aflezen.quote:
[..]
antwoordenboek zegt:
1 - W2 < x < 1 , 1 < x < 1 + W2
Doe jij het steeds op die manier..?quote:
[..]
Grafiek schetsen, daaruit kan je het vervolgens aflezen.
Grafiek schetsen van de twee mogelijkheden wat betreft het linkerlid?
Ja, dat is de opdracht ook. Niet zo lui zijn en gewoon schetsenquote:
[..]
Doe jij het steeds op die manier..?
Grafiek schetsen van de twee mogelijkheden wat betreft het linkerlid?
Voor compactheidquote:
Regard
Help?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Of lukte geslotenheid al niet?
Damn... ik haat daar overheen gelezen.quote:
[..]
Ja, dat is de opdracht ook. Niet zo lui zijn en gewoon schetsen
quote:
[..]
Voor compactheidZie mijn edit, informeel lukt geslotenheid me wel. Maar geen idee hoe ik dit rigoureus opschrijf...SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Of lukte geslotenheid al niet?
Maar jouw open cover, waarom mag je deze gebruiken? Als we het overzouden hebben, dan is hij logisch. Maar
en
zitten niet in
, moeten we ze dan niet helemaal achterwege laten?
[ Bericht 18% gewijzigd door Novermars op 05-05-2014 22:28:38 ]
Zij p is een limietpunt van E.quote:
[..]
Zie mijn edit, informeel lukt geslotenheid me wel. Maar geen idee hoe ik dit rigoureus opschrijf...
Maar jouw open cover, waarom mag je deze gebruiken? Als we het over
Dan voor elke ε > 0 bestaat er een x in E met p ongelijk aan x en |x-p| < ε.
Stel p zit niet in E. Stel bijvoorbeeld p > sqrt(3) (andere gevallen gaan analoog)
Laat ε = (p - sqrt{3})/2 in je definitie van limietpunt en je vind een tegenspraak.
Het gebruik van wortels kan je wel vermijden maar dan wordt het meer gepriegel denk ik omdat je steeds naar p^2 kijkt ipv naar p.
En Heine-Borel geldt dus alleen voor R^n, dat zal het idee van de opgave wel zijn.
Ja, dat heb ik ook al meermaals opgemerkt. Zoals gezegd, een goede (ouderwetse) leraar die ook echt les geeft blijft onvervangbaar. Maar daarnaast liggen de oorzaken van de dramatische achteruitgang van het niveau van het wiskunde onderwijs ook bij het lager onderwijs. Kinderen die nooit goed hebben leren rekenen (met uitsluitend pen en papier alsmede uit het hoofd, wel te verstaan) missen ook de benodigde vaardigheden om bijvoorbeeld eenvoudige algebraïsche herleidingen tot een goed einde te brengen. Dat wordt treffend geïllustreerd door het volgende plaatje op de website van Liesbeth van der Plas:quote:
[..]
Er moet ook gezegd worden dat het boek bijzonder ongeschikt is voor zelfstudie..
Ze merkt daarbij op: Als een kind niet in staat is het getalsommetje probleemloos uit te rekenen, is de algebra-opgave ook veel te hoog gegrepen. Op haar site is ook een interessante PDF te vinden waar ze het onderwijs dat ze zelf kreeg in de elementaire algebra en de vlakke meetkunde vergelijkt met het onderwijs dat haar dochter op school kreeg over deze zelfde onderwerpen, en de consequenties die dat heeft.
Maar goed, ik kan me voorstellen dat diegenen die zich nu op een toets voorbereiden en dit lezen zullen zeggen dat ze hier op dit moment niets mee opschieten, en daarom wil ik jullie ook niet het bos insturen maar toch wat goede en concrete adviezen meegeven.
Zoals gezegd is een goede leraar onvervangbaar, en dat betekent dat je eigenlijk een cursus zou moeten gaan volgen als je ernst maakt met je (vervolg)studie. Als je dat niet kunt bekostigen of anderszins niet in de gelegenheid bent om dat te gaan doen, dan zou je wellicht op zoek kunnen gaan naar iemand die bereid is je tegen een schappelijk tarief bijles te geven. Is ook dat geen reële mogelijkheid, dan blijft uiteraard alleen zelfstudie over. Maar dan kun je beter niet beginnen met het boek van Van de Craats, want dat is meer een opfriscursus en oefenboek, en daarmee bijzonder ongeschikt voor zelfstudie als je de stof nog nooit eerder hebt gezien. Ik zou dan aanraden te beginnen met de spijkers. Dat is een reeks van zeven boekjes die veel beter geschikt zijn voor zelfstudie en waaruit je de basistechnieken ook echt kunt leren. Je moet dan wel beginnen met het eerste boekje over rekenen en uiteindelijk alle zeven delen doorwerken. Dat moet te doen zijn, voor elk deeltje staat volgens de auteur van deze boekjes zo'n 10 à 20 uur studie. En ook al lijkt me dat wat optimistisch, dan nog moet het mogelijk zijn in enkele honderden uren zelfstudie deze gehele reeks door te werken en je de stof in zijn geheel eigen te maken. Pas in een tweede ronde zou je dan kunnen overwegen als herhaling nog wat extra opgaven te maken uit het boek van Van de Craats.
Inderdaad zeer interessant! Ik klikte op de link en heb 't gelijk grotendeels doorgelezen. Ik viel bijna om van verbazing om de verschillen tussen toen en nu en de relevantie van PISA en Cito. Nu begrijp ik ook beter wat ik laatst meemaakte: bij bijles was een jongetje dat een vier stond voor wiskunde in de brugklas. Hij begreep dingen en had inzicht, maar de rekenregels waren hem blijkbaar nooit goed uitgelegd.quote:
[...]
Op haar site is ook een interessante PDF te vinden waar ze het onderwijs dat ze zelf kreeg in de elementaire algebra en de vlakke meetkunde vergelijkt met het onderwijs dat haar dochter op school kreeg over deze zelfde onderwerpen, en de consequenties die dat heeft.
Hmm interessant artikel. Ik moet zeggen dat ik inderdaad het breuken gedeelte in het basisboek wiskunde heb doorgewerkt om weer op niveau te komen. Wist ik veel dat wanneer je breuken deelt je omgekeerd vermenigvuldigtquote:
[..]
Ja, dat heb ik ook al meermaals opgemerkt. Zoals gezegd, een goede (ouderwetse) leraar die ook echt les geeft blijft onvervangbaar. Maar daarnaast liggen de oorzaken van de dramatische achteruitgang van het niveau van het wiskunde onderwijs ook bij het lager onderwijs. Kinderen die nooit goed hebben leren rekenen (met uitsluitend pen en papier alsmede uit het hoofd, wel te verstaan) missen ook de benodigde vaardigheden om bijvoorbeeld eenvoudige algebraïsche herleidingen tot een goed einde te brengen. Dat wordt treffend geïllustreerd door het volgende plaatje op de website van Liesbeth van der Plas:
[ afbeelding ]
Ze merkt daarbij op: Als een kind niet in staat is het getalsommetje probleemloos uit te rekenen, is de algebra-opgave ook veel te hoog gegrepen. Op haar site is ook een interessante PDF te vinden waar ze het onderwijs dat ze zelf kreeg in de elementaire algebra en de vlakke meetkunde vergelijkt met het onderwijs dat haar dochter op school kreeg over deze zelfde onderwerpen, en de consequenties die dat heeft.
Maar goed, ik kan me voorstellen dat diegenen die zich nu op een toets voorbereiden en dit lezen zullen zeggen dat ze hier op dit moment niets mee opschieten, en daarom wil ik jullie ook niet het bos insturen maar toch wat goede en concrete adviezen meegeven.
Zoals gezegd is een goede leraar onvervangbaar, en dat betekent dat je eigenlijk een cursus zou moeten gaan volgen als je ernst maakt met je (vervolg)studie. Als je dat niet kunt bekostigen of anderszins niet in de gelegenheid bent om dat te gaan doen, dan zou je wellicht op zoek kunnen gaan naar iemand die bereid is je tegen een schappelijk tarief bijles te geven. Is ook dat geen reële mogelijkheid, dan blijft uiteraard alleen zelfstudie over. Maar dan kun je beter niet beginnen met het boek van Van de Craats, want dat is meer een opfriscursus en oefenboek, en daarmee bijzonder ongeschikt voor zelfstudie als je de stof nog nooit eerder hebt gezien. Ik zou dan aanraden te beginnen met de spijkers. Dat is een reeks van zeven boekjes die veel beter geschikt zijn voor zelfstudie en waaruit je de basistechnieken ook echt kunt leren. Je moet dan wel beginnen met het eerste boekje over rekenen en uiteindelijk alle zeven delen doorwerken. Dat moet te doen zijn, voor elk deeltje staat volgens de auteur van deze boekjes zo'n 10 à 20 uur studie. En ook al lijkt me dat wat optimistisch, dan nog moet het mogelijk zijn in enkele honderden uren zelfstudie deze gehele reeks door te werken en je de stof in zijn geheel eigen te maken. Pas in een tweede ronde zou je dan kunnen overwegen als herhaling nog wat extra opgaven te maken uit het boek van Van de Craats.
Het optellen van breuken heb ik wel eerder gehad. Hoofdstuk 1 in het basisboek wiskunde bestaat trouwens uit handmatig vermenigvuldigen en delen. Ik liet mijn ouders een vermenigvuldigenopgave maken en die deden dat toch beduidend sneller dan dat ik deed. Ik moest eerst het voorbeeld bestuderen voordat ik aan de opgaven kon beginnen, ik wist simpelweg niet wat de bedoeling was. De staartdelingen gingen mij trouwens wat beter af, deze kan ik me dan ook nog goed herinneren van de basisschool
Over de zelfstudie. Tja, die cursussen zijn inderdaad flink aan de prijs.. En voor mij is de afstand naar de universiteit waar ik wil gaan studeren geen pretje. Verder heb ik wel iemand die mij eventueel bijles kan geven. Maar ik vind het onnodig om hulp in te schakelen zolang ik het zelf nog red.
Voor mij is het nu aan de late kant om nog een andere methode te gaan proberen. Ik zit nu bij het laatste onderdeel van de examenstof (calcalus: differentiëren). Met alleen het boek had ik het niet gered. Maar in combinatie met khanacademy.org (aanrader!), youtubekanaal wiskundeacademie (behandelt dingen als differentieren niet maar wel parabolen, kwadratische vergelijking, snijpunten + asymptoten etc.) is het al goed te doen. Daarnaast kan je de opgave googlen + het woord wiskundeforum, daar zijn namelijk een hoop topics over de moeilijkere vragen uit het basisboek van mensen die er ook niet uitkwamen. En anders is er nog de mogelijkheid om zelf een vraag te stellen op een forum.
Ik heb je hier al het advies gegeven om bij het oplossen van wat lastiger ongelijkheden te werken met tekenschema's. Ik geef zo'n advies niet voor niets, het is de bedoeling dat je dat ook ter harte neemt.quote:
| x^2 - 2x | < 1
Ik deed
[snip]
Nu heb ik wel de goede antwoorden, maar heb ik niet de juiste combinatie van oplossingen bij elkaar en onjuiste ongelijkheidstekens...? Wat doe ik fout..?
Als de absolute waarde van een (reële) grootheid kleiner is dan 1, dan ligt de waarde van die grootheid zelf tussen −1 en +1. De ongelijkheid
| x2 − 2x | < 1
is dus equivalent met
−1 < x2 − 2x < 1
en dit is weer equivalent met
−1 < x2 − 2x ∧ x2 − 2x < 1
oftewel
x2 − 2x > −1 ∧ x2 − 2x < 1
en dus
x2 − 2x + 1 > 0 ∧ x2 − 2x − 1 < 0
Nu hebben we dus een combinatie van twee kwadratische ongelijkheden met een rechterlid herleid op nul en waaraan tegelijkertijd moet worden voldaan. Deze kwadratische ongelijkheden lossen we op door eerst de nulpunten te bepalen van de kwadratische veeltermen in het linkerlid van deze ongelijkheden. En daar heb je de abc-formule helemaal niet bij nodig. De bepaling van de nulpunten van de eerste kwadratische veelterm is wel heel eenvoudig. Hiervoor vinden we
x2 − 2x + 1 = 0
(x − 1)2 = 0
x − 1 = 0
x = 1
Voor de bepaling van de nulpunten van de tweede kwadratische veelterm kunnen we kwadraatafsplitsing gebruiken. Dan vinden we
x2 − 2x − 1 = 0
(x − 1)2 − 1 − 1 = 0
(x − 1)2 = 2
x − 1 = √2 ∨ x − 1 = −√2
x = 1 + √2 ∨ x = 1 − √2
Nu moet je zelf maar even twee tekenschema's maken (één voor elk van beide kwadratische ongelijkheden) waarbij je deze tekenschema's uitgelijnd onder elkaar plaatst. Maar strict genomen is dit hier niet eens nodig.
De grafiek van y = x2 − 2x + 1 is een dalparabool waarvan de top met coördinaten (1; 0) de x-as raakt, zodat we hebben x2 − 2x + 1 > 0 voor elke x ≠ 1.
De grafiek van y = x2 − 2x − 1 is een dalparabool die de x-as snijdt in de punten met coördinaten (1 − √2; 0) en (1 + √2; 0), zodat we hebben x2 − 2x − 1 < 0 voor 1 − √2 < x < 1 + √2.
Voor de waarden van x die aan de oorspronkelijke ongelijkheid voldoen vinden we dus de voorwaarde
x ≠ 1 ∧ 1 − √2 < x < 1 + √2
Het open interval (1 − √2, 1 + √2) waarop x moet liggen om aan de ongelijkheid te voldoen wordt hier dus in twee delen geknipt doordat de waarde x = 1 niet mee mag doen. Deze knip geeft aldus twee open intervallen. Je kunt de oplossing van de ongelijkheid nu noteren als
1 − √2 < x < 1 ∨ 1 < x < 1 + √2
of als
x ∈ (1 − √2, 1) ∪ (1, 1 + √2)
[ Bericht 0% gewijzigd door Riparius op 06-05-2014 00:16:00 ]
Differentieer met behulp van quotientregel:
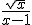
Ik kom dan tot:
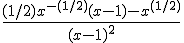
Maar het moet nog vereenvoudigd worden tot:
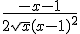
Hoe pak ik dit aan?
[ Bericht 14% gewijzigd door nodig op 06-05-2014 00:58:10 ]
Ik kom dan tot:
Maar het moet nog vereenvoudigd worden tot:
Hoe pak ik dit aan?
[ Bericht 14% gewijzigd door nodig op 06-05-2014 00:58:10 ]
Dit is alvast niet goed, je bent een kwadraat in de noemer vergeten. De quotiëntregel luidt in symbolische vormquote:
Differentieer met behulp van quotientregel:
Ik kom dan tot:
(f/g)' = (f'g − fg')/g2
Woops sorry, verkeerd overgenomenquote:
[..]
Dit is alvast niet goed, je bent een kwadraat in de noemer vergeten. De quotiëntregel luidt in symbolische vorm
(f/g)' = (f'g − fg')/g2
De kwadraat had ik wel in mijn schrift staan.De correctie:
Ook aangepast in eerste post.
Goed. Vermenigvuldig nu teller en noemer van je oorspronkelijke quotiënt met 2·x1/2 en pas daarna rekenregels voor het werken met exponenten toe.quote:
[..]
Woops sorry, verkeerd overgenomen
De correctie:
Ook aangepast in eerste post.
De noemer is dan duidelijk. Maar van de teller kan ik weinig maken. Wat bedoel je met oorspronkelijke quotiënt?quote:
[..]
Goed. Vermenigvuldig nu teller en noemer van je oorspronkelijke quotiënt met 2·x1/2 en pas daarna rekenregels voor het werken met exponenten toe.
Met het oorspronkelijke quotiënt bedoel ik de breuk zoals je die krijgt direct na toepassing van de quotiëntregel en zoals je die hierboven (gecorrigeerd) weergeeft.quote:
[..]
De noemer is dan duidelijk. Maar van de teller kan ik weinig maken. Wat bedoel je met oorspronkelijke quotiënt?
Goed, de noemer is je duidelijk. Nu gaan we kijken wat je krijgt als je de teller vermenigvuldigt met 2·x1/2. Hiervoor krijgen we dan
2·x1/2·(½·x−1/2·(x−1) − x1/2) = 2·½·x1/2·x−1/2·(x−1) − 2·x1/2·x1/2 = 1·x0·(x−1) − 2·x1 = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1
Ik maak hier gebruik van de distributiviteit van vermenigvuldiging t.o.v. optelling (en aftrekking), dus
a(b+c) = ab + ac
a(b−c) = ab − ac
alsmede van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal, dus
ap·aq = ap+q
Ook maak ik nog gebruik van de eigenschap dat de nulde macht van een getal gelijk is aan 1, dus
a0 = 1
Dit laatste volgt ook direct uit de regel ap·aq = ap+q met q = 0, want dan krijg je ap·a0 = ap zodat vermenigvuldiging met a0 niets verandert en a0 dus wel 1 moet zijn.
Q is een deelverzameling van R en heeft als zodanig de deeltopologie van de standaardtopologie op R. Dat wil zeggen dat S een open resp. gesloten deel van Q is in deze topologie precies als S geschreven kan worden als de doorsnede van Q met een open resp. gesloten deel van R.quote:
[..]
Zie mijn edit, informeel lukt geslotenheid me wel. Maar geen idee hoe ik dit rigoureus opschrijf...
Maar jouw open cover, waarom mag je deze gebruiken? Als we het over
Danku!quote:
[..]
Met het oorspronkelijke quotiënt bedoel ik de breuk zoals je die krijgt direct na toepassing van de quotiëntregel en zoals je die hierboven (gecorrigeerd) weergeeft.
Goed, de noemer is je duidelijk. Nu gaan we kijken wat je krijgt als je de teller vermenigvuldigt met 2·x1/2. Hiervoor krijgen we dan
2·x1/2·(½·x−1/2·(x−1) − x1/2) = 2·½·x1/2·x−1/2·(x−1) − 2·x1/2·x1/2 = 1·x0·(x−1) − 2·x1 = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1
Ik maak hier gebruik van de distributiviteit van vermenigvuldiging t.o.v. optelling (en aftrekking), dus
a(b+c) = ab + ac
a(b−c) = ab − ac
alsmede van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal, dus
ap·aq = ap+q
Ook maak ik nog gebruik van de eigenschap dat de nulde macht van een getal gelijk is aan 1, dus
a0 = 1
Dit laatste volgt ook direct uit de regel ap·aq = ap+q met q = 0, want dan krijg je ap·a0 = ap zodat vermenigvuldiging met a0 niets verandert en a0 dus wel 1 moet zijn.
Ik heb het even uitgeschreven op papier en begrijp het inderdaad. Ga de opgave nu nog een keer maken
. In je laatste 3 stappen: = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1
Moet de één-na-laatste stap niet gewoon x - 1 - 2x zijn? Ik zat de hele tijd die haakjes uit te werken maar dat komt niet uit. Die haakjes mag je toch weghalen omdat er in de stap ervoor de haakjes al uitgewerkt zijn?
Hoe meen je die haakjes weg te werken? Er staat in feite een 1 voor. 1(x-1) - 2x = x - 1 - 2x = -x -1. Het is dus hetzelfde.quote:
[..]
Danku!
Ik heb het even uitgeschreven op papier en begrijp het inderdaad. Ga de opgave nu nog een keer maken
In je laatste 3 stappen: = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1
Moet de één-na-laatste stap niet gewoon x - 1 - 2x zijn? Ik zat de hele tijd die haakjes uit te werken maar dat komt niet uit. Die haakjes mag je toch weghalen omdat er in de stap ervoor de haakjes al uitgewerkt zijn?
Daar had ik nog niet aan gedachtquote:
[..]
Hoe meen je die haakjes weg te werken? Er staat in feite een 1 voor. 1(x-1) - 2x = x - 1 - 2x = -x -1. Het is dus hetzelfde.
Ik zat te vermenigvuldigen met die -2x
Bedankt! Hartstikke handige methode! Ik maak er nu een grafiektekening bij, vind ik opzicht wel handiger!quote:
[..]
Ik heb je hier al het advies gegeven om bij het oplossen van wat lastiger ongelijkheden te werken met tekenschema's. Ik geef zo'n advies niet voor niets, het is de bedoeling dat je dat ook ter harte neemt.
Als de absolute waarde van een (reële) grootheid kleiner is dan 1, dan ligt de waarde van die grootheid zelf tussen −1 en +1. De ongelijkheid
| x2 − 2x | < 1
is dus equivalent met
−1 < x2 − 2x < 1
en dit is weer equivalent met
−1 < x2 − 2x ∧ x2 − 2x < 1
oftewel
x2 − 2x > −1 ∧ x2 − 2x < 1
en dus
x2 − 2x + 1 > 0 ∧ x2 − 2x − 1 < 0
Nu hebben we dus een combinatie van twee kwadratische ongelijkheden met een rechterlid herleid op nul en waaraan tegelijkertijd moet worden voldaan. Deze kwadratische ongelijkheden lossen we op door eerst de nulpunten te bepalen van de kwadratische veeltermen in het linkerlid van deze ongelijkheden. En daar heb je de abc-formule helemaal niet bij nodig. De bepaling van de nulpunten van de eerste kwadratische veelterm is wel heel eenvoudig. Hiervoor vinden we
x2 − 2x + 1 = 0
(x − 1)2 = 0
x − 1 = 0
x = 1
Voor de bepaling van de nulpunten van de tweede kwadratische veelterm kunnen we kwadraatafsplitsing gebruiken. Dan vinden we
x2 − 2x − 1 = 0
(x − 1)2 − 1 − 1 = 0
(x − 1)2 = 2
x − 1 = √2 ∨ x − 1 = −√2
x = 1 + √2 ∨ x = 1 − √2
Nu moet je zelf maar even twee tekenschema's maken (één voor elk van beide kwadratische ongelijkheden) waarbij je deze tekenschema's uitgelijnd onder elkaar plaatst. Maar strict genomen is dit hier niet eens nodig.
De grafiek van y = x2 − 2x + 1 is een dalparabool waarvan de top met coördinaten (1; 0) de x-as raakt, zodat we hebben x2 − 2x + 1 > 0 voor elke x ≠ 1.
De grafiek van y = x2 − 2x − 1 is een dalparabool die de x-as snijdt in de punten met coördinaten (1 − √2; 0) en (1 + √2; 0), zodat we hebben x2 − 2x − 1 < 0 voor 1 − √2 < x < 1 + √2.
Voor de waarden van x die aan de oorspronkelijke ongelijkheid voldoen vinden we dus de voorwaarde
x ≠ 1 ∧ 1 − √2 < x < 1 + √2
Het open interval (1 − √2, 1 + √2) waarop x moet liggen om aan de ongelijkheid te voldoen wordt hier dus in twee delen geknipt doordat de waarde x = 1 niet mee mag doen. Deze knip geeft aldus twee open intervallen. Je kunt de oplossing van de ongelijkheid nu noteren als
1 − √2 < x < 1 ∨ 1 < x < 1 + √2
of als
x ∈ (1 − √2, 1) ∪ (1, 1 + √2)
Dat klopt dus niet hèquote:Op dinsdag 6 mei 2014 15:39 schreef nodig het volgende:
[..]
Daar had ik nog niet aan gedacht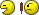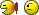
Ik zat te vermenigvuldigen met die -2x
Oké, nog een vraagje:
Differentieer:
![ln \sqrt[3]{1-x}](https://forum.fok.nl/lib/mimetex.cgi?ln%20%5Csqrt%5B3%5D%7B1-x%7D)
Nu kom ik tot:
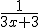
Maar het moet uiteindelijk worden:
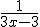
Wat doe ik fout?
Bij de volgende opgaven zijn de plus en minnen ook omgedraaid?
[ Bericht 7% gewijzigd door nodig op 06-05-2014 20:07:27 ]
Differentieer:
Nu kom ik tot:
Maar het moet uiteindelijk worden:
Wat doe ik fout?
Bij de volgende opgaven zijn de plus en minnen ook omgedraaid?
[ Bericht 7% gewijzigd door nodig op 06-05-2014 20:07:27 ]
Zie hieronder.quote:
Oké, nog een vraagje:
Differentieer:
Nu kom ik tot:
Maar het moet uiteindelijk worden:
Wat doe ik fout?
[ Bericht 17% gewijzigd door MrRiot op 06-05-2014 20:14:17 ]
Nope
quote:
Oké, nog een vraagje:
Differentieer:
Nu kom ik tot:
Maar het moet uiteindelijk worden:
Wat doe ik fout?
Bij de volgende opgaven zijn de plus en minnen ook omgedraaid?
Kan je via de logaritmeregels schrijven als:
Als je nu de kettingregel toepast krijg je als afgeleide:
quote:
Dankje! Ik denk dat ik met deze informatie een heel eind verder ga komenquote:
[..]
Kan je via de logaritmeregels schrijven als:
Als je nu de kettingregel toepast krijg je als afgeleide:
Wat zag je hier niet in? Ik vind het nogal veel op die andere som lijkenquote:
[..]
[..]
Dankje! Ik denk dat ik met deze informatie een heel eind verder ga komen
Ik kwam er niet op om die (1/3) voor de ln te zettenquote:
[..]
Wat zag je hier niet in? Ik vind het nogal veel op die andere som lijken
Maar inderdaad is dat gisteren ook al gezegd nu ik terug lees:
quote:
Jouw afgeleide van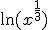
klopt niet.
Je vergeet de kettingregel.
Maar de kettingregel kan je vermijden.
Hint:
Bepaal met een staartdeling het polynoom g(x) waarvoor geldt f(x) = (x - a) g(x)
a = -1
f(x) = x^3 + 1
ik had
(x + 1) / x^3 + 1 \ x^2 - x + 1
Maar ik doe volgens mij iets fout want ik kom op ook uit op " rest 1"... dus er gaat wat in het uitschrijven fout.. hoe zouden jullie het doen?
en tenslotte:
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3)
ik denk dat dat wordt:
(2 - 1/x + 2/x^2 - 1/x^3 ) / ( 3 - 3/x - 3/x^2 + 3/x^3)
Echter weet ik niet hoe ik het verder moet oplossen om achter de nulpunten te komen
[ Bericht 28% gewijzigd door Super-B op 06-05-2014 21:07:54 ]
a = -1
f(x) = x^3 + 1
ik had
(x + 1) / x^3 + 1 \ x^2 - x + 1
Maar ik doe volgens mij iets fout want ik kom op ook uit op " rest 1"... dus er gaat wat in het uitschrijven fout.. hoe zouden jullie het doen?
en tenslotte:
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3)
ik denk dat dat wordt:
(2 - 1/x + 2/x^2 - 1/x^3 ) / ( 3 - 3/x - 3/x^2 + 3/x^3)
Echter weet ik niet hoe ik het verder moet oplossen om achter de nulpunten te komen
[ Bericht 28% gewijzigd door Super-B op 06-05-2014 21:07:54 ]
Dit klopt gewoon.quote:
Bepaal met een staartdeling het polynoom g(x) waarvoor geldt f(x) = (x - a) g(x)
a = -1
f(x) = x^3 + 1
ik had
(x + 1) / x^3 + 1 \ x^2 - x + 1
Maar ik doe volgens mij iets fout want ik kom op ook uit op " rest 1"... dus er gaat wat in het uitschrijven fout.. hoe zouden jullie het doen?
(x^2 -x + 1)(x+1) = x^3 + 1
Zou je de staartdeling kunnen uitwerken voor me? Daar gaat het mis bij mij..quote:
[..]
Dit klopt gewoon.
(x^2 -x + 1)(x+1) = x^3 + 1
Thanks!! Zou je me ook kunnen helpen met mijn tweede vraagstuk in de post?quote:
[ afbeelding ]
Zoiets. Maar misschien is mijn notatie anders dan de jouwe.
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3) = 0
'Gewoon' de nulpunten van de teller bepalen en controleren of het ook niet toevallig nulpunten van de noemer zijn.
Anders even invullen bij Wolfram Alpha om de ontbindingen te bepalen als het je zelf niet lukt.
'Gewoon' de nulpunten van de teller bepalen en controleren of het ook niet toevallig nulpunten van de noemer zijn.
Anders even invullen bij Wolfram Alpha om de ontbindingen te bepalen als het je zelf niet lukt.
Hoe bedoel je? Ik snap het niet..? Hebben de teller en noemer allebei eigen nulpunten? Maar het is samen 1 functie toch..?quote:
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3) = 0
'Gewoon' de nulpunten van de teller bepalen en controleren of het ook niet toevallig nulpunten van de noemer zijn.
Anders even invullen bij Wolfram Alpha om de ontbindingen te bepalen als het je zelf niet lukt.
Ik zit even te kijken in dat boek van Craats
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
"Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten van f (x)."
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
"Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten van f (x)."
Exact! Ik schrijf mee en probeer wat dingetjes uit, maar het wil niet helemaal lukken. Het boek is echt boek voor naslagwerk...quote:
Ik zit even te kijken in dat boek van Craats
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
Grotendeels heb ik het hulp van jullie nodig en dan willen de puzzelstukjes goed samenvallen.
Waarom zijn de nulpunten van de noemer niet ook de nulpunten van f(x) ? Dat heb ik niet zo begrepen, want zowel de teller en noemer horen toch bij elkaar en het is toch 1 functie? Die twee kun je toch niet los van elkaar zien?quote:
Ik zit even te kijken in dat boek van Craats
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
"Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten van f (x)."
''Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten
van f(x). De nulpunten van de noemer b(x) heten dan de polen van f(x). Bij
elke pool hoort een verticale asymptoot.''
Ik heb er werkelijk niks van begrepen wat er staat.
f(x) = a(x) / b(x)
Een rationale functie is altijd een samenstelling van twee andere functies (de teller a(x) en de noemer b(x))
f(x) = a(x) / b(x) = 0
Vermenigvuldig beide kanten met b(x)....
Dus de nulpunten van a(x) zijn de nulpunten van f(x)
Alleen a(x) = b(x) = 0 is een speciaal geval omdat je niet mag delen door 0.
Maar als a(x) en b(x) hetzelfde nulpunt c hebben dan kan je a(x) schrijven als a(x) = (x-c)g(x) en b(x) als b(x) = (x-c) q(x).
Oftewel dan kan je de term (x-c) wegdelen en heb je het probleem verholpen
f(x) = a(x) / b(x) = (x-c)g(x) / ((x-c)q(x)) = g(x)/q(x).
Een rationale functie is altijd een samenstelling van twee andere functies (de teller a(x) en de noemer b(x))
f(x) = a(x) / b(x) = 0
Vermenigvuldig beide kanten met b(x)....
Dus de nulpunten van a(x) zijn de nulpunten van f(x)
Alleen a(x) = b(x) = 0 is een speciaal geval omdat je niet mag delen door 0.
Maar als a(x) en b(x) hetzelfde nulpunt c hebben dan kan je a(x) schrijven als a(x) = (x-c)g(x) en b(x) als b(x) = (x-c) q(x).
Oftewel dan kan je de term (x-c) wegdelen en heb je het probleem verholpen
f(x) = a(x) / b(x) = (x-c)g(x) / ((x-c)q(x)) = g(x)/q(x).
Tja, dat krijg je als je een boek gaat doornemen dat niet geschikt is als leerboek en je bovendien de stof nog nooit eerder hebt gezien en kennelijk ook de nodige voorkennis mist, zoals rekenen met breuken (zie de site en de PDF van Liesbeth van der Plas waarnaar ik hierboven verwijs).quote:
[..]
Waarom zijn de nulpunten van de noemer niet ook de nulpunten van f(x) ? Dat heb ik niet zo begrepen, want zowel de teller en noemer horen toch bij elkaar en het is toch 1 functie? Die twee kun je toch niet los van elkaar zien?
''Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten
van f(x). De nulpunten van de noemer b(x) heten dan de polen van f(x). Bij
elke pool hoort een verticale asymptoot.''
Ik heb er werkelijk niks van begrepen wat er staat.
Delen door nul is niet gedefinieerd (onmogelijk), dus een breuk waarvan de noemer nul is heeft geen betekenis (geen waarde). Een breuk heeft alleen de waarde nul als de teller nul is terwijl de noemer niet nul is.
Als je dus een rationale functie hebt, dat is een functie met het functievoorschrift
f(x) = a(x)/b(x)
waarbij a(x) en b(x) veeltermen (polynomen) zijn in x, dan kan f(x) alleen nul zijn als a(x) nul is terwijl b(x) niet nul is.
Als je de omgekeerde situatie hebt, dus dat b(x) voor een zekere waarde x = x0 gelijk is aan nul terwijl a(x0) ≠ 0, dan neemt de absolute waarde van het quotiënt a(x)/b(x) en dus |f(x)| onbeperkt toe naarmate je x dichter in de buurt van die waarde x = x0 kiest, maar voor de waarde x = x0 zelf is de functiewaarde dan onbepaald. In dit geval heeft de grafiek van y = f(x) een verticale asymptoot bij x = x0, en men zegt dan ook dat de functie f een pool x = x0 heeft. Een verticale asymptoot is, eenvoudig gezegd, een verticale rechte lijn waar de grafiek van de functie steeds dichter tegenaan kruipt naarmate je x dichter bij x0 laat komen, maar dan zonder dat de grafiek van de functie ooit samenvalt met deze lijn.
[ Bericht 1% gewijzigd door Riparius op 07-05-2014 01:09:25 ]
Vereenvoudig zo ver mogelijk:
2^(1+x) 3^x
ik had 2^(1+x) * 3^x dat wordt dan 6^(2x)
Maar het antwoord is 2 * 6^x
hoe..?
[ Bericht 1% gewijzigd door RustCohle op 08-05-2014 12:14:42 ]
2^(1+x) 3^x
ik had 2^(1+x) * 3^x dat wordt dan 6^(2x)
Maar het antwoord is 2 * 6^x
hoe..?
[ Bericht 1% gewijzigd door RustCohle op 08-05-2014 12:14:42 ]
Het is 3^x neem ik aan?quote:
Vereenvoudig zo ver mogelijk:
2^(1+x) 3x
ik had 2^(1+x) * 3x dat wordt dan 6^(x^2)
Maar het antwoord is 2 * 6^x
hoe..?
2^(1+x) = 2^1 * 2^x = 2 * 2^x
Dit * 3^x geeft 2 * 2^x * 3^x = 2 * 6^x
Ja het is 3^x.quote:
[..]
Het is 3^x neem ik aan?
2^(1+x) = 2^1 * 2^x = 2 * 2^x
Dit * 3^x geeft 2 * 2^x * 3^x = 2 * 6^x
Waarom worden ze apart genomen? Ik dacht eerst 2^1 is 2 en dan 2^x.. en dat vermenigvuldigen met 3^x maakt 6^2x
weet je ook hoe je deelt met machten?quote:
[..]
Het is 3^x neem ik aan?
2^(1+x) = 2^1 * 2^x = 2 * 2^x
Dit * 3^x geeft 2 * 2^x * 3^x = 2 * 6^x
4(^2x) / 2x
ik deed alles delen door 2x maakt 2^x.. echter is het antwoord 2^(3x) of 8^x
Gewoon braaf rekenregels voor machten toepassen:quote:
Vereenvoudig zo ver mogelijk:
2^(1+x) 3^x
hoe..?
ap·aq = ap+q
ap·bp = (a·b)p
Bedenk dat je deze regels ook van rechts naar links kunt gebruiken.
http://nl.wikipedia.org/wiki/Machtsverheffen#Rekenen_met_machtenquote:
[..]
Ja het is 3^x.
Waarom worden ze apart genomen? Ik dacht eerst 2^1 is 2 en dan 2^x.. en dat vermenigvuldigen met 3^x maakt 6^2x
Hier ook weer zo"n pittige...
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
[ Bericht 0% gewijzigd door RustCohle op 08-05-2014 12:53:22 ]
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
[ Bericht 0% gewijzigd door RustCohle op 08-05-2014 12:53:22 ]
En dat is fout. Je begrijp er nog niet veel van.quote:
W(10^(20x+10))
De w is wel een vijfdemachtswortel..
ik zelf kwam uit op 100^20x
Je hebt (1020x+10)1/5 = 10(20x+10)·(1/5) = 104x+2
En gebruik superscript voor exponenten. Die carets zijn nergens voor nodig.
ohhh ik dacht dat je bovenop die superscript van 20x+10 nog een superscript moest doen met ^(1/5)quote:
[..]
En dat is fout. Je begrijp er nog niet veel van.
Je hebt (1020x+10)1/5 = 10(20x+10)·(1/5) = 104x+2
En gebruik superscript voor exponenten. Die carets zijn nergens voor nodig.
(10^-2x)^2
ik kwam uit op 100^-4x..
toch is het 10000^-x
Ik zit op mijn mobiel vandaar dat ik geen superscript doe.
ik kwam uit op 100^-4x..
toch is het 10000^-x
Ik zit op mijn mobiel vandaar dat ik geen superscript doe.
(10−2x)2 = 10−2x·2 = 10−4x = (104)−x = 10000−xquote:
(10^-2x)^2
ik kwam uit op 100^-4x..
toch is het 10000^-x
Ik zit op mijn mobiel vandaar dat ik geen superscript doe.
Die overgang.. snap ik niet.. dus van 10^-4x naar (10^4)^xquote:
[..]
(10−2x)2 = 10−2x·2 = 10−4x = (104)−x = 10000−x
Heel eenvoudig, −4x kun je ook schrijven als het product van +4 en −x, dus 4·(−x). En dus hebben wequote:
[..]
Die overgang.. snap ik niet.. dus van 10^-4x naar (10^4)^x
10−4x = 104·−x = (104)−x
Echt, dit is doodsimpele brugklas algebra.
Waarom kan dit niet bij 10^(4x +2) dat je dan gewoon 10^2 hebt en dus 100^4x?quote:
[..]
Heel eenvoudig, −4x kun je ook schrijven als het product van +4 en −x, dus 4·(−x). En dus hebben we
10−4x = 104·−x = (104)−x
Echt, dit is doodsimpele brugklas algebra.
quote:
Hier ook weer zo"n pittige...
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
Je hebt 104x+2 = 104x·102 = 104x·100 = 100·104xquote:
[..]
Waarom kan dit niet bij 10^(4x +2) dat je dan gewoon 10^2 hebt en dus 100^4x?
maar dit is niet hetzelfde als 1004x want dan zou 100 gelijk moeten zijn aan 104x, en dat is in het algemeen niet zo, behalve als x = ½.
Herschrijf hier eerst alle factoren als machten van 2, en bedenk ook dat delen door 8x = 23x hetzelfde is als vermenigvuldigen met het omgekeerde, dus vermenigvuldigen met 2−3x.quote:
Hier ook weer zo"n pittige...
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
even kijken.. dan kom ik als eerst uit totquote:
[..]
Herschrijf hier eerst alle factoren als machten van 2, en bedenk ook dat delen door 8x = 23x hetzelfde is als vermenigvuldigen met het omgekeerde, dus vermenigvuldigen met 2−3x.
2^x * 2^(1-2x) : 2^3x
en dat resulteert tot
2^(1-x) : 2^3x
Dat is niet goed. We hebbenquote:
[..]
even kijken.. dan kom ik als eerst uit tot
2^x * 2^(1-2x) : 2^3x
en dat resulteert tot
2^(1-x) : 2^3x
2x·41−x·2−3x = 2x·22−2x·2−3x = 2x+2−2x−3x = 22−4x
waarom alles vermenigvuldigen? Er is toch ook een deelsom? Opeens is het een vermenigvuldiging?quote:
[..]
Dat is niet goed. We hebben
2x·41−x·2−3x = 2x·22−2x·2−3x = 2x+2−2x−3x = 22−4x
en hoezo 2^(2-2x) ik zou denken 2^(2-x)
Omdat ik dan gebruik kan maken van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van machten met hetzelfde grondtal.quote:
Jazeker, maar ik heb je al gezegd dat delen hetzelfde is als vermenigvuldiging met het omgekeerde. En ik wil juist een vermenigvuldiging hebben omdat ik de exponenten dan kan optellen.quote:Er is toch ook een deelsom?
Nee, niet opeens, maar om de bovengenoemde reden.quote:Opeens is het een vermenigvuldiging?
Nee, want 2(1−x) = 2 − 2x (distributiviteit van vermenigvuldiging ten opzichte van optelling).quote:en hoezo 2^(2-2x) ik zou denken 2^(2-x)
Dat snap ik niet.. xdquote:
[..]
Omdat ik dan gebruik kan maken van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van machten met hetzelfde grondtal.
[..]
Jazeker, maar ik heb je al gezegd dat delen hetzelfde is als vermenigvuldiging met het omgekeerde. En ik wil juist een vermenigvuldiging hebben omdat ik de exponenten dan kan optellen.
[..]
Nee, niet opeens, maar om de bovengenoemde reden.
[..]
Nee, want 2(1−x) = 2 − 2x (distributiviteit van vermenigvuldiging ten opzichte van optelling).
Je hebtquote:
a(b + c) = ab + ac
a(b − c) = ab − ac
Je gaat me toch niet vertellen dat je dat nog nooit hebt gezien?
Ik bedoelde de tekst distributiviteit van de optelling..quote:
[..]
Je hebt
a(b + c) = ab + ac
a(b − c) = ab − ac
Je gaat me toch niet vertellen dat je dat nog nooit hebt gezien?
Snap jij 10log(2^6) - 10log 1/5
ik deed 10log 64/0,5 is 10log 128
Echter is het 7 10log2...
Aftrekken van een getal is hetzelfde als het tegengestelde van dat getal optellen.quote:
[..]
Ik bedoelde de tekst distributiviteit van de optelling..
Waarom denk je dat ik het mogelijk niet zou snappen?quote:Snap jij 10log(2^6) - 10log 1/5
Dat is fout want delen door 1/5 is niet hetzelfde als delen door 1/2 maar wel hetzelfde als vermenigvuldigen met 5.quote:Ik deed 10log 64/0,5 is 10log 128
10log(26) − 10log(1/5) = 6·10log 2 − (10log 2 − 10log 10) = 5·10log 2 + 1quote:Echter is het 7 10log2...
het was 1/2 niet 1/5quote:
[..]
Aftrekken van een getal is hetzelfde als het tegengestelde van dat getal optellen.
[..]
Waarom denk je dat ik het mogelijk niet zou snappen?
[..]
Dat is fout want delen door 1/5 is niet hetzelfde als delen door 1/2 maar wel hetzelfde als vermenigvuldigen met 5.
[..]
10log(26) − 10log(1/5) = 6·10log 2 − (10log 2 − 10log 10) = 5·10log 2 + 1
ik snap het niet.. ik weet wel dat 10log(2^6) het volgende wordt:quote:
[..]
Aftrekken van een getal is hetzelfde als het tegengestelde van dat getal optellen.
[..]
Waarom denk je dat ik het mogelijk niet zou snappen?
[..]
Dat is fout want delen door 1/5 is niet hetzelfde als delen door 1/2 maar wel hetzelfde als vermenigvuldigen met 5.
[..]
10log(26) − 10log(1/5) = 6·10log 2 − (10log 2 − 10log 10) = 5·10log 2 + 1
6 10log2 maar daarna weet ik het niet meer.. als je logs van elkaar aftrekt is hrt eigenlijk delen toch?
Dus 6 10log2 - 10log(1/2) is dan 6 10log4?
5log 8 + 5log 4 = 5log(23) + 5log(22) = 3·5log 2 + 2·5log 2 = 5·5log 2quote:
Net als dat 5log8 + 5log4 = 5 5log2 terwijl ik 5log20 heb.
Nee, hier heb jequote:
[..]
ik snap het niet.. ik weet wel dat 10log(2^6) het volgende wordt:
6 10log2 maar daarna weet ik het niet meer.. als je logs van elkaar aftrekt is het eigenlijk delen toch?
Dus 6 10log2 - 10log(1/2) is dan 6 10log4?
6·10log 2 − 10log(1/2) = 6·10log 2 + 10log 2 = 7·10log 2
Ik zie nu dat je hierboven een typo hebt, je schreef namelijk 1/5 terwijl je kennelijk 1/2 bedoelde.
Jep.. waar komt die 7 vandaan?quote:
[..]
Nee, hier heb je
6·10log 2 − 10log(1/2) = 6·10log 2 + 10log 2 = 7·10log 2
Ik zie nu dat je hierboven een typo hebt, je schreef namelijk 1/5 terwijl je kennelijk 1/2 bedoelde.
Heel eenvoudig, logaritmen van getallen die elkaars inverse zijn, zijn elkaars tegengestelde. Oftewel, je hebtquote:
glog(1/a) = −glog a
Dit is uiteraard een eenvoudig gevolg van de rekenregel
glog(a/b) = glog a − glog b
en
glog 1 = 0
Dus hebben we
6·10log 2 − 10log(1/2) = 6·10log 2 − (−10log 2) = 6·10log 2 + 10log 2 = 7·10log 2
Wat doe je eigenlijk bij het vermenigvuldigen van logaritmen?quote:
[..]
Heel eenvoudig, logaritmen van getallen die elkaars inverse zijn, zijn elkaars tegengestelde. Oftewel, je hebt
glog(1/a) = −glog a
Dit is uiteraard een eenvoudig gevolg van de rekenregel
glog(a/b) = glog a − glog b
en
glog 1 = 0
Dus hebben we
6·10log 2 − 10log(1/2) = 6·10log 2 − (−10log 2) = 6·10log 2 + 10log 2 = 7·10log 2
Schrijf 8 en 4 als machten van twee.
Hoe kom jij aan 5log 12?
Je dacht log(ab) = log(a) + log (b) dus dan zal log(a)log(b) wel gelijk zijn aan log(a+b)? Nee dus.
[ Bericht 35% gewijzigd door Anoonumos op 08-05-2014 18:35:40 ]
Hoe kom jij aan 5log 12?
Je dacht log(ab) = log(a) + log (b) dus dan zal log(a)log(b) wel gelijk zijn aan log(a+b)? Nee dus.
[ Bericht 35% gewijzigd door Anoonumos op 08-05-2014 18:35:40 ]
Ja... is toch zo? Wat moet je anders.. gewoon vermenigvuldigen uiteindelijk?quote:Op donderdag 8 mei 2014 18:26 schreef Anoonumos het volgende:
Schrijf 8 en 4 als machten van twee.
Hoe kom jij aan 5log 12?
Je dacht log(ab) = log(a) + log (b) dus dan zal log(a)log(b) wel gelijk zijn aan log(a+b)? Nee dus.
2^3 en 2^2maar kom er echt niet uit.quote:
Schrijf 8 en 4 als machten van twee.
Hoe kom jij aan 5log 12?
Je dacht log(ab) = log(a) + log (b) dus dan zal log(a)log(b) wel gelijk zijn aan log(a+b)? Nee dus.
Gewoon vermenigvuldigen ja
5log8 = 5log(23 )= 3 5log2
En net zo
5log 4 = 2 5log2
En dat met elkaar vermenigvuldigen geeft het antwoord
5log8 = 5log(23 )= 3 5log2
En net zo
5log 4 = 2 5log2
En dat met elkaar vermenigvuldigen geeft het antwoord
Thanks.... grof gezegd.... dat boek van Craats is een kut boek.quote:
Gewoon vermenigvuldigen ja
5log8 = 5log(23 )= 3 5log2
En net zo
5log 4 = 2 5log2
En dat met elkaar vermenigvuldigen geeft het antwoord
Hoe doe je 10^2x = 25
ik had 25log10 - 2 , maar dat is fout...
5log8 : 5log4
3 5log2 : 2 5log2 --> dus ik dacht
3/2 5log2 ... Is fout...
(1/2)log5 + 2log5 --> geen idee.
10^2x = 25
log25 / log10 --> antwoord / 2 het is goed, echter moet het geschreven worden als 10log5 ?!
Geen idee hoe ze op 5 komen? Waarschijnlijk 25^(1/2) maar ik weet niet waarom???
2logx2 = 3
ik had :
2³ = x² wordt dus 8 dus 22
Dit is deels goed, echter staat er +/- 22 ? Hoezo dat?
[ Bericht 17% gewijzigd door RustCohle op 08-05-2014 20:12:32 ]
3 5log2 : 2 5log2 --> dus ik dacht
3/2 5log2 ... Is fout...
(1/2)log5 + 2log5 --> geen idee.
10^2x = 25
log25 / log10 --> antwoord / 2 het is goed, echter moet het geschreven worden als 10log5 ?!
Geen idee hoe ze op 5 komen? Waarschijnlijk 25^(1/2) maar ik weet niet waarom???
2logx2 = 3
ik had :
2³ = x² wordt dus 8 dus 22
Dit is deels goed, echter staat er +/- 22 ? Hoezo dat?
[ Bericht 17% gewijzigd door RustCohle op 08-05-2014 20:12:32 ]
De 5log2 wordt weggedeeld.quote:
5log8 : 5log4
3 5log2 : 2 5log2 --> dus ik dacht
3/2 5log2
Hier gewoon de definitie van logaritmes gebruiken.quote:
102x = 25
en dus (definitie)
2x = 10log25
en dit verder uitwerken.
Logaritmen met de hand uitrekenen (benaderen) is erg lastig en veel werk, en dat wil je niet (en kun je ook niet, ook al zou ik je laten zien hoe het gaat). Vroeger gebruikte men logaritmentafels, maar je kunt nu een rekenmachine gebruiken. Elke simpele zakjapanner kan dat, en als je die niet bij de hand hebt kun je ook prima de calculator van Windows gebruiken, of eventueel een online calculator.quote:
Hoe kan ik die logaritmen benaderen om het beter te snappen? Ik kom namelijk nu ook vergelijkingen tegen..
Het is wel van belang dat je weet hoe je logaritmen omzet naar logaritmen met een ander grondtal, want calculators geven doorgaans alleen logaritmen met het grondtal 10 (de zogeheten gewone of Briggse logaritmen, aangeduid met log) en logaritmen met het speciale grondtal e (de zogeheten natuurlijke logaritmen, aangeduid met ln).
Als je een logaritme van een getal a met grondtal g om wil zetten in een logaritme van a met grondtal b (deze letter kies ik omdat een grondtal van een logaritme in het Engels een base heet) dan kun je gebruik maken van de betrekking
glog a = blog a / blog g
Deze betrekking kun je ook opschrijven in de gemakkelijker te onthouden zogeheten kettingvorm
blog a = blog g · glog a
Dat had ik! Het antwoord in getallen is goed (1,39....) echter de schrijfwijze niet!quote:
[..]
De 5log2 wordt weggedeeld.
[..]
Hier gewoon de definitie van logaritmes gebruiken.
102x = 25
en dus (definitie)
2x = 10log25
en dit verder uitwerken.
Weggedeeld?
Dankjewel!! Jij en de rest in dit topic zullen een totaal aandeelpercentage hebben van 80% als ik slaag voor de intaketoets.quote:
[..]
Logaritmen met de hand uitrekenen (benaderen) is erg lastig en veel werk, en dat wil je niet (en kun je ook niet, ook al zou ik je laten zien hoe het gaat). Vroeger gebruikte men logaritmentafels, maar je kunt nu een rekenmachine gebruiken. Elke simpele zakjapanner kan dat, en als je die niet bij de hand hebt kun je ook prima de calculator van Windows gebruiken, of eventueel een online calculator.
Het is wel van belang dat je weet hoe je logaritmen omzet naar logaritmen met een ander grondtal, want calculators geven doorgaans alleen logaritmen met het grondtal 10 (de zogeheten gewone of Briggse logaritmen, aangeduid met log) en logaritmen met het speciale grondtal e (zo zogeheten natuurlijke logaritmen, aangeduid met ln).
Als je een logaritme van een getal a met grondtal g om wil zetten in een logaritme van a met grondtal b (deze letter kies ik omdat een grondtal van een logaritme in het Engels een base heet) dan kun je gebruik maken van de betrekking
glog a = blog a / blog g
Deze betrekking kun je ook opschrijven in de gemakkelijker te onthouden zogeheten kettingvorm
blog a = blog g · glog a
2logx2 = 3
ik had :
2³ = x² wordt dus 8 dus 22
Dit is deels goed, echter staat er +/- 22 ? Hoezo dat?
Hier gaat het nodige mis met je notatie. De vergelijking luidtquote:
[..]
Dankjewel!! Jij en de rest in dit topic zullen een totaal aandeelpercentage hebben van 80% als ik slaag voor de intaketoets.
2logx2 = 3
ik had :
2³ = x² wordt dus 8 dus 22
Dit is deels goed, echter staat er +/- 22 ? Hoezo dat?
2log x2 = 3
Dan hebben we dus
x2 = 8
x = √8 ∨ x = −√8
x = 2√2 ∨ x = −2√2
Ja weggedeeld als in 5log2 / 5log2 = 1.quote:
[..]
Dat had ik! Het antwoord in getallen is goed (1,39....) echter de schrijfwijze niet!
Weggedeeld?
En voor 2x = 10log25
Gebruik dat 25 = 52 ...
Het is hier dus nodig om veel kwadraten en andere machten uit je hoofd te weten voor kleine getallen.
Aha.. Ik snap de of of situatie hier niet? Die kan ik dus hier niet inzien... wat ik dus wel kan bij tweedegraadsvergelijkingen.. met eventueel de discrimintant etc..quote:
[..]
Hier gaat het nodige mis met je notatie. De vergelijking luidt
2log x2 = 3
Dan hebben we dus
x2 = 8
x = √8 ∨ x = −√8
x = 2√2 ∨ x = −2√2
Oh hier wordt die 25 al van te voren weggedeeld in de zin van 25^(1/2) waardoor die 2 bij 2x weggewerkt wordt?quote:
[..]
Ja weggedeeld als in 5log2 / 5log2 = 1.
En voor 2x = 10log25
Gebruik dat 25 = 52 ...
Het is hier dus nodig om veel kwadraten en andere machten uit je hoofd te weten voor kleine getallen.
Dat kan ja, maar het hoeft niet per se van tevoren.quote:
[..]
Oh hier wordt die 25 al van te voren weggedeeld in de zin van 25^(1/2) waardoor die 2 bij 2x weggewerkt wordt?
2x = 10log25 = 10log(52) = 2 10log5
Deel beide kanten door 2
x = 10log5
Je hoeft hier de discriminant er niet met de haren bij te slepen. Als je bijvoorbeeld hebtquote:
[..]
Aha.. Ik snap de of of situatie hier niet? Die kan ik dus hier niet inzien... wat ik dus wel kan bij tweedegraadsvergelijkingen.. met eventueel de discriminant etc..
x2 = 4
dan is
x = 2 ∨ x = −2
Immers, vanwege de rekenregel 'min maal min geeft plus' is 4 niet alleen het kwadraat van 2 maar tevens het kwadraat van −2.
Verder moet je begrijpen dat
√8 = √4·√2 = 2√2
Dankje! Snap jij ook de functie e^x en de natuurlijke logaritme?quote:
[..]
Je hoeft hier de discriminant er niet met de haren bij te slepen. Als je bijvoorbeeld hebt
x2 = 4
dan is
x = 2 ∨ x = −2
Immers, vanwege de rekenregel 'min maal min geeft plus' is 4 niet alleen het kwadraat van 2 maar tevens het kwadraat van −2.
Verder moet je begrijpen dat
√8 = √4·√2 = 2√2
Ik snap niet echt wat ze hier willen zeggen vanaf het punt ''Zelfs geldt dat (e^(x - 1)) / x = 1 ''
en waarvoor die lim ( x --> 0 ) staat?
Pagina 153.
https://googledrive.com/h(...)met%20Antwoorden.pdf
[ Bericht 9% gewijzigd door RustCohle op 08-05-2014 22:21:57 ]
Ik zou je nog maar niet bezighouden met limieten, als je vrij basale dingen nog niet perfect onder de de knie hebt.
Ik moet wel doorzetten op dit moment, anders red ik de intaketoets niet.quote:
Ik zou je nog maar niet bezighouden met limieten, als je vrij basale dingen nog niet perfect onder de de knie hebt.
Ik kan dus nu niet bezighouden met het finetunen van de basale kennis... Dat doe ik wel als ik tijd heb..
De opgaven van logaritmen ging goed op de opgaven na waar het even fout ging, maar heb het wel door.. Dus dat is wel een pluspunt...
Waarom denk je dat ik dat wellicht niet zou begrijpen? Of bedoel je of ik het jou ook in jip-en-janneketaal uit kan leggen?quote:
[..]
Dankje! Snap jij ook de functie e^x en de natuurlijke logaritme?
Ik sluit me aan bij de opvatting van Novermars dat je niet met analyse (differentiaal- en integraalrekening) moet beginnen als je nog steeds volkomen vastloopt met simpele brugklas algebra.quote:Ik snap niet echt wat ze hier willen zeggen vanaf het punt ''Zelfs geldt dat (e^(x - 1)) / x = 1 ''
en waarvoor die lim ( x --> 0 ) staat?
Pagina 153.
https://googledrive.com/h(...)met%20Antwoorden.pdf
[ Bericht 0% gewijzigd door Riparius op 09-05-2014 00:07:55 ]
Of je het mij in jip en janneke taal kunt uitleggen inderdaad..quote:
[..]
Waarom denk je dat ik dat wellicht niet zou begrijpen? Of bedoel je of ik het jou ook in Jip & Janneke taal uit kan leggen?
[..]
Ik sluit me aan bij de opvatting van Novermars dat je niet met analyse (differentiaal- en integraalrekening) moet beginnen als je nog steeds volkomen vastloopt met simpele brugklas algebra.
Ik ben het volledig met je eens, maar ik heb, zoals ik al zei, te weinig tijd om de basale kennis te finetunen... Ik moet dus even doordreinen met de stof en kijk bij afloop alles na... voor de tweede keer.
Ik wil best een heel verhaal gaan typen over limieten, maar het jammere is dat je er toch niks van zal begrijpen. Ik weet niet wanneer je die toets hebt, maar je bent een half jaar te laat begonnen met leren.
19 meiquote:
Ik wil best een heel verhaal gaan typen over limieten, maar het jammere is dat je er toch niks van zal begrijpen. Ik weet niet wanneer je die toets hebt, maar je bent een half jaar te laat begonnen met leren.
Ik moet toch echt voorbij die bladzijde... Ik heb echt geen keus...quote:
Ik wil best een heel verhaal gaan typen over limieten, maar het jammere is dat je er toch niks van zal begrijpen. Ik weet niet wanneer je die toets hebt, maar je bent een half jaar te laat begonnen met leren.
Bij een limiet is alles in de buurt van een punt belangrijk, maar niet het punt zelf.quote:
[..]
Ik moet toch echt voorbij die bladzijde... Ik heb echt geen keus...
Voorbeeld: f(x) = 1/x
In x = 0 bestaat deze functie niet. Je kunt wel over een limiet naar x = 0 praten, dus alles heeeel dicht in de buurt van 0. Als deze functie dan convergeert, dus naar een waarde nadert, kun je zeggen dat deze limiet bestaat.
In mijn voorbeeld niet, want ∞ is geen getal.
Fervent tegenstander van het korps lasergamers.
quote:
[..]
Bij een limiet is alles in de buurt van een punt belangrijk, maar niet het punt zelf.
Voorbeeld: f(x) = 1/x
In x = 0 bestaat deze functie niet. Je kunt wel over een limiet naar x = 0 praten, dus alles heeeel dicht in de buurt van 0. Als deze functie dan convergeert, dus naar een waarde nadert, kun je zeggen dat deze limiet bestaat.
In mijn voorbeeld niet, want ∞ is geen getal.
En als we naar de extended real line gaan, bestaat de limiet dan opeens wel?
Dankje duidelijk! Zou je me blz 153 uit kunnen leggen van de geposte link? Ik quote het even hieronder..quote:
[..]
Bij een limiet is alles in de buurt van een punt belangrijk, maar niet het punt zelf.
Voorbeeld: f(x) = 1/x
In x = 0 bestaat deze functie niet. Je kunt wel over een limiet naar x = 0 praten, dus alles heeeel dicht in de buurt van 0. Als deze functie dan convergeert, dus naar een waarde nadert, kun je zeggen dat deze limiet bestaat.
In mijn voorbeeld niet, want ∞ is geen getal.
Dus eigenlijk vanaf dat punt (vanaf de helft) snap ik niet wat ze bedoelen... en wat er uberhaupt staat..quote:
[..]
Dankje! Snap jij ook de functie e^x en de natuurlijke logaritme?
Ik snap niet echt wat ze hier willen zeggen vanaf het punt ''Zelfs geldt dat (e^(x - 1)) / x = 1 ''
en waarvoor die lim ( x --> 0 ) staat?
Pagina 153.
https://googledrive.com/h(...)met%20Antwoorden.pdf
Waarom is dit nu weerquote:
[..]
En als we naar de extended real line gaan, bestaat de limiet dan opeens wel?
Ik leg hem het principe van een limiet uit zonder formele ε,δ definities. Jij vertelt helemaal niks, en die extended real line mag je diep in je endeldarm steken.
Fervent tegenstander van het korps lasergamers.
Het jip-en-jannekeverhaal (zo schrijf je dat toch volgens het witte/groene boekje?quote:
[..]
Dankje! Snap jij ook de functie e^x en de natuurlijke logaritme?
Ik snap niet echt wat ze hier willen zeggen vanaf het punt ''Zelfs geldt dat (e^(x - 1)) / x = 1 ''
en waarvoor die lim ( x --> 0 ) staat?
Pagina 153.
https://googledrive.com/h(...)met%20Antwoorden.pdf
) erachter is dat als je een getal dichtbij 0 invult, dat er dan ongeveer 1 uitkomt. Hoe dichter je het getal bij 0 kiest, hoe dichter de uitkomst bij 1 ligt. Probeer maar eens x=0.1, x=0.01, x=0.001, en of x=-0.1, x=-0.01, x=-0.001, etc, in te vullen in de formule, en kijk wat er gebeurt.
De reden dat je x=0 zelf niet invult, is natuurlijk dat je niet door 0 kan delen.
PS: je hebt de haakjes verkeerd getypt, het moet zijn (e^x - 1) / x.
Het kan best zo zijn dat het nu lijkt dat ik deze reeks terroriseer met onnozele en in jullie ogen wellicht hele domme vragen, maar ik hoop dat jullie begrijpen dat ik niet een ster ben in vwo wiskunde en een aantal basale wiskunde stof.
Dus hierbij mijn excuses.
Overigens werk ik me al twee weken de naad uit om mij de stof eigen te maken.. om kosten wat het kost die toets te halen.. ik ben al sinds ik begonnen ben met leren niet naar buiten gegaan (voor vrije tijd/socializen met vrienden)... alleen maar bikkelen..
Dus hierbij mijn excuses.
Overigens werk ik me al twee weken de naad uit om mij de stof eigen te maken.. om kosten wat het kost die toets te halen.. ik ben al sinds ik begonnen ben met leren niet naar buiten gegaan (voor vrije tijd/socializen met vrienden)... alleen maar bikkelen..
Je hoeft je niet te verontschuldigen. Sommige mensen in dit topic komen sowieso nooit buiten, dus dan krijg je wat gefrustreerde reactiesquote:
Het kan best zo zijn dat het nu lijkt dat ik deze reeks terroriseer met onnozele en in jullie ogen wellicht hele domme vragen, maar ik hoop dat jullie begrijpen dat ik niet een ster ben in vwo wiskunde en een aantal basale wiskunde stof.
Dus hierbij mijn excuses.
Overigens werk ik me al twee weken de naad uit om mij de stof eigen te maken.. om kosten wat het kost die toets te halen.. ik ben al sinds ik begonnen ben met leren niet naar buiten gegaan (voor vrije tijd/socializen met vrienden)... alleen maar bikkelen..
.
Precies.quote:
[..]
Je hoeft je niet te verontschuldigen. Sommige mensen in dit topic komen sowieso nooit buiten, dus dan krijg je wat gefrustreerde reacties
Met z'n extended real line.
Fervent tegenstander van het korps lasergamers.
Jij zegt dat de limiet enkel en alleen niet bestaat omdatquote:
[..]
Waarom is dit nu weer
Ik leg hem het principe van een limiet uit zonder formele ε,δ definities. Jij vertelt helemaal niks, en die extended real line mag je diep in je endeldarm steken.
Dus de 'waarde' is afhankelijk van het pad dat je neemt, dus kan je niks zinnigs zeggen over de algemene limiet
Nog niet eens. Ik zeg dat de limiet niet bestaat als hij niet convergeert, volgens die definitie bestaat die limiet niet. Voorts wijs ik hem erop dat ∞ geen getal is, voldoende studenten die dat nog wel eens willen zeggen.quote:
[..]
Jij zegt dat de limiet enkel en alleen niet bestaat omdatgeen getal is. In essentie natuurlijk niet fout, maar mijns inziens behoorlijk ontoereikend.
Dus de 'waarde' is afhankelijk van het pad dat je neemt, dus kan je niks zinnigs zeggen over de algemene limiet
Fervent tegenstander van het korps lasergamers.
Ohhhh ja dan wordt het wel geheel duidelijk... Als je even meekijkt op de link dan is er onderin nog een functiequote:
[..]
Het jip-en-jannekeverhaal (zo schrijf je dat toch volgens het witte/groene boekje?
Probeer maar eens x=0.1, x=0.01, x=0.001, en of x=-0.1, x=-0.01, x=-0.001, etc, in te vullen in de formule, en kijk wat er gebeurt.
De reden dat je x=0 zelf niet invult, is natuurlijk dat je niet door 0 kan delen.
PS: je hebt de haakjes verkeerd getypt, het moet zijn (e^x - 1) / x.
a^x = e ^(x ln a) zou je die ook kunnen uitleggen, evenals het daar onderstaande vanaf '' als eerste toepassing leiden we af...''
En daarom zeg ik ook, stel datquote:
[..]
Nog niet eens. Ik zeg dat de limiet niet bestaat als hij niet convergeert, volgens die definitie bestaat die limiet niet. Voorts wijs ik hem erop dat ∞ geen getal is, voldoende studenten die dat nog wel eens willen zeggen.
Ik heb dat stuk begrepen hoor! Top dankjewel! Die ∞ is inderdaad oneindig... Maar dat teken trof ik eerder bij het onderwerp asymptoten, maar dat teken ontcijferen was niet zo lastig.quote:
[..]
Nog niet eens. Ik zeg dat de limiet niet bestaat als hij niet convergeert, volgens die definitie bestaat die limiet niet. Voorts wijs ik hem erop dat ∞ geen getal is, voldoende studenten die dat nog wel eens willen zeggen.
Neen, natuurlijk niet. De limiet convergeert niet eenduidig.quote:
[..]
En daarom zeg ik ook, stel datwel een getal is, wat er dus gebeurd in de extended real line, convergeert de limiet dan opeens wel?
Fervent tegenstander van het korps lasergamers.
Gebruik e ^(x ln a) = (e^ln(a))^x. In het bewijsje gebruiken ze simpelweg die limiet waar we het net over hadden. Probeer het zelf even.quote:
[..]
Ohhhh ja dan wordt het wel geheel duidelijk... Als je even meekijkt op de link dan is er onderin nog een functie
a^x = e ^(x ln a) zou je die ook kunnen uitleggen, evenals het daar onderstaande vanaf '' als eerste toepassing leiden we af...''
En was het niet veel duidelijk geweest als je dat meteen had gezegd?quote:
[..]
Neen, natuurlijk niet. De limiet convergeert niet eenduidig.
Limieten zijn trouwens goed te vergelijken met een reis in het echte leven: Het gaat niet om de eindbestemming maar om de weg er na toe.
Wat snap je niet aan het begrip 'convergentie'?quote:
[..]
En was het niet veel duidelijk geweest als je dat meteen had gezegd?
Limieten zijn trouwens goed te vergelijken met een reis in het echte leven: Het gaat niet om de eindbestemming maar om de weg er na toe.
Fervent tegenstander van het korps lasergamers.
sorry niet gelukt. Snap er geen pepernoot van.quote:
[..]
Gebruik e ^(x ln a) = (e^ln(a))^x. In het bewijsje gebruiken ze simpelweg die limiet waar we het net over hadden. Probeer het zelf even.
Wat ik gewoon niet snap is het volgende:
*Wat is die ln x nou? Waarvoor dient het ?
*e-macht en de natuurlijke logaritme zijn elkaars inverse dus geldt dat x = e^(ln x).. ---> wat is de e-macht? En ik snap de formule ook niet..? Je berekent x ? Wat zegt die x?
*als je bovenstaande toepast op a^x ipv op x dan krijg je a^x = e^ln x --> waarvoor dient dit? En wat voor verband heeft die a^x met die e opeens..?! Het was toch maar een raaklijn..? Waarom is een exponentieel formule opeens gelijk aan iets wat ik niet weet wat het is? Sowieso al raar...
a^x - 1 / x = ln a
ik snap gewoon niet wat de a^x met de ln te maken heeft en de ln a etc. En wat ze allemaal inhouden en de verbanden... ik snap het gewoon allemaal niet meer...
*Wat is die ln x nou? Waarvoor dient het ?
*e-macht en de natuurlijke logaritme zijn elkaars inverse dus geldt dat x = e^(ln x).. ---> wat is de e-macht? En ik snap de formule ook niet..? Je berekent x ? Wat zegt die x?
*als je bovenstaande toepast op a^x ipv op x dan krijg je a^x = e^ln x --> waarvoor dient dit? En wat voor verband heeft die a^x met die e opeens..?! Het was toch maar een raaklijn..? Waarom is een exponentieel formule opeens gelijk aan iets wat ik niet weet wat het is? Sowieso al raar...
a^x - 1 / x = ln a
ik snap gewoon niet wat de a^x met de ln te maken heeft en de ln a etc. En wat ze allemaal inhouden en de verbanden... ik snap het gewoon allemaal niet meer...
De vraag is waarom je deze toelatingstoets wil afleggen. Waarschijnlijk om te kunnen beginnen met één of andere vervolgstudie waarvoor dit wordt geëist. Maar zo'n toelatingsexamen is er niet voor niets. Men wil namelijk weten of studenten wel een bepaald niveau hebben, gewoon omdat je dat nodig hebt om de studie in kwestie te kunnen volgen en een redelijke kans te hebben de studie ook succesvol af te kunnen ronden. En dat niveau heb je gewoon niet en over pakweg 10 dagen (want dat is de tijd die je nog hebt) zul je dat niveau ook niet hebben. Afgaande op wat ik gezien heb van je kennis en vaardigheden (of laat ik zeggen het manifeste gebrek daaraan) zul je die toets echt niet kunnen halen.quote:
Het kan best zo zijn dat het nu lijkt dat ik deze reeks terroriseer met onnozele en in jullie ogen wellicht hele domme vragen, maar ik hoop dat jullie begrijpen dat ik niet een ster ben in vwo wiskunde en een aantal basale wiskunde stof.
Je zult nog op zijn minst enkele honderden uren studie nodig hebben om je de stof eigen te maken. Zelfs als je vanaf dit moment 24 uur per etmaal zou kunnen studeren zonder verlies van concentratie, dan nog heb je niet voldoende tijd omdat je nog maar zo'n 240 uur hebt te gaan.quote:Dus hierbij mijn excuses.
Overigens werk ik me al twee weken de naad uit om mij de stof eigen te maken.. om kosten wat het kost die toets te halen.. ik ben al sinds ik begonnen ben met leren niet naar buiten gegaan (voor vrije tijd/socializen met vrienden)... alleen maar bikkelen..
Van de oefentoets die online gepubliceerd is, kan ik 6 vd 9 opgaven foutloos maken.quote:
[..]
De vraag is waarom je deze toelatingstoets wil afleggen. Waarschijnlijk om te kunnen beginnen met één of andere vervolgstudie waarvoor dit wordt geëist. Maar zo'n toelatingsexamen is er niet voor niets. Men wil namelijk weten of studenten wel een bepaald niveau hebben, gewoon omdat je dat nodig hebt om de studie in kwestie te kunnen volgen en een redelijke kans te hebben de studie ook succesvol af te kunnen ronden. En dat niveau heb je gewoon niet en over pakweg 10 dagen (want dat is de tijd die je nog hebt) zul je dat niveau ook niet hebben. Afgaande op wat ik gezien heb van je kennis en vaardigheden (of laat ik zeggen het manifeste gebrek daaraan) zul je die toets echt niet kunnen halen.
[..]
Je zult nog op zijn minst enkele honderden uren studie nodig hebben om je de stof eigen te maken. Zelfs als je vanaf dit moment 24 uur per etmaal zou kunnen studeren zonder verlies van concentratie, dan nog heb je niet voldoende tijd omdat je nog maar zo'n 240 uur hebt te gaan.
Ik zit nu in het laatste hoofdstuk en ik ben er van overtuigd dat ik het ga halen, mits ik de laatste hoofdstuk er doorheen kom (natuurlijke logaritmen, differentieren en foutenschatting)
Nú, in een vrijwel stressloze omgeving, kan die toets 'voldoende' maken. Maar wanneer je daar zit, zul je zien dat je opeens een black-out hebt.
Sommige dingen hebben tijd nodig om te zinken. Gun het die tijd dan ook.
Sommige dingen hebben tijd nodig om te zinken. Gun het die tijd dan ook.
Die 'e' van de e-macht is gewoon een getal, namelijk: e = 2,7182...quote:
Wat ik gewoon niet snap is het volgende:
*Wat is die ln x nou? Waarvoor dient het ?
*e-macht en de natuurlijke logaritme zijn elkaars inverse dus geldt dat x = e^(ln x).. ---> wat is de e-macht? En ik snap de formule ook niet..? Je berekent x ? Wat zegt die x?
*als je bovenstaande toepast op a^x ipv op x dan krijg je a^x = e^ln x --> waarvoor dient dit? En wat voor verband heeft die a^x met die e opeens..?! Het was toch maar een raaklijn..? Waarom is een exponentieel formule opeens gelijk aan iets wat ik niet weet wat het is? Sowieso al raar...
a^x - 1 / x = ln a
ik snap gewoon niet wat de a^x met de ln te maken heeft en de ln a etc. En wat ze allemaal inhouden en de verbanden... ik snap het gewoon allemaal niet meer...
Dus als er staat: e2, dan is dat gewoon (2,7182...)2
ex is dus een getal tot de macht x.
Dit getal e is wel speciaal, maar de reden hiervoor is op dit moment niet zo belangrijk.
Dan komt de 'ln'.
Je kent als het goed is de logaritme. Deze kun je schrijven als glog(a). Voor het grondtal (de 'g') in deze formule kun je ieder getal gebruiken. Vaak wordt hier 10 voor gebruikt.
Een getal wat vaak als grondtal wordt gebruikt is het speciale getal e. Je kunt dus een opgave hebben als: elog(x) = 3. Dit heeft dan als oplossing: x = e3 volgens de normale logaritmeregels.
Deze vorm van het logaritme is zelfs zo speciaal dat er een speciale naam en notatie voor is. Dit heet een natuurlijk logaritme en heeft als afkorting 'ln' ipv 'log'
Dit wil zeggen: elog(2) = ln(2)
ln is dus een korte schrijfwijze voor een logaritme met grondtal e.
Dan het probleem met x = eln(x).
Deze schrijfwijze wil alleen maar zeggen dat de ln functie en de e-macht inverse functies zijn. Dit is vergelijkbaar met de wortelfunctie en het kwadraat, deze zijn ook elkaars inverse functie. Dus:
Je moet x = eln(x) op precies dezelfde manier lezen: eerst de natuurlijke logaritme van een getal nemen en de uitkomst hiervan als exponent van een e-macht gebruiken doet netto niets met het getal.
Dit lijkt me voorlopig even genoeg
[quote] Op vrijdag 9 mei 2014 00:08 schreef Novermars het volgende:
Nú, in een vrijwel stressloze omgeving, kan die toets 'voldoende' maken. Maar wanneer je daar zit, zul je zien dat je opeens een black-out hebt.
Sommige dingen hebben tijd nodig om te zinken. Gun het die tijd dan ook.
[/quote
Heb sowieso nog een herkansing. Maar ik ga het maximale eruithalen de eerste x.. alleen heb grotendeels jullie hulp nodig...
hun literatuurverwijzing vd eur is zwaar kut.
Op vrijdag 9 mei 2014 00:08 schreef Novermars het volgende:Nú, in een vrijwel stressloze omgeving, kan die toets 'voldoende' maken. Maar wanneer je daar zit, zul je zien dat je opeens een black-out hebt.
Sommige dingen hebben tijd nodig om te zinken. Gun het die tijd dan ook.
[/quote
Heb sowieso nog een herkansing. Maar ik ga het maximale eruithalen de eerste x.. alleen heb grotendeels jullie hulp nodig...
hun literatuurverwijzing vd eur is zwaar kut.
Dat soort argumenten maken op mij nooit indruk. Dat is net zoiets als met die mensen die thuis op de bank zeggen dat ze bijna alle vragen van een televisiekwis kunnen beantwoorden, maar als ze dan zelf in de studio zitten bakken ze er niets van.quote:
[..]
Van de oefentoets die online gepubliceerd is, kan ik 6 vd 9 opgaven foutloos maken.
Laat op 19 mei hier maar even weten hoe het je is vergaan.quote:Ik zit nu in het laatste hoofdstuk en ik ben er van overtuigd dat ik het ga halen, mits ik de laatste hoofdstukken er doorheen kom (natuurlijke logaritmen, differentiëren en foutenschatting)
Iemand die mij kan vertellen waarom x = -1
Ik kom op x = -3/2
Mijn aanpak was gewoon alles ^2 zodat de wortel zou verdwijnen. Echter toch niet.
Het heeft ongetwijfeld met die x^2 onder de wortel te maken..
Je bent echt een held. Dankjewel.quote:
[..]
Die 'e' van de e-macht is gewoon een getal, namelijk: e = 2,7182...
Dus als er staat: e2, dan is dat gewoon (2,7182...)2
ex is dus een getal tot de macht x.
Dit getal e is wel speciaal, maar de reden hiervoor is op dit moment niet zo belangrijk.
Dan komt de 'ln'.
Je kent als het goed is de logaritme. Deze kun je schrijven als glog(a). Voor het grondtal (de 'g') in deze formule kun je ieder getal gebruiken. Vaak wordt hier 10 voor gebruikt.
Een getal wat vaak als grondtal wordt gebruikt is het speciale getal e. Je kunt dus een opgave hebben als: elog(x) = 3. Dit heeft dan als oplossing: x = e3 volgens de normale logaritmeregels.
Deze vorm van het logaritme is zelfs zo speciaal dat er een speciale naam en notatie voor is. Dit heet een natuurlijk logaritme en heeft als afkorting 'ln' ipv 'log'
Dit wil zeggen: elog(2) = ln(2)
ln is dus een korte schrijfwijze voor een logaritme met grondtal e.
Dan het probleem met x = eln(x).
Deze schrijfwijze wil alleen maar zeggen dat de ln functie en de e-macht inverse functies zijn. Dit is vergelijkbaar met de wortelfunctie en het kwadraat, deze zijn ook elkaars inverse functie. Dus:
Je moet x = eln(x) op precies dezelfde manier lezen: eerst de natuurlijke logaritme van een getal nemen en de uitkomst hiervan als exponent van een e-macht gebruiken doet netto niets met het getal.
Dit lijkt me voorlopig even genoeg
ik kan mijn dank echt niet verwoorden...vetgedrukte klinkt nog krom voor mij.. althans hoe ik moet starten.. bij a^x = y is het simpel om er een log van te maken en het op te lossen, maar deze... pittig hoor!
Let op met kwadrateren. Haal eerst de losse x naar de andere kant en kwadrateer dan beide kanten. Let hierbij op dat je (x+5)2 doet, en niet x2 + 52quote:
Iemand die mij kan vertellen waarom x = -1
Ik kom op x = -3/2
Mijn aanpak was gewoon alles ^2 zodat de wortel zou verdwijnen. Echter toch niet.
Het heeft ongetwijfeld met die x^2 onder de wortel te maken..
Eerst de wortel isoleren, dan pas kwadrateren. Anders krijg je allerlei mengtermen. Probeer dat eens en post je uitwerking. Veelgemaakte denkfout met dergelijke wortelvragen en hersenloos gelijk kwadrateren: (x+a)2 IS NIET GELIJK AAN x2 + a2.quote:
Iemand die mij kan vertellen waarom x = -1
Ik kom op x = -3/2
Mijn aanpak was gewoon alles ^2 zodat de wortel zou verdwijnen. Echter toch niet.
Het heeft ongetwijfeld met die x^2 onder de wortel te maken..
Verder: kan je echt geen docent regelen?? Succes met je toets. Erg benieuwd naar de uitkomst...
Zie het al.quote:
Iemand die mij kan vertellen waarom x = -1
Ik kom op x = -3/2
Mijn aanpak was gewoon alles ^2 zodat de wortel zou verdwijnen. Echter toch niet.
Het heeft ongetwijfeld met die x^2 onder de wortel te maken..
quote:
Iemand die mij kan vertellen waarom x = -1
Ik kom op x = -3/2
Mijn aanpak was gewoon alles ^2 zodat de wortel zou verdwijnen. Echter toch niet.
Het heeft ongetwijfeld met die x^2 onder de wortel te maken..
quote:
[..]
Let op met kwadrateren. Haal eerst de losse x naar de andere kant en kwadrateer dan beide kanten. Let hierbij op dat je (x+5)2 doet, en niet x2 + 52
Ahh, hij is geluktquote:
[..]
Eerst de wortel isoleren, dan pas kwadrateren. Anders krijg je allerlei mengtermen. Probeer dat eens en post je uitwerking. Veelgemaakte denkfout met dergelijke wortelvragen en hersenloos gelijk kwadrateren: (x+a)2 IS NIET GELIJK AAN x2 + a2.
Verder: kan je echt geen docent regelen?? Succes met je toets. Erg benieuwd naar de uitkomst...
Bedankt. Hmm, voor een eventuele herkansing ga ik wss bijles nemen. Wil het eerst zo maar eens proberen.
Jep, zo heb ik hem uiteindelijk ook gedaanquote:
Ik heb al door dat ik er nog even flink wat tijd in moet gaan stoppen
Voor ieder getal geldt deze relatie, dus eln(2) = 2, eln(4952) = 4952, etc. Net zoalsquote:
[..]
Je bent echt een held. Dankjewel.
vetgedrukte klinkt nog krom voor mij.. althans hoe ik moet starten.. bij a^x = y is het simpel om er een log van te maken en het op te lossen, maar deze... pittig hoor!
Als ik het voorbeeld van kwadraat & wortel even doortrek, kun je natuurlijk zeggen:
Maar ook:
De volgorde van de functies maakt dus niet uit, ze cancellen elkaar op allebei de manieren
Dit kun je ook gebruiken voor e-machten en natuurlijke logaritmes.
Deze manier vind ik inzichtelijker en dit kun je ook met je huidige kennis begrijpen.
Als we de twee functies omdraaien krijgen we:
ln(ex) = elog(ex) = x * elog(e) = x*1 = x
Als je een van deze stappen niet snapt hoor ik het graag.
Bepaal de vergelijking van de rechte lijn door het punt (10;3),die evenwijdig loopt aan
de lijn
y=(2/5)x + 13
Ik kom op (2/5)x - 1
Immers 2/5=0,4
0,4 x 10 = 4
Dus om tot 3 te komen 4 -1
Nu is het antwoord: (2/5)x + 1
Kan aan mij liggen maar dan komt er toch echt y = 5 bij x =10 en niet y=3 ?
de lijn
y=(2/5)x + 13
Ik kom op (2/5)x - 1
Immers 2/5=0,4
0,4 x 10 = 4
Dus om tot 3 te komen 4 -1
Nu is het antwoord: (2/5)x + 1
Kan aan mij liggen maar dan komt er toch echt y = 5 bij x =10 en niet y=3 ?
glog a is per definitie de exponent waartoe je g moet verheffen om a te krijgen. De uitspraak glog a = p is dus equivalent met gp = a.quote:
[..]
vetgedrukte klinkt nog krom voor mij.. althans hoe ik moet starten.. bij a^x = y is het simpel om er een log van te maken en het op te lossen, maar deze... pittig hoor!
Ja, natuurlijk. Heb je helemaal gelijk in, maar dit gaat even om het idee van inverse functies en dit is nou eenmaal een handig voorbeeld. (Ik ben een natuurkundige, dus ik doe over het algemeen niet zo moeilijk over dit soort dingenquote:
Mag ik nog even opmerkingen datals, en slechts als
en dat
voor alle
.
)Dit probleem heb je natuurlijk ook bij de logaritme. Die is alleen maar voor getallen groter dan 0 gedefinieerd.
Hint: de cartesische vergelijking van een rechte lijn met richtingscoëfficiënt m door het punt (x0;y0) isquote:
Bepaal de vergelijking van de rechte lijn door het punt (10;3),die evenwijdig loopt aan
de lijn
y=(2/5)x + 13
Ik kom op (2/5)x - 1
Immers 2/5=0,4
0,4 x 10 = 4
Dus om tot 3 te komen 4 -1
Nu is het antwoord: (2/5)x + 1
Kan aan mij liggen maar dan komt er toch echt y = 5 bij x =10 en niet y=3 ?
y − y0 = m(x − x0)
quote:
Bepaal de vergelijking van de rechte lijn door het punt (10;3),die evenwijdig loopt aan
de lijn
y=(2/5)x + 13
Ik kom op (2/5)x - 1
Immers 2/5=0,4
0,4 x 10 = 4
Dus om tot 3 te komen 4 -1
Nu is het antwoord: (2/5)x + 1
Kan aan mij liggen maar dan komt er toch echt y = 5 bij x =10 en niet y=3 ?
Wolfram geeft je gelijk
Ik zie de fout in je redenering ook niet. Of het woord evenwijdig heeft ineens een andere betekenis gekregen...
Ik heb het ook echt 5x ingevuld op mijn RMquote:
[..]
[ afbeelding ]
Wolfram geeft je gelijk
Ik zie de fout in je redenering ook niet. Of het woord evenwijdig heeft ineens een andere betekenis gekregen...
Dit hebben wij niet behandeld. Dan krijg ik dus 2 variabelen in mijn formule. Wat moet ik daar vervolgens mee doen?quote:
[..]
Hint: de cartesische vergelijking van een rechte lijn met richtingscoëfficiënt m door het punt (x0;y0) is
y − y0 = m(x − x0)
Ik snap er ook niks meer van, of het antwoord is in het antwoordmodel fout of ik interpreteer de vraag verkeerd?quote:
[..]
[ afbeelding ]
Wolfram geeft je gelijk
Ik zie de fout in je redenering ook niet. Of het woord evenwijdig heeft ineens een andere betekenis gekregen...
Het antwoordmodel is fout (of de vraag is verkeerd). Jij hebt het goed.quote:
[..]
Ik snap er ook niks meer van, of het antwoord is in het antwoordmodel fout of ik interpreteer de vraag verkeerd?
Maak het jezelf niet zo moeilijk. Je zoekt de vergelijking van een lijn die parallel is met een lijn waarvan de richtingscoëfficiënt 0,4 bedraagt, dus m = 0,4.Verder moet de lijn door het punt (10; 3) gaan, dus x0 = 10 en y0 = 3. Invullen geeft danquote:
[..]
Ik heb het ook echt 5x ingevuld op mijn RM
[..]
Dit hebben wij niet behandeld. Dan krijg ik dus 2 variabelen in mijn formule. Wat moet ik daar vervolgens mee doen?
[..]
y − 3 = 0,4·(x − 10)
y − 3 = 0,4·x − 4
y = 0,4·x − 1
Het antwoordmodel is fout. Helaas gaat er ontzettend veel tijd verloren doordat leerlingen proberen foutieve antwoorden te reproduceren of te rechtvaardigen, maar daar leer je niets van. Nog een argument tegen antwoordenboekjes.quote:Ik snap er ook niks meer van, of het antwoord is in het antwoordmodel fout of ik interpreteer de vraag verkeerd?
Woehoee. Dit is al de tweede keer dat ik mijn hoofd brak over die vraagquote:
[..]
Het antwoordmodel is fout (of de vraag is verkeerd). Jij hebt het goed.
Ah, ik snap hem, schrijf hem even op, dankuquote:
[..]
Maak het jezelf niet zo moeilijk. Je zoekt de vergelijking van een lijn die parallel is met een lijn waarvan de richtingscoëfficiënt 0,4 bedraagt, dus m = 0,4.Verder moet de lijn door het punt (10; 3) gaan, dus x0 = 10 en y0 = 3. Invullen geeft dan
y − 3 = 0,4·(x − 10)
y − 3 = 0,4·x − 4
y = 0,4·x − 1
[..]
Het antwoordmodel is fout. Helaas gaat er ontzettend veel tijd verloren doordat leerlingen proberen foutieve antwoorden te reproduceren of te rechtvaardigen, maar daar leer je niets van. Nog een argument tegen antwoordenboekjes.
Zonder antwoordgedeelte in 'basisboek wiskunde' was het helemaal een verloren strijd geweest
Vroeger leerde je bij analytische meetkunde gewoon een aantal standaardformules voor bijvoorbeeld rechte lijnen. Vind jij het ook zo gek dat dit soort klassieke dingen niet meer worden geleerd terwijl je er wel opgaven over krijgt (waarbij dan vervolgens onnodig moeilijk wordt gedaan)?quote:Op vrijdag 9 mei 2014 01:21 schreef nodig het volgende:
[..]
Ah, ik snap hem, schrijf hem even op, danku
Daar ben ik het niet mee eens. Antwoordenboekjes hebben een nefaste invloed op het leerproces. Het is dodelijk voor het ontwikkelen van je creatieve talenten en studenten krijgen de neiging om zichzelf te leren achterstevoren te redeneren, doordat men eerst gaat kijken wat het antwoord moet zijn en dan van daaruit gaat proberen terug te redeneren naar de opgave. De gevolgen daarvan zijn desastreus. Ik zie heel vaak mensen die oorzaak en gevolg omwisselen, ook bij zaken die (op het eerste gezicht) niets met wiskunde te maken hebben.quote:Zonder antwoordgedeelte in 'basisboek wiskunde' was het helemaal een verloren strijd geweest
Het is inderdaad vreemd. Misschien word ik trouwens wel geacht om die formule te weten. Maar ik kan hem nergens van herinnerenquote:
[..]
Vroeger leerde je bij analytische meetkunde gewoon een aantal standaardformules voor bijvoorbeeld rechte lijnen. Vind jij het ook zo gek dat dit soort klassieke dingen niet meer worden geleerd terwijl je er wel opgaven over krijgt (waarbij dan vervolgens onnodig moeilijk wordt gedaan)?
Tjah, ik doe het ook bij basisboek wiskunde.. Ik doe niet altijd gelijk kijken maar als ik een slecht gevoel heb over de eerste opgave dan controleer ik hem wel gelijk. Anders maak ik de rest ook verkeerd, leer ik het misschien nog verkeerd aanquote:[..]
Daar ben ik het niet mee eens. Antwoordenboekjes hebben een nefaste invloed op het leerproces. Het is dodelijk voor het ontwikkelen van je creatieve talenten en studenten krijgen de neiging om zichzelf te leren achterstevoren te redeneren, doordat men eerst gaat kijken wat het antwoord moet zijn en dan van daaruit gaat proberen terug te redeneren naar de opgave. De gevolgen daarvan zijn desastreus. Ik zie heel vaak mensen die oorzaak en gevolg omwisselen, ook bij zaken die (op het eerste gezicht) niets met wiskunde te maken hebben.
En dan nog moet ik soms geruime tijd het antwoord bestuderen voordat ik achter kom wat nou eigenlijk de bedoeling was
Ik ga nu trouwens slapen, fijne nachtrust
ik snap niet dat de ln in de macht staat van e.. en er niet gewoon naast.. en het vetgedrukte. Ik probeer de verbanden te zien tussen alles met een = teken..quote:
[..]
Voor ieder getal geldt deze relatie, dus eln(2) = 2, eln(4952) = 4952, etc. Net zoals
Als ik het voorbeeld van kwadraat & wortel even doortrek, kun je natuurlijk zeggen:
Maar ook:
De volgorde van de functies maakt dus niet uit, ze cancellen elkaar op allebei de manieren
Dit kun je ook gebruiken voor e-machten en natuurlijke logaritmes.
Deze manier vind ik inzichtelijker en dit kun je ook met je huidige kennis begrijpen.
Als we de twee functies omdraaien krijgen we:
ln(ex) = elog(ex) = x * elog(e) = x*1 = x
Als je een van deze stappen niet snapt hoor ik het graag.
ln en e zijn geen multiplicatieve inverse van elkaar, maar inverse functies. Het is ook niet zo dat x² * sqrt(x) = x.quote:
[..]
ik snap niet dat de ln in de macht staat van e.. en er niet gewoon naast.. en het vetgedrukte. Ik probeer de verbanden te zien tussen alles met een = teken..
Gebruik voor de duidelijkheid eens de notatie exp(x)=e^x.
Dan e^ln(x) = exp(ln(x)).
Als f en g inverse functies zijn, dan geldt per definitie f(g(x))=x. Nu zijn exp en ln inverse functies, dus exp(ln(x))=x en ln(exp(x))=x. Oftewel e^ln(x) = x en ln(e^x) = x.
We willen kijken wat er gebeurt als we eerst e tot de macht x nemen, en daar dan weer de natuurlijke logaritme van nemen. Dat is wat er helemaal links staat, ln(ex). De eerste gelijkheid, ln(ex) = elog(ex), is simpelweg invullen dat de ln de logaritme met grondtal e is, dus ln(x) = elog(x). Daarna gebruiken we de rekenregel log(ex) = x * log(e). Dat is precies de volgende gelijkheid, waarbij we als grondtal e gebruiken. elog(e) = 1, dat is makkelijk in te zien, dus vinden we dat ln(ex) = x. In woorden, als we van een getal x eerst de exponent nemen (ex), en daarvan weer de natuurlijke logaritme nemen, krijgen we x weer terug. Dat is precies wat er bedoeld wordt met inverse functies, zoals thenxero hierboven ook al uitlegt.quote:
[..]
ik snap niet dat de ln in de macht staat van e.. en er niet gewoon naast.. en het vetgedrukte. Ik probeer de verbanden te zien tussen alles met een = teken..
The biggest argument against democracy is a five minute discussion with the average voter.
hoe primitiveer je eigenlijk ?
mijn antwoordenboek geeft dit, maar snap hem niet helemaal:
mijn antwoordenboek geeft dit, maar snap hem niet helemaal:
Chairman of taskforce against 'omosexuality in Uganda.
Aha ! Dankje! Weet ne tenslotte het verschil tussenquote:
[..]
We willen kijken wat er gebeurt als we eerst e tot de macht x nemen, en daar dan weer de natuurlijke logaritme van nemen. Dat is wat er helemaal links staat, ln(ex). De eerste gelijkheid, ln(ex) = elog(ex), is simpelweg invullen dat de ln de logaritme met grondtal e is, dus ln(x) = elog(x). Daarna gebruiken we de rekenregel log(ex) = x * log(e). Dat is precies de volgende gelijkheid, waarbij we als grondtal e gebruiken. elog(e) = 1, dat is makkelijk in te zien, dus vinden we dat ln(ex) = x. In woorden, als we van een getal x eerst de exponent nemen (ex), en daarvan weer de natuurlijke logaritme nemen, krijgen we x weer terug. Dat is precies wat er bedoeld wordt met inverse functies, zoals thenxero hierboven ook al uitlegt.
a^(a log x) = x en a log x = y?
En natuurlijk wat ik moet doen bij de volgende vergelijkinf:
Lim x -> 0 (e^(-x) - 1) / x
De afgeleide van ax is ax ln a voor alle a > 0.quote:
hoe primitiveer je eigenlijk [ afbeelding ] ?
mijn antwoordenboek geeft dit, maar snap hem niet helemaal:
[ afbeelding ]
Dat had Thenxero hier toch uitgelegd.quote:
[..]
En natuurlijk wat ik moet doen bij de volgende vergelijkinf:
Lim x -> 0 (e^(-x) - 1) / x
SES / [Bèta wiskunde] Huiswerk- en vragentopic
Als je dat begrijpt is het goed. Ze zullen niet verwachten dat je in dit geval zelf de limiet kan uitrekenen want dat is geen middelbare schoolstof.
Maak er een e-macht van. Je hebt 3 = eln 3 en dus kun je voorquote:
hoe primitiveer je eigenlijk [ afbeelding ] ?
mijn antwoordenboek geeft dit, maar snap hem niet helemaal:
[ afbeelding ]
f(x) = 32x
schrijven
f(x) = e(2·ln 3)·x
Kun je dit wel primitiveren?
Oké ik heb nu letterlijk twee volle dagen aan één bladzijde gezeten en ik heb nu gerichte en misschien wat betere en duidelijkere vragen..
*Wat houdt die ln (natuurlijke logaritme) nou precies in? Ik snap dat a^x = e^ln a^x maar ik snap dus het verband niet echt...? Ik ben namelijk gewoon gewend a^x = y --> a log x = y
*Waarom is a^x = e^ln a^x hetzelfde als a^x = e^ln a ?
*Hoe kun je uit a^x = e^ln a het volgende afleiden: lim x -> 0 (a^x - 1 / x) = ln a .... waar komt die -1 vandaan en hoezo is die exponent van ln a achter de = teken gekomen en waarom delen door x ? Ik begrijp wel dat ze bedoelen met het limiet dat hoe dichter x bij de 0 is hoe meer de vergelijking gelijk aan elkaar wordt.
*Hoe loos ik vergelijkingen op als:
lim x --> 0 (e^-x -1 ) / x
lim x --> 1 (e^x - e ) / (x -1 )
Ik kan het verband met de theorie niet vinden..
[ Bericht 15% gewijzigd door RustCohle op 09-05-2014 19:57:58 ]
*Wat houdt die ln (natuurlijke logaritme) nou precies in? Ik snap dat a^x = e^ln a^x maar ik snap dus het verband niet echt...? Ik ben namelijk gewoon gewend a^x = y --> a log x = y
*Waarom is a^x = e^ln a^x hetzelfde als a^x = e^ln a ?
*Hoe kun je uit a^x = e^ln a het volgende afleiden: lim x -> 0 (a^x - 1 / x) = ln a .... waar komt die -1 vandaan en hoezo is die exponent van ln a achter de = teken gekomen en waarom delen door x ? Ik begrijp wel dat ze bedoelen met het limiet dat hoe dichter x bij de 0 is hoe meer de vergelijking gelijk aan elkaar wordt.
*Hoe loos ik vergelijkingen op als:
lim x --> 0 (e^-x -1 ) / x
lim x --> 1 (e^x - e ) / (x -1 )
Ik kan het verband met de theorie niet vinden..
[ Bericht 15% gewijzigd door RustCohle op 09-05-2014 19:57:58 ]
Hier gaat het al meteen fout. Ik had je hierboven al gezegd dat glog a is gedefinieerd als de exponent waartoe je g moet verheffen om a te krijgen. Dusquote:
Oké ik heb nu letterlijk twee volle dagen aan één bladzijde gezeten en ik heb nu gerichte en misschien wat betere en duidelijkere vragen..
*Wat houdt die ln (natuurlijke logaritme) nou precies in? Ik snap dat a^x = e^ln a^x maar ik snap dus het verband niet echt...? Ik ben namelijk gewoon gewend a^x = y --> a log x = y
glog a = x
is equivalent met
gx = a
De uitspraak ax = y is dus equivalent met alog y = x en niet met alog x = y zoals jij hier beweert.
Dit klopt ook al niet. Voor een a > 0 heb je a = eln a, want volgens de definitie van de logaritme is ln a immers de exponent waartoe je dat bijzondere grondtal e moet verheffen om a te krijgen. En als we hebbenquote:*Waarom is a^x = e^ln a^x hetzelfde als a^x = e^ln a ?
a = eln a
dan is ook
ax = (eln a)x
en volgens de regenregels voor het werken met machten kunnen we dit schrijven als
ax = ex·ln a
Een limiet is geen vergelijking. Het voert wat te ver om hier te laten zien waarom je hebtquote:*Hoe kun je uit a^x = e^ln a het volgende afleiden: lim x -> 0 (a^x - 1 / x) = ln a .... waar komt die -1 vandaan en hoezo is die exponent van ln a achter de = teken gekomen en waarom delen door x ? Ik begrijp wel dat ze bedoelen met het limiet dat hoe dichter x bij de 0 is hoe meer de vergelijking gelijk aan elkaar wordt.
limh→0 (ah − 1)/h = ln a
en als ik het uit zou gaan leggen zou je het toch niet begrijpen. Daarvoor moet je eerst het nodige weten van analyse en begrijpen wat de definitie van een afgeleide is, zodat je bijvoorbeeld kunt gaan zien dat deze limiet gelijk is aan de afgeleide van de functie f(x) = ax in het punt x = 0 aangezien 1 = a0.
Nogmaals, dit zijn geen vergelijkingen. Dit zijn limieten. Er zal je hoogstwaarschijnlijk op de toets niet gevraagd worden dergelijke limieten te bepalen. Je kunt deze limieten overigens wel eenvoudig herleiden tot de standaardlimietquote:*Hoe los ik vergelijkingen op als:
lim x --> 0 (e^-x -1 ) / x
lim x --> 1 (e^x - e ) / (x -1 )
Ik kan het verband met de theorie niet vinden..
limh→0 (eh − 1)/h = 1
Deze limiet is uiteraard een bijzonder geval van de hierboven gegeven limiet limh→0 (ah − 1)/h = ln a voor a = e.
[ Bericht 0% gewijzigd door Riparius op 09-05-2014 20:35:28 ]
Duidelijk... Natuurlijk niet alles.. Vetgedrukte is toch een !?!quote:
[..]
Hier gaat het al meteen fout. Ik had je hierboven al gezegd dat glog a is gedefinieerd als de exponent waartoe je g moet verheffen om a te krijgen. Dus
glog a = x
is equivalent met
gx = a
De uitspraak ax = y is dus equivalent met alog y = x en niet met alog x = y zoals jij hier beweert.
[..]
Dit klopt ook al niet. Voor een a > 0 heb je a = eln a, want volgens de definitie van de logaritme is ln a immers de exponent waartoe je dat bijzondere grondtal e moet verheffen om a te krijgen. En als we hebben
a = eln a
dan is ook
ax = (eln a)x
en volgens de regenregels voor het werken met machten kunnen we dit schrijven als
ax = ex·ln a
[..]
Een limiet is geen vergelijking. Het voert wat te ver om hier te laten zien waarom je hebt
limh→0 (ah − 1)/h = ln a
en als ik het uit zou gaan leggen zou je het toch niet begrijpen. Daarvoor moet je eerst het nodige weten van analyse en begrijpen wat de definitie van een afgeleide is, zodat je bijvoorbeeld kunt gaan zien dat deze limiet gelijk is aan de afgeleide van de functie f(x) = ax in het punt x = 0 aangezien 1 = a0.
[..]
Nogmaals, dit zijn geen vergelijkingen. Dit zijn limieten. Er zal je hoogstwaarschijnlijk op de toets niet gevraagd worden dergelijke limieten te bepalen. Je kunt deze limieten overigens wel eenvoudig herleiden tot de standaardlimiet
limh→0 (eh − 1)/h = 1
Deze limiet is uiteraard een bijzonder geval van de hierboven gegeven limiet limh→0 (ah − 1)/h = ln a voor a = e.
Het is niet dat ik een behoorlijke leeghoofd ben. Jullie zullen zich wellicht afvragen waarom ik hbo doe als ik dit soort makkelijke dingen niet snap... Dat is hem juist het snappen, ik kan het wel klakkenloos aannemen, maar wil het begrijpen en snappen ipv het trucje leren.
Dit zijn bijvoorbeeld de vergelijkingen in de oefentoets:
Differentieer de volgende functie:
* f(x) = ln(x² - 6x) - ln(x)
los de volgende vergelijking op:
ln(x^4 - 24x²) - ln(x²) = 0
Weer die klote logaritmen.
Wat snap je aan de eerste niet? Hoef je enkel een rekenregel (neem aan dat je ze hebt doorgenomen) te gebruiken (en te weten hoe je logaritmen differentiëert).quote:
[..]
Duidelijk... Natuurlijk niet alles.. Vetgedrukte is toch een !?!
Het is niet dat ik een behoorlijke leeghoofd ben. Jullie zullen zich wellicht afvragen waarom ik hbo doe als ik dit soort makkelijke dingen niet snap... Dat is hem juist het snappen, ik kan het wel klakkenloos aannemen, maar wil het begrijpen en snappen ipv het trucje leren.
Dit zijn bijvoorbeeld de vergelijkingen in de oefentoets:
Differentieer de volgende functie:
* f(x) = ln(x² - 6x) - ln(x)
los de volgende vergelijking op:
ln(x^4 - 24x²) - ln(x²) = 0
Weer die klote logaritmen.
f(x) = ln(x² - 6x) - ln(x)
f(x) = ln((x² - 6x)/x)
f(x) = ln(x - 6)
f'(x) = 1/(x-6)
Bij de tweede kan je een substitutie gebruiken om het jezelf makkelijker te maken (hoeft niet). Daarna lijkt ie me ook wel te doen.
ln(x^4 - 24x²) - ln(x²) = 0
Stel x2 = t
ln(t2 - 24t) - ln(t) = 0
ln((t2 - 24t)/t) = 0
ln(t - 24) = 0
t - 24 = e0 (e0 = 1)
t = 25
x2 = 25
x = 5 v x = -5
[ Bericht 4% gewijzigd door jordyqwerty op 09-05-2014 21:32:04 ]
Ik zou ten eerste alle logaritme regels goed uit je hoofd leren.quote:
[..]
los de volgende vergelijking op:
ln(x^4 - 24x²) - ln(x²) = 0
Weer die klote logaritmen.
(1) glog(a) + glog(b) = glog(a*b)
(2) glog(a) - glog(b) = glog(a/b)
(3) glog(an) = n*glog(a)
Deze regels werken voor elk grondtal g.
De tweede regel kan je bij deze vergelijking goed gebruiken. Als je dat hebt gedaan krijg je uiteindelijk iets in de vorm:
ln(a) = b
Dit kan je dan oplossen door aan beide kanten de e-macht te nemen.
eln(a) = eb
Als je nu de definitie van de logaritme toepast: (eln(a)=a)
a = eb
Dit zijn de stappen die je moet toepassen om zulk soort vergelijkingen op te lossen. Vaak is het dus een kwestie van de regels toepassen om de logaritmen samen te nemen, daarna de e-macht nemen aan beide kanten, en dan is het slechts een kwestie van netjes uitwerken.
Ik ben net ook met die vraag aan de slag gegaan.quote:
[..]
f(x) = ln(x² - 6x) - ln(x)
f(x) = ln((x² - 6x)/x)
f(x) = ln(x - 6)
f'(x) = 1/(x-6)
ln(x^4 - 24x²) - ln(x²) = 0
Stel x2 = t
ln(t2 - 24t) - ln(t) = 0
ln((t2 - 24t)/t) = 0
ln(t - 24) = 0
t - 24 = e0 (e0 = 1)
t = 25
x2 = 25
x = 5 v x = -5
Eerst kwam ik op een verkeerd antwoord uit. 2e keer dat ik hem berekende kwam die goed uit. Ik ben bang dat ik daar misschien op af ga, denken dat ik goed zit terwijl het toch anders moest
Maar aan de andere kant, je kan je antwoord natuurlijk invullen in de formule
Nvm, onzekerheidsniveau is gedaald
EDIT: Oké, zojuist die 1e opgave die gevraagd werd ook gemaakt. Zonder naar de uitwerking hier te hebben gekeken ofc. Deze had ik zelfs in 1x goed
Super easy... Echter door die ln etc. raak ik in de war...quote:
[..]
Wat snap je aan de eerste niet? Hoef je enkel een rekenregel (neem aan dat je ze hebt doorgenomen) te gebruiken (en te weten hoe je logaritmen differentiëert).
f(x) = ln(x² - 6x) - ln(x)
f(x) = ln((x² - 6x)/x)
f(x) = ln(x - 6)
f'(x) = 1/(x-6)
Bij de tweede kan je een substitutie gebruiken om het jezelf makkelijker te maken (hoeft niet). Daarna lijkt ie me ook wel te doen.
ln(x^4 - 24x²) - ln(x²) = 0
Stel x2 = t
ln(t2 - 24t) - ln(t) = 0
ln((t2 - 24t)/t) = 0
ln(t - 24) = 0
t - 24 = e0 (e0 = 1)
t = 25
x2 = 25
x = 5 v x = -5
Denk dat het aan de regels ligt... die er nog niet goed inzitten...Kennen jullie een goede plek om differentieren te leren?
Ik vind het boek dat ik heb daar zeer zwak in.
Hoe heb jij het hoofdstuk differentieren geleerd? Ik vind het boek daar heel zwak in...quote:
[..]
Ik ben net ook met die vraag aan de slag gegaan.
Eerst kwam ik op een verkeerd antwoord uit. 2e keer dat ik hem berekende kwam die goed uit. Ik ben bang dat ik daar misschien op af ga, denken dat ik goed zit terwijl het toch anders moest
Maar aan de andere kant, je kan je antwoord natuurlijk invullen in de formule
Nvm, onzekerheidsniveau is gedaald
EDIT: Oké, zojuist die 1e opgave die gevraagd werd ook gemaakt. Zonder naar de uitwerking hier te hebben gekeken ofc. Deze had ik zelfs in 1x goed
Bij wiskundeacademie doen ze het anders...
en ik snap al niet wat ze bedoelen met
( c f(x))' = x f' (x) voor elke constante c
Dan zou ik die nog eens goed doornemen, het zijn in feite vier 'regels' die je moet weten, die Ensemble al heeft opgesomd.quote:
[..]
Super easy... Echter door die ln etc. raak ik in de war...
Kennen jullie een goede plek om differentieren te leren?
Ik vind het boek dat ik heb daar zeer zwak in.
Heb je het dan enkel over logaritmen differentiëren of ook quotiënten, producten etc?
Je zou hier natuurlijk termsgewijs kunnen differentiëren en dan bij de eerste term de kettingregel kunnen gebruiken en tenslotte het eindresultaat herleiden tot één breuk, maar dat is allemaal niet slim. Je hebt namelijkquote:
[..]
Dit zijn bijvoorbeeld de vergelijkingen in de oefentoets:
Differentieer de volgende functie:
* f(x) = ln(x² - 6x) - ln(x)
x2 − 6x = x(x −6)
en dus hebben we
f(x) = ln x + ln(x − 6) − ln x
en dus
f(x) = ln(x − 6)
zodat
f'(x) = 1/(x − 6)
Ben je mal, de opgave hierboven laat je zien hoe elegant je met logaritmen kunt werken. Voor deze opgave hebben we twee logaritmen die gelijk moeten zijn, aangezien hun verschil nul bedraagt. Maar dan moeten de getallen waarvan we de logaritmen nemen ook gelijk zijn, en hebben we dusquote:los de volgende vergelijking op:
ln(x^4 - 24x²) - ln(x²) = 0
Weer die klote logaritmen.
x4 − 24x2 = x2
x4 − 25x2 = 0
x2(x2 − 25) = 0
x = 0 ∨ x = 5 ∨ x = − 5
Maar nu moet je even opletten, logaritmen zijn (binnen de reële getallen) alleen gedefinieerd voor positieve getallen. Immers, ln a = b is equivalent met eb = a, maar aangezien eb positief is voor elke b ∈ R moet a ook positief zijn.
De oplossing x = 0 komt dus te vervallen en we houden over
x = 5 ∨ x = −5
Daar snap ik ook geen flikker vanquote:
[..]
Hoe heb jij het hoofdstuk differentieren geleerd? Ik vind het boek daar heel zwak in...
Bij wiskundeacademie doen ze het anders...
en ik snap al niet wat ze bedoelen met
( c f(x))' = x f' (x) voor elke constante c
De andere formules die daar onder staan snap ik overigens wel allemaal. Ik moet wel toegeven dat ik lang heb moeten stoeien met de ln en log differentiaties. Ook komen er in dit hoofdstuk meerdere rekenregels die je hebt gehad bij elkaar.
Dan heb ik het over het uitleggen van differentieren.. De gedachte snap ik, maar ik snap niet wat ik moet doen qua berekening en de regels worden in der mate uitgelegd in het boek alsof ik het eerder heb gezien... zoalsquote:
[..]
Dan zou ik die nog eens goed doornemen, het zijn in feite vier 'regels' die je moet weten, die Ensemble al heeft opgesomd.
Heb je het dan enkel over logaritmen differentiëren of ook quotiënten, producten etc?
(c f(x))' = c f' (x) voor elke constante c
(f(x) + g (x))' = f'(x) + g'(x)
etc... al die regels..
Ik snap nu letterlijk alles... op het volgende na:quote:
[..]
Daar snap ik ook geen flikker van
De andere formules die daar onder staan snap ik overigens wel allemaal. Ik moet wel toegeven dat ik lang heb moeten stoeien met de ln en log differentiaties. Ook komen er in dit hoofdstuk meerdere rekenregels die je hebt gehad bij elkaar.
*Natuurlijke logaritmen, differentieren. --> H24 en h25 weet ik niet, want daar ben ik nog niet.
* rekenen met verschillende wortels, dus een derdemachtswortel delen door een tweedemachtswortel, maar goed dit is makkelijker aan te leren dan natuurlijke logaritmen en differentieren.
Ik zit al twee dagen te stoeien met natuurlijke logaritmen en differentieren. Ik stress me kapot hier.... Het gaat er maar om dat ik die toets overleef, daarna ga ik in de zomervakantie hard zelfstuderen.quote:
[..]
Daar snap ik ook geen flikker van
De andere formules die daar onder staan snap ik overigens wel allemaal. Ik moet wel toegeven dat ik lang heb moeten stoeien met de ln en log differentiaties. Ook komen er in dit hoofdstuk meerdere rekenregels die je hebt gehad bij elkaar.
Ik voel me letterlijk zo:
Volgens mij vertelt die 2e regel dat bijv:quote:
[..]
Dan heb ik het over het uitleggen van differentieren.. De gedachte snap ik, maar ik snap niet wat ik moet doen qua berekening en de regels worden in der mate uitgelegd in het boek alsof ik het eerder heb gezien... zoals
(c f(x))' = c f' (x) voor elke constante c
(f(x) + g (x))' = f'(x) + g'(x)
etc... al die regels..
2x^2 + x
Dan wordt 2x^2 genomen als f(x) en x als g(x)
Die 2 vervolgens differentieren en optellen: 4x + 1
Neem dit trouwens maar niet van mij aan voordat iemand dit kan bevestigen
[ Bericht 0% gewijzigd door nodig op 09-05-2014 21:47:26 (fout aangepast) ]
Oké, ik loop met differentieren iets voor op jou denk ik. Maar ik heb de paragraaf rationele functies en polynomen dan ook overgeslagenquote:
[..]
Ik snap nu letterlijk alles... op het volgende na:
*Natuurlijke logaritmen, differentieren. --> H24 en h25 weet ik niet, want daar ben ik nog niet.
* rekenen met verschillende wortels, dus een derdemachtswortel delen door een tweedemachtswortel, maar goed dit is makkelijker aan te leren dan natuurlijke logaritmen en differentieren.
Ach, dat heb ik ook gedaanquote:
[..]
Ik zit al twee dagen te stoeien met natuurlijke logaritmen en differentieren. Ik stress me kapot hier.... Het gaat er maar om dat ik die toets overleef, daarna ga ik in de zomervakantie hard zelfstuderen.
Ik voel me letterlijk zo:
Ik denk dat ik sommige opgaves nu wel 3x heb gedaan
Wat snap je niet aan die notatie?quote:
[..]
Dan heb ik het over het uitleggen van differentieren.. De gedachte snap ik, maar ik snap niet wat ik moet doen qua berekening en de regels worden in der mate uitgelegd in het boek alsof ik het eerder heb gezien... zoals
(c f(x))' = c f' (x) voor elke constante c
(f(x) + g (x))' = f'(x) + g'(x)
etc... al die regels..
Als je hebt f(x) = 5x², dan is de constante dus vijf. Differentieer je deze functie, dan krijg je dus (volgens de machtregel, ken je die?) f'(x) = 5 * 2x = 10x, dus inderdaad (cf(x))' = cf' (x).
Je kan in plaats van vijf daar bijvoorbeeld ook een willekeurige variabele neerzetten, zoals a (of c volgens de definitie).
Behalve dat 4x de afgeleide van 2x2 is wegens die eerste regel.quote:
[..]
Volgens mij vertelt die 2e regel dat bijv:
2x^2 + x
Dan wordt 2x^2 genomen als f(x) en x als g(x)
Die 2 vervolgens differentieren en optellen: 2x + 1
Neem dit trouwens maar niet van mij aan voordat iemand dit kan bevestigen
Die tweede zegt dat als bijvoorbeeld 2x2 + x hebt, dat je dan elke term in de som los mag differentieren.quote:
[..]
Volgens mij vertelt die 2e regel dat bijv:
2x^2 + x
Dan wordt 2x^2 genomen als f(x) en x als g(x)
Die 2 vervolgens differentieren en optellen: 2x + 1
Neem dit trouwens maar niet van mij aan voordat iemand dit kan bevestigen
Dus f(x) = 2x2 en g(x) = x
=> ( 2x2 + x)' = ((f(x) + g(x))' = f'(x) + g'(x) = 4x + 1
4x + 1 bedoel jequote:
[..]
Volgens mij vertelt die 2e regel dat bijv:
2x^2 + x
Dan wordt 2x^2 genomen als f(x) en x als g(x)
Die 2 vervolgens differentieren en optellen: 2x + 1
Neem dit trouwens maar niet van mij aan voordat iemand dit kan bevestigen
quote:
[..]
Behalve dat 4x de afgeleide van 2x2 is wegens die eerste regel.
quote:
[..]
Die tweede zegt dat als bijvoorbeeld 2x2 + x hebt, dat je dan elke term in de som los mag differentieren.
Dus f(x) = 2x2 en g(x) = x
=> ( 2x2 + x)' = ((f(x) + g(x))' = f'(x) + g'(x) = 4x + 1
Mijn fout inderdaad. Vergeten dat ik er een 2 voor had gezetquote:
Polynomen vond ik juist erg makkelijk. Rationale functies ook om te huilen, maar in mindere maten dan natuurlijke logaritmen en differentieren.quote:
[..]
Oké, ik loop met differentieren iets voor op jou denk ik. Maar ik heb de paragraaf rationele functies en polynomen dan ook overgeslagen
Ik snap de notaties gewoon niet.quote:
[..]
Wat snap je niet aan die notatie?
Als je hebt f(x) = 5x², dan is de constante dus vijf. Differentieer je deze functie, dan krijg je dus (volgens de machtregel, ken je die?) f'(x) = 5 * 2x = 10x, dus inderdaad (cf(x))' = cf' (x).
Je kan in plaats van vijf daar bijvoorbeeld ook een willekeurige variabele neerzetten, zoals a (of c volgens de definitie).
Als je wordt toegelaten mag je bij je eerste wiskunde vak nog heel wat gaan differentiëren.quote:
[..]
Polynomen vond ik juist erg makkelijk. Rationale functies ook om te huilen, maar in mindere maten dan natuurlijke logaritmen en differentieren.
Dat is niet best, want dit volgt namelijk heel eenvoudig uit de definitie van de afgeleidequote:
f'(x) = limh→0 (f(x+h) − f(x))/h
Uiteraard zijn ook alle overige regels voor het differentiëren te bewijzen aan de hand van de definitie van de afgeleide alsmede een aantal eigenschappen van limieten (die je uiteraard ook eerst bewezen moet hebben aan de hand van de definitie van een limiet).
Ik snap waarvoor f(x) staat, dat is de functie zelf... c? Dat weet ik niet.... ' is de afgeleide...quote:
[..]
Wat niet? Waar f(x) voor staat, waar c voor staat, waar ' voor staat?
Maar f'(x) ?! Het is toch f(x) '?
En sowieso wordt er niks uitgelegd over differentieren of iets... In het boek staat er alleen maar regels opgesomd en wat uitleg wat een raaklijn is.. Dat laatste weet ik... gelukkig nog.......
Daarnaast is er ook een somregel (f(x) + g (x))' , wanneer weet ik wanneer ik dit moet gebruiken? Wat houdt dit in? Dat ik de afgeleide van de functie g(x) moet hebben en deze als het ware moet optellen met de normale f(x) functie? Hoe kan ik aan een functie zien wanneer ik de constante c moet gebruiken en de somregel?
Jip en Janneke taal graag, zodat Nodig en ik het kunnen begrijpen, in ieder geval ik.
Jip en Janneke taal graag, zodat Nodig en ik het kunnen begrijpen, in ieder geval ik.
Ik snap de C niet.quote:
[..]
Wat niet? Waar f(x) voor staat, waar c voor staat, waar ' voor staat?
Ja dat die voor 'constante' staat. Staat dat in bijv de formule: 3x + 4x^2 + 8
De 8 lijkt me dan de constante?
Of zeggen ze dat wanneer bijv. 8 * f(x)
De 8 wordt meegenomen in de afgeleide.
De somregel gebruik je als een functie wil differentieren waar een of meerdere + in staat.quote:
Daarnaast is er ook een somregel (f(x) + g (x))' , wanneer weet ik wanneer ik dit moet gebruiken? Wat houdt dit in? Dat ik de afgeleide van de functie g(x) moet hebben en deze als het ware moet optellen met de normale f(x) functie? Hoe kan ik aan een functie zien wanneer ik de constante c moet gebruiken en de somregel?
Jip en Janneke taal graag, zodat Nodig en ik het kunnen begrijpen, in ieder geval ik.
Dus stel je hebt f(x) = 2x2 + 3x
Als je van deze functie de afgeleide wil bepalen zegt de somregel dat je elk deel van de som, dus 2x2 en 3x, apart mag differentieren.
Dus f'(x) = (2x2)' + (3x)' = 4x + 3
c staat voor een constante.quote:
[..]
Ik snap waarvoor f(x) staat, dat is de functie zelf... c? Dat weet ik niet.... ' is de afgeleide...
Maar f'(x) ?! Het is toch f(x) '?
En sowieso wordt er niks uitgelegd over differentieren of iets... In het boek staat er alleen maar regels opgesomd en wat uitleg wat een raaklijn is.. Dat laatste weet ik... gelukkig nog.......
(cf(x))' = cf' (x) zegt dat als je een term waar een constante voor staat wilt differentiëren, je die term bij het differentiëren buiten beschouwing mag laten (uiteraard uiteindelijk wel mee vermenigvuldigen).
f(x) moet toch niet afgeleide zijn? Maar alleen g(x) ?quote:
[..]
De somregel gebruik je als een functie wil differentieren waar een of meerdere + in staat.
Dus stel je hebt f(x) = 2x2 + 3x
Als je van deze functie de afgeleide wil bepalen zegt de somregel dat je elk deel van de som, dus 2x2 en 3x, apart mag differentieren.
Dus f'(x) = (2x2)' + (3x)' = 4x + 3
Ik snap het niet hoor... Heel het differentieren niet, wat ben je nou aan het doen?!?
Ik weet wel wat je bedoelt nu met de somregel.
En de drie en vier dan?quote:
[..]
Ik snap de C niet.
Ja dat die voor 'constante' staat. Staat dat in bijv de formule: 3x + 4x^2 + 8
De 8 lijkt me dan de constante?
(3x)' + (4x2)' + 8' = 3 * x' + 4 * x2' + 8' = 3 * 1 + 4 * 2x = 3 + 8x
(f(x) + g(x))' betekent de afgeleide van f(x) + g(x)quote:
[..]
f(x) moet toch niet afgeleide zijn? Maar alleen g(x) ?
-edit- onzin
Nee, dat is de productregel.quote:
[..]
(f(x) + g(x))' betekent de afgeleide van f(x) + g(x)
overigens is dat gelijk aan f'(x) g(x) + f(x) g'(x)
Dat is de productregel.quote:
[..]
(f(x) + g(x))' betekent de afgeleide van f(x) + g(x)
overigens is dat gelijk aan f'(x) g(x) + f(x) g'(x)
Die c staat voor een constante. Bij het bepalen van de afgeleide van een functie die een product is van een constante en een andere functie gebeurt er niets met een constante factor. Voorbeeld: je hebtquote:
Daarnaast is er ook een somregel (f(x) + g (x))' , wanneer weet ik wanneer ik dit moet gebruiken? Wat houdt dit in? Dat ik de afgeleide van de functie g(x) moet hebben en deze als het ware moet optellen met de normale f(x) functie? Hoe kan ik aan een functie zien wanneer ik de constante c moet gebruiken en de somregel?
Jip en Janneke taal graag, zodat Nodig en ik het kunnen begrijpen, in ieder geval ik.
f(x) = x2
f'(x) = 2x
Maar dan heb je ook
g(x) = 3x2
g'(x) = 3·2x = 6x
De somregel (en verschilregel) impliceert dat je een veelterm kunt differentiëren door termsgewijs te differentiëren. Voorbeeld: je hebt
f(x) = 2x3
f'(x) = 2·3x2 = 6x2
g(x) = 5x2
g'(x) = 5·2x = 10x
Hebben we nu
h(x) = f(x) + g(x)
dan zegt de somregel dat we ook hebben
h'(x) = f'(x) + g'(x)
en dus
h(x) = 2x3 + 5x2
h'(x) = 6x2 + 10x
EDIT: zie het hierboven alquote:
[..]
En de drie en vier dan?
(3x)' + (4x2)' + 8' = 3 * x' + 4 * x2' + 8' = 3 * 1 + 4 * 2x = 3 + 8x
Aha en hoe moet je differentieren?quote:
[..]
Die c staat voor een constante. Bij het bepalen van de afgeleide van een functie die een product is van een constante en een andere functie gebeurt er niets met een constante factor. Voorbeeld: je hebt
f(x) = x2
f'(x) = 2x
Maar dan heb je ook
g(x) = 3x2
g'(x) = 3·2x = 6x
De somregel (en verschilregel) impliceert dat je een veelterm kunt differentiëren door termsgewijs te differentiëren. Voorbeeld: je hebt
f(x) = 2x3
f'(x) = 2·3x2 = 6x2
g(x) = 5x2
g'(x) = 5·2x = 10x
Hebben we nu
h(x) = f(x) + g(x)
dan zegt de somregel dat we ook hebben
h'(x) = f'(x) + g'(x)
en dus
h(x) = 2x3 + 5x2
h'(x) = 6x2 + 10x
Stel je hebt f(x)quote:
Dan is het gedifferentieerde, ook wel afgeleide genoemd, hiervan f'(x)
Lees nu nog is zijn post door misschien dat je het snapt?
Ja oke, maar hoe differentieer je?quote:
[..]
Stel je hebt f(x)
Dan is het gedifferentieerde, ook wel afgeleide genoemd, hiervan f'(x)
Lees nu nog is zijn post door misschien dat je het snapt?
quote:
Door die formules te gebruikenquote:
Hier wordt de regel toegepast dat de gedifferentieerde van a^x = xa^(x-1)
Dus 8x^3 wordt op deze manier 24x^2
Daar zijn weer allerlei regels voor (die uiteindelijk volgen uit de definitie van de afgeleide). Een belangrijke regel is bijvoorbeeld dat als je hebtquote:
f(x) = xn
dat dan geldt
f'(x) = nxn−1
Maar er zijn uiteraard nog veel meer regels die je moet kennen en moet kunnen gebruiken, bijvoorbeeld voor het differentiëren van exponentiële en logaritmische functies alsmede goniometrische functies. En dan heb je nog algemene regels, zoals de som- en verschilregel, de productregel, de quotiëntregel, en de kettingregel (voor samengestelde functies). Deze regels moet je in de praktijk ook vaak combineren bij het differentiëren. Er gaat echt wel wat tijd en oefening in zitten voordat je dat allemaal beheerst en vlot en foutloos uit kunt voeren.
xa?! Ax bedoel je?quote:
[..]
[..]
Door die formules te gebruiken
Hier wordt de regel toegepast dat de gedifferentieerde van a^x = xa^(x-1)
Dus 8x^3 wordt op deze manier 24x^2
hoe kom je sowieso al aan die info. Het boek is te krom..
Het principe van differentieren isquote:
Dus je berekent de helling van de raaklijn op punt x.
Die limieten willen we natuurlijk niet voor elke formule gaan uitrekenen.
Maar we kunnen dit doen voor algemenere standaard formules zoals bijvoorbeeld
Met zulke standaard formules en regels kan je dan de afgeleides van formules berekenen.
Aha! Dat is dus wat ik zocht die f'(x) = nxn−1quote:
[..]
Daar zijn weer allerlei regels voor (die uiteindelijk volgen uit de definitie van de afgeleide). Een belangrijke regel is bijvoorbeeld dat als je hebt
f(x) = xn
dat dan geldt
f'(x) = nxn−1
Maar er zijn uiteraard nog veel meer regels die je moet kennen en moet kunnen gebruiken, bijvoorbeeld voor het differentiëren van exponentiële en logaritmische functies alsmede goniometrische functies. En dan heb je nog algemene regels, zoals de som- en verschilregel, de productregel, de quotiëntregel, en de kettingregel (voor samengestelde functies). Deze regels moet je in de praktijk ook vaak combineren bij het differentiëren. Er gaat echt wel wat tijd en oefening in zitten voordat je dat allemaal beheerst en vlot en foutloos uit kunt voeren.
Ken je een goede website met dit soort regels en uitleg mbt differentieren?
Wat is die letter h etc?quote:
[..]
Het principe van differentieren is
Dus je berekent de helling van de raaklijn op punt x.
Die limieten willen we natuurlijk niet voor elke formule gaan uitrekenen.
Maar we kunnen dit doen voor algemenere standaard formules zoals bijvoorbeeld.
Met zulke standaard formules en regels kan je dan de afgeleides van formules berekenen.
Ik heb namelijk in mijn boek
m = lim x --> a f(x) - f(a) / (x-a)
m is dan de richtingscoefficient van de raaklijn.
substitueer h = (x-a)quote:
[..]
Wat is die letter h etc?
Ik heb namelijk in mijn boek
m = lim x --> a f(x) - f(a) / (x-a)
m is dan de richtingscoefficient van de raaklijn.
Maakt dit plaatje het duidelijk?
Je neemt het limiet van h naar 0. Dan krijg je dus de raaklijn op het punt x.
Die regel zal toch wel in het boek staan?quote:
[..]
Aha! Dat is dus wat ik zocht die f'(x) = nxn−1
Ken je een goede website met dit soort regels en uitleg mbt differentieren?
quote:
[..]
De afgeleide van ax is ax ln a voor alle a > 0.
oh ik ben er al uit, alhoewel de fundamenten van de onderstaande niet helemaal begrijp, maar dat is nu niet zo heel belangrijk.quote:
[..]
Maak er een e-macht van. Je hebt 3 = eln 3 en dus kun je voor
f(x) = 32x
schrijven
f(x) = e(2·ln 3)·x
Kun je dit wel primitiveren?
het boek stelt:
dus is dit mijn uitwerking
Chairman of taskforce against 'omosexuality in Uganda.
Nee... Echter heb ik wel twee opgaven mbt differentieren foutloos gemaakt dankzij die regel... van Riparius met n-1quote:
[..]
Die regel zal toch wel in het boek staan?
Blz 171 van je googledrive link.quote:
[..]
Nee... Echter heb ik wel twee opgaven mbt differentieren foutloos gemaakt dankzij die regel... van Riparius met n-1
Is f(x+h) dan gewoon een punt?quote:
[..]
substitueer h = (x-a)
Maakt dit plaatje het duidelijk?
[ afbeelding ]
Je neemt dus het limiet van h naar 0. Dan krijg je dus de raaklijn op het punt x.
f(x+h) in dit geval Y en x+h dan een X punt? Of is f(x) een lijn en f(x+h) een lijn?
Ik snap het plaatje wel, maar ik snap die H niet en wat je daarmee moet in die formuleregel die je uiteindelijk moet gebruiken..
Ik zit op bladzijde 167 de hele tijd. Misschien dat ik het daardoor niet snap? Zie de blauwgekleurde formule op blz 167 in de googledrive link.quote:
https://googledrive.com/h(...)met%20Antwoorden.pdf
f is de functie, f(x) is de functie waarde op punt x, f(x+h) is de functie waarde op punt x + h.quote:
[..]
Is f(x+h) dan gewoon een punt?
f(x+h) in dit geval Y en x+h dan een X punt? Of is f(x) een lijn en f(x+h) een lijn?
Ik snap het plaatje wel, maar ik snap die H niet en wat je daarmee moet in die formuleregel die je uiteindelijk moet gebruiken..
Geeft je de helling van de lijn tussen f(x) en f(x+h).
Neem je het limiet van h naar 0 krijg je de helling op x.
Meer Jip en Janneke taal daarvoor?quote:
[..]
f is de functie f(x) is de functie waar op punt x, f(x+h) is de functie waarde op punt x + h.
Geeft je de helling van de lijn tussen f(x) en f(x+h).
Neem je het limiet van h naar 0 krijg je de helling op x.
BLZ 166
https://googledrive.com/h(...)met%20Antwoorden.pdf
20.1, 20.2 en 20.3 helemaal foutloos!!!!!!
https://googledrive.com/h(...)met%20Antwoorden.pdf
20.1, 20.2 en 20.3 helemaal foutloos!!!!!!
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |