[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op maandag 5 mei 2014 21:49 schreef Riparius het volgende:

[..]

Dat zegt niet veel. Mensen die aan zelfstudie doen voor een toelatingsexamen wiskunde studeren vaak bijzonder inefficiënt en vliegen voordurend uit de bocht, zo heb ik gemerkt. Een goede leraar die ook echt les geeft is onvervangbaar. Voor welke toets bereid je je voor, en welke boeken gebruik je daarbij?

Er moet ook gezegd worden dat het boek bijzonder ongeschikt is voor zelfstudie..

quote:

Op maandag 5 mei 2014 21:58 schreef Super-B het volgende:

[..]

Snap jij opgave 16.34 e?

Zowel de - als de + versie van het linkerlid berekenen?

Regard 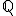as a metric space, with 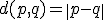. Let 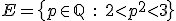. Show that 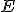is closed and bounded in 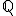, but that 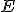is not compact. Is 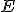open in ?

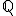Help?

Overduidelijk,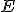 is begrensd. Dat was het makkelijke gedeelte. Volgens de definitie is een set closed iff als zij al haar limietpunten bevat. Omdat 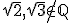, lijkt me dat deze set is gesloten is. Waarom mag ik Heine-Borel niet 'invoken'?

[ Bericht 18% gewijzigd door Novermars op 05-05-2014 22:22:26 ]

quote:

Op maandag 5 mei 2014 22:00 schreef Super-B het volgende:

[..]

antwoordenboek zegt:

1 - W2 < x < 1 , 1 < x < 1 + W2

Grafiek schetsen, daaruit kan je het vervolgens aflezen.

quote:

Op maandag 5 mei 2014 22:05 schreef Super-B het volgende:

[..]

Doe jij het steeds op die manier..?

Grafiek schetsen van de twee mogelijkheden wat betreft het linkerlid?

Ja, dat is de opdracht ook. Niet zo lui zijn en gewoon schetsen

quote:

Op maandag 5 mei 2014 22:04 schreef Novermars het volgende:
Regard as a metric space, with . Let . Show that is closed and bounded in , but that is not compact. Is open in ?

Help?

Voor compactheid

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

Of lukte geslotenheid al niet?

quote:

Op maandag 5 mei 2014 22:20 schreef Anoonumos het volgende:

[..]

Voor compactheid

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

Of lukte geslotenheid al niet?

Zie mijn edit, informeel lukt geslotenheid me wel. Maar geen idee hoe ik dit rigoureus opschrijf...

Maar jouw open cover, waarom mag je deze gebruiken? Als we het over zouden hebben, dan is hij logisch. Maar en zitten niet in , moeten we ze dan niet helemaal achterwege laten?

[ Bericht 18% gewijzigd door Novermars op 05-05-2014 22:28:38 ]

quote:

Op maandag 5 mei 2014 22:23 schreef Novermars het volgende:

[..]

Zie mijn edit, informeel lukt geslotenheid me wel. Maar geen idee hoe ik dit rigoureus opschrijf...

Maar jouw open cover, waarom mag je deze gebruiken? Als we het over zouden hebben, dan is hij logisch. Maar en zitten niet in , moeten we ze dan niet helemaal achterwege laten?

Zij p is een limietpunt van E.
Dan voor elke ε > 0 bestaat er een x in E met p ongelijk aan x en |x-p| < ε.

Stel p zit niet in E. Stel bijvoorbeeld p > sqrt(3) (andere gevallen gaan analoog)
Laat ε = (p - sqrt{3})/2 in je definitie van limietpunt en je vind een tegenspraak.

Het gebruik van wortels kan je wel vermijden maar dan wordt het meer gepriegel denk ik omdat je steeds naar p^2 kijkt ipv naar p.

En Heine-Borel geldt dus alleen voor R^n, dat zal het idee van de opgave wel zijn.

quote:

Op maandag 5 mei 2014 21:53 schreef nodig het volgende:

[..]

Er moet ook gezegd worden dat het boek bijzonder ongeschikt is voor zelfstudie..

Ja, dat heb ik ook al meermaals opgemerkt. Zoals gezegd, een goede (ouderwetse) leraar die ook echt les geeft blijft onvervangbaar. Maar daarnaast liggen de oorzaken van de dramatische achteruitgang van het niveau van het wiskunde onderwijs ook bij het lager onderwijs. Kinderen die nooit goed hebben leren rekenen (met uitsluitend pen en papier alsmede uit het hoofd, wel te verstaan) missen ook de benodigde vaardigheden om bijvoorbeeld eenvoudige algebraïsche herleidingen tot een goed einde te brengen. Dat wordt treffend geïllustreerd door het volgende plaatje op de website van Liesbeth van der Plas:



Ze merkt daarbij op: Als een kind niet in staat is het getalsommetje probleemloos uit te rekenen, is de algebra-opgave ook veel te hoog gegrepen. Op haar site is ook een interessante PDF te vinden waar ze het onderwijs dat ze zelf kreeg in de elementaire algebra en de vlakke meetkunde vergelijkt met het onderwijs dat haar dochter op school kreeg over deze zelfde onderwerpen, en de consequenties die dat heeft.

Maar goed, ik kan me voorstellen dat diegenen die zich nu op een toets voorbereiden en dit lezen zullen zeggen dat ze hier op dit moment niets mee opschieten, en daarom wil ik jullie ook niet het bos insturen maar toch wat goede en concrete adviezen meegeven.

Zoals gezegd is een goede leraar onvervangbaar, en dat betekent dat je eigenlijk een cursus zou moeten gaan volgen als je ernst maakt met je (vervolg)studie. Als je dat niet kunt bekostigen of anderszins niet in de gelegenheid bent om dat te gaan doen, dan zou je wellicht op zoek kunnen gaan naar iemand die bereid is je tegen een schappelijk tarief bijles te geven. Is ook dat geen reële mogelijkheid, dan blijft uiteraard alleen zelfstudie over. Maar dan kun je beter niet beginnen met het boek van Van de Craats, want dat is meer een opfriscursus en oefenboek, en daarmee bijzonder ongeschikt voor zelfstudie als je de stof nog nooit eerder hebt gezien. Ik zou dan aanraden te beginnen met de spijkers. Dat is een reeks van zeven boekjes die veel beter geschikt zijn voor zelfstudie en waaruit je de basistechnieken ook echt kunt leren. Je moet dan wel beginnen met het eerste boekje over rekenen en uiteindelijk alle zeven delen doorwerken. Dat moet te doen zijn, voor elk deeltje staat volgens de auteur van deze boekjes zo'n 10 à 20 uur studie. En ook al lijkt me dat wat optimistisch, dan nog moet het mogelijk zijn in enkele honderden uren zelfstudie deze gehele reeks door te werken en je de stof in zijn geheel eigen te maken. Pas in een tweede ronde zou je dan kunnen overwegen als herhaling nog wat extra opgaven te maken uit het boek van Van de Craats.

quote:

Op maandag 5 mei 2014 22:50 schreef Riparius het volgende:

[...]

Op haar site is ook een interessante PDF te vinden waar ze het onderwijs dat ze zelf kreeg in de elementaire algebra en de vlakke meetkunde vergelijkt met het onderwijs dat haar dochter op school kreeg over deze zelfde onderwerpen, en de consequenties die dat heeft.

Inderdaad zeer interessant! Ik klikte op de link en heb 't gelijk grotendeels doorgelezen. Ik viel bijna om van verbazing om de verschillen tussen toen en nu en de relevantie van PISA en Cito. Nu begrijp ik ook beter wat ik laatst meemaakte: bij bijles was een jongetje dat een vier stond voor wiskunde in de brugklas. Hij begreep dingen en had inzicht, maar de rekenregels waren hem blijkbaar nooit goed uitgelegd.

quote:

Op maandag 5 mei 2014 22:50 schreef Riparius het volgende:

[..]

Ja, dat heb ik ook al meermaals opgemerkt. Zoals gezegd, een goede (ouderwetse) leraar die ook echt les geeft blijft onvervangbaar. Maar daarnaast liggen de oorzaken van de dramatische achteruitgang van het niveau van het wiskunde onderwijs ook bij het lager onderwijs. Kinderen die nooit goed hebben leren rekenen (met uitsluitend pen en papier alsmede uit het hoofd, wel te verstaan) missen ook de benodigde vaardigheden om bijvoorbeeld eenvoudige algebraïsche herleidingen tot een goed einde te brengen. Dat wordt treffend geïllustreerd door het volgende plaatje op de website van Liesbeth van der Plas:

[ afbeelding ]

Ze merkt daarbij op: Als een kind niet in staat is het getalsommetje probleemloos uit te rekenen, is de algebra-opgave ook veel te hoog gegrepen. Op haar site is ook een interessante PDF te vinden waar ze het onderwijs dat ze zelf kreeg in de elementaire algebra en de vlakke meetkunde vergelijkt met het onderwijs dat haar dochter op school kreeg over deze zelfde onderwerpen, en de consequenties die dat heeft.

Maar goed, ik kan me voorstellen dat diegenen die zich nu op een toets voorbereiden en dit lezen zullen zeggen dat ze hier op dit moment niets mee opschieten, en daarom wil ik jullie ook niet het bos insturen maar toch wat goede en concrete adviezen meegeven.

Zoals gezegd is een goede leraar onvervangbaar, en dat betekent dat je eigenlijk een cursus zou moeten gaan volgen als je ernst maakt met je (vervolg)studie. Als je dat niet kunt bekostigen of anderszins niet in de gelegenheid bent om dat te gaan doen, dan zou je wellicht op zoek kunnen gaan naar iemand die bereid is je tegen een schappelijk tarief bijles te geven. Is ook dat geen reële mogelijkheid, dan blijft uiteraard alleen zelfstudie over. Maar dan kun je beter niet beginnen met het boek van Van de Craats, want dat is meer een opfriscursus en oefenboek, en daarmee bijzonder ongeschikt voor zelfstudie als je de stof nog nooit eerder hebt gezien. Ik zou dan aanraden te beginnen met de spijkers. Dat is een reeks van zeven boekjes die veel beter geschikt zijn voor zelfstudie en waaruit je de basistechnieken ook echt kunt leren. Je moet dan wel beginnen met het eerste boekje over rekenen en uiteindelijk alle zeven delen doorwerken. Dat moet te doen zijn, voor elk deeltje staat volgens de auteur van deze boekjes zo'n 10 à 20 uur studie. En ook al lijkt me dat wat optimistisch, dan nog moet het mogelijk zijn in enkele honderden uren zelfstudie deze gehele reeks door te werken en je de stof in zijn geheel eigen te maken. Pas in een tweede ronde zou je dan kunnen overwegen als herhaling nog wat extra opgaven te maken uit het boek van Van de Craats.

Hmm interessant artikel. Ik moet zeggen dat ik inderdaad het breuken gedeelte in het basisboek wiskunde heb doorgewerkt om weer op niveau te komen. Wist ik veel dat wanneer je breuken deelt je omgekeerd vermenigvuldigt Het optellen van breuken heb ik wel eerder gehad.

Hoofdstuk 1 in het basisboek wiskunde bestaat trouwens uit handmatig vermenigvuldigen en delen. Ik liet mijn ouders een vermenigvuldigenopgave maken en die deden dat toch beduidend sneller dan dat ik deed. Ik moest eerst het voorbeeld bestuderen voordat ik aan de opgaven kon beginnen, ik wist simpelweg niet wat de bedoeling was. De staartdelingen gingen mij trouwens wat beter af, deze kan ik me dan ook nog goed herinneren van de basisschool

Over de zelfstudie. Tja, die cursussen zijn inderdaad flink aan de prijs.. En voor mij is de afstand naar de universiteit waar ik wil gaan studeren geen pretje. Verder heb ik wel iemand die mij eventueel bijles kan geven. Maar ik vind het onnodig om hulp in te schakelen zolang ik het zelf nog red.

Voor mij is het nu aan de late kant om nog een andere methode te gaan proberen. Ik zit nu bij het laatste onderdeel van de examenstof (calcalus: differentiëren). Met alleen het boek had ik het niet gered. Maar in combinatie met khanacademy.org (aanrader!), youtubekanaal wiskundeacademie (behandelt dingen als differentieren niet maar wel parabolen, kwadratische vergelijking, snijpunten + asymptoten etc.) is het al goed te doen. Daarnaast kan je de opgave googlen + het woord wiskundeforum, daar zijn namelijk een hoop topics over de moeilijkere vragen uit het basisboek van mensen die er ook niet uitkwamen. En anders is er nog de mogelijkheid om zelf een vraag te stellen op een forum.

quote:

Op maandag 5 mei 2014 21:30 schreef Super-B het volgende:
| x^2 - 2x | < 1

Ik deed

[snip]

Nu heb ik wel de goede antwoorden, maar heb ik niet de juiste combinatie van oplossingen bij elkaar en onjuiste ongelijkheidstekens...? Wat doe ik fout..?

Ik heb je hier al het advies gegeven om bij het oplossen van wat lastiger ongelijkheden te werken met tekenschema's. Ik geef zo'n advies niet voor niets, het is de bedoeling dat je dat ook ter harte neemt.

Als de absolute waarde van een (reële) grootheid kleiner is dan 1, dan ligt de waarde van die grootheid zelf tussen −1 en +1. De ongelijkheid

| x² − 2x | < 1

is dus equivalent met

−1 < x² − 2x < 1

en dit is weer equivalent met

−1 < x² − 2x ∧ x² − 2x < 1

oftewel

x² − 2x > −1 ∧ x² − 2x < 1

en dus

x² − 2x + 1 > 0 ∧ x² − 2x − 1 < 0

Nu hebben we dus een combinatie van twee kwadratische ongelijkheden met een rechterlid herleid op nul en waaraan tegelijkertijd moet worden voldaan. Deze kwadratische ongelijkheden lossen we op door eerst de nulpunten te bepalen van de kwadratische veeltermen in het linkerlid van deze ongelijkheden. En daar heb je de abc-formule helemaal niet bij nodig. De bepaling van de nulpunten van de eerste kwadratische veelterm is wel heel eenvoudig. Hiervoor vinden we

x² − 2x + 1 = 0
(x − 1)² = 0
x − 1 = 0
x = 1

Voor de bepaling van de nulpunten van de tweede kwadratische veelterm kunnen we kwadraatafsplitsing gebruiken. Dan vinden we

x² − 2x − 1 = 0
(x − 1)² − 1 − 1 = 0
(x − 1)² = 2
x − 1 = √2 ∨ x − 1 = −√2
x = 1 + √2 ∨ x = 1 − √2

Nu moet je zelf maar even twee tekenschema's maken (één voor elk van beide kwadratische ongelijkheden) waarbij je deze tekenschema's uitgelijnd onder elkaar plaatst. Maar strict genomen is dit hier niet eens nodig.

De grafiek van y = x² − 2x + 1 is een dalparabool waarvan de top met coördinaten (1; 0) de x-as raakt, zodat we hebben x² − 2x + 1 > 0 voor elke x ≠ 1.

De grafiek van y = x² − 2x − 1 is een dalparabool die de x-as snijdt in de punten met coördinaten (1 − √2; 0) en (1 + √2; 0), zodat we hebben x² − 2x − 1 < 0 voor 1 − √2 < x < 1 + √2.

Voor de waarden van x die aan de oorspronkelijke ongelijkheid voldoen vinden we dus de voorwaarde

x ≠ 1 ∧ 1 − √2 < x < 1 + √2

Het open interval (1 − √2, 1 + √2) waarop x moet liggen om aan de ongelijkheid te voldoen wordt hier dus in twee delen geknipt doordat de waarde x = 1 niet mee mag doen. Deze knip geeft aldus twee open intervallen. Je kunt de oplossing van de ongelijkheid nu noteren als

1 − √2 < x < 1 ∨ 1 < x < 1 + √2

of als

x ∈ (1 − √2, 1) ∪ (1, 1 + √2)

[ Bericht 0% gewijzigd door Riparius op 06-05-2014 00:16:00 ]

Differentieer met behulp van quotientregel:


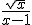
Ik kom dan tot:


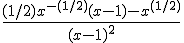
Maar het moet nog vereenvoudigd worden tot:


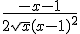
Hoe pak ik dit aan?

[ Bericht 14% gewijzigd door nodig op 06-05-2014 00:58:10 ]

quote:

Op dinsdag 6 mei 2014 00:46 schreef nodig het volgende:
Differentieer met behulp van quotientregel:


Ik kom dan tot:

Dit is alvast niet goed, je bent een kwadraat in de noemer vergeten. De quotiëntregel luidt in symbolische vorm

(f/g)' = (f'g − fg')/g²

quote:

Op dinsdag 6 mei 2014 00:53 schreef Riparius het volgende:

[..]

Dit is alvast niet goed, je bent een kwadraat in de noemer vergeten. De quotiëntregel luidt in symbolische vorm

(f/g)' = (f'g − fg')/g²

Woops sorry, verkeerd overgenomen De kwadraat had ik wel in mijn schrift staan.
De correctie:

Ook aangepast in eerste post.

quote:

Op dinsdag 6 mei 2014 00:55 schreef nodig het volgende:

[..]

Woops sorry, verkeerd overgenomen De kwadraat had ik wel in mijn schrift staan.
De correctie:

Ook aangepast in eerste post.

Goed. Vermenigvuldig nu teller en noemer van je oorspronkelijke quotiënt met 2·x^1/2 en pas daarna rekenregels voor het werken met exponenten toe.

quote:

Op dinsdag 6 mei 2014 01:02 schreef Riparius het volgende:

[..]

Goed. Vermenigvuldig nu teller en noemer van je oorspronkelijke quotiënt met 2·x^1/2 en pas daarna rekenregels voor het werken met exponenten toe.

De noemer is dan duidelijk. Maar van de teller kan ik weinig maken. Wat bedoel je met oorspronkelijke quotiënt?

quote:

Op dinsdag 6 mei 2014 01:13 schreef nodig het volgende:

[..]

De noemer is dan duidelijk. Maar van de teller kan ik weinig maken. Wat bedoel je met oorspronkelijke quotiënt?

Met het oorspronkelijke quotiënt bedoel ik de breuk zoals je die krijgt direct na toepassing van de quotiëntregel en zoals je die hierboven (gecorrigeerd) weergeeft.

Goed, de noemer is je duidelijk. Nu gaan we kijken wat je krijgt als je de teller vermenigvuldigt met 2·x^1/2. Hiervoor krijgen we dan

2·x^1/2·(½·x^−1/2·(x−1) − x^1/2) = 2·½·x^1/2·x^−1/2·(x−1) − 2·x^1/2·x^1/2 = 1·x⁰·(x−1) − 2·x¹ = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1

Ik maak hier gebruik van de distributiviteit van vermenigvuldiging t.o.v. optelling (en aftrekking), dus

a(b+c) = ab + ac
a(b−c) = ab − ac

alsmede van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal, dus

a^p·a^q = a^p+q

Ook maak ik nog gebruik van de eigenschap dat de nulde macht van een getal gelijk is aan 1, dus

a⁰ = 1

Dit laatste volgt ook direct uit de regel a^p·a^q = a^p+q met q = 0, want dan krijg je a^p·a⁰ = a^p zodat vermenigvuldiging met a⁰ niets verandert en a⁰ dus wel 1 moet zijn.

quote:

Op maandag 5 mei 2014 22:23 schreef Novermars het volgende:

[..]

Zie mijn edit, informeel lukt geslotenheid me wel. Maar geen idee hoe ik dit rigoureus opschrijf...

Maar jouw open cover, waarom mag je deze gebruiken? Als we het over zouden hebben, dan is hij logisch. Maar en zitten niet in , moeten we ze dan niet helemaal achterwege laten?

Q is een deelverzameling van R en heeft als zodanig de deeltopologie van de standaardtopologie op R. Dat wil zeggen dat S een open resp. gesloten deel van Q is in deze topologie precies als S geschreven kan worden als de doorsnede van Q met een open resp. gesloten deel van R.
is gesloten in R, en jouw verzameling is daarvan de doorsnede met Q.

quote:

Op dinsdag 6 mei 2014 01:49 schreef Riparius het volgende:

[..]

Met het oorspronkelijke quotiënt bedoel ik de breuk zoals je die krijgt direct na toepassing van de quotiëntregel en zoals je die hierboven (gecorrigeerd) weergeeft.

Goed, de noemer is je duidelijk. Nu gaan we kijken wat je krijgt als je de teller vermenigvuldigt met 2·x^1/2. Hiervoor krijgen we dan

2·x^1/2·(½·x^−1/2·(x−1) − x^1/2) = 2·½·x^1/2·x^−1/2·(x−1) − 2·x^1/2·x^1/2 = 1·x⁰·(x−1) − 2·x¹ = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1

Ik maak hier gebruik van de distributiviteit van vermenigvuldiging t.o.v. optelling (en aftrekking), dus

a(b+c) = ab + ac
a(b−c) = ab − ac

alsmede van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van twee machten van hetzelfde grondtal, dus

a^p·a^q = a^p+q

Ook maak ik nog gebruik van de eigenschap dat de nulde macht van een getal gelijk is aan 1, dus

a⁰ = 1

Dit laatste volgt ook direct uit de regel a^p·a^q = a^p+q met q = 0, want dan krijg je a^p·a⁰ = a^p zodat vermenigvuldiging met a⁰ niets verandert en a⁰ dus wel 1 moet zijn.

Danku!

Ik heb het even uitgeschreven op papier en begrijp het inderdaad. Ga de opgave nu nog een keer maken .

In je laatste 3 stappen: = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1
Moet de één-na-laatste stap niet gewoon x - 1 - 2x zijn? Ik zat de hele tijd die haakjes uit te werken maar dat komt niet uit. Die haakjes mag je toch weghalen omdat er in de stap ervoor de haakjes al uitgewerkt zijn?