SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Nee, aan de oplossing van je opgave komt geen trial and error te pas.quote:Op zondag 4 mei 2014 19:23 schreef Super-B het volgende:
[..]
De discriminant berekenen en werken volgens de trial and error methode. Waarden blijven invoeren bij de b variabelen totdat de uitkomsten lager dan 0 zijn... en alle waarden die een uitkomst hebben lager dan 0 zijn de antwoorden. Dat denk ik dan.
Maar even een gedachtenkronkel;
Het gaat toch om het feit het snijpunt met de x-as.. waarom betreft het oplossen van de vraag over de discriminant en de oplossing van de vergelijking? Zelf zou ik denken dat het iets te maken heeft met dat y niet 0 mag zijn.
De algemene gedaante van een kwadratische functie isquote:Want het oplossingsmogelijkheden van de grafiek //abc formule, kwadratische oplosmethode etc. // gaan allemaal over x en niet over y..
Dus dat is even een gedachtenkronkel. Zou je dat kunnen ophelderen voor mij?
(1) f(x) = ax2 + bx + c
Hierbij zijn a,b,c vaste (reële) getallen, en tevens is a ≠ 0, anders zou je geen kwadratische term meer hebben en dus ook geen kwadratische functie.
De grafiek van een kwadratische functie is altijd een parabool met een verticale symmetrie-as. Het is een dalparabool als a > 0 en een bergparabool als a < 0.
De grafiek van de kwadratische functie kan de x-as snijden in twee punten, de x-as raken in één punt of geheel en al boven of onder de x-as liggen.
Heeft de grafiek van de kwadratische functie punten die op de x-as liggen, dan zijn er waarden van x waarvoor de bijbehorende functiewaarde y = f(x) gelijk is aan nul, dus
(2) f(x) = 0
Uit (1) en (2) volgt dat je dan hebt
(3) ax2 + bx + c = 0
Dit is een tweedegraads vergelijking oftewel een kwadratische vergelijking, ook wel een vierkantsvergelijking genoemd (het woord kwadraat komt van het Latijnse quadratus dat 'vierkant' betekent).
Om nu de x-coördinaten van de snijpunten van de grafiek van de kwadratische functie met de x-as oftewel de nulpunten van f(x) te vinden moeten bekijken voor welke waarde(n) van x aan (3) wordt voldaan en dus vergelijking (3) oplossen.
De kwadratische vergelijking (3) kan óf 2 óf 1 óf 0 (reële) oplossingen hebben. Het aantal (reële) oplossingen wordt bepaald door de zogeheten discriminant van (3). De discriminant wordt gewoonlijk aangegeven met de hoofdletter D en is gelijk aan b2 − 4ac, dus
(4) D = b2 − 4ac
Er zijn nu drie mogelijkheden, de discriminant D kan positief zijn, nul, of negatief, en deze drie mogelijkheden corresponderen precies met het aantal (reële) oplossingen van de vierkantsvergelijking (3), als volgt
D > 0 : twee oplossingen
D = 0 : één oplossing
D < 0 : geen oplossingen
Als je wil weten waarom dit zo is, en tevens hoe de vermaarde abc-formule voor het oplossen van vierkantsvergelijkingen kan worden afgeleid, dan moet je deze post van mij eens goed bestuderen.
Nu je opgave. Gegeven is de functie
(5) f(x) = x2 + px + 1
waarbij een p een vast getal voorstelt (een zogeheten parameter, vandaar de keuze voor de letter p). Gevraagd wordt nu voor welke (reële) waarden van p de grafiek van de functie f geen punten gemeen heeft met de x-as. De grafiek van f is een dalparabool, aangezien de coëfficiënt van de kwadratische term gelijk is aan 1, en dus positief. Als de grafiek van f geen punten gemeen heeft met de x-as dan zal deze dalparabool dus geheel boven de x-as moeten liggen. Aangezien er geen waarden van x moeten zijn waarvoor f(x) = 0, moet de vergelijking
(6) x2 + px + 1 = 0
dan geen (reële) oplossingen hebben. Dat is het geval als de discriminant van (6) negatief is. Welnu, als je (6) vergelijkt met de standaardvorm (3), dan zie je dat we hier hebben a = 1, b = p, c = 1. De discriminant Dp van (6) is dus
(7) Dp = p2 − 4
We duiden de discriminant hier aan met Dp, met een index p, om aan te geven dat de discriminant hier afhangt van de waarde van p. De vraag is nu voor welke waarden van p geldt
(8) Dp < 0
en dus
(9) p2 − 4 < 0
Nu zie je dat (9) een kwadratische ongelijkheid is in de onbekende p, en deze ongelijkheid moeten we oplossen. Hoe doe je dat? Wel, je zou eerst kunnen kijken voor welke waarde(n) van p het linkerlid p2 − 4 precies gelijk is aan nul. Dan moet p2 = 4 zijn en hebben we dus p = 2 óf p = − 2. Je kunt nu gemakkelijk nagaan dat aan de ongelijkheid (9) wordt voldaan als p tussen deze waarden −2 en +2 in ligt, dus als p groter is dan −2 maar tevens kleiner dan +2. Dat kunnen we heel compact noteren als volgt
(10) −2 < p < 2
En daarmee is je opgave opgelost: de grafiek van de functie f(x) = x2 + px + 1 heeft geen snijpunten met de x-as als p op het open interval (−2, 2) ligt. Met een open interval bedoelen we een interval waarbij de eindpunten niet meedoen.
Hartstikke duidelijk! Jeetje, zelf getypt of van het internet bij elkaar gesprokkeld? Want het is werkelijk erg goed geschreven.. Wat voor opleiding volg je?quote:
[..]
Nee, aan de oplossing van je opgave komt geen trial and error te pas.
[..]
De algemene gedaante van een kwadratische functie is
(1) f(x) = ax2 + bx + c
Hierbij zijn a,b,c vaste (reële) getallen, en tevens is a ≠ 0, anders zou je geen kwadratische term meer hebben en dus ook geen kwadratische functie.
De grafiek van een kwadratische functie is altijd een parabool met een verticale symmetrie-as. Het is een dalparabool als a > 0 en een bergparabool als a < 0.
De grafiek van de kwadratische functie kan de x-as snijden in twee punten, de x-as raken in één punt of geheel en al boven of onder de x-as liggen.
Heeft de grafiek van de kwadratische functie punten die op de x-as liggen, dan zijn er waarden van x waarvoor de bijbehorende functiewaarde y = f(x) gelijk is aan nul, dus
(2) f(x) = 0
Uit (1) en (2) volgt dat je dan hebt
(3) ax2 + bx + c = 0
Dit is een tweedegraads vergelijking oftewel een kwadratische vergelijking, ook wel een vierkantsvergelijking genoemd (het woord kwadraat komt van het Latijnse quadratus dat 'vierkant' betekent).
Om nu de x-coördinaten van de snijpunten van de grafiek van de kwadratische functie met de x-as oftewel de nulpunten van f(x) te vinden moeten bekijken voor welke waarde(n) van x aan (3) wordt voldaan en dus vergelijking (3) oplossen.
De kwadratische vergelijking (3) kan óf 2 óf 1 óf 0 (reële) oplossingen hebben. Het aantal (reële) oplossingen wordt bepaald door de zogeheten discriminant van (3). De discriminant wordt gewoonlijk aangegeven met de hoofdletter D en is gelijk aan b2 − 4ac, dus
(4) D = b2 − 4ac
Er zijn nu drie mogelijkheden, de discriminant D kan positief zijn, nul, of negatief, en deze drie mogelijkheden corresponderen precies met het aantal (reële) oplossingen van de vierkantsvergelijking (3), als volgt
D > 0 : twee oplossingen
D = 0 : één oplossing
D < 0 : geen oplossingen
Als je wil weten waarom dit zo is, en tevens hoe de vermaarde abc-formule voor het oplossen van vierkantsvergelijkingen kan worden afgeleid, dan moet je deze post van mij eens goed bestuderen.
Nu je opgave. Gegeven is de functie
(5) f(x) = x2 + px + 1
waarbij een p een vast getal voorstelt (een zogeheten parameter, vandaar de keuze voor de letter p). Gevraagd wordt nu voor welke (reële) waarden van p de grafiek van de functie f geen punten gemeen heeft met de x-as. De grafiek van f is een dalparabool, aangezien de coëfficiënt van de kwadratische term gelijk is aan 1, en dus positief. Als de grafiek van f geen punten gemeen heeft met de x-as dan zal deze dalparabool dus geheel boven de x-as moeten liggen. Aangezien er geen waarden van x moeten zijn waarvoor f(x) = 0, moet de vergelijking
(6) x2 + px + 1 = 0
dan geen (reële) oplossingen hebben. Dat is het geval als de discriminant van (6) negatief is. Welnu, als je (6) vergelijkt met de standaardvorm (3), dan zie je dat we hier hebben a = 1, b = p, c = 1. De discriminant Dp van (6) is dus
(7) Dp = p2 − 4
We duiden de discriminant hier aan met Dp, met een index p, om aan te geven dat de discriminant hier afhangt van de waarde van p. De vraag is nu voor welke waarden van p geldt
(8) Dp < 0
en dus
(9) p2 − 4 < 0
Nu zie je dat (9) een kwadratische ongelijkheid is in de onbekende p, en deze ongelijkheid moeten we oplossen. Hoe doe je dat? Wel, je zou eerst kunnen kijken voor welke waarde(n) van p het linkerlid p2 − 4 precies gelijk is aan nul. Dan moet p2 = 4 zijn en hebben we dus p = 2 óf p = − 2. Je kunt nu gemakkelijk nagaan dat aan de ongelijkheid (9) wordt voldaan als p tussen deze waarden −2 en +2 in ligt, dus als p groter is dan −2 maar tevens kleiner dan +2. Dat kunnen we heel compact noteren als volgt
(10) −2 < p < 2
En daarmee is je opgave opgelost: de grafiek van de functie f(x) = x2 + px + 1 heeft geen snijpunten met de x-as als p op het open interval (−2, 2) ligt. Met een open interval bedoelen we een interval waarbij de eindpunten niet meedoen.
Het vetgedrukte is echter nog niet helemaal helder voor mij...
En hoe kan de oplossing x < 2 of x > -2 zijn? p² = 4 en de wortel daarvan is 2, dus dan kan p toch alleen maar < 2 ?
Daarnaast heb ik nog een vraag:
Zou ik ook i.p.v. een ongelijkheid ervan maken gewoon in de vergelijking -1 kunnen vullen, want alles onder <0 heeft geen oplossing:
x² + px + 1 = -1
Nee. Je wilt alle waarden van p weten waarvoor voor alle x geldt dat f(x) niet 0 is.quote:
[..]
Hartstikke duidelijk! Jeetje, zelf getypt of van het internet bij elkaar gesprokkeld? Want het is werkelijk erg goed geschreven.. Wat voor opleiding volg je?
Het vetgedrukte is echter nog niet helemaal helder voor mij...
En hoe kan de oplossing x < 2 of x > -2 zijn? p² = 4 en de wortel daarvan is 2, dus dan kan p toch alleen maar < 2 ?
Daarnaast heb ik nog een vraag:
Zou ik ook i.p.v. een ongelijkheid ervan maken gewoon in de vergelijking -1 kunnen vullen, want alles onder <0 heeft geen oplossing:
x² + px + 1 = -1
Bestudeer de hoofdstelling van de algebra eens, dan zul je zien dat in het algemene geval geldt dat voor f(x) = 0 met f(x) een polynoom van graad n geldt dat f(x) n oplossingen heeft. Deze kunnen complex zijn en met ten hoogste multipliciteit n. x2 - 4 = 0 is een polynoom van graad 2, dus heeft deze 2 oplossingen. Om dit te controleren moet je -2 eens kwadrateren. Daar komt 4 uit toch?
Verder is 3 posts hierboven duidelijk gemaakt dat Riparius geen antwoord geeft op privévragen, om maar even als persoonlijke secretaresse op te treden.
quote:
[ Bericht 3% gewijzigd door #ANONIEM op 04-05-2014 21:12:11 ]
Oké bedankt!quote:Op zondag 4 mei 2014 21:11 schreef Amoeba het volgende:
[..]
Nee. Je wilt alle waarden van p weten waarvoor voor alle x geldt dat f(x) niet 0 is.
Bestudeer de hoofdstelling van de algebra eens, dan zul je zien dat in het algemene geval geldt dat voor f(x) = 0 met f(x) een polynoom van graad n geldt dat f(x) n oplossingen heeft. Deze kunnen complex zijn en met ten hoogste multipliciteit n. x2 - 4 = 0 is een polynoom van graad 2, dus heeft deze 2 oplossingen. Om dit te controleren moet je -2 eens kwadrateren. Daar komt 4 uit toch?
Verder is 3 posts hierboven duidelijk gemaakt dat Riparius geen antwoord geeft op privévragen, om maar even als persoonlijke secretaresse op te treden.
[..]
Hier een iets lastigere:
x² + px + p
p² + 4p < 0
p² < -4p
Ik twijfel nu om het te delen door p waardoor je p < -4 krijgt... maar daarnaast denk ik dat het niet klopt, want in het antwoordenmodel staat wat anders dan p < -4.
D = b^2− 4acquote:
[..]
Oké bedankt!
Hier een iets lastigere:
x² + px + p
p² + 4p < 0
p² < -4p
Ik twijfel nu om het te delen door p waardoor je p < -4 krijgt... maar daarnaast denk ik dat het niet klopt, want in het antwoordenmodel staat wat anders dan p < -4.
Je bent de min vergeten.
Je maakt al een fout. De discriminant D is gelijk aan b^2 - 4acquote:
[..]
Oké bedankt!
Hier een iets lastigere:
x² + px + p
p² + 4p < 0
p² < -4p
Ik twijfel nu om het te delen door p waardoor je p < -4 krijgt... maar daarnaast denk ik dat het niet klopt, want in het antwoordenmodel staat wat anders dan p < -4.
Dan krijg je p^2 -4p < 0
Dus p(p-4) < 0
Volg je het nu?
Oeps ik zie het al!quote:
[..]
Je maakt al een fout. De discriminant D is gelijk aan b^2 - 4ac
Dan krijg je p^2 -4p < 0
Dus p(p-4) < 0
Volg je het nu?
Nee het vetgedrukte niet. Wiskunde blijft een interessant vak.
Ik zou zelf denken p² - 4p < 0 en dus p² < 4p en vervolgens beide kanten delen door p waardoor je krijgt p < 4
Maar mag dat wel altijd, delen door een getal?quote:
[..]
Oeps ik zie het al!
Nee het vetgedrukte niet. Wiskunde blijft een interessant vak.
Ik zou zelf denken p² - 4p < 0 en dus p² < 4p en vervolgens beide kanten delen door p waardoor je krijgt p < 4
Ja toch? In ieder geval letters wel toch om de letter - exponent weg te werken, althans bij breuken etc?quote:
[..]
Maar mag dat wel altijd, delen door een getal?
Nog een pittige hoor... 
Alleen dit keer ''voor welke reële getallen p snijdt de grafiek van f de x-as in twee verschillende punten?''
f (x) = x²+ 2px - 1
Vervolgens deed ik:
D = b²- 4ac wat resulteert tot 2p² + 4p > 0
Daarna deelde ik zowel links als rechts door 2, wat resulteert tot p²+ 2p > 0 (0/2 blijft 0).
p ( p + 2)
p = 0 of p = -2 du -2 < p < 0
Echter zegt het antwoordenmodel: ''voor alle p''
Alleen dit keer ''voor welke reële getallen p snijdt de grafiek van f de x-as in twee verschillende punten?''
f (x) = x²+ 2px - 1
Vervolgens deed ik:
D = b²- 4ac wat resulteert tot 2p² + 4p > 0
Daarna deelde ik zowel links als rechts door 2, wat resulteert tot p²+ 2p > 0 (0/2 blijft 0).
p ( p + 2)
p = 0 of p = -2 du -2 < p < 0
Echter zegt het antwoordenmodel: ''voor alle p''
Zolang je er bij het antwoord neer zet dat de oplossing alleen geldt indien de "letter" niet gelijk aan is aan nul wel.quote:
[..]
Ja toch? In ieder geval letters wel toch om de letter - exponent weg te werken, althans bij breuken etc?
In dit geval is dat dus precies de oplossing die je mist voor p² - 4p > 0. Je kunt hier een p "buiten haakjes halen", waardoor je dus p(p-4) > 0 krijgt. En dan gelijk kunt zien dat de grensgevallen p=0 V p=4 zijn.
Nee, tot 4p^2 + 4 > 0quote:
Nog een pittige hoor...
Alleen dit keer ''voor welke reële getallen p snijdt de grafiek van f de x-as in twee verschillende punten?''
f (x) = x²+ 2px - 1
Vervolgens deed ik:
D = b²- 4ac wat resulteert tot 2p² + 4p > 0
Voor welke reële getallen p snijdt de grafiek van f de x-as in twee verschillende punten?'
f (x) = x²+ 2px - 1
D = b²- 4ac dus als 4p² + 4 > 0 dan zijn er twee verschillende snijpunten
En p² is altijd groter of gelijk aan 0 voor elke p dus D > 0 voor elke p
f (x) = x²+ 2px - 1
D = b²- 4ac dus als 4p² + 4 > 0 dan zijn er twee verschillende snijpunten
En p² is altijd groter of gelijk aan 0 voor elke p dus D > 0 voor elke p
Hoe weet je direct dat p² altijd of gelijk is aan 0? Moet je het niet eerst oplossen of wat?quote:
Voor welke reële getallen p snijdt de grafiek van f de x-as in twee verschillende punten?'
f (x) = x²+ 2px - 1
D = b²- 4ac dus als 4p² + 4 > 0 dan zijn er twee verschillende snijpunten
En p² is altijd groter of gelijk aan 0 voor elke p dus D > 0 voor elke p
En het gaat toch om de hele formule dat >0 moet zijn?
p wordt gekwadrateerd, dus het resultaat is altijd groter dan 0.quote:
[..]
Hoe weet je direct dat p² altijd of gelijk is aan 0? Moet je het niet eerst oplossen of wat?
En het gaat toch om de hele formule dat >0 moet zijn?
Maar als p = 0 dan niet.. Het is wel een lastig onderwerp...quote:
[..]
p wordt gekwadrateerd, dus het resultaat is altijd groter dan 0.
f (x) = ax²+ bx + c
D = b²- 4ac
Nu
f (x) = x²+ 2px - 1
Dus a = 1 , b = 2p , c = -1
D = (2p)² - 4 * 1 * (-1) = 4p² + 4 = 4(p²+1)
Er zijn twee verschillende snijpunten met de x-as als D > 0.
Voor elke p geldt dat p² ≥ 0.
En dus geldt voor elke p dat p² + 1 > 0
Dus D > 0 voor alle p.
Dus voor elke p zijn er twee verschillende snijpunten met de x-as.
D = b²- 4ac
Nu
f (x) = x²+ 2px - 1
Dus a = 1 , b = 2p , c = -1
D = (2p)² - 4 * 1 * (-1) = 4p² + 4 = 4(p²+1)
Er zijn twee verschillende snijpunten met de x-as als D > 0.
Voor elke p geldt dat p² ≥ 0.
En dus geldt voor elke p dat p² + 1 > 0
Dus D > 0 voor alle p.
Dus voor elke p zijn er twee verschillende snijpunten met de x-as.
Dan is de oplossing toch alsnog groter dan 0, want er staat +4 achter ... Dus dat maakt niet uit.quote:
[..]
Maar als p = 0 dan niet.. Het is wel een lastig onderwerp...
Aha.. Je gaat nu van een ax²+ bx + c vergelijking uit.quote:
f (x) = ax²+ bx + c
D = b²- 4ac
Nu
f (x) = x²+ 2px - 1
Dus a = 1 , b = 2p , c = -1
D = (2p)² - 4 * 1 * (-1) = 4p² + 4 = 4(p²+1)
Er zijn twee verschillende snijpunten met de x-as als D > 0.
Voor elke p geldt dat p² ≥ 0.
En dus geldt voor elke p dat p² + 1 > 0
Dus D > 0 voor alle p.
Dus voor elke p zijn er twee verschillende snijpunten met de x-as.
Hoe zou jet het bij een vergelijking als bijvoorbeeld -x² + x + p + 1 doen? Hoe weet je dan wat b en c is?
Je kunt dat toch gewoon invullen? Wat staat er bij x², wat staat er bij x, en waar staat geen x bij.quote:
[..]
Aha.. Je gaat nu van een ax²+ bx + c vergelijking uit.
Hoe zou jet het bij een vergelijking als bijvoorbeeld -x² + x + p + 1 doen? Hoe weet je dan wat b en c is?
Ja maar ik raak in de war van de p -1quote:
[..]
Je kunt dat toch gewoon invullen? Wat staat er bij x², wat staat er bij x, en waar staat geen x bij.
Kan iemand hier de juiste berekening van geven? Ik kom wel op de juiste antwoorden maar volgens mij niet op de juiste manier..
Hoe kun je aan de oplossing zelf zien dat de oplossing is ''alle p'' ?quote:
f (x) = ax²+ bx + c
D = b²- 4ac
Nu
f (x) = x²+ 2px - 1
Dus a = 1 , b = 2p , c = -1
D = (2p)² - 4 * 1 * (-1) = 4p² + 4 = 4(p²+1)
Er zijn twee verschillende snijpunten met de x-as als D > 0.
Voor elke p geldt dat p² ≥ 0.
En dus geldt voor elke p dat p² + 1 > 0
Dus D > 0 voor alle p.
Dus voor elke p zijn er twee verschillende snijpunten met de x-as.
Aan 4(p² + 1) kan ik dat niet zo direct zien.
Waarom? Er staat geen x bij. p kun je in dit geval zien als niets meer dan een willekeurig getal.quote:
Voor elke p geldt toch dat het resulterende getal groter is dan 0?quote:
[..]
Hoe kun je aan de oplossing zelf zien dat de oplossing is ''alle p'' ?
Aan 4(p² + 1) kan ik dat niet zo direct zien.
Een kwadraat kan niet negatief zijn. Dus is p2 altijd groter dan of gelijk aan nul. Maar dan is p2 + 1 dus altijd tenminste 1 en 4(p2 + 1) dus altijd tenminste 4. De discriminant is dus altijd positief, en de corresponderende kwadratische vergelijking heeft dus altijd twee (verschillende) oplossingen.quote:
[..]
Hoe kun je aan de oplossing zelf zien dat de oplossing is ''alle p'' ?
Aan 4(p² + 1) kan ik dat niet zo direct zien.
Ja de merkwaardige producten ben ik eerder tegengekomen:quote:
[..]
Nee. Zorg dat je je merkwaardige producten kent. Zie ook hier.
4p^2 + 4
Als het p² - 4 was had ik geweten dat het een merkwaardig product was: (p-2)(p+2)
Maar ik weet niet hoe ik het merkwaardig kan oplossen bij zowel p² + 4 als 4p² + 4.
Wat is jouw manier?quote:
Kan iemand hier de juiste berekening van geven? Ik kom wel op de juiste antwoorden maar volgens mij niet op de juiste manier..
Dat is het punt niet. Je dacht hierboven dat jequote:
[..]
Ja de merkwaardige producten ben ik eerder tegengekomen:
4p^2 + 4
Als het p² - 4 was had ik geweten dat het een merkwaardig product was: (p-2)(p+2)
Maar ik weet niet hoe ik het merkwaardig kan oplossen bij zowel p² + 4 als 4p² + 4.
p2 + 1
kon herschrijven als
(p−1)(p+1)
maar dat klopt niet. Je had direct moeten zien dat als (p−1)(p+1) gelijk is aan p2 − 1 dat (p−1)(p+1) dan niet gelijk kan zijn aan p2 + 1.
Oh zo..quote:
[..]
Dat is het punt niet. Je dacht hierboven dat je
p2 + 1
kon herschrijven als
(p−1)(p+1)
maar dat klopt niet. Je had direct moeten zien dat als (p−1)(p+1) gelijk is aan p2 − 1 dat (p−1)(p+1) dan niet gelijk kan zijn aan p2 + 1.
Hoe los je dit op de ''merkwaardigheids'' manier op dan? 4p^2 + 4
Of kan dat niet opgelost worden en is de enige mogelijkheid om in te zien dat alle p's kunnen?
Je kunt p2 + 1 niet schrijven als een product van twee lineaire factoren, althans niet binnen de reële getallen. Maar het is hier voldoende om je te realiseren dat p2 + 1 niet kleiner kan zijn dan 1 en dus dat 4(p2 + 1) niet kleiner kan zijn dan 4. De uitdrukking 4(p2 + 1) is dus positief voor elke (reële) waarde van p.quote:
[..]
Oh zo..
Hoe los je dit op de ''merkwaardigheids'' manier op dan? 4p^2 + 4
Of kan dat niet opgelost worden en is de enige mogelijkheid om in te zien dat alle p's kunnen?
Wiskunde wordt als hulpmiddel gebruikt, net als bij alle andere bèta-opleidingen buiten wiskunde. Dat is niet te vergelijken met wiskunde zelf studeren, je krijgt wat gemeenschappelijke basisvakken en that's it.quote:
[..]
Ik geloof dat jij er de ballen verstand van hebt. Informatica is wel zeker een opleiding waar zeer veel wiskunde behandeld wordt.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ah kijk, duidelijkquote:
[..]
Wiskunde wordt als hulpmiddel gebruikt, net als bij alle andere bèta-opleidingen buiten wiskunde. Dat is niet te vergelijken met wiskunde zelf studeren, je krijgt wat gemeenschappelijke basisvakken en that's it.
Dan kunnen we er dus wel van uit gaan dat de wiskundekennis van een informatica-student gemiddeld gezien hoger is dan een niet-beta opleiding.
Blijft het natuurlijk een feit dat dit 'middelbareschoolwiskunde' is, een vwo-leerling, die uitblinkt in wiskunde bezit voor dit soort vragen ook genoeg kennis.
Dat is fout. Je weet namelijk helemaal niet of je onbekende p positief of negatief is. Als je bij een ongelijkheid beide leden deelt door een negatief getal, dan klapt het teken van de ongelijkheid om. Maar aangezien je in principe niet weet of je hier door een positief of negatief getal deelt kun je dus ook niet weten of je het ongelijkheidsteken wel of niet om moet klappen. Daarom is je aanpak fout.quote:
[..]
Oeps ik zie het al!
Nee het vetgedrukte niet. Wiskunde blijft een interessant vak.
Ik zou zelf denken p² - 4p < 0 en dus p² < 4p en vervolgens beide kanten delen door p waardoor je krijgt p < 4
Wat je moet doen is eerst de gelijkheid (vergelijking) p2 − 4p = 0 oplossen. Dan vind je p = 0 ∨ p = 4. Vervolgens maak je een tekenschema.
| 1 2 3 | ++++++++++++++++++++0--------------------0++++++++++++++++++++ ____________________|____________________|____________________ 0 4 |
Een tekenschema bestaat uit een getallenlijn waarop je de getallen aangeeft waarvoor je uitdrukking p2 − 4p gelijk is aan nul, hier dus de getallen 0 en 4. Boven deze getallen op de getallenlijn plaats je een 0 om aan te geven dat de waarde van p2 − 4p hier nul is. Verder zet je plustekens boven de getallenlijn daar waar p2 − 4p positief is en mintekens boven de getallenlijn daar waar p2 − 4p negatief is. Nu zie je in één oogopslag in het tekenschema dat p2 − 4p < 0 voor 0 < p < 4.
Uiteraard is het in een eenvoudig geval als dit ook zonder tekenschema direct in te zien dat p2 − 4p alleen negatief kan zijn als p tussen 0 en 4 in ligt: de grafiek van q = p2 − 4p (met p langs de horizontale as en q langs de verticale as) is immers een dalparabool die de p-as snijdt in de punten (0;0) en (4;0). Het deel van de grafiek tussen deze snijpunten ligt onder de p-as, zodat de waarde van q = p2 − 4p negatief is voor waarden van p tussen 0 en 4, en elders niet.
Bij het oplossen van ingewikkelder ongelijkheden kan een tekenschema goede diensten bewijzen. Als je bijvoorbeeld een ongelijkheid hebt met in het linkerlid een breuk waarbij de onbekende zowel in de teller als in de noemer voorkomt terwijl je het rechterlid al hebt herleid op nul, dan kun je twee afzonderlijke tekenschema's maken, namelijk één voor de teller en één voor de noemer, en deze tekenschema's uitgelijnd onder elkaar plaatsen. Als de waarde van de breuk als geheel dan bijvoorbeeld kleiner dan nul moet zijn, dan kan dat alleen hetzij als de teller negatief is en tevens de noemer positief hetzij als de teller positief is en tevens de noemer negatief. Uit het gecombineerde tekenschema van de teller en de noemer kun je dan aflezen voor welke waarden van de onbekende dit het geval is.
[ Bericht 0% gewijzigd door Riparius op 05-05-2014 08:19:12 ]
Laat eerst maar eens zien wat je hebt gedaan.quote:
Kan iemand hier de juiste berekening van geven? Ik kom wel op de juiste antwoorden maar volgens mij niet op de juiste manier..
Hint: voor elke x ∈ R heb je x4 = |x|4 en ook |³√x| = |x|1/3.
Geloof mij nu maar dat je met een informatica studie nog steeds de ballen verstand hebt van wiskunde.quote:
[..]
Ah kijk, duidelijk
Dan kunnen we er dus wel van uit gaan dat de wiskundekennis van een informatica-student gemiddeld gezien hoger is dan een niet-beta opleiding.
Blijft het natuurlijk een feit dat dit 'middelbareschoolwiskunde' is, een vwo-leerling, die uitblinkt in wiskunde bezit voor dit soort vragen ook genoeg kennis.
Weten jullie wat er met het volgende bedoelt wordt?:
f (x) = (2x + 4) / (x - 3)
Voor x = 3 wordt de noemer nul, en dan kan f(x) niet berekend worden. Nadert x boven tot 3, dan nadert f(x) tot +∞ , nadert x van onder tot 3, dan nadert f(x) tot -∞ .
Snappen jullie dit? Ik snap het niet echt.. wat maakt het uit als het antwoord op 0 komt bij asymptoten? Dan is het coördinaat van y gewoon 0 toch? Dat kan in principe toch gewoon?
Neem me niet kwalijk voor de vele vragen, maar het is voor mij een voorbereiding voor een intaketoets en dit zijn vrijwel vervaagde onderwerpen voor mij.
f (x) = (2x + 4) / (x - 3)
Voor x = 3 wordt de noemer nul, en dan kan f(x) niet berekend worden. Nadert x boven tot 3, dan nadert f(x) tot +∞ , nadert x van onder tot 3, dan nadert f(x) tot -∞ .
Snappen jullie dit? Ik snap het niet echt.. wat maakt het uit als het antwoord op 0 komt bij asymptoten? Dan is het coördinaat van y gewoon 0 toch? Dat kan in principe toch gewoon?
Neem me niet kwalijk voor de vele vragen, maar het is voor mij een voorbereiding voor een intaketoets en dit zijn vrijwel vervaagde onderwerpen voor mij.
Dat beide lijnen langzamerhand recht naar boven toe gaan wijzen en nooit de x = 3 raken, maar er wel dichtbij tegenaan hangen.quote:
Gaan ze echt beiden recht naar boven? Kijk eens beter.
Verder, wat is het verschil als je van onder ('links') en van boven ('rechts') naar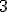
gaat?
Verder, wat is het verschil als je van onder ('links') en van boven ('rechts') naar
Oeps typfout, de één gaat naar boven (rechter) en de linker gaat naar beneden, maar ze raken beide nooit de x =3 (onzichtbare lijn)quote:
Gaan ze echt beiden recht naar boven? Kijk eens beter.
Verder, wat is het verschil als je van onder ('links') en van boven ('rechts') naar
Goeie vraag, heb geen flauw idee.quote:
En waarom zit er een gat (discontinuïteit) bij?
