SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Hoe meen je die haakjes weg te werken? Er staat in feite een 1 voor. 1(x-1) - 2x = x - 1 - 2x = -x -1. Het is dus hetzelfde.quote:Op dinsdag 6 mei 2014 14:49 schreef nodig het volgende:
[..]
Danku!
Ik heb het even uitgeschreven op papier en begrijp het inderdaad. Ga de opgave nu nog een keer maken.
In je laatste 3 stappen: = 1·1·(x−1) − 2x = (x−1) − 2x = −x −1
Moet de één-na-laatste stap niet gewoon x - 1 - 2x zijn? Ik zat de hele tijd die haakjes uit te werken maar dat komt niet uit. Die haakjes mag je toch weghalen omdat er in de stap ervoor de haakjes al uitgewerkt zijn?
Daar had ik nog niet aan gedachtquote:Op dinsdag 6 mei 2014 15:33 schreef jordyqwerty het volgende:
[..]
Hoe meen je die haakjes weg te werken? Er staat in feite een 1 voor. 1(x-1) - 2x = x - 1 - 2x = -x -1. Het is dus hetzelfde.
Ik zat te vermenigvuldigen met die -2x
Bedankt! Hartstikke handige methode! Ik maak er nu een grafiektekening bij, vind ik opzicht wel handiger!quote:
[..]
Ik heb je hier al het advies gegeven om bij het oplossen van wat lastiger ongelijkheden te werken met tekenschema's. Ik geef zo'n advies niet voor niets, het is de bedoeling dat je dat ook ter harte neemt.
Als de absolute waarde van een (reële) grootheid kleiner is dan 1, dan ligt de waarde van die grootheid zelf tussen −1 en +1. De ongelijkheid
| x2 − 2x | < 1
is dus equivalent met
−1 < x2 − 2x < 1
en dit is weer equivalent met
−1 < x2 − 2x ∧ x2 − 2x < 1
oftewel
x2 − 2x > −1 ∧ x2 − 2x < 1
en dus
x2 − 2x + 1 > 0 ∧ x2 − 2x − 1 < 0
Nu hebben we dus een combinatie van twee kwadratische ongelijkheden met een rechterlid herleid op nul en waaraan tegelijkertijd moet worden voldaan. Deze kwadratische ongelijkheden lossen we op door eerst de nulpunten te bepalen van de kwadratische veeltermen in het linkerlid van deze ongelijkheden. En daar heb je de abc-formule helemaal niet bij nodig. De bepaling van de nulpunten van de eerste kwadratische veelterm is wel heel eenvoudig. Hiervoor vinden we
x2 − 2x + 1 = 0
(x − 1)2 = 0
x − 1 = 0
x = 1
Voor de bepaling van de nulpunten van de tweede kwadratische veelterm kunnen we kwadraatafsplitsing gebruiken. Dan vinden we
x2 − 2x − 1 = 0
(x − 1)2 − 1 − 1 = 0
(x − 1)2 = 2
x − 1 = √2 ∨ x − 1 = −√2
x = 1 + √2 ∨ x = 1 − √2
Nu moet je zelf maar even twee tekenschema's maken (één voor elk van beide kwadratische ongelijkheden) waarbij je deze tekenschema's uitgelijnd onder elkaar plaatst. Maar strict genomen is dit hier niet eens nodig.
De grafiek van y = x2 − 2x + 1 is een dalparabool waarvan de top met coördinaten (1; 0) de x-as raakt, zodat we hebben x2 − 2x + 1 > 0 voor elke x ≠ 1.
De grafiek van y = x2 − 2x − 1 is een dalparabool die de x-as snijdt in de punten met coördinaten (1 − √2; 0) en (1 + √2; 0), zodat we hebben x2 − 2x − 1 < 0 voor 1 − √2 < x < 1 + √2.
Voor de waarden van x die aan de oorspronkelijke ongelijkheid voldoen vinden we dus de voorwaarde
x ≠ 1 ∧ 1 − √2 < x < 1 + √2
Het open interval (1 − √2, 1 + √2) waarop x moet liggen om aan de ongelijkheid te voldoen wordt hier dus in twee delen geknipt doordat de waarde x = 1 niet mee mag doen. Deze knip geeft aldus twee open intervallen. Je kunt de oplossing van de ongelijkheid nu noteren als
1 − √2 < x < 1 ∨ 1 < x < 1 + √2
of als
x ∈ (1 − √2, 1) ∪ (1, 1 + √2)
Dat klopt dus niet hèquote:Op dinsdag 6 mei 2014 15:39 schreef nodig het volgende:
[..]
Daar had ik nog niet aan gedacht
Ik zat te vermenigvuldigen met die -2x
Oké, nog een vraagje:
Differentieer:
![ln \sqrt[3]{1-x}](https://forum.fok.nl/lib/mimetex.cgi?ln%20%5Csqrt%5B3%5D%7B1-x%7D)
Nu kom ik tot:
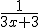
Maar het moet uiteindelijk worden:
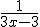
Wat doe ik fout?
Bij de volgende opgaven zijn de plus en minnen ook omgedraaid?
[ Bericht 7% gewijzigd door nodig op 06-05-2014 20:07:27 ]
Differentieer:
Nu kom ik tot:
Maar het moet uiteindelijk worden:
Wat doe ik fout?
Bij de volgende opgaven zijn de plus en minnen ook omgedraaid?
[ Bericht 7% gewijzigd door nodig op 06-05-2014 20:07:27 ]
Zie hieronder.quote:
Oké, nog een vraagje:
Differentieer:
Nu kom ik tot:
Maar het moet uiteindelijk worden:
Wat doe ik fout?
[ Bericht 17% gewijzigd door MrRiot op 06-05-2014 20:14:17 ]
Nope
quote:
Oké, nog een vraagje:
Differentieer:
Nu kom ik tot:
Maar het moet uiteindelijk worden:
Wat doe ik fout?
Bij de volgende opgaven zijn de plus en minnen ook omgedraaid?
Kan je via de logaritmeregels schrijven als:
Als je nu de kettingregel toepast krijg je als afgeleide:
quote:
Dankje! Ik denk dat ik met deze informatie een heel eind verder ga komenquote:
[..]
Kan je via de logaritmeregels schrijven als:
Als je nu de kettingregel toepast krijg je als afgeleide:
Wat zag je hier niet in? Ik vind het nogal veel op die andere som lijkenquote:
[..]
[..]
Dankje! Ik denk dat ik met deze informatie een heel eind verder ga komen
Ik kwam er niet op om die (1/3) voor de ln te zettenquote:
[..]
Wat zag je hier niet in? Ik vind het nogal veel op die andere som lijken
Maar inderdaad is dat gisteren ook al gezegd nu ik terug lees:
quote:
Jouw afgeleide van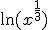
klopt niet.
Je vergeet de kettingregel.
Maar de kettingregel kan je vermijden.
Hint:
Bepaal met een staartdeling het polynoom g(x) waarvoor geldt f(x) = (x - a) g(x)
a = -1
f(x) = x^3 + 1
ik had
(x + 1) / x^3 + 1 \ x^2 - x + 1
Maar ik doe volgens mij iets fout want ik kom op ook uit op " rest 1"... dus er gaat wat in het uitschrijven fout.. hoe zouden jullie het doen?
en tenslotte:
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3)
ik denk dat dat wordt:
(2 - 1/x + 2/x^2 - 1/x^3 ) / ( 3 - 3/x - 3/x^2 + 3/x^3)
Echter weet ik niet hoe ik het verder moet oplossen om achter de nulpunten te komen
[ Bericht 28% gewijzigd door Super-B op 06-05-2014 21:07:54 ]
a = -1
f(x) = x^3 + 1
ik had
(x + 1) / x^3 + 1 \ x^2 - x + 1
Maar ik doe volgens mij iets fout want ik kom op ook uit op " rest 1"... dus er gaat wat in het uitschrijven fout.. hoe zouden jullie het doen?
en tenslotte:
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3)
ik denk dat dat wordt:
(2 - 1/x + 2/x^2 - 1/x^3 ) / ( 3 - 3/x - 3/x^2 + 3/x^3)
Echter weet ik niet hoe ik het verder moet oplossen om achter de nulpunten te komen
[ Bericht 28% gewijzigd door Super-B op 06-05-2014 21:07:54 ]
Dit klopt gewoon.quote:Op dinsdag 6 mei 2014 20:55 schreef Super-B het volgende:
Bepaal met een staartdeling het polynoom g(x) waarvoor geldt f(x) = (x - a) g(x)
a = -1
f(x) = x^3 + 1
ik had
(x + 1) / x^3 + 1 \ x^2 - x + 1
Maar ik doe volgens mij iets fout want ik kom op ook uit op " rest 1"... dus er gaat wat in het uitschrijven fout.. hoe zouden jullie het doen?
(x^2 -x + 1)(x+1) = x^3 + 1
Zou je de staartdeling kunnen uitwerken voor me? Daar gaat het mis bij mij..quote:
[..]
Dit klopt gewoon.
(x^2 -x + 1)(x+1) = x^3 + 1
Thanks!! Zou je me ook kunnen helpen met mijn tweede vraagstuk in de post?quote:
[ afbeelding ]
Zoiets. Maar misschien is mijn notatie anders dan de jouwe.
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3) = 0
'Gewoon' de nulpunten van de teller bepalen en controleren of het ook niet toevallig nulpunten van de noemer zijn.
Anders even invullen bij Wolfram Alpha om de ontbindingen te bepalen als het je zelf niet lukt.
'Gewoon' de nulpunten van de teller bepalen en controleren of het ook niet toevallig nulpunten van de noemer zijn.
Anders even invullen bij Wolfram Alpha om de ontbindingen te bepalen als het je zelf niet lukt.
Hoe bedoel je? Ik snap het niet..? Hebben de teller en noemer allebei eigen nulpunten? Maar het is samen 1 functie toch..?quote:
(2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3) = 0
'Gewoon' de nulpunten van de teller bepalen en controleren of het ook niet toevallig nulpunten van de noemer zijn.
Anders even invullen bij Wolfram Alpha om de ontbindingen te bepalen als het je zelf niet lukt.
Ik zit even te kijken in dat boek van Craats
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
"Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten van f (x)."
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
"Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten van f (x)."
Exact! Ik schrijf mee en probeer wat dingetjes uit, maar het wil niet helemaal lukken. Het boek is echt boek voor naslagwerk...quote:
Ik zit even te kijken in dat boek van Craats
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
Grotendeels heb ik het hulp van jullie nodig en dan willen de puzzelstukjes goed samenvallen.
Waarom zijn de nulpunten van de noemer niet ook de nulpunten van f(x) ? Dat heb ik niet zo begrepen, want zowel de teller en noemer horen toch bij elkaar en het is toch 1 functie? Die twee kun je toch niet los van elkaar zien?quote:
Ik zit even te kijken in dat boek van Craats
(Deze versie althans http://staff.science.uva.nl/~craats/BasisboekWiskunde2HP.pdf)
En dit staat toch gewoon op de pagina van 'Rationale functies' ?
Die functie f(x) = (x^2 + 1)(2x-1) / (3(x-1)^2(x+1)) die daar bovenaan de bladzijde staat is precies
gelijk aan jouw (2x^3 - x^2 + 2x - 1) / (3x^3 - 3x^2 - 3x + 3).
"Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten van f (x)."
''Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten
van f(x). De nulpunten van de noemer b(x) heten dan de polen van f(x). Bij
elke pool hoort een verticale asymptoot.''
Ik heb er werkelijk niks van begrepen wat er staat.
f(x) = a(x) / b(x)
Een rationale functie is altijd een samenstelling van twee andere functies (de teller a(x) en de noemer b(x))
f(x) = a(x) / b(x) = 0
Vermenigvuldig beide kanten met b(x)....
Dus de nulpunten van a(x) zijn de nulpunten van f(x)
Alleen a(x) = b(x) = 0 is een speciaal geval omdat je niet mag delen door 0.
Maar als a(x) en b(x) hetzelfde nulpunt c hebben dan kan je a(x) schrijven als a(x) = (x-c)g(x) en b(x) als b(x) = (x-c) q(x).
Oftewel dan kan je de term (x-c) wegdelen en heb je het probleem verholpen
f(x) = a(x) / b(x) = (x-c)g(x) / ((x-c)q(x)) = g(x)/q(x).
Een rationale functie is altijd een samenstelling van twee andere functies (de teller a(x) en de noemer b(x))
f(x) = a(x) / b(x) = 0
Vermenigvuldig beide kanten met b(x)....
Dus de nulpunten van a(x) zijn de nulpunten van f(x)
Alleen a(x) = b(x) = 0 is een speciaal geval omdat je niet mag delen door 0.
Maar als a(x) en b(x) hetzelfde nulpunt c hebben dan kan je a(x) schrijven als a(x) = (x-c)g(x) en b(x) als b(x) = (x-c) q(x).
Oftewel dan kan je de term (x-c) wegdelen en heb je het probleem verholpen
f(x) = a(x) / b(x) = (x-c)g(x) / ((x-c)q(x)) = g(x)/q(x).
Tja, dat krijg je als je een boek gaat doornemen dat niet geschikt is als leerboek en je bovendien de stof nog nooit eerder hebt gezien en kennelijk ook de nodige voorkennis mist, zoals rekenen met breuken (zie de site en de PDF van Liesbeth van der Plas waarnaar ik hierboven verwijs).quote:
[..]
Waarom zijn de nulpunten van de noemer niet ook de nulpunten van f(x) ? Dat heb ik niet zo begrepen, want zowel de teller en noemer horen toch bij elkaar en het is toch 1 functie? Die twee kun je toch niet los van elkaar zien?
''Als dat gebeurd is, zijn de nulpunten van de teller a(x) ook de nulpunten
van f(x). De nulpunten van de noemer b(x) heten dan de polen van f(x). Bij
elke pool hoort een verticale asymptoot.''
Ik heb er werkelijk niks van begrepen wat er staat.
Delen door nul is niet gedefinieerd (onmogelijk), dus een breuk waarvan de noemer nul is heeft geen betekenis (geen waarde). Een breuk heeft alleen de waarde nul als de teller nul is terwijl de noemer niet nul is.
Als je dus een rationale functie hebt, dat is een functie met het functievoorschrift
f(x) = a(x)/b(x)
waarbij a(x) en b(x) veeltermen (polynomen) zijn in x, dan kan f(x) alleen nul zijn als a(x) nul is terwijl b(x) niet nul is.
Als je de omgekeerde situatie hebt, dus dat b(x) voor een zekere waarde x = x0 gelijk is aan nul terwijl a(x0) ≠ 0, dan neemt de absolute waarde van het quotiënt a(x)/b(x) en dus |f(x)| onbeperkt toe naarmate je x dichter in de buurt van die waarde x = x0 kiest, maar voor de waarde x = x0 zelf is de functiewaarde dan onbepaald. In dit geval heeft de grafiek van y = f(x) een verticale asymptoot bij x = x0, en men zegt dan ook dat de functie f een pool x = x0 heeft. Een verticale asymptoot is, eenvoudig gezegd, een verticale rechte lijn waar de grafiek van de functie steeds dichter tegenaan kruipt naarmate je x dichter bij x0 laat komen, maar dan zonder dat de grafiek van de functie ooit samenvalt met deze lijn.
[ Bericht 1% gewijzigd door Riparius op 07-05-2014 01:09:25 ]
Vereenvoudig zo ver mogelijk:
2^(1+x) 3^x
ik had 2^(1+x) * 3^x dat wordt dan 6^(2x)
Maar het antwoord is 2 * 6^x
hoe..?
[ Bericht 1% gewijzigd door RustCohle op 08-05-2014 12:14:42 ]
2^(1+x) 3^x
ik had 2^(1+x) * 3^x dat wordt dan 6^(2x)
Maar het antwoord is 2 * 6^x
hoe..?
[ Bericht 1% gewijzigd door RustCohle op 08-05-2014 12:14:42 ]
Het is 3^x neem ik aan?quote:
Vereenvoudig zo ver mogelijk:
2^(1+x) 3x
ik had 2^(1+x) * 3x dat wordt dan 6^(x^2)
Maar het antwoord is 2 * 6^x
hoe..?
2^(1+x) = 2^1 * 2^x = 2 * 2^x
Dit * 3^x geeft 2 * 2^x * 3^x = 2 * 6^x
Ja het is 3^x.quote:
[..]
Het is 3^x neem ik aan?
2^(1+x) = 2^1 * 2^x = 2 * 2^x
Dit * 3^x geeft 2 * 2^x * 3^x = 2 * 6^x
Waarom worden ze apart genomen? Ik dacht eerst 2^1 is 2 en dan 2^x.. en dat vermenigvuldigen met 3^x maakt 6^2x
weet je ook hoe je deelt met machten?quote:
[..]
Het is 3^x neem ik aan?
2^(1+x) = 2^1 * 2^x = 2 * 2^x
Dit * 3^x geeft 2 * 2^x * 3^x = 2 * 6^x
4(^2x) / 2x
ik deed alles delen door 2x maakt 2^x.. echter is het antwoord 2^(3x) of 8^x
Gewoon braaf rekenregels voor machten toepassen:quote:
Vereenvoudig zo ver mogelijk:
2^(1+x) 3^x
hoe..?
ap·aq = ap+q
ap·bp = (a·b)p
Bedenk dat je deze regels ook van rechts naar links kunt gebruiken.
http://nl.wikipedia.org/wiki/Machtsverheffen#Rekenen_met_machtenquote:
[..]
Ja het is 3^x.
Waarom worden ze apart genomen? Ik dacht eerst 2^1 is 2 en dan 2^x.. en dat vermenigvuldigen met 3^x maakt 6^2x
Hier ook weer zo"n pittige...
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
[ Bericht 0% gewijzigd door RustCohle op 08-05-2014 12:53:22 ]
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
[ Bericht 0% gewijzigd door RustCohle op 08-05-2014 12:53:22 ]
En dat is fout. Je begrijp er nog niet veel van.quote:
W(10^(20x+10))
De w is wel een vijfdemachtswortel..
ik zelf kwam uit op 100^20x
Je hebt (1020x+10)1/5 = 10(20x+10)·(1/5) = 104x+2
En gebruik superscript voor exponenten. Die carets zijn nergens voor nodig.
ohhh ik dacht dat je bovenop die superscript van 20x+10 nog een superscript moest doen met ^(1/5)quote:
[..]
En dat is fout. Je begrijp er nog niet veel van.
Je hebt (1020x+10)1/5 = 10(20x+10)·(1/5) = 104x+2
En gebruik superscript voor exponenten. Die carets zijn nergens voor nodig.
(10^-2x)^2
ik kwam uit op 100^-4x..
toch is het 10000^-x
Ik zit op mijn mobiel vandaar dat ik geen superscript doe.
ik kwam uit op 100^-4x..
toch is het 10000^-x
Ik zit op mijn mobiel vandaar dat ik geen superscript doe.
(10−2x)2 = 10−2x·2 = 10−4x = (104)−x = 10000−xquote:
(10^-2x)^2
ik kwam uit op 100^-4x..
toch is het 10000^-x
Ik zit op mijn mobiel vandaar dat ik geen superscript doe.
Die overgang.. snap ik niet.. dus van 10^-4x naar (10^4)^xquote:
[..]
(10−2x)2 = 10−2x·2 = 10−4x = (104)−x = 10000−x
Heel eenvoudig, −4x kun je ook schrijven als het product van +4 en −x, dus 4·(−x). En dus hebben wequote:
[..]
Die overgang.. snap ik niet.. dus van 10^-4x naar (10^4)^x
10−4x = 104·−x = (104)−x
Echt, dit is doodsimpele brugklas algebra.
Waarom kan dit niet bij 10^(4x +2) dat je dan gewoon 10^2 hebt en dus 100^4x?quote:
[..]
Heel eenvoudig, −4x kun je ook schrijven als het product van +4 en −x, dus 4·(−x). En dus hebben we
10−4x = 104·−x = (104)−x
Echt, dit is doodsimpele brugklas algebra.
quote:
Hier ook weer zo"n pittige...
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
Je hebt 104x+2 = 104x·102 = 104x·100 = 100·104xquote:
[..]
Waarom kan dit niet bij 10^(4x +2) dat je dan gewoon 10^2 hebt en dus 100^4x?
maar dit is niet hetzelfde als 1004x want dan zou 100 gelijk moeten zijn aan 104x, en dat is in het algemeen niet zo, behalve als x = ½.
Herschrijf hier eerst alle factoren als machten van 2, en bedenk ook dat delen door 8x = 23x hetzelfde is als vermenigvuldigen met het omgekeerde, dus vermenigvuldigen met 2−3x.quote:
Hier ook weer zo"n pittige...
2^x * 4^(1-x) : 8^x
Sowieso is het eerst het delen.. maar dan weet ik het niet meer.
even kijken.. dan kom ik als eerst uit totquote:
[..]
Herschrijf hier eerst alle factoren als machten van 2, en bedenk ook dat delen door 8x = 23x hetzelfde is als vermenigvuldigen met het omgekeerde, dus vermenigvuldigen met 2−3x.
2^x * 2^(1-2x) : 2^3x
en dat resulteert tot
2^(1-x) : 2^3x
Dat is niet goed. We hebbenquote:
[..]
even kijken.. dan kom ik als eerst uit tot
2^x * 2^(1-2x) : 2^3x
en dat resulteert tot
2^(1-x) : 2^3x
2x·41−x·2−3x = 2x·22−2x·2−3x = 2x+2−2x−3x = 22−4x
waarom alles vermenigvuldigen? Er is toch ook een deelsom? Opeens is het een vermenigvuldiging?quote:
[..]
Dat is niet goed. We hebben
2x·41−x·2−3x = 2x·22−2x·2−3x = 2x+2−2x−3x = 22−4x
en hoezo 2^(2-2x) ik zou denken 2^(2-x)
Omdat ik dan gebruik kan maken van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van machten met hetzelfde grondtal.quote:
Jazeker, maar ik heb je al gezegd dat delen hetzelfde is als vermenigvuldiging met het omgekeerde. En ik wil juist een vermenigvuldiging hebben omdat ik de exponenten dan kan optellen.quote:Er is toch ook een deelsom?
Nee, niet opeens, maar om de bovengenoemde reden.quote:Opeens is het een vermenigvuldiging?
Nee, want 2(1−x) = 2 − 2x (distributiviteit van vermenigvuldiging ten opzichte van optelling).quote:en hoezo 2^(2-2x) ik zou denken 2^(2-x)
Dat snap ik niet.. xdquote:
[..]
Omdat ik dan gebruik kan maken van de rekenregel die zegt dat exponenten optellen bij vermenigvuldiging van machten met hetzelfde grondtal.
[..]
Jazeker, maar ik heb je al gezegd dat delen hetzelfde is als vermenigvuldiging met het omgekeerde. En ik wil juist een vermenigvuldiging hebben omdat ik de exponenten dan kan optellen.
[..]
Nee, niet opeens, maar om de bovengenoemde reden.
[..]
Nee, want 2(1−x) = 2 − 2x (distributiviteit van vermenigvuldiging ten opzichte van optelling).
Je hebtquote:
a(b + c) = ab + ac
a(b − c) = ab − ac
Je gaat me toch niet vertellen dat je dat nog nooit hebt gezien?
Ik bedoelde de tekst distributiviteit van de optelling..quote:
[..]
Je hebt
a(b + c) = ab + ac
a(b − c) = ab − ac
Je gaat me toch niet vertellen dat je dat nog nooit hebt gezien?
Snap jij 10log(2^6) - 10log 1/5
ik deed 10log 64/0,5 is 10log 128
Echter is het 7 10log2...
