SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Links:
Opmaak:
• http://betahw.mine.nu/index.php: site van GlowMouse om formules te kunnen gebruiken in je posts (op basis van Latexcode wordt een plaatje gegenereerd dat je vervolgens via het aangegeven linkje kunt opnemen).
Een uitleg over LaTeX-code kun je hier vinden, en je kunt deze site gebruiken om een hele post met verschillende stukken Latex-code erin ineens te laten parsen door betahw.mine.nu.
Wiskundig inhoudelijk:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben nog altijd op zoek naar een beetje hulp met dit vraagstuk:
[Bèta wiskunde] Huiswerk- en vragentopic
Ik heb een frequentie/phase/amplitude. Nou zou ik via kuramoto's model er voor moeten zorgen dat de phases vergelijkbaar worden, zodoende dat ze gaan synchroniseren. Alleen gaat dit synchronisatie op basis van frequentie over de tijd, en tot nu toe heb ik weinig succes geboekt met ze mooi samen te laten lopen, kortom ik doe iets fout in Matlab of hoe ik frequentie bereken aan de hand van kuramotos model.
[Bèta wiskunde] Huiswerk- en vragentopic
Ik heb een frequentie/phase/amplitude. Nou zou ik via kuramoto's model er voor moeten zorgen dat de phases vergelijkbaar worden, zodoende dat ze gaan synchroniseren. Alleen gaat dit synchronisatie op basis van frequentie over de tijd, en tot nu toe heb ik weinig succes geboekt met ze mooi samen te laten lopen, kortom ik doe iets fout in Matlab of hoe ik frequentie bereken aan de hand van kuramotos model.


quote:Ik ben bezig met oefenen voor me wiskunde B examens en loop vast op het volgende:
In het correctie voorschrift staat dat je van "f'(x)=2cos x ⋅ (1+ sin x) + 2sin x ⋅cos x" dit "f'(x)=2cos x + 4cos x ⋅sin x" kan maken. Alleen ik weet niet hoe???
a(b+c) = ab + acquote:Ja, dan krijg ik f'(x)=2cos x * 2cos x * sin x + 2sin x * cos x
En dat kan je ook schrijven als f'(x)=4cos x * sin x + 2sin x * cos x
En nu?
Waar haal jij 2cos(x)*2cos(x)*sin(x) vandaan??
Tip (serieus!): werk zoveel mogelijk met de hand en zo weinig mogelijk met je grafische rekenmachientje. Het is waarschijnlijk aan dat apparaatje te wijten dat je hier moeite mee hebt.
By the way: 2*cos(x)*2*cos(x)*sin(x) is 4*cos²(x)*sin(x), zo schrijf je dat dan op (maar normaal gesproken zonder die * of punt aangezien dat voor zich spreekt) net zoals je 8 schrijft in plaats van 4*2.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Kan iemand mijn antwoord controleren van de volgende dubbele integraal op het gebied D:
f(x,y)= 1/(1+x+y)
D =[0,1] x [0,1]
Mijn antwoord is: 3ln(3) - 4ln(2)
f(x,y)= 1/(1+x+y)
D =[0,1] x [0,1]
Mijn antwoord is: 3ln(3) - 4ln(2)


Ik krijg een bonus als ik binnen een minuut antwoord en een malus als het antwoord niet klopt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


In dat geval:
D=[0,1]x[0,1]
f(x,y)=xy voor 1/4<=x2+y2<=1
f(x,y)=0 anders.
Mijn antwoord is 9/64
Ik neem aan dat de bedoeling is om D in twee gebieden op te delen zodat f binnen die gebieden continu is en je de integralen van f binnen die gebieden bij elkaar kan optellen?
Als gebieden heb ik:
D1: [0,1/2] x[0,1/2]
D2: [1/2,1]x[1/2,1]
D=[0,1]x[0,1]
f(x,y)=xy voor 1/4<=x2+y2<=1
f(x,y)=0 anders.
Mijn antwoord is 9/64
Ik neem aan dat de bedoeling is om D in twee gebieden op te delen zodat f binnen die gebieden continu is en je de integralen van f binnen die gebieden bij elkaar kan optellen?
Als gebieden heb ik:
D1: [0,1/2] x[0,1/2]
D2: [1/2,1]x[1/2,1]


In welk gebied valt het punt (0,1)?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


GlowMouse heeft het antwoord niet binnen een minuut (en ik ook niet), maar het lijkt me dat je opdeling niets oplost, immers binnen D1 is je functie ook niet continu. Feitelijk moet je alleen integreren over een gebied dat uit een kwart van een cirkelring in het eerste kwadrant bestaat, omdat de functiewaarde daarbuiten 0 is. Gebruik dus poolcoördinaten, dan heb je ½ ≤ r ≤ 1 en 0 ≤ θ ≤ π/2.quote:Op dinsdag 10 mei 2011 14:16 schreef Siddartha het volgende:
In dat geval:
D=[0,1]x[0,1]
f(x,y)=xy voor 1/4<=x2+y2<=1
f(x,y)=0 anders.
Mijn antwoord is 9/64
Ik neem aan dat de bedoeling is om D in twee gebieden op te delen zodat f binnen die gebieden continu is en je de integralen van f binnen die gebieden bij elkaar kan optellen?
Als gebieden heb ik:
D1: [0,1/2] x[0,1/2]
D2: [1/2,1]x[1/2,1]


Poolcoördinaten staan pas volgende week op het programma, maar moet het gebied niet simpelweg :
D1: [0,W(1/2)]x[0,W(1/2)] (Met W als wortel)
D2: [W(1/2,1]x[W(1/2),1]
Zo geldt f(x,y)= 0 in voor alle x,y in gebied D1 en
f(x,y)=xy voor alle x,y in gebied D2.
D1: [0,W(1/2)]x[0,W(1/2)] (Met W als wortel)
D2: [W(1/2,1]x[W(1/2),1]
Zo geldt f(x,y)= 0 in voor alle x,y in gebied D1 en
f(x,y)=xy voor alle x,y in gebied D2.


Nee, zo werkt het niet, het gebied waarin je functiewaarde niet 0 is wordt niet begrensd door louter rechte lijnstukken. Maak maar eens een tekening.quote:Op dinsdag 10 mei 2011 14:43 schreef Siddartha het volgende:
Poolcoördinaten staan pas volgende week op het programma, maar moet het gebied niet simpelweg :
D1: [0,W(1/2)]x[0,W(1/2)] (Met W als wortel)
D2: [W(1/2,1]x[W(1/2),1]
Zo geldt f(x,y)= 0 in voor alle x,y in gebied D1 en
f(x,y)=xy voor alle x,y in gebied D2.
[ Bericht 0% gewijzigd door Riparius op 10-05-2011 15:51:55 ]


Dat het eerste gebied continu en begrensd is, is duidelijk.quote:Op dinsdag 10 mei 2011 14:47 schreef Riparius het volgende:
[..]
Nee, zo werkt het niet, het gebied waarin je functiewaarde niet 0 is wordt niet begrensd door louter rechte lijnstukken. Maar maar eens een tekening.
Maar het tweede gebied toch ook?
0<=f(x,y)<= 1 voor alle x,y in dat gebied, dus f is begrensd.
f is continu (duidelijk).
Dus f is integreerbaar in dat gebied.
Aangezien ik D in twee disjuncte gebieden heb opgedeeld, waarin f integreerbaar is, kan ik ze apart uitrekenen en uiteindelijk optellen.


In welk deel zit (0,1) nou?quote:Op dinsdag 10 mei 2011 14:56 schreef Siddartha het volgende:
[..]
Aangezien ik D in twee disjuncte gebieden heb opgedeeld, waarin f integreerbaar is, kan ik ze apart uitrekenen en uiteindelijk optellen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat wel, maar dat is het punt niet, want je zegt hierboven dat je het gebied met 0 ≤ x ≤ 1 en 0 ≤ y ≤ 1 wil opdelen in twee deelgebieden zodanig dat f(x,y) continu is binnen elk deelgebied. Maar je doet niet wat je zegt te doen.quote:Op dinsdag 10 mei 2011 14:56 schreef Siddartha het volgende:
[..]
[quote]
Dat het eerste gebied continu en begrensd is, is duidelijk.
Maar het tweede gebied toch ook?
Nee, dat laatste is niet zo.quote:0<=f(x,y)<= 1 voor alle x,y in dat gebied, dus f is begrensd.
f is continu (duidelijk).
Nee, f(x,y) is wel integreerbaar over je gebied D, maar niet continu over D.quote:Dus f is integreerbaar in dat gebied.
Ga hier nog maar eens goed over nadenken.quote:Aangezien ik D in twee disjuncte gebieden heb opgedeeld, waarin f integreerbaar is, kan ik ze apart uitrekenen en uiteindelijk optellen.


Ok, ik snap dat het niet klopt wat ik doe (goed voorbeeld Glowmouse!).
Laat ik een stapje terug nemen:
Kan ik niet binnen D een gebied nemen, namelijk
E:= {(x,y)in R2| 1/4<=x2+y2<=1}
Dan is f binnen E begrensd en continu, terwijl E ook x/y-simpel is.
Laat ik een stapje terug nemen:
Kan ik niet binnen D een gebied nemen, namelijk
E:= {(x,y)in R2| 1/4<=x2+y2<=1}
Dan is f binnen E begrensd en continu, terwijl E ook x/y-simpel is.


Dit is inderdaad het idee, de integraal van f(x,y) over E is gelijk aan die over D omdat de functiewaarde in het deel van D dat geen deel uitmaakt van E gelijk is aan nul en dus geen bijdrage levert aan de integraal. Maar simpel is anders als je geen poolcoördinaten mag of wil gebruiken. Je moet dan E alsnog opsplitsen.quote:Op dinsdag 10 mei 2011 15:13 schreef Siddartha het volgende:
Ok, ik snap dat het niet klopt wat ik doe (goed voorbeeld Glowmouse!).
Laat ik een stapje terug nemen:
Kan ik niet binnen D een gebied nemen, namelijk
E:= {(x,y)in R2| 1/4<=x2+y2<=1}
Dan is f binnen E begrensd en continu, terwijl E ook x/y-simpel is.


Of F(1)-F(1/2) voor F(r) de integraal van (x,y) -> xy over {(x,y) | x \geq 0, y \geq 0, x^2+y^2 \leq r^2} = {(x,y) | x \in [0,r], y \in [0,\sqrt{r^2-x^2}]}.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Dat kan inderdaad ook. Wat ik hierboven suggereer, even snel met Wolfram Alpha uitgerekend, is dit vermeerderd met dit, wat dus 3/64 + 9/128 = 15/128 oplevert.quote:Op woensdag 11 mei 2011 02:19 schreef keesjeislief het volgende:
Of F(1)-F(1/2) voor F(r) de integraal van (x,y) -> xy over {(x,y) | x \geq 0, y \geq 0, x^2+y^2 \leq r^2} = {(x,y) | x \in [0,r], y \in [0,\sqrt{r^2-x^2}]}.
Wat jij doet is dit verminderd met dit, wat dus 1/8 - 1/128 = 15/128 oplevert.
Veel verschil maakt het niet, want in beide gevallen moet je twee dubbelintegralen uitrekenen. Mooier is het om over te gaan op poolcoördinaten, dan krijgen we dit en hebben we meteen het antwoord.


Ik snap het nu trouwens en heb het met de hand nagerekend, heel erg bedankt voor de uitleg.
(Nu ik de tijden van de posts zie: Horen die ongoddelijke tijden bij wiskundigen?)
(Nu ik de tijden van de posts zie: Horen die ongoddelijke tijden bij wiskundigen?)


In dat opzicht heb ik dan iig de potentie wiskundige te wordenquote:
Finally, someone let me out of my cage


Nee, met mijn methode hoef je maar een dubbelintegraal uit te rekenen.quote:Op woensdag 11 mei 2011 06:01 schreef Riparius het volgende:
[..]
Dat kan inderdaad ook. Wat ik hierboven suggereer, even snel met Wolfram Alpha uitgerekend, is dit vermeerderd met dit, wat dus 3/64 + 9/128 = 15/128 oplevert.
Wat jij doet is dit verminderd met dit, wat dus 1/8 - 1/128 = 15/128 oplevert.
Veel verschil maakt het niet, want in beide gevallen moet je twee dubbelintegralen uitrekenen. Mooier is het om over te gaan op poolcoördinaten, dan krijgen we dit en hebben we meteen het antwoord.
Ik woon in de UK. Desalniettemin is de nacht wel heerlijk rustig. Ik verdenk Riparius ervan dat het calvinisme zo diep in zijn ziel verankerd zit dat hij voor dag en dauw opstaat en hele lange dagen maakt.quote:Op woensdag 11 mei 2011 11:14 schreef Siddartha het volgende:
Ik snap het nu trouwens en heb het met de hand nagerekend, heel erg bedankt voor de uitleg.
(Nu ik de tijden van de posts zie: Horen die ongoddelijke tijden bij wiskundigen?)
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Nee, want je geeft hierboven zelf aan dat je het verschil bepaalt van de integralen F(1) en F(1/2). Uitrekenen als één dubbelintegraal gaat wel met poolcoördinaten, maar dat was niet de bedoeling van Siddartha.quote:Op woensdag 11 mei 2011 19:40 schreef keesjeislief het volgende:
[..]
Nee, met mijn methode hoef je maar een dubbelintegraal uit te rekenen..
[..]
Hoe kom je daar nu bij? Je weet als wiskundige toch dat je geen ongefundeerde aannames moet doen?quote:Ik woon in de UK. Desalniettemin is de nacht wel heerlijk rustig. Ik verdenk Riparius ervan dat het calvinisme zo diep in zijn ziel verankerd zit dat hij voor dag en dauw opstaat en hele lange dagen maakt..


Nee, ik zeg dat je eerst een formule voor de functie F kunt bepalen (eenmaal dubbelintegraal uitrekenen) en vervolgens F(1)-F(1/2).quote:Op woensdag 11 mei 2011 20:50 schreef Riparius het volgende:
[..]
Nee, want je geeft hierboven zelf aan dat je het verschil bepaalt van de integralen F(1) en F(1/2). Uitrekenen als één dubbelintegraal gaat wel met poolcoördinaten, maar dat was niet de bedoeling van Siddartha.
Nvm, poging tot geintje.quote:Hoe kom je daar nu bij? Je weet als wiskundige toch dat je geen ongefundeerde aannames moet doen?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Ah, ik zie het al, dan bedoel je met F(r) dus dit, zodat F(r) = r4/8 en dus F(1) - F(1/2) = 15/128.quote:Op donderdag 12 mei 2011 00:21 schreef keesjeislief het volgende:
[..]
Nee, ik zeg dat je eerst een formule voor de functie F kunt bepalen (eenmaal dubbelintegraal uitrekenen) en vervolgens F(1)-F(1/2).


Dan vraag ik me wel af hoe je de verschillende gebieden daarin kan verwerken zonder stiekem toch met twee dubbele integralen te werken? Want de parametrisering van de dubbele integraal is verschillend, als je bijvoorbeeld x in y gaat uitdrukken, dan heb je voor het gebied x2+y2<=2 natuurlijk dat x=W(1-y2), maar voor het andere gebied heb je een andere functie, namelijk x=W(1/4-y2).quote:Op donderdag 12 mei 2011 00:21 schreef keesjeislief het volgende:
[..]
Nee, ik zeg dat je eerst een formule voor de functie F kunt bepalen (eenmaal dubbelintegraal uitrekenen) en vervolgens F(1)-F(1/2).
Dus daar zal je onderscheid in moeten maken ín de dubbele integraal.


Zie hierboven. Was iets waar ik zelf eerst ook niet aan gedacht had.quote:Op donderdag 12 mei 2011 01:05 schreef Siddartha het volgende:
[..]
Dan vraag ik me wel af hoe je de verschillende gebieden daarin kan verwerken zonder stiekem toch met twee dubbele integralen te werken?


Even een (waarschijnlijk onnozel) vraagje. Ik ben bezig met meetkunde en nu gebruiken ze twee symbolen in het antwoordenboek die ik niet kan plaatsen:
Wat betekenen deze precies? Ik heb wel een vermoeden, maar kan er geen duidelijkheid over krijgen via Wikipedia/Google.
Wat betekenen deze precies? Ik heb wel een vermoeden, maar kan er geen duidelijkheid over krijgen via Wikipedia/Google.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Aah zó. Bedankt!quote:Op donderdag 12 mei 2011 13:26 schreef thabit het volgende:
Het linkersymbool betekent "loodrecht" en het rechtersymbool betekent "evenwijdig".
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Wij hebben het linkersymbool ook geleerd als 'bottom' of false (in de boleaanse algebra).quote:Op donderdag 12 mei 2011 13:25 schreef Pipo1234 het volgende:
Even een (waarschijnlijk onnozel) vraagje. Ik ben bezig met meetkunde en nu gebruiken ze twee symbolen in het antwoordenboek die ik niet kan plaatsen: [ afbeelding ]
Wat betekenen deze precies? Ik heb wel een vermoeden, maar kan er geen duidelijkheid over krijgen via Wikipedia/Google.
Hoe kan je het verschil uitdrukken tussen twee vergelijkingen die allebei oneindig zijn, maar een orde (ik weet niet of dat de goede naam is, al die termen zijn een beetje weggezakt) verschillen? Bijvoorbeeld: Als lijnen dezelfde formule hebben, zijn er oneindig veel punten waarop de lijnen gelijk zijn. Als twee ruimtelijke figuren 'dezelfde formule hebben', hebben ze ook oneindig punten gelijk, maar nu zijn er als het ware twee parameters die allebei oneindig waarden aan kunnen nemen. Ik heb het tot nu toe beantwoordt als R (voor het maximaal aantal punten dat twee lijnen gemeen hebben) en R2 voor het aantal punten dat twee bollen maximaal gelijk kunnen hebben (R is natuurlijk het symbool voor de reële getallen). Dit lijkt me goed, maar ik wou het nog even checken
Ik heb ook dingen geleerd over aleph 0 en aleph 1 maar dat moest je dacht ik alleen gebruiken bij het het verschil tussen natuurlijke getallen en reële getallen.
Finally, someone let me out of my cage


R en R2 zijn als verzameling even groot. Je zal een extra structuur moeten opleggen om te kunnen zeggen dat R2 groter is dan R. Je kan in dit geval bijvoorbeeld de structuur van een vectorruimte gebruiken; in die zin heeft R dimensie 1 en R2 heeft dimensie 2.


Ok, maar even concreet, hoe zou je de volgende vraag correct moeten beantwoorden, met onderscheid tussen het geval waar de twee 'planes' (de punten waarvoor geldt ax+by+cz=d voor een zeker a, b, c, d uit R) dezelfde waarden voor a b c en d hebben, en het geval waarin de planes slechts een lijn 'delen':quote:Op vrijdag 13 mei 2011 18:20 schreef thabit het volgende:
R en R2 zijn als verzameling even groot. Je zal een extra structuur moeten opleggen om te kunnen zeggen dat R2 groter is dan R. Je kan in dit geval bijvoorbeeld de structuur van een vectorruimte gebruiken; in die zin heeft R dimensie 1 en R2 heeft dimensie 2.
In R3, how many points do two planes have in common? (Give all possible cases)
Finally, someone let me out of my cage


Kan je dan niet een bijectie van de oplossingen maken naar R en R2?
Of de vergelijking van oplossingen (een lijn of het vlak) in vectoren weergeven en dan over dimensies beginnen?
Of de vergelijking van oplossingen (een lijn of het vlak) in vectoren weergeven en dan over dimensies beginnen?


Dat zou kunnen, ik denk overigens dat de bedoeling is om gewoon met geometrische interpretaties te komen, dus met punten, lijnen of oppervlakten.quote:Op vrijdag 13 mei 2011 18:33 schreef Siddartha het volgende:
Kan je dan niet een bijectie van de oplossingen maken naar R en R2?
Of de vergelijking van oplossingen (een lijn of het vlak) in vectoren weergeven en dan over dimensies beginnen?
Ik vind het wel vreemd overigens: Je kan toch geen bijectie maken van R naar R2? Dan zijn R en R2 toch niet gelijkmachtig?
Finally, someone let me out of my cage


Ja, je kan wel een bijectie maken van R naar R2. Je kan een reëel getal decimaal uitschrijven en dan om en om cijfers kiezen om er 2 reële getallen van te maken (modulo wat details).


De bedoeling is denk ik dat je gewoon zegt dat het er oneindig veel zijn en dat de twee mogelijkheden zijn dat de twee vlakken ofwel gelijk zijn ofwel elkaar in een lijn snijden.quote:Op vrijdag 13 mei 2011 18:25 schreef minibeer het volgende:
[..]
Ok, maar even concreet, hoe zou je de volgende vraag correct moeten beantwoorden, met onderscheid tussen het geval waar de twee 'planes' (de punten waarvoor geldt ax+by+cz=d voor een zeker a, b, c, d uit R) dezelfde waarden voor a b c en d hebben, en het geval waarin de planes slechts een lijn 'delen':
In R3, how many points do two planes have in common? (Give all possible cases)


quote:Op vrijdag 13 mei 2011 18:52 schreef thabit het volgende:
Ja, je kan wel een bijectie maken van R naar R2. Je kan een reëel getal decimaal uitschrijven en dan om en om cijfers kiezen om er 2 reële getallen van te maken (modulo wat details).
Finally, someone let me out of my cage


Je antwoord is onleesbaar en waarschijnlijk fout.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zie het ja, er zit een foutje in. Ik kan niet zo goed met die codes werken. De vraag is overigens wel goed getypt 
Of niet?


quote:Op zaterdag 14 mei 2011 11:05 schreef Self-Catering het volgende:
Als ik deze moet differentieren:
[ afbeelding ]
Krijg ik dan als antwoord:
[ afbeelding ]
?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Produktregel gebruiken:quote:Op zaterdag 14 mei 2011 11:05 schreef Self-Catering het volgende:
Als ik deze moet differentieren:
[ afbeelding ]
Krijg ik dan als antwoord:
[ afbeelding ]
?
F'(x) = 1*sqrt(x) + (x+1)*1/(2*sqrt(x)) = (2*x)/(2*sqrt(x)) + (x+1)*1/(2*sqrt(x)) = (3*x+1)/(2*sqrt(x))
(laatste twee stappen optioneel).
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Ik moet volgens mijn opgave algebraïsch aan het antwoord van een aantal formules komen met betrekking tot sinus en cosinus. Nu zet ik alleen vraagtekens bij mijn methode... Is het zo dat jij bij dergelijke formules de daadwerkelijk omrekening van radiaal naar sinus/cosinus en visa versa hoofdzakelijk met de rekenmachine gedaan kan worden? Ik versta zelf namelijk onder algebraïsch dat het zoveel mogelijk zonder rekenmachine gedaan dient te worden.
Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord. Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord. Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


1. Algebraïsch = zonder rekenmachine. Wat bedoel je precies met omrekenen tussen radialen en sinus/cosinussen?quote:Op zaterdag 14 mei 2011 15:02 schreef Pipo1234 het volgende:
Ik moet volgens mijn opgave algebraïsch aan het antwoord van een aantal formules komen met betrekking tot sinus en cosinus. Nu zet ik alleen vraagtekens bij mijn methode... Is het zo dat jij bij dergelijke formules de daadwerkelijk omrekening van radiaal naar sinus/cosinus en visa versa hoofdzakelijk met de rekenmachine gedaan kan worden? Ik versta zelf namelijk onder algebraïsch dat het zoveel mogelijk zonder rekenmachine gedaan dient te worden.
Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord. Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
2. Oplossingen van cos x = cos a zijn inderdaad x=a en x=-a. Echter, omdat de cosinus 2pi - periodiek is, kan je bij de oplossing een willekeurig veelvoud van 2pi optellen en dan heb je weer een oplossing. Dus x=-a en x=a zijn nog lang niet alle oplossingen. Alle oplossingen worden gegeven door:
(1) x = a + 2*k*pi;
(2) x = -a + 2*k*pi,
waarbij k een willekeurig geheel getal is. Dit beantwoord ook direct je volgende vraag, denk daar maar even over na.
Note: Ik denk dat ze het in je boek hebben over alle oplossingen in het interval [0,2pi]


Je vraag is niet echt duidelijk. De rekenmachine gebruik je uitsluitend ter vervanging van papieren goniometrische tafels (ja, zo ging dat vroeger zonder rekenmachines). Als je dus een vraagstuk oplost (uitrekent) en je hebt (bijvoorbeeld) een benaderde waarde van de sinus (of cosinus of tangens) van 20 graden nodig, dan gebruik je daarvoor de rekenmachine.quote:Op zaterdag 14 mei 2011 15:02 schreef Pipo1234 het volgende:
Ik moet volgens mijn opgave algebraïsch aan het antwoord van een aantal formules komen met betrekking tot sinus en cosinus. Nu zet ik alleen vraagtekens bij mijn methode... Is het zo dat jij bij dergelijke formules de daadwerkelijk omrekening van radiaal naar sinus/cosinus en visa versa hoofdzakelijk met de rekenmachine gedaan kan worden? Ik versta zelf namelijk onder algebraïsch dat het zoveel mogelijk zonder rekenmachine gedaan dient te worden.
Er zijn echter een aantal standaardhoeken (0, 30, 45, 60 en 90 graden) waarvan je de exacte waarde van de sinus en cosinus uit het blote hoofd moet kennen. Daar is overigens een eenvoudig ezelsbruggetje voor: voor de sinus is dit de helft van de vierkantswortel uit resp. 0, 1, 2, 3 en 4 en voor de cosinus hetzelfde rijtje in omgekeerde volgorde.
Bij herleidingen van goniometrische formules en identiteiten gebruik je uiteraard geen rekenmachine.
Of je het echt begrijpt betwijfel ik, want wat je boek beweert is in zijn algemeenheid niet juist. De cosinus is immers een periodieke functie met periode 2π, dus er zijn oneindig veel oplossingen als je R als domein neemt.quote:Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord.
Dit is nu het gevolg van die periodiciteit. Ik neem aan dat je vertrouwd bent met de definities van sinus en cosinus aan de hand van de eenheidscirkel? Welnu, een rotatie van het uitgangspunt (1;0) om de oorsprong over een hoek van (7/6)∙π radialen levert hetzelfde beeldpunt op als een rotatie over een hoek van -(5/6)∙π radialen. Maak even een schetsje van de eenheidscirkel in een cartesisch assenstelsel om dit gemakkelijk te zien. Aangezien de cosinus en de sinus per definitie de x- resp. de y-coördinaat zijn van het beeldpunt van (1;0) bij rotatie over een willekeurige hoek, is het duidelijk dat (7/6)∙π en -(5/6)∙π dezelfde cosinus én dezelfde sinus hebben.quote:Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
Vanwege het feit dat de eenheidscirkel een omtrek heeft van 2π en je dus met een rotatie over een hoek van 2π radialen hetzij in positieve zin (tegen de wijzers van de klok in) hetzij in negatieve zin (met de wijzers van de klok mee) precies eenmaal rond bent geweest geldt dus voor elke willekeurige α (in radialen) en voor elk geheel getal k:
cos(α + 2∙k∙π) = cos α en sin(α + 2∙k∙π) = sin α
[ Bericht 0% gewijzigd door Riparius op 14-05-2011 16:49:58 ]


Omrekenen als in de tegenhanger vinden van een radiaal of omgekeerd. Feitelijk is het geen rekenen natuurlijk.quote:Op zaterdag 14 mei 2011 15:17 schreef thenxero het volgende:
[..]
1. Algebraïsch = zonder rekenmachine. Wat bedoel je precies met omrekenen tussen radialen en sinus/cosinussen?
In mijn boek wordt de formule gevraagd die jij ook noemt. Misschien had ik mijn vraag iets uitgebreider moeten stellen.quote:Op zaterdag 14 mei 2011 15:17 schreef thenxero het volgende:
2. Oplossingen van cos x = cos a zijn inderdaad x=a en x=-a. Echter, omdat de cosinus 2pi - periodiek is, kan je bij de oplossing een willekeurig veelvoud van 2pi optellen en dan heb je weer een oplossing. Dus x=-a en x=a zijn nog lang niet alle oplossingen. Alle oplossingen worden gegeven door:
(1) x = a + 2*k*pi;
(2) x = -a + 2*k*pi,
waarbij k een willekeurig geheel getal is. Dit beantwoord ook direct je volgende vraag, denk daar maar even over na.
Note: Ik denk dat ze het in je boek hebben over alle oplossingen in het interval [0,2pi]
Wat ik mij met name afvraag is het volgende:
Gevraagd wordt naar x van cosinus. (Ik heb de formules even in LATEX gezet om het wat duidelijker te maken). Volgens het principe x = a en x=-a krijg je het volgende antwoord:
Echter is volgens het boek dit het juiste antwoord:
Ik zie niet in waarom hierbij die regel niet opgaat. Het is trouwens wel opvallend dat in beide gevallen het antwoord is te herleiden naar een deel van pi, maar dat zou voor mij geen reden zijn om het antwoord anders te geven.
[ Bericht 4% gewijzigd door Pipo1234 op 14-05-2011 18:29:20 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


De formules voor omrekenen zijn heel makkelijk, van graden naar radialen doe je het aantal graden*pi/180, omgedraaid doe je het aantal radialen*180/pi.quote:Op zaterdag 14 mei 2011 18:23 schreef Pipo1234 het volgende:
[..]
Omrekenen als in de tegenhanger vinden van een radiaal of omgekeerd. Feitelijk is het geen rekenen natuurlijk.
Het antwoord is (als het goed is) 7/6 pi +k*2pi. Als je bij jouw antwoord k=1 invult krijg je precies 7/6 pi, de antwoorden zijn gelijk, alleen is de schrijfwijze andersquote:[..]
In mijn boek wordt de formule gevraagd die jij ook noemt. Misschien had ik mijn vraag iets uitgebreider moeten stellen.
Wat ik mij met name afvraag is het volgende:
Gevraagd wordt naar x van cosinus. (Ik heb de formules even en LATEX gezet om het wat duidelijker te maken). Volgens het principe x = a en x=-a krijg je het volgende antwoord:
[ afbeelding ]
Echter is volgens het boek dit het juiste antwoord:
[ afbeelding ]
Ik zie niet in waarom hierbij die regel niet opgaat. Het is trouwens wel opvallend dat in beide gevallen het antwoord is te herleiden naar een deel van pi, maar dat zou voor mij geen reden zijn om het antwoord anders te geven.
The biggest argument against democracy is a five minute discussion with the average voter.


Ik zie nu dat er bij de delingen nog pi moet staan...quote:Op zaterdag 14 mei 2011 18:33 schreef M.rak het volgende:
[..]
De formules voor omrekenen zijn heel makkelijk, van graden naar radialen doe je het aantal graden*pi/180, omgedraaid doe je het aantal radialen*180/pi.
[..]
Het antwoord is (als het goed is) 7/6 pi +k*2pi. Als je bij jouw antwoord k=1 invult krijg je precies 7/6 pi, de antwoorden zijn gelijk, alleen is de schrijfwijze anders.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Op het interval [0,2pi] is het equivalent, maar niet op |R.quote:Op zaterdag 14 mei 2011 18:33 schreef M.rak het volgende:
Het antwoord is (als het goed is) 7/6 pi +k*2pi. Als je bij jouw antwoord k=1 invult krijg je precies 7/6 pi, de antwoorden zijn gelijk, alleen is de schrijfwijze anders.


Hoe bedoel je?quote:Op zaterdag 14 mei 2011 18:36 schreef thenxero het volgende:
[..]
Op het interval [0,2pi] is het equivalent, maar niet op |R.
The biggest argument against democracy is a five minute discussion with the average voter.


Beide antwoorden zijn juist en gelijkwaardig, als je tenminste achter die breuken nog een factor π toevoegt, want zoals je het nu opschrijft is het gewoon fout. Immers, k is een willekeurig geheel getal, en als je eenmaal 2π optelt bij (-5/6)∙π krijg je (7/6)∙π. De verzameling van alle reële getallen van de gedaante (-5/6)∙π + k∙2π (met k geheel) is dus precies dezelfde als de verzameling van alle reële getallen van de gedaante (7/6)∙π + k∙2π (met k geheel).quote:Op zaterdag 14 mei 2011 18:23 schreef Pipo1234 het volgende:
Wat ik mij met name afvraag is het volgende:
Gevraagd wordt naar x van cosinus. (Ik heb de formules even in LATEX gezet om het wat duidelijker te maken). Volgens het principe x = a en x=-a krijg je het volgende antwoord:
[ afbeelding ]
Echter is volgens het boek dit het juiste antwoord:
[ afbeelding ]
Ik zie niet in waarom hierbij die regel niet opgaat. Het is trouwens wel opvallend dat in beide gevallen het antwoord is te herleiden naar een deel van pi, maar dat zou voor mij geen reden zijn om het antwoord anders te geven.


Kunstproductie en lijsten is dat een assortiment groep?
en klopt dit?
Assortiment groep Multimedia
Artikelgroep Foto s
Artikelsoort Canvas
Assortiment groep opname apparatuur
Artikelgroep Foto-apparatuur
Artikelsoort Digitale compact camera s
en klopt dit?
Assortiment groep Multimedia
Artikelgroep Foto s
Artikelsoort Canvas
Assortiment groep opname apparatuur
Artikelgroep Foto-apparatuur
Artikelsoort Digitale compact camera s


Klopt, was een beetje onduidelijk opgeschreven. Ik bedoelde te zeggen dat als je k=1 invult je 7/6 pi krijgt. De twee antwoorden zijn dus identiek (ze bevatten dezelfde getallen).quote:Op zaterdag 14 mei 2011 19:01 schreef thenxero het volgende:
[..]
Op [0,2pi] moet gelden k=1, op |R is k willekeurig.
The biggest argument against democracy is a five minute discussion with the average voter.


Neem X1, ... , Xn random sample van uniforme verdeling Xi~( θ-1, θ+1)
a) Laat zien dat sample mean, X- een unbiased estimator is van θ.
Is dit correct?
Laat zien dat E[ X- ]=θ
E[ X- ] = E[ 1/nΣnXi ]
= 1/n {Σn E(Xi)} en E(Xi=θ)
= 1/n {Σn(θ)}
= 1/n * nθ
= θ
a) Laat zien dat sample mean, X- een unbiased estimator is van θ.
Is dit correct?
Laat zien dat E[ X- ]=θ
E[ X- ] = E[ 1/nΣnXi ]
= 1/n {Σn E(Xi)} en E(Xi=θ)
= 1/n {Σn(θ)}
= 1/n * nθ
= θ
Beneath the gold, bitter steel


Hoe los je de volgende vergelijking op (met de hand):
12x^3 - 24x^2 + 6x = 0
En nog een vraag
Bepaal de lokale minima en maxima op het gegeven domein:
f:[-1/2,1] -> 1/(x^5+x+1)
dan kom ik tot f'(x) = (-5x^4-1)/((x^5+x+1)^2)
f'(x) = 0 geeft -5x^4-1 = 0 geeft x^4 = -1/5
Welke in het reëele vlak geen oplossingen heeft.
Maar is dit wel de manier om lokale minima/maxima te berekenen?
[ Bericht 38% gewijzigd door .aeon op 15-05-2011 19:50:10 ]
12x^3 - 24x^2 + 6x = 0
En nog een vraag
Bepaal de lokale minima en maxima op het gegeven domein:
f:[-1/2,1] -> 1/(x^5+x+1)
dan kom ik tot f'(x) = (-5x^4-1)/((x^5+x+1)^2)
f'(x) = 0 geeft -5x^4-1 = 0 geeft x^4 = -1/5
Welke in het reëele vlak geen oplossingen heeft.
Maar is dit wel de manier om lokale minima/maxima te berekenen?
[ Bericht 38% gewijzigd door .aeon op 15-05-2011 19:50:10 ]


De afgeleide wordt niet nul op dit interval, dat betekent dat de functie ofwel constant stijgt, ofwel constant daalt. Vul x=0 in in de afgeleide en je ziet dat de afgeleide daar negatief is, wat een constante daling aangeeft. Hieruit kan je concluderen dat het maximum op dat domein aangenomen wordt in het linkergrenspunt (-1/2) en het minimum op het rechtergrenspunt (1).quote:Op zondag 15 mei 2011 19:27 schreef .aeon het volgende:
Hoe los je de volgende vergelijking op (met de hand):
12x^3 - 24x^2 + 6x = 0
En nog een vraag
Bepaal de lokale minima en maxima op het gegeven domein:
f:[-1/2,1] -> 1/(x^5+x+1)
dan kom ik tot f'(x) = (-5x^4-1)/((x^5+x+1)^2)
f'(x) = 0 geeft -5x^4-1 = 0 geeft x^4 = -1/5
Welke in het reëele vlak geen oplossingen heeft.
Maar is dit wel de manier om lokale minima/maxima te berekenen?
The biggest argument against democracy is a five minute discussion with the average voter.


Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X² + Y² + Z² | X + Y + Z = 0?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?


Correctquote:Op zondag 15 mei 2011 14:36 schreef Fingon het volgende:
Neem X1, ... , Xn random sample van uniforme verdeling Xi~( θ-1, θ+1)
a) Laat zien dat sample mean, X- een unbiased estimator is van θ.
Is dit correct?
Laat zien dat E[ X- ]=θ
E[ X- ] = E[ 1/nΣnXi ]
= 1/n {Σn E(Xi)} en E(Xi=θ)
= 1/n {Σn(θ)}
= 1/n * nθ
= θ


hmm.. dit ziet er vreemd uit. X+Y+Z is N(0,3) verdeeld en nu conditioneer je de verdeling van de chi-kwadraatverdeling door deze normale verdeling op nul te stellen. Dat suggereert dat de kansdichtsheidsfunctie van deze verdeling blijkbaar gelijk is aan nul en dan krijg je toch een probleem als je de kansdichtsheidsfunctie van de geconditioneerde verdeling wilt bepalen.quote:Op zondag 15 mei 2011 21:32 schreef thenxero het volgende:
Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X² + Y² + Z² | X + Y + Z = 0?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?


Ik moet de dubbele integraal berekenen over f(x,y)= 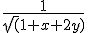 met gebied D=[0,1]x[0,1].
met gebied D=[0,1]x[0,1].
Kan ik een substitutie maken met
g: (r,a)= (rcos(a),2rsin(a)) ?
Dat levert dan de dubbele integraal over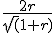 .
.
Kan ik een substitutie maken met
g: (r,a)= (rcos(a),2rsin(a)) ?
Dat levert dan de dubbele integraal over


waarom zou je dat willen? Je moet over een vierkant integreren en dan is het gebruik van cilindercoordinaten niet echt optimaal. Deze integraal kun je rechtstreeks doen, zonder substituties:quote:Op maandag 16 mei 2011 15:15 schreef Siddartha het volgende:
Ik moet de dubbele integraal berekenen over f(x,y)= [ afbeelding ] met gebied D=[0,1]x[0,1].
Kan ik een substitutie maken met
g: (r,a)= (rcos(a),2rsin(a)) ?
Dat levert dan de dubbele integraal over [ afbeelding ].


Ik had deze integraal graag met poolcoordinaten willen doen, puur om te oefenen. Wat dat betreft: Was mijn methode wel goed?quote:Op maandag 16 mei 2011 15:33 schreef Don_Vanelli het volgende:
[..]
waarom zou je dat willen? Je moet over een vierkant integreren en dan is het gebruik van cilindercoordinaten niet echt optimaal. Deze integraal kun je rechtstreeks doen, zonder substituties:
[ afbeelding ]


in principe mag je elke transformatie doen die je wil, maar wat worden je nieuwe grenzen dan?quote:Op maandag 16 mei 2011 16:02 schreef Siddartha het volgende:
[..]
Ik had deze integraal graag met poolcoordinaten willen doen, puur om te oefenen. Wat dat betreft: Was mijn methode wel goed?


'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.quote:Op maandag 16 mei 2011 16:09 schreef Don_Vanelli het volgende:
[..]
in principe mag je elke transformatie doen die je wil, maar wat worden je nieuwe grenzen dan?


Dat is zo niet te beantwoorden, je geeft je nieuwe integratiegrenzen namelijk niet. Maar met poolcoördinaten gaan integreren over een vierkant? Dan moet je eerst maar eens uitvogelen hoe je dan r als functie van θ beschrijft voor de beide zijden van het vierkant die niet langs de coördinaatassen liggen. Dan moet je dus eerst vergelijkingen in poolcoördinaten gaan opstellen voor de rechte lijnen met de cartesische vergelijkingen x=1 en y=1 en dan moet je alsnog gaan opsplitsen in twee integralen met resp. 0 ≤ θ ≤ π/4 en π/4 ≤ θ ≤ π/2.quote:Op maandag 16 mei 2011 16:02 schreef Siddartha het volgende:
[..]
Ik had deze integraal graag met poolcoordinaten willen doen, puur om te oefenen. Wat dat betreft: Was mijn methode wel goed?


Nee!quote:Op maandag 16 mei 2011 16:11 schreef Siddartha het volgende:
[..]
'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.


Vervang x door -y-zquote:Op zondag 15 mei 2011 21:32 schreef thenxero het volgende:
Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X² + Y² + Z² | X + Y + Z = 0?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben gewoon dom bezig, ik probeer een deel van de functie ipv een gebied/D te beschrijven. Wat nergens op slaat of in ieder geval niet handig is.quote:Op maandag 16 mei 2011 16:17 schreef Riparius het volgende:
[..]
Dat is zo niet te beantwoorden, je geeft je nieuwe integratiegrenzen namelijk niet. Maar met poolcoördinaten gaan integreren over een vierkant? Dan moet je eerst maar eens uitvogelen hoe je dan r als functie van θ beschrijft voor de beide zijden van het vierkant die niet langs de coördinaatassen liggen. Dan moet je dus eerst vergelijkingen in poolcoördinaten gaan opstellen voor de rechte lijnen met de cartesische vergelijkingen x=1 en y=1 en dan moet je alsnog gaan opsplitsen in twee integralen met resp. 0 ≤ θ ≤ π/4 en π/4 ≤ θ ≤ π/2.


Als je zo je cilindercoordinaten kiest is dat equivalent met een integraal over het gebied dat voldoet aanquote:Op maandag 16 mei 2011 16:11 schreef Siddartha het volgende:
[..]
'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.
en dat is iets anders dan een vierkant.


Ik ben even de weg kwijt... wie kan mij een aanwijzing geven hoe dit op te lossen? Volgens mijn boek moet ik de formules sin2 x + cos2 x = 1 en sin x/cos x = tan x gebruiken, maar daar kom ik niet verder mee. Alvast bedankt voor alle hulp!
quote:Los algebraïsch op: cos2 x = sin x
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


die tweede formule heb je niet eens nodig.. Schrijf de cosinus om in een sinus met behulp van de eerste regel en je krijgt een vergelijking in termen van sinussen die prima op te lossen is met een schaduwvergelijking.
edit: je kan ook alleen de tweede regel gebruiken en sin(x) = tan(x)*cos(x) schrijven, dan staat er aan beide kanten een factor cos(x) in die je buiten haakjes kan halen.
edit: je kan ook alleen de tweede regel gebruiken en sin(x) = tan(x)*cos(x) schrijven, dan staat er aan beide kanten een factor cos(x) in die je buiten haakjes kan halen.


Gebruik de 1e formule en herleid op 0. Vervang dan sin x door een letter.
I asked God for a bike, but I know God doesn't work that way.
So I stole a bike and asked for forgiveness.
So I stole a bike and asked for forgiveness.


Eens kijken of ik het nu beter begrijp:
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?


Als je cartesische coördinaten transformeert naar poolcoördinaten, dan moet je ook voor de beide nieuwe coördinaten (r en θ) de condities aangeven die gelden voor het gebied waarover je wil gaan integreren, en dus niet alleen voor θ.quote:Op maandag 16 mei 2011 16:44 schreef Siddartha het volgende:
Eens kijken of ik het nu beter begrijp:
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
Maak eerst eens een tekening van het bedoelde gebied en bedenk dan hoe je dit in poolcoördinaten kunt karakteriseren.quote:en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?


Klopt, r: [0,1].quote:Op maandag 16 mei 2011 16:52 schreef Riparius het volgende:
[..]
Als je cartesische coördinaten transformeert naar poolcoördinaten, dan moet je ook voor de beide nieuwe coördinaten (r en θ) de condities aangeven die gelden voor het gebied waarover je wil gaan integreren, en dus niet alleen voor θ.
D is het gebied tussen de cirkel met straal 1 en de lijn die loopt van y=1 tot x=1.quote:Maak eerst eens een tekening van het bedoelde gebied en bedenk dan hoe je dit in poolcoördinaten kunt karakteriseren.
Kan ik dan D weergeven door gebied (1) te pakken, maar dan te beperken tot:
a:[0,1/2Pi], r:[0,1] ?


Ik heb de oplossing gevonden van de vergelijking. Het was even lastig (aangezien ik niet zo goed ben in oplossen via algebraïsche weg.)
Het volgende heb ik gedaan: Ik heb eerst cosinus herleid naar sinus via de eerste formule. Toen heb ik de formule naar een tweedegraadsvergelijking herleid en hem met behulp van de ABC-formule opgelost. De weg die ik (ongeveer) gevolgd heb:
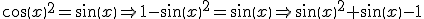
Het volgende heb ik gedaan: Ik heb eerst cosinus herleid naar sinus via de eerste formule. Toen heb ik de formule naar een tweedegraadsvergelijking herleid en hem met behulp van de ABC-formule opgelost. De weg die ik (ongeveer) gevolgd heb:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je hebt het rechterlid van je vergelijking wel netjes herleid op nul, maar bent vervolgens die nul weer vergeten, en dat is niet goed want dan is het geen vergelijking meer. De vergelijking die je krijgt is:quote:Op maandag 16 mei 2011 17:29 schreef Pipo1234 het volgende:
Ik heb de oplossing gevonden van de vergelijking. Het was even lastig (aangezien ik niet zo goed ben in oplossen via algebraïsche weg.)
Het volgende heb ik gedaan: Ik heb eerst cosinus herleid naar sinus via de eerste formule. Toen heb ik de formule naar een tweedegraadsvergelijking herleid en hem met behulp van de ABC-formule opgelost. De weg die ik (ongeveer) gevolgd heb:
[ afbeelding ]
sin2x + sin x - 1 = 0
Dit is een kwadratische vergelijking in sin x. Maar nu moet je uiteindelijk hieruit x oplossen. Hoe ben je nu verder gegaan? En wat was je uitkomst? Deze vergelijking komt niet 'mooi' uit.


Mijn oplossing was afgerond 0,67 en 3,81 en dat zijn ook degene die ik zocht. Ik moest er overigens wel nog een aantal dingen mee doen voordat ik op die waarden uitkwam, aangezien de waarden uit een ABC-formule niet direct op x slaan.quote:Op maandag 16 mei 2011 17:35 schreef Riparius het volgende:
[..]
Je hebt het rechterlid van je vergelijking wel netjes herleid op nul, maar bent vervolgens die nul weer vergeten, en dat is niet goed want dan is het geen vergelijking meer. De vergelijking die je krijgt is:
sin2x + sin x - 1 = 0
Dit is een kwadratische vergelijking in sin x. Maar nu moet je uiteindelijk hieruit x oplossen. Hoe ben je nu verder gegaan? En wat was je uitkomst? Deze vergelijking komt niet 'mooi' uit.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Nee, dit klopt niet. In cartesische coördinaten wordt het gebied waarover je wil gaan integreren gekarakteriseerd door:quote:
x2 + y2 ≤ 1 en tevens x + y ≥ 1
Maar dan is het duidelijk dat je r niet over het interval [0,1] kunt nemen. Immers, er ligt geen enkel punt in het bedoelde gebied met r < ½√2.
Nee dus. Stel nu eerst eens een vergelijking in poolcoördinaten op van de lijn met de cartesische vergelijking x + y = 1.quote:D is het gebied tussen de cirkel met straal 1 en de lijn die loopt van y=1 tot x=1.
Kan ik dan D weergeven door gebied (1) te pakken, maar dan te beperken tot:
a:[0,1/2Pi], r:[0,1] ?


Daar was ik al bang voor. Je hebt het niet goed gedaan. Je hebt weliswaar de kwadratische vergelijking in sin x opgelost, maar daarmee ben je er nog niet, want x wordt gevraagd, niet sin x. Verder moet je bedenken dat de sinus (voor reële x) alleen waarden tussen -1 en +1 aan kan nemen, dus één van de beide oplossingen van je vierkantsvergelijking is onbruikbaar.quote:Op maandag 16 mei 2011 17:46 schreef Pipo1234 het volgende:
[..]
Mijn oplossing was afgerond 0,67 en 3,81 en dat zijn ook degene die ik zocht. Ik moest er overigens wel nog een aantal dingen mee doen voordat ik op die waarden uitkwam, aangezien de waarden uit een ABC-formule niet direct op x slaan.


Het is uiteindelijk toch gelukt en ik kwam erop uit dat het chi-kwadraat verdeeld is met twee vrijheidsgraden... de kansdichtheidsfunctie is zeker geen nulquote:Op maandag 16 mei 2011 11:43 schreef Don_Vanelli het volgende:
[..]
hmm.. dit ziet er vreemd uit. X+Y+Z is N(0,3) verdeeld en nu conditioneer je de verdeling van de chi-kwadraatverdeling door deze normale verdeling op nul te stellen. Dat suggereert dat de kansdichtsheidsfunctie van deze verdeling blijkbaar gelijk is aan nul en dan krijg je toch een probleem als je de kansdichtsheidsfunctie van de geconditioneerde verdeling wilt bepalen.


Een schets maken en rechtstreeks de randvoorwaarden invullen geeft eigenlijk al meteen duidelijkheid inderdaad. (iets met een cirkelsegment in het positieve kwadrant)quote:Op maandag 16 mei 2011 17:54 schreef Riparius het volgende:
[..]
Nee, dit klopt niet. In cartesische coördinaten wordt het gebied waarover je wil gaan integreren gekarakteriseerd door:
x2 + y2 ≤ 1 en tevens x + y ≥ 1
Maar dan is het duidelijk dat je r niet over het interval [0,1] kunt nemen. Immers, er ligt geen enkel punt in het bedoelde gebied met r < ½√2.
[..]
Nee dus. Stel nu eerst eens een vergelijking in poolcoördinaten op van de lijn met de cartesische vergelijking x + y = 1.


Ik zal je toch maar even op weg helpen, want ik denk dat je de berekening hiervan een beetje onderschat. Ook zie ik dat je steeds probeert om bij het gebied waarover je wil integreren vaste onder- en bovengrenzen te bepalen voor je beide integratievariabelen terwijl dat in zijn algemeenheid niet gaat, ook hier niet.quote:Op maandag 16 mei 2011 16:44 schreef Siddartha het volgende:
Eens kijken of ik het nu beter begrijp:
Ik heb de functie f(x,y)= 1/(x2+y2)2
met gebied D={(x,y)| x2+y2<=1, x+y>=1}
Kan ik dan de twee eisen als volgt weergeven:
(1) x2+y2<=1 word x=rcos(a), y=rsin(a) met grenzen [0,2Pi]
en
(2) x+y>=1 als een x simpel gebied zien: x=L(y)=1-y.
Waarmee ik de dubbele integraal kan bepalen door er twee dubbele integralen van te maken en die van elkaar af te trekken? Dus de dubbele integraal over gebied (1) min de dubbele integraal over gebied (2)?
Laten we eerst eens kijken hoe je de integraal van
(1) f(x,y) = 1/(x2+y2)2
over het gebied
(2) D := {(x;y) ∈ R2 | x2 + y2 ≤ 1 ∧ x + y ≥ 1}
kunt opschrijven in cartesische coördinaten, dus zonder transformatie naar poolcoördinaten.
Het gebied D is een cirkelsegment dat, uitgezonderd de beide randpunten (1;0) en (0;1), geheel in het eerste kwadrant ligt en dat wordt begrensd door het deel van de eenheidscirkel dat zich in het eerste kwadrant bevindt en het lijnstuk dat de beide punten (1;0) en (0;1) verbindt.
Als we nu variabele x het interval [0,1] laten doorlopen, dan behoort daarbij voor elke waarde van x uit dit interval een interval voor y waarvan de ondergrens wordt bepaald door de lijn met vergelijking x + y = 1 en de bovengrens door de cirkel met vergelijking x2 + y2 = 1. Aangezien D in het eerste kwadrant ligt geldt hierbij in ieder geval y ≥ 0. Uit x + y = 1 volgt:
(3) y = 1 - x
En uit x2 + y2 = 1 volgt in combinatie met y ≥ 0:
(4) y = √(1 - x2)
Voor elke x zodanig dat 0 ≤ x ≤ 1 is dus 1 - x ≤ y ≤ √(1 - x2), en dus kunnen we het gebied D ook als volgt definiëren:
(5) D := {(x;y) ∈ R2 | 0 ≤ x ≤ 1 ∧ 1 - x ≤ y ≤ √(1 - x2)}
Kijk voor een plaatje even hier.
De clou is natuurlijk dat we nu de integraal van f(x,y) over D (dankzij het theorema van Fubini) kunnen schrijven als een herhaalde integraal, als volgt:
Ik zou je niet aanraden deze integraal met de hand uit te rekenen. We kunnen de berekening beter hanteerbaar maken door over te gaan op poolcoördinaten. Om dit te kunnen doen moeten we eerst het gebied D definiëren in poolcoördinaten, maar dan wel zó dat we de integraal van f(x,y) over D weer kunnen schrijven als een herhaalde integraal.
Aangezien het gebied D, uitgezonderd de punten met coördinaten (1;0) en (0;1), geheel in het eerste kwadrant ligt, weten we al dat bij gebruik van poolcoördinaten geldt:
(6) 0 ≤ θ ≤ π/2
Maar nu moeten we voor elke waarde van θ op het interval [0, π/2] een onder- en een bovengrens voor r bepalen. Voor de beide punten (1;0) en (0;1) op de rand van D die corresponderen met resp. θ = 0 en θ = π/2 is dit gemakkelijk: hier geldt r = 1, zodat we kunnen zeggen dat de onder- en bovengrens van r hier zijn samengevallen. Maar voor de andere waarden van θ en dus op het open interval (0, π/2) geldt dit niet.
Nemen we bijvoorbeeld θ = π/4, dus precies halverwege het interval [0, π/2], dan zitten we op een lijn die een hoek maakt van 45 graden met de positieve x-as. Dit is uiteraard de lijn met vergelijking x = y, voor zover deze in het eerste kwadrant ligt. Deze lijn snijdt de lijn met vergelijking x + y = 1 in het punt met coördinaten (½;½) en de eenheidscirkel in het punt met coördinaten (½√2;½√2). Het interval waarover r moet lopen voor θ = π/4 wordt nu bepaald door de afstanden tot de oorsprong van deze twee snijpunten.
De bovengrens is eenvoudig, want voor elk punt op de eenheidscirkel is immers r = 1. De bovengrens van het interval waarover r moet lopen voor een gegeven waarde van θ op het interval [0, π/2] ligt dus vast. Maar voor de ondergrens geldt dat niet: de afstand van de oorsprong tot een punt op het lijnstuk dat de punten (0;1) en (0;1) verbindt is variabel en afhankelijk van θ. In het speciale geval θ = π/4 dat we nu bekijken is de afstand van het snijpunt (½;½) tot de oorsprong gelijk aan ½√2, zodat we kunnen concluderen dat voor θ = π/4 geldt ½√2 ≤ r ≤ 1.
Maar dit is niet voldoende: we moeten voor elke waarde van θ op het open interval (0, π/2) de ondergrens van het interval waarover r moet lopen bepalen, in functie van θ. Anders gezegd, we moeten voor elk punt P op het lijnstuk dat de punten met coördinaten (1;0) en (0;1) verbindt de afstand OP = r tot de oorsprong bepalen als functie van de hoek θ die OP maakt met de positieve x-as. Dit betekent niets anders dan dat we een vergelijking in poolcoördinaten moeten opstellen van de lijn met de cartesische vergelijking x + y = 1.
Laten we het punt met de coördinaten (1;0) punt A noemen, en zij P een willekeurig punt (anders dan A) op het lijnstuk van A naar het punt (0;1). In driehoek OAP hebben we nu:
(7) ∠AOP = θ en ∠PAO = π/4
En aangezien de som van de hoeken van een driehoek π (radialen) bedraagt, hebben we dus ook:
(8) ∠OPA = π - (π/4 + θ) = ¾π - θ
Volgens de sinusregel hebben we nu in driehoek OAP:
(9) OP : sin ∠PAO = OA : sin ∠OPA
En aangezien OP = r en OA =1 volgt met (7) en (8) dus uit (9) dat:
(10) r : sin(π/4) = 1 : sin(¾π - θ)
En aangezien sin(π/4) = ½√2 hebben we dus:
(11) r = √2/(2∙sin(¾π - θ))
Dit is dus een vergelijking in poolcoördinaten van de lijn waarvan de vergelijking in cartesische coördinaten x + y = 1 luidt. Je kunt gemakkelijk nagaan dat voor θ = 0 en θ = π/2 geldt r = 1, terwijl voor θ = π/4 geldt r = ½√2, in overeenstemming met wat we eerder hadden gevonden. Voor het gebied D hebben we nu in poolcoördinaten:
(12) 0 ≤ θ ≤ π/2, √2/(2∙sin(¾π - θ)) ≤ r ≤ 1
Nu kunnen we de integraal van f(x,y) = 1/(x2 + y2)2 over D transformeren in een herhaalde integraal in poolcoördinaten. We hebben x2 + y2 = r2 en dus 1/(x2 + y2)2 = 1/r4. Bij een variabele substitutie van een integraal in meerdere variabelen moeten we ook nog rekening houden met de determinant van de Jacobiaan, die de schaalfactor geeft voor de transformatie. Bij een transformatie van cartesische coördinaten naar poolcoördinaten is dit eenvoudig r, zodat dxdy = dydx vervangen wordt door rdrdθ. We krijgen dan:
Zoals verwacht, is de uitkomst 1/2. Probeer nu zelf deze integraal wel met de hand uit te werken. Als je het goed doet vind je na integratie met r als variabele en na wat goniometrische herleidingen voor de binnenste integraal sin θ∙cos θ, wat je dan nog moet integreren over het interval [0, π/2] met θ als variabele om deze uitkomst te verkrijgen.
[ Bericht 0% gewijzigd door Riparius op 17-05-2011 06:40:01 ]


Persoonlijk vind ik dat je nogal moeilijk doet om de integratiegrenzen voor r te bepalen. Uit de voorwaarde x+y <= 1 is al meteen op te maken dat je voor als ondergrens voor r kunt kiezen voorquote:Op dinsdag 17 mei 2011 06:31 schreef Riparius het volgende:
[..]
Ik zal je toch maar even op weg helpen, want ik denk dat je de berekening hiervan een beetje onderschat. Ook zie ik dat je steeds probeert om bij het gebied waarover je wil integreren vaste onder- en bovengrenzen te bepalen voor je beide integratievariabelen terwijl dat in zijn algemeenheid niet gaat, ook hier niet.
Laten we eerst eens kijken hoe je de integraal van
(1) f(x,y) = 1/(x2+y2)2
over het gebied
(2) D := {(x;y) ∈ R2 | x2 + y2 ≤ 1 ∧ x + y ≥ 1}
kunt opschrijven in cartesische coördinaten, dus zonder transformatie naar poolcoördinaten.
Het gebied D is een cirkelsegment dat, uitgezonderd de beide randpunten (1;0) en (0;1), geheel in het eerste kwadrant ligt en dat wordt begrensd door het deel van de eenheidscirkel dat zich in het eerste kwadrant bevindt en het lijnstuk dat de beide punten (1;0) en (0;1) verbindt.
Als we nu variabele x het interval [0,1] laten doorlopen, dan behoort daarbij voor elke waarde van x uit dit interval een interval voor y waarvan de ondergrens wordt bepaald door de lijn met vergelijking x + y = 1 en de bovengrens door de cirkel met vergelijking x2 + y2 = 1. Aangezien D in het eerste kwadrant ligt geldt hierbij in ieder geval y ≥ 0. Uit x + y = 1 volgt:
(3) y = 1 - x
En uit x2 + y2 = 1 volgt in combinatie met y ≥ 0:
(4) y = √(1 - x2)
Voor elke x zodanig dat 0 ≤ x ≤ 1 is dus 1 - x ≤ y ≤ √(1 - x2), en dus kunnen we het gebied D ook als volgt definiëren:
(5) D := {(x;y) ∈ R2 | 0 ≤ x ≤ 1 ∧ 1 - x ≤ y ≤ √(1 - x2)}
Kijk voor een plaatje even hier.
De clou is natuurlijk dat we nu de integraal van f(x,y) over D (dankzij het theorema van Fubini) kunnen schrijven als een herhaalde integraal, als volgt:
[ afbeelding ]
Ik zou je niet aanraden deze integraal met de hand uit te rekenen. We kunnen de berekening beter hanteerbaar maken door over te gaan op poolcoördinaten. Om dit te kunnen doen moeten we eerst het gebied D definiëren in poolcoördinaten, maar dan wel zó dat we de integraal van f(x,y) over D weer kunnen schrijven als een herhaalde integraal.
Aangezien het gebied D, uitgezonderd de punten met coördinaten (1;0) en (0;1), geheel in het eerste kwadrant ligt, weten we al dat bij gebruik van poolcoördinaten geldt:
(6) 0 ≤ θ ≤ π/2
Maar nu moeten we voor elke waarde van θ op het interval [0, π/2] een onder- en een bovengrens voor r bepalen. Voor de beide punten (1;0) en (0;1) op de rand van D die corresponderen met resp. θ = 0 en θ = π/2 is dit gemakkelijk: hier geldt r = 1, zodat we kunnen zeggen dat de onder- en bovengrens van r hier zijn samengevallen. Maar voor de andere waarden van θ en dus op het open interval (0, π/2) geldt dit niet.
Nemen we bijvoorbeeld θ = π/4, dus precies halverwege het interval [0, π/2], dan zitten we op een lijn die een hoek maakt van 45 graden met de positieve x-as. Dit is uiteraard de lijn met vergelijking x = y, voor zover deze in het eerste kwadrant ligt. Deze lijn snijdt de lijn met vergelijking x + y = 1 in het punt met coördinaten (½;½) en de eenheidscirkel in het punt met coördinaten (½√2;½√2). Het interval waarover r moet lopen voor θ = π/4 wordt nu bepaald door de afstanden tot de oorsprong van deze twee snijpunten.
De bovengrens is eenvoudig, want voor elk punt op de eenheidscirkel is immers r = 1. De bovengrens van het interval waarover r moet lopen voor een gegeven waarde van θ op het interval [0, π/2] ligt dus vast. Maar voor de ondergrens geldt dat niet: de afstand van de oorsprong tot een punt op het lijnstuk dat de punten (0;1) en (0;1) verbindt is variabel en afhankelijk van θ. In het speciale geval θ = π/4 dat we nu bekijken is de afstand van het snijpunt (½;½) tot de oorsprong gelijk aan ½√2, zodat we kunnen concluderen dat voor θ = π/4 geldt ½√2 ≤ r ≤ 1.
Maar dit is niet voldoende: we moeten voor elke waarde van θ op het open interval (0, π/2) de ondergrens van het interval waarover r moet lopen bepalen, in functie van θ. Anders gezegd, we moeten voor elk punt P op het lijnstuk dat de punten met coördinaten (1;0) en (0;1) verbindt de afstand OP = r tot de oorsprong bepalen als functie van de hoek θ die OP maakt met de positieve x-as. Dit betekent niets anders dan dat we een vergelijking in poolcoördinaten moeten opstellen van de lijn met de cartesische vergelijking x + y = 1.
Laten we het punt met de coördinaten (1;0) punt A noemen, en zij P een willekeurig punt (anders dan A) op het lijnstuk van A naar het punt (0;1). In driehoek OAP hebben we nu:
(7) ∠AOP = θ en ∠PAO = π/4
En aangezien de som van de hoeken van een driehoek π (radialen) bedraagt, hebben we dus ook:
(8) ∠OPA = π - (π/4 + θ) = ¾π - θ
Volgens de sinusregel hebben we nu in driehoek OAP:
(9) OP : sin ∠PAO = OA : sin ∠OPA
En aangezien OP = r en OA =1 volgt met (7) en (8) dus uit (9) dat:
(10) r : sin(π/4) = 1 : sin(¾π - θ)
En aangezien sin(π/4) = ½√2 hebben we dus:
(11) r = √2/(2∙sin(¾π - θ))
Dit is dus een vergelijking in poolcoördinaten van de lijn waarvan de vergelijking in cartesische coördinaten x + y = 1 luidt. Je kunt gemakkelijk nagaan dat voor θ = 0 en θ = π/2 geldt r = 1, terwijl voor θ = π/4 geldt r = ½√2, in overeenstemming met wat we eerder hadden gevonden. Voor het gebied D hebben we nu in poolcoördinaten:
(12) 0 ≤ θ ≤ π/2, √2/(2∙sin(¾π - θ)) ≤ r ≤ 1
Nu kunnen we de integraal van f(x,y) = 1/(x2 + y2)2 over D transformeren in een herhaalde integraal in poolcoördinaten. We hebben x2 + y2 = r2 en dus 1/(x2 + y2)2 = 1/r4. Bij een variabele substitutie van een integraal in meerdere variabelen moeten we ook nog rekening houden met de determinant van de Jacobiaan, die de schaalfactor geeft voor de transformatie. Bij een transformatie van cartesische coördinaten naar poolcoördinaten is dit eenvoudig r, zodat dxdy = dydx vervangen wordt door rdrdθ. We krijgen dan:
[ afbeelding ]
Zoals verwacht, is de uitkomst 1/2. Probeer nu zelf deze integraal wel met de hand uit te werken. Als je het goed doet vind je na integratie met r als variabele en na wat goniometrische herleidingen voor de binnenste integraal sin θ∙cos θ, wat je dan nog moet integreren over het interval [0, π/2] met θ als variabele om deze uitkomst te verkrijgen.
1/(cosθ + sin θ)


Hier was ik weer. 
Ik heb er nu eentje waar ik dus echt niet uitkom: tan2 x = sin x. Zodra ik tan2 wil vervangen met behulp van sin/cos=tan (met de kwadratering erin) loop ik vast en andersom (sin x vervangen met cos x keer tan x) ook. Wie kan mij vertellen hoe ik dit op moet lossen? Ik kan er helaas bar weinig over vinden op internet (en in mij boek staat ook niet echt een toelichting). Met vastlopen bedoel ik dat ik er met ontbinden en de ABC-formule niet uitkom, enzovoorts.
Ik heb er nu eentje waar ik dus echt niet uitkom: tan2 x = sin x. Zodra ik tan2 wil vervangen met behulp van sin/cos=tan (met de kwadratering erin) loop ik vast en andersom (sin x vervangen met cos x keer tan x) ook. Wie kan mij vertellen hoe ik dit op moet lossen? Ik kan er helaas bar weinig over vinden op internet (en in mij boek staat ook niet echt een toelichting). Met vastlopen bedoel ik dat ik er met ontbinden en de ABC-formule niet uitkom, enzovoorts.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je hebt volkomen gelijk. Ik doe dit soort dingen te weinig.quote:Op dinsdag 17 mei 2011 07:54 schreef Don_Vanelli het volgende:
[..]
Persoonlijk vind ik dat je nogal moeilijk doet om de integratiegrenzen voor r te bepalen. Uit de voorwaarde x+y <= 1 is al meteen op te maken dat je voor als ondergrens voor r kunt kiezen voor
1/(cosθ + sin θ)
Uit x + y = 1, x = r∙cos θ, y = r∙sin θ volgt direct r∙(cos θ + sin θ) = 1 en dus r = 1/(cos θ + sin θ).
En inderdaad krijgen we dan:
[ Bericht 9% gewijzigd door Riparius op 17-05-2011 09:09:34 ]


Wat dacht je van:quote:Op dinsdag 17 mei 2011 08:16 schreef Pipo1234 het volgende:
Hier was ik weer.
Ik heb er nu eentje waar ik dus echt niet uitkom: tan2 x = sin x. Zodra ik tan2 wil vervangen met behulp van sin/cos=tan (met de kwadratering erin) loop ik vast en andersom (sin x vervangen met cos x keer tan x) ook. Wie kan mij vertellen hoe ik dit op moet lossen? Ik kan er helaas bar weinig over vinden op internet (en in mij boek staat ook niet echt een toelichting). Met vastlopen bedoel ik dat ik er met ontbinden en de ABC-formule niet uitkom, enzovoorts.
tan2x = sin2x / cos2x = sin2x / (1 - sin2x)
Dan krijgen we dus:
sin2x / (1 - sin2x) = sin x
En dus:
sin2x = sin x ∙(1 - sin2x)
Haakjes uitwerken:
sin2x = sin x - sin3x
Herleiden op nul:
sin3x + sin2x - sin x = 0
Factor sin x buiten haakjes halen:
sin x∙(sin2x + sin x - 1) = 0
Nu jij weer. Bedenk dat een product van twee factoren alleen nul kan zijn als (tenminste) één van de factoren zelf nul is.


Het was mij vooral onduidelijk wát ik nou wilde doen, wat ik wil weergeven. Gisteravond heb ik hier ook nog aan gezeten en de moeilijkheid voor mij zit in het weergeven van het gebied (in poolcoordinaten). Met deze uitleg is het (denk ik) een stuk duidelijker geworden, ik probeer het even in mijn eigen woorden weer te geven:quote:
Ik heb een functie in een gebied dat duidelijk niet rechthoekig is: Het is een deel van een cirkel dat afgesneden word door een rechte lijn (de schets van het gebied had ik goed).
Wat ik dus wil, is een ('redelijke') bijectie te geven van een simpeler gebied naar D.
Aangezien D een deel van een cirkel is en de uitdrukking x2+y2<=1 erin voorkomt, ligt het voor de hand om D in poolcoordinaten weer te geven.
Neem het gebied E, dat gevormd word door de r-as en de a-as.
Ik zoek een afbeelding g:(r,a)|-->(???, ??) zodat ik daarmee gebied D kan beschrijven.
Dus g:E-->D via een redelijke bijectie.
Aangezien D in poolcoordinaten word uitgedrukt, moet ik x/y uitdrukken in de hoek en de straal.
Dus x=rcos(a) en y=rsin(a). Aangezien ik weet hoe de afbeelding eruit ziet, weet ik dat de hoek over het gebied [0,1/2Pi] gaat: Dit zijn de randvoorwaarden voor de hoek ( oftewel: a loopt van 0 naar 1/2Pi).
De randvoorwaarden voor r zijn moeilijker:
Voor de bovengrens zie ik dat de punten worden weergegeven door een cirkel: r is dus constant. Om precies te zijn word de cirkel weergegeven door x2+y2=1, duidelijk is dat r=1 deze lijn beschrijft (het gaat ook met invullen zoals ik in de volgende stap doe).
Voor de ondergrens geldt: x+y>=1, dus x+y=1. Invullen van x=rcos(a) en y=rsin(a) geeft
r= 1/ (cos(a)+sin(a)).
Nu weet ik dus het gebied en kan ik in de oorspronkelijke formule x en y substitueren door respectievelijk rcos(a) en rsin(a) met gebied E als een rechtoek: [0,1/2Pi] x [1/(sin(a)+cos(a)),1] waardoor ik dus de theorema van Fubini kan gebruiken om te integreren.
Edit: Ik kom alleen niet uit met de integraal.
Ik krijg dus de functie 1/r^3, dat word -1/2 r^(-2). Randvoorwaarde van r invullen geeft dan:
1/2((cos(a)+sin(a))^3 -1)
Maar als ik die opsplits blijf ik met de integraal van -1/2a zitten, waar dus een getal met Pi uitkomt. Hoe moet ik dan op een half uitkomen?
[ Bericht 6% gewijzigd door Siddartha op 17-05-2011 14:29:07 ]


Dit gaat niet goed. We moeten eerst r-3 primitiveren naar r. Zoals je correct opmerkt is een primitieve hiervan:quote:Op dinsdag 17 mei 2011 12:03 schreef Siddartha het volgende:
[..]
Edit: Ik kom alleen niet uit met de integraal.
Ik krijg dus de functie 1/r^3, dat wordt -1/2 r^(-2). Randvoorwaarde van r invullen geeft dan:
1/2((cos(a)+sin(a))^3 -1)
Maar als ik die opsplits blijf ik met de integraal van -1/2a zitten, waar dus een getal met Pi uitkomt. Hoe moet ik dan op een half uitkomen?
(1) -½∙r-2
Het interval waarover we integreren is [1/(cos θ + sin θ), 1].
Dus krijgen we:
(2) [-½∙r-2]1/(cos θ + sin θ)1 = -½ + ½∙(cos θ + sin θ)2
Nu is:
(3) (cos θ + sin θ)2 = cos2θ + 2∙cosθ∙sin θ + sin2θ = 1 + 2∙cosθ∙sin θ
En dus hebben we voor (2):
(4) -½ + ½ + ½∙2∙cosθ∙sin θ = cosθ∙sin θ
Nu moeten we cosθ∙sin θ weer integreren met als variabele θ over het interval [0, π/2]. Om cosθ∙sin θ te primitiveren maken we gebruik van de identiteit:
(5) sin 2θ = 2∙cosθ∙sin θ
Zodoende is cosθ∙sin θ = ½∙sin 2θ, en een primitieve hiervan is -¼∙cos 2θ. Dus krijgen we uiteindelijk:
(6) [-¼∙cos 2θ]0π/2 = (-¼∙-1) - (-¼∙1) = ¼ + ¼ = ½.
That's all.
[ Bericht 0% gewijzigd door Riparius op 17-05-2011 16:45:37 ]


Ah, om de een of andere reden herleide ik wel de integraal tot -1/2r-2, maar ging ik daarna meteen weer verder met -1/2r-3 als integraal. Een stom foutje, denk ik.quote:Op dinsdag 17 mei 2011 16:08 schreef Riparius het volgende:
[..]
Dit gaat niet goed. We moeten eerst r-3 primitiveren naar r. Zoals je correct opmerkt is een primitieve hiervan:
(1) -½∙r-2
Heel erg bedankt voor de uitgebreide uitleg (en het geduld)!


Oké
Ik ga het nog eens proberen.
Mijn probleem is dat ik niet de resultaten kan reproduceren als in de volgende paper (PDF!):
http://suppes-corpus.stanford.edu/article.html?id=450
( Learning Pattern Recognition through Quasi-Synchronization of Phase Oscillators )
Ik heb een figure hiervan ff in jpg gezet met hun kuramotos model en een assumptie:
Ik gebruik hiervoor Matlab, maar enige hulp bij wat ik fout kan doen is maar al te graag gewild
Dus klik nog niet weg!
Als je kijkt bij figure 1 en 2 (2e pagina rechts in PDF, de eerste figure is vergelijkbaar met 2 alleen is er geen synchronizatie want ze liggen te ver van elkaar), zie je 6 lijnen. Deze lijnen zijn gemaakt mbv frequency, amplitude en phase. De phase hier is als ik het goed heb random distributed op [0,2pi], frequencies zijn aangegeven en amplitude is 1.
Links van de figures zie je een grote equation (1). In het stukje daarboven geven ze een beschrijving hoe ze een Oscillator O_n (dat getypeerd door zijn frequency is) kan worden beschreven dmv x_n(t) = A_n(t)*cos Phase_n(t).
Dit probeerde ik te gebruiken om de figures 1 en 2 te reproduceren d.m.v. equation 1 en de instellingen.
Hetzelfde trachtte ik met de gebruikelijke formule om een lijn te verkrijgen met ampli/freq/phase:
punt = Amplitude*sin(2*pi*Frequency*Tijd + Phase)
Tevergeefs wilt dit niet lukken en ik vermoed dat dit komt doordat ik de verkeerde formules gebruik om een lijn te tekenen.
Bij mij gaan de lijnen naar elkaar (synchronizatie) enkel wanneer ze alles hetzelfde hebben behalve de phase. Maar als ik ze andere frequenties geef (zoals in de paper), dan krijg ik op den duur 'regelmatige' golven. Zie hier het resultaat:
Dit is het enige wat er in de buurt van komt, maar hier zie je geen frequencies aangegeven.
Met een andere poging krijg ik dit :
Mijn grote vraag dus is:
Als ik kuramoto's model gebruik (die in equation 1 van paper staat vermeld) en de andere stuff heb, welke formule(s) gebruik ik om een mooie lijn te tekenen van de frequency over de tijd?
Ik ga het nog eens proberen.
Mijn probleem is dat ik niet de resultaten kan reproduceren als in de volgende paper (PDF!):
http://suppes-corpus.stanford.edu/article.html?id=450
( Learning Pattern Recognition through Quasi-Synchronization of Phase Oscillators )
Ik heb een figure hiervan ff in jpg gezet met hun kuramotos model en een assumptie:
Ik gebruik hiervoor Matlab, maar enige hulp bij wat ik fout kan doen is maar al te graag gewild
Dus klik nog niet weg!
Als je kijkt bij figure 1 en 2 (2e pagina rechts in PDF, de eerste figure is vergelijkbaar met 2 alleen is er geen synchronizatie want ze liggen te ver van elkaar), zie je 6 lijnen. Deze lijnen zijn gemaakt mbv frequency, amplitude en phase. De phase hier is als ik het goed heb random distributed op [0,2pi], frequencies zijn aangegeven en amplitude is 1.
Links van de figures zie je een grote equation (1). In het stukje daarboven geven ze een beschrijving hoe ze een Oscillator O_n (dat getypeerd door zijn frequency is) kan worden beschreven dmv x_n(t) = A_n(t)*cos Phase_n(t).
Dit probeerde ik te gebruiken om de figures 1 en 2 te reproduceren d.m.v. equation 1 en de instellingen.
Hetzelfde trachtte ik met de gebruikelijke formule om een lijn te verkrijgen met ampli/freq/phase:
punt = Amplitude*sin(2*pi*Frequency*Tijd + Phase)
Tevergeefs wilt dit niet lukken en ik vermoed dat dit komt doordat ik de verkeerde formules gebruik om een lijn te tekenen.
Bij mij gaan de lijnen naar elkaar (synchronizatie) enkel wanneer ze alles hetzelfde hebben behalve de phase. Maar als ik ze andere frequenties geef (zoals in de paper), dan krijg ik op den duur 'regelmatige' golven. Zie hier het resultaat:
Dit is het enige wat er in de buurt van komt, maar hier zie je geen frequencies aangegeven.
Met een andere poging krijg ik dit :
Mijn grote vraag dus is:
Als ik kuramoto's model gebruik (die in equation 1 van paper staat vermeld) en de andere stuff heb, welke formule(s) gebruik ik om een mooie lijn te tekenen van de frequency over de tijd?


"Hetzelfde trachtte ik met de gebruikelijke formule om een lijn te verkrijgen met ampli/freq/phase:
punt = Amplitude*sin(2*pi*Frequency*Tijd + Phase)"
Misschien moet je hier ook Cosinus gebruiken aangezien de fase voor On gedefinieerd is voor een cosinus functie? Anders weet ik het ook niet, het ziet er vrij complex uit.
punt = Amplitude*sin(2*pi*Frequency*Tijd + Phase)"
Misschien moet je hier ook Cosinus gebruiken aangezien de fase voor On gedefinieerd is voor een cosinus functie? Anders weet ik het ook niet, het ziet er vrij complex uit.


Voor zover ik weet is dat een andere methode om een lijn te tekenen met behulp van Amp/Freq/Phase. Maar ik weet dus vrij weinig af van sinusoidale functies aangezien ik ze nooit in me studie heb gehad. Ik denk dus dat mijn probleem meer ligt in hoe ik de functies moet doen.
In principe zou elke functie die ervoor zorgt dat je een frequentie over tijd ziet voldoen, enkel dat hierbij de phase verandert over de tijd (via kuramotos model).
In principe zou elke functie die ervoor zorgt dat je een frequentie over tijd ziet voldoen, enkel dat hierbij de phase verandert over de tijd (via kuramotos model).


Wat doe ik hier verkeerd (partiële afgeleiden)?
[x2/y]' = (y(2x))-(x2(0))/(y2) = (y(2x))/(y2)
Volgens mij moet de y niet in de teller staan, maar waarom?
NAT-TAN/(N2) geeft (y*2x)-(x2*0)/(y2) niet?
[ Bericht 10% gewijzigd door .aeon op 18-05-2011 12:42:45 ]
[x2/y]' = (y(2x))-(x2(0))/(y2) = (y(2x))/(y2)
Volgens mij moet de y niet in de teller staan, maar waarom?
NAT-TAN/(N2) geeft (y*2x)-(x2*0)/(y2) niet?
[ Bericht 10% gewijzigd door .aeon op 18-05-2011 12:42:45 ]


Als je naar x differentieert is y een constante en vice versa, een constante kan je gewoon laten staan. De term x^2/y kan je zien als 1/y * x^2, je doet niets met 1/y dus krijg je als afgeleide gewoon 1/y * 2x = 2x/y en niet 2yx/y^2.
Als je dit voor elke term toepast en gewoon de somregel toepast krijg je
df(x,y)/dx = 2x/y - y^2/x^2
df(x,y)/dy = 2y/x - x^2/y^2
Als je dit voor elke term toepast en gewoon de somregel toepast krijg je
df(x,y)/dx = 2x/y - y^2/x^2
df(x,y)/dy = 2y/x - x^2/y^2


2x/y is toch hetzelfde als 2yx/y^2??quote:Op woensdag 18 mei 2011 12:47 schreef bert_van_dirkjan het volgende:
De term x^2/y kan je zien als 1/y * x^2, je doet niets met 1/y dus krijg je als afgeleide gewoon 1/y * 2x = 2x/y en niet 2yx/y^2.
Ik snap het nog steeds niet.
Even ter verduidelijking, de afbeelding in mijn vorige post is mijn antwoord, en de docent heeft met rood cirkels gezet (op de plek waar ik ze na heb getekend) en mij 0 punten toegekend.
[ Bericht 7% gewijzigd door .aeon op 18-05-2011 14:31:50 ]


Dan zag hij het kwadraat in de noemer niet.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ah wat stom van mij, is natuurlijk hetzelfde, maar het is altijd verstandig om je antwoord zo eenvoudig mogelijk te schrijven


Weet niet of het het juiste topic is maar vraag me af of jullie dit kunnen bereken.
Stel ik heb een bingo spel met 80 getallen waarvan 20 getallen getrokken worden.
Je kan op met een lot voor 1 of 2 getallen kiezen, als ik dus 80 loten neem met elk 1 cijfer heb ik natuurlijk 20 goed.
Hoeveel moet ik er dan nemen om alle combinaties goed te hebben met 2 getallen?
Stel ik heb een bingo spel met 80 getallen waarvan 20 getallen getrokken worden.
Je kan op met een lot voor 1 of 2 getallen kiezen, als ik dus 80 loten neem met elk 1 cijfer heb ik natuurlijk 20 goed.
Hoeveel moet ik er dan nemen om alle combinaties goed te hebben met 2 getallen?


Als de volgorde van belang is zou je in principe  verschillende combinaties kunnen maken. Echter, als wij bijvoorbeeld de combi (37,74) hebben, dan is dat natuurlijk hetzelfde als (74,37). Daarom moeten we het aantal mogelijke combinaties nog door twee delen. Dus krijgen we:
verschillende combinaties kunnen maken. Echter, als wij bijvoorbeeld de combi (37,74) hebben, dan is dat natuurlijk hetzelfde als (74,37). Daarom moeten we het aantal mogelijke combinaties nog door twee delen. Dus krijgen we:
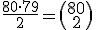
In het algemeen:
Als we k (in jouw voorbeeld k=2) getallen moeten kiezen uit een totaal van n (in jouw voorbeeld n=80), waarbij de volgorde van de keuze niet van belang is, krijgen we:
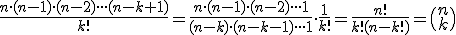
In het algemeen:
Als we k (in jouw voorbeeld k=2) getallen moeten kiezen uit een totaal van n (in jouw voorbeeld n=80), waarbij de volgorde van de keuze niet van belang is, krijgen we:


ok, nu een makkelijke vraag (t.o.v. de rest van de problemen die ik hier zie  )
)
ik heb twee vergelijkingen,
(ik moet dus Fb en Fc bepalen)
maar als ik het met substitutie probeer, komen er verkeerde antwoorden uit
de antwoorden staan in de spoiler (ik heb wel antwoorden maar geen uitwerkingen )
)
ik heb twee vergelijkingen,
(ik moet dus Fb en Fc bepalen)
maar als ik het met substitutie probeer, komen er verkeerde antwoorden uit
de antwoorden staan in de spoiler (ik heb wel antwoorden maar geen uitwerkingen
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.ik weet bijna zeker dat ik echt een stomme fout maak of iets over het hoofd zie, maar het is alweer een tijdje geleden voor me The only things that start on time are those that you're late for.
The only things that start on time are those that you're late for.


Je doet iets fout in de stap van 2,75=sin.... naar 2,75*cos(30)..... Voor de rest ziet het er goed uit.
Als je nou eerst deze stap neemt: 2,75 = (4/5 * sin(30)/cos(30) + 3/5) * Fc, lukt het dan wel?
Als je nou eerst deze stap neemt: 2,75 = (4/5 * sin(30)/cos(30) + 3/5) * Fc, lukt het dan wel?


ik kan die 3/5 toch niet zomaar onder de deelstreep zetten? of hoort die ernaast?quote:Op donderdag 19 mei 2011 00:39 schreef bert_van_dirkjan het volgende:
Als je nou eerst deze stap neemt: 2,75 = (4/5 * sin(30)/cos(30) + 3/5) * Fc, lukt het dan wel?
of bedoel je niet dit:
The only things that start on time are those that you're late for.


Uit de tweede vgl krijg jequote:Op donderdag 19 mei 2011 00:49 schreef t0sti het volgende:
[..]
ik kan die 3/5 toch niet zomaar onder de deelstreep zetten? of hoort die ernaast?
of bedoel je niet dit:
[ afbeelding ]
2.75 = (sin(30)*(4/5)/cos(30)+3/5)*Fc
en dus
Fc = 2.75/(sin(30)*(4/5)/cos(30)+3/5).
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


ik begrijp alleen niet hoe je uit die tweede vglquote:Op donderdag 19 mei 2011 00:57 schreef keesjeislief het volgende:
[..]
Uit de tweede vgl krijg je
2.75 = (sin(30)*(4/5)/cos(30)+3/5)*Fc
en dus
Fc = 2.75/(sin(30)*(4/5)/cos(30)+3/5).
2.75 = (sin(30)*(4/5)/cos(30)+3/5)*Fc
krijgt: ik zie boven de deelstreep Fc verdwijnen, en onder de deelstreep +3/5 erbij komen
EDIT: ik zie nu wel wat ik fout heb gedaan: die +3/5Fc had ik niet boven de deelstreep mogen zetten, maar ik snap bovenstaande nog steeds niet
[ Bericht 13% gewijzigd door t0sti op 19-05-2011 01:23:34 ]
The only things that start on time are those that you're late for.


Gewoon Fc buiten haakjes halen: Bla1*Fc/Bla2+Bla3*Fc = (Bla1/Bla2+Bla3)*Fc.quote:Op donderdag 19 mei 2011 01:08 schreef t0sti het volgende:
[..]
ik begrijp alleen niet hoe je uit die tweede vgl
2.75 = (sin(30)*(4/5)/cos(30)+3/5)*Fc
krijgt: ik zie boven de deelstreep Fc verdwijnen, en onder de deelstreep +3/5 erbij komen
EDIT: ik zie nu wel wat ik fout heb gedaan: die +3/5Fc had ik niet boven de deelstreep mogen zetten, maar ik snap bovenstaande nog steeds niet
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


ja, maar dan zet je dus de 3/5 Fc onder de deelstreep, terwijl dat volgens mijn logica helemaal niet kan/magquote:Op donderdag 19 mei 2011 01:45 schreef keesjeislief het volgende:
[..]
Gewoon Fc buiten haakjes halen: Bla1*Fc/Bla2+Bla3*Fc = (Bla1/Bla2+Bla3)*Fc.
(Dat is dus die +Bla3*Fc, die stond eerst achter de breuk)
The only things that start on time are those that you're late for.


Die staat nog steeds achter de breuk:quote:Op donderdag 19 mei 2011 01:56 schreef t0sti het volgende:
[..]
ja, maar dan zet je dus de 3/5 Fc onder de deelstreep, terwijl dat volgens mijn logica helemaal niet kan/mag
(Dat is dus die +Bla3*Fc, die stond eerst achter de breuk)
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


quote:Op donderdag 19 mei 2011 00:27 schreef t0sti het volgende:
ok, nu een makkelijke vraag (t.o.v. de rest van de problemen die ik hier zie)
ik heb twee vergelijkingen,
[ afbeelding ]
(ik moet dus Fb en Fc bepalen)
maar als ik het met substitutie probeer, komen er verkeerde antwoorden uit
[ afbeelding ]
de antwoorden staan in de spoiler (ik heb wel antwoorden maar geen uitwerkingen)
Je kunt kennelijk niet rekenen met breuken.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.ik weet bijna zeker dat ik echt een stomme fout maak of iets over het hoofd zie, maar het is alweer een tijdje geleden voor me
Als je twee breuken hebt waarvan de eerste een noemer cos 30° heeft en de tweede een noemer 5 heeft en je wil die breuken bij elkaar optellen, dan moet je die breuken eerst gelijknamig maken. Dat doe je door teller en noemer van de eerste breuk met 5 en teller en noemer van de tweede breuk met cos 30° te vermenigvuldigen.
Maar het kan een stuk overzichtelijker door eerst de breuken uit je oorspronkelijke vergelijkingen te elimineren. Als je beide leden van je eerste vergelijking met 15 vermenigvuldigt, en beide leden van je tweede vergelijking met 20, dan krijg je:
(1) 0 = -15∙cos 30°∙Fb + 12∙Fc
(2) 55 = 20∙sin 30°∙Fb + 12∙Fc
Door nu de leden van de eerste vergelijking van de leden van de tweede vergelijking af te trekken valt Fc weg en krijg je:
(3) 55 = (15∙cos 30° + 20∙sin 30°)∙Fb
Door substitutie van de exacte waarden cos 30° = ½∙√3 en sin 30° = ½ in (3) vinden we dan:
(4) Fb = 22/(4 + 3∙√3)
Bovendien volgt uit (1) na substitutie van cos 30° = ½∙√3 dat:
(5) Fc = (5/8)∙√3∙Fb
Zodat uit (4) en (5) volgt:
(6) Fc = 55∙√3/(16 + 12∙√3)
[ Bericht 1% gewijzigd door Riparius op 19-05-2011 06:05:53 ]


Riparius, altijd streng doch rechtvaardigquote:Op donderdag 19 mei 2011 05:52 schreef Riparius het volgende:
[..]
Je kunt kennelijk niet rekenen met breuken.


Ik moet de dubbele integraal uitrekenen van:
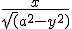 dydx met gebied [0,1]x[0,a]
dydx met gebied [0,1]x[0,a]
Als gebied heb ik gekozen: En={(x,y)| 0<=x>=1, 0<=y<=a-1/n}
Dan krijg ik als 'eerste'integraal (de integraal over y):
xarcsin(y/a)
Invullen over gebied En geeft xarcsin(1-1/n).
etc, etc, geeft als antwoord 1/4 Pi.
Het gaat me dus om de stappen voor etc, etc en het antwoord. Klopt dat?
[ Bericht 100% gewijzigd door Siddartha op 19-05-2011 11:58:36 ]
Als gebied heb ik gekozen: En={(x,y)| 0<=x>=1, 0<=y<=a-1/n}
Dan krijg ik als 'eerste'integraal (de integraal over y):
xarcsin(y/a)
Invullen over gebied En geeft xarcsin(1-1/n).
etc, etc, geeft als antwoord 1/4 Pi.
Het gaat me dus om de stappen voor etc, etc en het antwoord. Klopt dat?
[ Bericht 100% gewijzigd door Siddartha op 19-05-2011 11:58:36 ]


@bert_van_dirkjan
@keesjeislief
@Riparius
bedankt! voor het geduld en de uitleg (ook gezien de tijdstippen )
)




[ Bericht 8% gewijzigd door t0sti op 19-05-2011 12:24:23 ]
@keesjeislief
@Riparius
bedankt! voor het geduld en de uitleg (ook gezien de tijdstippen
[ Bericht 8% gewijzigd door t0sti op 19-05-2011 12:24:23 ]
The only things that start on time are those that you're late for.


Dit lijkt me juist. Wolfram Alpha verslikt zich in deze integraal (met a in de integrand), maar x∙arcsin(y/a) is inderdaad een primitieve naar y van x/√(a2 - y2). Het is weliswaar een oneigenlijke integraal omdat de functiewaarde onbepaald is voor y = a, maar je hoeft hier geen limietovergang te gebruiken. Integreren met y als variabele over [0,a] geeft:quote:Op donderdag 19 mei 2011 11:47 schreef Siddartha het volgende:
Ik moet de dubbele integraal uitrekenen van:
[ afbeelding ] dydx met gebied [0,1]x[0,a]
Als gebied heb ik gekozen: En={(x,y)| 0<=x>=1, 0<=y<=a-1/n}
Dan krijg ik als 'eerste'integraal (de integraal over y):
xarcsin(y/a)
Invullen over gebied En geeft xarcsin(1-1/n).
etc, etc, geeft als antwoord 1/4 Pi.
Het gaat me dus om de stappen voor etc, etc en het antwoord. Klopt dat?
[x∙arcsin(y/a)]0a = x∙arcsin(a/a) - x∙arcsin(0) = x∙arcsin(1) = x∙π/2.
Een primitieve hiervan naar x is (π/4)∙x2 zodat we inderdaad krijgen:
[(π/4)∙x2]01 = π/4 - 0 = π/4.


Dus hoeveel verschillende loten zou je kunnen hebben?quote:Op woensdag 18 mei 2011 23:02 schreef Don_Vanelli het volgende:
Als de volgorde van belang is zou je in principe [ afbeelding ] verschillende combinaties kunnen maken. Echter, als wij bijvoorbeeld de combi (37,74) hebben, dan is dat natuurlijk hetzelfde als (74,37). Daarom moeten we het aantal mogelijke combinaties nog door twee delen. Dus krijgen we:
[ afbeelding ]
In het algemeen:
Als we k (in jouw voorbeeld k=2) getallen moeten kiezen uit een totaal van n (in jouw voorbeeld n=80), waarbij de volgorde van de keuze niet van belang is, krijgen we:
[ afbeelding ]
Er zit geen verschil tussen 37,74 of 74,37 dat is hetzelfde.


Don_Vanelli heeft je toch al het antwoord gegeven? Het aantal is (80∙79)/2 = 3160. Te lui om dit even zelf uit te rekenen?quote:Op donderdag 19 mei 2011 16:26 schreef Kadooosh het volgende:
[..]
Dus hoeveel verschillende loten zou je kunnen hebben?
Er zit geen verschil tussen 37,74 of 74,37 dat is hetzelfde.


Volgens mij moet ik wel een limiet nemen (het eigenlijke gebied D is immers met y=a).quote:Op donderdag 19 mei 2011 16:01 schreef Riparius het volgende:
[..]
Dit lijkt me juist. Wolfram Alpha verslikt zich in deze integraal (met a in de integrand), maar x∙arcsin(y/a) is inderdaad een primitieve naar y van x/√(a2 - y2). Het is weliswaar een oneigenlijke integraal omdat de functiewaarde onbepaald is voor y = a, maar je hoeft hier geen limietovergang te gebruiken. Integreren met y als variabele over [0,a] geeft:
[x∙arcsin(y/a)]0a = x∙arcsin(a/a) - x∙arcsin(0) = x∙arcsin(1) = x∙π/2.
Een primitieve hiervan naar x is (π/4)∙x2 zodat we inderdaad krijgen:
[(π/4)∙x2]01 = π/4 - 0 = π/4.
Daarom pak ik ook het kleinere gebied En met y=a-1/n, zodat ik door het limiet van n->oneindig te nemen het gebied D kan uitputten met lim (En).
Het maakt verder geen verschil (de 1/n valt gewoon weg in de uiteindelijke integraal).


Ik begrijp je redenering wel, en die is ook correct, maar de primitieve naar y van x/√(a2 - y2) oftewel x∙arcsin(y/a) + C is wel gedefinieerd voor y=a, zodat je je een limietovergang naar het integratieinterval [0, a] kunt besparen.quote:Op donderdag 19 mei 2011 17:18 schreef Siddartha het volgende:
[..]
Volgens mij moet ik wel een limiet nemen (het eigenlijke gebied D is immers met y=a).
Daarom pak ik ook het kleinere gebied En met y=a-1/n, zodat ik door het limiet van n->oneindig te nemen het gebied D kan uitputten met lim (En).
Het maakt verder geen verschil (de 1/n valt gewoon weg in de uiteindelijke integraal).


"Voor elk priemgetal p is de commutatieve ring (Z/pZ) een eindig lichaam
van p elementen."
Nu word er voor deze stelling bewezen dat elk element/restklasse a die niet deelbaar door p is, een inverse heeft. Dat snap ik wel redelijk, maar hoe moet ik me die inverse voorstellen?
En hoe volgt daaruit dat er p elementen zijn?
van p elementen."
Nu word er voor deze stelling bewezen dat elk element/restklasse a die niet deelbaar door p is, een inverse heeft. Dat snap ik wel redelijk, maar hoe moet ik me die inverse voorstellen?
En hoe volgt daaruit dat er p elementen zijn?


Ok, bedankt!quote:Op donderdag 19 mei 2011 17:29 schreef Riparius het volgende:
[..]
Ik begrijp je redenering wel, en die is ook correct, maar de primitieve naar y van x/√(a2 - y2) oftewel x∙arcsin(y/a) + C is wel gedefinieerd voor y=a, zodat je je een limietovergang naar het integratieinterval [0, a] kunt besparen.
Al voelt het wel vreemd aan, dat de integraal wel goed gedefineerd is in het gehele gebied, terwijl de functie zelf dat niet is.


Nog bedankt voor je duidelijk uitleg. Het is me uiteindelijk gelukt om die opgaven enigszins door te krijgen.quote:
Nu heb ik alleen even een andere vraag over hetzelfde onderwerp. (Ik begin een beetje gefrustreerd te raken door al die algebra, aangezien ik er blijkbaar niet zo goed in ben en mijn boek totaal geen uitleg of uitwerking biedt.) Ik moet vergelijkingen zoals de volgenden oplossen: sin 3x = sin 2(x - 3) en sin 2x = sin 3x. Nu krijg ik het niet voor elkaar om hier een bruikbaar antwoord uit te krijgen. Ik zie het gewoon niet denk ik. Dat probleem had ik eerder ook al bij het oplossen van sin x = cos x enzovoorts. Helaas heb ik nog niet de routine om dit soort vergelijkingen "even" op te lossen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


De elk geheel getal heeft een rest bij deling door p. De restklassen hebben representanten 0, 1, ... p-1. Dat zijn er p in totaal. Er zijn ook geen identificaties tussen deze restklassen want het verschil tussen elk tweetal van deze representanten is minder dan p.quote:Op donderdag 19 mei 2011 17:32 schreef Siddartha het volgende:
"Voor elk priemgetal p is de commutatieve ring (Z/pZ) een eindig lichaam
van p elementen."
Nu word er voor deze stelling bewezen dat elk element/restklasse a die niet deelbaar door p is, een inverse heeft. Dat snap ik wel redelijk, maar hoe moet ik me die inverse voorstellen?
En hoe volgt daaruit dat er p elementen zijn?
Die inverse, dat moet je gewoon als deling zien. Formeel gezien betekent a/b = c dat c de unieke oplossing van de vergelijking bx = a is. In Z/pZ is op die manier a/b altijd goed gedefinieerd als b niet 0 is en voldoet ook gewoon aan standaard rekenregels.


Ik ga me vraag anders proberen te formuleren, ik heb namelijk het gevoel dat het erg simpel is. Immers, het wordt nergens echt in papers vermeldt hoe/wat.
Ik heb het volgende:
Een fase
Een amplitude
Een frequentie.
Ik verander de fase over de tijd geleidelijk.
Hoe krijg ik nu een frequentie tegenover tijd grafiek? Waarbij vanwege de veranderende fase, de golf dus niet perfect hetzelfde volgt. Wat er verder gebeurt is dat die lijn dus om de oorspronkelijk frequentie heen danst, b.v. 20 freq heeft een lijn dat vervolgens tussen 17 en 23 schommelt (vanwege andere oscillators)
Iemand?
Ik heb het volgende:
Een fase
Een amplitude
Een frequentie.
Ik verander de fase over de tijd geleidelijk.
Hoe krijg ik nu een frequentie tegenover tijd grafiek? Waarbij vanwege de veranderende fase, de golf dus niet perfect hetzelfde volgt. Wat er verder gebeurt is dat die lijn dus om de oorspronkelijk frequentie heen danst, b.v. 20 freq heeft een lijn dat vervolgens tussen 17 en 23 schommelt (vanwege andere oscillators)
Iemand?


OK. De sinus is (evenals de cosinus) een periodieke functie met een periode 2π. Dat betekent dus dat twee hoeken (rotaties) die een geheel veelvoud van 2π (radialen) van elkaar verschillen steeds dezelfde sinus (en dezelfde cosinus) hebben. Dus:quote:Op donderdag 19 mei 2011 19:47 schreef Pipo1234 het volgende:
[..]
Nog bedankt voor je duidelijk uitleg. Het is me uiteindelijk gelukt om die opgaven enigszins door te krijgen.
Nu heb ik alleen even een andere vraag over hetzelfde onderwerp. (Ik begin een beetje gefrustreerd te raken door al die algebra, aangezien ik er blijkbaar niet zo goed in ben en mijn boek totaal geen uitleg of uitwerking biedt.) Ik moet vergelijkingen zoals de volgenden oplossen: sin 3x = sin 2(x - 3) en sin 2x = sin 3x. Nu krijg ik het niet voor elkaar om hier een bruikbaar antwoord uit te krijgen. Ik zie het gewoon niet denk ik. Dat probleem had ik eerder ook al bij het oplossen van sin x = cos x enzovoorts. Helaas heb ik nog niet de routine om dit soort vergelijkingen "even" op te lossen.
(1) sin(α + 2κπ) = sin α en cos(α + 2κπ) = cos α voor elke k ∈ Z
Daarnaast is het ook nog eens zo dat supplementaire hoeken of rotaties (d.w.z. twee hoeken of rotaties die samen 180 graden zijn ofwel π radialen) ook dezelfde sinus hebben. Dat kun je gemakkelijk zien als je even een schetsje maakt met een assenkruis en de eenheidscirkel. De sinus van α is per definitie de y-coördinaat van het beeldpunt van (1;0) bij rotatie over een hoek α, en je ziet in een tekening gemakkelijk dat de beeldpunten van (1;0) bij rotatie over α en bij rotatie over π - α symmetrisch liggen t.o.v. de y-as ('even hoog') en dus dezelfde y-coördinaat hebben, en daarmee ook dezelfde sinus. Dus:
(2) sin(π - α) = sin α
Bij de cosinus werkt het anders. Dit is per definitie de x-coördinaat van het beeldpunt van (1;0) bij rotatie over een hoek α. En omdat de beeldpunten van (1;0) bij rotatie over α en bij rotatie over π - α symmetrisch liggen t.o.v. de y-as en dus tegengestelde x-coördinaten hebben, en daarmee ook een tegengestelde cosinus, geldt dus:
(3) cos(π - α) = -cos α
Nu kunnen we (1) en (2) combineren: als we weten dat twee hoeken (rotaties) dezelfde sinus hebben, dan kunnen we dus zeggen dat deze twee hoeken - op een geheel veelvoud van 2π na - ofwel dezelfde zijn ofwel supplementair zijn. Dus vinden we dat geldt:
(4) sin α = sin β ⇔ α = β + 2kπ ∨ α = (π - β) + 2kπ, k∈Z
Voor de cosinus geldt dat cos(-α) = cos α voor elke willekeurige hoek (rotatie) α, aangezien de beeldpunten van (1;0) bij rotaties over -α en α symmetrisch liggen t.o.v. de x-as en dus dezelfde x-coördinaat hebben. Zo vinden we ook dat geldt:
(5) cos α = cos β ⇔ α = β + 2kπ ∨ α = (- β) + 2kπ, k∈Z
Moeten we nu een vergelijking als sin 3x = sin 2(x-3) oplossen over R, dan kunnen we dus direct zeggen dat moet gelden:
3x = 2(x - 3) + 2kπ ∨3x = π - 2(x - 3) + 2kπ
Dit geeft:
3x = 2x - 6 + 2kπ ∨3x = π - 2x + 6 + 2kπ
En dus:
x = -6 + 2kπ ∨5x = 6 + (2k+1)π
Dus:
x = -6 + 2kπ ∨x = 6/5 + ((2k+1)/5)∙π, k∈Z
[ Bericht 0% gewijzigd door Riparius op 19-05-2011 21:54:54 ]


Wat voor soort vragen kan je verwachten op Examen Aardrijkskunde? Meer inzichts vragen of gewoon toepassingsvragen of wat voor soort dan ook?
Alvast bedankt
Kut, verkeerde topique
Alvast bedankt
Kut, verkeerde topique
RvP; Feyenoord
Op maandag 17 juni 2013 00:00 schreef alors het volgende:
Ik hoop dat Suarez er huilend afgaat met rood.
Op maandag 17 juni 2013 00:00 schreef alors het volgende:
Ik hoop dat Suarez er huilend afgaat met rood.


Lijkt me toch wel juist, mits je a0 = 1 neemt. Immers, het is triviaal dat a1 = 3, a2 = 9 en a3 = 26 (omdat alleen de sequentie 000 niet mee mag doen). Dan krijgen we dus volgens je recursieformule a4 = 2∙(26 + 9 + 3) = 2∙38 = 76, en dat klopt. Immers de sequentie 0000 mag niet meedoen, en ook x000 en 000x met x=1 of x=2 mogen niet meedoen, zodat a4 = 34 - 5 = 81 - 5 = 76.quote:Op donderdag 19 mei 2011 20:51 schreef Fingon het volgende:
an = 0,1,2, rijtjes van lengte n zonder 3 opeenvolgende nullen (000).
Stel de recurrente betrekking op voor aantal rijtjes:
[ link | afbeelding ]
an = 2*an-1 + 2*an-2 + 2*an-3
is dit enigzins correct? ik heb toch het idee dat het niet helemaal goed is..


Ok, maar wat voor manier gebruik jij daar dan, is die ook recursief of is dat een andere manier van tellen?quote:Op donderdag 19 mei 2011 21:35 schreef Riparius het volgende:
[..]
Lijkt me toch wel juist, mits je a0 = 1 neemt. Immers, het is triviaal dat a1 = 3, a2 = 9 en a3 = 26 (omdat alleen de sequentie 000 niet mee mag doen). Dan krijgen we dus volgens je recursieformule a4 = 2∙(26 + 9 + 3) = 2∙38 = 76, en dat klopt. Immers de sequentie 0000 mag niet meedoen, en ook x000 en 000x met x=1 of x=2 mogen niet meedoen, zodat a4 = 34 - 5 = 81 - 5 = 76.
Beneath the gold, bitter steel


Het totaal aantal sequenties van n maal een 0,1 of 2 is 3n. Bij a1 en a2 zijn er geen uitvallers omdat je dan geen drie nullen achter elkaar kunt hebben, dus a1 = 31 = 3 en a2 = 32 = 9. Bij a3 is er maar één uitvaller, want alleen 000 mag niet. Dus is a3 = 33 - 1 = 26. Met deze gegevens kun je aan de hand van je recursieformule a4 uitrekenen, en dan kom je op 76, wat inderdaad klopt. Voor a3 klopt de recursieformule ook, als we a0 = 1 nemen.quote:Op [url=http://forum.fok.nl/topic/1649235/3/50#9705229http://i.fokzine.net/temp(...)r/sub.png1]donderdag 19 mei 2011 22:08[/url] schreef Fingon het volgende:
[..]
Ok, maar wat voor manier gebruik jij daar dan, is die ook recursief of is dat een andere manier van tellen?


Maar de restklasses zelf bevatten wel meer elementen, toch? Als ik 7 als p pak, dan bevat de restklasse R1 de elementen 2 en 6.quote:Op donderdag 19 mei 2011 20:15 schreef thabit het volgende:
[..]
De elk geheel getal heeft een rest bij deling door p. De restklassen hebben representanten 0, 1, ... p-1. Dat zijn er p in totaal. Er zijn ook geen identificaties tussen deze restklassen want het verschil tussen elk tweetal van deze representanten is minder dan p.
Die inverse, dat moet je gewoon als deling zien. Formeel gezien betekent a/b = c dat c de unieke oplossing van de vergelijking bx = a is. In Z/pZ is op die manier a/b altijd goed gedefinieerd als b niet 0 is en voldoet ook gewoon aan standaard rekenregels.
En als het puur om die restklassen gaat, geldt dat dan niet voor elke commutatieve ring (Z/mZ) met m>0 natuurlijk getal?
Bij de inverse gaat het er toch om dat de 'x' niet gedefineerd is als de gebruikelijke 'keer', maar als een bewerking die voldoet aan bepaalde axioma's? Dus kan je in een lichaam van 2 elementen hebben dat 1 de inverse is van 1 (oid).


Elke restklasse bevat oneindig veel elementen. Voor p = 7 zit 2 niet in dezelfde restklasse als 6 maar wel in dezelfde restklasse als 9. En ja, voor m>0 heeft Z/mZ precies m elementen.quote:Op vrijdag 20 mei 2011 09:14 schreef Siddartha het volgende:
[..]
Maar de restklasses zelf bevatten wel meer elementen, toch? Als ik 7 als p pak, dan bevat de restklasse R1 de elementen 2 en 6.
En als het puur om die restklassen gaat, geldt dat dan niet voor elke commutatieve ring (Z/mZ) met m>0 natuurlijk getal?


Ja, inderdaad, maar de vermenigvuldiging op Z/mZ is gewoon gedefinieerd als de reductie modulo m van de vermenigvuldiging op Z.quote:Op vrijdag 20 mei 2011 09:14 schreef Siddartha het volgende:
[..]
Bij de inverse gaat het er toch om dat de 'x' niet gedefineerd is als de gebruikelijke 'keer', maar als een bewerking die voldoet aan bepaalde axioma's? Dus kan je in een lichaam van 2 elementen hebben dat 1 de inverse is van 1 (oid).


Bedankt voor je heldere uitleg. Spontaan viel het kwartje bij mij...quote:Op donderdag 19 mei 2011 21:15 schreef Riparius het volgende:
[..]
OK. De sinus is (evenals de cosinus) een periodieke functie met een periode 2π. Dat betekent dus dat twee hoeken (rotaties) die een geheel veelvoud van 2π (radialen) van elkaar verschillen steeds dezelfde sinus (en dezelfde cosinus) hebben. Dus:
...
Ik even even een uitgewerkte opgave in Latex gezet om te zien of ik het begrijp:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dat gaat best goed zo, alleen heb je bij de tweede mogelijkheid een (vaak voorkomende) tekenfout gemaakt.quote:Op vrijdag 20 mei 2011 13:16 schreef Pipo1234 het volgende:
[..]
Bedankt voor je heldere uitleg. Spontaan viel het kwartje bij mij...
Ik even even een uitgewerkte opgave in Latex gezet om te zien of ik het begrijp:
[ afbeelding ]
Je hebt:
πx = (½πx - ½π) + 2kπ ∨ πx = π - (½πx - ½π) + 2kπ
En dat wordt:
πx = ½πx - ½π + 2kπ ∨ πx = π - ½πx + ½π + 2kπ
Daarna verander je π - ½π zomaar in π + ½π, waardoor het antwoord uiteindelijk wel klopt. Maar twee fouten maken die elkaar opheffen betekent niet dat het foutloos is.
[ Bericht 2% gewijzigd door Riparius op 20-05-2011 14:03:16 ]


Bedoel je dat het eigenlijk tussen haakjes had moeten staan, zodat het correct is dat die halve pi plus wordt?quote:Op vrijdag 20 mei 2011 13:52 schreef Riparius het volgende:
[..]
Dat gaat best goed zo, alleen heb je bij de tweede mogelijkheid een (vaak voorkomende) tekenfout gemaakt.
Je hebt:
πx = (½πx - ½π) + 2kπ ∨ πx = π - (½πx - ½π) + 2kπ
En dat wordt:
πx = ½πx - ½π + 2kπ ∨ πx = π - ½πx + ½π + 2kπ
Daarna verander je π - ½π zomaar in π + ½π, waardoor het antwoord uiteindelijk wel klopt. Maar twee fouten maken die elkaar opheffen betekent niet dat het foutloos is.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ja, want π - (½πx - ½π) + 2kπ is niet hetzelfde als π - ½πx - ½π + 2kπ.quote:Op vrijdag 20 mei 2011 15:12 schreef Pipo1234 het volgende:
[..]
Bedoel je dat het eigenlijk tussen haakjes had moeten staan, zodat het correct is dat die halve pi plus wordt?


Oké. Ik snap het en dat is een heel goed punt. Bedankt!quote:Op vrijdag 20 mei 2011 15:26 schreef Riparius het volgende:
[..]
Ja, want π - (½πx - ½π) + 2kπ is niet hetzelfde als π - ½πx - ½π + 2kπ.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Domme vraag misschien, maar hoe krijg je die tekens van pi, 1/2 enzovoorts in een post? Ik neem aan dat daar een makkelijkere manier voor is dan de tekens uit je hoofd leren?quote:Op vrijdag 20 mei 2011 15:26 schreef Riparius het volgende:
[..]
Ja, want π - (½πx - ½π) + 2kπ is niet hetzelfde als π - ½πx - ½π + 2kπ.
The biggest argument against democracy is a five minute discussion with the average voter.


Fok ondersteunt Unicode, dus met een geschikt toetsenbord layout programma (of een geschikte keyboard layout van Windows zelf) kun je alles typen wat je wil zonder ingewikkelde codes. Ik gebruik zelf Tavultesoft Keyman omdat ik o.a. ook klassiek Grieks wil kunnen typen. Voor ¼, ½ en ¾ kun je (met de standaard toetsenbord indeling VS internationaal) gewoon Ctrl-Alt 6, Ctrl-Alt 7 en Ctrl-Alt 8 gebruiken (of AltGr met 6, 7, 8).quote:Op vrijdag 20 mei 2011 19:42 schreef M.rak het volgende:
[..]
Domme vraag misschien, maar hoe krijg je die tekens van pi, 1/2 enzovoorts in een post? Ik neem aan dat daar een makkelijkere manier voor is dan de tekens uit je hoofd leren?


Thanks, mooi programmaquote:Op vrijdag 20 mei 2011 20:09 schreef Riparius het volgende:
[..]
Fok ondersteunt Unicode, dus met een geschikt toetsenbord layout programma (of een geschikte keyboard layout van Windows zelf) kun je alles typen wat je wil zonder ingewikkelde codes. Ik gebruik zelf Tavultesoft Keyman omdat ik o.a. ook klassiek Grieks wil kunnen typen. Voor ¼, ½ en ¾ kun je (met de standaard toetsenbord indeling VS internationaal) gewoon Ctrl-Alt 6, Ctrl-Alt 7 en Ctrl-Alt 8 gebruiken (of AltGr met 6, 7, 8).
The biggest argument against democracy is a five minute discussion with the average voter.


Ik moet van de volgende functie het minimum vinden:
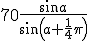
Nu weet ik dat sinus altijd op vaste plekken een maximum en minimum hebben zitten. En na een beetje rekenen kom ik op het minimum: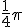 , aangezien bij de afgeleide de noemer maximaal is op dat punt. Dat is logisch aangezien
, aangezien bij de afgeleide de noemer maximaal is op dat punt. Dat is logisch aangezien 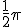 de plek is waar sinus maximaal is. Nu is alleen mijn vraag of dit de meest correcte manier is om dit te benaderen? Ik weet namelijk niet hoe ik bij sinus etc. het beste de maxima/minima kan benaderen, als de afgeleide niet 0 is en er een formule aan vast hang waarbij niet helemaal duidelijk is of het maximum/minimum bepalend is.
de plek is waar sinus maximaal is. Nu is alleen mijn vraag of dit de meest correcte manier is om dit te benaderen? Ik weet namelijk niet hoe ik bij sinus etc. het beste de maxima/minima kan benaderen, als de afgeleide niet 0 is en er een formule aan vast hang waarbij niet helemaal duidelijk is of het maximum/minimum bepalend is.
[ Bericht 8% gewijzigd door Pipo1234 op 21-05-2011 17:11:52 ]
Nu weet ik dat sinus altijd op vaste plekken een maximum en minimum hebben zitten. En na een beetje rekenen kom ik op het minimum:
[ Bericht 8% gewijzigd door Pipo1234 op 21-05-2011 17:11:52 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Weet je zeker dat dit de goede functie is? Als je dit namelijk op Wolfram Alpha invoert (zie hier), dan zegt hij dat er geen minima zijn, dat komt ook terug in de afgeleide die nooit nul is. Heb je niet te maken met een beperkt interval waarin je moet zoeken?quote:Op zaterdag 21 mei 2011 16:56 schreef Pipo1234 het volgende:
Ik moet van de volgende functie het minimum vinden:
[ afbeelding ]
Nu weet ik dat sinus altijd op vaste plekken een maximum en minimum hebben zitten. En na een beetje rekenen kom ik op het minimum: [ afbeelding ], aangezien bij de afgeleide de noemer maximaal is op dat punt. Dat is logisch aangezien [ afbeelding ] de plek is waar sinus maximaal is. Nu is alleen mijn vraag of dit de meest correcte manier is om dit te benaderen? Ik weet namelijk niet hoe ik bij sinus etc. het beste de maxima/minima kan benaderen, als de afgeleide niet 0 is en er een formule aan vast hang waarbij niet helemaal duidelijk is of het maximum/minimum bepalend is.
The biggest argument against democracy is a five minute discussion with the average voter.


Verdorie. Het had ¼π moeten zijn. Heb hem aangepast.quote:Op zaterdag 21 mei 2011 17:08 schreef M.rak het volgende:
[..]
Weet je zeker dat dit de goede functie is? Als je dit namelijk op Wolfram Alpha invoert (zie hier), dan zegt hij dat er geen minima zijn, dat komt ook terug in de afgeleide die nooit nul is. Heb je niet te maken met een beperkt interval waarin je moet zoeken?
[ Bericht 0% gewijzigd door Pipo1234 op 21-05-2011 17:26:03 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dan blijf je het zelfde probleem houden, kijk hier maar (beetje naar beneden scrollen voor de afgeleide, die wordt nooit nul).quote:Op zaterdag 21 mei 2011 17:11 schreef Pipo1234 het volgende:
[..]
Verdorie. Het had 1/4 pi moeten zijn. Heb hem aangepast.
The biggest argument against democracy is a five minute discussion with the average voter.


Je hebt gelijk. Dat is ook zo, aangezien ik het punt moet vinden waar de uitkomst van de afgeleide van die functie het kleinste is. Op dat punt is namelijk de toename het kleinste en dat heeft weer te maken met de opdracht. Ik raak er zelf een beetje van in de war, dus misschien had ik het niet toegelicht.quote:Op zaterdag 21 mei 2011 17:17 schreef M.rak het volgende:
[..]
Dan blijf je het zelfde probleem houden, kijk hier maar (beetje naar beneden scrollen voor de afgeleide, die wordt nooit nul).
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik bedacht me net dat ik in het geval van deze vraag ook even naar de uitwerkingen kan kijken van het betreffende examen. Dit was namelijk een vraag in mijn boek, dat in een examen zat. Het blijkt dus dat ik te ver heb doorgedacht, aangezien het antwoord eigenlijk het maximum van sin is.
Ik ieder geval bedankt.
Ik ieder geval bedankt.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ok, het is nu allemaal duidelijk dus?quote:Op zaterdag 21 mei 2011 17:30 schreef Pipo1234 het volgende:
Ik bedacht me net dat ik in het geval van deze vraag ook even naar de uitwerkingen kan kijken van het betreffende examen. Dit was namelijk een vraag in mijn boek, dat in een examen zat. Het blijkt dus dat ik te ver heb doorgedacht, aangezien het antwoord eigenlijk het maximum van sin is.
Ik ieder geval bedankt.
The biggest argument against democracy is a five minute discussion with the average voter.


Als je op zoek bent naar punten waar de afgeleide van een functie een minimum of een maximum bereikt, dan kun je kijken waar de afgeleide van de afgeleide oftewel de tweede afgeleide f''(x) van de oorspronkelijke functie f(x) gelijk is aan nul. In de grafiek van f(x) zijn dergelijke punten buigpunten, en die heeft de grafiek van je functie inderdaad.quote:Op zaterdag 21 mei 2011 17:23 schreef Pipo1234 het volgende:
[..]
Je hebt gelijk. Dat is ook zo, aangezien ik het punt moet vinden waar de uitkomst van de afgeleide van die functie het kleinste is. Op dat punt is namelijk de toename het kleinste en dat heeft weer te maken met de opdracht. Ik raak er zelf een beetje van in de war, dus misschien had ik het niet toegelicht.


Ik zal deze toch maar even voordoen, want ik zie nu dat je voor deze opgave niet persé de tweede afgeleide nodig hebt.quote:Op zaterdag 21 mei 2011 17:51 schreef Riparius het volgende:
[..]
Als je op zoek bent naar punten waar de afgeleide van een functie een minimum of een maximum bereikt, dan kun je kijken waar de afgeleide van de afgeleide oftewel de tweede afgeleide f''(x) van de oorspronkelijke functie f(x) gelijk is aan nul. In de grafiek van f(x) zijn dergelijke punten buigpunten, en die heeft de grafiek van je functie inderdaad.
De functie die je hebt is:
(1) f(x) = (70∙sin x)/sin(x + ¼π)
Afgeleide bepalen met de quotiëntregel levert:
(2) f'(x) = (70∙cos x∙sin(x + ¼π) - 70∙sin x∙cos(x + ¼π))/sin2(x + ¼π)
Nu kunnen we in de teller van dit quotiënt een factor 70 buiten haakjes halen. Bovendien geldt:
(3) sin(α-β) = sin α∙cos β - cos α∙sin β
En dus:
(4) cos x∙sin(x + ¼π) - sin x∙cos(x + ¼π) = sin((x + ¼π) - x) = sin(¼π) = ½√2
De afgeleide wordt dus:
(5) f'(x) = (35∙√2)/sin2(x + ¼π)
Deze afgeleide kan niet nul worden, maar bereikt wel een minimum als geldt:
(6) sin2(x + ¼π) = 1
En dus:
(7) sin(x + ¼π) = 1 ∨sin(x + ¼π) = -1
En dus:
(8) x + ¼∙π = ½∙π + 2∙k∙π ∨ x + ¼∙π = (3/2)∙π + 2∙k∙π
Dus:
(9) x = ¼∙π + 2∙k∙π ∨ x = (5/4)∙π + 2∙k∙π, k ∈ Z


Oké. Dan heb ik in ieder geval goed benaderd, alleen had ik het wordt beter moeten uitwerken geloof ik. Wat er bij punt 3 gebeurd is mij trouwens onbekend, hoewel ik deze regel herken van logaritmen, maar ik wist niet dat dit ook gold bij sin/cos.quote:Op zaterdag 21 mei 2011 19:14 schreef Riparius het volgende:
[..]
Ik zal deze toch maar even voordoen, want ik zie nu dat je voor deze opgave niet persé de tweede afgeleide nodig hebt.
De functie die je hebt is:
...
Bedankt voor de uitwerking!
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je bedoelt log(x+y)=log(x) log(y)? Dat is wel wat anders dan dit... Riparius gebruikt een standaard goniometrische identiteiten:quote:Op zaterdag 21 mei 2011 19:29 schreef Pipo1234 het volgende:
[..]
Oké. Dan heb ik in ieder geval goed benaderd, alleen had ik het wordt beter moeten uitwerken geloof ik. Wat er bij punt 3 gebeurd is mij trouwens onbekend, hoewel ik deze regel herken van logaritmen, maar ik wist niet dat dit ook gold bij sin/cos.
Bedankt voor de uitwerking!
sin(a+b) = sin(a) cos(b) + cos(a) sin(b)
samen met
sin(-a)=-sin(a)


Oké. Dacht even dat het hetzelfde wasquote:Op zaterdag 21 mei 2011 19:32 schreef thenxero het volgende:
[..]
Je bedoelt log(x+y)=log(x) log(y)? Dat is wel wat anders dan dit... Riparius gebruikt een standaard goniometrische identiteiten:
sin(a+b) = sin(a) cos(b) + cos(a) sin(b)
samen met
sin(-a)=-sin(a)
Edit: Ik zit even in mijn boek te kijken en zie net dat ik dat in het aankomende hoofdstuk ga krijgen. Vandaar dat ik het nog niet echt kende, had het wel langs zien komen toen ik e.e.a. op internet opzocht.
[ Bericht 7% gewijzigd door Pipo1234 op 21-05-2011 19:43:57 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dat niet, maar het grappige is dat je op een dieper niveau toch wel enigszins gelijk hebt. De zogeheten additietheorema's uit de goniometrie hangen samen met de exponentiële (en dus ook logaritmische) functie. Maar dat verband is alleen te begrijpen middels complexe getallen.quote:Op zaterdag 21 mei 2011 19:36 schreef Pipo1234 het volgende:
[..]
Oké. Dacht even dat het hetzelfde was
De additietheorema's uit de goniometrie worden tegenwoordig beroerd (of helemaal niet) uitgelegd in schoolboeken terwijl ze wel fundamenteel zijn. Bestudeer dit maar eens als je een bewijs wil zien voor deze formules.quote:Edit: Ik zit even in mijn boek te kijken en zie net dat ik dat in het aankomende hoofdstuk ga krijgen. Vandaar dat ik het nog niet echt kende, had het wel langs zien komen toen ik e.e.a. op internet opzocht.
[ Bericht 0% gewijzigd door Riparius op 21-05-2011 22:37:55 ]


Andere vraag, wellicht dat dit makkelijker is:
stel ik heb 2 reeksen van getallen in het domein [0,2pi]
Dus reeks 1 heeft een aantal getallen, en reeks 2 heeft aantal getallen. We nemen aan dat ze evenveel hebben.
Nou zou je het volgende kunnen zeggen:
var(sin(reeks 1 - reeks 2)) = 0, als ze perfect gelijk lopen, en 0.5 als dat compleet niet zo is.
Ik snap niet echt hoe ze dit doen, of hoe ze (paper) een benadering hiervan maken, ze melden recursive numerical approximation... ik heb dat nog niet eerder gezien in me AI studie.. :|
Iemand die me gemakkelijk kan uitleggen hoe/wat? Want hun variance is niet de gebruikelijke als ze menen 0.5 als maximaal te krijgen (met wat simpele experimentjes haal je zo 2.2 etc b.v. met zelfde soort getallen).
stel ik heb 2 reeksen van getallen in het domein [0,2pi]
Dus reeks 1 heeft een aantal getallen, en reeks 2 heeft aantal getallen. We nemen aan dat ze evenveel hebben.
Nou zou je het volgende kunnen zeggen:
var(sin(reeks 1 - reeks 2)) = 0, als ze perfect gelijk lopen, en 0.5 als dat compleet niet zo is.
Ik snap niet echt hoe ze dit doen, of hoe ze (paper) een benadering hiervan maken, ze melden recursive numerical approximation... ik heb dat nog niet eerder gezien in me AI studie.. :|
Iemand die me gemakkelijk kan uitleggen hoe/wat? Want hun variance is niet de gebruikelijke als ze menen 0.5 als maximaal te krijgen (met wat simpele experimentjes haal je zo 2.2 etc b.v. met zelfde soort getallen).


Ze hoeven niet perfect gelijk te lopen (als in alle termen zijn gelijk) om te krijgen dat sin(reeks1 - reeks2)=0. En waarom anders 1/2?
Bovendien, wat zijn je stochastische variabelen?
Bovendien, wat zijn je stochastische variabelen?


Ik begrijp een bepaald wiskundig stukje niet van een wikipedia artikel...
http://en.wikipedia.org/w(...)_distance#Definition
Het betreft zich om: t is half the number of transpositiont
http://en.wikipedia.org/w(...)_distance#Definition
Het betreft zich om: t is half the number of transpositiont
Wat wordt er bedoeld met transpositiont? Waarom is dus in het bovenstaande voorbeeld t=0 en verder in het artikel bij de voorbeelden, MARTHA en MARHTA t=2?quote:Two characters from s1 and s2 respectively, are considered matching only if they are not farther than .
Each character of s1 is compared with all its matching characters in s2. The number of matching (but different sequence order) characters divided by the numeric value '2' defines the number of transpositions. For example. in comparing CRATE with TRACE, only 'R' 'A' 'E' are the matching characters, i.e, m=3. Although 'C', 'T' appear in both strings, they are farther than 1.5, i.e., (5/2)-1=1.5. Therefore, t=0 . In DwAyNE versus DuANE the matching letters are already in the same order D-A-N-E, so no transpositions are needed.


Das de grap, het enige wat ze vermelden is hetgene wat ik opnoemde. En idd, ze hoeven niet perfect te lopen. Het hele paper lijkt achteraf nogal vreemd, gebruik hun stuff, maar kan op geen enkele manier iets reproduceren zoals zij hebben :| en dan dit var(sin(phi - rho)) enzo :|quote:Op zondag 22 mei 2011 00:54 schreef thenxero het volgende:
Ze hoeven niet perfect gelijk te lopen (als in alle termen zijn gelijk) om te krijgen dat sin(reeks1 - reeks2)=0. En waarom anders 1/2?
Bovendien, wat zijn je stochastische variabelen?


Een transpositie is een verwisseling van twee letters. In dat stukje gaan ze matchende letters in de juiste volgorde zetten, de overige letters niet. Eerst kijken ze welke letters matchen, en bij CRATE/TRACE is dat alleen RAE en dat staat al in beide woorden al in dezelfde volgorde dus hoef je ook niks te verwisselen om het in de juiste volgorde te krijgen.quote:Op zondag 22 mei 2011 02:05 schreef Dale. het volgende:
Ik begrijp een bepaald wiskundig stukje niet van een wikipedia artikel...
http://en.wikipedia.org/w(...)_distance#Definition
Het betreft zich om: t is half the number of transpositiont
[..]
Wat wordt er bedoeld met transpositiont? Waarom is dus in het bovenstaande voorbeeld t=0 en verder in het artikel bij de voorbeelden, MARTHA en MARHTA t=2?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dus als ik het goed begrijp is bij MARTHA en MARHTA t=1 omdat....quote:Op zondag 22 mei 2011 10:45 schreef GlowMouse het volgende:
[..]
Een transpositie is een verwisseling van twee letters. In dat stukje gaan ze matchende letters in de juiste volgorde zetten, de overige letters niet. Eerst kijken ze welke letters matchen, en bij CRATE/TRACE is dat alleen RAE en dat staat al in beide woorden al in dezelfde volgorde dus hoef je ook niks te verwisselen om het in de juiste volgorde te krijgen.
floor(6/2)-1 = 2, letters worden gezien als matching als ze binnen een range van [i-2,i+2], i is de index van de huidige letter. T/H en H/T voldoen hierbeide aan en worden dus als matching gezien dus m = 6. Verder omdat beide letters 2 keer verwisseld moeten worden T/H & H/T is het aantal transposities dus 2. Vervolgens delen door 2, 2/2 = 1 = t.
??
Is het dan ook zo dat het aantal transposities bij MAHTRA en MARTHA daar ook 2 is? H/R en R/H, dus 2/2 = 1 = t


Wikipedia legt het fout uit, zie http://www.amstat.org/sec(...)/papers/1990_056.pdf pag. 3 bovenaan voor de originele uitleg: het aantal transposities t wordt gedefinieerd als het aantal mismatches gedeeld door 2 (dit wijkt af van wat ik normaal onder transposities zou verstaan). Wikipedia zegt "t is half the number of transpositions" en dat klopt dus niet.
Bij MARTHA / MARHTA vergelijk je MARTHA met MARHTA, 2 mismatches, t=1.
Bij MAHTRA / MARTHA vergelijk je MAHTRA met MARTHA, 2 mismatches, t=1.
Bij MARTHA / MARHTA vergelijk je MARTHA met MARHTA, 2 mismatches, t=1.
Bij MAHTRA / MARTHA vergelijk je MAHTRA met MARTHA, 2 mismatches, t=1.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Okquote:Op zondag 22 mei 2011 13:40 schreef GlowMouse het volgende:
Wikipedia legt het fout uit, zie http://www.amstat.org/sec(...)/papers/1990_056.pdf pag. 3 bovenaan voor de originele uitleg: het aantal transposities t wordt gedefinieerd als het aantal mismatches gedeeld door 2 (dit wijkt af van wat ik normaal onder transposities zou verstaan). Wikipedia zegt "t is half the number of transpositions" en dat klopt dus niet.
Bij MARTHA / MARHTA vergelijk je MARTHA met MARHTA, 2 mismatches, t=1.
Bij MAHTRA / MARTHA vergelijk je MAHTRA met MARTHA, 2 mismatches, t=1.


Nee, de convergentiesnelheid kan van a afhangen, zoek maar een voorbeeldje.quote:Op zondag 22 mei 2011 13:46 schreef thenxero het volgende:
Als iets uniform convergeert op (-a,a) voor iedere a in |R, convergeert het dan ook uniform op |R?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja, dat dacht ik ook.
Ik wil bewijzen dat de MacLaurin reeks van de sin en cos uniform convergeren. Heb je een hint?
Ik wil bewijzen dat de MacLaurin reeks van de sin en cos uniform convergeren. Heb je een hint?


Ik doelde op bv. fn(x) = x/n.
Hint: om iets te bewijzen, moet het allereerst waar zijn.
Hint: om iets te bewijzen, moet het allereerst waar zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Is het niet zo dan?quote:Op zondag 22 mei 2011 14:00 schreef GlowMouse het volgende:
Ik doelde op bv. fn(x) = x/n.
Hint: om iets te bewijzen, moet het allereerst waar zijn.


Kun je mij een n geven zodanig dat de fout tussen de reeks van de eerste n termen en de echte sinus ten hoogste 1 is?quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oh hij convergeert denk ik toch niet uniform. Als je de grafiek bekijkt van de eerste k termen zie je een aantal golfjes maar daarna gaat hij gewoon naar +inf en -inf. Als je x heel groot maakt wordt de afwijking voor een eindig aantal termen oneindig groot. Dus hij convergeert niet uniform.
Zou wel stom zijn... mijn werkcollegebegeleider zei dat ik dat kon bewijzen om zo aan te tonen dat de afgeleide van de sinus de cosinus is, want met uniforme convergentie mag je de afgeleide binnen de som halen en is het duidelijk.
Hmmm....
Zou wel stom zijn... mijn werkcollegebegeleider zei dat ik dat kon bewijzen om zo aan te tonen dat de afgeleide van de sinus de cosinus is, want met uniforme convergentie mag je de afgeleide binnen de som halen en is het duidelijk.
Hmmm....


Je probeert iets te bewijzen wat niet klopt op R (of C). Kijk eens naar de Weierstraß M-test.quote:Op zondag 22 mei 2011 13:54 schreef thenxero het volgende:
Ja, dat dacht ik ook.
Ik wil bewijzen dat de MacLaurin reeks van de sin en cos uniform convergeren. Heb je een hint?


Laatste keer of ik het echt goed vat:quote:The number of transpositions is computed as follows: The first assigned character on one string is compared to the first assigned character on the other string. If the characters are not the same, half of a transpositions has occured. Then the second assigned character on one string is compared to the second assigned character on the other string, etc. The number of mismatched characters is divided by two to yield the number of transpositions.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | MARTHA MARHTA ------ xx (2 mismatches, t = 1) cunningham cunnigham ---------- xxxxx (5 mismatches, t = 2.5) dixon dicksonx -------- xxxxxx (6 mismatches, t = 3) |


ik heb ff een snelle (redelijk makkelijke) vraag;
ik moet voor me scripties veel van dit soort formules maken.
welke functie is dat in microsoft word?
ik moet voor me scripties veel van dit soort formules maken.
welke functie is dat in microsoft word?


Leer latex, gaat heel wat gemakkelijkerquote:Op zondag 22 mei 2011 14:28 schreef ukga het volgende:
ik heb ff een snelle (redelijk makkelijke) vraag;
ik moet voor me scripties veel van dit soort formules maken.
[ link | afbeelding ]
welke functie is dat in microsoft word?


latex?quote:Op zondag 22 mei 2011 14:29 schreef koffiegast het volgende:
[..]
Leer latex, gaat heel wat gemakkelijker
edit; hm ff gegoogled


Ja die zocht ik. maar die moet ik dus installeren want die staat niet tussen het lijstje van 'objecten'quote:


Ik heb het door. Is er een andere manier om te rechtvaardigen om de d/dx binnen de som gehaald mag worden zonder uniforme convergentie te hebben?quote:Op zondag 22 mei 2011 14:22 schreef Riparius het volgende:
[..]
Je probeert iets te bewijzen wat niet klopt op R (of C). Kijk eens naar de Weierstraß M-test.


Ik gebruik voor het betere formulewerk Texmaker op Ubuntu. Die is crossplatform, dus je kunt hem ook in Windows gebruiken. Moet je wel even Latex leren, maar dat is niet zo moeilijk en het levert je een hoop gemak op. Mocht je een vraag hebben dan is hier vast wel iemand die je wil helpen.
http://www.xm1math.net/texmaker/
http://www.xm1math.net/texmaker/
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je hebt op elk begrensd interval [-a, a] wel uniforme convergentie.quote:Op zondag 22 mei 2011 14:55 schreef thenxero het volgende:
[..]
Ik heb het door. Is er een andere manier om te rechtvaardigen om de d/dx binnen de som gehaald mag worden zonder uniforme convergentie te hebben?


Zoals ik zelf net al noemde. Maar wat heb ik daaraan?quote:Op zondag 22 mei 2011 14:58 schreef thabit het volgende:
[..]
Je hebt op elk begrensd interval [-a, a] wel uniforme convergentie.
edit: ik heb dus op [-pi,pi] uniforme convergentie en ik heb al bewezen dat de sinusreeks 2pi-periodiek is dus is de afgeleide ook 2pi periodiek. Op [-pi,pi] is de afgeleide gelijk aan cosinus dus overal gelijk aan cosinus?


Oke top man! thanks. ik heb het zojuist geinstalleerd (vanaf de officie cd)quote:Op zondag 22 mei 2011 14:57 schreef Ron.Jeremy het volgende:
http://www.denhulster.nl/(...)Formule%20editor.pdf
Hier staat hoe die geactiveerd moet worden.


Nee, je kunt alleen strings van gelijke lengte vergelijken.quote:Op zondag 22 mei 2011 14:28 schreef Dale. het volgende:
[..]
Laatste keer of ik het echt goed vat:
[ code verwijderd ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Daar lees ik niks over...?quote:Op zondag 22 mei 2011 15:12 schreef GlowMouse het volgende:
[..]
Nee, je kunt alleen strings van gelijke lengte vergelijken.


Of beter nog: hij is termsgewijs differentieerbaar in [-a,a] voor iedere a dus termsgewijs diffbaar voor iedere x in |R. Want differentieerbaarheid is wel een puntsgewijze eigenschap.quote:Op zondag 22 mei 2011 15:03 schreef thenxero het volgende:
[..]
Zoals ik zelf net al noemde. Maar wat heb ik daaraan?
edit: ik heb dus op [-pi,pi] uniforme convergentie en ik heb al bewezen dat de sinusreeks 2pi-periodiek is dus is de afgeleide ook 2pi periodiek. Op [-pi,pi] is de afgeleide gelijk aan cosinus dus overal gelijk aan cosinus?


http://www.amstat.org/sec(...)/papers/1990_056.pdf pag. 3 tweede kolom, bovenaan.quote:
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben bezig met somformules en verdubbelingsformules. Nu moet ik de volgende opgave met behulp van die twee dingen oplossen, alleen zie ik het even niet: tan t = sin 2t
Wil iemand mij een aanwezig geven? Ik kom niet verder dan tan naar sin/cos te herleiden en sin 2t naar 2 sin t keer cos t.
Wil iemand mij een aanwezig geven? Ik kom niet verder dan tan naar sin/cos te herleiden en sin 2t naar 2 sin t keer cos t.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik loop vast met partieel integreren,
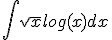
als ik neem
g = x^(1/2)
f' = log(x)
met de regel (fg) - int(g'f)
dan krijg ik
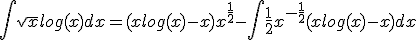
Die tweede integraal lijkt me nog moeilijker op te lossen dan sqrt(x)log(x), niet?
En als ik g en f' andersom neem, dus:
g = log(x)
f' = x^(1/2)
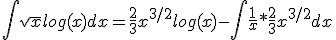
Wat er ook niet veel makkelijker uit ziet..
als ik neem
g = x^(1/2)
f' = log(x)
met de regel (fg) - int(g'f)
dan krijg ik
Die tweede integraal lijkt me nog moeilijker op te lossen dan sqrt(x)log(x), niet?
En als ik g en f' andersom neem, dus:
g = log(x)
f' = x^(1/2)
Wat er ook niet veel makkelijker uit ziet..


Die tweede term (1/x)*x2/3 kun je schrijven als
x-1 x2/3 = x-1/3.
x-1 x2/3 = x-1/3.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik kan je ook MathType aanraden, ik vind dat zelf nog wat fijner werken.quote:Op zondag 22 mei 2011 15:07 schreef ukga het volgende:
[..]
Oke top man! thanks. ik heb het zojuist geinstalleerd (vanaf de officie cd)
Beneath the gold, bitter steel


Wel, laten we eens kijken ...quote:Op zondag 22 mei 2011 21:09 schreef Pipo1234 het volgende:
Ik ben bezig met somformules en verdubbelingsformules. Nu moet ik de volgende opgave met behulp van die twee dingen oplossen, alleen zie ik het even niet: tan t = sin 2t
Wil iemand mij een aanwezig geven? Ik kom niet verder dan tan naar sin/cos te herleiden en sin 2t naar 2 sin t keer cos t.
De vergelijking is:
(1) tan t = sin 2t
Gebruik van tan t = sin t / cos t en sin 2t = 2∙sin t∙cos t geeft, zoals je zelf al had gevonden:
(2) sin t / cos t = 2∙sin t∙cos t
Nu wil ik de breuk in het linkerlid kwijt raken. Dat kunnen we doen door beide leden met cos t te vermenigvuldigen. Dit geeft:
(3) sin t = 2∙sin t∙cos2t
Hierbij is cos2t de conventionele notatie voor het kwadraat van cos t. Nu herleiden we het rechterlid op nul door van beide leden 2∙sint∙cos2t af te trekken. Dit geeft:
(4) sin t - 2∙sin t∙cos2t = 0
Nu hebben de twee termen in het linkerlid een factor sin t gemeenschappelijk, die ik dus buiten haakjes kan halen. Dit geeft:
(5) sin t∙(1 - 2∙cos2t) = 0
Hier stop ik even. Bedenk nu zelf hoe je deze vergelijking verder (exact) oplost.


Cos2 herleid naar 1 - sin2:quote:Op zondag 22 mei 2011 21:32 schreef Riparius het volgende:
...
Hier stop ik even. Bedenk nu zelf hoe je deze vergelijking verder (exact) oplost.
(6) sin t ∙ (1 - 2(1 - sin2t)) = 0
Vereenvoudigd/vermenigvuldigd:
(7) -sin t + 2sin3t = 0
Ontbonden in factoren:
(8) ( sin t )( -1 + 2sin t2 ) => sin t = 0 v -1 + 2sin2 t = 0
Antwoord:
t = k ∙ 2π v t = ¼π + k ∙ 2π
Is dit iets? Ik geloof overigens dat ik bij stap 5 vastzat, want dat zag ik eerst niet.
[ Bericht 0% gewijzigd door Pipo1234 op 22-05-2011 22:21:20 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Tot en met stap (8) klopt het (behalve dat het 2sin2 t moet zijn ipv 2t2, maar dat is een typfout geloof ik). Het antwoord wat je er daarna uitkrijgt zou ik nog eens goed nakijkenquote:Op zondag 22 mei 2011 22:10 schreef Pipo1234 het volgende:
[..]
Cos2 herleid naar 1 - sin2:
(6) sin t ∙ (1 - 2(1 - sin2t)) = 0
Vereenvoudigd/vermenigvuldigd:
(7) -sin t + 2sin3t = 0
Ontbonden in factoren:
(8) ( sin t )( -1 + 2t2 ) => sin t = 0 v -1 + 2sin2 t = 0
Antwoord:
t = k ∙ 2π v t = ¼ + k ∙ 2π
Is dit iets? Ik geloof overigens dat ik bij stap 5 vastzat, want dat zag ik eerst niet.
Edit: Let trouwens goed op, sin2 t betekent (sin(t))2, dus sin t * t2 is niet sin3 t, maar t2*sin(t). Ik weet niet of je dat dacht, of dat het inderdaad een typfout was, maar let er goed op.
The biggest argument against democracy is a five minute discussion with the average voter.


Há. Het moet 1/4 pi zijn. Het is alweer laat... Bedank voor de opmerkzaamheid.quote:Op zondag 22 mei 2011 22:17 schreef M.rak het volgende:
[..]
Tot en met stap (8) klopt het (behalve dat het 2sin2 t moet zijn ipv 2t2, maar dat is een typfout geloof ik). Het antwoord wat je er daarna uitkrijgt zou ik nog eens goed nakijken.
Het is trouwens gewoon een typfout.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


waarom niet gelijk cos²t = 1/2 oplossen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Goede vraag? Ik ben nog redelijk onbekend met dit soort dingen, dus ik weet niet wat je bedoelt.quote:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dan is (5) ook nulquote:Op zondag 22 mei 2011 22:23 schreef Pipo1234 het volgende:
[..]
Goede vraag? Ik ben nog redelijk onbekend met dit soort dingen, dus ik weet niet wat je bedoelt.


Na riparius heb je sin t = 0 V 2-cos t = 0.quote:Op zondag 22 mei 2011 22:23 schreef Pipo1234 het volgende:
[..]
Goede vraag? Ik ben nog redelijk onbekend met dit soort dingen, dus ik weet niet wat je bedoelt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Natuurlijk.quote:Op zondag 22 mei 2011 22:24 schreef GlowMouse het volgende:
[..]
Na riparius heb je sin t = 0 V 2-cos t = 0.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


In ieder geval bedankt allemaal! Ik ga maar eens richting mijn bed. Morgen weer een dag vol met wiskunde. 
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik zou morgen trouwens wel nog eens naar je oplossing vanquote:Op zondag 22 mei 2011 22:28 schreef Pipo1234 het volgende:
In ieder geval bedankt allemaal! Ik ga maar eens richting mijn bed. Morgen weer een dag vol met wiskunde.
hier kijken, met jouw oplossing heb je namelijk niet alle oplossingen gevondenquote:Ontbonden in factoren:
(8) ( sin t )( -1 + 2sin t2 ) => sin t = 0 v -1 + 2sin2 t = 0
Antwoord:
t = k ∙ 2π v t = ¼π + k ∙ 2π
The biggest argument against democracy is a five minute discussion with the average voter.


Je bent wel goed op weg, hoewel je het jezelf enerzijds wat te moeilijk maakt en anderzijds ook nogal wat vergeet en stappen overslaat.quote:Op zondag 22 mei 2011 22:10 schreef Pipo1234 het volgende:
[..]
Cos2 herleid naar 1 - sin2:
(6) sin t ∙ (1 - 2(1 - sin2t)) = 0
Vereenvoudigd/vermenigvuldigd:
(7) -sin t + 2sin3t = 0
Ontbonden in factoren:
(8) ( sin t )( -1 + 2sin2t ) => sin t = 0 v -1 + 2sin2 t = 0
Antwoord:
t = k ∙ 2π v t = ¼π + k ∙ 2π
Is dit iets? Ik geloof overigens dat ik bij stap 5 vastzat, want dat zag ik eerst niet.
Na de (overbodige!) substitutie cos2t = 1 - sin2t kom je inderdaad uit op
sin t = 0 ∨ -1 + 2∙sin2t = 0
Maar nu vergeet je een deel van de mogelijke oplossingen, want als:
sin t = 0 ∨sin2t = ½
Dan geldt:
sin t = 0 ∨sin t = ½√2 ∨sin t = -½√2
Verder vergeet je te bedenken dat sin t niet alleen nul is voor t = 2kπ maar voor t = kπ. Maak weer even een schetsje van de eenheidcirkel als je dit niet ziet. Als oplossingen krijgen we nu:
t = kπ ∨ t = ¼π + 2kπ ∨ t = ¾π + 2kπ ∨ t = -¼π + 2kπ ∨ t = -¾π + 2kπ, k∈Z
En dit kun je weer vereenvoudigen tot:
t = kπ ∨ t = ¼π + kπ ∨ t = ¾π + kπ, k∈Z
En dit kun je nog combineren tot:
t = kπ ∨ t = ¼π + ½kπ, k∈Z
Maar: het kan veel eleganter. Je hebt net de formules voor de dubbele hoek geleerd. Door β=α te nemen in de somformule voor cos(α+β) vinden we:
(1) cos 2α = cos2α - sin2α
Er zijn nog twee andere nuttige formules voor de cosinus van de dubbele hoek, die we vinden door sin2α = 1 - cos2α resp. cos2α = 1 - sin2α te substitueren in (1). Dit geeft:
(2) cos 2α = 2∙cos2α - 1
En:
(3) cos 2α = 1 - 2∙sin2α
Hier kunnen we gebruik maken van (2). De vergelijking wordt dan:
(4) sin t∙(-cos 2t) = 0
En dus:
(5) sin t∙cos 2t = 0
En dus:
(6) sin t = 0 ∨cos 2t = 0
Werk dit even verder uit.
[ Bericht 0% gewijzigd door Riparius op 23-05-2011 02:23:44 ]


Dat gaat helaas te ver voor mij. Ik zie namelijk niet wat ik na stap 6 moet doen... Ik krijg het idee dat ik hier echt ballen van snap, want ik ben totaal vastgelopen in mijn stof. Zit nu al een uur naar deze opgave te staren: Stel een formule voor cos 3t op waarin alleen cos t en machten van cos t voorkomen. Vervolgens kom ik niet verder dan: cos 2t + t => cos 2t · cos t - sin 2t · sin t.quote:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Als je nu cos2t en sin2t omschrijft, ben je er al bijna hoor.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Bedoel je zo:quote:Op maandag 23 mei 2011 14:13 schreef GlowMouse het volgende:
Als je nu cos2t en sin2t omschrijft, ben je er al bijna hoor.
cos 3t = (1 - 2 sin2 t) · cos t - (2 sin t · cos t) · sin t
Ik zie eerlijk gezegd niet hoe ik hier verder mee moet... vooral dat tweede deel kan ik niks mee.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


OK. Niet in paniek raken of gaan wanhopen. Ik ga eerst nog even de bespreking van de vergelijking van gisteren afronden. Ik pak de draad weer even op bij mijn eerste post hierover. Ik was gekomen tot:quote:Op maandag 23 mei 2011 14:00 schreef Pipo1234 het volgende:
[..]
Dat gaat helaas te ver voor mij. Ik zie namelijk niet wat ik na stap 6 moet doen... Ik krijg het idee dat ik hier echt ballen van snap, want ik ben totaal vastgelopen in mijn stof. Zit nu al een uur naar deze opgave te staren: Stel een formule voor cos 3t op waarin alleen cos t en machten van cos t voorkomen. Vervolgens kom ik niet verder dan: cos 2t + t => cos 2t · cos t - sin 2t · sin t.
(5) sin t∙(1 - 2∙cos2t) = 0
Een product van twee factoren kan alleen nul zijn als (tenminste) één van de twee factoren nul is, dus dit levert dan op sin t = 0 óf cos2t = ½ waaruit weer volgt sin t = 0 óf cos t = ½√2 óf cos t = -½√2. Drie mogelijkheden dus, en voor elk van deze drie mogelijkheden moet je dan nagaan welke waarden van t voldoen.
Maar, zoals gezegd, het kan eleganter. Met behulp van de identiteit cos 2t = 2∙cos2t - 1 herleiden we (5) tot:
(6) sin t∙cos 2t = 0
En dus geldt:
(7) sin t = 0 ∨cos 2t = 0
Aan de hand van de eenheidscirkel zien we gemakkelijk dat de sinus (y-coördinaat) nul wordt voor kπ en dat de cosinus (x-coördinaat) nul wordt voor ½π + kπ. Dus krijgen we:
(8) t = kπ ∨2t = ½π + kπ
En dus:
(9) t = kπ ∨t = ¼π + ½kπ, k∈Z
Zo eenvoudig kan het dus. We hoeven nu niet alle oplossingen die we op de andere manier voor cos2t = ½ krijgen apart te bekijken.
Nu je vraag over de herleiding van een identiteit voor cos 3t uitgedrukt in cos t. Deze opgave sluit trouwens naadloos aan bij wat ik gisteren al opmerkte over de drie verschillende identiteiten voor de cosinus van de dubbele hoek, dus ik vraag me toch af of je mijn antwoorden wel goed bestudeert.
Maar goed. We gaan nog even uit van de somformule voor cos(α+β). Deze luidt, zoals bekend:
(10) cos(α+β) = cos α∙cos β - sin α∙sin β
We nemen nu α = 2t en β = t, zodat α+β = 3t. Dit geeft:
(11) cos 3t = cos 2t∙cos t - sin 2t∙sin t
Nu weet je ook dat geldt:
(12) cost 2t = 2∙cos2t - 1 en sin 2t = 2∙sin t∙cos t
Substitutie van (12) in (11) levert:
(13) cos 3t = (2∙cos2t - 1)∙cos t - 2∙sin t∙cos t∙sin t
Uitwerken geeft:
(14) cos 3t = 2∙cos3t - cos t - 2∙sin2t∙cos t
Nu is ook:
(15) sin2t = 1 - cos2t
Substitutie van (15) in (14) geeft dus:
(16) cos 3t = 2∙cos3t - cos t - 2∙(1 - cos2t)∙cos t
Weer haakjes uitwerken:
(17) cos 3t = 2∙cos3t - cos t - 2∙cos t + 2∙cos3t
Nu nog termen met dezelfde macht samennemen, en we krijgen:
(18) cos 3t = 4∙cos3t - 3∙cos t
[ Bericht 0% gewijzigd door Riparius op 23-05-2011 15:47:20 ]


als je de haakjes wegwerkt dan heb je alleen nog maar cos t en sin²t (en wat 1'en en 2'en). Die sin²t kun je makkelijk omzetten in cos²t.quote:Op maandag 23 mei 2011 14:32 schreef Pipo1234 het volgende:
[..]
Bedoel je zo:
cos 3t = (1 - 2 sin2 t) · cos t - (2 sin t · cos t) · sin t
Ik zie eerlijk gezegd niet hoe ik hier verder mee moet... vooral dat tweede deel kan ik niks mee.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Oké. Het lijkt zo simpel als jij het zo uitlegt, maar ik raak altijd in de war door alle haakjes en vermenigvuldigingen. Ik lees trouwens al jouw uitleg uitvoerig, want ik wil Wiskunde B graag halen en heb al gemerkt dat jij er zeer veel van weet. Daarvoor mijn dank. Helaas blijft niet alles altijd even goed hangen en gaan sommige dingen nog te ver voor mij om het te snappen.quote:Op maandag 23 mei 2011 14:35 schreef Riparius het volgende:
[..]
...
Nu nog termen met dezelfde macht samennemen, en we krijgen:
(18) cos 3t = 4∙cos3t - 3∙cos t
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dat alles zo simpel lijkt als ik het uitleg is iets wat ik veel vaker hoor. Het zouden didactische kwaliteiten kunnen zijn, maar ik heb eerder het idee dat er tegenwoordig niet meer goed les wordt gegeven, en van veel 'uitleg' (of wat dat voor door moet gaan) in Nederlandse (school)boeken gaan mijn haren ook recht overeind staan. Verder lijken veel dingen niet alleen simpel, ze zijn het ook. Je moet alleen wel heel consequent te werk gaan.quote:Op maandag 23 mei 2011 15:10 schreef Pipo1234 het volgende:
[..]
Oké. Het lijkt zo simpel als jij het zo uitlegt, maar ik raak altijd in de war door alle haakjes en vermenigvuldigingen.
Waar heb je deze wiskunde voor nodig als ik vragen mag? Om meer inzicht te krijgen moet je een goede balans zien te vinden tussen het doornemen en begrijpen van de 'theorie' en het maken van opgaven. Als je je pas in een stukje theorie gaat verdiepen op het moment dat je merkt dat je even niet verder komt met een opgave dan krijg je een veel te fragmentarisch beeld van de stof. Anderzijds is het ook zo dat je inderdaad veel moet oefenen en niet alleen maar kijken hoe anderen (of antwoordenboekjes) het doen. Je kunt ook geen profvoetballer worden door elke avond met een krat bier voor de TV te gaan zitten en naar voetbalwedstrijden te kijken.quote:Ik lees trouwens al jouw uitleg uitvoerig, want ik wil Wiskunde B graag halen en heb al gemerkt dat jij er zeer veel van weet. Daarvoor mijn dank. Helaas blijft niet alles altijd even goed hangen en gaan sommige dingen nog te ver voor mij om het te snappen.


Het verschil zit hem erin dat zelf doen lastiger is dan iets volgen dat voorgedaan wordt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


goddomme, leraar heeft 2 oefenopgaven gemaakt maar snap er geen kut van;
1: bij de rij Un=3n²+2n+4 hoort een recursieve formule van de vorm Un=Un-1+an-1 met U0=4.
Bereken a.
2: gegeven is de rij Wn=an+5 en 4ΣK=0 Wk = 49. Bereken a.
iemand die me dit kan uitleggen ?
1: bij de rij Un=3n²+2n+4 hoort een recursieve formule van de vorm Un=Un-1+an-1 met U0=4.
Bereken a.
2: gegeven is de rij Wn=an+5 en 4ΣK=0 Wk = 49. Bereken a.
iemand die me dit kan uitleggen ?


1. schrijf de formule voor Un-1 eens uit, en los dan de vergelijking Un=Un-1+an-1 op.
2. wat is 4ΣK?
2. wat is 4ΣK?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Wiskunde gaat een stuk beter als je (a) geen krachttermen gebruikt en (b) een beetje moeite doet voor een begrijpelijke en correcte notatie.quote:Op maandag 23 mei 2011 17:18 schreef Buschetta1 het volgende:
goddomme, leraar heeft 2 oefenopgaven gemaakt maar snap er geen kut van;
1: bij de rij Un=3n²+2n+4 hoort een recursieve formule van de vorm Un=Un-1+an-1 met U0=4.
Bereken a.
2: gegeven is de rij Wn=an+5 en 4ΣK=0 Wk = 49. Bereken a.
iemand die me dit kan uitleggen ?
Eerste opgave.
We hebben het voorschrift:
(1) Un = 3n2 + 2n + 4
Substitutie van (n-1) voor n in (1) geeft:
(2) Un-1 = 3(n-1)2 + 2(n-1) + 4 = 3n2 - 6n +3 + 2n - 2 + 4 = 3n2 - 4n + 5
Trekken we nu (2) van (1) af, dan krijgen we:
(3) Un - Un-1 = (3n2 + 2n + 4) - (3n2 - 4n + 5) = 6n - 1
Gegeven is dat geldt:
(4) Un - Un-1 = an - 1
Uit een vergelijking van (3) met (4) volgt nu direct dat a = 6
Tweede opgave.
Gegeven is
(5) Wn = an + 5
Uit je beroerde notatie maak ik op dat de termen Wk met k = 0..4 bij elkaar 49 opleveren. Dit zijn vijf termen van een rekenkundige rij.
De som van een aantal opeenvolgende termen van een rekenkundige rij is gelijk aan het gemiddelde van de eerste en de laatste term vermenigvuldigd met het aantal termen. Dus krijgen we:
(6) 5∙(5 + (4a + 5))/2 =49
(7) 5∙(4a + 10)/2 = 49
(8) 5∙(2a + 5) = 49
(9) 10a + 25 = 49
(10) 10a = 24
a = 2,4


Blijkbaar heeft Theodor Kaluza geleerd om te zwemmen uit een boekquote:Op maandag 23 mei 2011 15:42 schreef Riparius het volgende:
Je kunt ook geen profvoetballer worden door elke avond met een krat bier voor de TV te gaan zitten en naar voetbalwedstrijden te kijken.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Tja, iets met uitzonderingen die de regel bevestigen? Hoeveel mensen zouden er verzuipen als je ze in het diepe gooit na alleen het doorwerken van wat verhandelingen over hogere zwemkunst? Maar verdiep je je altijd in de biografie van mathematici (of fysici) die je 'tegenkomt'? Moet je eens een kijkje nemen (voor wiskundigen dan) op MacTutor. Ik kan me trouwens wel voorstellen waarom Kaluza je aanspreekt.quote:Op maandag 23 mei 2011 18:09 schreef Haushofer het volgende:
[..]
Blijkbaar heeft Theodor Kaluza geleerd om te zwemmen uit een boek


Voor een universitaire studie Informatica.quote:Op maandag 23 mei 2011 15:42 schreef Riparius het volgende:
[..]
Waar heb je deze wiskunde voor nodig als ik vragen mag? Om meer inzicht te krijgen moet je een goede balans zien te vinden tussen het doornemen en begrijpen van de 'theorie' en het maken van opgaven. Als je je pas in een stukje theorie gaat verdiepen op het moment dat je merkt dat je even niet verder komt met een opgave dan krijg je een veel te fragmentarisch beeld van de stof. Anderzijds is het ook zo dat je inderdaad veel moet oefenen en niet alleen maar kijken hoe anderen (of antwoordenboekjes) het doen. Je kunt ook geen profvoetballer worden door elke avond met een krat bier voor de TV te gaan zitten en naar voetbalwedstrijden te kijken.
Er wordt mij niets voorgedaan, afgezien van voorbeelden in mijn boek. Het enige dat me voorgedaan wordt, is hetgeen dat hier beschreven worden. Vandaar mijn consequente aanwezigheid hier.quote:Op maandag 23 mei 2011 15:49 schreef GlowMouse het volgende:
Het verschil zit hem erin dat zelf doen lastiger is dan iets volgen dat voorgedaan wordt.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Zware studie. Ik weet niet of je al eens wat aan programmeren hebt gedaan, maar daarbij moet je ook goed op de haakjes letten ... (en nog op veel meer natuurlijk).quote:Op maandag 23 mei 2011 19:41 schreef Pipo1234 het volgende:
[..]
Voor een universitaire studie Informatica.
Goede boeken voor zelfstudie zijn dun gezaaid in het Nederlandse taalgebied. De vaak genoemde boeken van Van De Craats bijvoorbeeld vind ik helemaal niet zo goed. Beter zijn wat publicaties van de OU die vroeger gewoon vrij op internet stonden, maar daar zat dacht ik geen of weinig goniometrie bij. Je zou voor een beknopt overzichtje wel even deze syllabus van een Vlaamse zomercursus door kunnen nemen. En dan heb je ook nog die zogeheten spijkerreeks. Deze bijvoorbeeld voor goniometrie.quote:Ik verdiep me in de theorie als het wordt beschreven in mijn boek. En dat is denk ik het probleem in mijn geval, want het is echt een boek voor de middelbare school. De meeste dingen gaan best goed, alleen is loop ik hier een beetje vast. Weet niet goed waarom, misschien is het gewoon het moment of ik doe gewoon moeilijk.
[..]
Tja, dan mis je toch wel een 'echte' docent. Eentje die ouderwets les geeft bedoel ik, geen veredelde cipier.quote:Er wordt mij niets voorgedaan, afgezien van voorbeelden in mijn boek. Het enige dat me voorgedaan wordt, is hetgeen dat hier beschreven worden. Vandaar mijn consequente aanwezigheid hier.


Van sin/cosinus moet je hoe dan ook eerst twee delen snappen, wil je die opgaven met verstand kunnen oplossen (en niet door willekeurig identiteiten toe te passen):quote:Op maandag 23 mei 2011 19:41 schreef Pipo1234 het volgende:
[..]
Voor een universitaire studie Informatica.Ik verdiep me in de theorie als het wordt beschreven in mijn boek. En dat is denk ik het probleem in mijn geval, want het is echt een boek voor de middelbare school. De meeste dingen gaan best goed, alleen is loop ik hier een beetje vast. Weet niet goed waarom, misschien is het gewoon het moment of ik doe gewoon moeilijk.
Heb je een grafische rekenmachine?
Pak pen en papier, teken twee x/y-assen onder elkaar, de x-as loopt van 0 tot 2Pi, de y-as van -3 naar 3. Een gebruik je voor de sinus, de ander voor de cosinus.
Voor de sinus teken je eerst de functie sin(x):
Zoals je ziet zijn belangrijke x-waardes:0, Pi/2, Pi, 3Pi/2, 2Pi.
De (daarbij behorende) belangrijke y-waardes zijn: 0,1,0,-1,0.
Nu ga je bekijken wat er met sinus gebeurt als je a,b,c of e gaat veranderen in de functie:
asin(e+bx)+c
Bekijk bijvoorbeeld eens hoe de functie 2sin(x) eruit ziet en teken die. Vraag je nu af wat de belangrijke x-waardes zijn en wat de belangrijke y-waardes. Vervang 'a' weer eens door een andere waarde dan 2 op je rekenmachine, hoe ziet die functie er dan uit? Trek hieruit een conclusie.
Hetzelfde doe je voor b,c en e. Nu kun je dus ook beredeneren hoe de functie 3sin(x/2 + 4)+1 uit moet zien.
En dit hele gedoe kun je ook doen voor de cosinus-functie.
Daarna kun je bijvoorbeeld in een afbeelding cos en sin tekenen en bepaalde identiteiten afleiden:
Waarom is sin(Pi/2-a)= cos(a) bijvoorbeeld ?
Nu kun je daarna ook nog eens de x-as gaan verlengen (naar bijvoorbeeld -2Pi): Wat gebeurt er nu met je functie asin(e+bx)+c en resp cosinus?
Zie je nu ook waarom de vraag: 'Voor welke x geld sin(x)=1' niet alleen x=Pi/2 als antwoord heeft, maar nog veel meer? Waar hangt het echte antwoord vanaf?
Tweede gedeelte gaat over de eenheidscirkel:
Volgens mij had je hier al wat info over gekregen dus zal ik daar kort over zijn:
Ga eens met de 'pijl' mee langs de cirkel en beschrijf wat er met sin en cos gebeurt.


Ik "programmeer" al heel lang. Begonnen in BASIC, later overgestapt op PHP en tegenwoordig voornamelijk BASH. Echt een serieuze taal zoals JAVA of C heb ik nooit geleerd, maar dat is vooral omdat het niet hoefde. Wil het wel graag, maar je gaat niet even C leren als je je verveeld. Mijn probleem is vooral dat ik de slordig ben. Van a naar b hobbel. Als ik bijvoorbeeld een recursieve functie schrijf, maak ik vaak fouten die makkelijk voorkomen konden worden. Maar dat met haakjes ken ik wel, echter ben ik gewend om daar heel strikt mee te zijn en dat hoeft in wiskunde ook niet altijd.quote:Op maandag 23 mei 2011 20:19 schreef Riparius het volgende:
[..]
Zware studie. Ik weet niet of je al eens wat aan programmeren hebt gedaan, maar daarbij moet je ook goed op de haakjes letten ... (en nog op veel meer natuurlijk).
Ja die mis ik zeker. Gelukkig lukt het me aardig zonder, alleen vereist het een hoop wilskracht en discipline om door te gaan. Helaas heb ik niet de juist vooropleiding om onvoorwaardelijk toegelaten te worden tot de genoemde studie. Ik heb alleen maar een propedeuse van een niet gerelateerde HBO-studie, dus dat is niet genoeg als je geen Wiskunde B hebt gedaan op de middelbare school. Ik heb de MAVO gedaan, dus dat schiet niet op.quote:Op maandag 23 mei 2011 20:19 schreef Riparius het volgende:
[..]
Tja, dan mis je toch wel een 'echte' docent. Eentje die ouderwets les geeft bedoel ik, geen veredelde cipier.
[ Bericht 2% gewijzigd door Pipo1234 op 23-05-2011 21:27:30 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ah, zo. Maar heb je wel eens wat programma's geschreven om (eenvoudige) wiskundige vraagstellingen op te lossen? Bijvoorbeeld het genereren van een lijst priemgetallen, of het ontbinden in priemfactoren van een getal (mooi met recursie te doen!), of het genereren van primitieve Pythagoreïsche tripletten of zo?quote:Op maandag 23 mei 2011 21:22 schreef Pipo1234 het volgende:
[..]
Ik "programmeer" al heel lang. Begonnen in BASIC, later overgestapt op PHP en tegenwoordig voornamelijk BASH. Echt een serieuze taal zoals JAVA of C heb ik nooit geleerd, maar dat is vooral omdat het niet hoefde. Wil het wel graag, maar je gaat niet even C leren als je je verveeld. Mijn probleem is vooral dat ik de slordig ben. Van a naar b hobbel. Als ik bijvoorbeeld een recursieve functie schrijf, maak ik vaak fouten die makkelijk voorkomen konden worden. Maar dat met haakjes ken ik wel, echter ben ik gewend om daar heel strikt mee te zijn en dat hoeft in wiskunde ook niet altijd.
[..]
Wat voor onderwerpen worden er gevraagd voor wat betreft wiskundige voorkennis? Ik ben niet zo op de hoogte met de huidige lesprogramma's.quote:Ja die mis ik zeker. Gelukkig lukt het me aardig zonder, alleen vereist het een hoop wilskracht en discipline om door te gaan. Helaas heb ik niet de juist vooropleiding om onvoorwaardelijk toegelaten te worden tot de genoemde studie. Ik heb alleen maar een propedeuse van een niet gerelateerde HBO-studie, dus dat is niet genoeg als je geen Wiskunde B hebt gedaan op de middelbare school. Ik heb de MAVO gedaan, dus dat schiet niet op.Ik snap overigens heel goed waarom deze eis er is en heb ik geen probleem mee. Helaas zit ik met een beperkt tijdsvenster, want er zijn nog maar twee examens dit jaar.


Het stomme is dat ik wat jij nu beschrijft herken en redelijk begrijp. Ik heb dit behandeld in het vorige hoofdstuk van mijn boek en dat ging best goed. Het is ook best een interessant onderwerp overigens, vooral omdat je sinussen kunt aanpassen naar gelang de situatie. Alleen raak ik nu in de war bij opdrachten waar niet zozeer het om de sinus gaat, dan wel om vergelijkingen oplossen.quote:Op maandag 23 mei 2011 20:34 schreef Siddartha het volgende:
[..]
...
Volgens mij had je hier al wat info over gekregen dus zal ik daar kort over zijn:
Ga eens met de 'pijl' mee langs de cirkel en beschrijf wat er met sin en cos gebeurt.
Ik heb nog nooit bewust iets geschreven om wiskundige vraagstellingen op te lossen. Ooit eens een script geschreven dat op basis van vier coördinaten (hemelsbreed) een afstand berekende, maar ik weet niet in hoeverre ik dat wiskundige heb gedaan. Ik denk dat ik met de kennis die ik tot nu toe heb opgedaan veel beter in staat ben om iets wiskundigs te schrijven. Helaas heb ik daar op het moment (i.v.m. de wiskunde) nog geen tijd voor, maar zodra ik die wel heb ga ik er zeker mee spelen. Het lijkt mij erg interessant om iets te schrijven dat iets doet wat voor een mens te complex wordt.quote:Op maandag 23 mei 2011 21:51 schreef Riparius het volgende:
[..]
Ah, zo. Maar heb je wel eens wat programma's geschreven om (eenvoudige) wiskundige vraagstellingen op te lossen? Bijvoorbeeld het genereren van een lijst priemgetallen, of het ontbinden in priemfactoren van een getal (mooi met recursie te doen!), of het genereren van primitieve Pythagoreïsche tripletten of zo?
Laat ik voorop stellen dat ik ruim tien jaar vrij weinig met wiskunde heb gedaan. Ik heb er examen voor gedaan op de MAVO, maar dat niveau komt geenszins in de buurt van het wat ik nu behandel. Op het HBO heb ik wel statistiek gehad, maar dat was van niveau lik-me-vestje en heb ik op mijn pantoffels gehaald.
Ik moet de volgende onderwerpen beheersen waar het gaat om het examen dat ik ga doen. (Het gaat eigenlijk gewoon om Wiskunde B voor het VWO):quote:Op maandag 23 mei 2011 21:51 schreef Riparius het volgende:
[..]
Wat voor onderwerpen worden er gevraagd voor wat betreft wiskundige voorkennis? Ik ben niet zo op de hoogte met de huidige lesprogramma's.
Differentiaalrekenen
• Differentiëren
• Exponenten en logaritmen
• De kettingregel
• Twee afgeleiden
• Integreren
• Toepassingen
Voortgezette meetkkunde
• Bewijzen in driehoeken
• Driehoeken en cirkels
• Vierhoeken en cirkels
• Conflictlijnen
Goniometrie
• Goniometrie
• Goniometrische functies
• Goniometrische formules
• Lissajous-figuren
Het zijn eigenlijk twee boeken en ik ben nu in het laatste hoofdstuk van het eerste boek, dus goniometrische functies. Daarna moet ik nog vijf hoofdstukken behandelen: "Integreren" en "Toepassingen" van differentiaalrekenen, "Vierhoeken en cirkels" en "Conflictlijnen" van voortgezette meetkunde en "Lissajous-figuren" van goniometrie.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dat wordt het natuurlijk al gauw. Zelfs π berekenen wordt een mens al gauw te veel. Maar ook zo iets maken valt niet mee. Ik heb wel eens de broncode van een Pascal programmaatje bestudeerd dat dat deed tot zo'n 150.000 decimalen (binnen een minuut op mijn slome PC). Het basisidee (de formule van Machin) was simpel, maar de routines (deels in assembly) om met getallen met (heel) veel significante cijfers te kunnen werken waren niet bepaald simpel.quote:Op dinsdag 24 mei 2011 06:31 schreef Pipo1234 het volgende:
Ik heb nog nooit bewust iets geschreven om wiskundige vraagstellingen op te lossen. Ooit eens een script geschreven dat op basis van vier coördinaten (hemelsbreed) een afstand berekende, maar ik weet niet in hoeverre ik dat wiskundige heb gedaan. Ik denk dat ik met de kennis die ik tot nu toe heb opgedaan veel beter in staat ben om iets wiskundigs te schrijven. Helaas heb ik daar op het moment (i.v.m. de wiskunde) nog geen tijd voor, maar zodra ik die wel heb ga ik er zeker mee spelen. Het lijkt mij erg interessant om iets te schrijven dat iets doet wat voor een mens te complex wordt.
Dat is allemaal erg elementair. Ik heb me alleen verbaasd over de term 'conflictlijn'. Dat vind ik maar een idiote benaming die kennelijk recent in de mode is gekomen. In geen enkel ander land gebruiken ze dat, ook niet in Vlaanderen. Ik begrijp na lezing van dit stukje wel wat ermee wordt bedoeld, maar het is een bijzonder slecht idee om middelloodlijnen, middenparallellen, bissectrices en parabolen zo op één hoop te gooien.quote:Laat ik voorop stellen dat ik ruim tien jaar vrij weinig met wiskunde heb gedaan. Ik heb er examen voor gedaan op de MAVO, maar dat niveau komt geenszins in de buurt van het wat ik nu behandel. Op het HBO heb ik wel statistiek gehad, maar dat was van niveau lik-me-vestje en heb ik op mijn pantoffels gehaald.
[..]
Ik moet de volgende onderwerpen beheersen waar het gaat om het examen dat ik ga doen. (Het gaat eigenlijk gewoon om Wiskunde B voor het VWO):
Differentiaalrekenen
• Differentiëren
• Exponenten en logaritmen
• De kettingregel
• Twee afgeleiden
• Integreren
• Toepassingen
Voortgezette meetkunde
• Bewijzen in driehoeken
• Driehoeken en cirkels
• Vierhoeken en cirkels
• Conflictlijnen
Goniometrie
• Goniometrie
• Goniometrische functies
• Goniometrische formules
• Lissajous-figuren
Trek maar wat extra tijd uit voor vlakke meetkunde, want bewijzen worden meestal nogal lastig gevonden. Ik zie vaak dat mensen daar tegenwoordig niks meer van bakken.quote:Het zijn eigenlijk twee boeken en ik ben nu in het laatste hoofdstuk van het eerste boek, dus goniometrische functies. Daarna moet ik nog vijf hoofdstukken behandelen: "Integreren" en "Toepassingen" van differentiaalrekenen, "Vierhoeken en cirkels" en "Conflictlijnen" van voortgezette meetkunde en "Lissajous-figuren" van goniometrie.


Dat het elementair is, is waarschijnlijk helemaal waar. Gelukkig wel, want anders kwam ik er niet doorheen. 
De eerste twee hoofdstukken over dit onderwerp vielen mij alles behalve tegen. Ik vloog er zo doorheen, alleen ben ik bang dat daar ook de manco zit voor mij. Het is namelijk heel erg veel denken in vaste regels en die moet dus allemaal onthouden.quote:Op dinsdag 24 mei 2011 07:59 schreef Riparius het volgende:
[..]
Trek maar wat extra tijd uit voor vlakke meetkunde, want bewijzen worden meestal nogal lastig gevonden. Ik zie vaak dat mensen daar tegenwoordig niks meer van bakken.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik weet niet of je ook echt hebt gedaan wat ik zei, maar ik kan het je heel erg aanraden. Ik weet dat je dit wel snapt, dat je het ook in je hoofd kan bedenken, maar het kan voor zoveel meer begrip zorgen.quote:Op dinsdag 24 mei 2011 06:31 schreef Pipo1234 het volgende:
[..]
Het stomme is dat ik wat jij nu beschrijft herken en redelijk begrijp. Ik heb dit behandeld in het vorige hoofdstuk van mijn boek en dat ging best goed. Het is ook best een interessant onderwerp overigens, vooral omdat je sinussen kunt aanpassen naar gelang de situatie. Alleen raak ik nu in de war bij opdrachten waar niet zozeer het om de sinus gaat, dan wel om vergelijkingen oplossen.
Ik zou zeggen: Heb je wat vrije tijd, doe het dan gewoon. Het kost je vrijwel geen moeite (het is echt niet moeilijk, zeker niet met een grafische rekenmachine erbij), het kost alleen een beetje tijd.
Het is niet zozeer dat je meteen inzichten hiervan krijgt (waarschijnlijk wel trouwens, ik heb dit ook gedaan bij mensen die in 6 vwo zaten en me bezworen dat ze de sinus/cosinus begrepen...Dat viel erg tegen.), maar het echte inzicht krijg je daarna, als je opgaven gaat maken. Dan begrijp je ook de methode waarmee je zo'n opgaven moet oplossen.
Voor de goniometrische vergelijkingen die je moet oplossen mooet je gewoon de tijd nemen. Hou in het begin gewoon de lijst met identiteiten erbij en ga puzzelen: wat kan ik anders opschrijven en wat krijg ik dan?


Wederom schakel ik nog een keer de hulp in van de velen wiskundigen hier op Fok! 
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.
Toon aan met behulp van de eenheidscirkel:
cos (α-0.5π) = sin(α)
sin(α+π) = - sin(α)
Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijken zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.
Toon aan met behulp van de eenheidscirkel:
cos (α-0.5π) = sin(α)
sin(α+π) = - sin(α)
Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijken zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.


Wel, bedenk dan eerst maar eens wat sinus en cosinus met de eenheidscirkel te maken hebben.quote:Op dinsdag 24 mei 2011 18:47 schreef Uchiha1911 het volgende:
Wederom schakel ik nog een keer de hulp in van de velen wiskundigen hier op Fok!
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.
Toon aan met behulp van de eenheidscirkel:
cos (α-0.5π) = sin(α)
sin(α+π) = - sin(α)
Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijken zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.


Driehoeken binnen de cirkel?quote:Op dinsdag 24 mei 2011 18:51 schreef thabit het volgende:
[..]
Wel, bedenk dan eerst maar eens wat sinus en cosinus met de eenheidscirkel te maken hebben.


Bestudeer dit maar eens, en dan meer bepaald blz. 5. Overigens vraag ik mij wel af hoe goed je nu echt begrijpt waarom de afgeleiden van sin en cos zijn zoals ze zijn als je hier al moeite mee hebt. Probeer voor jezelf eens helder te krijgen aan de hand van de eenheidscirkel waarom het zo is dat:quote:Op dinsdag 24 mei 2011 18:47 schreef Uchiha1911 het volgende:
Wederom schakel ik nog een keer de hulp in van de velen wiskundigen hier op Fok!
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.
Toon aan met behulp van de eenheidscirkel:
cos (α-½π) = sin(α)
sin(α+π) = - sin(α)
Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijk zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.
d(cos t)/dt = cos(t + ½π) en d(sin t)/dt = sin(t + ½π)


Ik heb na een dagje hard blokken maar eens een eenheidscirkel uitgeprint om mee te spelen en wat meer inzicht te krijgen in de zaken waar ik recent met een aantal van jullie over gesproken heb. Nu heb ik een aantal dingen uitgevonden en graag verneem ik of ik het bij het juist eind heb. Ik hoop dat ik het begrijpelijk genoeg uitleg, want je moet het eigenlijk op zo'n cirkel zien.
Ik heb de twee formules bekeken: sin (½π - x) = cos x en cos (½π - x) = sin x.
En het volgende heb ik bevonden bij sinus (en bij cosinus): Wanneer je vanaf punt ½π x aftrekt krijg je een driehoek die identiek is aan degene bij sinus zonder de ½π. Het verschil zit hem in het feit dat x en y omgewisseld zijn en dus de waarde van sinus aan cosinus is gegeven en vica versa. Dus: sin (½π - x) = cos x (en cos (½π - x) = sin x)
Ik heb ook naar de somformule sin (t + u) = sin t · cos u + cus t · sin u gekeken. Alleen ik kom niet verder dan de conclusie dat daar het oppervlak van de driehoeken wordt berekent.
Ik heb de twee formules bekeken: sin (½π - x) = cos x en cos (½π - x) = sin x.
En het volgende heb ik bevonden bij sinus (en bij cosinus): Wanneer je vanaf punt ½π x aftrekt krijg je een driehoek die identiek is aan degene bij sinus zonder de ½π. Het verschil zit hem in het feit dat x en y omgewisseld zijn en dus de waarde van sinus aan cosinus is gegeven en vica versa. Dus: sin (½π - x) = cos x (en cos (½π - x) = sin x)
Ik heb ook naar de somformule sin (t + u) = sin t · cos u + cus t · sin u gekeken. Alleen ik kom niet verder dan de conclusie dat daar het oppervlak van de driehoeken wordt berekent.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik vind zelf die eenheidscirkel een beetje omslachtig. Als je kijkt naar de grafieken dan vind ik het veel makkelijker. Uit het plaatje zie je dan direct dat als je het golfje van de cos een half pi naar rechts verplaatst krijg je de sin. Dus dan heb je cos(x - pi/2) = sin(x). Verder weet je dat (of zie je ook makkelijk uit de grafiek ervan) dat cos(x)=cos(-x). Dus dan heb je sin(x) = cos(x-pi/2)= cos(-(x-pi/2))=cos(pi/2 -x), en dus sin(x) = cos(pi/2 - x).
Andersom kan je ook het golfje van de sin verplaatsen om de cos te krijgen, dat werkt dan ongeveer hetzelfde en krijg je de andere formule. Probeer maar.
Ik zeg niet dat dit een betere manier is maar het is wel eenvoudig als je eenmaal het cos en sin grafiekje uit je hoofd kent met een paar belangrijke punten.
Andersom kan je ook het golfje van de sin verplaatsen om de cos te krijgen, dat werkt dan ongeveer hetzelfde en krijg je de andere formule. Probeer maar.
Ik zeg niet dat dit een betere manier is maar het is wel eenvoudig als je eenmaal het cos en sin grafiekje uit je hoofd kent met een paar belangrijke punten.


Kijk ook even hier, blz. 5 voor een plaatje. Je kunt ook bedenken dat een rotatie over α gevolgd door spiegeling in de lijn met vergelijking x=y hetzelfde is als een rotatie over ½π - α, en bij spiegeling in de lijn met vergelijking x=y worden de x- en y- coördinaten van een punt omgewisseld.quote:Op dinsdag 24 mei 2011 23:13 schreef Pipo1234 het volgende:
Ik heb na een dagje hard blokken maar eens een eenheidscirkel uitgeprint om mee te spelen en wat meer inzicht te krijgen in de zaken waar ik recent met een aantal van jullie over gesproken heb. Nu heb ik een aantal dingen uitgevonden en graag verneem ik of ik het bij het juist eind heb. Ik hoop dat ik het begrijpelijk genoeg uitleg, want je moet het eigenlijk op zo'n cirkel zien.
Ik heb de twee formules bekeken: sin (½π - x) = cos x en cos (½π - x) = sin x.
En het volgende heb ik bevonden bij sinus (en bij cosinus): Wanneer je vanaf punt ½π x aftrekt krijg je een driehoek die identiek is aan degene bij sinus zonder de ½π. Het verschil zit hem in het feit dat x en y omgewisseld zijn en dus de waarde van sinus aan cosinus is gegeven en vica versa. Dus: sin (½π - x) = cos x (en cos (½π - x) = sin x)
Nee, dit stelt geen oppervlakte voor. Probeer eens of je mijn bewijs voor de additietheorema's kunt begrijpen.quote:Ik heb ook naar de somformule sin (t + u) = sin t · cos u + cos t · sin u gekeken. Alleen ik kom niet verder dan de conclusie dat daar het oppervlak van de driehoeken wordt berekend.


Ik had al naar die PDF gekeken, maar kon er weinig van maken. Ik heb een cirkel uitgeprint en uitgebreid zitten puzzelen en toen zag ik het op een gegevens moment. Nu ik naar dat bestand kijk zie ik het ook...quote:Op dinsdag 24 mei 2011 23:46 schreef Riparius het volgende:
[..]
Kijk ook even hier, blz. 5 voor een plaatje. Je kunt ook bedenken dat een rotatie over α gevolgd door spiegeling in de lijn met vergelijking x=y hetzelfde is als een rotatie over ½π - α, en bij spiegeling in de lijn met vergelijking x=y worden de x- en y- coördinaten van een punt omgewisseld.
Die tekst is voor mij helaas te complex.quote:Op dinsdag 24 mei 2011 23:46 schreef Riparius het volgende:
[..]
Nee, dit stelt geen oppervlakte voor. Probeer eens of je mijn bewijs voor de additietheorema's kunt begrijpen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Inderdaad, plaatjes helpen altijd bij goniometrie.quote:Op woensdag 25 mei 2011 00:10 schreef Pipo1234 het volgende:
[..]
Ik had al naar die PDF gekeken, maar kon er weinig van maken. Ik heb een cirkel uitgeprint en uitgebreid zitten puzzelen en toen zag ik het op een gegevens moment. Nu ik naar dat bestand kijk zie ik het ook...
[..]
Ik heb dit bewijs vaak genoeg met succes uitgelegd aan VWO leerlingen, dus het moet te doen zijn. Er zit niets in dat niet tot de stof voor het VWO behoort. Maar inderdaad is een goed plaatje erbij wel bijna onmisbaar voor een goed begrip. Jammer genoeg heeft er (nog) niemand gereageerd op mijn suggestie om hier een duidelijk plaatje bij te maken.quote:Die tekst is voor mij helaas te complex.


Als ik het snapte maakte ik wel een plaatje.quote:Op woensdag 25 mei 2011 00:21 schreef Riparius het volgende:
[..]
Inderdaad, plaatjes helpen altijd bij goniometrie.
[..]
Ik heb dit bewijs vaak genoeg met succes uitgelegd aan VWO leerlingen, dus het moet te doen zijn. Er zit niets in dat niet tot de stof voor het VWO behoort. Maar inderdaad is een goed plaatje erbij wel bijna onmisbaar voor een goed begrip. Jammer genoeg heeft er (nog) niemand gereageerd op mijn suggestie om hier een duidelijk plaatje bij te maken.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik wil van de volgende verzameling aantonen dat die gesloten is;
Dit is de zogenaamde LeastCore, en V staat voor de maximum operator, en M de index set van alle reëelwaardige functies F op Pi.
Ik heb getracht een rij in LC te maken, maar dat ging nergens heen....
Dit is de zogenaamde LeastCore, en V staat voor de maximum operator, en M de index set van alle reëelwaardige functies F op Pi.
Ik heb getracht een rij in LC te maken, maar dat ging nergens heen....


Ik ben op het moment bezig met opgaven maken voor integraalrekenen. Nu lukt dat allemaal wel, alleen loop ik nu tegen iets aan wat ik me eigenlijk afvraag. Op internet kan ik er even geen goede uitleg over vinden.
Ik vroeg mij af wat ik moet verstaan onder partieel differentiëren? Is dat differentiëren volgens een bepaalde regel(, net zoals bij de productregel/kettingregel) of moet ik er iets anders onder verstaan? Ik vroeg mij dit af omdat ik een opgave aan het maken ben waarin ik moet aantonen dat F(x) = x ln x - x dat primitieve is van f(x) = ln x en ik las ergens dat je het dan partieel moet differentiëren. Alleen rept mijn lesboek nergens over deze term/methode...
Ik vroeg mij af wat ik moet verstaan onder partieel differentiëren? Is dat differentiëren volgens een bepaalde regel(, net zoals bij de productregel/kettingregel) of moet ik er iets anders onder verstaan? Ik vroeg mij dit af omdat ik een opgave aan het maken ben waarin ik moet aantonen dat F(x) = x ln x - x dat primitieve is van f(x) = ln x en ik las ergens dat je het dan partieel moet differentiëren. Alleen rept mijn lesboek nergens over deze term/methode...
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Voor elke afzonderlijke y staat daar een ongelijkheid. Die definieert een verzameling. Toon maar eens aan dat die gesloten is. Dan neem je de doorsnede over alle y, die is dan ook weer gesloten.quote:


Ik kijk eigenlijk zelden op Wikipedia, omdat de uitleg daar vaak te beknopt is en in dit geval dus ook. Ik heb echter elders een goede uitleg gevonden over dit onderwerp. Nu zit ik alleen een beetje te puzzelen met een voorbeeld, aangezien ik niet helemaal krijg wat er als antwoord staat. Op pagina drie staat onderaan namelijk 1/16de in het antwoord, terwijl ik niet verder kom dan 1/4de.quote:Op woensdag 25 mei 2011 13:14 schreef GlowMouse het volgende:
http://nl.wikipedia.org/wiki/Parti%C3%ABle_integratie
http://members.multimania.nl/jwhakvoort/partiele%20integratie.pdf
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Er staat al 1/4, en als je dan x³ primitiveert, komt daar nog 1/4 bij.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ow natuurlijk...quote:Op woensdag 25 mei 2011 14:49 schreef GlowMouse het volgende:
Er staat al 1/4, en als je dan x³ primitiveert, komt daar nog 1/4 bij.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Zou je me willen uitleggen waarom?quote:Op woensdag 25 mei 2011 17:59 schreef thenxero het volgende:
Partiëel differentiëren is wel heel wat anders trouwens
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Partiële differentiatie gebruik je in formule die van meerdere variabelen afhangen, bijvoorbeeld f(x,y)=3x2-y (ik zal niet uitleggen hoe het werkt, aangezien dat niet tot de stof behoort die je hoeft te kennen). Partiëel integreren is integreren met de methode die je zelf al aandroeg. Het belangrijke verschil is dus dat de ene methode werkt voor differentiëren, en de andere voor integreren. Het heeft verder ook niets met elkaar te maken (voor zover ik weet), toevallig hebben ze een vergelijkbare naamquote:
The biggest argument against democracy is a five minute discussion with the average voter.


Differentiëren en integreren (eigenlijk: primitiveren) zijn elkaars inverse bewerking, net zoiets als vermenigvuldigen en delen, dus het is om te beginnen al een wat vreemde vraag.quote:
Maar: partieel differentiëren is iets totaal anders dan partieel integreren. Eigenlijk is de benaming partieel integreren wat ongelukkig, maar dat heb je wel vaker in de wiskunde, omdat het nu eenmaal een vakgebied is met een hele lange traditie waarin bovendien oude resultaten en inzichten gewoon geldig blijven, anders dan bijvoorbeeld bij natuurwetenschappen.
Van partieel differentiëren spreekt men bij de bepaling van afgeleiden van functies van meer dan één variabele. Heb je bijvoorbeeld een functie z = f(x,y), dan kun je kijken hoe de waarde van z afhangt van x wanneer y constant blijft, en hoe de waarde van z afhangt van y wanneer x constant blijft. Je kijkt dan naar de partiële afgeleiden ∂z/∂x = fx(x,y) resp. ∂z/∂y = fy(x,y).
En om de verwarring misschien nog wat groter te maken bestaat er ook een integratietechniek die splitsing in partiële breuken wordt genoemd. Daarbij wordt een rationale functie herschreven als een som van deelbreuken, die dan elk apart zijn te integreren (primitiveren).
[ Bericht 0% gewijzigd door Riparius op 25-05-2011 19:34:11 ]


Vraagje ik zoek info over hoe ik zeer grote (groter dan 64 bit) getallen kan optellen, vemenigvuldigen, aftrekken etc... Nu zoek ik dus geen library ofzo maar gewoon info hoe het 't meest wordt toegepast.


Dit is geen wiskundevraag. Maar goed, de manier is om getallen op te slaan in ééndimensionale array's in het werkgeheugen. Als de grootte van zo'n array N bytes is dan kun je werken met binaire getallen tot N*23 bits oftewel met decimale getallen tot zo'n N*8*10log(2) significante cijfers.quote:Op donderdag 26 mei 2011 02:19 schreef Dale. het volgende:
Vraagje ik zoek info over hoe ik zeer grote (groter dan 64 bit) getallen kan optellen, vemenigvuldigen, aftrekken etc... Nu zoek ik dus geen library ofzo maar gewoon info hoe het 't meest wordt toegepast.
Als je eens een implementatie van zo iets wil zien dan kun je de broncode van dit stokoude Pascal (MS-DOS) programmaatje voor de berekening van π eens bekijken. Omdat de grootte van een array in Turbo Pascal beperkt was (en is) tot 64 kB, kan het programma decimale getallen tot maximaal zo'n 157000 significante cijfers verwerken.


http://en.wikipedia.org/w(...)er_transform_methodsquote:Op donderdag 26 mei 2011 02:19 schreef Dale. het volgende:
Vraagje ik zoek info over hoe ik zeer grote (groter dan 64 bit) getallen kan optellen, vemenigvuldigen, aftrekken etc... Nu zoek ik dus geen library ofzo maar gewoon info hoe het 't meest wordt toegepast.


Bedankt voor je tip Thabit.
Nog maar een vraagje... een vraag uit mijn topologie en homotopie theorie tentamen van vorige week, waar ik niet uitkwam:
Dit stukje van de theorie was sowieso al chinees voor me, maar nu zelfs met het boek erbij kom ik er niet echt uit. Iemand die me kan helpen?

Nog maar een vraagje... een vraag uit mijn topologie en homotopie theorie tentamen van vorige week, waar ik niet uitkwam:
Dit stukje van de theorie was sowieso al chinees voor me, maar nu zelfs met het boek erbij kom ik er niet echt uit. Iemand die me kan helpen?


Ik studeer zelf geen wiskunde, maar heb wel een paar vakken gevolgd uit interesse. Dit soort shit is echt chinees voor me, terwijl 'normale' wiskunde me toch erg makkelijk af gaat.quote:Op donderdag 26 mei 2011 11:56 schreef FergieOliver het volgende:
Bedankt voor je tip Thabit.
Nog maar een vraagje... een vraag uit mijn topologie en homotopie theorie tentamen van vorige week, waar ik niet uitkwam:
Dit stukje van de theorie was sowieso al chinees voor me, maar nu zelfs met het boek erbij kom ik er niet echt uit. Iemand die me kan helpen?
[ afbeelding ]


Uit het feit dat Y padsamenhangend is en f een overdekking volgt in elk geval dat X ook padsamenhangend is (want f is surjectief). Lokaal is f in elk geval een homeomorfisme (want het is een overdekking) dus het enige wat je moet bewijzen is dat f injectief is.quote:Op donderdag 26 mei 2011 11:56 schreef FergieOliver het volgende:
Bedankt voor je tip Thabit.
Nog maar een vraagje... een vraag uit mijn topologie en homotopie theorie tentamen van vorige week, waar ik niet uitkwam:
Dit stukje van de theorie was sowieso al chinees voor me, maar nu zelfs met het boek erbij kom ik er niet echt uit. Iemand die me kan helpen?
[ afbeelding ]
Omdat X padsamenhangend is, maar het niet uit welk basispunt x0 je kiest voor de structuur van de fundamentaalgroep; die zal altijd triviaal zijn.
Stel nu dat f niet injectief is, dan kunnen we zvva aannemen dat de vezel boven x0 uit meer dan 1 punt bestaat, zeg dat y en z in deze vezel zitten. Omdat Y samenhangend is, bestaat er een pad van y0 naar y. Als we f toepassen op dat pad, dan krijgen we een lus op x0 in X. De fundamentaalgroep van X is triviaal, dus deze lus is homotoop met een constante lus op x0. Houden we y0 als basispunt aan in Y, dan kunnen we zo'n homotopie altijd liften om een homotopie in Y te krijgen. Dit impliceert dat het constante pad in y0 homotoop is met het pad van y0 naar y.
Dit betekent dat in de vezel boven x0 er een pad van y0 naar y is. Maar f is een overdekkingsafbeelding dus deze vezel is discreet. Hieruit volgt dat y gelijk moet zijn aan y0 en dus dat alle vezels uit 1 punt bestaan.


Hoe ben je zo briljant hé....quote:Op donderdag 26 mei 2011 13:30 schreef thabit het volgende:
[..]
Uit het feit dat Y padsamenhangend is en f een overdekking volgt in elk geval dat X ook padsamenhangend is (want f is surjectief). Lokaal is f in elk geval een homeomorfisme (want het is een overdekking) dus het enige wat je moet bewijzen is dat f injectief is.
Omdat X padsamenhangend is, maar het niet uit welk basispunt x0 je kiest voor de structuur van de fundamentaalgroep; die zal altijd triviaal zijn.
Stel nu dat f niet injectief is, dan kunnen we zvva aannemen dat de vezel boven x0 uit meer dan 1 punt bestaat, zeg dat y en z in deze vezel zitten. Omdat Y samenhangend is, bestaat er een pad van y0 naar y. Als we f toepassen op dat pad, dan krijgen we een lus op x0 in X. De fundamentaalgroep van X is triviaal, dus deze lus is homotoop met een constante lus op x0. Houden we y0 als basispunt aan in Y, dan kunnen we zo'n homotopie altijd liften om een homotopie in Y te krijgen. Dit impliceert dat het constante pad in y0 homotoop is met het pad van y0 naar y.
Dit betekent dat in de vezel boven x0 er een pad van y0 naar y is. Maar f is een overdekkingsafbeelding dus deze vezel is discreet. Hieruit volgt dat y gelijk moet zijn aan y0 en dus dat alle vezels uit 1 punt bestaan.
Heel erg bedankt. Ik ga het uitschrijven met m'n boek derbij en kijken of ik het vat


Ik ken Urysohns lemma. Hoe gebruik ik die om het volgende te bewijzen?
Ik bedoel je kan met zo'n Urysohn functie een gesloten verzameling naar 0 sturen en een disjuncte andere gesloten verzameling naar 1.
En dan? Wat willen ze eigenlijk precies in deze opgave? Laten zien dat je om de gesloten verzameling open verzamelingen kan leggen die nog steeds disjunct zijn ?
Ik bedoel je kan met zo'n Urysohn functie een gesloten verzameling naar 0 sturen en een disjuncte andere gesloten verzameling naar 1.
En dan? Wat willen ze eigenlijk precies in deze opgave? Laten zien dat je om de gesloten verzameling open verzamelingen kan leggen die nog steeds disjunct zijn ?


Sterker nog, hun afsluitingen moeten zelfs disjunct zijn.quote:Op donderdag 26 mei 2011 14:45 schreef Hypnagogia het volgende:
Ik ken Urysohns lemma. Hoe gebruik ik die om het volgende te bewijzen?
[ afbeelding ]
Ik bedoel je kan met zo'n Urysohn functie een gesloten verzameling naar 0 sturen en een disjuncte andere gesloten verzameling naar 1.
En dan? Wat willen ze eigenlijk precies in deze opgave? Laten zien dat je om de gesloten verzameling open verzamelingen kan leggen die nog steeds disjunct zijn ?
Misschien kun je, uitgaande van die Urysohnfuncties die je voor elk tweetal hebt, een functie f: T -> R proberen te maken met f(Ci) = {i} voor elke i.
*EDIT* Dit idee is iets te simpel. Je kunt beginnen met bewijzen dat een willekeurige vereniging van Ci'tjes gesloten is.
[ Bericht 6% gewijzigd door thabit op 27-05-2011 10:43:27 ]


hoeveel rente moet ik in totaal betalen wanneer ik voor 3 jaar een lening afsluit van 500e/maand met 1.5% rente die ik in 15 jaar mag aflossen. dus hoeveel rente heb ik totaal betaald na die 15 jaar aflossingsfase?
[ Bericht 0% gewijzigd door kingofthepokerface op 26-05-2011 17:35:45 ]
[ Bericht 0% gewijzigd door kingofthepokerface op 26-05-2011 17:35:45 ]
Wheter you think you can or you can't, either way you are right.


Je leent drie jaar lang elke maand 500 euro die je vervolgens in 15 jaar gaat aflossen? Hoeveel wil per jaar gaan aflossen?quote:Op donderdag 26 mei 2011 16:12 schreef kingofthepokerface het volgende:
hoeveel rente moet ik in totaal betalen wanneer ik voor 3 jaar een lening afsluit van 500e/maand met 1.5% rente die ik in 15 jaar mag aflossen. dus hoeveel rente heb ik totaal betaald na die 15 jaar aflossingsfase?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dat hangt er helemaal van af hoe je wilt aflossen. Des te groter de bedragen die je in het begin aflost, des te kleiner het uiteindelijk betaalde bedrag aan rente. Als je elk jaar een vast bedrag x, bestaande uit een deel aflossing en een deel rente, wilt terugbetalen kun je makkelijk een vergelijking opstellen om x uit op te lossen. Heb je dat al geprobeerd?quote:Op donderdag 26 mei 2011 16:12 schreef kingofthepokerface het volgende:
hoeveel rente moet ik in totaal betalen wanneer ik voor 3 jaar een lening afsluit van 500e/maand met 1.5% rente die ik in 15 jaar mag aflossen. dus hoeveel rente heb ik totaal betaald na die 15 jaar aflossingsfase?
Dat is normale wiskunde.quote:Op donderdag 26 mei 2011 12:17 schreef bert_van_dirkjan het volgende:
[..]
Ik studeer zelf geen wiskunde, maar heb wel een paar vakken gevolgd uit interesse. Dit soort shit is echt chinees voor me, terwijl 'normale' wiskunde me toch erg makkelijk af gaat.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Wat is de verdeling van Y als Y = lim n->inf [product van Xi van 1 tot n ]
en Xi~LOGN(mu, 2)?
Volgens mij wordt dat volgens de CLT toch weer een lognormale verdeling met mu=0 en variantie=1?
De exacte reden hiervoor weet ik niet meer, als iemand dat even kan oplepelen waardeer ik dat zeer
en Xi~LOGN(mu, 2)?
Volgens mij wordt dat volgens de CLT toch weer een lognormale verdeling met mu=0 en variantie=1?
De exacte reden hiervoor weet ik niet meer, als iemand dat even kan oplepelen waardeer ik dat zeer
Beneath the gold, bitter steel


het product is hetzelfde als de exponent van de som van de log
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dus zeg A=product van Xi van i=1 tot nquote:Op donderdag 26 mei 2011 20:48 schreef GlowMouse het volgende:
het product is hetzelfde als de exponent van de som van de log
dus A = exp{ln [A]}
ln[A] = som i=1 tot n van ln(Xi)
ik vind uiteindelijk dat dit met substitutie etc. is dat ln[Xi]=Zi~N(mu, 4) verdeeld
dan is Y=exp[som i=1 tot n van Zi]
dus Y is lognormaal verdeeld met ~(n*mu, n*4)
Maar als ik dan n-> inf doe gaat het beetje vreemd, ik mis een stuk parate theorie vrees ik
Beneath the gold, bitter steel


tussen 100 en 200 euro maar ga maar uit van 150quote:Op donderdag 26 mei 2011 19:29 schreef Pipo1234 het volgende:
[..]
Je leent drie jaar lang elke maand 500 euro die je vervolgens in 15 jaar gaat aflossen? Hoeveel wil per jaar gaan aflossen?
Wheter you think you can or you can't, either way you are right.


Ik neem aan dat je 150 euro per maand bedoelt? Dus samenvattend ga je 3 drie jaar lang elke maand 500 euro lenen en vervolgens ga je na die drie jaar elke maand 150 euro afbetalen?quote:Op donderdag 26 mei 2011 21:46 schreef kingofthepokerface het volgende:
[..]
tussen 100 en 200 euro maar ga maar uit van 150
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik ben op zoek naar de primitieve van de volgende functie: (4 - ex)2. Het gaat hier om een gekwadrateerde functie, aangezien ik bezig ben met lichamen berekenen. Ik krijg het niet voor elkaar om de juiste primitieve te vinden. Dit komt vooral door de kwadratering, aangezien ik het zonder kwadratering al gevonden heb. Ik ben ook niet zo sterk in afleiden van abstracte termen als LN en e.
Wil iemand mij een aanwezig geven hoe ik de primtieve kan vinden? Ik kom niet verder dan iets van 1/3 (4 - ex)3 i.c.m. met de kettingregel om de functie te herleiden, alleen dit lukt me dus niet.
Wil iemand mij een aanwezig geven hoe ik de primtieve kan vinden? Ik kom niet verder dan iets van 1/3 (4 - ex)3 i.c.m. met de kettingregel om de functie te herleiden, alleen dit lukt me dus niet.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Je kunt eerst de haakjes wegwerken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Dat heb ik geprobeerd, maar dan krijg ik 16 - 8ex + (ex)2 en wanneer ik dat herleid naar de primitieve 16x - 8ex + 1/3(ex)3 klopt het niet. Is mijn primitieve überhaupt goed?quote:
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Dat meen je niet.quote:
Ik heb nu de primitieve 16x - 8ex + 1/2 e2x en het volume dat ik daarmee krijg klopt helemaal.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Die machtregel geldt niet alleen voor e, maar altijd.quote:Op vrijdag 27 mei 2011 13:22 schreef Pipo1234 het volgende:
[..]
Dat meen je niet.Ik ben ook zo beroerd als het neerkomt op e en ln.
Bedankt.
Ik heb nu de primitieve 16x - 8ex + 1/2 e2x en het volume dat ik daarmee krijg klopt helemaal.
(a^p)^q = a^{pq}


Vraagje over radix conversie... Uit "art of Computer Programming" volume 2. Hier staat het volgende over radix conversie...
Nu snap ik niet de methode 1b. Ik heb bijvoorbeeld het getal 10 met als basis 10 (decimaal dus) Nu wil ik dit getal 10 met basis 10 omschrijven naar een getal met basis 256 (word). Hoe moet ik dit nou doen volgende de methode bij 1b? Enkel wat ik lees is dat je de polynoom, voor decimaal getal 345
3*10^2 + 4*10^1 + 5*10^0 = 345 opstelt en dat je dit kunt schrijven naar (3*10 + 4)*10) + 5
Waar is de conversie gebleven naar me nieuwe basis 256?
Nu snap ik niet de methode 1b. Ik heb bijvoorbeeld het getal 10 met als basis 10 (decimaal dus) Nu wil ik dit getal 10 met basis 10 omschrijven naar een getal met basis 256 (word). Hoe moet ik dit nou doen volgende de methode bij 1b? Enkel wat ik lees is dat je de polynoom, voor decimaal getal 345
3*10^2 + 4*10^1 + 5*10^0 = 345 opstelt en dat je dit kunt schrijven naar (3*10 + 4)*10) + 5
Waar is de conversie gebleven naar me nieuwe basis 256?


Stel je hebt de formule:
(9x-2)(x^2-2x)
Dan differentieer ik dit met de productregel en krijg ik:
9 * (x^2-2x) + (9x-2) * (2x-2)
Tot zover snap ik het allemaal. Maar nu loop ik tegen het probleem aan, hoe vereenvoudig ik dit? De volgende stappen onderneem ik altijd:
• -2 * -2 = +4
• 9 * -2x + 9x * -2 = -36x
Zoals je ziet klopt dit voor geen kant, want ik weet dat -36x -40x moet zijn. Om nog maar te zwijgen over hoe ze aan 27x^2 komen.
Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.
(9x-2)(x^2-2x)
Dan differentieer ik dit met de productregel en krijg ik:
9 * (x^2-2x) + (9x-2) * (2x-2)
Tot zover snap ik het allemaal. Maar nu loop ik tegen het probleem aan, hoe vereenvoudig ik dit? De volgende stappen onderneem ik altijd:
• -2 * -2 = +4
• 9 * -2x + 9x * -2 = -36x
Zoals je ziet klopt dit voor geen kant, want ik weet dat -36x -40x moet zijn. Om nog maar te zwijgen over hoe ze aan 27x^2 komen.
Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.


Het idee is dat je de berekening (3*10 + 4)*10 + 5 simpelweg in basis 256 uitvoert, ervan uitgaande dat je methodes voorhanden hebt om in basis 256 te rekenen.quote:Op vrijdag 27 mei 2011 14:38 schreef Dale. het volgende:
Vraagje over radix conversie... Uit "art of Computer Programming" volume 2. Hier staat het volgende over radix conversie...
[ afbeelding ]
Nu snap ik niet de methode 1b. Ik heb bijvoorbeeld het getal 10 met als basis 10 (decimaal dus) Nu wil ik dit getal 10 met basis 10 omschrijven naar een getal met basis 256 (word). Hoe moet ik dit nou doen volgende de methode bij 1b? Enkel wat ik lees is dat je de polynoom, voor decimaal getal 345
3*10^2 + 4*10^1 + 5*10^0 = 345 opstelt en dat je dit kunt schrijven naar (3*10 + 4)*10) + 5
Waar is de conversie gebleven naar me nieuwe basis 256?


http://mediatheek.thinkqu(...)kjes/page_uitleg.htmquote:Op vrijdag 27 mei 2011 15:02 schreef spanje1986 het volgende:
Stel je hebt de formule:
(9x-2)(x^2-2x)
Dan differentieer ik dit met de productregel en krijg ik:
9 * (x^2-2x) + (9x-2) * (2x-2)
Tot zover snap ik het allemaal. Maar nu loop ik tegen het probleem aan, hoe vereenvoudig ik dit? De volgende stappen onderneem ik altijd:
• -2 * -2 = +4
• 9 * -2x + 9x * -2 = -36x
Zoals je ziet klopt dit voor geen kant, want ik weet dat -36x -40x moet zijn. Om nog maar te zwijgen over hoe ze aan 27x^2 komen.
Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Volgens mij maak jij dezelfde denkfout als dat ik eerst deed. Je moet opletten dat je alle waarden met elkaar vermenigvuldigd.quote:Op vrijdag 27 mei 2011 15:02 schreef spanje1986 het volgende:
...
Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.
Dit is wat je krijgt via de productregel:
9 · (x2 - 2x) + (9x - 2) · (2x - 2)
Vervolgens vermenigvuldig je alles met elkaar (rekening houdend met de plus/min):
(9 · x2) - (9 · 2x) + (9x · 2x) - (9x · 2) - (2 · 2x) + (2 · 2)
Daarna heb je het volgende:
9x2 - 18x + 18x2 - 18x - 4x + 4
En na vereenvoudiging heb je de volgende afgeleide:
27x2 - 40x + 4
[ Bericht 0% gewijzigd door Pipo1234 op 28-05-2011 10:34:51 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Ik zoek de primitieve van deze functie: 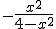
Ik weet niet goed hoe ik deze kan krijgen en heb al van alles geprobeerd. Hetgeen dat het meeste in de buurt kwam (maar niet klopte verder) was ln(4-x2). Iemand een tip hoe ik aan de primitieve kom?
Ik weet niet goed hoe ik deze kan krijgen en heb al van alles geprobeerd. Hetgeen dat het meeste in de buurt kwam (maar niet klopte verder) was ln(4-x2). Iemand een tip hoe ik aan de primitieve kom?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Breuksplitsen!quote:Op zaterdag 28 mei 2011 14:33 schreef Pipo1234 het volgende:
Ik zoek de primitieve van deze functie: [ afbeelding ]
Ik weet niet goed hoe ik deze kan krijgen en heb al van alles geprobeerd. Hetgeen dat het meeste in de buurt kwam (maar niet klopte verder) was ln(4-x2). Iemand een tip hoe ik aan de primitieve kom?


Na dat gedaan te hebben kom ik alsnog niet verder. Ik heb nu:quote:
Het probleem is dat ik het niet voor elkaar krijg om een primitieve te vinden waar die breuken de afgeleide van zijn. Ik zoek het via de machtsfunctie, aangezien ik niet weet hoe ik het anders moet doen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Begin eens met:quote:Op zaterdag 28 mei 2011 15:22 schreef Pipo1234 het volgende:
[..]
Na dat gedaan te hebben kom ik alsnog niet verder. Ik heb nu:
[ afbeelding ]
Het probleem is dat ik het niet voor elkaar krijg om een primitieve te vinden waar die breuken de afgeleide van zijn. Ik zoek het via de machtsfunctie, aangezien ik niet weet hoe ik het anders moet doen.
-x2/(4 - x2) = x2/(x2 -4) = (x2 - 4 + 4)/(x2 - 4) = (x2 - 4)/(x2 - 4) + 4/(x2 - 4) = 1 + 4/(x2 - 4).


Ik krijg de primitieve van deze formule maar niet te pakken. Als ik het met ln(x2-4) probeer kom ik in de knoop i.v.m. de kettingregel.quote:Op zaterdag 28 mei 2011 15:30 schreef Riparius het volgende:
[..]
Begin eens met:
-x2/(4 - x2) = x2/(x2 -4) = (x2 - 4 + 4)/(x2 - 4) = (x2 - 4)/(x2 - 4) + 4/(x2 - 4) = 1 + 4/(x2 - 4).
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


4/(x2 - 4) moet je nog vereenvoudigen door middel van breuksplitsen, nu heb je echter geen last meer van een x in de teller, waardoor het primitiveren na het breuksplitsen relatief eenvoudig is.quote:Op zaterdag 28 mei 2011 16:18 schreef Pipo1234 het volgende:
[..]
Ik krijg de primitieve van deze formule maar niet te pakken. Als ik het met ln(x2-4) probeer kom ik in de knoop i.v.m. de kettingregel.
The biggest argument against democracy is a five minute discussion with the average voter.


Dus toch...quote:Op zaterdag 28 mei 2011 16:26 schreef M.rak het volgende:
[..]
4/(x2 - 4) moet je nog vereenvoudigen door middel van breuksplitsen, nu heb je echter geen last meer van een x in de teller, waardoor het primitiveren na het breuksplitsen relatief eenvoudig is.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


OK. We hadden al gevonden dat:quote:Op zaterdag 28 mei 2011 16:18 schreef Pipo1234 het volgende:
[..]
Ik krijg de primitieve van deze formule maar niet te pakken. Als ik het met ln(x2-4) probeer kom ik in de knoop i.v.m. de kettingregel.
(1) -x2/(4 - x2) = 1 + 4/(x2 - 4).
Een primitieve van 1 is x, dus nu resteert nog de bepaling van een primitieve van 4/(x2 - 4). Hiervoor gaan we breuksplitsing oftewel splitsing in partiële breuken toepassen.
Het idee is - heel kort door de bocht - dat we een breuk gaan herschrijven als een som van deelbreuken waarbij de noemer telkens een factor is van de noemer van de oorspronkelijke breuk.
Als je 1/2 + 1/3 wil optellen, dan moet je deze breuken eerst gelijknamig maken:
1/2 + 1/3 = (3∙1)/(3∙2) + (2∙1)/(2∙3) = 3/6 + 2/6 = (3 + 2)/6 = 5/6
Maar stel nu eens dat we het omgekeerde zouden willen doen, dus 5/6 herleiden naar 1/2 + 1/3. Dan moeten we dus deze breuk opsplitsen in deelbreuken waarvan de noemers telkens één van van de (priem)factoren zijn van 6 = 2∙3. Dit is - heel kort - het achterliggende idee.
Nu gaan we 4/(x2 - 4) opsplitsen in deelbreuken. Daarvoor moeten we dus eerst de factoren van de noemer x2 - 4 bepalen. Dit is heel gemakkelijk, want je kent het merkwaardige product a2 - b2 = (a-b)(a+b). Dus hebben we:
(2) x2 - 4 = (x - 2)(x + 2)
De bedoeling is nu dat we zoiets krijgen:
(3) 4/(x2 - 4) = A/(x - 2) + B/(x + 2)
De kunst is nu om A en B te bepalen. Hiertoe vermenigvuldigen we beide leden van (3) met de noemer van de breuk in het linkerlid, dus met x2 - 4 = (x - 2)(x + 2) , zodat we alle breuken kwijtraken. Dan krijgen we:
(4) 4 = A(x + 2) + B(x - 2)
Uitwerken geeft:
(5) 4 = Ax + 2A + Bx - 2B
Hergroeperen van de termen in het rechterlid naar machten van x geeft:
(6) 4 = (A + B)x + 2(A - B)
Nu zou je in gedachten kunnen houden dat je het linkerlid van (6) ook kunt schrijven als 0∙x +4. Aan voorwaarde (6) kan alleen voldaan worden voor elke x indien de coëfficiënten van de veeltermen in het linkerlid en rechterlid paarsgewijs aan elkaar gelijk zijn. Dus krijgen we als voorwaarden:
(7a) A + B = 0
(7b) A - B = 2
Dit is een stelsel lineaire vergelijkingen in A en B, dat je op de gebruikelijke wijze(n) op kunt lossen. Door optelling van de leden van (7a) en (7b) verkrijgen we 2A = 2 en dus A = 1, en dus B = -1. Voor (3) kunnen we nu dus schrijven:
(8) 4/(x2 - 4) = 1/(x - 2) - 1/(x + 2)
Nu zijn we er bijna en kunnen we (8) primitiveren, maar toch moet je nog even opletten al naargelang de waarden die x aanneemt in je vraagstuk. Een primitieve van 1/x is ln(x), maar dit geldt alleen voor x > 0. De functie f(x) = 1/x is echter ook gedefinieerd voor x < 0. In dat geval kun je ln(-x) als primitieve nemen, immers volgens de kettingregel is de afgeleide hiervan (1/(-x))∙(-1) = 1/x, zoals gewenst. We kunnen beide mogelijkheden samen nemen door te zeggen dat ln |x| een primitieve is van 1/x voor x > 0 of x < 0.
Alles samengevat hebben we nu:
(9) -x2/(4 - x2) = 1 + 1/(x - 2) - 1/(x + 2)
En een primitieve hiervan is:
(10) x + ln |x - 2| - ln |x + 2| + C
That's it!
Als je meer wil weten over splitsing in deelbreuken kan ik je deze reader aanbevelen.
[ Bericht 0% gewijzigd door Riparius op 28-05-2011 17:11:53 ]


Ik heb het gevonden en snap nu wat ik verkeerd deed. Bedankt allemaal!
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |


















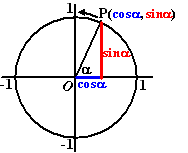


 Op
Op 

