[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op donderdag 19 mei 2011 00:27 schreef t0sti het volgende:
ok, nu een makkelijke vraag (t.o.v. de rest van de problemen die ik hier zie )

ik heb twee vergelijkingen,
[ afbeelding ]
(ik moet dus Fb en Fc bepalen)
maar als ik het met substitutie probeer, komen er verkeerde antwoorden uit
[ afbeelding ]
de antwoorden staan in de spoiler (ik heb wel antwoorden maar geen uitwerkingen )

SPOILER

Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

ik weet bijna zeker dat ik echt een stomme fout maak of iets over het hoofd zie, maar het is alweer een tijdje geleden voor me

Je kunt kennelijk niet rekenen met breuken.

Als je twee breuken hebt waarvan de eerste een noemer cos 30° heeft en de tweede een noemer 5 heeft en je wil die breuken bij elkaar optellen, dan moet je die breuken eerst gelijknamig maken. Dat doe je door teller en noemer van de eerste breuk met 5 en teller en noemer van de tweede breuk met cos 30° te vermenigvuldigen.

Maar het kan een stuk overzichtelijker door eerst de breuken uit je oorspronkelijke vergelijkingen te elimineren. Als je beide leden van je eerste vergelijking met 15 vermenigvuldigt, en beide leden van je tweede vergelijking met 20, dan krijg je:

(1) 0 = -15∙cos 30°∙F_b + 12∙F_c
(2) 55 = 20∙sin 30°∙F_b + 12∙F_c

Door nu de leden van de eerste vergelijking van de leden van de tweede vergelijking af te trekken valt F_c weg en krijg je:

(3) 55 = (15∙cos 30° + 20∙sin 30°)∙F_b

Door substitutie van de exacte waarden cos 30° = ½∙√3 en sin 30° = ½ in (3) vinden we dan:

(4) F_b = 22/(4 + 3∙√3)

Bovendien volgt uit (1) na substitutie van cos 30° = ½∙√3 dat:

(5) F_c = (5/8)∙√3∙F_b

Zodat uit (4) en (5) volgt:

(6) F_c = 55∙√3/(16 + 12∙√3)

[ Bericht 1% gewijzigd door Riparius op 19-05-2011 06:05:53 ]

quote:

Op donderdag 19 mei 2011 05:52 schreef Riparius het volgende:

[..]

Je kunt kennelijk niet rekenen met breuken.

Riparius, altijd streng doch rechtvaardig

Ik moet de dubbele integraal uitrekenen van:
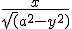dydx met gebied [0,1]x[0,a]

Als gebied heb ik gekozen: E_n={(x,y)| 0<=x>=1, 0<=y<=a-1/n}

Dan krijg ik als 'eerste'integraal (de integraal over y):
xarcsin(y/a)
Invullen over gebied E_n geeft xarcsin(1-1/n).
etc, etc, geeft als antwoord 1/4 Pi.
Het gaat me dus om de stappen voor etc, etc en het antwoord. Klopt dat?

[ Bericht 100% gewijzigd door Siddartha op 19-05-2011 11:58:36 ]

@bert_van_dirkjan
@keesjeislief
@Riparius

bedankt! voor het geduld en de uitleg (ook gezien de tijdstippen )


[ Bericht 8% gewijzigd door t0sti op 19-05-2011 12:24:23 ]

quote:

Op donderdag 19 mei 2011 11:47 schreef Siddartha het volgende:
Ik moet de dubbele integraal uitrekenen van:
[ afbeelding ] dydx met gebied [0,1]x[0,a]

Als gebied heb ik gekozen: E_n={(x,y)| 0<=x>=1, 0<=y<=a-1/n}

Dan krijg ik als 'eerste'integraal (de integraal over y):
xarcsin(y/a)
Invullen over gebied E_n geeft xarcsin(1-1/n).
etc, etc, geeft als antwoord 1/4 Pi.
Het gaat me dus om de stappen voor etc, etc en het antwoord. Klopt dat?

Dit lijkt me juist. Wolfram Alpha verslikt zich in deze integraal (met a in de integrand), maar x∙arcsin(y/a) is inderdaad een primitieve naar y van x/√(a² - y²). Het is weliswaar een oneigenlijke integraal omdat de functiewaarde onbepaald is voor y = a, maar je hoeft hier geen limietovergang te gebruiken. Integreren met y als variabele over [0,a] geeft:

[x∙arcsin(y/a)]₀^a = x∙arcsin(a/a) - x∙arcsin(0) = x∙arcsin(1) = x∙π/2.

Een primitieve hiervan naar x is (π/4)∙x² zodat we inderdaad krijgen:

[(π/4)∙x²]₀¹ = π/4 - 0 = π/4.

quote:

Op woensdag 18 mei 2011 23:02 schreef Don_Vanelli het volgende:
Als de volgorde van belang is zou je in principe [ afbeelding ] verschillende combinaties kunnen maken. Echter, als wij bijvoorbeeld de combi (37,74) hebben, dan is dat natuurlijk hetzelfde als (74,37). Daarom moeten we het aantal mogelijke combinaties nog door twee delen. Dus krijgen we:

[ afbeelding ]

In het algemeen:
Als we k (in jouw voorbeeld k=2) getallen moeten kiezen uit een totaal van n (in jouw voorbeeld n=80), waarbij de volgorde van de keuze niet van belang is, krijgen we:
[ afbeelding ]

Dus hoeveel verschillende loten zou je kunnen hebben?
Er zit geen verschil tussen 37,74 of 74,37 dat is hetzelfde.

quote:

Op donderdag 19 mei 2011 16:26 schreef Kadooosh het volgende:

[..]

Dus hoeveel verschillende loten zou je kunnen hebben?
Er zit geen verschil tussen 37,74 of 74,37 dat is hetzelfde.

Don_Vanelli heeft je toch al het antwoord gegeven? Het aantal is (80∙79)/2 = 3160. Te lui om dit even zelf uit te rekenen?

quote:

Op donderdag 19 mei 2011 16:01 schreef Riparius het volgende:

[..]

Dit lijkt me juist. Wolfram Alpha verslikt zich in deze integraal (met a in de integrand), maar x∙arcsin(y/a) is inderdaad een primitieve naar y van x/√(a² - y²). Het is weliswaar een oneigenlijke integraal omdat de functiewaarde onbepaald is voor y = a, maar je hoeft hier geen limietovergang te gebruiken. Integreren met y als variabele over [0,a] geeft:

[x∙arcsin(y/a)]₀^a = x∙arcsin(a/a) - x∙arcsin(0) = x∙arcsin(1) = x∙π/2.

Een primitieve hiervan naar x is (π/4)∙x² zodat we inderdaad krijgen:

[(π/4)∙x²]₀¹ = π/4 - 0 = π/4.

Volgens mij moet ik wel een limiet nemen (het eigenlijke gebied D is immers met y=a).
Daarom pak ik ook het kleinere gebied E_n met y=a-1/n, zodat ik door het limiet van n->oneindig te nemen het gebied D kan uitputten met lim (E_n).
Het maakt verder geen verschil (de 1/n valt gewoon weg in de uiteindelijke integraal).

quote:

Op donderdag 19 mei 2011 17:18 schreef Siddartha het volgende:

[..]

Volgens mij moet ik wel een limiet nemen (het eigenlijke gebied D is immers met y=a).
Daarom pak ik ook het kleinere gebied E_n met y=a-1/n, zodat ik door het limiet van n->oneindig te nemen het gebied D kan uitputten met lim (E_n).
Het maakt verder geen verschil (de 1/n valt gewoon weg in de uiteindelijke integraal).

Ik begrijp je redenering wel, en die is ook correct, maar de primitieve naar y van x/√(a² - y²) oftewel x∙arcsin(y/a) + C is wel gedefinieerd voor y=a, zodat je je een limietovergang naar het integratieinterval [0, a] kunt besparen.

"Voor elk priemgetal p is de commutatieve ring (Z/pZ) een eindig lichaam
van p elementen."

Nu word er voor deze stelling bewezen dat elk element/restklasse a die niet deelbaar door p is, een inverse heeft. Dat snap ik wel redelijk, maar hoe moet ik me die inverse voorstellen?
En hoe volgt daaruit dat er p elementen zijn?

quote:

Op donderdag 19 mei 2011 17:29 schreef Riparius het volgende:

[..]

Ik begrijp je redenering wel, en die is ook correct, maar de primitieve naar y van x/√(a² - y²) oftewel x∙arcsin(y/a) + C is wel gedefinieerd voor y=a, zodat je je een limietovergang naar het integratieinterval [0, a] kunt besparen.

Ok, bedankt!
Al voelt het wel vreemd aan, dat de integraal wel goed gedefineerd is in het gehele gebied, terwijl de functie zelf dat niet is.

quote:

Op dinsdag 17 mei 2011 08:42 schreef Riparius het volgende:

[..]

Wat dacht je van:
...

Nog bedankt voor je duidelijk uitleg. Het is me uiteindelijk gelukt om die opgaven enigszins door te krijgen.

Nu heb ik alleen even een andere vraag over hetzelfde onderwerp. (Ik begin een beetje gefrustreerd te raken door al die algebra, aangezien ik er blijkbaar niet zo goed in ben en mijn boek totaal geen uitleg of uitwerking biedt.) Ik moet vergelijkingen zoals de volgenden oplossen: sin 3x = sin 2(x - 3) en sin 2x = sin 3x. Nu krijg ik het niet voor elkaar om hier een bruikbaar antwoord uit te krijgen. Ik zie het gewoon niet denk ik. Dat probleem had ik eerder ook al bij het oplossen van sin x = cos x enzovoorts. Helaas heb ik nog niet de routine om dit soort vergelijkingen "even" op te lossen.

quote:

Op donderdag 19 mei 2011 17:32 schreef Siddartha het volgende:
"Voor elk priemgetal p is de commutatieve ring (Z/pZ) een eindig lichaam
van p elementen."

Nu word er voor deze stelling bewezen dat elk element/restklasse a die niet deelbaar door p is, een inverse heeft. Dat snap ik wel redelijk, maar hoe moet ik me die inverse voorstellen?
En hoe volgt daaruit dat er p elementen zijn?

De elk geheel getal heeft een rest bij deling door p. De restklassen hebben representanten 0, 1, ... p-1. Dat zijn er p in totaal. Er zijn ook geen identificaties tussen deze restklassen want het verschil tussen elk tweetal van deze representanten is minder dan p.

Die inverse, dat moet je gewoon als deling zien. Formeel gezien betekent a/b = c dat c de unieke oplossing van de vergelijking bx = a is. In Z/pZ is op die manier a/b altijd goed gedefinieerd als b niet 0 is en voldoet ook gewoon aan standaard rekenregels.

Ik ga me vraag anders proberen te formuleren, ik heb namelijk het gevoel dat het erg simpel is. Immers, het wordt nergens echt in papers vermeldt hoe/wat.

Ik heb het volgende:
Een fase
Een amplitude
Een frequentie.
Ik verander de fase over de tijd geleidelijk.
Hoe krijg ik nu een frequentie tegenover tijd grafiek? Waarbij vanwege de veranderende fase, de golf dus niet perfect hetzelfde volgt. Wat er verder gebeurt is dat die lijn dus om de oorspronkelijk frequentie heen danst, b.v. 20 freq heeft een lijn dat vervolgens tussen 17 en 23 schommelt (vanwege andere oscillators)

Iemand?

a_n = 0,1,2, rijtjes van lengte n zonder 3 opeenvolgende nullen (000).
Stel de recurrente betrekking op voor aantal rijtjes:

a_n = 2*a_n-1 + 2*a_n-2 + 2*a_n-3
is dit enigzins correct? ik heb toch het idee dat het niet helemaal goed is..

quote:

Op donderdag 19 mei 2011 19:47 schreef Pipo1234 het volgende:

[..]

Nog bedankt voor je duidelijk uitleg. Het is me uiteindelijk gelukt om die opgaven enigszins door te krijgen.

Nu heb ik alleen even een andere vraag over hetzelfde onderwerp. (Ik begin een beetje gefrustreerd te raken door al die algebra, aangezien ik er blijkbaar niet zo goed in ben en mijn boek totaal geen uitleg of uitwerking biedt.) Ik moet vergelijkingen zoals de volgenden oplossen: sin 3x = sin 2(x - 3) en sin 2x = sin 3x. Nu krijg ik het niet voor elkaar om hier een bruikbaar antwoord uit te krijgen. Ik zie het gewoon niet denk ik. Dat probleem had ik eerder ook al bij het oplossen van sin x = cos x enzovoorts. Helaas heb ik nog niet de routine om dit soort vergelijkingen "even" op te lossen.

OK. De sinus is (evenals de cosinus) een periodieke functie met een periode 2π. Dat betekent dus dat twee hoeken (rotaties) die een geheel veelvoud van 2π (radialen) van elkaar verschillen steeds dezelfde sinus (en dezelfde cosinus) hebben. Dus:

(1) sin(α + 2κπ) = sin α en cos(α + 2κπ) = cos α voor elke k ∈ Z

Daarnaast is het ook nog eens zo dat supplementaire hoeken of rotaties (d.w.z. twee hoeken of rotaties die samen 180 graden zijn ofwel π radialen) ook dezelfde sinus hebben. Dat kun je gemakkelijk zien als je even een schetsje maakt met een assenkruis en de eenheidscirkel. De sinus van α is per definitie de y-coördinaat van het beeldpunt van (1;0) bij rotatie over een hoek α, en je ziet in een tekening gemakkelijk dat de beeldpunten van (1;0) bij rotatie over α en bij rotatie over π - α symmetrisch liggen t.o.v. de y-as ('even hoog') en dus dezelfde y-coördinaat hebben, en daarmee ook dezelfde sinus. Dus:

(2) sin(π - α) = sin α

Bij de cosinus werkt het anders. Dit is per definitie de x-coördinaat van het beeldpunt van (1;0) bij rotatie over een hoek α. En omdat de beeldpunten van (1;0) bij rotatie over α en bij rotatie over π - α symmetrisch liggen t.o.v. de y-as en dus tegengestelde x-coördinaten hebben, en daarmee ook een tegengestelde cosinus, geldt dus:

(3) cos(π - α) = -cos α

Nu kunnen we (1) en (2) combineren: als we weten dat twee hoeken (rotaties) dezelfde sinus hebben, dan kunnen we dus zeggen dat deze twee hoeken - op een geheel veelvoud van 2π na - ofwel dezelfde zijn ofwel supplementair zijn. Dus vinden we dat geldt:

(4) sin α = sin β ⇔ α = β + 2kπ ∨ α = (π - β) + 2kπ, k∈Z

Voor de cosinus geldt dat cos(-α) = cos α voor elke willekeurige hoek (rotatie) α, aangezien de beeldpunten van (1;0) bij rotaties over -α en α symmetrisch liggen t.o.v. de x-as en dus dezelfde x-coördinaat hebben. Zo vinden we ook dat geldt:

(5) cos α = cos β ⇔ α = β + 2kπ ∨ α = (- β) + 2kπ, k∈Z

Moeten we nu een vergelijking als sin 3x = sin 2(x-3) oplossen over R, dan kunnen we dus direct zeggen dat moet gelden:

3x = 2(x - 3) + 2kπ ∨3x = π - 2(x - 3) + 2kπ

Dit geeft:

3x = 2x - 6 + 2kπ ∨3x = π - 2x + 6 + 2kπ

En dus:

x = -6 + 2kπ ∨5x = 6 + (2k+1)π

Dus:

x = -6 + 2kπ ∨x = 6/5 + ((2k+1)/5)∙π, k∈Z

[ Bericht 0% gewijzigd door Riparius op 19-05-2011 21:54:54 ]

Wat voor soort vragen kan je verwachten op Examen Aardrijkskunde? Meer inzichts vragen of gewoon toepassingsvragen of wat voor soort dan ook?

Alvast bedankt

Kut, verkeerde topique

quote:

Op donderdag 19 mei 2011 20:51 schreef Fingon het volgende:
a_n = 0,1,2, rijtjes van lengte n zonder 3 opeenvolgende nullen (000).
Stel de recurrente betrekking op voor aantal rijtjes:
[ link | afbeelding ]
a_n = 2*a_n-1 + 2*a_n-2 + 2*a_n-3
is dit enigzins correct? ik heb toch het idee dat het niet helemaal goed is..

Lijkt me toch wel juist, mits je a₀ = 1 neemt. Immers, het is triviaal dat a₁ = 3, a₂ = 9 en a₃ = 26 (omdat alleen de sequentie 000 niet mee mag doen). Dan krijgen we dus volgens je recursieformule a₄ = 2∙(26 + 9 + 3) = 2∙38 = 76, en dat klopt. Immers de sequentie 0000 mag niet meedoen, en ook x000 en 000x met x=1 of x=2 mogen niet meedoen, zodat a₄ = 3⁴ - 5 = 81 - 5 = 76.

quote:

Op donderdag 19 mei 2011 21:35 schreef Riparius het volgende:

[..]

Lijkt me toch wel juist, mits je a₀ = 1 neemt. Immers, het is triviaal dat a₁ = 3, a₂ = 9 en a₃ = 26 (omdat alleen de sequentie 000 niet mee mag doen). Dan krijgen we dus volgens je recursieformule a₄ = 2∙(26 + 9 + 3) = 2∙38 = 76, en dat klopt. Immers de sequentie 0000 mag niet meedoen, en ook x000 en 000x met x=1 of x=2 mogen niet meedoen, zodat a₄ = 3⁴ - 5 = 81 - 5 = 76.

Ok, maar wat voor manier gebruik jij daar dan, is die ook recursief of is dat een andere manier van tellen?

quote:

Op [url=http://forum.fok.nl/topic/1649235/3/50#9705229http://i.fokzine.net/temp(...)r/sub.png1]donderdag 19 mei 2011 22:08[/url] schreef Fingon het volgende:

[..]

Ok, maar wat voor manier gebruik jij daar dan, is die ook recursief of is dat een andere manier van tellen?

Het totaal aantal sequenties van n maal een 0,1 of 2 is 3ⁿ. Bij a₁ en a₂ zijn er geen uitvallers omdat je dan geen drie nullen achter elkaar kunt hebben, dus a₁ = 3¹ = 3 en a₂ = 3² = 9. Bij a₃ is er maar één uitvaller, want alleen 000 mag niet. Dus is a₃ = 3³ - 1 = 26. Met deze gegevens kun je aan de hand van je recursieformule a₄ uitrekenen, en dan kom je op 76, wat inderdaad klopt. Voor a₃ klopt de recursieformule ook, als we a₀ = 1 nemen.

quote:

Op donderdag 19 mei 2011 20:15 schreef thabit het volgende:

[..]

De elk geheel getal heeft een rest bij deling door p. De restklassen hebben representanten 0, 1, ... p-1. Dat zijn er p in totaal. Er zijn ook geen identificaties tussen deze restklassen want het verschil tussen elk tweetal van deze representanten is minder dan p.

Die inverse, dat moet je gewoon als deling zien. Formeel gezien betekent a/b = c dat c de unieke oplossing van de vergelijking bx = a is. In Z/pZ is op die manier a/b altijd goed gedefinieerd als b niet 0 is en voldoet ook gewoon aan standaard rekenregels.

Maar de restklasses zelf bevatten wel meer elementen, toch? Als ik 7 als p pak, dan bevat de restklasse R₁ de elementen 2 en 6.
En als het puur om die restklassen gaat, geldt dat dan niet voor elke commutatieve ring (Z/mZ) met m>0 natuurlijk getal?

Bij de inverse gaat het er toch om dat de 'x' niet gedefineerd is als de gebruikelijke 'keer', maar als een bewerking die voldoet aan bepaalde axioma's? Dus kan je in een lichaam van 2 elementen hebben dat 1 de inverse is van 1 (oid).

quote:

Op vrijdag 20 mei 2011 09:14 schreef Siddartha het volgende:

[..]

Maar de restklasses zelf bevatten wel meer elementen, toch? Als ik 7 als p pak, dan bevat de restklasse R₁ de elementen 2 en 6.
En als het puur om die restklassen gaat, geldt dat dan niet voor elke commutatieve ring (Z/mZ) met m>0 natuurlijk getal?

Elke restklasse bevat oneindig veel elementen. Voor p = 7 zit 2 niet in dezelfde restklasse als 6 maar wel in dezelfde restklasse als 9. En ja, voor m>0 heeft Z/mZ precies m elementen.

quote:

Op vrijdag 20 mei 2011 09:14 schreef Siddartha het volgende:

[..]

Bij de inverse gaat het er toch om dat de 'x' niet gedefineerd is als de gebruikelijke 'keer', maar als een bewerking die voldoet aan bepaalde axioma's? Dus kan je in een lichaam van 2 elementen hebben dat 1 de inverse is van 1 (oid).

Ja, inderdaad, maar de vermenigvuldiging op Z/mZ is gewoon gedefinieerd als de reductie modulo m van de vermenigvuldiging op Z.

quote:

Op donderdag 19 mei 2011 21:15 schreef Riparius het volgende:

[..]

OK. De sinus is (evenals de cosinus) een periodieke functie met een periode 2π. Dat betekent dus dat twee hoeken (rotaties) die een geheel veelvoud van 2π (radialen) van elkaar verschillen steeds dezelfde sinus (en dezelfde cosinus) hebben. Dus:

...

Bedankt voor je heldere uitleg. Spontaan viel het kwartje bij mij...

Ik even even een uitgewerkte opgave in Latex gezet om te zien of ik het begrijp:

quote:

Op vrijdag 20 mei 2011 13:16 schreef Pipo1234 het volgende:

[..]

Bedankt voor je heldere uitleg. Spontaan viel het kwartje bij mij...

Ik even even een uitgewerkte opgave in Latex gezet om te zien of ik het begrijp:
[ afbeelding ]

Dat gaat best goed zo, alleen heb je bij de tweede mogelijkheid een (vaak voorkomende) tekenfout gemaakt.

Je hebt:

πx = (½πx - ½π) + 2kπ ∨ πx = π - (½πx - ½π) + 2kπ

En dat wordt:

πx = ½πx - ½π + 2kπ ∨ πx = π - ½πx + ½π + 2kπ

Daarna verander je π - ½π zomaar in π + ½π, waardoor het antwoord uiteindelijk wel klopt. Maar twee fouten maken die elkaar opheffen betekent niet dat het foutloos is.

[ Bericht 2% gewijzigd door Riparius op 20-05-2011 14:03:16 ]

quote:

Op vrijdag 20 mei 2011 13:52 schreef Riparius het volgende:

[..]

Dat gaat best goed zo, alleen heb je bij de tweede mogelijkheid een (vaak voorkomende) tekenfout gemaakt.

Je hebt:

πx = (½πx - ½π) + 2kπ ∨ πx = π - (½πx - ½π) + 2kπ

En dat wordt:

πx = ½πx - ½π + 2kπ ∨ πx = π - ½πx + ½π + 2kπ

Daarna verander je π - ½π zomaar in π + ½π, waardoor het antwoord uiteindelijk wel klopt. Maar twee fouten maken die elkaar opheffen betekent niet dat het foutloos is.

Bedoel je dat het eigenlijk tussen haakjes had moeten staan, zodat het correct is dat die halve pi plus wordt?

quote:

Op vrijdag 20 mei 2011 15:12 schreef Pipo1234 het volgende:

[..]

Bedoel je dat het eigenlijk tussen haakjes had moeten staan, zodat het correct is dat die halve pi plus wordt?

Ja, want π - (½πx - ½π) + 2kπ is niet hetzelfde als π - ½πx - ½π + 2kπ.

quote:

Op vrijdag 20 mei 2011 15:26 schreef Riparius het volgende:

[..]

Ja, want π - (½πx - ½π) + 2kπ is niet hetzelfde als π - ½πx - ½π + 2kπ.

Oké. Ik snap het en dat is een heel goed punt. Bedankt!

quote:

Op vrijdag 20 mei 2011 15:26 schreef Riparius het volgende:

[..]

Ja, want π - (½πx - ½π) + 2kπ is niet hetzelfde als π - ½πx - ½π + 2kπ.

Domme vraag misschien, maar hoe krijg je die tekens van pi, 1/2 enzovoorts in een post? Ik neem aan dat daar een makkelijkere manier voor is dan de tekens uit je hoofd leren?

quote:

Op vrijdag 20 mei 2011 19:42 schreef M.rak het volgende:

[..]

Domme vraag misschien, maar hoe krijg je die tekens van pi, 1/2 enzovoorts in een post? Ik neem aan dat daar een makkelijkere manier voor is dan de tekens uit je hoofd leren?

Fok ondersteunt Unicode, dus met een geschikt toetsenbord layout programma (of een geschikte keyboard layout van Windows zelf) kun je alles typen wat je wil zonder ingewikkelde codes. Ik gebruik zelf Tavultesoft Keyman omdat ik o.a. ook klassiek Grieks wil kunnen typen. Voor ¼, ½ en ¾ kun je (met de standaard toetsenbord indeling VS internationaal) gewoon Ctrl-Alt 6, Ctrl-Alt 7 en Ctrl-Alt 8 gebruiken (of AltGr met 6, 7, 8).

quote:

Op vrijdag 20 mei 2011 20:09 schreef Riparius het volgende:

[..]

Fok ondersteunt Unicode, dus met een geschikt toetsenbord layout programma (of een geschikte keyboard layout van Windows zelf) kun je alles typen wat je wil zonder ingewikkelde codes. Ik gebruik zelf Tavultesoft Keyman omdat ik o.a. ook klassiek Grieks wil kunnen typen. Voor ¼, ½ en ¾ kun je (met de standaard toetsenbord indeling VS internationaal) gewoon Ctrl-Alt 6, Ctrl-Alt 7 en Ctrl-Alt 8 gebruiken (of AltGr met 6, 7, 8).

Thanks, mooi programma .

Ik moet van de volgende functie het minimum vinden:

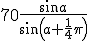
Nu weet ik dat sinus altijd op vaste plekken een maximum en minimum hebben zitten. En na een beetje rekenen kom ik op het minimum: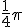 , aangezien bij de afgeleide de noemer maximaal is op dat punt. Dat is logisch aangezien 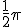de plek is waar sinus maximaal is. Nu is alleen mijn vraag of dit de meest correcte manier is om dit te benaderen? Ik weet namelijk niet hoe ik bij sinus etc. het beste de maxima/minima kan benaderen, als de afgeleide niet 0 is en er een formule aan vast hang waarbij niet helemaal duidelijk is of het maximum/minimum bepalend is.

[ Bericht 8% gewijzigd door Pipo1234 op 21-05-2011 17:11:52 ]

quote:

Op zaterdag 21 mei 2011 16:56 schreef Pipo1234 het volgende:
Ik moet van de volgende functie het minimum vinden:
[ afbeelding ]
Nu weet ik dat sinus altijd op vaste plekken een maximum en minimum hebben zitten. En na een beetje rekenen kom ik op het minimum: [ afbeelding ], aangezien bij de afgeleide de noemer maximaal is op dat punt. Dat is logisch aangezien [ afbeelding ] de plek is waar sinus maximaal is. Nu is alleen mijn vraag of dit de meest correcte manier is om dit te benaderen? Ik weet namelijk niet hoe ik bij sinus etc. het beste de maxima/minima kan benaderen, als de afgeleide niet 0 is en er een formule aan vast hang waarbij niet helemaal duidelijk is of het maximum/minimum bepalend is.

Weet je zeker dat dit de goede functie is? Als je dit namelijk op Wolfram Alpha invoert (zie hier), dan zegt hij dat er geen minima zijn, dat komt ook terug in de afgeleide die nooit nul is. Heb je niet te maken met een beperkt interval waarin je moet zoeken?

quote:

Op zaterdag 21 mei 2011 17:08 schreef M.rak het volgende:

[..]

Weet je zeker dat dit de goede functie is? Als je dit namelijk op Wolfram Alpha invoert (zie hier), dan zegt hij dat er geen minima zijn, dat komt ook terug in de afgeleide die nooit nul is. Heb je niet te maken met een beperkt interval waarin je moet zoeken?

Verdorie. Het had ¼π moeten zijn. Heb hem aangepast.

[ Bericht 0% gewijzigd door Pipo1234 op 21-05-2011 17:26:03 ]

quote:

Op zaterdag 21 mei 2011 17:11 schreef Pipo1234 het volgende:

[..]

Verdorie. Het had 1/4 pi moeten zijn. Heb hem aangepast.

Dan blijf je het zelfde probleem houden, kijk hier maar (beetje naar beneden scrollen voor de afgeleide, die wordt nooit nul).

quote:

Op zaterdag 21 mei 2011 17:17 schreef M.rak het volgende:

[..]

Dan blijf je het zelfde probleem houden, kijk hier maar (beetje naar beneden scrollen voor de afgeleide, die wordt nooit nul).

Je hebt gelijk. Dat is ook zo, aangezien ik het punt moet vinden waar de uitkomst van de afgeleide van die functie het kleinste is. Op dat punt is namelijk de toename het kleinste en dat heeft weer te maken met de opdracht. Ik raak er zelf een beetje van in de war, dus misschien had ik het niet toegelicht.

Ik bedacht me net dat ik in het geval van deze vraag ook even naar de uitwerkingen kan kijken van het betreffende examen. Dit was namelijk een vraag in mijn boek, dat in een examen zat. Het blijkt dus dat ik te ver heb doorgedacht, aangezien het antwoord eigenlijk het maximum van sin is.

Ik ieder geval bedankt.

quote:

Op zaterdag 21 mei 2011 17:30 schreef Pipo1234 het volgende:
Ik bedacht me net dat ik in het geval van deze vraag ook even naar de uitwerkingen kan kijken van het betreffende examen. Dit was namelijk een vraag in mijn boek, dat in een examen zat. Het blijkt dus dat ik te ver heb doorgedacht, aangezien het antwoord eigenlijk het maximum van sin is.

Ik ieder geval bedankt.

Ok, het is nu allemaal duidelijk dus?

quote:

Op zaterdag 21 mei 2011 17:23 schreef Pipo1234 het volgende:

[..]

Je hebt gelijk. Dat is ook zo, aangezien ik het punt moet vinden waar de uitkomst van de afgeleide van die functie het kleinste is. Op dat punt is namelijk de toename het kleinste en dat heeft weer te maken met de opdracht. Ik raak er zelf een beetje van in de war, dus misschien had ik het niet toegelicht.

Als je op zoek bent naar punten waar de afgeleide van een functie een minimum of een maximum bereikt, dan kun je kijken waar de afgeleide van de afgeleide oftewel de tweede afgeleide f''(x) van de oorspronkelijke functie f(x) gelijk is aan nul. In de grafiek van f(x) zijn dergelijke punten buigpunten, en die heeft de grafiek van je functie inderdaad.

quote:

Op zaterdag 21 mei 2011 17:51 schreef Riparius het volgende:

[..]

Als je op zoek bent naar punten waar de afgeleide van een functie een minimum of een maximum bereikt, dan kun je kijken waar de afgeleide van de afgeleide oftewel de tweede afgeleide f''(x) van de oorspronkelijke functie f(x) gelijk is aan nul. In de grafiek van f(x) zijn dergelijke punten buigpunten, en die heeft de grafiek van je functie inderdaad.

Ik zal deze toch maar even voordoen, want ik zie nu dat je voor deze opgave niet persé de tweede afgeleide nodig hebt.

De functie die je hebt is:

(1) f(x) = (70∙sin x)/sin(x + ¼π)

Afgeleide bepalen met de quotiëntregel levert:

(2) f'(x) = (70∙cos x∙sin(x + ¼π) - 70∙sin x∙cos(x + ¼π))/sin²(x + ¼π)

Nu kunnen we in de teller van dit quotiënt een factor 70 buiten haakjes halen. Bovendien geldt:

(3) sin(α-β) = sin α∙cos β - cos α∙sin β

En dus:

(4) cos x∙sin(x + ¼π) - sin x∙cos(x + ¼π) = sin((x + ¼π) - x) = sin(¼π) = ½√2

De afgeleide wordt dus:

(5) f'(x) = (35∙√2)/sin²(x + ¼π)

Deze afgeleide kan niet nul worden, maar bereikt wel een minimum als geldt:

(6) sin²(x + ¼π) = 1

En dus:

(7) sin(x + ¼π) = 1 ∨sin(x + ¼π) = -1

En dus:

(8) x + ¼∙π = ½∙π + 2∙k∙π ∨ x + ¼∙π = (3/2)∙π + 2∙k∙π

Dus:

(9) x = ¼∙π + 2∙k∙π ∨ x = (5/4)∙π + 2∙k∙π, k ∈ Z