SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



quote:Op vrijdag 13 mei 2011 18:52 schreef thabit het volgende:
Ja, je kan wel een bijectie maken van R naar R2. Je kan een reëel getal decimaal uitschrijven en dan om en om cijfers kiezen om er 2 reële getallen van te maken (modulo wat details).
Finally, someone let me out of my cage


Je antwoord is onleesbaar en waarschijnlijk fout.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik zie het ja, er zit een foutje in. Ik kan niet zo goed met die codes werken. De vraag is overigens wel goed getypt 
Of niet?


quote:Op zaterdag 14 mei 2011 11:05 schreef Self-Catering het volgende:
Als ik deze moet differentieren:
[ afbeelding ]
Krijg ik dan als antwoord:
[ afbeelding ]
?
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]


Produktregel gebruiken:quote:Op zaterdag 14 mei 2011 11:05 schreef Self-Catering het volgende:
Als ik deze moet differentieren:
[ afbeelding ]
Krijg ik dan als antwoord:
[ afbeelding ]
?
F'(x) = 1*sqrt(x) + (x+1)*1/(2*sqrt(x)) = (2*x)/(2*sqrt(x)) + (x+1)*1/(2*sqrt(x)) = (3*x+1)/(2*sqrt(x))
(laatste twee stappen optioneel).
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek


Ik moet volgens mijn opgave algebraïsch aan het antwoord van een aantal formules komen met betrekking tot sinus en cosinus. Nu zet ik alleen vraagtekens bij mijn methode... Is het zo dat jij bij dergelijke formules de daadwerkelijk omrekening van radiaal naar sinus/cosinus en visa versa hoofdzakelijk met de rekenmachine gedaan kan worden? Ik versta zelf namelijk onder algebraïsch dat het zoveel mogelijk zonder rekenmachine gedaan dient te worden.
Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord. Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord. Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


1. Algebraïsch = zonder rekenmachine. Wat bedoel je precies met omrekenen tussen radialen en sinus/cosinussen?quote:Op zaterdag 14 mei 2011 15:02 schreef Pipo1234 het volgende:
Ik moet volgens mijn opgave algebraïsch aan het antwoord van een aantal formules komen met betrekking tot sinus en cosinus. Nu zet ik alleen vraagtekens bij mijn methode... Is het zo dat jij bij dergelijke formules de daadwerkelijk omrekening van radiaal naar sinus/cosinus en visa versa hoofdzakelijk met de rekenmachine gedaan kan worden? Ik versta zelf namelijk onder algebraïsch dat het zoveel mogelijk zonder rekenmachine gedaan dient te worden.
Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord. Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
2. Oplossingen van cos x = cos a zijn inderdaad x=a en x=-a. Echter, omdat de cosinus 2pi - periodiek is, kan je bij de oplossing een willekeurig veelvoud van 2pi optellen en dan heb je weer een oplossing. Dus x=-a en x=a zijn nog lang niet alle oplossingen. Alle oplossingen worden gegeven door:
(1) x = a + 2*k*pi;
(2) x = -a + 2*k*pi,
waarbij k een willekeurig geheel getal is. Dit beantwoord ook direct je volgende vraag, denk daar maar even over na.
Note: Ik denk dat ze het in je boek hebben over alle oplossingen in het interval [0,2pi]


Je vraag is niet echt duidelijk. De rekenmachine gebruik je uitsluitend ter vervanging van papieren goniometrische tafels (ja, zo ging dat vroeger zonder rekenmachines). Als je dus een vraagstuk oplost (uitrekent) en je hebt (bijvoorbeeld) een benaderde waarde van de sinus (of cosinus of tangens) van 20 graden nodig, dan gebruik je daarvoor de rekenmachine.quote:Op zaterdag 14 mei 2011 15:02 schreef Pipo1234 het volgende:
Ik moet volgens mijn opgave algebraïsch aan het antwoord van een aantal formules komen met betrekking tot sinus en cosinus. Nu zet ik alleen vraagtekens bij mijn methode... Is het zo dat jij bij dergelijke formules de daadwerkelijk omrekening van radiaal naar sinus/cosinus en visa versa hoofdzakelijk met de rekenmachine gedaan kan worden? Ik versta zelf namelijk onder algebraïsch dat het zoveel mogelijk zonder rekenmachine gedaan dient te worden.
Er zijn echter een aantal standaardhoeken (0, 30, 45, 60 en 90 graden) waarvan je de exacte waarde van de sinus en cosinus uit het blote hoofd moet kennen. Daar is overigens een eenvoudig ezelsbruggetje voor: voor de sinus is dit de helft van de vierkantswortel uit resp. 0, 1, 2, 3 en 4 en voor de cosinus hetzelfde rijtje in omgekeerde volgorde.
Bij herleidingen van goniometrische formules en identiteiten gebruik je uiteraard geen rekenmachine.
Of je het echt begrijpt betwijfel ik, want wat je boek beweert is in zijn algemeenheid niet juist. De cosinus is immers een periodieke functie met periode 2π, dus er zijn oneindig veel oplossingen als je R als domein neemt.quote:Nog even een andere vraag over dit onderwerp: In mijn boek staat dat de oplossing van van de "standaardvergelijking" cos x = cos a twee oplossingen heeft, namelijk x = a en x = -a. Nu snap ik dat op zich wel, alleen is er bij één vraag een vreemd antwoord.
Dit is nu het gevolg van die periodiciteit. Ik neem aan dat je vertrouwd bent met de definities van sinus en cosinus aan de hand van de eenheidscirkel? Welnu, een rotatie van het uitgangspunt (1;0) om de oorsprong over een hoek van (7/6)∙π radialen levert hetzelfde beeldpunt op als een rotatie over een hoek van -(5/6)∙π radialen. Maak even een schetsje van de eenheidscirkel in een cartesisch assenstelsel om dit gemakkelijk te zien. Aangezien de cosinus en de sinus per definitie de x- resp. de y-coördinaat zijn van het beeldpunt van (1;0) bij rotatie over een willekeurige hoek, is het duidelijk dat (7/6)∙π en -(5/6)∙π dezelfde cosinus én dezelfde sinus hebben.quote:Daar is het antwoord namelijk 5/6pi en 1 1/6 pi, wat ook logisch is, alleen is 1 1/6 pi niet -5/6 pi, terwijl dat wel hetzelfde antwoord geeft. (Dit gaat trouwens over de symmetrie van sinus, enzovoorts.)
Vanwege het feit dat de eenheidscirkel een omtrek heeft van 2π en je dus met een rotatie over een hoek van 2π radialen hetzij in positieve zin (tegen de wijzers van de klok in) hetzij in negatieve zin (met de wijzers van de klok mee) precies eenmaal rond bent geweest geldt dus voor elke willekeurige α (in radialen) en voor elk geheel getal k:
cos(α + 2∙k∙π) = cos α en sin(α + 2∙k∙π) = sin α
[ Bericht 0% gewijzigd door Riparius op 14-05-2011 16:49:58 ]


Omrekenen als in de tegenhanger vinden van een radiaal of omgekeerd. Feitelijk is het geen rekenen natuurlijk.quote:Op zaterdag 14 mei 2011 15:17 schreef thenxero het volgende:
[..]
1. Algebraïsch = zonder rekenmachine. Wat bedoel je precies met omrekenen tussen radialen en sinus/cosinussen?
In mijn boek wordt de formule gevraagd die jij ook noemt. Misschien had ik mijn vraag iets uitgebreider moeten stellen.quote:Op zaterdag 14 mei 2011 15:17 schreef thenxero het volgende:
2. Oplossingen van cos x = cos a zijn inderdaad x=a en x=-a. Echter, omdat de cosinus 2pi - periodiek is, kan je bij de oplossing een willekeurig veelvoud van 2pi optellen en dan heb je weer een oplossing. Dus x=-a en x=a zijn nog lang niet alle oplossingen. Alle oplossingen worden gegeven door:
(1) x = a + 2*k*pi;
(2) x = -a + 2*k*pi,
waarbij k een willekeurig geheel getal is. Dit beantwoord ook direct je volgende vraag, denk daar maar even over na.
Note: Ik denk dat ze het in je boek hebben over alle oplossingen in het interval [0,2pi]
Wat ik mij met name afvraag is het volgende:
Gevraagd wordt naar x van cosinus. (Ik heb de formules even in LATEX gezet om het wat duidelijker te maken). Volgens het principe x = a en x=-a krijg je het volgende antwoord:
Echter is volgens het boek dit het juiste antwoord:
Ik zie niet in waarom hierbij die regel niet opgaat. Het is trouwens wel opvallend dat in beide gevallen het antwoord is te herleiden naar een deel van pi, maar dat zou voor mij geen reden zijn om het antwoord anders te geven.
[ Bericht 4% gewijzigd door Pipo1234 op 14-05-2011 18:29:20 ]
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


De formules voor omrekenen zijn heel makkelijk, van graden naar radialen doe je het aantal graden*pi/180, omgedraaid doe je het aantal radialen*180/pi.quote:Op zaterdag 14 mei 2011 18:23 schreef Pipo1234 het volgende:
[..]
Omrekenen als in de tegenhanger vinden van een radiaal of omgekeerd. Feitelijk is het geen rekenen natuurlijk.
Het antwoord is (als het goed is) 7/6 pi +k*2pi. Als je bij jouw antwoord k=1 invult krijg je precies 7/6 pi, de antwoorden zijn gelijk, alleen is de schrijfwijze andersquote:[..]
In mijn boek wordt de formule gevraagd die jij ook noemt. Misschien had ik mijn vraag iets uitgebreider moeten stellen.
Wat ik mij met name afvraag is het volgende:
Gevraagd wordt naar x van cosinus. (Ik heb de formules even en LATEX gezet om het wat duidelijker te maken). Volgens het principe x = a en x=-a krijg je het volgende antwoord:
[ afbeelding ]
Echter is volgens het boek dit het juiste antwoord:
[ afbeelding ]
Ik zie niet in waarom hierbij die regel niet opgaat. Het is trouwens wel opvallend dat in beide gevallen het antwoord is te herleiden naar een deel van pi, maar dat zou voor mij geen reden zijn om het antwoord anders te geven.
The biggest argument against democracy is a five minute discussion with the average voter.


Ik zie nu dat er bij de delingen nog pi moet staan...quote:Op zaterdag 14 mei 2011 18:33 schreef M.rak het volgende:
[..]
De formules voor omrekenen zijn heel makkelijk, van graden naar radialen doe je het aantal graden*pi/180, omgedraaid doe je het aantal radialen*180/pi.
[..]
Het antwoord is (als het goed is) 7/6 pi +k*2pi. Als je bij jouw antwoord k=1 invult krijg je precies 7/6 pi, de antwoorden zijn gelijk, alleen is de schrijfwijze anders.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


Op het interval [0,2pi] is het equivalent, maar niet op |R.quote:Op zaterdag 14 mei 2011 18:33 schreef M.rak het volgende:
Het antwoord is (als het goed is) 7/6 pi +k*2pi. Als je bij jouw antwoord k=1 invult krijg je precies 7/6 pi, de antwoorden zijn gelijk, alleen is de schrijfwijze anders.


Hoe bedoel je?quote:Op zaterdag 14 mei 2011 18:36 schreef thenxero het volgende:
[..]
Op het interval [0,2pi] is het equivalent, maar niet op |R.
The biggest argument against democracy is a five minute discussion with the average voter.


Beide antwoorden zijn juist en gelijkwaardig, als je tenminste achter die breuken nog een factor π toevoegt, want zoals je het nu opschrijft is het gewoon fout. Immers, k is een willekeurig geheel getal, en als je eenmaal 2π optelt bij (-5/6)∙π krijg je (7/6)∙π. De verzameling van alle reële getallen van de gedaante (-5/6)∙π + k∙2π (met k geheel) is dus precies dezelfde als de verzameling van alle reële getallen van de gedaante (7/6)∙π + k∙2π (met k geheel).quote:Op zaterdag 14 mei 2011 18:23 schreef Pipo1234 het volgende:
Wat ik mij met name afvraag is het volgende:
Gevraagd wordt naar x van cosinus. (Ik heb de formules even in LATEX gezet om het wat duidelijker te maken). Volgens het principe x = a en x=-a krijg je het volgende antwoord:
[ afbeelding ]
Echter is volgens het boek dit het juiste antwoord:
[ afbeelding ]
Ik zie niet in waarom hierbij die regel niet opgaat. Het is trouwens wel opvallend dat in beide gevallen het antwoord is te herleiden naar een deel van pi, maar dat zou voor mij geen reden zijn om het antwoord anders te geven.


Kunstproductie en lijsten is dat een assortiment groep?
en klopt dit?
Assortiment groep Multimedia
Artikelgroep Foto s
Artikelsoort Canvas
Assortiment groep opname apparatuur
Artikelgroep Foto-apparatuur
Artikelsoort Digitale compact camera s
en klopt dit?
Assortiment groep Multimedia
Artikelgroep Foto s
Artikelsoort Canvas
Assortiment groep opname apparatuur
Artikelgroep Foto-apparatuur
Artikelsoort Digitale compact camera s


Klopt, was een beetje onduidelijk opgeschreven. Ik bedoelde te zeggen dat als je k=1 invult je 7/6 pi krijgt. De twee antwoorden zijn dus identiek (ze bevatten dezelfde getallen).quote:Op zaterdag 14 mei 2011 19:01 schreef thenxero het volgende:
[..]
Op [0,2pi] moet gelden k=1, op |R is k willekeurig.
The biggest argument against democracy is a five minute discussion with the average voter.


Neem X1, ... , Xn random sample van uniforme verdeling Xi~( θ-1, θ+1)
a) Laat zien dat sample mean, X- een unbiased estimator is van θ.
Is dit correct?
Laat zien dat E[ X- ]=θ
E[ X- ] = E[ 1/nΣnXi ]
= 1/n {Σn E(Xi)} en E(Xi=θ)
= 1/n {Σn(θ)}
= 1/n * nθ
= θ
a) Laat zien dat sample mean, X- een unbiased estimator is van θ.
Is dit correct?
Laat zien dat E[ X- ]=θ
E[ X- ] = E[ 1/nΣnXi ]
= 1/n {Σn E(Xi)} en E(Xi=θ)
= 1/n {Σn(θ)}
= 1/n * nθ
= θ
Beneath the gold, bitter steel


Hoe los je de volgende vergelijking op (met de hand):
12x^3 - 24x^2 + 6x = 0
En nog een vraag
Bepaal de lokale minima en maxima op het gegeven domein:
f:[-1/2,1] -> 1/(x^5+x+1)
dan kom ik tot f'(x) = (-5x^4-1)/((x^5+x+1)^2)
f'(x) = 0 geeft -5x^4-1 = 0 geeft x^4 = -1/5
Welke in het reëele vlak geen oplossingen heeft.
Maar is dit wel de manier om lokale minima/maxima te berekenen?
[ Bericht 38% gewijzigd door .aeon op 15-05-2011 19:50:10 ]
12x^3 - 24x^2 + 6x = 0
En nog een vraag
Bepaal de lokale minima en maxima op het gegeven domein:
f:[-1/2,1] -> 1/(x^5+x+1)
dan kom ik tot f'(x) = (-5x^4-1)/((x^5+x+1)^2)
f'(x) = 0 geeft -5x^4-1 = 0 geeft x^4 = -1/5
Welke in het reëele vlak geen oplossingen heeft.
Maar is dit wel de manier om lokale minima/maxima te berekenen?
[ Bericht 38% gewijzigd door .aeon op 15-05-2011 19:50:10 ]


De afgeleide wordt niet nul op dit interval, dat betekent dat de functie ofwel constant stijgt, ofwel constant daalt. Vul x=0 in in de afgeleide en je ziet dat de afgeleide daar negatief is, wat een constante daling aangeeft. Hieruit kan je concluderen dat het maximum op dat domein aangenomen wordt in het linkergrenspunt (-1/2) en het minimum op het rechtergrenspunt (1).quote:Op zondag 15 mei 2011 19:27 schreef .aeon het volgende:
Hoe los je de volgende vergelijking op (met de hand):
12x^3 - 24x^2 + 6x = 0
En nog een vraag
Bepaal de lokale minima en maxima op het gegeven domein:
f:[-1/2,1] -> 1/(x^5+x+1)
dan kom ik tot f'(x) = (-5x^4-1)/((x^5+x+1)^2)
f'(x) = 0 geeft -5x^4-1 = 0 geeft x^4 = -1/5
Welke in het reëele vlak geen oplossingen heeft.
Maar is dit wel de manier om lokale minima/maxima te berekenen?
The biggest argument against democracy is a five minute discussion with the average voter.


Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X² + Y² + Z² | X + Y + Z = 0?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?


Correctquote:Op zondag 15 mei 2011 14:36 schreef Fingon het volgende:
Neem X1, ... , Xn random sample van uniforme verdeling Xi~( θ-1, θ+1)
a) Laat zien dat sample mean, X- een unbiased estimator is van θ.
Is dit correct?
Laat zien dat E[ X- ]=θ
E[ X- ] = E[ 1/nΣnXi ]
= 1/n {Σn E(Xi)} en E(Xi=θ)
= 1/n {Σn(θ)}
= 1/n * nθ
= θ


hmm.. dit ziet er vreemd uit. X+Y+Z is N(0,3) verdeeld en nu conditioneer je de verdeling van de chi-kwadraatverdeling door deze normale verdeling op nul te stellen. Dat suggereert dat de kansdichtsheidsfunctie van deze verdeling blijkbaar gelijk is aan nul en dan krijg je toch een probleem als je de kansdichtsheidsfunctie van de geconditioneerde verdeling wilt bepalen.quote:Op zondag 15 mei 2011 21:32 schreef thenxero het volgende:
Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X² + Y² + Z² | X + Y + Z = 0?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?


Ik moet de dubbele integraal berekenen over f(x,y)= 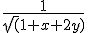 met gebied D=[0,1]x[0,1].
met gebied D=[0,1]x[0,1].
Kan ik een substitutie maken met
g: (r,a)= (rcos(a),2rsin(a)) ?
Dat levert dan de dubbele integraal over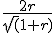 .
.
Kan ik een substitutie maken met
g: (r,a)= (rcos(a),2rsin(a)) ?
Dat levert dan de dubbele integraal over


waarom zou je dat willen? Je moet over een vierkant integreren en dan is het gebruik van cilindercoordinaten niet echt optimaal. Deze integraal kun je rechtstreeks doen, zonder substituties:quote:Op maandag 16 mei 2011 15:15 schreef Siddartha het volgende:
Ik moet de dubbele integraal berekenen over f(x,y)= [ afbeelding ] met gebied D=[0,1]x[0,1].
Kan ik een substitutie maken met
g: (r,a)= (rcos(a),2rsin(a)) ?
Dat levert dan de dubbele integraal over [ afbeelding ].


Ik had deze integraal graag met poolcoordinaten willen doen, puur om te oefenen. Wat dat betreft: Was mijn methode wel goed?quote:Op maandag 16 mei 2011 15:33 schreef Don_Vanelli het volgende:
[..]
waarom zou je dat willen? Je moet over een vierkant integreren en dan is het gebruik van cilindercoordinaten niet echt optimaal. Deze integraal kun je rechtstreeks doen, zonder substituties:
[ afbeelding ]


in principe mag je elke transformatie doen die je wil, maar wat worden je nieuwe grenzen dan?quote:Op maandag 16 mei 2011 16:02 schreef Siddartha het volgende:
[..]
Ik had deze integraal graag met poolcoordinaten willen doen, puur om te oefenen. Wat dat betreft: Was mijn methode wel goed?


'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.quote:Op maandag 16 mei 2011 16:09 schreef Don_Vanelli het volgende:
[..]
in principe mag je elke transformatie doen die je wil, maar wat worden je nieuwe grenzen dan?


Dat is zo niet te beantwoorden, je geeft je nieuwe integratiegrenzen namelijk niet. Maar met poolcoördinaten gaan integreren over een vierkant? Dan moet je eerst maar eens uitvogelen hoe je dan r als functie van θ beschrijft voor de beide zijden van het vierkant die niet langs de coördinaatassen liggen. Dan moet je dus eerst vergelijkingen in poolcoördinaten gaan opstellen voor de rechte lijnen met de cartesische vergelijkingen x=1 en y=1 en dan moet je alsnog gaan opsplitsen in twee integralen met resp. 0 ≤ θ ≤ π/4 en π/4 ≤ θ ≤ π/2.quote:Op maandag 16 mei 2011 16:02 schreef Siddartha het volgende:
[..]
Ik had deze integraal graag met poolcoordinaten willen doen, puur om te oefenen. Wat dat betreft: Was mijn methode wel goed?


Nee!quote:Op maandag 16 mei 2011 16:11 schreef Siddartha het volgende:
[..]
'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.


Vervang x door -y-zquote:Op zondag 15 mei 2011 21:32 schreef thenxero het volgende:
Als X,Y,Z i.i.d. N(0,1) verdeeld zijn, hoe vind ik dan de verdeling van X² + Y² + Z² | X + Y + Z = 0?
Ik weet dat X² + Y² + Z² chi-kwadraat verdeeld is met drie vrijheidsgraden, kan ik daar iets mee?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ik ben gewoon dom bezig, ik probeer een deel van de functie ipv een gebied/D te beschrijven. Wat nergens op slaat of in ieder geval niet handig is.quote:Op maandag 16 mei 2011 16:17 schreef Riparius het volgende:
[..]
Dat is zo niet te beantwoorden, je geeft je nieuwe integratiegrenzen namelijk niet. Maar met poolcoördinaten gaan integreren over een vierkant? Dan moet je eerst maar eens uitvogelen hoe je dan r als functie van θ beschrijft voor de beide zijden van het vierkant die niet langs de coördinaatassen liggen. Dan moet je dus eerst vergelijkingen in poolcoördinaten gaan opstellen voor de rechte lijnen met de cartesische vergelijkingen x=1 en y=1 en dan moet je alsnog gaan opsplitsen in twee integralen met resp. 0 ≤ θ ≤ π/4 en π/4 ≤ θ ≤ π/2.


Als je zo je cilindercoordinaten kiest is dat equivalent met een integraal over het gebied dat voldoet aanquote:Op maandag 16 mei 2011 16:11 schreef Siddartha het volgende:
[..]
'Binnenste' integraal van 0 naar r, buitenste integraal van 0 naar 2Pi.
en dat is iets anders dan een vierkant.


Ik ben even de weg kwijt... wie kan mij een aanwijzing geven hoe dit op te lossen? Volgens mijn boek moet ik de formules sin2 x + cos2 x = 1 en sin x/cos x = tan x gebruiken, maar daar kom ik niet verder mee. Alvast bedankt voor alle hulp!
quote:Los algebraïsch op: cos2 x = sin x
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.


die tweede formule heb je niet eens nodig.. Schrijf de cosinus om in een sinus met behulp van de eerste regel en je krijgt een vergelijking in termen van sinussen die prima op te lossen is met een schaduwvergelijking.
edit: je kan ook alleen de tweede regel gebruiken en sin(x) = tan(x)*cos(x) schrijven, dan staat er aan beide kanten een factor cos(x) in die je buiten haakjes kan halen.
edit: je kan ook alleen de tweede regel gebruiken en sin(x) = tan(x)*cos(x) schrijven, dan staat er aan beide kanten een factor cos(x) in die je buiten haakjes kan halen.


