[Bèta wiskunde] Huiswerk- en vragentopic

Wat is de verdeling van Y als Y = lim n->inf [product van Xi van 1 tot n ]
en Xi~LOGN(mu, 2)?
Volgens mij wordt dat volgens de CLT toch weer een lognormale verdeling met mu=0 en variantie=1?
De exacte reden hiervoor weet ik niet meer, als iemand dat even kan oplepelen waardeer ik dat zeer

quote:

Op donderdag 26 mei 2011 20:48 schreef GlowMouse het volgende:
het product is hetzelfde als de exponent van de som van de log

Dus zeg A=product van Xi van i=1 tot n
dus A = exp{ln [A]}
ln[A] = som i=1 tot n van ln(Xi)
ik vind uiteindelijk dat dit met substitutie etc. is dat ln[Xi]=Zi~N(mu, 4) verdeeld
dan is Y=exp[som i=1 tot n van Zi]
dus Y is lognormaal verdeeld met ~(n*mu, n*4)
Maar als ik dan n-> inf doe gaat het beetje vreemd, ik mis een stuk parate theorie vrees ik

quote:

Op donderdag 26 mei 2011 19:29 schreef Pipo1234 het volgende:

[..]

Je leent drie jaar lang elke maand 500 euro die je vervolgens in 15 jaar gaat aflossen? Hoeveel wil per jaar gaan aflossen?

tussen 100 en 200 euro maar ga maar uit van 150

quote:

Op donderdag 26 mei 2011 21:46 schreef kingofthepokerface het volgende:

[..]

tussen 100 en 200 euro maar ga maar uit van 150

Ik neem aan dat je 150 euro per maand bedoelt? Dus samenvattend ga je 3 drie jaar lang elke maand 500 euro lenen en vervolgens ga je na die drie jaar elke maand 150 euro afbetalen?

Ik ben op zoek naar de primitieve van de volgende functie: (4 - e^x)². Het gaat hier om een gekwadrateerde functie, aangezien ik bezig ben met lichamen berekenen. Ik krijg het niet voor elkaar om de juiste primitieve te vinden. Dit komt vooral door de kwadratering, aangezien ik het zonder kwadratering al gevonden heb. Ik ben ook niet zo sterk in afleiden van abstracte termen als LN en e.

Wil iemand mij een aanwezig geven hoe ik de primtieve kan vinden? Ik kom niet verder dan iets van 1/3 (4 - e^x)³ i.c.m. met de kettingregel om de functie te herleiden, alleen dit lukt me dus niet.

quote:

Op vrijdag 27 mei 2011 12:43 schreef GlowMouse het volgende:
Je kunt eerst de haakjes wegwerken.

Dat heb ik geprobeerd, maar dan krijg ik 16 - 8e^x + (e^x)² en wanneer ik dat herleid naar de primitieve 16x - 8e^x + 1/3(e^x)³ klopt het niet. Is mijn primitieve überhaupt goed?

quote:

Op vrijdag 27 mei 2011 13:01 schreef GlowMouse het volgende:
(e^x)² = e^2x

Dat meen je niet. Ik ben ook zo beroerd als het neerkomt op e en ln. Bedankt.

Ik heb nu de primitieve 16x - 8e^x + 1/2 e^2x en het volume dat ik daarmee krijg klopt helemaal.

quote:

Op vrijdag 27 mei 2011 13:22 schreef Pipo1234 het volgende:

[..]

Dat meen je niet. Ik ben ook zo beroerd als het neerkomt op e en ln. Bedankt.

Ik heb nu de primitieve 16x - 8e^x + 1/2 e^2x en het volume dat ik daarmee krijg klopt helemaal.

Die machtregel geldt niet alleen voor e, maar altijd.

(a^p)^q = a^{pq}

Vraagje over radix conversie... Uit "art of Computer Programming" volume 2. Hier staat het volgende over radix conversie...



Nu snap ik niet de methode 1b. Ik heb bijvoorbeeld het getal 10 met als basis 10 (decimaal dus) Nu wil ik dit getal 10 met basis 10 omschrijven naar een getal met basis 256 (word). Hoe moet ik dit nou doen volgende de methode bij 1b? Enkel wat ik lees is dat je de polynoom, voor decimaal getal 345

3*10^2 + 4*10^1 + 5*10^0 = 345 opstelt en dat je dit kunt schrijven naar (3*10 + 4)*10) + 5

Waar is de conversie gebleven naar me nieuwe basis 256?

Stel je hebt de formule:

(9x-2)(x^2-2x)

Dan differentieer ik dit met de productregel en krijg ik:

9 * (x^2-2x) + (9x-2) * (2x-2)

Tot zover snap ik het allemaal. Maar nu loop ik tegen het probleem aan, hoe vereenvoudig ik dit? De volgende stappen onderneem ik altijd:

• -2 * -2 = +4
• 9 * -2x + 9x * -2 = -36x

Zoals je ziet klopt dit voor geen kant, want ik weet dat -36x -40x moet zijn. Om nog maar te zwijgen over hoe ze aan 27x^2 komen.

Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.

quote:

Op vrijdag 27 mei 2011 14:38 schreef Dale. het volgende:
Vraagje over radix conversie... Uit "art of Computer Programming" volume 2. Hier staat het volgende over radix conversie...

[ afbeelding ]

Nu snap ik niet de methode 1b. Ik heb bijvoorbeeld het getal 10 met als basis 10 (decimaal dus) Nu wil ik dit getal 10 met basis 10 omschrijven naar een getal met basis 256 (word). Hoe moet ik dit nou doen volgende de methode bij 1b? Enkel wat ik lees is dat je de polynoom, voor decimaal getal 345

3*10^2 + 4*10^1 + 5*10^0 = 345 opstelt en dat je dit kunt schrijven naar (3*10 + 4)*10) + 5

Waar is de conversie gebleven naar me nieuwe basis 256?

Het idee is dat je de berekening (3*10 + 4)*10 + 5 simpelweg in basis 256 uitvoert, ervan uitgaande dat je methodes voorhanden hebt om in basis 256 te rekenen.

quote:

Op vrijdag 27 mei 2011 15:02 schreef spanje1986 het volgende:
Stel je hebt de formule:

(9x-2)(x^2-2x)

Dan differentieer ik dit met de productregel en krijg ik:

9 * (x^2-2x) + (9x-2) * (2x-2)

Tot zover snap ik het allemaal. Maar nu loop ik tegen het probleem aan, hoe vereenvoudig ik dit? De volgende stappen onderneem ik altijd:

• -2 * -2 = +4
• 9 * -2x + 9x * -2 = -36x

Zoals je ziet klopt dit voor geen kant, want ik weet dat -36x -40x moet zijn. Om nog maar te zwijgen over hoe ze aan 27x^2 komen.

Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.

http://mediatheek.thinkqu(...)kjes/page_uitleg.htm

quote:

Op vrijdag 27 mei 2011 15:02 schreef spanje1986 het volgende:
...

Wie o wie kan mij verder helpen, loop hier al een tijd lang tegen aan.

Volgens mij maak jij dezelfde denkfout als dat ik eerst deed. Je moet opletten dat je alle waarden met elkaar vermenigvuldigd.

Dit is wat je krijgt via de productregel:
9 · (x² - 2x) + (9x - 2) · (2x - 2)

Vervolgens vermenigvuldig je alles met elkaar (rekening houdend met de plus/min):
(9 · x²) - (9 · 2x) + (9x · 2x) - (9x · 2) - (2 · 2x) + (2 · 2)

Daarna heb je het volgende:
9x² - 18x + 18x² - 18x - 4x + 4

En na vereenvoudiging heb je de volgende afgeleide:
27x² - 40x + 4

[ Bericht 0% gewijzigd door Pipo1234 op 28-05-2011 10:34:51 ]

Ik zoek de primitieve van deze functie: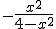

Ik weet niet goed hoe ik deze kan krijgen en heb al van alles geprobeerd. Hetgeen dat het meeste in de buurt kwam (maar niet klopte verder) was ln(4-x²). Iemand een tip hoe ik aan de primitieve kom?

quote:

Op zaterdag 28 mei 2011 14:33 schreef Pipo1234 het volgende:
Ik zoek de primitieve van deze functie: [ afbeelding ]

Ik weet niet goed hoe ik deze kan krijgen en heb al van alles geprobeerd. Hetgeen dat het meeste in de buurt kwam (maar niet klopte verder) was ln(4-x²). Iemand een tip hoe ik aan de primitieve kom?

Breuksplitsen!

quote:

Op zaterdag 28 mei 2011 14:39 schreef thabit het volgende:

[..]

Breuksplitsen!

Na dat gedaan te hebben kom ik alsnog niet verder. Ik heb nu:


Het probleem is dat ik het niet voor elkaar krijg om een primitieve te vinden waar die breuken de afgeleide van zijn. Ik zoek het via de machtsfunctie, aangezien ik niet weet hoe ik het anders moet doen.

Je kan die breuken nog iets anders schrijven: je kan de x in de teller wegwerken.

quote:

Op zaterdag 28 mei 2011 15:22 schreef Pipo1234 het volgende:

[..]

Na dat gedaan te hebben kom ik alsnog niet verder. Ik heb nu:
[ afbeelding ]

Het probleem is dat ik het niet voor elkaar krijg om een primitieve te vinden waar die breuken de afgeleide van zijn. Ik zoek het via de machtsfunctie, aangezien ik niet weet hoe ik het anders moet doen.

Begin eens met:

-x²/(4 - x²) = x²/(x² -4) = (x² - 4 + 4)/(x² - 4) = (x² - 4)/(x² - 4) + 4/(x² - 4) = 1 + 4/(x² - 4).

quote:

Op zaterdag 28 mei 2011 15:30 schreef Riparius het volgende:

[..]

Begin eens met:

-x²/(4 - x²) = x²/(x² -4) = (x² - 4 + 4)/(x² - 4) = (x² - 4)/(x² - 4) + 4/(x² - 4) = 1 + 4/(x² - 4).

Ik krijg de primitieve van deze formule maar niet te pakken. Als ik het met ln(x²-4) probeer kom ik in de knoop i.v.m. de kettingregel.

quote:

Op zaterdag 28 mei 2011 16:18 schreef Pipo1234 het volgende:

[..]

Ik krijg de primitieve van deze formule maar niet te pakken. Als ik het met ln(x²-4) probeer kom ik in de knoop i.v.m. de kettingregel.

4/(x² - 4) moet je nog vereenvoudigen door middel van breuksplitsen, nu heb je echter geen last meer van een x in de teller, waardoor het primitiveren na het breuksplitsen relatief eenvoudig is.

quote:

Op zaterdag 28 mei 2011 16:26 schreef M.rak het volgende:

[..]

4/(x² - 4) moet je nog vereenvoudigen door middel van breuksplitsen, nu heb je echter geen last meer van een x in de teller, waardoor het primitiveren na het breuksplitsen relatief eenvoudig is.

Dus toch... Ga ik dat eens proberen.

quote:

Op zaterdag 28 mei 2011 16:18 schreef Pipo1234 het volgende:

[..]

Ik krijg de primitieve van deze formule maar niet te pakken. Als ik het met ln(x²-4) probeer kom ik in de knoop i.v.m. de kettingregel.

OK. We hadden al gevonden dat:

(1) -x²/(4 - x²) = 1 + 4/(x² - 4).

Een primitieve van 1 is x, dus nu resteert nog de bepaling van een primitieve van 4/(x² - 4). Hiervoor gaan we breuksplitsing oftewel splitsing in partiële breuken toepassen.

Het idee is - heel kort door de bocht - dat we een breuk gaan herschrijven als een som van deelbreuken waarbij de noemer telkens een factor is van de noemer van de oorspronkelijke breuk.

Als je 1/2 + 1/3 wil optellen, dan moet je deze breuken eerst gelijknamig maken:

1/2 + 1/3 = (3∙1)/(3∙2) + (2∙1)/(2∙3) = 3/6 + 2/6 = (3 + 2)/6 = 5/6

Maar stel nu eens dat we het omgekeerde zouden willen doen, dus 5/6 herleiden naar 1/2 + 1/3. Dan moeten we dus deze breuk opsplitsen in deelbreuken waarvan de noemers telkens één van van de (priem)factoren zijn van 6 = 2∙3. Dit is - heel kort - het achterliggende idee.

Nu gaan we 4/(x² - 4) opsplitsen in deelbreuken. Daarvoor moeten we dus eerst de factoren van de noemer x² - 4 bepalen. Dit is heel gemakkelijk, want je kent het merkwaardige product a² - b² = (a-b)(a+b). Dus hebben we:

(2) x² - 4 = (x - 2)(x + 2)

De bedoeling is nu dat we zoiets krijgen:

(3) 4/(x² - 4) = A/(x - 2) + B/(x + 2)

De kunst is nu om A en B te bepalen. Hiertoe vermenigvuldigen we beide leden van (3) met de noemer van de breuk in het linkerlid, dus met x² - 4 = (x - 2)(x + 2) , zodat we alle breuken kwijtraken. Dan krijgen we:

(4) 4 = A(x + 2) + B(x - 2)

Uitwerken geeft:

(5) 4 = Ax + 2A + Bx - 2B

Hergroeperen van de termen in het rechterlid naar machten van x geeft:

(6) 4 = (A + B)x + 2(A - B)

Nu zou je in gedachten kunnen houden dat je het linkerlid van (6) ook kunt schrijven als 0∙x +4. Aan voorwaarde (6) kan alleen voldaan worden voor elke x indien de coëfficiënten van de veeltermen in het linkerlid en rechterlid paarsgewijs aan elkaar gelijk zijn. Dus krijgen we als voorwaarden:

(7a) A + B = 0
(7b) A - B = 2

Dit is een stelsel lineaire vergelijkingen in A en B, dat je op de gebruikelijke wijze(n) op kunt lossen. Door optelling van de leden van (7a) en (7b) verkrijgen we 2A = 2 en dus A = 1, en dus B = -1. Voor (3) kunnen we nu dus schrijven:

(8) 4/(x² - 4) = 1/(x - 2) - 1/(x + 2)

Nu zijn we er bijna en kunnen we (8) primitiveren, maar toch moet je nog even opletten al naargelang de waarden die x aanneemt in je vraagstuk. Een primitieve van 1/x is ln(x), maar dit geldt alleen voor x > 0. De functie f(x) = 1/x is echter ook gedefinieerd voor x < 0. In dat geval kun je ln(-x) als primitieve nemen, immers volgens de kettingregel is de afgeleide hiervan (1/(-x))∙(-1) = 1/x, zoals gewenst. We kunnen beide mogelijkheden samen nemen door te zeggen dat ln |x| een primitieve is van 1/x voor x > 0 of x < 0.

Alles samengevat hebben we nu:

(9) -x²/(4 - x²) = 1 + 1/(x - 2) - 1/(x + 2)

En een primitieve hiervan is:

(10) x + ln |x - 2| - ln |x + 2| + C

That's it!

Als je meer wil weten over splitsing in deelbreuken kan ik je deze reader aanbevelen.

[ Bericht 0% gewijzigd door Riparius op 28-05-2011 17:11:53 ]