[Bèta wiskunde] Huiswerk- en vragentopic

Die tweede term (1/x)*x^2/3 kun je schrijven als

x^-1 x^2/3 = x^-1/3.

Oh ja natuurlijk, ik ben te lang bezig
Bedankt!

quote:

Op zondag 22 mei 2011 15:07 schreef ukga het volgende:

[..]

Oke top man! thanks. ik heb het zojuist geinstalleerd (vanaf de officie cd)

Ik kan je ook MathType aanraden, ik vind dat zelf nog wat fijner werken.

quote:

Op zondag 22 mei 2011 21:09 schreef Pipo1234 het volgende:
Ik ben bezig met somformules en verdubbelingsformules. Nu moet ik de volgende opgave met behulp van die twee dingen oplossen, alleen zie ik het even niet: tan t = sin 2t

Wil iemand mij een aanwezig geven? Ik kom niet verder dan tan naar sin/cos te herleiden en sin 2t naar 2 sin t keer cos t.

Wel, laten we eens kijken ...

De vergelijking is:

(1) tan t = sin 2t

Gebruik van tan t = sin t / cos t en sin 2t = 2∙sin t∙cos t geeft, zoals je zelf al had gevonden:

(2) sin t / cos t = 2∙sin t∙cos t

Nu wil ik de breuk in het linkerlid kwijt raken. Dat kunnen we doen door beide leden met cos t te vermenigvuldigen. Dit geeft:

(3) sin t = 2∙sin t∙cos²t

Hierbij is cos²t de conventionele notatie voor het kwadraat van cos t. Nu herleiden we het rechterlid op nul door van beide leden 2∙sint∙cos²t af te trekken. Dit geeft:

(4) sin t - 2∙sin t∙cos²t = 0

Nu hebben de twee termen in het linkerlid een factor sin t gemeenschappelijk, die ik dus buiten haakjes kan halen. Dit geeft:

(5) sin t∙(1 - 2∙cos²t) = 0

Hier stop ik even. Bedenk nu zelf hoe je deze vergelijking verder (exact) oplost.

quote:

Op zondag 22 mei 2011 21:32 schreef Riparius het volgende:

...
Hier stop ik even. Bedenk nu zelf hoe je deze vergelijking verder (exact) oplost.

Cos² herleid naar 1 - sin²:
(6) sin t ∙ (1 - 2(1 - sin²t)) = 0

Vereenvoudigd/vermenigvuldigd:
(7) -sin t + 2sin³t = 0

Ontbonden in factoren:
(8) ( sin t )( -1 + 2sin t² ) => sin t = 0 v -1 + 2sin² t = 0

Antwoord:
t = k ∙ 2π v t = ¼π + k ∙ 2π

Is dit iets? Ik geloof overigens dat ik bij stap 5 vastzat, want dat zag ik eerst niet.

[ Bericht 0% gewijzigd door Pipo1234 op 22-05-2011 22:21:20 ]

quote:

Op zondag 22 mei 2011 22:10 schreef Pipo1234 het volgende:

[..]

Cos² herleid naar 1 - sin²:
(6) sin t ∙ (1 - 2(1 - sin²t)) = 0

Vereenvoudigd/vermenigvuldigd:
(7) -sin t + 2sin³t = 0

Ontbonden in factoren:
(8) ( sin t )( -1 + 2t² ) => sin t = 0 v -1 + 2sin² t = 0

Antwoord:
t = k ∙ 2π v t = ¼ + k ∙ 2π

Is dit iets? Ik geloof overigens dat ik bij stap 5 vastzat, want dat zag ik eerst niet.

Tot en met stap (8) klopt het (behalve dat het 2sin² t moet zijn ipv 2t², maar dat is een typfout geloof ik). Het antwoord wat je er daarna uitkrijgt zou ik nog eens goed nakijken .

Edit: Let trouwens goed op, sin² t betekent (sin(t))², dus sin t * t² is niet sin³ t, maar t²*sin(t). Ik weet niet of je dat dacht, of dat het inderdaad een typfout was, maar let er goed op.

quote:

Op zondag 22 mei 2011 22:17 schreef M.rak het volgende:

[..]

Tot en met stap (8) klopt het (behalve dat het 2sin² t moet zijn ipv 2t², maar dat is een typfout geloof ik). Het antwoord wat je er daarna uitkrijgt zou ik nog eens goed nakijken .

Há. Het moet 1/4 pi zijn. Het is alweer laat... Bedank voor de opmerkzaamheid.

Het is trouwens gewoon een typfout.

quote:

Op zondag 22 mei 2011 22:21 schreef GlowMouse het volgende:
waarom niet gelijk cos²t = 1/2 oplossen?

Goede vraag? Ik ben nog redelijk onbekend met dit soort dingen, dus ik weet niet wat je bedoelt.

quote:

Op zondag 22 mei 2011 22:23 schreef Pipo1234 het volgende:

[..]

Goede vraag? Ik ben nog redelijk onbekend met dit soort dingen, dus ik weet niet wat je bedoelt.

Dan is (5) ook nul

quote:

Op zondag 22 mei 2011 22:24 schreef GlowMouse het volgende:

[..]

Na riparius heb je sin t = 0 V 2-cos t = 0.

Natuurlijk. Dat is feitelijk hetzelfde. Ik probeer dingen zo uitgebreid mogelijk te doen, omdat ik de oefening wel kan gebruiken. Dus ik kijk niet zo naar de kortste weg.

In ieder geval bedankt allemaal! Ik ga maar eens richting mijn bed. Morgen weer een dag vol met wiskunde.

quote:

Op zondag 22 mei 2011 22:28 schreef Pipo1234 het volgende:
In ieder geval bedankt allemaal! Ik ga maar eens richting mijn bed. Morgen weer een dag vol met wiskunde.

Ik zou morgen trouwens wel nog eens naar je oplossing van

quote:

Ontbonden in factoren:
(8) ( sin t )( -1 + 2sin t² ) => sin t = 0 v -1 + 2sin² t = 0

Antwoord:
t = k ∙ 2π v t = ¼π + k ∙ 2π

hier kijken, met jouw oplossing heb je namelijk niet alle oplossingen gevonden .

quote:

Op zondag 22 mei 2011 22:10 schreef Pipo1234 het volgende:

[..]

Cos² herleid naar 1 - sin²:
(6) sin t ∙ (1 - 2(1 - sin²t)) = 0

Vereenvoudigd/vermenigvuldigd:
(7) -sin t + 2sin³t = 0

Ontbonden in factoren:
(8) ( sin t )( -1 + 2sin²t ) => sin t = 0 v -1 + 2sin² t = 0

Antwoord:
t = k ∙ 2π v t = ¼π + k ∙ 2π

Is dit iets? Ik geloof overigens dat ik bij stap 5 vastzat, want dat zag ik eerst niet.

Je bent wel goed op weg, hoewel je het jezelf enerzijds wat te moeilijk maakt en anderzijds ook nogal wat vergeet en stappen overslaat.

Na de (overbodige!) substitutie cos²t = 1 - sin²t kom je inderdaad uit op

sin t = 0 ∨ -1 + 2∙sin²t = 0

Maar nu vergeet je een deel van de mogelijke oplossingen, want als:

sin t = 0 ∨sin²t = ½

Dan geldt:

sin t = 0 ∨sin t = ½√2 ∨sin t = -½√2

Verder vergeet je te bedenken dat sin t niet alleen nul is voor t = 2kπ maar voor t = kπ. Maak weer even een schetsje van de eenheidcirkel als je dit niet ziet. Als oplossingen krijgen we nu:

t = kπ ∨ t = ¼π + 2kπ ∨ t = ¾π + 2kπ ∨ t = -¼π + 2kπ ∨ t = -¾π + 2kπ, k∈Z

En dit kun je weer vereenvoudigen tot:

t = kπ ∨ t = ¼π + kπ ∨ t = ¾π + kπ, k∈Z

En dit kun je nog combineren tot:

t = kπ ∨ t = ¼π + ½kπ, k∈Z

Maar: het kan veel eleganter. Je hebt net de formules voor de dubbele hoek geleerd. Door β=α te nemen in de somformule voor cos(α+β) vinden we:

(1) cos 2α = cos²α - sin²α

Er zijn nog twee andere nuttige formules voor de cosinus van de dubbele hoek, die we vinden door sin²α = 1 - cos²α resp. cos²α = 1 - sin²α te substitueren in (1). Dit geeft:

(2) cos 2α = 2∙cos²α - 1

En:

(3) cos 2α = 1 - 2∙sin²α

Hier kunnen we gebruik maken van (2). De vergelijking wordt dan:

(4) sin t∙(-cos 2t) = 0

En dus:

(5) sin t∙cos 2t = 0

En dus:

(6) sin t = 0 ∨cos 2t = 0

Werk dit even verder uit.

[ Bericht 0% gewijzigd door Riparius op 23-05-2011 02:23:44 ]

quote:

Op zondag 22 mei 2011 22:38 schreef Riparius het volgende:

[..]

...

Werk dit even verder uit.

Dat gaat helaas te ver voor mij. Ik zie namelijk niet wat ik na stap 6 moet doen... Ik krijg het idee dat ik hier echt ballen van snap, want ik ben totaal vastgelopen in mijn stof. Zit nu al een uur naar deze opgave te staren: Stel een formule voor cos 3t op waarin alleen cos t en machten van cos t voorkomen. Vervolgens kom ik niet verder dan: cos 2t + t => cos 2t · cos t - sin 2t · sin t.

quote:

Op maandag 23 mei 2011 14:13 schreef GlowMouse het volgende:
Als je nu cos2t en sin2t omschrijft, ben je er al bijna hoor.

Bedoel je zo:

cos 3t = (1 - 2 sin² t) · cos t - (2 sin t · cos t) · sin t

Ik zie eerlijk gezegd niet hoe ik hier verder mee moet... vooral dat tweede deel kan ik niks mee.

quote:

Op maandag 23 mei 2011 14:00 schreef Pipo1234 het volgende:

[..]

Dat gaat helaas te ver voor mij. Ik zie namelijk niet wat ik na stap 6 moet doen... Ik krijg het idee dat ik hier echt ballen van snap, want ik ben totaal vastgelopen in mijn stof. Zit nu al een uur naar deze opgave te staren: Stel een formule voor cos 3t op waarin alleen cos t en machten van cos t voorkomen. Vervolgens kom ik niet verder dan: cos 2t + t => cos 2t · cos t - sin 2t · sin t.

OK. Niet in paniek raken of gaan wanhopen. Ik ga eerst nog even de bespreking van de vergelijking van gisteren afronden. Ik pak de draad weer even op bij mijn eerste post hierover. Ik was gekomen tot:

(5) sin t∙(1 - 2∙cos²t) = 0

Een product van twee factoren kan alleen nul zijn als (tenminste) één van de twee factoren nul is, dus dit levert dan op sin t = 0 óf cos²t = ½ waaruit weer volgt sin t = 0 óf cos t = ½√2 óf cos t = -½√2. Drie mogelijkheden dus, en voor elk van deze drie mogelijkheden moet je dan nagaan welke waarden van t voldoen.

Maar, zoals gezegd, het kan eleganter. Met behulp van de identiteit cos 2t = 2∙cos²t - 1 herleiden we (5) tot:

(6) sin t∙cos 2t = 0

En dus geldt:

(7) sin t = 0 ∨cos 2t = 0

Aan de hand van de eenheidscirkel zien we gemakkelijk dat de sinus (y-coördinaat) nul wordt voor kπ en dat de cosinus (x-coördinaat) nul wordt voor ½π + kπ. Dus krijgen we:

(8) t = kπ ∨2t = ½π + kπ

En dus:

(9) t = kπ ∨t = ¼π + ½kπ, k∈Z

Zo eenvoudig kan het dus. We hoeven nu niet alle oplossingen die we op de andere manier voor cos²t = ½ krijgen apart te bekijken.

Nu je vraag over de herleiding van een identiteit voor cos 3t uitgedrukt in cos t. Deze opgave sluit trouwens naadloos aan bij wat ik gisteren al opmerkte over de drie verschillende identiteiten voor de cosinus van de dubbele hoek, dus ik vraag me toch af of je mijn antwoorden wel goed bestudeert.

Maar goed. We gaan nog even uit van de somformule voor cos(α+β). Deze luidt, zoals bekend:

(10) cos(α+β) = cos α∙cos β - sin α∙sin β

We nemen nu α = 2t en β = t, zodat α+β = 3t. Dit geeft:

(11) cos 3t = cos 2t∙cos t - sin 2t∙sin t

Nu weet je ook dat geldt:

(12) cost 2t = 2∙cos²t - 1 en sin 2t = 2∙sin t∙cos t

Substitutie van (12) in (11) levert:

(13) cos 3t = (2∙cos²t - 1)∙cos t - 2∙sin t∙cos t∙sin t

Uitwerken geeft:

(14) cos 3t = 2∙cos³t - cos t - 2∙sin²t∙cos t

Nu is ook:

(15) sin²t = 1 - cos²t

Substitutie van (15) in (14) geeft dus:

(16) cos 3t = 2∙cos³t - cos t - 2∙(1 - cos²t)∙cos t

Weer haakjes uitwerken:

(17) cos 3t = 2∙cos³t - cos t - 2∙cos t + 2∙cos³t

Nu nog termen met dezelfde macht samennemen, en we krijgen:

(18) cos 3t = 4∙cos³t - 3∙cos t

[ Bericht 0% gewijzigd door Riparius op 23-05-2011 15:47:20 ]

quote:

Op maandag 23 mei 2011 14:35 schreef Riparius het volgende:

[..]

...
Nu nog termen met dezelfde macht samennemen, en we krijgen:

(18) cos 3t = 4∙cos³t - 3∙cos t

Oké. Het lijkt zo simpel als jij het zo uitlegt, maar ik raak altijd in de war door alle haakjes en vermenigvuldigingen. Ik lees trouwens al jouw uitleg uitvoerig, want ik wil Wiskunde B graag halen en heb al gemerkt dat jij er zeer veel van weet. Daarvoor mijn dank. Helaas blijft niet alles altijd even goed hangen en gaan sommige dingen nog te ver voor mij om het te snappen.

quote:

Op maandag 23 mei 2011 15:10 schreef Pipo1234 het volgende:

[..]

Oké. Het lijkt zo simpel als jij het zo uitlegt, maar ik raak altijd in de war door alle haakjes en vermenigvuldigingen.

Dat alles zo simpel lijkt als ik het uitleg is iets wat ik veel vaker hoor. Het zouden didactische kwaliteiten kunnen zijn, maar ik heb eerder het idee dat er tegenwoordig niet meer goed les wordt gegeven, en van veel 'uitleg' (of wat dat voor door moet gaan) in Nederlandse (school)boeken gaan mijn haren ook recht overeind staan. Verder lijken veel dingen niet alleen simpel, ze zijn het ook. Je moet alleen wel heel consequent te werk gaan.

quote:

Ik lees trouwens al jouw uitleg uitvoerig, want ik wil Wiskunde B graag halen en heb al gemerkt dat jij er zeer veel van weet. Daarvoor mijn dank. Helaas blijft niet alles altijd even goed hangen en gaan sommige dingen nog te ver voor mij om het te snappen.

Waar heb je deze wiskunde voor nodig als ik vragen mag? Om meer inzicht te krijgen moet je een goede balans zien te vinden tussen het doornemen en begrijpen van de 'theorie' en het maken van opgaven. Als je je pas in een stukje theorie gaat verdiepen op het moment dat je merkt dat je even niet verder komt met een opgave dan krijg je een veel te fragmentarisch beeld van de stof. Anderzijds is het ook zo dat je inderdaad veel moet oefenen en niet alleen maar kijken hoe anderen (of antwoordenboekjes) het doen. Je kunt ook geen profvoetballer worden door elke avond met een krat bier voor de TV te gaan zitten en naar voetbalwedstrijden te kijken.

goddomme, leraar heeft 2 oefenopgaven gemaakt maar snap er geen kut van;
1: bij de rij Un=3n²+2n+4 hoort een recursieve formule van de vorm Un=Un-1+an-1 met U0=4.
Bereken a.

2: gegeven is de rij Wn=an+5 en 4ΣK=0 Wk = 49. Bereken a.

iemand die me dit kan uitleggen ?

ik heb het al, bedankt voor de hulp:)

quote:

Op maandag 23 mei 2011 17:18 schreef Buschetta1 het volgende:
goddomme, leraar heeft 2 oefenopgaven gemaakt maar snap er geen kut van;
1: bij de rij Un=3n²+2n+4 hoort een recursieve formule van de vorm Un=Un-1+an-1 met U0=4.
Bereken a.

2: gegeven is de rij Wn=an+5 en 4ΣK=0 Wk = 49. Bereken a.

iemand die me dit kan uitleggen ?

Wiskunde gaat een stuk beter als je (a) geen krachttermen gebruikt en (b) een beetje moeite doet voor een begrijpelijke en correcte notatie.

Eerste opgave.

We hebben het voorschrift:

(1) U_n = 3n² + 2n + 4

Substitutie van (n-1) voor n in (1) geeft:

(2) U_n-1 = 3(n-1)² + 2(n-1) + 4 = 3n² - 6n +3 + 2n - 2 + 4 = 3n² - 4n + 5

Trekken we nu (2) van (1) af, dan krijgen we:

(3) U_n - U_n-1 = (3n² + 2n + 4) - (3n² - 4n + 5) = 6n - 1

Gegeven is dat geldt:

(4) U_n - U_n-1 = an - 1

Uit een vergelijking van (3) met (4) volgt nu direct dat a = 6

Tweede opgave.

Gegeven is

(5) W_n = an + 5

Uit je beroerde notatie maak ik op dat de termen W_k met k = 0..4 bij elkaar 49 opleveren. Dit zijn vijf termen van een rekenkundige rij.

De som van een aantal opeenvolgende termen van een rekenkundige rij is gelijk aan het gemiddelde van de eerste en de laatste term vermenigvuldigd met het aantal termen. Dus krijgen we:

(6) 5∙(5 + (4a + 5))/2 =49

(7) 5∙(4a + 10)/2 = 49

(8) 5∙(2a + 5) = 49

(9) 10a + 25 = 49

(10) 10a = 24

a = 2,4

quote:

Op maandag 23 mei 2011 15:42 schreef Riparius het volgende:
Je kunt ook geen profvoetballer worden door elke avond met een krat bier voor de TV te gaan zitten en naar voetbalwedstrijden te kijken.

Blijkbaar heeft Theodor Kaluza geleerd om te zwemmen uit een boek

quote:

Op maandag 23 mei 2011 18:09 schreef Haushofer het volgende:

[..]

Blijkbaar heeft Theodor Kaluza geleerd om te zwemmen uit een boek

Tja, iets met uitzonderingen die de regel bevestigen? Hoeveel mensen zouden er verzuipen als je ze in het diepe gooit na alleen het doorwerken van wat verhandelingen over hogere zwemkunst? Maar verdiep je je altijd in de biografie van mathematici (of fysici) die je 'tegenkomt'? Moet je eens een kijkje nemen (voor wiskundigen dan) op MacTutor. Ik kan me trouwens wel voorstellen waarom Kaluza je aanspreekt.

quote:

Op maandag 23 mei 2011 15:42 schreef Riparius het volgende:

[..]

Waar heb je deze wiskunde voor nodig als ik vragen mag? Om meer inzicht te krijgen moet je een goede balans zien te vinden tussen het doornemen en begrijpen van de 'theorie' en het maken van opgaven. Als je je pas in een stukje theorie gaat verdiepen op het moment dat je merkt dat je even niet verder komt met een opgave dan krijg je een veel te fragmentarisch beeld van de stof. Anderzijds is het ook zo dat je inderdaad veel moet oefenen en niet alleen maar kijken hoe anderen (of antwoordenboekjes) het doen. Je kunt ook geen profvoetballer worden door elke avond met een krat bier voor de TV te gaan zitten en naar voetbalwedstrijden te kijken.

Voor een universitaire studie Informatica. Ik verdiep me in de theorie als het wordt beschreven in mijn boek. En dat is denk ik het probleem in mijn geval, want het is echt een boek voor de middelbare school. De meeste dingen gaan best goed, alleen is loop ik hier een beetje vast. Weet niet goed waarom, misschien is het gewoon het moment of ik doe gewoon moeilijk.

quote:

Op maandag 23 mei 2011 15:49 schreef GlowMouse het volgende:
Het verschil zit hem erin dat zelf doen lastiger is dan iets volgen dat voorgedaan wordt.

Er wordt mij niets voorgedaan, afgezien van voorbeelden in mijn boek. Het enige dat me voorgedaan wordt, is hetgeen dat hier beschreven worden. Vandaar mijn consequente aanwezigheid hier.

quote:

Op maandag 23 mei 2011 19:41 schreef Pipo1234 het volgende:

[..]

Voor een universitaire studie Informatica.

Zware studie. Ik weet niet of je al eens wat aan programmeren hebt gedaan, maar daarbij moet je ook goed op de haakjes letten ... (en nog op veel meer natuurlijk).

quote:

Ik verdiep me in de theorie als het wordt beschreven in mijn boek. En dat is denk ik het probleem in mijn geval, want het is echt een boek voor de middelbare school. De meeste dingen gaan best goed, alleen is loop ik hier een beetje vast. Weet niet goed waarom, misschien is het gewoon het moment of ik doe gewoon moeilijk.

[..]

Goede boeken voor zelfstudie zijn dun gezaaid in het Nederlandse taalgebied. De vaak genoemde boeken van Van De Craats bijvoorbeeld vind ik helemaal niet zo goed. Beter zijn wat publicaties van de OU die vroeger gewoon vrij op internet stonden, maar daar zat dacht ik geen of weinig goniometrie bij. Je zou voor een beknopt overzichtje wel even deze syllabus van een Vlaamse zomercursus door kunnen nemen. En dan heb je ook nog die zogeheten spijkerreeks. Deze bijvoorbeeld voor goniometrie.

quote:

Er wordt mij niets voorgedaan, afgezien van voorbeelden in mijn boek. Het enige dat me voorgedaan wordt, is hetgeen dat hier beschreven worden. Vandaar mijn consequente aanwezigheid hier.

Tja, dan mis je toch wel een 'echte' docent. Eentje die ouderwets les geeft bedoel ik, geen veredelde cipier.

quote:

Op maandag 23 mei 2011 19:41 schreef Pipo1234 het volgende:

[..]

Voor een universitaire studie Informatica. Ik verdiep me in de theorie als het wordt beschreven in mijn boek. En dat is denk ik het probleem in mijn geval, want het is echt een boek voor de middelbare school. De meeste dingen gaan best goed, alleen is loop ik hier een beetje vast. Weet niet goed waarom, misschien is het gewoon het moment of ik doe gewoon moeilijk.

Van sin/cosinus moet je hoe dan ook eerst twee delen snappen, wil je die opgaven met verstand kunnen oplossen (en niet door willekeurig identiteiten toe te passen):

Heb je een grafische rekenmachine?
Pak pen en papier, teken twee x/y-assen onder elkaar, de x-as loopt van 0 tot 2Pi, de y-as van -3 naar 3. Een gebruik je voor de sinus, de ander voor de cosinus.
Voor de sinus teken je eerst de functie sin(x):
Zoals je ziet zijn belangrijke x-waardes:0, Pi/2, Pi, 3Pi/2, 2Pi.
De (daarbij behorende) belangrijke y-waardes zijn: 0,1,0,-1,0.
Nu ga je bekijken wat er met sinus gebeurt als je a,b,c of e gaat veranderen in de functie:
asin(e+bx)+c
Bekijk bijvoorbeeld eens hoe de functie 2sin(x) eruit ziet en teken die. Vraag je nu af wat de belangrijke x-waardes zijn en wat de belangrijke y-waardes. Vervang 'a' weer eens door een andere waarde dan 2 op je rekenmachine, hoe ziet die functie er dan uit? Trek hieruit een conclusie.
Hetzelfde doe je voor b,c en e. Nu kun je dus ook beredeneren hoe de functie 3sin(x/2 + 4)+1 uit moet zien.
En dit hele gedoe kun je ook doen voor de cosinus-functie.
Daarna kun je bijvoorbeeld in een afbeelding cos en sin tekenen en bepaalde identiteiten afleiden:
Waarom is sin(Pi/2-a)= cos(a) bijvoorbeeld ?
Nu kun je daarna ook nog eens de x-as gaan verlengen (naar bijvoorbeeld -2Pi): Wat gebeurt er nu met je functie asin(e+bx)+c en resp cosinus?
Zie je nu ook waarom de vraag: 'Voor welke x geld sin(x)=1' niet alleen x=Pi/2 als antwoord heeft, maar nog veel meer? Waar hangt het echte antwoord vanaf?

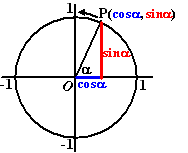
Tweede gedeelte gaat over de eenheidscirkel:

Volgens mij had je hier al wat info over gekregen dus zal ik daar kort over zijn:
Ga eens met de 'pijl' mee langs de cirkel en beschrijf wat er met sin en cos gebeurt.

quote:

Op maandag 23 mei 2011 20:19 schreef Riparius het volgende:

[..]

Zware studie. Ik weet niet of je al eens wat aan programmeren hebt gedaan, maar daarbij moet je ook goed op de haakjes letten ... (en nog op veel meer natuurlijk).

Ik "programmeer" al heel lang. Begonnen in BASIC, later overgestapt op PHP en tegenwoordig voornamelijk BASH. Echt een serieuze taal zoals JAVA of C heb ik nooit geleerd, maar dat is vooral omdat het niet hoefde. Wil het wel graag, maar je gaat niet even C leren als je je verveeld. Mijn probleem is vooral dat ik de slordig ben. Van a naar b hobbel. Als ik bijvoorbeeld een recursieve functie schrijf, maak ik vaak fouten die makkelijk voorkomen konden worden. Maar dat met haakjes ken ik wel, echter ben ik gewend om daar heel strikt mee te zijn en dat hoeft in wiskunde ook niet altijd.

quote:

Op maandag 23 mei 2011 20:19 schreef Riparius het volgende:

[..]

Tja, dan mis je toch wel een 'echte' docent. Eentje die ouderwets les geeft bedoel ik, geen veredelde cipier.

Ja die mis ik zeker. Gelukkig lukt het me aardig zonder, alleen vereist het een hoop wilskracht en discipline om door te gaan. Helaas heb ik niet de juist vooropleiding om onvoorwaardelijk toegelaten te worden tot de genoemde studie. Ik heb alleen maar een propedeuse van een niet gerelateerde HBO-studie, dus dat is niet genoeg als je geen Wiskunde B hebt gedaan op de middelbare school. Ik heb de MAVO gedaan, dus dat schiet niet op. Ik snap overigens heel goed waarom deze eis er is en heb ik geen probleem mee. Helaas zit ik met een beperkt tijdsvenster, want er zijn nog maar twee examens dit jaar.

[ Bericht 2% gewijzigd door Pipo1234 op 23-05-2011 21:27:30 ]

quote:

Op maandag 23 mei 2011 21:22 schreef Pipo1234 het volgende:

[..]

Ik "programmeer" al heel lang. Begonnen in BASIC, later overgestapt op PHP en tegenwoordig voornamelijk BASH. Echt een serieuze taal zoals JAVA of C heb ik nooit geleerd, maar dat is vooral omdat het niet hoefde. Wil het wel graag, maar je gaat niet even C leren als je je verveeld. Mijn probleem is vooral dat ik de slordig ben. Van a naar b hobbel. Als ik bijvoorbeeld een recursieve functie schrijf, maak ik vaak fouten die makkelijk voorkomen konden worden. Maar dat met haakjes ken ik wel, echter ben ik gewend om daar heel strikt mee te zijn en dat hoeft in wiskunde ook niet altijd.

[..]

Ah, zo. Maar heb je wel eens wat programma's geschreven om (eenvoudige) wiskundige vraagstellingen op te lossen? Bijvoorbeeld het genereren van een lijst priemgetallen, of het ontbinden in priemfactoren van een getal (mooi met recursie te doen!), of het genereren van primitieve Pythagoreïsche tripletten of zo?

quote:

Ja die mis ik zeker. Gelukkig lukt het me aardig zonder, alleen vereist het een hoop wilskracht en discipline om door te gaan. Helaas heb ik niet de juist vooropleiding om onvoorwaardelijk toegelaten te worden tot de genoemde studie. Ik heb alleen maar een propedeuse van een niet gerelateerde HBO-studie, dus dat is niet genoeg als je geen Wiskunde B hebt gedaan op de middelbare school. Ik heb de MAVO gedaan, dus dat schiet niet op. Ik snap overigens heel goed waarom deze eis er is en heb ik geen probleem mee. Helaas zit ik met een beperkt tijdsvenster, want er zijn nog maar twee examens dit jaar.

Wat voor onderwerpen worden er gevraagd voor wat betreft wiskundige voorkennis? Ik ben niet zo op de hoogte met de huidige lesprogramma's.

quote:

Op maandag 23 mei 2011 20:34 schreef Siddartha het volgende:

[..]

...

Volgens mij had je hier al wat info over gekregen dus zal ik daar kort over zijn:
Ga eens met de 'pijl' mee langs de cirkel en beschrijf wat er met sin en cos gebeurt.

Het stomme is dat ik wat jij nu beschrijft herken en redelijk begrijp. Ik heb dit behandeld in het vorige hoofdstuk van mijn boek en dat ging best goed. Het is ook best een interessant onderwerp overigens, vooral omdat je sinussen kunt aanpassen naar gelang de situatie. Alleen raak ik nu in de war bij opdrachten waar niet zozeer het om de sinus gaat, dan wel om vergelijkingen oplossen.

quote:

Op maandag 23 mei 2011 21:51 schreef Riparius het volgende:

[..]

Ah, zo. Maar heb je wel eens wat programma's geschreven om (eenvoudige) wiskundige vraagstellingen op te lossen? Bijvoorbeeld het genereren van een lijst priemgetallen, of het ontbinden in priemfactoren van een getal (mooi met recursie te doen!), of het genereren van primitieve Pythagoreïsche tripletten of zo?

Ik heb nog nooit bewust iets geschreven om wiskundige vraagstellingen op te lossen. Ooit eens een script geschreven dat op basis van vier coördinaten (hemelsbreed) een afstand berekende, maar ik weet niet in hoeverre ik dat wiskundige heb gedaan. Ik denk dat ik met de kennis die ik tot nu toe heb opgedaan veel beter in staat ben om iets wiskundigs te schrijven. Helaas heb ik daar op het moment (i.v.m. de wiskunde) nog geen tijd voor, maar zodra ik die wel heb ga ik er zeker mee spelen. Het lijkt mij erg interessant om iets te schrijven dat iets doet wat voor een mens te complex wordt.

Laat ik voorop stellen dat ik ruim tien jaar vrij weinig met wiskunde heb gedaan. Ik heb er examen voor gedaan op de MAVO, maar dat niveau komt geenszins in de buurt van het wat ik nu behandel. Op het HBO heb ik wel statistiek gehad, maar dat was van niveau lik-me-vestje en heb ik op mijn pantoffels gehaald.

quote:

Op maandag 23 mei 2011 21:51 schreef Riparius het volgende:

[..]

Wat voor onderwerpen worden er gevraagd voor wat betreft wiskundige voorkennis? Ik ben niet zo op de hoogte met de huidige lesprogramma's.

Ik moet de volgende onderwerpen beheersen waar het gaat om het examen dat ik ga doen. (Het gaat eigenlijk gewoon om Wiskunde B voor het VWO):

Differentiaalrekenen
• Differentiëren
• Exponenten en logaritmen
• De kettingregel
• Twee afgeleiden
• Integreren
• Toepassingen
Voortgezette meetkkunde
• Bewijzen in driehoeken
• Driehoeken en cirkels
• Vierhoeken en cirkels
• Conflictlijnen
Goniometrie
• Goniometrie
• Goniometrische functies
• Goniometrische formules
• Lissajous-figuren

Het zijn eigenlijk twee boeken en ik ben nu in het laatste hoofdstuk van het eerste boek, dus goniometrische functies. Daarna moet ik nog vijf hoofdstukken behandelen: "Integreren" en "Toepassingen" van differentiaalrekenen, "Vierhoeken en cirkels" en "Conflictlijnen" van voortgezette meetkunde en "Lissajous-figuren" van goniometrie.

quote:

Op dinsdag 24 mei 2011 06:31 schreef Pipo1234 het volgende:

Ik heb nog nooit bewust iets geschreven om wiskundige vraagstellingen op te lossen. Ooit eens een script geschreven dat op basis van vier coördinaten (hemelsbreed) een afstand berekende, maar ik weet niet in hoeverre ik dat wiskundige heb gedaan. Ik denk dat ik met de kennis die ik tot nu toe heb opgedaan veel beter in staat ben om iets wiskundigs te schrijven. Helaas heb ik daar op het moment (i.v.m. de wiskunde) nog geen tijd voor, maar zodra ik die wel heb ga ik er zeker mee spelen. Het lijkt mij erg interessant om iets te schrijven dat iets doet wat voor een mens te complex wordt.

Dat wordt het natuurlijk al gauw. Zelfs π berekenen wordt een mens al gauw te veel. Maar ook zo iets maken valt niet mee. Ik heb wel eens de broncode van een Pascal programmaatje bestudeerd dat dat deed tot zo'n 150.000 decimalen (binnen een minuut op mijn slome PC). Het basisidee (de formule van Machin) was simpel, maar de routines (deels in assembly) om met getallen met (heel) veel significante cijfers te kunnen werken waren niet bepaald simpel.

quote:

Laat ik voorop stellen dat ik ruim tien jaar vrij weinig met wiskunde heb gedaan. Ik heb er examen voor gedaan op de MAVO, maar dat niveau komt geenszins in de buurt van het wat ik nu behandel. Op het HBO heb ik wel statistiek gehad, maar dat was van niveau lik-me-vestje en heb ik op mijn pantoffels gehaald.

[..]

Ik moet de volgende onderwerpen beheersen waar het gaat om het examen dat ik ga doen. (Het gaat eigenlijk gewoon om Wiskunde B voor het VWO):

Differentiaalrekenen
• Differentiëren
• Exponenten en logaritmen
• De kettingregel
• Twee afgeleiden
• Integreren
• Toepassingen
Voortgezette meetkunde
• Bewijzen in driehoeken
• Driehoeken en cirkels
• Vierhoeken en cirkels
• Conflictlijnen
Goniometrie
• Goniometrie
• Goniometrische functies
• Goniometrische formules
• Lissajous-figuren

Dat is allemaal erg elementair. Ik heb me alleen verbaasd over de term 'conflictlijn'. Dat vind ik maar een idiote benaming die kennelijk recent in de mode is gekomen. In geen enkel ander land gebruiken ze dat, ook niet in Vlaanderen. Ik begrijp na lezing van dit stukje wel wat ermee wordt bedoeld, maar het is een bijzonder slecht idee om middelloodlijnen, middenparallellen, bissectrices en parabolen zo op één hoop te gooien.

quote:

Het zijn eigenlijk twee boeken en ik ben nu in het laatste hoofdstuk van het eerste boek, dus goniometrische functies. Daarna moet ik nog vijf hoofdstukken behandelen: "Integreren" en "Toepassingen" van differentiaalrekenen, "Vierhoeken en cirkels" en "Conflictlijnen" van voortgezette meetkunde en "Lissajous-figuren" van goniometrie.

Trek maar wat extra tijd uit voor vlakke meetkunde, want bewijzen worden meestal nogal lastig gevonden. Ik zie vaak dat mensen daar tegenwoordig niks meer van bakken.

Dat het elementair is, is waarschijnlijk helemaal waar. Gelukkig wel, want anders kwam ik er niet doorheen.

quote:

Op dinsdag 24 mei 2011 07:59 schreef Riparius het volgende:

[..]

Trek maar wat extra tijd uit voor vlakke meetkunde, want bewijzen worden meestal nogal lastig gevonden. Ik zie vaak dat mensen daar tegenwoordig niks meer van bakken.

De eerste twee hoofdstukken over dit onderwerp vielen mij alles behalve tegen. Ik vloog er zo doorheen, alleen ben ik bang dat daar ook de manco zit voor mij. Het is namelijk heel erg veel denken in vaste regels en die moet dus allemaal onthouden.

quote:

Op dinsdag 24 mei 2011 06:31 schreef Pipo1234 het volgende:

[..]

Het stomme is dat ik wat jij nu beschrijft herken en redelijk begrijp. Ik heb dit behandeld in het vorige hoofdstuk van mijn boek en dat ging best goed. Het is ook best een interessant onderwerp overigens, vooral omdat je sinussen kunt aanpassen naar gelang de situatie. Alleen raak ik nu in de war bij opdrachten waar niet zozeer het om de sinus gaat, dan wel om vergelijkingen oplossen.

Ik weet niet of je ook echt hebt gedaan wat ik zei, maar ik kan het je heel erg aanraden. Ik weet dat je dit wel snapt, dat je het ook in je hoofd kan bedenken, maar het kan voor zoveel meer begrip zorgen.
Ik zou zeggen: Heb je wat vrije tijd, doe het dan gewoon. Het kost je vrijwel geen moeite (het is echt niet moeilijk, zeker niet met een grafische rekenmachine erbij), het kost alleen een beetje tijd.
Het is niet zozeer dat je meteen inzichten hiervan krijgt (waarschijnlijk wel trouwens, ik heb dit ook gedaan bij mensen die in 6 vwo zaten en me bezworen dat ze de sinus/cosinus begrepen...Dat viel erg tegen.), maar het echte inzicht krijg je daarna, als je opgaven gaat maken. Dan begrijp je ook de methode waarmee je zo'n opgaven moet oplossen.

Voor de goniometrische vergelijkingen die je moet oplossen mooet je gewoon de tijd nemen. Hou in het begin gewoon de lijst met identiteiten erbij en ga puzzelen: wat kan ik anders opschrijven en wat krijg ik dan?

Wederom schakel ik nog een keer de hulp in van de velen wiskundigen hier op Fok!
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.

Toon aan met behulp van de eenheidscirkel:

cos (α-0.5π) = sin(α)
sin(α+π) = - sin(α)

Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijken zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.

quote:

Op dinsdag 24 mei 2011 18:47 schreef Uchiha1911 het volgende:
Wederom schakel ik nog een keer de hulp in van de velen wiskundigen hier op Fok!
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.

Toon aan met behulp van de eenheidscirkel:

cos (α-0.5π) = sin(α)
sin(α+π) = - sin(α)

Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijken zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.

Wel, bedenk dan eerst maar eens wat sinus en cosinus met de eenheidscirkel te maken hebben.

quote:

Op dinsdag 24 mei 2011 18:51 schreef thabit het volgende:

[..]

Wel, bedenk dan eerst maar eens wat sinus en cosinus met de eenheidscirkel te maken hebben.

Driehoeken binnen de cirkel?

quote:

Op dinsdag 24 mei 2011 18:54 schreef Uchiha1911 het volgende:

[..]

Driehoeken binnen de cirkel?

Misschien moet je even omhoogscrollen in dit topic.

quote:

Op dinsdag 24 mei 2011 18:47 schreef Uchiha1911 het volgende:
Wederom schakel ik nog een keer de hulp in van de velen wiskundigen hier op Fok!
Ik zit met een klein probleempje, wat waarschijnlijk erg makkelijk op te lossen is maar wat ik dus niet begrijp.

Toon aan met behulp van de eenheidscirkel:

cos (α-½π) = sin(α)
sin(α+π) = - sin(α)

Zou iemand mij uit kunnen leggen hoe ik dit zo kan laten zien? Ik ben al een stuk verder.. ben goniometrische functies aan het differentiëren en primitiveren.. maar nu ik terug kijk zie ik eigenlijk niet hoe het mogelijk is dit 'aan te tonen'.

Bestudeer dit maar eens, en dan meer bepaald blz. 5. Overigens vraag ik mij wel af hoe goed je nu echt begrijpt waarom de afgeleiden van sin en cos zijn zoals ze zijn als je hier al moeite mee hebt. Probeer voor jezelf eens helder te krijgen aan de hand van de eenheidscirkel waarom het zo is dat:

d(cos t)/dt = cos(t + ½π) en d(sin t)/dt = sin(t + ½π)

Ik heb na een dagje hard blokken maar eens een eenheidscirkel uitgeprint om mee te spelen en wat meer inzicht te krijgen in de zaken waar ik recent met een aantal van jullie over gesproken heb. Nu heb ik een aantal dingen uitgevonden en graag verneem ik of ik het bij het juist eind heb. Ik hoop dat ik het begrijpelijk genoeg uitleg, want je moet het eigenlijk op zo'n cirkel zien.

Ik heb de twee formules bekeken: sin (½π - x) = cos x en cos (½π - x) = sin x.

En het volgende heb ik bevonden bij sinus (en bij cosinus): Wanneer je vanaf punt ½π x aftrekt krijg je een driehoek die identiek is aan degene bij sinus zonder de ½π. Het verschil zit hem in het feit dat x en y omgewisseld zijn en dus de waarde van sinus aan cosinus is gegeven en vica versa. Dus: sin (½π - x) = cos x (en cos (½π - x) = sin x)

Ik heb ook naar de somformule sin (t + u) = sin t · cos u + cus t · sin u gekeken. Alleen ik kom niet verder dan de conclusie dat daar het oppervlak van de driehoeken wordt berekent.

Ik vind zelf die eenheidscirkel een beetje omslachtig. Als je kijkt naar de grafieken dan vind ik het veel makkelijker. Uit het plaatje zie je dan direct dat als je het golfje van de cos een half pi naar rechts verplaatst krijg je de sin. Dus dan heb je cos(x - pi/2) = sin(x). Verder weet je dat (of zie je ook makkelijk uit de grafiek ervan) dat cos(x)=cos(-x). Dus dan heb je sin(x) = cos(x-pi/2)= cos(-(x-pi/2))=cos(pi/2 -x), en dus sin(x) = cos(pi/2 - x).

Andersom kan je ook het golfje van de sin verplaatsen om de cos te krijgen, dat werkt dan ongeveer hetzelfde en krijg je de andere formule. Probeer maar.

Ik zeg niet dat dit een betere manier is maar het is wel eenvoudig als je eenmaal het cos en sin grafiekje uit je hoofd kent met een paar belangrijke punten.

quote:

Op dinsdag 24 mei 2011 23:13 schreef Pipo1234 het volgende:
Ik heb na een dagje hard blokken maar eens een eenheidscirkel uitgeprint om mee te spelen en wat meer inzicht te krijgen in de zaken waar ik recent met een aantal van jullie over gesproken heb. Nu heb ik een aantal dingen uitgevonden en graag verneem ik of ik het bij het juist eind heb. Ik hoop dat ik het begrijpelijk genoeg uitleg, want je moet het eigenlijk op zo'n cirkel zien.

Ik heb de twee formules bekeken: sin (½π - x) = cos x en cos (½π - x) = sin x.

En het volgende heb ik bevonden bij sinus (en bij cosinus): Wanneer je vanaf punt ½π x aftrekt krijg je een driehoek die identiek is aan degene bij sinus zonder de ½π. Het verschil zit hem in het feit dat x en y omgewisseld zijn en dus de waarde van sinus aan cosinus is gegeven en vica versa. Dus: sin (½π - x) = cos x (en cos (½π - x) = sin x)

Kijk ook even hier, blz. 5 voor een plaatje. Je kunt ook bedenken dat een rotatie over α gevolgd door spiegeling in de lijn met vergelijking x=y hetzelfde is als een rotatie over ½π - α, en bij spiegeling in de lijn met vergelijking x=y worden de x- en y- coördinaten van een punt omgewisseld.

quote:

Ik heb ook naar de somformule sin (t + u) = sin t · cos u + cos t · sin u gekeken. Alleen ik kom niet verder dan de conclusie dat daar het oppervlak van de driehoeken wordt berekend.

Nee, dit stelt geen oppervlakte voor. Probeer eens of je mijn bewijs voor de additietheorema's kunt begrijpen.

quote:

Op dinsdag 24 mei 2011 23:46 schreef Riparius het volgende:

[..]

Kijk ook even hier, blz. 5 voor een plaatje. Je kunt ook bedenken dat een rotatie over α gevolgd door spiegeling in de lijn met vergelijking x=y hetzelfde is als een rotatie over ½π - α, en bij spiegeling in de lijn met vergelijking x=y worden de x- en y- coördinaten van een punt omgewisseld.

Ik had al naar die PDF gekeken, maar kon er weinig van maken. Ik heb een cirkel uitgeprint en uitgebreid zitten puzzelen en toen zag ik het op een gegevens moment. Nu ik naar dat bestand kijk zie ik het ook...

quote:

Op dinsdag 24 mei 2011 23:46 schreef Riparius het volgende:
[..]

Nee, dit stelt geen oppervlakte voor. Probeer eens of je mijn bewijs voor de additietheorema's kunt begrijpen.

Die tekst is voor mij helaas te complex.

quote:

Op woensdag 25 mei 2011 00:10 schreef Pipo1234 het volgende:

[..]

Ik had al naar die PDF gekeken, maar kon er weinig van maken. Ik heb een cirkel uitgeprint en uitgebreid zitten puzzelen en toen zag ik het op een gegevens moment. Nu ik naar dat bestand kijk zie ik het ook...

[..]

Inderdaad, plaatjes helpen altijd bij goniometrie.

quote:

Die tekst is voor mij helaas te complex.

Ik heb dit bewijs vaak genoeg met succes uitgelegd aan VWO leerlingen, dus het moet te doen zijn. Er zit niets in dat niet tot de stof voor het VWO behoort. Maar inderdaad is een goed plaatje erbij wel bijna onmisbaar voor een goed begrip. Jammer genoeg heeft er (nog) niemand gereageerd op mijn suggestie om hier een duidelijk plaatje bij te maken.

quote:

Op woensdag 25 mei 2011 00:21 schreef Riparius het volgende:

[..]

Inderdaad, plaatjes helpen altijd bij goniometrie.

[..]

Ik heb dit bewijs vaak genoeg met succes uitgelegd aan VWO leerlingen, dus het moet te doen zijn. Er zit niets in dat niet tot de stof voor het VWO behoort. Maar inderdaad is een goed plaatje erbij wel bijna onmisbaar voor een goed begrip. Jammer genoeg heeft er (nog) niemand gereageerd op mijn suggestie om hier een duidelijk plaatje bij te maken.

Als ik het snapte maakte ik wel een plaatje. Morgen maar eens een poging doen om het te snappen.

Ik wil van de volgende verzameling aantonen dat die gesloten is;



Dit is de zogenaamde LeastCore, en V staat voor de maximum operator, en M de index set van alle reëelwaardige functies F op Pi.
Ik heb getracht een rij in LC te maken, maar dat ging nergens heen....