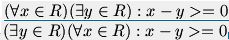SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Als vervolg op voorgaande topics.
Vorige topics:
[Centraal] Wiskunde-vragen, deel omega
Voor nog veel meer wiskunde vragen 3
Voor nog veel meer wiskunde vragen 2
Voor nog meer vragen over wiskunde.
Voor al uw vragen over wiskunde.
[ Bericht 45% gewijzigd door Anthraxx op 30-01-2005 12:01:17 ]
Vorige topics:
[Centraal] Wiskunde-vragen, deel omega
Voor nog veel meer wiskunde vragen 3
Voor nog veel meer wiskunde vragen 2
Voor nog meer vragen over wiskunde.
Voor al uw vragen over wiskunde.
[ Bericht 45% gewijzigd door Anthraxx op 30-01-2005 12:01:17 ]


Bij de limiet van
(ln ln(x)) / x
met x-> oneinding
Onder de deelstreep ga je naar oneindig, maar boven de deelstreep ook. De regel van l'hospital is dan van toepassing. De boel moet dan boven en onder gedifferentiëerd worden. Dan krijg je boven de deelstreep voglens mij (1/x)/ln(x) ---> dus 1/(x*ln(x)) Onder de deelstreep houd je natuurlijk 1 over.
Dan staat er bijna 0 gedeeld door 1, wat zou duiden op 0. Maar klopt dit dan ook?
M'n andere topic is gesloten, maar hier ga ik fijn verder
(ln ln(x)) / x
met x-> oneinding
Onder de deelstreep ga je naar oneindig, maar boven de deelstreep ook. De regel van l'hospital is dan van toepassing. De boel moet dan boven en onder gedifferentiëerd worden. Dan krijg je boven de deelstreep voglens mij (1/x)/ln(x) ---> dus 1/(x*ln(x)) Onder de deelstreep houd je natuurlijk 1 over.
Dan staat er bijna 0 gedeeld door 1, wat zou duiden op 0. Maar klopt dit dan ook?
M'n andere topic is gesloten, maar hier ga ik fijn verder


Ik vermoed dat je gelijk hebt ja... Ik had net een hele beschouwing getypt over dat het om een andere reden 0 was, maar toen zag ik dat ik over 1 van je ln's heengelezen had...
"Huh?" dacht hij nog net, voor hij zijn boek opensloeg.


Haha, zonde van het typewerk. Volgende keer zal ik weer een plaatje als formule posten aangezien dat stukken beter leestquote:Op zondag 31 oktober 2004 10:43 schreef xootje het volgende:
Ik vermoed dat je gelijk hebt ja... Ik had net een hele beschouwing getypt over dat het om een andere reden 0 was, maar toen zag ik dat ik over 1 van je ln's heengelezen had...
M'n GR lijkt inderdaad ook naar 0 te gaan, maar dat wil niet altijd iets zeggen natuurlijk. Hartstikke bedankt alvast voor de hulp, soms zie ik het even niet meer terwijl het helemaal niet moeilijk is... dan ben je te gefixeerd op iets.


Tja... Ik vond trouwens calculus een erg leuk vak toen ik dat in m'n eerste jaar had, dus ik doe het voor de lol ofzo
"Huh?" dacht hij nog net, voor hij zijn boek opensloeg.


Ik ben 4ejaars en ik moet nog al m'n wiskunde uit het eerste jaarquote:Op zondag 31 oktober 2004 10:47 schreef xootje het volgende:
Tja... Ik vond trouwens calculus een erg leuk vak toen ik dat in m'n eerste jaar had, dus ik doe het voor de lol ofzo
Wiskundig inzicht heb ik wel (al zou je het niet zeggen) maar de motivatie ontbreekt een beetje.


Uiteindelijk ben ik er zelf opgekomen door een beetje logisch na te denken over hoe de integraal er ongeveer uit zou moeten zien, maar de logische stappen heb ik niet. Voor een net iets ander probleem heb ik dus weinig aan m'n oplossing
f(x)=sin(2x)/sin(x) -------> F(x)= 2sin(x)+C Dat is, als ik me niet vergis
Zou je de F(x) weer afleiden kom je aan 2cos(x) wat dan gelijk zou moeten zijn aan de f(x). Waarom is dit zo, en hoe kan je dus in logische stappen naar deze integraal toewerken?
f(x)=sin(2x)/sin(x) -------> F(x)= 2sin(x)+C Dat is, als ik me niet vergis
Zou je de F(x) weer afleiden kom je aan 2cos(x) wat dan gelijk zou moeten zijn aan de f(x). Waarom is dit zo, en hoe kan je dus in logische stappen naar deze integraal toewerken?


Iemand?
Ow, ik zie nu dat een kickje helemaal geen zin heeft... Als sticky post staat het niet erg handig omdat het niet erg opvalt zo tussen de rode envelopjes! Mensen lezen vaak over de sticky's heen
Ow, ik zie nu dat een kickje helemaal geen zin heeft... Als sticky post staat het niet erg handig omdat het niet erg opvalt zo tussen de rode envelopjes! Mensen lezen vaak over de sticky's heen


lieverd,
sin(2x)=2sin(x)cos(x)
maak hier gebruik van.
sin(2x)=2sin(x)cos(x)
maak hier gebruik van.
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


aha, die rekenregel wist ik niet meer. Dat verklaart een en ander! Bedankt.quote:Op zondag 31 oktober 2004 20:16 schreef zurich het volgende:
lieverd,
sin(2x)=2sin(x)cos(x)
maak hier gebruik van.


Misschien dom hoor, maar hoe moet je
X^0.55 = 20
oplossen?
X^0.55 = 20
oplossen?
Ik ook_____Ik ook_____Ik ook_____Ik ook
____Ik ook_____Ik ook_____Ik ook_____
Ik ook_____Ik ook_____Ik ook_____Ik ook
____Ik ook_____Ik ook_____Ik ook_____
Ik ook_____Ik ook_____Ik ook_____Ik ook


met zoiets: x^a =b geeft x=b^(1/a) als a niet geljik aan nul is.....
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Dank je, het is gelukt!!
Ik ook_____Ik ook_____Ik ook_____Ik ook
____Ik ook_____Ik ook_____Ik ook_____
Ik ook_____Ik ook_____Ik ook_____Ik ook
____Ik ook_____Ik ook_____Ik ook_____
Ik ook_____Ik ook_____Ik ook_____Ik ook


[edit]Je hebt 't al gevonden dus mijn antwoord is overbodig en daarom gewist[/edit]quote:Op maandag 1 november 2004 21:33 schreef Intergalactrick het volgende:
Misschien dom hoor, maar hoe moet je
X^0.55 = 20
oplossen?
[ Bericht 22% gewijzigd door MarkA op 01-11-2004 22:41:08 ]


Wie kan mij het begrip puntelasticiteit uitleggen?
Som:
Het verband tussen de prijs p in euro's en de vraag q naar snorfietsen wordt vastgelegd door de formule:
q = 9000000/p - 3500.
Op 1 januari kost een zeker merk 1000 euro. Bereken de prijselasticiteit van de vraag bij deze prijs.
Bij de prijselasticiteit met procentuele verschillen in vraag/aanbod is het makkelijk. Dan deel je de procentuele vraag toe-/afname door de procentuele prijs toe-/afname. Maar hierbij weet ik niet hoe ik het moet doen. .
Het wiskundeboek snap ik niet, mijn economieboek niet en zelfs mijn aantekening erover niet.
Som:
Het verband tussen de prijs p in euro's en de vraag q naar snorfietsen wordt vastgelegd door de formule:
q = 9000000/p - 3500.
Op 1 januari kost een zeker merk 1000 euro. Bereken de prijselasticiteit van de vraag bij deze prijs.
Bij de prijselasticiteit met procentuele verschillen in vraag/aanbod is het makkelijk. Dan deel je de procentuele vraag toe-/afname door de procentuele prijs toe-/afname. Maar hierbij weet ik niet hoe ik het moet doen. .
Het wiskundeboek snap ik niet, mijn economieboek niet en zelfs mijn aantekening erover niet.


Oeh, bedankt! .quote:Op woensdag 3 november 2004 21:54 schreef mrbombastic het volgende:
Al weer een tijdje geleden dat ik dit gehad heb, maar volgens mij was het als volgt.
[afbeelding]
Maar nog 1 vraagje. Er staat dan - 9000000/p² x p/q = -9000000/p x 1/q. Dat snap ik niet helemaal, waarom wordt die p² een p?


9000000/p² x p/q = -9000000/p x 1/qquote:Op woensdag 3 november 2004 22:10 schreef Tom_Tom- het volgende:
[..]
Oeh, bedankt! .
Maar nog 1 vraagje. Er staat dan - 9000000/p² x p/q = -9000000/p x 1/q. Dat snap ik niet helemaal, waarom wordt die p² een p?
Aan de linkerkant van de vergelijking zie je in de rechterterm een p boven de deelstreep staan, en in de linkerterm een p kwadraat. Deze deel je op elkaar weg. Kijk maar, er staat namelijk ineens 1/q rechts van de vergelijking


Ah okay. . Jij ook bedankt!quote:Op woensdag 3 november 2004 22:15 schreef 205_Lacoste het volgende:
9000000/p² x p/q = -9000000/p x 1/q
Aan de linkerkant van de vergelijking zie je in de rechterterm een p boven de deelstreep staan, en in de linkerterm een p kwadraat. Deze deel je op elkaar weg. Kijk maar, er staat namelijk ineens 1/q rechts van de vergelijking
Ik kan best wel differentieren enzo hoor, maar er moeten niet te moeilijke minmachten staan, dan vind ik het niet meer leuk. .


Tot de macht 3 doen. ---> H/(C^2).
Maar dan is de functie natuurlijk ook tot de macht 3. Iets anders zou ik niet kunnen verzinnen.
Maar dan is de functie natuurlijk ook tot de macht 3. Iets anders zou ik niet kunnen verzinnen.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik heb al een aantal mensen gevraagd hoe ie moest, maar ik zag er geen duidelijke oplossing bij, en iedereen had een verschillende... Ik hoop dat een van jullie me ermee kan helpen ik want ik heb maandag een tentamen wiskunde.
[ Bericht 5% gewijzigd door j_bos op 04-11-2004 22:18:22 ]


lengte = x+12; breedte = yquote:Op donderdag 4 november 2004 22:10 schreef j_bos het volgende:
[afbeelding]
Ik heb al een aantal mensen gevraagd hoe ie moest, maar ik zag er geen duidelijke oplossing bij, en iedereen had een verschillende... Ik hoop dat een van jullie me ermee kan helpen ik want ik heb maandag een tentamen wiskunde.
Vergelijking 1: omtrek = 2*x+12+2*y =100 (er hoeft geen hek op de plaats van de muur)
Vergelijking 2: oppervlakte = (x+12)*y
De rest laat ik aan jou over als oefening.
Werkwijze:
schrijf vergelijking 1 in de vorm y = ax+b en stop dat in vergelijking 2.
Je krijgt nu een kwadratische vergelijking in x en ik neem aan dat je weet hoe je daar het maximum van kunt bepalen.
Mijn antwoord: x=16, y=28 (precies een vierkant!)
[ Bericht 1% gewijzigd door MarkA op 05-11-2004 01:46:57 ]


Algemeen: stel een functie op, differentieer deze en stel deze op 0. Dan weet je waar het maximum ligt. En dus ook welke x je moet nemen. Hier wordt dat dus een oppervlakfunctie.quote:Op donderdag 4 november 2004 22:10 schreef j_bos het volgende:
[afbeelding]
Ik heb al een aantal mensen gevraagd hoe ie moest, maar ik zag er geen duidelijke oplossing bij, en iedereen had een verschillende... Ik hoop dat een van jullie me ermee kan helpen ik want ik heb maandag een tentamen wiskunde.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


hoihohoh... weer een vraagje hopelijk krijg ik een snelle reacite.
x is reeel en n is een positief geheel getal
toon aan [[x]/n] =[x/n] .
ik dacht
stel dat [x/n]=p
dan
p<=x/n<p+1 geeft np<=x<np+n ===> [x]=np
en dus [x]/n=p dat betekent dat [[x]/n]=p of [[x]/n]=p-1
hoe ga ik nu verder.
is er een betere aanpak?
kan ik bijv. [[nx]/n]=[x] gebruiken?
alvast bedankt.
x is reeel en n is een positief geheel getal
toon aan [[x]/n] =[x/n] .
ik dacht
stel dat [x/n]=p
dan
p<=x/n<p+1 geeft np<=x<np+n ===> [x]=np
en dus [x]/n=p dat betekent dat [[x]/n]=p of [[x]/n]=p-1
hoe ga ik nu verder.
is er een betere aanpak?
kan ik bijv. [[nx]/n]=[x] gebruiken?
alvast bedankt.
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


De onderstreepte conclusie lijkt me niet geheel juist en moet vervangen worden door [x]=np+k waarbij k een geheel getal in de verzameling {0,...,n-1} is. Om aan te tonen dat [[x]/n]=p moet je bewijzen dat p<=[[x]/n]<p+1 (je weet immers al dat p geheel is omdat het van de vorm [blabla] is), ofwel dat p<=(np+k)/n<p+1. Dat laatste lijkt me niet zo moeilijk meer. .quote:Op maandag 8 november 2004 14:20 schreef zurich het volgende:
hoihohoh... weer een vraagje hopelijk krijg ik een snelle reacite.
x is reeel en n is een positief geheel getal
toon aan [[x]/n] =[x/n] .
ik dacht
stel dat [x/n]=p
dan
p<=x/n<p+1 geeft np<=x<np+n ===> [x]=np


die laatste geeft np<=np+k<=np+n
0<=k, en k<n en beide zijn waar
een ander idee..
voordat ik de genoemde gelijkheid moest bewijzen, moest ik eerst aantonen dat [[nx]/n]=[x] , de opdrachten zijn onafhankelijk van elkaar. toch had ik gedacht dat ik deze gelijkheid kan toepassen..
we kunnen altijd y vinden zodat x=y/n met y reeel.
stel dat x=y/n dan geldt [[ny/n]/n]=[y/n] dus [[y]/n]=[y/n] dus de gelijkheid is waar voor elk reeel getal. .. klopt het hier een beetje?
0<=k, en k<n en beide zijn waar
een ander idee..
voordat ik de genoemde gelijkheid moest bewijzen, moest ik eerst aantonen dat [[nx]/n]=[x] , de opdrachten zijn onafhankelijk van elkaar. toch had ik gedacht dat ik deze gelijkheid kan toepassen..
we kunnen altijd y vinden zodat x=y/n met y reeel.
stel dat x=y/n dan geldt [[ny/n]/n]=[y/n] dus [[y]/n]=[y/n] dus de gelijkheid is waar voor elk reeel getal. .. klopt het hier een beetje?
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


De implicatie "dus" moet de andere kant op:quote:Op dinsdag 9 november 2004 22:14 schreef zurich het volgende:
die laatste geeft np<=np+k<=np+n
0<=k, en k<n en beide zijn waar
een ander idee..
voordat ik de genoemde gelijkheid moest bewijzen, moest ik eerst aantonen dat [[nx]/n]=[x] , de opdrachten zijn onafhankelijk van elkaar. toch had ik gedacht dat ik deze gelijkheid kan toepassen..
we kunnen altijd y vinden zodat x=y/n met y reeel.
stel dat x=y/n dan geldt [[ny/n]/n]=[y/n] dus [[y]/n]=[y/n] dus de gelijkheid is waar voor elk reeel getal. .. klopt het hier een beetje?
[[y]/n]=[y/n] dus [[ny/n]/n]=[y/n] dus [[nx]/n]=[x].
Verder klopt het.


zo zo .. gelukkig
ik ben geen [x]-fanatiek.. maar in mijn hobby kom ik af en toe een paar van die sommen tegen waarbij men geen raad weet..
n weer geheel postief.
wat is het kleinste n zodat [10^n /x]=1989 mintens één gehele oplossing heeft..
x* 1989<=10^n<x1990
ik weet al dat ik dacht 1989=3²*13*17 ..maar of dat really helpt. enige tip?
ik ben geen [x]-fanatiek.. maar in mijn hobby kom ik af en toe een paar van die sommen tegen waarbij men geen raad weet..
n weer geheel postief.
wat is het kleinste n zodat [10^n /x]=1989 mintens één gehele oplossing heeft..
x* 1989<=10^n<x1990
ik weet al dat ik dacht 1989=3²*13*17 ..maar of dat really helpt. enige tip?
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


oh..ff wachten
ik heb ontdekt dat ik weer dezelfde fout maakt bij x* 1989<=10^n<x1990 als die van p<=x/n<p+1 geeft np<=x<np+n ===> [x]=np
mm.. k ga nu verder werken....
ik heb ontdekt dat ik weer dezelfde fout maakt bij x* 1989<=10^n<x1990 als die van p<=x/n<p+1 geeft np<=x<np+n ===> [x]=np
mm.. k ga nu verder werken....
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Niet zo'n moeilijke waarschijnlijk, maar ik snap um ff niet:
Hoe kun je bijv. een 3e graads polynoomfunctie uitdelen als een van de oplossingen x = 1 is, zoals bijv:
x-1 / 3x^3 + x^2 + x - 3 \ ????
Hoe kun je bijv. een 3e graads polynoomfunctie uitdelen als een van de oplossingen x = 1 is, zoals bijv:
x-1 / 3x^3 + x^2 + x - 3 \ ????


mm bedoel je met uidelen ... factoriseren of zoiets?! in elk geval
x=1 is een nulpunt en er bestaat dus een 2e graads uitdrukking zodat
(x-1)*(ax²+bx+c)=3x^3 + x^2 + x - 3
er bestaan verschillende manieren om die 2e graads uitdrukking te vinden..o.a het uitschrijven van (x-1)*(ax²+bx+c) en het vinden van de getallen a,b,c
x=1 is een nulpunt en er bestaat dus een 2e graads uitdrukking zodat
(x-1)*(ax²+bx+c)=3x^3 + x^2 + x - 3
er bestaan verschillende manieren om die 2e graads uitdrukking te vinden..o.a het uitschrijven van (x-1)*(ax²+bx+c) en het vinden van de getallen a,b,c
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Met een staartdeling. Je begint dus met 3x^2 en haalt dan 3x^2(x-1) van 3x^3 + x^2 + x - 3 af en zo ga je door totdat je niet meer verder kunt. Net als bij een staartdeling met getallen.quote:Op donderdag 11 november 2004 14:11 schreef M.M het volgende:
Niet zo'n moeilijke waarschijnlijk, maar ik snap um ff niet:
Hoe kun je bijv. een 3e graads polynoomfunctie uitdelen als een van de oplossingen x = 1 is, zoals bijv:
x-1 / 3x^3 + x^2 + x - 3 \ ????


Als je x=1 invult, krijg je 2 uit. Ik heb een voorbeeld gemaakt van zo'n staartdeling, ik heb van + x een - x gemaakt. Dan komt er wel 0 uit als je x=1 invult.quote:Op donderdag 11 november 2004 14:11 schreef M.M het volgende:
Niet zo'n moeilijke waarschijnlijk, maar ik snap um ff niet:
Hoe kun je bijv. een 3e graads polynoomfunctie uitdelen als een van de oplossingen x = 1 is, zoals bijv:
x-1 / 3x^3 + x^2 + x - 3 \ ????
Ik hoop dat je pdf-files kunt bekijken...
http://www.geocities.com/mansewy/staartdeling.pdf
.: Let epsilon be smaller than zero :.


Ik heb het inderdaad iets te snel gedaan.quote:
Maar jouw kruis is ook fout.
Er moet ipv -3x-3 3x-3 staan
En bovenin 3x^2+4x+3.
Maar het is verder duidelijk, hoop ik. :-(
.: Let epsilon be smaller than zero :.


Volgens mij is het goed zo.quote:Op vrijdag 12 november 2004 21:22 schreef MizzEnroe het volgende:
Maar jouw kruis is ook fout.
Je hebt gelijk dat x=1 geen oplossing is van de vergelijking 3x^3 + x^2 + x - 3 =0, die M.M. heeft aangedragen.quote:Maar het is verder duidelijk, hoop ik. :-(
[ Bericht 11% gewijzigd door MarkA op 13-11-2004 08:10:15 ]


Ben bezig met het zogenaamde Liquid Drop Model, met subatomaire fysica, en daar wordt het volgende gesteld:
Als je kern uit gelijke bollen bestaat, dan zal elke bol 12 contactpunten bevatten ( diep genoeg in de kern, op het oppervlak zal dit natuurlijk minder zijn) Hoe toon je zoiets aan?
Als je kern uit gelijke bollen bestaat, dan zal elke bol 12 contactpunten bevatten ( diep genoeg in de kern, op het oppervlak zal dit natuurlijk minder zijn) Hoe toon je zoiets aan?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


ik neem aan dat de kern ook even groot is als de bollen.quote:Op zondag 21 november 2004 16:56 schreef Haushofer het volgende:
Ben bezig met het zogenaamde Liquid Drop Model, met subatomaire fysica, en daar wordt het volgende gesteld:
Als je kern uit gelijke bollen bestaat, dan zal elke bol 12 contactpunten bevatten ( diep genoeg in de kern, op het oppervlak zal dit natuurlijk minder zijn) Hoe toon je zoiets aan?
zoiets bedoel je?quote:If you lay around one (red) sphere six equal spheres and lay in the dips three more spheres above and below, then the centres of the (grey) spheres are the corners of a cuboctahedron.
his leads to the closest packing of spheres in space. 12 spheres touch a central sphere.
In 2D six circles touch a central circle. 24 hyperspheres touch a central hyperspheres in the fourdimensional case.
Numbers like 6,12,24 are called "kissing numbers".
http://www.mathematische-basteleien.de/cuboctahedron.htm
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Ja, idd. Alleen ik hoopte dat het bewijs er voor nogal makkelijk zou zijn.
(of ik zoek niet goed genoeg) Iig bedankt.
(of ik zoek niet goed genoeg) Iig bedankt.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik snap iets niet van wiskunde. (Zit in 3VWO)
Stel je hebt de volgende tabel:
x -3 -2 -1 0 1 2
y -2 -5 -6 -5 -2 3
Wat is de formule hierbij? Ik weet dat ie kwadratische is, maar aangezien x = 0 niet de top is van de grafiek snap ik het ff niet meer......
x -3 -2 -1 0 1 2
y 4,5 2 0,5 0 0,5 2
Kijk deze snap ik dan weer wel, omdat de top gewoon bij x = 0 ligt, deze is dus y = 0,5x²
Kan iemand mij helpen? Bedankt!`
Edit: ik zie dat de tabel een beetje verneukt is, ik hoop dat jullie het kunnen lezen
Stel je hebt de volgende tabel:
x -3 -2 -1 0 1 2
y -2 -5 -6 -5 -2 3
Wat is de formule hierbij? Ik weet dat ie kwadratische is, maar aangezien x = 0 niet de top is van de grafiek snap ik het ff niet meer......
x -3 -2 -1 0 1 2
y 4,5 2 0,5 0 0,5 2
Kijk deze snap ik dan weer wel, omdat de top gewoon bij x = 0 ligt, deze is dus y = 0,5x²
Kan iemand mij helpen? Bedankt!`
Edit: ik zie dat de tabel een beetje verneukt is, ik hoop dat jullie het kunnen lezen


Bij dit soort vragen is er altijd een standaard aanpak.quote:Op maandag 22 november 2004 20:27 schreef basalphenaar het volgende:
Ik snap iets niet van wiskunde. (Zit in 3VWO)
Stel je hebt de volgende tabel:
x -3 -2 -1 0 1 2
y -2 -5 -6 -5 -2 3
Wat is de formule hierbij? Ik weet dat ie kwadratische is, maar aangezien x = 0 niet de top is van de grafiek snap ik het ff niet meer......
x -3 -2 -1 0 1 2
y 4,5 2 0,5 0 0,5 2
Kijk deze snap ik dan weer wel, omdat de top gewoon bij x = 0 ligt, deze is dus y = 0,5x²
Kan iemand mij helpen? Bedankt!`
Edit: ik zie dat de tabel een beetje verneukt is, ik hoop dat jullie het kunnen lezen
Zoals je al terecht hebt opgemerkt is de functie van de vorm f(x) = a*(x+b)2+c.
De opdracht is nu om de a, b en c te vinden.
- Laten we eerst maar b gaan bepalen. b geeft aan hoeveel de functie verschoven is ten opzichte van het nulpunt. Er moet gelden dat x+b = 0 voor de x-coordinaat van de top van de grafiek. De top ligt bij x=-1. Dus staat er -1+b=0, dus b = 1.
- Nu moeten we c gaan bepalen.
c is de y-coordinaat bij x=0. Als x=0 dan is y=-5, dus c=-5.
- Tenslotte moeten we de a nog bepalen.
Daarvoor kijken we hoeveel de functie stijgt/daalt als je voor x één stapje naar rechts gaat als je in de top begint. De top is x=-1, dus één stapje naar rechts gaan is naar x=0 gaan.
We zien dan dat de functie (-5 - -6 =) 1 stijgt. Dit is de waarde voor a.
Dus het eindantwoord is f(x) = (x+1)2-5.


Sin x / n = 6????
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.My white lines go a long way
Either up your nose or through your vein
With nothin to gain except killin' your brain


Kan iemand mij helpen met ( uitwerking ) het oplossen van
deze limiet?
bvd.
[ Bericht 12% gewijzigd door pfaf op 24-11-2004 14:30:54 ]
deze limiet?
bvd.
[ Bericht 12% gewijzigd door pfaf op 24-11-2004 14:30:54 ]


Ik denk dat er een fout in de vraag zit, ik zie immers geen x in de formule staan.quote:Op woensdag 24 november 2004 14:18 schreef pfaf het volgende:
Kan iemand mij helpen met ( uitwerking ) het oplossen van [afbeelding]
deze limiet?
bvd.


Tja, er vallen een hoop factoren tegenelkaar weg. Je houdt (n+1)/(2(2n+1)) over. De limiet is dus 1/4.


Ok, een kwart kan kloppen. Dan is de reeks convergent. En dat was de uitkomst.
De excacte uitwerking zal ( hopelijk ) wel lukken.
merci
De excacte uitwerking zal ( hopelijk ) wel lukken.
merci


Een faculteit is een product van factoren. n!=1*2*...*n. Dus als er op die manier boven en onder dezelfde factoren komen te staan kun je die tegenelkaar wegdelen. Zo is (n+1)!/n!=n+1.


Go Pfaf go! Heb vorig kwartaal nog bijles analyse gegeven. Mooi vakquote:Op woensdag 24 november 2004 14:36 schreef pfaf het volgende:
Ok, een kwart kan kloppen. Dan is de reeks [afbeelding] convergent. En dat was de uitkomst.
De excacte uitwerking zal ( hopelijk ) wel lukken.
merci
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Wiskunde-humor:
ex en de differentiaaloperator zitten op een bankje. Zegt de differentiaaloperator tegen ex: "Zal ik jouw eens lekker differentieren?" Zegt ex: "Ga je gang, er gebeurt toch niks."
"Dat had je gedacht; ik ben d/dy."
ex en de differentiaaloperator zitten op een bankje. Zegt de differentiaaloperator tegen ex: "Zal ik jouw eens lekker differentieren?" Zegt ex: "Ga je gang, er gebeurt toch niks."
"Dat had je gedacht; ik ben d/dy."
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


Waarom begon ik ook nog te lachen toe ik het las?quote:Op woensdag 24 november 2004 15:43 schreef IvdSangen het volgende:
Wiskunde-humor:
ex en de differentiaaloperator zitten op een bankje. Zegt de differentiaaloperator tegen ex: "Zal ik jouw eens lekker differentieren?" Zegt ex: "Ga je gang, er gebeurt toch niks."
"Dat had je gedacht; ik ben d/dy."


Mooie openingszin in de kroeg tegen een meisje: Wil je mijn eigenvector es zien?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


zou iemand mij een formule kunnen geven bij de volgende tabel?
5 teams is 6 wedstrijden
6 teams is 8 wedstrijden
7 teams is 11 wedstrijden
8 teams is 15 wedstrijden
Per extra team neemt het aantal wedstrijden toe met respectievelijk
+1
+2
+2
+4
wat is nu de formule van de somrij?
un+1 = >?
5 teams is 6 wedstrijden
6 teams is 8 wedstrijden
7 teams is 11 wedstrijden
8 teams is 15 wedstrijden
Per extra team neemt het aantal wedstrijden toe met respectievelijk
+1
+2
+2
+4
wat is nu de formule van de somrij?
un+1 = >?
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


Als ik het goed begrijp is 5 teams 6 wedstrijden, en 4 teams dan 5 wedstrijden??? Ik snap dat wedstrijdschema niet helemaal, maar:
(1+2+3+4+...+n)= (n+1)*(n/2)
Dus als n = 1, dan is het aantal teams 4 en het aantal wedstrijden 5. Dus voor een formule voor jouw probleem krijg je dan:
n teams= (n+1)*(n/2)+4 wedstrijden
(1+2+3+4+...+n)= (n+1)*(n/2)
Dus als n = 1, dan is het aantal teams 4 en het aantal wedstrijden 5. Dus voor een formule voor jouw probleem krijg je dan:
n teams= (n+1)*(n/2)+4 wedstrijden


Mijn docent kon de volgende formules niet uitleggen zonder het te plotten op een GR.
Maar ik wil ze dus op de 'ouderwetse' manier kunnen uitrekenen
0.01 X 1.3^x = 0.01x^3
en
0.5x^1.5 = 0.5 X 1.5^x
X staat voor maal, x staat voor onbekende
Alvast bedankt
Maar ik wil ze dus op de 'ouderwetse' manier kunnen uitrekenen
0.01 X 1.3^x = 0.01x^3
en
0.5x^1.5 = 0.5 X 1.5^x
X staat voor maal, x staat voor onbekende
Alvast bedankt
..................................................................................................................................................


1,3^x = x^3
e^(x*log(1,3))=e^(3*logx)
log(1,3)*x=3*log(x)
x/log(x)=3/log(1,3)
Wordt je niets wijzer van. Probeer maar es een Newton Raphson iteratie of iets dergelijks.
e^(x*log(1,3))=e^(3*logx)
log(1,3)*x=3*log(x)
x/log(x)=3/log(1,3)
Wordt je niets wijzer van. Probeer maar es een Newton Raphson iteratie of iets dergelijks.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


quote:Op woensdag 24 november 2004 15:43 schreef IvdSangen het volgende:
Wiskunde-humor:
ex en de differentiaaloperator zitten op een bankje. Zegt de differentiaaloperator tegen ex: "Zal ik jouw eens lekker differentieren?" Zegt ex: "Ga je gang, er gebeurt toch niks."
"Dat had je gedacht; ik ben d/dy."
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Begrijp ik het goed dat de factor 0.01 en 0,5 respectievelijk niet van invloed is op stelling?quote:Op zaterdag 27 november 2004 18:15 schreef s0k het volgende:
Mijn docent kon de volgende formules niet uitleggen zonder het te plotten op een GR.
Maar ik wil ze dus op de 'ouderwetse' manier kunnen uitrekenen
0.01 X 1.3^x = 0.01x^3
en
0.5x^1.5 = 0.5 X 1.5^x
X staat voor maal, x staat voor onbekende
Alvast bedankt
Edit: Er klopt niks van. Vul maar eens 4 in voor x bij de onderste. Dan krijg je links 8 en rechts 81/16 en 8 <> 81/16.
[ Bericht 7% gewijzigd door IvdSangen op 30-11-2004 02:25:54 ]
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


De bedoeling is de x te vinden waarvoor het wel geldt.quote:Op maandag 29 november 2004 21:02 schreef IvdSangen het volgende:
Edit: Er klopt niks van. Vul maar eens 4 in voor x bij de onderste. Dan krijg je links 8 en rechts 81/16 en 8 <> 81/16.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Dat heet nou algebra ...quote:Op maandag 29 november 2004 21:02 schreef IvdSangen het volgende:
[..]
Begrijp ik het goed dat de factor 0.01 en 0,5 respectievelijk niet van invloed is op stelling?
Edit: Er klopt niks van. Vul maar eens 4 in voor x bij de onderste. Dan krijg je links 8 en rechts 81/16 en 8 <> 81/16.
Oplossen van een wiskundige vergelijking, een waarde vinden voor x waarvoor dit geldt. Wiskunde is niet je sterkste punt?


Aha, er stond niet bij dat hij een oplossing zocht. Hij noemde enkel de formules en ik dacht dat hij er een bewijs voor zocht.
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


Het bewijs is de oplossingquote:Op dinsdag 30 november 2004 19:44 schreef IvdSangen het volgende:
Aha, er stond niet bij dat hij een oplossing zocht. Hij noemde enkel de formules en ik dacht dat hij er een bewijs voor zocht.


Mischien beetje stomme combinatoriek vraag maar ik kom er even niet aan uit
Wat is het aantal manieren om T ballen over N vazen te verdelen? Je hebt geen onderscheid tussen de ballen en de vazen mogen gewoon leeg zijn.
Wat is het aantal manieren om T ballen over N vazen te verdelen? Je hebt geen onderscheid tussen de ballen en de vazen mogen gewoon leeg zijn.
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Leg de T ballen op een rij en teken er N-1 strepen tussen, waarbij er best meerdere strepen op dezelfde plek mogen. Dit is hetzelfde probleem. Je moet dus N-1 strepen verdelen over T+1 plekken, waarbij 2 strepen op dezelfde plek mogen. Dit aantal is (N-1+T+1-1 boven N-1)=(N+T-1 boven N-1).


Op die manier kom ik eigenlijk nog steeds niet uit mijn oorspronkelijke probleem.
Ik zal het probleem even hier zetten:
Je hebt een markovketen met overgangsmatrix p_ij = p als i=j en p_ij = q als j=i - 1.
Dit is dus een keten waarbij je alleen naar links toe kan gaan.
Nu moet ik de kansen f_i0^(t) berekenen waarbij f_i0^(t) de kans is dat je in t stappen vanuit toestand i naar toestand 0 komt.
f_i0^(t) is zowiezo gelijk aan 0 als t < i omdat je minstens i stappen nodig hebt om van i naar 0 te komen. Beschouw nu t >= i. Als je van i naar 0 wilt gaan in t stappen moet je i keer met kans q naar links gaan en t-i keer ergens blijven zitten (waar je blijft zitten maakt niet veel uit).
Dus ik denk nu dat f_i0^(t) voor t>=1 gegeven wordt door f_i0^(t) = q^i * p^(t-i) * (aantal manieren om t - i keer te blijven zitten op de toestanden ongelijk aan 0).
Maar als ik dan jouw formule toepas op deze kans, en ik probeer te sommeren over al die kansen f_i0^(t) met t = 1 .. oneindig, krijg ik er een ondoenlijke uitdrukking uit en ik verwacht ook dat die niet naar 1 sommeert, wat wel zou moeten
Ik zal het probleem even hier zetten:
Je hebt een markovketen met overgangsmatrix p_ij = p als i=j en p_ij = q als j=i - 1.
Dit is dus een keten waarbij je alleen naar links toe kan gaan.
Nu moet ik de kansen f_i0^(t) berekenen waarbij f_i0^(t) de kans is dat je in t stappen vanuit toestand i naar toestand 0 komt.
f_i0^(t) is zowiezo gelijk aan 0 als t < i omdat je minstens i stappen nodig hebt om van i naar 0 te komen. Beschouw nu t >= i. Als je van i naar 0 wilt gaan in t stappen moet je i keer met kans q naar links gaan en t-i keer ergens blijven zitten (waar je blijft zitten maakt niet veel uit).
Dus ik denk nu dat f_i0^(t) voor t>=1 gegeven wordt door f_i0^(t) = q^i * p^(t-i) * (aantal manieren om t - i keer te blijven zitten op de toestanden ongelijk aan 0).
Maar als ik dan jouw formule toepas op deze kans, en ik probeer te sommeren over al die kansen f_i0^(t) met t = 1 .. oneindig, krijg ik er een ondoenlijke uitdrukking uit en ik verwacht ook dat die niet naar 1 sommeert, wat wel zou moeten
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Ok, als ik nu voor T = t - i en N = i gebruik en jouw bovenstaande formule toepas, krijg ik de volgende sommatie:
f_i0 = Som_{t=i}^inf f_i0^(t) = Som_{t=i}^inf ( t - 1 boven i - 1 ) * q^i * p^(t-i)
Met p + q = 1 uiteraard. En hier moet 1 uitkomen volgens de opgave
f_i0 = Som_{t=i}^inf f_i0^(t) = Som_{t=i}^inf ( t - 1 boven i - 1 ) * q^i * p^(t-i)
Met p + q = 1 uiteraard. En hier moet 1 uitkomen volgens de opgave
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Die sommatie kun je wel uitrekenen. Differentieer de identiteit
1/(1-x)=1+x+x^2+...
maar eens i-1 keer.
1/(1-x)=1+x+x^2+...
maar eens i-1 keer.


Handige symbolen:
є μ → ≈ ∩ ∞ √ ∑ ∏ ∆ ≡ ≥ ≤ ⌡ ⌠ ≠ ∫ < > § ± ² ³ Ω ∂ ← ¬ π
— voor breuken
Voorbeeld:
∞
∑ x2
i=2
1 є Ω
A → B
¬A ← ¬B
1 ≈ 1.00001
A ∩ B
√2
∏
∆x
52 ≡ 4 (mod 7)
1 ≥ 1
1 ≤ 4872494
1 ≠ 0
⌠
⌡
∫ x dμ
Ω
1 < 10
1 > -1
§ 10.9 met al mijn kut moeilijke opgaven
±1
² en ³ voor als sub en sup te ingewikkeld is
∂x
—
∂t
1 + x2
———
2 + x
π = 3.141592...
Thabit heb jij de N, Z, Q, R, C en de implicatie symbolen?
[ Bericht 32% gewijzigd door Landmass op 03-12-2004 00:49:30 ]
є μ → ≈ ∩ ∞ √ ∑ ∏ ∆ ≡ ≥ ≤ ⌡ ⌠ ≠ ∫ < > § ± ² ³ Ω ∂ ← ¬ π
— voor breuken
Voorbeeld:
∞
∑ x2
i=2
1 є Ω
A → B
¬A ← ¬B
1 ≈ 1.00001
A ∩ B
√2
∏
∆x
52 ≡ 4 (mod 7)
1 ≥ 1
1 ≤ 4872494
1 ≠ 0
⌠
⌡
∫ x dμ
Ω
1 < 10
1 > -1
§ 10.9 met al mijn kut moeilijke opgaven
±1
² en ³ voor als sub en sup te ingewikkeld is
∂x
—
∂t
1 + x2
———
2 + x
π = 3.141592...
Thabit heb jij de N, Z, Q, R, C en de implicatie symbolen?
[ Bericht 32% gewijzigd door Landmass op 03-12-2004 00:49:30 ]
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Ik zou niet weten hoe je die moet intikken. Eigenlijk zouden ze [latex]-tags moeten invoeren op het forum.


Ze zitten bij Speciale Tekens. Het probleem is alleen dat je dan een hele grote tabel krijgt waar het ergens tussen staat, je moet nogal zoeken. Niet echt toegankelijk dus.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Start/programmas/buro-accesoires/Systheemwerkset
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Hier mijn economisch/wiskundig vraag stuk. Snap er helemaal niets van.
In 2004 behaalde LAMEL N.V. een resultaat na belasting dat 60.125,- hoger was dan in 2003. De belasting over de winst is 35%. De constante kosten waren in 2004 met ¤ 9.250,- gestegen ten opzichte van 2003. De variabele kosten zijn in 2003 en 2004 50% van de omzet. In 2004 was de verkoopprijs met 5% gestegen ten opzichte van 2003. De afzet was 3% minder dan in 2003.
a. Bereken de omzet in 2003.
b. Bereken de variabele kosten in 2004.
In 2004 behaalde LAMEL N.V. een resultaat na belasting dat 60.125,- hoger was dan in 2003. De belasting over de winst is 35%. De constante kosten waren in 2004 met ¤ 9.250,- gestegen ten opzichte van 2003. De variabele kosten zijn in 2003 en 2004 50% van de omzet. In 2004 was de verkoopprijs met 5% gestegen ten opzichte van 2003. De afzet was 3% minder dan in 2003.
a. Bereken de omzet in 2003.
b. Bereken de variabele kosten in 2004.


quote:Op vrijdag 3 december 2004 12:26 schreef yuiert het volgende:
Hier mijn economisch/wiskundig vraag stuk. Snap er helemaal niets van.
In 2004 behaalde LAMEL N.V. een resultaat na belasting dat 60.125,- hoger was dan in 2003. De belasting over de winst is 35%.
Dus:
Resultaat2004 = 60125 + resultaat2003
= 0.65 * Winst2004 = 0.65 * (Omzet2004 - Kosten2004).
quote:De constante kosten waren in 2004 met ¤ 9.250,- gestegen ten opzichte van 2003.
Dus:
ConstKosten2004 = ConstKosten2003 + 9250
quote:De variabele kosten zijn in 2003 en 2004 50% van de omzet.
Dit is onduidelijk. De omzet over welk jaar? 2004? 2003? Of ieder voor zijn eigen jaar?
VarKosten2004 = 0.50 * Omzet?
VarKosten2003 = 0.50 * Omzet?
quote:In 2004 was de verkoopprijs met 5% gestegen ten opzichte van 2003. De afzet was 3% minder dan in 2003.
Dus:
Omzet2004 = 1.05 * Prijs2003 * 0.97 * Afzet2003
= 1.0185 * Prijs2003 * Afzet2003
quote:
a. Bereken de omzet in 2003.
b. Bereken de variabele kosten in 2004.
[ Bericht 0% gewijzigd door Landmass op 03-12-2004 17:54:46 ]
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


quote:Op donderdag 2 december 2004 22:16 schreef thabit het volgende:
Die sommatie kun je wel uitrekenen. Differentieer de identiteit
1/(1-x)=1+x+x^2+...
maar eens i-1 keer.
Woehoe het is gelukt, en er komt mooi 1 uit!
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Een vraagje. Hoe bepaal je de minimum afstand tussen 2 lijnen M en L? Ik dacht het volgende:
Parametriseren van M: x1+(x2-x1)t
L : y1+(y2-y1)s
R 2 = de afstanden tussen de componenten van L en M afzonderlijk gekwadrateerd.
En dan.....hoe moet je precies de "afgeleide" van R op 0 zetten? De gradienten componentsgewijs op 0 zetten? Heb wel een uitdrukking gevonden maar die is nogal lang en vervelend, dus als iemand een mooie ingeving heeft...
Parametriseren van M: x1+(x2-x1)t
L : y1+(y2-y1)s
R 2 = de afstanden tussen de componenten van L en M afzonderlijk gekwadrateerd.
En dan.....hoe moet je precies de "afgeleide" van R op 0 zetten? De gradienten componentsgewijs op 0 zetten? Heb wel een uitdrukking gevonden maar die is nogal lang en vervelend, dus als iemand een mooie ingeving heeft...
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ì{¦!B♣k☺☺☻♥♦♠•◘•9•◘○♂♀♪♫☼►◄↕┼♀¶§▬↨↑↓→←∟↔▲ !"##$%&'()*+,-./01,23¥┐└┴┬├─┼ãÃ╚ËÊÊ╔╩Ê╦╠═╬¤ð¶○ËK♀ÍÎÎÏ┘┌█▄¦Ì▀ÓßÔßGÓßÔ2ÒõÕ&µþÞÚÛ├ýÙßÔ▬5▀╬▬56▬6▬
ALT +(dec-getal) geeft de gewenste letter.
alfa doet het niet bij mij..:(
ALT +(dec-getal) geeft de gewenste letter.
alfa doet het niet bij mij..:(
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Bedankt voor de volledige uitwerking van de vorige, maar het gaat me er vooral om dat jullie me opweg helpen....
De volgende die ik totaal niet begrijp...
Korenaar N.V. beschikt voor de begroting van 2004 over de volgende gegevens voor product K-2.
Begrote kosten
Fabricagekosten Verkoopkosten
Variabel ¤ 250.000,- ¤ 100.000,-
Constant ¤ 450.000,- ¤ 180.000,-
De normale productie en afzet is 45.000 stuks per jaar.
De verwachte productie en afzet is 50.000 stuks voor 2004.
a. Bereken de fabricagekostprijs en de commerciele kostprijs van product K-2.
Voor de verwachte afzet heeft een marketingbureau het volgende overzicht opgesteld.
Verkoopprijs per stuk Verwachte afzet
¤ 26,- 41.000 stuks
¤ 25,- 46.000 stuks
¤ 24,- 50.000 stuks
¤ 23,- 53.000 stuks
¤ 22,- 55.000 stuks
b. Bereken bij welke verwachte afzet de winst voor Korenaar N.V. maximaal is.
Voor het eerste kwartaal van 2004 gelden de volgende gegevens:
Werkelijke productie: 11.000 stuks
Werkelijke afzet : 10.000 stuks
Verkoopprijs: ¤ 24,- per stuk
c. Bereken het perioderesultaat over kwartaal 1 2004 volgens absorption costing.
d. Bereken het perioderesultaat over kwartaal 1 2004 volgens variable costing
De volgende die ik totaal niet begrijp...
Korenaar N.V. beschikt voor de begroting van 2004 over de volgende gegevens voor product K-2.
Begrote kosten
Fabricagekosten Verkoopkosten
Variabel ¤ 250.000,- ¤ 100.000,-
Constant ¤ 450.000,- ¤ 180.000,-
De normale productie en afzet is 45.000 stuks per jaar.
De verwachte productie en afzet is 50.000 stuks voor 2004.
a. Bereken de fabricagekostprijs en de commerciele kostprijs van product K-2.
Voor de verwachte afzet heeft een marketingbureau het volgende overzicht opgesteld.
Verkoopprijs per stuk Verwachte afzet
¤ 26,- 41.000 stuks
¤ 25,- 46.000 stuks
¤ 24,- 50.000 stuks
¤ 23,- 53.000 stuks
¤ 22,- 55.000 stuks
b. Bereken bij welke verwachte afzet de winst voor Korenaar N.V. maximaal is.
Voor het eerste kwartaal van 2004 gelden de volgende gegevens:
Werkelijke productie: 11.000 stuks
Werkelijke afzet : 10.000 stuks
Verkoopprijs: ¤ 24,- per stuk
c. Bereken het perioderesultaat over kwartaal 1 2004 volgens absorption costing.
d. Bereken het perioderesultaat over kwartaal 1 2004 volgens variable costing


mm.. even een vraag stellen.. misschien heb ik de vraag al eerder gesteld.. k niet meer weten..
stel: a0 ,a1,...,an zodat
a0>=a1>=...>=an>0 en r een nulpunt van de polynoom
P(x)=a0xn+a1xn-1+...+an
A) bereken rP(r)-P(r)
en concludeer eruit dat:
|a0rn+1-an|=|(a1-a0)rr+...+(an-an-1)r|
B) stel dat |r|>1
toon aan dat |a0rn+1-an|> rn+1(a0-an)
en dat
|(a1-a0)rr+...+(an-an-1)r|<=(a0-an)rn
c) concludeer dat r<=1
ik zit een beetje vast bij B...
vooral de eerste ongelijkheid..
kan iemand hier een handje helpen..
stel: a0 ,a1,...,an zodat
a0>=a1>=...>=an>0 en r een nulpunt van de polynoom
P(x)=a0xn+a1xn-1+...+an
A) bereken rP(r)-P(r)
en concludeer eruit dat:
|a0rn+1-an|=|(a1-a0)rr+...+(an-an-1)r|
B) stel dat |r|>1
toon aan dat |a0rn+1-an|> rn+1(a0-an)
en dat
|(a1-a0)rr+...+(an-an-1)r|<=(a0-an)rn
c) concludeer dat r<=1
ik zit een beetje vast bij B...
vooral de eerste ongelijkheid..
kan iemand hier een handje helpen..
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


hmm, volgens mij kan je stellen dat als |r| > 1 --> r^(n+1) > 1 --> stel n is even en r< 0 --> |a0r^(n+1)-an| = -a0r^(n+1)+anquote:Op dinsdag 7 december 2004 19:15 schreef zurich het volgende:
mm.. even een vraag stellen.. misschien heb ik de vraag al eerder gesteld.. k niet meer weten..
stel: a0 ,a1,...,an zodat
a0>=a1>=...>=an>0 en r een nulpunt van de polynoom
P(x)=a0xn+a1xn-1+...+an
A) bereken rP(r)-P(r)
en concludeer eruit dat:
|a0rn+1-an|=|(a1-a0)rr+...+(an-an-1)r|
B) stel dat |r|>1
toon aan dat |a0rn+1-an|> rn+1(a0-an)
en dat
|(a1-a0)rr+...+(an-an-1)r|<=(a0-an)rn
c) concludeer dat r<=1
ik zit een beetje vast bij B...
vooral de eerste ongelijkheid..
kan iemand hier een handje helpen..
en ad rechterkant
a0r^(n+1)-anr^(n+1) --> an > 0
dus -a0r^(n+1)+an > 0 en a0r^(n+1)-anr^(n+1) < 0
stel n is oneven dan maakt het nix uit of r > 0 of r< 0
|a0r^(n+1)-an| = a0r^(n+1)-an > 0r^(n+1)-anr^(n+1) --> want r^(n+1) > 1 want |r| > 1
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


volgens mijquote:Op maandag 6 december 2004 19:16 schreef yuiert het volgende:
Bedankt voor de volledige uitwerking van de vorige, maar het gaat me er vooral om dat jullie me opweg helpen....
De volgende die ik totaal niet begrijp...
Korenaar N.V. beschikt voor de begroting van 2004 over de volgende gegevens voor product K-2.
Begrote kosten
Fabricagekosten Verkoopkosten
Variabel ¤ 250.000,- ¤ 100.000,-
Constant ¤ 450.000,- ¤ 180.000,-
De normale productie en afzet is 45.000 stuks per jaar.
De verwachte productie en afzet is 50.000 stuks voor 2004.
a. Bereken de fabricagekostprijs en de commerciele kostprijs van product K-2.
Voor de verwachte afzet heeft een marketingbureau het volgende overzicht opgesteld.
Verkoopprijs per stuk Verwachte afzet
¤ 26,- 41.000 stuks
¤ 25,- 46.000 stuks
¤ 24,- 50.000 stuks
¤ 23,- 53.000 stuks
¤ 22,- 55.000 stuks
b. Bereken bij welke verwachte afzet de winst voor Korenaar N.V. maximaal is.
Voor het eerste kwartaal van 2004 gelden de volgende gegevens:
Werkelijke productie: 11.000 stuks
Werkelijke afzet : 10.000 stuks
Verkoopprijs: ¤ 24,- per stuk
c. Bereken het perioderesultaat over kwartaal 1 2004 volgens absorption costing.
d. Bereken het perioderesultaat over kwartaal 1 2004 volgens variable costing
variabel is totaal 350.000/50.000 = 7/stuk
vast is totaal 630.000
dus tc = 630.000 + 7x (met x aantal verkochte goederen)
dus nu fab = 250.000/50.000 = 5/stuk
en ver = 100.000/50.000 = 2/stuk
b)
¤ 26,- 41.000 stuks = 41.000*19 - 630.000 = 149.000
¤ 25,- 46.000 stuks = 46.000*18 - 630.000 = 198.000
¤ 24,- 50.000 stuks = 50.000*17 - 630.000 = 220.000 --> meeste winst
¤ 23,- 53.000 stuks = 53.000*16 - 630.000 = 218.000
¤ 22,- 55.000 stuks = 55.000*15 - 630.000 = 195.000
c)
weet niet meer precies, kd8 dat je hier de werkelijke # verkochte goederen moet nemen, dus achteraf
dus vaste kosten worden 650.000/10.000 = 65 / 4 = 16,25
16,25 + var.kosten = 23,25 --> 10.000*0.75 = 7.500
d)
nu dus # geproduceerde goederen nemen
dus vaste kosten wordt 650.000/11.000 = 59.1 / 4 =14.77
14.77 + 7 = 21.77 --> 10.000*2.23 = 22.300
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Wellicht heb je het al gevonden, maar in het onderstaande document staat een mooie uitwerking voor een situatie in R3:quote:Op vrijdag 3 december 2004 14:33 schreef Haushofer het volgende:
Een vraagje. Hoe bepaal je de minimum afstand tussen 2 lijnen M en L?
...
http://www.mc.edu/campus/(...)g2001/bard.himel.pdf


Ik neem aan dat je de afstand tussen twee lijnsegmenten bedoelt? Het verschil is dat lijnen onbegrensd zijn, ze hebben geen eindpunten en gaan dus tot in het oneindige door. Lijnsegmenten hebben 2 eindpunten.quote:Op vrijdag 3 december 2004 14:33 schreef Haushofer het volgende:
Een vraagje. Hoe bepaal je de minimum afstand tussen 2 lijnen M en L? Ik dacht het volgende:
Parametriseren van M: x1+(x2-x1)t
L : y1+(y2-y1)s
R 2 = de afstanden tussen de componenten van L en M afzonderlijk gekwadrateerd.
En dan.....hoe moet je precies de "afgeleide" van R op 0 zetten? De gradienten componentsgewijs op 0 zetten? Heb wel een uitdrukking gevonden maar die is nogal lang en vervelend, dus als iemand een mooie ingeving heeft...
Het antwoord w.b. lijnen is dan ook heel makkelijk: als de lijnen parallel lopen, is de minimum afstand overal even groot, als de lijnen niet parallel lopen zullen ze elkaar ergens snijden en dus zal de minimum afstand 0 zijn.
En even een vraagje tussendoor: wil je een puur wiskundig resultaat of mag het ook een procedureel stappenplan (een algoritme zijn)? Algoritmes zijn doorgaans makkelijker te vinden / schrijven dan 1 enkele wiskundige formule. Dus als je de uitkomst bijv. in een programma gaat gebruiken, volstaat een algoritme.
Ik heb het wiskundige resultaat eens bekeken, en het is idd een behoorlijk pittige functie, of iig, er zitten veel termen in.
Wat betreft het algoritme: volgens mij is het zo, dat het lijnsegment K dat de kortste afstand vormt tussen de lijnsegmenten L en M, K altijd tenminste een van de 4 eindpunten van L of M gebruikt als eindpunt. Of andersom: K zal nooit ergens op het midden* van zowel L als M liggen (tenzij L en M parallel lopen). Kan het niet helemaal helder krijgen, maar volgens mij geldt dit.
Mocht dit idd zo zijn, dan kan je voor elk van de 4 eindpunten kijken wat de kleinste cirkel is (met het middelpunt op dat eindpunt) die het andere lijnsegment raakt. De kleinste van deze 4 cirkels is dan je antwoord.
* dwz, "midden" = "alles behalve de eindpunten"
--edit--
Ik kan geen tegenvoorbeeld vinden, dus volgens mij klopt mijn aanname, mits L en M elkaar niet snijden.
De formule om de kortste afstand tussen een punt (px, py) en een lijn
lx := sx + (ex-sx)*t
ly := sy + (ey-sy)*t
te vinden is:
| 1 2 3 4 5 | 2 2 -ex sx + sx + ex px - sx px - ey sy + sy + ey py - sy py t := ---------------------------------------------------------- 2 2 2 2 ex - 2 ex sx + sx + ey - 2 ey sy + sy |
N.B. dit resultaat moet je dan nog wel 'clampen' naar het bereik [0, 1], m.a.w als t < 0, dan t=0 en als t > 1, dan t = 1.
[ Bericht 10% gewijzigd door HenryHill op 08-12-2004 20:13:43 (Kortste afstand punt-lijn toegevoegd) ]
So this is how liberty dies... with thunderous applause.
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world


Mja, was meer nieuwsgierig hoe je die afgeleide definieerde.quote:En even een vraagje tussendoor: wil je een puur wiskundig resultaat of mag het ook een procedureel stappenplan (een algoritme zijn)?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ok, hier ga je dus niks aan hebben maar just for the fun of it heb ik het ff laten uitwerken door de computer. Stel dat je volgende formules hebt voor de lijnen M en L:quote:Op donderdag 9 december 2004 10:49 schreef Haushofer het volgende:
[..]
Mja, was meer nieuwsgierig hoe je die afgeleide definieerde.
line_mx := mx1 + (mx2 - mx1) mt
line_my := my1 + (my2 - my1) mt
line_lx := lx1 + (lx2 - lx1) lt
line_ly := ly1 + (ly2 - ly1) lt
De afstand op tijden (mt, lt) is dan gedefinieerd als:
dist := ((line_mx - line_lx)^2 + (line_my - line_ly)^2)^(1/2)
Uitgewerkt geeft dit (nb de macht tot een half "^(1/2)" is hetzelfde als de wortel):
dist := (-2*mt*mx2*lt*lx2 + 2*mt*mx2*lt*lx1 + 2*mt*mx1*lt*lx2 - 2*mt*mx1*lt*lx1 - 2*mt*my2*lt*ly2 + 2*mt*my2*lt*ly1 + mx1^2 - 2*mt*mx1^2 - 2*mx1*lx1 + mt^2*mx2^2 + mt^2*mx1^2 + lx1^2 - 2*lt*lx1^2 + lt^2*lx2^2 + lt^2*lx1^2 + my1^2 - 2*mt*my1^2 - 2*my1*ly1 + mt^2*my2^2 + mt^2*my1^2 + ly1^2 - 2*lt*ly1^2 + lt^2*ly2^2 + lt^2*ly1^2 - 2*mt^2*mx2*mx1 - 2*lt^2*lx2*lx1 + 2*mx1*mt*mx2 - 2*mx1*lt*lx2 + 2*mx1*lt*lx1 - 2*mt*mx2*lx1 + 2*mt*mx1*lx1 + 2*lx1*lt*lx2 - 2*mt^2*my2*my1 - 2*lt^2*ly2*ly1 + 2*my1*mt*my2 - 2*my1*lt*ly2 + 2*my1*lt*ly1 - 2*mt*my2*ly1 + 2*mt*my1*ly1 + 2*ly1*lt*ly2 + 2*mt*my1*lt*ly2 - 2*mt*my1*lt*ly1)^(1/2)
Als je deze formule differentieert naar mt (maw de afgeleide neemt) krijg je:
dist_diff_mt := 1/2*(-2*mx2*lt*lx2 + 2*mx2*lt*lx1 + 2*mx1*lt*lx2 - 2*mx1*lt*lx1 - 2*my2*lt*ly2 + 2*my2*lt*ly1 - 2*mx1^2 + 2*mt*mx2^2 + 2*mt*mx1^2 - 2*my1^2 + 2*mt*my2^2 + 2*mt*my1^2 - 4*mx1*mt*mx2 + 2*mx2*mx1 - 2*mx2*lx1 + 2*mx1*lx1 - 4*my1*mt*my2 + 2*my2*my1 - 2*my2*ly1 + 2*my1*ly1 + 2*my1*lt*ly2 - 2*my1*lt*ly1)/( - 2*mt*mx2*lt*lx2 + 2*mt*mx2*lt*lx1 + 2*mt*mx1*lt*lx2 - 2*mt*mx1*lt*lx1 - 2*mt*my2*lt*ly2 + 2*mt*my2*lt*ly1 + mx1^2 - 2*mt*mx1^2 - 2*mx1*lx1 + mt^2*mx2^2 + mt^2*mx1^2 + lx1^2 - 2*lt*lx1^2 + lt^2*lx2^2 + lt^2*lx1^2 + my1^2 - 2*mt*my1^2 - 2*my1*ly1 + mt^2*my2^2 + mt^2*my1^2 + ly1^2 - 2*lt*ly1^2 + lt^2*ly2^2 + lt^2*ly1^2 - 2*mt^2*mx2*mx1 - 2*lt^2*lx2*lx1 + 2*mx1*mt*mx2 - 2*mx1*lt*lx2 + 2*mx1*lt*lx1 - 2*mt*mx2*lx1 + 2*mt*mx1*lx1 + 2*lx1*lt*lx2 - 2*mt^2*my2*my1 - 2*lt^2*ly2*ly1 + 2*my1*mt*my2 - 2*my1*lt*ly2 + 2*my1*lt*ly1 - 2*mt*my2*ly1 + 2*mt*my1*ly1 + 2*ly1*lt*ly2 + 2*mt*my1*lt*ly2 - 2*mt*my1*lt*ly1)^(1/2)
De waarde van mt waarop de afgeleide 0 is (en "dist" dus minimaal) is dan:
mt := (mx2*lt*lx2 - mx2*lt*lx1 - mx1*lt*lx2 + mx1*lt*lx1 + my2*lt*ly2 - my2*lt*ly1 + mx1^2 + my1^2 - mx2*mx1 + mx2*lx1 - mx1*lx1 - my2*my1 + my2*ly1 - my1*ly1 - my1*lt*ly2 + my1*lt*ly1)/(mx2^2 + mx1^2 + my2^2 + my1^2 - 2*mx2*mx1 - 2*my2*my1)
N.B. je kunt "dist" ook nog differentieren naar lt, zodat je de waarde van lt kan bepalen waar "dist" minimaal is. De waarde van lt is dan:
lt := (mt*mx2*lx2 - mt*mx2*lx1 - mt*mx1*lx2 + mt*mx1*lx1 + mt*my2*ly2 - mt*my2*ly1 + lx1^2 + ly1^2 + mx1*lx2 - mx1*lx1 - lx1*lx2 + my1*ly2 - my1*ly1 - ly1*ly2 - mt*my1*ly2 + mt*my1*ly1)/(lx2^2 + lx1^2 + ly2^2 + ly1^2 - 2*lx1*lx2 - 2*ly1*ly2)
Dusse... veel plezier ermee
So this is how liberty dies... with thunderous applause.
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world


Ik kom er niet uit
................................mate van wandelen
tuinbezit........weinig......regelmatig.....veel......totaal
----------------------------------------------------------------
geen tuin........ 376.............183............47........1030
----------------------------------------------------------------
wel tuin...........136.............290............68.........494
----------------------------------------------------------------
totaal...............512.............473...........539.......1524
Som:
Bereken gamma , en spreek op basis van de uitkomst een oordeel uit over de hypothese van de onderzoekers.
................................mate van wandelen
tuinbezit........weinig......regelmatig.....veel......totaal
----------------------------------------------------------------
geen tuin........ 376.............183............47........1030
----------------------------------------------------------------
wel tuin...........136.............290............68.........494
----------------------------------------------------------------
totaal...............512.............473...........539.......1524
Som:
Bereken gamma , en spreek op basis van de uitkomst een oordeel uit over de hypothese van de onderzoekers.


Het lijkt me dat 47 in de eerste rij getallen en derde rij kolommen 471 moet zijn.quote:Op donderdag 9 december 2004 21:21 schreef Mokos het volgende:
Ik kom er niet uit
................................mate van wandelen
tuinbezit........weinig......regelmatig.....veel......totaal
----------------------------------------------------------------
geen tuin........ 376.............183............47........1030
----------------------------------------------------------------
wel tuin...........136.............290............68.........494
----------------------------------------------------------------
totaal...............512.............473...........539.......1524
Som:
Bereken gamma , en spreek op basis van de uitkomst een oordeel uit over de hypothese van de onderzoekers.
Dan zijn de totalen meer in overeenstemming.
[ Bericht 0% gewijzigd door Yosomite op 10-12-2004 17:09:40 ]


Ah, je hebt gelijk 47 moet het getal 471 zijn, wat stom van mij zeg.quote:Op donderdag 9 december 2004 23:08 schreef Yosomite het volgende:
Het lijkt met dat 47 in de eerste rij getallen en derde rij kolommen 471 moet zijn.
Dan zijn de totalen meer in overeenstemming.
Had het nog zo goed nagekeken.
misschien ben ik ook niet zo bij, voel me niet zo lekker


Op de vraag wat is het schaalniveau van de variabelen, heb ik trouwens het antwoord: 'ordinale variabele' gegeven. Zal dat goed zijn?
Verdorrie, ik kom er echt niet uit en moet morgen rond 10 uur weg en het dan inleveren.
had zelfs al een, vond het zelf wel een creatieve, poging in onzin gedaan om mensen hiernaar toe te lokken
Verdorrie, ik kom er echt niet uit en moet morgen rond 10 uur weg en het dan inleveren.
had zelfs al een, vond het zelf wel een creatieve, poging in onzin gedaan om mensen hiernaar toe te lokken


Ben je d'r verder nog uitgekomen?quote:Op donderdag 9 december 2004 23:31 schreef Mokos het volgende:
Op de vraag wat is het schaalniveau van de variabelen, heb ik trouwens het antwoord: 'ordinale variabele' gegeven. Zal dat goed zijn?
Verdorrie, ik kom er echt niet uit en moet morgen rond 10 uur weg en het dan inleveren.
had zelfs al een, vond het zelf wel een creatieve, poging in onzin gedaan om mensen hiernaar toe te lokken
De variabelen zijn nog niet geschaald, want je hebt alleen de nominale antwoorden, maar wel geordend. Dus ordinaal.


Ja, het is me uiteindelijk toch nog gelukt, opeens zag ik het lichtquote:Op vrijdag 10 december 2004 17:29 schreef Yosomite het volgende:
Ben je d'r verder nog uitgekomen?
De variabelen zijn nog niet geschaald, want je hebt alleen de nominale antwoorden, maar wel geordend. Dus ordinaal.
Schaalniveau heb ik dus ordinale variabele genoemd idd.
Gamma, kwam ik uit op: - 0,21
En eigenlijk was het uiteindelijk helemaal niet zo moeilijk, maar ik moest het even zien en gelukkig en hopelijk zag ik het uiteindelijk goed. Even puzzelen en doordenken. Had nog 2 vragen en die heb ik ook maar snel even gemaakt, opeens zat ik er gewoon in .


hoi.
als f(n)=n! wat is dan de inverse functie hiervan?...
met andere woorden als n!=m, hoe moet je n uitdrukken in m?
als f(n)=n! wat is dan de inverse functie hiervan?...
met andere woorden als n!=m, hoe moet je n uitdrukken in m?
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Ik ken niet het probleem waar je mee zit maar het lijkt me dat als je op zoek bent naar de inverse van die functie dat je op de verkeerde weg zit want die inverse is er niet (behoudens dat er nu een wskunde prof met iets heel vaags en abstracts komt aan zetten).quote:Op zondag 12 december 2004 21:23 schreef zurich het volgende:
hoi.
als f(n)=n! wat is dan de inverse functie hiervan?...
met andere woorden als n!=m, hoe moet je n uitdrukken in m?
Wat zou namelijk de inverse van 25 zijn?. Precies die is er niet.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Ik zou haast zeggen n= m/(n-1)!quote:Op zondag 12 december 2004 21:23 schreef zurich het volgende:
hoi.
als f(n)=n! wat is dan de inverse functie hiervan?...
met andere woorden als n!=m, hoe moet je n uitdrukken in m?
Aangezien n/(n-1)!=n oplevert... correct me if I'm wrong
Je schiet hier alleen niet veel me op, aangezien de n factor aan twee kanten voorkomt nu, anders zou ik het niet weten denk ik.


Het gaat natuurlijk om gehele getallen. Je hebt op zich gelijk alleen op deze manier krijg je breuken in het verhaal (en hoe definieer je de ! van een breuk ik weet het wel alleen betwijfel ik of het probleem het nodig heeft). Ik weet dus niet hoe zeer dat de bedoeling gaat zijn.quote:Op zondag 12 december 2004 21:28 schreef 205_Lacoste het volgende:
[..]
Ik zou haast zeggen n= m/(n-1)!
Aangezien n/(n-1)!=n oplevert... correct me if I'm wrong
Je schiet hier alleen niet veel me op, aangezien de n factor aan twee kanten voorkomt nu, anders zou ik het niet weten denk ik.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Ik ben wel erg benieuwd naar de 'ware' oplossing, ik vraag me namelijk af of die er wel is, anders dan ik gaf. Je zit hier met 2 onbekenden en een 'ingewikkelde' functie als faculteit genomen over één hiervan.


jammer dat n! niet te schrijven is als een soort polynoom ofzo, maar ja, bedankt..quote:Op maandag 13 december 2004 07:40 schreef 205_Lacoste het volgende:
Ik ben wel erg benieuwd naar de 'ware' oplossing, ik vraag me namelijk af of die er wel is, anders dan ik gaf. Je zit hier met 2 onbekenden en een 'ingewikkelde' functie als faculteit genomen over één hiervan.
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Afhankelijk van de operatie, het kan -25 of 1/25 zijn.quote:Op zondag 12 december 2004 21:27 schreef Landmass het volgende:
Wat zou namelijk de inverse van 25 zijn?. Precies die is er niet.
Als m = n! dan is de inverse: n = m*1/2*1/3*...*1/(n-1) = m/((n-1)! ) , maar dat schiet niet echt op.
Edit: Laatste pagina niet gezien, bij schrijven.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


waar staat die t voor.. als ik vragen mag!:)quote:Op maandag 13 december 2004 10:03 schreef Landmass het volgende:
http://mathworld.wolfram.com/Factorial.html
[afbeelding]
lijkt me een heel leuke mooi uitziende formule.. maar ik vrees dat ik alleen benadering krijg?
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Daar ga je over integreren.quote:Op maandag 13 december 2004 17:29 schreef zurich het volgende:
[..]
waar staat die t voor.. als ik vragen mag!:)
Wat wil je dan?quote:lijkt me een heel leuke mooi uitziende formule.. maar ik vrees dat ik alleen benadering krijg?
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


bijv. als n!=24 dan moet gelden dat n=4
.. en als n!=3628800 dan moet gelden dat n=10..
ect..
.. en als n!=3628800 dan moet gelden dat n=10..
ect..
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Een algoritme is makkelijk te vinden. Stel dat n! = m, danquote:Op maandag 13 december 2004 18:29 schreef zurich het volgende:
bijv. als n!=24 dan moet gelden dat n=4
.. en als n!=3628800 dan moet gelden dat n=10..
ect..
| 1 2 3 4 5 6 7 8 | In: de faculteit m Uit: De waarde van n n <- 1 while m != 1 do begin n <- n+1 m <- m / n end return n |
So this is how liberty dies... with thunderous applause.
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world


Laat me raden, je moet een informatica opdracht doen.quote:Op maandag 13 december 2004 18:29 schreef zurich het volgende:
bijv. als n!=24 dan moet gelden dat n=4
.. en als n!=3628800 dan moet gelden dat n=10..
ect..
Als je nou eens alle faculteiten afgaat totdat je dat gegeven getal overschreden hebt. Is dat geen goed idee.
vb1:
1! = 1 < 3628800
2! = 2 < 3628800
3! = 6 < 3628800
4! = 24 < 3628800
.
.
.
9! = 362880 < 3628800
10! = 3628800 BINGO
vb2:
1! = 1 < 3628801
2! = 2 < 3628801
.
.
.
10! = 3628800 < 3628801
11! = 39 916 800 > 3628801 JE ZAL GEEN WAARDE VINDEN
Het kan misschien sneller maar ik denk niet dat dat nodig is.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


1. Hoe doe je die code tag?quote:Op maandag 13 december 2004 18:37 schreef HenryHill het volgende:
[..]
Een algoritme is makkelijk te vinden. Stel dat n! = m, dan
[ code verwijderd ]
2. Je krijgt breuken met jouw progje, volgens mij is dat niet de bedoeling. Er is ook kans dat je in een oneindige loop komt.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


[ code ] (maar dan zonder de spaties natuurlijk)quote:Op maandag 13 december 2004 18:40 schreef Landmass het volgende:
[..]
1. Hoe doe je die code tag?
2. Je krijgt breuken met jouw progje, volgens mij is dat niet de bedoeling. Er is ook kans dat je in een oneindige loop komt.
Klopt, er wordt geen foutafhandeling gedaan, dus het gaat er heel naief vanuit dat de gegeven m idd het resultaat is van een faculteit (dwz, dat m terug te herleiden is naar de vorm n!). Als dat zo is, levert het echter geen breuken op (de rest bij de deling zal altijd 0 zijn), en zal het niet in een oneindige loop komen.
Mijn bedoeling was dan ook meer om kort en bondig een mogelijke aanpak te schetsen, niet om een waterdichte methode te geven.
So this is how liberty dies... with thunderous applause.
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world
Truth? What's so great about the truth? Try lying for a change, it's the currency of the world


even denken,.. het is niet echt een informatica/programmering opdracht..
ik was gewoon nieuwsgierig.. het viel me op dat ik nog nooit een inverse functie van f(n)=n! heb gezien. Kan dat niet met priemgetallen? ..dat je bijv. n! factoriseert ect..
ik was gewoon nieuwsgierig.. het viel me op dat ik nog nooit een inverse functie van f(n)=n! heb gezien. Kan dat niet met priemgetallen? ..dat je bijv. n! factoriseert ect..
chat with me on
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1
http://www.pandorabots.com/pandora/talk?botid=f5d922d97e345aa1


Voor de getallen tussen 4! = 24 en 5! = 120 zijn er dus geen inverse.quote:Op maandag 13 december 2004 19:56 schreef zurich het volgende:
het viel me op dat ik nog nooit een inverse functie van f(n)=n! heb gezien. Kan dat niet met priemgetallen? ..dat je bijv. n! factoriseert ect..
Tussen 5! = 120 en 6! 720 ook niet. etc.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


De normale faculteit is trouwens niet eens gedefinieerd voor breuken, alleen voor gehele positieve getallen. Als je het met de gamma functie wilt gaan doen, kan je hem bijvoorbeeld in een machtreeks schrijven, dit kan gewoon aangezien hij analytisch is, en van die machtreeks de inverse te bepalenquote:Op maandag 13 december 2004 18:40 schreef Landmass het volgende:
[..]
1. Hoe doe je die code tag?
2. Je krijgt breuken met jouw progje, volgens mij is dat niet de bedoeling. Er is ook kans dat je in een oneindige loop komt.
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


De Gamma functie is niet analytisch op de punten z=0,-1,-2,-3,... dus een algemene Taylorreeks bestaat niet (vanwege convergentiestraal).quote:Op dinsdag 14 december 2004 10:27 schreef Pietjuh het volgende:
[..]
De normale faculteit is trouwens niet eens gedefinieerd voor breuken, alleen voor gehele positieve getallen. Als je het met de gamma functie wilt gaan doen, kan je hem bijvoorbeeld in een machtreeks schrijven, dit kan gewoon aangezien hij analytisch is, en van die machtreeks de inverse te bepalen
Maar zo voor de hand liggend is werken met de gammafunctie niet. En werken met de inverse dus ook niet. Dat zou deze site toch wel moeten bewijzen. Daar zie je bijvoorbeeld dit staan:
met:
En dat is slechts voor 1 enkele waarde van de gamma functie...
O.o


Ik heb een vraag, wat betekend algebra in de volgende situatie?
Als
x - (x + y) >= 0 //>= is groter of gelijk aan
algebra:
y <= 0
Betekend algebra in dit geval vereenvoudigen?
Hebben jullie links waar hier meer over uit wordt gelegd?
Als
x - (x + y) >= 0 //>= is groter of gelijk aan
algebra:
y <= 0
Betekend algebra in dit geval vereenvoudigen?
Hebben jullie links waar hier meer over uit wordt gelegd?
Are you nuts??


Moet je niet gewoon het algebraïsch oplossen, dus alle mogelijkheden voor Y geven, daar lijkt het namelijk wel gewoon op.


-y >= 0
nu verm met -1 en dan draait het teken om dus
y =< 0
nu verm met -1 en dan draait het teken om dus
y =< 0
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Een algebra is een ring met een eenheid
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


algebraïsch oplossenquote:Op dinsdag 21 december 2004 20:08 schreef 205_Lacoste het volgende:
Moet je niet gewoon het algebraïsch oplossen, dus alle mogelijkheden voor Y geven, daar lijkt het namelijk wel gewoon op.
Wat is het verschil met gewoon oplossen? Of stel ik nu een hele domme vraag?
Ter info: vroeger heb ik op de MAVO wiskunde gehad, dus mijn wiskunde kennis is niet erg breed.
Are you nuts??


Dit begrijp ik dan wel weer wel.quote:Op dinsdag 21 december 2004 20:22 schreef Landmass het volgende:
-y >= 0
nu verm met -1 en dan draait het teken om dus
y =< 0
Maar hoe vallen de x-en in dit voorbeeld precies tegen elkaar weg?
Betekend in dit geval algebra dat je het moet vereenvoudigen?
Are you nuts??


Hehe, oké ik begrijp de situatie
En de oplossing bestaat dus in dit geval niet uit een absoluut getal.
Volgens Van Dale.quote:al·ge·bra (de ~ (v.))
1 wiskunde die zich bezighoudt met de betrekkingen van door letters en tekens aangeduide grootheden => stelkunde
al·ge·bra·ïsch (bn.)
1 van, uit, zoals gebruikelijk in de algebra
En de oplossing bestaat dus in dit geval niet uit een absoluut getal.


Ze willen gewoon dat je het oplost. Doordat het hier variabelen betreft gaan ze het algebraisch noemen. Trek je er niks van aan. JE oplossing was goed.quote:algebraïsch oplossen
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


x - (x + y) =quote:Op dinsdag 21 december 2004 21:11 schreef whosvegas het volgende:
[..]
Dit begrijp ik dan wel weer wel.
Maar hoe vallen de x-en in dit voorbeeld precies tegen elkaar weg?
Betekend in dit geval algebra dat je het moet vereenvoudigen?
x - x - y =
0 - y =
- y
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Mischien handig om te weten. a - b is notatie voor a + -b (belangrijk).
Op die manier ga je niet in de fout met haakjes zetten. Want wat zou a - b - c zijn. Moet je eerst a - b doen en darna -c of eerst b- c en dat van a aftrekken.
Zo moet het dus a - b - c is notatie voor a + -b + -c. Het is dus gewoon optellen en daar maakt de volgorde niet uit.
Op die manier ga je niet in de fout met haakjes zetten. Want wat zou a - b - c zijn. Moet je eerst a - b doen en darna -c of eerst b- c en dat van a aftrekken.
Zo moet het dus a - b - c is notatie voor a + -b + -c. Het is dus gewoon optellen en daar maakt de volgorde niet uit.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Oke, bedankt!quote:Op dinsdag 21 december 2004 21:11 schreef Landmass het volgende:
[..]
Ze willen gewoon dat je het oplost. Doordat het hier variabelen betreft gaan ze het algebraisch noemen. Trek je er niks van aan. JE oplossing was goed.
Ik wist niet precies wat ze met die term bedoelde
Morgen als ik weer aan de studie ga, zal ik het nog eens bestuderen. Nu geen zin meer in.
Are you nuts??


Ik versta toch iets anders onder een algebra hoorquote:Op dinsdag 21 december 2004 20:32 schreef Haushofer het volgende:
Een algebra is een ring met een eenheid
Namelijk een module over een lichaam met daarop een vermenigvuldiging gedefinieerd. Voorbeeldje ervan, die je waarschijnlijk wel kent is de Banach algebra. Dit is een genormeerde vectorruimte met || x y || <= || x || || y ||
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Ik heb zelf trouwens ook nog een vraagje, wat ik vandaag op mijn tentamen analyse 3 tegenkwam, maar waar ik niet aan kwam
Je hebt zeg maar een rij functies fn (x) = 1/n * ln(1+x/n).
Nu moest ik bewijzen dat de reeks som(f_n, n=1..oneindig) puntsgewijs convergeert voor x in [0, oneindig) en uniform convergeert voor x in [0,A] voor alle A>0. Dit heb ik kunnen bewijzen door onder andere f_n af te schatten als f_n < = 1/n * x/n = x/n^2, en som(x/n^2) convergeert naar x*Pi^2/6, dus som(f_n) convergeert ook.
Nu moest ik bij de volgende deelopgave echter ook aantonen dat som(f_n) niet uniform convergeert voor x in [0,oneindig), maar ik zou niet echt weten hoe ik dat moet doen
Je hebt zeg maar een rij functies fn (x) = 1/n * ln(1+x/n).
Nu moest ik bewijzen dat de reeks som(f_n, n=1..oneindig) puntsgewijs convergeert voor x in [0, oneindig) en uniform convergeert voor x in [0,A] voor alle A>0. Dit heb ik kunnen bewijzen door onder andere f_n af te schatten als f_n < = 1/n * x/n = x/n^2, en som(x/n^2) convergeert naar x*Pi^2/6, dus som(f_n) convergeert ook.
Nu moest ik bij de volgende deelopgave echter ook aantonen dat som(f_n) niet uniform convergeert voor x in [0,oneindig), maar ik zou niet echt weten hoe ik dat moet doen
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Uniforme convergentie is sowieso iets wat je bekijkt op compacte delen. We zeggen dat een reeks "normaal" convergeert op een verzameling U als-ie absoluut en uniform op elk compact deel van U convergeert.


Zat jij in dat lokaal dat recht naast de wc's zit? Want dan heb ik je waarschijnlijk uit dat lokaal zien lopen na afloop van het tentamen Ik zat zelf in lokaal er recht tegenover bij Renier Broker.quote:Op woensdag 22 december 2004 14:51 schreef thabit het volgende:
Hee, dat tentamen moest ik surveilleren. .
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Ik ben maar wat aan het oefenen geslagen met algebra, op deze site staat over diverse onderwerpen goede uitleg:
http://www.pandd.demon.nl/wiskunde.htm
Ook een goede:
http://nl.wikipedia.org/wiki/Hoofdpagina
Hebben jullie maar sites met wiskunde uileg?
Voor de opleiding (AMBI SE) die ik nu doe heb je eigenlijk HAVO wiskunde nodig, ik heb MAVO, maar tot nu toe kan ik het goed volgen. Vooral als ik wat sites heb met wat extra uitleg en natuurlijk Fok
http://www.pandd.demon.nl/wiskunde.htm
Ook een goede:
http://nl.wikipedia.org/wiki/Hoofdpagina
Hebben jullie maar sites met wiskunde uileg?
Voor de opleiding (AMBI SE) die ik nu doe heb je eigenlijk HAVO wiskunde nodig, ik heb MAVO, maar tot nu toe kan ik het goed volgen. Vooral als ik wat sites heb met wat extra uitleg en natuurlijk Fok
Are you nuts??


http://forum.scholieren.com/ (ga naar de afdeling exacte vakken)
http://www.wisfaq.nl/
Of vraag het anders hier.
We hebben hier een over ijverige maar uitermate behulpzame promovendi wiskunde in ons midden.
......................................................................
Voor het VWO heb je boekjes die beknopt het hele VWO programma wiskunde geven. Zoiets is er voor de HAVO misschien ook wel. Kan helpen.
http://www.wisfaq.nl/
Of vraag het anders hier.
We hebben hier een over ijverige maar uitermate behulpzame promovendi wiskunde in ons midden.
......................................................................
Voor het VWO heb je boekjes die beknopt het hele VWO programma wiskunde geven. Zoiets is er voor de HAVO misschien ook wel. Kan helpen.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Bedankt, zo moet ik er uit kunnen komenquote:Op donderdag 23 december 2004 20:58 schreef Landmass het volgende:
http://forum.scholieren.com/ (ga naar de afdeling exacte vakken)
http://www.wisfaq.nl/
Of vraag het anders hier.
We hebben hier een over ijverige maar uitermate behulpzame promovendi wiskunde in ons midden.
......................................................................
Voor het VWO heb je boekjes die beknopt het hele VWO programma wiskunde geven. Zoiets is er voor de HAVO misschien ook wel. Kan helpen.
Ik zal eens naar zo'n boekje voor de HAVO op zoek gaan.
Are you nuts??


Ja, daar zat ik. .quote:Op donderdag 23 december 2004 17:36 schreef Pietjuh het volgende:
[..]
Zat jij in dat lokaal dat recht naast de wc's zit? Want dan heb ik je waarschijnlijk uit dat lokaal zien lopen na afloop van het tentamen Ik zat zelf in lokaal er recht tegenover bij Renier Broker.
Wat vond je van het tentamen? Persoonljik vond ik er teveel differentiaalvergelijkingen tussenzitten. Maar goed, ik heb dan ook een natuurlijke voorkeur voor de wat meer theoretisch getinte vragen, waarbij studenten echt moeten laten zien dat ze de stof begrepen hebben, zoals het convergentiegedrag enzo.


Ja wel redelijk veel differentiaalvergelijkingen, waarbij je ook bijna niet over hoeft na te denken om ze op te kunnen lossen, vooral die ene eerste orde d.v. (y' + ycos(t) = cos(t) ) en die vraag met de laplace transformatie. Die vraag met de fourierreeks berekenen was gewoon ronduit irritant, want je had er een dik half uur voor nodig om al die partiele integraties uit te voerenquote:Op vrijdag 24 december 2004 17:59 schreef thabit het volgende:
Ja, daar zat ik. .
Wat vond je van het tentamen? Persoonljik vond ik er teveel differentiaalvergelijkingen tussenzitten. Maar goed, ik heb dan ook een natuurlijke voorkeur voor de wat meer theoretisch getinte vragen, waarbij studenten echt moeten laten zien dat ze de stof begrepen hebben, zoals het convergentiegedrag enzo.
Het nadruk waarop het vak gegeven werd, was ook voornamelijk differentiaalvergelijkingen. We hebben alleen in de eerste paar weken aandacht besteed aan convergentiecriteria zoals uniforme convergentie, absolute convergentie enz. Daarna hebben we de rest van de tijd ons alleen bezig gehouden met d.v's, wat opzich ook vrij handig is (bij natuurkunde heb je het ontzettend vaak nodig), maar wat meer over convergentiegedrag zou leuk geweest zijn Het zal waarschijnlijk ook wel komen omdat de docent (Verduyn-Lunel) zo'n enorme d.v. verslaafde is
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Offtopic: Ik ben nu met algemene relativiteit bezig, en moet zeggen dat het allemaal goed te doen is. Wel veel differentiaalgeometrie, en die tensorcalculus is gewoon de indices in de gaten houden. Heb zelf het boek van Ray D'Inverno, en college aantekeningen van Sean Carroll gedown'd, die allebei goed bevallen. Vooral die laatste. Eerste paar weken alleen wiskunde gehad, maar na die paar weken valt dan eindelijk het woord "zwaartekracht". Vind het zelf ook altijd wel leuk om de wiskundige achtergrond te kennen, hoewel veel natuurkundigen de details maar wat graag aannemen.quote:
Dacht dat het je misschien wel interesseerde.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Hier kan je ook nog een dictaat van het vak Meetkunde downloaden dat in leiden voor 3e jaars wordt gegevenquote:Op zaterdag 25 december 2004 13:12 schreef Haushofer het volgende:
[..]
Offtopic: Ik ben nu met algemene relativiteit bezig, en moet zeggen dat het allemaal goed te doen is. Wel veel differentiaalgeometrie, en die tensorcalculus is gewoon de indices in de gaten houden. Heb zelf het boek van Ray D'Inverno, en college aantekeningen van Sean Carroll gedown'd, die allebei goed bevallen. Vooral die laatste. Eerste paar weken alleen wiskunde gehad, maar na die paar weken valt dan eindelijk het woord "zwaartekracht". Vind het zelf ook altijd wel leuk om de wiskundige achtergrond te kennen, hoewel veel natuurkundigen de details maar wat graag aannemen.
Dacht dat het je misschien wel interesseerde.
http://www.math.leidenuniv.nl/~edix/meetk2002/index.html
En hier is het dictaat van meetkunde 2:
http://www.math.leidenuniv.nl/~edix/meetk2003/diktmeetk2.ps
Ik ga het volgende semester ook een vak volgen, genaamd "wiskundige methoden van de natuurkunde". Daar worden tensoren, distributies en greense functies, en lie groepen en representatietheorie behandeld. Dat vak is denk ik best wel een goede voorbereiding op de hogere jaars natuurkunde vakken, vooral quantumveldentheorie
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Dat vak wat jij beschrijft wordt bij ons idd ook gegeven, heet geloof ik mathematische methodes voor fysici ofzo. Die links ga ik denk ik wel even doorbladeren, heb zelf een PDF van Wulf Rossman, bevalt wel. Iig bedankt.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Hoi!
Ik heb drie vragen over Goniometrische Functies.
1. Hoe differentier ik: y = tan (3x)
tan (3x) = sin (3x) / cos (3x) => 3 cos (3x) / -3 sin (3x)
En toen?
2. Je hebt een functie: y=2 cos (x) - cos (2x) waarvan je de buigpunten moet uitrekenen.
y' = -2 sin (x) + 2 sin (2x)
y" = -2 cos (x) + 4 cos (2x)
y'' = 0
En dan doen ze opeens 8 cos^2 (x) - 2 cos (x) - 4 = 0 en dat m.b.v. abc-formule oplossen.
Hoe kom je aan deze formule? Oplossen verder lukt wel, maar hoe kom je aan 8 cos^2 (x) en de rest? cos kwadraat?????
3. Bereken van y = (2 - cos (x)) . (1 + cos (x)) de extremen.
Eerst even buiten haakjes halen; y = -cos^2 (x) + cos (x) + 2
Dan de afgeleide functie bepalen; y' = hoe doe ik dat?
Hoe bepaal ik de afgeleide van -cos^2 (x) ?
Daar kwam ik niet uit, kan iemand me helpen?
Ik heb drie vragen over Goniometrische Functies.
1. Hoe differentier ik: y = tan (3x)
tan (3x) = sin (3x) / cos (3x) => 3 cos (3x) / -3 sin (3x)
En toen?
2. Je hebt een functie: y=2 cos (x) - cos (2x) waarvan je de buigpunten moet uitrekenen.
y' = -2 sin (x) + 2 sin (2x)
y" = -2 cos (x) + 4 cos (2x)
y'' = 0
En dan doen ze opeens 8 cos^2 (x) - 2 cos (x) - 4 = 0 en dat m.b.v. abc-formule oplossen.
Hoe kom je aan deze formule? Oplossen verder lukt wel, maar hoe kom je aan 8 cos^2 (x) en de rest? cos kwadraat?????
3. Bereken van y = (2 - cos (x)) . (1 + cos (x)) de extremen.
Eerst even buiten haakjes halen; y = -cos^2 (x) + cos (x) + 2
Dan de afgeleide functie bepalen; y' = hoe doe ik dat?
Hoe bepaal ik de afgeleide van -cos^2 (x) ?
Daar kwam ik niet uit, kan iemand me helpen?


cos(2a) = 2cos^2(a) -1 dus x4 is jouw antwoord (rekenregels voor cosinus)quote:Op maandag 27 december 2004 16:58 schreef OldJeller het volgende:
Hoi!
Ik heb drie vragen over Goniometrische Functies.
1. Hoe differentier ik: y = tan (3x)
tan (3x) = sin (3x) / cos (3x) => 3 cos (3x) / -3 sin (3x)
En toen?
2. Je hebt een functie: y=2 cos (x) - cos (2x) waarvan je de buigpunten moet uitrekenen.
y' = -2 sin (x) + 2 sin (2x)
y" = -2 cos (x) + 4 cos (2x)
y'' = 0
En dan doen ze opeens 8 cos^2 (x) - 2 cos (x) - 4 = 0 en dat m.b.v. abc-formule oplossen.
Hoe kom je aan deze formule? Oplossen verder lukt wel, maar hoe kom je aan 8 cos^2 (x) en de rest? cos kwadraat?????
3. Bereken van y = (2 - cos (x)) . (1 + cos (x)) de extremen.
Eerst even buiten haakjes halen; y = -cos^2 (x) + cos (x) + 2
Dan de afgeleide functie bepalen; y' = hoe doe ik dat?
Hoe bepaal ik de afgeleide van -cos^2 (x) ?
Daar kwam ik niet uit, kan iemand me helpen?
cos^2(a) = (1+cos(2a)) / 2 (rekenregels cosinus)
en voor die tan(3x) kan je toch gewoon quotientregel gebruiken voor differentieren...
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Voor breuken bestaat de zogenoemde qoutiënt regel:quote:Op maandag 27 december 2004 16:58 schreef OldJeller het volgende:
Hoi!
Ik heb drie vragen over Goniometrische Functies.
1. Hoe differentier ik: y = tan (3x)
tan (3x) = sin (3x) / cos (3x) => 3 cos (3x) / -3 sin (3x)
En toen?
[t/n]' = ( n * t' - t * n' )/ (n^2)
Hier wordt dat dus t = sin(3x), n = cos(3x), t' = 3 cos (3x) en n' = -3 sin (3x)
De afgeleide wordt dan:
( 3 cos2 (3x) + 3 sin2 (3x)) / ( cos2 (3x)) [netjes uitwerken geeft]
= 3 + 3 * tan2 (3x)
Ze gebruiken de dubbele hoek formules:quote:2. Je hebt een functie: y=2 cos (x) - cos (2x) waarvan je de buigpunten moet uitrekenen.
y' = -2 sin (x) + 2 sin (2x)
y" = -2 cos (x) + 4 cos (2x)
y'' = 0
En dan doen ze opeens 8 cos^2 (x) - 2 cos (x) - 4 = 0 en dat m.b.v. abc-formule oplossen.
Hoe kom je aan deze formule? Oplossen verder lukt wel, maar hoe kom je aan 8 cos^2 (x) en de rest? cos kwadraat?????
sin (2x) = 2 * cos(x) * sin(x)
cos (2x) = cos2 (2x) - sin2 (2x) = 2*cos2 (2x) - 1 = 1 - sin2 (2x)
Hiervoor kan je het beste de kettingregel gebruiken, (of eventueel; de cos^2 omzetten dmv de dubbele hoekformules)quote:3. Bereken van y = (2 - cos (x)) . (1 + cos (x)) de extremen.
Eerst even buiten haakjes halen; y = -cos^2 (x) + cos (x) + 2
Dan de afgeleide functie bepalen; y' = hoe doe ik dat?
Hoe bepaal ik de afgeleide van -cos^2 (x) ?
Daar kwam ik niet uit, kan iemand me helpen?
d -cos2 (2x) / dx = - (2 *cos (x)) * (- sin (x)) = 2*cos(x)*sin(x)
Ik vrees voor je dat het niveau van je wiskundeleraar/wiskundeboek te laag is. In de 2e fase leert men de leerlingen liever trucjes dan regels, waardoor de wiskunde nodeloos ingewikkeld wordt.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Hey bedankt!
En je hebt gelijk.. dan probeer je een vraagstuk op te lossen.. en dan kom je er niet uit.. vraag je het aan de docent.. 'Ja, dat moet met deze regel...'
'Huh, die staat niet in het boek en heeft u ook nooit wat over gemeld?'
'Oh'
En zo gaat het dus dagelijks.
Maar nu kan ik iedergeval verder!
Thank you!
En je hebt gelijk.. dan probeer je een vraagstuk op te lossen.. en dan kom je er niet uit.. vraag je het aan de docent.. 'Ja, dat moet met deze regel...'
'Huh, die staat niet in het boek en heeft u ook nooit wat over gemeld?'
'Oh'
En zo gaat het dus dagelijks.
Maar nu kan ik iedergeval verder!
Thank you!


sin 3x / cos 3xquote:Op maandag 27 december 2004 19:17 schreef Wackyduck het volgende:
[..]
Voor breuken bestaat de zogenoemde qoutiënt regel:
[t/n]' = ( n * t' - t * n' )/ (n^2)
Hier wordt dat dus t = sin(3x), n = cos(3x), t' = 3 cos (3x) en n' = -3 sin (3x)
De afgeleide wordt dan:
( 3 cos2 (3x) + 3 sin2 (3x)) / ( cos2 (3x)) [netjes uitwerken geeft]
= 3 + 3 * tan2 (3x)
quotiënt regel: ( 3 cos (3x) * cos (3x) - sin (3x) * 3 sin (3x) ) / cos^2 (3x) wordt =>
( 3 cos2(3x) - 3 sin2(3x) ) / cos2(3x)
En er moet volgens het antwoordenboekje uitkomen: 3 / cos2(3x) uitkomen.. dat komt er alleen bij mij uit.. als het ( 3 cos2(3x) + 3 sin2(3x) ) / cos2(3x) is
En niet MIN: ( 3 cos2(3x) - 3 sin2(3x) ) / cos2(3x)
Want als het plus is, komt er inderdaad drie uit.. want 3 cos2(3x) + 3 sin2(3x) = 3, min elkaar is het 2,9 of whatever.
[ Bericht 5% gewijzigd door OldJeller op 27-12-2004 21:13:31 ]


Het is + , je bent namelijk de min van de afgeleide van de cosinus vergeten.quote:Op maandag 27 december 2004 21:07 schreef OldJeller het volgende:
[..]
sin 3x / cos 3x
quotiënt regel: ( 3 cos (3x) * cos (3x) - sin (3x) * 3 sin (3x) ) / cos^2 (3x) wordt =>
( 3 cos2(3x) - 3 sin2(3x) ) / cos2(3x)
En er moet volgens het antwoordenboekje uitkomen: 3 / cos2(3x) uitkomen.. dat komt er alleen bij mij uit.. als het ( 3 cos2(3x) + 3 sin2(3x) ) / cos2(3x) is
En niet MIN: ( 3 cos2(3x) - 3 sin2(3x) ) / cos2(3x)
Want als het plus is, komt er inderdaad drie uit.. want 3 cos2(3x) + 3 sin2(3x) = 3, min elkaar is het 2,9 of whatever.
Alle eendjes zwemmen in het water. :)
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...
Anatidaephobia is altijd terecht! Wij zijn de beste stalkers...


Je hebt gelijk..quote:Op maandag 27 december 2004 21:53 schreef Wackyduck het volgende:
[..]
Het is + , je bent namelijk de min van de afgeleide van de cosinus vergeten.
Ik heb nog een vraagje..
Je hebt de functie L = 1 / sin (alfa) + 2 / cos (alfa)
Hierbij is L de lengte van een gang waardoor een balk heen moet.. nu moet je uitrekenen wat de maximale breedte/lengte is van de gang.
Dus moet je de afgeleide gelijk aan 0 stellen. L' = 0
In het antwoordenboekje staat als afgeleide: L' = -cos(alfa) / sin2(alfa) + 2 sin(alfa) / cos2(alfa)
Hoe komen ze daaraan? De quotiëntregel werkt niet hierbij.. welke regel moet ik wel toepassen?


Oh jawel, de quotiëntenregel werkt hier ook.
Je moet niet vergeten hem los te laten op de constante "1" van de eerste term en de constante "2" van de tweede term. De afgeleides zijn nul. Dus die vallen weg.
Misschien wordt het makkelijker als je schrijft:
1/ sin(x) = sin-1(x)
Dan wordt het een macht, die je gewoon kunt differentiëren en vervolgens de kettingregel toepassen.
De afgeleide wordt dan: - sin-2(x)cos(x) = -cos(x) / sin2(x)
Je moet niet vergeten hem los te laten op de constante "1" van de eerste term en de constante "2" van de tweede term. De afgeleides zijn nul. Dus die vallen weg.
Misschien wordt het makkelijker als je schrijft:
1/ sin(x) = sin-1(x)
Dan wordt het een macht, die je gewoon kunt differentiëren en vervolgens de kettingregel toepassen.
De afgeleide wordt dan: - sin-2(x)cos(x) = -cos(x) / sin2(x)


Nadeel van deze notatie is wel dat in de meeste wiskunde boeken op het vwo sin-1(x) staat voor arcsin(x). Dit zou dus mischien voor verwarring kunnen zorgenquote:Op dinsdag 28 december 2004 14:42 schreef Yosomite het volgende:
Oh jawel, de quotiëntenregel werkt hier ook.
Je moet niet vergeten hem los te laten op de constante "1" van de eerste term en de constante "2" van de tweede term. De afgeleides zijn nul. Dus die vallen weg.
Misschien wordt het makkelijker als je schrijft:
1/ sin(x) = sin-1(x)
Dan wordt het een macht, die je gewoon kunt differentiëren en vervolgens de kettingregel toepassen.
De afgeleide wordt dan: - sin-2(x)cos(x) = -cos(x) / sin2(x)
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Je hebt gelijk! Hij kan inderdaad met de quotiëntregel..quote:Op dinsdag 28 december 2004 14:42 schreef Yosomite het volgende:
Oh jawel, de quotiëntenregel werkt hier ook.
Je moet niet vergeten hem los te laten op de constante "1" van de eerste term en de constante "2" van de tweede term. De afgeleides zijn nul. Dus die vallen weg.
Misschien wordt het makkelijker als je schrijft:
1/ sin(x) = sin-1(x)
Dan wordt het een macht, die je gewoon kunt differentiëren en vervolgens de kettingregel toepassen.
De afgeleide wordt dan: - sin-2(x)cos(x) = -cos(x) / sin2(x)
Door dat soort slordigheidsfouten raak ik altijd tijd kwijt.
Maar bedankt!


Ik ben programmeer opgaven aan het maken, op dit moment ben ik een opgaven aan het maken dat je een programma moet schrijven die een getal ontbind in priemfactoren. Ik heb een functie IsPriem() geschreven die moet vaststellen op een getal een priemgel is of niet.
Bij het testen van de functie komt het getal 91 naar voren als priem getal, maar dit getal komt niet in dit lijstje voor:
http://nl.wikipedia.org/wiki/Priemgetal
Er wordt genoemd dat een priemgetal 6n+1 of 6n-1 is. In het geval van 91:
6 * 15 + 1 = 91
Is 91 nou wel of geen priemgetal?
Bij het testen van de functie komt het getal 91 naar voren als priem getal, maar dit getal komt niet in dit lijstje voor:
http://nl.wikipedia.org/wiki/Priemgetal
Er wordt genoemd dat een priemgetal 6n+1 of 6n-1 is. In het geval van 91:
6 * 15 + 1 = 91
Is 91 nou wel of geen priemgetal?
Are you nuts??


91 = 7 * 13 dus 97 is GEEN priemgetal.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Bedankt!quote:Op dinsdag 28 december 2004 20:40 schreef Landmass het volgende:
91 = 7 * 13 dus 97 is GEEN priemgetal.
Are you nuts??


Nu weer even een vraagje voor mijzelf
Ik ben nu een soort van 2-dimensionale recursieve vergelijking tegengekomen, maar ik weet dus niet echt hoe ik dat soort dingen aan moet pakken om op te lossen. Voor normale recursieve vergelijkingen heb ik al een aantal technieken geleerd waaronder genererende functies enz.
Het betreft hier de volgende recursieve vergelijking:
ak,m = ak-1,m + ak-2,m-1.
Deze vergelijking heb ik verkregen uit een recursieve vergelijkingen voor polynomen:
Lk(x) = Lk-1(x) + xLk-2(x).
L0(x) = 1
L1(x) = 1 + x
ak,m is hier dus de coefficient van xm in Lk(x)
Zou iemand mij een hint kunnen geven van hoe ik dit probleem aan moet pakken?
Ik ben nu een soort van 2-dimensionale recursieve vergelijking tegengekomen, maar ik weet dus niet echt hoe ik dat soort dingen aan moet pakken om op te lossen. Voor normale recursieve vergelijkingen heb ik al een aantal technieken geleerd waaronder genererende functies enz.
Het betreft hier de volgende recursieve vergelijking:
ak,m = ak-1,m + ak-2,m-1.
Deze vergelijking heb ik verkregen uit een recursieve vergelijkingen voor polynomen:
Lk(x) = Lk-1(x) + xLk-2(x).
L0(x) = 1
L1(x) = 1 + x
ak,m is hier dus de coefficient van xm in Lk(x)
Zou iemand mij een hint kunnen geven van hoe ik dit probleem aan moet pakken?
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Bij dit soort vergelijkingen keek ik of er symmetrie in het probleem zit. En dan probeerde ik via een transformatie naar de geijkte polynomen te komen.quote:Op woensdag 29 december 2004 09:55 schreef Pietjuh het volgende:
Nu weer even een vraagje voor mijzelf
Ik ben nu een soort van 2-dimensionale recursieve vergelijking tegengekomen, maar ik weet dus niet echt hoe ik dat soort dingen aan moet pakken om op te lossen. Voor normale recursieve vergelijkingen heb ik al een aantal technieken geleerd waaronder genererende functies enz.
Het betreft hier de volgende recursieve vergelijking:
ak,m = ak-1,m + ak-2,m-1.
Deze vergelijking heb ik verkregen uit een recursieve vergelijkingen voor polynomen:
Lk(x) = Lk-1(x) + xLk-2(x).
L0(x) = 1
L1(x) = 1 + x
ak,m is hier dus de coefficient van xm in Lk(x)
Zou iemand mij een hint kunnen geven van hoe ik dit probleem aan moet pakken?
vb De eigenfuncties van de harmonische oscillator:
Hn+1(x) - 2x Hn(x) + 2n Hn-1(x) = 0
zijn de Hermite polynomen. Maar de vergelijking van jou krijg ik net niet in deze vorm gegoten.
Ik viel al snel terug op "Abramowitz and Stegun" of "Hankel", waar dit soort recursieve vergelijkingen staan.
Jouw vergelijking heeft wat weg van de Legendre polynomen.
Heb je de oorspronkelijke DV nog, of moet je het hier mee doen?


De recursieformule komt niet van een DV vandaan in mijn probleem. Het is afgeleid uit de torenveeltermexpansie van het Lucas probleem, wat een combinatorisch probleem is.quote:Op woensdag 29 december 2004 11:51 schreef Yosomite het volgende:
Bij dit soort vergelijkingen keek ik of er symmetrie in het probleem zit. En dan probeerde ik via een transformatie naar de geijkte polynomen te komen.
vb De eigenfuncties van de harmonische oscillator:
Hn+1(x) - 2x Hn(x) + 2n Hn-1(x) = 0
zijn de Hermite polynomen. Maar de vergelijking van jou krijg ik net niet in deze vorm gegoten.
Ik viel al snel terug op "Abramowitz and Stegun" of "Hankel", waar dit soort recursieve vergelijkingen staan.
Jouw vergelijking heeft wat weg van de Legendre polynomen.
Heb je de oorspronkelijke DV nog, of moet je het hier mee doen?
Ik heb wel iets kunnen vinden over Lucas w-polynomen op mathworld. Dat zijn polynomen die voldoen aan wn(x) = p(x)wn-1 + q(x)wn-2
http://mathworld.wolfram.com/LucasPolynomialSequence.html
maar daar staat jammergenoeg niet beschreven hoe je die reeks ook daadwerkelijk oplost
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Bij welk vak ben je hem tegengekomen?
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Woehoe ik heb al wat vooruitgang kunnen boeken!
Ik definieer nu f(y;x) = somk=0inf Lk yk.
Door nu de recurrente betrekking in te vullen heb ik hieruit verkregen dat
f(y;x) = (1+ xy) / (1 - y - xy^2)
Nu moet ik dus f(y;x) naar een machtreeks zien te ontwikkelen in y. Ik denk dat ik dat wel op moet kunnen lossen door eerst breuksplitsing toe te passen, en dan iets als de meetkundige reeks te gebruiken Of hebben jullie suggesties hoe het makkelijker zou kunnen?
Ik definieer nu f(y;x) = somk=0inf Lk yk.
Door nu de recurrente betrekking in te vullen heb ik hieruit verkregen dat
f(y;x) = (1+ xy) / (1 - y - xy^2)
Nu moet ik dus f(y;x) naar een machtreeks zien te ontwikkelen in y. Ik denk dat ik dat wel op moet kunnen lossen door eerst breuksplitsing toe te passen, en dan iets als de meetkundige reeks te gebruiken Of hebben jullie suggesties hoe het makkelijker zou kunnen?
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Dit is toch voldoende.quote:Op woensdag 29 december 2004 12:38 schreef Pietjuh het volgende:
Woehoe ik heb al wat vooruitgang kunnen boeken!
Ik definieer nu f(y;x) = somk=0inf Lk yk.
Door nu de recurrente betrekking in te vullen heb ik hieruit verkregen dat
f(y;x) = (1+ xy) / (1 - y - xy^2)
Nu moet ik dus f(y;x) naar een machtreeks zien te ontwikkelen in y. Ik denk dat ik dat wel op moet kunnen lossen door eerst breuksplitsing toe te passen, en dan iets als de meetkundige reeks te gebruiken Of hebben jullie suggesties hoe het makkelijker zou kunnen?
voor x =1 genereer je de functie (1+y)/ (1-y-y^2) en dat lijkt op de (2-y)/ (1-y-y^2) die ik in de link hieronder vond (maar niet helemaal).
Ik moest zelf eerst googlen, want afgezien van een relatie met de Fibonacci getallen ken ik de Lucas nummers niet.
In http://math.haifa.ac.il/toufik/toupap04/pap0408.pdf vond ik de genererende functies.
Misschien heb je er wat aan. Ik moet me eerst de stof eigen maken. Maar ik vind het interessant genoeg om erin te duiken.


Ok heb nu iig gevonden dat f(x,y) = somk=0inf (1 + xy)(y + xy^2)kquote:Op woensdag 29 december 2004 13:02 schreef Yosomite het volgende:
Dit is toch voldoende.
voor x =1 genereer je de functie (1+y)/ (1-y-y^2) en dat lijkt op de (2-y)/ (1-y-y^2) die ik in de link hieronder vond (maar niet helemaal).
Ik moest zelf eerst googlen, want afgezien van een relatie met de Fibonacci getallen ken ik de Lucas nummers niet.
In http://math.haifa.ac.il/toufik/toupap04/pap0408.pdf vond ik de genererende functies.
Misschien heb je er wat aan. Ik moet me eerst de stof eigen maken. Maar ik vind het interessant genoeg om erin te duiken.
Als ik nu (y + xy^2)k ontwikkel met het binomium van newton, en alles probeer te herschikken naar y's, dan lukt het allemaal wel denk ik
Ik moet namelijk wel echt een uitdrukking zien te vinden voor die coefficienten van xm van Lk(x) dus met x=1 invullen is het niet voldoende.
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Onvoorstelbaar dat mensen zoiets leuk kunnen vinden. Nouja, volgend semester mag ik assisteren bij analyse 4, over complexe functies, zo'n beetje de enige leuke soort analyse. . De docent (Pik) zei tegen mij dat-ie de nadruk toch wat meer op begrip wilde gaan leggen en wat minder op het rekenen, dus we zullen zien. .quote:Op zaterdag 25 december 2004 10:27 schreef Pietjuh het volgende:
[..]
Ja wel redelijk veel differentiaalvergelijkingen, waarbij je ook bijna niet over hoeft na te denken om ze op te kunnen lossen, vooral die ene eerste orde d.v. (y' + ycos(t) = cos(t) ) en die vraag met de laplace transformatie. Die vraag met de fourierreeks berekenen was gewoon ronduit irritant, want je had er een dik half uur voor nodig om al die partiele integraties uit te voeren
Het nadruk waarop het vak gegeven werd, was ook voornamelijk differentiaalvergelijkingen. We hebben alleen in de eerste paar weken aandacht besteed aan convergentiecriteria zoals uniforme convergentie, absolute convergentie enz. Daarna hebben we de rest van de tijd ons alleen bezig gehouden met d.v's, wat opzich ook vrij handig is (bij natuurkunde heb je het ontzettend vaak nodig), maar wat meer over convergentiegedrag zou leuk geweest zijn Het zal waarschijnlijk ook wel komen omdat de docent (Verduyn-Lunel) zo'n enorme d.v. verslaafde is


Die docent heeft bij analyse 3 ook 1 keer in moeten vallen voor onze normale docent, en ik vond hem wel een stuk gestructureerder uitleggen, dus het gaat denk ik wel interessanter worden dan bij analyse 3! Ik heb namelijk ook de stof al een beetje bekeken in de studiegids, en het lijkt me best interessantquote:Op donderdag 30 december 2004 16:59 schreef thabit het volgende:
Onvoorstelbaar dat mensen zoiets leuk kunnen vinden. Nouja, volgend semester mag ik assisteren bij analyse 4, over complexe functies, zo'n beetje de enige leuke soort analyse. . De docent (Pik) zei tegen mij dat-ie de nadruk toch wat meer op begrip wilde gaan leggen en wat minder op het rekenen, dus we zullen zien. .
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


ff een vraagje: als tanx=2b/(a-c)
toon aan dat y en z onafhankelijk zijn van de waarde van x.
y=a.cos²x+2b.sinx.cosx+c.sin²x
z=a.sin²x - 2b.sinx.cosx+c.cos²x
als tip wordt gegeven: bereken y+z en y-z.
y+z=a(cos²x+sin²x)+c(cos²x+sin²x)=a+c
y-z=a(cos²x-sin²x)+4bsinx.cosx+c(sin²x-cos²x)
als ik y-z verder vereenvoudig (o.a door gebruik te maken van sinx/cosx=2b/(a-c), dan krijg ik uiteindelijk weer een uitdrukking met sin²x of cos²x.. maar dat moet niet, ik denk dat alleen de getallen a,b en c moeten staan. .. kan iemand hier me helpen ...!?
another one:
als 0<a<pi/2 bepaal dan de waarde van a als tana= (√3+ 1)/(√3- 1)
ik heb geprobeerd tan(2a) te gebruiken maar.. nog geen nuttige resultaten...
alvast bedankt
toon aan dat y en z onafhankelijk zijn van de waarde van x.
y=a.cos²x+2b.sinx.cosx+c.sin²x
z=a.sin²x - 2b.sinx.cosx+c.cos²x
als tip wordt gegeven: bereken y+z en y-z.
y+z=a(cos²x+sin²x)+c(cos²x+sin²x)=a+c
y-z=a(cos²x-sin²x)+4bsinx.cosx+c(sin²x-cos²x)
als ik y-z verder vereenvoudig (o.a door gebruik te maken van sinx/cosx=2b/(a-c), dan krijg ik uiteindelijk weer een uitdrukking met sin²x of cos²x.. maar dat moet niet, ik denk dat alleen de getallen a,b en c moeten staan. .. kan iemand hier me helpen ...!?
another one:
als 0<a<pi/2 bepaal dan de waarde van a als tana= (√3+ 1)/(√3- 1)
ik heb geprobeerd tan(2a) te gebruiken maar.. nog geen nuttige resultaten...
alvast bedankt
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Eerste opgave:
Als je in de vergelijking voor y en z cos2x buiten haakjes haalt en gebruik maakt van de gegeven waarde voor tan x vind je:
y = cos2x*K1
z = cos2x*K2, met K1 en K2 onafhankelijk van x
y+z= cos2x*(K1+K2) = a+c
De waarde van cos2x is dus een constante en daarmee zijn dus ook y en z onafhankelijk van x
Tweede opgave, het handigste is natuurlijk een rekenmachine, maar zo kan 't ook:
tan(-x-y) = -{ (tan x + tan y) / (1 - tan x tan y)}
Met tan x = 1 en tan y = √3, krijgen we a = -arctan 1 - arctan √3 = -105° + kπ,
met a tussen 0 en π volgt a = 75°
[ Bericht 1% gewijzigd door MarkA op 02-01-2005 03:24:00 ]
Als je in de vergelijking voor y en z cos2x buiten haakjes haalt en gebruik maakt van de gegeven waarde voor tan x vind je:
y = cos2x*K1
z = cos2x*K2, met K1 en K2 onafhankelijk van x
y+z= cos2x*(K1+K2) = a+c
De waarde van cos2x is dus een constante en daarmee zijn dus ook y en z onafhankelijk van x
Tweede opgave, het handigste is natuurlijk een rekenmachine, maar zo kan 't ook:
tan(-x-y) = -{ (tan x + tan y) / (1 - tan x tan y)}
Met tan x = 1 en tan y = √3, krijgen we a = -arctan 1 - arctan √3 = -105° + kπ,
met a tussen 0 en π volgt a = 75°
[ Bericht 1% gewijzigd door MarkA op 02-01-2005 03:24:00 ]


mm ..even wachten . die arctan heb ik nog niet gehad, maar kan dat iet op een andere manier..ook al een stukje minder mooi...?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Als tan x = a, dan is x de hoek, waarbij de tangens gelijk is aan a,.quote:Op zondag 2 januari 2005 09:43 schreef achtbaan het volgende:
mm ..even wachten . die arctan heb ik nog niet gehad, maar kan dat iet op een andere manier..ook al een stukje minder mooi...?
Men schrijft dan x = arctan(a) of soms x = tan -1(a) (maar de laatste notatie vind ik nogal verwarrend)
Hopelijk kom je er zo uit.


mm, k weet wel wat dat is, maar ik dacht.. laten we maar er zonder het probleem oplossen..quote:Op zondag 2 januari 2005 10:37 schreef MarkA het volgende:
[..]
Als tan x = a, dan is x de hoek, waarbij de tangens gelijk is aan a,.
Men schrijft dan x = arctan(a) of soms x = tan -1(a) (maar de laatste notatie vind ik nogal verwarrend)
Hopelijk kom je er zo uit.
maar ja.. 'de' andere oplossing is voor mij niet zichtbaar maar ja.. ik denk niet dat dat echt de moeite waarde is om te onderzoeken
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Misschien heb ik het niet goed uitgelegd:
De formule:
tan(x+y) = (tan x + tan y) / (1 - tan x tan y) is een standaardformule en die heb ik dus niet zelf afgeleid. Je kunt ze in de meeste wiskunde boeken vinden en zo niet, gebruik Google dan maar eens.
Verder heb ik gebruik gemaakt van de eigenschap dat tan(x) = -tan(-x).
De bovenstaande standaardformule wordt dan tan(-x-y) = -{ (tan x + tan y) / (1 - tan x tan y)}
Als je nu stelt dat tan x = 1 en tan y = √3 in het rechterdeel van deze vergelijking krijg je precies het rechterdeel van de vergelijking die gegeven is.
De gevraagde a is dan -x-y = -arctan 1 - arctan √3
Het lijkt dus moeilijker dan het is.
De formule:
tan(x+y) = (tan x + tan y) / (1 - tan x tan y) is een standaardformule en die heb ik dus niet zelf afgeleid. Je kunt ze in de meeste wiskunde boeken vinden en zo niet, gebruik Google dan maar eens.
Verder heb ik gebruik gemaakt van de eigenschap dat tan(x) = -tan(-x).
De bovenstaande standaardformule wordt dan tan(-x-y) = -{ (tan x + tan y) / (1 - tan x tan y)}
Als je nu stelt dat tan x = 1 en tan y = √3 in het rechterdeel van deze vergelijking krijg je precies het rechterdeel van de vergelijking die gegeven is.
De gevraagde a is dan -x-y = -arctan 1 - arctan √3
Het lijkt dus moeilijker dan het is.


mm.. zo zo..
dus jij stel dat a=x+y en daarna vind je dat -x-y=-arctan1-arctan √3 dus a=arctan1 +arctan√3
mm oke.. het is inderdaad moeilijk,
ik had niet in gedachten dat ik moest stellen dat a=x+y... had ik niet verwacht ...
dus jij stel dat a=x+y en daarna vind je dat -x-y=-arctan1-arctan √3 dus a=arctan1 +arctan√3
mm oke.. het is inderdaad moeilijk,
ik had niet in gedachten dat ik moest stellen dat a=x+y... had ik niet verwacht ...
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


trouwens, in alle schoolboeken die ik ben tegenkomen zie ik vaak dat de regels voor exponenten alleen voor rationele machten gelden en niet voor reele getallen?
bijv. ar.ar'=ar+r met a reeel en groter dan 0 en r,r' elementen van Q
waarom zijn er geen regels voor r en r' reele getallen? of zijn die er wel?
bijv. ar.ar'=ar+r met a reeel en groter dan 0 en r,r' elementen van Q
waarom zijn er geen regels voor r en r' reele getallen? of zijn die er wel?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Hallo!
Van een lineaire afbeelding T: [R]³ ---> [R]³ wordt het beeld van een vector a als volgt verkregen: Eerst wordt a gedraaid over een hoek van 60° om de x-as (tegen de klok), vervolgens wordt de vector met een factor 4 vermenigvuldigd, en tenslotte wordt er gespiegeld in het vlak x=0 (het yz-vlak dus).
Vraag: Bepaal de matrix A van T.
Ik weet wel hoe ik dit moet aanpakken, maar ik weet niet hoe ik die 3 deelmatrices moet maken. Kan iemand mij stap voor stap (grafisch) uitleggen hoe ik die deelmatrices maak?
Bvd!
Van een lineaire afbeelding T: [R]³ ---> [R]³ wordt het beeld van een vector a als volgt verkregen: Eerst wordt a gedraaid over een hoek van 60° om de x-as (tegen de klok), vervolgens wordt de vector met een factor 4 vermenigvuldigd, en tenslotte wordt er gespiegeld in het vlak x=0 (het yz-vlak dus).
Vraag: Bepaal de matrix A van T.
Ik weet wel hoe ik dit moet aanpakken, maar ik weet niet hoe ik die 3 deelmatrices moet maken. Kan iemand mij stap voor stap (grafisch) uitleggen hoe ik die deelmatrices maak?
Bvd!
Cowabunga!!


Waarom zou dat niet gelden voor reele getallen?quote:Op maandag 3 januari 2005 21:38 schreef achtbaan het volgende:
trouwens, in alle schoolboeken die ik ben tegenkomen zie ik vaak dat de regels voor exponenten alleen voor rationele machten gelden en niet voor reele getallen?
bijv. ar.ar'=ar+r met a reeel en groter dan 0 en r,r' elementen van Q
waarom zijn er geen regels voor r en r' reele getallen? of zijn die er wel?


Die matrix van de rotatie is gewoon:quote:Op maandag 3 januari 2005 23:40 schreef F1-GRANdMAStER het volgende:
Hallo!
Van een lineaire afbeelding T: [R]³ ---> [R]³ wordt het beeld van een vector a als volgt verkregen: Eerst wordt a gedraaid over een hoek van 60° om de x-as (tegen de klok), vervolgens wordt de vector met een factor 4 vermenigvuldigd, en tenslotte wordt er gespiegeld in het vlak x=0 (het yz-vlak dus).
Vraag: Bepaal de matrix A van T.
Ik weet wel hoe ik dit moet aanpakken, maar ik weet niet hoe ik die 3 deelmatrices moet maken. Kan iemand mij stap voor stap (grafisch) uitleggen hoe ik die deelmatrices maak?
Bvd!
De vector met een factor 4 vermenigvuldigen is hetzelfde als vermenigvuldigen met de matrix 4I met I de identiteitsmatrix.
Spiegelen in het yz vlak is hetzelfde als de matrix (want x moet naar -x gestuurd worden)
[ -1 0 0 ]
[ 0 1 0 ]
[ 0 0 1 ]
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


ik zeg niet dat dat niet geldt voor reele dingen. Maar ik dacht: omdat er duidelijk staat dat r en r' geen reele getallen zijn maar gewoon getallen uit Q, heeft R iets speciaals en daarom staat niet dat r en r' reele getallen zijn... en ik dacht misschien gelden de regels niet voor reele exponenten.. maar zo te zien had ik ongelijkquote:Op dinsdag 4 januari 2005 10:34 schreef thabit het volgende:
[..]
Waarom zou dat niet gelden voor reele getallen?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


De 2 sinussen omgedraaid neem ik aan, want er wordt tegen de klok ingedraaidquote:Op dinsdag 4 januari 2005 10:42 schreef Pietjuh het volgende:
[..]
Die matrix van de rotatie is gewoon:
[afbeelding]
Cowabunga!!


Je hebt gelijk, ik had even snel over het hoofd gezien hoe mathworld de rotatiehoek defineert Nu moet in deze matrix sin(alpha) vervangen worden door sin(-alpha) = - sin(alpha)quote:Op dinsdag 4 januari 2005 19:23 schreef F1-GRANdMAStER het volgende:
[..]
De 2 sinussen omgedraaid neem ik aan, want er wordt tegen de klok ingedraaid
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Even een makkelijke vraag tussendoor
Stel ik heb een vergelijking die ik op wil lossen, dan moet ik ff weten hoe ik dat moet doen...
dus...
hoe kom ik dan op r uit?
Stel ik heb een vergelijking die ik op wil lossen, dan moet ik ff weten hoe ik dat moet doen...
dus...
| 1 | R^12-1 = 0.05899 |
hoe kom ik dan op r uit?


Ik moet de Wronskiaan bepalen van de volgende homogene differentiaalvergelijking:
(cos x)*u"(x)+(sin x)u'(x)-xu(x)=0
Ik kan met reductie van de orde wel een tweede lineair onafhankelijke oplossing bepalen, maar hoe bepaal ik een eerste oplossing?
netjes van een site gekopieerd, kan ieman dme helpen met het vinen van de oplossing/aanpak voor de vraag?
(cos x)*u"(x)+(sin x)u'(x)-xu(x)=0
Ik kan met reductie van de orde wel een tweede lineair onafhankelijke oplossing bepalen, maar hoe bepaal ik een eerste oplossing?
netjes van een site gekopieerd, kan ieman dme helpen met het vinen van de oplossing/aanpak voor de vraag?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Ik heb een vraagje, misschien dat Tabit raad weet.
Als eis stel je dat de covariante afgeleide van een scalaire functie reduceert tot een gewone partiele afgeleide. Wat je nu wilt, is weten wat het verband is tussen de connectie coefficienten van de covariante afgeleide op een contra- en een covariante vector. Hiervoor ga je de covariante afgeleide nemen van een contractie tussen een contra- en covariante vector ( een scalar dus )
Dus de covariante afgeleide van (wi vi ) = di (wi vi ) , met di is d/dxi, die laatste kun je makkelijk uitrekenen met de productregel ( Leibniz )
De linkerkant ga je uitschrijven met de gebruikelijke partiele afgeleide en de connectiecoefficienten, en stel je gelijk aan de rechterkant. Wat je dan krijgt: ( met G en K als de connectiecoefficiente )
wi Gijk vk +
vi Klji wl = 0
Nu stellen ze ( dummy indices ) dat dit gelijk is aan
Glji wlvi +
Klj i wlvi =0.
Waarna ze de vectoren w en v ellimineren, en K gelijk aan -G stellen. Maar waarom mag deze stap? Je verandert zo de contracties toch?
Als eis stel je dat de covariante afgeleide van een scalaire functie reduceert tot een gewone partiele afgeleide. Wat je nu wilt, is weten wat het verband is tussen de connectie coefficienten van de covariante afgeleide op een contra- en een covariante vector. Hiervoor ga je de covariante afgeleide nemen van een contractie tussen een contra- en covariante vector ( een scalar dus )
Dus de covariante afgeleide van (wi vi ) = di (wi vi ) , met di is d/dxi, die laatste kun je makkelijk uitrekenen met de productregel ( Leibniz )
De linkerkant ga je uitschrijven met de gebruikelijke partiele afgeleide en de connectiecoefficienten, en stel je gelijk aan de rechterkant. Wat je dan krijgt: ( met G en K als de connectiecoefficiente )
wi Gijk vk +
vi Klji wl = 0
Nu stellen ze ( dummy indices ) dat dit gelijk is aan
Glji wlvi +
Klj i wlvi =0.
Waarna ze de vectoren w en v ellimineren, en K gelijk aan -G stellen. Maar waarom mag deze stap? Je verandert zo de contracties toch?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ik zie geen contracties veranderen... Alleen in de eerste term (i,j,k)->(l,j,i). Dat zijn toch maar dummy indices, als die namen daarvan veranderen verandert de contractie toch niet?
Aangenomen trouwens dat je vi bedoelde waar je vi schreef
Aangenomen trouwens dat je vi bedoelde waar je vi schreef


Ej ja, ik zie het, volgorde maakt natuurlijk niet uit (vKw=Kwv etc ). Heb nog wat moeite met die dummy indices, geloof ik. En idd, die v moet contravariant zijn. Dank dank.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Hiernaast zijn de percentages van de verschillende soorten verkeersslachtoffers weergegeven die in een ziekenhuis worden behandeld. Op een dag worden in dat ziekenhuis 5 verkeersslachtoffers binnengebracht/
A: Maak een schatting van de kansverdeling van het aantal slachtoffers van bromfietsongevallen die die dag in dat ziekenhuis behandeld worden.
B: Schat de kans op minstens drie bromfietsongevallen die dag.
Hoe reken ik dit uit met mijn rekenmachine
| 1 2 3 4 5 6 7 | Soort Vervoer | Percentage -------------------------- te voet | 10.8 fiets | 28.9 bromfiets | 12.2 motor/scooter | 2.9 auto | 45.3 |
A: Maak een schatting van de kansverdeling van het aantal slachtoffers van bromfietsongevallen die die dag in dat ziekenhuis behandeld worden.
B: Schat de kans op minstens drie bromfietsongevallen die dag.
Hoe reken ik dit uit met mijn rekenmachine


bij A moet je dus een kansverdeling maken in deze tabel, alleen ik weet niet hoe ik moet beginen
| 1 2 3 4 5 6 7 8 | aantal | kans ------------ 0 | ? 1 | ? 2 | ? 3 | ? 4 | ? 5 | ? |


Laten we niet teveel in getallen denken. Daar gaat het fout. Noem de kans op een brommerongeval p. In ons geval is dus p=0.122. Wat is de kans op 5 brommerongevallen, uitgedrukt in p?


Wel, je hebt 5 patienten waarvan 1 brommer (b) en 4 anders (a). Zo krijg je 5 mogelijkheden: baaaa,abaaa,aabaa,aaaba,aaaab. Wat is nu de kans op elk van die mogelijkheden?


ljikt me typisch een geval van een binomiale verdeling
p = kans brommerslachtoffer
1-p = kans geen brommer slachtoffer
N = aantal slachtoffers dat is binnegebracht (in dit geval 5)
k = #brommerslachtoffers als er n patienten zijn binnengebracht die dag
gevraagd:
P(k=0), P(k=1), P(k=2), P(k=3), P(k=4), P(k=5)
hoe deden we dit ook alweer, binomiaal
P(k=n) = (N boven n)*p^n*(1-p)^N-n
en om de kans van minstens 3 uit te rekenen moet je dus gaan optellen
P(k= minstens n) = P(k=n)+P(k=n+1)+...+P(k=N)
idg n=3 en N=5
P(k= minstens 3) = P(k=3)+P(k=4)+P(k=5)
[ Bericht 18% gewijzigd door superbient op 13-01-2005 10:54:08 ]
p = kans brommerslachtoffer
1-p = kans geen brommer slachtoffer
N = aantal slachtoffers dat is binnegebracht (in dit geval 5)
k = #brommerslachtoffers als er n patienten zijn binnengebracht die dag
gevraagd:
P(k=0), P(k=1), P(k=2), P(k=3), P(k=4), P(k=5)
hoe deden we dit ook alweer, binomiaal
P(k=n) = (N boven n)*p^n*(1-p)^N-n
en om de kans van minstens 3 uit te rekenen moet je dus gaan optellen
P(k= minstens n) = P(k=n)+P(k=n+1)+...+P(k=N)
idg n=3 en N=5
P(k= minstens 3) = P(k=3)+P(k=4)+P(k=5)
[ Bericht 18% gewijzigd door superbient op 13-01-2005 10:54:08 ]
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Ik heb liever dat je er zelf achterkomt hoe het moet in plaats van een hapklare formule die je klakkeloos kunt invullen zonder te hoeven begrijpen waarom die geldt.


hoi mensen
hier komt ie:'
hoe lost men de vergelijking van Pell op die in vorm is van x²-my²=1 op ?(een andere oplossing dan (1,0) ?
toepassing
los op in N²
x² -8y²=1
alvast bedankt
hier komt ie:'
hoe lost men de vergelijking van Pell op die in vorm is van x²-my²=1 op ?(een andere oplossing dan (1,0) ?
toepassing
los op in N²
x² -8y²=1
alvast bedankt
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Maar snap je em ook?quote:Op donderdag 13 januari 2005 11:33 schreef rotskibo het volgende:
Kijk, daar hebben we tenminste wat aan
Dat is de grootste fout die leerlingen tegenwoordig maken. Niet snappen waarom! Ze voeren de formules in de GR en kijken wat er uitkomt, zonder te begrijpen hoe het echt in elkaar zit.
Nu even een makkelijke die ik vandaag bij een wiskunde SE fout had ( )
Hoe haal je kwadraten uit logaritmische vergelijkingen? Deze kreeg ik vandaag:
(ln (x))^2 = ln e^(x) + 4
En ik kwam er gewoon niet uit, alle moeilijke opgaven wel, maar deze niet


thnx
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Weet je zeker dat daar log(e^x) hoort te staan? (ik schrijf hier log omdat dat de echte notatie is voor de e-log en niet de 10-log. 10-loggen zijn door natuurkundigen bedacht omdat ze geen wiskunde begrijpen).quote:Op vrijdag 14 januari 2005 17:53 schreef MeneerGiraffe het volgende:
[..]
Maar snap je em ook?
Dat is de grootste fout die leerlingen tegenwoordig maken. Niet snappen waarom! Ze voeren de formules in de GR en kijken wat er uitkomt, zonder te begrijpen hoe het echt in elkaar zit.
Nu even een makkelijke die ik vandaag bij een wiskunde SE fout had ( )
Hoe haal je kwadraten uit logaritmische vergelijkingen? Deze kreeg ik vandaag:
(ln (x))^2 = ln e^(x) + 4
En ik kwam er gewoon niet uit, alle moeilijke opgaven wel, maar deze niet


quote:Op vrijdag 14 januari 2005 18:05 schreef thabit het volgende:
[..]
....10-loggen zijn door natuurkundigen bedacht omdat ze geen wiskunde begrijpen).
Mooi vak hè, natuurkunde!


Ohja dat klopt, het was:quote:Op vrijdag 14 januari 2005 18:05 schreef thabit het volgende:
[..]
Weet je zeker dat daar log(e^x) hoort te staan? (ik schrijf hier log omdat dat de echte notatie is voor de e-log en niet de 10-log. 10-loggen zijn door natuurkundigen bedacht omdat ze geen wiskunde begrijpen).
(ln (x))^2 = 3 ln (x) + 4
(die e had ik er perongeluk in gezet omdat ik er zeker een kwartier op gezeten heb
met ln e^x zou hij net wat te makkelijk zijn )


stel y = ln(x) , met y > 0quote:Op vrijdag 14 januari 2005 19:11 schreef MeneerGiraffe het volgende:
[..]
Ohja dat klopt, het was:
(ln (x))^2 = 3 ln (x) + 4
(die e had ik er perongeluk in gezet omdat ik er zeker een kwartier op gezeten heb
met ln e^x zou hij net wat te makkelijk zijn )
er ontstaat een vgl in y, die makkelijk op te lossen is.
Dan terugtransformeren naar x


Ah, dat is het, bedankt, dat ik daar zelf niet aan heb gedacht.quote:Op vrijdag 14 januari 2005 19:15 schreef Yosomite het volgende:
[..]
stel y = ln(x) , met y > 0
er ontstaat een vgl in y, die makkelijk op te lossen is.
Dan terugtransformeren naar x
Substitueren noemen wij het trouwens


Dat is het juiste woord!quote:Op vrijdag 14 januari 2005 19:25 schreef MeneerGiraffe het volgende:
Substitueren noemen wij het trouwens


Dat mag je uitleggen. Ben heel benieuwd.quote:Op vrijdag 14 januari 2005 19:38 schreef thabit het volgende:
[..]
Dat zeker. Ik vind het alleen zo jammer dat die schoenmakers niet bij hun leest blijven.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Natuurkundemod to the rescuequote:Op vrijdag 14 januari 2005 21:24 schreef Haushofer het volgende:
[..]
Dat mag je uitleggen. Ben heel benieuwd.


Ik snap deze som niet:
In jeugdsoos 'De Grot' vindt wekelijks een loterij plaats.
Elke week zijn er 50 loten en 6 prijzen.
a. Maarten heeft 5 loten gekocht. Bereken in drie decimalen nauwkeurig de kans dat hij precies twee prijzen wint.
b. Gert heeft zes loten gekocht. Bereken in drie decimalen nauwkeurig de kans dat hij minstens 1 prijs wint.
c. Anneloes speelt 20 weken achter elkaar mee. Zij koopt elke keer 4 loten. Bereken in drie decimalen nauwkeurig de kans dat zij precies zeven keer minstens 1 prijs wint.
d. Hoeveel weken achtereen moet je vier loten kopen opdat de kans op het minstens 5 keer winnen van minstens 1 prijs groter is dan 0.5?
Wij moeten dit dan doen met onze Grafische Rekenmachine, met het menu: Stat - dist - binm en dan bpd en bcd
Ik heb de antwoorden ook! Zal ik deze gelijk posten of nog even wachten?
In jeugdsoos 'De Grot' vindt wekelijks een loterij plaats.
Elke week zijn er 50 loten en 6 prijzen.
a. Maarten heeft 5 loten gekocht. Bereken in drie decimalen nauwkeurig de kans dat hij precies twee prijzen wint.
b. Gert heeft zes loten gekocht. Bereken in drie decimalen nauwkeurig de kans dat hij minstens 1 prijs wint.
c. Anneloes speelt 20 weken achter elkaar mee. Zij koopt elke keer 4 loten. Bereken in drie decimalen nauwkeurig de kans dat zij precies zeven keer minstens 1 prijs wint.
d. Hoeveel weken achtereen moet je vier loten kopen opdat de kans op het minstens 5 keer winnen van minstens 1 prijs groter is dan 0.5?
Wij moeten dit dan doen met onze Grafische Rekenmachine, met het menu: Stat - dist - binm en dan bpd en bcd
Ik heb de antwoorden ook! Zal ik deze gelijk posten of nog even wachten?


a. succeskans p = 5/50 = 0.1
Dit geeft: (6 boven 2) * 0.1^2 * 0.9^4 = 0.098
b. succeskans p = 6/50 = 0.12
P(minstens 1 prijs) = 1- P(0 prijzen) = 1- (6 boven 0) * 0.12^0 * 0.88^6 = 0.536
c. Eerst bereken je de kans dat Anneloes minstens 1 prijs wint als ze 1 keer meespeelt.
succeskans p = 4/50 = 0.08
P(minstens 1 prijs) = 1- P(0 prijzen) = 1- (6 boven 0) * 0.08^0 * 0.92^6 = 0.394
Nu bereken je de kans dat ze precies 7 keer 1 prijs wint.
succeskans p = 0,394
P(7 keer minstens 1 prijs) = (20 boven 7) * 0.394^7 * 0.606^13 = 0.170
d. De kans dat je minstens 1 prijs wint als je 1x meespeelt is 0.394 (zie c).
Je wilt nu uitrekenen hoe vaak je mee moet spelen opdat de kans dat je minimaal 5 keer minstens 1 prijs winst groter dan 0.5 is.
P(minstens 5 keer minstens 1 prijs) = 1 - som{i=0}{4} P(i keer minstens 1 prijs) = 1 - som{i=0}{4} (x boven i) * 0.394^i * 0.606^(x-i) > 0.5
Als je dit oplost krijg je x >= 12.
[ Bericht 7% gewijzigd door mrbombastic op 15-01-2005 14:26:36 ]
Dit geeft: (6 boven 2) * 0.1^2 * 0.9^4 = 0.098
b. succeskans p = 6/50 = 0.12
P(minstens 1 prijs) = 1- P(0 prijzen) = 1- (6 boven 0) * 0.12^0 * 0.88^6 = 0.536
c. Eerst bereken je de kans dat Anneloes minstens 1 prijs wint als ze 1 keer meespeelt.
succeskans p = 4/50 = 0.08
P(minstens 1 prijs) = 1- P(0 prijzen) = 1- (6 boven 0) * 0.08^0 * 0.92^6 = 0.394
Nu bereken je de kans dat ze precies 7 keer 1 prijs wint.
succeskans p = 0,394
P(7 keer minstens 1 prijs) = (20 boven 7) * 0.394^7 * 0.606^13 = 0.170
d. De kans dat je minstens 1 prijs wint als je 1x meespeelt is 0.394 (zie c).
Je wilt nu uitrekenen hoe vaak je mee moet spelen opdat de kans dat je minimaal 5 keer minstens 1 prijs winst groter dan 0.5 is.
P(minstens 5 keer minstens 1 prijs) = 1 - som{i=0}{4} P(i keer minstens 1 prijs) = 1 - som{i=0}{4} (x boven i) * 0.394^i * 0.606^(x-i) > 0.5
Als je dit oplost krijg je x >= 12.
[ Bericht 7% gewijzigd door mrbombastic op 15-01-2005 14:26:36 ]


Uhm, de antwoorden zijn
a. 0.094 (die heb je dus goed, zal wel de afronding zijn)
b. 0.556 (daar zit je wel iets meer vanaf..)
c. 0.158
d. minstens 12 weken
a. 0.094 (die heb je dus goed, zal wel de afronding zijn)
b. 0.556 (daar zit je wel iets meer vanaf..)
c. 0.158
d. minstens 12 weken


Ik ben er al uit....quote:Op zaterdag 15 januari 2005 15:58 schreef VoreG het volgende:
Ok even een hele stomme vraag maar
hoe teken je x >= y in een grafiek? .


a stel het je voor dat er 50 ballen zijn in een zak, 6 ballen leveren een prijs op en 44 niet, Maarten koopt 5 loten, heel belangrijk is hier, zonder terugleggen. Dus trekt zeg maar 5 ballen uit de zak.om precies 2 prijzen te winnen moeten dus 2 van die ballen de succesballen zijn en 3 van die ballen een niet-succesbal zijn. dit kan dus op ((6 boven 2)*(44 boven 3))/(50 boven 5) manieren = 0,094quote:Op zaterdag 15 januari 2005 13:29 schreef KiwiTjuHh het volgende:
Ik snap deze som niet:
In jeugdsoos 'De Grot' vindt wekelijks een loterij plaats.
Elke week zijn er 50 loten en 6 prijzen.
a. Maarten heeft 5 loten gekocht. Bereken in drie decimalen nauwkeurig de kans dat hij precies twee prijzen wint.
b. Gert heeft zes loten gekocht. Bereken in drie decimalen nauwkeurig de kans dat hij minstens 1 prijs wint.
c. Anneloes speelt 20 weken achter elkaar mee. Zij koopt elke keer 4 loten. Bereken in drie decimalen nauwkeurig de kans dat zij precies zeven keer minstens 1 prijs wint.
d. Hoeveel weken achtereen moet je vier loten kopen opdat de kans op het minstens 5 keer winnen van minstens 1 prijs groter is dan 0.5?
Wij moeten dit dan doen met onze Grafische Rekenmachine, met het menu: Stat - dist - binm en dan bpd en bcd
Ik heb de antwoorden ook! Zal ik deze gelijk posten of nog even wachten?
(zie dit dus als het #mogelijkheden dat je 2 succesballen uit de 6 kan trekken en 3 niet-succesballen uit de 44 dit zijn de totale mogelijke combinaties om precies 2 succes te trekken, dit moet je dan delen door het aantal mogelijke manieren om 5 ballen uit een totaal van 50 te trekken)
b minstens 1 prijs is gelijjk aan 1 - kans dat hij geen prijs wint, indien hij geen prijs wint, heeft hij dus alleen ballen uit de 44 niet-succesballen getrokken, weer zonder terugleggen
(44 boven 6)/(50 boven 6) = 0,444
1- 0,444 = 0,556
c
wat is de kan dat ze minstens 1 prijs wint --> 1 - ((44 boven 4)/(50 boven 4)) = 0,411
ze speelt 20 weken mee en wil precies 7 keer minstens 1 prijs winnen, dit is wel binomiaal met p = 0,411 en 1-p = 0,589
nu kan ze in die 20 weken 7 keer winnen op 20 boven 7 manieren dus
(20 boven 7)*0,411^7*0,589^13 = 0,158
d
we zien nu weer hetzelfde, kans op minstens 1 prijs = p = 0,411 en 1-p = geen prijs = 0,589
dit moet denk ik ff proberen worden, kd8 met de gr zoiets van binomcdf(n,p,k) = de kans dat je bij n keer een experiment doet met succeskans p hoogstens k successen hebt
idg zou dat dan
1- binomcdf(n,0,411,4) = kans minstens 5 > 0,5 zijn, dit zou dan bij n=12 zijn
*weet dit niet zeker, gr is weggezakt nadat we hem niet meer mochten gebruiken
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Kijk, natuurkundigen hebben uiteraard wiskunde nodig. Ze gebruiken het dus, tot zover nog geen probleem. Het probleem komt pas zodra ze zelf allerlei wiskunde gaan bedenken. Dan komen ze met allerlei theorieen geformuleerd in notaties aanzetten die getuigen van een zienswijze en wiskundige naiviteit waarvan je denkt "tja, schoenmaker, als je tegenwoordig wiskunde wilt doen op een manier die 100 jaar geleden actueel was, blijf dan liever bij je leest."quote:Op vrijdag 14 januari 2005 21:24 schreef Haushofer het volgende:
[..]
Dat mag je uitleggen. Ben heel benieuwd.


Heel goed geformuleerd. Ik voel me ook veel meer thuis in de natuurkunde dan in de wiskunde. Verbanden zien, redeneren, logisch nadenken kan ik allemaal wel, maar ik moet toch een soort houvast hebben, en puur wiskundig lukt het me niet echtquote:Op zaterdag 15 januari 2005 19:26 schreef thabit het volgende:
[..]
Kijk, natuurkundigen hebben uiteraard wiskunde nodig. Ze gebruiken het dus, tot zover nog geen probleem. Het probleem komt pas zodra ze zelf allerlei wiskunde gaan bedenken. Dan komen ze met allerlei theorieen geformuleerd in notaties aanzetten die getuigen van een zienswijze en wiskundige naiviteit waarvan je denkt "tja, schoenmaker, als je tegenwoordig wiskunde wilt doen op een manier die 100 jaar geleden actueel was, blijf dan liever bij je leest."
we hebben een reëel probleem, dus we zoeken naar reële oplossingen
in dit specifieke geval maken twee helften één
in dit specifieke geval maken twee helften één


Maar je begrijpt het verschil tussen natuurkunde en wiskunde toch wel? Waarom zouden natuurkundigen de wiskunde zo gebruiken als jullie? Da's klare onzin.quote:Op zaterdag 15 januari 2005 19:26 schreef thabit het volgende:
[..]
Kijk, natuurkundigen hebben uiteraard wiskunde nodig. Ze gebruiken het dus, tot zover nog geen probleem. Het probleem komt pas zodra ze zelf allerlei wiskunde gaan bedenken. Dan komen ze met allerlei theorieen geformuleerd in notaties aanzetten die getuigen van een zienswijze en wiskundige naiviteit waarvan je denkt "tja, schoenmaker, als je tegenwoordig wiskunde wilt doen op een manier die 100 jaar geleden actueel was, blijf dan liever bij je leest."
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Ze mogen wiskunde gebruiken zoals ze dat willen. . Ze moeten alleen geen wiskunde gaan bedenken, inclusief het invoeren van notaties en terminologie op een manier die wiskundigen niet zo snel zouden doen. .quote:Op zaterdag 15 januari 2005 22:25 schreef Haushofer het volgende:
[..]
Maar je begrijpt het verschil tussen natuurkunde en wiskunde toch wel? Waarom zouden natuurkundigen de wiskunde zo gebruiken als jullie? Da's klare onzin.


Hier waarschijnlijk een vrij domme vraag over taylorreeksontwikklingen van functies.
Zoals iedereen wel weet worden de coefficienten van xn in deze ontwikkeling van f(x) gegeven door f(n)(c) / n!
Wat ik nu vaak ben tegengekomen en eigenlijk zelf ook altijd gedaan heb, maar waar ik nu eigenlijk niet goed begrijp waarom is het volgende. Stel je wilt de taylorreeksontwikkeling maken van f(g(x)).
Bijvoorbeeld als f(x) = e^x en g(x) = x^2. Dan wordt bijna overal deze ontwikkeling bepaald door simpelweg x^2 te substitueren in de ontwikkeling van f(x) = e^x.
Maar als ik nu volgens de bekende formule de coefficienten wil berekenen krijg ik hier niet dezelfde coefficienten uit, want er verschijnen nu allemaal extra termen door de kettingregel.
Nu vraag ik me dus af waarom deze 2 op het oog verschillende ontwikkelingen convergeren naar dezelfde functie f(g(x)) ?
Zoals iedereen wel weet worden de coefficienten van xn in deze ontwikkeling van f(x) gegeven door f(n)(c) / n!
Wat ik nu vaak ben tegengekomen en eigenlijk zelf ook altijd gedaan heb, maar waar ik nu eigenlijk niet goed begrijp waarom is het volgende. Stel je wilt de taylorreeksontwikkeling maken van f(g(x)).
Bijvoorbeeld als f(x) = e^x en g(x) = x^2. Dan wordt bijna overal deze ontwikkeling bepaald door simpelweg x^2 te substitueren in de ontwikkeling van f(x) = e^x.
Maar als ik nu volgens de bekende formule de coefficienten wil berekenen krijg ik hier niet dezelfde coefficienten uit, want er verschijnen nu allemaal extra termen door de kettingregel.
Nu vraag ik me dus af waarom deze 2 op het oog verschillende ontwikkelingen convergeren naar dezelfde functie f(g(x)) ?
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Dus natuurkundigen moet slaafs op wiskundigen wachten of ze de benodigde wiskunde krijgen?quote:Op zaterdag 15 januari 2005 22:29 schreef thabit het volgende:
[..]
Ze mogen wiskunde gebruiken zoals ze dat willen. . Ze moeten alleen geen wiskunde gaan bedenken, inclusief het invoeren van notaties en terminologie op een manier die wiskundigen niet zo snel zouden doen. .
. Ej, het mag je misschien zijn ontschoten, maar natuurkundigen zijn bezig met een ander wereldje dan de wiskundigen. Verwacht jij dat een natuurkundige tensoren zo gaat gebruiken en begrijpen als een wiskundige? Een natuurkundige geeft niet altijd veel om de achterliggende wiskunde; hij wil het gereedschap gewoon gebruiken, en alle rompslomp is leuk erbij, maar niet altijd nodig. De manier waarop ik bijvoorbeeld het idee "tensoralgebra" begrijp en gebruik is in jou ogen misschien primitief, maar anders was ik wel wiskunde gaan studeren. Net zo bij het idee vectorruimte; als een natuurkundige met quantummechanica bezig ben, wil-ie niet eerst ellenlange berekeningen maken om te kijken of de ruimte wel volledig is ed. Daar hebben we wiskundigen voor
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Nog een stomme vraag ...
Stel je hebt x+y+z < 30
en x+y moet minstens de helft zijn van het totale bedrag
hoe schrijf je dat op als een vergelijking?
Stel je hebt x+y+z < 30
en x+y moet minstens de helft zijn van het totale bedrag
hoe schrijf je dat op als een vergelijking?


x + y >= 15 (er van uitgaande dat het totale bedrag 30 is zoals je sugggereert in je post)
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Dan heb je dus:quote:Op zondag 16 januari 2005 14:23 schreef VoreG het volgende:
Nog een stomme vraag ...
Stel je hebt x+y+z < 30
en x+y moet minstens de helft zijn van het totale bedrag
hoe schrijf je dat op als een vergelijking?
x+y+z<30
x+y>=15
Dus z<14.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Nu we toch bezig zijn...
Er geldt
x+y+z = 200
13x+y+10z <= 1700
Winst = Opbrengst - kosten = (uiteindelijk) 107x+71y+86z
En daaruit moet ik weten wanneer de winst maximaal is ... hoe krijg je dat in godsnaam voormekaar?!
Er geldt
x+y+z = 200
13x+y+10z <= 1700
Winst = Opbrengst - kosten = (uiteindelijk) 107x+71y+86z
En daaruit moet ik weten wanneer de winst maximaal is ... hoe krijg je dat in godsnaam voormekaar?!


x+y+z is kleiner dan 30.
Maar x+y is groter/gelijk aan 15.
Dat kan alleen maar als z kleiner is dan 14.
Anders:
x+y<30-z EN
x+y>=15
Dus z<30-(x+y), dus z<14.
Dus bijvoorbeeld x=8, y=8, z=13. Of zie ik nou wat over het hoofd?
Maar x+y is groter/gelijk aan 15.
Dat kan alleen maar als z kleiner is dan 14.
Anders:
x+y<30-z EN
x+y>=15
Dus z<30-(x+y), dus z<14.
Dus bijvoorbeeld x=8, y=8, z=13. Of zie ik nou wat over het hoofd?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Als ik het antwoord volledig opschrijf wordt het dit:quote:Op zondag 16 januari 2005 14:58 schreef Haushofer het volgende:
x+y+z is kleiner dan 30.
Maar x+y is groter/gelijk aan 15.
Dat kan alleen maar als z kleiner is dan 14.
Anders:
x+y<30-z EN
x+y>=15
Dus z<30-(x+y), dus z<14.
Dus bijvoorbeeld x=8, y=8, z=13. Of zie ik nou wat over het hoofd?
x+y+z <= 30
x >= 3
y >= 3
z >= 3
x+y-z >= 0
x <= 2y
De opdracht was
Een pensioenfonds gaat een bedrag ter waarde van maximaal 30 miljoen euro beleggen in aandelen, obligaties en onroerend goed. De regels blabla.
Minstends 3 miljoen moet in elk van de fondsen aandelen, obligaties en onroerend goed belegd worden.
Tenminste de helft van het totale bedrag moet worden geinvesteerd in aandelen en obligaties
Het bedrag dat voor aandelen wordt besteed mag niet het edubbele van het bedrag aan obligaties overschrijden.
Het dikgedrukte deel kom ik niet uit.


Het gaat denk ik fout op het moment dat de functie g die je substitueert een constante term heeft die ongelijk is aan 0. Dan convergeert de som die je krijgt voor f(g(x)) niet in de machtreeksring C[[x]]. En zelfs al convergeert hij bij elke coefficient gewoon in C, dan nog kan het zijn dat je een reeks eruit krijgt die convergentiestraal gelijk aan 0 heeft bijvoorbeeld.quote:Op zondag 16 januari 2005 14:19 schreef Pietjuh het volgende:
Hier waarschijnlijk een vrij domme vraag over taylorreeksontwikklingen van functies.
Zoals iedereen wel weet worden de coefficienten van xn in deze ontwikkeling van f(x) gegeven door f(n)(c) / n!
Wat ik nu vaak ben tegengekomen en eigenlijk zelf ook altijd gedaan heb, maar waar ik nu eigenlijk niet goed begrijp waarom is het volgende. Stel je wilt de taylorreeksontwikkeling maken van f(g(x)).
Bijvoorbeeld als f(x) = e^x en g(x) = x^2. Dan wordt bijna overal deze ontwikkeling bepaald door simpelweg x^2 te substitueren in de ontwikkeling van f(x) = e^x.
Maar als ik nu volgens de bekende formule de coefficienten wil berekenen krijg ik hier niet dezelfde coefficienten uit, want er verschijnen nu allemaal extra termen door de kettingregel.
Nu vraag ik me dus af waarom deze 2 op het oog verschillende ontwikkelingen convergeren naar dezelfde functie f(g(x)) ?


hoi ik heb een vraagje:
bepaal het aantal oplossing van deze vergelijking (in N*)
a+b+c=2005
a<b<c
ik dacht
1+2+2002
1+3+2001
1+4+2000
is ook een oplossing
ect....
is een oplossing en je kan ook meerdere oplossingen bedenken..
alleen hoe bepaal je het Aantal oplossingen?
dit heet te maken met telproblemen ofzo.. maar alleen hoe pas ik die kennis toe?
bepaal het aantal oplossing van deze vergelijking (in N*)
a+b+c=2005
a<b<c
ik dacht
1+2+2002
1+3+2001
1+4+2000
is ook een oplossing
ect....
is een oplossing en je kan ook meerdere oplossingen bedenken..
alleen hoe bepaal je het Aantal oplossingen?
dit heet te maken met telproblemen ofzo.. maar alleen hoe pas ik die kennis toe?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


wat ik merk is dat dat de eerste kolom kan (2005-1) keer het getal '1' bevatten
en de tweede kolom kan 2001 getallen bevatten '2,3,...,2002'
de derde kolom kan volgens deze redenering ook 2001 getallen bevatten
alleen op een gegeven moment is bi=ci
want daarna is bi > ci maar ermoet gelden dat b<c.
dus er zijn niet 2001 mogelijkheden voor b en c.. hoe moet ik het dan aanpakken?
voor de getallen a, is het ook moeilijk, je begint eerst met 1 en dan met 2 en dan.... tot een bepaald getal, dus het geval voordat a=b wordt bereikt.
en de tweede kolom kan 2001 getallen bevatten '2,3,...,2002'
de derde kolom kan volgens deze redenering ook 2001 getallen bevatten
alleen op een gegeven moment is bi=ci
want daarna is bi > ci maar ermoet gelden dat b<c.
dus er zijn niet 2001 mogelijkheden voor b en c.. hoe moet ik het dan aanpakken?
voor de getallen a, is het ook moeilijk, je begint eerst met 1 en dan met 2 en dan.... tot een bepaald getal, dus het geval voordat a=b wordt bereikt.
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Okee, we gaan het als volgt doen. We gaan eerst het aantal oplossingen tellen met alleen de voorwaarden a,b,c geheel en 0<a,b,c, maar nog niet meteen met 0<a<b<c. Dan trekken we daarvan af het aantal oplossingen waarbij 2 of meer getallen aan elkaar gelijk zijn. In de verzameling die je overhoudt komt elke oplossing van de vgl met 0<a<b<c precies 6 keer voor (elk drietal heeft immers 6 volgordes), dus delen we dat aantal door 6 en we hebben het antwoord.
Leg 2005 kralen op een rij. Als je nu in 2 tussenruimten van de kralen een streepje zet, dan krijg je een opdelen van 2005 in 3 getallen. Er zijn 2004 tussenruimten dus het aantal dat we zo krijgen is (2004 boven 2)=1002*2003.
Nu moeten we alle mogelijkheden tellen met 2 dezelfde erin. Dus het aantal paren (a,b,b) zeg maar. Elk paar komt 3 keer voor: ook nog als (b,a,b), (b,b,a). Als a oneven is en <2005 kun je het eraf trekken en zo is b uniek bepaald. Het gaat dus om het aantal oneven getallen van 1 t/m 2003. Dit is 1002. Maar dat moet dus nog keer 3. Dus we houden (1002*2003-1002*3)=1002*2000 over. Maar dit moet nog door 6 gedeeld worden.
En dat is 334000.
Leg 2005 kralen op een rij. Als je nu in 2 tussenruimten van de kralen een streepje zet, dan krijg je een opdelen van 2005 in 3 getallen. Er zijn 2004 tussenruimten dus het aantal dat we zo krijgen is (2004 boven 2)=1002*2003.
Nu moeten we alle mogelijkheden tellen met 2 dezelfde erin. Dus het aantal paren (a,b,b) zeg maar. Elk paar komt 3 keer voor: ook nog als (b,a,b), (b,b,a). Als a oneven is en <2005 kun je het eraf trekken en zo is b uniek bepaald. Het gaat dus om het aantal oneven getallen van 1 t/m 2003. Dit is 1002. Maar dat moet dus nog keer 3. Dus we houden (1002*2003-1002*3)=1002*2000 over. Maar dit moet nog door 6 gedeeld worden.
En dat is 334000.


oh waw
geef me de tijd tot morgen.. dan zal ik het proberen te snappen..
geef me de tijd tot morgen.. dan zal ik het proberen te snappen..
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


mm ik denk dat het een beetje snap, alleen waarom wordt het geval a-even niet behandeld?:S
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


thanx!
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


thanx
nu wordt het pas interessant...
bestaat er een algemene formule voor het vinden van het aantal oplossingen van een vergelijken in de vorm van
x1+x2....xn-1+xn=m
met
m geheel en groter dan nul
0<x1<x2<...<xn en al die xi zijn ook geheel.
ik denk dat je aanpak ook bruikbaar is in dit geval? n'est ce pas?
nu wordt het pas interessant...
bestaat er een algemene formule voor het vinden van het aantal oplossingen van een vergelijken in de vorm van
x1+x2....xn-1+xn=m
met
m geheel en groter dan nul
0<x1<x2<...<xn en al die xi zijn ook geheel.
ik denk dat je aanpak ook bruikbaar is in dit geval? n'est ce pas?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Misschien is de aanpak wel bruikbaar, maar een gesloten formule vinden zal iets lastiger worden, omdat je meer inclusie-exclusie hebt. Het aantal termen in de formule groeit als n groeit. Het volgende is ook een idee (geen idee of het hierdoor makkelijker wordt maar het is wel aardig om te vermelden).
Als we elke xi precies i minder maken kunnen we m met 1+...+n=n(n+1)/2 verlagen en de eis 0<x1<...<xn veranderen in 0<=x1<=...<=xn. Het probleem verandert hierdoor niet. Het gaat dus nu om het aantal manieren om m te schrijven als som van hooguit n getallen. We kunnen zo'n manier ook tekenen. Bekijk bijvoorbeed 10=5+3+2 als mogelijkheid om 10 te schrijven met 3 getallen. Dat ziet er zo uit:
XXXXX
XXX
XX
We kunnen het diagram spiegelen in de diagonaal.
XXX
XXX
XX
X
X
En we komen op 3+3+2+1+1 en dit is een mogelijkheid om 10 te schrijven als som van getallen die hooguit 3 zijn. Via dit truukje kun je het volgende dus zeggen. Het aantal mogelijke manieren om m te schrijven als som van hooguit n getallen is gelijk aan het aantal manieren om m te schrijven als som van getallen die hooguit n zijn.
[ Bericht 0% gewijzigd door thabit op 17-01-2005 15:37:27 ]
Als we elke xi precies i minder maken kunnen we m met 1+...+n=n(n+1)/2 verlagen en de eis 0<x1<...<xn veranderen in 0<=x1<=...<=xn. Het probleem verandert hierdoor niet. Het gaat dus nu om het aantal manieren om m te schrijven als som van hooguit n getallen. We kunnen zo'n manier ook tekenen. Bekijk bijvoorbeed 10=5+3+2 als mogelijkheid om 10 te schrijven met 3 getallen. Dat ziet er zo uit:
XXXXX
XXX
XX
We kunnen het diagram spiegelen in de diagonaal.
XXX
XXX
XX
X
X
En we komen op 3+3+2+1+1 en dit is een mogelijkheid om 10 te schrijven als som van getallen die hooguit 3 zijn. Via dit truukje kun je het volgende dus zeggen. Het aantal mogelijke manieren om m te schrijven als som van hooguit n getallen is gelijk aan het aantal manieren om m te schrijven als som van getallen die hooguit n zijn.
[ Bericht 0% gewijzigd door thabit op 17-01-2005 15:37:27 ]


Een lineair algebra vraagje. Wat zijn de nulpunten van
-x3+6x2-20x+16=0 ?
Ik heb gekeken naar de factorisatie van 16, en die factoren proberen in te vullen bij x, maar dan heb je natuurlijk oneindig veel mogelijkheden. (1*16=2*8=4*4=1/2*32....)
Nou heb je ook de formules van Cardano, maar kun je ook op een snuggere/snellere manier hieruit komen?
-x3+6x2-20x+16=0 ?
Ik heb gekeken naar de factorisatie van 16, en die factoren proberen in te vullen bij x, maar dan heb je natuurlijk oneindig veel mogelijkheden. (1*16=2*8=4*4=1/2*32....)
Nou heb je ook de formules van Cardano, maar kun je ook op een snuggere/snellere manier hieruit komen?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


De rationale nulpunten moeten geheel zijn, omdat de kopcoefficient gelijk is aan (+/-)1. Als de delers van 16 niet werken (zowel positief als negatief), dan heeft het ding geen rationale nulpunten. Een expliciete formule voor de nulpunten is in dat geval ook niet echt interessant.


Iemand?
Een onderzoeker denkt dat het percentage werklozen onder de uit veertigduizend mensen bestaande beroepsbevolking van een gemeente boven de 5 zal liggen. In een aselecte steekproef van 400 mensen uit de betreffende beroepsbevolking blijken er 26 werkloos te zijn.
Geef aan of de verwachting van de onderzoeker is bevestigd bij α = 0.10
Een onderzoeker denkt dat het percentage werklozen onder de uit veertigduizend mensen bestaande beroepsbevolking van een gemeente boven de 5 zal liggen. In een aselecte steekproef van 400 mensen uit de betreffende beroepsbevolking blijken er 26 werkloos te zijn.
Geef aan of de verwachting van de onderzoeker is bevestigd bij α = 0.10


In een vaas zitten 14 knikkers, 4 rood en 10 blauw. Robert pak zonder terugleggen een voor een knikkers uit de vaast. Hij stopt hiermee zodra hij een blauwe knikker pakt. Stel de kansverdeling op van het aantal keer dat Robert een knikker pakt. Geef de kansen in 4 decimalen nauwkeurig.
Aantal keer 1-2-3-4-5
kans 0,7143-?-?-?-?
P(x=1) 1- 4boven1 * 10 boven 0 gedeeld door 14 boven 1
maar bij 2 keer kom ik er al niet meer uit!
Help!
Aantal keer 1-2-3-4-5
kans 0,7143-?-?-?-?
P(x=1) 1- 4boven1 * 10 boven 0 gedeeld door 14 boven 1
maar bij 2 keer kom ik er al niet meer uit!
Help!


quote:Op dinsdag 18 januari 2005 11:16 schreef KiwiTjuHh het volgende:
In een vaas zitten 14 knikkers, 4 rood en 10 blauw. Robert pak zonder terugleggen een voor een knikkers uit de vaast. Hij stopt hiermee zodra hij een blauwe knikker pakt. Stel de kansverdeling op van het aantal keer dat Robert een knikker pakt. Geef de kansen in 4 decimalen nauwkeurig.
Aantal keer 1-2-3-4-5
kans 0,7143-?-?-?-?
P(x=1) 1- 4boven1 * 10 boven 0 gedeeld door 14 boven 1
maar bij 2 keer kom ik er al niet meer uit!
Help!
ok, 4 rood en 10 blauw, stopconditie is bij een blauwe bal
dus wanneer stoppen we na 1 bal, als we gelijk 1 blauwe trekken
zonder terugleggen
blauw kan op 10 manieren en 1 bal trekken op 14 manieren --> 10/14
kans dat we 2 ballen trekken dat betekent 1ste bal rood 2de bal blauw
kan op 4*10 manieren, totaal 2 ballen trekken kan op 14*13 manieren
dus --> 4*10/14*13 = 20/91
kans dat we 3 ballen trekken --> 2 rood dan 1 blauw is (4*3*10)/(14*13*12) = 5/91
kans dat we 4 ballen trekken --> 3 rood dan 1 blauw is (4*3*2*10)/(14*13*12*11) = 10/1001
kans dat we 5 ballen trekken --> 4 rood dan 1 blauw is (4*3*2*1*10)/(14*13*12*11*10) = 2/2002 = 1/1001
maar wat eigenlijk belangrijker is bij kansrekening is dat je het model begrijpt, het anwtoord is niet eens zo heel belangrijk, maar wel dat je begrijpt wat er gebeurt als er wordt gepraat over ZONDER terugleggen en wat bijvoorbeeld het model is bij 4 knikkers, dat je dan dus eerst 3 rode hebt getrokken en daarna 1 blauwe trekt
suc6
[ Bericht 5% gewijzigd door superbient op 18-01-2005 12:05:15 ]
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Ik ben het helemaal met je eens superbient, dat is ook de manier waarop ik dat altijd doe.. maar het antwoord met het antwoordenboekje komt gewoon niet overeen
Zij zeggen:
P(x=1) = 0.7143
P(x=2) = 0.2198
P(x=3) = 0.0549
P(x=4) = 0.0100
P(x=5) = 0.0100
Zij zeggen:
P(x=1) = 0.7143
P(x=2) = 0.2198
P(x=3) = 0.0549
P(x=4) = 0.0100
P(x=5) = 0.0100


afgerond klopt dat toch?? behalve bij P(x=5) is het een beetje vreemd --> dat moet 0.0010 zijn, maar waarom afgerond doen als het in breuken juist mooi precies kanquote:Op dinsdag 18 januari 2005 11:45 schreef KiwiTjuHh het volgende:
Ik ben het helemaal met je eens superbient, dat is ook de manier waarop ik dat altijd doe.. maar het antwoord met het antwoordenboekje komt gewoon niet overeen
Zij zeggen:
P(x=1) = 0.7143
P(x=2) = 0.2198
P(x=3) = 0.0549
P(x=4) = 0.0100
P(x=5) = 0.0100
en om nog even op jouw manier terug te komen,
hoe bereken je bijv P(x=3) uit, dat zou dan zijn eerst 2 rode en dan 1 blauwe
belangrijk hier is dat de 2 rode eerst moeten komen
kans op 2 rode en 1 blauwe willekeurig zonder terugleggen is bijv ((4 boven 2)*(10 boven 1))/(14 boven 3)
maar nu moeten eerst de rode ballen eruit dus
((4 boven 2)/(14 boven 2))*((10 boven 1)/(12 boven 1))
of ook wel
P(x=n) = ((4 boven n-1)/(14 boven n-1))*(10/(14-(n-1)))
[ Bericht 24% gewijzigd door superbient op 18-01-2005 12:02:38 ]
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


vermenigvuldigenquote:Op dinsdag 18 januari 2005 12:00 schreef KiwiTjuHh het volgende:
Wat bedoel jij met * dan?
en ik heb er nog ff haakjes bij gezet;)
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Stel p is priem. Wat zijn de inverteerbare elementen van Z/p2Z?
Ik dacht zelf: 1, p-1, p+1, p2-1
Dat zijn ze niet per definitie allemaal. Hoe kan ik ze allemaal te weten komen?
Ik dacht zelf: 1, p-1, p+1, p2-1
Dat zijn ze niet per definitie allemaal. Hoe kan ik ze allemaal te weten komen?
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


is het mogelijk om de kwatoren hieruit weg te halen?zo ja? hoe doe je dat ?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Volgens mij gaat je dat niet lukken en mij ook niet.
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


oh ..
want soms zijn ze overbodig...
want soms zijn ze overbodig...
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Ik zie niet direct iets. Sorry.quote:Op vrijdag 21 januari 2005 20:50 schreef achtbaan het volgende:
is het mogelijk om de kwatoren hieruit weg te halen?zo ja? hoe doe je dat ?
[afbeelding]
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


het komt goed..quote:
nog een vraagje, nu over de volgorde:
er is een verschil tussen de twee regels hier:
eentje is waar en de andere is fout..
in dit soort lastige gevallen, wat is de beste manier om te determineren dat zoiets logisch (wiskundig) gezien niet klopt ?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Als R de reeele getallen zijn dan is de bovenste goed en de onderste fout.quote:Op zondag 23 januari 2005 00:39 schreef achtbaan het volgende:
[..]
het komt goed..
nog een vraagje, nu over de volgorde:
er is een verschil tussen de twee regels hier:
eentje is waar en de andere is fout..
in dit soort lastige gevallen, wat is de beste manier om te determineren dat zoiets logisch (wiskundig) gezien niet klopt ?
Wat je natuurlijk meteen doet is x - y >= 0 schrijven als x >= y en dan gewoon lezen wat er staat.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


dus de onderste betekent dat er een getal y bestaat dat groter is dan alle getallen in R..
en dat is natuurlijk fout..
:S erg misleidend!
heb je meer van dit voorbeelden/
en dat is natuurlijk fout..
:S erg misleidend!
heb je meer van dit voorbeelden/
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


KLEINER maar het is dan nog steeds fout jaquote:Op zondag 23 januari 2005 09:41 schreef achtbaan het volgende:
dus de onderste betekent dat er een getal y bestaat dat groter is dan alle getallen in R..
en dat is natuurlijk fout..
:S erg misleidend!
Ik zal eens in mijn logica boek kijken. Ik heb het nu niet bij de hand.quote:heb je meer van dit voorbeelden/
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Hier heb je er een
(VoorAlle n uit N)(ErIsEen m uit N): n + m = 0
met N = {0, 1, 2, 3, 4, . . .}
(VoorAlle n uit N)(ErIsEen m uit N): n + m = 0
met N = {0, 1, 2, 3, 4, . . .}
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


De wiskundeleerkracht waar ik mee zit legt alles onvoldoende uit waardoor ik met zelfstudie er toch probeer te geraken. We zitten nu aan toepassingen van de Bepaalde integraal en meer over oppervlakteberekening bij cirkels.
Het lukt mij niet deze oefening te beginnen, laat staan op te lossen.
Geg: Twee cirkelschijven hebben een gelijke straal r en de afstand tussen de middelpunten is r*(2)^1/2
Gevr: Bereken het maatgetal van de oppervlakte van het gemeenschappelijk vlakdeel
Het lukt mij niet deze oefening te beginnen, laat staan op te lossen.
Geg: Twee cirkelschijven hebben een gelijke straal r en de afstand tussen de middelpunten is r*(2)^1/2
Gevr: Bereken het maatgetal van de oppervlakte van het gemeenschappelijk vlakdeel


dit is volgens mij niet waar, geldt toch alleen maar voor n = 0 --> want dan is m ook 0, anders kan het al nietquote:Op zondag 23 januari 2005 11:12 schreef Landmass het volgende:
Hier heb je er een
(VoorAlle n uit N)(ErIsEen m uit N): n + m = 0
met N = {0, 1, 2, 3, 4, . . .}
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Inderdaad, dat is ook de reden dat de natuurlijke getallen geen additieve groep vormen. Als je de natuurlijke getallen uitbreid tot de gehele getallen geldt bovenstaande bewering natuurlijk welquote:Op zondag 23 januari 2005 12:53 schreef superbient het volgende:
dit is volgens mij niet waar, geldt toch alleen maar voor n = 0 --> want dan is m ook 0, anders kan het al niet
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Ik zou zeggen. Trek een lijn door de 2 punten waar de cirkels elkaar snijden en probeer nu van 1 zo'n gebiedje het opp te berekenen. Dan hoef je het alleen nog maar maal 2 te doen.quote:Op zondag 23 januari 2005 11:40 schreef Reikoo het volgende:
De wiskundeleerkracht waar ik mee zit legt alles onvoldoende uit waardoor ik met zelfstudie er toch probeer te geraken. We zitten nu aan toepassingen van de Bepaalde integraal en meer over oppervlakteberekening bij cirkels.
Het lukt mij niet deze oefening te beginnen, laat staan op te lossen.
Geg: Twee cirkelschijven hebben een gelijke straal r en de afstand tussen de middelpunten is r*(2)^1/2
Gevr: Bereken het maatgetal van de oppervlakte van het gemeenschappelijk vlakdeel
Is dit VWO, HBO, Havo?
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


In België ASO Wiskunde 6u, ik zou het niet weten met welk Nederlands systeem ik het zou mee moeten vergelijken.


weer een vraagje over logica
nu over implicatie: 5+3>6 ==> pi is irrationeel
:S deze implicatie klopt maar.. wat is in godsnaam het verband tussen de linkere ongelijkheid en de uitspraak t aan de rechtere kant?
A ==> B
waarom moeten Negatief-A en B niet kloppen zodat de implicatie onjuist wordt?
stel A en B zijn onjuist, is het in dit geval onbeslisbaar of
A==B correct of incorrect is?
nu over implicatie: 5+3>6 ==> pi is irrationeel
:S deze implicatie klopt maar.. wat is in godsnaam het verband tussen de linkere ongelijkheid en de uitspraak t aan de rechtere kant?
A ==> B
waarom moeten Negatief-A en B niet kloppen zodat de implicatie onjuist wordt?
stel A en B zijn onjuist, is het in dit geval onbeslisbaar of
A==B correct of incorrect is?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


mssn domme vraag maar kan iemand mij een uitleg geven over wat nu eigenlijk een limiet is?? alvast bedankt!


als je bijv een rij hebt 1/n
met n = {0,1,2,3,...}
lim (n --> inf) 1/n = 0
algemeen:
rij{An} n>0 --> lim (n --> inf) An = L
definitie is zoiets als: voor alle epsilon > 0 is er een N(epsilon) zodanig dat voor alle n > N(epsilon) geldt |L - An| < epsilon
je moet het maar zien dat je als je verder in de irj loopt je steeds dicht bij de limiet L komt en je dus voor n = oneindig willekeurig dicht bij L zit
met n = {0,1,2,3,...}
lim (n --> inf) 1/n = 0
algemeen:
rij{An} n>0 --> lim (n --> inf) An = L
definitie is zoiets als: voor alle epsilon > 0 is er een N(epsilon) zodanig dat voor alle n > N(epsilon) geldt |L - An| < epsilon
je moet het maar zien dat je als je verder in de irj loopt je steeds dicht bij de limiet L komt en je dus voor n = oneindig willekeurig dicht bij L zit
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Misschien dat je dan beter even kan vertellen waarom je het wilt weten. Is het uit interesse of is het voor je opleiding en wat is die opleiding dan.quote:Op maandag 24 januari 2005 11:56 schreef andre17 het volgende:
mssn domme vraag maar kan iemand mij een uitleg geven over wat nu eigenlijk een limiet is?? alvast bedankt!
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Bij een normaal verdeelde toevalsvariabele X = úx=50 en óx=5
ú=gemiddelde
ó=standaardafwijking.
A
Bereken in vier decimalen de kans dat een waarneming meer dan 4 van úx afwijkt.
B
We doen 30 waarnemingen en bereken de gemiddelde X.
Bereken in 4 decimalen nauwkeurig de kans dat X meer dan 3 van úx afwijkt.
=============
A kom ik op dit uit:
Z= (X - úx) / óx
z= X - 50 / 5
P(X wijkt meer dan drie af) = P(X<47) of P(X>53)
Dit is hetzelfde als
2*(P<47)
2*(47-50/5) = 2*(-0,6).
Terugzoeken geeft 0,5485.
Dit klopt ook..
opgave B is het probleem
Het gaat nu om gemiddelde waarden.. Wat is nou de regel hiervoor?
[ Bericht 77% gewijzigd door Skv op 24-01-2005 14:34:03 ]
ú=gemiddelde
ó=standaardafwijking.
A
Bereken in vier decimalen de kans dat een waarneming meer dan 4 van úx afwijkt.
B
We doen 30 waarnemingen en bereken de gemiddelde X.
Bereken in 4 decimalen nauwkeurig de kans dat X meer dan 3 van úx afwijkt.
=============
A kom ik op dit uit:
Z= (X - úx) / óx
z= X - 50 / 5
P(X wijkt meer dan drie af) = P(X<47) of P(X>53)
Dit is hetzelfde als
2*(P<47)
2*(47-50/5) = 2*(-0,6).
Terugzoeken geeft 0,5485.
Dit klopt ook..
opgave B is het probleem
Het gaat nu om gemiddelde waarden.. Wat is nou de regel hiervoor?
[ Bericht 77% gewijzigd door Skv op 24-01-2005 14:34:03 ]
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


Help
[ Bericht 12% gewijzigd door Skv op 24-01-2005 14:34:45 ]
[ Bericht 12% gewijzigd door Skv op 24-01-2005 14:34:45 ]
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


voor a zou ik nog even nakijken als ik jou was, want id opgave staat dat je 4 van ux afwijkt....quote:Op maandag 24 januari 2005 13:22 schreef Skv het volgende:
Bij een normaal verdeelde toevalsvariabele X = úx=50 en óx=5
ú=gemiddelde
ó=standaardafwijking.
A
Bereken in vier decimalen de kans dat een waarneming meer dan 4 van úx afwijkt.
B
We doen 30 waarnemingen en bereken de gemiddelde X.
Bereken in 4 decimalen nauwkeurig de kans dat X meer dan 3 van úx afwijkt.
=============
A kom ik op dit uit:
Z= (X - úx) / óx
z= X - 50 / 5
P(X wijkt meer dan drie af) = P(X<47) of P(X>53)
Dit is hetzelfde als
2*(P<47)
2*(47-50/5) = 2*(-0,6).
Terugzoeken geeft 0,5485.
Dit klopt ook..
opgave B is het probleem
Het gaat nu om gemiddelde waarden.. Wat is nou de regel hiervoor?
nu b
we moeten nu ook meenemen dat het een gemiddelde is van 30 trekkingen, de kans dat zo'n gemiddelde meer dan 3 van een gemiddelde(vd verdeling) afligt is natuurlijk kleiner dan dat 1 trekking meer dan 3 van een gemiddelde aflegt, je zou immers denken dat het gemiddelde van 30 trekkingen de afwijkingen positief en negatief compenseert
we gaan als volgt te werk
standaardafwijking = sigma = 5
gemiddelde = mu = 50
aantal trekkingen = n = 30
we nemen een X-gemiddeld waar
we moeten berekenen P(x<47)+P(x>53) = 2*P(x<47)
Z = wortel(n)*((X-gem - mu)/sigma) --> is N(0,1) verdeeld
invullen levert 5.48*((47-50)/5) = 5.48*3/5 = -3.29
opzoeken levert P(X>3.29) = 1- P(x <3.29) = 0.0005
0.0005*2 = 0.001 = 0.1%
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Ik heb het als volgt opgelost:
A klopt; had een typefoutje hierboven, het moet 3 afwijking zijn.
Oplossing A:
2*normalcdf(-10^99,47,50,5) = 0,548
Oplossing B: (ik wist dus niet dat je gemiddelde óx berekende door óx door wortel N te delen).
2*normalcdf(-10^99,47,50,5/(wortel 30)) = 0,0010
Klopt dit ook? antwoord is iig hetzelfde
A klopt; had een typefoutje hierboven, het moet 3 afwijking zijn.
Oplossing A:
2*normalcdf(-10^99,47,50,5) = 0,548
Oplossing B: (ik wist dus niet dat je gemiddelde óx berekende door óx door wortel N te delen).
2*normalcdf(-10^99,47,50,5/(wortel 30)) = 0,0010
Klopt dit ook? antwoord is iig hetzelfde
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


ja dat klopt, op de gr moet t zo, nu ik op de uni zit moet t echter weer met het tabellenboekje, de standaardafwijking wordt idd kleiner naarmate je meer trekkingen neemt in het gemiddelde, als je dat logisch vindt, dan gaat het goedquote:Op maandag 24 januari 2005 18:35 schreef Skv het volgende:
Ik heb het als volgt opgelost:
A klopt; had een typefoutje hierboven, het moet 3 afwijking zijn.
Oplossing A:
2*normalcdf(-10^99,47,50,5) = 0,548
Oplossing B: (ik wist dus niet dat je gemiddelde óx berekende door óx door wortel N te delen).
2*normalcdf(-10^99,47,50,5/(wortel 30)) = 0,0010
Klopt dit ook? antwoord is iig hetzelfde
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Wat studeer je dan, dat je dit snapt?
Moet ik dat iig niet gaan doen
bedankt iig
Moet ik dat iig niet gaan doen
bedankt iig
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


Die eerste implicatie begrijp ik ook niet.quote:Op zondag 23 januari 2005 19:39 schreef achtbaan het volgende:
weer een vraagje over logica
nu over implicatie: 5+3>6 ==> pi is irrationeel
:S deze implicatie klopt maar.. wat is in godsnaam het verband tussen de linkere ongelijkheid en de uitspraak t aan de rechtere kant?
A ==> B
waarom moeten Negatief-A en B niet kloppen zodat de implicatie onjuist wordt?
stel A en B zijn onjuist, is het in dit geval onbeslisbaar of
A==B correct of incorrect is?
(Ik neem aan dat uje met onjuist False bedoelt en niet contingentie)
Stel A en B zijn onjuist, dan is A=>B waar, want False => X is True voor alle X. Het is namelijk zo dat een implicatie tautoloog is, zodra de 1-en van het linkerlid worden doorgegeven aan het rechterlid. Aangezien False uit enkel 0-en bestaat, worden deze automatisch doorgegeven.
Edit: Het kan ook zijn dat je bedoelt dat A en B in dit geval onjuist zijn, de regel blijft dan het zelfde alleen voor 1 rij uit de waarheidstabel. In dit tweede geval is het inderdaad onbeslisbaar of A=B waar is, in het eerste was dit overduidelijk wel het geval, daarom denk ik ook dat ik je verkeerd interpreteerde.
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


oh ja, er staat per definitie van implicatie, dat je vanuit A en B de 'uitspraak' (B Of -A) krijgt.
in ieder geval, hoe moet je dit toepassen bij het bewijzen dat
(voor alle (x,y,z) uit R³) : x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
?
alvast bedankt
in ieder geval, hoe moet je dit toepassen bij het bewijzen dat
(voor alle (x,y,z) uit R³) : x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
?
alvast bedankt
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


laten we het doen zoals je typte:
x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
x+y+z=0 ==> |x-y|+y+x+y+x+y+x>=1/2(x+y+x+y)
==>|x-y|+3x+3y>=x+y
==> |x-y|>=-2x-2y
en dit klopt want |x-y|>=0 en -2x-2y<=0
zo bedoel je?
x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
x+y+z=0 ==> |x-y|+y+x+y+x+y+x>=1/2(x+y+x+y)
==>|x-y|+3x+3y>=x+y
==> |x-y|>=-2x-2y
en dit klopt want |x-y|>=0 en -2x-2y<=0
zo bedoel je?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


wanneer is er geen 'verlies van algemeengheid'? hoe zie je dat aan de nieuwe gelijkheden/ongelijkheden die je krijgt als je een bepaalde handeling(en) uitvoert op bepaalde wiskundige dingen?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Deze redenering is correct als je haar van onder naar boven leest.quote:Op dinsdag 25 januari 2005 19:49 schreef achtbaan het volgende:
laten we het doen zoals je typte:
x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
x+y+z=0 ==> |x-y|+y+x+y+x+y+x>=1/2(x+y+x+y)
==>|x-y|+3x+3y>=x+y
==> |x-y|>=-2x-2y
en dit klopt want |x-y|>=0 en -2x-2y<=0
zo bedoel je?


Er is geen verlies van algemeenheid als het algemene geval uit het speciale geval volgt waar je veronderstelt in te zitten. In dit geval speelt de symmetreische wijze waarop de variabelen in de formules aanwezig zijn daar een belangrijke rol in. Ook het feit dat er niets aan de waarheid van de formules verandert als je x,y,z vervangt door -x,-y,-z is hier van belang om te kunnen specialiseren.quote:Op dinsdag 25 januari 2005 19:51 schreef achtbaan het volgende:
wanneer is er geen 'verlies van algemeengheid'? hoe zie je dat aan de nieuwe gelijkheden/ongelijkheden die je krijgt als je een bepaalde handeling(en) uitvoert op bepaalde wiskundige dingen?


hoi ,
ik heb een vraagje over breuken vereenvoudigen (het is namelijk alweer zolang geleden voor mij )
ik moet de volgende breuken eereenvoudigen:
115 / 180e
325 / 180e
1200 / 180e
wat is nou de simpelse manier om dat te doen?
ik heb een vraagje over breuken vereenvoudigen (het is namelijk alweer zolang geleden voor mij )
ik moet de volgende breuken eereenvoudigen:
115 / 180e
325 / 180e
1200 / 180e
wat is nou de simpelse manier om dat te doen?


ha mn oude rekenmachine doet het automatisch dus dat probleem is opgelost nu zit ik met een ander probleem.
ik moet soommige dingen om rkenen in graden zoals:
1/3 pie rad
7/12 pie rad
2 rad
0,68 rad
die 1e 2 lukken me wel dat is gewoon 1/3 x 180
maar die wat geen pie rad is maar gewone rad kom ik niet uit?
ik moet soommige dingen om rkenen in graden zoals:
1/3 pie rad
7/12 pie rad
2 rad
0,68 rad
die 1e 2 lukken me wel dat is gewoon 1/3 x 180
maar die wat geen pie rad is maar gewone rad kom ik niet uit?


Dan reken je 2 om naar een breuk van pi en dan doe je dat maal 180?quote:Op woensdag 26 januari 2005 22:55 schreef BaggerUser het volgende:
ha mn oude rekenmachine doet het automatisch dus dat probleem is opgelost nu zit ik met een ander probleem.
ik moet soommige dingen om rkenen in graden zoals:
1/3 pie rad
7/12 pie rad
2 rad
0,68 rad
die 1e 2 lukken me wel dat is gewoon 1/3 x 180
maar die wat geen pie rad is maar gewone rad kom ik niet uit?
Dus x * (180/pi) = y


Mja, 2pi radialen=360 graden. Dus 1 radiaal is ca 57 graden (360/6,28). Nou moet t niet meer zo moeilijk zijn.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Hoe bereken je de inhoud van een druppel met een doorsnede van 4 mm?
Geldt dan de regel pi * straal^2
Geldt dan de regel pi * straal^2
...drop it like it's hot...


ik zou zeggen opsplitsen in halve bol en kegel en de inhouden daarvan bij elkaar optellen
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Nee dat is de oppervlakte van een cirkelquote:Op zaterdag 29 januari 2005 12:38 schreef Nyluzzz het volgende:
Hoe bereken je de inhoud van een druppel met een doorsnede van 4 mm?
Geldt dan de regel pi * straal^2
Het volume van een bol wordt gegeven door 4 / 3 Pi r^3
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


oh ja dat was de formule,]quote:Op zaterdag 29 januari 2005 13:50 schreef Pietjuh het volgende:
[..]
Nee dat is de oppervlakte van een cirkel
Het volume van een bol wordt gegeven door 4 / 3 Pi r^3
thanx pietjuh
...drop it like it's hot...
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |




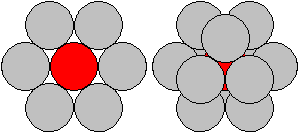


 convergent. En dat was de uitkomst.
convergent. En dat was de uitkomst.