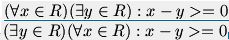SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Een lineair algebra vraagje. Wat zijn de nulpunten van
-x3+6x2-20x+16=0 ?
Ik heb gekeken naar de factorisatie van 16, en die factoren proberen in te vullen bij x, maar dan heb je natuurlijk oneindig veel mogelijkheden. (1*16=2*8=4*4=1/2*32....)
Nou heb je ook de formules van Cardano, maar kun je ook op een snuggere/snellere manier hieruit komen?
-x3+6x2-20x+16=0 ?
Ik heb gekeken naar de factorisatie van 16, en die factoren proberen in te vullen bij x, maar dan heb je natuurlijk oneindig veel mogelijkheden. (1*16=2*8=4*4=1/2*32....)
Nou heb je ook de formules van Cardano, maar kun je ook op een snuggere/snellere manier hieruit komen?
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


De rationale nulpunten moeten geheel zijn, omdat de kopcoefficient gelijk is aan (+/-)1. Als de delers van 16 niet werken (zowel positief als negatief), dan heeft het ding geen rationale nulpunten. Een expliciete formule voor de nulpunten is in dat geval ook niet echt interessant.


Iemand?
Een onderzoeker denkt dat het percentage werklozen onder de uit veertigduizend mensen bestaande beroepsbevolking van een gemeente boven de 5 zal liggen. In een aselecte steekproef van 400 mensen uit de betreffende beroepsbevolking blijken er 26 werkloos te zijn.
Geef aan of de verwachting van de onderzoeker is bevestigd bij α = 0.10
Een onderzoeker denkt dat het percentage werklozen onder de uit veertigduizend mensen bestaande beroepsbevolking van een gemeente boven de 5 zal liggen. In een aselecte steekproef van 400 mensen uit de betreffende beroepsbevolking blijken er 26 werkloos te zijn.
Geef aan of de verwachting van de onderzoeker is bevestigd bij α = 0.10


In een vaas zitten 14 knikkers, 4 rood en 10 blauw. Robert pak zonder terugleggen een voor een knikkers uit de vaast. Hij stopt hiermee zodra hij een blauwe knikker pakt. Stel de kansverdeling op van het aantal keer dat Robert een knikker pakt. Geef de kansen in 4 decimalen nauwkeurig.
Aantal keer 1-2-3-4-5
kans 0,7143-?-?-?-?
P(x=1) 1- 4boven1 * 10 boven 0 gedeeld door 14 boven 1
maar bij 2 keer kom ik er al niet meer uit!
Help!
Aantal keer 1-2-3-4-5
kans 0,7143-?-?-?-?
P(x=1) 1- 4boven1 * 10 boven 0 gedeeld door 14 boven 1
maar bij 2 keer kom ik er al niet meer uit!
Help!


quote:Op dinsdag 18 januari 2005 11:16 schreef KiwiTjuHh het volgende:
In een vaas zitten 14 knikkers, 4 rood en 10 blauw. Robert pak zonder terugleggen een voor een knikkers uit de vaast. Hij stopt hiermee zodra hij een blauwe knikker pakt. Stel de kansverdeling op van het aantal keer dat Robert een knikker pakt. Geef de kansen in 4 decimalen nauwkeurig.
Aantal keer 1-2-3-4-5
kans 0,7143-?-?-?-?
P(x=1) 1- 4boven1 * 10 boven 0 gedeeld door 14 boven 1
maar bij 2 keer kom ik er al niet meer uit!
Help!
ok, 4 rood en 10 blauw, stopconditie is bij een blauwe bal
dus wanneer stoppen we na 1 bal, als we gelijk 1 blauwe trekken
zonder terugleggen
blauw kan op 10 manieren en 1 bal trekken op 14 manieren --> 10/14
kans dat we 2 ballen trekken dat betekent 1ste bal rood 2de bal blauw
kan op 4*10 manieren, totaal 2 ballen trekken kan op 14*13 manieren
dus --> 4*10/14*13 = 20/91
kans dat we 3 ballen trekken --> 2 rood dan 1 blauw is (4*3*10)/(14*13*12) = 5/91
kans dat we 4 ballen trekken --> 3 rood dan 1 blauw is (4*3*2*10)/(14*13*12*11) = 10/1001
kans dat we 5 ballen trekken --> 4 rood dan 1 blauw is (4*3*2*1*10)/(14*13*12*11*10) = 2/2002 = 1/1001
maar wat eigenlijk belangrijker is bij kansrekening is dat je het model begrijpt, het anwtoord is niet eens zo heel belangrijk, maar wel dat je begrijpt wat er gebeurt als er wordt gepraat over ZONDER terugleggen en wat bijvoorbeeld het model is bij 4 knikkers, dat je dan dus eerst 3 rode hebt getrokken en daarna 1 blauwe trekt
suc6
[ Bericht 5% gewijzigd door superbient op 18-01-2005 12:05:15 ]
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Ik ben het helemaal met je eens superbient, dat is ook de manier waarop ik dat altijd doe.. maar het antwoord met het antwoordenboekje komt gewoon niet overeen
Zij zeggen:
P(x=1) = 0.7143
P(x=2) = 0.2198
P(x=3) = 0.0549
P(x=4) = 0.0100
P(x=5) = 0.0100
Zij zeggen:
P(x=1) = 0.7143
P(x=2) = 0.2198
P(x=3) = 0.0549
P(x=4) = 0.0100
P(x=5) = 0.0100


afgerond klopt dat toch?? behalve bij P(x=5) is het een beetje vreemd --> dat moet 0.0010 zijn, maar waarom afgerond doen als het in breuken juist mooi precies kanquote:Op dinsdag 18 januari 2005 11:45 schreef KiwiTjuHh het volgende:
Ik ben het helemaal met je eens superbient, dat is ook de manier waarop ik dat altijd doe.. maar het antwoord met het antwoordenboekje komt gewoon niet overeen
Zij zeggen:
P(x=1) = 0.7143
P(x=2) = 0.2198
P(x=3) = 0.0549
P(x=4) = 0.0100
P(x=5) = 0.0100
en om nog even op jouw manier terug te komen,
hoe bereken je bijv P(x=3) uit, dat zou dan zijn eerst 2 rode en dan 1 blauwe
belangrijk hier is dat de 2 rode eerst moeten komen
kans op 2 rode en 1 blauwe willekeurig zonder terugleggen is bijv ((4 boven 2)*(10 boven 1))/(14 boven 3)
maar nu moeten eerst de rode ballen eruit dus
((4 boven 2)/(14 boven 2))*((10 boven 1)/(12 boven 1))
of ook wel
P(x=n) = ((4 boven n-1)/(14 boven n-1))*(10/(14-(n-1)))
[ Bericht 24% gewijzigd door superbient op 18-01-2005 12:02:38 ]
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


vermenigvuldigenquote:Op dinsdag 18 januari 2005 12:00 schreef KiwiTjuHh het volgende:
Wat bedoel jij met * dan?
en ik heb er nog ff haakjes bij gezet;)
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Stel p is priem. Wat zijn de inverteerbare elementen van Z/p2Z?
Ik dacht zelf: 1, p-1, p+1, p2-1
Dat zijn ze niet per definitie allemaal. Hoe kan ik ze allemaal te weten komen?
Ik dacht zelf: 1, p-1, p+1, p2-1
Dat zijn ze niet per definitie allemaal. Hoe kan ik ze allemaal te weten komen?
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


is het mogelijk om de kwatoren hieruit weg te halen?zo ja? hoe doe je dat ?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Volgens mij gaat je dat niet lukken en mij ook niet.
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


oh ..
want soms zijn ze overbodig...
want soms zijn ze overbodig...
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Ik zie niet direct iets. Sorry.quote:Op vrijdag 21 januari 2005 20:50 schreef achtbaan het volgende:
is het mogelijk om de kwatoren hieruit weg te halen?zo ja? hoe doe je dat ?
[afbeelding]
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


het komt goed..quote:
nog een vraagje, nu over de volgorde:
er is een verschil tussen de twee regels hier:
eentje is waar en de andere is fout..
in dit soort lastige gevallen, wat is de beste manier om te determineren dat zoiets logisch (wiskundig) gezien niet klopt ?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Als R de reeele getallen zijn dan is de bovenste goed en de onderste fout.quote:Op zondag 23 januari 2005 00:39 schreef achtbaan het volgende:
[..]
het komt goed..
nog een vraagje, nu over de volgorde:
er is een verschil tussen de twee regels hier:
eentje is waar en de andere is fout..
in dit soort lastige gevallen, wat is de beste manier om te determineren dat zoiets logisch (wiskundig) gezien niet klopt ?
Wat je natuurlijk meteen doet is x - y >= 0 schrijven als x >= y en dan gewoon lezen wat er staat.
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


dus de onderste betekent dat er een getal y bestaat dat groter is dan alle getallen in R..
en dat is natuurlijk fout..
:S erg misleidend!
heb je meer van dit voorbeelden/
en dat is natuurlijk fout..
:S erg misleidend!
heb je meer van dit voorbeelden/
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


KLEINER maar het is dan nog steeds fout jaquote:Op zondag 23 januari 2005 09:41 schreef achtbaan het volgende:
dus de onderste betekent dat er een getal y bestaat dat groter is dan alle getallen in R..
en dat is natuurlijk fout..
:S erg misleidend!
Ik zal eens in mijn logica boek kijken. Ik heb het nu niet bij de hand.quote:heb je meer van dit voorbeelden/
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Hier heb je er een
(VoorAlle n uit N)(ErIsEen m uit N): n + m = 0
met N = {0, 1, 2, 3, 4, . . .}
(VoorAlle n uit N)(ErIsEen m uit N): n + m = 0
met N = {0, 1, 2, 3, 4, . . .}
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


De wiskundeleerkracht waar ik mee zit legt alles onvoldoende uit waardoor ik met zelfstudie er toch probeer te geraken. We zitten nu aan toepassingen van de Bepaalde integraal en meer over oppervlakteberekening bij cirkels.
Het lukt mij niet deze oefening te beginnen, laat staan op te lossen.
Geg: Twee cirkelschijven hebben een gelijke straal r en de afstand tussen de middelpunten is r*(2)^1/2
Gevr: Bereken het maatgetal van de oppervlakte van het gemeenschappelijk vlakdeel
Het lukt mij niet deze oefening te beginnen, laat staan op te lossen.
Geg: Twee cirkelschijven hebben een gelijke straal r en de afstand tussen de middelpunten is r*(2)^1/2
Gevr: Bereken het maatgetal van de oppervlakte van het gemeenschappelijk vlakdeel


dit is volgens mij niet waar, geldt toch alleen maar voor n = 0 --> want dan is m ook 0, anders kan het al nietquote:Op zondag 23 januari 2005 11:12 schreef Landmass het volgende:
Hier heb je er een
(VoorAlle n uit N)(ErIsEen m uit N): n + m = 0
met N = {0, 1, 2, 3, 4, . . .}
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Inderdaad, dat is ook de reden dat de natuurlijke getallen geen additieve groep vormen. Als je de natuurlijke getallen uitbreid tot de gehele getallen geldt bovenstaande bewering natuurlijk welquote:Op zondag 23 januari 2005 12:53 schreef superbient het volgende:
dit is volgens mij niet waar, geldt toch alleen maar voor n = 0 --> want dan is m ook 0, anders kan het al niet
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen


Ik zou zeggen. Trek een lijn door de 2 punten waar de cirkels elkaar snijden en probeer nu van 1 zo'n gebiedje het opp te berekenen. Dan hoef je het alleen nog maar maal 2 te doen.quote:Op zondag 23 januari 2005 11:40 schreef Reikoo het volgende:
De wiskundeleerkracht waar ik mee zit legt alles onvoldoende uit waardoor ik met zelfstudie er toch probeer te geraken. We zitten nu aan toepassingen van de Bepaalde integraal en meer over oppervlakteberekening bij cirkels.
Het lukt mij niet deze oefening te beginnen, laat staan op te lossen.
Geg: Twee cirkelschijven hebben een gelijke straal r en de afstand tussen de middelpunten is r*(2)^1/2
Gevr: Bereken het maatgetal van de oppervlakte van het gemeenschappelijk vlakdeel
Is dit VWO, HBO, Havo?
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


In België ASO Wiskunde 6u, ik zou het niet weten met welk Nederlands systeem ik het zou mee moeten vergelijken.


weer een vraagje over logica
nu over implicatie: 5+3>6 ==> pi is irrationeel
:S deze implicatie klopt maar.. wat is in godsnaam het verband tussen de linkere ongelijkheid en de uitspraak t aan de rechtere kant?
A ==> B
waarom moeten Negatief-A en B niet kloppen zodat de implicatie onjuist wordt?
stel A en B zijn onjuist, is het in dit geval onbeslisbaar of
A==B correct of incorrect is?
nu over implicatie: 5+3>6 ==> pi is irrationeel
:S deze implicatie klopt maar.. wat is in godsnaam het verband tussen de linkere ongelijkheid en de uitspraak t aan de rechtere kant?
A ==> B
waarom moeten Negatief-A en B niet kloppen zodat de implicatie onjuist wordt?
stel A en B zijn onjuist, is het in dit geval onbeslisbaar of
A==B correct of incorrect is?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


mssn domme vraag maar kan iemand mij een uitleg geven over wat nu eigenlijk een limiet is?? alvast bedankt!


als je bijv een rij hebt 1/n
met n = {0,1,2,3,...}
lim (n --> inf) 1/n = 0
algemeen:
rij{An} n>0 --> lim (n --> inf) An = L
definitie is zoiets als: voor alle epsilon > 0 is er een N(epsilon) zodanig dat voor alle n > N(epsilon) geldt |L - An| < epsilon
je moet het maar zien dat je als je verder in de irj loopt je steeds dicht bij de limiet L komt en je dus voor n = oneindig willekeurig dicht bij L zit
met n = {0,1,2,3,...}
lim (n --> inf) 1/n = 0
algemeen:
rij{An} n>0 --> lim (n --> inf) An = L
definitie is zoiets als: voor alle epsilon > 0 is er een N(epsilon) zodanig dat voor alle n > N(epsilon) geldt |L - An| < epsilon
je moet het maar zien dat je als je verder in de irj loopt je steeds dicht bij de limiet L komt en je dus voor n = oneindig willekeurig dicht bij L zit
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Misschien dat je dan beter even kan vertellen waarom je het wilt weten. Is het uit interesse of is het voor je opleiding en wat is die opleiding dan.quote:Op maandag 24 januari 2005 11:56 schreef andre17 het volgende:
mssn domme vraag maar kan iemand mij een uitleg geven over wat nu eigenlijk een limiet is?? alvast bedankt!
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Bij een normaal verdeelde toevalsvariabele X = úx=50 en óx=5
ú=gemiddelde
ó=standaardafwijking.
A
Bereken in vier decimalen de kans dat een waarneming meer dan 4 van úx afwijkt.
B
We doen 30 waarnemingen en bereken de gemiddelde X.
Bereken in 4 decimalen nauwkeurig de kans dat X meer dan 3 van úx afwijkt.
=============
A kom ik op dit uit:
Z= (X - úx) / óx
z= X - 50 / 5
P(X wijkt meer dan drie af) = P(X<47) of P(X>53)
Dit is hetzelfde als
2*(P<47)
2*(47-50/5) = 2*(-0,6).
Terugzoeken geeft 0,5485.
Dit klopt ook..
opgave B is het probleem
Het gaat nu om gemiddelde waarden.. Wat is nou de regel hiervoor?
[ Bericht 77% gewijzigd door Skv op 24-01-2005 14:34:03 ]
ú=gemiddelde
ó=standaardafwijking.
A
Bereken in vier decimalen de kans dat een waarneming meer dan 4 van úx afwijkt.
B
We doen 30 waarnemingen en bereken de gemiddelde X.
Bereken in 4 decimalen nauwkeurig de kans dat X meer dan 3 van úx afwijkt.
=============
A kom ik op dit uit:
Z= (X - úx) / óx
z= X - 50 / 5
P(X wijkt meer dan drie af) = P(X<47) of P(X>53)
Dit is hetzelfde als
2*(P<47)
2*(47-50/5) = 2*(-0,6).
Terugzoeken geeft 0,5485.
Dit klopt ook..
opgave B is het probleem
Het gaat nu om gemiddelde waarden.. Wat is nou de regel hiervoor?
[ Bericht 77% gewijzigd door Skv op 24-01-2005 14:34:03 ]
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


Help
[ Bericht 12% gewijzigd door Skv op 24-01-2005 14:34:45 ]
[ Bericht 12% gewijzigd door Skv op 24-01-2005 14:34:45 ]
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


voor a zou ik nog even nakijken als ik jou was, want id opgave staat dat je 4 van ux afwijkt....quote:Op maandag 24 januari 2005 13:22 schreef Skv het volgende:
Bij een normaal verdeelde toevalsvariabele X = úx=50 en óx=5
ú=gemiddelde
ó=standaardafwijking.
A
Bereken in vier decimalen de kans dat een waarneming meer dan 4 van úx afwijkt.
B
We doen 30 waarnemingen en bereken de gemiddelde X.
Bereken in 4 decimalen nauwkeurig de kans dat X meer dan 3 van úx afwijkt.
=============
A kom ik op dit uit:
Z= (X - úx) / óx
z= X - 50 / 5
P(X wijkt meer dan drie af) = P(X<47) of P(X>53)
Dit is hetzelfde als
2*(P<47)
2*(47-50/5) = 2*(-0,6).
Terugzoeken geeft 0,5485.
Dit klopt ook..
opgave B is het probleem
Het gaat nu om gemiddelde waarden.. Wat is nou de regel hiervoor?
nu b
we moeten nu ook meenemen dat het een gemiddelde is van 30 trekkingen, de kans dat zo'n gemiddelde meer dan 3 van een gemiddelde(vd verdeling) afligt is natuurlijk kleiner dan dat 1 trekking meer dan 3 van een gemiddelde aflegt, je zou immers denken dat het gemiddelde van 30 trekkingen de afwijkingen positief en negatief compenseert
we gaan als volgt te werk
standaardafwijking = sigma = 5
gemiddelde = mu = 50
aantal trekkingen = n = 30
we nemen een X-gemiddeld waar
we moeten berekenen P(x<47)+P(x>53) = 2*P(x<47)
Z = wortel(n)*((X-gem - mu)/sigma) --> is N(0,1) verdeeld
invullen levert 5.48*((47-50)/5) = 5.48*3/5 = -3.29
opzoeken levert P(X>3.29) = 1- P(x <3.29) = 0.0005
0.0005*2 = 0.001 = 0.1%
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Ik heb het als volgt opgelost:
A klopt; had een typefoutje hierboven, het moet 3 afwijking zijn.
Oplossing A:
2*normalcdf(-10^99,47,50,5) = 0,548
Oplossing B: (ik wist dus niet dat je gemiddelde óx berekende door óx door wortel N te delen).
2*normalcdf(-10^99,47,50,5/(wortel 30)) = 0,0010
Klopt dit ook? antwoord is iig hetzelfde
A klopt; had een typefoutje hierboven, het moet 3 afwijking zijn.
Oplossing A:
2*normalcdf(-10^99,47,50,5) = 0,548
Oplossing B: (ik wist dus niet dat je gemiddelde óx berekende door óx door wortel N te delen).
2*normalcdf(-10^99,47,50,5/(wortel 30)) = 0,0010
Klopt dit ook? antwoord is iig hetzelfde
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


ja dat klopt, op de gr moet t zo, nu ik op de uni zit moet t echter weer met het tabellenboekje, de standaardafwijking wordt idd kleiner naarmate je meer trekkingen neemt in het gemiddelde, als je dat logisch vindt, dan gaat het goedquote:Op maandag 24 januari 2005 18:35 schreef Skv het volgende:
Ik heb het als volgt opgelost:
A klopt; had een typefoutje hierboven, het moet 3 afwijking zijn.
Oplossing A:
2*normalcdf(-10^99,47,50,5) = 0,548
Oplossing B: (ik wist dus niet dat je gemiddelde óx berekende door óx door wortel N te delen).
2*normalcdf(-10^99,47,50,5/(wortel 30)) = 0,0010
Klopt dit ook? antwoord is iig hetzelfde
"Winning is a funny thing, it's one of those rare commodities on earth that money cannot buy, until you called me!"


Wat studeer je dan, dat je dit snapt?
Moet ik dat iig niet gaan doen
bedankt iig
Moet ik dat iig niet gaan doen
bedankt iig
Ons soort mensen, trapt reeds jaren blij van zin, het vuile plebs de modder in.
Ons soort mensen, steunpilaar van vaderland en koningin.
Ons soort mensen, steunpilaar van vaderland en koningin.


Die eerste implicatie begrijp ik ook niet.quote:Op zondag 23 januari 2005 19:39 schreef achtbaan het volgende:
weer een vraagje over logica
nu over implicatie: 5+3>6 ==> pi is irrationeel
:S deze implicatie klopt maar.. wat is in godsnaam het verband tussen de linkere ongelijkheid en de uitspraak t aan de rechtere kant?
A ==> B
waarom moeten Negatief-A en B niet kloppen zodat de implicatie onjuist wordt?
stel A en B zijn onjuist, is het in dit geval onbeslisbaar of
A==B correct of incorrect is?
(Ik neem aan dat uje met onjuist False bedoelt en niet contingentie)
Stel A en B zijn onjuist, dan is A=>B waar, want False => X is True voor alle X. Het is namelijk zo dat een implicatie tautoloog is, zodra de 1-en van het linkerlid worden doorgegeven aan het rechterlid. Aangezien False uit enkel 0-en bestaat, worden deze automatisch doorgegeven.
Edit: Het kan ook zijn dat je bedoelt dat A en B in dit geval onjuist zijn, de regel blijft dan het zelfde alleen voor 1 rij uit de waarheidstabel. In dit tweede geval is het inderdaad onbeslisbaar of A=B waar is, in het eerste was dit overduidelijk wel het geval, daarom denk ik ook dat ik je verkeerd interpreteerde.
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!
Limburgs dierbaar oord!
Daar is mijn Vaderland,
Limburgs dierbaar oord!


oh ja, er staat per definitie van implicatie, dat je vanuit A en B de 'uitspraak' (B Of -A) krijgt.
in ieder geval, hoe moet je dit toepassen bij het bewijzen dat
(voor alle (x,y,z) uit R³) : x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
?
alvast bedankt
in ieder geval, hoe moet je dit toepassen bij het bewijzen dat
(voor alle (x,y,z) uit R³) : x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
?
alvast bedankt
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


laten we het doen zoals je typte:
x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
x+y+z=0 ==> |x-y|+y+x+y+x+y+x>=1/2(x+y+x+y)
==>|x-y|+3x+3y>=x+y
==> |x-y|>=-2x-2y
en dit klopt want |x-y|>=0 en -2x-2y<=0
zo bedoel je?
x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
x+y+z=0 ==> |x-y|+y+x+y+x+y+x>=1/2(x+y+x+y)
==>|x-y|+3x+3y>=x+y
==> |x-y|>=-2x-2y
en dit klopt want |x-y|>=0 en -2x-2y<=0
zo bedoel je?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


wanneer is er geen 'verlies van algemeengheid'? hoe zie je dat aan de nieuwe gelijkheden/ongelijkheden die je krijgt als je een bepaalde handeling(en) uitvoert op bepaalde wiskundige dingen?
There ain't no mountain high enough
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you
Ain't no valley low enough
Ain't no river wide enough
To keep me from getting to you


Deze redenering is correct als je haar van onder naar boven leest.quote:Op dinsdag 25 januari 2005 19:49 schreef achtbaan het volgende:
laten we het doen zoals je typte:
x+y+z=0 ==> |x-y|+|y-z|+|z-x|>=1/2 (|x|+|y|+|z|)
x+y+z=0 ==> |x-y|+y+x+y+x+y+x>=1/2(x+y+x+y)
==>|x-y|+3x+3y>=x+y
==> |x-y|>=-2x-2y
en dit klopt want |x-y|>=0 en -2x-2y<=0
zo bedoel je?


Er is geen verlies van algemeenheid als het algemene geval uit het speciale geval volgt waar je veronderstelt in te zitten. In dit geval speelt de symmetreische wijze waarop de variabelen in de formules aanwezig zijn daar een belangrijke rol in. Ook het feit dat er niets aan de waarheid van de formules verandert als je x,y,z vervangt door -x,-y,-z is hier van belang om te kunnen specialiseren.quote:Op dinsdag 25 januari 2005 19:51 schreef achtbaan het volgende:
wanneer is er geen 'verlies van algemeengheid'? hoe zie je dat aan de nieuwe gelijkheden/ongelijkheden die je krijgt als je een bepaalde handeling(en) uitvoert op bepaalde wiskundige dingen?


hoi ,
ik heb een vraagje over breuken vereenvoudigen (het is namelijk alweer zolang geleden voor mij )
ik moet de volgende breuken eereenvoudigen:
115 / 180e
325 / 180e
1200 / 180e
wat is nou de simpelse manier om dat te doen?
ik heb een vraagje over breuken vereenvoudigen (het is namelijk alweer zolang geleden voor mij )
ik moet de volgende breuken eereenvoudigen:
115 / 180e
325 / 180e
1200 / 180e
wat is nou de simpelse manier om dat te doen?


ha mn oude rekenmachine doet het automatisch dus dat probleem is opgelost nu zit ik met een ander probleem.
ik moet soommige dingen om rkenen in graden zoals:
1/3 pie rad
7/12 pie rad
2 rad
0,68 rad
die 1e 2 lukken me wel dat is gewoon 1/3 x 180
maar die wat geen pie rad is maar gewone rad kom ik niet uit?
ik moet soommige dingen om rkenen in graden zoals:
1/3 pie rad
7/12 pie rad
2 rad
0,68 rad
die 1e 2 lukken me wel dat is gewoon 1/3 x 180
maar die wat geen pie rad is maar gewone rad kom ik niet uit?


Dan reken je 2 om naar een breuk van pi en dan doe je dat maal 180?quote:Op woensdag 26 januari 2005 22:55 schreef BaggerUser het volgende:
ha mn oude rekenmachine doet het automatisch dus dat probleem is opgelost nu zit ik met een ander probleem.
ik moet soommige dingen om rkenen in graden zoals:
1/3 pie rad
7/12 pie rad
2 rad
0,68 rad
die 1e 2 lukken me wel dat is gewoon 1/3 x 180
maar die wat geen pie rad is maar gewone rad kom ik niet uit?
Dus x * (180/pi) = y


Mja, 2pi radialen=360 graden. Dus 1 radiaal is ca 57 graden (360/6,28). Nou moet t niet meer zo moeilijk zijn.
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071


Hoe bereken je de inhoud van een druppel met een doorsnede van 4 mm?
Geldt dan de regel pi * straal^2
Geldt dan de regel pi * straal^2
...drop it like it's hot...


ik zou zeggen opsplitsen in halve bol en kegel en de inhouden daarvan bij elkaar optellen
Fok! presents
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL
GOOD MOD, BAD MOD
starring Sizzler & Sidekick
nu in POL


Nee dat is de oppervlakte van een cirkelquote:Op zaterdag 29 januari 2005 12:38 schreef Nyluzzz het volgende:
Hoe bereken je de inhoud van een druppel met een doorsnede van 4 mm?
Geldt dan de regel pi * straal^2
Het volume van een bol wordt gegeven door 4 / 3 Pi r^3
"If i think, it all seems absurd to me; if i feel, it all seems strange; if i desire, he who desires is something inside of me." Fernando Pessoa - The Book of Disquiet
Wandelen in Noorwegen
Wandelen in Noorwegen