Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Stel dat x een geheel positief getal is. Merk op dat
Echter,
Dus
Anders zie ik de fout niet.
Normaliter kun je d(f(x)+g(x))/dx opvatten als d(f(x))/dx + d(g(x))/dx, ofwel termsgewijs differentiëren.quote:
[ Bericht 100% gewijzigd door MrRiot op 18-01-2014 15:37:12 ]
)Ie, mag dit zomaar?
[ Bericht 5% gewijzigd door Fsmxi op 18-01-2014 16:06:31 (Foutje in plaatje gefixed) ]
Alleen in dit geval is het geen som van een constant aantal termen, maar is het een som van een variabel aantal termen.quote:Op zaterdag 18 januari 2014 14:39 schreef Amoeba het volgende:
[..]
Normaliter kun je d(f(x)+g(x))/dx opvatten als d(f(x))/dx + d(g(x))/dx, ofwel termsgewijs differentiëren.
Eigenlijk staat er dat
Ah, inderdaad. Daarom is termsgewijs differentiëren hier niet toegestaan.quote:Op zaterdag 18 januari 2014 16:47 schreef freiss het volgende:
[..]
Alleen in dit geval is het geen som van een constant aantal termen, maar is het een som van een variabel aantal termen.
Eigenlijk staat er dat, wat natuurlijk onwaar is.
Dit kan inderdaad nietquote:Op zaterdag 18 januari 2014 16:05 schreef Fsmxi het volgende:
Is differentiëren over een som een commutatief iets? (Of hoe het precies heet, ben geen wiskundige
Ie, mag dit zomaar?
[ afbeelding ]
De fout is dat je identiteit alleen geldt voor een x ∈ N, maar dan kun je dus niet differentiëren naar x. Je zou hooguit een differentiequotiënt kunnen bepalen.quote:
Leuke truc:
Stel dat x een geheel positief getal is. Merk op dat
[snip bogus]
Toch moet ik toegeven dat ik zelf even raar zat te kijken
.
Mijn eerste intuïtie is 9, immers zijn er 9 vrijheidsgraden en in het algemeen heb je dan 9 vergelijkingen nodig om dit op te lossen. Maar dan is er nog die foutcorrectie, dus wellicht heb je aan 8 vergelijkingen voldoende.
Kan iemand dit nader toelichten?
Ik ga hier vanavond eens naar kijken.
't Is lineaire algebra over F11. De vector (c1, ..., c9) is bepaald op een scalaire vermenigvuldiging na. Je moet dus een 1-dimensionale deelruimte van een 9-dimensionale ruimte bepalen. Hiervoor zijn 8 vergelijkingen nodig.quote:
[ afbeelding ]
Mijn eerste intuïtie is 9, immers zijn er 9 vrijheidsgraden en in het algemeen heb je dan 9 vergelijkingen nodig om dit op te lossen. Maar dan is er nog die foutcorrectie, dus wellicht heb je aan 8 vergelijkingen voldoende.
Kan iemand dit nader toelichten?
Kun je dit iets nader toelichten?quote:
[..]
't Is lineaire algebra over F11. De vector (c1, ..., c9) is bepaald op een scalaire vermenigvuldiging na. Je moet dus een 1-dimensionale deelruimte van een 9-dimensionale ruimte bepalen. Hiervoor zijn 8 vergelijkingen nodig.
Mijn redenatie is als volgt: Je moet 8 c'tjes bepalen, en die andere kun je met behulp van een foutcorrectie vinden. Immers, de 'modular equation' is in staat om één fout te corrigeren.
Doe eerst maar even of het allemaal reële getallen zijn, in plaats van een modulaire vergelijking. Hoe zou je het dan aanpakken?quote:
[..]
Kun je dit iets nader toelichten?
Mijn redenatie is als volgt: Je moet 8 c'tjes bepalen, en die andere kun je met behulp van een foutcorrectie vinden. Immers, de 'modular equation' is in staat om één fout te corrigeren.
Volgens mij heb je dan wél 9 vergelijkingen nodig toch? Je zet ze allemaal in een matrix en een beetje vegen doet wonderen.quote:
[..]
Doe eerst maar even of het allemaal reële getallen zijn, in plaats van een modulaire vergelijking. Hoe zou je het dan aanpakken?
Die vergelijkingen eindigen allemaal op "=0".quote:
[..]
Volgens mij heb je dan wél 9 vergelijkingen nodig toch? Je zet ze allemaal in een matrix en een beetje vegen doet wonderen.
Ah, je stelt ze allemaal aan elkaar gelijk.quote:
[..]
Die vergelijkingen eindigen allemaal op "=0".
Wut?quote:
[..]
Ah, je stelt ze allemaal aan elkaar gelijk.
In de oorspronkelijke opgave staat ook overal "=0 (mod 11)".
Ik heb geen idee.quote:
[..]
Wut?
In de oorspronkelijke opgave staat ook overal "=0 (mod 11)".
Voor een vergelijking met n onbekenden geldt dat er normaliter n condities nodig zijn om dit op te lossen.. Verder ga ik even echt niet komen.
Ja, maar als al die vergelijkingen op "=0" eindigen, zal de oplossing in zo'n geval ook 0 zijn. En dat is hier natuurlijk niet de bedoeling.quote:
[..]
Ik heb geen idee.
Voor een vergelijking met n onbekenden geldt dat er normaliter n condities nodig zijn om dit op te lossen.. Verder ga ik even echt niet komen.
Aaah zo. Dit kan alleen als c1 t/m c9 allen gelijk 0 zijn, in een niet-modulaire omgeving.quote:
[..]
Ja, maar als al die vergelijkingen op "=0" eindigen, zal de oplossing in zo'n geval ook 0 zijn. En dat is hier natuurlijk niet de bedoeling.
Het grappige is dat als je modulo een priemgetal werkt, dat dat soort dingen dan ook gewoon gelden.quote:
[..]
Aaah zo. Dit kan alleen als c1 t/m c9 allen gelijk 0 zijn, in een niet-modulaire omgeving.
quote:
[..]
Het grappige is dat als je modulo een priemgetal werkt, dat dat soort dingen dan ook gewoon gelden.
Dus feitelijk is deze opgave een smadelijk harde grap aangezien c1 tm c9 gewoon allemaal nul moeten wezen?
Nee. Je hebt gewoon geen 9 vergelijkingen nodig.quote:
[..]
Dus feitelijk is deze opgave een smadelijk harde grap aangezien c1 tm c9 gewoon allemaal nul moeten wezen?
Dat had ik bij mezelf voordat ik deze vraag op het forum stelde ook al bedacht. Nu snap ik nog niet waarom mijn antwoord van 8 goed was, maar ongetwijfeld mijn uitleg fout.quote:
[..]
Nee. Je hebt gewoon geen 9 vergelijkingen nodig.
Als je 8 (lineair onafhankelijke) vergelijkingen hebt in 9 onbekenden, dan heb je een 1-dimensionale oplossingsruimte. Dat wil zeggen dat er 1 vector (c1, ..., c9) != 0 is, zodanig dat elke oplossing een veelvoud van die vector is. Dus als (1,2,3,4,5,6,7,8,9) een oplossing is, dan is (2,4,6,8,10,12,14,16,18) dat bijvoorbeeld ook. Meer dan dat kun je ook niet doen, want als alle vergelijkingen op "=0" eindigen, is er altijd sprake van een oplossingsruimte.quote:
[..]
Dat had ik bij mezelf voordat ik deze vraag op het forum stelde ook al bedacht. Nu snap ik nog niet waarom mijn antwoord van 8 goed was, maar ongetwijfeld mijn uitleg fout.
[ Bericht 19% gewijzigd door thabit op 20-01-2014 21:09:22 ]
Bedankt voor de uitleg, best verwarrend allemaal.quote:
[..]
Als je 8 (lineair onafhankelijke) vergelijkingen hebt in 9 onbekenden, dan heb je een 1-dimensionale oplossingsruimte. Dat wil zeggen dat er 1 vector (c1, ..., c9) != 0 is, zodanig dat elke oplossing een veelvoud van die vector is. Dus als (1,2,3,4,5,6,7,8,9) een oplossing is, dan is (2,4,6,8,10,12,14,16,18) dat bijvoorbeeld ook. Meer dan dat kun je ook niet doen, want als alle vergelijkingen op "=0" eindigen, is er altijd sprake van een oplossingsruimte.
(Het kan natuurlijk ook dat de oorsprong de oplossing is van een stelsel vergelijkingen die eindigen op "= 0"
)Maar dat is een triviale oplossing en tevens een veelvoud van iedere oplossing (c1, c2, ... c9).quote:
[..]
Bedankt voor de uitleg, best verwarrend allemaal.
(Het kan natuurlijk ook dat de oorsprong de oplossing is van een stelsel vergelijkingen die eindigen op "= 0"
Ja, maar geen oplossingsruimte.quote:
[..]
Maar dat is een triviale oplossing en tevens een veelvoud van iedere oplossing (c1, c2, ... c9).
Dat is waar. Maar als de oorsprong de oplossing is, dan is ieder bankbiljetnummer geldig.quote:
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
Je weet dat:quote:
[ afbeelding ]
[ afbeelding ]
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
En het argument (
Dan is het snel in te zien dat in jouw geval voor z3 geldt dat het argument pi is.
Oh ja, want het is e^arg natuurlijk. Stom dat ik dat niet zag.quote:
[..]
Je weet dat:
En het argument () van een complex getal c voldoet aan:
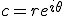
Dan is het snel in te zien dat in jouw geval voor z3 geldt dat het argument pi is.
Bedankt.Bedenk wel dat je zo niet alle oplossingen vindt, de uitwerking is niet volledig. Het argument van −1 is niet π maar π + 2kπ, k ∈ Z omdat in het complexe vlak het beeldpunt van 1 overgaat in het beeldpunt van −1 bij een rotatie om de oorsprong over een halve slag plus of min een geheel aantal slagen. Je krijgt dusquote:
[ afbeelding ]
[ afbeelding ]
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
z3 = (1/27)·e(π+2kπ)i, k ∈ Z
en dat geeft
z = (1/3)·e(⅓π+⅔kπ)i, k ∈ Z
Je kunt nu drie opeenvolgende gehele waarden voor k invullen (bijvoorbeeld −1, 0, 1), en dan krijg je drie verschillende oplossingen, die je zelf nog maar even in de vorm a+bi met a,b ∈ R moet herschrijven. De beeldpunten van de oplossingen vormen in het complexe vlak de hoekpunten van een gelijkzijdige driehoek en liggen op een cirkel met het middelpunt in de oorsprong en een straal 1/3.
[ Bericht 5% gewijzigd door Riparius op 21-01-2014 21:35:29 ]
Die screenshot van dat plaatje is dan ook maar een deel van de uitwerking.quote:
[..]
Bedenk wel dat je zo niet alle oplossingen vindt, de uitwerking is niet volledig. Het argument van −1 is niet π maar π + 2kπ, k ∈ Z omdat in het complexe vlak het beeldpunt van 1 overgaat in het beeldpunt van −1 bij een rotatie om de oorsprong over een halve slag plus of min een geheel aantal slagen. Je krijgt dus
z3 = (1/27)·e(π+2kπ)i, k ∈ Z
en dat geeft
z = (1/3)·e(⅓π+⅔kπ)i, k ∈ Z
Je kunt nu drie opeenvolgende gehele waarden voor k invullen (bijvoorbeeld −1, 0, 1), en dan krijg je drie verschillende oplossingen, die je zelf nog maar even in de vorm a+bi met a,b ∈ R moet herschrijven. De beeldpunten van de oplossingen vormen in het complexe vlak de hoekpunten van een gelijkzijdige driehoek en liggen op een cirkel met het middelpunt in de oorsprong en een straal 1/3.
Volgende stap was inderdaad die 2*k*pi. Maar ik begrijp nu wel wat beter waar ik mee bezig ben. Zoals gewoonlijk erg bedankt.Nu snap ik zijn uitwerking wel, maar waarom zou je zo moeilijk doen? Als je oneindig invult wordt die 1/x nul, sin(0) is nul, dus krijg je oneindig tot 0, waardoor het limiet 1 is? Lijkt me logisch toch?SPOILER: Uitwerking volgens de docent
Om dezelfde reden kun je ook niet zomaar zeggen dat om maar heel simpel en niet supergerelateerd voorbeeld te geven:
Oneindig/oneindig is niet altijd 1
lim(x->infinity) x^2/x = oneindig/oneindig maar deze limiet convergeert toch niet naar een getal.
zou dan ook
moeten zijn
Als mensen zonder al te veel nadenken beweren dat iets 'logisch' is, dan is dat doorgaans een indicatie dat het beweerde nu juist niet logisch is, en dat is hier ook het geval. Je doet me denken aan (beginnende) studenten die nogal eens schijnen te veronderstellen dat de limiet vanquote:
Ik moet het de limiet vanbepalen waarbij x naar oneindig gaat.
Nu snap ik zijn uitwerking wel, maar waarom zou je zo moeilijk doen? Als je oneindig invult wordt die 1/x nul, sin(0) is nul, dus krijg je oneindig tot 0, waardoor het limiet 1 is? Lijkt me logisch toch?SPOILER: Uitwerking volgens de docent[ afbeelding ]
voor n → ∞ gelijk is aan 1, immers (1 + 1/n) gaat naar 1, en elke macht van 1 is 1 toch? Maar je weet - hopelijk - wel dat dit niet klopt, de bedoelde limiet is namelijk e en ligt tussen 2 en 3.
Voor de limiet die je moet bepalen heb je de regel van l'Hôpital helemaal niet nodig, en wellicht is het beter voor je inzicht om eens te laten zien hoe je deze limiet langs elementaire weg aan kunt tonen. Voor 0 < θ < π/2 hebben we 0 < sin(θ) < θ < tan(θ) zodat we in ieder geval voor x > 1 hebben
en aangezien ln x > 0 voor x > 1 hebben we dan ook
Maar nu weet je ook dat ln x voor x > 1 de oppervlakte is onder de curve y = 1/x over het interval [1,x], zodat voor x > 1 geldt 0 < ln x < x−1 < x. Daarmee is voor x > 1 ook ln(x)/x = ln((√x)2)/x = 2∙ln(√x)/x < 2∙(√x)/x en dus
Combineren van deze ongelijkheden geeft voor x > 1
en aangezien 2/√x naar 0 gaat voor x → ∞ en ln(x)·sin(1/x) zit ingeklemd tussen 0 en 2/√x is het evident dat ln(x)·sin(1/x) ook naar 0 moet gaan voor x → ∞, ergo
De e-macht van ln(x)·sin(1/x) gaat dus naar e0 = 1 voor x → ∞, oftewel we hebben
QED
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 17:17:44 ]
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.
Als je het snapt probeer het ons eens uit te leggen.quote:
Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.
Kom je vanzelf op een bewijs.
Voortaan gewoon niet te simpel denken dus. Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').quote:
Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoordt tot een bewijs begrijp ik niet.
Alvast dank.
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
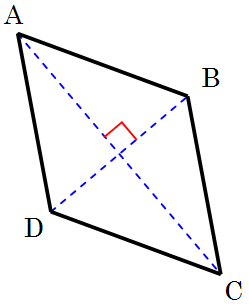
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wát je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
[ Bericht 4% gewijzigd door Riparius op 23-01-2014 06:38:17 ]
Concreet: Hoe bewijs je bijvoorbeeld
Als topologische ruimtes boven je niveau zijn, dan heb je wel een behoorlijk pittig voorbeeld gekozen. Bewijs eerst maar dat [0,1] compact is.quote:
Als je moet bewijzen dat een bepaalde set compact is met de (Finite) Open Cover definitie, hoe doe je dit? Ik snap wel hoe ik een tegenvoorbeeld moet bedenken en dit te noteren als een set niet compact is, maar het omgekeerde bewijzen lukt nog niet. Een zoektocht op Google heeft ook weinig opgeleverd, veelal hebben ze het over allerlei topologisch ruimtes en dat is nog boven mijn niveau.
Concreet: Hoe bewijs je bijvoorbeeldcompact is?
Of kan ik het beter laten zitten en maar Heine-Borel misbruiken?
O, maar als je dat eenmaal weet, dan hoef je alleen nog maar te bewijzen dat het product van twee compacte ruimten compact is.quote:
Dat bewijs staat in mijn boek en kan ik goed volgen. Is er misschien enig leesvoer dat relatief snel te begrijpen is zodat ik mijn voorbeeld kan oplossen?
Of kan ik het beter laten zitten en maar Heine-Borel misbruiken?
Verklaar je nader en leg uit! Ik geniet echt van dit soort wiskunde. Hopelijk ga ik het nog vaker tegenkomen tijdens Ectrie, maar ik vrees het ergste...quote:
[..]
O, maar als je dat eenmaal weet, dan hoef je alleen nog maar te bewijzen dat het product van twee compacte ruimten compact is.
Die verzameling W van jou is het product van twee intervallen: [-1,1] x [-1,1].quote:
[..]
Verklaar je nader en leg uit! Ik geniet echt van dit soort wiskunde. Hopelijk ga ik het nog vaker tegenkomen tijdens Ectrie, maar ik vrees het ergste...
Zeno is een beroemd kweker van schildpadden; door Zeno gekweekte schildpadden worden door liefhebbers in heel Nederland gekocht. Om gezonde schildpadden te kweken, doet Zeno veel onderzoek.
Zo heeft hij een recursieve formule bedacht om uit te rekenen hoe snel een populatie schildpadden zich uitbreidt:
un = un–1*2 + 4
hierin is u¬n het aantal schildpadden na n maanden.
Van een populatie is bekend dat in het begin (na 0 maanden dus) 4 schildpadden zijn
4 (3p) Gebruik de formule om te berekenen hoeveel schildpadden er zijn na 8 maanden. Beschrijf nauwkeurig hoe je te werk gaat.
Ik als wiskunde leek snap hier niets van. Hoe moet ik hier te werk gaan ?
@Thabit Zou je het misschien kunnen uitwerken? En misschien nog wel handiger, als je bijvoorbeeld een set
[ Bericht 14% gewijzigd door Novermars op 23-01-2014 21:56:14 ]
De un-1 is de populatie van de vorige maand waarmee je de huidige populatie kan berekenen. Om het aantal schildpadden na acht maanden te berekenen begin je met het invullen van de startpopulatie (dat zijn die vier schildpadden dus). Het antwoord wat daar uitkomt vul je in waar je eerst die 4 invulde, waardoor je het aantal schildpadden na 2 maanden weet. En dat tot je de populatie na 8 maanden weet.quote:
OPGAVE II Zeno de schildpaddenkweker
Zeno is een beroemd kweker van schildpadden; door Zeno gekweekte schildpadden worden door liefhebbers in heel Nederland gekocht. Om gezonde schildpadden te kweken, doet Zeno veel onderzoek.
Zo heeft hij een recursieve formule bedacht om uit te rekenen hoe snel een populatie schildpadden zich uitbreidt:
un = un–1*2 + 4
hierin is u¬n het aantal schildpadden na n maanden.
Van een populatie is bekend dat in het begin (na 0 maanden dus) 4 schildpadden zijn
4 (3p) Gebruik de formule om te berekenen hoeveel schildpadden er zijn na 8 maanden. Beschrijf nauwkeurig hoe je te werk gaat.
Ik als wiskunde leek snap hier niets van. Hoe moet ik hier te werk gaan ?
Bedankt ik snap het, was gewoon totaal niet logisch aan het nadenken.quote:
[..]
De un-1 is de populatie van de vorige maand waarmee je de huidige populatie kan berekenen. Om het aantal schildpadden na acht maanden te berekenen begin je met het invullen van de startpopulatie (dat zijn die vier schildpadden dus). Het antwoord wat daar uitkomt vul je in waar je eerst die 4 invulde, waardoor je het aantal schildpadden na 2 maanden weet. En dat tot je de populatie na 8 maanden weet.
Antwoordenmodel gaf het ook een beetje raar weer:
SPOILERFormule invoeren in de GR: nMin = 0, u(n) = u(n¬–1)*2 + 4
en u(nMin) = 4 2
u(8) = 2044 1
Ik snap dat antwoordenmodel ook niet. Je kan het wel via de GR berekenen, maar dan moet je met ans werken.quote:
[..]
Bedankt ik snap het, was gewoon totaal niet logisch aan het nadenken.
Antwoordenmodel gaf het ook een beetje raar weer:SPOILERFormule invoeren in de GR: nMin = 0, u(n) = u(n¬–1)*2 + 4
en u(nMin) = 4 2
u(8) = 2044 1
Het wordt natuurlijk pas echt een leuke opgave als je het aantal schildpadden na 100 maanden of zo moet berekenen. En nee, geen rekenmachines. Dan moet je dus een gesloten uitdrukking afleiden voor un.quote:
[..]
De un-1 is de populatie van de vorige maand waarmee je de huidige populatie kan berekenen. Om het aantal schildpadden na acht maanden te berekenen begin je met het invullen van de startpopulatie (dat zijn die vier schildpadden dus). Het antwoord wat daar uitkomt vul je in waar je eerst die 4 invulde, waardoor je het aantal schildpadden na 2 maanden weet. En dat tot je de populatie na 8 maanden weet.
Ja, maar denk niet dat hij daar al aan toe is.quote:
[..]
Het wordt natuurlijk pas echt een leuke opgave als je het aantal schildpadden na 100 maanden of zo moet berekenen. En nee, geen rekenmachines. Dan moet je dus een gesloten uitdrukking afleiden voor un.
Is trouwens best wel makkelijk vergeleken met de stof die hier normaal gesproken langs komt, je krijgt het zelfs bij wiskunde A. Of algemeen bewijzen dat elk gesloten interval [a,b] compact is.quote:
Je bedoelt?
@Thabit Zou je het misschien kunnen uitwerken? En misschien nog wel handiger, als je bijvoorbeeld een sethebt, hoe zou je het dan doen? Eerst bewijzen dat
en
compact zijn?
Het bewijs dat een product van twee compacte ruimten compact is, is ongetwijfeld met Google wel te vinden, dus ik weet niet in hoeverre het iets toevoegt om dat hier helemaal te gaan lopen uitspellen. Als je er zelf over na wilt denken, dan kan ik wel af en toe een hint geven.
Als je eenmaal weet dat producten van gesloten intervallen [a,b] compact zijn, dan is het tijd voor de volgende stelling: een gesloten deel van een compacte ruimte is compact. Bewijs die eerst maar; die is namelijk wat eenvoudiger.quote:
Inhomogene lineaire recursies bij wiskunde A? Leg jij iemand met alleen wiskunde A dan maar even uit hoe je hier op un = 2n+3 − 4 komt.quote:
[..]
Ja, maar denk niet dat hij daar al aan toe is.
Tot op een bepaald niveau, het moet natuurlijk niet de algebrakennis van A'ers overstijgen.quote:
[..]
Inhomogene lineaire recursies bij wiskunde A? Leg jij iemand met alleen wiskunde A dan maar even uit hoe je hier op un = 2n+3 + 4 komt.
Ik kan me herinneren dat ik heb geleerd hoe van je een recursieve formule een directe formule kan maken, kan dat kloppen? Ik weet eigenlijk niet meer zoveel van A.
Gaat 'm niet lukken. Volgens mij krijg je de inhomogene varianten niet eens bij wiskunde D.quote:
[..]
Inhomogene lineaire recursies bij wiskunde A? Leg jij iemand met alleen wiskunde A dan maar even uit hoe je hier op un = 2n+3 − 4 komt.
Ik haal dan termen door elkaar waarschijnlijk.quote:
[..]
Gaat 'm niet lukken. Volgens mij krijg je de inhomogene varianten niet eens bij wiskunde D.
Dat is juist, maar bij mijn weten geen inhomogene variant.quote:
[..]
Tot op een bepaald niveau, het moet natuurlijk niet de algebrakennis van A'ers overstijgen.
Ik kan me herinneren dat ik heb geleerd hoe van je een recursieve formule een directe formule kan maken, kan dat kloppen? Ik weet eigenlijk niet meer zoveel van A.
Waar had ik het over inhomogeen?quote:Op donderdag 23 januari 2014 22:15 schreef Amoeba het volgende:
[..]
Dat is juist, maar bij mijn weten geen inhomogene variant.
Mag ik gebruiken dat een set compact is iff gesloten en begrensd (aka Heine-Borel)? Of krijg ik dan een cirkelredenering omdat Heine-Borel leunt op het bewijs dat een gesloten subset compact is?quote:
[..]
Als je eenmaal weet dat producten van gesloten intervallen [a,b] compact zijn, dan is het tijd voor de volgende stelling: een gesloten deel van een compacte ruimte is compact. Bewijs die eerst maar; die is namelijk wat eenvoudiger.
Dan krijg je een cirkelredenering. Je wilt Heine-Borel immers bewijzen vanuit het basisgeval dat [a,b] compact is.quote:
[..]
Mag ik gebruiken dat een set compact is iff gesloten en begrensd (aka Heine-Borel)? Of krijg ik dan een cirkelredenering omdat Heine-Borel leunt op het bewijs dat een gesloten subset compact is?
Ik heb het bewijs maar opgezocht. Ik was wel goed op weg met hetgeen ik zelf bedacht had, maar ik blijf dit soort dingen moeilijk vinden om zelf te verzinnen zonder hints etc.quote:
[..]
Dan krijg je een cirkelredenering. Je wilt Heine-Borel immers bewijzen vanuit het basisgeval dat [a,b] compact is.
En als deze al eenvoudiger is, dan heb ik nog veel werk te verrichten :p
Het zou kunnen dat je dat geleerd hebt bij wiskunde A (maar het zal waarschijnlijk alleen om lineaire recurrentievergelijkingen gaan, of nog simpelere gevallen). Voor wat ingewikkeldere recurrenties worden vaak voortbrengende functies (bekender onder de Engelse term generating functions) gebruikt, een techniek waarbij je een polynoom met u0, u1, u2, ... als coëfficiënten gebruikt. Best een aparte techniek, maar vaak wel handig.quote:
[..]
Tot op een bepaald niveau, het moet natuurlijk niet de algebrakennis van A'ers overstijgen.
Ik kan me herinneren dat ik heb geleerd hoe van je een recursieve formule een directe formule kan maken, kan dat kloppen? Ik weet eigenlijk niet meer zoveel van A.
Voor de geinteresseerden: generatingfunctionology is een gratis pdf'je met een hele zooi informatie over voortbrengende functies (ik moet bekennen dat ik hem zelf nooit uitgelezen heb, maar zelfs alleen het eerste hoofdstuk bevat al erg veel informatie).
Als je de formule x0+x1+x2+...+xn=xn-1/(x+1) kent, kan je gewoon u1, u2, u3, u4, ... etc. uitschrijven (uitdrukken in u0) en kijken of je een patroon ziet. Een beproefde techniek, toegepast door vele beroemde wiskundigen
[ Bericht 13% gewijzigd door randomo op 23-01-2014 23:21:03 ]
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.
Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.quote:
[..]
Het zou kunnen dat je dat geleerd hebt bij wiskunde A (maar het zal waarschijnlijk alleen om lineaire recurrentievergelijkingen gaan, of nog simpelere gevallen). Voor wat ingewikkeldere recurrenties worden vaak voortbrengende functies (bekender onder de Engelse term generating functions) gebruikt, een techniek waarbij je een polynoom met u0, u1, u2, ... als coëfficiënten gebruikt. Best een aparte techniek, maar vaak wel handig.
Voor de geinteresseerden: generatingfunctionology is een gratis pdf'je met een hele zooi informatie over voortbrengende functies (ik moet bekennen dat ik hem zelf nooit uitgelezen heb, maar zelfs alleen het eerste hoofdstuk bevat al erg veel informatie).
Als je de formule x0+x1+x2+...+xn=xn-1/(x+1) kent, kan je gewoon u1, u2, u3, u4, ... etc. uitschrijven (uitdrukken in u0) en kijken of je een patroon ziet. Een beproefde techniek, toegepast door vele beroemde wiskundigen
Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.quote:
Ik heb de volgende opdracht:
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.
Voor lineare recursievergelijkingen is inderdaad wat eenvoudiger (er is niet voor niets een heel boek over geschreven), maar volgens mij zijn voortbrengende functies ook nuttig voor ingewikkeldere functies, en hebben ze meer functies dan alleen het oplossen van de recursievergelijking.quote:
[..]
Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...quote:
Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x²) dan moet je Stillwell, Mathematics and Its History, ³2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
[ Bericht 0% gewijzigd door Riparius op 24-01-2014 07:51:28 ]
Oh…quote:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x²) dan moet je Stillwell, Mathematics and Its History, ³2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Mooie post wel. Nog eens oprakelen dan maar.
Bedankt voor je antwoord.quote:
[..]
Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?
Gebruik de ε,δ definitie van de limiet om te laten zien dat limh→0 (f(1+h) − f(1))/h niet bestaat, dan heb je bewezen dat f niet differentieerbaar is in het punt x = 1. Verder wijst Thabit er terecht op dat je niet zomaar (impliciet of expliciet) aan mag nemen dat de afgeleide continu is in die punten waar je functie wel differentieerbaar is.quote:
[..]
Bedankt voor je antwoord.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 02:35:13 ]
Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.quote:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x²) dan moet je Stillwell, Mathematics and Its History, ³2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.
De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coëfficiënten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...quote:
[..]
Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.
Met voortbrengende functies kan je laten zien dat als de karakteristieke vergelijking kwadratisch is en een dubbel nulpunt heeft (dus van de vorm (x - c)2 = 0 is), een gesloten uitdrukking voor de recursie ak = kck-1a1 - (k - 1)cka0 is. Maar ik verwacht stiekem wel dat Riparius nog met een andere manier op de proppen komtquote:
[..]
De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coëfficiënten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...
Ik bedenk me nu pas dat je natuurlijk ook een kwadratische vergelijking kan hebben met alleen complexe nulpunten, dat is denk ik ook een moeilijkheid als je de methode van de karakteristieke vergelijking gebruikt (of niet? Ik denk er morgen misschien nog maar eens over na, het is inmiddels al half twee hier...)
Ik meen me ook een dergelijke uitdrukking te herinneren voor het oplossen van lineaire homogene differentiaalvergelijkingen met constante coëfficiënten. Als je een differentiaalvergelijking hebt van de vorm:
x'' = ax' + bx
kan je oplossingen van de vorm eλx veronderstellen, zodat je een karakteristiek polynoom krijgt:
λ2eλx = ac eλx + beλx
delen door eλx en alles naar de linkerkant brengen geeft:
λ2 - aλ - b = 0
Het idee is nu hetzelfde: vindt de twee oplossingen, door ze te combineren kan je een oplossing met de gewenste randvoorwaarde vinden. Ik meen me te herinneren (verbeter me als ik ernaast zit) dat als je een oplossing λ vindt met multipliciteit 2, je ipv van eλx, je xeλx en eλx als oplossingen vindt.
Ik blijf het allemaal een beetje mysterieus vinden...
Kan iemand me iets meer inzicht bijbrengen?[ Bericht 1% gewijzigd door randomo op 25-01-2014 10:31:31 ]
Zeer veel dank!!quote:
[..]
Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
[ afbeelding ]
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wát je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
Het is me een stuk duidelijker geworden door deze uitleg.
meestal
of
bedoeld?
Laten we eens uitgaan van een rij {un}, n∈ N0 met louter reële termen die aan een homogene lineaire tweede orde recursie met constante en reële coëfficiënten voldoet, en welquote:
Ik blijf het allemaal een beetje mysterieus vinden...
(1) a·un + b·un−1 + c·un−2 = 0
Hierbij moeten we a ≠ 0 en tevens c ≠ 0 veronderstellen, aangezien we anders geen tweede orde recursie hebben.
Zoals bekend kunnen we in beginsel gesloten uitdrukkingen vinden voor de algemene term un van rijen die aan het recursievoorschrift (1) voldoen door op zoek te gaan naar meetkundige rijen die aan dit voorschrift voldoen. Hebben we een meetkundige rij {un} met als eerste term u0 en reden λ, dan is
(2) un = u0·λn
Substitutie van (2) in geeft voor n > 1
(3) u0·λn−2(aλ2 + bλ + c) = 0
Nu is het duidelijk dat un = 0, i.e. een rij die uit louter nullen bestaat, een triviale oplossing is van het recursievoorschrift (1) en dat we daarom op grond van (2) zowel u0 ≠ 0 als λ ≠ 0 moeten veronderstellen om andere oplossingen naast deze triviale oplossing te vinden. Maar dan kan uitsluitend aan (3) worden voldaan als de uitdrukking tussen haakjes gelijk is aan nul, dus
(4) aλ2 + bλ + c = 0
Dit is de zogeheten karakteristieke vergelijking van het recursievoorschrift (1). We noemen het polynoom
(5) P(λ) = aλ2 + bλ + c
ook het karakteristieke polynoom van het recursievoorschrift (1). Nu is (4) een vierkantsvergelijking in λ, en zoals bekend wordt de aard van de nulpunten van P(λ) en daarmee van de oplossingen van (4) bepaald door de discriminant
(6) D = b2 − 4ac
van dit polynoom. We onderscheiden nu drie mogelijkheden.
1. D > 0. Nu heeft P(λ) twee verschillende reële nulpunten λ1 en λ2 en zijn de meetkundige rijen gedefinieerd door un = u0·λ1n en un = u0·λ2n twee (lineair onafhankelijke) oplossingen van (1). En omdat elke lineaire combinatie {cn} met cn = α·an + β·bn van twee rijen {an} en {bn} die voldoen aan (1) ook weer voldoet aan (1) krijgen we als algemene oplossing van het recursievoorschrift
(7) un = α·λ1n+ β·λ2n
waarin α en β willekeurige (reële) constanten zijn. Het is eenvoudig na te gaan dat (7) ook inderdaad de volledige oplossing geeft van het recursievoorschrift (1). Een rij die voldoet aan een tweede orde recursie ligt volledig vast als twee opeenvolgende termen van de rij zijn gegeven. Welnu, substitutie in (7) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ1 ≠ 0 en tevens λ2 ≠ 0, terwijl uit D ≠ 0 volgt dat λ1 ≠ λ2, zodat de determinant van het stelsel ongelijk is aan nul.
2. D < 0. Nu heeft P(λ) twee toegevoegd complexe nulpunten λ1 en λ2 maar de situatie verschilt niet wezenlijk van die voor D > 0. Ook nu geldt dat (7) de algemene oplossing geeft van het recursievoorschrift (1), en ook nu levert substitutie in (7) van twee opeenvolgende termen van een specifieke rij een stelsel van twee lineaire vergelijkingen in α en β met een unieke oplossing. Echter, niet alleen λ1 en λ2 maar ook α en β zijn nu in het algemeen (toegevoegd) complex, zodat het niet mogelijk is een gesloten algebraïsche uitdrukking voor de algemene term van de recursieve rij te geven zonder gebruik van complexe getallen, en dat terwijl alle termen van de rij zelf wel degelijk reëel zijn. Maar, zoals ik wel eens heb laten zien, is het in dit geval altijd mogelijk een goniometrische uitdrukking te geven voor algemene term van de rij zonder gebruik van complexe getallen.
3. D = 0. Nu heeft P(λ) één reëel nulpunt met multipliciteit 2, dat ik aan zal geven met λ0. Aangezien λ0 voldoet aan (4) is het duidelijk dat
(8) un = α·λ0n
met een willekeurige α in ieder geval een oplossing is van het recursievoorschrift (1). Maar het is evenzeer duidelijk dat (8) nu niet de volledige oplossing kan zijn van (1) omdat we bij het recursievoorschrift (1) de waarden van u0 en u1 steeds vrij kunnen kiezen, terwijl (8) alleen een oplossing biedt als u1 = λ0u0.
Een elegante methode om toch de volledige oplossing van (1) te verkrijgen als D = 0 berust op het gebruik van differentiaalrekening. Daarvoor hebben we de volgende stelling nodig:
Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.
Het bewijs van deze stelling gaat het eenvoudigst als we eerst even twee lemmata bewijzen.
Lemma 1. Als een niet-constant polynoom P(x) een enkelvoudig nulpunt x = x0 heeft, dan is P'(x0) ≠ 0.
Bewijs: volgens de factorstelling volgt uit P(x0) = 0 dat P(x) een factor (x − x0) bevat zodat P(x) = (x −x0)·Q(x). Aangezien x = x0 een enkelvoudig nulpunt is van P(x) kan het polynoom Q(x) geen verdere factoren (x − x0) bevatten zodat, wederom volgens de factorstelling, Q(x0) ≠ 0. De afgeleide van P(x) = (x −x0)·Q(x) is P'(x) = Q(x) + (x − x0)·Q'(x) zodat P'(x0) = Q(x0) + 0·Q'(x0) = Q(x0) ≠ 0, QED.
Lemma 2. Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1 dan heeft de afgeleide P'(x) een nulpunt x = x0 met een multipliciteit (m − 1).
Bewijs: aangezien P(x) een nulpunt x = x0 heeft met multipliciteit m > 1 is P(x) = (x − x0)m·Q(x) waarbij het polynoom Q(x) geen verdere factoren (x − x0) bevat zodat volgens de factorstelling Q(x0) ≠ 0. De afgeleide van P(x) = (x − x0)m·Q(x) is P'(x) = m·(x − x0)m−1·Q(x) + (x − x0)m·Q'(x) waarvoor we kunnen schrijven P'(x) = (x − x0)m−1·(m·Q(x) + (x − x0)·Q'(x)). Voor x = x0 is de factor (m·Q(x) + (x − x0)·Q'(x)) gelijk aan m·Q(x0) ≠ 0 zodat (m·Q(x) + (x − x0)·Q'(x)) volgens de factorstelling geen factor (x − x0) bevat en de multipliciteit van het nulpunt x = x0 van P'(x) dus gelijk is aan (m − 1), QED.
Het bewijs van bovenstaande stelling is nu uiteraard eenvoudig: heeft een niet-constant polynoom P(x) een nulpunt x = x0 met multipliciteit m > 1, dan geeft (herhaalde) toepassing van lemma 2 dat P(i)(x) voor i = 1 .. (m − 1) een nulpunt x = x0 heeft met een multipliciteit (m − i), zodat P(m−1)(x) een enkelvoudig nulpunt x = x0 heeft. En volgens lemma 1 is dan P(m)(x0) ≠ 0, QED.
Goed, nu de volledige oplossing van (1) als D = 0. Vermenigvuldigen we beide leden van (5) met λn−2, dan hebben we voor n > 1
(9) a·λn + b·λn−1 + c·λn−2 = λn−2·P(λ)
Differentiëren naar λ geeft nu
(10) a·n·λn−1 + b·(n−1)·λn−2 + c·(n−2)·λn−3 = (n−2)·λn−3·P(λ) + λn−2·P'(λ)
En beide leden vermenigvuldigen met λ geeft dan
(11) a·n·λn + b·(n−1)·λn−1 + c·(n−2)·λn−2 = (n−2)·λn−2·P(λ) + λn−1·P'(λ)
Nu is λ = λ0 een nulpunt van P(λ) met multipliciteit 2, zodat niet alleen P(λ0) = 0 maar tevens P'(λ0) = 0. Substutie van λ = λ0 in (11) geeft dus
(12) a·n·λ0n + b·(n−1)·λ0n−1 + c·(n−2)·λ0n−2 = 0
zodat we kunnen concluderen dat un = n·λ0n aan het recursievoorschrift (1) voldoet. Eerder vonden we al dat un = λ0n voldoet, zodat ook elke lineaire combinatie van deze oplossingen aan het recursievoorschrift voldoet en we dus krijgen
(13) un = (α + β·n)·λ0n
Het is weer gemakkelijk na te gaan dat deze oplossing inderdaad volledig is. Substitutie in (13) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ0 ≠ 0 zodat de determinant van het stelsel ongelijk is aan nul.
Het aardige van deze methode is dat deze eenvoudig is te generaliseren naar homogene lineaire recursies met constante coëfficiënten van hogere ordes. Heeft het karakteristieke polynoom P(λ) van zo'n hogere orde recursie van orde N namelijk een meervoudig nulpunt λ = λ0 met multipliciteit m, dan kun je door P(λ) te vermenigvuldigen met λn−N en daarna telkens om beurten te differentiëren en weer te vermenigvuldigen met λ gemakkelijk laten zien dat naast un = λ0n ook un = ni·λ0n voor i = 1 .. (m − 1) een oplossing geeft van de recursie. Zo geeft elk meervoudig nulpunt met een multipliciteit m dus precies m lineair onafhankelijke oplossingen.
Wil je niet gebruik maken van differentiaalrekening, dan is er in ieder geval voor tweede orde recursies waarbij de discriminant van de karakteristieke vergelijking gelijk is aan nul ook een goed bruikbare elementaire methode die bekend staat als de variatie van de constante. Het idee hierbij is dat je uitgaat van (8) maar dat je veronderstelt dat α niet constant is maar een functie van n. Dat wil dus zeggen dat je een rij {αn} zoekt zodanig dat
(14) un = αn·λ0n
een oplossing is van de recursie (1). Welnu, invullen van (14) in (1) geeft voor n > 1
(15) λ0n−2(a·αn·λ02 + b·αn−1·λ0 + c·αn−2) = 0
en aangezien λ0 ≠ 0 geeft dit
(16) a·αn·λ02 + b·αn−1·λ0 + c·αn−2 = 0
Nu weten we echter ook dat λ0 = −b/2a (en dus b ≠ 0 aangezien λ0 ≠ 0). Substitutie hiervan in (16) en gebruik maken van D = b2 − 4ac = 0 (en dus 4ac = b2) levert dan na wat herleiding
(17) αn − αn−1 = αn−1 − αn−2
In woorden: het verschil tussen elk tweetal opeenvolgende termen van de rij {αn} is constant. De rij {αn} is dus een willekeurige rekenkundige rij, en de algemene gedaante van αn is dus
(18) αn = α + n·β
waarbij α en β willekeurige constanten zijn. Substitutie van (18) in (14) geeft nu
(19) un = (α + n·β)·λ0n
en dit stemt geheel overeen met de eerder gevonden algemene oplossing (13).
That's all.
Iemand die mij vraag 12 kan uitleggen.
Wat snap je er niet aan? Wat snap je al wel?quote:
http://tinypic.com/r/11snpc2/5
Iemand die mij vraag 12 kan uitleggen.
Het gaat hier om een driehoek met een rechte hoek. Gegeven is de lengte van één van de zijdes die aan deze rechte hoek grenst (10). De andere zijde die aan de rechte hoek grenst wordt lengte a gesteld. Het gevraagde is de lengte van de langste zijde, dat is (op grond van de driehoeksongelijkheid) de schuine zijde van deze driehoek. Kun je hier iets mee? Hint: Pythagoras.
Als je dat doorhebt weet je waar de formule vandaan komt. De opdracht is simpeler: je moet drie keer een waarde voor a invullen in de formule.
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]
Top! Zoals gewoonlijk weer een uitstekende uitlegquote:
Die stelling was inderdaad uiteindelijk de missing link
Veel dank en hulde!quote:Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.
Dit is metawiskundig gezien wel een interessante vraag, want hoe definieer je de topologie op RxR? Enerzijds kun je de Euclidische metriek nemen en van daar uit werken. Anderzijds bestaat er ook een categorie-theoretische definitie van producten en kun je bewijzen dat producten bestaan in de categorie van topologische ruimten. De twee topologieën die je zo krijgt blijken hetzelfde te zijn, iets wat niet vanzelfsprekend is!quote:
Stel je hebt twee open sets, zeg maar. Is het Cartesian Product
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door Amoeba op 28-01-2014 21:48:45 ]
Je mist een accentje.quote:
Ik krijg koppijn van dit vraagstuk
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
[ afbeelding ]
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
Excuus, ik heb er eentje te veel gezet.quote:
http://www.win.tue.nl/~gprokert/opcoll14.pdf
Opgave 3
Ja die is gegarandeerd fout. Ik weet niet hoe ik de coëfficiënten van mijn expansie terugkrijg.quote:
Ik snap niet hoe je bij die laatste formule komt.
ak = 1, 3, 6*3, 9*6*3, 12*9*6*3...
Ja, dat wil zeggen:quote:
Er staat ck = -ck-3/k, dus er zal iets met faculteiten in de noemers moeten komen.
met
quote:
Maar niet in de eerste, die is namelijk 1.quote:
Nou, in elk van die factoren zit telkens een factor 3. Haal die er eerst maar eens uit.
1 is het lege product, dus die heeft geen factoren.quote:
[..]
Maar niet in de eerste, die is namelijk 1.
Okay.quote:
[..]
1 is het lege product, dus die heeft geen factoren.
Maar mijn berekening tot dusverre,
met
is juist?
Mijn vraag komt er echt op neer wat (ak) in gesloten vorm is..
3 1
3 3 2 1
4 3 3 3 3 2 1
dus uhm
[ Bericht 2% gewijzigd door Amoeba op 28-01-2014 22:20:29 ]
=>
Volgens Cauchy's Ratio Test convergeert y(x) op heel R, en dan nu die gesloten uitdrukking nog. Left for tomorrow I suppose.
Thabit, mijn dank.
Ik ben natuurlijk vergeten dat c0 ongelijk 0 is, anders is alles flauw.
[ Bericht 33% gewijzigd door Amoeba op 28-01-2014 22:37:57 ]
Jij bedoelt met ak iets anders dan in de oorspronkelijke opgave, en dat moet je natuurlijk niet doen. De oplossing van je DV is uiteraard y(x) = e−x³/3, dus het is gemakkelijk na te gaan wat de coëfficiënten van je machtreeks zouden moeten zijn.quote:
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...
Het gaat mis rond het punt 0. Kijk eens wat er gebeurt als je bijvoorbeeld x=1/n neemt.quote:
http://imgur.com/CS9i9Y4
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...
Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle xquote:
[..]
Het gaat mis rond het punt 0. Kijk eens wat er gebeurt als je bijvoorbeeld x=1/n neemt.
Je moet gewoon netjes de definities toepassen van puntsgewijze convergentie en uniforme convergentie. Puntsgewijze convergentie van je functierij {fn} naar een functie f* op R betekent dat je voor elke x ∈ R hebtquote:
[..]
Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
limn→∞ fn(x) = f*(x)
Bij a) word je gevraagd na te gaan dat dit inderdaad het geval is en f* te bepalen.
Uniforme convergentie van je functierij {fn} naar de bij a) bepaalde functie f* op R zou inhouden dat er voor elke ε > 0 een N ∈ N bestaat zodanig dat voor elke n > N en elke x ∈ R geldt
| fn(x) − f*(x) | < ε
Bij b) word je gevraagd aan te tonen dat dit niet het geval is voor jouw functierij {fn} en de bij a) bepaalde functie f*.
Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.
Fijne site, maar niet heus. Ik zie niet in waarom zoiets weggestopt moet worden achter een login, en mijn browser loopt ook nog eens vast op een script op de site wanneer ik een lijst probeer op te vragen van het cursusaanbod.quote:
Voor de liefhebbers, op Coursera is een course 'Functional Analysis' begonnen. https://class.coursera.org/functionalanalysis-001
Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.
https://www.dropbox.com/s(...)alysis-week01-V2.pdfquote:
[..]
Fijne site, maar niet heus. Ik zie niet in waarom zoiets weggestopt moet worden achter een login, en mijn browser loopt ook nog eens vast op een script op de site wanneer ik een lijst probeer op te vragen van het cursusaanbod.
Syllabus:
Week 1: Topology; continuity and convergence of a sequence in a topological space.
Week 2: Metric and normed spaces; completeness
Week 3: Banach spaces; linear continuous functions; weak topology
Week 4: Hilbert spaces; The Riesz representation theorem
Week 5: The Lax-Milgram Lemma
Week 6: Lp spaces; Fischer-Riesz
Week 7: Sobolev spaces
Week 8: Use of functional analysis for Partial Differential Equations
Zoiets, maar dit is nog wat te vaag (en ook twijfelachtig, de puntsgewijze limiet is overal 0 dus je hebt wel continuïteit). Mijn punt was eigenlijk: voordat je een bewijs gaat opstellen wil je eerst kijken naar wat er (in dit geval) misgaat. Als je eenmaal geïdentificeerd hebt dat het rond x=0 misgaat (wat je dus kan inzien door x=1/n in te vullen), kan je een rigoureus bewijs geven.quote:
[..]
Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
Neem epsilon = sin(1)/e. Laat N in N willekeurig zijn. Neem n=N en x=1/n, dan |f_n(x)-0|>= epsilon. Klaar.
quote:
[..]
Je moet gewoon netjes de definities toepassen van puntsgewijze convergentie en uniforme convergentie. Puntsgewijze convergentie van je functierij {fn} naar een functie f* op R betekent dat je voor elke x ∈ R hebt
limn→∞ fn(x) = f*(x)
Bij a) word je gevraagd na te gaan dat dit inderdaad het geval is en f* te bepalen.
Uniforme convergentie van je functierij {fn} naar de bij a) bepaalde functie f* op R zou inhouden dat er voor elke ε > 0 een N ∈ N bestaat zodanig dat voor elke n > N en elke x ∈ R geldt
| fn(x) − f*(x) | < ε
Bij b) word je gevraagd aan te tonen dat dit niet het geval is voor jouw functierij {fn} en de bij a) bepaalde functie f*.
Ah natuurlijk je moet gewoon de logische ontkenning van de definitie bewijzen, bedankt beiden!quote:
[..]
Zoiets, maar dit is nog wat te vaag (en ook twijfelachtig, de puntsgewijze limiet is overal 0 dus je hebt wel continuïteit). Mijn punt was eigenlijk: voordat je een bewijs gaat opstellen wil je eerst kijken naar wat er (in dit geval) misgaat. Als je eenmaal geïdentificeerd hebt dat het rond x=0 misgaat (wat je dus kan inzien door x=1/n in te vullen), kan je een rigoureus bewijs geven.
Neem epsilon = sin(1)/e. Laat N in N willekeurig zijn. Neem n=N en x=1/n, dan |f_n(x)-0|>= epsilon. Klaar.
10^(2*logD)
(10^logD)2
Ik snap niet hoe het kan dat het eerst keer 2 is en vervolgens tot de macht 2. Is er misschien een tussenstap gedaan?
Weet je zeker dat de tweede regel niet 10log(D^2) moet zijn? xlog(y) is immers log(y^x)quote:
In een deel van de uitwerking van een som staat dit:
10^(2*logD)
(10^logD)2
Ik snap niet hoe het kan dat het eerst keer 2 is en vervolgens tot de macht 2. Is er misschien een tussenstap gedaan?
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
| 1 2 3 4 5 6 7 8 | D=b^2-4ac a = p b = p+2 c = 3 D = (p+2)(p+2)-4*p*3 D = p^2+4p+4- 12p D = p^2-8p+4 |
| 1 2 | D = b^2 - 4ac D = 64-16 = 48 |
Invullen van bovenstaande toegepaste ABC formule geeft:
| 1 | p = (64+sqrt{48})/2 v p = (64-sqrt{48})/2 |
Maarfijn, nu loop ik vast. Ik zou zeggen dat het antwoord onderstaand zou zijn:
| 1 | (64+sqrt{48})/2 < p < (64-sqrt{48})/2 |
| 1 | 0 < p < (64-sqrt{48})/2 v p > (64+sqrt{48})/2 |
Ik hoop dat het enigszins duidelijk en overzichtelijk was, en dat iemand mij zou kunnen helpen. Tips over hoe de volgende keer beter een vraag te stellen natuurlijk ook altijd welkom!
Wat je hier doet klopt niet, en de rest van je uitwerking dus ook niet. De discriminant is afhankelijk van p, en daarmee een functie van p. Maar hier doe jij opeens alsof de discriminant een constante waarde heeft, maar dit is de discriminant van de vierkantsvergelijking in p, en dat is wat anders. Je kunt een index p gebruiken om aan te geven dat de discriminant van je oorspronkelijke kwadratische veelterm afhangt van p, dusquote:
Ik ga in mei een staatsexamen wiskunde B VWO doen waarin ik mij voorbereid d.m.v. de Getal en Ruimte reeks. Dit is mijn eerste post hier, en ik heb zo'n 10 minuten geprobeerd mijn functie op te stellen met behulp van de Equation Editor maar krijg het helaas niet voor elkaar. Nu loop ik vast op het volgende vraagstuk:
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
[ code verwijderd ]
Tot hier volg ik het helemaal. Maar nu gebeurt er het volgende in de uitwerkingen: Op deze discriminant wordt de ABC-formule weer toegepast om de nulpunten van p te vinden. Oke, kan ik me nog in vinden. Echter, deze wordt weer als volgt genoteerd.
[ code verwijderd ]
Vraag 1: Zou het toegestaan zijn om het zo te noteren? Ik zou namelijk wel inzien dat dit verwarrend is omdat we twee keer een discriminant benaderen.
Dp = p2 − 8p + 4
Je bepaalt nu eerst de waarden van p waarvoor geldt Dp = 0, zodat je vervolgens een tekenschema kunt maken van Dp als functie van p. Je vindt dan dat Dp > 0 voor p < 4 − 2√3 ∨ p > 4 + 2√3.
Voor de eerste opgave zijn de voorwaarden p > 0 ∧ Dp > 0 en dat is het geval voor 0 < p < 4 − 2√3 ∨ p > 4 + 2√3.
Verder: gebruik geen code tags als je daar toch niets zinnigs mee doet, dit maakt het quoten van specifieke passages namelijk onnodig lastig. Gebruik Unicode of HTML entities of TeX.
Die tweede discriminant heb je helemaal niet nodig. (als in apart definiëren)quote:
Gegeven zijn de functies
[formule]Fp(x) = px^2 + (p+2)x + 3[/formule]
Bereken exact de waarden van p waarvoor
a)Fp een negatief minimum heeft
b)Fp een positief maximum heeft
Ik hoop dat de vraagstelling duidelijk is. Zover kom ik:
a) Negatief minimum voor p>0 (want dan dalparabool) en D>0
[ code verwijderd ]
Tot hier volg ik het helemaal. Maar nu gebeurt er het volgende in de uitwerkingen: Op deze discriminant wordt de ABC-formule weer toegepast om de nulpunten van p te vinden. Oke, kan ik me nog in vinden. Echter, deze wordt weer als volgt genoteerd.
[ code verwijderd ]
Vraag 1: Zou het toegestaan zijn om het zo te noteren? Ik zou namelijk wel inzien dat dit verwarrend is omdat we twee keer een discriminant benaderen.
Daarnaast als je alleen D opschrijft is het natuurlijk niet duidelijk.
Je mag echter ook Nederlands gebruiken.
En zoals Riparius zei een subscript gebruiken, of een totaal ander symbool. Als je maar duidelijk maakt wat het symbool is.
En dat antwoordenboek klopt volgens mij niet, tenzij 64/2 opeens gelijk is aan 4.
Dat 64/2 zal mijn fout zijn, geen idee hoe ik er bij kom, aangezien er in het boek gewoon 8 staat. Zal het om wat voor reden dan ook gekwadrateerd hebben. Afijn, erg bedankt
Ik denk eerder dat je nog met die 64 in je hoofd zat van je berekening van de discriminant van je vierkantsvergelijking in p. Maar, als ik je een tip mag geven: gebruik niet de abc-formule als dat niet echt nodig is. Je kunt die vierkantsvergelijking in p ook gemakkelijk oplossen via kwadraatafsplitsing, zodat je hier geen discriminant op had hoeven schrijven:quote:
Riparius en t4rt4rus enorm bedankt voor jullie inbreng, het is me een stuk duidelijker geworden! Als ik nog ergens een keer mee zit weet ik waar ik moet zijn.
Dat 64/2 zal mijn fout zijn, geen idee hoe ik er bij kom, aangezien er in het boek gewoon 8 staat. Zal het om wat voor reden dan ook gekwadrateerd hebben. Afijn, erg bedankt
p2 − 8p + 4 = 0
(p − 4)2 − 16 + 4 = 0
(p − 4)2 = 12
p − 4 = 2√3 ∨ p − 4 = −2√3
p = 4 + 2√3 ∨ p = 4 − 2√3
Ik hoop dat je bedoelt dat het juist overzichtelijker is ...quote:
Ik zie wat je doet ja, oogt een stuk sneller, eenvoudiger, en minder overzichtelijk. Ik zal er op letten, bedankt!
Ik moet over een week een verslag voor natuurkunde inleven over twee vragen die zij heeft gesteld, Maar ik weet niet hoe ik dat allemaal moet berekenen.
Dit zijn de twee vragen die ik heb uitgevoerd:
1. Bepaling van de soortelijke warmte van een metaal.
Die 200 Ml water in de joulemeter (C = 60 J/ 'C). Roer 1 Min en meet daarna de begin- temperatuur. Breng een blokje metaal van 200 gram en 100 'C in de joulemeter. Roer totdat de temperatuur niet meer veranderd. Meet de eind- temperatuur.
Bereken de soortelijke warmte van het metaal. Zoek in de BINAS op welk metaal het is.
Water zonder metaal: 19 'C
Water met Metaal: 25 'C
2. Bepaling van de massa van een blokje ijzer.
Deo 200 Ml water in de joulemeter (C = 60 J/ 'C). Roer 1 Min en meet daarna de begin- temperatuur. Breng een blokje ijzen van 100 'C in de joulemeter. Roer totdat de temperatuur niet meer verandert. Meet de eind- temperatuur.
Bereken de massa van het blokje ijzer.
Water zonder ijzer: 19 'C
Water met ijzer: 29'C
Formules die we hebben gekregen:
(met * bedoel ik "keer")
Q = M * c * delta T
Q = C * delta T
Q op = Q af
Kan iemand met helpen met die berekening?
Ja, maar ik doe het niet. Maak eerst maar eens een fatsoenlijke post en plaats die in het juiste topic, dus niet hier. Als je zoveel belachelijke typo's in je post laat staan, dan geef je impliciet al aan dat je er geen enkele moeite voor wenst te doen. Geef in je herziene post duidelijk aan wat je zelf al hebt geprobeerd en waarom je niet verder komt of waarom je denkt dat de verkregen uitkomsten niet kunnen kloppen.quote:
Kan iemand met helpen met die berekening?
Hij stond ook al in het beta overige topic, alleen had meneer geen geduld.quote:
[..]
Ja, maar ik doe het niet. Maak eerst maar eens een fatsoenlijke post en plaats die in het juiste topic, dus niet hier. Als je zoveel belachelijke typo's in je post laat staan, dan geef je impliciet al aan dat je er geen enkele moeite voor wenst te doen. Geef in je herziene post duidelijk aan wat je zelf al hebt geprobeerd en waarom je niet verder komt of waarom je denkt dat de verkregen uitkomsten niet kunnen kloppen.
Opgave 4
Even wat notatie, die A met een streep is de kleinst mogelijke verzameling van A die gesloten is, d.w.z. de afsluiting van A. - A met een open rondje erboven is het inwendige van A. dA staat voor de rand van A.
Ik heb een 'bewijs' geschreven. In het kort laat ik zien dat z in 3 mogelijke deelverzamelingen van Rd kan zitten, en dat voor 2 deelverzamelingen geldt dat dist(z,A) = 0 en voor die andere laat ik zien dat die afstand altijd groter is dan 0. Op basis van die 3 zaken volgt dan de bewering.
Vooral bij de tweede deelverzameling dA weet ik niet zeker of dit bewijs wiskundig juist is. M.a.w. ik weet niet zeker hoe ik dat mathematisch juist opschrijf.. Iemand die daar iets over kan zeggen?
Hier mijn bewijs:
Misschien moet ik het anders verwoorden:
dist(z2, x~) < epsilon
=> dist(z2, x~) -> 0
moet ik opschrijven
| z2 - x~ | < epsilon
En omdat dist(z2, x~) het infimum van die verzameling is geldt:
dist(z2, x~) = 0?
[ Bericht 4% gewijzigd door Amoeba op 13-02-2014 00:13:53 ]
Het antwoord op 2c is: -3
http://i57.tinypic.com/8wh24l.png
Tip: kijk eens goed naar de grenzen van de integralen in de opdracht en dan naar die bij de vraag zelf.quote:
Hey kan iemand me met bijvoorbeeld vraag 2c helpen :
Het antwoord op 2c is: -3
http://i57.tinypic.com/8wh24l.png
nee sorry ik kom er niet uit.. misschien iets met 4-7 = -3 ?quote:
[..]
Tip: kijk eens goed naar de grenzen van de integralen in de opdracht en dan naar die bij de vraag zelf.
Weet je wel wat een integraal voorstelt? Wat je daarmee uitrekent?quote:
[..]
nee sorry ik kom er niet uit.. misschien iets met 4-7 = -3 ?
De oppervlakte onder een grafiek, de grenzen geven de grenzen van de x-as waarbinnen de oppervlakte wordt uitgerekend.. de rest van de sommen vind ik verder prima te doen hoor.. alleen voor opgave 2 staat nergens echt duidelijk uitgelegd in t boek ..quote:
[..]
Weet je wel wat een integraal voorstelt? Wat je daarmee uitrekent?
Als je dat begrijpt is de som heel simpel. Je wil de oppervlakte weten op het interval 4,6 en je weet de oppervlaktes op de intervallen 1,4 en 1,6. De rest is heel simpel (en heb je hierboven ook al goed gegoktquote:
[..]
De oppervlakte onder een grafiek, de grenzen geven de grenzen van de x-as waarbinnen de oppervlakte wordt uitgerekend.. de rest van de sommen vind ik verder prima te doen hoor.. alleen voor opgave 2 staat nergens echt duidelijk uitgelegd in t boek ..
)Aha dankjewel ! dan snap ik ze nu allemaal behalve 2e.. ik gok weer iets op 5*4 + 9 = 29 .. alleen t zou mij logisch lijken om dit te doen: 5+4 = 9quote:
[..]
Als je dat begrijpt is de som heel simpel. Je wil de oppervlakte weten op het interval 4,6 en je weet de oppervlaktes op de intervallen 1,4 en 1,6. De rest is heel simpel (en heb je hierboven ook al goed gegokt
Hint:quote:
[..]
Aha dankjewel ! dan snap ik ze nu allemaal behalve 2e.. ik gok weer iets op 5*4 + 9 = 29 .. alleen t zou mij logisch lijken om dit te doen: 5+4 = 9
ja daar liep ik vast.. doe iets fout :quote:
(integraal op interval 1 tot 6) 5 dx + (integraal op interval 1 tot 6) f(x) dx
Dat klopt gewoon. Dat eerste deel kun je dan volgens de normale integratieregels oplossen, dat tweede deel is gegeven, dus dat weet je ook.quote:
[..]
ja daar liep ik vast.. doe iets fout :
(integraal op interval 1 tot 6) 5 dx + (integraal op interval 1 tot 6) f(x) dx
Aha, wordt dus dan: (6 * 5) - 5 = 25.quote:Op dinsdag 18 februari 2014 11:50 schreef Alrac4 het volgende:
[..]
Dat klopt gewoon. Dat eerste deel kun je dan volgens de normale integratieregels oplossen, dat tweede deel is gegeven, dus dat weet je ook.
Dat eerste deel wel ja. En dan nog +4 van het tweede deel en je bent erquote:
[..]
Aha, wordt dus dan: (6 * 5) - 5 = 25.
Ja, thankss !quote:
[..]
Dat eerste deel wel ja. En dan nog +4 van het tweede deel en je bent er
Het gaat om het volgende; ik moet groei van 16% uitsmeren over vier periodes. Iets zegt mij dat een groei van 16% over een jaar niet hetzelfde is als een groei van 4% per kwartaal. Want:
1.16 is niet hetzelfde als 1 x 1.044 is niet hetzelfde. Of wel?
In ieder geval, hoe doe ik dat dan?
Die laatste zin klopt inderdaad, kan je uit die laatste vergelijking halen wat het wel zou moeten zijn?quote:
Het gaat om het volgende; ik moet groei van 16% uitsmeren over vier periodes. Iets zegt mij dat een groei van 16% over een jaar niet hetzelfde is als een groei van 4% per kwartaal. Want:
1.16 is niet hetzelfde als 1 x 1.044 is niet hetzelfde. Of wel?
.quote:Op woensdag 19 februari 2014 16:54 schreef JAM het volgende:
Als ik dat zou kunnen, dan had ik het niet gevraagd.
Dus 16% per jaar is 3.78% per kwartaal
quote:
[..]
Dus 16% per jaar is 3.78% per kwartaal
. 3. Dank. .3?quote:
Typ dan gewoon ♥quote:Op donderdag 20 februari 2014 11:03 schreef JAM het volgende:
Ja, daar stond eerst. <3. Da bleek geen hartje te zijn.
Hint: HTML Entities.
met a = (1,2,1,1,2) en b = (1,2,2,2,1).
A(a) = (2,4,3,3,3) = c en A(b) = (5,10,6,6,9) = d
a) Laat zien W = <a,b> is een invariante deelruimte voor A: W → W
Goed, simpel c = a+b en d = 4a+b, toppie. Dus iedere lineaire combinatie van c en d zit weer in W, zo invariant als maar wezen kan.
b) Bepaal de eigenwaarden en eigenruimten van W.
De matrix Aw wordt dan gegeven door
Eigenwaarden: λ1 = 3, λ2 = -1 zijn de nulpunten van het karakteristiek polynoom. De bijbehorende eigenruimten zijn dan
Eλ1 = < (2,1) >
Eλ2 = < (-2,1) >
De hoeveelheid rekenwerk is hiervoor niet zo belangrijk, Mathematica geeft mijn resultaat groen licht, dus beland ik bij opgave c. Mocht ik toch fouten maken, vandaar mijn toelichting tot dit alles.
c) Laat zien dat W een basis heeft bestaande uit eigenvectoren. Geef ook de bijbehorende matrix.
Maar hier loopt het spaak.. Ik heb een basis voor W die een vlak in R5 omvat, met de reeds berekende eigenruimten gaat het dan mis. Ik moet dus 2 eigenvectoren hebben met 5 componenten, anders is het geen basis voor W. Toch?
[ Bericht 1% gewijzigd door Amoeba op 21-02-2014 22:44:28 ]
A is een lineaire afbeelding en daar hoort een matrix bij. Ik moet dus een basis van eigenvectoren verzinnen voor die invariante deelruimte W en vervolgens de diagonaalmatrix opstellen.quote:
Heb je (c) niet eigenlijk al bij (b) opgelost? Wat wordt er met "bijbehorende matrix" bedoeld? De definitie daarvan is mij niet duidelijk.
[ Bericht 6% gewijzigd door Amoeba op 23-02-2014 16:50:52 ]
Maar je hebt de eigenwaarden en eigenvectoren al bij (b) uitgerekend, dus wat valt er hier dan verder nog te doen?quote:
[..]
A is een lineaire afbeelding en daar hoort een matrix bij. Ik moet dus een basis van eigenvectoren verzinnen voor die invariante deelruimte W en vervolgens de diagonaalmatrix opstellen.
Ik denk trouwens niet dat het om de diagonaalmatrix gaat. Maar die eigenvectoren hebben ieder 2 componenten, terwijl W een vlak is in de R^5 (dus 5 componenten).quote:Op zondag 23 februari 2014 16:50 schreef thabit het volgende:
[..]
Maar je hebt de eigenwaarden en eigenvectoren al bij (b) uitgerekend, dus wat valt er hier dan verder nog te doen?
Ik snap dat niet. Of moet ik A: W -> W zien als R^2 -> R^2?
Ja.quote:
[..]
Of moet ik A: W -> W zien als R^2 -> R^2?
Ah okay, dan snap ik het.quote:
Dank.
. Vriendin heeft besloten Facebook te onderzoeken voor der studie en komt op de volgende 2 vragen uit. 1) Hoe reken ik het maximaal aantal connecties uit bij X aantal vrienden? Wat we zelf gevonden hebben is het volgende http://www.wisfaq.nl/showfaq3.asp?Id=18443. Maar hoe dit nu exact moet
?2) Hoe reken ik het aantal realistische connecties uit? Bijvoorbeeld aantal vrienden is X en gemiddeld aantal gemeenschappelijke vrienden is Y.
De laatste keer dat ik rekenwerk als dit had was ik 16 dus het is allemaal diep diep weggezakt
. Een kip en klaar antwoord is niet direct nodig (zal wel handig zijn). Verwijzing naar een goede bron zou ook tof zijn. We zien door de bomen het bos niet meer echtWat bedoel je met connecties? Bedoel je daarmee dat als je een collectie van X mensen hebt, en iedereen is met elkaar bevriend, hoeveel relaties dit dan zijn?quote:
Tis vast een makkelijk vraag voor de wiskundehelden maar ik kom er zelf niet uit
1) Hoe reken ik het maximaal aantal connecties uit bij X aantal vrienden? Wat we zelf gevonden hebben is het volgende http://www.wisfaq.nl/showfaq3.asp?Id=18443. Maar hoe dit nu exact moet
2) Hoe reken ik het aantal realistische connecties uit? Bijvoorbeeld aantal vrienden is X en gemiddeld aantal gemeenschappelijke vrienden is Y.
De laatste keer dat ik rekenwerk als dit had was ik 16 dus het is allemaal diep diep weggezakt
Ja, dat bedoel ik exact. 2 mensen is maximaal 1 connectie. 3 mensen is maximaal 3 connecties. 4 connecties is maximaal 6 connecties.quote:
[..]
Wat bedoel je met connecties? Bedoel je daarmee dat als je een collectie van X mensen hebt, en iedereen is met elkaar bevriend, hoeveel relaties dit dan zijn?
En dan zie ik een A-B connectie hetzelfde als een B-A connectie.
aantal connecties = [N*(N-1)]/2quote:
[..]
Ja, dat bedoel ik exact. 2 mensen is maximaal 1 connectie. 3 mensen is maximaal 3 connecties. 4 connecties is maximaal 6 connecties.
En dan zie ik een A-B connectie hetzelfde als een B-A connectie.
waar N is het aantal vrienden
Voor 3 is het dus: 3*2/2 = 3
Voor 4 is het dus: 4*3/2 = 6
Voor 239 is het dus: 239*238/2 = 28441
Baas, nu ik hem lees is die ook direct volstrekt logischquote:
[..]
aantal connecties = [N*(N-1)]/2
waar N is het aantal vrienden
Voor 3 is het dus: 3*2/2 = 3
Voor 4 is het dus: 4*3/2 = 6
Voor 239 is het dus: 239*238/2 = 28441
. Heb je ook nog antwoord op mijn volgende vraag? Stel je voor dat het gemiddeld aantal gemeenschappelijk vrienden 25 is. Hoeveel connecties zijn er dan? Bij bij bijvoorbeeld 200 vrienden?
Je zult je vraag wat beter moeten formuleren. Je bekijkt een groep met 200 mensen die alleen connecties binnen die groep hebben? En je geeft alleen het gemiddelde aantal gemeenschappelijke vrienden, maar dat is wellicht niet genoeg informatie om tot een eenduidig antwoord te komen.quote:
[..]
Baas, nu ik hem lees is die ook direct volstrekt logisch
Heb je ook nog antwoord op mijn volgende vraag? Stel je voor dat het gemiddeld aantal gemeenschappelijk vrienden 25 is. Hoeveel connecties zijn er dan? Bij bij bijvoorbeeld 200 vrienden?
Wat je ook precies bedoelt, het zal waarschijnlijk een lastige vraag zijn. Maar het is altijd goed om eerst het probleem helder te formuleren. Bullshit in = bullshit out.
Ik zal morgen ff aan der vragen, nu ik het zo lees besef ik mezelf ook dat het op meerder manieren geïnterpreteerd kan worden.quote:
[..]
Je zult je vraag wat beter moeten formuleren. Je bekijkt een groep met 200 mensen die alleen connecties binnen die groep hebben? En je geeft alleen het gemiddelde aantal gemeenschappelijke vrienden, maar dat is wellicht niet genoeg informatie om tot een eenduidig antwoord te komen.
Wat je ook precies bedoelt, het zal waarschijnlijk een lastige vraag zijn. Maar het is altijd goed om eerst het probleem helder te formuleren. Bullshit in = bullshit out.
. Formuleren van de vraagstelling zal sowieso nog een hel van een karwei worden. Ik heb hotelschool gedaan 
, ik ben te oud voor deze shizzle. Sowieso alvast bedankt voor de feedback tot nu toe
, zeer waarschijnlijk gaan we nog wel 1-3 pogingen nodig hebben voordat de vraag helder genoeg geformuleerd zal zijn .6x - x^2/100 = 0
Deze moet ik afleiden, ik krijg dan: 6 - 2x/100, maar dat is niet goed. Wat vergeet ik?
Die 1*x schrijven we voor het gemak als x, de 1 laten we weg. Die breuk zoals hierboven omschrijven doe je gewoon door boven en onder de streep te delen door 2.
vergeten te vereenvoudigen dus 
Je moet hier de nulpunten van een polynoom van graad 2 oplossen.quote:
dit is obv. vrij easy maar geen idee..:
6x - x^2/100 = 0
Deze moet ik afleiden, ik krijg dan: 6 - 2x/100, maar dat is niet goed. Wat vergeet ik?
Dus, p(x) = -x2/100 + 6x
Nu ben je zo te zien geïnteresseerd in de nulpunten van p(x), dus
-x2/100 + 6x = 0 dan en slechts dan als 6x = x2/100
Dus x = 0 v 6 = -x/100 => x = -600
Dus je oplossingen zijn x = 0 en x = -600
Heeft me eens een keer een 10 gekost op de middelbare. Schreef op 4/6 ipv 2/3quote:Op maandag 24 februari 2014 22:00 schreef OllieWilliams het volgende:
2/100 is overigens niet fout, maar het kan "mooier" en daardoor is het ook beter te begrijpen; 1/2 is bijv duidelijker dan 32/64.
Ik heb een keerquote:
[..]
Heeft me eens een keer een 10 gekost op de middelbare. Schreef op 4/6 ipv 2/3
Baas!quote:
Tekening met pen (0,1 aftrek) en soms een rekenfoutje zoals 2*3=5. Zonde dat soort fouten... Ik let nu gelukkig al meer op slordigheidsfouten, maar het blijft lastig. 'k Zal nooit een 10 halen denk ik.quote:
[..]
Heeft me eens een keer een 10 gekost op de middelbare. Schreef op 4/6 ipv 2/3
(x-3)(x-2)(x-1) = 3
dus
x-3 = 3 v x-2 = 3 v x-1 = 3
Ik lachte me rot.
Blijft voorspelbaar. Gewoon truukje nadoen en verder niet nadenken.
Jaja. En galant als je bent loste jij die kubische vergelijking toen natuurlijk even vlot voor haar op.quote:
Ik zag vandaag een studente dit doen. Ik herhaal, wiskunde studente.
(x-3)(x-2)(x-1) = 3
dus
x-3 = 3 v x-2 = 3 v x-1 = 3
Ik lachte me rot.
Ik zag de noodzaak daar niet van in. Wat ik wel nodig vond was om de determinant van haar matrix juist te bepalen, dat leverde uiteraard ook een kubische vergelijking op, die ik galant als ik ben vlot oploste. En daarvoor had ik 0 rekenwerk voor nodig aangezien die in de vormquote:
[..]
Jaja. En galant als je bent loste jij die kubische vergelijking toen natuurlijk even vlot voor haar op.
(x-2)(x^2-1) - 3(x-2) = 0 eruit kwam rollen.
Je bent docent wiskunde? Dat bewijs mbv resttermen is op het middelbare wel te doen toch?quote:
Hehehehe, vandaag nog in de klas uitgelegd.
Blijft voorspelbaar. Gewoon truukje nadoen en verder niet nadenken.
Vroeger leerde je netjes (mét bewijs) dat een polynoom P(x) bij deling door (x − a) een rest P(a) oplevert, en dat de deling dus opgaat dan en slechts dan als P(a) = 0, maar ik betwijfel of -J-D- dat nog mag uitleggen, want stel je voor dat ze echt iets zouden leren ...quote:
[..]
Je bent docent wiskunde? Dat bewijs mbv resttermen is op het middelbare wel te doen toch?
Er zijn amper belemmeringen vanuit school wat ik mag of niet mag uitleggen. Zou ook te ridicuul voor woorden zijn.quote:
[..]
Vroeger leerde je netjes (mét bewijs) dat een polynoom P(x) bij deling door (x − a) een rest P(a) oplevert, en dat de deling dus opgaat dan en slechts dan als P(a) = 0, maar ik betwijfel of -J-D- dat nog mag uitleggen, want stel je voor dat ze echt iets zouden leren ...
Helaas is het zo dat we de leerlingen dienen voor te bereiden op een eindexamen en dus wel wat zaken vastliggen. Maar er is nog genoeg ruimte over om tot degelijke bewijsvoering te komen. Gelukkig mogen ze in het onderwijs nog steeds echt iets leren.
Begin eens met een lesje continuïteit van functies op R naar R.quote:
[..]
Er zijn amper belemmeringen vanuit school wat ik mag of niet mag uitleggen. Zou ook te ridicuul voor woorden zijn.
Helaas is het zo dat we de leerlingen dienen voor te bereiden op een eindexamen en dus wel wat zaken vastliggen. Maar er is nog genoeg ruimte over om tot degelijke bewijsvoering te komen. Gelukkig mogen ze in het onderwijs nog steeds echt iets leren.
Zeker mensen met wiskunde B moeten eigenlijk eens begrijpen dat zaken als differentieerbaarheid niet vanzelfsprekend zijn.Zeker. Dat moet zeker onderdeel zijn van de lessen. Buigpunten berekenen en dergelijke kunnen ze op een gegeven moment wel, maar dat onderdeel smeekt er haast om om wat dieper uitgespit te worden.quote:
[..]
Begin eens met een lesje continuïteit van functies op R naar R.
En in het verlengde kun je dan de middelwaardestelling en de maximum/minimum stelling bewijzen.quote:
[..]
Zeker. Dat moet zeker onderdeel zijn van de lessen. Buigpunten berekenen en dergelijke kunnen ze op een gegeven moment wel, maar dat onderdeel smeekt er haast om om wat dieper uitgespit te worden.
heeft ingevoerd. Ook verwijzingen naar bronnen waar ik misschien het antwoord kan vinden zijn welkom
De formule die je geeft wordt wel toegeschreven aan Leibniz (echter niet in deze notatie) en is dus ouder dan Cauchy. Er is een artikel van Binet geschreven in 1812 maar gepubliceerd in 1813 (lees online) waarin hij de vermenigvuldiging van determinanten bespreekt, maar niet in de thans gebruikelijke notatie. In de daarop volgende jaargang van hetzelfde tijdschrift staat de verhandeling van Cauchy die je kennelijk bedoelt (lees online), eveneens geschreven in 1812 en voorgedragen op dezelfde dag als die van Binet, maar pas gepubliceerd in 1815. In dit artikel introduceert Cauchy de moderne rangschikking van de elementen van een determinant in een vierkant en de dubbele subscript notatie. Hij gebruikt alleen nog niet de verticale strepen, die werden in 1841 geïntroduceerd door Cayley. De scan van het artikel van Cauchy is helaas slecht te lezen, maar de passage waarin hij het woord determinant in de huidige betekenis introduceert staat op p. 51:quote:
Heeft iemand een idee van wie de definitie van de determinant van nxn matrices is? Ik weet dat Cauchy in 1812 een verhandeling over determinanten heeft geschreven en het woord "determinant" in zijn huidige betekenis heeft ingevoerd. Ik weet alleen niet of hij ook de definitie
[ afbeelding ]
heeft ingevoerd. Ook verwijzingen naar bronnen waar ik misschien het antwoord kan vinden zijn welkom
M. Gauss s'en est servi avec avantage dans ses Recherches analytiques, pour découvrir les propriétés générales des formes du second degré, c'est-à-dire, des polynomes du second degré à deux ou à plusieurs variables; et il a désigné ces mêmes fonctions sous le nom de déterminans. Je conserverai cette dénomination qui fournit un moyen facile d'énoncer les résultats; j'observerai seulement qu'on donne aussi quelquefois aux fonctions dont il s'agit le nom de résultantes à deux ou à plusieurs lettres. Ainsi les deux expressions suivantes, déterminant et résultante, devront être regardées comme synonymes.
Cauchy verwijst dus naar Gauss (om precies te zijn, naar diens Disquisitiones arithmeticae, § 154, lees online).
Er zijn erg veel mensen die bijdragen hebben geleverd aan de theorie van de determinanten, te veel om hier de revue te laten passeren. Het standaardwerk op dit gebied is Thomas Muir, The Theory of Determinants in the Historical Order of Development, 1906-1923, 4 vols. Samen meer dan duizend bladzijden(!) en ook beschikbaar als Dover reprint (1960). Aangezien er geen copyright meer op dit werk rust, is het ook legaal beschikbaar via archive.org (lees online of download als PDF of als DjVu).
Een overzicht vind je verder in Morris Kline, Mathematical Thought from Ancient to Modern Times, 1972, vol. 2, hoofdstuk 33: Determinants and Matrices. Beslist raadplegen, hier vind je veel verwijzingen naar primaire bronnen die je in de meeste gevallen ook weer online kunt vinden.
[ Bericht 0% gewijzigd door Riparius op 06-03-2014 06:04:24 ]
waarom niet dan? Mis ik iets ?quote:
Ik ben zijn secretaresse niet, maar hij beantwoordt geen privé vragen (tot op heden). Lees zijn PoHi maar eens door, dan kun je je antwoord zelf verzinnen.quote:
dan zal hij dat wel niet willen vertellen, en dat betekent ook dat ik er geen vraag meer over stel. Duidelijk is voor mij wel dat we het niet over de gemiddelde wiskunde student hebben en meer richting gepromoveerde wiskundige met geschiedkundige interesses moeten denken.quote:
[..]
Ik ben zijn secretaresse niet, maar hij beantwoordt geen privé vragen (tot op heden). Lees zijn PoHi maar eens door, dan kun je je antwoord zelf verzinnen.
voor de kwaliteitsreacties En juist daar trek je te snel conclusies.quote:
[..]
dan zal hij dat wel niet willen vertellen, en dat betekent ook dat ik er geen vraag meer over stel. Duidelijk is voor mij wel dat we het niet over de gemiddelde wiskunde student hebben en meer richting gepromoveerde wiskundige met geschiedkundige interesses moeten denken.
prima, ik neem dat van je aan maar laten we het daar bij houden. Ter voorkoming van verdere topicvervuiling en ivm mogelijke privacywens.quote:Op dinsdag 4 maart 2014 18:52 schreef Amoeba het volgende:
[..]
En juist daar trek je te snel conclusies.
Zij
en
gegeven door
Mijn opdracht is om het beeld van S onder phi te vinden. Omdat
hoef ik (1/2,1) niet te bekijken, en verder vond ik dat
wat ellipsen zijn als je |z| vast neemt en theta laat lopen. Als |z| = 1 krijgen we als beeld het interval [2,-2] en als |z| = 2 krijgen we een ellips waar alle andere ellipsen binnen liggen. Het is nu intuitief wel duidelijk uit de continuiteit van phi dat alle punten binnen die grote ellips in phi(S) liggen, maar is er een elegante manier om dit hard te maken? Een stelling uit de topologie misschien? Ik heb nog nauwelijks topologie gehad, en ik heb het gevoel dat dit er mee te maken heeft. Ik vind het vrij vervelend om voor elk punt een ellips in het beeld waar dat punt op ligt te construeren...
[ Bericht 0% gewijzigd door JWF op 04-03-2014 20:31:36 ]
Daar moeten cirkels uit komen, geen 'algemene' ellipsen.quote:
Hallo allemaal,
Zij
en
gegeven door.
Mijn opdracht is om het beeld van S onder phi te vinden. Omdat
hoef ik (1/2,1) niet te bekijken, en verder vond ik dat,
wat ellipsen zijn als je |z| vast neemt en theta laat lopen. Als |z| = 1 krijgen we als beeld het interval [2,-2] en als |z| = 2 krijgen we een ellips waar alle andere ellipsen binnen liggen. Het is nu intuitief wel duidelijk uit de continuiteit van phi dat alle punten binnen die grote ellips in phi(S) liggen, maar is er een elegante manier om dit hard te maken? Een stelling uit de topologie misschien? Ik heb nog nauwelijks topologie gehad, en ik heb het gevoel dat dit er mee te maken heeft. Ik vind het vrij vervelend om voor elk punt een ellips in het beeld waar dat punt op ligt te construeren...
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.
Als je hebtquote:
Hoe dat zo? Je hebt toch
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.
w = z + 1/z
dan is
w = (r + 1/r)·cos φ + i·(r − 1/r)·sin φ
voor
z = r·eiφ
Als je r constant houdt, dan krijg je voor r ≠ 1 en tevens r ≠ 0 inderdaad een ellips in het w-vlak als beeld van z = r·eiφ, als je φ het interval [0, 2π] laat doorlopen, terwijl de eenheidscirkel in het w-vlak wordt afgebeeld op het reële interval [−2, 2]. Houd je daarentegen φ constant dan geeft z = r·eiφ in het w-vlak een hyperbool als je r het interval (0, ∞) laat doorlopen mits φ ≠ k·½π, k ∈ Z. Zo geeft je polaire grid in het z-vlak dus een set ellipsen en een set hyperbolen in het w-vlak die elkaar allemaal loodrecht snijden en die ook allemaal dezelfde brandpunten hebben, namelijk de beeldpunten van −2 en 2.
Laat maar, ik had de vraag verkeerd gelezen.quote:
Hoe dat zo? Je hebt toch
(met theta natuurlijk het argument en |z| de modulus). Er gaat dan hierboven iets fout, want dat zijn echt geen cirkels.
Top, fantastische post! In de laatste referentie die je noemt staat inderdaad een Franse brief + vertaling van Leibniz waarin hij inderdaad een determinant lijkt te berekenen. Dit wil natuurlijk niet zeggen dat hij ook de eerste is die die formule bedacht heeft (of dat hij überhaupt die formule bedacht heeft), maar maakt het wel aannemelijk dat hij er een aandeel in heeft gehad.quote:
[..]
Een overzicht vind je verder in Morris Kline, Mathematical Thought from Ancient to Modern Times, 1972, vol. 2, hoofdstuk 33: Determinants and Matrices. Beslist raadplegen, hier vind je veel verwijzingen naar primaire bronnen die je in de meeste gevallen ook weer online kunt vinden.
Dat is inderdaad het artikel waar ik het over had
In het boek wat ik voor het vak "History of Mathematics" gebruik ("A History of Mathematics" van Uta Merzbach en Carl Boyer), werden deze artikelen genoemd. Voor de rest staat er helaas niet zoveel in over determinanten.
Ik zal vooral de laatste bron gebruiken, mijn Frans is helaas onder middelbare-school niveau
huh hoe dan?
6 / 2 = 3quote:
Echt!?quote:
Dat snap ik, maar de rekenkundige bewerking vind ik lastig. Hoe maak ik dit stap voor stap kleiner?quote:
1/ 3 ^3sqrtu^2 * (3x^2+3)
Gevonden. Dank jullie wel!
Je bedoelde kennelijk dit, maar je herleiding klopt niet. Ga eerst maar eens deze cursus doorwerken.quote:
Op Volgens mij hoort die drie in de noemer bij de wortel. Dan klopt 't toch wel?quote:
[..]
Je bedoelde kennelijk dit, maar je herleiding klopt niet. Ga eerst maar eens deze cursus doorwerken.
Kijk zelf even. Iets met delen door 3 enzoquote:
Had m'n bericht al aangepast.quote:
[..]
Kijk zelf even. Iets met delen door 3 enzo
Denk dat 'rareziekte' de derdemachtswortel bedoelt, in de noemer.Dat staat er niet. Zet dan haken, maak zorg dat de gebruikte notatie voor geen enkele verwarring kan zorgen.quote:
[..]
Had m'n bericht al aangepast.
Da's waar. Maar omdat'ie "Gevonden" typte, neem ik aan dat'ie bedoelt dat'ie het juiste antwoord (het antwoord uit het antwoordenboek o.i.d.) heeft "gevonden". Dan hoort de drie kennelijk bij de wortelquote:
[..]
Dat staat er niet. Zet dan haken, maak zorg dat de gebruikte notatie voor geen enkele verwarring kan zorgen.
.Dan is de volgende les dat hij ook op het internet eenduidige notatie gebruikt.quote:
[..]
Da's waar. Maar omdat'ie "Gevonden" typte, neem ik aan dat'ie bedoelt dat'ie het juiste antwoord (het antwoord uit het antwoordenboek o.i.d.) heeft "gevonden". Dan hoort de drie kennelijk bij de wortel
Zo blijft het raden wat de vragensteller bedoelt, en kennelijk ziet hij zelf ook niet in dat zijn notatie ambigu of domweg fout is. In ieder geval mag je niet sqrt(u) schrijven als je cbrt(u) bedoelt. Dan wil hij dus dit aangeven in plaats van dit.quote:
[..]
Da's waar. Maar omdat'ie "Gevonden" typte, neem ik aan dat'ie bedoelt dat'ie het juiste antwoord (het antwoord uit het antwoordenboek o.i.d.) heeft "gevonden". Dan hoort de drie kennelijk bij de wortel
Kan iemand mij helpen met de volgende opgave:
-Waar ik dus niet uitkom is het volgende; ik weet niet waar "b" voor staat
-Steeds probeer ik met her Cartesisch product van A te werken A²= 49 elementen {[1,1], [1,2], .....[7,7]
-De kardinaliteit is eveneens [49]
-R is een deelverzameling van A²
Verder kom ik echt niet..
Hopelijk is er iemand die mij wat wegwijs kan maken.
De uitleg die ik hier heb behelst maar 5 regels, verder kom ik geen stap vooruit.
Frustrerend!
Bij voorbaat dank!!
Misschien moet je je leerboek eens beter bestuderen, of zelf even op het net op zoek gaan naar wat een binaire relatie nu eigenlijk is. De binaire relatie R is hier een deelverzameling van A × A en a en b stellen elementen voor van A. Gegeven is dat aRb oftewel (a,b) ∈ R dan en slechts dan als b − a = 1. Dan is het toch niet moeilijk alle elementen van R te geven?quote:
Beste mensen,
Kan iemand mij helpen met de volgende opgave:
[ afbeelding ]
-Waar ik dus niet uitkom is het volgende; ik weet niet waar "b" voor staat
-Steeds probeer ik met her Cartesisch product van A te werken A²= 49 elementen {[1,1], [1,2], .....[7,7]
-De kardinaliteit is eveneens [49]
-R is een deelverzameling van A²
Verder kom ik echt niet..
Hopelijk is er iemand die mij wat wegwijs kan maken.
De uitleg die ik hier heb behelst maar 5 regels, verder kom ik geen stap vooruit.
Frustrerend!
Bij voorbaat dank!!
Ik heb het allemaal even op een rijtje gezet, ik kom hier uit:quote:
[..]
Misschien moet je je leerboek eens beter bestuderen, of zelf even op het net op zoek gaan naar wat een binaire relatie nu eigenlijk is. De binaire relatie R is hier een deelverzameling van A × A en a en b stellen elementen voor van A. Gegeven is dat aRb oftewel (a,b) ∈ R dan en slechts dan als b − a = 1. Dan is het toch niet moeilijk alle elementen van R te geven?
{[2,1], [3,2], [4,3], [5,4], [6,5], [7,6]}
In de veronderstelling dat b - a steeds 1 moet zijn?
Nee, je hebt a en b omgewisseld, oftewel je doet nu net of aRb dan en slechts dan als b − a = −1. Gebruik verder ronde haakjes om geordende paren aan te geven.quote:
[..]
Ik heb het allemaal even op een rijtje gezet, ik kom hier uit:
{[2,1], [3,2], [4,3], [5,4], [6,5], [7,6]}
In de veronderstelling dat b - a steeds 1 moet zijn?
"A^2 bevat 49 tweetallen.
R is een relatie op A^2, en bevat juist die tweetallen (a,b) zodanig dat b - a = 1.
Voor welke tweetallen uit A^2 geldt dat laatste?"
Ik houd voor a, b telkens verzameling A aan.
Aangezien ik in mijn votige post a en heb heb omgewisseld,
{{1,2}, (2,3), (4,5), (6,7)}
Sorry van de rechte haakjes, dit is de manier waarop ik het online moet invoeren, vandaar.
Ik voel me echt een uilskuiken op dit moment, dit jaar ga ik na 4 jaar weer een opleiding volgen
Je vergeet nu ook nog twee elementen van R op te schrijven.quote:
Ik voel me echt een uilskuiken op dit moment, dit jaar ga ik na 4 jaar weer een opleiding volgen
Ik heb nu volgens mij het juiste antwoord:quote:
[..]
Je vergeet nu ook nog twee elementen van R op te schrijven.
{(1,2, (2,3), (3,4), (4,5), (5,6), (6,7)}
Ik moet nog wennen aan de manier waarop je bij wiskunde dient te denken, pfff
Ja, dat is het, afgezien van een vergeten haakje. Maar dit was toch doodsimpel? Voor welke opleiding is dit als ik vragen mag?quote:
[..]
Ik heb nu volgens mij het juiste antwoord:
{(1,2), (2,3), (3,4), (4,5), (5,6), (6,7)}
Ik moet nog wennen aan de manier waarop je bij wiskunde dient te denken, pfff
Dit is voor de opleiding Bedrijfskundige Informatica.quote:
[..]
Ja, dat is het, afgezien van een vergeten haakje. Maar dit was toch doodsimpel? Voor welke opleiding is dit als ik vragen mag?
Ik ben voornemens in september te starten, ik volg nu een cursus waarbij ik de wiskundestof uit de propedeuse behandel.
Indien ik voor alle tentamens een voldoende haal, heb ik tijdens de propedeuse vrijstelling voor het vak wiskunde.
[ Bericht 31% gewijzigd door rick949 op 22-03-2014 19:58:41 ]
Zij f: [a,b] -> R Riemann integreerbaar op [a.b], waar [a,b] een gesloten interval op R is. Verder zij a∫bf(x)dx > 0.
Bewijs de volgende bewering: Er is een interval I binnen [a,b] met lengte groter dan 0, er is een eps z.d.d. f(x) > eps voor alle x in I.
Nu heb ik dit:
Maar ik vrees dat mijn keuze voor een partitie Q om deze als een oneindige vereniging te definiëren misschien niet helemaal juist is..
Je mag je partitie inderdaad niet oneindig kiezen. In Riemann integratie is een partitie eindig. Je kiest het eindig en kan het eventueel later in het bewijs willekeurig groot (wel aftelbaar!) maken.quote:
Vraagje.
Zij f: [a,b] -> R Riemann integreerbaar op [a.b], waar [a,b] een gesloten interval op R is. Verder zij a∫bf(x)dx > 0.
Bewijs de volgende bewering: Er is een interval I binnen [a,b] met lengte groter dan 0, er is een eps z.d.d. f(x) > eps voor alle x in I.
Nu heb ik dit:
[ afbeelding ]
Maar ik vrees dat mijn keuze voor een partitie Q om deze als een oneindige vereniging te definiëren misschien niet helemaal juist is..
[ Bericht 2% gewijzigd door Mathemaat op 22-03-2014 23:29:45 ]
Ohja, even supremum noemen. Foutje.quote:
Het supremum van alle ondersommen genomen over alle eindige partities is gelijk aan de integraal, die groter dan 0 is. Er is dus een partitie waarvoor de ondersom groter dan 0 is. Die partitie moet minstens 1 interval hebben waarvoor de onderwaarde (infimum) groter dan 0 is.
Ik denk dat ik het wel weet dan. Even een kwestie van iets anders opschrijven.
Dank.
Maar dan mag ik niet meer spreken van L(Q,f) = sup(L(P,f) | P een partitie)quote:
[..]
Je mag je partitie inderdaad niet oneindig kiezen. In Riemann integratie is een partitie eindig. Je kiest het eindig en kan het eventueel later in het bewijs willekeurig groot (wel aftelbaar!) maken.
Nee dit moet anders en ik zie al hoe.
Ze willen dat je dat even netjes uitwerkt.quote:
Inderdaad je Q is geen partitie. Maar je hoeft geen specifieke partitie te kiezen, gebruik het antwoord van Thabit.quote:
[..]
Maar dan mag ik niet meer spreken van L(Q,f) = sup(L(P,f) | P een partitie)
Nee dit moet anders en ik zie al hoe.
Ga ik doen.quote:
[..]
Inderdaad je Q is geen partitie. Maar je hoeft geen specifieke partitie te kiezen, gebruik het antwoord van Thabit.
Eerste zin heb je vast als stelling in je dictaat, en de rest volgt direct uit tegenspraak.quote:
[..]
Ze willen dat je dat even netjes uitwerkt.
Ja inderdaad. Toen ik Thabits post las had ik het bewijs voor mezelf al rond.quote:
[..]
Eerste zin heb je vast als stelling in je dictaat, en de rest volgt direct uit tegenspraak.
g(τ)=ECC/ECL= (-750τ)/((1/8 τ^2-2τ+2) )
Deze geeft voor de waardes tussen 2 en 8:
1000
782,6086957
750
769,2307692
818,1818182
893,6170213
1000
Voor de tweede afgeleide kom ik handmatig én met wolfram op:
(12000(τ^3-48τ+256))/(τ^2-16τ+16)^3
Voor de convexity check moet dit altijd positief zijn (of iig in het gedeelte 2-8)
Maar dat is het niet, de waardes zijn namelijk:
-1305,555556
-166,6803649
-61,5234375
-38,63854751
-34,37265214
-38,48858153
-50,34722222
Wat doe ik hier fout? Klopt de hele convexity check an sich misschien niet?
Volgens mij ben je een minnetje vergeten.quote:
Ik heb de volgende formule:
g(τ)=ECC/ECL= (-750τ)/((1/8 τ^2-2τ+2) )
Voor de tweede afgeleide kom ik handmatig én met wolfram op:
(12000(τ^3-48τ+256))/(τ^2-16τ+16)^3
Voor de convexity check moet dit altijd positief zijn (of iig in het gedeelte 2-8)
Wat doe ik hier fout? Klopt de hele convexity check an sich misschien niet?
[ Bericht 16% gewijzigd door t4rt4rus op 27-03-2014 18:23:01 ]
Nog 3 keer gechecked en jahoor een min moest er nog voor. Bedankt.quote:
[..]
Volgens mij ben je een minnetje vergeten.
In het geval van
Maar bijvoorbeeld
Je vraag is niet echt duidelijk, beter formuleren dus. Je moet om te beginnen niet dezelfde letter x gebruiken voor de (rotatie)hoek, uitgedrukt in radialen, waarvan je de cosinus neemt, en de waarde van die cosinus. Je vraagt kennelijk naar een methode om voor een gegeven parameter θ de waarde van cos θ en sin θ te berekenen, en dat kan, althans in een willekeurig goede benadering, via reeksontwikkelingen. Het is omgekeerd ook mogelijk om voor een gegeven waarde op het interval [−1, 1] te bepalen voor welke (rotatie)hoeken cos θ of sin θ dan gelijk is aan de gegeven waarde. Maar omdat de sinus en de cosinus periodieke functies zijn met een periode 2π, zijn de gevonden waarden van θ dan niet eenduidig, maar slechts tot op een geheel veelvoud van 2π bepaald. Ik zou je aanraden om dit eens door te nemen.quote:
Heb wat zitten leren voor die parameters (x=cosx & y=sinx enzo). Ik vroeg me af, kun je uit een gegeven parameter ook die x en y functies uithalen?
[ Bericht 0% gewijzigd door Riparius op 27-03-2014 21:44:34 ]
Sorry dat het wat vaag is, maar bedankt voor je bazenpostquote:
[..]
Je vraag is niet echt duidelijk, beter formuleren dus. Je moet om te beginnen niet dezelfde letter x gebruiken voor de (rotatie)hoek, uitgedrukt in radialen, waarvan je de cosinus neemt, en de waarde van die cosinus. Je vraagt kennelijk naar een methode om voor een gegeven parameter θ de waarde van cos θ en sin θ te berekenen, en dat kan, althans in een willekeurig goede benadering, via reeksontwikkelingen. Het is omgekeerd ook mogelijk om voor een gegeven waarde op het interval [−1, 1] te bepalen voor welke (rotatie)hoeken cos θ of sin θ dan gelijk is aan de gegeven waarde. Maar omdat de sinus en de cosinus periodieke functies zijn met een periode 2π, zijn de gevonden waarden van θ dan niet eenduidig, maar slechts tot op een geheel veelvoud van 2π bepaald. Ik zou je aanraden om dit eens door te nemen.
. Wat ik me precies afvroeg was of het mogelijk was om van een gegeven grafiek dat een parameter is, de x- en y-functies 'eruithalen'.
Bijvoorbeeld:
"De onderstaande parameter is gegeven. Bereken exact wat de x- en y-functies zijn die deze parameter vormen"
Is dit mogelijk om te doen? Dat is wat ik mij afvraag.
Je vraag is zo niet goed te beantwoorden. Je zult in ieder geval de parametervoorstellingen moeten geven die bovenstaande grafiek opleveren. Verder is niet geheel duidelijk wat je met x- en y-functies bedoelt. Uiteraard zijn x en y beide functies van een parameter (zeg t) wanneer deze parametervoorstellingen zijn gegeven. Maar je ziet ook dat de grafiek niet de grafiek van een functie kan zijn, want dan zou er bij elke x-waarde ten hoogste één y-waarde horen voor een punt dat op de grafiek ligt, en dat is niet zo: je hebt verticale lijnen die de grafiek in twee punten snijden.quote:
[..]
Sorry dat het wat vaag is, maar bedankt voor je bazenpost
Wat ik me precies afvroeg was of het mogelijk was om van een gegeven grafiek dat een parameter is, de x- en y-functies 'eruithalen'.
Bijvoorbeeld:
"De onderstaande parameter is gegeven. Bereken exact wat de x- en y-functies zijn die deze parameter vormen"
[ afbeelding ]
Is dit mogelijk om te doen? Dat is wat ik mij afvraag.
Maar goed, je bent kennelijk bezig met het onderwerp Lissajousfiguren, en de bedoeling is klaarblijkelijk dat je uit de figuur afleest dat je hier hebt:
x = 2·sin t
y = sin 2t
Je kunt in WolframAlpha controleren dat deze parametervoorstelling inderdaad jouw grafiek oplevert.
De volgende vraag is dan wellicht wat de cartesische vergelijking is van deze kromme, dus de vergelijking in x en y die je krijgt als je t uit bovenstaande parametervoorstelling elimineert. Welnu, dat mag je zelf even proberen. Als je het goed doet vind je dan als cartesische vergelijking van je kromme:
x4 − 4x2 + 4y2 = 0
Ook dit kun je weer controleren met WolframAlpha.
[ Bericht 5% gewijzigd door Riparius op 27-03-2014 23:50:38 ]
Nee, dat kan niet. Dit heeft te maken in jouw voorbeeld met het feit dat de grafiek rondquote:
[..]
Sorry dat het wat vaag is, maar bedankt voor je bazenpost
Wat ik me precies afvroeg was of het mogelijk was om van een gegeven grafiek dat een parameter is, de x- en y-functies 'eruithalen'.
Bijvoorbeeld:
"De onderstaande parameter is gegeven. Bereken exact wat de x- en y-functies zijn die deze parameter vormen"
[ afbeelding ]
Is dit mogelijk om te doen? Dat is wat ik mij afvraag.
twee variabelen nodig heeft. Als de grafiek overal één variabele nodig had, dan kon je bijvoorbeeld de y functie afhankelijk van x bepalen, dus y(x) bepalen.
[ Bericht 1% gewijzigd door Mathemaat op 28-03-2014 10:59:48 ]
Als ik de functie f(x) = 1/x wil primitiveren, waarom is dan de primitieve F(x) = ln(|x|) +c? Waarom is ln absoluut? Ik begrijp dat variabele x in ln(x) niet negatief kan zijn, maar waarom wordt er bijvoorbeeld niet gesproken over F(x) = ln (x) +c met x>0?
Alvast super bedankt!
[ Bericht 0% gewijzigd door Maarten9191 op 28-03-2014 15:21:50 ]
Ze willen een primitieve geven van f(x) = 1/x die zowel geldt voor x > 0 als voor x < 0. Welnu, als x < 0, dan is ln x niet gedefinieerd (in R) en kan dit dus ook geen primitieve zijn.quote:
Ik ga in mei een staatsexamen wiskunde B doen met als voorbereiding een zelfstudie. Alles gaat gelukkig vrij soepel, alleen nu zit ik met wat (ogenschijnlijk simpels) wat ik niet helemaal begrijp.
Als ik de functie f(x) = 1/x wil primitiveren, waarom is dan de primitieve F(x) = ln(|x|) +c? Waarom is ln absoluut? Ik begrijp dat variabele x in ln(x) niet negatief kan zijn, maar waarom wordt er bijvoorbeeld niet gesproken over F(x) = ln (x) +c met x>0?
Alvast super bedankt!
Maar, als x < 0, dan is −x > 0, zodat ln(−x) dan wel is gedefineerd. Als je nu (voor x < 0) de afgeleide bepaalt van F(x) = ln(−x) + C, dan krijg je met behulp van de kettingregel
F'(x) = (−x)−1·(−1) = 1/x
en dat is precies wat we zochten.
Nu is verder |x| = x voor x > 0 en |x| = −x voor x < 0, dus kun je de twee gevallen x > 0 en x < 0 mooi samenvoegen door te schrijven
F(x) = ln(|x|) + C
Krijg ik van de Universiteit Utrecht een documentje om door te werken, over volledige inductie. Handig, dat heb ik bij het boekje over grondslagen en bewijzen voor mijn mondeling wiskunde al gehad. Begint me ondertussen op te vallen dat bewijzen en verzamelingen wel erg populair zijn voor open dagen en meeloopdagen. Leuk als introductie, maar als je de basis al 'n keer gehoord hebt...
Gisteren trouwens de film 'A Beautiful Mind' gezien, over wiskundige (en econoom) John Nash. Aanrader!
Schitterende film inderdaad.quote:
Volgende week vrijdag matching voor de studie wiskunde, hoera!
Krijg ik van de Universiteit Utrecht een documentje om door te werken, over volledige inductie. Handig, dat heb ik bij het boekje over grondslagen en bewijzen voor mijn mondeling wiskunde al gehad. Begint me ondertussen op te vallen dat bewijzen en verzamelingen wel erg populair zijn voor open dagen en meeloopdagen. Leuk als introductie, maar als je de basis al 'n keer gehoord hebt...
Gisteren trouwens de film 'A Beautiful Mind' gezien, over wiskundige (en econoom) John Nash. Aanrader!
Een aannemer vervaardigt hardhouten kozijnen. De kostprijs van een ongekeurd kozijn bedraagt 195. Normaliter valt 10% van de kozijnen bij de kwaliteitscontrole uit. De afgekeurde kozijnen worden voor 80 per stuk aan derden verkocht. Bereken de kostprijs van een goedgekeurd kozijn
Ik zet de vraag dan om naar 100% en ga uit van 100 producten, dus
195 * 90 = 17550 = 90%
80 * 10 = 800 = 10%
Totaal = 18350 voor 100%
18350 / 90 = 203,89
Echter weet ik niet of dit juist is omdat er normaal gezien een "rond" getal uitkomt. Zou iemand dit na willen berekenen?
Volgens mij klopt je antwoord niet.quote:
Zou iemand me hierbij kunnen helpen? Ik weet niet of ik het goed doe en ik heb geen uitwerking hiervan.
Een aannemer vervaardigt hardhouten kozijnen. De kostprijs van een ongekeurd kozijn bedraagt 195. Normaliter valt 10% van de kozijnen bij de kwaliteitscontrole uit. De afgekeurde kozijnen worden voor 80 per stuk aan derden verkocht. Bereken de kostprijs van een goedgekeurd kozijn
Ik zet de vraag dan om naar 100% en ga uit van 100 producten, dus
195 * 90 = 17550 = 90%
80 * 10 = 800 = 10%
Totaal = 18350 voor 100%
18350 / 90 = 203,89
Echter weet ik niet of dit juist is omdat er normaal gezien een "rond" getal uitkomt. Zou iemand dit na willen berekenen?
Stel de aannemer produceert 100 kozijnen, dan maakt hij 100*195 = 19500 aan kosten.
10% wordt afgekeurd en daarvoor wordt slechts 80 euro per stuk gevangen: 10*80 = 800.
Dan blijft er aan kosten over: 19500 - 800 - 18700 euro. Dit moet worden terugverdiend op 90 kozijnen: 18700/90 = 207,78 per goedgekeurd kozijn.
Bedankt, klinkt een stuk beter...quote:
[..]
Volgens mij klopt je antwoord niet.
Stel de aannemer produceert 100 kozijnen, dan maakt hij 100*195 = 19500 aan kosten.
10% wordt afgekeurd en daarvoor wordt slechts 80 euro per stuk gevangen: 10*80 = 800.
Dan blijft er aan kosten over: 19500 - 800 - 18700 euro. Dit moet worden terugverdiend op 90 kozijnen: 18700/90 = 207,78 per goedgekeurd kozijn.
Tja, als je de productiekosten van je afgekeurde kozijnen verdoezelt en de opbrengst van de verkoop daarvan dan als kosten opvoert ...quote:
[..]
Bedankt, klinkt een stuk beter...
[ Bericht 96% gewijzigd door 2thmx op 01-04-2014 22:27:29 (ik ben blind.) ]
200 graden Celsius?quote:
ff een klein vraagje tussendoor: wat is de temperatuur van de blauwe vlam bij scheikunde (niet ruisend). heb al even op internet opgezocht en de antwoorden variëren enorm. ik snap dat het ook aan de gaskraan etc. ligt maar weet iemand dat ongeveer? (zag ook dat het eerst in de binas stond maar heb dit niet kunnen vinden)
SES / [Bèta overig] Huiswerk- en vragentopicquote:
ff een klein vraagje tussendoor: wat is de temperatuur van de blauwe vlam bij scheikunde (niet ruisend). heb al even op internet opgezocht en de antwoorden variëren enorm. ik snap dat het ook aan de gaskraan etc. ligt maar weet iemand dat ongeveer? (zag ook dat het eerst in de binas stond maar heb dit niet kunnen vinden)
Ik dacht rond de 500Cquote:
ff een klein vraagje tussendoor: wat is de temperatuur van de blauwe vlam bij scheikunde (niet ruisend). heb al even op internet opgezocht en de antwoorden variëren enorm. ik snap dat het ook aan de gaskraan etc. ligt maar weet iemand dat ongeveer? (zag ook dat het eerst in de binas stond maar heb dit niet kunnen vinden)
intikt op wolframalpha? herschrijven van de formule/stap terug naar de integraal lukt wel.
bedoel je? Dat F(b) - F(a) kan je toch zelf intypen?
Als je een bepaalde (definiete) integraal wil laten berekenen door WolframAlpha, dan hoef je niet zelf een primitieve van de integrand in te voeren, maar kun je bijvoorbeeld zoiets doen. Maar het is helaas niet erg duidelijk wat je precies probeert te doen.quote:
geprobeerd, lukt niet helaas
herschrijven van de formule/stap terug naar de integraal lukt wel.
Ik moet voor mijn tentamen a.s. donderdag de beschikking hebben over skills in het uitrekenen van meervoudige integralen mbv coördinatentransformaties, en dan met name cilindrische, sferische en poolcoördinaten.
Opgave 13:
Zij T de driehoek in het cartesisch vlak ingesloten door de punten (0,0), (1,0) en (1,1).
Bereken de dubbelintegraal:
∫∫T (x2 + y2)dA
Nu wil ik dit graag met poolcoördinaten doen (er zullen vast betere alternatieven zijn ~ lineaire transformaties, maar ik maak het mezelf graag onnodig lastig)
Dus x = rcos(φ), y = rsin(φ)
De absolute waarde van de Jacobiaan is dan zoals bekend r, maar ik zie niet helemaal hoe de grenzen na mijn transformatie eruit zien.
Het is duidelijk dat φ van 0 tot π/4 loopt en r van 0 tot √2, maar r is overduidelijk afhankelijk van φ en ik zie die relatie niet. Help?
Want als r > 1, dan is er helemaal geen cirkelschijf meer..
[ Bericht 2% gewijzigd door Amoeba op 04-04-2014 10:40:18 ]
Ik was je voor met mijn ninjaedit. Nee, want je wilt integreren over een driehoek.quote:
is r niet van 0 tot 1? Je krijgt toch een pizzapuntje met 0<r<1 en 0<φ<π/4
Ik zat te denken om die integraal op te splitsen in de som van 2 integralen. 0 < r < 1 en 1 < r(φ) < √2
Die eerste is niet afhankelijk van φ, dus die mag ik erbuiten halen, maar die tweede weet ik nog steeds niet. ( r loopt van 1 tot sec(φ))?
En dit klopt inderdaad. Antwoord geeft me 1/3, maar zo te zien is poolcoordinaten niet the way to go. Het integreren van een vierdemachtssecans is niet zo handig.
[ Bericht 8% gewijzigd door Amoeba op 04-04-2014 11:00:13 ]
Dan integreer je een vierkant. Zou een factor ½ dat oplossen? Edit: dat werkt omdat x en y in deze symmetrisch zijn. Dus f(x,y) = f(y,x) topquote:
Helemaal geen transformatie nodig toch? Gewoon x van y tot 1 en dan y van 0 tot 1.
Dan integreer je over je driehoek
Waarom dacht ik zo lastig.quote:
Je kunt het met poolcoördinaten doen, maar de vergelijking van de straal afhankelijk van de hoek is flink ingewikkelder.quote:
Niet als je 'm opsplitst zoals ik deed. Dan r = sec(φ)quote:
[..]
Je kunt het met poolcoördinaten doen, maar de vergelijking van de straal afhankelijk van de hoek is flink ingewikkelder.
Aha, ik keek naar het verkeerde integratiegebied. Sry,quote:
[..]
Niet als je 'm opsplitst zoals ik deed. Dan r = sec(φ)
. Het antwoord is danJe hoeft overigens niets op te splitsen.
Ja ik snap waarom (algebraïsch), intuïtief is een splitsing net even dat stapje wat ik nodig had.quote:
[..]
Aha, ik keek naar het verkeerde integratiegebied. Sry,.
Je hoeft overigens niets op te splitsen.
Weet iemand wat ik hier fout doe ? :
http://i57.tinypic.com/vp7qtz.jpg
quote:
Heey,
Weet iemand wat ik hier fout doe ? :
http://i57.tinypic.com/vp7qtz.jpg
Als
Thanks! kom goed uit (Y)quote:
[..]
[ afbeelding ]
Alsdan is
de primitieve daarvan
Kan iemand hier mij de eerste stap uitleggen? Hoe kan je van keer naar plus gaan?
Dit kun je doen met breuksplitsen:quote:
[ afbeelding ]
Kan iemand hier mij de eerste stap uitleggen? Hoe kan je van keer naar plus gaan?
http://www.purplemath.com/modules/partfrac.htm
Ik kan de filmpjes van PatrickJMT ook erg aanraden:quote:
[..]
Dit kun je doen met breuksplitsen:
http://www.purplemath.com/modules/partfrac.htm
https://www.youtube.com/r(...)action+decomposition
Ah, dat eerste kon ik al, maar de andere kant op had ik nog nooit gehad.quote:
[..]
Dit kun je doen met breuksplitsen:
http://www.purplemath.com/modules/partfrac.htm
Het is nu gelukt, bedankt.http://nl.tinypic.com/r/kb52mt/8
Het goede antwoord moet 59 (3/5) zijn.