SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 1% gewijzigd door #ANONIEM op 18-01-2014 00:32:17 ]
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 1% gewijzigd door #ANONIEM op 18-01-2014 00:32:17 ]


Voorts ben ik van mening dat het termsgewijs differentiëren hier niet is toegestaan.
Anders zie ik de fout niet.
Anders zie ik de fout niet.


Normaliter kun je d(f(x)+g(x))/dx opvatten als d(f(x))/dx + d(g(x))/dx, ofwel termsgewijs differentiëren.quote:


Volgens mij heeft het er iets mee te maken dat je notatie niet eenduidig is ofzo, en 'mag' je alleen de standaardregels toepassen op niet multi-interpretabele notaties.
Your opinion of me is none of my business.


Alleen in dit geval is het geen som van een constant aantal termen, maar is het een som van een variabel aantal termen.quote:Op zaterdag 18 januari 2014 14:39 schreef Amoeba het volgende:
[..]
Normaliter kun je d(f(x)+g(x))/dx opvatten als d(f(x))/dx + d(g(x))/dx, ofwel termsgewijs differentiëren.
Eigenlijk staat er dat
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Ah, inderdaad. Daarom is termsgewijs differentiëren hier niet toegestaan.quote:Op zaterdag 18 januari 2014 16:47 schreef freiss het volgende:
[..]
Alleen in dit geval is het geen som van een constant aantal termen, maar is het een som van een variabel aantal termen.
Eigenlijk staat er dat, wat natuurlijk onwaar is.


Dit kan inderdaad nietquote:Op zaterdag 18 januari 2014 16:05 schreef Fsmxi het volgende:
Is differentiëren over een som een commutatief iets? (Of hoe het precies heet, ben geen wiskundige)
Ie, mag dit zomaar?
[ afbeelding ]


De fout is dat je identiteit alleen geldt voor een x ∈ N, maar dan kun je dus niet differentiëren naar x. Je zou hooguit een differentiequotiënt kunnen bepalen.quote:Op zaterdag 18 januari 2014 14:16 schreef thenxero het volgende:
Leuke truc:
Stel dat x een geheel positief getal is. Merk op dat
[snip bogus]


Het goede antwoord is al voorbij gekomen zie ik. Er zijn meerdere manieren om het uit te leggen. Het komt erop neer dat niet alleen de x'en in de som, maar ook het x aantal termen moet je variabel nemen. Maar je kan natuurlijk niet een niet-natuurlijk aantal termen hebben, dus op die manier differentiëren is complete onzin.
Toch moet ik toegeven dat ik zelf even raar zat te kijken .
.
Toch moet ik toegeven dat ik zelf even raar zat te kijken


't Is lineaire algebra over F11. De vector (c1, ..., c9) is bepaald op een scalaire vermenigvuldiging na. Je moet dus een 1-dimensionale deelruimte van een 9-dimensionale ruimte bepalen. Hiervoor zijn 8 vergelijkingen nodig.quote:Op maandag 20 januari 2014 15:35 schreef Amoeba het volgende:
[ afbeelding ]
Mijn eerste intuïtie is 9, immers zijn er 9 vrijheidsgraden en in het algemeen heb je dan 9 vergelijkingen nodig om dit op te lossen. Maar dan is er nog die foutcorrectie, dus wellicht heb je aan 8 vergelijkingen voldoende.
Kan iemand dit nader toelichten?


Kun je dit iets nader toelichten?quote:Op maandag 20 januari 2014 20:35 schreef thabit het volgende:
[..]
't Is lineaire algebra over F11. De vector (c1, ..., c9) is bepaald op een scalaire vermenigvuldiging na. Je moet dus een 1-dimensionale deelruimte van een 9-dimensionale ruimte bepalen. Hiervoor zijn 8 vergelijkingen nodig.
Mijn redenatie is als volgt: Je moet 8 c'tjes bepalen, en die andere kun je met behulp van een foutcorrectie vinden. Immers, de 'modular equation' is in staat om één fout te corrigeren.


Doe eerst maar even of het allemaal reële getallen zijn, in plaats van een modulaire vergelijking. Hoe zou je het dan aanpakken?quote:Op maandag 20 januari 2014 20:37 schreef Amoeba het volgende:
[..]
Kun je dit iets nader toelichten?
Mijn redenatie is als volgt: Je moet 8 c'tjes bepalen, en die andere kun je met behulp van een foutcorrectie vinden. Immers, de 'modular equation' is in staat om één fout te corrigeren.


Volgens mij heb je dan wél 9 vergelijkingen nodig toch? Je zet ze allemaal in een matrix en een beetje vegen doet wonderen.quote:Op maandag 20 januari 2014 20:39 schreef thabit het volgende:
[..]
Doe eerst maar even of het allemaal reële getallen zijn, in plaats van een modulaire vergelijking. Hoe zou je het dan aanpakken?


Die vergelijkingen eindigen allemaal op "=0".quote:Op maandag 20 januari 2014 20:41 schreef Amoeba het volgende:
[..]
Volgens mij heb je dan wél 9 vergelijkingen nodig toch? Je zet ze allemaal in een matrix en een beetje vegen doet wonderen.


Ah, je stelt ze allemaal aan elkaar gelijk.quote:Op maandag 20 januari 2014 20:43 schreef thabit het volgende:
[..]
Die vergelijkingen eindigen allemaal op "=0".


Wut?quote:Op maandag 20 januari 2014 20:44 schreef Amoeba het volgende:
[..]
Ah, je stelt ze allemaal aan elkaar gelijk.
In de oorspronkelijke opgave staat ook overal "=0 (mod 11)".


Ik heb geen idee.quote:Op maandag 20 januari 2014 20:45 schreef thabit het volgende:
[..]
Wut?
In de oorspronkelijke opgave staat ook overal "=0 (mod 11)".
Voor een vergelijking met n onbekenden geldt dat er normaliter n condities nodig zijn om dit op te lossen.. Verder ga ik even echt niet komen.


Ja, maar als al die vergelijkingen op "=0" eindigen, zal de oplossing in zo'n geval ook 0 zijn. En dat is hier natuurlijk niet de bedoeling.quote:Op maandag 20 januari 2014 20:47 schreef Amoeba het volgende:
[..]
Ik heb geen idee.
Voor een vergelijking met n onbekenden geldt dat er normaliter n condities nodig zijn om dit op te lossen.. Verder ga ik even echt niet komen.


Aaah zo. Dit kan alleen als c1 t/m c9 allen gelijk 0 zijn, in een niet-modulaire omgeving.quote:Op maandag 20 januari 2014 20:49 schreef thabit het volgende:
[..]
Ja, maar als al die vergelijkingen op "=0" eindigen, zal de oplossing in zo'n geval ook 0 zijn. En dat is hier natuurlijk niet de bedoeling.


Het grappige is dat als je modulo een priemgetal werkt, dat dat soort dingen dan ook gewoon gelden.quote:Op maandag 20 januari 2014 20:52 schreef Amoeba het volgende:
[..]
Aaah zo. Dit kan alleen als c1 t/m c9 allen gelijk 0 zijn, in een niet-modulaire omgeving.


quote:Op maandag 20 januari 2014 20:53 schreef thabit het volgende:
[..]
Het grappige is dat als je modulo een priemgetal werkt, dat dat soort dingen dan ook gewoon gelden.
Dus feitelijk is deze opgave een smadelijk harde grap aangezien c1 tm c9 gewoon allemaal nul moeten wezen?


Nee. Je hebt gewoon geen 9 vergelijkingen nodig.quote:Op maandag 20 januari 2014 20:56 schreef Amoeba het volgende:
[..]
Dus feitelijk is deze opgave een smadelijk harde grap aangezien c1 tm c9 gewoon allemaal nul moeten wezen?


Dat had ik bij mezelf voordat ik deze vraag op het forum stelde ook al bedacht. Nu snap ik nog niet waarom mijn antwoord van 8 goed was, maar ongetwijfeld mijn uitleg fout.quote:Op maandag 20 januari 2014 20:57 schreef thabit het volgende:
[..]
Nee. Je hebt gewoon geen 9 vergelijkingen nodig.


Als je 8 (lineair onafhankelijke) vergelijkingen hebt in 9 onbekenden, dan heb je een 1-dimensionale oplossingsruimte. Dat wil zeggen dat er 1 vector (c1, ..., c9) != 0 is, zodanig dat elke oplossing een veelvoud van die vector is. Dus als (1,2,3,4,5,6,7,8,9) een oplossing is, dan is (2,4,6,8,10,12,14,16,18) dat bijvoorbeeld ook. Meer dan dat kun je ook niet doen, want als alle vergelijkingen op "=0" eindigen, is er altijd sprake van een oplossingsruimte.quote:Op maandag 20 januari 2014 21:00 schreef Amoeba het volgende:
[..]
Dat had ik bij mezelf voordat ik deze vraag op het forum stelde ook al bedacht. Nu snap ik nog niet waarom mijn antwoord van 8 goed was, maar ongetwijfeld mijn uitleg fout.
[ Bericht 19% gewijzigd door thabit op 20-01-2014 21:09:22 ]


Bedankt voor de uitleg, best verwarrend allemaal.quote:Op maandag 20 januari 2014 21:02 schreef thabit het volgende:
[..]
Als je 8 (lineair onafhankelijke) vergelijkingen hebt in 9 onbekenden, dan heb je een 1-dimensionale oplossingsruimte. Dat wil zeggen dat er 1 vector (c1, ..., c9) != 0 is, zodanig dat elke oplossing een veelvoud van die vector is. Dus als (1,2,3,4,5,6,7,8,9) een oplossing is, dan is (2,4,6,8,10,12,14,16,18) dat bijvoorbeeld ook. Meer dan dat kun je ook niet doen, want als alle vergelijkingen op "=0" eindigen, is er altijd sprake van een oplossingsruimte.
(Het kan natuurlijk ook dat de oorsprong de oplossing is van een stelsel vergelijkingen die eindigen op "= 0"


Maar dat is een triviale oplossing en tevens een veelvoud van iedere oplossing (c1, c2, ... c9).quote:Op maandag 20 januari 2014 21:16 schreef randomo het volgende:
[..]
Bedankt voor de uitleg, best verwarrend allemaal.
(Het kan natuurlijk ook dat de oorsprong de oplossing is van een stelsel vergelijkingen die eindigen op "= 0")


Ja, maar geen oplossingsruimte.quote:Op maandag 20 januari 2014 21:17 schreef Amoeba het volgende:
[..]
Maar dat is een triviale oplossing en tevens een veelvoud van iedere oplossing (c1, c2, ... c9).


Dat is waar. Maar als de oorsprong de oplossing is, dan is ieder bankbiljetnummer geldig.quote:
[ Bericht 8% gewijzigd door #ANONIEM op 20-01-2014 23:21:44 ]


Je weet dat:quote:Op dinsdag 21 januari 2014 18:48 schreef Rezania het volgende:
[ afbeelding ]
[ afbeelding ]
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
En het argument (
Dan is het snel in te zien dat in jouw geval voor z3 geldt dat het argument pi is.


Oh ja, want het is e^arg natuurlijk. Stom dat ik dat niet zag.quote:Op dinsdag 21 januari 2014 18:56 schreef Alrac4 het volgende:
[..]
Je weet dat:
En het argument () van een complex getal c voldoet aan:
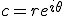
Dan is het snel in te zien dat in jouw geval voor z3 geldt dat het argument pi is.
Gist is liefde, gist is leven. Vooral in een vagijn.


Bedenk wel dat je zo niet alle oplossingen vindt, de uitwerking is niet volledig. Het argument van −1 is niet π maar π + 2kπ, k ∈ Z omdat in het complexe vlak het beeldpunt van 1 overgaat in het beeldpunt van −1 bij een rotatie om de oorsprong over een halve slag plus of min een geheel aantal slagen. Je krijgt dusquote:Op dinsdag 21 januari 2014 18:48 schreef Rezania het volgende:
[ afbeelding ]
[ afbeelding ]
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
z3 = (1/27)·e(π+2kπ)i, k ∈ Z
en dat geeft
z = (1/3)·e(⅓π+⅔kπ)i, k ∈ Z
Je kunt nu drie opeenvolgende gehele waarden voor k invullen (bijvoorbeeld −1, 0, 1), en dan krijg je drie verschillende oplossingen, die je zelf nog maar even in de vorm a+bi met a,b ∈ R moet herschrijven. De beeldpunten van de oplossingen vormen in het complexe vlak de hoekpunten van een gelijkzijdige driehoek en liggen op een cirkel met het middelpunt in de oorsprong en een straal 1/3.
[ Bericht 5% gewijzigd door Riparius op 21-01-2014 21:35:29 ]


Die screenshot van dat plaatje is dan ook maar een deel van de uitwerking.quote:Op dinsdag 21 januari 2014 19:24 schreef Riparius het volgende:
[..]
Bedenk wel dat je zo niet alle oplossingen vindt, de uitwerking is niet volledig. Het argument van −1 is niet π maar π + 2kπ, k ∈ Z omdat in het complexe vlak het beeldpunt van 1 overgaat in het beeldpunt van −1 bij een rotatie om de oorsprong over een halve slag plus of min een geheel aantal slagen. Je krijgt dus
z3 = (1/27)·e(π+2kπ)i, k ∈ Z
en dat geeft
z = (1/3)·e(⅓π+⅔kπ)i, k ∈ Z
Je kunt nu drie opeenvolgende gehele waarden voor k invullen (bijvoorbeeld −1, 0, 1), en dan krijg je drie verschillende oplossingen, die je zelf nog maar even in de vorm a+bi met a,b ∈ R moet herschrijven. De beeldpunten van de oplossingen vormen in het complexe vlak de hoekpunten van een gelijkzijdige driehoek en liggen op een cirkel met het middelpunt in de oorsprong en een straal 1/3.
Gist is liefde, gist is leven. Vooral in een vagijn.


Ik moet het limiet van 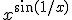 bepalen waarbij x naar oneindig gaat.
bepalen waarbij x naar oneindig gaat.
SPOILER: Uitwerking volgens de docentOm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Nu snap ik zijn uitwerking wel, maar waarom zou je zo moeilijk doen? Als je oneindig invult wordt die 1/x nul, sin(0) is nul, dus krijg je oneindig tot 0, waardoor het limiet 1 is? Lijkt me logisch toch?Gist is liefde, gist is leven. Vooral in een vagijn.


Nee, want je mag niet er zomaar vanuitgaan dat de sin(1/x) "harder naar nul gaat dan x naar oneindig" als ik het me goed herinner, dwz, sin(1/x) wordt voor grotere x steeds kleiner en steeds dichter bij 0, maar x word ook steeds groter, waardoor je niet kunt zeggen dat het zomaar 1 wordt.
Om dezelfde reden kun je ook niet zomaar zeggen dat om maar heel simpel en niet supergerelateerd voorbeeld te geven:
Oneindig/oneindig is niet altijd 1
lim(x->infinity) x^2/x = oneindig/oneindig maar deze limiet convergeert toch niet naar een getal.
Om dezelfde reden kun je ook niet zomaar zeggen dat om maar heel simpel en niet supergerelateerd voorbeeld te geven:
Oneindig/oneindig is niet altijd 1
lim(x->infinity) x^2/x = oneindig/oneindig maar deze limiet convergeert toch niet naar een getal.


Hmm, blijkbaar snap ik de uitwerking toch niet helemaal. De docent heeft het op een gegeven moment over oneindig gedeeld door oneindig, waardoor je L'Hop mag toepassen. Maar ik snap niet hoe hij aan oneindig in de noemer komt. Er staat 1/sin(1/x) in de noemer, vul je dan oneindig in krijg je toch 1/0? En iets delen door nul kan gewoon niet, dus dat kan dan ook geen oneindig als antwoord opleveren.
Gist is liefde, gist is leven. Vooral in een vagijn.


In de noemer staat 1/sin(1/x), niet sin(1/x), en het tweede gaat dusdanig naar nul dat het eerste naar oneindig gaat.


quote:Op woensdag 22 januari 2014 18:57 schreef Rezania het volgende:
Ik moet het de limiet vanbepalen waarbij x naar oneindig gaat.
Als mensen zonder al te veel nadenken beweren dat iets 'logisch' is, dan is dat doorgaans een indicatie dat het beweerde nu juist niet logisch is, en dat is hier ook het geval. Je doet me denken aan (beginnende) studenten die nogal eens schijnen te veronderstellen dat de limiet vanSPOILER: Uitwerking volgens de docentOm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Nu snap ik zijn uitwerking wel, maar waarom zou je zo moeilijk doen? Als je oneindig invult wordt die 1/x nul, sin(0) is nul, dus krijg je oneindig tot 0, waardoor het limiet 1 is? Lijkt me logisch toch?
voor n → ∞ gelijk is aan 1, immers (1 + 1/n) gaat naar 1, en elke macht van 1 is 1 toch? Maar je weet - hopelijk - wel dat dit niet klopt, de bedoelde limiet is namelijk e en ligt tussen 2 en 3.
Voor de limiet die je moet bepalen heb je de regel van l'Hôpital helemaal niet nodig, en wellicht is het beter voor je inzicht om eens te laten zien hoe je deze limiet langs elementaire weg aan kunt tonen. Voor 0 < θ < π/2 hebben we 0 < sin(θ) < θ < tan(θ) zodat we in ieder geval voor x > 1 hebben
en aangezien ln x > 0 voor x > 1 hebben we dan ook
Maar nu weet je ook dat ln x voor x > 1 de oppervlakte is onder de curve y = 1/x over het interval [1,x], zodat voor x > 1 geldt 0 < ln x < x−1 < x. Daarmee is voor x > 1 ook ln(x)/x = ln((√x)2)/x = 2∙ln(√x)/x < 2∙(√x)/x en dus
Combineren van deze ongelijkheden geeft voor x > 1
en aangezien 2/√x naar 0 gaat voor x → ∞ en ln(x)·sin(1/x) zit ingeklemd tussen 0 en 2/√x is het evident dat ln(x)·sin(1/x) ook naar 0 moet gaan voor x → ∞, ergo
De e-macht van ln(x)·sin(1/x) gaat dus naar e0 = 1 voor x → ∞, oftewel we hebben
QED
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 17:17:44 ]


Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
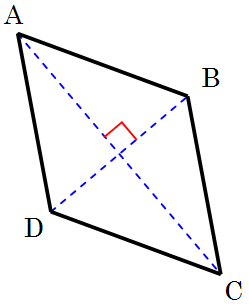
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.


Als je het snapt probeer het ons eens uit te leggen.quote:Op woensdag 22 januari 2014 21:58 schreef Aarch het volgende:
Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.
Kom je vanzelf op een bewijs.


Bedankt voor de antwoorden.  Voortaan gewoon niet te simpel denken dus.
Voortaan gewoon niet te simpel denken dus. 
Gist is liefde, gist is leven. Vooral in een vagijn.


Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').quote:Op woensdag 22 januari 2014 21:58 schreef Aarch het volgende:
Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoordt tot een bewijs begrijp ik niet.
Alvast dank.
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wát je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
[ Bericht 4% gewijzigd door Riparius op 23-01-2014 06:38:17 ]


Als je moet bewijzen dat een bepaalde set compact is met de (Finite) Open Cover definitie, hoe doe je dit? Ik snap wel hoe ik een tegenvoorbeeld moet bedenken en dit te noteren als een set niet compact is, maar het omgekeerde bewijzen lukt nog niet. Een zoektocht op Google heeft ook weinig opgeleverd, veelal hebben ze het over allerlei topologisch ruimtes en dat is nog boven mijn niveau.
Concreet: Hoe bewijs je bijvoorbeeld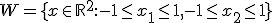 compact is?
compact is?
Concreet: Hoe bewijs je bijvoorbeeld
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |