SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan ťťn of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 1% gewijzigd door #ANONIEM op 18-01-2014 00:32:17 ]
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan ťťn of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 1% gewijzigd door #ANONIEM op 18-01-2014 00:32:17 ]


Voorts ben ik van mening dat het termsgewijs differentiŽren hier niet is toegestaan.
Anders zie ik de fout niet.
Anders zie ik de fout niet.


Normaliter kun je d(f(x)+g(x))/dx opvatten als d(f(x))/dx + d(g(x))/dx, ofwel termsgewijs differentiŽren.quote:


Volgens mij heeft het er iets mee te maken dat je notatie niet eenduidig is ofzo, en 'mag' je alleen de standaardregels toepassen op niet multi-interpretabele notaties.
Your opinion of me is none of my business.


Alleen in dit geval is het geen som van een constant aantal termen, maar is het een som van een variabel aantal termen.quote:Op zaterdag 18 januari 2014 14:39 schreef Amoeba het volgende:
[..]
Normaliter kun je d(f(x)+g(x))/dx opvatten als d(f(x))/dx + d(g(x))/dx, ofwel termsgewijs differentiŽren.
Eigenlijk staat er dat
HJ 14-punt-gift.
Lijst met rukmateriaal!
Lijst met rukmateriaal!


Ah, inderdaad. Daarom is termsgewijs differentiŽren hier niet toegestaan.quote:Op zaterdag 18 januari 2014 16:47 schreef freiss het volgende:
[..]
Alleen in dit geval is het geen som van een constant aantal termen, maar is het een som van een variabel aantal termen.
Eigenlijk staat er dat, wat natuurlijk onwaar is.


Dit kan inderdaad nietquote:Op zaterdag 18 januari 2014 16:05 schreef Fsmxi het volgende:
Is differentiŽren over een som een commutatief iets? (Of hoe het precies heet, ben geen wiskundige)
Ie, mag dit zomaar?
[ afbeelding ]


De fout is dat je identiteit alleen geldt voor een x ∈ N, maar dan kun je dus niet differentiŽren naar x. Je zou hooguit een differentiequotiŽnt kunnen bepalen.quote:Op zaterdag 18 januari 2014 14:16 schreef thenxero het volgende:
Leuke truc:
Stel dat x een geheel positief getal is. Merk op dat
[snip bogus]


Het goede antwoord is al voorbij gekomen zie ik. Er zijn meerdere manieren om het uit te leggen. Het komt erop neer dat niet alleen de x'en in de som, maar ook het x aantal termen moet je variabel nemen. Maar je kan natuurlijk niet een niet-natuurlijk aantal termen hebben, dus op die manier differentiŽren is complete onzin.
Toch moet ik toegeven dat ik zelf even raar zat te kijken .
.
Toch moet ik toegeven dat ik zelf even raar zat te kijken


't Is lineaire algebra over F11. De vector (c1, ..., c9) is bepaald op een scalaire vermenigvuldiging na. Je moet dus een 1-dimensionale deelruimte van een 9-dimensionale ruimte bepalen. Hiervoor zijn 8 vergelijkingen nodig.quote:Op maandag 20 januari 2014 15:35 schreef Amoeba het volgende:
[ afbeelding ]
Mijn eerste intuÔtie is 9, immers zijn er 9 vrijheidsgraden en in het algemeen heb je dan 9 vergelijkingen nodig om dit op te lossen. Maar dan is er nog die foutcorrectie, dus wellicht heb je aan 8 vergelijkingen voldoende.
Kan iemand dit nader toelichten?


Kun je dit iets nader toelichten?quote:Op maandag 20 januari 2014 20:35 schreef thabit het volgende:
[..]
't Is lineaire algebra over F11. De vector (c1, ..., c9) is bepaald op een scalaire vermenigvuldiging na. Je moet dus een 1-dimensionale deelruimte van een 9-dimensionale ruimte bepalen. Hiervoor zijn 8 vergelijkingen nodig.
Mijn redenatie is als volgt: Je moet 8 c'tjes bepalen, en die andere kun je met behulp van een foutcorrectie vinden. Immers, de 'modular equation' is in staat om ťťn fout te corrigeren.


Doe eerst maar even of het allemaal reŽle getallen zijn, in plaats van een modulaire vergelijking. Hoe zou je het dan aanpakken?quote:Op maandag 20 januari 2014 20:37 schreef Amoeba het volgende:
[..]
Kun je dit iets nader toelichten?
Mijn redenatie is als volgt: Je moet 8 c'tjes bepalen, en die andere kun je met behulp van een foutcorrectie vinden. Immers, de 'modular equation' is in staat om ťťn fout te corrigeren.


Volgens mij heb je dan wťl 9 vergelijkingen nodig toch? Je zet ze allemaal in een matrix en een beetje vegen doet wonderen.quote:Op maandag 20 januari 2014 20:39 schreef thabit het volgende:
[..]
Doe eerst maar even of het allemaal reŽle getallen zijn, in plaats van een modulaire vergelijking. Hoe zou je het dan aanpakken?


Die vergelijkingen eindigen allemaal op "=0".quote:Op maandag 20 januari 2014 20:41 schreef Amoeba het volgende:
[..]
Volgens mij heb je dan wťl 9 vergelijkingen nodig toch? Je zet ze allemaal in een matrix en een beetje vegen doet wonderen.


Ah, je stelt ze allemaal aan elkaar gelijk.quote:Op maandag 20 januari 2014 20:43 schreef thabit het volgende:
[..]
Die vergelijkingen eindigen allemaal op "=0".


Wut?quote:Op maandag 20 januari 2014 20:44 schreef Amoeba het volgende:
[..]
Ah, je stelt ze allemaal aan elkaar gelijk.
In de oorspronkelijke opgave staat ook overal "=0 (mod 11)".


Ik heb geen idee.quote:Op maandag 20 januari 2014 20:45 schreef thabit het volgende:
[..]
Wut?
In de oorspronkelijke opgave staat ook overal "=0 (mod 11)".
Voor een vergelijking met n onbekenden geldt dat er normaliter n condities nodig zijn om dit op te lossen.. Verder ga ik even echt niet komen.


Ja, maar als al die vergelijkingen op "=0" eindigen, zal de oplossing in zo'n geval ook 0 zijn. En dat is hier natuurlijk niet de bedoeling.quote:Op maandag 20 januari 2014 20:47 schreef Amoeba het volgende:
[..]
Ik heb geen idee.
Voor een vergelijking met n onbekenden geldt dat er normaliter n condities nodig zijn om dit op te lossen.. Verder ga ik even echt niet komen.


Aaah zo. Dit kan alleen als c1 t/m c9 allen gelijk 0 zijn, in een niet-modulaire omgeving.quote:Op maandag 20 januari 2014 20:49 schreef thabit het volgende:
[..]
Ja, maar als al die vergelijkingen op "=0" eindigen, zal de oplossing in zo'n geval ook 0 zijn. En dat is hier natuurlijk niet de bedoeling.


Het grappige is dat als je modulo een priemgetal werkt, dat dat soort dingen dan ook gewoon gelden.quote:Op maandag 20 januari 2014 20:52 schreef Amoeba het volgende:
[..]
Aaah zo. Dit kan alleen als c1 t/m c9 allen gelijk 0 zijn, in een niet-modulaire omgeving.


quote:Op maandag 20 januari 2014 20:53 schreef thabit het volgende:
[..]
Het grappige is dat als je modulo een priemgetal werkt, dat dat soort dingen dan ook gewoon gelden.
Dus feitelijk is deze opgave een smadelijk harde grap aangezien c1 tm c9 gewoon allemaal nul moeten wezen?


Nee. Je hebt gewoon geen 9 vergelijkingen nodig.quote:Op maandag 20 januari 2014 20:56 schreef Amoeba het volgende:
[..]
Dus feitelijk is deze opgave een smadelijk harde grap aangezien c1 tm c9 gewoon allemaal nul moeten wezen?


Dat had ik bij mezelf voordat ik deze vraag op het forum stelde ook al bedacht. Nu snap ik nog niet waarom mijn antwoord van 8 goed was, maar ongetwijfeld mijn uitleg fout.quote:Op maandag 20 januari 2014 20:57 schreef thabit het volgende:
[..]
Nee. Je hebt gewoon geen 9 vergelijkingen nodig.


Als je 8 (lineair onafhankelijke) vergelijkingen hebt in 9 onbekenden, dan heb je een 1-dimensionale oplossingsruimte. Dat wil zeggen dat er 1 vector (c1, ..., c9) != 0 is, zodanig dat elke oplossing een veelvoud van die vector is. Dus als (1,2,3,4,5,6,7,8,9) een oplossing is, dan is (2,4,6,8,10,12,14,16,18) dat bijvoorbeeld ook. Meer dan dat kun je ook niet doen, want als alle vergelijkingen op "=0" eindigen, is er altijd sprake van een oplossingsruimte.quote:Op maandag 20 januari 2014 21:00 schreef Amoeba het volgende:
[..]
Dat had ik bij mezelf voordat ik deze vraag op het forum stelde ook al bedacht. Nu snap ik nog niet waarom mijn antwoord van 8 goed was, maar ongetwijfeld mijn uitleg fout.
[ Bericht 19% gewijzigd door thabit op 20-01-2014 21:09:22 ]


Bedankt voor de uitleg, best verwarrend allemaal.quote:Op maandag 20 januari 2014 21:02 schreef thabit het volgende:
[..]
Als je 8 (lineair onafhankelijke) vergelijkingen hebt in 9 onbekenden, dan heb je een 1-dimensionale oplossingsruimte. Dat wil zeggen dat er 1 vector (c1, ..., c9) != 0 is, zodanig dat elke oplossing een veelvoud van die vector is. Dus als (1,2,3,4,5,6,7,8,9) een oplossing is, dan is (2,4,6,8,10,12,14,16,18) dat bijvoorbeeld ook. Meer dan dat kun je ook niet doen, want als alle vergelijkingen op "=0" eindigen, is er altijd sprake van een oplossingsruimte.
(Het kan natuurlijk ook dat de oorsprong de oplossing is van een stelsel vergelijkingen die eindigen op "= 0"


Maar dat is een triviale oplossing en tevens een veelvoud van iedere oplossing (c1, c2, ... c9).quote:Op maandag 20 januari 2014 21:16 schreef randomo het volgende:
[..]
Bedankt voor de uitleg, best verwarrend allemaal.
(Het kan natuurlijk ook dat de oorsprong de oplossing is van een stelsel vergelijkingen die eindigen op "= 0")


Ja, maar geen oplossingsruimte.quote:Op maandag 20 januari 2014 21:17 schreef Amoeba het volgende:
[..]
Maar dat is een triviale oplossing en tevens een veelvoud van iedere oplossing (c1, c2, ... c9).


Dat is waar. Maar als de oorsprong de oplossing is, dan is ieder bankbiljetnummer geldig.quote:
[ Bericht 8% gewijzigd door #ANONIEM op 20-01-2014 23:21:44 ]


Je weet dat:quote:Op dinsdag 21 januari 2014 18:48 schreef Rezania het volgende:
[ afbeelding ]
[ afbeelding ]
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
En het argument (
Dan is het snel in te zien dat in jouw geval voor z3 geldt dat het argument pi is.


Oh ja, want het is e^arg natuurlijk. Stom dat ik dat niet zag.quote:Op dinsdag 21 januari 2014 18:56 schreef Alrac4 het volgende:
[..]
Je weet dat:
En het argument () van een complex getal c voldoet aan:
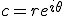
Dan is het snel in te zien dat in jouw geval voor z3 geldt dat het argument pi is.
Gist is liefde, gist is leven. Vooral in een vagijn.


Bedenk wel dat je zo niet alle oplossingen vindt, de uitwerking is niet volledig. Het argument van −1 is niet π maar π + 2kπ, k ∈ Z omdat in het complexe vlak het beeldpunt van 1 overgaat in het beeldpunt van −1 bij een rotatie om de oorsprong over een halve slag plus of min een geheel aantal slagen. Je krijgt dusquote:Op dinsdag 21 januari 2014 18:48 schreef Rezania het volgende:
[ afbeelding ]
[ afbeelding ]
Die eerste stappen snap ik wel, maar die laatste stap, hoe heeft hij bepaald dat pi het argument van z3 is?
z3 = (1/27)·e(π+2kπ)i, k ∈ Z
en dat geeft
z = (1/3)·e(⅓π+⅔kπ)i, k ∈ Z
Je kunt nu drie opeenvolgende gehele waarden voor k invullen (bijvoorbeeld −1, 0, 1), en dan krijg je drie verschillende oplossingen, die je zelf nog maar even in de vorm a+bi met a,b ∈ R moet herschrijven. De beeldpunten van de oplossingen vormen in het complexe vlak de hoekpunten van een gelijkzijdige driehoek en liggen op een cirkel met het middelpunt in de oorsprong en een straal 1/3.
[ Bericht 5% gewijzigd door Riparius op 21-01-2014 21:35:29 ]


Die screenshot van dat plaatje is dan ook maar een deel van de uitwerking.quote:Op dinsdag 21 januari 2014 19:24 schreef Riparius het volgende:
[..]
Bedenk wel dat je zo niet alle oplossingen vindt, de uitwerking is niet volledig. Het argument van −1 is niet π maar π + 2kπ, k ∈ Z omdat in het complexe vlak het beeldpunt van 1 overgaat in het beeldpunt van −1 bij een rotatie om de oorsprong over een halve slag plus of min een geheel aantal slagen. Je krijgt dus
z3 = (1/27)∑e(π+2kπ)i, k ∈ Z
en dat geeft
z = (1/3)∑e(⅓π+⅔kπ)i, k ∈ Z
Je kunt nu drie opeenvolgende gehele waarden voor k invullen (bijvoorbeeld −1, 0, 1), en dan krijg je drie verschillende oplossingen, die je zelf nog maar even in de vorm a+bi met a,b ∈ R moet herschrijven. De beeldpunten van de oplossingen vormen in het complexe vlak de hoekpunten van een gelijkzijdige driehoek en liggen op een cirkel met het middelpunt in de oorsprong en een straal 1/3.
Gist is liefde, gist is leven. Vooral in een vagijn.


Ik moet het limiet van 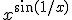 bepalen waarbij x naar oneindig gaat.
bepalen waarbij x naar oneindig gaat.
SPOILER: Uitwerking volgens de docentOm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Nu snap ik zijn uitwerking wel, maar waarom zou je zo moeilijk doen? Als je oneindig invult wordt die 1/x nul, sin(0) is nul, dus krijg je oneindig tot 0, waardoor het limiet 1 is? Lijkt me logisch toch?Gist is liefde, gist is leven. Vooral in een vagijn.


Nee, want je mag niet er zomaar vanuitgaan dat de sin(1/x) "harder naar nul gaat dan x naar oneindig" als ik het me goed herinner, dwz, sin(1/x) wordt voor grotere x steeds kleiner en steeds dichter bij 0, maar x word ook steeds groter, waardoor je niet kunt zeggen dat het zomaar 1 wordt.
Om dezelfde reden kun je ook niet zomaar zeggen dat om maar heel simpel en niet supergerelateerd voorbeeld te geven:
Oneindig/oneindig is niet altijd 1
lim(x->infinity) x^2/x = oneindig/oneindig maar deze limiet convergeert toch niet naar een getal.
Om dezelfde reden kun je ook niet zomaar zeggen dat om maar heel simpel en niet supergerelateerd voorbeeld te geven:
Oneindig/oneindig is niet altijd 1
lim(x->infinity) x^2/x = oneindig/oneindig maar deze limiet convergeert toch niet naar een getal.


Hmm, blijkbaar snap ik de uitwerking toch niet helemaal. De docent heeft het op een gegeven moment over oneindig gedeeld door oneindig, waardoor je L'Hop mag toepassen. Maar ik snap niet hoe hij aan oneindig in de noemer komt. Er staat 1/sin(1/x) in de noemer, vul je dan oneindig in krijg je toch 1/0? En iets delen door nul kan gewoon niet, dus dat kan dan ook geen oneindig als antwoord opleveren.
Gist is liefde, gist is leven. Vooral in een vagijn.


In de noemer staat 1/sin(1/x), niet sin(1/x), en het tweede gaat dusdanig naar nul dat het eerste naar oneindig gaat.


quote:Op woensdag 22 januari 2014 18:57 schreef Rezania het volgende:
Ik moet het de limiet vanbepalen waarbij x naar oneindig gaat.
Als mensen zonder al te veel nadenken beweren dat iets 'logisch' is, dan is dat doorgaans een indicatie dat het beweerde nu juist niet logisch is, en dat is hier ook het geval. Je doet me denken aan (beginnende) studenten die nogal eens schijnen te veronderstellen dat de limiet vanSPOILER: Uitwerking volgens de docentOm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Nu snap ik zijn uitwerking wel, maar waarom zou je zo moeilijk doen? Als je oneindig invult wordt die 1/x nul, sin(0) is nul, dus krijg je oneindig tot 0, waardoor het limiet 1 is? Lijkt me logisch toch?
voor n → ∞ gelijk is aan 1, immers (1 + 1/n) gaat naar 1, en elke macht van 1 is 1 toch? Maar je weet - hopelijk - wel dat dit niet klopt, de bedoelde limiet is namelijk e en ligt tussen 2 en 3.
Voor de limiet die je moet bepalen heb je de regel van l'HŰpital helemaal niet nodig, en wellicht is het beter voor je inzicht om eens te laten zien hoe je deze limiet langs elementaire weg aan kunt tonen. Voor 0 < θ < π/2 hebben we 0 < sin(θ) < θ < tan(θ) zodat we in ieder geval voor x > 1 hebben
en aangezien ln x > 0 voor x > 1 hebben we dan ook
Maar nu weet je ook dat ln x voor x > 1 de oppervlakte is onder de curve y = 1/x over het interval [1,x], zodat voor x > 1 geldt 0 < ln x < x−1 < x. Daarmee is voor x > 1 ook ln(x)/x = ln((√x)2)/x = 2∙ln(√x)/x < 2∙(√x)/x en dus
Combineren van deze ongelijkheden geeft voor x > 1
en aangezien 2/√x naar 0 gaat voor x → ∞ en ln(x)·sin(1/x) zit ingeklemd tussen 0 en 2/√x is het evident dat ln(x)·sin(1/x) ook naar 0 moet gaan voor x → ∞, ergo
De e-macht van ln(x)·sin(1/x) gaat dus naar e0 = 1 voor x → ∞, oftewel we hebben
QED
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 17:17:44 ]


Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.


Als je het snapt probeer het ons eens uit te leggen.quote:Op woensdag 22 januari 2014 21:58 schreef Aarch het volgende:
Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoord tot een bewijs begrijp ik niet.
Alvast dank.
Kom je vanzelf op een bewijs.


Bedankt voor de antwoorden.  Voortaan gewoon niet te simpel denken dus.
Voortaan gewoon niet te simpel denken dus. 
Gist is liefde, gist is leven. Vooral in een vagijn.


Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').quote:Op woensdag 22 januari 2014 21:58 schreef Aarch het volgende:
Ik zit vast voor een toets, dus ik hoop dat ik hier geholpen kan worden.
We zijn bezig met bewijzen van stellingen, maar het verwoorden is erg lastig.
Bijvoorbeeld hier:
Bewijs dat de diagonalen van een ruit ook bissectrices zijn.
Dat is iets wat ik allang wist en ook snap, maar hoe je zoiets verwoordt tot een bewijs begrijp ik niet.
Alvast dank.
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
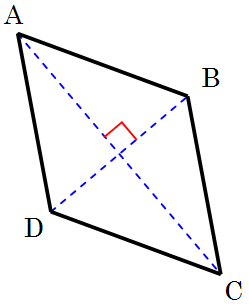
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wŠt je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
[ Bericht 4% gewijzigd door Riparius op 23-01-2014 06:38:17 ]


Als je moet bewijzen dat een bepaalde set compact is met de (Finite) Open Cover definitie, hoe doe je dit? Ik snap wel hoe ik een tegenvoorbeeld moet bedenken en dit te noteren als een set niet compact is, maar het omgekeerde bewijzen lukt nog niet. Een zoektocht op Google heeft ook weinig opgeleverd, veelal hebben ze het over allerlei topologisch ruimtes en dat is nog boven mijn niveau.
Concreet: Hoe bewijs je bijvoorbeeld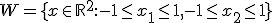 compact is?
compact is?
Concreet: Hoe bewijs je bijvoorbeeld


Als topologische ruimtes boven je niveau zijn, dan heb je wel een behoorlijk pittig voorbeeld gekozen. Bewijs eerst maar dat [0,1] compact is.quote:Op donderdag 23 januari 2014 21:07 schreef Novermars het volgende:
Als je moet bewijzen dat een bepaalde set compact is met de (Finite) Open Cover definitie, hoe doe je dit? Ik snap wel hoe ik een tegenvoorbeeld moet bedenken en dit te noteren als een set niet compact is, maar het omgekeerde bewijzen lukt nog niet. Een zoektocht op Google heeft ook weinig opgeleverd, veelal hebben ze het over allerlei topologisch ruimtes en dat is nog boven mijn niveau.
Concreet: Hoe bewijs je bijvoorbeeldcompact is?


Dat bewijs staat in mijn boek en kan ik goed volgen. Is er misschien enig leesvoer dat relatief snel te begrijpen is zodat ik mijn voorbeeld kan oplossen?
Of kan ik het beter laten zitten en maar Heine-Borel misbruiken?
Of kan ik het beter laten zitten en maar Heine-Borel misbruiken?


O, maar als je dat eenmaal weet, dan hoef je alleen nog maar te bewijzen dat het product van twee compacte ruimten compact is.quote:Op donderdag 23 januari 2014 21:36 schreef Novermars het volgende:
Dat bewijs staat in mijn boek en kan ik goed volgen. Is er misschien enig leesvoer dat relatief snel te begrijpen is zodat ik mijn voorbeeld kan oplossen?
Of kan ik het beter laten zitten en maar Heine-Borel misbruiken?


Verklaar je nader en leg uit! Ik geniet echt van dit soort wiskunde. Hopelijk ga ik het nog vaker tegenkomen tijdens Ectrie, maar ik vrees het ergste...quote:Op donderdag 23 januari 2014 21:38 schreef thabit het volgende:
[..]
O, maar als je dat eenmaal weet, dan hoef je alleen nog maar te bewijzen dat het product van twee compacte ruimten compact is.


Die verzameling W van jou is het product van twee intervallen: [-1,1] x [-1,1].quote:Op donderdag 23 januari 2014 21:41 schreef Novermars het volgende:
[..]
Verklaar je nader en leg uit! Ik geniet echt van dit soort wiskunde. Hopelijk ga ik het nog vaker tegenkomen tijdens Ectrie, maar ik vrees het ergste...


OPGAVE II Zeno de schildpaddenkweker
Zeno is een beroemd kweker van schildpadden; door Zeno gekweekte schildpadden worden door liefhebbers in heel Nederland gekocht. Om gezonde schildpadden te kweken, doet Zeno veel onderzoek.
Zo heeft hij een recursieve formule bedacht om uit te rekenen hoe snel een populatie schildpadden zich uitbreidt:
un = un–1*2 + 4
hierin is u¨n het aantal schildpadden na n maanden.
Van een populatie is bekend dat in het begin (na 0 maanden dus) 4 schildpadden zijn
4 (3p) Gebruik de formule om te berekenen hoeveel schildpadden er zijn na 8 maanden. Beschrijf nauwkeurig hoe je te werk gaat.
Ik als wiskunde leek snap hier niets van. Hoe moet ik hier te werk gaan ?
Zeno is een beroemd kweker van schildpadden; door Zeno gekweekte schildpadden worden door liefhebbers in heel Nederland gekocht. Om gezonde schildpadden te kweken, doet Zeno veel onderzoek.
Zo heeft hij een recursieve formule bedacht om uit te rekenen hoe snel een populatie schildpadden zich uitbreidt:
un = un–1*2 + 4
hierin is u¨n het aantal schildpadden na n maanden.
Van een populatie is bekend dat in het begin (na 0 maanden dus) 4 schildpadden zijn
4 (3p) Gebruik de formule om te berekenen hoeveel schildpadden er zijn na 8 maanden. Beschrijf nauwkeurig hoe je te werk gaat.
Ik als wiskunde leek snap hier niets van. Hoe moet ik hier te werk gaan ?
"the greatest enemy of knowledge is not ignorance, it is the illusion of knowledge." -Stephen W. Hawking


Je bedoelt 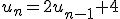 ?
?
@Thabit Zou je het misschien kunnen uitwerken? En misschien nog wel handiger, als je bijvoorbeeld een set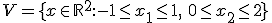 hebt, hoe zou je het dan doen? Eerst bewijzen dat
hebt, hoe zou je het dan doen? Eerst bewijzen dat![[-1,1]](https://forum.fok.nl/lib/mimetex.cgi?%20%5B-1%2C1%5D%20) en
en ![[0,2]](https://forum.fok.nl/lib/mimetex.cgi?%20%5B0%2C2%5D%20) compact zijn? Of nog exotischer,
compact zijn? Of nog exotischer, 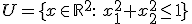 .
.
[ Bericht 14% gewijzigd door Novermars op 23-01-2014 21:56:14 ]
@Thabit Zou je het misschien kunnen uitwerken? En misschien nog wel handiger, als je bijvoorbeeld een set
[ Bericht 14% gewijzigd door Novermars op 23-01-2014 21:56:14 ]


De un-1 is de populatie van de vorige maand waarmee je de huidige populatie kan berekenen. Om het aantal schildpadden na acht maanden te berekenen begin je met het invullen van de startpopulatie (dat zijn die vier schildpadden dus). Het antwoord wat daar uitkomt vul je in waar je eerst die 4 invulde, waardoor je het aantal schildpadden na 2 maanden weet. En dat tot je de populatie na 8 maanden weet.quote:Op donderdag 23 januari 2014 21:43 schreef Drolflap het volgende:
OPGAVE II Zeno de schildpaddenkweker
Zeno is een beroemd kweker van schildpadden; door Zeno gekweekte schildpadden worden door liefhebbers in heel Nederland gekocht. Om gezonde schildpadden te kweken, doet Zeno veel onderzoek.
Zo heeft hij een recursieve formule bedacht om uit te rekenen hoe snel een populatie schildpadden zich uitbreidt:
un = un–1*2 + 4
hierin is u¨n het aantal schildpadden na n maanden.
Van een populatie is bekend dat in het begin (na 0 maanden dus) 4 schildpadden zijn
4 (3p) Gebruik de formule om te berekenen hoeveel schildpadden er zijn na 8 maanden. Beschrijf nauwkeurig hoe je te werk gaat.
Ik als wiskunde leek snap hier niets van. Hoe moet ik hier te werk gaan ?
Gist is liefde, gist is leven. Vooral in een vagijn.


Bedankt ik snap het, was gewoon totaal niet logisch aan het nadenken.quote:Op donderdag 23 januari 2014 21:51 schreef Rezania het volgende:
[..]
De un-1 is de populatie van de vorige maand waarmee je de huidige populatie kan berekenen. Om het aantal schildpadden na acht maanden te berekenen begin je met het invullen van de startpopulatie (dat zijn die vier schildpadden dus). Het antwoord wat daar uitkomt vul je in waar je eerst die 4 invulde, waardoor je het aantal schildpadden na 2 maanden weet. En dat tot je de populatie na 8 maanden weet.
Antwoordenmodel gaf het ook een beetje raar weer:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt."the greatest enemy of knowledge is not ignorance, it is the illusion of knowledge." -Stephen W. Hawking


quote:Op donderdag 23 januari 2014 21:53 schreef Drolflap het volgende:
[..]
Bedankt ik snap het, was gewoon totaal niet logisch aan het nadenken.
Antwoordenmodel gaf het ook een beetje raar weer:Ik snap dat antwoordenmodel ook niet. Je kan het wel via de GR berekenen, maar dan moet je met ans werken.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Gist is liefde, gist is leven. Vooral in een vagijn.


Het wordt natuurlijk pas echt een leuke opgave als je het aantal schildpadden na 100 maanden of zo moet berekenen. En nee, geen rekenmachines. Dan moet je dus een gesloten uitdrukking afleiden voor un.quote:Op donderdag 23 januari 2014 21:51 schreef Rezania het volgende:
[..]
De un-1 is de populatie van de vorige maand waarmee je de huidige populatie kan berekenen. Om het aantal schildpadden na acht maanden te berekenen begin je met het invullen van de startpopulatie (dat zijn die vier schildpadden dus). Het antwoord wat daar uitkomt vul je in waar je eerst die 4 invulde, waardoor je het aantal schildpadden na 2 maanden weet. En dat tot je de populatie na 8 maanden weet.


Ja, maar denk niet dat hij daar al aan toe is.quote:Op donderdag 23 januari 2014 21:56 schreef Riparius het volgende:
[..]
Het wordt natuurlijk pas echt een leuke opgave als je het aantal schildpadden na 100 maanden of zo moet berekenen. En nee, geen rekenmachines. Dan moet je dus een gesloten uitdrukking afleiden voor un.
Gist is liefde, gist is leven. Vooral in een vagijn.


Of algemeen bewijzen dat elk gesloten interval [a,b] compact is.quote:Op donderdag 23 januari 2014 21:50 schreef Novermars het volgende:
Je bedoelt?
@Thabit Zou je het misschien kunnen uitwerken? En misschien nog wel handiger, als je bijvoorbeeld een sethebt, hoe zou je het dan doen? Eerst bewijzen dat
en
compact zijn?
Het bewijs dat een product van twee compacte ruimten compact is, is ongetwijfeld met Google wel te vinden, dus ik weet niet in hoeverre het iets toevoegt om dat hier helemaal te gaan lopen uitspellen. Als je er zelf over na wilt denken, dan kan ik wel af en toe een hint geven.


Als je eenmaal weet dat producten van gesloten intervallen [a,b] compact zijn, dan is het tijd voor de volgende stelling: een gesloten deel van een compacte ruimte is compact. Bewijs die eerst maar; die is namelijk wat eenvoudiger.quote:


Inhomogene lineaire recursies bij wiskunde A? Leg jij iemand met alleen wiskunde A dan maar even uit hoe je hier op un = 2n+3 − 4 komt.quote:Op donderdag 23 januari 2014 21:57 schreef Rezania het volgende:
[..]
Ja, maar denk niet dat hij daar al aan toe is.Is trouwens best wel makkelijk vergeleken met de stof die hier normaal gesproken langs komt, je krijgt het zelfs bij wiskunde A.


Tot op een bepaald niveau, het moet natuurlijk niet de algebrakennis van A'ers overstijgen.quote:Op donderdag 23 januari 2014 22:08 schreef Riparius het volgende:
[..]
Inhomogene lineaire recursies bij wiskunde A? Leg jij iemand met alleen wiskunde A dan maar even uit hoe je hier op un = 2n+3 + 4 komt.
Ik kan me herinneren dat ik heb geleerd hoe van je een recursieve formule een directe formule kan maken, kan dat kloppen? Ik weet eigenlijk niet meer zoveel van A.
Gist is liefde, gist is leven. Vooral in een vagijn.


Gaat 'm niet lukken. Volgens mij krijg je de inhomogene varianten niet eens bij wiskunde D.quote:Op donderdag 23 januari 2014 22:08 schreef Riparius het volgende:
[..]
Inhomogene lineaire recursies bij wiskunde A? Leg jij iemand met alleen wiskunde A dan maar even uit hoe je hier op un = 2n+3 − 4 komt.


Ik haal dan termen door elkaar waarschijnlijk.quote:Op donderdag 23 januari 2014 22:15 schreef Amoeba het volgende:
[..]
Gaat 'm niet lukken. Volgens mij krijg je de inhomogene varianten niet eens bij wiskunde D.
Gist is liefde, gist is leven. Vooral in een vagijn.


Dat is juist, maar bij mijn weten geen inhomogene variant.quote:Op donderdag 23 januari 2014 22:14 schreef Rezania het volgende:
[..]
Tot op een bepaald niveau, het moet natuurlijk niet de algebrakennis van A'ers overstijgen.
Ik kan me herinneren dat ik heb geleerd hoe van je een recursieve formule een directe formule kan maken, kan dat kloppen? Ik weet eigenlijk niet meer zoveel van A.


Waar had ik het over inhomogeen?quote:Op donderdag 23 januari 2014 22:15 schreef Amoeba het volgende:
[..]
Dat is juist, maar bij mijn weten geen inhomogene variant.
Gist is liefde, gist is leven. Vooral in een vagijn.


Mag ik gebruiken dat een set compact is iff gesloten en begrensd (aka Heine-Borel)? Of krijg ik dan een cirkelredenering omdat Heine-Borel leunt op het bewijs dat een gesloten subset compact is?quote:Op donderdag 23 januari 2014 22:01 schreef thabit het volgende:
[..]
Als je eenmaal weet dat producten van gesloten intervallen [a,b] compact zijn, dan is het tijd voor de volgende stelling: een gesloten deel van een compacte ruimte is compact. Bewijs die eerst maar; die is namelijk wat eenvoudiger.


Dan krijg je een cirkelredenering. Je wilt Heine-Borel immers bewijzen vanuit het basisgeval dat [a,b] compact is.quote:Op donderdag 23 januari 2014 22:30 schreef Novermars het volgende:
[..]
Mag ik gebruiken dat een set compact is iff gesloten en begrensd (aka Heine-Borel)? Of krijg ik dan een cirkelredenering omdat Heine-Borel leunt op het bewijs dat een gesloten subset compact is?


Ik heb het bewijs maar opgezocht. Ik was wel goed op weg met hetgeen ik zelf bedacht had, maar ik blijf dit soort dingen moeilijk vinden om zelf te verzinnen zonder hints etc.quote:Op donderdag 23 januari 2014 22:32 schreef thabit het volgende:
[..]
Dan krijg je een cirkelredenering. Je wilt Heine-Borel immers bewijzen vanuit het basisgeval dat [a,b] compact is.
En als deze al eenvoudiger is, dan heb ik nog veel werk te verrichten :p


Het zou kunnen dat je dat geleerd hebt bij wiskunde A (maar het zal waarschijnlijk alleen om lineaire recurrentievergelijkingen gaan, of nog simpelere gevallen). Voor wat ingewikkeldere recurrenties worden vaak voortbrengende functies (bekender onder de Engelse term generating functions) gebruikt, een techniek waarbij je een polynoom met u0, u1, u2, ... als coŽfficiŽnten gebruikt. Best een aparte techniek, maar vaak wel handig.quote:Op donderdag 23 januari 2014 22:14 schreef Rezania het volgende:
[..]
Tot op een bepaald niveau, het moet natuurlijk niet de algebrakennis van A'ers overstijgen.
Ik kan me herinneren dat ik heb geleerd hoe van je een recursieve formule een directe formule kan maken, kan dat kloppen? Ik weet eigenlijk niet meer zoveel van A.
Voor de geinteresseerden: generatingfunctionology is een gratis pdf'je met een hele zooi informatie over voortbrengende functies (ik moet bekennen dat ik hem zelf nooit uitgelezen heb, maar zelfs alleen het eerste hoofdstuk bevat al erg veel informatie).
Als je de formule x0+x1+x2+...+xn=xn-1/(x+1) kent, kan je gewoon u1, u2, u3, u4, ... etc. uitschrijven (uitdrukken in u0) en kijken of je een patroon ziet. Een beproefde techniek, toegepast door vele beroemde wiskundigen
[ Bericht 13% gewijzigd door randomo op 23-01-2014 23:21:03 ]


Ik heb de volgende opdracht:
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
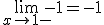
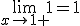
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.


Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.quote:Op donderdag 23 januari 2014 23:12 schreef randomo het volgende:
[..]
Het zou kunnen dat je dat geleerd hebt bij wiskunde A (maar het zal waarschijnlijk alleen om lineaire recurrentievergelijkingen gaan, of nog simpelere gevallen). Voor wat ingewikkeldere recurrenties worden vaak voortbrengende functies (bekender onder de Engelse term generating functions) gebruikt, een techniek waarbij je een polynoom met u0, u1, u2, ... als coŽfficiŽnten gebruikt. Best een aparte techniek, maar vaak wel handig.
Voor de geinteresseerden: generatingfunctionology is een gratis pdf'je met een hele zooi informatie over voortbrengende functies (ik moet bekennen dat ik hem zelf nooit uitgelezen heb, maar zelfs alleen het eerste hoofdstuk bevat al erg veel informatie).
Als je de formule x0+x1+x2+...+xn=xn-1/(x+1) kent, kan je gewoon u1, u2, u3, u4, ... etc. uitschrijven (uitdrukken in u0) en kijken of je een patroon ziet. Een beproefde techniek, toegepast door vele beroemde wiskundigen


Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.quote:Op donderdag 23 januari 2014 23:31 schreef Miraculously het volgende:
Ik heb de volgende opdracht:
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.


Voor lineare recursievergelijkingen is inderdaad wat eenvoudiger (er is niet voor niets een heel boek over geschreven), maar volgens mij zijn voortbrengende functies ook nuttig voor ingewikkeldere functies, en hebben ze meer functies dan alleen het oplossen van de recursievergelijking.quote:Op donderdag 23 januari 2014 23:31 schreef Riparius het volgende:
[..]
Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.


Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.


Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...quote:Op vrijdag 24 januari 2014 07:13 schreef Amoeba het volgende:
Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
[ Bericht 0% gewijzigd door Riparius op 24-01-2014 07:51:28 ]


Oh…quote:Op vrijdag 24 januari 2014 07:43 schreef Riparius het volgende:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Mooie post wel. Nog eens oprakelen dan maar.


Bedankt voor je antwoord.quote:Op vrijdag 24 januari 2014 00:11 schreef thabit het volgende:
[..]
Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?


Gebruik de ε,δ definitie van de limiet om te laten zien dat limh→0 (f(1+h) − f(1))/h niet bestaat, dan heb je bewezen dat f niet differentieerbaar is in het punt x = 1. Verder wijst Thabit er terecht op dat je niet zomaar (impliciet of expliciet) aan mag nemen dat de afgeleide continu is in die punten waar je functie wel differentieerbaar is.quote:Op vrijdag 24 januari 2014 19:46 schreef Miraculously het volgende:
[..]
Bedankt voor je antwoord.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 02:35:13 ]


Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.quote:Op vrijdag 24 januari 2014 07:43 schreef Riparius het volgende:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.


De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coŽfficiŽnten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...quote:Op vrijdag 24 januari 2014 20:31 schreef randomo het volgende:
[..]
Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.


Met voortbrengende functies kan je laten zien dat als de karakteristieke vergelijking kwadratisch is en een dubbel nulpunt heeft (dus van de vorm (x - c)2 = 0 is), een gesloten uitdrukking voor de recursie ak = kck-1a1 - (k - 1)cka0 is. Maar ik verwacht stiekem wel dat Riparius nog met een andere manier op de proppen komtquote:Op vrijdag 24 januari 2014 20:42 schreef Riparius het volgende:
[..]
De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coŽfficiŽnten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...
Ik bedenk me nu pas dat je natuurlijk ook een kwadratische vergelijking kan hebben met alleen complexe nulpunten, dat is denk ik ook een moeilijkheid als je de methode van de karakteristieke vergelijking gebruikt (of niet? Ik denk er morgen misschien nog maar eens over na, het is inmiddels al half twee hier...)
Ik meen me ook een dergelijke uitdrukking te herinneren voor het oplossen van lineaire homogene differentiaalvergelijkingen met constante coŽfficiŽnten. Als je een differentiaalvergelijking hebt van de vorm:
x'' = ax' + bx
kan je oplossingen van de vorm eλx veronderstellen, zodat je een karakteristiek polynoom krijgt:
λ2eλx = ac eλx + beλx
delen door eλx en alles naar de linkerkant brengen geeft:
λ2 - aλ - b = 0
Het idee is nu hetzelfde: vindt de twee oplossingen, door ze te combineren kan je een oplossing met de gewenste randvoorwaarde vinden. Ik meen me te herinneren (verbeter me als ik ernaast zit) dat als je een oplossing λ vindt met multipliciteit 2, je ipv van eλx, je xeλx en eλx als oplossingen vindt.
Ik blijf het allemaal een beetje mysterieus vinden...
[ Bericht 1% gewijzigd door randomo op 25-01-2014 10:31:31 ]


Zeer veel dank!!quote:Op woensdag 22 januari 2014 22:33 schreef Riparius het volgende:
[..]
Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
[ afbeelding ]
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wŠt je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
Het is me een stuk duidelijker geworden door deze uitleg.


Laten we eens uitgaan van een rij {un}, n∈ N0 met louter reŽle termen die aan een homogene lineaire tweede orde recursie met constante en reŽle coŽfficiŽnten voldoet, en welquote:Op zaterdag 25 januari 2014 10:17 schreef randomo het volgende:
Ik blijf het allemaal een beetje mysterieus vinden...Kan iemand me iets meer inzicht bijbrengen?
(1) a·un + b·un−1 + c·un−2 = 0
Hierbij moeten we a ≠ 0 en tevens c ≠ 0 veronderstellen, aangezien we anders geen tweede orde recursie hebben.
Zoals bekend kunnen we in beginsel gesloten uitdrukkingen vinden voor de algemene term un van rijen die aan het recursievoorschrift (1) voldoen door op zoek te gaan naar meetkundige rijen die aan dit voorschrift voldoen. Hebben we een meetkundige rij {un} met als eerste term u0 en reden λ, dan is
(2) un = u0·λn
Substitutie van (2) in geeft voor n > 1
(3) u0·λn−2(aλ2 + bλ + c) = 0
Nu is het duidelijk dat un = 0, i.e. een rij die uit louter nullen bestaat, een triviale oplossing is van het recursievoorschrift (1) en dat we daarom op grond van (2) zowel u0 ≠ 0 als λ ≠ 0 moeten veronderstellen om andere oplossingen naast deze triviale oplossing te vinden. Maar dan kan uitsluitend aan (3) worden voldaan als de uitdrukking tussen haakjes gelijk is aan nul, dus
(4) aλ2 + bλ + c = 0
Dit is de zogeheten karakteristieke vergelijking van het recursievoorschrift (1). We noemen het polynoom
(5) P(λ) = aλ2 + bλ + c
ook het karakteristieke polynoom van het recursievoorschrift (1). Nu is (4) een vierkantsvergelijking in λ, en zoals bekend wordt de aard van de nulpunten van P(λ) en daarmee van de oplossingen van (4) bepaald door de discriminant
(6) D = b2 − 4ac
van dit polynoom. We onderscheiden nu drie mogelijkheden.
1. D > 0. Nu heeft P(λ) twee verschillende reŽle nulpunten λ1 en λ2 en zijn de meetkundige rijen gedefinieerd door un = u0·λ1n en un = u0·λ2n twee (lineair onafhankelijke) oplossingen van (1). En omdat elke lineaire combinatie {cn} met cn = α·an + β·bn van twee rijen {an} en {bn} die voldoen aan (1) ook weer voldoet aan (1) krijgen we als algemene oplossing van het recursievoorschrift
(7) un = α·λ1n+ β·λ2n
waarin α en β willekeurige (reŽle) constanten zijn. Het is eenvoudig na te gaan dat (7) ook inderdaad de volledige oplossing geeft van het recursievoorschrift (1). Een rij die voldoet aan een tweede orde recursie ligt volledig vast als twee opeenvolgende termen van de rij zijn gegeven. Welnu, substitutie in (7) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ1 ≠ 0 en tevens λ2 ≠ 0, terwijl uit D ≠ 0 volgt dat λ1 ≠ λ2, zodat de determinant van het stelsel ongelijk is aan nul.
2. D < 0. Nu heeft P(λ) twee toegevoegd complexe nulpunten λ1 en λ2 maar de situatie verschilt niet wezenlijk van die voor D > 0. Ook nu geldt dat (7) de algemene oplossing geeft van het recursievoorschrift (1), en ook nu levert substitutie in (7) van twee opeenvolgende termen van een specifieke rij een stelsel van twee lineaire vergelijkingen in α en β met een unieke oplossing. Echter, niet alleen λ1 en λ2 maar ook α en β zijn nu in het algemeen (toegevoegd) complex, zodat het niet mogelijk is een gesloten algebraÔsche uitdrukking voor de algemene term van de recursieve rij te geven zonder gebruik van complexe getallen, en dat terwijl alle termen van de rij zelf wel degelijk reŽel zijn. Maar, zoals ik wel eens heb laten zien, is het in dit geval altijd mogelijk een goniometrische uitdrukking te geven voor algemene term van de rij zonder gebruik van complexe getallen.
3. D = 0. Nu heeft P(λ) ťťn reŽel nulpunt met multipliciteit 2, dat ik aan zal geven met λ0. Aangezien λ0 voldoet aan (4) is het duidelijk dat
(8) un = α·λ0n
met een willekeurige α in ieder geval een oplossing is van het recursievoorschrift (1). Maar het is evenzeer duidelijk dat (8) nu niet de volledige oplossing kan zijn van (1) omdat we bij het recursievoorschrift (1) de waarden van u0 en u1 steeds vrij kunnen kiezen, terwijl (8) alleen een oplossing biedt als u1 = λ0u0.
Een elegante methode om toch de volledige oplossing van (1) te verkrijgen als D = 0 berust op het gebruik van differentiaalrekening. Daarvoor hebben we de volgende stelling nodig:
Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.
Het bewijs van deze stelling gaat het eenvoudigst als we eerst even twee lemmata bewijzen.
Lemma 1. Als een niet-constant polynoom P(x) een enkelvoudig nulpunt x = x0 heeft, dan is P'(x0) ≠ 0.
Bewijs: volgens de factorstelling volgt uit P(x0) = 0 dat P(x) een factor (x − x0) bevat zodat P(x) = (x −x0)·Q(x). Aangezien x = x0 een enkelvoudig nulpunt is van P(x) kan het polynoom Q(x) geen verdere factoren (x − x0) bevatten zodat, wederom volgens de factorstelling, Q(x0) ≠ 0. De afgeleide van P(x) = (x −x0)·Q(x) is P'(x) = Q(x) + (x − x0)·Q'(x) zodat P'(x0) = Q(x0) + 0·Q'(x0) = Q(x0) ≠ 0, QED.
Lemma 2. Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1 dan heeft de afgeleide P'(x) een nulpunt x = x0 met een multipliciteit (m − 1).
Bewijs: aangezien P(x) een nulpunt x = x0 heeft met multipliciteit m > 1 is P(x) = (x − x0)m·Q(x) waarbij het polynoom Q(x) geen verdere factoren (x − x0) bevat zodat volgens de factorstelling Q(x0) ≠ 0. De afgeleide van P(x) = (x − x0)m·Q(x) is P'(x) = m·(x − x0)m−1·Q(x) + (x − x0)m·Q'(x) waarvoor we kunnen schrijven P'(x) = (x − x0)m−1·(m·Q(x) + (x − x0)·Q'(x)). Voor x = x0 is de factor (m·Q(x) + (x − x0)·Q'(x)) gelijk aan m·Q(x0) ≠ 0 zodat (m·Q(x) + (x − x0)·Q'(x)) volgens de factorstelling geen factor (x − x0) bevat en de multipliciteit van het nulpunt x = x0 van P'(x) dus gelijk is aan (m − 1), QED.
Het bewijs van bovenstaande stelling is nu uiteraard eenvoudig: heeft een niet-constant polynoom P(x) een nulpunt x = x0 met multipliciteit m > 1, dan geeft (herhaalde) toepassing van lemma 2 dat P(i)(x) voor i = 1 .. (m − 1) een nulpunt x = x0 heeft met een multipliciteit (m − i), zodat P(m−1)(x) een enkelvoudig nulpunt x = x0 heeft. En volgens lemma 1 is dan P(m)(x0) ≠ 0, QED.
Goed, nu de volledige oplossing van (1) als D = 0. Vermenigvuldigen we beide leden van (5) met λn−2, dan hebben we voor n > 1
(9) a·λn + b·λn−1 + c·λn−2 = λn−2·P(λ)
DifferentiŽren naar λ geeft nu
(10) a·n·λn−1 + b·(n−1)·λn−2 + c·(n−2)·λn−3 = (n−2)·λn−3·P(λ) + λn−2·P'(λ)
En beide leden vermenigvuldigen met λ geeft dan
(11) a·n·λn + b·(n−1)·λn−1 + c·(n−2)·λn−2 = (n−2)·λn−2·P(λ) + λn−1·P'(λ)
Nu is λ = λ0 een nulpunt van P(λ) met multipliciteit 2, zodat niet alleen P(λ0) = 0 maar tevens P'(λ0) = 0. Substutie van λ = λ0 in (11) geeft dus
(12) a·n·λ0n + b·(n−1)·λ0n−1 + c·(n−2)·λ0n−2 = 0
zodat we kunnen concluderen dat un = n·λ0n aan het recursievoorschrift (1) voldoet. Eerder vonden we al dat un = λ0n voldoet, zodat ook elke lineaire combinatie van deze oplossingen aan het recursievoorschrift voldoet en we dus krijgen
(13) un = (α + β·n)·λ0n
Het is weer gemakkelijk na te gaan dat deze oplossing inderdaad volledig is. Substitutie in (13) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ0 ≠ 0 zodat de determinant van het stelsel ongelijk is aan nul.
Het aardige van deze methode is dat deze eenvoudig is te generaliseren naar homogene lineaire recursies met constante coŽfficiŽnten van hogere ordes. Heeft het karakteristieke polynoom P(λ) van zo'n hogere orde recursie van orde N namelijk een meervoudig nulpunt λ = λ0 met multipliciteit m, dan kun je door P(λ) te vermenigvuldigen met λn−N en daarna telkens om beurten te differentiŽren en weer te vermenigvuldigen met λ gemakkelijk laten zien dat naast un = λ0n ook un = ni·λ0n voor i = 1 .. (m − 1) een oplossing geeft van de recursie. Zo geeft elk meervoudig nulpunt met een multipliciteit m dus precies m lineair onafhankelijke oplossingen.
Wil je niet gebruik maken van differentiaalrekening, dan is er in ieder geval voor tweede orde recursies waarbij de discriminant van de karakteristieke vergelijking gelijk is aan nul ook een goed bruikbare elementaire methode die bekend staat als de variatie van de constante. Het idee hierbij is dat je uitgaat van (8) maar dat je veronderstelt dat α niet constant is maar een functie van n. Dat wil dus zeggen dat je een rij {αn} zoekt zodanig dat
(14) un = αn·λ0n
een oplossing is van de recursie (1). Welnu, invullen van (14) in (1) geeft voor n > 1
(15) λ0n−2(a·αn·λ02 + b·αn−1·λ0 + c·αn−2) = 0
en aangezien λ0 ≠ 0 geeft dit
(16) a·αn·λ02 + b·αn−1·λ0 + c·αn−2 = 0
Nu weten we echter ook dat λ0 = −b/2a (en dus b ≠ 0 aangezien λ0 ≠ 0). Substitutie hiervan in (16) en gebruik maken van D = b2 − 4ac = 0 (en dus 4ac = b2) levert dan na wat herleiding
(17) αn − αn−1 = αn−1 − αn−2
In woorden: het verschil tussen elk tweetal opeenvolgende termen van de rij {αn} is constant. De rij {αn} is dus een willekeurige rekenkundige rij, en de algemene gedaante van αn is dus
(18) αn = α + n·β
waarbij α en β willekeurige constanten zijn. Substitutie van (18) in (14) geeft nu
(19) un = (α + n·β)·λ0n
en dit stemt geheel overeen met de eerder gevonden algemene oplossing (13).
That's all.


Wat snap je er niet aan? Wat snap je al wel?quote:Op zondag 26 januari 2014 12:17 schreef Beverwijker het volgende:
http://tinypic.com/r/11snpc2/5
Iemand die mij vraag 12 kan uitleggen.
Het gaat hier om een driehoek met een rechte hoek. Gegeven is de lengte van ťťn van de zijdes die aan deze rechte hoek grenst (10). De andere zijde die aan de rechte hoek grenst wordt lengte a gesteld. Het gevraagde is de lengte van de langste zijde, dat is (op grond van de driehoeksongelijkheid) de schuine zijde van deze driehoek. Kun je hier iets mee? Hint: Pythagoras.
Als je dat doorhebt weet je waar de formule vandaan komt. De opdracht is simpeler: je moet drie keer een waarde voor a invullen in de formule.


Stel je hebt twee open sets, zeg maar 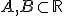 . Is het Cartesian Product
. Is het Cartesian Product 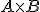 dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]


Top! Zoals gewoonlijk weer een uitstekende uitlegquote:
Die stelling was inderdaad uiteindelijk de missing link
Veel dank en hulde!quote:Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.


Dit is metawiskundig gezien wel een interessante vraag, want hoe definieer je de topologie op RxR? Enerzijds kun je de Euclidische metriek nemen en van daar uit werken. Anderzijds bestaat er ook een categorie-theoretische definitie van producten en kun je bewijzen dat producten bestaan in de categorie van topologische ruimten. De twee topologieŽn die je zo krijgt blijken hetzelfde te zijn, iets wat niet vanzelfsprekend is!quote:Op zondag 26 januari 2014 22:03 schreef Novermars het volgende:
Stel je hebt twee open sets, zeg maar. Is het Cartesian Product
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700


Ik krijg koppijn van dit vraagstuk
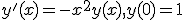
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 21:48:45 ]
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 21:48:45 ]


Je mist een accentje.quote:Op dinsdag 28 januari 2014 21:40 schreef Amoeba het volgende:
Ik krijg koppijn van dit vraagstuk
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
[ afbeelding ]
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?


Excuus, ik heb er eentje te veel gezet.quote:
http://www.win.tue.nl/~gprokert/opcoll14.pdf
Opgave 3
[ Bericht 6% gewijzigd door #ANONIEM op 28-01-2014 21:49:42 ]
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |