SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.quote:Op donderdag 23 januari 2014 23:12 schreef randomo het volgende:
[..]
Het zou kunnen dat je dat geleerd hebt bij wiskunde A (maar het zal waarschijnlijk alleen om lineaire recurrentievergelijkingen gaan, of nog simpelere gevallen). Voor wat ingewikkeldere recurrenties worden vaak voortbrengende functies (bekender onder de Engelse term generating functions) gebruikt, een techniek waarbij je een polynoom met u0, u1, u2, ... als coŽfficiŽnten gebruikt. Best een aparte techniek, maar vaak wel handig.
Voor de geinteresseerden: generatingfunctionology is een gratis pdf'je met een hele zooi informatie over voortbrengende functies (ik moet bekennen dat ik hem zelf nooit uitgelezen heb, maar zelfs alleen het eerste hoofdstuk bevat al erg veel informatie).
Als je de formule x0+x1+x2+...+xn=xn-1/(x+1) kent, kan je gewoon u1, u2, u3, u4, ... etc. uitschrijven (uitdrukken in u0) en kijken of je een patroon ziet. Een beproefde techniek, toegepast door vele beroemde wiskundigen


Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.quote:Op donderdag 23 januari 2014 23:31 schreef Miraculously het volgende:
Ik heb de volgende opdracht:
Onderzoek bij de volgende functies voor welke x ze wel gedefinieerd, maar niet differentieerbaar zijn.
f(x) = |x-1|.
Ik weet dat geldt voor f(x) = |x-1| { -(x-1) voor x<1 en x-1 voor x>1 (iemand die weet hoe ik deze stuksgewijs krijg, lukte me niet met LaTex).
Verder weet ik dat het minimum, en dus de knik, zit op het punt (1,0) waar de functie niet differentieerbaar is.
Is het nu voldoende (en klopt het ook) als ik zeg dat:
f'(x) = |x-1|' { -1 voor x<1 en 1 voor x>1
Waardoor we krijgen dat
Waardoor dus f(x)=|x-1| niet differentieerbaar is in het punt x=1.


Voor lineare recursievergelijkingen is inderdaad wat eenvoudiger (er is niet voor niets een heel boek over geschreven), maar volgens mij zijn voortbrengende functies ook nuttig voor ingewikkeldere functies, en hebben ze meer functies dan alleen het oplossen van de recursievergelijking.quote:Op donderdag 23 januari 2014 23:31 schreef Riparius het volgende:
[..]
Ik vind die voortbrengende functies helemaal niet handig om een eenvoudige lineaire recursie op te lossen. Met de methode van de zogeheten karakteristieke vergelijking gaat het veel eenvoudiger.


Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.


Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...quote:Op vrijdag 24 januari 2014 07:13 schreef Amoeba het volgende:
Die karakteristieke vergelijking staat me nog iets van bij. Misschien komt dat dus wel bij wiskunde D aan de orde.
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
[ Bericht 0% gewijzigd door Riparius op 24-01-2014 07:51:28 ]


Oh…quote:Op vrijdag 24 januari 2014 07:43 schreef Riparius het volgende:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Mooie post wel. Nog eens oprakelen dan maar.


Bedankt voor je antwoord.quote:Op vrijdag 24 januari 2014 00:11 schreef thabit het volgende:
[..]
Ik weet niet in hoeveel detail het bewezen dient te worden, maar je hebt op dit punt enkel bewezen dat de functie niet continu differentieerbaar is. Okee, als je wat stellingen gebruikt heb je ook bewezen dat f niet differentieerbaar is, maar het is wel belangrijk om te beseffen dat de afgeleide van een differentieerbare functie niet continu hoeft te zijn. Ik zou in elk geval direct de definitie van afgeleide toepassen hier.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?


Gebruik de ε,δ definitie van de limiet om te laten zien dat limh→0 (f(1+h) − f(1))/h niet bestaat, dan heb je bewezen dat f niet differentieerbaar is in het punt x = 1. Verder wijst Thabit er terecht op dat je niet zomaar (impliciet of expliciet) aan mag nemen dat de afgeleide continu is in die punten waar je functie wel differentieerbaar is.quote:Op vrijdag 24 januari 2014 19:46 schreef Miraculously het volgende:
[..]
Bedankt voor je antwoord.
Met de definitie van de afgeleide bedoel je f'(a) = limx→a (f(x) - f(a)) / (x - a) neem ik aan?
[ Bericht 0% gewijzigd door Riparius op 25-01-2014 02:35:13 ]


Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.quote:Op vrijdag 24 januari 2014 07:43 schreef Riparius het volgende:
[..]
Als dat alles is wat er van mijn uitleg destijds is blijven hangen, dan is dat niet veel ...
Wil je weten hoe je de gesloten uitdrukking voor de termen van de rij van Fibonacci afleidt met behulp van de voortbrengende functie F(x) = x/(1 − x − x≤) dan moet je Stillwell, Mathematics and Its History, ≥2010, p. 192-194 maar eens raadplegen. Die schrijft het helemaal uit (wat ik hier niet ga doen) en dan zie je dat het niet handig is. Neemt natuurlijk niet weg dat je met voortbrengende functies nog heel wat andere interessante dingen kunt doen.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.


De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coŽfficiŽnten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...quote:Op vrijdag 24 januari 2014 20:31 schreef randomo het volgende:
[..]
Dat voorbeeld (een gesloten uitdrukking voor de termen van de rij van Fibonacci) staat overigens ook in de link die ik gaf. Ze gaan er daar wel redelijk snel doorheen (in ongeveer een bladzijde). Waarmee ik overigens niet bedoel dat het een handige manier is.
Ik moet bekennen dat ik zelf ook weer even moest nadenken hoe die methode van de karakteristieke vergelijking ook al weer werkte. Maar eigenlijk is het heel simpel: je neemt aan dat xn een oplossing is, daaruit vindt je een kwadratische vergelijking met (hopelijk) twee oplossingen. Door een lineaire combinatie van deze twee oplossingen te maken kan je een nieuwe oplossing maken, die voldoet aan een randvoorwaarde. Als je alleen de eerste stap onthoudt (het aannemen dat er een oplossing van de vorm xn is), volgt de rest vrij natuurlijk.


Met voortbrengende functies kan je laten zien dat als de karakteristieke vergelijking kwadratisch is en een dubbel nulpunt heeft (dus van de vorm (x - c)2 = 0 is), een gesloten uitdrukking voor de recursie ak = kck-1a1 - (k - 1)cka0 is. Maar ik verwacht stiekem wel dat Riparius nog met een andere manier op de proppen komtquote:Op vrijdag 24 januari 2014 20:42 schreef Riparius het volgende:
[..]
De vierkantsvergelijking die je krijgt bij een homogene tweede orde lineaire recursie met constante coŽfficiŽnten heeft altijd twee oplossingen. Het wordt alleen iets lastiger als de twee oplossingen samenvallen. Wat je dan moet doen is niet helemaal triviaal, en dat heb ik destijds met opzet ook niet uitgelegd. Ik had gehoopt dat Amoeba daar wel een kritische vraag over zou stellen, maar dat gebeurde niet ...
Ik bedenk me nu pas dat je natuurlijk ook een kwadratische vergelijking kan hebben met alleen complexe nulpunten, dat is denk ik ook een moeilijkheid als je de methode van de karakteristieke vergelijking gebruikt (of niet? Ik denk er morgen misschien nog maar eens over na, het is inmiddels al half twee hier...)
Ik meen me ook een dergelijke uitdrukking te herinneren voor het oplossen van lineaire homogene differentiaalvergelijkingen met constante coŽfficiŽnten. Als je een differentiaalvergelijking hebt van de vorm:
x'' = ax' + bx
kan je oplossingen van de vorm eλx veronderstellen, zodat je een karakteristiek polynoom krijgt:
λ2eλx = ac eλx + beλx
delen door eλx en alles naar de linkerkant brengen geeft:
λ2 - aλ - b = 0
Het idee is nu hetzelfde: vindt de twee oplossingen, door ze te combineren kan je een oplossing met de gewenste randvoorwaarde vinden. Ik meen me te herinneren (verbeter me als ik ernaast zit) dat als je een oplossing λ vindt met multipliciteit 2, je ipv van eλx, je xeλx en eλx als oplossingen vindt.
Ik blijf het allemaal een beetje mysterieus vinden...
[ Bericht 1% gewijzigd door randomo op 25-01-2014 10:31:31 ]


Zeer veel dank!!quote:Op woensdag 22 januari 2014 22:33 schreef Riparius het volgende:
[..]
Een klassiek meetkundig bewijs verloopt volgens een vast stramien: Gegeven: ..., Te bewijzen: ..., Bewijs: ..., en eindigt natuurlijk met QED (Quod Erat Demonstrandum 'hetgeen te bewijzen was').
Je moet dus eerst bedenken wat je precies als gegeven wil veronderstellen (ja, een ruit natuurlijk) en wat je dan precies wil aantonen. Begin met te bedenken wat de definitie is van een ruit. Dat is niet evident, want er worden verschillende definities gehanteerd voor een ruit. In oudere meetkundeboeken (en bijvoorbeeld ook nog in de Franse Wikipedia) definieert men een ruit als een parallellogram waarvan twee aanliggende zijden gelijk zijn, maar een ruit wordt tegenwoordig meestal gedefinieerd als een vierhoek met vier gelijke zijden (zo bijvoorbeeld in de Nederlandse en de Engelse Wikipedia). De gekozen definitie heeft uiteraard consequenties, want als je de oude definitie hanteert, dan is de eigenschap dat een ruit vier gelijke zijden heeft een stelling, evenals het omgekeerde, namelijk dat een vierhoek met vier gelijke zijden een ruit is. En, vice versa, met de nieuwe definitie van een ruit is de bewering dat een ruit een parallellogram is weer een stelling.
Maar goed, teken een plaatje van een ruit en duid daarbij de hoekpunten aan met de letters A t/m D:
[ afbeelding ]
Teken ook de beide diagonalen AC en BD van de ruit.
Het is niet voldoende om alleen een plaatje te tekenen, je moet hier ook in woorden bij aangeven wat je precies als zijnde gegeven veronderstelt:
Gegeven: een ruit ABCD met diagonalen AC en BD.
Vervolgens moet je precies formuleren wŠt je nu eigenlijk wil bewijzen, waarbij je uiteraard kunt (en moet) refereren aan hetgeen je als gegeven hebt verondersteld. In dit geval zou je dus kunnen zeggen:
Te bewijzen: ∠BAC = ∠CAD.
Nu komt het echte werk. Bedenk dat je bij een bewijs een beroep mag doen op eerder bewezen stellingen.
Bewijs: Op grond van de definitie van een ruit is AB = BC, zodat driehoek ABC gelijkbenig is. In een gelijkbenige driehoek zijn de basishoeken gelijk, zodat
∠BAC = ∠BCA.
Aangezien een ruit een parallellogram is en in een parallellogram overstaande zijden evenwijdig zijn, is zijde BC evenwijdig aan zijde AD. Dus zijn ∠BCA en ∠CAD verwisselende binnenhoeken (Z-hoeken) en deze zijn ook gelijk, dus
∠BCA = ∠CAD.
Ergo
∠BAC = ∠CAD,
QED
Het bewijs voor elk van de drie andere hoekpunten verloopt uiteraard geheel analoog.
Het is me een stuk duidelijker geworden door deze uitleg.


Laten we eens uitgaan van een rij {un}, n∈ N0 met louter reŽle termen die aan een homogene lineaire tweede orde recursie met constante en reŽle coŽfficiŽnten voldoet, en welquote:Op zaterdag 25 januari 2014 10:17 schreef randomo het volgende:
Ik blijf het allemaal een beetje mysterieus vinden...Kan iemand me iets meer inzicht bijbrengen?
(1) a·un + b·un−1 + c·un−2 = 0
Hierbij moeten we a ≠ 0 en tevens c ≠ 0 veronderstellen, aangezien we anders geen tweede orde recursie hebben.
Zoals bekend kunnen we in beginsel gesloten uitdrukkingen vinden voor de algemene term un van rijen die aan het recursievoorschrift (1) voldoen door op zoek te gaan naar meetkundige rijen die aan dit voorschrift voldoen. Hebben we een meetkundige rij {un} met als eerste term u0 en reden λ, dan is
(2) un = u0·λn
Substitutie van (2) in geeft voor n > 1
(3) u0·λn−2(aλ2 + bλ + c) = 0
Nu is het duidelijk dat un = 0, i.e. een rij die uit louter nullen bestaat, een triviale oplossing is van het recursievoorschrift (1) en dat we daarom op grond van (2) zowel u0 ≠ 0 als λ ≠ 0 moeten veronderstellen om andere oplossingen naast deze triviale oplossing te vinden. Maar dan kan uitsluitend aan (3) worden voldaan als de uitdrukking tussen haakjes gelijk is aan nul, dus
(4) aλ2 + bλ + c = 0
Dit is de zogeheten karakteristieke vergelijking van het recursievoorschrift (1). We noemen het polynoom
(5) P(λ) = aλ2 + bλ + c
ook het karakteristieke polynoom van het recursievoorschrift (1). Nu is (4) een vierkantsvergelijking in λ, en zoals bekend wordt de aard van de nulpunten van P(λ) en daarmee van de oplossingen van (4) bepaald door de discriminant
(6) D = b2 − 4ac
van dit polynoom. We onderscheiden nu drie mogelijkheden.
1. D > 0. Nu heeft P(λ) twee verschillende reŽle nulpunten λ1 en λ2 en zijn de meetkundige rijen gedefinieerd door un = u0·λ1n en un = u0·λ2n twee (lineair onafhankelijke) oplossingen van (1). En omdat elke lineaire combinatie {cn} met cn = α·an + β·bn van twee rijen {an} en {bn} die voldoen aan (1) ook weer voldoet aan (1) krijgen we als algemene oplossing van het recursievoorschrift
(7) un = α·λ1n+ β·λ2n
waarin α en β willekeurige (reŽle) constanten zijn. Het is eenvoudig na te gaan dat (7) ook inderdaad de volledige oplossing geeft van het recursievoorschrift (1). Een rij die voldoet aan een tweede orde recursie ligt volledig vast als twee opeenvolgende termen van de rij zijn gegeven. Welnu, substitutie in (7) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ1 ≠ 0 en tevens λ2 ≠ 0, terwijl uit D ≠ 0 volgt dat λ1 ≠ λ2, zodat de determinant van het stelsel ongelijk is aan nul.
2. D < 0. Nu heeft P(λ) twee toegevoegd complexe nulpunten λ1 en λ2 maar de situatie verschilt niet wezenlijk van die voor D > 0. Ook nu geldt dat (7) de algemene oplossing geeft van het recursievoorschrift (1), en ook nu levert substitutie in (7) van twee opeenvolgende termen van een specifieke rij een stelsel van twee lineaire vergelijkingen in α en β met een unieke oplossing. Echter, niet alleen λ1 en λ2 maar ook α en β zijn nu in het algemeen (toegevoegd) complex, zodat het niet mogelijk is een gesloten algebraÔsche uitdrukking voor de algemene term van de recursieve rij te geven zonder gebruik van complexe getallen, en dat terwijl alle termen van de rij zelf wel degelijk reŽel zijn. Maar, zoals ik wel eens heb laten zien, is het in dit geval altijd mogelijk een goniometrische uitdrukking te geven voor algemene term van de rij zonder gebruik van complexe getallen.
3. D = 0. Nu heeft P(λ) ťťn reŽel nulpunt met multipliciteit 2, dat ik aan zal geven met λ0. Aangezien λ0 voldoet aan (4) is het duidelijk dat
(8) un = α·λ0n
met een willekeurige α in ieder geval een oplossing is van het recursievoorschrift (1). Maar het is evenzeer duidelijk dat (8) nu niet de volledige oplossing kan zijn van (1) omdat we bij het recursievoorschrift (1) de waarden van u0 en u1 steeds vrij kunnen kiezen, terwijl (8) alleen een oplossing biedt als u1 = λ0u0.
Een elegante methode om toch de volledige oplossing van (1) te verkrijgen als D = 0 berust op het gebruik van differentiaalrekening. Daarvoor hebben we de volgende stelling nodig:
Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.
Het bewijs van deze stelling gaat het eenvoudigst als we eerst even twee lemmata bewijzen.
Lemma 1. Als een niet-constant polynoom P(x) een enkelvoudig nulpunt x = x0 heeft, dan is P'(x0) ≠ 0.
Bewijs: volgens de factorstelling volgt uit P(x0) = 0 dat P(x) een factor (x − x0) bevat zodat P(x) = (x −x0)·Q(x). Aangezien x = x0 een enkelvoudig nulpunt is van P(x) kan het polynoom Q(x) geen verdere factoren (x − x0) bevatten zodat, wederom volgens de factorstelling, Q(x0) ≠ 0. De afgeleide van P(x) = (x −x0)·Q(x) is P'(x) = Q(x) + (x − x0)·Q'(x) zodat P'(x0) = Q(x0) + 0·Q'(x0) = Q(x0) ≠ 0, QED.
Lemma 2. Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1 dan heeft de afgeleide P'(x) een nulpunt x = x0 met een multipliciteit (m − 1).
Bewijs: aangezien P(x) een nulpunt x = x0 heeft met multipliciteit m > 1 is P(x) = (x − x0)m·Q(x) waarbij het polynoom Q(x) geen verdere factoren (x − x0) bevat zodat volgens de factorstelling Q(x0) ≠ 0. De afgeleide van P(x) = (x − x0)m·Q(x) is P'(x) = m·(x − x0)m−1·Q(x) + (x − x0)m·Q'(x) waarvoor we kunnen schrijven P'(x) = (x − x0)m−1·(m·Q(x) + (x − x0)·Q'(x)). Voor x = x0 is de factor (m·Q(x) + (x − x0)·Q'(x)) gelijk aan m·Q(x0) ≠ 0 zodat (m·Q(x) + (x − x0)·Q'(x)) volgens de factorstelling geen factor (x − x0) bevat en de multipliciteit van het nulpunt x = x0 van P'(x) dus gelijk is aan (m − 1), QED.
Het bewijs van bovenstaande stelling is nu uiteraard eenvoudig: heeft een niet-constant polynoom P(x) een nulpunt x = x0 met multipliciteit m > 1, dan geeft (herhaalde) toepassing van lemma 2 dat P(i)(x) voor i = 1 .. (m − 1) een nulpunt x = x0 heeft met een multipliciteit (m − i), zodat P(m−1)(x) een enkelvoudig nulpunt x = x0 heeft. En volgens lemma 1 is dan P(m)(x0) ≠ 0, QED.
Goed, nu de volledige oplossing van (1) als D = 0. Vermenigvuldigen we beide leden van (5) met λn−2, dan hebben we voor n > 1
(9) a·λn + b·λn−1 + c·λn−2 = λn−2·P(λ)
DifferentiŽren naar λ geeft nu
(10) a·n·λn−1 + b·(n−1)·λn−2 + c·(n−2)·λn−3 = (n−2)·λn−3·P(λ) + λn−2·P'(λ)
En beide leden vermenigvuldigen met λ geeft dan
(11) a·n·λn + b·(n−1)·λn−1 + c·(n−2)·λn−2 = (n−2)·λn−2·P(λ) + λn−1·P'(λ)
Nu is λ = λ0 een nulpunt van P(λ) met multipliciteit 2, zodat niet alleen P(λ0) = 0 maar tevens P'(λ0) = 0. Substutie van λ = λ0 in (11) geeft dus
(12) a·n·λ0n + b·(n−1)·λ0n−1 + c·(n−2)·λ0n−2 = 0
zodat we kunnen concluderen dat un = n·λ0n aan het recursievoorschrift (1) voldoet. Eerder vonden we al dat un = λ0n voldoet, zodat ook elke lineaire combinatie van deze oplossingen aan het recursievoorschrift voldoet en we dus krijgen
(13) un = (α + β·n)·λ0n
Het is weer gemakkelijk na te gaan dat deze oplossing inderdaad volledig is. Substitutie in (13) van twee opeenvolgende termen van een specifieke rij die aan (1) voldoet levert een stelsel van twee lineaire vergelijkingen in α en β en dit stelsel bezit een unieke oplossing aangezien uit c ≠ 0 in (1) volgt dat λ0 ≠ 0 zodat de determinant van het stelsel ongelijk is aan nul.
Het aardige van deze methode is dat deze eenvoudig is te generaliseren naar homogene lineaire recursies met constante coŽfficiŽnten van hogere ordes. Heeft het karakteristieke polynoom P(λ) van zo'n hogere orde recursie van orde N namelijk een meervoudig nulpunt λ = λ0 met multipliciteit m, dan kun je door P(λ) te vermenigvuldigen met λn−N en daarna telkens om beurten te differentiŽren en weer te vermenigvuldigen met λ gemakkelijk laten zien dat naast un = λ0n ook un = ni·λ0n voor i = 1 .. (m − 1) een oplossing geeft van de recursie. Zo geeft elk meervoudig nulpunt met een multipliciteit m dus precies m lineair onafhankelijke oplossingen.
Wil je niet gebruik maken van differentiaalrekening, dan is er in ieder geval voor tweede orde recursies waarbij de discriminant van de karakteristieke vergelijking gelijk is aan nul ook een goed bruikbare elementaire methode die bekend staat als de variatie van de constante. Het idee hierbij is dat je uitgaat van (8) maar dat je veronderstelt dat α niet constant is maar een functie van n. Dat wil dus zeggen dat je een rij {αn} zoekt zodanig dat
(14) un = αn·λ0n
een oplossing is van de recursie (1). Welnu, invullen van (14) in (1) geeft voor n > 1
(15) λ0n−2(a·αn·λ02 + b·αn−1·λ0 + c·αn−2) = 0
en aangezien λ0 ≠ 0 geeft dit
(16) a·αn·λ02 + b·αn−1·λ0 + c·αn−2 = 0
Nu weten we echter ook dat λ0 = −b/2a (en dus b ≠ 0 aangezien λ0 ≠ 0). Substitutie hiervan in (16) en gebruik maken van D = b2 − 4ac = 0 (en dus 4ac = b2) levert dan na wat herleiding
(17) αn − αn−1 = αn−1 − αn−2
In woorden: het verschil tussen elk tweetal opeenvolgende termen van de rij {αn} is constant. De rij {αn} is dus een willekeurige rekenkundige rij, en de algemene gedaante van αn is dus
(18) αn = α + n·β
waarbij α en β willekeurige constanten zijn. Substitutie van (18) in (14) geeft nu
(19) un = (α + n·β)·λ0n
en dit stemt geheel overeen met de eerder gevonden algemene oplossing (13).
That's all.


Wat snap je er niet aan? Wat snap je al wel?quote:Op zondag 26 januari 2014 12:17 schreef Beverwijker het volgende:
http://tinypic.com/r/11snpc2/5
Iemand die mij vraag 12 kan uitleggen.
Het gaat hier om een driehoek met een rechte hoek. Gegeven is de lengte van ťťn van de zijdes die aan deze rechte hoek grenst (10). De andere zijde die aan de rechte hoek grenst wordt lengte a gesteld. Het gevraagde is de lengte van de langste zijde, dat is (op grond van de driehoeksongelijkheid) de schuine zijde van deze driehoek. Kun je hier iets mee? Hint: Pythagoras.
Als je dat doorhebt weet je waar de formule vandaan komt. De opdracht is simpeler: je moet drie keer een waarde voor a invullen in de formule.


Stel je hebt twee open sets, zeg maar 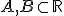 . Is het Cartesian Product
. Is het Cartesian Product 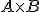 dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700
[ Bericht 17% gewijzigd door Novermars op 27-01-2014 16:06:44 ]


Top! Zoals gewoonlijk weer een uitstekende uitlegquote:
Die stelling was inderdaad uiteindelijk de missing link
Veel dank en hulde!quote:Als een niet-constant polynoom P(x) een nulpunt x = x0 heeft met een multipliciteit m > 1, dan is P(i)(x0) = 0 voor i = 1 .. (m − 1) terwijl P(m)(x0) ≠ 0.


Dit is metawiskundig gezien wel een interessante vraag, want hoe definieer je de topologie op RxR? Enerzijds kun je de Euclidische metriek nemen en van daar uit werken. Anderzijds bestaat er ook een categorie-theoretische definitie van producten en kun je bewijzen dat producten bestaan in de categorie van topologische ruimten. De twee topologieŽn die je zo krijgt blijken hetzelfde te zijn, iets wat niet vanzelfsprekend is!quote:Op zondag 26 januari 2014 22:03 schreef Novermars het volgende:
Stel je hebt twee open sets, zeg maar. Is het Cartesian Product
dan ook open? En zoja, hoe kan ik het beste hiervan een bewijs leveren?
Edit: Zie hier het antwoord + bewijs: http://math.stackexchange.com/q/653106/96700


Ik krijg koppijn van dit vraagstuk
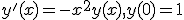
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 21:48:45 ]
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?
[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 21:48:45 ]


Je mist een accentje.quote:Op dinsdag 28 januari 2014 21:40 schreef Amoeba het volgende:
Ik krijg koppijn van dit vraagstuk
Nu moet ik dit oplossen mbv machtreeksen, vervolgens de convergentiestraal van de gevonden machtreeks bepalen en daarna een gesloten uitdrukking voor die machtreeks geven.
Tot nu toe was ik zo ver:
[ afbeelding ]
Waarbij ik zeker weet dat die onderste vergelijking niet klopt, immers gaat delen door k+3 na de eerste stap al fout..
Wat doe ik fout / wat mis ik?


Excuus, ik heb er eentje te veel gezet.quote:
http://www.win.tue.nl/~gprokert/opcoll14.pdf
Opgave 3
[ Bericht 6% gewijzigd door #ANONIEM op 28-01-2014 21:49:42 ]



